fractions to percentages problem solving

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled stories
• Sight words
• Sentences & passages
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

Fractions to percents

Download & Print Only $4.80

Convert fractions to percents worksheets

Students convert fractions to percentages , starting with the simplest case (proper fractions with denominators of 10 or 100) and proceeding to mixed numbers and other denominators.

Denominators of 10 or 100:

Mixed numbers:

Other denominators:

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Fraction to percent

Here you will learn about converting fractions to percentages.

Students will first learn about converting fractions to percentages in 6th grade math as part of their work with ratios and proportional relationships and will expand that knowledge to solving problems finding the whole given a part and the percent, or finding a part given the whole and the percent.

This will later be used to find the percent increase/decrease in 7th grade.

What is fraction to percent?

Converting a fraction to a percent is representing the fraction as a percentage without changing its value. 

For example,

\begin{aligned} \cfrac{1}{4}&=25 \% \\\\ \cfrac{9}{20}&=45 \% \\\\ \cfrac{1}{3}&=33.3 \% \\\\ \cfrac{4}{5}&=80 \% \end{aligned}

Common Core State Standards

How does this apply to 6th grade math and 7th grade math?

• Grade 6: Ratios and Proportional Relationships (6.RP.A.3a) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. a. Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.
• Grade 7: The Number System (7.NS.A.2d) Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0 s or eventually repeats.

How to convert fractions to percentages

In order to convert from a fraction to a percent:

Determine if the denominator is a factor or multiple of \bf{100} .

If it is follow these steps:

2 Convert the fraction so the denominator is \bf{100} .

3 Write the numerator as a percentage by using the percent symbol ( \bf{\%} ) because it is now ‘out of \bf{100} ’.

4 Clearly state the answer showing the ‘fraction’ = ‘percentage’.

If the denominator is not a factor or multiple of 100 follow these steps:

2 Divide the numerator by the denominator.

3 Multiply by \bf{100} to convert to a percentage (in cases with a decimal number, this involves moving the decimal point two spaces to the right of the decimal).

[FREE] Converting Fractions, Decimals and Percents Check for Understanding Quiz (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of converting fractions, decimals and percents. 10+ questions with answers covering a range of 4th, 5th and 6th grade converting fractions, decimals and percents topics to identify areas of strength and support!

Converting fractions to percentages examples

Example 1: converting a simple fraction to a percentage, where the denominator is a factor of 100.

Convert \, \cfrac{3}{4} \, to a percent.

See if the denominator is a factor or multiple of \bf{100} .

4 is a factor of 100 \; ( because 4 \times 25=100) .

4 needs to be multiplied by 25 to make 100, so we are going to multiply the denominator and numerator by 25 (this ensures they are equivalent fractions).

\cfrac{3}{4}

\cfrac{3 \, \times \, 25}{4 \, \times \, 25}

\cfrac{75}{100}

3 Write the numerator as a percent. 

\cfrac{75}{100}=75\% \; because \% means out of 100.

4 Clearly state the answer showing the ‘fraction’ = ‘percent’.

\cfrac{3}{4}=75\%

Example 2: converting a fraction to a percentage, where the denominator is a multiple of 100

Convert \, \cfrac{60}{200} \, to a percent.

200 is a multiple of 100 because 200 \div 2 = 100.

Convert the fraction so the denominator is \bf{100} .

200 needs to be divided by 2 to make 100, so we are going to divide the denominator and numerator by 2.

Note that we are not dividing by the greatest common factor (GCF) here because the intention is to make the denominator 100, not to simplify the fraction to the lowest terms.

\cfrac{60}{200}

\cfrac{60 \, \div \, 2}{200 \, \div \, 2}

\cfrac{30}{100}

Because we are converting to a percent, we only need to simplify the fraction so that the denominator is 100. The fraction is not in its simplest form.

Write the numerator as a percent.

\cfrac{30}{100}=30\% \; because \% means out of 100.

Clearly state the answer showing the ‘fraction’ = ‘percent’.

\cfrac{60}{200}=30\%

Example 3: converting an improper fraction to a percent

Convert \, \cfrac{25}{20} \, to a percent.

20 is a multiple of 100 because 20 \times 5 = 100.

20 needs to be multiplied by 5 to make 100, so we are going to multiply the denominator and numerator by 5.

\cfrac{25}{20}

\cfrac{25 \, \times \, 5}{20 \, \times \, 5}

\cfrac{125}{100}

\cfrac{125}{100}=125\% \; because \% means out of 100.

\cfrac{25}{20}=125\%

Example 4: converting a fraction to a percentage, where the denominator is not a factor/multiple of 100

Convert \, \cfrac{5}{8} \, to a percent.

8 is not a factor or multiple of 100.

Divide the numerator by the denominator.

\cfrac{5}{8}

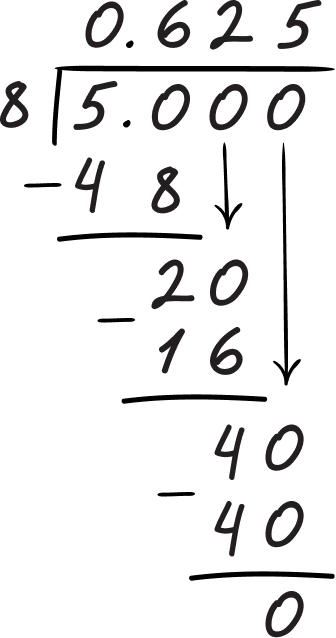
\cfrac{5}{8}=0.625

Multiply by \bf{100} to convert to a percent.

0.625 \times 100

\cfrac{5}{8}=62.5\%

Example 5: converting a fraction to a percentage, where the denominator is not a factor/multiple of 100 – involving a repeating decimal

Convert \, \cfrac{2}{9} \, to a percent.

9 is not a factor or multiple of 100 \; ( because 9 cannot be multiplied by an integer to make 100).

\cfrac{2}{9}

You can use your written method for division here. This example will show the ‘long division method’.

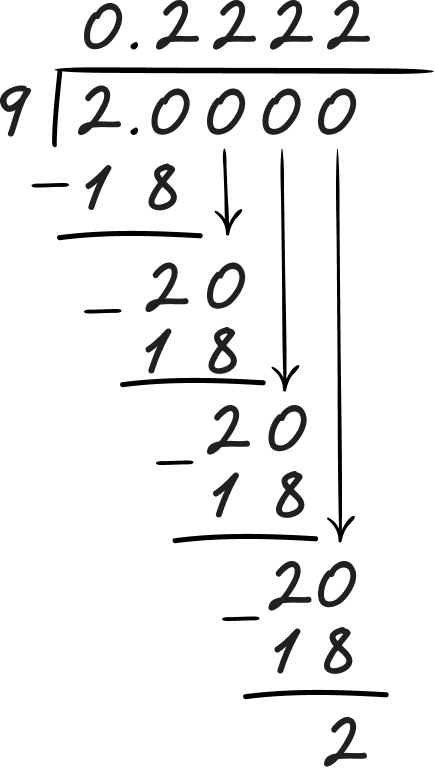
\cfrac{2}{9}=0.22222...=0.\overline{2}

0.\overline{2} \times 100 = 22.\overline{2}\%

\cfrac{2}{9}=22.\overline{2}\%

Example 6: converting a mixed number to a percentage

Convert 4 \, \cfrac{5}{16} \, to a percent.

Added step – convert to an improper fraction first .

4\, \cfrac{5}{16}=\cfrac{69}{16}

16 is not a factor or multiple of 100 \; ( because 16 cannot be multiplied by an integer to make 100).

\cfrac{69}{16}

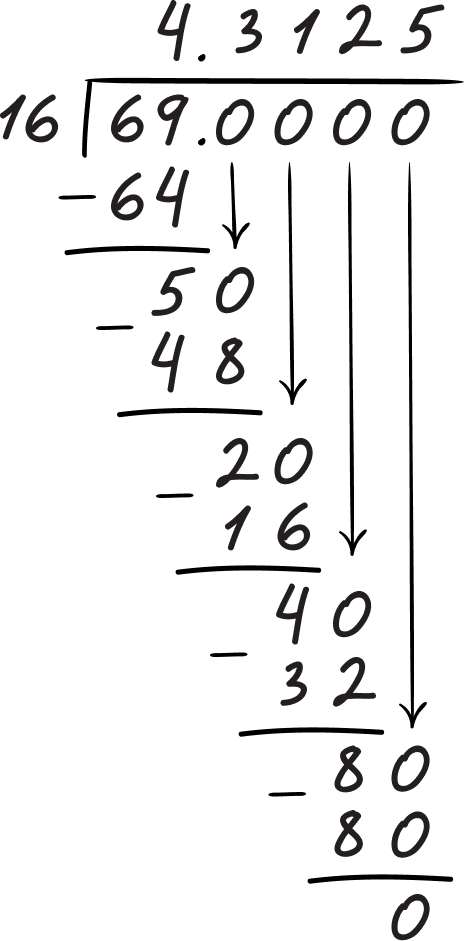
\cfrac{69}{16}=4.3125

4.3125 \times 100

\cfrac{69}{16}=431.25\%

Teaching tips for converting fractions to percents

• Use visual models such as hundreds grids or pie charts to illustrate the equivalence of fractions and percents and to demonstrate how both forms are ways to represent a part of a whole or a rate.
• Use real world contexts to demonstrate how fractions can be thought of as percentages.
• Worksheets for converting fractions to percentages have their place, but make sure that students have a conceptual understanding of the relationship between percentages and fractions.

Easy mistakes to make

• Mistakes with written division Often, mistakes are made when implementing a form of written division. For example, a common mistake with long division is mixing up the number being divided (dividend) by the number you are dividing by (divisor). The numerator is the dividend and therefore goes underneath the division symbol.
• Not multiplying by \bf{100} to make a percentage The percent sign means the number is given out of 100; therefore, we need to multiply the result of the division (the quotient) by 100 when writing it as a percentage. Example, \cfrac{3}{4}=0.75=75\%
• Not noticing a repeating decimal Sometimes a repeating decimal is not immediately obvious. For example, \cfrac{1}{7}=0.142857142857142857... Therefore, \cfrac{1}{7}= 0.\overline{142857}\

Related lessons on converting fractions, decimals, and percentages

• Percent to fraction
• Percent to decimal
• Decimal to percent
• Decimal to fractions
• Fraction to decimal
• Repeating decimal to fraction

Practice converting fractions to percentages questions

1. Convert \, \cfrac{1}{10} \, to a percent.

Start by making an equivalent fraction with a denominator of 100.

\cfrac{1}{10} \, is equal to \, \cfrac{10}{100} \, by multiplying the numerator and denominator by 10.

Write the numerator as a percent with the percent symbol (\%).

This gives you 10\%.

2. Convert \, \cfrac{4}{10} \, to a percent.

\cfrac{4}{10} \, is equal to \, \cfrac{40}{100} \, by multiplying the numerator and denominator by 10.

This gives you 40\%.

3. Convert \, \cfrac{11}{10} \, to a percent.

\cfrac{11}{10} \, is equal to \, \cfrac{110}{100} \, by multiplying the numerator and denominator by 10.

This gives you 110\%.

4. Convert \, \cfrac{6}{1000} \, to a percent.

\cfrac{6}{1000} \, is equal to \, \cfrac{0.6}{100} \, by dividing the numerator and denominator by 10.

This gives you 0.6\%.

5. Convert \, \cfrac{601}{20} \, to a percent.

\cfrac{601}{20} \, is equal to \, \cfrac{3005}{100} \, by multiplying the numerator and denominator by 5.

This gives you 3005\%.

6. Convert \, \cfrac{15}{16} \, to a percent.

Start by dividing your numerator by your denominator.

15 \div 16=0.9375

Multiply your quotient by 100 and write this product as a percentage.

This gives you 93.75\%.

Fraction to percent FAQs

Yes, this method will always work. However, it may be simpler to first check to see if the denominator is a factor or multiple of 100 to make an equivalent fraction with a denominator of 100.

If you have a repeating decimal, you can write the strand of digits that repeat (or just one digit if that digit repeats) and put a line over it that means it will repeat infinitely. If you do not have a repeating decimal, you can either round the number to the nearest tenth or hundredth place and write it as a percentage.

You can still divide the numerator by this factor, you will just not have a whole number as the answer. You can still express the numerator as a percentage with a decimal number.

The next lessons are

• Compound measures
• Properties of equality

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Halloween Color By Number
• Halloween Dot to Dot
• Kindergarten Halloween Sheets
• 1st Grade Halloween Sheets
• Puzzles & Challenges
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• Kindergarten Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Convert Fraction to Percent Support Page

Welcome to our Convert Fraction to Percent support page.

Here you will find some simple information and support about how to convert a fraction to a percentage.

We also have a calculator which will not only do the work for you, but also show you all the working out along the way!

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Convert Fraction to Percent

Fraction to percentage calculator.

If you need help on how to convert a fraction to a percentage, there is more help further down!

How It Works

To enter a fraction, you have to enter the numerator followed by '/' followed by the denominator. E.g. 4/5 or 23/7

To enter a mixed fraction, first type the whole number followed by space followed by the numerator followed by '/' followed by the denominator. E.g. 3 1/4 (3 and a quarter).

Press the Convert button and the fraction will be converted to a decimal and also a percentage.

Need to convert a percentage to a fraction? Use the link below.

• Convert Percent to Fraction

How to Convert Fractions to Percentages

There are two main ways to convert a fraction into a percent:

• The Denominator Way - converting the fraction to an equivalent fraction with a denominator of 100
• The Decimal Way - converting the fraction to a decimal and then converting the decimal to a percent

Method 1 - The Denominator Way

This way is a great way to use if the fraction has a denominator which is a factor of 100.

Here are the two quick steps you need to follow:

• Divide 100 by the denominator to find the multiplier.
• Multiply the numerator and denominator of the fraction by the multiplier to give you an equivalent fraction with a denominator of 100.

Examples using the Denominator Way

Example 1) convert into a percentage the fraction: \[ {3 \over 5} \].

You will notice that the denominator, which is 5, is a factor of 100.

100 ÷ 5 = 20, so 20 is our multiplier.

So we need to multiply the numerator and denominator by 20 to give us an equivalent fraction with a denominator of 100.

\[ {3 \over 5 } = {3 \times 20 \over 5 \times 20} = {60 \over 100} \]

Because a percentage is simply a fraction with a denominator of 100, we have found our percentage which is 60%.

So our answer is: \[ {3 \over 5} \; = \; 60\% \]

Example 2) Convert into a percentage the fraction: \[ {7 \over 20} \]

The denominator is 20, which is a factor of 100.

100 ÷ 20 = 5, so our multiplier is 5.

This gives us: \[ {7 \over 20} = {7 \times 5 \over 20 \times 5} = {35 \over 100} \]

Because a percentage is simply a fraction with a denominator of 100, we have found our percentage which is 35%.

So the answer is: \[ {7 \over 20} \; = \; 35\% \]

Method 2 - The Decimal Conversion Way

This method works well for any fraction, and it is the way our Fraction to Percentage calculator uses.

Step 1) Convert your fraction to a decimal by dividing the numerator by the denominator if you have a calculator this is easy, otherwise you need to use a dvision method.

Step 2) Multiply the decimal by 100 to change it into a percent.

You have now changed your fraction to a percentage.

Examples using the Decimal Conversion Way

Example 1) convert into a percentage the fraction: \[{3 \over 5} \].

To convert the fraction to a decimal we divide the numerator by the denominator.

So we calculate 3 ÷ 5 = 0.6

Multiply by 100 to change it to a percentage.

0.6 x 100 = 60%

This means that: \[{3 \over 5} \; = \; 60\% \]

Example 2) Convert into a percentage the fraction: \[{14 \over 9} \]

First, we calculate 14 ÷ 9 = 1.556 (this decimal has been rounded to 3 decimal places)

Next multiply by 100 to change it to a percentage.

1.556 x 100 = 155.6%

Final answer: \[{14 \over 9} \; = \; 155.6\% \; (to \;1dp) \]

Example 3) Convert into a percentage the fraction: \[{7 \over 8} \]

First, we calculate 7 ÷ 8 = 0.875

0.875 x 100 = 87.5%

Final answer: \[{7 \over 8} \; = \; 87.5\% \]

Convert Fraction to Percent printable sheets

Use this printable support sheet below if you would like a more printer-friendly version of this page.

• Converting Fraction to Percent Support Sheet
• PDF version

Convert Fraction to Percent Practice

Here you will find a printable sheet where you can practice your math skills at converting fractions to percentages.

The first two sheets get students to use the denominator method to create an equivalent fraction with a denominator of 100.

The third sheet uses the Decimal Conversion method to convert the fraction to a decimal then multiply by 100. Calculator recommended.

• Converting Fractions to Percent Sheet 1
• Sheet 1 Answers
• Converting Fractions to Percent Sheet 2
• Sheet 2 Answers
• Converting Fractions to Percent Sheet 3
• Sheet 3 Answers

Converting Percentages to Fractions

Here you will find some simple information and advice about how to convert a percentage to a fraction.

You will also find a printable resource sheet and some practice sheets which will help you understand and practice this math skill.

• Fractions Decimals Percents Worksheets

Looking to convert between fractions, decimals and percentages?

We have a wide range of worksheets to meet your needs!

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to Fraction Worksheets

Return to Conversion Charts

Return from Convert Fraction to Percent page to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Percentages and Fractions Practice Questions

Click here for questions, click here for answers.

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Converting Fractions to Percent: Steps, Formula, Table, Examples, FAQs

What is fractions to percents conversion, how to convert a fraction to a percent, fraction to percent conversion table, solved examples on converting fractions to percent, practice problems on fractions to percent conversion, frequently asked questions about converting  fractions to percent.

Fractions to percents conversion is the method of expressing a given fraction as a percentage. 

A fraction represents a part of the whole. A fraction $\frac{p}{q}$ consists of the numerator (p: top number) that represents the number of parts taken and denominator (q: bottom number), which represents the total number of parts the whole is divided into. For example, $\frac{2}{5}$ means 2 parts taken out of 5 equal parts. 

A percentage is a fraction expressed as a fraction with a denominator of 100. In other words, percentage means a part per hundred. By “per cent” we mean “per 100.” Percent is represented by the symbol “$\%$.” 

Converting fractions to percentages helps in comparing and ordering two quantities easily. Fractions, decimals, and percentages are all interrelated concepts. To convert a fraction to a percent, we can first convert it into a decimal. Multiply the given decimal by 100 to get the percentage value.

Recommended Games

To convert a fraction to a percent, simply convert fraction to decimal, multiply the decimal by 100, and add $\%$ sign. Another way to convert a fraction to a percentage is multiplying the fraction by 100, simplifying it, and adding$\%$ sign. 

Step 1: Convert the fraction into a decimal number. To do this, divide the numerator by the denominator.

Step 2: To get a percent value, multiply the obtained decimal number by 100. The result is the fraction as a percent. Write the percent with $\%$ symbol next to the answer.

Another way is to multiply the fraction by 100 and simplify. The result is the fraction as a percent. Add the $\%$ symbol to the answer.

$\frac{4}{7} = (\frac{4}{7} \times 100)\% = \frac{400}{7}\% = 57.1428…\%$

Recommended Worksheets

More Worksheets

Fraction to Percentage Formula

To convert a fraction to percent, we convert it to a decimal number and multiply it by 100 followed by the symbol $\%$. 

The formula to convert fraction m n to percentage is:

Percentage $= \frac{m}{n}\times100$

where, $m =$ numerator

            $n =$ denominator

Do not forget to add the “$\%$” sign after the final answer.

Take a look at the fractions to percent conversion chart.

Facts about Fractions to Percent Conversion

• Fractions can be expressed as decimals by dividing the numerator (top number) by the denominator (bottom number) using the long division method.
• To change a fraction to a percentage, divide the numerator by the denominator, and then multiply the result by 100. Alternatively, you can also multiply the numerator by 100 first, then divide the result by the denominator of the fraction.
• You can convert a fraction to percent by making the denominator 100, or by converting the fraction into $\frac{?}{100}$ form. $\frac{4}{5} = \frac{4 \times 20}{5 \times 20} = \frac{80}{100} = 80\%$
• A mixed fraction or a mixed number is always greater than (or equal to) 1. Thus, we always get a percent greater than 100 on converting a mixed number to a percentage. $2\frac{4}{5} = \frac{14}{5} =  \frac{14}{5} \times 100= 280\%$
• To convert percent to fraction , remove the % sign, divide by 100, and simplify if required.
• $100\% = \frac{100}{100} = 1$

In this article, we have learned about fractions and percentages and their conversions. Conversion of fractions and decimals to percentages are very important. They make fractions and percentages of amounts much simpler to visualize and compare. Now, let’s apply the knowledge to solve some examples and practice problems.

1. Convert each of the fractions to percentages.

•      $\frac{3}{10}$                   (b)     $\frac{1}{4}$                   (c)     $\frac{1}{2}$

Solution: 

To convert fractions to percentages, we can first convert it to a decimal form and then multiply it by 100.

(a)  $\frac{3}{10}$              

$\frac{3}{10} = 0.3$                

Multiply it by 100 to get the percentage value.                                   

$\frac{3}{10} = (0.3 \times 100)\% = 30\%$                                                             

(b) $\frac{1}{4} = (0.25 \times 100)\% = 25\%$ 

 (c) $\frac{1}{2} = (0.50 \times 100)\% = 50\%$

2. Compare the fractions $\frac{3}{4}$ and $\frac{4}{5}$ by converting them into percentages.

Let’s convert these fractions to percentages.

$\frac{3}{4} = (\frac{3}{4} \times 100)\% = (0.75 \times 100)\% = 75\%$    

$\frac{4}{5} = (\frac{4}{5} \times 100)\% = (0.8 \times 100)\% = 80\%$

$75\% \lt 80\%$

Thus, $\frac{3}{4} \lt \frac{4}{5}$

3. Kids at a birthday party finished 6 out of 10 slices of pizza. What percentage of pizza was eaten by kids?

6 out of $10 = \frac{6}{10}$

To change this fraction to percentage, we will multiply the fraction by 100.

$\frac{6}{10} = (\frac{6}{10} \times 100)\% = 60\%$

Thus, $60\%$ pizza was consumed.

4. Convert $\frac{3}{25}$ into a percentage.

$\frac{3}{25} =  (\frac{3}{25} \times 100)\%$ 

$\frac{3}{25} = \frac{300}{25}\%$

$\frac{3}{25} = 12\%$

Attend this quiz & Test your knowledge.

Which option defines the gray shaded portion of the circle?

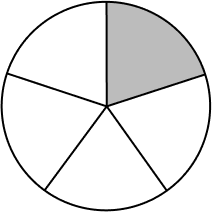
$\frac{3}{4}$ is equivalent to

For converting fraction to percent, we __________., $22\%$ can be written as the following decimal and fraction., convert the fraction to a percent: $\frac{7}{8}$.

Why do we need to convert a fraction to percent?

We need to convert a decimal to percent for comparing the quantities instantly. For example, if we have to compare the decimals of $\frac{1}{2},\; \frac{61}{100},\; \frac{987}{1000}$, we will not be able to make any sense of the values at first glance. If these fractions are converted into percentages as $50\%,\; 61\%,\; 98.7\%$, we will be able to compare them easily.

What are the steps to convert percent to fraction?

Step 1: Write down the given percent value like this: $\frac{Percent value}{100}$

Step 2: Simplify (or reduce) the fraction to its lowest term.

For example: Convert $20\%$ to fraction

$20\% = \frac{20}{100} = \frac{20}{100} \div \frac{20}{20} = \frac{1}{5}$

Thus, $20\% = \frac{1}{5}$

How do you convert a mixed number to a percentage?

To convert a mixed number to a percentage, first convert the mixed number to an improper fraction , and then convert the important fraction to a percentage.

$1\frac{2}{10} = \frac{12}{10} = \frac{12}{10} \times 100 = 120\%$

How do you convert an improper fraction to a percentage?

Divide the numerator by the denominator to get the decimal, and then multiply the decimal by 100.

Example: $\frac{7}{5} = 1.4$

$1.4 \times 100 = 140\%$

RELATED POSTS

• What Is a Constant? Definition, Solved Examples, Facts
• Cardinality of a Set: Definition, Symbol, Examples, Facts, FAQs
• Median of Triangle: Definition with Examples
• Set in Math – Definition, Types, Properties, Examples
• Exterior Angle Theorem: Definition, Proof, Examples, Facts, FAQs

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free