- Skip to main content
- Skip to primary sidebar
- Skip to footer

Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry
Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
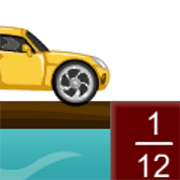
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”
Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents
- Prodigy Math
- Prodigy English
- Is a Premium Membership Worth It?
- Promote a Growth Mindset
- Help Your Child Who's Struggling with Math
- Parent's Guide to Prodigy
- Assessments
- Math Curriculum Coverage
- English Curriculum Coverage
- Administrators
- Game Portal
120 Math Word Problems To Challenge Students Grades 1 to 8

Written by Marcus Guido
Hey teachers! 👋
Use Prodigy to spark a love for math in your students – including when solving word problems!
- Teaching Tools
- Subtraction
- Multiplication
- Mixed operations
- Ordering and number sense
- Comparing and sequencing
- Physical measurement
- Ratios and percentages
- Probability and data relationships
You sit at your desk, ready to put a math quiz, test or activity together. The questions flow onto the document until you hit a section for word problems.
A jolt of creativity would help. But it doesn’t come.
Whether you’re a 3rd grade teacher or an 8th grade teacher preparing students for high school, translating math concepts into real world examples can certainly be a challenge.
This resource is your jolt of creativity. It provides examples and templates of math word problems for 1st to 8th grade classes.
There are 120 examples in total.
The list of examples is supplemented by tips to create engaging and challenging math word problems.
120 Math word problems, categorized by skill
Addition word problems.

Best for: 1st grade, 2nd grade
1. Adding to 10: Ariel was playing basketball. 1 of her shots went in the hoop. 2 of her shots did not go in the hoop. How many shots were there in total?
2. Adding to 20: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store to get 3 more pieces of gum. How many pieces of gum does Adrianna have now?
3. Adding to 100: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store and got 70 pieces of strawberry gum and 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?
4. Adding Slightly over 100: The restaurant has 175 normal chairs and 20 chairs for babies. How many chairs does the restaurant have in total?
5. Adding to 1,000: How many cookies did you sell if you sold 320 chocolate cookies and 270 vanilla cookies?
6. Adding to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In June, the hobby store sold 15,498 more trading cards than normal. In total, how many trading cards did the hobby store sell in June?
7. Adding 3 Numbers: Billy had 2 books at home. He went to the library to take out 2 more books. He then bought 1 book. How many books does Billy have now?
8. Adding 3 Numbers to and over 100: Ashley bought a big bag of candy. The bag had 102 blue candies, 100 red candies and 94 green candies. How many candies were there in total?
Subtraction word problems
Best for: 1st grade, second grade
9. Subtracting to 10: There were 3 pizzas in total at the pizza shop. A customer bought 1 pizza. How many pizzas are left?
10. Subtracting to 20: Your friend said she had 11 stickers. When you helped her clean her desk, she only had a total of 10 stickers. How many stickers are missing?
11. Subtracting to 100: Adrianna has 100 pieces of gum to share with her friends. When she went to the park, she shared 10 pieces of strawberry gum. When she left the park, Adrianna shared another 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

Practice math word problems with Prodigy Math
Join millions of teachers using Prodigy to make learning fun and differentiate instruction as they answer in-game questions, including math word problems from 1st to 8th grade!
12. Subtracting Slightly over 100: Your team scored a total of 123 points. 67 points were scored in the first half. How many were scored in the second half?
13. Subtracting to 1,000: Nathan has a big ant farm. He decided to sell some of his ants. He started with 965 ants. He sold 213. How many ants does he have now?
14. Subtracting to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In July, the hobby store sold a total of 20,777 trading cards. How many more trading cards did the hobby store sell in July compared with a normal month?
15. Subtracting 3 Numbers: Charlene had a pack of 35 pencil crayons. She gave 6 to her friend Theresa. She gave 3 to her friend Mandy. How many pencil crayons does Charlene have left?
16. Subtracting 3 Numbers to and over 100: Ashley bought a big bag of candy to share with her friends. In total, there were 296 candies. She gave 105 candies to Marissa. She also gave 86 candies to Kayla. How many candies were left?
Multiplication word problems

Best for: 2nd grade, 3rd grade
17. Multiplying 1-Digit Integers: Adrianna needs to cut a pan of brownies into pieces. She cuts 6 even columns and 3 even rows into the pan. How many brownies does she have?
18. Multiplying 2-Digit Integers: A movie theatre has 25 rows of seats with 20 seats in each row. How many seats are there in total?
19. Multiplying Integers Ending with 0: A clothing company has 4 different kinds of sweatshirts. Each year, the company makes 60,000 of each kind of sweatshirt. How many sweatshirts does the company make each year?
20. Multiplying 3 Integers: A bricklayer stacks bricks in 2 rows, with 10 bricks in each row. On top of each row, there is a stack of 6 bricks. How many bricks are there in total?
21. Multiplying 4 Integers: Cayley earns $5 an hour by delivering newspapers. She delivers newspapers 3 days each week, for 4 hours at a time. After delivering newspapers for 8 weeks, how much money will Cayley earn?
Division word problems
Best for: 3rd grade, 4th grade, 5th grade
22. Dividing 1-Digit Integers: If you have 4 pieces of candy split evenly into 2 bags, how many pieces of candy are in each bag?
23. Dividing 2-Digit Integers: If you have 80 tickets for the fair and each ride costs 5 tickets, how many rides can you go on?
24. Dividing Numbers Ending with 0: The school has $20,000 to buy new computer equipment. If each piece of equipment costs $50, how many pieces can the school buy in total?
25. Dividing 3 Integers: Melissa buys 2 packs of tennis balls for $12 in total. All together, there are 6 tennis balls. How much does 1 pack of tennis balls cost? How much does 1 tennis ball cost?
26. Interpreting Remainders: An Italian restaurant receives a shipment of 86 veal cutlets. If it takes 3 cutlets to make a dish, how many cutlets will the restaurant have left over after making as many dishes as possible?
Mixed operations word problems

27. Mixing Addition and Subtraction: There are 235 books in a library. On Monday, 123 books are taken out. On Tuesday, 56 books are brought back. How many books are there now?
28. Mixing Multiplication and Division: There is a group of 10 people who are ordering pizza. If each person gets 2 slices and each pizza has 4 slices, how many pizzas should they order?
29. Mixing Multiplication, Addition and Subtraction: Lana has 2 bags with 2 marbles in each bag. Markus has 2 bags with 3 marbles in each bag. How many more marbles does Markus have?
30. Mixing Division, Addition and Subtraction: Lana has 3 bags with the same amount of marbles in them, totaling 12 marbles. Markus has 3 bags with the same amount of marbles in them, totaling 18 marbles. How many more marbles does Markus have in each bag?
Ordering and number sense word problems
31. Counting to Preview Multiplication: There are 2 chalkboards in your classroom. If each chalkboard needs 2 pieces of chalk, how many pieces do you need in total?
32. Counting to Preview Division: There are 3 chalkboards in your classroom. Each chalkboard has 2 pieces of chalk. This means there are 6 pieces of chalk in total. If you take 1 piece of chalk away from each chalkboard, how many will there be in total?
33. Composing Numbers: What number is 6 tens and 10 ones?
34. Guessing Numbers: I have a 7 in the tens place. I have an even number in the ones place. I am lower than 74. What number am I?
35. Finding the Order: In the hockey game, Mitchell scored more points than William but fewer points than Auston. Who scored the most points? Who scored the fewest points?
Fractions word problems

Best for: 3rd grade, 4th grade, 5th grade, 6th grade
36. Finding Fractions of a Group: Julia went to 10 houses on her street for Halloween. 5 of the houses gave her a chocolate bar. What fraction of houses on Julia’s street gave her a chocolate bar?
37. Finding Unit Fractions: Heather is painting a portrait of her best friend, Lisa. To make it easier, she divides the portrait into 6 equal parts. What fraction represents each part of the portrait?
38. Adding Fractions with Like Denominators: Noah walks ⅓ of a kilometre to school each day. He also walks ⅓ of a kilometre to get home after school. How many kilometres does he walk in total?
39. Subtracting Fractions with Like Denominators: Last week, Whitney counted the number of juice boxes she had for school lunches. She had ⅗ of a case. This week, it’s down to ⅕ of a case. How much of the case did Whitney drink?
40. Adding Whole Numbers and Fractions with Like Denominators: At lunchtime, an ice cream parlor served 6 ¼ scoops of chocolate ice cream, 5 ¾ scoops of vanilla and 2 ¾ scoops of strawberry. How many scoops of ice cream did the parlor serve in total?
41. Subtracting Whole Numbers and Fractions with Like Denominators: For a party, Jaime had 5 ⅓ bottles of cola for her friends to drink. She drank ⅓ of a bottle herself. Her friends drank 3 ⅓. How many bottles of cola does Jaime have left?
42. Adding Fractions with Unlike Denominators: Kevin completed ½ of an assignment at school. When he was home that evening, he completed ⅚ of another assignment. How many assignments did Kevin complete?
43. Subtracting Fractions with Unlike Denominators: Packing school lunches for her kids, Patty used ⅞ of a package of ham. She also used ½ of a package of turkey. How much more ham than turkey did Patty use?
44. Multiplying Fractions: During gym class on Wednesday, the students ran for ¼ of a kilometre. On Thursday, they ran ½ as many kilometres as on Wednesday. How many kilometres did the students run on Thursday? Write your answer as a fraction.
45. Dividing Fractions: A clothing manufacturer uses ⅕ of a bottle of colour dye to make one pair of pants. The manufacturer used ⅘ of a bottle yesterday. How many pairs of pants did the manufacturer make?
46. Multiplying Fractions with Whole Numbers: Mark drank ⅚ of a carton of milk this week. Frank drank 7 times more milk than Mark. How many cartons of milk did Frank drink? Write your answer as a fraction, or as a whole or mixed number.
Decimals word problems
Best for: 4th grade, 5th grade
47. Adding Decimals: You have 2.6 grams of yogurt in your bowl and you add another spoonful of 1.3 grams. How much yogurt do you have in total?
48. Subtracting Decimals: Gemma had 25.75 grams of frosting to make a cake. She decided to use only 15.5 grams of the frosting. How much frosting does Gemma have left?
49. Multiplying Decimals with Whole Numbers: Marshall walks a total of 0.9 kilometres to and from school each day. After 4 days, how many kilometres will he have walked?
50. Dividing Decimals by Whole Numbers: To make the Leaning Tower of Pisa from spaghetti, Mrs. Robinson bought 2.5 kilograms of spaghetti. Her students were able to make 10 leaning towers in total. How many kilograms of spaghetti does it take to make 1 leaning tower?
51. Mixing Addition and Subtraction of Decimals: Rocco has 1.5 litres of orange soda and 2.25 litres of grape soda in his fridge. Antonio has 1.15 litres of orange soda and 0.62 litres of grape soda. How much more soda does Rocco have than Angelo?
52. Mixing Multiplication and Division of Decimals: 4 days a week, Laura practices martial arts for 1.5 hours. Considering a week is 7 days, what is her average practice time per day each week?
Comparing and sequencing word problems

Best for: Kindergarten, 1st grade, 2nd grade
53. Comparing 1-Digit Integers: You have 3 apples and your friend has 5 apples. Who has more?
54. Comparing 2-Digit Integers: You have 50 candies and your friend has 75 candies. Who has more?
55. Comparing Different Variables: There are 5 basketballs on the playground. There are 7 footballs on the playground. Are there more basketballs or footballs?
56. Sequencing 1-Digit Integers: Erik has 0 stickers. Every day he gets 1 more sticker. How many days until he gets 3 stickers?
57. Skip-Counting by Odd Numbers: Natalie began at 5. She skip-counted by fives. Could she have said the number 20?
58. Skip-Counting by Even Numbers: Natasha began at 0. She skip-counted by eights. Could she have said the number 36?
59. Sequencing 2-Digit Numbers: Each month, Jeremy adds the same number of cards to his baseball card collection. In January, he had 36. 48 in February. 60 in March. How many baseball cards will Jeremy have in April?
Time word problems
66. Converting Hours into Minutes: Jeremy helped his mom for 1 hour. For how many minutes was he helping her?
69. Adding Time: If you wake up at 7:00 a.m. and it takes you 1 hour and 30 minutes to get ready and walk to school, at what time will you get to school?
70. Subtracting Time: If a train departs at 2:00 p.m. and arrives at 4:00 p.m., how long were passengers on the train for?
71. Finding Start and End Times: Rebecca left her dad’s store to go home at twenty to seven in the evening. Forty minutes later, she was home. What time was it when she arrived home?
Money word problems
Best for: 1st grade, 2nd grade, 3rd grade, 4th grade, 5th grade
60. Adding Money: Thomas and Matthew are saving up money to buy a video game together. Thomas has saved $30. Matthew has saved $35. How much money have they saved up together in total?
61. Subtracting Money: Thomas has $80 saved up. He uses his money to buy a video game. The video game costs $67. How much money does he have left?
62. Multiplying Money: Tim gets $5 for delivering the paper. How much money will he have after delivering the paper 3 times?
63. Dividing Money: Robert spent $184.59 to buy 3 hockey sticks. If each hockey stick was the same price, how much did 1 cost?
64. Adding Money with Decimals: You went to the store and bought gum for $1.25 and a sucker for $0.50. How much was your total?
65. Subtracting Money with Decimals: You went to the store with $5.50. You bought gum for $1.25, a chocolate bar for $1.15 and a sucker for $0.50. How much money do you have left?
67. Applying Proportional Relationships to Money: Jakob wants to invite 20 friends to his birthday, which will cost his parents $250. If he decides to invite 15 friends instead, how much money will it cost his parents? Assume the relationship is directly proportional.
68. Applying Percentages to Money: Retta put $100.00 in a bank account that gains 20% interest annually. How much interest will be accumulated in 1 year? And if she makes no withdrawals, how much money will be in the account after 1 year?
Physical measurement word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade
72. Comparing Measurements: Cassandra’s ruler is 22 centimetres long. April’s ruler is 30 centimetres long. How many centimetres longer is April’s ruler?
73. Contextualizing Measurements: Picture a school bus. Which unit of measurement would best describe the length of the bus? Centimetres, metres or kilometres?
74. Adding Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Last year, Micha’s dad used 100 litres of gas. This year, her dad used 90 litres of gas. How much gas did he use in total for the two years?
75. Subtracting Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Over the past two years, Micha’s dad used 200 litres of gas. This year, he used 100 litres of gas. How much gas did he use last year?
76. Multiplying Volume and Mass: Kiera wants to make sure she has strong bones, so she drinks 2 litres of milk every week. After 3 weeks, how many litres of milk will Kiera drink?
77. Dividing Volume and Mass: Lillian is doing some gardening, so she bought 1 kilogram of soil. She wants to spread the soil evenly between her 2 plants. How much will each plant get?
78. Converting Mass: Inger goes to the grocery store and buys 3 squashes that each weigh 500 grams. How many kilograms of squash did Inger buy?
79. Converting Volume: Shad has a lemonade stand and sold 20 cups of lemonade. Each cup was 500 millilitres. How many litres did Shad sell in total?
80. Converting Length: Stacy and Milda are comparing their heights. Stacy is 1.5 meters tall. Milda is 10 centimetres taller than Stacy. What is Milda’s height in centimetres?
81. Understanding Distance and Direction: A bus leaves the school to take students on a field trip. The bus travels 10 kilometres south, 10 kilometres west, another 5 kilometres south and 15 kilometres north. To return to the school, in which direction does the bus have to travel? How many kilometres must it travel in that direction?
Ratios and percentages word problems
Best for: 4th grade, 5th grade, 6th grade
82. Finding a Missing Number: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. Jenny has 28 trophies. How many does Meredith have?
83. Finding Missing Numbers: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. The difference between the numbers is 12. What are the numbers?
84. Comparing Ratios: The school’s junior band has 10 saxophone players and 20 trumpet players. The school’s senior band has 18 saxophone players and 29 trumpet players. Which band has the higher ratio of trumpet to saxophone players?
85. Determining Percentages: Mary surveyed students in her school to find out what their favourite sports were. Out of 1,200 students, 455 said hockey was their favourite sport. What percentage of students said hockey was their favourite sport?
86. Determining Percent of Change: A decade ago, Oakville’s population was 67,624 people. Now, it is 190% larger. What is Oakville’s current population?
87. Determining Percents of Numbers: At the ice skate rental stand, 60% of 120 skates are for boys. If the rest of the skates are for girls, how many are there?
88. Calculating Averages: For 4 weeks, William volunteered as a helper for swimming classes. The first week, he volunteered for 8 hours. He volunteered for 12 hours in the second week, and another 12 hours in the third week. The fourth week, he volunteered for 9 hours. For how many hours did he volunteer per week, on average?
Probability and data relationships word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade
89. Understanding the Premise of Probability: John wants to know his class’s favourite TV show, so he surveys all of the boys. Will the sample be representative or biased?
90. Understanding Tangible Probability: The faces on a fair number die are labelled 1, 2, 3, 4, 5 and 6. You roll the die 12 times. How many times should you expect to roll a 1?
91. Exploring Complementary Events: The numbers 1 to 50 are in a hat. If the probability of drawing an even number is 25/50, what is the probability of NOT drawing an even number? Express this probability as a fraction.
92. Exploring Experimental Probability: A pizza shop has recently sold 15 pizzas. 5 of those pizzas were pepperoni. Answering with a fraction, what is the experimental probability that he next pizza will be pepperoni?
93. Introducing Data Relationships: Maurita and Felice each take 4 tests. Here are the results of Maurita’s 4 tests: 4, 4, 4, 4. Here are the results for 3 of Felice’s 4 tests: 3, 3, 3. If Maurita’s mean for the 4 tests is 1 point higher than Felice’s, what’s the score of Felice’s 4th test?
94. Introducing Proportional Relationships: Store A is selling 7 pounds of bananas for $7.00. Store B is selling 3 pounds of bananas for $6.00. Which store has the better deal?
95. Writing Equations for Proportional Relationships: Lionel loves soccer, but has trouble motivating himself to practice. So, he incentivizes himself through video games. There is a proportional relationship between the amount of drills Lionel completes, in x , and for how many hours he plays video games, in y . When Lionel completes 10 drills, he plays video games for 30 minutes. Write the equation for the relationship between x and y .
Geometry word problems
Best for: 4th grade, 5th grade, 6th grade, 7th grade, 8th grade
96. Introducing Perimeter: The theatre has 4 chairs in a row. There are 5 rows. Using rows as your unit of measurement, what is the perimeter?
97. Introducing Area: The theatre has 4 chairs in a row. There are 5 rows. How many chairs are there in total?
98. Introducing Volume: Aaron wants to know how much candy his container can hold. The container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. What is the container’s volume?
99. Understanding 2D Shapes: Kevin draws a shape with 4 equal sides. What shape did he draw?
100. Finding the Perimeter of 2D Shapes: Mitchell wrote his homework questions on a piece of square paper. Each side of the paper is 8 centimetres. What is the perimeter?
101. Determining the Area of 2D Shapes: A single trading card is 9 centimetres long by 6 centimetres wide. What is its area?
102. Understanding 3D Shapes: Martha draws a shape that has 6 square faces. What shape did she draw?
103. Determining the Surface Area of 3D Shapes: What is the surface area of a cube that has a width of 2cm, height of 2 cm and length of 2 cm?
104. Determining the Volume of 3D Shapes: Aaron’s candy container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. Bruce’s container is 25 centimetres tall, 9 centimetres long and 9 centimetres wide. Find the volume of each container. Based on volume, whose container can hold more candy?
105. Identifying Right-Angled Triangles: A triangle has the following side lengths: 3 cm, 4 cm and 5 cm. Is this triangle a right-angled triangle?
106. Identifying Equilateral Triangles: A triangle has the following side lengths: 4 cm, 4 cm and 4 cm. What kind of triangle is it?
107. Identifying Isosceles Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 5 cm. What kind of triangle is it?
108. Identifying Scalene Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 6 cm. What kind of triangle is it?
109. Finding the Perimeter of Triangles: Luigi built a tent in the shape of an equilateral triangle. The perimeter is 21 metres. What is the length of each of the tent’s sides?
110. Determining the Area of Triangles: What is the area of a triangle with a base of 2 units and a height of 3 units?
111. Applying Pythagorean Theorem: A right triangle has one non-hypotenuse side length of 3 inches and the hypotenuse measures 5 inches. What is the length of the other non-hypotenuse side?
112. Finding a Circle’s Diameter: Jasmin bought a new round backpack. Its area is 370 square centimetres. What is the round backpack’s diameter?
113. Finding a Circle's Area: Captain America’s circular shield has a diameter of 76.2 centimetres. What is the area of his shield?
114. Finding a Circle’s Radius: Skylar lives on a farm, where his dad keeps a circular corn maze. The corn maze has a diameter of 2 kilometres. What is the maze’s radius?
Variables word problems

Best for: 6th grade, 7th grade, 8th grade
115. Identifying Independent and Dependent Variables: Victoria is baking muffins for her class. The number of muffins she makes is based on how many classmates she has. For this equation, m is the number of muffins and c is the number of classmates. Which variable is independent and which variable is dependent?
116. Writing Variable Expressions for Addition: Last soccer season, Trish scored g goals. Alexa scored 4 more goals than Trish. Write an expression that shows how many goals Alexa scored.
117. Writing Variable Expressions for Subtraction: Elizabeth eats a healthy, balanced breakfast b times a week. Madison sometimes skips breakfast. In total, Madison eats 3 fewer breakfasts a week than Elizabeth. Write an expression that shows how many times a week Madison eats breakfast.
118. Writing Variable Expressions for Multiplication: Last hockey season, Jack scored g goals. Patrik scored twice as many goals than Jack. Write an expression that shows how many goals Patrik scored.
119. Writing Variable Expressions for Division: Amanda has c chocolate bars. She wants to distribute the chocolate bars evenly among 3 friends. Write an expression that shows how many chocolate bars 1 of her friends will receive.
120. Solving Two-Variable Equations: This equation shows how the amount Lucas earns from his after-school job depends on how many hours he works: e = 12h . The variable h represents how many hours he works. The variable e represents how much money he earns. How much money will Lucas earn after working for 6 hours?
How to easily make your own math word problems & word problems worksheets

Armed with 120 examples to spark ideas, making your own math word problems can engage your students and ensure alignment with lessons. Do:
- Link to Student Interests: By framing your word problems with student interests, you’ll likely grab attention. For example, if most of your class loves American football, a measurement problem could involve the throwing distance of a famous quarterback.
- Make Questions Topical: Writing a word problem that reflects current events or issues can engage students by giving them a clear, tangible way to apply their knowledge.
- Include Student Names: Naming a question’s characters after your students is an easy way make subject matter relatable, helping them work through the problem.
- Be Explicit: Repeating keywords distills the question, helping students focus on the core problem.
- Test Reading Comprehension: Flowery word choice and long sentences can hide a question’s key elements. Instead, use concise phrasing and grade-level vocabulary.
- Focus on Similar Interests: Framing too many questions with related interests -- such as football and basketball -- can alienate or disengage some students.
- Feature Red Herrings: Including unnecessary information introduces another problem-solving element, overwhelming many elementary students.
A key to differentiated instruction , word problems that students can relate to and contextualize will capture interest more than generic and abstract ones.
Final thoughts about math word problems
You’ll likely get the most out of this resource by using the problems as templates, slightly modifying them by applying the above tips. In doing so, they’ll be more relevant to -- and engaging for -- your students.
Regardless, having 120 curriculum-aligned math word problems at your fingertips should help you deliver skill-building challenges and thought-provoking assessments.
The result?
A greater understanding of how your students process content and demonstrate understanding, informing your ongoing teaching approach.













































































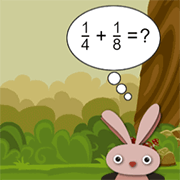





























































































































IMAGES
VIDEO
COMMENTS
Find over 100,000 free practice questions on various math topics and grade levels. Learn how to solve problems with interactive and fun exercises on Khan Academy.
Find 120 examples of math word problems for different skills and levels, from addition to division. Learn how to create engaging and challenging word problems with tips and templates.
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step-by-step explanations, just like a math tutor. ... Step-by-Step Examples. Basic Math. Long Arithmetic. Adding Using Long Addition. Long Subtraction. Long Multiplication. ... Solving the System of Equations Using an Inverse ...
Learn more than what the answer is - with the math helper app, you'll learn the steps behind it too. Benefits. Even simple math problems become easier to solve when broken down into steps. From basic additions to calculus, the process of problem solving usually takes a lot of practice before answers could come easily.
GeoGebra Math Practice. Math Practice is a tool for mastering algebraic notation. It supports students in their step-by-step math work, let's them explore different solution paths, and helps build confidence, fluency, and understanding. Getting started as a teacher or student.
Learn various problem solving strategies for math word problems, such as verbal model, algebraic model, guess and check, and find a pattern. See video lessons, examples, solutions and practice problems with step-by-step explanations.
Wolfram for Education. Wolfram Demonstrations. Mathematica. MathWorld. Online practice problems with answers for students and teachers. Pick a topic and start practicing, or print a worksheet for study sessions or quizzes.
Unit 1 Introduction to algebra. Unit 2 Solving basic equations & inequalities (one variable, linear) Unit 3 Linear equations, functions, & graphs. Unit 4 Sequences. Unit 5 System of equations. Unit 6 Two-variable inequalities. Unit 7 Functions. Unit 8 Absolute value equations, functions, & inequalities. Unit 9 Quadratic equations & functions.
To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem. ... Related Symbolab blog posts. Practice, practice, practice. Math can be an intimidating subject. Each new topic ...
MathPapa Practice offers practice problems to help you learn algebra. You can choose from different topics such as basic arithmetic, fractions, decimals, percentages, and puzzles.
This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. ... Problem Solving Strategy 3 (Using a variable to find the sum of a sequence.) Gauss's strategy for sequences. last term = fixed number (n-1) + first term.
Free math problem solver answers your algebra homework questions with step-by-step explanations.
Problems for 5th Grade. Multi-digit multiplication. Dividing completely. Writing expressions. Rounding whole numbers. Inequalities on a number line. Linear equation and inequality word problems. Linear equation word problems. Linear equation word problems.
Art of Problem Solving offers two other multifaceted programs. Beast Academy is our comic-based online math curriculum for students ages 6-13. And AoPS Academy brings our methodology to students grades 2-12 through small, in-person classes at local campuses. Through our three programs, AoPS offers the most comprehensive honors math pathway ...
Click to see solution. Problem 17. A biker covered half the distance between two towns in 2 hr 30 min. After that he increased his speed by 2 km/hr. He covered the second half of the distance in 2 hr 20 min. Find the distance between the two towns and the initial speed of the biker. Click to see solution. Problem 18.
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do. Here are some things we can do: Add or Subtract the same value from both sides; Clear out any fractions by Multiplying every term by the bottom parts; Divide every term by the same nonzero value; Combine Like Terms; Factoring
Solving algebraic word problems requires us to combine our ability to create equations and solve them. To solve an algebraic word problem: Define a variable. Write an equation using the variable. Solve the equation. If the variable is not the answer to the word problem, use the variable to calculate the answer.
Solve geometry problems, proofs, and draw geometric shapes Math Help Tailored For You Practice Practice and improve your math skills through interactive personalized exercises and quizzes Also Includes Dashboard Track your progress with detailed performance reports and analytics
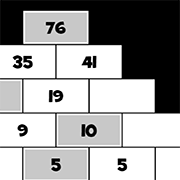
Picture math puzzles Do the math. BrainSnack. Enter numbers in each row and column to arrive at the end totals. Only numbers 1 through 9 are used, and each only once. Answer: BrainSnack. Tricky ...
Integration. ∫ 01 xe−x2dx. Limits. x→−3lim x2 + 2x − 3x2 − 9. Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
Multiplication, division, fractions, and logic games that boost fourth grade math skills. Level 4 Math Games Game Spotlight: Division Derby Multiplayer Math Games Tug Multiplication. Pony Pull Division. Grand Prix ... Logic and Problem Solving Games Icy Super Slide. Arcade Golf. Rabbit Samurai 2. Duck Life 4. Icy Purple Head 2. Duck Life Space ...
Learn third grade math—fractions, area, arithmetic, and so much more. This course is aligned with Common Core standards. ... Arithmetic patterns and problem solving One and two-step word problems: Arithmetic patterns and problem solving. Patterns in arithmetic: Arithmetic patterns and problem solving. Unit 9: Quadrilaterals. Quadrilaterals ...