
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.8 Hypothesis Tests for a Population Proportion
Learning objectives.
- Conduct and interpret hypothesis tests for a population proportion.
Some notes about conducting a hypothesis test:
- The null hypothesis [latex]H_0[/latex] is always an “equal to.” The null hypothesis is the original claim about the population parameter.
- The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.” The form of the alternative hypothesis depends on the context of the question.
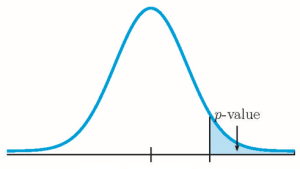
- If the alternative hypothesis is a “less than”, then the test is left-tail. The p -value is the area in the left-tail of the distribution.
- If the alternative hypothesis is a “greater than”, then the test is right-tail. The p -value is the area in the right-tail of the distribution.
- If the alternative hypothesis is a “not equal to”, then the test is two-tail. The p -value is the sum of the area in the two-tails of the distribution. Each tail represents exactly half of the p -value.
- Think about the meaning of the p -value. A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of 0.05. Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
- The significance level must be identified before collecting the sample data and conducting the test. Generally, the significance level will be included in the question. If no significance level is given, a common standard is to use a significance level of 5%.
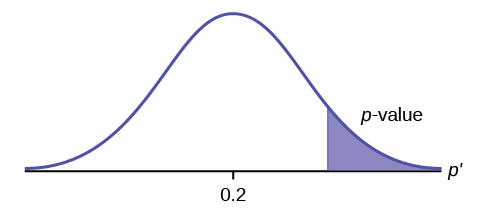
Suppose the hypotheses for a hypothesis test are:
[latex]\begin{eqnarray*} H_0: & & p=20 \% \\ H_a: & & p \gt 20\% \end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\gt[/latex], this is a right-tail test. The p -value is the area in the right-tail of the distribution.
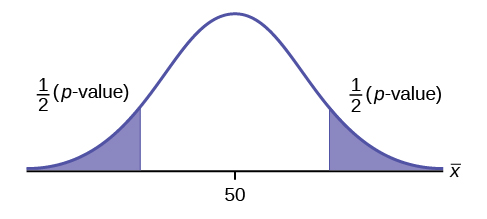
[latex]\begin{eqnarray*} H_0: & & p=50 \% \\ H_a: & & p \neq 50\% \end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tail test. The p -value is the sum of the areas in the two tails of the distribution. Each tail contains exactly half of the p -value.
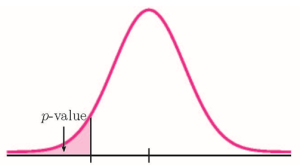
[latex]\begin{eqnarray*} H_0: & & p=10\% \\ H_a: & & p \lt 10\% \end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tail test. The p -value is the area in the left-tail of the distribution.
Steps to Conduct a Hypothesis Test for a Population Proportion
- Write down the null and alternative hypotheses in terms of the population proportion [latex]p[/latex]. Include appropriate units with the values of the proportion.
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level.
- If [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution with [latex]\displaystyle{z=\frac{\hat{p}-p}{\sqrt{\frac{p \times (1-p)}{n}}}}[/latex].
- If one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use a binomial distribution.
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- Write down a concluding sentence specific to the context of the question.
USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION PROPORTION
The p -value for a hypothesis test on a population proportion is the area in the tail(s) of distribution of the sample proportion. If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution to find the p -value. If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use the binomial distribution to find the p -value.
If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex]:
- For x , enter the value for [latex]\hat{p}[/latex].
- For [latex]\mu[/latex] , enter the mean of the sample proportions [latex]p[/latex]. Note: Because the test is run assuming the null hypothesis is true, the value for [latex]p[/latex] is the claim from the null hypothesis.
- For [latex]\sigma[/latex] , enter the standard error of the proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
- For the logic operator , enter true . Note: Because we are calculating the area under the curve, we always enter true for the logic operator.
- Use the appropriate technique with the norm.dist function to find the area in the left-tail or the area in the right-tail.
If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex]:
- The p -value is found using the binomial distribution.
- For x , enter the number of successes.
- For n , enter the sample size.
- For p , enter the the value of the population proportion [latex]p[/latex] from the null hypothesis.
- For the logic operator , enter true . Note: Because we are calculating an at most probability, the logic operator is always true.
- For p , enter the the value of the population proportion [latex]p[/latex] in the null hypothesis.
- For the logic operator , enter true . Note: Because we are calculating an at least probability, the logic operator is always true.
Marketers believe that 92% of adults own a cell phone. A cell phone manufacturer believes that number is actually lower. In a sample of 200 adults, 87% own a cell phone. At the 1% significance level, determine if the proportion of adults that own a cell phone is lower than the marketers’ claim.
Hypotheses:
[latex]\begin{eqnarray*} H_0: & & p=92\% \mbox{ of adults own a cell phone} \\ H_a: & & p \lt 92\% \mbox{ of adults own a cell phone} \end{eqnarray*}[/latex]
From the question, we have [latex]n=200[/latex], [latex]\hat{p}=0.87[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.92[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 200 \times 0.92=184 \geq 5 \\ n \times (1-p) & = & 200 \times (1-0.92)=16 \geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left tail of the distribution.
| norm.dist | ||
| 0.87 | 0.0046 | |
| 0.92 | ||
| sqrt(0.92*(1-0.92)/200) | ||
| true |
So the p -value[latex]=0.0046[/latex].
Conclusion:
Because p -value[latex]=0.0046 \lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 1% significance level there is enough evidence to suggest that the proportion of adults who own a cell phone is lower than 92%.
- The null hypothesis [latex]p=92\%[/latex] is the claim that 92% of adults own a cell phone.
- The alternative hypothesis [latex]p \lt 92\%[/latex] is the claim that less than 92% of adults own a cell phone.
- The function is norm.dist because we are finding the area in the left tail of a normal distribution.
- Field 1 is the value of [latex]\hat{p}[/latex].
- Field 2 is the value of [latex]p[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.92[/latex].
- Field 3 is the standard deviation for the sample proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
- The p -value of 0.0046 tells us that under the assumption that 92% of adults own a cell phone (the null hypothesis), there is only a 0.46% chance that the proportion of adults who own a cell phone in a sample of 200 is 87% or less. This is a small probability, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of adults who own a cell phone is most likely less than 92%.
A consumer group claims that the proportion of households that have at least three cell phones is 30%. A cell phone company has reason to believe that the proportion of households with at least three cell phones is much higher. Before they start a big advertising campaign based on the proportion of households that have at least three cell phones, they want to test their claim. Their marketing people survey 150 households with the result that 54 of the households have at least three cell phones. At the 1% significance level, determine if the proportion of households that have at least three cell phones is less than 30%.
[latex]\begin{eqnarray*} H_0: & & p=30\% \mbox{ of household have at least 3 cell phones} \\ H_a: & & p \gt 30\% \mbox{ of household have at least 3 cell phones} \end{eqnarray*}[/latex]
From the question, we have [latex]n=150[/latex], [latex]\displaystyle{\hat{p}=\frac{54}{150}=0.36}[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.3[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 150 \times 0.3=45 \geq 5 \\ n \times (1-p) & = & 150 \times (1-0.3)=105 \geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.
| 1-norm.dist | ||
| 0.36 | 0.0544 | |
| 0.3 | ||
| sqrt(0.3*(1-0.3)/150) | ||
| true |
So the p -value[latex]=0.0544[/latex].
Because p -value[latex]=0.0544 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the 1% significance level there is not enough evidence to suggest that the proportion of households with at least three cell phones is more than 30%.
- The null hypothesis [latex]p=30\%[/latex] is the claim that 30% of households have at least three cell phones.
- The alternative hypothesis [latex]p \gt 30\%[/latex] is the claim that more than 30% of households have at least three cell phones.
- The function is 1-norm.dist because we are finding the area in the right tail of a normal distribution.
- Field 2 is the value of [latex]p[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.3[/latex].
- The p -value of 0.0544 tells us that under the assumption that 30% of households have at least three cell phones (the null hypothesis), there is a 5.44% chance that the proportion of households with at least three cell phones in a sample of 150 is 36% or more. Compared to the 1% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the claim that 30% of households have at least three cell phones is most likely correct.
A teacher believes that 70% of students in the class will want to go on a field trip to the local zoo. The students in the class believe the proportion is much higher and ask the teacher to verify her claim. The teacher samples 50 students and 39 reply that they would want to go to the zoo. At the 5% significance level, determine if the proportion of students who want to go on the field trip is higher than 70%.
[latex]\begin{eqnarray*} H_0: & & p = 70\% \mbox{ of students want to go on the field trip} \\ H_a: & & p \gt 70\% \mbox{ of students want to go on the field trip} \end{eqnarray*}[/latex]
From the question, we have [latex]n=50[/latex], [latex]\displaystyle{\hat{p}=\frac{39}{50}=0.78}[/latex], and [latex]\alpha=0.05[/latex].
[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.7=35 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.7)=15 \geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.
| 1-norm.dist | ||
| 0.78 | 0.1085 | |
| 0.7 | ||
| sqrt(0.7*(1-0.7)/50) | ||
| true |
So the p -value[latex]=0.1085[/latex].
Because p -value[latex]=0.1085 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that the proportion of students who want to go on the field trip is higher than 70%.
- The null hypothesis [latex]p=70\%[/latex] is the claim that 70% of the students want to go on the field trip.
- The alternative hypothesis [latex]p \gt 70\%[/latex] is the claim that more than 70% of students want to go on the field trip.
- The p -value of 0.1085 tells us that under the assumption that 70% of students want to go on the field trip (the null hypothesis), there is a 10.85% chance that the proportion of students who want to go on the field trip in a sample of 50 students is 78% or more. Compared to the 5% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the teacher’s claim that 70% of students want to go on the field trip is most likely correct.
Joan believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50%. Joan samples 100 first-time brides and 56 reply that they are younger than their grooms. Use a 5% significance level.
[latex]\begin{eqnarray*} H_0: & & p=50\% \mbox{ of first-time brides are younger than the groom} \\ H_a: & & p \neq 50\% \mbox{ of first-time brides are younger than the groom} \end{eqnarray*}[/latex]
From the question, we have [latex]n=100[/latex], [latex]\displaystyle{\hat{p}=\frac{56}{100}=0.56}[/latex], and [latex]\alpha=0.05[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.5[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 100 \times 0.5=50 \geq 5 \\ n \times (1-p) & = & 100 \times (1-0.5)=50 \geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.
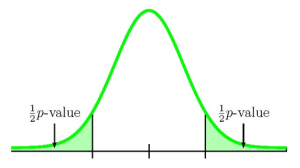
Because there is only one sample, we only have information relating to one of the two tails, either the left or the right. We need to know if the sample relates to the left or right tail because that will determine how we calculate out the area of that tail using the normal distribution. In this case, the sample proportion [latex]\hat{p}=0.56[/latex] is greater than the value of the population proportion in the null hypothesis [latex]p=0.5[/latex] ([latex]\hat{p}=0.56>0.5=p[/latex]), so the sample information relates to the right-tail of the normal distribution. This means that we will calculate out the area in the right tail using 1-norm.dist . However, this is a two-tailed test where the p -value is the sum of the area in the two tails and the area in the right-tail is only one half of the p -value. The area in the left tail equals the area in the right tail and the p -value is the sum of these two areas.
| 1-norm.dist | ||
| 0.56 | 0.1151 | |
| 0.5 | ||
| sqrt(0.5*(1-0.5)/100) | ||
| true |
So the area in the right tail is 0.1151 and [latex]\frac{1}{2}[/latex]( p -value)[latex]=0.1151[/latex]. This is also the area in the left tail, so
p -value[latex]=0.1151+0.1151=0.2302[/latex]
Because p -value[latex]=0.2302 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that the proportion of first-time brides that are younger than the groom is different from 50%.
- The null hypothesis [latex]p=50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is 50%.
- The alternative hypothesis [latex]p \neq 50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is different from 50%.
- We use norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the left tail. The area in the right tail equals the area in the left tail, so we can find the p -value by adding the output from this function to itself.
- We use 1-norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the right tail. The area in the left tail equals the area in the right tail, so we can find the p -value by adding the output from this function to itself.
- The p -value of 0.2302 is a large probability compared to the 5% significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the claim that the proportion of first-time brides who are younger than the groom is most likely correct.
Watch this video: Hypothesis Testing for Proportions: z -test by ExcelIsFun [7:27]
An online retailer believes that 93% of the visitors to its website will make a purchase. A researcher in the marketing department thinks the actual percent is lower than claimed. The researcher examines a sample of 50 visits to the website and finds that 45 of the visits resulted in a purchase. At the 1% significance level, determine if the proportion of visits to the website that result in a purchase is lower than claimed.
[latex]\begin{eqnarray*} H_0: & & p=93\% \mbox{ of visitors make a purchase} \\ H_a: & & p \lt 93\% \mbox{ of visitors make a purchase} \end{eqnarray*}[/latex]
From the question, we have [latex]n=50[/latex], [latex]x=45[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.93[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.93=46.5 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.93)=3.5 \lt 5\end{eqnarray*}[/latex]
Because [latex]n \times (1-p) \lt 5[/latex] we use a binomial distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the probability of getting at most 45 successes in 50 trials.
| binom.dist | ||
| 45 | 0.2710 | |
| 50 | ||
| 0.93 | ||
| true |
So the p -value[latex]=0.2710[/latex].
Because p -value[latex]=0.2710 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the 1% significance level there is not enough evidence to suggest that the proportion of visitors who make a purchase is lower than 93%.
- The null hypothesis [latex]p=93\%[/latex] is the claim that 93% of visitors to the website make a purchase.
- The alternative hypothesis [latex]p \lt 93\%[/latex] is the claim that less than 93% of visitors to the website make a purchase.
- The function is binom.dist because we are finding the probability of at most 45 successes.
- Field 1 is the number of successes [latex]x[/latex].
- Field 2 is the sample size [latex]n[/latex].
- Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.93[/latex].
- The p -value of 0.2710 tells us that under the assumption that 93% of visitors make a purchase (the null hypothesis), there is a 27.10% chance that the number of visitors in a sample of 50 who make a purchase is 45 or less. This is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the proportion of visitors to the website who make a purchase adults is most likely 93%.
A drug company claims that only 4% of people who take their new drug experience any side effects from the drug. A researcher believes that the percent is higher than drug company’s claim. The researcher takes a sample of 80 people who take the drug and finds that 10% of the people in the sample experience side effects from the drug. At the 5% significance level, determine if the proportion of people who experience side effects from taking the drug is higher than claimed.
[latex]\begin{eqnarray*} H_0: & & p=4\% \mbox{ of people experience side effects} \\ H_a: & & p \gt 4\% \mbox{ of people experience side effects} \end{eqnarray*}[/latex]
From the question, we have [latex]n=80[/latex], [latex]\hat{p}=0.1[/latex], and [latex]\alpha=0.05[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.04[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 80 \times 0.04=3.2 \lt 5\end{eqnarray*}[/latex]
Because [latex]n \times p \lt 5[/latex] we use a binomial distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the probability of getting at least 8 successes in 80 trials. (Note: In the sample of size 80, 10% have the characteristic of interest, so this means that [latex]80 \times 0.1=8[/latex] people in the sample have the characteristic of interest.)
| 1-binom.dist | ||
| 7 | 0.0147 | |
| 80 | ||
| 0.04 | ||
| true |
So the p -value[latex]=0.0147[/latex].
Because p -value[latex]=0.0147 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that the proportion of people who experience side effects from taking the drug is higher than 4%.
- The null hypothesis [latex]p=4\%[/latex] is the claim that 4% of the people experience side effects from taking the drug.
- The alternative hypothesis [latex]p \gt 4\%[/latex] is the claim that more than 4% of the people experience side effects from taking the drug.
- The function is 1-binom.dist because we are finding the probability of at least 8 successes.
- Field 1 is [latex]x-1[/latex] where [latex]x[/latex] is the number of successes. In this case, we are using the compliment rule to change the probability of at least 8 successes into 1 minus the probability of at most 7 successes.
- Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.04[/latex].
- The p -value of 0.0147 tells us that under the assumption that 4% of people experience side effects (the null hypothesis), there is a 1.47% chance that the number of people in a sample of 80 who experience side effects is 8 or more. This is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of people who experience side effects is most likely greater than 4%.
Concept Review
The hypothesis test for a population proportion is a well-established process:
- Find the p -value (the area in the corresponding tail) for the test using the appropriate distribution (normal or binomial).
- Compare the p -value to the significance level and state the outcome of the test.
Attribution
“ 9.6 Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.
Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Section 10.2: Hypothesis Tests for a Population Proportion
- 10.1 The Language of Hypothesis Testing
- 10.2 Hypothesis Tests for a Population Proportion
- 10.3 Hypothesis Tests for a Population Mean
- 10.4 Hypothesis Tests for a Population Standard Deviation
- 10.5 Putting It Together: Which Method Do I Use?
By the end of this lesson, you will be able to...
- explain the logic of hypothesis testing
- test hypotheses about a population proportion
- test hypotheses about a population proportion using the binomial probability distribution
For a quick overview of this section, watch this short video summary:
The Logic of Hypothesis Testing
Once we have our null and alternative hypotheses chosen, and our sample data collected, how do we choose whether or not to reject the null hypothesis? In a nutshell, it's this:
If the observed results are unlikely assuming that the null hypothesis is true, we say the result is statistically significant , and we reject the null hypothesis. In other words, the observed results are so unusual, that our original assumption in the null hypothesis must not have been correct.
There are generally three different methods for testing hypotheses:
- the classical approach
- confidence intervals
Because P -values are so much more widely used, we will be focusing on this method. You will be required to include P -values for your homework and exams. We will also frequently look at both P -values and confidence intervals to make sure the two methods align.
In general, we define the P -value this way:
The P -value is the probability of observing a sample statistic as extreme or more extreme than the one observed in the sample assuming that the null hypothesis is true.
The Sample Proportion
In Section 8.2, we learned about the distribution of the sample proportion, so let's do a quick review of that now.
We also learned some information about how the sample proportion is distributed:
Sampling Distribution of
For a random sample of size n such that n≤0.05N (in other words, the sample is less than 5% of the population),
So what we do is create a test statistic based on our sample, and then use a table or technology to find the probability of what we observed. Here are the details.
Testing Claims Regarding the Population Proportion Using P -Values
In this first section, we assume we are testing some claim about the population proportion. As usual, the following two conditions must be true:
- np(1-p)≥10, and
Step 1 : State the null and alternative hypotheses.
| H : p = p H : p ≠ p | H : p = p H : p < p | H : p = p H : p > p |
Step 2 : Decide on a level of significance, α , depending on the seriousness of making a Type I error. ( α will often be given as part of a test or homework question, but this will not be the case in the outside world.)
Step 4 : Determine the P -value.
Step 5 : Reject the null hypothesis if the P -value is less than the level of significance, α.
Step 6 : State the conclusion.
Calculating P -Values
Right-tailed tests.

Left-Tailed Tests

Two-Tailed Tests
In a two-tailed test, the P -value = 2P(Z > |z o |).

It may seem odd to multiply the probability by two, since "or more extreme" seems to imply the area in the tail only. The reason why we do multiply by two is that even though the result was on one side, we didn't know before collecting the data , on which side it would be.
The Strength of the Evidence
Since the P -value represents the probability of observing our result or more extreme, the smaller the P -value, the more unusual our observation was. Another way to look at it is this:
The smaller the P -value, the stronger the evidence supporting the alternative hypothesis. We can use the following guideline:
- P -value < 0.01: very strong evidence supporting the alternative hypothesis
- 0.01 ≤ P -value < 0.05: strong evidence supporting the alternative hypothesis
- 0.05 ≤ P -value < 0.1: some evidence supporting the alternative hypothesis
- P -value ≥ 0.1: weak to no evidence supporting the alternative hypothesis
These values are not hard lines, of course, but they can give us a general idea of the strength of the evidence.
But wait! There is an important caveat here, which was mentioned earlier in the section about The Controversy Regarding Hypothesis Testing . The problem is that it's relatively easy to get a large p-value - just get a really large sample size! So the chart above is really with the caveat " assuming equal sample sizes in comparable studies , ... "
This isn't something every statistics text will mention, nor will every instructor mention, but it's important.
According to the Elgin Community College website , approximately 56% of ECC students are female. Suppose we wonder if the same proportion is true for math courses. If we collect a sample of 200 ECC students enrolled in math courses and find that 105 of them are female, do we have enough evidence at the 10% level of significance to say that the proportion of math students who are female is different from the general population?
Note: Be sure to check that the conditions for performing the hypothesis test are met.
[ reveal answer ]
Before we begin, we need to make sure that our sample is less than 5% of the population, and that np 0 (1-p 0 )≥10.
Since there are roughly 16,000 students at ECC (source: www.elgin.edu ), our sample of 200 is clearly less than 5% of the population. Also, np 0 (1-p 0 ) = 200(0.56)(1-0.56) = 49.28 > 10
Step 1 : H 0 : p = 0.56 H 1 : p ≠ 0.56
Step 2 : α = 0.1
Step 4 : P -value = 2•P(Z < -1.00) ≈ 0.3187 (Note that this is a 2-tailed test.)
Step 5 : Since P -value > α , we do not reject H 0 .
Step 6 : There is not enough evidence at the 5% level of significance to support the claim that the proportion of students in math courses who are female is different from the general population.
Hypothesis Testing Regarding p Using StatCrunch
> > > and H , then click . > > > and H , then click . * To get the counts, first create a frequency table. If you have a grouping variable, use a contingency table. |
Consider the excerpt shown below (also used in Example 1 , in Section 9.3) from a poll conducted by Pew Research:
Stem cell, marijuana proposals lead in Mich. poll A recent poll shows voter support leading opposition for ballot proposals to loosen Michigan's restrictions on embryonic stem cell research and allow medical use of marijuana. The EPIC-MRA poll conducted for The Detroit News and television stations WXYZ, WILX, WOOD and WJRT found 50 percent of likely Michigan voters support the stem cell proposal , 32 percent against and 18 percent undecided. The telephone poll of 602 likely Michigan voters was conducted Sept. 22 through Wednesday. It has a margin of sampling error of plus or minus 4 percentage points. (Source: Associated Press )
Suppose we wonder if the percent of Elgin Community College students who support stem cell research is different from this. If 61 of 100 randomly selected ECC students support stem cell research, is there enough evidence at the 5% level of signficance to support our claim?
Since there are roughly 16,000 students at ECC (source: www.elgin.edu ), our sample of 100 is clearly less than 5% of the population. Also, np 0 (1-p 0 ) = 100(0.50)(1-0.50) = 25 > 10
Step 1 : H 0 : p = 0.5 H 1 : p ≠ 0.5
Step 2 : α = 0.05
Step 3 : We'll use StatCrunch.
Step 4 : Using StatCrunch:

Step 5 : Since P -value < α , we reject H 0 .
Step 6 : Based on this sample, there is enough evidence at the 5% level of significance to support the claim that the proportion of ECC students who support stem cell research is different from the Michigan poll.
One question you might have is, "What do we do if the conditions for the hypothesis test about p aren't met?" Great question!
A Binomial Refresher
The binomial probability distribution function.
The probability of obtaining x successes in n independent trials of a binomial experiment, where the probability of success is p, is given by
Where x = 0, 1, 2, ... , n
Using Technology to Calculate Binomial Probabilities
Here's a quick overview of the formulas for finding binomial probabilities in StatCrunch.
Click on > > Enter n, p, the appropriate equality/inequality, and x. The figure below shows P(X≥3) if n=4 and p=0.25.
|
Hypothesis Testing Using the Binomial Distribution
Traditionally, about 70% of students in a particular Statistics course at ECC are successful. If only 15 students in a class of 28 randomly selected students are successful, is there enough evidence at the 5% level of significance to say that students of that particular instructor are successful at a rate less than 70%?
Step 1 : H 0 : p = 0.7 H 1 : p < 0.7
Step 4 : If we let X = the number of students who were successful, X follows the binomial distribution. For this example, n=28 and p=0.70, and we want P(X≤15). Using StatCrunch:
Step 5 : Since P -value < α (though it's very close), we reject H 0 .
Step 6 : Based on this sample, there is enough evidence at the 5% level of significance to support the claim that the proportion of students who are successful in this professor's classes are less than 70%. (Keep in mind that this assumes the students were randomly assigned to that class, which is never the case in reality!)
<< previous section | next section >>

Chapter 8: Inference for One Proportion
Hypothesis test for a population proportion (3 of 3), learning objectives.
- Conduct a hypothesis test for a population proportion. State a conclusion in context.
- Interpret the P-value as a conditional probability in the context of a hypothesis test about a population proportion.
- Distinguish statistical significance from practical importance.
- From a description of a study, evaluate whether the conclusion of a hypothesis test is reasonable.
More about the P-Value
The P-value is a probability that describes the likelihood of the data if the null hypothesis is true. More specifically, the P-value is the probability that sample results are as extreme as or more extreme than the data if the null hypothesis is true. The phrase “as extreme as or more extreme than” means farther from the center of the sampling distribution in the direction of the alternative hypothesis.
More generally, we view the P-value a description of the strength of the evidence against the null hypothesis and in support of the alternative hypothesis. But the P-value is a probability about sample results, not about the null or alternative hypothesis.
One More Note about P-Values and the Significance Level
You may wonder why 5% is often selected as the significance level in hypothesis testing and why 1% is also a commonly used level. It is largely due to just convenience and tradition. When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly, these are arbitrary levels.
The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics. But it’s important to remember that there is really a continuous range of increasing confidence toward the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between the P-values 0.049 and 0.051, and it would be foolish to declare one case definitely a “real” effect and the other case definitely a “random” effect. In either case, the study results are roughly 5% likely by chance if there’s no actual effect.
Whether such a P-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision and the extent to which the hypothesized effect might contradict our prior experience or previous studies.
Sample Size and Hypothesis Testing
Consider our earlier example about teenagers and Internet access. According to the Kaiser Family Foundation, 84% of U.S. children ages 8 to 18 had Internet access at home as of August 2009. Researchers wonder if this number has changed since then. The hypotheses we tested were:
- H 0 : p = 0.84
- H a : p ≠ 0.84
The original sample consisted of 500 children, and 86% of them had Internet access at home. The P-value was about 0.22, which was not strong enough to reject the null hypothesis. There was not enough evidence to show that the proportion of all U.S. children ages 8 to 18 have Internet access at home.
Suppose we sampled 2,000 children and the sample proportion was still 86%. Our test statistic would be Z ≈ 2.44, and our P-value would be about 0.015. The larger sample size would allow us to reject the null hypothesis even though the sample proportion was the same.

Why does this happen? Larger samples vary less, so a sample proportion of 0.86 is more unusual with larger samples than with smaller samples if the population proportion is really 0.84. This means that if the alternative hypothesis is true, a larger sample size will make it more likely that we reject the null. Therefore, we generally prefer a larger sample as we have seen previously.
Drawing Conclusions from Hypothesis Tests
It is tempting to get involved in the details of a hypothesis test without thinking about how the data was collected. Whether we are calculating a confidence interval or performing a hypothesis test, the results are meaningless without a properly designed study. Consider the following exercises about how data collection can affect the results of a study.
Learn By Doing
Let’s summarize.
In this section, we looked at the four steps of a hypothesis test as they relate to a claim about a population proportion.
Step 1: Determine the hypotheses.
- The hypotheses are claims about the population proportion, p .
- The null hypothesis is a hypothesis that the proportion equals a specific value, p 0 .
- The alternative hypothesis is the competing claim that the parameter is less than, greater than, or not equal to p 0 .
Step 2: Collect the data.
Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the sample proportion can be np ≥ 10 and n (1 − p ) ≥ 10.
Step 3: Assess the evidence.
- Determine the test statistic which is the z -score for the sample proportion. The formula is: [latex]Z=\frac{\stackrel{ˆ}{p}-{p}_{0}}{\sqrt{\frac{{p}_{0}(1-{p}_{0})}{n}}}[/latex]
- Use the test statistic, together with the alternative hypothesis to determine the P-value. You can use a standard normal table (or Z -table) or technology (such as the simulations on the second page of this topic) to find the P-value.
- If the alternative hypothesis is greater than, the P-value is the area to the right of the test statistic. If the alternative hypothesis is less than, the P-value is the area to the left of the test statistic. If the alternative hypothesis is not equal to, the P-value is equal to double the tail area beyond the test statistic.
Step 4: Give the conclusion.
- A small P-value says the data is unlikely to occur if the null is true. If the P-value is less than or equal to the significance level, we reject the null hypothesis and accept the alternative hypothesis instead.
- If the P-value is greater than the significance level, we say we “fail to reject” the null hypothesis. We never say that we “accept” the null hypothesis. We just say that we don’t have enough evidence to reject it. This is equivalent to saying we don’t have enough evidence to support the alternative hypothesis.
- We write the conclusion in the context of the research question. Our conclusion is usually a statement about the alternative hypothesis (we accept H a or fail to accept H a ) and should include the P-value.
Other Hypothesis Testing Notes
Remember that the P-value is the probability of seeing a sample proportion as extreme as the one observed from the data if the null hypothesis is true. The probability is about the random sample, not about the null or alternative hypothesis.
A larger sample size makes it more likely that we will reject the null hypothesis if the alternative is true. Another way of thinking about this is that increasing the sample size will decrease the likelihood of a type II error. Recall that a type II error is failing to reject the null hypothesis when the alternative is true.
Increasing the sample size can have the unintended effect of making the test sensitive to differences so small they don’t matter. A statistically significant difference is one large enough that it is unlikely to be due to sampling variability alone. Even a difference so small that it is not important can be statistically significant if the sample size is big enough.
Finally, remember the phrase “garbage in, garbage out.” If the data collection methods are poor, then the results of a hypothesis test are meaningless. No statistical methods can create useful information if our data comes from convenience or voluntary response samples. Additionally, the results of a hypothesis test apply only to the population from whom the sample was chosen.
- Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Privacy Policy

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

8.7: Hypothesis Test of Single Population Proportion with Examples
- Last updated
- Save as PDF
- Page ID 130292

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Steps for performing Hypothesis Test for a Single Population Proportion
Step 1: State your hypotheses about the population proportion. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure
- \(\hat{P}=\frac{X}{n}\)
- Sample is random with independent observations .
- Sample is large. Check that the sample has 5 or more expected successes and 5 or more expected failures
- Population is large relative to the sample size . The population size is at least 10 times bigger than the sample size.
Step 3: Perform the procedure
- Find the Standard Error (SE) based on the assumption that \(H_{0}\) is true.
- Compute the observed value of the test statistic \(Z_{obs}\).
- Find the p-value in order to measure your level of surprise.
Step 4: Make a decision about \(H_{0}\) and \(H_{a}\)
- Do you reject or not reject your null hypothesis? What about the alternative hypothesis?
Step 5 : Make a conclusion.
- What does this mean in the context of the data?
Examples: Hypothesis Test for a Single Population Proportion
Example \(\pageindex{1}\).
Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.
Set up the hypothesis test:
The 1% level of significance means that α = 0.01. This is a test of a single population proportion .
\(H_{0}: p = 0.50\) \(H_{a}: p \neq 0.50\)
The words "is the same or different from" tell you this is a two-tailed test.
Calculate the distribution needed:
Random variable: \(\hat{P} =\) the percent of of first-time brides who are younger than their grooms.
Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the Normal distribution for \hat{P} , the estimated proportion.
\[ \hat{P} - N\left(p, \sqrt{\frac{p(1-p)}{n}}\right)\nonumber \]
\[ \hat{P} - N\left(0.5, \sqrt{\frac{0.5(0.5)}{100}}\right)\nonumber \]
where \(p = 0.50, q = 1−p = 0.50\), and \(n = 100\)
Calculate the p -value using the normal distribution for proportions:
\[p\text{-value} = P( \hat{P} < 0.47 \space or \space \hat{P} > 0.53) = 0.5485\nonumber \]
where \[x = 53, \hat{P} = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].
Interpretation of the p-value: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \( \hat{P} \) is 0.53 or more OR 0.47 or less (see the graph in Figure).
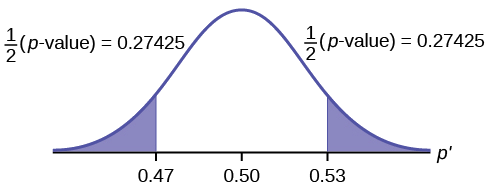
\(\mu = p = 0.50\) comes from \(H_{0}\), the null hypothesis.
\( \hat{P} = 0.53\). Since the curve is symmetrical and the test is two-tailed, the \( \hat{P} \) for the left tail is equal to \(0.50 – 0.03 = 0.47\) where \(\mu = p = 0.50\). (0.03 is the difference between 0.53 and 0.50.)
Compare \(\alpha\) and the \(p\text{-value}\):
Since \(\alpha = 0.01\) and \(p\text{-value} = 0.5485\). \(\alpha < p\text{-value}\).
Make a decision: Since \(\alpha < p\text{-value}\), you cannot reject \(H_{0}\).
Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.
The \(p\text{-value}\) can easily be calculated.
Press STAT and arrow over to TESTS . Press 5:1-PropZTest . Enter .5 for \(p_{0}\), 53 for \(x\) and 100 for \(n\). Arrow down to Prop and arrow to not equals \(p_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator calculates the \(p\text{-value}\) (\(p = 0.5485\)) and the test statistic (\(z\)-score). Prop not equals .5 is the alternate hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(z = 0.6\) (test statistic) and \(p = 0.5485\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.
The Type I and Type II errors are as follows:
The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).
The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)
Exercise \(\PageIndex{1}\)
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
First, determine what type of test this is, set up the hypothesis test, find the \(p\text{-value}\), sketch the graph, and state your conclusion.
Since the problem is about percentages, this is a test of single population proportions.
- \(H_{0} : p = 0.85\)
- \(H_{a}: p \neq 0.85\)
- \(p-value = 0.7554\)
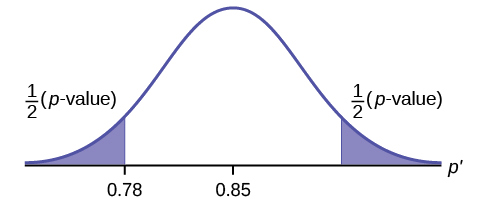
Because \(p > \alpha\), we fail to reject the null hypothesis. There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.
Example \(\PageIndex{2}\)
Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.
Set up the Hypothesis Test:
\(H_{0}: p = 0.30, H_{a}: p \neq 0.30\)
Determine the distribution needed:
The random variable is \( \hat{P} =\) proportion of households that have three cell phones.
The distribution for the hypothesis test is \( \hat{P} - N\left(0.30, \sqrt{\frac{0.30 \cdot (0.70)}{150}}\right)\)
Exercise \(\PageIndex{2}\).2
a. The value that helps determine the \(p\text{-value}\) is \( \hat{P} \). Calculate \( \hat{P} \).
a. \( \hat{P} = \frac{x}{n}\) where \(x\) is the number of successes and \(n\) is the total number in the sample.
\(x = 43, n = 150\)
\( \hat{P} = 43/150=0.2867\)
Exercise \(\PageIndex{2}\).3
b. What is a success for this problem?
b. A success is having three cell phones in a household.
Exercise \(\PageIndex{2}\).4
c. What is the level of significance?
c. The level of significance is the preset \(\alpha\). Since \(\alpha\) is not given, assume that \(\alpha = 0.05\).
Exercise \(\PageIndex{2}\).5
d. Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.
Calculate the \(p\text{-value}\).
d. \(p\text{-value} = 0.7216\)
Exercise \(\PageIndex{2}\).6
e. Make a decision. _____________(Reject/Do not reject) \(H_{0}\) because____________.
e. Assuming that \(\alpha = 0.05, \alpha < p\text{-value}\). The decision is do not reject \(H_{0}\) because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.
Exercise \(\PageIndex{2}\)
Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.
- \(H_{0}: p = 0.92\)
- \(H_{a}: p < 0.92\)
- \(p\text{-value} = 0.0046\)
Because \(p < 0.05\), we reject the null hypothesis. There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.
- Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
- Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).
The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter \(p\). The distribution for the test is normal. The estimated proportion \(\hat{p}\) is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived \(\alpha = 0.01\), for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

Example \(\PageIndex{3}\)
My dog has so many fleas,
They do not come off with ease. As for shampoo, I have tried many types Even one called Bubble Hype, Which only killed 25% of the fleas, Unfortunately I was not pleased.
I've used all kinds of soap, Until I had given up hope Until one day I saw An ad that put me in awe.
A shampoo used for dogs Called GOOD ENOUGH to Clean a Hog Guaranteed to kill more fleas.
I gave Fido a bath And after doing the math His number of fleas Started dropping by 3's! Before his shampoo I counted 42.
At the end of his bath, I redid the math And the new shampoo had killed 17 fleas. So now I was pleased.
Now it is time for you to have some fun With the level of significance being .01, You must help me figure out
Use the new shampoo or go without?
\(H_{0}: p \leq 0.25\) \(H_{a}: p > 0.25\)
In words, CLEARLY state what your random variable \(\bar{X}\) or \( \hat{P} \) represents.
\( \hat{P} =\) The proportion of fleas that are killed by the new shampoo
State the distribution to use for the test.
\[N\left(0.25, \sqrt{\frac{0.25 \cdot (1-0.25)}{42}}\right)\nonumber \]
Test Statistic: \(z_{obs} = 2.3163\)
Calculate the \(p\text{-value}\) using the normal distribution for proportions:
\[p\text{-value} = 0.0103\nonumber \]
In one to two complete sentences, explain what the p -value means for this problem.
If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more.
Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the \(p\text{-value}\).
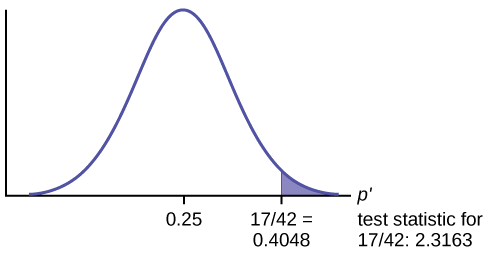
Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.
| 0.01 | Do not reject \(H_{0}\) | \(\alpha < p\text{-value}\) |
Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.
Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation. Label the point estimate and the lower and upper bounds of the confidence interval.
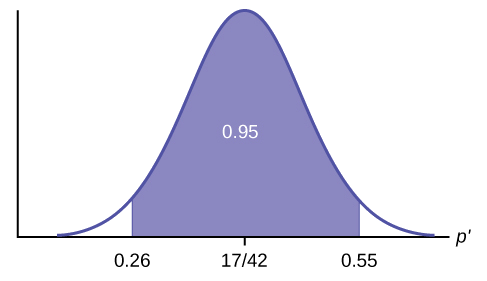
Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.
This test result is not very definitive since the \(p\text{-value}\) is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.
Example \(\PageIndex{4}\)
In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
We will follow the four-step process.
If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.
- \(H_{0}: p \leq 0.00034\)
- \(H_{a}: p > 0.00034\)
- \(\hat{P}=\frac{172}{420,019}=0.00041\).
- The sample is sufficiently large because we have \(np = 420,019(0.00034) = 142.8\), \(nq = 420,019(0.99966) = 419,876.2\) both greater than five. Sample is random with independent observations. Thus we will be able to generalize our results to the population.
- \(SE=\sqrt{\frac{0.00034(1-0.00034)}{420,019}}=0.000028\)
- \(Z_{obs}=\frac{0.00041-0.00034}{0.000028}=2.5\)
- \(p\text{-value} = 1-P(Z<2.5)=0.0062\)
- Since the \(p\text{-value} = 0.0062\) is greater than our alpha value \(= 0.005\), we cannot reject the null and cannot support alternative.
- Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.
Example \(\PageIndex{5}\)
According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.
We will follow the five-step plan.
- We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
- \(H_{0}: p = 0.00078\)
- \(H_{a}: p \neq 0.00078\)
- \(p\text{-value} = 0.00063\)
- Since the \(p\text{-value} = 0.00063\), is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis.
- In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.
The hypothesis test itself has an established process. This can be summarized as follows:
- Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
- Determine the random variable.
- Determine the distribution for the test.
- Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score (\(Z_{obs}\) is an example of test statistics.)
- Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.
Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.
- Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
- Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
- Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
- Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
- Data from Growing by Degrees by Allen and Seaman.
- Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
- Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
- Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
- Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
- Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
- Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
- Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
- Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
- Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
- Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
- “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
- Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
- Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
Prevent plagiarism. Run a free check.
The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved June 24, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 13.
- Comparing population proportions 1
- Comparing population proportions 2
Hypothesis test comparing population proportions
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics
- Probability and Statistics
How to Perform Hypothesis Testing for a Proportion
Last Updated: July 31, 2023
This article was co-authored by Joseph Quinones . Joseph Quinones is a High School Physics Teacher working at South Bronx Community Charter High School. Joseph specializes in astronomy and astrophysics and is interested in science education and science outreach, currently practicing ways to make physics accessible to more students with the goal of bringing more students of color into the STEM fields. He has experience working on Astrophysics research projects at the Museum of Natural History (AMNH). Joseph recieved his Bachelor's degree in Physics from Lehman College and his Masters in Physics Education from City College of New York (CCNY). He is also a member of a network called New York City Men Teach. This article has been viewed 35,001 times.
Hypothesis testing for a proportion is used to determine if a sampled proportion is significantly different from a specified population proportion. For example, if you expect the proportion of male births to be 50 percent, but the actual proportion of male births is 53 percent in a sample of 1000 births. Is this significantly different from the hypothesized population parameter? To find out, follow these steps.

- Are there more than 50 percent of Americans who self-identify as liberal?
- Is the percentage of defects in a given manufacturing plant more than 5%?
- Is the proportion of babies born male different from 50 percent?
- Are there more Americans who self-identify as liberal than as conservative? (Use hypothesis testing for 2 proportions instead.)
- Is the mean number of defects in a given manufacturing plant more than 50 per month? (Use hypothesis testing for one sample t-test instead.)
- Are male births related to paternal age? (Use chi-square test for independence instead.)

- Simple random sampling is used.
- Each sample point can result in only one of two possible outcomes. These outcomes are called successes and failures.
- The sample includes at least 10 successes and 10 failures.
- The population size is at least 20 times as big as the sample size.

- Right-tailed: Research question: Is the sample proportion greater than the hypothesized population proportion? Your hypotheses would be stated as follows: H0: p<=p0; Ha: p>p0.
- Left-tailed: Research question: Is the sample proportion less than the hypothesized population proportion? Your hypotheses would be stated as follows: H0: p>=p0; Ha: p<p0.
- Two-tailed: Research question: Is the sample proportion different from the hypothesized population proportion? Your hypotheses would be stated as follows: H0: p=p0; Ha: p<>p0.
- In your example, you can use a two-tailed test to see if the sample proportion of male births, 0.53, is different from the hypothesized population proportion of 0.50. So H0: p=0.50; Ha: p<>0.50. Typically, if there is no a priori reason to believe that any differences must be unidirectional, the two-tailed test is preferred as it is a more stringent test.

- In our example, p=0.53, p0=0.50, and n=1000. s = sqrt(0.50*(1-0.50)/1000) = 0.0158. the test statistic is z = (0.53-0.50)/0.0158 = 1.8974.

- Normal distribution probability z table. It is important to read the table description to note what probability is listed by the table. Some tables list cumulative (left side) area, others list right tail area, still others list only area from mean up to a positive z value.
- Excel. The excel function =norm.s.dist(z,cumulative). Substitute the numeric value for z and "true" for cumulative. This excel formula gives cumulative area to the left of a given z value. For your example, you would use the formula =norm.s.dist(1.8974,true) to find the cumulative left side area, which includes the left tail and the body. (Body is the area from -z to z.) You can subtract this from 1 to find the right tail area. Since your example is 2-tailed, you would then multiply by 2. A formula for p can be =2*(1-norm.s.dist(1.8974,true)). The output is 0.0578.
- Texas Instrument calculator, such as TI-83 or TI-84.
- Online normal distribution calculators.

Expert Q&A
You Might Also Like

Expert Interview

Thanks for reading our article! If you’d like to learn more about teaching, check out our in-depth interview with Joseph Quinones .
- ↑ http://stattrek.com/hypothesis-test/proportion.aspx?tutorial=ap
- ↑ http://blog.minitab.com/blog/michelle-paret/alphas-p-values-confidence-intervals-oh-my
About This Article

- Send fan mail to authors
Reader Success Stories
Shanaya Malik
Jun 29, 2019
Did this article help you?

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
Don’t miss out! Sign up for
wikiHow’s newsletter
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
5.5 - hypothesis testing for two-sample proportions.
We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test follows the same steps as one group.
These notes are going to go into a little bit of math and formulas to help demonstrate the logic behind hypothesis testing for two groups. If this starts to get a little confusion, just skim over it for a general understanding! Remember we can rely on the software to do the calculations for us, but it is good to have a basic understanding of the logic!
We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval.
For a test for two proportions, we are interested in the difference between two groups. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be:
\(H_0\colon p_1-p_2=0\)
Another way to look at it is \(H_0\colon p_1=p_2\). This is worth stopping to think about. Remember, in hypothesis testing, we assume the null hypothesis is true. In this case, it means that \(p_1\) and \(p_2\) are equal. Under this assumption, then \(\hat{p}_1\) and \(\hat{p}_2\) are both estimating the same proportion. Think of this proportion as \(p^*\).
Therefore, the sampling distribution of both proportions, \(\hat{p}_1\) and \(\hat{p}_2\), will, under certain conditions, be approximately normal centered around \(p^*\), with standard error \(\sqrt{\dfrac{p^*(1-p^*)}{n_i}}\), for \(i=1, 2\).
We take this into account by finding an estimate for this \(p^*\) using the two-sample proportions. We can calculate an estimate of \(p^*\) using the following formula:
\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\)
This value is the total number in the desired categories \((x_1+x_2)\) from both samples over the total number of sampling units in the combined sample \((n_1+n_2)\).
Putting everything together, if we assume \(p_1=p_2\), then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) will be approximately normal with mean 0 and standard error of \(\sqrt{p^*(1-p^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\), under certain conditions.
\(z^*=\dfrac{(\hat{p}_1-\hat{p}_2)-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)
...will follow a standard normal distribution.
Finally, we can develop our hypothesis test for \(p_1-p_2\).
Hypothesis Testing for Two-Sample Proportions
Conditions :
\(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five
Test Statistic:
\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)
...where \(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\).
The critical values, p-values, and decisions will all follow the same steps as those from a hypothesis test for a one-sample proportion.
Hypothesis Testing: Proportion Example
Hypothesis testing is a crucial statistical method used to determine whether there is enough evidence to reject a null hypothesis. It’s a fundamental tool in research and decision-making, helping us make informed conclusions based on data.
In this article, we’ll delve into hypothesis testing with a specific example involving proportions. We’ll explore the steps involved and how to interpret the results.
Understanding the Concepts
Before diving into the example, let’s define some key concepts:
- Null Hypothesis (H 0 ): This is a statement about the population parameter that we assume to be true. It’s typically the status quo or the default assumption.
- Alternative Hypothesis (H 1 ): This is the statement that we want to test. It contradicts the null hypothesis.
- Test Statistic: A value calculated from the sample data that measures how far the sample result deviates from what we’d expect under the null hypothesis.
- P-value: The probability of obtaining a test statistic as extreme as the one observed, assuming the null hypothesis is true.
- Significance Level (α): A threshold value that determines the level of evidence needed to reject the null hypothesis. Typically, α is set at 0.05, meaning we’re willing to accept a 5% chance of making a wrong decision.
Example: Coin Toss
Let’s consider a simple example. We want to test whether a coin is fair. Our null hypothesis is that the coin is fair, meaning the probability of getting heads (p) is 0.5. Our alternative hypothesis is that the coin is not fair, meaning p ≠ 0.5.
We toss the coin 100 times and observe 60 heads. Our sample proportion (p̂) is 60/100 = 0.6. Now, we need to determine if this sample proportion provides enough evidence to reject the null hypothesis.
Steps of Hypothesis Testing
The hypothesis testing process involves the following steps:
- State the null and alternative hypotheses:
- H 0 : p = 0.5
- H 1 : p ≠ 0.5
- Choose a significance level (α):
- Let α = 0.05
- Calculate the test statistic:
- For proportions, we use the z-statistic:
- z = (p̂ – p) / √(p(1-p)/n)
- z = (0.6 – 0.5) / √(0.5(1-0.5)/100) = 2
- Determine the p-value:
- The p-value is the probability of observing a z-statistic as extreme as 2, assuming the null hypothesis is true.
- Using a z-table or statistical software, we find the p-value to be approximately 0.0456.
- Make a decision:
- Since the p-value (0.0456) is less than the significance level (0.05), we reject the null hypothesis.
- This means there is enough evidence to conclude that the coin is not fair.
In this example, we successfully performed a hypothesis test for a proportion. We found enough evidence to reject the null hypothesis that the coin is fair. This process demonstrates the power of hypothesis testing in drawing conclusions from data and making informed decisions.
Remember, hypothesis testing is a crucial tool in various fields, from scientific research to business analysis. By understanding the concepts and steps involved, you can effectively analyze data and make informed judgments.
Research Methods
© 2024 by SchoolTube
Username or Email Address
Remember Me
Forgot password?
Enter your account data and we will send you a link to reset your password.
Your password reset link appears to be invalid or expired.
Privacy policy.
To use social login you have to agree with the storage and handling of your data by this website. Privacy Policy
Add to Collection
Public collection title
Private collection title
No Collections
Here you'll find all collections you've created before.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

29: Hypothesis Test for a Population Proportion Calculator
- Last updated
- Save as PDF
- Page ID 8351

- Larry Green
- Lake Tahoe Community College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
hypothesis test for a population Proportion calculator
Fill in the sample size, n, the number of successes, x, the hypothesized population proportion \(p_0\), and indicate if the test is left tailed, <, right tailed, >, or two tailed, \(\neq\). Then hit "Calculate" and the test statistic and p-Value will be calculated for you.
| n: | x: | \(p_0\): |
 |
IMAGES
VIDEO
COMMENTS
The p -value for a hypothesis test on a population proportion is the area in the tail (s) of distribution of the sample proportion. If both n× p ≥ 5 n × p ≥ 5 and n ×(1− p) ≥ 5 n × ( 1 − p) ≥ 5, use the normal distribution to find the p -value. If at least one of n× p < 5 n × p < 5 or n×(1 −p) < 5 n × ( 1 − p) < 5, use ...
Step 3) Compute the test statistic. The test statistic is the number of standard deviations the sample proportion is from the known proportion. It is also a Z-score, just like the critical value. z = ˆp − p √p(1 − p) n. For this problem, the test statistic is: z = 0.403 − 0.32 √0.32 ( 1 − 0.32) 196 = 2.49.
For the hypothesis test, she uses a 1% level of significance. Answer. Set up the hypothesis test: The 1% level of significance means that α = 0.01. This is a test of a single population proportion. \(H_{0}: p = 0.50\) \(H_{a}: p \neq 0.50\) The words "is the same or different from" tell you this is a two-tailed test. Calculate the distribution ...
test hypotheses about a population proportion; test hypotheses about a population proportion using the binomial probability distribution; ... Step 5: Reject the null hypothesis if the P-value is less than the level of significance, α. Step 6: State the conclusion. Calculating P-Values Right-Tailed Tests.
Step 1: Check assumptions and write hypotheses. When conducting a chi-square goodness-of-fit test, it makes the most sense to write the hypotheses first. The hypotheses will depend on the research question. The null hypothesis will always contain the equalities and the alternative hypothesis will be that at least one population proportion is ...
The examples on the following pages use the five step hypothesis testing procedure outlined below. This is the same procedure that we used to conduct a hypothesis test for a single mean, single proportion, difference in two means, and difference in two proportions. ... then there is not enough evidence that any of the population proportions are ...
Our sample proportion was 0.02 above the population proportion from the null hypothesis. In a sample of size 500, we would observe a sample proportion 0.02 or more away from 0.84 about 22% of the time by chance alone. Step 4: State a conclusion. Again we compare the P-value to the level of significance, α = 0.05.
At this point you should be more comfortable with the steps of a hypothesis test and not have to number each step, but know what each step means. Critical Value Method . Step 1: State the hypotheses: The key words in this example, "proportion" and "differs," give the hypotheses: H 0: p = 0.856. H 1: p ≠ 0.856 (claim)
Hypothesis Test for Proportions: Step 5 (cont.) •For a left tailed test: 𝐻𝑎: < 0 We have rejection regions for 𝐻 are as follows •Note: all of the rejection region is in the left tail, where is much smaller than 0 Confidence Reject (test stat) Reject (p-value) 0.90 Test-stat<-1.282 P-value<.1 0.95 Test-stat<-1.645 P-value<.05
Step 2: Collect the data. Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the sample proportion can be np ≥ 10 and n (1 − p) ≥ 10. Step 3: Assess the evidence. Determine the test statistic which is the z -score for the sample proportion.
The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. ... This is a single sample proportion test. We want to know if the population proportion is different from 0.5, so this is a two-tailed test. Our hypotheses are: \(H_0:p=0.5\) ... Step 4: \(p>0.05\), we should fail to reject the ...
Step 2: Collect the data. Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the sample proportion can be np ≥ 10 and n (1 − p) ≥ 10. Step 3: Assess the evidence.
Know the formula for the one-proportion z-test statistic Section 8.2 Hypothesis Testing in Four Steps Write the vocabulary terms in this section on 3 x 5 cards and study them. Important terms include: two-tailed p-value Be sure to also read and study the key points, highlighted in the blue boxes in the text. Know the four steps of hypothesis ...
! ! page!3! STA!205!Notes! Buckley! Fall!2016! Example'2:''In!2013,!18%!of!all!Kentucky!adults!were!uninsured.!With!the!passing!of!the!Affordable!Healthcare!Act,!one ...
Steps for performing Hypothesis Test for a Single Population Proportion. Step 1: State your hypotheses about the population proportion. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure. P^ = X n P ^ = X n. Conditions for the test:
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
The first step in hypothesis testing is to set up two competing hypotheses. The hypotheses are the most important aspect. If the hypotheses are incorrect, your conclusion will also be incorrect. ... Therefore, assuming the true population proportion is 0.5, a sample proportion of 0.556 is 2.504 standard deviations above the mean. The \(z^*\) ...
Solution. We will use the critical value approach to perform the test. The same test will be performed using the p -value approach in Example 8.5.3. We must check that the sample is sufficiently large to validly perform the test. Since ˆp = 270 / 500 = 0.54, √ˆp(1 − ˆp) n = √(0.54)(0.46) 500 ≈ 0.02. hence.
Our alternative hypothesis is that there is a difference. Or that P1 does not equal P2. Or that P1 minus P2, the proportion of men voting minus the proportion of women voting, the true population proportions, do not equal 0. And we're going to do the hypothesis test with a significance level of 5%.
In your example, you can use a two-tailed test to see if the sample proportion of male births, 0.53, is different from the hypothesized population proportion of 0.50. So H0: p=0.50; Ha: p<>0.50. Typically, if there is no a priori reason to believe that any differences must be unidirectional, the two-tailed test is preferred as it is a more ...
Statistics and Probability questions and answers. Step 5: Hypothesis Test for the Population Proportion Suppose the management claims that the proportion of games that your team wins when scoring 80 or more points is 0.50. Test this claim using a 5% level of significance. Make the following edits to the code block below: 1.
5.5 - Hypothesis Testing for Two-Sample Proportions. We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test follows the same steps as one group. These notes are going to go into a little bit of math and formulas to help demonstrate the logic behind hypothesis testing ...
Question: 5. Hypothesis Test for the Population Proportion Suppose the management claims that the proportion of games that your team wins when scoring 20 or more points is 0.50. You tested this claim using a 5% level of significance. Explain the steps you took to test this problem and interpret your results. See Step 5 in the Python script to ...
We toss the coin 100 times and observe 60 heads. Our sample proportion (p̂) is 60/100 = 0.6. Now, we need to determine if this sample proportion provides enough evidence to reject the null hypothesis. Steps of Hypothesis Testing. The hypothesis testing process involves the following steps: State the null and alternative hypotheses: H 0: p = 0.5
3/8/2020. 94% (98) View full document. Step 5: Hypothesis Test for the Population Proportion ¶ Suppose the management claims that the proportion of games that your team wins when scoring 80 or more points is 0.50. Test this claim using a 5% level of significance. Make the following edits to the code block below:
A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions. The difference of two proportions follows an approximate normal distribution. Generally, the null hypothesis states that the two proportions are the same. That is, \(H_{0}: p_{A} = p_{B}\).
hypothesis test for a population Proportion calculator. Fill in the sample size, n, the number of successes, x, the hypothesized population proportion p0 p 0, and indicate if the test is left tailed, <, right tailed, >, or two tailed, ≠ ≠ . Then hit "Calculate" and the test statistic and p-Value will be calculated for you. n: x: p0 p 0