
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 8: Rational Expressions

8.8 Rate Word Problems: Speed, Distance and Time
Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .
[latex]r\cdot t=d[/latex]
For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.
The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:
| Who or What | Rate | Time | Distance |
|---|---|---|---|
The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.
Example 8.8.1
Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Natasha | [latex]r[/latex] | [latex]\text{3 h}[/latex] | [latex]\text{3 h}(r)[/latex] |
| Joey | [latex]r + 2[/latex] | [latex]\text{3 h}[/latex] | [latex]\text{3 h}(r + 2)[/latex] |
The distance travelled by both is 30 km. Therefore, the equation to be solved is:
[latex]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}[/latex]
This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.
Example 8.8.2
Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Downstream | [latex]\text{12 km/h}[/latex] | [latex]t[/latex] | [latex]\text{12 km/h } (t)[/latex] |
| Upstream | [latex]\text{4 km/h}[/latex] | [latex](1 - t)[/latex] | [latex]\text{4 km/h } (1 - t)[/latex] |
The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:
[latex]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]
This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.
Example 8.8.3
Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Terry | [latex]\text{20 km/h}[/latex] | [latex]t[/latex] | [latex]\text{20 km/h }(t)[/latex] |
| Sally | [latex]\text{80 km/h}[/latex] | [latex](t - \text{6 h})[/latex] | [latex]\text{80 km/h }(t - \text {6 h})[/latex] |
The distance travelled by both is the same. Therefore, the equation to be solved is:
[latex]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]
This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.
Example 8.8.4
On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Fifty-five | [latex]\text{55 km/h}[/latex] | [latex]t[/latex] | [latex]\text{55 km/h }(t)[/latex] |
| Forty | [latex]\text{40 km/h}[/latex] | [latex](\text{2.5 h}-t)[/latex] | [latex]\text{40 km/h }(\text{2.5 h}-t)[/latex] |
[latex]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]
This means that the time spent travelling at 40 km/h was 0.5 h.
Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.
For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.
- A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
- Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
- Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
- Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
- A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
- Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
- A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
- A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?
Solve Questions 9 to 22.
- A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
- A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
- A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
- As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
- Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
- A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
- A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
- A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
- Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
- Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
- Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
- Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
- On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
- Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.
Answer Key 8.8
Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
- Pre-algebra lessons
- Pre-algebra word problems
- Algebra lessons
- Algebra word problems
- Algebra proofs
- Advanced algebra
- Geometry lessons
- Geometry word problems
- Geometry proofs
- Trigonometry lessons
- Consumer math
- Baseball math
- Math for nurses
- Statistics made easy
- High school physics
- Basic mathematics store
- SAT Math Prep
- Math skills by grade level
- Ask an expert
- Other websites
- K-12 worksheets
- Worksheets generator
- Algebra worksheets
- Geometry worksheets
- Free math problem solver
- Pre-algebra calculators
- Algebra Calculators
- Geometry Calculators
- Math puzzles
- Math tricks
- Member login
Distance rate time problems
Distance rate time problems involve object moving at a constant rate and this is called uniform motion. The formula d = r × t is the formula to use to solve problems related to distance, rate, and time.
Examples showing how to solve distance rate time problems
It may be obvious that for this type of problem, the distance is the same since you left the same place (your house) and are going to the same location.
Suppose that you went to no other places, the distance then to go back to your house is again the same.
Therefore, when solving distance rate time problems involving opposite direction travel, you can add the distances to get the total distance.
Study also the distance rate time problem in the figure below carefully

Mixture word problems
Recent Articles
How to divide any number by 5 in 2 seconds.
Feb 28, 24 11:07 AM
Math Trick to Square Numbers from 50 to 59
Feb 23, 24 04:46 AM
Sum of Consecutive Odd Numbers
Feb 22, 24 10:07 AM
100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

Recommended
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved
Algebra: Distance Problems
In these lessons, we will learn to solve word problems involving distance, rate (speed) and time.
Related Pages Rate Distance Time Word Problems Distance Word Problems Average Speed Problems
What Are Distance Word Problems Or Distance Rate Time Problems?
Distance problems are word problems that involve the distance an object will travel at a certain average rate for a given period of time .
The formula for distance problems is: distance = rate × time or d = r × t
Things to watch out for: Make sure that you change the units when necessary. For example, if the rate is given in miles per hour and the time is given in minutes then change the units appropriately.
It would be helpful to use a table to organize the information for distance problems. A table helps you to think about one number at a time instead being confused by the question.
The following diagrams give the steps to solve Distance-Rate-Time Problems. Scroll down the page for examples and solutions.

We will show you how to solve distance problems by the following examples:
- Traveling At Different Rates
- Traveling In Different Directions
- Given Total Time
- Wind and Current Problems
How To Solve Distance Problems: Traveling At Different Rates
Example: A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?
Solution: Step 1: Set up a rtd table.
| r | t | d | |
| Case 1 | |||
| Case 2 |
Step 2: Fill in the table with information given in the question.
A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours. If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make the trip?
Let t = time to make the trip in Case 2.
| r | t | d | |
| Case 1 | 50 | 6 | |
| Case 2 | 45 | t |
Step 3: Fill in the values for d using the formula d = rt
| r | t | d | |
| Case 1 | 50 | 6 | 50 × 6 = 300 |
| Case 2 | 45 | t | 45t |
Step 4: Since the distances traveled in both cases are the same, we get the equation:
Step 5: Beware - the question asked for “how many more minutes would it have taken to make the trip”, so we need to deduct the original 6 hours taken.
Answer: The time taken would have been 40 minutes longer.
How To Solve Distance Problems: Two Objects Traveling In The Same Direction
Example: This motion problem (or distance rate time problem or uniform rate problem) involves traveling in the same direction, solving for “how long” one moving object traveling until it meets up with the second moving object.
It uses d = rt (distance equals rate times time).
Car 1 starts from point A and heads for point B at 60 mph. Fifteen minutes later, car 2 leaves the same point A and heads for point B at 75 mph. How long before car 2 overtakes car 1?
How To Solve Distance Problems: Two Objects Traveling In The Opposite Directions
Example: A bus and a car leave the same place and traveled in opposite directions. If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?
| r | t | d | |
| bus | |||
| car |
If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?
Let t = time when they are 210 miles apart.
| r | t | d | |
| bus | 50 | t | |
| car | 55 | t |
| r | t | d | |
| bus | 50 | t | 50t |
| car | 55 | t | 55t |
Step 4: Since the total distance is 210, we get the equation:
50t + 55t = 210 105t = 210
Answer: They will be 210 miles apart in 2 hours.
Objects Traveling At Opposite Directions, Calculate How Long It Takes For Them To Be A Given Distance Apart
This motion problem (or distance rate time problem or uniform rate problem) involves one object traveling in one direction and the other in the opposite direction, solving for “how long” (or the amount of time) two moving objects traveling until they are certain distance apart.
Example: Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at 450 mph. How long will they be 1400 miles apart? At what time will they be 1400 miles apart? How far has each plane traveled?
How To Solve Distance Problems: Given The Total Time
Example: John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph. If he spent a total of 7 hours traveling, what is the distance traveled by John?
John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph. If he spent a total of 7 hours traveling, what is the distance traveled by John?
Let t = time to travel to town.
7 – t = time to return from town.
| r | t | d | |
| Case 1 | 40 | t | |
| Case 2 | 30 | 7 – t |
| r | t | d | |
| Case 1 | 40 | t | 40t |
| Case 2 | 30 | 7 – t | 30(7 – t) |
40t = 30(7 – t) Use distributive property 40t = 210 – 30t
Step 5: The distance traveled by John to town is
40t = 120 The distance traveled by John to go back is also 120 So, the total distance traveled by John is 240
Answer: The distance traveled by John is 240 miles.
How To Find The Total Distance Given Total Time And Two Rates?
Example: Roy took 5 hours to complete a journey. For the first 2 hours, he traveled at an average speed of 65 km/h. For the rest of the journey, he traveled at an average speed of 78 km/h. What was the total distance of the journey?
Study Guides > Prealgebra
Using the distance, rate, and time formula, learning outcomes.
- Use the problem-solving method to solve problems using the distance, rate, and time formula
Distance, Rate, and Time
| Step 1. the problem. You may want to create a mini-chart to summarize the information in the problem. | [latex]d=?[/latex] [latex-display]r=12\text{mph}[/latex-display] [latex]t=3\frac{1}{2}\text{hours}[/latex] |
| Step 2. what you are looking for. | distance traveled |
| Step 3. Choose a variable to represent it. | let = distance |
| Step 4. Write the appropriate formula for the situation. Substitute in the given information. | [latex]d=rt[/latex] [latex]d=12\cdot 3\frac{1}{2}[/latex] |
| Step 5. the equation. | [latex]d=42\text{ miles}[/latex] |
| Step 6. Does 42 miles make sense? | |
| Step 7. the question with a complete sentence. | Jamal rode 42 miles. |
| Step 1. the problem. Summarize the information in the problem. | [latex]d=520[/latex] miles [latex]r=65[/latex] mph [latex]t=?[/latex] |
| Step 2. what you are looking for. | how many hours (time) |
| Step 3. Choose a variable to represent it. | let [latex]t[/latex] = time |
| Step 4. Write the appropriate formula. Substitute in the given information. | [latex]d=rt[/latex] [latex]520=65t[/latex] |
| Step 5. the equation. | [latex]t=8[/latex] |
| Step 6. Substitute the numbers into the formula and make sure the result is a true statement. [latex-display]d=rt[/latex-display] [latex-display]520\stackrel{?}{=}65\cdot 8[/latex-display] [latex]520=520\quad\checkmark [/latex] | |
| Step 7. the question with a complete sentence. We know the units of time will be hours because we divided miles by miles per hour. | Rey's trip will take [latex]8[/latex] hours. |
Licenses & Attributions
Cc licensed content, original.
- Question ID 145550, 145553,145619,145620. Authored by: Lumen Learning. License: CC BY: Attribution .
CC licensed content, Shared previously
- Ex: Find the Rate Given Distance and Time. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .
- Example: Solve a Problem using Distance = Rate x Time. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
Please add a message.
Message received. Thanks for the feedback.
Distance, Rate, and Time Worksheets
- Pre Algebra & Algebra
- Math Tutorials
- Exponential Decay
- Worksheets By Grade
In math, distance, rate, and time are three important concepts you can use to solve many problems if you know the formula. Distance is the length of space traveled by a moving object or the length measured between two points. It is usually denoted by d in math problems.
The rate is the speed at which an object or person travels. It is usually denoted by r in equations. Time is the measured or measurable period during which an action, process, or condition exists or continues. In distance, rate, and time problems , time is measured as the fraction in which a particular distance is traveled. Time is usually denoted by t in equations.
Use these free, printable worksheets to help students learn and master these important math concepts. Each slide provides the student worksheet, followed by an identical worksheet that includes the answers for ease of grading. Each worksheet provides three distance, rate, and time problems for students to solve.
Worksheet No. 1
Print the PDF: Distance, Rate, and Time Worksheet No. 1
When solving distance problems, explain to students that they will use the formula:
or rate (speed) times time equals distance. For example, the first problem states:
The Prince David ship headed south at an average speed of 20 mph. Later the Prince Albert traveled north with an average speed of 20 mph. After the Prince David ship had traveled for eight hours, the ships were 280 miles apart. How many hours did the Prince David Ship Travel?
Students should find that the ship traveled for six hours.
Worksheet No. 2
Print the PDF: Distance, Rate, and Time Worksheet No. 2
If students are struggling, explain that to solve these problems, they will apply the formula that solves distance, rate, and time, which is distance = rate x tim e. It is abbreviated as:
The formula can also be rearranged as:
r = d/t or t = d/r
Let students know that there are many examples where you might use this formula in real life. For example, if you know the time and rate a person is traveling on a train, you can quickly calculate how far he traveled. And if you know the time and distance a passenger traveled on a plane, you could quickly figure the distance she traveled simply by reconfiguring the formula.
Worksheet No. 3
Print the PDF: Distance, Rate, Time Worksheet No. 3
On this worksheet, students will solve problems such as:
Two sisters Anna and Shay left the home at the same time. They headed out in opposite directions toward their destinations. Shay drove 50 mph faster than her sister Anna. Two hours later, they were 220 mph apart from each other. What was Anna’s average speed?
The students should find that Anna's average speed was 30 mph.
Worksheet No. 4
Print the PDF: Distance, Rate, Time Worksheet No. 4
Ryan left home and drove to his friend's house driving 28 mph. Warren left an hour after Ryan traveling at 35 mph hoping to catch up with Ryan. How long did Ryan drive before Warren caught up to him?
Students should find that Ryan drove for five hours before Warren caught up to him.

Worksheet No. 5
Print the PDF: Distance, Rate, and Time Worksheet No. 5
On this final worksheet, students will solve problems including:
Pam drove to the mall and back. It took one hour longer to go there than it did to come back home. The average speed she was traveling on the trip there was 32 mph. The average speed on the way back was 40 mph. How many hours did the trip there take?
They should find that Pam's trip took five hours.
- Solving Problems Involving Distance, Rate, and Time
- Realistic Math Problems Help 6th-graders Solve Real-Life Questions
- 4th-Grade Math Word Problems
- Rate of Change Worksheet with Solutions
- What Is Velocity in Physics?
- Help Kids Calculate the Area and Circumference of Circles
- Simple Interest Worksheets With Answers
- What Speed Actually Means in Physics
- Free Math Word Problem Worksheets for Fifth-Graders
- Quiz 8th-Graders With These Math Word Problems
- 3-Digit Addition Worksheets
- Geometry Practice: Perimeter Worksheets
- Second Grade Math: Solving Word Problems
- Newspaper Printables
- Free Christmas Math Worksheets
- Worksheets for Teaching Ordinal Numbers

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
"Distance" Word Problems
Explanation More Examples
What is a "distance" word problem?
"Distance" word problems, often also called "uniform rate" problems, involve something travelling at some fixed and steady ("uniform") pace ("rate", "velocity", or "speed"), or else you are told to regard to object as moving at some average speed.
Content Continues Below
MathHelp.com
Distance Word Problems
Whenever you read a problem that involves "how fast", "how far", or "for how long", you should think of the distance equation, d = rt , where d stands for distance, r stands for the (constant or average) rate of speed, and t stands for time.
Make sure that the units for time and distance agree with the units for the rate. For instance, if they give you a rate of feet per second, then your time must be in seconds and your distance must be in feet. Sometimes they try to trick you by using mis-matched units, and you have to catch this and convert to the correct units.
In case you're wondering, this type of exercise requires that the rate be fixed and steady (that is, unchanging) for the d = rt formula to work. The only way you can deal with a speed that might be changing over time is to take the average speed over the time or distance in question. Working directly with changing speeds will be something you'll encounter in calculus, as it requires calculus-based (or more advanced) methods.
What is the difference between a fixed speed and an average speed?
A fixed-speed exercise is one in which the car, say, is always going exactly sixty miles an hour; in three hours, the car, on cruise-control, will have gone 180 miles. An average-speed exercise is one in which the car, say, averaged forty miles an hour, but this average includes the different speeds related to stop lights, highways, and back roads; in three hours the car went 120 miles, though the car's speed was not constant. Most of the exercises you'll see will be fixed-speed exercises, but obviously they're not very "real world". It's a simplification they do in order to make the situation feasible using only algebraic methods.
What is an example of a "distance" word problem?
- A 555 -mile, 5 -hour plane trip was flown at two speeds. For the first part of the trip, the average speed was 105 mph. Then the tailwind picked up, and the remainder of the trip was flown at an average speed of 115 mph. For how long did the plane fly at each speed?
There is a method for setting up and solving these exercises that I first encountered well after I'd actually been doing them while taking a class as an undergraduate. But, as soon as I was introduced to the method, I switched over, because it is *so* way easier.
First I set up a grid, with the columns being labelled with the variables from the "distance" formula, and the rows being labelled with the "parts" involved:
|
|
|
|
|---|---|---|---|
first part |
|
|
|
second part |
|
|
|
total |
|
|
|
In the first part, the plane covered some distance. I don't know how much, so I'll need a variable to stand for this unknown value. I'll use the variable they give me in the distance equation:
They gave me the speed, or rate, for this part, so I'll add this to my table:
|
|
|
|
|---|---|---|---|
first part |
| 105 |
|
second part |
|
|
|
total |
|
|
|
The plane flew for some amount of time during this first part, but I don't know how long that was. So I need a variable to stand for this unknown value; I'll use the variable from the distance equation:
For the second part, the plane travelled the rest of the total distance. I don't know the exact distance that was flown during this second part, but I do know that it was "however much was left of the 555 miles, after the first d miles were flown in the first part. "How much was left after [some amount] was taken out" is expressed with subtraction: I take the amount that has been taken care of already, and subtract this from whatever was the total. Adding this to my table, I get:
|
|
|
|
|---|---|---|---|
first part |
| 105 |
|
second part | 555 − |
|
|
total |
|
|
|
They've given me the speed, or rate, for the second part, and I can use the same "How much is left?" construction for whatever was the time for this second part. So now my table looks like this:
|
|
|
|
|---|---|---|---|
first part |
| 105 |
|
second part | 555 − | 115 | 5 − |
total |
|
|
|
For the "total" row, I add down (or take info from the exercise statement):
|
|
|
|
|---|---|---|---|
first part |
| 105 |
|
second part | 555 − | 115 | 5 − |
total | 555 | --- | 5 |
Advertisement
Why did I not add down in the "rate" column? Because I cannot add rates! In this exercise, adding the rates would have said that the average rate for the entire trip was 105 + 115 = 220 miles per hour. But obviously this makes no sense.
The genius of this table-based method of set-up is that I can now create equations from the rows and columns. In this exercise, there is more than one way to proceed. I'll work with the "distance" equation to create expressions for the distances covered in each part.
Multiplying across, the first row tells me that the distance covered in the first part of the flight was:
1st part distance: 105 t
Again multiplying across, the second row tells me that the distance covered in the second part of the flight was:
2nd part distance: 115(5 − t )
I can add these two partial-distance expressions, and set them equal to the known total distance:
105 t + 115(5 − t ) = 555
This is an equation in one variable, which I can solve:
105 t + 115(5 − t ) = 555 105 t + 575 − 115 t = 555 575 − 10 t = 555 20 = 10 t 2 = t
Looking back at my table, I see the I had defined t to be the time that the plane spent in the air on the first part of its journey. Looking back at the original exercise, I see that they want to know the times that the plane spent at each of the two speeds.
I now have the time for the first part of the flight; the time was two hours. The exercise said that the entire trip was five hours, so the second part must have taken three hours (found by subtracting the first-part time from the total time). They haven't asked for the partial distances, so I now have all the information I need; no further computations are necessary. My answer is:
first part: 2 hours second part: 3 hours
When I was setting up my equation, I mentioned that there was more than one way to proceed. What was the other way? I could have used the table to create an expression for each of the two partial times, added, set the result equal to the given total, and solved for the variable d . Since the distance equation is d = rt , then the expressions for the partial times would be created by solving the equation for t = . My work would have looked like this:
first part: d /105
second part: (555 − d )/115
adding: d /105 + (555 − d )/115 = 5 23 d + 11,655 − 21 d = 12,075 2 d = 420 d = 210
Looking back at my table, I would have seen that this gives me the distance covered in the first half of the flight. Looking back at the exercise, I would have seeing that they are wanting times, not distances. So I would have back-solved for the time for the first part, and then done the subtraction to find the time for the second part. My work would have had more steps, but my answer would have been the same.
There are three things that I hope you take from the above example:
- Using a table or grid to keep track of what you're doing can be incredibly helpful.
- It is important to clearly define your variables, so you know (by the end) what you'd meant (back in the beginning), so you can apply your results correctly.
- You should always check the original exercise, so you can be sure that you're answering the question that they'd actually asked.
(My value for the distance, found above, is correct, but was not what they'd asked for.) But even more important to understand is this:
NEVER TRY TO ADD RATES! Think about it: If you drive 20 mph on one street, and 40 mph on another street, does that mean you averaged 60 mph? Of course not.
Can I even average the rates? If I drove at 20 mph for one hour, and then drove 60 mph for two hours, then I would have travelled 140 miles in three hours, or a little under 47 mph. But 47 is not the average of 20 and 60 .
As you can see, the actual math involved in solving this type of exercise is often quite simple. It's the set-up that's the hard part. So what follows are some more examples, but with just the set-up displayed. Try your hand at solving, and click on the links to get pop-ups from which to check your equations and solutions.
- An executive drove from home at an average speed of 30 mph to an airport where a helicopter was waiting. The executive boarded the helicopter and flew to the corporate offices at an average speed of 60 mph. The entire distance was 150 miles; the entire trip took three hours. Find the distance from the airport to the corporate offices.
I will start in the usual way, by setting up my table:
|
|
|
|
|---|---|---|---|
driving |
|
|
|
flying |
|
|
|
total |
|
|
|
I have labelled my rows so it's clear how they relate to the exercise. Now I need to fill in the rows. As before, I don't know the distance or the time for the part where the executive was driving, so I'll use variables for these unknowns, along with the given rate.
|
|
|
|
|---|---|---|---|
driving |
| 30 |
|
flying |
|
|
|
total |
|
|
|
For the flying portion of the trip, I'll use the "how much is left" construction, along with the given rate, to fill in my second row. I'll also fill in the totals.
|
|
|
|
|---|---|---|---|
driving |
| 30 |
| flying | 150 − | 60 | 3 − |
total | 150 | --- | 3 |
The first row gives me the equation d = 30 t . The second row is messier, giving me the equation:
150 − d = 60(3 − t )
There are various ways I can go from here; I think I'll solve this second equation for the variable d , and then set the results equal to each other.
150 − d = 60(3 − t ) 150 − 60(3 − t ) = d
Setting equal these two expressions for d , I get:
30 t = 150 − 60(3 − t )
Solve for t ; interpret the value; state the final answer.

- A car and a bus set out at 2 p.m. from the same point, headed in the same direction. The average speed of the car is 30 mph slower than twice the speed of the bus. In two hours, the car is 20 miles ahead of the bus. Find the rate of the car.
Both vehicles travelled for the same amount of time.
|
|
|
|
|---|---|---|---|
car |
|
| 2 |
bus |
|
| 2 |
total |
| --- |
|
The car's values are expressed in terms of the bus' values, so I'll use variables for the bus' unknowns, and then define the car in terms of the bus' variables. This gives me:
|
|
|
|
|---|---|---|---|
car | + 20 | 2 − 30 | 2 |
bus |
|
| 2 |
total | --- | --- | --- |
(As it turns out, I won't need the "total" row this time.) The car's row gives me:
d + 20 = 2(2 r − 30)
This is not terribly helpful. The second row gives me:
I'll use the second equation to simplify the first equation by substituting " 2 r " from the second equation in for the " d " in the first equation. Then I'll solve the equation for the value of " r ". Finally, I'll need to interpret this value within the context of the exercise, and then I'll state the final answer.
(Remember that the expression for the car's speed, from the table, was 2 r − 30 , so all you need to do is find the numerical value of this expression. Just evaluate; don't try to solve — again — for the value of r .)
URL: https://www.purplemath.com/modules/distance.htm
Page 1 Page 2
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- Privacy / Cookies
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
DISTANCE = RATE X TIME
Explore the formula d = rt by starting with unit conversion problems. Mathletes will solve for distance, rate and time by paying attention to the units given in the problem and using the appropriate equivalent version of the formula: d = rt , r = d / t or t = d / r .
Download Mathlete handout.
Download coach version with solutions.
Download The Problems PowerPoint.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 6.8: Rate Word Problems: Speed, Distance and Time
Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .
For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.
The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:
| Who or What | Rate | Time | Distance |
|---|---|---|---|
The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.
Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Natasha | |||
| Joey |
The distance travelled by both is 30 km. Therefore, the equation to be solved is:
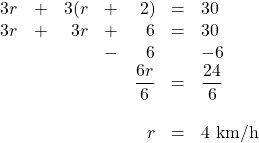
This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.
Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Downstream | |||
| Upstream |
The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:
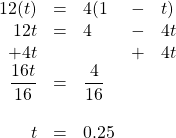
This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.
Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Terry | |||
| Sally |
The distance travelled by both is the same. Therefore, the equation to be solved is:
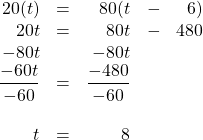
This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.
On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Fifty-five | |||
| Forty |
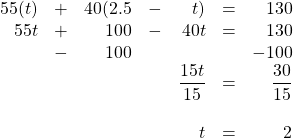
This means that the time spent travelling at 40 km/h was 0.5 h.
Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.
For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.
- A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
- Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
- Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
- Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
- A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
- Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
- A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
- A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?
Solve Questions 9 to 22.
- A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
- A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
- A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
- As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
- Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
- A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
- A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
- A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
- Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
- Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
- Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
- Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
- On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
- Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.
Answers to odd questions
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| A | |||
| B |
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| T | |||
| T |
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| P | |||
| F |
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| Away | |||
| Return |
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| Away | |||
| Back |
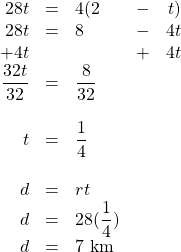
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| To resort | |||
| Return |
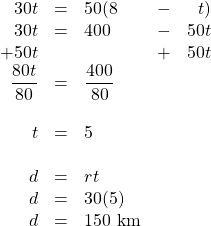
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| Sam | |||
| Sue |
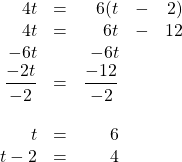
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| MB | |||
| CC |
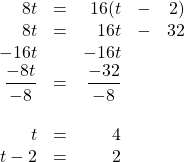
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| M | |||
| M |

| Who or What | Rate | Time | Equation |
|---|---|---|---|
| C | |||
| C |
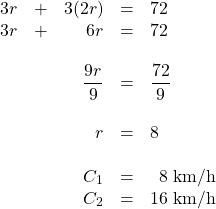
| Who or What | Rate | Time | Equation |
|---|---|---|---|
| S | |||
| S |
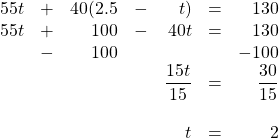
Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Solving Distance, Rate, and Time Word Problems
Distance, rate, and time problems are a common type of word problem in algebra. These problems involve objects moving at a constant speed, and we need to figure out how far they travel, how long it takes them to travel a certain distance, or how fast they are traveling.
The key to solving these problems is to understand the relationship between distance, rate, and time. The formula that connects these three is:
Distance = Rate × Time
This formula can be rearranged to solve for any of the three variables:
- Rate = Distance / Time
- Time = Distance / Rate
Setting Up the Equation
When solving distance, rate, and time word problems, it’s helpful to set up a table to organize the information. The table should have columns for distance, rate, and time, and rows for each object or situation involved in the problem.
For example, consider the following problem:
Two cars leave from the same point at the same time. Car A travels east at 60 miles per hour, and Car B travels west at 70 miles per hour. How long will it take for the cars to be 260 miles apart?
Here’s how we can set up a table to organize the information:
| Distance | Rate | Time | |
|---|---|---|---|
| Car A | d | 60 | t |
| Car B | 260 – d | 70 | t |
We know the rate of each car and the total distance they need to be apart. We are trying to find the time it takes for them to reach that distance. We can use the formula Distance = Rate × Time to create equations for each car:
- Car A: d = 60t
- Car B: 260 – d = 70t
We now have a system of two equations with two unknowns. We can solve for d and t using substitution or elimination.
Solving the Equation
In this case, we’ll use substitution. From the first equation, we know that d = 60 t . We can substitute this value of d into the second equation:
260 – 60 t = 70 t
Simplifying the equation:
260 = 130 t
Solving for t :
t = 260 / 130 = 2 hours
Therefore, it will take 2 hours for the cars to be 260 miles apart.
Key Points to Remember
- Make sure you understand the relationship between distance, rate, and time.
- Set up a table to organize the information in the problem.
- Use the formula Distance = Rate × Time to create equations.
- Solve the system of equations using substitution or elimination.
By following these steps, you can solve any distance, rate, and time word problem.
Distance Rate time
© 2024 by SchoolTube
Username or Email Address
Remember Me
Forgot password?
Enter your account data and we will send you a link to reset your password.
Your password reset link appears to be invalid or expired.
Privacy policy.
To use social login you have to agree with the storage and handling of your data by this website. Privacy Policy
Add to Collection
Public collection title
Private collection title
No Collections
Here you'll find all collections you've created before.
Module 5: Multi-Step Linear Equations
Using the distance, rate, and time formula, learning outcomes.
- Use the problem-solving method to solve problems using the distance, rate, and time formula
One formula you’ll use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant speed. The basic idea is probably already familiar to you. Do you know what distance you traveled if you drove at a steady rate of [latex]60[/latex] miles per hour for [latex]2[/latex] hours? (This might happen if you use your car’s cruise control while driving on the Interstate.) If you said [latex]120[/latex] miles, you already know how to use this formula!
The math to calculate the distance might look like this:
[latex]\begin{array}{}\\ \text{distance}=\left(\Large\frac{60\text{ miles}}{1\text{ hour}}\normalsize\right)\left(2\text{ hours}\right)\hfill \\ \text{distance}=120\text{ miles}\hfill \end{array}[/latex]
In general, the formula relating distance, rate, and time is
[latex]\text{distance}\text{=}\text{rate}\cdot \text{time}[/latex]
Distance, Rate, and Time
For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula
[latex]d=rt[/latex]
where [latex]d=[/latex] distance, [latex]r=[/latex] rate, and [latex]t=[/latex] time.
Notice that the units we used above for the rate were miles per hour, which we can write as a ratio [latex]\Large\frac{miles}{hour}[/latex]. Then when we multiplied by the time, in hours, the common units “hour” divided out. The answer was in miles.
Jamal rides his bike at a uniform rate of [latex]12[/latex] miles per hour for [latex]3\Large\frac{1}{2}[/latex] hours. How much distance has he traveled?
| Step 1. the problem. You may want to create a mini-chart to summarize the | [latex]d=?[/latex] [latex]r=12\text{mph}[/latex] [latex]t=3 \Large\frac{1}{2}\normalsize\text{hours}[/latex] |
| Step 2. what you are looking for. | distance traveled |
| Step 3. Choose a variable to represent it. | let = distance |
| Step 4. Write the appropriate formula for the situation. Substitute in the given information. | [latex]d=rt[/latex] [latex]d=12\cdot 3\Large\frac{1}{2}[/latex] |
| Step 5. the equation. | [latex]d=42\text{ miles}[/latex] |
| Step 6. Does 42 miles make sense?
| |
| Step 7. the question with a complete sentence. | Jamal rode 42 miles. |
In the following video we provide another example of how to solve for distance given rate and time.
Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of [latex]520[/latex] miles. If he can drive at a steady rate of [latex]65[/latex] miles per hour, how many hours will the trip take?
Show Solution
| Step 1. the problem. Summarize the information in the problem. | [latex]d=520[/latex] miles [latex]r=65[/latex] mph [latex]t=?[/latex] |
| Step 2. what you are looking for. | how many hours (time) |
| Step 3. Choose a variable to represent it. | let [latex]t[/latex] = time |
| Step 4. Write the appropriate formula. Substitute in the given information. | [latex]d=rt[/latex] [latex]520=65t[/latex] |
| Step 5. the equation. | [latex]t=8[/latex] |
| Step 6. Substitute the numbers into the formula and make sure [latex]d=rt[/latex] [latex]520\stackrel{?}{=}65\cdot 8[/latex] [latex]520=520\quad\checkmark [/latex] | |
| Step 7. the question with a complete sentence. We know the units of time will be hours because | Rey’s trip will take [latex]8[/latex] hours. |
In the following video we show another example of how to find rate given distance and time.
- Question ID 145550, 145553,145619,145620. Authored by : Lumen Learning. License : CC BY: Attribution
- Ex: Find the Rate Given Distance and Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/3rYh32ErDaE . License : CC BY: Attribution
- Example: Solve a Problem using Distance = Rate x Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/lMO1L_CvH4Y . License : CC BY: Attribution
- Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Our website uses cookies and thereby collects information about your visit to improve our website (by analyzing), show you Social Media content and relevant advertisements. Please see our page for furher details or agree by clicking the 'Accept' button.
Cookie settings
Below you can choose which kind of cookies you allow on this website. Click on the "Save cookie settings" button to apply your choice.
Functional Our website uses functional cookies. These cookies are necessary to let our website work.
Analytical Our website uses analytical cookies to make it possible to analyze our website and optimize for the purpose of a.o. the usability.
Social media Our website places social media cookies to show you 3rd party content like YouTube and FaceBook. These cookies may track your personal data.
Advertising Our website places advertising cookies to show you 3rd party advertisements based on your interests. These cookies may track your personal data.
Other Our website places 3rd party cookies from other 3rd party services which aren't Analytical, Social media or Advertising.
Default cookie settings Save cookie settings
This content is blocked. Accept cookies within the '%CC%' category to view this content. click to accept all cookies Accept %CC% cookies
Word Problems- Distance Rate and Time
Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
\(\textbf{1)}\) When Mike rows his boat with the current, he travels 8 miles in 2 hours. Against the current, he can only travel 6 miles in the same time. How fast can Mike travel in still water? What is the rate of the current? Show Boat Speed Boat speed is 3.5 miles per hour Show Rate of the Current Rate of the current is .5 miles per hour Show Explanation Let b = speed of boat in still water. Let c = speed of current When Mike rows with the current, his effective speed is increased by the speed of the current, so his speed is “b + c” (rate of the boat plus rate of the current). When Mike rows against the current, his effective speed is decreased by the speed of the current, so his speed is “b – c” (rate of the boat minus rate of the current). Given the information: With the current: Distance = 8 miles, Time = 2 hours Against the current: Distance = 6 miles, Time = 2 hours We can use the formula: Distance = Rate × Time For rowing with the current: 8 = (b + c) × 2 For rowing against the current: 6 = (b – c) × 2 Now we have a system of two equations: 2b + 2c = 8 2b – 2c = 6 We can simplify these equations by dividing both sides of both equations by 2: b + c = 4 b – c = 3 Add the equations to eliminate c 2b = 7 b = 3.5 Now that we have b=3.5, we can substitute it into one of the equations to solve for the speed of the current: b + c = 4 3.5 + c = 4 c = 0.5 So, Mike can travel at a speed of 3.5 miles per hour in still water, and the speed of the current is 0.5 miles per hour.
\(\textbf{2)}\) with the wind, a plane can fly 1200 miles in 2 hours and 30 minutes. against the wind, the same plane can only fly 1000 miles in the same time. find the rate of the plane in still air and the rate of the wind. show plane speed plane speed is 440 miles per hour show wind speed wind speed is 40 miles per hour, \(\textbf{3)}\) a boat travels 30 miles upstream (against the current) in 3 hours. the boat travels the same distance downstream (with the current) in 2 hours. what is the rate of the boat in still water what is the rate of the current show boat speed boat speed is 12.5 miles per hour show rate of the current rate of the current is 2.5 miles per hour, \(\textbf{4)}\) a plane travels 2500 miles in 5 hours when it flies into the wind. when the same plane flies with the wind, it can travel the same distance in 4 hours. find the rate of the plane in still air and the rate of the wind. show plane speed plane speed is 562.5 miles per hour show wind speed wind speed is 62.5 miles per hour show explanation let p= speed of plane let w= speed of wind when the plane is flying into the wind, its effective speed is reduced by the speed of the wind, so the plane’s speed is “p – w”. when the plane is flying with the wind, its effective speed is increased by the speed of the wind, so the plane’s speed is “p + w”. given the information: flying into the wind: distance = 2500 miles, time = 5 hours flying with the wind: distance = 2500 miles, time = 4 hours we can use the formula: distance = rate × time for flying into the wind: 2500 = (p – w) × 5 for flying with the wind: 2500 = (p + w) × 4 now we have a system of two equations: 5p – 5w = 2500 4p + 4w = 2500 we can simplify these equations by dividing both sides of the second equation by 4: 5p – 5w = 2500 p + w = 625 now we can solve this system of equations. let’s solve the second equation for p: p = 625 – w substitute this value of p into the first equation: 5(625 – w) – 5w = 2500 3125 – 5w – 5w = 2500 -10w = -625 w = 62.5 now that we have the value of the wind speed, we can find the rate of the plane in still air by substituting w=62.5 into the equation p = 625 – w: p = 625 – 62.5 p = 562.5 so, the rate of the plane in still air is 562.5 miles per hour, and the rate of the wind is 62.5 miles per hour., \(\textbf{5)}\) two cars started at the same place. one car going north traveled \(50\) mph for \(2\) hours. the other car traveled south at \(60\) mph for \(1\) hour and \(15\) minutes. how far apart are the cars show answer the answer is \(175 \) miles, \(\textbf{6)}\) two cars started at the same place. one car going north traveled \(10\) mph for \(4\) hours. the other car traveled east at \(15\) mph for \(2\) hours. how far apart are the cars show answer the answer is \(50 \) miles, \(\textbf{7)}\) two cars started at the same place. both traveled north. one car traveled at \(50\) mph for \(2\) hours. the other car traveled at \(60\) mph for \(1\) hour and \(45\) minutes. how far apart are the cars show answer the answer is \(5\) miles, \(\textbf{8)}\) a car travels from city a to city b at 50 miles per hour. then they return to city a at 30 miles per hour. what was the average rate of speed of the two trips show answer the answer is \(37.5\) miles per hour show explanation to find the average rate of speed for the round trip from city a to city b and back, you can use the concept of harmonic mean. the harmonic mean is calculated as the reciprocal of the average of the reciprocals of the individual speeds. the formula for the harmonic mean of two speeds is: harmonic mean = \(\displaystyle\frac{2}{\frac{1}{50}+\frac{1}{30}}\) to add the fractions in the denominator, you need a common denominator, which is the least common multiple of 50 and 30, which is 1500: harmonic mean = \(\displaystyle\frac{2}{\frac{30}{1500}+\frac{50}{1500}}\) harmonic mean = \(\displaystyle\frac{2}{\frac{80}{1500}}\) harmonic mean = \(\displaystyle2\cdot\frac{1500}{80}\) harmonic mean = \(\displaystyle\frac{3000}{80}\) harmonic mean = \(\displaystyle 37.5\) so, the average rate of speed for the round trip is 37.5 miles per hour., \(\textbf{9)}\) sarah walked to work and it took 60 minutes. when she drove it took 6 minutes. she drives 36 mph faster than she walks. how far away is her work show answer the answer is \(4\) miles, see related pages\(\), \(\bullet\text{ word problems- linear equations}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- averages}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- consecutive integers}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- distance, rate and time}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- break even}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- ratios}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- age}\) \(\,\,\,\,\,\,\,\,\), \(\bullet\text{ word problems- mixtures and concentration}\) \(\,\,\,\,\,\,\,\,\), sure, here are eight seo optimized paragraphs about word problems involving distance, rate, and time: 1. introduction to word problems - distance, rate and time: word problems involving distance, rate, and time are a common type of problem found in math classes at all levels. these types of problems involve solving for one or more unknown quantities, such as distance, rate, or time, by using information about the relationships between these quantities. 2. definition of word problems - distance, rate and time: word problems involving distance, rate, and time are mathematical problems that involve calculating one or more unknown quantities by using information about the relationships between distance, rate, and time. these types of problems often involve situations that involve motion, such as a person walking or a car driving. 3. why do we learn about word problems - distance, rate and time: understanding how to solve word problems involving distance, rate, and time is important because these types of problems are common in real-life situations. for example, if you want to know how long it will take to drive to a destination, you need to know how to calculate the time based on the distance and the speed at which you are traveling. 4. what math class is word problems - distance, rate and time: word problems involving distance, rate, and time are typically covered in math classes at all levels, from elementary school through high school and beyond. these types of problems may be introduced in a variety of math classes, including algebra, geometry, and calculus. 5. common mistakes with word problems - distance, rate and time: one common mistake when solving word problems involving distance, rate, and time is not paying attention to the units of measurement. it is important to make sure that all quantities are expressed in the same units, such as miles per hour or kilometers per hour, to ensure that the final answer is correct. 6. fun fact about word problems - distance, rate and time: did you know that the ancient egyptians used a system of measurement based on the length of a person's arm this system, called the cubit, was used to measure distance, and it is still used in some parts of the world today. 7. who discovered word problems - distance, rate and time: the concept of solving problems involving distance, rate, and time has been around for centuries. it is likely that these types of problems were first used by ancient civilizations to solve practical problems, such as how long it would take to travel from one place to another. 8. related topics to word problems - distance, rate and time: other topics related to word problems involving distance, rate, and time include algebra, geometry, and calculus. these subjects involve using mathematical concepts and techniques to solve more complex problems involving variables and equations. 5 real world examples of word problems- distance, rate and time here are five real-world examples of word problems involving distance, rate, and time: 1. a car travels at a rate of 60 miles per hour for 3 hours. how far does the car travel in this problem, the rate is given in miles per hour, and the time is given in hours. to solve the problem, you need to multiply the rate by the time to find the distance traveled: 60 miles/hour * 3 hours = 180 miles. 2. a plane flies at a speed of 500 miles per hour for 4 hours. how far does the plane travel in this problem, the rate is given in miles per hour, and the time is given in hours. to solve the problem, you need to multiply the rate by the time to find the distance traveled: 500 miles/hour * 4 hours = 2000 miles. 3. a person walks at a rate of 3 miles per hour for 2 hours. how far does the person walk in this problem, the rate is given in miles per hour, and the time is given in hours. to solve the problem, you need to multiply the rate by the time to find the distance traveled: 3 miles/hour * 2 hours = 6 miles. 4. a train travels at a rate of 70 miles per hour for 5 hours. how far does the train travel in this problem, the rate is given in miles per hour, and the time is given in hours. to solve the problem, you need to multiply the rate by the time to find the distance traveled: 70 miles/hour * 5 hours = 350 miles. 5. a boat travels at a rate of 15 miles per hour for 8 hours. how far does the boat travel in this problem, the rate is given in miles per hour, and the time is given in hours. to solve the problem, you need to multiply the rate by the time to find the distance traveled: 15 miles/hour * 8 hours = 120 miles. 5 other math topics that use word problems- distance, rate and time here are five other math topics that use word problems involving distance, rate, and time: 1. algebra: algebra is a branch of mathematics that involves using letters and symbols to represent unknown quantities and using equations to solve for those quantities. word problems involving distance, rate, and time can be expressed using algebraic equations, and solving these equations can help you find the unknown quantities in the problem. 2. geometry: geometry is a branch of mathematics that deals with shapes and the properties of space. word problems involving distance, rate, and time can often involve geometric concepts, such as the distance between two points or the area of a particular shape. 3. trigonometry: trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. word problems involving distance, rate, and time can often involve trigonometric concepts, such as finding the distance between two points using the pythagorean theorem. 4. calculus: calculus is a branch of mathematics that deals with the study of change and the rates at which quantities change. word problems involving distance, rate, and time can often be expressed using calculus concepts, such as finding the average rate of change over a particular time period. 5. statistics: statistics is a branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. word problems involving distance, rate, and time can often involve statistical concepts, such as finding the mean, median, or mode of a set of data. i've put out a lot of practice problems, notes and videos on andymath.com. i hope it helps thank you, about andymath.com, andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. if you have any requests for additional content, please contact andy at [email protected] . he will promptly add the content. topics cover elementary math , middle school , algebra , geometry , algebra 2/pre-calculus/trig , calculus and probability/statistics . in the future, i hope to add physics and linear algebra content. visit me on youtube , tiktok , instagram and facebook . andymath content has a unique approach to presenting mathematics. the clear explanations, strong visuals mixed with dry humor regularly get millions of views. we are open to collaborations of all types, please contact andy at [email protected] for all enquiries. to offer financial support, visit my patreon page. let’s help students understand the math way of thinking thank you for visiting. how exciting.
- Architecture and Design
- Asian and Pacific Studies
- Business and Economics
- Classical and Ancient Near Eastern Studies
- Computer Sciences
- Cultural Studies
- Engineering
- General Interest
- Geosciences
- Industrial Chemistry
- Islamic and Middle Eastern Studies
- Jewish Studies
- Library and Information Science, Book Studies
- Life Sciences
- Linguistics and Semiotics
- Literary Studies
- Materials Sciences
- Mathematics
- Social Sciences
- Sports and Recreation
- Theology and Religion
- Publish your article
- The role of authors
- Promoting your article
- Abstracting & indexing
- Publishing Ethics
- Why publish with De Gruyter
- How to publish with De Gruyter
- Our book series
- Our subject areas
- Your digital product at De Gruyter
- Contribute to our reference works
- Product information
- Tools & resources
- Product Information
- Promotional Materials
- Orders and Inquiries
- FAQ for Library Suppliers and Book Sellers
- Repository Policy
- Free access policy
- Open Access agreements
- Database portals
- For Authors
- Customer service
- People + Culture
- Journal Management
- How to join us
- Working at De Gruyter
- Mission & Vision
- De Gruyter Foundation
- De Gruyter Ebound
- Our Responsibility
- Partner publishers

Your purchase has been completed. Your documents are now available to view.
Application of locally regularized extremal shift to the problem of realization of a prescribed motion
A controlled system of differential equations under the action of an unknown disturbance is considered. The problem discussed in the paper consists in constructing algorithms for forming a control that provides the realization of a prescribed motion for any admissible disturbance. Namely these algorithms should provide the closeness in the metric of the space of differentiable functions of a phase trajectory of a given controlled system and some etalon trajectory of an analogous system functioning when any outer actions are absent. As the space of admissible disturbances, we take the space of measurable square integrable (with respect to the Euclidean norm) functions. The cases of inaccurate measurements of phase trajectories of both systems at all times and at discrete times are under study. Two computer oriented algorithms for solving the problem are designed. The algorithms are based on the (well-known in the theory of guaranteed control) method of extremal shift. In the process, its local (at each time of control correction) regularization is performed by the method of smoothing functional (the Tikhonov method). In addition, estimates for algorithm’s convergence rate are presented.
[1] K. Abbaoui and Y. Cherruault, New ideas for solving identification and optimal control problems related to biomedical systems, Int. J. Biomed. Comput. 36 (1994), no. 3, 181–186. 10.1016/0020-7101(94)90052-3 Search in Google Scholar PubMed
[2] S. Arimoto, S. Kawamura and F. Miyazaki, Bettering operation of robots by learning, J. Robot. Syst. 1 (1984), no. 2, 123–140. 10.1002/rob.4620010203 Search in Google Scholar
[3] S. Arimoto, S. Kawamura, F. Miyazaki and S. Tamaki, Learning control theory for dynamical systems, 1985 24th IEEE Conference on Decision and Control, IEEE Press, Piscataway (1985), 1375–1380. 10.1109/CDC.1985.268737 Search in Google Scholar
[4] A. Astolfi, Tracking and Regulation in Linear Systems, Springer, London, 2014. 10.1007/978-1-4471-5102-9_198-1 Search in Google Scholar
[5] T. Berger, A. Ilchmann and E. P. Ryan, Funnel control of nonlinear systems, Math. Control Signals Systems 33 (2021), no. 1, 151–194. 10.1007/s00498-021-00277-z Search in Google Scholar
[6] Z. Bien and K. M. Huh, Higher-order iterative learning control algorithm, IEE Proc. D 136 (1989), no. 3, 105–112. 10.1049/ip-d.1989.0016 Search in Google Scholar
[7] W. H. Chen, J. Yang, L. Guo and S. Li, Disturbance observer-based control and related methods: An overview, IEEE Trans. Ind. Electron. 63 (2016), no. 2, 1083–1095. 10.1109/TIE.2015.2478397 Search in Google Scholar
[8] X. Deng, X. Sun and S. Liu, Retracted: High-order iterative learning consensus tracking of nonlinear multiagent systems with time-varying delays, Trans. Inst. Meas. Control 41 (2019), no. 4, NP2–NP11. 10.1177/0142331218799144 Search in Google Scholar
[9] M. Fabrizio, A. Favini and G. Marinoschi, An optimal control problem for a singular system of solid-liquid phase transition, Numer. Funct. Anal. Optim. 31 (2010), no. 7–9, 989–1022. 10.1080/01630563.2010.512691 Search in Google Scholar
[10] A. Favini and G. Marinoschi, Identification of the time derivative coefficient in a fast diffusion degenerate equation, J. Optim. Theory Appl. 145 (2010), no. 2, 249–269. 10.1007/s10957-009-9635-z Search in Google Scholar
[11] J. Hätönen, D. H. Owens and K. Feng, Basis functions and parameter optimisation in high-order iterative learning control, Automatica J. IFAC 42 (2006), no. 2, 287–294. 10.1016/j.automatica.2005.05.025 Search in Google Scholar
[12] S. I. Kabanikhin, Inverse and Ill-Posed Problems, Walter de Gruyter, Berlin, 2012. 10.1515/9783110224016 Search in Google Scholar
[13] S. Kindermann and A. Leitão, On regularization methods for inverse problems of dynamic type, Numer. Funct. Anal. Optim. 27 (2006), no. 2, 139–160. 10.1080/01630560600569973 Search in Google Scholar
[14] S. Kindermann and A. Leitão, On regularization methods based on dynamic programming techniques, Appl. Anal. 86 (2007), no. 5, 611–632. 10.1080/00036810701354953 Search in Google Scholar
[15] N. N. Krasovskiĭ and A. I. Subbotin, Game-Theoretical Control Problems, Springer Ser. Soviet Math., Springer, New York, 1988. 10.1007/978-1-4612-3716-7 Search in Google Scholar
[16] A. V. Kryazhimskiĭ and Y. S. Osipov, Stable solutions of inverse problems of the dynamics of controllable systems, Proc. Steklon Inst. Math. 185 (1988), 143–164. Search in Google Scholar
[17] M. M. Lavrentev, V. G. Romanov and S. P. Šišatskiĭ, Ill-posed Problems of Mathematical Physics and Analysis (in Russian), “Nauka”, Moscow, 1980. Search in Google Scholar
[18] S. Li, J. Yang, W. H. Chen and X. Chen, Generalized extended state observer based control for systems with mismatched uncertainties, IEEE Trans. Ind. Electron. 59 (2012), no. 12, 4792–4802. 10.1109/TIE.2011.2182011 Search in Google Scholar
[19] X. Li and J. Wang, Fault-tolerant tracking control for a class of nonlinear multi-agent systems, Systems Control Lett. 135 (2020), Article ID 104576. 10.1016/j.sysconle.2019.104576 Search in Google Scholar
[20] V. Maksimov, On stable solution of the problem of disturbance reduction in a linear dynamical system, Math. Control Signals Systems 36 (2024), no. 1, 177–211. 10.1007/s00498-023-00363-4 Search in Google Scholar
[21] V. I. Maksimov, Dynamical Inverse Problems of Distributed Systems, VSP, Utrecht, 2002. 10.1515/9783110944839 Search in Google Scholar
[22] V. I. Maksimov, On tracking a trajectory of a dynamical system, J. Appl. Math. Mech. 75 (2011), no. 6, 667–674. 10.1016/j.jappmathmech.2012.01.007 Search in Google Scholar
[23] V. I. Maksimov, On a stable solution of the problem of disturbance reduction, Int. J. Appl. Math. Comput. Sci. 31 (2021), no. 2, 187–194. 10.34768/amcs-2021-0013 Search in Google Scholar
[24] Y. S. Osipov and A. V. Kryazhimskii, Inverse Problems for Ordinary Differential Equations: Dynamical Solutions, Gordon and Breach Science, Basel, 1995. Search in Google Scholar
[25] E. P. Ryan, C. J. Sangwin and P. Townsend, Controlled functional differential equations: approximate and exact asymptotic tracking with prescribed transient performance, ESAIM Control Optim. Calc. Var. 15 (2009), no. 4, 745–762. 10.1051/cocv:2008045 Search in Google Scholar
[26] A. A. Samarskiĭ, Introduction in the Theory of Difference Schemes (in Russian), “Nauka”, Moscow, 1971. Search in Google Scholar
[27] Y. Wang, Y. Song and F. L. Lewis, Robust adaptive fault-tolerant control of multi-agent systems with uncertain nonidentical dynamics and undetectable actuation failures, IEEE Trans. Ind. Electron. 62 (2015), no. 6, 3978–3988. 10.1109/TIE.2015.2399400 Search in Google Scholar
[28] W. M. Wonham, Linear Multivariable Control: A Geometric Approach, Appl. Math. 10, Springer, New York, 1979. 10.1007/978-1-4684-0068-7 Search in Google Scholar
[29] X. Yang, A PD-type iterative learning control for a class of switched discrete-time systems with model uncertainties and external noises, Discrete Dyn. Nat. Soc. 2015 (2015), Article ID 410292. 10.1155/2015/410292 Search in Google Scholar
[30] M. Yu and S. Chai, Adaptive iterative learning control for discrete-time nonlinear systems with multiple iteration-varying high-order internal models, Internat. J. Robust Nonlinear Control 31 (2021), no. 15, 7390–7408. 10.1002/rnc.5690 Search in Google Scholar
[31] Y. Yuan, Z. Wang, Y. Yu, L. Guo and H. Yang, Active disturbance rejection control for a pneumatic motion platform subject to actuator saturation: an extended state observer approach, Automatica J. IFAC 107 (2019), 353–361. 10.1016/j.automatica.2019.05.056 Search in Google Scholar
[32] Z.-L. Zhao and B.-Z. Guo, A nonlinear extended state observer based on fractional power functions, Automatica J. IFAC 81 (2017), 286–296. 10.1016/j.automatica.2017.03.002 Search in Google Scholar
© 2024 Walter de Gruyter GmbH, Berlin/Boston
- X / Twitter
Supplementary Materials
Please login or register with De Gruyter to order this product.

IMAGES
VIDEO
COMMENTS
Distance, Rate, and Time. For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula. d= rt d = r t. where d = d = distance, r = r = rate, and t= t = time. Notice that the units we used above for the rate were miles per hour, which we can write as a ratio miles hour m i l ...
Before you can use the distance, rate, and time formula, D=RT, you need to make sure that your units for the distance and time are the same units as your rate. ... How to solve distance, rate, and time problems . Take the course Want to learn more about Algebra 2? I have a step-by-step course for that. :) Learn More Finding average rate given ...
Solving for Distance, Rate, or Time. When you are solving problems for distance, rate, and time, you will find it helpful to use diagrams or charts to organize the information and help you solve the problem. You will also apply the formula that solves distance, rate, and time, which is distance = rate x tim e. It is abbreviated as:
Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance. r⋅t = d r ⋅ t = d. For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h) (4h) = 120 km.
30. t. 30 × t. The total distance you and your wife travel is 45t + 30t = 75t and this must be equal to 225. 75 × t = 225. Since 75 times 3 = 225, t = 3. Therefore, you will be 225 miles apart after 3 hours. The above are great examples of distance rate time problems. Try to do some now in your math textbook.
The distance is 300,000 miles and the time is 4 hours. We will plug these values into the formula, like so. To solve it, we need to divide both sides by 4. This means it was traveling at 75,000 mph. Two Moving Objects. Sometimes two objects travel to cover a certain distance.
Rate-Time-Distance Problem. Solve this word problem using uniform motion rt = d formula: Example: Two cyclists start at the same corner and ride in opposite directions. One cyclist rides twice as fast as the other. In 3 hours, they are 81 miles apart. Find the rate of each cyclist. Show Video Lesson
Distance problems are word problems that involve the distance an object will travel at a certain average rate for a given period of time. The formula for distance problems is: distance = rate × time or. d = r × t. Things to watch out for: Make sure that you change the units when necessary. For example, if the rate is given in miles per hour ...
In this problem, you need to figure out the distance that the Murphy family traveled. Distance = rate × time. Next, take the given information from the problem and substitute that information into the formula. Distance = rate × time Distance = 53 m p h × 3.5 h. Then, calculate the distance by multiplying the rate by the time.
An application of linear equations can be found in distance problems. When solving distance problems we will use the relationship rt = d or rate (speed) times time equals distance. For example, if a person were to travel 30 mph for 4 hours. To find the total distance we would multiply rate times time or (30)(4) = 120.
Use the formula r = d/t. Your rate is 24 miles divided by 2 hours, so: r = 24 miles ÷ 2 hours = 12 miles per hour. Now let's say you rode your bike at a rate of 10 miles per hour for 4 hours. How many miles did you travel? This time, use the distance formula d = rt: d = 10 miles per hour × 4 hours = 40 miles. Next, you ride 18 miles and ...
Use the distance formula to solve for rate. Distance = 285 m i l e s. Time = 9.5 h o u r s. Rate = x. Solution: The answer is 30 mph. Example B Use the distance formula to solve for time. ... If the rate in the problem gives miles per hour (mph), then time must be in hours. If the time is given in minutes, divide by sixty to determine the ...
Distance, Rate, and Time. For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula d=rt d = rt where d= d = distance, r= r = rate, and t= t= time. Notice that the units we used above for the rate were miles per hour, which we can write as a ratio \frac {miles} {hour ...
In math, distance, rate, and time are three important concepts you can use to solve many problems if you know the formula. Distance is the length of space traveled by a moving object or the length measured between two points. It is usually denoted by d in math problems.. The rate is the speed at which an object or person travels. It is usually denoted by r in equations.
http://www.emathacademy.com/This video shows how to set up and solve distance rate time word problems for Algebra 1 and Algebra 2. To solve distance rate ti...
2nd part distance: 115 (5 − t) I can add these two partial-distance expressions, and set them equal to the known total distance: 105 t + 115 (5 − t) = 555. This is an equation in one variable, which I can solve: 105 t + 115 (5 − t) = 555. 105 t + 575 − 115 t = 555. 575 − 10 t = 555. 20 = 10 t.
DISTANCE = RATE X TIME. Explore the formula d = rt by starting with unit conversion problems. Mathletes will solve for distance, rate and time by paying attention to the units given in the problem and using the appropriate equivalent version of the formula: d = rt, r = d / t or t = d / r. Download Mathlete handout. Download coach version with ...
Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance. For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h) (4h) = 120 km.
Make sure you understand the relationship between distance, rate, and time. Set up a table to organize the information in the problem. Use the formula Distance = Rate × Time to create equations. Solve the system of equations using substitution or elimination. By following these steps, you can solve any distance, rate, and time word problem.
Follow the steps given here to solve a rate problem using a rational equation: Step 1: Determine which iteration of the rate equation you must use by analyzing the word problem. Step 2: Set up the ...
Distance, Rate, and Time. For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula. d= rt d = r t. where d = d = distance, r = r = rate, and t= t = time. Notice that the units we used above for the rate were miles per hour, which we can write as a ratio miles hour m i l ...
Flying with the wind: Distance = 2500 miles, Time = 4 hours We can use the formula: Distance = Rate × Time. For flying into the wind: 2500 = (p - w) × 5. For flying with the wind: 2500 = (p + w) × 4. Now we have a system of two equations: 5p - 5w = 2500 4p + 4w = 2500. We can simplify these equations by dividing both sides of the second ...
How to Solve Distance, Rate and Time Problems Using Systems of Linear Equations. Step 1: Fill out a distance, rate, and time (DRT) Table with the information given in the problem.. Step 2: Use the ...
Two computer oriented algorithms for solving the problem are designed. The algorithms are based on the (well-known in the theory of guaranteed control) method of extremal shift. In the process, its local (at each time of control correction) regularization is performed by the method of smoothing functional (the Tikhonov method).