homework 3 free fall and graphs

Free Fall Motion: Explanation, Review, and Examples

• The Albert Team
• Last Updated On: February 16, 2023

Free fall and projectile motion describe objects that are moving through the air and acted on only by gravity. In this post, we will describe this type of motion using both graphs and kinematic equations. Since projectile motion involves two dimensions, these problems can be complex. We will explain many examples so you can see how to solve different types of projectile motion. 

What We Review

An object that is moving under only the influence of gravity is in free fall. In order for an object to be in free fall, wind and air resistance must be ignored. On Earth, all objects in free fall accelerate downward at the rate of gravity or 9.81\text{ m/s}^2 .

Applying Free Fall to Kinematic Equations

When analyzing free fall motion, we can apply the same kinematic equations as we did for motion on the ground. We can then use these equations to determine properties such as distance, time, and velocity. 

How to Find Distance Fallen for an Object in Free Fall

If an object is in free fall, we can use kinematic equations to find the distance it falls during a certain time. You will typically use the following kinematic equation to calculate the distance fallen:

In order to use this equation, you need to know the initial velocity of the object and the time of flight. Remember that the acceleration of a free falling object is always equal to the acceleration due to gravity, 9.81\text{ m/s}^2 . 

Many free fall physics problems will include scenarios where objects are dropped from rest. In this case, the initial velocity is zero and the first term of the kinematic equation above will cancel out. 

If the time is not known, another method for calculating the distance fallen is to use the following kinematic equation:

In this case, you must know the final velocity v_f of the object. Then, you can solve the equation for the distance d .

How to Find Time for an Object in Free Fall

The amount of time an object is in free fall will depend on its velocity and the distance it falls. Similar to distance, there are two equations you can use to find the time, depending on what you know. 

If you know the initial and final velocity of the object, then the simplest way to calculate time is using the kinematic equation:

This equation can be solved for time. Then, you’ll only need to substitute the values for the velocities and the acceleration due to gravity.

Another method to find time if you do not know the object’s final velocity is to use the equation:

Note that in this equation there are two terms that include the time t . Unless the initial velocity is zero, this can make it more challenging to solve this equation for time. If using this equation, you may need to use the quadratic formula to solve for time.

How to Find Final Velocity for an Object in Free Fall

The final velocity of an object in free fall depends on the amount of time it falls. Due to the acceleration of gravity, the velocity will increase every second by 9.81\text{ m/s} . The final velocity can be calculated using the equation:

If you do not know the amount of time the object is falling, another method for calculating the final velocity is using the kinematic equation: 

This equation requires that you instead know the distance that the object falls. If you are using this equation to find the final velocity, remember that the final velocity is squared in this equation. That means you will need to take a square root as your final step to solve for the final velocity. 

Examples of Free Fall

In this next section, we’ll apply the methods you just learned to solve some problems about free fall motion.

Example 1: How to Find the Distance for an Object Dropped from Rest

For example, an object is dropped from rest from the top of a tall building. It hits the ground 5\text{ s} after it is dropped. What is the height of the building? 

In this scenario, we know that the object’s initial velocity is zero because it was dropped from rest. We also know that the acceleration is 9.81\text{ m/s}^2 . This problem is asking us to find the distance the object falls. This will be equal to the height of the building.

Based on this information, we can use the following kinematic equation to find the distance:

Substituting the given values produces:

Therefore, the height of the building is about 123\text{ m} .

Example 2: How to Find the Final Velocity for an Object with Initial Velocity

In another example, an object in free fall has an initial, downward velocity of 2\text{ m/s} and falls a distance of 45\text{ m} . What is the object’s final velocity? 

In this scenario, we are given the object’s initial velocity, v_i and the distance d . We also know that the acceleration is 9.81\text{ m/s}^2 . Based on this information, we can use the following kinematic equation to find the final velocity:

Since the initial velocity is in the same direction as the acceleration (downward) we can use the same sign for both values.

Our last step is to eliminate the square by taking the square root:

Therefore, the final velocity of the object is about 30\text{ m/s} .

Motion Graphs for Objects in Free Fall

In addition to using physics equations, we can also represent free fall motion with motion graphs. Position-time graphs, velocity-time graphs, and acceleration-time graphs can tell us a lot about the object’s motion over time. Want a more in-depth review of motion graphs? Check out this blog post !

Position-Time Graph for an Object in Free Fall

In terms of position, many objects in free fall start at a high position, or height off the ground, and move downward. Objects in free fall accelerate due to gravity. Therefore, the position-time graph for free fall motion must be curved. This means that objects in free fall start with a slow velocity and gradually speed up which is represented by the steep downward curve of the graph. 

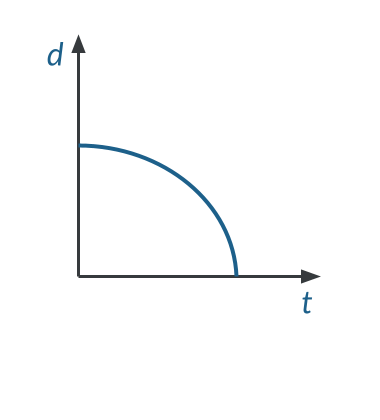
Velocity-Time Graph for an Object in Free Fall

As an object falls, its velocity increases due to the acceleration of gravity. This means that the velocity starts slow and steadily increases in the downward direction. The graph below shows the velocity-time for an object in free fall:

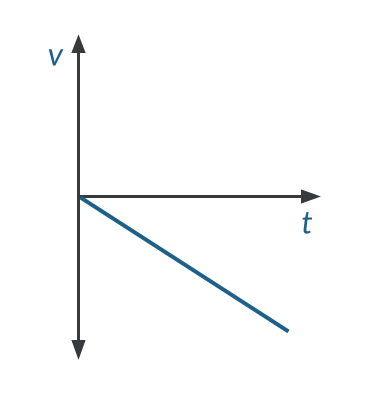
Note that the slope of this graph is constant and represents the acceleration due to gravity, or -9.81\text{ m/s}^2 .

Acceleration-Time Graph for an Object in Free Fall

Free fall acceleration is constant. Throughout the entire time that an object is falling, it is accelerating at a rate equal to the acceleration due to gravity, -9.81\text{ m/s}^2 . As shown in the graph below, the acceleration-time graph is a constant negative line. 

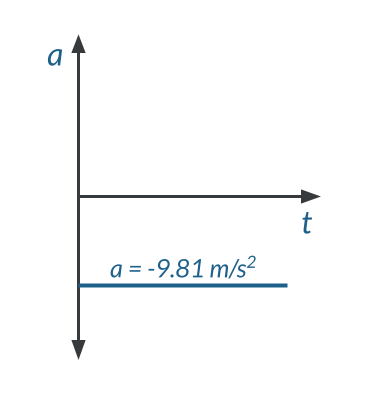
Projectile Motion

A projectile is an object that is launched or thrown into the air and then only influenced by gravity. Projectile motion has many similarities to free fall motion, however, projectiles may also travel a horizontal distance in addition to falling vertically down. 

Examples of Projectile Motion

The exact trajectory, or path, a projectile will take depends on how it is launched. However, all projectiles follow a curved trajectory such as in the image shown below:

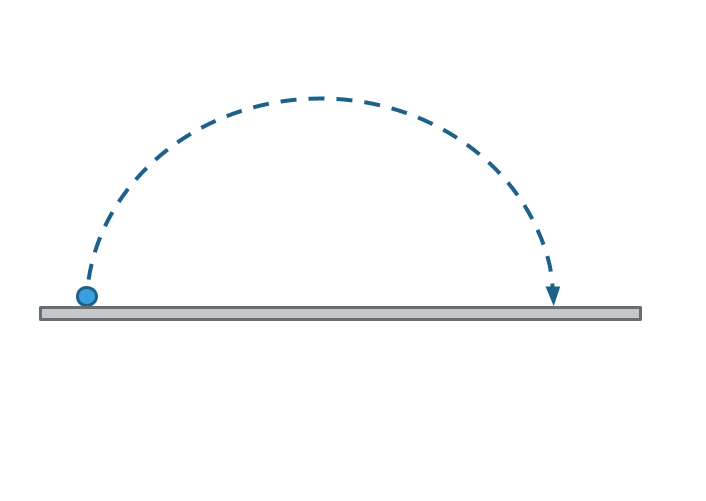
If you play or watch sports, you likely have already observed projectile motion. Projectile motion describes the arc of a basketball in a free throw, a fly ball in baseball, or a volleyball bumped over the net. 

Horizontal Component of Velocity

To analyze projectile motion, we must separate the motion into horizontal and vertical components. The horizontal component of a projectile’s velocity is independent of the vertical component of velocity. Since gravity acts vertically, there are no horizontal forces acting on projectiles. This means that the horizontal component of a projectile’s velocity remains constant throughout the entire flight. 

Example: Finding the Horizontal Component

For example, a projectile is launched from the ground with an initial speed of 8\text{ m/s} at a 60^{\circ} angle. What is the horizontal component of the projectile’s velocity?

We will need to use trig identities to determine the components of the velocity. We can visualize the components as a triangle where the hypotenuse is the initial velocity and the sides represent the horizontal, v_{ix} , and vertical, v_{iy} , components of the velocity.

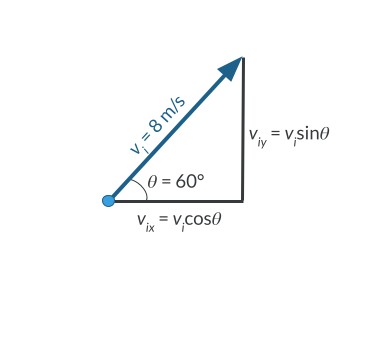
Cosine is defined as the adjacent side of the triangle divided by the hypotenuse. Since the horizontal component is adjacent to the angle, we can use cosine to find the horizontal component of velocity:

Therefore, the horizontal component of the initial velocity is 4\text{ m/s} .

Need to review your trig identities? Try out this resource from Khan Academy .

Vertical Component of Velocity

The vertical component of a projectile’s velocity will be influenced by gravity, which acts vertically on the object causing it to accelerate downward. Therefore, the vertical component of velocity will change throughout the projectile’s flight. We can calculate the vertical component of velocity at a particular time in a method similar to calculating the horizontal component. 

Example: Finding the Vertical Component

In the same example, a projectile is launched from the ground with an initial speed of 8\text{ m/s} at a 60^{\circ} angle. What is the vertical component of the projectile’s velocity?

As we visualize the velocity components, we are solving this time for the opposite side of the triangle. Sine is defined as the opposite side of the triangle divided by the hypotenuse. Therefore, the initial vertical velocity is:

Solving Projectile Motion Questions

Let’s apply what we’ve learned to some examples of projectile motion!

Example 1: Finding the Range of a Projectile

In this example, a projectile is fired horizontally with a speed of 5\text{ m/s} from a cliff with a height of 60\text{ m} . How far from the base of the cliff will the projectile land? 

In this scenario, we are given the initial horizontal velocity v_{ix}=5\text{ m/s} and the vertical change in position d_y=-60\text{ m} . Since the projectile is launched horizontally, the initial vertical velocity, v_{iy} , is zero. We also always know in projectile motion that the vertical acceleration is a_y=-9.81\text{ m/s}^2 and the horizontal acceleration, a_x , is zero.

This problem is asking us to find the horizontal displacement, or d_x . This is also referred to as the range . We can use the following kinematic equation to find the projectile’s final horizontal position:

Since the horizontal acceleration of a projectile is zero, this equation can be simplified to:

Before we can solve this equation, we must first determine the time of the projectile’s flight. We can actually use this same equation in the vertical direction to solve for time:

Since the initial vertical velocity is zero, this equation can be simplified to:

Solving for t :

Substituting the given values:

Now we can use this time to calculate the horizontal displacement of the projectile:

Therefore, the projectile will land about 17.5\text{ m} from the base of the cliff. 

Example 2: Finding the Maximum Height of a Projectile

As another example, a projectile is launched from the ground with an initial velocity of 25\text{ m/s} at an angle of 50^{\circ} . What is the projectile’s maximum height?

As a projectile travels upward, its vertical velocity becomes slower and slower due to the negative acceleration of gravity. At the maximum height of the trajectory, the projectile’s vertical velocity will momentarily be zero as the projectile stops and turns to move downward. Therefore, in this scenario, our final vertical velocity, v_{fy} , is zero.

We can use the following kinematic equation to solve for the maximum height, d_y :

Solving for d_y :

Before we can use this equation to calculate the height, we will need to use the sine trig identity to find the vertical component of the initial velocity:

Since the initial velocity is in the opposite direction as the acceleration, it’s really important to remember the sign here. If we define moving up as positive, then the initial velocity is positive and the acceleration is negative. Substituting this initial vertical velocity and the given values into the equation above gives:

Therefore, the projectile will reach a maximum height of about 18.7\text{ m} .

For more examples and an explanation of solving these types of projectile motion problems, check out this youtube video from Professor Dave . 

Understanding free fall and projectile motion allows you to solve some of the most complex problems you will encounter in introductory physics. All projectiles are acted on only by gravity, and the vertical and horizontal components of motion are independent of each other. This allows us to apply our kinematic equations to solve for a projectile’s time of flight, velocity, and displacement in each direction.  

Interested in a school license?​

Popular posts.

AP® Score Calculators

Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides

The ultimate review guides for AP® subjects to help you plan and structure your prep.

Core Subject Review Guides

Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator

See how scores on each section impacts your overall SAT® score

ACT® Score Calculator

See how scores on each section impacts your overall ACT® score

Grammar Review Hub

Comprehensive review of grammar skills

AP® Posters

Download updated posters summarizing the main topics and structure for each AP® exam.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.5: Free-Falling Objects

• Last updated
• Save as PDF
• Page ID 16932

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

learning objectives

• Solve basic problems concerning free fall and distinguish it from other kinds of motion

The motion of falling objects is the simplest and most common example of motion with changing velocity. If a coin and a piece of paper are simultaneously dropped side by side, the paper takes much longer to hit the ground. However, if you crumple the paper into a compact ball and drop the items again, it will look like both the coin and the paper hit the floor simultaneously. This is because the amount of force acting on an object is a function of not only its mass, but also area. Free fall is the motion of a body where its weight is the only force acting on an object.

Free Fall : This clip shows an object in free fall.

Galileo also observed this phenomena and realized that it disagreed with the Aristotle principle that heavier items fall more quickly. Galileo then hypothesized that there is an upward force exerted by air in addition to the downward force of gravity. If air resistance and friction are negligible, then in a given location (because gravity changes with location), all objects fall toward the center of Earth with the same constant acceleration , independent of their mass , that constant acceleration is gravity. Air resistance opposes the motion of an object through the air, while friction opposes motion between objects and the medium through which they are traveling. The acceleration of free-falling objects is referred to as the acceleration due to gravity gg. As we said earlier, gravity varies depending on location and altitude on Earth (or any other planet), but the average acceleration due to gravity on Earth is 9.8 \(\mathrm{\frac{m}{s^2}}\). This value is also often expressed as a negative acceleration in mathematical calculations due to the downward direction of gravity.

The best way to see the basic features of motion involving gravity is to start by considering straight up and down motion with no air resistance or friction. This means that if the object is dropped, we know the initial velocity is zero. Once the object is in motion, the object is in free-fall. Under these circumstances, the motion is one-dimensional and has constant acceleration, gg. The kinematic equations for objects experiencing free fall are:

\[\begin{align} \mathrm{v} & \mathrm{=v_0−gt} \\ \mathrm{y} & \mathrm{=y_0+v_0t−\frac{1}{2}gt^2} \\ \mathrm{v^2} & \mathrm{=v^2_0−2g(y−y_0),} \end{align}\]

where \(\mathrm{v=velocity, g=gravity, t=time,}\) and \(\mathrm{y=vertical \; displacement}\).

Video \(\PageIndex{1}\) : Free Fall Motion - Describes how to calculate the time for an object to fall if given the height and the height that an object fell if given the time to fall.

Example \(\PageIndex{1}\):

Some examples of objects that are in free fall include:

• A spacecraft in continuous orbit. The free fall would end once the propulsion devices turned on.
• An stone dropped down an empty well.
• An object, in projectile motion, on its descent.
• The acceleration of free-falling objects is called the acceleration due to gravity, since objects are pulled towards the center of the earth.
• The acceleration due to gravity is constant on the surface of the Earth and has the value of 9.80 \(\mathrm{\frac{m}{s^2}}\) .

The amount by which a speed or velocity changes within a certain period of time (and so a scalar quantity or a vector quantity).

CC LICENSED CONTENT, SHARED PREVIOUSLY

Regents Physics

Free Fall –> Up and Down Problems

• Acceleration vs. Velocity
• Pirates of the Caribbean Free Fall
• “The Rock” WS
• Drop Problems
• Castle Learning “FreeFall Physics” by 10/14
• Catapult Project (10/27)
• Finish Up & Down Problem Worksheet

HW: Up & Down Problems

1. An object is thrown straight into the air. When it reaches its highest point, its velocity is ________________ and its acceleration is _____________________.

2. An object is thrown from the ground into the air with a speed of 20 m/s.

a. What is its speed when it hits the ground?

b. What is the object’s total time in the air?

c. What is the maximum height will the object reach?

3. Lebron James slam dunks a basketball and a physics student observes that Lebron’s feet are 1.0 meter above the floor at the peak of his jump. At what upward speed must Lebron leave the floor with to achieve this?

4. A cheerleader is thrown into the air. She is in the air for a total of 2.0 seconds.

a. With what initial velocity was the cheerleader thrown into the air?

b. What was her maximum height?

5. An arrow is shot straight up into the air with a velocity of 50 m/s.

a. What is the total time the arrow is in the air?

b. What is the maximum height above the ground that the arrow reaches?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Algebra Based Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Representing Free Fall by Graphs
• Intro to Free Fall
• Acceleration of Gravity
• How Fast? and How Far?
• The BIG Misconception

Representing Free Fall by Position-Time Graphs

A position versus time graph for a free-falling object is shown below.

Observe that the line on the graph curves. As learned earlier , a curved line on a position versus time graph signifies an accelerated motion. Since a free-falling object is undergoing an acceleration (g = 9.8 m/s/s), it would be expected that its position-time graph would be curved. A further look at the position-time graph reveals that the object starts with a small velocity (slow) and finishes with a large velocity (fast). Since the slope of any position vs. time graph is the velocity of the object ( as learned in Lesson 3 ), the small initial slope indicates a small initial velocity and the large final slope indicates a large final velocity. Finally, the negative slope of the line indicates a negative (i.e., downward) velocity.

Representing Free Fall by Velocity-Time Graphs

A velocity versus time graph for a free-falling object is shown below.

Observe that the line on the graph is a straight, diagonal line. As learned earlier, a diagonal line on a velocity versus time graph signifies an accelerated motion. Since a free-falling object is undergoing an acceleration (g = 9,8 m/s/s, downward), it would be expected that its velocity-time graph would be diagonal. A further look at the velocity-time graph reveals that the object starts with a zero velocity (as read from the graph) and finishes with a large, negative velocity; that is, the object is moving in the negative direction and speeding up. An object that is moving in the negative direction and speeding up is said to have a negative acceleration (if necessary, review the vector nature of acceleration ). Since the slope of any velocity versus time graph is the acceleration of the object ( as learned in Lesson 4 ), the constant, negative slope indicates a constant, negative acceleration. This analysis of the slope on the graph is consistent with the motion of a free-falling object - an object moving with a constant acceleration of 9.8 m/s/s in the downward direction.  

• Kinematic Equations Introduction