define non routine problem solving

Mathematical Mysteries

Revealing the mysteries of mathematics

How to Solve Math Problems: Non-Routine Problems

Nonroutine Problem Solving , stresses the use of heuristics [3] and often requires little to no use of algorithms. Unlike algorithms, heuristics are procedures or strategies that do not guarantee a solution to a problem but provide a more highly probable method for discovering a solution. Building a model and drawing a picture of a problem are two basic problem-solving heuristics. Studying end-of-game situations provides students with experiences in using the heuristics of reducing the problem to a similar but simpler problem and working a problem backwards, i.e. from its resolution to its initial state. Other heuristics include describing the problem situation, classifying information, and finding irrelevant information. [1]

There Are Two Categories of Nonroutine Problem Solving: Static and Active

Static-Nonroutine  problems have a fixed, known goal and fixed, known elements that are used to resolve the problem. Solving a jigsaw puzzle is an example of a Static- Nonroutine problem. Given all pieces to a puzzle and a picture of the goal, learners are challenged to arrange the pieces to complete the picture. Various heuristics such as classifying the pieces by color, connecting the pieces that form the border, or connecting the pieces that form a salient feature to the puzzle, such as a flag pole, are typical ways in which people attempt to resolve such problems. [1]

Active-Nonroutine  problems may have a fixed goal with changing elements, a changing goal or alternative goals with fixed elements, or changing or alternative goals with changing elements. The heuristics used in this form of problem-solving are known as strategies. People who study such problems must learn to change or adapt their strategies as the problem unfolds. [1]

What is non-routine problem-solving in math?

A non-routine problem is any complex problem that requires some degree of creativity or originality to solve. Non-routine problems typically do not have an immediately apparent strategy for solving them. Often times, these problems can be solved in multiple ways.

Incorporating non-routine problem solving into your math program is one of the most impactful steps you can take as an educator. By consistently allowing your students to grapple with these challenging problems, you are helping them acquire essential problem-solving skills and the confidence needed to successfully execute them. [2]

Step 1: Understand

This is a time to just think! Allow yourself some time to get to know the problem. Read and reread. No pencil or paper necessary for this step. Remember, you cannot solve a problem until you know what the problem is!

• Does the problem give me enough information (or too much information)?
• What question is being asked of me?
• What do I know and what do I need to find out?
• What should my solution look like?
• What type of mathematics might be required?
• Can I restate the problem in my own words?
• Are there any terms or words that I am unfamiliar with?

Step 2: Plan

Now it’s time to decide on a plan of action! Choose a reasonable problem-solving strategy. Several are listed below. You may only need to use one strategy or a combination of strategies.

• Draw a picture or diagram
• Make an organized list
• Make a table
• Solve a simpler related problem
• Find a pattern
• Guess and check
• Act out a problem
• Work backward
• Write an equation
• Use manipulatives
• Break it into parts
• Use logical reasoning

Step 3: Execute

Alright! You understand the problem. You have a plan to solve the problem. Now it’s time to dig in and get to work! As you work, you may need to revise your plan. That’s okay! Your plan is not set in stone and can change anytime you see fit.

• Am I checking each step of my plan as I work?
• Am I keeping an accurate record of my work?
• Am I keeping my work organized so that I could explain my thinking to others?
• Am I going in the right direction? Is my plan working?
• Do I need to go back to Step 2 and find a new plan?
• Do I think I have the correct solution? If so, it’s time to move on to the next step!

Step 4: Review

You’ve come so far, but you’re not finished just yet! A mathematician must always go back and check his/her work. Reviewing your work is just as important as the first 3 steps! Before asking yourself the questions below, reread the problem and review all your work.

• Is my answer reasonable?
• Can I use estimation to check if my answer is reasonable?
• Is there another way to solve this problem?
• Can this problem be extended? Can I make a change to this problem to create a new one?
• I didn’t get the correct answer. What went wrong? Where did I make a mistake?

[1] “Pentathlon Institute Active Problem-Solving”. 2023.  mathpentath.org . https://www.mathpentath.org/active-problem-solving/ .

[2] Tallman, Melissa. 2015. “Problem Solving In Math • Teacher Thrive”. Teacher Thrive. https://teacherthrive.com/non-routine-problem-solving/ .

[3] A heuristic is  a mental shortcut commonly used to simplify problems and avoid cognitive overload .

Additional Reading

“101 Great Higher-Order Thinking Questions for Math”. 2023.  elementaryassessments.com . https://elementaryassessments.com/higher-order-thinking-questions-for-math/ .

⭐ “Developing Mathematics Thinking with HOTS (Higher Order Thinking Skills) Questions”. 2023. saydel.k12.ia.us . https://www.saydel.k12.ia.us/cms_files/resources/Developing%20Mathematics%20Thinking%20with%20HOTS%20Questions%20(from%20classroom%20observations)PDF.pdf .

“Higher Order Thinking Skills in Maths”. 2017.  education.gov.Scot . https://education.gov.scot/resources/higher-order-thinking-skills-in-maths/ .

“How to Increase Higher Order Thinking”. 2023.  Reading Rockets . https://www.readingrockets.org/topics/comprehension/articles/how-increase-higher-order-thinking .

⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.

Website Powered by WordPress.com .

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

Problem Solving in Math

  What is non-routine problem-solving in math?

A non-routine problem is any complex problem that requires some degree of creativity or originality to solve.  Non-routine problems typically do not have an immediately apparent strategy for solving them.  Often times, these problems can be solved in multiple ways.

Incorporating non-routine problem solving into your math program is one of the most impactful steps you can take as an educator. By consistently allowing your students to grapple with these challenging problems, you are helping them acquire essential problem-solving skills and the confidence needed to successfully execute them.

One of the best ways to prepare students for solving non-routine problems is by familiarizing them with the four steps of problem-solving. I have a set of questions and/or guides for each step, that students can use to engage in an inner-dialogue as they progress through the steps.  You can download this free Steps to Non-Routine Problem Solving Flip-Book {HERE}.

1. Understand: 

This is a time to just think! Allow yourself some time to get to know the problem.  Read and reread. No pencil or paper necessary for this step.  Remember, you cannot solve a problem until you know what the problem is!

• Does the problem give me enough information (or too much information)?
• What question is being asked of me?
• What do I know and what do I need to find out?
• What should my solution look like?
• What type of mathematics might be required?
• Can I restate the problem in my own words?
• Are there any terms or words that I am unfamiliar with?

Now it’s time to decide on a plan of action! Choose a reasonable problem-solving strategy. Several are listed below.  You may only need to use one strategy or a combination of strategies.

• draw a picture or diagram
• make an organized list
• make a table
• solve a simpler related problem
• find a pattern
• guess and check
• act out a problem
• work backward
• write an equation
• use manipulatives
• break it into parts
• use logical reasoning

3. Execute: 

Alright! You understand the problem.  You have a plan to solve the problem.  Now it’s time to dig in and get to work! As you work, you may need to revise your plan. That’s okay! Your plan is not set in stone and can change anytime you see fit.

• Am I checking each step of my plan as I work?
• Am I keeping an accurate record of my work?
• Am I keeping my work organized so that I could explain my thinking to others?
• Am I going in the right direction? Is my plan working?
• Do I need to go back to Step 2 and find a new plan?
• Do I think I have the correct solution? If so, it’s time to move on to the next step!

4. Review: 

You’ve come so far, but you’re not finished just yet!  A mathematician must always go back and check his/her work. Reviewing your work is just as important as the first 3 steps! Before asking yourself the questions below, reread the problem and review all your work.

• Is my answer reasonable?
• Can I use estimation to check if my answer is reasonable?
• Is there another way to solve this problem?
• Can this problem be extended? Can I make a change to this problem to create a new one?
• I didn’t get the correct answer.  What went wrong? Where did I make a mistake?

My Brain Power Math resources are the perfect compliment to this free flip-book.  Each book has a collection of non-routine math problems in a variety of formats.

• Depth and Complexity
• End of the School Year
• Reading Comprehension
• Reading Fluency
• Uncategorized

LATEST ON INSTAGRAM

• Search Menu
• Sign in through your institution
• Browse content in Arts and Humanities
• Browse content in Archaeology
• Anglo-Saxon and Medieval Archaeology
• Archaeological Methodology and Techniques
• Archaeology by Region
• Archaeology of Religion
• Archaeology of Trade and Exchange
• Biblical Archaeology
• Contemporary and Public Archaeology
• Environmental Archaeology
• Historical Archaeology
• History and Theory of Archaeology
• Industrial Archaeology
• Landscape Archaeology
• Mortuary Archaeology
• Prehistoric Archaeology
• Underwater Archaeology
• Urban Archaeology
• Zooarchaeology
• Browse content in Architecture
• Architectural Structure and Design
• History of Architecture
• Residential and Domestic Buildings
• Theory of Architecture
• Browse content in Art
• Art Subjects and Themes
• History of Art
• Industrial and Commercial Art
• Theory of Art
• Biographical Studies
• Byzantine Studies
• Browse content in Classical Studies
• Classical History
• Classical Philosophy
• Classical Mythology
• Classical Literature
• Classical Reception
• Classical Art and Architecture
• Classical Oratory and Rhetoric
• Greek and Roman Epigraphy
• Greek and Roman Law
• Greek and Roman Papyrology
• Greek and Roman Archaeology
• Late Antiquity
• Religion in the Ancient World
• Digital Humanities
• Browse content in History
• Colonialism and Imperialism
• Diplomatic History
• Environmental History
• Genealogy, Heraldry, Names, and Honours
• Genocide and Ethnic Cleansing
• Historical Geography
• History by Period
• History of Emotions
• History of Agriculture
• History of Education
• History of Gender and Sexuality
• Industrial History
• Intellectual History
• International History
• Labour History
• Legal and Constitutional History
• Local and Family History
• Maritime History
• Military History
• National Liberation and Post-Colonialism
• Oral History
• Political History
• Public History
• Regional and National History
• Revolutions and Rebellions
• Slavery and Abolition of Slavery
• Social and Cultural History
• Theory, Methods, and Historiography
• Urban History
• World History
• Browse content in Language Teaching and Learning
• Language Learning (Specific Skills)
• Language Teaching Theory and Methods
• Browse content in Linguistics
• Applied Linguistics
• Cognitive Linguistics
• Computational Linguistics
• Forensic Linguistics
• Grammar, Syntax and Morphology
• Historical and Diachronic Linguistics
• History of English
• Language Acquisition
• Language Evolution
• Language Reference
• Language Variation
• Language Families
• Lexicography
• Linguistic Anthropology
• Linguistic Theories
• Linguistic Typology
• Phonetics and Phonology
• Psycholinguistics
• Sociolinguistics
• Translation and Interpretation
• Writing Systems
• Browse content in Literature
• Bibliography
• Children's Literature Studies
• Literary Studies (Asian)
• Literary Studies (European)
• Literary Studies (Eco-criticism)
• Literary Studies (Romanticism)
• Literary Studies (American)
• Literary Studies (Modernism)
• Literary Studies - World
• Literary Studies (1500 to 1800)
• Literary Studies (19th Century)
• Literary Studies (20th Century onwards)
• Literary Studies (African American Literature)
• Literary Studies (British and Irish)
• Literary Studies (Early and Medieval)
• Literary Studies (Fiction, Novelists, and Prose Writers)
• Literary Studies (Gender Studies)
• Literary Studies (Graphic Novels)
• Literary Studies (History of the Book)
• Literary Studies (Plays and Playwrights)
• Literary Studies (Poetry and Poets)
• Literary Studies (Postcolonial Literature)
• Literary Studies (Queer Studies)
• Literary Studies (Science Fiction)
• Literary Studies (Travel Literature)
• Literary Studies (War Literature)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Browse content in Media Studies
• Browse content in Music
• Applied Music
• Dance and Music
• Ethics in Music
• Ethnomusicology
• Gender and Sexuality in Music
• Medicine and Music
• Music Cultures
• Music and Religion
• Music and Media
• Music and Culture
• Music Education and Pedagogy
• Music Theory and Analysis
• Musical Scores, Lyrics, and Libretti
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Performance Practice and Studies
• Race and Ethnicity in Music
• Sound Studies
• Browse content in Performing Arts
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• Epistemology
• Feminist Philosophy
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Non-Western Philosophy
• Philosophy of Science
• Philosophy of Language
• Philosophy of Mind
• Philosophy of Perception
• Philosophy of Action
• Philosophy of Law
• Philosophy of Religion
• Philosophy of Mathematics and Logic
• Practical Ethics
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• East Asian Religions
• History of Religion
• Judaism and Jewish Studies
• Qumran Studies
• Religion and Education
• Religion and Health
• Religion and Politics
• Religion and Science
• Religion and Law
• Religion and Art, Literature, and Music
• Religious Studies
• Browse content in Society and Culture
• Cookery, Food, and Drink
• Cultural Studies
• Customs and Traditions
• Ethical Issues and Debates
• Hobbies, Games, Arts and Crafts
• Lifestyle, Home, and Garden
• Natural world, Country Life, and Pets
• Popular Beliefs and Controversial Knowledge
• Sports and Outdoor Recreation
• Technology and Society
• Travel and Holiday
• Visual Culture
• Browse content in Law
• Arbitration
• Browse content in Company and Commercial Law
• Commercial Law
• Company Law
• Browse content in Comparative Law
• Systems of Law
• Competition Law
• Browse content in Constitutional and Administrative Law
• Government Powers
• Judicial Review
• Local Government Law
• Military and Defence Law
• Parliamentary and Legislative Practice
• Construction Law
• Contract Law
• Browse content in Criminal Law
• Criminal Procedure
• Criminal Evidence Law
• Sentencing and Punishment
• Employment and Labour Law
• Environment and Energy Law
• Browse content in Financial Law
• Banking Law
• Insolvency Law
• History of Law
• Human Rights and Immigration
• Intellectual Property Law
• Browse content in International Law
• Private International Law and Conflict of Laws
• Public International Law
• IT and Communications Law
• Jurisprudence and Philosophy of Law
• Law and Politics
• Law and Society
• Browse content in Legal System and Practice
• Courts and Procedure
• Legal Skills and Practice
• Primary Sources of Law
• Regulation of Legal Profession
• Medical and Healthcare Law
• Browse content in Policing
• Criminal Investigation and Detection
• Police and Security Services
• Police Procedure and Law
• Police Regional Planning
• Browse content in Property Law
• Personal Property Law
• Study and Revision
• Terrorism and National Security Law
• Browse content in Trusts Law
• Wills and Probate or Succession
• Browse content in Medicine and Health
• Browse content in Allied Health Professions
• Arts Therapies
• Clinical Science
• Dietetics and Nutrition
• Occupational Therapy
• Operating Department Practice
• Physiotherapy
• Radiography
• Speech and Language Therapy
• Browse content in Anaesthetics
• General Anaesthesia
• Neuroanaesthesia
• Browse content in Clinical Medicine
• Acute Medicine
• Cardiovascular Medicine
• Clinical Genetics
• Clinical Pharmacology and Therapeutics
• Dermatology
• Endocrinology and Diabetes
• Gastroenterology
• Genito-urinary Medicine
• Geriatric Medicine
• Infectious Diseases
• Medical Toxicology
• Medical Oncology
• Pain Medicine
• Palliative Medicine
• Rehabilitation Medicine
• Respiratory Medicine and Pulmonology
• Rheumatology
• Sleep Medicine
• Sports and Exercise Medicine
• Clinical Neuroscience
• Community Medical Services
• Critical Care
• Emergency Medicine
• Forensic Medicine
• Haematology
• History of Medicine
• Browse content in Medical Dentistry
• Oral and Maxillofacial Surgery
• Paediatric Dentistry
• Restorative Dentistry and Orthodontics
• Surgical Dentistry
• Browse content in Medical Skills
• Clinical Skills
• Communication Skills
• Nursing Skills
• Surgical Skills
• Medical Ethics
• Medical Statistics and Methodology
• Browse content in Neurology
• Clinical Neurophysiology
• Neuropathology
• Nursing Studies
• Browse content in Obstetrics and Gynaecology
• Gynaecology
• Occupational Medicine
• Ophthalmology
• Otolaryngology (ENT)
• Browse content in Paediatrics
• Neonatology
• Browse content in Pathology
• Chemical Pathology
• Clinical Cytogenetics and Molecular Genetics
• Histopathology
• Medical Microbiology and Virology
• Patient Education and Information
• Browse content in Pharmacology
• Psychopharmacology
• Browse content in Popular Health
• Caring for Others
• Complementary and Alternative Medicine
• Self-help and Personal Development
• Browse content in Preclinical Medicine
• Cell Biology
• Molecular Biology and Genetics
• Reproduction, Growth and Development
• Primary Care
• Professional Development in Medicine
• Browse content in Psychiatry
• Addiction Medicine
• Child and Adolescent Psychiatry
• Forensic Psychiatry
• Learning Disabilities
• Old Age Psychiatry
• Psychotherapy
• Browse content in Public Health and Epidemiology
• Epidemiology
• Public Health
• Browse content in Radiology
• Clinical Radiology
• Interventional Radiology
• Nuclear Medicine
• Radiation Oncology
• Reproductive Medicine
• Browse content in Surgery
• Cardiothoracic Surgery
• Gastro-intestinal and Colorectal Surgery
• General Surgery
• Neurosurgery
• Paediatric Surgery
• Peri-operative Care
• Plastic and Reconstructive Surgery
• Surgical Oncology
• Transplant Surgery
• Trauma and Orthopaedic Surgery
• Vascular Surgery
• Browse content in Science and Mathematics
• Browse content in Biological Sciences
• Aquatic Biology
• Biochemistry
• Bioinformatics and Computational Biology
• Developmental Biology
• Ecology and Conservation
• Evolutionary Biology
• Genetics and Genomics
• Microbiology
• Molecular and Cell Biology
• Natural History
• Plant Sciences and Forestry
• Research Methods in Life Sciences
• Structural Biology
• Systems Biology
• Zoology and Animal Sciences
• Browse content in Chemistry
• Analytical Chemistry
• Computational Chemistry
• Crystallography
• Environmental Chemistry
• Industrial Chemistry
• Inorganic Chemistry
• Materials Chemistry
• Medicinal Chemistry
• Mineralogy and Gems
• Organic Chemistry
• Physical Chemistry
• Polymer Chemistry
• Study and Communication Skills in Chemistry
• Theoretical Chemistry
• Browse content in Computer Science
• Artificial Intelligence
• Computer Architecture and Logic Design
• Game Studies
• Human-Computer Interaction
• Mathematical Theory of Computation
• Programming Languages
• Software Engineering
• Systems Analysis and Design
• Virtual Reality
• Browse content in Computing
• Business Applications
• Computer Security
• Computer Games
• Computer Networking and Communications
• Digital Lifestyle
• Graphical and Digital Media Applications
• Operating Systems
• Browse content in Earth Sciences and Geography
• Atmospheric Sciences
• Environmental Geography
• Geology and the Lithosphere
• Maps and Map-making
• Meteorology and Climatology
• Oceanography and Hydrology
• Palaeontology
• Physical Geography and Topography
• Regional Geography
• Soil Science
• Urban Geography
• Browse content in Engineering and Technology
• Agriculture and Farming
• Biological Engineering
• Civil Engineering, Surveying, and Building
• Electronics and Communications Engineering
• Energy Technology
• Engineering (General)
• Environmental Science, Engineering, and Technology
• History of Engineering and Technology
• Mechanical Engineering and Materials
• Technology of Industrial Chemistry
• Transport Technology and Trades
• Browse content in Environmental Science
• Applied Ecology (Environmental Science)
• Conservation of the Environment (Environmental Science)
• Environmental Sustainability
• Environmentalist Thought and Ideology (Environmental Science)
• Management of Land and Natural Resources (Environmental Science)
• Natural Disasters (Environmental Science)
• Nuclear Issues (Environmental Science)
• Pollution and Threats to the Environment (Environmental Science)
• Social Impact of Environmental Issues (Environmental Science)
• History of Science and Technology
• Browse content in Materials Science
• Ceramics and Glasses
• Composite Materials
• Metals, Alloying, and Corrosion
• Nanotechnology
• Browse content in Mathematics
• Applied Mathematics
• Biomathematics and Statistics
• History of Mathematics
• Mathematical Education
• Mathematical Finance
• Mathematical Analysis
• Numerical and Computational Mathematics
• Probability and Statistics
• Pure Mathematics
• Browse content in Neuroscience
• Cognition and Behavioural Neuroscience
• Development of the Nervous System
• Disorders of the Nervous System
• History of Neuroscience
• Invertebrate Neurobiology
• Molecular and Cellular Systems
• Neuroendocrinology and Autonomic Nervous System
• Neuroscientific Techniques
• Sensory and Motor Systems
• Browse content in Physics
• Astronomy and Astrophysics
• Atomic, Molecular, and Optical Physics
• Biological and Medical Physics
• Classical Mechanics
• Computational Physics
• Condensed Matter Physics
• Electromagnetism, Optics, and Acoustics
• History of Physics
• Mathematical and Statistical Physics
• Measurement Science
• Nuclear Physics
• Particles and Fields
• Plasma Physics
• Quantum Physics
• Relativity and Gravitation
• Semiconductor and Mesoscopic Physics
• Browse content in Psychology
• Affective Sciences
• Clinical Psychology
• Cognitive Psychology
• Cognitive Neuroscience
• Criminal and Forensic Psychology
• Developmental Psychology
• Educational Psychology
• Evolutionary Psychology
• Health Psychology
• History and Systems in Psychology
• Music Psychology
• Neuropsychology
• Organizational Psychology
• Psychological Assessment and Testing
• Psychology of Human-Technology Interaction
• Psychology Professional Development and Training
• Research Methods in Psychology
• Social Psychology
• Browse content in Social Sciences
• Browse content in Anthropology
• Anthropology of Religion
• Human Evolution
• Medical Anthropology
• Physical Anthropology
• Regional Anthropology
• Social and Cultural Anthropology
• Theory and Practice of Anthropology
• Browse content in Business and Management
• Business Strategy
• Business Ethics
• Business History
• Business and Government
• Business and Technology
• Business and the Environment
• Comparative Management
• Corporate Governance
• Corporate Social Responsibility
• Entrepreneurship
• Health Management
• Human Resource Management
• Industrial and Employment Relations
• Industry Studies
• Information and Communication Technologies
• International Business
• Knowledge Management
• Management and Management Techniques
• Operations Management
• Organizational Theory and Behaviour
• Pensions and Pension Management
• Public and Nonprofit Management
• Strategic Management
• Supply Chain Management
• Browse content in Criminology and Criminal Justice
• Criminal Justice
• Criminology
• Forms of Crime
• International and Comparative Criminology
• Youth Violence and Juvenile Justice
• Development Studies
• Browse content in Economics
• Agricultural, Environmental, and Natural Resource Economics
• Asian Economics
• Behavioural Finance
• Behavioural Economics and Neuroeconomics
• Econometrics and Mathematical Economics
• Economic Systems
• Economic History
• Economic Methodology
• Economic Development and Growth
• Financial Markets
• Financial Institutions and Services
• General Economics and Teaching
• Health, Education, and Welfare
• History of Economic Thought
• International Economics
• Labour and Demographic Economics
• Law and Economics
• Macroeconomics and Monetary Economics
• Microeconomics
• Public Economics
• Urban, Rural, and Regional Economics
• Welfare Economics
• Browse content in Education
• Adult Education and Continuous Learning
• Care and Counselling of Students
• Early Childhood and Elementary Education
• Educational Equipment and Technology
• Educational Strategies and Policy
• Higher and Further Education
• Organization and Management of Education
• Philosophy and Theory of Education
• Schools Studies
• Secondary Education
• Teaching of a Specific Subject
• Teaching of Specific Groups and Special Educational Needs
• Teaching Skills and Techniques
• Browse content in Environment
• Applied Ecology (Social Science)
• Climate Change
• Conservation of the Environment (Social Science)
• Environmentalist Thought and Ideology (Social Science)
• Natural Disasters (Environment)
• Social Impact of Environmental Issues (Social Science)
• Browse content in Human Geography
• Cultural Geography
• Economic Geography
• Political Geography
• Browse content in Interdisciplinary Studies
• Communication Studies
• Museums, Libraries, and Information Sciences
• Browse content in Politics
• African Politics
• Asian Politics
• Chinese Politics
• Comparative Politics
• Conflict Politics
• Elections and Electoral Studies
• Environmental Politics
• European Union
• Foreign Policy
• Gender and Politics
• Human Rights and Politics
• Indian Politics
• International Relations
• International Organization (Politics)
• International Political Economy
• Irish Politics
• Latin American Politics
• Middle Eastern Politics
• Political Methodology
• Political Communication
• Political Philosophy
• Political Sociology
• Political Behaviour
• Political Economy
• Political Institutions
• Political Theory
• Politics and Law
• Politics of Development
• Public Administration
• Public Policy
• Quantitative Political Methodology
• Regional Political Studies
• Russian Politics
• Security Studies
• State and Local Government
• UK Politics
• US Politics
• Browse content in Regional and Area Studies
• African Studies
• Asian Studies
• East Asian Studies
• Japanese Studies
• Latin American Studies
• Middle Eastern Studies
• Native American Studies
• Scottish Studies
• Browse content in Research and Information
• Research Methods
• Browse content in Social Work
• Addictions and Substance Misuse
• Adoption and Fostering
• Care of the Elderly
• Child and Adolescent Social Work
• Couple and Family Social Work
• Direct Practice and Clinical Social Work
• Emergency Services
• Human Behaviour and the Social Environment
• International and Global Issues in Social Work
• Mental and Behavioural Health
• Social Justice and Human Rights
• Social Policy and Advocacy
• Social Work and Crime and Justice
• Social Work Macro Practice
• Social Work Practice Settings
• Social Work Research and Evidence-based Practice
• Welfare and Benefit Systems
• Browse content in Sociology
• Childhood Studies
• Community Development
• Comparative and Historical Sociology
• Economic Sociology
• Gender and Sexuality
• Gerontology and Ageing
• Health, Illness, and Medicine
• Marriage and the Family
• Migration Studies
• Occupations, Professions, and Work
• Organizations
• Population and Demography
• Race and Ethnicity
• Social Theory
• Social Movements and Social Change
• Social Research and Statistics
• Social Stratification, Inequality, and Mobility
• Sociology of Religion
• Sociology of Education
• Sport and Leisure
• Urban and Rural Studies
• Browse content in Warfare and Defence
• Defence Strategy, Planning, and Research
• Land Forces and Warfare
• Military Administration
• Military Life and Institutions
• Naval Forces and Warfare
• Other Warfare and Defence Issues
• Peace Studies and Conflict Resolution
• Weapons and Equipment

• < Previous chapter
• Next chapter >

48 Problem Solving

Department of Psychological and Brain Sciences, University of California, Santa Barbara

• Published: 03 June 2013
• Cite Icon Cite
• Permissions Icon Permissions

Problem solving refers to cognitive processing directed at achieving a goal when the problem solver does not initially know a solution method. A problem exists when someone has a goal but does not know how to achieve it. Problems can be classified as routine or nonroutine, and as well defined or ill defined. The major cognitive processes in problem solving are representing, planning, executing, and monitoring. The major kinds of knowledge required for problem solving are facts, concepts, procedures, strategies, and beliefs. Classic theoretical approaches to the study of problem solving are associationism, Gestalt, and information processing. Current issues and suggested future issues include decision making, intelligence and creativity, teaching of thinking skills, expert problem solving, analogical reasoning, mathematical and scientific thinking, everyday thinking, and the cognitive neuroscience of problem solving. Common themes concern the domain specificity of problem solving and a focus on problem solving in authentic contexts.

The study of problem solving begins with defining problem solving, problem, and problem types. This introduction to problem solving is rounded out with an examination of cognitive processes in problem solving, the role of knowledge in problem solving, and historical approaches to the study of problem solving.

Definition of Problem Solving

Problem solving refers to cognitive processing directed at achieving a goal for which the problem solver does not initially know a solution method. This definition consists of four major elements (Mayer, 1992 ; Mayer & Wittrock, 2006 ):

Cognitive —Problem solving occurs within the problem solver’s cognitive system and can only be inferred indirectly from the problem solver’s behavior (including biological changes, introspections, and actions during problem solving). Process —Problem solving involves mental computations in which some operation is applied to a mental representation, sometimes resulting in the creation of a new mental representation. Directed —Problem solving is aimed at achieving a goal. Personal —Problem solving depends on the existing knowledge of the problem solver so that what is a problem for one problem solver may not be a problem for someone who already knows a solution method.

The definition is broad enough to include a wide array of cognitive activities such as deciding which apartment to rent, figuring out how to use a cell phone interface, playing a game of chess, making a medical diagnosis, finding the answer to an arithmetic word problem, or writing a chapter for a handbook. Problem solving is pervasive in human life and is crucial for human survival. Although this chapter focuses on problem solving in humans, problem solving also occurs in nonhuman animals and in intelligent machines.

How is problem solving related to other forms of high-level cognition processing, such as thinking and reasoning? Thinking refers to cognitive processing in individuals but includes both directed thinking (which corresponds to the definition of problem solving) and undirected thinking such as daydreaming (which does not correspond to the definition of problem solving). Thus, problem solving is a type of thinking (i.e., directed thinking).

Reasoning refers to problem solving within specific classes of problems, such as deductive reasoning or inductive reasoning. In deductive reasoning, the reasoner is given premises and must derive a conclusion by applying the rules of logic. For example, given that “A is greater than B” and “B is greater than C,” a reasoner can conclude that “A is greater than C.” In inductive reasoning, the reasoner is given (or has experienced) a collection of examples or instances and must infer a rule. For example, given that X, C, and V are in the “yes” group and x, c, and v are in the “no” group, the reasoning may conclude that B is in “yes” group because it is in uppercase format. Thus, reasoning is a type of problem solving.

Definition of Problem

A problem occurs when someone has a goal but does not know to achieve it. This definition is consistent with how the Gestalt psychologist Karl Duncker ( 1945 , p. 1) defined a problem in his classic monograph, On Problem Solving : “A problem arises when a living creature has a goal but does not know how this goal is to be reached.” However, today researchers recognize that the definition should be extended to include problem solving by intelligent machines. This definition can be clarified using an information processing approach by noting that a problem occurs when a situation is in the given state, the problem solver wants the situation to be in the goal state, and there is no obvious way to move from the given state to the goal state (Newell & Simon, 1972 ). Accordingly, the three main elements in describing a problem are the given state (i.e., the current state of the situation), the goal state (i.e., the desired state of the situation), and the set of allowable operators (i.e., the actions the problem solver is allowed to take). The definition of “problem” is broad enough to include the situation confronting a physician who wishes to make a diagnosis on the basis of preliminary tests and a patient examination, as well as a beginning physics student trying to solve a complex physics problem.

Types of Problems

It is customary in the problem-solving literature to make a distinction between routine and nonroutine problems. Routine problems are problems that are so familiar to the problem solver that the problem solver knows a solution method. For example, for most adults, “What is 365 divided by 12?” is a routine problem because they already know the procedure for long division. Nonroutine problems are so unfamiliar to the problem solver that the problem solver does not know a solution method. For example, figuring out the best way to set up a funding campaign for a nonprofit charity is a nonroutine problem for most volunteers. Technically, routine problems do not meet the definition of problem because the problem solver has a goal but knows how to achieve it. Much research on problem solving has focused on routine problems, although most interesting problems in life are nonroutine.

Another customary distinction is between well-defined and ill-defined problems. Well-defined problems have a clearly specified given state, goal state, and legal operators. Examples include arithmetic computation problems or games such as checkers or tic-tac-toe. Ill-defined problems have a poorly specified given state, goal state, or legal operators, or a combination of poorly defined features. Examples include solving the problem of global warming or finding a life partner. Although, ill-defined problems are more challenging, much research in problem solving has focused on well-defined problems.

Cognitive Processes in Problem Solving

The process of problem solving can be broken down into two main phases: problem representation , in which the problem solver builds a mental representation of the problem situation, and problem solution , in which the problem solver works to produce a solution. The major subprocess in problem representation is representing , which involves building a situation model —that is, a mental representation of the situation described in the problem. The major subprocesses in problem solution are planning , which involves devising a plan for how to solve the problem; executing , which involves carrying out the plan; and monitoring , which involves evaluating and adjusting one’s problem solving.

For example, given an arithmetic word problem such as “Alice has three marbles. Sarah has two more marbles than Alice. How many marbles does Sarah have?” the process of representing involves building a situation model in which Alice has a set of marbles, there is set of marbles for the difference between the two girls, and Sarah has a set of marbles that consists of Alice’s marbles and the difference set. In the planning process, the problem solver sets a goal of adding 3 and 2. In the executing process, the problem solver carries out the computation, yielding an answer of 5. In the monitoring process, the problem solver looks over what was done and concludes that 5 is a reasonable answer. In most complex problem-solving episodes, the four cognitive processes may not occur in linear order, but rather may interact with one another. Although some research focuses mainly on the execution process, problem solvers may tend to have more difficulty with the processes of representing, planning, and monitoring.

Knowledge for Problem Solving

An important theme in problem-solving research is that problem-solving proficiency on any task depends on the learner’s knowledge (Anderson et al., 2001 ; Mayer, 1992 ). Five kinds of knowledge are as follows:

Facts —factual knowledge about the characteristics of elements in the world, such as “Sacramento is the capital of California” Concepts —conceptual knowledge, including categories, schemas, or models, such as knowing the difference between plants and animals or knowing how a battery works Procedures —procedural knowledge of step-by-step processes, such as how to carry out long-division computations Strategies —strategic knowledge of general methods such as breaking a problem into parts or thinking of a related problem Beliefs —attitudinal knowledge about how one’s cognitive processing works such as thinking, “I’m good at this”

Although some research focuses mainly on the role of facts and procedures in problem solving, complex problem solving also depends on the problem solver’s concepts, strategies, and beliefs (Mayer, 1992 ).

Historical Approaches to Problem Solving

Psychological research on problem solving began in the early 1900s, as an outgrowth of mental philosophy (Humphrey, 1963 ; Mandler & Mandler, 1964 ). Throughout the 20th century four theoretical approaches developed: early conceptions, associationism, Gestalt psychology, and information processing.

Early Conceptions

The start of psychology as a science can be set at 1879—the year Wilhelm Wundt opened the first world’s psychology laboratory in Leipzig, Germany, and sought to train the world’s first cohort of experimental psychologists. Instead of relying solely on philosophical speculations about how the human mind works, Wundt sought to apply the methods of experimental science to issues addressed in mental philosophy. His theoretical approach became structuralism —the analysis of consciousness into its basic elements.

Wundt’s main contribution to the study of problem solving, however, was to call for its banishment. According to Wundt, complex cognitive processing was too complicated to be studied by experimental methods, so “nothing can be discovered in such experiments” (Wundt, 1911/1973 ). Despite his admonishments, however, a group of his former students began studying thinking mainly in Wurzburg, Germany. Using the method of introspection, subjects were asked to describe their thought process as they solved word association problems, such as finding the superordinate of “newspaper” (e.g., an answer is “publication”). Although the Wurzburg group—as they came to be called—did not produce a new theoretical approach, they found empirical evidence that challenged some of the key assumptions of mental philosophy. For example, Aristotle had proclaimed that all thinking involves mental imagery, but the Wurzburg group was able to find empirical evidence for imageless thought .

Associationism

The first major theoretical approach to take hold in the scientific study of problem solving was associationism —the idea that the cognitive representations in the mind consist of ideas and links between them and that cognitive processing in the mind involves following a chain of associations from one idea to the next (Mandler & Mandler, 1964 ; Mayer, 1992 ). For example, in a classic study, E. L. Thorndike ( 1911 ) placed a hungry cat in what he called a puzzle box—a wooden crate in which pulling a loop of string that hung from overhead would open a trap door to allow the cat to escape to a bowl of food outside the crate. Thorndike placed the cat in the puzzle box once a day for several weeks. On the first day, the cat engaged in many extraneous behaviors such as pouncing against the wall, pushing its paws through the slats, and meowing, but on successive days the number of extraneous behaviors tended to decrease. Overall, the time required to get out of the puzzle box decreased over the course of the experiment, indicating the cat was learning how to escape.

Thorndike’s explanation for how the cat learned to solve the puzzle box problem is based on an associationist view: The cat begins with a habit family hierarchy —a set of potential responses (e.g., pouncing, thrusting, meowing, etc.) all associated with the same stimulus (i.e., being hungry and confined) and ordered in terms of strength of association. When placed in the puzzle box, the cat executes its strongest response (e.g., perhaps pouncing against the wall), but when it fails, the strength of the association is weakened, and so on for each unsuccessful action. Eventually, the cat gets down to what was initially a weak response—waving its paw in the air—but when that response leads to accidentally pulling the string and getting out, it is strengthened. Over the course of many trials, the ineffective responses become weak and the successful response becomes strong. Thorndike refers to this process as the law of effect : Responses that lead to dissatisfaction become less associated with the situation and responses that lead to satisfaction become more associated with the situation. According to Thorndike’s associationist view, solving a problem is simply a matter of trial and error and accidental success. A major challenge to assocationist theory concerns the nature of transfer—that is, where does a problem solver find a creative solution that has never been performed before? Associationist conceptions of cognition can be seen in current research, including neural networks, connectionist models, and parallel distributed processing models (Rogers & McClelland, 2004 ).

Gestalt Psychology

The Gestalt approach to problem solving developed in the 1930s and 1940s as a counterbalance to the associationist approach. According to the Gestalt approach, cognitive representations consist of coherent structures (rather than individual associations) and the cognitive process of problem solving involves building a coherent structure (rather than strengthening and weakening of associations). For example, in a classic study, Kohler ( 1925 ) placed a hungry ape in a play yard that contained several empty shipping crates and a banana attached overhead but out of reach. Based on observing the ape in this situation, Kohler noted that the ape did not randomly try responses until one worked—as suggested by Thorndike’s associationist view. Instead, the ape stood under the banana, looked up at it, looked at the crates, and then in a flash of insight stacked the crates under the bananas as a ladder, and walked up the steps in order to reach the banana.

According to Kohler, the ape experienced a sudden visual reorganization in which the elements in the situation fit together in a way to solve the problem; that is, the crates could become a ladder that reduces the distance to the banana. Kohler referred to the underlying mechanism as insight —literally seeing into the structure of the situation. A major challenge of Gestalt theory is its lack of precision; for example, naming a process (i.e., insight) is not the same as explaining how it works. Gestalt conceptions can be seen in modern research on mental models and schemas (Gentner & Stevens, 1983 ).

Information Processing

The information processing approach to problem solving developed in the 1960s and 1970s and was based on the influence of the computer metaphor—the idea that humans are processors of information (Mayer, 2009 ). According to the information processing approach, problem solving involves a series of mental computations—each of which consists of applying a process to a mental representation (such as comparing two elements to determine whether they differ).

In their classic book, Human Problem Solving , Newell and Simon ( 1972 ) proposed that problem solving involved a problem space and search heuristics . A problem space is a mental representation of the initial state of the problem, the goal state of the problem, and all possible intervening states (based on applying allowable operators). Search heuristics are strategies for moving through the problem space from the given to the goal state. Newell and Simon focused on means-ends analysis , in which the problem solver continually sets goals and finds moves to accomplish goals.

Newell and Simon used computer simulation as a research method to test their conception of human problem solving. First, they asked human problem solvers to think aloud as they solved various problems such as logic problems, chess, and cryptarithmetic problems. Then, based on an information processing analysis, Newell and Simon created computer programs that solved these problems. In comparing the solution behavior of humans and computers, they found high similarity, suggesting that the computer programs were solving problems using the same thought processes as humans.

An important advantage of the information processing approach is that problem solving can be described with great clarity—as a computer program. An important limitation of the information processing approach is that it is most useful for describing problem solving for well-defined problems rather than ill-defined problems. The information processing conception of cognition lives on as a keystone of today’s cognitive science (Mayer, 2009 ).

Classic Issues in Problem Solving

Three classic issues in research on problem solving concern the nature of transfer (suggested by the associationist approach), the nature of insight (suggested by the Gestalt approach), and the role of problem-solving heuristics (suggested by the information processing approach).

Transfer refers to the effects of prior learning on new learning (or new problem solving). Positive transfer occurs when learning A helps someone learn B. Negative transfer occurs when learning A hinders someone from learning B. Neutral transfer occurs when learning A has no effect on learning B. Positive transfer is a central goal of education, but research shows that people often do not transfer what they learned to solving problems in new contexts (Mayer, 1992 ; Singley & Anderson, 1989 ).

Three conceptions of the mechanisms underlying transfer are specific transfer , general transfer , and specific transfer of general principles . Specific transfer refers to the idea that learning A will help someone learn B only if A and B have specific elements in common. For example, learning Spanish may help someone learn Latin because some of the vocabulary words are similar and the verb conjugation rules are similar. General transfer refers to the idea that learning A can help someone learn B even they have nothing specifically in common but A helps improve the learner’s mind in general. For example, learning Latin may help people learn “proper habits of mind” so they are better able to learn completely unrelated subjects as well. Specific transfer of general principles is the idea that learning A will help someone learn B if the same general principle or solution method is required for both even if the specific elements are different.

In a classic study, Thorndike and Woodworth ( 1901 ) found that students who learned Latin did not subsequently learn bookkeeping any better than students who had not learned Latin. They interpreted this finding as evidence for specific transfer—learning A did not transfer to learning B because A and B did not have specific elements in common. Modern research on problem-solving transfer continues to show that people often do not demonstrate general transfer (Mayer, 1992 ). However, it is possible to teach people a general strategy for solving a problem, so that when they see a new problem in a different context they are able to apply the strategy to the new problem (Judd, 1908 ; Mayer, 2008 )—so there is also research support for the idea of specific transfer of general principles.

Insight refers to a change in a problem solver’s mind from not knowing how to solve a problem to knowing how to solve it (Mayer, 1995 ; Metcalfe & Wiebe, 1987 ). In short, where does the idea for a creative solution come from? A central goal of problem-solving research is to determine the mechanisms underlying insight.

The search for insight has led to five major (but not mutually exclusive) explanatory mechanisms—insight as completing a schema, insight as suddenly reorganizing visual information, insight as reformulation of a problem, insight as removing mental blocks, and insight as finding a problem analog (Mayer, 1995 ). Completing a schema is exemplified in a study by Selz (Fridja & de Groot, 1982 ), in which people were asked to think aloud as they solved word association problems such as “What is the superordinate for newspaper?” To solve the problem, people sometimes thought of a coordinate, such as “magazine,” and then searched for a superordinate category that subsumed both terms, such as “publication.” According to Selz, finding a solution involved building a schema that consisted of a superordinate and two subordinate categories.

Reorganizing visual information is reflected in Kohler’s ( 1925 ) study described in a previous section in which a hungry ape figured out how to stack boxes as a ladder to reach a banana hanging above. According to Kohler, the ape looked around the yard and found the solution in a flash of insight by mentally seeing how the parts could be rearranged to accomplish the goal.

Reformulating a problem is reflected in a classic study by Duncker ( 1945 ) in which people are asked to think aloud as they solve the tumor problem—how can you destroy a tumor in a patient without destroying surrounding healthy tissue by using rays that at sufficient intensity will destroy any tissue in their path? In analyzing the thinking-aloud protocols—that is, transcripts of what the problem solvers said—Duncker concluded that people reformulated the goal in various ways (e.g., avoid contact with healthy tissue, immunize healthy tissue, have ray be weak in healthy tissue) until they hit upon a productive formulation that led to the solution (i.e., concentrating many weak rays on the tumor).

Removing mental blocks is reflected in classic studies by Duncker ( 1945 ) in which solving a problem involved thinking of a novel use for an object, and by Luchins ( 1942 ) in which solving a problem involved not using a procedure that had worked well on previous problems. Finding a problem analog is reflected in classic research by Wertheimer ( 1959 ) in which learning to find the area of a parallelogram is supported by the insight that one could cut off the triangle on one side and place it on the other side to form a rectangle—so a parallelogram is really a rectangle in disguise. The search for insight along each of these five lines continues in current problem-solving research.

Heuristics are problem-solving strategies, that is, general approaches to how to solve problems. Newell and Simon ( 1972 ) suggested three general problem-solving heuristics for moving from a given state to a goal state: random trial and error , hill climbing , and means-ends analysis . Random trial and error involves randomly selecting a legal move and applying it to create a new problem state, and repeating that process until the goal state is reached. Random trial and error may work for simple problems but is not efficient for complex ones. Hill climbing involves selecting the legal move that moves the problem solver closer to the goal state. Hill climbing will not work for problems in which the problem solver must take a move that temporarily moves away from the goal as is required in many problems.

Means-ends analysis involves creating goals and seeking moves that can accomplish the goal. If a goal cannot be directly accomplished, a subgoal is created to remove one or more obstacles. Newell and Simon ( 1972 ) successfully used means-ends analysis as the search heuristic in a computer program aimed at general problem solving, that is, solving a diverse collection of problems. However, people may also use specific heuristics that are designed to work for specific problem-solving situations (Gigerenzer, Todd, & ABC Research Group, 1999 ; Kahneman & Tversky, 1984 ).

Current and Future Issues in Problem Solving

Eight current issues in problem solving involve decision making, intelligence and creativity, teaching of thinking skills, expert problem solving, analogical reasoning, mathematical and scientific problem solving, everyday thinking, and the cognitive neuroscience of problem solving.

Decision Making

Decision making refers to the cognitive processing involved in choosing between two or more alternatives (Baron, 2000 ; Markman & Medin, 2002 ). For example, a decision-making task may involve choosing between getting $240 for sure or having a 25% change of getting $1000. According to economic theories such as expected value theory, people should chose the second option, which is worth $250 (i.e., .25 x $1000) rather than the first option, which is worth $240 (1.00 x $240), but psychological research shows that most people prefer the first option (Kahneman & Tversky, 1984 ).

Research on decision making has generated three classes of theories (Markman & Medin, 2002 ): descriptive theories, such as prospect theory (Kahneman & Tversky), which are based on the ideas that people prefer to overweight the cost of a loss and tend to overestimate small probabilities; heuristic theories, which are based on the idea that people use a collection of short-cut strategies such as the availability heuristic (Gigerenzer et al., 1999 ; Kahneman & Tversky, 2000 ); and constructive theories, such as mental accounting (Kahneman & Tversky, 2000 ), in which people build a narrative to justify their choices to themselves. Future research is needed to examine decision making in more realistic settings.

Intelligence and Creativity

Although researchers do not have complete consensus on the definition of intelligence (Sternberg, 1990 ), it is reasonable to view intelligence as the ability to learn or adapt to new situations. Fluid intelligence refers to the potential to solve problems without any relevant knowledge, whereas crystallized intelligence refers to the potential to solve problems based on relevant prior knowledge (Sternberg & Gregorenko, 2003 ). As people gain more experience in a field, their problem-solving performance depends more on crystallized intelligence (i.e., domain knowledge) than on fluid intelligence (i.e., general ability) (Sternberg & Gregorenko, 2003 ). The ability to monitor and manage one’s cognitive processing during problem solving—which can be called metacognition —is an important aspect of intelligence (Sternberg, 1990 ). Research is needed to pinpoint the knowledge that is needed to support intelligent performance on problem-solving tasks.

Creativity refers to the ability to generate ideas that are original (i.e., other people do not think of the same idea) and functional (i.e., the idea works; Sternberg, 1999 ). Creativity is often measured using tests of divergent thinking —that is, generating as many solutions as possible for a problem (Guilford, 1967 ). For example, the uses test asks people to list as many uses as they can think of for a brick. Creativity is different from intelligence, and it is at the heart of creative problem solving—generating a novel solution to a problem that the problem solver has never seen before. An important research question concerns whether creative problem solving depends on specific knowledge or creativity ability in general.

Teaching of Thinking Skills

How can people learn to be better problem solvers? Mayer ( 2008 ) proposes four questions concerning teaching of thinking skills:

What to teach —Successful programs attempt to teach small component skills (such as how to generate and evaluate hypotheses) rather than improve the mind as a single monolithic skill (Covington, Crutchfield, Davies, & Olton, 1974 ). How to teach —Successful programs focus on modeling the process of problem solving rather than solely reinforcing the product of problem solving (Bloom & Broder, 1950 ). Where to teach —Successful programs teach problem-solving skills within the specific context they will be used rather than within a general course on how to solve problems (Nickerson, 1999 ). When to teach —Successful programs teaching higher order skills early rather than waiting until lower order skills are completely mastered (Tharp & Gallimore, 1988 ).

Overall, research on teaching of thinking skills points to the domain specificity of problem solving; that is, successful problem solving depends on the problem solver having domain knowledge that is relevant to the problem-solving task.

Expert Problem Solving

Research on expertise is concerned with differences between how experts and novices solve problems (Ericsson, Feltovich, & Hoffman, 2006 ). Expertise can be defined in terms of time (e.g., 10 years of concentrated experience in a field), performance (e.g., earning a perfect score on an assessment), or recognition (e.g., receiving a Nobel Prize or becoming Grand Master in chess). For example, in classic research conducted in the 1940s, de Groot ( 1965 ) found that chess experts did not have better general memory than chess novices, but they did have better domain-specific memory for the arrangement of chess pieces on the board. Chase and Simon ( 1973 ) replicated this result in a better controlled experiment. An explanation is that experts have developed schemas that allow them to chunk collections of pieces into a single configuration.

In another landmark study, Larkin et al. ( 1980 ) compared how experts (e.g., physics professors) and novices (e.g., first-year physics students) solved textbook physics problems about motion. Experts tended to work forward from the given information to the goal, whereas novices tended to work backward from the goal to the givens using a means-ends analysis strategy. Experts tended to store their knowledge in an integrated way, whereas novices tended to store their knowledge in isolated fragments. In another study, Chi, Feltovich, and Glaser ( 1981 ) found that experts tended to focus on the underlying physics concepts (such as conservation of energy), whereas novices tended to focus on the surface features of the problem (such as inclined planes or springs). Overall, research on expertise is useful in pinpointing what experts know that is different from what novices know. An important theme is that experts rely on domain-specific knowledge rather than solely general cognitive ability.

Analogical Reasoning

Analogical reasoning occurs when people solve one problem by using their knowledge about another problem (Holyoak, 2005 ). For example, suppose a problem solver learns how to solve a problem in one context using one solution method and then is given a problem in another context that requires the same solution method. In this case, the problem solver must recognize that the new problem has structural similarity to the old problem (i.e., it may be solved by the same method), even though they do not have surface similarity (i.e., the cover stories are different). Three steps in analogical reasoning are recognizing —seeing that a new problem is similar to a previously solved problem; abstracting —finding the general method used to solve the old problem; and mapping —using that general method to solve the new problem.

Research on analogical reasoning shows that people often do not recognize that a new problem can be solved by the same method as a previously solved problem (Holyoak, 2005 ). However, research also shows that successful analogical transfer to a new problem is more likely when the problem solver has experience with two old problems that have the same underlying structural features (i.e., they are solved by the same principle) but different surface features (i.e., they have different cover stories) (Holyoak, 2005 ). This finding is consistent with the idea of specific transfer of general principles as described in the section on “Transfer.”

Mathematical and Scientific Problem Solving

Research on mathematical problem solving suggests that five kinds of knowledge are needed to solve arithmetic word problems (Mayer, 2008 ):

Factual knowledge —knowledge about the characteristics of problem elements, such as knowing that there are 100 cents in a dollar Schematic knowledge —knowledge of problem types, such as being able to recognize time-rate-distance problems Strategic knowledge —knowledge of general methods, such as how to break a problem into parts Procedural knowledge —knowledge of processes, such as how to carry our arithmetic operations Attitudinal knowledge —beliefs about one’s mathematical problem-solving ability, such as thinking, “I am good at this”

People generally possess adequate procedural knowledge but may have difficulty in solving mathematics problems because they lack factual, schematic, strategic, or attitudinal knowledge (Mayer, 2008 ). Research is needed to pinpoint the role of domain knowledge in mathematical problem solving.

Research on scientific problem solving shows that people harbor misconceptions, such as believing that a force is needed to keep an object in motion (McCloskey, 1983 ). Learning to solve science problems involves conceptual change, in which the problem solver comes to recognize that previous conceptions are wrong (Mayer, 2008 ). Students can be taught to engage in scientific reasoning such as hypothesis testing through direct instruction in how to control for variables (Chen & Klahr, 1999 ). A central theme of research on scientific problem solving concerns the role of domain knowledge.

Everyday Thinking

Everyday thinking refers to problem solving in the context of one’s life outside of school. For example, children who are street vendors tend to use different procedures for solving arithmetic problems when they are working on the streets than when they are in school (Nunes, Schlieman, & Carraher, 1993 ). This line of research highlights the role of situated cognition —the idea that thinking always is shaped by the physical and social context in which it occurs (Robbins & Aydede, 2009 ). Research is needed to determine how people solve problems in authentic contexts.

Cognitive Neuroscience of Problem Solving

The cognitive neuroscience of problem solving is concerned with the brain activity that occurs during problem solving. For example, using fMRI brain imaging methodology, Goel ( 2005 ) found that people used the language areas of the brain to solve logical reasoning problems presented in sentences (e.g., “All dogs are pets…”) and used the spatial areas of the brain to solve logical reasoning problems presented in abstract letters (e.g., “All D are P…”). Cognitive neuroscience holds the potential to make unique contributions to the study of problem solving.

Problem solving has always been a topic at the fringe of cognitive psychology—too complicated to study intensively but too important to completely ignore. Problem solving—especially in realistic environments—is messy in comparison to studying elementary processes in cognition. The field remains fragmented in the sense that topics such as decision making, reasoning, intelligence, expertise, mathematical problem solving, everyday thinking, and the like are considered to be separate topics, each with its own separate literature. Yet some recurring themes are the role of domain-specific knowledge in problem solving and the advantages of studying problem solving in authentic contexts.

Future Directions

Some important issues for future research include the three classic issues examined in this chapter—the nature of problem-solving transfer (i.e., How are people able to use what they know about previous problem solving to help them in new problem solving?), the nature of insight (e.g., What is the mechanism by which a creative solution is constructed?), and heuristics (e.g., What are some teachable strategies for problem solving?). In addition, future research in problem solving should continue to pinpoint the role of domain-specific knowledge in problem solving, the nature of cognitive ability in problem solving, how to help people develop proficiency in solving problems, and how to provide aids for problem solving.

Anderson L. W. , Krathwohl D. R. , Airasian P. W. , Cruikshank K. A. , Mayer R. E. , Pintrich P. R. , Raths, J., & Wittrock M. C. ( 2001 ). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s taxonomy of educational objectives. New York : Longman.

Baron J. ( 2000 ). Thinking and deciding (3rd ed.). New York : Cambridge University Press.

Google Scholar

Google Preview

Bloom B. S. , & Broder B. J. ( 1950 ). Problem-solving processes of college students: An exploratory investigation. Chicago : University of Chicago Press.

Chase W. G. , & Simon H. A. ( 1973 ). Perception in chess.   Cognitive Psychology, 4, 55–81.

Chen Z. , & Klahr D. ( 1999 ). All other things being equal: Acquisition and transfer of the control of variable strategy . Child Development, 70, 1098–1120.

Chi M. T. H. , Feltovich P. J. , & Glaser R. ( 1981 ). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121–152.

Covington M. V. , Crutchfield R. S. , Davies L. B. , & Olton R. M. ( 1974 ). The productive thinking program. Columbus, OH : Merrill.

de Groot A. D. ( 1965 ). Thought and choice in chess. The Hague, The Netherlands : Mouton.

Duncker K. ( 1945 ). On problem solving.   Psychological Monographs, 58 (3) (Whole No. 270).

Ericsson K. A. , Feltovich P. J. , & Hoffman R. R. (Eds.). ( 2006 ). The Cambridge handbook of expertise and expert performance. New York : Cambridge University Press.

Fridja N. H. , & de Groot A. D. ( 1982 ). Otto Selz: His contribution to psychology. The Hague, The Netherlands : Mouton.

Gentner D. , & Stevens A. L. (Eds.). ( 1983 ). Mental models. Hillsdale, NJ : Erlbaum.

Gigerenzer G. , Todd P. M. , & ABC Research Group (Eds.). ( 1999 ). Simple heuristics that make us smart. Oxford, England : Oxford University Press.

Goel V. ( 2005 ). Cognitive neuroscience of deductive reasoning. In K. J. Holyoak & R. G. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 475–492). New York : Cambridge University Press.

Guilford J. P. ( 1967 ). The nature of human intelligence. New York : McGraw-Hill.

Holyoak K. J. ( 2005 ). Analogy. In K. J. Holyoak & R. G. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 117–142). New York : Cambridge University Press.

Humphrey G. ( 1963 ). Thinking: An introduction to experimental psychology. New York : Wiley.

Judd C. H. ( 1908 ). The relation of special training and general intelligence. Educational Review, 36, 28–42.

Kahneman D. , & Tversky A. ( 1984 ). Choices, values, and frames. American Psychologist, 39, 341–350.

Kahneman D. , & Tversky A. (Eds.). ( 2000 ). Choices, values, and frames. New York : Cambridge University Press.

Kohler W. ( 1925 ). The mentality of apes. New York : Liveright.

Larkin J. H. , McDermott J. , Simon D. P. , & Simon H. A. ( 1980 ). Expert and novice performance in solving physics problems. Science, 208, 1335–1342.

Luchins A. ( 1942 ). Mechanization in problem solving.   Psychological Monographs, 54 (6) (Whole No. 248).

Mandler J. M. , & Mandler G. ( 1964 ). Thinking from associationism to Gestalt. New York : Wiley.

Markman A. B. , & Medin D. L. ( 2002 ). Decision making. In D. Medin (Ed.), Stevens’ handbook of experimental psychology, Vol. 2. Memory and cognitive processes (2nd ed., pp. 413–466). New York : Wiley.

Mayer R. E. ( 1992 ). Thinking, problem solving, cognition (2nd ed). New York : Freeman.

Mayer R. E. ( 1995 ). The search for insight: Grappling with Gestalt psychology’s unanswered questions. In R. J. Sternberg & J. E. Davidson (Eds.), The nature of insight (pp. 3–32). Cambridge, MA : MIT Press.

Mayer R. E. ( 2008 ). Learning and instruction. Upper Saddle River, NJ : Merrill Prentice Hall.

Mayer R. E. ( 2009 ). Information processing. In T. L. Good (Ed.), 21st century education: A reference handbook (pp. 168–174). Thousand Oaks, CA : Sage.

Mayer R. E. , & Wittrock M. C. ( 2006 ). Problem solving. In P. A. Alexander & P. H. Winne (Eds.), Handbook of educational psychology (2nd ed., pp. 287–304). Mahwah, NJ : Erlbaum.

McCloskey M. ( 1983 ). Intuitive physics.   Scientific American, 248 (4), 122–130.

Metcalfe J. , & Wiebe D. ( 1987 ). Intuition in insight and non-insight problem solving. Memory and Cognition, 15, 238–246.

Newell A. , & Simon H. A. ( 1972 ). Human problem solving. Englewood Cliffs, NJ : Prentice-Hall.

Nickerson R. S. ( 1999 ). Enhancing creativity. In R. J. Sternberg (Ed.), Handbook of creativity (pp. 392–430). New York : Cambridge University Press.

Nunes T. , Schliemann A. D. , & Carraher D. W , ( 1993 ). Street mathematics and school mathematics. Cambridge, England : Cambridge University Press.

Robbins P. , & Aydede M. (Eds.). ( 2009 ). The Cambridge handbook of situated cognition. New York : Cambridge University Press.

Rogers T. T. , & McClelland J. L. ( 2004 ). Semantic cognition: A parallel distributed processing approach. Cambridge, MA : MIT Press.

Singley M. K. , & Anderson J. R. ( 1989 ). The transfer of cognitive skill. Cambridge, MA : Harvard University Press.

Sternberg R. J. ( 1990 ). Metaphors of mind: Conceptions of the nature of intelligence. New York : Cambridge University Press.

Sternberg R. J. ( 1999 ). Handbook of creativity. New York : Cambridge University Press.

Sternberg R. J. , & Gregorenko E. L. (Eds.). ( 2003 ). The psychology of abilities, competencies, and expertise. New York : Cambridge University Press.

Tharp R. G. , & Gallimore R. ( 1988 ). Rousing minds to life: Teaching, learning, and schooling in social context. New York : Cambridge University Press.

Thorndike E. L. ( 1911 ). Animal intelligence. New York: Hafner.

Thorndike E. L. , & Woodworth R. S. ( 1901 ). The influence of improvement in one mental function upon the efficiency of other functions. Psychological Review, 8, 247–261.

Wertheimer M. ( 1959 ). Productive thinking. New York : Harper and Collins.

Wundt W. ( 1973 ). An introduction to experimental psychology. New York : Arno Press. (Original work published in 1911).

Further Reading

Baron, J. ( 2008 ). Thinking and deciding (4th ed). New York: Cambridge University Press.

Duncker, K. ( 1945 ). On problem solving. Psychological Monographs , 58(3) (Whole No. 270).

Holyoak, K. J. , & Morrison, R. G. ( 2005 ). The Cambridge handbook of thinking and reasoning . New York: Cambridge University Press.

Mayer, R. E. , & Wittrock, M. C. ( 2006 ). Problem solving. In P. A. Alexander & P. H. Winne (Eds.), Handbook of educational psychology (2nd ed., pp. 287–304). Mahwah, NJ: Erlbaum.

Sternberg, R. J. , & Ben-Zeev, T. ( 2001 ). Complex cognition: The psychology of human thought . New York: Oxford University Press.

Weisberg, R. W. ( 2006 ). Creativity . New York: Wiley.

• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Donate | Contact Us

NATIONAL CONTACT INFORMATION (317) 356-6284 FAX 317-356-6680 [email protected]

Our National Office is located at: 1412 Sadlier Circle East Drive Indianapolis, IN 46239 Get Directions

Pentathlon Institute

Active Problem-Solving

Learning to resolve problems that are continually undergoing change.

The Mathematics Pentathlon ® Program provides experiences in thought processes necessary for Active Problem Solving. The series of 20 Mathematics Pentathlon games provide K-7 students with experiences in deductive and inductive reasoning through the repeated use of sequential thought as well as nonlinear, intuitive thinking. Exposure to such forms of thought helps students relate to real-life problem-solving situations and learn to “think on their feet.”

The Four Sections below explain the following: Active Problem Solving Defined, What is Mathematics, Three Types of Mathematical Thought, and Conceptual Understanding Using Concrete and Pictorial Models.

Active-Problem Solving Defined

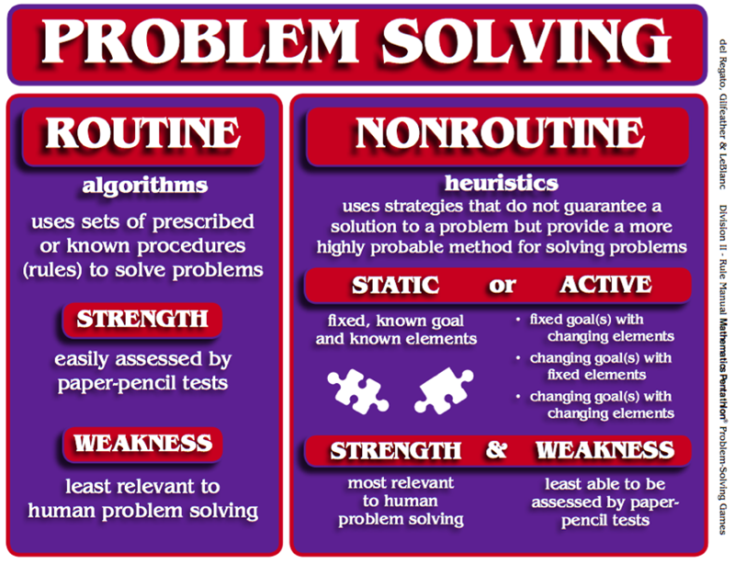
Problem solving can be divided into two categories:, routine & non-routine.

Routine Problem Solving , stresses the use of sets of known or prescribed procedures (algorithms) to solve problems. The strength of this approach is that it is easily assessed by paper-pencil tests. Since today’s computers and calculators can quickly and accurately perform the most complex arrangements of algorithms for multi-step routine problems, the typical workplace does not require a high level of proficiency in Routine Problem Solving. However, today’s workplace does require many employees to be proficient in Nonroutine Problem Solving.

Nonroutine Problem Solving , stresses the use of heuristics and often requires little to no use of algorithms. Unlike algorithms, heuristics are procedures or strategies that do not guarantee a solution to a problem but provide a more highly probable method for discovering a solution. Building a model and drawing a picture of a problem are two basic problem-solving heuristics. Studying end-of-game situations provides students with experiences in using the heuristics of reducing the problem to a similar but simpler problem and working a problem backwards, i.e. from its resolution to its initial state. Other heuristics include describing the problem situation, classifying information, and finding irrelevant information.

There Are Two Categories of Nonroutine Problem Solving:

Static and active.

Static-Nonroutine problems have a fixed, known goal and fixed, known elements that are used to resolve the problem. Solving a jigsaw puzzle is an example of a Static- Nonroutine problem. Given all pieces to a puzzle and a picture of the goal, learners are challenged to arrange the pieces to complete the picture. Various heuristics such as classifying the pieces by color, connecting the pieces that form the border, or connecting the pieces that form a salient feature to the puzzle, such as a flag pole, are typical ways in which people attempt to resolve such problems.

Active-Nonroutine problems may have a fixed goal with changing elements, a changing goal or alternative goals with fixed elements, or changing or alternative goals with changing elements. The heuristics used in this form of problem-solving are known as strategies. People who study such problems must learn to change or adapt their strategies as the problem unfolds.

What is Mathematics?

There is a growing belief in the mathematics community, as well as society in general, that the study of mathematics must develop in all students an understanding of mathematics that continues throughout one’s lifetime and evolves to meet ever-changing situations and variables. From our perspective, mathematics is an area of investigation that develops the ability to critically observe, classify, describe, and analyze data in a logical manner using both inductive and deductive methods. In contrast to the sterilized and unrelated manner in which school mathematics has often been taught, mathematics is a creative and aesthetic study of patterns and geometric and numerical relationships. It is dynamic rather than passive in nature and should involve students in strategic thinking by exploring multiple possibilities and variables that continually change, much like life.

The Mathematics Pentathlon® Program, which integrates Adventures in Problem Solving, Activity Books I & II, the Mathematics Pentathlon® Games and Investigation Exercises, Books I & II was designed to implement the definition of mathematics described above. The games are organized into four division levels by grade, K-1, 2-3, 4- 5, and 6-7 with five games at each level. The name of the Program, Mathematics Pentathlon®, was coined to liken it to a worldwide series of athletic events, the Decathlon component of the Olympics. In the world of athletics the Decathlon is appreciated for valuing and rewarding individuals who have developed a diverse range of athletic abilities. In contrast, the mathematics community as a whole has rarely valued or rewarded individuals with a diverse range of mathematics abilities. The Mathematics Pentathlon® Games promote diversity in mathematical thinking by integrating spatial/ geometric, arithmetic/computational, and logical/scientific reasoning at each division level. Since each of the 5 games requires students to broaden their thought processes, it attracts students from a wide range of ability levels, from those considered “gifted and talented” to “average” to “at-risk.”

The format of games was chosen for two reasons. First, games that are of a strategic nature require students to consider multiple options and formulate strategies based on expected countermoves from the other player. The Mathematics Pentathlon® further promotes this type of thought by organizing students into groups of four and teams of two. Teams alternate taking turns and team partners alternate making decisions about particular plays by discussing aloud the various options and possibilities. In this manner, all group members grow in their understanding of multiple options and strategies. As students play these games over the course of time, they learn to make a plan based on better available options as well as to reassess and adjust this plan based on what the other team acted upon to change their prior ideas. Through this interactive process of sharing ideas and possibilities, students learn to think many steps ahead, blending both inductive and deductive thinking. Second, games were chosen as a format since they are a powerful motivational tool that attracts students from a diverse range of abilities and interest levels to spend more time on task developing basic skills as well as problem-solving skills. While race-type games based on chance are commonly used in classrooms, they do not typically capture students’ curiosity for long periods of time. Students may play such games once or twice, but then lose interest since they are not seriously challenged. The Mathematics Pentathlon® Games have seriously challenged students to mature in their ability to think strategically and resolve problems that are continually undergoing change. As a result, we view active-problem solving and strategic thinking as described above as a critical focal point of the mathematics curriculum.

3 Types of Mathematical Thought

Integration of spatial/geometric, computational, and logical/scientific reasoning.

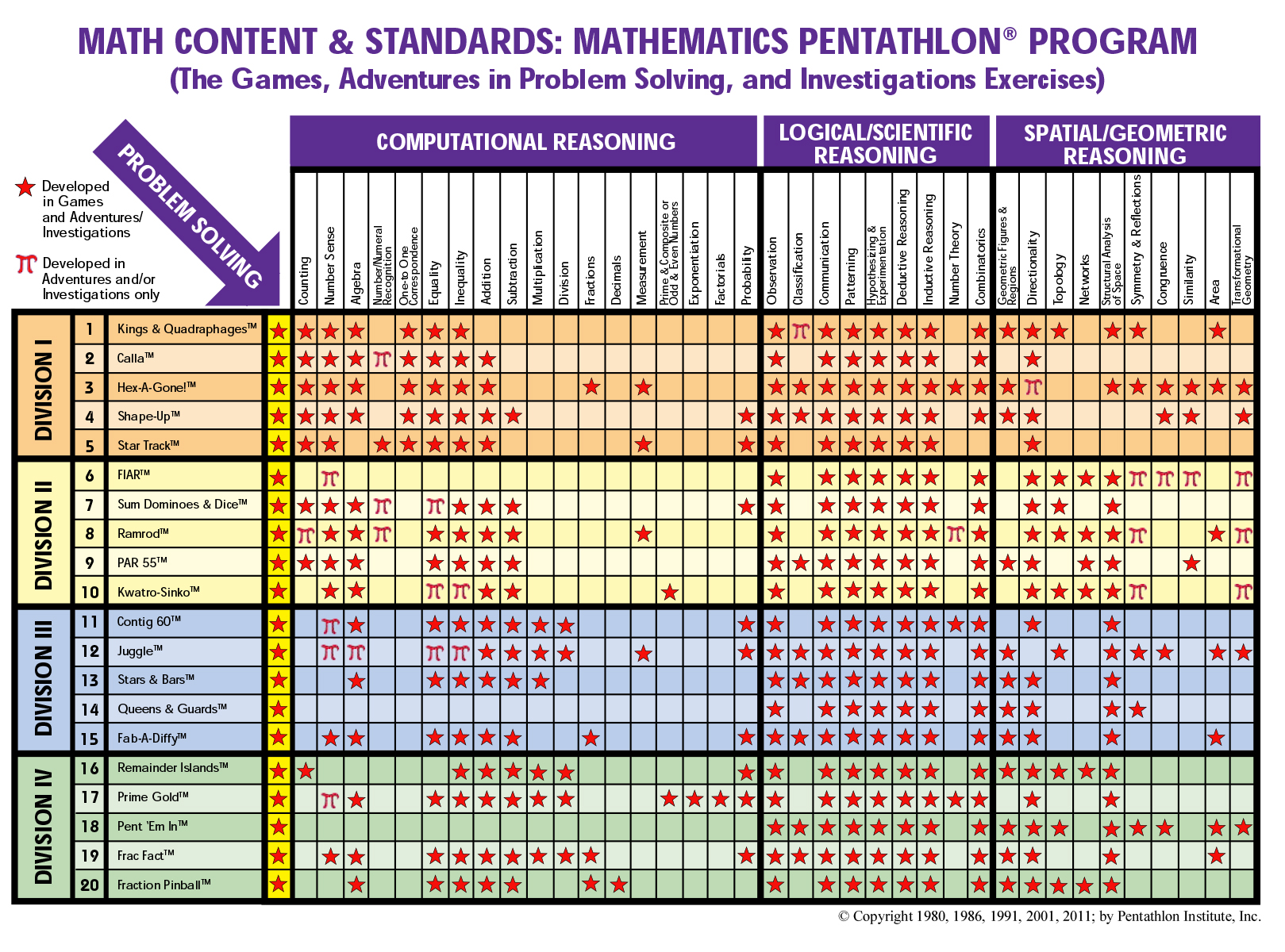
Most mathematics instruction stresses students’ knowledge of basic arithmetic facts. While the Mathematics Pentathlon Program provides a great deal of practice with mastery of the basic facts, it goes far beyond learning arithmetic skills. The Mathematics Content and Standards Chart for the 20 Mathematics Pentathlon Games shows how each game addresses several mathematical content and process objectives (see inside back cover of manual). These objectives have been clustered into logical/scientific reasoning, computational reasoning, and spatial/geometric reasoning. Each of these categories is described below.

Spatial/Geometric Reasoning

Spatial visualization involves the ability to image objects and pictures in the mind’s eye and to be able to mentally transform the positions and examine the properties of these objects/pictures. A large body of mathematics research concludes that spatial reasoning ability is highly related to higher-level mathematical problem-solving and geometric skills as well as students’ overall achievement in mathematics. Many of the Mathematics Pentathlon Games stress spatial reasoning and several integrate this form of thinking with logical and computational reasoning.

Computational Reasoning

Many of the Mathematics Pentathlon Games incorporate computation into the game structure. More time-on-task practicing arithmetic skills does indeed result in students’ increased performance in the classroom as well as on standardized tests. But in the Mathematics Pentathlon Games that stress computation, it is not sufficient to rely on arithmetic skills alone. To be successful in these games, students must also use their logical reasoning abilities to consider several options and to decide which ones will maximize their ability to reach the game’s goal(s).

Logical/Scientific Reasoning

One of the most important life skills, not to mention mathematical skills, is the ability to think logically. The process of observation, classification, hypothesizing, experimentation, and inductive and deductive thought are required for logical reasoning. Yet where do children learn these fundamental life skills? Strategic games provide students the opportunity to develop this form of thinking. Each of the Mathematics Pentathlon Games is a strategy game that develops students’ logical reasoning skills through the process of investigating a variety of options and choosing better options.  At the same time students develop scientific reasoning skills by learning how to be better observers of game-playing variables and options. Playing the games over the course of time allows for hypothetical reasoning to evolve since students analyze sequences of “if-then” situations and make choices based on linking inductive and deductive thought.

While each of the 20 games may stress one form of the mathematical thinking over another, each game integrates at least two categories of mathematical thinking. Furthermore, the five games at each Divisional level balance the three types of reasoning.

Conceptual Understanding Using Concrete and Pictorial Models Understanding

Since its inception, the National Council of Teachers of Mathematics (NCTM) has called for a conceptually-based curriculum in schools throughout the country. The most recent psychological and educational research has shown that conceptual understanding is a key attribute of individuals who are proficient in mathematics. Furthermore, a large body of research over the last four decades suggests that effective use of physical and pictorial models of mathematics concepts improves students’ conceptual understanding, problem-solving skills, and overall achievement in mathematics. Research also indicates that the use of concrete and pictorial models improves spatial visualization and geometric thinking.

The  Mathematics Pentathlon ®   Program  incorporates a variety of concrete and pictorial models to develop students’ conceptual understanding of many important mathematics concepts that involve computational, spatial, and logical reasoning. In addition, by playing these games in cooperative groups, as suggested in this publication, students also improve their oral and written communication skills through their discussion of mathematical ideas and relationships.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Springer Nature - PMC COVID-19 Collection

Improving Students’ Problem-Solving Flexibility in Non-routine Mathematics

Huy a. nguyen.

Carnegie Mellon University, Pittsburgh, PA 15213 USA

John Stamper

Bruce m. mclaren.

A key issue in mathematics education is supporting students in developing general problem-solving skills that can be applied to novel, non-routine situations. However, typical mathematics instruction in the U.S. too often is dominated by rote learning, without exposing students to the underlying reasoning or alternate ways to solve problems. As a first step in addressing this problem, we present a cognitive task analysis study that investigates how students without a mathematics-related background solve novel non-routine problems. We found that most students were able to identify the underlying pattern that yields the final solution in each problem. Furthermore, they tended to use various forms of visualization in their draft work, but occasionally made computational mistakes. Based on these results, we propose our plan for developing an instructional platform that leverages learning science principles to train students in problem-solving abilities.

Introduction

The ability to tackle non-routine problems – those that cannot be solved with a known method or formula and require analysis and synthesis as well as creativity [ 9 ] – is becoming increasingly important in the 21st century [ 5 ]. However, when faced with a non-routine problem, U.S. students tend to apply memorized procedures incorrectly rather than modify them or develop new solutions [ 8 ]. One possible source for this difficulty is the typical instructional focus in U.S. schools on memorization and application of routine procedures [ 2 , 6 , 7 ]. Such an approach makes students proficient at executing rote procedures, but it does little to help them understand the conceptual basis for the procedures or to think creatively about novel problems - both of which are essential for developing problem-solving flexibility.

An important first step in addressing this issue is to assess how students currently approach non-routine problem solving, so that we can design the appropriate learning interventions. In this work, we present an empirical cognitive task analysis where participants were asked to think aloud while solving a series of non-routine problems from discrete mathematics. We chose this domain because discrete math problems can often be tackled from multiple perspectives while not requiring any advanced background beyond the high school curriculum [ 3 ]. Based on the findings from this study, we propose our plan for developing a tutoring system for non-routine problem-solving ability. Then, we discuss the system’s broader implications and the challenges we need to address in deploying this system at scale.

Assessing Students’ Problem-Solving Skills

We conducted interview sessions with three students at a private university in a midwest US city. None of the students had a mathematics-related background. The participants were asked to solve three non-routine mathematics problems on paper in one hour. They were also encouraged to think aloud and write down their draft work. The three problems in our study, taken from [ 3 ], and a brief summary of their sample solutions, are as follows.

In an air show there are twenty rows. The first row contains one seat, the second three seats, the third five seats, the fourth seventh seats, and so on. How many seats are there in total ?

Sample solution: In the first row there is 1 seat. In the first two rows there are 1 + 3 =  4 seats. In the first three rows there are 1 + 3 + 5 =  9 seats. In the first four rows there are 1 + 3 + 5 + 7 =  16 seats. In the first five rows there are 1 + 3 + 5 + 7 + 9 =  25 seats. Based on this pattern, in the first k rows there are k 2 seats. In our case, there are 20 rows and therefore 400 seats in total.

Find all integers between 1 and 99 (inclusive) with all distinct digits.

Sample solution: there are 99 integers between 1 and 99 in total, and 9 of them have non-distinct digits, namely 11, 22, 33, …, 88, 99. Hence, the remaining 90 integers have distinct digits.

What is the digit in the ones place of 2 57 ?

Sample solution: Looking at the sequence of powers of 2–2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, … – we see that the corresponding sequence of digits in the ones places is 2, 4, 8, 6, 2, 4, 8, 6, 2, 4, … In other words, this sequence is a cycle of length 4. Therefore the last digit of 2 57 is that of 2 53 , which is that of 2 49 , …, which is that of 2 1 , which is 2.

We then analyzed recordings of the participants’ think-aloud and their draftwork, from which we derived the following insights:

Pattern Identification.

Participants were aware that they had to find a pattern or formula to solve the problems, because it was not feasible to directly compute the final answer. All participants were able to identify the expected pattern for each problem as outlined above, except for one student who failed to do so for Problem 1 . While this participant realized that the number of seats on row k is the k-th positive odd number, this pattern alone was insufficient to solve the problem.

Visualization.

Participants tended to visualize the problem by drawing examples and making lists or tables (Fig.  1 ). They expressed that these visualizations were crucial in helping them identify the correct pattern and solve the problem.

Participants’ attempts at visualizing the problem in their draftworks.

Computation.

Participants occasionally made computational mistakes while calculating the initial sequence values, especially in Problem 3 . As a consequence, they could not identify any pattern based on the wrong values, and took some time to realize the mistake. All students who corrected their mistakes were able to subsequently solve the problem.

In summary, we found that participants were aware of the idea behind identifying patterns, and they all did so via some kind of visualization. On the other hand, computational mistakes, while not directly related to our learning objectives, can be detrimental to the overall problem-solving process. From these insights, we propose the following next steps.

Developing a Tutoring System for Flexible Problem-Solving

Moving forward, our plan is to iteratively conduct more cognitive task analysis interviews and develop a prototype of the system. Our initial conceptualization of how the system will work is as follows. A single round of exercise in the system incorporates four learning stages, all of which are built on established learning principles: 1) Reviewing a worked example of a non-routine mathematics problem, 2) Explaining the worked example to a partner, 3) Solving a new problem which is isomorphic to the worked example problem, and 4) Explaining the isomorphic solution to a partner. Between rounds, the student can review previous solutions, look at materials related to the problem space, or practice basic math skills. This design is intended to (1) formally introduce students to a complete solution through worked examples, (2) reinforce their understanding of the worked example through self-explanation, and (3) assess students’ learning through an isomorphic problem. Our hypothesis is that through the learning system, students will get a better sense of how to approach a novel non-routine problem, so that in case they have not yet found the solution – for example, like the participant in our study who did not identify the true pattern in Problem 1 – they can still adopt a different viewpoint and explore other strategies.

We have already begun mapping the problem space by developing a non-routine problem-solving flowchart and identifying sets of potential non-routine problem solutions. Once we have tested our solution space, we will develop and pilot a low fidelity paper prototype version of the system with college students to further refine the mathematical content and identify areas for revision to the design. We are also looking at which technological features could be useful for students learning in this domain. As a first step, our system will include a canvas for students to perform their draftwork on, as well as a simple calculator interface with basic arithmetic operations to help students avoid computational mistakes. An important follow-up question is whether students’ draftwork can be analyzed to infer their thinking process, which could in turn guide the design of appropriate feedback mechanics. While this task has previously been performed manually by domain experts [ 1 ], employing a machine learning technique to automate it to some extent would greatly enhance the system’s adaptive support functionality and scalability.

This research will provide concrete, generalizable evidence about the utility and implementation of worked examples, multiple solutions, and self-explanation to promote skills in non-routine problem solving. Results will inform future tutoring system design by identifying how and when the instructional features are most beneficial for developing problem-solving skills. We also intend to have a practical impact by distributing a tutoring system that is accessible to a wide range of students, including lower-performing students who would typically not be exposed to these types of problems and strategies [ 1 , 4 ]. In addition, we will provide a teacher’s guide to support educators in using the system adaptively to support their instructional goals.

Contributor Information

Ig Ibert Bittencourt, Email: [email protected] .

Mutlu Cukurova, Email: [email protected] .

Kasia Muldner, Email: [email protected] .

Rose Luckin, Email: [email protected] .

Eva Millán, Email: se.amu.ccl@ave .

Mathelogical

Home Non-Routine Mathematics

Introduction to Non-Routine Mathematics / Non-Routine Problem Solving

Creative problem solving or Non-Routine Mathematics involves finding solutions for unseen problems or situations that are different from structured Maths problems. There are no set formulae or strategies to solve them , and it takes creativity, flexibility  and originality to do so. This can be done by creating our own ways to assess the problem at hand and reach a solution. We need to find our own solutions and sometimes derive our own formulae too.

A non-routine problem can have multiple solutions at times, the way each one of us  has different approach and different solutions for our real-life problems.

Why non-routine Mathematics

• It’s an engaging and interesting way to introduce problem solving to kids and grown-ups.
• Its helps boost the brain power.
• It encourages us to think beyond obvious and analyse a situation with more clarity.
• Encourages us to be more flexible and creative in our approach and to think and analyse from an extremely basic level, rather than just learning Mathematical formulae and trying to fit them in all situations.
• Brings out originality, independent thought process and analytical skills as one must investigate a problem, reach a solution, and explain it too.

How to Analyse a Non-Routine Problem :

• Read the problem well and make note of the data given to you.
• Figure out clearly what is asked or what is expected from you.
• Take note of all the conditions and restrictions . This will help you get more clarity.
• Break up the problem into smaller parts , try to solve these smaller problems first.
• Make a note of data and properties or any similar situations ( faced earlier)
• Look for a pattern or think about a logical way of reaching a solution. Make a model or devise a strategy .
• Use this strategy and your knowledge to reach a solution.

Let’s try a few examples!

There are 50 chairs and stools altogether in a restaurant. Find the number of chairs and the number of stools, if each chair has 4 legs and each stool has 3 legs and there are 180 wooden legs in the restaurant?

First thing that comes to our mind is that we have two algebraic equations here and solving simultaneous equations is the only way to get a solution.

Not really! A small child and a Non-Math student can solve it too.

Logic: Each piece of furniture has at least 3 legs (stools-3 legs, chairs -4 legs).

So, minimum number of legs (for 50 pcs of furniture) in the restaurant = 3 X 50  = 150 legs  if there are only stools in the restaurant.                                                                       

Chairs have 4 legs i.e., each extra leg belongs to a chair.

(we have already taken 3 legs of each chair and stool into account)

Number of extra wooden legs in the restaurant

 =  total number – minimum possible number of legs for 50 pcs of furniture                  

 = 180 -150  = 30 legs

Each extra leg (4 th leg) belongs to a chair.

Therefore, the number of chairs in the restaurant = 30

So, number of stools = 50-30=20

For more on this topic: Solving without Simultaneous Equations

A cube is painted from all sides. It is then cut into 27 equal small cubes. How many cubes

• Have 1 side painted?
• Have 3 sides painted?

The cube is cut into 27 equal cubes of equal size that means it’s a 3x3x3 cube. Visualise the cube (have included 3x3x3 Rubix cube pic for reference)

a) Only the cubes at the centre of each face (that are located neither at corners nor along the edges) will have just one side painted.

In a 3 x 3 cube there is only one cube on each face which is located neither at corners nor along the edges.

There are 6 faces in any cube.

Therefore, 6 cubes have only one side painted.

b)The small cubes at the corners of the big cube have 3 sides painted.

There are 8 small corner cubes in the big cube.

Therefore, 8 cubes have 3 sides painted.

• Worksheet 1 - Rabbit and Chicken
• Introduction - Regions made by intersecting lines
• Intro Number of trees planted along a road

More Related Topics

• Using Models to Solve Problems
• Number of Trees Planted Along a Road
• How to Solve Without Algebraic Equations
• Man-Hours Word Problems
• Regions Made by Intersecting Circles
• Regions Made by Intersecting Lines

Non-routine Algebra Problems

(a new problem of the week).

Last week I mentioned “non-routine problems” in connection with the idea of “guessing” at a method. Let’s look at a recent discussion in which the same issues came up. How do you approach a problem when you have no idea where to start? We’ll consider some interesting implications for problem solving in general, with an emphasis on George Pólya’s outline.

First problem: mindless manipulation?

This came to us in March, from a student who identified him/herself as “J”:

Hi, Recently I had to solve a problem If (a + md) / (a + nd) = (a + nd) / (a + rd) and (1 / n) – (1 / m) = (1 / r) – (1/n) , then (d / a) = -(2 / n) i.e. Given the two expressions above I need to prove the last equality. I don’t understand problems like these. Basic Algebra books talk about problems like equation solving or word problems, but those are easy because there’s always some method you can use . For example regarding equation solving you move x’s to the left, numbers to the right; word problems can be solved using equalities like distance = rate * time. But a problem like the one above it seems has no method; it seems like you’re supposed to just manipulate the symbols until you get the answer . For example I tried to solve it like this: Regarding the first expression, after multiplying numerator of the first fraction by the denominator of the second I get (d / a) = ((m + r – 2n) / (n^2 – mr)) and 2mr = nm – nr then substitute for mr in the first expression. I reached the solution by luck; I just manipulated the symbols and it took me a lot of time . So is there a more efficient way to solve problems like these? How to think about these problems? Am I supposed to just mindlessly manipulate the symbols until I get lucky? Finally are there any books that deal with problems like these ? Because like I mentioned it seems like most precalculus books talk about equation solving etc., problems which have a clear method. Thanks.

The solution

Before we deal with the question, let’s look more closely at his solution.

We are given two equations:

$$\displaystyle\frac{a + md}{a + nd} = \frac{a + nd}{a + rd}$$

$$\displaystyle\frac{1}{n} – \frac{1}{m} = \frac{1}{r} – \frac{1}{n}$$

We need to conclude that

$$\displaystyle\frac{d}{a} = -\frac{2}{n}.$$

J gave only a brief outline of what he did; can we fill in the gaps?

My version is to first “cross-multiply” in each equation to eliminate fractions, and do a little simplification:

The first becomes $$(a + md)(a + rd) = (a + nd) (a + nd),$$ which expands to $$a^2 + rda + mda + mrd^2 = a^2 + 2nda + n^2d^2,$$ then $$rda + mda – 2nda = n^2d^2 – mrd^2,$$ which factors to yield $$(r + m – 2n)da = (n^2 – mr)d^2.$$ Dividing, we get $$\displaystyle\frac{d}{a} = \frac{r + m – 2n}{n^2 – mr}.$$

(You may notice here that in dividing both sides by d , we obscured the fact that the line before is true whenever d = 0. I’ll be mentioning this below.)

The second equation, multiplied by \(mnr\), becomes $$mr – nr = nm – mr,$$ which easily becomes $$2mr = nm + nr.$$ (J had a sign error here.)

Now, replacing \(mr\) with \(\displaystyle\frac{nm + nr}{2}\), we get $$\displaystyle\frac{d}{a} = \frac{r + m – 2n}{n^2 – \frac{nm + nr}{2}} = \frac{2(r + m – 2n)}{2n^2 – nm – nr} = \frac{2(r + m – 2n)}{-n(r + m – 2n)} = -\frac{2}{n}.$$

How to solve it

Taking the question myself, I replied:

I tried the problem without looking at your work, and ended up doing almost exactly the same things. That took me just a few minutes. So probably it is not your method itself, but your way of finding it , that needs improvement. In my case, I did the “obvious” things (clearing fractions, expanding, factoring) to both given equations, keeping my eyes open for points at which they might be linked together , and found one. It may be mostly experience that allowed me to find it quickly. That is, I didn’t “mind lessly manipulate”, but “mind fully  manipulated”. And the more ideas there are in your mind, the more easily that can happen. So maybe just doing a lot of (different) problems is the main key.

I added a few more thoughts about strategies:

There may be a better method for solving this, but finding it would take me a longer time than what I did. So perseverance at trying things is necessary , regardless. Solutions to hard problems don’t just jump out at you (unless they are already in your mind from past experience); you have to explore . The ideas I describe for working out a proof apply here as well: Building a Geometric Proof I like to think of a proof as a bridge, or maybe a path through a forest: you have to start with some facts you are given, and find a way to your destination. You have to start out by looking over the territory, getting a feel for where you are and where you have to go – what direction you have to head, what landmarks you might find on the way, how you’ll know when you’re getting close. (By the way, in my work I also found that d/a = 0 gives a solution, so that if d=0 (and a ≠ 0), the conclusion is not necessarily true. Did you omit a condition that all variables are nonzero?) You are probably right that too many textbooks and courses focus on routine methods, and don’t give enough training in non-routine problem solving . They may include some “challenge problems” or “critical thinking exercises”, but don’t really teach that. One source of this sort of training is in books or websites (such as artofproblemsolving.com ) that are aimed at preparation for contests. Books like Pólya’s   How to Solve It  (and newer books with similar titles) are also helpful. Here are a few pages I found in our archives that have at least some relevance: Defining “Problem Solving” Giving Myself a Challenge Preparing for a Math Olympiad Learning Proofs What Is Mathematical Thinking? Others of us may have ideas to add.

Some these have been mentioned in previous posts such as How to Write a Proof: The Big Picture and  Studying Math: Want a Challenge? .

Another problem: following Pólya

The next day, J wrote in with another problem, having already followed up on my suggestions:

Hi. I posted here recently asking about problem solving and algebra and I was recommended a book called “How to solve it” by Pólya . I bought that book and now I am trying to solve some algebra exercises using it. Today I came across this problem If bz + cy = cx + az = ay + bx and (x + y +z)^2 = 0 , then a +/- b +/- c. (The sign +/- was a bit confusing to me since it’s not brought up anywhere in the book besides this problem, but Wikipedia says that a +/- b = 0 is a + b =0 or a – b = 0.) In the book “How to solve it” Pólya says that first it’s important to understand the problem and restate it . So my interpretation of a problem is this: If numbers x, y, z are such that (x + y + z)^2 = 0 and bz + cy = cx + az and bz + cy = ay + bx, then the numbers a, b, c are such that a + b + c = 0 or a – b – c =0 Next Pólya says to devise a plan . To do that he says you need to look at a hypothesis and conclusion and think of a similar problem or a theorem. The best I could think of is an elimination problem, i.e. when you’re given a certain set of equations and you can find a relationship between constants. Can you think of any other similar problems which could help me solve this problem?

I first responded to the last question:

Hi again, J. I would say that the last question you asked was “similar” to this, so the same general approach will help. That’s essentially what you said in your last paragraph, I think. I know that isn’t very helpful, but it’s all I can think of myself. You’d like to have seen a problem that is more specifically like this one, such as having (x + y + z) 2  = 0 in it, perhaps, so you could get more specific ideas. I only know that I have seen a lot of problems like this involving symmetrical equations (where each variable is used in the same ways), and I suspect those problems can be solved by similar methods. But I don’t know one method that would work for this one.

I’ll get back to that question. But let’s focus first on Pólya.

Here is what Pólya says (p. 5) when he introduces his famous four steps of problem solving:

In order to group conveniently the questions and suggestions of our list, we shall distinguish four phases of the work. First, we have to understand the problem; we have to see clearly what is required. Second, we have to see how the various items are connected, how the unknown is linked to the data, in order to obtain the idea of the solution, to make a plan . third, we carry out our plan. Fourth, we look back at the completed solution, we review and discuss it.

This process is then explained in more detail, and used as an organizing principle in the rest of the book. It can be amazing to see how many students jump into a problem before they understand what it is asking, or do calculations without having made any plans . On the other hand, it would be wrong to think of these four steps as a routine to be followed exactly; often you don’t fully understand a problem until you have started doing something , perhaps carrying out a half-formed plan and then realizing that you had a wrong impression of some part.

Understanding the problem

And J has here a good example of a misunderstanding. This problem uses the plus-or-minus symbol (±) in a rare way, which in this case requires asking (not explicitly one of Pólya’s recommendations, but valuable!).

The problem says this:

$$\text{If } bz + cy = cx + az = ay + bx \text{ and } (x + y + z)^2 = 0 \text{, then } a \pm b \pm c.$$

(No, that doesn’t quite make sense! We’ll be fixing that shortly.)

What does it mean when there are two of the same symbol? The Wikipedia page J found says, “In mathematical formulas, the ± symbol may be used to indicate a symbol that may be replaced by either the + or − symbols, allowing the formula to represent two values or two equations.” They give an example (the quadratic formula), where either sign yields a valid answer; then an example with two of the same sign (the addition/subtraction identity for sines) in which both must be replaced with the same sign ; and third example (a Taylor series) where the reader has to determine which sign is appropriate for a given term. Later they introduce the minus-or-plus sign (\(\mp\)), which explicitly indicates the opposite sign from an already-used ±.

But here, we have two ±’s with no clear reason why they should be the same, or should be different. Is this a special case? J has assumed they are the same, so that it means “\(a + b + c = 0\) or \(a – b – c = 0\)“. This is the first issue I had to deal with:

First, though, did you mean to say that the conclusion is a ± b ± c  = 0 ? That wouldn’t quite mean what you said about it, because the two signs need not be the same. Rather, it means that  either  a + b + c = 0, or a + b – c = 0, or a – b + c = 0, or a – b – c = 0: any possible combination  of the signs.

Now, how did I know that, when it goes against what Wikipedia seems to be saying? I’m not sure! There is actually some ambiguity; really, we just shouldn’t rule out this possibility . But I saw from the start that if the two signs are the same, then the problem has an odd asymmetry , requiring b and c to have the same sign in this equation, but not a . That simply seems unlikely, considering the symmetry elsewhere.

Sometimes we discover, as we proceed through the solving process, that we have to interpret the statement one way or another in order for it to be true – an example of my comment that understanding can come after doing some work. (That was actually the case here. But the problem really should have been written to make this clear!)

Hints toward a solution

What this means is that we don’t know the signs of the numbers. One thing that suggests is that we might be able to show some fact about a 2 ,  b 2 , and c 2 , so that we would have to take  square roots , requiring us to use ± before each of a, b, and c. It’s also interesting that they said that (x + y + z) 2  = 0, which means nothing more than x + y + z = 0. That also makes me curious, and at the least puts squares into my mind for a second reason.

Here I am just letting my mind wander around the problem, pondering what the givens suggest. This is part of both the understanding phase, and the “looking for connections” Pólya talked about.

Not even being sure of the conclusion, I just tried manipulating the equations any way I could, just to make their meanings more visible; and then I solved x + y + z = 0 for z and put that into my derived equations, eliminating z. That took me eventually to a very simple equation that involved a, b, x 2 , and y 2 . And that gave a route to the ± I’d had in mind.

We could say that my initial plan is, as I suggested at the top, to explore ! We can refine the plan as we see more connections. (As I said, Pólya has to be followed flexibly.)

There’s a lot of detail I’ve omitted, in part because much of my work was undirected, so you may well find a better way. But the key was to have some thoughts in mind before I did a lot of work, in hope of recognizing a useful form when I ran across it . The other key was perseverance , because things got very complicated before they became simple again! (I suspect that as I go through this again, I’ll see some better choices to make, knowing better where I’m headed.) I don’t think you told us where these problems came from; they seem like contest-type problems, which you can expect to be highly non-routine. As I said last time, until you’ve done a lot of these, you just need to keep your eyes open so that you are learning things that will be useful in future problems! I am not a contest expert, as a couple of us are, so I hope they will add some input.

Since we never got back to the details of this problem, let’s finish it now. Frankly, I had to look in my stack of scrap paper to find what I did in March, because I wasn’t making any progress when I tried it again just now. Clearly I could have given a better hint! I was hoping that just the encouragement that it could be done would lead to J finding a nicer approach than mine.

But here’s what I find in my incomplete notes from then. First, I rewrote the equality of three expressions as two equations, and eliminated c; I’ll use a different pair of equations than I did then, with that goal in mind: $$cx + az = ay + bx\; \rightarrow\; c = \frac{ay-az+bx}{x}$$ $$ay + bx = bz + cy\; \rightarrow\; c = \frac{ay-bz+bx}{y}$$

Setting these equal to eliminate c, $$\frac{ay-az+bx}{x} = \frac{ay-bz+bx}{y}$$

Cross-multiplying, $$ay^2-ayz+bxy = axy-bxz+bx^2$$

Solving \(x + y + z = 0\) for z and substituting, $$ay^2-ay(-x-y)+bxy = axy-bx(-x-y)+bx^2$$

Expanding, $$ay^2 + axy + ay^2 + bxy = axy + bx^2 + bxy + bx^2$$

Canceling like terms on both sides, $$2ay^2 = 2bx^2$$

Therefore, $$\frac{x^2}{a} = \frac{y^2}{b}$$

We could do the same thing with different variables and find that this is also equal to \(\frac{z^2}{c}\). So we have $$\frac{x^2}{a} = \frac{y^2}{b} = \frac{z^2}{c} = k$$

Now we’re at the place I foresaw, where we can take square roots: $$x = \pm\sqrt{ak}$$ $$y = \pm\sqrt{bk}$$ $$z = \pm\sqrt{ck}$$

Therefore, since \(x+y+z=0\), we know that $$\pm\sqrt{ak}+\pm\sqrt{bk}+\pm\sqrt{ck}=0$$

and, dividing by \(\sqrt{k}\), we have $$\pm\sqrt{a}\pm\sqrt{b}\pm\sqrt{c}=0$$

In March, it turns out, I stopped short of the answer, thinking I saw it coming. But in fact, I didn’t attain the goal! I hoped that a , b , and c would be squared before we have to take the roots. We seem, however, to have proved that they must all be positive , which makes the conclusion impossible!

I’m wondering if the problem, which was never quite actually stated, might have been different from what I assumed. In fact, armed with this suspicion, I tried to find an example or a counterexample, and found that if $$\begin{pmatrix}a & b & c\\ x & y & z\end{pmatrix}= \begin{pmatrix}1 & 4 & 1\\ 1 & -2 & 1\end{pmatrix}$$ satisfies the conditions, with $$bz + cy = cx + az = ay + bx = 2,$$ but no combination of signed a , b , and c add up to 0. So the real problem must have been something else …

Remembering how to solve a problem

At this point J abandoned that path, and closed with a side issue:

Hi Doctor. I have one more question about problem solving. I spent some more time on the problem we discussed then I skipped it and decided to focus on other problems instead. I managed to solve a few of them but then I took a long break when I came back I couldn’t remember the solutions without looking at my work . I don’t know if you read How to solve it by Pólya. I ask since at the beginning of that book Pólya gives an example of a mathematical problem. The problem in question is this: Find the diagonal of a rectangular parallelepiped if the length, width, and height are known. He asks the reader to consider the auxiliary problem of finding the diagonal of the right triangle using Pythagoras theorem. I am telling you this because the solution to this problem is very clear; I can recall it even long after I finished reading. I do not feel the same about algebra problems. I solve them, do the obvious things, and then I almost immediately forget. Does that happen to you? If not how do you remember the solution? I just want to know if you find these algebra problems as unintuitive as I do.

My memory is as bad as anyone’s! I replied,

I wouldn’t say that I remember every solution I’ve done, or every solution I’ve read. The example you give is a classic that stands out, particularly the overall strategy. Others are more ad-hoc and don’t feel universal (in the sense of being applicable to a large class of problems), so they don’t stick in the memory. I don’t have my copy of Pólya with me (I’ve been meaning to look for it), but I recall that one of his principles is to take time after solving a problem to focus on what you did and think about how it might be of use for other problems. This is something like looking around before I leave my car in a parking lot to be sure I will recognize where I left it when I come back from another direction. I want to fix the good idea in my mind and be able to recognize future times when it will fit. But even though I do have that habit, there are some problem types that I recognize over and over, but keep forgetting what the trick is. (Maybe sometimes it’s because I’ve seen two different tricks, and they get mixed up in my mind.) So you’re not alone. For me, though, it’s not such much being unintuitive , as just not being memorable , or being too complex for me to have focused on them enough to remember.

So Pólya recognized the likelihood of forgetting (failing to learn from what you have done), and the need to make a deliberate effort there!

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Teaching problem solving using non-routine tasks

[email protected]

[email protected]

[email protected]

• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Maureen Siew Fang Chong , Masitah Shahrill , Ratu Ilma Indra Putri , Zulkardi; Teaching problem solving using non-routine tasks. AIP Conf. Proc. 24 April 2018; 1952 (1): 020020. https://doi.org/10.1063/1.5031982

Download citation file:

• Ris (Zotero)
• Reference Manager

Non-routine problems are related to real-life context and require some realistic considerations and real-world knowledge in order to resolve them. This study examines several activity tasks incorporated with non-routine problems through the use of an emerging mathematics framework, at two junior colleges in Brunei Darussalam. The three sampled teachers in this study assisted in selecting the topics and the lesson plan designs. They also recommended the development of the four activity tasks: incorporating the use of technology; simulation of a reality television show; designing real-life sized car park spaces for the school; and a classroom activity to design a real-life sized dustpan. Data collected from all four of the activity tasks were analyzed based on the students’ group work. The findings revealed that the most effective activity task in teaching problem solving was to design a real-life sized car park. This was because the use of real data gave students the opportunity to explore, gather information and give or receive feedback on the effect of their reasons and proposed solutions. The second most effective activity task was incorporating the use of technology as it enhanced the students’ understanding of the concepts learnt in the classroom. This was followed by the classroom activity that used real data as it allowed students to work and assess the results mathematically. The simulation of a television show was found to be the least effective since it was viewed as not sufficiently challenging to the students.

Sign in via your Institution

Citing articles via, publish with us - request a quote.

Sign up for alerts

• Online ISSN 1551-7616
• Print ISSN 0094-243X
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

Difficulties in Solving Non-Routine Problems: Preliminary Analysis and Results

ASM Science Journal

Students have been taught to solve problems since primary school. However, they still have been having difficulties in solving mathematics problems, especially non-routine problems. By searching errors in mathematics skills and cognitive abilities that have been causing difficulties in solving non-routine problems, this study aims to determine the dominant difficulties that high-achieving students commonly face. A problem-solving test (PST) that comprises four non-routine problems involving algebra was distributed to 56 Form Four selected students through purposive sampling. Each problem is followed by a reflection that allows students to describe the difficulties they face while solving the problem. Hence, the qualitative and quantitative analysis of answer scripts as well as students’ reflection shows that the dominant difficulties faced by high-achieving students when solving non-routine problems are language and information management skills. Poor mastery of these two skills ha...

Related Papers

Ericka Quindiagan

In Malaysia, like many other countries, problem solving is one of major aspect in mathematics curriculum which required students to apply and to integrate many mathematical concepts and skills as well as making decision. However, students were reported to have difficulties in mathematics problem solving. The focus of this study is to discuss the major mathematics skills and cognitive abilities in learning that caused the difficulties in mathematics problems-solving among students from students' point of view. The study was carried out on three focused group samples that were selected through purposeful sampling. A mixed qualitative and quantitative approach is used in order to have clearer understanding. Apart from the questionnaire given, focused group interviews were carried out. Interviews were recorded and transcribed. Data finding was analyzed descriptively. Data findings showed that respondents lacked in many mathematics skills such as number-fact, visual-spatial and information skills. Information skill was the most critical. The deficiency of these mathematics skills and also of cognitive abilities in learning inhibits the mathematics problem-solving. This understanding on how the deficits influenced the problem-solving is expected to give effective guide lines in preparing diagnostic instruments and learning modules in order to develop the mathematics skills.

Universal Journal of Educational Research

Horizon Research Publishing(HRPUB) Kevin Nelson

Algebraic problem-solving is a way of thinking and reasoning that allows students to create models, study relationships, and solve problems. However, students only have a little understanding of formulating and solving algebraic problems. This study aims to determine the predominant difficulties that Year Six students face when learning algebraic problem-solving. This study used a quantitative research design involving 80 students selected by purposive sampling. The instruments used in this study include criterion-referenced tests consisting of word and diagram algebraic problem-solving items. Data were analysed using GNU PSPP software. The descriptive statistics showed that the predominant difficulty that Year Six students faced when solving algebraic word problems was text difficulties and unfamiliar contexts. For diagrammatic algebraic problem-solving, students encountered the most difficulty with visual-spatial awareness. The Chi-Square test was used to identify the statistical correlation coefficient between gender and difficulties in solving algebraic problems. The result showed a positive association between gender and recognition difficulties and gender and sign substitution error. The findings of this study may encourage students to better learn algebraic problem-solving skills. Moreover, this study also provides important information for teachers to better teach algebraic problem-solving to Year Six students.

IOSR Journals publish within 3 days

Solving problems in algebra depicts the ability of students to be able to understand, plan, execute the plan in any given routine and non-routine algebraic problems. Algebra as one of the most important aspect of mathematics is very fundamental for success in secondary school mathematics. This paper discuss attitude of secondary school students towards solving algebraic problems. It is recommended that these negative attitude needs to be overcome, so that later in life these students will not suffer lack of algebraic problem solving skills which is very important and fundamental in their future employment success and everyday life.

Africa Development and Resources Research Institute ADRRI

Solving word problems is one of the major challenges in algebra facing majority of the first year students of Tamale College of Education in Ghana. Action research design using George Polya's Problem Solving Model was applied to assist the students solve word problems in mathematics. The census sampling technique was used to select 55 first year students of Tamale College of Education in the Sagnerigu District of Northern Region of Ghana. The data collection tools involved the use of observation, interviews, pre-test (diagnostic test) and post-test (post-intervention test). Data was analysis in frequency distribution, percentages, paired sample t-test and eta square for data interpretation. The findings of the study show that the mean of the pre-test scores was 2.33 (SD = 1.491) compared with the mean of the post-test scores of 7.36 (SD = 1.682). The difference between the two means and their respective standard deviations is an indication that there is a statistically significant increase in students' achievement after the intervention process. The eta squared value of 0.97 implies that the intervention has great impact on students' performance of solving word problems.

JRAMathEdu (Journal of Research and Advances in Mathematics Education)

One of the topics within the course of Essential Concepts in School Mathematics (ECSM) for prospective mathematics teachers concerns maximum and minimum problems. This type of problems requires mathematization, i.e., the activity of transforming a problem into a symbolic mathematics problem and of reorganizing within the mathematical system, in the solution process. This research aims to investigate the implementation of the learning and teaching process of the ECSM course that strengthen prospective mathematics teachers’ conceptual understanding and problem solving abilities through mathematization activities. To reach this aim, this qualitative study was conducted through an observation of the learning and teaching process, including the formative written assessment, for the case of maximum and minimum problems, involving 19 students of mathematics education program. The results of this study revealed that the learning and teaching process is implemented by emphasizing the use of...

INTERNATIONAL ONLINE CONFERENCE ON MATHEMATICS EDUCATION

Thinking is the process of deciding what to believe or what to do by making sense of the current situation as an action that keeps the brain functioning continuously (Cüceloğlu, 1999). Thinking, which is a mental product, realizes thanks to the interactions between elements that exist in the mind, and if adaptation, reasoning or judgment is to be made, it reaches the result by activating affective inputs in mental processes (Jones, 2019). Environmental factors, education level and social environment are important factors in the development of an individual's thinking skills (Özdemir, 2005). It is divided into many different types in terms of thinking, purpose and skills. For example; creative thinking, critical thinking, analytical thinking, metacognitive thinking, divergent thinking, convergent thinking, lateral thinking, algorithmic thinking and critical thinking (Çiftçi, 2017). According to NACE (2017), employers rated the need for critical thinking/problem solving as the most needed competency for career readiness. During the last two decades students at higher education are being more exposed to the concept of critical thinking as a way to improve not only their professional skills, but their personal competencies as members of a global community (Altuve, 2010; Crenshaw, Hale, & Harper, 2011; Facione, 2013; Moore, 2013; Villarini, 2003). Halpern (2014) warns that in our era, in which a myriad of knowledge can be easily accessed at one click, it is important to teach students to be critical and effective thinkers. Critical thinking is usually related to other skills that are considered key in the 21st century in students’ learning process, with stakeholders, andin everyone’s family life: metacognition, motivation, and creativity (Moeti, Mgawi, & Mealosi, 2017). Critical thinking is a competence student need in their personal and professional lives. Therefore, universities should do their best to include this in their teaching programs and classroom practice. Since there is no clear definition of critical thinking competence and many new methodologies need to be developed to develop this skill, it seems to be an issue that educators should focus on for many years (Bezanilla, et al., 2019). This study was conducted on the classroom teacher candidates' levels of using critical thinking skills through advertisements. This work was carried out with 14 teacher candidates in 3rd grade, the classroom education department of a university in South Anatolia region in Turkey. Before the data were collected, a questionnaire study was carried out on how to reflect their critical thinking skills to prospective teachers in the most comfortable way. This survey included topics such as social problems, covid-19 process, cultural values, our education life, personal development, individual needs, global problems, communication problems and advertisements. Since it was concluded that more than half of the students participating in the study chose the subject of advertising, this study was conducted on advertisements. The opinions and critical approaches of the advertisements given to the pre-service teachers to watch and interpret were analyzed. When the results were examined, it was concluded that the advertisements of the teacher candidates were generally gathered in the themes such as violation of ethical values, products that do not reflect the truth, subliminal messages, gender inequality, and women's body preemptive of products. In general, it can be said that pre-service teachers can look at advertisements critically, but some of them have very superficial implications. The reason for the pre-service teachers' such shallow answers may be that they have not received any thinking training throughout their education. For this, at least after high school education, it can be suggested that the courses with the content of thinking education should be included in the curriculum.

Jurnal Pendidikan Matematika

Mardiana Yusuf

There are many difficulties that can be identified when students solve mathematic problems especially in solving probability word problems. This study was conducted to identify the major obstacles faced by matriculation college students while solving the probability of an event word problems. Seven college students were the sample for this case study. Clinical interviews are used as a data collection. This data collection technique was selected based on the researcher’s observation on the participants as they answered the probability word problem task. The task was given during the interview session. Semi structured interviews are used to obtain in depth information. Think-aloud analysis involves observations leading to individual behaviours in the oral or nonverbal form of participants and the researcher’s field notes. Participants were found to have difficulty interpreting probabilities. There are three categories of difficulties that have been identified, namely not knowing the m...

Mathematics and Statistics

This study is focused on investigating errors made by students and the various causal factors in working on trigonometry problems by applying sine and cosine rules. Samples were taken randomly from high school students. Data were collected in two ways, namely a written test that was referred to Polya's strategy and interviews with students who made mistakes. Students' errors were analyzed with the Newman concept. The results show that all types of errors occurred with a distribution of 3.83, 19.15, 24.74, 24.89 and 27.39% for reading errors (RE), comprehension error (CE), transformation errors (TE), process skill errors (PSE), and encoding errors (EE), respectively. The RE, CE, TE, PSE, and EE are marked by errors in reading symbols or important information, misunderstanding information and not understanding what is known and questioned, cannot change problems into mathematical models and also incorrectly use signs in arithmetic operations, student inaccuracies in the process of answering and also their lack of understanding in fraction operations, and the inability to deduce answers, respectively. An anomaly occurs because it turns out students who have medium trigonometry achievements make more mistakes than students who have low achievement.

TJPRC Publication

The purpose of this study is to analyze the ability and students' difficulties in solving mathematical problems. This study is a qualitative research with the number of participants-32 students consisting of 16 male students and 16 female students with an age range of 12-13 years. Data were collected by observation, interviews, and tests of social arithmetic problems. The results showed that junior high school students have low ability in solving mathematical problems. The low ability of students' mathematical problem solving is caused by several factors, namely (1) students can not understand the keyword of social arithmetic problem; (2) students can not develop problem solving strategy based on problem in question; (3) students easily give up in the face of every difficulty and error; (4) students do not like to read long and unclear questions in reading questions; (5) students are not careful in the calculation process; (6) the student is wrong in taking and determining the concept or strategy of completion; and (7) the students did not verify either in terms of concepts, strategies, calculations, and answers. In subsequent research, our objective is to focus more on student activities in solving mathematical problems.

The study investigated the effects of Solve-Reflect-Pose Strategy (SRP) on pre-service mathematics teachers’ algebraic knowledge for teaching in Nigeria. A pre-test-post-test quasi experimental design was employed. Intact classes were used and in all, 182 pre-service mathematics teachers’ participated in the study (92 in the experimental group taught with the SRP and 90 in the control group taught using the Modified Conventional Method (MCM). One research instrument manipulated at three levels namely: Conceptual Knowledge Test (CKT), Procedural Knowledge Test (PKT) and Flexible Procedural Knowledge Test (FPKT), was used for the quantitative data and interview protocol for qualitative data. The two research questions formulated were analysed using descriptive statistics while independent sample t-test was used to analyse the two hypotheses. Results showed that there were statistically significant differences in the mean post-test achievement scores on conceptual knowledge test, proce...

RELATED PAPERS

Jurnal Math Educator Nusantara: Wahana Publikasi Karya Tulis Ilmiah di Bidang Pendidikan Matematika

suryo widodo

South African Journal of Education

Mohd Hilmi Hamzah

Categories of intuitive reasoning and GeoGebra 3D: an experience with Brazilian students

Renata T E Ó F I L O de Sousa

International Electronic Journal of Mathematics Education

Sharifah Osman

Prof Mdu Ndlovu

Restu Anjarwati

Jurnal Riset Pendidikan Matematika Jakarta

Muiz Ghifari

Phebby Teoh

Al-Jabar : Jurnal Pendidikan Matematika

justin eduardo simarmata

Rahmat Eko Sanjaya

Shiau Wei Chan

World Academy of Research in Science and Engineering

WARSE The World Academy of Research in Science and Engineering

International Electronic Journal of Elementary Education

Sheunghyun Yeo

International Journal of Statistics and Applied Mathematics

MARK REN Villaflor

Journal of Computers in Education

Ju-Ling Shih

Australian Journal of Middle Years of Schooling

Michelle Ronksley-Pavia , Michelle Neumann

Rural Special Education Quarterly

Joseph C A L V I N Gagnon

Joseph C A L V I N Gagnon , Jonte A. Myers

International Journal of Learning and Teaching

Effects of Numerous Seatworks on the Academic Performance of Grade 9 Students in Mathematics in the Philippines

Eriel Chang

Tamika A McLean

Adolescent Success Dec Volume 20 1

Lorraine Day

Research in Science Education

Jeroen Spandaw

World Journal on Educational Technology: Current Issues

WJET Journal

Asia Pacific Journal of Educational Perspectives

Genaro Nocete de Mesa, Jr.

Journal on Mathematics Education

Eddie Aparicio

Large-scale Assessments in Education

Christopher Agard

Journal on Efficiency and Responsibility in Education and Science, 11(3), 53-64

Melanie Gurat

Journal of Education and Learning Mathematics Research (JELMaR)

fatqurhohman fatqurhohman

Education Sciences

Alice Lemmo

Infinity Journal

Elvis Napitupulu

Education Sciences , Osama Swidan

Indonesian Journal on Learning and Advanced Education (IJOLAE)

Subanji Subanji

International Journal for Research in Applied Sciences and Biotechnology

Resty C Samosa

Journal for Multicultural Education

Silvana Watson

Eurasia Journal of Mathematics, Science and Technology Education

Wajeeh Daher

ACADEMIC STUDIES IN EDUCATIONAL SCIENCES

Atilla Ergin

Journal of Education and Learning

Putcharee Junpeng

Nonmanut Pongsakdi

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

Self-Esteem

It’s ok you can’t solve every problem, trying to “fix" everything can leave you feeling like a failure..

Updated May 10, 2024 | Reviewed by Ray Parker

• What Is Self-Esteem?
• Find a therapist near me
• Your intrinsic value is more than what you can do for other people.

You are still worthwhile and can be successful, even if you don’t have all the solutions.

• Consider which decision will make you feel you’ve stayed true to your values.

In coaching others, I often discuss problem-solving strategies to help individuals think creatively and consider many options when they are faced with challenging situations.

Problem solving 1-2 includes the following:

• Define the problem, identify obstacles, and set realistic goals .
• Generate a variety of alternative solutions to overcome obstacles identified.
• Choose which idea has the highest likelihood to achieve the goal.
• Try out the solution in real-life and see if it worked or not.

Problem-solving strategies can be helpful in many situations. Thinking creatively and testing out different potential solutions can help you come up with alternative ways of solving your problems.

While many problems can be solved, there are also situations in which there is no “perfect” solution or in which what seems to be the best solution still leaves you feeling unsatisfied or like you’re not doing enough.

I encourage you to increase your comfort around the following three truths:

1. You can’t always solve everyone else’s problems.

2. You can’t always solve all of your own problems.

3. You are not a failure if you can’t solve every problem.

You can’t always solve everyone else’s problems.

When someone around you needs help, do you feel compelled to find solutions to their problem?

Are you seen as the problem solver at your job or in your close relationships?

Does it feel uncomfortable for you to listen to someone tell you about a problem and not offer solutions?

There are times when others come to you because they know you can help them solve a problem. There are also times when the other person is coming to you not for a solution to their problem, but for support, empathy, and a listening ear.

Your relationships may be negatively impacted if others feel that you don’t fully listen and only try to “fix” everything for them. While this may feel like a noble act, it may lead the other person to feel like they have failed or that you think they are unable to solve their own problems.

Consider approaching such situations with curiosity by saying to the other person:

• As you share this information with me, tell me how I can best support you.
• What would be most helpful right now? Are you looking for an empathetic ear or want to brainstorm potential next steps?
• I want to be sure I am as helpful as I can be right now; what are you hoping to get out of our conversation?

You can’t always solve all of your own problems.

We are taught from a young age that problems have a solution. For example, while solving word problems in math class may not have been your favorite thing to do, you knew there was ultimately a “right” answer. Many times, the real world is much more complex, and many of the problems that you face do not have clear or “right” answers.

You may often be faced with finding solutions that do the most good for the most amount of people, but you know that others may still be left out or feel unsatisfied with the result.

Your beliefs about yourself, other people, and the world can sometimes help you make decisions in such circumstances. You may ask for help from others. Some may consider their faith or spirituality for guidance. While others may consider philosophical theories.

Knowing that there often isn’t a “perfect” solution, you may consider asking yourself some of the following questions:

• What’s the healthiest decision I can make? The healthiest decision for yourself and for those who will be impacted.
• Imagine yourself 10 years in the future, looking back on the situation: What do you think the future-you would encourage you to do?
• What would a wise person do?
• What decision will allow you to feel like you’ve stayed true to your values?

You are not a failure if you can’t solve all of the problems.

If you have internalized feeling like you need to be able to solve every problem that comes across your path, you may feel like a failure each time you don’t.

It’s impossible to solve every problem.

Your intrinsic value is more than what you can do for other people. You have value because you are you.

Consider creating more realistic and adaptive thoughts around your ability to help others and solve problems.

Some examples include:

• I am capable, even without solving all of the problems.
• I am worthwhile, even if I’m not perfect.
• What I do for others does not define my worth.
• In living my values, I know I’ve done my best.

I hope you utilize the information above to consider how you can coach yourself the next time you:

• Start to solve someone else’s problem without being asked.
• Feel stuck in deciding the best next steps.
• Judge yourself negatively.

1. D'zurilla, T. J., & Goldfried, M. R. (1971). Problem solving and behavior modification. Journal of abnormal psychology, 78(1), 107.

2. D’Zurilla, T. J., & Nezu, A. M. (2010). Problem-solving therapy. Handbook of cognitive-behavioral therapies, 3(1), 197-225.

Julie Radico, Psy.D. ABPP, is a board-certified clinical psychologist and coauthor of You Will Get Through This: A Mental Health First-Aid Kit.

• Find a Therapist
• Find a Treatment Center
• Find a Psychiatrist
• Find a Support Group
• Find Online Therapy
• United States
• Brooklyn, NY
• Chicago, IL
• Houston, TX
• Los Angeles, CA
• New York, NY
• Portland, OR
• San Diego, CA
• San Francisco, CA
• Seattle, WA
• Washington, DC
• Asperger's
• Bipolar Disorder
• Chronic Pain
• Eating Disorders
• Passive Aggression
• Personality
• Goal Setting
• Positive Psychology
• Stopping Smoking
• Low Sexual Desire
• Relationships
• Child Development
• Self Tests NEW
• Therapy Center
• Diagnosis Dictionary
• Types of Therapy

At any moment, someone’s aggravating behavior or our own bad luck can set us off on an emotional spiral that threatens to derail our entire day. Here’s how we can face our triggers with less reactivity so that we can get on with our lives.

• Emotional Intelligence
• Gaslighting
• Affective Forecasting
• Neuroscience