problem solving involving surface area

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.8: Volume and Surface Area

• Last updated
• Save as PDF
• Page ID 129646

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

After completing this section, you should be able to:

• Calculate the surface area of right prisms and cylinders.
• Calculate the volume of right prisms and cylinders.
• Solve application problems involving surface area and volume.

Volume and surface area are two measurements that are part of our daily lives. We use volume every day, even though we do not focus on it. When you purchase groceries, volume is the key to pricing. Judging how much paint to buy or how many square feet of siding to purchase is based on surface area. The list goes on. An example is a three-dimensional rendering of a floor plan. These types of drawings make building layouts far easier to understand for the client. It allows the viewer a realistic idea of the product at completion; you can see the natural space, the volume of the rooms. This section gives you practical information you will use consistently. You may not remember every formula, but you will remember the concepts, and you will know where to go should you want to calculate volume or surface area in the future.

We will concentrate on a few particular types of three-dimensional objects: right prisms and right cylinders. The adjective “right” refers to objects such that the sides form a right angle with the base. We will look at right rectangular prisms, right triangular prisms, right hexagonal prisms, right octagonal prisms, and right cylinders. Although, the principles learned here apply to all right prisms.

Three-Dimensional Objects

In geometry, three-dimensional objects are called geometric solids . Surface area refers to the flat surfaces that surround the solid and is measured in square units. Volume refers to the space inside the solid and is measured in cubic units. Imagine that you have a square flat surface with width and length. Adding the third dimension adds depth or height, depending on your viewpoint, and now you have a box. One way to view this concept is in the Cartesian coordinate three-dimensional space. The x Figure 10.161.

Here is another view taking the two-dimensional square to a third dimension. See Figure 10.162.

To study objects in three dimensions, we need to consider the formulas for surface area and volume. For example, suppose you have a box (Figure 10.163) with a hinged lid that you want to use for keeping photos, and you want to cover the box with a decorative paper. You would need to find the surface area to calculate how much paper is needed. Suppose you need to know how much water will fill your swimming pool. In that case, you would need to calculate the volume of the pool. These are just a couple of examples of why these concepts should be understood, and familiarity with the formulas will allow you to make use of these ideas as related to right prisms and right cylinders.

Right Prisms

A right prism is a particular type of three-dimensional object. It has a polygon-shaped base and a congruent, regular polygon-shaped top, which are connected by the height of its lateral sides, as shown in Figure 10.164. The lateral sides form a right angle with the base and the top. There are rectangular prisms, hexagonal prisms, octagonal prisms, triangular prisms, and so on.

Generally, to calculate surface area, we find the area of each side of the object and add the areas together. To calculate volume, we calculate the space inside the solid bounded by its sides.

The formula for the surface area of a right prism is equal to twice the area of the base plus the perimeter of the base times the height, S A = 2 B + p h , S A = 2 B + p h , where B B is equal to the area of the base and top, p p is the perimeter of the base, and h h is the height.

The formula for the volume of a rectangular prism, given in cubic units, is equal to the area of the base times the height, V = B ⋅ h , V = B ⋅ h , where B B is the area of the base and h h is the height.

Example 10.56

Calculating surface area and volume of a rectangular prism.

Find the surface area and volume of the rectangular prism that has a width of 10 cm, a length of 5 cm, and a height of 3 cm (Figure 10.165).

The surface area is S A = 2 ( 10 ) ( 5 ) + 2 ( 5 ) ( 3 ) + 2 ( 10 ) ( 3 ) = 190 cm 2 . S A = 2 ( 10 ) ( 5 ) + 2 ( 5 ) ( 3 ) + 2 ( 10 ) ( 3 ) = 190 cm 2 .

The volume is V = 10 ( 5 ) ( 3 ) = 150 cm 3 . V = 10 ( 5 ) ( 3 ) = 150 cm 3 .

Your Turn 10.56

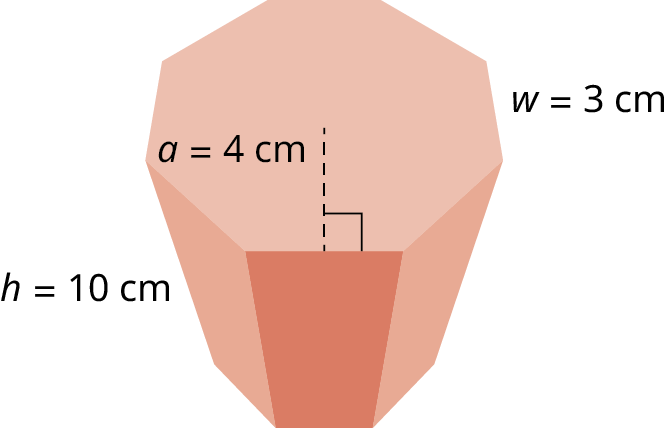
In Figure 10.167, we have three views of a right hexagonal prism. The regular hexagon is the base and top, and the lateral faces are the rectangular regions perpendicular to the base. We call it a right prism because the angle formed by the lateral sides to the base is 90 ∘ . Figure 10.164.

The first image is a view of the figure straight on with no rotation in any direction. The middle figure is the base or the top. The last figure shows you the solid in three dimensions. To calculate the surface area of the right prism shown in Figure 10.167, we first determine the area of the hexagonal base and multiply that by 2, and then add the perimeter of the base times the height. Recall the area of a regular polygon is given as A = 1 2 a p , A = 1 2 a p , where a a is the apothem and p p is the perimeter. We have that

A b a s e = 1 2 ( 5.2 ) ( 36 ) = 93.6 cm 2 A b a s e = 1 2 ( 5.2 ) ( 36 ) = 93.6 cm 2

Then, the surface area of the hexagonal prism is

S A = 2 ( 93.6 ) + 36 ( 20 ) = 907.2 in 2 S A = 2 ( 93.6 ) + 36 ( 20 ) = 907.2 in 2

To find the volume of the right hexagonal prism, we multiply the area of the base by the height using the formula V = B h . V = B h . The base is 93.6 cm 2 , 93.6 cm 2 , and the height is 20 cm cm . Thus,

V = 93.6 ( 20 ) = 1872 cm 3 . V = 93.6 ( 20 ) = 1872 cm 3 .

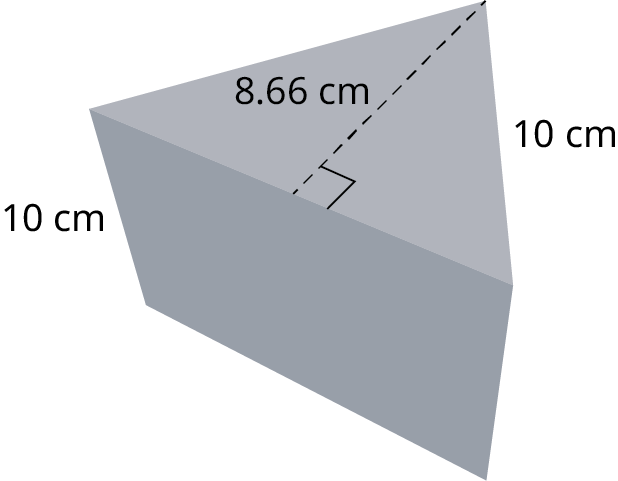
Example 10.57

Calculating the surface area of a right triangular prism.

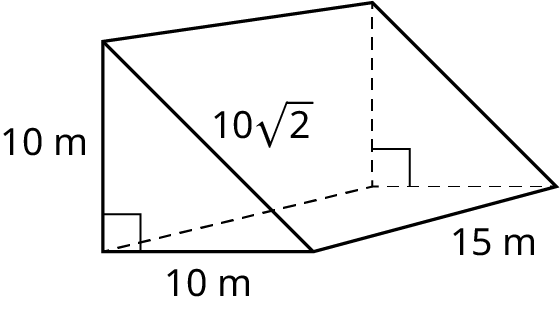
Find the surface area of the triangular prism (Figure 10.168).

The area of the triangular base is A b a s e = 1 2 ( 12 ) ( 6 ) = 36 in 2 A b a s e = 1 2 ( 12 ) ( 6 ) = 36 in 2 . The perimeter of the base is p = 12 + 8.49 + 8.49 = 28.98 in . p = 12 + 8.49 + 8.49 = 28.98 in . Then, the surface area of the triangular prism is S A = 2 ( 36 ) + 28.98 ( 10 ) = 361.8 in 2 . S A = 2 ( 36 ) + 28.98 ( 10 ) = 361.8 in 2 .

Your Turn 10.57

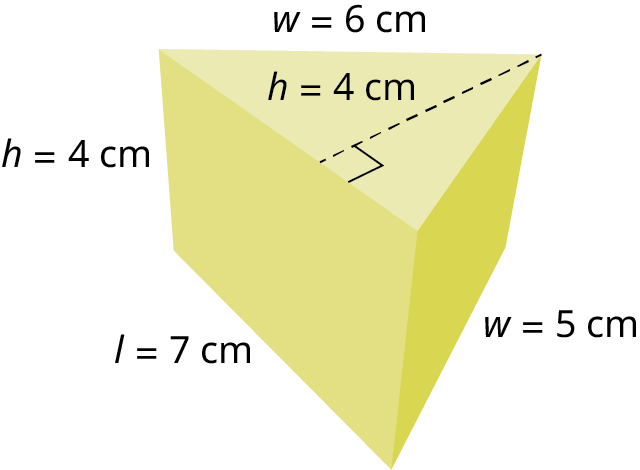
Example 10.58

Finding the surface area and volume.

Find the surface area and the volume of the right triangular prism with an equilateral triangle as the base and height (Figure 10.170).

The area of the triangular base is A b a s e = 1 2 ( 6 ) ( 10.39 ) = 31.17 cm 2 A b a s e = 1 2 ( 6 ) ( 10.39 ) = 31.17 cm 2 . Then, the surface area is S A = 2 ( 31.17 ) + 36 ( 10 ) = 422.34 cm 2 . S A = 2 ( 31.17 ) + 36 ( 10 ) = 422.34 cm 2 .

The volume formula is found by multiplying the area of the base by the height. We have that V = B ⋅ h = ( 31.17 ) ( 10 ) = 311.7 cm 3 . V = B ⋅ h = ( 31.17 ) ( 10 ) = 311.7 cm 3 .

Your Turn 10.58

Example 10.59

Determining surface area application.

Katherine and Romano built a greenhouse made of glass with a metal roof (Figure 10.172). In order to determine the heating and cooling requirements, the surface area must be known. Calculate the total surface area of the greenhouse.

The area of the long side measures 95 ft × 6.5 ft = 1,235 ft 2 . 95 ft × 6.5 ft = 1,235 ft 2 . Multiplying by 2 gives 2,470 ft 2 . 2,470 ft 2 . The front (minus the triangular area) measures 22 ft × 6.5 ft = 286 ft 2 . 22 ft × 6.5 ft = 286 ft 2 . Multiplying by 2 gives 572 ft 2 . 572 ft 2 . The floor measures 95 ft × 22 ft = 2,090 ft 2 . 95 ft × 22 ft = 2,090 ft 2 . Each triangular region measures A = 1 2 ( 22 ) ( 5 ) = 55 ft 2 . A = 1 2 ( 22 ) ( 5 ) = 55 ft 2 . Multiplying by 2 gives 110 ft 2 . 110 ft 2 . Finally, one side of the roof measures 12.1 ft × 95 ft = 1,149.5 ft 2 . 12.1 ft × 95 ft = 1,149.5 ft 2 . Multiplying by 2 gives 2299 ft 2 . 2299 ft 2 . Add them up and we have S A = 2,470 + 572 + 2,090 + 110 + 2,299 = 7,541 ft 2 . S A = 2,470 + 572 + 2,090 + 110 + 2,299 = 7,541 ft 2 .

Your Turn 10.59

Right cylinders.

There are similarities between a prism and a cylinder. While a prism has parallel congruent polygons as the top and the base, a right cylinder is a three-dimensional object with congruent circles as the top and the base. The lateral sides of a right prism make a 90 ∘ 90 ∘ angle with the polygonal base, and the side of a cylinder, which unwraps as a rectangle, makes a 90 ∘ 90 ∘ angle with the circular base.

Right cylinders are very common in everyday life. Think about soup cans, juice cans, soft drink cans, pipes, air hoses, and the list goes on.

In Figure 10.173, imagine that the cylinder is cut down the 12-inch side and rolled out. We can see that the cylinder side when flat forms a rectangle. The S A S A formula includes the area of the circular base, the circular top, and the area of the rectangular side. The length of the rectangular side is the circumference of the circular base. Thus, we have the formula for total surface area of a right cylinder.

The surface area of a right cylinder is given as S A = 2 π r 2 + 2 π r h . S A = 2 π r 2 + 2 π r h .

To find the volume of the cylinder, we multiply the area of the base with the height.

The volume of a right cylinder is given as V = π r 2 h . V = π r 2 h .

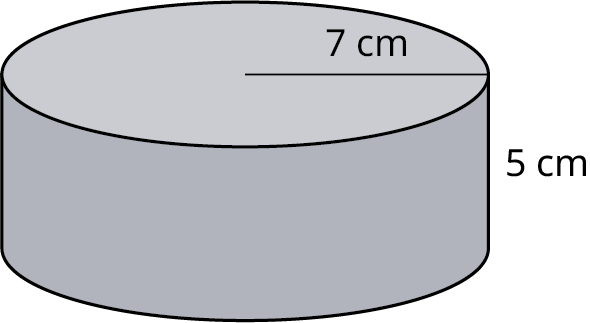
Example 10.60

Finding the surface area and volume of a cylinder.

Given the cylinder in Figure 10.173, which has a radius of 5 inches and a height of 12 inches, find the surface area and the volume.

Step 1: We begin with the areas of the base and the top. The area of the circular base is

A b a s e = π ( 5 ) 2 = 25 π = 78.5 in 2 . A b a s e = π ( 5 ) 2 = 25 π = 78.5 in 2 .

Step 2: The base and the top are congruent parallel planes. Therefore, the area for the base and the top is

A = 2 ( 78.5 ) = 157 in 2 . A = 2 ( 78.5 ) = 157 in 2 .

Step 3: The area of the rectangular side is equal to the circumference of the base times the height:

A = 2 π ( 5 ) ( 12 ) = 377 in 2 A = 2 π ( 5 ) ( 12 ) = 377 in 2

Step 4: We add the area of the side to the areas of the base and the top to get the total surface area. We have

S A = 157 + 377 = 534 in 2 S A = 157 + 377 = 534 in 2 .

Step 5: The volume is equal to the area of the base times the height. Then,

Your Turn 10.60

Applications of Surface Area and Volume

The following are just a small handful of the types of applications in which surface area and volume are critical factors. Give this a little thought and you will realize many more practical uses for these procedures.

Example 10.61

Applying a calculation of volume.

A can of apple pie filling has a radius of 4 cm and a height of 10 cm. How many cans are needed to fill a pie pan (Figure 10.175) measuring 22 cm in diameter and 3 cm deep?

The volume of the can of apple pie filling is V = π ( 4 ) 2 ( 10 ) = 502.7 cm 3 . V = π ( 4 ) 2 ( 10 ) = 502.7 cm 3 . The volume of the pan is V = π ( 11 ) 2 ( 3 ) = 1140.4 cm 3 . V = π ( 11 ) 2 ( 3 ) = 1140.4 cm 3 . To find the number of cans of apple pie filling, we divide the volume of the pan by the volume of a can of apple pie filling. Thus, 1140 ÷ 502.7 = 2.3. 1140 ÷ 502.7 = 2.3. We will need 2.3 cans of apple pie filling to fill the pan.

Your Turn 10.61

Optimization.

Problems that involve optimization are ones that look for the best solution to a situation under some given conditions. Generally, one looks to calculus to solve these problems. However, many geometric applications can be solved with the tools learned in this section. Suppose you want to make some throw pillows for your sofa, but you have a limited amount of fabric. You want to make the largest pillows you can from the fabric you have, so you would need to figure out the dimensions of the pillows that will fit these criteria. Another situation might be that you want to fence off an area in your backyard for a garden. You have a limited amount of fencing available, but you would like the garden to be as large as possible. How would you determine the shape and size of the garden? Perhaps you are looking for maximum volume or minimum surface area. Minimum cost is also a popular application of optimization. Let’s explore a few examples.

Example 10.62

Maximizing area.

Suppose you have 150 meters of fencing that you plan to use for the enclosure of a corral on a ranch. What shape would give the greatest possible area?

So, how would we start? Let’s look at this on a smaller scale. Say that you have 30 inches of string and you experiment with different shapes. The rectangle in Figure 10.176 measures 12 in long by 3 in wide. We have a perimeter of P = 2 ( 12 ) + 2 ( 3 ) = 30 in Figure 10.176, measures 8 in long and 7 in wide. The perimeter is P = 2 ( 8 ) + 2 ( 7 ) = 30 in Figure 10.176, the square measures 7.5 in on each side. The perimeter is then P = 4 ( 7.5 ) = 30 in Figure 10.176, we would consider a circumference of 30 = 2 π r , 30 = 2 π r , which gives a radius of 30 ÷ 2 π = 4.77 in 30 ÷ 2 π = 4.77 in and an area of A = π ( 4.77 ) 2 = 71.5 in 2 . A = π ( 4.77 ) 2 = 71.5 in 2 .

We see that the circular shape gives the maximum area relative to a circumference of 30 in. So, a circular corral with a circumference of 150 meters and a radius of 23.87 meters gives a maximum area of 1,790.5 m 2 . 1,790.5 m 2 .

Your Turn 10.62

Example 10.63, designing for cost.

Suppose you want to design a crate built out of wood in the shape of a rectangular prism (Figure 10.177). It must have a volume of 3 cubic meters. The cost of wood is $15 per square meter. What dimensions give the most economical design while providing the necessary volume?

To choose the optimal shape for this container, you can start by experimenting with different sizes of boxes that will hold 3 cubic meters. It turns out that, similar to the maximum rectangular area example where a square gives the maximum area, a cube gives the maximum volume and the minimum surface area.

As all six sides are the same, we can use a simplified volume formula:

V = s 3 , V = s 3 ,

where s s is the length of a side. Then, to find the length of a side, we take the cube root of the volume.

3 = s 3 3 3 = s = 1.4422 m 3 = s 3 3 3 = s = 1.4422 m

The surface area is equal to the sum of the areas of the six sides. The area of one side is A = ( 1.4422 ) 2 = 2.08 m 2 . A = ( 1.4422 ) 2 = 2.08 m 2 . So, the surface area of the crate is S A = 6 ( 2.08 ) = 12.5 m 2 S A = 6 ( 2.08 ) = 12.5 m 2 . At $15 a square meter, the cost comes to 12.5 ( $ 15 ) = $ 187.50. 12.5 ( $ 15 ) = $ 187.50. Checking the volume, we have V = ( 1.4422 ) 3 = 2.99 m 3 V = ( 1.4422 ) 3 = 2.99 m 3 .

Your Turn 10.63

Check your understanding.

Section 10.7 Exercises

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Geometry >

Surface Area Worksheets

Surface area worksheets comprise an enormous collection of exercises on different solid figures. The large chunk of exercises is categorized based on a step-by-step approach involving counting unit squares to determine the SA, finding the surface area of nets, and then computing the surface area of geometrical shapes like cubes, cones, cylinders, rectangular prisms, L-shaped prisms, spheres, hemispheres, pyramids, and composite figures, catering to the needs of students in 5th grade through high school. Revisiting surface area is easy with our mixed 3D shapes revision pdfs. Count on our free printable SA worksheets for a great start!

List of Surface Area Worksheets

• Surface Area of 3D Figures Using Nets
• Surface Area by Counting Squares
• Surface Area of Cubes
• Surface Area of Rectangular Prisms
• Surface Area of L-Shaped Prisms
• Surface Area of Triangular Prisms
• Surface Area of Cylinders
• Surface Area of Prisms and Cylinders
• Surface Area of Cones
• Surface Area of Spheres and Hemispheres
• Surface Area of Pyramids
• Surface Area of Mixed Solid Shapes
• Surface Area of Composite Figures

Explore the Surface Area Worksheets in Detail

Surface Area of 3D Figures Using Nets Worksheets

Finding the surface area of 3D figures using nets worksheets assist students in visualizing the surface of solid shapes whose nets are sketched on grids. Add on to their practice in determining the SA of the nets of 3D shapes like cylinders, cones, and pyramids, and in drawing the nets of solid figures too.

Surface Area by Counting Squares Worksheets

Start off with counting unit squares on an isometric paper, follow up by drawing the correct number of squares, and then find the SA of rectangular prisms by counting the squares scaled to varied units. These interesting exercises make the surface area by counting squares pdfs a compulsive print for your grade 5 and grade 6 students.

Surface Area of Cubes Worksheets

Page through these surface area of a cube exercises to practice computing the total area occupied by the cubes with edge length offered as integers, decimals and fractions. Included here are pdfs to find the missing edge length using the SA and more.

Surface Area of Rectangular Prisms Worksheets

Surface area of rectangular prisms handouts are a sure-fire hit in every grade 6, grade 7, and grade 8 geometry curriculum. Find the SA using the height, width, and length, and extend your practice to finding the missing dimensions as well.

Surface Area of L-Shaped Prisms Worksheets

Lay a strong foundation in decomposing shapes with these printable surface area of L-shaped rectangular prism worksheets. Solve for surface area of independent 3D shapes, add them, and subtract the area of the face that connects the rectangular blocks.

Surface Area of Triangular Prisms Worksheets

Expedite practice calculating the surface area of triangular prisms with these worksheet pdfs, rendering the attributes of the triangular bases and rectangular side faces of the figure, in integers and decimals.

Surface Area of Cylinders Worksheets

The surface area of a cylinder pdfs feature solid shapes, each made up of a curved surface with two circular bases. Recall the formula for SA of a cylinder, plug in the integer, decimal, or fractional radius measures in the formula 2πrh + 2πr 2 and compute.

Surface Area of Prisms and Cylinders Worksheets

A mix of rectangular prisms, triangular prisms, and cylinders is what these printable worksheets have in store for your middle and high school learners. Consider memorizing the SA formulas, apply the one relevant to the solid shape, substitute the dimensions and solve.

Surface Area of Cones Worksheets

Give your 6th grade, 7th grade, and 8th grade students an edge over their peers with these surface area of cones exercises. Supplying the values of the dimensions in the formula and calculating the surface area of cones is all that is expected of learners.

Surface Area of Spheres and Hemispheres Worksheets

Build fluency and competence with this collection of surface area of spheres and hemispheres worksheets. Get students to find the TSA of the hemispheres and CSA of the spheres by substituting the dimensions in relevant formulas.

Surface Area of Pyramids Worksheets

Handle these printable surface area of pyramid practice sheets with great dexterity. Learn the know-how of finding the surface area of pyramids applying relevant formulas and substituting the dimensions accordingly.

Surface Area of Mixed Solid Shapes Worksheets

How well do your 8th grade and high school students remember the SA formulas of solid shapes like cubes, cones, cylinders, spheres, hemispheres, prisms and pyramids? Check for yourself with these surface area of solid shapes revision pdfs.

Surface Area of Composite Figures Worksheets

Tee up to decompose each combined shape, find the sum of the SA of individual 3D shapes, subtract the area of the common parts, and determine the SA like a pro with this set of printable surface area of composite shapes worksheets.

Sample Worksheets

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

Surface Area Questions

Surface Area of a Cuboid

Click here for Questions and Answers

Surface Area of a Prism

Surface Area of a Cylinder

Surface Area of a Sphere

Surface Area of a Cone

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 6th grade   >   Unit 10

• Expressions to find surface area

Surface area

• Surface area versus volume
• Surface area word problem example
• Surface area word problems
• Surface area review
• 3D figures FAQ

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Surface Area and Volume in the Real World

New york state common core math grade 6, module 5, lesson 19.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Practice problems of the surface area

Number of problems found: 978.

• all math problems 18875
• solid geometry 2293
• surface area 978
• pyramid 134
• cylinder 116
• spherical cap 15
• hemisphere 11

• New math problems
• Popular math problems
• Harder math problems
• The easiest word problems

Engage your students with effective distance learning resources. ACCESS RESOURCES>>

Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

Grade 6 Mathematics Module: Solving Word Problems Involving Measurement of Surface Area

This Self-Learning Module (SLM) is prepared so that you, our dear learners, can continue your studies and learn while at home. Activities, questions, directions, exercises, and discussions are carefully stated for you to understand each lesson.

Each SLM is composed of different parts. Each part shall guide you step-by-step as you discover and understand the lesson prepared for you.

Pre-tests are provided to measure your prior knowledge on lessons in each SLM. This will tell you if you need to proceed on completing this module or if you need to ask your facilitator or your teacher’s assistance for better understanding of the lesson. At the end of each module, you need to answer the post-test to self-check your learning. Answer keys are provided for each activity and test. We trust that you will be honest in using these.

Please use this module with care. Do not put unnecessary marks on any part of this SLM. Use a separate sheet of paper in answering the exercises and tests. And read the instructions carefully before performing each task.

This module was designed and written with you in mind. It is here to help you master the skills in solving word problems involving surface area. this module allows you to use it in various learning situations. The language used recognizes your vocabulary level. The lessons are arranged to follow the standard sequence of your course. But the order in which you read them can be changed to match with the textbook you are now using.

After going through this module, you are expected to be able to solve word problems involving measurement of surface area of different solid objects.

Grade 6 Mathematics Quarter 3 Self-Learning Module: Solving Word Problems Involving Measurement of Surface Area

Can't find what you're looking for.

We are here to help - please use the search box below.

Leave a Comment Cancel reply

Area of Composite Figures Word Problems

The area of composite shapes is the area that is covered by any composite shape. The composite shape is a shape in which few polygons are put together to form a required shape. These shapes or figures can be made up of a combination of triangles, squares, and quadrilaterals, etc. Divide a composite shape into basic shapes like square, triangle, rectangle, hexagon, etc. to determine the area of composite shapes.

1. Read the word problem and decompose the composite figure into simpler shapes of which you can find the area. 2. Write down the area formulas of the simpler shapes. 3. Substitute the given values into the formulas. 4. Add or subtract the areas of the simple shapes as needed and state the correct square units.

The area is composed of a square and two semicircles (one whole circle).

Area of the pool = Area of a circle + Area of a square

= πr 2 + s 2

= 3.14 (18.25 m) 2 + (36.5 m) 2

= 1045.81 m 2 + 1332.25 m 2

= 2378.1 m 2

Practice Area of Composite Figures Word Problems

Practice Problem 1

Practice Problem 2

Practice Problem 3

Composite figure – a figure created by adding two or more shapes.

Area – the space occupied by a flat shape or the surface of an object.

Pre-requisite Skills Measurement – Perimeter Measurement – Area Circumference and Area of Circles Circles: Diameter, Radius, Circumference Area of a parallelogram Area of a triangle

Related Skills Surface Area of Prisms Surface Area of Pyramids Surface Area of Cylinders Surface Area of Cones Surface Area of Rectangular Prisms Surface Area of Composite Figures