null hypothesis scientific definition

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Null Hypothesis Examples

The null hypothesis (H 0 ) is the hypothesis that states there is no statistical difference between two sample sets. In other words, it assumes the independent variable does not have an effect on the dependent variable in a scientific experiment .

The null hypothesis is the most powerful type of hypothesis in the scientific method because it’s the easiest one to test with a high confidence level using statistics. If the null hypothesis is accepted, then it’s evidence any observed differences between two experiment groups are due to random chance. If the null hypothesis is rejected, then it’s strong evidence there is a true difference between test sets or that the independent variable affects the dependent variable.

• The null hypothesis is a nullifiable hypothesis. A researcher seeks to reject it because this result strongly indicates observed differences are real and not just due to chance.
• The null hypothesis may be accepted or rejected, but not proven. There is always a level of confidence in the outcome.

What Is the Null Hypothesis?

The null hypothesis is written as H 0 , which is read as H-zero, H-nought, or H-null. It is associated with another hypothesis, called the alternate or alternative hypothesis H A or H 1 . When the null hypothesis and alternate hypothesis are written mathematically, they cover all possible outcomes of an experiment.

An experimenter tests the null hypothesis with a statistical analysis called a significance test. The significance test determines the likelihood that the results of the test are not due to chance. Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01). But, even if the confidence in the test is high, there is always a small chance the outcome is incorrect. This means you can’t prove a null hypothesis. It’s also a good reason why it’s important to repeat experiments.

Exact and Inexact Null Hypothesis

The most common type of null hypothesis assumes no difference between two samples or groups or no measurable effect of a treatment. This is the exact hypothesis . If you’re asked to state a null hypothesis for a science class, this is the one to write. It is the easiest type of hypothesis to test and is the only one accepted for certain types of analysis. Examples include:

There is no difference between two groups H 0 : μ 1  = μ 2 (where H 0  = the null hypothesis, μ 1  = the mean of population 1, and μ 2  = the mean of population 2)

Both groups have value of 100 (or any number or quality) H 0 : μ = 100

However, sometimes a researcher may test an inexact hypothesis . This type of hypothesis specifies ranges or intervals. Examples include:

Recovery time from a treatment is the same or worse than a placebo: H 0 : μ ≥ placebo time

There is a 5% or less difference between two groups: H 0 : 95 ≤ μ ≤ 105

An inexact hypothesis offers “directionality” about a phenomenon. For example, an exact hypothesis can indicate whether or not a treatment has an effect, while an inexact hypothesis can tell whether an effect is positive of negative. However, an inexact hypothesis may be harder to test and some scientists and statisticians disagree about whether it’s a true null hypothesis .

How to State the Null Hypothesis

To state the null hypothesis, first state what you expect the experiment to show. Then, rephrase the statement in a form that assumes there is no relationship between the variables or that a treatment has no effect.

Example: A researcher tests whether a new drug speeds recovery time from a certain disease. The average recovery time without treatment is 3 weeks.

• State the goal of the experiment: “I hope the average recovery time with the new drug will be less than 3 weeks.”
• Rephrase the hypothesis to assume the treatment has no effect: “If the drug doesn’t shorten recovery time, then the average time will be 3 weeks or longer.” Mathematically: H 0 : μ ≥ 3

This null hypothesis (inexact hypothesis) covers both the scenario in which the drug has no effect and the one in which the drugs makes the recovery time longer. The alternate hypothesis is that average recovery time will be less than three weeks:

H A : μ < 3

Of course, the researcher could test the no-effect hypothesis (exact null hypothesis): H 0 : μ = 3

The danger of testing this hypothesis is that rejecting it only implies the drug affected recovery time (not whether it made it better or worse). This is because the alternate hypothesis is:

H A : μ ≠ 3 (which includes μ <3 and μ >3)

Even though the no-effect null hypothesis yields less information, it’s used because it’s easier to test using statistics. Basically, testing whether something is unchanged/changed is easier than trying to quantify the nature of the change.

Remember, a researcher hopes to reject the null hypothesis because this supports the alternate hypothesis. Also, be sure the null and alternate hypothesis cover all outcomes. Finally, remember a simple true/false, equal/unequal, yes/no exact hypothesis is easier to test than a more complex inexact hypothesis.

• Adèr, H. J.; Mellenbergh, G. J. & Hand, D. J. (2007).  Advising on Research Methods: A Consultant’s Companion . Huizen, The Netherlands: Johannes van Kessel Publishing. ISBN  978-90-79418-01-5 .
• Cox, D. R. (2006).  Principles of Statistical Inference . Cambridge University Press. ISBN  978-0-521-68567-2 .
• Everitt, Brian (1998).  The Cambridge Dictionary of Statistics . Cambridge, UK New York: Cambridge University Press. ISBN 978-0521593465.
• Weiss, Neil A. (1999).  Introductory Statistics  (5th ed.). ISBN 9780201598773.

Related Posts

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 14 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Null hypothesis

Null hypothesis n., plural: null hypotheses [nʌl haɪˈpɒθɪsɪs] Definition: a hypothesis that is valid or presumed true until invalidated by a statistical test

Table of Contents

Null Hypothesis Definition

Null hypothesis is defined as “the commonly accepted fact (such as the sky is blue) and researcher aim to reject or nullify this fact”.

More formally, we can define a null hypothesis as “a statistical theory suggesting that no statistical relationship exists between given observed variables” .

In biology , the null hypothesis is used to nullify or reject a common belief. The researcher carries out the research which is aimed at rejecting the commonly accepted belief.

What Is a Null Hypothesis?

A hypothesis is defined as a theory or an assumption that is based on inadequate evidence. It needs and requires more experiments and testing for confirmation. There are two possibilities that by doing more experiments and testing, a hypothesis can be false or true. It means it can either prove wrong or true (Blackwelder, 1982).

For example, Susie assumes that mineral water helps in the better growth and nourishment of plants over distilled water. To prove this hypothesis, she performs this experiment for almost a month. She watered some plants with mineral water and some with distilled water.

In a hypothesis when there are no statistically significant relationships among the two variables, the hypothesis is said to be a null hypothesis. The investigator is trying to disprove such a hypothesis. In the above example of plants, the null hypothesis is:

There are no statistical relationships among the forms of water that are given to plants for growth and nourishment.

Usually, an investigator tries to prove the null hypothesis wrong and tries to explain a relation and association between the two variables.

An opposite and reverse of the null hypothesis are known as the alternate hypothesis . In the example of plants the alternate hypothesis is:

There are statistical relationships among the forms of water that are given to plants for growth and nourishment.

The example below shows the difference between null vs alternative hypotheses:

Alternate Hypothesis: The world is round Null Hypothesis: The world is not round.

Copernicus and many other scientists try to prove the null hypothesis wrong and false. By their experiments and testing, they make people believe that alternate hypotheses are correct and true. If they do not prove the null hypothesis experimentally wrong then people will not believe them and never consider the alternative hypothesis true and correct.

The alternative and null hypothesis for Susie’s assumption is:

• Null Hypothesis: If one plant is watered with distilled water and the other with mineral water, then there is no difference in the growth and nourishment of these two plants.
• Alternative Hypothesis:  If one plant is watered with distilled water and the other with mineral water, then the plant with mineral water shows better growth and nourishment.

The null hypothesis suggests that there is no significant or statistical relationship. The relation can either be in a single set of variables or among two sets of variables.

Most people consider the null hypothesis true and correct. Scientists work and perform different experiments and do a variety of research so that they can prove the null hypothesis wrong or nullify it. For this purpose, they design an alternate hypothesis that they think is correct or true. The null hypothesis symbol is H 0 (it is read as H null or H zero ).

Why is it named the “Null”?

The name null is given to this hypothesis to clarify and explain that the scientists are working to prove it false i.e. to nullify the hypothesis. Sometimes it confuses the readers; they might misunderstand it and think that statement has nothing. It is blank but, actually, it is not. It is more appropriate and suitable to call it a nullifiable hypothesis instead of the null hypothesis.

Why do we need to assess it? Why not just verify an alternate one?

In science, the scientific method is used. It involves a series of different steps. Scientists perform these steps so that a hypothesis can be proved false or true. Scientists do this to confirm that there will be any limitation or inadequacy in the new hypothesis. Experiments are done by considering both alternative and null hypotheses, which makes the research safe. It gives a negative as well as a bad impact on research if a null hypothesis is not included or a part of the study. It seems like you are not taking your research seriously and not concerned about it and just want to impose your results as correct and true if the null hypothesis is not a part of the study.

Development of the Null

In statistics, firstly it is necessary to design alternate and null hypotheses from the given problem. Splitting the problem into small steps makes the pathway towards the solution easier and less challenging. how to write a null hypothesis?

Writing a null hypothesis consists of two steps:

• Firstly, initiate by asking a question.
• Secondly, restate the question in such a way that it seems there are no relationships among the variables.

In other words, assume in such a way that the treatment does not have any effect.

The usual recovery duration after knee surgery is considered almost 8 weeks.

A researcher thinks that the recovery period may get elongated if patients go to a physiotherapist for rehabilitation twice per week, instead of thrice per week, i.e. recovery duration reduces if the patient goes three times for rehabilitation instead of two times.

Step 1: Look for the problem in the hypothesis. The hypothesis either be a word or can be a statement. In the above example the hypothesis is:

“The expected recovery period in knee rehabilitation is more than 8 weeks”

Step 2: Make a mathematical statement from the hypothesis. Averages can also be represented as μ, thus the null hypothesis formula will be.

In the above equation, the hypothesis is equivalent to H1, the average is denoted by μ and > that the average is greater than eight.

Step 3: Explain what will come up if the hypothesis does not come right i.e., the rehabilitation period may not proceed more than 08 weeks.

There are two options: either the recovery will be less than or equal to 8 weeks.

H 0 : μ ≤ 8

In the above equation, the null hypothesis is equivalent to H 0 , the average is denoted by μ and ≤ represents that the average is less than or equal to eight.

What will happen if the scientist does not have any knowledge about the outcome?

Problem: An investigator investigates the post-operative impact and influence of radical exercise on patients who have operative procedures of the knee. The chances are either the exercise will improve the recovery or will make it worse. The usual time for recovery is 8 weeks.

Step 1: Make a null hypothesis i.e. the exercise does not show any effect and the recovery time remains almost 8 weeks.

H 0 : μ = 8

In the above equation, the null hypothesis is equivalent to H 0 , the average is denoted by μ, and the equal sign (=) shows that the average is equal to eight.

Step 2: Make the alternate hypothesis which is the reverse of the null hypothesis. Particularly what will happen if treatment (exercise) makes an impact?

In the above equation, the alternate hypothesis is equivalent to H1, the average is denoted by μ and not equal sign (≠) represents that the average is not equal to eight.

Significance Tests

To get a reasonable and probable clarification of statistics (data), a significance test is performed. The null hypothesis does not have data. It is a piece of information or statement which contains numerical figures about the population. The data can be in different forms like in means or proportions. It can either be the difference of proportions and means or any odd ratio.

The following table will explain the symbols:

P-value is the chief statistical final result of the significance test of the null hypothesis.

• P-value = Pr(data or data more extreme | H 0 true)
• | = “given”
• Pr = probability
• H 0 = the null hypothesis

The first stage of Null Hypothesis Significance Testing (NHST) is to form an alternate and null hypothesis. By this, the research question can be briefly explained.

Null Hypothesis = no effect of treatment, no difference, no association Alternative Hypothesis = effective treatment, difference, association

When to reject the null hypothesis?

Researchers will reject the null hypothesis if it is proven wrong after experimentation. Researchers accept null hypothesis to be true and correct until it is proven wrong or false. On the other hand, the researchers try to strengthen the alternate hypothesis. The binomial test is performed on a sample and after that, a series of tests were performed (Frick, 1995).

Step 1: Evaluate and read the research question carefully and consciously and make a null hypothesis. Verify the sample that supports the binomial proportion. If there is no difference then find out the value of the binomial parameter.

Show the null hypothesis as:

H 0 :p= the value of p if H 0 is true

To find out how much it varies from the proposed data and the value of the null hypothesis, calculate the sample proportion.

Step 2: In test statistics, find the binomial test that comes under the null hypothesis. The test must be based on precise and thorough probabilities. Also make a list of pmf that apply, when the null hypothesis proves true and correct.

When H 0 is true, X~b(n, p)

N = size of the sample

P = assume value if H 0 proves true.

Step 3: Find out the value of P. P-value is the probability of data that is under observation.

Rise or increase in the P value = Pr(X ≥ x)

X = observed number of successes

P value = Pr(X ≤ x).

Step 4: Demonstrate the findings or outcomes in a descriptive detailed way.

• Sample proportion
• The direction of difference (either increases or decreases)

Perceived Problems With the Null Hypothesis

Variable or model selection and less information in some cases are the chief important issues that affect the testing of the null hypothesis. Statistical tests of the null hypothesis are reasonably not strong. There is randomization about significance. (Gill, 1999) The main issue with the testing of the null hypothesis is that they all are wrong or false on a ground basis.

There is another problem with the a-level . This is an ignored but also a well-known problem. The value of a-level is without a theoretical basis and thus there is randomization in conventional values, most commonly 0.q, 0.5, or 0.01. If a fixed value of a is used, it will result in the formation of two categories (significant and non-significant) The issue of a randomized rejection or non-rejection is also present when there is a practical matter which is the strong point of the evidence related to a scientific matter.

The P-value has the foremost importance in the testing of null hypothesis but as an inferential tool and for interpretation, it has a problem. The P-value is the probability of getting a test statistic at least as extreme as the observed one.

The main point about the definition is: Observed results are not based on a-value

Moreover, the evidence against the null hypothesis was overstated due to unobserved results. A-value has importance more than just being a statement. It is a precise statement about the evidence from the observed results or data. Similarly, researchers found that P-values are objectionable. They do not prefer null hypotheses in testing. It is also clear that the P-value is strictly dependent on the null hypothesis. It is computer-based statistics. In some precise experiments, the null hypothesis statistics and actual sampling distribution are closely related but this does not become possible in observational studies.

Some researchers pointed out that the P-value is depending on the sample size. If the true and exact difference is small, a null hypothesis even of a large sample may get rejected. This shows the difference between biological importance and statistical significance. (Killeen, 2005)

Another issue is the fix a-level, i.e., 0.1. On the basis, if a-level a null hypothesis of a large sample may get accepted or rejected. If the size of simple is infinity and the null hypothesis is proved true there are still chances of Type I error. That is the reason this approach or method is not considered consistent and reliable. There is also another problem that the exact information about the precision and size of the estimated effect cannot be known. The only solution is to state the size of the effect and its precision.

Null Hypothesis Examples

Here are some examples:

Example 1: Hypotheses with One Sample of One Categorical Variable

Among all the population of humans, almost 10% of people prefer to do their task with their left hand i.e. left-handed. Let suppose, a researcher in the Penn States says that the population of students at the College of Arts and Architecture is mostly left-handed as compared to the general population of humans in general public society. In this case, there is only a sample and there is a comparison among the known population values to the population proportion of sample value.

• Research Question: Do artists more expected to be left-handed as compared to the common population persons in society?
• Response Variable: Sorting the student into two categories. One category has left-handed persons and the other category have right-handed persons.
• Form Null Hypothesis: Arts and Architecture college students are no more predicted to be lefty as compared to the common population persons in society (Lefty students of Arts and Architecture college population is 10% or p= 0.10)

Example 2: Hypotheses with One Sample of One Measurement Variable

A generic brand of antihistamine Diphenhydramine making medicine in the form of a capsule, having a 50mg dose. The maker of the medicines is concerned that the machine has come out of calibration and is not making more capsules with the suitable and appropriate dose.

• Research Question: Does the statistical data recommended about the mean and average dosage of the population differ from 50mg?
• Response Variable: Chemical assay used to find the appropriate dosage of the active ingredient.
• Null Hypothesis: Usually, the 50mg dosage of capsules of this trade name (population average and means dosage =50 mg).

Example 3: Hypotheses with Two Samples of One Categorical Variable

Several people choose vegetarian meals on a daily basis. Typically, the researcher thought that females like vegetarian meals more than males.

• Research Question: Does the data recommend that females (women) prefer vegetarian meals more than males (men) regularly?
• Response Variable: Cataloguing the persons into vegetarian and non-vegetarian categories. Grouping Variable: Gender
• Null Hypothesis: Gender is not linked to those who like vegetarian meals. (Population percent of women who eat vegetarian meals regularly = population percent of men who eat vegetarian meals regularly or p women = p men).

Example 4: Hypotheses with Two Samples of One Measurement Variable

Nowadays obesity and being overweight is one of the major and dangerous health issues. Research is performed to confirm that a low carbohydrates diet leads to faster weight loss than a low-fat diet.

• Research Question: Does the given data recommend that usually, a low-carbohydrate diet helps in losing weight faster as compared to a low-fat diet?
• Response Variable: Weight loss (pounds)
• Explanatory Variable: Form of diet either low carbohydrate or low fat
• Null Hypothesis: There is no significant difference when comparing the mean loss of weight of people using a low carbohydrate diet to people using a diet having low fat. (population means loss of weight on a low carbohydrate diet = population means loss of weight on a diet containing low fat).

Example 5: Hypotheses about the relationship between Two Categorical Variables

A case-control study was performed. The study contains nonsmokers, stroke patients, and controls. The subjects are of the same occupation and age and the question was asked if someone at their home or close surrounding smokes?

• Research Question: Did second-hand smoke enhance the chances of stroke?
• Variables: There are 02 diverse categories of variables. (Controls and stroke patients) (whether the smoker lives in the same house). The chances of having a stroke will be increased if a person is living with a smoker.
• Null Hypothesis: There is no significant relationship between a passive smoker and stroke or brain attack. (odds ratio between stroke and the passive smoker is equal to 1).

Example 6: Hypotheses about the relationship between Two Measurement Variables

A financial expert observes that there is somehow a positive and effective relationship between the variation in stock rate price and the quantity of stock bought by non-management employees

• Response variable- Regular alteration in price
• Explanatory Variable- Stock bought by non-management employees
• Null Hypothesis: The association and relationship between the regular stock price alteration ($) and the daily stock-buying by non-management employees ($) = 0.

Example 7: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples

• Research Question: Is the relation between the bill paid in a restaurant and the tip given to the waiter, is linear? Is this relation different for dining and family restaurants?
• Explanatory Variable- total bill amount
• Response Variable- the amount of tip
• Null Hypothesis: The relationship and association between the total bill quantity at a family or dining restaurant and the tip, is the same.

Try to answer the quiz below to check what you have learned so far about the null hypothesis.

Choose the best answer. 

Send Your Results (Optional)

• Blackwelder, W. C. (1982). “Proving the null hypothesis” in clinical trials. Controlled Clinical Trials , 3(4), 345–353.
• Frick, R. W. (1995). Accepting the null hypothesis. Memory & Cognition, 23(1), 132–138.
• Gill, J. (1999). The insignificance of null hypothesis significance testing. Political Research Quarterly , 52(3), 647–674.
• Killeen, P. R. (2005). An alternative to null-hypothesis significance tests. Psychological Science, 16(5), 345–353.

©BiologyOnline.com. Content provided and moderated by Biology Online Editors.

Last updated on June 16th, 2022

You will also like...

IQ, Creativity and Learning

Human intelligence provided the means to utilize abstract ideas and implement reasoning. This tutorial takes a further l..

Effect of Chemicals on Growth & Development in Organisms

Plants and animals need elements, such as nitrogen, phosphorus, potassium, and magnesium for proper growth and developme..

Running Water Freshwater Communities

This tutorial introduces flowing water communities, which bring new and dithering factors into the equation for possible..

Freshwater Communities & Lentic Waters

Lentic or still water communities can vary greatly in appearance -- from a small temporary puddle to a large lake. The s..

New Zealand’s Unique Fauna

Meet some of New Zealand's unique fauna, including endemic insects, frogs, reptiles, birds, and mammals, and investigate..

Origins of Life on Earth

Earth was created around 4.5 billion years ago and life began not long after. Primitive life likely possessed the elemen..

Related Articles...

No related articles found

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating ​ the dependent variable or due to random chance. 

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

When do we reject the null hypothesis .

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. 

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables. 

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a  p  -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

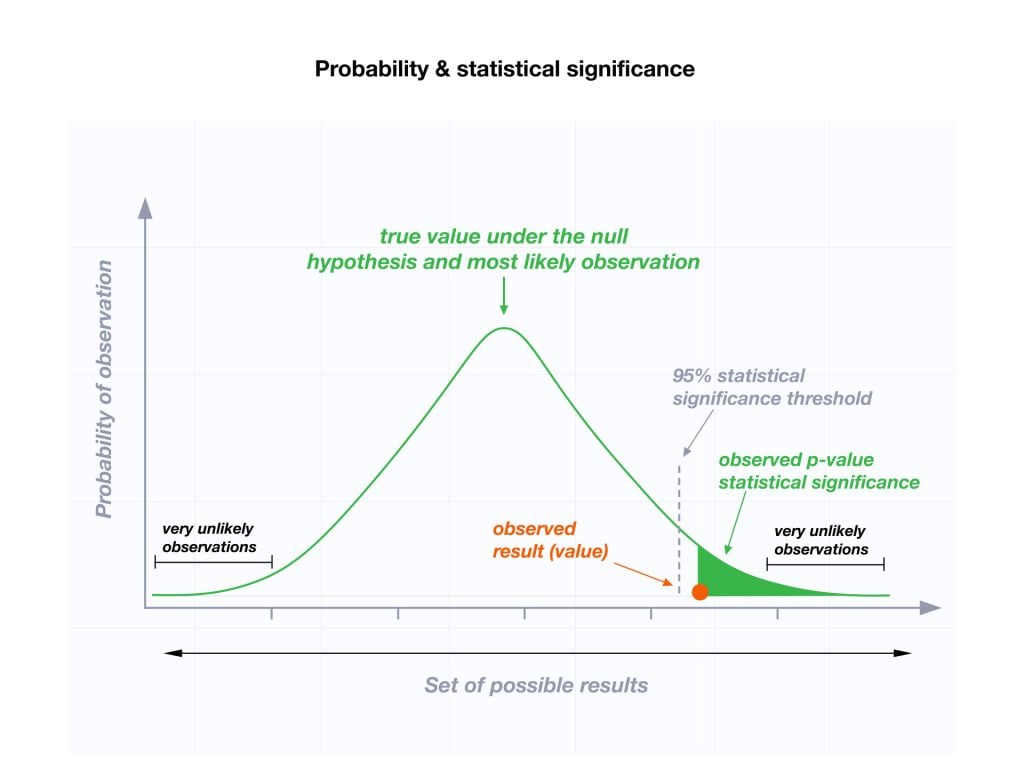
Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. 

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null. 

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists. 

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter. 

Purpose of a Null Hypothesis 

• The primary purpose of the null hypothesis is to disprove an assumption. 
• Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
• A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true. 

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables. 

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study. 

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”).  However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing.  Political research quarterly ,  52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method.  American Psychologist ,  56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing.  Behavior research methods ,  43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy.  Psychological methods ,  5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.  Psychological bulletin ,  57 (5), 416.

Related Articles

Research Methodology

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

Convergent Validity: Definition and Examples

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing

Examples of null and alternative hypotheses

• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.3: The Research Hypothesis and the Null Hypothesis

• Last updated
• Save as PDF
• Page ID 18038

• Michelle Oja
• Taft College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Hypotheses are predictions of expected findings.

The Research Hypothesis

A research hypothesis is a mathematical way of stating a research question.  A research hypothesis names the groups (we'll start with a sample and a population), what was measured, and which we think will have a higher mean.  The last one gives the research hypothesis a direction.  In other words, a research hypothesis should include:

• The name of the groups being compared.  This is sometimes considered the IV.
• What was measured.  This is the DV.
• Which group are we predicting will have the higher mean.  

There are two types of research hypotheses related to sample means and population means:  Directional Research Hypotheses and Non-Directional Research Hypotheses

Directional Research Hypothesis

If we expect our obtained sample mean to be above or below the other group's mean (the population mean, for example), we have a directional hypothesis. There are two options:

• Symbol:       \( \displaystyle \bar{X} > \mu \)
• (The mean of the sample is greater than than the mean of the population.)
• Symbol:     \( \displaystyle \bar{X} < \mu \)
• (The mean of the sample is less than than mean of the population.)

Example \(\PageIndex{1}\)

A study by Blackwell, Trzesniewski, and Dweck (2007) measured growth mindset and how long the junior high student participants spent on their math homework.  What’s a directional hypothesis for how scoring higher on growth mindset (compared to the population of junior high students) would be related to how long students spent on their homework?  Write this out in words and symbols.

Answer in Words:            Students who scored high on growth mindset would spend more time on their homework than the population of junior high students.

Answer in Symbols:         \( \displaystyle \bar{X} > \mu \) 

Non-Directional Research Hypothesis

A non-directional hypothesis states that the means will be different, but does not specify which will be higher.  In reality, there is rarely a situation in which we actually don't want one group to be higher than the other, so we will focus on directional research hypotheses.  There is only one option for a non-directional research hypothesis: "The sample mean differs from the population mean."  These types of research hypotheses don’t give a direction, the hypothesis doesn’t say which will be higher or lower.

A non-directional research hypothesis in symbols should look like this:    \( \displaystyle \bar{X} \neq \mu \) (The mean of the sample is not equal to the mean of the population).

Exercise \(\PageIndex{1}\)

What’s a non-directional hypothesis for how scoring higher on growth mindset higher on growth mindset (compared to the population of junior high students) would be related to how long students spent on their homework (Blackwell, Trzesniewski, & Dweck, 2007)?  Write this out in words and symbols.

Answer in Words:            Students who scored high on growth mindset would spend a different amount of time on their homework than the population of junior high students.

Answer in Symbols:        \( \displaystyle \bar{X} \neq \mu \) 

See how a non-directional research hypothesis doesn't really make sense?  The big issue is not if the two groups differ, but if one group seems to improve what was measured (if having a growth mindset leads to more time spent on math homework).  This textbook will only use directional research hypotheses because researchers almost always have a predicted direction (meaning that we almost always know which group we think will score higher).

The Null Hypothesis

The hypothesis that an apparent effect is due to chance is called the null hypothesis, written \(H_0\) (“H-naught”). We usually test this through comparing an experimental group to a comparison (control) group.  This null hypothesis can be written as:

\[\mathrm{H}_{0}: \bar{X} = \mu \nonumber \]

For most of this textbook, the null hypothesis is that the means of the two groups are similar.  Much later, the null hypothesis will be that there is no relationship between the two groups.  Either way, remember that a null hypothesis is always saying that nothing is different.  

This is where descriptive statistics diverge from inferential statistics.  We know what the value of \(\overline{\mathrm{X}}\) is – it’s not a mystery or a question, it is what we observed from the sample.  What we are using inferential statistics to do is infer whether this sample's descriptive statistics probably represents the population's descriptive statistics.  This is the null hypothesis, that the two groups are similar.  

Keep in mind that the null hypothesis is typically the opposite of the research hypothesis. A research hypothesis for the ESP example is that those in my sample who say that they have ESP would get more correct answers than the population would get correct, while the null hypothesis is that the average number correct for the two groups will be similar. 

In general, the null hypothesis is the idea that nothing is going on: there is no effect of our treatment, no relation between our variables, and no difference in our sample mean from what we expected about the population mean. This is always our baseline starting assumption, and it is what we seek to reject. If we are trying to treat depression, we want to find a difference in average symptoms between our treatment and control groups. If we are trying to predict job performance, we want to find a relation between conscientiousness and evaluation scores. However, until we have evidence against it, we must use the null hypothesis as our starting point.

In sum, the null hypothesis is always : There is no difference between the groups’ means OR There is no relationship between the variables .

In the next chapter, the null hypothesis is that there’s no difference between the sample mean   and population mean.  In other words:

• There is no mean difference between the sample and population.
• The mean of the sample is the same as the mean of a specific population.
• \(\mathrm{H}_{0}: \bar{X} = \mu \nonumber \)
• We expect our sample’s mean to be same as the population mean.

Exercise \(\PageIndex{2}\)

A study by Blackwell, Trzesniewski, and Dweck (2007) measured growth mindset and how long the junior high student participants spent on their math homework.  What’s the null hypothesis for scoring higher on growth mindset (compared to the population of junior high students) and how long students spent on their homework?  Write this out in words and symbols.

Answer in Words:            Students who scored high on growth mindset would spend a similar amount of time on their homework as the population of junior high students.

Answer in Symbols:    \( \bar{X} = \mu \)

Contributors and Attributions

Foster et al.  (University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus)

Dr. MO ( Taft College )

What Is a Hypothesis? (Science)

If...,Then...

Angela Lumsden/Getty Images

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

A hypothesis (plural hypotheses) is a proposed explanation for an observation. The definition depends on the subject.

In science, a hypothesis is part of the scientific method. It is a prediction or explanation that is tested by an experiment. Observations and experiments may disprove a scientific hypothesis, but can never entirely prove one.

In the study of logic, a hypothesis is an if-then proposition, typically written in the form, "If X , then Y ."

In common usage, a hypothesis is simply a proposed explanation or prediction, which may or may not be tested.

Writing a Hypothesis

Most scientific hypotheses are proposed in the if-then format because it's easy to design an experiment to see whether or not a cause and effect relationship exists between the independent variable and the dependent variable . The hypothesis is written as a prediction of the outcome of the experiment.

• Null Hypothesis and Alternative Hypothesis

Statistically, it's easier to show there is no relationship between two variables than to support their connection. So, scientists often propose the null hypothesis . The null hypothesis assumes changing the independent variable will have no effect on the dependent variable.

In contrast, the alternative hypothesis suggests changing the independent variable will have an effect on the dependent variable. Designing an experiment to test this hypothesis can be trickier because there are many ways to state an alternative hypothesis.

For example, consider a possible relationship between getting a good night's sleep and getting good grades. The null hypothesis might be stated: "The number of hours of sleep students get is unrelated to their grades" or "There is no correlation between hours of sleep and grades."

An experiment to test this hypothesis might involve collecting data, recording average hours of sleep for each student and grades. If a student who gets eight hours of sleep generally does better than students who get four hours of sleep or 10 hours of sleep, the hypothesis might be rejected.

But the alternative hypothesis is harder to propose and test. The most general statement would be: "The amount of sleep students get affects their grades." The hypothesis might also be stated as "If you get more sleep, your grades will improve" or "Students who get nine hours of sleep have better grades than those who get more or less sleep."

In an experiment, you can collect the same data, but the statistical analysis is less likely to give you a high confidence limit.

Usually, a scientist starts out with the null hypothesis. From there, it may be possible to propose and test an alternative hypothesis, to narrow down the relationship between the variables.

Example of a Hypothesis

Examples of a hypothesis include:

• If you drop a rock and a feather, (then) they will fall at the same rate.
• Plants need sunlight in order to live. (if sunlight, then life)
• Eating sugar gives you energy. (if sugar, then energy)
• White, Jay D.  Research in Public Administration . Conn., 1998.
• Schick, Theodore, and Lewis Vaughn.  How to Think about Weird Things: Critical Thinking for a New Age . McGraw-Hill Higher Education, 2002.
• Null Hypothesis Definition and Examples
• Definition of a Hypothesis
• What Are the Elements of a Good Hypothesis?
• Six Steps of the Scientific Method
• Independent Variable Definition and Examples
• What Are Examples of a Hypothesis?
• Understanding Simple vs Controlled Experiments
• Scientific Method Flow Chart
• Scientific Method Vocabulary Terms
• What Is a Testable Hypothesis?
• Null Hypothesis Examples
• What 'Fail to Reject' Means in a Hypothesis Test
• How To Design a Science Fair Experiment
• What Is an Experiment? Definition and Design
• Hypothesis Test for the Difference of Two Population Proportions

Best Practices in Science

The Null Hypothesis

Show Topics

Publications

• Journals and Blogs

The null hypothesis, as described by Anthony Greenwald in ‘Consequences of Prejudice Against the Null Hypothesis,’ is the hypothesis of no difference between treatment effects or of no association between variables. Unfortunately in academia, the ‘null’ is often associated with ‘insignificant,’ ‘no value,’ or ‘invalid.’ This association is due to the bias against papers that accept the null hypothesis by journals. This prejudice by journals to only accept papers that show ‘significant’ results (also known as rejecting this ‘null hypothesis’) puts added pressure on those working in academia, especially with their relevance and salaries often depend on publications. This pressure may also be correlated with increased scientific misconduct, which you can also read more about on this website by clicking here . If you would like to read publication, journal articles, and blogs about the null hypothesis, views on rejecting and accepting the null, and journal bias against the null hypothesis, please see the resources we have linked below.

Most scientific journals are prejudiced against papers that demonstrate support for null hypotheses and are unlikely to publish such papers and articles. This phenomenon leads to selective publishing of papers and ensures that the portion of articles that do get published is unrepresentative of the total research in the field.

Anderson, D. R., Burnham, K. P., & Thompson, W. L. (2000). Null hypothesis testing: problems, prevalence, and an alternative. The journal of wildlife management , 912-923.

Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the royal statistical society . Series B (Methodological), 289-300.

Berger, J. O., & Sellke, T. (1987). Testing a point null hypothesis: The irreconcilability of p values and evidence. Journal of the American statistical Association , 82 (397), 112-122.

Blackwelder, W. C. (1982). “Proving the null hypothesis” in clinical trials. Controlled clinical trials , 3 (4), 345-353.

Dirnagl, U. (2010). Fighting publication bias: introducing the Negative Results section. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism , 30 (7), 1263.

Dickersin, K., Chan, S. S., Chalmersx, T. C., Sacks, H. S., & Smith, H. (1987). Publication bias and clinical trials. Controlled clinical trials , 8 (4), 343-353.

Efron, B. (2004). Large-scale simultaneous hypothesis testing: the choice of a null hypothesis. Journal of the American Statistical Association , 99 (465), 96-104.

Fanelli, D. (2010). Do pressures to publish increase scientists’ bias? An empirical support from US States Data. PloS one , 5 (4), e10271.

Fanelli, D. (2011). Negative results are disappearing from most disciplines and countries. Scientometrics , 90 (3), 891-904.

Greenwald, A. G. (1975). Consequences of Prejudice Against the Null Hypothesis. Psychological Bulletin , 82 (1).

Hubbard, R., & Armstrong, J. S. (1997). Publication bias against null results. Psychological Reports , 80 (1), 337-338.

I’ve Got Your Impact Factor Right Here (Science, February 24, 2012)

Johnson, R. T., & Dickersin, K. (2007). Publication bias against negative results from clinical trials: three of the seven deadly sins. Nature Clinical Practice Neurology , 3 (11), 590-591.

Keep negativity out of politics. We need more of it in journals (STAT, October 14, 2016)

Knight, J. (2003). Negative results: Null and void. Nature , 422 (6932), 554-555.

Koren, G., & Klein, N. (1991). Bias against negative studies in newspaper reports of medical research. Jama , 266 (13), 1824-1826.

Koren, G., Shear, H., Graham, K., & Einarson, T. (1989). Bias against the null hypothesis: the reproductive hazards of cocaine. The Lancet , 334 (8677), 1440-1442.

Krantz, D. (2012).  The Null Hypothesis Testing Controversy in Psychology. Journal of American Statistical Association .

Lash, T. (2017). The Harm Done to Reproducibility by the Culture of Null Hypothesis Significance Testing. American Journal of Epidemiology .

Mahoney, M. J. (1977). Publication prejudices: An experimental study of confirmatory bias in the peer review system. Cognitive therapy and research , 1 (2), 161-175.

Matosin, N., Frank, E., Engel, M., Lum, J. S., & Newell, K. A. (2014). Negativity towards negative results: a discussion of the disconnect between scientific worth and scientific culture.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.

No result is worthless: the value of negative results in science (BioMed Central, October 10, 2012)

Negative Results: The Dark Matter of Research (American Journal Experts)

Neil Malhotra: Why No News Is Still Important News in Research (Stanford Graduate School of Business, October 27, 2014)

Null Hypothesis Definition and Example (Statistics How To, November 5, 2012)

Null Hypothesis Glossary Definition (Statlect Digital Textbook)

Opinion: Publish Negative Results (The Scientist, January 15, 2013)

Positives in negative results: when finding ‘nothing’ means something (The Conversation, September 24, 2014)

Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic bulletin & review , 16 (2), 225-237.

Unknown Unknowns: The War on Null and Negative Results (social science space, September 19, 2014)

Valuing Null and Negative Results in Scientific Publishing (Scholastica, November 4, 2015)

Vasilev, M. R. (2013). Negative results in European psychology journals. Europe’s Journal of Psychology , 9 (4), 717-730

Where have all the negative results gone? (bioethics.net, December 4, 2013)

Where to publish negative results (BitesizeBio, November 27, 2013)

Why it’s time to publish research “failures” (Elsevier, May 5, 2015)

Woolson, R. F., & Kleinman, J. C. (1989). Perspectives on statistical significance testing. Annual review of public health , 10 (1), 423-440.

Would you publish your negative results? If no, why? (ResearchGate, October 26, 2012)

• More from M-W
• To save this word, you'll need to log in. Log In

null hypothesis

Definition of null hypothesis

Examples of null hypothesis in a sentence.

These examples are programmatically compiled from various online sources to illustrate current usage of the word 'null hypothesis.' Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.

Word History

1935, in the meaning defined above

Dictionary Entries Near null hypothesis

Nullarbor Plain

Cite this Entry

“Null hypothesis.” Merriam-Webster.com Dictionary , Merriam-Webster, https://www.merriam-webster.com/dictionary/null%20hypothesis. Accessed 17 May. 2024.

More from Merriam-Webster on null hypothesis

Britannica.com: Encyclopedia article about null hypothesis

Subscribe to America's largest dictionary and get thousands more definitions and advanced search—ad free!

Can you solve 4 words at once?

Word of the day.

See Definitions and Examples »

Get Word of the Day daily email!

Popular in Grammar & Usage

More commonly misspelled words, your vs. you're: how to use them correctly, every letter is silent, sometimes: a-z list of examples, more commonly mispronounced words, how to use em dashes (—), en dashes (–) , and hyphens (-), popular in wordplay, the words of the week - may 17, birds say the darndest things, a great big list of bread words, 10 scrabble words without any vowels, 12 more bird names that sound like insults (and sometimes are), games & quizzes.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List

• PMC5635437.1 ; 2015 Aug 25
• PMC5635437.2 ; 2016 Jul 13
• ➤ PMC5635437.3; 2016 Oct 10

Null hypothesis significance testing: a short tutorial

Cyril pernet.

1 Centre for Clinical Brain Sciences (CCBS), Neuroimaging Sciences, The University of Edinburgh, Edinburgh, UK

Version Changes

Revised. amendments from version 2.

This v3 includes minor changes that reflect the 3rd reviewers' comments - in particular the theoretical vs. practical difference between Fisher and Neyman-Pearson. Additional information and reference is also included regarding the interpretation of p-value for low powered studies.

Peer Review Summary

Although thoroughly criticized, null hypothesis significance testing (NHST) remains the statistical method of choice used to provide evidence for an effect, in biological, biomedical and social sciences. In this short tutorial, I first summarize the concepts behind the method, distinguishing test of significance (Fisher) and test of acceptance (Newman-Pearson) and point to common interpretation errors regarding the p-value. I then present the related concepts of confidence intervals and again point to common interpretation errors. Finally, I discuss what should be reported in which context. The goal is to clarify concepts to avoid interpretation errors and propose reporting practices.

The Null Hypothesis Significance Testing framework

NHST is a method of statistical inference by which an experimental factor is tested against a hypothesis of no effect or no relationship based on a given observation. The method is a combination of the concepts of significance testing developed by Fisher in 1925 and of acceptance based on critical rejection regions developed by Neyman & Pearson in 1928 . In the following I am first presenting each approach, highlighting the key differences and common misconceptions that result from their combination into the NHST framework (for a more mathematical comparison, along with the Bayesian method, see Christensen, 2005 ). I next present the related concept of confidence intervals. I finish by discussing practical aspects in using NHST and reporting practice.

Fisher, significance testing, and the p-value

The method developed by ( Fisher, 1934 ; Fisher, 1955 ; Fisher, 1959 ) allows to compute the probability of observing a result at least as extreme as a test statistic (e.g. t value), assuming the null hypothesis of no effect is true. This probability or p-value reflects (1) the conditional probability of achieving the observed outcome or larger: p(Obs≥t|H0), and (2) is therefore a cumulative probability rather than a point estimate. It is equal to the area under the null probability distribution curve from the observed test statistic to the tail of the null distribution ( Turkheimer et al. , 2004 ). The approach proposed is of ‘proof by contradiction’ ( Christensen, 2005 ), we pose the null model and test if data conform to it.

In practice, it is recommended to set a level of significance (a theoretical p-value) that acts as a reference point to identify significant results, that is to identify results that differ from the null-hypothesis of no effect. Fisher recommended using p=0.05 to judge whether an effect is significant or not as it is roughly two standard deviations away from the mean for the normal distribution ( Fisher, 1934 page 45: ‘The value for which p=.05, or 1 in 20, is 1.96 or nearly 2; it is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not’). A key aspect of Fishers’ theory is that only the null-hypothesis is tested, and therefore p-values are meant to be used in a graded manner to decide whether the evidence is worth additional investigation and/or replication ( Fisher, 1971 page 13: ‘it is open to the experimenter to be more or less exacting in respect of the smallness of the probability he would require […]’ and ‘no isolated experiment, however significant in itself, can suffice for the experimental demonstration of any natural phenomenon’). How small the level of significance is, is thus left to researchers.

What is not a p-value? Common mistakes

The p-value is not an indication of the strength or magnitude of an effect . Any interpretation of the p-value in relation to the effect under study (strength, reliability, probability) is wrong, since p-values are conditioned on H0. In addition, while p-values are randomly distributed (if all the assumptions of the test are met) when there is no effect, their distribution depends of both the population effect size and the number of participants, making impossible to infer strength of effect from them.

Similarly, 1-p is not the probability to replicate an effect . Often, a small value of p is considered to mean a strong likelihood of getting the same results on another try, but again this cannot be obtained because the p-value is not informative on the effect itself ( Miller, 2009 ). Because the p-value depends on the number of subjects, it can only be used in high powered studies to interpret results. In low powered studies (typically small number of subjects), the p-value has a large variance across repeated samples, making it unreliable to estimate replication ( Halsey et al. , 2015 ).

A (small) p-value is not an indication favouring a given hypothesis . Because a low p-value only indicates a misfit of the null hypothesis to the data, it cannot be taken as evidence in favour of a specific alternative hypothesis more than any other possible alternatives such as measurement error and selection bias ( Gelman, 2013 ). Some authors have even argued that the more (a priori) implausible the alternative hypothesis, the greater the chance that a finding is a false alarm ( Krzywinski & Altman, 2013 ; Nuzzo, 2014 ).

The p-value is not the probability of the null hypothesis p(H0), of being true, ( Krzywinski & Altman, 2013 ). This common misconception arises from a confusion between the probability of an observation given the null p(Obs≥t|H0) and the probability of the null given an observation p(H0|Obs≥t) that is then taken as an indication for p(H0) (see Nickerson, 2000 ).

Neyman-Pearson, hypothesis testing, and the α-value

Neyman & Pearson (1933) proposed a framework of statistical inference for applied decision making and quality control. In such framework, two hypotheses are proposed: the null hypothesis of no effect and the alternative hypothesis of an effect, along with a control of the long run probabilities of making errors. The first key concept in this approach, is the establishment of an alternative hypothesis along with an a priori effect size. This differs markedly from Fisher who proposed a general approach for scientific inference conditioned on the null hypothesis only. The second key concept is the control of error rates . Neyman & Pearson (1928) introduced the notion of critical intervals, therefore dichotomizing the space of possible observations into correct vs. incorrect zones. This dichotomization allows distinguishing correct results (rejecting H0 when there is an effect and not rejecting H0 when there is no effect) from errors (rejecting H0 when there is no effect, the type I error, and not rejecting H0 when there is an effect, the type II error). In this context, alpha is the probability of committing a Type I error in the long run. Alternatively, Beta is the probability of committing a Type II error in the long run.

The (theoretical) difference in terms of hypothesis testing between Fisher and Neyman-Pearson is illustrated on Figure 1 . In the 1 st case, we choose a level of significance for observed data of 5%, and compute the p-value. If the p-value is below the level of significance, it is used to reject H0. In the 2 nd case, we set a critical interval based on the a priori effect size and error rates. If an observed statistic value is below and above the critical values (the bounds of the confidence region), it is deemed significantly different from H0. In the NHST framework, the level of significance is (in practice) assimilated to the alpha level, which appears as a simple decision rule: if the p-value is less or equal to alpha, the null is rejected. It is however a common mistake to assimilate these two concepts. The level of significance set for a given sample is not the same as the frequency of acceptance alpha found on repeated sampling because alpha (a point estimate) is meant to reflect the long run probability whilst the p-value (a cumulative estimate) reflects the current probability ( Fisher, 1955 ; Hubbard & Bayarri, 2003 ).

The figure was prepared with G-power for a one-sided one-sample t-test, with a sample size of 32 subjects, an effect size of 0.45, and error rates alpha=0.049 and beta=0.80. In Fisher’s procedure, only the nil-hypothesis is posed, and the observed p-value is compared to an a priori level of significance. If the observed p-value is below this level (here p=0.05), one rejects H0. In Neyman-Pearson’s procedure, the null and alternative hypotheses are specified along with an a priori level of acceptance. If the observed statistical value is outside the critical region (here [-∞ +1.69]), one rejects H0.

Acceptance or rejection of H0?

The acceptance level α can also be viewed as the maximum probability that a test statistic falls into the rejection region when the null hypothesis is true ( Johnson, 2013 ). Therefore, one can only reject the null hypothesis if the test statistics falls into the critical region(s), or fail to reject this hypothesis. In the latter case, all we can say is that no significant effect was observed, but one cannot conclude that the null hypothesis is true. This is another common mistake in using NHST: there is a profound difference between accepting the null hypothesis and simply failing to reject it ( Killeen, 2005 ). By failing to reject, we simply continue to assume that H0 is true, which implies that one cannot argue against a theory from a non-significant result (absence of evidence is not evidence of absence). To accept the null hypothesis, tests of equivalence ( Walker & Nowacki, 2011 ) or Bayesian approaches ( Dienes, 2014 ; Kruschke, 2011 ) must be used.

Confidence intervals

Confidence intervals (CI) are builds that fail to cover the true value at a rate of alpha, the Type I error rate ( Morey & Rouder, 2011 ) and therefore indicate if observed values can be rejected by a (two tailed) test with a given alpha. CI have been advocated as alternatives to p-values because (i) they allow judging the statistical significance and (ii) provide estimates of effect size. Assuming the CI (a)symmetry and width are correct (but see Wilcox, 2012 ), they also give some indication about the likelihood that a similar value can be observed in future studies. For future studies of the same sample size, 95% CI give about 83% chance of replication success ( Cumming & Maillardet, 2006 ). If sample sizes however differ between studies, CI do not however warranty any a priori coverage.

Although CI provide more information, they are not less subject to interpretation errors (see Savalei & Dunn, 2015 for a review). The most common mistake is to interpret CI as the probability that a parameter (e.g. the population mean) will fall in that interval X% of the time. The correct interpretation is that, for repeated measurements with the same sample sizes, taken from the same population, X% of times the CI obtained will contain the true parameter value ( Tan & Tan, 2010 ). The alpha value has the same interpretation as testing against H0, i.e. we accept that 1-alpha CI are wrong in alpha percent of the times in the long run. This implies that CI do not allow to make strong statements about the parameter of interest (e.g. the mean difference) or about H1 ( Hoekstra et al. , 2014 ). To make a statement about the probability of a parameter of interest (e.g. the probability of the mean), Bayesian intervals must be used.

The (correct) use of NHST

NHST has always been criticized, and yet is still used every day in scientific reports ( Nickerson, 2000 ). One question to ask oneself is what is the goal of a scientific experiment at hand? If the goal is to establish a discrepancy with the null hypothesis and/or establish a pattern of order, because both requires ruling out equivalence, then NHST is a good tool ( Frick, 1996 ; Walker & Nowacki, 2011 ). If the goal is to test the presence of an effect and/or establish some quantitative values related to an effect, then NHST is not the method of choice since testing is conditioned on H0.

While a Bayesian analysis is suited to estimate that the probability that a hypothesis is correct, like NHST, it does not prove a theory on itself, but adds its plausibility ( Lindley, 2000 ). No matter what testing procedure is used and how strong results are, ( Fisher, 1959 p13) reminds us that ‘ […] no isolated experiment, however significant in itself, can suffice for the experimental demonstration of any natural phenomenon'. Similarly, the recent statement of the American Statistical Association ( Wasserstein & Lazar, 2016 ) makes it clear that conclusions should be based on the researchers understanding of the problem in context, along with all summary data and tests, and that no single value (being p-values, Bayesian factor or else) can be used support or invalidate a theory.

What to report and how?

Considering that quantitative reports will always have more information content than binary (significant or not) reports, we can always argue that raw and/or normalized effect size, confidence intervals, or Bayes factor must be reported. Reporting everything can however hinder the communication of the main result(s), and we should aim at giving only the information needed, at least in the core of a manuscript. Here I propose to adopt optimal reporting in the result section to keep the message clear, but have detailed supplementary material. When the hypothesis is about the presence/absence or order of an effect, and providing that a study has sufficient power, NHST is appropriate and it is sufficient to report in the text the actual p-value since it conveys the information needed to rule out equivalence. When the hypothesis and/or the discussion involve some quantitative value, and because p-values do not inform on the effect, it is essential to report on effect sizes ( Lakens, 2013 ), preferably accompanied with confidence or credible intervals. The reasoning is simply that one cannot predict and/or discuss quantities without accounting for variability. For the reader to understand and fully appreciate the results, nothing else is needed.

Because science progress is obtained by cumulating evidence ( Rosenthal, 1991 ), scientists should also consider the secondary use of the data. With today’s electronic articles, there are no reasons for not including all of derived data: mean, standard deviations, effect size, CI, Bayes factor should always be included as supplementary tables (or even better also share raw data). It is also essential to report the context in which tests were performed – that is to report all of the tests performed (all t, F, p values) because of the increase type one error rate due to selective reporting (multiple comparisons and p-hacking problems - Ioannidis, 2005 ). Providing all of this information allows (i) other researchers to directly and effectively compare their results in quantitative terms (replication of effects beyond significance, Open Science Collaboration, 2015 ), (ii) to compute power to future studies ( Lakens & Evers, 2014 ), and (iii) to aggregate results for meta-analyses whilst minimizing publication bias ( van Assen et al. , 2014 ).

[version 3; referees: 1 approved

Funding Statement

The author(s) declared that no grants were involved in supporting this work.

• Christensen R: Testing Fisher, Neyman, Pearson, and Bayes. The American Statistician. 2005; 59 ( 2 ):121–126. 10.1198/000313005X20871 [ CrossRef ] [ Google Scholar ]
• Cumming G, Maillardet R: Confidence intervals and replication: Where will the next mean fall? Psychological Methods. 2006; 11 ( 3 ):217–227. 10.1037/1082-989X.11.3.217 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dienes Z: Using Bayes to get the most out of non-significant results. Front Psychol. 2014; 5 :781. 10.3389/fpsyg.2014.00781 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fisher RA: Statistical Methods for Research Workers . (Vol. 5th Edition). Edinburgh, UK: Oliver and Boyd.1934. Reference Source [ Google Scholar ]
• Fisher RA: Statistical Methods and Scientific Induction. Journal of the Royal Statistical Society, Series B. 1955; 17 ( 1 ):69–78. Reference Source [ Google Scholar ]
• Fisher RA: Statistical methods and scientific inference . (2nd ed.). NewYork: Hafner Publishing,1959. Reference Source [ Google Scholar ]
• Fisher RA: The Design of Experiments . Hafner Publishing Company, New-York.1971. Reference Source [ Google Scholar ]
• Frick RW: The appropriate use of null hypothesis testing. Psychol Methods. 1996; 1 ( 4 ):379–390. 10.1037/1082-989X.1.4.379 [ CrossRef ] [ Google Scholar ]
• Gelman A: P values and statistical practice. Epidemiology. 2013; 24 ( 1 ):69–72. 10.1097/EDE.0b013e31827886f7 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Halsey LG, Curran-Everett D, Vowler SL, et al.: The fickle P value generates irreproducible results. Nat Methods. 2015; 12 ( 3 ):179–85. 10.1038/nmeth.3288 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hoekstra R, Morey RD, Rouder JN, et al.: Robust misinterpretation of confidence intervals. Psychon Bull Rev. 2014; 21 ( 5 ):1157–1164. 10.3758/s13423-013-0572-3 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hubbard R, Bayarri MJ: Confusion over measures of evidence (p’s) versus errors ([alpha]’s) in classical statistical testing. The American Statistician. 2003; 57 ( 3 ):171–182. 10.1198/0003130031856 [ CrossRef ] [ Google Scholar ]
• Ioannidis JP: Why most published research findings are false. PLoS Med. 2005; 2 ( 8 ):e124. 10.1371/journal.pmed.0020124 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Johnson VE: Revised standards for statistical evidence. Proc Natl Acad Sci U S A. 2013; 110 ( 48 ):19313–19317. 10.1073/pnas.1313476110 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Killeen PR: An alternative to null-hypothesis significance tests. Psychol Sci. 2005; 16 ( 5 ):345–353. 10.1111/j.0956-7976.2005.01538.x [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kruschke JK: Bayesian Assessment of Null Values Via Parameter Estimation and Model Comparison. Perspect Psychol Sci. 2011; 6 ( 3 ):299–312. 10.1177/1745691611406925 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Krzywinski M, Altman N: Points of significance: Significance, P values and t -tests. Nat Methods. 2013; 10 ( 11 ):1041–1042. 10.1038/nmeth.2698 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lakens D: Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t -tests and ANOVAs. Front Psychol. 2013; 4 :863. 10.3389/fpsyg.2013.00863 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lakens D, Evers ER: Sailing From the Seas of Chaos Into the Corridor of Stability: Practical Recommendations to Increase the Informational Value of Studies. Perspect Psychol Sci. 2014; 9 ( 3 ):278–292. 10.1177/1745691614528520 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lindley D: The philosophy of statistics. Journal of the Royal Statistical Society. 2000; 49 ( 3 ):293–337. 10.1111/1467-9884.00238 [ CrossRef ] [ Google Scholar ]
• Miller J: What is the probability of replicating a statistically significant effect? Psychon Bull Rev. 2009; 16 ( 4 ):617–640. 10.3758/PBR.16.4.617 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Morey RD, Rouder JN: Bayes factor approaches for testing interval null hypotheses. Psychol Methods. 2011; 16 ( 4 ):406–419. 10.1037/a0024377 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Neyman J, Pearson ES: On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference: Part I. Biometrika. 1928; 20A ( 1/2 ):175–240. 10.3389/fpsyg.2015.00245 [ CrossRef ] [ Google Scholar ]
• Neyman J, Pearson ES: On the problem of the most efficient tests of statistical hypotheses. Philos Trans R Soc Lond Ser A. 1933; 231 ( 694–706 ):289–337. 10.1098/rsta.1933.0009 [ CrossRef ] [ Google Scholar ]
• Nickerson RS: Null hypothesis significance testing: a review of an old and continuing controversy. Psychol Methods. 2000; 5 ( 2 ):241–301. 10.1037/1082-989X.5.2.241 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Nuzzo R: Scientific method: statistical errors. Nature. 2014; 506 ( 7487 ):150–152. 10.1038/506150a [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Open Science Collaboration. PSYCHOLOGY. Estimating the reproducibility of psychological science. Science. 2015; 349 ( 6251 ):aac4716. 10.1126/science.aac4716 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Rosenthal R: Cumulating psychology: an appreciation of Donald T. Campbell. Psychol Sci. 1991; 2 ( 4 ):213–221. 10.1111/j.1467-9280.1991.tb00138.x [ CrossRef ] [ Google Scholar ]
• Savalei V, Dunn E: Is the call to abandon p -values the red herring of the replicability crisis? Front Psychol. 2015; 6 :245. 10.3389/fpsyg.2015.00245 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Tan SH, Tan SB: The Correct Interpretation of Confidence Intervals. Proceedings of Singapore Healthcare. 2010; 19 ( 3 ):276–278. 10.1177/201010581001900316 [ CrossRef ] [ Google Scholar ]
• Turkheimer FE, Aston JA, Cunningham VJ: On the logic of hypothesis testing in functional imaging. Eur J Nucl Med Mol Imaging. 2004; 31 ( 5 ):725–732. 10.1007/s00259-003-1387-7 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• van Assen MA, van Aert RC, Nuijten MB, et al.: Why Publishing Everything Is More Effective than Selective Publishing of Statistically Significant Results. PLoS One. 2014; 9 ( 1 ):e84896. 10.1371/journal.pone.0084896 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Walker E, Nowacki AS: Understanding equivalence and noninferiority testing. J Gen Intern Med. 2011; 26 ( 2 ):192–196. 10.1007/s11606-010-1513-8 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wasserstein RL, Lazar NA: The ASA’s Statement on p -Values: Context, Process, and Purpose. The American Statistician. 2016; 70 ( 2 ):129–133. 10.1080/00031305.2016.1154108 [ CrossRef ] [ Google Scholar ]
• Wilcox R: Introduction to Robust Estimation and Hypothesis Testing . Edition 3, Academic Press, Elsevier: Oxford, UK, ISBN: 978-0-12-386983-8.2012. Reference Source [ Google Scholar ]

Referee response for version 3

Dorothy vera margaret bishop.

1 Department of Experimental Psychology, University of Oxford, Oxford, UK

I can see from the history of this paper that the author has already been very responsive to reviewer comments, and that the process of revising has now been quite protracted.

That makes me reluctant to suggest much more, but I do see potential here for making the paper more impactful. So my overall view is that, once a few typos are fixed (see below), this could be published as is, but I think there is an issue with the potential readership and that further revision could overcome this.

I suspect my take on this is rather different from other reviewers, as I do not regard myself as a statistics expert, though I am on the more quantitative end of the continuum of psychologists and I try to keep up to date. I think I am quite close to the target readership , insofar as I am someone who was taught about statistics ages ago and uses stats a lot, but never got adequate training in the kinds of topic covered by this paper. The fact that I am aware of controversies around the interpretation of confidence intervals etc is simply because I follow some discussions of this on social media. I am therefore very interested to have a clear account of these issues.

This paper contains helpful information for someone in this position, but it is not always clear, and I felt the relevance of some of the content was uncertain. So here are some recommendations:

• As one previous reviewer noted, it’s questionable that there is a need for a tutorial introduction, and the limited length of this article does not lend itself to a full explanation. So it might be better to just focus on explaining as clearly as possible the problems people have had in interpreting key concepts. I think a title that made it clear this was the content would be more appealing than the current one.
• P 3, col 1, para 3, last sentence. Although statisticians always emphasise the arbitrary nature of p < .05, we all know that in practice authors who use other values are likely to have their analyses queried. I wondered whether it would be useful here to note that in some disciplines different cutoffs are traditional, e.g. particle physics. Or you could cite David Colquhoun’s paper in which he recommends using p < .001 ( http://rsos.royalsocietypublishing.org/content/1/3/140216) - just to be clear that the traditional p < .05 has been challenged.

What I can’t work out is how you would explain the alpha from Neyman-Pearson in the same way (though I can see from Figure 1 that with N-P you could test an alternative hypothesis, such as the idea that the coin would be heads 75% of the time).

‘By failing to reject, we simply continue to assume that H0 is true, which implies that one cannot….’ have ‘In failing to reject, we do not assume that H0 is true; one cannot argue against a theory from a non-significant result.’

I felt most readers would be interested to read about tests of equivalence and Bayesian approaches, but many would be unfamiliar with these and might like to see an example of how they work in practice – if space permitted.

• Confidence intervals: I simply could not understand the first sentence – I wondered what was meant by ‘builds’ here. I understand about difficulties in comparing CI across studies when sample sizes differ, but I did not find the last sentence on p 4 easy to understand.
• P 5: The sentence starting: ‘The alpha value has the same interpretation’ was also hard to understand, especially the term ‘1-alpha CI’. Here too I felt some concrete illustration might be helpful to the reader. And again, I also found the reference to Bayesian intervals tantalising – I think many readers won’t know how to compute these and something like a figure comparing a traditional CI with a Bayesian interval and giving a source for those who want to read on would be very helpful. The reference to ‘credible intervals’ in the penultimate paragraph is very unclear and needs a supporting reference – most readers will not be familiar with this concept.

P 3, col 1, para 2, line 2; “allows us to compute”

P 3, col 2, para 2, ‘probability of replicating’

P 3, col 2, para 2, line 4 ‘informative about’

P 3, col 2, para 4, line 2 delete ‘of’

P 3, col 2, para 5, line 9 – ‘conditioned’ is either wrong or too technical here: would ‘based’ be acceptable as alternative wording

P 3, col 2, para 5, line 13 ‘This dichotomisation allows one to distinguish’

P 3, col 2, para 5, last sentence, delete ‘Alternatively’.

P 3, col 2, last para line 2 ‘first’

P 4, col 2, para 2, last sentence is hard to understand; not sure if this is better: ‘If sample sizes differ between studies, the distribution of CIs cannot be specified a priori’

P 5, col 1, para 2, ‘a pattern of order’ – I did not understand what was meant by this

P 5, col 1, para 2, last sentence unclear: possible rewording: “If the goal is to test the size of an effect then NHST is not the method of choice, since testing can only reject the null hypothesis.’ (??)

P 5, col 1, para 3, line 1 delete ‘that’

P 5, col 1, para 3, line 3 ‘on’ -> ‘by’

P 5, col 2, para 1, line 4 , rather than ‘Here I propose to adopt’ I suggest ‘I recommend adopting’

P 5, col 2, para 1, line 13 ‘with’ -> ‘by’

P 5, col 2, para 1 – recommend deleting last sentence

P 5, col 2, para 2, line 2 ‘consider’ -> ‘anticipate’

P 5, col 2, para 2, delete ‘should always be included’

P 5, col 2, para 2, ‘type one’ -> ‘Type I’

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

The University of Edinburgh, UK

I wondered about changing the focus slightly and modifying the title to reflect this to say something like: Null hypothesis significance testing: a guide to commonly misunderstood concepts and recommendations for good practice

Thank you for the suggestion – you indeed saw the intention behind the ‘tutorial’ style of the paper.

• P 3, col 1, para 3, last sentence. Although statisticians always emphasise the arbitrary nature of p < .05, we all know that in practice authors who use other values are likely to have their analyses queried. I wondered whether it would be useful here to note that in some disciplines different cutoffs are traditional, e.g. particle physics. Or you could cite David Colquhoun’s paper in which he recommends using p < .001 ( http://rsos.royalsocietypublishing.org/content/1/3/140216)  - just to be clear that the traditional p < .05 has been challenged.

I have added a sentence on this citing Colquhoun 2014 and the new Benjamin 2017 on using .005.

I agree that this point is always hard to appreciate, especially because it seems like in practice it makes little difference. I added a paragraph but using reaction times rather than a coin toss – thanks for the suggestion.

Added an example based on new table 1, following figure 1 – giving CI, equivalence tests and Bayes Factor (with refs to easy to use tools)

Changed builds to constructs (this simply means they are something we build) and added that the implication that probability coverage is not warranty when sample size change, is that we cannot compare CI.

I changed ‘ i.e. we accept that 1-alpha CI are wrong in alpha percent of the times in the long run’ to ‘, ‘e.g. a 95% CI is wrong in 5% of the times in the long run (i.e. if we repeat the experiment many times).’ – for Bayesian intervals I simply re-cited Morey & Rouder, 2011.

It is not the CI cannot be specified, it’s that the interval is not predictive of anything anymore! I changed it to ‘If sample sizes, however, differ between studies, there is no warranty that a CI from one study will be true at the rate alpha in a different study, which implies that CI cannot be compared across studies at this is rarely the same sample sizes’

I added (i.e. establish that A > B) – we test that conditions are ordered, but without further specification of the probability of that effect nor its size

Yes it works – thx

P 5, col 2, para 2, ‘type one’ -> ‘Type I’ 

Typos fixed, and suggestions accepted – thanks for that.

Stephen J. Senn

1 Luxembourg Institute of Health, Strassen, L-1445, Luxembourg

The revisions are OK for me, and I have changed my status to Approved.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Referee response for version 2

On the whole I think that this article is reasonable, my main reservation being that I have my doubts on whether the literature needs yet another tutorial on this subject.

A further reservation I have is that the author, following others, stresses what in my mind is a relatively unimportant distinction between the Fisherian and Neyman-Pearson (NP) approaches. The distinction stressed by many is that the NP approach leads to a dichotomy accept/reject based on probabilities established in advance, whereas the Fisherian approach uses tail area probabilities calculated from the observed statistic. I see this as being unimportant and not even true. Unless one considers that the person carrying out a hypothesis test (original tester) is mandated to come to a conclusion on behalf of all scientific posterity, then one must accept that any remote scientist can come to his or her conclusion depending on the personal type I error favoured. To operate the results of an NP test carried out by the original tester, the remote scientist then needs to know the p-value. The type I error rate is then compared to this to come to a personal accept or reject decision (1). In fact Lehmann (2), who was an important developer of and proponent of the NP system, describes exactly this approach as being good practice. (See Testing Statistical Hypotheses, 2nd edition P70). Thus using tail-area probabilities calculated from the observed statistics does not constitute an operational difference between the two systems.

A more important distinction between the Fisherian and NP systems is that the former does not use alternative hypotheses(3). Fisher's opinion was that the null hypothesis was more primitive than the test statistic but that the test statistic was more primitive than the alternative hypothesis. Thus, alternative hypotheses could not be used to justify choice of test statistic. Only experience could do that.

Further distinctions between the NP and Fisherian approach are to do with conditioning and whether a null hypothesis can ever be accepted.

I have one minor quibble about terminology. As far as I can see, the author uses the usual term 'null hypothesis' and the eccentric term 'nil hypothesis' interchangeably. It would be simpler if the latter were abandoned.

Referee response for version 1

Marcel alm van assen.

1 Department of Methodology and Statistics, Tilburgh University, Tilburg, Netherlands

Null hypothesis significance testing (NHST) is a difficult topic, with misunderstandings arising easily. Many texts, including basic statistics books, deal with the topic, and attempt to explain it to students and anyone else interested. I would refer to a good basic text book, for a detailed explanation of NHST, or to a specialized article when wishing an explaining the background of NHST. So, what is the added value of a new text on NHST? In any case, the added value should be described at the start of this text. Moreover, the topic is so delicate and difficult that errors, misinterpretations, and disagreements are easy. I attempted to show this by giving comments to many sentences in the text.

Abstract: “null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences to investigate if an effect is likely”. No, NHST is the method to test the hypothesis of no effect.

Intro: “Null hypothesis significance testing (NHST) is a method of statistical inference by which an observation is tested against a hypothesis of no effect or no relationship.” What is an ‘observation’? NHST is difficult to describe in one sentence, particularly here. I would skip this sentence entirely, here.

Section on Fisher; also explain the one-tailed test.

Section on Fisher; p(Obs|H0) does not reflect the verbal definition (the ‘or more extreme’ part).

Section on Fisher; use a reference and citation to Fisher’s interpretation of the p-value

Section on Fisher; “This was however only intended to be used as an indication that there is something in the data that deserves further investigation. The reason for this is that only H0 is tested whilst the effect under study is not itself being investigated.” First sentence, can you give a reference? Many people say a lot about Fisher’s intentions, but the good man is dead and cannot reply… Second sentence is a bit awkward, because the effect is investigated in a way, by testing the H0.

Section on p-value; Layout and structure can be improved greatly, by first again stating what the p-value is, and then statement by statement, what it is not, using separate lines for each statement. Consider adding that the p-value is randomly distributed under H0 (if all the assumptions of the test are met), and that under H1 the p-value is a function of population effect size and N; the larger each is, the smaller the p-value generally is.

Skip the sentence “If there is no effect, we should replicate the absence of effect with a probability equal to 1-p”. Not insightful, and you did not discuss the concept ‘replicate’ (and do not need to).

Skip the sentence “The total probability of false positives can also be obtained by aggregating results ( Ioannidis, 2005 ).” Not strongly related to p-values, and introduces unnecessary concepts ‘false positives’ (perhaps later useful) and ‘aggregation’.

Consider deleting; “If there is an effect however, the probability to replicate is a function of the (unknown) population effect size with no good way to know this from a single experiment ( Killeen, 2005 ).”

The following sentence; “ Finally, a (small) p-value  is not an indication favouring a hypothesis . A low p-value indicates a misfit of the null hypothesis to the data and cannot be taken as evidence in favour of a specific alternative hypothesis more than any other possible alternatives such as measurement error and selection bias ( Gelman, 2013 ).” is surely not mainstream thinking about NHST; I would surely delete that sentence. In NHST, a p-value is used for testing the H0. Why did you not yet discuss significance level? Yes, before discussing what is not a p-value, I would explain NHST (i.e., what it is and how it is used). 

Also the next sentence “The more (a priori) implausible the alternative hypothesis, the greater the chance that a finding is a false alarm ( Krzywinski & Altman, 2013 ;  Nuzzo, 2014 ).“ is not fully clear to me. This is a Bayesian statement. In NHST, no likelihoods are attributed to hypotheses; the reasoning is “IF H0 is true, then…”.

Last sentence: “As  Nickerson (2000)  puts it ‘theory corroboration requires the testing of multiple predictions because the chance of getting statistically significant results for the wrong reasons in any given case is high’.” What is relation of this sentence to the contents of this section, precisely?

Next section: “For instance, we can estimate that the probability of a given F value to be in the critical interval [+2 +∞] is less than 5%” This depends on the degrees of freedom.

“When there is no effect (H0 is true), the erroneous rejection of H0 is known as type I error and is equal to the p-value.” Strange sentence. The Type I error is the probability of erroneously rejecting the H0 (so, when it is true). The p-value is … well, you explained it before; it surely does not equal the Type I error.

Consider adding a figure explaining the distinction between Fisher’s logic and that of Neyman and Pearson.

“When the test statistics falls outside the critical region(s)” What is outside?

“There is a profound difference between accepting the null hypothesis and simply failing to reject it ( Killeen, 2005 )” I agree with you, but perhaps you may add that some statisticians simply define “accept H0’” as obtaining a p-value larger than the significance level. Did you already discuss the significance level, and it’s mostly used values?

“To accept or reject equally the null hypothesis, Bayesian approaches ( Dienes, 2014 ;  Kruschke, 2011 ) or confidence intervals must be used.” Is ‘reject equally’ appropriate English? Also using Cis, one cannot accept the H0.

Do you start discussing alpha only in the context of Cis?

“CI also indicates the precision of the estimate of effect size, but unless using a percentile bootstrap approach, they require assumptions about distributions which can lead to serious biases in particular regarding the symmetry and width of the intervals ( Wilcox, 2012 ).” Too difficult, using new concepts. Consider deleting.

“Assuming the CI (a)symmetry and width are correct, this gives some indication about the likelihood that a similar value can be observed in future studies, with 95% CI giving about 83% chance of replication success ( Lakens & Evers, 2014 ).” This statement is, in general, completely false. It very much depends on the sample sizes of both studies. If the replication study has a much, much, much larger N, then the probability that the original CI will contain the effect size of the replication approaches (1-alpha)*100%. If the original study has a much, much, much larger N, then the probability that the original Ci will contain the effect size of the replication study approaches 0%.

“Finally, contrary to p-values, CI can be used to accept H0. Typically, if a CI includes 0, we cannot reject H0. If a critical null region is specified rather than a single point estimate, for instance [-2 +2] and the CI is included within the critical null region, then H0 can be accepted. Importantly, the critical region must be specified a priori and cannot be determined from the data themselves.” No. H0 cannot be accepted with Cis.

“The (posterior) probability of an effect can however not be obtained using a frequentist framework.” Frequentist framework? You did not discuss that, yet.

“X% of times the CI obtained will contain the same parameter value”. The same? True, you mean?

“e.g. X% of the times the CI contains the same mean” I do not understand; which mean?

“The alpha value has the same interpretation as when using H0, i.e. we accept that 1-alpha CI are wrong in alpha percent of the times. “ What do you mean, CI are wrong? Consider rephrasing.

“To make a statement about the probability of a parameter of interest, likelihood intervals (maximum likelihood) and credibility intervals (Bayes) are better suited.” ML gives the likelihood of the data given the parameter, not the other way around.

“Many of the disagreements are not on the method itself but on its use.” Bayesians may disagree.

“If the goal is to establish the likelihood of an effect and/or establish a pattern of order, because both requires ruling out equivalence, then NHST is a good tool ( Frick, 1996 )” NHST does not provide evidence on the likelihood of an effect.

“If the goal is to establish some quantitative values, then NHST is not the method of choice.” P-values are also quantitative… this is not a precise sentence. And NHST may be used in combination with effect size estimation (this is even recommended by, e.g., the American Psychological Association (APA)).

“Because results are conditioned on H0, NHST cannot be used to establish beliefs.” It can reinforce some beliefs, e.g., if H0 or any other hypothesis, is true.

“To estimate the probability of a hypothesis, a Bayesian analysis is a better alternative.” It is the only alternative?

“Note however that even when a specific quantitative prediction from a hypothesis is shown to be true (typically testing H1 using Bayes), it does not prove the hypothesis itself, it only adds to its plausibility.” How can we show something is true?

I do not agree on the contents of the last section on ‘minimal reporting’. I prefer ‘optimal reporting’ instead, i.e., the reporting the information that is essential to the interpretation of the result, to any ready, which may have other goals than the writer of the article. This reporting includes, for sure, an estimate of effect size, and preferably a confidence interval, which is in line with recommendations of the APA.

I have read this submission. I believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

The idea of this short review was to point to common interpretation errors (stressing again and again that we are under H0) being in using p-values or CI, and also proposing reporting practices to avoid bias. This is now stated at the end of abstract.

Regarding text books, it is clear that many fail to clearly distinguish Fisher/Pearson/NHST, see Glinet et al (2012) J. Exp Education 71, 83-92. If you have 1 or 2 in mind that you know to be good, I’m happy to include them.

I agree – yet people use it to investigate (not test) if an effect is likely. The issue here is wording. What about adding this distinction at the end of the sentence?: ‘null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences used to investigate if an effect is likely, even though it actually tests for the hypothesis of no effect’.

I think a definition is needed, as it offers a starting point. What about the following: ‘NHST is a method of statistical inference by which an experimental factor is tested against a hypothesis of no effect or no relationship based on a given observation’

The section on Fisher has been modified (more or less) as suggested: (1) avoiding talking about one or two tailed tests (2) updating for p(Obs≥t|H0) and (3) referring to Fisher more explicitly (ie pages from articles and book) ; I cannot tell his intentions but these quotes leave little space to alternative interpretations.

The reasoning here is as you state yourself, part 1: ‘a p-value is used for testing the H0; and part 2: ‘no likelihoods are attributed to hypotheses’ it follows we cannot favour a hypothesis. It might seems contentious but this is the case that all we can is to reject the null – how could we favour a specific alternative hypothesis from there? This is explored further down the manuscript (and I now point to that) – note that we do not need to be Bayesian to favour a specific H1, all I’m saying is this cannot be attained with a p-value.

The point was to emphasise that a p value is not there to tell us a given H1 is true and can only be achieved through multiple predictions and experiments. I deleted it for clarity.

This sentence has been removed

Indeed, you are right and I have modified the text accordingly. When there is no effect (H0 is true), the erroneous rejection of H0 is known as type 1 error. Importantly, the type 1 error rate, or alpha value is determined a priori. It is a common mistake but the level of significance (for a given sample) is not the same as the frequency of acceptance alpha found on repeated sampling (Fisher, 1955).

A figure is now presented – with levels of acceptance, critical region, level of significance and p-value.

I should have clarified further here – as I was having in mind tests of equivalence. To clarify, I simply states now: ‘To accept the null hypothesis, tests of equivalence or Bayesian approaches must be used.’

It is now presented in the paragraph before.

Yes, you are right, I completely overlooked this problem. The corrected sentence (with more accurate ref) is now “Assuming the CI (a)symmetry and width are correct, this gives some indication about the likelihood that a similar value can be observed in future studies. For future studies of the same sample size, 95% CI giving about 83% chance of replication success (Cumming and Mallardet, 2006). If sample sizes differ between studies, CI do not however warranty any a priori coverage”.

Again, I had in mind equivalence testing, but in both cases you are right we can only reject and I therefore removed that sentence.

Yes, p-values must be interpreted in context with effect size, but this is not what people do. The point here is to be pragmatic, does and don’t. The sentence was changed.

Not for testing, but for probability, I am not aware of anything else.

Cumulative evidence is, in my opinion, the only way to show it. Even in hard science like physics multiple experiments. In the recent CERN study on finding Higgs bosons, 2 different and complementary experiments ran in parallel – and the cumulative evidence was taken as a proof of the true existence of Higgs bosons.

Daniel Lakens

1 School of Innovation Sciences, Eindhoven University of Technology, Eindhoven, Netherlands

I appreciate the author's attempt to write a short tutorial on NHST. Many people don't know how to use it, so attempts to educate people are always worthwhile. However, I don't think the current article reaches it's aim. For one, I think it might be practically impossible to explain a lot in such an ultra short paper - every section would require more than 2 pages to explain, and there are many sections. Furthermore, there are some excellent overviews, which, although more extensive, are also much clearer (e.g., Nickerson, 2000 ). Finally, I found many statements to be unclear, and perhaps even incorrect (noted below). Because there is nothing worse than creating more confusion on such a topic, I have extremely high standards before I think such a short primer should be indexed. I note some examples of unclear or incorrect statements below. I'm sorry I can't make a more positive recommendation.

“investigate if an effect is likely” – ambiguous statement. I think you mean, whether the observed DATA is probable, assuming there is no effect?

The Fisher (1959) reference is not correct – Fischer developed his method much earlier.

“This p-value thus reflects the conditional probability of achieving the observed outcome or larger, p(Obs|H0)” – please add 'assuming the null-hypothesis is true'.

“p(Obs|H0)” – explain this notation for novices.

“Following Fisher, the smaller the p-value, the greater the likelihood that the null hypothesis is false.”  This is wrong, and any statement about this needs to be much more precise. I would suggest direct quotes.

“there is something in the data that deserves further investigation” –unclear sentence.

“The reason for this” – unclear what ‘this’ refers to.

“ not the probability of the null hypothesis of being true, p(H0)” – second of can be removed?

“Any interpretation of the p-value in relation to the effect under study (strength, reliability, probability) is indeed

wrong, since the p-value is conditioned on H0”  - incorrect. A big problem is that it depends on the sample size, and that the probability of a theory depends on the prior.

“If there is no effect, we should replicate the absence of effect with a probability equal to 1-p.” I don’t understand this, but I think it is incorrect.

“The total probability of false positives can also be obtained by aggregating results (Ioannidis, 2005).” Unclear, and probably incorrect.

“By failing to reject, we simply continue to assume that H0 is true, which implies that one cannot, from a nonsignificant result, argue against a theory” – according to which theory? From a NP perspective, you can ACT as if the theory is false.

“(Lakens & Evers, 2014”) – we are not the original source, which should be cited instead.

“ Typically, if a CI includes 0, we cannot reject H0.”  - when would this not be the case? This assumes a CI of 1-alpha.

“If a critical null region is specified rather than a single point estimate, for instance [-2 +2] and the CI is included within the critical null region, then H0 can be accepted.” – you mean practically, or formally? I’m pretty sure only the former.

The section on ‘The (correct) use of NHST’ seems to conclude only Bayesian statistics should be used. I don’t really agree.

“ we can always argue that effect size, power, etc. must be reported.” – which power? Post-hoc power? Surely not? Other types are unknown. So what do you mean?

The recommendation on what to report remains vague, and it is unclear why what should be reported.

This sentence was changed, following as well the other reviewer, to ‘null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences to investigate if an effect is likely, even though it actually tests whether the observed data are probable, assuming there is no effect’

Changed, refers to Fisher 1925

I changed a little the sentence structure, which should make explicit that this is the condition probability.

This has been changed to ‘[…] to decide whether the evidence is worth additional investigation and/or replication (Fisher, 1971 p13)’

my mistake – the sentence structure is now ‘ not the probability of the null hypothesis p(H0), of being true,’ ; hope this makes more sense (and this way refers back to p(Obs>t|H0)

Fair enough – my point was to stress the fact that p value and effect size or H1 have very little in common, but yes that the part in common has to do with sample size. I left the conditioning on H0 but also point out the dependency on sample size.

The whole paragraph was changed to reflect a more philosophical take on scientific induction/reasoning. I hope this is clearer.

Changed to refer to equivalence testing

I rewrote this, as to show frequentist analysis can be used  - I’m trying to sell Bayes more than any other approach.

I’m arguing we should report it all, that’s why there is no exhausting list – I can if needed.

• Math Article

Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .

In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.

Table of contents:

• Comparison with Alternative Hypothesis

Null Hypothesis Definition

The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .

Null Hypothesis Symbol

In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .

Null Hypothesis Principle

The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.

Null Hypothesis Formula

Here, the hypothesis test formulas are given below for reference.

The formula for the null hypothesis is:

H 0 :  p = p 0

The formula for the alternative hypothesis is:

H a = p >p 0 , < p 0 ≠ p 0

The formula for the test static is:

Remember that,  p 0  is the null hypothesis and p – hat is the sample proportion.

Also, read:

Types of Null Hypothesis

There are different types of hypothesis. They are:

Simple Hypothesis

It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.

Composite Hypothesis

The composite hypothesis is one that does not completely specify the population distribution.

Exact Hypothesis

Exact hypothesis defines the exact value of the parameter. For example μ= 50

Inexact Hypothesis

This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60

Null Hypothesis Rejection

Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.

How do you Find the Null Hypothesis?

The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).

When is Null Hypothesis Rejected?

The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.

Null Hypothesis and Alternative Hypothesis

Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.

Null Hypothesis Examples

Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.

If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.

Few more examples are:

1). Are there is 100% chance of getting affected by dengue?

Ans: There could be chances of getting affected by dengue but not 100%.

2). Do teenagers are using mobile phones more than grown-ups to access the internet?

Ans: Age has no limit on using mobile phones to access the internet.

3). Does having apple daily will not cause fever?

Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.

4). Do the children more good in doing mathematical calculations than grown-ups?

Ans: Age has no effect on Mathematical skills.

In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives. 

The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data. 

Frequently Asked Questions on Null Hypothesis

What is meant by the null hypothesis.

In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.

What are the benefits of hypothesis testing?

Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.

When a null hypothesis is accepted and rejected?

The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.

Why is the null hypothesis important?

The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.

How to accept or reject the null hypothesis in the chi-square test?

If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Alternative Dispute Resolution (ADR): Meaning, Types and FAQs
• Level of Significance-Definition, Steps and Examples
• Difference Between Hypothesis And Theory
• What is Dihybrid Cross? Examples and an Overview
• Real-life Applications of Hypothesis Testing
• T-Test in Statistics: Formula, Types and Steps
• Hypothesis Testing Formula
• Independent Sample t Test in R
• Alternate Interior Angles
• How do you define and measure your product hypothesis?
• Difference between Alternate and Alternative
• Introduction to Power Analysis in Python
• Difference between Null and Alternate Hypothesis
• Inductive Reasoning | Definition, Types, & Examples
• Python unittest - assertIn() function
• Python unittest - assertNotIsInstance() function
• Python unittest - assertIsNone() function
• Python unittest - assertIsInstance() function

Alternative Hypothesis: Definition, Types and Examples

In statistical hypothesis testing, the alternative hypothesis is an important proposition in the hypothesis test. The goal of the hypothesis test is to demonstrate that in the given condition, there is sufficient evidence supporting the credibility of the alternative hypothesis instead of the default assumption made by the null hypothesis.

Alternative Hypotheses

Both hypotheses include statements with the same purpose of providing the researcher with a basic guideline. The researcher uses the statement from each hypothesis to guide their research. In statistics, alternative hypothesis is often denoted as H a or H 1 .

Table of Content

What is a Hypothesis?

Alternative hypothesis, types of alternative hypothesis, difference between null and alternative hypothesis, formulating an alternative hypothesis, example of alternative hypothesis, application of alternative hypothesis.

“A hypothesis is a statement of a relationship between two or more variables.” It is a working statement or theory that is based on insufficient evidence.

While experimenting, researchers often make a claim, that they can test. These claims are often based on the relationship between two or more variables. “What causes what?” and “Up to what extent?” are a few of the questions that a hypothesis focuses on answering. The hypothesis can be true or false, based on complete evidence.

While there are different hypotheses, we discuss only null and alternate hypotheses. The null hypothesis, denoted H o , is the default position where variables do not have a relation with each other. That means the null hypothesis is assumed true until evidence indicates otherwise. The alternative hypothesis, denoted H 1 , on the other hand, opposes the null hypothesis. It assumes a relation between the variables and serves as evidence to reject the null hypothesis.

Example of Hypothesis:

Mean age of all college students is 20.4 years. (simple hypothesis).

An Alternative Hypothesis is a claim or a complement to the null hypothesis. If the null hypothesis predicts a statement to be true, the Alternative Hypothesis predicts it to be false. Let’s say the null hypothesis states there is no difference between height and shoe size then the alternative hypothesis will oppose the claim by stating that there is a relation.

We see that the null hypothesis assumes no relationship between the variables whereas an alternative hypothesis proposes a significant relation between variables. An alternative theory is the one tested by the researcher and if the researcher gathers enough data to support it, then the alternative hypothesis replaces the null hypothesis.

Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

There are a few types of alternative hypothesis that we will see:

1. One-tailed test H 1 : A one-tailed alternative hypothesis focuses on only one region of rejection of the sampling distribution. The region of rejection can be upper or lower.

• Upper-tailed test H 1 : Population characteristic > Hypothesized value
• Lower-tailed test H 1 : Population characteristic < Hypothesized value

2. Two-tailed test H 1 : A two-tailed alternative hypothesis is concerned with both regions of rejection of the sampling distribution.

3. Non-directional test H 1 : A non-directional alternative hypothesis is not concerned with either region of rejection; rather, it is only concerned that null hypothesis is not true.

4. Point test H 1 : Point alternative hypotheses occur when the hypothesis test is framed so that the population distribution under the alternative hypothesis is a fully defined distribution, with no unknown parameters; such hypotheses are usually of no practical interest but are fundamental to theoretical considerations of statistical inference and are the basis of the Neyman–Pearson lemma.

the differences between Null Hypothesis and Alternative Hypothesis is explained in the table below:

Formulating an alternative hypothesis means identifying the relationships, effects or condition being studied. Based on the data we conclude that there is a different inference from the null-hypothesis being considered.

• Understand the null hypothesis.
• Consider the alternate hypothesis
• Choose the type of alternate hypothesis (one-tailed or two-tailed)

Alternative hypothesis must be true when the null hypothesis is false. When trying to identify the information need for alternate hypothesis statement, look for the following phrases:

• “Is it reasonable to conclude…”
• “Is there enough evidence to substantiate…”
• “Does the evidence suggest…”
• “Has there been a significant…”

When alternative hypotheses in mathematical terms, they always include an inequality ( usually ≠, but sometimes < or >) . When writing the alternate hypothesis, make sure it never includes an “=” symbol.

To help you write your hypotheses, you can use the template sentences below.

Does independent variable affect dependent variable?

• Null Hypothesis (H 0 ): Independent variable does not affect dependent variable.
• Alternative Hypothesis (H a ): Independent variable affects dependent variable.

Various examples of Alternative Hypothesis includes:

Two-Tailed Example

• Research Question : Do home games affect a team’s performance?
• Null-Hypothesis: Home games do not affect a team’s performance.
• Alternative Hypothesis: Home games have an effect on team’s performance.
• Research Question: Does sleeping less lead to depression?
• Null-Hypothesis: Sleeping less does not have an effect on depression.
• Alternative Hypothesis : Sleeping less has an effect on depression.

One-Tailed Example

• Research Question: Are candidates with experience likely to get a job?
• Null-Hypothesis: Experience does not matter in getting a job.
• Alternative Hypothesis: Candidates with work experience are more likely to receive an interview.
• Alternative Hypothesis : Teams with home advantage are more likely to win a match.

Some applications of Alternative Hypothesis includes:

• Rejecting Null-Hypothesis : A researcher performs additional research to find flaws in the null hypothesis. Following the research, which uses the alternative hypothesis as a guide, they may decide whether they have enough evidence to reject the null hypothesis.
• Guideline for Research : An alternative and null hypothesis include statements with the same purpose of providing the researcher with a basic guideline. The researcher uses the statement from each hypothesis to guide their research.
• New Theories : Alternative hypotheses can provide the opportunity to discover new theories that a researcher can use to disprove an existing theory that may not have been backed up by evidence.

We defined the relationship that exist between null-hypothesis and alternative hypothesis. While the null hypothesis is always a default assumption about our test data, the alternative hypothesis puts in all the effort to make sure the null hypothesis is disproved.

Null-hypothesis always explores new relationships between the independent variables to find potential outcomes from our test data. We should note that for every null hypothesis, one or more alternate hypotheses can be developed.

Also Check:

Mathematics Maths Formulas Branches of Mathematics

FAQs on Alternative Hypothesis

What is hypothesis.

A hypothesis is a statement of a relationship between two or more variables.” It is a working statement or theory that is based on insufficient evidence.

What is an Alternative Hypothesis?

Alternative hypothesis, denoted by H 1 , opposes the null-hypothesis. It assumes a relation between the variables and serves as an evidence to reject the null-hypothesis.

What is the Difference between Null-Hypothesis and Alternative Hypothesis?

Null hypothesis is the default claim that assumes no relationship between variables while alternative hypothesis is the opposite claim which considers statistical significance between the variables.

What is Alternative and Experimental Hypothesis?

Null hypothesis (H 0 ) states there is no effect or difference, while the alternative hypothesis (H 1 or H a ) asserts the presence of an effect, difference, or relationship between variables. In hypothesis testing, we seek evidence to either reject the null hypothesis in favor of the alternative hypothesis or fail to do so.

Please Login to comment...

Similar reads.

• Math-Statistics
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Open access
• Published: 13 May 2024

SCIPAC: quantitative estimation of cell-phenotype associations

• Dailin Gan 1 ,
• Yini Zhu 2 ,
• Xin Lu 2 , 3 &
• Jun Li   ORCID: orcid.org/0000-0003-4353-5761 1  

Genome Biology volume  25 , Article number:  119 ( 2024 ) Cite this article

175 Accesses

2 Altmetric

Metrics details

Numerous algorithms have been proposed to identify cell types in single-cell RNA sequencing data, yet a fundamental problem remains: determining associations between cells and phenotypes such as cancer. We develop SCIPAC, the first algorithm that quantitatively estimates the association between each cell in single-cell data and a phenotype. SCIPAC also provides a p -value for each association and applies to data with virtually any type of phenotype. We demonstrate SCIPAC’s accuracy in simulated data. On four real cancerous or noncancerous datasets, insights from SCIPAC help interpret the data and generate new hypotheses. SCIPAC requires minimum tuning and is computationally very fast.

Single-cell RNA sequencing (scRNA-seq) technologies are revolutionizing biomedical research by providing comprehensive characterizations of diverse cell populations in heterogeneous tissues [ 1 , 2 ]. Unlike bulk RNA sequencing (RNA-seq), which measures the average expression profile of the whole tissue, scRNA-seq gives the expression profiles of thousands of individual cells in the tissue [ 3 , 4 , 5 , 6 , 7 ]. Based on this rich data, cell types may be discovered/determined in an unsupervised (e.g., [ 8 , 9 ]), semi-supervised (e.g., [ 10 , 11 , 12 , 13 ]), or supervised manner (e.g., [ 14 , 15 , 16 ]). Despite the fast development, there are still limitations with scRNA-seq technologies. Notably, the cost for each scRNA-seq experiment is still high; as a result, most scRNA-seq data are from a single or a few biological samples/tissues. Very few datasets consist of large numbers of samples with different phenotypes, e.g., cancer vs. normal. This places great difficulties in determining how a cell type contributes to a phenotype based on single-cell studies (especially if the cell type is discovered in a completely unsupervised manner or if people have limited knowledge of this cell type). For example, without having single-cell data from multiple cancer patients and multiple normal controls, it could be hard to computationally infer whether a cell type may promote or inhibit cancer development. However, such association can be critical for cancer research [ 17 ], disease diagnosis [ 18 ], cell-type targeted therapy development [ 19 ], etc.

Fortunately, this difficulty may be overcome by borrowing information from bulk RNA-seq data. Over the past decade, a considerable amount of bulk RNA-seq data from a large number of samples with different phenotypes have been accumulated and made available through databases like The Cancer Genome Atlas (TCGA) [ 20 ] and cBioPortal [ 21 , 22 ]. Data in these databases often contain comprehensive patient phenotype information, such as cancer status, cancer stages, survival status and time, and tumor metastasis. Combining single-cell data from a single or a few individuals and bulk data from a relatively large number of individuals regarding a particular phenotype can be a cost-effective way to determine how a cell type contributes to the phenotype. A recent method Scissor [ 23 ] took an essential step in this direction. It uses single-cell and bulk RNA-seq data with phenotype information to classify the cells into three discrete categories: Scissor+, Scissor−, and null cells, corresponding to cells that are positively associated, negatively associated, and not associated with the phenotype.

Here, we present a method that takes another big step in this direction, which is called Single-Cell and bulk data-based Identifier for Phenotype Associated Cells or SCIPAC for short. SCIPAC enables quantitative estimation of the strength of association between each cell in a scRNA-seq data and a phenotype, with the help of bulk RNA-seq data with phenotype information. Moreover, SCIPAC also enables the estimation of the statistical significance of the association. That is, it gives a p -value for the association between each cell and the phenotype. Furthermore, SCIPAC enables the estimation of association between cells and an ordinal phenotype (e.g., different stages of cancer), which could be informative as people may not only be interested in the emergence/existence of cancer (cancer vs. healthy, a binary problem) but also in the progression of cancer (different stages of cancer, an ordinal problem).

To study the performance of SCIPAC, we first apply SCIPAC to simulated data under three schemes. SCIPAC shows high accuracy with low false positive rates. We further show the broad applicability of SCIPAC on real datasets across various diseases, including prostate cancer, breast cancer, lung cancer, and muscular dystrophy. The association inferred by SCIPAC is highly informative. In real datasets, some cell types have definite and well-studied functions, while others are less well-understood: their functions may be disease-dependent or tissue-dependent, and they may contain different sub-types with distinct functions. In the former case, SCIPAC’s results agree with current biological knowledge. In the latter case, SCIPAC’s discoveries inspire the generation of new hypotheses regarding the roles and functions of cells under different conditions.

An overview of the SCIPAC algorithm

SCIPAC is a computational method that identifies cells in single-cell data that are associated with a given phenotype. This phenotype can be binary (e.g., cancer vs. normal), ordinal (e.g., cancer stage), continuous (e.g., quantitative traits), or survival (i.e., survival time and status). SCIPAC uses input data consisting of three parts: single-cell RNA-seq data that measures the expression of p genes in m cells, bulk RNA-seq data that measures the expression of the same set of p genes in n samples/tissues, and the statuses/values of the phenotype of the n bulk samples/tissues. The output of SCIPAC is the strength and the p -value of the association between each cell and the phenotype.

SCIPAC proposes the following definition of “association” between a cell and a phenotype: A group of cells that are likely to play a similar role in the phenotype (such as cells of a specific cell type or sub-type, cells in a particular state, cells in a cluster, cells with similar expression profiles, or cells with similar functions) is considered to be positively/negatively associated with a phenotype if an increase in their proportion within the tissue likely indicates an increased/decreased probability of the phenotype’s presence. SCIPAC assigns the same association to all cells within such a group. Taking cancer as the phenotype as an example, if increasing the proportion of a cell type indicates a higher chance of having cancer (binary), having a higher cancer stage (ordinal), or a higher hazard rate (survival), all cells in this cell type is positively associated with cancer.

The algorithm of SCIPAC follows the following four steps. First, the cells in the single-cell data are grouped into clusters according to their expression profiles. The Louvain algorithm from the Seurat package [ 24 , 25 ] is used as the default clustering algorithm, but the user may choose any clustering algorithm they prefer. Or if information of the cell types or other groupings of cells is available a priori, it may be supplied to SCIPAC as the cell clusters, and this clustering step can be skipped. In the second step, a regression model is learned from bulk gene expression data with the phenotype. Depending on the type of the phenotype, this model can be logistic regression, ordinary linear regression, proportional odds model, or Cox proportional hazards model. To achieve a higher prediction power with less variance, by default, the elastic net (a blender of Lasso and ridge regression [ 26 ]) is used to fit the model. In the third step, SCIPAC computes the association strength \(\Lambda\) between each cell cluster and the phenotype based on a mathematical formula that we derive. Finally, the p -values are computed. The association strength and its p -value between a cell cluster and the phenotype are given to all cells in the cluster.

SCIPAC requires minimum tuning. When the cell-type information is given in step 1, SCIPAC does not have any (hyper)parameter. Otherwise, the Louvain algorithm used in step 1 has a “resolution” parameter that controls the number of cell clusters: a larger resolution results in more clusters. SCIPAC inherits this parameter as its only parameter. Since SCIPAC gives the same association strength and p -value to cells from the same cluster, this parameter also determines the resolution of results provided by SCIPAC. Thus, we still call it “resolution” in SCIPAC. Because of its meaning, we recommend setting it so that the number of cell clusters given by the clustering algorithm is comparable to, or reasonably larger than, the number of cell types (or sub-types) in the data. We will see that the performance of SCIPAC is insensitive to this resolution parameter, and the default value 2.0 typically works well.

The details of the SCIPAC algorithm are given in the “ Methods ” section.

Performance in simulated data

We assess the performance of SCIPAC in simulated data under three different schemes. The first scheme is simple and consists of only three cell types. The second scheme is more complicated and consists of seven cell types, which better imitates actual scRNA-seq data. In the third scheme, we simulate cells under different cell development stages to test the performance of SCIPAC under an ordinal phenotype. Details of the simulation are given in Additional file 1.

Simulation scheme I

Under this scheme, the single-cell data consists of three cell types: one is positively associated with the phenotype, one is negatively associated, and the third is not associated (we call it “null”). Figure 1 a gives the UMAP [ 27 ] plot of the three cell types, and Fig. 1 b gives the true associations of these three cell types with the phenotype, with red, blue, and light gray denoting positive, negative, and null associations.

UMAP visualization and numeric measures of the simulated data under scheme I. All the plots in a–e  are scatterplots of the two dimensional single-cell data given by UMAP. The x and y axes represent the two dimensions, and their scales are not shown as their specific values are not directly relevant. Points in the plots represents single cells, and they are colored differently in each subplot to reflect different information/results. a  Cell types. b  True associations. The association between cell types 1, 2, and 3 and the phenotype are positive, negative, and null, respectively. c  Association strengths \(\Lambda\) given by SCIPAC under different resolutions. Red/blue represents the sign of \(\Lambda\) , and the shade gives the absolute value of \(\Lambda\) . Every cell is colored red or blue since no \(\Lambda\) is exactly zero. Below each subplot, Res stands for resolution, and K stands for the number of cell clusters given by this resolution. d   p -values given by SCIPAC. Only cells with p -value \(< 0.05\) are colored red (positive association) or blue (negative association); others are colored white. e  Results given by Scissor under different \(\alpha\) values. Red, blue, and light gray stands for Scissor+, Scissor−, and background (i.e., null) cells. f  F1 scores and g  FSC for SCIPAC and Scissor under different parameter values. For SCIPAC, each bar is the value under a resolution/number of clusters. For Scissor, each bar is the value under an \(\alpha\)

We apply SCIPAC to the simulated data. For the resolution parameter (see the “ Methods ” section), values 0.5, 1.0, and 1.5 give 3, 4, and 4 clusters, respectively, close to the actual number of cell types. They are good choices based on the guidance for choosing this parameter. To show how SCIPAC behaves under parameter misspecification, we also set the resolution up to 4.0, which gives a whopping 61 clusters. Figure 1 c and d give the association strengths \(\Lambda\) and the p -values given by four different resolutions (results under other resolutions are provided in Additional file 1: Fig. S1 and S2). In Fig. 1 c, red and blue denote positive and negative associations, respectively, and the shade of the color represents the strength of the association, i.e., the absolute value of \(\Lambda\) . Every cell is colored blue or red, as none of \(\Lambda\) is exactly zero. In Fig. 1 d, red and blue denote positive and negative associations that are statistically significant ( p -value \(< 0.05\) ). Cells whose associations are not statistically significant ( p -value \(\ge 0.05\) ) are shown in white. To avoid confusion, it is worth repeating that cells that are colored in red/blue in Fig. 1 c are shown in red/blue in Fig. 1 d only if they are statistically significant; otherwise, they are colored white in Fig. 1 d.

From Fig. 1 c, d (as well as Additional file 1: Fig. S1 and S2), it is clear that the results of SCIPAC are highly consistent under different resolution values, including both the estimated association strengths and the p -values. It is also clear that SCIPAC is highly accurate: most truly associated cells are identified as significant, and most, if not all, truly null cells are identified as null.

As the first algorithm that quantitatively estimates the association strength and the first algorithm that gives the p -value of the association, SCIPAC does not have a real competitor. A previous algorithm, Scissor, is able to classify cells into three discrete categories according to their associations with the phenotype. So, we compare SCIPAC with Scissor in respect of the ability to differentiate positively associated, negatively associated, and null cells.

Running Scissor requires tuning a parameter called \(\alpha\) , which is a number between 0 and 1 that balances the amount of regularization for the smoothness and for the sparsity of the associations. The Scissor R package does not provide a default value for this \(\alpha\) or a function to help select this value. The Scissor paper suggests the following criterion: “the number of Scissor-selected cells should not exceed a certain percentage of total cells (default 20%) in the single-cell data. In each experiment, a search on the above searching list is performed from the smallest to the largest until a value of \(\alpha\) meets the above criteria.” In practice, we have found that this criterion does not often work properly, as the truly associated cells may not compose 20% of all cells in actual data. Therefore, instead of setting \(\alpha\) to any particular value, we set \(\alpha\) values that span the whole range of \(\alpha\) to see the best possible performance of Scissor.

The performance of Scissor in our simulation data under four different \(\alpha\) values are shown in Fig. 1 e, and results under more \(\alpha\) values are shown in Additional file 1: Fig. S3. In the figures, red, blue, and light gray denote Scissor+, Scissor−, and null (called “background” in Scissor) cells, respectively. The results of Scissor have several characteristics different from SCIPAC. First, Scissor does not give the strength or statistical significance of the association, and thus the colors of the cells in the figures do not have different shades. Second, different \(\alpha\) values give very different results. Greater \(\alpha\) values generally give fewer Scissor+ and Scissor− cells, but there are additional complexities. One complexity is that the Scissor+ (or Scissor−) cells under a greater \(\alpha\) value are not a strict subset of Scissor+ (or Scissor−) cells under a smaller \(\alpha\) value. For example, the number of truly negatively associated cells detected as Scissor− increases when \(\alpha\) increases from 0.01 to 0.30. Another complexity is that the direction of the association may flip as \(\alpha\) increases. For example, most cells of cell type 2 are identified as Scissor+ under \(\alpha =0.01\) , but many of them are identified as Scissor− under larger \(\alpha\) values. Third, Scissor does not achieve high power and low false-positive rate at the same time under any \(\alpha\) . No matter what the \(\alpha\) value is, there is only a small proportion of cells from cell type 2 that are correctly identified as negatively associated, and there is always a non-negligible proportion of null cells (i.e., cells from cell type 3) that are incorrectly identified as positively or negatively associated. Fourth, Scissor+ and Scissor− cells can be close to each other in the figure, even under a large \(\alpha\) value. This means that cells with nearly identical expression profiles are detected to be associated with the phenotype in opposite directions, which can place difficulties in interpreting the results.

SCIPAC overcomes the difficulties of Scissor and gives results that are more informative (quantitative strengths with p -values), more accurate (both high power and low false-positive rate), less sensitive to the tuning parameter, and easier to interpret (cells with similar expression typically have similar associations to the phenotype).

SCIPAC’s higher accuracy in differentiating positively associated, negatively associated, and null cells than Scissors can also be measured numerically using the F1 score and the fraction of sign correctness (FSC). F1, which is the harmonic mean of precision and recall, is a commonly used measure of calling accuracy. Note that precision and recall are only defined for two-class problems, which try to classify desired signals/discoveries (so-called “positives”) against noises/trivial results (so-called “negatives”). Our case, on the other hand, is a three-class problem: positive association, negative association, and null. To compute F1, we combine the positive and negative associations and treat them as “positives,” and treat null as “negatives.” This F1 score ignores the direction of the association; thus, it alone is not enough to describe the performance of an association-detection algorithm. For example, an algorithm may have a perfect F1 score even if it incorrectly calls all negative associations positive. To measure an algorithm’s ability to determine the direction of the association, we propose a statistic called FSC, defined as the fraction of true discoveries that also have the correct direction of the association. The F1 score and FSC are numbers between 0 and 1, and higher values are preferred. A mathematical definition of these two measures is given in Additional file 1.

Figure 1 f, g show the F1 score and FSC of SCIPAC and Scissor under different values of tuning parameters. The F1 score of Scissor is between 0.2 and 0.7 under different \(\alpha\) ’s. The FSC of Scissor increases from around 0.5 to nearly 1 as \(\alpha\) increases, but Scissor does not achieve high F1 and FSC scores at the same time under any \(\alpha\) . On the other hand, the F1 score of SCIPAC is close to perfection when the resolution parameter is properly set, and it is still above 0.90 even if the resolution parameter is set too large. The FSC of SCIPAC is always above 0.96 under different resolutions. That is, SCIPAC achieves high F1 and FSC scores simultaneously under a wide range of resolutions, representing a much higher accuracy than Scissor.

Simulation scheme II

This more complicated simulation scheme has seven cell types, which are shown in Fig. 2 a. As shown in Fig. 2 b, cell types 1 and 3 are negatively associated (colored blue), 2 and 4 are positively associated (colored red), and 5, 6, and 7 are not associated (colored light gray).

UMAP visualization of the simulated data under a–g  scheme II and h–k  scheme III. a  Cell types. b  True associations. c , d  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. e  Results given by Scissor under different \(\alpha\) values. f  F1 scores and g  FSC for SCIPAC and Scissor under different parameter values. h  Cell differentiation paths. The four paths have the same starting location, which is in the center, but different ending locations. This can be considered as a progenitor cell type differentiating into four specialized cell types. i  Cell differentiation steps. These steps are used to create four stages, each containing 500 steps. Thus, this plot of differentiation steps can also be viewed as the plot of true association strengths. j , k  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution

The association strengths and p -values given by SCIPAC under the default resolution are illustrated in Fig. 2 c, d, respectively. Results under several other resolutions are given in Additional file 1: Fig. S4 and S5. Again, we find that SCIPAC gives highly consistent results under different resolutions. SCIPAC successfully identifies three out of the four truly associated cell types. For the other truly associated cell type, cell type 1, SCIPAC correctly recognizes its association with the phenotype as negative, although the p -values are not significant enough. The F1 score is 0.85, and the FSC is greater than 0.99, as shown in Fig. 2 f, g.

The results of Scissor under four different \(\alpha\) values are given in Fig. 2 e. (More shown in Additional file 1: Fig. S6.) Under this highly challenging simulation scheme, Scissor can only identify one out of four truly associated cell types. Its F1 score is below 0.4.

Simulation scheme III

This simulation scheme is to assess the performance of SCIPAC for ordinal phenotypes. We simulate cells along four cell-differentiation paths with the same starting location but different ending locations, as shown in Fig. 2 h. These cells can be considered as a progenitor cell population differentiating into four specialized cell types. In Fig. 2 i, the “step” reflects their position in the differentiation path, with step 0 meaning the start and step 2000 meaning the end of the differentiation. Then, the “stage” is generated according to the step: cells in steps 0 \(\sim\) 500, 501 \(\sim\) 1000, 1001 \(\sim\) 1500, and 1501 \(\sim\) 2000 are assigned to stages I, II, III, and IV, respectively. This stage is treated as the ordinal phenotype. Under this simulation scheme, Fig. 2 i also gives the actual associations, and all cells are associated with the phenotype.

The results of SCIPAC under the default resolution are shown in Fig. 2 j, k. Clearly, the associations SCIPAC identifies are highly consistent with the truth. Particularly, it successfully identifies the cells in the center as early-stage cells and most cells at the end of branches as last-stage cells. The results of SCIPAC under other resolutions are given in Additional file 1: Fig. S7 and S8, which are highly consistent. Scissor does not work with ordinal phenotypes; thus, no results are reported here.

Performance in real data

We consider four real datasets: a prostate cancer dataset, a breast cancer dataset, a lung cancer dataset, and a muscular dystrophy dataset. The bulk RNA-seq data of the three cancer datasets are obtained from the TCGA database, and that of the muscular dystrophy dataset is obtained from a published paper [ 28 ]. A detailed description of these datasets is given in Additional file 1. We will use these datasets to assess the performance of SCIPAC on different types of phenotypes. The cell type information (i.e., which cell belongs to which cell type) is available for the first three datasets, but we ignore this information so that we can make a fair comparison with Scissor, which cannot utilize this information.

Prostate cancer data with a binary phenotype

We use the single-cell expression of 8,700 cells from prostate-cancer tumors sequenced by [ 29 ]. The cell types of these cells are known and given in Fig. 3 a. The bulk data comprises 550 TCGA-PRAD (prostate adenocarcinoma) samples with phenotype (cancer vs. normal) information. Here the phenotype is cancer, and it is binary: present or absent.

UMAP visualization of the prostate cancer data, with a zoom-in view for the red-circled region (cell type MNP). a  True cell types. BE, HE, and CE stand for basal, hillock, club epithelial cells, LE-KLK3 and LE-KLK4 stand for luminal epithelial cells with high levels of kallikrein related peptidase 3 and 4, and MNP stands for mononuclear phagocytes. In the zoom-in view, the sub-types of MNP cells are given. b  Association strengths \(\Lambda\) given by SCIPAC under the default resolution. The cyan-circled cells are B cells, which are estimated by SCIPAC as negatively associated with cancer but estimated by Scissor as Scissor+ or null. c   p -values given by SCIPAC. The MNP cell type, which is red-circled in the plot, is estimated by SCIPAC to be strongly negatively associated with cancer but estimated by Scissor to be positively associated with cancer. d  Results given by Scissor under different \(\alpha\) values

Results from SCIPAC with the default resolution are shown in Fig. 3 b, c (results with other resolutions, given in Additional file 1: Fig. S9 and S10, are highly consistent with results here.) Compared with results from Scissor, shown in Fig. 3 d, results from SCIPAC again show three advantages. First, results from SCIPAC are richer and more comprehensive. SCIPAC gives estimated associations and the corresponding p -values, and the estimated associations are quantitative (shown in Fig. 3 b as different shades to the red or blue color) instead of discrete (shown in Fig. 3 d as a uniform shade to the red, blue, or light gray color). Second, SCIPAC’s results can be easier to interpret as the red and blue colors are more block-wise instead of scattered. Third, unlike Scissor, which produces multiple sets of results varying based on the parameter \(\alpha\) —a parameter without a default value or tuning guidance—typically, a single set of results from SCIPAC under its default settings suffices.

Comparing the results from our SCIPAC method with those from Scissor is non-trivial, as the latter’s outcomes are scattered and include multiple sets. We propose the following solutions to summarize the inferred association of a known cell type with the phenotype using a specific method (Scissor under a specific \(\alpha\) value, or SCIPAC with the default setting). We first calculate the proportion of cells in this cell type identified as Scissor+ (by Scissor at a specific \(\alpha\) value) or as significantly positively associated (by SCIPAC), denoted by \(p_{+}\) . We also calculate the proportion of all cells, encompassing any cell type, which are identified as Scissor+ or significantly positively associated, serving as the average background strength, denoted by \(p_{a}\) . Then, we compute the log odds ratio for this cell type to be positively associated with the phenotype compared to the background, represented as:

Similarly, the log odds ratio for the cell type to be negatively associated with the phenotype, \(\rho _-\) , is computed in a parallel manner.

For SCIPAC, a cell type is summarized as positively associated with the phenotype if \(\rho _+ \ge 1\) and \(\rho _- < 1\)  and negatively associated if \(\rho _- \ge 1\) and \(\rho _+ < 1\) . If neither condition is met, the association is inconclusive. For Scissor, we apply it under six different \(\alpha\) values: 0.01, 0.05, 0.10, 0.15, 0.20, and 0.25. A cell type is summarized as positively associated with the phenotype if \(\rho _+ \ge 1\) and \(\rho _- < 1\) in at least four of these \(\alpha\) values and negatively associated if \(\rho _- \ge 1\) and \(\rho _+ < 1\) in at least four \(\alpha\) values. If these criteria are not met, the association is deemed inconclusive. The above computation of log odds ratios and the determination of associations are performed only on cell types that each compose at least 1% of the cell population, to ensure adequate power.

For the prostate cancer data, the log odds ratios for each cell type using each method are presented in Tables S1 and S2. The final associations determined for each cell type are summarized in Table S3. In the last column of this table, we also indicate whether the conclusions drawn from SCIPAC and Scissor are consistent or not.

We find that SCIPAC’s results agree with Scissor on most cell types. However, there are three exceptions: mononuclear phagocytes (MNPs), B cells, and LE-KLK4.

MNPs are red-circled and zoomed in in each sub-figure of Fig. 3 . Most cells in this cell type are colored red in Fig. 3 d but colored dark blue in Fig. 3 b. In other words, while Scissor determines that this cell type is Scissor+, SCIPAC makes the opposite inference. Moreover, SCIPAC is confident about its judgment by giving small p -values, as shown in Fig. 3 c. To see which inference is closer to the biological fact is not easy, as biologically MNPs contain a number of sub-types that each have different functions [ 30 , 31 ]. Fortunately, this cell population has been studied in detail in the original paper that generated this dataset [ 29 ], and the sub-type information of each cell is provided there: this MNP population contains six sub-types, which are dendritic cells (DC), M1 macrophages (Mac1), metallothionein-expressing macrophages (Mac-MT), M2 macrophages (Mac2), proliferating macrophages (Mac-cycling), and monocytes (Mono), as shown in the zoom-in view of Fig. 3 a. Among these six sub-types, DC, Mac1, and Mac-MT are believed to inhibit cancer development and can serve as targets in cancer immunotherapy [ 29 ]; they compose more than 60% of all MNP cells in this dataset. SCIPAC makes the correct inference on this majority of MNP cells. Another cell type, Mac2, is reported to promote tumor development [ 32 ], but it only composes less than \(15\%\) of the MNPs. How the other two cell types, Mac-cycling and Mono, are associated with cancer is less studied. Overall, the results given by SCIPAC are more consistent with the current biological knowledge.

B cells are cyan-circled in Fig. 3 b. B cells are generally believed to have anti-tumor activity by producing tumor-reactive antibodies and forming tertiary lymphoid structures [ 29 , 33 ]. This means that B cells are likely to be negatively associated with cancer. SCIPAC successfully identifies this negative association, while Scissor fails.

LE-KLK4, a subtype of cancer cells, is thought to be positively associated with the tumor phenotype [ 29 ]. SCIPAC successfully identified this positive association, in contrast to Scissor, which failed to do so (in the figure, a proportion of LE-KLK4 cells are identified as Scissor+, especially under the smallest \(\alpha\) value; however, this proportion is not significantly higher than the background Scissor+ level under the majority of \(\alpha\) values).

In summary, across all three cell types, the results from SCIPAC appear to be more consistent with current biological knowledge. For more discussions regarding this dataset, refer to Additional file 1.

Breast cancer data with an ordinal phenotype

The scRNA-seq data for breast cancer are from [ 34 ], and we use the 19,311 cells from the five HER2+ tumor tissues. The true cell types are shown in Fig. 4 a. The bulk data include 1215 TCGA-BRCA samples with information on the cancer stage (I, II, III, or IV), which is treated as an ordinal phenotype.

UMAP visualization of the breast cancer data. a  True cell types. CAFs stand for cancer-associated fibroblasts, PB stands for plasmablasts and PVL stands for perivascular-like cells. b , c  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. Cyan-circled are a group of T cells that are estimated by SCIPAC to be most significantly associated with the cancer stage in the negative direction, and orange-circled are a group of T cells that are estimated by SCIPAC to be significantly positively associated with the cancer stage. d  DE analysis of the cyan-circled T cells vs. all the other T cells. e  DE analysis of the cyan-circled T cells vs. all the other cells. f  Expression of CD8+ T cell marker genes in the cyan-circled cells and all the other cells. g  DE analysis of the orange-circled T cells vs. all the other cells. h  Expression of regulatory T cell marker genes in the orange-circled cells and all the other cells

Association strengths and p -values given by SCIPAC under the default resolution are shown in Fig. 4 b, c. Results under other resolutions are given in Additional file 1: Fig. S11 and S12, and again they are highly consistent with results under the default resolution. We do not present the results from Scissor, as Scissor does not take ordinal phenotypes.

In the SCIPAC results, cells that are most strongly and statistically significantly associated with the phenotype in the positive direction are the cancer-associated fibroblasts (CAFs). This finding agrees with the literature: CAFs contribute to therapy resistance and metastasis of cancer cells via the production of secreted factors and direct interaction with cancer cells [ 35 ], and they are also active players in breast cancer initiation and progression [ 36 , 37 , 38 , 39 ]. Another large group of cells identified as positively associated with the phenotype is the cancer epithelial cells. They are malignant cells in breast cancer tissues and are thus expected to be associated with severe cancer stages.

Of the cells identified as negatively associated with severe cancer stages, a large portion of T cells is the most noticeable. Biologically, T cells contain many sub-types, including CD4+, CD8+, regulatory T cells, and more, and their functions are diverse in the tumor microenvironment [ 40 ]. To explore SCIPAC’s discoveries, we compare T cells that are identified as most statistically significant, with p -values \(< 10^{-6}\) and circled in Fig. 4 d, with the other T cells. Differential expression (DE) analysis (details about DE analysis and other analyses are given in Additional file 1) identifies seven genes upregulated in these most significant T cells. Of these seven genes, at least five are supported by the literature: CCL4, XCL1, IFNG, and GZMB are associated with CD8+ T cell infiltration; they have been shown to have anti-tumor functions and are involved in cancer immunotherapy [ 41 , 42 , 43 ]. Also, IL2 has been shown to serve an important role in combination therapies for autoimmunity and cancer [ 44 ]. We also perform an enrichment analysis [ 45 ], in which a pathway called Myc stands out with a \(\textit{p}\text{-value}<10^{-7}\) , much smaller than all other pathways. Myc is downregulated in the T cells that are identified as most negatively associated with cancer stage progress. This agrees with current biological knowledge about this pathway: Myc is known to contribute to malignant cell transformation and tumor metastasis [ 46 , 47 , 48 ].

On the above, we have compared T cells that are most significantly associated with cancer stages in the negative direction with the other T cells using DE and pathway analysis, and the results could suggest that these cells are tumor-infiltrated CD8+ T cells with tumor-inhibition functions. To check this hypothesis, we perform DE analysis of these cells against all other cells (i.e., the other T cells and all the other cell types). The DE genes are shown in Fig. 4 e. It can be noted that CD8+ T cell marker genes such as CD8A, CD8B, and GZMK are upregulated. We further obtain CD8+ T cell marker genes from CellMarker [ 49 ] and check their expression, as illustrated in Fig. 4 f. Marker genes CD8A, CD8B, CD3D, GZMK, and CD7 show significantly higher expression in these T cells. This again supports our hypothesis that these cells are tumor-infiltrated CD8+ T cells that have anti-tumor functions.

Interestingly, not all T cells are identified as negatively associated with severe cancer stages; a group of T cells is identified as positively associated, as circled in Fig. 4 c. To explore the function of this group of T cells, we perform DE analysis of these T cells against the other T cells. The DE genes are shown in Fig. 4 g. Based on the literature, six out of eight over-expressed genes are associated with cancer development. The high expression of NUSAP1 gene is associated with poor patient overall survival, and this gene also serves as a prognostic factor in breast cancer [ 50 , 51 , 52 ]. Gene MKI67 has been treated as a candidate prognostic prediction for cancer proliferation [ 53 , 54 ]. The over-expression of RRM2 has been linked to higher proliferation and invasiveness of malignant cells [ 55 , 56 ], and the upregulation of RRM2 in breast cancer suggests it to be a possible prognostic indicator [ 57 , 58 , 59 , 60 , 61 , 62 ]. The high expression of UBE2C gene always occurs in cancers with a high degree of malignancy, low differentiation, and high metastatic tendency [ 63 ]. For gene TOP2A, it has been proposed that the HER2 amplification in HER2 breast cancers may be a direct result of the frequent co-amplification of TOP2A [ 64 , 65 , 66 ], and there is a high correlation between the high expressions of TOP2A and the oncogene HER2 [ 67 , 68 ]. Gene CENPF is a cell cycle-associated gene, and it has been identified as a marker of cell proliferation in breast cancers [ 69 ]. The over-expression of these genes strongly supports the correctness of the association identified by SCIPAC. To further validate this positive association, we perform DE analysis of these cells against all the other cells. We find that the top marker genes obtained from CellMarker [ 49 ] for the regulatory T cells, which are known to be immunosuppressive and promote cancer progression [ 70 ], are over-expressed with statistical significance, as shown in Fig. 4 h. This finding again provides strong evidence that the positive association identified by SCIPAC for this group of T cells is correct.

Lung cancer data with survival information

The scRNA-seq data for lung cancer are from [ 71 ], and we use two lung adenocarcinoma (LUAD) patients’ data with 29,888 cells. The true cell types are shown in Fig. 5 a. The bulk data consist of 576 TCGA-LUAD samples with survival status and time.

UMAP visualization of a–d  the lung cancer data and e–g  the muscular dystrophy data. a  True cell types. b , c  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. d  Results given by Scissor under different \(\alpha\) values. e , f  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. Circled are a group of cells that are identified by SCIPAC as significantly positively associated with the disease but identified by Scissor as null. g  Results given by Scissor under different \(\alpha\) values

Association strengths and p -values given by SCIPAC are given in Fig. 5 b, c (results under other resolutions are given in Additional file 1: Fig. S13 and S14). In Fig. 5 c, most cells with statistically significant associations are CD4+ T cells or B cells. These associations are negative, meaning that the abundance of these cells is associated with a reduced death rate, i.e., longer survival time. This agrees with the literature: CD4+ T cells primarily mediate anti-tumor immunity and are associated with favorable prognosis in lung cancer patients [ 72 , 73 , 74 ]; B cells also show anti-tumor functions in all stages of human lung cancer development and play an essential role in anti-tumor responses [ 75 , 76 ].

The results by Scissor under different \(\alpha\) values are shown in Fig. 5 d. The highly scattered Scissor+ and Scissor− cells make identifying and interpreting meaningful phenotype-associated cell groups difficult.

Muscular dystrophy data with a binary phenotype

This dataset contains cells from four facioscapulohumeral muscular dystrophy (FSHD) samples and two control samples [ 77 ]. We pool all the 7047 cells from these six samples together. The true cell types of these cells are unknown. The bulk data consists of 27 FSHD patients and eight controls from [ 28 ]. Here the phenotype is FSHD, and it is binary: present or absent.

The results of SCIPAC with the default resolution are given in Fig. 5 e, f. Results under other resolutions are highly similar (shown in Additional file 1: Fig. S15 and S16). For comparison, results given by Scissor under different \(\alpha\) values are presented in Fig. 5 g. The agreements between the results of SCIPAC and Scissor are clear. For example, both methods identify cells located at the top and lower left part of UMAP plots to be negatively associated with FSHD, and cells located at the center and right parts of UMAP plots to be positively associated. However, the discrepancies in their results are also evident. The most pronounced one is a large group of cells (circled in Fig. 5 f) that are identified by SCIPAC as significantly positively associated but are completely ignored by Scissor. Checking into this group of cells, we find that over 90% (424 out of 469) come from the FSHD patients, and less than 10% come from the control samples. However, cells from FSHD patients only compose 73% (5133) of all the 7047 cells. This statistically significant ( p -value \(<10^{-15}\) , Fisher’s exact test) over-representation (odds ratio = 3.51) suggests that the positive association identified SCIPAC is likely to be correct.

SCIPAC is computationally highly efficient. On an 8-core machine with 2.50 GHz CPU and 16 GB RAM, SCIPAC takes 7, 24, and 2 s to finish all the computation and give the estimated association strengths and p -values on the prostate cancer, lung cancer, and muscular dystrophy datasets, respectively. As a reference, Scissor takes 314, 539, and 171 seconds, respectively.

SCIPAC works with various phenotype types, including binary, continuous, survival, and ordinal. It can easily accommodate other types by using a proper regression model with a systematic component in the form of Eq. 3 (see the “ Methods ” section). For example, a Poisson or negative binomial log-linear model can be used if the phenotype is a count (i.e., non-negative integer).

In SCIPAC’s definition of association, a cell type is associated with the phenotype if increasing the proportion of this cell type leads to a change of probability of the phenotype occurring. The strength of association represents the extent of the increase or decrease in this probability. In the case of binary-response, this change is measured by the log odds ratio. For example, if the association strength of cell type A is twice that of cell type B, increasing cell type A by a certain proportion leads to twice the amount of change in the log odds ratio of having the phenotype compared to increasing cell type B by the same proportion. The association strength under other types of phenotypes can be interpreted similarly, with the major difference lying in the measure of change in probability. For quantitative, ordinal, and survival outcomes, the difference in the quantitative outcome, log odds ratio of the right-tail probability, and log hazard ratio respectively are used. Despite the differences in the exact form of the association strength under different types of phenotypes, the underlying concept remains the same: a larger (absolute value of) association strength indicates that the same increase/decrease in a cell type leads to a larger change in the occurrence of the phenotype.

As SCIPAC utilizes both bulk RNA-seq data with phenotype and single-cell RNA-seq data, the estimated associations for the cells are influenced by the choice of the bulk data. Although different bulk data can yield varying estimations of the association for the same single cells, the estimated associations appear to be reasonably robust even when minor changes are made to the bulk data. See Additional file 1 for further discussions.

When using the Louvain algorithm in the Seurat package to cluster cells, SCIPAC’s default resolution is 2.0, larger than the default setting of Seurat. This allows for the identification of potential subtypes within the major cell type and enables the estimation of individual association strengths. Consequently, a more detailed and comprehensive description of the association between single cells and the phenotype can be obtained by SCIPAC.

When applying SCIPAC to real datasets, we made a deliberate choice to disregard the cell annotation provided by the original publications and instead relied on the inferred cell clusters produced by the Louvain algorithm. We made this decision for several reasons. Firstly, we aimed to ensure a fair comparison with Scissor, as it does not utilize cell-type annotations. Secondly, the original annotation might not be sufficiently comprehensive or detailed. Presumed cell types could potentially encompass multiple subtypes, each of which may exhibit distinct associations with the phenotype under investigation. In such cases, employing the Louvain algorithm with a relatively high resolution, which is the default setting in SCIPAC, enables us to differentiate between these subtypes and allows SCIPAC to assign varying association strengths to each subtype.

SCIPAC fits the regression model using the elastic net, a machine-learning algorithm that maximizes a penalized version of the likelihood. The elastic net can be replaced by other penalized estimates of regression models, such as SCAD [ 78 ], without altering the rest of the SCIPAC algorithm. The combination of a regression model and a penalized estimation algorithm such as the elastic net has shown comparable or higher prediction power than other sophisticated methods such as random forests, boosting, or neural networks in numerous applications, especially for gene expression data [ 79 ]. However, there can still be datasets where other models have higher prediction power. It will be future work to incorporate these models into SCIPAC.

The use of metacells is becoming an efficient way to handle large single-cell datasets [ 80 , 81 , 82 , 83 ]. Conceptually, SCIPAC can incorporate metacells and their representatives as an alternative to its default setting of using cell clusters/types and their centroids. We have explored this aspect using metacells provided by SEACells [ 81 ]. Details are given in Additional file 1. Our comparative analysis reveals that combining SCIPAC with SEACells results in significantly reduced performance compared to using SCIPAC directly on original single-cell data. The primary reason for this appears to be the subpar performance of SEACells in cell grouping, especially when contrasted with the Louvain algorithm. Given these findings, we do not suggest using metacells provided by SEACells for SCIPAC applications in the current stage.

Conclusions

SCIPAC is a novel algorithm for studying the associations between cells and phenotypes. Compared to the previous algorithm, SCIPAC gives a much more detailed and comprehensive description of the associations by enabling a quantitative estimation of the association strength and by providing a quality control—the p -value. Underlying SCIPAC are a general statistical model that accommodates virtually all types of phenotypes, including ordinal (and potentially count) phenotypes that have never been considered before, and a concise and closed-form mathematical formula that quantifies the association, which minimizes the computational load. The mathematical conciseness also largely frees SCIPAC from parameter tuning. The only parameter (i.e., the resolution) barely changes the results given by SCIPAC. Overall, compared with its predecessor, SCIPAC represents a substantially more capable software by being much more informative, versatile, robust, and user-friendly.

The improvement in accuracy is also remarkable. In simulated data, SCIPAC achieves high power and low false positives, which is evident from the UMAP plot, F1 score, and FSC score. In real data, SCIPAC gives results that are consistent with current biological knowledge for cell types whose functions are well understood. For cell types whose functions are less studied or more multifaceted, SCIPAC gives support to certain biological hypotheses or helps identify/discover cell sub-types.

SCIPAC’s identification of cell-phenotype associations closely follows its definition of association: when increasing the fraction of a cell type increases (or decreases) the probability for a phenotype to be present, this cell type is positively (or negatively) associated with the phenotype.

The increase of the fraction of a cell type

For a bulk sample, let vector \(\varvec{G} \in \mathbb {R}^p\) be its expression profile, that is, its expression on the p genes. Suppose there are K cell types in the tissue, and let \(\varvec{g}_{k}\) be the representative expression of the k ’th cell type. Usually, people assume that \(\varvec{G}\) can be decomposed by

where \(\gamma _{k}\) is the proportion of cell type k in the bulk tissue, with \(\sum _{k = 1}^{K}\gamma _{k} = 1\) . This equation links the bulk and single-cell expression data.

Now consider increasing cells from cell type k by \(\Delta \gamma\) proportion of the original number of cells. Then, the new proportion of cell type k becomes \(\frac{\gamma _{k} + \Delta \gamma }{1 + \Delta \gamma }\) , and the new proportion of cell type \(j \ne k\) becomes \(\frac{\gamma _{j}}{1 + \Delta \gamma }\)  (note that the new proportions of all cell types should still add up to 1). Thus, the bulk expression profile with the increase of cell type k becomes

Plugging Eq. 1 , we get

Interestingly, this expression of \(\varvec{G}^*\) does not include \(\gamma _{1}, \ldots , \gamma _{K}\) . This means that there is no need actually to compute \(\gamma _{1}, \ldots , \gamma _{K}\) in Eq. 1 , which could otherwise be done using a cell-type-decomposition software, but an accurate and robust decomposition is non-trivial [ 84 , 85 , 86 ]. See Additional file 1 for a more in-depth discussion on the connections of SCIPAC with decomposition/deconvolution.

The change in chance of a phenotype

In this section, we consider how the increase in the fraction of a cell type will change the chance for a binary phenotype such as cancer to occur. Other types of phenotypes will be considered in the next section.

Let \(\pi (\varvec{G})\) be the chance of an individual with gene expression profile \(\varvec{G}\) for this phenotype to occur. We assume a logistic regression model to describe the relationship between \(\pi (\varvec{G})\) and \(\varvec{G}\) :

here the left-hand side is the log odds of \(\pi (\varvec{G})\) , \(\beta _{0}\) is the intercept, and \(\varvec{\beta }\) is a length- p vector of coefficients. In the section after the next, we will describe how we obtain \(\beta _{0}\) and \(\varvec{\beta }\) from the data.

When increasing cells from cell type k by \(\Delta \gamma\) , \(\varvec{G}\) becomes \(\varvec{G}^*\) in Eq. 3 . Plugging Eq. 2 , we get

We further take the difference between Eqs. 4 and 3 and get

The left-hand side of this equation is the log odds ratio (i.e., the change of log odds). On the right-hand side, \(\frac{\Delta \gamma }{1 + \Delta \gamma }\) is an increasing function with respect to \(\Delta \gamma\) , and \(\varvec{\beta }^T(\varvec{g}_{k} - \varvec{G})\) is independent of \(\Delta \gamma\) . This indicates that given any specific \(\Delta \gamma\) , the log odds ratio under over-representation of cell type k is proportional to

\(\lambda _k\) describes the strength of the effect of increasing cell type k to a bulk sample with expression profile \(\varvec{G}\) . Given the presence of numerous bulk samples, employing multiple \(\lambda _k\) ’s could be cumbersome and obscure the overall effect of a particular cell type. To concisely summarize the association of cell type k , we propose averaging their effects. The average effect on all bulk samples can be obtained by

where \(\bar{\varvec{G}}\) is the average expression profile of all bulk samples.

\(\Lambda _k\) gives an overall impression of how strong the effect is when cell type k over-represents to the probability for the phenotype to be present. Its sign represents the direction of the change: a positive value means an increase in probability, and a negative value means a decrease in probability. Its absolute value represents the strength of the effect. In SCIPAC, we call \(\Lambda _k\) the association strength of cell type k and the phenotype.

Note that this derivation does not involve likelihood, although the computation of \(\varvec{\beta }\) does. Here, it serves more as a definitional approach.

Definition of the association strength for other types of phenotype

Our definition of \(\Lambda _k\) relies on vector \(\varvec{\beta }\) . In the case of a binary phenotype, \(\varvec{\beta }\) are the coefficients of a logistic regression that describes a linear relationship between the expression profile and the log odds of having the phenotype, as shown in Eq. 3 . For other types of phenotype, \(\varvec{\beta }\) can be defined/computed similarly.

For a quantitative (i.e., continuous) phenotype, an ordinary linear regression can be used, and the left-hand side of Eq. 3 is changed to the quantitative value of the phenotype.

For a survival phenotype, a Cox proportional hazards model can be used, and the left-hand side of Eq. 3 is changed to the log hazard ratio.

For an ordinal phenotype, we use a proportional odds model

where \(j \in \{1, 2, ..., (J - 1)\}\) and J is the number of ordinal levels. It should be noted that here we use the right-tail probability \(\Pr (Y_{i} \ge j + 1 | X)\) instead of the commonly used cumulative probability (left-tail probability) \(\Pr (Y_{i} \le j | X)\) . Such a change makes the interpretation consistent with other types of phenotypes: in our model, a larger value on the right-hand side indicates a larger chance for \(Y_{i}\) to have a higher level, which in turn guarantees that the sign of the association strength defined according to this \(\varvec{\beta }\) has the usual meaning: a positive \(\Lambda _k\) value means a positive association with the phenotype-using the cancer stage as an example. A positive \(\Lambda _k\) means the over-representation of cell type k increases the chance of a higher cancer stage. In contrast, using the commonly used cumulative probability leads to a counter-intuitive, reversed interpretation.

Computation of the association strength in practice

In practice, \(\varvec{\beta }\) in Eq. 3 needs to be learned from the bulk data. By default, SCIPAC uses the elastic net, a popular and powerful penalized regression method:

In this model, \(l(\beta _{0}, \varvec{\beta })\) is a log-likelihood of the linear model (i.e., logistic regression for a binary phenotype, ordinary linear regression for a quantitative phenotype, Cox proportional odds model for a survival phenotype, and proportional odds model for an ordinal phenotype). \(\alpha\) is a number between 0 and 1, denoting a combination of \(\ell _1\) and \(\ell _2\) penalties, and \(\lambda\) is the penalty strength. SCIPAC fixes \(\alpha\) to be 0.4 (see Additional file 1 for discussions on this choice) and uses 10-fold cross-validation to decide \(\lambda\) automatically. This way, they do not become hyperparameters.

In SCIPAC, the fitting and cross-validation of the elastic net are done by calling the ordinalNet [ 87 ] R package for the ordinal phenotype and by calling the glmnet R package [ 88 , 89 , 90 , 91 ] for other types of phenotypes.

The computation of the association strength, as defined by Eq. 7 , does not only require \(\varvec{\beta }\) , but also \(\varvec{g}_k\) and \(\bar{\varvec{G}}\) . \(\bar{\varvec{G}}\) is simply the average expression profile of all bulk samples. On the other hand, \(\varvec{g}_k\) requires knowing the cell type of each cell. By default, SCIPAC does not assume this information to be given, and it uses the Louvain clustering implemented in the Seurat [ 24 , 25 ] R package to infer it. This clustering algorithm has one tuning parameter called “resolution.” SCIPAC sets its default value as 2.0, and the user can use other values. With the inferred or given cell types, \(\varvec{g}_k\) is computed as the centroid (i.e., the mean expression profile) of cells in cluster k .

Given \(\varvec{\beta }\) , \(\bar{\varvec{G}}\) , and \(\varvec{g}_k\) , the association strength can be computed using Eq. 7 . Knowing the association strength for each cell type and the cell-type label for each cell, we also know the association strength for every single cell. In practice, we standardize the association strengths for all cells. That is, we compute the mean and standard deviation of the association strengths of all cells and use them to centralize and scale the association strength, respectively. We have found such standardization makes SCIPAC more robust to the possible unbalance in sample size of bulk data in different phenotype groups.

Computation of the p -value

SCIPAC uses non-parametric bootstrap [ 92 ] to compute the standard deviation and hence the p -value of the association. Fifty bootstrap samples, which are believed to be enough to compute the standard error of most statistics [ 93 ], are generated for the bulk expression data, and each is used to compute (standardized) \(\Lambda\) values for all the cells. For cell i , let its original \(\Lambda\) values be \(\Lambda _i\) , and the bootstrapped values be \(\Lambda _i^{(1)}, \ldots , \Lambda _i^{(50)}\) . A z -score is then computed using

and then the p -value is computed according to the cumulative distribution function of the standard Gaussian distribution. See Additional file 1 for more discussions on the calculation of p -value.

Availability of data and materials

The simulated datasets [ 94 ] under three schemes are available at Zenodo with DOI 10.5281/zenodo.11013320 [ 95 ]. The SCIPAC package is available at GitHub website https://github.com/RavenGan/SCIPAC under the MIT license [ 96 ]. The source code of SCIPAC is also deposited at Zenodo with DOI 10.5281/zenodo.11013696 [ 97 ]. A vignette of the R package is available on the GitHub page and in the Additional file 2. The prostate cancer scRNA-seq data is obtained from the Prostate Cell Atlas https://www.prostatecellatlas.org [ 29 ]; the scRNA-seq data for the breast cancer are from the Gene Expression Omnibus (GEO) under accession number GSE176078 [ 34 , 98 ]; the scRNA-seq data for the lung cancer are from E-MTAB-6149 [ 99 ] and E-MTAB-6653 [ 71 , 100 ]; the scRNA-seq data for facioscapulohumeral muscular dystrophy data are from the GEO under accession number GSE122873 [ 101 ]. The bulk RNA-seq data are obtained from the TCGA database via TCGAbiolinks (ver. 2.25.2) R package [ 102 ]. More details about the simulated and real scRNA-seq and bulk RNA-seq data can be found in the Additional file 1.

Yofe I, Dahan R, Amit I. Single-cell genomic approaches for developing the next generation of immunotherapies. Nat Med. 2020;26(2):171–7.

Article   CAS   PubMed   Google Scholar  

Zhang Q, He Y, Luo N, Patel SJ, Han Y, Gao R, et al. Landscape and dynamics of single immune cells in hepatocellular carcinoma. Cell. 2019;179(4):829–45.

Fan J, Slowikowski K, Zhang F. Single-cell transcriptomics in cancer: computational challenges and opportunities. Exp Mol Med. 2020;52(9):1452–65.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Klein AM, Mazutis L, Akartuna I, Tallapragada N, Veres A, Li V, et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell. 2015;161(5):1187–201.

Macosko EZ, Basu A, Satija R, Nemesh J, Shekhar K, Goldman M, et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell. 2015;161(5):1202–14.

Rosenberg AB, Roco CM, Muscat RA, Kuchina A, Sample P, Yao Z, et al. Single-cell profiling of the developing mouse brain and spinal cord with split-pool barcoding. Science. 2018;360(6385):176–82.

Zheng GX, Terry JM, Belgrader P, Ryvkin P, Bent ZW, Wilson R, et al. Massively parallel digital transcriptional profiling of single cells. Nat Commun. 2017;8(1):1–12.

Article   Google Scholar  

Abdelaal T, Michielsen L, Cats D, Hoogduin D, Mei H, Reinders MJ, et al. A comparison of automatic cell identification methods for single-cell RNA sequencing data. Genome Biol. 2019;20(1):1–19.

Article   CAS   Google Scholar  

Luecken MD, Theis FJ. Current best practices in single-cell RNA-seq analysis: a tutorial. Mol Syst Biol. 2019;15(6):e8746.

Article   PubMed   PubMed Central   Google Scholar  

Guo H, Li J. scSorter: assigning cells to known cell types according to marker genes. Genome Biol. 2021;22(1):1–18.

Pliner HA, Shendure J, Trapnell C. Supervised classification enables rapid annotation of cell atlases. Nat Methods. 2019;16(10):983–6.

Zhang AW, O’Flanagan C, Chavez EA, Lim JL, Ceglia N, McPherson A, et al. Probabilistic cell-type assignment of single-cell RNA-seq for tumor microenvironment profiling. Nat Methods. 2019;16(10):1007–15.

Zhang Z, Luo D, Zhong X, Choi JH, Ma Y, Wang S, et al. SCINA: a semi-supervised subtyping algorithm of single cells and bulk samples. Genes. 2019;10(7):531.

Johnson TS, Wang T, Huang Z, Yu CY, Wu Y, Han Y, et al. LAmbDA: label ambiguous domain adaptation dataset integration reduces batch effects and improves subtype detection. Bioinformatics. 2019;35(22):4696–706.

Ma F, Pellegrini M. ACTINN: automated identification of cell types in single cell RNA sequencing. Bioinformatics. 2020;36(2):533–8.

Tan Y, Cahan P. SingleCellNet: a computational tool to classify single cell RNA-Seq data across platforms and across species. Cell Syst. 2019;9(2):207–13.

Salcher S, Sturm G, Horvath L, Untergasser G, Kuempers C, Fotakis G, et al. High-resolution single-cell atlas reveals diversity and plasticity of tissue-resident neutrophils in non-small cell lung cancer. Cancer Cell. 2022;40(12):1503–20.

Good Z, Sarno J, Jager A, Samusik N, Aghaeepour N, Simonds EF, et al. Single-cell developmental classification of B cell precursor acute lymphoblastic leukemia at diagnosis reveals predictors of relapse. Nat Med. 2018;24(4):474–83.

Wagner J, Rapsomaniki MA, Chevrier S, Anzeneder T, Langwieder C, Dykgers A, et al. A single-cell atlas of the tumor and immune ecosystem of human breast cancer. Cell. 2019;177(5):1330–45.

Weinstein JN, Collisson EA, Mills GB, Shaw KR, Ozenberger BA, Ellrott K, et al. The cancer genome atlas pan-cancer analysis project. Nat Genet. 2013;45(10):1113–20.

Cerami E, Gao J, Dogrusoz U, Gross BE, Sumer SO, Aksoy BA, et al. The cBio cancer genomics portal: an open platform for exploring multidimensional cancer genomics data. Cancer Disc. 2012;2(5):401–4.

Gao J, Aksoy BA, Dogrusoz U, Dresdner G, Gross B, Sumer SO, et al. Integrative analysis of complex cancer genomics and clinical profiles using the cBioPortal. Sci Signal. 2013;6(269):1.

Sun D, Guan X, Moran AE, Wu LY, Qian DZ, Schedin P, et al. Identifying phenotype-associated subpopulations by integrating bulk and single-cell sequencing data. Nat Biotechnol. 2022;40(4):527–38.

Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks. J Stat Mech Theory Exp. 2008;2008(10):P10008.

Stuart T, Butler A, Hoffman P, Hafemeister C, Papalexi E, Mauck WM III, et al. Comprehensive integration of single-cell data. Cell. 2019;177(7):1888–902.

Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol. 2005;67(2):301–20.

McInnes L, Healy J, Melville J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. 2018. arXiv preprint arXiv:1802.03426 .

Wong CJ, Wang LH, Friedman SD, Shaw D, Campbell AE, Budech CB, et al. Longitudinal measures of RNA expression and disease activity in FSHD muscle biopsies. Hum Mol Genet. 2020;29(6):1030–43.

Tuong ZK, Loudon KW, Berry B, Richoz N, Jones J, Tan X, et al. Resolving the immune landscape of human prostate at a single-cell level in health and cancer. Cell Rep. 2021;37(12):110132.

Hume DA. The mononuclear phagocyte system. Curr Opin Immunol. 2006;18(1):49–53.

Hume DA, Ross IL, Himes SR, Sasmono RT, Wells CA, Ravasi T. The mononuclear phagocyte system revisited. J Leukoc Biol. 2002;72(4):621–7.

Raggi F, Bosco MC. Targeting mononuclear phagocyte receptors in cancer immunotherapy: new perspectives of the triggering receptor expressed on myeloid cells (TREM-1). Cancers. 2020;12(5):1337.

Largeot A, Pagano G, Gonder S, Moussay E, Paggetti J. The B-side of cancer immunity: the underrated tune. Cells. 2019;8(5):449.

Wu SZ, Al-Eryani G, Roden DL, Junankar S, Harvey K, Andersson A, et al. A single-cell and spatially resolved atlas of human breast cancers. Nat Genet. 2021;53(9):1334–47.

Fernández-Nogueira P, Fuster G, Gutierrez-Uzquiza Á, Gascón P, Carbó N, Bragado P. Cancer-associated fibroblasts in breast cancer treatment response and metastasis. Cancers. 2021;13(13):3146.

Ao Z, Shah SH, Machlin LM, Parajuli R, Miller PC, Rawal S, et al. Identification of cancer-associated fibroblasts in circulating blood from patients with metastatic breast cancer. Identification of cCAFs from metastatic cancer patients. Cancer Res. 2015;75(22):4681–7.

Arcucci A, Ruocco MR, Granato G, Sacco AM, Montagnani S. Cancer: an oxidative crosstalk between solid tumor cells and cancer associated fibroblasts. BioMed Res Int. 2016;2016.  https://pubmed.ncbi.nlm.nih.gov/27595103/ .

Buchsbaum RJ, Oh SY. Breast cancer-associated fibroblasts: where we are and where we need to go. Cancers. 2016;8(2):19.

Ruocco MR, Avagliano A, Granato G, Imparato V, Masone S, Masullo M, et al. Involvement of breast cancer-associated fibroblasts in tumor development, therapy resistance and evaluation of potential therapeutic strategies. Curr Med Chem. 2018;25(29):3414–34.

Savas P, Virassamy B, Ye C, Salim A, Mintoff CP, Caramia F, et al. Single-cell profiling of breast cancer T cells reveals a tissue-resident memory subset associated with improved prognosis. Nat Med. 2018;24(7):986–93.

Bassez A, Vos H, Van Dyck L, Floris G, Arijs I, Desmedt C, et al. A single-cell map of intratumoral changes during anti-PD1 treatment of patients with breast cancer. Nat Med. 2021;27(5):820–32.

Romero JM, Grünwald B, Jang GH, Bavi PP, Jhaveri A, Masoomian M, et al. A four-chemokine signature is associated with a T-cell-inflamed phenotype in primary and metastatic pancreatic cancer. Chemokines in Pancreatic Cancer. Clin Cancer Res. 2020;26(8):1997–2010.

Tamura R, Yoshihara K, Nakaoka H, Yachida N, Yamaguchi M, Suda K, et al. XCL1 expression correlates with CD8-positive T cells infiltration and PD-L1 expression in squamous cell carcinoma arising from mature cystic teratoma of the ovary. Oncogene. 2020;39(17):3541–54.

Hernandez R, Põder J, LaPorte KM, Malek TR. Engineering IL-2 for immunotherapy of autoimmunity and cancer. Nat Rev Immunol. 2022:22:1–15.  https://pubmed.ncbi.nlm.nih.gov/35217787/ .

Korotkevich G, Sukhov V, Budin N, Shpak B, Artyomov MN, Sergushichev A. Fast gene set enrichment analysis. BioRxiv. 2016:060012.  https://www.biorxiv.org/content/10.1101/060012v3.abstract .

Dang CV. MYC on the path to cancer. Cell. 2012;149(1):22–35.

Gnanaprakasam JR, Wang R. MYC in regulating immunity: metabolism and beyond. Genes. 2017;8(3):88.

Oshi M, Takahashi H, Tokumaru Y, Yan L, Rashid OM, Matsuyama R, et al. G2M cell cycle pathway score as a prognostic biomarker of metastasis in estrogen receptor (ER)-positive breast cancer. Int J Mol Sci. 2020;21(8):2921.

Zhang X, Lan Y, Xu J, Quan F, Zhao E, Deng C, et al. Cell Marker: a manually curated resource of cell markers in human and mouse. Nucleic Acids Res. 2019;47(D1):D721–8.

Chen L, Yang L, Qiao F, Hu X, Li S, Yao L, et al. High levels of nucleolar spindle-associated protein and reduced levels of BRCA1 expression predict poor prognosis in triple-negative breast cancer. PLoS ONE. 2015;10(10):e0140572.

Li M, Yang B. Prognostic value of NUSAP1 and its correlation with immune infiltrates in human breast cancer. Crit Rev TM Eukaryot Gene Expr. 2022;32(3).  https://pubmed.ncbi.nlm.nih.gov/35695609/ .

Zhang X, Pan Y, Fu H, Zhang J. Nucleolar and spindle associated protein 1 (NUSAP1) inhibits cell proliferation and enhances susceptibility to epirubicin in invasive breast cancer cells by regulating cyclin D kinase (CDK1) and DLGAP5 expression. Med Sci Monit: Int Med J Exp Clin Res. 2018;24:8553.

Geyer FC, Rodrigues DN, Weigelt B, Reis-Filho JS. Molecular classification of estrogen receptor-positive/luminal breast cancers. Adv Anat Pathol. 2012;19(1):39–53.

Karamitopoulou E, Perentes E, Tolnay M, Probst A. Prognostic significance of MIB-1, p53, and bcl-2 immunoreactivity in meningiomas. Hum Pathol. 1998;29(2):140–5.

Duxbury MS, Whang EE. RRM2 induces NF- \(\kappa\) B-dependent MMP-9 activation and enhances cellular invasiveness. Biochem Biophys Res Commun. 2007;354(1):190–6.

Zhou BS, Tsai P, Ker R, Tsai J, Ho R, Yu J, et al. Overexpression of transfected human ribonucleotide reductase M2 subunit in human cancer cells enhances their invasive potential. Clin Exp Metastasis. 1998;16(1):43–9.

Zhang H, Liu X, Warden CD, Huang Y, Loera S, Xue L, et al. Prognostic and therapeutic significance of ribonucleotide reductase small subunit M2 in estrogen-negative breast cancers. BMC Cancer. 2014;14(1):1–16.

Putluri N, Maity S, Kommagani R, Creighton CJ, Putluri V, Chen F, et al. Pathway-centric integrative analysis identifies RRM2 as a prognostic marker in breast cancer associated with poor survival and tamoxifen resistance. Neoplasia. 2014;16(5):390–402.

Koleck TA, Conley YP. Identification and prioritization of candidate genes for symptom variability in breast cancer survivors based on disease characteristics at the cellular level. Breast Cancer Targets Ther. 2016;8:29.

Li Jp, Zhang Xm, Zhang Z, Zheng Lh, Jindal S, Liu Yj. Association of p53 expression with poor prognosis in patients with triple-negative breast invasive ductal carcinoma. Medicine. 2019;98(18).  https://pubmed.ncbi.nlm.nih.gov/31045815/ .

Gong MT, Ye SD, Lv WW, He K, Li WX. Comprehensive integrated analysis of gene expression datasets identifies key anti-cancer targets in different stages of breast cancer. Exp Ther Med. 2018;16(2):802–10.

PubMed   PubMed Central   Google Scholar  

Chen Wx, Yang Lg, Xu Ly, Cheng L, Qian Q, Sun L, et al. Bioinformatics analysis revealing prognostic significance of RRM2 gene in breast cancer. Biosci Rep. 2019;39(4).  https://pubmed.ncbi.nlm.nih.gov/30898978/ .

Hao Z, Zhang H, Cowell J. Ubiquitin-conjugating enzyme UBE2C: molecular biology, role in tumorigenesis, and potential as a biomarker. Tumor Biol. 2012;33(3):723–30.

Arriola E, Rodriguez-Pinilla SM, Lambros MB, Jones RL, James M, Savage K, et al. Topoisomerase II alpha amplification may predict benefit from adjuvant anthracyclines in HER2 positive early breast cancer. Breast Cancer Res Treat. 2007;106(2):181–9.

Knoop AS, Knudsen H, Balslev E, Rasmussen BB, Overgaard J, Nielsen KV, et al. Retrospective analysis of topoisomerase IIa amplifications and deletions as predictive markers in primary breast cancer patients randomly assigned to cyclophosphamide, methotrexate, and fluorouracil or cyclophosphamide, epirubicin, and fluorouracil: Danish Breast Cancer Cooperative Group. J Clin Oncol. 2005;23(30):7483–90.

Tanner M, Isola J, Wiklund T, Erikstein B, Kellokumpu-Lehtinen P, Malmstrom P, et al. Topoisomerase II \(\alpha\) gene amplification predicts favorable treatment response to tailored and dose-escalated anthracycline-based adjuvant chemotherapy in HER-2/neu-amplified breast cancer: Scandinavian Breast Group Trial 9401. J Clin Oncol. 2006;24(16):2428–36.

Arriola E, Moreno A, Varela M, Serra JM, Falo C, Benito E, et al. Predictive value of HER-2 and topoisomerase II \(\alpha\) in response to primary doxorubicin in breast cancer. Eur J Cancer. 2006;42(17):2954–60.

Järvinen TA, Tanner M, Bärlund M, Borg Å, Isola J. Characterization of topoisomerase II \(\alpha\) gene amplification and deletion in breast cancer. Gene Chromosome Cancer. 1999;26(2):142–50.

Landberg G, Erlanson M, Roos G, Tan EM, Casiano CA. Nuclear autoantigen p330d/CENP-F: a marker for cell proliferation in human malignancies. Cytom J Int Soc Anal Cytol. 1996;25(1):90–8.

CAS   Google Scholar  

Bettelli E, Carrier Y, Gao W, Korn T, Strom TB, Oukka M, et al. Reciprocal developmental pathways for the generation of pathogenic effector TH17 and regulatory T cells. Nature. 2006;441(7090):235–8.

Lambrechts D, Wauters E, Boeckx B, Aibar S, Nittner D, Burton O, et al. Phenotype molding of stromal cells in the lung tumor microenvironment. Nat Med. 2018;24(8):1277–89.

Bremnes RM, Busund LT, Kilvær TL, Andersen S, Richardsen E, Paulsen EE, et al. The role of tumor-infiltrating lymphocytes in development, progression, and prognosis of non-small cell lung cancer. J Thorac Oncol. 2016;11(6):789–800.

Article   PubMed   Google Scholar  

Schalper KA, Brown J, Carvajal-Hausdorf D, McLaughlin J, Velcheti V, Syrigos KN, et al. Objective measurement and clinical significance of TILs in non–small cell lung cancer. J Natl Cancer Inst. 2015;107(3):dju435.

Tay RE, Richardson EK, Toh HC. Revisiting the role of CD4+ T cells in cancer immunotherapy—new insights into old paradigms. Cancer Gene Ther. 2021;28(1):5–17.

Dieu-Nosjean MC, Goc J, Giraldo NA, Sautès-Fridman C, Fridman WH. Tertiary lymphoid structures in cancer and beyond. Trends Immunol. 2014;35(11):571–80.

Wang Ss, Liu W, Ly D, Xu H, Qu L, Zhang L. Tumor-infiltrating B cells: their role and application in anti-tumor immunity in lung cancer. Cell Mol Immunol. 2019;16(1):6–18.

van den Heuvel A, Mahfouz A, Kloet SL, Balog J, van Engelen BG, Tawil R, et al. Single-cell RNA sequencing in facioscapulohumeral muscular dystrophy disease etiology and development. Hum Mol Genet. 2019;28(7):1064–75.

Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. J Am Stat Assoc. 2001;96(456):1348–60.

Hastie T, Tibshirani R, Friedman JH, Friedman JH. The elements of statistical learning: data mining, inference, and prediction, vol. 2. New York: Springer; 2009.

Book   Google Scholar  

Baran Y, Bercovich A, Sebe-Pedros A, Lubling Y, Giladi A, Chomsky E, et al. MetaCell: analysis of single-cell RNA-seq data using K-nn graph partitions. Genome Biol. 2019;20(1):1–19.

Persad S, Choo ZN, Dien C, Sohail N, Masilionis I, Chaligné R, et al. SEACells infers transcriptional and epigenomic cellular states from single-cell genomics data. Nat Biotechnol. 2023;41:1–12.  https://pubmed.ncbi.nlm.nih.gov/36973557/ .

Ben-Kiki O, Bercovich A, Lifshitz A, Tanay A. Metacell-2: a divide-and-conquer metacell algorithm for scalable scRNA-seq analysis. Genome Biol. 2022;23(1):100.

Bilous M, Tran L, Cianciaruso C, Gabriel A, Michel H, Carmona SJ, et al. Metacells untangle large and complex single-cell transcriptome networks. BMC Bioinformatics. 2022;23(1):336.

Avila Cobos F, Alquicira-Hernandez J, Powell JE, Mestdagh P, De Preter K. Benchmarking of cell type deconvolution pipelines for transcriptomics data. Nat Commun. 2020;11(1):1–14.

Jin H, Liu Z. A benchmark for RNA-seq deconvolution analysis under dynamic testing environments. Genome Biol. 2021;22(1):1–23.

Wang X, Park J, Susztak K, Zhang NR, Li M. Bulk tissue cell type deconvolution with multi-subject single-cell expression reference. Nat Commun. 2019;10(1):380.

Wurm MJ, Rathouz PJ, Hanlon BM. Regularized ordinal regression and the ordinalNet R package. 2017. arXiv preprint arXiv:1706.05003 .

Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw. 2010;33(1):1.

Simon N, Friedman J, Hastie T. A blockwise descent algorithm for group-penalized multiresponse and multinomial regression. 2013. arXiv preprint arXiv:1311.6529 .

Simon N, Friedman J, Hastie T, Tibshirani R. Regularization paths for Cox’s proportional hazards model via coordinate descent. J Stat Softw. 2011;39(5):1.

Tibshirani R, Bien J, Friedman J, Hastie T, Simon N, Taylor J, et al. Strong rules for discarding predictors in lasso-type problems. J R Stat Soc Ser B Stat Methodol. 2012;74(2):245–66.

Efron B. Bootstrap methods: another look at the jackknife. In: Breakthroughs in statistics. New York: Springer; 1992. pp. 569–593.

Efron B, Tibshirani RJ. An introduction to the bootstrap. London: CRC Press; 1994.

Zappia L, Phipson B, Oshlack A. Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 2017;18(1):174.

Gan D, Zhu Y, Lu X, Li J. Simulated datasets used in SCIPAC analysis. Zenodo. 2024. https://doi.org/10.5281/zenodo.11013320 .

Gan D, Zhu Y, Lu X, Li J. SCIPAC R package. GitHub. 2024. https://github.com/RavenGan/SCIPAC . Accessed 24 Apr 2024.

Gan D, Zhu Y, Lu X, Li J. SCIPAC source code. Zenodo. 2024. https://doi.org/10.5281/zenodo.11013696 .

Wu SZ, Al-Eryani G, Roden DL, Junankar S, Harvey K, Andersson A, et al. A single-cell and spatially resolved atlas of human breast cancers. Datasets. 2021. https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE176078 . Gene Expression Omnibus. Accessed 1 Oct 2022.

Lambrechts D, Wauters E, Boeckx B, Aibar S, Nittner D, Burton O, et al. Phenotype molding of stromal cells in the lung tumor microenvironment. Datasets. 2018. https://www.ebi.ac.uk/biostudies/arrayexpress/studies/E-MTAB-6149 . ArrayExpress. Accessed 24 July 2022.

Lambrechts D, Wauters E, Boeckx B, Aibar S, Nittner D, Burton O, et al. Phenotype molding of stromal cells in the lung tumor microenvironment. Datasets. 2018. https://www.ebi.ac.uk/biostudies/arrayexpress/studies/E-MTAB-6653 . ArrayExpress. Accessed 24 July 2022.

van den Heuvel A, Mahfouz A, Kloet SL, Balog J, van Engelen BG, Tawil R, et al. Single-cell RNA sequencing in facioscapulohumeral muscular dystrophy disease etiology and development. Datasets. 2019. https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE122873 . Gene Expression Omnibus. Accessed 13 Aug 2022.

Colaprico A, Silva TC, Olsen C, Garofano L, Cava C, Garolini D, et al. TCGAbiolinks: an R/Bioconductor package for integrative analysis of TCGA data. Nucleic Acids Res. 2016;44(8):e71.

Download references

Review history

The review history is available as Additional file 3.

Peer review information

Veronique van den Berghe was the primary editor of this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.

This work is supported by the National Institutes of Health (R01CA280097 to X.L. and J.L, R01CA252878 to J.L.) and the DOD BCRP Breakthrough Award, Level 2 (W81XWH2110432 to J.L.).

Author information

Authors and affiliations.

Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, 46556, IN, USA

Dailin Gan & Jun Li

Department of Biological Sciences, Boler-Parseghian Center for Rare and Neglected Diseases, Harper Cancer Research Institute, Integrated Biomedical Sciences Graduate Program, University of Notre Dame, Notre Dame, 46556, IN, USA

Yini Zhu & Xin Lu

Tumor Microenvironment and Metastasis Program, Indiana University Melvin and Bren Simon Comprehensive Cancer Center, Indianapolis, 46202, IN, USA

You can also search for this author in PubMed   Google Scholar

Contributions

J.L. conceived and supervised the study. J.L. and D.G. proposed the methods. D.G. implemented the methods and analyzed the data. D.G. and J.L. drafted the paper. D.G., Y.Z., X.L., and J.L. interpreted the results and revised the paper.

Corresponding author

Correspondence to Jun Li .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Additional file 1. supplementary materials that include additional results and plots., additional file 2. a vignette of the scipac package., additional file 3. review history., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Gan, D., Zhu, Y., Lu, X. et al. SCIPAC: quantitative estimation of cell-phenotype associations. Genome Biol 25 , 119 (2024). https://doi.org/10.1186/s13059-024-03263-1

Download citation

Received : 30 January 2023

Accepted : 30 April 2024

Published : 13 May 2024

DOI : https://doi.org/10.1186/s13059-024-03263-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Phenotype association
• Single cell
• RNA sequencing
• Cancer research

Genome Biology

ISSN: 1474-760X

• Submission enquiries: [email protected]
• General enquiries: [email protected]