

Problem Solving Strategies
The following are some examples of problem solving strategies.
Explore it//Act it/Try it (EAT) method (Basic)
Explore it//Act it/Try it (EAT) method (Intermediate )
Explore it//Act it/Try it (EAT) method (Advanced)
Finding a Pattern (Basic)
Finding a Pattern (Intermediate)
Finding a Pattern (Advanced)
Explore It/Act It/Try It (EAT) Method (Basic)
In this lesson, we will look at some basic examples of the Explore it//Act it/Try it (EAT) method of problem solving strategy.
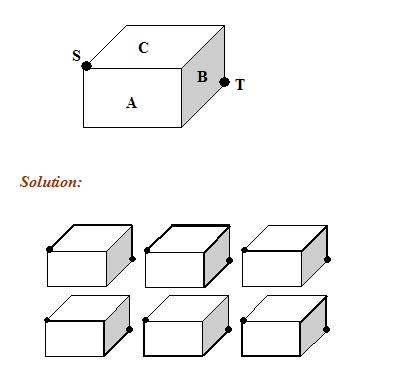
A plumber has to connect a pipe from a storage tank at the corner, S , of the roof to a tap at the diagonally opposite corner, T , in the figure below. Find the number of paths for the pipe if the pipe can only run along the edges of walls A , B , or roof C .
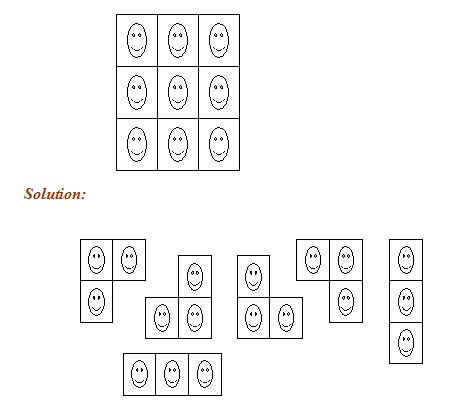
Three stamps are to be torn from a sheet of nine stamps as shown below. The three stamps must be intact so that each stamp is joined to another stamp along at least one edge. Find the possible patterns for these three stamps.
Rachel has to spend exactly $100 on the following gifts. What are the combinations of gifts that she can buy?
B, E, F or B, D
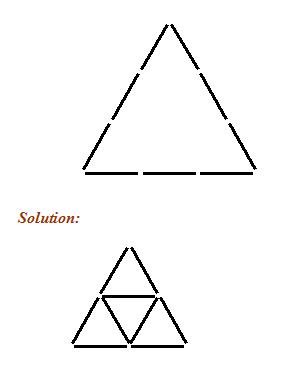
The figure below shows 9 matchsticks arranged as an equilateral triangle. Rearrange exactly 5 of the matchsticks to form 5 equilateral triangles, without leaving any stray matchsticks.
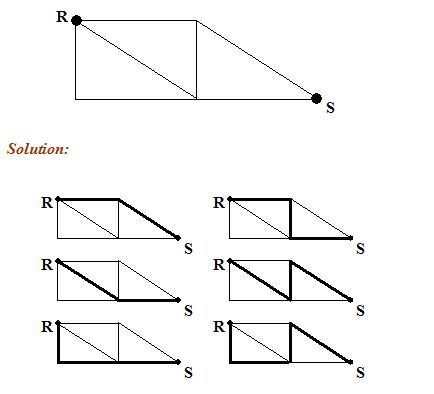
The figure below shows the roads linking cities R and S . What are the different routes to travel from R to S ?
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
| | > >
First Edition |
Chapter 1, Lesson 5: A Plan for Problem Solving
- Extra Examples
- Parent and Student Study Guide
- Self-Check Quizzes
The resource you requested requires you to enter a username and password below:
| Password: | |
Please read our Terms of Use and Privacy Policy before you explore our Web site. To report a technical problem with this Web site, please contact the site producer .

- Toggle navigation
Mathematics Department Course Hub
- Project Profile
- Course Outline
- Faculty Announcements
- Course Coordination
- Training and Support
- Lesson 5: Problem-Solving Strategies
Hi Everyone!
On this page you will find some material about Lesson 5. Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Table of Contents
In this section you will find some important information about the specific resources related to this lesson:
- the learning outcomes,
- the section in the textbook,
- the homework,
- supporting video.
Learning Outcomes. (extracted from the textbook)
- State the four steps in the basic problem-solving procedure.
- Divide radical expressions.
- Solve problems using a diagram.
- Solve problems using trial and error.
- Solve problems involving money.
- Solve problems using calculation.
Topic . This lesson covers
Section 1.3: Problem-Solving Strategies
pages 29-35, ex. 1-6.
Practice Homework:
page 36: 19, 21, 25, 35, 38, 41, 43
ALEKS Assignment
Warmup Questions
These are questions on fundamental concepts that you need to know before you can embark on this lesson. Don’t skip them! Take your time to do them, and check your answer by clicking on the “Show Answer” tab.
Warmup Question 1
$$(2\sqrt{5a})(-4\sqrt{5a}).$$
Show Answer 1
$$(2\sqrt{5a})(-4\sqrt{5a})= -8\sqrt{(5a)^2}=-8(5a)=-40a$$
Warmup Question 2
$$(\sqrt 3-6)(\sqrt 3+6).$$
Show Answer 2
$$(\sqrt 3-6)(\sqrt 3+6)= (\sqrt 3)^2-6^2 = 3 – 36 = -33$$
If you are not comfortable with the Warmup Questions, don’t give up! Click on the indicated lesson for a quick catchup. A brief review will help you boost your confidence to start the new lesson, and that’s perfectly fine.
Need a review? Check Lesson 6 .
Quick Intro
This is like a mini-lesson with an overview of the main objects of study. It will often contain a list of key words, definitions and properties – all that is new in this lesson. We will use this opportunity to make connections with other concepts. It can be also used as a review of the lesson.
A Quick Intro to Division of Radicals and Rationalization
Key Words. Radicals, division of radicals, simplified form, rationalization, conjugate.
When dividing radical terms, the following property can be very helpful.
Division Property
$$\dfrac{\sqrt[n]a}{\sqrt[n]b}=\sqrt[n]{\dfrac{a}{b}}$$
If not, it may be necessary to rationalize the denominator. On Lesson 5 we listed three conditions for a radical expression to be in simplified form. The third one is:
There should be no radicals in the denominator of a fraction.
$\bigstar$ We gave $\dfrac{1}{\sqrt 2}$ as an example that fails this condition. To simplify it, we multiply both the numerator and the denominator by $\sqrt 2$.
$$\underbrace{\dfrac{1}{\sqrt 2}}_{\text{radical in the denominator}}=\dfrac{1}{\sqrt 2}\cdot\dfrac{\sqrt 2}{\sqrt 2}=\dfrac{1\cdot\sqrt 2}{\sqrt 2\cdot\sqrt 2}=\underbrace{\dfrac{\sqrt 2}{2}}_{\text{no radical in the denominator}}$$
$\bigstar$ The process of removing a radical from the denominator is called rationalization .
$\bigstar$ The key idea was to multiply the original denominator by another copy of it, since squaring eliminates the radical.
$$(\sqrt a)(\sqrt a) = (\sqrt a)^2=a.$$
$\bigstar$ But what if we have $\dfrac{1}{\sqrt 3 -6}$? Squaring $\sqrt{3}-6$ will not help (try it!). In the Warmup Question #2 we saw that
$$(\sqrt 3 -6)(\sqrt 3 +6)=-33$$
results in a number free of radical. So
$$\underbrace{\dfrac{1}{\sqrt 3 -6}}_{\text{radical in the denominator}}=\dfrac{1}{\sqrt 3 -6}\cdot\dfrac{\sqrt 3 +6}{\sqrt 3 +6}$$
$$=\dfrac{1\cdot(\sqrt 3 +6)}{(\sqrt 3 -6)\cdot(\sqrt 3 +6)}=\underbrace{-\dfrac{\sqrt 3 +6}{33}}_{\text{no radical in the denominator}}$$
$\bigstar$ This happens because the above product is a difference of squares
$$(a-b)(a+b)=a^2-b^2,$$
and squaring a single radical eliminates the radical.
$\bigstar$ We say that $a-b$ and $a+b$ are conjugates . So if the denominator is $\sqrt 3 -6$, we rationalize it by multiplying the numerator and the denominator by its conjugate $\sqrt 3+6$.
Video Lesson
Many times the mini-lesson will not be enough for you to start working on the problems. You need to see someone explaining the material to you. In the video you will find a variety of examples, solved step-by-step – starting from a simple one to a more complex one. Feel free to play them as many times as you need. Pause, rewind, replay, stop… follow your pace!
A description of the video
In the video you will see the following radical expressions.
- $\dfrac{3\sqrt x+1}{2\sqrt x}$
- $\dfrac{3\sqrt 5 + 1}{2\sqrt 7 -3}$
Try Questions
Now that you have read the material and watched the video, it is your turn to put in practice what you have learned. We encourage you to try the Try Questions on your own. When you are done, click on the “Show answer” tab to see if you got the correct answer.
Try Question 1
Simplify $$\dfrac{\sqrt{15}}{5\sqrt{20}}.$$
$$\dfrac{\sqrt{15}}{5\sqrt{20}} = \dfrac{\sqrt{15}}{5\sqrt{20}}\cdot \dfrac{\sqrt{20}}{\sqrt{20}}$$
$$= \dfrac{\sqrt{15}\sqrt{20}}{5\cdot 20} = \dfrac{\sqrt{15} \cdot 2\sqrt{5}}{5\cdot 20}$$
$$= \dfrac{\sqrt {5\cdot 15}}{5\cdot 10} = \dfrac{5\sqrt {3}}{50} = \dfrac{\sqrt 3}{10}$$
Try Question 2
Simplify $$\dfrac{3}{4+2\sqrt 5}.$$
$$\dfrac{3}{4+2\sqrt 5}=\dfrac{3}{4+2\sqrt 5}\cdot \dfrac{4-2\sqrt 5}{4-2\sqrt 5}$$
$$= \dfrac{3(4-2\sqrt 5)}{(4+2\sqrt 5)(4-2\sqrt 5)}= \dfrac{12-6\sqrt 5}{16-20}$$
$$=\dfrac{12-6\sqrt 5}{-4} = \dfrac{-6+3\sqrt 5}{2} $$
Try Question 3
Rationalize and simplify
$$\dfrac{1+3\sqrt 2}{1-\sqrt 2}+\sqrt 2.$$
Show Answer 3
$$\dfrac{1+3\sqrt 2}{1-\sqrt 2}+\sqrt 2= \dfrac{1+3\sqrt 2}{1-\sqrt 2}\cdot\dfrac{1+\sqrt 2}{1+\sqrt 2}+\sqrt 2$$
$$=\dfrac{(1+3\sqrt 2)(1+\sqrt 2)}{(1-\sqrt 2)(1+\sqrt 2)} +\sqrt 2 = \dfrac{1+\sqrt 2+3\sqrt 2 +3\cdot 2}{1-2}+\sqrt 2 $$
$$=\dfrac{7+4\sqrt 2}{-1}+\sqrt 2 = -7-4\sqrt 2+\sqrt 2 = -7-3\sqrt 2$$
You should now be ready to start working on the homework problems. Doing the homework is an essential part of learning. It will help you practice the lesson and reinforce your knowledge.
It is time to do the homework on WeBWork:
RationalizeDenominators
When you are done, come back to this page for the Exit Questions.
Exit Questions
After doing the WeBWorK problems, come back to this page. The Exit Questions include vocabulary checking and conceptual questions. Knowing the vocabulary accurately is important for us to communicate. You will also find one last problem. All these questions will give you an idea as to whether or not you have mastered the material. Remember: the “Show Answer” tab is there for you to check your work!
- What is the goal in rationalizing the denominator?
- Why does the ‘conjugate’ play a role in accomplishing this?
$\bigstar$ Simplify
(a) $\dfrac{3-3\sqrt{3a}}{4\sqrt{8a}}$
(b) $\dfrac{\sqrt{5}+3}{4-\sqrt 5}$
Show Answer
(a) $$\dfrac{3-3\sqrt{3a}}{4\sqrt{8a}}=\dfrac{3-3\sqrt{3a}}{4\cdot 2 \sqrt{2a}} $$
$$= \dfrac{3-3\sqrt{3a}}{8\sqrt{2a}}\cdot\dfrac{\sqrt{2a}}{\sqrt{2a}} =\dfrac{(3-3\sqrt{3a}) \sqrt{2a}}{8\cdot 2a} $$
$$= \dfrac{3\sqrt{2a}-3\sqrt{6a^2}}{16a} =\dfrac{3\sqrt{2a}-3a\sqrt 6}{16a}$$
(b) $$\dfrac{\sqrt{5}+3}{4-\sqrt 5}= \dfrac{\sqrt{5}+3}{4-\sqrt 5}\cdot \dfrac{4+\sqrt 5}{4+\sqrt 5} $$
$$= \dfrac{(\sqrt{5}+3)(4+\sqrt 5)}{(4-\sqrt 5)(4-\sqrt 5)}=\dfrac{4\sqrt{5}+5+12+3\sqrt 5}{16-5}$$
$$ =\dfrac{7\sqrt 5+17}{11}$$
Need more help?
Don’t wait too long to do the following.
- Watch the additional video resources.
- Talk to your instructor.
- Form a study group.
- Visit a tutor. For more information, check the tutoring page .
Lessons Menu
- Lesson 1: Applications of Linear Equations
- Lesson 2: Ratio, Proportion, and Variation
- Lesson 3: The Nature of Mathematical Reasoning
- Lesson 4: Estimation and Interpreting Graphs
- Lesson 6: Statement and Quantifiers
- Lesson 7: Measures of Length: Converting Units and the Metric System
- Lesson 8: Measures of Area, Volume, and Capacity
- Lesson 9: Measures of Weight & Temperature
- Lesson 10: Percents
- Lesson 11: Simple Interest
- Lesson 12: Compound Interest
- Lesson 13: Basic Concepts of Probability
- Lesson 14: Tree Diagrams, Tables and Sample Spaces
- Lesson 15: Gathering and Organizing Data/Picturing Data
- Lesson 16: Measures of Average
- Lesson 17: Measures of Variation
- Lesson 18: Measures of Position
- Lesson 19: The Normal Distribution/Applications of the Normal Distribution
- Lesson 20: Correlation and Regression Analysis
- Lesson 21: Points, Lines, Planes & Angles
- Lesson 22: Triangles
- Lesson 23: Polygons and Perimeter/Areas of Polygons and Circles
© 2024 MAT 1190 Course Hub
Theme by Anders Noren — Up ↑
The OpenLab at City Tech: A place to learn, work, and share
The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.

New York City College of Technology | City University of New York
Accessibility
Our goal is to make the OpenLab accessible for all users.
Learn more about accessibility on the OpenLab
Creative Commons
- - Attribution
- - NonCommercial
- - ShareAlike

© New York City College of Technology | City University of New York
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
5th grade (Eureka Math/EngageNY)
Unit 1: module 1: place value and decimal fractions, unit 2: module 2: multi-digit whole number and decimal fraction operations, unit 3: module 3: addition and subtractions of fractions, unit 4: module 4: multiplication and division of fractions and decimal fractions, unit 5: module 5: addition and multiplication with volume and area, unit 6: module 6: problem solving with the coordinate plane.

How it works
Transform your enterprise with the scalable mindsets, skills, & behavior change that drive performance.
Explore how BetterUp connects to your core business systems.
We pair AI with the latest in human-centered coaching to drive powerful, lasting learning and behavior change.
Build leaders that accelerate team performance and engagement.
Unlock performance potential at scale with AI-powered curated growth journeys.
Build resilience, well-being and agility to drive performance across your entire enterprise.
Transform your business, starting with your sales leaders.
Unlock business impact from the top with executive coaching.
Foster a culture of inclusion and belonging.
Accelerate the performance and potential of your agencies and employees.
See how innovative organizations use BetterUp to build a thriving workforce.
Discover how BetterUp measurably impacts key business outcomes for organizations like yours.
A demo is the first step to transforming your business. Meet with us to develop a plan for attaining your goals.

- What is coaching?
Learn how 1:1 coaching works, who its for, and if it's right for you.
Accelerate your personal and professional growth with the expert guidance of a BetterUp Coach.
Types of Coaching
Navigate career transitions, accelerate your professional growth, and achieve your career goals with expert coaching.
Enhance your communication skills for better personal and professional relationships, with tailored coaching that focuses on your needs.
Find balance, resilience, and well-being in all areas of your life with holistic coaching designed to empower you.
Discover your perfect match : Take our 5-minute assessment and let us pair you with one of our top Coaches tailored just for you.

Research, expert insights, and resources to develop courageous leaders within your organization.
Best practices, research, and tools to fuel individual and business growth.
View on-demand BetterUp events and learn about upcoming live discussions.
The latest insights and ideas for building a high-performing workplace.
- BetterUp Briefing
The online magazine that helps you understand tomorrow's workforce trends, today.
Innovative research featured in peer-reviewed journals, press, and more.
Founded in 2022 to deepen the understanding of the intersection of well-being, purpose, and performance
We're on a mission to help everyone live with clarity, purpose, and passion.
Join us and create impactful change.
Read the buzz about BetterUp.
Meet the leadership that's passionate about empowering your workforce.
For Business
For Individuals
10 Problem-solving strategies to turn challenges on their head

Jump to section
What is an example of problem-solving?
What are the 5 steps to problem-solving, 10 effective problem-solving strategies, what skills do efficient problem solvers have, how to improve your problem-solving skills.
Problems come in all shapes and sizes — from workplace conflict to budget cuts.
Creative problem-solving is one of the most in-demand skills in all roles and industries. It can boost an organization’s human capital and give it a competitive edge.
Problem-solving strategies are ways of approaching problems that can help you look beyond the obvious answers and find the best solution to your problem .
Let’s take a look at a five-step problem-solving process and how to combine it with proven problem-solving strategies. This will give you the tools and skills to solve even your most complex problems.
Good problem-solving is an essential part of the decision-making process . To see what a problem-solving process might look like in real life, let’s take a common problem for SaaS brands — decreasing customer churn rates.
To solve this problem, the company must first identify it. In this case, the problem is that the churn rate is too high.
Next, they need to identify the root causes of the problem. This could be anything from their customer service experience to their email marketing campaigns. If there are several problems, they will need a separate problem-solving process for each one.
Let’s say the problem is with email marketing — they’re not nurturing existing customers. Now that they’ve identified the problem, they can start using problem-solving strategies to look for solutions.
This might look like coming up with special offers, discounts, or bonuses for existing customers. They need to find ways to remind them to use their products and services while providing added value. This will encourage customers to keep paying their monthly subscriptions.
They might also want to add incentives, such as access to a premium service at no extra cost after 12 months of membership. They could publish blog posts that help their customers solve common problems and share them as an email newsletter.
The company should set targets and a time frame in which to achieve them. This will allow leaders to measure progress and identify which actions yield the best results.

Perhaps you’ve got a problem you need to tackle. Or maybe you want to be prepared the next time one arises. Either way, it’s a good idea to get familiar with the five steps of problem-solving.
Use this step-by-step problem-solving method with the strategies in the following section to find possible solutions to your problem.
1. Identify the problem
The first step is to know which problem you need to solve. Then, you need to find the root cause of the problem.
The best course of action is to gather as much data as possible, speak to the people involved, and separate facts from opinions.
Once this is done, formulate a statement that describes the problem. Use rational persuasion to make sure your team agrees .
2. Break the problem down
Identifying the problem allows you to see which steps need to be taken to solve it.
First, break the problem down into achievable blocks. Then, use strategic planning to set a time frame in which to solve the problem and establish a timeline for the completion of each stage.
3. Generate potential solutions
At this stage, the aim isn’t to evaluate possible solutions but to generate as many ideas as possible.
Encourage your team to use creative thinking and be patient — the best solution may not be the first or most obvious one.
Use one or more of the different strategies in the following section to help come up with solutions — the more creative, the better.
4. Evaluate the possible solutions
Once you’ve generated potential solutions, narrow them down to a shortlist. Then, evaluate the options on your shortlist.
There are usually many factors to consider. So when evaluating a solution, ask yourself the following questions:
- Will my team be on board with the proposition?
- Does the solution align with organizational goals ?
- Is the solution likely to achieve the desired outcomes?
- Is the solution realistic and possible with current resources and constraints?
- Will the solution solve the problem without causing additional unintended problems?

5. Implement and monitor the solutions
Once you’ve identified your solution and got buy-in from your team, it’s time to implement it.
But the work doesn’t stop there. You need to monitor your solution to see whether it actually solves your problem.
Request regular feedback from the team members involved and have a monitoring and evaluation plan in place to measure progress.
If the solution doesn’t achieve your desired results, start this step-by-step process again.
There are many different ways to approach problem-solving. Each is suitable for different types of problems.
The most appropriate problem-solving techniques will depend on your specific problem. You may need to experiment with several strategies before you find a workable solution.
Here are 10 effective problem-solving strategies for you to try:
- Use a solution that worked before
- Brainstorming
- Work backward
- Use the Kipling method
- Draw the problem
- Use trial and error
- Sleep on it
- Get advice from your peers
- Use the Pareto principle
- Add successful solutions to your toolkit
Let’s break each of these down.
1. Use a solution that worked before
It might seem obvious, but if you’ve faced similar problems in the past, look back to what worked then. See if any of the solutions could apply to your current situation and, if so, replicate them.
2. Brainstorming
The more people you enlist to help solve the problem, the more potential solutions you can come up with.
Use different brainstorming techniques to workshop potential solutions with your team. They’ll likely bring something you haven’t thought of to the table.
3. Work backward
Working backward is a way to reverse engineer your problem. Imagine your problem has been solved, and make that the starting point.
Then, retrace your steps back to where you are now. This can help you see which course of action may be most effective.
4. Use the Kipling method
This is a method that poses six questions based on Rudyard Kipling’s poem, “ I Keep Six Honest Serving Men .”
- What is the problem?
- Why is the problem important?
- When did the problem arise, and when does it need to be solved?
- How did the problem happen?
- Where is the problem occurring?
- Who does the problem affect?
Answering these questions can help you identify possible solutions.
5. Draw the problem
Sometimes it can be difficult to visualize all the components and moving parts of a problem and its solution. Drawing a diagram can help.
This technique is particularly helpful for solving process-related problems. For example, a product development team might want to decrease the time they take to fix bugs and create new iterations. Drawing the processes involved can help you see where improvements can be made.

6. Use trial-and-error
A trial-and-error approach can be useful when you have several possible solutions and want to test them to see which one works best.
7. Sleep on it
Finding the best solution to a problem is a process. Remember to take breaks and get enough rest . Sometimes, a walk around the block can bring inspiration, but you should sleep on it if possible.
A good night’s sleep helps us find creative solutions to problems. This is because when you sleep, your brain sorts through the day’s events and stores them as memories. This enables you to process your ideas at a subconscious level.
If possible, give yourself a few days to develop and analyze possible solutions. You may find you have greater clarity after sleeping on it. Your mind will also be fresh, so you’ll be able to make better decisions.
8. Get advice from your peers
Getting input from a group of people can help you find solutions you may not have thought of on your own.
For solo entrepreneurs or freelancers, this might look like hiring a coach or mentor or joining a mastermind group.
For leaders , it might be consulting other members of the leadership team or working with a business coach .
It’s important to recognize you might not have all the skills, experience, or knowledge necessary to find a solution alone.
9. Use the Pareto principle
The Pareto principle — also known as the 80/20 rule — can help you identify possible root causes and potential solutions for your problems.
Although it’s not a mathematical law, it’s a principle found throughout many aspects of business and life. For example, 20% of the sales reps in a company might close 80% of the sales.
You may be able to narrow down the causes of your problem by applying the Pareto principle. This can also help you identify the most appropriate solutions.

10. Add successful solutions to your toolkit
Every situation is different, and the same solutions might not always work. But by keeping a record of successful problem-solving strategies, you can build up a solutions toolkit.
These solutions may be applicable to future problems. Even if not, they may save you some of the time and work needed to come up with a new solution.

Improving problem-solving skills is essential for professional development — both yours and your team’s. Here are some of the key skills of effective problem solvers:
- Critical thinking and analytical skills
- Communication skills , including active listening
- Decision-making
- Planning and prioritization
- Emotional intelligence , including empathy and emotional regulation
- Time management
- Data analysis
- Research skills
- Project management
And they see problems as opportunities. Everyone is born with problem-solving skills. But accessing these abilities depends on how we view problems. Effective problem-solvers see problems as opportunities to learn and improve.
Ready to work on your problem-solving abilities? Get started with these seven tips.
1. Build your problem-solving skills
One of the best ways to improve your problem-solving skills is to learn from experts. Consider enrolling in organizational training , shadowing a mentor , or working with a coach .
2. Practice
Practice using your new problem-solving skills by applying them to smaller problems you might encounter in your daily life.
Alternatively, imagine problematic scenarios that might arise at work and use problem-solving strategies to find hypothetical solutions.
3. Don’t try to find a solution right away
Often, the first solution you think of to solve a problem isn’t the most appropriate or effective.
Instead of thinking on the spot, give yourself time and use one or more of the problem-solving strategies above to activate your creative thinking.

4. Ask for feedback
Receiving feedback is always important for learning and growth. Your perception of your problem-solving skills may be different from that of your colleagues. They can provide insights that help you improve.
5. Learn new approaches and methodologies
There are entire books written about problem-solving methodologies if you want to take a deep dive into the subject.
We recommend starting with “ Fixed — How to Perfect the Fine Art of Problem Solving ” by Amy E. Herman.
6. Experiment
Tried-and-tested problem-solving techniques can be useful. However, they don’t teach you how to innovate and develop your own problem-solving approaches.
Sometimes, an unconventional approach can lead to the development of a brilliant new idea or strategy. So don’t be afraid to suggest your most “out there” ideas.
7. Analyze the success of your competitors
Do you have competitors who have already solved the problem you’re facing? Look at what they did, and work backward to solve your own problem.
For example, Netflix started in the 1990s as a DVD mail-rental company. Its main competitor at the time was Blockbuster.
But when streaming became the norm in the early 2000s, both companies faced a crisis. Netflix innovated, unveiling its streaming service in 2007.
If Blockbuster had followed Netflix’s example, it might have survived. Instead, it declared bankruptcy in 2010.
Use problem-solving strategies to uplevel your business
When facing a problem, it’s worth taking the time to find the right solution.
Otherwise, we risk either running away from our problems or headlong into solutions. When we do this, we might miss out on other, better options.
Use the problem-solving strategies outlined above to find innovative solutions to your business’ most perplexing problems.
If you’re ready to take problem-solving to the next level, request a demo with BetterUp . Our expert coaches specialize in helping teams develop and implement strategies that work.
Boost your productivity
Maximize your time and productivity with strategies from our expert coaches.
Elizabeth Perry, ACC
Elizabeth Perry is a Coach Community Manager at BetterUp. She uses strategic engagement strategies to cultivate a learning community across a global network of Coaches through in-person and virtual experiences, technology-enabled platforms, and strategic coaching industry partnerships. With over 3 years of coaching experience and a certification in transformative leadership and life coaching from Sofia University, Elizabeth leverages transpersonal psychology expertise to help coaches and clients gain awareness of their behavioral and thought patterns, discover their purpose and passions, and elevate their potential. She is a lifelong student of psychology, personal growth, and human potential as well as an ICF-certified ACC transpersonal life and leadership Coach.
8 creative solutions to your most challenging problems
5 problem-solving questions to prepare you for your next interview, what are metacognitive skills examples in everyday life, what is lateral thinking 7 techniques to encourage creative ideas, 31 examples of problem solving performance review phrases, learn what process mapping is and how to create one (+ examples), leadership activities that encourage employee engagement, how much do distractions cost 8 effects of lack of focus, can dreams help you solve problems 6 ways to try, similar articles, the pareto principle: how the 80/20 rule can help you do more with less, thinking outside the box: 8 ways to become a creative problem solver, 3 problem statement examples and steps to write your own, contingency planning: 4 steps to prepare for the unexpected, learn to sweat the small stuff: how to improve attention to detail, stay connected with betterup, get our newsletter, event invites, plus product insights and research..
3100 E 5th Street, Suite 350 Austin, TX 78702
- Platform Overview
- Integrations
- Powered by AI
- BetterUp Lead™
- BetterUp Manage™
- BetterUp Care®
- Sales Performance
- Diversity & Inclusion
- Case Studies
- Why BetterUp?
- About Coaching
- Find your Coach
- Career Coaching
- Communication Coaching
- Life Coaching
- News and Press
- Leadership Team
- Become a BetterUp Coach
- BetterUp Labs
- Center for Purpose & Performance
- Leadership Training
- Business Coaching
- Contact Support
- Contact Sales
- Privacy Policy
- Acceptable Use Policy
- Trust & Security
- Cookie Preferences

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

5.3: Problem Solving Strategies
- Last updated
- Save as PDF
- Page ID 32466

- Michelle Manes
- University of Hawaii
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.
Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.
How to Solve It
George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985. [1]

George Pólya, circa 1973
- Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 ( http://creativecommons.org/licenses/by/2.0 )], via Wikimedia Commons ↵
In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:
- First, you have to understand the problem.
- After understanding, then make a plan.
- Carry out the plan.
- Look back on your work. How could it be better?
This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.
Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!
We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:
- What if the picture was different?
- What if the numbers were simpler?
- What if I just made up some numbers?
You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.
This brings us to the most important problem solving strategy of all:
Problem Solving Strategy 2 (Try Something!).
If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.
And equally important: If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.
Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what he had left after paying Brianna. Finally, Alex saw David and gave him 1/2 of what he had remaining. Who got the most money from Alex?
Think/Pair/Share
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.
Problem Solving Strategy 3 (Draw a Picture).
Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?
Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?
After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.
Problem Solving Strategy 4 (Make Up Numbers).
Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!
You can work forwards: Assume Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person. Or you can work backwards: suppose he has some specific amount left at the end, like $10. Since he gave Chris half of what he had left, that means he had $20 before running into Chris. Now, work backwards and figure out how much each person got.
Watch the solution only after you tried this strategy for yourself.
If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!
(Squares on a Chess Board)
How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)
Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!
Think / Pair / Share
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?
It is clear that you want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. You should never ask the teacher, “Is this right?” Instead, you should declare, “Here’s my answer, and here is why I know it is correct!”
Problem Solving Strategy 5 (Try a Simpler Problem).
Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?
Of course the ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).
Problem Solving Strategy 6 (Work Systematically).
If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.
For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:
| 1 | 0 | 0 | 0 | ||
| 4 | 1 | 0 | 0 | ||
| 9 | 4 | 1 | 0 | ||
Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate).
Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!
For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.
Problem Solving Strategy 8 (Look for and Explain Patterns).
Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.
If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:
- Describe all of the patterns you see in the table.
- Can you explain and justify any of the patterns you see? How can you be sure they will continue?
- What calculation would you do to find the total number of squares on a 100 × 100 chess board?
(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)
(Broken Clock)
This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)
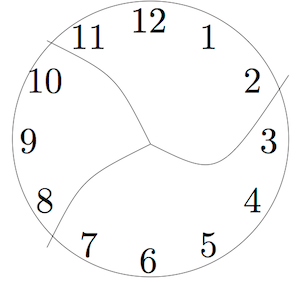
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2.)
Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What progress have you made?
Problem Solving Strategy 9 (Find the Math, Remove the Context).
Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:
- What is the sum of all the numbers on the clock’s face?
- Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
- How do I know when I am done? When should I stop looking?
Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.
Problem Solving Strategy 10 (Check Your Assumptions).
When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?
In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:
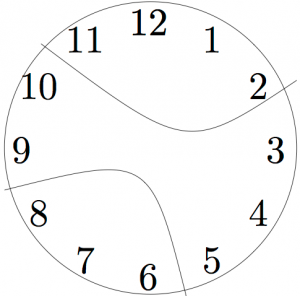
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.
- Inspiration
| Patterns with Exponents and Powers of 10 | ||
| Patterns with Exponents and Powers of 10 | ||
| Understand Whole-Number Place Value | ||
| Understand Whole-Number Place Value | ||
| Decimals to Thousandths | ||
| Decimals to Thousandths | ||
| Understand Decimal Place Value | ||
| Understand Decimal Place Value | ||
| Compare Decimals | ||
| Compare Decimals | ||
| Round Decimals | ||
| Round Decimals | ||
| Look For and Use Structure | ||
| Look For and Use Structure | ||
| Mental Math | ||
| Mental Math | ||
| Estimate Sums and Differences of Decimals | ||
| Estimate Sums and Differences of Decimals | ||
| Use Models to Add and Subtract Decimals | ||
| Use Models to Add and Subtract Decimals | ||
| Use Strategies to Add Decimals | ||
| Use Strategies to Add Decimals | ||
| Use Strategies to Subtract Decimals | ||
| Use Strategies to Subtract Decimals | ||
| Model with Math | ||
| Model with Math | ||
| Multiply Greater Numbers by Powers of 10 | ||
| Multiply Greater Numbers by Powers of 10 | ||
| Estimate Products | ||
| Estimate Products | ||
| Multiply by 1-Digit Numbers | ||
| Multiply by 1-Digit Numbers | ||
| Multiply 2-Digit by 2-Digit Numbers | ||
| Multiply 2-Digit by 2-Digit Numbers | ||
| Multiply 3-Digit by 2-Digit numbers | ||
| Multiply 3-Digit by 2-Digit numbers | ||
| Multiply Whole Numbers with Zeros | ||
| Multiply Whole Numbers with Zeros | ||
| Practice Multiplying Multi-Digit Numbers | ||
| Practice Multiplying Multi-Digit Numbers | ||
| Solve Word Problems Using Multiplication | ||
| Solve Word Problems Using Multiplication | ||
| Critique Reasoning | ||
| Critique Reasoning | ||
| Multiply Decimals by Powers of 10 | ||
| Multiply Decimals by Powers of 10 | ||
| Estimate the Product of a Decimal and a Whole Number | ||
| Estimate the Product of a Decimal and a Whole Number | ||
| Use Models to Multiply a Decimal by a Whole Number | ||
| Use Models to Multiply a Decimal by a Whole Number | ||
| Multiply a Decimal and a Whole Number | ||
| Multiply a Decimal and a Whole Number | ||
| Use Models to Multiply a Decimal and a Decimal | ||
| Use Models to Multiply a Decimal and a Decimal | ||
| Multiply Decimals Using Partial Products | ||
| Multiply Decimals Using Partial Products | ||
| Use Properties to Multiply Decimals | ||
| Use Properties to Multiply Decimals | ||
| Use Number Sense to Multiply Decimals | ||
| Use Number Sense to Multiply Decimals | ||
| Model with Math | ||
| Model with Math | ||
| Use Patterns and Mental Math to Divide | ||
| Use Patterns and Mental Math to Divide | ||
| Estimate Quotients with 2-Digit Divisors | ||
| Estimate Quotients with 2-Digit Divisors | ||
| Use Models and Properties to Divide with 2-Digit Divisors | ||
| Use Models and Properties to Divide with 2-Digit Divisors | ||
| Use Partial Quotients to Divide | ||
| Use Partial Quotients to Divide | ||
| Use Sharing to Divide: 2-Digit Divisors | ||
| Use Sharing to Divide: 2-Digit Divisors | ||
| Use Sharing to Divide: Greater Dividends | ||
| Use Sharing to Divide: Greater Dividends | ||
| Choose a Strategy to Divide | ||
| Choose a Strategy to Divide | ||
| Make Sense and Persevere | ||
| Make Sense and Persevere | ||
| Patterns for Dividing with Decimals | ||
| Patterns for Dividing with Decimals | ||
| Estimate Decimal Quotients | ||
| Estimate Decimal Quotients | ||
| Use Models to Divide by a 1-Digit Whole Number | ||
| Use Models to Divide by a 1-Digit Whole Number | ||
| Divide by a 2-Digit Whole Number | ||
| Divide by a 2-Digit Whole Number | ||
| Divide by a Decimal | ||
| Divide by a Decimal | ||
| Reasoning | ||
| Reasoning | ||
| Estimate Sums and Differences of Fractions | ||
| Estimate Sums and Differences of Fractions | ||
| Find Common Denominators | ||
| Find Common Denominators | ||
| Add Fractions with Unlike Denominators | ||
| Add Fractions with Unlike Denominators | ||
| Subtract Fractions with Unlike Denominators | ||
| Subtract Fractions with Unlike Denominators | ||
| Add and Subtract Fractions | ||
| Add and Subtract Fractions | ||
| Estimate Sums and Differences of Mixed Numbers | ||
| Estimate Sums and Differences of Mixed Numbers | ||
| Use Models to Add Mixed Numbers | ||
| Use Models to Add Mixed Numbers | ||
| Add Mixed Numbers | ||
| Add Mixed Numbers | ||
| Use Models to Subtract Mixed Numbers | ||
| Use Models to Subtract Mixed Numbers | ||
| Subtract Mixed Numbers | ||
| Subtract Mixed Numbers | ||
| Add and Subtract Mixed Numbers | ||
| Add and Subtract Mixed Numbers | ||
| Model with Math | ||
| Model with Math | ||
| Multiply a Fraction by a Whole Number | ||
| Multiply a Fraction by a Whole Number | ||
| Multiply a Whole Number by a Fraction | ||
| Multiply a Whole Number by a Fraction | ||
| Multiply Fractions and Whole Numbers | ||
| Multiply Fractions and Whole Numbers | ||
| Use Models to Multiply Two Fractions | ||
| Use Models to Multiply Two Fractions | ||
| Multiply Two Fractions | ||
| Multiply Two Fractions | ||
| Area of a Rectangle | ||
| Area of a Rectangle | ||
| Multiply Mixed Numbers | ||
| Multiply Mixed Numbers | ||
| Multiplication as Scaling | ||
| Multiplication as Scaling | ||
| Make Sense and Persevere | ||
| Make Sense and Persevere | ||
| Fractions and Division | ||
| Fractions and Division | ||
| Fractions and Mixed Numbers as Quotients | ||
| Fractions and Mixed Numbers as Quotients | ||
| Use Multiplication to Divide | ||
| Use Multiplication to Divide | ||
| Divide Whole Numbers by Unit Fractions | ||
| Divide Whole Numbers by Unit Fractions | ||
| Divide Unit Fractions by Non-Zero Whole Numbers | ||
| Divide Unit Fractions by Non-Zero Whole Numbers | ||
| Divide Whole Numbers and Unit Fractions | ||
| Divide Whole Numbers and Unit Fractions | ||
| Solve Problems Using Division | ||
| Solve Problems Using Division | ||
| Repeated Reasoning | ||
| Repeated Reasoning | ||
| Analyze Line Plots | ||
| Analyze Line Plots | ||
| Make Line Plots | ||
| Make Line Plots | ||
| Solve Word Problems Using Measurement Data | ||
| Solve Word Problems Using Measurement Data | ||
| Critique Reasoning | ||
| Critique Reasoning | ||
| Model Volume | ||
| Model Volume | ||
| Develop a Volume Formula | ||
| Develop a Volume Formula | ||
| Combine Volume of Prisms | ||
| Combine Volume of Prisms | ||
| Solve Word Problems Using Volume | ||
| Solve Word Problems Using Volume | ||
| Use Appropriate Tools | ||
| Use Appropriate Tools | ||
| Convert Customary Units of Length | ||
| Convert Customary Units of Length | ||
| Convert Customary Units of Capacity | ||
| Convert Customary Units of Capacity | ||
| Convert Customary Units of Weight | ||
| Convert Customary Units of Weight | ||
| Convert Metric Units of Length | ||
| Convert Metric Units of Length | ||
| Convert Metric Units of Capacity | ||
| Convert Metric Units of Capacity | ||
| Convert Metric Units of Mass | ||
| Convert Metric Units of Mass | ||
| Convert Units of Time | ||
| Convert Units of Time | ||
| Solve Word Problems Using Measurement Conversions | ||
| Solve Word Problems Using Measurement Conversions | ||
| Precision | ||
| Precision | ||
| Evaluate Expressions | ||
| Evaluate Expressions | ||
| Write Numerical Expressions | ||
| Write Numerical Expressions | ||
| Interpret Numerical Expressions | ||
| Interpret Numerical Expressions | ||
| Reasoning | ||
| Reasoning | ||
| The Coordinate System | ||
| The Coordinate System | ||
| Graph Data Using Ordered Pairs | ||
| Graph Data Using Ordered Pairs | ||
| Solve Problems Using Ordered Pairs | ||
| Solve Problems Using Ordered Pairs | ||
| Reasoning | ||
| Reasoning | ||
| Numerical Patterns | ||
| Numerical Patterns | ||
| More Numerical Patterns | ||
| More Numerical Patterns | ||
| Analyze and Graph Relationships | ||
| Analyze and Graph Relationships | ||
| Make Sense and Persevere | ||
| Make Sense and Persevere | ||
| Classify Triangles | ||
| Classify Triangles | ||
| Classify Quadrilaterals | ||
| Classify Quadrilaterals | ||
| Continue to Classify Quadrilaterals | ||
| Continue to Classify Quadrilaterals | ||
| Construct Arguments | ||
| Construct Arguments | ||
| Understand Division of Fractions | ||
| Understand Division of Fractions | ||
| Understand Integers | ||
| Understand Integers | ||
| Rational Numbers on the Coordinate Plane | ||
| Rational Numbers on the Coordinate Plane | ||
| Understand and Represent Exponents | ||
| Understand and Represent Exponents | ||
| Understand Equations and Solutions | ||
| Understand Equations and Solutions | ||
| Understand Ratios | ||
| Understand Ratios | ||
| Understand Rates and Unit Rates | ||
| Understand Rates and Unit Rates | ||
| Understand Percent | ||
| Understand Percent | ||
| Relate Fractions, Decimals, and Percents | ||
| Relate Fractions, Decimals, and Percents | ||
| Find Areas of Parallelograms and Rhombuses | ||
| Find Areas of Parallelograms and Rhombuses | ||
- For Parents
- For Teachers
- Teaching Topics

- Kindergarten
- EM3/CCSS at Home
- Family Letters
- Student Gallery
- Understanding EM
- Algorithms/ Computation
- Student Links
EM4 at Home
Fractions and multiplication strategies.
Lesson | Vocabulary | Home Link Help | Games |
|---|---|---|---|
| Exploring Equal Parts, Fractions of Different Wholes, and Area | Home Link 5-1
| ||
| Representing Fractions | Home Link 5-2
| ||
| Equivalent Fractions | Home Link 5-3
| ||
| Recognizing Helper Facts | Home Link 5-4
| ||
| Multiplication Facts Strategies: Doubling, Part 1 | Home Link 5-5
| ||
| Multiplication Facts Strategies: Doubling, Part 2 | Home Link 5-6
| ||
| Patterns in Products | Home Link 5-7
| ||
| Finding Missing Factors | Home Link 5-8
| ||
| Multiplication Facts Strategies: Near Squares | Home Link 5-9
| ||
| Open Response and Reengagement: Button Dolls: Solving a Number Story | Home Link 5-10
| ||
| Multiplication Fact Strategies: Decomposing Factors | Home Link 5-11
| ||
| Unit 5 Progress Check | Home Link 5-12 |

Everyday Mathematics for Parents: What You Need to Know to Help Your Child Succeed
The University of Chicago School Mathematics Project
University of Chicago Press
Learn more >>
Related Links
Help with algorithms.
Access video tutorials, practice exercises, and information on the research basis and development of various algorithms.
Everyday Mathematics Online
With a login provided by your child's teacher, access resources to help your child with homework or brush up on your math skills.
Parent Connections on Publisher's site
McGraw-Hill Education offers many resources for parents, including tips, activities, and helpful links.
Parent Resources on EverydayMath.com
EverydayMath.com features activity ideas, literature lists, and family resources for the EM curriculum.
Understanding Everyday Mathematics for Parents
Learn more about the EM curriculum and how to assist your child.


- Share on Facebook
- Tweet This Resource
- Pin This Resource

Problem-Soving Strategies, Practice 1: Sample
This problem-soving strategies, practice 1: sample worksheet also includes:.
- Join to access all included materials
A variety of word problems help your learners examine the ways that they find solutions. Each question provides opportunities to add, subtract, and multiply time, measurements, and money.
Additional Tags
Instructional ideas.
- Add to your homework packet for the week when preparing for a math standardized test
- Use the resource to assess skill levels of incoming learners
- A good class quiz after learning about different ways to solve the problems
Classroom Considerations
- Designed for 5th and 6th graders, but could work for younger learners in need of a challenge
- Promotes critical thinking in a multiple-choice format
- Includes a sample worksheet with explanations for each answer, as well as an answer key for the assessment
Start Your Free Trial
Save time and discover engaging curriculum for your classroom. Reviewed and rated by trusted, credentialed teachers.
- Collection Types
- Activities & Projects
- Assessments
- Graphics & Images
- Handouts & References
- Interactives
- Lab Resources
- Learning Games
- Lesson Plans
- Presentations
- Primary Sources
- Printables & Templates
- Professional Documents
- Study Guides
- Instructional Videos
- Performance Tasks
- Graphic Organizers
- Writing Prompts
- Constructed Response Items
- AP Test Preps
- Lesson Planet Articles
- Online Courses
- Interactive Whiteboards
- Home Letters
- Unknown Types
- Stock Footages
- All Resource Types
See similar resources:
Math stars: a problem-solving newsletter grade 6, addition and subtraction word problems #1, multiplication grade 3 formative assessment lesson, word problems, christmas fraction word problems, multiplication & division word problems, mental math, adding decimals, multiplication facts, practice: word problems, problem-solving strategies.

COMMENTS
Algebra questions and answers; 1.9022 Topic 1: Exploring problem-solving strategies 33 LESSON 5: HOMEWORK Notes or additional instructions based on whole-class discussion of homework assignment: 1. Classify the following sequences as either arithmetic or geometric. Then state the common difference or ratio and find the missing terms.
solving. They will then answer a free response question in which they analyze a strategy in a Worked Example for solving an equation in the form y 5 x2 1 d that uses factoring. Adapted Virtual Facilitation Notes Lesson 5: The Root of the Problem • 1 A2_M01_T02_L05_Adapted Virtual TIG.indd 1 5/20/21 11:59 AM
Topic 1: Exploring problem-solving strategies 1.1 CONSOLIDATION ACTIVITY For the following problems, work with your partner to rewrite the shape equations using letters as variables. You can decide which letters to use for your variables. Example: using shapes ax A -12 Equations using shapes o -13 7 Equations using shapes 0+0 = 24 Equations ...
In this lesson, we will look at some basic examples of the Explore it//Act it/Try it (EAT) method of problem solving strategy. Example: A plumber has to connect a pipe from a storage tank at the corner, S, of the roof to a tap at the diagonally opposite corner, T, in the figure below. Find the number of paths for the pipe if the pipe can only ...
1 m 1 m 2 m 1.7 m 1.7 m 2 m 60° 60° 30° 30° E D F 12.1 cm 8.4 cm 7.9 cm A B C 7.9 cm 8.5 cm 12.1 cm there is a pair of corresponding sides that are not congruent. DE 12.1 DE ¯ DF ¯ DF ¯ 7.9 EF Moe dul 5 221 on sLse 1 DO NOT EDIT--Changes must be made through "File info" CorrectionKey=NL-B;CA-B GE_MNLESE385795_U2M05L1.indd 221 5/22/14 ...
Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
Problem-Solving Strategy Updates Scavenger Hunt Recording Sheet ... Data Updates Problem of the Week Cards TAKS Test Practice Lesson Resources Extra Examples Parent and Student Study Guide Self-Check Quizzes ... First Edition Chapter 1, Lesson 5: A Plan for Problem Solving. Extra Examples; Parent and Student Study Guide; Self-Check Quizzes; Log ...
Introductory Algebra Lesson 5 - Problem Solving Strategies Writing Equations Step 1: Read and understand the problem. Underline the givens and circle the goal. Step 2: Form a strategy to solve the problem. Step 3: Choose a variable to represent the unknown quantity. Step 4: Read every word in the problem, and translate the given information ...
Lesson 1: Applications of Linear Equations; Lesson 2: Ratio, Proportion, and Variation; Lesson 3: The Nature of Mathematical Reasoning; Lesson 4: Estimation and Interpreting Graphs; Lesson 5: Problem-Solving Strategies; Lesson 6: Statement and Quantifiers; Lesson 7: Measures of Length: Converting Units and the Metric System
Getting started with Algebra. Topic 1 - Exploring problem-solving strategies. Lesson 1.1: Collaborating around mathematics. 1. Model decimals and fractions. 2. Solve proportions: word problems. 3. Estimate sums and differences of decimals.
Topic 1: Exploring problem-solving strategies Textbook section IXL skills Lesson 1.1: Collaborating around mathematics 1.Model decimals and fractions X59 ... Lesson 1.5: Exploring sequences 1.Identify arithmetic and geometric sequences X76 2.Arithmetic sequences ALG 3.Geometric sequences HLJ Agile Mind - Intensified Algebra 1 ...
Unit 5: Module 5: Addition and multiplication with volume and area. 0/1400 Mastery points. Topic A: Concepts of volume Topic B: Volume and the operations of multiplication and addition Topic C: Area of rectangular figures with fractional side lengths. Topic D: Drawing, analysis, and classification of two-dimensional shapes.
function that models a problem situation and use it to answer a question about the situation. Lesson Video(s): The aligned lesson overview video(s) provide additional instruction for students on the key concepts in this lesson and can be found alongside the digital interactive student lesson. TEKS: 2A.3A, 2A.3B, 2A.4A, 2A.4D, 2A.7B
One of the best ways to improve your problem-solving skills is to learn from experts. Consider enrolling in organizational training, shadowing a mentor, or working with a coach. 2. Practice. Practice using your new problem-solving skills by applying them to smaller problems you might encounter in your daily life.
Instructional Day Topic 1-2 Introduce data collection and problem solving. 3 Introduce the four steps of the problem solving process. 4-6 Apply the problem solving process. Use different strategies to plan and carry out the plan to solve several problems. 7-9 Reinforce the four steps of the problems solving process.
In insight problem-solving, the cognitive processes that help you solve a problem happen outside your conscious awareness. 4. Working backward. Working backward is a problem-solving approach often ...
Make sense of problems and persevere in solving them. Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway ...
Problem Solving Strategy 9 (Find the Math, Remove the Context). Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
problem situation and use it to answer a question about the situation. 5 The Root of the Problem: Solving Quadratic Equations 2A.4F 2 Students solve quadratic equations of the form y 5 ax2 1 bx 1 c. They first factor trinomials and use the Zero Product Property. Students then use the method of completing the square
1. Divide by 2-digit numbers using partial quotients. Lesson 5-5: Use Sharing to Divide: 2-Digit Divisors. 1. Divide 2-digit and 3-digit numbers by 2-digit numbers. 2. Divide 2-digit and 3-digit numbers by 2-digit numbers: word problems. Lesson 5-5: Use Sharing to Divide: 2-Digit Divisors.
PRACTICING SKILLS & CONCEPTS 1. Solve the shape equation puzzle: 2. Continue this pattern of shapes for three more steps. Explain the pattern or how you continued it: PREPARING FOR UPCOMING LESSONS 3. If the large square represents one whole, what fraction is represented by the shaded area? Answer with supporting work: 4. To get ready for a field trip, students and adults were put into groups.
Multiplication Facts Strategies: Near Squares. Home Link 5-9 English Español Selected Answers. 5-10. Open Response and Reengagement: Button Dolls: Solving a Number Story. Home Link 5-10 English Español Selected Answers. 5-11. Multiplication Fact Strategies: Decomposing Factors. Home Link 5-11 English Español Selected Answers. 5-12. Unit 5 ...
This Problem-Soving Strategies, Practice 1: Sample Worksheet is suitable for 2nd - 5th Grade. ... Educator Edition Save time lesson planning by exploring our library of educator reviews to over 550,000 open educational ... Includes a sample worksheet with explanations for each answer, as well as an answer key for the assessment; Cons. None ...