the hypothesis and conclusion of each statement

Statistics Made Easy

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Truth Tables- Conditional, Biconditional

• Last updated
• Save as PDF
• Page ID 52962

• David Lippman
• Pierce College via The OpenTextBookStore

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Conditional

A conditional is a logical compound statement in which a statement \(p\), called the hypothesis, implies a statement \(q\), called the conclusion.

A conditional is written as \(p \rightarrow q\) and is translated as "if \(p\), then \(q\)".

The English statement “If it is raining, then there are clouds is the sky” is a conditional statement. It makes sense because if the hypothesis “it is raining” is true, then the conclusion “there are clouds in the sky” must also be true.

Notice that the statement tells us nothing of what to expect if it is not raining; there might be clouds in the sky, or there might not. If the hypothesis is false, then the conclusion becomes irrelevant.

Suppose you order a team jersey online on Tuesday and want to receive it by Friday so you can wear it to Saturday’s game. The website says that if you pay for expedited shipping, you will receive the jersey by Friday. In what situation is the website telling a lie?

There are four possible outcomes:

• You pay for expedited shipping and receive the jersey by Friday
• You pay for expedited shipping and don’t receive the jersey by Friday
• You don’t pay for expedited shipping and receive the jersey by Friday
• You don’t pay for expedited shipping and don’t receive the jersey by Friday

Only one of these outcomes proves that the website was lying: the second outcome in which you pay for expedited shipping but don’t receive the jersey by Friday. The first outcome is exactly what was promised, so there’s no problem with that. The third outcome is not a lie because the website never said what would happen if you didn’t pay for expedited shipping; maybe the jersey would arrive by Friday whether you paid for expedited shipping or not. The fourth outcome is not a lie because, again, the website didn’t make any promises about when the jersey would arrive if you didn’t pay for expedited shipping.

It may seem strange that the third outcome in the previous example, in which the first part is false but the second part is true, is not a lie. Remember, though, that if the hypothesis is false, we cannot make any judgment about the conclusion. The website never said that paying for expedited shipping was the only way to receive the jersey by Friday.

A friend tells you “If you upload that picture to Facebook, you’ll lose your job.” Under what conditions can you say that your friend was wrong?

• You upload the picture and lose your job
• You upload the picture and don’t lose your job
• You don’t upload the picture and lose your job
• You don’t upload the picture and don’t lose your job

There is only one possible case in which you can say your friend was wrong: the second outcome in which you upload the picture but still keep your job. In the last two cases, your friend didn’t say anything about what would happen if you didn’t upload the picture, so you can’t say that their statement was wrong. Even if you didn’t upload the picture and lost your job anyway, your friend never said that you were guaranteed to keep your job if you didn’t upload the picture; you might lose your job for missing a shift or punching your boss instead.

Truth Table for the Conditional

\(\begin{array}{|c|c|c|} \hline p & q & p \rightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Again, if the hypothesis \(p\) is false, we cannot prove that the statement is a lie, so the result of the third and fourth rows is true.

Construct a truth table for the statement \((m \wedge \sim p) \rightarrow r\)

We start by constructing a truth table with 8 rows to cover all possible scenarios. Next, we can focus on the hypothesis, \(m \wedge \sim p\).

\(\begin{array}{|c|c|c|} \hline m & p & r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline m & p & r & \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

Now we can create a column for the conditional. Because it can be confusing to keep track of all the Ts and \(\mathrm{Fs}\), why don't we copy the column for \(r\) to the right of the column for \(m \wedge \sim p\) ? This makes it a lot easier to read the conditional from left to right.

\(\begin{array}{|c|c|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p & r & (m \wedge \sim p) \rightarrow r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

When \(m\) is true, \(p\) is false, and \(r\) is false- -the fourth row of the table-then the hypothesis \(m \wedge \sim p\) will be true but the conclusion false, resulting in an invalid conditional; every other case gives a valid conditional.

If you want a real-life situation that could be modeled by \((m \wedge \sim p) \rightarrow r\), consider this: let \(m=\) we order meatballs, \(p=\) we order pasta, and \(r=\) Rob is happy. The statement \((m \wedge \sim p) \rightarrow r\) is "if we order meatballs and don't order pasta, then Rob is happy". If \(m\) is true (we order meatballs), \(p\) is false (we don't order pasta), and \(r\) is false (Rob is not happy), then the statement is false, because we satisfied the hypothesis but Rob did not satisfy the conclusion.

For any conditional, there are three related statements, the converse, the inverse, and the contrapositive.

Derived Forms of a Conditional

The original conditional is \(\quad\) "if \(p,\) then \(q^{\prime \prime} \quad p \rightarrow q\)

The converse is \(\quad\) "if \(q,\) then \(p^{\prime \prime} \quad q \rightarrow p\)

The inverse is \(\quad\) "if not \(p,\) then not \(q^{\prime \prime} \quad \sim p \rightarrow \sim q\)

The contrapositive is "if not \(q,\) then not \(p^{\prime \prime} \quad \sim q \rightarrow \sim p\)

Consider again the conditional “If it is raining, then there are clouds in the sky.” It seems reasonable to assume that this is true.

The converse would be “If there are clouds in the sky, then it is raining.” This is not always true.

The inverse would be “If it is not raining, then there are not clouds in the sky.” Likewise, this is not always true.

The contrapositive would be “If there are not clouds in the sky, then it is not raining.” This statement is true, and is equivalent to the original conditional.

Looking at truth tables, we can see that the original conditional and the contrapositive are logically equivalent, and that the converse and inverse are logically equivalent.

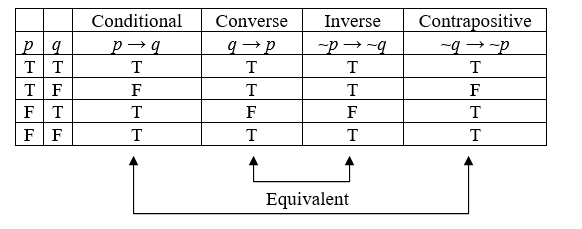
Equivalence

A conditional statement and its contrapositive are logically equivalent.

The converse and inverse of a conditional statement are logically equivalent.

In other words, the original statement and the contrapositive must agree with each other; they must both be true, or they must both be false. Similarly, the converse and the inverse must agree with each other; they must both be true, or they must both be false.

We typically represent the conditional using the words, "if ..., then ...," but there are other ways this logical connective can be represented in English. Consider the conditional from Example 5: "If it is raining, then there are clouds in the sky." We could equivalently write, "It is raining only if there are clouds in the sky." You can probably imagine how these two statements are saying the same thing - whenever it's raining outside, it is a safe conclusion there are clouds in the sky as well. Some other wordings that communicate the same information use either "sufficient" or "necessary." For example, "Raining is a sufficient condition for it to be cloudy," and "Being cloudy is a necessary condition for it to be raining." Here is a table summarizing the different wordings.

Different Wordings of the Conditional

The following statements are equivalent:

• If \(p\), then \(q\).
• \(q\) only if \(p\).
• \(p\) is sufficient for \(q\).
• \(q\) is necessary for \(p\).

In everyday life, we often have a stronger meaning in mind when we use a conditional statement. Consider “If you submit your hours today, then you will be paid next Friday.” What the payroll rep really means is “If you submit your hours today, then you will be paid next Friday, and if you don’t submit your hours today, then you won’t be paid next Friday.” The conditional statement if t , then p also includes the inverse of the statement: if not t , then not p . A more compact way to express this statement is “You will be paid next Friday if and only if you submit your timesheet today.” A statement of this form is called a biconditional .

Biconditional

A biconditional is a logical conditional statement in which the hypothesis and conclusion are interchangeable.

A biconditional is written as \(p \leftrightarrow q\) and is translated as " \(p\) if and only if \(q^{\prime \prime}\).

Because a biconditional statement \(p \leftrightarrow q\) is equivalent to \((p \rightarrow q) \wedge(q \rightarrow p),\) we may think of it as a conditional statement combined with its converse: if \(p\), then \(q\) and if \(q\), then \(p\). The double-headed arrow shows that the conditional statement goes from left to right and from right to left. A biconditional is considered true as long as the hypothesis and the conclusion have the same truth value; that is, they are either both true or both false.

Truth Table for the Biconditional

\(\begin{array}{|c|c|c|} \hline p & q & p \leftrightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Notice that the fourth row, where both components are false, is true; if you don’t submit your timesheet and you don’t get paid, the person from payroll told you the truth.

Suppose this statement is true: “The garbage truck comes down my street if and only if it is Thursday morning.” Which of the following statements could be true?

• It is noon on Thursday and the garbage truck did not come down my street this morning.
• It is Monday and the garbage truck is coming down my street.
• It is Wednesday at 11:59PM and the garbage truck did not come down my street today.
• This cannot be true. This is like the second row of the truth table; it is true that I just experienced Thursday morning, but it is false that the garbage truck came.
• This cannot be true. This is like the third row of the truth table; it is false that it is Thursday, but it is true that the garbage truck came.
• This could be true. This is like the fourth row of the truth table; it is false that it is Thursday, but it is also false that the garbage truck came, so everything worked out like it should.

Try it Now 1

Suppose this statement is true: “I wear my running shoes if and only if I am exercising.” Determine whether each of the following statements must be true or false.

• I am exercising and I am not wearing my running shoes.
• I am wearing my running shoes and I am not exercising.
• I am not exercising and I am not wearing my running shoes.

Choices a & b are false; c is true.

Create a truth table for the statement \((A \vee B) \leftrightarrow \sim C\)

Whenever we have three component statements, we start by listing all the possible truth value combinations for \(A, B,\) and \(C .\) After creating those three columns, we can create a fourth column for the hypothesis, \(A \vee B\). Now we will temporarily ignore the column for \(C\) and focus on \(A\) and \(B\), writing the truth values for \(A \vee B\).

\(\begin{array}{|c|c|c|} \hline A & B & C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline A & B & C & A \vee B \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

Next we can create a column for the negation of \(C\). (Ignore the \(A \vee B\) column and simply negate the values in the \(C\) column.)

\(\begin{array}{|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Finally, we find the truth values of \((A \vee B) \leftrightarrow \sim C\). Remember, a biconditional is true when the truth value of the two parts match, but it is false when the truth values do not match.

\(\begin{array}{|c|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C & (A \vee B) \leftrightarrow \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

To illustrate this situation, suppose your boss needs you to do either project \(A\) or project \(B\) (or both, if you have the time). If you do one of the projects, you will not get a crummy review ( \(C\) is for crummy). So \((A \vee B) \leftrightarrow \sim C\) means "You will not get a crummy review if and only if you do project \(A\) or project \(B\)." Looking at a few of the rows of the truth table, we can see how this works out. In the first row, \(A, B,\) and \(C\) are all true: you did both projects and got a crummy review, which is not what your boss told you would happen! That is why the final result of the first row is false. In the fourth row, \(A\) is true, \(B\) is false, and \(C\) is false: you did project \(A\) and did not get a crummy review. This is what your boss said would happen, so the final result of this row is true. And in the eighth row, \(A, B\), and \(C\) are all false: you didn't do either project and did not get a crummy review. This is not what your boss said would happen, so the final result of this row is false. (Even though you may be happy that your boss didn't follow through on the threat, the truth table shows that your boss lied about what would happen.)

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

How to Write a Great Hypothesis

Hypothesis Definition, Format, Examples, and Tips

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk,  "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.

Verywell / Alex Dos Diaz

• The Scientific Method

Hypothesis Format

Falsifiability of a hypothesis.

• Operationalization

Hypothesis Types

Hypotheses examples.

• Collecting Data

A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process.

Consider a study designed to examine the relationship between sleep deprivation and test performance. The hypothesis might be: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."

At a Glance

A hypothesis is crucial to scientific research because it offers a clear direction for what the researchers are looking to find. This allows them to design experiments to test their predictions and add to our scientific knowledge about the world. This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.

The Hypothesis in the Scientific Method

In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:

• Forming a question
• Performing background research
• Creating a hypothesis
• Designing an experiment
• Collecting data
• Analyzing the results
• Drawing conclusions
• Communicating the results

The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. At this point, researchers then begin to develop a testable hypothesis.

Unless you are creating an exploratory study, your hypothesis should always explain what you  expect  to happen.

In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.

Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore numerous factors to determine which ones might contribute to the ultimate outcome.

In many cases, researchers may find that the results of an experiment  do not  support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.

In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."

In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk adage that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."

Elements of a Good Hypothesis

So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:

• Is your hypothesis based on your research on a topic?
• Can your hypothesis be tested?
• Does your hypothesis include independent and dependent variables?

Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the  journal articles you read . Many authors will suggest questions that still need to be explored.

How to Formulate a Good Hypothesis

To form a hypothesis, you should take these steps:

• Collect as many observations about a topic or problem as you can.
• Evaluate these observations and look for possible causes of the problem.
• Create a list of possible explanations that you might want to explore.
• After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.

In the scientific method ,  falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.

Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that  if  something was false, then it is possible to demonstrate that it is false.

One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.

The Importance of Operational Definitions

A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.

Operational definitions are specific definitions for all relevant factors in a study. This process helps make vague or ambiguous concepts detailed and measurable.

For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.

These precise descriptions are important because many things can be measured in various ways. Clearly defining these variables and how they are measured helps ensure that other researchers can replicate your results.

Replicability

One of the basic principles of any type of scientific research is that the results must be replicable.

Replication means repeating an experiment in the same way to produce the same results. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.

Some variables are more difficult than others to define. For example, how would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.

To measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming others. The researcher might utilize a simulated task to measure aggressiveness in this situation.

Hypothesis Checklist

• Does your hypothesis focus on something that you can actually test?
• Does your hypothesis include both an independent and dependent variable?
• Can you manipulate the variables?
• Can your hypothesis be tested without violating ethical standards?

The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:

• Simple hypothesis : This type of hypothesis suggests there is a relationship between one independent variable and one dependent variable.
• Complex hypothesis : This type suggests a relationship between three or more variables, such as two independent and dependent variables.
• Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
• Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
• Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative population sample and then generalizes the findings to the larger group.
• Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.

A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the  dependent variable  if you change the  independent variable .

The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."

A few examples of simple hypotheses:

• "Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
• "Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."​
• "Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."
• "Children who receive a new reading intervention will have higher reading scores than students who do not receive the intervention."

Examples of a complex hypothesis include:

• "People with high-sugar diets and sedentary activity levels are more likely to develop depression."
• "Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."

Examples of a null hypothesis include:

• "There is no difference in anxiety levels between people who take St. John's wort supplements and those who do not."
• "There is no difference in scores on a memory recall task between children and adults."
• "There is no difference in aggression levels between children who play first-person shooter games and those who do not."

Examples of an alternative hypothesis:

• "People who take St. John's wort supplements will have less anxiety than those who do not."
• "Adults will perform better on a memory task than children."
• "Children who play first-person shooter games will show higher levels of aggression than children who do not." 

Collecting Data on Your Hypothesis

Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.

Descriptive Research Methods

Descriptive research such as  case studies ,  naturalistic observations , and surveys are often used when  conducting an experiment is difficult or impossible. These methods are best used to describe different aspects of a behavior or psychological phenomenon.

Once a researcher has collected data using descriptive methods, a  correlational study  can examine how the variables are related. This research method might be used to investigate a hypothesis that is difficult to test experimentally.

Experimental Research Methods

Experimental methods  are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).

Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually  cause  another to change.

The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.

Thompson WH, Skau S. On the scope of scientific hypotheses .  R Soc Open Sci . 2023;10(8):230607. doi:10.1098/rsos.230607

Taran S, Adhikari NKJ, Fan E. Falsifiability in medicine: what clinicians can learn from Karl Popper [published correction appears in Intensive Care Med. 2021 Jun 17;:].  Intensive Care Med . 2021;47(9):1054-1056. doi:10.1007/s00134-021-06432-z

Eyler AA. Research Methods for Public Health . 1st ed. Springer Publishing Company; 2020. doi:10.1891/9780826182067.0004

Nosek BA, Errington TM. What is replication ?  PLoS Biol . 2020;18(3):e3000691. doi:10.1371/journal.pbio.3000691

Aggarwal R, Ranganathan P. Study designs: Part 2 - Descriptive studies .  Perspect Clin Res . 2019;10(1):34-36. doi:10.4103/picr.PICR_154_18

Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

Choose Your Test

Sat / act prep online guides and tips, what is a hypothesis and how do i write one.

General Education

Think about something strange and unexplainable in your life. Maybe you get a headache right before it rains, or maybe you think your favorite sports team wins when you wear a certain color. If you wanted to see whether these are just coincidences or scientific fact, you would form a hypothesis, then create an experiment to see whether that hypothesis is true or not.

But what is a hypothesis, anyway? If you’re not sure about what a hypothesis is--or how to test for one!--you’re in the right place. This article will teach you everything you need to know about hypotheses, including: 

• Defining the term “hypothesis” 
• Providing hypothesis examples 
• Giving you tips for how to write your own hypothesis

So let’s get started!

What Is a Hypothesis?

Merriam Webster defines a hypothesis as “an assumption or concession made for the sake of argument.” In other words, a hypothesis is an educated guess . Scientists make a reasonable assumption--or a hypothesis--then design an experiment to test whether it’s true or not. Keep in mind that in science, a hypothesis should be testable. You have to be able to design an experiment that tests your hypothesis in order for it to be valid. 

As you could assume from that statement, it’s easy to make a bad hypothesis. But when you’re holding an experiment, it’s even more important that your guesses be good...after all, you’re spending time (and maybe money!) to figure out more about your observation. That’s why we refer to a hypothesis as an educated guess--good hypotheses are based on existing data and research to make them as sound as possible.

Hypotheses are one part of what’s called the scientific method .  Every (good) experiment or study is based in the scientific method. The scientific method gives order and structure to experiments and ensures that interference from scientists or outside influences does not skew the results. It’s important that you understand the concepts of the scientific method before holding your own experiment. Though it may vary among scientists, the scientific method is generally made up of six steps (in order):

• Observation
• Asking questions
• Forming a hypothesis
• Analyze the data
• Communicate your results

You’ll notice that the hypothesis comes pretty early on when conducting an experiment. That’s because experiments work best when they’re trying to answer one specific question. And you can’t conduct an experiment until you know what you’re trying to prove!

Independent and Dependent Variables 

After doing your research, you’re ready for another important step in forming your hypothesis: identifying variables. Variables are basically any factor that could influence the outcome of your experiment . Variables have to be measurable and related to the topic being studied.

There are two types of variables:  independent variables and dependent variables. I ndependent variables remain constant . For example, age is an independent variable; it will stay the same, and researchers can look at different ages to see if it has an effect on the dependent variable. 

Speaking of dependent variables... dependent variables are subject to the influence of the independent variable , meaning that they are not constant. Let’s say you want to test whether a person’s age affects how much sleep they need. In that case, the independent variable is age (like we mentioned above), and the dependent variable is how much sleep a person gets. 

Variables will be crucial in writing your hypothesis. You need to be able to identify which variable is which, as both the independent and dependent variables will be written into your hypothesis. For instance, in a study about exercise, the independent variable might be the speed at which the respondents walk for thirty minutes, and the dependent variable would be their heart rate. In your study and in your hypothesis, you’re trying to understand the relationship between the two variables.

Elements of a Good Hypothesis

The best hypotheses start by asking the right questions . For instance, if you’ve observed that the grass is greener when it rains twice a week, you could ask what kind of grass it is, what elevation it’s at, and if the grass across the street responds to rain in the same way. Any of these questions could become the backbone of experiments to test why the grass gets greener when it rains fairly frequently.

As you’re asking more questions about your first observation, make sure you’re also making more observations . If it doesn’t rain for two weeks and the grass still looks green, that’s an important observation that could influence your hypothesis. You'll continue observing all throughout your experiment, but until the hypothesis is finalized, every observation should be noted.

Finally, you should consult secondary research before writing your hypothesis . Secondary research is comprised of results found and published by other people. You can usually find this information online or at your library. Additionally, m ake sure the research you find is credible and related to your topic. If you’re studying the correlation between rain and grass growth, it would help you to research rain patterns over the past twenty years for your county, published by a local agricultural association. You should also research the types of grass common in your area, the type of grass in your lawn, and whether anyone else has conducted experiments about your hypothesis. Also be sure you’re checking the quality of your research . Research done by a middle school student about what minerals can be found in rainwater would be less useful than an article published by a local university.

Writing Your Hypothesis

Once you’ve considered all of the factors above, you’re ready to start writing your hypothesis. Hypotheses usually take a certain form when they’re written out in a research report.

When you boil down your hypothesis statement, you are writing down your best guess and not the question at hand . This means that your statement should be written as if it is fact already, even though you are simply testing it.

The reason for this is that, after you have completed your study, you'll either accept or reject your if-then or your null hypothesis. All hypothesis testing examples should be measurable and able to be confirmed or denied. You cannot confirm a question, only a statement! 

In fact, you come up with hypothesis examples all the time! For instance, when you guess on the outcome of a basketball game, you don’t say, “Will the Miami Heat beat the Boston Celtics?” but instead, “I think the Miami Heat will beat the Boston Celtics.” You state it as if it is already true, even if it turns out you’re wrong. You do the same thing when writing your hypothesis.

Additionally, keep in mind that hypotheses can range from very specific to very broad.  These hypotheses can be specific, but if your hypothesis testing examples involve a broad range of causes and effects, your hypothesis can also be broad.  

The Two Types of Hypotheses

Now that you understand what goes into a hypothesis, it’s time to look more closely at the two most common types of hypothesis: the if-then hypothesis and the null hypothesis.

#1: If-Then Hypotheses

First of all, if-then hypotheses typically follow this formula:

If ____ happens, then ____ will happen.

The goal of this type of hypothesis is to test the causal relationship between the independent and dependent variable. It’s fairly simple, and each hypothesis can vary in how detailed it can be. We create if-then hypotheses all the time with our daily predictions. Here are some examples of hypotheses that use an if-then structure from daily life: 

• If I get enough sleep, I’ll be able to get more work done tomorrow.
• If the bus is on time, I can make it to my friend’s birthday party. 
• If I study every night this week, I’ll get a better grade on my exam. 

In each of these situations, you’re making a guess on how an independent variable (sleep, time, or studying) will affect a dependent variable (the amount of work you can do, making it to a party on time, or getting better grades). 

You may still be asking, “What is an example of a hypothesis used in scientific research?” Take one of the hypothesis examples from a real-world study on whether using technology before bed affects children’s sleep patterns. The hypothesis read s:

“We hypothesized that increased hours of tablet- and phone-based screen time at bedtime would be inversely correlated with sleep quality and child attention.”

It might not look like it, but this is an if-then statement. The researchers basically said, “If children have more screen usage at bedtime, then their quality of sleep and attention will be worse.” The sleep quality and attention are the dependent variables and the screen usage is the independent variable. (Usually, the independent variable comes after the “if” and the dependent variable comes after the “then,” as it is the independent variable that affects the dependent variable.) This is an excellent example of how flexible hypothesis statements can be, as long as the general idea of “if-then” and the independent and dependent variables are present.

#2: Null Hypotheses

Your if-then hypothesis is not the only one needed to complete a successful experiment, however. You also need a null hypothesis to test it against. In its most basic form, the null hypothesis is the opposite of your if-then hypothesis . When you write your null hypothesis, you are writing a hypothesis that suggests that your guess is not true, and that the independent and dependent variables have no relationship .

One null hypothesis for the cell phone and sleep study from the last section might say: 

“If children have more screen usage at bedtime, their quality of sleep and attention will not be worse.” 

In this case, this is a null hypothesis because it’s asking the opposite of the original thesis! 

Conversely, if your if-then hypothesis suggests that your two variables have no relationship, then your null hypothesis would suggest that there is one. So, pretend that there is a study that is asking the question, “Does the amount of followers on Instagram influence how long people spend on the app?” The independent variable is the amount of followers, and the dependent variable is the time spent. But if you, as the researcher, don’t think there is a relationship between the number of followers and time spent, you might write an if-then hypothesis that reads:

“If people have many followers on Instagram, they will not spend more time on the app than people who have less.”

In this case, the if-then suggests there isn’t a relationship between the variables. In that case, one of the null hypothesis examples might say:

“If people have many followers on Instagram, they will spend more time on the app than people who have less.”

You then test both the if-then and the null hypothesis to gauge if there is a relationship between the variables, and if so, how much of a relationship. 

4 Tips to Write the Best Hypothesis

If you’re going to take the time to hold an experiment, whether in school or by yourself, you’re also going to want to take the time to make sure your hypothesis is a good one. The best hypotheses have four major elements in common: plausibility, defined concepts, observability, and general explanation.

#1: Plausibility

At first glance, this quality of a hypothesis might seem obvious. When your hypothesis is plausible, that means it’s possible given what we know about science and general common sense. However, improbable hypotheses are more common than you might think. 

Imagine you’re studying weight gain and television watching habits. If you hypothesize that people who watch more than  twenty hours of television a week will gain two hundred pounds or more over the course of a year, this might be improbable (though it’s potentially possible). Consequently, c ommon sense can tell us the results of the study before the study even begins.

Improbable hypotheses generally go against  science, as well. Take this hypothesis example: 

“If a person smokes one cigarette a day, then they will have lungs just as healthy as the average person’s.” 

This hypothesis is obviously untrue, as studies have shown again and again that cigarettes negatively affect lung health. You must be careful that your hypotheses do not reflect your own personal opinion more than they do scientifically-supported findings. This plausibility points to the necessity of research before the hypothesis is written to make sure that your hypothesis has not already been disproven.

#2: Defined Concepts

The more advanced you are in your studies, the more likely that the terms you’re using in your hypothesis are specific to a limited set of knowledge. One of the hypothesis testing examples might include the readability of printed text in newspapers, where you might use words like “kerning” and “x-height.” Unless your readers have a background in graphic design, it’s likely that they won’t know what you mean by these terms. Thus, it’s important to either write what they mean in the hypothesis itself or in the report before the hypothesis.

Here’s what we mean. Which of the following sentences makes more sense to the common person?

If the kerning is greater than average, more words will be read per minute.

If the space between letters is greater than average, more words will be read per minute.

For people reading your report that are not experts in typography, simply adding a few more words will be helpful in clarifying exactly what the experiment is all about. It’s always a good idea to make your research and findings as accessible as possible. 

Good hypotheses ensure that you can observe the results. 

#3: Observability

In order to measure the truth or falsity of your hypothesis, you must be able to see your variables and the way they interact. For instance, if your hypothesis is that the flight patterns of satellites affect the strength of certain television signals, yet you don’t have a telescope to view the satellites or a television to monitor the signal strength, you cannot properly observe your hypothesis and thus cannot continue your study.

Some variables may seem easy to observe, but if you do not have a system of measurement in place, you cannot observe your hypothesis properly. Here’s an example: if you’re experimenting on the effect of healthy food on overall happiness, but you don’t have a way to monitor and measure what “overall happiness” means, your results will not reflect the truth. Monitoring how often someone smiles for a whole day is not reasonably observable, but having the participants state how happy they feel on a scale of one to ten is more observable. 

In writing your hypothesis, always keep in mind how you'll execute the experiment.

#4: Generalizability 

Perhaps you’d like to study what color your best friend wears the most often by observing and documenting the colors she wears each day of the week. This might be fun information for her and you to know, but beyond you two, there aren’t many people who could benefit from this experiment. When you start an experiment, you should note how generalizable your findings may be if they are confirmed. Generalizability is basically how common a particular phenomenon is to other people’s everyday life.

Let’s say you’re asking a question about the health benefits of eating an apple for one day only, you need to realize that the experiment may be too specific to be helpful. It does not help to explain a phenomenon that many people experience. If you find yourself with too specific of a hypothesis, go back to asking the big question: what is it that you want to know, and what do you think will happen between your two variables?

Hypothesis Testing Examples

We know it can be hard to write a good hypothesis unless you’ve seen some good hypothesis examples. We’ve included four hypothesis examples based on some made-up experiments. Use these as templates or launch pads for coming up with your own hypotheses.

Experiment #1: Students Studying Outside (Writing a Hypothesis)

You are a student at PrepScholar University. When you walk around campus, you notice that, when the temperature is above 60 degrees, more students study in the quad. You want to know when your fellow students are more likely to study outside. With this information, how do you make the best hypothesis possible?

You must remember to make additional observations and do secondary research before writing your hypothesis. In doing so, you notice that no one studies outside when it’s 75 degrees and raining, so this should be included in your experiment. Also, studies done on the topic beforehand suggested that students are more likely to study in temperatures less than 85 degrees. With this in mind, you feel confident that you can identify your variables and write your hypotheses:

If-then: “If the temperature in Fahrenheit is less than 60 degrees, significantly fewer students will study outside.”

Null: “If the temperature in Fahrenheit is less than 60 degrees, the same number of students will study outside as when it is more than 60 degrees.”

These hypotheses are plausible, as the temperatures are reasonably within the bounds of what is possible. The number of people in the quad is also easily observable. It is also not a phenomenon specific to only one person or at one time, but instead can explain a phenomenon for a broader group of people.

To complete this experiment, you pick the month of October to observe the quad. Every day (except on the days where it’s raining)from 3 to 4 PM, when most classes have released for the day, you observe how many people are on the quad. You measure how many people come  and how many leave. You also write down the temperature on the hour. 

After writing down all of your observations and putting them on a graph, you find that the most students study on the quad when it is 70 degrees outside, and that the number of students drops a lot once the temperature reaches 60 degrees or below. In this case, your research report would state that you accept or “failed to reject” your first hypothesis with your findings.

Experiment #2: The Cupcake Store (Forming a Simple Experiment)

Let’s say that you work at a bakery. You specialize in cupcakes, and you make only two colors of frosting: yellow and purple. You want to know what kind of customers are more likely to buy what kind of cupcake, so you set up an experiment. Your independent variable is the customer’s gender, and the dependent variable is the color of the frosting. What is an example of a hypothesis that might answer the question of this study?

Here’s what your hypotheses might look like: 

If-then: “If customers’ gender is female, then they will buy more yellow cupcakes than purple cupcakes.”

Null: “If customers’ gender is female, then they will be just as likely to buy purple cupcakes as yellow cupcakes.”

This is a pretty simple experiment! It passes the test of plausibility (there could easily be a difference), defined concepts (there’s nothing complicated about cupcakes!), observability (both color and gender can be easily observed), and general explanation ( this would potentially help you make better business decisions ).

Experiment #3: Backyard Bird Feeders (Integrating Multiple Variables and Rejecting the If-Then Hypothesis)

While watching your backyard bird feeder, you realized that different birds come on the days when you change the types of seeds. You decide that you want to see more cardinals in your backyard, so you decide to see what type of food they like the best and set up an experiment. 

However, one morning, you notice that, while some cardinals are present, blue jays are eating out of your backyard feeder filled with millet. You decide that, of all of the other birds, you would like to see the blue jays the least. This means you'll have more than one variable in your hypothesis. Your new hypotheses might look like this: 

If-then: “If sunflower seeds are placed in the bird feeders, then more cardinals will come than blue jays. If millet is placed in the bird feeders, then more blue jays will come than cardinals.”

Null: “If either sunflower seeds or millet are placed in the bird, equal numbers of cardinals and blue jays will come.”

Through simple observation, you actually find that cardinals come as often as blue jays when sunflower seeds or millet is in the bird feeder. In this case, you would reject your “if-then” hypothesis and “fail to reject” your null hypothesis . You cannot accept your first hypothesis, because it’s clearly not true. Instead you found that there was actually no relation between your different variables. Consequently, you would need to run more experiments with different variables to see if the new variables impact the results.

Experiment #4: In-Class Survey (Including an Alternative Hypothesis)

You’re about to give a speech in one of your classes about the importance of paying attention. You want to take this opportunity to test a hypothesis you’ve had for a while: 

If-then: If students sit in the first two rows of the classroom, then they will listen better than students who do not.

Null: If students sit in the first two rows of the classroom, then they will not listen better or worse than students who do not.

You give your speech and then ask your teacher if you can hand out a short survey to the class. On the survey, you’ve included questions about some of the topics you talked about. When you get back the results, you’re surprised to see that not only do the students in the first two rows not pay better attention, but they also scored worse than students in other parts of the classroom! Here, both your if-then and your null hypotheses are not representative of your findings. What do you do?

This is when you reject both your if-then and null hypotheses and instead create an alternative hypothesis . This type of hypothesis is used in the rare circumstance that neither of your hypotheses is able to capture your findings . Now you can use what you’ve learned to draft new hypotheses and test again! 

Key Takeaways: Hypothesis Writing

The more comfortable you become with writing hypotheses, the better they will become. The structure of hypotheses is flexible and may need to be changed depending on what topic you are studying. The most important thing to remember is the purpose of your hypothesis and the difference between the if-then and the null . From there, in forming your hypothesis, you should constantly be asking questions, making observations, doing secondary research, and considering your variables. After you have written your hypothesis, be sure to edit it so that it is plausible, clearly defined, observable, and helpful in explaining a general phenomenon.

Writing a hypothesis is something that everyone, from elementary school children competing in a science fair to professional scientists in a lab, needs to know how to do. Hypotheses are vital in experiments and in properly executing the scientific method . When done correctly, hypotheses will set up your studies for success and help you to understand the world a little better, one experiment at a time.

What’s Next?

If you’re studying for the science portion of the ACT, there’s definitely a lot you need to know. We’ve got the tools to help, though! Start by checking out our ultimate study guide for the ACT Science subject test. Once you read through that, be sure to download our recommended ACT Science practice tests , since they’re one of the most foolproof ways to improve your score. (And don’t forget to check out our expert guide book , too.)

If you love science and want to major in a scientific field, you should start preparing in high school . Here are the science classes you should take to set yourself up for success.

If you’re trying to think of science experiments you can do for class (or for a science fair!), here’s a list of 37 awesome science experiments you can do at home

Ashley Sufflé Robinson has a Ph.D. in 19th Century English Literature. As a content writer for PrepScholar, Ashley is passionate about giving college-bound students the in-depth information they need to get into the school of their dreams.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

• Privacy Policy

Home » What is a Hypothesis – Types, Examples and Writing Guide

What is a Hypothesis – Types, Examples and Writing Guide

Table of Contents

Definition:

Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation.

Hypothesis is often used in scientific research to guide the design of experiments and the collection and analysis of data. It is an essential element of the scientific method, as it allows researchers to make predictions about the outcome of their experiments and to test those predictions to determine their accuracy.

Types of Hypothesis

Types of Hypothesis are as follows:

Research Hypothesis

A research hypothesis is a statement that predicts a relationship between variables. It is usually formulated as a specific statement that can be tested through research, and it is often used in scientific research to guide the design of experiments.

Null Hypothesis

The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.

Alternative Hypothesis

An alternative hypothesis is a statement that assumes there is a significant difference or relationship between variables. It is often used as an alternative to the null hypothesis and is tested against the null hypothesis to determine which statement is more accurate.

Directional Hypothesis

A directional hypothesis is a statement that predicts the direction of the relationship between variables. For example, a researcher might predict that increasing the amount of exercise will result in a decrease in body weight.

Non-directional Hypothesis

A non-directional hypothesis is a statement that predicts the relationship between variables but does not specify the direction. For example, a researcher might predict that there is a relationship between the amount of exercise and body weight, but they do not specify whether increasing or decreasing exercise will affect body weight.

Statistical Hypothesis

A statistical hypothesis is a statement that assumes a particular statistical model or distribution for the data. It is often used in statistical analysis to test the significance of a particular result.

Composite Hypothesis

A composite hypothesis is a statement that assumes more than one condition or outcome. It can be divided into several sub-hypotheses, each of which represents a different possible outcome.

Empirical Hypothesis

An empirical hypothesis is a statement that is based on observed phenomena or data. It is often used in scientific research to develop theories or models that explain the observed phenomena.

Simple Hypothesis

A simple hypothesis is a statement that assumes only one outcome or condition. It is often used in scientific research to test a single variable or factor.

Complex Hypothesis

A complex hypothesis is a statement that assumes multiple outcomes or conditions. It is often used in scientific research to test the effects of multiple variables or factors on a particular outcome.

Applications of Hypothesis

Hypotheses are used in various fields to guide research and make predictions about the outcomes of experiments or observations. Here are some examples of how hypotheses are applied in different fields:

• Science : In scientific research, hypotheses are used to test the validity of theories and models that explain natural phenomena. For example, a hypothesis might be formulated to test the effects of a particular variable on a natural system, such as the effects of climate change on an ecosystem.
• Medicine : In medical research, hypotheses are used to test the effectiveness of treatments and therapies for specific conditions. For example, a hypothesis might be formulated to test the effects of a new drug on a particular disease.
• Psychology : In psychology, hypotheses are used to test theories and models of human behavior and cognition. For example, a hypothesis might be formulated to test the effects of a particular stimulus on the brain or behavior.
• Sociology : In sociology, hypotheses are used to test theories and models of social phenomena, such as the effects of social structures or institutions on human behavior. For example, a hypothesis might be formulated to test the effects of income inequality on crime rates.
• Business : In business research, hypotheses are used to test the validity of theories and models that explain business phenomena, such as consumer behavior or market trends. For example, a hypothesis might be formulated to test the effects of a new marketing campaign on consumer buying behavior.
• Engineering : In engineering, hypotheses are used to test the effectiveness of new technologies or designs. For example, a hypothesis might be formulated to test the efficiency of a new solar panel design.

How to write a Hypothesis

Here are the steps to follow when writing a hypothesis:

Identify the Research Question

The first step is to identify the research question that you want to answer through your study. This question should be clear, specific, and focused. It should be something that can be investigated empirically and that has some relevance or significance in the field.

Conduct a Literature Review

Before writing your hypothesis, it’s essential to conduct a thorough literature review to understand what is already known about the topic. This will help you to identify the research gap and formulate a hypothesis that builds on existing knowledge.

Determine the Variables

The next step is to identify the variables involved in the research question. A variable is any characteristic or factor that can vary or change. There are two types of variables: independent and dependent. The independent variable is the one that is manipulated or changed by the researcher, while the dependent variable is the one that is measured or observed as a result of the independent variable.

Formulate the Hypothesis

Based on the research question and the variables involved, you can now formulate your hypothesis. A hypothesis should be a clear and concise statement that predicts the relationship between the variables. It should be testable through empirical research and based on existing theory or evidence.

Write the Null Hypothesis

The null hypothesis is the opposite of the alternative hypothesis, which is the hypothesis that you are testing. The null hypothesis states that there is no significant difference or relationship between the variables. It is important to write the null hypothesis because it allows you to compare your results with what would be expected by chance.

Refine the Hypothesis

After formulating the hypothesis, it’s important to refine it and make it more precise. This may involve clarifying the variables, specifying the direction of the relationship, or making the hypothesis more testable.

Examples of Hypothesis

Here are a few examples of hypotheses in different fields:

• Psychology : “Increased exposure to violent video games leads to increased aggressive behavior in adolescents.”
• Biology : “Higher levels of carbon dioxide in the atmosphere will lead to increased plant growth.”
• Sociology : “Individuals who grow up in households with higher socioeconomic status will have higher levels of education and income as adults.”
• Education : “Implementing a new teaching method will result in higher student achievement scores.”
• Marketing : “Customers who receive a personalized email will be more likely to make a purchase than those who receive a generic email.”
• Physics : “An increase in temperature will cause an increase in the volume of a gas, assuming all other variables remain constant.”
• Medicine : “Consuming a diet high in saturated fats will increase the risk of developing heart disease.”

Purpose of Hypothesis

The purpose of a hypothesis is to provide a testable explanation for an observed phenomenon or a prediction of a future outcome based on existing knowledge or theories. A hypothesis is an essential part of the scientific method and helps to guide the research process by providing a clear focus for investigation. It enables scientists to design experiments or studies to gather evidence and data that can support or refute the proposed explanation or prediction.

The formulation of a hypothesis is based on existing knowledge, observations, and theories, and it should be specific, testable, and falsifiable. A specific hypothesis helps to define the research question, which is important in the research process as it guides the selection of an appropriate research design and methodology. Testability of the hypothesis means that it can be proven or disproven through empirical data collection and analysis. Falsifiability means that the hypothesis should be formulated in such a way that it can be proven wrong if it is incorrect.

In addition to guiding the research process, the testing of hypotheses can lead to new discoveries and advancements in scientific knowledge. When a hypothesis is supported by the data, it can be used to develop new theories or models to explain the observed phenomenon. When a hypothesis is not supported by the data, it can help to refine existing theories or prompt the development of new hypotheses to explain the phenomenon.

When to use Hypothesis

Here are some common situations in which hypotheses are used:

• In scientific research , hypotheses are used to guide the design of experiments and to help researchers make predictions about the outcomes of those experiments.
• In social science research , hypotheses are used to test theories about human behavior, social relationships, and other phenomena.
• I n business , hypotheses can be used to guide decisions about marketing, product development, and other areas. For example, a hypothesis might be that a new product will sell well in a particular market, and this hypothesis can be tested through market research.

Characteristics of Hypothesis

Here are some common characteristics of a hypothesis:

• Testable : A hypothesis must be able to be tested through observation or experimentation. This means that it must be possible to collect data that will either support or refute the hypothesis.
• Falsifiable : A hypothesis must be able to be proven false if it is not supported by the data. If a hypothesis cannot be falsified, then it is not a scientific hypothesis.
• Clear and concise : A hypothesis should be stated in a clear and concise manner so that it can be easily understood and tested.
• Based on existing knowledge : A hypothesis should be based on existing knowledge and research in the field. It should not be based on personal beliefs or opinions.
• Specific : A hypothesis should be specific in terms of the variables being tested and the predicted outcome. This will help to ensure that the research is focused and well-designed.
• Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion.
• Relevant : A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.

Advantages of Hypothesis

Hypotheses have several advantages in scientific research and experimentation:

• Guides research: A hypothesis provides a clear and specific direction for research. It helps to focus the research question, select appropriate methods and variables, and interpret the results.
• Predictive powe r: A hypothesis makes predictions about the outcome of research, which can be tested through experimentation. This allows researchers to evaluate the validity of the hypothesis and make new discoveries.
• Facilitates communication: A hypothesis provides a common language and framework for scientists to communicate with one another about their research. This helps to facilitate the exchange of ideas and promotes collaboration.
• Efficient use of resources: A hypothesis helps researchers to use their time, resources, and funding efficiently by directing them towards specific research questions and methods that are most likely to yield results.
• Provides a basis for further research: A hypothesis that is supported by data provides a basis for further research and exploration. It can lead to new hypotheses, theories, and discoveries.
• Increases objectivity: A hypothesis can help to increase objectivity in research by providing a clear and specific framework for testing and interpreting results. This can reduce bias and increase the reliability of research findings.

Limitations of Hypothesis

Some Limitations of the Hypothesis are as follows:

• Limited to observable phenomena: Hypotheses are limited to observable phenomena and cannot account for unobservable or intangible factors. This means that some research questions may not be amenable to hypothesis testing.
• May be inaccurate or incomplete: Hypotheses are based on existing knowledge and research, which may be incomplete or inaccurate. This can lead to flawed hypotheses and erroneous conclusions.
• May be biased: Hypotheses may be biased by the researcher’s own beliefs, values, or assumptions. This can lead to selective interpretation of data and a lack of objectivity in research.
• Cannot prove causation: A hypothesis can only show a correlation between variables, but it cannot prove causation. This requires further experimentation and analysis.
• Limited to specific contexts: Hypotheses are limited to specific contexts and may not be generalizable to other situations or populations. This means that results may not be applicable in other contexts or may require further testing.
• May be affected by chance : Hypotheses may be affected by chance or random variation, which can obscure or distort the true relationship between variables.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

Conditional Statement – Definition, Truth Table, Examples, FAQs

What is a conditional statement, how to write a conditional statement, what is a biconditional statement, solved examples on conditional statements, practice problems on conditional statements, frequently asked questions about conditional statements.

A conditional statement is a statement that is written in the “If p, then q” format. Here, the statement p is called the hypothesis and q is called the conclusion. It is a fundamental concept in logic and mathematics. 

Conditional statement symbol :  p → q

A conditional statement consists of two parts.

• The “if” clause, which presents a condition or hypothesis.
• The “then” clause, which indicates the consequence or result that follows if the condition is true. 

Example : If you brush your teeth, then you won’t get cavities.

Hypothesis (Condition): If you brush your teeth

Conclusion (Consequence): then you won’t get cavities 

Conditional Statement: Definition

A conditional statement is characterized by the presence of “if” as an antecedent and “then” as a consequent. A conditional statement, also known as an “if-then” statement consists of two parts:

• The “if” clause (hypothesis): This part presents a condition, situation, or assertion. It is the initial condition that is being considered.
• The “then” clause (conclusion): This part indicates the consequence, result, or action that will occur if the condition presented in the “if” clause is true or satisfied. 

Related Worksheets

Representation of Conditional Statement

The conditional statement of the form ‘If p, then q” is represented as p → q. 

It is pronounced as “p implies q.”

Different ways to express a conditional statement are:

• p implies q
• p is sufficient for q
• q is necessary for p

Parts of a Conditional Statement

There are two parts of conditional statements, hypothesis and conclusion. The hypothesis or condition will begin with the “if” part, and the conclusion or action will begin with the “then” part. A conditional statement is also called “implication.”

Conditional Statements Examples:

Example 1: If it is Sunday, then you can go to play. 

Hypothesis: If it is Sunday

Conclusion: then you can go to play. 

Example 2: If you eat all vegetables, then you can have the dessert.

Condition: If you eat all vegetables

Conclusion: then you can have the dessert 

To form a conditional statement, follow these concise steps:

Step 1 : Identify the condition (antecedent or “if” part) and the consequence (consequent or “then” part) of the statement.

Step 2 : Use the “if… then…” structure to connect the condition and consequence.

Step 3 : Ensure the statement expresses a logical relationship where the condition leads to the consequence.

Example 1 : “If you study (condition), then you will pass the exam (consequence).” 

This conditional statement asserts that studying leads to passing the exam. If you study (condition is true), then you will pass the exam (consequence is also true).

Example 2 : If you arrange the numbers from smallest to largest, then you will have an ascending order.

Hypothesis: If you arrange the numbers from smallest to largest

Conclusion: then you will have an ascending order

Truth Table for Conditional Statement

The truth table for a conditional statement is a table used in logic to explore the relationship between the truth values of two statements. It lists all possible combinations of truth values for “p” and “q” and determines whether the conditional statement is true or false for each combination. 

The truth value of p → q is false only when p is true and q is False. 

If the condition is false, the consequence doesn’t affect the truth of the conditional; it’s always true.

In all the other cases, it is true.

The truth table is helpful in the analysis of possible combinations of truth values for hypothesis or condition and conclusion or action. It is useful to understand the presence of truth or false statements. 

Converse, Inverse, and Contrapositive

The converse, inverse, and contrapositive are three related conditional statements that are derived from an original conditional statement “p → q.” 

Consider a conditional statement: If I run, then I feel great.

• Converse: 

The converse of “p → q” is “q → p.” It reverses the order of the original statement. While the original statement says “if p, then q,” the converse says “if q, then p.” 

Converse: If I feel great, then I run.

• Inverse: 

The inverse of “p → q” is “~p → ~q,” where “” denotes negation (opposite). It negates both the antecedent (p) and the consequent (q). So, if the original statement says “if p, then q,” the inverse says “if not p, then not q.”

Inverse : If I don’t run, then I don’t feel great.

• Contrapositive: 

The contrapositive of “p → q” is “~q → ~p.” It reverses the order and also negates both the statements. So, if the original statement says “if p, then q,” the contrapositive says “if not q, then not p.”

Contrapositive: If I don’t feel great, then I don’t run.

A biconditional statement is a type of compound statement in logic that expresses a bidirectional or two-way relationship between two statements. It asserts that “p” is true if and only if “q” is true, and vice versa. In symbolic notation, a biconditional statement is represented as “p ⟺ q.”

In simpler terms, a biconditional statement means that the truth of “p” and “q” are interdependent. 

If “p” is true, then “q” must also be true, and if “q” is true, then “p” must be true. Conversely, if “p” is false, then “q” must be false, and if “q” is false, then “p” must be false. 

Biconditional statements are often used to express equality, equivalence, or conditions where two statements are mutually dependent for their truth values. 

Examples : 

• I will stop my bike if and only if the traffic light is red.  
• I will stay if and only if you play my favorite song.

Facts about Conditional Statements

• The negation of a conditional statement “p → q” is expressed as “p and not q.” It is denoted as “𝑝 ∧ ∼𝑞.” 
• The conditional statement is not logically equivalent to its converse and inverse.
• The conditional statement is logically equivalent to its contrapositive. 
• Thus, we can write p → q ∼q → ∼p

In this article, we learned about the fundamentals of conditional statements in mathematical logic, including their structure, parts, truth tables, conditional logic examples, and various related concepts. Understanding conditional statements is key to logical reasoning and problem-solving. Now, let’s solve a few examples and practice MCQs for better comprehension.

Example 1: Identify the hypothesis and conclusion. 

If you sing, then I will dance.

Solution : 

Given statement: If you sing, then I will dance.

Here, the antecedent or the hypothesis is “if you sing.”

The conclusion is “then I will dance.”

Example 2: State the converse of the statement: “If the switch is off, then the machine won’t work.” 

Here, p: The switch is off

q: The machine won’t work.

The conditional statement can be denoted as p → q.

Converse of p → q is written by reversing the order of p and q in the original statement.

Converse of  p → q is q → p.

Converse of  p → q: q → p: If the machine won’t work, then the switch is off.

Example 3: What is the truth value of the given conditional statement? 

If 2+2=5 , then pigs can fly.

Solution:  

q: Pigs can fly.

The statement p is false. Now regardless of the truth value of statement q, the overall statement will be true. 

F → F = T

Hence, the truth value of the statement is true. 

Conditional Statement - Definition, Truth Table, Examples, FAQs

Attend this quiz & Test your knowledge.

What is the antecedent in the given conditional statement? If it’s sunny, then I’ll go to the beach.

A conditional statement can be expressed as, what is the converse of “a → b”, when the antecedent is true and the consequent is false, the conditional statement is.

What is the meaning of conditional statements?

Conditional statements, also known as “if-then” statements, express a cause-and-effect or logical relationship between two propositions.

When does the truth value of a conditional statement is F?

A conditional statement is considered false when the antecedent is true and the consequent is false.

What is the contrapositive of a conditional statement?

The contrapositive reverses the order of the statements and also negates both the statements. It is equivalent in truth value to the original statement.

RELATED POSTS

• Ordering Decimals: Definition, Types, Examples
• Decimal to Octal: Steps, Methods, Conversion Table
• Lattice Multiplication – Definition, Method, Examples, Facts, FAQs
• X Intercept – Definition, Formula, Graph, Examples
• Lateral Face – Definition With Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.11: If Then Statements

• Last updated
• Save as PDF
• Page ID 2144

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Hypothesis followed by a conclusion in a conditional statement.

Conditional Statements

A conditional statement (also called an if-then statement ) is a statement with a hypothesis followed by a conclusion . The hypothesis is the first, or “if,” part of a conditional statement. The conclusion is the second, or “then,” part of a conditional statement. The conclusion is the result of a hypothesis.

If-then statements might not always be written in the “if-then” form. Here are some examples of conditional statements:

• Statement 1: If you work overtime, then you’ll be paid time-and-a-half.
• Statement 2: I’ll wash the car if the weather is nice.
• Statement 3: If 2 divides evenly into \(x\), then \(x\) is an even number.
• Statement 4: I’ll be a millionaire when I win the lottery.
• Statement 5: All equiangular triangles are equilateral.

Statements 1 and 3 are written in the “if-then” form. The hypothesis of Statement 1 is “you work overtime.” The conclusion is “you’ll be paid time-and-a-half.” Statement 2 has the hypothesis after the conclusion. If the word “if” is in the middle of the statement, then the hypothesis is after it. The statement can be rewritten: If the weather is nice, then I will wash the car. Statement 4 uses the word “when” instead of “if” and is like Statement 2. It can be written: If I win the lottery, then I will be a millionaire. Statement 5 “if” and “then” are not there. It can be rewritten: If a triangle is equiangular, then it is equilateral.

What if you were given a statement like "All squares are rectangles"? How could you determine the hypothesis and conclusion of this statement?

Example \(\PageIndex{1}\)

Determine the hypothesis and conclusion: I'll bring an umbrella if it rains.

Hypothesis: "It rains." Conclusion: "I'll bring an umbrella."

Example \(\PageIndex{2}\)

Determine the hypothesis and conclusion: All right angles are \(90^{\circ}\).

Hypothesis: "An angle is right." Conclusion: "It is \(90^{\circ}\)."

Example \(\PageIndex{3}\)

Use the statement: I will graduate when I pass Calculus.

Rewrite in if-then form and determine the hypothesis and conclusion.

This statement can be rewritten as If I pass Calculus, then I will graduate. The hypothesis is “I pass Calculus,” and the conclusion is “I will graduate.”

Example \(\PageIndex{4}\)

Use the statement: All prime numbers are odd.

Rewrite in if-then form, determine the hypothesis and conclusion, and determine whether this is a true statement.

This statement can be rewritten as If a number is prime, then it is odd. The hypothesis is "a number is prime" and the conclusion is "it is odd". This is not a true statement (remember that not all conditional statements will be true!) since 2 is a prime number but it is not odd.

Example \(\PageIndex{5}\)

Determine the hypothesis and conclusion: Sarah will go to the store if Riley does the laundry.

The statement can be rewritten as "If Riley does the laundry then Sarah will go to the store." The hypothesis is "Riley does the laundry" and the conclusion is "Sarah will go to the store."

Determine the hypothesis and the conclusion for each statement.

• If 5 divides evenly into \(x\), then \(x\) ends in 0 or 5.
• If a triangle has three congruent sides, it is an equilateral triangle.
• Three points are coplanar if they all lie in the same plane.
• If \(x=3\), then \(x^2=9\).
• If you take yoga, then you are relaxed.
• All baseball players wear hats.
• I'll learn how to drive when I am 16 years old.
• If you do your homework, then you can watch TV.
• Alternate interior angles are congruent if lines are parallel.
• All kids like ice cream.

Additional Resources

Video: If-Then Statements Principles - Basic

Activities: If-Then Statements Discussion Questions

Study Aids: Conditional Statements Study Guide

Practice: If Then Statements

Real World: If Then Statements

The Scientific Method by Science Made Simple

Understanding and using the scientific method.

The Scientific Method is a process used to design and perform experiments. It's important to minimize experimental errors and bias, and increase confidence in the accuracy of your results.

In the previous sections, we talked about how to pick a good topic and specific question to investigate. Now we will discuss how to carry out your investigation.

Steps of the Scientific Method

• Observation/Research
• Experimentation

Now that you have settled on the question you want to ask, it's time to use the Scientific Method to design an experiment to answer that question.

If your experiment isn't designed well, you may not get the correct answer. You may not even get any definitive answer at all!

The Scientific Method is a logical and rational order of steps by which scientists come to conclusions about the world around them. The Scientific Method helps to organize thoughts and procedures so that scientists can be confident in the answers they find.

OBSERVATION is first step, so that you know how you want to go about your research.

HYPOTHESIS is the answer you think you'll find.

PREDICTION is your specific belief about the scientific idea: If my hypothesis is true, then I predict we will discover this.

EXPERIMENT is the tool that you invent to answer the question, and

CONCLUSION is the answer that the experiment gives.

Don't worry, it isn't that complicated. Let's take a closer look at each one of these steps. Then you can understand the tools scientists use for their science experiments, and use them for your own.

OBSERVATION

This step could also be called "research." It is the first stage in understanding the problem.

After you decide on topic, and narrow it down to a specific question, you will need to research everything that you can find about it. You can collect information from your own experiences, books, the internet, or even smaller "unofficial" experiments.

Let's continue the example of a science fair idea about tomatoes in the garden. You like to garden, and notice that some tomatoes are bigger than others and wonder why.

Because of this personal experience and an interest in the problem, you decide to learn more about what makes plants grow.

For this stage of the Scientific Method, it's important to use as many sources as you can find. The more information you have on your science fair topic, the better the design of your experiment is going to be, and the better your science fair project is going to be overall.

Also try to get information from your teachers or librarians, or professionals who know something about your science fair project. They can help to guide you to a solid experimental setup.

The next stage of the Scientific Method is known as the "hypothesis." This word basically means "a possible solution to a problem, based on knowledge and research."

The hypothesis is a simple statement that defines what you think the outcome of your experiment will be.

All of the first stage of the Scientific Method -- the observation, or research stage -- is designed to help you express a problem in a single question ("Does the amount of sunlight in a garden affect tomato size?") and propose an answer to the question based on what you know. The experiment that you will design is done to test the hypothesis.

Using the example of the tomato experiment, here is an example of a hypothesis:

TOPIC: "Does the amount of sunlight a tomato plant receives affect the size of the tomatoes?"

HYPOTHESIS: "I believe that the more sunlight a tomato plant receives, the larger the tomatoes will grow.

This hypothesis is based on:

(1) Tomato plants need sunshine to make food through photosynthesis, and logically, more sun means more food, and;

(2) Through informal, exploratory observations of plants in a garden, those with more sunlight appear to grow bigger.

The hypothesis is your general statement of how you think the scientific phenomenon in question works.

Your prediction lets you get specific -- how will you demonstrate that your hypothesis is true? The experiment that you will design is done to test the prediction.

An important thing to remember during this stage of the scientific method is that once you develop a hypothesis and a prediction, you shouldn't change it, even if the results of your experiment show that you were wrong.

An incorrect prediction does NOT mean that you "failed." It just means that the experiment brought some new facts to light that maybe you hadn't thought about before.

Continuing our tomato plant example, a good prediction would be: Increasing the amount of sunlight tomato plants in my experiment receive will cause an increase in their size compared to identical plants that received the same care but less light.

This is the part of the scientific method that tests your hypothesis. An experiment is a tool that you design to find out if your ideas about your topic are right or wrong.

It is absolutely necessary to design a science fair experiment that will accurately test your hypothesis. The experiment is the most important part of the scientific method. It's the logical process that lets scientists learn about the world.

On the next page, we'll discuss the ways that you can go about designing a science fair experiment idea.

The final step in the scientific method is the conclusion. This is a summary of the experiment's results, and how those results match up to your hypothesis.

You have two options for your conclusions: based on your results, either:

(1) YOU CAN REJECT the hypothesis, or

(2) YOU CAN NOT REJECT the hypothesis.

This is an important point!

You can not PROVE the hypothesis with a single experiment, because there is a chance that you made an error somewhere along the way.

What you can say is that your results SUPPORT the original hypothesis.

If your original hypothesis didn't match up with the final results of your experiment, don't change the hypothesis.

Instead, try to explain what might have been wrong with your original hypothesis. What information were you missing when you made your prediction? What are the possible reasons the hypothesis and experimental results didn't match up?

Remember, a science fair experiment isn't a failure simply because does not agree with your hypothesis. No one will take points off if your prediction wasn't accurate. Many important scientific discoveries were made as a result of experiments gone wrong!

A science fair experiment is only a failure if its design is flawed. A flawed experiment is one that (1) doesn't keep its variables under control, and (2) doesn't sufficiently answer the question that you asked of it.

Search This Site:

Science Fairs

• Introduction
• Project Ideas
• Types of Projects
• Pick a Topic
• Scientific Method
• Design Your Experiment
• Present Your Project
• What Judges Want
• Parent Info

Recommended *

• Sample Science Projects - botany, ecology, microbiology, nutrition

* This site contains affiliate links to carefully chosen, high quality products. We may receive a commission for purchases made through these links.

• Terms of Service

Copyright © 2006 - 2023, Science Made Simple, Inc. All Rights Reserved.

The science fair projects & ideas, science articles and all other material on this website are covered by copyright laws and may not be reproduced without permission.

Understanding Logical Statements

Learning Objectives

• Identify the hypothesis and conclusion in a logical statement.
• Determine whether mathematical statements involving linear, quadratic, absolute value expressions, equations, or inequalities are always, sometimes, or never true.
• Use counterexamples to show that a statement is false, and recognize that a single counterexample is sufficient.

Introduction

Logic is an essential part of the study of mathematics. Much of mathematics is concerned with the characteristics of numbers and other mathematical objects (such as geometric figures or variables), and being able to make decisions about what must be true based on known characteristics and other facts is vital.

The Parts of a Logical Statement

A logical statement A statement that allows drawing a conclusion or result based on a hypothesis or premise. is a statement that, when true, allows us to take a known set of facts and infer (or assume) a new fact from them. Logical statements have two parts: The hypothesis The part of a logical statement that provides the premise on which the conclusion is based. In a statement “If `x` then `y` ,” the hypothesis is `x` . , which is the premise or set of facts that we start with, and the conclusion The part of a logical statement that provides the result or consequences of the hypothesis. In a statement “If `x` then `y` ,” the conclusion is `y` . , which is the new fact that we can infer when the hypothesis is true. (Note: If you've used hypothesis in science class, you've probably noticed that this is a fairly different definition. Be careful not to get confused!)

Consider this statement:

If you go outside without any rain gear or cover when it’s pouring rain, you will get wet.

Here, the hypothesis is “you go outside without any rain gear or cover when it’s pouring rain.” The hypothesis must be completely true before we can use the statement to infer anything new from it. What does this statement say about someone who doesn’t go outside? About someone who uses an umbrella? About what happens to someone when it’s not pouring rain? Nothing. This statement doesn't apply to anyone in those cases.

The conclusion of this statement is “you will get wet.” Suppose it’s raining, and someone walks outside, and doesn't have any rain gear or other kind of cover—what will happen? All the parts of the hypothesis have been met, so—if the statement is true—we can infer that the person is going to get wet. It certainly seems reasonable that they would!

Note that in this example, if the hypothesis isn’t true, the person still could get wet. On a sunny day with no rain, someone might go outside to wash his car and get sprayed by the hose. Someone else might go swimming, and then they would really get wet! The statement says nothing when the hypothesis is false. It's only helpful when the hypothesis is true.

Not all logical statements are written as “If (something is true) then (something else is true).” To identify the hypothesis and conclusion, you may need to try to rewrite a statement in an “if-then” format.

Logical statements can also be about mathematics, of course! Anything that lets us infer a new fact about something mathematical from given information is a logical statement. For example, “The diagonals of a rectangle have the same length” is a logical statement. The hypothesis is the part that can help us if we know it’s true. When could this statement be useful?

With algebraic statements, the hypothesis is often an assumption about what values are allowed for a variable. For example, you might have seen a statement like “ `a + b = b + a` , where `a`  and `b` are real numbers.” Let's treat this equation as a logical statement:

Testing for Truth

Critical thinking is important, not just in mathematics but in everyday life. Have you ever heard someone make a statement and then thought, “Wait. Is that true?” Sometimes people have reasons for thinking something is true even though it isn’t. Determining if a statement is true is a great skill to have!

When determining if a statement is true, most people start by looking for examples A situation that suggests a logical statement may be true. , which are situations for which the statement does turn out to be true (both the hypothesis and the conclusion are true). A more powerful situation to find, if one exists, is a counterexample A situation that provides evidence that a logical statement is false. , a situation for which the statement turns out to be false (the hypothesis is true, but the conclusion is false). Why are counterexamples so powerful?

Consider a person who sees the moon many times at night and then thinks: I’ve never seen the moon during the day. The person might then make the statement, “The moon only comes out at night.” As an if-then statement, this is the same as “If the moon is out, then it’s night.” We can all probably think of many times when we saw the moon out, and it was nighttime. These are examples, situations when the statement was true.

But in fact, the statement is not always true, and we only need to see the moon during the day once —only one counterexample—to know that the statement is not true. Many, many examples cannot prove the statement is true, but we only need one counterexample to prove it’s not!

For a given statement, then, we have three possibilities:

So how can we be sure if something is true (or never true for that matter), if we can’t rely on lots of examples? With algebraic statements, sometimes we can turn to a graph for help:

Another way to decide if something is always, sometimes, or never true is reasoning from other things we know are true. We can start with something we know is true and try to create the original statement. Let’s try this with the same example above:

When we try to put together logical arguments like that, the biggest problem can be knowing where to start. There's a good chance our first attempt(s) will run into a dead end, and we'll need to start over. Practice does make it easier. Sometimes it helps to work backward: start by assuming the conclusion is true, try to think of a related statement known to be true (or false), and then connect them. Let’s take one last look at the example above:

Another way to test the truth of a statement is to look for counterexamples. Graphs can help us there, too:

Although we know  `|-x| = -x` is not always true if `x` is any real number, we also know that it is sometimes true. In fact, we can specify when it’s true—using the graph from the example, we can see it’s true when `x<=0` . We can use that fact to create a new statement:

If `x<=0` , then `|-x| = -x` .

Because of the narrower hypothesis, this statement is always true.

Special Cases

When we look for examples, and particularly for counterexamples, there are some special cases that are easy to overlook. Keeping these cases in mind is often very helpful. Look through some special cases and consider if any of them provides a counterexample for this statement: “When two numbers are multiplied, the product is larger than each of the factors.”

Here are some more examples. Consider the special cases above as you read through these.

Logical statements have two parts, a hypothesis that presents facts that the statement needs to be true, and a conclusion that presents a new fact we can infer when the hypothesis is true.

For a statement to be always true, there must be no counterexamples for which the hypothesis is true and the conclusion is false. If there are examples for which the statement is true, but there are also counterexamples, then the statement is sometimes true. These sometimes true statements can be made into always true statements by changing the hypothesis. A statement is never true if there are no examples for which both the hypothesis and the conclusion are true. When looking for counterexamples and examples, there are some special cases (such as negative numbers and fractions) that should be considered.

A free service from Mattecentrum

If-then statement

• Logical correct I
• Logical correct II

When we previously discussed inductive reasoning we based our reasoning on examples and on data from earlier events. If we instead use facts, rules and definitions then it's called deductive reasoning.

We will explain this by using an example.

If you get good grades then you will get into a good college.

The part after the "if": you get good grades - is called a hypotheses and the part after the "then" - you will get into a good college - is called a conclusion.

Hypotheses followed by a conclusion is called an If-then statement or a conditional statement.

This is noted as

$$p \to q$$

This is read - if p then q.

A conditional statement is false if hypothesis is true and the conclusion is false. The example above would be false if it said "if you get good grades then you will not get into a good college".

If we re-arrange a conditional statement or change parts of it then we have what is called a related conditional.

Our conditional statement is: if a population consists of 50% men then 50% of the population must be women.

If we exchange the position of the hypothesis and the conclusion we get a converse statemen t: if a population consists of 50% women then 50% of the population must be men.

$$q\rightarrow p$$

If both statements are true or if both statements are false then the converse is true. A conditional and its converse do not mean the same thing

If we negate both the hypothesis and the conclusion we get a inverse statemen t: if a population do not consist of 50% men then the population do not consist of 50% women.

$$\sim p\rightarrow \: \sim q$$

The inverse is not true juest because the conditional is true. The inverse always has the same truth value as the converse.

We could also negate a converse statement, this is called a contrapositive statemen t:  if a population do not consist of 50% women then the population do not consist of 50% men.

$$\sim q\rightarrow \: \sim p$$

The contrapositive does always have the same truth value as the conditional. If the conditional is true then the contrapositive is true.

A pattern of reaoning is a true assumption if it always lead to a true conclusion. The most common patterns of reasoning are detachment and syllogism.

If we turn of the water in the shower, then the water will stop pouring.

If we call the first part p and the second part q then we know that p results in q. This means that if p is true then q will also be true. This is called the law of detachment and is noted:

$$\left [ (p \to q)\wedge p \right ] \to q$$

The law of syllogism tells us that if p → q and q → r then p → r is also true.

This is noted:

$$\left [ (p \to q)\wedge (q \to r ) \right ] \to (p \to r)$$

If the following statements are true:

If we turn of the water (p), then the water will stop pouring (q). If the water stops pouring (q) then we don't get wet any more (r).

Then the law of syllogism tells us that if we turn of the water (p) then we don't get wet (r) must be true.

Video lesson

Write a converse, inverse and contrapositive to the conditional

"If you eat a whole pint of ice cream, then you won't be hungry"

• Angles, parallel lines and transversals
• Congruent triangles
• More about triangles
• Inequalities
• Mean and geometry
• The converse of the Pythagorean theorem and special triangles
• Properties of parallelograms
• Common types of transformation
• Transformation using matrices
• Basic information about circles
• Inscribed angles and polygons
• Advanced information about circles
• Parallelogram, triangles etc
• The surface area and the volume of pyramids, prisms, cylinders and cones
• SAT Overview
• ACT Overview

Trump’s lawyer charges Michael Cohen lied to jury

Angry defense lawyer shouts in confrontation with Donald Trump’s former fixer, who stayed calm in his third day of testimony.

NEW YORK — The central witness against Donald Trump withstood a withering cross-examination Thursday from the former president’s defense lawyer, who accused Michael Cohen of lying as recently as two days ago to realize his dreams of revenge against his ex-boss.

The confrontation between Cohen and Trump lawyer Todd Blanche was the most anticipated moment in the month-long trial, which is now speeding toward a conclusion. Because the trial is off Friday, the jurors will have three days to weigh Cohen’s answers. His cross-examination will continue Monday morning, setting the stage for closing arguments next week.

New York Supreme Court Justice Juan Merchan told the lawyers that he would try to make sure those arguments don’t stretch out over more than one day, but he warned that they might because of scheduling demands of the jurors and other logistics issues.

The day’s testimony was closely watched by a cadre of Trump’s political allies sitting behind him in court, including Reps. Matt Gaetz (R-Fla.) and Lauren Boebert (R-Colo.). There were so many congressional Republicans in court in New York that a House Oversight Committee hearing in Washington was delayed .

Trump, who paid close attention Thursday to Blanche’s questioning of Cohen, has still not decided whether he will take the stand, Blanche told the judge. Most defendants do not testify at their trials, believing the risks of being questioned by prosecutors under oath are simply too great.

Trump hush money trial

In his third day on the witness stand, Cohen remained calm and quiet — speaking in a slow, sometimes raspy voice as Blanche challenged his truthfulness again and again. At one point, Blanche shouted that Cohen was a liar.

Cohen’s ability to keep his cool under pressure is an important measuring stick for the prosecutors’ chances of success.

Perhaps more importantly, the jury must decide whether they believe the only witness who directly ties Trump to an alleged scheme to falsify business records to cover up hush money payments to a porn star.

Cohen, a disbarred and convicted former lawyer , has admitted that he lied for Trump for years; it would be a far more serious threat to the prosecution case if jurors came to suspect he lied to them.

Trump is charged with 34 felony counts of falsifying business records by Manhattan District Attorney Alvin Bragg . The indictment accuses Trump of creating a false paper trail to hide the fact that adult-film star Stormy Daniels was paid $130,000 in October 2016 to stay silent about her claim to have had sex with Trump years earlier. Trump denies the two had sex.

Cohen is instrumental to the prosecution case because he paid Daniels with his own money; the following year, the lawyer was given monthly payments from Trump in what prosecutors say was a corrupt scheme to reimburse him and keep Daniels’s allegations under wraps. Cohen is the only witness who has described conversations with Trump in which he said it was clear that his boss understood they would create the false paper trail.

The angriest and potentially most consequential moment in Thursday’s testimony came when Blanche confronted Cohen over his claim that he spoke to Trump on the evening of Oct. 24, 2016, when he called the phone of Trump’s security chief, Keith Schiller.

Cohen testified Tuesday that during the phone call, he told Trump the plan to pay hush money to Daniels was moving forward.

Blanche, however, presented text messages between Schiller and Cohen that preceded that call and suggested an entirely different reason for the conversation. In those texts, Cohen complained about getting harassing phone calls and asked for Schiller’s help. “Call me,” Schiller replied.

After hours of mild-mannered and patient questioning of Cohen, Blanche erupted as he confronted Cohen over the Schiller texts. Accusing Cohen of fabricating key evidence against his client, the lawyer angrily grabbed the microphone and raised his voice.

“That was a lie! You did not talk to President Trump that night!” Blanche bellowed.

Blanche suggested the call was simply too short for it to have included Schiller handing his phone to his boss so he and Cohen could discuss a financial transaction that would ultimately be the genesis of criminal charges against Trump.

“I’m not sure that’s accurate,” Cohen said.

He tried to revise his earlier account, saying he “also spoke to Mr. Trump and told him that everything regarding the Stormy Daniels matter was being worked on and it’s going to be resolved.”

The back-and-forth was the most tense moment yet of Cohen’s cross-examination, and of the entire trial.

But a quieter exchange may prove more damaging to Cohen’s credibility. It happened when Blanche asked Cohen if he had been willing to lie under oath while pleading guilty to tax crimes “because the stakes affected you personally.”

Cohen agreed that he had been.

A few minutes later, Blanche asked Cohen whether “the outcome of this trial affects you personally.”

Again, Cohen said: “Yes.”

Throughout the day, Blanche tried to methodically rip apart the prosecution portrait of Cohen as a remorseful, reformed henchman , using elements of Cohen’s prior testimony to suggest to the jury that he is a singularly selfish person .

Wearing a pale yellow tie, dark suit and dark-rimmed glasses, Cohen met Blanche’s indignation with a calm insistence that whatever his faults, his story about Trump’s guilt was true.

Yet he also struggled to explain why he told a congressional committee in 2019 that he never sought and would never seek a pardon from Trump, when his lawyer was doing just that . (Cohen called it a “misstatement.”) Or how he could claim to have accepted responsibility for financial crimes, but also call the prosecutor and judge in that case corrupt.

On the stand, Cohen said the fault for what happened lay with his bank, his accountant and others.

“You’ve blamed a lot of people over the years for the conduct you were convicted of, yes?” Blanche asked.

“I blame people, yes,” he replied.

Cohen also admitted that he often recorded his conversations with people without their knowledge, including at one point Trump, who at the time was his legal client.

Blanche played for the jury two short recordings of a bombastic Cohen talking about how joyful he was over Trump’s indictment and the prospect of the former president possibly going to jail. Cohen has continued to rail publicly against Trump, on podcasts, social media and in news interviews, despite repeated entreaties from the prosecutors for him to stop.

“I truly f---ing hope that this man ends up in prison,” Cohen said on a podcast excerpt played for the jury Thursday. “Revenge is a dish best served cold, and you best believe I want this man to go down and rot inside for what he did to my family.”

In another podcast clip, this one from May of last year, weeks after Trump’s indictment in this case, Cohen declared: “I want to thank the Manhattan district attorney’s office and their fearless leader Alvin Bragg, with whom I spent countless hours.”

On the witness stand, Cohen conceded that he had not in fact met or spent time with Bragg.

The district attorney has attended the trial intermittently but was not in court Thursday. The trial is off Friday so that Trump can attend his son’s high school graduation.

Just before court ended for the day, Blanche asked about a 2016 conversation in which Cohen reassured a reporter that the story about a Trump-Daniels encounter was false. In the phone call, Cohen told the reporter to believe Cohen because he is “a really bad liar.”

On the stand, Cohen acknowledged that he was lying at the time.

Trump New York hush money case

Former president Donald Trump’s criminal hush money trial is underway in New York. Follow live updates from the trial .

Key witnesses: Several key witnesses, including David Pecker and Stormy Daniels, have taken the stand. Here’s what Daniels said during her testimony . Read full transcripts from the trial .

Gag order: New York Supreme Court Justice Juan Merchan has twice ruled that Trump violated his gag order , which prohibits him from commenting on jurors and witnesses in the case, among others. Here are all of the times Trump has violated the gag order .

The case: The investigation involves a $130,000 payment made to Daniels, an adult-film actress , during the 2016 presidential campaign. It’s one of many ongoing investigations involving Trump . Here are some of the key people in the case .

The charges: Trump is charged with 34 felony counts of falsifying business records. Falsifying business records is a felony in New York when there is an “intent to defraud” that includes an intent to “commit another crime or to aid or conceal” another crime. He has pleaded not guilty . Here’s what to know about the charges — and any potential sentence .