

User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
S.3.3 hypothesis testing examples.
- Example: Right-Tailed Test
- Example: Left-Tailed Test
- Example: Two-Tailed Test
Brinell Hardness Scores
An engineer measured the Brinell hardness of 25 pieces of ductile iron that were subcritically annealed. The resulting data were:
| Brinell Hardness of 25 Pieces of Ductile Iron | ||||||||
|---|---|---|---|---|---|---|---|---|
| 170 | 167 | 174 | 179 | 179 | 187 | 179 | 183 | 179 |
| 156 | 163 | 156 | 187 | 156 | 167 | 156 | 174 | 170 |
| 183 | 179 | 174 | 179 | 170 | 159 | 187 | ||
The engineer hypothesized that the mean Brinell hardness of all such ductile iron pieces is greater than 170. Therefore, he was interested in testing the hypotheses:
H 0 : μ = 170 H A : μ > 170
The engineer entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:
Descriptive Statistics
| N | Mean | StDev | SE Mean | 95% Lower Bound |
|---|---|---|---|---|
| 25 | 172.52 | 10.31 | 2.06 | 168.99 |
$\mu$: mean of Brinelli
Null hypothesis H₀: $\mu$ = 170 Alternative hypothesis H₁: $\mu$ > 170
| T-Value | P-Value |
|---|---|
| 1.22 | 0.117 |
The output tells us that the average Brinell hardness of the n = 25 pieces of ductile iron was 172.52 with a standard deviation of 10.31. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 10.31 by the square root of n = 25, is 2.06). The test statistic t * is 1.22, and the P -value is 0.117.
If the engineer set his significance level α at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were greater than 1.7109 (determined using statistical software or a t -table):
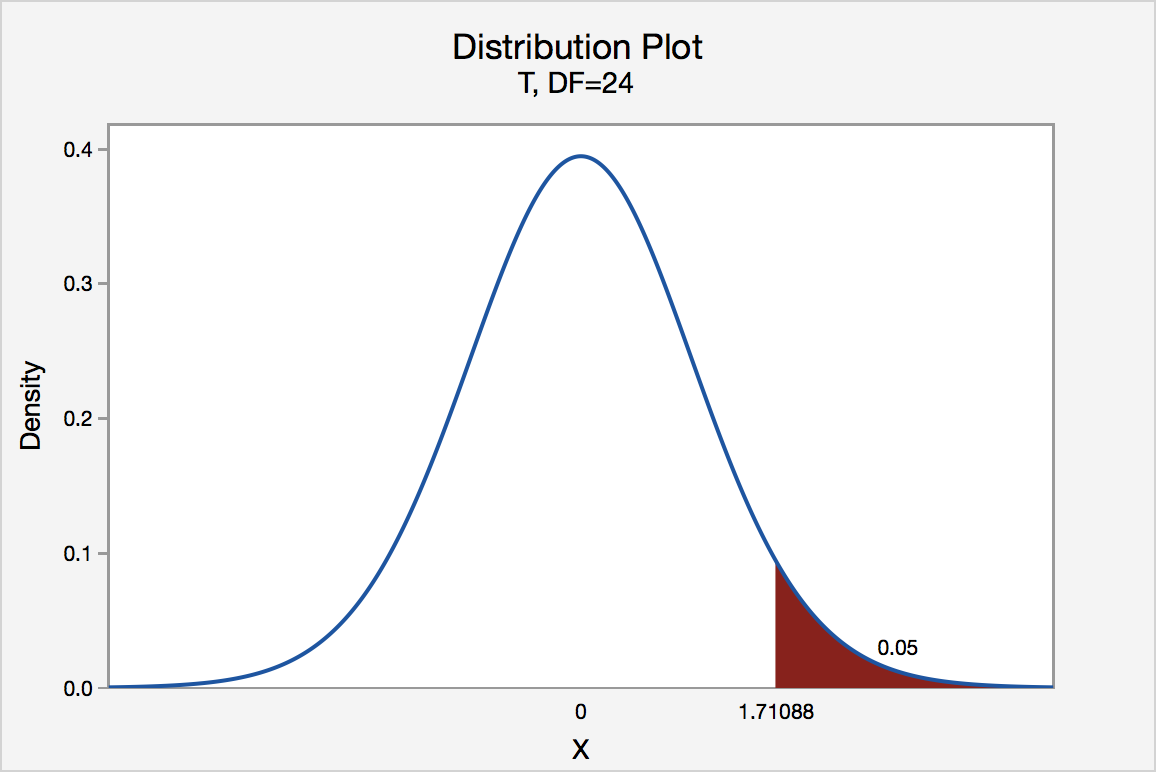
Since the engineer's test statistic, t * = 1.22, is not greater than 1.7109, the engineer fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.
If the engineer used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 24 curve and to the right of the test statistic t * = 1.22:
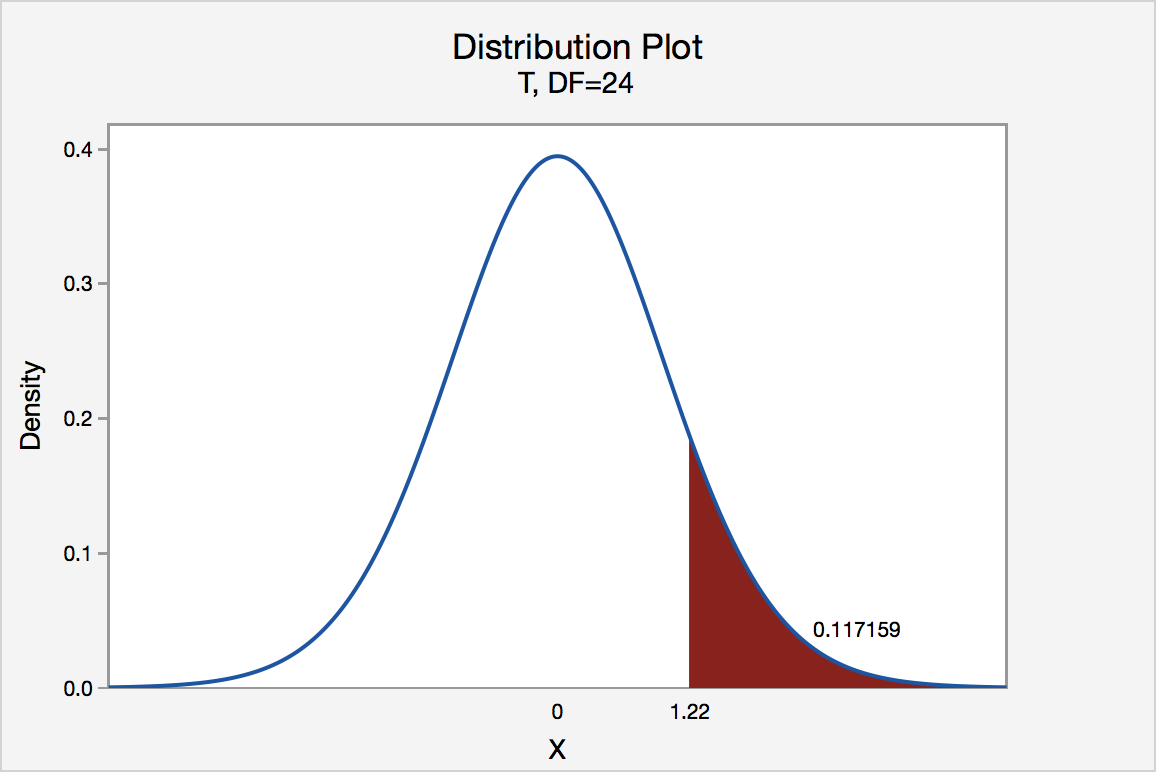
In the output above, Minitab reports that the P -value is 0.117. Since the P -value, 0.117, is greater than \(\alpha\) = 0.05, the engineer fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.
Note that the engineer obtains the same scientific conclusion regardless of the approach used. This will always be the case.
Height of Sunflowers
A biologist was interested in determining whether sunflower seedlings treated with an extract from Vinca minor roots resulted in a lower average height of sunflower seedlings than the standard height of 15.7 cm. The biologist treated a random sample of n = 33 seedlings with the extract and subsequently obtained the following heights:
| Heights of 33 Sunflower Seedlings | ||||||||
|---|---|---|---|---|---|---|---|---|
| 11.5 | 11.8 | 15.7 | 16.1 | 14.1 | 10.5 | 9.3 | 15.0 | 11.1 |
| 15.2 | 19.0 | 12.8 | 12.4 | 19.2 | 13.5 | 12.2 | 13.3 | |
| 16.5 | 13.5 | 14.4 | 16.7 | 10.9 | 13.0 | 10.3 | 15.8 | |
| 15.1 | 17.1 | 13.3 | 12.4 | 8.5 | 14.3 | 12.9 | 13.5 | |
The biologist's hypotheses are:
H 0 : μ = 15.7 H A : μ < 15.7
The biologist entered her data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. She obtained the following output:
| N | Mean | StDev | SE Mean | 95% Upper Bound |
|---|---|---|---|---|
| 33 | 13.664 | 2.544 | 0.443 | 14.414 |
$\mu$: mean of Height
Null hypothesis H₀: $\mu$ = 15.7 Alternative hypothesis H₁: $\mu$ < 15.7
| T-Value | P-Value |
|---|---|
| -4.60 | 0.000 |
The output tells us that the average height of the n = 33 sunflower seedlings was 13.664 with a standard deviation of 2.544. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 13.664 by the square root of n = 33, is 0.443). The test statistic t * is -4.60, and the P -value, 0.000, is to three decimal places.
Minitab Note. Minitab will always report P -values to only 3 decimal places. If Minitab reports the P -value as 0.000, it really means that the P -value is 0.000....something. Throughout this course (and your future research!), when you see that Minitab reports the P -value as 0.000, you should report the P -value as being "< 0.001."
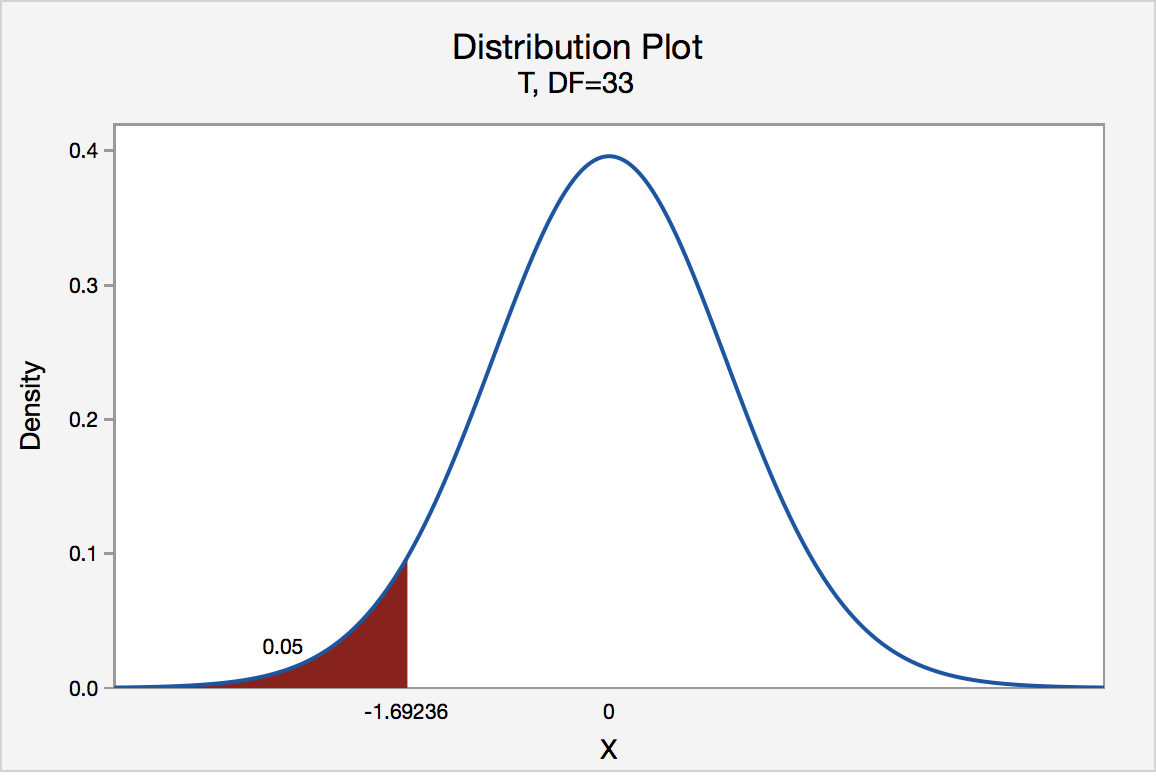
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t * were less than -1.6939 (determined using statistical software or a t -table):s-3-3
Since the biologist's test statistic, t * = -4.60, is less than -1.6939, the biologist rejects the null hypothesis. That is, the test statistic falls in the "critical region." There is sufficient evidence, at the α = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.
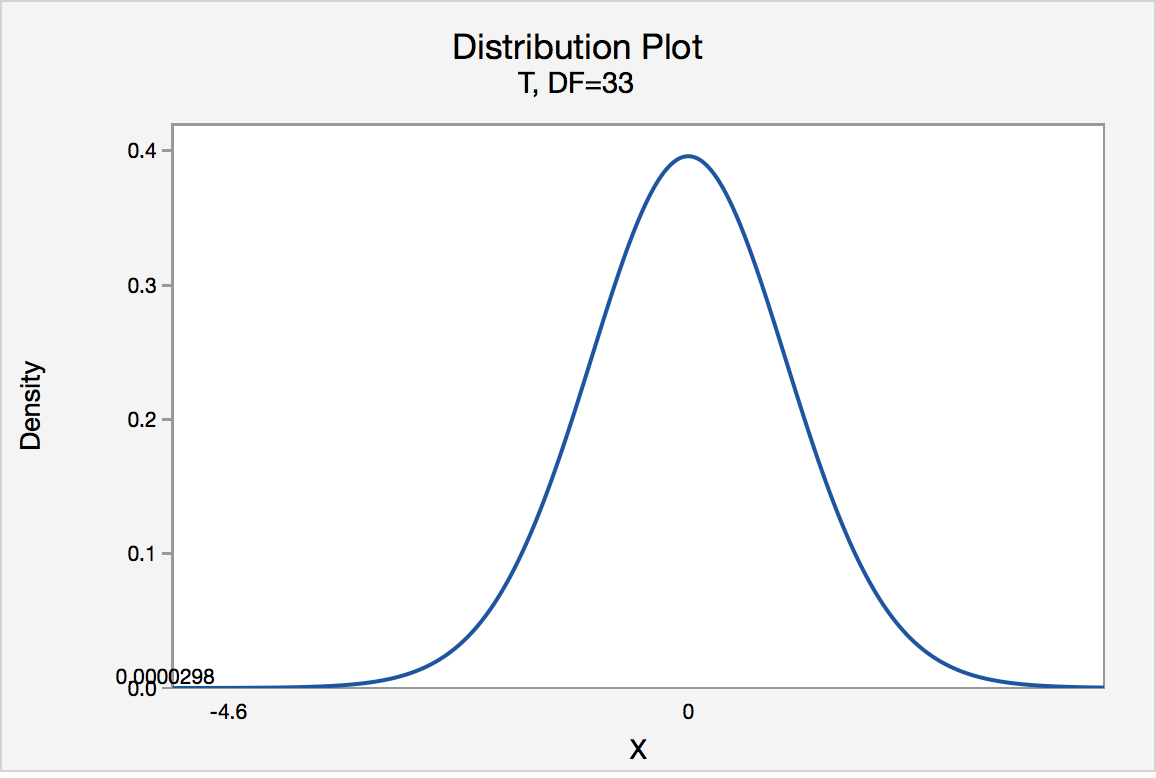
If the biologist used the P -value approach to conduct her hypothesis test, she would determine the area under a t n - 1 = t 32 curve and to the left of the test statistic t * = -4.60:
In the output above, Minitab reports that the P -value is 0.000, which we take to mean < 0.001. Since the P -value is less than 0.001, it is clearly less than \(\alpha\) = 0.05, and the biologist rejects the null hypothesis. There is sufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.
Note again that the biologist obtains the same scientific conclusion regardless of the approach used. This will always be the case.
Gum Thickness
A manufacturer claims that the thickness of the spearmint gum it produces is 7.5 one-hundredths of an inch. A quality control specialist regularly checks this claim. On one production run, he took a random sample of n = 10 pieces of gum and measured their thickness. He obtained:
| Thicknesses of 10 Pieces of Gum | ||||
|---|---|---|---|---|
| 7.65 | 7.60 | 7.65 | 7.70 | 7.55 |
| 7.55 | 7.40 | 7.40 | 7.50 | 7.50 |
The quality control specialist's hypotheses are:
H 0 : μ = 7.5 H A : μ ≠ 7.5
The quality control specialist entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:
| N | Mean | StDev | SE Mean | 95% CI for $\mu$ |
|---|---|---|---|---|
| 10 | 7.550 | 0.1027 | 0.0325 | (7.4765, 7.6235) |
$\mu$: mean of Thickness
Null hypothesis H₀: $\mu$ = 7.5 Alternative hypothesis H₁: $\mu \ne$ 7.5
| T-Value | P-Value |
|---|---|
| 1.54 | 0.158 |
The output tells us that the average thickness of the n = 10 pieces of gums was 7.55 one-hundredths of an inch with a standard deviation of 0.1027. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 0.1027 by the square root of n = 10, is 0.0325). The test statistic t * is 1.54, and the P -value is 0.158.
If the quality control specialist sets his significance level \(\alpha\) at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were less than -2.2616 or greater than 2.2616 (determined using statistical software or a t -table):
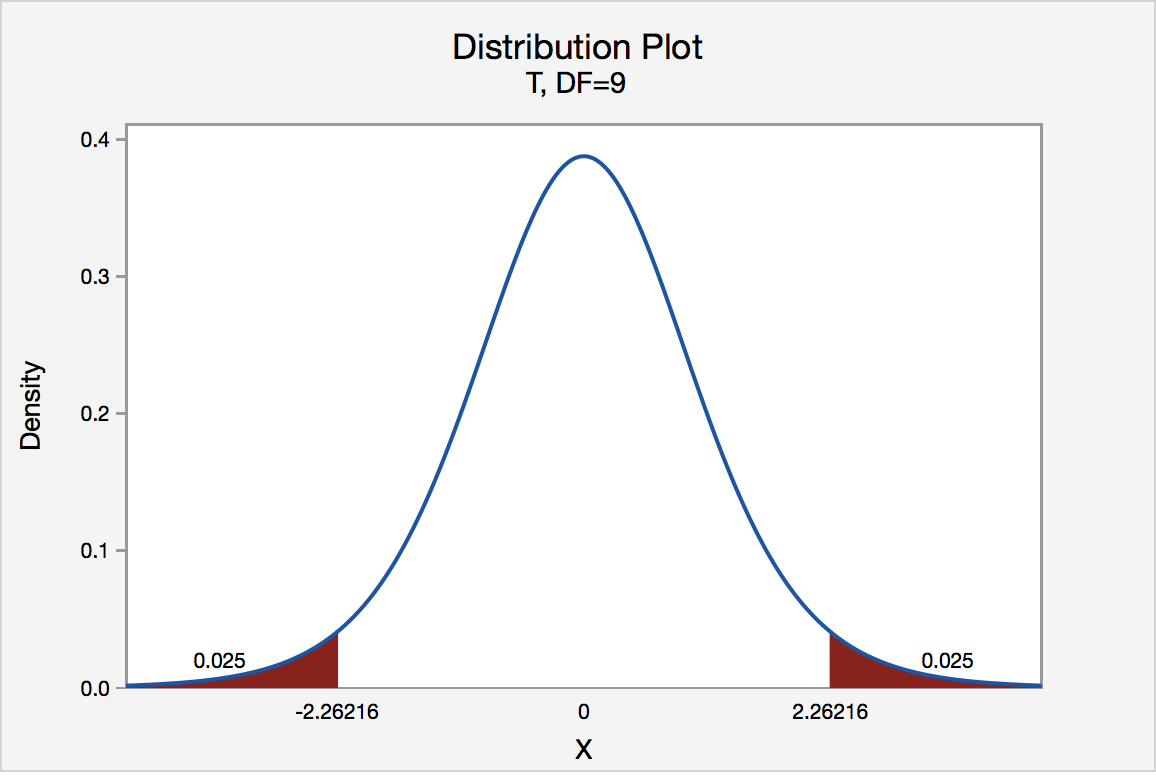
Since the quality control specialist's test statistic, t * = 1.54, is not less than -2.2616 nor greater than 2.2616, the quality control specialist fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all of the manufacturer's spearmint gum differs from 7.5 one-hundredths of an inch.
If the quality control specialist used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 9 curve, to the right of 1.54 and to the left of -1.54:
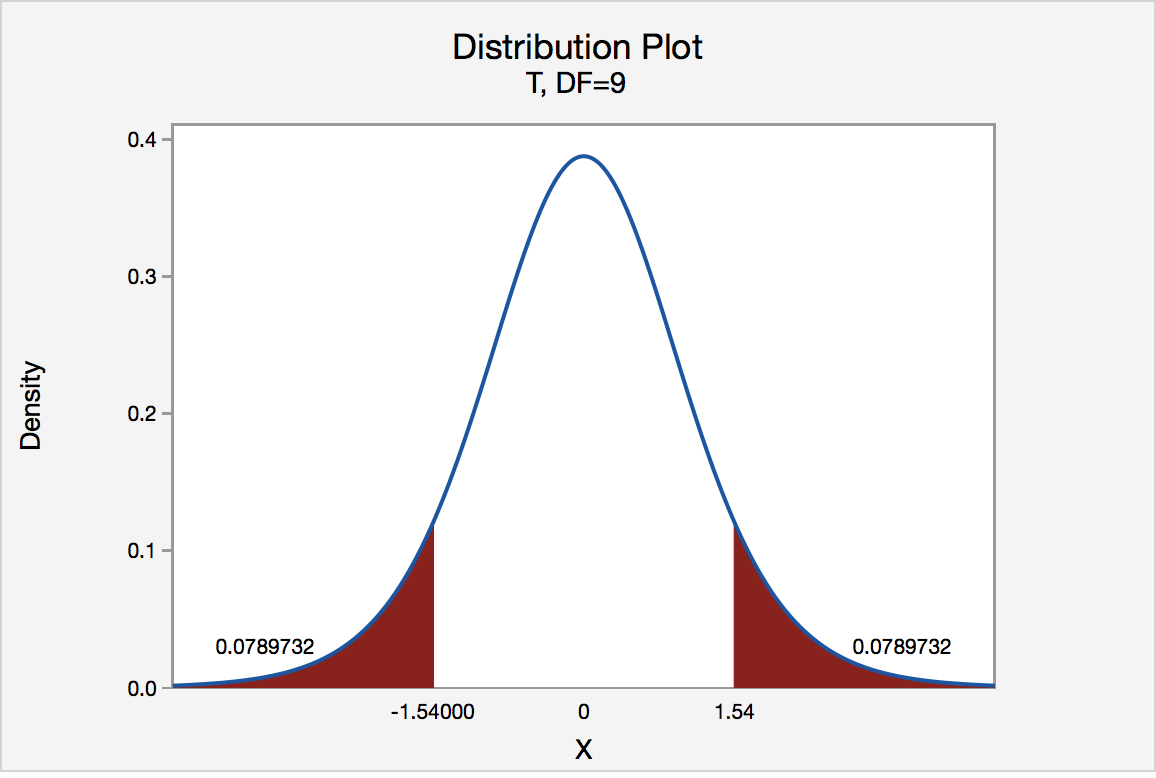
In the output above, Minitab reports that the P -value is 0.158. Since the P -value, 0.158, is greater than \(\alpha\) = 0.05, the quality control specialist fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all pieces of spearmint gum differs from 7.5 one-hundredths of an inch.
Note that the quality control specialist obtains the same scientific conclusion regardless of the approach used. This will always be the case.
In our review of hypothesis tests, we have focused on just one particular hypothesis test, namely that concerning the population mean \(\mu\). The important thing to recognize is that the topics discussed here — the general idea of hypothesis tests, errors in hypothesis testing, the critical value approach, and the P -value approach — generally extend to all of the hypothesis tests you will encounter.

Statistics Made Easy
4 Examples of Hypothesis Testing in Real Life
In statistics, hypothesis tests are used to test whether or not some hypothesis about a population parameter is true.
To perform a hypothesis test in the real world, researchers will obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:
- Null Hypothesis (H 0 ): The sample data occurs purely from chance.
- Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.
If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we can reject the null hypothesis and conclude that we have sufficient evidence to say that the alternative hypothesis is true.
The following examples provide several situations where hypothesis tests are used in the real world.
Example 1: Biology
Hypothesis tests are often used in biology to determine whether some new treatment, fertilizer, pesticide, chemical, etc. causes increased growth, stamina, immunity, etc. in plants or animals.
For example, suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.
She then performs a hypothesis test using the following hypotheses:
- H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
- H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)
If the p-value of the test is less than some significance level (e.g. α = .05), then she can reject the null hypothesis and conclude that the fertilizer leads to increased plant growth.
Example 2: Clinical Trials
Hypothesis tests are often used in clinical trials to determine whether some new treatment, drug, procedure, etc. causes improved outcomes in patients.
For example, suppose a doctor believes that a new drug is able to reduce blood pressure in obese patients. To test this, he may measure the blood pressure of 40 patients before and after using the new drug for one month.
He then performs a hypothesis test using the following hypotheses:
- H 0 : μ after = μ before (the mean blood pressure is the same before and after using the drug)
- H A : μ after < μ before (the mean blood pressure is less after using the drug)
If the p-value of the test is less than some significance level (e.g. α = .05), then he can reject the null hypothesis and conclude that the new drug leads to reduced blood pressure.
Example 3: Advertising Spend
Hypothesis tests are often used in business to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales.
For example, suppose a company believes that spending more money on digital advertising leads to increased sales. To test this, the company may increase money spent on digital advertising during a two-month period and collect data to see if overall sales have increased.
They may perform a hypothesis test using the following hypotheses:
- H 0 : μ after = μ before (the mean sales is the same before and after spending more on advertising)
- H A : μ after > μ before (the mean sales increased after spending more on advertising)
If the p-value of the test is less than some significance level (e.g. α = .05), then the company can reject the null hypothesis and conclude that increased digital advertising leads to increased sales.
Example 4: Manufacturing
Hypothesis tests are also used often in manufacturing plants to determine if some new process, technique, method, etc. causes a change in the number of defective products produced.
For example, suppose a certain manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, they may measure the mean number of defective widgets produced before and after using the new method for one month.
They can then perform a hypothesis test using the following hypotheses:
- H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
- H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)
If the p-value of the test is less than some significance level (e.g. α = .05), then the plant can reject the null hypothesis and conclude that the new method leads to a change in the number of defective widgets produced per month.
Additional Resources
Introduction to Hypothesis Testing Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Hypothesis Testing: Uses, Steps & Example
By Jim Frost 4 Comments
What is Hypothesis Testing?
Hypothesis testing in statistics uses sample data to infer the properties of a whole population . These tests determine whether a random sample provides sufficient evidence to conclude an effect or relationship exists in the population. Researchers use them to help separate genuine population-level effects from false effects that random chance can create in samples. These methods are also known as significance testing.

For example, researchers are testing a new medication to see if it lowers blood pressure. They compare a group taking the drug to a control group taking a placebo. If their hypothesis test results are statistically significant, the medication’s effect of lowering blood pressure likely exists in the broader population, not just the sample studied.
Using Hypothesis Tests
A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement the sample data best supports. These two statements are called the null hypothesis and the alternative hypothesis . The following are typical examples:
- Null Hypothesis : The effect does not exist in the population.
- Alternative Hypothesis : The effect does exist in the population.
Hypothesis testing accounts for the inherent uncertainty of using a sample to draw conclusions about a population, which reduces the chances of false discoveries. These procedures determine whether the sample data are sufficiently inconsistent with the null hypothesis that you can reject it. If you can reject the null, your data favor the alternative statement that an effect exists in the population.
Statistical significance in hypothesis testing indicates that an effect you see in sample data also likely exists in the population after accounting for random sampling error , variability, and sample size. Your results are statistically significant when the p-value is less than your significance level or, equivalently, when your confidence interval excludes the null hypothesis value.
Conversely, non-significant results indicate that despite an apparent sample effect, you can’t be sure it exists in the population. It could be chance variation in the sample and not a genuine effect.
Learn more about Failing to Reject the Null .
5 Steps of Significance Testing
Hypothesis testing involves five key steps, each critical to validating a research hypothesis using statistical methods:
- Formulate the Hypotheses : Write your research hypotheses as a null hypothesis (H 0 ) and an alternative hypothesis (H A ).
- Data Collection : Gather data specifically aimed at testing the hypothesis.
- Conduct A Test : Use a suitable statistical test to analyze your data.
- Make a Decision : Based on the statistical test results, decide whether to reject the null hypothesis or fail to reject it.
- Report the Results : Summarize and present the outcomes in your report’s results and discussion sections.
While the specifics of these steps can vary depending on the research context and the data type, the fundamental process of hypothesis testing remains consistent across different studies.
Let’s work through these steps in an example!
Hypothesis Testing Example
Researchers want to determine if a new educational program improves student performance on standardized tests. They randomly assign 30 students to a control group , which follows the standard curriculum, and another 30 students to a treatment group, which participates in the new educational program. After a semester, they compare the test scores of both groups.
Download the CSV data file to perform the hypothesis testing yourself: Hypothesis_Testing .
The researchers write their hypotheses. These statements apply to the population, so they use the mu (μ) symbol for the population mean parameter .
- Null Hypothesis (H 0 ) : The population means of the test scores for the two groups are equal (μ 1 = μ 2 ).
- Alternative Hypothesis (H A ) : The population means of the test scores for the two groups are unequal (μ 1 ≠ μ 2 ).
Choosing the correct hypothesis test depends on attributes such as data type and number of groups. Because they’re using continuous data and comparing two means, the researchers use a 2-sample t-test .
Here are the results.

The treatment group’s mean is 58.70, compared to the control group’s mean of 48.12. The mean difference is 10.67 points. Use the test’s p-value and significance level to determine whether this difference is likely a product of random fluctuation in the sample or a genuine population effect.
Because the p-value (0.000) is less than the standard significance level of 0.05, the results are statistically significant, and we can reject the null hypothesis. The sample data provides sufficient evidence to conclude that the new program’s effect exists in the population.
Limitations
Hypothesis testing improves your effectiveness in making data-driven decisions. However, it is not 100% accurate because random samples occasionally produce fluky results. Hypothesis tests have two types of errors, both relating to drawing incorrect conclusions.
- Type I error: The test rejects a true null hypothesis—a false positive.
- Type II error: The test fails to reject a false null hypothesis—a false negative.
Learn more about Type I and Type II Errors .
Our exploration of hypothesis testing using a practical example of an educational program reveals its powerful ability to guide decisions based on statistical evidence. Whether you’re a student, researcher, or professional, understanding and applying these procedures can open new doors to discovering insights and making informed decisions. Let this tool empower your analytical endeavors as you navigate through the vast seas of data.
Learn more about the Hypothesis Tests for Various Data Types .
Share this:

Reader Interactions
June 10, 2024 at 10:51 am
Thank you, Jim, for another helpful article; timely too since I have started reading your new book on hypothesis testing and, now that we are at the end of the school year, my district is asking me to perform a number of evaluations on instructional programs. This is where my question/concern comes in. You mention that hypothesis testing is all about testing samples. However, I use all the students in my district when I make these comparisons. Since I am using the entire “population” in my evaluations (I don’t select a sample of third grade students, for example, but I use all 700 third graders), am I somehow misusing the tests? Or can I rest assured that my district’s student population is only a sample of the universal population of students?
June 10, 2024 at 1:50 pm
I hope you are finding the book helpful!
Yes, the purpose of hypothesis testing is to infer the properties of a population while accounting for random sampling error.
In your case, it comes down to how you want to use the results. Who do you want the results to apply to?
If you’re summarizing the sample, looking for trends and patterns, or evaluating those students and don’t plan to apply those results to other students, you don’t need hypothesis testing because there is no sampling error. They are the population and you can just use descriptive statistics. In this case, you’d only need to focus on the practical significance of the effect sizes.
On the other hand, if you want to apply the results from this group to other students, you’ll need hypothesis testing. However, there is the complicating issue of what population your sample of students represent. I’m sure your district has its own unique characteristics, demographics, etc. Your district’s students probably don’t adequately represent a universal population. At the very least, you’d need to recognize any special attributes of your district and how they could bias the results when trying to apply them outside the district. Or they might apply to similar districts in your region.
However, I’d imagine your 3rd graders probably adequately represent future classes of 3rd graders in your district. You need to be alert to changing demographics. At least in the short run I’d imagine they’d be representative of future classes.
Think about how these results will be used. Do they just apply to the students you measured? Then you don’t need hypothesis tests. However, if the results are being used to infer things about other students outside of the sample, you’ll need hypothesis testing along with considering how well your students represent the other students and how they differ.
I hope that helps!
June 10, 2024 at 3:21 pm
Thank you so much, Jim, for the suggestions in terms of what I need to think about and consider! You are always so clear in your explanations!!!!
June 10, 2024 at 3:22 pm
You’re very welcome! Best of luck with your evaluations!
Comments and Questions Cancel reply
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 12: Significance tests (hypothesis testing)
About this unit.
Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.
The idea of significance tests
- Simple hypothesis testing (Opens a modal)
- Idea behind hypothesis testing (Opens a modal)
- Examples of null and alternative hypotheses (Opens a modal)
- P-values and significance tests (Opens a modal)
- Comparing P-values to different significance levels (Opens a modal)
- Estimating a P-value from a simulation (Opens a modal)
- Using P-values to make conclusions (Opens a modal)
- Simple hypothesis testing Get 3 of 4 questions to level up!
- Writing null and alternative hypotheses Get 3 of 4 questions to level up!
- Estimating P-values from simulations Get 3 of 4 questions to level up!
Error probabilities and power
- Introduction to Type I and Type II errors (Opens a modal)
- Type 1 errors (Opens a modal)
- Examples identifying Type I and Type II errors (Opens a modal)
- Introduction to power in significance tests (Opens a modal)
- Examples thinking about power in significance tests (Opens a modal)
- Consequences of errors and significance (Opens a modal)
- Type I vs Type II error Get 3 of 4 questions to level up!
- Error probabilities and power Get 3 of 4 questions to level up!
Tests about a population proportion
- Constructing hypotheses for a significance test about a proportion (Opens a modal)
- Conditions for a z test about a proportion (Opens a modal)
- Reference: Conditions for inference on a proportion (Opens a modal)
- Calculating a z statistic in a test about a proportion (Opens a modal)
- Calculating a P-value given a z statistic (Opens a modal)
- Making conclusions in a test about a proportion (Opens a modal)
- Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
- Conditions for a z test about a proportion Get 3 of 4 questions to level up!
- Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
- Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
- Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!
Tests about a population mean
- Writing hypotheses for a significance test about a mean (Opens a modal)
- Conditions for a t test about a mean (Opens a modal)
- Reference: Conditions for inference on a mean (Opens a modal)
- When to use z or t statistics in significance tests (Opens a modal)
- Example calculating t statistic for a test about a mean (Opens a modal)
- Using TI calculator for P-value from t statistic (Opens a modal)
- Using a table to estimate P-value from t statistic (Opens a modal)
- Comparing P-value from t statistic to significance level (Opens a modal)
- Free response example: Significance test for a mean (Opens a modal)
- Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
- Conditions for a t test about a mean Get 3 of 4 questions to level up!
- Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
- Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
- Making conclusions in a t test for a mean Get 3 of 4 questions to level up!
More significance testing videos
- Hypothesis testing and p-values (Opens a modal)
- One-tailed and two-tailed tests (Opens a modal)
- Z-statistics vs. T-statistics (Opens a modal)
- Small sample hypothesis test (Opens a modal)
- Large sample proportion hypothesis testing (Opens a modal)
Hypothesis Testing
Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.
A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. |
What is Hypothesis Testing in Statistics?
Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.
Hypothesis Testing Definition
Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.
Null Hypothesis
The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.
Alternative Hypothesis
The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.
Hypothesis Testing P Value
In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.
Hypothesis Testing Critical region
All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.
Hypothesis Testing Formula
Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:
- z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
- t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
- \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.
We will learn more about these test statistics in the upcoming section.
Types of Hypothesis Testing
Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.
Hypothesis Testing Z Test
A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:
- One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
- Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).
Hypothesis Testing t Test
The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.
- One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
- Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).
Hypothesis Testing Chi Square
The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.
One Tailed Hypothesis Testing
One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.
Right Tailed Hypothesis Testing
The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:
\(H_{0}\): The population parameter is ≤ some value
\(H_{1}\): The population parameter is > some value.
If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing
The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:
\(H_{0}\): The population parameter is ≥ some value
\(H_{1}\): The population parameter is < some value.
The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing
In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:
\(H_{0}\): the population parameter = some value
\(H_{1}\): the population parameter ≠ some value
The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps
Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:
- Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
- Step 2: Set up the alternative hypothesis.
- Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
- Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
- Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.
Hypothesis Testing Example
The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.
Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.
Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.
Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.
1 - \(\alpha\) = 1 - 0.05 = 0.95
0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.
Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.
z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15
z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56
Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.
Hypothesis Testing and Confidence Intervals
Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.
Related Articles:
- Probability and Statistics
- Data Handling
Important Notes on Hypothesis Testing
- Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
- It involves the setting up of a null hypothesis and an alternate hypothesis.
- There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
- Hypothesis testing can be classified as right tail, left tail, and two tail tests.
Examples on Hypothesis Testing
- Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
- Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
- Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.
go to slide go to slide go to slide

Book a Free Trial Class
FAQs on Hypothesis Testing
What is hypothesis testing.
Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.
What is the z Test in Hypothesis Testing?
The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.
What is the t Test in Hypothesis Testing?
The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.
What is the formula for z test in Hypothesis Testing?
The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).
What is the p Value in Hypothesis Testing?
The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.
What is One Tail Hypothesis Testing?
When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.
What is the Alpha Level in Two Tail Hypothesis Testing?
To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.
9.4 Full Hypothesis Test Examples
Tests on means, example 9.8.
Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05. Assume that the swim times for the 25-yard freestyle are normal.
Set up the Hypothesis Test:
Since the problem is about a mean, this is a test of a single population mean .
H 0 : μ = 16.43 H a : μ < 16.43
For Jeffrey to swim faster, his time will be less than 16.43 seconds. The "<" tells you this is left-tailed.
Determine the distribution needed:
Random variable: X ¯ X ¯ = the mean time to swim the 25-yard freestyle.
Distribution for the test: X ¯ X ¯ is normal (population standard deviation is known: σ = 0.8)
X ¯ ~ N ( μ , σ X n ) X ¯ ~ N ( μ , σ X n ) Therefore, X ¯ ~ N ( 16.43 , 0.8 15 ) X ¯ ~ N ( 16.43 , 0.8 15 )
μ = 16.43 comes from H 0 and not the data. σ = 0.8, and n = 15.
Calculate the p -value using the normal distribution for a mean:
p -value = P ( x ¯ x ¯ < 16) = 0.0187 where the sample mean in the problem is given as 16.
p -value = 0.0187 (This is called the actual level of significance .) The p -value is the area to the left of the sample mean is given as 16.
μ = 16.43 comes from H 0 . Our assumption is μ = 16.43.
Interpretation of the p -value: If H 0 is true , there is a 0.0187 probability (1.87%)that Jeffrey's mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It is a rare event.
Compare α and the p -value:
α = 0.05 p -value = 0.0187 α > p -value
Make a decision: Since α > α > p -value, reject H 0 .
This indicates that you reject the null hypothesis that the mean time to swim the 25-yard freestyle is at least 16.43 seconds.
Conclusion: At the 5% significance level, there is sufficient evidence that Jeffrey's mean time to swim the 25-yard freestyle is less than 16.43 seconds. Thus, based on the sample data, we conclude that Jeffrey swims faster using the new goggles.
The Type I and Type II errors for this problem are as follows: The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in at least 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)
The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)
The mean throwing distance of a football for Marco, a high school quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.
First, determine what type of test this is, set up the hypothesis test, find the p -value, sketch the graph, and state your conclusion.
Example 9.9
Jasmine has just begun her new job on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least 100 dollars against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jasmine has met this requirement at the significance level of 95%?
- H 0 : µ ≤ 100 H a : µ > 100 The null and alternative hypothesis are for the parameter µ because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.
- Test statistic: t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67 t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67
- Critical value: t a = 1.753 t a = 1.753 with n-1 degrees of freedom= 15
The test statistic is a Student's t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t t ( t a ) ( t a ) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jasmine's performance meets company standards.
It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, state your conclusion, and identify the Type I errors.
Example 9.10
A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, s 2 s 2 . Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of significance in the analysis should be 99%.
Again we will follow the steps in our analysis of this problem.
STEP 1 : Set the Null and Alternative Hypothesis. The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:
STEP 2 : Decide the level of significance and draw the graph showing the critical value.
This problem has already set the level of significance at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because this is a continuous random variable and we are interested in the mean, and the sample size is greater than 30, the appropriate distribution is the normal distribution and the relevant critical value is 2.575 from the normal table or the t-table at 0.005 column and infinite degrees of freedom. We draw the graph and mark these points.
STEP 3 : Calculate sample parameters and the test statistic. The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, s, is 0.173. With this information we calculate the test statistic as -3.07, and mark it on the graph.
STEP 4 : Compare test statistic and the critical values Now we compare the test statistic and the critical value by placing the test statistic on the graph. We see that the test statistic is in the tail, decidedly greater than the critical value of 2.575. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard deviations. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3 plus standard deviations away and thus we cannot accept the null hypothesis.
STEP 5 : Reach a Conclusion
Three standard deviations of a test statistic will guarantee that the test will fail. The probability that anything is within three standard deviations is almost zero. Actually it is 0.0026 on the normal distribution, which is certainly almost zero in a practical sense. Our formal conclusion would be “ At a 99% level of significance we cannot accept the hypothesis that the sample mean came from a distribution with a mean of 8 ounces” Or less formally, and getting to the point, “At a 99% level of significance we conclude that the machine is under filling the bottles and is in need of repair”.
Try It 9.10
A company records the mean time of employees working in a day. The mean comes out to be 475 minutes, with a standard deviation of 45 minutes. A manager recorded times of 20 employees. The times of working were (frequencies are in parentheses) 460(3); 465(2); 470(3); 475(1); 480(6); 485(3); 490(2).
Conduct a hypothesis test using a 2.5% level of significance to determine if the mean time is more than 475 .
Hypothesis Test for Proportions
Just as there were confidence intervals for proportions, or more formally, the population parameter p of the binomial distribution, there is the ability to test hypotheses concerning p .
The population parameter for the binomial is p . The estimated value (point estimate) for p is p′ where p′ = x/n , x is the number of successes in the sample and n is the sample size.
When you perform a hypothesis test of a population proportion p , you take a simple random sample from the population. The conditions for a binomial distribution must be met, which are: there are a certain number n of independent trials meaning random sampling, the outcomes of any trial are binary, success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np′ and nq′ must both be greater than five ( np′ > 5 and nq′ > 5). In this case the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = np μ = np and σ = npq σ = npq . Remember that q = 1 – p q = 1 – p . There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we first were estimating confidence intervals for p .
Again, we begin with the standardizing formula modified because this is the distribution of a binomial.
Substituting p 0 p 0 , the hypothesized value of p , we have:
This is the test statistic for testing hypothesized values of p , where the null and alternative hypotheses take one of the following forms:
| Two-tailed test | One-tailed test | One-tailed test |
|---|---|---|
| H : p = p | H : p ≤ p | H : p ≥ p |
| H : p ≠ p | H : p > p | H : p < p |
The decision rule stated above applies here also: if the calculated value of Z c shows that the sample proportion is "too many" standard deviations from the hypothesized proportion, the null hypothesis cannot be accepted. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.
Example 9.11
The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is the same or different from 50% . They sample 100 first-time borrowers and find 53 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.
STEP 1 : Set the null and alternative hypothesis.
H 0 : p = 0.50 H a : p ≠ 0.50
The words "is the same or different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)
STEP 2 : Decide the level of significance and draw the graph showing the critical value
The level of significance has been set by the problem at the 5% level. Because this is two-tailed test one-half of the alpha value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the student’s t-table at the very bottom at infinite degrees of freedom remembering that at infinity the t-distribution is the normal distribution. Of course the value can also be found on the normal table but you have go looking for one-half of 95 (0.475) inside the body of the table and then read out to the sides and top for the number of standard deviations.
STEP 3 : Calculate the sample parameters and critical value of the test statistic.
The test statistic is a normal distribution, Z, for testing proportions and is:
For this case, the sample of 100 found 53 of these loans were smaller than those of other borrowers. The sample proportion, p′ = 53/100= 0.53 The test question, therefore, is : “Is 0.53 significantly different from .50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard deviations away from .50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard deviations.
STEP 4 : Compare the test statistic and the critical value.
The calculated value is well within the critical values of ± 1.96 standard deviations and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evident of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard deviations.
STEP 5 : Reach a conclusion
The formal conclusion would be “At a 5% level of significance we cannot reject the null hypothesis that 50% of first-time borrowers take out smaller loans than other borrowers.” Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians, for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know, and the data constrain the conclusion to be within the metes and bounds of the data.
Try It 9.11
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. The teacher performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
Example 9.12
Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.
Here is an abbreviate version of the system to solve hypothesis tests applied to a test on a proportions.
Try It 9.12
Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.
Example 9.13
The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.
1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98; 1.02; .95; .95 Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05.
Let’s follow a four-step process to answer this statistical question.
- H 0 : μ ≤ 1
- H a : μ > 1
- Plan : We are testing a sample mean without a known population standard deviation with less than 30 observations. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
- Do the calculations and draw the graph .
- State the Conclusions : We cannot accept the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.
Try It 9.13
The boiling point of a specific liquid is measured for 15 samples, and the boiling points are obtained as follows:
205; 206; 206; 202; 199; 194; 197; 198; 198; 201; 201; 202; 207; 211; 205
Is there convincing evidence that the average boiling point is greater than 200? Use a significance level of 0.1. Assume the population is normal.

Example 9.14
In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
- H 0 : p ≤ 0.00034
- H a : p > 0.00034
If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.
- We will be testing a sample proportion with x = 172 and n = 420,019. The sample is sufficiently large because we have np' = 420,019(0.00034) = 142.8, nq' = 420,019(0.99966) = 419,876.2, two independent outcomes, and a fixed probability of success p' = 0.00034. Thus we will be able to generalize our results to the population.
Try It 9.14
In a study of 390,000 moisturizer users, 138 of the subjects developed skin diseases. Test the claim that moisturizer users developed skin diseases at a greater rate than that for non-moisturizer users (the rate of skin diseases for non-moisturizer users is 0.041%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-business-statistics-2e/pages/1-introduction
- Authors: Alexander Holmes, Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Business Statistics 2e
- Publication date: Dec 13, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-business-statistics-2e/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-business-statistics-2e/pages/9-4-full-hypothesis-test-examples
© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
11 Hypothesis Testing with One Sample
Student learning outcomes.
By the end of this chapter, the student should be able to:
- Be able to identify and develop the null and alternative hypothesis
- Identify the consequences of Type I and Type II error.
- Be able to perform an one-tailed and two-tailed hypothesis test using the critical value method
- Be able to perform a hypothesis test using the p-value method
- Be able to write conclusions based on hypothesis tests.
Introduction
Now we are down to the bread and butter work of the statistician: developing and testing hypotheses. It is important to put this material in a broader context so that the method by which a hypothesis is formed is understood completely. Using textbook examples often clouds the real source of statistical hypotheses.
Statistical testing is part of a much larger process known as the scientific method. This method was developed more than two centuries ago as the accepted way that new knowledge could be created. Until then, and unfortunately even today, among some, “knowledge” could be created simply by some authority saying something was so, ipso dicta . Superstition and conspiracy theories were (are?) accepted uncritically.
The scientific method, briefly, states that only by following a careful and specific process can some assertion be included in the accepted body of knowledge. This process begins with a set of assumptions upon which a theory, sometimes called a model, is built. This theory, if it has any validity, will lead to predictions; what we call hypotheses.
As an example, in Microeconomics the theory of consumer choice begins with certain assumption concerning human behavior. From these assumptions a theory of how consumers make choices using indifference curves and the budget line. This theory gave rise to a very important prediction, namely, that there was an inverse relationship between price and quantity demanded. This relationship was known as the demand curve. The negative slope of the demand curve is really just a prediction, or a hypothesis, that can be tested with statistical tools.
Unless hundreds and hundreds of statistical tests of this hypothesis had not confirmed this relationship, the so-called Law of Demand would have been discarded years ago. This is the role of statistics, to test the hypotheses of various theories to determine if they should be admitted into the accepted body of knowledge; how we understand our world. Once admitted, however, they may be later discarded if new theories come along that make better predictions.
Not long ago two scientists claimed that they could get more energy out of a process than was put in. This caused a tremendous stir for obvious reasons. They were on the cover of Time and were offered extravagant sums to bring their research work to private industry and any number of universities. It was not long until their work was subjected to the rigorous tests of the scientific method and found to be a failure. No other lab could replicate their findings. Consequently they have sunk into obscurity and their theory discarded. It may surface again when someone can pass the tests of the hypotheses required by the scientific method, but until then it is just a curiosity. Many pure frauds have been attempted over time, but most have been found out by applying the process of the scientific method.
This discussion is meant to show just where in this process statistics falls. Statistics and statisticians are not necessarily in the business of developing theories, but in the business of testing others’ theories. Hypotheses come from these theories based upon an explicit set of assumptions and sound logic. The hypothesis comes first, before any data are gathered. Data do not create hypotheses; they are used to test them. If we bear this in mind as we study this section the process of forming and testing hypotheses will make more sense.
One job of a statistician is to make statistical inferences about populations based on samples taken from the population. Confidence intervals are one way to estimate a population parameter. Another way to make a statistical inference is to make a decision about the value of a specific parameter. For instance, a car dealer advertises that its new small truck gets 35 miles per gallon, on average. A tutoring service claims that its method of tutoring helps 90% of its students get an A or a B. A company says that women managers in their company earn an average of $60,000 per year.
A statistician will make a decision about these claims. This process is called ” hypothesis testing .” A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analyses of the data, to reject the null hypothesis.
In this chapter, you will conduct hypothesis tests on single means and single proportions. You will also learn about the errors associated with these tests.
Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
Table 1 presents the various hypotheses in the relevant pairs. For example, if the null hypothesis is equal to some value, the alternative has to be not equal to that value.
| equal (=) | not equal (≠) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
NOTE
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
Outcomes and the Type I and Type II Errors
| True | False | |
| Correct Outcome | Type II error | |
| Type I Error | Correct Outcome |
The four possible outcomes in the table are:
Each of the errors occurs with a particular probability. The Greek letters α and β represent the probabilities.
By way of example, the American judicial system begins with the concept that a defendant is “presumed innocent”. This is the status quo and is the null hypothesis. The judge will tell the jury that they can not find the defendant guilty unless the evidence indicates guilt beyond a “reasonable doubt” which is usually defined in criminal cases as 95% certainty of guilt. If the jury cannot accept the null, innocent, then action will be taken, jail time. The burden of proof always lies with the alternative hypothesis. (In civil cases, the jury needs only to be more than 50% certain of wrongdoing to find culpability, called “a preponderance of the evidence”).
The example above was for a test of a mean, but the same logic applies to tests of hypotheses for all statistical parameters one may wish to test.
The following are examples of Type I and Type II errors.
Type I error : Frank thinks that his rock climbing equipment may not be safe when, in fact, it really is safe.
Type II error : Frank thinks that his rock climbing equipment may be safe when, in fact, it is not safe.
Notice that, in this case, the error with the greater consequence is the Type II error. (If Frank thinks his rock climbing equipment is safe, he will go ahead and use it.)
This is a situation described as “accepting a false null”.
Type I error : The emergency crew thinks that the victim is dead when, in fact, the victim is alive. Type II error : The emergency crew does not know if the victim is alive when, in fact, the victim is dead.
The error with the greater consequence is the Type I error. (If the emergency crew thinks the victim is dead, they will not treat him.)
Distribution Needed for Hypothesis Testing
Particular distributions are associated with hypothesis testing.We will perform hypotheses tests of a population mean using a normal distribution or a Student’s t -distribution. (Remember, use a Student’s t -distribution when the population standard deviation is unknown and the sample size is small, where small is considered to be less than 30 observations.) We perform tests of a population proportion using a normal distribution when we can assume that the distribution is normally distributed. We consider this to be true if the sample proportion, p ‘ , times the sample size is greater than 5 and 1- p ‘ times the sample size is also greater then 5. This is the same rule of thumb we used when developing the formula for the confidence interval for a population proportion.
Hypothesis Test for the Mean
Going back to the standardizing formula we can derive the test statistic for testing hypotheses concerning means.
This gives us the decision rule for testing a hypothesis for a two-tailed test:
| If |
| If |
P-Value Approach
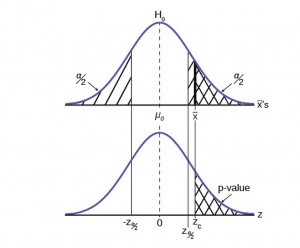
Both decision rules will result in the same decision and it is a matter of preference which one is used.
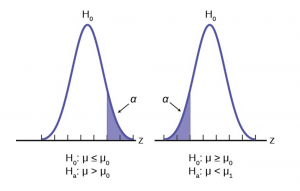
One and Two-tailed Tests
The claim would be in the alternative hypothesis. The burden of proof in hypothesis testing is carried in the alternative. This is because failing to reject the null, the status quo, must be accomplished with 90 or 95 percent significance that it cannot be maintained. Said another way, we want to have only a 5 or 10 percent probability of making a Type I error, rejecting a good null; overthrowing the status quo.
Figure 5 shows the two possible cases and the form of the null and alternative hypothesis that give rise to them.
Effects of Sample Size on Test Statistic
Table 3 summarizes test statistics for varying sample sizes and population standard deviation known and unknown.
| < 30 (σ unknown) | |
| < 30 (σ known) | |
| > 30 (σ unknown) | |
| > 30 (σ known) |
A Systematic Approach for Testing A Hypothesis
A systematic approach to hypothesis testing follows the following steps and in this order. This template will work for all hypotheses that you will ever test.
- Set up the null and alternative hypothesis. This is typically the hardest part of the process. Here the question being asked is reviewed. What parameter is being tested, a mean, a proportion, differences in means, etc. Is this a one-tailed test or two-tailed test? Remember, if someone is making a claim it will always be a one-tailed test.
- Decide the level of significance required for this particular case and determine the critical value. These can be found in the appropriate statistical table. The levels of confidence typical for the social sciences are 90, 95 and 99. However, the level of significance is a policy decision and should be based upon the risk of making a Type I error, rejecting a good null. Consider the consequences of making a Type I error.
- Take a sample(s) and calculate the relevant parameters: sample mean, standard deviation, or proportion. Using the formula for the test statistic from above in step 2, now calculate the test statistic for this particular case using the parameters you have just calculated.
- Compare the calculated test statistic and the critical value. Marking these on the graph will give a good visual picture of the situation. There are now only two situations:
a. The test statistic is in the tail: Cannot Accept the null, the probability that this sample mean (proportion) came from the hypothesized distribution is too small to believe that it is the real home of these sample data.
b. The test statistic is not in the tail: Cannot Reject the null, the sample data are compatible with the hypothesized population parameter.
- Reach a conclusion. It is best to articulate the conclusion two different ways. First a formal statistical conclusion such as “With a 95 % level of significance we cannot accept the null hypotheses that the population mean is equal to XX (units of measurement)”. The second statement of the conclusion is less formal and states the action, or lack of action, required. If the formal conclusion was that above, then the informal one might be, “The machine is broken and we need to shut it down and call for repairs”.
All hypotheses tested will go through this same process. The only changes are the relevant formulas and those are determined by the hypothesis required to answer the original question.
Full Hypothesis Test Examples
Tests on means.
Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey’s mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05.
Solution – Example 6
Set up the Hypothesis Test:
Since the problem is about a mean, this is a test of a single population mean . Set the null and alternative hypothesis:
In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95 % confidence. The null and alternative hypotheses are thus:
For Jeffrey to swim faster, his time will be less than 16.43 seconds. The “<” tells you this is left-tailed. Determine the distribution needed:
Distribution for the test statistic:
The sample size is less than 30 and we do not know the population standard deviation so this is a t-test and the proper formula is:
Our step 2, setting the level of significance, has already been determined by the problem, .05 for a 95 % significance level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffery’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.
To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t-test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t-distribution and mark the critical value (Figure 6). For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t-table we find 1.761. This is the critical value and we can put this on our graph.
Step 3 is the calculation of the test statistic using the formula we have selected.
We find that the calculated test statistic is 2.08, meaning that the sample mean is 2.08 standard deviations away from the hypothesized mean of 16.43.
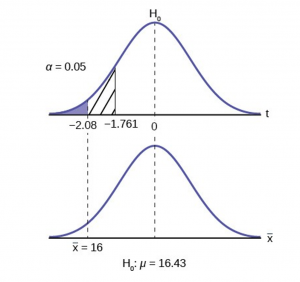
Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely for us to accept the null hypothesis. We cannot accept the null.
Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of significance we cannot accept the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% significance we believe that the goggles improves swimming speed”
If we wished to use the p-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard deviations from the mean on a t-distribution. This value is .0187. Comparing this to the α-level of .05 we see that we cannot accept the null. The p-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the alpha level of 0.05. Both methods reach the same conclusion that we cannot accept the null hypothesis.
Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of $108 with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least $100 against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 95%?
Solution – Example 7
STEP 1 : Set the Null and Alternative Hypothesis.
STEP 2 : Decide the level of significance and draw the graph (Figure 7) showing the critical value.
STEP 3 : Calculate sample parameters and the test statistic.
STEP 4 : Compare test statistic and the critical values
STEP 5 : Reach a Conclusion
The test statistic is a Student’s t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t ( t a ) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jane’s performance meets company standards.
Again we will follow the steps in our analysis of this problem.
Solution – Example 8
STEP 1 : Set the Null and Alternative Hypothesis. The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:
STEP 2 : Decide the level of significance and draw the graph showing the critical value.
This problem has already set the level of significance at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because this is a continuous random variable and we are interested in the mean, and the sample size is greater than 30, the appropriate distribution is the normal distribution and the relevant critical value is 2.575 from the normal table or the t-table at 0.005 column and infinite degrees of freedom. We draw the graph and mark these points (Figure 8).
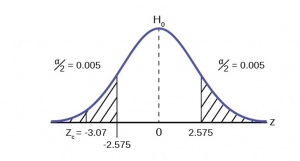
STEP 3 : Calculate sample parameters and the test statistic. The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, s, is 0.173. With this information we calculate the test statistic as -3.07, and mark it on the graph.
STEP 4 : Compare test statistic and the critical values Now we compare the test statistic and the critical value by placing the test statistic on the graph. We see that the test statistic is in the tail, decidedly greater than the critical value of 2.575. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard deviations. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3 plus standard deviations away and thus we cannot accept the null hypothesis.
Three standard deviations of a test statistic will guarantee that the test will fail. The probability that anything is within three standard deviations is almost zero. Actually it is 0.0026 on the normal distribution, which is certainly almost zero in a practical sense. Our formal conclusion would be “ At a 99% level of significance we cannot accept the hypothesis that the sample mean came from a distribution with a mean of 8 ounces” Or less formally, and getting to the point, “At a 99% level of significance we conclude that the machine is under filling the bottles and is in need of repair”.
Media Attributions
- Type1Type2Error
- HypTestFig2
- HypTestFig3
- HypTestPValue
- OneTailTestFig5
- HypTestExam7
- HypTestExam8
Quantitative Analysis for Business Copyright © by Margo Bergman is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
The Genius Blog
Hypothesis Testing Solved Examples(Questions and Solutions)
Here is a list hypothesis testing exercises and solutions. Try to solve a question by yourself first before you look at the solution.
Question 1 In the population, the average IQ is 100 with a standard deviation of 15. A team of scientists want to test a new medication to see if it has either a positive or negative effect on intelligence, or not effect at all. A sample of 30 participants who have taken the medication has a mean of 140. Did the medication affect intelligence? View Solution to Question 1
A professor wants to know if her introductory statistics class has a good grasp of basic math. Six students are chosen at random from the class and given a math proficiency test. The professor wants the class to be able to score above 70 on the test. The six students get the following scores:62, 92, 75, 68, 83, 95. Can the professor have 90% confidence that the mean score for the class on the test would be above 70. Solution to Question 2
Question 3 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.
| 42.1 | 42.7 |
| 41 | 43.6 |
| 41.3 | 43.8 |
| 41.8 | 43.3 |
| 42.4 | 42.5 |
| 42.8 | 43.5 |
| 43.2 | 43.1 |
| 42.3 | 41.7 |
| 41.8 | 44 |
| 42.7 | 44.1 |
Do the data provide sufficient evidence to conclude that, on the average, the new machine packs faster? Perform the required hypothesis test at the 5% level of significance. Solution to Question 3
Question 4 We want to compare the heights in inches of two groups of individuals. Here are the measurements: X: 175, 168, 168, 190, 156, 181, 182, 175, 174, 179 Y: 120, 180, 125, 188, 130, 190, 110, 185, 112, 188 Solution to Question 4
Question 5 A clinic provides a program to help their clients lose weight and asks a consumer agency to investigate the effectiveness of the program. The agency takes a sample of 15 people, weighing each person in the sample before the program begins and 3 months later. The results a tabulated below
Determine is the program is effective. Solution to Question 5
Question 6 A sample of 20 students were selected and given a diagnostic module prior to studying for a test. And then they were given the test again after completing the module. . The result of the students scores in the test before and after the test is tabulated below.
We want to see if there is significant improvement in the student’s performance due to this teaching method Solution to Question 6
Question 7 A study was performed to test wether cars get better mileage on premium gas than on regular gas. Each of 10 cars was first filled with regular or premium gas, decided by a coin toss, and the mileage for the tank was recorded. The mileage was recorded again for the same cars using other kind of gasoline. Determine wether cars get significantly better mileage with premium gas.
Mileage with regular gas: 16,20,21,22,23,22,27,25,27,28 Mileage with premium gas: 19, 22,24,24,25,25,26,26,28,32 Solution to Question 7
Question 8 An automatic cutter machine must cut steel strips of 1200 mm length. From a preliminary data, we checked that the lengths of the pieces produced by the machine can be considered as normal random variables with a 3mm standard deviation. We want to make sure that the machine is set correctly. Therefore 16 pieces of the products are randomly selected and weight. The figures were in mm: 1193,1196,1198,1195,1198,1199,1204,1193,1203,1201,1196,1200,1191,1196,1198,1191 Examine wether there is any significant deviation from the required size Solution to Question 8
Question 9 Blood pressure reading of ten patients before and after medication for reducing the blood pressure are as follows
Patient: 1,2,3,4,5,6,7,8,9,10 Before treatment: 86,84,78,90,92,77,89,90,90,86 After treatment: 80,80,92,79,92,82,88,89,92,83
Test the null hypothesis of no effect agains the alternate hypothesis that medication is effective. Execute it with Wilcoxon test Solution to Question 9
Question on ANOVA Sussan Sound predicts that students will learn most effectively with a constant background sound, as opposed to an unpredictable sound or no sound at all. She randomly divides 24 students into three groups of 8 each. All students study a passage of text for 30 minutes. Those in group 1 study with background sound at a constant volume in the background. Those in group 2 study with nose that changes volume periodically. Those in group 3 study with no sound at all. After studying, all students take a 10 point multiple choice test over the material. Their scores are tabulated below.
Group1: Constant sound: 7,4,6,8,6,6,2,9 Group 2: Random sound: 5,5,3,4,4,7,2,2 Group 3: No sound at all: 2,4,7,1,2,1,5,5 Solution to Question 10
Question 11 Using the following three groups of data, perform a one-way analysis of variance using α = 0.05.
| 51 | 23 | 56 |
| 45 | 43 | 76 |
| 33 | 23 | 74 |
| 45 | 43 | 87 |
| 67 | 45 | 56 |
Solution to Question 11
Question 12 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.
New Machine: 42,41,41.3,41.8,42.4,42.8,43.2,42.3,41.8,42.7 Old Machine: 42.7,43.6,43.8,43.3,42.5,43.5,43.1,41.7,44,44.1
Perform an F-test to determine if the null hypothesis should be accepted. Solution to Question 12
Question 13 A random sample 500 U.S adults are questioned about their political affiliation and opinion on a tax reform bill. We need to test if the political affiliation and their opinon on a tax reform bill are dependent, at 5% level of significance. The observed contingency table is given below.
| total | ||||
| 138 | 83 | 64 | 285 | |
| 64 | 67 | 84 | 215 | |
| total | 202 | 150 | 148 | 500 |
Solution to Question 13
Question 14 Can a dice be considered regular which is showing the following frequency distribution during 1000 throws?
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 182 | 154 | 162 | 175 | 151 | 176 |
Solution to Question 14
Solution to Question 15
Question 16 A newly developed muesli contains five types of seeds (A, B, C, D and E). The percentage of which is 35%, 25%, 20%, 10% and 10% according to the product information. In a randomly selected muesli, the following volume distribution was found.
| Component | A | B | C | D | E |
| Number of Pieces | 184 | 145 | 100 | 63 | 63 |
Lets us decide about the null hypothesis whether the composition of the sample corresponds to the distribution indicated on the packaging at alpha = 0.1 significance level. Solution to Question 16
Question 17 A research team investigated whether there was any significant correlation between the severity of a certain disease runoff and the age of the patients. During the study, data for n = 200 patients were collected and grouped according to the severity of the disease and the age of the patient. The table below shows the result
| 41 | 34 | 9 | ||
| 25 | 25 | 12 | ||
| 6 | 33 | 15 | ||
Let us decided about the correlation between the age of the patients and the severity of disease progression. Solution to Question 17
Question 18 A publisher is interested in determine which of three book cover is most attractive. He interviews 400 people in each of the three states (California, Illinois and New York), and asks each person which of the cover he or she prefers. The number of preference for each cover is as follows:
| 81 | 60 | 182 | 323 | |
| 78 | 93 | 95 | 266 | |
| 241 | 247 | 123 | 611 | |
| 400 | 400 | 400 | 1200 |
Do these data indicate that there are regional differences in people’s preferences concerning these covers? Use the 0.05 level of significance. Solution to Question 18
Question 19 Trees planted along the road were checked for which ones are healthy(H) or diseased (D) and the following arrangement of the trees were obtained:
H H H H D D D H H H H H H H D D H H D D D
Test at the = 0.05 significance wether this arrangement may be regarded as random
Solution to Question 19
Question 20 Suppose we flip a coin n = 15 times and come up with the following arrangements
H T T T H H T T T T H H T H H
(H = head, T = tail)
Test at the alpha = 0.05 significance level whether this arrangement may be regarded as random.
Solution to Question 20
kindsonthegenius
You might also like, one-way anova(analysis of variance) problem – question 11, chi-square goodness of fit test – question 16 ( a newly developed muesli…), how to perform mann-witney u test(step by step) – hypothesis testing.
I am really impressed with your writing abilities as well as with the structure to your weblog. Is this a paid subject matter or did you modify it yourself?
Either way stay up the excellent high quality writing, it’s uncommon to look a great blog like this one these days..
Below are given the gain in weights (in lbs.) of pigs fed on two diet A and B Dieta 25 32 30 34 24 14 32 24 30 31 35 25 – – DietB 44 34 22 10 47 31 40 30 32 35 18 21 35 29
- Business Essentials
- Leadership & Management
- Credential of Leadership, Impact, and Management in Business (CLIMB)
- Entrepreneurship & Innovation
- Digital Transformation
- Finance & Accounting
- Business in Society
- For Organizations
- Support Portal
- Media Coverage
- Founding Donors
- Leadership Team

- Harvard Business School →
- HBS Online →
- Business Insights →
Business Insights
Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.
- Career Development
- Communication
- Decision-Making
- Earning Your MBA
- Negotiation
- News & Events
- Productivity
- Staff Spotlight
- Student Profiles
- Work-Life Balance
- AI Essentials for Business
- Alternative Investments
- Business Analytics
- Business Strategy
- Business and Climate Change
- Design Thinking and Innovation
- Digital Marketing Strategy
- Disruptive Strategy
- Economics for Managers
- Entrepreneurship Essentials
- Financial Accounting
- Global Business
- Launching Tech Ventures
- Leadership Principles
- Leadership, Ethics, and Corporate Accountability
- Leading Change and Organizational Renewal
- Leading with Finance
- Management Essentials
- Negotiation Mastery
- Organizational Leadership
- Power and Influence for Positive Impact
- Strategy Execution
- Sustainable Business Strategy
- Sustainable Investing
- Winning with Digital Platforms
A Beginner’s Guide to Hypothesis Testing in Business

- 30 Mar 2021
Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.
If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.
Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.
Access your free e-book today.
What Is Hypothesis Testing?
To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.
A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”
Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.
Hypothesis Testing in Business
When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.
The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.
As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.
In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.
Related: 9 Fundamental Data Science Skills for Business Professionals
Key Considerations for Hypothesis Testing
1. alternative hypothesis and null hypothesis.
In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.
For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.
In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”
The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.
Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.
2. Significance Level and P-Value
Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.
In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.
3. One-Sided vs. Two-Sided Testing
When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.
Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

4. Sampling
To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.
A survey involves asking a series of questions to a random population sample and recording self-reported responses.
Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.
Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

Learn How to Perform Hypothesis Testing
Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.
If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.
Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- How to Write a Strong Hypothesis | Steps & Examples
How to Write a Strong Hypothesis | Steps & Examples
Published on May 6, 2022 by Shona McCombes . Revised on November 20, 2023.
A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection .
Example: Hypothesis
Daily apple consumption leads to fewer doctor’s visits.
Table of contents
What is a hypothesis, developing a hypothesis (with example), hypothesis examples, other interesting articles, frequently asked questions about writing hypotheses.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Variables in hypotheses
Hypotheses propose a relationship between two or more types of variables .
- An independent variable is something the researcher changes or controls.
- A dependent variable is something the researcher observes and measures.
If there are any control variables , extraneous variables , or confounding variables , be sure to jot those down as you go to minimize the chances that research bias will affect your results.
In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
Step 1. Ask a question
Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.
Step 2. Do some preliminary research
Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.
At this stage, you might construct a conceptual framework to ensure that you’re embarking on a relevant topic . This can also help you identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalize more complex constructs.
Step 3. Formulate your hypothesis
Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.
4. Refine your hypothesis
You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:
- The relevant variables
- The specific group being studied
- The predicted outcome of the experiment or analysis
5. Phrase your hypothesis in three ways
To identify the variables, you can write a simple prediction in if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable.
In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.
If you are comparing two groups, the hypothesis can state what difference you expect to find between them.
6. Write a null hypothesis
If your research involves statistical hypothesis testing , you will also have to write a null hypothesis . The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .
- H 0 : The number of lectures attended by first-year students has no effect on their final exam scores.
- H 1 : The number of lectures attended by first-year students has a positive effect on their final exam scores.
| Research question | Hypothesis | Null hypothesis |
|---|---|---|
| What are the health benefits of eating an apple a day? | Increasing apple consumption in over-60s will result in decreasing frequency of doctor’s visits. | Increasing apple consumption in over-60s will have no effect on frequency of doctor’s visits. |
| Which airlines have the most delays? | Low-cost airlines are more likely to have delays than premium airlines. | Low-cost and premium airlines are equally likely to have delays. |
| Can flexible work arrangements improve job satisfaction? | Employees who have flexible working hours will report greater job satisfaction than employees who work fixed hours. | There is no relationship between working hour flexibility and job satisfaction. |
| How effective is high school sex education at reducing teen pregnancies? | Teenagers who received sex education lessons throughout high school will have lower rates of unplanned pregnancy teenagers who did not receive any sex education. | High school sex education has no effect on teen pregnancy rates. |
| What effect does daily use of social media have on the attention span of under-16s? | There is a negative between time spent on social media and attention span in under-16s. | There is no relationship between social media use and attention span in under-16s. |
If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.
- Sampling methods
- Simple random sampling
- Stratified sampling
- Cluster sampling
- Likert scales
- Reproducibility
Statistics
- Null hypothesis
- Statistical power
- Probability distribution
- Effect size
- Poisson distribution
Research bias
- Optimism bias
- Cognitive bias
- Implicit bias
- Hawthorne effect
- Anchoring bias
- Explicit bias
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
McCombes, S. (2023, November 20). How to Write a Strong Hypothesis | Steps & Examples. Scribbr. Retrieved June 28, 2024, from https://www.scribbr.com/methodology/hypothesis/
Is this article helpful?
Shona McCombes
Other students also liked, construct validity | definition, types, & examples, what is a conceptual framework | tips & examples, operationalization | a guide with examples, pros & cons, "i thought ai proofreading was useless but..".
I've been using Scribbr for years now and I know it's a service that won't disappoint. It does a good job spotting mistakes”
- Bipolar Disorder
- Therapy Center
- When To See a Therapist
- Types of Therapy
- Best Online Therapy
- Best Couples Therapy
- Best Family Therapy
- Managing Stress
- Sleep and Dreaming
- Understanding Emotions
- Self-Improvement
- Healthy Relationships
- Student Resources
- Personality Types
- Guided Meditations
- Verywell Mind Insights
- 2024 Verywell Mind 25
- Mental Health in the Classroom
- Editorial Process
- Meet Our Review Board
- Crisis Support
How to Write a Great Hypothesis
Hypothesis Definition, Format, Examples, and Tips
Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
:max_bytes(150000):strip_icc():format(webp)/IMG_9791-89504ab694d54b66bbd72cb84ffb860e.jpg)
Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk, "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.
:max_bytes(150000):strip_icc():format(webp)/VW-MIND-Amy-2b338105f1ee493f94d7e333e410fa76.jpg)
Verywell / Alex Dos Diaz
- The Scientific Method
Hypothesis Format
Falsifiability of a hypothesis.
- Operationalization
Hypothesis Types
Hypotheses examples.
- Collecting Data
A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process.
Consider a study designed to examine the relationship between sleep deprivation and test performance. The hypothesis might be: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."
At a Glance
A hypothesis is crucial to scientific research because it offers a clear direction for what the researchers are looking to find. This allows them to design experiments to test their predictions and add to our scientific knowledge about the world. This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.
The Hypothesis in the Scientific Method
In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:
- Forming a question
- Performing background research
- Creating a hypothesis
- Designing an experiment
- Collecting data
- Analyzing the results
- Drawing conclusions
- Communicating the results
The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. At this point, researchers then begin to develop a testable hypothesis.
Unless you are creating an exploratory study, your hypothesis should always explain what you expect to happen.
In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.
Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore numerous factors to determine which ones might contribute to the ultimate outcome.
In many cases, researchers may find that the results of an experiment do not support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.
In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."
In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk adage that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."
Elements of a Good Hypothesis
So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:
- Is your hypothesis based on your research on a topic?
- Can your hypothesis be tested?
- Does your hypothesis include independent and dependent variables?
Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the journal articles you read . Many authors will suggest questions that still need to be explored.
How to Formulate a Good Hypothesis
To form a hypothesis, you should take these steps:
- Collect as many observations about a topic or problem as you can.
- Evaluate these observations and look for possible causes of the problem.
- Create a list of possible explanations that you might want to explore.
- After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.
In the scientific method , falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.
Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that if something was false, then it is possible to demonstrate that it is false.
One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.
The Importance of Operational Definitions
A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.
Operational definitions are specific definitions for all relevant factors in a study. This process helps make vague or ambiguous concepts detailed and measurable.
For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.
These precise descriptions are important because many things can be measured in various ways. Clearly defining these variables and how they are measured helps ensure that other researchers can replicate your results.
Replicability
One of the basic principles of any type of scientific research is that the results must be replicable.
Replication means repeating an experiment in the same way to produce the same results. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.
Some variables are more difficult than others to define. For example, how would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.
To measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming others. The researcher might utilize a simulated task to measure aggressiveness in this situation.
Hypothesis Checklist
- Does your hypothesis focus on something that you can actually test?
- Does your hypothesis include both an independent and dependent variable?
- Can you manipulate the variables?
- Can your hypothesis be tested without violating ethical standards?
The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:
- Simple hypothesis : This type of hypothesis suggests there is a relationship between one independent variable and one dependent variable.
- Complex hypothesis : This type suggests a relationship between three or more variables, such as two independent and dependent variables.
- Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
- Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
- Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative population sample and then generalizes the findings to the larger group.
- Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.
A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the dependent variable if you change the independent variable .
The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."
A few examples of simple hypotheses:
- "Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
- "Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."
- "Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."
- "Children who receive a new reading intervention will have higher reading scores than students who do not receive the intervention."
Examples of a complex hypothesis include:
- "People with high-sugar diets and sedentary activity levels are more likely to develop depression."
- "Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."
Examples of a null hypothesis include:
- "There is no difference in anxiety levels between people who take St. John's wort supplements and those who do not."
- "There is no difference in scores on a memory recall task between children and adults."
- "There is no difference in aggression levels between children who play first-person shooter games and those who do not."
Examples of an alternative hypothesis:
- "People who take St. John's wort supplements will have less anxiety than those who do not."
- "Adults will perform better on a memory task than children."
- "Children who play first-person shooter games will show higher levels of aggression than children who do not."
Collecting Data on Your Hypothesis
Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.
Descriptive Research Methods
Descriptive research such as case studies , naturalistic observations , and surveys are often used when conducting an experiment is difficult or impossible. These methods are best used to describe different aspects of a behavior or psychological phenomenon.
Once a researcher has collected data using descriptive methods, a correlational study can examine how the variables are related. This research method might be used to investigate a hypothesis that is difficult to test experimentally.
Experimental Research Methods
Experimental methods are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).
Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually cause another to change.
The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.
Thompson WH, Skau S. On the scope of scientific hypotheses . R Soc Open Sci . 2023;10(8):230607. doi:10.1098/rsos.230607
Taran S, Adhikari NKJ, Fan E. Falsifiability in medicine: what clinicians can learn from Karl Popper [published correction appears in Intensive Care Med. 2021 Jun 17;:]. Intensive Care Med . 2021;47(9):1054-1056. doi:10.1007/s00134-021-06432-z
Eyler AA. Research Methods for Public Health . 1st ed. Springer Publishing Company; 2020. doi:10.1891/9780826182067.0004
Nosek BA, Errington TM. What is replication ? PLoS Biol . 2020;18(3):e3000691. doi:10.1371/journal.pbio.3000691
Aggarwal R, Ranganathan P. Study designs: Part 2 - Descriptive studies . Perspect Clin Res . 2019;10(1):34-36. doi:10.4103/picr.PICR_154_18
Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.
By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
- Search Search Please fill out this field.
What Is Hypothesis Testing?
Step 1: define the hypothesis, step 2: set the criteria, step 3: calculate the statistic, step 4: reach a conclusion, types of errors, the bottom line.
- Trading Skills
- Trading Basic Education
Hypothesis Testing in Finance: Concept and Examples
Charlene Rhinehart is a CPA , CFE, chair of an Illinois CPA Society committee, and has a degree in accounting and finance from DePaul University.
:max_bytes(150000):strip_icc():format(webp)/CharleneRhinehartHeadshot-CharleneRhinehart-ca4b769506e94a92bc29e4acc6f0f9a5.jpg)
Your investment advisor proposes you a monthly income investment plan that promises a variable return each month. You will invest in it only if you are assured of an average $180 monthly income. Your advisor also tells you that for the past 300 months, the scheme had investment returns with an average value of $190 and a standard deviation of $75. Should you invest in this scheme? Hypothesis testing comes to the aid for such decision-making.
Key Takeaways
- Hypothesis testing is a mathematical tool for confirming a financial or business claim or idea.
- Hypothesis testing is useful for investors trying to decide what to invest in and whether the instrument is likely to provide a satisfactory return.
- Despite the existence of different methodologies of hypothesis testing, the same four steps are used: define the hypothesis, set the criteria, calculate the statistic, and reach a conclusion.
- This mathematical model, like most statistical tools and models, has limitations and is prone to certain errors, necessitating investors also considering other models in conjunction with this one
Hypothesis or significance testing is a mathematical model for testing a claim, idea or hypothesis about a parameter of interest in a given population set, using data measured in a sample set. Calculations are performed on selected samples to gather more decisive information about the characteristics of the entire population, which enables a systematic way to test claims or ideas about the entire dataset.
Here is a simple example: A school principal reports that students in their school score an average of 7 out of 10 in exams. To test this “hypothesis,” we record marks of say 30 students (sample) from the entire student population of the school (say 300) and calculate the mean of that sample. We can then compare the (calculated) sample mean to the (reported) population mean and attempt to confirm the hypothesis.
To take another example, the annual return of a particular mutual fund is 8%. Assume that mutual fund has been in existence for 20 years. We take a random sample of annual returns of the mutual fund for, say, five years (sample) and calculate its mean. We then compare the (calculated) sample mean to the (claimed) population mean to verify the hypothesis.
This article assumes readers' familiarity with concepts of a normal distribution table, formula, p-value and related basics of statistics.
Different methodologies exist for hypothesis testing, but the same four basic steps are involved:
Usually, the reported value (or the claim statistics) is stated as the hypothesis and presumed to be true. For the above examples, the hypothesis will be:
- Example A: Students in the school score an average of 7 out of 10 in exams.
- Example B: The annual return of the mutual fund is 8% per annum.
This stated description constitutes the “ Null Hypothesis (H 0 ) ” and is assumed to be true – the way a defendant in a jury trial is presumed innocent until proven guilty by the evidence presented in court. Similarly, hypothesis testing starts by stating and assuming a “ null hypothesis ,” and then the process determines whether the assumption is likely to be true or false.
The important point to note is that we are testing the null hypothesis because there is an element of doubt about its validity. Whatever information that is against the stated null hypothesis is captured in the Alternative Hypothesis (H 1 ). For the above examples, the alternative hypothesis will be:
- Students score an average that is not equal to 7.
- The annual return of the mutual fund is not equal to 8% per annum.
In other words, the alternative hypothesis is a direct contradiction of the null hypothesis.
As in a trial, the jury assumes the defendant's innocence (null hypothesis). The prosecutor has to prove otherwise (alternative hypothesis). Similarly, the researcher has to prove that the null hypothesis is either true or false. If the prosecutor fails to prove the alternative hypothesis, the jury has to let the defendant go (basing the decision on the null hypothesis). Similarly, if the researcher fails to prove an alternative hypothesis (or simply does nothing), then the null hypothesis is assumed to be true.
The decision-making criteria have to be based on certain parameters of datasets.
The decision-making criteria have to be based on certain parameters of datasets and this is where the connection to normal distribution comes into the picture.
As per the standard statistics postulate about sampling distribution , for any sample size n, the sampling distribution of X is normal if the X from which the sample is drawn is normally distributed. Hence, the probabilities of all other possible sample mean that one could select are normally distributed.
For e.g., determine if the average daily return, of any stock listed on XYZ stock market , around New Year's Day is greater than 2%.
H 0 : Null Hypothesis: mean = 2%
H 1 : Alternative Hypothesis: mean > 2% (this is what we want to prove)
Take the sample (say of 50 stocks out of total 500) and compute the mean of the sample.
For a normal distribution, 95% of the values lie within two standard deviations of the population mean. Hence, this normal distribution and central limit assumption for the sample dataset allows us to establish 5% as a significance level. It makes sense as, under this assumption, there is less than a 5% probability (100-95) of getting outliers that are beyond two standard deviations from the population mean. Depending upon the nature of datasets, other significance levels can be taken at 1%, 5% or 10%. For financial calculations (including behavioral finance), 5% is the generally accepted limit. If we find any calculations that go beyond the usual two standard deviations, then we have a strong case of outliers to reject the null hypothesis.
Graphically, it is represented as follows:
In the above example, if the mean of the sample is much larger than 2% (say 3.5%), then we reject the null hypothesis. The alternative hypothesis (mean >2%) is accepted, which confirms that the average daily return of the stocks is indeed above 2%.
However, if the mean of the sample is not likely to be significantly greater than 2% (and remains at, say, around 2.2%), then we CANNOT reject the null hypothesis. The challenge comes on how to decide on such close range cases. To make a conclusion from selected samples and results, a level of significance is to be determined, which enables a conclusion to be made about the null hypothesis. The alternative hypothesis enables establishing the level of significance or the "critical value” concept for deciding on such close range cases.
According to the textbook standard definition, “A critical value is a cutoff value that defines the boundaries beyond which less than 5% of sample means can be obtained if the null hypothesis is true. Sample means obtained beyond a critical value will result in a decision to reject the null hypothesis." In the above example, if we have defined the critical value as 2.1%, and the calculated mean comes to 2.2%, then we reject the null hypothesis. A critical value establishes a clear demarcation about acceptance or rejection.
This step involves calculating the required figure(s), known as test statistics (like mean, z-score , p-value , etc.), for the selected sample. (We'll get to these in a later section.)
With the computed value(s), decide on the null hypothesis. If the probability of getting a sample mean is less than 5%, then the conclusion is to reject the null hypothesis. Otherwise, accept and retain the null hypothesis.
There can be four possible outcomes in sample-based decision-making, with regard to the correct applicability to the entire population:
|
| |
| Correct | Incorrect (TYPE 1 Error - a) |
| Incorrect (TYPE 2 Error - b) | Correct |
The “Correct” cases are the ones where the decisions taken on the samples are truly applicable to the entire population. The cases of errors arise when one decides to retain (or reject) the null hypothesis based on the sample calculations, but that decision does not really apply for the entire population. These cases constitute Type 1 ( alpha ) and Type 2 ( beta ) errors, as indicated in the table above.
Selecting the correct critical value allows eliminating the type-1 alpha errors or limiting them to an acceptable range.
Alpha denotes the error on the level of significance and is determined by the researcher. To maintain the standard 5% significance or confidence level for probability calculations, this is retained at 5%.
According to the applicable decision-making benchmarks and definitions:
- “This (alpha) criterion is usually set at 0.05 (a = 0.05), and we compare the alpha level to the p-value. When the probability of a Type I error is less than 5% (p < 0.05), we decide to reject the null hypothesis; otherwise, we retain the null hypothesis.”
- The technical term used for this probability is the p-value . It is defined as “the probability of obtaining a sample outcome, given that the value stated in the null hypothesis is true. The p-value for obtaining a sample outcome is compared to the level of significance."
- A Type II error, or beta error, is defined as the probability of incorrectly retaining the null hypothesis, when in fact it is not applicable to the entire population.
A few more examples will demonstrate this and other calculations.
A monthly income investment scheme exists that promises variable monthly returns. An investor will invest in it only if they are assured of an average $180 monthly income. The investor has a sample of 300 months’ returns which has a mean of $190 and a standard deviation of $75. Should they invest in this scheme?
Let’s set up the problem. The investor will invest in the scheme if they are assured of the investor's desired $180 average return.
H 0 : Null Hypothesis: mean = 180
H 1 : Alternative Hypothesis: mean > 180
Method 1: Critical Value Approach
Identify a critical value X L for the sample mean, which is large enough to reject the null hypothesis – i.e. reject the null hypothesis if the sample mean >= critical value X L
P (identify a Type I alpha error) = P (reject H 0 given that H 0 is true),
This would be achieved when the sample mean exceeds the critical limits.
= P (given that H 0 is true) = alpha
Graphically, it appears as follows:
Taking alpha = 0.05 (i.e. 5% significance level), Z 0.05 = 1.645 (from the Z-table or normal distribution table)
= > X L = 180 +1.645*(75/sqrt(300)) = 187.12
Since the sample mean (190) is greater than the critical value (187.12), the null hypothesis is rejected, and the conclusion is that the average monthly return is indeed greater than $180, so the investor can consider investing in this scheme.
Method 2: Using Standardized Test Statistics
One can also use standardized value z.
Test Statistic, Z = (sample mean – population mean) / (std-dev / sqrt (no. of samples).
Then, the rejection region becomes the following:
Z= (190 – 180) / (75 / sqrt (300)) = 2.309
Our rejection region at 5% significance level is Z> Z 0.05 = 1.645.
Since Z= 2.309 is greater than 1.645, the null hypothesis can be rejected with a similar conclusion mentioned above.
Method 3: P-value Calculation
We aim to identify P (sample mean >= 190, when mean = 180).
= P (Z >= (190- 180) / (75 / sqrt (300))
= P (Z >= 2.309) = 0.0084 = 0.84%
The following table to infer p-value calculations concludes that there is confirmed evidence of average monthly returns being higher than 180:
p-value | Inference |
less than 1% | supporting alternative hypothesis |
between 1% and 5% | supporting alternative hypothesis |
between 5% and 10% | supporting alternative hypothesis |
greater than 10% | supporting alternative hypothesis |
A new stockbroker (XYZ) claims that their brokerage fees are lower than that of your current stock broker's (ABC). Data available from an independent research firm indicates that the mean and std-dev of all ABC broker clients are $18 and $6, respectively.
A sample of 100 clients of ABC is taken and brokerage charges are calculated with the new rates of XYZ broker. If the mean of the sample is $18.75 and std-dev is the same ($6), can any inference be made about the difference in the average brokerage bill between ABC and XYZ broker?
H 0 : Null Hypothesis: mean = 18
H 1 : Alternative Hypothesis: mean <> 18 (This is what we want to prove.)
Rejection region: Z <= - Z 2.5 and Z>=Z 2.5 (assuming 5% significance level, split 2.5 each on either side).
Z = (sample mean – mean) / (std-dev / sqrt (no. of samples))
= (18.75 – 18) / (6/(sqrt(100)) = 1.25
This calculated Z value falls between the two limits defined by:
- Z 2.5 = -1.96 and Z 2.5 = 1.96.
This concludes that there is insufficient evidence to infer that there is any difference between the rates of your existing broker and the new broker.
Alternatively, The p-value = P(Z< -1.25)+P(Z >1.25)
= 2 * 0.1056 = 0.2112 = 21.12% which is greater than 0.05 or 5%, leading to the same conclusion.
Graphically, it is represented by the following:
Criticism Points for the Hypothetical Testing Method:
- A statistical method based on assumptions
- Error-prone as detailed in terms of alpha and beta errors
- Interpretation of p-value can be ambiguous, leading to confusing results
Hypothesis testing allows a mathematical model to validate a claim or idea with a certain confidence level. However, like the majority of statistical tools and models, it is bound by a few limitations. The use of this model for making financial decisions should be considered with a critical eye, keeping all dependencies in mind. Alternate methods like Bayesian Inference are also worth exploring for similar analysis.
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 4-5.
Rice University, OpenStax. " Introductory Statistics 2e: 7.1 The Central Limit Theorem for Sample Means (Averages) ."
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 5-6.
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 13.
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 6.
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 6-7.
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 10.
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 11.
Gregory J. Privitera. " Chapter 8: Introduction to Hypothesis Testing ." Statistics for Behavioral Sciences, Part III: Probability and the Foundations of Inferential Statistics. Sage Publications , pp. 7, 10-11.
:max_bytes(150000):strip_icc():format(webp)/clearing.asp_final-9c343dd51008415295777bff228db769.png)
- Terms of Service
- Editorial Policy
- Privacy Policy
Perform Hypothesis testing with NumPy and SciPy's Stats module
Numpy: integration with scipy exercise-7 with solution.
Write a NumPy program to generate random samples and perform a hypothesis test using SciPy's stats module.
Sample Solution:
Python Code:
Explanation:
- Import necessary libraries:
- Import NumPy for generating random samples and SciPy's stats module for hypothesis testing.
- Generate two sets of random samples using NumPy:
- Create two normally distributed samples with different means (loc) but the same standard deviation (scale).
- Perform an independent t-test using SciPy's stats module:
- Use ttest_ind to perform a t-test to compare the means of the two samples.
- Print the results of the hypothesis test:
- Display the t-statistic and p-value to determine if there is a significant difference between the two samples.
Python-Numpy Code Editor:
Have another way to solve this solution? Contribute your code (and comments) through Disqus.
Previous: Fit a curve to sample data using NumPy and SciPy's curve_fit. Next: Ordinary differential equations with NumPy and SciPy.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
Follow us on Facebook and Twitter for latest update.
- Weekly Trends and Language Statistics

IMAGES
VIDEO
COMMENTS
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t* were less than -1.6939 (determined using statistical software or a t-table):s-3-3. Since the biologist's test statistic, t* = -4.60, is less than -1.6939, the biologist rejects the null hypothesis.
Present the findings in your results and discussion section. Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps. Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test.
In statistics, hypothesis tests are used to test whether or not some hypothesis about a population parameter is true. To perform a hypothesis test in the real world, researchers will obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:. Null Hypothesis (H 0): The sample data occurs purely from chance.
The treatment group's mean is 58.70, compared to the control group's mean of 48.12. The mean difference is 10.67 points. Use the test's p-value and significance level to determine whether this difference is likely a product of random fluctuation in the sample or a genuine population effect.. Because the p-value (0.000) is less than the standard significance level of 0.05, the results are ...
Example 3: Public Opinion About President Step 1. Determine the null and alternative hypotheses. Null hypothesis: There is no clear winning opinion on this issue; the proportions who would answer yes or no are each 0.50. Alternative hypothesis: Fewer than 0.50, or 50%, of the population would answer yes to this question.
Registered nurses earned an average annual salary of $69,110. For that same year, a survey was conducted of 41 California registered nurses to determine if the annual salary is higher than $69,110 for California nurses. The sample average was $71,121 with a sample standard deviation of $7,489. Conduct a hypothesis test.
Unit 12: Significance tests (hypothesis testing) Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values ...
Full Hypothesis Test Examples. Example 8.6.4 8.6. 4. Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71.
Test Statistic: z = x¯¯¯ −μo σ/ n−−√ z = x ¯ − μ o σ / n since it is calculated as part of the testing of the hypothesis. Definition 7.1.4 7.1. 4. p - value: probability that the test statistic will take on more extreme values than the observed test statistic, given that the null hypothesis is true.
where μ μ denotes the mean distance between the holes. Step 2. The sample is small and the population standard deviation is unknown. Thus the test statistic is. T = x¯ −μ0 s/ n−−√ T = x ¯ − μ 0 s / n. and has the Student t t -distribution with n − 1 = 4 − 1 = 3 n − 1 = 4 − 1 = 3 degrees of freedom. Step 3.
Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant. It involves the setting up of a null hypothesis and an alternate hypothesis. There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. The teacher performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
It tests the null hypothesis that the population variances are equal (called homogeneity of variance or homoscedasticity). Suppose the resulting p-value of Levene's test is less than the significance level (typically 0.05).In that case, the obtained differences in sample variances are unlikely to have occurred based on random sampling from a population with equal variances.
Full Hypothesis Test Examples Tests on Means. Example 6. Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds. His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles.
View Solution to Question 1. Question 2. A professor wants to know if her introductory statistics class has a good grasp of basic math. Six students are chosen at random from the class and given a math proficiency test. The professor wants the class to be able to score above 70 on the test. The six students get the following scores:62, 92, 75 ...
3. One-Sided vs. Two-Sided Testing. When it's time to test your hypothesis, it's important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests, or one-tailed and two-tailed tests, respectively. Typically, you'd leverage a one-sided test when you have a strong conviction ...
Developing a hypothesis (with example) Step 1. Ask a question. Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project. Example: Research question.
(A z-score and a t-score are examples of test statistics.) Compare the preconceived α with the p-value, make a decision (reject or do not reject H0), and write a clear conclusion. 10.7: Hypothesis Testing of a Single Mean and Single Proportion (Worksheet) A statistics Worksheet: The student will select the appropriate distributions to use in ...
The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset \(\alpha = 0.05\). Assume the throw distances for footballs are normal. First, determine what type of test this is, set up the hypothesis test, find the p-value, sketch the graph, and state your conclusion.
A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process. Consider a study designed to examine the relationship between sleep deprivation and test ...
9.1: Prelude to Hypothesis Testing. A statistician will make a decision about claims via a process called "hypothesis testing." A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analysis of the data, to reject ...
Hypothesis or significance testing is a mathematical model for testing a claim, idea or hypothesis about a parameter of interest in a given population set, using data measured in a sample set.
A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions. 10.5: Matched or Paired Samples When using a hypothesis test for matched or paired samples, the following characteristics should be present: Simple random sampling is used. Sample sizes are often small.
Create two normally distributed samples with different means (loc) but the same standard deviation (scale). Perform an independent t-test using SciPy's stats module: Use ttest_ind to perform a t-test to compare the means of the two samples. Print the results of the hypothesis test: Display the t-statistic and p-value to determine if there is a ...
8.1: Introduction to Two-Sample Tests; 8.2: Comparing Two Independent Population Means; 8.3: Cohen's Standards for Small, Medium, and Large Effect Sizes; 8.4: Test for Differences in Means- Assuming Equal Population Variances; 8.5: Comparing Two Independent Population Proportions; 8.6: Two Population Means with Known Standard Deviations