research paper statistics example

Purdue Online Writing Lab Purdue OWL® College of Liberal Arts

Writing with Descriptive Statistics

Welcome to the Purdue OWL

This page is brought to you by the OWL at Purdue University. When printing this page, you must include the entire legal notice.

Copyright ©1995-2018 by The Writing Lab & The OWL at Purdue and Purdue University. All rights reserved. This material may not be published, reproduced, broadcast, rewritten, or redistributed without permission. Use of this site constitutes acceptance of our terms and conditions of fair use.

Usually there is no good way to write a statistic. It rarely sounds good, and often interrupts the structure or flow of your writing. Oftentimes the best way to write descriptive statistics is to be direct. If you are citing several statistics about the same topic, it may be best to include them all in the same paragraph or section.

The mean of exam two is 77.7. The median is 75, and the mode is 79. Exam two had a standard deviation of 11.6.

Overall the company had another excellent year. We shipped 14.3 tons of fertilizer for the year, and averaged 1.7 tons of fertilizer during the summer months. This is an increase over last year, where we shipped only 13.1 tons of fertilizer, and averaged only 1.4 tons during the summer months. (Standard deviations were as followed: this summer .3 tons, last summer .4 tons).

Some fields prefer to put means and standard deviations in parentheses like this:

If you have lots of statistics to report, you should strongly consider presenting them in tables or some other visual form. You would then highlight statistics of interest in your text, but would not report all of the statistics. See the section on statistics and visuals for more details.

If you have a data set that you are using (such as all the scores from an exam) it would be unusual to include all of the scores in a paper or article. One of the reasons to use statistics is to condense large amounts of information into more manageable chunks; presenting your entire data set defeats this purpose.

At the bare minimum, if you are presenting statistics on a data set, it should include the mean and probably the standard deviation. This is the minimum information needed to get an idea of what the distribution of your data set might look like. How much additional information you include is entirely up to you. In general, don't include information if it is irrelevant to your argument or purpose. If you include statistics that many of your readers would not understand, consider adding the statistics in a footnote or appendix that explains it in more detail.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Indian J Anaesth
• v.60(9); 2016 Sep

Basic statistical tools in research and data analysis

Zulfiqar ali.

Department of Anaesthesiology, Division of Neuroanaesthesiology, Sheri Kashmir Institute of Medical Sciences, Soura, Srinagar, Jammu and Kashmir, India

S Bala Bhaskar

1 Department of Anaesthesiology and Critical Care, Vijayanagar Institute of Medical Sciences, Bellary, Karnataka, India

Statistical methods involved in carrying out a study include planning, designing, collecting data, analysing, drawing meaningful interpretation and reporting of the research findings. The statistical analysis gives meaning to the meaningless numbers, thereby breathing life into a lifeless data. The results and inferences are precise only if proper statistical tests are used. This article will try to acquaint the reader with the basic research tools that are utilised while conducting various studies. The article covers a brief outline of the variables, an understanding of quantitative and qualitative variables and the measures of central tendency. An idea of the sample size estimation, power analysis and the statistical errors is given. Finally, there is a summary of parametric and non-parametric tests used for data analysis.

INTRODUCTION

Statistics is a branch of science that deals with the collection, organisation, analysis of data and drawing of inferences from the samples to the whole population.[ 1 ] This requires a proper design of the study, an appropriate selection of the study sample and choice of a suitable statistical test. An adequate knowledge of statistics is necessary for proper designing of an epidemiological study or a clinical trial. Improper statistical methods may result in erroneous conclusions which may lead to unethical practice.[ 2 ]

Variable is a characteristic that varies from one individual member of population to another individual.[ 3 ] Variables such as height and weight are measured by some type of scale, convey quantitative information and are called as quantitative variables. Sex and eye colour give qualitative information and are called as qualitative variables[ 3 ] [ Figure 1 ].

Classification of variables

Quantitative variables

Quantitative or numerical data are subdivided into discrete and continuous measurements. Discrete numerical data are recorded as a whole number such as 0, 1, 2, 3,… (integer), whereas continuous data can assume any value. Observations that can be counted constitute the discrete data and observations that can be measured constitute the continuous data. Examples of discrete data are number of episodes of respiratory arrests or the number of re-intubations in an intensive care unit. Similarly, examples of continuous data are the serial serum glucose levels, partial pressure of oxygen in arterial blood and the oesophageal temperature.

A hierarchical scale of increasing precision can be used for observing and recording the data which is based on categorical, ordinal, interval and ratio scales [ Figure 1 ].

Categorical or nominal variables are unordered. The data are merely classified into categories and cannot be arranged in any particular order. If only two categories exist (as in gender male and female), it is called as a dichotomous (or binary) data. The various causes of re-intubation in an intensive care unit due to upper airway obstruction, impaired clearance of secretions, hypoxemia, hypercapnia, pulmonary oedema and neurological impairment are examples of categorical variables.

Ordinal variables have a clear ordering between the variables. However, the ordered data may not have equal intervals. Examples are the American Society of Anesthesiologists status or Richmond agitation-sedation scale.

Interval variables are similar to an ordinal variable, except that the intervals between the values of the interval variable are equally spaced. A good example of an interval scale is the Fahrenheit degree scale used to measure temperature. With the Fahrenheit scale, the difference between 70° and 75° is equal to the difference between 80° and 85°: The units of measurement are equal throughout the full range of the scale.

Ratio scales are similar to interval scales, in that equal differences between scale values have equal quantitative meaning. However, ratio scales also have a true zero point, which gives them an additional property. For example, the system of centimetres is an example of a ratio scale. There is a true zero point and the value of 0 cm means a complete absence of length. The thyromental distance of 6 cm in an adult may be twice that of a child in whom it may be 3 cm.

STATISTICS: DESCRIPTIVE AND INFERENTIAL STATISTICS

Descriptive statistics[ 4 ] try to describe the relationship between variables in a sample or population. Descriptive statistics provide a summary of data in the form of mean, median and mode. Inferential statistics[ 4 ] use a random sample of data taken from a population to describe and make inferences about the whole population. It is valuable when it is not possible to examine each member of an entire population. The examples if descriptive and inferential statistics are illustrated in Table 1 .

Example of descriptive and inferential statistics

Descriptive statistics

The extent to which the observations cluster around a central location is described by the central tendency and the spread towards the extremes is described by the degree of dispersion.

Measures of central tendency

The measures of central tendency are mean, median and mode.[ 6 ] Mean (or the arithmetic average) is the sum of all the scores divided by the number of scores. Mean may be influenced profoundly by the extreme variables. For example, the average stay of organophosphorus poisoning patients in ICU may be influenced by a single patient who stays in ICU for around 5 months because of septicaemia. The extreme values are called outliers. The formula for the mean is

where x = each observation and n = number of observations. Median[ 6 ] is defined as the middle of a distribution in a ranked data (with half of the variables in the sample above and half below the median value) while mode is the most frequently occurring variable in a distribution. Range defines the spread, or variability, of a sample.[ 7 ] It is described by the minimum and maximum values of the variables. If we rank the data and after ranking, group the observations into percentiles, we can get better information of the pattern of spread of the variables. In percentiles, we rank the observations into 100 equal parts. We can then describe 25%, 50%, 75% or any other percentile amount. The median is the 50 th percentile. The interquartile range will be the observations in the middle 50% of the observations about the median (25 th -75 th percentile). Variance[ 7 ] is a measure of how spread out is the distribution. It gives an indication of how close an individual observation clusters about the mean value. The variance of a population is defined by the following formula:

where σ 2 is the population variance, X is the population mean, X i is the i th element from the population and N is the number of elements in the population. The variance of a sample is defined by slightly different formula:

where s 2 is the sample variance, x is the sample mean, x i is the i th element from the sample and n is the number of elements in the sample. The formula for the variance of a population has the value ‘ n ’ as the denominator. The expression ‘ n −1’ is known as the degrees of freedom and is one less than the number of parameters. Each observation is free to vary, except the last one which must be a defined value. The variance is measured in squared units. To make the interpretation of the data simple and to retain the basic unit of observation, the square root of variance is used. The square root of the variance is the standard deviation (SD).[ 8 ] The SD of a population is defined by the following formula:

where σ is the population SD, X is the population mean, X i is the i th element from the population and N is the number of elements in the population. The SD of a sample is defined by slightly different formula:

where s is the sample SD, x is the sample mean, x i is the i th element from the sample and n is the number of elements in the sample. An example for calculation of variation and SD is illustrated in Table 2 .

Example of mean, variance, standard deviation

Normal distribution or Gaussian distribution

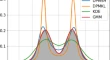
Most of the biological variables usually cluster around a central value, with symmetrical positive and negative deviations about this point.[ 1 ] The standard normal distribution curve is a symmetrical bell-shaped. In a normal distribution curve, about 68% of the scores are within 1 SD of the mean. Around 95% of the scores are within 2 SDs of the mean and 99% within 3 SDs of the mean [ Figure 2 ].

Normal distribution curve

Skewed distribution

It is a distribution with an asymmetry of the variables about its mean. In a negatively skewed distribution [ Figure 3 ], the mass of the distribution is concentrated on the right of Figure 1 . In a positively skewed distribution [ Figure 3 ], the mass of the distribution is concentrated on the left of the figure leading to a longer right tail.

Curves showing negatively skewed and positively skewed distribution

Inferential statistics

In inferential statistics, data are analysed from a sample to make inferences in the larger collection of the population. The purpose is to answer or test the hypotheses. A hypothesis (plural hypotheses) is a proposed explanation for a phenomenon. Hypothesis tests are thus procedures for making rational decisions about the reality of observed effects.

Probability is the measure of the likelihood that an event will occur. Probability is quantified as a number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty).

In inferential statistics, the term ‘null hypothesis’ ( H 0 ‘ H-naught ,’ ‘ H-null ’) denotes that there is no relationship (difference) between the population variables in question.[ 9 ]

Alternative hypothesis ( H 1 and H a ) denotes that a statement between the variables is expected to be true.[ 9 ]

The P value (or the calculated probability) is the probability of the event occurring by chance if the null hypothesis is true. The P value is a numerical between 0 and 1 and is interpreted by researchers in deciding whether to reject or retain the null hypothesis [ Table 3 ].

P values with interpretation

If P value is less than the arbitrarily chosen value (known as α or the significance level), the null hypothesis (H0) is rejected [ Table 4 ]. However, if null hypotheses (H0) is incorrectly rejected, this is known as a Type I error.[ 11 ] Further details regarding alpha error, beta error and sample size calculation and factors influencing them are dealt with in another section of this issue by Das S et al .[ 12 ]

Illustration for null hypothesis

PARAMETRIC AND NON-PARAMETRIC TESTS

Numerical data (quantitative variables) that are normally distributed are analysed with parametric tests.[ 13 ]

Two most basic prerequisites for parametric statistical analysis are:

• The assumption of normality which specifies that the means of the sample group are normally distributed
• The assumption of equal variance which specifies that the variances of the samples and of their corresponding population are equal.

However, if the distribution of the sample is skewed towards one side or the distribution is unknown due to the small sample size, non-parametric[ 14 ] statistical techniques are used. Non-parametric tests are used to analyse ordinal and categorical data.

Parametric tests

The parametric tests assume that the data are on a quantitative (numerical) scale, with a normal distribution of the underlying population. The samples have the same variance (homogeneity of variances). The samples are randomly drawn from the population, and the observations within a group are independent of each other. The commonly used parametric tests are the Student's t -test, analysis of variance (ANOVA) and repeated measures ANOVA.

Student's t -test

Student's t -test is used to test the null hypothesis that there is no difference between the means of the two groups. It is used in three circumstances:

where X = sample mean, u = population mean and SE = standard error of mean

where X 1 − X 2 is the difference between the means of the two groups and SE denotes the standard error of the difference.

• To test if the population means estimated by two dependent samples differ significantly (the paired t -test). A usual setting for paired t -test is when measurements are made on the same subjects before and after a treatment.

The formula for paired t -test is:

where d is the mean difference and SE denotes the standard error of this difference.

The group variances can be compared using the F -test. The F -test is the ratio of variances (var l/var 2). If F differs significantly from 1.0, then it is concluded that the group variances differ significantly.

Analysis of variance

The Student's t -test cannot be used for comparison of three or more groups. The purpose of ANOVA is to test if there is any significant difference between the means of two or more groups.

In ANOVA, we study two variances – (a) between-group variability and (b) within-group variability. The within-group variability (error variance) is the variation that cannot be accounted for in the study design. It is based on random differences present in our samples.

However, the between-group (or effect variance) is the result of our treatment. These two estimates of variances are compared using the F-test.

A simplified formula for the F statistic is:

where MS b is the mean squares between the groups and MS w is the mean squares within groups.

Repeated measures analysis of variance

As with ANOVA, repeated measures ANOVA analyses the equality of means of three or more groups. However, a repeated measure ANOVA is used when all variables of a sample are measured under different conditions or at different points in time.

As the variables are measured from a sample at different points of time, the measurement of the dependent variable is repeated. Using a standard ANOVA in this case is not appropriate because it fails to model the correlation between the repeated measures: The data violate the ANOVA assumption of independence. Hence, in the measurement of repeated dependent variables, repeated measures ANOVA should be used.

Non-parametric tests

When the assumptions of normality are not met, and the sample means are not normally, distributed parametric tests can lead to erroneous results. Non-parametric tests (distribution-free test) are used in such situation as they do not require the normality assumption.[ 15 ] Non-parametric tests may fail to detect a significant difference when compared with a parametric test. That is, they usually have less power.

As is done for the parametric tests, the test statistic is compared with known values for the sampling distribution of that statistic and the null hypothesis is accepted or rejected. The types of non-parametric analysis techniques and the corresponding parametric analysis techniques are delineated in Table 5 .

Analogue of parametric and non-parametric tests

Median test for one sample: The sign test and Wilcoxon's signed rank test

The sign test and Wilcoxon's signed rank test are used for median tests of one sample. These tests examine whether one instance of sample data is greater or smaller than the median reference value.

This test examines the hypothesis about the median θ0 of a population. It tests the null hypothesis H0 = θ0. When the observed value (Xi) is greater than the reference value (θ0), it is marked as+. If the observed value is smaller than the reference value, it is marked as − sign. If the observed value is equal to the reference value (θ0), it is eliminated from the sample.

If the null hypothesis is true, there will be an equal number of + signs and − signs.

The sign test ignores the actual values of the data and only uses + or − signs. Therefore, it is useful when it is difficult to measure the values.

Wilcoxon's signed rank test

There is a major limitation of sign test as we lose the quantitative information of the given data and merely use the + or – signs. Wilcoxon's signed rank test not only examines the observed values in comparison with θ0 but also takes into consideration the relative sizes, adding more statistical power to the test. As in the sign test, if there is an observed value that is equal to the reference value θ0, this observed value is eliminated from the sample.

Wilcoxon's rank sum test ranks all data points in order, calculates the rank sum of each sample and compares the difference in the rank sums.

Mann-Whitney test

It is used to test the null hypothesis that two samples have the same median or, alternatively, whether observations in one sample tend to be larger than observations in the other.

Mann–Whitney test compares all data (xi) belonging to the X group and all data (yi) belonging to the Y group and calculates the probability of xi being greater than yi: P (xi > yi). The null hypothesis states that P (xi > yi) = P (xi < yi) =1/2 while the alternative hypothesis states that P (xi > yi) ≠1/2.

Kolmogorov-Smirnov test

The two-sample Kolmogorov-Smirnov (KS) test was designed as a generic method to test whether two random samples are drawn from the same distribution. The null hypothesis of the KS test is that both distributions are identical. The statistic of the KS test is a distance between the two empirical distributions, computed as the maximum absolute difference between their cumulative curves.

Kruskal-Wallis test

The Kruskal–Wallis test is a non-parametric test to analyse the variance.[ 14 ] It analyses if there is any difference in the median values of three or more independent samples. The data values are ranked in an increasing order, and the rank sums calculated followed by calculation of the test statistic.

Jonckheere test

In contrast to Kruskal–Wallis test, in Jonckheere test, there is an a priori ordering that gives it a more statistical power than the Kruskal–Wallis test.[ 14 ]

Friedman test

The Friedman test is a non-parametric test for testing the difference between several related samples. The Friedman test is an alternative for repeated measures ANOVAs which is used when the same parameter has been measured under different conditions on the same subjects.[ 13 ]

Tests to analyse the categorical data

Chi-square test, Fischer's exact test and McNemar's test are used to analyse the categorical or nominal variables. The Chi-square test compares the frequencies and tests whether the observed data differ significantly from that of the expected data if there were no differences between groups (i.e., the null hypothesis). It is calculated by the sum of the squared difference between observed ( O ) and the expected ( E ) data (or the deviation, d ) divided by the expected data by the following formula:

A Yates correction factor is used when the sample size is small. Fischer's exact test is used to determine if there are non-random associations between two categorical variables. It does not assume random sampling, and instead of referring a calculated statistic to a sampling distribution, it calculates an exact probability. McNemar's test is used for paired nominal data. It is applied to 2 × 2 table with paired-dependent samples. It is used to determine whether the row and column frequencies are equal (that is, whether there is ‘marginal homogeneity’). The null hypothesis is that the paired proportions are equal. The Mantel-Haenszel Chi-square test is a multivariate test as it analyses multiple grouping variables. It stratifies according to the nominated confounding variables and identifies any that affects the primary outcome variable. If the outcome variable is dichotomous, then logistic regression is used.

SOFTWARES AVAILABLE FOR STATISTICS, SAMPLE SIZE CALCULATION AND POWER ANALYSIS

Numerous statistical software systems are available currently. The commonly used software systems are Statistical Package for the Social Sciences (SPSS – manufactured by IBM corporation), Statistical Analysis System ((SAS – developed by SAS Institute North Carolina, United States of America), R (designed by Ross Ihaka and Robert Gentleman from R core team), Minitab (developed by Minitab Inc), Stata (developed by StataCorp) and the MS Excel (developed by Microsoft).

There are a number of web resources which are related to statistical power analyses. A few are:

• StatPages.net – provides links to a number of online power calculators
• G-Power – provides a downloadable power analysis program that runs under DOS
• Power analysis for ANOVA designs an interactive site that calculates power or sample size needed to attain a given power for one effect in a factorial ANOVA design
• SPSS makes a program called SamplePower. It gives an output of a complete report on the computer screen which can be cut and paste into another document.

It is important that a researcher knows the concepts of the basic statistical methods used for conduct of a research study. This will help to conduct an appropriately well-designed study leading to valid and reliable results. Inappropriate use of statistical techniques may lead to faulty conclusions, inducing errors and undermining the significance of the article. Bad statistics may lead to bad research, and bad research may lead to unethical practice. Hence, an adequate knowledge of statistics and the appropriate use of statistical tests are important. An appropriate knowledge about the basic statistical methods will go a long way in improving the research designs and producing quality medical research which can be utilised for formulating the evidence-based guidelines.

Financial support and sponsorship

Conflicts of interest.

There are no conflicts of interest.

Statistical Papers

Statistical Papers is a forum for presentation and critical assessment of statistical methods encouraging the discussion of methodological foundations and potential applications.

• The Journal stresses statistical methods that have broad applications, giving special attention to those relevant to the economic and social sciences.
• Covers all topics of modern data science, such as frequentist and Bayesian design and inference as well as statistical learning.
• Contains original research papers (regular articles), survey articles, short communications, reports on statistical software, and book reviews.
• High author satisfaction with 90% likely to publish in the journal again.
• Werner G. Müller,
• Carsten Jentsch,
• Shuangzhe Liu,
• Ulrike Schneider

Latest issue

Volume 65, Issue 2

Latest articles

Covariance structure tests for multivariate t -distribution.

• Katarzyna Filipiak

A non-classical parameterization for density estimation using sample moments

• Anders Lindquist

Geometric infinitely divisible autoregressive models

• Monika S. Dhull

A mixture distribution for modelling bivariate ordinal data

• Ryan H. L. Ip
• K. Y. K. Wu

Analyzing quantitative performance: Bayesian estimation of 3-component mixture geometric distributions based on Kumaraswamy prior

• Nadeem Akhtar
• Sajjad Ahmad Khan
• Haifa Alqahtani

Journal updates

Write & submit: overleaf latex template.

Overleaf LaTeX Template

Journal information

• Australian Business Deans Council (ABDC) Journal Quality List
• Current Index to Statistics
• Google Scholar
• Japanese Science and Technology Agency (JST)
• Mathematical Reviews
• Norwegian Register for Scientific Journals and Series
• OCLC WorldCat Discovery Service
• Research Papers in Economics (RePEc)
• Science Citation Index Expanded (SCIE)
• TD Net Discovery Service
• UGC-CARE List (India)

Rights and permissions

Editorial policies

© Springer-Verlag GmbH Germany, part of Springer Nature

• Find a journal
• Publish with us
• Track your research

Statistical Research Questions: Five Examples for Quantitative Analysis

Table of contents, introduction.

How are statistical research questions for quantitative analysis written? This article provides five examples of statistical research questions that will allow statistical analysis to take place.

In quantitative research projects, writing statistical research questions requires a good understanding and the ability to discern the type of data that you will analyze. This knowledge is elemental in framing research questions that shall guide you in identifying the appropriate statistical test to use in your research.

Thus, before writing your statistical research questions and reading the examples in this article, read first the article that enumerates the  four types of measurement scales . Knowing the four types of measurement scales will enable you to appreciate the formulation or structuring of research questions.

Once you feel confident that you can correctly identify the nature of your data, the following examples of statistical research questions will strengthen your understanding. Asking these questions can help you unravel unexpected outcomes or discoveries particularly while doing exploratory data analysis .

Five Examples of Statistical Research Questions

In writing the statistical research questions, I provide a topic that shows the variables of the study, the study description, and a link to the original scientific article to give you a glimpse of the real-world examples.

Topic 1: Physical Fitness and Academic Achievement

A study was conducted to determine the relationship between physical fitness and academic achievement. The subjects of the study include school children in urban schools.

Statistical Research Question No. 1

Is there a significant relationship between physical fitness and academic achievement?

Notice that this study correlated two variables, namely 1) physical fitness, and 2) academic achievement.

To allow statistical analysis to take place, there is a need to define what is physical fitness, as well as academic achievement. The researchers measured physical fitness in terms of  the number of physical fitness tests  that the students passed during their physical education class. It’s simply counting the ‘number of PE tests passed.’

On the other hand, the researchers measured academic achievement in terms of a passing score in Mathematics and English. The variable is the  number of passing scores  in both Mathematics and English.

Both variables are ratio variables. 

Given the statistical research question, the appropriate statistical test can be applied to determine the relationship. A Pearson correlation coefficient test will test the significance and degree of the relationship. But the more sophisticated higher level statistical test can be applied if there is a need to correlate with other variables.

In the particular study mentioned, the researchers used  multivariate logistic regression analyses  to assess the probability of passing the tests, controlling for students’ weight status, ethnicity, gender, grade, and socioeconomic status. For the novice researcher, this requires further study of multivariate (or many variables) statistical tests. You may study it on your own.

Most of what I discuss in the statistics articles I wrote came from self-study. It’s easier to understand concepts now as there are a lot of resource materials available online. Videos and ebooks from places like Youtube, Veoh, The Internet Archives, among others, provide free educational materials. Online education will be the norm of the future. I describe this situation in my post about  Education 4.0 .

The following video sheds light on the frequently used statistical tests and their selection. It is an excellent resource for beginners. Just maintain an open mind to get rid of your dislike for numbers; that is, if you are one of those who have a hard time understanding mathematical concepts. My ebook on  statistical tests and their selection  provides many examples.

Source: Chomitz et al. (2009)

Topic 2: Climate Conditions and Consumption of Bottled Water

This study attempted to correlate climate conditions with the decision of people in Ecuador to consume bottled water, including the volume consumed. Specifically, the researchers investigated if the increase in average ambient temperature affects the consumption of bottled water.

Statistical Research Question No. 2

Is there a significant relationship between average temperature and amount of bottled water consumed?

In this instance, the variables measured include the  average temperature in the areas studied  and the  volume of water consumed . Temperature is an  interval variable,  while volume is a  ratio variable .

In this example, the variables include the  average temperature  and  volume of bottled water . The first variable (average temperature) is an interval variable, and the latter (volume of water) is a ratio variable.

Now, it’s easy to identify the statistical test to analyze the relationship between the two variables. You may refer to my previous post titled  Parametric Statistics: Four Widely Used Parametric Tests and When to Use Them . Using the figure supplied in that article, the appropriate test to use is, again, Pearson’s Correlation Coefficient.

Source: Zapata (2021)

Topic 3: Nursing Home Staff Size and Number of COVID-19 Cases

An investigation sought to determine if the size of nursing home staff and the number of COVID-19 cases are correlated. Specifically, they looked into the number of unique employees working daily, and the outcomes include weekly counts of confirmed COVID-19 cases among residents and staff and weekly COVID-19 deaths among residents.

Statistical Research Question No. 3

Is there a significant relationship between the number of unique employees working in skilled nursing homes and the following:

• number of weekly confirmed COVID-19 cases among residents and staff, and
• number of weekly COVID-19 deaths among residents.

Note that this study on COVID-19 looked into three variables, namely 1) number of unique employees working in skilled nursing homes, 2) number of weekly confirmed cases among residents and staff, and 3) number of weekly COVID-19 deaths among residents.

We call the variable  number of unique employees  the  independent variable , and the other two variables ( number of weekly confirmed cases among residents and staff  and  number of weekly COVID-19 deaths among residents ) as the  dependent variables .

This correlation study determined if the number of staff members in nursing homes influences the number of COVID-19 cases and deaths. It aims to understand if staffing has got to do with the transmission of the deadly coronavirus. Thus, the study’s outcome could inform policy on staffing in nursing homes during the pandemic.

A simple Pearson test may be used to correlate one variable with another variable. But the study used multiple variables. Hence, they produced  regression models  that show how multiple variables affect the outcome. Some of the variables in the study may be redundant, meaning, those variables may represent the same attribute of a population.  Stepwise multiple regression models  take care of those redundancies. Using this statistical test requires further study and experience.

Source: McGarry et al. (2021)

Topic 4: Surrounding Greenness, Stress, and Memory

Scientific evidence has shown that surrounding greenness has multiple health-related benefits. Health benefits include better cognitive functioning or better intellectual activity such as thinking, reasoning, or remembering things. These findings, however, are not well understood. A study, therefore, analyzed the relationship between surrounding greenness and memory performance, with stress as a mediating variable.

Statistical Research Question No. 4

Is there a significant relationship between exposure to and use of natural environments, stress, and memory performance?

As this article is behind a paywall and we cannot see the full article, we can content ourselves with the knowledge that three major variables were explored in this study. These are 1) exposure to and use of natural environments, 2) stress, and 3) memory performance.

Referring to the abstract of this study,  exposure to and use of natural environments  as a variable of the study may be measured in terms of the days spent by the respondent in green surroundings. That will be a ratio variable as we can count it and has an absolute zero point. Stress levels can be measured using standardized instruments like the  Perceived Stress Scale . The third variable, i.e., memory performance in terms of short-term, working memory, and overall memory may be measured using a variety of  memory assessment tools as described by Murray (2016) .

As you become more familiar and well-versed in identifying the variables you would like to investigate in your study, reading studies like this requires reading the method or methodology section. This section will tell you how the researchers measured the variables of their study. Knowing how those variables are quantified can help you design your research and formulate the appropriate statistical research questions.

Source: Lega et al. (2021)

Topic 5: Income and Happiness

This recent finding is an interesting read and is available online. Just click on the link I provide as the source below. The study sought to determine if income plays a role in people’s happiness across three age groups: young (18-30 years), middle (31-64 years), and old (65 or older). The literature review suggests that income has a positive effect on an individual’s sense of happiness. That’s because more money increases opportunities to fulfill dreams and buy more goods and services.

Reading the abstract, we can readily identify one of the variables used in the study, i.e., money. It’s easy to count that. But for happiness, that is a largely subjective matter. Happiness varies between individuals. So how did the researcher measured happiness? As previously mentioned, we need to see the methodology portion to find out why.

If you click on the link to the full text of the paper on pages 10 and 11, you will read that the researcher measured happiness using a 10-point scale. The scale was categorized into three namely, 1) unhappy, 2) happy, and 3) very happy.

An investigation was conducted to determine if the size of nursing home staff and the number of COVID-19 cases are correlated. Specifically, they looked into the number of unique employees working daily, and the outcomes include weekly counts of confirmed COVID-19 cases among residents and staff and weekly COVID-19 deaths among residents.

Statistical Research Question No. 5

Is there a significant relationship between income and happiness?

Source: Måseide (2021)

Now the statistical test used by the researcher is, honestly, beyond me. I may be able to understand it how to use it but doing so requires further study. Although I have initially did some readings on logit models, ordered logit model and generalized ordered logit model are way beyond my self-study in statistics.

Anyhow, those variables found with asterisk (***, **, and **) on page 24 tell us that there are significant relationships between income and happiness. You just have to look at the probability values and refer to the bottom of the table for the level of significance of those relationships.

I do hope that upon reaching this part of the article, you are now well familiar on how to write statistical research questions. Practice makes perfect.

References:

Chomitz, V. R., Slining, M. M., McGowan, R. J., Mitchell, S. E., Dawson, G. F., & Hacker, K. A. (2009). Is there a relationship between physical fitness and academic achievement? Positive results from public school children in the northeastern United States.  Journal of School Health ,  79 (1), 30-37.

Lega, C., Gidlow, C., Jones, M., Ellis, N., & Hurst, G. (2021). The relationship between surrounding greenness, stress and memory.  Urban Forestry & Urban Greening ,  59 , 126974.

Måseide, H. (2021). Income and Happiness: Does the relationship vary with age?

McGarry, B. E., Gandhi, A. D., Grabowski, D. C., & Barnett, M. L. (2021). Larger Nursing Home Staff Size Linked To Higher Number Of COVID-19 Cases In 2020: Study examines the relationship between staff size and COVID-19 cases in nursing homes and skilled nursing facilities. Health Affairs, 40(8), 1261-1269.

Zapata, O. (2021). The relationship between climate conditions and consumption of bottled water: A potential link between climate change and plastic pollution. Ecological Economics, 187, 107090.

© P. A. Regoniel 12 October 2021 | Updated 08 January 2024

Related Posts

Gnumeric 1.12.50: Free Spreadsheet Software Like Excel

Mango Pulp Weevil: A Pest Control Problem in Palawan Island

Writing a research article: how to paraphrase, about the author, patrick regoniel.

Dr. Regoniel, a faculty member of the graduate school, served as consultant to various environmental research and development projects covering issues and concerns on climate change, coral reef resources and management, economic valuation of environmental and natural resources, mining, and waste management and pollution. He has extensive experience on applied statistics, systems modelling and analysis, an avid practitioner of LaTeX, and a multidisciplinary web developer. He leverages pioneering AI-powered content creation tools to produce unique and comprehensive articles in this website.

SimplyEducate.Me Privacy Policy

Statistics Made Easy

The Importance of Statistics in Research (With Examples)

The field of statistics is concerned with collecting, analyzing, interpreting, and presenting data.

In the field of research, statistics is important for the following reasons:

Reason 1 : Statistics allows researchers to design studies such that the findings from the studies can be extrapolated to a larger population.

Reason 2 : Statistics allows researchers to perform hypothesis tests to determine if some claim about a new drug, new procedure, new manufacturing method, etc. is true.

Reason 3 : Statistics allows researchers to create confidence intervals to capture uncertainty around population estimates.

In the rest of this article, we elaborate on each of these reasons.

Reason 1: Statistics Allows Researchers to Design Studies

Researchers are often interested in answering questions about populations like:

• What is the average weight of a certain species of bird?
• What is the average height of a certain species of plant?
• What percentage of citizens in a certain city support a certain law?

One way to answer these questions is to go around and collect data on every single individual in the population of interest.

However, this is typically too costly and time-consuming which is why researchers instead take a  sample  of the population and use the data from the sample to draw conclusions about the population as a whole.

There are many different methods researchers can potentially use to obtain individuals to be in a sample. These are known as  sampling methods .

There are two classes of sampling methods:

• Probability sampling methods : Every member in a population has an equal probability of being selected to be in the sample.
• Non-probability sampling methods : Not every member in a population has an equal probability of being selected to be in the sample.

By using probability sampling methods, researchers can maximize the chances that they obtain a sample that is representative of the overall population.

This allows researchers to extrapolate the findings from the sample to the overall population.

Read more about the two classes of sampling methods here .

Reason 2: Statistics Allows Researchers to Perform Hypothesis Tests

Another way that statistics is used in research is in the form of hypothesis tests .

These are tests that researchers can use to determine if there is a statistical significance between different medical procedures or treatments.

For example, suppose a scientist believes that a new drug is able to reduce blood pressure in obese patients. To test this, he measures the blood pressure of 30 patients before and after using the new drug for one month.

He then performs a paired samples t- test using the following hypotheses:

• H 0 : μ after = μ before (the mean blood pressure is the same before and after using the drug)
• H A : μ after < μ before (the mean blood pressure is less after using the drug)

If the p-value of the test is less than some significance level (e.g. α = .05), then he can reject the null hypothesis and conclude that the new drug leads to reduced blood pressure.

Note : This is just one example of a hypothesis test that is used in research. Other common tests include a one sample t-test , two sample t-test , one-way ANOVA , and two-way ANOVA .

Reason 3: Statistics Allows Researchers to Create Confidence Intervals

Another way that statistics is used in research is in the form of confidence intervals .

A confidence interval is a range of values that is likely to contain a population parameter with a certain level of confidence.

For example, suppose researchers are interested in estimating the mean weight of a certain species of turtle.

Instead of going around and weighing every single turtle in the population, researchers may instead take a simple random sample of turtles with the following information:

• Sample size  n = 25
• Sample mean weight  x  = 300
• Sample standard deviation  s = 18.5

Using the confidence interval for a mean formula , researchers may then construct the following 95% confidence interval:

95% Confidence Interval:  300 +/-  1.96*(18.5/√ 25 ) =  [292.75, 307.25]

The researchers would then claim that they’re 95% confident that the true mean weight for this population of turtles is between 292.75 pounds and 307.25 pounds.

Additional Resources

The following articles explain the importance of statistics in other fields:

The Importance of Statistics in Healthcare The Importance of Statistics in Nursing The Importance of Statistics in Business The Importance of Statistics in Economics The Importance of Statistics in Education

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Official Writing
• Report Writing

How to Write a Statistical Report

Last Updated: March 6, 2024 Fact Checked

This article was reviewed by Grace Imson, MA and by wikiHow staff writer, Jennifer Mueller, JD . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 403,468 times.

A statistical report informs readers about a particular subject or project. You can write a successful statistical report by formatting your report properly and including all the necessary information your readers need. [1] X Research source

A Beginner’s Guide to Statistical Report Writing

Use other statistical reports as a guide to format your own. Type your report in an easy-to-read font, include all the information that your reader needs, and present your results in a table or graph.

Formatting Your Report

• If you're completing your report for a class, your instructor or professor may be willing to show you some reports submitted by previous students if you ask.
• University libraries also have copies of statistical reports created by students and faculty researchers on file. Ask the research librarian to help you locate one in your field of study.
• You also may be able to find statistical reports online that were created for business or marketing research, as well as those filed for government agencies.
• Be careful following samples exactly, particularly if they were completed for research in another field. Different fields of study have their own conventions regarding how a statistical report should look and what it should contain. For example, a statistical report by a mathematician may look incredibly different than one created by a market researcher for a retail business.

• You typically want to have 1-inch margins around all sides of your report. Be careful when adding visual elements such as charts and graphs to your report, and make sure they don't bleed over the margins or your report may not print properly and will look sloppy.
• You may want to have a 1.5-inch margin on the left-hand side of the page if you anticipate putting your study into a folder or binder, so all the words can be read comfortably when the pages are turned.
• Don't double-space your report unless you're writing it for a class assignment and the instructor or professor specifically tells you to do so.
• Use headers to add the page number to every page. You may also want to add your last name or the title of the study along with the page number.

• Citation methods typically are included in style manuals, which not only detail how you should cite your references but also have rules on acceptable punctuation and abbreviations, headings, and the general formatting of your report.
• For example, if you're writing a statistical report based on a psychological study, you typically must use the style manual published by the American Psychological Association (APA).
• Your citation method is all the more important if you anticipate your statistical report will be published in a particular trade or professional journal.

• If you're creating your statistical report for a class, a cover sheet may be required. Check with your instructor or professor or look on your assignment sheet to find out whether a cover sheet is required and what should be included on it.
• For longer statistical reports, you may also want to include a table of contents. You won't be able to format this until after you've finished the report, but it will list each section of your report and the page on which that section starts.

• If you decide to create section headings, they should be bold-faced and set off in such a way that they stand out from the rest of the text. For example, you may want to center bold-faced headings and use a slightly larger font size.
• Make sure a section heading doesn't fall at the bottom of the page. You should have at least a few lines of text, if not a full paragraph, below each section heading before the page break.

• Check the margins around visual elements and make sure the text lines up and is not too close to the visual element. You want it to be clear where the text ends and the words associated with the visual element (such as the axis labels for a graph) begin.
• Visual elements can cause your text to shift, so you'll need to double-check your section headings after your report is complete and make sure none of them are at the bottom of a page.
• Where possible, you also want to change your page breaks to eliminate situations in which the last line of a page is the first line of a paragraph, or the first line of a page is the last line of a paragraph. These are difficult to read.

Creating Your Content

• Avoid overly scientific or statistical language in your abstract as much as possible. Your abstract should be understandable to a larger audience than those who will be reading the entire report.
• It can help to think of your abstract as an elevator pitch. If you were in an elevator with someone and they asked you what your project was about, your abstract is what you would say to that person to describe your project.
• Even though your abstract appears first in your report, it's often easier to write it last, after you've completed the entire report.

• Aim for clear and concise language to set the tone for your report. Put your project in layperson's terms rather than using overly statistical language, regardless of the target audience of your report.
• If your report is based on a series of scientific experiments or data drawn from polls or demographic data, state your hypothesis or expectations going into the project.
• If other work has been done in the field regarding the same subject or similar questions, it's also appropriate to include a brief review of that work after your introduction. Explain why your work is different or what you hope to add to the existing body of work through your research.

• Include a description of any particular methods you used to track results, particularly if your experiments or studies were longer-term or observational in nature.
• If you had to make any adjustments during the development of the project, identify those adjustments and explain what required you to make them.
• List any software, resources, or other materials you used in the course of your research. If you used any textbook material, a reference is sufficient – there's no need to summarize that material in your report.

• Start with your main results, then include subsidiary results or interesting facts or trends you discovered.
• Generally you want to stay away from reporting results that have nothing to do with your original expectations or hypotheses. However, if you discovered something startling and unexpected through your research, you may want to at least mention it.
• This typically will be the longest section of your report, with the most detailed statistics. It also will be the driest and most difficult section for your readers to get through, especially if they are not statisticians.
• Small graphs or charts often show your results more clearly than you can write them in text.

• When you get to this section of your report, leave the heavy, statistical language behind. This section should be easy for anyone to understand, even if they skipped over your results section.
• If any additional research or study is necessary to further explore your hypotheses or answer questions that arose in the context of your project, describe that as well.

• It is often the case that you see things in hindsight that would have made data-gathering easier or more efficient. This is the place to discuss those. Since the scientific method is designed so that others can repeat your study, you want to pass on to future researchers your insights.
• Any speculation you have, or additional questions that came to mind over the course of your study, also are appropriate here. Just make sure you keep it to a minimum – you don't want your personal opinions and speculation to overtake the project itself.

• For example, if you compared your study to a similar study conducted in another city the year before yours, you would want to include a citation to that report in your references.
• Cite your references using the appropriate citation method for your discipline or field of study.
• Avoid citing any references that you did not mention in your report. For example, you may have done some background reading in preparation for your project. However, if you didn't end up directly citing any of those sources in your report, there's no need to list them in your references.

• Avoid trade "terms of art" or industry jargon if your report will be read mainly by people outside your particular industry.
• Make sure the terms of art and statistical terms that you do use in your report are used correctly. For example, you shouldn't use the word "average" in a statistical report because people often use that word to refer to different measures. Instead, use "mean," "median," or "mode" – whichever is correct.

Presenting Your Data

• This is particularly important if you're submitting your report for publication in a trade journal. If the pages are different sizes than the paper you print your report on, your visual elements won't line up the same way in the journal as they do in your manuscript.
• This also can be a factor if your report will be published online, since different display sizes can cause visual elements to display differently.
• The easiest way to label your visual elements is "Figure," followed by a number. Then you simply number each element sequentially in the order in which they appear in your report.
• Your title describes the information presented by the visual element. For example, if you've created a bar graph that shows the test scores of students on the chemistry class final, you might title it "Chemistry Final Test Scores, Fall 2016."

• Make sure each visual element is large enough in size that your readers can see everything they need to see without squinting. If you have to shrink down a graph to the point that readers can't make out the labels, it won't be very helpful to them.
• Create your visual elements using a format that you can easily import into your word-processing file. Importing using some graphics formats can distort the image or result in extremely low resolution.

• For example, if you have hundreds of samples, your x axis will be cluttered if you display each sample individually as a bar. However, you can move the measure on the y axis to the x axis, and use the y axis to measure the frequency.
• When your data include percentages, only go out to fractions of a percentage if your research demands it. If the smallest difference between your subjects is two percentage points, there's no need to display more than the whole percentage. However, if the difference between your subjects comes down to hundredths of a percent, you would need to display percentages to two decimal places so the graph would show the difference.
• For example, if your report includes a bar graph of the distribution of test scores for a chemistry class, and those scores are 97.56, 97.52, 97.46, and 97.61, your x axis would be each of the students and your y axis would start at 97 and go up to 98. This would highlight the differences in the students' scores.

• Be careful that your appendix does not overwhelm your report. You don't necessarily want to include every data sheet or other document you created over the course of your project.
• Rather, you only want to include documents that reasonably expand and lead to a further understanding of your report.
• For example, when describing your methods you state that a survey was conducted of students in a chemistry class to determine how they studied for the final exam. You might include a copy of the questions the students were asked in an appendix. However, you wouldn't necessarily need to include a copy of each student's answers to those questions.

Statistical Report Outline

Community Q&A

You Might Also Like

• ↑ https://www.ibm.com/docs/en/iotdm/11.3?topic=SSMLQ4_11.3.0/com.ibm.nex.optimd.dg.doc/11arcperf/oparcuse-r-statistical_reports.html
• ↑ https://www.examples.com/business/report/statistics-report.html
• ↑ https://collaboratory.ucr.edu/sites/g/files/rcwecm2761/files/2019-04/Final_Report_dan.pdf
• ↑ https://tex.stackexchange.com/questions/49386/what-is-the-recommended-font-to-use-for-a-statistical-table-in-an-academic-journ
• ↑ https://psychology.ucsd.edu/undergraduate-program/undergraduate-resources/academic-writing-resources/writing-research-papers/citing-references.html
• ↑ https://www.youtube.com/watch?v=kl3JOCmuil4

About This Article

Start your statistical report with an introduction explaining the purpose of your research. Then, dive into your research methods, how you collected data, and the experiments you conducted. Present you results with any necessary charts and graphs, but do not discuss or analyze the numbers -- in a statistical report, all analysis should happen in the conclusion. Once you’ve finished writing your report, draft a 200 word abstract and create a cover sheet with your name, the date, and the report title. Don’t forget to cite the appropriate references when necessary! For more formatting help, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Dorothy Walter

Jan 15, 2017

Did this article help you?

Sarvath Ali

Feb 10, 2017

Mar 8, 2018

Sonam Sharma

Apr 30, 2019

Ashley Persaud

Jan 23, 2018

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

• Dissertation
• PowerPoint Presentation
• Book Report/Review
• Research Proposal
• Math Problems
• Proofreading
• Movie Review
• Cover Letter Writing
• Personal Statement
• Nursing Paper
• Argumentative Essay
• Research Paper
• Discussion Board Post

How To Write A Statistics Research Paper?

Table of Contents

Naturally, all-encompassing information about the slightest details of the statistical paper writing cannot be stuffed into one guideline. Still, we will provide a glimpse of the basics of the stats research paper.

What is a stats research paper?

One of the main problems of stats academic research papers is that not all students understand what it is. Put it bluntly, it is an essay that provides an analysis of the gathered statistical data to induce the key points of a specified research issue. Thus, the author of the paper creates a construct of the topic by explaining the statistical data.

Writing a statistics research paper is quite challenging because the sources of data for statistical analysis are quite numerous. These are data mining, biostatistics, quality control, surveys, statistical modelling, etc.

Collecting data for the college research paper analysis is another headache. Research papers of this type call for the data taken from the most reliable and relevant sources because no indeterminate information is inadmissible here.

How to create the perfect statistics research paper example?

If you want to create the paper that can serve as a research paper writing example of well-written statistics research paper example, then here is a guideline that will help you to master this task.

Select the topic

Obviously, work can’t be written without a topic. Therefore, it is essential to come up with the theme that promises interesting statistics, and a possibility to gather enough data for the research. Access to the reliable sources of the research data is also a must.

If you are not confident about the availability of several sources concerning the chosen topic, you’d better choose something else.

Remember to jot down all the needed information for the proper referencing when you use a resource

Data collection

The duration of this stage depends on the number of data sources and the chosen methodology of the data collection. Mind that once you have chosen the method, you should stick to it. Naturally, it is essential to explain your choice of the methodology in your statistics research paper.

Outlining the paper

Creating a rough draft of the paper is your chance to save some time and nerves. Once you’ve done it, you get a clear picture of what to write about and what points should be worked through.

The intro section

This is, perhaps, the most important part of the paper. As this is the most scientific paper from all the papers you will have to write in your studies, it calls for the most logical and clear approach. Thus, your intro should consist of:

• Opening remarks about the field of the research.
• Credits to other researchers who worked on this theme.
• The scientific motivation for the new research .
• An explanation of why existing researches are not sufficient.
• The thesis statement , aka the core idea of the text.

The body of the text (research report, as they say in statistics)

Believe it or not, but many professional writers start such papers from the body. Here you have to place the Methodology Section where you establish the methods of data collection and the results of it. Usually, all main graphs or charts are placed here as a way to convey the results. All additional materials are gathered in the appendices.

The next paragraph of the paper will be the Evaluation of the gathered data . And that’s where the knowledge on how to read statistics in a research paper can come in handy. If you have no clue how to do it, you’re in trouble, to be honest. At least, you should know three concepts: odds ratios, confidence intervals, and p values. You can start searching for them on the web or in B.S.Everitt’s Dictionary of Statistics.

And the last section of the body is Discussion . Here, as the name suggests, you have to discuss the analysis and the results of the research.

The conclusion

This section requires only several sentences where you summarise the findings and highlight the importance of the research. You may also include a suggestion on how to continue or deepen the research of the issue.

Tips on how to write a statistics paper example

Here are some life hacks and shortcuts that you may use to boost your paper:

• Many sources where you take the statistical data , do offer it with the interpretation. Do not waste time on calculations and take the interpretation from there.
• Visuals are the must: always include a graph, chart, or a table to visualize your words.
• If you do not know the statistical procedure and how to interpret the results , never use it in the paper.
• Always put the statistics at the end of the sentence.
• If your paper requires the presentation of your calculations and you are not confident with it, ask a pro to help you.
• Different types of statistical data require proper formatting. Cite statistics properly according to the chosen format.

…Final thoughts

We hope that our guideline on how to write a statistics paper example unveiled the mystery of writing such papers.

But, in the case you still dread stats essays, here is a sound solution: entrust your task to the professionals! Order a paper at trustworthy writing service and enjoy saved time and the great result.

Psst… You can hand this work to a writer and have a completely stress-free evening. It would take like 3 minutes. And your perfect statistics research paper would be done on time!

Research Paper

Category: statistics research paper examples.

Browse statistics research paper examples below.

Standardized Tests Research Paper Example

• Youth Program
• Wharton Online

Research Papers / Publications

Statistics Research Paper

View sample Statistics Research Paper. Browse other  research paper examples and check the list of research paper topics for more inspiration. If you need a religion research paper written according to all the academic standards, you can always turn to our experienced writers for help. This is how your paper can get an A! Feel free to contact our custom writing service s for professional assistance. We offer high-quality assignments for reasonable rates.

Academic Writing, Editing, Proofreading, And Problem Solving Services

Get 10% off with 24start discount code, more statistics research papers:.

• Time Series Research Paper
• Crime Statistics Research Paper
• Economic Statistics Research Paper
• Education Statistics Research Paper
• Health Statistics Research Paper
• Labor Statistics Research Paper
• History of Statistics Research Paper
• Survey Sampling Research Paper
• Multidimensional Scaling Research Paper
• Sequential Statistical Methods Research Paper
• Simultaneous Equation Estimation Research Paper
• Statistical Clustering Research Paper
• Statistical Sufficiency Research Paper
• Censuses Of Population Research Paper
• Stochastic Models Research Paper
• Stock Market Predictability Research Paper
• Structural Equation Modeling Research Paper
• Survival Analysis Research Paper
• Systems Modeling Research Paper
• Nonprobability Sampling Research Paper

1. Introduction

Statistics is a body of quantitative methods associated with empirical observation. A primary goal of these methods is coping with uncertainty. Most formal statistical methods rely on probability theory to express this uncertainty and to provide a formal mathematical basis for data description and for analysis. The notion of variability associated with data, expressed through probability, plays a fundamental role in this theory. As a consequence, much statistical effort is focused on how to control and measure variability and/or how to assign it to its sources.

Almost all characterizations of statistics as a field include the following elements:

(a) Designing experiments, surveys, and other systematic forms of empirical study.

(b) Summarizing and extracting information from data.

(c) Drawing formal inferences from empirical data through the use of probability.

(d) Communicating the results of statistical investigations to others, including scientists, policy makers, and the public.

This research paper describes a number of these elements, and the historical context out of which they grew. It provides a broad overview of the field, that can serve as a starting point to many of the other statistical entries in this encyclopedia.

2. The Origins Of The Field of Statistics

The word ‘statistics’ is related to the word ‘state’ and the original activity that was labeled as statistics was social in nature and related to elements of society through the organization of economic, demographic, and political facts. Paralleling this work to some extent was the development of the probability calculus and the theory of errors, typically associated with the physical sciences. These traditions came together in the nineteenth century and led to the notion of statistics as a collection of methods for the analysis of scientific data and the drawing of inferences therefrom.

As Hacking (1990) has noted: ‘By the end of the century chance had attained the respectability of a Victorian valet, ready to be the logical servant of the natural, biological and social sciences’ ( p. 2). At the beginning of the twentieth century, we see the emergence of statistics as a field under the leadership of Karl Pearson, George Udny Yule, Francis Y. Edgeworth, and others of the ‘English’ statistical school. As Stigler (1986) suggests:

Before 1900 we see many scientists of different fields developing and using techniques we now recognize as belonging to modern statistics. After 1900 we begin to see identifiable statisticians developing such techniques into a unified logic of empirical science that goes far beyond its component parts. There was no sharp moment of birth; but with Pearson and Yule and the growing number of students in Pearson’s laboratory, the infant discipline may be said to have arrived. (p. 361)

Pearson’s laboratory at University College, London quickly became the first statistics department in the world and it was to influence subsequent developments in a profound fashion for the next three decades. Pearson and his colleagues founded the first methodologically-oriented statistics journal, Biometrika, and they stimulated the development of new approaches to statistical methods. What remained before statistics could legitimately take on the mantle of a field of inquiry, separate from mathematics or the use of statistical approaches in other fields, was the development of the formal foundations of theories of inference from observations, rooted in an axiomatic theory of probability.

Beginning at least with the Rev. Thomas Bayes and Pierre Simon Laplace in the eighteenth century, most early efforts at statistical inference used what was known as the method of inverse probability to update a prior probability using the observed data in what we now refer to as Bayes’ Theorem. (For a discussion of who really invented Bayes’ Theorem, see Stigler 1999, Chap. 15). Inverse probability came under challenge in the nineteenth century, but viable alternative approaches gained little currency. It was only with the work of R. A. Fisher on statistical models, estimation, and significance tests, and Jerzy Neyman and Egon Pearson, in the 1920s and 1930s, on tests of hypotheses, that alternative approaches were fully articulated and given a formal foundation. Neyman’s advocacy of the role of probability in the structuring of a frequency-based approach to sample surveys in 1934 and his development of confidence intervals further consolidated this effort at the development of a foundation for inference (cf. Statistical Methods, History of: Post- 1900 and the discussion of ‘The inference experts’ in Gigerenzer et al. 1989).

At about the same time Kolmogorov presented his famous axiomatic treatment of probability, and thus by the end of the 1930s, all of the requisite elements were finally in place for the identification of statistics as a field. Not coincidentally, the first statistical society devoted to the mathematical underpinnings of the field, The Institute of Mathematical Statistics, was created in the United States in the mid-1930s. It was during this same period that departments of statistics and statistical laboratories and groups were first formed in universities in the United States.

3. Emergence Of Statistics As A Field

3.1 the role of world war ii.

Perhaps the greatest catalysts to the emergence of statistics as a field were two major social events: the Great Depression of the 1930s and World War II. In the United States, one of the responses to the depression was the development of large-scale probability-based surveys to measure employment and unemployment. This was followed by the institutionalization of sampling as part of the 1940 US decennial census. But with World War II raging in Europe and in Asia, mathematicians and statisticians were drawn into the war effort, and as a consequence they turned their attention to a broad array of new problems. In particular, multiple statistical groups were established in both England and the US specifically to develop new methods and to provide consulting. (See Wallis 1980, on statistical groups in the US; Barnard and Plackett 1985, for related efforts in the United Kingdom; and Fienberg 1985). These groups not only created imaginative new techniques such as sequential analysis and statistical decision theory, but they also developed a shared research agenda. That agenda led to a blossoming of statistics after the war, and in the 1950s and 1960s to the creation of departments of statistics at universities—from coast to coast in the US, and to a lesser extent in England and elsewhere.

3.2 The Neo-Bayesian Revival

Although inverse probability came under challenge in the 1920s and 1930s, it was not totally abandoned. John Maynard Keynes (1921) wrote A Treatise on Probability that was rooted in this tradition, and Frank Ramsey (1926) provided an early effort at justifying the subjective nature of prior distributions and suggested the importance of utility functions as an adjunct to statistical inference. Bruno de Finetti provided further development of these ideas in the 1930s, while Harold Jeffreys (1938) created a separate ‘objective’ development of these and other statistical ideas on inverse probability.

Yet as statistics flourished in the post-World War II era, it was largely based on the developments of Fisher, Neyman and Pearson, as well as the decision theory methods of Abraham Wald (1950). L. J. Savage revived interest in the inverse probability approach with The Foundations of Statistics (1954) in which he attempted to provide the axiomatic foundation from the subjective perspective. In an essentially independent effort, Raiffa and Schlaifer (1961) attempted to provide inverse probability counterparts to many of the then existing frequentist tools, referring to these alternatives as ‘Bayesian.’ By 1960, the term ‘Bayesian inference’ had become standard usage in the statistical literature, the theoretical interest in the development of Bayesian approaches began to take hold, and the neo-Bayesian revival was underway. But the movement from Bayesian theory to statistical practice was slow, in large part because the computations associated with posterior distributions were an overwhelming stumbling block for those who were interested in the methods. Only in the 1980s and 1990s did new computational approaches revolutionize both Bayesian methods, and the interest in them, in a broad array of areas of application.

3.3 The Role Of Computation In Statistics

From the days of Pearson and Fisher, computation played a crucial role in the development and application of statistics. Pearson’s laboratory employed dozens of women who used mechanical devices to carry out the careful and painstaking calculations required to tabulate values from various probability distributions. This effort ultimately led to the creation of the Biometrika Tables for Statisticians that were so widely used by others applying tools such as chisquare tests and the like. Similarly, Fisher also developed his own set of statistical tables with Frank Yates when he worked at Rothamsted Experiment Station in the 1920s and 1930s. One of the most famous pictures of Fisher shows him seated at Whittingehame Lodge, working at his desk calculator (see Box 1978).

The development of the modern computer revolutionized statistical calculation and practice, beginning with the creation of the first statistical packages in the 1960s—such as the BMDP package for biological and medical applications, and Datatext for statistical work in the social sciences. Other packages soon followed—such as SAS and SPSS for both data management and production-like statistical analyses, and MINITAB for the teaching of statistics. In 2001, in the era of the desktop personal computer, almost everyone has easy access to interactive statistical programs that can implement complex statistical procedures and produce publication-quality graphics. And there is a new generation of statistical tools that rely upon statistical simulation such as the bootstrap and Markov Chain Monte Carlo methods. Complementing the traditional production-like packages for statistical analysis are more methodologically oriented languages such as S and S-PLUS, and symbolic and algebraic calculation packages. Statistical journals and those in various fields of application devote considerable space to descriptions of such tools.

4. Statistics At The End Of The Twentieth Century

It is widely recognized that any statistical analysis can only be as good as the underlying data. Consequently, statisticians take great care in the the design of methods for data collection and in their actual implementation. Some of the most important modes of statistical data collection include censuses, experiments, observational studies, and sample Surveys, all of which are discussed elsewhere in this encyclopedia. Statistical experiments gain their strength and validity both through the random assignment of treatments to units and through the control of nontreatment variables. Similarly sample surveys gain their validity for generalization through the careful design of survey questionnaires and probability methods used for the selection of the sample units. Approaches to cope with the failure to fully implement randomization in experiments or random selection in sample surveys are discussed in Experimental Design: Compliance and Nonsampling Errors.

Data in some statistical studies are collected essentially at a single point in time (cross-sectional studies), while in others they are collected repeatedly at several time points or even continuously, while in yet others observations are collected sequentially, until sufficient information is available for inferential purposes. Different entries discuss these options and their strengths and weaknesses.

After a century of formal development, statistics as a field has developed a number of different approaches that rely on probability theory as a mathematical basis for description, analysis, and statistical inference. We provide an overview of some of these in the remainder of this section and provide some links to other entries in this encyclopedia.

4.1 Data Analysis

The least formal approach to inference is often the first employed. Its name stems from a famous article by John Tukey (1962), but it is rooted in the more traditional forms of descriptive statistical methods used for centuries.

Today, data analysis relies heavily on graphical methods and there are different traditions, such as those associated with

(a) The ‘exploratory data analysis’ methods suggested by Tukey and others.

(b) The more stylized correspondence analysis techniques of Benzecri and the French school.

(c) The alphabet soup of computer-based multivariate methods that have emerged over the past decade such as ACE, MARS, CART, etc.

No matter which ‘school’ of data analysis someone adheres to, the spirit of the methods is typically to encourage the data to ‘speak for themselves.’ While no theory of data analysis has emerged, and perhaps none is to be expected, the flexibility of thought and method embodied in the data analytic ideas have influenced all of the other approaches.

4.2 Frequentism

The name of this group of methods refers to a hypothetical infinite sequence of data sets generated as was the data set in question. Inferences are to be made with respect to this hypothetical infinite sequence. (For details, see Frequentist Inference).

One of the leading frequentist methods is significance testing, formalized initially by R. A. Fisher (1925) and subsequently elaborated upon and extended by Neyman and Pearson and others (see below). Here a null hypothesis is chosen, for example, that the mean, µ, of a normally distributed set of observations is 0. Fisher suggested the choice of a test statistic, e.g., based on the sample mean, x, and the calculation of the likelihood of observing an outcome as or more extreme as x is from µ 0, a quantity usually labeled as the p-value. When p is small (e.g., less than 5 percent), either a rare event has occurred or the null hypothesis is false. Within this theory, no probability can be given for which of these two conclusions is the case.

A related set of methods is testing hypotheses, as proposed by Neyman and Pearson (1928, 1932). In this approach, procedures are sought having the property that, for an infinite sequence of such sets, in only (say) 5 percent for would the null hypothesis be rejected if the null hypothesis were true. Often the infinite sequence is restricted to sets having the same sample size, but this is unnecessary. Here, in addition to the null hypothesis, an alternative hypothesis is specified. This permits the definition of a power curve, reflecting the frequency of rejecting the null hypothesis when the specified alternative is the case. But, as with the Fisherian approach, no probability can be given to either the null or the alternative hypotheses.

The construction of confidence intervals, following the proposal of Neyman (1934), is intimately related to testing hypotheses; indeed a 95 percent confidence interval may be regarded as the set of null hypotheses which, had they been tested at the 5 percent level of significance, would not have been rejected. A confidence interval is a random interval, having the property that the specified proportion (say 95 percent) of the infinite sequence, of random intervals would have covered the true value. For example, an interval that 95 percent of the time (by auxiliary randomization) is the whole real line, and 5 percent of the time is the empty set, is a valid 95 percent confidence interval.

Estimation of parameters—i.e., choosing a single value of the parameters that is in some sense best—is also an important frequentist method. Many methods have been proposed, both for particular models and as general approaches regardless of model, and their frequentist properties explored. These methods usually extended to intervals of values through inversion of test statistics or via other related devices. The resulting confidence intervals share many of the frequentist theoretical properties of the corresponding test procedures.

Frequentist statisticians have explored a number of general properties thought to be desirable in a procedure, such as invariance, unbiasedness, sufficiency, conditioning on ancillary statistics, etc. While each of these properties has examples in which it appears to produce satisfactory recommendations, there are others in which it does not. Additionally, these properties can conflict with each other. No general frequentist theory has emerged that proposes a hierarchy of desirable properties, leaving a frequentist without guidance in facing a new problem.

4.3 Likelihood Methods

The likelihood function (first studied systematically by R. A. Fisher) is the probability density of the data, viewed as a function of the parameters. It occupies an interesting middle ground in the philosophical debate, as it is used both by frequentists (as in maximum likelihood estimation) and by Bayesians in the transition from prior distributions to posterior distributions. A small group of scholars (among them G. A. Barnard, A. W. F. Edwards, R. Royall, D. Sprott) have proposed the likelihood function as an independent basis for inference. The issue of nuisance parameters has perplexed this group, since maximization, as would be consistent with maximum likelihood estimation, leads to different results in general than does integration, which would be consistent with Bayesian ideas.

4.4 Bayesian Methods

Both frequentists and Bayesians accept Bayes’ Theorem as correct, but Bayesians use it far more heavily. Bayesian analysis proceeds from the idea that probability is personal or subjective, reflecting the views of a particular person at a particular point in time. These views are summarized in the prior distribution over the parameter space. Together the prior distribution and the likelihood function define the joint distribution of the parameters and the data. This joint distribution can alternatively be factored as the product of the posterior distribution of the parameter given the data times the predictive distribution of the data.

In the past, Bayesian methods were deemed to be controversial because of the avowedly subjective nature of the prior distribution. But the controversy surrounding their use has lessened as recognition of the subjective nature of the likelihood has spread. Unlike frequentist methods, Bayesian methods are, in principle, free of the paradoxes and counterexamples that make classical statistics so perplexing. The development of hierarchical modeling and Markov Chain Monte Carlo (MCMC) methods have further added to the current popularity of the Bayesian approach, as they allow analyses of models that would otherwise be intractable.

Bayesian decision theory, which interacts closely with Bayesian statistical methods, is a useful way of modeling and addressing decision problems of experimental designs and data analysis and inference. It introduces the notion of utilities and the optimum decision combines probabilities of events with utilities by the calculation of expected utility and maximizing the latter (e.g., see the discussion in Lindley 2000).

Current research is attempting to use the Bayesian approach to hypothesis testing to provide tests and pvalues with good frequentist properties (see Bayarri and Berger 2000).

4.5 Broad Models: Nonparametrics And Semiparametrics

These models include parameter spaces of infinite dimensions, whether addressed in a frequentist or Bayesian manner. In a sense, these models put more inferential weight on the assumption of conditional independence than does an ordinary parametric model.

4.6 Some Cross-Cutting Themes

Often different fields of application of statistics need to address similar issues. For example, dimensionality of the parameter space is often a problem. As more parameters are added, the model will in general fit better (at least no worse). Is the apparent gain in accuracy worth the reduction in parsimony? There are many different ways to address this question in the various applied areas of statistics.

Another common theme, in some sense the obverse of the previous one, is the question of model selection and goodness of fit. In what sense can one say that a set of observations is well-approximated by a particular distribution? (cf. Goodness of Fit: Overview). All statistical theory relies at some level on the use of formal models, and the appropriateness of those models and their detailed specification are of concern to users of statistical methods, no matter which school of statistical inference they choose to work within.

5. Statistics In The Twenty-first Century

5.1 adapting and generalizing methodology.

Statistics as a field provides scientists with the basis for dealing with uncertainty, and, among other things, for generalizing from a sample to a population. There is a parallel sense in which statistics provides a basis for generalization: when similar tools are developed within specific substantive fields, such as experimental design methodology in agriculture and medicine, and sample surveys in economics and sociology. Statisticians have long recognized the common elements of such methodologies and have sought to develop generalized tools and theories to deal with these separate approaches (see e.g., Fienberg and Tanur 1989).

One hallmark of modern statistical science is the development of general frameworks that unify methodology. Thus the tools of Generalized Linear Models draw together methods for linear regression and analysis of various models with normal errors and those log-linear and logistic models for categorical data, in a broader and richer framework. Similarly, graphical models developed in the 1970s and 1980s use concepts of independence to integrate work in covariance section, decomposable log-linear models, and Markov random field models, and produce new methodology as a consequence. And the latent variable approaches from psychometrics and sociology have been tied with simultaneous equation and measurement error models from econometrics into a broader theory of covariance analysis and structural equations models.

Another hallmark of modern statistical science is the borrowing of methods in one field for application in another. One example is provided by Markov Chain Monte Carlo methods, now used widely in Bayesian statistics, which were first used in physics. Survival analysis, used in biostatistics to model the disease-free time or time-to-mortality of medical patients, and analyzed as reliability in quality control studies, are now used in econometrics to measure the time until an unemployed person gets a job. We anticipate that this trend of methodological borrowing will continue across fields of application.

5.2 Where Will New Statistical Developments Be Focused ?

In the issues of its year 2000 volume, the Journal of the American Statistical Association explored both the state of the art of statistics in diverse areas of application, and that of theory and methods, through a series of vignettes or short articles. These essays provide an excellent supplement to the entries of this encyclopedia on a wide range of topics, not only presenting a snapshot of the current state of play in selected areas of the field but also affecting some speculation on the next generation of developments. In an afterword to the last set of these vignettes, Casella (2000) summarizes five overarching themes that he observed in reading through the entire collection:

(a) Large datasets.

(b) High-dimensional/nonparametric models.

(c) Accessible computing.

(d) Bayes/frequentist/who cares?

(e) Theory/applied/why differentiate?

Not surprisingly, these themes fit well those that one can read into the statistical entries in this encyclopedia. The coming together of Bayesian and frequentist methods, for example, is illustrated by the movement of frequentists towards the use of hierarchical models and the regular consideration of frequentist properties of Bayesian procedures (e.g., Bayarri and Berger 2000). Similarly, MCMC methods are being widely used in non-Bayesian settings and, because they focus on long-run sequences of dependent draws from multivariate probability distributions, there are frequentist elements that are brought to bear in the study of the convergence of MCMC procedures. Thus the oft-made distinction between the different schools of statistical inference (suggested in the preceding section) is not always clear in the context of real applications.

5.3 The Growing Importance Of Statistics Across The Social And Behavioral Sciences

Statistics touches on an increasing number of fields of application, in the social sciences as in other areas of scholarship. Historically, the closest links have been with economics; together these fields share parentage of econometrics. There are now vigorous interactions with political science, law, sociology, psychology, anthropology, archeology, history, and many others.

In some fields, the development of statistical methods has not been universally welcomed. Using these methods well and knowledgeably requires an understanding both of the substantive field and of statistical methods. Sometimes this combination of skills has been difficult to develop.

Statistical methods are having increasing success in addressing questions throughout the social and behavioral sciences. Data are being collected and analyzed on an increasing variety of subjects, and the analyses are becoming increasingly sharply focused on the issues of interest.

We do not anticipate, nor would we find desirable, a future in which only statistical evidence was accepted in the social and behavioral sciences. There is room for, and need for, many different approaches. Nonetheless, we expect the excellent progress made in statistical methods in the social and behavioral sciences in recent decades to continue and intensify.

Bibliography:

• Barnard G A, Plackett R L 1985 Statistics in the United Kingdom, 1939–1945. In: Atkinson A C, Fienberg S E (eds.) A Celebration of Statistics: The ISI Centennial Volume. Springer-Verlag, New York, pp. 31–55
• Bayarri M J, Berger J O 2000 P values for composite null models (with discussion). Journal of the American Statistical Association 95: 1127–72
• Box J 1978 R. A. Fisher, The Life of a Scientist. Wiley, New York
• Casella G 2000 Afterword. Journal of the American Statistical Association 95: 1388
• Fienberg S E 1985 Statistical developments in World War II: An international perspective. In: Anthony C, Atkinson A C, Fienberg S E (eds.) A Celebration of Statistics: The ISI Centennial Volume. Springer-Verlag, New York, pp. 25–30
• Fienberg S E, Tanur J M 1989 Combining cognitive and statistical approaches to survey design. Science 243: 1017–22
• Fisher R A 1925 Statistical Methods for Research Workers. Oliver and Boyd, London
• Gigerenzer G, Swijtink Z, Porter T, Daston L, Beatty J, Kruger L 1989 The Empire of Chance. Cambridge University Press, Cambridge, UK
• Hacking I 1990 The Taming of Chance. Cambridge University Press, Cambridge, UK
• Jeffreys H 1938 Theory of Probability, 2nd edn. Clarendon Press, Oxford, UK
• Keynes J 1921 A Treatise on Probability. Macmillan, London
• Lindley D V 2000/1932 The philosophy of statistics (with discussion). The Statistician 49: 293–337
• Neyman J 1934 On the two different aspects of the representative method: the method of stratified sampling and the method of purposive selection (with discussion). Journal of the Royal Statistical Society 97: 558–625
• Neyman J, Pearson E S 1928 On the use and interpretation of certain test criteria for purposes of statistical inference. Part I. Biometrika 20A: 175–240
• Neyman J, Pearson E S 1932 On the problem of the most efficient tests of statistical hypotheses. Philosophical Transactions of the Royal Society, Series. A 231: 289–337
• Raiffa H, Schlaifer R 1961 Applied Statistical Decision Theory. Harvard Business School, Boston
• Ramsey F P 1926 Truth and probability. In: The Foundations of Mathematics and Other Logical Essays. Kegan Paul, London, pp.
• Savage L J 1954 The Foundations of Statistics. Wiley, New York
• Stigler S M 1986 The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press, Cambridge, MA
• Stigler S M 1999 Statistics on the Table: The History of Statistical Concepts and Methods. Harvard University Press, Cambridge, MA
• Tukey John W 1962 The future of data analysis. Annals of Mathematical Statistics 33: 1–67
• Wald A 1950 Statistical Decision Functions. Wiley, New York
• Wallis W 1980 The Statistical Research Group, 1942–1945 (with discussion). Journal of the American Statistical Association 75: 320–35

ORDER HIGH QUALITY CUSTOM PAPER

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

1.4 - example: descriptive statistics, example 1-5: women's health survey (descriptive statistics) section  .

Let us take a look at an example. In 1985, the USDA commissioned a study of women’s nutrition. Nutrient intake was measured for a random sample of 737 women aged 25-50 years. The following variables were measured:

• Calcium(mg)
• Vitamin A(μg)
• Vitamin C(mg)

Using Technology

•   Example

We will use the SAS program to carry out the calculations that we would like to see.

Download the data file: nutrient.csv

The lines of this program are saved in a simple text file with a .sas file extension. If you have SAS installed on the machine on which you have downloaded this file, it should launch SAS and open the program within the SAS application. Marking up a printout of the SAS program is also a good strategy for learning how this program is put together.

Note : In the upper right-hand corner of the code block you will have the option of copying (   ) the code to your clipboard or downloading (   ) the file to your computer.

The first part of this SAS output, (download below), is the results of the Means Procedure - proc means. Because the SAS output is usually a relatively long document, printing these pages of output out and marking them with notes is highly recommended if not required!

Example: Nutrient Intake Data - Descriptive Statistics

The MEANS Procedure

The Means Procedure

Summary statistics.

Download the SAS Output file: nutrient2.lst

The first column of the Means Procedure table above gives the variable name. The second column reports the sample size. This is then followed by the sample means (third column) and the sample standard deviations (fourth column) for each variable. I have copied these values into the table below. I have also rounded these numbers a bit to make them easier to use for this example.

Here are the steps to find the descriptive statistics for the Women's Nutrition dataset in Minitab:

Descriptive Statistics in Minitab

• Go to File > Open > Worksheet [open nutrient_tf.csv ]
• Highlight and select C2 through C6 and choose ‘Select ’ to move the variables into the window on the right.
• Select ‘ Statistics... ’, and check the boxes for the statistics of interest.

Descriptive Statistics

A summary of the descriptive statistics is given here for ease of reference.

Notice that the standard deviations are large relative to their respective means, especially for Vitamin A & C. This would indicate a high variability among women in nutrient intake. However, whether the standard deviations are relatively large or not, will depend on the context of the application. Skill in interpreting the statistical analysis depends very much on the researcher's subject matter knowledge.

The variance-covariance matrix is also copied into the matrix below.

\[S = \left(\begin{array}{RRRRR}157829.4 & 940.1 & 6075.8 & 102411.1 & 6701.6 \\ 940.1 & 35.8 & 114.1 & 2383.2 & 137.7 \\ 6075.8 & 114.1 & 934.9 & 7330.1 & 477.2 \\ 102411.1 & 2383.2 & 7330.1 & 2668452.4 & 22063.3 \\ 6701.6 & 137.7 & 477.2 & 22063.3 & 5416.3 \end{array}\right)\]

Interpretation

Because this covariance is positive, we see that calcium intake tends to increase with increasing iron intake. The strength of this positive association can only be judged by comparing s 12 to the product of the sample standard deviations for calcium and iron. This comparison is most readily accomplished by looking at the sample correlation between the two variables.

• The sample variances are given by the diagonal elements of S . For example, the variance of iron intake is \(s_{2}^{2}\). 35. 8 mg 2 .
• The covariances are given by the off-diagonal elements of S . For example, the covariance between calcium and iron intake is \(s_{12}\)= 940. 1.
• Note that, the covariances are all positive, indicating that the daily intake of each nutrient increases with increased intake of the remaining nutrients.

Sample Correlations

The sample correlations are included in the table below.

Here we can see that the correlation between each of the variables and themselves is all equal to one, and the off-diagonal elements give the correlation between each of the pairs of variables.

Generally, we look for the strongest correlations first. The results above suggest that protein, iron, and calcium are all positively associated. Each of these three nutrient increases with increasing values of the remaining two.

The coefficient of determination is another measure of association and is simply equal to the square of the correlation. For example, in this case, the coefficient of determination between protein and iron is \((0.623)^2\) or about 0.388.

\[r^2_{23} = 0.62337^2 = 0.38859\]

This says that about 39% of the variation in iron intake is explained by protein intake. Or, conversely, 39% of the protein intake is explained by the variation in the iron intake. Both interpretations are equivalent.

Review of Related Literature (RRL) in Research Paper

Ai generator.

1. Introduction: This review examines how technology affects education, focusing on student engagement, learning outcomes, and teacher practices over the past decade.

2. Theoretical Framework: Based on Constructivist Learning Theory and TPACK, this review explores how technology integration enhances education.

3. Review of Empirical Studies

Student Engagement

• Interactive Whiteboards : Smith & Jones (2015) found increased student participation in 20 elementary classrooms using interactive whiteboards.
• Gamification : Lee & Hammer (2011) reported improved motivation and engagement with educational games in 300 middle school students.

Learning Outcomes

• Online Learning Platforms : Johnson & Brown (2017) observed better standardized test performance among 500 high school students using online platforms.
• Blended Learning : Clark & Mayer (2016) found higher academic achievement in 200 college students in blended learning environments.

Teacher Practices

• Professional Development : Williams & Davis (2018) highlighted improved instructional practices from ongoing tech training in 150 teachers.
• Digital Assessment Tools : Thompson & Peterson (2019) showed enhanced instructional strategies using digital tools in 30 high school classrooms.

4. Methodological Review: Studies used surveys, experiments, and longitudinal designs. Surveys provided broad data but had self-report biases. Experiments showed causation but lacked ecological validity. Longitudinal studies provided long-term data but were resource-intensive.

5. Synthesis and Critique: Technology positively impacts engagement, outcomes, and practices. Challenges include digital divide and training. More longitudinal and experimental research is needed.

6. Conclusion: Research shows technology’s potential to enhance education but highlights the need for further study on sustainable implementation and overcoming barriers.

7. References :

• Clark, R. C., & Mayer, R. E. (2016). E-learning and the Science of Instruction . Wiley.
• Johnson, L., & Brown, A. (2017). Impact of Online Learning on Student Performance . Journal of Educational Technology, 12(3), 45-56.
• Lee, J. J., & Hammer, J. (2011). Gamification in Education . Academic Exchange Quarterly, 15(2), 1-5.
• Smith, K., & Jones, L. (2015). Interactive Whiteboards in Elementary Education . Educational Technology Research, 63(4), 123-135.
• Thompson, M., & Peterson, D. (2019). Digital Assessment Tools in High Schools . Journal of Education, 14(1), 78-89.
• Williams, P., & Davis, R. (2018). Professional Development for Technology Integration . Journal of Teacher Education, 20(4), 100-110.

Text prompt

• Instructive
• Professional

10 Examples of Public speaking

20 Examples of Gas lighting

• Future Annual Meetings
• 2024 Annual Meeting
• 2023 Annual Meeting
• 2022 Annual Meeting
• 2021 Annual Meeting
• April 19 AERA Gathering and Presidential Presentation
• 2019 Annual Meeting
• 2018 Annual Meeting
• 2017 Annual Meeting
• 2016 Annual Meeting
• 2015 Annual Meeting
• 2014 Annual Meeting
• Leveraged Knowledge and Cyclical Inequality
• Demonizing the Undeserving Poor
• Does that Sound Like Meritocracy to You?
• A Global “HEADS UP”
• What’s Race Got to Do with It
• Education Policy is Social Policy
• Reading History and Learning about Policy and Peop
• Poverty and Impoverishment in the Bay Area of Cali
• Poverty and Education: Reflections on the AERA Con
• Trying to Fix an Urban School - 2013 AM Theme
• The Poverty of Capitalism
• Myth of Poverty
• On Poverty and Systemic Collapse
• Poverty has an iPhone
• Media at Annual Meeting
• 2012 Annual Meeting
• 2011 Annual Meeting
• Past Brown Lectures
• Virtual Events
• AERA Centennial
• Webcasts of Lectures & Events

Share