methods for traffic assignment

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

13 Last Step of Four Step Modeling (Trip Assignment Models)

Chapter overview.

Chapter 13 presents trip assignment, the last step of the Four-Step travel demand Model (FSM). This step determines which paths travelers choose for moving between each pair of zones. Additionally, this step can yield numerous results, such as traffic volumes in different transportation corridors, the patterns of vehicular movements, total vehicle miles traveled (VMT) and vehicle travel time (VTT) in the network, and zone-to-zone travel costs. Identification of the heavily congested links is crucial for transportation planning and engineering practitioners. This chapter begins with some fundamental concepts, such as the link cost functions. Next, it presents some common and useful trip assignment methods with relevant examples. The methods covered in this chapter include all-or-nothing (AON), user equilibrium (UE), system optimum (SO), feedback loop between distribution and assignment (LDA),  incremental increase assignment, capacity restrained assignment, and stochastic user equilibrium assignment.

Learning Objectives

•  Describe the reasons for performing trip assignment models in FSM and relate these models’ foundation through the cost-function concept.
• Compare static and dynamic trip assignment models and infer the appropriateness of each model for different situations.
• Explain Wardrop principles and relate them to traffic assignment algorithms.
• Complete simple network traffic assignment models using static models such as the all-or-nothing and user equilibrium models.
• Solve modal split analyses manually for small samples using the discrete choice modeling framework and multinominal logit models.

Introduction

In this chapter, we continue the discussion about FSM and elaborate on different methods of traffic assignment, the last step in the FSM model after trip generation, trip distribution, and modal split. The traffic assignment step, which is also called route assignment or route choice , simulates the choice of route selection from a set of alternatives between the origin and the destination zones (Levinson et al., 2014). The first three FSM steps determine the number of trips produced between each zone and the proportion completed by different transportation modes. The purpose of the final step is to determine the routes or links in the study area that are likely to be used. For example, when updating a Regional Transportation Plan (RTP), traffic assignment is helpful in determining how much shift or diversion in daily traffic happens with the introduction an additional transit line or extension a highway corridor (Levinson et al., 2014). The output from the last step can provide modelers with numerous valuable results. By analyzing the results, the planner can gain insight into the strengths and weaknesses of different transportation plans. The results of trip assignment analysis can be:

• The traffic flows in the transportation system and the pattern of vehicular movements.
• The volume of traffic on network links.
• Travel costs between trip origins and destinations (O-D).
• Aggregated network metrics such as total vehicle flow, vehicle miles traveled (VMT) , and vehicle travel time (VTT).
• Zone-to-zone travel costs (travel time) for a given level of demand.
• Modeled link flows highlighting congested corridors.
• Analysis of turning movements for future intersection design.
• Determining the Origin-Destination (O-D) pairs using a specific link or path.
• Simulation of the individual choice for each pair of origins and destinations (Mathew & Rao, 2006).

Link Performance Function

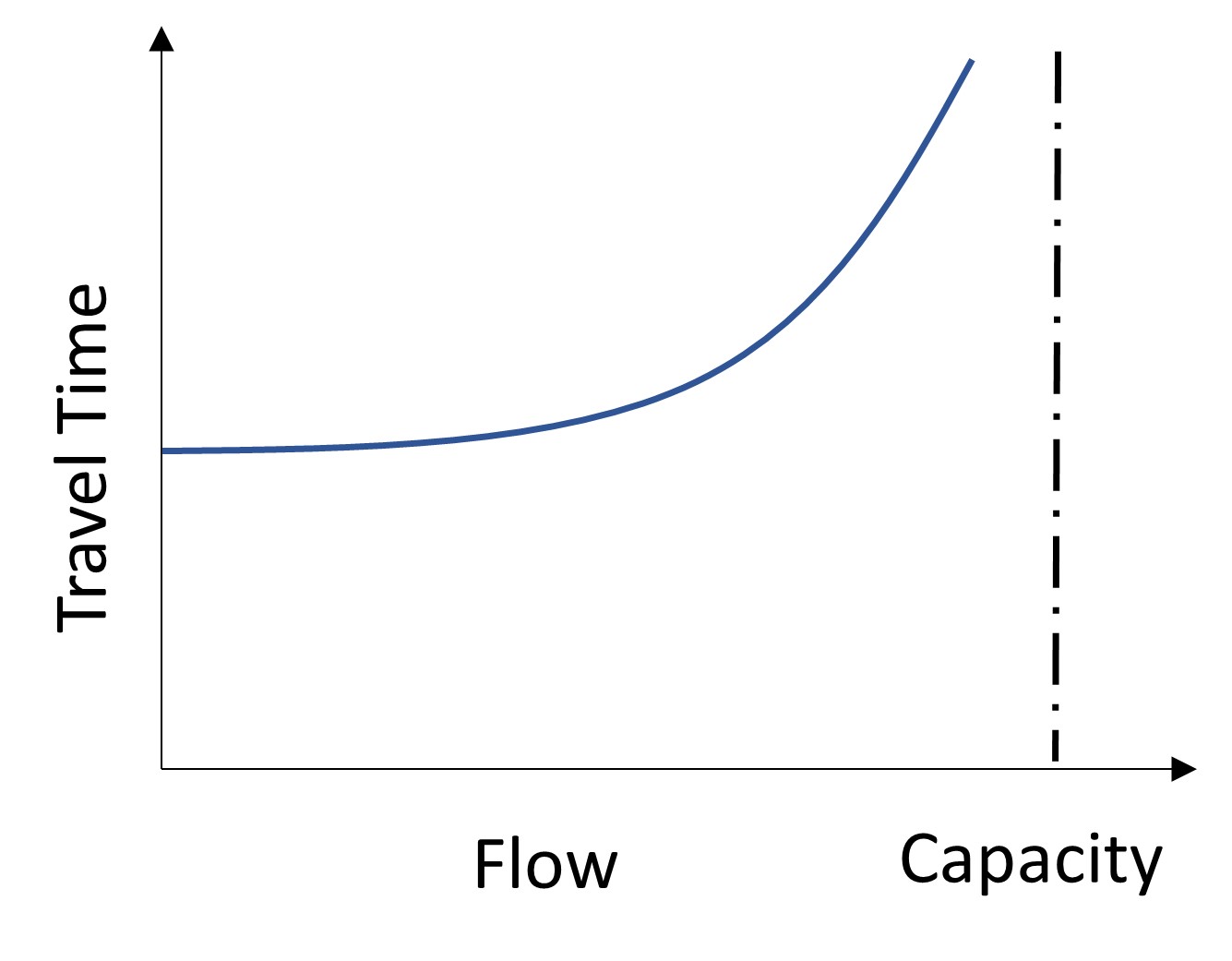
Building a link performance function is one of the most important and fundamental concepts of the traffic assignment process. This function is usually used for estimating travel time, travel cost, and speed on the network based on the relationship between speed and travel flow. While this function can take different forms, such as linear, polynomial , exponential , and hyperbolic , one of the most common functions is the link performance function which represents generalized travel costs (United States Bureau of Public Roads, 1964). This equation estimates travel time on a free-flow road (travel with speed limit) adding a function that exponentially increases travel time as the road gets more congested. The road volume-to-capacity ratio can represent congestion (Meyer, 2016).

While transportation planners now recognize that intersection delays contribute to link delays, the following sections will focus on the traditional function. Equation (1) is the most common and general formula for the link performance function.

• t and x are the travel time and vehicle flow;
• t 0 is the link free flow travel time;
• k is the link capacity;
• α and β are parameters for specific type of links and calibrated using the field data. In the absence of any field data, it is usually assumed = 0.15, and β= 4.0.

α and β are the coefficients for this formula and can take different values (model parameters). However, most studies and planning practices use the same value for them. These values can be locally calibrated for the most efficient results.

Figure 13.1 demonstrates capacity as the relationship between flow and travel time. In this plot, the travel time remains constant as vehicle volumes increase until the turning point , which indicates that the link’s volume is approaching its capacity.

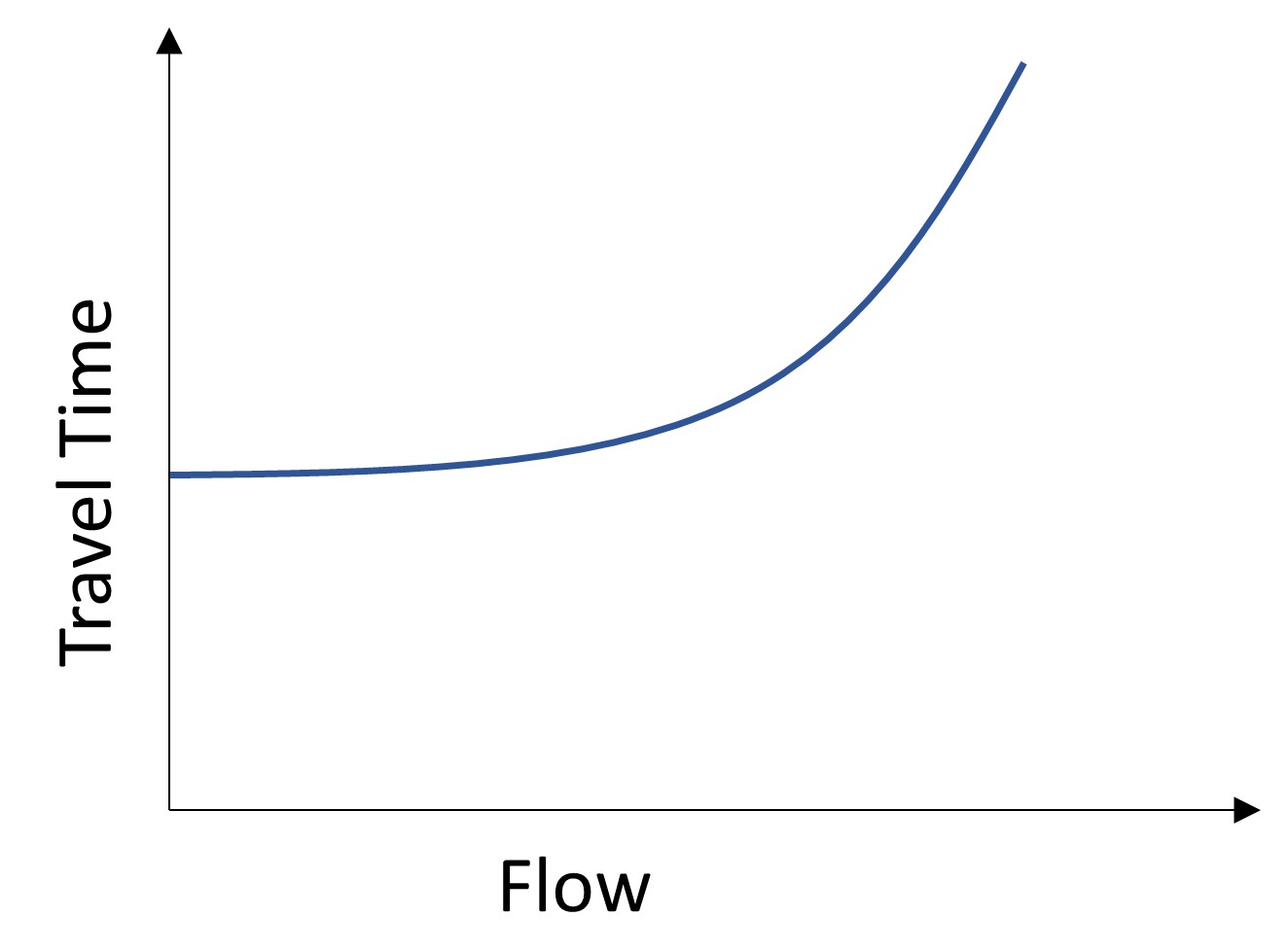
The following example shows how the link performance function helps us to determine the travel time according to flow and capacity.

Performance Function Example

Assume the traffic volume on a path between zone i and j was 525. The travel time recorded on this path is 15 minutes. If the capacity of this path would be 550, then calculate the new travel time for future iteration of the model.

Based on the link performance function, we have:

Now we have to plug in the numbers into the formula to determine the new travel time:

Traffic Assignment Models

Typically, traffic assignment is calculated for private cars and transit systems independently. Recall that the impedance function differs for drivers and riders, and thus simulating utility maximization behavior should be approached differently. For public transit assignment, variables such as fare, stop or transfer, waiting time, and trip times define the utility (equilibrium) (Sheffi, 1985). For private car assignment, however, in some cases, the two networks are related when public buses share highways with cars, and congestion can also affect the performance.

Typically, private car traffic assignment models the path choice of trip makers using:

• algorithms like all-or-nothing
• user equilibrium
• system optimum assignment

Of the assignment models listed above, user equilibrium is widely adopted in the U.S. (Meyer, 2016). User equilibrium relies on the premise that travelers aim to minimize their travel costs. This algorithm achieves equilibrium when no user can decrease their travel time or cost by altering their travel path.

• incremental
• capacity-restrained
• iterative feedback loop
• Stochastic user equilibrium assignment
• Dynamic traffic assignment

All-or-nothing Model

Through the all-or-nothing (AON) assignment, it is assumed that the impedance of a road or path between each origin and destination is constant and equal to the free-flow level of service. This means that the traffic time is not affected by the traffic flow on the path. The only logic behind this model is that each traveler uses the shortest path from his or her origin to the destination, and no vehicle is assigned to other paths (Hui, 2014). This method is called the all-or-nothing assignment model and is the simplest one among all assignment models. This method is also called the 0-1 assignment model, and its advantage is its simple procedure and calculation. The assumptions of this method are:

• Congestion does not affect travel time or cost, meaning that no matter how much traffic is loaded on the route, congestion does not take place.
• Since the method assigns one route to any travel between each pair of OD, all travelers traveling from a particular zone to another particular zone choose the same route (Hui, 2014).

To run the AON model, the following process can be followed:

• Step 0: Initialization. Use free flow travel costs Ca=Ca(0) , for each link a on the empty network. Ɐ
• Step 1: Path finding. Find the shortest path P for each zonal pair.
• Step 2: Path flows assigning. Assign both passenger trips (hppod) and freight trips (hfpod) in PCEs from zonal o to d to path P.
• Step 3: Link flows computing. Sum the flows on all paths going through a link as total flows of this link.

Example 2 illustrates the above-mentioned process for the AON model

All-or-nothing Example

Table 13.1 shows a trip distribution matrix with 4 zones. Using the travel costs between each pair of them shown in Figure 13.2, assign the traffic to the network. Load the vehicle trips from the trip distribution table shown below using the AON technique. After assigning the traffic, illustrate the links and the traffic volume on each on them.

Table 13.1 Trip Distribution Results.

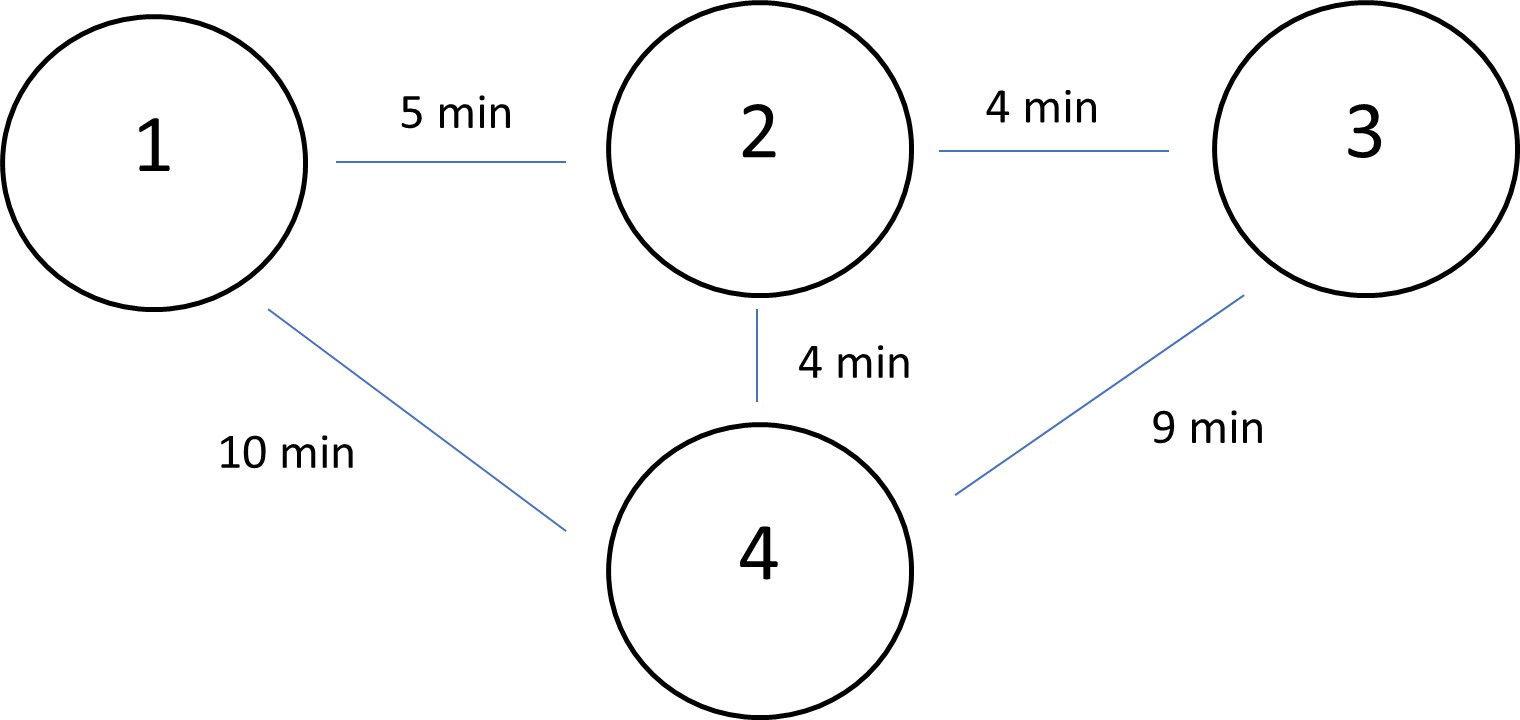
To solve this problem, we need to find the shortest path among all alternatives for each pair of zones. The result of this procedure would be 10 routes in total, each of which bears a specific amount of travels. For instance, the shortest path between zone 1 and 2 is the straight line with 5 min travel time. All other routes like 1 to 4 to 2 or 1 to 4 to 3 to 2 would be empty from travelers going from zone 1 to zone 2. The results are shown in Table 13.2.

As you can see, some of the routes remained unused. This is because in all-or-nothing if a route has longer travel time or higher costs, then it is assumed it would not be used at all.

User Equilibrium

The next method for traffic assignment is called User Equilibrium (UE). The rule or algorithm is adapted from the well-known Wardrop equilibrium (1952) conditions (Correa & Stier-Moses, 2011). In this algorithm, it is assumed that travelers will always choose the shortest path, and equilibrium conditions are realized when no traveler is able to decrease their travel impedance by changing paths (Levinson et al., 2014).

As we discussed, the UE method is based on the first principle of Wardrop : “for each origin- destination (OD) pair, with UE, the travel time on all used paths is equal and less than or equally to the travel time that would be experienced by a single vehicle on any unused path”( Jeihani Koohbanani, 2004, p. 10). The mathematical format of this principle is shown in equation (3):

For a given OD pair, the UE condition can be expressed in equation (3):

This model assumes that all paths have equal travel time. Additionally, the model includes the following general assumptions:

• The users possess all the knowledge needed about different paths.
• The users have perfect knowledge of the path cost.
• Travel time in a route is subject to change only by the cost flow function of that route.
• Travel times increases as we load travel into the network (Mathew & Rao, 2006).

Hence, the UE assignment comes to an optimization problem that can be formulated using equation (4):

k  is the path x a equilibrium flow in link a t a  travel time on link a f k rs  flow on path  connecting OD pairs q rs  trip rate between  and δ a, k rs is constraint function defined as 1 if link a belongs to path k and 0 otherwise

Example 3 shows how the UE method can be applied for the traffic assignment step. This example is a very simple network consisting of two zones with two possible paths between them.

UE Example 

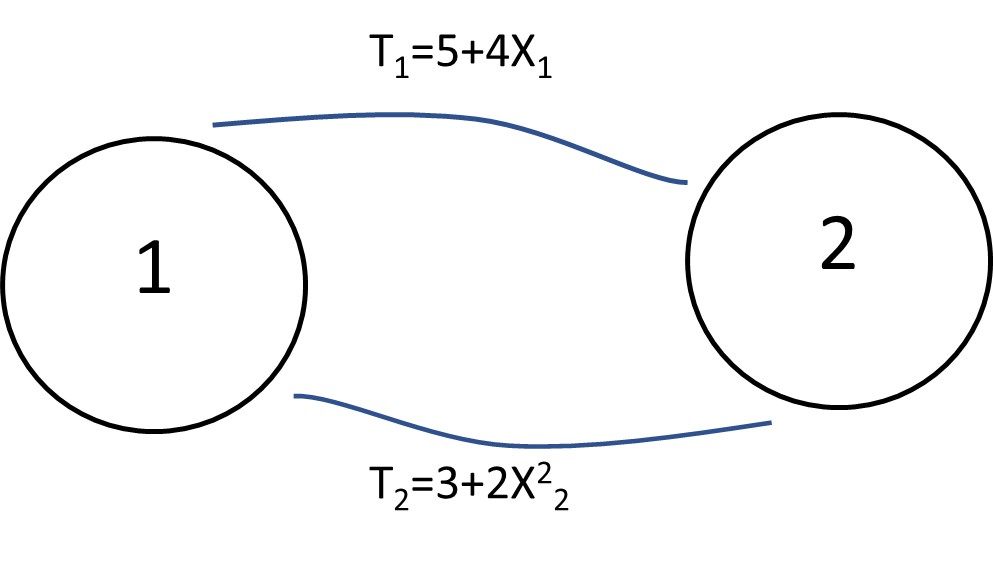
In this example, t 1 and t 2 are travel times measured by min on each route, and x 1 and x 2 are traffic flows on each route measured by (Veh/Hour).

Using the UE method, assign 4,500 Veh/Hour to the network and calculate travel time on each route after assignment, traffic volume, and system total travel time.

According to the information provided, total flow (X 1 +X 2 ) is equal to 4,500 (4.5).

First, we need to check, with all traffic assigned to one route, whether that route is still the shortest path. Thus we have:

T 1 (4.5)=23min

T 2 (0)=3min

if all traffic is assigned to route 2:

T 1 (0)=3min

T 2 (4.5)=43.5 min

Step 2: Wardrope equilibrium rule: t 1 =t 2        5+4x 1 =3+ 2x 2 2         and we have x 1 =4.5-x 2

Now the equilibrium equation can be written as: 6 + 4(4.5 − x2)=4+ x222

x 1 = 4.5 − x 2 = 1.58

Now the updated average travel times are: t 1 =5+4(1.58)=11.3min and T 2 =3+2(2.92)2=20.05min

Now the total system travel time is:

Z(x)=X 1 T 1 (X 1 )+X 2 T 2 (X 2 )=2920 veh/hr(11.32)+1585 veh/hr(20.05)=33054+31779=64833 min

System Optimum Assignment

One traffic assignment model is similar to the previous one and is called system optimum (SO). The second principle of the Wardrop defines the model’s logic. Based on this principle, drivers’ rationale for choosing a path is to minimize total system costs with one another to minimize total system travel time (Mathew & Rao, 2006). Using the SO traffic assignment, one can solve various problems, such as optimizing the departure time for a single commuting route, minimizing the total travel time from multiple origins to a single destination, or minimizing travel time in stochastic time-dependent O-D flows from several origins to a single destination ( Jeihani & Koohbanani, 2004).

One other traffic assignment model similar to the previous one is called system optimum (SO) in which the second principle of the Wardrop defines the logic of the model. Based on this principle, drivers’ rationale for choosing a path is to minimize total system costs with one another in order to minimize total system travel time (Mathew & Rao, 2006). Using the SO traffic assignment, problems like optimizing departure time for a single commuting route, minimizing total travels from multiple origins to one destination, or minimizing travel time in stochastic time-dependent OD flows from several origins to a single destination can be solved (Jeihani Koohbanani, 2004).

The basic mathematical formula for this model that satisfies the principle of the model is shown in equation (5):

In example 4, we will use the same network we described in the UE example in order to compare the results for the two models.

In that simple two-zone network, we had:

T 1 =5+4X 1    T2=3+2X 2 2

Now, based on the principle of the model we have:

Z(x)=x 1 t 1 (x 1 )+x 2 t 2 (x 2 )

Z(x)=x 1 (5+4x 1 )+x 2 (3+2x 2 2 )

Z(x)=5x 1 +4x 1 2 +3x 2 +2x 2 3

From the flow conservation. we have: x 1 +x 2 =4.5     x 1 =4.5-x 2

Z(x)=5(4.5-x 2 )+4(4.5-x 2 )2+4x 2 +x 2 3

Z(x)=x 3 2 +4x 2 2 -27x 2 +103.5

In order to minimize the above equation, we have to take derivatives and equate it to zero. After doing the calculations, we have:

Based on our finding, the system travel time would be:

T 1 =5+4*1.94=12.76min     T 2 =3+ 2(2.56)2=10.52 min

And the total travel time of the system would be:

Z(x)=X 1 T 1 (X 1 )+X 2 T 2 (X 2 )=1940 veh/hr(12.76)+2560 veh/hr(10.52)=24754+26931=51685 min

Incremental Increase model

Incremental increase is based on the logic of the AON model and models a process designed with multiple steps. In each step or level, a fraction of the total traffic volume is assigned, and travel time is calculated based on the allocated traffic volume. Through this incremental addition of traffic, the travel time of each route in step (n) is the updated travel time from the previous step (n-1) (Rojo, 2020).

The steps for the incremental increase traffic assignment model are:

• Finding the shortest path between each pair of O-Ds (Origin Destination).
• Assigning a portion of the trips according to the matrix (usually 40, 30, 20 and 10 percent to the shortest path).
• Updating the travel time after each iteration (each incremental increase).
• Continuing until all trips are assigned.
• Summing the results.

The example below illustrates the implementation process of this method.

A hypothetical network accommodates two zones with three possible links between them. Perform an incremental increase traffic assignment model for assigning 200 trips between the two zones with increments of: 30%, 30%, 20%, 20%. (The capacity is 50 trips.)

Incremental Increase Example

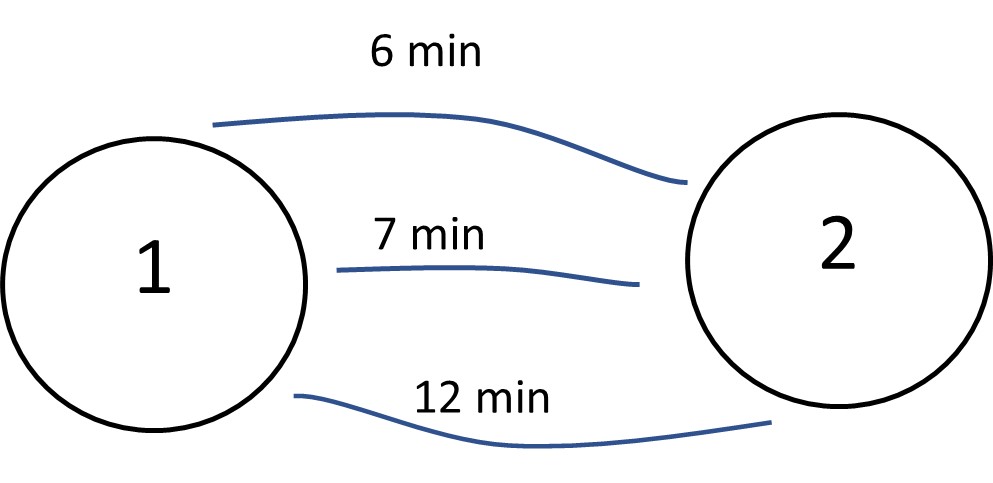
Step 1 (first iteration): Using the method of AON, we now assign the flow to the network using the function below:

Since the first route has the shortest travel time, the first 30% of the trips will be assigned to route 1. The updated travel time for this path would be:

And the remaining route will be empty, and thus their travel times are unchanged.

Step 2 (second iteration): Now, we can see that the second route has the shortest travel time, with 30% of the trips being assigned to this route, and the new travel time would be:

Step 3 (third iteration): In the third step, the 20% of the remaining trips will be assigned to the shortest path, which in this case is the first route again. The updated travel time for this route is:

Step 4 (fourth iteration): In the last iteration, the remaining 10% would be assigned to first route, and the time is:

Finally, we can see that route 1 has a total of 140 trips with a 8.85 travel time, the second route has a total of 60 trips with a 9.17 travel time, and the third route was never used.

Capacity Restraint Assignment

So far, all the presented algorithms or rules have considered the model’s link capacity. The flow is assigned to a link based on travel time as the only factor. In this model, after each iteration, the total number of trips is compared with the capacity to observe how much increase in travel time was realized by the added volume. In this model, the iteration stops if the added volume in step (n) does not change the travel time updated in step (n-1). With the incorporation of such a constraint, the cost or performance function would be different from the cost functions discussed in previous algorithms (Mathew & Rao, 2006). Figure 13.6 visualizes the relationship between flow and travel time with a capacity constraint.

Based on this capacity constraint specific to each link, the α, β can be readjusted for different links such as highways, freeways, and other roads.

Feedback Loop Model (Combined Traffic Assignment and Trip Distribution)

The feedback loop model defines an interaction between the trip distribution route choice step with several iterations. The model allows travelers to change their destination if a route is congested. For example, the feedback loop models that the traveler has a choice of similar destinations, such as shopping malls, in the area. In other words, in a real-world situation, travelers usually simultaneously decide about their travel characteristics (Qasim, 2012).

The chart below shows how the combination of these two modes can take place:

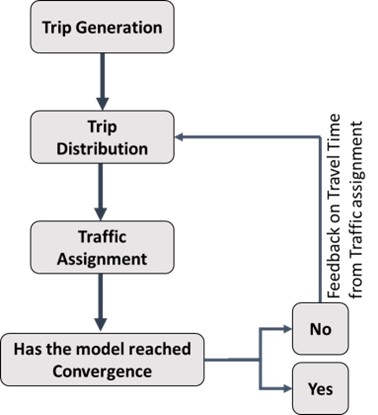
Equation (6), shown below for this model, ensures convergence at the end of the model is:

where C a (t) is the same as previous

P a   is total personal trip flows on link a,

f a   is total freight trip flows on link a,

T od is the total flow from node o to node d,

p od is personal trip from node o to node d,

F od is freight trip from node o to node d,

ζ is a parameter estimated from empirical data,

K is a parameter depending on the type of gravity model used to calculate T od , Evans (1976) proved that K’ equals to 1 for distribution using doubly constrained gravity model and it equals to 1 plus attractiveness for distribution using singly constrained model. Florian et al. (1975) ignored K for distribution using a doubly constrained gravity model because it is a constant.

Stochastic User Equilibrium Traffic Assignment

Stochastic user equilibrium traffic assignment is a sophisticated and more realistic model in which the level of uncertainty regarding which link should be used based on a measurement of utility function is introduced. This model performs a discrete choice analysis through a logistic model. Based on the first Wardrop principle, this model assumes that all drivers perceive the costs of traveling in each link identically and choose the route with minimum cost. In stochastic UE, however, the model allows different individuals to have different perceptions about the costs, and thus, they may choose non-minimum cost routes (Mathew & Rao, 2006). In this model, flow is assigned to all links from the beginning, unlike previous models, which is closer to reality. The probability of using each path is calculated with the following logit formula shown in equation (7):

P i is the probability of using path i

U i is the utility function for path i

In the following, an example of a simple network is presented.

Stochastic User Equilibrium Example

There is a flow of 200 trips between two points and their possible path, each of which has a travel time specified in Figure 13.7.

Using the mentioned logit formula for these paths, we have:

Based on the calculated probabilities, the distribution of the traffic flow would be:

Q 1 =175 trips

Q 2 =24 trips

Q 3 =1 trips

Dynamic Traffic Assignment

Recall the first Wardrop principle, in which travelers are believed to choose their routes with the minimum cost. Dynamic traffic assignment is based on the same rule, but the difference is that delays result from congestion. In this way, not only travelers’ route choice affects the network’s level of service, but also the network’s level of service affects travelers’ choice. However, it is not theoretically proven that an equilibrium would result under such conditions (Mathew & Rao, 2006).

Today, various algorithms are developed to solve traffic assignment problems. In any urban transportation system, travelers’ route choice and different links’ level of service have a dynamic feedback loop and affect each other simultaneously. However, a lot of these rules are not present in the models presented here. In real world cases, there can be more than thousands of nodes and links in the network, and therefore more sensitivity to dynamic changes is required for a realistic traffic assignment (Meyer, 2016). Also, the travel demand model applies a linear sequence of the four steps, which is unlike reality. Additionally, travelers may have only a limited knowledge of all possible paths, modes, and opportunities and may not make rational decisions.

In this last chapter of land-use/transportation modeling book, we reviewed the basic concepts and principles of traffic assignment models as the last step in travel demand modeling. Modeling the route choice and other components of travel behavior and demand for transportation proven to be very challenging and can incorporate multiple factors. For instance, going from AON to incremental increase assignment, we factor in the capacity and volume (and resulting delays) relationship in the assignment to make more realistic models.  Multiple-time-period assignments for multiple classes, separate specification of facilities like high-occupancy vehicle (HOV) and high-occupancy toll (HOT) lanes; and, independent transit assignment using congested highway travel times to estimate a bus ridership assignment, are some of the new extensions and variation of algorithms that take into account more realities within transportation network. A new prospect in traffic assignment models that adds several capabilities for such efforts is emergence of ITS such as data that can be collected from connected vehicles or autonomous vehicles. Using these data, perceived utility or impedances of different modes or infrastructure from individuals perspective can be modeled accurately, leading to more accurate assignment models, which are crucial planning studies such as growth and land use control efforts, environmental studies, transportation economies, etc.

Route choice is the process of choosing a certain path for a trip from a very large choice sets.

Regional Transportation Plan is long term planning document for a region’s transportation usually updated every five years.

• Vehicles (VMT) is the aggregate number of miles driven from in an area in particular time of day.
• Total vehicle travel time is the aggregate amount of time spent in transportation usually in minutes.

Link performance function is function used for estimating travel time, travel cost, and speed on the network based on the relationship between speed and travel flow.

Hyperbolic function is a function used for linear differential equations like calculating distances and angels in hyperbolic geometry.

Free-flow road is situation where vehicles can travel with the maximum allowed travel speed.

• Algorithms like all-or-nothing an assignment model where we assume that the impedance of a road or path between each origin and destination is constant and is equal to free-flow level of service, meaning that the traffic time is not affected by the traffic flow on the path.

Capacity-restrained is a model which takes into account the capacity of a road compared to volume and updates travel times.

User equilibrium is a traffic assignment model where we assume that travelers will always choose the shortest path and equilibrium condition would be realized when no traveler is able to decrease their travel impedance by changing paths.

System optimum assignment is an assignment model based on the principle that drivers’ rationale for choosing a path is to minimize total system costs with one another in order to minimize total system travel time.

• Static user-equilibrium assignment algorithm is an iterative traffic assignment process which assumes that travelers chooses the travel path with minimum travel time subject to constraints.
• Iterative feedback loop is a model that iterates between trip distribution and route choice step based on the rational that if a path gets too congested, the travel may alter travel destination.

First principle of Wardrop is the assumption that for each origin-destination (OD) pair, with UE, the travel time on all used paths is equal and less than or equally to the travel time that would be experienced by a single vehicle on any unused path.

System optimum (SO) is a condition in trip assignment model where total travel time for the whole area is at a minimum.

• Stochastic time-dependent OD is a modeling framework where generation and distribution of trips are randomly assigned to the area.

Incremental increase is AON-based model with multiple steps in each of which, a fraction of the total traffic volume is assigned, and travel time is calculated based on the allocated traffic volume.

Stochastic user equilibrium traffic assignment employs a probability distribution function that controls for uncertainties when drivers compare alternative routes and make decisions.

Dynamic traffic assignment is a model based on Wardrop first principle in which delays resulted from congestion is incorporated in the algorithm.

Key Takeaways

In this chapter, we covered:

• Traffic assignment is the last step of FSM, and the link cost function is a fundamental concept for traffic assignment.
• Different static and dynamic assignments and how to perform them using a simplistic transportation network.
• Incorporating stochastic decision-making about route choice and how to solve assignment problems with regard to this feature.

Prep/quiz/assessments

• Explain what the link performance function is in trip assignment models and how it is related to link capacity.
• Name a few static and dynamic traffic assignment models and discuss how different their rules or algorithms are.
• How does stochastic decision-making on route choice affect the transportation level of service, and how it is incorporated into traffic assignment problems?
• Name one extension of the all-or-nothing assignment model and explain how this extension improves the model results.

Correa, J.R., & Stier-Moses, N.E.(2010).Wardrope equilibria. In J.J. Cochran( Ed.), Wiley encyclopedia of operations research and management science (pp.1–12). Hoboken, NJ: John Wiley & Sons. http://dii.uchile.cl/~jcorrea/papers/Chapters/CS2010.pdf

Hui, C. (2014). Application study of all-or-nothing assignment method for determination of logistic transport route in urban planning. Computer Modelling & New Technologies , 18 , 932–937. http://www.cmnt.lv/upload-files/ns_25crt_170vr.pdf

Jeihani Koohbanani, M. (2004).  Enhancements to transportation analysis and simulation systems (Unpublished Doctoral dissertation, Virginia Tech). https://vtechworks.lib.vt.edu/bitstream/handle/10919/30092/dissertation-final.pdf?sequence=1&isAllowed=y

Levinson, D., Liu, H., Garrison, W., Hickman, M., Danczyk, A., Corbett, M., & Dixon, K. (2014). Fundamentals of transportation . Wikimedia. https://upload.wikimedia.org/wikipedia/commons/7/79/Fundamentals_of_Transportation.pdf

Mathew, T. V., & Rao, K. K. (2006). Introduction to transportation engineering. Civil engineering–Transportation engineering. IIT Bombay, NPTEL ONLINE, Http://Www. Cdeep. Iitb. Ac. in/Nptel/Civil% 20Engineering .

Meyer, M. D. (2016). Transportation planning handbook . John Wiley & Sons.

Qasim, G. (2015). Travel demand modeling: AL-Amarah city as a case study . [Unpublished Doctoral dissertation , the Engineering College University of Baghdad]

Rojo, M. (2020). Evaluation of traffic assignment models through simulation. Sustainability , 12 (14), 5536. https://doi.org/10.3390/su12145536

Sheffi, Y. (1985). Urban transportation networks: Equilibrium analysis with mathematical programming method . Prentice-Hall. http://web.mit.edu/sheffi/www/selectedMedia/sheffi_urban_trans_networks.pdf

US Bureau of Public Roads.  (1964). Traffic assignment manual for application with a large, high speed computer . U.S. Department of Commerce, Bureau of Public Roads, Office of Planning, Urban Planning Division.

https://books.google.com/books/about/Traffic_Assignment_Manual_for_Applicatio.html?id=gkNZAAAAMAAJ

Wang, X., & Hofe, R. (2008). Research methods in urban and regional planning . Springer Science & Business Media.

Vehicles (VMT) is the aggregate number of miles deriven from in an area in particular time of day.

Polynomial is distribution that involves the non-negative integer powers of a variable.

Hyperbolic function is a function that the uses the variable values as the power to the constant of e.

A point on the curve where the derivation of the function becomes either maximum or minimum.

all-or-nothing is an assignment model where we assume that the impedance of a road or path between each origin and destination is constant and is equal to free-flow level

Incremental model is a model that the predictions or estimates or fed into the model for forecasting incrementally to account for changes that may occur during each increment.

Iterative feedback loop is a model that iterates between trip distribution and route choice step based on the rational that if a path gets too congested, the travel may alter travel destination

Wardrop equilibrium is a state in traffic assignment model where are drivers are reluctant to change their path because the average travel time is at a minimum.

second principle of the Wardrop is a principle that assumes drivers’ rationale for choosing a path is to minimize total system costs with one another in order to minimize total system travel time

Stochastic time-dependent OD is a modeling framework where generation and distribution of trips are randomly assigned to the area

feedback loop model is type of dynamic traffic assignment model where an iteration between route choice and traffic assignment step is peformed, based on the assumption that if a particular route gets heavily congested, the travel may change the destination (like another shopping center).

Transportation Land-Use Modeling & Policy Copyright © by Mavs Open Press. All Rights Reserved.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.6: 3-6 Route Choice

• Last updated
• Save as PDF
• Page ID 48085

• David Levinson et al.
• Associate Professor (Engineering) via Wikipedia

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Route assignment , route choice , or traffic assignment concerns the selection of routes (alternative called paths) between origins and destinations in transportation networks. It is the fourth step in the conventional transportation forecasting model, following Trip Generation, Destination Choice, and Mode Choice. The zonal interchange analysis of trip distribution provides origin-destination trip tables. Mode choice analysis tells which travelers will use which mode. To determine facility needs and costs and benefits, we need to know the number of travelers on each route and link of the network (a route is simply a chain of links between an origin and destination). We need to undertake traffic (or trip) assignment. Suppose there is a network of highways and transit systems and a proposed addition. We first want to know the present pattern of travel times and flows and then what would happen if the addition were made.

Link Performance Function

The cost that a driver imposes on others is called the marginal cost. However, when making decisions, a driver only faces his own cost (the average cost) and ignores any costs imposed on others (the marginal cost).

• \[AverageCost=\dfrac{S_T}{Q}\]
• \[MarginalCost=\dfrac{\delta S_T}{\delta Q}\]

where \(S_T\) is the total cost, and \(Q\) is the flow.

BPR Link Performance Function

Suppose we are considering a highway network. For each link there is a function stating the relationship between resistance and volume of traffic. The Bureau of Public Roads (BPR) developed a link (arc) congestion (or volume-delay, or link performance) function, which we will term S a (Q a )

\[S_a(Q_a)=t_a(1+0.15\dfrac ({Q_a}{c_a})^4)\]

t a = free-flow travel time on link a per unit of time

Q a = flow (or volume) of traffic on link a per unit of time (somewhat more accurately: flow attempting to use link a )

c a = capacity of link a per unit of time

S a (Q a ) is the average travel time for a vehicle on link a

There are other congestion functions. The CATS has long used a function different from that used by the BPR, but there seems to be little difference between results when the CATS and BPR functions are compared.

Can Flow Exceed Capacity?

On a link, the capacity is thought of as “outflow.” Demand is inflow.

If inflow > outflow for a period of time, there is queueing (and delay).

For Example, for a 1 hour period, if 2100 cars arrive and 2000 depart, 100 are still there. The link performance function tries to represent that phenomenon in a simple way.

Wardrop's Principles of Equilibrium

User Equilibrium

Each user acts to minimize his/her own cost, subject to every other user doing the same. Travel times are equal on all used routes and lower than on any unused route.

• System optimal

Each user acts to minimize the total travel time on the system.

Price of Anarchy

The reason we have congestion is that people are selfish. The cost of that selfishness (when people behave according to their own interest rather than society's) is the price of anarchy .

The ratio of system-wide travel time under User Equilibrium and System Optimal conditions.

For a two-link network with linear link performance functions (latency functions), Price of Anarchy is < 4/3.

Is this too much? Should something be done, or is 33% waste acceptable? [The loss may be larger/smaller in other cases, under different assumptions, etc.]

Conservation of Flow

An important factor in road assignment is the conservation of flow. This means that the number of vehicles entering the intersection (link segment) equals the number of vehicles exiting the intersection for a given period of time (except for sources and sinks).

Similarly, the number of vehicles entering the back of the link equals the number exiting the front (over a long period of time).

Auto assignment

Long-standing techniques.

The above examples are adequate for a problem of two links, however real networks are much more complicated. The problem of estimating how many users are on each route is long standing. Planners started looking hard at it as freeways and expressways (motorways) began to be developed. The freeway offered a superior level of service over the local street system and diverted traffic from the local system. At first, diversion was the technique. Ratios of travel time were used, tempered by considerations of costs, comfort, and level of service.

The Chicago Area Transportation Study (CATS) researchers developed diversion curves for freeways versus local streets. There was much work in California also, for California had early experiences with freeway planning. In addition to work of a diversion sort, the CATS attacked some technical problems that arise when one works with complex networks. One result was the Moore algorithm for finding shortest paths on networks.

The issue the diversion approach didn’t handle was the feedback from the quantity of traffic on links and routes. If a lot of vehicles try to use a facility, the facility becomes congested and travel time increases. Absent some way to consider feedback, early planning studies (actually, most in the period 1960-1975) ignored feedback. They used the Moore algorithm to determine shortest paths and assigned all traffic to shortest paths. That’s called all or nothing assignment because either all of the traffic from i to j moves along a route or it does not.

The all-or-nothing or shortest path assignment is not trivial from a technical-computational view. Each traffic zone is connected to n - 1 zones, so there are numerous paths to be considered. In addition, we are ultimately interested in traffic on links. A link may be a part of several paths, and traffic along paths has to be summed link by link.

An argument can be made favoring the all-or-nothing approach. It goes this way: The planning study is to support investments so that a good level of service is available on all links. Using the travel times associated with the planned level of service, calculations indicate how traffic will flow once improvements are in place. Knowing the quantities of traffic on links, the capacity to be supplied to meet the desired level of service can be calculated.

Heuristic procedures

To take account of the affect of traffic loading on travel times and traffic equilibria, several heuristic calculation procedures were developed. One heuristic proceeds incrementally. The traffic to be assigned is divided into parts (usually 4). Assign the first part of the traffic. Compute new travel times and assign the next part of the traffic. The last step is repeated until all the traffic is assigned. The CATS used a variation on this; it assigned row by row in the O-D table.

The heuristic included in the FHWA collection of computer programs proceeds another way.

• Step 0: Start by loading all traffic using an all or nothing procedure.
• Step 1: Compute the resulting travel times and reassign traffic.
• Step 2: Now, begin to reassign using weights. Compute the weighted travel times in the previous two loadings and use those for the next assignment. The latest iteration gets a weight of 0.25 and the previous gets a weight of 0.75.
• Step 3. Continue.

These procedures seem to work “pretty well,” but they are not exact.

Frank-Wolfe algorithm

Dafermos (1968) applied the Frank-Wolfe algorithm (1956, Florian 1976), which can be used to deal with the traffic equilibrium problem.

Equilibrium Assignment

To assign traffic to paths and links we have to have rules, and there are the well-known Wardrop equilibrium (1952) conditions. The essence of these is that travelers will strive to find the shortest (least resistance) path from origin to destination, and network equilibrium occurs when no traveler can decrease travel effort by shifting to a new path. These are termed user optimal conditions, for no user will gain from changing travel paths once the system is in equilibrium.

The user optimum equilibrium can be found by solving the following nonlinear programming problem

\[min \displaystyle \sum_{a} \displaystyle\int\limits_{0}^{v_a}S_a(Q_a)\, dx\]

subject to:

\[Q_a=\displaystyle\sum_{i}\displaystyle\sum_{j}\displaystyle\sum_{r}\alpha_{ij}^{ar}Q_{ij}^r\]

\[sum_{r}Q_{ij}^r=Q_{ij}\]

\[Q_a\ge 0, Q_{ij}^r\ge 0\]

where \(Q_{ij}^r\) is the number of vehicles on path r from origin i to destination j . So constraint (2) says that all travel must take place: i = 1 ... n; j = 1 ... n

\(\alpha_{ij}^{ar}\)= 1 if link a is on path r from i to j ; zero otherwise.

So constraint (1) sums traffic on each link. There is a constraint for each link on the network. Constraint (3) assures no negative traffic.

Transit assignment

There are also methods that have been developed to assign passengers to transit vehicles. In an effort to increase the accuracy of transit assignment estimates, a number of assumptions are generally made. Examples of these include the following:

• All transit trips are run on a set and predefined schedule that is known or readily available to the users.
• There is a fixed capacity associated with the transit service (car/trolley/bus capacity).

Solve for the flows on Links a and b in the Simple Network of two parallel links just shown if the link performance function on link a :

\(S_a=5+2*Q_a\)

and the function on link b :

\(S_b=10+Q_b\)

where total flow between the origin and destination is 1000 trips.

Time (Cost) is equal on all used routes so \(S_a=S_b\)

And we have Conservation of flow so, \(Q_a+Q_b=Q_o=Q_d=1000\)

\(5+2*(1000-Q_b)=10+Q_b\)

\(1995=3Q_b\)

\(Q_b=665;Q_a=335\)

An example from Eash, Janson, and Boyce (1979) will illustrate the solution to the nonlinear program problem. There are two links from node 1 to node 2, and there is a resistance function for each link (see Figure 1). Areas under the curves in Figure 2 correspond to the integration from 0 to a in equation 1, they sum to 220,674. Note that the function for link b is plotted in the reverse direction.

\(S_a=15(1+0.15(\dfrac{Q_a}{1000})^4)\)

\(S_b=20(1+0.15(\dfrac{Q_a}{3000})^4)\)

\(Q_a+Q_b=8000\)

Show graphically the equilibrium result.

At equilibrium there are 2,152 vehicles on link a and 5,847 on link b . Travel time is the same on each route: about 63.

Figure 3 illustrates an allocation of vehicles that is not consistent with the equilibrium solution. The curves are unchanged, but with the new allocation of vehicles to routes the shaded area has to be included in the solution, so the Figure 3 solution is larger than the solution in Figure 2 by the area of the shaded area.

Assume the traffic flow from Milwaukee to Chicago, is 15000 vehicles per hour. The flow is divided between two parallel facilities, a freeway and an arterial. Flow on the freeway is denoted \(Q_f\), and flow on the two-lane arterial is denoted \(Q_a\).

The travel time (in minutes) on the freeway (\(C_f\)) is given by:

\(C_f=10+Q_f/1500\)

\(C_a=15+Q_a/1000\)

Apply Wardrop's User Equilibrium Principle, and determine the flow and travel time on both routes.

The travel times are set equal to one another

\(C_f=C_a\)

\(10+Q_f/1500=15+Q_a/1000\)

The total traffic flow is equal to 15000

\(Q_f+Q_a=15000\)

\(Q_a=15000-Q_f\)

\(10+Q_f/1500=15+(15000-Q_f)/1000\)

Solve for \(Q_f\)

\(Q_f=60000/5=12000\)

\(Q_a=15000-Q_f=3000\)

Thought Questions

• How can we get drivers to consider their marginal cost?
• Alternatively: How can we get drivers to behave in a “System Optimal” way?

Sample Problems

Given a flow of six (6) units from origin “o” to destination “r”. Flow on each route ab is designated with Qab in the Time Function. Apply Wardrop's Network Equilibrium Principle (Users Equalize Travel Times on all used routes)

A. What is the flow and travel time on each link? (complete the table below) for Network A

Link Attributes

B. What is the system optimal assignment?

C. What is the Price of Anarchy?

What is the flow and travel time on each link? Complete the table below for Network A:

These four links are really 2 links O-P-R and O-Q-R, because by conservation of flow Qop = Qpr and Qoq = Qqr.

By Wardrop's Equilibrium Principle, the travel time (cost) on each used route must be equal. Therefore \(C_{opr}=C_{oqr}\)

OR \(25+6*Q_{opr}=20+7*Q_{oqr}\)

\(5+6*Q_{opr}=7*Q_{oqr}\)

\(Q_{oqr}=5/7+6*Q_{opr}/7\)

By the conservation of flow principle

\(Q_{oqr}+Q_{opr}=6\)

\(Q_{opr}=6-Q_{oqr}\)

By substitution

\Q_{oqr}=5/7+6/7(6-Q_{oqr})=41/7-6*Q_{oqr}/7\)

\(13*Q_{oqr}=41\)

\(Q_{oqr}=41/13=3.15\)

\(Q_{opr}=2.84\)

\(42.01=25+6(2.84)\)

\(42.05=20+7(3.15)\)

Check (within rounding error)

or expanding back to the original table:

User Equilibrium: Total Delay = 42.01 * 6 = 252.06

What is the system optimal assignment?

Conservation of Flow:

\(Q_{opr}+Q_{oqr}=6\)

\(TotalDelay=Q_{opr}(25+6*Q_{oqr})+Q_{oqr}(20+7*Q_{oqr})\)

\(25Q_{opr}+6Q_{opr}^2+(6_Q_{opr})(20+7(6-Q_{opr}))\)

\(25Q_{opr}+6Q_{opr}^2+(6_Q_{opr})(62-7Q_{opr}))\)

\(25Q_{opr}+6Q_{opr}^2+372-62Q_{opr}-42Q_{opr}+7Q_{opr}^2\)

\(13Q_{opr}^2-79Q_{opr}+372\)

Analytic Solution requires minimizing total delay

\(\deltaC/\deltaQ=26Q_{opr}-79=0\)

\(Q_{opr}=79/26-3.04\)

\(Q_{oqr}=6-Q_{opr}=2.96\)

And we can compute the SO travel times on each path

\(C_{opr,SO}=25+6*3.04=43.24\)

\(C_{opr,SO}=20+7*2.96=40.72\)

Note that unlike the UE solution, \(C_{opr,SO}\g C_{oqr,SO}\)

Total Delay = 3.04(25+ 6*3.04) + 2.96(20+7*2.96) = 131.45+120.53= 251.98

Note: one could also use software such as a "Solver" algorithm to find this solution.

What is the Price of Anarchy?

User Equilibrium: Total Delay =252.06 System Optimal: Total Delay = 251.98

Price of Anarchy = 252.06/251.98 = 1.0003 < 4/3

The Marcytown - Rivertown corridor was served by 3 bridges, according to the attached map. The bridge over the River on the route directly connecting Marcytown and Citytown collapsed, leaving two alternatives, via Donkeytown and a direct. Assume the travel time functions Cij in minutes, Qij in vehicles/hour, on the five links routes are as given.

Marcytown - Rivertown Cmr = 5 + Qmr/1000

Marcytown - Citytown (prior to collapse) Cmc = 5 + Qmc/1000

Marcytown - Citytown (after collapse) Cmr = ∞

Citytown - Rivertown Ccr = 1 + Qcr/500

Marcytown - Donkeytown Cmd = 7 + Qmd/500

Donkeytown - Rivertown Cdr = 9 + Qdr/1000

Also assume there are 10000 vehicles per hour that want to make the trip. If travelers behave according to Wardrops user equilibrium principle.

A) Prior to the collapse, how many vehicles used each route?

Route A (Marcytown-Rivertown) = Ca = 5 + Qa/1000

Route B (Marcytown-Citytown-Rivertown) = Cb = 5 + Qb/1000 + 1 + Qb/500 = 6 + 3Qb/1000

Route C (Marcytown-Donkeytown-Rivertown)= Cc = 7 + Qc/500 + 9 + Qc/1000 = 16 + 3Qc/1000

At equilibrium the travel time on all three used routes will be the same: Ca = Cb = Cc

We also know that Qa + Qb + Qc = 10000

Solving the above set of equations will provide the following results:

Qa = 8467;Qb = 2267;Qc = −867

We know that flow cannot be negative. By looking at the travel time equations we can see a pattern.

Even with a flow of 0 vehicles the travel time on route C(16 minutes) is higher than A or B. This indicates that vehicles will choose route A or B and we can ignore Route C.

Solving the following equations:

Route A (Marcytown-Rivertown) = Ca = 5 + Qa /1000

Route B (Marcytown-Citytown-Rivertown) = Cb = 6 + 3Qb /1000

Qa + Qb = 10000

We can the following values:

Qa = 7750; Qb = 2250; Qc = 0

B) After the collapse, how many vehicles used each route?

We now have only two routes, route A and C since Route B is no longer possible. We could solve the following equations:

Route C (Marcytown- Donkeytown-Rivertown) = Cc = 16 + 3Qc /1000

Qa+ Qc= 10000

But we know from above table that Route C is going to be more expensive in terms of travel time even with zero vehicles using that route. We can therefore assume that Route A is the only option and allocate all the 10,000 vehicles to Route A.

If we actually solve the problem using the above set of equations, you will get the following results:

Qa = 10250; Qc = -250

which again indicates that route C is not an option since flow cannot be negative.

C) After the collapse, public officials want to reduce inefficiencies in the system, how many vehicles would have to be shifted between routes? What is the “price of anarchy” in this case?

TotalDelayUE =(15)(10,000)=150,000

System Optimal

TotalDelaySO =(Qa)(5+Qa/1000)+(Qc)(16+3Qc/1000)

Using Qa + Qc = 10,000

TotalDelaySO =(Qa2)/250−71Qa+460000

Minimize total delay ∂((Qa2)/250 − 71Qa + 460000)/∂Qa = 0

Qa/125−7 → Qa = 8875 Qc = 1125 Ca = 13,875 Cc = 19,375

TotalDelaySO =144938

Price of Anarchy = 150,000/144,938 = 1.035

• \(C_T\) - total cost
• \(C_k\) - travel cost on link \(k\)
• \(Q_k\) - flow (volume) on link \(k\)

Abbreviations

• VDF - Volume Delay Function
• LPF - Link Performance Function
• BPR - Bureau of Public Roads
• UE - User Equilbrium
• SO - System Optimal
• DTA - Dynamic Traffic Assignment
• DUE - Deterministic User Equilibrium
• SUE - Stochastic User Equilibrium
• AC - Average Cost
• MC - Marginal Cost
• Route assignment, route choice, auto assignment
• Volume-delay function, link performance function
• User equilibrium
• Conservation of flow
• Average cost
• Marginal cost

External Exercises

Use the ADAM software at the STREET website and try Assignment #3 to learn how changes in network characteristics impact route choice.

Additional Questions

1. If trip distribution depends on travel times, and travel times depend on the trip table (resulting from trip distribution) that is assigned to the road network, how do we solve this problem (conceptually)?

2. Do drivers behave in a system optimal or a user optimal way? How can you get them to move from one to the other.

3. Identify a mechanism that can ensure the system optimal outcome is achieved in route assignment, rather than the user equilibrium. Why would we want such an outcome? What are the drawbacks to the mechanism you identified?

4. Assume the flow from Dakotopolis to New Fargo, is 5300 vehicles per hour. The flow is divided between two parallel facilities, a freeway and an arterial. Flow on the freeway is denoted \(Q_f\), and flow on the two-lane arterial is denoted \(Q_r\). The travel time on the freeway \(C_f\) is given by:

\(C_f=5+Q_f/1000\)

The travel time on the arterial (Cr) is given by

\(C_r=7+Q_r/500\)

(a) Apply Wardrop's User Equilibrium Principle, and determine the flow and travel time on both routes from Dakotopolis to New Fargo.

(b) Solve for the System Optimal Solution and determine the flow and travel time on both routes.

5. Given a flow of 10,000 vehicles from origin to destination traveling on three parallel routes. Flow on each route A, B, or C is designated with \(Q_a\), \(Q_b\), \(Q_c\) in the Time Function Respectively. Apply Wardrop's Network Equilibrium Principle (Users Equalize Travel Times on all used routes), and determine the flow on each route.

\(T_A=500+20Q_A\)

\(T_B=1000+10Q_B\)

\(T_C=2000+30Q_C\)

• How does average cost differ from marginal cost?
• How do System Optimal and User Equilibrium travel time differ?
• Why do we want people to behave in an SO way?
• How can you get people to behave in an SO way?
• Who was John Glen Wardrop?
• What are Wardrop’s Two Principles?
• What does conservation of flow require in route assignment?
• Can Variable Message Signs be used to encourage System Optimal behavior?
• What is freeflow travel time?
• If a problem has more than two routes, where does the extra equation come from?
• How can you determine if a route is unused?
• What is the difference between capacity and flow
• Draw a typical volume-delay function for a deterministic, static user equilibrium assignment.
• Can Q be negative?
• What is route assignment?
• Is it important that the output travel times from route choice be consistent with the input travel times for destination choice and mode choice? Why?

• Help & FAQ

Traffic assignment: A survey of mathematical models and techniques

• Civil and Urban Engineering
• Center for Interacting Urban Networks

Research output : Chapter in Book/Report/Conference proceeding › Chapter

This chapter presents the fundamentals of the theory and techniques of traffic assignment problem. It first presents the steady-state traffic assignment problem formulation which is also called static assignment, followed by Dynamic Traffic Assignment (DTA), where the traffic demand on the network is time varying. The static assignment problem is shown in a mathematical programming setting for two different objectives to be satisfied. The first one where all users experience same travel times in alternate used routes is called user-equilibrium and another setting called system optimum in which the assignment attempts to minimize the total travel time. The alternate formulation uses variational inequality method which is also presented. Dynamic travel routing problem is also reviewed in the variational inequality setting. DTA problem is shown in discrete and continuous time in terms of lumped parameters as well as in a macroscopic setting, where partial differential equations are used for the link traffic dynamics. A Hamilton–Jacobi- based travel time dynamics model is also presented for the links and routes, which is integrated with the macroscopic traffic dynamics. Simulation-based DTA method is also very briefly reviewed. This chapter is taken from the following Springer publication and is reproduced here, with permission and with minor changes: Pushkin Kachroo, and Neveen Shlayan, “Dynamic traffic assignment: A survey of mathematical models and technique,” Advances in Dynamic Network Modeling in Complex Transportation Systems (Editor: Satish V. Ukkusuri and Kaan Özbay) Springer New York, 2013. 1-25.

Publication series

Asjc scopus subject areas.

• Control and Systems Engineering
• Automotive Engineering
• Aerospace Engineering
• Industrial and Manufacturing Engineering

Access to Document

• 10.1007/978-3-319-69231-9_2

Other files and links

• Link to publication in Scopus
• Link to the citations in Scopus

Traffic Assignment Problem

Traffic assignment problems usually consider two dimensions.

• Generation and attraction . A place of origin generates movements that are bound (attracted) to a place of destination. The relationship between traffic generation and attraction is commonly labeled as spatial interaction. The above example considers one origin/generation and destination/attraction, but the majority of traffic assignment problems consider several origins and destinations.
• Path selection . Traffic assignment considers which paths are to be selected and the amount of traffic using these paths (if more than one unit). For simple problems, a single path will be selected, while for complex problems, several paths could be used. Factors behind the choice of traffic assignment may include cost, time, or the number of connections.

Share this:

Network assignment

What is Network Assignment?

Role of Network Assignment in Travel Forecasting

Overview of Methods for Traffic Assignment for Highways

All-or-nothing Assignments

Incremental assignment

Brief History of Traffic Equilibrium Concepts

Calculating Generalized Costs from Delays

Challenges for Highway Traffic Assignment

Transit Assignment

Latest Developments

Page categories

Topic Circles

Trip Based Models

More pages in this category:

# what is network assignment.

In the metropolitan transportation planning and analysis, the network assignment specifically involves estimating travelers’ route choice behavior when travel destinations and mode of travel are known. Origin-destination travel demand are assigned to a transportation network in order to estimate traffic flows and network travel conditions such as travel time. These estimated outputs from network assignment are compared against observed data such as traffic counts for model validation .

Network assignment is a mathematical problem which is solved by a solution algorithm through the use of computer. It is usually resolved as a travel cost optimization problem for each origin-destination pair on a model network. For every origin-destination pair, a path is selected that typically minimizes travel costs. The simplest kind of travel cost is travel time from beginning to end of the trip. A more complex form of travel cost, called generalized cost, may include combinations of other costs of travel such as toll cost and auto operating cost on highway networks. Transit networks may include within generalized cost weights to emphasize out-of-vehicle time and penalties to represent onerous tasks. Usually, monetary costs of travel, such as tolls and fares, are converted to time equivalent based on an estimated value of time. The shortest path is found using a path finding algorithm .

The surface transportation network can include the auto network, bus network, passenger rail network, bicycle network, pedestrian network, freight rail network, and truck network. Traditionally, passenger modes are handled separately from vehicular modes. For example, trucks and passenger cars may be assigned to the same network, but bus riders often are assigned to a separate transit network, even though buses travel over roads. Computing traffic volume on any of these networks first requires estimating network specific origin-destination demand. In metropolitan transportation planning practice in the United States, the most common network assignments employed are automobile, truck, bus, and passenger rail. Bicycle, pedestrian, and freight rail network assignments are not as frequently practiced.

# Role of Network Assignment in Travel Forecasting

The urban travel forecasting process is analyzed within the context of four decision choices:

• Personal Daily Activity
• Locations to Perform those Activities
• Mode of Travel to Activity Locations, and
• Travel Route to the Activity Locations.

Usually, these four decision choices are named as Trip Generation , Trip Distribution , Mode Choice , and Traffic Assignment. There are variations in techniques on how these travel decision choices are modeled both in practice and in research. Generalized cost, which is typically in units of time and is an output of the path-choice step of the network assignment process, is the single most important travel input to other travel decision choices, such as where to travel and by which mode. Thus, the whole urban travel forecasting process relies heavily on network assignment. Generalized cost is also a major factor in predicting socio-demographic and spatial changes. To ensure consistency in generalized cost between all travel model components in a congested network, travel cost may be fed back to the earlier steps in the model chain. Such feedback is considered “best practice” for urban regional models. Outputs from network assignment are also inputs for estimating mobile source emissions as part of a review of metropolitan area transportation plans, a requirement under the Clean Air Act Amendments of 1990 for areas not in attainment of the National Ambient Air Quality Standard.

# Overview of Methods for Traffic Assignment for Highways

This topic deals principally with an overview of static traffic assignment. The dynamic traffic assignment is discussed elsewhere.

There are a large number of traffic assignment methods, but they all have at their core a procedure called “all-or-nothing” (AON) traffic assignment. All-or-nothing traffic assignment places all trips between an origin and destination on the shortest path between that origin and destination and no trips on any other possible path (compare path finding algorithm for a step-by-step introduction). Shortest paths may be determined by a well-known algorithm by Dijkstra; however, when there are turn penalties in the network a different algorithm, called Vine building , must be used instead.

# All-or-nothing Assignments

The simplest assignment algorithm is the all-or-nothing traffic assignment. In this algorithm, flows from every origin to every destination are assigned using the path finding algorithm , and travel time remains unchanged regardless of travel volumes.

All-or-nothing traffic assignment may be used when delays are unimportant for a network. Another alternative to the user-equilibrium technique is the stochastic traffic assignment technique, which assumes variation in link level travel time.

One of the earliest, computationally efficient stochastic traffic assignment algorithms was developed by Robert Dial. [1] More recently the k-shortest paths algorithm has gained popularity.

The biggest disadvantage of the all-or-nothing assignment and the stochastic assignment is that congestion cannot be considered. In uncongested networks, these algorithms are very useful. In congested conditions, however, these algorithm miss that some travelers would change routes to avoid congestion.

# Incremental assignment

The incremental assignment method is the simplest way to (somewhat rudimentary) consider congestion. In this method, a certain share of all trips (such as half of all trips) is assigned to the network. Then, travel times are recalculated using a volume-delay function , or VDF. Next, a smaller share (such as 25% of all trips) is assigned based using the revised travel times. Using the demand of 50% + 25%, travel times are recalculated again. Next, another smaller share of trips (such as 10% of all trips) is assigned using the latest travel times.

A large benefit of the incremental assignment is model runtime. Usually, flows are assigned within 5 to 10 iterations. Most user-equilibrium assignment methods (see below) require dozens of iterations, which increases the runtime proportionally.

In the incremental assignment, the first share of trips is assigned based on free-flow conditions. Following iterations see some congestion, on only the very last trip to be assigned will consider true congestion levels. This is reasonable for lightly congested networks, as a large number of travelers could travel at free-flow speed.

The incremental assignment works unsatisfactorily in heavily congested networks, as even 50% of the travel demand may lead to congestion on selected roads. The incremental assignment will miss the fact that a portion of the 50% is likely to select different routes.

# Brief History of Traffic Equilibrium Concepts

Traffic assignment theory today largely traces its origins to a single principle of “user equilibrium” by Wardrop [2] in 1952. Wardrop’s “first” principle simply states (slightly paraphrased) that at equilibrium not a single driver may change paths without incurring a greater travel impedance . That is, any used path between an origin and destination must have a shortest travel time between the origin and destination, and all other paths must have a greater travel impedance. There may be multiple paths between an origin and destination with the same shortest travel impedance, and all of these paths may be used.

Prior to the early 1970’s there were many algorithms that attempted to solve for Wardrop’s user equilibrium on large networks. All of these algorithms failed because they either did not converge properly or they were too slow computationally. The first algorithm to be able to consistently find a correct user equilibrium on a large traffic network was conceived by a research group at Northwestern University (LeBlanc, Morlok and Pierskalla) in 1973. [3] This algorithm was called “Frank-Wolfe decomposition” after the name of a more general optimization technique that was adapted, and it found the minimum of an “objective function” that came directly from theory attributed to Beckmann from 1956. [4] The Frank-Wolfe decomposition formulation was extended to the combined distribution/assignment problem by Evans in 1974. [5]

A lack of extensibility of these algorithms to more realistic traffic assignments prompted model developers to seek more general methods of traffic assignment. A major development of the 1980s was a realization that user equilibrium traffic assignment is a “variational inequality” and not a minimization problem. [6] An algorithm called the method of successive averages (MSA) has become a popular replacement for Frank-Wolfe decomposition because of MSA’s ability to handle very complicated relations between speed and volume and to handle the combined distribution/mode-split/assignment problem. The convergence properties of MSA were proven for elementary traffic assignments by Powell and Sheffi and in 1982. [7] MSA is known to be slower on elementary traffic assignment problems than Frank-Wolfe decomposition, although MSA can solve a wider range of traffic assignment formulations allowing for greater realism.

A number of enhancements to the overall theme of Wardop’s first principle have been implemented in various software packages. These enhancements include: faster algorithms for elementary traffic assignments, stochastic multiple paths, OD table spatial disaggregation and multiple vehicle classes.

# Calculating Generalized Costs from Delays

Equilibrium traffic assignment needs a method (or series of methods) for calculating impedances (which is another term for generalized costs) on all links (and nodes) of the network, considering how those links (and nodes) were loaded with traffic. Elementary traffic assignments rely on volume-delay functions (VDFs), such as the well-known “BPR curve” (see NCHRP Report 365), [8] that expressed travel time as a function of link volume and link capacity. The 1985 US Highway Capacity Manual (and later editions through 2010) made it clear to transportation planners that delays on large portions of urban networks occur mainly at intersections, which are nodes on a network, and that the delay on any given intersection approach relates to what is happening on all other approaches. VDFs are not suitable for situations where there is conflicting and opposing traffic that affects delays. Software for implementing trip-based models are now incorporating more sophisticated delay relationships from the Highway Capacity Manual and other sources, although many MPO forecasting models still use VDFs, exclusively.

# Challenges for Highway Traffic Assignment

Numerous practical and theoretical inadequacies pertaining to Static User Equilibrium network assignment technique are reported in the literature. Among them, most widely noted concerns and challenges are:

• Inadequate network convergence;
• Continued use of legacy slow convergent network algorithm, despite availability of faster solution methods and computers;
• Non-unique route flows and link flows for multi-class assignments and for assignment on networks that include delays from opposing and conflicting traffic;
• Continued use of VDFs , when superior delay estimation techniques are available;
• Unlikeness of a steady-state network condition;
• Impractical assumption that all drivers have flawless route information and are acting without bias;
• Every driver travels at the same congested speed, no vehicle traveling on the same link overtakes another vehicle;
• Oncoming traffic does not affect traffic flows;
• Interruptions, such as accidents or inclement weather, are not represented;
• Traffic does not form queues;
• Continued use of multi-hour time periods, when finer temporal detail gives better estimates of delay and path choice.

# Transit Assignment

Most transit network assignment in implementation is allocation of known transit network specific demand based on routes, vehicle frequency, stop location, transfer point location and running times. Transit assignments are not equilibrium, but can be either all-or-nothing or stochastic. Algorithms often use complicated expressions of generalized cost which include the different effects of waiting time, transfer time, walking time (for both access and egress), riding time and fare structures. Estimated transit travel time is not directly dependent on transit passenger volume on routes and at stations (unlike estimated highway travel times, which are dependent on vehicular volumes on roads and at intersection). The possibility of many choices available to riders, such as modes of access to transit and overlaps in services between transit lines for a portion of trip segments, add further complexity to these problems.

# Latest Developments

With the increased emphasis on assessment of travel demand management strategies in the US, there have been some notable increases in the implementation of disaggregated modeling of individual travel demand behavior. Similar efforts to simulate travel route choice on dynamic transportation network have been proposed, primarily to support the much needed realistic representation of time and duration of roadway congestion. Successful examples of a shift in the network assignment paradigm to include dynamic traffic assignment on a larger network have emerged in practice. Dynamic traffic assignments are able to follow UE principles. An even newer topic is the incorporation of travel time reliability into path building.

# References

Dial , Robert Barkley, Probabilistic Assignment; a Multipath Traffic Assignment Model Which Obviates Path Enumeration, Thesis (Ph.D.), University of Washington, 1971. ↩︎

Wardrop, J. C., Some Theoretical Aspects of Road Traffic Research, Proceedings, Institution of Civil Engineers Part 2, 9, pp. 325–378. 1952. ↩︎

LeBlanc, Larry J., Morlok, Edward K., Pierskalla, William P., An Efficient Approach to Solving the Road Network Equilibrium Traffic Assignment Problem, Transportation Research 9, 1975, 9, 309–318. ↩︎

(opens new window) ) ↩︎

Evans, Suzanne P., Derivation and Analysis of Some Models for Combining Trip Distribution and Assignment, Transportation Research, Vol 10, pp 37–57 1976. ↩︎

Dafermos, S.C., Traffic Equilibrium and Variational Inequalities, Transportation Science 14, 1980, pp. 42-54. ↩︎

Powell, Warren B. and Sheffi, Yosef, The Convergence of Equilibrium Algorithms with Predetermined Step Sizes, Transportation Science, February 1, 1982, pp. 45-55. ↩︎

(opens new window) ). ↩︎

← Mode choice Dynamic Traffic Assignment →

This site uses cookies to learn which topics interest our readers.

To read this content please select one of the options below:

Please note you do not have access to teaching notes, traffic assignment methods.

Handbook of Transport Geography and Spatial Systems

ISBN : 978-0-080-44108-5 , eISBN : 978-1-615-83253-8

Publication date: 24 August 2004

Acknowledgements

Acknowledgment.

This study is mainly supported by two grants from the Research Grants Council of the Hong Kong Special Administration Region awarded to the Hong Kong Polytechnic University (Project Nos. PolyU 5046/00E and N_PolyU 515/01).

Lam, W.H.K. and Lo, H.K. (2004), "Traffic Assignment Methods", Hensher, D.A. , Button, K.J. , Haynes, K.E. and Stopher, P.R. (Ed.) Handbook of Transport Geography and Spatial Systems ( , Vol. 5 ), Emerald Group Publishing Limited, Leeds, pp. 609-625. https://doi.org/10.1108/9781615832538-034

Emerald Group Publishing Limited

Copyright © 2008 Emerald Group Publishing Limited

We’re listening — tell us what you think

Something didn’t work….

Report bugs here

All feedback is valuable

Please share your general feedback

Join us on our journey

Platform update page.

Visit emeraldpublishing.com/platformupdate to discover the latest news and updates

Questions & More Information

Answers to the most commonly asked questions here

• Newsletters

IE 11 Not Supported

• Special: Constituents

Can AI Help Agencies Save Money on Traffic Studies?

As agencies get more comfortable with new ways of analyzing data, urbanlogiq is betting officials will prefer ai-powered tools over typical traffic-counting methods. already one city has started using such a product..

Evaluating the Effect of Multiple Data Types on a Large Scale Static Origin–Destination Matrix Estimation, Case Study of Tehran, Iran

• Research Paper
• Published: 28 May 2024

Cite this article

• Ali Farzaneh Movahed 1 &
• Mahmoud Mesbah   ORCID: orcid.org/0000-0002-3344-1350 1 , 2  

15 Accesses

Explore all metrics

The purpose of this study is to estimate the Origin–Destination Matrix (ODM) of Tehran city which is a large scale network, using three types of field data of count links, partial paths flows, and the difference in incoming and outgoing flows to/from the central traffic area. The data was collected from 482 Automatic Number Plate Recognition cameras on two cordon lines and 1957 inductive loop detectors at signalized intersections. A bi-level iterative model is used to estimate the static ODM. The upper level minimized an error term based on the multiple field measurements and the lower level formulates a user equilibrium traffic assignment. The results showed that the R-squared value of the fitted line, which regressed the observed and estimated values of the field data, was increased from 0.5 before an ODM estimation to 0.74 afterwards. The value of the PRMSE after estimating the ODM decreased by 37% compared to the before scenario. These results indicate that the estimated ODM is significantly better than the base ODM. In conclusion, this study demonstrated an efficient approach to estimate the ODM in a large scale network and successfully estimated the ODM of Tehran city.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Estimation of origin–destination matrices using link counts and partial path data

Estimation of an Urban OD Matrix Using Different Information Sources

A Bayesian Markov Model for Station-Level Origin-Destination Matrix Reconstruction

Abrahamsson T (1998) Estimation of origin-destination matrices using traffic counts-a literature survey. Travel behaviour research: updating the state of play. Elsevier, Amsterdam, pp 199–220

Google Scholar  

Afandizadeh Zargari S, Memarnejad A, Mirzahossein H (2021) Hourly origin–destination matrix estimation using intelligent transportation systems data and deep learning. Sensors 21(21):7080

Article   Google Scholar  

Alsger A, Tavassoli A, Mesbah M, Ferreira L (2017) Evaluation of effects from sample-size origin-destination estimation using smart card fare data. J Transp Eng Part A Syst 143(4):4017003

Bananiardecani F, Mahmoudzadeh A, Mesbah M (2024) Fuzing multiple erroneous sensors to estimate travel time. J Intell Transp Syst. https://doi.org/10.1080/15472450.2024.2315514

Bell MGH (1991) The estimation of origin-destination matrices by constrained generalised least squares. Transp Res Part B Methodol 25(1):13–22

Article   MathSciNet   Google Scholar  

Byrd RH, Hribar ME, Nocedal J (1999) An interior point algorithm for large-scale nonlinear programming. SIAM J Optim 9(4):877–900

Byrd RH, Gilbert JC, Nocedal J (2000) A trust region method based on interior point techniques for nonlinear programming. Math Program 89:149–185

Caggiani L, Ottomanelli M, Sassanelli D (2013) A fixed point approach to origin–destination matrices estimation using uncertain data and fuzzy programming on congested networks. Transp Res Part C Emerg Technol 28:130–141

Ceccato R, Gecchele G, Rossi R, Gastaldi M (2022) Cost-effectiveness analysis of origin-destination matrices estimation using floating car data. Experimental results from two real cases. Transp Res Procedia 62:541–548

Cipriani E, Florian M, Mahut M, Nigro M (2011) A gradient approximation approach for adjusting temporal origin–destination matrices. Transp Res Part C Emerg Technol 19(2):270–282

Cipriani E, Gemma A, Mannini L, Carrese S, Crisalli U (2021) Traffic demand estimation using path information from Bluetooth data. Transp Res Part C Emerg Technol 133:103443

de Villa AR, Casas J, Breen M, Perarnau J (2014) Static OD estimation minimizing the relative error and the GEH index. Procedia-Soc Behav Sci 111:810–818

Djahel S, Doolan R, Muntean G-M, Murphy J (2014) A communications-oriented perspective on traffic management systems for smart cities: challenges and innovative approaches. IEEE Commun Surv Tutorials 17(1):125–151

Englezou Y, Timotheou S, and Panayiotou CG (2021), Estimating the origin-destination matrix using link count observations from unmanned aerial vehicles. In: 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), pp. 3539–3544.

Gholi H, Mamdoohi AR, Babazadeh A (2022) An application of stochastic user equilibrium assignment in the origin-destination matrix estimation. Sharif J Civ Eng 38(11):99–108

Kim H, Nam D, Suh W, Cheon SH (2018) Origin-destination trip table estimation based on subarea network OD flow and vehicle trajectory data. Transp Plan Technol 41(3):265–285

Landau U, Hauer E, Geva I (1981) Estimation of cross-cordon origin-destination flows from cordon studies. Transp Res Rec 891:5–10

Lundgren JT, Peterson A (2008) A heuristic for the bilevel origin–destination-matrix estimation problem. Transp Res Part B Methodol 42(4):339–354

Mahpour A, Mamdoohi AR (2019) Evaluating the effect of traffic assignment method on the accuracy of the origin-destination matrix correction results in traffic fuzzy flow method. J Transp Res 16(3):1–9

Mesbah M, Mollajafari M, Golroo A, Pakdaman Z (2021) Fusion of travel time data in Niayesh tunnel using Bayesian inference. Amirkabir J Civ Eng 53(10):4205–4218

Mesbah M, Bourbour S, Faroqi H, Ghaffari A, and Ghassemi S (2022) A data-driven approach to estimate dynamic and multimodal urban origin-destination matrices

Parry K, Hazelton ML (2012) Estimation of origin–destination matrices from link counts and sporadic routing data. Transp Res Part B Methodol 46(1):175–188

Patil SN, Behara KNS, Khadhir A, Bhaskar A (2023) Methods to enhance the quality of bi-level origin–destination matrix adjustment process. Transp Lett 15(2):77–86

Rao W, Wu Y-J, Xia J, Ou J, Kluger R (2018) Origin-destination pattern estimation based on trajectory reconstruction using automatic license plate recognition data. Transp Res Part C Emerg Technol 95:29–46

Research project of updating multi-modal hourly OD matrices for Tehran City Network,” Tehran, 2020.

Rostami Nasab M, Shafahi Y (2020) Estimation of origin–destination matrices using link counts and partial path data. Transportation (Amst) 47(6):2923–2950

Sbaï A, Van Zuylen HJ, Li J, Zheng F, and Ghadi F (2017), Estimation of an urban OD matrix using different information sources. In: Computational Science and Its Applications–ICCSA 2017: 17th International Conference, Trieste, Italy, July 3-6, 2017, Proceedings, Part II 17, pp. 183–198.

Shafiei S, Saberi M, Vu HL (2020) Integration of departure time choice modeling and dynamic origin–destination demand estimation in a large-scale network. Transp Res Rec 2674(9):972–981

Sheffi Y (1985) Urban transportation networks, vol 6. Prentice-Hall, Englewood Cliffs

Shen W, Wynter L (2012) A new one-level convex optimization approach for estimating origin–destination demand. Transp Res Part B Methodol 46(10):1535–1555

H. Spiess (1990) A gradient approach for the OD matrix adjustment problem. a∈ ˆA , vol. 1, p. 2

Sun C, Chang Y, Luan X, Tu Q, Tang W (2020) Origin-destination demand reconstruction using observed travel time under congested network. Netw Spat Econ 20:733–755

Teimouri M, Sheikhmohammady M, Husseinzadeh Kashan A, Shojaie AA (2021) Developing an iterative procedure to estimate origin-destination matrix based on two-point license plate tracking system. Sci Iran 28(4):2361–2373

Tympakianaki A, Koutsopoulos HN, Jenelius E (2015) c-SPSA: cluster-wise simultaneous perturbation stochastic approximation algorithm and its application to dynamic origin–destination matrix estimation. Transp Res Part C Emerg Technol 55:231–245

Van Der Zijpp NJ (1997) Dynamic origin-destination matrix estimation from traffic counts and automated vehicle identification data. Transp Res Rec 1607(1):87–94

Wei C, Asakura Y (2013) A Bayesian approach to traffic estimation in stochastic user equilibrium networks. Transp Res Part C Emerg Technol 36:446–459

L. G. Willumsen (1978), Estimation of an OD matrix from traffic counts–a review

Xie C, Kockelman KM, Waller ST (2011) A maximum entropy-least squares estimator for elastic origin-destination trip matrix estimation. Procedia-Social Behav Sci 17:189–212

Xiong X, Ozbay K, Jin L, Feng C (2020) Dynamic origin–destination matrix prediction with line graph neural networks and kalman filter. Transp Res Rec 2674(8):491–503

Yang H (1995) Heuristic algorithms for the bilevel origin-destination matrix estimation problem. Transp Res Part B Methodol 29(4):231–242

Yang H, Sasaki T, Iida Y, Asakura Y (1992) Estimation of origin-destination matrices from link traffic counts on congested networks. Transp Res Part B Methodol 26(6):417–434

Download references

No funding was received to assist with the preparation of this manuscript.

Author information

Authors and affiliations.

Department of Civil and Environmental Engineering, Amirkabir University of Technology (Tehran Polytechnic), Hafez St., Tehran, 15875-4413, Iran

Ali Farzaneh Movahed & Mahmoud Mesbah

School of Civil Engineering, The University of Queensland, Brisbane, 4072, Australia

Mahmoud Mesbah

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Mahmoud Mesbah .

Ethics declarations

Conflict of interest.

The authors have no relevant financial or non-financial interests to disclose.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Farzaneh Movahed, A., Mesbah, M. Evaluating the Effect of Multiple Data Types on a Large Scale Static Origin–Destination Matrix Estimation, Case Study of Tehran, Iran. Iran J Sci Technol Trans Civ Eng (2024). https://doi.org/10.1007/s40996-024-01460-3

Download citation

Received : 08 October 2023

Accepted : 04 May 2024

Published : 28 May 2024

DOI : https://doi.org/10.1007/s40996-024-01460-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Static origin–destination matrix estimation
• Multiple field data
• Large scale networks
• Automatic Number Plate Recognition (ANPR) cameras
• Cordon line
• Find a journal
• Publish with us
• Track your research