hypothesis testing confidence interval

Warning: The NCBI web site requires JavaScript to function. more...

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings
Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1] When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3] Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4] When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5] One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6] Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7] The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3] In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12] Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13] A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14] Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15] confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14] A larger width indicates a smaller sample size or a larger variability. [16] A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15] Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14] In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13] An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14] Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4] Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care.

Review Questions
Access free multiple choice questions on this topic.
Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

Bulk download StatPearls data from FTP

Related information

PMC PubMed Central citations
PubMed Links to PubMed

Recent Activity

Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

Skip to secondary menu
Skip to main content
Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

Confidence Intervals: Interpreting, Finding & Formulas

By Jim Frost 10 Comments

What is a Confidence Interval?

A confidence interval (CI) is a range of values that is likely to contain the value of an unknown population parameter . These intervals represent a plausible domain for the parameter given the characteristics of your sample data. Confidence intervals are derived from sample statistics and are calculated using a specified confidence level.

Population parameters are typically unknown because it is usually impossible to measure entire populations. By using a sample, you can estimate these parameters. However, the estimates rarely equal the parameter precisely thanks to random sampling error . Fortunately, inferential statistics procedures can evaluate a sample and incorporate the uncertainty inherent when using samples. Confidence intervals place a margin of error around the point estimate to help us understand how wrong the estimate might be.

You’ll frequently use confidence intervals to bound the sample mean and standard deviation parameters. But you can also create them for regression coefficients , proportions, rates of occurrence (Poisson), and the differences between populations.

Related post : Populations, Parameters, and Samples in Inferential Statistics

What is the Confidence Level?

The confidence level is the long-run probability that a series of confidence intervals will contain the true value of the population parameter.

Different random samples drawn from the same population are likely to produce slightly different intervals. If you draw many random samples and calculate a confidence interval for each sample, a percentage of them will contain the parameter.

The confidence level is the percentage of the intervals that contain the parameter. For 95% confidence intervals, an average of 19 out of 20 include the population parameter, as shown below.

Interval plot that displays 20 confidence intervals. 19 of them contain the population parameter.

The image above shows a hypothetical series of 20 confidence intervals from a study that draws multiple random samples from the same population. The horizontal red dashed line is the population parameter, which is usually unknown. Each blue dot is a the sample’s point estimate for the population parameter. Green lines represent CIs that contain the parameter, while the red line is a CI that does not contain it. The graph illustrates how confidence intervals are not perfect but usually correct.

The CI procedure provides meaningful estimates because it produces ranges that usually contain the parameter. Hence, they present plausible values for the parameter.

Technically, you can create CIs using any confidence level between 0 and 100%. However, the most common confidence level is 95%. Analysts occasionally use 99% and 90%.

Related posts : Populations and Samples and Parameters vs. Statistics ,

How to Interpret Confidence Intervals

A confidence interval indicates where the population parameter is likely to reside. For example, a 95% confidence interval of the mean [9 11] suggests you can be 95% confident that the population mean is between 9 and 11.

Confidence intervals also help you navigate the uncertainty of how well a sample estimates a value for an entire population.

These intervals start with the point estimate for the sample and add a margin of error around it. The point estimate is the best guess for the parameter value. The margin of error accounts for the uncertainty involved when using a sample to estimate an entire population.

The width of the confidence interval around the point estimate reveals the precision. If the range is narrow, the margin of error is small, and there is only a tiny range of plausible values. That’s a precise estimate. However, if the interval is wide, the margin of error is large, and the actual parameter value is likely to fall somewhere within that more extensive range . That’s an imprecise estimate.

Ideally, you’d like a narrow confidence interval because you’ll have a much better idea of the actual population value!

For example, imagine we have two different samples with a sample mean of 10. It appears both estimates are the same. Now let’s assess the 95% confidence intervals. One interval is [5 15] while the other is [9 11]. The latter range is narrower, suggesting a more precise estimate.

That’s how CIs provide more information than the point estimate (e.g., sample mean) alone.

Confidence Intervals for Effect Sizes

Confidence intervals are similarly helpful for understanding an effect size. For example, if you assess a treatment and control group, the mean difference between these groups is the estimated effect size. A 2-sample t-test can construct a confidence interval for the mean difference.

In this scenario, consider both the size and precision of the estimated effect. Ideally, an estimated effect is both large enough to be meaningful and sufficiently precise for you to trust. CIs allow you to assess both of these considerations! Learn more about this distinction in my post about Practical vs. Statistical Significance .

Learn more about how confidence intervals and hypothesis tests are similar .

Related post : Effect Sizes in Statistics

Avoid a Common Misinterpretation of Confidence Intervals

A frequent misuse is applying confidence intervals to the distribution of sample values. Remember that these ranges apply only to population parameters, not the data values.

For example, a 95% confidence interval [10 15] indicates that we can be 95% confident that the parameter is within that range.

However, it does NOT indicate that 95% of the sample values occur in that range.

If you need to use your sample to find the proportion of data values likely to fall within a range, use a tolerance interval instead.

Related post : See how confidence intervals compare to prediction intervals and tolerance intervals .

What Affects the Widths of Confidence Intervals?

Ok, so you want narrower CIs for their greater precision. What conditions produce tighter ranges?

Sample size, variability, and the confidence level affect the widths of confidence intervals. The first two are characteristics of your sample, which I’ll cover first.

Sample Variability

Variability present in your data affects the precision of the estimate. Your confidence intervals will be broader when your sample standard deviation is high.

It makes sense when you think about it. When there is a lot of variability present in your sample, you’re going to be less sure about the estimates it produces. After all, a high standard deviation means your sample data are really bouncing around! That’s not conducive for finding precise estimates.

Unfortunately, you often don’t have much control over data variability. You can institute measurement and data collection procedures that reduce outside sources of variability, but after that, you’re at the mercy of the variability inherent in your subject area. But, if you can reduce external sources of variation, that’ll help you reduce the width of your confidence intervals.

Sample Size

Increasing your sample size is the primary way to reduce the widths of confidence intervals because, in most cases, you can control it more than the variability. If you don’t change anything else and only increase the sample size, the ranges tend to narrow. Need even tighter CIs? Just increase the sample size some more!

Theoretically, there is no limit, and you can dramatically increase the sample size to produce remarkably narrow ranges. However, logistics, time, and cost issues will constrain your maximum sample size in the real world.

In summary, larger sample sizes and lower variability reduce the margin of error around the point estimate and create narrower confidence intervals. I’ll point out these factors again when we get to the formula later in this post.

Related post : Sample Statistics Are Always Wrong (to Some Extent)!

Changing the Confidence Level

The confidence level also affects the confidence interval width. However, this factor is a methodology choice separate from your sample’s characteristics.

If you increase the confidence level (e.g., 95% to 99%) while holding the sample size and variability constant, the confidence interval widens. Conversely, decreasing the confidence level (e.g., 95% to 90%) narrows the range.

I’ve found that many students find the effect of changing the confidence level on the width of the range to be counterintuitive.

Imagine you take your knowledge of a subject area and indicate you’re 95% confident that the correct answer lies between 15 and 20. Then I ask you to give me your confidence for it falling between 17 and 18. The correct answer is less likely to fall within the narrower interval, so your confidence naturally decreases.

Conversely, I ask you about your confidence that it’s between 10 and 30. That’s a much wider range, and the correct value is more likely to be in it. Consequently, your confidence grows.

Confidence levels involve a tradeoff between confidence and the interval’s spread. To have more confidence that the parameter falls within the interval, you must widen the interval. Conversely, your confidence necessarily decreases if you use a narrower range.

Confidence Interval Formula

Confidence intervals account for sampling uncertainty by using critical values, sampling distributions, and standard errors. The precise formula depends on the type of parameter you’re evaluating. The most common type is for the mean, so I’ll stick with that.

You’ll use critical Z-values or t-values to calculate your confidence interval of the mean. T-values produce more accurate confidence intervals when you do not know the population standard deviation. That’s particularly true for sample sizes smaller than 30. For larger samples, the two methods produce similar results. In practice, you’d usually use a t-value.

Below are the confidence interval formulas for both Z and t. However, you’d only use one of them.

x̄ = the sample mean, which is the point estimate.
Z = the critical z-value
t = the critical t-value
s = the sample standard deviation
s / √n = the standard error of the mean

The only difference between the two formulas is the critical value. If you’re using the critical z-value, you’ll always use 1.96 for 95% confidence intervals. However, for the t-value, you’ll need to know the degrees of freedom and then look up the critical value in a t-table or online calculator.

To calculate a confidence interval, take the critical value (Z or t) and multiply it by the standard error of the mean (SEM). This value is known as the margin of error (MOE) . Then add and subtract the MOE from the sample mean (x̄) to produce the upper and lower limits of the range.

Related posts : Critical Values , Standard Error of the Mean , and Sampling Distributions

Interval Widths Revisited

Think back to the discussion about the factors affecting the confidence interval widths. The formula helps you understand how that works. Recall that the critical value * SEM = MOE.

Smaller margins of error produce narrower confidence intervals. By looking at this equation, you can see that the following conditions create a smaller MOE:

Smaller critical values, which you obtain by decreasing the confidence level.
Smaller standard deviations, because they’re in the numerator of the SEM.
Large samples sizes, because its square root is in the denominator of the SEM.

How to Find a Confidence Interval

Let’s move on to using these formulas to find a confidence interval! For this example, I’ll use a fuel cost dataset that I’ve used in other posts: FuelCosts . The dataset contains a random sample of 25 fuel costs. We want to calculate the 95% confidence interval of the mean.

However, imagine we have only the following summary information instead of the dataset.

Sample mean: 330.6
Standard deviation: 154.2

Fortunately, that’s all we need to calculate our 95% confidence interval of the mean.

We need to decide on using the critical Z or t-value. I’ll use a critical t-value because the sample size (25) is less than 30. However, if the summary didn’t provide the sample size, we could use the Z-value method for an approximation.

My next step is to look up the critical t-value using my t-table. In the table, I’ll choose the alpha that equals 1 – the confidence level (1 – 0.95 = 0.05) for a two-sided test. Below is a truncated version of the t-table. Click for the full t-distribution table .

In the table, I see that for a two-sided interval with 25 – 1 = 24 degrees of freedom and an alpha of 0.05, the critical value is 2.064.

Entering Values into the Confidence Interval Formula

Let’s enter all of this information into the formula.

First, I’ll calculate the margin of error:

Example calculations for the confidence interval.

Next, I’ll take the sample mean and add and subtract the margin of error from it:

330.6 + 63.6 = 394.2
330.6 – 63.6 = 267.0

The 95% confidence interval of the mean for fuel costs is 267.0 – 394.2. We can be 95% confident that the population mean falls within this range.

If you had used the critical z-value (1.96), you would enter that into the formula instead of the t-value (2.064) and obtain a slightly different confidence interval. However, t-values produce more accurate results, particularly for smaller samples like this one.

As an aside, the Z-value method always produces narrower confidence intervals than t-values when your sample size is less than infinity. So, basically always! However, that’s not good because Z-values underestimate the uncertainty when you’re using a sample estimate of the standard deviation rather than the actual population value. And you practically never know the population standard deviation.

Neyman, J. (1937). Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability . Philosophical Transactions of the Royal Society A . 236 (767): 333–380.

Reader Interactions

April 23, 2024 at 8:37 am

February 24, 2024 at 8:29 am

Thank you so much

February 14, 2024 at 1:56 pm

If I take a sample and create a confidence interval for the mean, can I say that 95% of the mean of the other samples I will take can be found in this range?

February 23, 2024 at 8:40 pm

Unfortunately, that would be an invalid statement. The CI formula uses your sample to estimate the properties of the population to construct the CI. Your estimates are bound to be off by at least a little bit. If you knew the precise properties of the population, you could determine the range in which 95% of random samples from that population would fall. However, again, you don’t know the precise properties of the population. You just have estimates based on your sample.

September 29, 2023 at 6:55 pm

Hi Jim, My confusion is similar to one comment. What I cannot seem to understand is the concept of individual and many CIs and therefore statements such as X% of the CIs.

For a sampling distribution, which itself requires many samples to produce, we try to find a confidence interval. Then how come there are multiple CIs. More specifically “Different random samples drawn from the same population are likely to produce slightly different intervals. If you draw many random samples and calculate a confidence interval for each sample, a percentage of them will contain the parameter.” this is what confuses me. Is interval here represents the range of the samples drawn? If that is true, why is the term CI or interval used for sample range? If not, could you please explain what is mean by an individual CI or how are we calculating confidence interval for each sample? In the image depicting 19 out of 20 will have population parameter, is the green line the range of individual samples or the confidence interval?

Please try to sort this confusion out for me. I find your website really helpful for clearing my statistical concepts. Thank you in advance for helping out. Regards.

September 30, 2023 at 1:52 am

A key point to remember is that inferential statistics occur in the context of drawing many random samples from the same population. Of course, a single study typically draws a single sample. However, if that study were to draw another random sample, it would be somewhat different than the first sample. A third sample would be somewhat different as well. That produces the sampling distribution, which helps you calculate p-values and construct CIs. Inferential statistics procedures use the idea of many samples to incorporate random sampling error into the results.

For CIs, if you were to collect many random samples, a certain percentage of them will contain the population parameter. That percentage is the confidence interval. Again, a single study will only collect a single sample. However, picturing many CIs helps you understand the concept of the confidence level. In practice, a study generates one CI per parameter estimate. But the graph with multiple CIs is just to help you understand the concept of confidence level.

Alternatively, you can think of CIs as an object class. Suppose 100 disparate studies produce 95% CIs. You can assume that about 95 of those CIs actually contain the population parameter. Using statistical procedures, you can estimate the sampling distribution using the sample itself without collecting many samples.

I don’t know what you mean by “Interval here represents the range of samples drawn.” As I write in this article, the CI is an interval of values that likely contain the population parameter. Reread the section titled How to Interpret Confidence Intervals to understand what each one means.

Each CI is estimated from a single sample and a study generates one CI per parameter estimate. However, again, understanding the concept of the confidence level is easier when you picture multiple CIs. But if a single study were to collect multiple samples and produces multiple CIs, that graph is what you’d expect to see. Although, in the real world, you never know for sure whether a CI actually contains the parameter or not.

The green lines represent CIs that contain the population parameter. Red lines represent CIs that do not contain the population parameter. The graph illustrates how CIs are not perfect but they are usually correct. I’ve added text to the article to clarify that image.

I also show you how to calculate the CI for a mean in this article. I’m not sure what more you need to understand there? I’m happy to clarify any part of that.

I hope that helps!

July 6, 2023 at 10:14 am

Hi Jim, This was an excellent article, thank you! I have a question: when computing a CI in its single-sample t-test module, SPSS appears to use the difference between population and sample means as a starting point (so the formula would be (X-bar-mu) +/- tcv(SEM)). I’ve consulted multiple stats books, but none of them compute a CI that way for a single-sample t-test. Maybe I’m just missing something and this is a perfectly acceptable way of doing things (I mean, SPSS does it :-)), but it yields substantially different lower and upper bounds from a CI that uses the traditional X-bar as a starting point. Do you have any insights? Many thanks in advance! Stephen

July 7, 2023 at 2:56 am

Hi Stephen,

I’m not an SPSS user but that formula is confusing. They presented this formula as being for the CI of a sample mean?

I’m not sure why they’re subtracting Mu. For one thing, you almost never know what Mu is because you’d have to measure the entire population. And, if you knew Mu, you wouldn’t need to perform a t-test! Why would you use a sample mean (X-bar) if you knew the population mean? None of it makes sense to me. It must be an error of some kind even if just of documentation.

October 13, 2022 at 8:33 am

Are there strict distinctions between the terms “confident”, “likely”, and “probability”? I’ve seen a number of other sources exclaim that for a given calculated confidence interval, the frequentist interpretation of that is the parameter is either in or not in that interval. They say another frequent misinterpretation is that the parameter lies within a calculated interval with a 95% probability.

It’s very confusing to balance that notion with practical casual communication of data in non-research settings.

October 13, 2022 at 5:43 pm

It is a confusing issue.

In this strictest technical sense, the confidence level is probability that applies to the process but NOT an individual confidence interval. There are several reasons for that.

In the frequentist framework, the probability that an individual CI contains the parameter is either 100% or 0%. It’s either in it or out. The parameter is not a random variable. However, because you don’t know the parameter value, you don’t know which of those two conditions is correct. That’s the conceptual approach. And the mathematics behind the scenes are complementary to that. There’s just no way to calculate the probability that an individual CI contains the parameter.

On the other hand, the process behind creating the intervals will cause X% of the CIs at the Xth confidence level to include that parameter. So, for all 95% CIs, you’d expect 95% of them to contain the parameter value. The confidence level applies to the process, not the individual CIs. Statisticians intentionally used the term “confidence” to describe that as opposed to “probability” hoping to make that distinction.

So, the 95% confidence applies the process but not individual CIs.

However, if you’re thinking that if 95% of many CIs contain the parameter, then surely a single CI has a 95% probability. From a technical standpoint, that is NOT true. However, it sure sounds logical. Most statistics make intuitive sense to me, but I struggle with that one myself. I’ve asked other statisticians to get their take on it. The basic gist of their answers is that there might be other information available which can alter the actual probability. Not all CIs produced by the process have the same probability. For example, if an individual CI is a bit higher or lower than most other CIs for the same thing, the CIs with the unusual values will have lower probabilities for containing the parameters.

I think that makes sense. The only problem is that you often don’t know where your individual CI fits in. That means you don’t know the probability for it specifically. But you do know the overall probability for the process.

The answer for this question is never totally satisfying. Just remember that there is no mathematical way in the frequentist framework to calculate the probability that an individual CI contains the parameter. However, the overall process is designed such that all CIs using a particular confidence level will have the specified proportion containing the parameter. However, you can’t apply that overall proportion to your individual CI because on the technical side there’s no mathematical way to do that and conceptually, you don’t know where your individual CI fits in the entire distribution of CIs.

Comments and Questions Cancel reply

Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .

Payment Plans
Product List
Partnerships

Try Free Trial
Study Packages
Levels I, II & III Lifetime Package
Video Lessons
Study Notes
Practice Questions
Levels II & III Lifetime Package
About the Exam
About your Instructor
Part I Study Packages
Parts I & II Packages
Part I & Part II Lifetime Package
Part II Study Packages
Exams P & FM Lifetime Package
Quantitative Questions
Verbal Questions
Data Insight Questions
Live Tutoring
About your Instructors
EA Practice Questions
Data Sufficiency Questions
Integrated Reasoning Questions

Hypothesis Testing

After completing this reading, you should be able to:

Construct an appropriate null hypothesis and alternative hypothesis and distinguish between the two.
Construct and apply confidence intervals for one-sided and two-sided hypothesis tests, and interpret the results of hypothesis tests with a specific level of confidence.
Differentiate between a one-sided and a two-sided test and identify when to use each test.
Explain the difference between Type I and Type II errors and how these relate to the size and power of a test.
Understand how a hypothesis test and a confidence interval are related.
Explain what the p-value of a hypothesis test measures.
Interpret the results of hypothesis tests with a specific level of confidence.
Identify the steps to test a hypothesis about the difference between two population means.
Explain the problem of multiple testing and how it can bias results.

Hypothesis testing is defined as a process of determining whether a hypothesis is in line with the sample data. Hypothesis testing tries to test whether the observed data of the hypothesis is true. Hypothesis testing starts by stating the null hypothesis and the alternative hypothesis. The null hypothesis is an assumption of the population parameter. On the other hand, the alternative hypothesis states the parameter values (critical values) at which the null hypothesis is rejected. The critical values are determined by the distribution of the test statistic (when the null hypothesis is true) and the size of the test (which gives the size at which we reject the null hypothesis).

Components of the Hypothesis Testing

The elements of the test hypothesis include:

The null hypothesis.
The alternative hypothesis.
The test statistic.
The size of the hypothesis test and errors
The critical value.
The decision rule.

The Null hypothesis

As stated earlier, the first stage of the hypothesis test is the statement of the null hypothesis. The null hypothesis is the statement concerning the population parameter values. It brings out the notion that “there is nothing about the data.”

The null hypothesis , denoted as H 0 , represents the current state of knowledge about the population parameter that’s the subject of the test. In other words, it represents the “status quo.” For example, the U.S Food and Drug Administration may walk into a cooking oil manufacturing plant intending to confirm that each 1 kg oil package has, say, 0.15% cholesterol and not more. The inspectors will formulate a hypothesis like:

H 0 : Each 1 kg package has 0.15% cholesterol.

A test would then be carried out to confirm or reject the null hypothesis.

Other typical statements of H 0 include:

$$H_0:\mu={\mu}_0$$

$$H_0:\mu≤{\mu}_0$$

$μ$ = true population mean and,

$μ_0$= the hypothesized population mean.

The Alternative Hypothesis

The alternative hypothesis , denoted H 1 , is a contradiction of the null hypothesis. The null hypothesis determines the values of the population parameter at which the null hypothesis is rejected. Thus, rejecting the H 0 makes H 1 valid. We accept the alternative hypothesis when the “status quo” is discredited and found to be untrue.

Using our FDA example above, the alternative hypothesis would be:

H 1 : Each 1 kg package does not have 0.15% cholesterol.

The typical statements of H1 include:

$$H_1:\mu \neq {\mu}_0$$

$$H_1:\mu > {\mu}_0$$

Note that we have stated the alternative hypothesis, which contradicted the above statement of the null hypothesis.

The Test Statistic

A test statistic is a standardized value computed from sample information when testing hypotheses. It compares the given data with what we would expect under the null hypothesis. Thus, it is a major determinant when deciding whether to reject H 0 , the null hypothesis.

We use the test statistic to gauge the degree of agreement between sample data and the null hypothesis. Analysts use the following formula when calculating the test statistic.

$$ \text{Test Statistic}= \frac{(\text{Sample Statistic–Hypothesized Value})}{(\text{Standard Error of the Sample Statistic})}$$

The test statistic is a random variable that changes from one sample to another. Test statistics assume a variety of distributions. We shall focus on normally distributed test statistics because it is used hypotheses concerning the means, regression coefficients, and other econometric models.

We shall consider the hypothesis test on the mean. Consider a null hypothesis $H_0:μ=μ_0$. Assume that the data used is iid, and asymptotic normally distributed as:

$$\sqrt{n} (\hat{\mu}-\mu) \sim N(0, {\sigma}^2)$$

Where ${\sigma}^2$ is the variance of the sequence of the iid random variable used. The asymptotic distribution leads to the test statistic:

$$T=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{\hat{\sigma}^2}{n}}}\sim N(0,1)$$

Note this is consistent with our initial definition of the test statistic.

The following table gives a brief outline of the various test statistics used regularly, based on the distribution that the data is assumed to follow:

$$\begin{array}{ll} \textbf{Hypothesis Test} & \textbf{Test Statistic}\\ \text{Z-test} & \text{z-statistic} \\ \text{Chi-Square Test} & \text{Chi-Square statistic}\\ \text{t-test} & \text{t-statistic} \\ \text{ANOVA} & \text{F-statistic}\\ \end{array}$$ We can subdivide the set of values that can be taken by the test statistic into two regions: One is called the non-rejection region, which is consistent with H 0 and the rejection region (critical region), which is inconsistent with H 0 . If the test statistic has a value found within the critical region, we reject H 0 .

Just like with any other statistic, the distribution of the test statistic must be specified entirely under H 0 when H 0 is true.

The Size of the Hypothesis Test and the Type I and Type II Errors

While using sample statistics to draw conclusions about the parameters of the population as a whole, there is always the possibility that the sample collected does not accurately represent the population. Consequently, statistical tests carried out using such sample data may yield incorrect results that may lead to erroneous rejection (or lack thereof) of the null hypothesis. We have two types of errors:

Type I Error

Type I error occurs when we reject a true null hypothesis. For example, a type I error would manifest in the form of rejecting H 0 = 0 when it is actually zero.

Type II Error

Type II error occurs when we fail to reject a false null hypothesis. In such a scenario, the test provides insufficient evidence to reject the null hypothesis when it’s false.

The level of significance denoted by α represents the probability of making a type I error, i.e., rejecting the null hypothesis when, in fact, it’s true. α is the direct opposite of β, which is taken to be the probability of making a type II error within the bounds of statistical testing. The ideal but practically impossible statistical test would be one that simultaneously minimizes α and β. We use α to determine critical values that subdivide the distribution into the rejection and the non-rejection regions.

The Critical Value and the Decision Rule

The decision to reject or not to reject the null hypothesis is based on the distribution assumed by the test statistic. This means if the variable involved follows a normal distribution, we use the level of significance (α) of the test to come up with critical values that lie along with the standard normal distribution.

The decision rule is a result of combining the critical value (denoted by $C_α$), the alternative hypothesis, and the test statistic (T). The decision rule is to whether to reject the null hypothesis in favor of the alternative hypothesis or fail to reject the null hypothesis.

For the t-test, the decision rule is dependent on the alternative hypothesis. When testing the two-side alternative, the decision is to reject the null hypothesis if $|T|>C_α$. That is, reject the null hypothesis if the absolute value of the test statistic is greater than the critical value. When testing on the one-sided, decision rule, reject the null hypothesis if $T<C_α$ when using a one-sided lower alternative and if $T>C_α$ when using a one-sided upper alternative. When a null hypothesis is rejected at an α significance level, we say that the result is significant at α significance level.

Note that prior to decision-making, one must decide whether the test should be one-tailed or two-tailed. The following is a brief summary of the decision rules under different scenarios:

Left One-tailed Test

H 1 : parameter < X

Decision rule: Reject H 0 if the test statistic is less than the critical value. Otherwise, do not reject H 0.

Right One-tailed Test

H 1 : parameter > X

Decision rule: Reject H 0 if the test statistic is greater than the critical value. Otherwise, do not reject H 0.

Two-tailed Test

H 1 : parameter ≠ X (not equal to X)

Decision rule: Reject H 0 if the test statistic is greater than the upper critical value or less than the lower critical value.

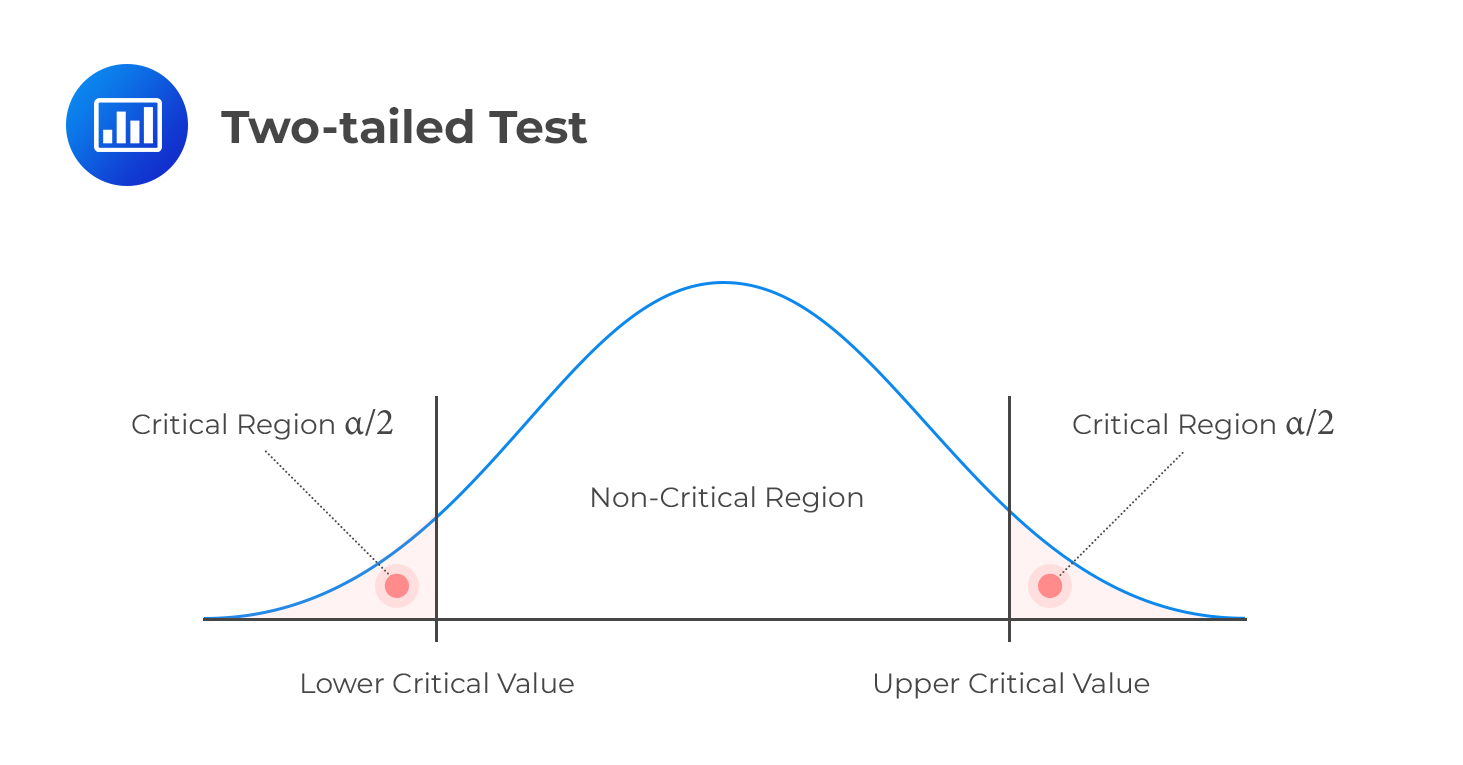
H 0 : μ < μ 0 vs. H 1 : μ > μ 0.

The second graph represents the rejection region when the alternative is a one-sided upper. The null hypothesis, in this case, is stated as:

H 0 : μ > μ 0 vs. H 1 : μ < μ 0.

Example: Hypothesis Test on the Mean

Consider the returns from a portfolio $X=(x_1,x_2,\dots, x_n)$ from 1980 through 2020. The approximated mean of the returns is 7.50%, with a standard deviation of 17%. We wish to determine whether the expected value of the return is different from 0 at a 5% significance level.

We start by stating the two-sided hypothesis test:

H 0 : μ =0 vs. H 1 : μ ≠ 0

The test statistic is:

$$T=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{\hat{\sigma}^2}{n}}} \sim N(0,1)$$

In this case, we have,

$\hat{μ}$=0.075

$\hat{\sigma}^2$=0.17 2

$$T=\frac{0.075-0}{\sqrt{\frac{0.17^2}{40}}} \approx 2.79$$

At the significance level, $α=5\%$,the critical value is $±1.96$. Since this is a two-sided test, the rejection regions are ( $-\infty,-1.96$ ) and ($1.96, \infty $ ) as shown in the diagram below:

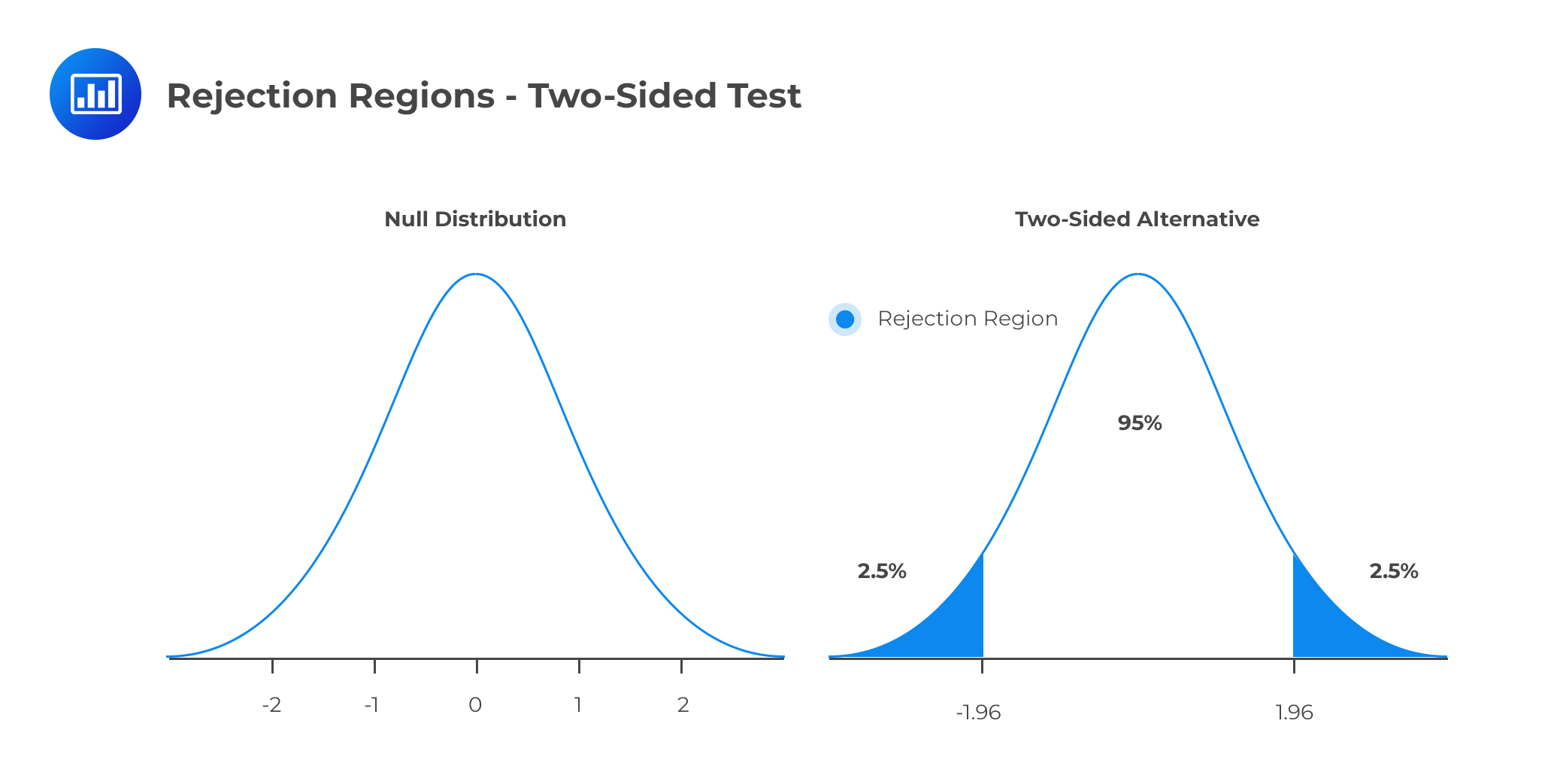
The example above is an example of a Z-test (which is mostly emphasized in this chapter and immediately follows from the central limit theorem (CLT)). However, we can use the Student’s t-distribution if the random variables are iid and normally distributed and that the sample size is small (n<30).

In Student’s t-distribution, we used the unbiased estimator of variance. That is:

$$s^2=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{s^2}{n}}}$$

Therefore the test statistic for $H_0=μ_0$ is given by:

$$T=\frac{\hat{\mu}-{\mu}_0}{\sqrt{\frac{s^2}{n}}} \sim t_{n-1}$$

The Type II Error and the Test Power

The power of a test is the direct opposite of the level of significance. While the level of relevance gives us the probability of rejecting the null hypothesis when it’s, in fact, true, the power of a test gives the probability of correctly discrediting and rejecting the null hypothesis when it is false. In other words, it gives the likelihood of rejecting H 0 when, indeed, it’s false. Denoting the probability of type II error by $\beta$, the power test is given by:

$$ \text{Power of a Test}=1–\beta $$

The power test measures the likelihood that the false null hypothesis is rejected. It is influenced by the sample size, the length between the hypothesized parameter and the true value, and the size of the test.

Confidence Intervals

A confidence interval can be defined as the range of parameters at which the true parameter can be found at a confidence level. For instance, a 95% confidence interval constitutes the set of parameter values where the null hypothesis cannot be rejected when using a 5% test size. Therefore, a 1-α confidence interval contains values that cannot be disregarded at a test size of α.

It is important to note that the confidence interval depends on the alternative hypothesis statement in the test. Let us start with the two-sided test alternatives.

$$ H_0:μ=0$$

$$H_1:μ≠0$$

Then the $1-α$ confidence interval is given by:

$$\left[\hat{\mu} -C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} ,\hat{\mu} + C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} \right]$$

$C_α$ is the critical value at $α$ test size.

Example: Calculating Two-Sided Alternative Confidence Intervals

Consider the returns from a portfolio $X=(x_1,x_2,…, x_n)$ from 1980 through 2020. The approximated mean of the returns is 7.50%, with a standard deviation of 17%. Calculate the 95% confidence interval for the portfolio return.

The $1-\alpha$ confidence interval is given by:

$$\begin{align*}&\left[\hat{\mu}-C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} ,\hat{\mu} + C_{\alpha} \times \frac{\hat {\sigma}}{\sqrt{n}} \right]\\& =\left[0.0750-1.96 \times \frac{0.17}{\sqrt{40}}, 0.0750+1.96 \times \frac{0.17}{\sqrt{40}} \right]\\&=[0.02232,0.1277]\end{align*}$$

Thus, the confidence intervals imply any value of the null between 2.23% and 12.77% cannot be rejected against the alternative.

One-Sided Alternative

For the one-sided alternative, the confidence interval is given by either:

$$\left(-\infty ,\hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}} \right )$$

for the lower alternative

$$\left ( \hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}},\infty \right )$$

for the upper alternative.

Example: Calculating the One-Sided Alternative Confidence Interval

Assume that we were conducting the following one-sided test:

$H_0:μ≤0$

$H_1:μ>0$

The 95% confidence interval for the portfolio return is:

$$\begin{align*}&=\left(-\infty ,\hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}} \right )\\&=\left(-\infty ,0.0750+1.645\times \frac{0.17}{\sqrt{40}}\right)\\&=(-\infty, 0.1192)\end{align*}$$

On the other hand, if the hypothesis test was:

$H_0:μ>0$

$H_1:μ≤0$

The 95% confidence interval would be:

$$=\left(-\infty ,\hat{\mu} +C_{\alpha} \times \frac{\hat{\sigma}}{\sqrt{n}} \right )$$

$$=\left(-\infty ,0.0750+1.645\times \frac{0.17}{\sqrt{40}}\right)=(0.1192, \infty)$$

Note that the critical value decreased from 1.96 to 1.645 due to a change in the direction of the change.

The p-Value

When carrying out a statistical test with a fixed value of the significance level (α), we merely compare the observed test statistic with some critical value. For example, we might “reject H 0 using a 5% test” or “reject H 0 at 1% significance level”. The problem with this ‘classical’ approach is that it does not give us details about the strength of the evidence against the null hypothesis.

Determination of the p-value gives statisticians a more informative approach to hypothesis testing. The p-value is the lowest level at which we can reject H 0 . This means that the strength of the evidence against H 0 increases as the p-value becomes smaller. The test statistic depends on the alternative.

The p-Value for One-Tailed Test Alternative

For one-tailed tests, the p-value is given by the probability that lies below the calculated test statistic for left-tailed tests. Similarly, the likelihood that lies above the test statistic in right-tailed tests gives the p-value.

Denoting the test statistic by T, the p-value for $H_1:μ>0$ is given by:

$$P(Z>|T|)=1-P(Z≤|T|)=1- \Phi (|T|) $$

Conversely , for $H_1:μ≤0 $ the p-value is given by:

$$ P(Z≤|T|)= \Phi (|T|)$$

Where z is a standard normal random variable, the absolute value of T (|T|) ensures that the right tail is measured whether T is negative or positive.

The p-Value for Two-Tailed Test Alternative

If the test is two-tailed, this value is given by the sum of the probabilities in the two tails. We start by determining the probability lying below the negative value of the test statistic. Then, we add this to the probability lying above the positive value of the test statistic. That is the p-value for the two-tailed hypothesis test is given by:

$$2\left[1-\Phi [|T|\right]$$

Example 1: p-Value for One-Sided Alternative

Let θ represent the probability of obtaining a head when a coin is tossed. Suppose we toss the coin 200 times, and heads come up in 85 of the trials. Test the following hypothesis at 5% level of significance.

H 0 : θ = 0.5

H 1 : θ < 0.5

First, not that repeatedly tossing a coin follows a binomial distribution.

Our p-value will be given by P(X < 85) where X `binomial(200,0.5) with mean 100(np=200*0.5), assuming H 0 is true.

$$\begin{align*}P\left [ z< \frac{85.5-100}{\sqrt{50}} \right]&=P(Z<-2.05)\\&=1–0.97982=0.02018 \end{align*}$$

Recall that for a binomial distribution, the variance is given by:

$$np(1-p)=200(0.5)(1-0.5)=50$$

(We have applied the Central Limit Theorem by taking the binomial distribution as approx. normal)

Since the probability is less than 0.05, H 0 is extremely unlikely, and we actually have strong evidence against H 0 that favors H 1 . Thus, clearly expressing this result, we could say:

“There is very strong evidence against the hypothesis that the coin is fair. We, therefore, conclude that the coin is biased against heads.”

Remember, failure to reject H 0 does not mean it’s true. It means there’s insufficient evidence to justify rejecting H 0, given a certain level of significance.

Example 2: p-Value for Two-Sided Alternative

A CFA candidate conducts a statistical test about the mean value of a random variable X.

H 0 : μ = μ 0 vs. H 1 : μ ≠ μ 0

She obtains a test statistic of 2.2. Given a 5% significance level, determine and interpret the p-value

$$ \text{P-value}=2P(Z>2.2)=2[1–P(Z≤2.2)] =1.39\%×2=2.78\%$$

(We have multiplied by two since this is a two-tailed test)

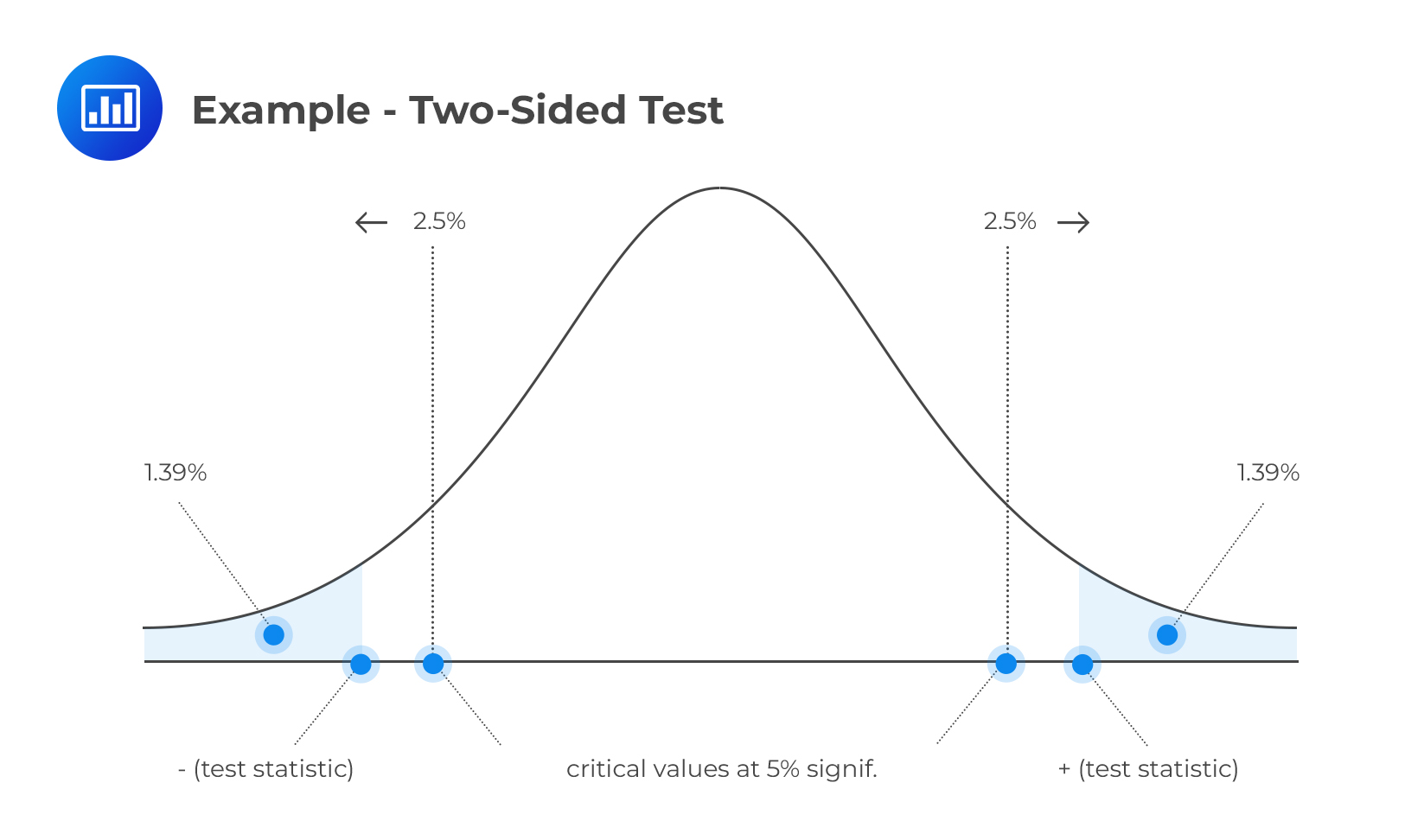
The p-value (2.78%) is less than the level of significance (5%). Therefore, we have sufficient evidence to reject H 0 . In fact, the evidence is so strong that we would also reject H 0 at significance levels of 4% and 3%. However, at significance levels of 2% or 1%, we would not reject H 0 since the p-value surpasses these values.

Hypothesis about the Difference between Two Population Means.

It’s common for analysts to be interested in establishing whether there exists a significant difference between the means of two different populations. For instance, they might want to know whether the average returns for two subsidiaries of a given company exhibit significant differences.

Now, consider a bivariate random variable:

$$W_i=[X_i,Y_i]$$

Assume that the components $X_i$ and $Y_i$are both iid and are correlated. That is: $\text{Corr} (X_i,Y_i )≠0$

Now, suppose that we want to test the hypothesis that:

$$H_0:μ_X=μ_Y$$

$$H_1:μ_X≠μ_Y$$

In other words, we want to test whether the constituent random variables have equal means. Note that the hypothesis statement above can be written as:

$$H_0:μ_X-μ_Y=0$$

$$H_1:μ_X-μ_Y≠0$$

To execute this test, consider the variable:

$$Z_i=X_i-Y_i$$

Therefore, considering the above random variable, if the null hypothesis is correct then,

$$E(Z_i)=E(X_i)-E(Y_i)=μ_X-μ_Y=0$$

Intuitively, this can be considered as a standard hypothesis test of

H 0 : μ Z =0 vs. H 1 : μ Z ≠ 0.

The tests statistic is given by:

$$T=\frac{\hat{\mu}_z}{\sqrt{\frac{\hat{\sigma}^2_z}{n}}} \sim N(0,1)$$

Note that the test statistic formula accounts for the correction between $X_i $ and $Y_i$. It is easy to see that:

$$V(Z_i)=V(X_i )+V(Y_i)-2COV(X_i, Y_i)$$

Which can be denoted as:

$$\hat{\sigma}^2_z =\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\sigma}_{XY}$$

$$ \hat{\mu}_z ={\mu}_X-{\mu}_Y $$

And thus the test statistic formula can be written as:

$$T=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\sigma}_{XY}}{n}}}$$

This formula indicates that correlation plays a crucial role in determining the magnitude of the test statistic.

Another special case of the test statistic is when $X_i$, and $Y_i$ are iid and independent. The test statistic is given by:

$$T=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X}{n_X}+\frac{\hat{\sigma}^2_Y}{n_Y}}}$$

Where $n_X$ and $n_Y$ are the sample sizes of $X_i$, and $Y_i$ respectively.

Example: Hypothesis Test on Two Means

An investment analyst wants to test whether there is a significant difference between the means of the two portfolios at a 95% level. The first portfolio X consists of 30 government-issued bonds and has a mean of 10% and a standard deviation of 2%. The second portfolio Y consists of 30 private bonds with a mean of 14% and a standard deviation of 3%. The correlation between the two portfolios is 0.7. Calculate the null hypothesis and state whether the null hypothesis is rejected or otherwise.

The hypothesis statement is given by:

H 0 : μ X – μ Y =0 vs. H 1 : μ X – μ Y ≠ 0.

Note that this is a two-tailed test. At 95% level, the test size is α=5% and thus the critical value $C_α=±1.96$.

Recall that:

$$Cov(X, Y)=σ_{XY}=ρ_{XY} σ_X σ_Y$$

Where ρ_XY is the correlation coefficient between X and Y.

Now the test statistic is given by:

$$T=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\sigma}_{XY}}{n}}}=\frac{{\mu}_X -{\mu}_Y}{\sqrt{\frac{\hat{\sigma}^2_X +\hat{\sigma}^2_Y – 2{\rho}_{XY} {\sigma}_X {\sigma}_Y}{n}}}$$

$$=\frac{0.10-0.14}{\sqrt{\frac{0.02^2 +0.03^2-2\times 0.7 \times 0.02 \times 0.03}{30}}}=-10.215$$

The test statistic is far much less than -1.96. Therefore the null hypothesis is rejected at a 95% level.

The Problem of Multiple Testing

Multiple testing occurs when multiple multiple hypothesis tests are conducted on the same data set. The reuse of data results in spurious results and unreliable conclusions that do not hold up to scrutiny. The fundamental problem with multiple testing is that the test size (i.e., the probability that a true null is rejected) is only applicable for a single test. However, repeated testing creates test sizes that are much larger than the assumed size of alpha and therefore increases the probability of a Type I error.

Some control methods have been developed to combat multiple testing. These include Bonferroni correction, the False Discovery Rate (FDR), and Familywise Error Rate (FWER).

Practice Question An experiment was done to find out the number of hours that candidates spend preparing for the FRM part 1 exam. For a sample of 10 students , the average study time was found to be 312.7 hours, with a standard deviation of 7.2 hours. What is the 95% confidence interval for the mean study time of all candidates? A. [307.5, 317.9] B. [310, 317] C. [300, 317] D. [307.5, 312.2] The correct answer is A. To calculate the 95% confidence interval for the mean study time of all candidates, we can use the formula for the confidence interval when the population variance is unknown: \[\text{Confidence Interval} = \bar{X} \pm t_{1-\frac{\alpha}{2}} \times \frac{s}{\sqrt{n}}\] Where: $\bar{X}$ is the sample mean $t_{1-\frac{\alpha}{2}}$ is the t-score corresponding to the desired confidence level and degrees of freedom $s$ is the sample standard deviation $n$ is the sample size In this case: $\bar{X} = 312.7$ hours (the average study time) $s = 7.2$ hours (the standard deviation of study time) $n = 10$ students (the sample size) To find the t-score ($t_{1-\frac{\alpha}{2}}$), we look at the t-table for the 95% confidence level (which corresponds to $\alpha = 0.05$) and 9 degrees of freedom ($n – 1 = 10 – 1 = 9$). The t-score is 2.262. Now, we can plug these values into the confidence interval formula: \[\text{Confidence Interval} = 312.7 \pm 2.262 \times \frac{7.2}{\sqrt{10}}\] Calculating the margin of error: \[\text{Margin of Error} = 2.262 \times \frac{7.2}{\sqrt{10}} \approx 5.2\] So the confidence interval is: \[\text{Confidence Interval} = 312.7 \pm 5.2 = [307.5, 317.9]\] Therefore, the 95% confidence interval for the mean study time of all candidates is [307.5, 317.9] hours.

Offered by AnalystPrep

Approaches to Asset Allocation

Applying the capm to performance measu ....

After completing this reading, you should be able to: Calculate, compare, and evaluate... Read More

Pricing Financial Forwards and Futures

After completing this reading, you should be able to: Define and describe financial... Read More

Measuring Credit Risk

After completing this reading, you should be able to: Explain the distinctions between... Read More

Modeling and Hedging Non-Parallel Term ...

After completing this reading you should be able to: Describe principal components analysis... Read More

8.6 Relationship Between Confidence Intervals and Hypothesis Tests

Confidence intervals (CI) and hypothesis tests should give consistent results: we should not reject [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if the corresponding [latex](1 - \alpha) \times 100\%[/latex] confidence interval contains the hypothesized value [latex]\mu_0[/latex]. Two-sided confidence intervals correspond to two-tailed tests, upper-tailed confidence intervals correspond to right-tailed tests, and lower-tailed confidence intervals correspond to left-tailed tests.

A [latex](1 - \alpha) \times 100\%[/latex] two-sided [latex]t[/latex] confidence interval is given in the form [latex](\bar{x} - t_{\alpha / 2} \frac{s}{\sqrt{n}}, \bar{x} + t_{\alpha / 2} \frac{s}{\sqrt{n}})[/latex]. A [latex](1 - \alpha) \times 100\%[/latex] upper-tailed t confidence interval is given by [latex](\bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}, \infty)[/latex] and the number [latex]\bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}[/latex] is called the lower bound of the interval. A [latex](1 - \alpha) \times 100\%[/latex] lower-tailed t confidence interval is given by [latex](- \infty, \bar{x} + t_{\alpha} \frac{s}{\sqrt{n}})[/latex] and the number [latex]\bar{x} + t_{\alpha} \frac{s}{\sqrt{n}}[/latex] is called the upper bound of the interval. We can also use confidence intervals to make conclusions about hypothesis tests: reject the null hypothesis [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if the corresponding [latex](1 - \alpha) \times 100\%[/latex] confidence interval does not contain the hypothesized value [latex]\mu_0[/latex]. The relationship is summarized in the following table.

Table 8.3 : Relationship Between Confidence Interval and Hypothesis Test

Null hypothesis	[latex]H_0: \mu = \mu_0[/latex]	[latex]H_0: \mu \leq \mu_0[/latex]	[latex]H_0: \mu \geq \mu_0[/latex]
Alternative	[latex]H_a: \mu \neq \mu_0[/latex]	[latex]H_a: \mu \: \gt \: \mu_0[/latex]	[latex]H_a: \mu
[latex](1 - \alpha) \times 100\%[/latex] CI	[latex](\bar{x} - t_{\alpha / 2} \frac{s}{\sqrt{n}}, \bar{x} + t_{\alpha / 2} \frac{s}{\sqrt{n}})[/latex]	[latex](\bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}, \infty)[/latex]	[latex](- \infty, \bar{x} + t_{\alpha} \frac{s}{\sqrt{n}})[/latex]
Decision

Here is the reason we should reject [latex]H_0[/latex] if [latex]\mu_0[/latex] is outside the corresponding confidence interval.

Take the right-tailed test for example, we should reject [latex]H_0[/latex] if the observed test statistic [latex]t_o[/latex] falls in the rejection region, that is if [latex]t_o \geq t_{\alpha}[/latex]. This implies [latex]t_o = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} \geq t_{\alpha} \Longrightarrow \mu_0 \leq \bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}.[/latex] Given that the upper-tailed confidence interval for a right-tailed test is [latex](\bar{x} - t_{\alpha / 2} \frac{s}{\sqrt{n}}, \infty)[/latex], [latex]\mu_0 \leq \bar{x} - t_{\alpha} \frac{s}{\sqrt{n}}[/latex] means the value of [latex]\mu_0[/latex] is outside the confidence interval. The same rationale applies to two-tailed and left-tailed tests. Therefore, we can reject [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if [latex]\mu_0[/latex] is outside the corresponding (1– [latex]\alpha[/latex] )×100% confidence interval.

Example: Relationship Between Confidence Intervals and Hypothesis Tests

The ankle-brachial index (ABI) compares the blood pressure of a patient’s arm to the blood pressure of the patient’s leg. The ABI can be an indicator of different diseases, including arterial diseases. A healthy (or normal) ABI is 0.9 or greater. Researchers obtained the ABI of 100 women with peripheral arterial disease and obtained a mean ABI of 0.64 with a standard deviation of 0.15.

Set up the hypotheses: [latex]H_0: \mu \geq 0.9[/latex] versus [latex]H_a: \mu < 0.9[/latex].
The significance level is [latex]\alpha = 0.05[/latex].
Compute the value of the test statistic: [latex]t_o = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} = \frac{0.64 - 0.9}{0.15 / \sqrt{100}} = \frac{-0.26}{0.015} = -17.333[/latex] with [latex]df = n-1 = 100 -1 = 99[/latex] (not given in Table IV, use 95, the closest one smaller than 99).
Find the P-value. For a left-tailed test, the P-value is the area to the left of the observed test statistic [latex]t_o[/latex]. [latex]\mbox{P-value} = P(t \leq t_o) = P(t \leq -17.333) = P(t \geq 17.333) 2.629(t_{0.005})[/latex].
Decision: Since the P- value [latex]< 0.005 < 0.05(\alpha)[/latex], we should reject the null hypothesis [latex]H_0[/latex].
Conclusion: At the 5% significance level, the data provide sufficient evidence that, on average, women with peripheral arterial disease have an unhealthy ABI.

[latex]\left( - \infty, \bar{x} + t_{\alpha} \frac{s}{\sqrt{n}} \right)= \left( - \infty, 0.64 + 1.661 \times \frac{0.15}{\sqrt{100}} \right) = (- \infty , 0.665)[/latex].

Does the interval in part b) support the conclusion in part a)? In part a), we reject [latex]H_0[/latex] and claim that the mean ABI is below 0.9 for women with peripheral arterial disease. In part b), we are 95% confident that the mean ABI is less than 0.9 since the entire confidence interval is below 0.9. In other words, the hypothesized value 0.9 is outside the corresponding confidence interval, we should reject the null. Therefore, the results obtained in parts a) and b) are consistent.

Quality Improvement
Talk To Minitab

Understanding Hypothesis Tests: Confidence Intervals and Confidence Levels

Topics: Hypothesis Testing , Data Analysis , Statistics

In this series of posts, I show how hypothesis tests and confidence intervals work by focusing on concepts and graphs rather than equations and numbers.

Previously, I used graphs to show what statistical significance really means . In this post, I’ll explain both confidence intervals and confidence levels, and how they’re closely related to P values and significance levels.

How to Correctly Interpret Confidence Intervals and Confidence Levels

A confidence interval is a range of values that is likely to contain an unknown population parameter. If you draw a random sample many times, a certain percentage of the confidence intervals will contain the population mean. This percentage is the confidence level.

Most frequently, you’ll use confidence intervals to bound the mean or standard deviation, but you can also obtain them for regression coefficients, proportions, rates of occurrence (Poisson), and for the differences between populations.

Just as there is a common misconception of how to interpret P values , there’s a common misconception of how to interpret confidence intervals. In this case, the confidence level is not the probability that a specific confidence interval contains the population parameter.

The confidence level represents the theoretical ability of the analysis to produce accurate intervals if you are able to assess many intervals and you know the value of the population parameter. For a specific confidence interval from one study, the interval either contains the population value or it does not—there’s no room for probabilities other than 0 or 1. And you can't choose between these two possibilities because you don’t know the value of the population parameter.

"The parameter is an unknown constant and no probability statement concerning its value may be made." —Jerzy Neyman, original developer of confidence intervals.

This will be easier to understand after we discuss the graph below . . .

With this in mind, how do you interpret confidence intervals?

Confidence intervals serve as good estimates of the population parameter because the procedure tends to produce intervals that contain the parameter. Confidence intervals are comprised of the point estimate (the most likely value) and a margin of error around that point estimate. The margin of error indicates the amount of uncertainty that surrounds the sample estimate of the population parameter.

In this vein, you can use confidence intervals to assess the precision of the sample estimate. For a specific variable, a narrower confidence interval [90 110] suggests a more precise estimate of the population parameter than a wider confidence interval [50 150].

Confidence Intervals and the Margin of Error

Let’s move on to see how confidence intervals account for that margin of error. To do this, we’ll use the same tools that we’ve been using to understand hypothesis tests. I’ll create a sampling distribution using probability distribution plots , the t-distribution , and the variability in our data. We'll base our confidence interval on the energy cost data set that we've been using.

When we looked at significance levels , the graphs displayed a sampling distribution centered on the null hypothesis value, and the outer 5% of the distribution was shaded. For confidence intervals, we need to shift the sampling distribution so that it is centered on the sample mean and shade the middle 95%.

Probability distribution plot that illustrates how a confidence interval works

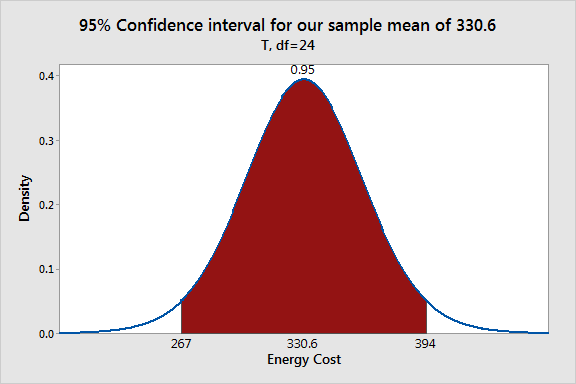
The shaded area shows the range of sample means that you’d obtain 95% of the time using our sample mean as the point estimate of the population mean. This range [267 394] is our 95% confidence interval.

Using the graph, it’s easier to understand how a specific confidence interval represents the margin of error, or the amount of uncertainty, around the point estimate. The sample mean is the most likely value for the population mean given the information that we have. However, the graph shows it would not be unusual at all for other random samples drawn from the same population to obtain different sample means within the shaded area. These other likely sample means all suggest different values for the population mean. Hence, the interval represents the inherent uncertainty that comes with using sample data.

You can use these graphs to calculate probabilities for specific values. However, notice that you can’t place the population mean on the graph because that value is unknown. Consequently, you can’t calculate probabilities for the population mean, just as Neyman said!

Why P Values and Confidence Intervals Always Agree About Statistical Significance

You can use either P values or confidence intervals to determine whether your results are statistically significant. If a hypothesis test produces both, these results will agree.

The confidence level is equivalent to 1 – the alpha level. So, if your significance level is 0.05, the corresponding confidence level is 95%.

If the P value is less than your significance (alpha) level, the hypothesis test is statistically significant.
If the confidence interval does not contain the null hypothesis value, the results are statistically significant.
If the P value is less than alpha, the confidence interval will not contain the null hypothesis value.

For our example, the P value (0.031) is less than the significance level (0.05), which indicates that our results are statistically significant. Similarly, our 95% confidence interval [267 394] does not include the null hypothesis mean of 260 and we draw the same conclusion.

To understand why the results always agree, let’s recall how both the significance level and confidence level work.

The significance level defines the distance the sample mean must be from the null hypothesis to be considered statistically significant.
The confidence level defines the distance for how close the confidence limits are to sample mean.

Both the significance level and the confidence level define a distance from a limit to a mean. Guess what? The distances in both cases are exactly the same!

The distance equals the critical t-value * standard error of the mean . For our energy cost example data, the distance works out to be $63.57.

Imagine this discussion between the null hypothesis mean and the sample mean:

Null hypothesis mean, hypothesis test representative : Hey buddy! I’ve found that you’re statistically significant because you’re more than $63.57 away from me!

Sample mean, confidence interval representative : Actually, I’m significant because you’re more than $63.57 away from me !

Very agreeable aren’t they? And, they always will agree as long as you compare the correct pairs of P values and confidence intervals. If you compare the incorrect pair, you can get conflicting results, as shown by common mistake #1 in this post .

Closing Thoughts

In statistical analyses, there tends to be a greater focus on P values and simply detecting a significant effect or difference. However, a statistically significant effect is not necessarily meaningful in the real world. For instance, the effect might be too small to be of any practical value.

It’s important to pay attention to the both the magnitude and the precision of the estimated effect. That’s why I'm rather fond of confidence intervals. They allow you to assess these important characteristics along with the statistical significance. You'd like to see a narrow confidence interval where the entire range represents an effect that is meaningful in the real world.

If you like this post, you might want to read the previous posts in this series that use the same graphical framework:

Part One: Why We Need to Use Hypothesis Tests
Part Two: Significance Levels (alpha) and P values

For more about confidence intervals, read my post where I compare them to tolerance intervals and prediction intervals .

If you'd like to see how I made the probability distribution plot, please read: How to Create a Graphical Version of the 1-sample t-Test .

Trust Center

Terms of Use
Privacy Policy
Cookies Settings

Confidence Intervals

Hypothesis testing is the approach to statistical inference that we use when we have two competing theories that we are trying to choose between. A second approach to statistical inference is confidence intervals, which allow us to present a range of reasonable values for our unknown population parameter. The range of reasonable values allows us to understand the corresponding population better without requiring any ideas to be fully specified.

General Motivation and Framework

We have access to our sample, but we would really like to make a statement about the corresponding population. For example, we can calculate that the median price per night for a Chicago Airbnb was \$126 for a sample. What we really want to know, though, is what the median price per night for a Chicago Airbnb is for the entire population of Airbnbs, so that we can make an appropriate statement for the population.

How can we extend our knowledge from the sample to the population? We can use confidence intervals to help us generate a range of reasonable values for our unknown parameter. This will help us to make reasonable conclusions that should extend to the population appropriately.

To do so, we will combine our knowledge of sampling distributions with our specific sample value. This has many similar flavors to hypothesis testing but is approaching the problem through a different framework. Below, we'll walk through an example followed by the process to generate a confidence interval.

Confidence Interval Example

Like mentioned above, the median price per night for a Chicago Airbnb was $126 in our sample. Can we generate a sampling distribution for the possible values that the median price per night could take from repeated random samples?

We will use the resampling approach to generating a sampling distribution as described previously.

Histogram of the sampling distribution for the median price of a Chicago Airbnb.

We've now generated our sampling distribution for sample median prices of Airbnbs in Chicago. Now, suppose that I want to create a range of reasonable values for the population median prices with 90% confidence (we'll define what 90% confidence means soon). To do so, I'll find the middle 90% of this distribution by calculating the 5th percentile and the 95th percentile.

For our simulated sampling distribution, the middle 90% are between \$120 and \$132 per night for a Chicago Airbnb.

At last, we'll make a jump from making statements about samples to making statements about populations. We could say that a range of reasonable values for the population median price per night of a Chicago Airbnb is between \$120 and \$132 per night.

Confidence Interval Steps

To generate a confidence interval, we follow the same set of steps. We do apply some steps differently depending on our specific parameter of interest.

To generate a confidence interval, we should:

Identify and define the parameter of interest
Determine the confidence level
Generate or use theory to specify the sampling distribution and check conditions
Calculate the middle region of your sampling distribution, according to your confidence level
Write a conclusion in the context of the problem.

Identify Parameter of Interest

We discussed identifying and defining the parameter of interest when we first described hypothesis testing. This is repeated for confidence intervals.

In this example, our population of interest is all Chicago Airbnbs. We likely would want to specify a time frame as well, and since we are using March 2023 data, we may specify that this is for all Chicago Airbnbs in March 2023.

Our parameter of interest (the summary measure) is the median. We may define the parameter of interest as $M$, the population median price per night for a Chicago Airbnb.

Determine the Confidence Level

The confidence level is analogous to the significance level. We'll provide a more exact definition and interpretation of the confidence level shortly. Confidence levels should be greater than 0% and less than 100%.

Confidence levels do not depend on the data and should be selected before observing the data. The confidence level is generally chosen based on the stakeholders and their requirements for the confidence in results. More confidence in the results are associated with higher confidence levels.

Common confidence levels include 90%, 95%, 98%, and 99%.

Determine the Sampling Distribution for the Sample Statistic

We again will use the sampling distribution of the sample statistic as the basis for our confidence interval calculation. To do so, we can follow the same process outlined for hypothesis testing. Recall, that we chose between a simulation-based resampling approach or a theory-based approach using the Central Limit Theorem to define the sampling distribution.

The biggest distinction between generating sampling distributions for confidence intervals compared to hypothesis testing is that we don't need to make any adjustments to our sampling distribution so that it is consistent with the null hypothesis. That is, recall that we wanted to adopt the skeptic's claim in hypothesis testing. When we were generating a sampling distribution, we would make any modifications necessary so that the sampling distribution fulfilled the condition of the null hypothesis. This distinction should be considered in two ways:

when generating the sampling distribution
when checking any necessary conditions

For example, if we were performing hypothesis testing with a simulation-based approach, we would need to first adjust the data so that the sample median was equal to the null value. However, without that condition for confidence intervals, we would use the data exactly as it is in the sample.

Similarly, some conditions for sampling distributions use information about the parameter of interest. For example, the theory-based approach with proportions requires that $n \times p$ and $n \times (1-p)$ are both at least 10. When we have a hypothesis, we should plug in the null value from the null hypothesis into these checks. With confidence intervals, if we don't have any requirements for the parameter, we can use our best estimate for $p$, which is often $\hat{p}$ when checking the conditions.

Again, the simulation-based approach requires the least number of assumptions. For our example, it is the only option for estimating the sampling distribution, since we haven't introduced theory that relates to the sampling distribution for a sample median.

Calculate the Confidence Interval

After we have determined the sampling distribution, we want to actually calculate the confidence interval, which is the range of reasonable values for our parameter of interest.

We want to find the central part of the sampling distribution that corresponds to our confidence level to generate the confidence interval, regardless of the approach for generating the sampling distribution. That is, if we want a 95% confidence interval, we will want to find the 2.5th percentile and the 97.5th percentile of the sampling distribution, so that the middle 95% is contained within those two values. In general, if we say that our confidence level is represented as CL%, then we want the (100-CL)/2 and (100+CL)/2 percentiles. We can find these percentiles both for a simulated sampling distribution or for a well-defined distribution, as long as we provide Python with the appropriate information.

This might seem counterintuitive, as we are using information about our sample to generate a guess about our population. To understand this, let's start by saying that this range would be a range of typical values for a sample statistic as calculated from our available data. Then, we're going to switch the order of the statement. This indicates that a sample statistic like the one we found would be reasonable if our parameter were anywhere in that range instead. Therefore, we'll say that the confidence interval that we calculated represents a range of reasonable values for the parameter.

Write a Conclusion in the Context of the Problem

Finally, we've generated our confidence interval and want to communicate our results to other stakeholders. What exactly does the confidence interval mean?

Informally, we might say something like: it is reasonable to claim that the population median price for a Chicago Airbnb is between \$120 and \$136 per night, with 90% confidence.

The formal interpretation is that we are 90% confident that the true population median price for a Chicago Airbnb falls in the range of \$120 and \$136 per night.

Confidence Interval Widths

Say that a stakeholder is not satisfied with a confidence interval. A common concern is that a confidence interval is too wide; that is, your stakeholder would like a narrower range of reasonable values. What can be changed to satisfy your stakeholder?

The two adjustable factors that affect the width of the confidence interval are the:

sample size
confidence level

Larger sample sizes result in narrower sampling distributions (recall this feature of the standard error from our sampling distribution module). This will also result in our confidence interval being narrower.

Larger confidence levels require a larger component of the sampling distribution to be included in the confidence interval. This will result in a wider confidence interval.

Therefore, if your stakeholder wants a narrower confidence interval, you could add more observations to your sample size or you could reduce your confidence level. It is also possible to estimate a desired sample size before gathering data that results in a confidence interval with limitations on the width of the confidence interval. We will skip over this calculation for our course, although you may encounter it in a future course.

Confidence Interval Misconceptions and Misinterpretations

We've discussed briefly what a confidence interval means. Equally important is what a confidence interval does not imply.

A confidence interval does not correspond to:

the probability that the parameter is in the confidence interval
a range of reasonable values for the sample data
a range of reasonable values for a sample statistic
a range of reasonable values for any future results from another sample

These last three misconceptions stem from misunderstanding that the confidence interval is about the parameter of interest and not about the sample or any of its corresponding characteristics.

For the first statement, consider that the population is already defined, and the corresponding parameter value for the population could then be calculated. It is a specific number, and it doesn't change. For example, it might be 120 or it could be 145. However, since the population is fixed, it is that exact number.

Once the confidence interval is calculated, then the confidence interval is also set and determined. It won't change. In this case, the parameter will either be contained in our confidence interval or it won't be, so the probability associated with the parameter being in the confidence interval is either 0 (the confidence interval isn't correct) or 1 (the confidence interval is correct).

Confidence Level Interpretation

We now understand how to calculate a confidence interval, what the confidence interval indicates, and what it doesn't indicate. However, we need to return to the second step where we set the confidence level for the interval. We know that this will have ramifications for the following steps of generating a confidence interval. But, what does it mean?

The confidence level means:

"If we gathered repeated random samples of the same size and calculated a CL% confidence interval for each, we would expect CL% of the resulting confidence intervals to contain the true parameter of interest."

Generally, this means that we expect CL% of our intervals to be correct. However, as we discussed above, we can't apply this reasoning to one specific interval after it's been calculated. This still does allow for variability and for different confidence intervals being generated from different samples.

Hypothesis Testing Decisions through Confidence Intervals

You may have noticed that many of the steps used for confidence intervals are shared with hypothesis testing. While there are distinctions between the two, we can also use confidence intervals to help us determine the result of a hypothesis test.

Suppose that a friend found it reported that the median price for all Chicago hotels is $160 per night. They suspect that Airbnbs are less expensive per night, and the population median price for Chicago Airbnbs is less expensive.

That is, the parameter of interest would be $M$ the population median price per night for all Chicago Airbnbs in March 2023. We can (and have) found the corresponding sample statistic, $m$ or the median price per night for the Chicago Airbnbs from our sample.

Because we don't have any data to analyze for Chicago hotels, we'll use this number as if it were true and treat this as a test for only one population. Our hypotheses would be:

$H_0: M = 160$

$H_a: M < 160$

What does the data say? If we've already generated a confidence interval, we don't need to repeat many of the steps for hypothesis testing. Instead, we can consider our calculated confidence interval as a range of reasonable values for our parameter. That is, it is reasonable that the population median price per night for all Chicago Airbnbs is between \$120 and \$136. In this case, the null value of 160 is not included in the range of reasonable values. Everything reasonable falls under the alternative hypothesis. We would want to reject the null hypothesis and adopt the alternative hypothesis as a more reasonable claim.

In this case, our confidence interval clearly supports our alternative hypothesis rather than our null hypothesis. However, in order to use confidence intervals to anticipate the decision for a hypothesis test, we need to ensure that we are using comparable confidence and significance levels:

for a two-sided alternative hypothesis, use a confidence level of $1-\alpha$
for a one-sided alternative hypothesis, use a confidence level of $1-2\times\alpha$

Confidence intervals and hypothesis testing

Understand the t value and Pr(>|t|) fields in the output of lm
Be able to think critically about the meaning and limitations of strict hypothesis tests

Confidence intervals and hypothesis tests

T-statistics.

Suppose we’re interested in the value $\beta_k$ , the $k$ –th entry of $\betav$ in for some regression $\y_n \sim \betav^\trans \xv_n$ . Recall that we have been finding $\v$ such that

\[ \sqrt{N} (\beta_k - \beta) \rightarrow \gauss{0, \v}. \]

For example, under homoskedastic assumptions with $\y_n = \xv_n^\trans \beta + \res_n$ , we have

\[ \begin{aligned} \v =& \sigma^2 (\Xcov^{-1})_{kk} \textrm{ where } \\ \Xcov =& \lim_{N \rightarrow \infty} \frac{1}{N} \X^\trans \X \textrm{ and } \\ \sigma^2 =& \var{\res_n}. \end{aligned} \]

Typically we don’t know $\v$ , but have $\hat\v$ such that $\hat\v \rightarrow \v$ as $N \rightarrow \infty$ . Again, under homoeskedastic assumptions,

\[ \begin{aligned} \hat\v =& \hat\sigma^2 \left(\frac{1}{N} \X^\trans \X \right)_{kk} \textrm{ where } \\ \hat\sigma^2 =& \frac{1}{N-P} \sumn \reshat_n^2. \end{aligned} \]

Putting all this together, the quantity

\[ \t = \frac{\sqrt{N} (\betahat_k - \beta_k)}{\sqrt{\hat\v}} = \frac{\betahat_k - \beta_k}{\sqrt{\hat\v / N}} \]

has an approximately standard normal distribution for large $N$ .

Quantities of this form are called “T–statistics,” since, under our normal assumptions, we have shown that

\[ \t \sim \studentt{N-P}, \]

exactly for all $N$ . Despite it’s name, it’s worth remembering that a T–statistic is actually not Student T distributed in general; it is asymptotically normal. Recall that for large $N$ , the Student T and standard normal distributions coincide.

Plugging in values for $\beta_k$

However, there’s something funny about a “T-statistic” — as written, you cannot compute it, because you don’t know $\beta_k$ . In fact, finding what values $\beta_k$ might plausibly take is the whole point of statistical inference.

So what good is a T–statistic? Informally, one way to reason about it is as follows. Let’s take some concrete values for an example. Suppose guess that $\beta_k^0$ is the value, and compute

\[ \betahat_k = 2 \quad\textrm{and}\quad \sqrt{\hat\v / N} = 3 \quad\textrm{so}\quad \t = \frac{2 - \beta_k^0}{3}. \]

We use the superscript $0$ to indicate that $\beta_k^0$ is our guess, not necessarily the true value.

Suppose we plug in some particular value, such as $\beta_k^0 = 32$ . Using this value, we compute our T–statistic, and find that it’s very large — in our example, we would have $\t = (2 - 32) / 3 = -30$ . It’s very unlikely to get a standard normal (or Student T) draw this large. Therefore, either:

We got a very (very very very very) unusual draw of our standard normal or
We guessed wrong, i.e. $\beta_k \ne \beta_k^0 = 32$ .

In this way, we might consider it plausible to “reject” the hypothesis that $\beta_k = 32$ .

There’s a subtle problem with the preceding reasoning, however. Suppose we do the same calculation with $\beta_k^0 = 1$ . Then $\t = (2 - 1) / 3 = 1/3$ . This is a much more typical value for a standard normal distribution. However, the probability of getting exactly $1/3$ — or, indeed, any particular value — is zero, since the normal distribution is continuous valued. (This problem is easiest to see with continuous random variables, but the same basic problem will occur when the distribution is discrete but spread over a large number of possible values.)

Rejection regions

To resolve this problem, we can specify regions that we consider implausible. That is, suppose we take a region $R$ such that, if $\t$ is standard normal (or Student-T), then

\[ \prob{\t \in R} \le \alpha \quad\textrm{form some small }\alpha. \]

For example, we might take $\Phi^{-1}(\cdot)$ to be the inverse CDF of $\t$ if $\beta_k = \beta_k^0$ . Then we can take

\[ R_{ts} = \{\t: \abs{t} \ge q \} \quad\textrm{where } q = \Phi^{-1}(\alpha / 2)\\ \]

where $q$ is an $\alpha / 2$ quantile of the distribution of $\t$ . But there are other choices, such as

\[ \begin{aligned} R_{u} ={}& \{\t: \t \ge q \} \quad\textrm{where } q = \Phi^{-1}(1 - \alpha) \\ R_{l} ={}& \{\t: \t \le q \} \quad\textrm{where } q = \Phi^{-1}(\alpha) \\ R_{m} ={}& \{\t: \abs{\t} \le q \} \quad\textrm{where } q = \Phi^{-1}(0.5 + \alpha / 2) \quad\textrm{(!!!)}\\ R_{\infty} ={}& \begin{cases} \emptyset & \textrm{ with independent probability } \alpha \\ (-\infty,\infty) & \textrm{ with independent probability } 1 - \alpha \\ \end{cases} \quad\textrm{(!!!)} \end{aligned} \]

The last two may seem silly, but they are still rejection regions into which $\t$ is unlikely to fall if it has a standard normal distribution.

How can we think about $\alpha$ , and about the choice of the region? Recall that

If $\t \in R$ , we “reject” the proposed value of $\beta_k^0$
If $\t \notin R$ , we “fail to reject” the given value of $\beta_k^0$ .

Of course, we don’t “accept” the value of $\beta_k^0$ in the sense of believing that $\beta_k^0 = \beta_k$ — if nothing else, there will always be multiple values of $\beta_k^0$ that we do not reject, and $\beta_k$ cannot be equal to all of them.

So there are two ways to make an error:

Type I error: We are correct and $\beta_k = \beta_k^0$ , but $\t \in R$ and we reject
Type II error: We are incorrect and $\beta_k \ne \beta_k^0$ , but $\t \notin R$ and we fail to reject

By definition of the region $R$ , we have that

\[ \prob{\textrm{Type I error}} \le \alpha. \]

This is true for all the regions above, including the silly ones!

What about the Type II error? It must depend on the “true” value of $\beta_k$ , and on the shape of the rejection region we choose. Note that

\[ \t = \frac{\betahat_k - \beta_k^0}{\sqrt{\hat\v / N}} = \frac{\betahat_k - \beta_k}{\sqrt{\hat\v / N}} + \frac{\beta_k - \beta_k^0}{\sqrt{\hat\v / N}} \]

So if the true value $\beta_k \gg \beta_k^0$ , then our $\t$ statistic is too large, and so on.

For example:

Then $\t$ is too large and positive.
$R_u$ and $R_{ts}$ will reject, but $R_l$ will not.
The Type II error of $R_u$ will be lowest, then $R_{ts}$ , then $R_l$ .
$R_l$ actually has greater Type II error than the silly regions, $R_\infty$ and $R_m$ .
Then $\t$ is too large and negative.
$R_l$ and $R_{ts}$ will reject, but $R_u$ will not.
The Type II error of $R_l$ will be lowest, then $R_{ts}$ , then $R_u$ .
$R_u$ actually has greater Type II error than the silly regions, $R_\infty$ and $R_m$ .
Then $\t$ has about the same distribution as when $\beta_k^0 = \beta_k$ .
All the regions reject just about as often as we commit a Type I error, that is, a proportion $\alpha$ of the time.

Thus the shape of the region determines which alternatives you are able to reject. The probability of “rejecting” under a particular alternative is called the “power” of a test; the power is one minus the Type II error rate.

The null and alternative

Statistics has some formal language to distinguish between the “guess” $\beta_k^0$ and other values.

Falsely rejecting the null hypothesis is called a Type I error
By construction, Type I errors occurs with probability at most $\alpha$
Falsely failling to reject the null hypothesis is called a Type II error
Type II errors’ probability depends on the alternative(s) and the rejection region shape.

The choice of a test statistic (here, $\t$ ), together with a rejection region (here, $R$ ) constitute a “test” of the null hypothesis. In general, one can imagine constructing many different tests, with different theoretical guarantees and power.

Confidence intervals

Often in applied statistics, a big deal is made about a single hypothesis test, particularly the null that $\beta_k^0 = 0$ . Often this is not a good idea. Typically, we do not care whether $\beta_k$ is precisely zero; rather, we care about the set of plausible values $\beta_k$ might take. The distinction can be expressed as the difference between statistical and practical significance:

Statistical significance is the size of an effect relative to sampling variability
Practical significance is the size of the effect in terms of its effect on reality.

For example, suppose that $\beta_k$ is nonzero but very small, but $\sqrt{\hat\v / N}$ is very small, too. We might reject the null hypothesis $\beta_k^0 = 0$ with a high degree of certainty, and call our result statistically significant . However, a small value of $\beta_k$ may still not be a meaningful effect size for the problem at hand, i.e., it may not be practically significant .

A remendy is confidence intervals, which are actually closely related to our hypothesis tests. Recall that we have been constructing intervals of the form

\[ \prob{\beta_k \in I} \ge 1-\alpha \]

\[ I = \left(\betahat_k \pm q \hat\v / \sqrt{N}\right), \]

where $q = \Phi^{-1}(\alpha / 2)$ , and $\Phi$ is the CDF of either the standard normal or Student T distribution. It turns out that $I$ is precisely the set of values that we would not reject with region $R_{ts}$ . And, indeed, given a confidence interval, a valid test of the hypothesis $\beta_k^0$ is given by rejecting if an only if $\beta_k^0 \in I$ .

This duality is entirely general:

The set of values that a valid test does not reject is a valid confidence interval
Checking whether a value falls in a valid confidence interval is a valid test

Source Code

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

4: confidence intervals.

Construct and interpret sampling distributions using StatKey
Explain the general form of a confidence interval
Interpret a confidence interval
Explain the process of bootstrapping
Construct bootstrap confidence intervals using the standard error method
Construct bootstrap confidence intervals using the percentile method in StatKey
Construct bootstrap confidence intervals using Minitab
Describe how sample size impacts a confidence interval

This lesson corresponds to Chapter 3 in the Lock 5 textbook. In Lessons 2 and Lesson 3 you learned about descriptive statistics. Lesson 4 begins our coverage of inferential statistics which use data from a sample to make an inference about a population. Confidence intervals use data collected from a sample to estimate a population parameter.

In this lesson we will be working with the following statistics and parameters:

	Population Parameter	Sample Statistic
Mean	$\mu$	$\overline x$
Difference in two means	$\mu_1 - \mu_2$	$\overline x_1 - \overline x_2$
Proportion	$p$	$\widehat p$
Difference in two proportions	$p_1 - p_2$	$\widehat p_1 - \widehat p_2$
Correlation	$\rho$	$r$
Slope (simple linear regression)	$\beta$	$b$

Before we being, let's review population parameters and sample statistics.

Population parameters are fixed values. We rarely know the parameter values because it is often difficult to obtain measures from the entire population.

Sample statistics are known values, but they are random variables because they vary from sample to sample.

Example: Campus Commuters Section

A survey is carried out at a university to estimate the proportion of undergraduate students who drive to campus to attend classes. One thousand students are randomly selected and asked whether they drive or not to campus to attend classes. The population is all of the undergraduates at that university. The sample is the group of 1000 undergraduate students surveyed. The parameter is the true proportion of all undergraduate students at that university who drive to campus to attend classes. The statistic is the proportion of the 1000 sampled undergraduates who drive to campus to attend classes.

Example: Annual Income in California Section

A study is conducted to estimate the true mean annual income of all adult residents of California. The study randomly selects 2000 adult residents of California. The population consists of all adult residents of California. The sample is the 2000 residents in the study. The parameter is the true mean annual income of all adult residents of California. The statistic is the mean of the 2000 residents in this sample.

Ultimately, we measure sample statistics and use them to draw conclusions about unknown population parameters. This is statistical inference.

Introduction to Statistics and Data Science

Chapter 16 confidence intervals and hypothesis testing, 16.1 relation to confidence intervals.

I have been hinting throughout our discussion of hypothesis testing that in many cases confidence intervals are a better approach. In fact for the single sample tests we have looked at so far we have little need for complications of hypothesis testing. R has been hinting that confidence intervals can also be used in the output from the t.test and prop.test commands.

16.1.1 Two sided tests

Lets start with two sided hypothesis tests. Recall we use two sided hypothesis tests when our alternative hypothesis is of the form $H_a: \mu \neq a$ or $H_a: p \neq b$ for the case of testing population proportions.

For example, lets look at the biased coin example from the last section again:

You will notice that R gives us a 95 percent confidence interval for $p$ given the data. This is the very same confidence interval we would get if we used the prop.test command to just get the confidence interval for the population proportion $p$ :

Notice that 0.5 is just outside the 95% confidence interval for $p$ . This means we would reject the null hypothesis at a significance level of $\alpha=0.05$ for any null hypothesis outside this 95% confidence interval (0.505.0.904). Therefore, conducting a two-sided hypothesis test with significance level $\alpha$ just amounts to forming a confidence interval at 1.0- $\alpha$ level and seeing if the confidence interval contains the null value.

If the 95% confidence interval formed based on our sample does not include the null hypothesis value $H_0: \mu=a$ or $H_0: p=b$ we would reject the null hypothesis at a $\alpha=0.05$ significance level.

This is important for a few reasons:

Generality: We saw how to form the confidence interval for any point estimator we want (median, variance, IQR, etc) using bootstrapping . You will notice we only learned how to do hypothesis tests for the population mean $\mu$ and proportion $p$ . Therefore, interpreting confidence intervals as hypothesis tests allows us to perform hypothesis tests on any point estimator $\hat{\theta}$ we want using bootstrapping.

Ease of Interpretations: By reporting the confidence interval rather than just the results of the hypothesis test we give the reader our our results much more information. This enables us to spot and correct many of the common mistakes we have discussed for hypothesis testing.

We find sufficient evidence to reject the null hypothesis here at a $\alpha=0.05$ significance level. This could be reported as finding a biased coin. However, if we were to report the confidence interval as $(0.485,0.49945)$ we can see that the only reason we find a “significant” difference here is because the sample size is very large. The reader can then make up their own mind as to what constitutes a significant difference.

We could then (falsely) claim that since we didn’t reject the null hypothesis this shows our coin isn’t biased. However, we say earlier that we might fail to reject the null hypothesis for two reasons. First because the null is actually true, but also because we haven’t collected enough data yet. Looking at the confidence interval here can give us an idea of which case we are in. The 95% confidence interval here is 0.1369306, 0.7263303 . This huge range on the confidence interval tells us we are in the not enough data regime.

A wide confidence interval indicates that we may have retained the null because we have insufficient evidence to perform any inference at all.

16.1.2 One-sided confidence intervals

When we learned about confidence intervals we saw that a typical 95% confidence interval $(s_1, s_2)$ is chosen so that

$s_1$ is the 2.5% quantile of the sampling distribution

$s_2$ is the 97.5% quantile of the sampling distribution

Thus we decide to take off the 5% from each side evenly. However, their is no particular reason that we have to do it this way. For example, we could leave off 5% by considering the intervals $(-\infty, h_1)$ or $(h_2, \infty)$ . Where $h_1$ is the 95% quantile of the sampling distribution and $h_2$ is the $5%$ quantile of the sampling distribution. This are called one-sided confidence intervals and are the confidence interval equivalent for hypothesis testing when are alternatives is sided (less, greater).

When we test a “less” alternative hypothesis like $H_a: \mu < 0.1$ or for proportions $H_a: p < 0.5$ , then the confidence interval to use is the left one sided interval $(-\infty, h_1)$ . If we use the t.test or prop.test commands in R , then R will automatically choose this for us. The confidence interval equivalent to a hypothesis test is to form your confidence interval (usually 95% or 99%) and see if it contains the null value. If it does then retain the null hypothesis at level (100-95, or 100-99).

The “greater” test is equilvalent to forming a right one sided interval $(h_2, \infty)$ . With the same interpretations as above.

Lets use the prop.test command to form a left sided confidence interval:

This confidence interval contains the null hypothesis so we cannot conclude that the true $p$ is less than 45% given this data.

Lets use a t.test command and interpret the confidence interval.

At the 95% level we see the confidence interval does not contain the null value (94) so we would reject the null hypothesis. However, we can see that if we raise the significance level to 1%, we get:

Now the null hypothesis value is contained in the confidence interval.

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

What is the difference between confidence intervals and hypothesis testing?

I have read about controversies regarding hypothesis testing with some commentators suggesting that hypothesis testing should not be used. Some commentators suggest that confidence intervals should be used instead.

What is the difference between confidence intervals and hypothesis testing? Explanation with reference and examples would be appreciated.
hypothesis-testing
confidence-interval

5 $\begingroup$ I think you wanted to ask why reporting the hypothesis testing results by showing confidence interval is better than just saying something is confirmed or rejected on some p-value level. $\endgroup$ – user88 Commented Oct 1, 2011 at 9:53
4 $\begingroup$ You should consider checking some of your other questions as answered. $\endgroup$ – Andy W Commented Oct 1, 2011 at 13:13
$\begingroup$ In simple words, when we are calculating confidence interval we use the observed proportion while when we are calculating the hypothesis test we use the expected mean. $\endgroup$ – Lerner Zhang Commented Aug 24, 2020 at 16:11

3 Answers 3

You can use a confidence interval (CI) for hypothesis testing. In the typical case, if the CI for an effect does not span 0 then you can reject the null hypothesis. But a CI can be used for more, whereas reporting whether it has been passed is the limit of the usefulness of a test.

The reason you're recommended to use CI instead of just a t-test, for example, is because then you can do more than just test hypotheses. You can make a statement about the range of effects you believe to be likely (the ones in the CI). You can't do that with just a t-test. You can also use it to make statements about the null, which you can't do with a t-test. If the t-test doesn't reject the null then you just say that you can't reject the null, which isn't saying much. But if you have a narrow confidence interval around the null then you can suggest that the null, or a value close to it, is likely the true value and suggest the effect of the treatment, or independent variable, is too small to be meaningful (or that your experiment doesn't have enough power and precision to detect an effect important to you because the CI includes both that effect and 0).

Added Later: I really should have said that, while you can use a CI like a test it isn't one. It's an estimate of a range where you think the parameter values lies. You can make test like inferences but you're just so much better off never talking about it that way.

Which is better?

A) The effect is 0.6, t (29) = 2.8, p < 0.05. This statistically significant effect is... (some discussion ensues about this statistical significance without any mention of or even strong ability to discuss the practical implication of the magnitude of the finding... under a Neyman-Pearson framework the magnitude of the t and p values is pretty much meaningless and all you can discuss is whether the effect is present or isn't found to be present. You can never really talk about there not actually being an effect based on the test.)

B) Using a 95% confidence interval I estimate the effect to be between 0.2 and 1.0. (some discussion ensues talking about the actual effect of interest, whether it's plausible values are ones that have any particular meaning and any use of the word significant for exactly what it's supposed to mean. In addition, the width of the CI can go directly to a discussion of whether this is a strong finding or whether you can only reach a more tentative conclusion)

If you took a basic statistics class you might initially gravitate toward A. And there may be some cases where it is a better way to report a result. But for most work B is by far and away superior. A range estimate is not a test.

$\begingroup$ One addition to @john 's comments: First, sometimes the key question is whether the CI spans 1, not 0 (e.g. logistic regression). $\endgroup$ – Peter Flom Commented Oct 1, 2011 at 9:23
$\begingroup$ Guys, it is 1 or is it 0? (This looks very illuminating to me, so I guess, I need to learn the correct value to look out for!) @John $\endgroup$ – Adhesh Josh Commented Oct 1, 2011 at 12:06
$\begingroup$ What is the relation between 95% CI and two-tailed testing hypothesis with alfa=0.05? are they same?If not then how? $\endgroup$ – love-stats Commented Oct 1, 2011 at 13:49
$\begingroup$ love-stats, when used the same they are the same. $\endgroup$ – John Commented Oct 1, 2011 at 14:51
$\begingroup$ Adhesh Josh, the null hypothesis can be any fixed value specified beforehand. That's another feature of the CI over straight NHST. It's very easy to use when you want to test against a hypothetical value other than 0. $\endgroup$ – John Commented Oct 1, 2011 at 14:53

There is an equivalence between hypothesis tests and confidence intervals. (See e.g. https://en.wikipedia.org/wiki/Confidence_interval#Hypothesis_testing )

I'll give a very specific example. Suppose we have sample $x_1, x_2, \ldots, x_n$ from a normal distribution with mean $\mu$ and variance 1, which we'll write as $\mathcal N(\mu,1)$ . Suppose we think that $\mu = m$ , and we want to test the null-hypothesis $H_0: \mu = m$ , at level $0.05.$ So we make a test statistic, which in this case we will take to be the sample average: $v = (x_1 + x_2 + \cdots + x_n ) / n$ . Now suppose $A(m)$ is the "acceptance region" for $v$ for this test. That means that $A(m)$ is the set of possible values of $v$ for which the null-hypothesis $\mu=m$ is accepted at level 0.05 (I use "accepted" as a shorthand for "not rejected" – I am not suggesting that you would conclude the null hypothesis is true.). For this example, we can look at the $\mathcal N(m,1)$ normal distribution and choose any set that has probability at least 0.95 under this distribution. Now, a 95% confidence region for $\mu$ is the set of all $m$ for which $v$ is in $A(m)$ . In other words, it is the set of all $m$ for which the null-hypothesis would be accepted for the observed $v$ . That's why John says "If the CI for an effect does not span $0$ then you can reject the null hypothesis." (John is referring to the case of testing $\mu = 0$ .)

A related topic is the p-value: The p-value is the smallest level for a test at which we would reject the null-hypothesis. To tie it in with the discussion of confidence intervals, suppose we get a particular sample average $v$ , from which we construct confidence intervals of different sizes. Suppose a 95% confidence interval for $\mu$ does not contain $m$ . Then we can reject the null-hypothesis $\mu=m$ at level $0.05.$ Then suppose we grow the confidence interval until it just touches (but doesn't include) the value $m$ , and suppose this is a 98% confidence interval. Then the p-value for the hypothesis $\mu=m$ is $0.02$ (which we get from $1-0.98$ ).

$\begingroup$ Please read this as p-value can't be interpreted as smallest level of test to reject null. "It has already been shown that interpreting p values in single (or ongoing) experiments is not permissible in a Neyman–Pearson hypothesis testing context. The calculation of a p value depends only on the truth of the null hypothesis. The p value does not measure the amount of evidence supporting HA; it is a measure of inductive evidence against H0." 'Source : ftp.stat.duke.edu/WorkingPapers/03-26.pdf $\endgroup$ – sree22 Commented Apr 13, 2018 at 6:51
$\begingroup$ @sree22 can you expand on this, or suggest a rewording? I was trying to give a definition of p-value in this context, not an interpretation. $\endgroup$ – DavidR Commented Jun 17, 2019 at 15:54

'Student' argued for confidence intervals on the grounds that they could show which effects were more important as well as which were more significant.

For example, if you found two effects where the first had a confidence interval for its financial impact from £5 to £6, while the second had a confidence interval from £200 to £2800. The first is more statistically significant but the second is probably more important.

Your Answer

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged hypothesis-testing confidence-interval or ask your own question .

Featured on Meta
Bringing clarity to status tag usage on meta sites
We've made changes to our Terms of Service & Privacy Policy - July 2024
Announcing a change to the data-dump process

Hot Network Questions

Topology on a module over a topological ring
Variable usage in arithmetic expansions
Completely introduce your friends
What is an intuitive way to rename a column in a Dataset?
Simple casino game
How do I safely remove a mystery cast iron pipe in my basement?
Equations for dual cubic curves
How to attach a 4x8 plywood to a air hockey table
Running fully sheathed romex through a media box
Can a rope thrower act as a propulsion method for land based craft?
DATEDIFF Rounding
Passport Carry in Taiwan
Change output language of internal commands like "lpstat"?
Do metal objects attract lightning?
Do the amplitude and frequency of gravitational waves emitted by binary stars change as the stars get closer together?
I'm trying to remember a novel about an asteroid threatening to destroy the earth. I remember seeing the phrase "SHIVA IS COMING" on the cover
How can these humans cross the ocean(s) at the first possible chance?
The answer is not wrong
Why does a halfing's racial trait lucky specify you must use the next roll?
How would increasing atomic bond strength affect nuclear physics?
Historical U.S. political party "realignments"?
What does it say in the inscriptions on Benjamin's doorway; A Canticle for Leibowitz
Would Camus say that any philosopher who denies the absurd is intellectually dishonest?
Who was the "Dutch author", "Bumstone Bumstone"?

Hypothesis Testing & Confidence Intervals in Statistics

COMMENTS

6.6
In other words, if the the 95% confidence interval contains the hypothesized parameter, then a hypothesis test at the 0.05 $\alpha$ level will almost always fail to reject the null hypothesis. If the 95% confidence interval does not contain the hypothesize parameter, then a hypothesis test at the 0.05 $\alpha$ level will almost always ...
Hypothesis Testing and Confidence Intervals
The relationship between the confidence level and the significance level for a hypothesis test is as follows: Confidence level = 1 - Significance level (alpha) For example, if your significance level is 0.05, the equivalent confidence level is 95%. Both of the following conditions represent statistically significant results: The P-value in a ...
Hypothesis Testing, P Values, Confidence Intervals, and Significance
Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting ...
Confidence Intervals: Interpreting, Finding & Formulas
Confidence intervals are similarly helpful for understanding an effect size. For example, if you assess a treatment and control group, the mean difference between these groups is the estimated effect size. A 2-sample t-test can construct a confidence interval for the mean difference.
Hypothesis Test vs. Confidence Interval: What's the Difference?
Here's the difference between the two: A hypothesis test is a formal statistical test that is used to determine if some hypothesis about a population parameter is true. A confidence interval is a range of values that is likely to contain a population parameter with a certain level of confidence. This tutorial shares a brief overview of each ...
PDF Chapter 5 Conﬁdence Intervals and Hypothesis Testing
1 α)% of the probability mass is within the i. terval. The interpretation of a (1 α)% confidence −interval [φ1, φ2] is that the probability that the mode. 95% HPD confidence interval. Symmetric 95% confidence interval. e intervals for a posterior distributed asBeta(5, 29)Of course, there is always more than one way of choosing the bounds ...
Hypothesis Testing and Confidence Intervals
The correct answer is A. To calculate the 95% confidence interval for the mean study time of all candidates, we can use the formula for the confidence interval when the population variance is unknown: Confidence Interval = ¯X ±t1−α 2 × s √n Confidence Interval = X ¯ ± t 1 − α 2 × s n. Where: ¯X X ¯ is the sample mean.
8.6 Relationship Between Confidence Intervals and Hypothesis Tests
We can also use confidence intervals to make conclusions about hypothesis tests: reject the null hypothesis [latex]H_0[/latex] at the significance level [latex]\alpha[/latex] if the corresponding [latex](1 - \alpha) \times 100\%[/latex] confidence interval does not contain the hypothesized value [latex]\mu_0[/latex]. The relationship is ...
Understanding Hypothesis Tests: Confidence Intervals and ...
You can use either P values or confidence intervals to determine whether your results are statistically significant. If a hypothesis test produces both, these results will agree. The confidence level is equivalent to 1 - the alpha level. So, if your significance level is 0.05, the corresponding confidence level is 95%.
The Relationship Between Hypothesis Testing and Confidence Intervals
Confidence intervals and hypothesis testing are both methods that look to infer some kind of population parameter from a sample of data drawn from that population. Confidence intervals gives us a range of possible values and an estimate of the precision for our parameter value.
Confidence Intervals
Hypothesis Testing Decisions through Confidence Intervals. You may have noticed that many of the steps used for confidence intervals are shared with hypothesis testing. While there are distinctions between the two, we can also use confidence intervals to help us determine the result of a hypothesis test.
Confidence intervals and hypothesis testing
And, indeed, given a confidence interval, a valid test of the hypothesis β k 0 is given by rejecting if an only if β k 0 ∈ I. This duality is entirely general: The set of values that a valid test does not reject is a valid confidence interval. Checking whether a value falls in a valid confidence interval is a valid test.
4: Confidence Intervals
This lesson corresponds to Chapter 3 in the Lock 5 textbook. In Lessons 2 and Lesson 3 you learned about descriptive statistics. Lesson 4 begins our coverage of inferential statistics which use data from a sample to make an inference about a population. Confidence intervals use data collected from a sample to estimate a population parameter.
The Ultimate Guide to Hypothesis Testing and Confidence Intervals in
We can test whether this sample is drawn from a population with mean equals to μ by checking whether Ᾱ differs significantly from μ. We can also estimation a 95% confidence interval for the population mean where this sample is drawn from. Hypothesis Testing. Here are the steps for conducting hypothesis testing: Step 1: Set up the null ...
PDF Lecture 10: Confidence intervals & Hypothesis testing
Testing claims based on a confidence interval (cont.) Using a confidence interval for hypothesis testing might be insufficient in some cases since it gives a yes/no (reject/don't reject) answer, as opposed to quantifying our decision with a probability. Formal hypothesis testing allows us to report a probability along with our decision.
11.8: Significance Testing and Confidence Intervals
There is a close relationship between confidence intervals and significance tests. Specifically, if a statistic is significantly different from 0 0 at the 0.05 0.05 level, then the 95% 95 % confidence interval will not contain 0 0. All values in the confidence interval are plausible values for the parameter, whereas values outside the interval ...
Hypothesis testing and confidence intervals
Hypothesis testing and confidence intervals are intrinsically related. This chapter discusses how to test statistical hypotheses, and then focuses on interval estimation. Special attention is given to explanation of major statistical concepts, such as the p-value, in layman's terms. The chapter provides two ad hoc examples where hypothesis ...
12: Confidence Intervals and Hypothesis Tests
12.1: Confidence Intervals. In this chapter, you will learn to construct and interpret confidence intervals. You will also learn a new distribution, the Student's-t, and how it is used with these intervals. Throughout the chapter, it is important to keep in mind that the confidence interval is a random variable.
Hypothesis Test vs. Confidence Interval
Hypothesis Testing (p value) and Confidence Interval: Comparing and contrasting hypothesis testing and confidence interval in research and statistics with ex...
Chapter 16 Confidence Intervals and Hypothesis Testing
The confidence interval equivalent to a hypothesis test is to form your confidence interval (usually 95% or 99%) and see if it contains the null value. If it does then retain the null hypothesis at level (100-95, or 100-99). The "greater" test is equilvalent to forming a right one sided interval (h2,∞) ( h 2, ∞).
What is the difference between confidence intervals and hypothesis testing?
25. You can use a confidence interval (CI) for hypothesis testing. In the typical case, if the CI for an effect does not span 0 then you can reject the null hypothesis. But a CI can be used for more, whereas reporting whether it has been passed is the limit of the usefulness of a test.
11: Hypothesis Testing and Confidence Intervals with Two Samples
11.5: Matched or Paired Samples. When using a hypothesis test for matched or paired samples, the following characteristics should be present: Simple random sampling is used. Sample sizes are often small. Two measurements (samples) are drawn from the same pair of individuals or objects. Differences are calculated from the matched or paired samples.
Hypothesis Testing & Confidence Intervals in Statistics
Hypothesis testing is a procedure based on sample evidence and probability theory to decide whether the hypothesis is a reasonable statement. ... We wish to construct a 95 percent confidence interval for the proportion of Internet users in the sampled population who have searched for information on experimental treatments or medicines.
Bootstrapping (statistics)
From this empirical distribution, one can derive a bootstrap confidence interval for the purpose of hypothesis testing. Regression. In regression problems, case resampling refers to the simple scheme of resampling individual cases - often rows of a data set. For regression problems, as long as the data set is fairly large, this simple scheme ...

	Population Parameter	Sample Statistic
Mean	\(\mu\)	\(\overline x\)
Difference in two means	\(\mu_1 - \mu_2\)	\(\overline x_1 - \overline x_2\)
Proportion	\(p\)	\(\widehat p\)
Difference in two proportions	\(p_1 - p_2\)	\(\widehat p_1 - \widehat p_2\)
Correlation	\(\rho\)	\(r\)
Slope (simple linear regression)	\(\beta\)	\(b\)

StatPearls [Internet].

Affiliations

In this Page

Related information

Similar articles in PubMed

Recent Activity

Confidence Intervals: Interpreting, Finding & Formulas

What is a Confidence Interval?

What is the Confidence Level?

How to Interpret Confidence Intervals

Confidence Intervals for Effect Sizes

Avoid a Common Misinterpretation of Confidence Intervals

What Affects the Widths of Confidence Intervals?

Sample Variability

Sample Size

Changing the Confidence Level

Confidence Interval Formula

Interval Widths Revisited

How to Find a Confidence Interval

Entering Values into the Confidence Interval Formula

Share this:

Reader Interactions

Comments and Questions Cancel reply

Hypothesis Testing

Components of the Hypothesis Testing

The Null hypothesis

The Alternative Hypothesis

The Test Statistic

The Size of the Hypothesis Test and the Type I and Type II Errors

Type I Error

Type II Error

The Critical Value and the Decision Rule

Left One-tailed Test

Right One-tailed Test

Two-tailed Test

Example: Hypothesis Test on the Mean

The Type II Error and the Test Power

Confidence Intervals

Example: Calculating Two-Sided Alternative Confidence Intervals

One-Sided Alternative

Example: Calculating the One-Sided Alternative Confidence Interval

The p-Value

The p-Value for One-Tailed Test Alternative

The p-Value for Two-Tailed Test Alternative

Example 1: p-Value for One-Sided Alternative

Example 2: p-Value for Two-Sided Alternative

Hypothesis about the Difference between Two Population Means.

Example: Hypothesis Test on Two Means

The Problem of Multiple Testing

Approaches to Asset Allocation

Pricing Financial Forwards and Futures

Measuring Credit Risk

Modeling and Hedging Non-Parallel Term ...

Leave a Comment Cancel reply

8.6 Relationship Between Confidence Intervals and Hypothesis Tests

Understanding Hypothesis Tests: Confidence Intervals and Confidence Levels

How to Correctly Interpret Confidence Intervals and Confidence Levels

Confidence Intervals and the Margin of Error

Why P Values and Confidence Intervals Always Agree About Statistical Significance

Closing Thoughts

You Might Also Like

Confidence Intervals

General Motivation and Framework

Confidence Interval Example

Confidence Interval Steps

Identify Parameter of Interest

Determine the Confidence Level

Determine the Sampling Distribution for the Sample Statistic

Calculate the Confidence Interval

Write a Conclusion in the Context of the Problem

Confidence Interval Widths

Confidence Interval Misconceptions and Misinterpretations

Confidence Level Interpretation

Hypothesis Testing Decisions through Confidence Intervals

Confidence intervals and hypothesis testing

Confidence intervals and hypothesis tests

Plugging in values for \(\beta_k\)

Rejection regions

The null and alternative

Confidence intervals