3 6 problem solving using charts answer key

• 888-309-8227
• 732-384-0146

New User Registration

Forgot Password

Textbook Resources

Textbook resources.

• Call us toll-free
• FAQs – Frequently Asked Questions
• Contact Lumos Learning – Proven Study Programs by Expert Teachers

Follow us: Lumos Learning -->

• 2024 © Lumos Learning
• Privacy Policy - Terms of Service - Disclaimers

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc... Read More

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc., the Partnership for the Assessment of Readiness for College and Careers, nor any state of the Union. Neither PARCC, Inc., nor The Partnership for the Assessment of Readiness for College and Careers, nor any member state has endorsed this product. No portion of any fees or charges paid for any products or services Lumos Learning offers will be paid or inure to the benefit of PARCC, Inc., or any state of the Union

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not aff... Read More

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not affiliated to Lumos Learning. The Regents of the University of California – Smarter Balanced Assessment Consortium, was not involved in the production of, and does not endorse these products or this site.

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC, was not... Read More

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC,was not involved in the production of, and does not endorse these products or this site.

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the... Read More

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the production of, and does not endorse these products or this site.

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the... Read More

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the production of, and does not endorse these products or this site.

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved... Read More

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved in the production of, and does not endorse these products or this site.

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the prod... Read More

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the production of, and does not endorse these products or this site.

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved... Read More

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved in the production of, and does not endorse these products or this site.

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved... Read More

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved in the production of, and does not endorse these products or this site.

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved... Read More

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved in the production of, and does not endorse these products or this site.

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved... Read More

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved in the production of, and does not endorse these products or this site.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: Use a Problem-Solving Strategy

• Last updated
• Save as PDF
• Page ID 15136

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Approach word problems with a positive attitude
• Use a problem-solving strategy for word problems
• Solve number problems

Before you get started, take this readiness quiz.

• Translate “6 less than twice x ” into an algebraic expression. If you missed this problem, review Exercise 1.3.43 .
• Solve: \(\frac{2}{3}x=24\). If you missed this problem, review Exercise 2.2.10 .
• Solve: \(3x+8=14\). If you missed this problem, review Exercise 2.3.1 .

Approach Word Problems with a Positive Attitude

“If you think you can… or think you can’t… you’re right.”—Henry Ford

The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion? How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?

Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below (Figure \(\PageIndex{1}\))?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.

Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in Figure \(\PageIndex{2}\) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!

Use a Problem-Solving Strategy for Word Problems

We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.

Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.

USE A PROBLEM-SOLVING STRATEGY TO SOLVE WORD PROBLEMS.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Example \(\PageIndex{1}\)

Pilar bought a purse on sale for \($18\), which is one-half of the original price. What was the original price of the purse?

Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.

Let p = the original price of the purse.

Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!

In this problem, the words “what was the original price of the purse” tell us what we need to find.

Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.

Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.

Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.

Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.

Step 6. Check the answer in the problem to make sure it makes sense. We solved the equation and found that \(p=36\),which means “the original price” was \($36\).

If this were a homework exercise, our work might look like this:

Pilar bought a purse on sale for \($18\), which is one-half the original price. What was the original price of the purse?

Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”

Try It \(\PageIndex{2}\)

Joaquin bought a bookcase on sale for \($120\), which was two-thirds of the original price. What was the original price of the bookcase?

Try It \(\PageIndex{3}\)

Two-fifths of the songs in Mariel’s playlist are country. If there are \(16\) country songs, what is the total number of songs in the playlist?

Let’s try this approach with another example.

Example \(\PageIndex{4}\)

Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were \(11\) girls in the study group. How many boys were in the study group?

Try It \(\PageIndex{5}\)

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was \(3\) more than twice the number of notebooks. He bought \(7\) textbooks. How many notebooks did he buy?

Try It \(\PageIndex{6}\)

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed \(22\) Sudoku puzzles. How many crossword puzzles did he do?

Solve Number Problems

Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.

Example \(\PageIndex{7}\)

The difference of a number and six is \(13\). Find the number.

Try It \(\PageIndex{8}\)

The difference of a number and eight is \(17\). Find the number.

Try It \(\PageIndex{9}\)

The difference of a number and eleven is \(−7\). Find the number.

Example \(\PageIndex{10}\)

The sum of twice a number and seven is \(15\). Find the number.

Try It \(\PageIndex{11}\)

The sum of four times a number and two is \(14\). Find the number.

Try It \(\PageIndex{12}\)

The sum of three times a number and seven is \(25\). Find the number.

​​​​​​ Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

Example \(\PageIndex{13}\)

One number is five more than another. The sum of the numbers is 21. Find the numbers.

Try It \(\PageIndex{14}\)

One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.

Try It \(\PageIndex{15}\)

The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.

Example \(\PageIndex{16}\)

The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.

Try It \(\PageIndex{17}\)

The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.

Try It \(\PageIndex{18}\)

The sum of two numbers is \(−18\). One number is \(40\) more than the other. Find the numbers.

Example \(\PageIndex{19}\)

One number is ten more than twice another. Their sum is one. Find the numbers.

Try It \(\PageIndex{20}\)

One number is eight more than twice another. Their sum is negative four. Find the numbers.

\(-4,\; 0\)

Try It \(\PageIndex{21}\)

One number is three more than three times another. Their sum is \(−5\). Find the numbers.

\(-3,\; -2\)

Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:

\[\begin{array}{l}{1,2,3,4} \\ {-10,-9,-8,-7} \\ {150,151,152,153}\end{array}\]

Notice that each number is one more than the number preceding it. So if we define the first integer as \(n\), the next consecutive integer is \(n+1\). The one after that is one more than \(n+1\), so it is \(n+1+1\), which is \(n+2\). \[\begin{array}{ll}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text { consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

Example \(\PageIndex{22}\)

The sum of two consecutive integers is \(47\). Find the numbers.

Try It \(\PageIndex{23}\)

The sum of two consecutive integers is 95. Find the numbers.

Try It \(\PageIndex{24}\)

The sum of two consecutive integers is −31. Find the numbers.

Example \(\PageIndex{25}\)

Find three consecutive integers whose sum is −42.

Try It \(\PageIndex{26}\)

Find three consecutive integers whose sum is −96.

-33, -32, -31

Try It \(\PageIndex{27}\)

Find three consecutive integers whose sum is −36.

-13, -12, -11

Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

\[\begin{array}{l}{18,20,22} \\ {64,66,68} \\ {-12,-10,-8}\end{array}\]

Notice each integer is \(2\) more than the number preceding it. If we call the first one \(n\), then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\). \[\begin{array}{cll}{n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers \(77\), \(79\), and \(81\).

\[\begin{array}{l}{77,79,81} \\ {n, n+2, n+4}\end{array}\]

\[\begin{array}{cll}{n} & {1^{\text { st }} \text {odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?

Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2.

Example \(\PageIndex{28}\)

Find three consecutive even integers whose sum is 84.

\[\begin{array}{ll} {\textbf{Step 1. Read} \text{ the problem.}} & {} \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} & {\text{three consecutive even integers}} \\ {\textbf{Step 3. Name} \text{ the integers.}} & {\text{Let } n = 1^{st} \text{ even integers.}} \\ {} &{n + 2 = 2^{nd} \text{ consecutive even integer}} \\ {} &{n + 4 = 3^{rd} \text{ consecutive even integer}} \\ {\textbf{Step 4. Translate.}} &{} \\ {\text{ Restate as one sentence. }} &{\text{The sum of the three even integers is 84.}} \\ {\text{Translate into an equation.}} &{n + n + 2 + n + 4 = 84} \\ {\textbf{Step 5. Solve} \text{ the equation. }} &{} \\ {\text{Combine like terms.}} &{n + n + 2 + n + 4 = 84} \\ {\text{Subtract 6 from each side.}} &{3n + 6 = 84} \\ {\text{Divide each side by 3.}} &{3n = 78} \\ {} &{n = 26 \space 1^{st} \text{ integer}} \\\\ {} &{n + 2\space 2^{nd} \text{ integer}} \\ {} &{26 + 2} \\ {} &{28} \\\\ {} &{n + 4\space 3^{rd} \text{ integer}} \\ {} &{26 + 4} \\ {} &{30} \\ {\textbf{Step 6. Check.}} &{} \\\\ {26 + 28 + 30 \stackrel{?}{=} 84} &{} \\ {84 = 84 \checkmark} & {} \\ {\textbf{Step 7. Answer} \text{ the question.}} &{\text{The three consecutive integers are 26, 28, and 30.}} \end{array}\]

Try It \(\PageIndex{29}\)

Find three consecutive even integers whose sum is 102.

Try It \(\PageIndex{30}\)

Find three consecutive even integers whose sum is −24.

−10,−8,−6

Example \(\PageIndex{31}\)

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

Try It \(\PageIndex{32}\)

According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,500. This was $1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?

Try It \(\PageIndex{33}\)

U.S. Census data shows that the median price of new home in the United States in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?

Key Concepts

• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.

\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text {consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

3.1 Functions and Function Notation

• ⓑ yes (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)

w = f ( d ) w = f ( d )

g ( 5 ) = 1 g ( 5 ) = 1

m = 8 m = 8

y = f ( x ) = x 3 2 y = f ( x ) = x 3 2

g ( 1 ) = 8 g ( 1 ) = 8

x = 0 x = 0 or x = 2 x = 2

• ⓐ yes, because each bank account has a single balance at any given time;
• ⓑ no, because several bank account numbers may have the same balance;
• ⓒ no, because the same output may correspond to more than one input.
• ⓐ Yes, letter grade is a function of percent grade;
• ⓑ No, it is not one-to-one. There are 100 different percent numbers we could get but only about five possible letter grades, so there cannot be only one percent number that corresponds to each letter grade.

No, because it does not pass the horizontal line test.

3.2 Domain and Range

{ − 5 , 0 , 5 , 10 , 15 } { − 5 , 0 , 5 , 10 , 15 }

( − ∞ , ∞ ) ( − ∞ , ∞ )

( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ ) ( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ )

[ − 5 2 , ∞ ) [ − 5 2 , ∞ )

• ⓐ values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3
• ⓑ { x | x ≤ − 2 or − 1 ≤ x < 3 } { x | x ≤ − 2 or − 1 ≤ x < 3 }
• ⓒ ( − ∞ , − 2 ] ∪ [ − 1 , 3 ) ( − ∞ , − 2 ] ∪ [ − 1 , 3 )

domain =[1950,2002] range = [47,000,000,89,000,000]

domain: ( − ∞ , 2 ] ; ( − ∞ , 2 ] ; range: ( − ∞ , 0 ] ( − ∞ , 0 ]

3.3 Rates of Change and Behavior of Graphs

$ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 $ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 per year.

a + 7 a + 7

The local maximum appears to occur at ( − 1 , 28 ) , ( − 1 , 28 ) , and the local minimum occurs at ( 5 , − 80 ) . ( 5 , − 80 ) . The function is increasing on ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) and decreasing on ( − 1 , 5 ) . ( − 1 , 5 ) .

3.4 Composition of Functions

( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2 ( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2

No, the functions are not the same.

A gravitational force is still a force, so a ( G ( r ) ) a ( G ( r ) ) makes sense as the acceleration of a planet at a distance r from the Sun (due to gravity), but G ( a ( F ) ) G ( a ( F ) ) does not make sense.

f ( g ( 1 ) ) = f ( 3 ) = 3 f ( g ( 1 ) ) = f ( 3 ) = 3 and g ( f ( 4 ) ) = g ( 1 ) = 3 g ( f ( 4 ) ) = g ( 1 ) = 3

g ( f ( 2 ) ) = g ( 5 ) = 3 g ( f ( 2 ) ) = g ( 5 ) = 3

[ − 4 , 0 ) ∪ ( 0 , ∞ ) [ − 4 , 0 ) ∪ ( 0 , ∞ )

Possible answer:

g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g

3.5 Transformation of Functions

The graphs of f ( x ) f ( x ) and g ( x ) g ( x ) are shown below. The transformation is a horizontal shift. The function is shifted to the left by 2 units.

g ( x ) = 1 x - 1 + 1 g ( x ) = 1 x - 1 + 1

g ( x ) = − f ( x ) g ( x ) = − f ( x )

h ( x ) = f ( − x ) h ( x ) = f ( − x )

Notice: g ( x ) = f ( − x ) g ( x ) = f ( − x ) looks the same as f ( x ) f ( x ) .

g ( x ) = 3 x - 2 g ( x ) = 3 x - 2

g ( x ) = f ( 1 3 x ) g ( x ) = f ( 1 3 x ) so using the square root function we get g ( x ) = 1 3 x g ( x ) = 1 3 x

3.6 Absolute Value Functions

using the variable p p for passing, | p − 80 | ≤ 20 | p − 80 | ≤ 20

f ( x ) = − | x + 2 | + 3 f ( x ) = − | x + 2 | + 3

x = − 1 x = − 1 or x = 2 x = 2

3.7 Inverse Functions

h ( 2 ) = 6 h ( 2 ) = 6

The domain of function f − 1 f − 1 is ( − ∞ , − 2 ) ( − ∞ , − 2 ) and the range of function f − 1 f − 1 is ( 1 , ∞ ) . ( 1 , ∞ ) .

• ⓐ f ( 60 ) = 50. f ( 60 ) = 50. In 60 minutes, 50 miles are traveled.
• ⓑ f − 1 ( 60 ) = 70. f − 1 ( 60 ) = 70. To travel 60 miles, it will take 70 minutes.

x = 3 y + 5 x = 3 y + 5

f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ] f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ]

3.1 Section Exercises

A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.

When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.

When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.

not a function

f ( − 3 ) = − 11 ; f ( − 3 ) = − 11 ; f ( 2 ) = − 1 ; f ( 2 ) = − 1 ; f ( − a ) = − 2 a − 5 ; f ( − a ) = − 2 a − 5 ; − f ( a ) = − 2 a + 5 ; − f ( a ) = − 2 a + 5 ; f ( a + h ) = 2 a + 2 h − 5 f ( a + h ) = 2 a + 2 h − 5

f ( − 3 ) = 5 + 5 ; f ( − 3 ) = 5 + 5 ; f ( 2 ) = 5 ; f ( 2 ) = 5 ; f ( − a ) = 2 + a + 5 ; f ( − a ) = 2 + a + 5 ; − f ( a ) = − 2 − a − 5 ; − f ( a ) = − 2 − a − 5 ; f ( a + h ) = 2 − a − h + 5 f ( a + h ) = 2 − a − h + 5

f ( − 3 ) = 2 ; f ( − 3 ) = 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( − a ) = | − a − 1 | − | − a + 1 | ; f ( − a ) = | − a − 1 | − | − a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; f ( a + h ) = | a + h − 1 | − | a + h + 1 | f ( a + h ) = | a + h − 1 | − | a + h + 1 |

g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a

a. f ( − 2 ) = 14 ; f ( − 2 ) = 14 ; b. x = 3 x = 3

a. f ( 5 ) = 10 ; f ( 5 ) = 10 ; b. x = − 1 x = − 1 or x = 4 x = 4

• ⓐ f ( t ) = 6 − 2 3 t ; f ( t ) = 6 − 2 3 t ;
• ⓑ f ( − 3 ) = 8 ; f ( − 3 ) = 8 ;
• ⓒ t = 6 t = 6
• ⓐ f ( 0 ) = 1 ; f ( 0 ) = 1 ;
• ⓑ f ( x ) = − 3 , x = − 2 f ( x ) = − 3 , x = − 2 or x = 2 x = 2

not a function so it is also not a one-to-one function

one-to- one function

function, but not one-to-one

f ( x ) = 1 , x = 2 f ( x ) = 1 , x = 2

f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2 f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2

f ( − 2 ) = 4 ;    f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236 f ( − 2 ) = 4 ;    f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236

f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9 f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9

[ 0 , 100 ] [ 0 , 100 ]

[ − 0.001 , 0 .001 ] [ − 0.001 , 0 .001 ]

[ − 1 , 000 , 000 , 1,000,000 ] [ − 1 , 000 , 000 , 1,000,000 ]

[ 0 , 10 ] [ 0 , 10 ]

[ −0.1 , 0.1 ] [ −0.1 , 0.1 ]

[ − 100 , 100 ] [ − 100 , 100 ]

• ⓐ g ( 5000 ) = 50 ; g ( 5000 ) = 50 ;
• ⓑ The number of cubic yards of dirt required for a garden of 100 square feet is 1.
• ⓐ The height of a rocket above ground after 1 second is 200 ft.
• ⓑ The height of a rocket above ground after 2 seconds is 350 ft.

3.2 Section Exercises

The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.

There is no restriction on x x for f ( x ) = x 3 f ( x ) = x 3 because you can take the cube root of any real number. So the domain is all real numbers, ( − ∞ , ∞ ) . ( − ∞ , ∞ ) . When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x x -values are restricted for f ( x ) = x f ( x ) = x to nonnegative numbers and the domain is [ 0 , ∞ ) . [ 0 , ∞ ) .

Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x x -axis and y y -axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate − ∞ − ∞ or ∞ . ∞ . Combine the graphs to find the graph of the piecewise function.

( − ∞ , 3 ] ( − ∞ , 3 ]

( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ ) ( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ )

( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ ) ( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ )

( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ ) ( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ )

( − ∞ , 5 ) ( − ∞ , 5 )

[ 6 , ∞ ) [ 6 , ∞ )

( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ ) ( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ )

domain: ( 2 , 8 ] , ( 2 , 8 ] , range [ 6 , 8 ) [ 6 , 8 )

domain: [ − 4 , 4], [ − 4 , 4], range: [ 0 , 2] [ 0 , 2]

domain: [ − 5 , 3 ) , [ − 5 , 3 ) , range: [ 0 , 2 ] [ 0 , 2 ]

domain: ( − ∞ , 1 ] , ( − ∞ , 1 ] , range: [ 0 , ∞ ) [ 0 , ∞ )

domain: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; range: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ]

domain: [ − 3 , ∞ ) ; [ − 3 , ∞ ) ; range: [ 0 , ∞ ) [ 0 , ∞ )

domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0 f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0

f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34 f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34

f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16 f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16

domain: ( − ∞ , 1 ) ∪ ( 1 , ∞ ) ( − ∞ , 1 ) ∪ ( 1 , ∞ )

window: [ − 0.5 , − 0.1 ] ; [ − 0.5 , − 0.1 ] ; range: [ 4 , 100 ] [ 4 , 100 ]

window: [ 0.1 , 0.5 ] ; [ 0.1 , 0.5 ] ; range: [ 4 , 100 ] [ 4 , 100 ]

[ 0 , 8 ] [ 0 , 8 ]

Many answers. One function is f ( x ) = 1 x − 2 . f ( x ) = 1 x − 2 .

• ⓐ The fixed cost is $500.
• ⓑ The cost of making 25 items is $750.
• ⓒ The domain is [0, 100] and the range is [500, 1500].

3.3 Section Exercises

Yes, the average rate of change of all linear functions is constant.

The absolute maximum and minimum relate to the entire graph, whereas the local extrema relate only to a specific region around an open interval.

4 ( b + 1 ) 4 ( b + 1 )

4 x + 2 h 4 x + 2 h

− 1 13 ( 13 + h ) − 1 13 ( 13 + h )

3 h 2 + 9 h + 9 3 h 2 + 9 h + 9

4 x + 2 h − 3 4 x + 2 h − 3

increasing on ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , decreasing on ( − 2.5 , 1 ) ( − 2.5 , 1 )

increasing on ( − ∞ , 1 ) ∪ ( 3 , 4 ) , ( − ∞ , 1 ) ∪ ( 3 , 4 ) , decreasing on ( 1 , 3 ) ∪ ( 4 , ∞ ) ( 1 , 3 ) ∪ ( 4 , ∞ )

local maximum: ( − 3 , 60 ) , ( − 3 , 60 ) , local minimum: ( 3 , − 60 ) ( 3 , − 60 )

absolute maximum at approximately ( 7 , 150 ) , ( 7 , 150 ) , absolute minimum at approximately ( −7.5 , −220 ) ( −7.5 , −220 )

Local minimum at ( 3 , − 22 ) , ( 3 , − 22 ) , decreasing on ( − ∞ , 3 ) , ( − ∞ , 3 ) , increasing on ( 3 , ∞ ) ( 3 , ∞ )

Local minimum at ( − 2 , − 2 ) , ( − 2 , − 2 ) , decreasing on ( − 3 , − 2 ) , ( − 3 , − 2 ) , increasing on ( − 2 , ∞ ) ( − 2 , ∞ )

Local maximum at ( − 0.5 , 6 ) , ( − 0.5 , 6 ) , local minima at ( − 3.25 , − 47 ) ( − 3.25 , − 47 ) and ( 2.1 , − 32 ) , ( 2.1 , − 32 ) , decreasing on ( − ∞ , − 3.25 ) ( − ∞ , − 3.25 ) and ( − 0.5 , 2.1 ) , ( − 0.5 , 2.1 ) , increasing on ( − 3.25 , − 0.5 ) ( − 3.25 , − 0.5 ) and ( 2.1 , ∞ ) ( 2.1 , ∞ )

b = 5 b = 5

2.7 gallons per minute

approximately –0.6 milligrams per day

3.4 Section Exercises

Find the numbers that make the function in the denominator g g equal to zero, and check for any other domain restrictions on f f and g , g , such as an even-indexed root or zeros in the denominator.

Yes. Sample answer: Let f ( x ) = x + 1 and  g ( x ) = x − 1. f ( x ) = x + 1 and  g ( x ) = x − 1. Then f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x and g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . So f ∘ g = g ∘ f . f ∘ g = g ∘ f .

( f + g ) ( x ) = 2 x + 6 , ( f + g ) ( x ) = 2 x + 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f − g ) ( x ) = 2 x 2 + 2 x − 6 , ( f − g ) ( x ) = 2 x 2 + 2 x − 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , ( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f g ) ( x ) = x 2 + 2 x 6 − x 2 , ( f g ) ( x ) = x 2 + 2 x 6 − x 2 , domain: ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ )

( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , ( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , ( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f g ) ( x ) = x + 2 , ( f g ) ( x ) = x + 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f g ) ( x ) = 4 x 3 + 8 x 2 , ( f g ) ( x ) = 4 x 3 + 8 x 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f + g ) ( x ) = 3 x 2 + x − 5 , ( f + g ) ( x ) = 3 x 2 + x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f − g ) ( x ) = 3 x 2 − x − 5 , ( f − g ) ( x ) = 3 x 2 − x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: ( 5 , ∞ ) ( 5 , ∞ )

• ⓑ f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1 f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1
• ⓒ f ( g ( x ) ) = 6 x 2 − 2 f ( g ( x ) ) = 6 x 2 − 2
• ⓓ ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20 ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20
• ⓔ ( f ∘ f ) ( − 2 ) = 163 ( f ∘ f ) ( − 2 ) = 163

f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7 f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7

f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x

( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4 ( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4

f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1 f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1

• ⓐ ( g ∘ f ) ( x ) = − 3 2 − 4 x ( g ∘ f ) ( x ) = − 3 2 − 4 x
• ⓑ ( − ∞ , 1 2 ) ( − ∞ , 1 2 )
• ⓐ ( 0 , 2 ) ∪ ( 2 , ∞ ) ; ( 0 , 2 ) ∪ ( 2 , ∞ ) ;
• ⓑ ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ; ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ;
• ⓒ ( 0 , ∞ ) ( 0 , ∞ )

( 1 , ∞ ) ( 1 , ∞ )

sample: f ( x ) = x 3 g ( x ) = x − 5 f ( x ) = x 3 g ( x ) = x − 5

sample: f ( x ) = 4 x g ( x ) = ( x + 2 ) 2 f ( x ) = 4 x g ( x ) = ( x + 2 ) 2

sample: f ( x ) = x 3 g ( x ) = 1 2 x − 3 f ( x ) = x 3 g ( x ) = 1 2 x − 3

sample: f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5 f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5

sample: f ( x ) = x g ( x ) = 2 x + 6 f ( x ) = x g ( x ) = 2 x + 6

sample: f ( x ) = x 3 g ( x ) = ( x − 1 ) f ( x ) = x 3 g ( x ) = ( x − 1 )

sample: f ( x ) = x 3 g ( x ) = 1 x − 2 f ( x ) = x 3 g ( x ) = 1 x − 2

sample: f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 f ( x ) = x g ( x ) = 2 x − 1 3 x + 4

f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94 f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94

f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5 f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5

18 x 2 + 60 x + 51 18 x 2 + 60 x + 51

g ∘ g ( x ) = 9 x + 20 g ∘ g ( x ) = 9 x + 20

( f ∘ g ) ( 6 ) = 6 ( f ∘ g ) ( 6 ) = 6 ; ( g ∘ f ) ( 6 ) = 6 ( g ∘ f ) ( 6 ) = 6

( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11 ( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11

A ( t ) = π ( 25 t + 2 ) 2 A ( t ) = π ( 25 t + 2 ) 2 and A ( 2 ) = π ( 25 4 ) 2 = 2500 π A ( 2 ) = π ( 25 4 ) 2 = 2500 π square inches

A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π square units

• ⓐ N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1 N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1
• ⓑ 3.38 hours

3.5 Section Exercises

A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.

A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.

For a function f , f , substitute ( − x ) ( − x ) for ( x ) ( x ) in f ( x ) . f ( x ) . Simplify. If the resulting function is the same as the original function, f ( − x ) = f ( x ) , f ( − x ) = f ( x ) , then the function is even. If the resulting function is the opposite of the original function, f ( − x ) = − f ( x ) , f ( − x ) = − f ( x ) , then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.

g ( x ) = | x - 1 | − 3 g ( x ) = | x - 1 | − 3

g ( x ) = 1 ( x + 4 ) 2 + 2 g ( x ) = 1 ( x + 4 ) 2 + 2

The graph of f ( x + 43 ) f ( x + 43 ) is a horizontal shift to the left 43 units of the graph of f . f .

The graph of f ( x - 4 ) f ( x - 4 ) is a horizontal shift to the right 4 units of the graph of f . f .

The graph of f ( x ) + 8 f ( x ) + 8 is a vertical shift up 8 units of the graph of f . f .

The graph of f ( x ) − 7 f ( x ) − 7 is a vertical shift down 7 units of the graph of f . f .

The graph of f ( x + 4 ) − 1 f ( x + 4 ) − 1 is a horizontal shift to the left 4 units and a vertical shift down 1 unit of the graph of f . f .

decreasing on ( − ∞ , − 3 ) ( − ∞ , − 3 ) and increasing on ( − 3 , ∞ ) ( − 3 , ∞ )

decreasing on ( 0 , ∞ ) ( 0 , ∞ )

g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1 g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1

f ( x ) = | x - 3 | − 2 f ( x ) = | x - 3 | − 2

f ( x ) = x + 3 − 1 f ( x ) = x + 3 − 1

f ( x ) = ( x - 2 ) 2 f ( x ) = ( x - 2 ) 2

f ( x ) = | x + 3 | − 2 f ( x ) = | x + 3 | − 2

f ( x ) = − x f ( x ) = − x

f ( x ) = − ( x + 1 ) 2 + 2 f ( x ) = − ( x + 1 ) 2 + 2

f ( x ) = − x + 1 f ( x ) = − x + 1

The graph of g g is a vertical reflection (across the x x -axis) of the graph of f . f .

The graph of g g is a vertical stretch by a factor of 4 of the graph of f . f .

The graph of g g is a horizontal compression by a factor of 1 5 1 5 of the graph of f . f .

The graph of g g is a horizontal stretch by a factor of 3 of the graph of f . f .

The graph of g g is a horizontal reflection across the y y -axis and a vertical stretch by a factor of 3 of the graph of f . f .

g ( x ) = | − 4 x | g ( x ) = | − 4 x |

g ( x ) = 1 3 ( x + 2 ) 2 − 3 g ( x ) = 1 3 ( x + 2 ) 2 − 3

g ( x ) = 1 2 ( x - 5 ) 2 + 1 g ( x ) = 1 2 ( x - 5 ) 2 + 1

The graph of the function f ( x ) = x 2 f ( x ) = x 2 is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.

The graph of f ( x ) = | x | f ( x ) = | x | is stretched vertically by a factor of 2, shifted horizontally 4 units to the right, reflected across the horizontal axis, and then shifted vertically 3 units up.

The graph of the function f ( x ) = x 3 f ( x ) = x 3 is compressed vertically by a factor of 1 2 . 1 2 .

The graph of the function is stretched horizontally by a factor of 3 and then shifted vertically downward by 3 units.

The graph of f ( x ) = x f ( x ) = x is shifted right 4 units and then reflected across the vertical line x = 4. x = 4.

3.6 Section Exercises

Isolate the absolute value term so that the equation is of the form | A | = B . | A | = B . Form one equation by setting the expression inside the absolute value symbol, A , A , equal to the expression on the other side of the equation, B . B . Form a second equation by setting A A equal to the opposite of the expression on the other side of the equation, − B . − B . Solve each equation for the variable.

The graph of the absolute value function does not cross the x x -axis, so the graph is either completely above or completely below the x x -axis.

The distance from x to 8 can be represented using the absolute value statement: ∣ x − 8 ∣ = 4.

∣ x − 10 ∣ ≥ 15

There are no x-intercepts.

(−4, 0) and (2, 0)

( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 ) ( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 )

( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 ) ( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 )

range: [ – 400 , 100 ] [ – 400 , 100 ]

There is no solution for a a that will keep the function from having a y y -intercept. The absolute value function always crosses the y y -intercept when x = 0. x = 0.

| p − 0.08 | ≤ 0.015 | p − 0.08 | ≤ 0.015

| x − 5.0 | ≤ 0.01 | x − 5.0 | ≤ 0.01

3.7 Section Exercises

Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that y y -values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no y y -values repeat and the function is one-to-one.

Yes. For example, f ( x ) = 1 x f ( x ) = 1 x is its own inverse.

Given a function y = f ( x ) , y = f ( x ) , solve for x x in terms of y . y . Interchange the x x and y . y . Solve the new equation for y . y . The expression for y y is the inverse, y = f − 1 ( x ) . y = f − 1 ( x ) .

f − 1 ( x ) = x − 3 f − 1 ( x ) = x − 3

f − 1 ( x ) = 2 − x f − 1 ( x ) = 2 − x

f − 1 ( x ) = − 2 x x − 1 f − 1 ( x ) = − 2 x x − 1

domain of f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7 f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7

domain of f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5 f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5

a. f ( g ( x ) ) = x f ( g ( x ) ) = x and g ( f ( x ) ) = x . g ( f ( x ) ) = x . b. This tells us that f f and g g are inverse functions

  f ( g ( x ) ) = x , g ( f ( x ) ) = x   f ( g ( x ) ) = x , g ( f ( x ) ) = x

not one-to-one

[ 2 , 10 ] [ 2 , 10 ]

f − 1 ( x ) = ( 1 + x ) 1 / 3 f − 1 ( x ) = ( 1 + x ) 1 / 3

f − 1 ( x ) = 5 9 ( x − 32 ) . f − 1 ( x ) = 5 9 ( x − 32 ) . Given the Fahrenheit temperature, x , x , this formula allows you to calculate the Celsius temperature.

t ( d ) = d 50 , t ( d ) = d 50 , t ( 180 ) = 180 50 . t ( 180 ) = 180 50 . The time for the car to travel 180 miles is 3.6 hours.

Review Exercises

f ( − 3 ) = − 27 ; f ( − 3 ) = − 27 ; f ( 2 ) = − 2 ; f ( 2 ) = − 2 ; f ( − a ) = − 2 a 2 − 3 a ; f ( − a ) = − 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2 f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2

x = − 1.8 x = − 1.8 or or  x = 1.8 or  x = 1.8

− 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64 − 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64

( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ )

increasing ( 2 , ∞ ) ; ( 2 , ∞ ) ; decreasing ( − ∞ , 2 ) ( − ∞ , 2 )

increasing ( − 3 , 1 ) ; ( − 3 , 1 ) ; constant ( − ∞ , − 3 ) ∪ ( 1 , ∞ ) ( − ∞ , − 3 ) ∪ ( 1 , ∞ )

local minimum ( − 2 , − 3 ) ; ( − 2 , − 3 ) ; local maximum ( 1 , 3 ) ( 1 , 3 )

( − 1.8 , 10 ) ( − 1.8 , 10 )

( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x ( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x

( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2 ( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2

( f ∘ g ) ( x ) = 1 + x 1 + 4 x ,   x ≠ 0 ,   x ≠ − 1 4 ( f ∘ g ) ( x ) = 1 + x 1 + 4 x ,   x ≠ 0 ,   x ≠ − 1 4

( f ∘ g ) ( x ) = 1 x , x > 0 ( f ∘ g ) ( x ) = 1 x , x > 0

sample: g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x

f ( x ) = | x − 3 | f ( x ) = | x − 3 |

f ( x ) = 1 2 | x + 2 | + 1 f ( x ) = 1 2 | x + 2 | + 1

f ( x ) = − 3 | x − 3 | + 3 f ( x ) = − 3 | x − 3 | + 3

f − 1 ( x ) = x - 9 10 f − 1 ( x ) = x - 9 10

f − 1 ( x ) = x - 1 f − 1 ( x ) = x - 1

The function is one-to-one.

Practice Test

The relation is a function.

The graph is a parabola and the graph fails the horizontal line test.

2 a 2 − a 2 a 2 − a

− 2 ( a + b ) + 1 − 2 ( a + b ) + 1

f − 1 ( x ) = x + 5 3 f − 1 ( x ) = x + 5 3

( − ∞ , − 1.1 ) and  ( 1.1 , ∞ ) ( − ∞ , − 1.1 ) and  ( 1.1 , ∞ )

( 1.1 , − 0.9 ) ( 1.1 , − 0.9 )

f ( 2 ) = 2 f ( 2 ) = 2

f ( x ) = { | x | if x ≤ 2 3 if x > 2 f ( x ) = { | x | if x ≤ 2 3 if x > 2

x = 2 x = 2

f − 1 ( x ) = − x − 11 2 f − 1 ( x ) = − x − 11 2

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra/pages/chapter-3

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

McGraw Hill My Math Grade 3 Chapter 2 Lesson 6 Answer Key Use Models to Add

All the solutions provided in McGraw Hill Math Grade 3 Answer Key PDF Chapter 2 Lesson 6 Use Models to Add  will give you a clear idea of the concepts.

McGraw-Hill My Math Grade 3 Answer Key Chapter 2 Lesson 6 Use Models to Add

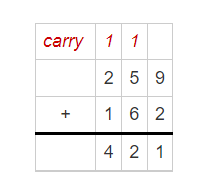
Use a place-value chart and base-ten blocks to model three-digit addition with regrouping. To regroup means to rename a number using place value.

Check for Reasonableness Ask yourself if the answer makes sense. Is your answer reasonable? 301 is close to the estimate of 300. It makes sense. The answer is reasonable.

Talk About It

Question 1. Explain how you know when you need to regroup. Answer: Regrouping in math is when you make groups of ten when performing operations such as addition or subtraction. This typically takes place when you work with double digits. Explanation: In the above example 10 ones are regrouped as one ten.

Question 2. Mathematical PRACTICE 6 Be Precise Why were the ones and tens regrouped? Answer: Regrouping is the current term for carrying in addition and borrowing in subtraction. In both operations, it simply means that either a ten is changing or a group of ones is changing. Explanation: In the above example 10 ones are regrouped as one ten and 10 tens are regrouped as one hundred.

Question 3. Tell whether or not you need to regroup when finding the sum of 147 and 214. Explain. Answer: Yes we need to regroup when finding the sum of 147 and 214. Explanation: 10 ones are regrouped as one ten 147 + 214 = 361

Practice It

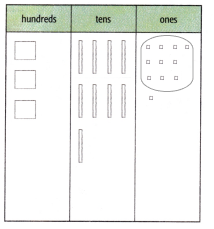
Use models to add. Draw the sum.

Use base-ten blocks, the table, and the information below to solve each problem.

Question 10. How many miles did the Smith family travel from Chicago, IL, to Memphis, TN? Write a number sentence. ____ + ____ = ____ total miles Answer: 181 + 464 = 645 Explanation: Chicago to Indianapolis they travelled 181 miles Indianapolis to Memphis they travelled 464 miles so total they travelled 645 miles

Question 11. To the nearest hundred, about how many miles did the Smith family travel round trip? ____ miles + ____ miles = ____ miles round trip Answer: To the nearest hundred , they travelled 600 miles. Explanation: total they travelled 645 miles. the nearest hundred of 645 is 600 miles.

Question 12. Mathematical PRACTICE 4 Model Math The Smith family spent a total of $2,345 on travel expenses and $500 on gasoline. About how much money did they spend altogether? Round to the nearest hundred. $____ + $___ = $_____ Answer: Total money they spend altogether is $2845 Explanation: Smith family spent a total of $2,345 on travel expenses $500 on gasoline $2345 + $500 = $2845 the nearest hundred of $2845 is $2800

Write About It

Question 13. How do I know if I need to regroup when finding a sum? Answer: When adding numbers, if the sum of the two numbers you are adding together is more than 20, you will need to regroup. Explanation: If you’re adding 7 + 5 you can make a ten by swapping the 7 and the 5. This is called regrouping.

McGraw Hill My Math Grade 3 Chapter 2 Lesson 6 My Homework Answer Key

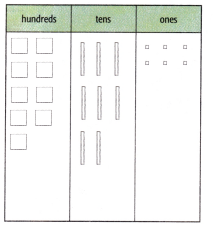
Draw place-value blocks to show the sum.

Problem Solving

Question 4. Mathematical PRACTICE 4 Model Math Luisa has 183 pennies. Her dad gives her 128 more. Write a number sentence to show how many pennies Luisa has now. Answer: Luisa has 311 pennies. Explanation: Luisa has 183 pennies Her dad gives her 128 more 183 + 128 = 311 total pennies Luisa has now is 311

Question 5. Jonah has read 265 pages. He has 147 more to read How many pages will he read in all? Answer: Total number of pages Jonah will read is 412 Explanation: Jonah has read 265 pages. He has to read more 147 pages 265 + 147 = 412 Jonah will read 412 pages in all.

Vocabulary Check

Choose the correct word to complete each sentence. reasonable   regroup     sum

Question 6. ____ means to rename a number using place value. Answer: regroup Explanation: regroup means to rename a number using place value

Question 7. The answer to an addition sentence is called the _____. Answer: Sum Explanation: The answer to an addition sentence is called the sum

Question 8. Estimate the exact answer before solving the problem to see if your answer is _____ Answer: reasonable Explanation: Estimate the exact answer before solving the problem to see if your answer is reasonable

Leave a Comment Cancel Reply

You must be logged in to post a comment.