example of distance formula problem solving

Distance Formula

In these lessons, we will learn

• how to derive the distance formula from the Pythagorean Theorem.
• how to use the distance formula.

Related Pages Pythagoras' Theorem Midpoint Formula Coordinate Geometry Geometry Lessons

Check out the distance formula calculator near the end of this page that can calculate the distance between two points. Use it to check your answers.

The following figures give the Distance Formula and how the Distance Formula is derived from the Pythagorean Theorem. Scroll down the page for more examples and solutions.

In the coordinate plane, we can use the distance formula to find the distance between any two points. The distance formula can be derived from the Pythagorean Theorem .

The distance between the two points (x 1 ,y 1 ) and (x 2 ,y 2 ) is given by the distance formula.

Example: To find the distance between the points P(2, 3) and Q(1, 1). We can sketch the right-angled triangle PQR with PQ as the hypotenuse.

Example: Find the distance between the points A(1, 2) and B(-3, -2).

Distance Formula Worksheet 1 Distance Formula Worksheet 2

How The Distance Formula Comes From The Pythagorean Theorem?

Example of finding the distance between two points.

The following videos show the Distance Formula and how to find the Distance Between Two Points

Example: Suppose you drive from point A(3,8) in a straight line to B(13,14); if you stop halfway how far would you be from point B?

The following video gives another example of using the distance formula

Distance Calculator This distance formula calculator can calculate the distance between two given points on the coordinate plane.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Problems on Distance Formula

We will discuss here how to solve the problems on distance formula.

The distance between two points A (x\(_{1}\), y\(_{1}\)) and B (x\(_{2}\), y\(_{2}\)) is given by the formula

AB = \(\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}\)

1.  If the distance between the points (5, - 2) and (1, a) is 5, find the values of a.

We know, the distance between (x\(_{1}\), y\(_{1}\)) and (x\(_{2}\), y\(_{2}\))

is \(\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}\)

Here, the distance = 5, x\(_{1}\) = 5, x\(_{2}\) = 1, y\(_{1}\) = -2 and y\(_{2}\) = a

Therefore, 5 = \(\sqrt{(5 - 1)^{2} + (-2 - a)^{2}}\)

⟹ 25 = 16 + (2 + a)\(^{2}\)

⟹ (2 + a)\(^{2}\) = 25 - 16

⟹ (2 + a)\(^{2}\) = 9

Taking square root, 2 + a = ±3

⟹ a = -2 ± 3

⟹ a = 1, -5

2. The co-ordinates of points on the x-axis which are at a distance of 5 units from the point (6, -3).

Let the co-ordinates of the point on the x-axis be (x, 0)

Since, distance = \(\sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}\)

Now taking (6, -3) = (x\(_{1}\), y\(_{1}\)) and (x, 0) = (x\(_{2}\), y\(_{2}\)), we get

5 = \(\sqrt{(x - 6)^{2} + (0 + 3)^{2}}\)

Squaring both sides we get

⟹ 25 = (x – 6)\(^{2}\) + 3\(^{2}\)

⟹ 25 = x\(^{2}\) – 12x + 36 + 9

⟹ 25 = x\(^{2}\) – 12x + 45

⟹ x\(^{2}\) – 12x + 45 – 25 = 0

⟹ x\(^{2}\) – 12x + 20 = 0

⟹ (x – 2)(x – 10) = 0

⟹ x = 2 or x = 10

Therefore, the required points on the x-axis are (2, 0) and (10, 0).

3. Which point on the y-axis is equidistance from the points (12, 3) and (-5, 10)?

Let the required point on the y-axis (0, y).

Given (0, y) is equidistance from (12, 3) and (-5, 10)

i.e., distance between (0, y) and (12, 3) = distance between (0, y) and (-5, 10)

⟹ \(\sqrt{(12 - 0)^{2} + (3 - y)^{2}}\) = \(\sqrt{(-5 - 0)^{2} + (10 - y)^{2}}\)

⟹ 144 + 9 + y\(^{2}\) – 6y = 25 + 100 + y\(^{2}\) – 20y

⟹ 14y = -28

Therefore, the required point on the y-axis = (0, -2)

4.  Find the values of a such that PQ = QR, where P, Q and R are the points whose coordinates are (6, - 1), (1, 3) and (a, 8) respectively.

PQ = \(\sqrt{(6 - 1)^{2} + (-1 - 3)^{2}}\)

     = \(\sqrt{5^{2} + (-4)^{2}}\)

     = \(\sqrt{25 + 16}\)

     = \(\sqrt{41}\)

QR = \(\sqrt{(1 - a)^{2} + (3 - 8)^{2}}\)

     = \(\sqrt{(1 - a)^{2} + (-5)^{2}}\)

     = \(\sqrt{(1 - a)^{2} + 25}\)

Therefore, PQ = QR

⟹ \(\sqrt{41}\) = \(\sqrt{(1 - a)^{2} + 25}\)

⟹ 41 = (1 - a)\(^{2}\) + 25

⟹ (1 - a)\(^{2}\) = 41 - 25

⟹ (1 - a)\(^{2}\) = 16

⟹ 1 - a = ±4

⟹ a = -3, 5

5.  Find the points on the y-axis, each of which is at a distance of 13 units from the point (-5, 7).

Let A (-5, 7) be the given point and let P (0, y) be the required point on the y-axis. Then,

PA = 13 units

⟹ PA\(^{2}\) = 169

⟹ (0 + 5)\(^{2}\) + (y - 7)\(^{2}\) = 169

⟹ 25 + y\(^{2}\) - 14y + 49 = 169

⟹ y\(^{2}\) – 14y + 74 = 169

⟹ y\(^{2}\) – 14y – 95 = 0

⟹ (y - 19)(y + 5) = 0

⟹ y – 19 = 0 or, y + 5 = 0

⟹ y = 19 or, y = -5

Hence, the required points are (0, 19) and (0, -5)

●   Distance and Section Formulae

• Distance Formula
• Distance Properties in some Geometrical Figures
• Conditions of Collinearity of Three Points
• Distance of a Point from the Origin
• Distance Formula in Geometry
• Section Formula
• Midpoint Formula
• Centroid of a Triangle
• Worksheet on Distance Formula
• Worksheet on Collinearity of Three Points
• Worksheet on Finding the Centroid of a Triangle
• Worksheet on Section Formula

10th Grade Math From Problems on Distance Formula to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Share this page: What’s this?

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Division of Two-Digit by a One-Digit Numbers | Dividing Larger Numbers

Oct 29, 24 01:27 PM

2nd Grade Multiplication Worksheet | 2-Digit by 1-Digit | 3-Digit by 1

Oct 29, 24 12:21 AM

Multiplication and Division are Related | Multiplication Fact|Division

Oct 29, 24 12:06 AM

Divide on a Number Line | Various Division Problems | Solved Examples

Oct 28, 24 12:53 AM

Facts about Division | Basic Division Facts | Learn Long Division

Oct 27, 24 03:33 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Distance Problems with Solutions

The concept of the distance between two points is an important one in mathematics. A set of distance problems with detailed solutions (at the bottom of this page) are presented.

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

In order to access this I need to be confident with:

This topic is relevant for:

Distance Formula

Here we will learn about the distance formula, including how to find the distance between two coordinates.

There are also distance formula worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

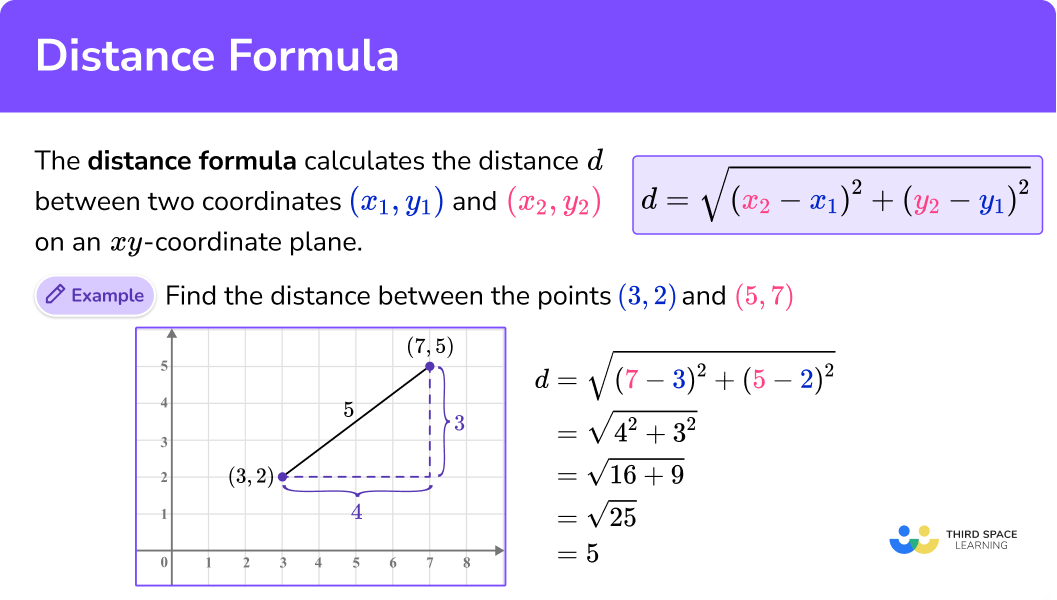
What is the distance formula?

The distance formula is an application of the Pythagorean theorem a^2+b^2=c^2 in coordinate geometry.

It will calculate the distance between two cartesian coordinates on an xy -coordinate plane.

To do this we find the differences between the x -coordinates and the difference between the y -coordinates, square them, then find the square root of the answer.

This can be written as the distance formula

d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2},

where d is the distance between the points \left(x_1, y_1\right) and \left(x_2, y_2\right) .

For example,

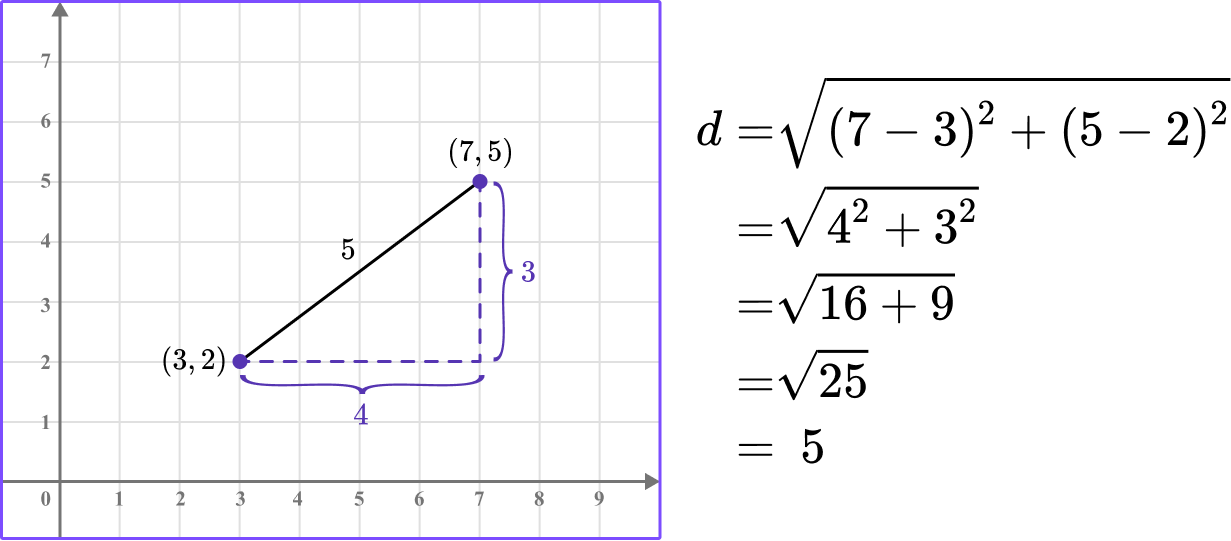
The line segment between the two points forms the hypotenuse of a right angled triangle.

The length of the hypotenuse is the distance between the two end points of the line segment.

How to use the distance formula

In order to find the distance between two points:

• Identify the two points and label them \bf{\left(x_1, y_1\right) } and \bf{\left(x_2, y_2\right)} .

Substitute the values into the formula \bf{d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}} .

Solve the equation.

Explain how to use the distance formula

Straight line graphs worksheet (includes distance formula)

Get your free distance formula worksheet of 20+ straight line graphs questions and answers. Includes reasoning and applied questions.

Related lessons on straight line graphs

Distance formula  is part of our series of lessons to support revision on  straight line graphs . You may find it helpful to start with the main straight line graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Straight line graphs
• Gradient of a line
• Equation of a line
• Coordinates maths
• How to find the y intercept and the x intercept
• How to find the midpoint
• Intersecting lines
• Linear graph
• Parallel and perpendicular lines

Distance formula examples

Example 1: distance between two points on a coordinate axes in the first quadrant.

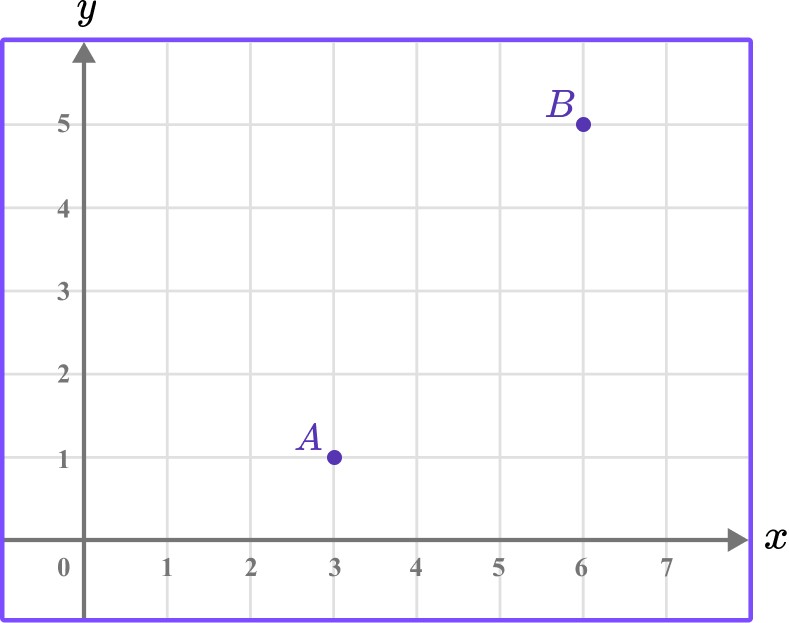
Find the distance between the points A and B.

Identify the two points and label them \bf{\left(x_1, y_1\right)} and \bf{\left(x_2, y_2\right)} .

A=(3,1) and B=(6, 5).

Let \left(x_1, y_1\right) =(3, 1) and \left(x_2, y_2\right) =(6, 5).

2 Substitute the values into the formula \bf{d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}} .

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ &=\sqrt{(6-3)^2+(5-1)^2} \end{aligned}

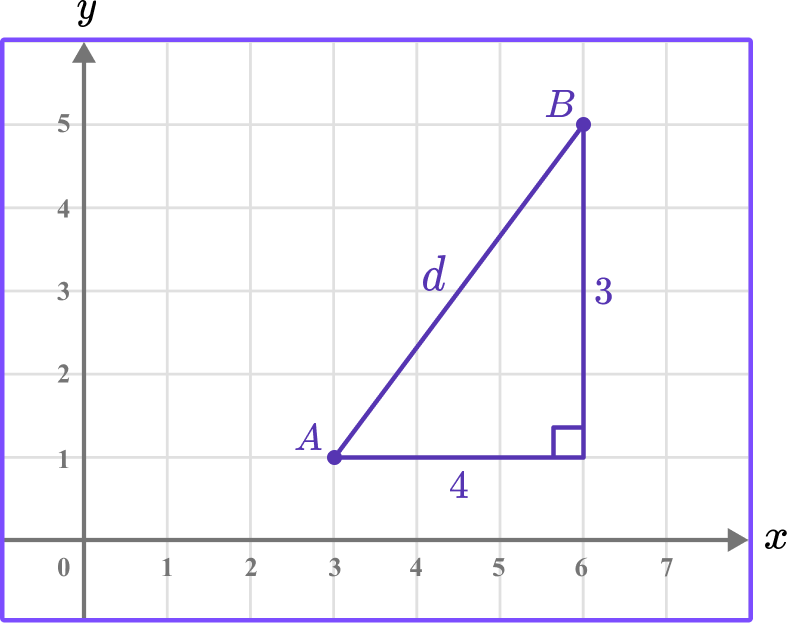
3 Solve the equation.

\begin{aligned} d&=\sqrt{(6-3)^2+(5-1)^2} \\\\ &=\sqrt{3^2+4^2} \\\\ &=\sqrt{9+16} \\\\ &=\sqrt{25} \\\\ &=5 \end{aligned}

Example 2: distance between two points on a coordinate axes

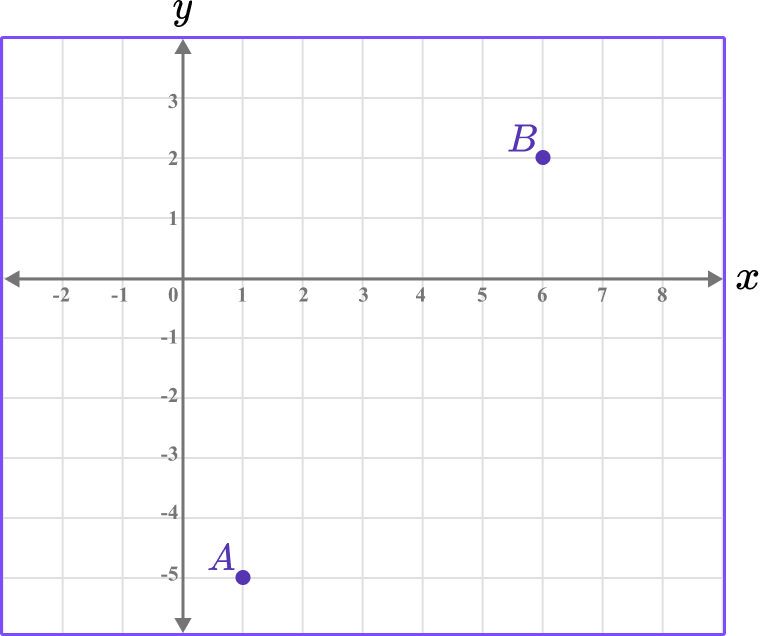
Give your answer to 1 decimal place.

A=(1, -5) and (B=6, 2).

Let \left(x_1, y_1\right)=(1, -5) and \left(x_2, y_2\right)=(6, 2).

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ &=\sqrt{(6-1)^2+(2-(-5))^2} \end{aligned}

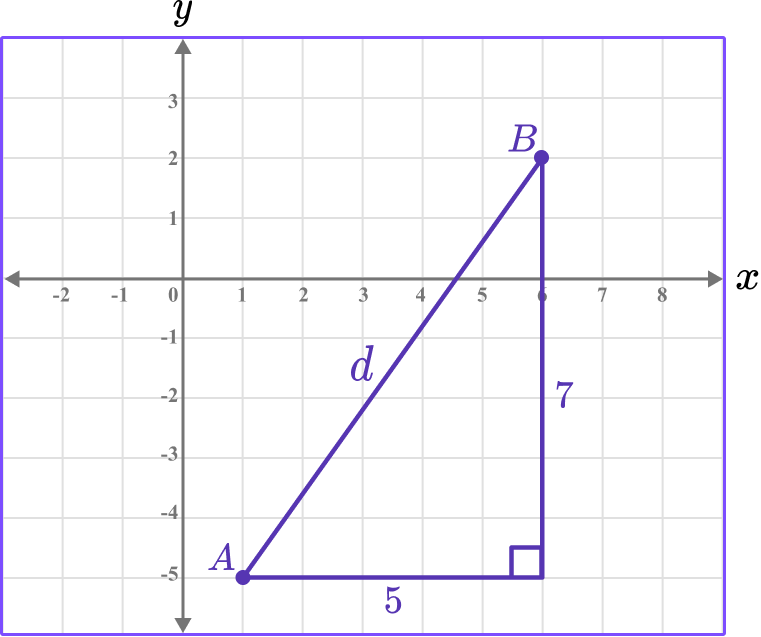
\begin{aligned} d&=\sqrt{(6-1)^2+(2-(-5))^2} \\\\ &=\sqrt{5^2+7^2} \\\\ &=\sqrt{25+49} \\\\ &=\sqrt{74} \\\\ &=8.6 \text { (1 d.p. }) \end{aligned}

Example 3: distance between two given points with positive coordinates

Find the distance between the points (1, 4) and (7, 12).

Let \left(x_1, y_1\right)=(1, 4) and \left(x_2, y_2\right)=(7, 12).

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ &=\sqrt{(7-1)^2+(12-4)^2} \end{aligned}

\begin{aligned} d&=\sqrt{(7-1)^2+(12-4)^2} \\\\ &=\sqrt{6^2+8^2} \\\\ &=\sqrt{36+64} \\\\ &=\sqrt{100} \\\\ &=10 \end{aligned}

Example 4: distance between any two given points

Find the distance between the points (-2, 5) and (6, -7).

Let \left(x_1, y_1\right)=(-2, 5) and \left(x_2, y_2\right)=(6, -7).

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ &=\sqrt{(6-(-2))^2+(-7-5)^2} \end{aligned}

\begin{aligned} d&=\sqrt{(6-(-2))^2+(-7-5)^2} \\\\ &=\sqrt{8^2+(-12)^2} \\\\ &=\sqrt{64+144} \\\\ &=\sqrt{208} \\\\ &=14.4 \text { (1 d.p.) } \end{aligned}

Example 5: finding a missing value given the distance

The distance between the points (1, 5) and (16, \, k) is 17.

Find the value of k, where k is negative.

Let \left(x_1, y_1\right)=(1, 5) and \left(x_2, y_2\right)=(16, \, k).

We also know that d=17.

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ 17&=\sqrt{(16-1)^2+(k-5)^2} \end{aligned}

\begin{aligned} 17&=\sqrt{(16-1)^2+(k-5)^2} \\\\ 17&=\sqrt{15^2+(k-5)^2} \\\\ 289&=225+(k-5)^2 \\\\ 64&=(k-5)^2 \\\\ \pm 8&=k-5 \\\\ k&= \pm 8+5 \end{aligned}

k=13 or k=-3

We know that k is negative so k=-3.

Common misconceptions

• Confusing the distance formula with the midpoint formula

A common error is to find the midpoint instead of the distance.

The midpoint formula is \left(\cfrac{x_1+x_2}{2}, \, \cfrac{y_1+y_2}{2}\right).

• Squaring negative numbers to give a negative

When using the distance formula, it is common to get negative values after the subtraction step. These values will be squared, so it is important to remember that the square of a negative value is positive. For example, (-3)^2=9.

Practice distance formula questions

1. Find the distance between the point (6, 8) and the origin.

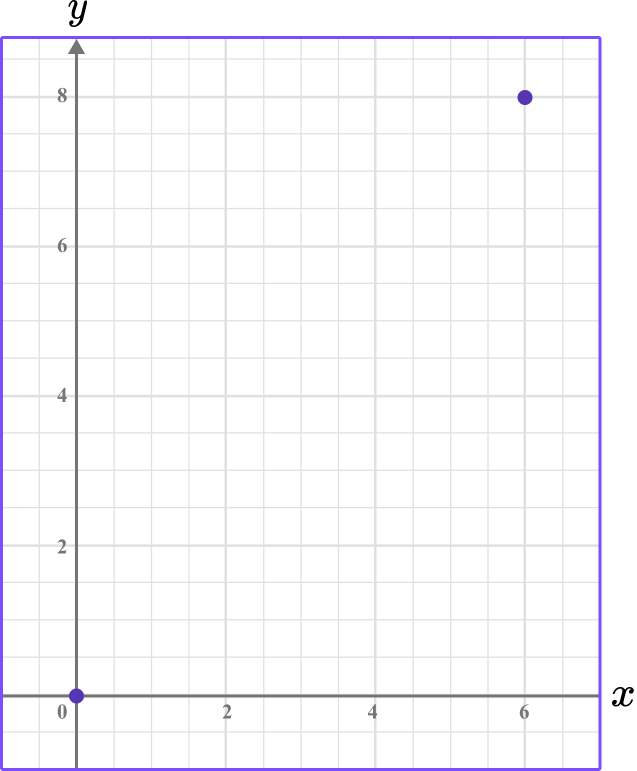
The origin is (0, 0) so let \left(x_1, y_1\right)=(0, 0) and \left(x_2, y_2\right)=(6, 8).

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(6-0)^2+(8-0)^2} \\\\ & =\sqrt{6^2+8^2} \\\\ & =\sqrt{36+64} \\\\ & =\sqrt{100} \\\\ & =10 \end{aligned}

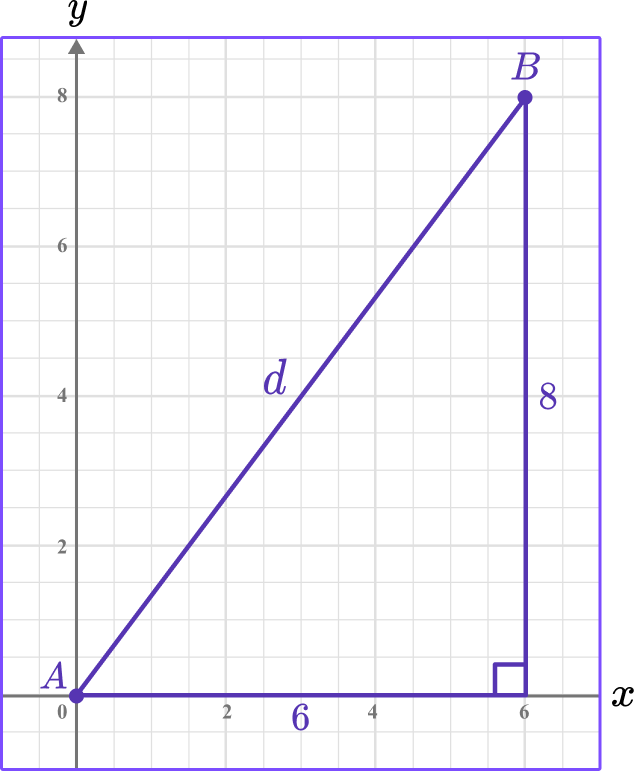
2. Find the distance between the point (0, 10) and (24, 0).

Let \left(x_1, y_1\right)=(0, 10) and \left(x_2, y_2\right)=(24, 0).

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(24-0)^2+(0-10)^2} \\\\ & =\sqrt{24^2+(-10)^2} \\\\ & =\sqrt{576+100} \\\\ & =\sqrt{676} \\\\ & =26 \end{aligned}

3. Find the distance between the points (5, 3) and (14, 10). Give your answer to 1 decimal place.

Let \left(x_1, y_1\right)=(5, 3) and \left(x_2, y_2\right)=(14, 10).

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(14-5)^2+(10-3)^2} \\\\ & =\sqrt{9^2+7^2} \\\\ & =\sqrt{81+49} \\\\ & =\sqrt{130} \\\\ & =11.4 \text { (1 d.p.) } \end{aligned}

4. Find the distance between the points (-2, 4) and (-8, -9). Give your answer to 1 decimal place.

Let \left(x_1, y_1\right)=(-2, 4) and \left(x_2, y_2\right)=(-8, -9).

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ & =\sqrt{(-8-(-2))^2+(-9-4)^2} \\\\ & =\sqrt{(-6)^2+(-13)^2} \\\\ & =\sqrt{36+169} \\\\ & =\sqrt{205} \\\\ & =14.3 \text { (1 d.p.) } \end{aligned}

5. The distance between the points (8,-3) and (15, a) is 25. Find the value of a, where a is positive.

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ 25&=\sqrt{(15-8)^2+(a-(-3))^2} \\\\ 25&=\sqrt{7^2+(a+3)^2} \\\\ 625&=49+(a+3)^2 \\\\ 576&=(a+3)^2 \\\\ \pm 24&=a+3 \\\\ a&=\pm 24-3 \end{aligned}

a=21 or a=-27

We know that a is positive so a=21.

6. The distance between the points (b, 4) and (6, -8) is 15. Find the value of b, where b is negative.

\begin{aligned} d&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} \\\\ 15&=\sqrt{(6-b)^2+(-8-4)^2} \\\\ 15&=\sqrt{(6-b)^2+(-12)^2} \\\\ 225&=(6-b)^2+144 \\\\ 81&=(6-b)^2 \\\\ \pm 9&=6-b \\\\ -b&=\pm 9-6 \end{aligned}   -b=3 or -b=-15   b=-3 or b=15

We know that b is negative so b=-3.

Distance formula GCSE questions

1. Find the distance between (0, 4) and (7, 18).

Give your answer to one decimal place.

Answer in the range of 15.6-15.7.

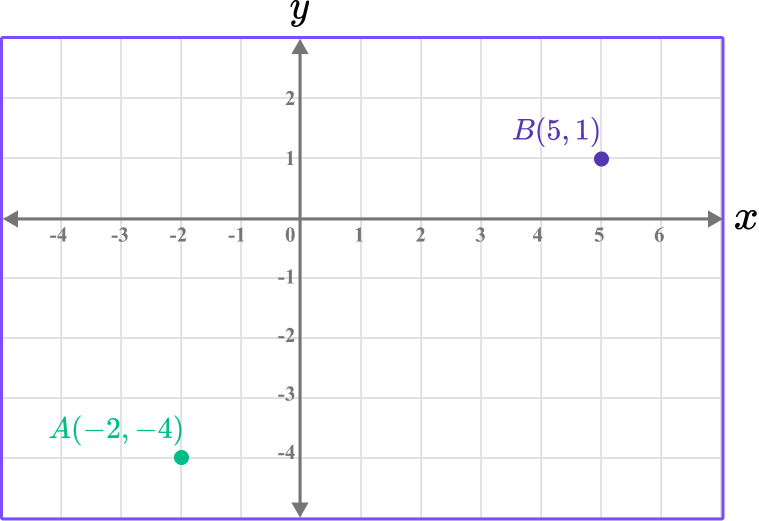
(a) Find the midpoint of AB.

(b) Find the distance AB.

x -value of 1.5.

y -value of -1.5.

Answer in the range of 8.6-8.7.

3. M(4,3) is the midpoint of the line segment PQ, where Q has the coordinates (-9, 7).

Find the distance PQ to one decimal place.

Process to find the point P \, (17,-1).

(17-(-9))=26 \, or \, (-1-7)=-8

26^2+(-8)^2=740

Alternatively, find the distance MQ and double it.

(4-(-9))=13 \, or \, (3-7)=-4

13^2+4^2=185

2\times \sqrt{185}

Learning checklist

You have now learned how to:

• Find the distance between two points on an xy -coordinate axes

The next lessons are

• Maths formulas
• Interpreting graphs
• Inequalities

Beyond GCSE

In A level mathematics, we look at coordinates in three dimensional space. The 2D distance formula can be adapted for a 3D coordinate system that has an x -axis, y -axis and z -axis with coordinates \left(x_1, y_1, z_1\right) and \left(x_2, y_2, z_2\right) .

d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview