properties of real numbers assignment

1.1 Real Numbers: Algebra Essentials

Learning objectives.

In this section, you will:

• Classify a real number as a natural, whole, integer, rational, or irrational number.
• Perform calculations using order of operations.
• Use the following properties of real numbers: commutative, associative, distributive, inverse, and identity.
• Evaluate algebraic expressions.
• Simplify algebraic expressions.

It is often said that mathematics is the language of science. If this is true, then an essential part of the language of mathematics is numbers. The earliest use of numbers occurred 100 centuries ago in the Middle East to count, or enumerate items. Farmers, cattle herders, and traders used tokens, stones, or markers to signify a single quantity—a sheaf of grain, a head of livestock, or a fixed length of cloth, for example. Doing so made commerce possible, leading to improved communications and the spread of civilization.

Three to four thousand years ago, Egyptians introduced fractions. They first used them to show reciprocals. Later, they used them to represent the amount when a quantity was divided into equal parts.

But what if there were no cattle to trade or an entire crop of grain was lost in a flood? How could someone indicate the existence of nothing? From earliest times, people had thought of a “base state” while counting and used various symbols to represent this null condition. However, it was not until about the fifth century CE in India that zero was added to the number system and used as a numeral in calculations.

Clearly, there was also a need for numbers to represent loss or debt. In India, in the seventh century CE, negative numbers were used as solutions to mathematical equations and commercial debts. The opposites of the counting numbers expanded the number system even further.

Because of the evolution of the number system, we can now perform complex calculations using these and other categories of real numbers. In this section, we will explore sets of numbers, calculations with different kinds of numbers, and the use of numbers in expressions.

Classifying a Real Number

The numbers we use for counting, or enumerating items, are the natural numbers : 1, 2, 3, 4, 5, and so on. We describe them in set notation as { 1 , 2 , 3 , ... } { 1 , 2 , 3 , ... } where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers . Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .

The set of integers adds the opposites of the natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

The set of rational numbers is written as { m n | m and  n are integers and  n ≠ 0 } . { m n | m and  n are integers and  n ≠ 0 } . Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.

Because they are fractions, any rational number can also be expressed as a terminating or repeating decimal. Any rational number can be represented as either:

• ⓐ a terminating decimal: 15 8 = 1.875 , 15 8 = 1.875 , or
• ⓑ a repeating decimal: 4 11 = 0.36363636 … = 0. 36 ¯ 4 11 = 0.36363636 … = 0. 36 ¯

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Writing Integers as Rational Numbers

Write each of the following as a rational number.

Write a fraction with the integer in the numerator and 1 in the denominator.

• ⓐ 7 = 7 1 7 = 7 1
• ⓑ 0 = 0 1 0 = 0 1
• ⓒ −8 = − 8 1 −8 = − 8 1

Identifying Rational Numbers

Write each of the following rational numbers as either a terminating or repeating decimal.

• ⓐ − 5 7 − 5 7
• ⓑ 15 5 15 5
• ⓒ 13 25 13 25

Write each fraction as a decimal by dividing the numerator by the denominator.

• ⓐ − 5 7 = −0. 714285 ——— , − 5 7 = −0. 714285 ——— , a repeating decimal
• ⓑ 15 5 = 3 15 5 = 3 (or 3.0), a terminating decimal
• ⓒ 13 25 = 0.52 , 13 25 = 0.52 , a terminating decimal
• ⓐ 68 17 68 17
• ⓑ 8 13 8 13
• ⓒ − 17 20 − 17 20

Irrational Numbers

At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even 3 2 , 3 2 , but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers . Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.

Differentiating Rational and Irrational Numbers

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

• ⓑ 33 9 33 9
• ⓓ 17 34 17 34
• ⓔ 0.3033033303333 … 0.3033033303333 …
• ⓐ 25 : 25 : This can be simplified as 25 = 5. 25 = 5. Therefore, 25 25 is rational.

So, 33 9 33 9 is rational and a repeating decimal.

• ⓒ 11 : 11 11 : 11 is irrational because 11 is not a perfect square and 11 11 cannot be expressed as a fraction.

So, 17 34 17 34 is rational and a terminating decimal.

• ⓔ 0.3033033303333 … 0.3033033303333 … is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.
• ⓐ 7 77 7 77
• ⓒ 4.27027002700027 … 4.27027002700027 …
• ⓓ 91 13 91 13

Real Numbers

Given any number n , we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers . As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line.The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line as shown in Figure 1 .

Classifying Real Numbers

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

• ⓐ − 10 3 − 10 3
• ⓒ − 289 − 289
• ⓓ −6 π −6 π
• ⓔ 0.615384615384 … 0.615384615384 …
• ⓐ − 10 3 − 10 3 is negative and rational. It lies to the left of 0 on the number line.
• ⓑ 5 5 is positive and irrational. It lies to the right of 0.
• ⓒ − 289 = − 17 2 = −17 − 289 = − 17 2 = −17 is negative and rational. It lies to the left of 0.
• ⓓ −6 π −6 π is negative and irrational. It lies to the left of 0.
• ⓔ 0.615384615384 … 0.615384615384 … is a repeating decimal so it is rational and positive. It lies to the right of 0.
• ⓑ −11.411411411 … −11.411411411 …
• ⓒ 47 19 47 19
• ⓓ − 5 2 − 5 2
• ⓔ 6.210735 6.210735

Sets of Numbers as Subsets

Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram, such as Figure 2 .

Sets of Numbers

The set of natural numbers includes the numbers used for counting: { 1 , 2 , 3 , ... } . { 1 , 2 , 3 , ... } .

The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .

The set of integers adds the negative natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } .

The set of rational numbers includes fractions written as { m n | m and  n are integers and  n ≠ 0 } . { m n | m and  n are integers and  n ≠ 0 } .

The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: { h | h is not a rational number } . { h | h is not a rational number } .

Differentiating the Sets of Numbers

Classify each number as being a natural number ( N ), whole number ( W ), integer ( I ), rational number ( Q ), and/or irrational number ( Q′ ).

• ⓔ 3.2121121112 … 3.2121121112 …
• ⓐ − 35 7 − 35 7
• ⓔ 4.763763763 … 4.763763763 …

Performing Calculations Using the Order of Operations

When we multiply a number by itself, we square it or raise it to a power of 2. For example, 4 2 = 4 ⋅ 4 = 16. 4 2 = 4 ⋅ 4 = 16. We can raise any number to any power. In general, the exponential notation a n a n means that the number or variable a a is used as a factor n n times.

In this notation, a n a n is read as the n th power of a , a , or a a to the n n where a a is called the base and n n is called the exponent . A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, 24 + 6 ⋅ 2 3 − 4 2 24 + 6 ⋅ 2 3 − 4 2 is a mathematical expression.

To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations . This is a sequence of rules for evaluating such expressions.

Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify 4 2 4 2 as 16.

Next, perform multiplication or division, left to right.

Lastly, perform addition or subtraction, left to right.

Therefore, 24 + 6 ⋅ 2 3 − 4 2 = 12. 24 + 6 ⋅ 2 3 − 4 2 = 12.

For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.

Order of Operations

Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS :

P (arentheses) E (xponents) M (ultiplication) and D (ivision) A (ddition) and S (ubtraction)

Given a mathematical expression, simplify it using the order of operations.

• Step 1. Simplify any expressions within grouping symbols.
• Step 2. Simplify any expressions containing exponents or radicals.
• Step 3. Perform any multiplication and division in order, from left to right.
• Step 4. Perform any addition and subtraction in order, from left to right.

Using the Order of Operations

Use the order of operations to evaluate each of the following expressions.

• ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 )
• ⓑ 5 2 − 4 7 − 11 − 2 5 2 − 4 7 − 11 − 2
• ⓒ 6 − | 5 − 8 | + 3 ( 4 − 1 ) 6 − | 5 − 8 | + 3 ( 4 − 1 )
• ⓓ 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2
• ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1
• ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction. ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction.

Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol so the numerator is considered to be grouped.

• ⓒ 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition. 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition.

In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

• ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add. 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add.
• ⓐ 5 2 − 4 2 + 7 ( 5 − 4 ) 2 5 2 − 4 2 + 7 ( 5 − 4 ) 2
• ⓑ 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6
• ⓒ | 1.8 − 4.3 | + 0.4 15 + 10 | 1.8 − 4.3 | + 0.4 15 + 10
• ⓓ 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2
• ⓔ [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 ) [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 )

Using Properties of Real Numbers

For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

We can better see this relationship when using real numbers.

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

Again, consider an example with real numbers.

It is important to note that neither subtraction nor division is commutative. For example, 17 − 5 17 − 5 is not the same as 5 − 17. 5 − 17. Similarly, 20 ÷ 5 ≠ 5 ÷ 20. 20 ÷ 5 ≠ 5 ÷ 20.

Associative Properties

The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.

Consider this example.

The associative property of addition tells us that numbers may be grouped differently without affecting the sum.

This property can be especially helpful when dealing with negative integers. Consider this example.

Are subtraction and division associative? Review these examples.

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference 12 − ( 5 + 3 ) . 12 − ( 5 + 3 ) . We can rewrite the difference of the two terms 12 and ( 5 + 3 ) ( 5 + 3 ) by turning the subtraction expression into addition of the opposite. So instead of subtracting ( 5 + 3 ) , ( 5 + 3 ) , we add the opposite.

Now, distribute −1 −1 and simplify the result.

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

For example, we have ( −6 ) + 0 = −6 ( −6 ) + 0 = −6 and 23 ⋅ 1 = 23. 23 ⋅ 1 = 23. There are no exceptions for these properties; they work for every real number, including 0 and 1.

Inverse Properties

The inverse property of addition states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted by (− a ), that, when added to the original number, results in the additive identity, 0.

For example, if a = −8 , a = −8 , the additive inverse is 8, since ( −8 ) + 8 = 0. ( −8 ) + 8 = 0.

The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted 1 a , 1 a , that, when multiplied by the original number, results in the multiplicative identity, 1.

For example, if a = − 2 3 , a = − 2 3 , the reciprocal, denoted 1 a , 1 a , is − 3 2 − 3 2 because

Properties of Real Numbers

The following properties hold for real numbers a , b , and c .

Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.

• ⓐ 3 ⋅ 6 + 3 ⋅ 4 3 ⋅ 6 + 3 ⋅ 4
• ⓑ ( 5 + 8 ) + ( −8 ) ( 5 + 8 ) + ( −8 )
• ⓒ 6 − ( 15 + 9 ) 6 − ( 15 + 9 )
• ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) 4 7 ⋅ ( 2 3 ⋅ 7 4 )
• ⓔ 100 ⋅ [ 0.75 + ( −2.38 ) ] 100 ⋅ [ 0.75 + ( −2.38 ) ]
• ⓐ 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify. 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify.
• ⓑ ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition. ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition.
• ⓒ 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify. 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify.
• ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication. 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication.
• ⓔ 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify. 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify.
• ⓐ ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ] ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ]
• ⓑ 5 ⋅ ( 6.2 + 0.4 ) 5 ⋅ ( 6.2 + 0.4 )
• ⓒ 18 − ( 7 −15 ) 18 − ( 7 −15 )
• ⓓ 17 18 + [ 4 9 + ( − 17 18 ) ] 17 18 + [ 4 9 + ( − 17 18 ) ]
• ⓔ 6 ⋅ ( −3 ) + 6 ⋅ 3 6 ⋅ ( −3 ) + 6 ⋅ 3

Evaluating Algebraic Expressions

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as x + 5 , 4 3 π r 3 , x + 5 , 4 3 π r 3 , or 2 m 3 n 2 . 2 m 3 n 2 . In the expression x + 5 , x + 5 , 5 is called a constant because it does not vary and x is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.

Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

• ⓑ 4 3 π r 3 4 3 π r 3
• ⓒ 2 m 3 n 2 2 m 3 n 2
• ⓐ 2 π r ( r + h ) 2 π r ( r + h )
• ⓑ 2( L + W )
• ⓒ 4 y 3 + y 4 y 3 + y

Evaluating an Algebraic Expression at Different Values

Evaluate the expression 2 x − 7 2 x − 7 for each value for x.

• ⓐ x = 0 x = 0
• ⓑ x = 1 x = 1
• ⓒ x = 1 2 x = 1 2
• ⓓ x = −4 x = −4
• ⓐ Substitute 0 for x . x . 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7
• ⓑ Substitute 1 for x . x . 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5
• ⓒ Substitute 1 2 1 2 for x . x . 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6
• ⓓ Substitute −4 −4 for x . x . 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15

Evaluate the expression 11 − 3 y 11 − 3 y for each value for y.

• ⓐ y = 2 y = 2
• ⓑ y = 0 y = 0
• ⓒ y = 2 3 y = 2 3
• ⓓ y = −5 y = −5

Evaluate each expression for the given values.

• ⓐ x + 5 x + 5 for x = −5 x = −5
• ⓑ t 2 t −1 t 2 t −1 for t = 10 t = 10
• ⓒ 4 3 π r 3 4 3 π r 3 for r = 5 r = 5
• ⓓ a + a b + b a + a b + b for a = 11 , b = −8 a = 11 , b = −8
• ⓔ 2 m 3 n 2 2 m 3 n 2 for m = 2 , n = 3 m = 2 , n = 3
• ⓐ Substitute −5 −5 for x . x . x + 5 = ( −5 ) + 5 = 0 x + 5 = ( −5 ) + 5 = 0
• ⓑ Substitute 10 for t . t . t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19 t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19
• ⓒ Substitute 5 for r . r . 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π
• ⓓ Substitute 11 for a a and –8 for b . b . a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85 a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85
• ⓔ Substitute 2 for m m and 3 for n . n . 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12
• ⓐ y + 3 y − 3 y + 3 y − 3 for y = 5 y = 5
• ⓑ 7 − 2 t 7 − 2 t for t = −2 t = −2
• ⓒ 1 3 π r 2 1 3 π r 2 for r = 11 r = 11
• ⓓ ( p 2 q ) 3 ( p 2 q ) 3 for p = −2 , q = 3 p = −2 , q = 3
• ⓔ 4 ( m − n ) − 5 ( n − m ) 4 ( m − n ) − 5 ( n − m ) for m = 2 3 , n = 1 3 m = 2 3 , n = 1 3

An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation 2 x + 1 = 7 2 x + 1 = 7 has the solution of 3 because when we substitute 3 for x x in the equation, we obtain the true statement 2 ( 3 ) + 1 = 7. 2 ( 3 ) + 1 = 7.

A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area A A of a circle in terms of the radius r r of the circle: A = π r 2 . A = π r 2 . For any value of r , r , the area A A can be found by evaluating the expression π r 2 . π r 2 .

Using a Formula

A right circular cylinder with radius r r and height h h has the surface area S S (in square units) given by the formula S = 2 π r ( r + h ) . S = 2 π r ( r + h ) . See Figure 3 . Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of π . π .

Evaluate the expression 2 π r ( r + h ) 2 π r ( r + h ) for r = 6 r = 6 and h = 9. h = 9.

The surface area is 180 π 180 π square inches.

A photograph with length L and width W is placed in a mat of width 8 centimeters (cm). The area of the mat (in square centimeters, or cm 2 ) is found to be A = ( L + 16 ) ( W + 16 ) − L ⋅ W . A = ( L + 16 ) ( W + 16 ) − L ⋅ W . See Figure 4 . Find the area of a mat for a photograph with length 32 cm and width 24 cm.

Simplifying Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.

Simplify each algebraic expression.

• ⓐ 3 x − 2 y + x − 3 y − 7 3 x − 2 y + x − 3 y − 7
• ⓑ 2 r − 5 ( 3 − r ) + 4 2 r − 5 ( 3 − r ) + 4
• ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) ( 4 t − 5 4 s ) − ( 2 3 t + 2 s )
• ⓓ 2 m n − 5 m + 3 m n + n 2 m n − 5 m + 3 m n + n
• ⓐ 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify. 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify.
• ⓑ 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify. 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify.
• ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify. ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify.
• ⓓ 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify. 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify.
• ⓐ 2 3 y − 2 ( 4 3 y + z ) 2 3 y − 2 ( 4 3 y + z )
• ⓑ 5 t − 2 − 3 t + 1 5 t − 2 − 3 t + 1
• ⓒ 4 p ( q − 1 ) + q ( 1 − p ) 4 p ( q − 1 ) + q ( 1 − p )
• ⓓ 9 r − ( s + 2 r ) + ( 6 − s ) 9 r − ( s + 2 r ) + ( 6 − s )

Simplifying a Formula

A rectangle with length L L and width W W has a perimeter P P given by P = L + W + L + W . P = L + W + L + W . Simplify this expression.

If the amount P P is deposited into an account paying simple interest r r for time t , t , the total value of the deposit A A is given by A = P + P r t . A = P + P r t . Simplify the expression. (This formula will be explored in more detail later in the course.)

Access these online resources for additional instruction and practice with real numbers.

• Simplify an Expression.
• Evaluate an Expression 1.
• Evaluate an Expression 2.

1.1 Section Exercises

Is 2 2 an example of a rational terminating, rational repeating, or irrational number? Tell why it fits that category.

What is the order of operations? What acronym is used to describe the order of operations, and what does it stand for?

What do the Associative Properties allow us to do when following the order of operations? Explain your answer.

For the following exercises, simplify the given expression.

10 + 2 × ( 5 − 3 ) 10 + 2 × ( 5 − 3 )

6 ÷ 2 − ( 81 ÷ 3 2 ) 6 ÷ 2 − ( 81 ÷ 3 2 )

18 + ( 6 − 8 ) 3 18 + ( 6 − 8 ) 3

−2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2 −2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2

4 − 6 + 2 × 7 4 − 6 + 2 × 7

3 ( 5 − 8 ) 3 ( 5 − 8 )

4 + 6 − 10 ÷ 2 4 + 6 − 10 ÷ 2

12 ÷ ( 36 ÷ 9 ) + 6 12 ÷ ( 36 ÷ 9 ) + 6

( 4 + 5 ) 2 ÷ 3 ( 4 + 5 ) 2 ÷ 3

3 − 12 × 2 + 19 3 − 12 × 2 + 19

2 + 8 × 7 ÷ 4 2 + 8 × 7 ÷ 4

5 + ( 6 + 4 ) − 11 5 + ( 6 + 4 ) − 11

9 − 18 ÷ 3 2 9 − 18 ÷ 3 2

14 × 3 ÷ 7 − 6 14 × 3 ÷ 7 − 6

9 − ( 3 + 11 ) × 2 9 − ( 3 + 11 ) × 2

6 + 2 × 2 − 1 6 + 2 × 2 − 1

64 ÷ ( 8 + 4 × 2 ) 64 ÷ ( 8 + 4 × 2 )

9 + 4 ( 2 2 ) 9 + 4 ( 2 2 )

( 12 ÷ 3 × 3 ) 2 ( 12 ÷ 3 × 3 ) 2

25 ÷ 5 2 − 7 25 ÷ 5 2 − 7

( 15 − 7 ) × ( 3 − 7 ) ( 15 − 7 ) × ( 3 − 7 )

2 × 4 − 9 ( −1 ) 2 × 4 − 9 ( −1 )

4 2 − 25 × 1 5 4 2 − 25 × 1 5

12 ( 3 − 1 ) ÷ 6 12 ( 3 − 1 ) ÷ 6

For the following exercises, evaluate the expression using the given value of the variable.

8 ( x + 3 ) – 64 8 ( x + 3 ) – 64 for x = 2 x = 2

4 y + 8 – 2 y 4 y + 8 – 2 y for y = 3 y = 3

( 11 a + 3 ) − 18 a + 4 ( 11 a + 3 ) − 18 a + 4 for a = –2 a = –2

4 z − 2 z ( 1 + 4 ) – 36 4 z − 2 z ( 1 + 4 ) – 36 for z = 5 z = 5

4 y ( 7 − 2 ) 2 + 200 4 y ( 7 − 2 ) 2 + 200 for y = –2 y = –2

− ( 2 x ) 2 + 1 + 3 − ( 2 x ) 2 + 1 + 3 for x = 2 x = 2

For the 8 ( 2 + 4 ) − 15 b + b 8 ( 2 + 4 ) − 15 b + b for b = –3 b = –3

2 ( 11 c − 4 ) – 36 2 ( 11 c − 4 ) – 36 for c = 0 c = 0

4 ( 3 − 1 ) x – 4 4 ( 3 − 1 ) x – 4 for x = 10 x = 10

1 4 ( 8 w − 4 2 ) 1 4 ( 8 w − 4 2 ) for w = 1 w = 1

For the following exercises, simplify the expression.

4 x + x ( 13 − 7 ) 4 x + x ( 13 − 7 )

2 y − ( 4 ) 2 y − 11 2 y − ( 4 ) 2 y − 11

a 2 3 ( 64 ) − 12 a ÷ 6 a 2 3 ( 64 ) − 12 a ÷ 6

8 b − 4 b ( 3 ) + 1 8 b − 4 b ( 3 ) + 1

5 l ÷ 3 l × ( 9 − 6 ) 5 l ÷ 3 l × ( 9 − 6 )

7 z − 3 + z × 6 2 7 z − 3 + z × 6 2

4 × 3 + 18 x ÷ 9 − 12 4 × 3 + 18 x ÷ 9 − 12

9 ( y + 8 ) − 27 9 ( y + 8 ) − 27

( 9 6 t − 4 ) 2 ( 9 6 t − 4 ) 2

6 + 12 b − 3 × 6 b 6 + 12 b − 3 × 6 b

18 y − 2 ( 1 + 7 y ) 18 y − 2 ( 1 + 7 y )

( 4 9 ) 2 × 27 x ( 4 9 ) 2 × 27 x

8 ( 3 − m ) + 1 ( − 8 ) 8 ( 3 − m ) + 1 ( − 8 )

9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x ) 9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x )

5 2 − 4 ( 3 x ) 5 2 − 4 ( 3 x )

Real-World Applications

For the following exercises, consider this scenario: Fred earns $40 at the community garden. He spends $10 on a streaming subscription, puts half of what is left in a savings account, and gets another $5 for walking his neighbor’s dog.

Write the expression that represents the number of dollars Fred keeps (and does not put in his savings account). Remember the order of operations.

How much money does Fred keep?

For the following exercises, solve the given problem.

According to the U.S. Mint, the diameter of a quarter is 0.955 inches. The circumference of the quarter would be the diameter multiplied by π . π . Is the circumference of a quarter a whole number, a rational number, or an irrational number?

Jessica and her roommate, Adriana, have decided to share a change jar for joint expenses. Jessica put her loose change in the jar first, and then Adriana put her change in the jar. We know that it does not matter in which order the change was added to the jar. What property of addition describes this fact?

For the following exercises, consider this scenario: There is a mound of g g pounds of gravel in a quarry. Throughout the day, 400 pounds of gravel is added to the mound. Two orders of 600 pounds are sold and the gravel is removed from the mound. At the end of the day, the mound has 1,200 pounds of gravel.

Write the equation that describes the situation.

Solve for g .

For the following exercise, solve the given problem.

Ramon runs the marketing department at their company. Their department gets a budget every year, and every year, they must spend the entire budget without going over. If they spend less than the budget, then the department gets a smaller budget the following year. At the beginning of this year, Ramon got $2.5 million for the annual marketing budget. They must spend the budget such that 2,500,000 − x = 0. 2,500,000 − x = 0. What property of addition tells us what the value of x must be?

For the following exercises, use a graphing calculator to solve for x . Round the answers to the nearest hundredth.

0.5 ( 12.3 ) 2 − 48 x = 3 5 0.5 ( 12.3 ) 2 − 48 x = 3 5

( 0.25 − 0.75 ) 2 x − 7.2 = 9.9 ( 0.25 − 0.75 ) 2 x − 7.2 = 9.9

If a whole number is not a natural number, what must the number be?

Determine whether the statement is true or false: The multiplicative inverse of a rational number is also rational.

Determine whether the statement is true or false: The product of a rational and irrational number is always irrational.

Determine whether the simplified expression is rational or irrational: −18 − 4 ( 5 ) ( −1 ) . −18 − 4 ( 5 ) ( −1 ) .

Determine whether the simplified expression is rational or irrational: −16 + 4 ( 5 ) + 5 . −16 + 4 ( 5 ) + 5 .

The division of two natural numbers will always result in what type of number?

What property of real numbers would simplify the following expression: 4 + 7 ( x − 1 ) ? 4 + 7 ( x − 1 ) ?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/1-1-real-numbers-algebra-essentials

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Real Number Properties

Real Numbers have properties!

Example: Multiplying by zero

When we multiply a real number by zero we get zero:

• 0 × 0.0001 = 0

It is called the "Zero Product Property", and is listed below.

Here are the main properties of the Real Numbers

Real Numbers are Commutative, Associative and Distributive :

Commutative example

a + b = b + a 2 + 6 = 6 + 2

ab = ba 4 × 2 = 2 × 4

Associative example

(a + b) + c = a + ( b + c ) (1 + 6) + 3 = 1 + (6 + 3)

(ab)c = a(bc) (4 × 2) × 5 = 4 × (2 × 5)

Distributive example

a × (b + c) = ab + ac 3 × (6+2) = 3 × 6 + 3 × 2

(b+c) × a = ba + ca (6+2) × 3 = 6 × 3 + 2 × 3

Real Numbers are closed (the result is also a real number) under addition and multiplication:

Closure example

a+b is real 2 + 3 = 5 is real

a×b is real 6 × 2 = 12 is real

Adding zero leaves the real number unchanged, likewise for multiplying by 1:

Identity example

a + 0 = a 6 + 0 = 6

a × 1 = a 6 × 1 = 6

For addition the inverse of a real number is its negative, and for multiplication the inverse is its reciprocal :

Additive Inverse example

a + (−a ) = 0 6 + (−6) = 0

Multiplicative Inverse example

a × (1/a) = 1 6 × (1/6) = 1

But not for 0 as 1/0 is undefined

Multiplying by zero gives zero (the Zero Product Property ):

Zero Product example

If ab = 0 then a=0 or b=0, or both  

a × 0 = 0 × a = 0 5 × 0 = 0 × 5 = 0

Multiplying two negatives make a positive , and multiplying a negative and a positive makes a negative:

Negation example

−1 × (−a) = −(−a) = a −1 × (−5) = −(−5) = 5

(−a)(−b) = ab (−3)(−6) = 3 × 6 = 18

(−a)(b) = (a)(−b) = −(ab) −3 × 6 = 3 × −6 = −18

• English Language Arts
• Graphic Organizers
• Social Studies
• Teacher Printables
• Foreign Language

Home > Math Worksheets > Integers > Properties of Real Numbers

Real numbers are just about any number you can think of including whole, rational, and irrational numbers. The only values that are not real numbers are imaginary and infinity. The most common properties of real numbers are the associative, commutative, closure, and distributive properties. They can go through many different types of basic operations and still retain their identity as a real number. Commutative property - Addition: When you add two values, their sum will be the same no matter which order you place arrange the values in. Multiplication: when you multiply two integers, their product will be the same no matter which orders you find the product in. Associative property - Addition: When you add two numbers, their sum will be the same no matter which way you group the sums. Multiplication: When you multiply three or more units, their product will be the same no matter which way you group the integers. Distributive property - This says that the sum of two number times a third number will be equal to the sum of each addend times the third number. Identity property -Addition: the sum of zero and any number will be that number. Multiplication: the product of one and any number is that number.

These worksheets explain how to identify the property associated with a given expression. The worksheets also go over certain properties of real numbers, such as the commutative property of addition, relate to actual equations. Your students will use these worksheets to review identifying the property associated with a given expression. Note: students should already be familiar with the list of the properties of real numbers. We also cover the topics of: commutative property of multiplication, the additive identity property, the distributive property, and the multiplicative inverse property.

Get Free Worksheets In Your Inbox!

Properties of real numbers worksheets, click the buttons to print each worksheet and answer key., properties of real numbers lesson and practice.

Determine the given example of which property in this situation. Two elements are interchanging; a x b = b x a, this is the hint that we needed.

Students will learn how to determine the property of a given expression. Ten problems are provided.

What property is displayed over this series of problems.

Review and Practice

This worksheet will practice this skill by completing the problems. A sample problem is solved and six practice problems are provided.

Properties of Real Numbers Quiz

Students demonstrate their proficiency recognizing properties of numbers. Ten problems are provided.

Skill Check

Students will identify properties over a series of problems the use a wide variety of operations. Three problems are provided, and space is included for students to copy the correct answer when given.

Identify the property of real numbers that is demonstrated in the following equation: x + 4y = 4y + x

Worksheet 1

Practice identifying these properties for each of these 10 equations. Example: (4a) b = 4 (ab) 2

Worksheet 2

Practice identifying properties of real numbers over the series of exercises that we show you here. Example: 8f + (-8f) = 0

Follow along with the steps given to identify the property of real numbers demonstrated in this equation: x + 8y = 8y + x

For each problem determine the property that is demonstrated, and then check your answers and record your total score below. Example: (x + 5) + (-x + -5) = 0.

Study Guides > College Algebra CoRequisite Course

Properties of real numbers, learning outcomes.

• Use the order of operations to simplify an algebraic expression.
• Use properties of real numbers to simplify algebraic expressions.

How was the fraction above simplified?

• [latex]\dfrac{a}{b}\cdot\dfrac{c}{d}=\dfrac{ac}{bd}[/latex]
• [latex]6\cdot\dfrac{2}{3}=\dfrac{6}{1}\cdot\dfrac{2}{3}=\dfrac{12}{3}=4[/latex]

A General Note: Order of Operations

How to: given a mathematical expression, simplify it using the order of operations..

• Simplify any expressions within grouping symbols.
• Simplify any expressions containing exponents or radicals.
• Perform any multiplication and division in order, from left to right.
• Perform any addition and subtraction in order, from left to right.

Example: Using the Order of Operations

• [latex]{\left(3\cdot 2\right)}^{2}-4\left(6+2\right)[/latex]
• [latex]\dfrac{{5}^{2}-4}{7}-\sqrt{11 - 2}[/latex]
• [latex]6-|5 - 8|+3\left(4 - 1\right)[/latex]
• [latex]\dfrac{14 - 3\cdot 2}{2\cdot 5-{3}^{2}}[/latex]
• [latex]7\left(5\cdot 3\right)-2\left[\left(6 - 3\right)-{4}^{2}\right]+1[/latex]

[latex]\begin{align}\left(3\cdot 2\right)^{2} & =\left(6\right)^{2}-4\left(8\right) && \text{Simplify parentheses} \\ & =36-4\left(8\right) && \text{Simplify exponent} \\ & =36-32 && \text{Simplify multiplication} \\ & =4 && \text{Simplify subtraction}\end{align}[/latex]

[latex]\begin{align}\frac{5^{2}-4}{7}-\sqrt{11-2} & =\frac{5^{2}-4}{7}-\sqrt{9} && \text{Simplify grouping systems (radical)} \\ & =\frac{5^{2}-4}{7}-3 && \text{Simplify radical} \\ & =\frac{25-4}{7}-3 && \text{Simplify exponent} \\ & =\frac{21}{7}-3 && \text{Simplify subtraction in numerator} \\ & =3-3 && \text{Simplify division} \\ & =0 && \text{Simplify subtraction}\end{align}[/latex]

[latex]\begin{align}6-|5-8|+3\left(4-1\right) & =6-|-3|+3\left(3\right) && \text{Simplify inside grouping system} \\ & =6-3+3\left(3\right) && \text{Simplify absolute value} \\ & =6-3+9 && \text{Simplify multiplication} \\ & =3+9 && \text{Simplify subtraction} \\ & =12 && \text{Simplify addition}\end{align}[/latex]

[latex]\begin{align}\frac{14-3\cdot2}{2\cdot5-3^{2}} & =\frac{14-3\cdot2}{2\cdot5-9} && \text{Simplify exponent} \\ & =\frac{14-6}{10-9} && \text{Simplify products} \\ & =\frac{8}{1} && \text{Simplify quotient} \\ & =8 && \text{Simplify quotient}\end{align}[/latex] In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

[latex]\begin{align}7\left(5\cdot3\right)-2[\left(6-3\right)-4^{2}]+1 & =7\left(15\right)-2[\left(3\right)-4^{2}]+1 && \text{Simplify inside parentheses} \\ & 7\left(15\right)-2\left(3-16\right)+1 && \text{Simplify exponent} \\ & =7\left(15\right)-2\left(-13\right)+1 && \text{Subtract} \\ & =105+26+1 && \text{Multiply} \\ & =132 && \text{Add}\end{align}[/latex]

Recall: simplifying fractions

Using properties of real numbers, commutative properties, associative properties, distributive property.

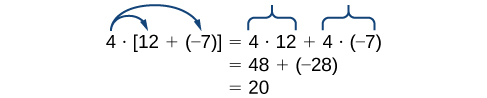
Identity Properties

Inverse properties, a general note: properties of real numbers, using the inverse property of numbers: simplifying fractions, example: using properties of real numbers.

• [latex]3\cdot 6+3\cdot 4[/latex]
• [latex]\left(5+8\right)+\left(-8\right)[/latex]
• [latex]6-\left(15+9\right)[/latex]
• [latex]\dfrac{4}{7}\cdot \left(\frac{2}{3}\cdot \dfrac{7}{4}\right)[/latex]
• [latex]100\cdot \left[0.75+\left(-2.38\right)\right][/latex]

Answer: 1. [latex-display]\begin{align}3\cdot6+3\cdot4 &=3\cdot\left(6+4\right) && \text{Distributive property} \\ &=3\cdot10 && \text{Simplify} \\ & =30 && \text{Simplify}\end{align}[/latex-display] 2. [latex-display]\begin{align}\left(5+8\right)+\left(-8\right) &=5+\left[8+\left(-8\right)\right] &&\text{Associative property of addition} \\ &=5+0 && \text{Inverse property of addition} \\ &=5 &&\text{Identity property of addition}\end{align}[/latex-display] 3. [latex-display]\begin{align}6-\left(15+9\right) & =6+(-15-9) && \text{Distributive property} \\ & =6+\left(-24\right) && \text{Simplify} \\ & =-18 && \text{Simplify}\end{align}[/latex-display] 4. [latex-display]\begin{align}\frac{4}{7}\cdot\left(\frac{2}{3}\cdot\frac{7}{4}\right) & =\frac{4}{7} \cdot\left(\frac{7}{4}\cdot\frac{2}{3}\right) && \text{Commutative property of multiplication} \\ & =\left(\frac{4}{7}\cdot\frac{7}{4}\right)\cdot\frac{2}{3} && \text{Associative property of multiplication} \\ & =1\cdot\frac{2}{3} && \text{Inverse property of multiplication} \\ & =\frac{2}{3} && \text{Identity property of multiplication}\end{align}[/latex-display] 5. [latex-display]\begin{align}100\cdot[0.75+\left(-2.38\right)] & =100\cdot0.75+100\cdot\left(-2.38\right) && \text{Distributive property} \\ & =75+\left(-238\right) && \text{Simplify} \\ & =-163 && \text{Simplify}\end{align}[/latex-display]

• [latex]\left(-\dfrac{23}{5}\right)\cdot \left[11\cdot \left(-\dfrac{5}{23}\right)\right][/latex]
• [latex]5\cdot \left(6.2+0.4\right)[/latex]
• [latex]18-\left(7 - 15\right)[/latex]
• [latex]\dfrac{17}{18}+\cdot \left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right][/latex]
• [latex]6\cdot \left(-3\right)+6\cdot 3[/latex]
• 11, commutative property of multiplication, associative property of multiplication, inverse property of multiplication, identity property of multiplication;
• 33, distributive property;
• 26, distributive property;
• [latex]\dfrac{4}{9}[/latex], commutative property of addition, associative property of addition, inverse property of addition, identity property of addition;
• 0, distributive property, inverse property of addition, identity property of addition

Licenses & Attributions

Cc licensed content, original.

• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .
• Evaluate a Mathematical Expression With the Desmos Calculator. Authored by: Lumen Learning. License: Public Domain: No Known Copyright .

CC licensed content, Shared previously

• Question ID 259. Authored by: Sousa, James. License: Other . License terms: IMathAS Community License CC-BY + GPL.
• Question ID 99379. Authored by: Davis, Desiree. License: Other . License terms: IMathAS Community License CC-BY + GPL.
• Question ID 92360. Authored by: Jenck, Michael for Lumen Learning. License: Other . License terms: IMathAS Community License CC-BY + GPL.
• Question ID 92361. Authored by: Jenck, Michael for Lumen Learning. License: Other . License terms: IMathAS Community License CC-BY + GPL.
• College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
• Simplifying Expressions With Square Roots. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .

CC licensed content, Specific attribution

• College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

Module 1: Real Numbers and Algebraic Expressions

Use properties of real numbers, learning outcomes.

• Define and use the commutative property of addition and multiplication
• Define and use the associative property of addition and multiplication
• Define and use the distributive property
• Define and use the identity property of addition and multiplication
• Define and use the inverse property of addition and multiplication

For some activities we perform, the order of certain processes does not matter, but the order of others do. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for addition and multiplication.

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

We can better see this relationship when using real numbers.

Show that numbers may be added in any order without affecting the sum. [latex]\left(-2\right)+7=5[/latex]

[latex]7+\left(-2\right)=5[/latex]

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

Again, consider an example with real numbers.

Show that numbers may be multiplied in any order without affecting the product.[latex]\left(-11\right)\cdot\left(-4\right)=44[/latex]

[latex]\left(-4\right)\cdot\left(-11\right)=44[/latex]

Caution! It is important to note that neither subtraction nor division is commutative. For example, [latex]17 - 5[/latex] is not the same as [latex]5 - 17[/latex]. Similarly, [latex]20\div 5\ne 5\div 20[/latex].

Associative Properties – Grouping

The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.

Consider this example.

Show that you can regroup numbers that are multiplied together and not affect the product.[latex]\left(3\cdot4\right)\cdot5=60[/latex]

[latex]3\cdot\left(4\cdot5\right)=60[/latex]

This property can be especially helpful when dealing with negative integers. Consider this example.

Show that regrouping addition does not affect the sum. [latex][15+\left(-9\right)]+23=29[/latex]

[latex]15+[\left(-9\right)+23]=29[/latex]

Are subtraction and division associative? Review these examples.

Use the associative property to explore whether subtraction and division are associative.

1) [latex]8-\left(3-15\right)\stackrel{?}{=}\left(8-3\right)-15[/latex]

2) [latex]64\div\left(8\div4\right)\stackrel{?}{=}\left(64\div8\right)\div4[/latex]

[latex]\,\,\,\,\,\,\,\,\,\,\,8-\left(-12\right)=5-15[/latex]

[latex]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,20\neq-10[/latex]

[latex]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,64\div2\stackrel{?}{=}8\div4[/latex]

[latex]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,32\neq 2[/latex]

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

Use the distributive property to show that [latex]4\cdot[12+(-7)]=20[/latex]

Note that [latex]4[/latex] is outside the grouping symbols, so we distribute the  [latex]4[/latex] by multiplying it by [latex]12[/latex], multiplying it by [latex]–7[/latex], and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition.

The reverse is not true as we can see in this example.

[latex]\begin{array}{ccc}\hfill 6+\left(3\cdot 5\right)& \stackrel{?}{=}& \left(6+3\right)\cdot \left(6+5\right) \\ \hfill 6+\left(15\right)& \stackrel{?}{=}& \left(9\right)\cdot \left(11\right)\hfill \\ \hfill 21& \ne & \text{ }99\hfill \end{array}[/latex]

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference [latex]12-\left(5+3\right)[/latex]. We can rewrite the difference of the two terms [latex]12[/latex] and [latex]\left(5+3\right)[/latex] by turning the subtraction expression into addition of the opposite. So instead of subtracting [latex]\left(5+3\right)[/latex], we add the opposite.

Now, distribute [latex]-1[/latex] and simplify the result.

Rewrite the last example by changing the sign of each term and adding the results.

[latex]\begin{array}{l}12-\left(5+3\right)=12+\left(-5-3\right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=12+\left(-8\right) \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=4\end{array}[/latex]

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms.

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

Show that the identity property of addition and multiplication are true for [latex]-6 \text{ and }23[/latex].

Show Solution

[latex]\left(-6\right)+0=-6[/latex]

[latex]23+0=23[/latex]

[latex]-6\cdot1=-6[/latex]

[latex]23\cdot 1=23[/latex]

There are no exceptions for these properties; they work for every real number, including [latex]0[/latex] and [latex]1[/latex].

Inverse Properties

The inverse property of addition states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted  a , that, when added to the original number, results in the additive identity, [latex]0[/latex].

For example, if [latex]a=-8[/latex], the additive inverse is [latex]8[/latex], since [latex]\left(-8\right)+8=0[/latex].

The inverse property of multiplication holds for all real numbers except [latex]0[/latex] because the reciprocal of [latex]0[/latex] is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\dfrac{1}{a}[/latex], that, when multiplied by the original number, results in the multiplicative identity, [latex]1[/latex].

1) Define the additive inverse of [latex]a=-8[/latex], and use it to illustrate the inverse property of addition.

2) Write the reciprocal of [latex]a=-\dfrac{2}{3}[/latex], and use it to illustrate the inverse property of multiplication.

1) The additive inverse is [latex]8[/latex], and [latex]\left(-8\right)+8=0[/latex]

2) The reciprocal is [latex]-\dfrac{3}{2}[/latex] and [latex]\left(-\dfrac{2}{3}\normalsize\right)\cdot \left(-\dfrac{3}{2}\normalsize\right)=1[/latex]

A General Note: Properties of Real Numbers

The following properties hold for real numbers a , b , and c .

Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.

• [latex]3\left(6+4\right)[/latex]
• [latex]\left(5+8\right)+\left(-8\right)[/latex]
• [latex]6-\left(15+9\right)[/latex]
• [latex]\dfrac{4}{7}\normalsize\cdot \left(\dfrac{2}{3}\normalsize\cdot\dfrac{7}{4}\normalsize\right)[/latex]
• [latex]100\cdot \left[0.75+\left(-2.38\right)\right][/latex]
• [latex]\begin{array}{l}\\\\3\cdot\left(6+4\right)=3\cdot6+3\cdot4\,\,\,\,\,\,\,\,\,\,\,\text{Distributive property} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=18+12\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Simplify} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=30\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Simplify}\end{array}[/latex]
• [latex]\begin{array}{l}\\\\\left(5+8\right)+\left(-8\right)=5+\left[8+\left(-8\right)\right]\,\,\,\,\,\,\,\,\,\,\,\text{Associative property of addition} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=5+0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Inverse property of addition} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{Identity property of addition}\end{array}[/latex]
• [latex]\begin{array}{l}\\\\6-\left(15+9\right) \hfill& =6+[\left(-15\right)+\left(-9\right)] \hfill& \text{Distributive property} \\ \hfill& =6+\left(-24\right) \hfill& \text{Simplify} \\ \hfill& =-18 \hfill& \text{Simplify}\end{array}[/latex]
• [latex]\begin{array}{l}\\\\\\\\\frac{4}{7}\cdot\left(\frac{2}{3}\cdot\frac{7}{4}\right) \hfill& =\frac{4}{7} \cdot\left(\frac{7}{4}\cdot\frac{2}{3}\right) \hfill& \text{Commutative property of multiplication} \\ \hfill& =\left(\frac{4}{7}\cdot\frac{7}{4}\right)\cdot\frac{2}{3}\hfill& \text{Associative property of multiplication} \\ \hfill& =1\cdot\frac{2}{3} \hfill& \text{Inverse property of multiplication} \\ \hfill& =\frac{2}{3} \hfill& \text{Identity property of multiplication}\end{array}[/latex]
• [latex]\begin{array}{l}\\\\100\cdot[0.75+\left(-2.38\right)] \hfill& =100\cdot0.75+100\cdot\left(-2.38\right)\hfill& \text{Distributive property} \\ \hfill& =75+\left(-238\right) \hfill& \text{Simplify} \\ \hfill& =-163 \hfill& \text{Simplify}\end{array}[/latex]

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Properties of Real Numbers. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/8SFm8Os_4C8 . License : CC BY: Attribution
• College Algebra: Using Properties of Real Numbers. Located at : https://courses.candelalearning.com/collegealgebra1xmaster/chapter/using-properties-of-real-numbers . License : CC BY: Attribution

• Math Article

Real Numbers

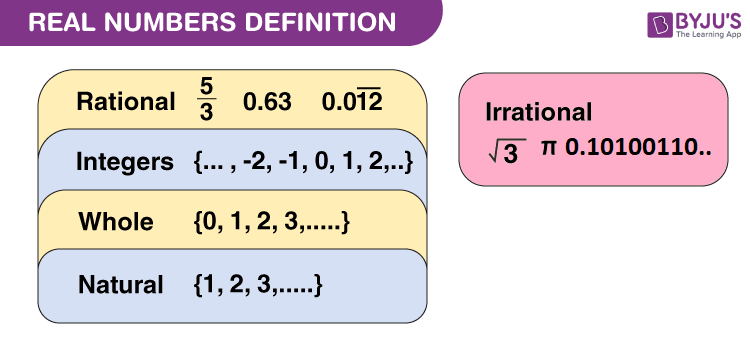
Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and are commonly used to represent a complex number . Some of the examples of real numbers are 23, -12, 6.99, 5/2, π, and so on. In this article, we are going to discuss the definition of real numbers, the properties of real numbers and the examples of real numbers with complete explanations.

Table of contents:

• Set of real numbers
• Commutative
• Associative
• Distributive

Solved Examples

Practice questions, real numbers definition.

Real numbers can be defined as the union of both rational and irrational numbers. They can be both positive or negative and are denoted by the symbol “R”. All the natural numbers, decimals and fractions come under this category. See the figure, given below, which shows the classification of real numerals.

Set of Real Numbers

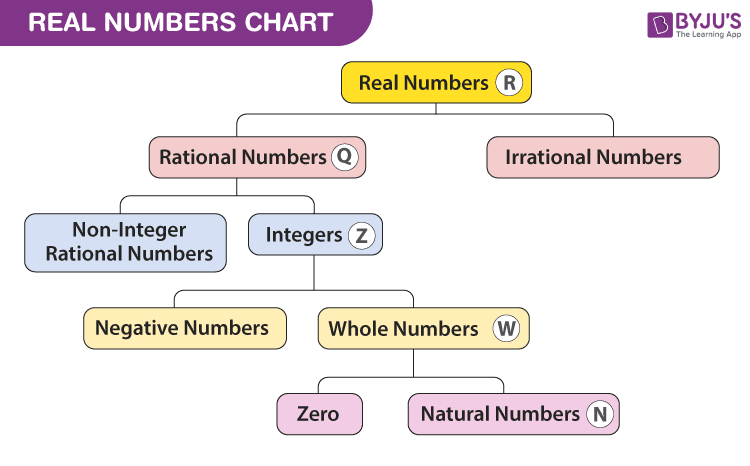
The set of real numbers consists of different categories, such as natural and whole numbers, integers, rational and irrational numbers. In the table given below, all the real numbers formulas (i.e.) the representation of the classification of real numbers are defined with examples.

Real Numbers Chart

The chart for the set of real numerals including all the types are given below:

Properties of Real Numbers

The following are the four main properties of real numbers:

• Commutative property
• Associative property
• Distributive property
• Identity property

Consider “m, n and r” are three real numbers. Then the above properties can be described using m, n, and r as shown below:

Commutative Property

If m and n are the numbers, then the general form will be m + n = n + m for addition and m.n = n.m for multiplication.

• Addition: m + n = n + m. For example, 5 + 3 = 3 + 5, 2 + 4 = 4 + 2.
• Multiplication: m × n = n × m. For example, 5 × 3 = 3 × 5, 2 × 4 = 4 × 2.

Associative Property

If m, n and r are the numbers. The general form will be m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication.

• Addition: The general form will be m + (n + r) = (m + n) + r. An example of additive associative property is 10 + (3 + 2) = (10 + 3) + 2.
• Multiplication: (mn) r = m (nr). An example of a multiplicative associative property is (2 × 3) 4 = 2 (3 × 4).

Distributive Property

For three numbers m, n, and r, which are real in nature, the distributive property is represented as:

m (n + r) = mn + mr and (m + n) r = mr + nr.

• Example of distributive property is: 5(2 + 3) = 5 × 2 + 5 × 3. Here, both sides will yield 25.

Identity Property

There are additive and multiplicative identities.

• For addition: m + 0 = m. (0 is the additive identity)
• For multiplication:  m × 1 = 1 × m = m. (1 is the multiplicative identity)

Video Lesson on Numbers

Find five rational numbers between 1/2 and 3/5.

We shall make the denominator same for both the given rational number

(1 × 5)/(2 × 5) = 5/10  and (3 × 2)/(5 × 2) = 6/10

Now, multiply both the numerator and denominator of both the rational number by 6, we have

(5 × 6)/(10 × 6) = 30/60  and (6 × 6)/(10 × 6) = 36/60

Five rational numbers between 1/2 = 30/60 and 3/5 = 36/60 are

31/60, 32/60, 33/60, 34/60, 35/60.  

Write the decimal equivalent of the following:

(i) 1/4  (ii) 5/8 (iii) 3/2

(i) 1/4 = (1 × 25)/(4 × 25) = 25/100 = 0.25

(ii) 5/8 = (5 × 125)/(8 × 125) = 625/1000 = 0.625

(iii) 3/2 = (3 × 5)/(2 × 5) = 15/10 = 1.5

What should be multiplied to 1.25 to get the answer 1?

Solution: 1.25 = 125/100 

Now if we multiply this by 100/125, we get

125/100 × 100/125 = 1

• Which is the smallest composite number?
• Prove that any positive odd integer is of the form 6x + 1, 6x + 3, or 6x + 5.
• Evaluate 2 + 3 × 6 – 5.
• What is the product of a non-zero rational number and an irrational number?

Can every positive integer be represented as 4x + 2 (where x is an integer)?

Real Numbers Class 9 and 10

In real numbers Class 9, the common concepts introduced include representing real numbers on a number line, operations on real numbers, properties of real numbers, and the law of exponents for real numbers. In Class 10, some advanced concepts related to real numbers are included. Apart from what are real numbers, students will also learn about the real numbers formulas and concepts such as Euclid’s Division Lemma, Euclid’s Division Algorithm and the fundamental theorem of arithmetic in class 10.

Frequently Asked Questions on Real Numbers

What are natural and real numbers.

Natural numbers are all positive integers starting from 1 to infinity. All natural numbers are integers but not all the integers are natural numbers. These are the set of all counting numbers such as 1, 2, 3, 4, 5, 6, 7, 8, 9, …….∞.

Real numbers are numbers that include both rational and irrational numbers. Rational numbers such as integers (-2, 0, 1), fractions(1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.

Is Zero a Real or an Imaginary Number?

Zero is considered to be both a real and an imaginary number. As we know, imaginary numbers are the square root of non-positive real numbers. And since 0 is also a non-positive number, therefore it fulfils the criteria of the imaginary number. Whereas 0 is also a rational number, which is defined in a number line and hence a real number.

Are there Real Numbers that are not Rational or Irrational?

No, there are no real numbers that are neither rational nor irrational. The definition of real numbers itself states that it is a combination of both rational and irrational numbers.

Is the real number a subset of a complex number?

Yes, because a complex number is the combination of a real and imaginary number. So, if the complex number is a set then the real and imaginary numbers are the subsets of it.

What are the properties of real numbers?

Is √3 a real number.

Yes, √3 is a real number. We know that a real number is a combination of both rational and irrational numbers. Since √3 is an irrational number, we can also say that √3 is a real number.

Is 3i a real number?

No, 3i is not a real number, as it has an imaginary part in it.

What are the different subsets of real numbers?

The subsets of real numbers include rational numbers, irrational numbers, natural numbers, and whole numbers.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

According to a new mathematical definition, whole numbers are divided into two sets, one of which is the merger of the sequence of prime numbers and numbers zero and one. Three other definitions, deduced from this first, subdivide the set of whole numbers into four classes of numbers with own and unique arithmetic properties. The geometric distribution of these different types of whole numbers, in various closed matrices, is organized into exact value ratios to 3/2 or 1/1.

can u use any real number of ur choice in mathematics

Where is the chat box?

please send explanation of this.

Sir,I want to know more about mathematics.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Introduction: Connecting Your Learning

Mathematics is no different. Once you have entered this world, you need to explore and discover the characteristics (properties) that make operations like addition, subtraction, multiplication, and division work. In this lesson, you will examine some of the properties of real numbers.

Focusing Your Learning

Lesson objectives.

By the end of this lesson, you should be able to:

• Identify the basic properties of real numbers.

Presentation

Basic properties of real numbers.

The basic properties of real numbers are used to determine the order in which you simplify math expressions. The basic properties of real numbers include the following:

• The Closure Property
• The Commutative Property
• The Associative Property

The Distributive Property

Take a closer look at each property.

The Closure Properties

Real numbers are closed under addition, subtraction, and multiplication.

That means if a and b are real numbers, then a + b is a unique real number, and a ⋅ b is a unique real number.

For example:

3 and 11 are real numbers.

Any time you add, subtract, or multiply two real numbers, the result will be a real number.

Although this property seems obvious, some collections are not closed under certain operations.

Here are some examples.

Natural numbers are not closed under subtraction. Although 8 is a natural number, 8 − 8 is not. (8 − 8 = 0, and 0 is not a natural number.)

Watch the following video for an additional explanation and examples of the Closure Property.

The Commutative Properties

The commutative properties tell you that two numbers can be added or multiplied in any order without affecting the result.

Let a and b represent real numbers.

Watch the following videos for a detailed explanation of the Commutative Properties.

Practice Exercise: Commutative Properties

It is time to practice what you have learned. You will need a piece of a paper and a pencil to complete the following activity . Write down the proper number or letter that goes in the parentheses to make the statement true. Use the commutative properties. When you are done, make sure to check your answers to see how well you did.

Practice Exercise

m + 12 = 12 + ( )

9 ⋅ 7 = ( ) ⋅ 9

6 a = a ( )

4 ( k − 5) = ( ) 4

(9 a −1)( ) = (2 b + 7)(9 a − 1)

Check Answers

• 6 + 5 = (5) + 6
• m + 12 = 12 + ( m )
• 9 ⋅ 7 = (7) ⋅ 9
• 6 a = a (6)
• 4( k - 5) = ( k - 5) 4
• (9 a - 1) (2 b + 7) = (2 b + 7)(9 a - 1)

Simplify (rearrange into a simpler form):     5 y 6 b 8 ac 4

According to the commutative property of multiplication, you can reorder the variables and numbers to and get all the numbers together and all the letters together.

Use the example above to complete the following practice exercise.

Simplify each of the following quantities.

3 a 7 y 9 d

6 b 8 acz 4 ⋅ 5

4 p 6 qr 3 ( a + b )

• 72 pqr ( a + b )

The Associative Properties

The associative properties tell you that you may group together the quantities in any way without affecting the result.

(Let a , b , and c represent real numbers.)

The following examples show how the Associative Properties of addition and multiplication can be used.

Watch the following videos for a detailed explanation of the Associative Properties.

Practice Exercise: Associative Properties

It is time to practice what you have learned about the Associative Properties. You will need to get out of a piece of a paper and a pencil to complete the following activity. Write down the proper number or letter that goes in the parentheses to make the statement true. Use the Associative Properties. When you are done make sure to check your answers to see how well you did.

(9 + 2) + 5 = 9 + ( )

x + (5 + y ) = ( )+ y

(11 a ) 6 = 11 ( )

• (9 + 2) + 5 = 9 + (2 + 5)
• x + (5 + y ) = ( x + 5) + y
• (11 a ) 6 = 11 ( a ⋅ 6)

The Distributive Properties

When you were first introduced to multiplication, you most likely recognized that it was developed as a description for repeated addition.

Consider this: 4 + 4 + 4 = 3 ⋅ 4

Notice that there are three 4s; that is, 4 appears three times. Hence, 3 times 4. Algebra is generalized arithmetic, and you can now make an important generalization.

When the number a is added repeatedly, meaning n times, we have a + a + a + ⋯ + a ( a appears n times)

Then, using multiplication as a description for repeated addition, you can replace a + a + a + ⋯ + a with n ( a ).

Example 1: x + x + x + x can be written as 4 x since x is repeatedly added 4 times.

x + x + x + x = 4 x

Example 2: r + r can be written as 2 r since r is repeatedly added 2 times.

r + r = 2 r

The distributive property involves both multiplication and addition. Take a look at the explanation below.

Rewrite 4( a + b ).

STEP 1: You proceed by reading 4( a + b ) as multiplication: 4 times the quantity ( a + b ).

• This directs you to write:

4( a + b ) = ( a + b ) + ( a + b ) + ( a + b ) + ( a + b ) = a + b + a + b + a + b + a + b

STEP 2: Now you use the commutative property of addition to collect all the a′s together and all the b′s together.

4( a + b ) = a + a + a + a + b + b + b + b

4 a ′s + 4 b ′s

STEP 3: Now, you use multiplication as a description for repeated addition.

• This directs us to write:

4( a + b ) = 4 a + 4 b

• You have distributed the 4 over the sum to both a and b .

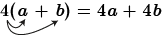
Because of the commutative property and the convention of writing the variables in alphabetical order, you can also write the following:

b ⋅ a + c ⋅ a as a ⋅ b + a ⋅ c , so ( b + c ) a = a ⋅ b + a ⋅ c too.

The distributive property is useful when you cannot or do not wish to perform operations inside parentheses.

Use the distributive property to rewrite each of the following quantities.

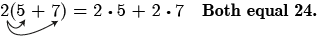
Watch the following videos for a detailed explanation of the Distributive Property.

Practice Exercise: Distributive Properties

Use the distributive property to rewrite each of the following quantities without the parentheses. When you perform operations using the distributive property, it is often called expanding the expression.

4 ( a + y )

1 ( x + y )

• 3 ⋅ 2 + 3 ⋅ 1
• 7 ⋅ x + 7 ⋅ 6
• 4 ⋅ a + 4 ⋅ y
• 9 ⋅ a + 2 ⋅ a
• a ⋅ x + 5 ⋅ a
• 1 ⋅ x + 1 ⋅ y

The Identity Properties

Additive Identity

The number 0 is called the additive identity since when it is added to any real number, it preserves the identity of that number. Zero is the only additive identity.

For example: 6 + 0 = 6

Multiplicative Identity

The number 1 is called the multiplicative identity since when 1 is multiplied by any real number, it preserves the identity of that number. One is the only multiplicative identity.

For example: 6 ⋅ 1 = 6.

The identity properties are summarized as follows.

Watch the following Khan Academy videos for an additional explanation and examples of the Identity Property.

The Inverse Properties

Additive Inverses

When two numbers are added together and the result is the additive identity, 0, the numbers are called additive inverses of each other.

When 3 is added to −3, the result is 0: that is 3 + (−3) = 0.

The numbers 3 and −3 are additive inverses of each other.

What is the additive inverse of −15?

For a more in-depth explanation of additive inverses, watch the following video by Khan Academy.

Multiplicative Inverses

When two numbers are multiplied together and the result is the multiplicative identity, 1, the numbers are called multiplicative inverses of each other.

The inverse properties are as follows.

For a more in-depth explanation of multiplicative inverses watch the following video by Khan Academy.

Exercise: Additive and Multiplicative Inverses

Summarizing your learning.

Did you know there were so many kinds of properties for real numbers? You should now be familiar with closure, commutative, associative, distributive, identity, and inverse properties. Literal explanations were included to make the symbolic explanations easier to interpret. Take a look at the following Web site for additional explanations of the properties of real numbers.

Properties of Real Numbers

Assessing Your Learning

• Complete the Arithmetic Review: Properties of Real Numbers.

“Basic Properties of Real Numbers: Properties of the Real Numbers” by Ellis, W., & Burzynski, D. © 2009 retrieved from http://cnx.org/content/m21894/1.4/ is used under a Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/ . This adaption of the lesson, “Properties of Real Numbers,” by the National Information Security and Geospatial Technologies Consortium (NISGTC) is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0 .

Additional Attributions

1-1 Properties of Real Numbers

Here is your free content for this lesson!

Properties of Real Numbers - Word Docs & PowerPoints

1-1 Assignment - Properties of Real Numbers 1-1 Bellwork - Properties of real numbers 1-1 Exit Quiz - Properties of Real Numbers 1-1 Guided Notes SE - Properties of Real Numbers 1-1 Guided Notes TE - Properties of Real Numbers 1-1 Lesson Plan - Properties of Real Numbers 1-1 Online Activity - Properties of Real Numbers 1-1 Slide Show - Properties of Real Numbers

Properties of Real Numbers - PDFs

1-1 Assignment SE - Properties of Real Numbers 1-1 Assignment - Properties of Real Numbers 1-1 Bellwork SE - Properties of real numbers 1-1 Bellwork - Properties of real numbers 1-1 Exit Quiz SE - Properties of Real Numbers 1-1 Exit Quiz - Properties of Real Numbers 1-1 Guided Notes TE - Properties of Real Numbers 1-1 Guided Notes SE - Properties of Real Numbers 1-1 Lesson Plan - Properties of Real Numbers 1-1 Online Activity - Properties of Real Numbers 1-1 Slide Show - Properties of Real Numbers

Want access to everything? Simply click the image below to GET ALL OF OUR LESSONS!

Want more Great Algebra 2 Lessons? Check out our other posts…

Matrix multiplication, the properties of parabolas, organizing data into matrices, modeling data with quadratic functions, teaching linear equations, graphing systems of equations, teaching relations and functions, solving systems of linear inequalities, solving equations (algebra 2), simplifying algebraic expressions (algebra 2), angles and the unit circle – time to eat, properties of real numbers – the importance of differentiating directions in algebra, absolute value functions and graphs – real world applications, rational functions and their graphs – group activity, algebraic expressions worksheet and activity – mazing, holiday algebra 2 activities, how to make your math class paperless, i stopped letting my students use calculators in class, algebra 2 teacher hacks, conditional probability – call it in the air, area under a curve – is your umbrella big enough, properties of logarithms, adding and subtracting matrices – using rainbows, the nightmare of exploring conic sections, probability of multiple events – a coin and a card, roots and radical expressions – why so negative, solving systems of equations by substitution – sports and algebra 2, permutations and combinations using magic card tricks, angry birds parabola project, subscribe to blog via email.

Enter your email address to subscribe to this blog and receive notifications of new posts by email.

Join 2,707 other subscribers

Email Address

Share this:

• Click to share on Facebook (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to email this to a friend (Opens in new window)
• Click to print (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Tumblr (Opens in new window)
• Click to share on WhatsApp (Opens in new window)
• Click to share on Skype (Opens in new window)
• Click to share on Telegram (Opens in new window)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: Properties of Real Numbers

• Last updated
• Save as PDF
• Page ID 30812

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Use the commutative and associative properties
• Use the properties of identity, inverse, and zero
• Simplify expressions using the Distributive Property

Use the Commutative and Associative Properties

The order we add two numbers doesn’t affect the result. If we add \(8+9\) or \(9+8\), the results are the same—they both equal 17. So, \(8+9=9+8\). The order in which we add does not matter!

Similarly, when multiplying two numbers, the order does not affect the result. If we multiply \(9·8\) or \(8·9\) the results are the same—they both equal 72. So, \(9·8=8·9\). The order in which we multiply does not matter! These examples illustrate the Commutative Property .

COMMUTATIVE PROPERTY

\[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \]

When adding or multiplying, changing the order gives the same result.

The Commutative Property has to do with order. We subtract \(9−8\) and \(8−9\), and see that \(9−8\neq 8−9\). Since changing the order of the subtraction does not give the same result, we know that subtraction is not commutative .

Division is not commutative either . Since \(12÷3\neq 3÷12\), changing the order of the division did not give the same result. The commutative properties apply only to addition and multiplication!

• Addition and multiplication are commutative.
• Subtraction and division are not commutative.

When adding three numbers, changing the grouping of the numbers gives the same result. For example,\((7+8)+2=7+(8+2)\), since each side of the equation equals 17.

This is true for multiplication, too. For example, \(\left(5·\frac{1}{3}\right)·3=5·\left(\frac{1}{3}·3\right)\), since each side of the equation equals 5.

These examples illustrate the Associative Property .

ASSOCIATIVE PROPERTY

\[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \]

When adding or multiplying, changing the grouping gives the same result.

The Associative Property has to do with grouping. If we change how the numbers are grouped, the result will be the same. Notice it is the same three numbers in the same order—the only difference is the grouping.

We saw that subtraction and division were not commutative. They are not associative either.

\[\begin{array}{cc} (10−3)−2\neq 10−(3−2) & (24÷4)÷2\neq 24÷(4÷2) \\ 7−2\neq 10−1 & 6÷2\neq 24÷2 \\ 5\neq 9 & 3\neq 12 \end{array}\]

When simplifying an expression, it is always a good idea to plan what the steps will be. In order to combine like terms in the next example, we will use the Commutative Property of addition to write the like terms together.

Example \(\PageIndex{1}\)

Simplify: \(18p+6q+15p+5q\).

\[\begin{array}{lc} \text{} & 18p+6q+15p+5q \\ \text{Use the Commutative Property of addition to} & 18p+15p+6q+5q \\ \text{reorder so that like terms are together.} & {} \\ \text{Add like terms.} & 33p+11q \end{array}\]

Example \(\PageIndex{2}\)

Simplify: \(23r+14s+9r+15s\).

\(32r+29s\)

Example \(\PageIndex{3}\)

Simplify: \(37m+21n+4m−15n\).

When we have to simplify algebraic expressions, we can often make the work easier by applying the Commutative Property or Associative Property first.

EXAMPLE \(\PageIndex{4}\)

Simplify: \((\frac{5}{13}+\frac{3}{4})+\frac{1}{4}\).

\( \begin{array}{lc} \text{} & (\frac{5}{13}+\frac{3}{4})+\frac{1}{4} \\ {\text{Notice that the last 2 terms have a common} \\ \text{denominator, so change the grouping.} } & \frac{5}{13}+(\frac{3}{4}+\frac{1}{4}) \\ \text{Add in parentheses first.} & \frac{5}{13}+(\frac{4}{4}) \\ \text{Simplify the fraction.} & \frac{5}{13}+1 \\ \text{Add.} & 1\frac{5}{13} \\ \text{Convert to an improper fraction.} & \frac{18}{13} \end{array}\)

EXAMPLE \(\PageIndex{5}\)

Simplify: \((\frac{7}{15}+\frac{5}{8})+\frac{3}{8}.\)

\(1 \frac{7}{15}\)

EXAMPLE \(\PageIndex{6}\)

Simplify: \((\frac{2}{9}+\frac{7}{12})+\frac{5}{12}\).

\(1\frac{2}{9}\)

Use the Properties of Identity, Inverse, and Zero

What happens when we add 0 to any number? Adding 0 doesn’t change the value. For this reason, we call 0 the additive identity . The Identity Property of Addition that states that for any real number \(a,a+0=a\) and \(0+a=a.\)

What happens when we multiply any number by one? Multiplying by 1 doesn’t change the value. So we call 1 the multiplicative identity. The Identity Property of Multiplication that states that for any real number \(a,a·1=a\) and \(1⋅a=a.\)

We summarize the Identity Properties here.

IDENTITY PROPERTY

\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \\ \\ \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \\ \\ \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\]

What number added to 5 gives the additive identity, 0? We know

The missing number was the opposite of the number!

We call \(−a\) the additive inverse of \(a\). The opposite of a number is its additive inverse. A number and its opposite add to zero, which is the additive identity. This leads to the Inverse Property of Addition that states for any real number \(a,a+(−a)=0.\)

What number multiplied by \(\frac{2}{3}\) gives the multiplicative identity, 1? In other words, \(\frac{2}{3}\) times what results in 1? We know

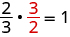
The missing number was the reciprocal of the number!

We call \(\frac{1}{a}\) the multiplicative inverse of a . The reciprocal of a number is its multiplicative inverse. This leads to the Inverse Property of Multiplication that states that for any real number \(a,a\neq 0,a·\frac{1}{a}=1.\)

We’ll formally state the inverse properties here.

INVERSE PROPERTY

\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\]

The Identity Property of addition says that when we add 0 to any number, the result is that same number. What happens when we multiply a number by 0? Multiplying by 0 makes the product equal zero.

What about division involving zero? What is \(0÷3\)? Think about a real example: If there are no cookies in the cookie jar and 3 people are to share them, how many cookies does each person get? There are no cookies to share, so each person gets 0 cookies. So, \(0÷3=0.\)

We can check division with the related multiplication fact. So we know \(0÷3=0\) because \(0·3=0\).

Now think about dividing by zero. What is the result of dividing 4 by 0? Think about the related multiplication fact:

Is there a number that multiplied by 0 gives 4? Since any real number multiplied by 0 gives 0, there is no real number that can be multiplied by 0 to obtain 4. We conclude that there is no answer to \(4÷0\) and so we say that division by 0 is undefined .

We summarize the properties of zero here.

PROPERTIES OF ZERO

Multiplication by Zero: For any real number a ,

\[a⋅0=0 \; \; \; 0⋅a=0 \; \; \; \; \text{The product of any number and 0 is 0.}\]

Division by Zero: For any real number a , \(a\neq 0\)

\[\begin{array}{cl} \dfrac{0}{a}=0 & \text{Zero divided by any real number, except itself, is zero.} \\ \dfrac{a}{0} \text{ is undefined} & \text{Division by zero is undefined.} \end{array}\]

We will now practice using the properties of identities, inverses, and zero to simplify expressions.

EXAMPLE \(\PageIndex{7}\)

Simplify: \(−84n+(−73n)+84n.\)

\(\begin{array}{lc} \text{} & −84n+(−73n)+84n \\ \text{Notice that the first and third terms are} \\ \text{opposites; use the Commutative Property of} & −84n+84n+(−73n) \\ \text{addition to re-order the terms.} \\ \text{Add left to right.} & 0+(−73n) \\ \text{Add.} & −73n \end{array}\)

EXAMPLE \(\PageIndex{8}\)

Simplify: \(−27a+(−48a)+27a\).

\(−48a\)

EXAMPLE \(\PageIndex{9}\)

Simplify: \(39x+(−92x)+(−39x)\).

\(−92x\)

Now we will see how recognizing reciprocals is helpful. Before multiplying left to right, look for reciprocals—their product is 1.

EXAMPLE \(\PageIndex{10}\)

Simplify: \(\frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7}\).

\(\begin{array}{lc} \text{} & \frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7} \\ \text{Notice the first and third terms} \\ {\text{are reciprocals, so use the Commutative} \\ \text{Property of multiplication to re-order the} \\ \text{factors.}} & \frac{7}{15}·\frac{15}{7}·\frac{8}{23} \\ \text{Multiply left to right.} & 1·\frac{8}{23} \\ \text{Multiply.} & \frac{8}{23} \end{array}\)

EXAMPLE \(\PageIndex{11}\)

Simplify: \(\frac{9}{16}⋅\frac{5}{49}⋅\frac{16}{9}\).

\(\frac{5}{49}\)

Simplify: \(\frac{6}{17}⋅\frac{11}{25}⋅\frac{17}{6}\).

\(\frac{11}{25}\)

The next example makes us aware of the distinction between dividing 0 by some number or some number being divided by 0.

Simplify: a. \(\frac{0}{n+5}\), where \(n\neq −5\) b. \(\frac{10−3p}{0}\) where \(10−3p\neq 0.\)

\(\begin{array}{lc} {} & \dfrac{0}{n+5} \\ \text{Zero divided by any real number except itself is 0.} & 0 \end{array}\)

\(\begin{array}{lc} {} & \dfrac{10−3p}{0} \\ \text{Division by 0 is undefined.} & \text{undefined} \end{array}\)

EXAMPLE \(\PageIndex{14}\)

Simplify: a. \(\frac{0}{m+7}\), where \(m\neq −7\) b. \(\frac{18−6c}{0}\), where \(18−6c\neq 0\).

a. 0 b. undefined

EXAMPLE \(\PageIndex{15}\)

Simplify: a. \(\frac{0}{d−4}\), where \(d\neq 4\) b. \(\frac{15−4q}{0}\), where \(15−4q\neq 0\).

Simplify Expressions Using the Distributive Property

Suppose that three friends are going to the movies. They each need $9.25—that’s 9 dollars and 1 quarter—to pay for their tickets. How much money do they need all together?

You can think about the dollars separately from the quarters. They need 3 times $9 so $27 and 3 times 1 quarter, so 75 cents. In total, they need $27.75. If you think about doing the math in this way, you are using the Distributive Property.

DISTRIBUTIVE PROPERTY

\(\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\)

In algebra, we use the Distributive Property to remove parentheses as we simplify expressions.

EXAMPLE \(\PageIndex{16}\)

Simplify: \(3(x+4)\).

\(\begin{array} {} & 3(x+4) \\ \text{Distribute.} \; \; \; \; \; \; \; \; & 3·x+3·4 \\ \text{Multiply.} & 3x+12 \end{array}\)

Simplify: \(4(x+2)\).

EXAMPLE \(\PageIndex{18}\)

Simplify: \(6(x+7)\).

Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in Example would look like this:

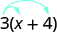
EXAMPLE \(\PageIndex{19}\)

Simplify: \(8(\frac{3}{8}x+\frac{1}{4})\).

EXAMPLE \(\PageIndex{20}\)

Simplify: \(6(\frac{5}{6}y+\frac{1}{2})\).

EXAMPLE \(\PageIndex{21}\)

Simplify: \(12(\frac{1}{3}n+\frac{3}{4})\)

Using the Distributive Property as shown in the next example will be very useful when we solve money applications in later chapters.

EXAMPLE \(\PageIndex{22}\)

Simplify: \(100(0.3+0.25q)\).

EXAMPLE \(\PageIndex{23}\)

Simplify: \(100(0.7+0.15p).\)

EXAMPLE \(\PageIndex{24}\)

Simplify: \(100(0.04+0.35d)\).

When we distribute a negative number, we need to be extra careful to get the signs correct!

EXAMPLE \(\PageIndex{25}\)

Simplify: \(−11(4−3a).\)

\(\begin{array}{lc} {} & −11(4−3a) \\ \text{Distribute. } \; \; \; \; \; \; \; \; \; \;& −11·4−(−11)·3a \\ \text{Multiply.} & −44−(−33a) \\ \text{Simplify.} & −44+33a \end{array}\)

Notice that you could also write the result as \(33a−44.\) Do you know why?

Simplify: \(−5(2−3a)\).

\(−10+15a\)

EXAMPLE \(\PageIndex{27}\)

Simplify: \(−7(8−15y).\)

\(−56+105y\)

In the next example, we will show how to use the Distributive Property to find the opposite of an expression.

Simplify: \(−(y+5)\).

\(\begin{array}{lc} {} & −(y+5) \\ \text{Multiplying by }−1 \text{ results in the opposite.}& −1(y+5) \\ \text{Distribute.} & −1·y+(−1)·5 \\ \text{Simplify.} & −y+(−5) \\ \text{Simplify.} & −y−5 \end{array} \)

EXAMPLE \(\PageIndex{29}\)

Simplify: \(−(z−11)\).

\(−z+11\)

EXAMPLE \(\PageIndex{30}\)

Simplify: \(−(x−4)\).

\(−x+4\)

There will be times when we’ll need to use the Distributive Property as part of the order of operations. Start by looking at the parentheses. If the expression inside the parentheses cannot be simplified, the next step would be multiply using the Distributive Property, which removes the parentheses. The next two examples will illustrate this.

EXAMPLE \(\PageIndex{31}\)

Simplify: \(8−2(x+3)\)

We follow the order of operations. Multiplication comes before subtraction, so we will distribute the 2 first and then subtract.

\(\begin{array}{lc} {} & \text{8−2(x+3)} \\ \text{Distribute.} & 8−2·x−2·3 \\ \text{Multiply.} & 8−2x−6 \\ \text{Combine like terms.} &−2x+2 \end{array}\)

EXAMPLE \(\PageIndex{32}\)

Simplify: \(9−3(x+2)\).

\(3−3x\)

EXAMPLE \(\PageIndex{33}\)

Simplify: \(7x−5(x+4)\).

\(2x−20\)

EXAMPLE \(\PageIndex{34}\)

Simplify: \(4(x−8)−(x+3)\).

\(\begin{array}{lc} {} & 4(x−8)−(x+3) \\ \text{Distribute.} & 4x−32−x−3 \\ \text{Combine like terms.} & 3x−35 \end{array}\)

EXAMPLE \(\PageIndex{35}\)

Simplify: \(6(x−9)−(x+12)\).

\(5x−66\)

EXAMPLE \(\PageIndex{36}\)

Simplify: \(8(x−1)−(x+5)\).

\(7x−13\)

All the properties of real numbers we have used in this chapter are summarized here.

Key Concepts