Numerical Problems on Poisson’s Ratio
- Post author By Hemant More
- Post date November 12, 2019
- 1 Comment on Numerical Problems on Poisson’s Ratio

Science > Physics > Elasticity > Numerical Problems on Poisson’s Ratio
In this article, we shall study the concept of poisson’s ratio and numerical problems on it. The concept of this constant (Poisson,s ratio) was introduced by physicist Simeon Poisson. When a rod or wire is subjected to tensile stress, its length increases in the direction of stress, but its transverse (lateral) dimensions decrease and vice-versa. i.e. when the length increase, the thickness decreases and vice-versa. In other words, we can say that the longitudinal strain is always accompanied by a transverse (lateral) strain.

The ratio of transverse strain to the corresponding longitudinal strain is called Poisson’s ratio. It is denoted by letter ‘m’. It has no unit. It is a dimensionless quantity.
Poisson’s Ratio = Lateral strain / Longitudinal strain
For homogeneous isotropic medium -1 ≤ m ≤ 0.5. In actual practice, Poisson’s ratio is always positive. There are some materials with a negative Poisson’s ratio. Poisson’s ratio of cork is zero, that of metal is 0.3 and that of rubber is 0.5.
Materials with a negative value of Poisson’s ratio are said to be auxetic. They grow larger in the transverse direction when stretched and smaller when compressed. Most auxetic materials are polymers with a crumpled, foamy structure. Pulling the foam causes the crumples to unfold and the whole network expands in the transverse direction.
Numerical Problems:
Example – 1:
When a brass rod of diameter 6 mm is subjected to a tension of 5 × 10 3 N, the diameter changes by 3.6 × 10 -4 cm. Calculate the longitudinal strain and Poisson’s ratio for brass given that Y for the brass is 9 × 10 10 N/m².
Given: Diameter of rod = D = 6 mm, Radius of wire = 6/2 = 3 mm = 3 × 10 -3 m, Load F = 5 × 10 3 N, Change in diameter = d = 3.6 × 10 -4 cm = 3.6 × 10 -6 m, Y for the brass is 9 × 10 10 N/m².
To Find: Longitudinal strain =? Poisson’s ratio = ?,
Y = Longitudinal Stress /Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Longitudinal Strain = F / (A × Y)
∴ Longitudinal Strain = F / (π r² × Y)
∴ Longitudinal Strain = 5 × 10 3 / (3.142 × (3 × 10 -3 )² × 9 × 10 10 )
∴ Longitudinal Strain = 5 × 10 3 / (3.142 × 9 × 10 -6 × 9 × 10 10 )
∴ Longitudinal Strain = 1.96 × 10 -3
Now, Lateral strain = d /D = (3.6 × 10 -6 )/ (6 × 10 -3 ) = 6 × 10 -4
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Poisson’s ratio = (6 × 10 -4 ) / (1.96 × 10 -3 ) = 0.31
Ans: Longitudinal strain is 1.96 × 10 -3 and Poisson’s ratio is 0.31.
Example – 2:
A metal wire of length 1.5 m is loaded and an elongation of 2 mm is produced. If the diameter of the wire is 1 mm, find the change in the diameter of the wire when elongated. σ = 0.24.
Given: Original length of wire = L = 1.5 m, Elongation in wire = 2 mm = 2 × 10 -3 m, Diameter of wire = D = 1 mm, Poisson’s ratio = σ = 0.24.
To Find: Change in diameter = d =?
Longitudinal strain = l/L = (2 × 10 -3 )/1.5 = 1.33 × 10 -3
Poisson’s ratio = Lateral strain / Longitudinal strain
∴ Lateral strain =Poisson’s ratio × Longitudinal strain
∴ Lateral strain = 0.24 × 1.33 × 10 -3 = 3.2 × 10 -4
Lateral strain = d / D
∴ d = Lateral strain × D = 3.2 × 10 -4 × 1 × 10 -3 = 3.2 × 10 -7 m
Ans: The change in diameter is 3.2 × 10 -7 m
Example – 3:
A metallic wire (Y = 20 × 10 10 N/m². and σ = 0.26) of length 3 m and diameter 0.1 cm is stretched by a load of 10 kg. Calculate the decrease in diameter of the wire.
Given: Original length of wire = L = 3 m, Diameter of wire = D = 0.1 cm = 0.1 × 10 -2 m = 1 × 10 -3 m, Radius of wire = r = 0.1/2 = 0.05 cm = 0.05 × 10 -2 m = 5 × 10 -4 m,, Stretching load = 10 kg = 10 x 9.8 N, Young’s modulus of elasticity = Y = 20 × 10 10 N/m², and Poisson’s ratio = σ = 0.26
To Find: Decrease in diameter = d =?
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × (5 × 10 -4 )² × 20 × 10 10 )
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × 25 × 10 -8 × 20 × 10 10 )
∴ Longitudinal Strain = 6.24 × 10 -4
∴ Lateral strain = 0.26 × 6.24 × 10 -4 = 1.62 × 10 -4
∴ d = Lateral strain × D = 1.62 × 10 -4 ×1 × 10 -3 = 1.62 × 10 -7 m
Ans: The decrease in diameter is 1.62 × 10 -7 m
Example – 4:
A copper wire 3m long and 1 mm² in cross-section is fixed at one end and a weight of 10 kg is attached at the free end. If Y for copper is 12.5 × 10 10 N/m² and σ = 0.25 find the extension, lateral strain and the lateral compression produced in the wire.
Given: Original length of wire = L = 3 m, Area of cross-section of wire = A = 1 mm² = 1 × 10 -6 m², Stretching load = 10 kg = 10 × 9.8 N, Young’s modulus of elasticity = Y = 12.5 × 10 10 N/m², and Poisson’s ratio = σ = 0.25
To Find: Extension = l =? Lateral strain = ?, Lateral compression = ?
∴ Longitudinal Strain = 10 × 9.8 / (1 × 10 -6 × 12.5 × 10 10 )
∴ Longitudinal Strain = 7.84 × 10 -4
Now, Longitudinal Strain = l/L
∴ l = Longitudinal strain × L
∴ l = 7.84 × 10 -4 × 3 =2.352 × 10 -3 m = 2.352 mm
∴ Lateral strain = 0.25 × 7.84 × 10 -4 = 1.96 × 10 -4
Area of cross-section = A = 1 × 10 -6 m²
∴ π r² = 1 × 10 -6
∴ r² = 1 × 10 -6 / π = = 1 × 10 -6 / 3.142
∴ r² = 0.3183 × 10 -6
∴ r = 5.64 × 10 -4 m
Diameter = D = 2r = 2 × 5.64 × 10 -4 m = 11.28 × 10 -4 m
Now, Lateral strain = d / D
∴ d = Lateral strain × D = 1.96 × 10 -4 × 11.28 × 10 -4 = 2.21 × 10 -7 m
Ans: Elongation = 2.352 mm, Lateral strain = 1.96 × 10 -4 , Lateral compression = 2.21 × 10 -7 m.
Example – 5:
A wire of diameter 2 mm and length 5 m is stretched by a load of 10 kg. Find the extension produced in the wire if Y = 12 × 10 10 N/m². If σ = 0.35 for the material of the wire, find the lateral contraction.
Given: Original length of wire = L = 5 m, Diameter of wire = D = 2 mm = 2 × 10 -3 m , Radius of wire = 2/2 = 1mm = 1 × 10 -3 m, Stretching load = 10 kg = 10 × 9.8 N, Young’s modulus of elasticity = Y = 12 × 10 10 N/m², and Poisson’s ratio = σ = 0.35
To Find: Lateral contraction =?
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × (1 × 10 -3 )² × 12 × 10 10 )
∴ Longitudinal Strain = (10 x 9.8) / (3.142 × 1 × 10 -6 × 12 × 10 10 )
∴ Longitudinal Strain = 2.6 × 10 -4
∴ l = 2.6 × 10 -4 × 5 = 1.3 × 10 -3 m = 1.3 mm
∴ Lateral strain = 0.35 ×2.6 × 10 -4 = 9.1 × 10 -5
∴ d = Lateral strain × D = 9.1 × 10 -5 × 2 × 10 -3 = 1.82 × 10 -7 m
Ans: Elongation = 1.3 mm, Lateral contraction = 1.82 × 10 -7 m
Example – 6:
Find the longitudinal stress to be studied to a wire to decrease its diameter uniformly by 1%. Poisson’s ratio = 0.25, Young’s modulus = 2 × 10 11 N/m².
Given: Lateral strain = 1 % = 1 × 10 -2 , Young’s modulus of elasticity = Y = 2 × 10 11 N/m² . and Poisson’s ratio = σ = 0.25
To Find: Longitudinal stress =?
∴ Longitudinal strain =Lateral strain / Poisson’s ratio
∴ Longitudinal strain = 1 × 10 -2 / 0.25 = 4 × 10 -2
∴ Longitudinal Stress = Longitudinal Strain × Y
∴ Longitudinal Stress = 4 × 10 -2 × 2 × 10 11 = 8 × 10 9 N/m² .
Ans: Longitudinal stress = 8 × 10 9 N/m²
Example – 7:
A copper wire 3 m long is stretched to increase its length by 0.3 cm. Find the lateral strain produced in the wire. If Poisson’s ratio for copper is 0.26.
Given: Length of wire = L = 3m, Increase in length = l = 0.3 cm = 0.3 × 10 -2 m = 3 × 10 -3 m, Poisson’s ratio = σ = 0.26
To Find: Lateral strain =?
Longitudinal strain = l/L = (3 × 10 -3 )/ 3 = 10 -3
∴ Lateral strain = 0.36 × 10 -3 = 3.6 × 10 -4
Ans: Lateral strain = 3.6 × 10 -4
Example – 8:
A steel wire having cross-sectional area 1 mm² is stretched by 10 N. Find the lateral strain produced in the wire. Young’s modulus for steel is 2 × 10 11 N/m² and Poisson’s ratio is 0.291.
Given: Area of cross-section = 1 mm² = 1 × 10 -6 m², Stretching Load = 10 N, Young’s modulus for steel= Y = 2 × 10 11 N/m², Poisson’s ratio = σ = 0.291
Y = Longitudinal Stress / Longitudinal Strain
∴ Y = F / (A × Longitudinal Strain)
∴ Longitudinal strain = F / (A × Y)
∴ Longitudinal strain = 10 / (1 × 10 -6 × 2 × 10 11 ) = 5 × 10 -5
∴ Lateral strain = 0.291 × 5 × 10 -5 = 1.455 × 10 -5
Ans: Lateral strain =1.455 × 10 -5
Example – 9:
A load 1 kg produces a certain extension in the wire of length 3 m and radius 5 × 10 -4 m. How much will be the lateral strain produced in the wire? Given Y = 7.48 × 10 10 N/m², σ = 0.291.
Given: Load attached = F = 1 kg = 1 × 9.8 N , Length of wire = L = 3 m, Radius of cross-section = r = 5 × 10 -4 m cross-section = 1 mm² = 1 × 10 -6 m², Stretching Load = 10 N, Young’s modulus = Y = 7.48 × 10 10 N/m², Poisson’s ratio = σ = 0.291
∴ Y = F / (A × Longitudinal Strain)
∴ Y = F / (π r² × Longitudinal Strain)
∴ Longitudinal strain = (1 × 9.8) /(3.142 × (5 × 10 -4 )² × 7.48 × 10 10 )
∴ Longitudinal strain = (1 × 9.8) /(3.142 × 25 × 10 -8 × 7.48 × 10 10 )
∴ Longitudinal strain = 1.67 × 10 -4
∴ Lateral strain = 0.291 × 1.67 × 10 -4 = 4.86 × 10 -5
Ans: Lateral strain = 4.86 × 10 -5
Previous Topic: Numerical Problems on Stress, Strain, and Young’s Modulus
Next Topic: Numerical Problems on Stresses and Strains in Composite Wires
- Tags Deformation , deforming force , Elastic material , Elasticity , Extension in wire , Hooke's law , Lateral strain , Longitudinal strain , Longitudinal stress , Modulus of elasticity , Plastic material , Plasticity , Rigid material , Rigidity , Strain , Stress , Young's modulus of elasticity
One reply on “Numerical Problems on Poisson’s Ratio”
I am happy now ,I can solve problems on poisson’s ratio .
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *

- Science Notes Posts
- Contact Science Notes
- Todd Helmenstine Biography
- Anne Helmenstine Biography
- Free Printable Periodic Tables (PDF and PNG)
- Periodic Table Wallpapers
- Interactive Periodic Table
- Periodic Table Posters
- Science Experiments for Kids
- How to Grow Crystals
- Chemistry Projects
- Fire and Flames Projects
- Holiday Science
- Chemistry Problems With Answers
- Physics Problems
- Unit Conversion Example Problems
- Chemistry Worksheets
- Biology Worksheets
- Periodic Table Worksheets
- Physical Science Worksheets
- Science Lab Worksheets
- My Amazon Books
Poisson’s Ratio

Poisson’s ratio (symbol ν or nu) or is a mechanical property of a material that is the measure of its deformation perpendicular to the direction of loading. In other words, it is the negative value of the ratio of transverse or lateral strain (x-direction) to axial or longitudinal strain (y-direction).
The ratio takes its name from French physicist and mathematician Siméon Poisson. It measures the Poisson effect , which is the tendency of a material to compress in the direction perpendicular to the applied force. For example, a rubber band becomes thinner when you stretch it or thicker when you compress it.
In simple terms, Poisson’s ratio measures a materials ability to thicken when compressed or thin when stretched.
Formula for Poisson’s Ratio
The reason the formula for Poisson’s ratio contains a negative sign is so the unitless scalar value is positive for most materials under tensile deformation. There are multiple ways of writing the formula:
Poisson’s ratio (ν) = transverse strain / longitudinal strain = – d ε trans / d ε axial = – d ε lat / d ε long
Here, strain ε is the change in length divided by original length:
What Poisson’s Ratio Means
Most materials have Poisson’s ratio values ranging between 0.0 and 0.5.
Soft materials, like rubber, have Poisson’s ratio values near 0.5. Steel and rigid polymers typically have values around 0.3. Porous materials typically have Poisson’s ratio values close to zero. This is because they collapse when compressed.
Auxetic materials have negative Poisson’s ratio values. In other words, they thicken when stretched and thin when compressed. Origami-folded materials and certain crystals are auxetic materials.
Is Poisson’s Ratio a Constant for a Material?
Poisson’s ratio is relatively constant within elastic limits for most materials. There are exceptions.
Poisson’s ratio is not necessarily the same for elongation versus compression. Also, the ratio may be isotropic or anisotropic . For a linear isotropic material, the deformation is the same regardless of the material’s axis. For an anisotropic material, Poisson’s ratio depends on the stress and strain axis.
Usually, Poisson’s ratio gradually increases with temperature, up to a certain peak temperature. In most cases, the overall effect is small because changing temperature affects both transverse and axial strain.
Table of Poisson’s Ratio Values
This table lists representative Poisson’s ratio values for a range of materials:
| Material | Poisson’s Ratio |
|---|---|
| cork | 0.0 |
| foam | 0.10-0.50 |
| glass | 0.18-0.30 |
| concrete | 0.1-0.2 |
| sand | 0.2-0.455 |
| magnesium | 0.252-0.289 |
| titanium | 0.265-0.34 |
| stainless steel | 0.30-0.31 |
| clay | 0.30-0.45 |
| aluminum alloy | 0.32 |
| copper | 0.33 |
| gold | 0.42-0.44 |
| rubber | 0.5 |
Auxetic Materials
Auxetic materials or auxetics display a negative Poisson’s ratio. They thicken when stretched. Examples of auxetics include certain molecules, macromolecules, bulk materials, and crystals. Usually, auxetics have high fracture resistance and energy absorption. This makes them useful as shock absorbers, packing materials, and body armor.
Here are some examples of auxetic materials:
- Crystalline Li, Na, K, Cu, Fe, and many other metallic elements
- Living bone (probably)
- Most types of paper
- Some types of polytetrafluoroethylene (e.g., Gore-Tex)
- Boresi, A. P.; Schmidt, R. J.; Sidebottom, O. M. (1993). Advanced Mechanics of Materials . Wiley.
- Epishin, A.I.; Lisovenko, D.S. (2016). “Extreme values of Poisson’s ratio of cubic crystals”. Technical Physics . 61 (10): 1516–1524. doi: 10.1016/j.mechmat.2019.03.017
- Gercek, H. (January 2007). “Poisson’s ratio values for rocks”. International Journal of Rock Mechanics and Mining Sciences . 44 (1): 1–13. doi: 10.1016/j.ijrmms.2006.04.011
- Jastrzebski, D. (1959). Nature and Properties of Engineering Materials (Wiley International ed.). John Wiley & Sons, Inc.
- Lakes, R.S. (1987). “Foam structures with a negative Poisson’s ratio”. Science . 235 (4792): 1038–40. doi: 10.1126/science.235.4792.1038
Related Posts
- Physics Class-11th Notes
- Physics Formulas
- Physics Symbol
- Application of Physics
- Class 8 Science
- Class 9 Science
- Class 10 Science
- Class 11 Science
- Class 12 Science
- Class 8 Study Material
- Class 9 Study Material
- Class 10 Study Material
- Class 11 Study Material
- Class 12 Study Material
- Physics: Definition, Branches, Topics and Application
- Rest and Motion
- What is Pressure?
- Inertia Meaning
- Newton's Laws of Motion | Formula, Examples and Questions
- Universal Law of Gravitation
- What is Gravity?
- Law of Conservation of Energy
- Free Body Diagram
- Inclined Plane
- Conservative Forces - Definition, Formula, Examples
- Frame of Reference
- Kinematics | Definition, Formula, Derivation, Problems
- What is Motion?
- Distance and Displacement
- Speed and Velocity
- Acceleration
- Momentum Formula
- Equations of Motion: Derivations and Examples
- Uniform Circular Motion
- Projectile Motion
- Relative Motion
Rotational Mechanics
- Concepts of Rotational Motion
- Angular Motion
- Angular Frequency
- Rotational Kinetic Energy
- Angular Momentum
- Centre of Mass
- Centre of Gravity
- Radius of Gyration
- Moment of Inertia
Fluid Mechanics
- Mechanical Properties of Fluids
- What is Viscosity?
- Buoyant Force
- Archimedes Principle
- Pascal's Law
- Reynolds Number
- Streamline Flow
- Laminar and Turbulent Flow
- Bernoulli's Principle
- Poiseuilles Law Formula
- Stoke's Law
Solid Mechanics
- What is Stress?
- Stress and Strain
- Stress-Strain Curve
- Elasticity and Plasticity
- Modulus of Elasticity
- Modulus of Rigidity
- Young's Modulus
- Bulk Modulus Formula
- Shear Modulus and Bulk Modulus
- Poisson's Ratio
- Stress, Strain and Elastic Potential Energy
Thermodynamics
- Basics Concepts of Thermodynamics
- Zeroth Law of Thermodynamics
- First Law of Thermodynamics
- Second Law of Thermodynamics
- Thermodynamic Cycles
- Thermodynamic State Variables and Equation of State
- Enthalpy: Definition, Formula and Reactions
- State Functions
- Carnot Engine
- Heat Engine - Definition, Working, PV Diagram, Efficiency, Types
Wave and Oscillation
- Introduction to Waves - Definition, Types, Properties
- Wave Motion
- Oscillation
- Oscillatory Motion Formula
- Amplitude Formula
- What is Frequency?
- Amplitude, Time Period and Frequency of a Vibration
- Energy of a Wave Formula
- Simple Harmonic Motion
- Displacement in Simple Harmonic Motion
- Production and Propagation of Sound
- What are the Characteristics of Sound Waves?
- Speed of Sound
- Reflection of Sound
- Refraction of Sound
- How do we hear?
- Audible and Inaudible Sounds
- Explain the Working and Application of SONAR
- Noise Pollution
- Doppler Effect - Definition, Formula, Examples
- Doppler Shift Formula
- Electrostatics
- Electric Charge
- Coulomb's Law
- Electric Dipole
- Dipole Moment
- Electrostatic Potential
- Electric Potential Energy
- Potential due to an Electric Dipole
- Equipotential Surfaces
- Capacitor and Capacitance
Current Electricity
- Electric Current
- Heating Effect of Electric Current
- Alternating Current
- Electrical Energy and Power
- Electric Circuit
Poisson’s Ratio
Poisson’s Ratio is the negative ratio of transversal strain or lateral strain to the longitudinal strain of a material under stress. When a material particularly a rubber-like material undergoes stress the deformation is not limited to only one direction, rather it happens along both transversal and longitudinal directions. In this situation, material scientists are curious to know the ratio of transversal and longitudinal deformation that occurred in the object to know about the strength of the material.
Table of Content
What is Poisson’s Ratio?
Poisson ratio definition, longitudinal and transversal strain, poisson’s ratio formula, poisson effect, poisson’s ratio values for different materials, poisson’s ratio range, people also view:, applications of poisson’s ratio, 1. poission’s ratio in bending, 2. poisson’s ratio in anisotropic material, 3. poisson’s ratio in viscoelastic material, 4. poisson’s ratio in phase transformation, poisson’s ratio – solved examples.
In this article, we will learn about the longitudinal and transversal strain, the calculation of the Poisson Ratio, and other related aspects in detail.
Poisson’s ratio is the ratio of the amount of transversal expansion to the amount of axial compression for small values of these changes.
Poisson Ratio is defined as the negative ratio of the transversal strain to the longitudinal strain. It basically compares the change in the breadth of an object with respect to the change in the length of the object. It gives an idea about the strength of a material.
When Stress is applied the change in dimension is seen along the direction of the stress applied and also the direction perpendicular to the stress applied. Let’s say when we apply tension stress on a horizontal bar, the length of the bar will increase along the direction of the applied stress. This is called Longitudinal Strain. Along with the increase in length, you will observe that the bar becomes thin in between i.e. the breadth of the bar decreases. This is what we call Transversal Strain. Both longitudinal and transversal strain go hand in hand but not at the same rate. To measure the relativeness of longitudinal and transversal strain we use Poisson’s Ratio.
Longitudinal Strain is given by ε l = ΔL / L and it is positive as there is an increase in length.
Transversal Strain is given by ε t = ΔB / B and it is negative as breadth decreases on applying tensile stress.
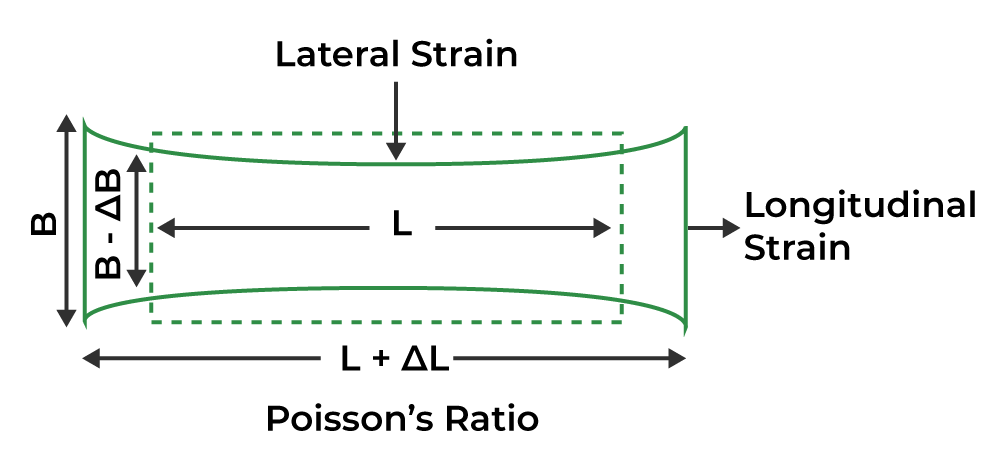
Now in the below sections, we will learn about Poisson Ratio in detail.
As stated in its definition, Poisson Ratio is given as the negative of the ratio of the transversal strain to the longitudinal strain its formula is mentioned below:
ν = -ε t /ε l Where , ν is Poisson’s Ratio ε t is Transversal Strain, and ε l is Longitudinal Strain.
The negative sign in the ratio is used to make the ratio positive because the numerator i.e. transversal strain is generally negative due to a decrease in breadth. Thus Poisson’s Ratio is generally positive in nature, however in the case of material whose thickness increases on applying tensile stress such as polymers then that material will have a negative Poisson Ratio. Poisson Ratio is an scalar quantity.
Unit of Poisson Ratio: Since the Poisson Ratio is a ratio change in the length along transversal and longitudinal directions it has no unit.
Dimension of Poisson Ratio: Since there is no unit of Poisson Ration, there is no dimension of Poisson Ratio.
The Poisson effect is a phenomenon in which a material expands in directions perpendicular to the direction of compression. Poisson’s ratio is a measure of this phenomenon. When a material is stretched rather than crushed, it tends to contract in directions that are transverse to the stretching direction.
Poisson’s Ratio is a scalar and a unitless quantity. It has a positive magnitude for tensile deformation while it has a negative value for auxetic materials like polymer.
The minus sign in Poisson’s Ratio formula indicates that the ratio of the transversal strain to the longitudinal strain is always positive.
The range of Poisson’s Ratio value lies between -1.0 to +0.5. However, the value of Poisson’s ratio for most materials is between 0 and 0.5.
For plastics, the Poisson’s Ratio is in the range of 0 to 0.5. When the Poisson’s Ratio is 0, there is no reduction in diameter or, to put it another way, no lateral contraction occurs when the material is elongated, but the density decreases.
When the diameter of the material drops during the elongation process or when the material is elastomeric, a value of 0.5 implies that the volume of the material or item will remain the same or constant.
The following table shows the various Poisson’s Ratios for various materials.
| Material | Poisson’s Ratio |
|---|---|
| Rubber | 0.49 |
| Gold | 0.43 |
| Clay | 0.37 |
| Copper | 0.33 |
| Aluminum | 0.32 |
| Cast Iron | 0.24 |
| Concrete | 0.2 |
| Cork | 0 |
Poisson’s Ratio is usually positive since most common materials get narrower in the opposite or cross direction when stretched. Most materials resist changes in volume, as defined by the bulk modulus K or also known as B, more than changes in shape, as determined by the shear modulus G. The shape distortion also causes the interatomic connections to realign.
Difference between Stress and Strain Hooke’s Law Young’s Law
Poisson’s Ratio is majorly used to analyze the strength of the material. However, it has got some other applications also which are mentioned below:
While bending a bar, the curvature of the bar perpendicular to the bending is governed by Poisson’s Ratio, while in the case of rubber anticlastic curvature i.e. convex along the longitudinal plane and concave along the perpendicular plane is observed.
Anisotropic Material is those which have direction-dependent properties. Examples include crystals, honeycombs, etc. In such objects, the Poisson’s Ratio is also direction dependent. Also, it can take any arbitrary large positive or negative value under the defined positive strain energy density.
The viscoelastic material goes under creep which is a time-dependent phenomenon. In this case, Poisson’s Ratio is a function of time and also the frequency and the phase angle if there is sinusoidal deformation in the viscoelastic material.
The Poisson’s Ratio of material is significantly affected by its phase transformation. At the point of phase transformation, the value of Poisson’s Ratio starts decreasing significantly and can even take a negative value as the bulk modulus of a material reduces at Phase Transformation Point.
Problem 1: The longitudinal strain for a wire is 0.02 and its Poisson ratio is 0.6. Find the lateral strain in the wire.
Given: Longitudinal strain of wire = 0.02 Poisson ratio = 0.6 The Poisson’s Ratio formula is as follows: ν = lateral strain/longitudinal strain Substitute the given values to find the lateral strain. 0.6 = Lateral strain / 0.02 Lateral strain = 0.012 Hence, the lateral strain in the wire is 0.012.
Problem 2: What is the maximum and minimum values of Poisson’s ratio for a metal?
The Poisson’s Ratio formula is as follows: ν = Lateral strain/longitudinal strain It is always positive because if we apply force in longitudinal strain, lateral strain always decreases for metals. It lies between 0 to 0.5 .
Problem 3: Is Poisson’s ratio affected by temperature?
In general, lower temperatures reduce both horizontal and vertical strain, while higher temperatures increase both horizontal and vertical strain. As a result, the net effect on Poisson’s Ratio is negligible because both horizontal and vertical strain change by the same amount.
Problem 4: A 2.0 m long metal wire is loaded, resulting in a 4 mm elongation. Find the change in diameter of wire when elongated if the diameter of wire is 1.5 mm and the Poisson’s ratio of wire is 0.24.
Given: Length of wire, L is 2.0 m. Change in length, ΔL is 4 mm = 0.004 m Diameter of wire, D is 1.5 mm. Poisson’s ratio, ν is 0.24. The longitudinal strain in the wire is given as: Longitudinal strain = ΔL/L = 0.004/2.0 = 0.002 The Poisson’s Ratio formula is as follows: ν = Lateral strain/longitudinal strain Substitute the given values to find the lateral strain. 0.24 = lateral strain / 0.002 Lateral strain = 0.00048 The lateral strain in a wire is given as: Lateral strain = ΔD / D 0.00048 = ΔD / 1.5 mm ΔD = 0.00072 mm Hence, the change in diameter of the wire is 0.00072 mm.
Problem 5: What if a material’s Poisson ratio is zero?
A Poisson’s ratio of 0 indicates that the material does not deform in either the lateral or axial directions in response to the application of force. Cork is an example of a material with a Poisson’s ratio of nearly 0 and no deformation under stress. Cork is applied as a seal in bottle stoppers because it expands and contracts under stress, protecting the substance inside.
Important Physics Related Links:
- Rolling Resistance Formula
- Diagram of Human Eye with Labeling
- What is Archimedes Principle
- Newton Action Reaction
- Define Fluid Flow
- Speed of Sound in km
- Electromagnetic Properties
- List of Heavenly Bodies
- Visible Rays
- SI Unit of Electricity
Poisson’s Ratio – FAQs
Poisson Ratio is the negative of the ratio of lateral strain to the longitudinal strain.
What is the Formula for Poisson’s Ratio?
The formula for Poisson’s Ratio is given as Poisson’s Ratio = – Transversal Strain/Longitudinal Strain
What is the Unit of Poisson’s Ratio?
Poisson’s Ratio has no units. It is a unitless scalar quantity.
What is Poisson’s Ratio of Steel?
The value of Poisson’s Ratio of Steel is 0.28.
What is Poisson’s Ratio of Concrete?
The value of Poisson’s Ratio of Concrete is 0.1 to 0.2.
Why is Poisson’s Ratio Negative?
The negative sign in the formula of Poisson’s Ratio is to make the ratio of transversal strain to the longitudinal strain positive.
Which Material has the Highest Poisson Ratio?
Elastic Rubber has the highest Poisson’s Ratio.
What does Poisson’s Ratio 0.5 signify?
The value of Poisson’s Ratio 0.5 signify that the material is incompressible but deformed within elastic limits.
Why Poisson’s Ratio of Cork is Zero?
The Zero value of Poisson’s Ratio of a Cork is because there is no deformation either in longitudinal or lateral direction on application of stress.
What is Poisson’s Ratio of Rubber?
Rubber has approximate Poisson’s Ratio of 0.5.
What is Poisson’s Ratio of Soil?
As soil is not same everywhere, for soft to stiff clay Poisson’s ratio fof 0.20–0.45 and for loose sand Poisson’s ratio is 0.15–0.35.
Please Login to comment...
Similar reads.
- Physics-Class-11
- School Learning
- School Physics
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

www.springer.com The European Mathematical Society
- StatProb Collection
- Recent changes
- Current events
- Random page
- Project talk
- Request account
- What links here
- Related changes
- Special pages
- Printable version
- Permanent link
- Page information
- View source
Poisson equation, numerical methods
Methods replacing the original boundary value problem for the Poisson equation
$$ \tag{1 } \Delta u ( x) \equiv \sum_{r=1}^ { d } \frac{\partial ^ {2} u ( x) }{\partial x _ {r} ^ {2} } = f ( x) ,\ x \equiv ( x _ {1} \dots x _ {d} ) , $$
by a system of $ N $ linear algebraic equations
$$ \tag{2 } L _ {N} ( \mathbf u _ {N} ) = \mathbf f _ {N} , $$
with a solution $ \mathbf u _ {N} \equiv ( u _ {1} \dots u _ {n} ) $ which makes it possible to construct a certain approximation $ p _ {N} \mathbf u ^ {N} $ to the solution of the original problem as $ N \rightarrow \infty $.
One defines such extremely important concepts as the error of the numerical method and bounds for the error (the accuracy) depending on the way one compares the solutions of the original problem (1) and the discrete problem (2). The algebraic properties of the system (2) (discrete analogues of boundary value problems) connected with the stability of solutions (the well-posedness of the discrete problems), the possibility of finding exact or approximate solutions of (2) by some direct or iterative method when carrying out the corresponding computation and corresponding demands on the computer memory (see Minimization of the labour of calculation ) give other characteristics of the numerical methods.
Numerical solutions of boundary value problems for the Poisson equation are important not only because these problems often arise in diverse branches of science and technology, but because they frequently are a means for solving more general boundary value problems for both equations and systems of equations of elliptic type as well as for various non-stationary systems. The basic numerical methods for solving the boundary value problems under discussion are projection methods and difference methods (see [1] – [13] ).
- 1 Projection methods.
- 2.1 References
- 2.2 Comments
- 2.3 References

Projection methods.
These encompass a number of methods: variational, least squares, Galerkin, projection-difference, projection-grid, and finite elements methods. In all of these one characteristically reduces the original boundary value problem to an operator equation
$$ \tag{3 } L ( u) = f $$
(the operator $ L $ acts, for example, from a Hilbert space $ H $ into $ H $) with subsequent choice of finite-dimensional subspaces $ H _ {N} $ and $ F _ {N} $( $ N \rightarrow \infty $): the problem (3) itself is replaced in these methods by the problem of finding a $ \widehat{u} _ {N} \in H _ {N} $ such that for any $ v \in F _ {N} $,
$$ ( L \widehat{u} _ {N} - f , v ) _ {H} = 0 . $$
Then, given bases in $ H _ {N} $ and $ F _ {N} $, the system (2) is a system for the coefficients in the expansion of $ \widehat{u} _ {N} $ with respect to the basis of $ H _ {N} $ and $ p _ {N} \mathbf u _ {N} $ can be taken as the function $ \widehat{u} _ {N} $ itself; it is natural to define the error in the method as $ \| u - \widehat{u} _ {N} \| _ {H} $. In the most important cases $ H $ is a certain subspace of the Sobolev space $ W _ {2} ^ { \prime } ( \Omega ) $, $ H _ {N} = F _ {N} $ and, if $ \psi _ {1} ( x) \dots \psi _ {N} ( x) $ is a basis of $ H _ {N} $, then the system (2) takes the form
$$ \tag{4 } \sum_{j=1}^ { N } u _ {j} \int\limits _ \Omega \mathop{\rm grad} \psi _ {j} ( x) \ \mathop{\rm grad} \psi _ {i} ( x) \ d x = \int\limits _ \Omega f ( x) \psi _ {i} ( x) d x , $$
$$ i = 1 \dots N . $$
The error in the method is estimated by the distance in $ H $ from the solution of the original problem to the subspace $ H _ {N} $( see [1] , [5] – [11] ). In modern variants of projection methods the subspaces $ H _ {N} $ tend to be chosen so that the functions $ \psi _ {i} ( x) $ have local supports and in each equation (4) only a finite number of coefficients are non-zero. Methods of this type are also called projection-grid methods (projection-difference, variational-difference, finite element methods) (see [1] , [4] , [7] – [11] ). The great merit of these methods is that they can be applied when the domain $ \Omega $ of the boundary value problem under consideration is geometrically fairly complicated. Methods which are also close to projection methods but relatively rarely applied are the collocation method , spectral methods and boundary element methods (see [13] – [15] ).
Difference (finite-difference) methods.
These use a certain grid domain $ \Omega _ {N} $ containing $ N $ nodes of a grid to approximate the original domain $ \Omega $ and usually lead to a system (2) by approximating the Poisson equation and the corresponding boundary conditions by their difference (grid) analogues, using only the values of the function at the chosen nodes (see [1] ). The error of the method is usually obtained by comparing the vector $ \mathbf u _ {N} $ and the vector obtained by restricting the required solution to the set of nodes under consideration. The well-posedness and approximation can be studied for various choices of norms; it is, in particular, possible to use the maximum principle; convergence is obtained as a corollary of well-posedness and approximation (see [1] – [4] ).
Systems (2) can be derived both by basing them on certain discrete analogues of the corresponding variational problems and by basing them on an approximation to certain integral relations (see [1] , [2] , [4] , [11] ); such approaches bring these variants of difference methods somewhat closer to projection-difference methods.
The most intensively studied methods for solving systems of grid equations (2) are the simplest difference analogues on a parallelepiped grid (see [1] , [10] ). In the case of two variables and when the domain $ \Omega $ in the plane is rectangular, direct methods are often applied for a number of boundary conditions; these direct methods enable one to find the solution of (2) at the cost of $ O ( N \mathop{\rm ln} N ) $ arithmetic operations. Such a method is that of separation of variables, which uses the discrete Fourier transform and the reduction method (cf. Separation of variables, method of ); methods are also known with a bound $ O ( N) $ on the numbers of operations (see [11] – [13] ). When $ d \geq 2 $ and one may use separation of variables (in this case $ \Omega $ is a parallelepiped), the solution of (2) can be found with accuracy $ \epsilon > 0 $ at the cost of $ O ( N \mathop{\rm ln} N | \mathop{\rm ln} \epsilon | ) $ operations by an iterative alternating-directions method (see [1] , [11] ); iterative methods with factorizable operators (methods of successive overrelaxation with symmetrization, incomplete matrix factorization, alternating-triangular methods) enable one to find the solution of (2) with accuracy $ \epsilon $ at a cost of $ O ( N ^ {1+1/2d} | \mathop{\rm ln} \epsilon | ) $ operations (see [11] , [12] ) in fairly general situations.
In the case of simply-connected and multiply-connected domains $ \Omega $ in the plane which are composed of a finite number of rectangles, the solution of the system (2) with accuracy $ \epsilon $ can be found at the cost of $ O ( N \mathop{\rm ln} N + N ^ {3/4} | \mathop{\rm ln} \epsilon | \mathop{\rm ln} N ) $ operations by cutting $ \Omega $ up into rectangles (see [11] , [13] ). Similar asymptotic solutions for discrete analogues of the Dirichlet problem can be obtained for certain domains using the methods of capacity and of fictitious unknowns (see [11] , [13] ). For a number of systems (2) which are projection-difference analogues of the original problem, computation lengths of the order $ O ( N \mathop{\rm ln} N | \mathop{\rm ln} \epsilon | ) $ and sometimes also $ O ( N \mathop{\rm ln} N ) $( when $ \epsilon $ is of order $ N ^ {- \alpha } $, $ \alpha > 0 $) can be achieved by iterative methods using the spectral equivalence of operators (see [11] , [13] ). In a number of cases the use of a sequence of grids enables one to obtain methods which give the solution to (2) with an accuracy of order $ N ^ {- \alpha } $, $ \alpha > 0 $, and with asymptotically-minimal computational work (the number of operations is $ O ( N) $) (see for example [1] , [10] , [11] ).
| [1] | S.K. Godunov, V.S. Ryaben'kii, "The theory of difference schemes" , North-Holland (1964) (Translated from Russian) |
| [2] | O.A. Ladyzhenskaya, "The boundary value problems of mathematical physics" , Springer (1986) (Translated from Russian) |
| [3] | G.I. Marchuk, V.V. Shaidurov, "Difference methods and their extrapolations" , Springer (1983) (Translated from Russian) |
| [4] | A.A. Samarskii, V.B. Andreev, "Méthodes aux différences pour équations elliptiques" , MIR (1978) (Translated from Russian) |
| [5] | S.G. Mikhlin, "The numerical performance of variational methods" , Wolters-Noordhoff (1971) (Translated from Russian) |
| [6] | M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [7] | J.P. Aubin, "Approximation of elliptic boundary value problems" , Wiley (1972) |
| [8] | G. Strang, J. Fix, "An analyse of the finite element method" , Prentice-Hall (1973) |
| [9] | P.G. Ciarlet, "The finite element method for elliptic problems" , North-Holland (1978) |
| [10] | W. Hackbush, "Multigrid methods and applications" , Springer (1985) |
| [11] | E.G. D'yakonov, "Minimization of computational work. Asymptotically-optimal algorithms" , Moscow (1989) (In Russian) |
| [12] | A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , , Birkhäuser (1989) (Translated from Russian) |
| [13] | R. Glowinski (ed.) G.H. Golub (ed.) G.A. Meurant (ed.) J. Periaux (ed.) , , SIAM (1988) |
| [14] | C. Canuto, M.Y. Hussaini, A. Quarteroni, T.A. Zang, "Spectral methods in fluid dynamics" , Springer (1988) |
| [15] | P.K. Banerjee, R. Butterfield, "Boundary element methods in engineering science" , McGraw-Hill (1981) |
During the last few years a new and very powerful class of methods has come up which have essentially an $ O( N) $ complexity. These so-called multigrid methods are based on employing smoothing effects of higher frequencies on courser grids and damping of lower frequencies on finer grids. They must be considered to be among the most powerful tools available today (1990) and can be used for finite-difference and finite-element discretization alike.
| [a1] | U. Trottenberg (ed.) , , , , Springer (1982) |
| [a2] | S.F. McCormick, "Multigrid methods" , SIAM (1987) |
| [a3] | G. Birkhoff, R.E. Lynch, "Numerical solution of elliptic problems" , SIAM (1984) |
| [a4] | C. Johnson, "Numerical solution of partial differential equations by the finite element method" , Cambridge Univ. Press (1987) |
| [a5] | G.D. Smith, "Numerical solution of partial differential equations: finite difference method" , Clarendon Press (1978) |
| [a6] | A.R. Mitchell, D.F. Griffiths, "The finite difference method in partial differential equations" , Wiley (1980) |
| [a7] | A.R. Mitchell, R. Wait, "Finite element analysis and applications" , Wiley (1985) |
- This page was last edited on 13 January 2024, at 13:06.
- Privacy policy
- About Encyclopedia of Mathematics
- Disclaimers
- Impressum-Legal
Find Study Materials for
- Explanations
- Business Studies
- Combined Science
- Computer Science
- Engineering
- English literature
- Environmental Science
- Human Geography
- Macroeconomics
- Microeconomics
- Social Studies
- Browse all subjects
- Textbook Solutions
- Read our Magazine
Create Study Materials
- Flashcards Create and find the best flashcards.
- Notes Create notes faster than ever before.
- Study Sets Everything you need for your studies in one place.
- Study Plans Stop procrastinating with our smart planner features.
Chapter 2: Problem 10
Define Poisson's ratio.
Short answer, step by step solution, definition of poisson's ratio, explanation of the parameters, key concepts.
These are the key concepts you need to understand to accurately answer the question.
Mechanical Engineering and Poisson's Ratio
Material deformation, lateral strain, longitudinal strain, one app. one place for learning..
All the tools & learning materials you need for study success - in one app.

Most popular questions from this chapter
Describe a nanometer.
What property of a material is a measure of its stiffness?
What is the difference between proportional limit and elastic limit?
Describe pultrusion, and list four shapes produced by this process.
What is the principal constituent of bronze?
Recommended explanations on Physics Textbooks
Fields in physics, electricity, particle model of matter, oscillations, turning points in physics.
What do you think about this solution?
We value your feedback to improve our textbook solutions.
Study anywhere. Anytime. Across all devices.
Privacy overview.

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

6.1: Poisson's Formula
- Last updated
- Save as PDF
- Page ID 2156

- Erich Miersemann
- University of Leipzig
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Assume \(u\) is a solution of (6.2), then, since Fourier transform is a linear mapping,
\[\widehat{u_t-\triangle u}=\hat{0}.\]
From properties of the Fourier transform, see Proposition 5.1, we have
\[\widehat{\triangle u}=\sum_{k=1}^n\widehat{\frac{\partial^2 u}{\partial x_k^2}}=\sum_{k=1}^n i^2\xi^2_k\widehat{u}(\xi),\]
provided the transforms exist. Thus we arrive at the ordinary differential equation for the Fourier transform of \(u\)
\[\frac{d\widehat{u}}{dt}+|\xi|^2\widehat{u}=0,\]
where \(\xi\) is considered as a parameter. The solution is
\[\widehat{u}(\xi,t)=\widehat{\phi}(\xi)e^{-|\xi|^2 t}\]
since \(\widehat{u}(\xi,0)=\widehat{\phi}(\xi)\). From Theorem 5.1 it follows
\begin{eqnarray*} u(x,t)&=&(2\pi)^{-n/2}\int_{\mathbb{R}^n}\ \widehat{\phi}(\xi)e^{-|\xi|^2t}e^{i\xi\cdot x}\ d\xi\\ &=&(2\pi)^{-n}\int_{\mathbb{R}^n}\ \phi(y)\left(\int_{\mathbb{R}^n}e^{i\xi\cdot (x-y)-|\xi|^2t}\ d\xi\right)\ dy. \end{eqnarray*}
$$K(x,y,t)=(2\pi)^{-n}\int_{\mathbb{R}^n}e^{i\xi\cdot (x-y)-|\xi|^2t}\ d\xi.\]
By the same calculations as in the proof of Theorem 5.1, step (vi), we find
\begin{equation} \label{kernel1} K(x,y,t)=(4\pi t)^{-n/2}e^{-|x-y|^2/4t}. \end{equation}
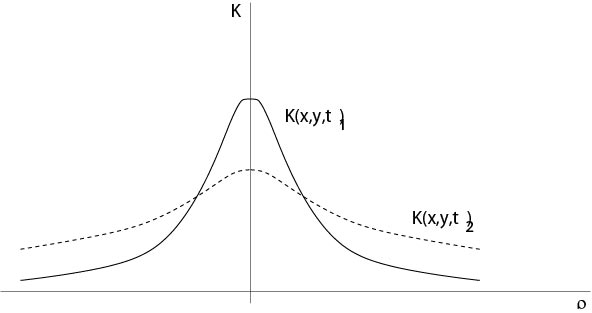
Figure 6.1.1: Kernel \(K(x,y,t)\), \(\rho=|x-y|\), \(t_1<t_2\)
Thus we have
\begin{equation} \label{poisson1} u(x,t)=\frac{1}{\left(2\sqrt{\pi t}\right)^n}\int_{\mathbb{R}^n}\ \phi (z)e^{-|x-z|^2/4t}\ dz. \end{equation}
Definition. Formula (\ref{poisson1}) is called Poisson's formula } and the function \(K\) defined by (\ref{kernel1}) is called heat kernel or fundamental solution of the heat equation.
Proposition 6.1 The kernel \(K\) has following properties:
- (i) \(K(x,y,t)\in C^\infty(\mathbb{R}^n\times\mathbb{R}^n\times\mathbb{R}^1_+)\),
- (ii) \((\partial/\partial t\ -\triangle)K(x,y,t)=0,\ t>0\),
- (iii) \(K(x,y,t)>0,\ t>0\),
- (iv) \(\int_{\mathbb{R}^n}\ K(x,y,t)\ dy=1\), \(x\in\mathbb{R}^n\), \(t>0\)
- \(\delta>0\):(v) For each fixed
$$\lim_{\begin{array}{l}t\to0\\ t>0\end{array}}\int_{\mathbb{R}^n\setminus B_\delta(x)}\ K(x,y,t)\ dy=0$$
uniformly for \(x\in\mathbb{R}\).
Proof. (i) and (iii) are obviously, and (ii) follows from the definition of \(K\). Equations (iv) and (v) hold since
\begin{eqnarray*} \int_{\mathbb{R}^n\setminus B_\delta(x)}\ K(x,y,t)\ dy&=& \int_{\mathbb{R}^n\setminus B_\delta(x)}\ (4\pi t)^{-n/2}e^{-|x-y|^2/4t}\ dy\\ &=&\pi^{-n/2}\int_{\mathbb{R}^n\setminus B_{\delta/\sqrt{4t}}(0)}e^{-|\eta|^2}\ d\eta \end{eqnarray*} by using the substitution \(y=x+(4t)^{1/2}\eta\). For fixed \(\delta>0\) it follows (v) and for \(\delta:=0\) we obtain (iv).
Theorem 6.1. Assume \(\phi\in C(\mathbb{R}^n)\) and \(\sup_{\mathbb{R}^n}|\phi(x)|<\infty\). Then \(u(x,t)\) given by Poisson's formula (\ref{poisson1}) is in \(C^{\infty}(\mathbb{R}^n\times\mathbb{R}^1_+)\), continuous on \(\mathbb{R}^n\times[0,\infty)\) and a solution of the initial value problem (6.2) , (6.3) .
Proof. It remains to show
$$ \lim_{\begin{array}{l}x\to\xi\\ t\to0\end{array}}u(x,t)=\phi(\xi). \]
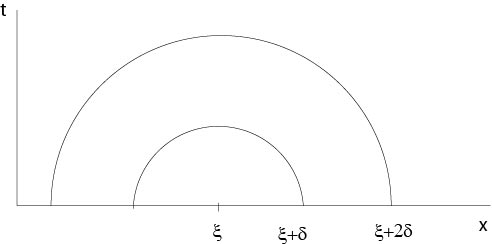
Figure 6.1.2: Figure to the proof of Theorem 6.1
Since \(\phi\) is continuous there exists for given \(\varepsilon>0\) a \(\delta=\delta(\varepsilon)\) such that \(|\phi(y)-\phi(\xi)|<\varepsilon\) if \(|y-\xi|<2\delta\). Set \(M:=\sup_{\mathbb{R}^n}|\phi(y)|\). Then, see Proposition 6.1, $$ u(x,t)-\phi(\xi)=\int_{\mathbb{R}^n}\ K(x,y,t)\left(\phi(y)-\phi(\xi)\right)\ dy. $$ It follows, if \(|x-\xi|<\delta\) and \(t>0\), that \begin{eqnarray*} |u(x,t)-\phi(\xi)|&\le&\int_{B_{\delta}(x)}\ K(x,y,t)\left|\phi(y)-\phi(\xi)\right|\ dy\\ &&+\int_{\mathbb{R}^n\setminus B_{\delta}(x)}\ K(x,y,t)\left|\phi(y)-\phi(\xi)\right|\ dy\\ &\le&\int_{B_{2\delta}(x)}\ K(x,y,t)\left|\phi(y)-\phi(\xi)\right|\ dy\\ &&+2M\int_{\mathbb{R}^n\setminus B_{\delta}(x)}\ K(x,y,t)\ dy\\ &\le&\varepsilon\int_{\mathbb{R}^n}\ K(x,y,t)\ dy+2M\int_{\mathbb{R}^n\setminus B_{\delta}(x)}\ K(x,y,t)\ dy\\ &<&2\varepsilon \end{eqnarray*} if \(0<t\le t_0\), \(t_0\) sufficiently small.
Remarks. 1. Uniqueness follows under the additional growth assumption $$ |u(x,t)|\le Me^{a|x|^2}\ \ \mbox{in}\ D_T, $$ where \(M\) and \(a\) are positive constants, see Proposition 6.2 below. In the one-dimensional case, one has uniqueness in the class \(u(x,t)\ge 0\) in \(D_T\), see [10], pp. 222.
2. \(u(x,t)\) defined by Poisson's formula depends on all values \(\phi(y)\), \(y\in\mathbb{R}^n\). That means, a perturbation of \(\phi\), even far from a fixed \(x\), has influence to the value \(u(x,t)\). This means that heat travels with infinite speed, in contrast to the experience.
Contributors and Attributions
- Prof. Dr. Erich Miersemann ( Universität Leipzig )
Integrated by Justin Marshall.
Poisson’s Ratio-Formula, Significance, Equation, Example
What is poisson’s ratio.
Poisson’s ratio of a material is a very important parameter in material science and engineering mechanics. When a force is applied to a bar it deforms (elongates or compresses) in the axial (longitudinal) direction. At the same time, a deformation is observed in the transverse (width) direction as well. Poisson’s ratio relates these changes in the transverse direction and axial direction. This effect is known as Poisson’s effect which is named after the French mathematician and physicist Simeon Poisson. The Poisson’s ratio is defined as the ratio of the transverse strain to that of the axial strain under the influence of the same force. It is a material property and remains constant.
Poisson’s Ratio Formula
Let’s deduce the formula for Poisson’s ratio. From the above definition, Poisson’s ratio can be expressed mathematically as
Poisson’s Ratio=Transverse (Lateral) Strain/Axial (Longitudinal) Strain
Let’s understand this philosophy using the example in Fig. 2. In this image, A tensile force (F) is applied in a bar of diameter do and length lo. With the action of this force F, the bar elongates and the final length is l. Also, the diameter reduces and the final diameter is d.
So from the above, Axial Strain, Longitudinal Strain, or Linear Strain= (Change in Length/Original Length)=(l-l o )/l o . Similarly, Lateral Strain or Transverse Strain=(Change in Diameter/Original base Diameter)=(d-d o )/d o . So, as per the definition, the equation of Poisson’s Ratio or Poisson’s ratio formula can be written as follows
Poisson’s Ratio=Lateral Strain/Longitudinal Strain={(d-d o )/d o }/((l-l o )/l o }= l o (d-d o )/d o (l-l o )
Poisson’s ratio example.
| Carbon Steel | 0.27–0.30 |
| Cast iron | 0.21–0.26 |
| Stainless steel | 0.30–0.31 |
| Aluminium-alloy | 0.32 |
| Copper | 0.33 |
| Inconel | 0.27-0.38 |
| Gold | 0.42–0.44 |
| Silver | 0.37 |
| Platinum | 0.39 |
| Glass | 0.18–0.3 |
| Foam | 0.10–0.50 |
| Sand | 0.20–0.455 |
| Molybdenum | 0.307 |
| Concrete | 0.1–0.2 |
| Clay | 0.30–0.45 |
| Tin | 0.33 |
| Titanium | 0.265–0.34 |
| Magnesium alloy | 0.252–0.289 |
| Rubber | 0.48-0.4999 |
| Brass | 0.331 |
| Bronze | 0.34 |
| Ice | 0.33 |
| Lead | 0.431 |
| Monel | 0.315 |
| Nickel | 0.31 |
| Polystyrene | 0.34 |
| Limestone | 0.2-0.3 |
| Nickel Steel | 0.291 |
| Tungsten | 0.28 |
| Metallic Glass | 0.276–0.409 |
| Boron | 0.08 |
| Beryllium | 0.03 |
| Cork | 0.0 |
| Re-entrant foam | -0.7 |
Unit of Poisson’s Ratio
Poisson’s ratio is the ratio of two strains. Both longitudinal and lateral strains are dimensionless. So Poisson’s Ratio is dimensionless. There is no unit for Poisson’s Ratio.
Symbol of Poisson’s Ratio
Poisson’s ratio is normally denoted by the Greek letter ν (nu). However, this is not standardized. So users can use any symbol for Poisson’s ratio at their discretion.
What is Negative Poisson’s Ratio?
In general, for common materials, the cross-section becomes narrower when stretched. So, Poisson’s ratio is positive for most materials. However, certain materials (Origami-folded materials, certain solid woods, and certain crystals) show a negative Poisson ratio. This means when they are stretched in the longitudinal axis, their cross-sectional area increases. The main reason behind such type of behavior is due to their uniquely oriented, hinged molecular bonds. These materials are known as auxetic materials. Note that, more than three hundred crystalline materials have negative Poisson’s ratio in certain states. Some of the typical examples of auxetic materials are Li, Cu, Rb, Na, K, Ag, Fe, Ni, Co, BAsO 4 , Cs, Au, Be, Ca, Zn Sr, Sb, MoS 2 , Living bone tissue, Non-carbon nanotubes, Auxetic polyurethane foam, Chain organic molecules, etc.
Applications of Poisson’s Ratio
Poisson’s ratio is a very important parameter of materials. In engineering mechanics, the strength of materials, structural engineering, machine design, and fluid flow problems, Poisson’s ratio finds wide application. Some of the common applications of Poisson’s ratio are listed below:
In pressurized pipeline flow problems, Poisson’s effect has a significant influence. The internal pressure creates hoop stress in the pipe material. Due to Poisson’s effect, this hoop stress causes the pipe to increase in diameter and slightly decrease in length.
The near-zero Poisson’s ratio for Cork material makes it ideal as bottle stoppers.
In structural engineering, Poisson’s ratio is essential for analyzing the deformation and stability of structures. It helps engineers predict how materials will respond to different load conditions.
Poisson’s ratio is crucial in the design and analysis of composite materials, where different materials are combined to achieve specific mechanical properties. Understanding how these materials deform is essential for their effective use.
FAQs related to Poisson’s Ratio
Poisson’s ratio of a material is defined as the ratio of the lateral strain (change in the width per unit width of a material) to the axial strain (change in its length per unit length) due to the action of a Force.
What does a Poisson ratio of 0.5 Means?
Poisson’s ratio of 0.5 signifies that due to the application of a force the deformation change in the width direction is half the deformation change in the axial direction. Normally, for perfectly incompressible isotropic materials the value of Poisson’s ratio is 0.5. Rubber is a typical example.
What is the Poisson’s Ratio of Steel?
Can poisson’s ratio be greater than 1, why poisson’s ratio is important.
Poisson’s ratio of a material is very important for studying the stress and deflection properties of engineering materials like pipes, beams, vessels, etc.
What if Poisson’s Ratio is Zero?
Which material has the highest poisson ratio, what is the poisson’s ratio of aluminum.
The Poisson’s ratio of Aluminum normally varies between 0.3 to 0.35.
What is the Poisson’s Ratio of Concrete?
Few more related articles for you. Introduction to Stress-Strain Curve (With PDF) Stress or Strain: Which comes first? Hooke’s Law: Statement, Equation, Graph, Applications, Limitations (With PDF) Young’s modulus: Young’s modulus of Steels [With PDF]
Related Posts:
5 thoughts on “ poisson’s ratio-formula, significance, equation, example ”.
Your books really helped me to understand various topics Thank you sir Keep continue this good work
Thanks Mr. Anup for your permission to use the figures. b r gupta
Leave a Reply Cancel reply
Recent posts.
- Materials Properties
Poisson’s Ratio
What is poisson’s ratio.
When a material is stretched by a tensile force, it usually undergoes a lateral contraction, and when it’s compressed, it usually undergoes a lateral expansion. That phenomenon of lateral contraction or expansion is known as the Poisson effect . The ratio of the lateral contraction or expansion and longitudinal extension or compression is called Poisson’s ratio .
Poisson’s ratio is defined as the ratio between lateral strain (the amount that a material deforms perpendicular to the applied force) and axial strain (the amount that it deforms parallel to the force). In other words, it’s a measure of how much something expands or contracts in response to being stretched or compressed along one axis.
Poisson’s ratio is not always the same for elongation versus compression.
Strain, Axial Strain, & Transverse Strain
Strain (ε) is the relative change in length to the original length Δ l l o
Axial strain is the strain along the direction of the applied force Δ l x l x
Transverse strain is the strain perpendicular to the direction of the applied force Δ l y l y
Poisson’s ratio range
Poisson’s ratio is a dimensionless quantity that ranges from -1 to 0.5, however for most materials the Poisson’s ratio is in the range of (0 - 0.5).
- A material with Poisson’s ratio between (0 < 𝜈 ≤ 0.5), would contract in the lateral direction when stretched, and expand laterally when compressed.
- A material with Poisson’s ratio equal to 0, would not deform in the lateral direction when stretched or compressed.
- A material with Poisson’s ratio between (-1 ≤ 𝜈 < 0), would expand in the lateral direction when stretched, and contract laterally when compressed.
You can find the Poisson’s ratio of common materials on this page: Poisson’s ratio values .
Formula & Units
Poisson’s Ratio ( 𝜈 ) = transverse strain / axial strain
- 𝜈 is the Poisson’s ratio
- ε lateral is the lateral strain (strain in the direction perpendicular to the direction of force)
- ε axial is the axial strain (strain along the direction of force)
Poisson’s ratio is a dimensionless quantity, which means that it does not have a unit of measurement.
By convention compressive deformation is considered negative, and tensile deformation is considered positive, thus the negative sign in the Poisson’s ratio formula is there, so that for a typical material, where the lateral deformation is opposite to the longitudinal deformation, the Poisson’s ratio value would be positive.
Factors Affecting Poisson’s Ratio
Several factors can affect the Poisson’s ratio of a material, including:
- Material composition: The Poisson’s ratio can vary depending on the chemical composition of the material, such as its crystalline structure, elemental composition, and bonding types.
- Temperature: The Poisson’s ratio can change with temperature due to changes in the material’s structure and bonding. Some materials may exhibit anomalous behavior, such as negative Poisson’s ratios, at certain temperatures.
- Strain rate: The Poisson’s ratio can also be affected by the rate at which the material is deformed. Some materials exhibit time-dependent behavior, where the Poisson’s ratio changes over time due to the rate of deformation.
- Loading conditions: The Poisson’s ratio can vary depending on the direction and magnitude of the applied stress. For example, the Poisson’s ratio may be different under tensile and compressive loads.
- Anisotropy: Materials that exhibit anisotropic behavior, where the mechanical properties vary depending on the direction of the applied force, may also exhibit different Poisson’s ratios depending on the direction of the deformation.
- Presence of defects: The presence of defects such as voids, cracks, and inclusions can also affect the Poisson’s ratio. Defects can lead to local changes in the material’s stiffness and may affect the way the material deforms under stress.
Applications of Poisson’s Ratio
Poisson’s ratio has numerous applications across various fields. Some of the main applications of Poisson’s ratio include:
- Material science: Poisson’s ratio is a fundamental mechanical property of materials, and it is widely used in material science to characterize the mechanical behavior of materials. It is used to determine the stiffness, strength, and ductility of materials, as well as to predict their behavior under different loading conditions.
- Engineering: Poisson’s ratio is used extensively in engineering to design and optimize structures and components. Engineers use it to determine the response of materials to different loading conditions, such as tension, compression, bending, and torsion.
- Manufacturing: Poisson’s ratio is used in manufacturing to improve the quality of products. It is used in quality control to ensure that the manufactured products meet the desired mechanical properties.
Overall, Poisson’s ratio is a key property that plays an important role in many areas of science and engineering. Its applications are widespread and varied, and it is a critical property to consider when designing and developing new materials and structures.
| Definition | The ratio between lateral deformation to axial deformation in a material when under uniaxial loading |
| Symbol | |
| Formula | |
| Units | Unitless |
Frequently Asked Questions
- Poisson’s Ratio Table
- Stiffness in Physics
- Stress & Strain
- Elasticity & Plasticity
- Ductility & Brittleness
- Young’s Modulus
- Shear Modulus
- Bulk Modulus
- Flexural Modulus
- Modulus of Toughness
- Modulus of Resilience

IMAGES
VIDEO
COMMENTS
Solution to Problem 222 Poisson's Ratio. A solid cylinder of diameter d carries an axial load P. Show that its change in diameter is 4 Pν / πEd. Solution 222.
Numerical Problems: Example - 1: When a brass rod of diameter 6 mm is subjected to a tension of 5 × 103 N, the diameter changes by 3.6 × 10-4 cm. Calculate the longitudinal strain and Poisson's ratio for brass given that Y for the brass is 9 × 1010 N/m². Given: Diameter of rod = D = 6 mm, Radius of wire = 6/2 = 3 mm = 3 × 10 -3 m, Load ...
The Poisson's Ratio for the given material is 0.1. Example 2. When a metallic rod of length 3 m and diameter 1 cm is subjected to a tension of 800 N, the diameter changes by 3 ×10−7m 3 × 10 − 7 m. Calculate the Poisson's ratio; longitudinal strain for the metal if it's Young's modulus is 10N/m2 10 N / m 2. Solution.
Subject - Strength of MaterialsVideo Name - Poisson's Ratio : Problem 1Chapter - Stress and StrainFaculty - Prof. Zafar ShaikhWatch the video lecture on Topi...
Solution to Problem 222 Poisson's Ratio. Problem 222. A solid cylinder of diameter d carries an axial load P. Show that its change in diameter is 4 Pν / πEd. Solution 222. Click here to show or hide the solution.
What Poisson's Ratio Means. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. Soft materials, like rubber, have Poisson's ratio values near 0.5. Steel and rigid polymers typically have values around 0.3. Porous materials typically have Poisson's ratio values close to zero. This is because they collapse when compressed.
Problem 2: What is the maximum and minimum values of Poisson's ratio for a metal? Solution: The Poisson's Ratio formula is as follows: ν = Lateral strain/longitudinal strain. It is always positive because if we apply force in longitudinal strain, lateral strain always decreases for metals. It lies between 0 to 0.5.
View solution > Consider the following two statements A and B and identify the correct answer. ... Modulus of Elasticity and Poisson's Ratio - Problems L2. Example Definitions Formulaes. Learn with Videos. Problems on Elasticity - I. ... Mindmap > Important Diagrams > Common Misconceptions > Memorization tricks > Problem solving tips ...
Poisson's ratio of a material defines the ratio of transverse strain (x direction) to the axial strain (y direction)In materials science and solid mechanics, Poisson's ratio ν is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the specific direction of loading.The value of Poisson's ratio is the negative of the ratio of ...
Or more precisely, the formula solving Poisson's equation with a special right hand side: − u = δ(x) (8) where δ(x) is the Dirac delta function. 1. Fundamental solution. We start by trying to solve − u= δ(x). (9) 1.1. The Dirac delta function. First we explain the rationale behind this strategy. That is, why solving this equation can ...
This video solves for the change in the length and diameter of a rod loaded in tension.
Now, we will solve a problem based on Young's modulus of elasticity and Poisson's ratio. Let's take a problem based on Young's modulus of elasticity and Poisson's ratio. Suppose, we have a copper wire of 0 . 2 c m 2 cross-sectional area under the tensile force of 3 0 N .
to which the solution is R= Ar n+Br −1. The general solution to Laplace's equation in the axisymmetric case is therefore (absorb-ing the constant Cinto Aand B) Φ(r,θ) = X∞ n=0 (A nrn +B nr −n 1)P n(cosθ). Non-axisymmetric Case [non-examinable] A similar analysis when Φ may depend on φ shows that the general solution is Φ(r,θ,φ ...
Numerical solutions of boundary value problems for the Poisson equation are important not only because these problems often arise in diverse branches of science and technology, but because they frequently are a means for solving more general boundary value problems for both equations and systems of equations of elliptic type as well as for ...
FREE SOLUTION: Problem 10 Define Poisson's ratio.... step by step explanations answered by teachers Vaia Original! ... Poisson's ratio provides a numerical value that engineers use to quantify the lateral strain. Accurately predicting lateral strain informs the design criteria for materials used in various mechanical applications. ...
Subject - Strength of MaterialsVideo Name - Problem 1 on Calculation of Poisson's RatioChapter - Simple Stress And StrainFaculty - Prof. Shravan GuptaUpskill...
Learn how to calculate Poisson's ratio using Poisson's ratio formula, and discover if a negative Poisson ratio is also possible. Updated: 11/21/2023 Table of Contents
6 Write down Poisson's equation ∇2Φ = −ρ/ 0, and let Φ(r,θ) = R(r)Θ(θ). In this case, you can pick a particular form for Θ so that each term in Poisson's equation contains exactly the same function of θ; hence Θ cancels throughout. This leaves you with the ordinary differential equation for R(r) given in the hint, with α = −1/
The LibreTexts libraries are Powered by NICE CXone Expert and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739.
solutions. However if l= 0 only equation 3 provides d= 0 which obviously must be true. It also provides the same result that was found in the counterexample above. Thus equation 3 is the exact solution of the problem. Conclusion Equation 3 can be used to calculate Poissons Ratio as a function of l(in the volume conservative case).
An example solution of Poisson's equation in 2-d. Let us now use the techniques discussed above to solve Poisson's equation in two dimensions. Suppose that the source term is. (181) for and . The boundary conditions at are , , and [see Eq. ( 147 )], whereas the boundary conditions at are , , and [see Eq. ( 148 )].
For these modules to have positive values, the Poisson's ratio of a stable, isotropic, linear elastic material must be between −1.0 and +0.5. The value of Poisson's ratio normally ranges between 0.0 and 0.5. The following table provides a few typical values (range) of Poisson's ratio for common materials.
Formula & Units. Poisson's Ratio (𝜈) = transverse strain / axial strain. 𝜈 =-𝜀 l a t e r a l 𝜀 a x i a l. Where: 𝜈 is the Poisson's ratio; ε lateral is the lateral strain (strain in the direction perpendicular to the direction of force); ε axial is the axial strain (strain along the direction of force); Poisson's ratio is a dimensionless quantity, which means that it ...