assignment method algorithm

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

The present assignment is optimal if each row and column has exactly one encircled zero.
The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

$\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} $

With 5 jobs and 5 men, the stated problem is balanced.

$\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} $

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

$\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} $

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

$\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} $

When the zeros are assigned, we get the following:

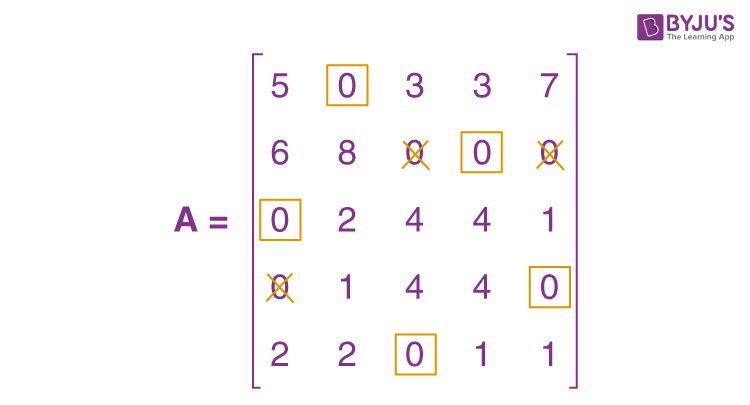
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

$\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} $

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

MATHS Related Links

Register with BYJU'S & Download Free PDFs

Data Structures
Linked List
Binary Tree
Binary Search Tree
Segment Tree
Disjoint Set Union
Fenwick Tree
Red-Black Tree
Advanced Data Structures

Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)

Given a 2D array , arr of size N*N where arr[i][j] denotes the cost to complete the j th job by the i th worker. Any worker can be assigned to perform any job. The task is to assign the jobs such that exactly one worker can perform exactly one job in such a way that the total cost of the assignment is minimized.

Input: arr[][] = {{3, 5}, {10, 1}} Output: 4 Explanation: The optimal assignment is to assign job 1 to the 1st worker, job 2 to the 2nd worker. Hence, the optimal cost is 3 + 1 = 4. Input: arr[][] = {{2500, 4000, 3500}, {4000, 6000, 3500}, {2000, 4000, 2500}} Output: 4 Explanation: The optimal assignment is to assign job 2 to the 1st worker, job 3 to the 2nd worker and job 1 to the 3rd worker. Hence, the optimal cost is 4000 + 3500 + 2000 = 9500.

Different approaches to solve this problem are discussed in this article .

Approach: The idea is to use the Hungarian Algorithm to solve this problem. The algorithm is as follows:

For each row of the matrix, find the smallest element and subtract it from every element in its row.
Repeat the step 1 for all columns.
Cover all zeros in the matrix using the minimum number of horizontal and vertical lines.
Test for Optimality : If the minimum number of covering lines is N , an optimal assignment is possible. Else if lines are lesser than N , an optimal assignment is not found and must proceed to step 5.
Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Consider an example to understand the approach:

Let the 2D array be: 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000 500 1000 0 0 500 500 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found. 2500 4000 3500 4000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 3500 + 2000 = 9500

For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library . This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3 ) time. It solves the optimal assignment problem.

Below is the implementation of the above approach:

Time Complexity: O(N 3 ) Auxiliary Space: O(N 2 )

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Index Assignment problem Hungarian algorithm Solve online

The assignment problem

The assignment problem deals with assigning machines to tasks, workers to jobs, soccer players to positions, and so on. The goal is to determine the optimum assignment that, for example, minimizes the total cost or maximizes the team effectiveness. The assignment problem is a fundamental problem in the area of combinatorial optimization.

Assume for example that we have four jobs that need to be executed by four workers. Because each worker has different skills, the time required to perform a job depends on the worker who is assigned to it.

The matrix below shows the time required (in minutes) for each combination of a worker and a job. The jobs are denoted by J1, J2, J3, and J4, the workers by W1, W2, W3, and W4.


82	83	69	92
77	37	49	92
11	69	5	86
8	9	98	23

Each worker should perform exactly one job and the objective is to minimize the total time required to perform all jobs.

It turns out to be optimal to assign worker 1 to job 3, worker 2 to job 2, worker 3 to job 1 and worker 4 to job 4. The total time required is then 69 + 37 + 11 + 23 = 140 minutes. All other assignments lead to a larger amount of time required.

The Hungarian algorithm can be used to find this optimal assignment. The steps of the Hungarian algorithm can be found here , and an explanation of the Hungarian algorithm based on the example above can be found here .

Hungarian Method: Assignment Problem

Hungarian Method is an efficient method for solving assignment problems .

This method is based on the following principle:

If a constant is added to, or subtracted from, every element of a row and/or a column of the given cost matrix of an assignment problem, the resulting assignment problem has the same optimal solution as the original problem.

Hungarian Algorithm

The objective of this section is to examine a computational method - an algorithm - for deriving solutions to the assignment problems. The following steps summarize the approach:

Steps in Hungarian Method

1. Identify the minimum element in each row and subtract it from every element of that row.

2. Identify the minimum element in each column and subtract it from every element of that column.

3. Make the assignments for the reduced matrix obtained from steps 1 and 2 in the following way:

For every zero that becomes assigned, cross out (X) all other zeros in the same row and the same column.
If for a row and a column, there are two or more zeros and one cannot be chosen by inspection, then you are at liberty to choose the cell arbitrarily for assignment.

4. An optimal assignment is found, if the number of assigned cells equals the number of rows (and columns). In case you have chosen a zero cell arbitrarily, there may be alternate optimal solutions. If no optimal solution is found, go to step 5.

5. Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix obtained from step 3 by adopting the following procedure:

Mark all the rows that do not have assignments.
Mark all the columns (not already marked) which have zeros in the marked rows.
Mark all the rows (not already marked) that have assignments in marked columns.
Repeat steps 5 (i) to (iii) until no more rows or columns can be marked.
Draw straight lines through all unmarked rows and marked columns.

You can also draw the minimum number of lines by inspection.

6. Select the smallest element from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment.

7. Go to step 3 and repeat the procedure until you arrive at an optimal assignment.

For the time being we assume that number of jobs is equal to number of machines or persons. Later in the chapter, we will remove this restrictive assumption and consider a special case where no. of facilities and tasks are not equal.

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

> > Assignment Problem calculator (Using Hungarian method-1)

"; for(j=1;j "; // if(getValue("txtJH"+j)=="") // S += " "; // else // S += " "; if(getValue("txtJH"+j)=="") { if(j==1) { CHead="A"; } else { var CAscii=(PHead.charCodeAt(0)+1);//gives 65+1 if(CAscii "; PHead = CHead; } S += ""; // "; // if(getValue("txtWH"+i)=="") // S += " "; // else // S += " "; if(getValue("txtWH"+i)=="") { if(i==1) { CHead="A"; } else { var CAscii=(PHead.charCodeAt(0)+1);//gives 65+1 if(CAscii "; PHead = CHead; for(j=1;j "; S += " "; } S += ""; } // "; } if(i


Method
Hungarian method

Type your data (either with heading or without heading), for seperator you can use space or tab for sample click random button

OR

Rows :





\	1	2	3
A	6	3	5
B	5	9	2
C	5	7	8

\	1	2	3	4	5
A	10	5	13	15	16
B	3	9	18	13	6
C	10	7	2	2	2
D	7	11	9	7	12
E	7	9	10	4	12

\	1	2	3	4	5
A	32	38	40	28	40
B	40	24	28	21	36
C	41	27	33	30	37
D	22	38	41	36	36
E	29	33	40	35	39

\	1	2	3	4
A	9	14	19	15
B	7	17	20	19
C	9	18	21	18
D	10	12	18	19
E	10	15	21	16

\	1	2	3	4	5
A	85	75	65	125	75
B	90	78	66	132	78
C	75	66	57	114	69
D	80	72	60	120	72
E	76	64	56	112	68

\	1	2	3	4	5
A	2	1	2	3	0
B	4	1	0	7	0
C	0	0	2	0	2
D	0	1	0	1	0
E	3	0	3	0	3

\	1	2	3	4
A	42	35	28	21
B	30	25	20	15
C	30	25	20	15
D	24	20	16	12

\	A	B	C	D	E
M1	9	11	15	10	11
M2	12	9	-	10	9
M3	-	11	14	11	7
M4	14	8	12	7	8

\	A	B	C	D	E
A	8	2	x	5	4
B	10	9	2	8	4
C	5	4	9	6	x
D	3	6	2	8	7
E	5	6	10	4	3

Solution

Hungarian method calculator

1. A computer centre has 3expert programmers. The centre wants 3 application programmes to be developed. The head of thecomputer centre, after studying carefully the programmes to be developed, estimates the computer time in minutes required by the experts for the application programmes as follows.

		Programmers
		A	B	C
Programmes	1	6	3	5
	2	5	9	2
	3	5	7	8

		Employees
		I	II	III	IV	V
Jobs	A	10	5	13	15	16
	B	3	9	18	13	6
	C	10	7	2	2	2
	D	7	11	9	7	12
	E	7	9	10	4	12

		Location
		A	B	C	D	E
Machine	M1	9	11	15	10	11
	M2	12	9	--	10	9
	M3	--	11	14	11	7
	M4	14	8	12	7	8

		Flight Number
		I	II	III	IV	V
Pilot	A	8	2	-	5	4
	B	10	9	2	8	4
	C	5	4	9	6	-
	D	3	6	2	8	7
	E	5	6	10	4	3

How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

Subtract the smallest entry in each row from all the entries of the row.
Subtract the smallest entry in each column from all the entries of the column.
Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

	Task 1	Task 2	Task 3
Emp 1	5	7	6
Emp 2	6	4	5
Emp 3	8	5	3

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

	Task 1	Task 2	Task 3
Emp 1	0	2	1
Emp 2	2	0	1
Emp 3	5	2	0

Next, we subtract the smallest entry in each column from all the entries of the column:

	Task 1	Task 2	Task 3
Emp 1	0	2	1
Emp 2	2	0	1
Emp 3	5	2	0
	0	0	0

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

Emp 1 to Task 3
Emp 2 to Task 2
Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

History of O.R.
Approach, Techniques and Tools
Phases and Processes of O.R. Study
Typical Applications of O.R
Limitations of Operations Research
Models in Operations Research
O.R. in real world

2 Linear Programming: Formulation and Graphical Method

General formulation of Linear Programming Problem
Optimisation Models
Basics of Graphic Method
Important steps to draw graph
Multiple, Unbounded Solution and Infeasible Problems
Solving Linear Programming Graphically Using Computer
Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

Principle of Simplex Method
Computational aspect of Simplex Method
Simplex Method with several Decision Variables
Two Phase and M-method
Multiple Solution, Unbounded Solution and Infeasible Problem
Sensitivity Analysis
Dual Linear Programming Problem

4 Transportation Problem

Basic Feasible Solution of a Transportation Problem
Modified Distribution Method
Stepping Stone Method
Unbalanced Transportation Problem
Degenerate Transportation Problem
Transhipment Problem
Maximisation in a Transportation Problem

5 Assignment Problem

Solution of the Assignment Problem
Unbalanced Assignment Problem
Problem with some Infeasible Assignments
Maximisation in an Assignment Problem
Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

Concepts of goal programming
Goal programming model formulation
Graphical method of goal programming
The simplex method of goal programming
Using Excel Solver to Solve Goal Programming Models
Application areas of goal programming

8 Integer Programming

Some Integer Programming Formulation Techniques
Binary Representation of General Integer Variables
Unimodularity
Cutting Plane Method
Branch and Bound Method
Solver Solution

9 Dynamic Programming

Dynamic Programming Methodology: An Example
Definitions and Notations
Dynamic Programming Applications

10 Non-Linear Programming

Solution of a Non-linear Programming Problem
Convex and Concave Functions
Kuhn-Tucker Conditions for Constrained Optimisation
Quadratic Programming
Separable Programming
NLP Models with Solver

11 Introduction to game theory and its Applications

Important terms in Game Theory
Saddle points
Mixed strategies: Games without saddle points
2 x n games
Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

Reasons for using simulation
Monte Carlo simulation
Limitations of simulation
Steps in the simulation process
Some practical applications of simulation
Two typical examples of hand-computed simulation
Computer simulation

13 Queueing Models

Characteristics of a queueing model
Notations and Symbols
Statistical methods in queueing
The M/M/I System
The M/M/C System
The M/Ek/I System
Decision problems in queueing

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

Is there a greedy algorithm to solve the assignment problem?

The assignment problem is defined as:

There are n people who need to be assigned to n jobs, one person per job. The cost that would accrue if the ith person is assigned to the jth job is a known quantity C[i,j] for each pair i, j = 1, 2, ..., n. The problem is to find an assignment with the minimum total cost.

There is a question asking to design a greedy algorithm to solve the problem. It also asks if the greedy algorithm always yields an optimal solution and for the performance class of the algorithm. Here is my attempt at designing an algorithm:

Am I correct in saying that my algorithm is of O(n^2)? Am I also correct in saying that a greedy algorithm does not always yield an optimal solution? I used my algorithm on the following cost matrix and it is clearly not the optimal solution. Did I Do something wrong?

Applying greedy algorithm to cost matrix

greedy-algorithms
assignment-problem

$\begingroup$ Algorithms for maximum weight bipartite maximum matching are unfortunately more complicated than that. They don't really follow the greedy paradigm. $\endgroup$ – Yuval Filmus Commented Apr 7, 2017 at 6:05

The answer of your post question (already given in Yuval comment) is that there is no greedy techniques providing you the optimal answer to an assignment problem.

The commonly used solution is the Hungarian algorithm, see

Harold W. Kuhn, "The Hungarian Method for the assignment problem", Naval Research Logistics Quarterly, 2: 83–97, 1955

for the original paper.

Otherwise your solution seems correct to me, and as usually with greedy algorithms, it will provide you a feasible solution which you may hope to not be "too far" from the global optimal solution.

Your Answer

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged algorithms greedy-algorithms assignment-problem or ask your own question .

Featured on Meta
Upcoming sign-up experiments related to tags

Hot Network Questions

Why can't LaTeX (seem to?) Support Arbitrary Text Sizes?
Remove assignment of [super] key from showing "activities" in Ubuntu 22.04
Cathay Pacific Online Booking: When to Enter Passport Details?
Viewport Shader Render different from 1 computer to another
What was the first game to intentionally use letterboxing to indicate a cutscene?
Artinian Gorenstein subrings with same socle degree
Is the zero vector necessary to do quantum mechanics?
Is Légal’s reported “psychological trick” considered fair play or unacceptable conduct under FIDE rules?
Different outdir directories in one Quantum ESPRESSO run
Have children's car seats not been proven to be more effective than seat belts alone for kids older than 24 months?
Predictable Network Interface Names: ensX vs enpXsY
Are combat sports ethical?
Why is it 'capacité d'observation' (without article) but 'sens de l'observation' (with article)?
Specific calligraphic font for lowercase g
Geometry question about a six-pack of beer
How to engagingly introduce a ton of history that happens in, subjectively, a moment?
Does Matthew 7:13-14 contradict Luke 13:22-29?
In equation (3) from lecture 7 in Leonard Susskind’s ‘Classical Mechanics’, should the derivatives be partial?
What is the translation of misgendering in French?
Sangaku problem involving eight circles
How to Pick Out Strings of a Specified Length
What is a positive coinductive type and why are they so bad?
Is it better to show fake sympathy to maintain a good atmosphere?
What kind of sequence is between an arithmetic and a geometric sequence?

Disaggregated spatiotemporal traffic assignment for road reservation service and supply-demand statistical analysis

Guo, Renzhong

This paper develops a disaggregated spatiotemporal traffic assignment method with a system-optimal (SO) orientation and analyzes the supply-demand matching degree with four statistical indexes under the background of a road reservation system. Three key issues are addressed. Firstly, the paper illustrates the service process of a road reservation system. It is essential to know how the road reservation system works and the difference between it and other reservation systems. Secondly, a spatiotemporal discretization expression method based on the system-optimal traffic assignment (SOTA) model with predictive origin-destination demand for link travel time is put forward to make the supply space could be reserved, and the demand would not be mutually interfering. Thirdly, the study proposes a reverse feasible spatiotemporal route searching algorithm based on the expected arrival time to individually assign the applicants on the road network. This route searching algorithm does not use the network topology but the spatiotemporal discretized links. The departure time preference was considered in the feasible spatiotemporal route searching algorithm. Moreover, as the real demand distribution of the whole reservation area is not difficult to obtain after a period of updates, it is possible to analyze the supply-demand matching degree of the road network. Thus, four statistical indexes are proposed to assess the state variation of the road network. Simulation results verify the effectiveness and efficiency of the proposed method. The novel reverse feasible routes searching algorithm has a system-optimal trend with inputting the demand individually and an acceptable calculating efficiency. The method proposed by this paper could ensure a reliable road reservation service with accurate demand prediction. Considering the departure time preference would not bring extra burden to the road reservation system but provide more user-friendly service. Through the analysis, the supply-demand matching degree of the road network is significantly influenced by the cohesive capacity connection of the upstream and downstream links. This indicates the network structure and road attributes optimization should be considered in enhancing the road reservation service.

Demand control;
Feasible spatiotemporal routes;
System-optimal orientation;
Supply-demand statistical analysis

IMAGES

assignment method algorithm
How to Solve an Assignment Problem Using the Hungarian Method
Objectives in Scheduling Loading Sequencing. Monitoring. Advanced
Target Assignment algorithm.
Grid assignment method 3. Algorithm analysis 3.1. Traditional A*
Assignment algorithm

VIDEO

Assignment Problem ( Brute force method) Design and Analysis of Algorithm
2. Minimal Assignment problem {Hungarian Method}
ASSIGNMENT PROBLEM: meaning, formulation, Hungarian method
"Mastering Assignment Operators in Python: A Comprehensive Guide"
Hungarian Method
BCS-042 SOLVED ASSIGNMENT 2023-24|Introduction to Algorithm design|IGNOU SOLVED ASSIGNMENT

COMMENTS

Assignment problem
Worked example of assigning tasks to an unequal number of workers using the Hungarian method. The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks.Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent ...
Hungarian Algorithm for Assignment Problem
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3). Space complexity : O(n^2), where n is the number of workers and jobs.This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional ...
PDF Lecture 8: Assignment Algorithms
Hungarian algorithm steps for minimization problem. Step 1: For each row, subtract the minimum number in that row from all numbers in that row. Step 2: For each column, subtract the minimum number in that column from all numbers in that column. Step 3: Draw the minimum number of lines to cover all zeroes.
Hungarian algorithm
The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
Hungarian Method
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
How to Solve an Assignment Problem Using the Hungarian Method
In this lesson we learn what is an assignment problem and how we can solve it using the Hungarian method.
Assignment Problem and Hungarian Algorithm
General description of the algorithm. This problem is known as the assignment problem. The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our problem is a special case of binary integer ...
PDF The Assignment Problem and the Hungarian Method
The Hungarian Method: The following algorithm applies the above theorem to a given n × n cost matrix to ﬁnd an optimal assignment. Step 1. Subtract the smallest entry in each row from all the entries of its row. Step 2. Subtract the smallest entry in each column from all the entries of its column. Step 3.
PDF Hungarian method for assignment problem
Hungarian method for assignment problem Step 1. Subtract the entries of each row by the row minimum. Step 2. Subtract the entries of each column by the column minimum. Step 3. Make an assignment to the zero entries in the resulting matrix. A = M 17 10 15 17 18 M 6 10 20 12 5 M 14 19 12 11 15 M 7 16 21 18 6 M −10
The Hungarian Algorithm for the Assignment Problem
The Hungarian method is a combinatorial optimization algorithm which solves the assignment problem in polynomial time . Later it was discovered that it was a primal-dual Simplex method.. It was developed and published by Harold Kuhn in 1955, who gave the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians: Denes Konig and Jeno ...
Hungarian Algorithm for Assignment Problem
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library. This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3) time. It solves the optimal assignment problem. Below is the implementation of the above approach:
The Assignment Problem (Using Hungarian Algorithm)
Total Cost= 2+8+4+6=20. Approach 3: Greedy Approach In this case, the algorithm will choose the lowest cost worker to be assigned to the task as the first assignment, then choose the next lowest ...
PDF The Hungarian method for the assignment problem
THE HUNGARIAN METHOD FOR THE ASSIGNMENT. PROBLEM'. H. W. Kuhn. Bryn Y a w College. Assuming that numerical scores are available for the perform- ance of each of n persons on each of n jobs, the "assignment problem" is the quest for an assignment of persons to jobs so that the sum of the. n scores so obtained is as large as possible.
An Assignment Problem solved using the Hungarian Algorithm
The Hungarian algorithm: An example. We consider an example where four jobs (J1, J2, J3, and J4) need to be executed by four workers (W1, W2, W3, and W4), one job per worker. The matrix below shows the cost of assigning a certain worker to a certain job. The objective is to minimize the total cost of the assignment.
Solve the assignment problem online
Solve an assignment problem online. Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given. Fill in the cost matrix (random cost matrix):
The Assignment Problem
The total time required is then 69 + 37 + 11 + 23 = 140 minutes. All other assignments lead to a larger amount of time required. The Hungarian algorithm can be used to find this optimal assignment. The steps of the Hungarian algorithm can be found here, and an explanation of the Hungarian algorithm based on the example above can be found here.
Assignment Problem, Maximization Example, Hungarian Method
The Hungarian Method can also solve such assignment problems, as it is easy to obtain an equivalent minimization problem by converting every number in the matrix to an opportunity loss. The conversion is accomplished by subtracting all the elements of the given matrix from the highest element. It turns out that minimizing opportunity loss ...
Hungarian Method, Assignment Problem, Hungarian Algorithm
Hungarian Algorithm. The objective of this section is to examine a computational method - an algorithm - for deriving solutions to the assignment problems. The following steps summarize the approach: Steps in Hungarian Method . 1. Identify the minimum element in each row and subtract it from every element of that row. 2.
PDF A Distributed Algorithm for the Assignment Problem
A Distributed Algorithm for the Assignment Problem Dimitri P. Bertsekas March 1979y Abstract This paper describes a new algorithm for solving the classical assign-ment problem. The algorithm is of a primal-dual nature and in some ways resembles the Hungarian and subgradient methods, but is substantially di erent in other respects.
Hungarian method calculator
Home > Operation Research calculators > Assignment Problem calculator (Using Hungarian method-1) Algorithm and examples. Method. Hungarian method. Type your data (either with heading or without heading), for seperator you can use space or tab. for sample click random button. OR.
How to Solve the Assignment Problem: A Complete Guide
The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps: Subtract the smallest entry in each row from all the entries of the row. Subtract the smallest entry in each column from all the entries of the column. Draw the minimum number of lines to cover ...
Is there a greedy algorithm to solve the assignment problem?
The answer of your post question (already given in Yuval comment) is that there is no greedy techniques providing you the optimal answer to an assignment problem. The commonly used solution is the Hungarian algorithm, see. Harold W. Kuhn, "The Hungarian Method for the assignment problem", Naval Research Logistics Quarterly, 2: 83-97, 1955.
Assignment Method
The simplex method can be solved as a linear programming problem using the simplex algorithm. The transportation method is a special case of the assignment problem. The method is, however, computationally inefficient for solving the assignment problem due to the solution's degeneracy problem.
Disaggregated spatiotemporal traffic assignment for road reservation
This paper develops a disaggregated spatiotemporal traffic assignment method with a system-optimal (SO) orientation and analyzes the supply-demand matching degree with four statistical indexes under the background of a road reservation system. Three key issues are addressed. Firstly, the paper illustrates the service process of a road reservation system.