Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.

What does the dot product of two vectors represent?
I know how to calculate the dot product of two vectors alright. However, it is not clear to me what, exactly, does the dot product represent .
The product of two numbers, $2$ and $3$, we say that it is $2$ added to itself $3$ times or something like that.
But when it comes to vectors $\vec{a} \cdot \vec{b}$, I'm not sure what to say. "It is $\vec{a}$ added to itself $\vec{b}$ times" which doesn't make much sense to me.
- 1 $\begingroup$ Adding $\vec{a}$ to itself $b$ times ($b$ being a number) is another operation, called the scalar product. The dot product involves two vectors and yields a number. $\endgroup$ – user65203 Commented May 22, 2014 at 22:40
- $\begingroup$ Something not mentioned but of interest is that the dot product is an example of a bilinear function , which can be considered a generalization of multiplication. $\endgroup$ – While I Am Commented Mar 15, 2021 at 23:34
- $\begingroup$ Does this answer your question? Meaning of Dot Products in Regards to Linear Algebra $\endgroup$ – Ketan Commented Mar 17, 2021 at 16:58
12 Answers 12
The dot product tells you what amount of one vector goes in the direction of another. For instance, if you pulled a box 10 meters at an inclined angle, there is a horizontal component and a vertical component to your force vector. So the dot product in this case would give you the amount of force going in the direction of the displacement, or in the direction that the box moved. This is important because work is defined to be force multiplied by displacement, but the force here is defined to be the force in the direction of the displacement.
http://youtu.be/KDHuWxy53uM
- 34 $\begingroup$ For this interpretation it's important that the vector you are projecting onto has unit length, otherwise you are getting the component of vector 1 along vector 2 scaled by the length of vector 2 $\endgroup$ – Ryan Vitale Commented May 22, 2014 at 22:52
- 1 $\begingroup$ Work is a good example of magnitude as well as direction. W = F.D , i.e work is the scalar product of the force and displacement vectors (assuming constant force and direction). $\endgroup$ – Tom Collinge Commented May 23, 2014 at 7:37
- 6 $\begingroup$ This answer is vague. As rVitale points out, your first sentence is only true if the "other" vector is a unit vector. When you say "[pull] a box 10 meters at an inclined angle", you need to be clearer about what the two vectors are: presumably, you mean the force vector and the vector along which the box moves. $\endgroup$ – David Richerby Commented May 23, 2014 at 9:08
- 12 $\begingroup$ Obviously it helped the OP. The criticism of the King is blasphemous. $\endgroup$ – King Squirrel Commented May 23, 2014 at 13:05
- 5 $\begingroup$ Oh this makes sense now. The dot product is zero when they're orthogonal because they don't have any common component! $\endgroup$ – Kenneth Worden Commented Sep 13, 2015 at 18:08
Geometric Meaning
As other answers have pointed out, the dot product $\vec{a} \cdot \vec{b}$ is related to the angle $\theta$ between $\vec{a}$ and $\vec{b}$ through:
$$\vec a \cdot \vec b = \Vert\vec a\Vert_2 \, \Vert\vec b\Vert_2 \, \cos \theta$$
Assuming that $a$ and $b$ point into similar directions, i.e., $\theta \leq 90°$ , we can visualize what this relationship means (skipping the vector arrows and Euclidean norm subscript from now on):

$p$ is the vector resulting from an orthogonal projection of $a$ onto $b$ . As the $\cos$ is the ratio between the adjacent leg ( $p$ ) and the hypotenuse ( $a$ ) in the right triangle, i.e.,
$$\cos \theta = \frac{\Vert p \Vert}{\Vert a \Vert},$$
we get for the inner product:
$$a \cdot b = \Vert a \Vert \, \Vert b \Vert \, \frac{\Vert p \Vert}{\Vert a \Vert} = \Vert p \Vert \Vert b \Vert$$
So, the inner product is the length of the vector $p$ , the projection of $a$ onto $b$ , multiplied by the length of $b$ . If $a$ and $b$ point into opposite directions, i.e., $90° < \theta \leq 180°$ , the dot product will be the negative: $a \cdot b = - \Vert p \Vert \Vert b \Vert$
The problem is that the relationship between the dot product and the angle $\theta$ is not inherently given. By definition:
$$a \cdot b = \sum_i a_i b_i$$
So, we need to find a link between this and the cosine. From the definition of the dot product, we can see that it scales proportionally with the input vectors, so for non-unit vectors $u$ and $v$ with the corresponding unit vectors $\hat{u}$ and $\hat{v}$ :
$$u \cdot v = \Vert u \Vert \hat{u} \cdot \Vert v \Vert \hat{v} = \Vert u \Vert \Vert v \Vert \hat{u} \cdot \hat{v}.$$
For simplicity, we will assume $a$ and $b$ to be unit vectors. Thus, we only need to show
$$a \cdot b = \cos \theta$$
or, by the definition of $\cos$ , we need to show:
$$a \cdot b = \Vert p \Vert $$
Let's calculate the length of the projection $p$ using $a$ and $b$ . We can start by using the Pythagorean theorem:

$$ \Vert p \Vert ^2 = \Vert a \Vert ^2 - \Vert c \Vert ^2$$
Because $a$ is a unit vector:
$$ \Vert p \Vert ^2 = 1 - \Vert c \Vert ^2$$
Now, we need to calculate the length of $c$ using the other rectangular triangle. Again, we use the fact that $b$ is a unit vector, i.e., $ \Vert b \Vert = 1$ .
$$ \begin{align} \Vert c \Vert ^2 &= \Vert d \Vert ^2 - (\Vert b \Vert - \Vert p \Vert)^2 \\ &= \Vert d \Vert ^2 - (1 - \Vert p \Vert)^2 \\ &= \Vert d \Vert ^2 - 1 + 2 \Vert p \Vert - \Vert p \Vert^2 \end{align} $$
Now, we can insert this term for $\Vert c \Vert ^2$ in the equation above:
$$ \begin{align} \Vert p \Vert ^2 &= 1 - \Vert d \Vert ^2 + 1 - 2 \Vert p \Vert + \Vert p \Vert^2 \\ 0 &= 2 - \Vert d \Vert ^2 - 2 \Vert p \Vert \\ 2 \Vert p \Vert &= 2 - \Vert d \Vert ^2 \end{align} $$
In the figure, we see that $\vec a + \vec d = \vec b$ . Therefore, $\vec d = \vec b - \vec a$ , or:
$$d_i = b_i - a_i$$
Thus, we can express $\Vert d \Vert^2$ as:
$$ \begin{align} \Vert d \Vert ^2 &= \sum_i d_i^2 \\ &= \sum_i (b_i - a_i)^2 \\ &= \sum_i b_i^2 - 2 b_i a_i + a_i^2 \\ &= \sum_i b_i^2 - \sum_i 2 b_i a_i + \sum_i a_i^2 \\ &= \Vert b \Vert^2 - \sum_i 2 b_i a_i + \Vert a \Vert^2 \\ &= 1 - \sum_i 2 b_i a_i + 1 \\ &= 2 - 2 \sum_i b_i a_i \end{align} $$
$$ \begin{align} 2 \Vert p \Vert &= 2 - \Vert d \Vert ^2 \\ &= 2 - (2 - 2 \sum_i b_i a_i) \\ &= 2 \sum_i b_i a_i \\ \Vert p \Vert &= \sum_i b_i a_i \end{align} $$
- 1 $\begingroup$ Hello Kilian - thanks for this. I'm not sure how you got the expression for \norm{c}^2 in the second step and how you got the expression for the \norm{p}^2 in the third step. Could you please clarify? $\endgroup$ – G. Khanna Commented Jan 26, 2020 at 17:00
- $\begingroup$ Same here, very interested in a clarification. $\endgroup$ – qreon Commented Oct 24, 2020 at 10:07
- $\begingroup$ I updated the equations to make it more clear. Let me know if you have any further questions! $\endgroup$ – Kilian Obermeier Commented Nov 15, 2020 at 12:11
- $\begingroup$ Thanks for such detailed answer.. helped me to clear many doubts and concepts. $\endgroup$ – ogirkar Commented Dec 27, 2020 at 8:46
- $\begingroup$ For me this post would be helped if you outlined what you are going to be proving, before the lenghy proof starts. Alternatively, I would put p is the vector resulting from an orthogonal projection of a onto b in bold. $\endgroup$ – DailyFrankPeter Commented Jan 21, 2021 at 12:00
I think of dot product as the "same-ness" of two vectors. If two vectors are orthogonal (90 degrees on one another) they are 'not at all the same' (dot product =0), and if they are parallel they are 'very much the same'. If you divide their dot product by the product of their magnitude, that is the argument for an arccosine function to find the angle between them. My application for the dot product is finding the angle between two vectors for calculating the force required to pull a cable through two or more pipes with a bend. It's hard to do this in a three dimensional world without knowing how to calculate the dot product. Math makes life really easy :)
It might help to think of multiplication of real numbers in a more geometric fashion. $2$ times $3$ is the length of the interval you get starting with an interval of length $3$ and then stretching the line by a factor of $2$.
For dot product, in addition to this stretching idea, you need another geometric idea, namely projection. Imagine the line $L$ parallel to $\vec b$ through the origin $O$. Now imagine projecting from the tip of the vector $\vec a$, along a line perpendicular to $L$, until hitting $L$ at a point $P$. The dot product $\vec a \cdot \vec b$ is the length of the line segment you get by starting with the line segment $OP$ and then stretching the plane by a factor equal to the length of $\vec b$.
I'm being a little careless about plus and minus signs, but those can be incorporated into this picture too.
- 5 $\begingroup$ What's the importance of this? What do we get from the product? I mean why we are so interested in finding this dot product? $\endgroup$ – Wasiq Noor Commented Jul 24, 2018 at 2:26
- $\begingroup$ Hi @LeeMosher please could you help out with math.stackexchange.com/q/4445701/585488 $\endgroup$ – linker Commented May 8, 2022 at 8:23
- $\begingroup$ Wasiq, the importance of this is that when we compute something like work (force in the direction of motion multiplied by the displacement) we can simply write this as $F\cdot d$ where $F$ and $d$ are both vectors. If the vectors are not in the same direction we need to find the component of force that is in the direction of motion. So if the force is being applied at an angle relative to the displacement, $|F|cos(\theta)$ gives us the force in the direction of motion and it is that which gets multiplied by $|d|$, not $|F|$ itself. It's a way of multiplying when the direction matters. $\endgroup$ – smichr Commented May 19 at 2:59
The dot product of two vectors u,v is the area of the parallelogram u,v' where v' is v rotated by 90 degrees.
- 1 $\begingroup$ This is the most interesting answer to me because it shows a link between cross product and dot product. I will give you the most I can which is one. $\endgroup$ – Sedumjoy Commented Jul 13, 2020 at 17:24
- $\begingroup$ Haha, thank you! $\endgroup$ – Jules Commented Jul 14, 2020 at 19:04
- $\begingroup$ @Jules You are confusing the dot product with the vector product $\endgroup$ – Black Mild Commented Jun 14, 2021 at 9:12
- 2 $\begingroup$ I'm not. The vector (cross) product has a similar interpretation, but without the 90 degree rotation. $\endgroup$ – Jules Commented Jun 15, 2021 at 10:40
- 1 $\begingroup$ Best answer, but (nitpicking) the dot product is the determinant of $u$ and $v'$, i.e, $$\langle u,v\rangle=\det(u,v').$$ $\endgroup$ – Michael Hoppe Commented Sep 5, 2023 at 18:54
First of all, if we write $\vec{a} = a \vec{u}$ and $\vec{b} = b \vec{v}$, where $a$ and $b$ are the length of $\vec{a}$ and $\vec{b}$ respectively, then $$\vec{a} \cdot \vec{b} = (a \vec{u})\cdot (b \vec{v}) = ab \,\, \vec{u} \cdot \vec{v};$$ this is a pretty natural property for a product to have.
Now as for $\vec{u} \cdot \vec{v}$, this is equal to $\cos \theta,$ where $\theta$ is the angle between $\vec{u}$ and $\vec{v}$.
As King Squirrel notes, this is also the length of the projection of $\vec{u}$ onto the line through $\vec{v}$, and also the length of the projection of $\vec{v}$ onto the line through $\vec{u}$.
So altogether we get
$$\vec{a} \cdot \vec{b} = a b \, \cos \theta,$$ and it has the interpretation in terms of projecting one vector onto another that King Squirrel discusses.
- $\begingroup$ does this meaning have any remnant when used over $\Bbb F_p$? $\endgroup$ – Turbo Commented Dec 9, 2014 at 7:18
Dot product is the product of magnitudes of 2 vectors with the Cosine of the angle between them. You can take the smaller or the larger angle between the vectors. That is if theta is the angle then you can take (360-theta) as well.
Geometrically, it will also be equal to (read it slowly) the product of “projection” of magnitude of one vector on the other and the magnitude of the 2nd vector.
In Physics, as an example, Mechanical Work is a scalar and a result of dot product of force and displacement vectors. Like-wise, Magnetic flux is the dot product of magnetic field and vector area
Let me try to explain this with an example. Say you wish to find the work done by a force F along X axis over a distance d. However the problem also tells you that the direction of the force is not along the X axis but at an angle of 60 degree with X axis.
Now you know that the work done is the product of force and displacement. But in this case you know that the force is not exactly totally acting in the direction of X axis, since it is inclined at 60 degree. So what you can do is, find what is the contribution of this force in the X direction. Well it turns out with simple trigonometry that it is F Cos60 in direction of X axis. Now you can say that the work done = F Cos 60 X d. This can also be represented as F.d = F d Cos 60. So you see, dot product gives us the magnitude of a certain entity (in this case work) by way of attributing a certain vector (in this case force F) in the direction of the other vector. Here "d" was the other vector along which work was being found
Dot product is a scalar quantity. Watch this video that I have made to understand this better-
What is Dot Product of Vectors
If you have two vectors of lengths $2$ and $3$ .
If they point in the same direction it is reasonable that the product would be $6$ .
If the one of length $2$ is rotated $180^\circ$ , then it becomes $-2$ and the other is still $3$ . It is reasonable that this product is $-6$ .
So the range of values is between $-6$ and $6$ .
Half way through the rotation at $90^\circ$ , the product is halfway between $-6$ and $6$ . The product is $0$ .
$$2 \cdot 3\cos0^\circ=2 \cdot 3 \cdot 1=6$$
$$2 \cdot 3\cos 90^\circ=2 \cdot 3 \cdot 0=0$$
$$2 \cdot 3\cos180^\circ=2 \cdot 3 \cdot -1=-6$$
Note the length is always positive.
When one calculates A.B , two measurements happen: measurement of how small the angle between them is, and how long A and B are. A.B basically means projection length of A on B , with this length then scaled by the absolute length of B .
One way to think about the interpretation of the dot product is to think how would one maximise or minimise the dot product between two vectors. Let's assume we are trying to maximise the dot product between two vectors that we can modify:
The dot product will be grow larger as the angle between two vector decreases. The dot product A.B will also grow larger as the absolute lengths of A and B increase. This is because as A gets larger, its projected length will be longer, and as B 's length gets larger, the scaling of A 's projection will grow larger, given that B 's absolute length will act as a scaler of A 's projection length.
- $\begingroup$ Please do not post the same answer more than once. If you find that the same answer will address multiple questions, then please flag the questions as duplicates. $\endgroup$ – Xander Henderson ♦ Commented Mar 17, 2021 at 16:04
These questions are better approached geometrically because they have very well defined applications and real world examples.
For example here we are mentioning the dot product which has a very direct application in calculating work for example.
Work should be force multiplied by the distance moved. This is in simple algebra but when you get to geometry and 3D. Both the force and displacement have directions.
So the dot product helps by projecting the force onto displacement to help you decide how did the force contribute in doing the work.
Three Scenarios:
1 - Force is in direction of displacement: means the force did positive work in moving the object.
2 - Force is perpendicular to displacement: means force did nothing in moving the object in this direction. Zero work.
3 - Force is in the opposite direction of displacement: means force did negative work in moving the object in this direction; slowed it down or stopped it.
When directions are considered, we essentially bring a new dimension to the perception of the entity. (Speed vs Velocity: 5km/h vs 5km/h towards east). Bringing the sense of direction, the question arises, how the entities interact?
In dot product, diagrammatically, what we find is, essentially, the area that is affected by the two entities taken together.
Consider Tetris. You have built a foundation already. Now, a new part is falling and you have the arrow keys to move it around. Two competing vectors, your movement and the falling of the brick/part, will determine how the new part is arranged. The area covered by the falling part would be determined by the dot product of the said vectors.
I don't think the dot product has a very obviously interesting visual interpretation.
I'm not a math teacher, but if I were asked to define the dot product in a course, I'd start by defining the scalar projection first. This has a very intuitive interpretation. And then you'd see immediately that, in order to compute the scalar projection, it's useful to compute the dot product.
So, in a normed vector space $E$ , let $u,v \in E$ two vectors such as $u, v \neq 0$ .
Formally, the scalar projection of $v$ over $u$ is the unique scalar $\alpha$ such as
$$ || \alpha u ||^2 + || v - \alpha u ||^2 = || v ||^2 $$
It might not be true in every normed vector space that such a unique scalar has to exist, but in $\mathbb{R}^n$ with the Euclidean norm at least, you can prove that it does exist and that it is indeed unique.
Intuitively/geometrically, you're fixing a point $P$ and you're trying to adjust the length and the orientation of a vector that goes in the same direction as $u$ , (that's $\alpha u$ ), so that the triangle formed by the points: $P, P+v, P+\alpha u$ satisfies the Pythagorean property of a right triangle of hypothenuse $[P, P+v]$ (that's what the property $|| \alpha u ||^2 + || v - \alpha u ||^2 = || v ||^2$ expresses).
If you expand the condition
$$||\alpha u||² + ||v - \alpha u||² = ||v||²$$
using the definition of the Euclidean norm, you'll see that $\alpha$ has to be equal to
$$ \frac{\sum\limits_{i=1}^{n} u_i v_i}{||u||}$$
(and that this quantity does satisfy the condition).
So geometrically, what is the scalar product of $u$ and $v$ ? I'd say that it is this quantity that when divided by $||u||$ gives you the scalar projection of $v$ over $u$ .
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged geometry vectors ..
- Featured on Meta
- User activation: Learnings and opportunities
- Preventing unauthorized automated access to the network
- A Limited Advertising Test on this Site
Hot Network Questions
- Why does Lebanon apparently lack aerial defenses?
- displaylink-driver not installable with 6.1.0-25-amd64 kernel
- How does 自由に不自由していない work here?
- Can I redeem myself with a better research paper if my thesis sucks?
- Did Sauron refer to Morgoth as "Morgoth" (Sindarin for "Black Foe" or "Dark Tyrant")?
- Book where a parent recounts an anecdote about a painting of a Russian sled pursued by wolves
- How to format units inside math environment?
- Order of function transformations
- Bayesian inference in high-dimension for a non-linear multimodal model
- Help Understanding Op-Amp Mixing of Square Waves Swinging from 0V to 9V
- How can Mayday shoot webs without a web-shooter device?
- Informal "chats" with potential grad school advisors
- Will a Palm tree in Mars be approximately 2.5 times taller than the same tree on Earth?
- Which ancient philosopher compared thoughts to birds?
- Is it Possible to Successfully Do a PhD in the UK Without Formal University Enrolment?
- Used car dealership refused to let me use my OBDII on their car, is this a red flag?
- Would a stream cipher gain any benefit from a more complicated function than XOR?
- God the Father punished the Son as sin-bearer: how does that prove God’s righteousness?
- Where is this NPC's voice coming from?
- Why are METAR issued at 53 minutes of the hour?
- Score the science points in 7 Wonders
- How can I award a player an additional Feat?
- In what range does incrementing and decrementing Java doubles work?
- 2 NICs, PC is trying to use wrong one
Dot Product
A vector has magnitude (how long it is) and direction :
Here are two vectors:
They can be multiplied using the " Dot Product " (also see Cross Product ).
Calculating
The Dot Product is written using a central dot:
a · b This means the Dot Product of a and b
We can calculate the Dot Product of two vectors this way:
a · b = | a | × | b | × cos(θ)
Where: | a | is the magnitude (length) of vector a | b | is the magnitude (length) of vector b θ is the angle between a and b
So we multiply the length of a times the length of b , then multiply by the cosine of the angle between a and b
OR we can calculate it this way:
a · b = a x × b x + a y × b y
So we multiply the x's, multiply the y's, then add.
Both methods work!
And the result is a number (called a "scalar" to show it is not a vector).
Example: Calculate the dot product of vectors a and b :
Both methods came up with the same result (after rounding)
Also note that we used minus 6 for a x (it is heading in the negative x-direction)
Note: you can use the Vector Calculator to help you.
Why cos(θ) ?
OK, to multiply two vectors it makes sense to multiply their lengths together but only when they point in the same direction .
So we make one "point in the same direction" as the other by multiplying by cos(θ):
THEN we multiply !
It works exactly the same if we "projected" b alongside a then multiplied.
Because it doesn't matter which order we do the multiplication:
| a | × | b | × cos(θ) = | a | × cos(θ) × | b |
In effect, the dot product multiplies the aligned lengths.
Remembering Cos
To remember to multiply by cos(θ) think "dot cos" .
Right Angles
When two vectors are at right angles to each other the dot product is zero .
Example: calculate the dot product for:
or we can calculate it this way:
This can be a handy way to find out if two vectors are at right angles.
Same Direction
The dot product of two vectors that point in the same direction is the simple product of their lengths, because the angle is 0 degrees which has a cosine of 1
Right-Angled Triangle
Let's use the dot product on a right-angled triangle!
We just proved the Pythagorean Theorem !
Note: when we allow angles other than 90 degrees we can create the Law of Cosines . Have a go yourself, but be careful how you define the angle!
The Dot Product is used a lot in Physics
Example: Work
In Physics Work is force times distance, but only the aligned part.
So work is the dot product of force and distance.
Alex pushes a box 3 m straight forward using 200 N of force. But his push is a little upwards by 20°.
(Without cos θ, the wrong value would be 600 J)
Three or More Dimensions
This all works fine in 3 (or more) dimensions, too.
And can actually be very useful!
Example: Sam has measured the end-points of two poles, and wants to know the angle between them :
We have 3 dimensions, so don't forget the z-components:
a · b = a x × b x + a y × b y + a z × b z
Now for the other formula:
But what is | a | ? It is the magnitude, or length, of the vector a . We can use Pythagoras :
- | a | = √(4 2 + 8 2 + 10 2 )
- | a | = √(16 + 64 + 100)
- | a | = √180
Likewise for | b |:
- | b | = √(9 2 + 2 2 + 7 2 )
- | b | = √(81 + 4 + 49)
- | b | = √134
And we know from the calculation above that a · b = 122, so:
I tried a calculation like that once, but worked all in angles and distances ... it was very hard, involved lots of trigonometry, and my brain hurt. The method above is much easier.
Cross Product
The Dot Product gives a scalar (ordinary number) answer, and is sometimes called the scalar product .
But there is also the Cross Product which gives a vector as an answer, and is sometimes called the vector product .
MATH CHEMISTRY PHYSICS BIOLOGY EDUCATION
xaktly | Matrix algebra
Notes on notation.
Textbooks vary in how they designate which things are vectors , some using bold font, and others using arrow $(\, \vec v \,)$ notation. I use arrows.
Publications are also split on how they write vector components , some using angle brackets like $\vec v = \langle 1, 2, 3\rangle$, and some just using parentheses like $\vec v = (1, 2, 3)$. I'll use the latter because it's usually clear in context when we mean to write a vector.
Many textbooks write the length of vector $\vec v_1$ as $||\vec v_1 ||$. In these pages, I'll stick to the single bars representation, $|\vec v_1 |$. When we're working in the context of vectors, it's difficult to confuse this notation with the absolute value – and simpler and cleaner to write.
The angle between vectors
The dot product (also called the scalar product) gives us the angle between any two vectors. It's one of the most important relationships between vectors. In this section we'll define the dot product and show how it gives the angle between vectors for two- and three-dimensional vectors.
The dot product gives the angle between two vectors of any dimension. It's a tricky concept, but it's true. You can calculate the angle between 27-dimensional vectors.
Here's the definition of the dot product for two-dimensional vectors like $\vec v_1 = (x_1, y_1)$:
Dot product of 2-D vectors
$$ \begin{align} \vec v_1 &= (x_1, y_1) \\[3pt] \vec v_2 &= (x_2, y_2) \\[5pt] \vec v_1 \cdot \vec v_2 &= x_1 x_2 + y_1 y_2 \end{align}$$
Notice the the result of the dot product is not another vector – it's just another number or a scalar . That's why we often call the dot product the scalar product . We can easily extend the definition of the dot product to vectors of any dimension, as long as the two have the same dimension.
Dot product of $n$-D vectors
$$ \begin{align} \vec v_1 &= (a_1, a_2, \dots , a_n) \\[3pt] \vec v_2 &= (b_1, b_2, \dots , b_n) \\[5pt] \vec v_1 \cdot \vec v_2 &= a_1 b_1 + a_2 b_2 + \dots + a_n b_n \end{align}$$
Finally, the dot product can be thought of as a row vector (or a 1 × n matrix) multiplied by a column vector (an n × 1 matrix). Here's a picture of that for 2-D vectors:
$$ \begin{align} v_1 &\cdot v_2 = (x_1, y_1)\left( \begin{matrix} x_2 \\ y_2 \end{matrix} \right) = x_1 x_2 + y_1 y_2 \\[5pt] &\phantom{0000000} \color{#E90F89}{(1 \times 2)(2 \times 1) = 1 \times 1 \; \text{(scalar)}} \end{align}$$
The dot product, $\vec a \cdot \vec b$, is defined only for vectors of the same dimension.
Practice problems.
Calculate the dot product of these vectors. Roll over or tap each problem for the solution.

Connection between the dot product and angle
Consider two vectors, $\vec v_1$ and $\vec v_2$. Here they are:

The first thing we'll do is to translate them to the origin to make things easier. Remember that we can always do this because the only things about vectors that are important are their length and direction.

Now if we remember vector subtraction, we can construct the vector $\vec v_2 - \vec v_1$. Let's also draw in angle $\theta$ between $\vec v_1$ and $\vec v_2$:

We begin with the law of cosines (LOC), where $|\vec v_1|$ is the length of vector $\vec v_1$, $|\vec v_2|$ is the length of vector $\vec v_2$, and so on:
$$|\vec v_2 - \vec v_1| = |\vec v_1|^2 + |\vec v_2|^2 - 2|\vec v_1||v_2| cos(\theta)$$
Now let's take a look at that left side, $|\vec v_1 - \vec v_2|^2$. We can use the coordinates of the endpoints of $\vec v_2 - \vec v_1$, which are the coordinates of both ends of $\vec v_1$ and $\vec v_2$ to get
$$|\vec v_1 - \vec v_2|^2 = \left(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\right)^2$$
Here we're just using the distance formula (which is really just the Pythagorean theorem) with those coordinates. Now we have the square of a square root, so that right side is just
$$= (x_2 - x_1)^2 + (y_2 - y_1)^2$$
Now for the right side of our LOC equation. If we remember that the square of the length of a vector is
$$|v_1|^2 = \left(\sqrt{x_1^2 + y_1^2} \right)^2$$
$$ \begin{align} |v_1|^2 = x_1^2 + y_1^2 \\[5pt] |v_2|^2 = x_2^2 + y_2^2 \end{align}$$
Now we can rewrite both sides, and expand the binomials on the left to get:
$$ \begin{align} (x_2 &- x_1)^2 + (y_2 - y_1)^2 \\[5pt] &= x_1^2 + y_1^2 + x_2^2 + y_2^2 - 2|\vec v_1||\vec v_2| cos(\theta) \end{align}$$
If we expand the squared binomials on the left side, we notice that the squared terms containing purely $x$'s or $y$'s are represented on both sides of the equation, so we can eliminate them:
$$ \require{cancel} \begin{align} \cancel{x_2^2} &- 2x_1x_2 + \cancel{x_1^2} + \cancel{y_2^2} - 2y_1y_2 + \cancel{y_1^2} \\ &= \cancel{x_1^2} + \cancel{y_1^2} + \cancel{x_2^2} + \cancel{y_2^2} - 2|\vec v_1||\vec v_2| cos(\theta) \end{align}$$
Finally, we can divide all of those $-2$'s away:
$$\cancel{-2}x_1x_2 + \cancel{-2}y_1y_2 = \cancel{-2}|\vec v_1||\vec v_2| cos(\theta)$$
$$x_1x_2 + y_1y_2 = |\vec v_1||\vec v_2| cos(\theta)$$
Now all that remains is to recognize that $x_1 x_2 + y_1 y_2$ is just the definition of the dot product, so we've arrived at the relationship between the dot product of two vectors and the angle between them:
$$\vec v_1 \cdot \vec v_2 = |\vec v_1||\vec v_2| cos(\theta)$$
Definition of the dot product
Find the angle between vectors $v_1 = (-1, 2)$ and $v_2 = (2, 5)$
Solution : We begin by writing the dot-product equation and rearranging it to find the angle:
Solving for the angle, we get
$$\theta = cos^{-1} \left( \frac{\vec v_1 \cdot \vec v_2}{|\vec v_1||\vec v_2|} \right)$$
Now we just have to fill in the information. The dot product is the product of the x-coordinates plus the product of the y's:
$$\vec v_1 \cdot \vec v_2 = (-1)(2) + 2(5) = 8$$
The lengths of the vectors are found using the distance formula:
$$ \begin{align} |\vec v_1| &= ((-1)^2 + 2^2)^{1/2} = \sqrt{5} \\[5pt] |\vec v_2| &= (2^2 + 5^2)^{1/2} = \sqrt{29} \end{align}$$
And finally the angle:
$$\theta = cos^{-1}\left( \frac{8}{\sqrt{5\cdot 29}} \right) = 48.4˚$$
Find the angles between all of the unit vectors in $\mathbb{R}^3$, $\hat i = (1, 0, 0)$, $\hat j = (0, 1, 0)$ and $\hat k = (0, 0, 1)$.
Solution : These three vectors are the basis vectors of 3D Cartesian coordinates. The relevant dot products are
$$ \begin{align} \hat i \cdot \hat j &= (1, 0, 0) \cdot (0, 1, 0) = 0 \\[5pt] \hat i \cdot \hat k &= (1, 0, 0) \cdot (0, 0, 1) = 0 \\[5pt] \hat j \cdot \hat k &= (0, 1, 0) \cdot (0, 0, 1) = 0 \end{align}$$
All of our dot products are zero, and the angle with $cos(\theta) = 0$ is $\theta = 90^{\circ}$.
So the angles between these three unit vectors are all 90˚, just what we'd expect for the alignment of the axes of a rectilinear coordinate system.
Calculate the angle between each pair of vectors.
$(1, 2), \; (-1, 3)$
Let $\vec a = (1, 2)$ and $\vec b = (-1, 3).$ Then
$$\theta = cos^{-1}\left( \frac{\vec a\cdot \vec b}{|\vec a||\vec b|} \right)$$
$$ \begin{align} |\vec a| &= \sqrt{1^2 + 2^2} = \sqrt{5} \\[5pt] |\vec b| &= \sqrt{(-1)^2 + 3^2} = \sqrt{10} \\[5pt] \vec a \cdot \vec b &= 1(-1) + 2(3) = 5 \\[5pt] \theta &= cos^{-1}\left( \frac{5}{\sqrt{5}\sqrt{10}} \right) \\[5pt] &= cos^{-1} \left( \frac{\sqrt{2}}{2} \right) = \frac{\pi}{4} \end{align}$$
So the angle is 45˚. Let me expand that last step a bit. It was a way of recognizing a familiar sine or cosine value:
$$ \require{cancel} \frac{5}{\sqrt{5}\sqrt{10}} = \frac{\cancel{\sqrt{5}}\sqrt{5}}{\cancel{\sqrt{5}}\sqrt{10}} = \frac{\sqrt{5}}{\sqrt{10}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}$$
$(1, -1), \; (-1, 1)$
Let $\vec a = (1, 1)$ and $\vec b = (1, -1).$ Then
These vectors both have length $|\vec a| = |\vec b| = \sqrt{2},$ and the dot product is $\vec a \cdot \vec b = 1(1) + 1(-1) = 0,$ so the angle is
$$\theta = cos^{-1} \left( \frac{0}{\sqrt{2}}\right) = \frac{\pi}{2}$$
So the angle is 90˚. That's pretty clear from a graph of these two vectors. But it's good to solve problems we already know the answers to at first; it helps us to learn the method.
$(1, 2, -1), \; (2, 2, -3)$
Let $\vec a = (1, 2, -1)$ and $\vec b = (2, 2, -3).$ Then
$$\theta = cos^{-1}\left( \frac{a\cdot \vec b}{|\vec a||\vec b|} \right)$$
$$ \begin{align} |\vec a| &= \sqrt{1 + 4 + 1} = \sqrt{6} \\[5pt] |\vec b| &= \sqrt{4 + 4 + 9} = \sqrt{17} \\[5pt] \vec a \cdot \vec b &= 1(2) + 2(2) + (-1)(-3) = 9 \\[5pt] \theta &= cos^{-1}\left( \frac{9}{\sqrt{6}\sqrt{17}} \right) \\[5pt] &= cos^{-1} \left( \frac{9}{\sqrt{102}} \right) \approx 27˚ \end{align}$$
$(1, 1, 2, 1), \; (-2, 1, -1, 1)$
Let $\vec a = (1, 1, 2, 1)$ and $\vec b = (-2, 1, -1, 1).$ Then
$$ \begin{align} |\vec a| &= \sqrt{1 + 1 + 4 + 1} = \sqrt{7} \\[5pt] |\vec b| &= \sqrt{4 + 1 + 1 + 1} = \sqrt{7} \\[5pt] \vec a \cdot \vec b &= 1(-2) + 1(1) + 2(-1) + 1(1)= -2 \\[5pt] \theta &= cos^{-1}\left( \frac{-2}{\sqrt{7}\sqrt{7}} \right) \\[5pt] &= cos^{-1} \left( \frac{-2}{7} \right) \approx 107˚ \end{align}$$
It's difficult to visualize these vectors in a 4-dimensional space, but the angle between them is 107˚.
Properties of the dot product
Here are some key properties of the dot product that will come in handy when doing calculations. They can all be proved fairly easily using either the basic definition of the dot product, $\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + \dots + a_n + b_n,$ or the angle definition, $\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}| cos(\theta).$
| Property | Explanation |
|---|---|
| $\vec{a} \cdot \vec{a} = |\vec{a}|^2$ | The dot product of a vector with itself is equal to the square of its length, because $cos(0) = 1$. |
| $\vec{0} \cdot \vec{a} = 0$ | The dot product of a vector with the zero vector, $\vec{0} = (0, 0, \dots \ 0),$ is zero because the length of the zero vector is zero. That is, $(a_1, a_2, \dots a_n) \cdot (0, 0, \dots 0) = 0 + 0 + \dots + 0 = 0$. |
| $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$ | The dot product is commutative because multiplication is commutative. |
| $\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$ | The dot product is distributive. |
| $(k \vec{a}) \cdot \vec{b} = k(\vec{a} \cdot \vec{b})$ | ($k$ is a constant) Scalar multiplication and the dot product are commutative and associative. |
Example 3 – finding orthogonal vectors
Find a vector of length 1 that is perpendicular (orthogonal) to $(1, 0, 1).$
Solution : This kind of problem will have two main steps. First we'll find one vector that is perpendicular to $(1, 0, 1)$, but we'll have to remember that there are an infinite number of such vectors – all of different length. The second step will be to adjust the length of that vector to one – to make it a unit vector . Here's a picture of this 3-dimensional vector, which lives in the $x-z$ plane:

The magenta arrows just show the steps to drawing our vector – 1 unit along the $x$-axis, then one along the $z$.
Recall that the angle between perpendicular vectors (one known and one unknown in this case) has to be 90˚, and that the cosine of 90˚ is zero, so we'll start there:
$$cos(\theta) = \left( \frac{\vec v_1 \cdot \vec v_2}{|\vec v_1||\vec v_2|} \right)$$
We can get rid of the denominator because for this expression to equal zero, all that is required is that the dot product be zero:
$$\frac{\vec v_1 \cdot \vec v_2}{|\vec v_1||\vec v_2|} = 0$$
Now the dot product between $\vec v = (1, 0, 1)$ and an unknown vector $(x, y, z)$ of the same dimension is:
$$ \begin{align} 1(x) + 0(y) + 1(z) &= 0 \\[5pt] x + z &= 0 \\[5pt] x &= -z \end{align}$$
So all that is required of this vector is that $y = 0$ and $x = -z$.
$$\vec v_{\perp} = (1, \, 0, \, -1)$$
The vectors $(3, 0, -3)$ and $(4.5, 0, 4.5)$ would work just as well. They differ only in length, but they're perpendicular to $(1, 0, 1$). What we need to do now is to adjust the length of $(1, 0, 1)$ to $1$. First we need to find its current length:
$$|(1, 0, -1)| = (1^2 + 0^2 + (-1)^2)^{1/2} = \sqrt{2}$$
Now to adjust the length we just divide each component of our vector by that length. You can check for yourself that the length of this new vector is $1$.
$$\vec v_{\perp} = \left( \frac{1}{\sqrt{2}}, \, 0, \, \frac{-1}{\sqrt{2}} \right)$$
The process of adjusting the length of a vector to 1, or making it a unit vector , is called normalization .
Finally, if $(a, 0, -a)$ is perpendicular to $(1, 0, 1)$, then so is $(-a, 0, a)$. It also satisfies the requirement that $x = -z$, it just points in the opposite direction.

The diagram above shows our two vectors. They lie in the x-z plane. Notice that there are many other vectors perpendicular to $(1, 0, 1)$ outside of that plane.
Normalization of a vector
To normalize a vector (set its length to one), calculate the length of the vector, then divide each component of the vector by that length.
For each problem calculate the unit vector orthogonal to each of the vectors given. Remember that a unit vector has a length of 1.
$(2, -2, 1)$ and $(1, 0, 0)$
$$ \begin{align} 2x - 3y &= 0 \\[5pt] 2x &= 3y \\[5pt] x &= \frac{3}{2} y \end{align}$$
All we need is this relationship between x and y. They are not independent. Let $y = 1,$ then $x = \frac{3}{2},$ so one possible orthogonal vector is $v = \left(\frac{3}{2}, 1 \right).$ Now we need to normalize this vector. The first step is calculating its length:
$$|v| = \sqrt{\frac{9}{4} + 1} = \frac{\sqrt{13}}{2}$$
Now to normalize the vector, we divide each component by this length:
$$ \begin{align} v_n &= \left( \frac{3}{2}\frac{2}{\sqrt{13}}, \frac{2}{\sqrt{13}} \right) \\[5pt] &= \left( \frac{3}{\sqrt{13}}, \frac{2}{\sqrt{13}} \right) \end{align}$$
You can check for yourself that the length of the normalized vector is 1, and that its dot product with (2, -3) is zero.
$(1, 1, -1)$ and $(1, -1, 1)$
In this case we'll need to set up and solve two equations for our three unknowns. They are
$$ \begin{align} (1, 1, -1)\cdot (x, y, z) &= 0 \rightarrow x + y - z = 0 \\[5pt] (1, -1, 1) \cdot (x, y, z) &= 0 \rightarrow x - y + z = 0 \end{align}$$
If we add those two equations, we get $2x = 0,$ so $x = 0.$ Now plugging in x = 0 to the first equation gives $y - z = 0,$ so $y = z.$ If we let z = 1, then y = 1 and x = 0, so our "prototype" orthogonal vector is $(0, 1, 1).$
The length of this vector is
$$\sqrt{0^2 + 1^2 + 1^2} = \sqrt{2}.$$
Now dividing each component of $\vec{v}$ by $\sqrt{2}$ gives us our orthogonal unit vector:
$$v_n = \left( 1, \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)$$
$(1, 2, -1)$ and $(-1, -1, 0)$
$$ \begin{align} (1, 2, -1) \cdot (x, y, z) &= 0 \rightarrow x + 2y - z = 0 \\[5pt] (-1, -1, 0) \cdot (x, y, z) &= 0 \rightarrow -x - y = 0 \end{align}$$
This system isn't too difficult to solve. We already have $x = -y,$ so if we let $y = 1,$ then $x = -1,$ and (from the first equation), $z = x + 2y = 1,$ so our orthogonal vector (or one of them) is $(-1, 1, 1).$
The length of this vector is $\sqrt{3},$ so our normalized orthogonal vector (one of a kind) is
$$v_n = \left( \frac{-\sqrt{3}}{3}, \frac{\sqrt{3}}{3}, \frac{\sqrt{3}}{3} \right)$$
You can confirm that the dot products of this vector with the original two are zero, and that its length is 1.
$$ \begin{align} (2, -2, 1)\cdot (x, y, z) &= 0 \rightarrow 2x - 2y + z = 0 \\[5pt] (1, 0, 0) \cdot (x, y, z) &= 0 \rightarrow x = 0 \end{align}$$
Given that $x = 0,$ we have that $2y = z,$ or $y = \frac{1}{2}z,$ so if we let $z = 1,$ then our orthogonal vector is
$$v = (0, \frac{1}{2}, 1)$$
Now the length of this vector is $\sqrt{5}/2,$ so to normalize it, we divide all vector components by that length to get:
$$v = \left( 0, \frac{\sqrt{5}}{5}, \frac{2\sqrt{5}}{5} \right)$$
$(1, -1, -2, 1), \; (-2, -1, 1, 2), \; (2, 3, 4, 1)$
In this case we'll need to set up and solve three equations for our four unknowns. They are
$$ \begin{align} (1, -1, 2, 1)\cdot (w, x, y, z) &= 0 \rightarrow w - x + 2y + z = 0 \\[5pt] (2, 3, 4, 1)\cdot (w, x, y, z) &= 0 \rightarrow 2w + 3x + + 4y + z = 0 \\[5pt] (2, -1, 1, 2) \cdot (w, x, y, z) &= 0 \rightarrow 2w - x + y + 2z = 0 \end{align}$$
If we multiply the top equation by -2, we can set the three equations up to eliminate w:
$$ \begin{align} -2w + 2x - 4y - 2z &= 0 \\[4pt] 2w + 3x + 4y + z &= 0 \\[4pt] 2w - x + y + 2z &= 0 \end{align}$$
Adding the first equation to the second and to the third gives two new equations, reduced a bit:
$$ \begin{align} 5x - z = 0 \\[4pt] x - 3y = 0 \end{align}$$
Now we can find x, y and z in terms of one of those. It works out nicely if we let $y = 1,$ then $x = 3$ and $z = 5x = 15.$
Then w can be found from the first of the original equations:
$$ \begin{align} w &= x - 2y - z = 0 \\[4pt] &= 3 - 2 - 15 = 15 \end{align}$$
So one version of our orthogonal vector (the differ only in length) is
$$v = (w, x, y, z) = (-14, 3, 1, 15)$$
In order to normalize this vector, we need its length:
$$|v| = \sqrt{14^2 + 3^2 + 1 + 15^2} = \sqrt{431}$$
Our normalized orghogonal vector is
$$v_n = \left( \frac{-14}{20.76}, \frac{3}{20.76}, \frac{1}{20.76}, \frac{15}{20.76},\right),$$
where $20.76 \approx \sqrt{431}.$
$(2, 1, -2, -1), \; (1, 1, -1, 2), \; (0, 1, 1, 1)$
$$ \begin{align} (2, 1, -2, -1)\cdot (w, x, y, z) &= 0 \rightarrow 2w + x - 2y - z = 0 \\[5pt] (1, 1, -1, 2)\cdot (w, x, y, z) &= 0 \rightarrow w + x - y + 2z = 0 \\[5pt] (0, 1, 1, 1) \cdot (w, x, y, z) &= 0 \rightarrow x + y + z = 0 \end{align}$$
Now let's use the last equation to eliminate z in the first two, adding it to the first, subtracting 2 × it from the second to get:
$$ \begin{align} 2w + 2x - y &= 0 \\[5pt] -2w + 2x + 6y &= 0 \end{align}$$
Now add these to eliminate w and find a direct relationship between x and y:
$$4x + 5y = 0 \rightarrow x = \frac{-5}{4}$$
If we let $x = 1,$ then $y = \frac{-5}{4}.$
Now we can use one of the equations above to find w:
$$w = x + 3y = -\frac{5}{4} + 3 = \frac{7}{4}$$
Finally, we can use the last of our original equations to find z:
$$z = -x - y = \frac{5}{4} - 1 = \frac{1}{4},$$
So our vector is
$$v = \left( \frac{7}{4}, \frac{-5}{4}, 1, \frac{1}{4} \right)$$
Its length is $\sqrt{91}/4,$ so we obtain the normalized (unit length) vector by dividing each component of our orthogonal vector by this length.
$$ \begin{align} v_n &= \left( \frac{7}{4}\frac{4}{\sqrt{91}}, \frac{-5}{4}\frac{4}{\sqrt{91}}, 1\frac{4}{\sqrt{91}}, \frac{1}{4}\frac{4}{\sqrt{91}} \right) \\[5pt] &= \left( \frac{7}{\sqrt{91}}, \frac{-5}{\sqrt{91}}, \frac{4}{\sqrt{91}}, \frac{1}{\sqrt{91}} \right) \end{align}$$

You can think of matrix multiplication like taking lots of dot products
If matrix multiplication gets the best of you, it might help to think of it like taking a bunch of dot products, row vectors from the left matrix with column vectors with the right-hand matrix. Here's a 3-D matrix multiplication problem:

We'll think of the matrix on the left as a vertical list of row vectors (a column vector of row vectors ... but that's confusing), called a , b and c . The matrix on the right is a horizontal list of column vectors, x , y and z .
Now if we multiply the two matrices, we're just taking a series of dot products like this:
$$ = \begin{bmatrix} a \cdot x & a \cdot y & a \cdot z \\ b \cdot x & b \cdot y & b \cdot z \\ c \cdot x & c \cdot y & c \cdot z \end{bmatrix}$$
Now take a look at that matrix. The element in the second row, second column is just the dot product of the second row vector, b , and the second column vector, y . It's the same for each element in the result matrix. Here is the expanded result:
$$ \begin{bmatrix} a_1x_1 + a_2x_2 + a_3x_3 & a_1y_1 + a_2y_2 + a_3y_3 & a_1z_1 + a_2z_2 + a_3z_3 \\ b_1x_1 + b_2x_2 + b_3x_3 & b_1y_1 + b_2y_2 + b_3y_3 & b_1z_1 + b_2z_2 + b_3z_3 \\ c_1x_1 + c_2x_2 + c_3x_3 & c_1y_1 + c_2y_2 + c_3y_3 & c_1z_1 + c_2z_2 + c_3z_3 \end{bmatrix}$$
Vector transpose approach
There is another very valuable way to approach the dot product. It's the matrix product of the transpose of a vector with the vector itself. First, the transpose:
The transpose $(\, {\vec v}^T \,)$ of a vector is obtained by rewriting a column vector as a row or a row vector as a column.
Here are some examples. Let $\vec a = (a_1, a_2)$ and $\vec b = \left(\begin{matrix} b_1 \\ b_2 \end{matrix} \right)$. $\vec a$ is a row vector and $\vec b$ is a column vector. We write the transposes of these vectors as $\vec a^T$ and $\vec b^T$. Then we have
$$\begin{align} \vec a = (a_1, a_2) \phantom{0000} \vec a^T &= \left( \begin{matrix} a_1 \\ a_2 \end{matrix} \right) \\[5pt] \vec b = \left(\begin{matrix} b_1 \\ b_2 \end{matrix} \right) \phantom{0000} \vec b^T &= (b_1, b_2) \end{align}$$
Just as an aside, we can write the transpose of a matrix, too. Just consider a matrix as a row of column vectors or a column of row vectors. Here's a 2×2 example:
$$A = \left( \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \right) \phantom{000} A^T = \left( \begin{matrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{matrix} \right)$$
Now we make two slight changes to our thinking about vectors and the dot product.
- We write all vectors, by default, as column vectors . Let's let the column vector be our natural way to write any vector.
- The dot product of vectors $\vec a$ and $\vec b$ is then $\vec a^T \vec b$.
That is, if $\vec a = \left( \begin{matrix} a_1 \\ a_2 \end{matrix} \right)$ and $\vec b = \left( \begin{matrix} b_1 \\ b_2 \end{matrix} \right)$, then the dot product $\vec a \cdot \vec b$ is
$$\vec a \cdot \vec b = \vec a^T \vec b = (a_1, a_2) \left( \begin{matrix} b_1 \\ b_2 \end{matrix} \right) = a_1 b_1 + a+2 b_2$$.
Calculate the dot product of the 3-space vectors $\vec x = \left( \begin{matrix} 1 \\ 2 \\ -3 \end{matrix} \right)$ and $\vec y = \left( \begin{matrix} -2 \\ 2 \\ 3 \end{matrix} \right)$
Solution : The dot product is $\vec x^T \vec y$,
$$ = (1, 2, -3) \left( \begin{matrix} -2 \\ 2 \\ 3 \end{matrix} \right) = 1(-2) + 2(2) - 3(3) = -7$$
This form of the dot product works for any two vectors of any dimension as long as they're the same dimension.
Matrix multiplication works in the same way: we simply multiply each row vector in the left-side matrics by each column vector in the right-side matrix.

Back up and review vectors, then come back and learn the dot product.
The cross product
The cross product is related to the dot product.

In two dimensions, orthogonal means perpendicular . But when we proceed to three or more dimensions, "perpendicular" isn't good enough. In 3-D a line and a plane can be perpendicular when viewed from one direction, but not perpendicular when viewed from an angle 90˚ away on the plane. The word orthogonal means perpendicular in every conceivable direction, no matter how many dimensions.
Browse Course Material
Course info.
- Prof. Denis Auroux
Departments
- Mathematics
As Taught In
- Differential Equations
- Linear Algebra
Learning Resource Types
Multivariable calculus, session 2: dot products.
« Previous | Next »
In this session you will:
- Watch a lecture video clip and read board notes
- Read course notes and examples
- Do problems and use solutions to check your work
Lecture Video
Video excerpts.
Clip: Dot Products
The following images show the chalkboard contents from these video excerpts. Click each image to enlarge.
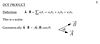
Reading and Examples
Dot Product (PDF)
Problems and Solutions
Problems: Dot Product (PDF)
Solutions (PDF)

You are leaving MIT OpenCourseWare
The Work (dot product) calculator uses the equation, W= F⋅d, to computes the work done when a force (F) is applied to move a mass some displacement (d).
INSTRUCTIONS: Choose the preferred units and enter the following:
- (`F_x`) - This is the force applied in the x direction
- (`F_y`) - This is the force applied in the y direction
- (`F_z`) - This is the force applied in the z direction
- (`d_x`) - This is the distance the mass is moved in the x direction
- (`d_y`) - This is the distance the mass is moved in the y direction
- (`d_z`) - This is the distance the mass is moved in the z direction
Work (w) : The calculator returns the work in Newton meters (N•m). However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
This specific work calculator is an example of using the dot product . The dot product is used to multiply two vectors and output a scalar quanitity. Since force and displacement are vectors, and work is the multiplication of those two vectors , we are left with using the dot product ! The dot product simply examines vectors in their specific cartesian directions, and then multiplies like terms to get a new vector in the appropriate direction. It is a powerful tool and is used commonly in Vector Calculus and Physics.
Related Calculators:
- Work(Fdcos)
- Kinetic Energy
- Potential Energy(mgh)
- Potential Energy(Fy)
References:
Light and Matter Textbook Chapter 13.7
Sorry, JavaScript must be enabled. Change your browser options, then try again .
Dot product
Study guide, related topics.
- Multivariable calculus (147 problems) Multivariable calculus (147 problems) -->
Practice problems
- Which have a positive dot product with $\mathbf{A}$?
- Which have a negative dot product with $\mathbf{A}$?
- Which have zero dot product with $\mathbf{A}$?
- Which has the largest dot product with $\mathbf{A}$?
- Which has the most negative dot product with $\mathbf{A}$?
- Directly (in the case of 3d vectors)
- By the dot product angle formula
- more problems
For corrections, suggestions, or feedback, please email [email protected]
- © 2014 Paul Hand
Profound Physics
Dot Product In Physics: What Is The Physical Meaning of It?
The dot product is a mathematical operation between two vectors that produces a scalar (number) as a result. It is also commonly used in physics, but what actually is the physical meaning of the dot product?
The physical meaning of the dot product is that it represents how much of any two vector quantities overlap. For example, the dot product between force and displacement describes the amount of force in the direction in which the position changes and this amounts to the work done by that force.
In this article, we’ll be discussing this in a lot more detail as well as looking at some examples of how dot products are used in physics.
We’ll also discuss some more general notions of dot products, which are useful for relativity and quantum mechanics , among other things.
If you’re interested in learning physics more deeply, you may enjoy my Advanced Math For Physics: A Complete Self-Study Course – it’s the perfect place to get started learning more advanced physics and math, as it begins from the very fundamentals.
Table of Contents
Significance of The Dot Product In Physics: Intuitive Explanation + Examples
In an intuitive sense, the dot product is a measure of how much two vectors are aligned . So, if we have two vectors, u and v, the dot product between these two would give the length of the vector v along the vector u , or if you will, the projection of v along u .
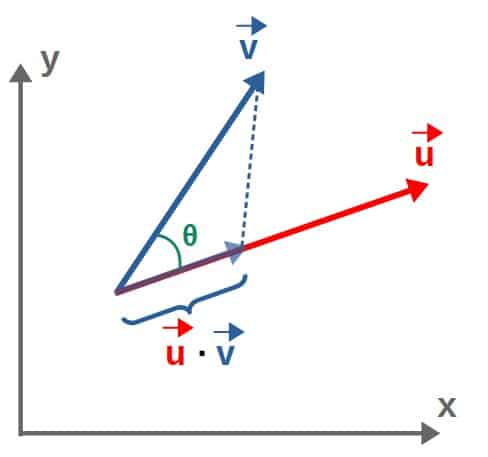
If we know the angle between the two vectors (θ in the above picture), the dot product can be calculated by the following formula:
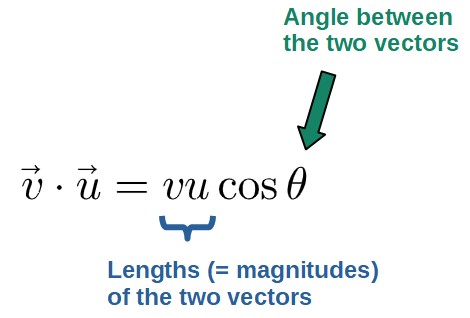
An interesting way to interpret this cos(θ) -factor is that it describes a kind of “percentage of alignment” between the two vectors; if cos(θ)=1, the vectors are fully aligned (since θ=0°) and if cos(θ)=0 (meaning θ=90°), the vectors don’t align at all. Moreover, something like cos(θ)=0.97 (θ≈15°) would correspond to the vectors being “almost aligned”.
The dot product can also be calculated in terms of the components of these vectors by using the following formula:
In general, this formula is valid for any number of dimensions, but here I’ve only written in in three dimensions.
Now, what’s the significance of all of this to physics? Well, many physical quantities are described by vectors (for example, velocity and forces), so it only makes sense that the dot product also has some physical significance.
In particular, the same geometric picture applies in physics as well; the dot product gives the length of one vector along another vector, but now, vectors represent something physical.
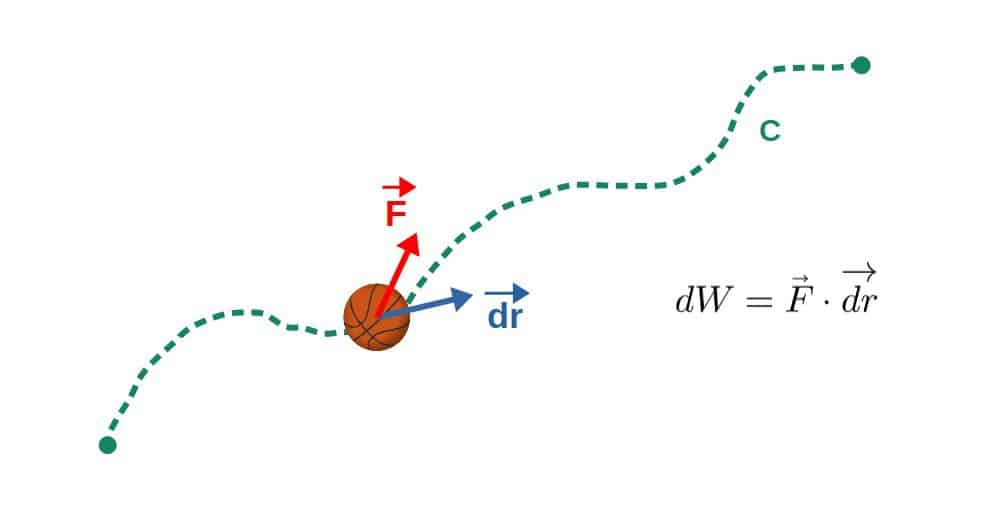
The best way to explain the physics of this is through an example. Namely, the dot product between a displacement vector and a force vector , which could be described as “the change in position (displacement) in the direction of the force”.
This quantity gives the work done by the force , which is essentially the change in energy caused by this force. More precisely, the work done along some path is actually given by a line integral of this dot product, which I explain in this article .
Hopefully this is enough motivation to establish why dot products are indeed useful in physics. There are thousands of different applications for the dot product ranging from basic mechanics to electromagnetism and even to graphic design and animations .
A nice explanation of this can be found in the video below:
Now, in higher-level physics , dot products are also useful but for slightly different reasons than the elementary geometric interpretation given above.
Namely, the dot product is useful because it has some nice mathematical properties that can be generalized very well to more abstract and more advanced areas of physics.
For example, the usual way to deal with mechanics problems is by using Newton’s laws, which are essentially vector equations.
However, an alternative way is to use only energies (which are scalars) and this is done in a formulation of mechanics called Lagrangian mechanics . I actually have a whole introductory article discussing Lagrangian mechanics, which you can find here .
Lagrangian mechanics is a highly elegant formulation of mechanics and part of that elegance comes from the fact that energy is a scalar quantity , which is partly due to the mathematical properties of the dot product.
This is because kinetic energy is a scalar since it involves only a dot product of velocities (I explain this and much more about the kinetic energy formula in this article ).
This directly brings us to one of the defining properties of the dot product; it is a mathematical operation that gives a scalar as a result .
This is particularly important since scalars are invariant quantities (I’ll explain this later) that have a lot of use in, for example, special and general relativity.
For our purposes, the main properties of the dot product are:
- The dot product is a scalar .
- The dot product is commutative (though this is not true for operators anymore; this fact is actually part of where the richness of quantum mechanics comes from).
- The dot product defines a notion of orthogonality (if the dot product between two quantities is zero).
We’ll talk about these properties more later, but it’s worth noting that while these may seem obvious when only looked at from the lens of this “basic” definition of the dot product, they really are what defines the dot product itself.
This is why these properties are important if we wish to generalize the notion of the dot product to more complicated situations, such as curved spacetime in general relativity . This is what we’ll talk about next.
Dot Product In Special And General Relativity
In general relativity, gravity and the motion of objects under the influence of gravity , is explained by spacetime (so both space and time) itself being curved, which results in the effects of gravity and gravitational acceleration.
Everything we’re interested in in general relativity, essentially takes place in curved spacetime . You could therefore think of the mathematics of general relativity as simply ordinary math but done in a “curved geometry”.
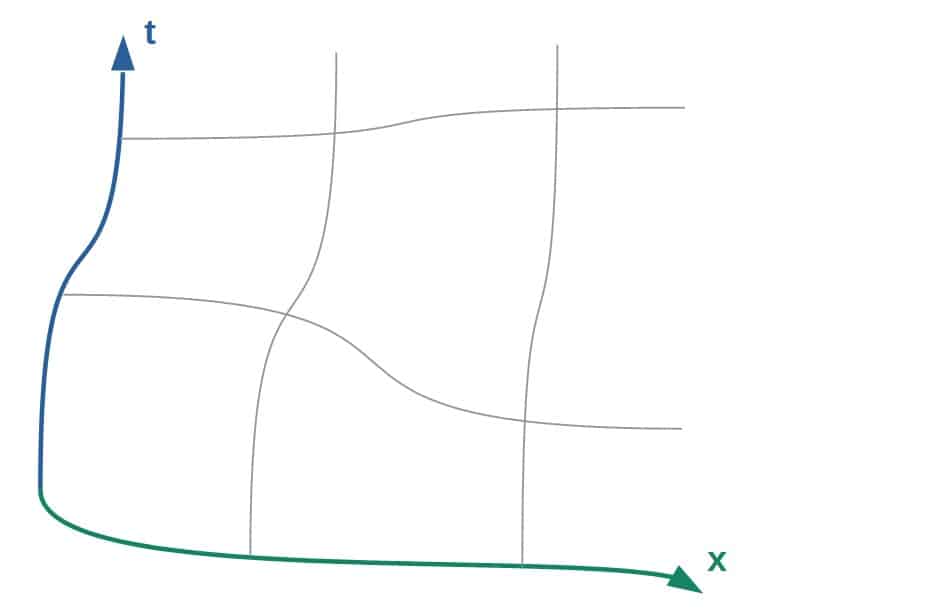
It’s worth noting that special relativity is really just a “special case” of general relativity, which is why we’ll discuss mostly general relativity here. If you’re interested in either of these topics, I recommend reading my introductory article on special relativity as well as my introductory article on general relativity . I also have a guide for learning general (and special) relativity , which is particularly aimed at those wanting to self-study these topics on their own.
Now, the difficulty of this comes from the fact that if we’re dealing with some arbitrarily curved spaces, how can there be any kind of a universal notion of a dot product ? The answer is that there cannot, at least not in the way we’re used to.
Really, the problem comes from the fact that in a curved spacetime, the basis vectors (which are used to express components of vectors) are not constant and may vary from place to place .
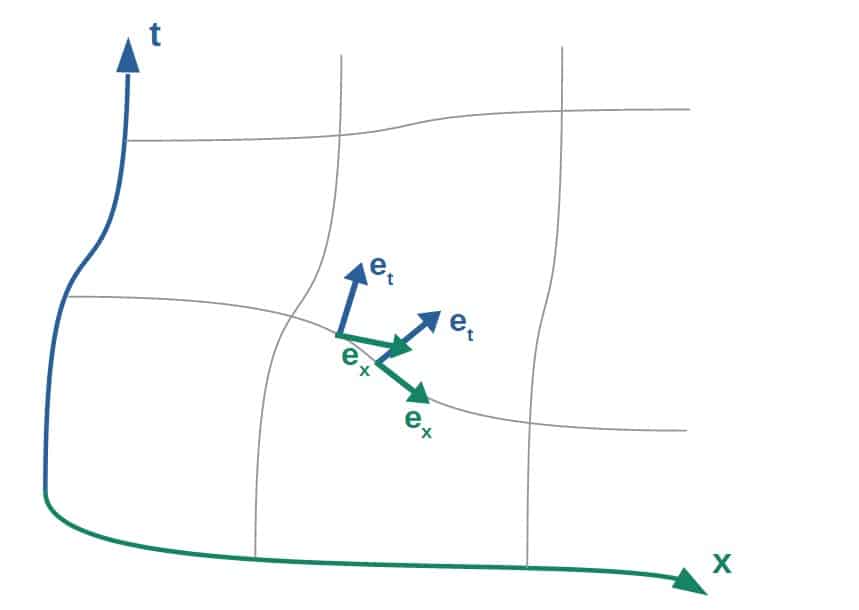
If the basis vectors are not constant, we can’t define the dot product as simply just the sum of the products of components:
Instead, we use an object called the metric tensor , which you can think of as adding a “correction factor” to each term in this dot product to account for the fact that the basis vectors may be different from place to place :
Note that these metric components (the g’s here) are actually components of a two-index tensor rather than vector components. This is why they have two indices. Moreover, the metric is generally a function that can also vary from place to place like the basis vectors.
More generally, the dot product can be written as:
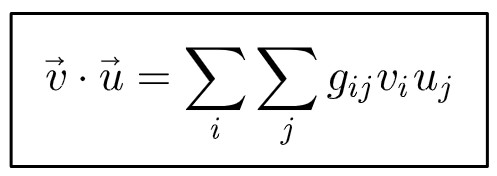
Instead of the usual dot product formula, we now have a double sum, which CAN actually have cross-terms involving products of the vector components such as v 1 u 2 . This is indeed possible if the basis vectors are not constant, but not in the typical Cartesian (x,y,z) coordinate system.
This is the formula for the dot product between two vectors in any arbitrary coordinate system or space (although there are some mathematical restrictions, which we won’t get into now).
Now, the metric for any given spacetime is typically calculated from the Einstein field equations of general relativity, which specifies the geometry of that spacetime by its energy and momentum content. This is the usual way of calculating different spacetime metrics in general relativity.
By using the metric, it’s possible to derive all kinds of physical results from general relativity, such as time dilation near a black hole . I discuss this and its geometric as well as physical interpretations in detail in this article .
Now, the bottom line with all of this is that it is possible to define a notion of the dot product in curved spaces and coordinate systems by using a metric tensor .
The physical meaning of this is more or less the same still; the dot product is a measure of how much two vectors align, although this is a bit more difficult to picture if we’re dealing with a curved geometry.
In any case, the mathematics of curved spaces (and differential geometry in general) is fascinating and holds so many interesting concepts which have applications in so many areas of physics too.
If you want to learn more about these, I recommend my article on the Christoffel symbols , one of the central mathematical tools used in general relativity, as well as my article on the Ricci tensor , which has an interesting physical meaning having to do with gravitational tides.
Dot Product In Quantum Mechanics (The Inner Product)
The dot product in quantum mechanics is quite a bit more abstract than any of the notions we talked about before.
Besides, it usually doesn’t even go by the name if a dot product, but rather the inner product (to be precise, the inner product actually refers to a more general “class” of mathematical operations than the dot product).
The inner product between two vectors is denoted by “sandwiching” together a bra vector (the thing on the left) and a ket vector (the thing on the right):
Now, this is equivalent to a typical dot product, except that in quantum mechanics, we’re usually dealing with complex numbers . So, this inner product is actually:
Here, the star denoted the complex conjugate of the components of v. Note that this is pretty much the same as the dot product for “ordinary” vectors, except generalized to complex numbers.
Now, these bra’s and ket’s (the v and u with these weird brackets around them) are indeed vectors . However, they are not the typical vectors in 3D space, but rather they are abstract state vectors in a complex vector space .
The physical meaning of them is that they represent quantum states of a system. Now, what this practically means will depend on the particular state vector. For example, we could have a state vector that represents a particle with some momentum and this would be a perfectly valid quantum state.
The dot product (or inner product) also has pretty much the same meaning, except that it is now a mathematical operation in an abstract vector space, so we cannot picture it geometrically.
An important application of these inner products in quantum mechanics is for basis states . These are analogous to basis vectors, but again they are abstract complex vectors. Basis states are defined by the following inner products:
The first equation here means that our basis state is normalized (its “square” is 1). This allows for a probabilistic interpretation in quantum mechanics.
The inner product here being equal to zero means that our two states are orthogonal . In quantum mechanics, this corresponds to these basis vectors representing distinct quantum states , for example, states of definite momenta (as opposed to a superposition of different momenta).
Now, these define a “basis” in this abstract vector space and we can indeed represent any possible quantum mechanical state by using these basis states (this is analogous to how any vector can be expressed in terms of basis vectors).
I'm the founder of Profound Physics, a website I created to help especially those trying to self-study physics as that is what I'm passionate about doing myself. I like to explain what I've learned in an understandable and laid-back way and I'll keep doing so as I learn more about the wonders of physics.
Similar Posts
Gradient in different coordinates (intuition & step-by-step examples).
The gradient is one of the most important differential operators often used…
Calculus of Variations For Dummies: An Intuitive Introduction
Most people have heard of basic calculus and know about its applications…
How To Learn Vector Calculus: A Step-By-Step Guide
In my opinion, if there is one area of mathematics you should…

Is Time Always The Independent Variable? (And When Is It Not?)
Usually time is treated as the independent variable when, for example, making…
Legendre Transformations For Dummies: Intuition & Examples
If you’ve studied thermodynamics or Hamiltonian mechanics, you’ve probably encountered the Legendre…

Is Time Actually A Vector or A Scalar? The Physics Explained
Often, we think of time as simply a number assigned to a…
- For educators
- English (US)
- English (India)
- English (UK)
- Greek Alphabet
This problem has been solved!
You'll get a detailed solution from a subject matter expert that helps you learn core concepts.
Question: For this assignment explain the following concepts: -Explain the concept of "dot product". Make sure to include an example (2 marks) -Can you explain the concept of "work" and how it relates to "dot product"( 2 marks) -Can you explain when the "work" is 0. Support your answer with an example. (2 marks) -Can you explain what we mean when we say the work is
For this assignment explain the following concepts:
-Explain the concept of "dot product". Make sure to include an example (2 marks)
-Can you explain the concept of "work" and how it relates to "dot product"( 2 marks)
-Can you explain when the "work" is 0. Support your answer with an example. (2 marks)
-Can you explain what we mean when we say the work is negative? Which force does the negative work? ( 2 marks)
-Explain the difference between "dot product" and "cross product" (2 marks)
- How could you use a wrench to explain "cross product". (2 marks)

Not the question you’re looking for?
Post any question and get expert help quickly.

COMMENTS
For those who need the help. Learn with flashcards, games, and more — for free.
Study with Quizlet and memorize flashcards containing terms like Given u = 1, 3 , v = 2, 1 , and cos(ϴ) = √2/2, where ϴ is the angle between the vectors, what is the scalar projection uv and the dot product u · v?, What is the relationship between vectors u = 1, 0 and v = 0, -3 ?, Given u = 3, 2 , v = 1, 5 , and the angle between the vectors is 45°, what is u · v? and more.
Quizlet has study tools to help you learn anything. Improve your grades and reach your goals with flashcards, practice tests and expert-written solutions today. ... practice tests and expert-written solutions today. Flashcards. 1 / 10 Dot Product and Work Assignment. Log in. Sign up. Get a hint. Find the dot product of u = 〈3, -4〉 and v ...
For exercises 13-18, find the measure of the angle between the three-dimensional vectors ⇀ a and ⇀ b. Express the answer in radians rounded to two decimal places, if it is not possible to express it exactly. 13) ⇀ a = 3, − 1, 2 , ⇀ b = 1, − 1, − 2 . Answer: 14) ⇀ a = 0, − 1, − 3 , ⇀ b = 2, 3, − 1 .
I know how to calculate the dot product of two vectors alright. However, it is not clear to me what, exactly, does the dot product represent. The product of two numbers, 2 and 3, we say that it is 2 added to itself 3 times or something like that. But when it comes to vectors →a ⋅ →b, I'm not sure what to say. "It is →a added to itself →b times" which doesn't make much sense to me.
Video Description: Herb Gross motivates the definition of the dot product: Work = Force x Distance. He also shows how to calculate the dot product of two vectors in 3-space. Other topics include projections, directional cosines, and the arithmetic structure of the dot product. Instructor/speaker: Prof. Herbert Gross
In Physics Work is force times distance, but only the aligned part. So work is the dot product of force and distance. Alex pushes a box 3 m straight forward using 200 N of force. But his push is a little upwards by 20°.
Assignment Read: Section 11.3 - Dot Products Lesson 3 in Study Guide
A constant force of F = 47i + 30j moves an object along a vector D = 13i - 8j, where units are in pounds and feet. Find the work done.
The dot product (also called the scalar product) gives us the angle between any two vectors. It's one of the most important relationships between vectors. In this section we'll define the dot product and show how it gives the angle between vectors for two- and three-dimensional vectors. The dot product gives the angle between two vectors of any dimension. It's a tricky concept, but it's true ...
This section provides materials for a session on dot products, including lecture video excerpts, board notes, readings and examples, and problems with solutions.
The Math / Science This specific work calculator is an example of using the dot product. The dot product is used to multiply two vectors and output a scalar quanitity. Since force and displacement are vectors, and work is the multiplication of those two vectors, we are left with using the dot product!
Solution. Suppose that two opposite sides of a quadrilateral are parallel and have equal length. Show that the quadrilateral is a parallelogram. Solution. Consider an arbitrary quadrilateral. The two blue line segments connect the midpoints of adjacent sides.
Question: Work (symbol: W) is defined as the dot product between a force (symbol: F) and a displaceme (symbol: An): W=F.AT Let's investigate the work that a ramp does as a box is pushed up the ramp. The force that the ramp exerts on the box is shown below, as well as the displacement of the box as it moves up the ramp. AF Framp Los 68° 22 Premel = 50 N 1471 = 13 m Two all one question please ...
Study with Quizlet and memorize flashcards containing terms like Find a b if a = 10i + 4j and b = 3i + 4j., The angle between a 180-pound force F and = 5i + 2j is 30. Find the work done by F in moving and object from A to B., Use the dot product to find when v = . and more.
Quizlet has study tools to help you learn anything. Improve your grades and reach your goals with flashcards, practice tests and expert-written solutions today. Match. Dot Product and Work Assignment. Log in. Sign up. Ready to play? Match all the terms with their definitions as fast as you can. Avoid wrong matches, they add extra time!
The physical meaning of the dot product is that it represents how much of any two vector quantities overlap. For example, the dot product between force and displacement describes the amount of force in the direction in which the position changes and this amounts to the work done by that force. In this article, we'll be discussing this in a ...
Quizlet has study tools to help you learn anything. Improve your grades and reach your goals with flashcards, practice tests and expert-written solutions today.
For this assignment explain the following concepts: -Explain the concept of "dot product". Make sure to include an example (2 marks) -Can you explain the concept of "work" and how it relates to "dot product" ( 2 marks) -Can you explain when the "work" is 0.