problem solving in acceleration with solutions

Physics Problems with Solutions

Acceleration: Tutorials with Examples

Examples with explanations on the concepts of acceleration of moving object are presented. More problems and their solutions can also be found in this website.

Average Acceleration

An object with initial velocity v 0 at time t 0 and final velocity v at time t has an average acceleration between t 0 and t given by

Examples with soltutions

What is the acceleration of an object that moves with uniform velocity? Solution: If the velocity is uniform, let us say V, then the initial and final velocities are both equal to V and the definition of the acceleration gives

A car accelerates from rest to a speed of 36 km/h in 20 seconds. What is the acceleration of the car in m/s 2 ? Solution: The initial velocity is 0 (from rest) and the final velocity is 36 km/h. Hence

Popular Pages

About me and why I created this physics website.

Acceleration Problems

Search Website

Real World Applications — for high school level and above

Amusement Parks
Battle & Weapons
Engineering
Miscellaneous

Education & Theory — for high school level and above

Useful Formulas
Physics Questions
Example Mechanics Problems
Learn Physics Compendium

Kids Section

Physics For Kids
Science Experiments
Science Fair Ideas
Science Quiz
Science Toys
Teacher Resources
Commercial Disclosure
Privacy Policy

problem solving in acceleration with solutions

Exam Center
Ticket Center
Flash Cards
Straight Line Motion

Solved Speed, Velocity, and Acceleration Problems

Simple problems on speed, velocity, and acceleration with descriptive answers are presented for the AP Physics 1 exam and college students. In each solution, you can find a brief tutorial.

Speed and velocity Problems:

Problem (1): What is the speed of a rocket that travels $8000\,{\rm m}$ in $13\,{\rm s}$?

Solution : Speed is defined in physics as the total distance divided by the elapsed time, so the rocket's speed is \[\text{speed}=\frac{8000}{13}=615.38\,{\rm m/s}\]

Problem (2): How long will it take if you travel $400\,{\rm km}$ with an average speed of $100\,{\rm m/s}$?

Solution : Average speed is the ratio of the total distance to the total time. Thus, the elapsed time is \begin{align*} t&=\frac{\text{total distance}}{\text{average speed}}\\ \\ &=\frac{400\times 10^{3}\,{\rm m}}{100\,{\rm m/s}}\\ \\ &=4000\,{\rm s}\end{align*} To convert it to hours, it must be divided by $3600\,{\rm s}$ which gives $t=1.11\,{\rm h}$.

Problem (3): A person walks $100\,{\rm m}$ in $5$ minutes, then $200\,{\rm m}$ in $7$ minutes, and finally $50\,{\rm m}$ in $4$ minutes. Find its average speed.

Solution : First find its total distance traveled ($D$) by summing all distances in each section, which gets $D=100+200+50=350\,{\rm m}$. Now, by definition of average speed, divide it by the total time elapsed $T=5+7+4=16$ minutes.

But keep in mind that since the distance is in SI units, so the time traveled must also be in SI units, which is $\rm s$. Therefore, we have\begin{align*}\text{average speed}&=\frac{\text{total distance} }{\text{total time} }\\ \\ &=\frac{350\,{\rm m}}{16\times 60\,{\rm s}}\\ \\&=0.36\,{\rm m/s}\end{align*}

Problem (4): A person walks $750\,{\rm m}$ due north, then $250\,{\rm m}$ due east. If the entire walk takes $12$ minutes, find the person's average velocity.

Solution : Average velocity , $\bar{v}=\frac{\Delta x}{\Delta t}$, is displacement divided by the elapsed time. Displacement is also a vector that obeys the addition vector rules. Thus, in this velocity problem, add each displacement to get the total displacement .

In the first part, displacement is $\Delta x_1=750\,\hat{j}$ (due north) and in the second part $\Delta x_2=250\,\hat{i}$ (due east). The total displacement vector is $\Delta x=\Delta x_1+\Delta x_2=750\,\hat{i}+250\,\hat{j}$ with magnitude of \begin{align*}|\Delta x|&=\sqrt{(750)^{2}+(250)^{2}}\\ \\&=790.5\,{\rm m}\end{align*} In addition, the total elapsed time is $t=12\times 60$ seconds. Therefore, the magnitude of the average velocity is \[\bar{v}=\frac{790.5}{12\times 60}=1.09\,{\rm m/s}\]

Problem (5): An object moves along a straight line. First, it travels at a velocity of $12\,{\rm m/s}$ for $5\,{\rm s}$ and then continues in the same direction with $20\,{\rm m/s}$ for $3\,{\rm s}$. What is its average speed?

Solution: Average velocity is displacement divided by elapsed time, i.e., $\bar{v}\equiv \frac{\Delta x_{tot}}{\Delta t_{tot}}$.

Here, the object goes through two stages with two different displacements, so add them to find the total displacement. Thus,\[\bar{v}=\frac{x_1 + x_2}{t_1 +t_2}\] Again, to find the displacement, we use the same equation as the average velocity formula, i.e., $x=vt$. Thus, displacements are obtained as $x_1=v_1\,t_1=12\times 5=60\,{\rm m}$ and $x_2=v_2\,t_2=20\times 3=60\,{\rm m}$. Therefore, we have \begin{align*} \bar{v}&=\frac{x_1+x_2}{t_1+t_2}\\ \\&=\frac{60+60}{5+3}\\ \\&=\boxed{15\,{\rm m/s}}\end{align*}

Problem (6): A plane flies the distance between two cities in $1$ hour and $30$ minutes with a velocity of $900\,{\rm km/h}$. Another plane covers that distance at $600\,{\rm km/h}$. What is the flight time of the second plane?

Solution: first find the distance between two cities using the average velocity formula $\bar{v}=\frac{\Delta x}{\Delta t}$ as below \begin{align*} x&=vt\\&=900\times 1.5\\&=1350\,{\rm km}\end{align*} where we wrote one hour and a half minutes as $1.5\,\rm h$. Now use again the same kinematic equation above to find the time required for another plane \begin{align*} t&=\frac xv\\ \\ &=\frac{1350\,\rm km}{600\,\rm km/h}\\ \\&=2.25\,{\rm h}\end{align*} Thus, the time for the second plane is $2$ hours and $0.25$ of an hour, which converts to minutes as $2$ hours and ($0.25\times 60=15$) minutes.

Problem (7): To reach a park located south of his jogging path, Henry runs along a 15-kilometer route. If he completes the journey in 1.5 hours, determine his speed and velocity.

Solution: Henry travels his route to the park without changing direction along a straight line. Therefore, the total distance traveled in one direction equals the displacement, i.e, \[\text{distance traveled}=\Delta x=15\,\rm km\]Velocity is displacement divided by the time of travel \begin{align*} \text{velocity}&=\frac{\text{displacement}}{\text{time of travel}} \\\\ &=\frac{15\,\rm km}{1.5\,\rm h} \\\\ &=\boxed{10\,\rm km/h}\end{align*} and by definition, its average speed is \begin{align*} \text{speed}&=\frac{\text{distance covered}}{\text{time interval}}\\\\&=\frac{15\,\rm km}{1.5\,\rm h}\\\\&=\boxed{10\,\rm km/h}\end{align*} Thus, Henry's velocity is $10\,\rm km/h$ to the south, and its speed is $10\,\rm km/h$. As you can see, speed is simply a positive number, with units but velocity specifies the direction in which the object is moving.

Problem (8): In 15 seconds, a football player covers the distance from his team's goal line to the opposing team's goal line and back to the midway point of the field having 100-yard-length. Find, (a) his average speed, and (b) the magnitude of the average velocity.

Solution: The total length of the football field is $100$ yards or in meters, $L=91.44\,\rm m$. Going from one goal's line to the other and back to the midpoint of the field takes $15\,\rm s$ and covers a distance of $D=100+50=150\,\rm yd$.

average speed and velocity at football field

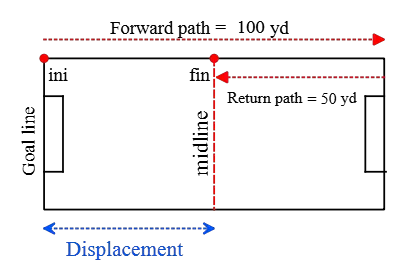
Distance divided by the time of travel gets the average speed, \[\text{speed}=\frac{150\times 0.91}{15}=9.1\,\rm m/s\] To find the average velocity, we must find the displacement of the player between the initial and final points.

The initial point is her own goal line and her final position is the midpoint of the field, so she has displaced a distance of $\Delta x=50\,\rm yd$ or $\Delta x=50\times 0.91=45.5\,\rm m$. Therefore, her velocity is calculated as follows \begin{align*} \text{velocity}&=\frac{\text{displacement}}{\text{time elapsed}} \\\\ &=\frac{45.5\,\rm m}{15\,\rm s} \\\\&=\boxed{3.03\quad \rm m/s}\end{align*} Contrary to the previous problem, here the motion is not in one direction, hence, the displacement is not equal to the distance traveled. Accordingly, the average speed is not equal to the magnitude of the average velocity.

Problem (9): You begin at a pillar and run towards the east (the positive $x$ direction) for $250\,\rm m$ at an average speed of $5\,\rm m/s$. After that, you run towards the west for $300\,\rm m$ at an average speed of $4\,\rm m/s$ until you reach a post. Calculate (a) your average speed from pillar to post, and (b) your average velocity from pillar to post.

Solution : First, you traveled a distance of $L_1=250\,\rm m$ toward east (or $+x$ direction) at $5\,\rm m/s$. Time of travel in this route is obtained as follows \begin{align*} t_1&=\frac{L_1}{v_1}\\\\ &=\frac{250}{5}\\\\&=50\,\rm s\end{align*} Likewise, traveling a distance of $L_2=300\,\rm m$ at $v_2=4\,\rm m/s$ takes \[t_2=\frac{300}{4}=75\,\rm s\] (a) Average speed is defined as the distance traveled (or path length) divided by the total time of travel \begin{align*} v&=\frac{\text{path length}}{\text{time of travel}} \\\\ &=\frac{L_1+L_2}{t_1+t_2}\\\\&=\frac{250+300}{50+75} \\\\&=4.4\,\rm m/s\end{align*} Therefore, you travel between these two pillars in $125\,\rm s$ and with an average speed of $4.4\,\rm m/s$.

(b) Average velocity requires finding the displacement between those two points. In the first case, you move $250\,\rm m$ toward $+x$ direction, i.e., $L_1=+250\,\rm m$. Similarly, on the way back, you move $300\,\rm m$ toward the west ($-x$ direction) or $L_2=-300\,\rm m$. Adding these two gives us the total displacement between the initial point and the final point, \begin{align*} L&=L_1+L_2 \\\\&=(+250)+(-300) \\\\ &=-50\,\rm m\end{align*} The minus sign indicates that you are generally displaced toward the west.

Finally, the average velocity is obtained as follows: \begin{align*} \text{average velocity}&=\frac{\text{displacement}}{\text{time of travel}} \\\\ &=\frac{-50}{125} \\\\&=-0.4\,\rm m/s\end{align*} A negative average velocity indicating motion to the left along the $x$-axis.

This speed problem better makes it clear to us the difference between average speed and average speed. Unlike average speed, which is always a positive number, the average velocity in a straight line can be either positive or negative.

Problem (10): What is the average speed for the round trip of a car moving uphill at 40 km/h and then back downhill at 60 km/h?

Solution : Assuming the length of the hill to be $L$, the total distance traveled during this round trip is $2L$ since $L_{up}=L_{down}=L$. However, the time taken for going uphill and downhill was not provided. We can write them in terms of the hill's length $L$ as $t=\frac L v$.

Applying the definition of average speed gives us \begin{align*} v&=\frac{\text{distance traveled}}{\text{total time}} \\\\ &=\frac{L_{up}+L_{down}}{t_{up}+t_{down}} \\\\ &=\cfrac{2L}{\cfrac{L}{v_{up}}+\cfrac{L}{v_{down}}} \end{align*} By reorganizing this expression, we obtain a formula that is useful for solving similar problems in the AP Physics 1 exams. \[\text{average speed}=\frac{2v_{up} \times v_{down}}{v_{up}+v_{down}}\] Substituting the numerical values into this, yields \begin{align*} v&=\frac{2(40\times 60)}{40+60} \\\\ &=\boxed{48\,\rm m/s}\end{align*} What if we were asked for the average velocity instead? During this round trip, the car returns to its original position, and thus its displacement, which defines the average velocity, is zero. Therefore, \[\text{average velocity}=0\,\rm m/s\]

Acceleration Problems

Problem (9): A car moves from rest to a speed of $45\,\rm m/s$ in a time interval of $15\,\rm s$. At what rate does the car accelerate?

Solution : The car is initially at rest, $v_1=0$, and finally reaches $v_2=45\,\rm m/s$ in a time interval $\Delta t=15\,\rm s$. Average acceleration is the change in velocity, $\Delta v=v_2-v_1$, divided by the elapsed time $\Delta t$, so \[\bar{a}=\frac{45-0}{15}=\boxed{3\,\rm m/s^2} \]

Problem (10): A car moving at a velocity of $15\,{\rm m/s}$, uniformly slows down. It comes to a complete stop in $10\,{\rm s}$. What is its acceleration?

Solution: Let the car's uniform velocity be $v_1$ and its final velocity $v_2=0$. Average acceleration is the difference in velocities divided by the time taken, so we have: \begin{align*}\bar{a}&=\frac{\Delta v}{\Delta t}\\\\&=\frac{v_2-v_1}{\Delta t}\\\\&=\frac{0-15}{10}\\\\ &=\boxed{-1.5\,{\rm m/s^2}}\end{align*}The minus sign indicates the direction of the acceleration vector, which is toward the $-x$ direction.

Problem (11): A car moves from rest to a speed of $72\,{\rm km/h}$ in $4\,{\rm s}$. Find the acceleration of the car.

Solution: Known: $v_1=0$, $v_2=72\,{\rm km/h}$, $\Delta t=4\,{\rm s}$. Average acceleration is defined as the difference in velocities divided by the time interval between those points \begin{align*}\bar{a}&=\frac{v_2-v_1}{t_2-t_1}\\\\&=\frac{20-0}{4}\\\\&=5\,{\rm m/s^2}\end{align*} In above, we converted $\rm km/h$ to the SI unit of velocity ($\rm m/s$) as \[1\,\frac{km}{h}=\frac {1000\,m}{3600\,s}=\frac{10}{36}\, \rm m/s\] so we get \[72\,\rm km/h=72\times \frac{10}{36}=20\,\rm m/s\]

Problem (12): A race car accelerates from an initial velocity of $v_i=10\,{\rm m/s}$ to a final velocity of $v_f = 30\,{\rm m/s}$ in a time interval of $2\,{\rm s}$. Determine its average acceleration.

Solution: A change in the velocity of an object $\Delta v$ over a time interval $\Delta t$ is defined as an average acceleration. Known: $v_i=10\,{\rm m/s}$, $v_f = 30\,{\rm m/s}$, $\Delta t=2\,{\rm s}$. Applying definition of average acceleration, we get \begin{align*}\bar{a}&=\frac{v_f-v_i}{\Delta t}\\&=\frac{30-10}{2}\\&=10\,{\rm m/s^2}\end{align*}

Problem (13): A motorcycle starts its trip along a straight line with a velocity of $10\,{\rm m/s}$ and ends with $20\,{\rm m/s}$ in the opposite direction in a time interval of $2\,{\rm s}$. What is the average acceleration of the car?

Solution: Known: $v_i=10\,{\rm m/s}$, $v_f=-20\,{\rm m/s}$, $\Delta t=2\,{\rm s}$, $\bar{a}=?$. Using average acceleration definition we have \begin{align*}\bar{a}&=\frac{v_f-v_i}{\Delta t}\\\\&=\frac{(-20)-10}{2}\\\\ &=\boxed{-15\,{\rm m/s^2}}\end{align*}Recall that in the definition above, velocities are vector quantities. The final velocity is in the opposite direction from the initial velocity so a negative must be included.

Problem (14): A ball is thrown vertically up into the air by a boy. After $4$ seconds, it reaches the highest point of its path. How fast does the ball leave the boy's hand?

Solution : At the highest point, the ball has zero speed, $v_2=0$. It takes the ball $4\,\rm s$ to reach that point. In this problem, our unknown is the initial speed of the ball, $v_1=?$. Here, the ball accelerates at a constant rate of $g=-9.8\,\rm m/s^2$ in the presence of gravity.

When the ball is tossed upward, the only external force that acts on it is the gravity force.

Using the average acceleration formula $\bar{a}=\frac{\Delta v}{\Delta t}$ and substituting the numerical values into this, we will have \begin{gather*} \bar{a}=\frac{\Delta v}{\Delta t} \\\\ -9.8=\frac{0-v_1}{4} \\\\ \Rightarrow \boxed{v_1=39.2\,\rm m/s} \end{gather*} Note that $\Delta v=v_2-v_1$.

Problem (15): A child drops crumpled paper from a window. The paper hit the ground in $3\,\rm s$. What is the velocity of the crumpled paper just before it strikes the ground?

Solution : The crumpled paper is initially in the child's hand, so $v_1=0$. Let its speed just before striking be $v_2$. In this case, we have an object accelerating down in the presence of gravitational force at a constant rate of $g=-9.8\,\rm m/s^2$. Using the definition of average acceleration, we can find $v_2$ as below \begin{gather*} \bar{a}=\frac{\Delta v}{\Delta t} \\\\ -9.8=\frac{v_2-0}{3} \\\\ \Rightarrow v_2=3\times (-9.8)=\boxed{-29.4\,\rm m/s} \end{gather*} The negative shows us that the velocity must be downward, as expected!

Problem (16): A car travels along the $x$-axis for $4\,{\rm s}$ at an average velocity of $10\,{\rm m/s}$ and $2\,{\rm s}$ with an average velocity of $30\,{\rm m/s}$ and finally $4\,{\rm s}$ with an average velocity $25\,{\rm m/s}$. What is its average velocity across the whole path?

Solution: There are three different parts with different average velocities. Assume each trip is done in one dimension without changing direction. Thus, displacements associated with each segment are the same as the distance traveled in that direction and is calculated as below: \begin{align*}\Delta x_1&=v_1\,\Delta t_1\\&=10\times 4=40\,{\rm m}\\ \\ \Delta x_2&=v_2\,\Delta t_2\\&=30\times 2=60\,{\rm m}\\ \\ \Delta x_3&=v_3\,\Delta t_3\\&=25\times 4=100\,{\rm m}\end{align*}Now use the definition of average velocity, $\bar{v}=\frac{\Delta x_{tot}}{\Delta t_{tot}}$, to find it over the whole path\begin{align*}\bar{v}&=\frac{\Delta x_{tot}}{\Delta t_{tot}}\\ \\&=\frac{\Delta x_1+\Delta x_2+\Delta x_3}{\Delta t_1+\Delta t_2+\Delta t_3}\\ \\&=\frac{40+60+100}{4+2+4}\\ \\ &=\boxed{20\,{\rm m/s}}\end{align*}

Problem (17): An object moving along a straight-line path. It travels with an average velocity $2\,{\rm m/s}$ for $20\,{\rm s}$ and $12\,{\rm m/s}$ for $t$ seconds. If the total average velocity across the whole path is $10\,{\rm m/s}$, then find the unknown time $t$.

Solution: In this velocity problem, the whole path $\Delta x$ is divided into two parts $\Delta x_1$ and $\Delta x_2$ with different average velocities and times elapsed, so the total average velocity across the whole path is obtained as \begin{align*}\bar{v}&=\frac{\Delta x}{\Delta t}\\\\&=\frac{\Delta x_1+\Delta x_2}{\Delta t_1+\Delta t_2}\\\\&=\frac{\bar{v}_1\,t_1+\bar{v}_2\,t_2}{t_1+t_2}\\\\10&=\frac{2\times 20+12\times t}{20+t}\\\Rightarrow t&=80\,{\rm s}\end{align*}

Note : whenever a moving object, covers distances $x_1,x_2,x_3,\cdots$ in $t_1,t_2,t_3,\cdots$ with constant or average velocities $v_1,v_2,v_3,\cdots$ along a straight-line without changing its direction, then its total average velocity across the whole path is obtained by one of the following formulas

Distances and times are known:\[\bar{v}=\frac{x_1+x_2+x_3+\cdots}{t_1+t_2+t_3+\cdots}\]
Velocities and times are known: \[\bar{v}=\frac{v_1\,t_1+v_2\,t_2+v_3\,t_3+\cdots}{t_1+t_2+t_3+\cdots}\]
Distances and velocities are known:\[\bar{v}=\frac{x_1+x_2+x_3+\cdots}{\frac{x_1}{v_1}+\frac{x_2}{v_2}+\frac{x_3}{v_3}+\cdots}\]

Problem (18): A car travels one-fourth of its path with a constant velocity of $10\,{\rm m/s}$, and the remaining with a constant velocity of $v_2$. If the total average velocity across the whole path is $16\,{\rm m/s}$, then find the $v_2$?

Solution: This is the third case of the preceding note. Let the length of the path be $L$ so \begin{align*}\bar{v}&=\frac{x_1+x_2}{\frac{x_1}{v_1}+\frac{x_2}{v_2}}\\\\16&=\frac{\frac 14\,L+\frac 34\,L}{\frac{\frac 14\,L}{10}+\frac{\frac 34\,L}{v_2}}\\\\\Rightarrow v_2&=20\,{\rm m/s}\end{align*}

Problem (19): An object moves along a straight-line path. It travels for $t_1$ seconds with an average velocity $50\,{\rm m/s}$ and $t_2$ seconds with a constant velocity of $25\,{\rm m/s}$. If the total average velocity across the whole path is $30\,{\rm m/s}$, then find the ratio $\frac{t_2}{t_1}$?

Solution: the velocities and times are known, so we have \begin{align*}\bar{v}&=\frac{v_1\,t_1+v_2\,t_2}{t_1+t_2}\\\\30&=\frac{50\,t_1+25\,t_2}{t_1+t_2}\\\\ \Rightarrow \frac{t_2}{t_1}&=4\end{align*}

Acceleration

Practice problem 1.

A car is said to go "zero to sixty in six point six seconds". What is its acceleration in m/s 2 ?
The driver can't release his foot from the gas pedal (a.k.a. the accelerator). How many additional seconds would it take for the driver to reach 80 mph assuming the aceleration remains constant?
A car moving at 80 mph has a speed of 35.8 m/s. What acceleration would it have if it took 5.0 s to come to a complete stop?

Well first of all, we shouldn't be dealing with English units. They're difficult to work with, so let's convert them straight away and then do the old "plug and chug".

Since the question asked for acceleration and acceleration is a vector quantity this answer is not complete. A proper answer must include a direction as well. This is quite easy to do. Since the car is starting from rest and moving forward, its acceleration must also be forward. The ultimate, complete answer to this problem is the car is accelerating at…

a = 4.06 m/s 2 forward

We should convert the final speed to SI units.

Use the fact that change equals rate times time, and then add that change to our velocity at the end of the previous problem. Algebra will do the rest for us.

Alternate solution. We don't need no stinkin' conversions with this method. The ratio of eighty to sixty is a simple one, namely 4 3 . From our definition of acceleration, it should be apparent that time is directly proportional to change in velocity when acceleration is constant. Thus…

This is not the answer. It is the time elapsed from the moment when the car began to move. The question was about the additional time needed, so we should subtract the time required to go from zero to sixty. Thus…

∆ t = 8.8 s − 6.6 s = 2.2 s

The two methods give essentially the same answer.

Quite simple. Let's do it.

Nothing surprising there except the negative sign. When a vector quantity is negative what does it mean? There are several interpretations of this, but I think mine is the best. When a vector has a negative value, it means that it points in a direction opposite that of the positive vectors. In this problem, since the positive vectors are assumed to point forward (What other direction would a normal car drive?) the acceleration must be backward. Thus the complete answer to this problem is that the car's acceleration is…

a = 7.16 m/s 2 backward

Although it is common to assign deceleration a negative value, negative acceleration does not automatically imply deceleration. When dealing with vector quantities, any direction can be assumed positive…

up, down, right, left, forward, backward, north, south, east, west

and the corresponding opposite direction assumed negative…

down, up, left, right, backward, forward, south, north, west, east.

It won't matter which you chose as long as you are consistent throughout a problem. Don't learn any rules for assigning signs to particular directions and don't let anyone tell you that a certain direction must be positive or must be negative.

practice problem 2

Acceleration is the rate of change of velocity with time. Since velocity is a vector, this definition means acceleration is also a vector. When it comes to vectors, direction matters as much as size. In a simple one-dimensional problem like this one, directions are indicated by algebraic sign. Every quantity that points away from the batter will be positive. Every quantity that points toward him will be negative. Thus, the ball comes in at −40 m/s and goes out at +50 m/s. If we didn't pay attention to this detail, we wouldn't get the right answer.

practice problem 3

Practice problem 4.

3.4 Motion with Constant Acceleration

Learning objectives.

By the end of this section, you will be able to:

Identify which equations of motion are to be used to solve for unknowns.
Use appropriate equations of motion to solve a two-body pursuit problem.

You might guess that the greater the acceleration of, say, a car moving away from a stop sign, the greater the car’s displacement in a given time. But, we have not developed a specific equation that relates acceleration and displacement. In this section, we look at some convenient equations for kinematic relationships, starting from the definitions of displacement, velocity, and acceleration. We first investigate a single object in motion, called single-body motion. Then we investigate the motion of two objects, called two-body pursuit problems .

First, let us make some simplifications in notation. Taking the initial time to be zero, as if time is measured with a stopwatch, is a great simplification. Since elapsed time is Δ t = t f − t 0 Δ t = t f − t 0 , taking t 0 = 0 t 0 = 0 means that Δ t = t f Δ t = t f , the final time on the stopwatch. When initial time is taken to be zero, we use the subscript 0 to denote initial values of position and velocity. That is, x 0 x 0 is the initial position and v 0 v 0 is the initial velocity . We put no subscripts on the final values. That is, t is the final time , x is the final position , and v is the final velocity . This gives a simpler expression for elapsed time, Δ t = t Δ t = t . It also simplifies the expression for x displacement, which is now Δ x = x − x 0 Δ x = x − x 0 . Also, it simplifies the expression for change in velocity, which is now Δ v = v − v 0 Δ v = v − v 0 . To summarize, using the simplified notation, with the initial time taken to be zero,

where the subscript 0 denotes an initial value and the absence of a subscript denotes a final value in whatever motion is under consideration.

We now make the important assumption that acceleration is constant . This assumption allows us to avoid using calculus to find instantaneous acceleration. Since acceleration is constant, the average and instantaneous accelerations are equal—that is,

Thus, we can use the symbol a for acceleration at all times. Assuming acceleration to be constant does not seriously limit the situations we can study nor does it degrade the accuracy of our treatment. For one thing, acceleration is constant in a great number of situations. Furthermore, in many other situations we can describe motion accurately by assuming a constant acceleration equal to the average acceleration for that motion. Lastly, for motion during which acceleration changes drastically, such as a car accelerating to top speed and then braking to a stop, motion can be considered in separate parts, each of which has its own constant acceleration.

Displacement and Position from Velocity

To get our first two equations, we start with the definition of average velocity:

Substituting the simplified notation for Δ x Δ x and Δ t Δ t yields

Solving for x gives us

where the average velocity is

The equation v – = v 0 + v 2 v – = v 0 + v 2 reflects the fact that when acceleration is constant, v – v – is just the simple average of the initial and final velocities. Figure 3.18 illustrates this concept graphically. In part (a) of the figure, acceleration is constant, with velocity increasing at a constant rate. The average velocity during the 1-h interval from 40 km/h to 80 km/h is 60 km/h:

In part (b), acceleration is not constant. During the 1-h interval, velocity is closer to 80 km/h than 40 km/h. Thus, the average velocity is greater than in part (a).

Solving for Final Velocity from Acceleration and Time

We can derive another useful equation by manipulating the definition of acceleration:

Substituting the simplified notation for Δ v Δ v and Δ t Δ t gives us

Solving for v yields

Example 3.7

Calculating final velocity.

Second, we identify the unknown; in this case, it is final velocity v f v f .

Last, we determine which equation to use. To do this we figure out which kinematic equation gives the unknown in terms of the knowns. We calculate the final velocity using Equation 3.12 , v = v 0 + a t v = v 0 + a t .

Figure 3.19 is a sketch that shows the acceleration and velocity vectors.

Significance

In addition to being useful in problem solving, the equation v = v 0 + a t v = v 0 + a t gives us insight into the relationships among velocity, acceleration, and time. We can see, for example, that

Final velocity depends on how large the acceleration is and how long it lasts
If the acceleration is zero, then the final velocity equals the initial velocity ( v = v 0 ), as expected (in other words, velocity is constant)
If a is negative, then the final velocity is less than the initial velocity

All these observations fit our intuition. Note that it is always useful to examine basic equations in light of our intuition and experience to check that they do indeed describe nature accurately.

Solving for Final Position with Constant Acceleration

We can combine the previous equations to find a third equation that allows us to calculate the final position of an object experiencing constant acceleration. We start with

Adding v 0 v 0 to each side of this equation and dividing by 2 gives

Since v 0 + v 2 = v – v 0 + v 2 = v – for constant acceleration, we have

Now we substitute this expression for v – v – into the equation for displacement, x = x 0 + v – t x = x 0 + v – t , yielding

Example 3.8

Calculating displacement of an accelerating object.

Second, we substitute the known values into the equation to solve for the unknown:

Since the initial position and velocity are both zero, this equation simplifies to

Substituting the identified values of a and t gives

What else can we learn by examining the equation x = x 0 + v 0 t + 1 2 a t 2 ? x = x 0 + v 0 t + 1 2 a t 2 ? We can see the following relationships:

Displacement depends on the square of the elapsed time when acceleration is not zero. In Example 3.8 , the dragster covers only one-fourth of the total distance in the first half of the elapsed time.
If acceleration is zero, then initial velocity equals average velocity ( v 0 = v – ) ( v 0 = v – ) , and x = x 0 + v 0 t + 1 2 a t 2 becomes x = x 0 + v 0 t . x = x 0 + v 0 t + 1 2 a t 2 becomes x = x 0 + v 0 t .

Solving for Final Velocity from Distance and Acceleration

A fourth useful equation can be obtained from another algebraic manipulation of previous equations. If we solve v = v 0 + a t v = v 0 + a t for t , we get

Substituting this and v – = v 0 + v 2 v – = v 0 + v 2 into x = x 0 + v – t x = x 0 + v – t , we get

Example 3.9

Second, we substitute the knowns into the equation v 2 = v 0 2 + 2 a ( x − x 0 ) v 2 = v 0 2 + 2 a ( x − x 0 ) and solve for v :

An examination of the equation v 2 = v 0 2 + 2 a ( x − x 0 ) v 2 = v 0 2 + 2 a ( x − x 0 ) can produce additional insights into the general relationships among physical quantities:

The final velocity depends on how large the acceleration is and the distance over which it acts.
For a fixed acceleration, a car that is going twice as fast doesn’t simply stop in twice the distance. It takes much farther to stop. (This is why we have reduced speed zones near schools.)

Putting Equations Together

In the following examples, we continue to explore one-dimensional motion, but in situations requiring slightly more algebraic manipulation. The examples also give insight into problem-solving techniques. The note that follows is provided for easy reference to the equations needed. Be aware that these equations are not independent. In many situations we have two unknowns and need two equations from the set to solve for the unknowns. We need as many equations as there are unknowns to solve a given situation.

Summary of Kinematic Equations (constant a )

Before we get into the examples, let’s look at some of the equations more closely to see the behavior of acceleration at extreme values. Rearranging Equation 3.12 , we have

From this we see that, for a finite time, if the difference between the initial and final velocities is small, the acceleration is small, approaching zero in the limit that the initial and final velocities are equal. On the contrary, in the limit t → 0 t → 0 for a finite difference between the initial and final velocities, acceleration becomes infinite.

Similarly, rearranging Equation 3.14 , we can express acceleration in terms of velocities and displacement:

Thus, for a finite difference between the initial and final velocities acceleration becomes infinite in the limit the displacement approaches zero. Acceleration approaches zero in the limit the difference in initial and final velocities approaches zero for a finite displacement.

Example 3.10

How far does a car go.

First, we need to identify the knowns and what we want to solve for. We know that v 0 = 30.0 m/s, v = 0, and a = −7.00 m/s 2 ( a is negative because it is in a direction opposite to velocity). We take x 0 to be zero. We are looking for displacement Δ x Δ x , or x − x 0 . Second, we identify the equation that will help us solve the problem. The best equation to use is v 2 = v 0 2 + 2 a ( x − x 0 ) . v 2 = v 0 2 + 2 a ( x − x 0 ) . This equation is best because it includes only one unknown, x . We know the values of all the other variables in this equation. (Other equations would allow us to solve for x , but they require us to know the stopping time, t , which we do not know. We could use them, but it would entail additional calculations.) Third, we rearrange the equation to solve for x : x − x 0 = v 2 − v 0 2 2 a x − x 0 = v 2 − v 0 2 2 a and substitute the known values: x − 0 = 0 2 − ( 30.0 m/s ) 2 2 ( −7.00 m/s 2 ) . x − 0 = 0 2 − ( 30.0 m/s ) 2 2 ( −7.00 m/s 2 ) . Thus, x = 64.3 m on dry concrete . x = 64.3 m on dry concrete .
This part can be solved in exactly the same manner as (a). The only difference is that the acceleration is −5.00 m/s 2 . The result is x wet = 90.0 m on wet concrete. x wet = 90.0 m on wet concrete.
When the driver reacts, the stopping distance is the same as it is in (a) and (b) for dry and wet concrete. So, to answer this question, we need to calculate how far the car travels during the reaction time, and then add that to the stopping time. It is reasonable to assume the velocity remains constant during the driver’s reaction time. To do this, we, again, identify the knowns and what we want to solve for. We know that v – = 30.0 m/s v – = 30.0 m/s , t reaction = 0.500 s t reaction = 0.500 s , and a reaction = 0 a reaction = 0 . We take x 0-reaction x 0-reaction to be zero. We are looking for x reaction x reaction . Second, as before, we identify the best equation to use. In this case, x = x 0 + v – t x = x 0 + v – t works well because the only unknown value is x , which is what we want to solve for. Third, we substitute the knowns to solve the equation: x = 0 + ( 3 0.0 m/s ) ( 0.500 s ) = 15 .0 m . x = 0 + ( 3 0.0 m/s ) ( 0.500 s ) = 15 .0 m . This means the car travels 15.0 m while the driver reacts, making the total displacements in the two cases of dry and wet concrete 15.0 m greater than if he reacted instantly. Last, we then add the displacement during the reaction time to the displacement when braking ( Figure 3.23 ), x braking + x reaction = x total , x braking + x reaction = x total , and find (a) to be 64.3 m + 15.0 m = 79.3 m when dry and (b) to be 90.0 m + 15.0 m = 105 m when wet.

Example 3.11

Calculating time.

We need to solve for t . The equation x = x 0 + v 0 t + 1 2 a t 2 x = x 0 + v 0 t + 1 2 a t 2 works best because the only unknown in the equation is the variable t , for which we need to solve. From this insight we see that when we input the knowns into the equation, we end up with a quadratic equation.

We need to rearrange the equation to solve for t , then substituting the knowns into the equation:

We then simplify the equation. The units of meters cancel because they are in each term. We can get the units of seconds to cancel by taking t = t s, where t is the magnitude of time and s is the unit. Doing so leaves

We then use the quadratic formula to solve for t ,

which yields two solutions: t = 10.0 and t = −20.0. A negative value for time is unreasonable, since it would mean the event happened 20 s before the motion began. We can discard that solution. Thus,

Check Your Understanding 3.5

A rocket accelerates at a rate of 20 m/s 2 during launch. How long does it take the rocket to reach a velocity of 400 m/s?

Example 3.12

Acceleration of a spaceship.

Then we substitute v 0 v 0 into v = v 0 + a t v = v 0 + a t to solve for the final velocity:

With the basics of kinematics established, we can go on to many other interesting examples and applications. In the process of developing kinematics, we have also glimpsed a general approach to problem solving that produces both correct answers and insights into physical relationships. The next level of complexity in our kinematics problems involves the motion of two interrelated bodies, called two-body pursuit problems .

Two-Body Pursuit Problems

Up until this point we have looked at examples of motion involving a single body. Even for the problem with two cars and the stopping distances on wet and dry roads, we divided this problem into two separate problems to find the answers. In a two-body pursuit problem , the motions of the objects are coupled—meaning, the unknown we seek depends on the motion of both objects. To solve these problems we write the equations of motion for each object and then solve them simultaneously to find the unknown. This is illustrated in Figure 3.25 .

The time and distance required for car 1 to catch car 2 depends on the initial distance car 1 is from car 2 as well as the velocities of both cars and the acceleration of car 1. The kinematic equations describing the motion of both cars must be solved to find these unknowns.

Consider the following example.

Example 3.13

Cheetah catching a gazelle.

Equation for the gazelle: The gazelle has a constant velocity, which is its average velocity, since it is not accelerating. Therefore, we use Equation 3.10 with x 0 = 0 x 0 = 0 : x = x 0 + v – t = v – t . x = x 0 + v – t = v – t . Equation for the cheetah: The cheetah is accelerating from rest, so we use Equation 3.13 with x 0 = 0 x 0 = 0 and v 0 = 0 v 0 = 0 : x = x 0 + v 0 t + 1 2 a t 2 = 1 2 a t 2 . x = x 0 + v 0 t + 1 2 a t 2 = 1 2 a t 2 . Now we have an equation of motion for each animal with a common parameter, which can be eliminated to find the solution. In this case, we solve for t : x = v – t = 1 2 a t 2 t = 2 v – a . x = v – t = 1 2 a t 2 t = 2 v – a . The gazelle has a constant velocity of 10 m/s, which is its average velocity. The acceleration of the cheetah is 4 m/s 2 . Evaluating t , the time for the cheetah to reach the gazelle, we have t = 2 v – a = 2 ( 10 m/s ) 4 m/s 2 = 5 s . t = 2 v – a = 2 ( 10 m/s ) 4 m/s 2 = 5 s .
To get the displacement, we use either the equation of motion for the cheetah or the gazelle, since they should both give the same answer. Displacement of the cheetah: x = 1 2 a t 2 = 1 2 ( 4 m/s 2 ) ( 5 ) 2 = 50 m . x = 1 2 a t 2 = 1 2 ( 4 m/s 2 ) ( 5 ) 2 = 50 m . Displacement of the gazelle: x = v – t = 10 m/s ( 5 ) = 50 m . x = v – t = 10 m/s ( 5 ) = 50 m . We see that both displacements are equal, as expected.

Check Your Understanding 3.6

A bicycle has a constant velocity of 10 m/s. A person starts from rest and begins to run to catch up to the bicycle in 30 s when the bicycle is at the same position as the person. What is the acceleration of the person?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

Authors: William Moebs, Samuel J. Ling, Jeff Sanny
Publisher/website: OpenStax
Book title: University Physics Volume 1
Publication date: Sep 19, 2016
Location: Houston, Texas
Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
Section URL: https://openstax.org/books/university-physics-volume-1/pages/3-4-motion-with-constant-acceleration

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

TPC and eLearning
What's NEW at TPC?
Read Watch Interact
Practice Review Test
Teacher-Tools
Subscription Selection
Seat Calculator
Ad Free Account
Edit Profile Settings
Classes (Version 2)
Student Progress Edit
Task Properties
Export Student Progress
Task, Activities, and Scores
Metric Conversions Questions
Metric System Questions
Metric Estimation Questions
Significant Digits Questions
Proportional Reasoning
Acceleration
Distance-Displacement
Dots and Graphs
Graph That Motion
Match That Graph
Name That Motion
Motion Diagrams
Pos'n Time Graphs Numerical
Pos'n Time Graphs Conceptual
Up And Down - Questions
Balanced vs. Unbalanced Forces
Change of State
Force and Motion
Mass and Weight
Match That Free-Body Diagram
Net Force (and Acceleration) Ranking Tasks
Newton's Second Law
Normal Force Card Sort
Recognizing Forces
Air Resistance and Skydiving
Solve It! with Newton's Second Law
Which One Doesn't Belong?
Component Addition Questions
Head-to-Tail Vector Addition
Projectile Mathematics
Trajectory - Angle Launched Projectiles
Trajectory - Horizontally Launched Projectiles
Vector Addition
Vector Direction
Which One Doesn't Belong? Projectile Motion
Forces in 2-Dimensions
Being Impulsive About Momentum
Explosions - Law Breakers
Hit and Stick Collisions - Law Breakers
Case Studies: Impulse and Force
Impulse-Momentum Change Table
Keeping Track of Momentum - Hit and Stick
Keeping Track of Momentum - Hit and Bounce
What's Up (and Down) with KE and PE?
Energy Conservation Questions
Energy Dissipation Questions
Energy Ranking Tasks
LOL Charts (a.k.a., Energy Bar Charts)
Match That Bar Chart
Words and Charts Questions
Name That Energy
Stepping Up with PE and KE Questions
Case Studies - Circular Motion
Circular Logic
Forces and Free-Body Diagrams in Circular Motion
Gravitational Field Strength
Universal Gravitation
Angular Position and Displacement
Linear and Angular Velocity
Angular Acceleration
Rotational Inertia
Balanced vs. Unbalanced Torques
Getting a Handle on Torque
Torque-ing About Rotation
Properties of Matter
Fluid Pressure
Buoyant Force
Sinking, Floating, and Hanging
Pascal's Principle
Flow Velocity
Bernoulli's Principle
Balloon Interactions
Charge and Charging
Charge Interactions
Charging by Induction
Conductors and Insulators
Coulombs Law
Electric Field
Electric Field Intensity
Polarization
Case Studies: Electric Power
Know Your Potential
Light Bulb Anatomy
I = ∆V/R Equations as a Guide to Thinking
Parallel Circuits - ∆V = I•R Calculations
Resistance Ranking Tasks
Series Circuits - ∆V = I•R Calculations
Series vs. Parallel Circuits
Equivalent Resistance
Period and Frequency of a Pendulum
Pendulum Motion: Velocity and Force
Energy of a Pendulum
Period and Frequency of a Mass on a Spring
Horizontal Springs: Velocity and Force
Vertical Springs: Velocity and Force
Energy of a Mass on a Spring
Decibel Scale
Frequency and Period
Closed-End Air Columns
Name That Harmonic: Strings
Rocking the Boat
Wave Basics
Matching Pairs: Wave Characteristics
Wave Interference
Waves - Case Studies
Color Addition and Subtraction
Color Filters
If This, Then That: Color Subtraction
Light Intensity
Color Pigments
Converging Lenses
Curved Mirror Images
Law of Reflection
Refraction and Lenses
Total Internal Reflection
Who Can See Who?
Formulas and Atom Counting
Atomic Models
Bond Polarity
Entropy Questions
Cell Voltage Questions
Heat of Formation Questions
Reduction Potential Questions
Oxidation States Questions
Measuring the Quantity of Heat
Hess's Law
Oxidation-Reduction Questions
Galvanic Cells Questions
Thermal Stoichiometry
Molecular Polarity
Quantum Mechanics
Balancing Chemical Equations
Bronsted-Lowry Model of Acids and Bases
Classification of Matter
Collision Model of Reaction Rates
Density Ranking Tasks
Dissociation Reactions
Complete Electron Configurations
Elemental Measures
Enthalpy Change Questions
Equilibrium Concept
Equilibrium Constant Expression
Equilibrium Calculations - Questions
Equilibrium ICE Table
Intermolecular Forces Questions
Ionic Bonding
Lewis Electron Dot Structures
Limiting Reactants
Line Spectra Questions
Mass Stoichiometry
Measurement and Numbers
Metals, Nonmetals, and Metalloids
Metric Estimations
Metric System
Molarity Ranking Tasks
Mole Conversions
Name That Element
Names to Formulas
Names to Formulas 2
Nuclear Decay
Particles, Words, and Formulas
Periodic Trends
Precipitation Reactions and Net Ionic Equations
Pressure Concepts
Pressure-Temperature Gas Law
Pressure-Volume Gas Law
Chemical Reaction Types
Significant Digits and Measurement
States Of Matter Exercise
Stoichiometry Law Breakers
Stoichiometry - Math Relationships
Subatomic Particles
Spontaneity and Driving Forces
Gibbs Free Energy
Volume-Temperature Gas Law
Acid-Base Properties
Energy and Chemical Reactions
Chemical and Physical Properties
Valence Shell Electron Pair Repulsion Theory
Writing Balanced Chemical Equations
Mission CG1
Mission CG10
Mission CG2
Mission CG3
Mission CG4
Mission CG5
Mission CG6
Mission CG7
Mission CG8
Mission CG9
Mission EC1
Mission EC10
Mission EC11
Mission EC12
Mission EC2
Mission EC3
Mission EC4
Mission EC5
Mission EC6
Mission EC7
Mission EC8
Mission EC9
Mission RL1
Mission RL2
Mission RL3
Mission RL4
Mission RL5
Mission RL6
Mission KG7
Mission RL8
Mission KG9
Mission RL10
Mission RL11
Mission RM1
Mission RM2
Mission RM3
Mission RM4
Mission RM5
Mission RM6
Mission RM8
Mission RM10
Mission LC1
Mission RM11
Mission LC2
Mission LC3
Mission LC4
Mission LC5
Mission LC6
Mission LC8
Mission SM1
Mission SM2
Mission SM3
Mission SM4
Mission SM5
Mission SM6
Mission SM8
Mission SM10
Mission KG10
Mission SM11
Mission KG2
Mission KG3
Mission KG4
Mission KG5
Mission KG6
Mission KG8
Mission KG11
Mission F2D1
Mission F2D2
Mission F2D3
Mission F2D4
Mission F2D5
Mission F2D6
Mission KC1
Mission KC2
Mission KC3
Mission KC4
Mission KC5
Mission KC6
Mission KC7
Mission KC8
Mission AAA
Mission SM9
Mission LC7
Mission LC9
Mission NL1
Mission NL2
Mission NL3
Mission NL4
Mission NL5
Mission NL6
Mission NL7
Mission NL8
Mission NL9
Mission NL10
Mission NL11
Mission NL12
Mission MC1
Mission MC10
Mission MC2
Mission MC3
Mission MC4
Mission MC5
Mission MC6
Mission MC7
Mission MC8
Mission MC9
Mission RM7
Mission RM9
Mission RL7
Mission RL9
Mission SM7
Mission SE1
Mission SE10
Mission SE11
Mission SE12
Mission SE2
Mission SE3
Mission SE4
Mission SE5
Mission SE6
Mission SE7
Mission SE8
Mission SE9
Mission VP1
Mission VP10
Mission VP2
Mission VP3
Mission VP4
Mission VP5
Mission VP6
Mission VP7
Mission VP8
Mission VP9
Mission WM1
Mission WM2
Mission WM3
Mission WM4
Mission WM5
Mission WM6
Mission WM7
Mission WM8
Mission WE1
Mission WE10
Mission WE2
Mission WE3
Mission WE4
Mission WE5
Mission WE6
Mission WE7
Mission WE8
Mission WE9
Vector Walk Interactive
Name That Motion Interactive
Kinematic Graphing 1 Concept Checker
Kinematic Graphing 2 Concept Checker
Graph That Motion Interactive
Two Stage Rocket Interactive
Rocket Sled Concept Checker
Force Concept Checker
Free-Body Diagrams Concept Checker
Free-Body Diagrams The Sequel Concept Checker
Skydiving Concept Checker
Elevator Ride Concept Checker
Vector Addition Concept Checker
Vector Walk in Two Dimensions Interactive
Name That Vector Interactive
River Boat Simulator Concept Checker
Projectile Simulator 2 Concept Checker
Projectile Simulator 3 Concept Checker
Hit the Target Interactive
Turd the Target 1 Interactive
Turd the Target 2 Interactive
Balance It Interactive
Go For The Gold Interactive
Egg Drop Concept Checker
Fish Catch Concept Checker
Exploding Carts Concept Checker
Collision Carts - Inelastic Collisions Concept Checker
Its All Uphill Concept Checker
Stopping Distance Concept Checker
Chart That Motion Interactive
Roller Coaster Model Concept Checker
Uniform Circular Motion Concept Checker
Horizontal Circle Simulation Concept Checker
Vertical Circle Simulation Concept Checker
Race Track Concept Checker
Gravitational Fields Concept Checker
Orbital Motion Concept Checker
Angular Acceleration Concept Checker
Balance Beam Concept Checker
Torque Balancer Concept Checker
Aluminum Can Polarization Concept Checker
Charging Concept Checker
Name That Charge Simulation
Coulomb's Law Concept Checker
Electric Field Lines Concept Checker
Put the Charge in the Goal Concept Checker
Circuit Builder Concept Checker (Series Circuits)
Circuit Builder Concept Checker (Parallel Circuits)
Circuit Builder Concept Checker (∆V-I-R)
Circuit Builder Concept Checker (Voltage Drop)
Equivalent Resistance Interactive
Pendulum Motion Simulation Concept Checker
Mass on a Spring Simulation Concept Checker
Particle Wave Simulation Concept Checker
Boundary Behavior Simulation Concept Checker
Slinky Wave Simulator Concept Checker
Simple Wave Simulator Concept Checker
Wave Addition Simulation Concept Checker
Standing Wave Maker Simulation Concept Checker
Color Addition Concept Checker
Painting With CMY Concept Checker
Stage Lighting Concept Checker
Filtering Away Concept Checker
InterferencePatterns Concept Checker
Young's Experiment Interactive
Plane Mirror Images Interactive
Who Can See Who Concept Checker
Optics Bench (Mirrors) Concept Checker
Name That Image (Mirrors) Interactive
Refraction Concept Checker
Total Internal Reflection Concept Checker
Optics Bench (Lenses) Concept Checker
Kinematics Preview
Velocity Time Graphs Preview
Moving Cart on an Inclined Plane Preview
Stopping Distance Preview
Cart, Bricks, and Bands Preview
Fan Cart Study Preview
Friction Preview
Coffee Filter Lab Preview
Friction, Speed, and Stopping Distance Preview
Up and Down Preview
Projectile Range Preview
Ballistics Preview
Juggling Preview
Marshmallow Launcher Preview
Air Bag Safety Preview
Colliding Carts Preview
Collisions Preview
Engineering Safer Helmets Preview
Push the Plow Preview
Its All Uphill Preview
Energy on an Incline Preview
Modeling Roller Coasters Preview
Hot Wheels Stopping Distance Preview
Ball Bat Collision Preview
Energy in Fields Preview
Weightlessness Training Preview
Roller Coaster Loops Preview
Universal Gravitation Preview
Keplers Laws Preview
Kepler's Third Law Preview
Charge Interactions Preview
Sticky Tape Experiments Preview
Wire Gauge Preview
Voltage, Current, and Resistance Preview
Light Bulb Resistance Preview
Series and Parallel Circuits Preview
Thermal Equilibrium Preview
Linear Expansion Preview
Heating Curves Preview
Electricity and Magnetism - Part 1 Preview
Electricity and Magnetism - Part 2 Preview
Vibrating Mass on a Spring Preview
Period of a Pendulum Preview
Wave Speed Preview
Slinky-Experiments Preview
Standing Waves in a Rope Preview
Sound as a Pressure Wave Preview
DeciBel Scale Preview
DeciBels, Phons, and Sones Preview
Sound of Music Preview
Shedding Light on Light Bulbs Preview
Models of Light Preview
Electromagnetic Radiation Preview
Electromagnetic Spectrum Preview
EM Wave Communication Preview
Digitized Data Preview
Light Intensity Preview
Concave Mirrors Preview
Object Image Relations Preview
Snells Law Preview
Reflection vs. Transmission Preview
Magnification Lab Preview
Reactivity Preview
Ions and the Periodic Table Preview
Periodic Trends Preview
Intermolecular Forces Preview
Melting Points and Boiling Points Preview
Reaction Rates Preview
Ammonia Factory Preview
Stoichiometry Preview
Nuclear Chemistry Preview
Gaining Teacher Access
Tasks and Classes
Tasks - Classic
Subscription
Subscription Locator
1-D Kinematics
Newton's Laws
Vectors - Motion and Forces in Two Dimensions
Momentum and Its Conservation
Work and Energy
Circular Motion and Satellite Motion
Thermal Physics
Static Electricity
Electric Circuits
Vibrations and Waves
Sound Waves and Music
Light and Color
Reflection and Mirrors
About the Physics Interactives
Task Tracker
Usage Policy
Newtons Laws
Vectors and Projectiles
Forces in 2D
Momentum and Collisions
Circular and Satellite Motion
Balance and Rotation
Electromagnetism
Waves and Sound
Atomic Physics
Forces in Two Dimensions
Work, Energy, and Power
Circular Motion and Gravitation
Sound Waves
1-Dimensional Kinematics
Circular, Satellite, and Rotational Motion
Einstein's Theory of Special Relativity
Waves, Sound and Light
QuickTime Movies
About the Concept Builders
Pricing For Schools
Directions for Version 2
Measurement and Units
Relationships and Graphs
Rotation and Balance
Vibrational Motion
Reflection and Refraction
Teacher Accounts
Task Tracker Directions
Kinematic Concepts
Kinematic Graphing
Wave Motion
Sound and Music
About CalcPad
1D Kinematics
Vectors and Forces in 2D
Simple Harmonic Motion
Rotational Kinematics
Rotation and Torque
Rotational Dynamics
Electric Fields, Potential, and Capacitance
Transient RC Circuits
Light Waves
Units and Measurement
Stoichiometry
Molarity and Solutions
Thermal Chemistry
Acids and Bases
Kinetics and Equilibrium
Solution Equilibria
Oxidation-Reduction
Nuclear Chemistry
Newton's Laws of Motion
Work and Energy Packet
Static Electricity Review
NGSS Alignments
1D-Kinematics
Projectiles
Circular Motion
Magnetism and Electromagnetism
Graphing Practice
About the ACT
ACT Preparation
For Teachers
Other Resources
Solutions Guide
Solutions Guide Digital Download
Motion in One Dimension
Work, Energy and Power
TaskTracker
Other Tools
Algebra Based Physics
Frequently Asked Questions
Purchasing the Download
Purchasing the CD
Purchasing the Digital Download
About the NGSS Corner
NGSS Search
Force and Motion DCIs - High School
Energy DCIs - High School
Wave Applications DCIs - High School
Force and Motion PEs - High School
Energy PEs - High School
Wave Applications PEs - High School
Crosscutting Concepts
The Practices
Physics Topics
NGSS Corner: Activity List
NGSS Corner: Infographics
About the Toolkits
Position-Velocity-Acceleration
Position-Time Graphs
Velocity-Time Graphs
Newton's First Law
Newton's Second Law
Newton's Third Law
Terminal Velocity
Projectile Motion
Forces in 2 Dimensions
Impulse and Momentum Change
Momentum Conservation
Work-Energy Fundamentals
Work-Energy Relationship
Roller Coaster Physics
Satellite Motion
Electric Fields
Circuit Concepts
Series Circuits
Parallel Circuits
Describing-Waves
Wave Behavior Toolkit
Standing Wave Patterns
Resonating Air Columns
Wave Model of Light
Plane Mirrors
Curved Mirrors
Teacher Guide
Using Lab Notebooks
Current Electricity
Light Waves and Color
Reflection and Ray Model of Light
Refraction and Ray Model of Light
Classes (Legacy Version)
Teacher Resources
Subscriptions

Newton's Laws
Einstein's Theory of Special Relativity
About Concept Checkers
School Pricing
Newton's Laws of Motion
Newton's First Law
Newton's Third Law

Kinematic Equations and Problem-Solving

Kinematic Equations Introduction
Solving Problems with Kinematic Equations
Kinematic Equations and Free Fall
Sample Problems and Solutions
Kinematic Equations and Kinematic Graphs

The four kinematic equations that describe the mathematical relationship between the parameters that describe an object's motion were introduced in the previous part of Lesson 6 . The four kinematic equations are:

In the above equations, the symbol d stands for the displacement of the object. The symbol t stands for the time for which the object moved. The symbol a stands for the acceleration of the object. And the symbol v stands for the instantaneous velocity of the object; a subscript of i after the v (as in v i ) indicates that the velocity value is the initial velocity value and a subscript of f (as in v f ) indicates that the velocity value is the final velocity value.

Problem-Solving Strategy

Construct an informative diagram of the physical situation.
Identify and list the given information in variable form.
Identify and list the unknown information in variable form.
Identify and list the equation that will be used to determine unknown information from known information.
Substitute known values into the equation and use appropriate algebraic steps to solve for the unknown information.
Check your answer to insure that it is reasonable and mathematically correct.

The use of this problem-solving strategy in the solution of the following problem is modeled in Examples A and B below.

Example Problem A

Ima Hurryin is approaching a stoplight moving with a velocity of +30.0 m/s. The light turns yellow, and Ima applies the brakes and skids to a stop. If Ima's acceleration is -8.00 m/s 2 , then determine the displacement of the car during the skidding process. (Note that the direction of the velocity and the acceleration vectors are denoted by a + and a - sign.)

The solution to this problem begins by the construction of an informative diagram of the physical situation. This is shown below. The second step involves the identification and listing of known information in variable form. Note that the v f value can be inferred to be 0 m/s since Ima's car comes to a stop. The initial velocity ( v i ) of the car is +30.0 m/s since this is the velocity at the beginning of the motion (the skidding motion). And the acceleration ( a ) of the car is given as - 8.00 m/s 2 . (Always pay careful attention to the + and - signs for the given quantities.) The next step of the strategy involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the displacement of the car. So d is the unknown quantity. The results of the first three steps are shown in the table below.

The next step of the strategy involves identifying a kinematic equation that would allow you to determine the unknown quantity. There are four kinematic equations to choose from. In general, you will always choose the equation that contains the three known and the one unknown variable. In this specific case, the three known variables and the one unknown variable are v f , v i , a , and d . Thus, you will look for an equation that has these four variables listed in it. An inspection of the four equations above reveals that the equation on the top right contains all four variables.

Once the equation is identified and written down, the next step of the strategy involves substituting known values into the equation and using proper algebraic steps to solve for the unknown information. This step is shown below.

(0 m/s) 2 = (30.0 m/s) 2 + 2 • (-8.00 m/s 2 ) • d

0 m 2 /s 2 = 900 m 2 /s 2 + (-16.0 m/s 2 ) • d

(16.0 m/s 2 ) • d = 900 m 2 /s 2 - 0 m 2 /s 2

(16.0 m/s 2 )*d = 900 m 2 /s 2

d = (900 m 2 /s 2 )/ (16.0 m/s 2 )

The solution above reveals that the car will skid a distance of 56.3 meters. (Note that this value is rounded to the third digit.)

The last step of the problem-solving strategy involves checking the answer to assure that it is both reasonable and accurate. The value seems reasonable enough. It takes a car a considerable distance to skid from 30.0 m/s (approximately 65 mi/hr) to a stop. The calculated distance is approximately one-half a football field, making this a very reasonable skidding distance. Checking for accuracy involves substituting the calculated value back into the equation for displacement and insuring that the left side of the equation is equal to the right side of the equation. Indeed it is!

Example Problem B

Ben Rushin is waiting at a stoplight. When it finally turns green, Ben accelerated from rest at a rate of a 6.00 m/s 2 for a time of 4.10 seconds. Determine the displacement of Ben's car during this time period.

Once more, the solution to this problem begins by the construction of an informative diagram of the physical situation. This is shown below. The second step of the strategy involves the identification and listing of known information in variable form. Note that the v i value can be inferred to be 0 m/s since Ben's car is initially at rest. The acceleration ( a ) of the car is 6.00 m/s 2 . And the time ( t ) is given as 4.10 s. The next step of the strategy involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the displacement of the car. So d is the unknown information. The results of the first three steps are shown in the table below.

The next step of the strategy involves identifying a kinematic equation that would allow you to determine the unknown quantity. There are four kinematic equations to choose from. Again, you will always search for an equation that contains the three known variables and the one unknown variable. In this specific case, the three known variables and the one unknown variable are t, v i , a, and d. An inspection of the four equations above reveals that the equation on the top left contains all four variables.

d = (0 m/s) • (4.1 s) + ½ • (6.00 m/s 2 ) • (4.10 s) 2

d = (0 m) + ½ • (6.00 m/s 2 ) • (16.81 s 2 )

d = 0 m + 50.43 m

The solution above reveals that the car will travel a distance of 50.4 meters. (Note that this value is rounded to the third digit.)

The last step of the problem-solving strategy involves checking the answer to assure that it is both reasonable and accurate. The value seems reasonable enough. A car with an acceleration of 6.00 m/s/s will reach a speed of approximately 24 m/s (approximately 50 mi/hr) in 4.10 s. The distance over which such a car would be displaced during this time period would be approximately one-half a football field, making this a very reasonable distance. Checking for accuracy involves substituting the calculated value back into the equation for displacement and insuring that the left side of the equation is equal to the right side of the equation. Indeed it is!

The two example problems above illustrate how the kinematic equations can be combined with a simple problem-solving strategy to predict unknown motion parameters for a moving object. Provided that three motion parameters are known, any of the remaining values can be determined. In the next part of Lesson 6 , we will see how this strategy can be applied to free fall situations. Or if interested, you can try some practice problems and check your answer against the given solutions.

Reset password New user? Sign up

Existing user? Log in

1D Kinematics Problem Solving

Already have an account? Log in here.

Recommended Course

Classical mechanics.

Hardcore training for the aspiring physicist.

The equations of 1D Kinematics are very useful in many situations. While they may seem minimal and straightforward at first glance, a surprising amount of subtlety belies these equations. And the number of physical scenarios to which they can be applied is vast. These problems may not be groundbreaking advances in modern physics, but they do represent very tangible everyday experiences: cars on roads, balls thrown in the air, hockey pucks on ice, and countless more examples can be modeled with these three relatively simple equations.

Equation Review

1d kinematics problems: easy, 1d kinematics problems: medium.

The three fundamental equations of kinematics in one dimension are:

\[v = v_0 + at,\]

\[x = x_0 + v_0 t + \frac12 at^2,\]

\[v^2 = v_0^2 + 2a(x-x_0).\]

The first gives the change in velocity under a constant acceleration given a change in time, the second gives the change in position under a constant acceleration given a change in time, and the third gives the change in velocity under a constant acceleration given a change in distance.

Here, the subscript "0" always refers to "initial". So, $v_0$ is the initial velocity, and $x_0$ is the initial position. Letters with no subscript indicate the quantity value after some time, $t$. So, in the first equation, $v$ is the velocity of an object that began at velocity $v_0$ and has moved with constant acceleration $a$ for an amount of time $t$.

Very often, rather than using the initial and final positions, we simply want to know the total change in position, the distance traveled. This change in position is always merely the initial position subtracted from the final position: $x-x_0$, often called $d$ for distance. In many problems, this simplifies things and makes it simpler to see what is being asked. With this change, the second and third equations are sometimes rewritten:

\[d = v_0 t + \frac12 at^2,\]

\[v^2 = v_0^2 + 2ad.\]

A ball is dropped from rest off a cliff of height $100 \text{ m}$. Assuming gravity accelerates masses uniformly on Earth's surface at $g = 9.8 \text{ m}/\text{s}^2$, how fast is the ball going when it hits the ground? How long does it take to hit the ground? Solution: The third kinematics equation gives the final speed as: \[v_f^2 = 2( 9.8 \text{ m}/\text{s}^2)(100 \text{ m}) \implies v_f \approx 44.3 \text{ m}/\text{s}.\] The first kinematical equation gives the time to accelerate up to this speed: \[t = \frac{v}{a} = \frac{44.3 \text{ m}/\text{s}}{9.8 \text{ m}/\text{s}^2} \approx 4.5 \text{ s}.\]

A soccer ball is kicked from rest at the penalty spot into the net $11 \text{ m}$ away. It takes $0.4 \text{ s}$ for the ball to hit the net. If the soccer ball does not accelerate after being kicked, how fast was it traveling immediately after being kicked? Solution: This is a straightforward application of the second equation of motion with $a = 0$, i.e $d = vt$: \[v = \frac{d}{t} = \frac{11 \text{ m}}{0.4 \text{ s}} = 27.5 \text{ m}/\text{s}.\]

A continuously accelerating car starts from rest as it zooms over a span of $100 \text{ m}$. If the final velocity of the car is $30 \text{ m}/\text{s}$, what is the acceleration of the car? Solution: Applying the third kinematical equation with $v_0 = 0$, \[v^2 = 2ad \implies a = \frac{v^2}{2d} = \frac{900}{200} \text{ m}/\text{s}^2 = 4.5 \text{ m}/\text{s}^2.\]

A basketball is dropped from a height of $10 \text{ m}$ above the surface of the moon, accelerating downwards at $1.6 \text { m}/\text{s}^2$. How long does it take to hit the surface, in seconds to the nearest tenth?

A train traveling at $40 \text{ m}/\text{s}$ is heading towards a station $400 \text{ m}$ away. If the train must slow down with constant deceleration $a$ into the station, how long does it take to come to a complete stop, in seconds? Answer to the nearest integer.

Sometimes kinematics problems require multiple steps of computation, which can make them more difficult. Below, some more challenging problems are explored.

A projectile is launched with speed $v_0$ at an angle $\theta$ to the horizontal and follows a trajectory under the influence of gravity. Find the range of the projectile. Solution: The projectile begins with velocity in the vertical direction of $v_0 \sin \theta$. To reach the apex of its trajectory, where the projectile is at rest, thus requires a time: \[t = \frac{v_0 \sin \theta}{g}.\] The time that it takes to fall back to the ground is therefore double this time, \[t = \frac{2v_0 \sin \theta}{g}.\] The range is the total distance in the horizontal direction traveled during this time. This is just the velocity in the x-direction times the time: \[R = v_x t = v_0 \cos \theta t = \frac{2v_0^2 \sin \theta \cos \theta}{g} = \frac{v_0^2 \sin 2 \theta}{g}.\]

A package is dropped from a cargo plane which is traveling at an altitude of $10000 \text{ m}$ with a horizontal velocity of $250 \text{ m}/\text{s}$ and no vertical component of the velocity. The package is initially at rest with respect to the plane. On the ground, a man is speeding along parallel to the plane in a $5 \text{ m}$ wide car traveling $40 \text{ m}/\text{s}$ trying to catch the package. The car starts a distance $X \text{ m}$ ahead of the plane. What does $X$ need to be for the man to succeed in catching the package? Solution: First, compute how long it takes for the package to hit the ground: \[d = \frac12gt^2 \implies t = \sqrt{\frac{2d}{g}} = \sqrt{\frac{20000 \text{ m}}{9.8 \text{ m}/\text{s}^2}} = 45.2 \text{ s}.\] How far does the package travel horizontally during that time? \[d_{\text{package}} = v_x t = (250 \text{ m}/\text{s})(45.2 \text{ s}) = 11300 \text{ m}.\] How far does the car travel during that time? \[d_{\text{car}} = v_x t = (40 \text{ m}/\text{s})(45.2 \text{ s}) = 1808 \text{ m}.\] If the package is caught, then $d_{\text{car}} + X = d_{\text{package}}$. This requires: \[X = (11300 - 1808) \text{ m} = 9492 \text{ m},\] or nearly $10$ kilometers! To be exact, the above quantity for $X$ can be shifted by up to $2.5 \text{ m}$ and still make contact with the car, because of the nonzero width of the car, but this is a negligible correction; $X$ is very large in comparison.

A pitcher throws a baseball towards home plate, a distance of $18 \text{ m}$ away, at $v = 40 \text{ m}/\text{s}$. Suppose the batter takes $.2 \text {s}$ to react before swinging. In swinging, the batter accelerates the end of the bat from rest through $2 \text{ m}$ at some constant acceleration $a$. Assuming that the end of the bat hits the ball if it crosses the plate within $. 05 \text{ s}$ of the ball crossing the plate, what is the minimum required $a$ in $\text{m}/\text{s}^2$ to the nearest tenth for the batter to hit the ball?

SpaceX is trying to land their next reusable rocket back on a drone ship. The drone ship is traveling due west in an ocean current at a constant speed of $5 \text{ m}/\text{s}$. The rocket is $2000 \text{ m}$ east of the drone ship and $5000 \text{ m}$ vertically above it, traveling vertically downwards at $100 \text{ m}/\text{s}$. If the rocket can apply vertical and horizontal thrusts to change the acceleration of the rocket in the vertical and horizontal directions, and must accelerate constantly in both directions, find the magnitude of the net acceleration (vector) required to land on the ship with no vertical velocity. Answer in $\text{ m}/\text{s}^2$ to the nearest tenth.

Master concepts like these

Learn more in our Classical Mechanics course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

Acceleration Examples

Acceleration is a vector quantity that measures a change in speed or direction. It is defined as a change in velocity per unit of time. Given below is the acceleration examples problems with solution for your reference to calculate acceleration in m / s 2 .

Acceleration Example Problems

Let us consider the acceleration practice problem: A car accelerates uniformly from 22.5 m/s to 46.1 m/s in 2.47 seconds. Determine the acceleration of the car.

We can calculate the Acceleration using the given formula.

Substituting the values in the formula,

Acceleration = (46.1 – 22.5 ) / 2.47 = 23.6 / 2.47 = 9.554 m/s 2

Therefore, the value of Acceleration is 9.554 m/s 2 .

Refer the below example of acceleration with solution. When an airplane accelerates down a runway at 3.20 m/s 2 to 5.41 m/s 2 for 28 s until is finally lifts off the ground, calculate its acceleration before its take off.

Substituting the values in the above given formula,

Acceleration = (5.41 – 3.20 ) / 28 = 2.21 / 28 = 0.078 m/s 2

Therefore, Acceleration is 0.078 m/s 2 .

Related Examples:

Potential Energy Examples
Young's Modulus Calculation Examples
Kinetic Energy Example
Force Examples
Work Physics Problems With Solutions
Synthetic Division Examples

Calculators and Converters

Classical Physics

Top Calculators

Popular calculators.

Derivative Calculator
Inverse of Matrix Calculator
Compound Interest Calculator
Pregnancy Calculator Online

Top Categories

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

6.3: Solving Problems with Newton's Laws (Part 2)

Last updated
Save as PDF
Page ID 5883

Newton’s Laws of Motion and Kinematics

Physics is most interesting and most powerful when applied to general situations that involve more than a narrow set of physical principles. Newton’s laws of motion can also be integrated with other concepts that have been discussed previously in this text to solve problems of motion. For example, forces produce accelerations, a topic of kinematics, and hence the relevance of earlier chapters.

When approaching problems that involve various types of forces, acceleration, velocity, and/or position, listing the givens and the quantities to be calculated will allow you to identify the principles involved. Then, you can refer to the chapters that deal with a particular topic and solve the problem using strategies outlined in the text. The following worked example illustrates how the problem-solving strategy given earlier in this chapter, as well as strategies presented in other chapters, is applied to an integrated concept problem.

Example 6.6: What Force Must a Soccer Player Exert to Reach Top Speed?

A soccer player starts at rest and accelerates forward, reaching a velocity of 8.00 m/s in 2.50 s. (a) What is her average acceleration? (b) What average force does the ground exert forward on the runner so that she achieves this acceleration? The player’s mass is 70.0 kg, and air resistance is negligible.

To find the answers to this problem, we use the problem-solving strategy given earlier in this chapter. The solutions to each part of the example illustrate how to apply specific problem-solving steps. In this case, we do not need to use all of the steps. We simply identify the physical principles, and thus the knowns and unknowns; apply Newton’s second law; and check to see whether the answer is reasonable.

We are given the initial and final velocities (zero and 8.00 m/s forward); thus, the change in velocity is $\Delta$v = 8.00 m/s . We are given the elapsed time, so $\Delta$t = 2.50 s. The unknown is acceleration, which can be found from its definition: $$a = \frac{\Delta v}{\Delta t} \ldotp$$Substituting the known values yields $$a = \frac{8.00\; m/s}{2.50\; s} = 3.20\; m/s^{2} \ldotp$$
Here we are asked to find the average force the ground exerts on the runner to produce this acceleration. (Remember that we are dealing with the force or forces acting on the object of interest.) This is the reaction force to that exerted by the player backward against the ground, by Newton’s third law. Neglecting air resistance, this would be equal in magnitude to the net external force on the player, since this force causes her acceleration. Since we now know the player’s acceleration and are given her mass, we can use Newton’s second law to find the force exerted. That is, $$F_{net} = ma \ldotp$$Substituting the known values of m and a gives $$F_{net} = (70.0\; kg)(3.20\; m/s^{2}) = 224\; N \ldotp$$

This is a reasonable result: The acceleration is attainable for an athlete in good condition. The force is about 50 pounds, a reasonable average force.

Significance

This example illustrates how to apply problem-solving strategies to situations that include topics from different chapters. The first step is to identify the physical principles, the knowns, and the unknowns involved in the problem. The second step is to solve for the unknown, in this case using Newton’s second law. Finally, we check our answer to ensure it is reasonable. These techniques for integrated concept problems will be useful in applications of physics outside of a physics course, such as in your profession, in other science disciplines, and in everyday life.

Exercise 6.4

The soccer player stops after completing the play described above, but now notices that the ball is in position to be stolen. If she now experiences a force of 126 N to attempt to steal the ball, which is 2.00 m away from her, how long will it take her to get to the ball?

Example 6.7: What Force Acts on a Model Helicopter?

A 1.50-kg model helicopter has a velocity of 5.00 $\hat{j}$ m/s at t = 0. It is accelerated at a constant rate for two seconds (2.00 s) after which it has a velocity of (6.00 $\hat{i}$ + 12.00 $\hat{j}$) m/s. What is the magnitude of the resultant force acting on the helicopter during this time interval?

We can easily set up a coordinate system in which the x-axis ($\hat{i}$ direction) is horizontal, and the y-axis ($\hat{j}$ direction) is vertical. We know that $\Delta$t = 2.00s and $\Delta$v = (6.00 $\hat{i}$ + 12.00 $\hat{j}$ m/s) − (5.00 $\hat{j}$ m/s). From this, we can calculate the acceleration by the definition; we can then apply Newton’s second law.

\[a = \frac{\Delta v}{\Delta t} = \frac{(6.00 \hat{i} + 12.00 \hat{j}\; m/s) - (5.00 \hat{j}\; m/s)}{2.00\; s} = 3.00 \hat{i} + 3.50 \hat{j}\; m/s^{2}$$ $$\sum \vec{F} = m \vec{a} = (1.50\; kg)(3.00 \hat{i} + 3.50 \hat{j}\; m/s^{2}) = 4.50 \hat{i} + 5.25 \hat{j}\; N \ldotp\]

The magnitude of the force is now easily found:

\[F = \sqrt{(4.50\; N)^{2} + (5.25\; N)^{2}} = 6.91\; N \ldotp\]

The original problem was stated in terms of $\hat{i}$ − $\hat{j}$ vector components, so we used vector methods. Compare this example with the previous example.

Exercise 6.5

Find the direction of the resultant for the 1.50-kg model helicopter.

Example 6.8: Baggage Tractor

Figure $\PageIndex{7}$(a) shows a baggage tractor pulling luggage carts from an airplane. The tractor has mass 650.0 kg, while cart A has mass 250.0 kg and cart B has mass 150.0 kg. The driving force acting for a brief period of time accelerates the system from rest and acts for 3.00 s. (a) If this driving force is given by F = (820.0t) N, find the speed after 3.00 seconds. (b) What is the horizontal force acting on the connecting cable between the tractor and cart A at this instant?

Figure (a) shows a baggage tractor driving to the left and pulling two luggage carts. The external forces on the system are shown. The forces on the tractor are F sub tractor, horizontally to the left, N sub tractor vertically up, and w sub tractor vertically down. The forces on the cart immediately behind the tractor, cart A, are N sub A vertically up, and w sub A vertically down. The forces on cart B, the one behind cart A, are N sub B vertically up, and w sub B vertically down. Figure (b) shows the free body diagram of the tractor, consisting of F sub tractor, horizontally to the left, N sub tractor vertically up, w sub tractor vertically down, and T horizontally to the right.

A free-body diagram shows the driving force of the tractor, which gives the system its acceleration. We only need to consider motion in the horizontal direction. The vertical forces balance each other and it is not necessary to consider them. For part b, we make use of a free-body diagram of the tractor alone to determine the force between it and cart A. This exposes the coupling force $\vec{T}$, which is our objective.

$$\sum F_{x} = m_{system} a_{x}\; and\; \sum F_{x} = 820.0t,$$so $$820.0t = (650.0 + 250.0 + 150.0)a$$ $$a = 0.7809t \ldotp$$Since acceleration is a function of time, we can determine the velocity of the tractor by using a = $\frac{dv}{dt}$ with the initial condition that v 0 = 0 at t = 0. We integrate from t = 0 to t = 3: $$\begin{split}dv & = adt \\ \int_{0}^{3} dv & = \int_{0}^{3.00} adt = \int_{0}^{3.00} 0.7809tdt \\ v & = 0.3905t^{2} \big]_{0}^{3.00} = 3.51\; m/s \ldotp \end{split}$$
Refer to the free-body diagram in Figure $\PageIndex{7}$(b) $$\begin{split} \sum F_{x} & = m_{tractor} a_{x} \\ 820.0t - T & = m_{tractor} (0.7805)t \\ (820.0)(3.00) - T & = (650.0)(0.7805)(3.00) \\ T & = 938\; N \ldotp \end{split}$$

Since the force varies with time, we must use calculus to solve this problem. Notice how the total mass of the system was important in solving Figure $\PageIndex{7}$(a), whereas only the mass of the truck (since it supplied the force) was of use in Figure $\PageIndex{7}$(b).

Recall that v = $\frac{ds}{dt}$ and a = $\frac{dv}{dt}$. If acceleration is a function of time, we can use the calculus forms developed in Motion Along a Straight Line , as shown in this example. However, sometimes acceleration is a function of displacement. In this case, we can derive an important result from these calculus relations. Solving for dt in each, we have dt = $\frac{ds}{v}$ and dt = $\frac{dv}{a}$. Now, equating these expressions, we have $\frac{ds}{v}$ = $\frac{dv}{a}$. We can rearrange this to obtain a ds = v dv.

Example 6.9: Motion of a Projectile Fired Vertically

A 10.0-kg mortar shell is fired vertically upward from the ground, with an initial velocity of 50.0 m/s (see Figure $\PageIndex{8}$). Determine the maximum height it will travel if atmospheric resistance is measured as F D = (0.0100 v 2 ) N, where v is the speed at any instant.

(a) A photograph of a soldier firing a mortar shell straight up. (b) A free body diagram of the mortar shell shows forces F sub D and w, both pointing vertically down. Force w is larger than force F sub D.

The known force on the mortar shell can be related to its acceleration using the equations of motion. Kinematics can then be used to relate the mortar shell’s acceleration to its position.

Initially, y 0 = 0 and v 0 = 50.0 m/s. At the maximum height y = h, v = 0. The free-body diagram shows F D to act downward, because it slows the upward motion of the mortar shell. Thus, we can write

\[\begin{split} \sum F_{y} & = ma_{y} \\ -F_{D} - w & = ma_{y} \\ -0.0100 v^{2} - 98.0 & = 10.0 a \\ a & = -0.00100 v^{2} - 9.80 \ldotp \end{split}\]

The acceleration depends on v and is therefore variable. Since a = f(v), we can relate a to v using the rearrangement described above,

\[a ds = v dv \ldotp\]

We replace ds with dy because we are dealing with the vertical direction,

\[\begin{split} ady & = vdv \\ (−0.00100v^{2} − 9.80)dy & = vdv \ldotp \end{split}\]

We now separate the variables (v’s and dv’s on one side; dy on the other):

\[\begin{split} \int_{0}^{h} dy & = \int_{50.0}^{0} \frac{vdv}{(-0.00100 v^{2} - 9.80)} \\ & = - \int_{50.0}^{0} \frac{vdv}{(-0.00100 v^{2} + 9.80)} \\ & = (-5 \times 10^{3}) \ln(0.00100v^{2} + 9.80) \Big|_{50.0}^{0} \ldotp \end{split}\]

Thus, h = 114 m.

Notice the need to apply calculus since the force is not constant, which also means that acceleration is not constant. To make matters worse, the force depends on v (not t), and so we must use the trick explained prior to the example. The answer for the height indicates a lower elevation if there were air resistance. We will deal with the effects of air resistance and other drag forces in greater detail in Drag Force and Terminal Speed .

Exercise 6.6

If atmospheric resistance is neglected, find the maximum height for the mortar shell. Is calculus required for this solution?

Explore the forces at work in this simulation when you try to push a filing cabinet. Create an applied force and see the resulting frictional force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a free-body diagram of all the forces (including gravitational and normal forces).

Physics Formulas

Acceleration Formula

One may have perceived that pushing a terminally ill bus can give it a sudden start. That’s because lift provides an upward push when it starts. Here velocity changes and this is acceleration! Henceforth, the frame accelerates. Acceleration is described as the rate of change of velocity of an object. A body’s acceleration is the final result of all the forces being applied to the body, as defined by Newton’s second law. Acceleration is a vector quantity that is described as the frequency at which a body’s velocity changes.

Formula of Acceleration

Acceleration is the rate of change in velocity to the change in time. It is denoted by symbol a and is articulated as-

$acceleration formula 1$

The S.I unit for acceleration is meter per second square or m/s 2 .

$velocity in terms of acceleration$

Final Velocity is v
Initial velocity is u
Acceleration is a
Time taken is t
Distance traveled is s

Acceleration Solved Examples

Underneath we have provided some sample numerical based on acceleration which might aid you to get an idea of how the formula is made use of:

Problem 1: A toy car accelerates from 3 m/s to 5 m/s in 5 s. What is its acceleration? Answer:

Given: Initial Velocity u = 3 m/s, Final Velocity v = 5m/s, Time taken t = 5s.

$Acceleration formula 5$

Problem 2: A stone is released into the river from a bridge. It takes 4s for the stone to touch the river’s water surface. Compute the height of the bridge from the water level.

(Initial Velocity) u = 0 (because the stone was at rest), t = 4s (t is Time taken) a = g = 9.8 m/s 2 , (a is Acceleration due to gravity) distance traveled by stone = Height of bridge = s The distance covered is articulated by

$Acceleration formula 9$

s = 0 + 1/2 × 9.8 × 4 = 19.6 m/s 2

Therefore, s = 19.6 m/s 2

Register with BYJU'S & Download Free PDFs

Talk to our experts

1800-120-456-456

Acceleration Formula

What is Acceleration?

When a stationary car starts suddenly, we get pushed up backward, and when brakes are applied, we get pushed forward against our seat, or when our car takes a sharp right turn, we get pushed towards the left. We experience these situations because our car is accelerating.

Simply when there is a change in Velocity, there will be Acceleration. Let’s understand the concept of Acceleration with illustrative examples.

Let’s suppose I have a car moving with a constant Velocity of 90 kmph along a straight line. I can see a helicopter flying at roughly a speed of 20,000 kmph. If I were to ask you that in these two cases, where do you find the Acceleration? Your answer will be surely no because both are moving at a constant pace, so no Acceleration in both cases.

Now, if I ask you that Acceleration is equal to high speed. What will be your answer? You may say yes, but that’s not true for sure. Want to know why? It’s because Acceleration is the rate of change of Velocity. Now, let’s understand the Acceleration formula.

General Formula of Acceleration

We already know that Velocity is a speed with direction; therefore, it is a vector quantity. The Acceleration ‘a’ is given as:

\[ a = \frac{\text{Change in Velocity}}{\text{Time Taken}}\]

This formula states that the rate of change in Velocity is the Acceleration, or if the Velocity of an object changes from its initial value ‘u’ to the final value ‘v’, then the expression can be simply written as:

\[a = \frac{(v - u)}{t}\]

Acceleration Formula in Physics

In Physics , Acceleration is described as the rate of change of Velocity of an object, irrespective of whether it speeds up or slows down. If it speeds up, Acceleration is taken as positive and if it slows down, the Acceleration is negative. It is caused by the net unbalanced force acting on the object, as per Newton’s Second Law. Acceleration is a vector quantity as it describes the time rate of change of Velocity, which is a vector quantity. Acceleration is denoted by a. Its SI unit is \[\frac{m}{s^{2}}\] and dimensions are \[[M^{0}L^{1}T^{–2}]\].

If \[v_{0}, v_{t}\] and t represents the initial Velocity, final Velocity and the time taken for the change in Velocity, then, the Acceleration is given by:

\[\overrightarrow{a} = \frac{\overrightarrow{v_t} - \overrightarrow{v_0}}{t}\]

In one dimensional motion, we can use;

\[a = \frac{v_t - v_0}{t}\]

If \[\overrightarrow{r} \]represents displacement vector and \[\overrightarrow{v} = \frac{\overrightarrow{\text{d}r}}{\text{d}t}\] represents the velocity, then;

Acceleration: \[\overrightarrow{a} = \frac{\overrightarrow{\text{d}v}}{\text{d}t} = \frac{\overrightarrow{\text{d}^{2}v}}{\text{d}^{2}t}\]

In one dimensional motion, where x is the displacement, and \[v = \frac{\text{d}r}{\text{d}t}\] is the Velocity, then;

\[a = \frac{\text{d}{v}}{\text{d}t} = \frac{\text{d}^{2}x}{\text{d}^{2}t}\]

A car starts from rest and achieves a speed of 54 \[\frac{km}{h}\] in 3 seconds. Find its Acceleration?

Solution: \[v_0\] = 0, \[v_t\] = 54 \[\frac{km}{h}\] = 15 \[\frac{m}{s}\], t = 3s, a = ?

Acceleration:

\[a = \frac{v_t - v_0}{t} = \frac{15 - 0}{3} = 5 \frac{m}{s^{2}}\]

A body moves along the x- axis according to the relation \[x = 1 – 2 t + 3t^{2}\], where x is in meters and t is in seconds. Find the Acceleration of the body when t = 3 s

We have: \[x = 1 – 2 t + 3t^{2}\]

then; Velocity \[v = \frac{\text{d}x}{\text{d}t} = -2 + 6t \]

Acceleration: \[v = \frac{\text{d}v}{\text{d}t} = 6 \frac{m}{s^{2}}\].

(We see that the Acceleration is constant here. Therefore, at t = 3s also, its value is 6 \[\frac{m}{s^{2}}\]).

Solved Questions Using Acceleration Formula:

1. What will be the Acceleration of a Car if it Slows from 90 \[\frac{km}{h}\] to a Stop in 10 sec?

Here, u = 90 \[\frac{km}{h}\] = \[ \frac{90 \times 5}{18} = 25 \frac{m}{s^{2}} \] because initially it was moving at a speed of 90 kmph then reached zero.

Final Velocity ‘v’ = 0 kmph, and t = 10 seconds

Now, applying the formula here:

\[a = \frac{(0 - 25)}{10} = (-) 2.5 \frac{m}{s^{2}} \]

2. A Girl Starts her Motion in a Straight Line at a Velocity of 30 \[\frac{m}{s}\], her Velocity is Changing at a Constant Rate. If She Stops after 60 s, What is her Acceleration?

Answer: Here, the initial Velocity of a girl was 30 \[\frac{m}{s}\] and stops, so her final Velocity will become 0 m/s. Now, the deceleration or retardation occurs, which is just the opposite of Acceleration and it can be determined as:

\[ a = \frac{(0 - 30)}{60} = (-) 0.5 \frac{m}{s^{2}} \]

Question 3: A Car Moves in a Circular Track with a Constant Velocity; will it Experience Acceleration?

Answer: Here, the speed is constant; however, the direction is continuously varying, which means the Velocity is also varying. It states that the car will experience Acceleration.

How to prepare for a test on Acceleration using Vedantu

You can log onto Vedantu and then go through the study material that’s present

You can click on Acceleration Formula with examples and solved problem

After going through this study matter, the concepts will get much clearer

You can also make notes of the above by writing down the important points

Carefully observe the solved examples

The matter will have ensured that you are preparing well for the exams

Why choose Vedantu?

Vedantu is a top e-learning platform that only keeps the best study material on its website. It is extremely dependable since all students bank on it before they sit down for revisions or tests. The study material on it is free of cost and can be downloaded and then gone through in the offline mode as well. You should choose Vedantu if you need to be smartly prepped up before your tests and learn all the complex concepts.

FAQs on Acceleration Formula

1. Where can I find sums on Acceleration?

You can find ample examples and sums on Acceleration if you choose to read Acceleration Formula with examples and solved problems on Vedantu. This has a detailed description of what Acceleration is, what its examples are, how it's related to speed and direction. You will find the kind of sums that will come for the tests here so that you can practice them and secure good marks. Do not skip reading any part as that might cause problems with understanding the concepts later on.

2. How do I clear my concepts related to Velocity and speed?

You should understand the very basics of what each is so that you can answer questions when they are asked. Go through Acceleration Formula with examples and solved problems available on this page on Vedantu as this is the ideal guide for those who are looking to clear their concepts.

Velocity is the speed with direction. The rate of change in Velocity would be termed Acceleration. Understanding this is key to solving the sums that come from this chapter and topic. You should go through the entire description along with its formulae and examples. Practice a few sums and then assess your understanding.

3. When a car suddenly halts, why do we get pushed forward against our seat?

As a car suddenly stops, we tend to get pushed forward as our car starts accelerating. As there is a change in the speed with direction (Velocity), Acceleration occurs. More about this is provided if you go to Acceleration Formula with examples and solved problem. This can be found on Vedantu and contains all the relevant details that need to be known. It has explained everything in an extremely simplified manner with the help of examples and is an ideal guidebook for those who are looking to clear their concepts related to Acceleration.

4. Is Acceleration the same as very high speed?

You may be partially correct in stating so but not entirely. Acceleration is more essentially the rate of change of Velocity. You can read from Acceleration Formula with examples and solve problems on Vedantu and then understand better. It has the description of Acceleration along with its sums and a lot of examples. It has a comprehensive description of the topic and its related concepts so that students do not get confused while learning about the topic. Acceleration as a concept is crucial for the higher classes as the Science and Maths study material that they come across then, will be based on these.

5. Can I skip the chapter and the sums on Acceleration when I am studying?

You should not skip anything at any point in time as it could lead to securing lower grades overall. If you have any queries regarding the concepts on Acceleration and its related problems, you can refer to Acceleration Formula with examples and solved problems on Vedantu’s platform. This will clear all your doubts so that you do not feel tempted to skip this chapter just because it's slightly tricky. Once you have completely scanned this page, you will be able to solve the sums that come for your tests and be more confident in tackling questions that come from the chapter.

JEE-IIT-NCERT Physics & Math

Widget atas posting, uniform acceleration motion problems and solutions.

Problem #1

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

By Bill Whitaker

May 5, 2024 / 7:00 PM EDT / CBS News

As the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years.

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything.

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students.

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told them was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah.

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it."

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson: So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash.

Bill Whitaker: Did you look at the problem?

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter)

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Bill Whitaker with Calcea Johnson and Ne'Kiya Jackson

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics.

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch.

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh)

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah.

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans.

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates.

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

St. Mary's Academy president and interim principal Pamela Rogers

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in.

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven.

Bill Whitaker: What do you mean by that?

Bill Whitaker and Gloria Ladson-Billings

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter)

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Heineken vows nearly $50 million to transform "tired pubs" in U.K.

Should you use a reverse mortgage to cover long-term care costs?

Afghan diplomat accused of smuggling gold into India resigns

How technology helped a nonspeaking autistic woman find her voice

ENVIRONMENT

Are the Great Lakes the key to solving America’s emissions conundrum?

A single cargo ship can carry enough goods to replace nearly 3,000 semi-trucks—that's why some are calling for a shipping boom in America's famous lakes.

The Mark W Barker coming into Sturgeon Bay through the shipping canal.

Nearly four decades had passed since the Great Lakes witnessed that unique ritual: the smashing of a bottle of champagne off the bow of a U.S.-flagged cargo ship.

When it finally happened in October 2021 with the launching of the MV Mark W. Barker, a 639-foot-long freighter, in Sturgeon Bay, Wisconsin, it marked a new dawn.

The first bulk carrier to enter service on the Great Lakes for 37 years, the ship can transport goods ranging from salt to wind turbine blades to shipping containers. Its hull design means it can hold 20 percent more cargo than vessels of a similar size. It’s also the first ship sailing the Great Lakes to meet the U.S. Environmental Protection Agency’s tier 4 emissions standards .

“It’s the most capable, most environmentally friendly asset we have,” says Brendan O’Connor, chief operations officer for the Interlake Steamship Company, which operates the MV Mark W. Barker.

The ship, and others like it, are a critical piece of the climate change puzzle. As the deadlines for meeting the Paris Climate Agreement’s emissions targets draw ever closer—with the goal for emissions to peak before 2025 and decline 43 percent by 2030—one industry is inducing panic: the transportation world.

America’s transportation industry is the country’s leading source of carbon emissions, responsible for a whopping 29 percent . And while privately-owned vehicles make up 58 percent of that, medium- and heavy-duty trucks carrying bulk materials account for 23 percent.

For Hungry Minds

Yet one weapon in the battle against emissions may be sitting in plain sight: the Great Lakes.

Linking Chicago, Detroit, Cleveland, Toronto, Buffalo, and other cities that are home to about 32 million people, Great Lakes shipping could play a significant role in helping the U.S. and Canada dramatically reduce their emissions footprints.

Transporting more goods with fewer vehicles

Today, several ports have projects that could help facilitate that change.

The Port of Cleveland on Lake Erie is set for a $32-million infrastructure upgrade . Farther west on Lake Superior, the Port of Duluth-Superior was recently expanded to handle international container freight . One survey of public and private investments found more than $8.4 billion has been committed to developing Great Lakes maritime infrastructure.

Road freight emits up to 100 times the amount of emissions of ships —a single Great Lakes vessel can carry as much bulk material as 2,800 semi-trucks or 700 rail cars . With gas prices raising trucking costs on average and rail strike threats growing in recent years, Great Lakes shipping could serve as a cleaner, more efficient way to transport many of the critical items America’s economy relies on.

Still, challenges abound. The two largest Great Lakes cities—Toronto and Chicago— currently both have comparatively small port infrastructure systems.

( Interested in an electric car? Here's what you should know. )

This small strait is essential to global shipping. Now it's the center of headlines.

NASA has a plan to clean up space junk—but is going green enough?

What exactly is lab-grown meat? Here’s what you need to know.

The Port of Toronto’s economic impact is dwarfed by ports in Montreal and Vancouver, while Chicago’s port has been falling into disrepair for decades. Despite this poor infrastructure, experts say the Port of Chicago has significant potential as a major hub because it is also connected to the Mississippi River by the Illinois Waterway, a network of canals, lakes, and rivers.

Not a perfect solution

Shipping hasn’t always been a cleaner alternative. In 2021, ships traversing the Great Lakes and St. Lawrence Seaway, the body of water that connects the lakes to the Atlantic Ocean, consumed 500,000 tons of fuel that emitted 1.6 million tons of carbon dioxide, according to one study . That’s the equivalent of around 380,000 cars.

Still, experts say that opportunities for change are growing.

“It’s technically feasible to decarbonize every ship in the fleet,” says Bryan Comer, marine program director at the International Council on Clean Transportation, a Washington, D.C.-based research institute. “The question is: What are the regulatory and economic drivers or incentives to do that?”

( How green can we make air travel? And how soon? )

Comer says that while there’s potential for electrifying smaller ships such as tugboats, to meet U.S. emissions targets, some larger ships will need new propulsion technologies that replace internal combustion engines with fuel cells that run on ‘green hydrogen,’ an energy resource made from renewable electricity.

“That is going to be the ingredient in all of the fuels that are used,” he says.

To help meet this transition, the U.S. Department of Energy has made $7 billion available to build up to 10 so-called ‘hydrogen hubs’ across the country .

“A lot of our efforts are in the scale-up of large-scale production of the clean hydrogen molecules—building out the infrastructure, the storage (and) the delivery,” says Neil Banwart of the Midwest Alliance for Clean Hydrogen , one of seven awardees of the federal funding.

“We certainly do hope that Great Lakes shipping is [a buyer], a use case for this clean hydrogen that we intend to produce.”

Small steps toward big change

In the meantime, Great Lakes ports and shipping companies are working on short-term ways to push the industry closer to net zero.

The Port of Cleveland’s infrastructure update includes an electrification plan and charging stations it hopes will help it fulfill its goal of becoming the first net-zero emissions port on the Great Lakes by 2050.

The Interlake Steamship Company hopes to cut its emissions footprint by 50 percent in the next decade.

“The engines are going to be the best way for us to move the needle,” says Brendan O’Connor.

“We’re not quite there yet but in the next two or three years I think we’ll see changes.”

The fungus in 'The Last of Us' is real—and it's very, very expensive

Here’s what worries engineers the most about U.S. infrastructure

10 simple ways to change your life in 2024

Heat waves are getting worse. Here’s how to prepare.

Dead whales are washing up on the East Coast. The reason remains a mystery.

Environment

History & Culture

History & Culture
Mind, Body, Wonder
Paid Content
Terms of Use
Privacy Policy
Your US State Privacy Rights
Children's Online Privacy Policy
Interest-Based Ads
About Nielsen Measurement
Do Not Sell or Share My Personal Information
Nat Geo Home
Attend a Live Event
Book a Trip
Inspire Your Kids
Shop Nat Geo
Visit the D.C. Museum
Learn About Our Impact
Support Our Mission
Advertise With Us
Customer Service
Renew Subscription
Manage Your Subscription
Work at Nat Geo
Sign Up for Our Newsletters
Contribute to Protect the Planet

Try Paramount+
Search shows
TV Provider

Teens surprise math world with Pythagorean Theorem trigonometry proof | 60 Minutes

Full Episodes

IMAGES

Acceleration Practice Problems with solutions
Solving problems for acceleration
How to solve simple acceleration problems
Solving Problems Calculating the Average Acceleration of an Object
Laws of Motion Problems with Solutions Six
1D KINEMATIC MOTION PRACTICE

VIDEO

Constant acceleration
Acceleration Solution
Physics. Problem solving. 01_10
How to Solve Uniformly Accelerated Linear Motion Problems Part I- Grade 12 Physics
Kinematics Problem Solving (Uniform Acceleration)
Top 4 Causes of Loss of Power While Acclerating

COMMENTS

Acceleration: Tutorials with Examples
Examples with explanations on the concepts of acceleration of moving object are presented. More problems and their solutions can also be found in this website.. Average Acceleration The average acceleration is a vector quantity (magnitude and direction) that describes the rate of change (with the time) of the velocity of a moving object.. An object with initial velocity v 0 at time t 0 and ...
Acceleration Problems
Problem # 1. A particle is moving in a straight line with a velocity given by 5 t2, where t is time. Find an expression for the acceleration of the particle. (Answer: 10 t ) Problem # 2. A particle travels in a straight line a distance of 2 m in a time of 0.01 seconds. It is known that the particle accelerates from rest with constant ...
Kinematic Equations: Sample Problems and Solutions
Kinematic equations relate the variables of motion to one another. Each equation contains four variables. The variables include acceleration (a), time (t), displacement (d), final velocity (vf), and initial velocity (vi). If values of three variables are known, then the others can be calculated using the equations. This page demonstrates the process with 20 sample problems and accompanying ...
Solved Speed, Velocity, and Acceleration Problems
Kinematics Equations: Problems and Solutions. Position vs. Time Graphs. Velocity vs. Time Graphs In the following section, some sample AP Physics 1 problems on acceleration are provided. Problem (20): An object moves with constant acceleration along a straight line.
Uniform Acceleration Motion: Problems with Solutions
Problem 10: To approximate the height of a water well, Martha and John drop a heavy rock into the well. 8 seconds after the rock is dropped, they hear a splash caused by the impact of the rock on the water. What is the height of the well. (Speed of sound in air is 340 m/s). Solution to Problem 10.
Acceleration and velocity (practice)
Acceleration and velocity. A rocket ship starts from rest and turns on its forward booster rockets, causing it to have a constant acceleration of 4 m s 2 rightward. After 3 s , what will be the velocity of the rocket ship? Answer using a coordinate system where rightward is positive. m s. Learn for free about math, art, computer programming ...
Acceleration
solution. Acceleration is the rate of change of velocity with time. Since velocity is a vector, this definition means acceleration is also a vector. When it comes to vectors, direction matters as much as size. In a simple one-dimensional problem like this one, directions are indicated by algebraic sign.
6.1 Solving Problems with Newton's Laws
Solve more complex acceleration problems; Apply calculus to more advanced dynamics problems; Success in problem solving is necessary to understand and apply physical principles. ... To find the answers to this problem, we use the problem-solving strategy given earlier in this chapter. The solutions to each part of the example illustrate how to ...
3.4 Motion with Constant Acceleration
Even for the problem with two cars and the stopping distances on wet and dry roads, we divided this problem into two separate problems to find the answers. In a two-body pursuit problem, the motions of the objects are coupled—meaning, the unknown we seek depends on the motion of both objects. To solve these problems we write the equations of ...
Position, velocity, acceleration problems and solutions
Position, velocity, acceleration problems and solutions. When solving a Physics problem in general and one of Kinematics in particular, it is important that you follow an order. Get used to being organized when you solve problems, and you will see how it gives good results. It is worth spending a little time on the previous analysis of a ...
Kinematic Equations and Problem-Solving
The use of this problem-solving strategy in the solution of the following problem is modeled in Examples A and B below. ... If Ima's acceleration is -8.00 m/s 2, then determine the displacement of the car during the skidding process. (Note that the direction of the velocity and the acceleration vectors are denoted by a + and a - sign.)
1D Kinematics Problem Solving
Equation Review. The three fundamental equations of kinematics in one dimension are: \ [v = v_0 + at,\] \ [x = x_0 + v_0 t + \frac12 at^2,\] \ [v^2 = v_0^2 + 2a (x-x_0).\] The first gives the change in velocity under a constant acceleration given a change in time, the second gives the change in position under a constant acceleration given a ...
2.5: Motion with Constant Acceleration (Part 1)
In part (b), acceleration is not constant. During the 1-h interval, velocity is closer to 80 km/h than 40 km/h. Thus, the average velocity is greater than in part (a). Figure 2.5.1 2.5. 1: (a) Velocity-versus-time graph with constant acceleration showing the initial and final velocities v 0 and v. The average velocity is 1 2 1 2 (v 0 + v) = 60 ...
6.2: Solving Problems with Newton's Laws (Part 1)
The angle is given by. θ = tan − 1(F2 F1) = tan − 1(3.6 × 105 N 2.7 × 105 N) = 53.1o. From Newton's first law, we know this is the same direction as the acceleration. We also know that →FD is in the opposite direction of →Fapp, since it acts to slow down the acceleration.
Acceleration Examples
Refer the below example of acceleration with solution. When an airplane accelerates down a runway at 3.20 m/s 2 to 5.41 m/s 2 for 28 s until is finally lifts off the ground, calculate its acceleration before its take off. Solution: Substituting the values in the above given formula, Acceleration = (5.41 - 3.20 ) / 28 = 2.21 / 28 = 0.078 m/s 2
Setting up problems with constant acceleration
Setting up problems with constant acceleration. Onur drops a basketball from a height of 10 m on Mars, where the acceleration due to gravity has a magnitude of 3.7 m s 2 . We want to know how many seconds the basketball is in the air before it hits the ground. We can ignore air resistance. Which kinematic formula would be most useful to solve ...
6.3: Solving Problems with Newton's Laws (Part 2)
Solution. We are given the initial and final velocities (zero and 8.00 m/s forward); thus, the change in velocity is Δ Δ v = 8.00 m/s . We are given the elapsed time, so Δ Δ t = 2.50 s. The unknown is acceleration, which can be found from its definition: a = Δv Δt. (6.3.1) (6.3.1) a = Δ v Δ t.
Acceleration Formula With Solved Examples
Answer: s = 0 + 1/2 × 9.8 × 4 = 19.6 m/s 2. Therefore, s = 19.6 m/s 2. Acceleration is the change in velocity per time. Acceleration formula can be expressed in terms of initial velocity, final velocity, time taken or distance travelled. Solved examples are useful in understanding the formula.
PDF 1.6 Solving Uniform Acceleration Problems
solving. One could also eliminate any variables with zero values, rearrange the equation, and then solve for the unknown. You will notice that when the time interval is the unknown variable and the appropriate equation is quadratic (the second and fifth equations in Table 1), the solution is much simpler if the initial or final velocity is zero.
Acceleration Formula with Examples and Solved Problems
Example 2: A body moves along the x- axis according to the relation , where x is in meters and t is in seconds. Find the Acceleration of the body when t = 3 s. Solution: We have: then; Velocity. Acceleration: . (We see that the Acceleration is constant here. Therefore, at t = 3s also, its value is 6 ).
PDF Solving Acceleration Problems
what you're supposed to find ("no solution" will not be the answer). Explicit information -information that you are told directly Check for understanding -In the following problem, identify the explicit information: A bullet comes to rest in a tree in .01 seconds, with an acceleration of -8000 m/s2. What was the bullet's velocity ...
Uniform acceleration motion Problems and Solutions
a = 15 m/s2. Problem #2. A car accelerates uniformly from 21,0 m/s to 35,0 m/s in 3,0 seconds. Determine the acceleration of the car and the distance traveled. Answer: Given: time t = 4,0 s, initial velocity vi = 21,0 m/s, and finale velocity vf = 35,0 m/s,
Solving Problems Calculating the Average Acceleration of an Object
Steps for Solving Problems Calculating the Average Acceleration of an object Algebraically. Step 1: Determine our known values for velocity and time. Step 2: Determine what we are being asked to ...
Teens come up with trigonometry proof for Pythagorean Theorem, a
A high school teacher didn't expect a solution when she set a 2,000-year-old Pythagorean Theorem problem in front of her students. Then Calcea Johnson and Ne'Kiya Jackson stepped up to the challenge.
Are the Great Lakes the key to solving America's emissions conundrum?
On January 21, 2023, the Mark W Barker arrived in Sturgeon Bay, Wisconsin for its first shipping season. Some experts say ships like these should be used to reduce the U.S.'s transportation footprint.
Watch 60 Minutes: Teens' innovative Pythagorean Theorem work
A high school teacher didn't expect a solution when she set a 2,000-year-old Pythagorean Theorem problem in front of her students. Then Calcea Johnson and Ne'Kiya Jackson stepped up to the challenge.

Physics Problems with Solutions

Average Acceleration

Examples with soltutions

More References and links

Popular Pages

Acceleration Problems

Real World Applications — for high school level and above

Education & Theory — for high school level and above

Kids Section

Solved Speed, Velocity, and Acceleration Problems

Speed and velocity Problems:

Acceleration Problems

Acceleration

practice problem 2

practice problem 3

3.4 Motion with Constant Acceleration

Displacement and Position from Velocity

Solving for Final Velocity from Acceleration and Time

Example 3.7

Significance

Solving for Final Position with Constant Acceleration

Example 3.8

Solving for Final Velocity from Distance and Acceleration

Example 3.9

Putting Equations Together

Summary of Kinematic Equations (constant a )

Example 3.10

Example 3.11

Check Your Understanding 3.5

Example 3.12

Two-Body Pursuit Problems

Example 3.13

Check Your Understanding 3.6

Kinematic Equations and Problem-Solving

Problem-Solving Strategy

Example Problem A

Example Problem B

1D Kinematics Problem Solving

Recommended Course

Equation Review

Master concepts like these

Acceleration Examples

Acceleration Example Problems

Related Examples:

Calculators and Converters

Top Calculators

Top Categories

6.3: Solving Problems with Newton's Laws (Part 2)

Newton’s Laws of Motion and Kinematics

Example 6.6: What Force Must a Soccer Player Exert to Reach Top Speed?

Exercise 6.4

Example 6.7: What Force Acts on a Model Helicopter?

Exercise 6.5

Example 6.8: Baggage Tractor

Example 6.9: Motion of a Projectile Fired Vertically

Exercise 6.6

Acceleration Formula

Formula of Acceleration

Acceleration Solved Examples

Leave a Comment Cancel reply

Register with BYJU'S & Download Free PDFs

Acceleration Formula

What is Acceleration?

General Formula of Acceleration

Acceleration Formula in Physics

Acceleration: \[\overrightarrow{a} = \frac{\overrightarrow{\text{d}v}}{\text{d}t} = \frac{\overrightarrow{\text{d}^{2}v}}{\text{d}^{2}t}\]

\[a = \frac{\text{d}{v}}{\text{d}t} = \frac{\text{d}^{2}x}{\text{d}^{2}t}\]

Solved Questions Using Acceleration Formula:

How to prepare for a test on Acceleration using Vedantu

Why choose Vedantu?

FAQs on Acceleration Formula

JEE-IIT-NCERT Physics & Math

Post a Comment for "Uniform acceleration motion Problems and Solutions"

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

More from CBS News

Heineken vows nearly $50 million to transform "tired pubs" in U.K.

Should you use a reverse mortgage to cover long-term care costs?

Afghan diplomat accused of smuggling gold into India resigns

How technology helped a nonspeaking autistic woman find her voice

Are the Great Lakes the key to solving America’s emissions conundrum?