

Fun teaching resources & tips to help you teach math with confidence

Math Strategies: Problem Solving by Finding a Pattern
One important math concept that children begin to learn and apply in elementary school is reading and using a table. This is essential knowledge, because we encounter tables of data all the time in our everyday lives! But it’s not just important that kids can read and answer questions based on information in a table, it’s also important that they know how to create their own table and then use it to solve problems, find patterns, graph equations, and so on. And while some may think of these as two different things, I think problem solving by making a table and finding a pattern go hand in hand!

–>Pssst! Do your kids need help making sense of and solving word problems? You might like this set of editable word problem solving templates ! Use these with any grade level, for any type of word problem :
Finding Patterns in Math Problems:
So when should kids use problem solving by finding a pattern ? Well, when the problem gives a set of data, or a pattern that is continuing and can be arranged in a table, it’s good to consider looking for the pattern and determining the “rule” of the pattern.
As I mentioned when I discussed problem solving by making a list , finding a pattern can be immensely helpful and save a lot of time when working on a word problem. Sometimes, however, a student may not recognize the pattern right away, or may get bogged down with all the details of the question.
Setting up a table and filling in the information given in the question is a great way to organize things and provide a visual so that the “rule” of the pattern can be determined. The “rule” can then be used to find the answer to the question. This removes the tedious work of completing a table, which is especially nice if a lot of computation is involved.
But a table is also great for kids who struggle with math, because it gives them a way to get to the solution even if they have a hard time finding the pattern, or aren’t confident that they are using the “rule” correctly.
Because even though using a known pattern can save you time, and eliminate the need to fill out the entire table, it’s not necessary. A student who is unsure could simply continue filling out their table until they reach the solution they’re looking for.
Helping students learn how to set up a table is also helpful because they can use it to organize information (much like making a list) even if there isn’t a pattern to be found, because it can be done in a systematic way, ensuring that nothing is left out.
If your students are just learning how to read and create tables, I would suggest having them circle their answer in the table to show that they understood the question and knew where in the table to find the answer.
If you have older students, encourage them to find a pattern in the table and explain it in words , and then also with mathematical symbols and/or an equation. This will help them form connections and increase number sense. It will also help them see how to use their “rule” or equation to solve the given question as well as make predictions about the data.
It’s also important for students to consider whether or not their pattern will continue predictably . In some instances, the pattern may look one way for the first few entries, then change, so this is important to consider as the problems get more challenging.
There are tons of examples of problems where creating a table and finding a pattern is a useful strategy, but here’s just one example for you:
Ben decides to prepare for a marathon by running ten minutes a day, six days a week. Each week, he increases his time running by two minutes per day. How many minutes will he run in week 8?
Included in the table is the week number (we’re looking at weeks 1-8), as well as the number of minutes per day and the total minutes for the week. The first step is to fill in the first couple of weeks by calculating the total time.
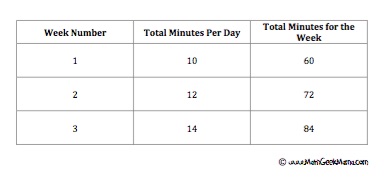
Once you’ve found weeks 1-3, you may see a pattern and be able to calculate the total minutes for week 8. For example, in this case, the total number of minutes increases by 12 each week, meaning in week 8 he will run for 144 minutes.
If not, however, simply continue with the table until you get to week 8, and then you will have your answer.
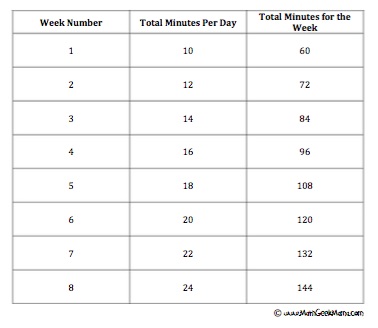
I think it is especially important to make it clear to students that it is perfectly acceptable to complete the entire table (or continue a given table) if they don’t see or don’t know how to use the pattern to solve the problem.
I was working with a student once and she was given a table, but was then asked a question about information not included in that table . She was able to tell me the pattern she saw, but wasn’t able to correctly use the “rule” to find the answer. I insisted that she simply extend the table until she found what she needed. Then I showed her how to use the “rule” of the pattern to get the same answer.
I hope you find this helpful! Looking for and finding patterns is such an essential part of mathematics education! If you’re looking for more ideas for exploring patterns with younger kids, check out this post for making patterns with Skittles candy .
And of course, don’t miss the other posts in this Math Problem Solving Series:
- Problem Solving by Solving an Easier Problem
- Problem Solving by Drawing a Picture
- Problem Solving by Working Backwards
- Problem Solving by Making a List
One Comment
I had so much trouble spotting patterns when I was in school. Fortunately for her, my daughter rocks at it! This technique will be helpful for her when she’s a bit older! #ThoughtfulSpot
Comments are closed.
Similar Posts

3D Shapes Activity Pack! {FREE Download!}

7 Math Fact Fluency Strategies for Students with Learning Disabilities

Creating Patterns With Skittles {FREE Printable!}
We have to give them homework.

Easy Christmas Tree Symmetry Craft!

8 Reasons Making Mistakes in Math is a GOOD Thing!
Find more resources to help make math engaging, join 165k+ parents & teachers.
Who learn new tips and strategies, as well as receive engaging resources to make math fun!

- Privacy Policy
Math Time Doesn't Have to End in Tears
Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

Pattern Problem Solving: Teach Students to Find a Pattern in Math Problems
Pattern analysis is a critical 21st century skill.
Need more tips and tricks for teaching math? You can find them in our math resources center .
| Add to Folder | |
|---|---|
| creative writing | |
| children's book | |
| activities | |
| classroom tools | |
| language arts and writing | |
| vocabulary |
Pattern problem solving
In this article, we’ll delve into the concept of pattern problem solving, a fundamental mathematical strategy that involves the identification of repeated sequences or elements to solve complex problems.
This method is instrumental in enhancing logical thinking and mathematical comprehension among students. Let's explore how this works, why it's important, and how to teach this critical skill effectively.

What is pattern problem solving?
Pattern problem solving is a mathematical strategy in which students look for patterns in data to solve a problem. To find a pattern, students search for repeated items, numbers, or series of events.
The following problem can be solved by finding the pattern:
There are 1000 lockers in a high school with 1000 students. The first student opens all 1000 lockers; next, the second student closes lockers 2, 4, 6, 8, 10, and so on up to locker 1000; the third student changes the state (opens lockers that are closed, closes lockers that are open) of lockers 3, 6, 9, 12, 15, and so on; the fourth student changes the state of lockers 4, 8, 12, 16, and so on. This continues until every student has had a turn. How many lockers will be open at the end?
For the answer, visit The Locker Problem from the Math Doctors
Why is pattern problem solving important?
Pattern problem solving is an important strategy for students as it encourages them to observe and understand patterns in data, which is a critical aspect of mathematical and logical thinking.
This strategy allows students to predict future data points or behaviors based on existing patterns. It helps students understand the inherent structure of data sets and mathematical problems, making them easier to solve.
Pattern recognition also aids in the understanding of multiplication facts, for example, recognizing that 4 x 7 is the same as 7 x 4. Overall, pattern problem solving fosters analytical thinking, problem-solving skills, and a deeper understanding of mathematics.
How to teach students to find the pattern in a math problem (using an example)
In the upcoming section, we will break down the steps on how to find a pattern in a math problem effectively. We will use a practical example to illustrate each step and provide helpful teaching tips throughout the process.
The goal is to offer a clear and comprehensible guide for educators teaching students about pattern problem solving in math.
Sample question: If you build a four-sided pyramid using basketballs and don't count the bottom as a side, how many balls will there be in a pyramid that has six layers?
Helpful teaching tip: Use cooperative learning groups to find solutions to the above problem. Cooperative learning groups help students verbalize their thinking, brainstorm ideas, discuss options, and justify their positions. After finding a solution, each group can present it to the class, explaining how they reached their solution and why they think it is correct. Or, students can explain their solutions in writing, and the teacher can display the solutions. Then students can circulate around the room to read each group's solution.
1. Ensure students understand the problem
Demonstrate that the first step to solving a problem is understanding it. This involves identifying the key pieces of information needed to find the answer. This may require students to read the problem several times or put the problem into their own words.
Sometimes you can solve a problem simply through pattern recognition, but more often you must extend the pattern to find the solution. Making a number table will help you see the pattern more clearly.
In this problem, students understand:
The top layer will have one basketball. I need to find how many balls there will be in each layer of a pyramid, from the first to the sixth. I need to find how many basketballs will be in the entire pyramid.
2. Choose a pattern problem solving strategy
To successfully find a pattern, you need to be sure that the pattern will continue.
Have students give reasons why they think the pattern is predictable and not based on probability. Problems that are solved most easily by finding a pattern include those that ask students to extend a sequence of numbers or to make a prediction based on data.
In this problem, students may also choose to make a table or draw a picture to organize and represent their thinking.
3. Solve the problem
Start with the top layer of the pyramid, one basketball. Determine how many balls must be under that ball to make the next layer or a pyramid. Let students use manipulatives if needed— they can use manipulatives of any kind, from coins to cubes to golf balls. Let students also draw pictures to help solve the problem, if needed.
If your students are in groups, you may want to have each group use a different manipulative and then compare their solutions. This will help you understand if different manipulatives affect the solution.
Helpful teaching tip: If students are younger, solve this problem with only three layers.
If it helps to visualize the pyramid, use manipulatives to create the third layer. Record the number and look for a pattern. The second layer adds 3 basketballs and the next adds 5 basketballs. Each time you add a new layer, the number of basketballs needed to create that layer increases by 2.
| 1 (top) | 1 | 1 |
| 2 | 3 | 4 (1 + 3 = 4) |
| 3 | 5 | 9 (4 + 5 = 9) |
| 4 | 7 | 16 (9 + 7 = 16) |
| 5 | 9 | 25 (16 + 9 = 25) |
| 6 | 11 | 36 (25 + 11 = 36) |
1 1 + 3 = 4 4 + 5 = 9
Continue until six layers are recorded. Once a pattern is found, students might not need to use manipulatives. 9 + 7 = 16
16 + 9 = 25 25 + 11 = 36
Then add the basketballs used to make all six layers.
The answer is 91 balls .
Look at the list to see if there is another pattern. The number of balls used in each level is the square of the layer number. So the 10th layer would have 10 x 10 = 100 balls .
4. Check your students' answers
Read the problem again to be sure the question was answered:
Yes, I found the total number of basketballs in the six-layer pyramid.
Also check the math to be sure it’s correct:
1 + 4 + 9 + 16 + 25 +36 = 91
Determine if the best strategy was chosen for this problem, or if there was another way to solve the problem:
Finding a pattern was a good way to solve this problem because the pattern was predictable.
5. Explain
Students should be able to explain the process they went through to find their answers. Students must be able to talk or write about their thinking. Demonstrate how to write a paragraph describing the steps they took and the decisions they made throughout.
I started with the first layer. I used blocks to make the pyramid and made a list of the number of blocks I used. Then I created a table to record the number of balls in each layer. I made four layers, then saw a pattern. I saw that or each layer, the number of balls used was the number of the layer multiplied by itself. I finished the pattern without the blocks, by multiplying the number of balls that would be in layers 5 and 6. Then I added up each layer. 1 + 4 + 9 + 16 + 25 +36 = 91. I got a total of 91 basketballs
How can you stretch this pattern problem solving strategy?

Math problems can be simple, with few criteria needed to solve them, or they can be multidimensional, requiring charts or tables to organize students' thinking and to record patterns.
In using patterns, it is important for students to find out if the pattern will continue predictably. Have students determine if there is a reason for the pattern to continue, and be sure students use logic when finding patterns to solve problems.
- For example, if it rains on Sunday, snows on Monday, rains on Tuesday, and snows on Wednesday, will it rain on Thursday?
- Another example: If Lauren won the first and third game of chess, and Walter won the second and fourth game, who will win the fifth game?
- Another example: If a plant grew 13 centimeters in the first week and 10 centimeters in the second week, how many centimeters will it grow in the third week?
Because these are questions of probability or nature, be sure students understand why patterns can't be used to find these answers.
Featured Middle School Resources

Related Resources
- PRINT TO PLAY
- DIGITAL GAMES

Problem-Solving Strategies
October 16, 2019
There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.
Problem-solving strategies
1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.
Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.
Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?
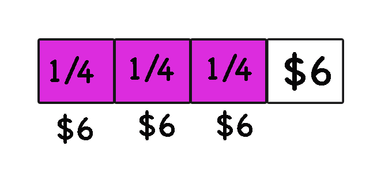
2. Guess and check
Teach students the same strategy research mathematicians use.
With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly. By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.
Find two numbers that have sum 11 and product 24.
Try/guess 5 and 6 the product is 30 too high
adjust to 4 and 7 with product 28 still high
adjust again 3 and 8 product 24
3. Make a table or a list
Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.
To make sure you are listing all the information correctly read the problem carefully.
Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.
Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?
A table or list is useful in solving logic problems.
| Thomas | Lucky | Not gray, the cat is black |
| Helen | Not Moo, not Buddy, not Lucky so Fifi | White |
| Bill | Moo | Gray |
| Mary | Buddy | Brown |
Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.
Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.
Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.
5. Find a pattern.
Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.
The “rule” can then be used to find the answer to the question and complete the table/list.
Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?
| Sunday | 5 |
| Monday | 10 |
| Tuesday | 20 |
| Wednesday | 40 |
| Thursday | |
| Friday | |
| Saturday |
6. Working backward
Problems that can be solved with this strategy are the ones that list a series of events or a sequence of steps .
In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.
Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.
For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.
The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.
8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took
8+31+5+4= 48 Answer: The box came with 48 pieces of candy.
Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.
Print and digital activities
I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.
sample below

How to use the activity cards
Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.
Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.
For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.
Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.
Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions
There are 2 versions of the resource
70 google slides with explanations + 70 printable task cards
70 google slides with explanations + 11 worksheets
You might also like
Multiplying fractions/mixed numbers/simplifying
Adding and subtracting fractions
AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities
Teaching area, ideas, games, print, and digital activities
Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems
Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division

Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike
Diving into Division -Teaching division conceptually

Expressions with arrays
Decimals, Decimal fractions, Percentages – print and digital
Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital
Check out our best selling card games now available at amazon.com and amazon.ca.

Chicken Escape
A multiplayer card game that makes mental math practice fun! Chicken Escape is a fast-paced multiplayer card game. While playing…

Dragon Times – A math Adventure card game
Dragon Times is an educational fantasy card game that aims to motivate children to practice multiplication and division facts while…
| > > Problem Solving Strategies |







IMAGES
VIDEO
COMMENTS
The first step is to fill in the first couple of weeks by calculating the total time. Once you've found weeks 1-3, you may see a pattern and be able to calculate the total minutes for week 8. For example, in this case, the total number of minutes increases by 12 each week, meaning in week 8 he will run for 144 minutes.
Pattern problem solving is a mathematical strategy in which students look for patterns in data to solve a problem. To find a pattern, students search for repeated items, numbers, or series of events. The following problem can be solved by finding the pattern: There are 1000 lockers in a high school with 1000 students.
Here we will look at some advanced examples of "Find a Pattern" method of problem solving strategy. Example: Each hexagon below is surrounded by 12 dots. a) Find the number of dots for a pattern with 6 hexagons in the first column. b) Find the pattern of hexagons with 229 dots. Solution:
Develop and use the strategy "look for a pattern." Plan and compare alternative approaches to solving a problem. Solve real-world problems using the above strategies as part of a plan. Introduction. In this section, we will apply the problem-solving plan you learned about in the last section to solve several real-world problems.
Problem Solving Strategy 8 (Look for and Explain Patterns). Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more ...
5. Find a pattern. Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the "find a pattern" problem-solving strategy.
5.6: Recognizing Patterns is shared under a license and was authored, remixed, and/or curated by LibreTexts. Recognizing patterns in mathematics is a fundamental skill that simplifies problem-solving by revealing underlying structures and relationships. This section explores various types of patterns, ….
LOOK FOR PATTERNS When students use this problem-solving strategy, they are required to analyze patterns in data and make predictions and generalizations based on their analysis. They then must check the generalization against the information in the problem and possibly make a prediction from, or extension of, the given information.
This foundations of math video explains the four-step process of problem solving: understanding the problem, devising a plan, carrying out the plan, and loo...
Problem Solving Strategies. Problem Solving Strategies. Look for a pattern. Example: Solution: Find the sum of the first 100 even positive numbers. The sum of the first 1 even positive numbers is 2 or 1 (1 +1) = 1 (2). The sum of the first 2 even positive numbers is 2 + 4 = 6 or 2 (2 +1) = 2 (3). The sum of the first 3 even positive numbers is ...
Problem Solving Strategy 8 (Look for and Explain Patterns). Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand!
In this video, we will see how finding a pattern in the word problem can help us solve it easily.This is another strategy of Problem Solving. Below is the pl...
A Problem Solving Strategy: Look for and Explain Patterns Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand!
In a review of literature on mathematical problem solving, looking for a pattern was recognized as a strategy in every article and publication. This is no coincidence. Identifying a pattern may shed more light on a solution than any other tactic. Consider the following problem:
This lesson focuses on two of the strategies introduced in the previous chapter: making a table and looking for a pattern. These are the most common strategies you have used before algebra. Let's review the four-step problem-solving plan from Lesson 1.7. Devise a plan - Translate. Come up with a way to solve the problem.
The following video shows more examples of using problem solving strategies and models. Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home ...
In this instance, "look for a pattern" would be especially helpful from the list of problem-solving strategies. Either write all numbers from 201 through 351 and notice the pattern that there are 5 in every set of 10 numbers (e.g. 201-210), and then count how many sets of 10 numbers there are and multiply that by 5, or simply write one set ...
Problem Solving Strategy 8 (Look for and Explain Patterns). Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand!
This discusses about looking for a pattern and working backward strategies. This is just a continuation of my video about Problem solving strategy. This discusses about looking for a pattern and ...
Step 1: Make a Table. The first step to look for a pattern is to make a table showing the relationships that are there. For example, suppose the problem were to find the next three numbers in the series 2, 4, 6, 8. They are related in a simple way, such that 2 +2 is 4 +2 is 6 +2 is 8. In order to extend the pattern, 8 +2 is 10, +2 is 12 +2 is 14.
A powerpoint outlining the universally accepted strategies to solve a problem - * look for a pattern * draw a sketch * make an organised list * simplify the problem * guess and check * make a table * write a number sentence * act out a problem Each strategy is accompanied by an example and a problem for student to try, plus solutions. Thanks ...
Learn how to look for patterns in a word problem to help you find a solution.We hope you are enjoying this video! For more in-depth learning, check out Miaca...
The document discusses the "Look for a Pattern" problem solving strategy. It suggests that problems are easier to solve when they share patterns, as patterns provide order and simplicity. An example is provided about a family cycling around an oval, with the number of circuits increasing by four each day. By recognizing this pattern of increasing by four, it is deduced that it will take the ...