User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts
10.1 - setting the hypotheses: examples.
A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.
Example 10.2: Hypotheses with One Sample of One Categorical Variable Section
About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.
- Research Question : Are artists more likely to be left-handed than people found in the general population?
- Response Variable : Classification of the student as either right-handed or left-handed
State Null and Alternative Hypotheses
- Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
- Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.
Example 10.3: Hypotheses with One Sample of One Measurement Variable Section

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.
- Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
- Response Variable : dosage of the active ingredient found by a chemical assay.
- Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
- Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.
Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.
- Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
- Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
- Explanatory (Grouping) Variable: Sex
- Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
- Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.
Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.
- Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
- Response Variable : Weight loss (pounds)
- Explanatory (Grouping) Variable : Type of diet
- Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
- Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.
Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section
- Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
- Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
- Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
- Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.
This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.
Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section
- Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
- Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
- Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
- Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.
Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section
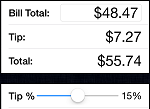
- Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
- Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
- Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
- Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.
Have a thesis expert improve your writing
Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null and Alternative Hypotheses | Definitions & Examples
Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis (H 0 ): There’s no effect in the population .
- Alternative hypothesis (H A ): There’s an effect in the population.
The effect is usually the effect of the independent variable on the dependent variable .
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question
- They both make claims about the population
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
- Alternative hypothesis (H A ): Independent variable affects dependent variable .
Test-specific
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 27 September 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/
Is this article helpful?

Shaun Turney
Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.
Module 9: Hypothesis Testing With One Sample
Null and alternative hypotheses, learning outcomes.
- Describe hypothesis testing in general and in practice
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make adecision. There are two options for a decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30
H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
H 0 : The drug reduces cholesterol by 25%. p = 0.25
H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
H 0 : μ = 2.0
H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66
- H 0 : μ = 66
- H a : μ ≠ 66
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
H 0 : μ ≥ 5
H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45
- H 0 : μ ≥ 45
- H a : μ < 45
In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
H 0 : p ≤ 0.066
H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40
- H 0 : p = 0.40
- H a : p > 0.40
Concept Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.
Formula Review
H 0 and H a are contradictory.
- OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
- Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License
Alternative hypothesis
by Marco Taboga , PhD
In a statistical test, observed data is used to decide whether or not to reject a restriction on the data-generating probability distribution.
The assumption that the restriction is true is called null hypothesis , while the statement that the restriction is not true is called alternative hypothesis.
A correct specification of the alternative hypothesis is essential to decide between one-tailed and two-tailed tests.
Table of contents
Mathematical setting
Choice between one-tailed and two-tailed tests, the critical region, the interpretation of the rejection, the interpretation must be coherent with the alternative hypothesis.
- Power function
Accepting the alternative
More details, keep reading the glossary.
In order to fully understand the concept of alternative hypothesis, we need to remember the essential elements of a statistical inference problem:
we observe a sample drawn from an unknown probability distribution;
in principle, any valid probability distribution could have generated the sample;
however, we usually place some a priori restrictions on the set of possible data-generating distributions;
A couple of simple examples follow.
When we conduct a statistical test, we formulate a null hypothesis as a restriction on the statistical model.
The alternative hypothesis is
The alternative hypothesis is used to decide whether a test should be one-tailed or two-tailed.
The null hypothesis is rejected if the test statistic falls within a critical region that has been chosen by the statistician.
The critical region is a set of values that may comprise:
only the left tail of the distribution or only the right tail (one-tailed test);
both the left and the right tail (two-tailed test).
The choice of the critical region depends on the alternative hypothesis. Let us see why.
The interpretation is different depending on the tail of the distribution in which the test statistic falls.
![alternative hypothesis example in statistics [eq7]](https://www.statlect.com/images/alternative-hypothesis__27.png)
The choice between a one-tailed or a two-tailed test needs to be done in such a way that the interpretation of a rejection is always coherent with the alternative hypothesis.
When we deal with the power function of a test, the term "alternative hypothesis" has a special meaning.
We conclude with a caveat about the interpretation of the outcome of a test of hypothesis.
The interpretation of a rejection of the null is controversial.
According to some statisticians, rejecting the null is equivalent to accepting the alternative.
However, others deem that rejecting the null does not necessarily imply accepting the alternative. In fact, it is possible to think of situations in which both hypotheses can be rejected. Let us see why.
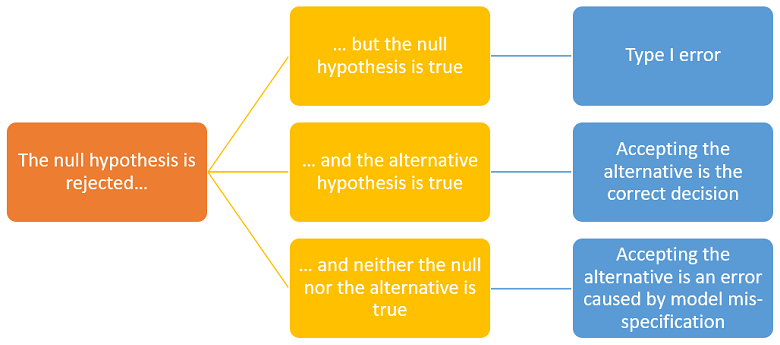
According to the conceptual framework illustrated by the images above, there are three possibilities:
the null is true;
the alternative is true;
neither the null nor the alternative is true because the true data-generating distribution has been excluded from the statistical model (we say that the model is mis-specified).
If we are in case 3, accepting the alternative after a rejection of the null is an incorrect decision. Moreover, a second test in which the alternative becomes the new null may lead us to another rejection.
You can find more details about the alternative hypothesis in the lecture on Hypothesis testing .
Previous entry: Almost sure
Next entry: Binomial coefficient
How to cite
Please cite as:
Taboga, Marco (2021). "Alternative hypothesis", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/alternative-hypothesis.
Most of the learning materials found on this website are now available in a traditional textbook format.
- Maximum likelihood
- Binomial distribution
- Beta distribution
- Convergence in probability
- Delta method
- Exponential distribution
- Chi-square distribution
- Set estimation
- Wishart distribution
- Mathematical tools
- Fundamentals of probability
- Probability distributions
- Asymptotic theory
- Fundamentals of statistics
- About Statlect
- Cookies, privacy and terms of use
- Precision matrix
- Loss function
- Integrable variable
- Critical value
- To enhance your privacy,
- we removed the social buttons,
- but don't forget to share .
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Alternative hypothesis
By Jim Frost
The alternative hypothesis is one of two mutually exclusive hypotheses in a hypothesis test. The alternative hypothesis states that a population parameter does not equal a specified value. Typically, this value is the null hypothesis value associated with no effect , such as zero. If your sample contains sufficient evidence, you can reject the null hypothesis and favor the alternative hypothesis. The alternative hypothesis is often denoted as H 1 or H A .
If you are performing a two-tailed hypothesis test, the alternative hypothesis states that the population parameter does not equal the null hypothesis value. For example, when the alternative hypothesis is H A : μ ≠ 0, the test can detect differences both greater than and less than the null value.
A one-tailed alternative hypothesis can test for a difference only in one direction. For example, H A : μ > 0 can only test for differences that are greater than zero.
- How Hypothesis Tests Work: Significance Levels (Alpha) and P values
- How to Identify the Distribution of Your Data
- When Can I Use One-Tailed Hypothesis Tests?
- Examples of Hypothesis Tests: Busting Myths about the Battle of the Sexes
- Failing to Reject the Null Hypothesis
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Hypothesis Testing with One Sample
Null and Alternative Hypotheses
OpenStaxCollege
[latexpage]
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
H 0 : The drug reduces cholesterol by 25%. p = 0.25
H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
H 0 : μ = 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ = 66
- H a : μ ≠ 66
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
H 0 : μ ≥ 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ ≥ 45
- H a : μ < 45
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
H 0 : p ≤ 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p = 0.40
- H a : p > 0.40
<!– ??? –>
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
Chapter Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:
Formula Review
H 0 and H a are contradictory.
| has: | equal (=) | greater than or equal to (≥) | less than or equal to (≤) |
| has: | not equal (≠) greater than (>) less than (<) | less than (<) | greater than (>) |
If α ≤ p -value, then do not reject H 0 .
If α > p -value, then reject H 0 .
α is preconceived. Its value is set before the hypothesis test starts. The p -value is calculated from the data.
You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. What is the random variable? Describe in words.
The random variable is the mean Internet speed in Megabits per second.
You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. State the null and alternative hypotheses.
The American family has an average of two children. What is the random variable? Describe in words.
The random variable is the mean number of children an American family has.
The mean entry level salary of an employee at a company is 💲58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.
A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.
The random variable is the proportion of people picked at random in Times Square visiting the city.
A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.
In a population of fish, approximately 42% are female. A test is conducted to see if, in fact, the proportion is less. State the null and alternative hypotheses.
Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.
A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?
- H 0 : __________
- H a : __________
- H 0 : μ = 15
- H a : μ ≠ 15
The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?
Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.
State the null hypothesis, H 0 , and the alternative hypothesis. H a , in terms of the appropriate parameter ( μ or p ).
- The mean number of years Americans work before retiring is 34.
- At most 60% of Americans vote in presidential elections.
- The mean starting salary for San Jose State University graduates is at least 💲100,000 per year.
- Twenty-nine percent of high school seniors get drunk each month.
- Fewer than 5% of adults ride the bus to work in Los Angeles.
- The mean number of cars a person owns in her lifetime is not more than ten.
- About half of Americans prefer to live away from cities, given the choice.
- Europeans have a mean paid vacation each year of six weeks.
- The chance of developing breast cancer is under 11% for women.
- Private universities’ mean tuition cost is more than 💲20,000 per year.
- H 0 : μ = 34; H a : μ ≠ 34
- H 0 : p ≤ 0.60; H a : p > 0.60
- H 0 : μ ≥ 100,000; H a : μ < 100,000
- H 0 : p = 0.29; H a : p ≠ 0.29
- H 0 : p = 0.05; H a : p < 0.05
- H 0 : μ ≤ 10; H a : μ > 10
- H 0 : p = 0.50; H a : p ≠ 0.50
- H 0 : μ = 6; H a : μ ≠ 6
- H 0 : p ≥ 0.11; H a : p < 0.11
- H 0 : μ ≤ 20,000; H a : μ > 20,000
Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:
- p < 0.30
- p > 0.30
A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:
- p > 0.20
- p < 0.20
Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:
- H o : \(\overline{x}\) = 4.5, H a : \(\overline{x}\) > 4.5
- H o : μ ≥ 4.5, H a : μ < 4.5
- H o : μ = 4.75, H a : μ > 4.75
- H o : μ = 4.5, H a : μ > 4.5
Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.
Null and Alternative Hypotheses Copyright © 2013 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
- Math Article
Alternative Hypothesis

Alternative hypothesis defines there is a statistically important relationship between two variables. Whereas null hypothesis states there is no statistical relationship between the two variables. In statistics, we usually come across various kinds of hypotheses. A statistical hypothesis is supposed to be a working statement which is assumed to be logical with given data. It should be noticed that a hypothesis is neither considered true nor false.
The alternative hypothesis is a statement used in statistical inference experiment. It is contradictory to the null hypothesis and denoted by H a or H 1 . We can also say that it is simply an alternative to the null. In hypothesis testing, an alternative theory is a statement which a researcher is testing. This statement is true from the researcher’s point of view and ultimately proves to reject the null to replace it with an alternative assumption. In this hypothesis, the difference between two or more variables is predicted by the researchers, such that the pattern of data observed in the test is not due to chance.
To check the water quality of a river for one year, the researchers are doing the observation. As per the null hypothesis, there is no change in water quality in the first half of the year as compared to the second half. But in the alternative hypothesis, the quality of water is poor in the second half when observed.
Difference Between Null and Alternative Hypothesis
|
|
|
| It denotes there is no relationship between two measured phenomena. | It’s a hypothesis that a random cause may influence the observed data or sample. |
| It is represented by H | It is represented by H or H |
| Example: Rohan will win at least Rs.100000 in lucky draw. | Example: Rohan will win less than Rs.100000 in lucky draw. |
Basically, there are three types of the alternative hypothesis, they are;
Left-Tailed : Here, it is expected that the sample proportion (π) is less than a specified value which is denoted by π 0 , such that;
H 1 : π < π 0
Right-Tailed: It represents that the sample proportion (π) is greater than some value, denoted by π 0 .
H 1 : π > π 0
Two-Tailed: According to this hypothesis, the sample proportion (denoted by π) is not equal to a specific value which is represented by π 0 .
H 1 : π ≠ π 0
Note: The null hypothesis for all the three alternative hypotheses, would be H 1 : π = π 0 .
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved September 23, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 . This is usually what the researcher is trying to prove.
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject H 0 " if the sample information favors the alternative hypothesis or "do not reject H 0 " or "decline to reject H 0 " if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ .30 H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66

Example 9.3
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Statistics 2e
- Publication date: Dec 13, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-statistics-2e/pages/9-1-null-and-alternative-hypotheses
© Jul 18, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
8.2 Null and Alternative Hypotheses
Learning objectives.
- Describe hypothesis testing in general and in practice.
A hypothesis test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints and only one of these hypotheses is true. The hypothesis test determines which hypothesis is most likely true.
- The null hypothesis is a claim that a population parameter equals some value. For example, [latex]H_0: \mu=5[/latex].
- The alternative hypothesis is a claim that a population parameter is greater than, less than, or not equal to some value. For example, [latex]H_a: \mu>5[/latex], [latex]H_a: \mu<5[/latex], or [latex]H_a: \mu \neq 5[/latex]. The form of the alternative hypothesis depends on the wording of the hypothesis test.
- An alternative notation for [latex]H_a[/latex] is [latex]H_1[/latex].
Because the null and alternative hypotheses are contradictory, we must examine evidence to decide if we have enough evidence to reject the null hypothesis or not reject the null hypothesis. The evidence is in the form of sample data. After we have determined which hypothesis the sample data supports, we make a decision. There are two options for a decision . They are “ reject [latex]H_0[/latex] ” if the sample information favors the alternative hypothesis or “ do not reject [latex]H_0[/latex] ” if the sample information is insufficient to reject the null hypothesis.
Watch this video: Simple hypothesis testing | Probability and Statistics | Khan Academy by Khan Academy [6:24]
A candidate in a local election claims that 30% of registered voters voted in a recent election. Information provided by the returning office suggests that the percentage is higher than the 30% claimed.
The parameter under study is the proportion of registered voters, so we use [latex]p[/latex] in the statements of the hypotheses. The hypotheses are
[latex]\begin{eqnarray*} \\ H_0: & & p=30\% \\ \\ H_a: & & p \gt 30\% \\ \\ \end{eqnarray*}[/latex]
- The null hypothesis [latex]H_0[/latex] is the claim that the proportion of registered voters that voted equals 30%.
- The alternative hypothesis [latex]H_a[/latex] is the claim that the proportion of registered voters that voted is greater than (i.e. higher) than 30%.
A medical researcher believes that a new medicine reduces cholesterol by 25%. A medical trial suggests that the percent reduction is different than claimed. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & p=25\% \\ \\ H_a: & & p \neq 25\% \end{eqnarray*}[/latex]
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & \mu=2 \mbox{ points} \\ \\ H_a: & & \mu \neq 2 \mbox{ points} \end{eqnarray*}[/latex]
We want to test whether or not the mean height of eighth graders is 66 inches. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & \mu=66 \mbox{ inches} \\ \\ H_a: & & \mu \neq 66 \mbox{ inches} \end{eqnarray*}[/latex]
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
[latex]\begin{eqnarray*} H_0: & & \mu=5 \mbox{ years} \\ \\ H_a: & & \mu \lt 5 \mbox{ years} \end{eqnarray*}[/latex]
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & \mu=45 \mbox{ minutes} \\ \\ H_a: & & \mu \lt 45 \mbox{ minutes} \end{eqnarray*}[/latex]
In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & p=6.6\% \\ \\ H_a: & & p \gt 6.6\% \end{eqnarray*}[/latex]
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. State the null and alternative hypotheses.
[latex]\begin{eqnarray*} H_0: & & p=40\% \\ \\ H_a: & & p \gt 40\% \end{eqnarray*}[/latex]
Concept Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we evaluate the null hypothesis , typically denoted with [latex]H_0[/latex]. The null hypothesis is not rejected unless the hypothesis test shows otherwise. The null hypothesis always contain an equal sign ([latex]=[/latex]). Always write the alternative hypothesis , typically denoted with [latex]H_a[/latex] or [latex]H_1[/latex], using less than, greater than, or not equals symbols ([latex]\lt[/latex], [latex]\gt[/latex], [latex]\neq[/latex]). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. But we can never state that a claim is proven true or false. All we can conclude from the hypothesis test is which of the hypothesis is most likely true. Because the underlying facts about hypothesis testing is based on probability laws, we can talk only in terms of non-absolute certainties.
Attribution
“ 9.1 Null and Alternative Hypotheses “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.
Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Statistics Resources
- Excel - Tutorials
- Basic Probability Rules
- Single Event Probability
- Complement Rule
- Intersections & Unions
- Compound Events
- Levels of Measurement
- Independent and Dependent Variables
- Entering Data
- Central Tendency
- Data and Tests
- Displaying Data
- Discussing Statistics In-text
- SEM and Confidence Intervals
- Two-Way Frequency Tables
- Empirical Rule
- Finding Probability
- Accessing SPSS
- Chart and Graphs
- Frequency Table and Distribution
- Descriptive Statistics
- Converting Raw Scores to Z-Scores
- Converting Z-scores to t-scores
- Split File/Split Output
- Sampling Methods
- Partial Eta Squared
- Downloading and Installing G*Power: Windows/PC
- Correlation
- Testing Parametric Assumptions
- One-Way ANOVA
- Two-Way ANOVA
- Repeated Measures ANOVA
- Goodness-of-Fit
- Test of Association
- Pearson's r
- Point Biserial
- Mediation and Moderation
- Simple Linear Regression
- Multiple Linear Regression
- Binomial Logistic Regression
- Multinomial Logistic Regression
- Independent Samples T-test
- Dependent Samples T-test
- Testing Assumptions
- T-tests using SPSS
- T-Test Practice
- Predictive Analytics This link opens in a new window
- Quantitative Research Questions
- Null & Alternative Hypotheses
- One-Tail vs. Two-Tail
- Alpha & Beta
- Associated Probability
- Decision Rule
- Statement of Conclusion
- Statistics Group Sessions
ASC Chat Hours
ASC Chat is usually available at the following times ( Pacific Time):
| Days | Hours (Pacific time) |
|---|---|
| Mon. | 9 am - 8 pm |
| Tue. | 7 am - 1 pm 3 pm - 10 pm |
| Wed. | 7 am - 1 pm 3 pm - 10 pm |
| Thurs. | 7 am - 1 pm 2 pm - 10 pm |
| Fri. | 9 am - 1 pm 3 pm - 5 pm 6 pm - 8 pm |
| Sat. | 7 am - 1 pm 6 pm - 9 pm |
| Sun. | 10 am - 1 pm 5 pm - 9 pm |
If there is not a coach on duty, submit your question via one of the below methods:
928-440-1325
Ask a Coach
Search our FAQs on the Academic Success Center's Ask a Coach page.
Once you have developed a clear and focused research question or set of research questions, you’ll be ready to conduct further research, a literature review, on the topic to help you make an educated guess about the answer to your question(s). This educated guess is called a hypothesis.
In research, there are two types of hypotheses: null and alternative. They work as a complementary pair, each stating that the other is wrong.
- Null Hypothesis (H 0 ) – This can be thought of as the implied hypothesis. “Null” meaning “nothing.” This hypothesis states that there is no difference between groups or no relationship between variables. The null hypothesis is a presumption of status quo or no change.
- Alternative Hypothesis (H a ) – This is also known as the claim. This hypothesis should state what you expect the data to show, based on your research on the topic. This is your answer to your research question.
Null Hypothesis: H 0 : There is no difference in the salary of factory workers based on gender. Alternative Hypothesis : H a : Male factory workers have a higher salary than female factory workers.
Null Hypothesis : H 0 : There is no relationship between height and shoe size. Alternative Hypothesis : H a : There is a positive relationship between height and shoe size.
Null Hypothesis : H 0 : Experience on the job has no impact on the quality of a brick mason’s work. Alternative Hypothesis : H a : The quality of a brick mason’s work is influenced by on-the-job experience.
Was this resource helpful?
- << Previous: Hypothesis Testing
- Next: One-Tail vs. Two-Tail >>
- Last Updated: Sep 23, 2024 5:42 PM
- URL: https://resources.nu.edu/statsresources

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- Open access
- Published: 27 September 2024
Altered molecular and cellular mechanisms in KIF5A -associated neurodegenerative or neurodevelopmental disorders
- Marta Cozzi ORCID: orcid.org/0000-0001-9428-7054 1 na1 ,
- Stefania Magri 2 na1 ,
- Barbara Tedesco ORCID: orcid.org/0000-0002-7077-3696 1 , 2 ,
- Guglielmo Patelli 1 , 2 ,
- Veronica Ferrari ORCID: orcid.org/0000-0003-2514-9445 1 ,
- Elena Casarotto 1 ,
- Marta Chierichetti 1 ,
- Paola Pramaggiore ORCID: orcid.org/0000-0003-1399-7973 1 ,
- Laura Cornaggia 1 ,
- Margherita Piccolella ORCID: orcid.org/0000-0002-5130-1116 1 ,
- Mariarita Galbiati ORCID: orcid.org/0000-0003-3250-5591 1 ,
- Paola Rusmini ORCID: orcid.org/0000-0001-9989-0733 1 ,
- Valeria Crippa ORCID: orcid.org/0000-0002-3058-5711 1 ,
- Jessica Mandrioli ORCID: orcid.org/0000-0002-9244-9782 3 , 4 ,
- Davide Pareyson ORCID: orcid.org/0000-0001-6854-765X 5 ,
- Chiara Pisciotta ORCID: orcid.org/0000-0002-3850-076X 5 ,
- Stefano D’Arrigo 6 ,
- Antonia Ratti ORCID: orcid.org/0000-0002-4264-6614 7 , 8 ,
- Lorenzo Nanetti ORCID: orcid.org/0000-0002-1952-4539 2 ,
- Caterina Mariotti 2 ,
- Elisa Sarto ORCID: orcid.org/0000-0002-0699-956X 2 ,
- Viviana Pensato ORCID: orcid.org/0000-0001-9798-2669 2 ,
- Cinzia Gellera 2 ,
- Daniela Di Bella ORCID: orcid.org/0000-0003-0912-5136 2 ,
- Riccardo M. Cristofani ORCID: orcid.org/0000-0003-2719-846X 1 na2 ,
- Franco Taroni 2 na2 &
- Angelo Poletti ORCID: orcid.org/0000-0002-8883-0468 1 na2
Cell Death & Disease volume 15 , Article number: 692 ( 2024 ) Cite this article
Metrics details
- Amyotrophic lateral sclerosis
Mutations targeting distinct domains of the neuron-specific kinesin KIF5A associate with different neurodegenerative/neurodevelopmental disorders, but the molecular bases of this clinical heterogeneity are unknown. We characterised five key mutants covering the whole spectrum of KIF5A -related phenotypes: spastic paraplegia (SPG, R17Q and R280C), Charcot-Marie-Tooth disease (CMT, R864*), amyotrophic lateral sclerosis (ALS, N999Vfs*40), and neonatal intractable myoclonus (NEIMY, C975Vfs*73) KIF5A mutants. CMT-R864*-KIF5A and ALS-N999Vfs*40-KIF5A showed impaired autoinhibition and peripheral localisation accompanied by altered mitochondrial distribution, suggesting transport competence disruption. ALS-N999Vfs*40-KIF5A formed SQSTM1/p62-positive inclusions sequestering WT-KIF5A, indicating a gain of toxic function. SPG-R17Q-KIF5A and ALS-N999Vfs*40-KIF5A evidenced a shorter half-life compared to WT-KIF5A, and proteasomal blockage determined their accumulation into detergent-insoluble inclusions. Interestingly, SPG-R280C-KIF5A and ALS-N999Vfs*40-KIF5A both competed for degradation with proteasomal substrates. Finally, NEIMY-C975Vfs*73-KIF5A displayed a similar, but more severe aberrant behaviour compared to ALS-N999Vfs*40-KIF5A; these two mutants share an abnormal tail but cause disorders on the opposite end of KIF5A -linked phenotypic spectrum. Thus, our observations support the pathogenicity of novel KIF5A mutants, highlight abnormalities of recurrent variants, and demonstrate that both unique and shared mechanisms underpin KIF5A -related diseases.
Similar content being viewed by others
Loss of function mutations in GEMIN5 cause a neurodevelopmental disorder

Bi-allelic variants in RNF170 are associated with hereditary spastic paraplegia
PCDHA9 as a candidate gene for amyotrophic lateral sclerosis
Introduction.
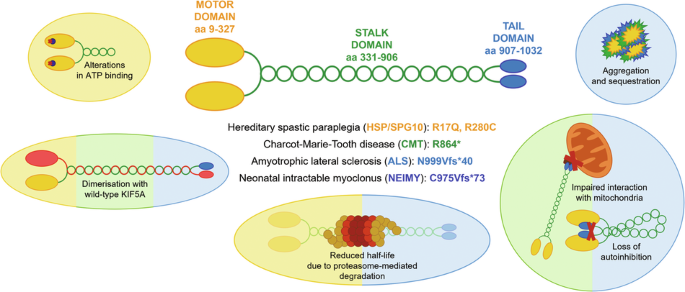
Kinesins are ATP-dependent molecular motors that transport cargoes towards microtubule plus-end participating in several cell functions, from intracellular trafficking to cell division [ 1 ]. The human kinesin family comprises more than 40 proteins divided into 15 subgroups. The three members of the KIF5 subfamily, KIF5A, KIF5B, and KIF5C, were the first ones to be identified. While KIF5B is ubiquitously expressed, KIF5A and KIF5C are neuron-specific [ 2 ]. KIF5s share a common structure comprising an N-terminal motor head, a central coiled-coil stalk, and a C-terminal globular tail (Fig. 1A ). The head domain binds microtubules and fuels transport through ATP hydrolysis. The stalk domain mediates KIF5 homodimerisation, conformational changes, and interaction with kinesin light chains. The tail domain is involved in cargo/adaptor binding, microtubule sliding/bundling, and autoinhibition [ 1 ]. Autoinhibition prevents unnecessary kinesin movements in the absence of cargo and is achieved through direct interaction between the KIF5 motor domain and an isoleucine-alanine-lysine (IAK) motif in the tail. This state is relieved upon interaction with cargoes or adaptors, that promotes KIF5 unfolding and stepping along microtubules [ 3 ]. KIF5s mediate the anterograde axonal transport of several cargoes, including proteins, RNA granules, and organelles [ 4 , 5 , 6 , 7 , 8 ].
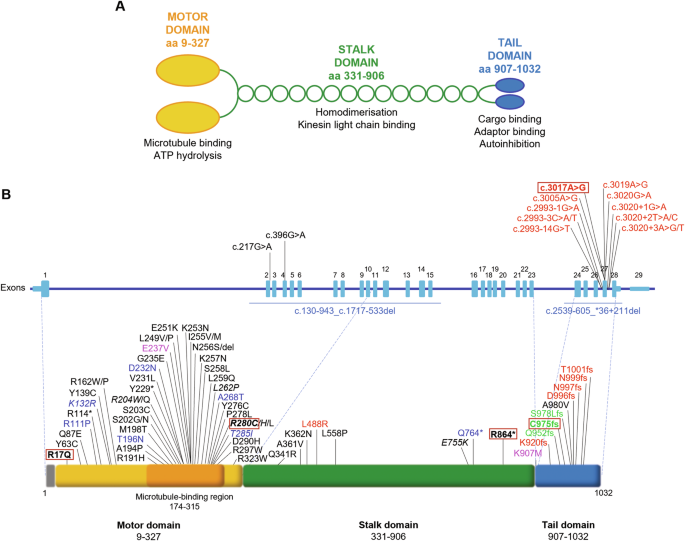
A Schematic representation of KIF5A structure, including KIF5A domains and their main functions. B Distribution of KIF5A pathogenic variants associated with HSP/SPG10 (black), CMT (blue), ALS (red), and NEIMY (green) phenotypes. The p.E237V and p.K907M variants (purple) are associated with West syndrome and severe global developmental delay, and Leber optic neuropathy, respectively. Variants associated with more than one disease are indicated in italics. The variants investigated in this study are indicated in bold and boxed. See Supplementary Table 1 for a detailed list of the variants and the associated phenotypes.
In the past 20 years, numerous disease-causing variants have been identified in the KIF5A gene (Fig. 1B and Supplementary Table 1 ). Heterozygous missense variants in the motor and stalk domains are associated with spastic paraplegia type 10 (SPG10, Mendelian Inheritance in Man (MIM) #604187), a form of hereditary spastic paraplegia (HSP) [ 9 ], and axonal Charcot-Marie-Tooth disease (CMT) [ 10 ]. Frameshift mutations targeting the KIF5A tail are instead linked to ALS (MIM#617921) [ 11 , 12 ] and to a complex infantile neurodevelopmental disorder with leukoencephalopathy named ne onatal i ntractable my oclonus (NEIMY, MIM#617235) [ 13 , 14 ]. To date, the molecular mechanisms whereby KIF5A mutations lead to neurodegeneration have been only partially characterised. Generally, variants in the motor domain impair microtubule binding and/or ATP hydrolysis, resulting in reduced KIF5A motility and/or anterograde transport [ 15 ]. On the other hand, mutations leading to tail elongation associated or not with exon 27 skipping (ΔExon27) abolish KIF5A autoinhibition and cause protein aggregation and limited cytoplasmic recycling, accompanied by WT KIF5A sequestration into inclusions [ 16 , 17 , 18 ]. Despite these findings, the exact pathogenic mechanisms whereby mutations in different KIF5A domains give rise to distinct phenotypes are yet to be resolved.
Here, we studied in our series of patients and selected for functional characterisation four variants associated with different KIF5A phenotypes—SPG10, CMT, and ALS—to gain insight into the unique and shared molecular mechanisms driving KIF5A -related pathologies. Based on the observations made on the ALS-associated ΔExon27 p.N999Vfs*40 KIF5A mutant [ 11 , 12 ], we then compared its behaviour with that of p.C975Vfs*73 KIF5A [ 14 ], a NEIMY-linked variant that shares its elongated tail.
Patients and KIF5A variants
Between 2008 and 2022, the KIF5A gene was analysed in ~2150 index cases referred for genetic testing to the Istituto Neurologico Carlo Besta. Clinical diagnosis was HSP in ~600 of them, CMT in ~700, ALS in ~400, and developmental epileptic encephalopathy (DEE) in ~450. Heterozygous pathogenic or likely pathogenic variants [ 19 ] were identified in 29 cases (19 HSP, 9 CMT, 1 ALS). In addition, novel missense variants of uncertain significance (VUS) located in the motor domain were found in four probands with a spastic paraplegia phenotype. No variants were found in the DEE group, where NEIMY patients are expected to be included.
For this study, we decided to compare the functional effects of the recurrent p.R280C variant, which was the most frequent in our series (7/29 index cases, Supplementary Table 2 ), the nonsense mutation p.R864*, previously reported in an HSP patient [ 20 ] and found by us in a CMT2 patient, the NEIMY-associated variant p.C975Vfs*73, the ALS-associated p.N999Vfs*40, and the c.50 G > A/p.R17Q [ 21 ], one of the 4 novel VUS identified in our series. This mutation lies in the motor domain and may represent the most N-terminal pathogenic variant in KIF5A. Although it is classified as VUS according to the American College of Medical Genetics and Genomics (ACMG) criteria [ 19 ], its potential pathological relevance is supported by the following points: (a) it is absent in population databases including gnomAD, TOPMed, 1000 Genomes (PM2); (b) it co-segregates with the disease in an autosomal dominant pattern (PP1; Supplementary Table 2 ); (c) the KIF5A gene is intolerant to missense variants (gnomAD missense constraint z-score = 3.6; PP2); (d) in silico aggregated scores predict a deleterious effect (REVEL [ 22 ]: Supporting pathogenic (0.74), CADD [ 23 ]: 29.4) and the variant affects a conserved residue in a conserved region of the protein (PP3; Supplementary Fig. 1 ). Interestingly, structural modelling shows that the arginine-17 residue lies in the ATP-binding pocket of the KIF5A motor domain and predicts that the p.R17Q substitution would hamper ATP/ADP binding (Fig. 2A ), thus altering the ability of mutant KIF5A to fuel transport.
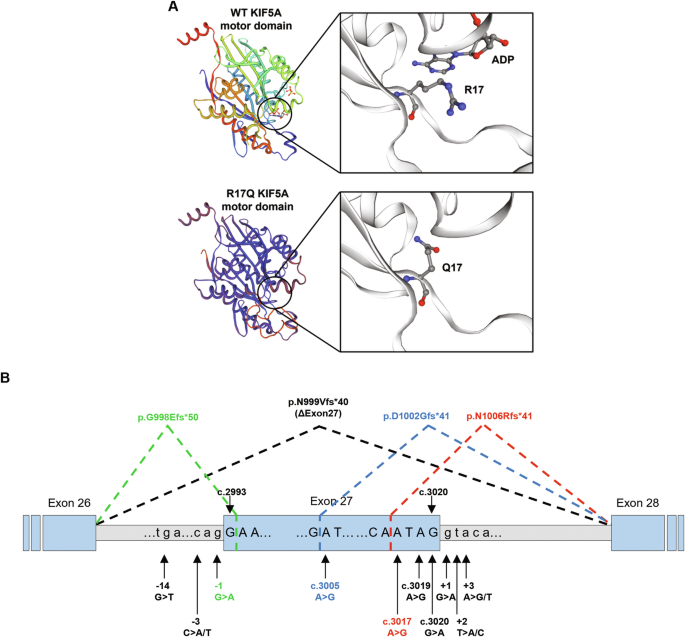
A p.R17Q KIF5A motor domain structure modelled by SWISS-MODEL ( https://swissmodel.expasy.org ) using wild-type (WT) KIF5A head as template (SMTL ID: 1mkj.1). Modelling predicts the loss of the ATP/ADP binding site in KIF5A motor domain as a consequence of the R17Q substitution. B Splicing prediction of variants identified in exon 27 and intron flanking regions. Diagram of the effect (either predicted or experimentally proven) of different splicing variants. The dotted lines indicate the probable aberrant effect on splicing based on the algorithms used. Variants that cause skipping of exon 27 (p.N999Vfs*40, ΔExon27) are indicated in black, the c.2993-1 G > A predicted to result in p.G998Efs*50 is in green, and the c.3005 A > G predicted to cause p.D1002Gfs*41 is in blue. The novel variant c.3017 A > G reported in this study is indicated in red.
In the ALS series, only one patient carried a KIF5A variant, a novel c.3017 A > G/p.N1006S substitution classified as likely pathogenic according to the ACMG criteria [ 19 ]: it is absent in population databases (gnomAD, TOPMed, 1000 Genomes (PM2)), and, most importantly, it is predicted by different tools to cause aberrant splicing (PP3). This variant lies in exon 27, that is strongly associated with ALS phenotypes [ 12 ] (Supplementary Table 1 ) and is predicted to attenuate/abolish the constitutive donor site of intron 27 and create a new GT donor site within exon 27 at position c.3017_3018 (Fig. 2B and Table 1 ). This would generate two possible transcripts, the recurrent form ΔExon27 (r.2993_3020del, p.N999Vfs*40) [ 11 , 12 , 16 , 18 ], and/or a novel frameshift form retaining part of exon 27 (r.(3017_3020del), p.(N1006Rfs*41)). The effects on the KIF5A protein are expected to be similar, as both transcripts would encode a common C-terminal tail (Supplementary Fig. 2 ). Unfortunately, the splicing effects could not be assessed at the mRNA level due to the lack of biological samples from this patient.
Clinical phenotypes of selected KIF5A mutation carriers
The detailed clinical and instrumental findings on the patients carrying the selected KIF5A variants are described in Supplementary Table 2 . There were seven women and six men. Autosomal dominant family history was reported in 3/10 families (six patients), two patients were adopted, and the remaining five subjects had a sporadic presentation. Age at onset was >34 years in the family with the p.R17Q variant and <30 years in patients with the p.R280C variant (range 2–29 years). Spastic paraplegia was the predominant phenotype in most patients with a variant in the motor domain (9/11, Patients 1–6, 8–10). Seven of them also exhibited axonal polyneuropathy (Patients 1, 2, 4, 5, 7, 10, 11). Two patients with the p.R280C variant presented with a CMT5 phenotype, an autosomal dominant form of axonal CMT with pyramidal involvement (Patients 7 and 11). The patient with the p.R864* variant (Patient 12) presented three episodes of Parsonage-Turner syndrome in upper limbs at age 14, 16, and 20 and axonal sensory neuropathy in lower limbs at age 20. The patient carrying the p.(N1006R) variant (Patient 13) was diagnosed with ALS at the age of 60 after a 12-month history of right arm muscle weakness and atrophy, and widespread cramps. Family history was negative. Neurological examination showed upper limb weakness with hypotrophy and widespread fasciculations, marked lower limb hyperreflexia, and right Babinski sign. Respiratory function was normal (forced vital capacity 87%), and the revised ALS functional rating scale [ 24 ] score was 37/48. Disease progression was fast and characterised by rapidly worsening four limbs weakness, widespread upper and lower motor neuron signs, and bulbar and respiratory involvement, which occurred 5 months after diagnosis. The patient accepted non-invasive ventilation but refused other supports and died from respiratory insufficiency 3 months later (20 months after symptoms onset).
KIF5A mutants display altered localisation, levels, and solubility
We initially characterised the intracellular distribution of the selected variants (hereafter: R17Q, R280C, R864*, N999Vfs*40, or C975Vfs*73 KIF5A) in NSC-34 cells. As expected, wild-type (WT) KIF5A appeared diffused across the cytoplasm, including neurites. The SPG10-related R17Q and R280C KIF5A mutants showed a similar distribution (Fig. 3A ), even if the latter also accumulated into perinuclear puncta in a few cells (Supplementary Fig. 3A ). Conversely, both the CMT-linked R864* and the ALS-associated N999Vfs*40 KIF5A mutants preferentially localised within neurites, but with a distinct distribution pattern: the R864* mutant appeared diffused in neurites, while N999Vfs*40 KIF5A formed inclusions at neurite tips (Fig. 3A and quantification in Supplementary Fig. 3B ). The intracellular distribution found for the R864* and N999Vfs*40 KIF5A mutants is consistent with the impairment of kinesin autoinhibitory function, respectively depending on the loss and the modification of the KIF5A tail [ 3 ]. For the ALS-linked N999Vfs*40 KIF5A mutant, this abnormal protein distribution has already been associated with accumulation at microtubule plus-ends [ 16 , 17 , 18 ].
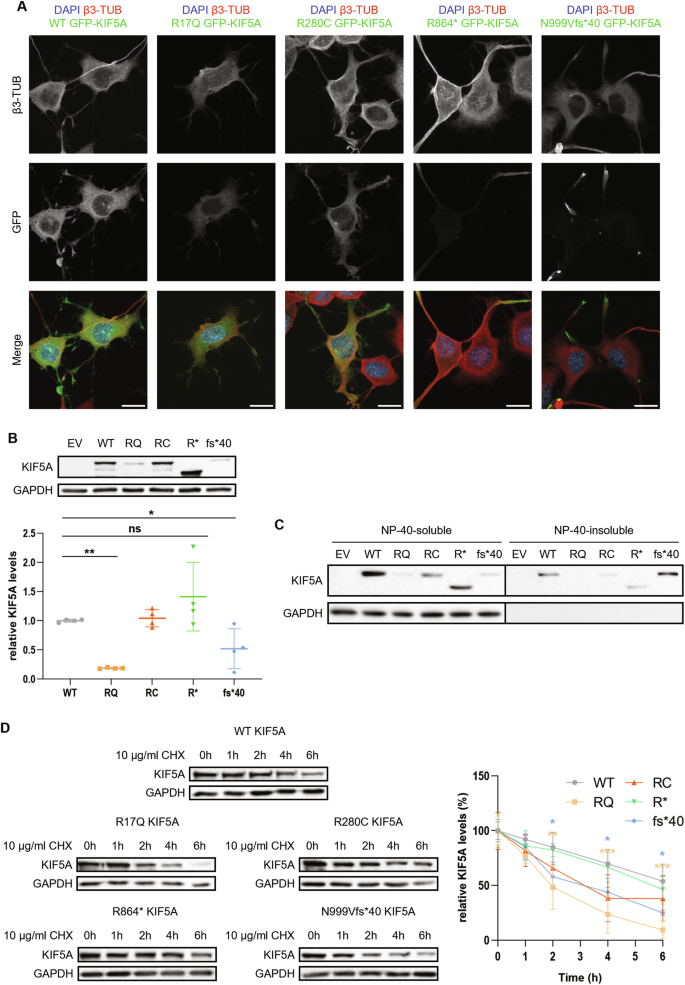
A Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently transfected with WT or mutant pGFP-KIF5A constructs. Endogenous β3-tubulin was stained in red. Nuclei were stained with DAPI. Scale bar 20 µm. B Western blot analysis of KIF5A protein levels in SH-SY5Y cells transiently transfected with WT or mutant pKIF5A constructs ( N = 4). An empty vector (EV) was used as a transfection mock. GAPDH protein levels were used for normalisation. The graph represents mean optical densities relative to samples overexpressing WT KIF5A ± SD. One-way ANOVA with Fisher’s LSD post-test was performed. ns not significant; * P < 0.05; ** P < 0.01. C Western blot analysis of KIF5A fractionation between the NP-40–soluble and the NP-40–insoluble protein fractions deriving from the same whole cell lysate of SH-SY5Y cells transiently transfected with WT or mutant pKIF5A constructs. D Western blot analysis of KIF5A protein levels in SH-SY5Y cells transiently transfected with WT or mutant pKIF5A constructs and treated with 10 µg/ml CHX for 1-2-4-6 h ( N = 3). GAPDH protein levels were used for normalisation. The graph represents mean optical densities expressed as percentages of either WT or mutant KIF5A baseline (i.e., 0 h) levels ± SD. Two-way ANOVA with Sidak’s post-test was performed comparing WT and mutant KIF5A protein levels at each time point. * P < 0.05; ** P < 0.01; *** P < 0.001.
In parallel, we compared WT and mutant KIF5A protein levels upon SH-SY5Y cell transfection. While WT and R280C KIF5A levels were similar, significantly lower protein levels were detected for the R17Q and N999Vfs*40 mutants and a tendency to display higher protein levels was found for the R864* mutant with respect to WT KIF5A (Fig. 3B ). We also tested KIF5A solubility by fractionating proteins in the mild detergent NP-40. As shown in Fig. 3C , N999Vfs*40 KIF5A was enriched in the insoluble protein fraction, differently from the other KIF5A mutants under analysis and the WT protein, that all resulted largely soluble in NP-40. This is in line with the aggregation-prone behaviour observed in immunofluorescence and suggests a potential gain of toxic function for N999Vfs*40 KIF5A. Since the RT-qPCR analysis showed comparable KIF5A mRNA levels between cells overexpressing WT or mutant KIF5A (Supplementary Fig. 3C ), we hypothesised that the observed changes in KIF5A protein levels may depend on an altered turnover of the R17Q and N999Vfs*40 mutants compared to that of WT KIF5A. This was confirmed by cycloheximide (CHX) chase assay: overexpressed WT KIF5A displayed a ~6 h half-life in CHX-treated cells, while the protein levels of the R17Q and N999Vfs*40 KIF5A mutants were respectively reduced to ~10 and ~25% in the same time interval. On the contrary, WT, R280C, and R864* KIF5A showed comparable degradation profiles (Fig. 3D ). Therefore, we observed a reduction in protein levels caused by protein instability and potentially restricting the pool of KIF5A motors available for anterograde transport for R17Q and N999Vfs*40 KIF5A, but not for the other mutants included in our study.
Mutant KIF5A interaction with WT KIF5A and mitochondria
In neurons, KIF5A works as a homodimer [ 25 ]. To assess whether the investigated KIF5A mutants were capable of dimerising with the WT protein, we co-transfected NSC-34 cells with equal amounts of WT pmRFP-KIF5A and pGFP-KIF5A constructs to test for WT and mutant KIF5A reciprocal distribution. As shown in Fig. 4A , the WT protein co-distributed with all KIF5A mutants. Notably, both R864* and N999Vfs*40 KIF5A partially sequestered the WT protein to the cell periphery (quantification in Supplementary Fig. 4A ), a finding in line with previous reports on ΔExon27 KIF5A variants [ 16 , 17 , 18 ]. The interaction between WT and mutant KIF5A was also confirmed by co-immunoprecipitation in SH-SY5Y cells (Supplementary Fig. 4B ). Therefore, these results suggest a possible dominant-negative effect of R864* and N999Vfs*40 KIF5A on the WT protein.
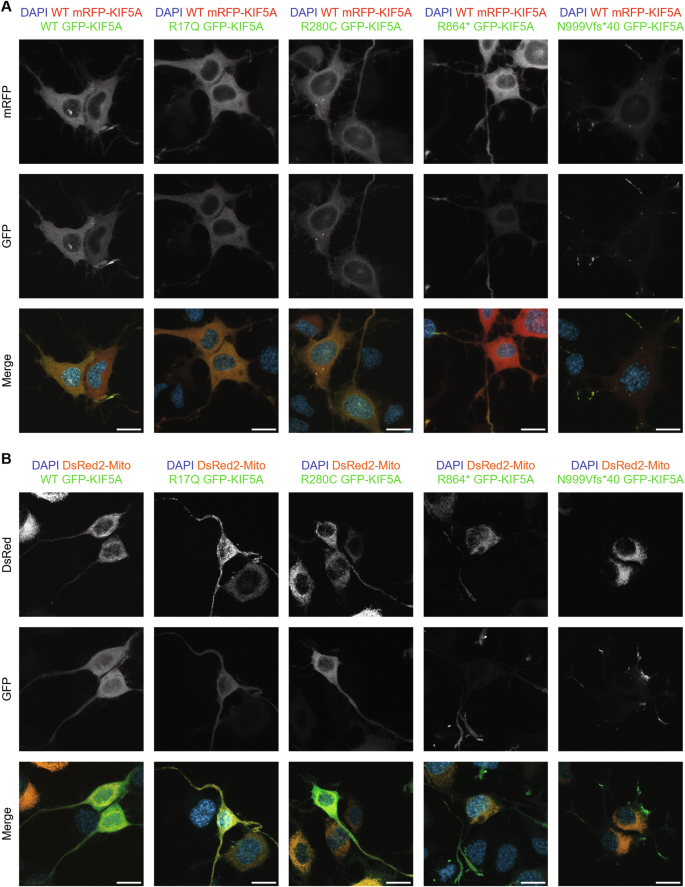
A Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently co-transfected with equal amounts of WT or mutant pGFP-KIF5A and WT pmRFP-KIF5A constructs. Nuclei were stained with DAPI. Scale bar 20 µm. B Confocal microscopy analysis (63× magnification) of NSC-34 transiently co-transfected with WT or mutant pGFP-KIF5A constructs and pDsRed2-Mito. Nuclei were stained with DAPI. Scale bar 20 µm.
KIF5A transports mitochondria along axonal and dendritic processes [ 6 , 7 ] and proper mitochondrial distribution and metabolism are essential to ensure neuronal homoeostasis. Based on these premises, we evaluated the reciprocal distribution of mitochondria and mutant KIF5A by co-transfecting NSC-34 cells with the mitochondrial reporter pDsRed2-Mito and pGFP-KIF5A constructs. Upon overexpression of R864* or N999Vfs*40 KIF5A, just a small fraction of mitochondria co-distributed with mutant KIF5A within neurites and very few organelles were found close to N999Vfs*40 KIF5A aggregates; instead, R17Q and R280C KIF5A showed a reciprocal distribution with their cargo similar to that of the WT protein (Fig. 4B ). This observation hints that the R864* and N999Vfs*40 KIF5A mutants might display a defective interaction with the mitochondrion, with potentially pathogenic effects. Indeed, mitochondrial dysfunction has been associated with several neurodegenerative diseases, including KIF5A -related conditions [ 26 ]. Notably, a similar alteration in mitochondrial distribution was reported in an ALS-KIF5A Drosophila model [ 27 ].
KIF5A mutants do not alter the basal autophagy flux
KIF5s participate in lysosomal transport and autophagy [ 8 , 28 ]. The latter is one of the main protein degradation pathways, and its dysfunction is often involved in the pathogenesis of neurodegenerative diseases, including HSP and ALS [ 29 , 30 ]. Since we observed an enhanced degradation rate and/or an aggregation-prone behaviour for some of the KIF5A mutants under investigation (Fig. 3 ), we analysed the possible interplay between mutant KIF5A and autophagy. We initially evaluated the basal protein levels of two autophagy markers, SQSTM1/p62 and MAP1LC3 [ 31 ], in KIF5A-overexpressing cells. Both SQSTM1/p62 and MAP1LC3 protein levels remained unchanged in all tested conditions in western blot (Fig. 5A ) and immunofluorescence analysis showed no alterations in endogenous MAP1LC3 localisation (Fig. 5B ). SQSTM1/p62 distribution, too, was unaltered, except for N999Vfs*40 KIF5A-overexpressing cells, in which mutant KIF5A inclusions resulted positive for this autophagy receptor (Fig. 5C ). The direct interaction between N999Vfs*40 KIF5A and SQSTM1/p62 was confirmed by co-immunoprecipitation (Supplementary Fig. 4B ). This aberrant interaction is consistent with previous reports [ 16 , 18 ] and may indicate that the aggregation-prone, short-lived N999Vfs*40 KIF5A mutant is targeted to autophagy-mediated degradation by SQSTM1/p62. However, by treating KIF5A-overexpressing cells with the autophagosome-lysosome fusion inhibitor NH 4 Cl to assess the impact of autophagy blockage on KIF5A turnover, we did not observe any significant alteration in KIF5A protein levels and distribution, despite the expected increase in SQSTM1/p62 and MAP1LC3-II protein levels that confirms autophagy inhibition (Fig. 5D and Supplementary Fig. 5A ).
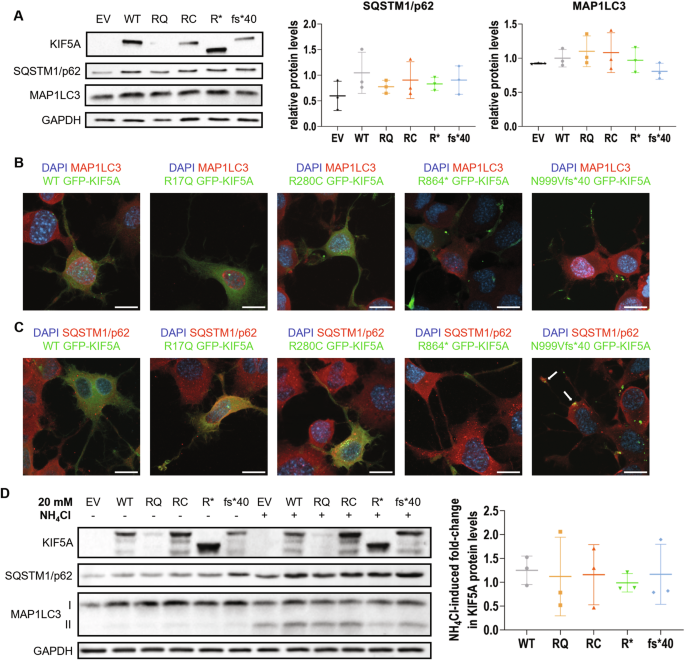
A Western blot analysis of basal SQSTM1/p62 and MAP1LC3 protein levels in SH-SY5Y cells transiently transfected with WT or mutant pKIF5A constructs ( N = 3). An empty vector (EV) was used as a transfection mock. GAPDH protein levels were used for normalisation. Graphs represent mean SQSTM1/p62 (left graph) and MAP1LC3 (right graph) optical densities relative to samples overexpressing WT KIF5A ± SD. One-way ANOVA with Fisher’s LSD post-test was performed. B Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently transfected with WT or mutant pGFP-KIF5A constructs. Endogenous MAP1LC3 was stained in red. Nuclei were stained with DAPI. Scale bar 20 µm. C Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently transfected with WT or mutant pGFP-KIF5A constructs. Endogenous SQSTM1/p62 was stained in red. Nuclei were stained with DAPI. Arrows highlight co-localisation between N999Vfs*40 KIF5A and SQSTM1/p62. Scale bar 20 µm. D Western blot analysis of KIF5A protein levels in SH-SY5Y cells transiently transfected with WT or mutant pKIF5A constructs and treated with 20 mM NH 4 Cl for 16 h ( N = 3). The graph represents the mean fold-change of GAPDH-normalised WT or mutant KIF5A protein levels induced by the treatment ± SD. One-way ANOVA with Fisher’s LSD post-test was performed.
Altogether, these results indicate that mutant KIF5A overexpression does not alter basal autophagy, that in turn does not represent the preferential degradation route for WT and mutant KIF5A, despite the abnormal interaction observed between SQSTM1/p62 and the ALS-linked N999Vfs*40 KIF5A mutant.
WT and mutant KIF5A degradation is mainly mediated by the ubiquitin-proteasome system
We then tested whether the enhanced protein turnover observed for R17Q and N999Vfs*40 KIF5A (Fig. 3D ) could depend on the activity of the other main protein degradation route in cells, the ubiquitin-proteasome system (UPS). Notably, SQSTM1/p62 is a ubiquitin-binding protein acting both as an autophagy receptor [ 31 ] and in the delivery of ubiquitinated substrates to the UPS by direct interaction with the 26S proteasome [ 32 ]. SQSTM1/p62 co-localisation with the aggregation-prone N999Vfs*40 KIF5A mutant could, therefore, be indicative of its targeting to the UPS instead of autophagy. To test this hypothesis, we treated KIF5A-overexpressing SH-SY5Y cells with the 26S proteasome inhibitor MG132 and observed an increase in protein levels for both WT and mutant KIF5A upon treatment. Interestingly, MG132-induced accumulation (i.e. fold-change of GAPDH-normalised KIF5A protein levels induced by the treatment) resulted statistically higher for the short-lived R17Q and N999Vfs*40 KIF5A mutants than for the WT protein (Fig. 6A ). Moreover, proteasomal blockage induced the preferential partitioning of both R17Q and N999Vfs*40 KIF5A in the NP-40–insoluble protein fraction. Such transitioning was particularly relevant for the R17Q mutant, which appeared completely NP-40–soluble in basal conditions, and for the N999Vfs*40 mutant (Fig. 6B ). Immunofluorescence analysis of NSC-34 cells treated with MG132 showed distribution into abundant perinuclear puncta for both R17Q and N999Vfs*40 KIF5A upon UPS blockage, differently from the other KIF5A mutants under analysis and from the WT protein, that remained largely diffused (Supplementary Fig. 5B ). These results strongly suggest that R17Q and N999Vfs*40 KIF5A form potentially harmful inclusions in neurons when proteostasis is impaired.
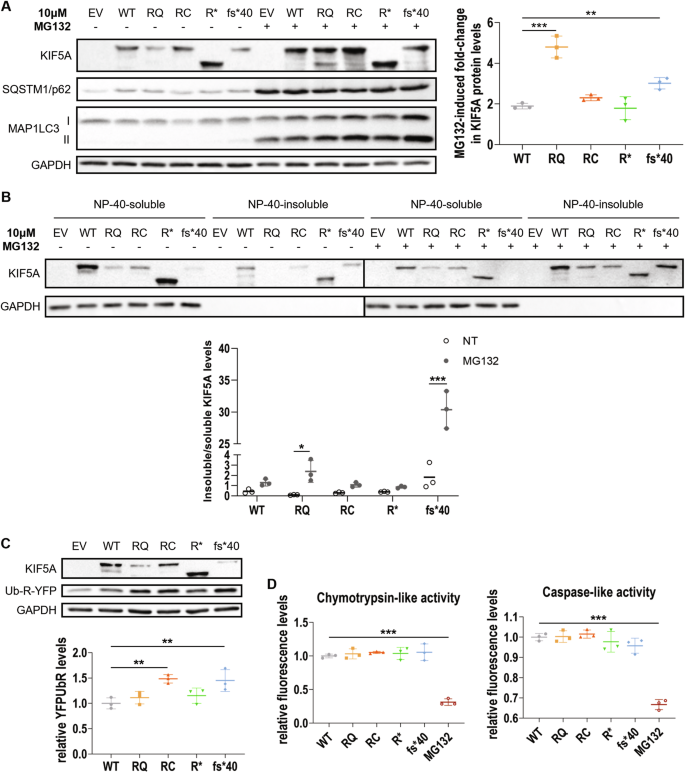
A Western blot analysis of KIF5A protein levels in SH-SY5Y cells transiently transfected with WT or mutant pKIF5A constructs and treated with 10 µM MG132 for 16 h ( N = 3). An empty vector (EV) was used as a transfection mock. The graph represents the mean fold-change of GAPDH-normalised WT or mutant KIF5A protein levels induced by the treatment ± SD. One-way ANOVA with Fisher’s LSD post-test was performed. * P < 0.05; *** P < 0.001. B Western blot analysis of KIF5A fractionation between the NP-40–soluble and the NP-40–insoluble protein fractions deriving from the same whole cell lysate of SH-SY5Y transiently transfected with WT or mutant pKIF5A constructs and treated with 10 µM MG132 for 16 h ( N = 3). The graph represents mean ratio between KIF5A insoluble and soluble protein levels in each experimental condition ± SD. Two-way ANOVA with Fisher’s LSD post-test was performed comparing insoluble/soluble KIF5A ratio between untreated (NT) and treated (MG132) samples for each KIF5A condition. * P < 0.05; *** P < 0.001. C Western blot analysis of Ub-R-YFP protein levels in SH-SY5Y transiently co-transfected with WT or mutant pKIF5A constructs and Ub-R-YFP ( N = 3). GAPDH protein levels were used for normalisation. The graph represents mean Ub-R-YFP optical densities relative to samples overexpressing WT KIF5A ± SD. One-way ANOVA with Fisher’s LSD post-test was performed. ** P < 0.01. D Proteasome activity analysis in SH-SY5Y cells overexpressing WT or mutant pKIF5A constructs ( N = 3). Specific AMC-conjugated peptides (N-Suc-LLVY-AMC and Z-LLE-AMC) were used to evaluate chymotrypsin-like (top graph) and caspase-like (bottom graph) proteasome activities. Samples treated with 1 µM MG132 for 16 h were used as control. Graphs represent mean fluorescence levels relative to samples overexpressing WT KIF5A ± SD. One-way ANOVA with Fisher’s LSD post-test was performed. * P < 0.05; *** P < 0.001.
To further investigate the interplay between KIF5A and the UPS, we co-expressed the proteasome activity reporter Ub-R-YFP [ 33 ] and pKIF5A constructs in SH-SY5Y cells and observed that Ub-R-YFP significantly accumulated upon concomitant overexpression of either R280C or N999Vfs*40 KIF5A compared to cells overexpressing the WT protein (Fig. 6C ), suggesting that both KIF5A mutants might have a direct impact on the 26S proteasome activity. Ub-R-YFP accumulation in cells may occur either through proteasome inhibition or through competition between substrates destined for proteasomal degradation. To test which was the case upon mutant KIF5A overexpression, we assayed the enzymatic activity of the proteasome in KIF5A-overexpressing cells. In detail, we measured the conversion rate of the 7-amino-4-methyl coumarin (AMC)-conjugated substrates N -Suc-LLVY-AMC and Z-LLE-AMC, respectively targeted by the chymotrypsin-like and the caspase-like activities of the 26S proteasome. We found that the UPS was not inhibited by WT or mutant KIF5A overexpression (Fig. 6D ). Thus, R280C and N999Vfs*40 KIF5A might compete with Ub-R-YFP for proteasome-mediated degradation, resulting in its accumulation in cells.
Taken together, our observations indicate that WT and mutant KIF5A turnover mainly depends on the UPS.
NEIMY-KIF5A displays similar, but more severe defects compared to ALS-KIF5A
Frameshift mutations in the KIF5A tail domain have been associated with both ALS and NEIMY. Although these diseases are very different from one another, the underpinning KIF5A mutations are expected to produce partially overlapping effects on the corresponding protein [ 13 , 14 ]. Based on the results obtained in N999Vfs*40 KIF5A characterisation, we compared its behaviour with that of the NEIMY-linked C975Vfs*73 KIF5A variant [ 14 ]. The latter presents an elongated tail in comparison to WT KIF5A and shares the last 40 amino acids with the N999Vfs*40 mutant, despite not being affected by exon 27 skipping (Supplementary Fig. 6 ). Interestingly, CamSol analysis [ 34 ] confirmed the low intrinsic solubility of the 40-residue tail common to N999Vfs*40 and C975Vfs*73 KIF5A, but also revealed the presence of a poorly soluble sequence in the C975Vfs*73 mutant that is missing in both WT and N999Vfs*40 KIF5A. Remarkably, such sequence corresponds to the amino acids encoded by KIF5A exon 27 (Supplementary Fig. 7 ). This would indicate an even lower solubility of C975Vfs*73 KIF5A with respect to N999Vfs*40 KIF5A. Notably, two other NEIMY-linked KIF5A mutations reported in the literature, c.2854delC/p.Q952Rfs*96 and c.2934delG/p.S978Vfs*70 KIF5A [ 13 ], share the frame and the low-solubility sequences in their aberrant tail with C975Vfs*73 KIF5A (Supplementary Figs. 6 , 7 ), suggesting potential similarities in the behaviour of these variants.
On these bases, we compared the distribution of the two frameshift mutants and found that C975Vfs*73 KIF5A accumulated both in the cell body and within neurites into larger aggregates than those formed by the N999Vfs*40 mutant (Fig. 7A ), in line with the presence of an additional low-solubility amino acid sequence in C975Vfs*73 KIF5A tail. Moreover, aggregates formed by the NEIMY-associated mutant sequestered WT KIF5A to a higher extent compared to N999Vfs*40 KIF5A ones (Fig. 7B ), suggesting that C975Vfs*73 KIF5A might exert a more prominent dominant-negative effect on the WT protein. Additionally, as seen for N999Vfs*40 KIF5A, no co-distribution was observed between mitochondria and C975Vfs*73 KIF5A aggregates (Fig. 7C ), hinting at a shared loss of function between ALS- and NEIMY-KIF5A mutants that would be consistent with reports implicating mitochondrial dysfunction in both phenotypes [ 13 , 14 , 26 ]. Notably, SQSTM1/p62 was co-immunoprecipitated by both N999Vfs*40 and C975Vfs*73 KIF5A (Supplementary Fig. 8A ), but was found exclusively at the rim of NEIMY-KIF5A aggregates, while it was clearly observed within ALS-KIF5A ones (Supplementary Fig. 8B ). Consistently, NP-40–soluble/insoluble protein extraction showed that both ALS- and NEIMY-KIF5A are characterised by poor detergent solubility; however, the former sequestered a larger amount of SQSTM1/p62 protein in the insoluble fraction in comparison to the latter (Fig. 7D ). Finally, proteasomal blockage by MG132 induced C975Vfs*73 KIF5A accumulation, while autophagy inhibition did not significantly modify its protein levels, similarly to the N999Vfs*40 KIF5A mutant (Supplementary Fig. 8C ). In line with this observation, both ALS- and NEIMY-KIF5A aggregates were found to be ubiquitinated and positive for the ubiquitin-binding protein BAG1 (Supplementary Fig. 8D ).
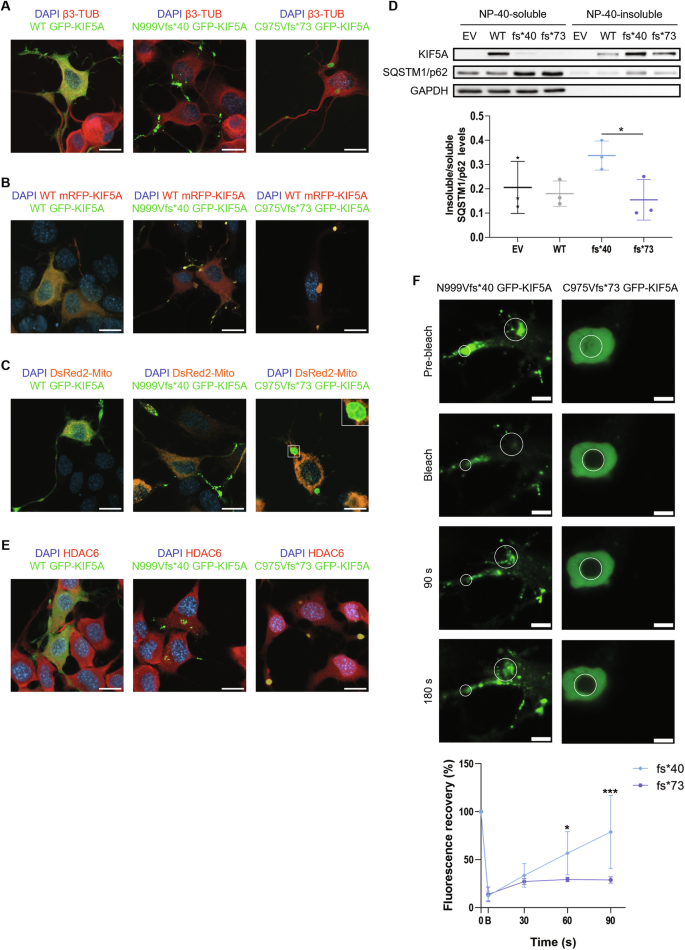
A Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently transfected with WT or frameshift pGFP-KIF5A constructs. Endogenous β3-tubulin was stained in red. Nuclei were stained with DAPI. Scale bar 20 µm. B Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently co-transfected with equal amounts of WT or frameshift pGFP-KIF5A and WT pmRFP-KIF5A constructs. Nuclei were stained with DAPI. Scale bar 20 µm. C Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently co-transfected with WT or frameshift pGFP-KIF5A constructs and pDsRed2-Mito. Nuclei were stained with DAPI. Scale bar 20 µm. D Western blot analysis of KIF5A and SQSTM1/p62 fractionation between the NP-40–soluble and the NP-40–insoluble protein fraction in SH-SY5Y cells transiently transfected with WT or frameshift pKIF5A constructs ( N = 3). An empty vector (EV) was used as a transfection mock. The graph represents mean ratio between SQSTM1/p62 insoluble and soluble protein levels in each experimental condition ± SD. Student’s t -test was performed comparing SQSTM1/p62 insoluble/soluble ratio in samples overexpressing N999Vfs*40 or C975Vfs*73 KIF5A. * P < 0.05. E Confocal microscopy analysis (63× magnification) of NSC-34 cells transiently transfected with WT or frameshift pGFP-KIF5A constructs. Endogenous HDAC6 was stained in red. Nuclei were stained with DAPI. Scale bar 20 µm. F Fluorescence recovery after photobleaching analysis of frameshift KIF5A aggregates in NSC-34 cells 48 h after transient transfection with pGFP-KIF5A constructs ( N = 3). Scale bar 5 µm. The graph represents the percentage of fluorescence recovery of each aggregate over time compared to the baseline (i.e. 0 s) ± SD. Two-way ANOVA with Sidak’s post-test was performed comparing N999Vfs*40 and C975Vfs*73 KIF5A fluorescence recovery levels at each time point. * P < 0.05; *** P < 0.001.
A deeper characterisation of frameshift KIF5A inclusions also revealed features that are unique to NEIMY-KIF5A. Specifically, C975Vfs*73 KIF5A aggregates, but not those of N999Vfs*40 KIF5A, resulted positive for HDAC6 and G3BP1 (Fig. 7E , Supplementary Fig. 9A, and Supplementary Table 3 ), known to be implicated in stress granule formation [ 35 ]. Interestingly, live imaging analysis showed that both ALS- and NEIMY-KIF5A aggregates were motile and dynamic 24 h after transfection, but at 48 h, the largest C975Vfs*73 KIF5A aggregates had lost most of their motility differently from N999Vfs*40 KIF5A aggregates (Supplementary Fig. 9B ). Consistently, while both ALS- and NEIMY-KIF5A aggregates recovered fluorescence following photobleaching 24 h after transfection (Supplementary Fig. 9C ), only N999fs*40 KIF5A aggregates retained this ability at 48 h (Fig. 7F ). This is in contrast with the extreme flexibility of stress granules and indicates that the initially dynamic C975fs*73 KIF5A-positive aggregates may mature into solid-like structures with time.
Together, these results suggest that most biochemical features characterising the ALS-linked N999Vfs*40 KIF5A mutant appear exacerbated for the NEIMY-related C975Vfs*73 KIF5A, providing a possible explanation for the higher severity of its associated neurodevelopmental phenotype compared to KIF5A-linked neurodegeneration.
Mutations targeting KIF5A give rise to distinct neurodegenerative and neurodevelopmental diseases depending on the affected protein domain, but the bases of this heterogeneity are unclear. Most mutations cluster in the motor domain and mainly associate with HSP/SPG10 [ 9 ] or CMT [ 10 ], while KIF5A tail variants associate with ALS [ 11 , 12 ] and NEIMY [ 13 , 14 ]. Variants in the stalk domain are less frequent and poorly characterised [ 36 ].
In this work, we investigated the biochemical behaviour of four disease-associated KIF5A mutants identified in a cohort of Italian patients, to discern the shared and unique pathogenic mechanisms underlying KIF5A-associated diseases. The clinical features of patients carrying the selected variants well illustrate the main aspects of phenotypic distinction and overlap characterising these disorders. A consistent phenotype is associated with motor domain variants (e.g. the recurrent p.R280C mutation), in which polyneuropathy with foot deformities and upper motor neuron signs are the main core features, often associated with ataxia and cognitive impairment. The occurrence of cognitive impairment in the two patients diagnosed with CMT5 further supports the notion that the clinical phenotypes associated with motor domain variants could be more appropriately described as complex HSP. Clinical heterogeneity is well illustrated by the cases of Patients 12 and 13. Patient 12, who carried the truncating variant p.R864* in the stalk domain, exhibited a mild neuropathic phenotype, while a previously reported patient with the same variant had a complex HSP [ 20 ]. Patient 13, carrying variant p.(N1006S), putatively belonging to the group of ALS-associated ΔExon27 frameshift tail mutations, had a late-onset and rapidly progressing ALS phenotype, unlike most patients with KIF5A tail mutations, who exhibit younger onset and slow course of the disease [ 11 , 12 ].
The variety of clinical phenotypes caused by mutant KIF5A, along with its multifaceted functions, prompts the need to dissect and compare the molecular mechanisms of different variants in a homogeneous experimental setting. Previous studies have focused on single mutants [ 11 , 15 , 37 ], lacking the possibility of direct comparison we wanted to pursue in our study.
The first shared biochemical feature we identified between the KIF5A mutants under investigation is the peripheral localisation of the C-terminal mutants R864* and N999Vfs*40 KIF5A, consistent with the loss of KIF5A autoinhibitory function. Either mutations or deletion of the IAK motif generate constitutively active kinesin motors [ 3 ]. The IAK motif is absent in R864* KIF5A, possibly explaining its altered intracellular distribution. Differently, the loss of KIF5A autoinhibition observed for N999Vfs*40 KIF5A has been previously described [ 16 , 17 , 18 ], and it has been attributed to the replacement of 7 negatively charged amino acids with 9 positively charged ones in mutant KIF5A C-terminal domain; such change is predicted to hinder the stability of the head-tail association state required for kinesin autoinhibition [ 16 ]. At the functional level, autoinhibition loss causes the rapid removal of dimers containing mutant KIF5A from the pool of cytoplasmic motors available for anterograde transport, which in turn could cause imbalances in axonal trafficking, as previously suggested for ALS-KIF5A [ 16 , 18 ]. Additionally, both R864* (by tail truncation) and N999Vfs*40 KIF5A (by translational frameshift of its cargo/adaptor-binding region) may lose their ability to interact with KIF5A-specific substrates. However, the adaptor binding sites on the stalk domain are not completely abolished by the R864* truncating mutation (e.g. kinesin light chain binding involves amino acids 770-811 [ 38 ]), thus its interaction with specific cargoes could be partially retained. Similarly, the ability of N999Vfs*40 KIF5A to transport cargo is debated. While Baron and colleagues [ 16 ] reported increased speed and percentage of moving mitochondria in ALS-KIF5A- compared to WT KIF5A-overexpressing primary motor neurons, Pant et al. [ 18 ] did not observe co-distribution between ALS-KIF5A inclusions and mitochondria in overexpressing primary cortical neurons, in line with our data. The absence of co-distribution between ALS-KIF5A and mitochondria does not necessarily reflect the inability of KIF5A motors to interact with their cargo, since this interaction may be lost only upon ALS-KIF5A oligomerisation and aggregation. While distal accumulation of mitochondria (or other KIF5A cargoes) may be promoted by soluble ALS-KIF5A motors or WT-mutant KIF5A heterodimers, the inability to recycle aggregated ALS-KIF5A to the cytoplasm might also cause an opposite effect of enhanced retrograde transport, introducing additional imbalances in axonal trafficking. Moreover, this effect may be exacerbated by WT KIF5A sequestration into ALS-KIF5A aggregates and might not be compensated by other kinesin motors. Alterations in transport equilibrium may also occur with the R864* KIF5A mutant, which could promote the fast dismissal of the WT protein from the cytoplasm via heterodimerisation, even if additional studies are required to better elucidate these aspects.
A second shared behaviour we observed is between the SPG10-related R17Q KIF5A mutant and N999Vfs*40 KIF5A, that both display a shorter turnover compared to the WT protein, with which they dimerise. Thus, the fast turnover of R17Q and N999Vfs*40 KIF5A may affect the clearance of both their homodimers and WT-mutant KIF5A heterodimers, restricting the pool of motors available for axonal transport. Concerning the R17Q KIF5A mutant, the alteration of its ATP-binding site predicted in silico may tamper with its ability to fuel transport, and also destabilise the protein, causing its premature degradation, in line with the reported loss of function for SPG10-related KIF5A variants [ 15 ]. Regarding the accelerated turnover of N999Vfs*40 KIF5A, this is in line with its lower levels compared to WT KIF5A in iPSC-derived motor neurons harbouring ALS-KIF5A mutations [ 16 , 39 ] and in ALS-KIF5A animal models [ 27 , 40 ].
The other SPG10-related mutant, R280C KIF5A, also shares similarities with other KIF5A variants in our study. The R280C substitution targets the microtubule-binding site of the KIF5A head, reducing its affinity for microtubule tracks without having a dominant-negative effect on the WT protein. Nonetheless, the R280C mutant competes with WT KIF5A for cargo binding, sequestering substrates to transport-incompetent KIF5A motors [ 15 ], a mechanism that could be shared with R17Q KIF5A, which has an inactive ATP-binding site but an intact tail. Notably, we found that R280C KIF5A forms small perinuclear puncta, potentially due to its inability to interact with microtubules, and competes with Ub-R-YFP for proteasomal degradation, that are features also described for N999Vfs*40 KIF5A.
Finally, we found that the NEIMY-linked C975Vfs*73 KIF5A mutant shares most of the abnormal behaviours observed for N999Vfs*40 KIF5A, including loss of autoinhibition and distal distribution, aggregation propensity, negative dominance on WT KIF5A, and lack of co-distribution between aggregates and mitochondria. Despite all these similarities, the N999Vfs*40 and C975Vfs*73 KIF5A mutants lead to strikingly different neurological conditions, respectively an adult-onset form of motor neuron degeneration and a complex and very severe early-onset neurodevelopmental phenotype. Such difference might be related to the higher aggregation propensity and sequestration potential characterising NEIMY-KIF5A compared to ALS-KIF5A. Based on our observations, it is conceavable that NEIMY-KIF5A inclusions may form similarly to stress granules and then evolve into solid-like aggregates, loosing their dynamic status and the ability to undergo liquid-liquid phase partitioning typical of ribonucleoprotein condensates [ 35 ]. Protein and/or mRNA sequestration into these solid-like structures could further exacerbate NEIMY-KIF5A toxicity through both gain- and loss-of-function mechanisms.
The clinical symptoms affecting NEIMY patients are similar regardless of the underpinning mutation [ 13 , 14 ], and they have been previously proposed to derive from mitochondrial dysfunction and altered excitatory/inhibitory equilibrium [ 13 , 14 , 41 ], defects that are in line with impaired KIF5A-dependent trafficking of mitochondria [ 6 , 7 ] and GABA A receptor subunits [ 42 ]. Interestingly, post-natal neuron-specific Kif5a depletion in conditional knock-out mice results in an epileptic phenotype [ 42 ] reminiscent of NEIMY patients, further supporting the hypothesis of a KIF5A loss of function component in this neurodevelopmental disease. Notably, accumulation of synaptic vesicles leading to alterations in synaptic transmission was recently observed in ALS-KIF5A Drosophila larvae [ 27 ], suggesting that this loss of function mechanism, too, could be shared between ALS and NEIMY. Altogether, our data on N999Vfs*40 and C975Vfs*73 KIF5A indicate that a combination of a loss of function in axonal transport and a toxic gain of function due to aggregation and WT KIF5A sequestration may underpin both NEIMY and KIF5A-linked ALS.
In conclusion, we performed a comprehensive functional study of a panel of KIF5A variants representative of the different KIF5A -related disorders. We demonstrated the pathogenicity of the novel p.R17Q variant, altered at the level of the ATP-binding site of the motor domain, and of the p.R864* variant, which is both one of the few mutations in the stalk domain and one of the very rare truncations in KIF5A. We also provided evidence for a combined gain/loss of function pathomechanism unexpectedly shared by two frameshift mutants associated with ALS and NEIMY, that would bridge the dichotomy between KIF5A -linked neurodevelopmental and neurodegenerative conditions.
Materials and methods
Genetic studies.
Patients were recruited by the Units of Medical Genetics and Neurogenetics, Rare Neurological Diseases, and Neurodevelopmental Disorders at the Istituto Neurologico Carlo Besta (Milan, Italy) and the Neurology Unit at the Azienda Ospedaliero-Universitaria di Modena (Modena, Italy).
Genetic analysis of the KIF5A gene was performed by Sanger sequencing or by targeted next generation sequencing approaches (single-gene amplicon-deep sequencing or disease gene panels) on Illumina MiSeq or NextSeq550 apparatuses (Illumina, Inc., San Diego, CA, USA). Novel variants were classified according to the guidelines of the ACMG [ 19 ]. In silico prediction of the exon 27 variant was evaluated by Alternative Splice Site Predictor [ 43 ], NNSplice [ 44 ], SpliceAI [ 45 ], and dbscSNV Ada/RF [ 46 ] tools. All variants are described in relation to the reference sequence NM_004984.4 and according to current Human Genome Variation Society recommendations for sequence variant nomenclature ( https://varnomen.hgvs.org/ ; Mutalyzer 3: https://mutalyzer.nl ).
Chemicals and antibodies
CHX (C6255), MG132 (C2211) and NH 4 Cl (254134) were purchased from Sigma-Aldrich (Saint Louis, MI, USA). 10 μg/ml CHX was used to treat cells for 1-2-4-6 h to block protein synthesis and evaluate KIF5A stability. 10 µM MG132 was used to treat cells for 16 h to block the 26S proteasome. 20 mM NH 4 Cl was used to treat cells for 16 h to inhibit autophagy.
All antibodies used in the present work are listed in Supplementary Table 4 .
pKIF5A plasmids for the transient overexpression of human WT or mutant (R17Q, R280C, R864*, N999Vfs*40, C975Vfs*73) KIF5A were generated by GenScript Biotech (Piscataway, NJ, USA) by cloning the cDNA sequences of interest into the backbone of the empty vector (EV) pcDNA3.1. pFLAG-KIF5A and pGFP-KIF5A were cloned starting from the pKIF5A constructs. A complete list of the plasmids used in this work is reported in Supplementary Table 5 .
Cell lines and transfection
The human neuroblastoma SH-SY5Y cell line was obtained from the American Type Culture Collection (ATCC, Rockville, MD, USA CRL-2266;). SH-SY5Y cells were cultured at 37 °C in 5% CO 2 in DMEM High Glucose (Euroclone S.p.A., Pero, Italy; ECB7501L) supplemented with 10% heat-inactivated foetal bovine serum (FBS; Sigma-Aldrich, Saint Louis, MI, USA; F7524), 1 mM l -glutamine (Euroclone S.p.A., Pero, Italy; ECB3004D), and antibiotics (SERVA Electrophoresis GmbH, Heidelberg, Germany; penicillin, 31749.04; streptomycin, 35500.01).
The murine motor neuron-like NSC-34 cell line was provided by Dr. Neil R. Cashman (University of British Columbia, Canada). NSC-34 cells were cultured at 37 °C in 5% CO 2 in DMEM High Glucose supplemented with 5% FBS, 1 mM l -glutamine and antibiotics.
The SH-SY5Y neuroblastoma cell line was chosen to investigate mutant KIF5A biochemical behaviour because of its human origin. The murine NSC-34 cell line was used to analyse mutant KIF5A distribution and motility in a bona fide motoneuronal model not requiring differentiation.
SH-SY5Y and NSC-34 cells were transfected with Lipofectamine™ 3000 Transfection Reagent (Thermo Fisher Scientific Inc., Waltham, MA, USA; L3000015) diluted in Opti-MEM™ (Thermo Fisher Scientific Inc., Waltham, MA, USA; 31985070) 24 h after seeding, according to the manufacturer’s instructions. The next day cells were directly processed (SH-SY5Y cells, co-immunoprecipitation or CHX assay), or the medium was changed to limit Lipofectamine™ 3000 toxicity.
Fluorescence microscopy and immunofluorescence
NSC-34 cells were seeded in 24-well plates onto 13-mm coverslips at 35,000 cells/well and transfected as previously described. 48 h after transfection, cells were fixed onto coverslips in a 1:1 solution of 4% paraformaldehyde and 4% sucrose in 0.2 M phosphate buffer (0.06 M KH 2 PO 4 , 0.31 M Na 2 HPO 4 ; pH 7.4) for 25 min at 37 °C. For fluorescence microscopy analyses, nuclei were stained with 0.02% DAPI in PBS and coverslips were mounted with Mowiol® 4-88 Reagent (Sigma-Aldrich, Saint Louis, MI, USA; 475904). For immunofluorescence analyses, cells were incubated in PBS added with 0.1% Triton X-100, 1% BSA (Sigma-Aldrich, Saint Louis, MI, USA; X100 and A7030), and 10% FBS for 45 min at room temperature for permeabilisation and blocking of nonspecific sites. Subsequently, cells were incubated with the required primary and then secondary antibodies diluted in PBS added with 0.1% BSA as reported in Supplementary Table 4 . Finally, nuclei were stained with DAPI, and coverslips were mounted as described. Images were acquired with an LSM 900 confocal microscope (Carl Zeiss Microscopy, Germany) and were processed using ImageJ/Fiji (version 2.9.0).
Western blot
SH-SY5Y cells were seeded in 12-well plates at 150,000 cells/well and transfected as previously described. At the time of harvesting, cells were collected in their own medium and centrifuged at 100× g for 5 min at 4 °C to remove the supernatant. Total proteins were then extracted and protein concentration was determined through bicinchoninic acid assay with the QPRO BCA Kit Standard (Cyanagen Srl, Bologna, Italy; PRTD1), following the manufacturer’s instructions. Subsequently, 15–20 μg total proteins were incubated in sample buffer (250 mM Tris, 40% glycerol, 8% SDS, 0.1% bromophenol blue) at 100 °C for 5 min for denaturation and loaded on 10–15% SDS-polyacrylamide gels. Separated proteins were then transferred to 0.45-µm nitrocellulose membranes (Euroclone S.p.A., Pero, Italy; GE10600002) using a Trans-Blot® Turbo TM Transfer System (Bio-Rad Laboratories, Hercules, CA, USA). For the immunochemical detection of proteins, membranes were initially incubated in 5% non-fat dried milk diluted in TBS-T (20 mM Tris-HCl pH 7.5, 0.5 M NaCl, 0.05% Tween 20; pH 7.6) to block nonspecific sites and then probed using the antibodies reported in Supplementary Table 4 . Immunoreactivity was detected using Westar chemiluminescent reagents (Cyanagen Srl, Bologna, Italy). Images were acquired using a ChemiDoc TM XRS+ System (Bio-Rad Laboratories, Hercules, CA, USA), and optical density was analysed with Image Lab TM Software (Bio-Rad Laboratories, Hercules, CA, USA; version 6.0.1).
To analyse KIF5A solubility, SH-SY5Y cells were harvested 48 h after transfection as described, resuspended in NP-40 lysis buffer (150 mM NaCl, 20 mM Tris base, 0.05% NP-40, 1.5 mM MgCl 2 , 3% glycerol; pH 7.4) added with 1 mM DTT (Sigma-Aldrich, Saint Louis, MI, USA; 3483-12-3) and Protease Inhibitor Cocktail (Sigma-Aldrich, Saint Louis, MI, USA; P8340), and passed 10 times through a syringe needle for lysis. Then, 20 μg total proteins were diluted in 15 μl NP-40 lysis buffer and were centrifuged at 16,100× g for 15 min at 4 °C. NP-40–soluble supernatants were collected, while NP-40–insoluble pellets were resuspended in the same volume of NP-40 lysis buffer (without protease inhibitor and DTT) and sonicated. Both NP-40–soluble and NP-40-insoluble fractions were then analysed.
To compare WT and mutant KIF5A turnover, 24 h after transfection SH-SY5Y cells were incubated with fresh medium added with CHX and collected at the previously indicated time points, except for control samples which were immediately harvested. After the last collection, cells were resuspended in PBS added with protease inhibitor and lysed through slight sonication to extract proteins.
In all other cases, SH-SY5Y cells were harvested 48 h after transfection and processed to extract proteins in PBS added with protease inhibitor as described.
RNA extraction from cells and RT-qPCR
SH-SY5Y cells were seeded in 12-well plates at 150,000 cells/well and transfected as previously described. 48 h after transfection, total RNA was extracted from cells using TRI Reagent® (Sigma-Aldrich, Saint Louis, MI, USA; T9424) and 1-bromo-3-chloropropane (Sigma-Aldrich, Saint Louis, MI, USA; B9673), following the manufacturer’s instructions. RNA quantification was performed using a NanoDrop 2000 (Thermo Fisher Scientific Inc., Waltham, MA, USA), after which 1 μg/sample RNA was treated with DNase I (Sigma-Aldrich, Saint Louis, MI, USA; AMPD1) and reverse transcribed to cDNA with the High-Capacity cDNA Reverse Transcription Kit (Thermo Fisher Scientific Inc., Waltham, MA, USA; 4368814). Subsequently, qPCR was performed using the iTaq SYBR Green Supermix (Bio-Rad Laboratories, Hercules, CA, USA; 1725124) in a total volume of 10 μl with 500 nmol primers. A CFX96 Real-Time System (Bio-Rad Laboratories, Hercules, CA, USA) was used according to the following cycling conditions: 94 °C for 10 min, 94 °C for 15 s (40 cycles), 6 °C for 1 min. Data were expressed as C t values and analysed with CFX Manager™ Software (Bio-Rad Laboratories, Hercules, CA, USA; version 3.1). Primers for qPCR were synthesised by Eurofins MWG-Biotech (Ebersberg, Germany) with the following sequences: hKIF5A 5′–GGAGAACATGGAAACGGAGCA–3′ (forward), 5′–TATTCTTTGCCTCGTCCAGCAC–3′ (reverse); hGAPDH 5′–GAAGGTGAAGGTCGGAGTC–3′ (forward), 5′ –TTGATGGCAACAATATCCACTT–3′ (reverse).
Co-immunoprecipitation
SH-SY5Y cells were seeded in 6-well plates at 300,000 cells/well and transfected as previously described. The next day, cells were harvested in their medium pooling three wells per experimental condition and centrifuged at 100× g for 5 min at 4 °C. Pellets were resuspended in RIPA buffer (150 mM NaCl, 0.5% Na-deoxycholate, 100 µM Na-orthovanadate, 50 mM NaF, 50 mM Tris-HCl pH 7.7, 10 mM EDTA pH 8, 0.08% SDS, 0.8% Triton X-100) added with cOmplete Protease Inhibitor Cocktail (Sigma-Aldrich, Saint Louis, MI, USA; 4693116001), incubated on ice for 20 min, and centrifuged at 16,000× g for 15 min at 4 °C for clearing. 100 μl/sample SureBeads TM Protein G Magnetic Beads (Bio-Rad Laboratories, Hercules, CA, USA; 1614023) were conjugated to 2 μg/sample mouse monoclonal anti-FLAG antibody (Sigma-Aldrich, Saint Louis, MI, USA; F1804) diluted in PBS-T (PBS, 0.1% Tween 20) for 10 min at room temperature and washed in PBS-T. Antibody–conjugated beads were then incubated with 250 μg/sample RIPA-soluble protein extracts for 1 h at 4 °C. After washing in PBS-T, immunoprecipitated proteins were eluted from the beads with Laemmli Sample Buffer (Bio-Rad Laboratories, Hercules, CA, USA; 1610737) added with 5% β-mercaptoethanol by incubating samples for 10 min at 70 °C. Immunoprecipitation, input, and output samples were then loaded on 7.5% gels and analysed through a western blot.
Proteasome activity assay
SH-SY5Y cells were seeded in 6-well plates at 300,000 cells/well and transfected as previously described. Un-transfected samples were treated with 1 μM MG132 for 16 h to block the 26S proteasome as control. 48 h after transfection, cells were harvested in their medium, centrifuged at 600× g for 5 min, and washed three times in PBS. Pellets were then homogenised in PBS added with 0.5% NP-40 and centrifuged at 1300× g for 15 min. Supernatants were subsequently collected and protein concentration was quantified as described. Reaction mixtures were prepared by diluting 50 μg total proteins in 50 mM HEPES-KOH pH 8.0 and added with 5 mM EGTA and 5 mM ATP to a final volume of 500 μl. 50 nM AMC-conjugated substrates were added to the reaction mixtures to quantify the chymotryptic-like (Sigma-Aldrich, Saint Louis, MI, USA; N -Suc-LLVY-AMC, S6510) and the caspase-like (Sigma-Aldrich, Saint Louis, MI, USA; Z-LLE-AMC, C0483) activities of the 26S proteasome. Finally, samples were incubated for 45 min at 37 °C and fluorescence was measured at 340 nm excitation and 460 nm emission wavelengths using an Enspire® Multimode Plate Reader (PerkinElmer, Inc., Waltham, MA, USA).
Protein solubility predictions
CamSol ( http://www-vendruscolo.ch.cam.ac.uk/camsolmethod.html ; accessed on November 20, 2022) was used to predict the intrinsic solubility profile of WT, N999Vfs*40, and C975Vfs*73 KIF5A C-terminal tails with the CamSol Intrinsic method [ 34 ]. The following sequences were used as input:
YFANSCTSSGATSSGGPLASYQKANMDNGNATDINDNRSDLPCGYEAEDQAKLFPLHQETAAS for WT KIF5A (amino acids 970–1032);
YFANSCTSSGATSSGGPLASYQKANMDNGVTCRVAMRLRTRPSFSLSTKRQQPANLPHPRLHTCTFSF for N999Vfs*40 KIF5A (amino acids 970–1037);
YFANSVPAVDPHLLAAPWLPTRRPTWTMDMPQISMTIGVTCRVAMRLRTRPSFSLSTKRQQPANLPHPRLHTCTFSF for C975Vfs*73 KIF5A (amino acids 970–1046).
Live imaging
NSC-34 cells were seeded in 35-mm glass bottom dishes at 50,000 cells/well and transfected as previously described. 24 h or 48 h after transfection, cells were imaged in their medium added with 20 mM HEPES pH 7.4 at 37 °C and 5% CO 2 with an LSM 900 confocal microscope using a 63× oil-immersion lens. Live imaging sequences were acquired at 1 frame every 1.5–2 s for up to 300 s. For fluorescence recovery after photobleaching, one pre-bleach image preceded photobleaching with a 5 mW 488 nm laser at 100% for 3 s. Images were processed using ImageJ/Fiji (version 2.9.0).
Unpaired two-sided Student’s t -test and one- or two-way ANOVA tests followed by Fisher’s LSD or Sidak’s post-tests were applied, according to figure captions. Gaussian distribution was assumed in all cases and equal variance was confirmed by Brown–Forsythe test. P < 0.05 was considered significant. All analyses were performed using GraphPad PRISM (version 8.0.2). For the CHX chase assay (Fig. 3D ), images in which bands corresponding to WT or mutant KIF5A baseline (i.e. 0 h) displayed comparable optical densities were chosen for data analysis in order to set a virtually identical reference value between the tested conditions, even if the images were acquired at different exposure times. For each experimental condition, mean normalised optical densities of the reference bands were set at 100 and all other mean values were plotted as a percentage of the reference values.
Data availability
Data supporting the findings of this study are available from the corresponding authors upon request. Anonymised data from this study are available at https://zenodo.org/communities/besta and will be shared by request from any qualified investigator.
Hirokawa N, Noda Y, Tanaka Y, Niwa S. Kinesin superfamily motor proteins and intracellular transport. Nat Rev Mol Cell Biol. 2009;10:682–96.
Article CAS PubMed Google Scholar
Miki H, Okada Y, Hirokawa N. Analysis of the kinesin superfamily: insights into structure and function. Trends Cell Biol. 2005;15:467–76.
Kaan HYK, Hackney DD, Frank K. The structure of the Kinesin-1 motor-tail complex reveals the mechanism of autoinhibition. Science. 2011;333:883–5.
Article CAS PubMed PubMed Central Google Scholar
Xia C-H, Roberts EA, Her L-S, Liu X, Williams DS, Cleveland DW, et al. Abnormal neurofilament transport caused by targeted disruption of neuronal kinesin heavy chain KIF5A. J Cell Biol. 2003;161:55–66.
Kanai Y, Dohmae N, Hirokawa N. Kinesin transports RNA: isolation and characterization of an RNA-transporting granule. Neuron. 2004;43:513–25.
Karle KN, Möckel D, Reid E, Schöls L. Axonal transport deficit in a KIF5A(-/-) mouse model. Neurogenetics. 2012;13:169–79.
Campbell PD, Shen K, Sapio MR, Glenn TD, Talbot WS, Marlow FL. Unique function of Kinesin Kif5A in localization of mitochondria in axons. J Neurosci. 2014;34:14717–32.
Article PubMed PubMed Central Google Scholar
Liu M, Pi H, Xi Y, Wang L, Tian L, Chen M, et al. KIF5A-dependent axonal transport deficiency disrupts autophagic flux in trimethyltin chloride-induced neurotoxicity. Autophagy. 2021;17:903–24.
Reid E, Kloos M, Ashley-Koch A, Hughes L, Bevan S, Svenson IK, et al. A kinesin heavy chain (KIF5A) mutation in hereditary spastic paraplegia (SPG10). Am J Hum Genet. 2002;71:1189–94.
Crimella C, Baschirotto C, Arnoldi A, Tonelli A, Tenderini E, Airoldi G, et al. Mutations in the motor and stalk domains of KIF5A in spastic paraplegia type 10 and in axonal Charcot-Marie-Tooth type 2. Clin Genet. 2012;82:157–64.
Nicolas A, Kenna KP, Renton AE, Ticozzi N, Faghri F, Chia R, et al. Genome-wide analyses identify KIF5A as a novel ALS gene. Neuron. 2018;97:1268–1283.e6.
Article CAS PubMed Central Google Scholar
Brenner D, Yilmaz R, Müller K, Grehl T, Petri S, Meyer T, et al. Hot-spot KIF5A mutations cause familial ALS. Brain. 2018;141:688–97.
Duis J, Dean S, Applegate C, Harper A, Xiao R, He W, et al. KIF5A mutations cause an infantile onset phenotype including severe myoclonus with evidence of mitochondrial dysfunction. Ann Neurol. 2016;80:633–7.
Rydzanicz M, Jagła M, Kosinska J, Tomasik T, Sobczak A, Pollak A, et al. KIF5A de novo mutation associated with myoclonic seizures and neonatal onset progressive leukoencephalopathy. Clin Genet. 2017;91:769–73.
Ebbing B, Mann K, Starosta A, Jaud J, Schöls L, Schüle R, et al. Effect of spastic paraplegia mutations in KIF5A kinesin on transport activity. Hum Mol Genet. 2008;17:1245–52.
Baron DM, Fenton AR, Saez-Atienzar S, Giampetruzzi A, Sreeram A. Shankaracharya et al. ALS-associated KIF5A mutations abolish autoinhibition resulting in a toxic gain of function. Cell Rep. 2022;39:110598.
Nakano J, Chiba K, Niwa S. An ALS‐associated KIF5A mutant forms oligomers and aggregates and induces neuronal toxicity. Genes Cells. 2022;27:421–35.
Pant DC, Parameswaran J, Rao L, Loss I, Chilukuri G, Parlato R, et al. ALS‐linked KIF5A ΔExon27 mutant causes neuronal toxicity through gain‐of‐function. EMBO Rep. 2022;23:e54234.
Richards S, Aziz N, Bale S, Bick D, Das S, Gastier-Foster J, et al. Standards and guidelines for the interpretation of sequence variants: a joint consensus recommendation of the American College of Medical Genetics and Genomics and the Association for Molecular Pathology. Genet Med. 2015;17:405–24.
Lynch DS, Koutsis G, Tucci A, Panas M, Baklou M, Breza M, et al. Hereditary spastic paraplegia in Greece: characterisation of a previously unexplored population using next-generation sequencing. Eur J Hum Genet. 2016;24:857–63.
Article PubMed Google Scholar
Santangelo S, Bossolasco P, Magri S, Colombrita C, Invernizzi S, Gellera C, et al. Generation of an iPSC line from a patient with spastic paraplegia type 10 carrying a novel mutation in KIF5A gene. Stem Cell Res. 2023;66:103008.
Ioannidis NM, Rothstein JH, Pejaver V, Middha S, McDonnell SK, Baheti S, et al. REVEL: an ensemble method for predicting the pathogenicity of rare missense variants. Am J Hum Genet. 2016;99:877–85.
Rentzsch P, Witten D, Cooper GM, Shendure J, Kircher M. CADD: predicting the deleteriousness of variants throughout the human genome. Nucleic Acids Res. 2019;47:D886–94.
Cedarbaum JM, Stambler N, Malta E, Fuller C, Hilt D, Thurmond B, et al. The ALSFRS-R: a revised ALS functional rating scale that incorporates assessments of respiratory function. J Neurol Sci. 1999;169:13–21.
DeBoer SR, You Y, Szodorai A, Kaminska A, Pigino G, Nwabuisi E, et al. Conventional kinesin holoenzymes are composed of heavy and light chain homodimers. Biochemistry. 2008;47:4535–43.
Pareyson D, Saveri P, Sagnelli A, Piscosquito G. Mitochondrial dynamics and inherited peripheral nerve diseases. Neurosci Lett. 2015;596:66–77.
Soustelle L, Aimond F, Andrés CL, Brugioti V, Raoul C, Layalle S. ALS-associated KIF5A mutation causes locomotor deficits associated with cytoplasmic inclusions, alterations of neuromuscular junctions and motor neuron loss. J Neurosci. 2023;43:8058–72.
Liu X, Klionsky DJ. Regulation of autophagic lysosome reformation by kinesin 1, clathrin and phosphatidylinositol-4,5-bisphosphate. Autophagy. 2018;14:1–2.
Toupenet Marchesi L, Leblanc M, Stevanin G. Current knowledge of endolysosomal and autophagy defects in hereditary spastic paraplegia. Cells 2021;10:1678.
Cozzi M, Ferrari V. Autophagy dysfunction in ALS: from transport to protein degradation. J Mol Neurosci. 2022;72:1456–81.
Pankiv S, Clausen TH, Lamark T, Brech A, Bruun J-A, Outzen H, et al. p62/SQSTM1 binds directly to Atg8/LC3 to facilitate degradation of ubiquitinated protein aggregates by autophagy. J Biol Chem. 2007;282:24131–45.
Myeku N, Figueiredo-Pereira ME. Dynamics of the degradation of ubiquitinated proteins by proteasomes and autophagy. J Biol Chem. 2011;286:22426–40.
Menéndez-Benito V, Verhoef LGGC, Masucci MG, Dantuma NP. Endoplasmic reticulum stress compromises the ubiquitin–proteasome system. Hum Mol Genet. 2005;14:2787–99.
Sormanni P, Vendruscolo M. Protein solubility predictions using the CamSol method in the study of protein homeostasis. Cold Spring Harb. Perspect. Biol. 2019;11:a033845.
Riggs CL, Kedersha N, Ivanov P, Anderson P. Mammalian stress granules and P bodies at a glance. J Cell Sci. 2020;133:jcs242487.
de Boer EMJ, van Rheenen W, Goedee HS, Kamsteeg E-J, Brilstra EH, Veldink JH, et al. Genotype-phenotype correlations of KIF5A stalk domain variants. Amyotroph Lateral Scler Frontotemporal Degener. 2021;22:561–70.
Dutta M, Diehl MR, Onuchic JN, Jana B. Structural consequences of hereditary spastic paraplegia disease-related mutations in kinesin. Proc Natl Acad Sci USA. 2018;115:E10822–29.
Diefenbach RJ, Mackay JP, Armati PJ, Cunningham AL. The C-terminal region of the stalk domain of ubiquitous human kinesin heavy chain contains the binding site for kinesin light chain. Biochemistry. 1998;37:16663–70.
Pino MG, Rich KA, Hall NJ, Jones ML, Fox A, Musier-Forsyth K, et al. Heterogeneous splicing patterns resulting from KIF5A variants associated with amyotrophic lateral sclerosis. Hum Mol Genet. 2023;32:3166–80.
Rich KA, Pino MG, Yalvac ME, Fox A, Harris H, Balch MHH, et al. Impaired motor unit recovery and maintenance in a knock-in mouse model of ALS-associated Kif5a variant. Neurobiol Dis. 2023;182:106148.
Fukuoka M, Okazaki S, Kim K, Nukui M, Inoue T, Kuki I, et al. Preliminary report for epilepsia open: a case of West syndrome with severe global developmental delay and confirmed KIF5A gene variant. Epilepsia Open. 2021;6:230–4.
Nakajima K, Yin X, Takei Y, Seog D-H, Homma N, Hirokawa N. Molecular motor KIF5A is essential for GABA(A) receptor transport, and KIF5A deletion causes epilepsy. Neuron. 2012;76:945–61.
Wang M, Marín A. Characterization and prediction of alternative splice sites. Gene. 2006;366:219–27.
Reese MG, Eeckman FH, Kulp D, Haussler D. Improved splice site detection in Genie. J Comput. Biol. 1997;4:311–23.
Jaganathan K, Kyriazopoulou Panagiotopoulou S, McRae JF, Darbandi SF, Knowles D, Li YI, et al. Predicting splicing from primary sequence with deep learning. Cell. 2019;176:535–548.e24.
Jian X, Boerwinkle E, Liu X. In silico prediction of splice-altering single nucleotide variants in the human genome. Nucleic Acids Res. 2014;42:13534–44.
Download references
Acknowledgements
The authors thank Prof. Giampietro Schiavo, Dr. James N. Sleigh and Dr. Jose Norberto Vargas (Department of Neuromuscular Diseases, Queen Square Institute of Neurology, University College London) for their support in live imaging experiments.
SM, LN, CM, CG, DDB and FT are members of the European Reference Network for Rare Neurological Disorders (project number 739510). This research was funded by: Italian Ministry of Health (grant RF-2018-12367768 and RRC 2023 to FT); Fondazione Regionale per la Ricerca Biomedica (grant CP 20/2018 (Care4NeuroRare) to FT). Additional support was received from: The Company of Biologists (Travelling Fellowship n. JCSTF2205742 to MCo); European Molecular Biology Organisation (Scientific Exchange Grant n. 9643 to MCo); Fondazione Telethon (n. GGP19128 to AP); Fondazione Cariplo (n. 2021-1544 to SM and RC); Association Française contre les Myopathies (AFM Telethon n. 23236 to AP); Ministero dell’Università e della Ricerca (MIUR)—Italy [PRIN—Progetti di ricerca di interesse nazionale (n. 2017F2A2C5 to AP; n. 2022EFLFL8 to AP; n. 2020PBS5MJ to VC; n. 2022KSJZF5 to VC); PRIN—Progetti di ricerca di interesse nazionale—bando 2022, PNRR finanziato dall’Unione europea—Next Generation EU, componente M4C2, investimento 1.1 (n. P2022B5J32 to RC and n. P20225R4Y5 to VC); CN3: RNA—Codice Proposta: CN_00000041; Tematica Sviluppo di terapia genica e farmaci con tecnologia a RNA (Centro Nazionale di Ricerca—CN3 National Center for Gene Therapy and Drugs based on RNA Technology to AP); Progetto Dipartimenti di Eccellenza to DiSFeB]; Università degli Studi di Milano (piano di sviluppo della ricerca (PSR) UNIMI - linea B to BT, VF and RC).
Author information
These authors contributed equally: Marta Cozzi, Stefania Magri.
These authors jointly supervised this work: Riccardo M. Cristofani, Franco Taroni, Angelo Poletti.
Authors and Affiliations
Department of Pharmacological and Biomolecular Sciences “Rodolfo Paoletti” (DiSFeB), Università degli Studi di Milano, 20133, Milan, Italy
Marta Cozzi, Barbara Tedesco, Guglielmo Patelli, Veronica Ferrari, Elena Casarotto, Marta Chierichetti, Paola Pramaggiore, Laura Cornaggia, Margherita Piccolella, Mariarita Galbiati, Paola Rusmini, Valeria Crippa, Riccardo M. Cristofani & Angelo Poletti
Unit of Medical Genetics and Neurogenetics, Fondazione IRCCS Istituto Neurologico Carlo Besta, 20133, Milan, Italy
Stefania Magri, Barbara Tedesco, Guglielmo Patelli, Lorenzo Nanetti, Caterina Mariotti, Elisa Sarto, Viviana Pensato, Cinzia Gellera, Daniela Di Bella & Franco Taroni
Department of Biomedical, Metabolic and Neural Sciences, University of Modena and Reggio Emilia, Centre for Neuroscience and Neurotechnology (CfNN), 41125, Modena, Italy
Jessica Mandrioli
Department of Neurosciences, Azienda Ospedaliero-Universitaria di Modena, 41126, Modena, Italy
Unit of Rare Neurological Diseases, Fondazione IRCCS Istituto Neurologico Carlo Besta, 20133, Milan, Italy
Davide Pareyson & Chiara Pisciotta
Department of Pediatric Neurosciences, Fondazione IRCCS Istituto Neurologico Carlo Besta, 20133, Milan, Italy
Stefano D’Arrigo
Department of Medical Biotechnology and Translational Medicine, Università degli Studi di Milano, 20054, Segrate, Italy
Antonia Ratti
Department of Neuroscience – Laboratory of Neuroscience, IRCCS Istituto Auxologico Italiano, 20095, Cusano Milanino, Italy
You can also search for this author in PubMed Google Scholar
Contributions
MCo, SM, BT, RC, FT and AP: study concept and design, writing and revision of the paper. MCo, SM, BT, GP and AR: acquisition of data and statistical analysis. MCo, SM, BT, GP, VF, EC, MCh, PP, LC, MP, MG, PR, VC, AR, VP, CG, RC, FT and AP: analysis and interpretation of data. SM, JM, DP, CP, SD, LN, CM, ES, VP, DDB and CG: clinical characterisation and genetic screening of patients. All authors read and approved the final paper.
Corresponding authors
Correspondence to Franco Taroni or Angelo Poletti .
Ethics declarations
Competing interests.
The authors declare no competing interests.
Each individual providing a biological sample for this study signed an informed consent approved by the Institutional Review Board of the Fondazione IRCCS Istituto Neurologico Carlo Besta, in agreement with the Declaration of Helsinki and the Belmont Report.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Edited by Paolo Pinton
Supplementary information
Supplementary figures, supplementary table 1 word format, supplementary table 2 word format, supplementary table 3 word format, supplementary table 4 word format, supplementary table 5 word format, supplementary immunofluorescence images, unedited blot images, rights and permissions.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Cite this article.
Cozzi, M., Magri, S., Tedesco, B. et al. Altered molecular and cellular mechanisms in KIF5A -associated neurodegenerative or neurodevelopmental disorders. Cell Death Dis 15 , 692 (2024). https://doi.org/10.1038/s41419-024-07096-5
Download citation
Received : 28 February 2024
Revised : 17 September 2024
Accepted : 19 September 2024
Published : 27 September 2024
DOI : https://doi.org/10.1038/s41419-024-07096-5
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies

IMAGES
VIDEO
COMMENTS
The null hypothesis (H0) answers "No, there's no effect in the population.". The alternative hypothesis (Ha) answers "Yes, there is an effect in the population.". The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
Null hypothesis: µ ≥ 70 inches. Alternative hypothesis: µ < 70 inches. A two-tailed hypothesis involves making an "equal to" or "not equal to" statement. For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null and alternative hypotheses in this case would be: Null hypothesis: µ = 70 inches.
The following are hypothetical examples of an alternative hypothesis. Years of kendo experience has a positive correlation with personal resilience.Coffee drinkers have higher average productivity than people who don't drink coffee.Temperature influences the volume of alcohol.Rain causes mud puddles.There is a positive correlation between the ...
Alternative hypothesis. Alternative hypothesis \(\left(H_{A}\right)\): If we conclude that the null hypothesis is false, or rather and more precisely, we find that we provisionally fail to reject the null hypothesis, then we provisionally accept the alternative hypothesis.The view then is that something other than random chance has influenced the sample observations.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
10.1 - Setting the Hypotheses: Examples. A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or ...
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There's no effect in the population. Alternative hypothesis (HA): There's an effect in the population. The effect is usually the effect of the independent variable on the dependent ...
H0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt. Ha: The alternative hypothesis: It is a claim about the population that is contradictory to H0 and what we conclude when we reject H0. Since the ...
Example Consider a test of hypothesis for the mean of a normal distribution, where we test . The test statistic is the z-statistic where is the sample mean, is the variance of the distribution and is the sample size. If we run a two-tailed test with critical value , the critical region is the union of the right and left tails of the ...
The alternative hypothesis is one of two mutually exclusive hypotheses in a hypothesis test. The alternative hypothesis states that a population parameter does not equal a specified value. Typically, this value is the null hypothesis value associated with no effect, such as zero.If your sample contains sufficient evidence, you can reject the null hypothesis and favor the alternative hypothesis.
Some of the following statements refer to the null hypothesis, some to the alternate hypothesis. State the null hypothesis, H 0, and the alternative hypothesis. H a, in terms of the appropriate parameter (μ or p). The mean number of years Americans work before retiring is 34. At most 60% of Americans vote in presidential elections.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement of no difference between the variables-they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
Types. Basically, there are three types of the alternative hypothesis, they are; Left-Tailed: Here, it is expected that the sample proportion (π) is less than a specified value which is denoted by π 0, such that; H 1 : π < π 0. Right-Tailed: It represents that the sample proportion (π) is greater than some value, denoted by π 0.
There are 5 main steps in hypothesis testing: State your research hypothesis as a null hypothesis and alternate hypothesis (H o) and (H a or H 1). Collect data in a way designed to test the hypothesis. Perform an appropriate statistical test. Decide whether to reject or fail to reject your null hypothesis. Present the findings in your results ...
The alternative hypothesis is a hypothesis used in significance testing which contains a strict inequality. A test of significance will result in either rejecting the null hypothesis (indicating ...
Lesson 3: The idea of significance tests. Idea behind hypothesis testing. Examples of null and alternative hypotheses. Writing null and alternative hypotheses. P-values and significance tests. Comparing P-values to different significance levels. Estimating a P-value from a simulation. Estimating P-values from simulations.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. \(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
The alternative hypothesis is a claim that a population parameter is greater than, less than, or not equal to some value. For example, H a: μ> 5 H a: μ> 5, H a: μ <5 H a: μ <5, or H a: μ ≠ 5 H a: μ ≠ 5. The form of the alternative hypothesis depends on the wording of the hypothesis test. An alternative notation for H a H a is H 1 H 1.
The alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. Thus, our alternative hypothesis is the mathematical way of stating our research question. If we expect our obtained sample mean to be above or below the null hypothesis value, which we call a ...
Null Hypothesis (H0) - This can be thought of as the implied hypothesis. "Null" meaning "nothing.". This hypothesis states that there is no difference between groups or no relationship between variables. The null hypothesis is a presumption of status quo or no change. Alternative Hypothesis (Ha) - This is also known as the claim.
Statistics Unpaired two-sided Student's t -test and one- or two-way ANOVA tests followed by Fisher's LSD or Sidak's post-tests were applied, according to figure captions.
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.