multiple linear regression analysis research paper

• Open access
• Published: 24 May 2022

Multiple regression model to analyze the total LOS for patients undergoing laparoscopic appendectomy

• Teresa Angela Trunfio 1 ,
• Arianna Scala 2 ,
• Cristiana Giglio 3 ,
• Giovanni Rossi 4 ,
• Anna Borrelli 4 ,
• Maria Romano 5 &
• Giovanni Improta 2 , 6  

BMC Medical Informatics and Decision Making volume  22 , Article number:  141 ( 2022 ) Cite this article

25k Accesses

31 Citations

Metrics details

The rapid growth in the complexity of services and stringent quality requirements present a challenge to all healthcare facilities, especially from an economic perspective. The goal is to implement different strategies that allows to enhance and obtain health processes closer to standards. The Length Of Stay (LOS) is a very useful parameter for the management of services within the hospital and is an index evaluated for the management of costs. In fact, a patient's LOS can be affected by a number of factors, including their particular condition, medical history, or medical needs. To reduce and better manage the LOS it is necessary to be able to predict this value.

In this study, a predictive model was built for the total LOS of patients undergoing laparoscopic appendectomy, one of the most common emergency procedures. Demographic and clinical data of the 357 patients admitted at “San Giovanni di Dio e Ruggi d’Aragona” University Hospital of Salerno (Italy) had used as independent variable of the multiple linear regression model.

The obtained model had an R 2 value of 0.570 and, among the independent variables, the significant variables that most influence the total LOS were Age, Pre-operative LOS, Presence of Complication and Complicated diagnosis.

This work designed an effective and automated strategy for improving the prediction of LOS, that can be useful for enhancing the preoperative pathways. In this way it is possible to characterize the demand and to be able to estimate a priori the occupation of the beds and other related hospital resources.

Peer Review reports

Introduction

The appendix is a protrusion of the large intestine, located where the large intestine joins the small intestine. The appendix performs some immunological functions, but it is not a fundamental organ [ 1 ]. When something, such as undigested food residues obstruct the internal lumen, it inflames, causing the "appendicitis".

In emergency surgery, one of the most common conditions that require a surgery is appendicitis [ 2 ]. Appendicitis is primarily a disease of adolescents and young adults with a peak incidence in the second and third decades of life. There is a slight male preponderance of 3:2 in teenagers and young adults. In adults, the incidence of appendicitis is approximately 1.4 times greater in men than in women [ 3 ]. In general, the risk for men and women is estimated at 8.6% and 6.7%, respectively [ 4 ]. Then, on 100,000 case of acute appendicitis, a range between 114.44 and 481.60 require a surgical procedure [ 5 ]. This value is a function of the socioeconomic level of the countries considered, in fact, the risk of appendicitis is rising sharply, especially in industrialized countries.

In the post-war period, thanks to the use of antibiotics and in particular penicillin, mortality was reduced (from over 40–2%). In the case of uncomplicated diagnosis, mortality is 0.08–0.4% while it rises to 12% in the case of perforation [ 6 ]. The diagnosis of acute appendicitis is predominantly clinical, in that is based on the accurate evaluation of the data provided by the anamnestic collection and on the patient's physical examination. It can be difficult, occasionally taxing the diagnostic skills of even the most experienced surgeon [ 7 ]. Early diagnosis is an essential condition for an effective treatment.

Appendectomy is a surgical procedure that can basically be performed in two ways: laparoscopic appendectomy (LA) and open appendectomy (OA). Both procedures can be decisive, and the choice is conditioned in the first place by the patient's age and the severity of appendicitis, also by the surgeon's skills and the availability of hospital resources [ 8 ].

Since its introduction in 1983, LA has quickly become a common and more adopted practice [ 9 ]. Nguyen et al. showed both an increased used of LA compared of OA and that patients undergoing LA have generally a no complicate diagnosis, a shorter length of stay (LOS) and fewer post-operative complications, without the increasing of healthcare costs [ 10 ]. Kwok KayYau et al., instead, showed the efficacy of LA in the complicated appendicitis [ 11 ]. LA proves once again to be feasible and safe, with a significantly shorter operative time, lower incidence of wound infection, and reduced LOS compared with OA.

The LOS—measured in days—is defined as the difference between the date of admission and the date of discharge of the patient. It is linked to the severity of the medical conditions, age of patient and any complication of the medical diagnosis, or the treatment received [ 12 ].

LOS is useful for planning admission and so a direct indicator of effectiveness and efficiency that has an impact on the organization and costs. For these reasons, in literature there are many works that have used LOS as an indicator of quality [ 13 , 14 , 15 ]. In all aspects of the healthcare sector, the extraction of clinical and organizational data for advanced analysis [ 16 , 17 , 18 , 19 ] and for process improvement [ 20 , 21 , 22 , 23 ] has proven to be a fundamental support in patient management.

LOS modeling is also not new in the literature. Verburg et al. [ 24 ] compared the performance of eight regression models when predicting intensive care unit LOS, failing to obtain optimal results for any of them, while Lee et al. [ 25 ] show the high performance of robust gamma mixed regression for the study of pediatric LOS. In addition to regression models, multiple linear regression was used to predict the LOS for patients undergoing valvuloplasty by considering their characteristics [ 26 ]. Austin et al. [ 27 ] use statistical analysis or analyzing LOS in a cohort of patients undergoing CABG surgery, while Scala et al. [ 28 ] show the benefits of implementing classifiers for predicting LOS [ 29 , 30 , 31 , 32 , 33 ].

In this study, a predictive model of the hospital stay of patients undergoing laparoscopic appendectomy was constructed to study how certain clinical and demographic variables affect the LOS prediction. The present research work is an extension of our previous work [ 34 ] in which the dataset considered was extended both in terms of years of observation and comorbidities considered, also evaluating the impact of comorbidities. The model used is multiple linear regression, which has proven effective in different healthcare implementations.

The dataset, used in this study, included the information of 357 patients who have undergone an appendectomy in the five years 2016–2020 at the University Hospital “San Giovanni di Dio e Ruggi d’Aragona” of Salerno (Italy). The following variables was extracted from the hospital information system QuaniSDO:

Gender (Male / Female);

Comorbidities;

Diagnostic Related Group (DRG);

Date of admission, discharge and LC procedure;

From these, the independent and dependent variables of the MLR model were obtained. In particular, from the analysis of DRG it was possible to identify if a patient had Complications during surgery or Complicated diagnosis. From the date, the pre-operative LOS (date of LC procedure—date of admission) and the total LOS was calculated. From the comorbidities, the following additional independent variables have been defined:

Presence of comorbidities (yes / no);

Heart Disease (yes / no);

Diabetes (yes / no);

Hypertension (yes / no);

Obesity (yes / no);

Peritonitis (yes / no);

Cancer (yes / no).

Table 1 shows the distribution of the features into the sample.

The frequency of the groups of identified comorbidities on the population was calculated (Table 2 ). Frequency is a measure of the frequency of a disease or health condition in a population at a particular point in time [ 35 ], in this case in the five years 2016–2020.

IBM SPSS (Statistical Package for Social Science) ver. 27 was used to build a MLR model used to predict the total LOS [ 36 ].

• Multiple linear regression

In the last years, several data analytics methodologies have been proposed for supporting different applications [ 37 , 38 ]. One of the most used one is the Multiple Linear Regression, that is a statistical technique that uses several explanatory variables to predict the outcome of a response variable. Multiple linear regression represents an extension of the simple linear regression model that uses just one explanatory variable. In this work, MLR model was implemented to predict the value of dependent variable Y (total LOS) starting from knowledge of several independent variables (Age, Gender, Pre-operative LOS, Complications during surgery, Complicated diagnosis, Presence of comorbidities, Heart Disease, Diabetes, Hypertension, Obesity, Peritonitis and Cancer).

The equation for a multiple linear regression is:

where Y is the total LOS, β 0 is intercept value, x i are the twelve independent variables (pre-operative LOS, presence of complications, complicated diagnosis, gender, age, presence of comorbidities, heart disease, diabetes, hypertension, obesity, peritonitis and cancer) and β i are the estimated regression coefficients of respective independent variables. \(\varepsilon\) is the model error, i.e. the variation of our estimate of Y with respect to the real value. Before creating the model, the following six hypotheses must be verified:

The linear relationship between the independent and dependent variable. It can be checked through the scatter plot.

Absence of multicollinearity. Multicollinearity determines important changes in the values of the regression coefficients. Tolerance = 1- \(R_{i}^{2}\) and Variance Inflation Factor (VIF) =  \(\frac{1}{{1 - R_{i}^{2} }}\) —where \(R_{i}^{2}\) is the proportion of the variation in the dependent variable that is predictable from the independent variables—are used to verify this assumption.

The independence of the residuals. In this case, the result of Durbin-Watson statistical test is analyzed.

The residuals have constant variance. It is possible to verify it by building the graph of "standardized residuals" against the "standardized predicted value".

The residuals are normally distributed. To verify this assumption a quantile–quantile (Q-Q) plot can be used.

Presence of outliers. The Cook's distance values always less than 1 guarantees the absence of outliers.

As a measure of the goodness of fit of a multiple regression model, the coefficient of determination, known as R 2 , is used. The linear determination index R 2 represents the fraction of variance of Y which is explainable by the X regressors included in the model.

R 2 shows how well the terms (data points) fit a curve or line but there is also Adjusted-R 2 that indicates how well terms fit a curve or line, but adjusts for the number of terms in a model. This is why in multiple linear regression with several predictors it is advisable to observe Adjusted-R 2 [ 39 ].

where n represents the total sample size and m is the number of predictors. In most cases it turns out: 0 ≥ R 2  ≥ 1. The \(R^{2}\) and \(\overline{{R^{2} }}\) tell whether the regressors are suitable for predicting the values of the dependent variable in the sample of data used. If \(R^{2}\) (or \(\overline{{R^{2} }}\) ) tends to one, the regressors produce good predictions of the dependent variable, if \(R^{2}\) (or \(\overline{{R^{2} }}\) ) tends to 0 the opposite is true. The level of significant α is equal to 0.05.

Before building the MLR model, the six hypotheses were tested. The result of Durbin-Watson test was 1.505 and it was between the acceptable range of [1.5; 2.5] to demonstrate the independence of residual. The Cook’s distance for each observation was less than 1, so there were not outliers in the dataset that negatively affect the estimate of the coefficients. For the 2nd assumption, Table 3 shows the values of VIF, and Tolerance obtained for each independent variable.

The VIF values were always less than 10 and the Tolerance values were always greater than 0.2, so the absence of multicollinearity was verified.

Figure  1 shows the Q-Q plot, a graph “observed value” against “expected normal value” used to test the normally distribution of the residual values.

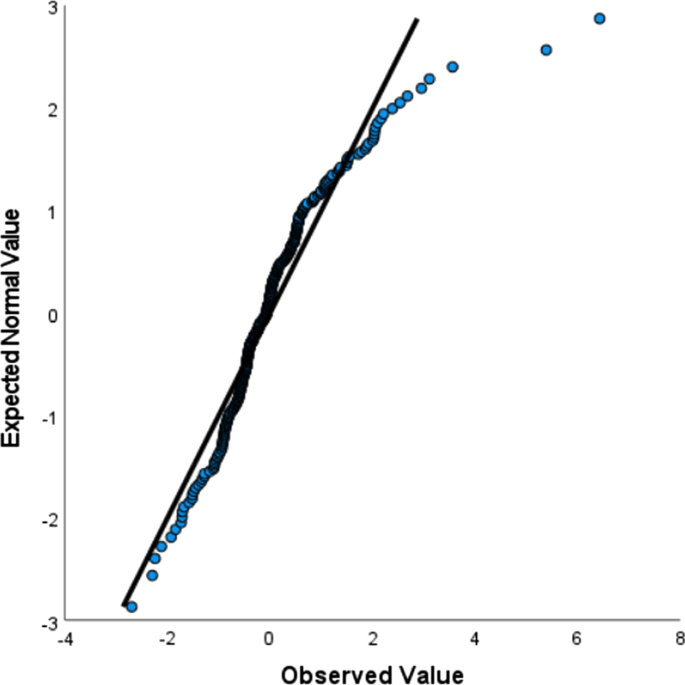
Normal Q-Q Plot of Standardized Residual

As can be seen from the Fig.  1 , the points are quite close to the line. There are few outliers, but which is proven not to affect the goodness of the coefficients estimation. In fact, Cook's distance was calculated for each point and the maximum value obtained was 0.8, which is well below the required threshold 1.

Figure  2 shows the graph of "standardized residuals" against the "standardized predicted value" used to verify that the variance of the residuals is constant.

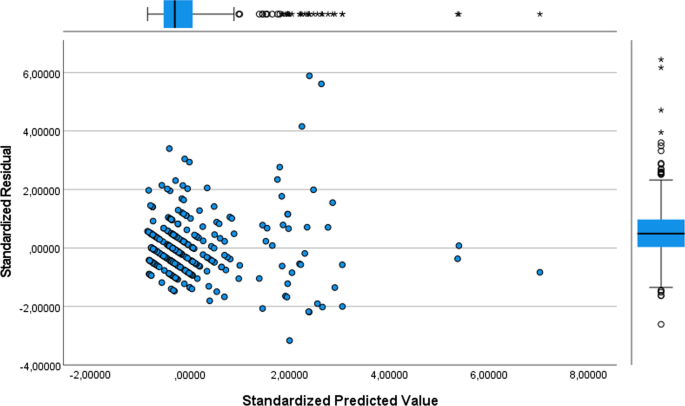
Plot of "standardized residuals" against the "standardized predicted value"

The variance of residuals was not constant across predicted values, so there was a moderate violation of homoscedasticity, which was however considered acceptable. In fact, Table 4 shows that the analysis of variance is significant, i.e. there is indeed a linear dependence between the dependent variable and the regressor variable (p-value < 0.05). Then, the MLR model was implemented. Table 4 shows the performance of the model.

The coefficient of determination (R 2 ) was greater than 0.5 so it can be considered a good preliminary model to represent the problem. The p-values below the alpha value are highlighted in bold.

Table 5 shows the coefficients of the model and the results of the t-test, used to study the significance of the regression coefficients (βi). P-values < 0.05 were considered statistically significant.

The p-value was less than 0.05 for the Pre-operative LOS, the Presence of complication, Complicated diagnosis and Age. Among these variables that significantly influence LOS, the pre-operative LOS has the highest coefficient in accordance with the definition of total LOS (pre-operative LOS + post-operative LOS).

The aim of this work was to build a predictive model, using the multiple linear regression, of the total LOS for patients undergoing a laparoscopic appendectomy at "San Giovanni di Dio e Ruggi d’Aragona" University Hospital of Salerno (Italy) in the five-year period 2016–2020. Starting from a group of selected information (Gender, Age, Comorbidities, Diagnostic Related Group (DRG), Date of admission, Date of discharge and Date of LC procedure) the independent variables of the model were obtained. In particular, the analysis of the comorbidities made it possible to divide patients into subgroups by categories of pathologies with higher frequency in our sample.

A simple model has been obtained with a value of R 2 equal to 0.570. The value of R 2 , even if slightly, exceeds the value of 0.5 that support its use for this task. In fact, the linear models have the advantage of being easy to understand and use during the activities carried out by healthcare staff. The results of t-test demonstrate that Pre-operative LOS, Presence of complication, Complicated Diagnosis and Age are the variables that most influence the total LOS. The Pre-operative LOS is a value that we expected because it is linked with the definition of LOS. The result of the influences is actually in line with what can be read from the literature on the topic. For example, Liu et al. [ 40 ] show how age is a factor influencing procedures related to 18 different DRGs. Remaining in the theme of appendectomy, Ponsiglione et al. [ 41 ] showed how in procedures performed in urgency there is a strong link between LOS and comorbidities, while Demir et al. [ 42 ] highlight how both postoperative and total LOS of the patients undergoing appendectomy are more likely to be affected by patients' demographic characteristics and clinical needs. In addition, other variables not included in this study have significant effects on LOS. For example, Crandall et al. [ 43 ] showed as the operative time of day was a surprisingly important determinant of hospital LOS while Cheong et al. [ 44 ] highlighted a significantly longer hospital stay was associated with open appendectomy, pediatric surgeon, and the Territories for simple appendicitis in pediatric patients.

The multi-year study showed a dependence of total LOS on age that was not evident in the previous model [ 30 ]. This information is important for the possible creation of pathways for specific age groups, for the management of complications or for the standardization of the pre-operative phase, as already done by the hospital for femur fracture in patients older than 65 years [ 45 ].

This work demonstrated that the MLR represents a valid preliminary support to characterize the demand and to be able to estimate a priori the occupation of the beds and the use of other hospital resources.

Although the work is novel in terms of sample size and number of comorbidities analyzed, it is not without limitations. In particular, the model is not validated through the use of datasets from other hospitals, the impact that other procedures, such as those related to possible complications, may have on LOS is not included, and the value of R. 2 is slightly above the 0.5 value and this makes it necessary to search for a more robust predictive model. For example, classification algorithms (such as Logistic Regression) could be a valid alternative [ 46 ].

In this work, the data of 357 patients undergoing LC at "San Giovanni di Dio e Ruggi d’Aragona" University Hospital of Salerno (Italy) in the five-year period 2016–2020 was study using MLR model, whose aim is to predict LOS on the basis of patients' clinical and demographic variables. Among the independent variables, Pre-operative LOS, presence of complication, complicated diagnosis and age are the variables that most influence the total LOS. The results are in line with what can be found in the scientific literature, in which the impact of age, complicated diagnoses, and complications is discussed for several clinical procedures including appendectomy. The model, in addition, has good performance that validates it as a prediction tool to be given for use by clinicians. The linear model, however, although very simple in its interpretation, could not be robust enough. Therefore, future developments will include validation of the model with multicenter studies as well as the use of advanced data processing tools.

Availability of data and materials

The datasets generated and/or analyzed during the current study are not publicly available for privacy reasons but are available from the corresponding author on reasonable request.

Abbreviations

Laparoscopic Appendectomy

Open Appendectomy

Length Of Stay

https://www.news-medical.net/health/Why-do-Humans-have-an-Appendix-(Italian).aspx .

Cervellin G, Mora R, Ticinesi A, et al. Epidemiology and outcomes of acute abdominal pain in a large urban Emergency Department: retrospective analysis of 5,340 cases. Ann Transl Med. 2016;4:362.

Article   Google Scholar  

Alvarado A. Clinical approach in the diagnosis of acute appendicitis. In: Garbuzenko D (ed) Current issues in the diagnostics and treatment of acute appendicitis. Intech Open;2018: p. 13–42.

Krzyzak M, Mulrooney SM. Acute appendicitis review: background, epidemiology, diagnosis, and treatment. Cureus. 2020;12(6):e8562. https://doi.org/10.7759/cureus.8562 .

Article   PubMed   PubMed Central   Google Scholar  

Salomon JA, Wang H, Freeman MK, Vos T, Flaxman AD, Lopez AD, Murray CJ. Healthy life expectancy for 187 countries, 1990–2010: a systematic analysis for the Global Burden Disease Study 2010. The Lancet. 2012;380(9859):2144–62.

Stein GY, Rath-Wolfson L, Zeidman A, et al. Sex differences in the epidemiology, seasonal variation, and trends in the management of patients with acute appendicitis. Langenbecks Arch Surg. 2012;397:1087–92. https://doi.org/10.1007/s00423-012-0958-0 .

Article   PubMed   Google Scholar  

Marudanayagam R, Williams GT, Rees BI. Review of the pathological results of 2660 appendicectomy specimens. J Gastroenterol. 2006;41(8):745–9. https://doi.org/10.1007/s00535-006-1855-5 .

Prystowsky JB, Pugh CM, Nagle AP. Appendicitis. Curr Probl Surg. 2005;42(10):694–742. https://doi.org/10.1067/j.cpsurg.2005.07.005 .

Mandrioli M, et al. Advances in laparoscopy for acute care surgery and trauma. World J Gastroenterol. 2016;22(2):668–80. https://doi.org/10.3748/wjg.v22.i2.668 .

Article   CAS   PubMed   PubMed Central   Google Scholar  

Nguyen NT, et al. Trends in utilization and outcomes of laparoscopic versus open appendectomy. Am J Surg. 2004;188(6):813–20.

Yau KK, et al. Laparoscopic versus open appendectomy for complicated appendicitis. J Am Coll Surg. 2007;205(1):60–5.

McAleese P, Odling-Smee W. The effect of complications on length of stay. Ann Surg. 1994;220(6):740.

Article   CAS   Google Scholar  

McVeigh TP, et al. Assessing the impact of an ageing population on complication rates and in-patient length of stay. Int J Surg. 2013;11(9):872–5.

Moore L, et al. Derivation and validation of a quality indicator of acute care length of stay to evaluate trauma care. Ann Surg. 2014;260(6):1121–7.

Picone I, Latessa I, Fiorillo A, Scala A, Angela Trunfio T, Triassi M (2021) Predicting length of stay using regression and Machine Learning models in Intensive Care Unit: a pilot study. In: 2021 11th international conference on biomedical engineering and technology; p. 52–8.

Ponsiglione AM, Cesarelli G, Amato F, Romano M. Optimization of an artificial neural network to study accelerations of foetal heart rhythm. In: 2021 IEEE 6th international forum on research and technology for society and industry (RTSI); 2021. p. 159–64. https://doi.org/10.1109/RTSI50628.2021.9597213 .

Cesarelli M, Romano M, Bifulco P, Improta G, D’Addio G. An application of symbolic dynamics for FHRV assessment. Stud Health Technol Inform. 2012;180:123–7.

PubMed   Google Scholar  

Improta G, Ponsiglione AM, Parente G, Romano M, Cesarelli G, Rea T et al. Evaluation of medical training courses satisfaction: Qualitative analysis and analytic hierarchy process. In: European medical and biological engineering conference; p. 518–26; 2020. Springer, Cham.

Cesarelli G, Scala A, Vecchione D, Ponsiglione AM, Guizzi G. An innovative business model for a multi-echelon supply chain inventory management pattern. J Phys Conf Ser. 2021;1828(1):012082.

Improta G, Luciano MA, Vecchione D, Cesarelli G, Rossano L, Santalucia I, Triassi M. Management of the diabetic patient in the diagnostic care pathway. In: Jarm T, Cvetkoska A, Mahnič-Kalamiza S, Miklavcic D (eds) 8th European medical and biological engineering conference. EMBEC 2020. IFMBE proceedings, vol 80;2021. Springer, Cham. https://doi.org/10.1007/978-3-030-64610-3_88

Converso G, Improta G, Mignano M, Santillo LC. A simulation approach for agile production logic implementation in a hospital emergency unit. In: Intelligent software methodologies, tools and techniques, vol. 532, p. 623–34;2015. Springer.

Trunfio TA, Scala A, Borrelli A, Sparano M, Triassi M, Improta G. Application of the Lean Six Sigma approach to the study of the LOS of patients who undergo laparoscopic cholecystectomy at the San Giovanni di Dio and Ruggi d'Aragona University Hospital. In 2021 5th international conference on medical and health informatics (ICMHI 2021). Association for Computing Machinery, New York, NY, USA, 50–54;2021. https://doi.org/10.1145/3472813.3472823

Raiola E, Triassi M, Improta G, Di Cicco MV, Montella E, Ferraro A, Cerchione R, Centobelli P. Implementation of lean practices to reduce healthcare associated infections. Int J Healthc Technol Manag. 2020;18:51. https://doi.org/10.1504/IJHTM.2020.10039887 .

Verburg IWM, et al. Comparison of regression methods for modeling intensive care length of stay. PLoS ONE. 2014;9(10):e109684.

Lee AH, et al. A robustified modeling approach to analyze pediatric length of stay. Ann Epidemiol. 2005;15(9):673–7.

Scala A, Trunfio TA, De Coppi L, Rossi G, Borrelli A, Triassi M, Improta G. Regression models to study the total LOS related to valvuloplasty. Int J Environ Res Public Health. 2022;19(5):3117.

Austin PC, Rothwell DM, Tu JV. A comparison of statistical modeling strategies for analyzing length of stay after CABG surgery. Health Serv Outcomes Res Method. 2002;3(2):107–33.

Scala A, Angela Trunfio T, Lombardi A, Giglio C, Borrelli A, Triassi M. A comparison of different Machine Learning algorithms for predicting the length of hospital stay for patients undergoing cataract surgery. In: 2021 International symposium on biomedical engineering and computational biology; p. 1–4.

Austin PC, Tu JV, Daly PA, Alter DA. The use of quantile regression in health care research: a case study examining gender differences in the timeliness of thrombolytic therapy. Stat Med. 2005;24(5):791–816.

Scala A, Trunfio TA, Borrelli A, Ferrucci G, Triassi M, Improta G. Modelling the hospital length of stay for patients undergoing laparoscopic cholecystectomy through a multiple regression model. In 2021 5th international conference on medical and health informatics (ICMHI 2021). Association for Computing Machinery, New York, NY, USA. P. 68–72; 2021. https://doi.org/10.1145/3472813.3472826 .

Trunfio TA, Maria Ponsiglione A, Ferrara A, Borrelli A, Gargiulo PA. Comparison of different regression and classification methods for predicting the length of hospital stay after cesarean sections. In: 2021 5th international conference on medical and health informatics. 2021.

Lukong AMY, Jafaru Y. Covid-19 pandemic challenges, coping strategies and resilience among healthcare workers: A multiple linear regression analysis. Afr J Health Nurs Midwif. 2021;4:16–27.

Google Scholar  

Turgeman L, May JH, Sciulli R. Insights from a machine learning model for predicting the hospital Length of Stay (LOS) at the time of admission. Expert Syst Appl. 2017;78:376–85.

Trunfio TA, Scala A, Giglio C, Rossi G, Borrelli A, Gargiulo P, Romano M. Modelling the hospital length of stay for patients undergoing laparoscopic appendectomy through a Multiple Regression Model. In 2021 International Symposium on Biomedical Engineering and Computational Biology (BECB 2021). Assoc Comput Mach. 2021;36:1–5. https://doi.org/10.1145/3502060.3503644 .

https://www.health-ni.gov.uk/articles/prevalence-statistics#:~:text=Prevalence%20is%20a%20measure%20of,within%20a%20particular%20time%20period .

IBM Corp. IBM SPSS statistics for windows; version 27.0; IBM Corp: Armonk, NY, USA, 2020.

Sperlí G. A deep learning based community detection approach. In: Proceedings of the 34th ACM/SIGAPP symposium on applied computing, p. 1107–1110. 2019. https://doi.org/10.1145/3297280.3297574 .

De Santo A, Galli A, Gravina M, Moscato V, Sperlì G. Deep Learning for HDD health assessment: an application based on LSTM. IEEE Trans Comput. 2020;71(1):69–80. https://doi.org/10.1109/TC.2020.3042053 .

Everitt BS, Skrondal A. The Cambridge dictionary of statistics. Cambridge: Cambridge University Press; 2010.

Book   Google Scholar  

Yingxin L, Jim PMC. Factors influencing patients’ length of stay. Aust Health Rev. 2001;24:63–70.

Maria Ponsiglione A., et al. Modeling the variation in length of stay for appendectomy and cholecystectomy interventions in the emergency general surgery. In: 2021 international symposium on biomedical engineering and computational biology. 2021.

Demir C, et al. The factors affecting length of stay of the patients undergoing appendectomy surgery in a military teaching hospital. Mil Med. 2007;172(6):634–9.

Crandall M, et al. Acute uncomplicated appendicitis: case time of day influences hospital length of stay. Surg Infect. 2009;10(1):65–9.

Cheong LHA, Emil S. Determinants of appendicitis outcomes in Canadian children. J Pediatr Surg. 2014;49(5):777–81.

Scala A, Ponsiglione AM, Loperto I, Della Vecchia A, Borrelli A, Russo G, Triassi M, Improta G. Lean six sigma approach for reducing length of hospital stay for patients with femur fracture in a University Hospital. Int J Environ Res Public Health. 2021;18:2843. https://doi.org/10.3390/ijerph18062843 .

Scala A, Loperto I, Carrano R, Federico S, Triassi M, Improta G. Assessment of proteinuria level in nephrology patients using a machine learning approach. In: 2021 5th international conference on medical and health informatics (ICMHI 2021). Association for Computing Machinery, New York, NY, USA, 13–16;2021. https://doi.org/10.1145/3472813.3472816 .

Download references

Acknowledgements

The authors thank the organizers of the 2021 International Symposium on Biomedical Engineering and Computational Biology (BECB 2021) for give us the opportunity to published the short version of this work. It was an important recognition that prompted us to continue and deepen our study.

Not applicable.

Author information

Authors and affiliations.

Department of Advanced Biomedical Sciences, University Hospital of Naples ‘Federico II’, Naples, Italy

Teresa Angela Trunfio

Department of Public Health, University of Naples “Federico II”, Naples, Italy

Arianna Scala & Giovanni Improta

University of Rome “La Sapienza”, Rome, Italy

Cristiana Giglio

“San Giovanni di Dio e Ruggi d’Aragona” University Hospital, Salerno, Italy

Giovanni Rossi & Anna Borrelli

Department of Electrical Engineering and Information Technology, University of Study of Naples “Federico II”, Naples, Italy

Maria Romano

Interdepartmental Center for Research in Healthcare Management and Innovation in Healthcare (CIRMIS), University of Naples “Federico II”, Naples, Italy

Giovanni Improta

You can also search for this author in PubMed   Google Scholar

Contributions

Conceptualization, A.B., G.R., M.R. and G.I.; methodology, A.S., C.G. and T.A.T.; validation, A.S. and T.A.T.: formal analysis, A.S. and T.A.T.; investigation, A.S., C.G. and T.A.T.; resources, A.B., M.R. and G.I.; data curation, A.L., A.S., C.G. and T.A.T.; writing—original draft preparation, A.S. and T.A.T; writing—review and editing, A.B., M.R. and G.I.; visualization, A.S. and T.A.T; supervision, A.B., M.R. and G.I.; project administration, A.B., M.R. and G.I. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Arianna Scala .

Ethics declarations

Ethics approval and consent to participate.

In compliance with the Declaration of Helsinki and with the Italian Legislative Decree 211/2003, Implementation of the 2001/20/CE directive, since no patients/children were involved in the study, the signed informed consent form and the ethical approval are not mandatory for these type of studies. Furthermore, in compliance with the regulations of the Italian National Institute of Health, our study is not reported among those needing assessment by the Ethical Committee of the Italian National Institute of Health. The hospital management authorised us to access and use the database and the hospital's medical director is listed as an author.

Consent to publication

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Trunfio, T.A., Scala, A., Giglio, C. et al. Multiple regression model to analyze the total LOS for patients undergoing laparoscopic appendectomy. BMC Med Inform Decis Mak 22 , 141 (2022). https://doi.org/10.1186/s12911-022-01884-9

Download citation

Received : 28 December 2021

Accepted : 16 May 2022

Published : 24 May 2022

DOI : https://doi.org/10.1186/s12911-022-01884-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Appendectomy
• Length of stay
• Public health

BMC Medical Informatics and Decision Making

ISSN: 1472-6947

• General enquiries: [email protected]

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 01 December 2015

Points of Significance

Multiple linear regression

• Martin Krzywinski 2 &
• Naomi Altman 1  

Nature Methods volume  12 ,  pages 1103–1104 ( 2015 ) Cite this article

47k Accesses

87 Citations

42 Altmetric

Metrics details

When multiple variables are associated with a response, the interpretation of a prediction equation is seldom simple.

You have full access to this article via your institution.

Last month we explored how to model a simple relationship between two variables, such as the dependence of weight on height 1 . In the more realistic scenario of dependence on several variables, we can use multiple linear regression (MLR). Although MLR is similar to linear regression, the interpretation of MLR correlation coefficients is confounded by the way in which the predictor variables relate to one another.

In simple linear regression 1 , we model how the mean of variable Y depends linearly on the value of a predictor variable X ; this relationship is expressed as the conditional expectation E( Y | X ) = β 0 + β 1 X . For more than one predictor variable X 1 , . . ., X p , this becomes β 0 + Σ β j X j . As for simple linear regression, one can use the least-squares estimator (LSE) to determine estimates b j of the β j regression parameters by minimizing the residual sum of squares, SSE = Σ( y i − ŷ i ) 2 , where ŷ i = b 0 + Σ j b j xij . When we use the regression sum of squares, SSR = Σ( ŷ i − Y − ) 2 , the ratio R 2 = SSR/(SSR + SSE) is the amount of variation explained by the regression model and in multiple regression is called the coefficient of determination.

The slope β j is the change in Y if predictor j is changed by one unit and others are held constant. When normality and independence assumptions are fulfilled, we can test whether any (or all) of the slopes are zero using a t -test (or regression F -test). Although the interpretation of β j seems to be identical to its interpretation in the simple linear regression model, the innocuous phrase “and others are held constant” turns out to have profound implications.

To illustrate MLR—and some of its perils—here we simulate predicting the weight ( W , in kilograms) of adult males from their height ( H , in centimeters) and their maximum jump height ( J , in centimeters). We use a model similar to that presented in our previous column 1 , but we now include the effect of J as E( W | H , J ) = β H H + β J J + β 0 + ε, with β H = 0.7, β J = −0.08, β 0 = −46.5 and normally distributed noise ε with zero mean and σ = 1 ( Table 1 ). We set β J negative because we expect a negative correlation between W and J when height is held constant (i.e., among men of the same height, lighter men will tend to jump higher). For this example we simulated a sample of size n = 40 with H and J normally distributed with means of 165 cm (σ = 3) and 50 cm (σ = 12.5), respectively.

Although the statistical theory for MLR seems similar to that for simple linear regression, the interpretation of the results is much more complex. Problems in interpretation arise entirely as a result of the sample correlation 2 among the predictors. We do, in fact, expect a positive correlation between H and J —tall men will tend to jump higher than short ones. To illustrate how this correlation can affect the results, we generated values using the model for weight with samples of J and H with different amounts of correlation.

Let's look first at the regression coefficients estimated when the predictors are uncorrelated, r ( H , J ) = 0, as evidenced by the zero slope in association between H and J ( Fig. 1a ). Here r is the Pearson correlation coefficient 2 . If we ignore the effect of J and regress W on H , we find Ŵ = 0.71 H − 51.7 ( R 2 = 0.66) ( Table 1 and Fig. 1b ). Ignoring H , we find Ŵ = −0.088 J + 69.3 ( R 2 = 0.19). If both predictors are fitted in the regression, we obtain Ŵ = 0.71 H − 0.088 J − 47.3 ( R 2 = 0.85). This regression fit is a plane in three dimensions ( H , J , W ) and is not shown in Figure 1 . In all three cases, the results of the F -test for zero slopes show high significance ( P ≤ 0.005).

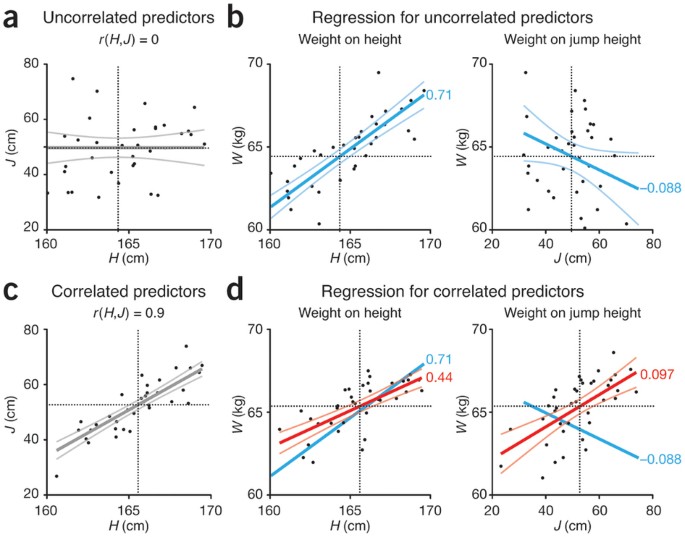
( a ) Simulated values of uncorrelated predictors, r ( H , J ) = 0. The thick gray line is the regression line, and thin gray lines show the 95% confidence interval of the fit. ( b ) Regression of weight ( W ) on height ( H ) and of weight on jump height ( J ) for uncorrelated predictors shown in a . Regression slopes are shown ( b H = 0.71, b J = −0.088). ( c ) Simulated values of correlated predictors, r ( H , J ) = 0.9. Regression and 95% confidence interval are denoted as in a . ( d ) Regression (red lines) using correlated predictors shown in c . Light red lines denote the 95% confidence interval. Notice that b J = 0.097 is now positive. The regression line from b is shown in blue. In all graphs, horizontal and vertical dotted lines show average values.

When the sample correlations of the predictors are exactly zero, the regression slopes ( b H and b J ) for the “one predictor at a time” regressions and the multiple regression are identical, and the simple regression R 2 sums to multiple regression R 2 (0.66 + 0.19 = 0.85; Fig. 2 ). The intercept changes when we add a predictor with a nonzero mean to satisfy the constraint that the least-squares regression line goes through the sample means, which is always true when the regression model includes an intercept.

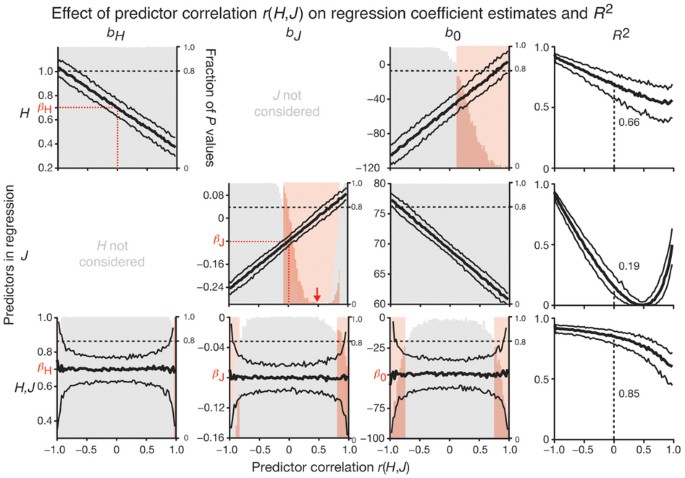
Shown are the values of regression coefficient estimates ( b H , b J , b 0 ) and R 2 and the significance of the test used to determine whether the coefficient is zero from 250 simulations at each value of predictor sample correlation −1 < r ( H , J ) < 1 for each scenario where either H or J or both H and J predictors are fitted in the regression. Thick and thin black curves show the coefficient estimate median and the boundaries of the 10th–90th percentile range, respectively. Histograms show the fraction of estimated P values in different significance ranges, and correlation intervals are highlighted in red where >20% of the P values are >0.01. Actual regression coefficients ( β H , β J , β 0 ) are marked on vertical axes. The decrease in significance for b J when jump height is the only predictor and r ( H , J ) is moderate (red arrow) is due to insufficient statistical power ( b J is close to zero). When predictors are uncorrelated, r ( H , J ) = 0, R 2 of individual regressions sum to R 2 of multiple regression (0.66 + 0.19 = 0.85). Panels are organized to correspond to Table 1 , which shows estimates of a single trial at two different predictor correlations.

Balanced factorial experiments show a sample correlation of zero among the predictors when their levels have been fixed. For example, we might fix three heights and three jump heights and select two men representative of each combination, for a total of 18 subjects to be weighed. But if we select the samples and then measure the predictors and response, the predictors are unlikely to have zero correlation.

When we simulate highly correlated predictors r ( H , J ) = 0.9 ( Fig. 1c ), we find that the regression parameters change depending on whether we use one or both predictors ( Table 1 and Fig. 1d ). If we consider only the effect of H , the coefficient β H = 0.7 is inaccurately estimated as b H = 0.44. If we include only J , we estimate β J = −0.08 inaccurately, and even with the wrong sign ( b J = 0.097). When we use both predictors, the estimates are quite close to the actual coefficients ( b H = 0.63, b J = −0.056).

In fact, as the correlation between predictors r ( H , J ) changes, the estimates of the slopes ( b H , b J ) and intercept ( b 0 ) vary greatly when only one predictor is fitted. We show the effects of this variation for all values of predictor correlation (both positive and negative) across 250 trials at each value ( Fig. 2 ). We include negative correlation because although J and H are likely to be positively correlated, other scenarios might use negatively correlated predictors (e.g., lung capacity and smoking habits). For example, if we include only H in the regression and ignore the effect of J , b H steadily decreases from about 1 to 0.35 as r ( H , J ) increases. Why is this? For a given height, larger values of J (an indicator of fitness) are associated with lower weight. If J and H are negatively correlated, as J increases, H decreases, and both changes result in a lower value of W . Conversely, as J decreases, H increases, and thus W increases. If we use only H as a predictor, J is lurking in the background, depressing W at low values of H and enhancing W at high levels of H , so that the effect of H is overestimated ( b H increases). The opposite effect occurs when J and H are positively correlated. A similar effect occurs for b J , which increases in magnitude (becomes more negative) when J and H are negatively correlated. Supplementary Figure 1 shows the effect of correlation when both regression coefficients are positive.

When both predictors are fitted ( Fig. 2 ), the regression coefficient estimates ( b H , b J , b 0 ) are centered at the actual coefficients ( β H , β J , β 0 ) with the correct sign and magnitude regardless of the correlation of the predictors. However, the standard error in the estimates steadily increases as the absolute value of the predictor correlation increases.

Neglecting important predictors has implications not only for R 2 , which is a measure of the predictive power of the regression, but also for interpretation of the regression coefficients. Unconsidered variables that may have a strong effect on the estimated regression coefficients are sometimes called 'lurking variables'. For example, muscle mass might be a lurking variable with a causal effect on both body weight and jump height. The results and interpretation of the regression will also change if other predictors are added.

Given that missing predictors can affect the regression, should we try to include as many predictors as possible? No, for three reasons. First, any correlation among predictors will increase the standard error of the estimated regression coefficients. Second, having more slope parameters in our model will reduce interpretability and cause problems with multiple testing. Third, the model may suffer from overfitting. As the number of predictors approaches the sample size, we begin fitting the model to the noise. As a result, we may seem to have a very good fit to the data but still make poor predictions.

MLR is powerful for incorporating many predictors and for estimating the effects of a predictor on the response in the presence of other covariates. However, the estimated regression coefficients depend on the predictors in the model, and they can be quite variable when the predictors are correlated. Accurate prediction of the response is not an indication that regression slopes reflect the true relationship between the predictors and the response.

Altman, N. & Krzywinski, M. Nat. Methods 12 , 999–1000 (2015).

Article   CAS   Google Scholar  

Altman, N. & Krzywinski, M. Nat. Methods 12 , 899–900 (2015).

Download references

Author information

Authors and affiliations.

Naomi Altman is a Professor of Statistics at The Pennsylvania State University.,

• Naomi Altman

Martin Krzywinski is a staff scientist at Canada's Michael Smith Genome Sciences Centre.,

Martin Krzywinski

You can also search for this author in PubMed   Google Scholar

Ethics declarations

Competing interests.

The authors declare no competing financial interests.

Integrated supplementary information

Supplementary figure 1 regression coefficients and r 2.

The significance and value of regression coefficients and R 2 for a model with both regression coefficients positive, E( W | H,J ) = 0.7 H + 0.08 J - 46.5 + ε. The format of the figure is the same as that of Figure 2 .

Supplementary information

Supplementary figure 1.

Regression coefficients and R 2 (PDF 299 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Krzywinski, M., Altman, N. Multiple linear regression. Nat Methods 12 , 1103–1104 (2015). https://doi.org/10.1038/nmeth.3665

Download citation

Published : 01 December 2015

Issue Date : December 2015

DOI : https://doi.org/10.1038/nmeth.3665

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Income and oral and general health-related quality of life: the modifying effect of sense of coherence, findings of a cross-sectional study.

• Mehrsa Zakershahrak
• Sergio Chrisopoulos
• David Brennan

Applied Research in Quality of Life (2023)

Outcomes of a novel all-inside arthroscopic anterior talofibular ligament repair for chronic ankle instability

• Xiao’ao Xue
• Yinghui Hua

International Orthopaedics (2023)

Predicting financial losses due to apartment construction accidents utilizing deep learning techniques

• Ji-Myong Kim
• Sang-Guk Yum

Scientific Reports (2022)

Regression modeling of time-to-event data with censoring

• Tanujit Dey
• Stuart R. Lipsitz

Nature Methods (2022)

A Systematic Analysis for Energy Performance Predictions in Residential Buildings Using Ensemble Learning

• Monika Goyal
• Mrinal Pandey

Arabian Journal for Science and Engineering (2021)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

multiple linear regression Recently Published Documents

Total documents.

• Latest Documents
• Most Cited Documents
• Contributed Authors
• Related Sources
• Related Keywords

The Effect of Conflict and Termination of Employment on Employee's Work Spirit

This study aims to find out the conflict and termination of employment both partially and simultaneously have a significant effect on the morale of employees at PT. The benefits of Medan Technique and how much it affects. The method used in this research is quantitative method with several tests namely reliability analysis, classical assumption deviation test and linear regression. Based on the results of primary data regression processed using SPSS 20, multiple linear regression equations were obtained as follows: Y = 1,031 + 0.329 X1+ 0.712 X2.In part, the conflict variable (X1)has a significant effect on the employee's work spirit (Y) at PT. Medan Technical Benefits. This means that the hypothesis in this study was accepted, proven from the value of t calculate > t table (3,952 < 2,052). While the variable termination of employment (X2) has a significant influence on the work spirit of employees (Y) in PT. Medan Technical Benefits. This means that the hypothesis in this study was accepted, proven from the value of t calculate > t table (7,681 > 2,052). Simultaneously, variable conflict (X1) and termination of employment (X2) have a significant influence on the morale of employees (Y) in PT. Medan Technical Benefits. This means that the hypothesis in this study was accepted, as evidenced by the calculated F value > F table (221,992 > 3.35). Conflict variables (X1) and termination of employment (X2) were able to contribute an influence on employee morale variables (Y) of 94.3% while the remaining 5.7% was influenced by other variables not studied in this study. From the above conclusions, the author advises that employees and leaders should reduce prolonged conflict so that the spirit of work can increase. Leaders should be more selective in severing employment relationships so that decent employees are not dismissed unilaterally. Employees should work in a high spirit so that the company can see the quality that employees have.

Prediction of Local Government Revenue using Data Mining Method

Local Government Revenue or commonly abbreviated as PAD is part of regional income which is a source of regional financing used to finance the running of government in a regional government. Each local government must plan Local Government Revenue for the coming year so that a forecasting method is needed to determine the Local Government Revenue value for the coming year. This study discusses several methods for predicting Local Government Revenue by using data on the realization of Local Government Revenue in the previous years. This study proposes three methods for forecasting local Government revenue. The three methods used in this research are Multiple Linear Regression, Artificial Neural Network, and Deep Learning. In this study, the data used is Local Revenue data from 2010 to 2020. The research was conducted using RapidMiner software and the CRISP-DM framework. The tests carried out showed an RMSE value of 97 billion when using the Multiple Linear Regression method and R2 of 0,942, the ANN method shows an RMSE value of 135 billion and R2 of 0.911, and the Deep Learning method shows the RMSE value of 104 billion and R2 of 0.846. This study shows that for the prediction of Local Government Revenue, the Multiple Linear Regression method is better than the ANN or Deep Learning method. Keywords— Local Government Revenue, Multiple Linear Regression, Artificial Neural Network, Deep Learning, Coefficient of Determination

Analisis Peran Motivasi sebagai Mediasi Pengaruh Trilogi Kepemimpinan dan Kepuasan Kerja terhadap Produktivitas Kerja Karyawan PT. Mataram Tunggal Garment

The purpose of this study is to find out the motivation to mediate the leadership trilogy and job satisfaction to employee work productivity at PT. Mataram Tunggal Garment. The method used in this study is quantitative. Primary data was obtained from questionnaires with 78 respondents with saturated sample techniques. Then the data is analyzed using descriptive analysis, multiple linear regression tests, t (partial) tests, coesifisien determination (R2) and sobel tests. The results showed that job satisfaction had a significant influence on motivation, leadership trilogy and job satisfaction had a significant influence on employee work productivity, leadership trilogy and motivation had no significant effect on employee work productivity, motivation mediated leadership trilogy and job satisfaction had no insignificant effect on employee work productivity.  Keywords: Leadership Trilogy, Motivation, Job Satisfaction and Employee Productivity.

Prevalence of asymptomatic hyperuricemia and its association with prediabetes, dyslipidemia and subclinical inflammation markers among young healthy adults in Qatar

Abstract Aim The aim of this study is to investigate the prevalence of asymptomatic hyperuricemia in Qatar and to examine its association with changes in markers of dyslipidemia, prediabetes and subclinical inflammation. Methods A cross-sectional study of young adult participants aged 18 - 40 years old devoid of comorbidities collected between 2012 and 2017. Exposure was defined as uric acid level, and outcomes were defined as levels of different blood markers. De-identified data were collected from Qatar Biobank. T-tests, correlation tests and multiple linear regression were all used to investigate the effects of hyperuricemia on blood markers. Statistical analyses were conducted using STATA 16. Results The prevalence of asymptomatic hyperuricemia is 21.2% among young adults in Qatar. Differences between hyperuricemic and normouricemic groups were observed using multiple linear regression analysis and found to be statistically and clinically significant after adjusting for age, gender, BMI, smoking and exercise. Significant associations were found between uric acid level and HDL-c p = 0.019 (correlation coefficient -0.07 (95% CI [-0.14, -0.01]); c-peptide p = 0.018 (correlation coefficient 0.38 (95% CI [0.06, 0.69]) and monocyte to HDL ratio (MHR) p = 0.026 (correlation coefficient 0.47 (95% CI [0.06, 0.89]). Conclusions Asymptomatic hyperuricemia is prevalent among young adults and associated with markers of prediabetes, dyslipidemia, and subclinical inflammation.

Screen Time, Age and Sunshine Duration Rather Than Outdoor Activity Time Are Related to Nutritional Vitamin D Status in Children With ASD

Objective: This study aimed to investigate the possible association among vitamin D, screen time and other factors that might affect the concentration of vitamin D in children with autism spectrum disorder (ASD).Methods: In total, 306 children with ASD were recruited, and data, including their age, sex, height, weight, screen time, time of outdoor activity, ASD symptoms [including Autism Behavior Checklist (ABC), Childhood Autism Rating Scale (CARS) and Autism Diagnostic Observation Schedule–Second Edition (ADOS-2)] and vitamin D concentrations, were collected. A multiple linear regression model was used to analyze the factors related to the vitamin D concentration.Results: A multiple linear regression analysis showed that screen time (β = −0.122, P = 0.032), age (β = −0.233, P &lt; 0.001), and blood collection month (reflecting sunshine duration) (β = 0.177, P = 0.004) were statistically significant. The vitamin D concentration in the children with ASD was negatively correlated with screen time and age and positively correlated with sunshine duration.Conclusion: The vitamin D levels in children with ASD are related to electronic screen time, age and sunshine duration. Since age and season are uncontrollable, identifying the length of screen time in children with ASD could provide a basis for the clinical management of their vitamin D nutritional status.

Determining Factors of Fraud in Local Government

The objectives of this research are to analyze determining factors of fraud in local government. This study used internal control effectiveness, compliance with accounting rules, compensation compliance, and unethical behavior as an independent variable, while fraud as the dependent variable. The research was conducted at Bantul local government (OPD). The sample of this research were 86 respondents. The sample uses a purposive sampling method. The respondent data is analyzed with multiple linear regression. The results showed: Internal control effectiveness has an impact on fraud. Compliance with accounting rules does not affect fraud. Compensations compliance does not affect fraud. Unethical behavior has an impact on fraud.

PENGARUH TINGKAT EFEKTIVITAS PERPUTARAN KAS, PIUTANG, DAN MODAL KERJA TERHADAP RENTABILITAS EKONOMI PADA KOPERASI PEDAGANG PASAR GROGOLAN BARU (KOPPASGOBA) PERIODE 2016-2020

This study aims to test and analyze the effect of effectiveness of cash turnover, receivables,and working capital on economic rentability in the New Grogolan Market Traders Cooperative of Pekalongan City from 2016 to 2020. The method used in this study was quantitative research method with documentation techniques and analyzed used multiple linear regression analysis. The results of this study showed (1) the effectiveness of cash turnover has no significant effect on economic rentability, (2) the effectiveness of receivables turnover has no significant effect on economic rentability, (3) the effectiveness of working capital turnover has a positive and significant effect on economic rentability, and (4) there is a positive and significant effect on the effectiveness of cash turnover, receivables, and working capital together on economic rentability. Keywords: Turnover of cash, turnover of receivables, turnover of working capital, and economic rentability.

Improvement of AHMES Using AI Algorithms

This research aims to improve the rationality and intelligence of AUTOMATICALLY HIGHER MATHEMATICALLY EXAM SYSTEM (AHMES) through some AI algorithms. AHMES is an intelligent and high-quality higher math examination solution for the Department of Computer Engineering at Pai Chai University. This research redesigned the difficulty system of AHMES and used some AI algorithms for initialization and continuous adjustment. This paper describes the multiple linear regression algorithm involved in this research and the AHMES learning (AL) algorithm improved by the Q-learning algorithm. The simulation test results of the upgraded AHMES show the effectiveness of these algorithms.

ANALISIS PENGARUH KUALITAS PELAYANAN, PROMOSI DAN HARGA TERHADAP KEPUASAN PELANGGAN PADA JASA PENGIRIMAN BARANG JNE DI BESUKI

This research was conducted to see the effect of service quality, promotion and price on customer satisfaction. This research was conducted at the Besuki branch of JNE. Sampling was done by random sampling technique where all the population was taken at random to be the research sample. This is done to increase customer satisfaction at JNE Besuki branch through service quality, promotion and price. The analytical tool used is multiple linear regression to determine service quality, promotion and price on customer satisfaction. The results show that service quality affects customer satisfaction, promotion affects customer satisfaction, price affects customer satisfaction. Keyword : service quality, promotion, price, customer satisfaction

PENGARUH KUALITAS PRODUK, HARGA DAN INFLUENCER MARKETING TERHADAP KEPUTUSAN PEMBELIAN SCARLETT BODY WHITENING

This research aimed to figure out the influence between product quality, price and marketing influencer with the purchasing decision of Scarlett Body Whitening in East Java. The research instrument employed questionnaire to collect data from Scarlett Body Whitening consumers in East Java. Since there was no valid data for number of the consumers, the research used Roscoe method to take the sample. Data analyzed using multiple linear regression test. Product quality and price have a positive and significant effect on purchasing decisions. Meanwhile, the marketing influencer had no significant effect on purchase decision for Scarlett Body Whitening. Need further research to ensure that marketing influencer had an effect on purchase decision.   Keywords: Product quality, price, marketing influencer, buying decision

Export Citation Format

Share document.

• {{subColumn.name}}

Applied Computing and Intelligence

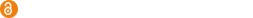
• {{newsColumn.name}}
• Share facebook twitter google linkedin

Using multiple linear regression for biochemical oxygen demand prediction in water

• Isaiah Kiprono Mutai 1,2 , 
• Kristof Van Laerhoven 3 , 
• Nancy Wangechi Karuri 1 , 
• Robert Kimutai Tewo 1 ,  , 
• 1. Department of Chemical Engineering, Dedan Kimathi University of Technology, Private bag 10143, Dedan Kimathi, Nyeri, Kenya
• 2. Department of Mechanical Engineering, Dedan Kimathi University of Technology, Private bag 10143, Dedan Kimathi, Nyeri, Kenya
• 3. Department of Ubiquitous Computing, University of Siegen, H-A 8110, Holderlin Str., Siegen, 57076, Germany
• Academic Editor: Azlan Ismail
• Received: 21 May 2024 Revised: 15 October 2024 Accepted: 16 October 2024 Published: 22 October 2024
• Full Text(HTML)
• Download PDF

Biochemical oxygen demand (BOD) is an important water quality measurement but takes five days or more to obtain. This may result in delays in taking corrective action in water treatment. Our goal was to develop a BOD predictive model that uses other water quality measurements that are quicker than BOD to obtain; namely pH, temperature, nitrogen, conductivity, dissolved oxygen, fecal coliform, and total coliform. Principal component analysis showed that the data spread was in the direction of the BOD eigenvector. The vectors for pH, temperature, and fecal coliform contributed the greatest to data variation, and dissolved oxygen negatively correlated to BOD. K-means clustering suggested three clusters, and t-distributed stochastic neighbor embedding showed that BOD had a strong influence on variation in the data. Pearson correlation coefficients indicated that the strongest positive correlations were between BOD, and fecal and total coliform, as well as nitrogen. The largest negative correlation was between dissolved oxygen, and BOD. Multiple linear regression (MLR) using fecal, and total coliform, dissolved oxygen, and nitrogen to predict BOD, and training/test data of 80%/20% and 90%/10% had performance indices of RMSE = 2.21 mg/L, r = 0.48 and accuracy of 50.1%, and RMSE = 2.18 mg/L, r = 0.54 and an accuracy of 55.5%, respectively. BOD prediction was better than previous MLR models. Increasing the percentage of the training set above 80% improved the model accuracy but did not significantly impact its prediction. Thus, MLR can be used successfully to estimate BOD in water using other water quality measurements that are quicker to obtain.

• machine learning ,
• multiple linear regression ,
• water treatment ,
• contamination

Citation: Isaiah Kiprono Mutai, Kristof Van Laerhoven, Nancy Wangechi Karuri, Robert Kimutai Tewo. Using multiple linear regression for biochemical oxygen demand prediction in water[J]. Applied Computing and Intelligence, 2024, 4(2): 125-137. doi: 10.3934/aci.2024008

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding author: Email: [email protected] ; Tel: +254723484716

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 73 ) PDF downloads( 7 ) Cited by( 0 )

Figures and Tables

Figures( 4 )  /  Tables( 4 )

Associated material

Other articles by authors.

• Isaiah Kiprono Mutai
• Kristof Van Laerhoven
• Nancy Wangechi Karuri
• Robert Kimutai Tewo

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

• Figure 1. PCA analysis of the water data showing the scree plot, a plot of the first two principal components, and a biplot of the first and second principal components
• Figure 2. K-Means clustering of the data. Three clusters selected in the data structure in line with the elbow rule
• Figure 3. t-Distributed Stochastic Neighbor Embedding using normalized BOD values as the target. The transformation on the right is based on low (0–0.3), medium (0.3–0.7), and high (0.7–1.0) normalized BOD levels
• Figure 4. Comparison of observed and predicted BOD values for the 80%/20% and the 90%/10% training/testing data split. An accuracy of 50.1% and 55.5%, RMSE of 2.21 mg/L and 2.18 mg/L, and r values of 0.48 and 0.54 were achieved for the for the 80%/20% and 90%/10% training/test data splits respectively

Regression Analysis of Dependent Current Status Data with Left-Truncation Under Linear Transformation Model

• Published: 21 October 2024

Cite this article

• Mengyue Zhang 1 ,
• Shishun Zhao 1 ,
• Tao Hu 3 &
• Jianguo Sun 4  

19 Accesses

Explore all metrics

The paper discusses the regression analysis of current status data, which is common in various fields such as tumorigenic research and demographic studies. Analyzing this type of data poses a significant challenge and has recently gained considerable interest. Furthermore, the authors consider an even more difficult scenario where, apart from censoring, one also faces left-truncation and informative censoring, meaning that there is a potential correlation between the examination time and the failure time of interest. The authors propose a sieve maximum likelihood estimation (MLE) method and in the proposed method for inference, a copula-based procedure is applied to depict the informative censoring. Also the authors utilise the splines to estimate the unknown nonparametric functions in the model, and the asymptotic properties of the proposed estimator are established. The simulation results indicate that the developed approach is effective in practice, and it has been successfully applied a set of real data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime

Price excludes VAT (USA) Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Regression analysis of current status data in the presence of a cured subgroup and dependent censoring.

A New Approach for Regression Analysis of Multivariate Current Status Data with Informative Censoring

Regression Analysis of Misclassified Current Status Data with Informative Observation Times

Huang J, Efficient estimation for the proportional hazards model with interval censoring, The Annals of Statistics , 1996, 24 (2): 540–568.

Article   MathSciNet   Google Scholar  

Zhang Z, Sun J, and Sun L, Statistical analysis of current status data with informative observation times, Statistics in Medicine , 2005, 24 (9): 1399–1407.

Sun J, The Statistical Analysis of Interval-Censored Failure Time Data , Springer, New York, 2006.

Google Scholar  

Wang C, Sun J, Sun L, et al., Nonparametric estimation of current status data with dependent censoring, Lifetime Data Analysis , 2012, 18 (4): 434–445.

Titman A C, A pool-adjacent-violators type algorithm for non-parametric estimation of current status data with dependent censoring, Lifetime Data Analysis , 2014, 20 (3): 444–458.

Rossini A J and Tsiatis A A, A semiparametric proportional odds regression model for the analysis of current status data, Journal of the American Statistical Association , 1996, 91 (434): 713–721.

Lin D Y, Oakes D, and Ying Z, Additive hazards regression with current status data, Biometrika , 1998, 85 (2): 289–298.

Sun J and Sun L, Semiparametric linear transformation models for current status data, Canadian Journal of Statistics , 2005, 33 (1): 85–96.

Zhang B, Tong X, Zhang J, et al., Efficient estimation for linear transformation models with current status data, Communications in Statistics-Theory and Methods , 2013, 42 (17): 3191–3203.

Cheng G and Wang X, Semiparametric additive transformation model under current status data, Electronic Journal of Statistics , 2011, 5 : 1735–1764.

Lu M, Liu Y, and Li C S, Efficient estimation of a linear transformation model for current status data via penalized splines, Statistical Methods in Medical Research , 2020, 29 (1): 3–14.

Chen C M, Lu T F C, Chen M H, et al., Semiparametric transformation models for current status data with informative censoring, Biometrical Journal , 2012, 54 (5): 641–656.

Ma L, Hu T, and Sun J, Sieve maximum likelihood regression analysis of dependent current status data, Biometrika , 2015, 102 (3): 731–738.

Luo L and Zhao H, Robust regression analysis for clustered interval-censored failure time data, Journal of Systems Science & Complexity , 2021, 34 (3): 1156–1174.

Zhao S, Hu T, Ma L, et al., Regression analysis of informative current status data with the additive hazards model, Lifetime Data Analysis , 2015, 21 (2): 241–258.

Xu D, Zhao S, Hu T, et al., Regression analysis of informative current status data with the semiparametric linear transformation model, Journal of Applied Statistics , 2019, 46 (2): 187–202.

Zhao S, Dong L, and Sun J, Regression analysis of interval-censored data with informative observation times under the accelerated failure time model, Journal of Systems Science & Complexity , 2022, 35 (4): 1520–1534.

Du M, Hu T, and Sun J, Semiparametric probit model for informative current status data, Statistics in Medicine , 2019, 38 (12): 2219–2227.

Xu D, Zhao S, and Sun J, Regression analysis of dependent current status data with the accelerated failure time model, Communications in Statistics-Simulation and Computation , 2022, 51 (10): 6188–6196.

Wang W, Xu D, Zhao S, et al., Regression analysis of misclassified current status data with informative observation times, Journal of Systems Science & Complexity , 2023, 36 (3): 1250–1264.

Bilker W B and Wang M C, A semiparametric extension of the Mann-Whitney test for randomly truncated data, Biometrics , 1996, 52 (1): 10–20.

Article   Google Scholar  

Rennert L and Xie S X, Bias induced by ignoring double truncation inherent in autopsy-confirmed survival studies of neurodegenerative diseases, Statistics in Medicine , 2019, 38 (19): 3599–3613.

Dorre A, Bayesian estimation of a lifetime distribution under double truncation caused by time-restricted data collection, Statistical Papers , 2020, 61 (3): 945–965.

Kim J S, Efficient estimation for the proportional hazards model with left-truncated and “case 1” interval-censored data, Statistica Sinica , 2003, 13 (2): 519–537.

MathSciNet   Google Scholar  

Wang P, Tong X, Zhao S, et al., Regression analysis of left-truncated and case I interval-censored data with the additive hazards model, Communications in Statistics-Theory and Methods , 2015, 44 (8): 1537–1551.

Dabrowska D M and Doksum K A, Partial likelihood in transformation models with censored data, Scandinavian Journal of Statistics , 1988, 15 : 1–23.

Zeng D and Lin D Y, Maximum likelihood estimation in semiparametric regression models with censored data, Journal of the Royal Statistical Society: Series B (Statistical Methodology) , 2007, 69 (4): 507–564.

Nelsen R B, An Introduction to Copulas , Springer, New York, 2006.

Lu M, Zhang Y, and Huang J, Estimation of the mean function with panel count data using monotone polynomial splines, Biometrika , 2007, 94 (3): 705–718.

Schumaker L L, Spline Functions: Basic Theory , Cambridge University Press, Cambridge, 1981.

De Gruttola V and Lagakos S W, Analysis of doubly-censored survival data, with application to AIDS, Biometrics , 1989, 45 (1): 1–11.

Kim M Y, De Gruttola V G, and Lagakos S W, Analyzing doubly censored data with covariates, with application to AIDS, Biometrics , 1993, 49 (1): 13–22.

Huang J and Rossini A J, Sieve estimation for the proportional odds failure-time regression model with interval censoring, Journal of the American Statistical Association , 1997, 92 (439): 960–967.

Zhang Y, Hua L, and Huang J, A spline-based semiparametric maximum likelihood estimation method for the cox model with interval-censored data, Scandinavian Journal of Statistics , 2010, 37 (2): 338–354.

Pollard D, Convergence of Stochastic Processes , Springer, New York, 1984.

Book   Google Scholar  

Shen X and Wong W H, Convergence rate of sieve estimates, The Annals of Statistics , 1994, 22 (2): 580–615.

van der Vaart A W and Wellner J A, Weak Convergence and Empirical Processes: With Applications to Statistics , Springer, New York, 1996.

Shen X, On methods of sieves and penalization, The Annals of Statistics , 1997, 25 (6): 2555–2591.

Chen X, Fan Y, and Tsyrennikov V, Efficient estimation of semiparametric multivariate copula models, Journal of the American Statistical Association , 2006, 101 (475): 1228–1240.

Download references

Author information

Authors and affiliations.

Center for Applied Statistical Research, School of Mathematics, Jilin University, Changchun, 130012, China

Mengyue Zhang & Shishun Zhao

Key Laboratory of Applied Statistics of MOE and School of Mathematics and Statistics, Northeast Normal University, Changchun, 130024, China

School of Mathematical Sciences, Capital Normal University, Beijing, 100048, China

Department of Statistics, University of Missouri, Columbia, MO, 65211, USA

Jianguo Sun

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Tao Hu .

Ethics declarations

The authors declare no conflict of interest.

Additional information

This research was supported by the National Natural Science Foundation of China under Grant Nos. 12171328, 12001093, 12231011, and 12071176, the National Key Research and Development Program of China under Grant No. 2020YFA0714102 and Beijing Natural Science Foundation under Grant No. Z210003.

Rights and permissions

Reprints and permissions

About this article

Zhang, M., Zhao, S., Xu, D. et al. Regression Analysis of Dependent Current Status Data with Left-Truncation Under Linear Transformation Model. J Syst Sci Complex (2024). https://doi.org/10.1007/s11424-024-3474-8

Download citation

Received : 03 November 2023

Revised : 25 December 2023

Published : 21 October 2024

DOI : https://doi.org/10.1007/s11424-024-3474-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• current status data
• informative observation
• left-truncation
• linear transformation model
• Find a journal
• Publish with us
• Track your research