Problem Solving in Mathematics
- Math Tutorials
- Pre Algebra & Algebra
- Exponential Decay
- Worksheets By Grade
The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.
Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures
Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.
Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.
Look for Clue Words
Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.
Common clue words for addition problems:
Common clue words for subtraction problems:
- How much more
Common clue words for multiplication problems:
Common clue words for division problems:
Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.
Read the Problem Carefully
This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:
- Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
- What did you need to do in that instance?
- What facts are you given about this problem?
- What facts do you still need to find out about this problem?
Develop a Plan and Review Your Work
Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:
- Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
- If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.
If it seems like you’ve solved the problem, ask yourself the following:
- Does your solution seem probable?
- Does it answer the initial question?
- Did you answer using the language in the question?
- Did you answer using the same units?
If you feel confident that the answer is “yes” to all questions, consider your problem solved.
Tips and Hints
Some key questions to consider as you approach the problem may be:
- What are the keywords in the problem?
- Do I need a data visual, such as a diagram, list, table, chart, or graph?
- Is there a formula or equation that I'll need? If so, which one?
- Will I need to use a calculator? Is there a pattern I can use or follow?
Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.
- Converting Cubic Meters to Liters
- 2nd Grade Math Word Problems
- 2020-21 Common Application Essay Option 4—Solving a Problem
- The Horse Problem: A Math Challenge
- How to Use Math Journals in Class
- The Frayer Model for Math
- Algorithms in Mathematics and Beyond
- "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
- Critical Thinking Definition, Skills, and Examples
- Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
- Graphic Organizers in Math
- College Interview Tips: "Tell Me About a Challenge You Overcame"
- Christmas Word Problem Worksheets
- Solving Problems Involving Distance, Rate, and Time
- Study Tips for Math Homework and Math Tests
- Innovative Ways to Teach Math
Mathematics Through Problem Solving
What Is A ‘Problem-Solving Approach’?

- interactions between students/students and teacher/students (Van Zoest et al., 1994)
- mathematical dialogue and consensus between students (Van Zoest et al., 1994)
- teachers providing just enough information to establish background/intent of the problem, and students clarifing, interpreting, and attempting to construct one or more solution processes (Cobb et al., 1991)
- teachers accepting right/wrong answers in a non-evaluative way (Cobb et al., 1991)
- teachers guiding, coaching, asking insightful questions and sharing in the process of solving problems (Lester et al., 1994)
- teachers knowing when it is appropriate to intervene, and when to step back and let the pupils make their own way (Lester et al., 1994)
- A further characteristic is that a problem-solving approach can be used to encourage students to make generalisations about rules and concepts, a process which is central to mathematics (Evan and Lappin, 1994).
Schoenfeld (in Olkin and Schoenfeld, 1994, p.43) described the way in which the use of problem solving in his teaching has changed since the 1970s:
My early problem-solving courses focused on problems amenable to solutions by Polya-type heuristics: draw a diagram, examine special cases or analogies, specialize, generalize, and so on. Over the years the courses evolved to the point where they focused less on heuristics per se and more on introducing students to fundamental ideas: the importance of mathematical reasoning and proof…, for example, and of sustained mathematical investigations (where my problems served as starting points for serious explorations, rather than tasks to be completed).
Schoenfeld also suggested that a good problem should be one which can be extended to lead to mathematical explorations and generalisations. He described three characteristics of mathematical thinking:
- valuing the processes of mathematization and abstraction and having the predilection to apply them
- developing competence with the tools of the trade and using those tools in the service of the goal of understanding structure – mathematical sense-making (Schoenfeld, 1994, p.60).
- As Cobb et al. (1991) suggested, the purpose for engaging in problem solving is not just to solve specific problems, but to ‘encourage the interiorization and reorganization of the involved schemes as a result of the activity’ (p.187). Not only does this approach develop students’ confidence in their own ability to think mathematically (Schifter and Fosnot, 1993), it is a vehicle for students to construct, evaluate and refine their own theories about mathematics and the theories of others (NCTM, 1989). Because it has become so predominant a requirement of teaching, it is important to consider the processes themselves in more detail.
The Role of Problem Solving in Teaching Mathematics as a Process
Problem solving is an important component of mathematics education because it is the single vehicle which seems to be able to achieve at school level all three of the values of mathematics listed at the outset of this article: functional, logical and aesthetic. Let us consider how problem solving is a useful medium for each of these.
It has already been pointed out that mathematics is an essential discipline because of its practical role to the individual and society. Through a problem-solving approach, this aspect of mathematics can be developed. Presenting a problem and developing the skills needed to solve that problem is more motivational than teaching the skills without a context. Such motivation gives problem solving special value as a vehicle for learning new concepts and skills or the reinforcement of skills already acquired (Stanic and Kilpatrick, 1989, NCTM, 1989). Approaching mathematics through problem solving can create a context which simulates real life and therefore justifies the mathematics rather than treating it as an end in itself. The National Council of Teachers of Mathematics (NCTM, 1980) recommended that problem solving be the focus of mathematics teaching because, they say, it encompasses skills and functions which are an important part of everyday life. Furthermore it can help people to adapt to changes and unexpected problems in their careers and other aspects of their lives. More recently the Council endorsed this recommendation (NCTM, 1989) with the statement that problem solving should underly all aspects of mathematics teaching in order to give students experience of the power of mathematics in the world around them. They see problem solving as a vehicle for students to construct, evaluate and refine their own theories about mathematics and the theories of others.
According to Resnick (1987) a problem-solving approach contributes to the practical use of mathematics by helping people to develop the facility to be adaptable when, for instance, technology breaks down. It can thus also help people to transfer into new work environments at this time when most are likely to be faced with several career changes during a working lifetime (NCTM, 1989). Resnick expressed the belief that ‘school should focus its efforts on preparing people to be good adaptive learners, so that they can perform effectively when situations are unpredictable and task demands change’ (p.18). Cockcroft (1982) also advocated problem solving as a means of developing mathematical thinking as a tool for daily living, saying that problem-solving ability lies ‘at the heart of mathematics’ (p.73) because it is the means by which mathematics can be applied to a variety of unfamiliar situations.
Problem solving is, however, more than a vehicle for teaching and reinforcing mathematical knowledge and helping to meet everyday challenges. It is also a skill which can enhance logical reasoning. Individuals can no longer function optimally in society by just knowing the rules to follow to obtain a correct answer. They also need to be able to decide through a process of logical deduction what algorithm, if any, a situation requires, and sometimes need to be able to develop their own rules in a situation where an algorithm cannot be directly applied. For these reasons problem solving can be developed as a valuable skill in itself, a way of thinking (NCTM, 1989), rather than just as the means to an end of finding the correct answer.
Many writers have emphasised the importance of problem solving as a means of developing the logical thinking aspect of mathematics. ‘If education fails to contribute to the development of the intelligence, it is obviously incomplete. Yet intelligence is essentially the ability to solve problems: everyday problems, personal problems … ‘(Polya, 1980, p.1). Modern definitions of intelligence (Gardner, 1985) talk about practical intelligence which enables ‘the individual to resolve genuine problems or difficulties that he or she encounters’ (p.60) and also encourages the individual to find or create problems ‘thereby laying the groundwork for the acquisition of new knowledge’ (p.85). As was pointed out earlier, standard mathematics, with the emphasis on the acquisition of knowledge, does not necessarily cater for these needs. Resnick (1987) described the discrepancies which exist between the algorithmic approaches taught in schools and the ‘invented’ strategies which most people use in the workforce in order to solve practical problems which do not always fit neatly into a taught algorithm. As she says, most people have developed ‘rules of thumb’ for calculating, for example, quantities, discounts or the amount of change they should give, and these rarely involve standard algorithms. Training in problem-solving techniques equips people more readily with the ability to adapt to such situations.
A further reason why a problem-solving approach is valuable is as an aesthetic form. Problem solving allows the student to experience a range of emotions associated with various stages in the solution process. Mathematicians who successfully solve problems say that the experience of having done so contributes to an appreciation for the ‘power and beauty of mathematics’ (NCTM, 1989, p.77), the “joy of banging your head against a mathematical wall, and then discovering that there might be ways of either going around or over that wall” (Olkin and Schoenfeld, 1994, p.43). They also speak of the willingness or even desire to engage with a task for a length of time which causes the task to cease being a ‘puzzle’ and allows it to become a problem. However, although it is this engagement which initially motivates the solver to pursue a problem, it is still necessary for certain techniques to be available for the involvement to continue successfully. Hence more needs to be understood about what these techniques are and how they can best be made available.
In the past decade it has been suggested that problem-solving techniques can be made available most effectively through making problem solving the focus of the mathematics curriculum. Although mathematical problems have traditionally been a part of the mathematics curriculum, it has been only comparatively recently that problem solving has come to be regarded as an important medium for teaching and learning mathematics (Stanic and Kilpatrick, 1989). In the past problem solving had a place in the mathematics classroom, but it was usually used in a token way as a starting point to obtain a single correct answer, usually by following a single ‘correct’ procedure. More recently, however, professional organisations such as the National Council of Teachers of Mathematics (NCTM, 1980 and 1989) have recommended that the mathematics curriculum should be organized around problem solving, focusing on:
- developing skills and the ability to apply these skills to unfamiliar situations
- gathering, organising, interpreting and communicating information
- formulating key questions, analyzing and conceptualizing problems, defining problems and goals, discovering patterns and similarities, seeking out appropriate data, experimenting, transferring skills and strategies to new situations
- developing curiosity, confidence and open-mindedness (NCTM, 1980, pp.2-3).
One of the aims of teaching through problem solving is to encourage students to refine and build onto their own processes over a period of time as their experiences allow them to discard some ideas and become aware of further possibilities (Carpenter, 1989). As well as developing knowledge, the students are also developing an understanding of when it is appropriate to use particular strategies. Through using this approach the emphasis is on making the students more responsible for their own learning rather than letting them feel that the algorithms they use are the inventions of some external and unknown ‘expert’. There is considerable importance placed on exploratory activities, observation and discovery, and trial and error. Students need to develop their own theories, test them, test the theories of others, discard them if they are not consistent, and try something else (NCTM, 1989). Students can become even more involved in problem solving by formulating and solving their own problems, or by rewriting problems in their own words in order to facilitate understanding. It is of particular importance to note that they are encouraged to discuss the processes which they are undertaking, in order to improve understanding, gain new insights into the problem and communicate their ideas (Thompson, 1985, Stacey and Groves, 1985).
It has been suggested in this chapter that there are many reasons why a problem-solving approach can contribute significantly to the outcomes of a mathematics education. Not only is it a vehicle for developing logical thinking, it can provide students with a context for learning mathematical knowledge, it can enhance transfer of skills to unfamiliar situations and it is an aesthetic form in itself. A problem-solving approach can provide a vehicle for students to construct their own ideas about mathematics and to take responsibility for their own learning. There is little doubt that the mathematics program can be enhanced by the establishment of an environment in which students are exposed to teaching via problem solving, as opposed to more traditional models of teaching about problem solving. The challenge for teachers, at all levels, is to develop the process of mathematical thinking alongside the knowledge and to seek opportunities to present even routine mathematics tasks in problem-solving contexts.
Example #1 – Mathematical Treasure Hunt
Objective – The objective of this activity is to encourage students to apply their problem-solving skills while having fun exploring mathematical concepts in a real-world context.
Materials Needed
Paper and pencils for each student Treasure map (could be a printed map or drawn by hand) Clues (math-related questions or puzzles) Optional: Small prizes or rewards for completing the treasure hunt Instructions:
Introduction (5 minutes)
Begin by introducing the activity to the students. Explain that they will be going on a mathematical treasure hunt where they will solve math problems to uncover hidden clues leading them to the treasure. Emphasize that this activity will require their problem-solving skills and teamwork.
Setting Up the Treasure Hunt (10 minutes)
Prepare a treasure map with different locations marked on it. These locations could be scattered around the classroom, school, or any other designated area. Hide clues at each location that will lead the students to the next destination.
Creating Clues (15 minutes)
Create math-related clues or puzzles that the students will need to solve to uncover the next location on the treasure map. The clues should be age-appropriate and aligned with the students’ math skills. For example:
Solve the following addition problem to reveal the next clue: 15 + 27 – 9 = ?
Count the number of chairs in the classroom and multiply by 3 to find the next location.
Find the area of the square-shaped rug in the library to unlock the next clue.
Starting the Treasure Hunt (5 minutes)
Divide the students into small groups or pairs, depending on the class size. Provide each group with a treasure map and the first clue. Explain the rules of the treasure hunt and encourage students to work together to solve the clues.
Exploring and Solving Clues (30 minutes)
Allow the students to begin the treasure hunt. As they solve each clue, they will uncover the location of the next clue on the treasure map. Encourage them to discuss and collaborate on the solutions to the math problems. Circulate around the room to provide assistance and guidance as needed.
Finding the Treasure (10 minutes)
Once the students have solved all the clues and reached the final location on the treasure map, they will discover the hidden treasure.
Congratulate them on their problem-solving skills and teamwork. You can optionally reward the students with small prizes or certificates for completing the treasure hunt successfully.
Reflection and Discussion (10 minutes)
After the treasure hunt, gather the students together for a brief reflection and discussion. Ask them about their favorite part of the activity, the challenges they faced, and what they learned from solving the math problems. Encourage them to share their strategies and insights with the class.
Extension Ideas
Create themed treasure hunts based on specific mathematical concepts such as geometry, fractions, or measurement.
Invite students to design their own treasure hunts for their classmates, incorporating math problems and creative clues.
Integrate technology by using QR codes or digital maps to lead students to each clue location.
By engaging students in a fun and interactive math problem-solving activity like the “Mathematical Treasure Hunt,” educators can foster a positive attitude towards mathematics while strengthening students’ critical thinking and collaboration skills.
Example #2 – Math Maze Adventure
Objective – The objective of this activity is to challenge students’ problem-solving abilities while navigating through a maze filled with math-related obstacles and puzzles.
Large maze layout (could be drawn on a poster board or printed) Dice Game tokens or markers for each student Math problem cards (with varying difficulty levels) Stopwatch or timer Optional: Prizes or rewards for completing the maze within a certain time limit
Instructions
Begin by introducing the “Math Maze Adventure” to the students. Explain that they will embark on a thrilling journey through a maze filled with mathematical challenges that they must overcome using their problem-solving skills.
Setting Up the Maze (10 minutes)
Create a large maze layout on a poster board or print one from a maze generator website. Designate a starting point and an endpoint within the maze. Place obstacles and challenges throughout the maze, such as math problems, riddles, or puzzles.
Preparing Math Problem Cards (15 minutes)
Create a set of math problem cards with varying difficulty levels. These problems could involve arithmetic operations, geometry concepts, fractions, or any other relevant math topics. Write each problem on a separate card and mix them up.
Starting the Adventure (5 minutes)
Divide the students into small groups or pairs, depending on the class size. Provide each group with a game token or marker to represent their position in the maze. Explain the rules of the game and how to navigate through the maze.
Navigating the Maze (30 minutes)
Start the timer and allow the students to begin their “Math Maze Adventure.” They will roll the dice to determine how many spaces they can move in the maze. When they land on a space with a math problem, they must draw a problem card and solve it correctly to proceed.
Solving Math Problems (30 minutes)
As students encounter math problems in the maze, they will work together to solve them. Encourage them to discuss strategies, share ideas, and check each other’s work. If they solve the problem correctly, they can continue moving through the maze. If not, they must stay in place until they solve it.
Reaching the Endpoint (10 minutes)
The goal of the “Math Maze Adventure” is to reach the endpoint of the maze within a certain time limit. Students must use their problem-solving skills and teamwork to overcome obstacles and challenges along the way. If they reach the endpoint before time runs out, they win the game!
After completing the maze, gather the students together for a reflection and discussion. Ask them about their experience navigating through the maze, the math problems they encountered, and the strategies they used to solve them. Encourage them to share their insights and lessons learned.
Create multiple versions of the maze with different layouts and levels of difficulty to provide ongoing challenges for students.
Integrate storytelling elements into the maze adventure, with each space representing a different part of the story that unfolds as students progress.
Incorporate technology by using a digital maze app or online platform to create and navigate through virtual mazes with math challenges.
The “Math Maze Adventure” offers an exciting and interactive way for students to practice their problem-solving skills while embarking on a thrilling journey through a maze filled with mathematical challenges. Through teamwork, critical thinking, and perseverance, students will navigate their way to success!
Carpenter, T. P. (1989). ‘Teaching as problem solving’. In R.I.Charles and E.A. Silver (Eds), The Teaching and Assessing of Mathematical Problem Solving, (pp.187-202). USA: National Council of Teachers of Mathematics.
Clarke, D. and McDonough, A. (1989). ‘The problems of the problem solving classroom’, The Australian Mathematics Teacher, 45, 3, 20-24.
Cobb, P., Wood, T. and Yackel, E. (1991). ‘A constructivist approach to second grade mathematics’. In von Glaserfield, E. (Ed.), Radical Constructivism in Mathematics Education, pp. 157-176. Dordrecht, The Netherlands: Kluwer Academic Publishers.
Cockcroft, W.H. (Ed.) (1982). Mathematics Counts. Report of the Committee of Inquiry into the Teaching of Mathematics in Schools, London: Her Majesty’s Stationery Office.
Evan, R. and Lappin, G. (1994). ‘Constructing meaningful understanding of mathematics content’, in Aichele, D. and Coxford, A. (Eds.) Professional Development for Teachers of Mathematics , pp. 128-143. Reston, Virginia: NCTM.
Gardner, Howard (1985). Frames of Mind. N.Y: Basic Books.
Lester, F.K.Jr., Masingila, J.O., Mau, S.T., Lambdin, D.V., dos Santon, V.M. and Raymond, A.M. (1994). ‘Learning how to teach via problem solving’. in Aichele, D. and Coxford, A. (Eds.) Professional Development for Teachers of Mathematics , pp. 152-166. Reston, Virginia: NCTM.
National Council of Teachers of Mathematics (NCTM) (1980). An Agenda for Action: Recommendations for School Mathematics of the 1980s, Reston, Virginia: NCTM.
National Council of Teachers of Mathematics (NCTM) (1989). Curriculum and Evaluation Standards for School Mathematics, Reston, Virginia: NCTM.
Olkin, I. & Schoenfeld, A. (1994). A discussion of Bruce Reznick’s chapter. In A. Schoenfeld (Ed.). Mathematical Thinking and Problem Solving. (pp. 39-51). Hillsdale, NJ: Lawrence Erlbaum Associates.
Polya, G. (1980). ‘On solving mathematical problems in high school’. In S. Krulik (Ed). Problem Solving in School Mathematics, (pp.1-2). Reston, Virginia: NCTM.
Resnick, L. B. (1987). ‘Learning in school and out’, Educational Researcher, 16, 13-20..
Romberg, T. (1994). Classroom instruction that fosters mathematical thinking and problem solving: connections between theory and practice. In A. Schoenfeld (Ed.). Mathematical Thinking and Problem Solving. (pp. 287-304). Hillsdale, NJ: Lawrence Erlbaum Associates.
Schifter, D. and Fosnot, C. (1993). Reconstructing Mathematics Education. NY: Teachers College Press.
Schoenfeld, A. (1994). Reflections on doing and teaching mathematics. In A. Schoenfeld (Ed.). Mathematical Thinking and Problem Solving. (pp. 53-69). Hillsdale, NJ: Lawrence Erlbaum Associates.
Stacey, K. and Groves, S. (1985). Strategies for Problem Solving, Melbourne, Victoria: VICTRACC.
Stanic, G. and Kilpatrick, J. (1989). ‘Historical perspectives on problem solving in the mathematics curriculum’. In R.I. Charles and E.A. Silver (Eds), The Teaching and Assessing of Mathematical Problem Solving, (pp.1-22). USA: National Council of Teachers of Mathematics.
Swafford, J.O. (1995). ‘Teacher preparation’. in Carl, I.M. (Ed.) Prospects for School Mathematics , pp. 157-174. Reston, Virginia: NCTM.
Thompson, P. W. (1985). ‘Experience, problem solving, and learning mathematics: considerations in developing mathematics curricula’. In E.A. Silver (Ed.), Teaching and Learning Mathematical Problem Solving: Multiple Research Perspectives, (pp.189-236). Hillsdale, N.J: Lawrence Erlbaum.
Van Zoest, L., Jones, G. and Thornton, C. (1994). ‘Beliefs about mathematics teaching held by pre-service teachers involved in a first grade mentorship program’. Mathematics Education Research Journal. 6(1): 37-55.
Related Article on Teaching Values | Other Articles

Or search by topic
Number and algebra
- The Number System and Place Value
- Calculations and Numerical Methods
- Fractions, Decimals, Percentages, Ratio and Proportion
- Properties of Numbers
- Patterns, Sequences and Structure
- Algebraic expressions, equations and formulae
- Coordinates, Functions and Graphs
Geometry and measure
- Angles, Polygons, and Geometrical Proof
- 3D Geometry, Shape and Space
- Measuring and calculating with units
- Transformations and constructions
- Pythagoras and Trigonometry
- Vectors and Matrices
Probability and statistics
- Handling, Processing and Representing Data
- Probability
Working mathematically
- Thinking mathematically
- Mathematical mindsets
- Cross-curricular contexts
- Physical and digital manipulatives
For younger learners
- Early Years Foundation Stage
Advanced mathematics
- Decision Mathematics and Combinatorics
- Advanced Probability and Statistics
Published 2017 Revised 2019
What's the Problem with Problem Solving?
| Word problems | We have a collection of short problems that would be ideal to fit into this category. While these problems sit within our secondary pages, the would be suitable for upper primary students. |
| Visual problems | and |
| Finding all possibilities | and |
| Logic problems | and |
| Rules and patterns | and |
| Pattern spotting | and |
| Working systematically | and |
| Using diagrams and pictorial information | and |
| Working backwards | and |
| Trial and improvement | and |
| Visualising | and |
| Conjecturing and generalising | and |
| Reasoning logically | and |
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 1: Algebra foundations
Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations
Graph your math problems
Practice, practice, practice

Get math help in your language
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Problem Solving
Problem or Exercise?
The main activity of mathematics is solving problems. However, what most people experience in most mathematics classrooms is practice exercises. An exercise is different from a problem.
In a problem , you probably don’t know at first how to approach solving it. You don’t know what mathematical ideas might be used in the solution. Part of solving a problem is understanding what is being asked, and knowing what a solution should look like. Problems often involve false starts, making mistakes, and lots of scratch paper!
In an exercise , you are often practicing a skill. You may have seen a teacher demonstrate a technique, or you may have read a worked example in the book. You then practice on very similar assignments, with the goal of mastering that skill.
Note: What is a problem for some people may be an exercise for other people who have more background knowledge! For a young student just learning addition, this might be a problem:
But for you, that is an exercise!
Both problems and exercises are important in mathematics learning. But we should never forget that the ultimate goal is to develop more and better skills (through exercises) so that we can solve harder and more interesting problems.
Learning math is a bit like learning to play a sport. You can practice a lot of skills:
- hitting hundreds of forehands in tennis so that you can place them in a particular spot in the court,
- breaking down strokes into the component pieces in swimming so that each part of the stroke is more efficient,
- keeping control of the ball while making quick turns in soccer,
- shooting free throws in basketball,
- catching high fly balls in baseball,
But the point of the sport is to play the game. You practice the skills so that you are better at playing the game. In mathematics, solving problems is playing the game!
On Your Own
For each question below, decide if it is a problem or an exercise . (You do not need to solve the problems! Just decide which category it fits for you.) After you have labeled each one, compare your answers with a partner.
1. This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers.(Note: Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15. )
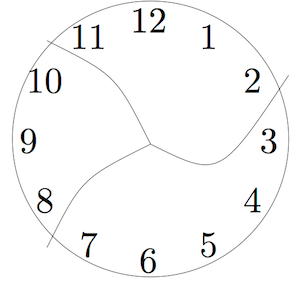
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2).
2. A soccer coach began the year with a $500 budget. By the end of December, the coach spent $450. How much money in the budget was not spent?
3. What is the product of 4,500 and 27?
4. Arrange the digits 1–6 into a “difference triangle” where each number in the row below is the difference of the two numbers above it.
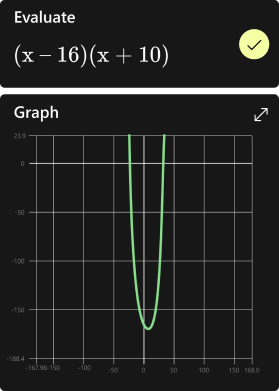
5. Simplify the following expression:
7. You have eight coins and a balance scale. The coins look alike, but one of them is a counterfeit. The counterfeit coin is lighter than the others. You may only use the balance scale two times. How can you find the counterfeit coin?

8. How many squares, of any possible size, are on a standard 8 × 8 chess board?
9. What number is 3 more than half of 20?
10. Find the largest eight-digit number made up of the digits 1, 1, 2, 2, 3, 3, 4, and 4 such that the 1’s are separated by one digit, the 2’s are separated by two digits, the 3’s by three digits, and the 4’s by four digits.
Mathematics for Elementary Teachers Copyright © 2018 by Michelle Manes is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Advertisement
What problem-solving knowledge is required in mathematical teaching? A curricular approach
- Research article
- Published: 21 October 2021
- Volume 42 , pages 1–12, ( 2022 )
Cite this article

- Juan Luis Piñeiro ORCID: orcid.org/0000-0002-9616-3925 1 ,
- Elena Castro-Rodríguez 2 &
- Enrique Castro 2
399 Accesses
6 Altmetric
Explore all metrics
This study explores the knowledge required for teachers to teach problem solving (PS) from a Primary Mathematics Curriculum Guidelines perspective. It analyzes six countries’ curricular guidelines for primary education using the Mathematical Problem-Solving Knowledge for Teaching model. To identify the PS knowledge required in each education system, the country guidelines were selected based on the country’s results in the 2012 Programme for International Student Assessment (PISA) survey. Data analysis revealed that PS-related knowledge included in the curricula is broad and challenging for teachers. Further, it is not always coherent and research-based. More specifically, the findings show that curricular guidelines emphasize problem classification and solving processes. Our analysis supports the conclusion that particularities in teachers’ knowledge become visible when we view it from the perspective of PS rather than of mathematical concepts.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions

Similar content being viewed by others

Teaching with digital technology

Research on early childhood mathematics teaching and learning

Trends in mathematics education and insights from a meta-review and bibliometric analysis of review studies
Agre, G. P. (1982). The concept of problem. Educational Studies, 13 (2), 121–142.
Article Google Scholar
Ball, D. L., Hill, H. C., & Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29 (1), 14–46.
Google Scholar
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59 (5), 389–407.
Bardin, L. (1996). Análisis de contenido . Akal.
Boote, S. K., & Boote, D. N. (2018). ABC problem in elementary mathematics education: Arithmetic before comprehension. Journal of Mathematics Teacher Education, 21 (2), 99–122.
Bromme, R. (1994). Beyond subject matter: A psychological topology of teachers’ professional knowledge. In R. Biehler, R. Scholz, R. Sträber, & B. Winkelmann (Eds.), Didactics of mathematics as a scientific discipline (pp. 73–88). Kluwer Academic Publishers.
Carrillo, J., Climent, N., Montes, M., Contreras, L. C., Flores-Medrano, E., Escudero-Ávila, D., … Muñoz-Catalán, M. C. (2018). The mathematics teacher’s specialised knowledge (MTSK) model. Research in Mathematics Education , 20 (3), 236–253.
Chapman, O. (2008). Instructional practices to facilitate prospective mathematics teachers’ learning of problem solving for teaching. In M. Santos-Trigo & Y. Schimizu (Eds.), ICME-11. Topic study group 19. Research and development in problem solving in mathematics education (pp. 158–167). ICME.
Chapman, O. (2012). Practice-based conception of secondary school teachers’ mathematical problem-solving for teaching. In En T.-Y. Tso (Ed.), Proceedings of the 36th conference of the international group for the psychology of mathematics education (Vol. 2, pp. 107–114). PME.
Chapman, O. (2015). Mathematics teachers’ knowledge for teaching problem solving. LUMAT, 3 (1), 19–36.
Chapman, O. (2016). An exemplary mathematics teacher’s ways of holding problem-solving knowledge for teaching. In C. Csíkos, A. Rausch, & J. Szitányi (Eds.), Proceedings of the 40th conference of the PME (Vol. 2, pp. 139–146). PME.
Christou, C., Mousoulides, N., Pittalis, M., Pitta-Pantazi, D., & Sriraman, B. (2005). An empirical taxonomy of problem posing processes. ZDM, 37 (3), 149–158.
Consejo Federal de Educación (2011a). Núcleos de aprendizajes prioritarios. 1° ciclo Educación Primaria. 1°, 2° y 3° Años . Ministerio de Educación de Argentina.
Consejo Federal de Educación (2011b). Núcleos de aprendizajes prioritarios. 2° ciclo Educación Primaria. 4°, 5° y 6° Años . Ministerio de Educación de Argentina.
Creswell, J. W. (2013). Research design: Qualitative, quantitative, and mixed methods approaches (4th ed.). SAGE.
Curriculum Planning and Development Division. (2007). Mathematics syllabus primary . Singapore Ministry of Education.
Deng, Z. (2018). Pedagogical content knowledge reconceived: Bringing curriculum thinking into the conversation on teachers’ content knowledge. Teaching and Teacher Education, 72 , 155–164.
Depaepe, F., De Corte, E., & Verschaffel, L. (2010). Teachers’ approaches towards word problem solving: Elaborating or restricting the problem context. Teaching and Teacher Education, 26 (2), 152–160.
Foster, C., Wake, G., & Swan, M. (2014). Mathematical knowledge for teaching problem solving: Lessons from lesson study. In S. Oesterle, P. Liljedahl, C. Nicol, & D. Allan (Eds.), Proceedings of the joint meeting of PME 38 and PME-NA 36 (Vol. 3, pp. 97–104). PME.
Grønmo, L. S., Lindquist, M., & Arora, A. (2014). TIMSS advanced 2015 mathematics framework. In I. V. S. Mullis & M. O. Martin (Eds.), TIMSS advanced 2015 assessment frameworks (pp. 9–16). TIMMS & PIRLS International Study Center, Lynch School of Education, Boston College and IEA.
Hernández, R., Fernández, C., & Baptista, P. (2014). Metodología de la investigación (6th ed.). McGraw-Hill Education.
Krippendorff, K. (2004). Content analysis: An introduction to its methodology (2nd ed.). Sage.
Kuckartz, U. (2019). Qualitative text analysis: A systematic approach. In G. Kaiser & N. Presmeg (Eds.), Compendium for early career researchers in mathematics education (pp. 181–198). Springer.
Chapter Google Scholar
Lester, F. K. (2013). Thoughts about research on mathematical problem-solving instruction. The Mathematics Enthusiast, 10 (1&2), 245–278.
Lester, F. K., & Cai, J. (2016). Can mathematical problem solving be taught? Preliminary answers from 30 years of research. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and solving mathematical problems (pp. 117–135). Springer.
Lin, F.-L., & Rowland, T. (2016). Pre-service and in-service mathematics teachers’ knowledge and professional development. In Á. Gutiérrez, G. C. Leder, & P. Boero (Eds.), The second handbook of research on the psychology of mathematics education (pp. 483–520). Sense.
Ministerio de Educación (2012). Bases curriculares Educación Básica. Unidad de Currículum y Evaluación.
Ministerio de Educación y Ciencia (2014). Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria, BOE , (52), 19349–19420.
National Core Curriculum for Basic Education (2004). National core curriculum for basic education intended for pupils in compulsory education. Finland National Board of Education.
NCTM (1980). An agenda for action: Recommendations for school mathematics of the l980’s. Author.
NCTM (2000). Principles and standards for school mathematics. Author.
NCTM. (2010). Making it happen. A guide to interpreting and implementing common core state standards for mathematics . Author.
O’Shea, J., & y Leavy, A. M. (2013). Teaching mathematical problem-solving from an emergent constructivist perspective: the experiences of Irish primary teachers. Journal of Mathematics Teacher Education, 16 (4), 293–318.
OECD. (2013). Draft PISA 2015 mathematics framework . Autor.
OECD. (2014). PISA 2012 results: What students know and can do . Autor.
Piñeiro, J. L. (2019). Conocimiento profesional de maestros en formación inicial sobre resolución de problemas en matemáticas (Doctoral dissertation). University of Granada. http://hdl.handle.net/10481/57450 .
Pólya, G. (1945). How to solve it . University Press.
Book Google Scholar
Rico, L. (2007). La competencia matemática en PISA. PNA, 1 (2), 47–66.
Rowland, T., Huckstep, P., & Thwaites, A. (2005). Elementary teachers’ mathematics subject knowledge: The knowledge quartet and the case of Naomi. Journal of Mathematics Teacher Education, 8 (3), 255–281.
Safrudiannur, & Rott, B. (2019). The different mathematics performances in PISA 2012 and a curricula comparison: Enriching the comparison by an analysis of the role of problem solving in intended learning processes. Mathematics Education Research Journal, 31 , 175–195.
Schmidt, W. H., McKnight, C. C., Valverde, G. A., Houang, R. T., & Wiley, D. E. (1997). Many visions, many aims. A cross-national investigation of curricular intentions in school mathematics (Vol. 1). Kluwer Academic.
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition and sense making in mathematics. In D. Grows (Ed.), Handbook for research on mathematics teaching and learning (pp. 334–370). Macmillan.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15 (2), 4–14.
Silver, E. A. (1994). On mathematical problem posing. For the Learning of Mathematics, 14 (1), 19–28.
Stacey, K. (2005). The place of problem solving in contemporary mathematics curriculum documents. The Journal of Mathematical Behavior, 24 (3–4), 341–350.
Weber, K., & Leikin, R. (2016). Recent advances in research on problem solving and problem posing. In Á. Gutiérrez, G. C. Leder, & P. Boero (Eds.), The second handbook of research on the psychology of mathematics education (pp. 353–382) . Routledge.
Download references
This work was supported by the Spanish Ministry of Science and Innovation’s National R&D + I Plan, funded under project PGC2018–095765-B-100; and the Government of Chile’s National Scientific and Technological Research Commission (CONICYT) [grant number 72170314].
Author information
Authors and affiliations.
Faculty of Philosophy and Education, Universidad Metropolitana de Ciencias de la Educación, Av. José Pedro Alessandri 774, Ñuñoa, Santiago, Chile
Juan Luis Piñeiro
Faculty of Education, Universidad de Granada, Cartuja Campus s/n, 18011, Granada, Spain
Elena Castro-Rodríguez & Enrique Castro
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Juan Luis Piñeiro .
Ethics declarations
Conflict of interest.
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Reprints and permissions
About this article
Piñeiro, J.L., Castro-Rodríguez, E. & Castro, E. What problem-solving knowledge is required in mathematical teaching? A curricular approach. Curric Perspect 42 , 1–12 (2022). https://doi.org/10.1007/s41297-021-00152-6
Download citation
Received : 03 December 2020
Revised : 24 September 2021
Accepted : 29 September 2021
Published : 21 October 2021
Issue Date : April 2022
DOI : https://doi.org/10.1007/s41297-021-00152-6
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Problem solving
- Teachers’ knowledge
- Primary teachers
- Curricular analysis
- Find a journal
- Publish with us
- Track your research

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

Module 1: Problem Solving Strategies
- Last updated
- Save as PDF
- Page ID 10352
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.
Pólya’s How to Solve It
George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1
1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:
First, you have to understand the problem.
After understanding, then make a plan.
Carry out the plan.
Look back on your work. How could it be better?
This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.
Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!
Problem Solving Strategy 1 (Guess and Test)
Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.
Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?
Step 1: Understanding the problem
We are given in the problem that there are 25 chickens and cows.
All together there are 76 feet.
Chickens have 2 feet and cows have 4 feet.
We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.
Step 2: Devise a plan
Going to use Guess and test along with making a tab
Many times the strategy below is used with guess and test.
Make a table and look for a pattern:
Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.
Step 3: Carry out the plan:
| Chickens | Cows | Number of chicken feet | Number of cow feet | Total number of feet |
| 20 | 5 | 40 | 20 | 60 |
| 21 | 4 | 42 | 16 | 58 |
Notice we are going in the wrong direction! The total number of feet is decreasing!
| 19 | 6 | 38 | 24 | 62 |
Better! The total number of feet are increasing!
| 15 | 10 | 30 | 40 | 70 |
| 12 | 13 | 24 | 52 | 76 |
Step 4: Looking back:
Check: 12 + 13 = 25 heads
24 + 52 = 76 feet.
We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.
Videos to watch:
1. Click on this link to see an example of “Guess and Test”
http://www.mathstories.com/strategies.htm
2. Click on this link to see another example of Guess and Test.
http://www.mathinaction.org/problem-solving-strategies.html
Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)
Check in question 2:
Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)
Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!
Videos to watch demonstrating how to use "Draw a Picture".
1. Click on this link to see an example of “Draw a Picture”
2. Click on this link to see another example of Draw a Picture.
Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)
Gauss's strategy for sequences.
last term = fixed number ( n -1) + first term
The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.
Ex: 2, 5, 8, ... Find the 200th term.
Last term = 3(200-1) +2
Last term is 599.
To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2
Sum = (2 + 599) (200) then divide by 2
Sum = 60,100
Check in question 3: (10 points)
Find the 320 th term of 7, 10, 13, 16 …
Then find the sum of the first 320 terms.
Problem Solving Strategy 4 (Working Backwards)
This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.
Videos to watch demonstrating of “Working Backwards”
https://www.youtube.com/watch?v=5FFWTsMEeJw
Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?
1. We start with 11 and work backwards.
2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.
3. The opposite of doubling something is dividing by 2. 18/2 = 9
4. This should be our answer. Looking back:
9 x 2 = 18 -7 = 11
5. We have the right answer.
Check in question 4:
Christina is thinking of a number.
If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)
Problem Solving Strategy 5 (Looking for a Pattern)
Definition: A sequence is a pattern involving an ordered arrangement of numbers.
We first need to find a pattern.
Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?
Example 1: 1, 4, 7, 10, 13…
Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.
Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.
So the next number would be
25 + 11 = 36
Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.
In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5
-5 – 3 = -8
Example 4: 1, 2, 4, 8 … find the next two numbers.
This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?
So each number is being multiplied by 2.
16 x 2 = 32
1. Click on this link to see an example of “Looking for a Pattern”
2. Click on this link to see another example of Looking for a Pattern.
Problem Solving Strategy 6 (Make a List)
Example 1 : Can perfect squares end in a 2 or a 3?
List all the squares of the numbers 1 to 20.
1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.
Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.
How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?
Quarter’s dimes
0 3 30 cents
1 2 45 cents
2 1 60 cents
3 0 75 cents
Videos demonstrating "Make a List"
Check in question 5:
How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)
Problem Solving Strategy 7 (Solve a Simpler Problem)
Geometric Sequences:
How would we find the nth term?
Solve a simpler problem:
1, 3, 9, 27.
1. To get from 1 to 3 what did we do?
2. To get from 3 to 9 what did we do?
Let’s set up a table:
Term Number what did we do
Looking back: How would you find the nth term?
Find the 10 th term of the above sequence.
Let L = the tenth term
Problem Solving Strategy 8 (Process of Elimination)
This strategy can be used when there is only one possible solution.
I’m thinking of a number.
The number is odd.
It is more than 1 but less than 100.
It is greater than 20.
It is less than 5 times 7.
The sum of the digits is 7.
It is evenly divisible by 5.
a. We know it is an odd number between 1 and 100.
b. It is greater than 20 but less than 35
21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.
c. The sum of the digits is 7
21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.
Check in question 6: (8 points)
Jose is thinking of a number.
The number is not odd.
The sum of the digits is divisible by 2.
The number is a multiple of 11.
It is greater than 5 times 4.
It is a multiple of 6
It is less than 7 times 8 +23
What is the number?
Click on this link for a quick review of the problem solving strategies.
https://garyhall.org.uk/maths-problem-solving-strategies.html
10 Hard Math Problems That Continue to Stump Even the Brightest Minds
Maybe you’ll have better luck.

For now, you can take a crack at the hardest math problems known to man, woman, and machine. For more puzzles and brainteasers, check out Puzzmo . ✅ More from Popular Mechanics :
- To Create His Geometric Artwork, M.C. Escher Had to Learn Math the Hard Way
- Fourier Transforms: The Math That Made Color TV Possible
- The Game of Trees is a Mad Math Theory That Is Impossible to Prove
The Collatz Conjecture

In September 2019, news broke regarding progress on this 82-year-old question, thanks to prolific mathematician Terence Tao. And while the story of Tao’s breakthrough is promising, the problem isn’t fully solved yet.
A refresher on the Collatz Conjecture : It’s all about that function f(n), shown above, which takes even numbers and cuts them in half, while odd numbers get tripled and then added to 1. Take any natural number, apply f, then apply f again and again. You eventually land on 1, for every number we’ve ever checked. The Conjecture is that this is true for all natural numbers (positive integers from 1 through infinity).
✅ Down the Rabbit Hole: The Math That Helps the James Webb Space Telescope Sit Steady in Space
Tao’s recent work is a near-solution to the Collatz Conjecture in some subtle ways. But he most likely can’t adapt his methods to yield a complete solution to the problem, as Tao subsequently explained. So, we might be working on it for decades longer.
The Conjecture lives in the math discipline known as Dynamical Systems , or the study of situations that change over time in semi-predictable ways. It looks like a simple, innocuous question, but that’s what makes it special. Why is such a basic question so hard to answer? It serves as a benchmark for our understanding; once we solve it, then we can proceed onto much more complicated matters.
The study of dynamical systems could become more robust than anyone today could imagine. But we’ll need to solve the Collatz Conjecture for the subject to flourish.
Goldbach’s Conjecture
One of the greatest unsolved mysteries in math is also very easy to write. Goldbach’s Conjecture is, “Every even number (greater than two) is the sum of two primes.” You check this in your head for small numbers: 18 is 13+5, and 42 is 23+19. Computers have checked the Conjecture for numbers up to some magnitude. But we need proof for all natural numbers.
Goldbach’s Conjecture precipitated from letters in 1742 between German mathematician Christian Goldbach and legendary Swiss mathematician Leonhard Euler , considered one of the greatest in math history. As Euler put it, “I regard [it] as a completely certain theorem, although I cannot prove it.”
✅ Dive In: The Math Behind Our Current Theory of Human Color Perception Is Wrong
Euler may have sensed what makes this problem counterintuitively hard to solve. When you look at larger numbers, they have more ways of being written as sums of primes, not less. Like how 3+5 is the only way to break 8 into two primes, but 42 can broken into 5+37, 11+31, 13+29, and 19+23. So it feels like Goldbach’s Conjecture is an understatement for very large numbers.
Still, a proof of the conjecture for all numbers eludes mathematicians to this day. It stands as one of the oldest open questions in all of math.

The Twin Prime Conjecture
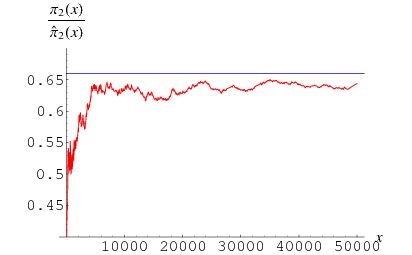
Together with Goldbach’s, the Twin Prime Conjecture is the most famous in Number Theory—or the study of natural numbers and their properties, frequently involving prime numbers. Since you've known these numbers since grade school, stating the conjectures is easy.
When two primes have a difference of 2, they’re called twin primes. So 11 and 13 are twin primes, as are 599 and 601. Now, it's a Day 1 Number Theory fact that there are infinitely many prime numbers. So, are there infinitely many twin primes? The Twin Prime Conjecture says yes.
Let’s go a bit deeper. The first in a pair of twin primes is, with one exception, always 1 less than a multiple of 6. And so the second twin prime is always 1 more than a multiple of 6. You can understand why, if you’re ready to follow a bit of heady Number Theory.
✅ Keep Learning: If We Draw Graphs Like This, We Can Change Computers Forever
All primes after 2 are odd. Even numbers are always 0, 2, or 4 more than a multiple of 6, while odd numbers are always 1, 3, or 5 more than a multiple of 6. Well, one of those three possibilities for odd numbers causes an issue. If a number is 3 more than a multiple of 6, then it has a factor of 3. Having a factor of 3 means a number isn’t prime (with the sole exception of 3 itself). And that's why every third odd number can't be prime.
How’s your head after that paragraph? Now imagine the headaches of everyone who has tried to solve this problem in the last 170 years.
The good news is that we’ve made some promising progress in the last decade. Mathematicians have managed to tackle closer and closer versions of the Twin Prime Conjecture. This was their idea: Trouble proving there are infinitely many primes with a difference of 2? How about proving there are infinitely many primes with a difference of 70,000,000? That was cleverly proven in 2013 by Yitang Zhang at the University of New Hampshire.
For the last six years, mathematicians have been improving that number in Zhang’s proof, from millions down to hundreds. Taking it down all the way to 2 will be the solution to the Twin Prime Conjecture. The closest we’ve come —given some subtle technical assumptions—is 6. Time will tell if the last step from 6 to 2 is right around the corner, or if that last part will challenge mathematicians for decades longer.
The Riemann Hypothesis
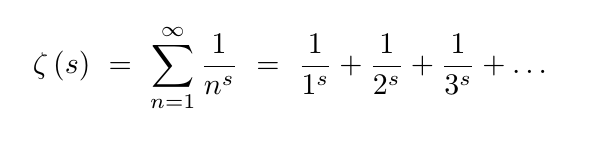
Today’s mathematicians would probably agree that the Riemann Hypothesis is the most significant open problem in all of math. It’s one of the seven Millennium Prize Problems , with $1 million reward for its solution. It has implications deep into various branches of math, but it’s also simple enough that we can explain the basic idea right here.
There is a function, called the Riemann zeta function, written in the image above.
For each s, this function gives an infinite sum, which takes some basic calculus to approach for even the simplest values of s. For example, if s=2, then 𝜁(s) is the well-known series 1 + 1/4 + 1/9 + 1/16 + …, which strangely adds up to exactly 𝜋²/6. When s is a complex number—one that looks like a+b𝑖, using the imaginary number 𝑖—finding 𝜁(s) gets tricky.
So tricky, in fact, that it’s become the ultimate math question. Specifically, the Riemann Hypothesis is about when 𝜁(s)=0; the official statement is, “Every nontrivial zero of the Riemann zeta function has real part 1/2.” On the plane of complex numbers, this means the function has a certain behavior along a special vertical line. The hypothesis is that the behavior continues along that line infinitely.
✅ Stay Curious: How to Paint a Room Using Math
The Hypothesis and the zeta function come from German mathematician Bernhard Riemann, who described them in 1859. Riemann developed them while studying prime numbers and their distribution. Our understanding of prime numbers has flourished in the 160 years since, and Riemann would never have imagined the power of supercomputers. But lacking a solution to the Riemann Hypothesis is a major setback.
If the Riemann Hypothesis were solved tomorrow, it would unlock an avalanche of further progress. It would be huge news throughout the subjects of Number Theory and Analysis. Until then, the Riemann Hypothesis remains one of the largest dams to the river of math research.
The Birch and Swinnerton-Dyer Conjecture
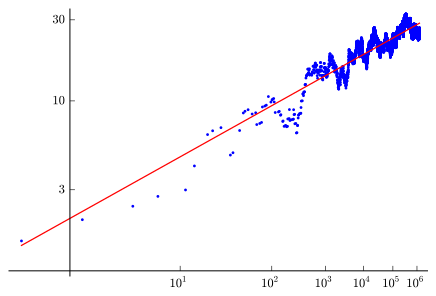
The Birch and Swinnerton-Dyer Conjecture is another of the six unsolved Millennium Prize Problems, and it’s the only other one we can remotely describe in plain English. This Conjecture involves the math topic known as Elliptic Curves.
When we recently wrote about the toughest math problems that have been solved , we mentioned one of the greatest achievements in 20th-century math: the solution to Fermat’s Last Theorem. Sir Andrew Wiles solved it using Elliptic Curves. So, you could call this a very powerful new branch of math.
✅ The Latest: Mathematicians Discovered Something Mind-Blowing About the Number 15
In a nutshell, an elliptic curve is a special kind of function. They take the unthreatening-looking form y²=x³+ax+b. It turns out functions like this have certain properties that cast insight into math topics like Algebra and Number Theory.
British mathematicians Bryan Birch and Peter Swinnerton-Dyer developed their conjecture in the 1960s. Its exact statement is very technical, and has evolved over the years. One of the main stewards of this evolution has been none other than Wiles. To see its current status and complexity, check out this famous update by Wells in 2006.
The Kissing Number Problem

A broad category of problems in math are called the Sphere Packing Problems. They range from pure math to practical applications, generally putting math terminology to the idea of stacking many spheres in a given space, like fruit at the grocery store. Some questions in this study have full solutions, while some simple ones leave us stumped, like the Kissing Number Problem.
When a bunch of spheres are packed in some region, each sphere has a Kissing Number, which is the number of other spheres it’s touching; if you’re touching 6 neighboring spheres, then your kissing number is 6. Nothing tricky. A packed bunch of spheres will have an average kissing number, which helps mathematically describe the situation. But a basic question about the kissing number stands unanswered.
✅ Miracles Happen: Mathematicians Finally Make a Breakthrough on the Ramsey Number
First, a note on dimensions. Dimensions have a specific meaning in math: they’re independent coordinate axes. The x-axis and y-axis show the two dimensions of a coordinate plane. When a character in a sci-fi show says they’re going to a different dimension, that doesn’t make mathematical sense. You can’t go to the x-axis.
A 1-dimensional thing is a line, and 2-dimensional thing is a plane. For these low numbers, mathematicians have proven the maximum possible kissing number for spheres of that many dimensions. It’s 2 when you’re on a 1-D line—one sphere to your left and the other to your right. There’s proof of an exact number for 3 dimensions, although that took until the 1950s.
Beyond 3 dimensions, the Kissing Problem is mostly unsolved. Mathematicians have slowly whittled the possibilities to fairly narrow ranges for up to 24 dimensions, with a few exactly known, as you can see on this chart . For larger numbers, or a general form, the problem is wide open. There are several hurdles to a full solution, including computational limitations. So expect incremental progress on this problem for years to come.
The Unknotting Problem
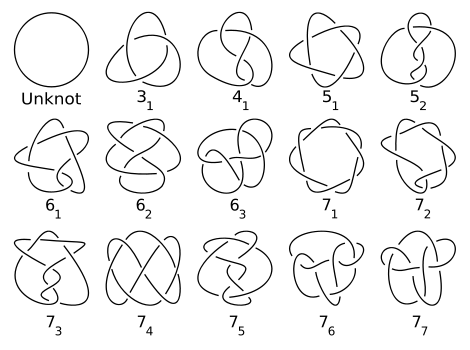
The simplest version of the Unknotting Problem has been solved, so there’s already some success with this story. Solving the full version of the problem will be an even bigger triumph.
You probably haven’t heard of the math subject Knot Theory . It ’s taught in virtually no high schools, and few colleges. The idea is to try and apply formal math ideas, like proofs, to knots, like … well, what you tie your shoes with.
For example, you might know how to tie a “square knot” and a “granny knot.” They have the same steps except that one twist is reversed from the square knot to the granny knot. But can you prove that those knots are different? Well, knot theorists can.
✅ Up Next: The Amazing Math Inside the Rubik’s Cube
Knot theorists’ holy grail problem was an algorithm to identify if some tangled mess is truly knotted, or if it can be disentangled to nothing. The cool news is that this has been accomplished! Several computer algorithms for this have been written in the last 20 years, and some of them even animate the process .
But the Unknotting Problem remains computational. In technical terms, it’s known that the Unknotting Problem is in NP, while we don ’ t know if it’s in P. That roughly means that we know our algorithms are capable of unknotting knots of any complexity, but that as they get more complicated, it starts to take an impossibly long time. For now.
If someone comes up with an algorithm that can unknot any knot in what’s called polynomial time, that will put the Unknotting Problem fully to rest. On the flip side, someone could prove that isn’t possible, and that the Unknotting Problem’s computational intensity is unavoidably profound. Eventually, we’ll find out.
The Large Cardinal Project

If you’ve never heard of Large Cardinals , get ready to learn. In the late 19th century, a German mathematician named Georg Cantor figured out that infinity comes in different sizes. Some infinite sets truly have more elements than others in a deep mathematical way, and Cantor proved it.
There is the first infinite size, the smallest infinity , which gets denoted ℵ₀. That’s a Hebrew letter aleph; it reads as “aleph-zero.” It’s the size of the set of natural numbers, so that gets written |ℕ|=ℵ₀.
Next, some common sets are larger than size ℵ₀. The major example Cantor proved is that the set of real numbers is bigger, written |ℝ|>ℵ₀. But the reals aren’t that big; we’re just getting started on the infinite sizes.
✅ More Mind-Blowing Stuff: Mathematicians Discovered a New 13-Sided Shape That Can Do Remarkable Things
For the really big stuff, mathematicians keep discovering larger and larger sizes, or what we call Large Cardinals. It’s a process of pure math that goes like this: Someone says, “I thought of a definition for a cardinal, and I can prove this cardinal is bigger than all the known cardinals.” Then, if their proof is good, that’s the new largest known cardinal. Until someone else comes up with a larger one.
Throughout the 20th century, the frontier of known large cardinals was steadily pushed forward. There’s now even a beautiful wiki of known large cardinals , named in honor of Cantor. So, will this ever end? The answer is broadly yes, although it gets very complicated.
In some senses, the top of the large cardinal hierarchy is in sight. Some theorems have been proven, which impose a sort of ceiling on the possibilities for large cardinals. But many open questions remain, and new cardinals have been nailed down as recently as 2019. It’s very possible we will be discovering more for decades to come. Hopefully we’ll eventually have a comprehensive list of all large cardinals.
What’s the Deal with 𝜋+e?
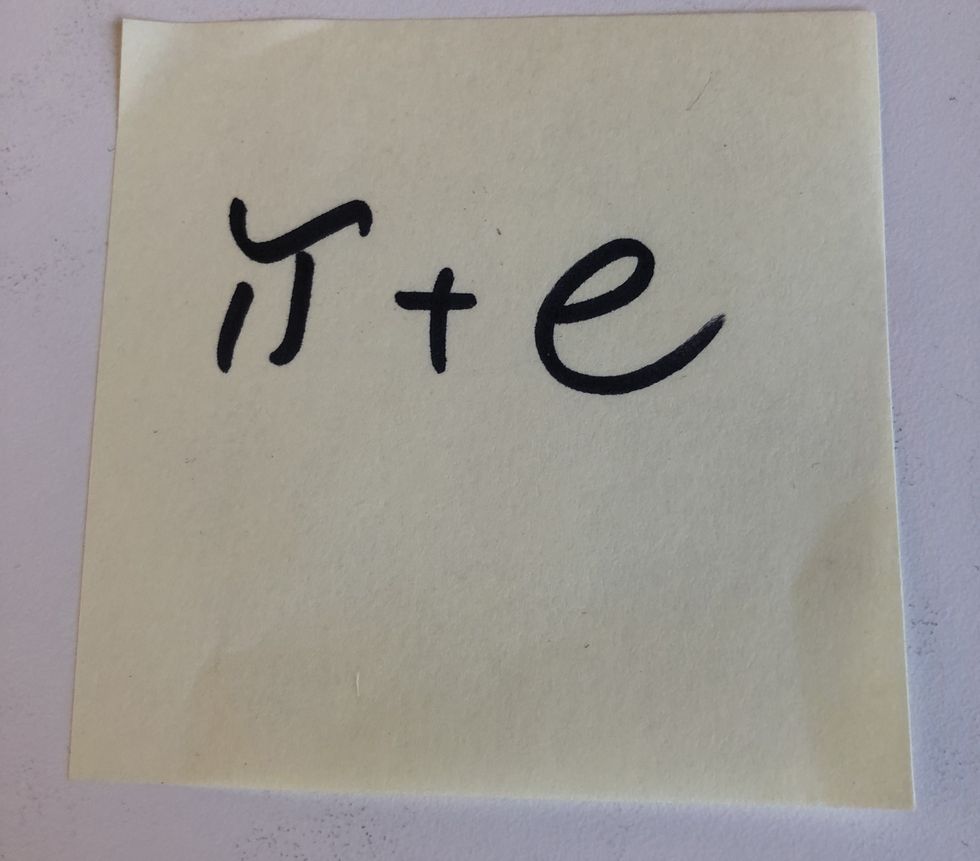
Given everything we know about two of math’s most famous constants, 𝜋 and e , it’s a bit surprising how lost we are when they’re added together.
This mystery is all about algebraic real numbers . The definition: A real number is algebraic if it’s the root of some polynomial with integer coefficients. For example, x²-6 is a polynomial with integer coefficients, since 1 and -6 are integers. The roots of x²-6=0 are x=√6 and x=-√6, so that means √6 and -√6 are algebraic numbers.
✅ Try It Yourself: Can You Solve This Viral Brain Teaser From TikTok?
All rational numbers, and roots of rational numbers, are algebraic. So it might feel like “most” real numbers are algebraic. Turns out, it’s actually the opposite. The antonym to algebraic is transcendental, and it turns out almost all real numbers are transcendental—for certain mathematical meanings of “almost all.” So who’s algebraic , and who’s transcendental?
The real number 𝜋 goes back to ancient math, while the number e has been around since the 17th century. You’ve probably heard of both, and you’d think we know the answer to every basic question to be asked about them, right?
Well, we do know that both 𝜋 and e are transcendental. But somehow it’s unknown whether 𝜋+e is algebraic or transcendental. Similarly, we don’t know about 𝜋e, 𝜋/e, and other simple combinations of them. So there are incredibly basic questions about numbers we’ve known for millennia that still remain mysterious.
Is 𝛾 Rational?
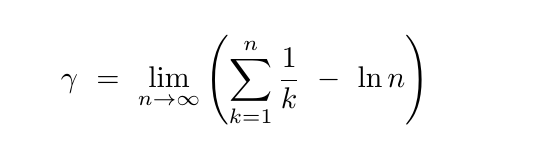
Here’s another problem that’s very easy to write, but hard to solve. All you need to recall is the definition of rational numbers.
Rational numbers can be written in the form p/q, where p and q are integers. So, 42 and -11/3 are rational, while 𝜋 and √2 are not. It’s a very basic property, so you’d think we can easily tell when a number is rational or not, right?
Meet the Euler-Mascheroni constant 𝛾, which is a lowercase Greek gamma. It’s a real number, approximately 0.5772, with a closed form that’s not terribly ugly; it looks like the image above.
✅ One More Thing: Teens Have Proven the Pythagorean Theorem With Trigonometry. That Should Be Impossible
The sleek way of putting words to those symbols is “gamma is the limit of the difference of the harmonic series and the natural log.” So, it’s a combination of two very well-understood mathematical objects. It has other neat closed forms, and appears in hundreds of formulas.
But somehow, we don’t even know if 𝛾 is rational. We’ve calculated it to half a trillion digits, yet nobody can prove if it’s rational or not. The popular prediction is that 𝛾 is irrational. Along with our previous example 𝜋+e, we have another question of a simple property for a well-known number, and we can’t even answer it.
Dave Linkletter is a Ph.D. candidate in Pure Mathematics at the University of Nevada, Las Vegas. His research is in Large Cardinal Set Theory. He also teaches undergrad classes, and enjoys breaking down popular math topics for wide audiences.

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Pop Mech Pro .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

North Korea Sends “Poop Balloons” Into South Korea

Plane Flown by 'Ace of Aces' Pilot Finally Found

The F-35 Is Still One of the Safest Planes

The Air Force’s Upcoming “Doomsday Plane” Replacem

Meet the Marines' New Kamikaze Drone

Did Russia Launch a Weapon Near a U.S. Satellite?

A Groundbreaking Discovery For Interstellar Travel

America's Missile Defense Has Entered a New Era

The Army’s Laser Isn’t All It’s Cracked Up To Be

What We Know About Russia’s Mystery Radio Signal

Corpses Found Under Hitler's Lair

Game Central
Inequalities, absolute value and rounding, related concepts.
share this!
April 29, 2024
This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
trusted source
Intervention based on science of reading and math boosts comprehension and word problem-solving skills
by University of Kansas
New research from the University of Kansas has found that an intervention based on the science of reading and math effectively helped English learners boost their comprehension, visualize and synthesize information, and make connections that significantly improved their math performance.
The intervention , performed for 30 minutes twice a week for 10 weeks with 66 third-grade English language learners who displayed math learning difficulties, improved students' performance when compared to students who received general instruction. This indicates that emphasizing cognitive concepts involved in the science of reading and math are key to helping students improve, according to researchers.
"Word problem-solving is influenced by both the science of reading and the science of math. Key components include number sense, decoding, language comprehension and working memory. Utilizing direct and explicit teaching methods enhances understanding and enables students to effectively connect these skills to solve math problems . This integrated approach ensures that students are equipped with necessary tools to navigate both the linguistic and numerical demands of word problems," said Michael Orosco, professor of educational psychology at KU and lead author of the study.
The intervention incorporates comprehension strategy instruction in both reading and math, focusing and decoding, phonological awareness, vocabulary development, inferential thinking, contextualized learning and numeracy.
"It is proving to be one of the most effective evidence-based practices available for this growing population," Orosco said.
The study, co-written with Deborah Reed of the University of Tennessee, was published in the journal Learning Disabilities Research and Practice .
For the research, trained tutors implemented the intervention, developed by Orosco and colleagues based on cognitive and culturally responsive research conducted over a span of 20 years. One example of an intervention session tested in the study included a script in which a tutor examined a word problem explaining that a person made a quesadilla for his friend Mario and gave him one-fourth of it, then asked students to determine how much remained.
The tutor first asked students if they remembered a class session in which they made quesadillas and what shape they were, and demonstrated concepts by drawing a circle on the board, dividing it into four equal pieces, having students repeat terms like numerator and denominator. The tutor explains that when a question asks how much is left, subtraction is required. The students also collaborated with peers to practice using important vocabulary in sentences. The approach both helps students learn and understand mathematical concepts while being culturally responsive.
"Word problems are complex because they require translating words into mathematical equations, and this involves integrating the science of reading and math through language concepts and differentiated instruction," Orosco said. "We have not extensively tested these approaches with this group of children. However, we are establishing an evidence-based framework that aids them in developing background knowledge and connecting it to their cultural contexts."
Orosco, director of KU's Center for Culturally Responsive Educational Neuroscience, emphasized the critical role of language in word problems, highlighting the importance of using culturally familiar terms. For instance, substituting "pastry" for "quesadilla" could significantly affect comprehension for students from diverse backgrounds. Failure to grasp the initial scenario could impede subsequent problem-solving efforts.
The study proved effective in improving students' problem-solving abilities, despite covariates including an individual's basic calculation skills, fluid intelligence and reading comprehension scores. That finding is key, as while ideally all students would begin on equal footing and there would be few variations in a classroom, in reality, covariates exist and are commonplace.
The study had trained tutors deliver the intervention, and its effectiveness should be further tested with working teachers, the authors wrote. Orosco said professional development to help teachers gain the skills is necessary, and it is vital for teacher preparation programs to train future teachers with such skills as well. And helping students at the elementary level is necessary to help ensure success in future higher-level math classes such as algebra.
The research builds on Orosco and colleagues' work in understanding and improving math instruction for English learners. Future work will continue to examine the role of cognitive functions such as working memory and brain science, as well as potential integration of artificial intelligence in teaching math.
"Comprehension strategy instruction helps students make connections, ask questions, visualize, synthesize and monitor their thinking about word problems," Orosco and Reed wrote. "Finally, applying comprehension strategy instruction supports ELs in integrating their reading, language and math cognition…. Focusing on relevant language in word problems and providing collaborative support significantly improved students' solution accuracy."
Provided by University of Kansas
Explore further
Feedback to editors

Virgin Galactic completes final spaceflight before two-year pause
3 hours ago

Study finds fresh water and key conditions for life appeared on Earth a half-billion years earlier than thought
18 hours ago

Saturday Citations: Praising dogs; the evolution of brown fat; how SSRIs relieve depression. Plus: Boeing's Starliner
Jun 8, 2024
Nonreciprocal quantum batteries exhibit remarkable capacities and efficiency

New method optimizes lithium extraction from seawater and groundwater

Rare 7-foot fish washed ashore on Oregon's coast garners worldwide attention
Jun 7, 2024

California wildfire pollution killed 52,000 in a decade: study

Quantum chemistry and simulation help characterize coordination complex of elusive element 61

A protein that enables smell in ants—and stops cell death
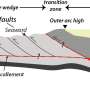
Cascadia Subduction Zone, one of Earth's top hazards, comes into sharper focus
Relevant physicsforums posts, how is physics taught without calculus.
16 hours ago
Is "College Algebra" really just high school "Algebra II"?
Uk school physics exam from 1967.
May 27, 2024
Physics education is 60 years out of date
May 16, 2024
Plagiarism & ChatGPT: Is Cheating with AI the New Normal?
May 13, 2024
Physics Instructor Minimum Education to Teach Community College
May 11, 2024
More from STEM Educators and Teaching
Related Stories

Study shows program improves teaching skills, students' word problem–solving
Jun 14, 2022
Study shows approach can help English learners improve at math word problems
Jun 19, 2018

Study examines role of working memory, cognitive functions in English learners learning to write
Oct 17, 2023

Cognitive study shows lack of bilingual education adversely affects English language learners' writing skills
Oct 14, 2021

How vocabulary breadth and depth influence bilingual reading comprehension
Aug 21, 2023

Study validates the simple view of reading for enhancing second and foreign language learners' experience
Aug 17, 2023
Recommended for you

First-generation medical students face unique challenges and need more targeted support, say researchers

Investigation reveals varied impact of preschool programs on long-term school success
May 2, 2024
Training of brain processes makes reading more efficient
Apr 18, 2024

Researchers find lower grades given to students with surnames that come later in alphabetical order
Apr 17, 2024

Earth, the sun and a bike wheel: Why your high-school textbook was wrong about the shape of Earth's orbit
Apr 8, 2024

Touchibo, a robot that fosters inclusion in education through touch
Apr 5, 2024
Let us know if there is a problem with our content
Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).
Please select the most appropriate category to facilitate processing of your request
Thank you for taking time to provide your feedback to the editors.
Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.
E-mail the story
Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.
Newsletter sign up
Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.
More information Privacy policy
Donate and enjoy an ad-free experience
We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.
E-mail newsletter
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&

IMAGES
VIDEO
COMMENTS
Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.
The very first Mathematical Practice is: Make sense of problems and persevere in solving them. Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of ...
What Is A 'Problem-Solving Approach'? As the emphasis has shifted from teaching problem solving to teaching via problem solving (Lester, Masingila, Mau, Lambdin, dos Santon and Raymond, 1994), many writers have attempted to clarify what is meant by a problem-solving approach to teaching mathematics.The focus is on teaching mathematical topics through problem-solving contexts and enquiry ...
To summarise: Master mathematics actively. In mathematics you are advised to actively consider problems and examples before writing tests and exams, to work out examples repeatedly, to study the theory thoroughly until you really understand it and to never think that memorising facts can replace the active solving of problems. Problem solving in
Perhaps another problem with problem solving is that children don't know how to solve problems. This four stage process is a helpful guide to scaffold the skills being developed, from getting started to thinking more deeply about the task. Stage 1: Getting started. Stage 2: Working on the problem.
The Algebra 1 course, often taught in the 9th grade, covers Linear equations, inequalities, functions, and graphs; Systems of equations and inequalities; Extension of the concept of a function; Exponential models; and Quadratic equations, functions, and graphs. Khan Academy's Algebra 1 course is built to deliver a comprehensive, illuminating, engaging, and Common Core aligned experience!
Get math help in your language. Works in Spanish, Hindi, German, and more. Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
122 Mathematical Problem Solving After solving the problem, the person should look back, which is the fourth stage. Therefore, the actual problem-solving process occurs in the second and third stages although problem solving should involve the first and fourth stages also: what the person should do before and after problem solving.
Abstract. Since problem solving became one of the foci of mathematics education, numerous studies have been performed to improve its teaching, develop students' higher-level skills, and evaluate its learning.
The main activity of mathematics is solving problems. However, what most people experience in most mathematics classrooms is practice exercises. An exercise is different from a problem. In a problem, you probably don't know at first how to approach solving it. You don't know what mathematical ideas might be used in the solution.
The term 'Problem-Solving' refers to one of the four main proficiency strands of mathematics, as outlined by the Australian Maths Curriculum. The Australian Maths Curriculum provides a definition, defining Problem-Solving as being: "The ability to make choices, interpret, formulate, model, and investigate problem situations, and communicate ...
Abstract and Figures. Problem solving in mathematics education has been a prominent research field that aims at understanding and relating the processes involved in solving problems to students ...
In this article I model the process of problem solving and thinking through a problem. The focus is on the problem solving process, using NRICH problems to highlight the processes. Needless to say, this is not how problems should be taught to a class! ... The NRICH Project aims to enrich the mathematical experiences of all learners. To support ...
Polya's (1957) four-step process has provided a model for the teaching and assessing. problem solving in mathematics classrooms: understanding the problem, devising a plan, carrying out the plan, and looking back. Other educators have adapted these steps, but the. essence of these adaptations is very similar to what Polya initially developed.
The paper concludes with a new model for the teaching and learning of Mathematics and problem solving from pre-school to higher education which could assist especially novice Mathematics teachers ...
"This edited book of 26 chapters is divided into four parts: defining the field; mathematical problem posing in the school curriculum, mathematical problem posing in teacher education, and concluding remarks. … there are many examples of problem-posing tasks scattered throughout the book's many chapters. … the book is for mathematics education graduate students, but it could also be ...
Mathematical problem-solving is necessary to encounter professional, 21st-century, and everyday challenges. The relevant context of mathematical problem-solving is related to science, which is presented using natural language. Mathematical problem-solving requires both mathematical skills and nonmathematical skills, e.g., science knowledge and ...
solving. Problem solving is not only the goal of learning mathematics but also an important way of doing mathematics (National Council of Teachers of Mathematics [NCTM], 2000). Since the 1940s, there has been a long history of interest in problem solving in the mathematics education
This study explores the knowledge required for teachers to teach problem solving (PS) from a Primary Mathematics Curriculum Guidelines perspective. It analyzes six countries' curricular guidelines for primary education using the Mathematical Problem-Solving Knowledge for Teaching model. To identify the PS knowledge required in each education system, the country guidelines were selected based ...
Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
In m athematics, a problem -situation is a learning situation. which the teacher imagin es in order to create a space f or reflection and analysis around a problem/ question to be. solved. This ...
Solving the full version of the problem will be an even bigger triumph. You probably haven't heard of the math subject Knot Theory. It's taught in virtually no high schools, and few colleges ...
He is, as he predicted, a mathematician at a university, teaching and solving previously unsolved math problems. "So yeah, I'm a postdoc at CMU (Carnegie Mellon University) right now," he ...
Type a math problem. Related Concepts. Polynomial. In mathematics, a polynomial is a mathematical expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate x is x² − 4x + 7
Problem solving plays an important role in mathematics and should have a prominent role in the mathematics education of K-12 students. However, knowing how to incorporate problem solving meaningfully into the mathematics curriculum is not necessarily obvious to mathematics teachers. (The term "problem solving" refers to mathematical tasks that ...
"Word problem-solving is influenced by both the science of reading and the science of math. Key components include number sense, decoding, language comprehension and working memory.
Free math problem solver answers your algebra homework questions with step-by-step explanations.
Kindergarten math is often too basic and that can be a problem. In Jodie Murphy's kindergarten class in Aston, Pennsylvania, math lessons go beyond the basics of counting and recognizing numbers ...