theoretical research topics neuroscience

The Center for Brain Science at Harvard is home to a vibrant community of theorists modeling neural circuits, behavior, and cognition. Our emphasis is on gathering people and ideas from many fields to understand the computational bases of intelligence in humans, other animals, and machines.

Computational neuroscience. Deep learning. Computational cognitive science — CBS faculty, postdocs, graduate students, and visitors are advancing the frontiers of all these areas.

We offer rigorous, interdisciplinary training for students and postdocs. We host seminars, symposia, workshops, journal clubs, debates, and social events.

Faculty and Associates

Jan Drugowitsch

Sam Gershman

Talia Konkle

Petros Koumoutsakos

Gabriel Kreiman

Cengiz Pehlevan

Hanspeter Pfister

Kanaka Rajan

Maurice Smith

Haim Sompolinsky

Hidenori Tanaka

Tomer Ullman

Leslie Valiant

NeuroTheory Initiative

The CBS NeuroTheory Initiative is a hub for Harvard scientists discovering the computational bases of intelligence in humans, other animals, and machines. We offer rigorous, interdisciplinary training for students and postdocs.

We host seminars, symposia, workshops, journal clubs, debates, and social events. We are bringing together ideas and talent from neuroscience, computer science, psychology, physics, applied mathematics, and statistics to understand the nature of intelligence. In addition to CBS faculty, we are joining forces with others from around Harvard.

With the astonishing successes of artificial intelligence in recent years—recognizing faces, translating languages, generating cogent text, driving cars—CBS scientists have increasingly turned to thorny problems of how our brains achieve intelligent cognition.

Advances in AI are proceeding at an historic pace, yet it is widely acknowledged that AI falls far short of the flexible intelligence evident in humans and animals. Animal brains—­­­­and human brains in particular—are nature’s existence proof that physical mechanisms can give rise to general intelligence.

The CBS effort to discover the bases of intelligent cognition draws together neuroscience, cognitive science, and computer science. As an essential first step towards this goal, we are building a coherent theoretical community aimed at understanding natural and machine intelligence. This group is closely allied with experimentalists studying the neural bases of intelligent cognition in humans and experimental animals. Theorists—with backgrounds in computer science, physics, statistics, mathematics, and psychology—engage in frequent interactions to build an intellectual framework for understanding the complexities of intelligence.

Our NeuroTheory Initiative is expanding the research and education at Harvard in the multidisciplinary field of theoretical neuroscience-cognition-AI.

Thanks to generous support from Dean of Science Christopher Stubbs, we have begun with a set of shared, interactive activities. We are building on faculty strength in these fields, which is spread across schools and departments but is focused in the FAS and SEAS. A robust Visitors program is establishing close ties to industry, where rapid advances in AI are being made.

We launched the NeuroTheory Initiative in the spring of 2022 with a kickoff event featuring posters, a panel discussion, and talks by George Alvarez, Nada Amin, Demba Ba, Boaz Barak, Jonathan Frankle, Sam Gershman, Sham Kakade, Talia Konkle, Hima Lakkaraju, David Nelson, Cengiz Pehlevan, Hanspeter Pfister, and Tomer Ullman.

Our colleagues from NTT Research at Harvard, Hidenori Tanaka and Gautam Reddy, host visiting graduate students and interns throughout the summer and continuing into the academic year. In August 2022, CBS hosted a 2-day workshop on Reinforcement Learning, featuring talks, posters, panel discussions, introductory tutorials, and many informal conversations. Speakers included Sam Gershman, Petros Koumoutsakos, Poornima Kumar, Lucy Lai, Jack Lindsey, Susan Murphy, Gautam Reddy, Sandra Romero Pinto, Maurice Smith, Anna Trella, Naoshige Uchida, and John Vastola.

We have assembled a group of Harvard scientists with a key research interest aimed at developing a theoretical understanding of intelligence. This group of faculty (listed below), with their trainees, forms the core of the NeuroTheory Initiative. They are drawn from Applied Math, Computer Science, Electrical Engineering, Mathematics, Neurobiology, Physics, Psychology, and Statistics. As in fields like physics with a mature theory-experiment tradition, the CBS NeuroTheory Initiative encourages close interactions with experimental neuroscientists and cognitive scientists.

In addition to the CBS Theory faculty listed above, others in the Harvard community are part of the CBS NeuroTheory Initiative.

George Angelo Alvarez

David Alvarez-Melis

Morgane Austern

Emery Neal Brown

Finale Doshi-Velez

Jonathan Frankle

Lucas Janson

Sham Kakade

Hima Lakkaraju

Susan Murphy

David Nelson

David Parkes

Horng-Tzer Yau

Swartz Postdoctoral Fellowships

We currently have one opening for a Swartz Postdoctoral Fellow, beginning in summer or fall of 2024 . The Fellow will join a vibrant group of theoretical and experimental neuroscientists and theorists in allied fields at Harvard’s Center for Brain Science.

Read more about the Swartz Program HERE .

Please read below for information about how to apply for a Swartz Fellowship.

We will have one postdoctoral opening, beginning summer or fall of 2024 . Interested applicants should immediately send a CV, statement of research interests, and arrange for three letters of reference to be sent to Haim Sompolinsky ( [email protected] ) or Kenneth Blum ( [email protected] ). Applications should have “Swartz Fellowship” in the subject line. Applications will be considered until the position is filled.

Harvard University is an equal opportunity employer, and all qualified applicants will receive consideration for employment without regard to race, color, sex, gender identity, sexual orientation, religion, creed, national origin, ancestry, age, protected veteran status, disability, genetic information, military service, pregnancy and pregnancy-related conditions, or other protected status.

The Center for Brain Science includes faculty doing research on a wide variety of topics, including neural mechanisms of rodent learning, decision-making, and sex-specific and social behaviors; human motor control; behavioral and fMRI studies of human cognition; large-scale reconstruction of detailed brain circuitry; circuit mechanisms of learning and behavior in worms, larval flies, and larval zebrafish; circuit mechanisms of individual differences in flies and humans; rodent and fly olfaction; inhibitory circuit development; and reinforcement learning in rodents and humans.

Graduate Programs

Graduate students in many Harvard programs are pursuing theoretical neuroscience from different directions. Follow these links to learn more about each program.

Applied Mathematics

Bioengineering, computer science, molecules, cells & organisms, program in neuroscience (pin).

These are representative courses drawn from many that are offered each semester.

Spring 2023

Upcoming events, news and publications.

• NTT Research gift establishes CBS-NTT Fellowship Program April 12, 2024 Gift supports postdoctoral research in the physics of intelligence…
• Swartz Postdoctoral Fellowship October 20, 2023 We have one opening for a Swartz Postdoctoral Fellow, beginning in summer or fall of 2024….
• Ba, Konkle, Pehlevan, and Sompolinsky named inaugural Kempner Institute Associate Faculty April 5, 2023 Demba Ba, Talia Konkle, Cengiz Pehlevan, and Haim Sompolinsky were named the Institute’s inaugural cohort of “associate faculty.”…

Ben Sorscher, S. Ganguli, H. Sompolinsky

• Haim Sompolinsky deepens ties to Harvard September 7, 2022 Haim Sompolinsky has joined Harvard full-time, as a Professor in Residence….
• RL at Harvard workshop September 1, 2022 Thank you to everyone, especially Paul Masset, for helping to make the CBS NeuroTheory workshop a success! Click on the link below to see some photos Souvik Mandal took at the event….
• Haim Sompolinsky wins Gruber Foundation Neuroscience Prize May 17, 2022 Haim has been awarded the Gruber Foundation Neuroscience Prize, along with Larry Abbott, Emery Brown, and Terry Sejnowski “for pioneering contributions to computational and theoretical neuroscience.”…

Faculty are in many locations. We have a suite of offices on the first floor of the Northwest Building where many theorists are gathered.

Northwest Building 52 Oxford Street Cambridge, MA 02138

The Kempner Institute

Seeking to understand the basis of intelligence in natural and artificial systems.

Kempner Fellows

The Kempner Institute has opened the application for the next cohort of Kempner Research Fellows. The application is open now and will close on  October 9, 2023 . The 3 year fellowship provides a generous stipend, funding for research, and access to our GPU cluster. We seek candidates who are working on or more of the following areas:

• Foundations of intelligence, including mathematical and computational models of intelligence, cognitive theories of intelligence, and the neurobiological basis of intelligence.
• Applications of artificial intelligence, including natural language processing, visual scene processing and analysis, and to the mechanistic analysis of high dimensional neural and behavioral data. The study of these applications can either be from an engineering standpoint (e.g., development of new methodologies or advancing the state of the art) as well as from a scientific one (e.g., achieving a better understanding of deep learning).

To be eligible, a candidate must be, at the earliest, in the final year of their Ph.D. training and at the latest, have received their PhD no earlier than 9/1/2021. See this link for more information and how to apply:  https://www.harvard.edu/kempner-institute/opportunities/the-kempner-institute-postdoctoral-fellowship/  

Email  [email protected]  for any questions about the position.

Theoretical neuroscience: a discipline within neuroscience that combines neuroscience data with general mathematical and physical principles in order to produce theories of brain function that are communicable in both natural language and in the language of mathematics.

Modern neuroscience has at its disposal many new tools for measuring brain activity, but far fewer tools for understanding these measurements in a larger theory of brain function. Our aim is to supply useful algorithms, statistical analysis, and theoretical ideas to both analyze measurements and guide further experimentation.

When it comes to understanding a system of such amazing complexity as the brain, theory can tell us where to look and what to look for. It becomes particularly indispensable in trying to fit together experimental results that span a wide range of spatial and temporal scales. One critical component of this enterprise is bridging the gap between cognitive science and neuroscience – the former having concrete things to say about what makes a system truly intelligent and the latter revealing the physical mechanisms of real systems in nature that behave intelligently. The job of theoretical neuroscience is to characterise the computational problems that such a system has to solve and to develop a theory of how a solution to those problems might be implemented by neurons in real brains. The sections below describe some of our past and current work along these lines.

Models of sensory coding

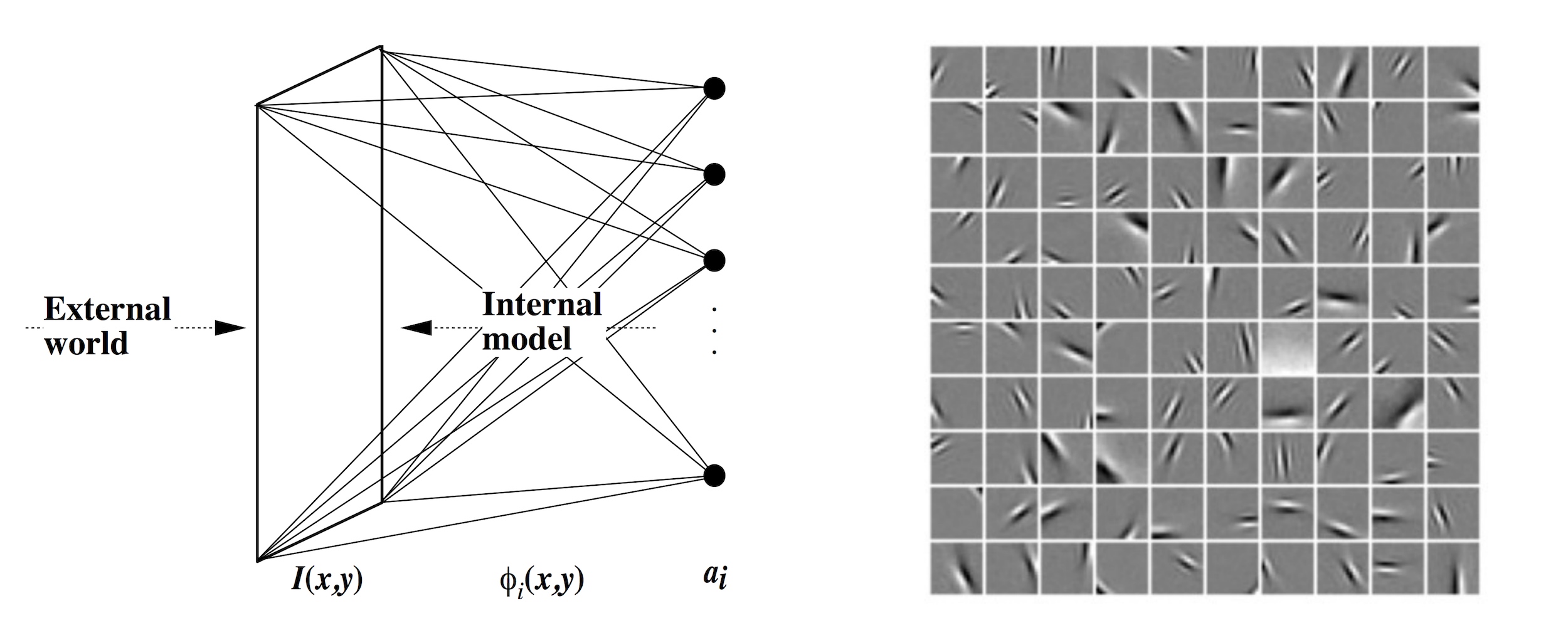
The process of perception requires an animal to integrate sensory information from a variety of organs in order to build a model of the world sufficient for survival. The signals from each of these senses possess somewhat specific statistical structure – a core theory in sensory neuroscience is that neurons adapt on a range of timescales to the structure in these signals. We work on both the characterization of natural signals and on developing models of sensory neural coding that can learn representations from data. Our efforts have focused primarily on unsupervised learning using principles of sparse coding and information theory. We are particularly interested in the roles of feedback and hierarchy in building representations of sensory data. While some theories of sensory coding are fairly general, the majority of our past and present work in this area has focused on models of the visual and auditory system.

In addition to modeling neural representation, we are investigating the potential for some of these models to serve as the basis for data compression schemes. We believe that neuroscience and psychophysics has a lot to offer in determining 1) good ways to sample sensory signals and 2) how to compactly represent the relevant information they contain. Given the amount of visual and audio data stored online, we believe that this may become an important application for our work in this area.

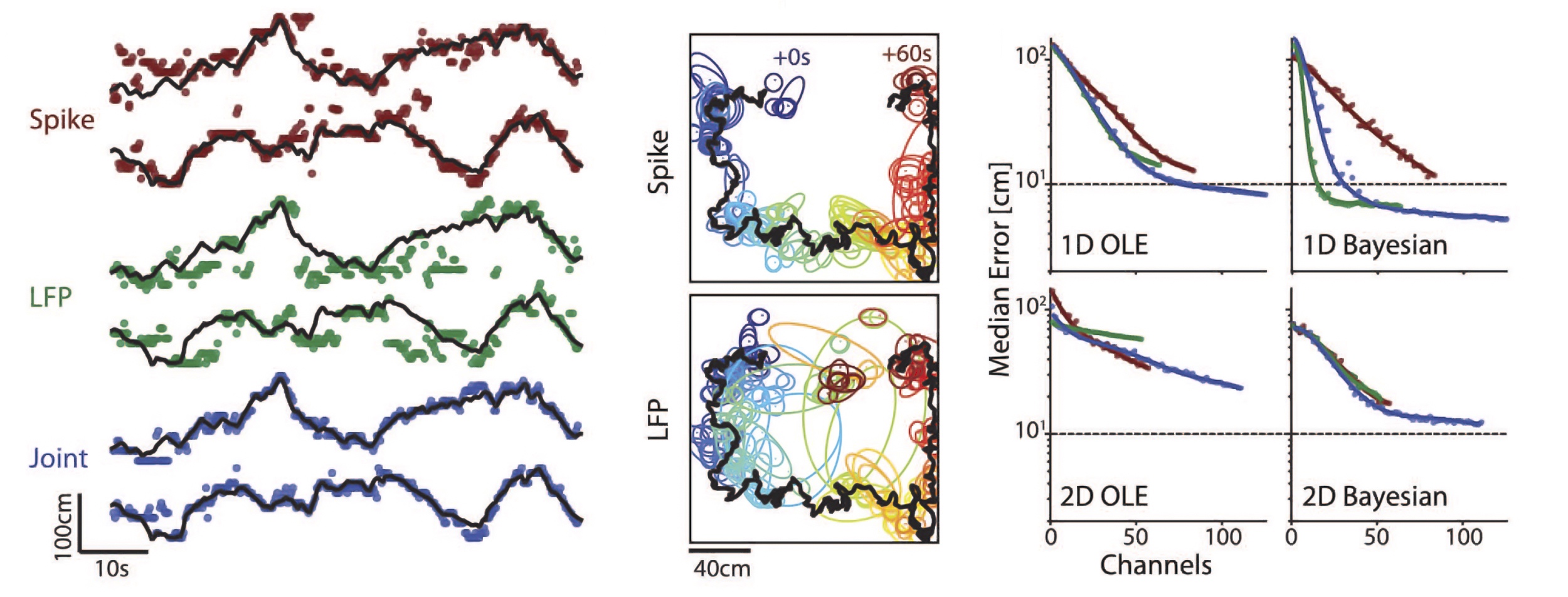
Analysis and modeling of neuroscience data

The quality and variety of neuroscience measurement techniques has dramatically improved over the last few decades and researchers now have access to huge multivariate neural datasets across a large range of spatial and temporal scales. Statistical methods for drawing meaningful conclusions from this data are still catching up to these innovations, and we are contributing to this effort. Our work is in both developing such methods and in applying them to the analysis of neural data, in particular in the hippocampus and visual cortex. Past work in this area has for example included an analysis of bi-modal firing behavior in thalamic relay cells, models of higher-order correlations within microcolumns in the primary visual cortex, and the discovery of place fields encoded by local field potential signals. The Redwood Center is also engaged in neuroinformatics and runs the Collaborative Research in Computational Neuroscience project (CRCNS) which hosts a wide variety of neuroscience datasets along with collaborative tools for sharing these datasets with the neuroscience community.

Computing with high-dimensional distributed representations

Several current projects at the Redwood Center are investigating theories of computation that utilize high-dimensional vectors as the atomic unit of representation. Whereas a modern computing architecture operates on 32 or 64 bit words, our theories rely on words that are 1000 or more bits long. Furthermore, information is distributed evenly across all the bits in a given word – systems that utilize this kind of representation exhibit behavior that is robust to significant perturbations to the underlying words. Models of vector symbolic algebra define a mathematical formalism for computing with these high-dimensional distributed representations and can be understood as abstractions of certain properties of real neural systems. What interests us about this work from a neuroscience perspective is that it represents an example of how high dimensional distributed representations like those found in the brain might be able to support robust symbolic computation.

This research also demonstrates a new paradigm for computing that may address challenges posed by the end of Moore’s Law. Collaborations we have with academic and industrial groups developing next-generation computing architectures have been centered on building efficient implementations of these models and early results demonstrate significant advantages over existing approaches. Physical systems that implement these models enjoy improvements in performance, energy efficiency, and robustness with simple algorithms that learn fast. We think this may be a path towards building the next generation of computing hardware.

Understanding neural networks

One long-standing research direction within theoretical neuroscience is the study of networks of artificial neurons which capture at some level the properties of neurons measured in real brains. This allows us to both investigate what kinds of tasks these networks are good at performing and also what might be missing from our current models. Over the past decade there has been a growing acceptance of the amazing capabilities of neural network models as general computational objects that can learn to represent and store patterns found in data from a wide variety of natural signals. While the applications of these models are compelling, we are far more interested in why these systems behave the way they do. We are attacking this question using ideas from random matrix theory, dynamical systems theory, and statistical mechanics.

Mainstream use of neural networks outside the field of neuroscience is based on a model of neurons that is now more than sixty years old. Neurons in real brains are capable of a much richer set of computations than these older models utilize. One of our objectives is to demonstrate the utility of using neural network models that incorporate a more modern view of neural computation.

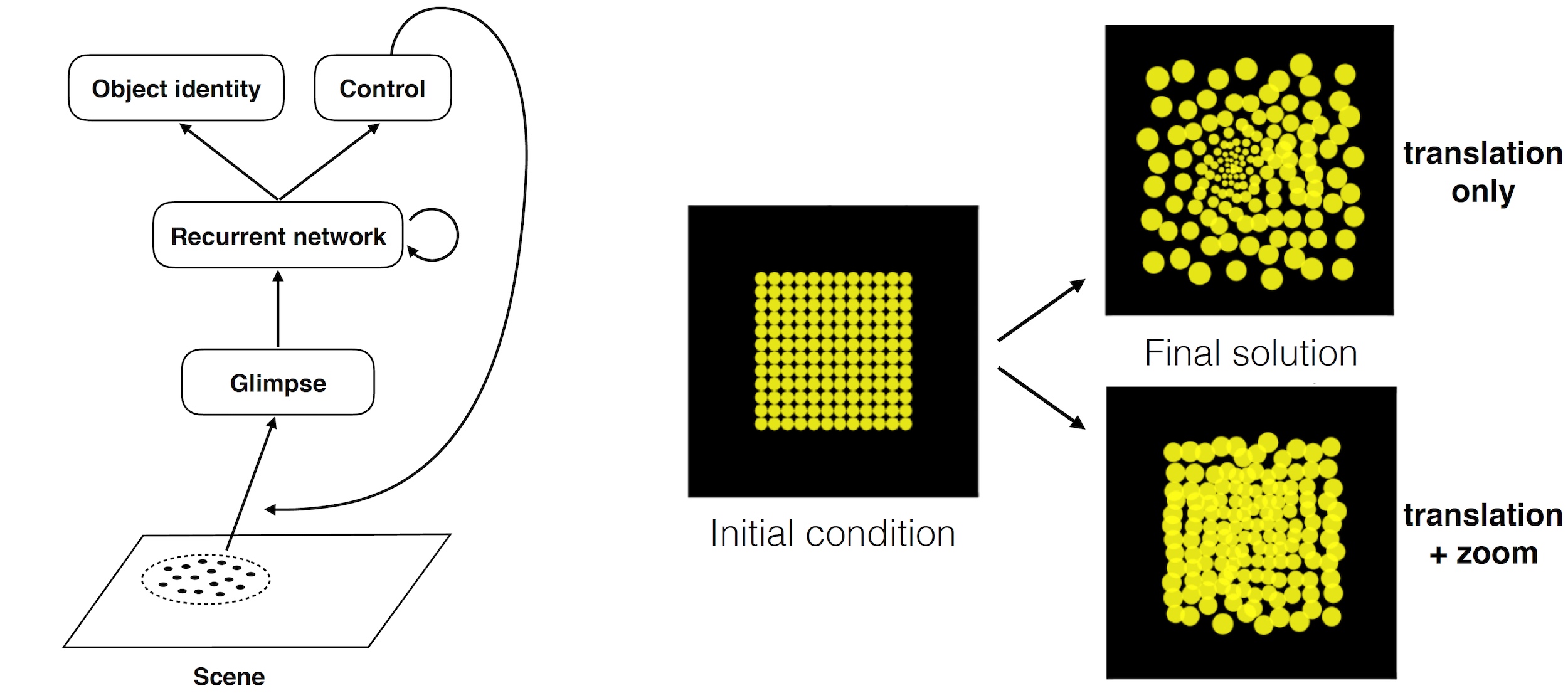
Active Perception

Much of the past work on perception has carried with it the implicit assumption of a passive observer collecting sensory information from the world. This reductionist approach, while valuable, leaves out a key functionality of biological visual systems which may be critical to understanding it as a whole – i.e., the purposeful and active acquisition of information about the world through eye, head and body movements.

As these movements occur, the information acquired from different fixations must somehow be assimilated and stored in working memory in order to enable actions that go beyond simple reflexes based on the immediate input. We are studying this problem along several different lines:

• Theories of attention that address where one should look or move
• Theories of optimal signal acquisition given constraints imposed by active perception
• Theories of working memory and representation that can build up a stable percept of the world from multiple fixations over time

In all of these works, our objective is to develop a neural architecture that functions in a robust and biologically-relevant manner.

Autonomous Systems

Humans and other animals are the only systems in existence capable of truly autonomous behavior despite decades of research on this topic within the robotics and computer science communities. We believe that sensing, navigating, remembering and acting in a rich three-dimensional environment is fundamentally more difficult than many researchers first realized and that a key component of deconstructing this problem is the study of nervous systems that have already solved it. Work from the neuroscience community that has something to offer here includes theories of sensorimotor loops, feedback, memory, and neural encodings of position and orientation in three-dimensional space. Our objective is to combine some of these theories with ideas from engineering, in particular Simultaneous Localization and Mapping to design systems that are robust, efficient, and general-purpose.

Topics in NeuroIS and a Taxonomy of Neuroscience Theories in NeuroIS

• First Online: 01 December 2015

Cite this chapter

• René Riedl 5 &
• Pierre-Majorique Léger 6  

Part of the book series: Studies in Neuroscience, Psychology and Behavioral Economics ((SNPBE))

2175 Accesses

1 Citations

This chapter provides a publications retrospective of NeuroIS topics, and outlines potential themes for future NeuroIS studies. We begin with a description of topics from 2007 NeuroIS publications, and then, based on research agendas and discussion papers, we present topics that can be investigated by applying neuroscience approaches. Next, we analyze the topics of one specific publication—the proceedings of the Gmunden Retreat on NeuroIS. Our identification of the research topics, and the neuroscience methods and tools presented in the proceedings, is based on analysis of 85 papers published between 2011 and 2014. We end the chapter by reflecting on applying neuroscience reference theories in NeuroIS research. Because current NeuroIS research rarely addresses the use of reference theories from neuroscience, this chapter suggests a taxonomy for neuroscience theories to promote such a discourse in NeuroIS research.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Adam, M. T. P., Gimpel, H., Maedche, A., & Riedl, R. (2014). Stress-sensitive adaptive enterprise systems: Theoretical foundations and design blueprint. In F. Davis, R. Riedl, J. vom Brocke, P. M. Léger & A. Randolph (Eds.), Proceedings of Gmunden Retreat on NeuroIS 2014, Gmunden, Austria (pp. 39–41).

Google Scholar  

Adam, M. T. P., Gimpel, H., Maedche, A., & Riedl, R. (2015). Design blueprint for stress-sensitive adaptive enterprise systems. Business and Information Systems Engineering (under review).

Astor, P. J., Adam, M. T. P., Jericic, P., Schaaff, K., & Weinhardt, C. (2013). Integrating biosignal into information systems: A NeuroIS tool for improving emotion regulation. Journal of Management Information Systems, 30 , 247–277.

Article   Google Scholar  

Backs, R. W., & Boucsein, W. (Eds.). (2000). Engineering psychophysiology: Issues and applications . New Jersey: Lawrence Erlbaum.

Baron-Cohen, S., Knickmeyer, R. C., & Belmonte, M. K. (2005). Sex differences in the brain: Implications for explaining autism. Science, 310 , 819–823.

Bechara, A., & Damasio, A. R. (2005). The somatic marker hypothesis: A neural theory of economic decision. Games and Economic Behavior, 52 , 336–372.

Article   MATH   Google Scholar  

Bechara, A., Damasio, H., & Damasio, A. R. (2000). Emotion, decision making and the orbitofrontal cortex. Cerebral Cortex, 10 , 295–307.

Bechara, A., Damasio, H., Damasio, A. R., & Lee, G. P. (1999). Different contributions of the human amygdala and ventromedial prefrontal cortex to decision-making. Journal of Neuroscience, 19 , 5473–5481.

Chesselet, M.-F. (2000). Mapping the basal ganglia. In A. W. Toga & J. C. Mazziotta (Eds.), Brain mapping: The systems (pp. 177–206). Massachusetts: Academic Press.

Derrick, D. C., Jenkins, J. L., & Nunamaker, J. F, Jr. (2011). Design principles for special purpose, embodied, conversational intelligence with environmental sensors (SPECIES) agents. AIS Transactions on Human-Computer Interaction, 3 , 62–81.

Dimoka, A., Banker, R. D., Benbasat, I., Davis, F. D., Dennis, A. R., Gefen, D., et al. (2012). On the use of neurophysiological tools in IS research: Developing a research agenda for NeuroIS. MIS Quarterly, 36 , 679–702.

Dimoka, A., Pavlou, P. A., & Davis, F. F. (2007). NEURO-IS: The potential of cognitive neuroscience for information systems research. In Twenty Eighth International Conference on Information Systems (pp. 1–20).

Dimoka, A., Pavlou, P. A., & Davis, F. D. (2011). NeuroIS: The potential of cognitive neuroscience for information systems research. Information Systems Research, 22 , 687–702.

Frank, M. J., Cohen, M. X., & Sanfey, A. G. (2009). Multiple systems in decision making—A neurocomputational perspective. Current Directions in Psychological Science, 18 , 73–77.

Gregor, S. (2006). The nature of theory in information systems. MIS Quarterly, 30 , 611–642.

Heinrich, L. J., & Riedl, R. (2013). Understanding the dominance and advocacy of the design-oriented research approach in the business informatics community: A history-based examination. Journal of Information Technology, 28 , 34–49.

Léger, P.-M., Riedl, R., & vom Brocke, J. (2014). Emotions and ERP information sourcing: The moderating role of expertise. Industrial Management & Data Systems, 114 , 456–471.

Loos, P., Riedl, R., Müller-Putz, G. R., vom Brocke, J., Davis, F. D., Banker, R. D., & Léger, P.-M. (2010). NeuroIS: Neuroscientific approaches in the investigation and development of information systems. Business & Information Systems Engineering, 2 , 395–401.

Moore, M. M., Storey, V. C., & Randolph, A. B. (2005). User profiles for facilitating conversations with locked-in users. In Proceedings of the International Conference on Information Systems (pp. 923–936).

Müller-Putz, G. R., Riedl, R., & Wriessnegger, S. C. (2015). Electroencephalography (EEG) as a research tool in the information systems discipline: Foundations, measurement, and applications. Communications of the Association for Information Systems, 37 .

Randolph, A. B., Karmakar, S., & Jackson, M. M. (2006). Toward predicting control of a brain-computer interface. In Proceedings of the International Conference on Information Systems (pp. 803–812).

Riedl, R. (2009). Zum Erkenntnispotenzial der kognitiven Neurowissenschaften für die Wirtschaftsinformatik: Überlegungen anhand exemplarischer Anwendungen. NeuroPsychoEconomics, 4 , 32–44.

Riedl, R. (2013). On the biology of technostress: Literature review and research agenda. DATA BASE for Advances in Information Systems, 44 , 18–55.

Riedl, R., Banker, R. D., Benbasat, I., Davis, F. D., Dennis, A. R., Dimoka, A., et al. (2010a). On the foundations of NeuroIS: Reflections on the Gmunden retreat 2009. Communications of the Association for Information Systems, 27 , 243–264.

Riedl, R., Davis, F. D., & Hevner, A. R. (2014a). Towards a NeuroIS research methodology: Intensifying the discussion on methods, tools, and measurement. Journal of the Association for Information Systems, 15 , Article 4.

Riedl, R., Hubert, M., & Kenning, P. (2010c). Are there neural gender differences in online trust? An fMRI study on the perceived trustworthiness of eBay offers. MIS Quarterly, 34 , 397–428.

Riedl, R., & Javor, A. (2012). The biology of trust: Integrating evidence from genetics, endocrinology, and functional brain imaging. Journal of Neuroscience, Psychology, and Economics, 5 , 63–91.

Riedl, R., Kindermann, H., Auinger, A., & Javor, A. (2012). Technostress from a neurobiological perspective: System breakdown increases the stress hormone cortisol in computer users. Business & Information Systems Engineering, 4 , 61–69.

Riedl, R., Kindermann, H., Auinger, A., & Javor, A. (2013). Computer breakdown as a stress factor during task completion under time pressure: Identifying gender differences based on skin conductance. Advances in Human-Computer Interaction, 2013 (Article ID 420169).

Riedl, R., Mohr, P., Kenning, P., Davis, F., & Heekeren, H. (2014b). Trusting humans and avatars: A brain imaging study based on evolution theory. Journal of Management Information Systems, 30 , 83–113.

Riedl, R., Randolph, A. B., vom Brocke, Jan., Léger, P.-M., & Dimoka, A. (2010b). The Potential of neuroscience for human-computer interaction research. In Proceedings of SIGHCI 2010, Paper 16 .

Riedl, R., & Roithmayr, F. (2007a). Human-computer interaction and neuroscience: Science or science fiction? In W. Hong & E. Loiacono (Eds.), Proceedings of the 6th Annual Workshop on HCI Research in MIS , 80.

Riedl, R., & Roithmayr, F. (2007b). Neuroscience and management information systems. In C. Middleton (Ed.), Proceedings of the International Federation for Information Processing Workshop on Organizations and Society in Information Systems (OASIS, IFIP 8.2) (pp. 36–38).

Satpute, A. B., & Lieberman, M. D. (2006). Integrating automatic and controlled processes into neurocognitive models of social cognition. Brain Research, 1079 , 86–97.

Sidorova, A., Evangelopoulos, N., Valacich, J. S., & Ramakrishnan, T. (2008). Uncovering the intellectual core of the information systems discipline. MIS Quarterly, 32 , 467–482.

Stanovich, K. E., & West, R. F. (2000). Individual differences in reasoning: Implications for the rationality debate? Behavioral and Brain Sciences, 23 , 645–726.

Steininger, K., Riedl, R., Roithmayr, F., & Mertens, P. (2009). Fads and trends in business and information systems engineering and information systems research: A comparative literature analysis. Business & Information Systems Engineering, 1 , 411–428.

Van Aken, J. (2004). Management research based on the paradigm of the design sciences: The quest for field-tested and grounded technological rules. Journal of Management Studies, 41 , 219–246.

vom Brocke, J., Riedl, R., & Léger, P.-M. (2013). Application strategies for neuroscience in information systems design science research. Journal of Computer Information Systems, 53 , 1–13.

Download references

Author information

Authors and affiliations.

University of Applied Sciences Upper Austria and University of Linz, Steyr/Linz, Austria

HEC Montréal, Montréal, QC, Canada

Pierre-Majorique Léger

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to René Riedl .

Rights and permissions

Reprints and permissions

Copyright information

© 2016 Springer-Verlag Berlin Heidelberg

About this chapter

Riedl, R., Léger, PM. (2016). Topics in NeuroIS and a Taxonomy of Neuroscience Theories in NeuroIS. In: Fundamentals of NeuroIS. Studies in Neuroscience, Psychology and Behavioral Economics. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-45091-8_4

Download citation

DOI : https://doi.org/10.1007/978-3-662-45091-8_4

Published : 01 December 2015

Publisher Name : Springer, Berlin, Heidelberg

Print ISBN : 978-3-662-45090-1

Online ISBN : 978-3-662-45091-8

eBook Packages : Computer Science Computer Science (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Research Topics & Ideas: Neuroscience

50 Topic Ideas To Kickstart Your Research Project

If you’re just starting out exploring neuroscience-related topics for your dissertation, thesis or research project, you’ve come to the right place. In this post, we’ll help kickstart your research by providing a hearty list of neuroscience-related research ideas , including examples from recent studies.

PS – This is just the start…

We know it’s exciting to run through a list of research topics, but please keep in mind that this list is just a starting point . These topic ideas provided here are intentionally broad and generic , so keep in mind that you will need to develop them further. Nevertheless, they should inspire some ideas for your project.

To develop a suitable research topic, you’ll need to identify a clear and convincing research gap , and a viable plan to fill that gap. If this sounds foreign to you, check out our free research topic webinar that explores how to find and refine a high-quality research topic, from scratch. Alternatively, consider our 1-on-1 coaching service .

Neuroscience-Related Research Topics

• Investigating the neural mechanisms underlying memory consolidation during sleep.
• The role of neuroplasticity in recovery from traumatic brain injury.
• Analyzing the impact of chronic stress on hippocampal function.
• The neural correlates of anxiety disorders: A functional MRI study.
• Investigating the effects of meditation on brain structure and function in mindfulness practitioners.
• The role of the gut-brain axis in the development of neurodegenerative diseases.
• Analyzing the neurobiological basis of addiction and its implications for treatment.
• The impact of prenatal exposure to environmental toxins on neurodevelopment.
• Investigating gender differences in brain aging and the risk of Alzheimer’s disease.
• The neural mechanisms of pain perception and its modulation by psychological factors.
• Analyzing the effects of bilingualism on cognitive flexibility and brain aging.
• The role of the endocannabinoid system in regulating mood and emotional responses.
• Investigating the neurobiological underpinnings of obsessive-compulsive disorder.
• The impact of virtual reality technology on cognitive rehabilitation in stroke patients.
• Analyzing the neural basis of social cognition deficits in autism spectrum disorders.
• The role of neuroinflammation in the progression of multiple sclerosis.
• Investigating the effects of dietary interventions on brain health and cognitive function.
• The neural substrates of decision-making under risk and uncertainty.
• Analyzing the impact of early life stress on brain development and mental health outcomes.
• The role of dopamine in motivation and reward processing in the human brain.
• Investigating neural circuitry changes in depression and response to antidepressants.
• The impact of sleep deprivation on cognitive performance and neural function.
• Analyzing the brain mechanisms involved in empathy and moral reasoning.
• The role of the prefrontal cortex in executive function and impulse control.
• Investigating the neurophysiological basis of schizophrenia.

Neuroscience Research Ideas (Continued)

• The impact of chronic pain on brain structure and connectivity.
• Analyzing the effects of physical exercise on neurogenesis and cognitive aging.
• The neural mechanisms underlying hallucinations in psychiatric and neurological disorders.
• Investigating the impact of music therapy on brain recovery post-stroke.
• The role of astrocytes in neural communication and brain homeostasis.
• Analyzing the effect of hormone fluctuations on mood and cognition in women.
• The impact of neurofeedback training on attention deficit hyperactivity disorder (ADHD).
• Investigating the neural basis of resilience to stress and trauma.
• The role of the cerebellum in non-motor cognitive and affective functions.
• Analyzing the contribution of genetics to individual differences in brain structure and function.
• The impact of air pollution on neurodevelopment and cognitive decline.
• Investigating the neural mechanisms of visual perception and visual illusions.
• The role of mirror neurons in empathy and social understanding.
• Analyzing the neural correlates of language development and language disorders.
• The impact of social isolation on neurocognitive health in the elderly.
• Investigating the brain mechanisms involved in chronic fatigue syndrome.
• The role of serotonin in mood regulation and its implications for antidepressant therapies.
• Analyzing the neural basis of impulsivity and its relation to risky behaviors.
• The impact of mobile technology usage on attention and brain function.
• Investigating the neural substrates of fear and anxiety-related disorders.
• The role of the olfactory system in memory and emotional processing.
• Analyzing the impact of gut microbiome alterations on central nervous system diseases.
• The neural mechanisms of placebo and nocebo effects.
• Investigating cortical reorganization following limb amputation and phantom limb pain.
• The role of epigenetics in neural development and neurodevelopmental disorders.

Recent Neuroscience Studies

While the ideas we’ve presented above are a decent starting point for finding a research topic, they are fairly generic and non-specific. So, it helps to look at actual studies in the neuroscience space to see how this all comes together in practice.

Below, we’ve included a selection of recent studies to help refine your thinking. These are actual studies,  so they can provide some useful insight as to what a research topic looks like in practice.

• The Neurodata Without Borders ecosystem for neurophysiological data science (Rübel et al., 2022)
• Genetic regulation of central synapse formation and organization in Drosophila melanogaster (Duhart & Mosca, 2022)
• Embracing brain and behaviour: Designing programs of complementary neurophysiological and behavioural studies (Kirwan et al., 2022).
• Neuroscience and Education (Georgieva, 2022)
• Why Wait? Neuroscience Is for Everyone! (Myslinski, 2022)
• Neuroscience Knowledge and Endorsement of Neuromyths among Educators: What Is the Scenario in Brazil? (Simoes et al., 2022)
• Design of Clinical Trials and Ethical Concerns in Neurosciences (Mehanna, 2022) Methodological Approaches and Considerations for Generating Evidence that Informs the Science of Learning (Anderson, 2022)
• Exploring the research on neuroscience as a basis to understand work-based outcomes and to formulate new insights into the effective management of human resources in the workplace: A review study (Menon & Bhagat, 2022)
• Neuroimaging Applications for Diagnosis and Therapy of Pathologies in the Central and Peripheral Nervous System (Middei, 2022)
• The Role of Human Communicative Competence in Post-Industrial Society (Ilishova et al., 2022)
• Gold nanostructures: synthesis, properties, and neurological applications (Zare et al., 2022)
• Interpretable Graph Neural Networks for Connectome-Based Brain Disorder Analysis (Cui et al., 2022)

As you can see, these research topics are a lot more focused than the generic topic ideas we presented earlier. So, for you to develop a high-quality research topic, you’ll need to get specific and laser-focused on a specific context with specific variables of interest.  In the video below, we explore some other important things you’ll need to consider when crafting your research topic.

Get 1-On-1 Help

If you’re still unsure about how to find a quality research topic, check out our Research Topic Kickstarter service, which is the perfect starting point for developing a unique, well-justified research topic.

You Might Also Like:

Submit a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Print Friendly

• Skip to main content
• Skip to navigation
• Skip to search
• Increase font size
• Decrease font size
• Sharpen color
• Invert color

Search form

You are here.

back to research topics

Theoretical and Computational Neuroscience

The brain is acting through the interaction of billions of neurons and myriads of action potentials that are criss-crossing within and between brain areas. To make sense of this complexity, one must use mathematical tools and sophisticated analysis methods in order to extract the important information and create reduced models of brain function. Together, faculty members and students at the Weizmann Institute, coming from diverse quantitative backgrounds such as physics, engineering, mathematics and computer science, are breaking new cutting-edge avenues in computational and theoretical neuroscience. We are using mathematical tools taken from Statistical Physics, Dynamicsl Systems, Machine Learning and Information Theory -- to name just a few -- in order to create new models and theories of brain function. Both analytical approaches and simulations are used heavily. By intense collaborations with experimental laboratories, these new theories and computational tools are put to the test, and then refined further. Our aim is to unravel the basic principles of brain operation and the underlying neural codes.

Related Groups

• Yarden Cohen
• Michal Ramot
• Takashi Kawashima
• Michail Tsodyks
• Elad Schneidman

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• HHS Author Manuscripts

Computational Neuroscience: Mathematical and Statistical Perspectives

Robert e. kass.

1 Carnegie Mellon University, Pittsburgh, PA, USA, 15213; email: ude.umc.tats@ssak

Shun-ichi Amari

2 RIKEN Brain Science Institute, Wako, Saitama Prefecture, Japan, 351-0198

Kensuke Arai

3 Boston University, Boston, MA, USA, 02215

Emery N. Brown

4 Massachusetts Institute of Technology, Cambridge, MA, USA, 02139

5 Harvard Medical School, Boston, MA, USA, 02115

Casey O. Diekman

6 New Jersey Institute of Technology, Newark, NJ, USA, 07102

Markus Diesmann

7 Jülich Research Centre, Jülich, Germany, 52428

8 RWTH Aachen University, Aachen, Germany, 52062

Brent Doiron

9 University of Pittsburgh, Pittsburgh, PA, USA, 15260

Uri T. Eden

Adrienne l. fairhall.

10 University of Washington, Seattle, WA, USA, 98105

Grant M. Fiddyment

Tomoki fukai, sonja grün, matthew t. harrison.

11 Brown University, Providence, RI, USA, 02912

Moritz Helias

Hiroyuki nakahara, jun-nosuke teramae.

12 Osaka University, Suita, Osaka Prefecture, Japan, 565-0871

Peter J. Thomas

13 Case Western Reserve University, Cleveland, OH, USA, 44106

Mark Reimers

14 Michigan State University, East Lansing, MI, USA, 48824

Jordan Rodu

Horacio g. rotstein, eric shea-brown, hideaki shimazaki.

15 Honda Research Institute Japan, Wako, Saitama Prefecture, Japan, 351-0188

16 Kyoto University, Kyoto, Kyoto Prefecture, Japan, 606-8502

Shigeru Shinomoto

Byron m. yu, mark a. kramer.

Mathematical and statistical models have played important roles in neuroscience, especially by describing the electrical activity of neurons recorded individually, or collectively across large networks. As the field moves forward rapidly, new challenges are emerging. For maximal effectiveness, those working to advance computational neuroscience will need to appreciate and exploit the complementary strengths of mechanistic theory and the statistical paradigm.

1. Introduction

Brain science seeks to understand the myriad functions of the brain in terms of principles that lead from molecular interactions to behavior. Although the complexity of the brain is daunting and the field seems brazenly ambitious, painstaking experimental efforts have made impressive progress. While investigations, being dependent on methods of measurement, have frequently been driven by clever use of the newest technologies, many diverse phenomena have been rendered comprehensible through interpretive analysis, which has often leaned heavily on mathematical and statistical ideas. These ideas are varied, but a central framing of the problem has been to “elucidate the representation and transmission of information in the nervous system” ( Perkel and Bullock 1968 ). In addition, new and improved measurement and storage devices have enabled increasingly detailed recordings, as well as methods of perturbing neural circuits, with many scientists feeling at once excited and overwhelmed by opportunities of learning from the ever-larger and more complex data sets they are collecting. Thus, computational neuroscience has come to encompass not only a program of modeling neural activity and brain function at all levels of detail and abstraction, from sub-cellular biophysics to human behavior, but also advanced methods for analysis of neural data.

In this article we focus on a fundamental component of computational neuroscience, the modeling of neural activity recorded in the form of action potentials (APs), known as spikes , and sequences of them known as spike trains (see Figure 1 ). In a living organism, each neuron is connected to many others through synapses , with the totality forming a large network. We discuss both mechanistic models formulated with differential equations and statistical models for data analysis, which use probability to describe variation. Mechanistic and statistical approaches are complementary, but their starting points are different, and their models have tended to incorporate different details. Mechanistic models aim to explain the dynamic evolution of neural activity based on hypotheses about the properties governing the dynamics. Statistical models aim to assess major drivers of neural activity by taking account of indeterminate sources of variability labeled as noise. These approaches have evolved separately, but are now being drawn together. For example, neurons can be either excitatory , causing depolarizing responses at downstream ( post-synaptic ) neurons (i.e., responses that push the voltage toward the firing threshold, as illustrated in Figure 1 ), or inhibitory , causing hyperpolarizing post-synaptic responses (that push the voltage away from threshold). This detail has been crucial for mechanistic models but, until relatively recently, has been largely ignored in statistical models. On the other hand, during experiments, neural activity changes while an animal reacts to a stimulus or produces a behavior. This kind of non-stationarity has been seen as a fundamental challenge in the statistical work we review here, while mechanistic approaches have tended to emphasize emergent behavior of the system. In current research, as the two perspectives are being combined increasingly often, the distinction has become blurred. Our purpose in this review is to provide a succinct summary of key ideas in both approaches, together with pointers to the literature, while emphasizing their scientific interactions. We introduce the subject with some historical background, and in subsequent sections describe mechanistic and statistical models of the activity of individual neurons and networks of neurons. We also highlight several domains where the two approaches have had fruitful interaction.

Action potential and spike trains. The left panel shows the voltage drop recorded across a neuron’s cell membrane. The voltage fluctuates stochastically, but tends to drift upward, and when it rises to a threshold level (dashed line) the neuron fires an action potential, after which it returns to a resting state; the neuron then responds to inputs that will again make its voltage drift upward toward the threshold. This is often modeled as drifting Brownian motion that results from excitatory and inhibitory Poisson process inputs ( Tuckwell 1988 ; Gerstein and Mandelbrot 1964 ). The right panel shows spike trains recorded from 4 neurons repeatedly across 3 experimental replications, known as trials . The spike times are irregular within trials, and there is substantial variation across trials, and across neurons.

1.1. The brain-as-computer metaphor

The modern notion of computation may be traced to a series of investigations in mathematical logic in the 1930s, including the Turing machine ( Turing 1937 ). Although we now understand logic as a mathematical subject existing separately from human cognitive processes, it was natural to conceptualize the rational aspects of thought in terms of logic (as in Boole’s 1854 Investigation of the Laws of Thought ( Boole 1854 , p. 1) which “aimed to investigate those operations of the mind by which reasoning is performed”), and this led to the 1943 proposal by Craik that the nervous system could be viewed “as a calculating machine capable of modeling or paralleling external events” ( Craik 1943 , p. 120) while Mc-Culloch and Pitts provided what they called “A logical calculus of the ideas immanent in nervous activity” ( McCulloch and Pitts 1943 ). In fact, while it was an outgrowth of preliminary investigations by a number of early theorists ( Piccinini 2004 ), the McCulloch and Pitts paper stands as a historical landmark for the origins of artificial intelligence, along with the notion that mind can be explained by neural activity through a formalism that aims to define the brain as a computational device; see Figure 2 . In the same year another noteworthy essay, by Norbert Wiener and colleagues, argued that in studying any behavior its purpose must be considered, and this requires recognition of the role of error correction in the form of feedback ( Rosenblueth et al. 1943 ). Soon after, Wiener consolidated these ideas in the term cybernetics ( Wiener 1948 ). Also, in 1948 Claude Shannon published his hugely influential work on information theory which, beyond its technical contributions, solidified information (the reduction of uncertainty) as an abstract quantification of the content being transmitted across communication channels, including those in brains and computers ( Shannon and Weaver 1949 ).

In the left diagram, McCulloch-Pitts neurons x 1 and x 2 each send binary activity to neuron y using the rule y = 1 if x 1 + x 2 > 1 and y = 0 otherwise; this corresponds to the logical AND operator; other logical operators NOT, OR, NOR may be similarly implemented by thresholding. In the right diagram, the general form of output is based on thresholding linear combinations, i.e., y =1 when ∑ w i x i > c and y = 0 otherwise. The values w i are called synaptic weights. However, because networks of perceptrons (and their more modern artificial neural network descendents) are far simpler than networks in the brain, each artificial neuron corresponds conceptually not to an individual neuron in the brain but, instead, to large collections of neurons in the brain.

The first computer program that could do something previously considered exclusively the product of human minds was the Logic Theorist of Newell and Simon ( Newell and Simon 1956 ), which succeeded in proving 38 of the 52 theorems concerning the logical foundations of arithmetic in Chapter 2 of Principia Mathematica ( Whitehead and Russell 1912 ). The program was written in a list-processing language they created (a precursor to LISP), and provided a hierarchical symbol manipulation framework together with various heuristics, which were formulated by analogy with human problem-solving ( Gugerty 2006 ). It was also based on serial processing, as envisioned by Turing and others.

A different kind of computational architecture, developed by Rosenblatt ( Rosenblatt 1958 ), combined the McCulloch-Pitts conception with a learning rule based on ideas articulated by Hebb in 1949 ( Hebb 1949 ), now known as Hebbian learning . Hebb’s rule was, “When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased” ( Hebb 1949 ), that is, the strengths of the synapses connecting the two neurons increase, which is sometimes stated colloquially as, “Neurons that fire together, wire together.” Rosenblatt called his primitive neurons perceptrons , and he created a rudimentary classifier, aimed at imitating biological decision making, from a network of perceptrons, see Figure 2 . This was the first artificial neural network that could carry out a non-trivial task.

As the foregoing historical outline indicates, the brain-as-computer metaphor was solidly in place by the end of the 1950s. It rested on a variety of technical specifications of the notions that (1) logical thinking is a form of information processing, (2) information processing is the purpose of computer programs, while, (3) information processing may be implemented by neural systems (explicitly in the case of McCulloch-Pitts model and its descendents, but implicitly otherwise). A crucial recapitulation of the information-processing framework, given later by David Marr ( Marr 1982 ), distinguished three levels of analysis: computation (“What is the goal of the computation, why is it appropriate, and what is the logic of the strategy by which it can be carried out?”), algorithm (“What is the representation for the input and output, and what is the algorithm for the transformation?”), and implementation (“How can the representation and algorithm be realized physically?”). This remains a very useful way to categorize descriptions of brain computation.

1.2. Neurons as electrical circuits

A rather different line of mathematical work, more closely related to neurobiology, had to do with the electrical properties of neurons. So-called “animal electricity” had been observed by Galvani in 1791 ( Galvani and Aldini 1792 ). The idea that the nervous system was made up of individual neurons was put forth by Cajal in 1886, the synaptic basis of communication across neurons was established by Sherrington in 1897 ( Sherrington 1897 ), and the notion that neurons were electrically excitable in a manner similar to a circuit involving capacitors and resistors in parallel was proposed by Hermann in 1905 ( Piccolino 1998 ). In 1907, Lapique gave an explicit solution to the resulting differential equation, in which the key constants could be determined from data, and he compared what is now known as the leaky integrate-and-fire model (LIF) with his own experimental results ( Abbott 1999 ; Brunel and Van Rossum 2007 ; Lapique 1907 ). This model, and variants of it, remain in use today ( Gerstner et al. 2014 ), and we return to it in Section 2 (see Figure 3 ). Then, a series of investigations by Adrian and colleagues established the “all or nothing” nature of the AP, so that increasing a stimulus intensity does not change the voltage profile of an AP but, instead, increases the neural firing rate ( Adrian and Zotterman 1926 ). The conception that stimulus or behavior is related to firing rate has become ubiquitous in neurophysiology. It is often called rate coding , in contrast to temporal coding , which involves the information carried in the precise timing of spikes ( Abeles 1982 ; Shadlen and Movshon 1999 ; Singer 1999 ).

(a) The LIF model is motivated by an equivalent circuit. The capacitor represents the cell membrane through which ions cannot pass. The resistor represents channels in the membrane (through which ions can pass) and the battery a difference in ion concentration across the membrane. (b) The equivalent circuit motivates the differential equation that describes voltage dynamics (gray box). When the voltage reaches a threshold value ( V threshold ), it is reset to a smaller value ( V reset ). In this model, the occurrence of a reset indicates an action potential; the rapid voltage dynamics of action potentials are not included in the model. (c) An example trace of the LIF model voltage (blue). When the input current ( I ) is large enough, the voltage increases until reaching the voltage threshold (red horizontal line), at which time the voltage is set to the reset voltage (green horizontal line). The times of reset are labeled as “AP”, denoting action potential. In the absence of an applied current ( I = 0) the voltage approaches a stable equilibrium value ( V rest ).

Following these fundamental descriptions, remaining puzzles about the details of action potential generation led to investigations by several neurophysiologists and, ultimately, to one of the great scientific triumphs, the Hodgkin-Huxley model . Published in 1952 ( Hodgkin and Huxley 1952 ), the model consisted of a differential equation for the neural membrane potential (in the squid giant axon) together with three subsidiary differential equations for the dynamic properties of the sodium and potassium ion channels. See Figure 4 . This work produced accurate predictions of the time courses of membrane conductances; the form of the action potential; the change in action potential form with varying concentrations of sodium; the number of sodium ions involved in inward flux across the membrane; the speed of action potential propagation; and the voltage curves for sodium and potassium ions ( Hille 2001 ; Hodgkin and Huxley 1952 ). Thus, by the time the brain-as-computer metaphor had been established, the power of biophysical modeling had also been demonstrated. Over the past 60 years, the Hodgkin-Huxley equations have been refined, but the model’s fundamental formulation has endured, and serves as the basis for many present-day models of single neuron activity; see Section 2.2 .

The Hodgkin-Huxley model provides a mathematical description of a neuron’s voltage dynamics in terms of changes in sodium (Na + ) and potassium (K + ) ion concentrations. The cartoon in (a) illustrates a cell body with membrane channels through which (Na + ) and (K + ) may pass. The model consists of four coupled nonlinear differential equations (b) that describe the voltage dynamics ( V ), which vary according to an input current ( I ), a potassium current, a sodium current, and a leak current. The conductances of the potassium ( n ) and sodium currents ( m , h ) vary in time, which controls the flow of sodium and potassium ions through the neural membrane. Each channel’s dynamics depends on (c) a steady state function and a time constant. The steady state functions range from 0 to 1, where 0 indicates that the channel is closed (so that ions cannot pass), and 1 indicates that the channel is open (ions can pass). One might visualize these channels as gates that swing open and closed, allowing ions to pass or impeding their flow; these gates are indicated in green and red in the cartoon (a). The steady state functions depend on the voltage; the vertical dashed line indicates the typical resting voltage value of a neuron. The time constants are less than 10 ms, and smallest for one component of the sodium channel (the sodium activation gate m ). (d) During an action potential, the voltage undergoes a rapid depolarization ( V increases) and then less rapid hyperpolarization ( V decreases), supported by the opening and closing of the membrane channels.

1.3. Receptive fields and tuning curves

In early recordings from the optic nerve of the Limulus (horseshoe crab), Hartline found that shining a light on the eye could drive individual neurons to fire, and that a neuron’s firing rate increased with the intensity of the light ( Hartline and Graham 1932 ). He called the location of the light that drove the neuron to fire the neuron’s receptive field . In primary visual cortex (known as area V1), the first part of cortex to get input from the retina, Hubel and Wiesel showed that bars of light moving across a particular part of the visual field, again labeled the receptive field, could drive a particular neuron to fire and, furthermore, that the orientation of the bar of light was important: many neurons were driven to fire most rapidly when the bar of light moved in one direction, and fired much more slowly when the orientation was rotated 90 degrees away ( Hubel and Wiesel 1959 ). When firing rate is considered as a function of orientation, this function has come to be known as a tuning curve ( Dayan and Abbott 2001 ). More recently, the terms “receptive field” and “tuning curve” have been generalized to refer to non-spatial features that drive neurons to fire. The notion of tuning curves, which could involve many dimensions of tuning simultaneously, widely applied in computational neuroscience.

1.4. Networks

Neuron-like artificial neural networks, advancing beyond perceptron networks, were developed during the 1960s and 1970s, especially in work on associative memory ( Amari 1977b ), where a memory is stored as a pattern of activity that can be recreated by a stimulus when it provides even a partial match to the pattern. To describe a given activation pattern, Hopfield applied statistical physics tools to introduce an energy function and showed that a simple update rule would decrease the energy so that the network would settle to a pattern-matching “attractor” state ( Hopfield 1982 ). Hopfield’s network model is an example of what statisticians call a two-way interaction model for N binary variables, where the energy function becomes the negative log-likelihood function. Hinton and Sejnowski provided a stochastic mechanism for optimization and the interpretation that a posterior distribution was being maximized, calling their method a Boltzmann machine because the probabilities they used were those of the Boltzmann distribution in statistical mechanics ( Hinton and Sejnowski 1983 ). Geman and Geman then provided a rigorous analysis together with their reformulation in terms of the Gibbs sampler ( Geman and Geman 1984 ). Additional tools from statistical mechanics were used to calculate memory capacity and other properties of memory retrieval ( Amit et al. 1987 ), which created further interest in these models among physicists.

Artificial neural networks gained traction as models of human cognition through a series of developments in the 1980s ( Medler 1998 ), producing the paradigm of parallel distributed processing (PDP). PDP models are multi-layered networks of nodes resembling those of their perceptron precursor, but they are interactive , or recurrent , in the sense that they are not necessarily feed-forward: connections between nodes can go in both directions, and they may have structured inhibition and excitation ( Rumelhart et al. 1986 ). In addition, training (i.e., estimating parameters by minimizing an optimization criterion such as the sum of squared errors across many training examples) is done by a form of gradient descent known as back propagation (because iterations involve steps backward from output errors toward input weights). While the nodes within these networks do not correspond to individual neurons, features of the networks, including back propagation, are usually considered to be biologically plausible. For example, synaptic connections between biological neurons are plastic, and change their strength following rules consistent with theoretical models (e.g., Hebb’s rule). Furthermore, PDP models can reproduce many behavioral phenomena, famously including generation of past tense for English verbs and making childlike errors before settling on correct forms ( McClelland and Rumelhart 1981 ). Currently, there is increased interest in neural network models through deep learning , which we will discuss briefly, below.

Analysis of the overall structure of network connectivity, exemplified in research on social networks (see Fienberg (2012) for historical overview), has received much attention following the 1998 observation that several very different kinds of networks, including the neural connectivity in the worm C. elegans , exhibit “small world” properties of short average path length between nodes, together with substantial clustering of nodes, and that these properties may be described by a relatively simple stochastic model ( Watts and Strogatz 1998 ). This style of network description has since been applied in many contexts involving brain measurement, mainly using structural and functional magnetic resonance imaging (MRI) ( Bassett and Bullmore 2016 ; Bullmore and Sporns 2009 ), though cautions have been issued regarding the difficulty of interpreting results physiologically ( Papo et al. 2016 ).

1.5. Statistical models

Stochastic considerations have been part of neuroscience since the first descriptions of neural activity, outlined briefly above, due to the statistical mechanics underlying the flow of ions across channels and synapses ( Colquhoun and Sakmann 1998 ; Destexhe et al. 1994 ). Spontaneous fluctuations in a neuron’s membrane potential are believed to arise from the random opening and closing of ion channels, and this spontaneous variability has been analyzed using a variety of statistical methods ( Sigworth 1980 ). Such analysis provides information about the numbers and properties of the ion channel populations responsible for excitability. Probability has also been used extensively in psychological theories of human behavior for more than 100 years, e.g., Stigler (1986 , Ch. 7). Especially popular theories used to account for behavior include Bayesian inference and reinforcement learning, which we will touch on below. A more recent interest is to determine signatures of statistical algorithms in neural function. For example, drifting diffusion to a threshold, which is used with LIF models ( Tuckwell 1988 ), has also been used to describe models of decision making based on neural recordings ( Gold and Shadlen 2007 ). However, these are all examples of ways that statistical models have been used to describe neural activity, which is very different from the role of statistics in data analysis. Before previewing our treatment of data analytic methods, we describe the types of data that are relevant to this article.

1.6. Recording modalities

Efforts to understand the nervous system must consider both anatomy (its constituents and their connectivity) and function (neural activity and its relationship to the apparent goals of an organism). Anatomy does not determine function, but does strongly constrain it. Anatomical methods range from a variety of microscopic methods to static, whole-brain MRI ( Fischl et al. 2002 ). Functional investigations range across spatial and temporal scales, beginning with recordings from ion channels, to action potentials, to local field potentials (LFPs) due to the activity of many thousands of neural synapses. Functional measurements outside the brain (still reflecting electrical activity within it), come from electroencephalography (EEG) ( Nunez and Srinivasan 2006 ) and magnetoencephalography (MEG) ( Hämäläinen et al. 1993 ), as well as indirect methods that measure a physiological or metabolic parameter closely associated with neural activity, including positron emission tomography (PET) ( Bailey et al. 2005 ), functional MRI (fMRI) ( Lazar 2008 ), and near-infrared resonance spectroscopy (NIRS) ( Villringer et al. 1993 ). These functional methods have timescales spanning milliseconds to minutes, and spatial scales ranging from a few cubic millimeters to many cubic centimeters.

While interesting mathematical and statistical problems arise in nearly every kind of neuroscience data, we focus here on neural spiking activity. Spike trains are sometimes recorded from individual neurons in tissue that has been extracted from an animal and maintained over hours in a functioning condition ( in vitro ). In this setting, the voltage drop across the membrane is nearly deterministic; then, when the neuron is driven with the same current input on each of many repeated trials, the timing of spikes is often replicated precisely across the trials ( Mainen and Sejnowski 1995 ), as seen in portions of the spike trains in Figure 5 . Recordings from brains of living animals ( in vivo ) show substantial irregularity in spike timing, as in Figure 1 . These recordings often come from electrodes that have been inserted into brain tissue near, but not on or in, the neuron generating a resulting spike train; that is, they are extracellular recordings. The data could come from one up to dozens, hundreds, or even thousands of electrodes. Because the voltage on each electrode is due to activity of many nearby neurons, with each neuron contributing its own voltage signature repeatedly, there is an interesting statistical clustering problem known as spike sorting ( Carlson et al. 2014 ; Rey et al. 2015 ), but we will ignore that here. Another important source of activity, recorded from many individual neurons simultaneously, is calcium imaging , in which light is emitted by fluorescent indicators in response to the flow of calcium ions into neurons when they fire ( Grienberger and Konnerth 2012 ). Calcium dynamics, and the nature of the indicator, limit temporal resolution to between tens and several hundred milliseconds. Signals can be collected using one-photon microscopy even from deep in the brain of a behaving animal; two-photon microscopy provides significantly higher spatial resolution but at the cost of limiting recordings to the brain surface. Due to the temporal smoothing, extraction of spiking data from calcium imaging poses its own set of statistical challenges ( Pnevmatikakis et al. 2016 ).

Left panel displays the current (“Stim,” for stimulus, at the top of the panel) injected into a mitral cell from the olfactory system of a mouse, together with the neural spiking response (MC) across many trials (each row displays the spike train for a particular trial). The response is highly regular across trials, but at some points in time it is somewhat variable. The right panel displays a stimulus filter fitted to the complete set of data using model ( 3 ), where the stimulus filter, i.e., the function g 0 ( s ), represents the contribution to the firing rate due to the current I ( t − s ) at s milliseconds prior to time t . Figure modified from ( Wang et al. 2015 )

Neural firing rates vary widely, depending on recording site and physiological circumstances, from quiescent (essentially 0 spikes per second) to as many as 200 spikes per second. The output of spike sorting is a sequence of spike times, typically at time resolution of 1 millisecond (the approximate width of an AP). While many analyses are based on spike counts across relatively long time intervals (numbers of spikes that occur in time bins of tens or hundreds of milliseconds), some are based on the more complete precise timing information provided by the spike trains.

In some special cases, mainly in networks recorded in vitro , neurons are densely sampled and it is possible to study the way activity of one neuron directly influences the activity of other neurons ( Pillow et al. 2008 ). However, in most experimental settings to date, a very small proportion of the neurons in the circuit are sampled.

1.7. Data analysis

In experiments involving behaving animals, each experimental condition is typically repeated across many trials. On any two trials, there will be at least slight differences in behavior, neural activity throughout the brain, and contributions from molecular noise, all of which results in considerable variability of spike timing. Thus, a spike train may be regarded as a point process , i.e., a stochastic sequence of event times, with the events being spikes. We discuss point process modeling below, but note here that the data are typically recorded as sparse binary time series in 1 millisecond time bins (1 if spike, 0 if no spike). When spike counts within broader time bins are considered, they may be assumed to form continuous-valued time series, and this is the framework for some of the methods referenced below. It is also possible to apply time series methods directly to the binary data, or smoothed versions of them, but see the caution in Kass et al. (2014 , Section 19.3.7). A common aim is to relate an observed pattern of activity to features of the experimental stimulus or behavior. However, in some settings predictive approaches are used, often under the rubric of decoding , in the sense that neural activity is “decoded” to predict the stimulus or behavior. In this case, tools associated with the field of statistical machine learning may be especially useful ( Ventura and Todorova 2015 ). We omit many interesting questions that arise in the course of analyzing biological neural networks, such as the distribution of the post-synaptic potentials that represent synaptic weights ( Buzsáki and Mizuseki 2014 ; Teramae et al. 2012 ).

Data analysis is performed by scientists with diverse backgrounds. Statistical approaches use frameworks built on probabilistic descriptions of variability, both for inductive reasoning and for analysis of procedures. The resulting foundation for data analysis has been called the statistical paradigm ( Kass et al. 2014 , Section 1.2 ).

1.8. Components of the nervous system

When we speak of neurons, or brains, we are indulging in sweeping generalities: properties may depend not only on what is happening to the organism during a study, but also on the component of the nervous system studied, and the type of animal being used. Popular organisms in neuroscience include worms, mollusks, insects, fish, birds, rodents, non-human primates, and, of course, humans. The nervous system of vertebrates comprises the brain, the spinal cord, and the peripheral system. The brain itself includes both the cerebral cortex and sub-cortical areas. Textbooks of neuroscience use varying organizational rubrics, but major topics include the molecular physiology of neurons, sensory systems, the motor system, and systems that support higher-order functions associated with complex and flexible behavior ( Kandel et al. 2013 ; Swanson 2012 ). Attempts at understanding computational properties of the nervous system have often focused on sensory systems: they are more easily accessed experimentally, controlled inputs to them can be based on naturally occurring inputs, and their response properties are comparatively simple. In addition, much attention has been given to the cerebral cortex, which is involved in higher-order functioning.

2. Single Neurons

Mathematical models typically aim to describe the way a given phenomenon arises from some architectural constraints. Statistical models typically are used to describe what a particular data set can say concerning the phenomenon, including the strength of evidence. We very briefly outline these approaches in the case of single neurons, and then review attempts to bring them together.

2.1. LIF models and their extensions

Originally proposed more than a century ago, the LIF model ( Figure 3 ) continues to serve an important role in neuroscience research ( Abbott 1999 ). Although LIF neurons are deterministic, they often mimic the variation in spike trains of real neurons recorded in vitro , such as those in Figure 5 . In the left panel of that figure, the same fluctuating current is applied repeatedly as input to the neuron, and this creates many instances of spike times that are highly precise in the sense of being replicated across trials; some other spike times are less precise. Precise spike times occur when a large slope in the input current leads to wide recruitment of ion channels ( Mainen and Sejnowski 1995 ). Temporal locking of spikes to high frequency inputs also can be seen in LIF models ( Goedeke and Diesmann 2008 ). Many extensions of the original leaky integrate-and-fire model have been developed to capture other features of observed neuronal activity ( Gerstner et al. 2014 ), including more realistic spike initiation through inclusion of a quadratic term, and incorporation of a second dynamical variable to simulate adaptation and to capture more diverse patterns of neuronal spiking and bursting. Even though these models ignore the biophysics of action potential generation (which involve the conductances generated by ion channels, as in the Hodgkin-Huxley model), they are able to capture the nonlinearities present in several biophysical neuronal models ( Rotstein 2015 ). The impact of stochastic effects due to the large number of synaptic inputs delivered to an LIF neuron has also been extensively studied using diffusion processes ( Lansky and Ditlevsen 2008 ).

2.2. Biophysical models

There are many extensions of the Hodgkin and Huxley framework outlined in Figure 4 . These include models that capture additional biological features, such as additional ionic currents ( Somjen 2004 ), and aspects of the neuron’s extracellular environment ( Wei et al. 2014 ), both of which introduce new fast and slow timescales to the dynamics. Contributions due to the extensive dendrites (which receive inputs to the neuron) have been simulated in detailed biophysical models ( Rall 1962 ). While increased biological realism necessitates additional mathematical complexity, especially when large populations of neurons are considered, the Hodgkin-Huxley model and its extensions remain fundamental to computational neuroscience research ( Markram et al. 2015 ; Traub et al. 2005 ).

Simplified mathematical models of single neuron activity have facilitated a dynamical understanding of neural behavior. The Fitzhugh-Nagumo model is a purely phenomenological model, based on geometric and dynamic principles, and not directly on the neuron’s biophysics ( Fitzhugh 1960 ; Nagumo et al. 1962 ). Because of its low dimensionality, it is amenable to phase-plane analysis using dynamical systems tools (e.g., examining the null-clines, equilibria and trajectories).

An alternative approach is to simplify the equations of a detailed neuronal model in ways that retain a biophysical interpretation ( Ermentrout and Terman 2010 ). For example, by making a steady-state approximation for the fast ionic sodium current activation in the Hodgkin-Huxley model ( m in Figure 4 ), and recasting two of the gating variables ( n and h ), it is possible to simplify the original Hodgkin-Huxley model to a two-dimensional model, which can be investigated more easily in the phase plane ( Gerstner et al. 2014 ). The development of simplified models is closely interwoven with bifurcation theory and the theory of normal forms within dynamical systems ( Izhikevich 2007 ). One well-studied reduction of the Hodgkin-Huxley equations to a 2-dimensional conductance-based model was developed by John Rinzel ( Rinzel 1985 ). In this case, the geometries of the phenomenological Fitzhugh-Nagumo model and the simplified Rinzel model are qualitatively similar. Yet another approach to dimensionality reduction consists of neglecting the spiking currents (fast sodium and delayed-rectifying potassium) and considering only the currents that are active in the sub-threshold regime ( Rotstein et al. 2006 ). This cannot be done in the original Hodgkin-Huxley model, because the only ionic currents are those that lead to spikes, but it is useful in models that include additional ionic currents in the sub-threshold regime.

2.3. Point process regression models of single neuron activity

Mathematically, the simplest model for an irregular spike train is a homogeneous Poisson process, for which the probability of spiking within a time interval ( t, t + Δ t ], for small Δ t , may be written

where λ represents the firing rate of the neuron and where disjoint intervals have independent spiking. This model, however, is often inadequate for many reasons. For one thing, neurons have noticeable refractory periods following a spike, during which the probability of spiking goes to zero (the absolute refractory period ) and then gradually increases, often over tens of milliseconds (the relative refractory period ). In this sense neurons exhibit memory effects, often called spike history effects. To capture those, and many other physiological effects, more general point processes must be used. We outline the key ideas underlying point process modeling of spike trains.

As we indicated in Section 1.2 , a fundamental result in neurophysiology is that neurons respond to a stimulus or contribute to an action by increasing their firing rates. The measured firing rate of a neuron within a time interval would be the number of spikes in the interval divided by the length of the interval (usually in units of seconds, so that the ratio is in spikes per second, abbreviated as Hz, for Hertz). The point process framework centers on the theoretical instantaneous firing rate, which takes the expected value of this ratio and passes to the limit as the length of the time interval goes to zero, giving an intensity function for the process. To accurately model a neuron’s spiking behavior, however, the intensity function typically must itself evolve over time depending on changing inputs and experimental conditions, the recent past spiking behavior of the neuron, the behavior of other neurons, the behavior of local field potentials, etc. It is therefore called a conditional intensity function and may be written in the form

where N ( t , t +Δ t ] is the number of spikes in the interval ( t , t + Δ t ] and where the vector X t includes both the past spiking history H t prior to time t and also any other quantities that affect the neuron’s current spiking behavior. In some special cases, the conditional intensity will be deterministic, but in general, because X t is random, the conditional intensity is also random. If X t includes unobserved random variables, the process is often called doubly stochastic . When the conditional intensity depends on the history H t , the process is often called self-exciting (though the effects may produce an inhibition of firing rate rather than an excitation). The vector X t may be high-dimensional. A mathematically tractable special case, where contributions to the intensity due to previous spikes enter additively in terms of a fixed kernel function, is the Hawkes process .

As a matter of interpretation, in sufficiently small time intervals the spike count is either zero or one, so we may replace the expectation with the probability of spiking and get

A statistical model for a spike train involves two things: (1) a simple, universal formula for the probability density of the spike train in terms of the conditional intensity function (which we omit here) and (2) a specification of the way the conditional intensity function depends on variables x t . An analogous statement is also true for multiple spike trains, possibly involving multiple neurons. Thus, when the data are resolved down to individual spikes, statistical analysis is primarily concerned with modeling the conditional intensity function in a form that can be implemented efficiently and that fits the data adequately well. That is, writing

the challenge is to identify within the variable x t all relevant effects, or features , in the terminology of machine learning, and then to find a suitable form for the function f , keeping in mind that, in practice, the dimension of x t may range from 1 to many millions. This identification of the components of x t that modulate the neuron’s firing rate is a key step in interpreting the function of a neural system. Details may be found in Kass et al. (2014 , Chapter 19), but see Amarasingham et al. (2015) for an important caution about the interpretation of neural firing rate through its representation as a point process intensity function.

A statistically tractable non-Poisson form involves log-additive models, the simplest case being

where s * ( t ) is the time of the immediately preceding spike, and g 0 and g 1 are functions that may be written in terms of some basis ( Kass and Ventura 2001 ). To include contributions from spikes that are earlier than the immediately preceding one, the term log g 1 ( t − s * ( t )) is replaced by a sum of terms of the form log g 1 j ( t − s j ( t )), where s j ( t ) is the j -th spike back in time preceding t , and a common simplification is to assume the functions g 1 j are all equal to a single function g 1 ( Pillow et al. 2008 ). The resulting probability density function for the set of spike times (which defines the likelihood function) is very similar to that of a Poisson generalized linear model (GLM) and, in fact, GLM software may be used to fit many point process models ( Kass et al. 2014 , Chapter 19). The use of the word “linear” may be misleading here because highly nonlinear functions may be involved, e.g., in Equation (2) , g 0 and g 1 are typically nonlinear. An alternative is to call these point process regression models. Nonetheless, the model in (2) is often said to specify a GLM neuron , as are other point process regression models.

2.4. Point process regression and leaky integrate-and-fire models

Assuming excitatory and inhibitory Poisson process inputs to an LIF neuron, the distribution of waiting times for a threshold crossing, which corresponds to the inter-spike interval (ISI), is found to be inverse Gaussian ( Tuckwell 1988 ) and this distribution often provides a good fit to experimental data when neurons are in steady state, as when they are isolated in vitro and spontaneous activity is examined ( Gerstein and Mandelbrot 1964 ). The inverse Gaussian distribution, within a biologically-reasonable range of coefficient of variations, turns out to be qualitatively very similar to ISI distributions generated by processes given by Equation (2) . Furthermore, spike trains generated from LIF models can be fitted well by these GLM-type models ( Kass et al. 2014 , Section 19.3.4 and references therein).

An additional connection between LIF and GLM neurons comes from considering the response of neurons to injected currents, as illustrated in Figure 5 . In this context, the first term in Equation (2) may be rewritten as a convolution with the current I ( t ) at time t , so that ( 2 ) becomes

Figure 5 shows the estimate of g 0 that results from fitting this model to data illustrated in that figure. Here, the function g 0 is often called a stimulus filter . On the other hand, following Gerstner et al. (2014 , Chapter 6), we may write a generalized version of LIF in integral form,

which those authors call a Spike Response Model (SRM). By equating the log conditional intensity to voltage in ( 4 ),

we thereby get a modified LIF neuron that is also a GLM neuron ( Paninski et al. 2009 ). Thus, both theory and empirical study indicate that GLM and LIF neurons are very similar, and both describe a variety of neural spiking patterns ( Weber and Pillow 2016 ).

It is interesting that these empirically-oriented SRMs, and variants that included an adaptive threshold ( Kobayashi et al. 2009 ), performed better than much more complicated biophysical models in a series of international competitions for reproducing and predicting recorded spike times of biological neurons under varying circumstances ( Gerstner and Naud 2009 ).

2.5. Multidimensional models

The one-dimensional LIF dynamic model in Figure 3b is inadequate when interactions of sub-threshold ion channel dynamics cause a neuron’s behavior to be more complicated than integration of inputs. Neurons can even behave as differentiators and respond only to fluctuations in input. Furthermore, as noted in Sections 1.3 and 2.3 , features that drive neural firing can be multidimensional. Multivariate dynamical systems are able to describe the ways that interacting, multivariate effects can bring the system to its firing threshold, as in the Hodgkin-Huxley model ( Hong et al. 2007 ). A number of model variants that aim to account for such multidimensional effects have been compared in predicting experimental data from sensory areas ( Aljadeff et al. 2016 ).

2.6. Statistical challenges in biophysical modeling

Conductance-based biophysical models pose problems of model identifiability and parameter estimation. The original Hodgkin-Huxley equations ( Hodgkin and Huxley 1952 ) contain on the order of two dozen numerical parameters describing the membrane capacitance, maximal conductances for the sodium and potassium ions, kinetics of ion channel activation and inactivation, and the ionic equilibrium potentials (at which the flow of ions due to imbalances of concentration across the cell membrane offsets that due to imbalances of electrical charge). Hodgkin and Huxley arrived at estimates of these parameters through a combination of extensive experimentation, biophysical reasoning, and regression techniques. Others have investigated the experimental information necessary to identify the model ( Walch and Eisenberg 2016 ). In early work, statistical analysis of nonstationary ensemble fluctuations was used to estimate the conductances of individual ion channels ( Sigworth 1977 ). Following the introduction of single-channel recording techniques ( Sakmann and Neher 1984 ), which typically report a binary projection of a multistate underlying Markovian ion channel process, many researchers expanded the theory of aggregated Markov processes to handle inference problems related to identifying the structure of the underlying Markov process and estimating transition rate parameters ( Qin et al. 1997 ).

More recently, parameter estimation challenges in biophysical models have been tackled using a variety of techniques under the rubric of “data assimilation,” where data results are combined with models algorithmically. Data assimilation methods illustrate the interplay of mathematical and statistical approaches in neuroscience. For example, in Meng et al. (2014) , the authors describe a state space modeling framework and a sequential Monte Carlo (particle filter) algorithm to estimate the parameters of a membrane current in the Hodgkin-Huxley model neuron. They applied this framework to spiking data recorded from rat layer V cortical neurons, and correctly identified the dynamics of a slow membrane current. Variations on this theme include the use of synchronization manifolds for parameter estimation in experimental neural systems driven by dynamically rich inputs ( Meliza et al. 2014 ), combined statistical and geometric methods ( Tien and Guckenheimer 2008 ), and other state space models ( Vavoulis et al. 2012 ).

3. Networks

3.1. mechanistic approaches for modeling small networks.

While biological neural networks typically involve anywhere from dozens to many millions of neurons, studies of small neural networks involving handfuls of cells have led to remarkably rich insights. We describe three such cases here, and the types of mechanistic models that drive them.

First, neural networks can produce rhythmic patterns of activity. Such rhythms, or oscillations, play clear roles in central pattern generators (CPGs) in which cell groups produce coordinated firing for, e.g., locomotion or breathing ( Grillner and Jessell 2009 ; Marder and Bucher 2001 ). Small network models have been remarkably successful in describing how such rhythms occur. For example, models involving pairs of cells have revealed how delays in connections among inhibitory cells, or reciprocal interactions between excitatory and inhibitory neurons, can lead to rhythms in the gamma range (30–80 Hz) associated with some aspects of cognitive processing. A general theory, beginning with two-cell models of this type, describes how synaptic and intrinsic cellular dynamics interact to determine when the underlying synchrony will and will not occur ( Kopell and Ermentrout 2002 ). Larger models involving three or more interacting cell types describe the origin of more complex rhythms, such as the triphasic rhythm in the stomatogastric ganglion (for digestion in certain invertebrates). This system in particular has revealed a rich interplay between the intrinsic dynamics in multiple cells and the synapses that connect them ( Marder and Bucher 2001 ). There turn out to be many highly distinct parameter combinations, lying in subsets of parameter space, that all produce the key target rhythm, but do so in very different ways ( Prinz et al. 2004 ). Understanding the origin of this flexibility, and how biological systems take advantage of it to produce robust function, is a topic of ongoing work.

The underlying mechanistic models for rhythmic phenomena are of Hodgkin-Huxley type, involving sodium and potassium channels ( Figure 4 ). For some phenomena, including respiratory and stomatogastric rhythms, additional ion channels that drive bursting in single cells play a key role. Dynamical systems tools for assessing the stability of periodic orbits may then be used to determine what patterns of rhythmic activity will be stably produced by a given network. Specifically, coupled systems of biophysical differential equations can often be reduced to interacting circular variables representing the phase of each neuron ( Ermentrout and Terman 2010 ). Such phase models yield to very elegant stability analyses that can often predict the dynamics of the original biophysical equations.

A second example concerns the origin of collective activity in irregularly spiking neural circuits. To understand the development of correlated spiking in such systems, stochastic differential equation models, or models driven by point process inputs, are typically used. This yields Fokker-Planck or population density equations ( Tranchina 2010 ; Tuck-well 1988 ) and these can be iterated across multiple layers or neural populations ( Doiron et al. 2006 ; Tranchina 2010 ). In many cases, such models can be approximated using linear response approaches, yielding analytical solutions and considerable mechanistic insight ( De La Rocha et al. 2007 ; Ostojic and Brunel 2011a ). A prominent example comes from the mechanisms of correlated firing in feedforward networks ( De La Rocha et al. 2007 ; Shadlen and Newsome 1998 ). Here, stochastically firing cells send diverging inputs to multiple neurons downstream. The downstream neurons thereby share some of their input fluctuations, and this, in turn, creates correlated activity that can have rich implications for information transmission ( De La Rocha et al. 2007 ; Doiron et al. 2016 ; Zylberberg et al. 2016 ).

A third case of highly influential small circuit modeling concerns neurons in the early visual cortex (early in the sense of being only a few synapses from the retina), which are responsive to visual stimuli (moving bars of light) with specific orientations that fall within their receptive field (see Section 1.3 ). Neurons having neighboring regions within their receptive field in which a stimulus excites or inhibits activity were called simple cells, and those without this kind of sub-division were complex cells. Hubel and Wiesel famously showed how simple circuit models can account for both the simple and complex cell responses ( Hubel and Wiesel 1959 ). Later work described this through one or several iterated algebraic equations that map input firing rates x i into outputs y = f (∑ i w i x i ), where w = ( w 1 , …, w N ) is a synaptic weight vector.

3.2. Statistical methods for small networks

Point process models for small networks begin with conditional intensity specifications similar to that in Equation (2) , and include coupling terms ( Kass et al. 2014 , Section 19.3.4, and references therein). They have been applied to CPGs described above, in Section 3.1 , to reconstruct known circuitry from spiking data ( Gerhard et al. 2013 ). In addition, many of the methods we discuss below, in Section 3.4 on large networks, have also been used with small networks.

3.3. Mechanistic models of large networks across scales and levels of complexity

There is a tremendous variety of mechanistic models of large neural networks. We here describe these in rough order of their complexity and scale.

3.3.1. Binary and firing rate models.

At the simplest level, binary models abstract the activity of each neuron as either active (taking the value 1) or silent (0) in a given time step. As mentioned in the Introduction, despite their simplicity, these models capture fundamental properties of network activity ( Renart et al. 2010 ; van Vreeswijk and Sompolinsky 1996 ) and explain network functions such as associative memory. The proportion of active neurons at a given time is governed by effective rate equations ( Ginzburg and Sompolinsky 1994 ; Wilson and Cowan 1972 ). Such firing rate models feature a continuous range of activity states, and often take the form of nonlinear ordinary or stochastic differential equations. Like binary models, these also implement associative memory ( Hopfield 1984 ), but are widely used to describe broader dynamical phenomena in networks, including predictions of oscillations in excitatory-inhibitory networks ( Wilson and Cowan 1972 ), transitions from fixed point to oscillatory to chaotic dynamics in randomly connected neural networks ( Bos et al. 2016 ), amplified selectivity to stimuli, and the formation of line attractors (a set of stable solutions on a line in state space) that gradually store and accumulate input signals ( Cain and Shea-Brown 2012 ).

Firing rate models have been a cornerstone of theoretical neuroscience. Their second order statistics can analytically be matched to more realistic spiking and binary models ( Grytskyy et al. 2013 ; Ostojic and Brunel 2011a ). We next describe how trial-varying dynamical fluctuations can emerge in networks of spiking neuron models.

3.3.2. Stochastic spiking activity in networks.

A beautiful body of work summarizes the network state in a population-density approach that describes the evolution of the probability density of states rather than individual neurons ( Amit and Brunel 1997 ). The theory is able to capture refractoriness ( Meyer and van Vreeswijk 2002 ) and adaptation ( Deger et al. 2014 ). Furthermore, although it loses the identity of individual neurons, it can faithfully capture collective activity states, such as oscillations ( Brunel 2000 ). Small synaptic amplitudes and weak correlations further reduce the time-evolution to a Fokker-Planck equation ( Brunel 2000 ; Ostojic et al. 2009 ). Network states beyond such diffusion approximations include neuronal avalanches , the collective and nearly synchronous firing of a large fraction of cells, often following power-law distributions ( Beggs and Plenz 2003 ). While early work focused on the firing rates of populations, later work clarified how more subtle patterns of correlated spiking develop. In particular, linear fluctuations about a stationary state determine population-averaged measures of correlations ( Helias et al. 2013 ; Ostojic et al. 2009 ; Tetzlaff et al. 2012 ; Trousdale et al. 2012 ).

At an even larger scale, a continuum of coupled population equations at each point in space lead to neuronal field equations ( Bressloff 2012 ). They predict stable “bumps” of activity, as well as traveling waves and spirals ( Amari 1977a ; Roxin et al. 2006 ). Intriguingly, when applied as a model of visual cortex and rearranged to reflect spatial layout of the retina, patterns induced in these continuum equations can resemble visual hallucinations ( Bressloff et al. 2001 ).

Analysis has provided insight into the ways that spiking networks can produce irregular spike times like those found in cortical recordings from behaving animals ( Shadlen and Newsome 1998 ), as in Figure 5 . Suppose we have a network of N E excitatory and N I inhibitory LIF neurons with connections occurring at random according to independent binary (Bernoulli) random variables, i.e., a connection exists when the binary random variable takes the value 1 and does not exist when it is 0. We denote the binary connectivity random variables by κ i j α β , where α and β take the values E or I , with κ i j α β = 1 when the output of neuron j in population β injects current into neuron i in population α . We let J αβ be the coupling strength (representing synaptic current) from a neuron in population β to a neuron in population α . Thus, the contribution to the current input of a neuron in population α generated at time t by a spike from neuron in population β at time s will be J α β κ i j α β δ ( t − s ) , where δ ( t − s ) is the Dirac delta function. The behavior of the network can be analyzed by letting N E → ∞ and N I → ∞. Based on reasonable simplifying assumptions, the mean M α and variance V α of the total current for population α have been derived ( Amit and Brunel 1997 ; Van Vreeswijk and Sompolinsky 1998 ), and these determine the regularity or irregularity in spiking activity.

We step through three possibilities, under three different conditions on the network, using a modification of the LIF equation found in Figure 3 . The set of equations, for all the neurons in the network, includes terms defined by network connectivity and also terms defined by external input fluctuations. Because the connectivity matrix may contain cycles (there may be a path from any neuron back to itself), network connectivity is called recurrent . Let us take the membrane potential of neuron i from population α to be

where t i k α is the k th spike time from neuron i of population α , τ α is the membrane dynamics time constant, and the external inputs include both a constant μ 0 and a fluctuating source σ 0 ξ( t ) where ξ( t ) is white noise (independent across neurons). This set of equations is supplemented with the spike reset rule that when V i α ( t ) = V T the voltage resets to V R < V T .

The firing rate of the average neuron in population α is λ α = ∑ j ∑ k δ ( t − t j k α ) / N α . For the network to remain stable, we take these firing rates to be bounded, i.e., λ α ~ O ( 1 ) . Similarly, to assure that the current input to each neuron remains bounded, some assumption must be made about the way coupling strengths J αβ scale as the number of inputs K increases. Let us take the scaling to be J αβ = j αβ / K γ , with j α β ~ O ( 1 ) , as K → ∞, where γ is a scaling exponent. We describe the resulting spiking behavior under scaling conditions γ =1 and γ = 1/2.

If we set γ = 1 then we have J ~ 1/ K , so that J K = j ~ O ( 1 ) . In this case we get M α ~ O ( 1 ) and V α = [ σ 0 α ] 2 + O ( 1 / K ) . If we further set σ 0 α = 0 , so that all fluctuations must be internal, then V α vanishes for large K . In such networks, after an initial transient, the neurons synchronize, and each fires with perfect rhythmicity (left part of panel A in Figure 6 ). This is very different than the irregularity seen in cortical recordings ( Figure 3 ). Therefore, some modification must be made.

Panel A displays plots of spike trains from 1000 excitatory neurons in a network having 1000 excitatory and 1000 inhibitory LIF neurons with connections determined from independent Bernoulli random variables having success probability of 0.2; on average K = 200 inputs per neuron with no synaptic dynamics. Each neuron receives a static depolarizing input; in absence of coupling each neuron fires repetitively. Left: Spike trains under weak coupling, current J ∝ K −1 . Middle: Spike trains under weak couplng, with additional uncorrelated noise applied to each cell. Right: Spike trains under strong coupling, J ∝ K − 1 2 . Panel B shows the distribution of firing rates across cells, and panel C the distribution of interspike interval (ISI) coefficient of variation across cells.

The first route to appropriate spike train irregularity keeps γ = 1 while setting [ σ 0 α ] 2 ~ O ( 1 ) so that V α no longer vanishes in the large K limit. Simulations of this network ( Figure 6A , middle) maintain realistic rates ( Figure 6B , red curve), but also show realistic irregularity ( Faisal et al. 2008 ), as quantified in Figure 6C by the coefficient of variation (CV) of the inter-spike intervals. Treating irregular spiking activity as the consequence of stochastic inputs has a long history ( Tuckwell 1988 ).

The second route does not rely on external input stochasticity, but instead increases the synaptic connection strengths by setting γ = 1/2. As a consequence we get V α ~ O ( 1 ) even if σ 0 α = 0 so that variability is internally generated through recurrent interactions ( Monteforte and Wolf 2012 ; Van Vreeswijk and Sompolinsky 1998 ), but to get M α ~ O ( 1 ) , an additional condition is needed. If the recurrent connectivity is dominated by inhibition, so that the network recurrence results in negative current, the activity dynamically settles into a state in which

where μ 0 α has been replaced by the constant μ α using μ 0 α = K μ α so that the mean external input is of order O ( K ) . The scaling γ = 1/2 now makes the total excitatory and the total inhibitory synaptic inputs individually large, i.e., O ( K ) , so that the V α is also large. However, given the balance condition in ( 6 ), excitation and inhibition mutually cancel and V α remains moderate. Simulations of the network with γ = 1/2 and σ 0 α = 0 shows an asynchronous network dynamic ( Figure 6A , right). Further, the firing rates stabilize at low mean levels ( Figure 6B , blue curve), while the inter-spike interval CV is large ( Figure 6C , blue curve).

These two mechanistic routes to high levels of neural variability differ strikingly in the degree of heterogeneity of the spiking statistics. For the weak coupling with γ = 1 the resulting distribution of firing rates and inter-spike interval CVs are narrow ( Figure 6B, C , red curves). At strong coupling with γ = 1/2, however, the spread of firing rates is large: over half of the neurons fire at rates below 1 Hz ( Figure 6B , blue curve), in line with observed cortical activity ( Roxin et al. 2011 ). The approximate dynamic balance between excitatory and inhibitory synaptic currents has been confirmed experimentally ( Okun and Lampl 2008 ) and is usually called balanced excitation and inhibition .

3.3.3. Asynchronous dynamics in recurrent networks.

The analysis above focused only on M α and V α , ignoring any correlated activity between the currents neurons in the network. The original justification for such asynchronous dynamics in Van Vreeswijk and Sompolinsky (1998) and Amit and Brunel (1997) relied on a sparse wiring assumption, i.e, K/N α → 0 as N α → ∞ for α ∈ ( E , I ). However, more recently it has been shown that the balanced mechanism required to keep firing rates moderate also ensures that network correlations vanish. Balance arises from the dominance of negative feedback which suppresses fluctuations in the population-averaged activity and hence causes small pairwise correlations ( Tetzlaff et al. 2012 ). As a consequence, fluctuations of excitatory and inhibitory synaptic currents are tightly locked so that Equation (6) is satisfied. The excitatory and inhibitory cancellation mechanism therefore extends to pairs of cells and operates even in networks with dense wiring, i.e., K / N α ~ O ( 1 ) ( Hertz 2010 ; Renart et al. 2010 ), so that input correlations are much weaker than expected by the number of shared inputs ( Shadlen and Newsome 1998 ; Shea-Brown et al. 2008 ). This suppression and cancellation of correlations holds in the same way for intrinsically-generated fluctuations that often even dominate the correlation structure ( Helias et al. 2014 ). Recent work has shown that the asynchronous state is more robustly realized in nonrandom networks than normally distributed random networks ( Litwin-Kumar and Doiron 2012 ; Teramae et al. 2012 ).

There is a large literature on how network connectivity, at the level of mechanistic models, leads to different covariance structures in network activity ( Ginzburg and Sompolinsky 1994 ). Highly local connectivity features scale up to determine global levels of covariance ( Doiron et al. 2016 ; Helias et al. 2013 ; Trousdale et al. 2012 ). Moreover, features of that connectivity that point specifically to low-dimensional structures of neural covariability can be isolated ( Doiron et al. 2016 ). An outstanding problem is to create model networks that mimic the low-dimensional covariance structure reported in experiments (see Section 3.4.1 ).

3.4. Statistical methods for large networks

New recording technologies should make it possible to track the flow of information across very large networks of neurons, but the details of how to do so have not yet been established. One tractable component of the problem ( Cohen and Kohn 2011 ) involves co-variation in spiking activity among many neurons (typically dozens to hundreds), which leads naturally to dimensionality reduction and to graphical representations (where neurons are nodes, and some definition of correlated activity determines edges). However, two fundamental complications affect most experiments. First, co-variation can occur at multiple timescales. A simplification is to consider either spike counts in coarse time bins (20 milliseconds or longer) or spike times with precision in the range of 1–5 milliseconds. We will discuss methods based on spike counts and precise spike timing separately, in the next two subsections. Second, experiments almost always involve some stimuli or behaviors that create evolving conditions within the network. Thus, methods that assume stationarity must be used with care, and analyses that allow for dynamic evolution will likely be useful. Fortunately, many experiments are conducted using multiple exposures to the same stimuli or behavioral cues, which creates a series of putatively independent replications (trials). While the responses across trials are variable, sometimes in systematic ways, the setting of multiple trials often makes tractable the analysis of non-stationary processes.

After reviewing techniques for analyzing co-variation of spike counts and precisely-timed spiking we will also briefly mention three general approaches to understanding network behavior: reinforcement learning, Bayesian inference, and deep learning. Reinforcement learning and Bayesian inference use a decision-theoretic foundation to define optimal actions of the neural system in achieving its goals, which is appealing insofar as evolution may drive organism design toward optimality.

3.4.1. Correlation and dimensionality reduction in spike counts.

Dimensionality reduction methods have been fruitfully applied to study decision-making, learning, motor control, olfaction, working memory, visual attention, audition, rule learning, speech, and other phenomena ( Cunningham and Yu 2014 ). Dimensionality reduction methods that have been used to study neural population activity include principal component analysis, factor analysis, latent dynamical systems, and non-linear methods such as Isomap and locally-linear embedding. Such methods can provide two types of insights. First, the time course of the neural response can vary substantially from one experimental trial to the next, even though the presented stimulus, or the behavior, is identical on each trial. In such settings, it is of interest to examine population activity on individual trials ( Churchland et al. 2007 ). Dimensionality reduction provides a way to summarize the population activity time course on individual experimental trials by leveraging the statistical power across neurons ( Yu et al. 2009 ). One can then study how the latent variables extracted by dimensionality reduction change across time or across experimental conditions. Second, the multivariate statistical structure in the population activity identified by dimensionality reduction may be indicative of the neural mechanisms underlying various brain functions. For example, one study suggested that a subject can imagine moving their arms, while not actually moving them, when neural activity related to motor preparation lies in a space orthogonal to that related to motor execution ( Kaufman et al. 2014 ). Furthermore, the multivariate structure of population activity can help explain why some tasks are easier to learn than others ( Sadtler et al. 2014 ) and how subjects respond differently to the same stimulus in different contexts ( Mante et al. 2013 ).

3.4.2. Correlated spiking activity at precise time scales.

In principle, very large quantities of information could be conveyed through the precise timing of spikes across groups of neurons. The idea that the nervous system might be able to recognize such patterns of precise timing is therefore an intriguing possibility ( Abeles 1982 ; Geman 2006 ; Singer and Gray 1995 ). However, it is very difficult to obtain strong experimental evidence in favor of a widespread computational role for precise timing (e.g., an accuracy within 1–5 milliseconds), beyond the influence of the high arrival rate of synaptic impulses when multiple input neurons fire nearly synchronously. Part of the issue is experimental, because precise timing may play an important role only in specialized circumstances, but part is statistical: under plausible point process models, patterns such as nearly synchronous firing will occur by chance, and it may be challenging to define a null model that captures the null concept without producing false positives. For example, when the firing rates of two neurons increase, the number of nearly synchronous spikes will increase even when the spike trains are otherwise independent; thus, a null model with constant firing rates could produce false positives for the null hypothesis of independence. This makes the detection of behaviorally-relevant spike patterns a subtle statistical problem ( Grün 2009 ; Harrison et al. 2013 ).

A strong indication that precise timing of spikes may be relevant to behavior came from an experiment involving hand movement, during which pairs of neurons in motor cortex fired synchronously (within 5 milliseconds of each other) more often than predicted by an independent Poisson process model and, furthermore, these events, called Unitary Events , clustered around times that were important to task performance ( Riehle et al. 1997 ). While this illustrated the potential role of precisely timed spikes, it also raised the issue of whether other plausible point process null models might lead to different results. Much work has been done to refine this methodology ( Albert et al. 2016 ; Gmn 2009 ; Torre et al. 2016 ). Related approaches replace the null assumption of independence with some order of correlation, using marked Poisson processes ( Staude et al. 2010 ).

There is a growing literature on dependent point processes. Some models do not include a specific mechanism for generating precise spike timing, but can still be used as null models for hypothesis tests of precise spike timing. On a coarse time scale, point process regression models as in Equation (1) can incorporate effects of one neuron’s spiking behavior on another ( Pillow et al. 2008 ; Truccolo 2010 ). On a fine time scale, one may instead consider multivariate binary processes (multiple sequences of 0s and 1s where 1s represent spikes). In the stationary case, a standard statistical tool for analyzing binary data involves loglinear models ( Agresti 1996 ), where the log of the joint probability of any particular pattern is represented as a sum of terms that involve successively higher-order interactions, i.e., terms that determine the probability of spiking within a given time bin for individual neurons, pairs of neurons, triples, etc. Two-way interaction models, also called maximum entropy models, which exclude higher than pairwise interactions, have been used in several studies and in some cases higher-order interactions have been examined ( Ohiorhenuan et al. 2010 ; Santos et al. 2010 ; Shimazaki et al. 2015 ), sometimes using information geometry ( Nakahara et al. 2006 ), though large amounts of data may be required to find small but plausibly interesting effects ( Kelly and Kass 2012 ). Extensions to non-stationary processes have also been developed ( Shimazaki et al. 2012 ; Zhou et al. 2015 ). Dichotomized Gaussian models, which instead produce binary outputs from threshold crossings of a latent multivariate Gaussian random variable, have also been used ( Amari et al. 2003 ; Shimazaki et al. 2015 ), as have Hawkes processes ( Jovanovic et al. 2015 ). A variety of correlation structures may be accommodated by analyzing cumulants ( Staude et al. 2010 ).

To test hypotheses about precise timing, several authors have suggested procedures akin to permutation tests or nonparametric bootstrap. The idea is to generate re-sampled data, also called pseudo-data or surrogate data , that preserves as many of the features of the original data as possible, but that lacks the feature of interest, such as precise spike timing. A simple case, called dithering or jittering , modifies the precise time of each spike by some random amount within a small interval, thereby preserving all coarse temporal structure and removing all fine temporal structure. Many variations on this theme have been explored ( Grün 2009 ; Harrison et al. 2013 ; Platkiewicz et al. 2017 ), and connections have been made with the well-established statistical notion of conditional inference ( Harrison et al. 2015 ).

3.4.3. Reinforcement learning.

Reinforcement learning (RL) grew from attempts to describe mathematically the way organisms learn in order to achieve repeatedly-presented goals. The motivating idea was spelled out in 1911 by Thorndike ( Thorndike 1911 , p. 244): when a behavioral response in some situation leads to reward (or discomfort) it becomes associated with that reward (or discomfort), so that the behavior becomes a learned response to the situation. While there were important precursors ( Bush and Mosteller 1955 ; Rescorla and Wagner 1972 ), the basic theory reached maturity with the 1998 publication of the book by Sutton and Barto ( Sutton and Barto 1998 ). Within neuroscience, a key discovery involved the behavior of dopamine neurons in certain tasks: they initially fire in response to a reward but, after learning, fire in response to a stimulus that predicts reward; this was consistent with predictions of RL ( Schultz et al. 1997 ). (Dopamine is a neuromodulator, meaning a substance that, when emitted from the synapses of neurons, modulates the synaptic effects of other neurons; a dopamine neuron is a neuron that emits dopamine; dopamine is known to play an essential role in goal-directed behavior.)

In brief, the mathematical framework is that of a Markov decision process, which is an action-dependent Markov chain (i.e., a stochastic process on a set of states where the probability of transitioning from one state to the next is action-dependent) together with rewards that depend on both state transition and action. When an agent (an abstract entity representing an organism, or some component of its nervous system) reaches stationarity after learning, the current value V t of an action may be represented in terms of its future-discounted expected reward:

where R t is the reward at time t . Thus, to drive the agent toward this stationarity condition, the current estimate of value V ^ t should be updated in such a way as to decrease the estimated magnitude of E ( R t + γV t +1 ) − V t , which is known as the reward prediction error (RPE),

This is also called the temporal difference learning error. RL algorithms accomplish learning by sequentially reducing the magnitude of the RPE. The essential interpretation of Schultz et al. (1997) , which remains widely influential, was that dopamine neurons signal RPE.

The RL-based description of the activity of dopamine neurons has been considered one of the great success stories in computational neuroscience, operating at the levels of computation and algorithm in Marr’s framework (see Section 1.1 ). A wide range of further studies have elaborated the basic framework and taken on topics such as the behavior of other neuromodulators; neuroeconomics; the distinction between model-based learning, where transition probabilities are learned explicitly, and model-free learning; social behavior and decision-making; and the role of time and internal models in learning ( Dayan and Nakahara 2017 ; Schultz 2015 ).

3.4.4. Bayesian inference.

Although statistical methods based on Bayes’ Theorem now play a major role in statistics, they were, until relatively recently, controversial ( McGrayne 2011 ). In neuroscience, Bayes’ Theorem has been used in many theoretical constructions in part because the brain must combine prior knowledge with current data somehow, and also because evolution may have led to neural network behavior that is, like Bayesian inference (under well specified conditions), optimal, or nearly so. Bayesian inference has played a prominent role in theories of human problem-solving ( Anderson 2009 ), visual perception ( Geisler 2011 ), sensory and motor integration ( Körding 2007 ; Wolpert et al. 2011 ), and general cortical processing ( Griffiths et al. 2012 ).

3.4.5. Deep learning.

Deep learning ( LeCun et al. 2015 ) is an outgrowth of PDP modeling (see Section 1.4 ). Two major architectures came out of the 1980’s and 1990’s, convolutional neural networks (CNNs) and long short term memory (LSTM). LSTM ( Hochreiter and Schmidhuber 1997 ) enables neural networks to take as input sequential data of arbitrary length and learn long-term dependencies by incorporating a memory module where information can be added or forgotten according to functions of the current input and state of the system. CNNs, which achieve state of the art results in many image classification tasks, take inspiration from the visual system by incorporating receptive fields and enforcing shift-invariance (physiological visual object recognition being invariant to shifts in location). In deep learning architectures, receptive fields ( LeCun et al. 2015 ) identify a very specific input pattern, or stimulus, in a small spatial region, using convolution to combine inputs. Receptive fields induce sparsity and lead to significant computational savings, which prompted early success with CNNs ( LeCun 1989 ). Shift invariance is achieved through a spatial smoothing operator known as pooling (a weighted average, or often the maximum value, over a local neighborhood of nodes). Because it introduces redundancies, pooling is often combined with downsampling. Many layers, each using convolution and pooling, are stacked to create a deep network, in rough analogy to multiple anatomical layers in the visual system of primates. Although artificial neural networks had largely fallen out of widespread use by the end of the 1990s, faster computers combined with availability of very large repositories of training data, and the innovation of greedy layer-wise training ( Bengio et al. 2007 ) brought large gains in performance and renewed attention, especially when ALEXNET ( Krizhevsky et al. 2012 ) was applied to the ImageNet database ( Deng et al. 2009 ). Rapid innovation has enabled the application of deep learning to a wide variety of problems of increasing size and complexity.

The success of deep learning in reaching near human-level performance on certain highly constrained prediction and classification tasks, particularly in the area of computer vision, has inspired interest in exploring the connections between deep neural networks and the brain. Studies have shown similarities between the internal representations of convolutional neural networks and representations in the primate visual system ( Kriegeskorte 2015 ; Yamins and DiCarlo 2016 ). Furthermore, the biological phenomenon of hippocampal replay during memory consolidation prompted innovation in artificial intelligence, in part through the incorporation of reinforcement learning (see Section 3.4.3 ) into deep learning architectures ( Mnih et al. 2015 ). On the other hand, some studies have shown cases in which biological vision and deep networks diverge in performance ( Nguyen et al. 2015 ; Ullman et al. 2016 ). Even though they are not biologically realistic, deep learning architectures may suggest new scientific hypotheses ( Pelillo et al. 2015 ).

3.5. Connecting mathematical and statistical approaches in large networks

3.5.1. bridging from dynamical to statistical models of neural spiking..

In Section 2.4 we made an explicit connection between an integrated form of LIF models and GLMs. An alternative is to derive from a mechanistic model, first, an instantaneous intensity by determining mean activity and, second, the variation around the mean. In binary models, the first step leads to a Gaussian integral ( Van Vreeswijk and Sompolinsky 1998 ) and the second to its derivative ( Helias et al. 2014 ; Renart et al. 2010 ). For spiking models, these steps are conceptually identical, but mathematically more involved. The firing rate follows from the mean first passage time for the membrane voltage to exceed the threshold ( Amit and Brunel 1997 ; Tuckwell 1988 ). Computing deviations of responses from the mean requires either perturbation theory applied to the Fokker-Planck equation ( Richardson 2008 ) or separation of timescales for slow currents ( Moreno-Bote and Parga 2010 ). These approaches may be united in an elegant framework to produce an equivalent GLM model ( Ostojic and Brunel 2011b ). Approximating the fluctuations in spiking and binary networks up to linear order, correlations are equivalent to those of linear stochastic differential equations driven by Gaussian noise ( Grytskyy et al. 2013 ). Extensions treat the mechanistic origins of stimulus adaptation in statistical models of neural responses ( Famulare and Fairhall 2010 ).

3.5.2. Multivariate relationships via latent variable models.

An important question is whether mechanistic models can reproduce features of recorded neural activity that go beyond population means and variances. This is especially challenging when, as is usually the case, recorded neurons represent only a very small sample from a vast network. Simple summary statistics, such as the variability of the activity of individual neurons or the correlation between pairs of neurons, can be a helpful first step ( Litwin-Kumar and Doiron 2012 ). A natural next step is to examine summaries based on dimensionality reduction, as in Section 3.4.1 , where the same multivariate statistical methods are applied to both the activity produced by the model and to the data. For example, spontaneous activity recorded in the primary visual cortex has been found to be more like activity produced by a spiking network model having clustered connections than that produced by a network with uniform random connectivity ( Williamson et al. 2016 ).

Mechanistic models can also help in characterizing the statistical tools used to study neural population activity by providing ground truth with which to judge performance of statistical methods ( Williamson et al. 2016 ). This includes determination of the amount of data needed in order to identify particular effects. From results outlined in Section 2.4 , when LIF models are used these ground truth data sets should be very similar to others generated using GLM neurons ( Zaytsev et al. 2015 ), and it is a topic for future research to take advantage of this relationship.

In addition to providing readers with an entry into the mathematical and statistical literature in computational neuroscience, we have also tried to highlight places where the two approaches go hand in hand, especially in Sections Section 2.4 , Section 2.5 , Section 2.6 , and 3.5 . Another concrete example of this interplay comes from anesthesia, where highly structured oscillations, readily visible in the EEG, change in a systematic way, depending on the dose of a given anesthetic and the molecular targets and neural circuits where the anesthetic acts ( Brown et al. 2011 ). One of the most widely used anesthetics, propofol, acts at multiple sites in the brain to enhance the activity of inhibitory neurons resulting initially in beta oscillations (13 – 25 Hz) followed within seconds by slow-delta oscillations (0.1 – 4 Hz), and then a combination of slow-delta oscillations with alpha oscillations (8 – 12 Hz) when the patient is unconscious. Multitaper spectral time series analysis showed that the alpha oscillations are highly coherent across the front of the scalp, and this was explained by a circuit model using Hodgkin-Huxley neurons ( Ching et al. 2010 ; Cimenser et al. 2011 ). Because all anesthetics create similar oscillations, the combination of careful statistical analysis and mechanistic modeling may be used to investigate the way other anesthetics create altered brain states.

As this example illustrates, computational neuroscience, like experimental neuroscience, aims to improve knowledge about the functioning of the nervous system. On the one hand, the statistical approach helps by introducing methods to summarize nervous system data. On the other hand, mathematical theory helps by introducing frameworks for describing nervous system behavior. Because both sides of computational neuroscience aim to build understanding from data, they complement each other: mechanistic models refine scientific questions, and can thereby guide development of statistical methods; statistical methods can find important features of data, and can suggest directions for modeling efforts. As the field tackles additional complexity in modeling and data analysis, it will become increasingly important for researchers in computational neuroscience to be cognizant of the essential ideas, tools, and approaches of both domains.

ACKNOWLEDGMENTS

This article was initiated during a workshop in October 2015 with support from the National Science Foundation under Grant DMS-1127914 to the Statistical and Applied Mathematical Sciences Institute. Additional conceptualization resulted from a second workshop in June, 2016, with support from the U.S.-Japan Brain Research Cooperative Program via NIMH grant MH064537, NSF grant DMS 1612914, and the Japan Society for the Promotion Science. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of these funding agencies. Additional work of individual authors was supported by individual research grants.

DISCLOSURE STATEMENT

The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.

LITERATURE CITED

• Abbott LF. 1999. Lapicque’s introduction of the integrate-and-fire model neuron (1907) . Brain research bulletin 50 :303—304 [ PubMed ] [ Google Scholar ]
• Abeles M 1982. Role of the cortical neuron: integrator or coincidence detector? Israel journal of medical sciences 18 :83—92 [ PubMed ] [ Google Scholar ]
• Adrian ED, Zotterman Y. 1926. The impulses produced by sensory nerve endings . The Journal of Physiology 61 :465–483 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Agresti A 1996. Categorical data analysis , volume 990 New York: John Wiley & Sons [ Google Scholar ]
• Albert M, Bouret Y, Fromont M, Reynaud-Bouret P. 2016. Surrogate data methods based on a shuffling of the trials for synchrony detection: the centering issue . Neural Comput . 28 :2352–2392 [ PubMed ] [ Google Scholar ]
• Aljadeff J, Lansdell BJ, Fairhall AL, Kleinfeld D. 2016. Analysis of neuronal spike trains, deconstructed . Neuron 91 :221–259 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Amarasingham A, Geman S, Harrison MT. 2015. Ambiguity and nonidentifiability in the statistical analysis of neural codes . Proc. Natl. Acad. Sci. U. S. A 112 :6455–6460 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Amari SI. 1977a. Dynamics of pattern formation in lateral-inhibition type neural fields . Biological Cybernetics 27 :77–87 [ PubMed ] [ Google Scholar ]
• Amari SI. 1977b. Neural theory of association and concept-formation . Biological Cybernetics 26 :175–185 [ PubMed ] [ Google Scholar ]
• Amari SI, Nakahara H, Wu S, Sakai Y. 2003. Synchronous firing and higher-order interactions in neuron pool . Neural Comput . 15 :127–142 [ PubMed ] [ Google Scholar ]
• Amit DJ, Brunel N. 1997. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex . Cerebral Cortex 7 :237–252 [ PubMed ] [ Google Scholar ]
• Amit DJ, Gutfreund H, Sompolinsky H. 1987. Information storage in neural networks with low levels of activity . Phys. Rev. A Gen. Phys 35 :2293–2303 [ PubMed ] [ Google Scholar ]
• Anderson JR. 2009. How can the human mind occur in the physical universe? Oxford University Press [ Google Scholar ]
• Bailey DL, Townsend DW, Valk PE, Maisey MN. 2005. Positron emission tomography . Springer [ Google Scholar ]
• Bassett DS, Bullmore ET. 2016. Small-World brain networks revisited . Neuroscientist [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Beggs JM, Plenz D. 2003. Neuronal avalanches in neocortical circuits . J. of Nuerosci 23 :11167–11177 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Bengio Y, Lamblin P, Popovici D, Larochelle H. 2007. Greedy Layer-Wise training of deep networks In Schölkopf PB, Platt JC, Hoffman T, editors, Advances in Neural Information Processing Systems 19 , pages 153–160. MIT Press [ Google Scholar ]
• Boole G 1854. An Investigation of the Laws of Thought on which are Founded the Mathematical Theories of Logic and Probabilities . Walton and Maberly [ Google Scholar ]
• Bos H, Diesmann M, Helias M. 2016. Identifying anatomical origins of coexisting oscillations in the cortical microcircuit . PLOS Computational Biology 12 :1–34 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Bressloff PC. 2012. Spatiotemporal dynamics of continuum neural fields . Journal of Physics A: Mathematical and Theoretical 45 [ Google Scholar ]
• Bressloff PC, Cowan JD, Golubitsky M, Thomas PJ, Wiener MC. 2001. Geometric visual hallucinations, euclidean symmetry and the functional architecture of striate cortex . Philosophical Transactions of the Royal Society B 356 :299—330 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Brown EN, Purdon PL, Van Dort CJ. 2011. General anesthesia and altered states of arousal: a systems neuroscience analysis . Annual review of neuroscience 34 :601—628 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Brunel N 2000. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons . Journal of Computational Neuroscience 8 :183—208 [ PubMed ] [ Google Scholar ]
• Brunel N, Van Rossum MC. 2007. Lapicques 1907 paper: from frogs to integrate-and-fire . Biological cybernetics 97 :337—339 [ PubMed ] [ Google Scholar ]
• Bullmore E, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems . Nat. Rev. Neurosci 10 :186—198 [ PubMed ] [ Google Scholar ]
• Bush RR, Mosteller F. 1955. Stochastic models for learning . John Wiley & Sons, Inc. [ Google Scholar ]
• Buzsáki G, Mizuseki K. 2014. The log-dynamic brain: how skewed distributions affect network operations . Nature Reviews Neuroscience 15 :264—278 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Cain N, Shea-Brown E. 2012. Computational models of decision making: integration, stability, and noise . Current opinion in neurobiology 22 :1047—1053 [ PubMed ] [ Google Scholar ]
• Carlson DE, Vogelstein JT, Wu Q, Lian W, Zhou M, Stoetzner CR, Kipke D, Weber D, Dunson DB, Carin L. 2014. Multichannel electrophysiological spike sorting via joint dictionary learning and mixture modeling . IEEE Transactions on Biomedical Engineering 61 :41—54 [ PubMed ] [ Google Scholar ]
• Ching S, Cimenser A, Purdon PL, Brown EN, Kopell NJ. 2010. Thalamocortical model for a propofol-induced α-rhythm associated with loss of consciousness . Proceedings of the National Academy of Sciences 107 :22665–22670 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Churchland MM, Yu BM, Sahani M, Shenoy KV. 2007. Techniques for extracting single-trial activity patterns from large-scale neural recordings . Curr. Opin. Neurobiol 17 :609–618 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Cimenser A, Purdon PL, Pierce ET, Walsh JL, Salazar-Gomez AF, Harrell PG, Tavares-Stoeckel C, Habeeb K, Brown EN. 2011. Tracking brain states under general anesthesia by using global coherence analysis . Proceedings of the National Academy of Sciences 108 :8832–8837 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Cohen MR, Kohn A. 2011. Measuring and interpreting neuronal correlations . Nat. Neurosci 14 :811–819 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Colquhoun D, Sakmann B. 1998. From muscle endplate to brain synapses: a short history of synapses and agonist-activated ion channels . Neuron 20 :381–387 [ PubMed ] [ Google Scholar ]
• Craik K 1943. The nature of explanation . Cambridge University, Cambridge UK [ Google Scholar ]
• Cunningham JP, Yu BM. 2014. Dimensionality reduction for large-scale neural recordings . Nat. Neurosci 17 :1500–1509 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Dayan P, Abbott LF. 2001. Theoretical neuroscience , volume 806 Cambridge, MA: MIT Press [ Google Scholar ]
• Dayan P, Nakahara H. 2017. Reconstruction of recurrent synaptic connectivity of thousands of neurons from simulated spiking activity . accepted [ PMC free article ] [ PubMed ]
• De La Rocha J, Doiron B, Shea-Brown E, Josić K, Reyes A. 2007. Correlation between neural spike trains increases with firing rate . Nature 448 :802–806 [ PubMed ] [ Google Scholar ]
• Deger M, Schwalger T, Naud R, Gerstner W. 2014. Fluctuations and information filtering in coupled populations of spiking neurons with adaptation . Physical Review E 90 :062704 [ PubMed ] [ Google Scholar ]
• Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L. 2009. ImageNet: A large-scale hierarchical image database . In 2009 IEEE Conference on Computer Vision and Pattern Recognition, pages 248–255 [ Google Scholar ]
• Destexhe A, Mainen ZF, Sejnowski TJ. 1994. Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism . J. Comput. Neurosci 1 :195–230 [ PubMed ] [ Google Scholar ]
• Doiron B, Litwin-Kumar A, Rosenbaum R, Ocker GK, Josic K. 2016. The mechanics of state-dependent neural correlations . Nature neuroscience 19 :383–393 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Doiron B, Rinzel J, Reyes A. 2006. Stochastic synchronization in finite size spiking networks . Physical Review E 74 :030903 [ PubMed ] [ Google Scholar ]
• Ermentrout B, Terman DH. 2010. Foundations of mathematical neuroscience . Citeseer [ Google Scholar ]
• Faisal AA, Selen LP, Wolpert DM. 2008. Noise in the nervous system . Nature Reviews Neuroscience 9 :292–303 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Famulare M, Fairhall A. 2010. Feature selection in simple neurons: how coding depends on spiking dynamics . Neural Comput . 22 :581–598 [ PubMed ] [ Google Scholar ]
• Fienberg SE. 2012. A brief history of statistical models for network analysis and open challenges . J. Comput. Graph. Stat 21 :825–839 [ Google Scholar ]
• Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, Van Der Kouwe A, Killiany R, Kennedy D, Klaveness S, et al. 2002. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain . Neuron 33 :341–355 [ PubMed ] [ Google Scholar ]
• Fitzhugh R 1960. Thresholds and plateaus in the Hodgkin-Huxley nerve equations . J. Gen. Physiol 43 :867–896 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Galvani L, Aldini G. 1792. De Viribus Electricitatis In Motu Musculari Comentarius Cum Joannis Aldini Dissertatione Et Notis; Accesserunt Epistolae ad animalis electricitatis theoriam perti- nentes . Apud Societatem Typographicam [ Google Scholar ]
• Geisler WS. 2011. Contributions of ideal observer theory to vision research . Vision research 51 :771–781 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Geman S 2006. Invariance and selectivity in the ventral visual pathway . Journal of Physiology-Paris 100 :212–224 [ PubMed ] [ Google Scholar ]
• Geman S, Geman D. 1984. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images . IEEE Trans. Pattern Anal. Mach. Intell 6 :721–741 [ PubMed ] [ Google Scholar ]
• Gerhard F, Kispersky T, Gutierrez GJ, Marder E, Kramer M, Eden U. 2013. Successful reconstruction of a physiological circuit with known connectivity from spiking activity alone . PLoS Comput Biol 9 :e1003138. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Gerstein GL, Mandelbrot B. 1964. Random walk models for the spike activity of a single neuron . Biophys. J 4 :41–68 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Gerstner W, Kistler WM, Naud R, Paninski L. 2014. Neuronal dynamics: From single neurons to networks and models of cognition . Cambridge University Press [ Google Scholar ]
• Gerstner W, Naud R. 2009. How good are neuron models? Science 326 :379–380 [ PubMed ] [ Google Scholar ]
• Ginzburg I, Sompolinsky H. 1994. Theory of correlations in stochastic neural networks . Phys Rev E 50 :3171–3191 [ PubMed ] [ Google Scholar ]
• Goedeke S, Diesmann M. 2008. The mechanism of synchronization in feed-forward neuronal networks . New Journal of Physics 10 :015007 [ Google Scholar ]
• Gold JI, Shadlen MN. 2007. The neural basis of decision making . Annu. Rev. Neurosci 30 :535–574 [ PubMed ] [ Google Scholar ]
• Grienberger C, Konnerth A. 2012. Imaging calcium in neurons . Neuron 73 :862–885 [ PubMed ] [ Google Scholar ]
• Griffiths TL, Chater N, Norris D, Pouget A. 2012. How the bayesians got their beliefs (and what those beliefs actually are): comment on bowers and davis (2012) . [ PubMed ]
• Grillner S, Jessell TM. 2009. Measured motion: searching for simplicity in spinal locomotor networks . Current opinion in neurobiology 19 :572–586 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Grün S 2009. Data-driven significance estimation for precise spike correlation . Journal of Neuro-physiology 101 :1126–1140 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Grytskyy D, Tetzlaff T, Diesmann M, Helias M. 2013. A unified view on weakly correlated recurrent networks . Frontiers in Computational Neuroscience 7 :131. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Gugerty L 2006. Newell and simon’s logic theorist: Historical background and impact on cognitive modeling . Proc. Hum. Fact. Ergon. Soc. Annu. Meet 50 :880–884 [ Google Scholar ]
• Hämäläinen M, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. 1993. Magnetoencephalographytheory, instrumentation, and applications to noninvasive studies of the working human brain . Reviews of modern Physics 65 :413 [ Google Scholar ]
• Harrison MT, Amarasingham A, Kass RE. 2013. Statistical identification of synchronous spiking . Spike Timing: Mechanisms and Function page 77 [ Google Scholar ]
• Harrison MT, Amarasingham A, Truccolo W. 2015. Spatiotemporal conditional inference and hypothesis tests for neural ensemble spiking precision . Neural Comput . 27 :104—150 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Hartline HK, Graham CH. 1932. Nerve impulses from single receptors in the eye . Journal of Cellular Physiology 1 :277—295 [ Google Scholar ]
• Hebb DO. 1949. The organization of behavior: A neuropsychological approach . John Wiley & Sons [ Google Scholar ]
• Helias M, Tetzlaff T, Diesmann M. 2013. Echoes in correlated neural systems . New Journal of Physics 15 :023002 [ Google Scholar ]
• Helias M, Tetzlaff T, Diesmann M. 2014. The correlation structure of local cortical networks intrinsically results from recurrent dynamics . PLOS Computational Biology 10 :e1003428. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Hertz J 2010. Cross-correlations in high-conductance states of a model cortical network . Neural Comput . 22 :427–447 [ PubMed ] [ Google Scholar ]
• Hille B 2001. Ionic Channels of Excitable Membranes . Sinauer [ Google Scholar ]
• Hinton GE, Sejnowski TJ. 1983. Optimal perceptual inference . In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 448–453 [ Google Scholar ]
• Hochreiter S, Schmidhuber J. 1997. Long short-term memory . Neural Comput . 9 :1735–1780 [ PubMed ] [ Google Scholar ]
• Hodgkin AL, Huxley AF. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve . J. Physiol 117 :500–544 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Hong S, A y Arcas B, Fairhall AL. 2007. Single neuron computation: from dynamical system to feature detector . Neural Comput . 19 :3133–3172 [ PubMed ] [ Google Scholar ]
• Hopfield JJ. 1982. Neural networks and physical systems with emergent collective computational abilities . Proc. Natl. Acad. Sci. U. S. A 79 :2554–2558 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Hopfield JJ. 1984. Neurons with graded response have collective computational properties like those of two-state neurons . Proceedings of the National Academy of Sciences 81 :3088–3092 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Hubel DH, Wiesel TN. 1959. Receptive fields of single neurones in the cat’s striate cortex . The Journal of physiology 148 :574–591 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Izhikevich EM. 2007. Dynamical systems in neuroscience . MIT press [ Google Scholar ]
• Jovanović S, Hertz J, Rotter S. 2015. Cumulants of hawkes point processes . Phys. Rev. E Stat. Nonlin. Soft Matter Phys 91 :042802. [ PubMed ] [ Google Scholar ]
• Kandel ER, Schwartz JH, Jessell TM, Siegelbaum SA, Hudspeth AJ. 2013. Principles of neural science . McGraw-hill; New York, 5 edition [ Google Scholar ]
• Kass RE, Eden UT, Brown EN. 2014. Analysis of Neural Data: . Springer Series in Statistics . Springer; New York [ Google Scholar ]
• Kass RE, Ventura V. 2001. A spike-train probability model . Neural Comput . 13 :1713–1720 [ PubMed ] [ Google Scholar ]
• Kaufman MT, Churchland MM, Ryu SI, Shenoy KV. 2014. Cortical activity in the null space: permitting preparation without movement . Nat. Neurosci 17 :440–448 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Kelly RC, Kass RE. 2012. A framework for evaluating pairwise and multiway synchrony among stimulus-driven neurons . Neural Comput . 24 :2007–2032 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Kobayashi R, Tsubo Y, Shinomoto S. 2009. Made-to-order spiking neuron model equipped with a multi-timescale adaptive threshold . Frontiers in computational neuroscience 3 :9. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Kopell N, Ermentrout G. 2002. Mechanisms of phase-locking and frequency control in pairs of coupled neural oscillators . Handbook of dynamical systems 2 :3–54 [ Google Scholar ]
• Körding K 2007. Decision theory: What” should” the nervous system do? Science 318 :606–610 [ PubMed ] [ Google Scholar ]
• Kriegeskorte N 2015. Deep neural networks: A new framework for modeling biological vision and brain information processing . Annual Review of Vision Science 1 :417–446 [ PubMed ] [ Google Scholar ]
• Krizhevsky A, Sutskever I, Hinton GE. 2012. ImageNet classification with deep convolutional neural networks In Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors, Advances in Neural Information Processing Systems 25 , pages 1097–1105. Curran Associates, Inc. [ Google Scholar ]
• Lansky P, Ditlevsen S. 2008. A review of the methods for signal estimation in stochastic diffusion leaky integrate-and-fire neuronal models . Biological cybernetics 99 :253–262 [ PubMed ] [ Google Scholar ]
• Lapique L 1907. Recherches quantitatives sur l’excitation electrique des nerfs traitee comme une polarization . J. Physiol. Pathol. Gen 9 :620–635 [ Google Scholar ]
• Lazar N 2008. The statistical analysis of functional MRI data . Springer Science & Business Media [ Google Scholar ]
• LeCun Y 1989. Generalization and network design strategies In Pfeifer R, Schreter Z, Fogelman Soulié F, Steels L, editors, Connectionism in perspective , pages 143—155. Zurich, Switzerland: Elsevier [ Google Scholar ]
• LeCun Y, Bengio Y, Hinton G. 2015. Deep learning . Nature 521 :436–444 [ PubMed ] [ Google Scholar ]
• Litwin-Kumar A, Doiron B. 2012. Slow dynamics and high variability in balanced cortical networks with clustered connections . Nat. Neurosci 15 :1498–1505 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Mainen ZF, Sejnowski TJ. 1995. Reliability of spike timing in neocortical neurons . Science 268 :1503–1506 [ PubMed ] [ Google Scholar ]
• Mante V, Sussillo D, Shenoy KV, Newsome WT. 2013. Context-dependent computation by recurrent dynamics in prefrontal cortex . Nature 503 :78–84 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Marder E, Bucher D. 2001. Central pattern generators and the control of rhythmic movements . Current biology 11 :R986–R996 [ PubMed ] [ Google Scholar ]
• Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA, Ailamaki A, Alonso-Nanclares L, Antille N, Arsever S, Kahou GAA, Berger TK, Bilgili A, Buncic N, Chalimourda A, Chindemi G, Courcol JD, Delalondre F, Delattre V, Druckmann S, Dumusc R, Dynes J, Eilemann S, Gal E, Gevaert ME, Ghobril JP, Gidon A, Graham JW, Gupta A, Haenel V, Hay E, Heinis T, Hernando JB, Hines M, Kanari L, Keller D, Kenyon J, Khazen G, Kim Y, King JG, Kisvarday Z, Kumbhar P, Lasserre S, Lé Be JV, Magalhães BRC, Merchán-Pérez A, Meystre J, Morrice BR, Muller J, Muñoz-Céspedes A, Muralidhar S, Muthurasa K, Nachbaur D, Newton TH, Nolte M, Ovcharenko A, Palacios J, Pastor L, Perin R, Ranjan R, Riachi I, Rodríguez JR, Riquelme JL, Rössert C, Sfyrakis K, Shi Y, Shillcock JC, Silberberg G, Silva R, Tauheed F, Telefont M, Toledo-Rodriguez M, Tränkler T, Van Geit W, Díaz JV, Walker R, Wang Y, Zaninetta SM, DeFelipe J, Hill SL, Segev I, Schürmann F. 2015. Reconstruction and simulation of neocortical microcircuitry . Cell 163 :456–492 [ PubMed ] [ Google Scholar ]
• Marr D. Vision: A computational approach. 1982.
• McClelland JL, Rumelhart DE. 1981. An interactive activation model of context effects in letter perception: I. an account of basic findings . Psychological review 88 :375 [ PubMed ] [ Google Scholar ]
• McCulloch WS, Pitts W. 1943. A logical calculus of the ideas immanent in nervous activity . Bull. Math. Biophys 5 :115–133 [ PubMed ] [ Google Scholar ]
• McGrayne SB. 2011. The theory that would not die: how Bayes’ rule cracked the enigma code, hunted down Russian submarines, & emerged triumphant from two centuries of controversy . Yale University Press [ Google Scholar ]
• Medler DA. 1998. A brief history of connectionism . Neural Computing Surveys 1 :18–72 [ Google Scholar ]
• Meliza CD, Kostuk M, Huang H, Nogaret A, Margoliash D, Abarbanel HD. 2014. Estimating parameters and predicting membrane voltages with conductance-based neuron models . Biological Cybernetics 108 :495–516 [ PubMed ] [ Google Scholar ]
• Meng L, Kramer MA, Middleton SJ, Whittington MA, Eden UT. 2014. A unified approach to linking experimental, statistical and computational analysis of spike train data . PloS one 9 :e85269. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Meyer C, van Vreeswijk C. 2002. Temporal correlations in stochastic networks of spiking neurons . Neural Comput . 14 :369–404 [ PubMed ] [ Google Scholar ]
• Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, Graves A, Riedmiller M, Fidjeland AK, Ostrovski G, et al. 2015. Human-level control through deep reinforcement learning . Nature 518 :529–533 [ PubMed ] [ Google Scholar ]
• Monteforte M, Wolf F. 2012. Dynamic flux tubes form reservoirs of stability in neuronal circuits . Phys. Rev. X page 041007 [ Google Scholar ]
• Moreno-Bote R, Parga N. 2010. Response of integrate-and-fire neurons to noisy inputs filtered by synapses with arbitrary timescales: Firing rate and correlations . Neural Comput . 22 :1528–1572 [ PubMed ] [ Google Scholar ]
• Nagumo J, Arimoto S, Yoshizawa S. 1962. An active pulse transmission line simulating nerve axon . Proceedings of the IRE 50 :2061–2070 [ Google Scholar ]
• Nakahara H, Amari Si, Richmond BJ. 2006. A comparison of descriptive models of a single spike train by information-geometric measure . Neural Comput . 18 :545–568 [ PubMed ] [ Google Scholar ]
• Newell A, Simon H. 1956. The logic theory machine-a complex information processing system . IEEE Trans. Inf. Theory 2 :61–79 [ Google Scholar ]
• Nguyen A, Yosinski J, Clune J. 2015. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images . In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , pages 427–436 [ Google Scholar ]
• Nunez PL, Srinivasan R. 2006. Electric Fields of the Brain: The Neurophysics of EEG . Oxford University Press, New York, NY [ Google Scholar ]
• Ohiorhenuan IE, Mechler F, Purpura KP, Schmid AM, Hu Q, Victor JD. 2010. Sparse coding and high-order correlations in fine-scale cortical networks . Nature 466 :617–621 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Okun M, Lampl I. 2008. Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities . Nature Neuroscience 11 :535–537 [ PubMed ] [ Google Scholar ]
• Ostojic S, Brunel N. 2011a. From spiking neuron models to linear-nonlinear models . PLOS Computational Biology 7 :e1001056. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Ostojic S, Brunel N. 2011b. From spiking neuron models to linear-nonlinear models . PLoS Comput Biol 7 :e1001056. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Ostojic S, Brunel N, Hakim V. 2009. How connectivity, background activity, and synaptic properties shape the cross-correlation between spike trains . J. of Nuerosci 29 :10234–10253 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Paninski L, Brown EN, Iyengar S, Kass RE. 2009. Statistical models of spike trains . Stochastic methods in neuroscience pages 278–303 [ Google Scholar ]
• Papo D, Zanin M, Martinez JH, Buldú JM. 2016. Beware of the Small-World neuroscientist! Front. Hum. Neurosci 10 :96. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Pelillo M, Scantamburlo T, Schiaffonati V. 2015. Pattern recognition between science and engineering: A red herring? Pattern Recognit. Lett 64 :3–10 [ Google Scholar ]
• Perkel DH, Bullock TH. 1968. Neural coding . Neurosci. Res. Program Bull [ Google Scholar ]
• Piccinini G 2004. The first computational theory of mind and brain: a close look at mcculloch and pitts’s logical calculus of ideas immanent in nervous activity . Synthese 141 :175–215 [ Google Scholar ]
• Piccolino M 1998. Animal electricity and the birth of electrophysiology: the legacy of luigi galvani . Brain Res. Bull 46 :381–407 [ PubMed ] [ Google Scholar ]
• Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, Simoncelli EP. 2008. Spatio-temporal correlations and visual signalling in a complete neuronal population . Nature 454 :995–999 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Platkiewicz J, Stark E, Amarasingham A. 2017. Spike-centered jitter can mistake temporal structure . Neural Comput . 29 :783–803 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W, et al. 2016. Simultaneous denoising, deconvolution, and demixing of calcium imaging data . Neuron 89 :285–299 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Prinz AA, Bucher D, Marder E. 2004. Similar network activity from disparate circuit parameters . Nature neuroscience 7 :1345–1352 [ PubMed ] [ Google Scholar ]
• Qin F, Auerbach A, Sachs F. 1997. Maximum likelihood estimation of aggregated markov processes . Proceedings of the Royal Society of London B: Biological Sciences 264 :375–383 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Rall W 1962. Theory of physiological properties of dendrites . Ann. N. Y. Acad. Sci 96 :1071–1092 [ PubMed ] [ Google Scholar ]
• Renart A, De La Rocha J, Bartho P, Hollender L, Parga N, Reyes A, Harris KD. 2010. The asynchronous state in cortical circuits . Science 327 :587–590 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Rescorla RA, Wagner AR. 1972. A theory of pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement In Black AH, Prokasy WF, editors, Classical conditioning II: Current research and theory , volume 2 , pages 64–99. New-York [ Google Scholar ]
• Rey HG, Pedreira C, Quiroga RQ. 2015. Past, present and future of spike sorting techniques . Brain research bulletin 119 :106–117 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Richardson MJE. 2008. Spike-train spectra and network response functions for non-linear integrate-and-fire neurons . Biological Cybernetics 99 :381–392 [ PubMed ] [ Google Scholar ]
• Riehle A, Grön S, Diesmann M, Aertsen A. 1997. Spike synchronization and rate modulation differentially involved in motor cortical function . Science 278 :1950–1953 [ PubMed ] [ Google Scholar ]
• Rinzel J 1985. Excitation dynamics: insights from simplified membrane models In Fed. Proc , volume 44 , pages 2944–2946 [ PubMed ] [ Google Scholar ]
• Rosenblatt F 1958. The perceptron: a probabilistic model for information storage and organization in the brain . Psychol. Rev 65 :386–408 [ PubMed ] [ Google Scholar ]
• Rosenblueth A, Wiener N, Bigelow J. 1943. Behavior, purpose and teleology . Philos. Sci 10 :18–24 [ Google Scholar ]
• Rotstein HG. 2015. Subthreshold amplitude and phase resonance in models of quadratic type: Nonlinear effects generated by the interplay of resonant and amplifying currents . Journal of computational neuroscience 38 :325–354 [ PubMed ] [ Google Scholar ]
• Rotstein HG, Oppermann T, White JA, Kopell N. 2006. A reduced model for medial entorhinal cortex stellate cells: subthreshold oscillations, spiking and synchronization . Journal of Computational Neuroscience 21 :271–292 [ PubMed ] [ Google Scholar ]
• Roxin A, Brunel N, Hansel D. 2006. Rate Models with Delays and the Dynamics of Large Networks of Spiking Neurons . Progress of Theoretical Physics Supplement 161 :68–85 [ Google Scholar ]
• Roxin A, Brunel N, Hansel D, Mongillo G, van Vreeswijk C. 2011. On the distribution of firing rates in networks of cortical neurons . J. of Nuerosci 31 :16217–16226 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Rumelhart DE, McClelland JL, PDP Research Group. 1986. Parallel distributed processing: Explorations in the microstructures of cognition. Volume 1: Foundations The MIT Press, Cambridge, MA [ Google Scholar ]
• Sadtler PT, Quick KM, Golub MD, Chase SM, Ryu SI, Tyler-Kabara EC, Yu BM, Batista AP. 2014. Neural constraints on learning . Nature 512 :423–426 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Sakmann B, Neher E. 1984. Patch clamp techniques for studying ionic channels in excitable membranes . Annual review of physiology 46 :455–472 [ PubMed ] [ Google Scholar ]
• Santos GS, Gireesh ED, Plenz D, Nakahara H. 2010. Hierarchical interaction structure of neural activities in cortical slice cultures . J. of Nuerosci 30 :8720–8733 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Schultz W 2015. Neuronal reward and decision signals: from theories to data . Physiological Reviews 95 :853–951 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Schultz W, Dayan P, Montague PR. 1997. A neural substrate of prediction and reward . Science 275 :1593–1599 [ PubMed ] [ Google Scholar ]
• Shadlen MN, Movshon JA. 1999. Synchrony unbound . Neuron 24 :67–77 [ PubMed ] [ Google Scholar ]
• Shadlen MN, Newsome WT. 1998. The variable discharge of cortical neurons: Implications for connectivity, computation, and information coding . J. of Nuerosci 18 :3870–3896 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Shannon CE, Weaver W. 1949. The Mathematical Theory of Information . University of Illinois Press [ Google Scholar ]
• Shea-Brown E, Josic K, de la Rocha J, Doiron B. 2008. Correlation and synchrony transfer in integrate-and-fire neurons: basic properties and consequences for coding . Physical Review Letters 100 :108102. [ PubMed ] [ Google Scholar ]
• Sherrington CS. 1897. The central nervous system . A Text-book of Physiology 3 :60 [ Google Scholar ]
• Shimazaki H, Amari SI, Brown EN, Grün S. 2012. State-space analysis of time-varying higher-order spike correlation for multiple neural spike train data . PLoS Comput. Biol 8 :e1002385. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Shimazaki H, Sadeghi K, Ishikawa T, Ikegaya Y, Toyoizumi T. 2015. Simultaneous silence organizes structured higher-order interactions in neural populations . Scientific reports 5 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Sigworth F 1977. Sodium channels in nerve apparently have two conductance states . Nature 270 :265–267 [ PubMed ] [ Google Scholar ]
• Sigworth F 1980. The variance of sodium current fluctuations at the node of ranvier . The Journal of physiology 307 :97. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Singer W 1999. Neuronal synchrony: a versatile code for the definition of relations? Neuron 24 :49–65, 111–25 [ PubMed ] [ Google Scholar ]
• Singer W, Gray CM. 1995. Visual feature integration and the temporal correlation hypothesis . Annual review of neuroscience 18 :555–586 [ PubMed ] [ Google Scholar ]
• Somjen GG. 2004. Ions in the brain: normal function, seizures, and stroke . Oxford University Press [ Google Scholar ]
• Staude B, Rotter S, Grün S. 2010. Cubic: cumulant based inference of higher-order correlations in massively parallel spike trains . Journal of computational neuroscience 29 :327–350 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Stigler SM. 1986. The history of statistics: The measurement of uncertainty before 1900 . Harvard University Press [ Google Scholar ]
• Sutton RS, Barto AG. 1998. Reinforcement learning: An introduction , volume 1 MIT press; Cambridge [ Google Scholar ]
• Swanson LW. 2012. Brain architecture: understanding the basic plan . Oxford University Press [ Google Scholar ]
• Teramae JN, Tsubo Y, Fukai T. 2012. Optimal spike-based communication in excitable networks with strong-sparse and weak-dense links . Sci. Rep 2 :485. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Tetzlaff T, Helias M, Einevoll G, Diesmann M. 2012. Decorrelation of neural-network activity by inhibitory feedback . PLOS Computational Biology 8 :e1002596. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Thorndike EL. 1911. Animal intelligence: Experimental studies . Macmillan [ Google Scholar ]
• Tien JH, Guckenheimer J. 2008. Parameter estimation for bursting neural models . Journal of Computational Neuroscience 24 :358–373 [ PubMed ] [ Google Scholar ]
• Torre E, Quaglio P, Denker M, Brochier T, Riehle A, Grün S. 2016. Synchronous spike patterns in macaque motor cortex during an instructed-delay reach-to-grasp task . J. of Nuerosci 36 :8329–8340 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Tranchina D 2010. Population density methods in large-scale neural network modelling In Stochastic Methods in Neuroscience . Oxford University Press [ Google Scholar ]
• Traub RD, Contreras D, Cunningham MO, Murray H, LeBeau FEN, Roopun A, Bibbig A, Wilent WB, Higley MJ, Whittington MA. 2005. Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts . J. Neurophysiol 93 :2194–2232 [ PubMed ] [ Google Scholar ]
• Trousdale J, Hu Y, Shea-Brown E, Josic K. 2012. Impact of network structure and cellular response on spike time correlations . PLOS Computational Biology 8 :e1002408. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Truccolo W 2010. Stochastic models for multivariate neural point processes: Collective dynamics and neural decoding In Analysis of parallel spike trains , pages 321–341. Springer [ Google Scholar ]
• Tuckwell HC. 1988. Introduction to Theoretical Neurobiology , volume 2 Cambridge University Press, Cambridge [ Google Scholar ]
• Turing AM. 1937. On computable numbers, with an application to the entscheidungsproblem . Proc. Lond. Math. Soc 2 :230–265 [ Google Scholar ]
• Ullman S, Assif L, Fetaya E, Harari D. 2016. Atoms of recognition in human and computer vision . Proc. Natl. Acad. Sci. U. S. A 113 :2744–2749 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• van Vreeswijk C, Sompolinsky H. 1996. Chaos in neuronal networks with balanced excitatory and inhibitory activity . Science 274 :1724–1726 [ PubMed ] [ Google Scholar ]
• Van Vreeswijk C, Sompolinsky H. 1998. Chaotic balanced state in a model of cortical circuits . Neural Comput . 10 :1321–1371 [ PubMed ] [ Google Scholar ]
• Vavoulis DV, Straub VA, Aston JA, Feng J. 2012. A self-organizing state-space-model approach for parameter estimation in hodgkin-huxley-type models of single neurons . PLoS Comput Biol 8 :e1002401. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Ventura V, Todorova S. 2015. A computationally efficient method for incorporating spike waveform information into decoding algorithms . Neural Comput . [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Villringer A, Planck J, Hock C, Schleinkofer L, Dirnagl U. 1993. Near infrared spectroscopy (nirs): a new tool to study hemodynamic changes during activation of brain function in human adults . Neuroscience letters 154 :101–104 [ PubMed ] [ Google Scholar ]
• Walch OJ, Eisenberg MC. 2016. Parameter identifiability and identifiable combinations in generalized hodgkin–huxley models . Neurocomputing 199 :137–143 [ Google Scholar ]
• Wang W, Tripathy SJ, Padmanabhan K, Urban NN, Kass RE. 2015. An empirical model for reliable spiking activity . Neural Comput . [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Watts DJ, Strogatz SH. 1998. Collective dynamics of small-worldnetworks . Nature 393 :440–442 [ PubMed ] [ Google Scholar ]
• Weber AI, Pillow JW. 2016. Capturing the dynamical repertoire of single neurons with generalized linear models . arXiv preprint arXiv:1602.07389 [ PubMed ] [ Google Scholar ]
• Wei Y, Ullah G, Schiff SJ. 2014. Unification of neuronal spikes, seizures, and spreading depression . J. Neurosci 34 :11733–11743 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Whitehead AN, Russell B. 1912. Principia Mathematica . University Press [ Google Scholar ]
• Wiener N 1948. Cybernetics: Control and communication in the animal and the machine . Wiley; New York [ Google Scholar ]
• Williamson RC, Cowley BR, Litwin-Kumar A, Doiron B, Kohn A, Smith MA, Yu BM. 2016. Scaling properties of dimensionality reduction for neural populations and network models . PLoS Comput. Biol 12 :e1005141. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Wilson HR, Cowan JD. 1972. Excitatory and inhibitory interactions in localized populations of model neurons . Biophysical Journal 12 :1–24 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Wolpert DM, Diedrichsen J, Flanagan JR. 2011. Principles of sensorimotor learning . Nature Reviews Neuroscience 12 :739–751 [ PubMed ] [ Google Scholar ]
• Yamins DLK, DiCarlo JJ. 2016. Using goal-driven deep learning models to understand sensory cortex . Nat. Neurosci 19 :356–365 [ PubMed ] [ Google Scholar ]
• Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, Sahani M. 2009. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity . J. Neurophysiol 102 :614–635 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Zaytsev YV, Morrison A, Deger M. 2015. Reconstruction of recurrent synaptic connectivity of thousands of neurons from simulated spiking activity . Journal of computational neuroscience 39 :77–103 [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Zhou P, Burton SD, Snyder AC, Smith MA, Urban NN, Kass RE. 2015. Establishing a statistical link between network oscillations and neural synchrony . PLoS Comput Biol 11 :e1004549. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Zylberberg J, Cafaro J, Turner MH, Shea-Brown E, Rieke F. 2016. Direction-selective circuits shape noise to ensure a precise population code . Neuron 89 :369–383 [ PMC free article ] [ PubMed ] [ Google Scholar ]

Center for Theoretical and Computational Neuroscience

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals

Cognitive neuroscience articles from across Nature Portfolio

Cognitive neuroscience is the field of study focusing on the neural substrates of mental processes. It is at the intersection of psychology and neuroscience, but also overlaps with physiological psychology, cognitive psychology and neuropsychology. It combines the theories of cognitive psychology and computational modelling with experimental data about the brain.

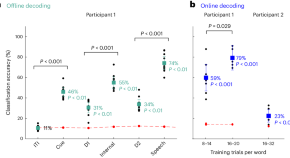
Brain–machine-interface device translates internal speech into text

For patients affected by speech disorders, brain–machine-interface (BMI) devices could restore their ability to verbally communicate. In this work, we captured neural activity associated with internal speech — words said within the mind with no associated movement or audio output — and translated these cortical signals into text in real time.

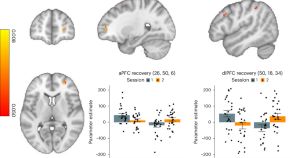
Prefrontal cortex activity increases after inpatient treatment for heroin addiction

Using task-based functional MRI, we examined inpatients with heroin use disorder. We found that 15 weeks of medication-assisted treatment (including supplemental group therapy) improved impaired anterior and dorsolateral prefrontal cortex function during an inhibitory control task. Inhibitory control, a core deficit in drug addiction, may be amenable to targeted prefrontal cortex interventions.

Related Subjects

• Cognitive control
• Consciousness
• Intelligence
• Personality
• Problem solving

Latest Research and Reviews

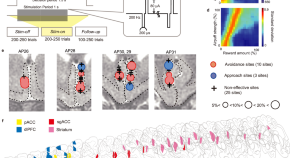
Cingulate microstimulation induces negative decision-making via reduced top-down influence on primate fronto-cingulo-striatal network

The neuronal mechanism of how the prefrontal cortex exerts top-down influence on the cingulo-striatal network during decision-making in depressive states is not fully understood. Here authors showed that negative bias in decision-making can be artificially induced via stimulating such neural network and they observed diminished top-down influences correlating with the depressive state.

• Satoko Amemori
• Ann M. Graybiel
• Ken-ichi Amemori

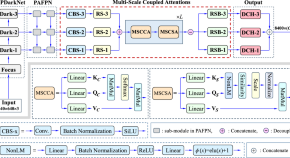
Multi-scale coupled attention for visual object detection

• Hongping Yan

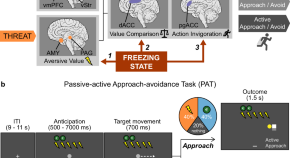
The neurocomputational link between defensive cardiac states and approach-avoidance arbitration under threat

A human fMRI study shows that defensive cardiac states moderate the neural computations of reward and threat value underlying approach-avoidance arbitration.

• Felix H. Klaassen
• Lycia D. de Voogd
• Karin Roelofs

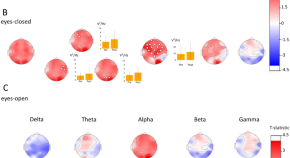
Short-term meditation training alters brain activity and sympathetic responses at rest, but not during meditation

• Anna Rusinova
• Maria Volodina
• Alexei Ossadtchi

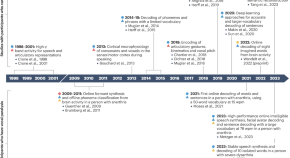
The speech neuroprosthesis

A clinically viable speech neuroprosthesis could restore natural speech to individuals with vocal-tract paralysis. In this Review, Silva et al. discuss rapid progress in neural interfaces and computational algorithms for decoding speech from cortical activity and propose evaluation metrics to help standardize speech neuroprostheses.

• Alexander B. Silva
• Kaylo T. Littlejohn
• Edward F. Chang

Association between household size and risk of incident dementia in the UK Biobank study

• Chao-Hua Cong
• Pan-Long Li
• Jing-Jing Su

News and Comment

Situational models of implicit bias.

• Maximilian A. Primbs

Mapping the claustrum to elucidate consciousness

• Navona Calarco

Prenatal alcohol exposure influences visual processing in infants

• Teresa Schubert

Attentional capture

A large network of brain regions is involved in salient distractor processing.

• Isobel Leake

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

• Frontiers in Behavioral Neuroscience
• Emotion Regulation and Processing
• Research Topics

Central and Autonomic Communication: Understanding the Functional Circuits Regulating Cognition, Emotion, and Visceral Functions

Total Downloads

Total Views and Downloads

About this Research Topic

The organism adapts to current demands via communication between the central (CNS) and autonomic (ANS) nervous systems which is achieved through complex and hierarchically organized neural processing. Before reaching the higher-order cortical regions representing the affective states, organ-specific information from sympathetic and parasympathetic afferents is integrated at different levels of brain organization. The top-down influences on the ANS critically depend on the accurate perception of interoceptive signals and correct predictive coding. Neurovisceral integration underlies the regulation of peripheral physiology, cognitive performance, and emotional/physical health. Central-autonomic miscommunication leads to various pathological conditions, such as, among others, anxiety disorder in the case of sympathetic hyperactivation. The Neurovisceral Integration Model explains how the bidirectional communication between CNS and ANS provides the adaptive response. The brainstem noradrenergic nucleus Locus Coeruleus (LC) is one of the key nodes within the central autonomic network. The LC is bidirectionally connected to both the autonomic nuclei and forebrain regions, including the prefrontal cortex and amygdala, that exert top-down regulation of the ANS. The LC activation results in a characteristic pattern of autonomic changes consistent with increased sympathetic tonus and vagal withdrawal. The control of arousal and autonomic function is thus inseparably linked, largely via the involvement of the LC. The LC has been identified as a key mediator of vagus nerve stimulation (VNS), which is being used increasingly as a treatment for conditions such as epilepsy, depression, inflammation, somatosensory rehabilitation, and also as a technique for cognitive enhancement. The CNS-ANS communication is reflected in the heart rate variability (HRV). Higher HRV corresponds to vagal/parasympathetic tonus and correlates with better physical health, emotion regulation, and cognitive control. Higher HRV also indexes glucose regulation, hypothalamic-adrenal-pituitary (HPA) axis function, inflammation, and reduced risk for cardiovascular disease. Lower HRV has been associated with affective disorders such as depression and anxiety. Thus, this non-invasive tool has the potential for a broader clinical application. This article collection aims to update and advance current views on the relationship between the body, emotion, and cognition. Besides the values of new fundamental knowledge, we highlight the importance of the body-brain interaction for mental and physical health. The development of new diagnostic methods and improving the analysis of the existing measurements, like the HRV, will make the clinical application of biomarkers of the ANS activity more reliable and increase their predictive power for therapeutic effectiveness. Finally, the influence of cognitive factors like learning, perception, or attention on the ANS in association with neural plasticity shall help correct various pathological states. In this Research Topic, we are looking to address key aspects of body-brain communication to promote discussion around this topic and to increase our understanding of the mechanisms underlying the development of affective disorders. The special focus is on the biomarkers of the ANS activity and the methods for ANS modulation. Theoretical and computational modeling help the emergence of testable hypotheses and inquiry for future experimental research. We welcome submission of Original Research, Review, Methods, and Perspective articles on the following sub-topics: • mechanisms of self-regulation and adaptability of the organism • functional connectivity within the central autonomic network • interoception and cognitive control • the locus coeruleus and autonomic function • vagus nerve stimulation (VNS) and modulation of brain activity • memory- and plasticity-enhancing effects of vagus nerve stimulation (VNS) • understanding the effectiveness of vagus nerve stimulation (VNS) • the locus coeruleus (LC) as a mediator of vagus nerve stimulation (VNS) • the state-of-the-art and the perspectives in methodological approaches to investigate the locus coeruleus organization and function • inputs to the locus coeruleus and link to neuropsychiatric and neurodegenerative disorders • psychosomatics and psychopathology • heart rate variability (HRV) as a diagnostic tool for psychiatric conditions • heart rate variability (HRV) as a biofeedback to promote cognitive enhancement • neurobiological basis for individual differences in the vagal regulation • computational models of the central-autonomic control

Keywords : HRV, locus cerules, psychopathology, psychiatric conditions, CNS, ANS, visceral functions, cognition, VNS

Important Note : All contributions to this Research Topic must be within the scope of the section and journal to which they are submitted, as defined in their mission statements. Frontiers reserves the right to guide an out-of-scope manuscript to a more suitable section or journal at any stage of peer review.

Topic Editors

Topic coordinators, submission deadlines, participating journals.

Manuscripts can be submitted to this Research Topic via the following journals:

total views

• Demographics

No records found

total views article views downloads topic views

Top countries

Top referring sites, about frontiers research topics.

With their unique mixes of varied contributions from Original Research to Review Articles, Research Topics unify the most influential researchers, the latest key findings and historical advances in a hot research area! Find out more on how to host your own Frontiers Research Topic or contribute to one as an author.

Scientists want to know how the smells of nature benefit our health

Spending time in nature is good for us. Studies have shown that contact with nature can lift our well-being by affecting emotions, influencing thoughts, reducing stress and improving physical health. Even brief exposure to nature can help. One well-known study found that hospital patients recovered faster if their room included a window view of a natural setting.

Knowing more about nature's effects on our bodies could not only help our well-being, but could also improve how we care for land, preserve ecosystems and design cities, homes and parks. Yet studies on the benefits of contact with nature have typically focused primarily on how seeing nature affects us. There has been less focus on what the nose knows. That is something a group of researchers wants to change.

"We are immersed in a world of odorants, and we have a sophisticated olfactory system that processes them, with resulting impacts on our emotions and behavior," said Gregory Bratman, a University of Washington assistant professor of environmental and forest sciences. "But compared to research on the benefits of seeing nature, we don't know nearly as much about how the impacts of nature's scents and olfactory cues affect us."

In a paper published May 15 in Science Advances , Bratman and colleagues from around the world outline ways to expand research into how odors and scents from natural settings impact our health and well-being. The interdisciplinary group of experts in olfaction, psychology, ecology, public health, atmospheric science and other fields are based at institutions in the U.S., the U.K., Taiwan, Germany, Poland and Cyprus.

At its core, the human sense of smell, or olfaction, is a complex chemical detection system in constant operation. The nose is packed with hundreds of olfactory receptors, which are sophisticated chemical sensors. Together, they can detect more than one trillion scents, and that information gets delivered directly to the nervous system for our minds to interpret -- consciously or otherwise.

The natural world releases a steady stream of chemical compounds to keep our olfactory system busy. Plants in particular exude volatile organic compounds, or VOCs, that can persist in the air for hours or days. VOCs perform many functions for plants, such as repelling herbivores or attracting pollinators. Some researchers have studied the impact of exposures to plant VOCs on people.

"We know bits and pieces of the overall picture," said Bratman. "But there is so much more to learn. We are proposing a framework, informed by important research from many others, on how to investigate the intimate links between olfaction, nature and human well-being."

Nature's smell-mediated impacts likely come through different routes, according to the authors. Some chemical compounds, including a subset of those from the invisible realm of plant VOCs, may be acting on us without our conscious knowledge. In these cases, olfactory receptors in the nose could be initiating a "subthreshold" response to molecules that people are largely unaware of. Bratman and his co-authors are calling for vastly expanded research on when, where and how these undetected biochemical processes related to natural VOCs may affect us.

Other olfactory cues are picked up consciously, but scientists still don't fully understand all their impacts on our health and well-being. Some scents, for example, may have "universal" interpretations to humans -- something that nearly always smells pleasant, like a sweet-smelling flower. Other scents are closely tied to specific memories, or have associations and interpretations that vary by culture and personal experience, as research by co-author Asifa Majid of the University of Oxford has shown.

"Understanding how olfaction mediates our relationships with the natural world and the benefits we receive from it are multi-disciplinary undertakings," said Bratman. "It involves insights from olfactory function research, Indigenous knowledge, Western psychology, anthropology, atmospheric chemistry, forest ecology, Shinrin-yoku -- or 'forest bathing' -- neuroscience, and more."

Investigation into the potential links between our sense of smell and positive experiences with nature includes research by co-author Cecilia Bembibre at University College London, which shows that the cultural significance of smells, including those from nature, can be passed down in communities to each new generation. Co-author Jieling Xiao at Birmingham City University has delved into the associations people have with scents in built environments and urban gardens.

Other co-authors have shown that nature leaves its signature in the very air we breathe. Forests, for example, release a complex chemical milieux into the air. Research by co-author Jonathan Williams at the Max Planck Institute for Chemistry and the Cyprus Institute shows how natural VOCs can react and mix in the atmosphere, with repercussions for olfactory environments.

The authors are also calling for more studies to investigate how human activity alters nature's olfactory footprint -- both by pollution, which can modify or destroy odorants in the air, and by reducing habitats that release beneficial scents.

"Human activity is modifying the environment so quickly in some cases that we're learning about these benefits while we're simultaneously making them more difficult for people to access," said Bratman. "As research illuminates more of these links, our hope is that we can make more informed decisions about our impacts on the natural world and the volatile organic compounds that come from it. As we say in the paper, we live within the chemical contexts that nature creates. Understanding this more can contribute to human well-being and advance efforts to protect the natural world."

• Medical Topics
• Psychology Research
• Diseases and Conditions
• Neuroscience
• Social Psychology
• Ecology Research
• Environmental Issues
• Geochemistry
• What is knowledge?
• Environmental impact assessment
• Temperature record of the past 1000 years
• Origin of life
• Psycholinguistics
• U.S. Navy Marine Mammal Program
• List of disasters
• Athletic training

Story Source:

Materials provided by University of Washington . Original written by James Urton. Note: Content may be edited for style and length.

Journal Reference :

• Gregory N. Bratman, Cecilia Bembibre, Gretchen C. Daily, Richard L. Doty, Thomas Hummel, Lucia F. Jacobs, Peter H. Kahn, Connor Lashus, Asifa Majid, John D. Miller, Anna Oleszkiewicz, Hector Olvera-Alvarez, Valentina Parma, Anne M. Riederer, Nancy Long Sieber, Jonathan Williams, Jieling Xiao, Chia-Pin Yu, John D. Spengler. Nature and human well-being: The olfactory pathway . Science Advances , 2024; 10 (20) DOI: 10.1126/sciadv.adn3028

Cite This Page :

Explore More

• Toward a Successful Vaccine for HIV
• Highly Efficient Thermoelectric Materials
• Toward Human Brain Gene Therapy
• Whale Families Learn Each Other's Vocal Style
• AI Can Answer Complex Physics Questions
• Otters Use Tools to Survive a Changing World
• Monogamy in Mice: Newly Evolved Type of Cell
• Sustainable Electronics, Doped With Air
• Male Vs Female Brain Structure
• Breeding 'Carbon Gobbling' Plants

Trending Topics

Strange & offbeat.