homework & practice 3 6

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

3 6 Homework

3 6 Homework - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are Eureka math homework helper 20152016 grade 3 module 1, Homework practice and problem solving practice workbook, Eureka math homework helper 20152016 grade 6 module 2, Algebra 2 work, Unit 3 chapter 6 polynomials and polynomial functions, Homework practice and problem solving practice workbook, Grade 3 verbs work, Practice and homework name lesson estimate fraction.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. Eureka Math Homework Helper 20152016 Grade 3 Module 1

2. homework practice and problem-solving practice workbook, 3. eureka math homework helper 20152016 grade 6 module 2, 4. algebra 2 1.3-1.6 worksheet, 5. unit 3 chapter 6 polynomials and polynomial functions, 6. homework practice and problem-solving practice workbook, 7. grade 3 verbs worksheets -, 8. practice and homework name lesson 6.3 estimate fraction ....

• 888-309-8227
• 732-384-0146

New User Registration

Forgot Password

Textbook Resources

Textbook resources.

• Call us toll-free
• FAQs – Frequently Asked Questions
• Contact Lumos Learning – Proven Study Programs by Expert Teachers

Follow us: Lumos Learning -->

• 2024 © Lumos Learning
• Privacy Policy - Terms of Service - Disclaimers

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc... Read More

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc., the Partnership for the Assessment of Readiness for College and Careers, nor any state of the Union. Neither PARCC, Inc., nor The Partnership for the Assessment of Readiness for College and Careers, nor any member state has endorsed this product. No portion of any fees or charges paid for any products or services Lumos Learning offers will be paid or inure to the benefit of PARCC, Inc., or any state of the Union

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not aff... Read More

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not affiliated to Lumos Learning. The Regents of the University of California – Smarter Balanced Assessment Consortium, was not involved in the production of, and does not endorse these products or this site.

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC, was not... Read More

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC,was not involved in the production of, and does not endorse these products or this site.

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the... Read More

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the production of, and does not endorse these products or this site.

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the... Read More

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the production of, and does not endorse these products or this site.

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved... Read More

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved in the production of, and does not endorse these products or this site.

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the prod... Read More

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the production of, and does not endorse these products or this site.

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved... Read More

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved in the production of, and does not endorse these products or this site.

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved... Read More

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved in the production of, and does not endorse these products or this site.

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved... Read More

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved in the production of, and does not endorse these products or this site.

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved... Read More

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved in the production of, and does not endorse these products or this site.

Home > CC3 > Chapter 6 > Lesson 6.2.3

Lesson 6.1.1, lesson 6.1.2, lesson 6.1.3, lesson 6.1.4, lesson 6.2.1, lesson 6.2.2, lesson 6.2.3, lesson 6.2.4, lesson 6.2.5, lesson 6.2.6.

© 2022 CPM Educational Program. All rights reserved.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.6: Chapter 3 Exercises with Solutions

• Last updated
• Save as PDF
• Page ID 24101

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

3.1 Exercises

Exercise \(\pageindex{1}\).

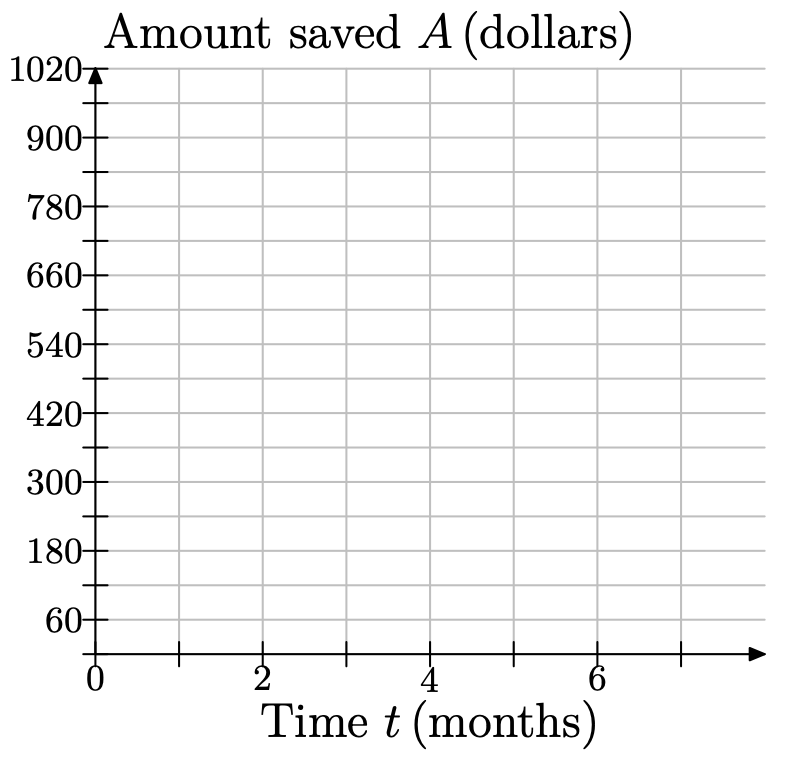
Jodiah is saving his money to buy a Playstation 3 gaming system. He estimates that he will need $950 to buy the unit itself, accessories, and a few games. He has $600 saved right now, and he can reasonably put $60 into his savings at the end of each month. Since the amount of money saved depends on how many months have passed, choose time, in months, as your independent variable and place it on the horizontal axis. Let t represent the number of months passed, and make a mark for every month. Choose money saved, in dollars, as your dependent variable and place it on the vertical axis. Let A represent the amount saved in dollars. Since Jodiah saves $60 each month, it will be convenient to let each box represent $60. Copy the following coordinate system onto a sheet of graph paper.

a) At month 0, Jodiah has $600 saved. This corresponds to the point (0, 600). Plot this point on your coordinate system.

b) For the next month, he saved $60 more. Beginning at point (0, 600), move 1 month to the right and $60 up and plot a new data point. What are the coordinates of this point?

c) Each time you go right 1 month, you must go up by $60 and plot a new data point. Repeat this process until you reach the edge of the coordinate system.

d) Keeping in mind that we are modeling this discrete situation continuously, draw a line through your data points.

e) Use your graph to estimate how much money Jodiah will have saved after 7 months. f) Using your graph, estimate how many months it will take him to have saved up enough money to buy his gaming system, accessories, and games.

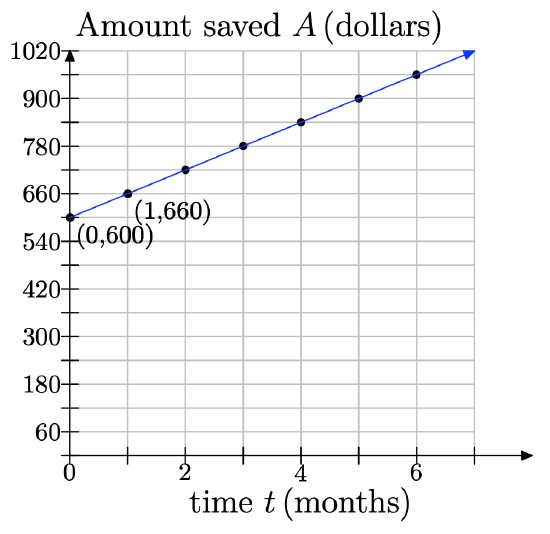
From the graph, when t = 7 months, he will have saved $1020.

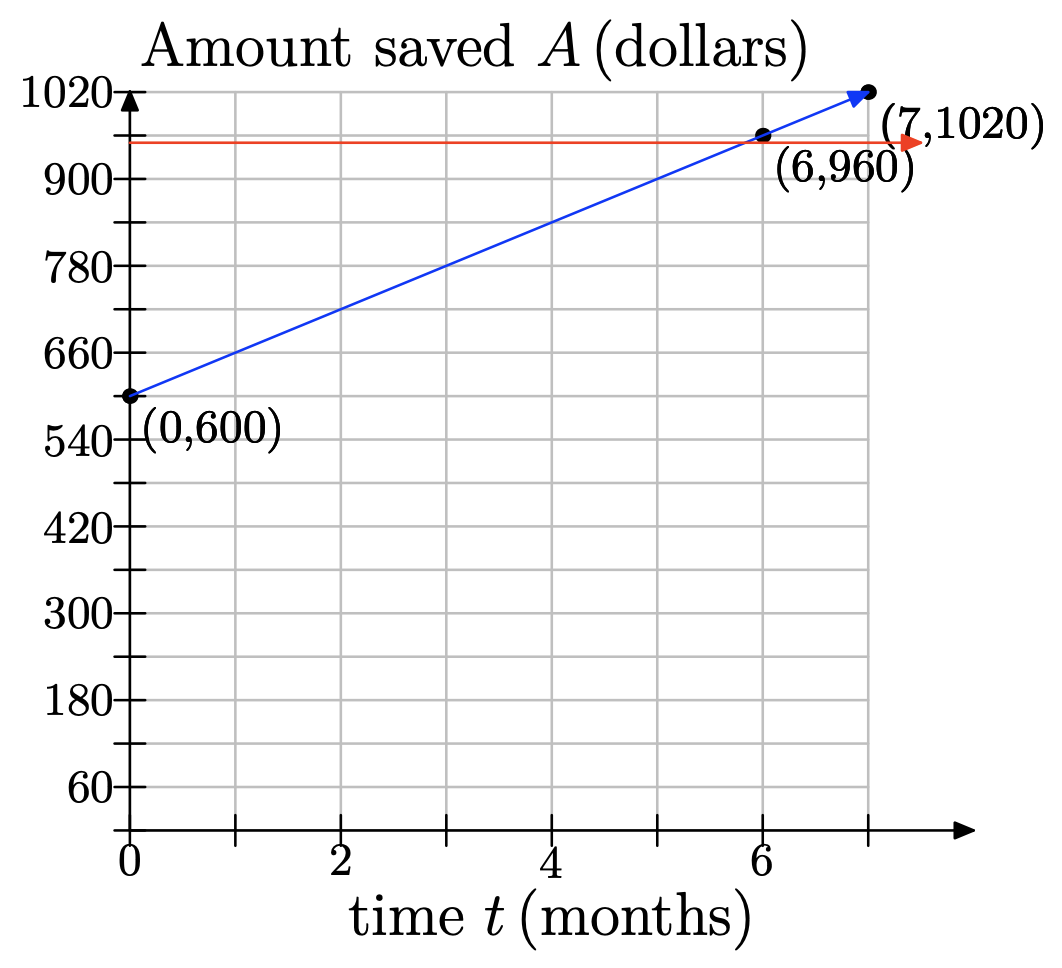
Note that we’ve modeled a discrete problem continuously: He saves $60 at the end of each month, and he will have $900 by the end of month five; and then $960 by the end of month six. There will be no time at which he has exactly $950, so the answer is 6 months, at which point he’ll have $960.

Exercise \(\PageIndex{2}\)

The sign above shows the prices for a taxi ride from Liberty Cab Company. Since the cost depends on the distance traveled, make the distance be the independent variable and place it on the horizontal axis. Let d represent the distance traveled, in miles. Because the cab company charges per 1/6 mile, it is convenient to mark every 1/6 mile. Make price, in $, your dependent variable and place it on the vertical axis. Let C represent the cost, in $. Because the cost occurs in increments of 40c, mark every 40c along the vertical axis. Copy the following coordinate system onto a sheet of graph paper.

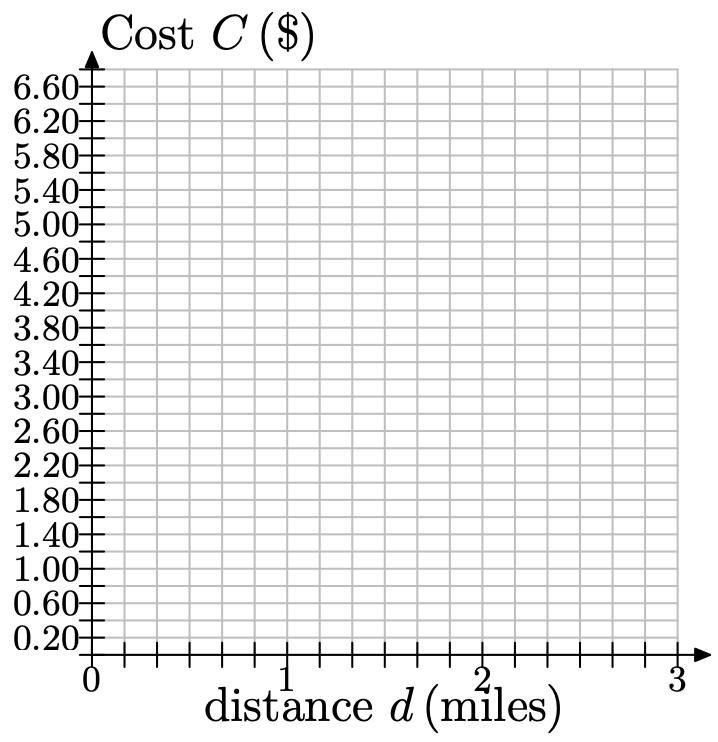
a) For the first 1/6 mile of travel, the cost is $2.30. This corresponds to the point (1/6,$2.30). Plot this point on your coordinate system.

b) For the next 1/6 of a mile, the cost goes up by 40\(\cent\). Beginning at point (1/6,$2.30), move 1/6 of a mile to the right and 40c up and plot a new data point. What are the coordinates of this point?

c) Each time you go right 1/6 of a mile, you must go up by 40\(\cent\) and plot a new data point. Repeat this process until you reach the edge of your coordinate system.

e) Melissa steps into a cab in the city of Niagara Falls, about 2 miles from Niagara Falls State Park. Use your graph to estimate the fare to the park.

f) Elsewhere in the area, Georgina takes a cab. She has only $5 for the fare. Use the graph to estimate how far she can travel, in miles, with only $5 for the fare.

Exercise \(\PageIndex{3}\)

A boat is 200 ft from a buoy at sea. It approaches the buoy at an average speed of 15 ft/s.

a) Choosing time, in seconds, as your independent variable and distance from the buoy, in feet, as your dependent variable, make a graph of a coordinate system on a sheet of graph paper showing the axes and units. Use tick marks to identify your scales.

b) At time t=0, the boat is 200 ft from the buoy. To what point does this correspond? Plot this point on your coordinate system.

c) After 1 second, the boat has drawn 15 ft closer to the buoy. Beginning at the previous point, move 1 second to the right and 15 ft down (since the distance is decreasing) and plot a new data point. What are the coordinates of this point?

d) Each time you go right 1 second, you must go down by 15 ft and plot a new data point. Repeat this process until you reach 12 seconds.

e) Draw a line through your data points.

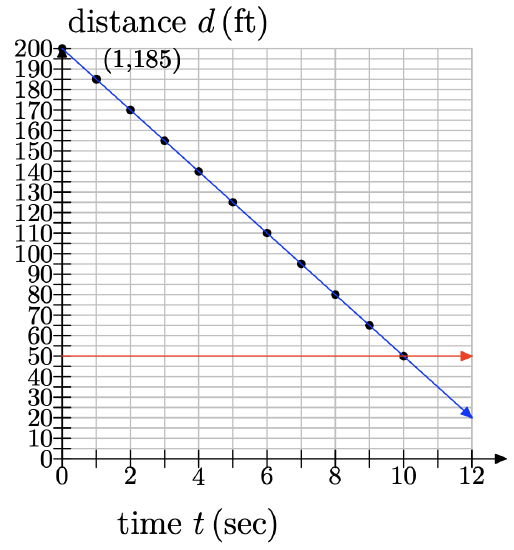
f) When the boat is within 50 feet of the buoy, the driver wants to begin to slow down. Use your graph to estimate how soon the boat will be within 50 feet of the buoy.

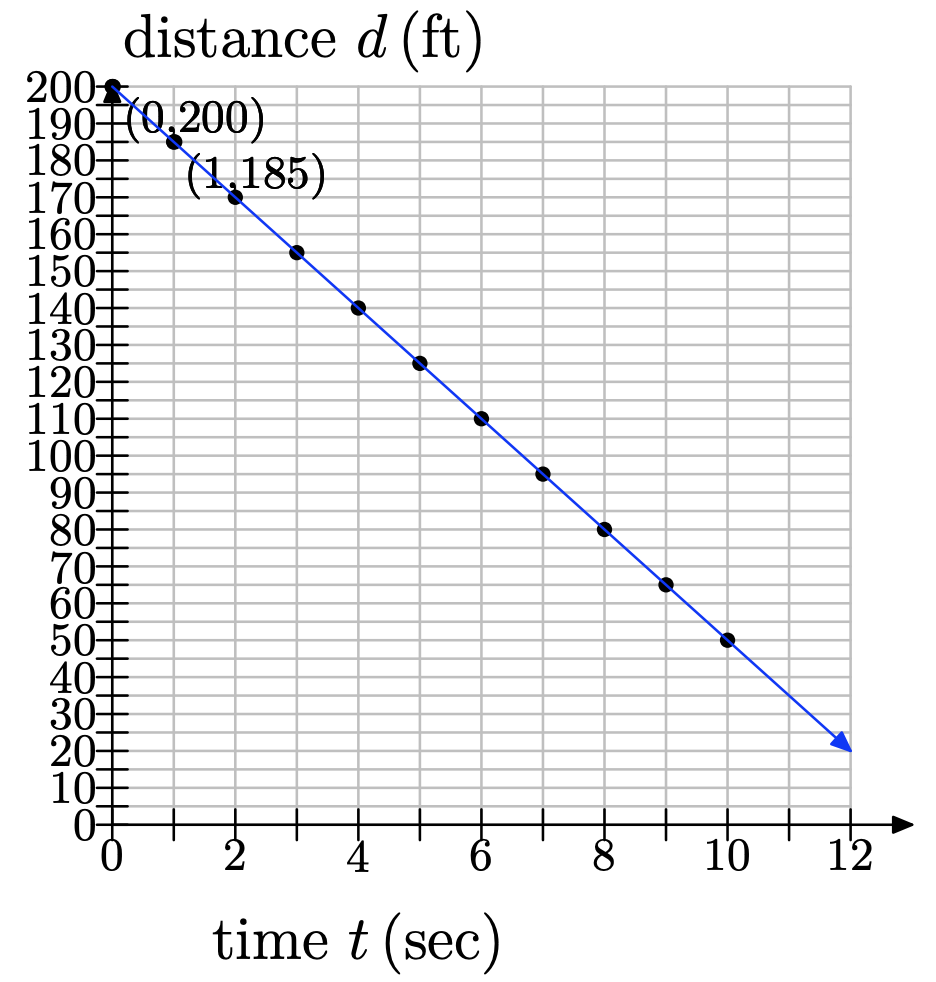
f) We draw a line at 50 ft and see that it occurs at 10 seconds:

Exercise \(\PageIndex{4}\)

Joe owes $24,000 in student loans. He has finished college and is now working. He can afford to pay $1500 per month toward his loans.

a) Choose time in months as your independent variable and amount owed, in $, as the dependent variable. On a sheet of graph paper, make a sketch of the coordinate system, using tick marks and labeling the axes appropriately.

b) At time t = 0, Joe has not yet paid anything toward his loans. To what point does this correspond? Plot this point on your coordinate system.

c) After one month, he pays $1500. Beginning at the previous point, move 1 month to the right and $1500 down (down because the debt is decreasing). Plot this point. What are its coordinates?

d) Each time you go 1 month to the right, you must move $1500 down. Continue doing this until his loans have been paid off.

e) Keeping in mind that we are modeling this discrete situation continuously, draw a line through your data points.

f) Use the graph to determine how many months it will take him to pay off the full amount of his loans.

Exercise \(\PageIndex{5}\)

Earl the squirrel has only ten more days until hibernation. He needs to save 50 more acorns. He is tired of collecting acorns and so he is only able to gather 8 acorns every 2 days.

a) Let t represent time in days and make it your independent variable. Let N represent the number of acorns collected and make it your dependent variable. Set up an appropriately scaled coordinate system on a sheet of graph paper.

b) At time t = 0, Earl has collected zero of the acorns he needs. To what point does this correspond? Plot this point on your coordinate system.

c) After two days (t = 2), Earl has collected 8 acorns. Beginning at the previous point, move 2 days to the right and 8 acorns up. Plot this point. What are its coordinates?

d) Each time you go 2 days to the right, you must move 8 acorns up and plot a point. Continue doing this until you reach 14 days.

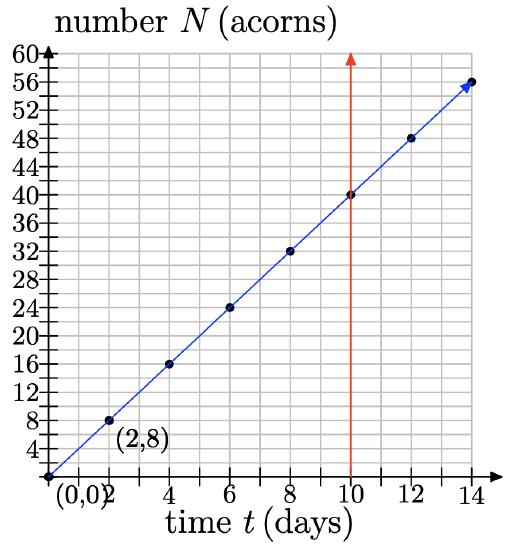
f) Use the graph to determine how many acorns he will have collected after 10 days. Will Earl have collected enough acorns for his winter hibernation?

g) Notice that the number of acorns collected is increasing at a rate of 8 acorns every 2 days. Reduce this to a rate that tells the average number of acorns that is collected each day.

h) The table below lists the number of acorns Earl will have collected at various times. Some of the entries have been completed for you. For example, at t = 0, Earl has no acorns, so N = 0. After one day, the amount increases by 4, so N = 0 + 4(1). After two days, two increases have occurred, so N = 0+4(2). The pattern continues. Fill in the missing entries.

i) Express the number of acorns collected, N, as a function of the time t, in days.

j) Use your function to predict the number of acorns that Earl will have after 10 days. Does this answer agree with your estimate from part (f)?

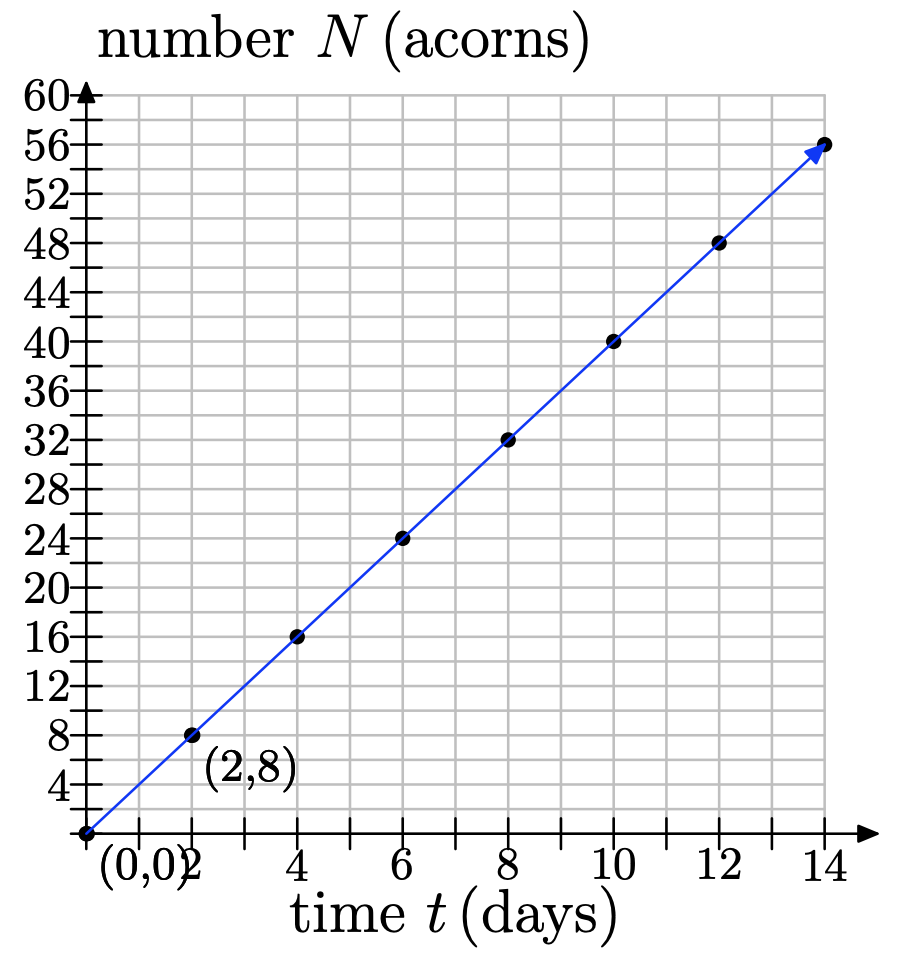
f) If you draw a line at 10 days, then you can see that he will have collected 40 acorns.

g) \(\frac{8}{2}\) acorns/day = 4 acorns/day

h) Following the pattern, we get:

i) N = 0 + 4t or N = 4t

j) At t = 10, N = 0 + 4(10) = 40 acorns.

Exercise \(\PageIndex{6}\)

On network television, a typical hour of programming contains 15 minutes of commercials and advertisements and 45 minutes of the program itself.

a) Choose amount of television watched as your independent variable and place it on the horizontal axis. Let T represent the amount of television watched, in hours. Choose total amount of commercials/ads watched as your dependent variable and place it on the vertical axis. Let C represent the total amount of commercials/ads watched, in minutes. Using a sheet of graph paper, make a sketch of a coordinate system and label appropriately.

b) For 0 hours of programming watched, 0 minutes of commercials have been watched. To what point does this correspond? Plot it on your coordinate system.

c) After watching 1 hour of program-ming, 15 minutes of commercials/ads have been watched. Beginning at the previous point, move 1 hour to the right and 15 minutes up. Plot this point. What are its coordinates?

d) Each time you go 1 hour to the right, you must move 15 minutes up and plot a point. Continue doing this until you reach 5 hours of programming.

f) Billy watches TV for five hours on Monday. Use the graph to determine how many minutes of commercials he has watched during this time.

g) Suppose a person has watched one hour of commercials/ads. Use the graph to estimate how many hours of television he watched.

h) The following table shows numbers of hours of programming watched as it relates to number of minutes of commercials/ads watched. For 0 hours of TV, 0 minutes of commercials/ads are watched. For each hour of TV watched, we must count 15 minutes of commercials/ads. So, for 1 hour, 0 + 15(1) minutes of commercials are watched. For 2 hours, 0 + 15(2) minutes; and so on. Fill in the missing entries.

i) Express the amount of commercials/ads watched, C, as a function of the amount of television watched T. Use your equation to predict the amount of commercials/ads watched for 5 hours of television programming. Does this answer agree with your estimate from part (f)?

Exercise \(\PageIndex{7}\)

According to NATO (the National Association of Theatre Owners), the average price of a movie ticket was 5.65 dollars in the year 2001. Since then, the average price has been rising each year by about 20\(\cents\).

a) Choose year, beginning with 2000, as the independent variable and make marks every year on the axis. Choose average ticket price, in dollars, as your dependent variable and begin at 5.65 dollars, with marks every 10\(\cents\) above. Make a sketch of a coordinate system and label appropriately.

b) In 2001, the average ticket price was 5.65 dollars, corresponding to the point (2001, 5.65). Plot it on your coordinate system.

c) In 2002, one year later, the average price rose by about 20\(\cents\). Beginning at the previous point, move right by 1 year and up by 20\(\cents\) and plot the point. What are its coordinates?

d) Each time you go 1 year to the right, you must move up by 20\(\cents\) and plot a point. Continue doing this until the year 2010.

f) Use the graph to estimate what year the average price of a ticket will pass 7.00 dollars.

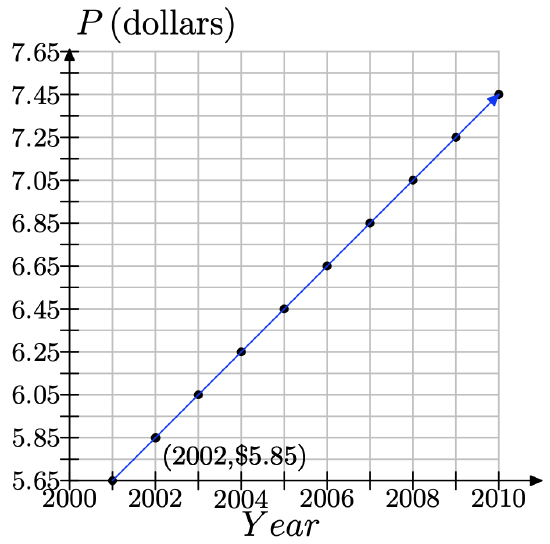
f) Draw a line for $7.00 and look for the year.

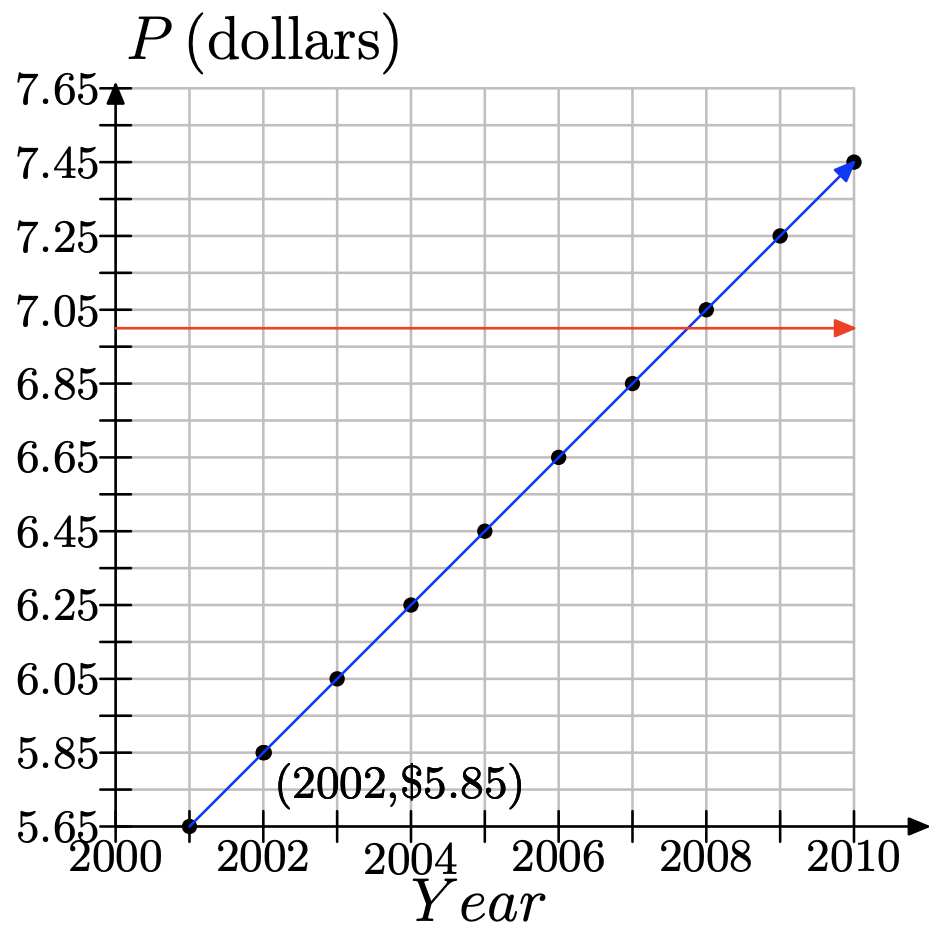
Notice that year is between 2007 and 2008. But this is a discrete problem, since we are only dealing with whole years. Thus, the answer is 2008.

Exercise \(\PageIndex{8}\)

When Jessica drives her car to a work-related conference, her employer reimburses her approximately 45 cents per mile to cover the cost of gas and the wear-and-tear on the vehicle.

a) Using distance traveled d, in miles, as the independent variable and amount reimbursed A, in dollars, as the dependent variable, make a sketch of a coordinate system and label appropriately. Mark distance every 5 miles and amount reimbursed every $0.45.

b) For traveling 0 miles, the reimbursement is 0. This corresponds to the point (0, 0). Plot it on your coordinate system.

c) For a trip that requires her to drive a total of 5 miles, she is reimbursed 5(0.45) = $2.25. This corresponds to the point (5, $2.25). Plot it.

d) For each 5 miles you go to the right, you must go up $2.25 and plot the point. Do this until you reach 20 miles.

f) In March, Jessica attends a conference that is only 5 miles away. Counting round trip, she travels 10 total miles. Use the graph to determine how much she is reimbursed.

g) In December, she attends a conference 10 miles away. How long is her trip in total? Use the graph to determine how much she will be reimbursed.

h) For longer trips, such as 200 total miles, you will probably need to make a much larger graph. And what if she travels 400 miles? Or further? It is limitations such as these that make it useful to find an equation that describes what the graph shows. To find the equation, we start with a table that helps us to understand the relationship between the dependent and independent variables. Complete the table below.

i) Use the table from part (h) to come up with an equation that relates d and A.

j) Now, use the equation to determine the reimbursement amounts for trips of 200 miles and 400 miles.

Exercise \(\PageIndex{9}\)

Temperature is typically measured in degrees Fahrenheit in the United States; but it is measured in degrees Celsius in many other countries. The relationship between Fahrenheit and Celsius is linear. Let’s choose the measurement of degrees in Celsius to be our independent variable and the measurement of degrees in Fahrenheit to be our dependent variable. Water freezes at 0 degrees Celsius, which corresponds to 32 degrees Fahrenheit; and water boils at 100 degrees Celsius, which corresponds to 212 degrees Fahrenheit. We can plot this information as the two points (0,32) and (100,212). The relationship is linear, so have the following graph:

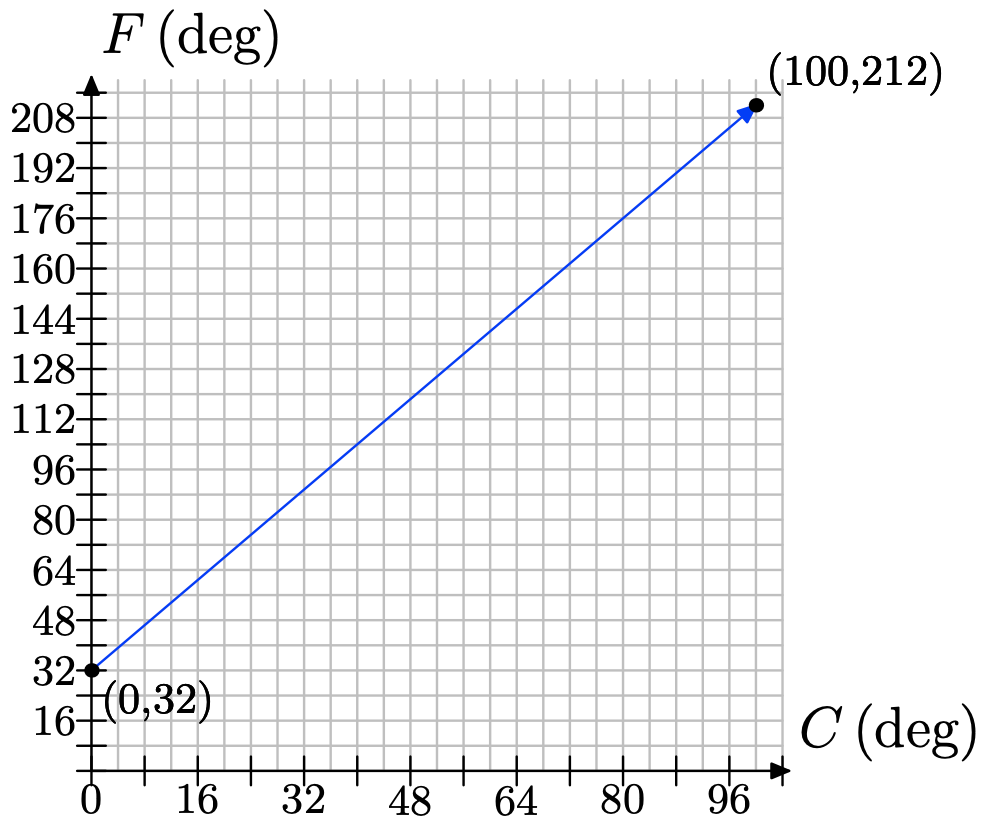
a) Use the graph to approximate the equivalent Fahrenheit temperature for 48 degree Celsius.

b) To determine the rate of change of Fahrenheit with respect to Celsius, we draw a right triangle with sides parallel to the axes that connects the two points we know...

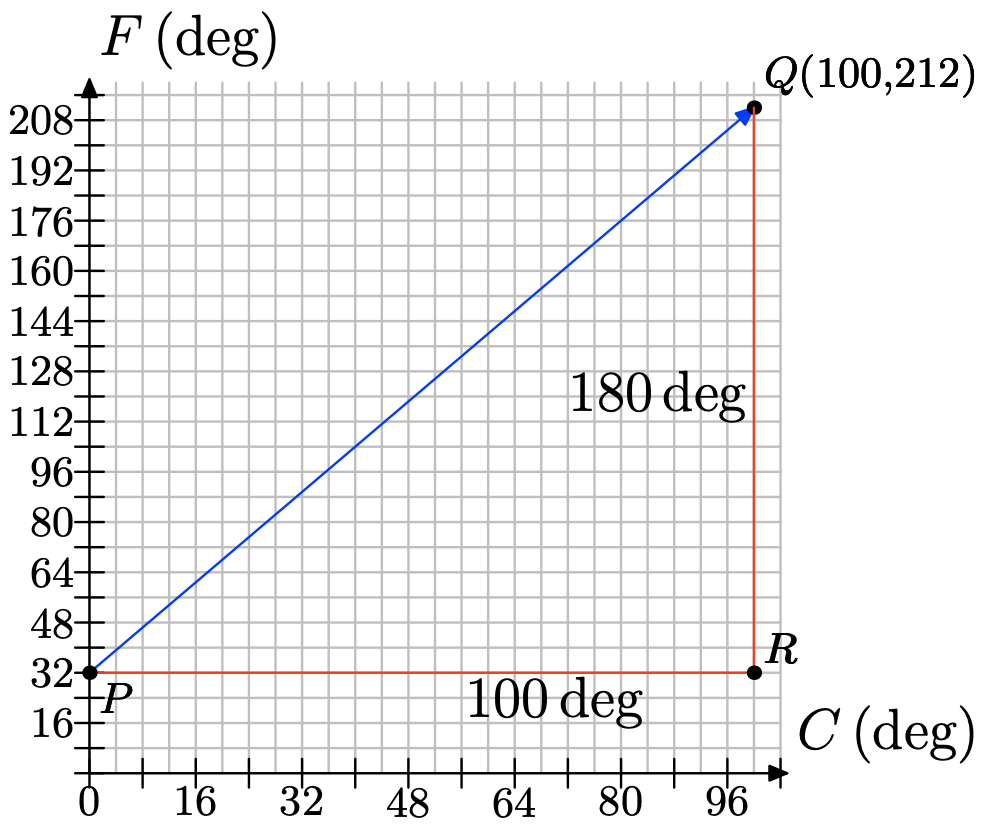
Side PR is 100 degrees long, representing an increase in 100 degrees Celsius. Side RQ is 180 degrees, representing an increase in 180 degrees Fahrenheit. Find the rate of increase of Fahrenheit per Celsius. c) The following table shows some values of temperatures in Celsius and their corresponding Fahrenheit readings. Zero degrees Celsius corresponds to 32 degrees Fahrenheit. Our rate is 9 degrees Fahrenheit for every 5 degrees Celsius, or 9/5 of a degree Fahrenheit for every 1 degree Celsius. So, for 1 degree Celsius, we increase the Fahrenheit reading by 9/5 degree, getting 32 + 9/5(1). For 2 degrees Celsius, we increase by two occurrences of 9/5 degree to get 32 + 9/5(2). Fill in the missing entries, following the pattern.

d) Use the table to form an equation that gives degrees Fahrenheit in terms of degrees Celsius.

a) We make a line at 48 degrees Celsius and read off the Fahrenheit estimate.

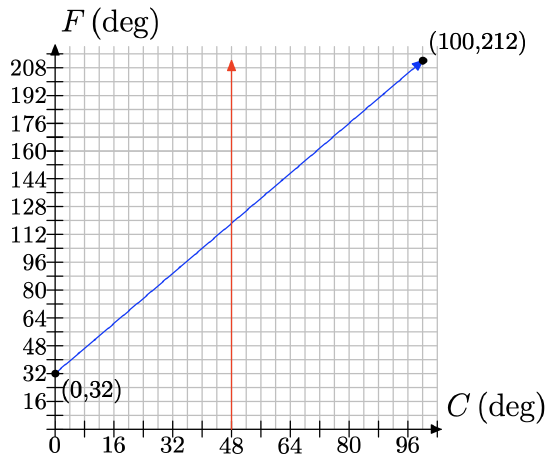
The estimate should be approximately 120 degrees Fahrenheit.

b) \(\dfrac{changeinF}{ changeinC} = \dfrac{180}{ 100 }= \dfrac{9}{ 5}\)

d) F = 9 5C + 32

Exercise \(\PageIndex{10}\)

On June 16, 2006, the conversion rate from Euro to U.S. dollars was approximately 0.8 to 1, meaning that every 0.8 Euros were worth 1 U.S. dollar.

a) Choosing dollars to be the independent variable and Euros to be the dependent variable, make a graph of co-ordinate system. Mark every dollar on the dollar axis and every 0.8 Euros on the Euro axis. Label appropriately.

b) Zero dollars are worth 0 Euros. This corresponds to the point (0, 0). Plot it on your coordinate system.

c) One dollar is worth 0.8 Euros. Plot this as a point on your coordinate system.

d) For every dollar you move to the right, you must go up 0.8 Euros and plot a point. Do this until you reach $10.

f) Use the graph to estimate how many Euros $8 are worth.

g) Use the graph to estimate how many dollars 5 Euros are worth.

h) The following table shows some values of dollars and their corresponding value in Euros. Fill in the missing entries.

i) Use the table to make an equation that can be used to convert dollars to Euros.

j) Use the equation from (i) to convert $8 to Euros. Does your answer agree with the answer from (f) that you obtained using the graph?

Exercise \(\PageIndex{11}\)

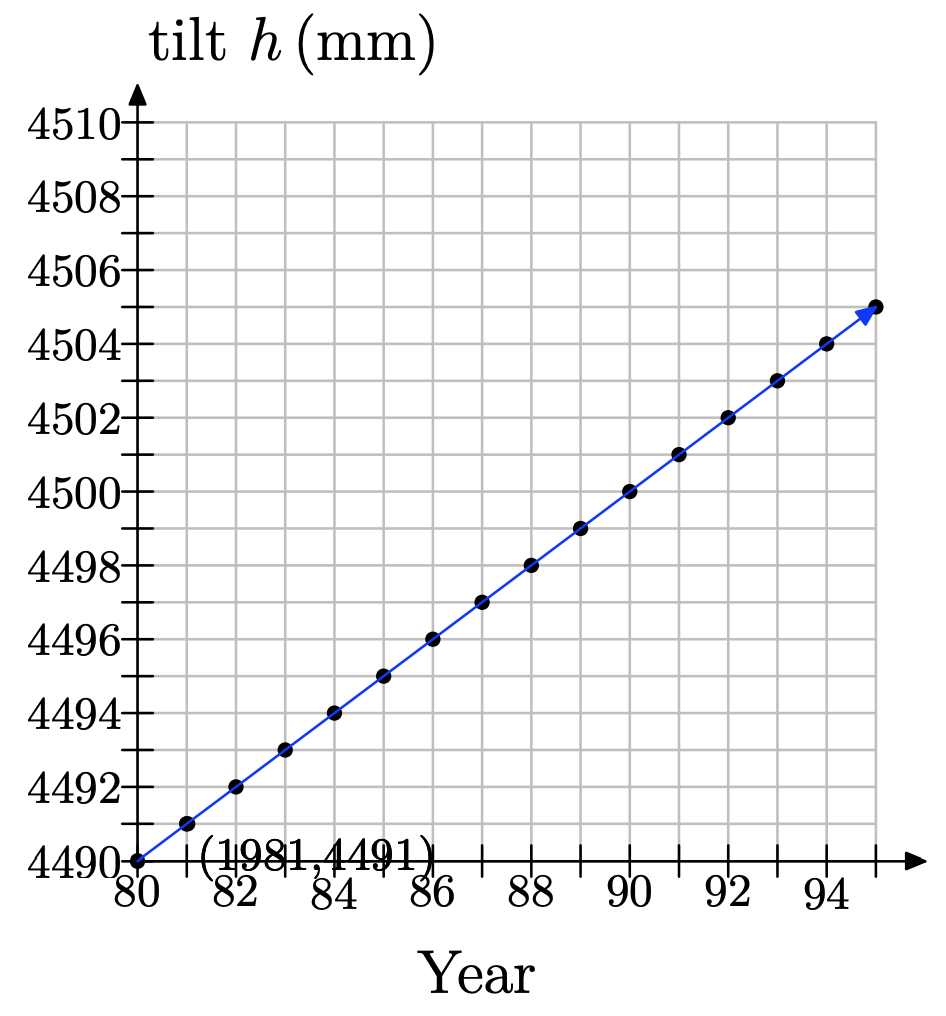
The Tower of Pisa in Italy has its famous lean to the south because the clay and sand ground on which it is built is softer on the south side than the north. The tilt is often found by measuring the distance that the upper part of the tower overhangs the base, indicated by h in the figure below. In 1980, the tower had a tilt of h = 4.49m, and this tilt was increasing by about 1 mm/year.

Figure \(\PageIndex{1}\). h measures the tilt of the Tower of Pisa.

We will investigate how the tilt of the tower changed from 1980 to 1995.

a) First, note that our units do not match: The tilt in 1980 was given as 4.49 m, but the annual increase in the tilt is given as 1 mm/year. Our first goal is to make the units the same. We will use millimeters (mm). Convert 4.49 m to mm.

b) Get a sheet of graph paper. Since the tilt of the tower depends on the year, make the year the independent variable and place it on the horizontal axis. Let t represent the year. Make the tilt the dependent variable and place it on the vertical axis. Let h represent the tilt, measured in millimeters (mm). Choose 1980 as the first year on the horizontal axis and mark every year thereafter, until 1995. Let the vertical axis begin at 4.49 m, converted to mm from part (a), since that was our first measurement; and then we mark every 1 mm thereafter up to 4510 mm.

c) Think of 1980 as the starting year. Together with the tilt measurement from that year, it forms a point. What are the coordinates of this point? Plot the point on your coordinate system.

d) Beginning at the first point, from part (c), move one year to the right (to 1981) and 1 mm up (because the tilt increases) and plot a new data point.

e) Each time you move one year to the right, you must move 1 mm up and plot a new point. Repeat this process until you reach the year 1995.

f) Keeping in mind that we are modeling this discrete situation continuously, draw a line through your data points. We can use this model to make predictions.

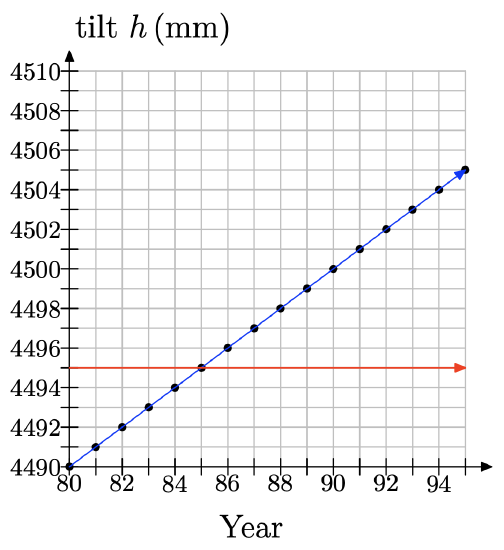
g) According to computer simulation models, which use sophisticated mathematics, the tower would be in danger of collapsing when h reaches about 4495 mm. Use your graph to estimate what year this would happen.

h) In reality, the tilt of the tower passed 4495 mm and the tower did not collapse. In fact, the tilt increased to 4500 mm before the tower was closed on January 7, 1990, to undergo renovations to decrease the tilt. (The tower was reopened in 2001, after engineers used weights and removed dirt from under the base to decrease the tilt by 450 mm.) What might be some reasons why the prediction of the computer model was wrong?

i) The following table lists the tilt of the tower, h, the year, and the number of years since 1980. In 1980, the tilt was 4490 mm and no occurrences of the 1 mm increase had happened yet, so we fill in 4490 + 0(1) = 4490. In 1981, one occurrence of the 1 mm increase had occurred because one year had passed since 1980. Therefore, the tilt was 4490 + 1(1). In 1982, two occurrences of the 1 mm increase had occurred, because 2 years had passed since 1980. Thus, the tilt was 4490 + 2(1). And the pattern continues in this manner. Fill in the remaining entries.

j) Let x represent the number of years since 1980 and h represent the tilt. Using the table above, write an equation that relates h and x.

k) Use your equation to predict the tilt in 1990. Does it agree with the actual value from 1990? Does it agree with the value that is shown on the graph you made?

l) In part (g), you used the graph to predict the year in which the tilt would be 4495mm. Use your equation to make the same prediction. Do the answers agree?

a) There are 1000mm in 1m, so 4.49 = 4.49(1000) = 4490 mm.

g) We draw a line for h = 4495 and see that it corresponds to 1985.

h) No model is perfect. The computer model must not have taken into consideration certain unexpected factors.

j) h = 4490 + 1x

k) In 1990, x = 10, and so h = 4490+1(10) = 4500mm. Yes, it agrees with the actual value in 1990.

l) To find when the tilt will be 4495, set h = 4495 and solve for x. 4495 = 4490 + 1x leads to 5 = x, and so our answer is 1985. This agrees with the answer from (g).

Exercise \(\PageIndex{12}\)

According to the Statistical Abstract of the United States (www.census.gov), there were approximately 31, 000 crimes reported in the United States in 1998, and this was dropping by a rate of about 2900 per year.

a) On a sheet of graph paper, make a coordinate system and plot the 1998 data as a point. Note that you will only need to graph the first quadrant of a coordinate system, since there are no data for years before 1998 and there cannot be a negative number of crimes reported. Use the given rate to find points for 1999 through 2006, and then draw a line through your data. We are constructing a continuous model for our discrete situation.

b) The following table lists the number of crimes reported, C, the year, and the number of years since 1998. In 1998, the number was 31, 000 and no occurrences of the 2900 decrease had happened yet, so we fill in 31000 − 2900(0). In 1999, one occurrence of the 2900 decrease had happened because one year had passed since 1998. Therefore, the number of crimes reported was 31000−2900(1). And the pattern continues in this manner. Fill in the remaining entries.

c) Observing the pattern in the table, we come up with the equation C = 31000 − 2900x to relate the number of crimes C to the number of years x after 1998. Here, C is a function of x, and so we can use the notation C(x) = 31000 − 2900x to emphasize this.

i. Compute C(5).

ii. In a complete sentence, explain what C(5) represents.

iii. Compute C(8).

iv. In a complete sentence, explain what C(8) represents.

Exercise \(\PageIndex{13}\)

According to the Statistical Abstract of the United States (www.census.gov), there were approximately 606, 000 inmates in United States prisons in 1999, and this was increasing by a rate of about 14, 000 per year.

a) On a sheet of graph paper, make a coordinate system and plot the 1999 data as a point. Note that you will only need to graph the first quadrant of a coordinate system, since there are no data for years before 1999 and there cannot be a negative number of crimes reported. Use the given rate to find points for 2000 through 2006, and then draw a line through your data. We are constructing a continuous model for our discrete situation.

b) The following table lists the number of inmates, N, the year, and the number of years since 1999. In 1999, the number was 606, 000 and no occurrences of the 14, 000 increase had happened yet, so we fill in 606000 + 14000(0). In 2000, one occurrence of the 14, 000 increase had happened because one year had passed since 1999. Therefore, the number of crimes reported was 606000 + 14000(1). And the pattern continues in this manner. Fill in the remaining entries.

c) Observing the pattern in the table, we come up with the equation N = 606000+14000x to relate the number of crimes C to the number of years x after 1999. Here, N is a function of x, and so we can use the notation N(x) = 606000+14000x to emphasis this.

i. Compute N(5).

ii. In a complete sentence, explain what N(5) represents.

iii. Compute N(7).

iv. In a complete sentence, explain what N(7) represents.

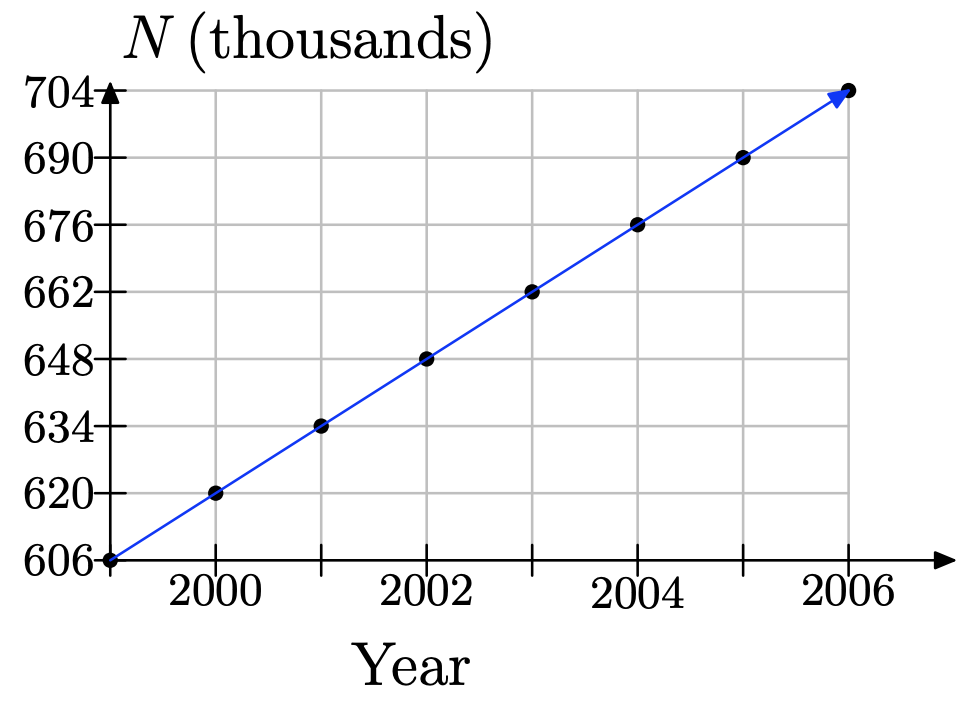
i. N(5) = 606000 + 14000(5) = 676000.

ii. It means that, according to our model, 5 years after 1999 (that is, in 2004), the number of inmates will be 676, 000.

iii. N(7) = 606000 + 14000(7) = 704000.

iv. It means that, according to our model, in 2006, the number of inmates will be 704, 000

3.2 Exercises

Suppose you are riding a bicycle up a hill as shown below.

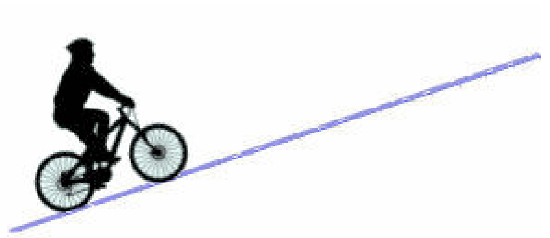
Figure \(\PageIndex{1}\). Riding a bicycle up a hill.

a) If the hill is straight as shown, consider the slant, or steepness, of its incline. As you ride up the hill, what can you say about the slant? Does it change? If so, how?

b) The slant is what mathematicians call the slope. To confirm your answer to part (a), you will place the hill on a coordinate system and compute its slope along various segments of the hill. See the figure below.

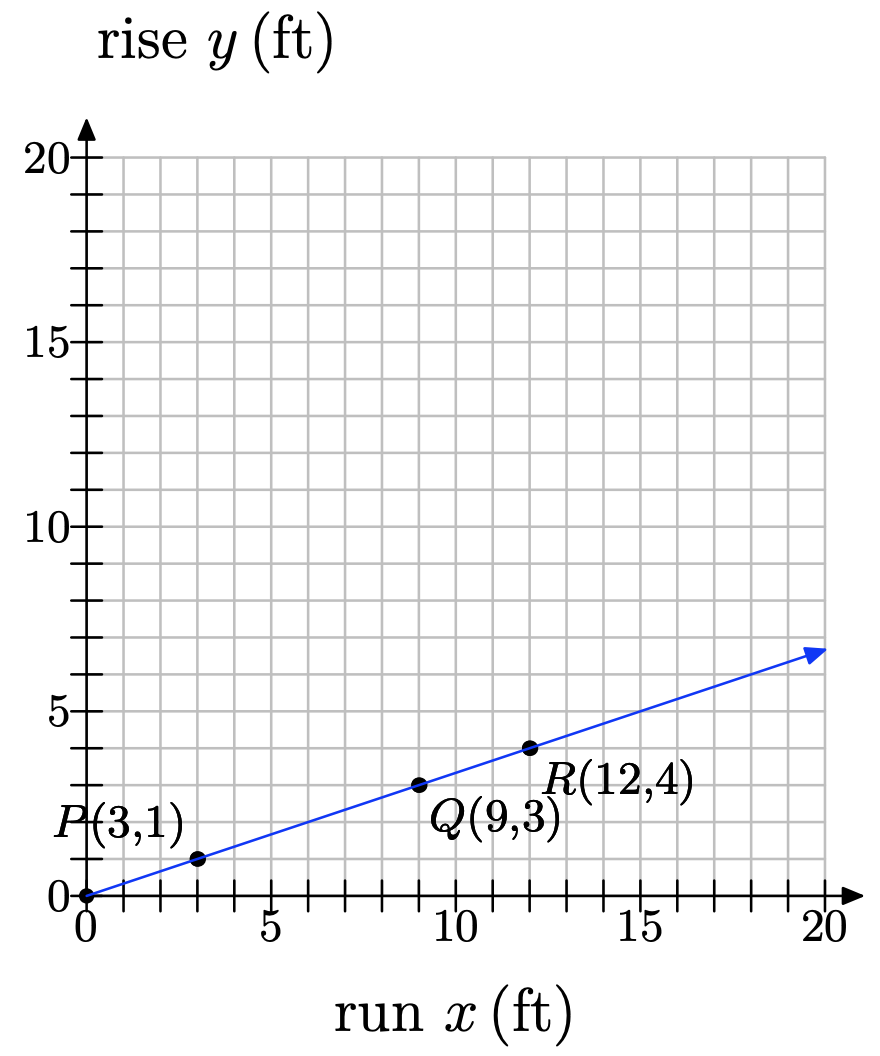
Three points–P, Q and R–have been labeled along the hill. We call the vertical distance (height) the rise and the horizontal distance the run. As you ride up the hill from point P to point Q, what is the rise? What is the run? Use these values to compute the slope from P to Q.

c) Now consider as you ride from P to R. What is the rise? What is the run? Use these values to compute the slope from P to R.

d) Finally, consider as you ride from Q to R. What is the rise? What is the run? Use these values to compute the slope from Q to R.

e) How do the values for slope from parts (b)-(d) compare? Do these results confirm your answer to part (a)?

f) Notice that the slope is positive in this example. In this context of riding a bicycle over a hill, what would negative slope mean?

a) No, it does not change. The slant is the same everywhere along the straight hill.

b) \(m_{PQ} = \dfrac{3−1 }{9−3} = \dfrac{2}{6} = \dfrac{1}{3}\)

c) \(m_{PR} = \dfrac{4−1 }{12−3} = \dfrac{3}{9} = \dfrac{1}{3}\)

d) \(m_{QR} = \dfrac{4-3}{12−9} = \dfrac{1}{3}\)

e) They are all the same. This makes sense because the slant or steepness of the hill is the same throughout.

f) Positive slope means that you are riding uphill; negative slope would mean that you are riding downhill.

Set up a coordinate system on a sheet of graph paper, plotting the points P(3, 4) and Q(−2, −7) and drawing the line through them.

a) What can you say about the slope of the line? Is it positive, zero, negative or undefined? Is the slope the same everywhere along the line, or does it change in places? If it does change, where are the slopes different?

b) Use your graph to determine the change in y (rise) and the change in x (run). Use these results to compute the slope of the line.

c) Use the slope formula to compute the slope of the line.

d) Does your numerical solution from part (c) agree with your graphical solution from part (b)? If not, check your work for errors.

Set up a coordinate system on a sheet of graph paper, plotting the points P(−1, 3) and Q(5, −3) and drawing the line through them.

a) The slope is negative because the line slants downhill. The slope is the same everywhere along the line because the slant of the line does not change.

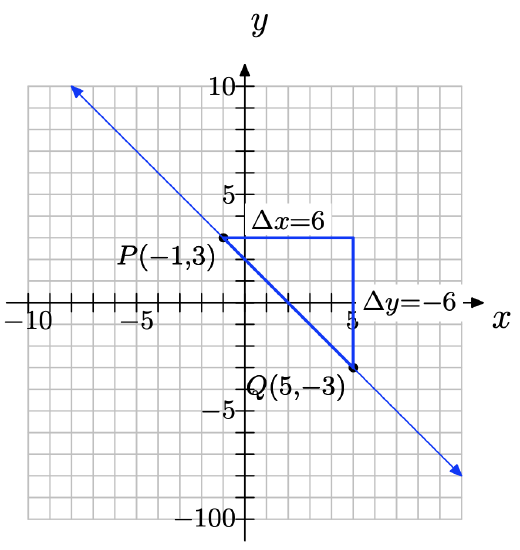
slope = −6/6 = −1

c) ∆y = −3 − (3) = −6; ∆x = 5 − (−1) = 6; slope = \dfrac{\delta y} {\delta x}\) =\( \dfrac{−6 }{6}\) = −1

In Exercises \(\PageIndex{4}\)-\(\PageIndex{10}\), perform each of the following tasks.

i. Make a sketch of a coordinate system; plot the given points, and draw the line through the points.

ii. Use the slope formula to compute the slope of the line through the given points. Reduce the slope where possible.

(0, 0) and (3, 4)

(−5, 2) and (0, 3)

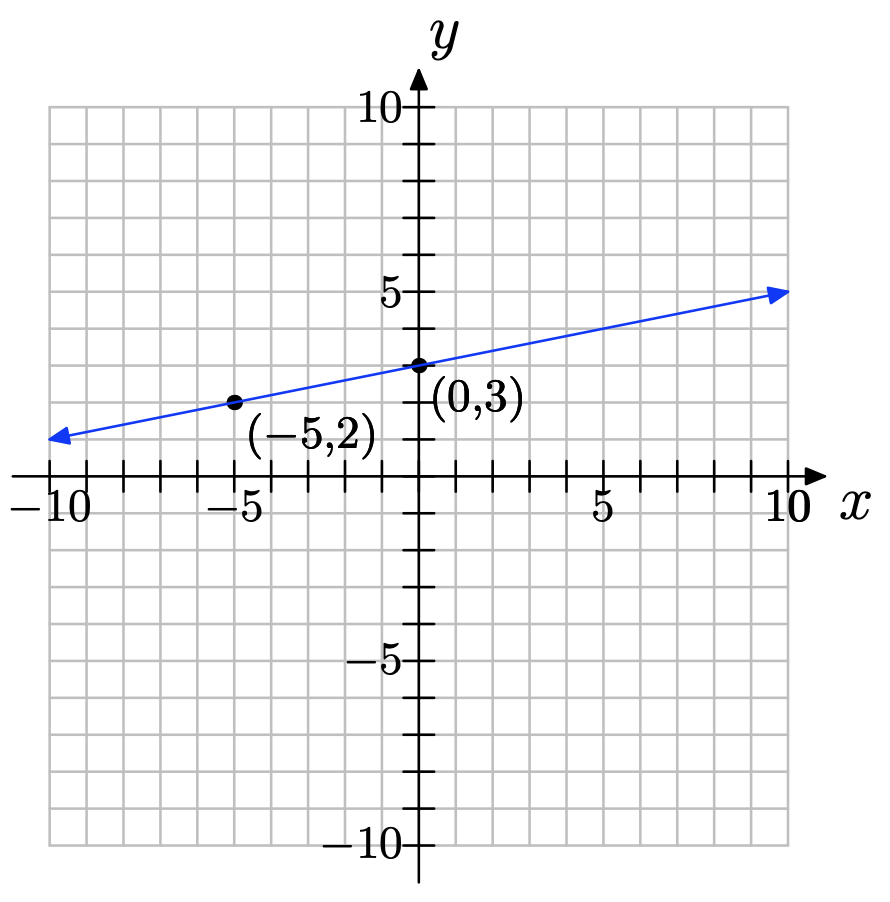
\(slope = \dfrac{3−2}{ 0−(−5)} = \dfrac{1}{5}\)

(−3, −3) and (6, −5)

(2, 0) and (2, 2)

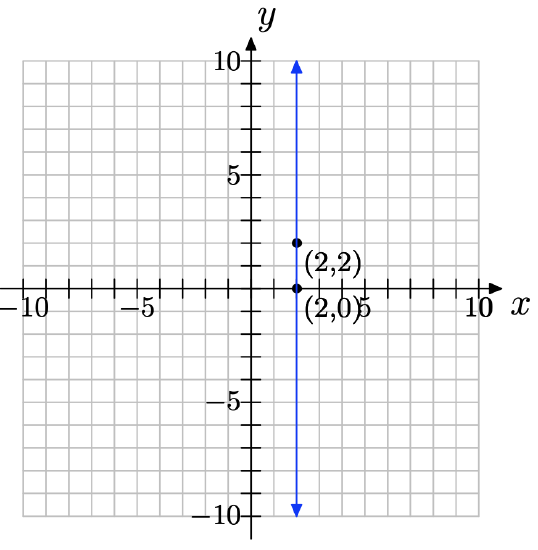
\(slope = \dfrac{2−0 }{2−2} = \dfrac{2}{0}\) = undefined

(−9, −3) and (6, −3)

(−8, 4) and (3, −8)

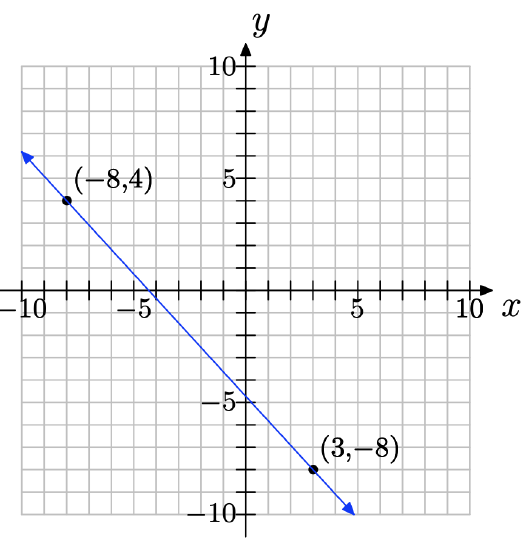
\(slope = \dfrac{−8−4}{ 3−(−8)} = \dfrac{−12}{ 11}\)

(−2, 6) and (5, −2)

For the following line, two convenient points P and Q have been chosen. We chose two points that were at the corners of boxes on our grid so their coordinates are easy to read.

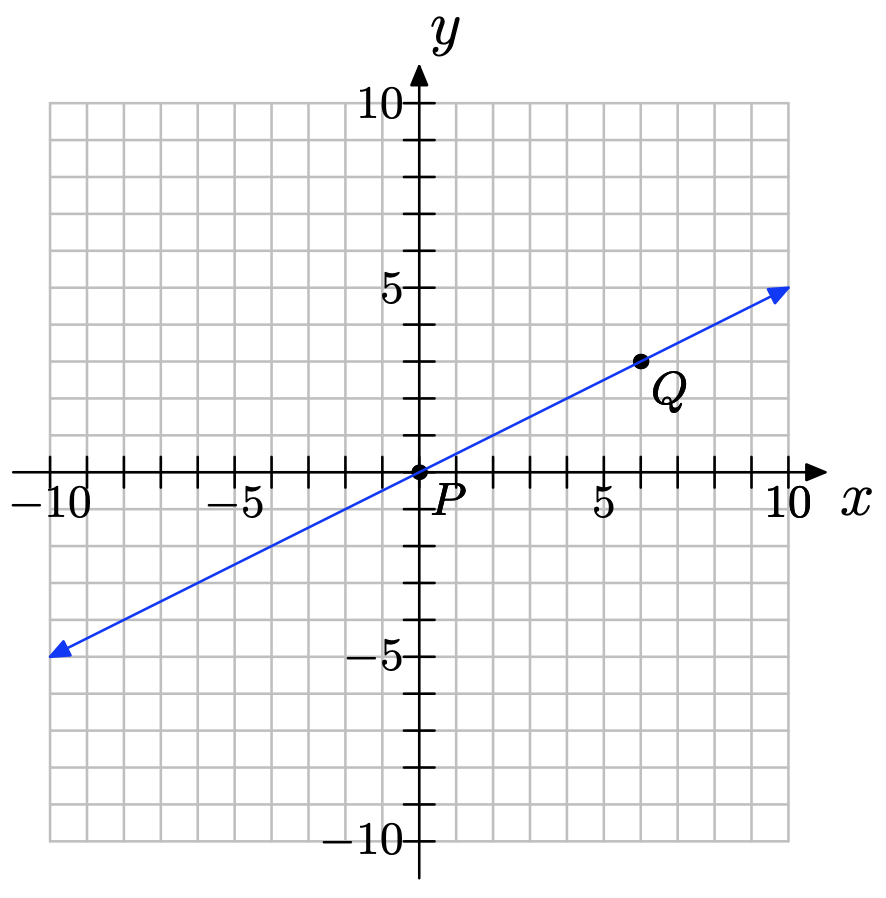
a) Label their coordinates.

b) Thinking of P as the starting point and Q as the ending point, draw a right triangle joining the points.

c) Clearly state the change in y (rise) and the change in x (run) from P to Q.

d) Compute the slope.

a) The points are (0, 0) and (6, 3).

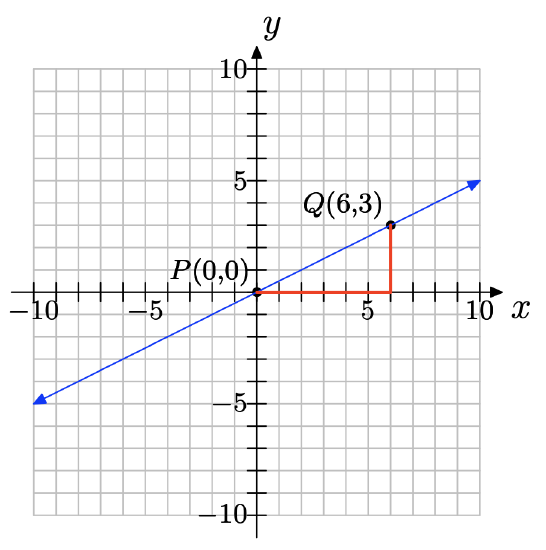
c) ∆y = 3 − 0 = 3; ∆x = 6 − 0 = 6

d) slope = \(\dfrac{\delta y}{\delta x} =\dfrac{3}{6} = \dfrac{1}{ 2}\)

For the following line, two convenient points A and B have been chosen. We chose two points that were at the corners of boxes on our grid so their coordinates are easy to read.

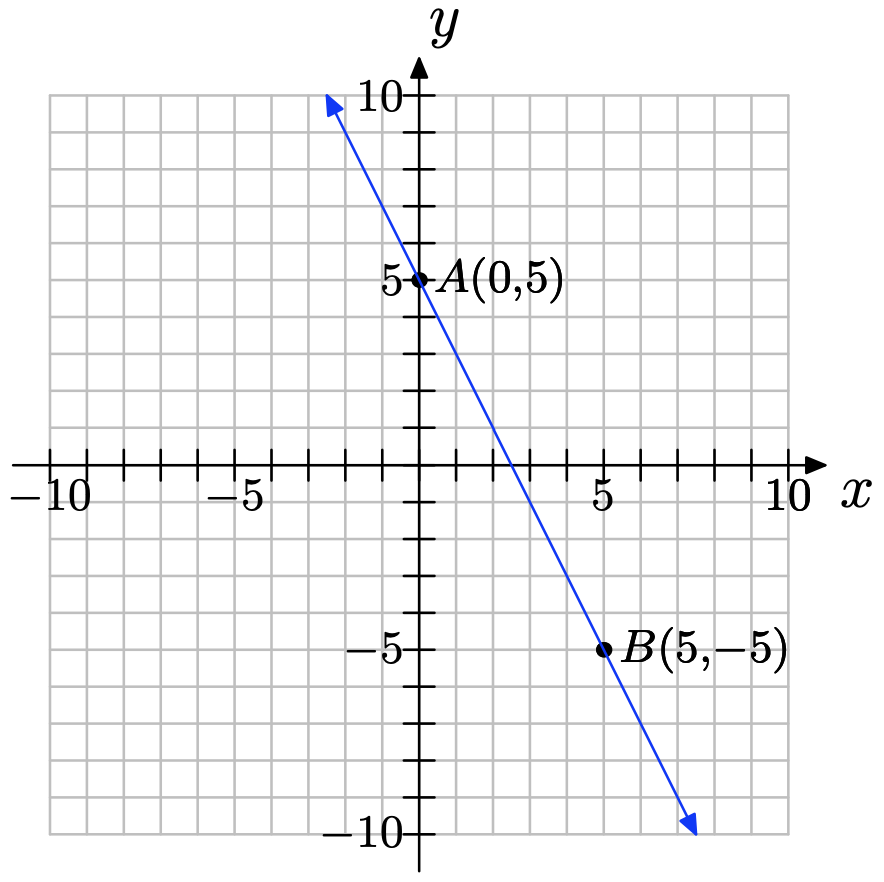
b) Thinking of A as the starting point and B as the ending point, draw a right triangle joining the points.

c) Clearly state the change in y (rise) and the change in x (run) from A to B.

Copy the coordinate system below onto a sheet of graph paper. Then do the following:

a) Select any two convenient points P and Q on the graph of the line. Label each point with its coordinates.

b) Clearly state the change in y (rise) and the change in x (run). Compute the slope of the line.

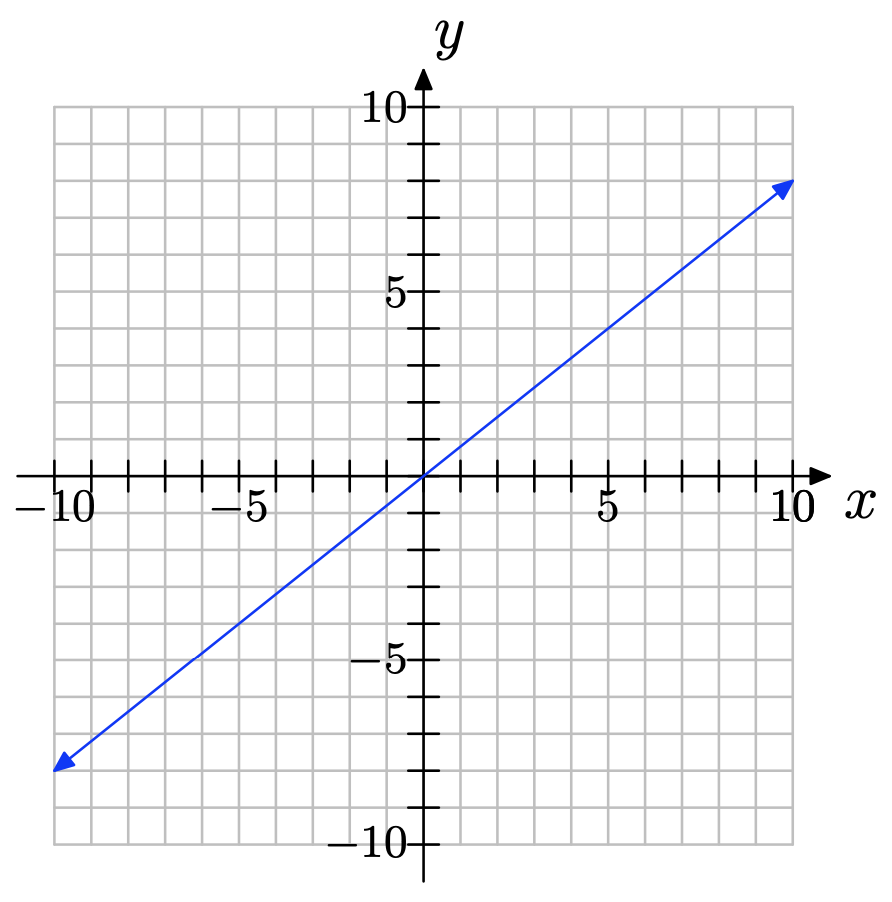
NOTE: Solutions may vary depending on which two convenient points were chosen.

a) You can pick any two points on the line; for example, (0, 0) and (5, 4) as shown below.

b) ∆y = 4 − 0 = 4; ∆x = 5 − 0 = 5; slope = \(\dfrac{\delta y }{\delta x} = \dfrac{4}{5}\)

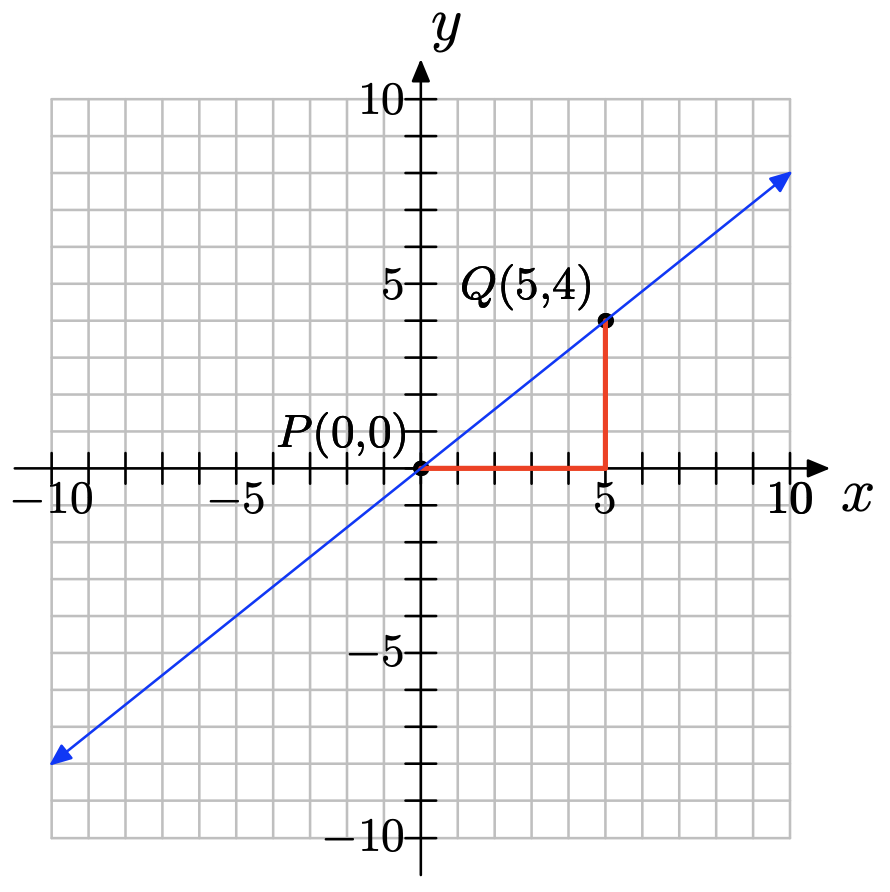
Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

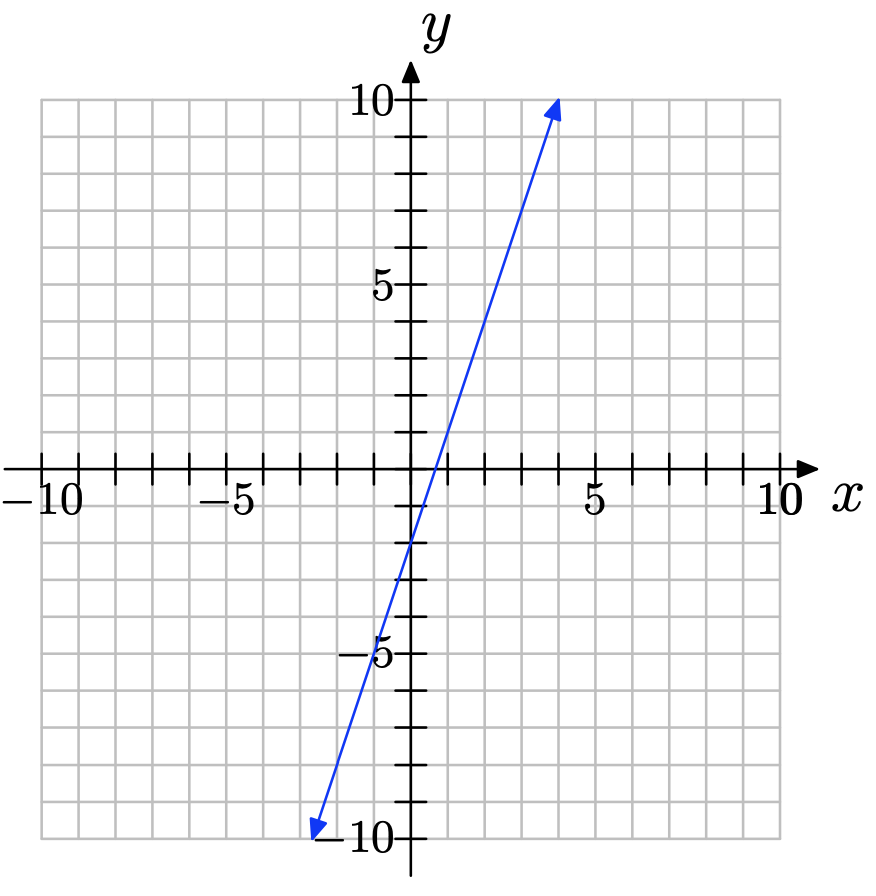
a) You can pick any two points on the line; for example, (1, 1) and (3, 7) as shown below.

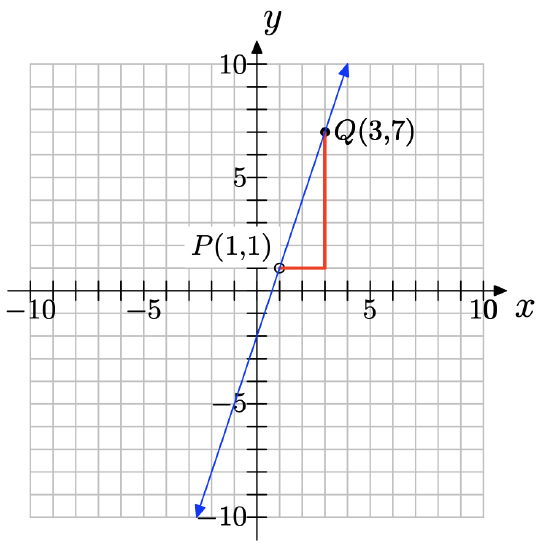
b) ∆y = 7 − 1 = 6; ∆x = 3 − 1 = 2; slope =\( \dfrac{\delta y }{\delta x} = \dfrac{6}{2} = 3\)

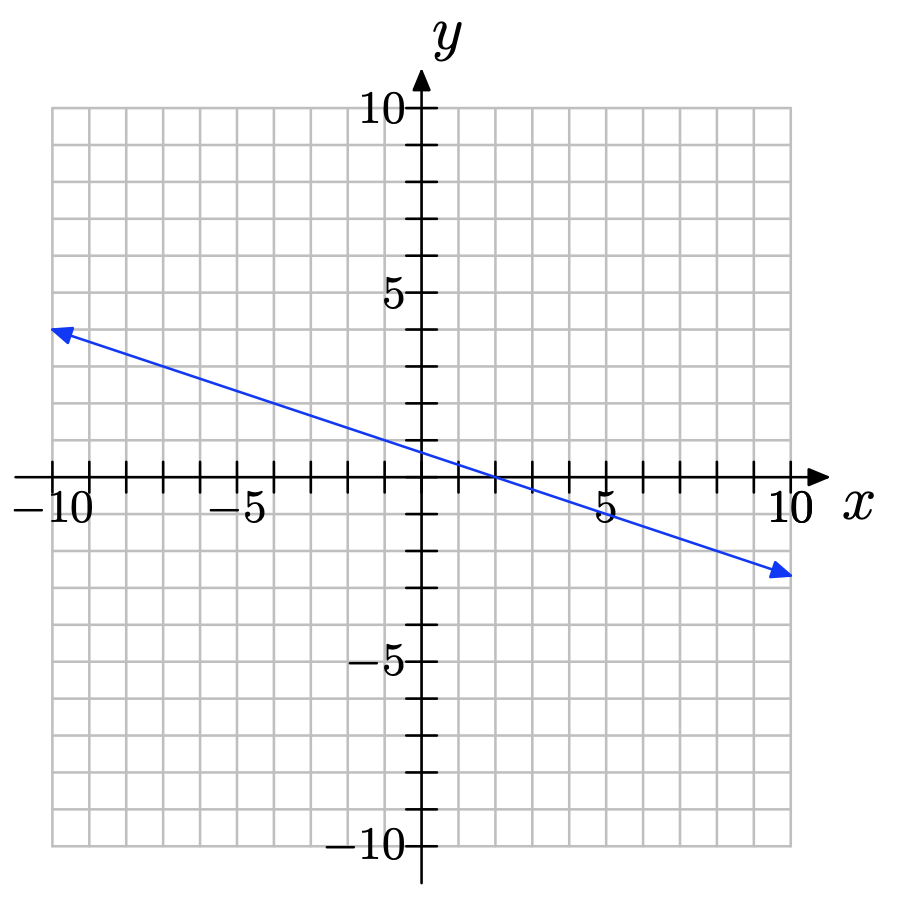
Exercise \(\PageIndex{16}\)

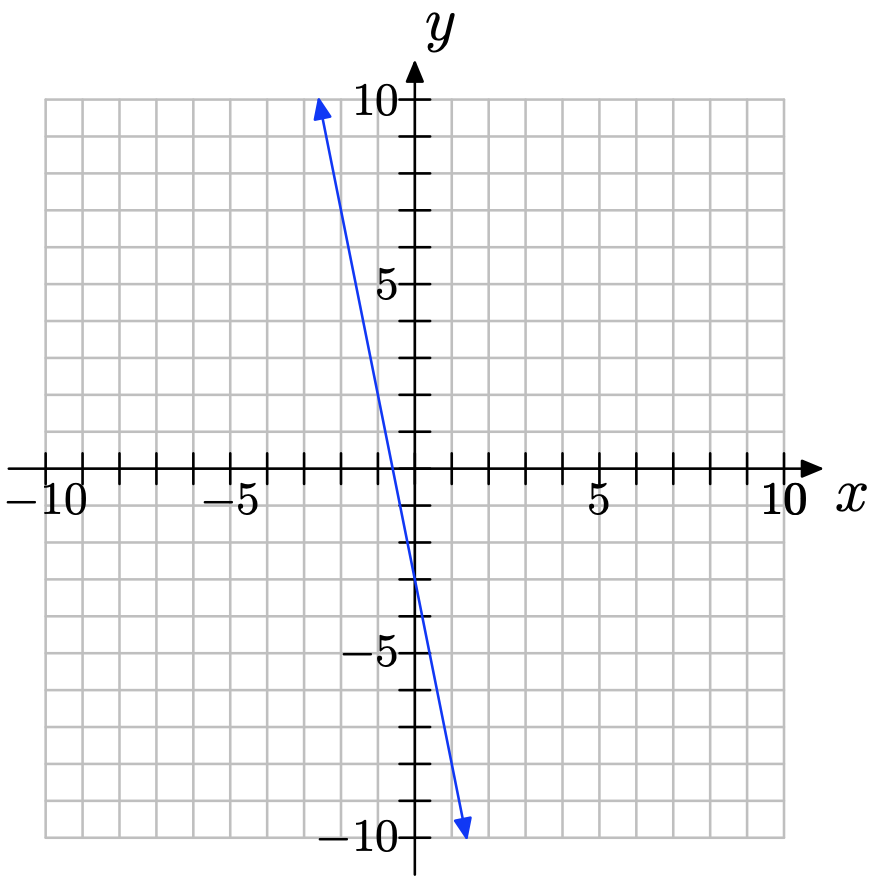
Exercise \(\PageIndex{17}\)

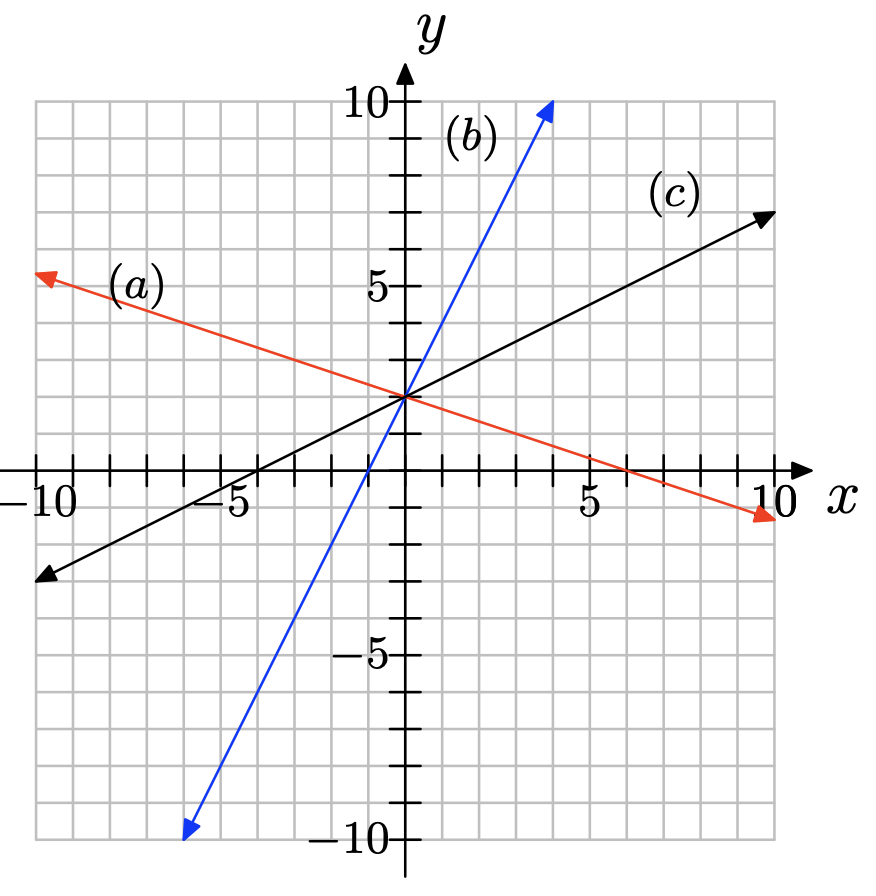
The following coordinate system shows the graphs of three lines, each with different slope. Match each slope with (a), (b), or (c) appropriately.

slope = 2/3

slope = −2

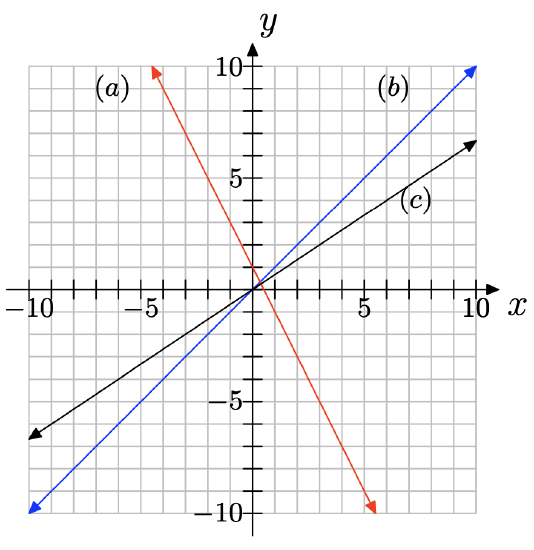
slope = 1: (b)

slope = 2/3: (c)

slope = −2: (a)

Exercise \(\PageIndex{18}\)

slope = −1/3

slope = 1/2

Exercise \(\PageIndex{19}\)

Draw a coordinate system on a sheet of graph paper for which the x- and y-axes both range from −10 to 10.

a) Draw a line that contains the point (0, 1) and has slope 2. Label the line as (a).

b) On the same coordinate system, draw a line that contains the point (0, 1) and has slope −1/2. Label it as (b).

c) Use the slopes of these two lines to show that they are perpendicular.

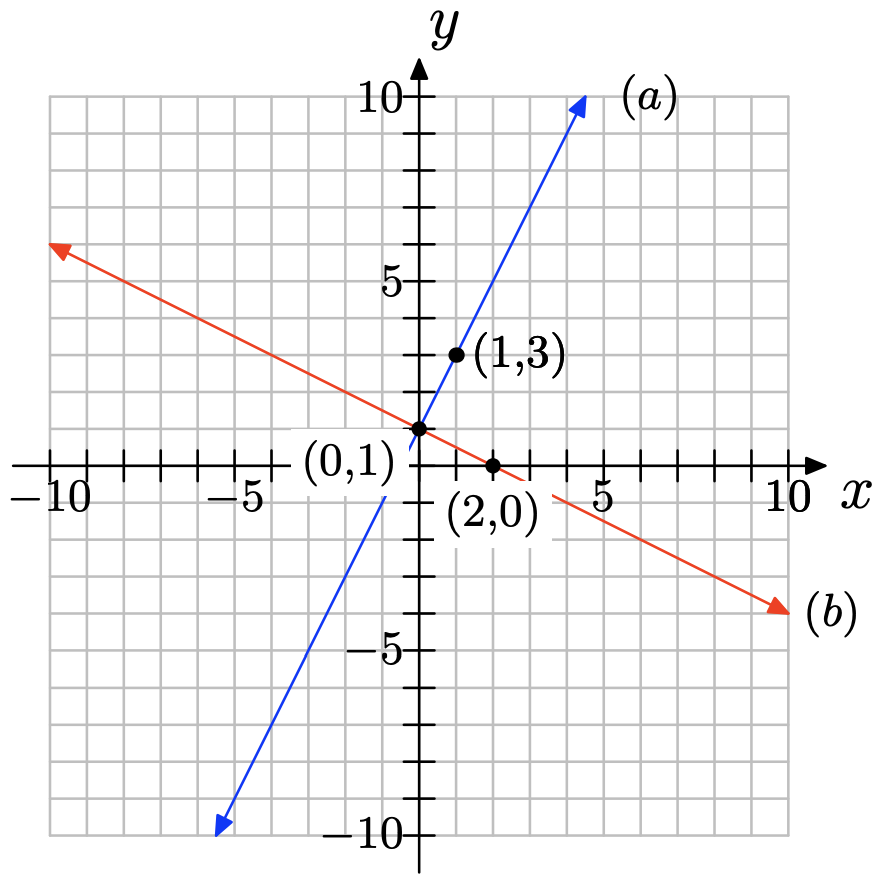
c) \(m_{1}m_{2} = 2(−1/2) = −1\), so the lines are perpendicular.

Exercise \(\PageIndex{20}\)

a) Draw a line that contains the point (1, −2) and has slope 1/3. Label the line as (a).

b) On the same coordinate system, draw a line that contains the point (0, 1) and has slope −3. Label it as (b).

Exercise \(\PageIndex{21}\)

Draw a line through the point P(1, 3) that is parallel to the line through the origin with slope −1/4.

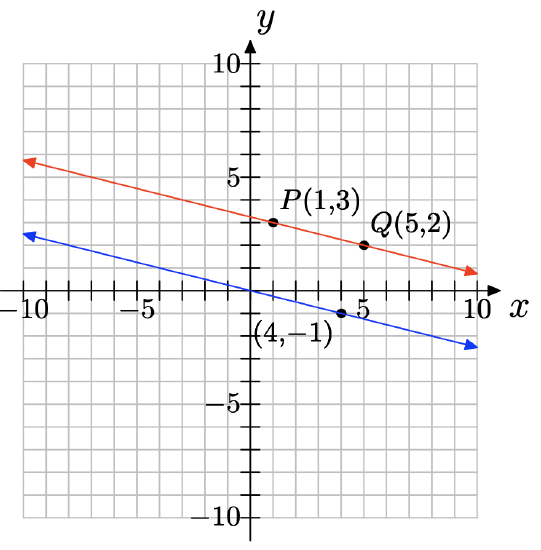
Exercise \(\PageIndex{22}\)

Draw a line through the point P(1,3) that is parallel to the line through the origin with slope 3/5.

Exercise \(\PageIndex{23}\)

a) Draw a line that contains the point (−1, −2) and has slope 3/4. Label the line as (a).

b) On the same coordinate system, draw a line that contains the point (0, 1) and has slope 4/3. Label it as (b).

c) Are these lines parallel, perpendicular or neither? Show using their slopes.

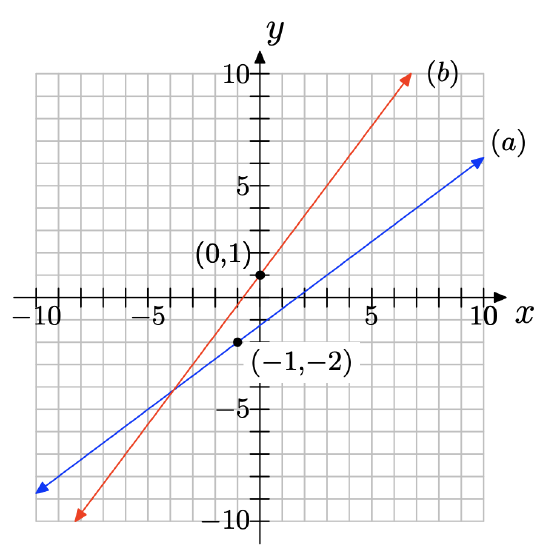
c) \(m_{1}m_{2} = (4/3)(3/4) = 1 \neq −1\), so the lines are not perpendicular; the slopes are not equal, so the lines are not parallel, either. Thus, the lines may be classified as neither parallel nor perpendicular.

Exercise \(\PageIndex{24}\)

Graph a coordinate system on a sheet of graph paper for which the x- and y-axes both range from −10 to 10.

a) Draw a line that contains the point (−4, 0) and has slope 1. Label the line as (a).

b) On the same coordinate system, draw a line that contains the point (0, 2) and has slope −1. Label it as (b).

Exercise \(\PageIndex{25}\)

Figure \(\PageIndex{2}\). A grade is a way of expressing slope.

On the road from Fort Bragg to Willits or from Fort Bragg to Santa Rosa, one often passes signs like that shown above. A grade is just slope expressed as a percent instead of a fraction or decimal. In other words, the grade measures the steepness of the road just as slope does.

a) An 80 /0 grade means that, for every horizontal distance of 100 ft, the road rises or drops 8 ft (depending on whether you are going uphill or downhill). Write 80 /0 grade as slope in reduced fractional form.

b) Suppose a hill drops 16 ft for every 180 ft horizontally. Find the grade of the hill to the nearest tenth of a percent.

c) Explain in a complete sentence or sentences what a grade of 00 /0 would represent.

a) grade \(=\dfrac{ 8}{ 100} = \dfrac{2}{ 25}\)

b) grade \(= \dfrac{16}{ 180} = \dfrac{4}{ 45} = 8.90 \)%

c) 0% grade represents no grade or slope; that is, a flat road.

3.3 Exercises

In Exercises \(\PageIndex{1}\)-\(\PageIndex{6}\), perform each of the following tasks for the given linear function.

i. Set up a coordinate system on a sheet of graph paper. Label and scale each axis. Remember to draw all lines with a ruler.

ii. Identify the slope and y-intercept of the graph of the given linear function.

iii. Use the slope and y-intercept to draw the graph of the given linear function on your coordinate system. Label the y-intercept with its coordinate and the graph with its equation.

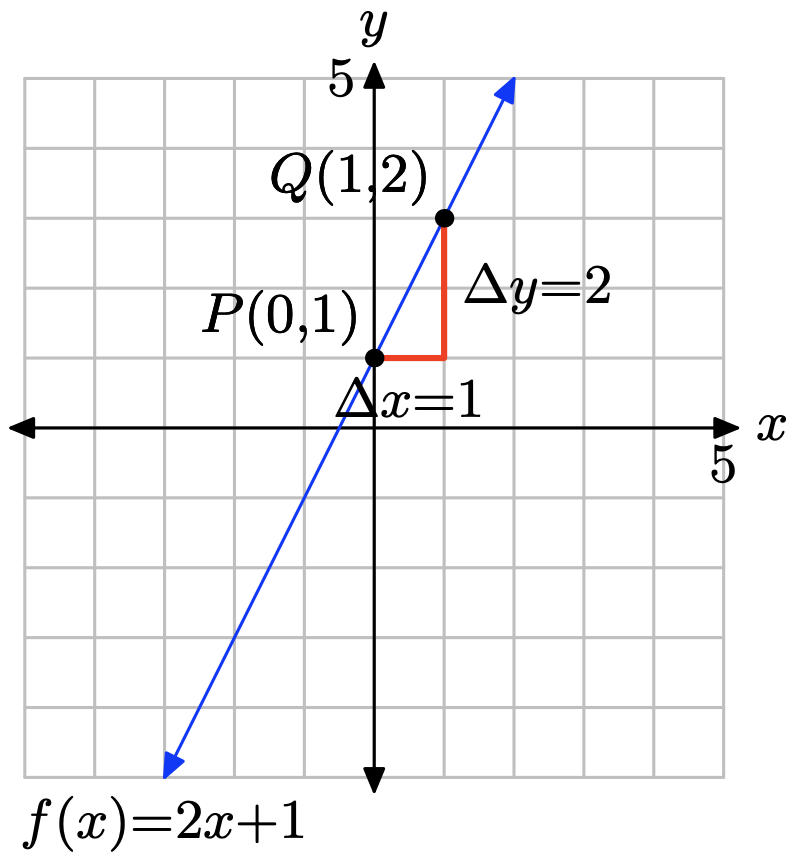
f(x) = 2x + 1

Compare f(x) = 2x + 1 with f(x) = mx + b. Note that the slope is m = 2 and the y-coordinate of the y-intercept is b = 1. Therefore, the y-intercept will be the point (0, 1). Plot the point P(0, 1). To obtain a line of slope m = 2/1, start at the point P(0, 1), then move 1 unit to the right and 2 units upward, arriving at the point Q(1, 3), as shown in the figure below. The line through the points P and Q is the required line.

f(x) = −2x + 3

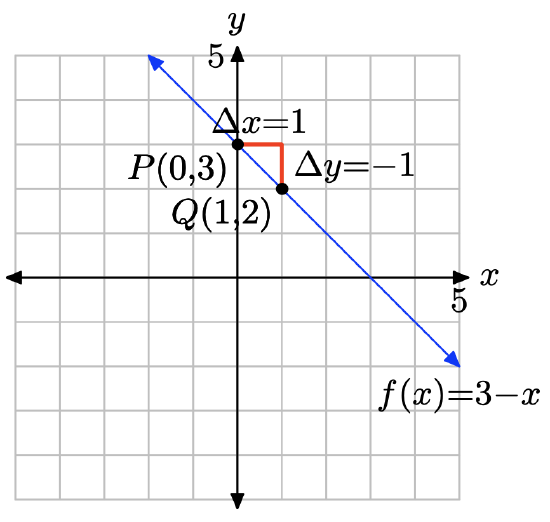
f(x) = 3 − x

Compare f(x) = 3 − x, or equivalently f(x) = −x + 3, with f(x) = mx + b. Note that the slope is m = −1 and the y-coordinate of the y-intercept is b = 3. Therefore, the y-intercept will be the point (0, 3). Plot the point P(0, 3). To obtain a line of slope m = −1, start at the point P(0, 3), then move 1 unit to the right and 1 units downward, arriving at the point Q(1, 2), as shown in the figure below. The line through the points P and Q is the required line.

f(x) = 2 − 3x

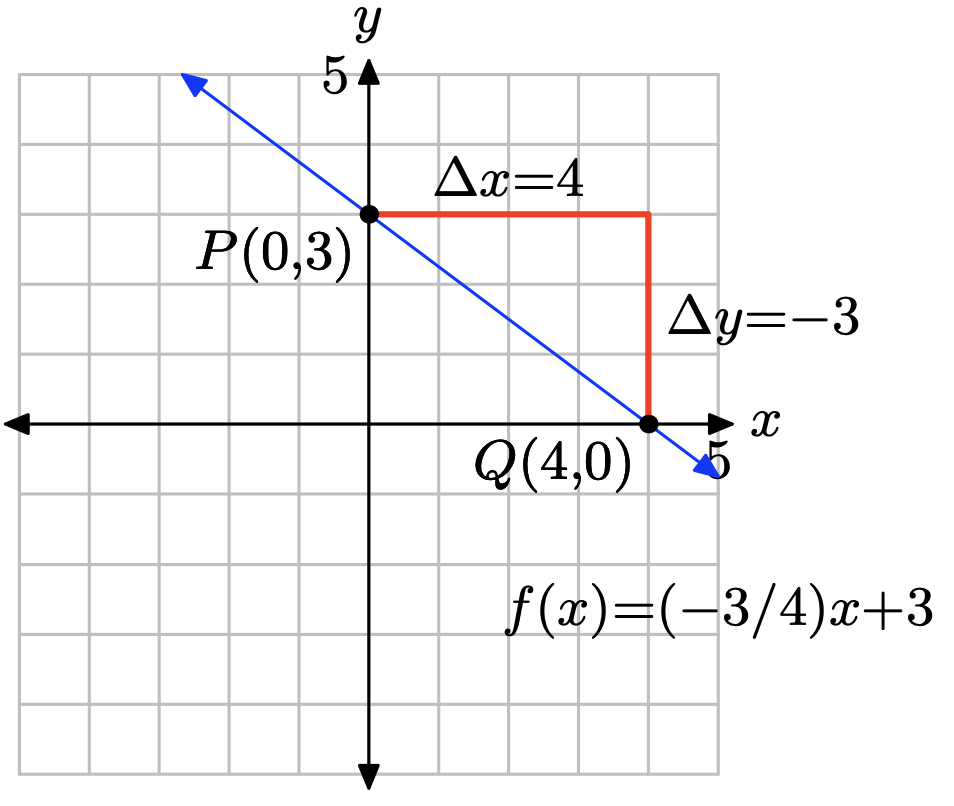
\(f(x) = −\frac{3}{4} x + 3\)

Compare f(x) = (−3/4)x+3 with f(x) = mx+b. Note that the slope is m = −3/4 and the y-coordinate of the y-intercept is b = 3. Therefore, the y-intercept will be the point (0, 3). Plot the point P(0, 3). To obtain a line of slope m = −3/4, start at the point P(0, 3), then move 4 units to the right and 3 units downward, arriving at the point Q(4, 0), as shown in the figure below. The line through the points P and Q is the required line.

\(f(x) = \frac{2}{3} x − 2\)

In Exercises \(\PageIndex{7}\)-\(\PageIndex{12}\), perform each of the following tasks.

i. Make a copy of the given graph on a sheet of graph paper.

ii. Label the y-intercept with its coordinates, then draw a right triangle and label the sides to help identify the slope.

iii. Label the line with its equation.

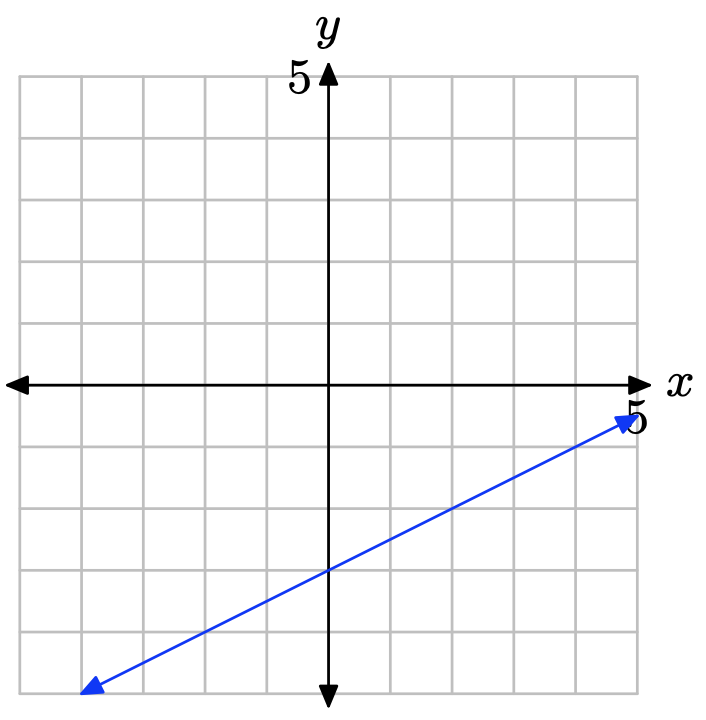
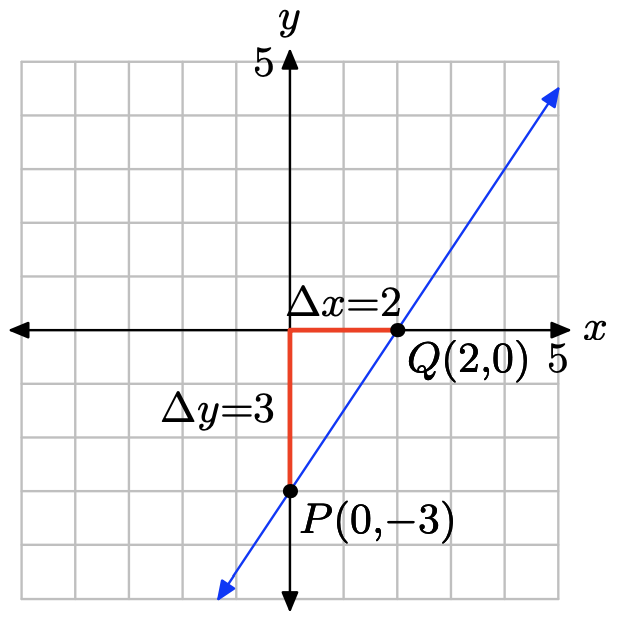
The slope is found by dividing the rise by the run (see figure). Hence, the slope is 1/2. The y-intercept is found by noting where the graph of the line crosses the y-axis (see figure), in this case, at (0, −3). Hence, m = 1/2 and b = −3, so the equation of the line in slope intercept form is

\[y = mx + b \quad \text{or} \quad y = \frac{1}{2}x − 3 \nonumber \]

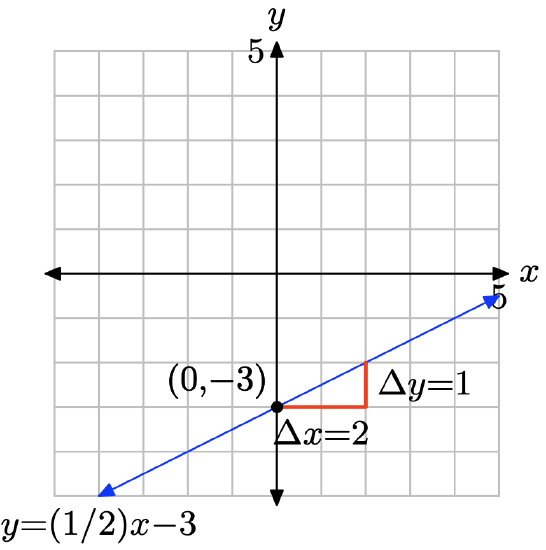
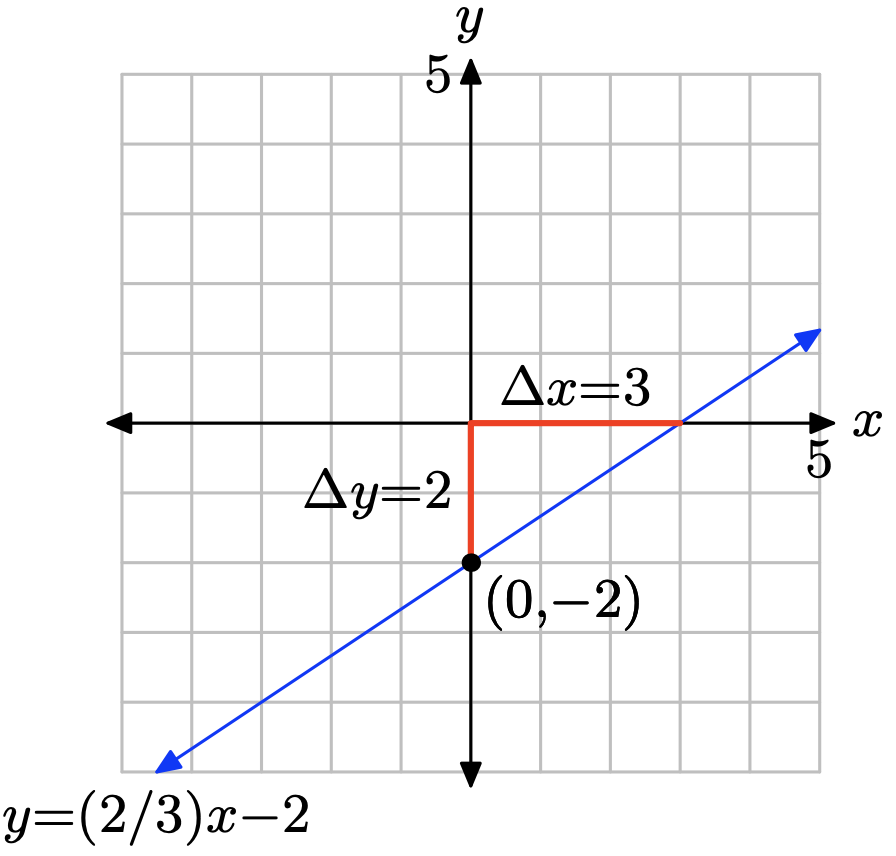
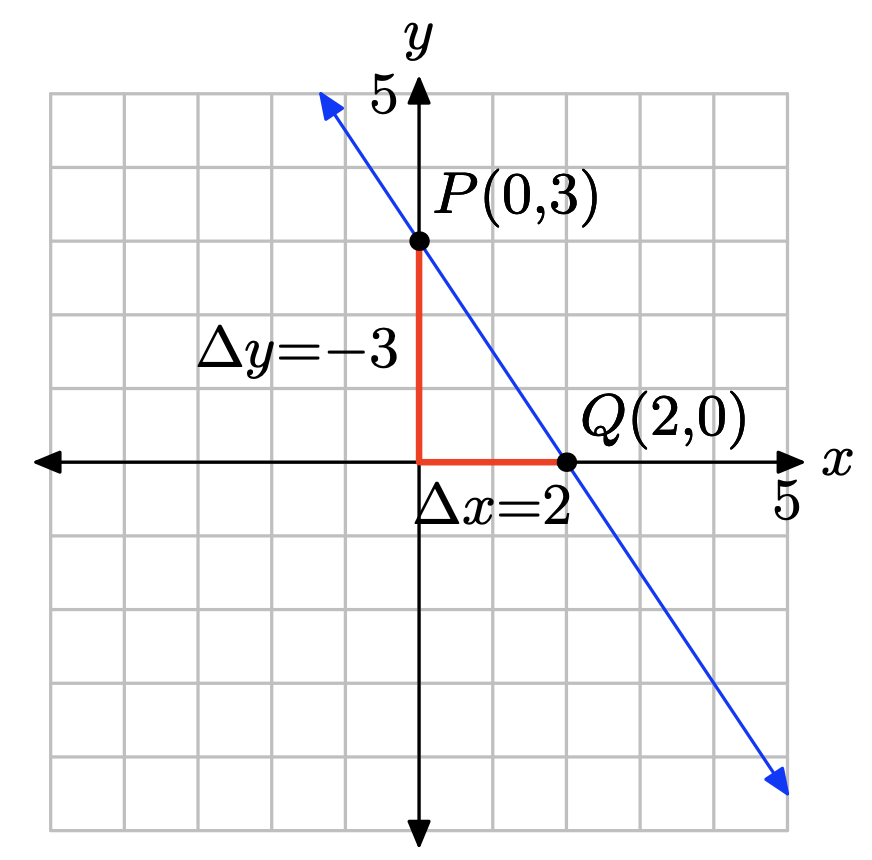
The slope is found by dividing the rise by the run (see figure). Hence, the slope is 2/3. The y-intercept is found by noting where the graph of the line crosses the y-axis (see figure), in this case, at (0, −2). Hence, m = 2/3 and b = −2, so the equation of the line in slope intercept form is

\[y = mx + b \quad \text{or} \quad y = \frac{2}{3}x − 2 \nonumber \]

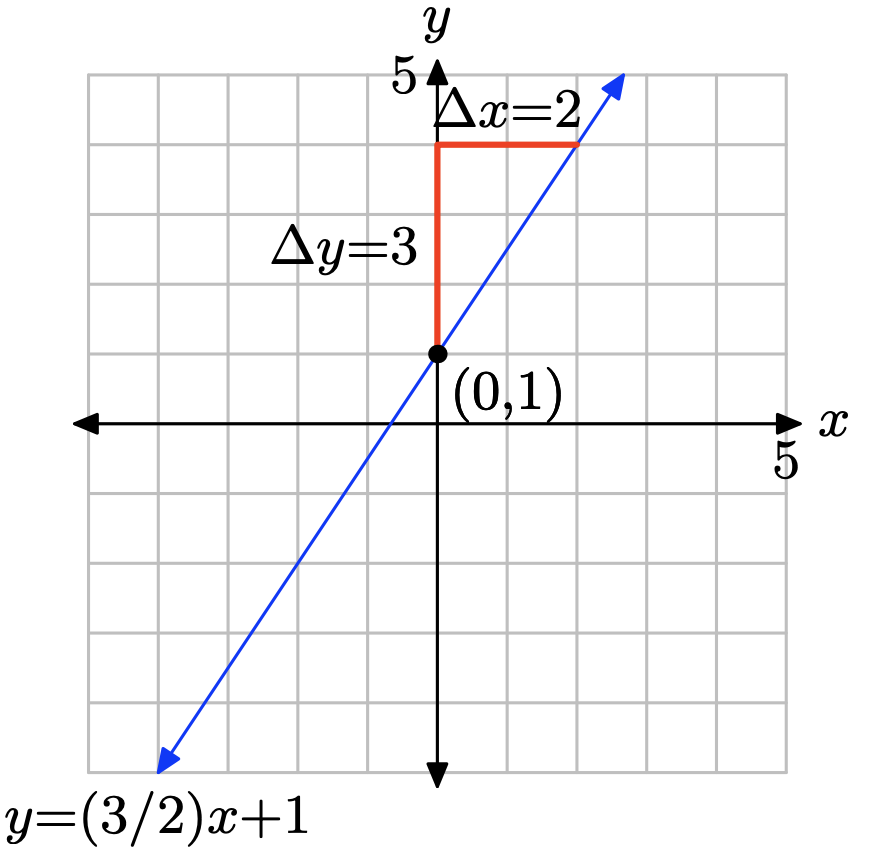
The slope is found by dividing the rise by the run (see figure). Hence, the slope is 3/2. The y-intercept is found by noting where the graph of the line crosses the y-axis (see figure), in this case, at (0, 1). Hence, m = 3/2 and b = 1, so the equation of the line in slope intercept form is

\[y = mx + b \quad \text{or} \quad y = \frac{3}{2}x + 1 \nonumber \]

Kate makes $39, 000 per year and gets a raise of $1000 each year. Since her salary depends on the year, let time t represent the year, with t = 0 being the present year, and place it along the horizontal axis. Let salary S, in thousands of dollars, be the dependent variable and place it along the vertical axis. We will assume that the rate of increase of $1000 per year is constant, so we can model this situation with a linear function.

a) On a sheet of graph paper, make a graph to model this situation, going as far as t = 10 years.

b) What is the S-intercept?

c) What is the slope?

d) Suppose we want to predict Kate’s salary in 20 years or 30 years. We cannot use the graphical model because it only shows up to t = 10 years. We could draw a larger graph, but what if we then wanted to predict 50 years into the future? The point is that a graphical model is limited to what it shows. A model algebraic function, however, can be used to predict for any year! Find the slope-intercept form of the linear function that models Kate’s salary.

e) Write the function using function notation, which emphasizes that S is a function of t.

f) Now use the algebraic model from (e) to predict Kate’s salary 10 years, 20 years, 30 years, and 50 years into the future.

g) Compute S(40).

h) In a complete sentence, explain what the value of S(40) from part (g) means in the context of the problem.

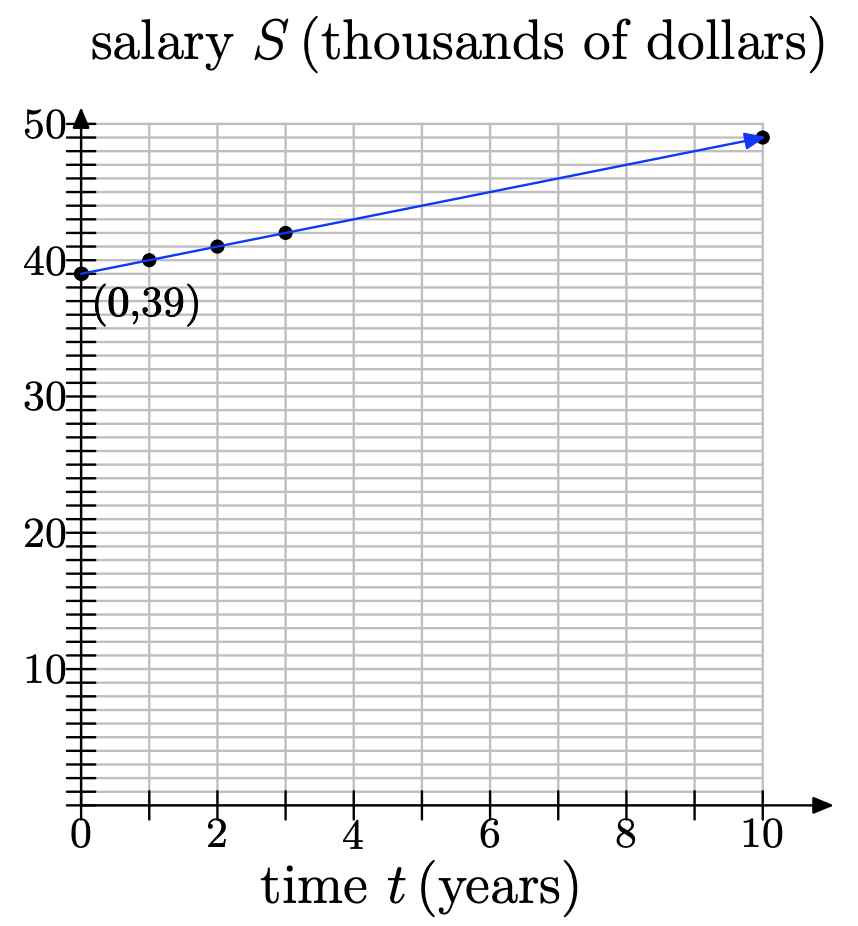
b) At t = 0 (present year), her salary is $39, 000. Since S is in thousands of dollars, S = 39 when t = 0. So the S-intercept is (0, 39).

c) The increase in Kate’s salary is $1, 000 per year, but S is in thousands of dollars, so the rate of increase in S is 1. That is, the slope is 1.

d) Using the slope-intercept form, we get S = t + 39.

e) S(t) = t + 39.

• To find Kate’s salary in 10 years, compute S(10) = 10 + 39 = 49, which means that she will be earning $49, 000 per year.
• To find Kate’s salary in 20 years, compute S(20) = 20 + 39 = 59, which means that she will be earning $59, 000 per year.
• To find Kate’s salary in 30 years, compute S(30) = 30 + 39 = 69, which means that she will be earning $69, 000 per year.
• To find Kate’s salary in 50 years, compute S(50) = 50 + 39 = 89, which means that she will be earning $89, 000 per year.

g) S(40) = 40 + 39 = 79. h) If the current rate of increase continues, in 40 years Kate’s salary will be $79, 000.

For each DVD that Blue Charles Co. sells, they make 5c profit. Profit depends on the number of DVD’s sold, so let number sold n be the independent variable and profit P, in $, be the dependent variable.

a) On a sheet of graph paper, make a graph to model this situation, going as far as n = 15.

b) Use the graph to predict the profit if n = 10 DVD’s are sold.

c) The graphical model is limited to predicting for values of n on your graph. Any larger value of n necessitates a larger graph, or a different kind of model. To begin finding an algebraic model, identify the P-intercept of the graph.

d) What is the slope of the line in your graphical model?

e) Find a slope-intercept form of a linear function that models Blue Charles Co.’s sales.

f) Write the function using function notation.

g) Explain why this model does not have the same limitation as the graphical model.

h) Find P(100), P(1000), and P(10000).

i) In complete sentences, explain what the values of P(100), P(1000), and P(10000) mean in the context of the problem.

Enrique had $1, 000 saved when he began to put away an additional $25 each month.

a) Let t represent time, in months, and S represent Enrique’s savings, in $. Identify which should be the independent and dependent variables.

b) To begin finding a linear function to model this situation, identify the S-intercept and slope.

c) Find a slope-intercept form of a linear function to model Enrique’s savings over time.

d) Write the linear function in function notation.

e) Use the function model to predict how much will be in his savings in one year.

f) Use the function model to predict when will he have $2000 saved.

g) Graph the function on a coordinate system.

h) At the same time, Anne-Marie also begins to save $25 per month, but she begins with $1200 already in her savings. Make a graphical model of her situation and place it on the same coordinate system as the graphical model for Enrique’s savings. Label it appropriately.

i) How do the lines compare to each other? Say something about their slopes.

j) Find a slope-intercept form of a linear function that models Anne-Marie’s savings. Use the same variables as you did for Enrique’s model.

k) Write the function using function notation.

l) Prove that the graphs of the two functions are parallel lines.

m) For Anne-Marie, looking at the graphs, do you think it will take her more time or less time than Enrique to save up $2000?

n) Use the linear function model for Anne-Marie to predict how long it will take her to save $2000. Does this agree with your expectation from (m)?

a) t should be the independent variable and S should be the dependent variable.

b) S-intercept = (0, 1000); slope = 25

c) S = 25t + 1000

d) S(t) = 25t + 1000

e) S(12) = 25(12) + 1000 = 1300

f) Set S=2000 and solve for t. 2000 = 25t + 1000 1000 = 25t 40 = t So it will take 40 months for him to reach $2000.

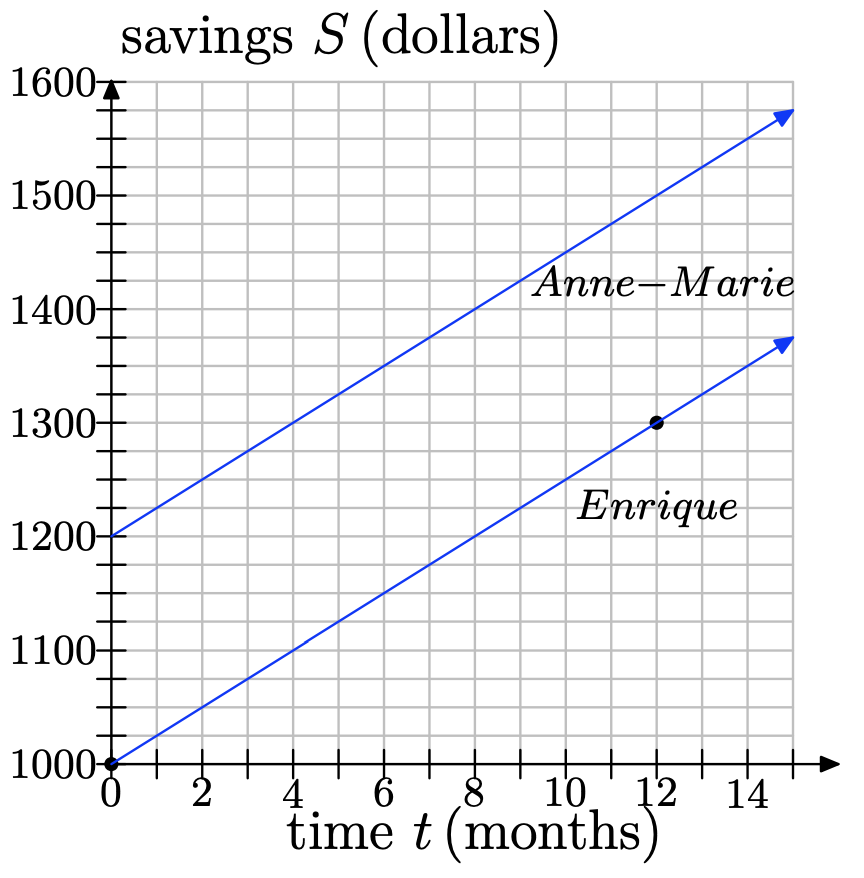
i) The lines have the same slope; they are parallel.

j) S = 25t + 1200

k) S(t) = 25t + 1200

l) They are lines because they are in the y = mx + b form. They are parallel because their slopes are equal (both are 25).

m) It should take her less time because her graph is above Enrique’s graph. This makes sense intuitively since she began with more money than he did.

n) Set S=2000 and solve for t. 2000 = 25t + 1200 800 = 25t 32 = t So it will take 32 months for her to reach $2000. This agrees with our expectation from (m): It takes her less time than Enrique

Jose is initially 400 meters away from the bus stop. He starts running toward the stop at a rate of 5 meters per second.

a) Express Jose’s distance d from the bus stop as a function of time t.

b) Use your model to determine Jose’s distance from the bus stop after one minute.

c) Use your model to determine the time it will take Jose to reach the bus stop.

A ball is dropped from rest above the surface of the earth. As it falls, its speed increases at a constant rate of 32 feet per second per second.

a) Express the speed v of the ball as a function of time t.

b) Use your model to determine the speed of the ball after 5 seconds.

c) Use your model to determine the time it will take for the ball to achieve a speed of 256 feet per second.

a) We will do a “rough” plot of speed v versus time t. Speed depends upon time, so we place the speed on the vertical axis and the time on the horizontal axis in the figure that follows. The intial speed is 0 ft/s, which give us the v-intercept at P(0, 0). The rate at which the speed is increasing (acceleration) is constant and will be the slope of the line; i.e., the slope of the line is m = 32 ft/s2 (32 feet per second per second).

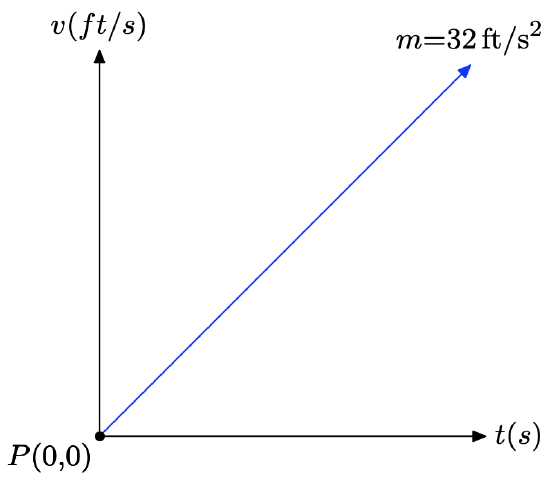
Because we know the slope and intercept of the line, we can use the slope intercept form y = mx + b and substitute m = 32 and b = 0 to obtain

\[y = mx + b\\ y = 32x + 0 \\y = 32x \nonumber \]

However, we are using v and t in place of y and x, so we replace these in the last formula to obtain

\[v = 32t \nonumber \]

or using function notation,

\[v(t) = 32t \nonumber \] b) To find the speed of the ball after 5 seconds, substitute t = 5 into the equation developed in the previous part.

\[v(t) = 32t \\ v(5) = 32(5) \\ v(5) = 160 \nonumber \]

Hence, the speed of the ball after 5 seconds is 160 feet per second.

c) To find the time it takes the ball to reach 256 feet per second, we must find t so that v(t) = 256.

\[v(t) = 256\\ 32t = 256\\ t = 8 \nonumber \]

Thus, it takes 8 seconds for the ball to attain a speed of 256 feet per second.

A ball is thrown into the air with an initial speed of 200 meters per second. It immediately begins to lose speed at a rate of 9.5 meters per second per second.

c) Use your model to determine the time it will take for the ball to achieve its maximum height.

In Exercises \(\PageIndex{19}\)-\(\PageIndex{24}\), a linear function is given in standard form Ax + By = C. In each case, solve the given equation for y, placing the equation in slope-intercept form. Use the slope and intercept to draw the graph of the equation on a sheet of graph paper.

3x − 2y = 6

Place 3x − 2y = 6 in slope-intercept form. First subtract 3x from both sides of the equation, then divide both sides of the resulting equation by −2.

\[\begin{array} {lll} 3x − 2y & = &6 −2 \\ y &=& −3x + 6 \\ y &= &\frac{3}{2}x − 3 \end{array} \nonumber \]

Compare y = (3/2)x − 3 with y = mx + b to see that the slope is m = 3/2 and the y-coordinate of the y-intercept is b = −3. Therefore, the y-intercept will be the point (0, −3). Plot the point P(0, −3). To obtain a line of slope m = 3/2, start at the point P(0, −3), then move 3 units up and 2 units to the right, arriving at the point Q(2, 0), as shown in the figure below. The line through the points P and Q is the required line.

3x + 5y = 15

3x + 2y = 6

Place 3x + 2y = 6 in slope-intercept form. First subtract 3x from both sides of the equation, then divide both sides of the resulting equation by 2.

\[\begin{array}{lll} 3x + 2y & =& 6 \\ 2y &=& −3x + 6 \\ y &=& −\frac{3}{2} x + 3 \end{array} \nonumber \]

Compare y = (−3/2)x + 3 with y = mx + b to see that the slope is m = −3/2 and the y-coordinate of the y-intercept is b = 3. Therefore, the y-intercept will be the point (0, 3). Plot the point P(0, 3). To obtain a line of slope m = −3/2, start at the point P(0, 3), then move 3 units downward and 2 units to the right, arriving at the point Q(2, 0), as shown in the figure below. The line through the points P and Q is the required line.

4x − y = 4

x − 3y = −3

Place x − 3y = −3 in slope-intercept form. First subtract x from both sides of the equation, then divide both sides of the resulting equation by −3.

\[\begin{array} {lll} x − 3y &=& −3 \\ −3y &=& −x − 3 \\ y &=& \frac{1}{3} x + 1 \end{array} \nonumber \]

Compare y = (1/3)x + 1 with y = mx + b to see that the slope is m = 1/3 and the y-coordinate of the y-intercept is b = 1. Therefore, the y-intercept will be the point (0, 1). Plot the point P(0, 1). To obtain a line of slope m = 1/3, start at the point P(0, 1), then move 1 unit upward and 3 units to the right, arriving at the point Q(3, 2), as shown in the figure below. The line through the points P and Q is the required line.

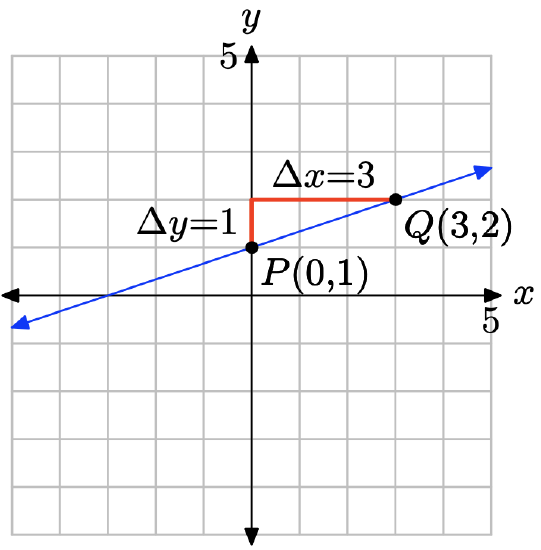
x + 4y = −4

In Exercises \(\PageIndex{25}\)-\(\PageIndex{30}\), you are given a linear function in slope-intercept form. Place the linear function in standard form Ax+ By = C, where A, B, and C are integers and A > 0.

\(y = \frac{2}{3}x − 5\)

Start with \[y =\frac{ 2}{ 3} x − 5 \nonumber \] and multiply both sides by 3 to clear the fractions.

\[3y = 2x − 15 \nonumber \]

Finally, subtract 3y from both sides of the equation, then add 15 to both sides of the equation to obtain \[15 = 2x − 3y \nonumber \], or equivalently, \[2x − 3y = 15 \nonumber \].

Exercise \(\PageIndex{26}\)

\(y = \frac{5}{6}x + 1\)

Exercise \(\PageIndex{27}\)

\(y = −\frac{4}{ 5} x + 3\)

Start with \[y = −\frac{4}{5} x + 3 \nonumber \] and multiply both sides by 5 to clear the fractions. \[5y = −4x + 15 \nonumber \]

Finally, add 4x to both sides of the equation.

\[4x + 5y = 15 \nonumber \]

Exercise \(\PageIndex{28}\)

\(y = −\frac{3}{7} x + 2\)

Exercise \(\PageIndex{29}\)

\(y = −\frac{2}{5} x − 3\)

Start with \[y = −\frac{2}{5} x − 3 \nonumber \] and multiply both sides by 5 to clear the fractions.

\[5y = −2x − 15 \nonumber \]

Finally, add 2x to both sides of the equation.

\[2x + 5y = −15 \nonumber \]

Exercise \(\PageIndex{30}\)

\(y = −\frac{1}{4}x + 2\)

Exercise \(\PageIndex{31}\)

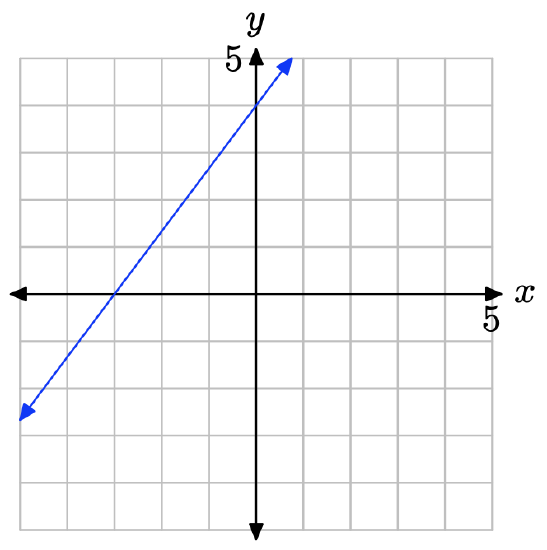
What is the x-intercept of the line?

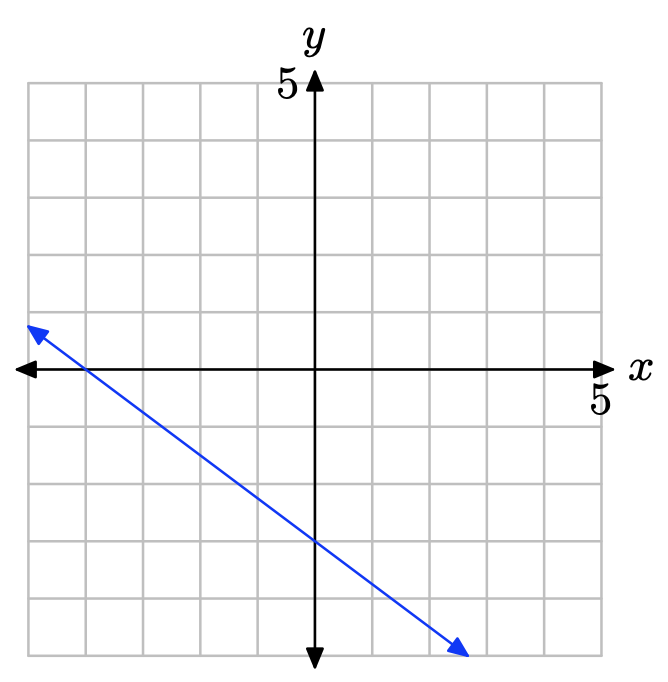
The x-intercept is the location where the line crosses the x-axis.

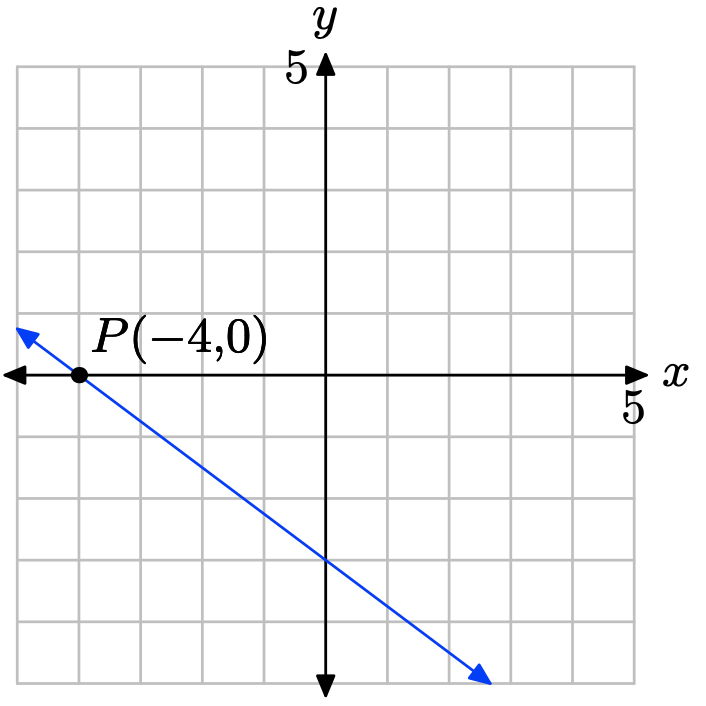
Therefore, the x-intercept is (−4, 0).

Exercise \(\PageIndex{32}\)

What is the y-intercept of the line?

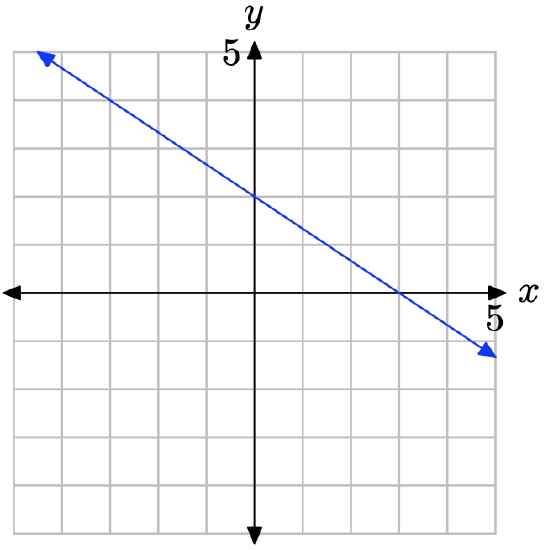
Exercise \(\PageIndex{33}\)

The y-intercept is the location where the line crosses the y-axis.

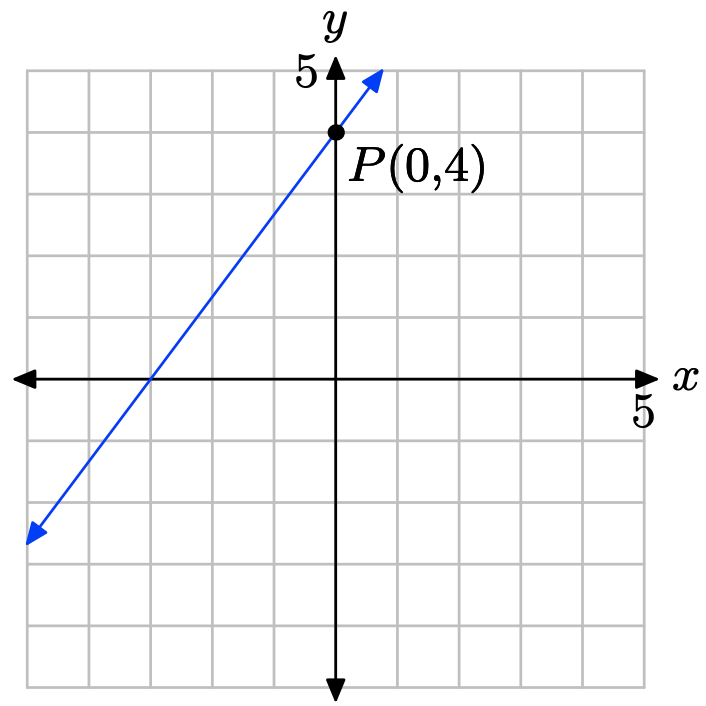
Therefore, the y-intercept is (0, 4).

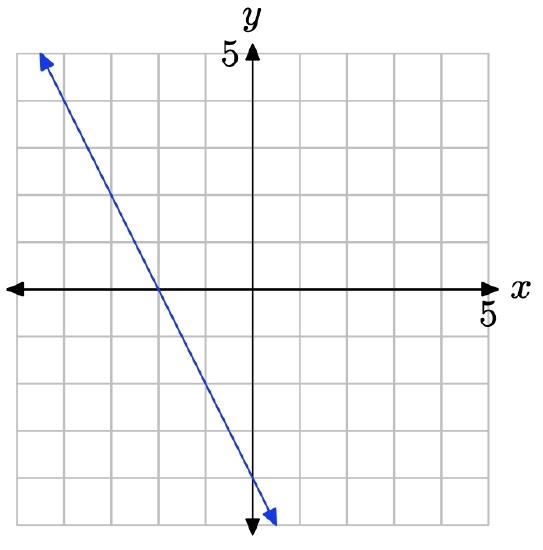
Exercise \(\PageIndex{34}\)

In Exercises \(\PageIndex{35}\)-\(\PageIndex{40}\), find the x- and y-intercepts of the linear function that is given in standard form. Use the intercepts to plot the graph of the line on a sheet of graph paper.

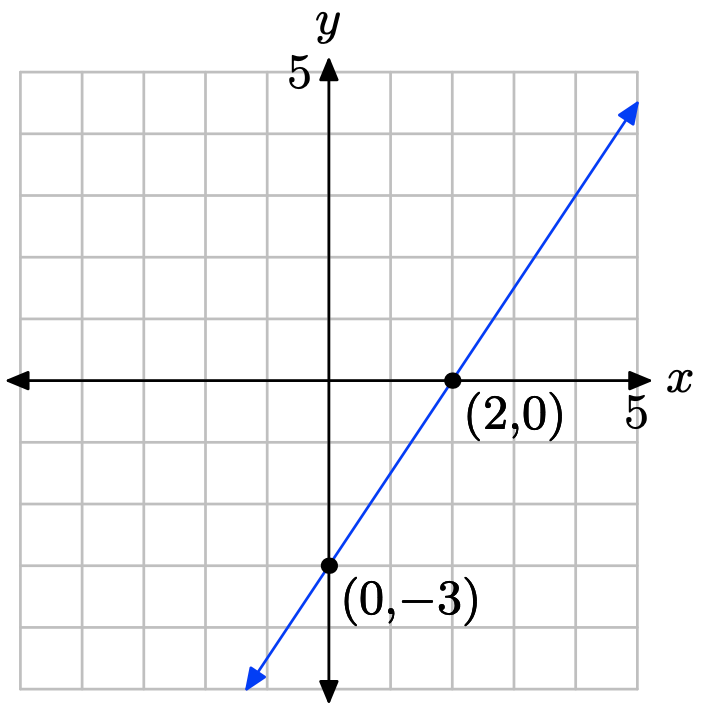
Exercise \(\PageIndex{35}\)

Set x = 0 in 3x − 2y = 6 to get −2y = 6 or y = −3. The y-intercept is (0, −3). Set y = 0 in 3x − 2y = 6 to get 3x = 6 or x = 2. The x-intercept is (2, 0). Plot the intercepts. The line through the intercepts is the required line.

Exercise \(\PageIndex{36}\)

4x + 5y = 20

Exercise \(\PageIndex{37}\)

x − 2y = −2

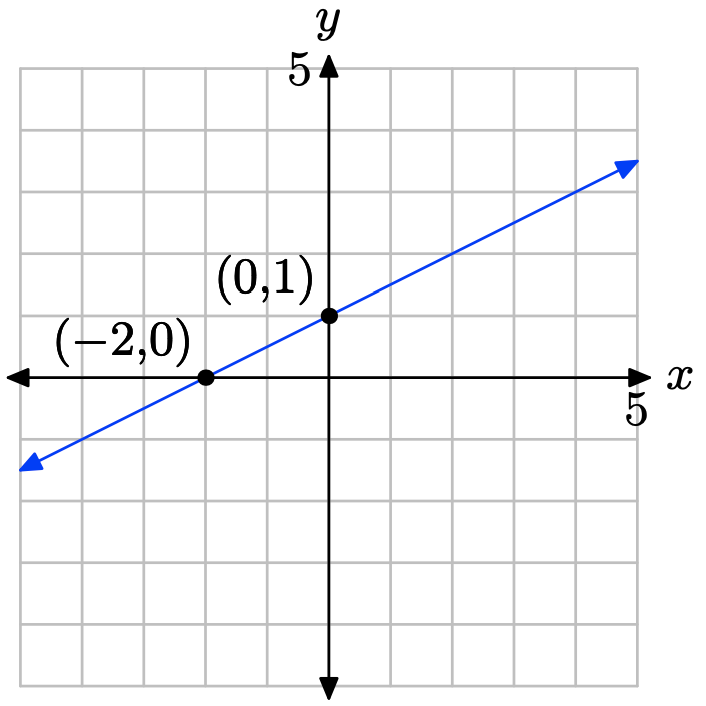
Set x = 0 in x−2y = −2 to get −2y = −2 or y = 1. The y-intercept is (0, 1). Set y = 0 in x − 2y = −2 to get x = −2. The x-intercept is (−2, 0). Plot the intercepts. The line through the intercepts is the required line.

Exercise \(\PageIndex{38}\)

6x + 5y = 30

Exercise \(\PageIndex{39}\)

2x − y = 4

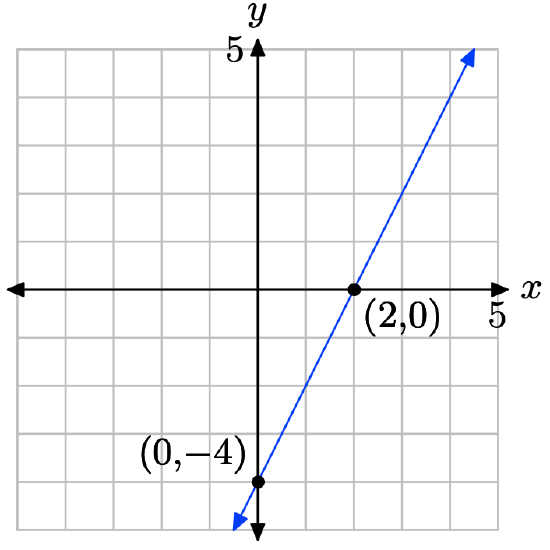
Set x = 0 in 2x − y = 4 to get −y = 4 or y = −4. The y-intercept is (0, −4). Set y = 0 in 2x − y = 4 to get 2x = 4. The x-intercept is (2, 0). Plot the intercepts. The line through the intercepts is the required line.

Exercise \(\PageIndex{40}\)

8x − 3y = 24

Exercise \(\PageIndex{41}\)

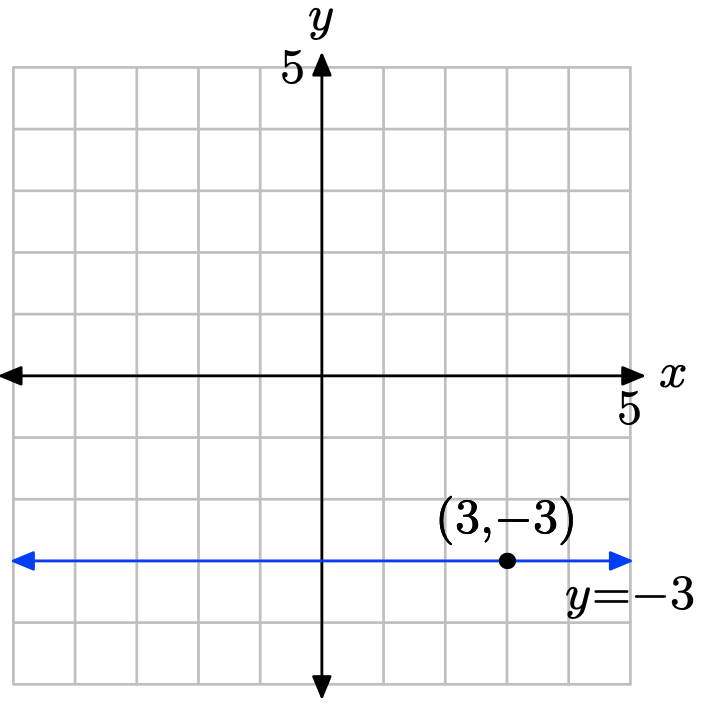
Sketch the graph of the horizontal line that passes through the point (3, −3). Label the line with its equation.

Every horizontal line has an equation of the form y = d. Since this line must pass through the point (3, −3), it follows that the equation is y = −3.

Exercise \(\PageIndex{42}\)

Sketch the graph of the horizontal line that passes through the point (−9, 9). Label the line with its equation.

Exercise \(\PageIndex{43}\)

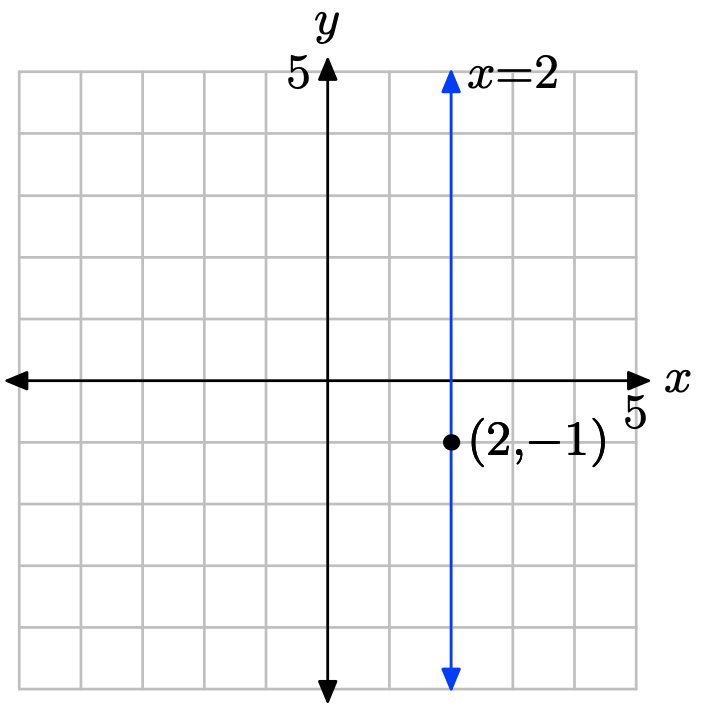
Sketch the graph of the vertical line that passes through the point (2, −1). Label the line with its equation.

Every vertical line has an equation of the form x = c. Since this line must pass through the point (2, −1), it follows that the equation is x = 2.

Exercise \(\PageIndex{44}\)

Sketch the graph of the vertical line that passes through the point (15, −16). Label the line with its equation.

In Exercises \(\PageIndex{45}\)-\(\PageIndex{48}\), find the domain and range of the given linear function.

Exercise \(\PageIndex{45}\)

f(x) = −37x − 86

The domain of every linear function is \((−\infty,\infty)\). Since the slope of the graph of f is \(−37 \neq 0\), the range is also \((−\infty,\infty)\).

Exercise \(\PageIndex{46}\)

Exercise \(\pageindex{47}\).

f(x) = −12

The domain of every linear function is \((−\infty,\infty)\). Since f(x) = −12 for every x, the range is {−12}.

Exercise \(\PageIndex{48}\)

f(x) = −2x + 8

3.4 Exercises

In Exercises \(\PageIndex{1}\)-\(\PageIndex{4}\), perform each of the following tasks.

i. Draw the line on a sheet of graph paper with the given slope m that passes through the given point \((x_{0}, y_{0})\).

ii. Estimate the y-intercept of the line.

iii. Use the point-slope form to determine the equation of the line. Place your answer in slope-intercept form by solving for y. Compare the exact value of the y-intercept with the approximation found in part (ii).

m = 2/3 and \((x_{0}, y_{0}) = (−1, −1)\)

Plot the point P(−1, −1). To draw a line through P with slope m = 2/3, start at the point P, then move up 2 units and right 3 units to the point Q(2, 1). The line through the points P and Q is the required line.

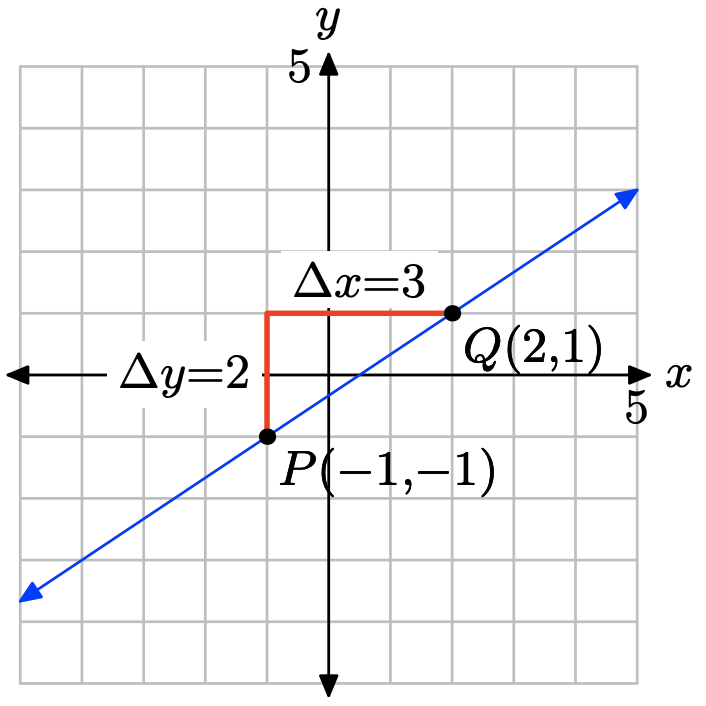
From the graph above, we would estimate the y-intercept as (0, −0.3). To find the equation of the line, substitute m = 2/3 and \((x_{0}, y_{0}) = (−1, −1)\) into the point-slope form of the line.

\[y − y0 = m(x − x0) \\ y − (−1) = \frac{2}{ 3} (x − (−1))\\ y + 1 = \frac{2}{ 3} (x + 1) \nonumber \]

To place this in slope-intercept form y = mx + b, solve for y.

\[y = \frac{2}{ 3} x + \frac{2}{ 3} − 1\\ y = \frac{2}{ 3} x + \frac{2}{ 3} − \frac{3}{ 3} \\ y = \frac{2}{ 3} x − \frac{1}{ 3} \nonumber \]

Comparing this result with y = mx + b, we see that the exact y-coordinate of the yintercept is b = −1/3, which is in close agreement with the approximation −0.3 found above.

m = -2/3 and \((x_{0}, y_{0}) = (1, −1)\)

m = -3/4 and \((x_{0}, y_{0}) = (−2, 3)\)

Plot the point P(−2, 3). To draw a line through P with slope m = −3/4, start at the point P, then move down 3 units and right 4 units to the point Q(2, 0). The line through the points P and Q is the required line.

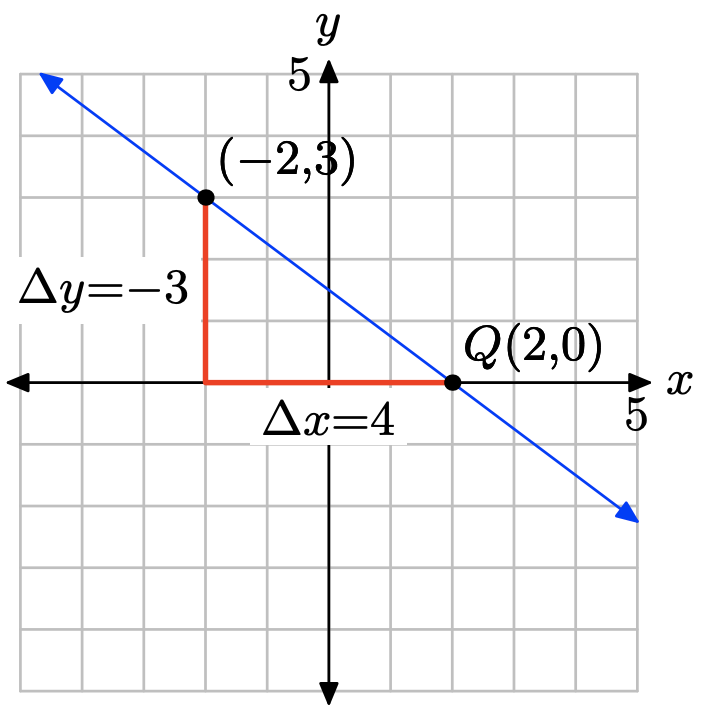
From the graph above, we would estimate the y-intercept as (0, 1.5). To find the equation of the line, substitute m = −3/4 and \((x_{0}, y_{0}) = (−2, 3)\) into the point-slope form of the line.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −\frac{3}{ 4} (x − (−2)) \\ y − 3 = −\frac{3}{ 4} (x + 2) \nonumber \]

\[y = −\frac{3}{ 4} x − \frac{3}{ 2} + 3 \\ y = −\frac{3}{ 4} x − \frac{3}{ 2} + \frac{6}{ 2} \\ y = −\frac{3}{ 4} x + \frac{3}{ 2} \nonumber \]

Comparing this result with y = mx + b, we see that the exact y-coordinate of the y-intercept is b = 3/2, which is in close agreement with the approximation 1.5 found above.

m = 2/5 and \((x_{0}, y_{0}) = (−3, -2)\)

Find the equation of the line in slope-intercept form that passes through the point (1, 3) and has a slope of 1.

Substitute 1 for m, 1 for \(x_{1}\), and 3 for \(y_{1}\) into the point-slope form \(y − y_{1} = m(x − x_{1})\) to obtain y − 3 = 1(x − 1). To place this in slope-intercept form y = mx + b, solve for y. \[y = x − 1 + 3 \\ y = x + 2 \nonumber \]

Find the equation of the line in slope-intercept form that passes through the point (0, 2) and has a slope of 1/4.

Find the equation of the line in slope-intercept form that passes through the point (1, 9) and has a slope of −2/3.

Substitute −2/3 for m, 1 for x1, and 9 for y1 into the point-slope form \(y − y_{1} = m(x − x_{1})\)

to obtain \[y − 9 = −\frac{2}{3} (x − 1) \nonumber \].

\[y = −\frac{2}{3} x + \frac{2}{3} + 9 \\ y = −\frac{2}{3} x + \frac{2}{3} + \frac{27}{3} \\ y = −\frac{2}{3} x + \frac{29}{3} \nonumber \]

Find the equation of the line in slope-intercept form that passes through the point (1, 9) and has a slope of −3/4.

In Exercises \(\PageIndex{9}\)-\(\PageIndex{12}\), perform each of the following tasks.

i. Set up a coordinate system on a sheet of graph paper and draw the line through the two given points.

ii. Use the point-slope form to determine the equation of the line.

iii. Place the equation of the line in standard form Ax+By = C, where A, B, and C are integers and A > 0. Label the line in your plot with this result.

(−2, −1) and (3, 2)

Plot the points P(−2, −1) and Q(3, 2) and draw a line through them.

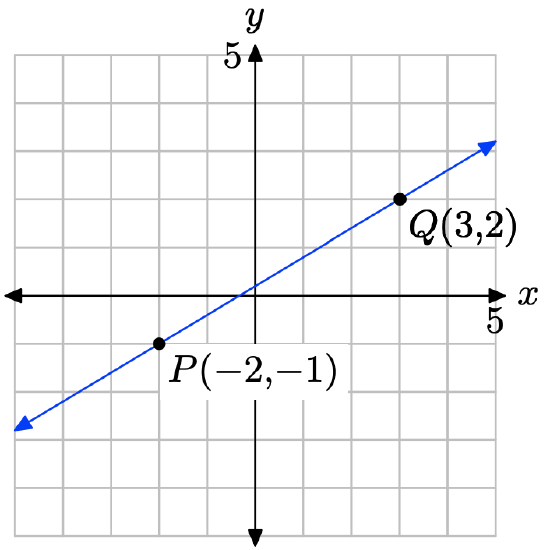
Calculate the slope of the line through the points P and Q.

\[m = \dfrac{\delta y }{\delta x} = \dfrac{2 − (−1)}{ 3 − (−2)} = \dfrac{3}{5} \nonumber \]

Substitute m = 3/5 and \((x_{0}, y_{0}) = (−2, −1)\) into the point-slope form of the line

\[y − y_{0} = m(x − x_{0}) \\ y − (−1) = \dfrac{3}{5} (x − (−2)) \\ y + 1 =\dfrac{3}{5} (x + 2) \nonumber \]

Place this result in Standard form. First clear the fractions by multiplying by 5.

\[y + 1 = \dfrac{3}{5} x + \dfrac{6}{5} \\ 5y + 5 = 3x + 6 \\ 3x − 5y = −1 \nonumber \]

Hence, the standard form of the line is 3x − 5y = −1.

(−1, 4) and (2, −3)

(−2, 3) and (4, −3)

Plot the points P(−2, 3) and Q(4, −3) and draw a line through them.

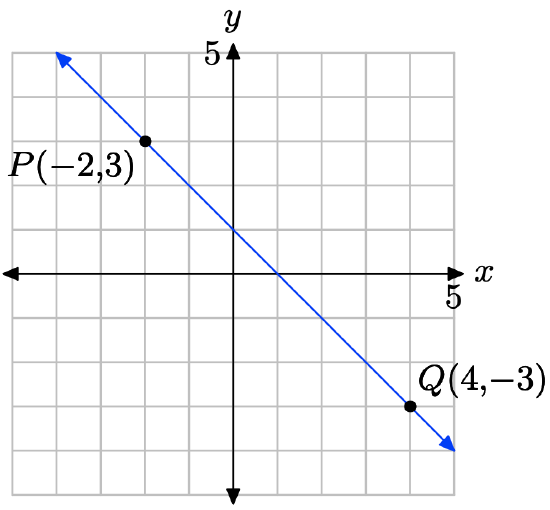
\[m = \dfrac{\delta y}{\delta x} = \dfrac{−3 − 3}{4 − (−2)}= \dfrac{−6}{ 6} = −1 \nonumber \]

Substitute m = −1 and \((x_{0}, y_{0}) = (−2, 3)\) into the point-slope form of the line.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −1(x − (−2)) \\ y − 3 = −1(x + 2) \nonumber \]

Place this result in Standard form.

\[y − 3 = −x − 2 \\ x + y = 1 \nonumber \]

Hence, the standard form of the line is x + y = 1.

(−4, 4) and (2, −4)

Find the equation of the line in slope-intercept form that passes through the points (−5, 5) and (6, 8).

Substitute 5 for \(y_{1}\), 8 for \(y_{2}\), −5 for \(x_{1}\), and 6 for \(x_{2}\) into the slope formula to find the slope m:

\[m = \dfrac{y_{1} − y_{2}}{x_{1} − x_{2} }= \dfrac{5 − 8}{−5 − 6} = \dfrac{3}{11} \nonumber \]

Now substitute \(\dfrac{3}{11}\) for m, −5 for x1, and 5 for y1 into the point-slope form

\[y − y_{1} = m(x − x_{1}) \nonumber \]

and then solve for y to obtain the equation

\[y = \dfrac{3}{ 11} x + \dfrac{70}{ 11} \nonumber \]

Find the equation of the line in slope-intercept form that passes through the points (6, −6) and (9, −7).

Find the equation of the line in slope-intercept form that passes through the points (−4, 6) and (2, −4).

Substitute 6 for \(y_{1}\), −4 for \(y_{2}\), −4 for \(x_{1}\), and 2 for \(x_{2}\) into the slope formula to find the slope m:

\[m = \dfrac{ y_{1} − y_{2}}{ x_{1} − x_{2} }= \dfrac{6 − (−4) }{−4 − 2} = \dfrac{−5}{ 3} \nonumber \]

Now substitute \(\dfrac{−5}{ 3}\) for m, −4 for x1, and 6 for \(y_{1}\) into the point-slope form

\[y = \dfrac{−5}{3} x − \dfrac{2}{ 3} \nonumber \]

Find the equation of the line in slope-intercept form that passes through the points (−1, 5) and (4, 4).

In Exercises \(\PageIndex{17}\)-\(\PageIndex{20}\), perform each of the following tasks.

i. Draw the graph of the given linear equation on graph paper and label it with its equation.

ii. Determine the slope of the given equation, then use this slope to draw a second line through the given point P that is parallel to the first line.

iii. Estimate the y-intercept of the second line from your graph.

iv. Use the point-slope form to determine the equation of the second line. Place this result in slope-intercept form y = mx + b, then state the exact value of the y-intercept. Label the second line with the slope-intercept form of its equation.

2x + 3y = 6, P = (−2, −3)

Plot the points Q(0, 2) and R(3, 0) and draw a line through them as shown in (a) below. You can calculate the slope of this line from the graph, or you can use the slope formula as follows.

\[m = \dfrac{\delta y}{\delta x} = \dfrac{0 − 2 }{3 − 0} = −\dfrac{2}{ 3} \nonumber \]

The second line must be parallel to the first, so it must have the same slope; namely, m = −2/3. The second line must pass through the point P(−2, −3), so plot the point P. To get the right slope, start at the point P, then move 3 units to the right and 2 units down, as shown in (b). It would appear that this line crosses the y-axis near (0, −4.3).

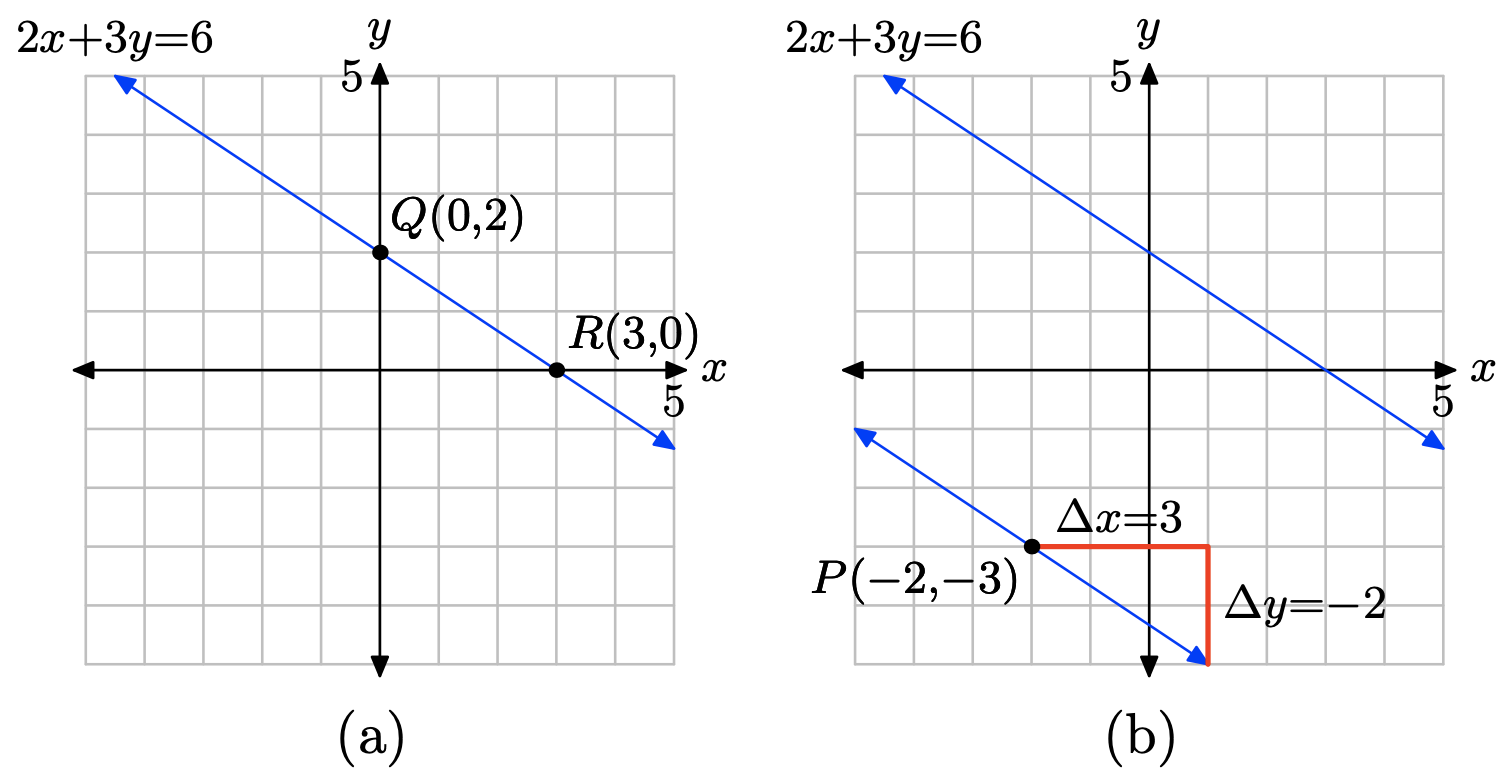
To find the equation of the second line, use the point slope form of the line and m = −2/3 and \((x_{0}, y_{0}) = (−2, −3)\), as follows.

\[y − y_{0} = m(x − x_{0}) \\ y − (−3) = −\dfrac{2}{ 3} (x − (−2)) \\ y + 3 = −\dfrac{2}{ 3}(x + 2) \nonumber \]

To place this in slope-intercept form y = mx + b, we must solve for y.

\[y + 3 = −\dfrac{2}{ 3}x − \dfrac{4}{ 3} \\ y = −\dfrac{2}{ 3} x − \dfrac{4}{ 3} − 3 \\ y = −\dfrac{2}{ 3} x − \dfrac{4}{ 3} −\dfrac{9}{ 3}\\ y = −\dfrac{2}{ 3} x − \dfrac{13}{ 3} \nonumber \]

Hence, the equation in slope-intercept form is y = (−2/3)x − 13/3, making the exact y-coordinate of the y-intercept b = −13/3, which is in pretty close agreement (check on your calculator) with our estimate of −4.3.

3x − 4y = 12, P = (−3, 4)

x + 2y = −4, P = (3, 3)

Plot the points Q(−4, 0) and R(0, −2) and draw a line through them as shown in (a) below. You can calculate the slope of this line from the graph, or you can use the slope formula as follows.

\[m = \dfrac{\delta y}{\delta x} = \dfrac{−2 − 0 }{0 − (−4)} = −\dfrac{1}{2} \nonumber \]

The second line must be parallel to the first, so it must have the same slope; namely, m = −1/2. The second line must pass through the point P(3, 3), so plot the point P. To get the right slope, start at the point P, then move 1 unit downward and 2 units to the right, as shown in (b). It would appear that this line crosses the y-axis near (0, 4.5).

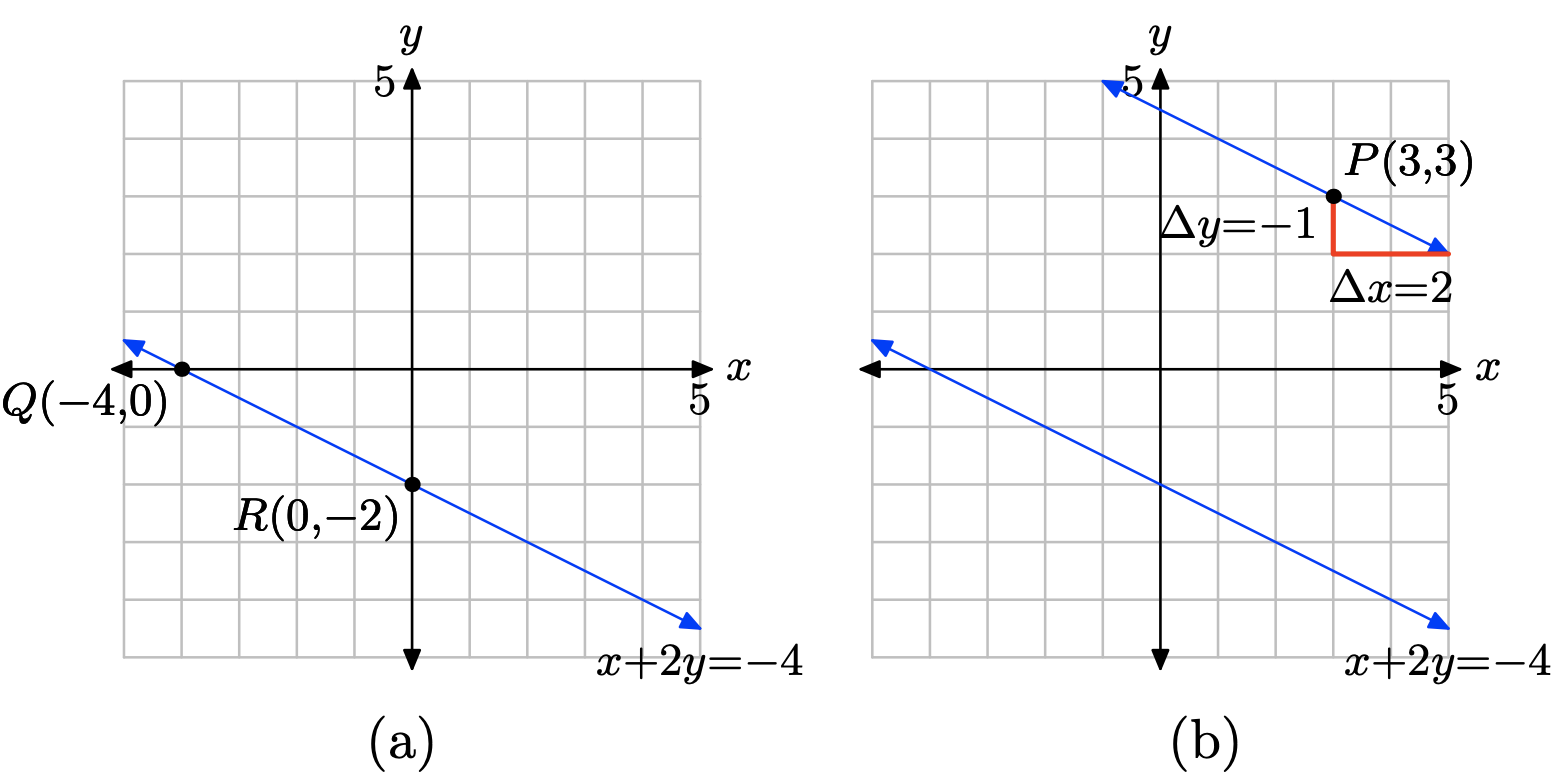
To find the equation of the second line, use the point slope form of the line and m = −1/2 and \((x_{0}, y_{0}) = (3, 3)\), as follows.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −\dfrac{1}{ 2} (x − 3) \nonumber \]

\[− 3 = −\dfrac{1}{ 2} x + \dfrac{3}{ 2} \\ y = −\dfrac{1}{ 2} x + \dfrac{3}{ 2} + 3 \\ y = −\dfrac{1}{ 2} x + \dfrac{3}{ 2} + \dfrac{6}{ 2} \\ y = −\dfrac{1}{ 2} x + \dfrac{9}{ 2} \nonumber \]

Hence, the equation in slope-intercept form is y = (−1/2)x + 9/2, making the exact y-coordinate of the y-intercept b = 9/2, which is in pretty close agreement (check on your calculator) with our estimate of 4.5.

5x + 2y = 10, P = (−3, −5)

In Exercises \(\PageIndex{21}\)-\(\PageIndex{24}\), perform each of the following tasks.

ii. Determine the slope of the given equation, then use this slope to draw a second line through the given point P that is prependicular to the first line.

iii. Use the point-slope form to determine the equation of the second line. Place this result in standard form Ax+By = C, where A, B, C are integers and A > 0. Label the second line with this standard form of its equation.

x − 2y = −2, P = (3, −4)

Let x = 0 in x − 2y = −2. Then −2y = −2 and y = 1. This calculation gives us the y-intercept R(0, 1). Let y = 0 in x − 2y = −2 and x = −2. This gives us the x-intercept Q(−2, 0). Plot the points Q(−2, 0) and R(0, 1) and draw a line through them as in (a) below.

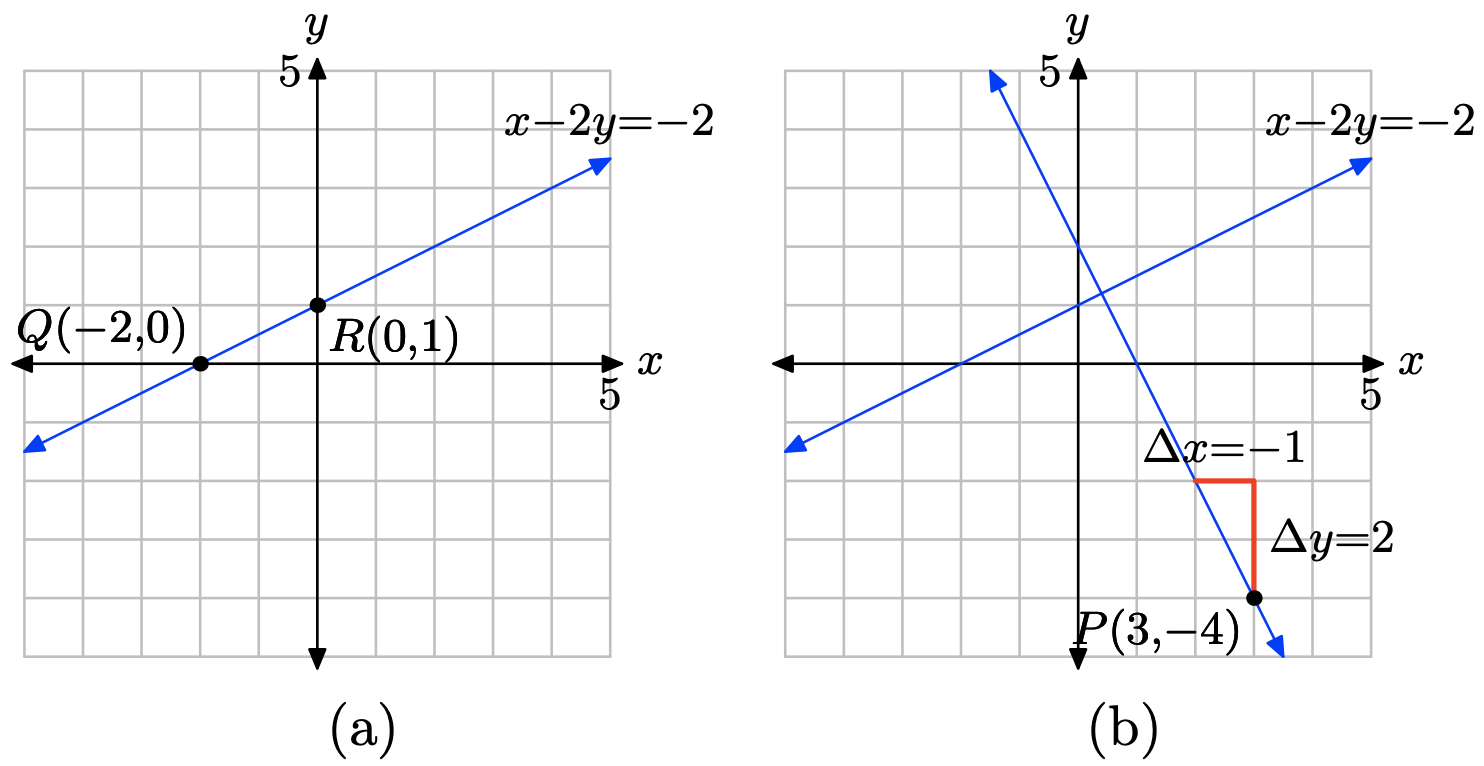
You can calculate the slope of the first line from the graph or you can obtain it with the slope formula as follows.

\[m1 = \dfrac{\delta y}{\delta x} = \dfrac{1 − 0}{ 0 − (−2)} = \dfrac{1}{ 2} \nonumber \]

The second line is perpendicular to this first line, so the slope of the second line must be the negative reciprocal of the slope of the first line; i.e., the slope of the second line should be \(m = −1/m_{2} = −1/(1/2)\), or m = −2. To draw a line through the point P(3, −4) that is perpendicular to the line in (a), first plot the point P(3, −4), then move upward 2 units and to the left 1 unit as shown in (b). This gives us a line through P(3, −4) with slope m = −2, so this line will be perpendicular to the first line. To find the equation of the perpendicular line, substitute m = −2 and \((x_{0}, y_{0}) = (3, −4)\) into the point-slope formula, then place the resulting equation in standard form.

\[y − y_{0} = m(x − x_{0}) \\ y − (−4) = −2(x − 3) \\ y + 4 = −2x + 6 \\ 2x + y = 2 \nonumber \]

Thus, the equation of the line that passes through P(3, −4) and is perpendicular to the line x − 2y = −2 is 2x + y = 2.

3x + y = 3, P = (−3, −4)

x − 2y = 4, P = (−3, 3)

Set x = 0 in x − 2y = 4 to obtain −2y = 4. Hence, y = −2 and the y-intercept is Q(0, −2). Set y = 0 in x − 2y = 4 to obtain x = 4. Hence, the x-intercept is R(4, 0). Plot Q(0, −2) and R(4, 0) and draw a line through them as in (a) below.

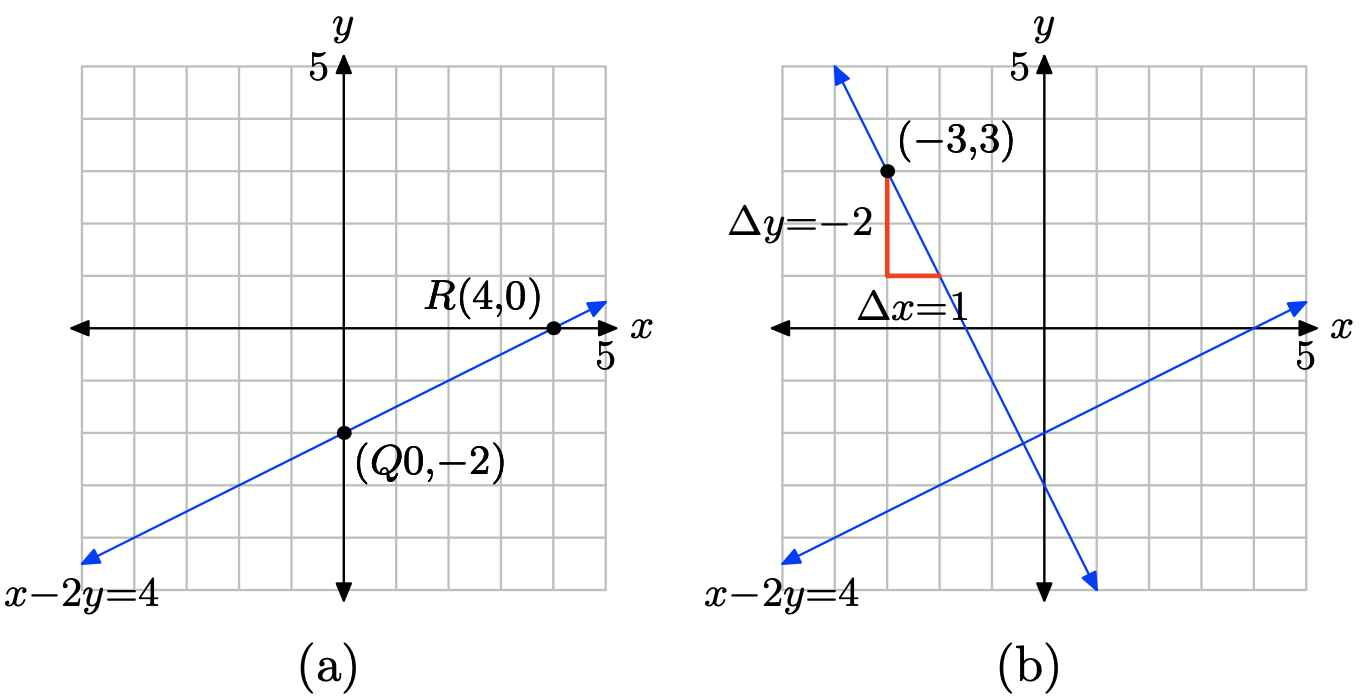
\[m_{1} = \dfrac{\delta y}{\delta x} = \dfrac{0 − (−2)}{ 4 − 0 }= \dfrac{1}{2} \nonumber \]

The second line is perpendicular to this first line, so the slope of the second line must be the negative reciprocal of the slope of the first line; i.e., the slope of the second line should be m = −1/m2 = −1/(1/2), or m = −2. To draw a line through the point P(−3, 3) that is perpendicular to the line in (a), first plot the point P(−3, 3), then move downward 2 units and to the right 1 unit as shown in (b). This gives us a line through P(−3, 3) with slope m = −2, so this line will be perpendicular to the first line. To find the equation of the perpendicular line, substitute m = −2 and \((x_{0}, y_{0}) = (−3, 3)\) into the point-slope formula, then place the resulting equation in standard form.

\[y − y_{0} = m(x − x_{0}) \\ y − 3 = −2(x − (−3)) \\ y − 3 = −2(x + 3) \\ y − 3 = −2x − 6 \\ 2x + y = −3 \nonumber \]

Thus, the equation of the line that passes through P(−3, 3) and is perpendicular to the line x − 2y = 4 is 2x + y = −3.

x − 4y = 4, P = (−3, 4)

Find the equation of the line in slope-intercept form that passes through the point (7, 8) and is parallel to the line x − 5y = 4.

First solve x − 5y = 4 for y to get \(y = \dfrac{1 }{5} x − \dfrac{4}{5} \) The slope of this line is \(\dfrac{1}{5}\). Therefore, every parallel line also has slope \(\dfrac{1}{5}\).

Now to find the equation of the parallel line that passes through the point (7, 8), substitute \(\dfrac{1}{5}\) for m, 7 for \(x_{1}\), and 8 for \(y_{1}\) into the point-slope form

\[y − y_{1} = m(x − x_{1}) \nonumber \] to obtain

\[y − 8 = \dfrac{1}{5}(x − 7) \nonumber \]. Then solve for y:

\[y = \dfrac{1}{5} x − \dfrac{7}{5} + 8 \\ y = \dfrac{1}{5}x − \dfrac{7}{5} +\dfrac{40}{5} y = \dfrac{1}{5} x + \dfrac{33}{5} \nonumber \]

Find the equation of the line in slope-intercept form that passes through the point (3, −7) and is perpendicular to the line 7x − 2y = −8.

Find the equation of the line in slope-intercept form that passes through the point (1, −2) and is perpendicular to the line −7x + 5y = 4.

First solve −7x + 5y = 4 for y to get

\[y = \dfrac{7}{5} x + 4 5 \nonumber \]

The slope of this line is \dfrac{7}{5}. Therefore, every perpendicular line has slope −\(\dfrac{7}{5}\) (the negative reciprocal of \(\dfrac{7}{5}\). Now to find the equation of the perpendicular line that passes through the point (1, −2), substitute −\dfrac{5}{7} for m, 1 for \(x_{1}\), and −2 for \(y_{1}\) into the point-slope form

\[y − y1 = m(x − x1) \nonumber \] to obtain \[y − (−2) = −\dfrac{5}{7} (x − 1) \nonumber \]. Then solve for y:

\[y = −\dfrac{5}{7}x +\dfrac{5}{7} − 2 \\ y = −\dfrac{5}{7} x + \dfrac{5}{7} − \dfrac{14}{7} \\ y = −\dfrac{5}{7} x − \dfrac{9}{7} \nonumber \]

Find the equation of the line in slope-intercept form that passes through the point (4, −9) and is parallel to the line 9x + 3y = 5.

Find the equation of the line in slope-intercept form that passes through the point (2, −9) and is perpendicular to the line −8x + 3y = 1.

First solve −8x + 3y = 1 for y to get \[y = \dfrac{8}{3} x + \dfrac{1}{3} \nonumber \]

The slope of this line is \(\dfrac{8}{3}\). Therefore, every perpendicular line has slope \(−\dfrac{3}{8}\) (the negative reciprocal of \(\dfrac{8}{3}\)). Now to find the equation of the perpendicular line that passes through the point (2, −9), substitute \(−\dfrac{3}{8}\) for m, 2 for \(x_{1}\), and −9 for \(y_{1}\) into the point-slope form \[y − y1 = m(x − x1) \nonumber \]

to obtain \[y − (−9) = −\dfrac{3}{8} (x − 2) \nonumber \]

Then solve for y:

\[y = −\dfrac{3}{8} x + \dfrac{3}{4} − 9 \\ y = −\dfrac{3}{8} x + \dfrac{3}{4}− \dfrac{36}{4} \\ y = −\dfrac{3}{8} x − \dfrac{33}{4} \nonumber \]

Find the equation of the line in slope-intercept form that passes through the point (−7, −7) and is parallel to the line 8x + y = 2.

Add texts here. Do not delete this text first.

A ball is thrown vertically upward on a distant planet. After 1 second, its velocity is 100 meters per second. After 5 seconds, the velocity is 50 meters per second. Assume that the velocity v of the ball is a linear function of the time t.

a) On graph paper, sketch the graph of the velocity v versus the time t. Assume that the velocity is the dependent variable and place it on the vertical axis.

b) Determine the slope of the line, including its units, then give a real world explanation of the meaning of this slope.

c) Determine an equation that models the velocity v of the ball as a function of time t.

d) Determine the time it takes the ball to reach its maximum height.

a) At 1 second, the speed is 100 meters per second. This is the point (1, 100) in the plot below. At 5 seconds, the speed is 50 meters per second. This is the point (5, 50) in the plot below.

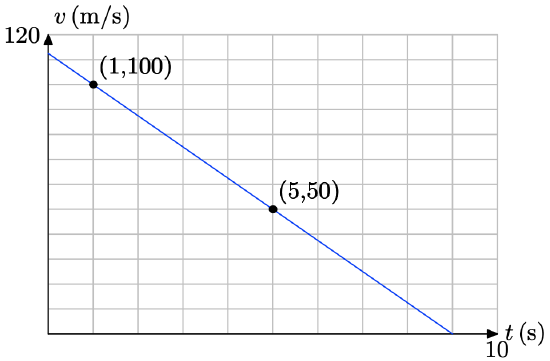
b) We’ll keep the units in our slope calculation to provide real-world meaning for the rate.

\[m = \dfrac{\delta v}{\delta t} = \dfrac{50 m/s − 100 m/s}{ 5 s − 1 s} = −12.5 (m/s)/s. \nonumber \]

That is, the slope is \(−12.5 m/s^2\). This is acceleration, the rate at which the speed is changing with respect to time. Every second, the speed decreases by 12.5 meters per second.

c) We use the point-slope form of the line, namely

\[y − y_{0} = m(x − x_{0}) \nonumber \]

However, v and t are taking the place of y and x, respectively, so the equation becomes \[v − v_{0} = m(t − t_{0}) \nonumber \], Now, substitute the slope m = −12.5 and the point \((t_{0}, v_{0}) = (1, 100)\) to obtain \[v − 100 = −12.5(t − 1) \nonumber \]. Solve this for v, obtaining \[v − 100 = −12.5t + 12.5 \\ v = −12.5t + 112.5 \nonumber \]. Equivalently, we could use function notation and write \[v(t) = −12.5t + 112.5 \nonumber \].

d) When the ball reaches its maximum height, its speed will equal zero. Consequently, to find the time of this event, we must solve v(t) = 0. Replace v(t) with −12.5t + 112.5 and solve for t. \[−12.5t + 112.5 = 0 \\ −12.5t = −112.5 \\ t = 9 \nonumber \]. Hence, it takes 9 seconds for the ball to reach its maximum height.

A ball is thrown vertically upward on a distant planet. After 2 seconds, its velocity is 320 feet per second. After 8 seconds, the velocity is 200 feet per second. Assume that the velocity v of the ball is a linear function of the time t.

An automobile is traveling down the autobahn and the driver applies its brakes. After 2 seconds, the car’s speed is 60 km/h. After 4 seconds, the car’s speed is 50 km/h.

c) Determine an equation that models the velocity v of the automobile as a function of time t. d) Determine the time it takes the automobile to stop.

a) After 2 seconds, the speed of the car is 60 km/h. This is the point (2, 60). After 4 seconds, the car’s speed is 50 km/h. This is the point (4, 50). Plot these two points and draw a line through them, as shown in the plot below.

\[m = \dfrac{\delta v}{\delta t} = \dfrac{50 km/h − 60 km/h}{ 4 s − 2 s }= −5 (km/h)/s \nonumber \]

That is, the slope is −5 (km/h)/s. This is acceleration, the rate at which the speed is changing with respect to time. Every second, the speed decreases by 5 kilometers per hour.

c) We use the point-slope form of the line, namely \[y − y_{0} = m(x − x_{0}) \nonumber \], However, v and t are taking the place of y and x, respectively, so the equation becomes \[v − v_{0} = m(t − t_{0}) \nonumber \], Now, substitute the slope m = −5 and the point \((t_{0}, v_{0}) = (2, 60)\) to obtain \[v − 60 = −5(t − 2) \nonumber \]. Solve this for v, obtaining \[v − 60 = −5t + 10 \\ v = −5t + 70 \nonumber \]. Equivalently, we could use function notation and write \[v(t) = −5t + 70 \nonumber \].

d) To find the time it takes the car to stop, we must determine the time t so that \[v(t) = 0 \nonumber \]. Replace v(t) with −5t + 70 and solve for t.

\[−5t + 70 = 0\\ −5t = −70 \\ t = 14 \nonumber \]. Hence, it takes 14 seconds for the to brake to a stop.

An automobile is traveling down the autobahn and its driver steps on the accelerator. After 2 seconds, the car’s velocity is 30 km/h. After 4 seconds, the car’s velocity is 40 km/h.

c) Determine an equation that models the velocity v of the automobile as a function of time t.

d) Determine the speed of the vehicle after 8 seconds.

Suppose that the demand d for a particular brand of teakettle is a linear function of its unit price p. When the unit price is fixed at $30, the demand for teakettles is 100. This means the public buys 100 teakettles. If the unit price is fixed at $50, then the demand for teakettles is 60.

a) On graph paper, sketch the graph of the demand d versus the unit price p. Assume that the demand is the dependent variable and place it on the vertical axis.

c) Determine an equation that models the demand d for teakettles as a function of unit price p.

d) Compute the demand if the unit price is set at $40.

a) When the unit price is $30, the demand is 100 teakettles. This is the point (30, 100). When the unit price is $50, the demand is 60 teakettles. This is the point (50, 60). Plot the points (30, 100) and (50, 60) and draw a line through them, as shown in the plot below.

\[m = \dfrac{\delta d}{\delta p} = \dfrac{60 teakettles − 100 teakettles}{ 50 dollars − 30 dollars } = −2 teakettles/dollar \nonumber \]

That is, the slope is −2 teakettles/dollar. This is the rate at which the demand is changing with respect to the unit price. For every increase in the unit price of one dollar, the demand is lowered by 2 teakettles (2 fewer teakettles are bought).

c) We use the point-slope form of the line, namely\[ y − y_{0} = m(x − x_{0}) \nonumber \], However, d and p are taking the place of y and x, respectively, so the equation becomes

\[d − d_{0} = m(p − p_{0}) \nonumber \]

Now, substitute the slope m = −2 and the point \((p_{0}, d_{0}) = (30, 100)\) to obtain \[d − 100 = −2(p − 30) \nonumber \]. Solve this for d, obtaining

\[d − 100 = −2p + 60 \\ d = −2p + 160 \nonumber \]

Equivalently, we could use function notation and write d(p) = −2p + 160.

d) To determine the demand if the unit price is $40, compute \[ d(40) = −2(40) + 160 = 80 \nonumber \]

Hence, the demand is for 80 teakettles if the price per kettle is set at $40.

It’s perfect kite-flying weather on the coast of Oregon. Annie grabs her kite, climbs up on the roof of her two story home, and begins playing out kite string. In 10 seconds, Annie’s kite is 120 feet above the ground. After 20 seconds, it is 220 feet above the ground. Assume that the height h of the kite above the ground is a linear function of the amount of time t that has passed since Annie began playing out kite string.

a) On graph paper, sketch the graph of the height h of the kite above ground versus the time t . Assume that the height is the dependent variable and place it on the vertical axis.

c) Determine an equation that models the height h of the kite as a function of time t.

d) Determine the height of the kite after 20 seconds.

e) Determine the height of Annie’s second story roof above ground.

3.5 Exercises

The following set of data about revolving consumer credit (debt) in the United States is from Google.com. This is primarily made up of credit card debt, but also includes other consumer non-mortgage credit, like those offered by commercial banks, credit unions, Sallie Mae, and the federal government.

a) Set up a coordinate system on graph paper, placing the credit C on the vertical axis, and the years x after 2001 on the horizontal axis. Label and scale each axis appropriately. Draw what you feel is the line of best fit. Remember to draw all lines with a ruler.

b) Select two points on your line of best fit that are not from the data table above. Use these two points to determine the slope of the line. Include units with your answer. Write a sentence or two explaining the real world significance of the slope of the line of best fit.

c) Use one of the two points on the line and the slope to determine the equation of the line of best fit in point-slope form. Use C and x for the dependent and independent variables, respectively. Solve the resulting equation for C and write your result using function notation.

d) Use the equation developed in part (c) to predict the revolving credit debt in the year 2008.

e) If the linear trend predicted by the line of best fit continues, in what year will the revolving credit debt reach 1.0 trillion dollars?

a) Scale and label the axes, plot the points, then draw the line of best fit.

b) Select two points, P(1.4, 750) and Q(2.8, 780) that are points on the line but not points in the original data table.

Use these two points to calculate the slope of the line of best fit.

\[m = \dfrac{\delta C}{\delta x} = \dfrac{780 − 750}{ 2.8 − 1.4} \nonumber \] billion dollars/year

Using a calculator, the slope is approximately 21.42 billion dollars per year. What this means is that the credit debt is increasing at a rate of 21.42 billion dollars per year. c) To find the equation of the line, use the point P(1.4, 750) and the slope m = 21.42 in the point-slope form of the line.

\[y − y_{0} = m(x − x_{0}) \\ y − 750 = 21.42(x − 1.4) \nonumber \]

Replace y and x with C and x, respectively, then solve for C in terms of x.

\[C − 750 = 21.42(x − 1.4) \\ C − 750 = 21.42x − 29.988 \\ C = 21.42x + 720.012 \nonumber \]

In function notation, C(x) = 21.42x + 720.012. Note: Answers will vary somewhat due to the subjective nature of drawing the line of best fit and picking points on the line.

d) The year 2008 gives x = 2008−2001 = 7 years since 2001. Hence, to find the credit debt in 2008, we use C(x) = 21.42x + 720.012 and evaluate

\[C(7) = 21.42(7) + 720.012 = 869.952 \nonumber \]

Hence, the credit debt in 2008 will be approximately 869 billion dollars.

e) A trillion dollars is 1000 billion dollars. Hence, to find when the credit debt is 1000 billion dollars, we must solve C(x) = 1000 for x.

\[C(x) = 1000 \\ 21.42x + 720.012 = 1000 \\ 21.42x = 279.988 \\ x \approx 13.07 \nonumber \] Hence, the credit debt will reach a trillion dollars approximately 13 years after the year 2001, or a little bit into the year 2014.

The following set of data about non-revolving credit (debt) in the United States is from Google.com. The largest component of non-revolving credit is automobile loans, but it is also includes student loans and other defined-term consumer loans.

a) Set up a coordinate system on graph paper, placing the non-revolving credit debt D on the vertical axis, and the years x after 2001 on the horizontal axis. Label and scale each axis appropriately. Draw what you feel is the line of best fit. Remember to draw all lines with a ruler.

c) Use one of the two points on the line and the slope to determine the equation of the line of best fit in pointslope form. Use D and x for the dependent and independent variables, respectively. Solve the resulting equation for D and write your result using function notation.

d) Use the equation developed in part (c) to predict the non-revolving credit debt in the year 2008. e) If the linear trend predicted by the line of best fit continues, in what year will the non-revolving credit debt reach 2.0 trillion dollars?

According to the U.S. Bureau of Transportation (www.bts.gov), retail sales of new cars declined every year from 2000- 2004, as shown in the following table.

a) Set up a coordinate system on graph paper, placing the sales S on the vertical axis, and the years x after 2000 on the horizontal axis. Label and scale each axis appropriately. Draw what you feel is the line of best fit. Remember to draw all lines with a ruler.

c) Use one of the two points on the line and the slope to determine the equation of the line of best fit in point-slope form. Use S and x for the dependent and independent variables, respectively. Solve the resulting equation for S and write your result using function notation.

d) Use the equation developed in part (c) to predict sales in the year 2006.

e) If the linear trend predicted by the line of best fit continues, when will sales drop to 7 million cars per year?

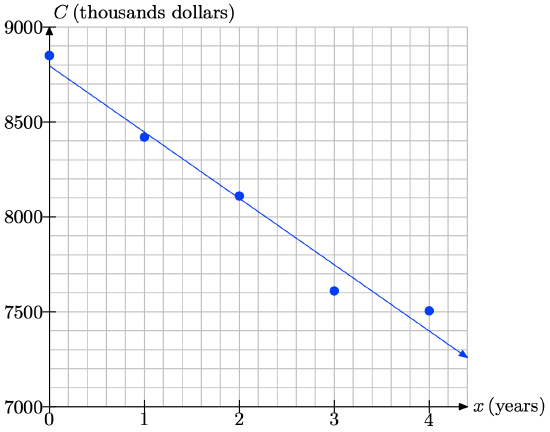
b) Select two points, P(1.4, 8300) and Q(4.0, 7400) that are points on the line but not points in the original data table.

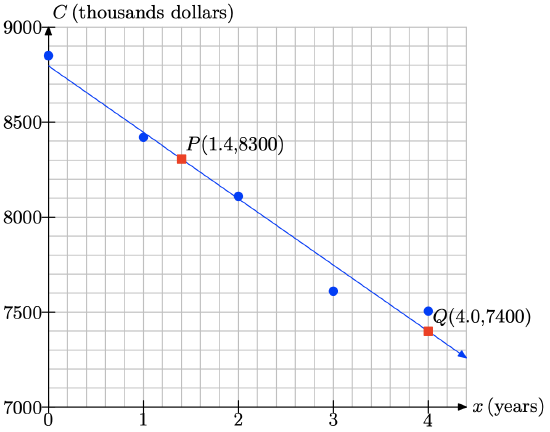
\[m = \dfrac{\delta C }{\delta x} = \dfrac{8300 − 7400 }{4.0 − 1.4} \nonumber \] thousand cars/year Using a calculator, the slope is approximately −346.15 thousand cars per year. What this means is that sales of new cars is decreasing at an approximate rate of 346 thousand cars per year.

c) To find the equation of the line, use the point P(1.4, 8300) and the slope m = −346.15 in the point-slope form of the line.

\[y − y_{0} = m(x − x_{0}) \\ y − 8300 = −346.15(x − 1.4) \nonumber \]

Replace y and x with S and x, respectively, then solve for S in terms of x.

\[S − 8300 = −346.15(x − 1.4) \\ S − 8300 = −346.15x + 484.61 \\ S = −346.15x + 8784.61 \nonumber \]

In function notation, S(x) = −346.15x + 8784.61. Note: Answers will vary somewhat due to the subjective nature of drawing the line of best fit and picking points on the line.

d) To determine the sales in 2006, evaluate S(x) = −346.15x+8784.61 at x = 2006− 2000 = 6.

\[S(6) = −346.15(6) + 8784.61 = 6707.71 \nonumber \]

Thus, the sales will be approximately 6,707,710 new cars.

e) To determine when sales of new cars will drop to 7 million, we must solve

\[S(x) = 7000. −346.15x + 8784.61 = 7000 \\ −346.15x = −1784.61 \\ x \approx 5.16 \nonumber \]

Hence, sales will reach 7 million cars somewhere in the year 2005-2006.

The following table shows total midyear population of the world according to the U.S. Census Bureau, (www.census.gov) for recent years.

a) Set up a coordinate system on graph paper, placing the population P on the vertical axis, and the years x after 2000 on the horizontal axis. Label and scale each axis appropriately. Draw what you feel is the line of best fit. Remember to draw all lines with a ruler.

c) Use one of the two points on the line and the slope to determine the equation of the line of best fit in point-slope form. Use P and x for the dependent and independent variables, respectively. Solve the resulting equation for P and write your result using function notation.

d) Use the equation developed in part (c) to predict the population in 2010.

e) If the linear trend predicted by the line of best fit continues, when will world population reach 7 billion?

The following table shows an excerpt from the U.S. Census Bureau’s 2005 data (www.census.gov) on annual sales of new homes in the United States.

We cannot use price ranges as coordinate values (we must have single values), so we replace each price range in the table with a single price in the middle of the range–the average value of a home in that range. This gives us the following modified table:

We can now plot the data on a coordinate system.

a) Enter the data into your calculator and make a scatter plot. Copy it down onto your paper, labeling appropriately.

b) Use your calculator to determine a line of best fit. This is called a linear demand function, because it allows you to predict the demand for houses with a certain price. Write it using function notation and round to the nearest thousandth. Graph it on your calculator and copy it onto your coordinate system.

c) Use the linear demand function to predict annual sales of homes priced at $200, 000. Try to use the TABLE feature on your calculator to make this prediction.

a) Select STAT, then 1:Edit and enter the data as shown in (a). Select 2nd STAT PLOT, then turn turn on Plot1 as shown in (b). Select scatterplot, choose the lists you used for the data, then a marker, as shown in (b). Finally, select 9:ZoomStat from the ZOOM menu to produce the plot in (c).

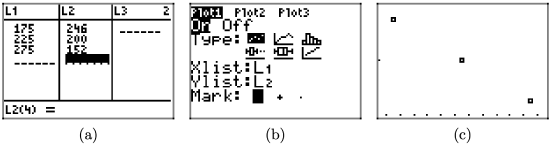
b) Push the STAT button, right-arrow to the CALC menu, then select 4:LinReg(ax+b), followed by L1, a comma, L2, a comma, and Y1 from the VARS menu (select Y-VARS then 1:Function submenus). The result is shown in (a). Press ENTER to produce the calculation shown in (b). This is the line of best fit. This procedure also stores the line of best fit in Y1, so pushing the GRAPH button produces the line of best fit shown in (c).

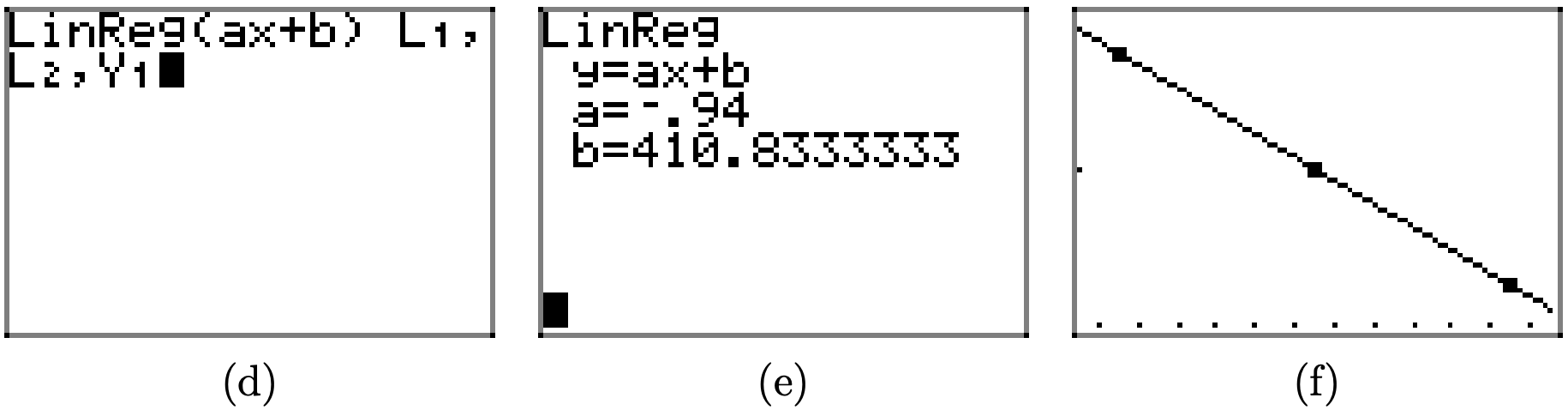
In (b) above, we see that the number sold N, as a function of average price P is given by the linear function N(P) = −0.94P + 410.833.

c) If all went well in part (b), then we can press 2nd TBL SET and set up the table parameters as shown in (g). Make sure the independent variable is set to ASK. Select 2nd TABLE, then enter 200 (which represents an average price p = $200, 000) as shown in (h).

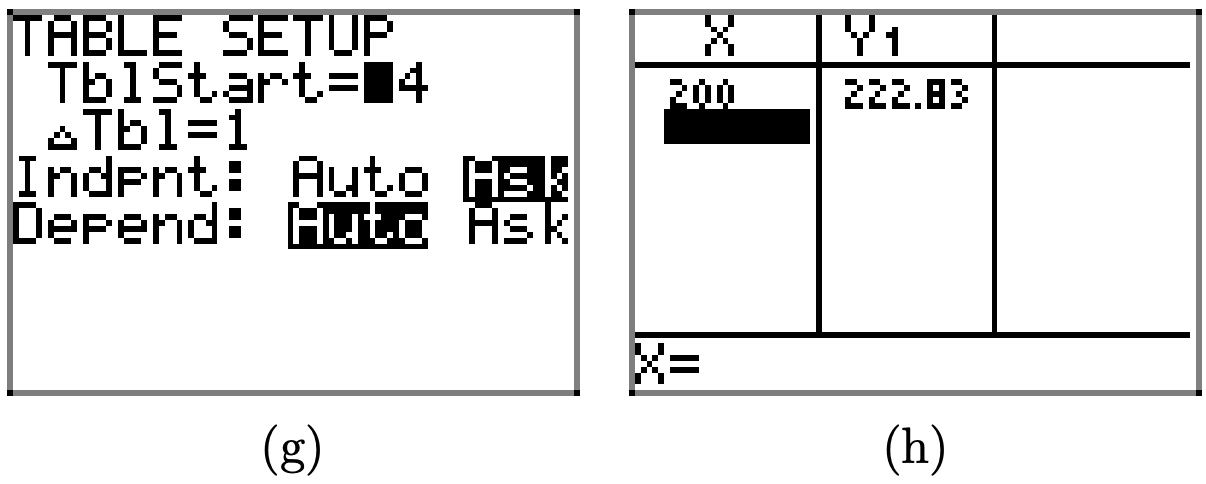
Thus, N(200) = 222.83, so approximately 222.83 thousand or 222, 830 homes are sold at the average price of $200,000.

The following table shows data from the National Association of Homebuilders (www.nahb.org), indicating the median price of new homes in the United States.

b) Use your calculator to determine a line of best fit that can be used to predict the median price of new homes in future years. Write it using function notation. Graph it on your calculator and copy it onto your coordinate system.

c) Use the linear demand function to predict the median price of a new home in 2010. Try to use the TABLE feature on your calculator to make this prediction.

d) Looking at the graph, do you think the linear demand function models the actual data points well? If not, why not? What does this mean about the prediction you made in part (c)?

Jim is hanging blocks of various mass on a spring in the physics lab. He notices that the spring will stretch further if he adds more mass to the end of the spring. He is soon convinced that the distance the spring will stretch depends on the amount of mass attached to it. He decides to take some measurements. He records the amount of mass attached to the end of the spring and then measures the distance that the spring stretched. Here is Jim’s data.

b) Use your calculator to determine a line of best fit that can be used to predict the distance the spring stretches. Write it using function notation. Graph it on your calculator and copy it onto your coordinate system.

c) Use the function from part (c) to predict the distance the spring will stretch if 175 grams is attached to the spring. Try to use the TABLE feature on your calculator to make this prediction.

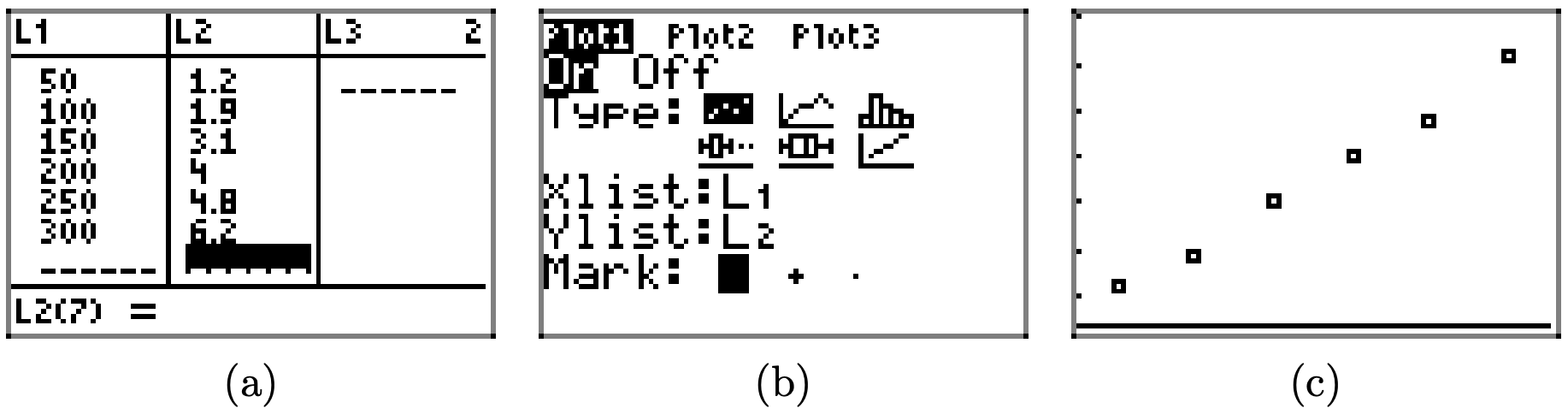
In (b) above, we see that the distance stretched d, as a function of mass m is given by the linear function d(m) = 0.01977m + 0.07333.

c) If all went well in part (b), then we can press 2nd TBL SET and set up the table parameters as shown in (g). Make sure the independent variable is set to ASK. Select 2nd TABLE, then enter 175 (which represents a mass of 175 grams) as shown in (h).

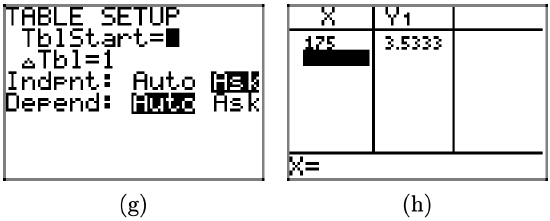
Thus, d(175) = 3.5333, so the spring stretches approximately 3.53 centimeters when a mass of 175 grams is attached.

Dave and Melody are lab partners in Tony Sartori’s afternoon chemistry lab. Professor Sartori has prepared an experiment to help them discover the relationship between the Celsius and Fahrenheit temperature scales. The experiment consists of a beaker full of ice and two thermometers, one calibrated in the Fahrenheit scale, the other in the Celsius scale. Dave and Melody use a Bunsen burner to heat the beaker, eventually bringing the water in the beaker to the boiling point. Every few minutees they make two temperature readings, one in Fahrenheit, one in Celsius. The data that they record during the laboratory session follows.

b) Use your calculator to determine a line of best fit that can be used to predict the Fahrenheit temperature as a function of the Celsius temperature. Write it using function notation. Graph it on your calculator and copy it onto your coordinate system.

c) Use the function from part (c) to predict the Fahrenheit temperature if the Celsius temperature is 40. Try to use the TABLE feature on your calculator to make this prediction.

d) Use the function from part (c) to predict the Celsius temperature if the Fahrenheit temperature is 100.

The following table shows data on home sales at the Mendocino Coast in 2005.

b) Use your calculator to determine a line of best fit. Write it using function notation and round to the nearest thousandth. Graph it on your calculator and copy it onto your coordinate system.

c) Use the linear function to predict the sales for houses in the price range $500, 000− $599, 000. Use the average price of $550, 000 for this estimate.

d) The actual number of houses sold in the price range $500, 000 − $599, 000 was 41. Plot this as a point on your coordinate system and compare it to your linear function model’s prediction. Notice that this actual value is pretty different from the prediction.

e) What this means is that a linear model is not very good for the data for home sales! Draw a simple curve that goes through each of the data points. Notice that it does not very closely resemble the shape of a line! More sophisticated functions are required to model this example–such as quadratic functions, which we study in a later chapter. The moral of the story here is that not every data set can be modeled linearly!

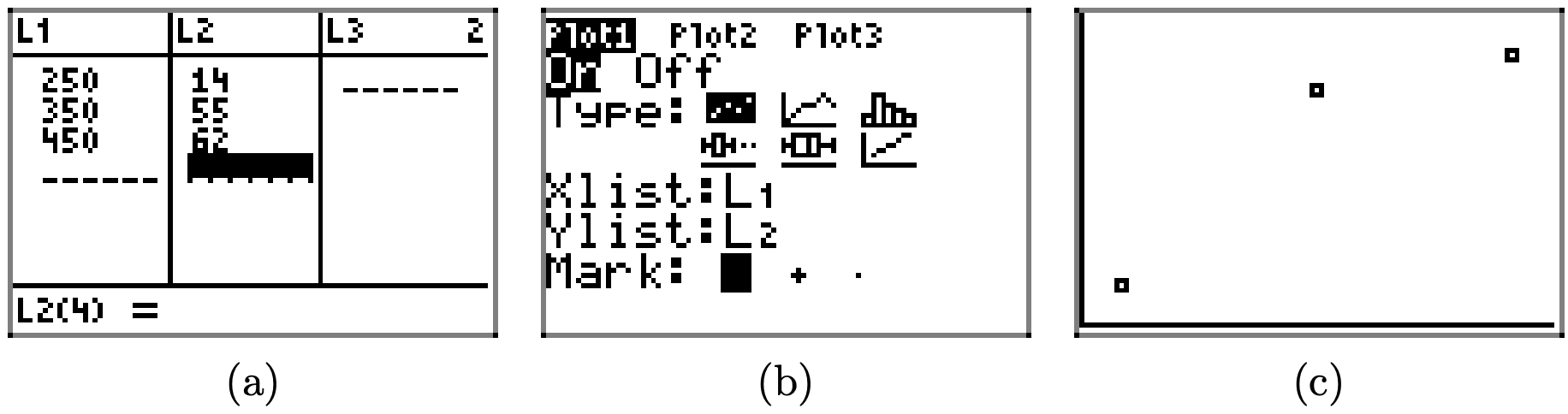
In (b) above, we see that the number sold N, as a function of average price P is given by the linear function N(P) = 0.24P − 40.33.

c) If all went well in part (b), then we can press 2nd TBL SET and set up the table parameters as shown in (g). Make sure the independent variable is set to ASK. Select 2nd TABLE, then enter 550 (which represents an average price P = $550, 000) as shown in (h).

Thus, N(550) = 91.667, so approximately 91.667 thousand or 91, 667 homes are sold at the average price of $550,000. d) Press the STAT button, select 1:Edit and add the point (550, 41) to the table, as shown in (i). Select 9:ZoomStat from the ZOOM menu to produce the image in (j). Note that the data no longer depicts a linear trend, but something more of a nonlinear (curvy) nature

e) In (k) we’ve drawn a smooth curve of best fit.

The following from the July 14, 2006 edition of the Beijing Today newspaper shows how high-heels affect the ball of the foot. The table shows the increase in percent of pressure on the ball of the foot for given heights of heels.

b) Notice that, because we have exactly two data points, the line of best fit is the line that goes through both points. To begin finding the equation, use the slope formula to compute the slope.

c) Use the point-slope form to find an equation for the line. Write it in slope-intercept form.

d) Use the linear function to predict the percent of stress increase for a 3-inch heel.

e) The actual percent of pressure increase for a 3-inch heel is 76 %. Plot this as a point on your coordinate system and compare it to your linear function model’s prediction. Notice that this actual value is pretty different from the prediction.

f) What this means is that a linear model is not very good for the data! Draw a simple curve that goes through each of the data points. Notice that it does not very closely resemble the shape of a line! More sophisticated functions are required to model this example. Not every data set should be modeled linearly!

3-6 Homework

$ 400.00 Original price was: $400.00. $ 79.00 Current price is: $79.00.

Our blackline masters have 3 years of meaningful work for the child and are extension lessons from the Montessori album.  This is a valuable resource allowing the directress time to focus attention on the child as opposed to stressing about creating thousands of follow up lessons across the Montessori curriculum.

• Description Description

Product Description

Blackline masters.

Creating appropriate homework that is challenging and inspiring is time consuming.  We all know a teacher’s time is precious, and that time is best spent with the students.

With these homework blacklines, you will not have to create appropriate homework ever again!  Enjoy!

• Three years of weekly homework sheets
• Topics covered: math, cultural, language, and practical life
• One sheet per week designed to minimize copy costs and eliminate dittos
• Allows students to continue the Montessori curriculum at home
• Introduces a three-part lesson to parents
• Includes sequenced word lists for individualization

Related products

6-9 Math Application

Classroom Job Board

6 Morning Routine Booklets 10 Pack

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Big Ideas Math Answers Grade 6 Chapter 3 Ratios and Rates

Free solutions to Big Ideas Math Grade 6 Chapter 3 Ratios and Rates are available here. So, the pupils those who are searching the Big Ideas Math Grade 6 Chapter 3 Ratios and Rates Solution Key can get them on this page. As per your convenience we have provided the solutions in the pdf format. So, Download Big Ideas Math Answers Grade 6 Chapter 3 Ratios and Rates pdf for free of cost.

Big Ideas Math Book 6th Grade Answer Key Chapter 3 Ratios and Rates

The list of topics covered in this chapter are Ratios, Using Tape Diagrams, Ratio tables, Graphing Ratio Relationships and so on.  Check out the topics and practice the problems number of times and score highest marks in the exams. 6th Grade Ratios and Rates Solution Key helps the students to complete the homework or assignment in time.

Performance Task

Ratios and Rates STEAM Video/Performance Task

Ratios and rates getting ready for chapter.

Lesson: 1 Ratios

Lesson 3.1 Ratios

Ratios homework & practice 3.1.

Lesson: 2 Using Tape Diagrams

Lesson 3.2 Using Tape Diagrams

Using tape diagrams homework & practice 3.2.

Lesson: 3 Using Ratio Tables

Lesson 3.3 Using Ratio Tables

Using ratio tables homework & practice 3.3.

Lesson: 4 Graphing Ratio Relationships

Lesson 3.4 Graphing Ratio Relationships

Graphing ratio relationships homework & practice 3.4.

Lesson: 5 Rates and Unit Rates

Lesson 3.5 Rates and Unit Rates

Rates and unit rates homework & practice 3.5.

Lesson: 6 Converting Measures

Lesson 3.6 Converting Measures

Converting measures homework & practice 3.6, ratios and rates connecting concepts, ratios and rates chapter review, ratios and rates practice test, ratios and rates cumulative practice.

STEAM Video

Answer: Enid says the heart pumps about 5 liters of blood each minute. 5 × 1 = 5 liters We have multiply number of minutes with 5

2. Explain how you can estimate the amount of blood your heart pumps in one heart beat.

Answer: Multiply your body surface area by the cardiac index to determine the liters of blood pumped by your heart in one minute.

Answer: 1 liter = 1000 ml The volume of Aorta and large arteries is 300 ml 300/1000 = 0.3 = 30% Small arteries = 0.4L 0.4 × 1000 = 400ml = 40% 40% of blood contained in small arteries Small veins = 2.43qt 2.43 qt = 2.299L Large Veins = 0.24 gal 0.24 gal = 0.908L

Chapter Exploration

Explanation: Count the red portion shown in the image out of 12 potions when we count we get Four-twelfths of the portion of the rectangle is red

Explanation: Count the red portion shown in the image out of 18 potion when we count we get Six out of eighteen of the portion of the rectangle is red

Explanation: Count the red portion shown in the image out of 9 potion when we count we get Five out of nine of the portion of the Square is red

Explanation: Count the red portion shown in the image out of 9 potion when we count we get four out of nine of the portion of the Square is red

Explanation: Count the red portion shown in the image out of 9 potion when we count we get six out of nine of the portion of the Square is red

Explanation: Count the red portion shown in the image out of 24 potion when we count we get sixteen out of twenty-four of the portion of the Rectangle is red

Explanation: Count the red portion shown in the image out of 12 potion when we count we get four out of twelve of the portion of the Rectangle is red

Explanation: Count the red portion shown in the image out of 12 potion when we count we get five out of twelve of the portion of the Rectangle is red

Explanation: Count the red portion shown in the image out of 6 potion when we count we get six out of six of the portion of the Rectangle is red

Explanation: a ratio indicates how many times one number contains another. so 5 : 6 of the tiles are blue.

Explanation: a ratio indicates how many times one number contains another. so 3 : 4 of the tiles are yellow

Explanation: a ratio indicates how many times one number contains another. so 4 : 5 of the tiles are green

Explanation: a ratio indicates how many times one number contains another. so 5 : 7 of the tiles are red

Question 15. MODELING REAL LIFE Work with a partner. The soccer committee has 8 girls and 6 boys. The tennis committee has 9 girls and 8 boys. A friend tells you that the tennis committee has a greater portion of girls than the soccer committee. Is your friend correct? Explain. If not, how many boys could you add to the soccer committee so that your friend is correct? Answer: Given, The soccer committee has 8 girls and 6 boys. The tennis committee has 9 girls and 8 boys. The ratio of soccer committee is 8:6 The ratio of tennis committee is 9:8 Compare both the ratios 8 < 9 Thus number of girls in tennis committee are more than soccer committee. Thus we can say that your friend is correct.

Vocabulary The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts. ratio rate equivalent rates equivalent ratios unit rate

Answer: Ratio – a ratio indicates how many times one number contains another. Rate – a measure, quantity, or frequency, typically one measured against another quantity or measure. Equivalent rates – Equivalent rates are rates that are equal. Equivalent ratio – Two ratios that have the same value are called equivalent ratios. Unit Rate – A unit rate is a rate with 1 in the denominator.

A ratio is a comparison of two quantities. Consider two quantities a and b. The ratio a : b indicates that there are a units of the first quantity for every b units of the second quantity.

EXPLORATION 1

Answer: 24 girls and 12 boys in the science class b. What comparisons can you make between your class and the science class? Can you determine which class has more girls? more boys? Explain your reasoning.

Answer: Number of girls and boys in your class are 42. Number of girls = 22 Number of boys = 20 Compare the number of girls in your class and science class 22: 24 Thus there are more girls in science class. 20:12 Thus there are more boys in your class.

c. Write three ratios that you observe in your classroom. Describe what each ratio represents. Answer: 36:42 – This represents number of students in science class and your class 22:24 – This represents number of girls in science class and your class 20:12 – This represents number of boys in science class and your class

EXPLORATION 2

Answer: 3 + 1: 1 + 1 4:2 No it will not change the taste of the mixture. b. Describe how you can make larger amounts without changing the taste. Answer: If the number of portions and the size of each portion change, you will have to find a conversion factor using a similar approach.

Write the indicated ratio using the coins in Example 1. Question 1. dimes to pennies Answer:  1 : 10

Explanation: we have to convert the coins from dimes to pennies. we know that A dime is worth 10 pennies. so the ratio is 1 : 10

Question 2. quarters to the total number of coins. Answer: 25 : 40

The number \(\frac{a}{b}\) associated with the ratio a : b is called the value of the ratio. It describes the multiplicative relationship between the quantities in a ratio.

Determine whether the ratios are equivalent. Question 4. 1 : 1 and 6 : 6 Answer:  The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 1 : 1 and 6 : 6 are Equivalent

Question 5. 1 : 2 and 3 : 4 Answer: The ratios are Not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. hence the 1 : 2 and 3 : 4 The ratios are Not Equivalent.

Question 6. 8 : 3 and 6 : 16 Answer: The ratios are Not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. hence the 8 : 3 and 6 : 16 ratios are Not Equivalent.

Self-Assessment for Concepts & Skills Solve each exercise. Then rate your understanding of the success criteria in your journal.

Explanation: a ratio indicates how many times one number contains another. so 4 : 5 of sharks to dolphins by observing the picture given

Question 8. dolphins : animals Answer: 5 : 0

Explanation: a ratio indicates how many times one number contains another. so 5 : 0 of dolphins: animals by observing the picture given

IDENTIFYING EQUIVALENT RATIOS Determine whether the ratios are equivalent. Explain your reasoning. Question 9. 2 : 3 and 24 : 36 Answer: The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 2 : 3 and 24 : 36 are Equivalent

Question 10. 5 : 7 and 20 : 28 Answer: The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 5 : 7 and 20 : 28 are Equivalent

Question 11. 3 : 10 and 9 : 25 Answer: The ratios are Not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. hence the 3 : 10 and 9 : 25 ratios are Not Equivalent.

Explanation: A ratio takes one number and divides it into another number to determine a decimal that can later be converted to a percentage if desired The ratio of wolves to cougars in a forest is 5 : 3 so the interpret the value of the ratio is 5 to 3.

Question 14. You are kayaking at a pace of 63 feet every 12 seconds. Your friend’s pace is 21 feet every 3 seconds. Are you and your friend kayaking at the same pace? If not, who is faster? Answer: No, Me and my friend kayaking are not at the same pace. my friend is faster.

Explanation: Given, You are kayaking at a pace of 63 feet every 12 seconds Your friend’s pace is 21 feet every 3 seconds So if I am kayaking at apace of 63 feet for every 12 seconds. then dividing 63 feet by 12 seconds we get 5.25 feet per second. In the same way friend’s pace is 21 feet every 3 seconds. the dividing 21 feet by 3 second we get 7 feet per second. Hence me and my friend are not at the same pace. 7 feet per second my friend is faster than me

Review & Refresh

Divide. Check your answer. Question 1. 15.4 ÷ 2.2 Answer: 7

Explanation: Given 15.4 ÷ 2.2 so divide 15.4 by 2.2 we get 7

Question 2. 56.07 ÷ 8.9 Answer: 6.9

Explanation: Given 56.07 ÷ 8.9 so divide 56.07 by 8.9 we get 6.9

Question 3. \(\sqrt [ 8.43 ]{ 12.645 } \) Answer: 0.8164

Explanation: Given \(\sqrt [ 8.43 ]{ 12.645 } \) so divide square root of 8.43 by 12.645 we get 0.8164

Question 4. \(\sqrt [ 11.6 ]{ 51.62 } \) Answer: 0.474

Explanation: Given \(\sqrt [ 11.6 ]{ 51.62 } \) so divide square root of 11.6 by 51.62 we get 0.474

Find the value of the power. Question 5. 8 2 Answer: 8 × 8 = 64

Explanation: given 8 2 so by multiplying 8 × 8, we get 64

Question 6. 1 6 Answer: 1

Explanation: given 1 power of 6 so by multiplying 1 × 1 × 1 ×1 × 1 × 1 we get 1

Question 7. 3 4 Answer: 81

Explanation: given 3 power of 4 so by multiplying 3 × 3 × 3 × 3 we get 81

Question 8. 2 6 Answer: 64

Explanation: given 2 power of 6 so by multiplying 2 × 2 × 2 ×2 × 2 × 2 we get 64

Concepts, Skills, & Problem Solving

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. There are two frogs and five turtles in the shown image. hence frogs to turtles is 2 : 5

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. There are six basketballs and four soccer balls in the shown image. hence basketballs to soccer balls are 6 : 4

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. There are two calculators and six pencils in the shown image. hence calculators : pencils are 2 : 6

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. There are three shirts and six pants in the shown image. hence shirts : pants are 3 : 6

Question 17. MODELING REAL LIFE Twelve of the 28 students in a class own a dog. What is the ratio of students who own a dog to students who do not? Answer: 12 : 28

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. Given Twelve of the 28 students in a class own a dog we get 12 students who have dogs out of 28 students so in the students who do not have dogs are 28 hence the ratio of students who own a dog to students who do not is 12 : 28

Question 18. LOGIC Name two things that you would like to have in a ratio of 5 : 1 but not in a ratio of 1 : 5. Explain your reasoning. Answer: 5 students in 1 class gives the ratio 5:1 It is not possible to have 1 student in 5 classes.

OPEN-ENDED Describe a real-life relationship that can be represented by the ratio. Question 19. 1 out of every 7 Answer: 1 : 7

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. hence 1 out of every 7 is 1 : 7

Question 20. 5 to 26 Answer: 5 : 26

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. hence 5 to 26 7 is   5 : 26

Question 21. 2 per 5 Answer: 2 : 5

Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b. hence 2 per 5 is 2 : 5

Question 22. 7 : 1 Answer:  7 out of  1

Explanation: a ratio indicates how many times one number contains another. Hence 7 : 1 is 7 out of  1

Answer: Let us consider the month be April The number of days in April are 30. 4:1 4 × 6 = 24 days 1 × 6 = 6 days 24 + 6 = 30 days b. In another month, the number of sunny days is 5 times the number of rainy days. Write the ratio of sunny days to rainy days. Answer: 5:1

Explanation: Given, In another month, the number of sunny days is 5 times the number of rainy days. The ratio of the sunny days to rainy days is 5 : 1

IDENTIFYING EQUIVALENT RATIOS Determine whether the ratios are equivalent. Question 24. 2 : 3 and 4 : 9

Answer: The ratios are Not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 2 : 3 and 4 : 9 are Not Equivalent

Question 25. 3 : 8 and 9 : 24

Answer: The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 3 : 8 and 9 : 24 are Equivalent

Question 26. 1 : 4 and 2 : 6

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 1 : 4 and 2 : 6 are Not Equivalent

Question 27. 5 : 3 and 15 : 12 Answer: The ratios are Not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 5 : 3 and 15 : 12 are Not Equivalent

Question 28. 6 : 10 and 12 : 20 Answer: The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 6 : 10 and 12 : 20 are Equivalent.

Question 29. 2 : 3 and 4 : 5 Answer: The ratios are not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 2 : 3 and 4 : 5 are not Equivalent.

Question 30. 28 : 32 and 7 : 8 Answer: The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 28 : 32 and 7 : 8 are Equivalent.

Question 31. 24 : 100 and 6 : 25 Answer: The ratios are Not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 28 : 32 and 7 : 8 are Not Equivalent.

Question 32. 85 : 210 and 340 : 735 Answer: The ratios are Not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 85 : 210 and 340 : 735  are Not Equivalent.

WRITING EQUIVALENT RATIOS Write a ratio that is equivalent to the given ratio. Justify your answer. Question 33. 3 : 1 Answer: 6: 2

Explanation: The equivalent ratio of 3:1 is 6:2 Two ratios that have the same value are called equivalent ratios. 6:2 = 3:1

Question 34. 7 : 2 Answer: 14: 4

Explanation: Two ratios that have the same value are called equivalent ratios. The equivalent ratio of 7 : 2 is 14:4 7 × 2 : 2 × 2 = 14:4

Question 35. 6 : 6 Answer: 12:12

Explanation: Two ratios that have the same value are called equivalent ratios. The equivalent ratio of 6:6 is 12:12 6 × 2 : 6 × 2 = 12:12

Question 36. 0 : 8 Answer: 0:16

Explanation: Two ratios that have the same value are called equivalent ratios. The equivalent ratio of 0:8 is 0:16 0 × 2: 8 × 2 = 0 : 16

Explanation: Since 3 : 9 = 6 : X Then we know 9/3 = X/6 Multiplying both sides by 6 cancels on the right 6 × (9/3) = (X/6) × 6 6 × (9/3) = X Then solving for X X = 6 × (9/3) X = 18 Therefore 3 : 9 = 6 : 18 Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.

Explanation: Since X : 6 = 7 : 2 Then we know X/6 = 7/2 Multiplying both sides by 6 cancels on the left 6 × (X/6) = (7/2) × 6 X = (7/2) × 6 Then solving for X X = 6 × (7/2) X = 21 Therefore 21 : 6 = 7 : 2 Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 4 : 8 and 8 : 12  are Not Equivalent. after add 4 each to the ratios

Question 41. OPEN-ENDED A non-Newtonian liquid demonstrates properties of both a solid and a liquid. A recipe for a non-Newtonian liquid calls for 1 cup of water and 2 cups of cornstarch. Find two possible combinations of water and cornstarch that you can use to make a larger batch. Justify your answer. Answer: Given, A non-Newtonian liquid demonstrates properties of both a solid and a liquid. A recipe for a non-Newtonian liquid calls for 1 cup of water and 2 cups of cornstarch The ratio of water and cornstarch is 1 : 2 The possible combinations of water and cornstarch are You can multiply 3 to each number in the first ratio to obtain the numbers in the second ratio, the ratios are equivalent. 1 × 3 : 2 × 3 = 3 : 6 You can multiply 5 to each number in the first ratio to obtain the numbers in the second ratio, the ratios are equivalent. 1 × 5 : 2 × 5 = 5 : 10

Question 42. PROBLEM SOLVING You are downloading songs to your tablet. The ratio of pop songs to rock songs is 5 : 4. You download 40 pop songs. How many rock songs do you download? Answer: 32

Explanation: Given, . The ratio of pop songs to rock songs is 5 : 4. You download 40 pop songs. Let number of rock songs be x 5 : 4 :: 40 :: x 5 × x = 4 × 40 5x = 160 x = 160/5 x = 32 Therefore, number of rock songs = 32.

Explanation: Given, the ratio of states that border an ocean to states that do not border an ocean is 7 : 9. So states that border an ocean is 7 and states that do not border an ocean is 9 hence the states border an ocean is 7

Question 44. REASONING The value of a ratio is \(\frac{4}{3}\). The second quantity in the ratio is how many times the first quantity in the ratio? Explain your reasoning. Answer: The second quantity is 1.3333 times the first quantity in the ratio.

Explanation: A ratio is given to us which is 4:3. What we need to find out is, the second quantity in the ratio is how many times the first quantity in the ratio. The definition of ratio is, the quantitative relation between two amounts showing the number of times one value contains or is contained within the other. So according to the definition of ratio we get: 4/3 = 1.33 So we can say that 4 contains 3, 1.3333 times in it. So the second quantity is 1.3333 times the first quantity in the ratio.

Explanation: Given A train moving at a constant speed travels 3 miles every 5 minutes. by dividing 3 miles by 5 minutes we get 0.6 miles per minute A car moving at a constant speed travels 12 miles every 20 minutes. by dividing 12 miles by 20 minutes we get 0.6 miles per minute Hence both vehicle have the same speed

Question 46. CRITICAL THINKING To win a relay race, you must swim 200 yards before your opponent swims 190 yards. You swim at a pace of 50 yards every 40 seconds. Your opponent swims at a pace of 10 yards every 8.5 seconds. Who wins the race? Justify your answer. Answer:

Explanation: Given You swim at a pace of 50 yards every 40 seconds By dividing 50 yards by 40 seconds we get 1.25 yards per second Your opponent swims at a pace of 10 yards every 8.5 seconds. By dividing 10 yards by 8.5 seconds we get 1.17 yards per second You swim at a pace of 50 yards every 40 seconds  for completing 200 yards you take 160 seconds your opponent swims at a pace of 10 yards every 8.5 seconds  for completing 190 yards you take 162.3  seconds hence you won the race by completing 200 yards in 160 seconds before your opponent completes 190 yards at 162.3 seconds

Question 47. DIG DEEPER! There are 3 boys for every 2 girls in a dance competition. Does it make sense for there to be a total of 9 people in the competition? Explain. Answer: No

Explanation: Given, There are 3 boys for every 2 girls in a dance competition. 3:2=5 so girls are 2:5 set up the proportion 2/5=x/9 5x=18 x=3.6 girls another way you can look at it is because there are 3 boys for every 2 girls, add 2 more girls, you’ll get 3 more boys that makes the total of 10 people so 9 is impossible

Answer: The ratio of the length of the blue rectangle to the length of the green rectangle is 2 : 4 The ratio of the width of the blue rectangle to the width of the green rectangle is 3 : 6 Perimeter of the rectangle = 2l + 2w Blue rectangle: 2(3) + 2(2) = 6 + 4 = 10 Green Rectangle: 2(6) + 2(4) = 12 + 8 = 20 Ratio of perimeter of blue rectangle to the green rectangle is 10 : 20 Area of the rectangle = lb Blue rectangle: A = 2 × 3 = 6 Green Rectangle: A = 4 × 6 = 24 Ratio of Area of blue rectangle to the green rectangle is 6 : 24 b. Compare your ratios in part(a). Answer: The ratio of the length of the blue rectangle to the length of the green rectangle is 2 : 4 equivalent to 1 : 2 The ratio of the width of the blue rectangle to the width of the green rectangle is 3 : 6 equivalent to 1 : 2 Ratio of perimeter of blue rectangle to the green rectangle is 10 : 20 equivalent to 1 : 2 Ratio of Area of blue rectangle to the green rectangle is 6 : 24 equivalent to 1 : 4

Question 49. STRUCTURE The ratio of the side lengths of a triangle is 2 : 3 : 4. The shortest side is 15 inches. What is the perimeter of the triangle? Explain. Answer: 67.5 inches

Explanation: Given that, The ratio of the side lengths of a triangle is 2 : 3 : 4. The shortest side is 15 inches. Let x = the first side y = the second side z = the third side We know that x/y = 2/3 y = 1.5x x/z = 2/4 z = 2x x = 15 inches Substitute the value of x in both the equations y = 1.5(15) = 22.5 in z = 2(15) = 30 in Now find the perimeter of the triangle P = x + y + z P = 15 + 22.5 + 30 = 67.5 inches

Question 51. DIG DEEPER! There are 12 boys and 10 girls in your gym class. If 6 boys joined the class, how many girls would need to join for the ratio of boys to girls to remain the same? Justify your answer. Answer: Given, There are 12 boys and 10 girls in your gym class. 12/10=6/5 6 boys joined: 18/(of girls)=6/5, #of girls=18×5/6=15 5 more girls will keep the same ratio 6/5

You can use a visual model, called a tape diagram, to represent the relationship between two quantities in a ratio.

Answer: We determine from the tape diagram that the beginner trail has one rectangle and the expert trial has four rectangles.

b. Choose a length for one of the trails. What conclusions can you make from the tape diagram? Explain your reasoning.

You can use tape diagrams to represent ratios and solve ratio problems.

Explanation: given The tape diagram represents the ratio of gifts received to gifts given. You received 4 gifts the ratio by observing the given image is 1 : 4 hence you gave 1 gift

Question 2. There are 8 bones in a large snake for every 3 bones in a small snake. The small snake has 150 bones. How many bones does the large snake have? Answer: 400

Explanation: Given, There are 8 bones in a large snake for every 3 bones in a small snake. The small snake has 150 bones. 150/3 = 50 bones 50 × 8 = 400 bones Thus the large snake has 400 bones.

Question 3. WHAT IF? Repeat Example 3 when the ratio of your monthly allowance to your friend’s monthly allowance is 2 to 3.

Question 5. REASONING You are given a tape diagram and the total value of the parts. How can you find the value of 1 part? Answer:

Question 6. DRAWING A TAPE DIAGRAM Describe two ways that you can represent the ratio 12 : 4 using a tape diagram. Answer:

Explanation: Number of winning tickets = 7 Number of losing tickets = 28 The ratio of winning tickets and losing tickets are 7 : 28 We get 1 : 4 Thus the answer is 7 : 28

Question 8. 80 tickets; 2 : 8 Answer: 16 : 64

Explanation: Total number of tickets = 80 The ratio of winning tickets to losing tickets is 2 : 8 Let 2x be the winning tickets and 8x be the losing tickets 2x + 8x = 80 10x = 80 x = 80/10 = 8 Number of winning tickets = 2x = 2(8) = 16 Number of losing tickets = 8x = 8(8) = 64 The ratio of winning tickets and losing tickets are 16 : 64

Question 11. DIG DEEPER! Your team wins 18 medals at a track meet. The medals are gold, silver, and bronze in a ratio of 2 : 2 : 5. How many of each medal were won by your team? Answer: The team won 4 gold medals, 4 silver medals and 10 bronze medals.

Explanation: Given, Total medals won = 18 Ratio of gold, silver and bronze = 2:2:5 Let, x be the original number. Therefore, Gold medals = 2x Silver medals = 2x Bronze medals = 5x According to given statement 2x + 2x + 5x = 18 9x = 18 x = 2 Gold medals = 2x = 2(2) = 4 Silver medals = 2x = 2(2) = 4 Bronze medals = 5x = 5(2) = 10

Determine whether the ratios are equivalent. Question 1. 11 : 4 and 22 : 8 Answer: The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 11 : 4 and 22 : 8 are Equivalent.

Question 2. 12 : 18 and 2 : 3 Answer: The ratios are Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 12 : 18 and 2 : 3 are Equivalent.

Question 3. 56 : 81 and 7 : 9 Answer: The ratios are not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 56 : 81 and 7 : 9 are not Equivalent.

Question 4. 2 : 12 and 6 : 24 Answer: The ratios are not Equivalent.

Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2. Hence the ratios 2 : 12 and 6 : 24 are not Equivalent.

Multiply. Write the answer in the simplest form. Question 5. \(\frac{7}{10}\) . \(\frac{5}{7}\) Answer: \(\frac{1}{2}\) For fraction multiplication, multiply the numerators and then multiply the denominators to get \(\frac{7}{10}\) . \(\frac{5}{7}\) This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 35 and 70 using GCF(35,70) = 35 35÷35 divided by 70÷35= \(\frac{1}{2}\) Therefore: \(\frac{7}{10}\) . \(\frac{5}{7}\) is 12

Question 6. 2\(\frac{1}{3}\) . \(\frac{3}{4}\) Answer: \(\frac{1}{2}\)

Explanation: For fraction multiplication, multiply the numerators and then multiply the denominators to get 1×33×4=312 This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 3 and 12 using GCF(3,12) = 3 3÷3 divided by 12÷3= \(\frac{1}{4}\) Therefore: as given in question 2\(\frac{1}{3}\) . \(\frac{3}{4}\) = 2 × \(\frac{1}{4}\) we get \(\frac{1}{2}\)

Question 7. 5\(\frac{3}{8}\) . 2\(\frac{1}{2}\) Answer: 13 \(\frac{7}{16}\)

Explanation: Convert any mixed numbers to fractions. 5\(\frac{3}{8}\) = \(\frac{43}{8}\) 2\(\frac{1}{2}\) = \(\frac{5}{2}\) \(\frac{43}{8}\) × \(\frac{5}{2}\) = \(\frac{215}{16}\) Now convert it into the mixed fractions \(\frac{215}{16}\) = 13 \(\frac{7}{16}\)

Question 8. Melissa earns $7.40 per hour working at a grocery store. She works 14.25 hours this week. How much does she earn? A. $83.13 B. $105.45 C. $156.75 D. $1054.50 Answer: $105.45

Explanation: Given, Melissa earns $7.40 per hour working at a grocery store. She works 14.25 hours this week. 14.25 × 7.40 = $105.45 Thus Melissa earns $105.45 this week

Question 10. The expert trail is 1200 meters long. How long is the beginner trail? Answer: For the beginner’s trail, there is only one rectangle. For Expert Trail, there are 4 rectangles. Then in total, we have 5 rectangles. We know that the combined length is 1200 meters, then the 5 rectangles are equivalent to 1200 meters. Then each rectangle will be equivalent to: 1200m/5 = 240m Now, we know that the beginner’s trail has one rectangle, then the length of the beginner’s trail is 240 meters long. The expert’s trail has 4 rectangles, then it is: 4×240m = 960m long.

Question 11. The combined length of the trails is 2000 meters. How long is each trail? Answer: For the beginner’s trail, there is only one rectangle. For Expert Trail, there are 4 rectangles. Then in total, we have 5 rectangles. We know that the combined length is 2000 meters, then the 5 rectangles are equivalent to 2000 meters. Then each rectangle will be equivalent to: 2000m/5 = 400m. Now, we know that the beginner’s trail has one rectangle, then the length of the beginner’s trail is 400 meters long. The expert’s trail has 4 rectangles, then it is: 4×400m = 1600m long.

Question 12. The expert trail is 750 meters longer than the beginner trail. How long is each trail? Answer: For the beginner’s trail, there is only one rectangle. For Expert Trail, there are 4 rectangles. Then in total, we have 5 rectangles. We know that the combined length is 750 meters, then the 5 rectangles are equivalent to 750 meters. Then each rectangle will be equivalent to: 750m/5 = 150m Now, we know that the beginner’s trail has one rectangle, then the length of the beginner’s trail is 150 meters long. The expert’s trail has 4 rectangles, then it is: 4×150m = 600m long.

DRAWING A TAPE DIAGRAM A bag contains red marbles and blue marbles. You are given the number of red marbles in the bag and the ratio of red marbles to blue marbles. Find the number of blue marbles in the bag. Question 15. 10 red marbles; 5 to 1 Answer: red : blue=5:1 red/blue=5 red= 10 so blue= 2

Question 16. 3 red marbles; 3 : 7 Answer: red : blue=3:7 red/blue=3/7 red= 3 so blue= 7

Question 17. 12 red marbles; 4 : 3 Answer: red : blue=4:3 red/blue= 12/9 red= 12 so blue= 9

Question 18. 6 red marbles; 2 for every 5 Answer: red : blue=2:5 red/blue= 2×3 : 5×3 red= 6 so blue= 15

Question 19. 18 red marbles; 6 to 9 Answer: red : blue=6:9 red/blue=18/27 red= 18 so blue= 27

Question 20. 12 red marbles; 3 : 4 Answer: red : blue=3:4 red/blue=12/16 red= 12 so blue= 16

USING A TAPE DIAGRAM A bowl contains blueberries and strawberries. You are given the total number of berries in the bowl and the ratio of blueberries to strawberries. How many of each berry are in the bowl? Question 21. 16 berries; 3 : 1 Answer: no of strawberries = 4 no of blueberries = 12

Explanation: total berries :- 16 ration :- 3:1 no of strawberries :- 1x no of blueberries :- 3x 3x + 1x = 16 4x = 16 x = 4

Question 22. 10 berries; 2 for every 3 Answer: no of strawberries :- 3x no of blueberries :- 2x 2x + 3x = 10 5x = 10 x = 2 no of strawberries :- 3x = 3(2) = 6 no of blueberries :- 2x = 2(2) = 4

Question 23. 12 berries; 1 to 2 Answer: no of strawberries :- 2x no of blueberries :- 1x 1x + 2x = 12 3x = 12 x = 4 no of strawberries :- 2x = 2(4) = 8 no of blueberries :- 1x = 1(4) = 4

Question 24. 20 berries; 4 : 1 Answer: no of strawberries :- 1x no of blueberries :- 4x 1x + 4x = 20 5x = 20 x = 4 no of strawberries :- 1x = 1(4) = 4 no of blueberries :- 4x = 4(4) = 16

Question 25. 48 berries; 9 to 3 Answer: no of strawberries :- 3x no of blueberries :- 9x 3x + 9x = 48 12x = 48 x = 4 no of strawberries :- 3x = 3(4) = 12 no of blueberries :- 9x = 9(4) = 36

Question 26. 46 berries; 11 for every 12 Answer: no of strawberries :- 12x no of blueberries :- 11x 12x + 11x = 46 23x = 46 x = 2 no of strawberries :- 12x = 12(2) = 24 no of blueberries :- 11x = 11(2) = 22

Question 29. MODELING REAL LIFE There are 8 more girls than boys in a school play. The ratio of boys to girls is 5 : 7. How many boys and how many girls are in the play? Answer: Given, There are 8 more girls than boys in a school play. The ratio of boys to girls is 5 : 7 5x = 5(4) = 20 boys 7x = 7(4) = 28 girls To find how many more girls there are than boys in the play, We have to subtract the number of girls and number of boys 28 – 20 = 8 Thus it means there are 8 more girls than boys in the school play.

Question 30. DIG DEEPER! A baseball team sells tickets for two games. The ratio of sold tickets to unsold tickets for the first game was 7 : 3. For the second game, the ratio was 13 : 2. There were 240 unsold tickets for the second game. How many tickets were sold for the first game? Answer: 1260 tickets were sold on the first game

Explanation: For the second game, the ratio was 13 : 2. Total ratio = 13 + 2 = 15 There were 240 unsold tickets for the second game. Let the total number of tickets for the second game be x. 240 = 2/15 × x 2x = 15 × 240 = 3600 x = 3600/2 = 1800 1800 tickets were sold for the second time. Assuming total number of tickets for the first game is equal to total number of tickets for the second game. Therefore total number of tickets sold for the first game is 1800 The ratio of sold tickets to unsold tickets for the first game was 7: 3 Total ratio 7 + 3 = 10 Number of tickets sold for the first game would be 7/10 × 1800 = 12600/10 = 1260 tickets

Explanation: We know that: You have $150 in a savings account. This is represented with two tiles. Then each tile represents: $150/2 = $75 And in cash you have 5 tiles, then in cash you have: 5×$75 = $375. Then the problem is: You have $150 in the savings account You have $375 in cash. You want to deposit a quantity such that you have twice the amount of money in your savings account as you have in cash. Suppose that you move a quantity X from cash to the savings account, then now we have the situation: Sav. Acc. = $150 + X Cash = $375 – X And we want that: Sav. Acc. = 2×Cash ($150 + X) = 2×($375 – X) Let’s solve this for X. $150 + X = $750 – 2×X 3×X = $750 – $150 = $600 X = $600/3 = $200 You should deposit $200 in the Savings account.

Explanation: A fish tank contains tetras, guppies, and minnows. The ratio of tetras to guppies is 4 : 2. The ratio of minnows to guppies is 1 : 3. There are 60 fish in the tank. Let number of tetras be t number of guppies be g number of minnows be m Ratio of tetras to guppies is 4:2, or reducing, 2:1 m = g/3 Also, total there are 60 fish t + g + m = 60 2g + g + g/3 = 60 Now finding t and m: m = g/3 = 18/3 = 6 m = 6 t = 2g t = 2(18) t = 36 There are 36 tetras and 6 minnows. So, there are 36 – 6 = 30 more tetras than minnows

You can also generate a ratio table by using subtraction or division. In summary, you can find equivalent ratios by: • adding or subtracting quantities in equivalent ratios. • multiplying or dividing each quantity in a ratio by the same number.

Question 8. WRITING Explain how creating a ratio table using repeated addition is similar to creating a ratio table using multiplication. Answer: Ratio tables are constructed in a special way. Each pair of values in the table will be equivalent to the same ratio. You can use repeated addition or multiplication to create a ratio table. There is a constant value that we can multiply the values in the first column by to get the values in the second column.

Question 9. You mix 7 tablespoons of vinegar for every 4 tablespoons of baking soda to produce a chemical reaction. You use 15 tablespoons of baking soda. How much vinegar do you use? Answer: Given, You mix 7 tablespoons of vinegar for every 4 tablespoons of baking soda to produce a chemical reaction. You use 15 tablespoons of baking soda. Case 1: Tablespoon of vinegar taken = 7 Tablespoon of baking soda taken = 4 The ratio between v and b = 7:4 Case 2: Tablespoon of vinegar taken = x Tablespoon of baking soda taken = 15 The ratio between v and b = x:15 7:4 : : x:15 7 × 15 = 4 × x 4x = 105 x = 105/4 x = 26.25 Thus you use 26.25 teaspoons.

A bag contains green tokens and black tokens. You are given the number of green tokens in the bag and the ratio of green tokens to black tokens. Find the number of black tokens in the bag. Question 1. green tokens; 4 for every 1 Answer: no of green tokens:- 4x no of black tokens:- 1x x = 1 no of green tokens:- 4x = 4(1) = 4 no of black tokens:- 1x = 1() = 1

Question 2. 6 green tokens; 2 : 7 Answer: no of green tokens:- 2x no of black tokens:- 7x 2x + 7x = 6 9x = 6 x = 6/9 x = 2/3 no of green tokens:- 2x = 2(2/3) = 4/3 no of black tokens:- 7x = 7(2/3) = 14/3

Question 3. 24 green tokens; 8 to 5 Answer: no of green tokens:- 8x no of black tokens:- 5x 8x + 5x = 24 13x = 24 x = 24/13 no of green tokens:- 8x = 8(24/13) = 14.7 no of black tokens:- 5x = 5(24/13) = 9.23

Question 4. 36 green tokens; 3 for every 4 Answer: no of green tokens:- 3x no of black tokens:- 4x 3x + 4x = 36 7x = 36 x = 36/7 no of green tokens:- 3x = 3(36/7) = 15.42 no of black tokens:- 4x = 4(36/7) = 20.57

Find the GCF of the numbers. Question 5. 8, 16 Answer: 8

Explanation: The factors of 8 are: 1, 2, 4, 8 The factors of 16 are: 1, 2, 4, 8, 16 Then the greatest common factor is 8.

Question 6. 48, 80 Answer: 16

Explanation: The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80 Then the greatest common factor is 16.

Question 7. 15, 45, 100 Answer: 5

Explanation: The factors of 15 are: 1, 3, 5, 15 The factors of 45 are: 1, 3, 5, 9, 15, 45 The factors of 100 are: 1, 2, 4, 5, 10, 20, 25, 50, 100 Then the greatest common factor is 5.

Evaluate the expression. Question 8. 35 – 2 × 4 2 Answer: 35 – 2 × 4 2 35 – 2 × 16 35 – 32 = 3

Question 9. 12 ÷ (1 + 3 3 – 2 4 ) Answer: 12 ÷ (1 + 3 3 – 2 4 ) 12 ÷ (1 + 27 – 16) 12 ÷ (28 – 16) 12 ÷ 12 = 1

Question 10. 8 2 ÷ [(11 – 3) . 2] Answer: 8 2 ÷ [(11 – 3) . 2] 8 2 ÷ [8 . 2] 8 2 ÷ 16 64 ÷ 16 = 4

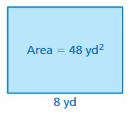
USING A RATIO TABLE Use a ratio table to find the number of calories in the indicated number of cups of milk from Exploration 1. Explain your method. (See Exploration 1, p. 121.) Question 13. 16 cups Answer: You buy milk that contains 180 calories per 2 cups. 1 cup = 180/2 = 90 calories 16 cups = 16 × 90 = 1440 calories

Question 14. 18 cups Answer: You buy milk that contains 180 calories per 2 cups. 1 cup = 180/2 = 90 calories 18 cups = 18 × 90 = 1620 calories

Question 15. 5.5 cups Answer: You buy milk that contains 180 calories per 2 cups. 1 cup = 180/2 = 90 calories 5.5 cups = 5.5 × 90 = 495 calories

Explanation: Given, First and second place in a contest use a ratio to share a cash prize. When first place pays $100, second place pays $60. Let x be the pay of the first place when the second place pays $36 100/60 = x/36 x = $60

Explanation: We know that for every 4 milligrams of copper, there are 15 milligrams of gold. if 48 milligrams of copper are used, we can separate them in “sets” of 4 milligrams. We have 48/4 = 12 sets. And for each one of these 12 sets, there are 15 milligrams of gold, then the total amount of gold in the alloy is: 12×15mg = 180 mg

Question 31. MODELING REAL LIFE You make candles by adding 2 fluid ounces of scented oil for every 22 fluid ounces of wax. Your friend makes candles by adding 3 fluid ounces of the same scented oil for every 37 fluid ounces of wax. Whose candles are more fragrant? Explain your reasoning. Answer: Your candles are more fragrant

Explanation: Given, You make candles by adding 2 fluid ounces of scented oil for every 22 fluid ounces of wax. Your friend makes candles by adding 3 fluid ounces of the same scented oil for every 37 fluid ounces of wax. Compare 2/22 and 3/37 2/22 > 3/37 By this we can say that your candles are more fragrant.

Question 32. MODELING REAL LIFE A mint milk shake contains 1.25 fluid ounces of milk for every 4 ounces of ice cream. A strawberry milk shake contains 1.75 fluid ounces of milk for every 5 ounces of ice cream. Which milk shake is thicker? Explain. Answer:

CRITICAL THINKING Two whole numbers A and B satisfy the following conditions. Find A and B. Question 33. A + B = 30 A : B is equivalent to 2 : 3. Answer: Let A = 2x Let B = 3x 2x + 3x = 30 5x = 30 x = 30/5 = 6 x = 6 A = 2x = 2(6) = 12 B = 3(6) = 18 A : B = 12 : 18

Question 34. A + B = 44 A : B is equivalent to 4 : 7. Answer: Let A = 4x Let B = 7x 4x + 7x = 44 11x = 44 x = 44/11 x = 4 A = 4x = 4(4) = 16 B = 7x = 7(4) = 28 A : B = 16 : 28

Question 35. A – B = 18 A : B is equivalent to 11 : 5. Answer: Let A = 11x Let B = 5x 11x – 5x = 18 6x = 18 x = 18/6 x = 3 A = 11x = 11(3) = 33 B = 5x = 5(3) = 15 33 – 15 = 18 A : B = 33 : 15

Question 36. A – B = 25 A : B is equivalent to 13 : 8. Answer: Let A = 13x Let B = 8x 13x – 8x = 25 5x = 25 x = 5 A = 13x = 13(5) = 65 B = 8(5) = 40 A : B = 65 : 40

Answer: There are 161 calories in 28 grams. You eat 9 cashews totaling 12 grams. We need to find out how many calories in 12 grams For that we make a proportion Calories/grams = calories/grams 161/28 = x/12 28x = 161 × 12 x = 1932/28 x = 69 There are 69 calories in 12 grams

b. How many cashews are in one serving? Answer: Divide 161 by 28 to get the calorie count for one gram Multiply that by 12 to work out how many calories you have eaten in the 9 cashews 161/28 = 5.75 5.75 x 12 = 69

Question 38. REASONING The ratio of three numbers is 4 : 5 : 3. The sum of the numbers is 54. What are the three numbers? Answer: Let it be x. 4x + 5x + 3x = 54 12x = 54 x = 54/12 x = 4.5 Now 4x = 4× 4.5 = 18 3x = 3 × 4.5 =13.5 5x = 5× 4.5 = 22.5

Question 39. CRITICAL THINKING Seven out of every 8 students surveyed own a bike. The difference between the number of students who own a bike and those who do not is 72. How many students were surveyed? Answer: So if x people were surveyed, 7/8 people owned a bike and 1/8 did not. The difference between them is 72 7/8 × x – 1/8 = 72 So, this means that, 6/8 x = 72 Let us simpify 3/4 × x = 72 1/4 × x = 24 and multiply by 4 x = 96 So 96 people were surveyed

Question 41. PROBLEM SOLVING You earn $72 for every 8 hours you spend shoveling snow. You earn $60 for every 5 hours you spend babysitting. For every 3 hours you spend babysitting, you spend 2 hours shoveling snow. You babysit for 15 hours in January. How much money do you earn in January? Answer: $90

Explanation: Earning for 8 hours shoveling snow = $72 Amount per hour = $72/8 = $9 3 hours of babysitting = 2 hours shoveling snow Babysitting hours in January = 15 hours Hours of shoveling snow in January = (15/3) x 2 = 10 hours Amount earned in January = Hours shoveling snow x Hourly Rate = 10 x $9 = $90 That is, you earn $90 in January.

Question 42. DIG DEEPER! You and a friend each have a collection of tokens. Initially, for every 8 tokens you had, your friend had 3. After you give half of your tokens to your friend, your friend now has 18 more tokens than you. Initially, how many more tokens did you have than your friend? Answer: 30 token

Explanation: Initially, for every 8 tokens I had, my friend had 3. Therefore, ratio of tokens that me and my friend is 8 : 3 Let I have 8 x tokens and my friend has 3 x tokens, where x is any number. Then again according to the question, After I gave half of your friend, my friend now has 18 more tokens than you. That is, (3x + 4x) – 4x = 18 7x – 4x = 18 3x = 18 x = 6 Therefore , Initially the difference between me and my friend’s token = 8 x – 3 x = 5 x = 5 × 6 = 30

For a ratio of two quantities, you can use equivalent ratios to create ordered pairs of the form (first quantity, second quantity). You can plot these ordered pairs in a coordinate plane and draw a line, starting at(0, 0), through the points.

Question 3. WHAT IF? Repeat Example 2 when the cost of the dark chocolate cashews is $15 per pound. Answer:

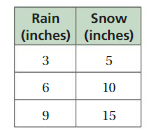
Question 5. CRITICAL THINKING Use what you know about equivalent ratios to explain why the graph of a ratio relationship passes through (0, 0). Answer:

Write the name of the decimal number. Question 3. 7.1 Answer: We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number. 7.1 can be written as seven and one.

Question 4. 3.54 Answer: We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number. 3.54 can be written as three and five four

Question 5. 13.6 Answer: We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number. 13.6 can be written as thirteen and six

Question 6. 8.132 Answer: We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number. 8.132 can be written as eight and one thirty two

Question 19. MODELING REAL LIFE A radio station collects donations for a new broadcast tower. The cost to construct the tower is $25.50 per inch. a. Represent the ratio relationship using a graph. b. How much does it cost to fund 4.5 inches of the construction? Answer:

Question 20. MODELING REAL LIFE Your school organizes a clothing drive as a fundraiser for a class trip. The school earns $100 for every 400 pounds of donated clothing. a. Represent the ratio relationship using a graph. b. How much money does your school earn for donating 2200 pounds of clothing? Answer:

Question 22. MODELING REAL LIFE An airplane traveling from Chicago to Los Angeles travels 15 miles every 2 minutes. On the return trip, the plane travels 25 miles every 3 minutes. Graph each ratio relationship in the same coordinate plane. Does the plane fly faster when traveling to Los Angeles or to Chicago? Answer:

Question 23. MODELING REAL LIFE Your freezer produces 8 ice cubes every 2 hours. Your friend’s freezer produces 24 ice cubes every 5 hours. Graph each ratio relationship in the same coordinate plane. Whose freezer produces ice faster? Answer:

Question 26. STRUCTURE The point (p, q) is on the graph of values from a ratio table. What are two additional points on the graph? Answer:

Question 1. WHAT IF? Repeat Example 1 when you add 4 pints of water for every 3 cups of concentrate. Answer:

Question 2. WHAT IF? Repeat Example 2 when the space junk travels 3 miles every 5 seconds. Answer:

FINDING UNIT RATES Write a unit rate for the situation. Question 3. revolutions in 50 seconds Answer:

Question 4. 1400 words for every 4 pages Answer: 1400 – 4 pages x – 1 page 4 × x = 1400 x = 1400/4 x = 350 Thus 350 words for every 1 page.

Explanation: 8 pounds for every 2 feet 8/2 = 4 feet 12 pounds per 3 feet 12/3 = 4 feet 20 pounds per 4 feet 20/4 = 5 feet 24 pounds for every 6 feet 24/6 = 4 feet

Question 6. You buy 10 pounds of birdseed at Store A for $11.50. Your friend buys 15 pounds of birdseed at Store B for $19.50. How much less would you spend by buying 20 pounds of birdseed at the store with the better deal? Answer: Store A

Explanation: Given, You buy 10 pounds of birdseed at Store A for $11.50. 10 pounds – $11.50 1 pound – $1.15 20 pounds = 20 × 1.15 = $23 Your friend buys 15 pounds of birdseed at Store B for $19.50. 15 pounds – $19.50 1 pound – $1.3 1.3 × 20 = $26 $23 < $26

Question 7. A person hikes 4 miles in 2.5 hours. Find the unit rate in miles per hour. Then find the unit rate in hours per mile. How is each unit rate useful in a real-life situation? Answer: 1.6 kilometer per hour

Explanation: The unit rate is the number of miles in 1 hour. Given, Distance = 4 miles Time = 2.5 hours So if he hike 4 miles in 2.5 hours then he will hike x mile in 1 hour x = 4/2.5 x = 1.6 miles per hour

Divide. Write the answer in simplest form. Question 5. \(\frac{1}{5}\) ÷ \(\frac{3}{10}\) Answer: \(\frac{2}{3}\)

Explanation: Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction. Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes \(\frac{1}{5}\) × \(\frac{10}{3}\) = \(\frac{10}{15}\) = \(\frac{2}{3}\)

Question 6. \(\frac{3}{8}\) ÷ 6 Answer: \(\frac{1}{16}\)

Explanation: Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction. Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes \(\frac{3}{8}\) × \(\frac{1}{6}\) = \(\frac{1}{16}\)

Question 7. 3\(\frac{1}{6}\) ÷ 2 Answer: 1 \(\frac{7}{12}\)

Explanation: Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction. Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes 3\(\frac{1}{6}\) = \(\frac{19}{6}\) \(\frac{19}{6}\) × \(\frac{1}{2}\) = 1 \(\frac{7}{12}\)

Question 8. 5\(\frac{1}{3}\) ÷ 2\(\frac{2}{3}\) Answer: 2

Explanation: Convert any mixed numbers to fractions. 5\(\frac{1}{3}\) = \(\frac{16}{3}\) 2\(\frac{2}{3}\) = \(\frac{8}{3}\) \(\frac{16}{3}\) × \(\frac{3}{8}\) = \(\frac{48}{24}\) = 2

Add or subtract. Question 9. 6.94 + 12.301 Answer: 19.241

Question 10. 8.753 – 7.71 Answer: 1.043

Question 11. 14.532 – 6.613 Answer: 7.919

Question 12. The winner in an election for class president received \(\frac{3}{4}\) of the 240 votes. How many votes did the winner receive? A. 60 B. 150 C. 180 D. 320 Answer: 180

Explanation: Given, The winner in an election for class president received \(\frac{3}{4}\) of the 240 votes. \(\frac{3}{4}\) × 240 = 180 The winner receive 180 votes. Thus the correct answer is option C

USING EQUIVALENT RATIOS Use the ratio in Exploration 2 to estimate the number of times you can clap your hands in the given amount of time. (See Exploration 2, p. 135.) Question 13. 0.5 minute Answer:

Question 14. 1.75 minutes Answer:

Question 15. 2.25 minutes Answer:

FINDING UNIT RATES Write a unit rate for the situation. Question 16. 24 animals in 2 square miles Answer: 12 animals

Explanation: Given, 24 animals in 2 square miles 24/2 = 12 12 animals in 1 square mile

Question 17. $100 for every 5 guests Answer: $20

Explanation: Given, $100 for every 5 guests 100/5 = $20 $20 per guest.

Question 18. $28 saved in 4 weeks Answer: $7

Explanation: Given, $28 saved in 4 weeks 28/4 = $7 $7 per week

Question 19. 18 necklaces made in 3 hours Answer: 6 necklaces

Explanation: Given, 18 necklaces made in 3 hours 18/3 = 6 6 necklaces made in 1 hour

Question 20. 270 miles in 6 hours Answer: 45 miles per hour

Explanation: Given, 270 miles in 6 hours 270/6 = 45 45 miles in 1 hour

Question 21. 228 students in 12 classes Answer: 24 students per class

Explanation: Given, 228 students in 12 classes 228/12 = 24 24 students in 1 class

Question 22. 2520 kilobytes in 18 seconds Answer: 140 kilobytes per second

Explanation: Given, 2520 kilobytes in 18 seconds 2520/18 = 140 kilobytes 140 kilobytes per second

Question 23. 880 calories in 8 servings Answer: 110 calories in 1 serving

Explanation: Given, 880 calories in 8 servings 880/8 = 110 110 calories in 1 serving

Question 24. 1080 miles on 15 gallons Answer: 72 miles in 1 gallon

Explanation: Given, 1080 miles on 15 gallons 1080/15 = 72 miles 72 miles in 1 gallon

Question 25. $12.50 for 5 ounces Answer: 2.5

Explanation: Given, $12.50 for 5 ounces 12.50/5 = 2.5 $2.5 per ounce

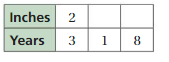
Question 29. MODELING REAL LIFE You earn $35 for washing 7 cars. a. How much do you earn for washing 4 cars?

Answer: Given, You earn $35 for washing 7 cars. 7 cars = $35 1 car = x x × 7 = $35 x = 35/7 = 5 Thus you earn $5 per car 4 cars = 4 × 5 = $20 You earn $20 for washing 4 cars..

b. You earn $45. How many cars did you wash? Answer: you earn $5 per car 45/5 = 9 You wash 9 cars for $45

COMPARING RATES Decide whether the rates are equivalent. Question 30. 24 laps in 6 minutes 72 laps in 18 minutes Answer: Yes

Explanation: 24:6 = 4 : 1 72 : 18 = 4 : 1 Thus the rates are equivalent.

Question 31. 126 points for every 3 games 210 points for every 5 games Answer: Yes

Explanation: Given 126 points for every 3 games 210 points for every 5 games 126 : 3 = 42 : 1 210 : 5 = 42 : 1 Thus the rates are equivalent.

Question 32. 15 breaths for every 36 seconds 90 breaths for every 3 minutes Answer: No

Explanation: Given 15 breaths for every 36 seconds 90 breaths for every 3 minutes 15 : 36 = 0.41 90 : 180 = 0.5 Thus the rates are not equivalent.

Question 33. $16 for 4 pounds $1 for 4 ounces Answer: Yes

Explanation: Given $16 for 4 pounds $1 for 4 ounces 1 pound = 16 ounces 4 pounds = 64 ounces 16 : 64 = 1 : 4 Thus the rates are equivalent.

Question 34. MODELING REAL LIFE An office printer prints 25 photos in 12.5 minutes. A home printer prints 15 photos in 6 minutes. Which printer is faster? How many more photos can you print in 12 minutes using the faster printer? Answer: The home printer is faster

Explanation: Given, An office printer prints 25 photos in 12.5 minutes. A home printer prints 15 photos in 6 minutes. 23 photos in 12.5 minutes 12.5 is half of 25 and therefore this is a two to one ratio So 2 photos print in 1 minute with the office printer. And 4 photos in 2 minutes. The home printer prints 15 photos in 6 minutes. Since 15 is not divisible by 6 without a remainder divide both by 3. So 5 photos in 2 minutes. This is faster than the office printer. This leaves you with an answer of 30 photos in 12 minutes.

Question 35. MODELING REAL LIFE You jog 2 kilometers in 12 minutes. Your friend jogs 3 kilometers in 16.5 minutes. Who jogs faster? How much sooner will the faster jogger finish a five-kilometer race? Answer: First, we have to calculate the speed of person 1 and 2. Speed = Distance/time Speed of person 1 = 2/12 = 0.167 km/min Speed of person 2 = 3/16.5 = 0.182 km/min From this we conclude that, person 2 jogs faster as compared to person 1. Now we have to calculate the time taken by the faster jogger to finish a 5 kilometer race. Faster jogger speed = 0.182 km/min Distance = 5 km S = d/t Time = 27.5 min Thus, the time taken by the faster jogger finish a 5 kilometer race will be, 27.5 minutes.

Question 36. PROBLEM SOLVING A softball team has a budget of $200 for visors. The athletic director pays $90 for 12 sun visors. Is there enough money in the budget to purchase 15 more sun visors? Explain your reasoning. Answer: $112.5

Explanation: An athletic director pays $90 for 12 sun visors for the softball team. The rate per sun visor is equal to $90/12 = $7.5 So the athletic director should pay $7.5 × 15 = $112.5

Question 39. DIG DEEPER! You can complete one-half of a job in an hour. Your friend can complete one-third of the same job in an hour. How long will it take to complete the job if you work together? Answer: Given, You can complete one-half of a job in an hour. Your friend can complete one-third of the same job in an hour 1 1/2 + 1 1/3 = 1/x has to be between 1/4 min to 1/6 hours. first guess is about (1/2)(1/4+1/6) = 5/24= 0.21 hours 2 + 3 = 1/x 5 = 1/x x = 1/5 = 0.20 hours

The U.S. customary system is a system of measurement that contains units for length, capacity, and weight. The metric system is a decimal system of measurement, based on powers of 10, that contains units for length, capacity, and mass. Key Vocabulary U.S. customary system, p. 142 metric system,p. 142 You can use unit rates and ratio tables to convert measures within the same system and between systems.

Question 1. Convert 48 feet to yards. Answer: 16 yards

Explanation: Convert from feets to yards We know that 1 yard = 3 feet So, 48 feet = 48/3 = 16 yards

Question 2. Convert 7 miles to kilometers. Round to the nearest hundredth if necessary. Answer: Convert from miles to kilometers. 1 mile = 1.6 km 7 miles = 7 × 1.6 = 11.2 kilometers

Question 3. Convert 20 quarts to liters. Round to the nearest hundredth if necessary. Answer: Convert from quarts to liters. 1 quart = 0.94 liters 20 quarts = 20 × 0.94 = 18.92 liters

Question 4. Convert 60 kilometers per hour to miles per hour. Round to the nearest hundredth if necessary. Answer: Convert from kilometers per hour to miles per hour. 1 kilometer per hour = 0.621 miles per hour 60 kilometer per hour = 37.28 miles per hour

Self-Assessment for Concepts & Skills Solve each exercise. Then rate your understanding of the success criteria in your journal

Question 8. Will all of the water from a full two-liter bottle fit into a two-quart pitcher? Explain. Answer: 1 liter = 1.05669 quarts q/L = 1.05669/1 q/2 = 1.05669/1 q = 2 × 1.05669 q = 2.11338

Question 9. DIG DEEPER! The speed of light is about 300,000 kilometers per second. The Sun is about 93 million miles from Earth. How many minutes does it take for sunlight to reach Earth? Answer:

Write a unit rate for the situation. Question 1. 102 beats per 2 minutes Answer: 51 per minute

Explanation: 102 beats per 2 minutes 102/2 = 51 beats per minute

Question 2. 60 shirts for every 5 clothing racks Answer: 12 for 1 clothing racks

Explanation: 60 shirts for every 5 clothing racks 60/5 = 12 12 for 1 clothing racks

Question 3. $100 donated for every 5 volunteers Answer: 20 for 1 volunteer

Explanation: $100 donated for every 5 volunteers 100/5 = 20 $20 donated for 1 volunteer

Question 4. 30 milliliters every 4 hours Answer: 7.5 ml per hour

Explanation: 30 milliliters every 4 hours 30/4 = 7.5 So, 7.5 ml per hour

Question 5. What is the LCM of 6, 12, and 18? A. 6 B. 18 C. 36 D. 72 Answer: C

Explanation: Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple. Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48 Multiples of 12: 12, 24, 36, 48, 60 Multiples of 18: 18, 36, 54, 72 Therefore, LCM(6, 12, 18) = 36 Thus the correct answer is option C.

Write the prime factorization of the number. Question 6. 56 Answer: 2 x 2 x 2 x 7

Explanation: 56 = 2 × 28 = 2 × 2 × 14 = 2 × 2 × 2 × 7 Thus the prime factorization of the number 56 is 2 x 2 x 2 x 7

Question 7. 74 Answer: 2 × 37

Explanation: 74 = 2 × 37 Thus the prime factorization of the number 74 is 2 x 37

Question 8. 63 Answer: 3 × 3 × 7

Explanation: 63 = 3 × 21 = 3 × 3 × 7 Thus the prime factorization of the number 63 is 3 × 3 × 7

Question 9. 132 Answer: 2 x 2 x 3 x 11

Explanation: 132 = 2 × 66 = 2 × 2 × 33 = 2 × 2 × 3 × 11 Thus the prime factorization of the number 132 is 2 x 2 x 3 x 11

Write the product as a power. Question 10. 6 × 6 Answer: The product of 6×6 is 6²

Question 11. 18 × 18 × 18 × 18 Answer: The product of 18×18×18×18 is 18⁴

Question 12. 12 × 12 × 12 × 12 × 12 Answer: The product of 12×12×12×12×12 is 12⁵

COMPARING MEASURES Answer the question. Explain your answer. (See Explorations 1 & 2, p. 141.) Question 13. Which juice container is larger: 2 L or 1 gal? Answer: Convert from liters to gal 1 liter = 0.26 gal 2 liter = 0.52 gal 1 gal = 3.78 liter Thus the juice container with 1 gal is larger

Question 14. Which is longer:1 in. or 2 cm? Answer: 1 inch is longer than 2 cm

Explanation: Convert from inches to cm 1 inch = 2.54 cm 2.54 cm > 2 cm

Explanation: Convert from pints to cups. 1 pint = 2 cups 3 pints = 3 × 2 cups = 6 cups

Explanation: Convert from mL to L 1000 mL = 1 L 1500 mL = 1.5 L

Explanation: Convert from ounces to lb 1 ounce = 0.0625 40 oz = 2.5 lb

Explanation: Convert from feet to inches. 1 feet = 12 inches 5 feet = 5 × 12 = 60 inches So, 5 ft = 60 in.

Explanation: Convert from gallons to quarts 1 gal = 4 qt 6 gal = 6 × 4 qt = 24 qt So, 6 gal = 24 qt

Explanation: Convert from cm to mm 1 cm = 10 mm 48 cm = 48 × 10 mm = 480 mm So, 48 cm = 480 mm

Explanation: Convert from cm to m 1 cm = 0.01 m 500 cm = 500 × 0.01 m = 5 meters So, 500 cm = 5 meters

Explanation: Convert from grams to kilograms 1 kg = 1000 g 6000g = 6 kg

Explanation: Convert from fl ounce to cups 1 fl oz = 0.125 cups 32 fl ouz = 4 cups

Explanation: Convert from liters to quarts. 1 L = 1.05 qt 12 L = 12.608 qt 12 L ≈ 13 qt

Explanation: Convert from meters to feet 1 meter = 3.28 feet 14 meter = 45.93 feet 14 m ≈ 46 feet

Explanation: Convert from feet to meter 1 feet = 0.3 m 4 feet = 1.21 m 4 ft ≈ 1 m

Explanation: Convert from lb to kgs. 1 lb = 0.45 kg 64 lb = 29.02 kg 64 lb ≈ 29 kg

Explanation: Convert from kg to miles 1 km = 0.621 miles 0.3 km = 0.186 miles

Explanation: Convert from inches to centimeters. 1 inch = 2.54 centimeter 75.2 inch = 191.008 centimeter 75.2 in ≈ 191 cm

Explanation: Convert from kg to lb 1 kg = 2.20 lb 17 kg = 37.47 lb 17 kg ≈ 34 lb

Explanation: Convert from cm to inches. 1 cm = 0.39 in 15 cm = 5.90 in 15 cm ≈ 6 in

Explanation: Convert from miles to kilometers 1 mile = 1.609 km 9 miles = 14.48 km 9 miles ≈ 14 km

Question 33. GRAPHING RELATIONSHIPS Represent the relationship between each pair of units in a coordinate plane. a. feet and yards b. pounds and kilograms Answer:

Question 34. MODELING REAL LIFE Earth travels 30 kilometers each second as it revolves around the Sun. How many miles does Earth travel in 1 second? Answer:

Explanation: Convert from cubic feet to the gallon 1 cu ft = 7.48 gal 12 cu ft = 12 × 7.48 gal = 89.76 gal 12 cu ft ≈ 90 gal

Explanation: Convert from quart to liter 1 qt = 0.94 L 6 qt = 5.67 L 6 qt ≈ 6 L

Explanation: Convert from liters to gal 1 L = 0.264 gal 5 L = 5 × 0.264 gal = 1.32 gal 5 L ≈ 1 gal

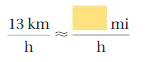
Explanation: Convert from km per hour to miles per hour 1 km per hour = 0.621 miles per hour 13 km per hour = 8.07 miles per hour

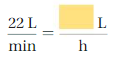
Explanation: Convert from liter per minute to liter per hour 1 liter per minute = 60 liter per hour 22 liter per minute = 1320 liter per hour

Explanation: Convert from miles per hour to miles per second. 1 miles per hour = 0.0002 miles per second 63 miles per hour = 0.175 miles per second

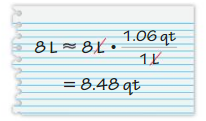
Answer: 1 hour = 60 minutes The heart pumps 5 quarts of blood per minute 1 min = 5 quarts 60 min = 60 × 5 quarts = 300 quarts Thus the heart pumps 300 quarts of blood per hour.

b. How many liters of blood does the human heart pump per minute? Answer: Given, The heart pumps 5 quarts of blood per minute Convert from quarts to liters 1 quart = 0.94 L 5 quarts = 4.73 L Thus it pumps 4.73 L of blood per minute.

Explanation: Convert from ounce to kg 1 oz = 0.02kg 30 oz = 0.85kg Thus 30 oz < 8 kg

Explanation: Convert from feet to centimeter 1 feet = 30.48 cm 6 feet = 182.88 Thus 6 feet < 300 cm

Explanation: Convert from gal to liter 1 gal = 3.78L 3 gal = 11.35L Thus 3 gal > 6L

Explanation: Convert from inches to mm. 1 in = 25.4mm 10 in = 254 mm Thus 254mm > 200 mm

Explanation: Convert from lb to grams 1 lb = 453.5g 5 lb = 2268g 2268g > 1200g Thus 5 lb > 1200g

Explanation: Convert from meters to feet 1 meter = 3.28 ft 1500 meter = 4921.26 ft 4921.26 ft > 3000 ft Thus 1500 m > 3000 ft

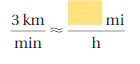
Explanation: Convert from km per min to miles per hour 1 km per min = 37.28 miles per hour 3 km per min = 111.84 miles per hour 3 km per min ≈ 112 miles per hour

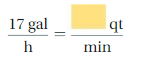
Explanation: Convert from gal per hour to qt per minute 1 gal per hour = 0.06 qt per minute 17 gal per hour = 1.13 qt per minute

Explanation: Convert from cm per minute to inches per second 1 cm per minute = 0.006 inches per second 600 cm per minute = 3.93 inches per second 600 cm per minute ≈ 4 inches per second

Question 54. MODELING REAL LIFE You are riding on a zip line. Your speed is 15 miles per hour. What is your speed in feet per second? Answer: 22 feet per second

Explanation: Given, You are riding on a zip line. Your speed is 15 miles per hour. Convert from mile per hour to feet per second 1 mile per hour = 1.46 feet per second 15 miles per hour = 22 feet per second

Question 55. PROBLEM SOLVING Thunder is the sound caused by lightning. You hear thunder 5 seconds after a lightning strike. The speed of sound is about 1225 kilometers per hour. About how many miles away was the lightning? Answer:

Question 57. DIG DEEPER! You travel 4000 feet every minute on a snowmobile. a. The evening speed limit for snowmobiles in your state is 55 miles per hour. Is your speed less than or equal to the speed limit? Justify your answer. b. What is your pace in minutes per mile? c. You are 22 miles from your house at 6:00 P.M. If you continue to travel at this speed, do you reach your house in time for dinner at 6:30 P.M.? Answer:

Question 59. STRUCTURE Consider the conversion facts 1 inch = 2.54 centimeters and 1 centimeter ≈ 0.39 inch. a. Write an expression for the exact number of inches in 1 centimeter. b. Use a calculator to evaluate your expression in part(a). Explain why measurement conversions may be slightly different when converting between metric units and U.S. customary units using the conversion facts in the back of the book. Answer:

Question 60. DIG DEEPER! One liter of paint covers 100 square feet. How many gallons of paint does it take to cover a room whose walls have an area of 800 square meters? Answer: Given, One liter of paint covers 100 square feet. First, convert 800 square meters to square feet. I calculated it to be 8611.13 sq ft 100 sq.ft/1 L x L = 8611.13. Now convert L to gallons. 1gallon = 3.785 L

Using the Problem-Solving Plan

Make a plan. Represent the ratio 3 : 1 : 2 using a tape diagram. Because there are 6 parts that represent 0.75 gallon, divide 0.75 by6 to find the value of one part of the tape diagram. Then use the value of one part to find the number of gallons of each ingredient you should use.

Solve and check. Use the plan to solve the problem. Then check your solution. Answer:

Question 3. The greatest common factor of two whole numbers is 9. The ratio of the greater number to the lesser number is 6 : 5. What are the two numbers? Justify your answer. Answer:

Review Vocabulary

Chapter Self-Assessment

3.1 Ratios (pp. 107–114) Learning Target: Understand the concepts of ratios and equivalent ratios.

Explanation: There are 3 butterflies and 2 caterpillars Thus the ratio is 3 : 2

Explanation: There are 6 saxophones and 3 trumpets Thus the ratio is 6: 3 and the equivalent ratio is 1 : 2

Determine whether the ratios are equivalent. Question 4. 5 : 2 and 30 : 12 Answer: Yes

Explanation: 30/12 = 5/2 5 : 2 = 5 : 2 Thus the ratios are equivalent

Question 5. 4 : 3 and 8 : 7 Answer: No

Explanation: 4/3 ≠ 8/7 Thus the ratios are not equivalent

Question 6. 6 : 4 and 18 : 6 Answer: No

Explanation: 6 : 4 and 18 : 6 6/4 = 3/2 18/6 = 3 3/2 ≠ 3 Thus the ratios are not equivalent

Question 7. 18 : 12 and 3 : 2 Answer: Yes

Explanation: 18 : 12 and 3 : 2 18/12 = 3/2 3 : 2 = 3 : 2 Thus the ratios are equivalent

Question 8. Write two equivalent ratios that have values of \(\frac{5}{7}\) Answer: \(\frac{10}{14}\) and \(\frac{15}{21}\)

Question 9. During a chess match, there are 12 pieces left on the board. The ratio of white pieces to black pieces is 2 : 1. How many white pieces are on the board? Answer:

Question 10. You run at a pace of 2 miles every 17 minutes. Your friend runs at a pace of 3 miles every 24 minutes. Are you and your friend running at the same pace? If not, who is running faster? Answer:

3.2 Using Tape Diagram (pp. 115-120) Learning Target: Use tape diagrams to model and solve ratio problems.

A container has peppermint gum and spearmint gum. You are given the number of pieces of peppermint gum in the container and the ratio of peppermint gum to spearmint gum. Find the number of pieces of spearmint gum in the container. Question 14. 24 peppermint; 8 to 5 Answer: Let the total number of peppermint gum and spearmint gum in the container = x The ratio is 8 : 5 8 + 5 = 13 8/13 × x = 24 x = 24 × 13/8 x = 39 5/13 × 39 = 15

Question 15. 18 peppermint; 2 : 3 Answer: Let the total number of peppermint gum and spearmint gum in the container = x The ratio is 2 : 3 2 + 3 = 5 2/5 × x = 18 x = 18 × 5/2 x = 45 Number of spearmint gum will be now Ratio of spearmint/total ratio × total number of gums = number of spearmint 3/5 × 45 = 27 Thus the number of spearmint gum = 27

Question 16. 32 peppermint; 8 to 7 Answer: Let the total number of peppermint gum and spearmint gum in the container = x The ratio is 8 : 7 8 + 7 = 15 8/15 × x = 32 x = 32 × 15/8 x = 4 × 15 x = 60 Number of spearmint gum will be now Ratio of spearmint/total ratio × total number of gums = number of spearmint 7/15 × 60 = 28

Question 17. 40 peppermint; 5 : 2 Answer: Let the total number of peppermint gum and spearmint gum in the container = x The ratio is 5 : 2 5 + 2 = 7 5/7 × x = 40 x = 40 × 7/5 x = 8 × 7 x = 56 Number of spearmint gum will be now Ratio of spearmint/total ratio × total number of gums = number of spearmint 2/7 × 56 = 16

Question 19. 165 tickets; 8 to 7 Answer: The ratio of adult tickets sold to student tickets sold is 8 : 7 8 + 7 = 15 8/15 = x/165 8 × 165 = x × 15 1320 = 15x x = 1320/15 x = 88 The number of student tickets would be 165 – 88 = 77 student tickets

Question 20. 210 tickets; 16 : 5 Answer: The ratio of adult tickets sold to student tickets sold is 16 : 5 16 + 5 = 21 16/21 = x/210 16 × 210 = x × 21 3360 = 21x x = 3360/21 x = 160 The number of student tickets would be 210 – 160 = 50 student tickets

Question 21. 248 tickets; 5 : 3 Answer: The ratio of adult tickets sold to student tickets sold is 5 : 3 5 + 3 = 8 5/8 = x/248 5 × 248 = 8 × x 1240 = 8x x = 1240/8 x = 155 The number of student tickets would be 248 – 155 = 93 student tickets

Question 22. You perform 7 sit-ups for every 2 pull-ups as part of an exercise routine. You perform 25 more sit-ups than pull-ups. How many sit-ups and how many pull-ups do you perform? Answer: 35 sit ups and 10 pullups

Explanation: Given, You perform 7 sit-ups for every 2 pull-ups as part of an exercise routine. You perform 25 more sit-ups than pull-ups. so we know that for 7 situps you do 2 pullups so the possible values would be 7,2 14,4 21, 6 28, 8 35, 10, and so on so now you just look at which two numbers have a difference of 25 when subtracting them, you’ll notice that 35 and 10 have a difference of 25.

3.3 Using Ratio Tables (pp. 121-128) Learning Target: Use ratio tables to represent equivalent ratios and solve ratio problems.

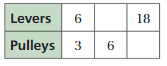
Question 30. A song has 12 beats every 5 seconds. How many beats are there in 30 seconds? Answer: 72 beats in 30 seconds

Explanation: Given, A song has 12 beats every 5 seconds. 5 seconds = 12 beats 1 second = 12/5 = 2.4 beats 30 seconds = 30 × 2.4 beats = 72 beats Thus 72 beats are there in 30 seconds.

Question 31. On New Year’sEve, the Times Square ball is lowered 47 feet every 20 seconds. How long does it take for the ball to be lowered 141 feet? Answer: 60 seconds

Explanation: On New Year’sEve, the Times Square ball is lowered 47 feet every 20 seconds. All you have to do is cross multiply and isolate x. 47/20 × 141/x 47x = 2820 x = 60 seconds

Question 33. You make lemonade by adding 11 cups of water for every 3 cups of lemon juice. Your friend makes lemonade by adding 9 cups of water for every 2 cups of lemon juice. Whose lemonade is more watered down? Answer: Well first I did was I found out that both 3 and 2 go into 12. 2 goes into 12 6 times. 9 × 6 is 54. 3 goes into 12 four times. 11 × 4 is 44. 54 is greater than 44 therefore the answer would be your friend.

3.4 Graphing Ratio Relationships (pp. 129-134) Learning Target: Represent ratio relationships in a coordinate plane.

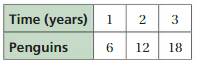
Question 36. You buy magnesium sulfate for $1.50 per pound. a. Represent the ratio relationship using a graph. b. How much does 3.5 pounds of magnesium sulfate cost? Answer:

3.5 Rates and Unit Rates (pp. 135–140) Learning Target: Understand the concept of a unit rate and solve rate problems.

Write a unit rate for the situation. Question 38. 12 stunts in 4 movies Answer: 3

Explanation: 12 stunts in 4 movies 12/4 = 3 3 stunts in 1 movie

Question 39. 3600 stitches in 3 minutes Answer: 1200

Explanation: 3600 stitches in 3 minutes 3600/3 = 1200 1200 stiches in 1 minute

Question 40. $18 for 6 pounds Answer: 3

Explanation: $18 for 6 pounds 18/6 = 3 $3 for 1 pound

Question 41. 240 people in 5 buses Answer: 48

Explanation: 240 people in 5 buses 240/5 = 48 48 people in 1 bus

Question 42. A train travels 120 miles in 3 hours. Write two unit rates that describe the relationship between the number of miles and the number of hours the train travels. Answer:

Question 43. Mercury orbits the Sun 3 times in 264 days. a. How many times does Mercury orbit the Sun in 440 days? b. How many days does it take Mercury to orbit the Sun 8 times? Answer:

Question 44. A cyclist travels 4 miles in 20 minutes. At this rate, how many miles does the cyclist travel in 30 minutes? Answer: Given, A cyclist travels 4 miles in 20 minutes. 20/4 = 5 minutes 1 mile in 5 minutes 30 minutes divided by 5 30/5 = 6 minutes So, 6 miles in 6 minutes

Decide whether the rates are equivalent. Question 45. 18 keystrokes in 3 seconds 48 keystrokes in 16 seconds Answer: No

Explanation: 18 keystrokes in 3 seconds 48 keystrokes in 16 seconds 18 : 3 :: 48 : 16 6 : 1 :: 3 : 1 The rates are not equivalent

Question 46. 210 miles in 3 hours 780 miles in 12 hours Answer: No

Explanation: 210 miles in 3 hours 780 miles in 12 hours 210 : 3 = 70 780 : 12 = 65 The rates are not equivalent

Question 47. You and a friend are picking up trash on a beach. You fill 2 bags with trash in 28 minutes. Your friend fills 3 bags with trash in 48 minutes. Who fills bags with trash faster? How much sooner will the faster person fill 7 bags with trash?

3.6 Converting Measures (pp. 141–148) Learning Target: Use ratio reasoning to convert units of measure.

Explanation: Convert from cups to fluid ounces 1 cup = 8 fluid ounce 2.5 cups = 20 fluid ounces

Explanation: Convert from feet to yards 1 feet = 0.33 yard 12 feet = 4 yards

Explanation: Convert from milligrams to grams 1 mg = 0.001 g 3500 mg = 3.5 grams

Explanation: Convert from inches to centimeters 1 in = 2.54 cm 9.2 in = 23.36 cm 9.2 in ≈ 23 cm

Explanation: Convert from lb to kg 1 lb = 0.45 kg 15 lb = 6.80 kg 15 lb ≈ 7 kg

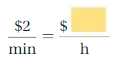
Explanation: Convert from hours to minutes 1 hour = 60 minutes 1 min = $2 60 min = x x = 60 × 2 x = $120

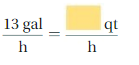
Explanation: Convert from gal to qt 1 gal = 4 qt 13 gal = 52 qt

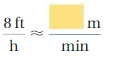
Question 57. Explain how to use conversion factors to find the number of fluid ounces in any given number of quarts of a liquid. Answer:

Question 58. Water flows through a pipe at a rate of 10 gallons per minute. How many gallons of water flow through the pipe in an hour? Answer: Given, Water flows through a pipe at a rate of 10 gallons per minute. 1 hour = 60 minute 1 minute = 10 gallon 60 minutes = 60 × 10 gallon = 600 gallon Thus 600 gallons of water flow through the pipe in an hour.

Question 60. The distance between two stars increases at a rate of 3 centimeters per month. What is the rate in inches per year? Answer: 14.17 inches

Explanation: Given, The distance between two stars increases at a rate of 3 centimeters per month. 3 cm – 1 month 1 year = 12 months 3 × 12 = 36 centimeters Convert from centimeters to inches 36 centimeters = 14.17 inches

Question 2. Determine whether the ratios 8 : 7 and 15 : 14 are equivalent. Answer: The ratios 8 : 7 and 15 : 14 are not equivalent. The equivalent ratio of 8:7 is 16 : 14.

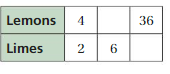
Question 6. You travel 224 miles in 4 hours. Find the unit rate. Answer: 56

Explanation: Given, You travel 224 miles in 4 hours. 1 hour = x 4 × x = 224 x = 224/4 x = 56 miles The unit rate is 56 miles.

Explanation: Convert from centimeters to inches. 1 cm = 0.39 6 cm = 6 × 0.39 6 cm = 2.34 inches

Explanation: Convert from liters to gal 1 liter = 0.26 gal 30 liter = 7.92 gal

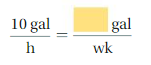
Explanation: Convert from hours to week 1 hour = 0.005 = 5/1000 10 gal/h = 2000/wk

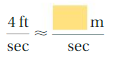
Explanation: Convert from feet to meters 1 feet = 0.30m 4 feet = 1.21 m 4 ft ≈ 1m

Question 11. During a baseball season, Team A scores 9 runs for every 7 runs that Team B scores. The total number of runs scored by both teams is 1440. How many runs does each team score? Answer: Team A scores 810 Team B scores 630

Explanation: During a baseball season, Team A scores 9 runs for every 7 runs that Team B scores. The total number of runs scored by both teams is 1440. Let b scores x runs Then a scores x + (2 × x/7) Because every 7 runs of b, a is scores more 2 runs. Total number of runs scored by both teams is 1440 a + b = 1440 x + (2 × x/7) + x = 1440 (16 × x)/7 = 1440 16 × x = 1440 × 7 16x = 10080 x = 10080/16 x = 630 Thus team b scores 630 runs Team a scores is x + (2 × x/7) = 810 runs

Question 12. At a movie theater, the ratio of filled seats to empty seats is 6 : 5. There are 120 empty seats. How many seats are filled? Answer: 144

Explanation: Given, At a movie theater, the ratio of filled seats to empty seats is 6 : 5. There are 120 empty seats. Number of filled = 6 Number of empty = 5 120/5 = 24 then multiply it by 6 to get 144. Thus the number of filled seats = 144

Question 13. You and your friend mix water and citric acid. You add 3 cups of citric acid for every 16 cups of water. Your friend adds 2 cups of citric acid for every 12 cups of water. Whose mixture is more acidic? Answer: A’s mixture is more acidic

Explanation: Given, You and your friend mix water and citric acid. You add 3 cups of citric acid for every 16 cups of water. Your friend adds 2 cups of citric acid for every 12 cups of water. A add 3 cups of citric acid for every 16 cups of water, the ratio = 3/16 B adds 2 cups of citric acid for every 12 cups of water = 2/12 LCM of 16 and 12 are 48 16 – 16, 32, 48, 64, 80, 96 12 – 12, 24, 36, 48, 60, 72 A – 3/16 × 3/3 = 9/48 B – 2/12 × 4/4 = 8/48 We found that in terms of 48 cups of water, friend A mixes 9 cups of acid while friend B mixes 8 cups of acid, means A is adding more acid than B and hence friend A’s mixture is more acidic.

Question 15. In a rectangle, the ratio of the length to the width is 5 : 2. The length of the rectangle is 13.875 feet greater than the width. What are the perimeter and the area of the rectangle? Answer: P = 64.75 feet A = 213.91 feet

Explanation: Given, In a rectangle, the ratio of the length to the width is 5 : 2. The length of the rectangle is 13.875 feet greater than the width. 13.875 ÷ 3 = 4.625 feet 4.625 × 5 = 23.125 feet So, the length of the rectangle is 23.125 feet 4.625 × 2 = 9.25 feet So, the width of the rectangle is 9.25 feet We know that, Perimeter of the rectangle = 2l + 2w P = 2(23.125) + 2(9.25) P = 64.75 feet Area of the rectangle = l × w A = 23.125 × 9.25 Area = 213.91 sq. feet

Explanation: Dividing two fractions is the same as multiplying the first fraction by the reciprocal (inverse) of the second fraction. Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes \(\frac{2}{9}\) × \(\frac{5}{4}\) = \(\frac{10}{36}\) This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 10 and 36 using GCF is 2 \(\frac{10}{36}\) ÷ \(\frac{2}{2}\) = \(\frac{5}{18}\) Thus the correct answer is option B.

Explanation: Given, Your speed while waterskiing is 22 miles per hour. Convert from miles to kilometers 1 mile = 1.609 kilometer 22 miles = 22 × 1.609 = 35.40 kilometers

Question 3. Which number is equivalent to the expression below? 2 . 4 2 + 3(6 ÷ 2) F. 25 G. 41 H. 73 I. 105 Answer: 2 . 4 2 + 3(6 ÷ 2) 2 . 4 2 + 3(3) 2 . 4 2 + 9 2 × 16 + 9 32+9 = 41 Thus the correct answer is option G.

Explanation: Given, The tape diagram models the ratio of red beads to green beads in a bracelet. The bracelet uses 12 red beads. From the above figure we observe that there are 3 3 × 4 = 12 1 box = 4 beads There are 2 green boxes 2 × 4 = 8 Thus there 8 green beads in the bracelet.

Question 5. What is the least common multiple of 8, 12, and 20? F. 24 G. 40 H. 60 I. 120 Answer: 120

Explanation: Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple. Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136 Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144 Multiples of 20: 20, 40, 60, 80, 100, 120, 140, 160 Therefore, LCM(8, 12, 20) = 120 Thus the correct answer is option I.

Question 6. Which number is equivalent to 2.34 × 1.08 × 5.6? A. 12.787632 B. 14.15232 C. 23.5872 D. 14,152.32 Answer: 14.15232

Explanation: Multiply the three numbers 2.34 × 1.08 × 5.6 we get 14.15232 Thus the correct answer is option B.

Explanation: Given, The school store sells 4 pencils for $0.50. Cost of 1 pencil is 0.50/4 = 0.125 0.125 × 10 = 1.25 Thus the cost of 10 pencils is $1.25

Explanation: By seeing the above figure we can write the ratio from frogs to snakes. There are 8 frogs There are 4 snakes 8:4 Thus the correct answer is option C.

Question 10. Which expression is equivalent to 3 6 ? F. 3 × 3 × 3 × 3 × 3 G. 3 × 5 H. 5 × 5 × 5 I. 3 + 3 + 3 + 3 + 3 Answer: 3 × 3 × 3 × 3 × 3 The expression equivalent to 3 6 is 3 × 3 × 3 × 3 × 3 Thus the correct answer is option F.

Explanation: The correct order of operations when evaluating 5 + 4 × 2 3 is Add 5 and 4, Multiply 9 and 2 and Evaluate 18³ Thus the correct answer is option A.

Conclusion:

You can Download Middle School Big Ideas Math Answers Grade 6 Chapter 3 Ratios and Rates through the direct links provided here. Make use of the links and practice well for the exams. Keep in touch with our site to get the latest updates regarding the BIM 6th Grade Answer Key Chapter wise.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

Watch CBS News

New England Patriots start first OTAs with Jerod Mayo and Drake Maye

By Matt Geagan

Updated on: May 20, 2024 / 6:56 AM EDT / CBS Boston

FOXBORO -- The Patriots' offseason program will really kick into high gear on Monday when Jerod Mayo and company host their first OTA practice in Foxboro.

This will be the first of 10 days of organized team practice activity (OTAs for short) that the team will hold over the next few weeks. And the first session just so happens to be open to the media, so we'll get our first look at Drake Maye with the full team after he took the field for last weekend's rookie minicamp.

We'll also hear from new head coach Jerod Mayo at 11:30 a.m., with the practice session set to kick off at noon. After the Patriots are done on the field, a handful of players will chat with reporters as well.

Monday afternoon will have a training-camp sorta feel to it behind Gillette Stadium. Minus players hitting each other on the field, of course. That still isn't allowed.

While OTAs are voluntary, most of the 2024 Patriots have been in Foxboro for the first phases of the offseason. Phase One included meetings and strength and conditioning, while Phase Two was made up of on-field workouts, drills, and walkthroughs. While players still can't lay any licks on each other during Phase Three, teams can do 7-on-7, 9-on-7 and 11-on-11 drills as the offseason program ramps up. 

While the Patriots will be hitting the field a number of times over the next several weeks, only three other sessions are open to the media after Monday: May 29, June 3, and June 7.

The offseason program will culminate with New England's mandatory minicamp, which will be held from June 10-12. Fittingly, minicamp will end on the day that Tom Brady will be enshrined in the Patriots Hall of Fame. 

Matthew Geagan is a sports writer and producer for CBS Boston and wbz.com. He has been part of the WBZ sports team for nearly 20 years.

Featured Local Savings

More from cbs news.

Celtics will face Pacers in Eastern Conference Finals

Tim Thomas gets Bruins fans fired up ahead of Game 6

Devers homers for 5th straight game, lifts Red Sox to 11-3 win

Boston's professional women's hockey team wins in front of sold out crowd

Indy 500 practice recap: Team Penske tops speed chart on Fast Friday

It's Fast Friday at Indianapolis Motor Speedway. Speeds among the 34 drivers seeking a spot in the 2024 Indianapolis 500 will jump today as race officials give them a 100-horsepower boost for this weekend's qualifying.

Pato O'Ward and Scott McLaughlin have had the fastest laps in this week's practice, which has been frequently interrupted by rain. Marcus Ericsson and Linus Lundqvist have sustained accidents. NASCAR star Kyle Larson continues his effort to race 1,100 miles in one day.

Nathan Brown is your best Indy 500 follow, and we will have updates throughout practice. Please remember to refresh .

Mix of young and old: Ganassi vets prepare rookie class for first Indy 500

A big setback: IndyCar rookie Nolan Siegel crashes on Fast Friday at IMS

6 p.m.: Team Penske dominates Indy 500 Fast Friday practice

Team Penske rules Fast Friday.

Defending Indy 500 champion Josef Newgarden, Scott McLaughlin and 2018 race champ Will Power – all from Roger Penske's team – have the best 4-lap qualifying simulation runs in Fast Friday practice. 

Newgarden goes 234.063 mph over a 10-mile run on the 2.5-mile Indianapolis Motor Speedway oval. McLaughlin, Power and Arrow McLaren's Alexander Rossi and Pato O'Ward all top 233.

Katherine Legge has the lowest 4-lap run among those reaching qualifying speed (229.984). Rookie Nolan Siegel, who crashed on Friday, did not reach a 200 mph average over a 4-lap run.

Colton Herta had the best single lap (234.974) and Kyle Larson was No. 2 (234.271).

Qualifying for the May 26 race begins Saturday, when race positions 13-30 will be settled. The front 4 rows and the back row will be determined Sunday. One of the 34 entries will not make the race.

Indy 500 Fast Friday practice recap 

With car number, driver, engine, team, mph over a 4-lap simulated qualifying run

• (2) Josef Newgarden, Chevrolet, Penske, 234.063
• (3) Scott McLaughlin, Chevrolet, Penske, 233.623
• (12) Will Power, Chevrolet, Penske, 233.451
• (7) Alexander Rossi, Chevrolet, Arrow McLaren, 233.355
• (5) Pato O'Ward, Chevrolet, Arrow McLaren, 233.043
• (60) Felix Rosenqvist, Honda, Meyer Shank, 232.906
• (27) Kyle Kirkwood, Honda, Andretti Global, 232.893
• (78) Agustin Canapino, Chevrolet, Juncos Hollinger Racing, 232.875
• (14) Santino Ferrucci, Chevrolet, AJ Foyt Racing, 232.867
• (17) Kyle Larson, Chevrolet, Arrow McLaren, 232.549
• (26) Colton Herta, Honda, Andretti Global, 232.548
• (21) Rinus VeeKay, Chevrolet, Ed Carpenter Racing, 232.517
• (41) Sting Ray Robb, Chevrolet, AJ Foyt Racing, 232.207
• (06) Helio Castroneves, Honda, Meyer Shank, 232.200
• (98) Marco Andretti, Honda, Andretti Global, 232.083
• (45) Christian Lundgaard, Honda, Rahal Letterman Lanigan, 232.025
• (10) Alex Palou, Honda, Chip Ganassi Racing, 231.972
• (23) Ryan Hunter-Reay, Chevrolet, Dreyer & Reinbold/Cusick, 231.658
• (9) Scott Dixon, Honda, Chip Ganassi Racing, 231.546
• (20) Ed Carpenter, Chevrolet, Ed Carpenter Racing, 231.546
• (6) Callum Ilott, Chevrolet, Arrow McLaren, 231.430
• (30) Pietro Fittipaldi, Honda, Rahal Letterman Lanigan, 231.319
• (28) Marcus Ericsson, Honda, Andretti Global, 231.298
• (11) Marcus Armstrong, Honda, Chip Ganassi Racing, 231.219
• (8) Linus Lundqvist, Honda, Chip Ganassi Racing, 231.107
• (33) Christian Rasmussen, Chevrolet, Ed Carpenter Racing, 231.070
• (66) Tom Blomqvist, Honda, Meyer Shank, 230.945
• (15) Graham Rahal, Honda, Rahal Letterman Lanigan, 230.867
• (75) Takuma Sato, Honda, Rahal Letterman Lanigan, 230.833
• (77) Romain Grosjean, Chevrolet, Juncos Hollinger Racing, 230.740
• (24) Conor Daly, Chevrolet, Dreyer & Reinbold/Cusick, 230.490
• (4) Kyffin Simpson, Honda, Chip Ganassi Racing, 230.340
• (51) Katherine Legge, Honda, Dale Coyne Racing, 229.984
• (18) Nolan Siegel, Honda, Dale Coyne Racing, 199.413

5:30 p.m.: Graham Rahal discusses Indy 500 qualifying

Graham Rahal had the 25th best 4-lap qualifying simulation run as he sat on pit road with about 35 minutes remaining in practice. He feels more confident than last year, when he failed to make the race in qualifying, but got in after a post-qualifying crash that injured Stefan Wilson.

"We're in a safer spot," Rahal said. "We've still got work to do."

5:15 p.m.: Kyle Larson says Fast Friday not 'scary fast'

The NASCAR Cup star drives 34 laps, with the 2nd-best single lap at 234.271 mph. His best 4-lap qualifying simulation run is 232.549, which is 9th heading into the closing 45 minutes of practice.

"I expected it to feel like we were going way faster than before. It definitely feels faster, but not scary fast," he said on pit road. "Pretty comfortable."

5 p.m.: It's Happy Hour at Fast Friday

Here's where we stand heading into the final hour of Indianapolis 500 practice.

• (60) Felix Rosenqvist, Honda, Meyer Shank, 232.857
• (27) Kyle Kirkwood, Honda, Andretti Global, 232.663
• (5) Pato O'Ward, Chevrolet, Arrow McLaren, 232.565

∎ Pietro Fittipaldi suffers a mechanical issue and coasts into the pits.

∎ Colton Herta has the fastest single lap at 234.974 mph.

Track conditions : 75 degrees, cloudy, wind out of the southwest; track temperature 107 degrees and dropping.

4 p.m.: How IndyCar teams are faring on Fast Friday

Team Penske still has 3 of the top 4 4-lap qualifying simulation runs. Arrow McLaren (2nd, 6th, 7th, 16th), Andretti Global (8th, 10th, 12th) and Meyer Shank (5th, 11th, 21st) are also strong.

Kyle Larson, driving for Arrow McLaren, has the day's top single lap at 234.271 mph, but he doesn't complete a simulated qualifying run.

Pato O'Ward, an Arrow McLaren driver who stands 6th, said in Gasoline Alley he isn't considered with chasing the speed of the Penske cars for qualifying. He said any car starting in the top 15 is capable of winning.

Noticeably missing from the top of the speed chart: Chip Ganassi Racing (Scott Dixon is best at 13th); Rahal Letterman Lanigan (Graham Rahal is 22nd; he was initially bumped from the field last year as the team struggled mightily; Rahal ended up in the field on another team after a post-qualifying crash).

3:15 p.m.: Alex Palou suffers a mechanical issue

The IndyCar Series points leader who won on the IMS road course last weekend brings out a caution as his engine appears to encounter a problem on the back stretch. He started last year's race from the pole and finished 4th.

3 p.m.: Halfway through Fast Friday Indy 500 qualifying practice

Marcus Ericsson and Linus Lundqvist, who crashed Thursday, are back on the track.

• (2) Josef Newgarden, Chevrolet, Penske, 234.063 mph; this 4-lap qualifying simulation run is just completed. Alex Palou's 2023 pole speed was 234.217.
• (12) Will Power, Chevrolet, Penske, 233.172
• (3) Scott McLaughlin, Chevrolet, Penske, 233.054
• (7) Alexander Rossi, Chevrolet, Arrow McLaren, 232.916
• (21) Rinus VeeKay, Chevrolet, Ed Carpenter Racing, 232.448
• (06) Helio Castroneves, Honda, Meyer Shank, 231.743

Track conditions : 75 degree air temperature, cloudy skies; 111 degree track temp

Newgarden tries to temper his excitement after his fast run: "It'll be harder tomorrow and even harder on Sunday." He notes his poor qualifying draws (which will be done after Friday's practice) and potential changes in weather and track conditions during the weekend.

2 p.m.: Snake on the track?! Snake on the track

Alexander Rossi stands third in 4-lap qualifying simulation runs through 2 hours, despite an unusual encounter .

1:37 p.m.: Indy 500 rookie Nolan Siegel crashes

The 19-year-old spins in Turn 2, hits the outside wall and gets airborne before coming to rest on the back straight upside down. He immediately apologized to his crew on the team radio and said he was all right. Safety crew members tip the car right side up.

"Feel bad for the team," he said after being cleared to drive at the infield medical center.

1 p.m.: Penske drivers have best simulated 4-lap qualifying runs

This is from the first hour of practice. Drivers say their setups are conservative, so expect speeds to climb.

• (2) Josef Newgarden, Chevrolet, Penske, 233.259 mph
• (12) Will Power, Chevrolet, Penske, 232.561
• (98) Marco Andretti, Honda, Andretti Global, 231.734
• (5) Pato O'Ward, Chevrolet, Arrow McLaren, 231.696
• (17) Kyle Larson, Chevrolet, Arrow McLaren, 231.560
• (14) Santino Ferrucci, Chevrolet, AJ Foyt Racing, 231.395

12:35 p.m.: Kyle Larson has a hot lap

Kyle Larson, who is trying to complete the Indy 500-NASCAR double this month, has a lap of 232.493 mph, 7th fastest in the first half-hour.

"He's a pro, but he's very much not used to it," said Tony Kanaan, the 2013 Indy 500 winner who is coaching Larson through his first Indy 500 experience.

12:02 p.m.: Josef Newgarden is fast out of the box

Last year's Indy 500 winner turns a lap at 233.868 mph just after the green flag flies.

"It felt OK," he said on pit lane a few minutes later, noting he doesn't expect to turn a lot of laps today. "Wasn't perfect. It's difficult to tell where everything's going to land (tomorrow)."

Indy 500 news from IndyStar

Indy 500's first lady Beth Boles: World champion jet skier, state winning lacrosse coach

Friend of IndyCar: Eddie Gossage, iconic racing promoter & former Texas Motor Speedway president, dies at 65

Indy 500 qualifying schedule

All sessions will be on  Peacock , IndyCar Live, IndyCar Radio and  SiriusXM Channel 218 ; all times ET

May 18, Saturday

8:30-9:30 a.m. : Indy 500 full field practice

11 a.m.-6 p.m. : Indy 500 qualifying

May 19, Sunday

Noon-2 p.m. : Indy 500 practice

3-6 p.m. : Indy 500 qualifying, also on NBC

Monday, May 20

1-3 p.m. : Indy 500 full field practice

Friday, May 24

11 a.m.-1 p.m. : Carb Day, Indy 500 full field practice

2:30-4 p.m. : Pit stop competition

More From Forbes

10 ways hr leaders can improve union communication.

• Share to Facebook
• Share to Twitter
• Share to Linkedin

When it comes to working for a union, having effective communication between HR leaders and union representatives is key to developing a positive workplace environment. Through an understanding of union members’ perspectives and concerns, HR can build a foundation of trust and mutual respect that is beneficial to all those involved.

Below, Forbes Human Resources Council members explore strategies for HR leaders to improve their communication skills with union representatives. They also look at successful examples from a range of industries where improved communication has led to positive outcomes for both employees and management.

1. Talk And Listen To One Another

Having worked for unions and management, the most important way to communicate with union reps is just that—communicate. Communication requires that people don't just "hear" what the other is saying, but be active listeners, be responsive and be authentic. If you cannot provide an answer, explain why or provide a time frame to reconvene. Recognize and respect people, and be a good human. - Ilyssa DeCasperis , LA County Metro

2. Be Open To Collaboration

HR leaders can best engage unions with transparency, active listening and collaboration. Successful negotiations on fair wages, working conditions or dispute resolution build trust and boost productivity, fostering stronger partnerships. While it can’t be done overnight, the healthy dynamic between unions and HR can be priceless. - William Stonehouse , Crawford Thomas Recruiting

3. Practice Honesty And Transparency

As a teen, I worked for a company where the union berated the line and HR leaders, and then told them out of employees' earshot, "You know it's just for show, so they can cool off." That was not okay for the employees or the leaders, and I had no problem saying that to them all. Be transparent and honest behind open and closed doors—work together for the employees. The them versus us game is dead. - Nakisha Dixon , Vercara

Top CEO Bets On A Shock Biden Crypto Flip As Congress Hurtles Toward A Crucial Vote That Could Blow Up The Price Of Bitcoin Ethereum And XRP

Iphone 16 pro max all new design upgrade promised insider claims, who is ebrahim raisi iran’s president—nicknamed ‘butcher of tehran’—dies in helicopter crash., 4. bridge understanding through neutral facilitators.

Utilize neutral facilitators to help bridge gaps in understanding. This will ensure that both sides are heard and understood. - Britton Bloch , Navy Federal

5. Have A Say In Contracting

Get involved in negotiating the contract. Doing so allows HR to show union leaders that mutual (union and co) interest in supporting employees’ needs and desires is of utmost importance. This builds an initial foundation of trust and respect making subsequent interactions less adversarial, especially when disagreement between company leadership and union officials ensues. The 2020 NYCTA-TWU is an example. - Laci Loew

Forbes Human Resources Council is an invitation-only organization for HR executives across all industries. Do I qualify?

6. Act As Partners

Having been in a union and an HR leader in a unionized environment, and serving on a Civil Service Board, the number one thing HR can do to improve the relationship is to reduce friction. Think of yourselves as partners in the employee's career, and do your best to work with the union rep to have the right processes in place. You all want the same thing; a great place for members to thrive! - Tracy Cote , StockX

7. Hold Joint Sessions

Organize regular joint sessions that focus on future trends impacting the industry, such as automation, globalization and new employment models. By exploring future challenges together, HR and union leaders can collaboratively strategize on adapting and thriving. This approach shifts the dynamic from adversarial to cooperative, leading to more productive outcomes. - Katrina Jones

8. Respect One Anothers’ Perspectives

HR leaders should be transparent and respectful and understand union representatives' perspectives to communicate better with them. Establishing a good relationship, listening to their feedback and working collaboratively to address their concerns can improve outcomes. When a company's HR leader meets regularly with union representatives, this leads to improved employee morale and productivity. - Reema Akhtar , Seer Solutions

9. Make Communication A Regular Thing

Michigan HR leaders can enhance communication with union reps by embracing transparency and regular dialogue. An example: A Detroit manufacturing firm held quarterly meetings with union leaders, discussing concerns openly. This led to a negotiated agreement that improved worker benefits and productivity, boosting company morale and operational efficiency. - CJ Eason , JobFairGiant.com

10. Learn From Those Around You

Effective communication between HR leaders and union representatives is paramount to cultivating a positive and productive work environment. By implementing strategic communication practices and learning from real-world examples, HR leaders can significantly enhance their interactions with union representatives, leading to improved collaboration, trust and outcomes for all stakeholders. - Jessica Kriegel , Culture Partners

• Editorial Standards
• Reprints & Permissions

Recap: Scott McLaughlin leads Team Penske front row sweep for 2024 Indianapolis 500

Pole position for the  2024 Indianapolis 500  will be determined Sunday, May 19. The best qualifier gets to lead the field at the start of the May 26 race. Rows 1-4 and 11 will be determined today. Rows 5-10 are set.

Team Penske's drivers – Will Power, Scott McLaughlin and defending race winner Josef Newgarden – had the best qualifying runs Saturday. Kyle Larson , who is trying to complete the Indy 500-NASCAR Cup double, also has a shot at pole position.

Alex Palou 's pole-winning 4-lap average of 234.217 mph from 2023 is the pole position run in Speedway history. Arie Luyendyk set the qualifying record of 236.986 in 1996, but qualifying rules at the time dictated he start further back.

Please follow  Nathan Brown  all season for IndyCar news and analysis. We'll have every qualifying run here.

First day recap:  Team Penske, Kyle Larson headline Indy 500 qualifying, will go for pole position

What is a plenum event? Inside the glitch that hampered Chevy drivers in Day 1 of Indy 500 qualifying

5:50 p.m.: Scott McLaughlin, Team Penske dominate Indy 500 qualifying

Scott McLaughlin has the fastest pole-winning run in race history at 234.220 mph as Team Penske sweeps the front row for the first time since 1988.

Will Power and Josef Newgarden will join McLaughlin on the front row next Sunday.

The second row includes Alexander Rossi, NASCAR star Kyle Larson and Santino Ferrucci.

Penske drivers Rick Mears, Al Unser and Danny Sullivan swept the front row for Penske in 1988, and Mears won.

This is Penske's 19th pole position here, and the first since Simon Pagenaud in 2019. Pagenaud is the last pole-sitter to also win the race.

INDY 500 LINEUP: A complete guide to the 33-car starting field

5:20 p.m.: Indy 500 Fast 6 qualifying

With car number, driver, engine, team, 4-lap speed average in mph

(3) Scott McLaughlin, Chevrolet, Penske, 234.220

(12) Will Power, Chevrolet, Penske, 233.917

(2) Josef Newgarden, Chevrolet, Penske, 233.808

(7) Alexander Rossi, Chevrolet, Arrow McLaren, 233.090 ("I'm annoyed, but I'm motivated," he says of Team Penske)

(17) Kyle Larson, Chevrolet, Arrow McLaren, 232.846; he thanks his team and is off to North Wilkesboro, N.C., for Sunday night's NASCAR All-Star Race.

(14) Santino Ferrucci, Chevrolet, Foyt, 232.692

Track conditions : 90 degrees, sunny; track temperature 126.7

4:05 p.m.: Indy 500 last chance qualifying

Nolan Siegel, after being released from the infield medical center: "I'm going home because I did everything I possibly could. ... It led me into the wall."

Row 11 qualifiers : Katherine Legge, Marcus Ericsson, Graham Rahal.

With car number, driver, engine, team, 4-lap speed average in mph; drivers can make multiple attempts

Nolan Siegel crashes between Turns 1 and 2 on the 2nd lap of his final qualifying attempt and will miss the Indy 500. He gets out of the car under his own power. Along pit road, Graham Rahal, who qualifies 33rd, empathizes with Siegel. Rahal failed to qualify in 2023, but got into the race field after a post-qualifying crash involving Stefan Wilson.

(28) Marcus Ericsson, Honda, Andretti, 230.027; bumps Nolan Siegel

(15) Graham Rahal, Honda, RLL, 229.974; Marcus Ericsson is out the outside of the field at the moment.

(51) Katherine Legge, Honda, Coyne, 230.092 (She has a wiggle on the warm-up lap, and almost loses control on Lap 4; post-race comment: "Terrifying," adding she's a big bad car racer who also wants to cry.)

(28) Marcus Ericsson, Honda, Andretti, 220.702 (last lap is at 195.411; he decelerates heading into Turn 1 on Lap 4, believing his run is complete, and loses momentum); race officials disallow the run.

(18) Nolan Siegel, Honda, Coyne, 229.566

Track conditions : 88 degrees, partly cloudy; track temperatures 124

3:05 p.m.: Fast 12 Indy 500 qualifying

With car number, driver, engine, team, 4-lap speed average in mph; *-advances to Fast 6

Fast 6 : Team Penske's Scott McLaughlin, Will Power and Josef Newgarden, as well as Alexander Rossi, Kyle Larson and Santino Ferrucci. All are Chevrolets.

Row 3 : Rinus VeeKay, Pato O'Ward, Felix Rosenqvist; Row 4 : Takuma Sato, Kyle Kirkwood, Ryan Hunter-Reay.

(12) Will Power, Chevrolet, Penske, 233.483*

(3) Scott McLaughlin, Chevrolet, Penske, 233.492*

(2) Josef Newgarden, Chevrolet, Penske, 233.286*

(7) Alexander Rossi, Chevrolet, Arrow McLaren, 233.071*

(27) Kyle Kirkwood, Honda, Andretti, 230.993 ("I know we've got a good race car and good starting position.")

(17) Kyle Larson, Chevrolet, Arrow McLaren, 232.788* ("Happy with how the day's going." He plans to compete in the NASCAR Cup All-Star race at North Wilkesboro, N.C., later Sunday, but first he will be in the Fast 6.)

(60) Felix Rosenqvist, Honda, Meyer Shank, 232.305

(14) Santino Ferrucci, Chevrolet, Foyt, 232.723*

(75) Takuma Sato, Honda, RLL, 232.171

(5) Pato O'Ward, Chevrolet, Arrow McLaren, 232.584 ("The happiest balance in qualifying" set up.)

(21) Rinus VeeKay, Chevrolet, Carpenter, 232.610 ("This feels like a bonus lap," in the wake of Saturday's early crash and recovery to reach the top 12.)

(23) Ryan Hunter-Reay, Chevrolet, D&R-Cusick, 230.567 (Post-run comment: "That was pretty terrible.")

Track conditions : 87 degrees, partly cloudy; track temperature 124.5

1:45 p.m.: Last row qualifiers practice

Qualifying simulations : Katherine Legge (231.011); Marcus Ericsson (230.532); Graham Rahal (229.073); Nolan Siegel (228.955).

1 p.m.: Indy 500 Top 12 practice is complete

Here are the best 4-lap qualifying simulation runs, in average mph

• (3) Josef Newgarden, 233.707
• (60) Felix Rosenqvist, 232.848
• (3) Scott McLaughlin, 232.655
• (5) Pato O'Ward, 232.637
• (7) Alexander Rossi, 232.495
• (27) Kyle Kirkwood, 232.335
• (17) Kyle Larson, 232.091
• (12) Will Power, 231.688
• (75) Takuma Sato, 228.852
• (23) Ryan Hunter-Reay, 225.365

Kyle Larson acknowledges the constant tweaking in search of qualifying speed is frustrating, considering the qualifying process in NASCAR is much simpler.

12:30 p.m.: Josef Newgarden has top qualifying practice run

Qualifying simulations : Josef Newgarden (233.707) and Felix Rosenqvist (232.848) have topped O'Ward's previous run.

NASCAR star Kyle Larson started a simulated qualifying run, but backed out after briefly sliding.

12:15 p.m.: Indy 500 Top 12 practice

Qualifying simulations : Pato O'Ward (232.637); Alexander Rossi (232.495); Kyle Kirkwood (232.335); Will Power (231.688)

Track conditions : 84 degrees, sunny; track temperature 114.4

Fast 12 Indianapolis 500 qualifiers

With car number, driver, engine, team and 4-lap speed average; all cars use Dallara chassis and Firestone tires (W-race winner; R-race rookie)

One round of qualifying will cut this group to the Fast Six, and a second round will determine the top six starters

• (12) Will Power (W), Chevrolet, Penske, 233.758 mph
• (3) Scott McLaughlin, Chevrolet, Penske, 233.332
• (2) Josef Newgarden (W), Chevrolet, Penske, 233.293
• (7) Alexander Rossi (W), Chevrolet, Arrow McLaren, 233.069
• (27) Kyle Kirkwood, Honda, Andretti Global, 232.764
• (17) Kyle Larson (R), Chevrolet, Arrow McLaren 232.563
• (60) Felix Rosenqvist, Honda, Meyer Shank, 232.547
• (14) Santino Ferrucci, Chevrolet, AJ Foyt, 232.496
• (75) Takuma Sato (W), Honda, Rahal Letterman Lanigan, 232.473
• (6) Pato O'Ward, Chevrolet, Arrow McLaren, 232.434
• (21) Rinus VeeKay, Chevrolet, Ed Carpenter, 232.419
• (23) Ryan Hunter-Reay (W), Chevrolet, Dreyer & Reinbold-Cusick, 232.385

2024 Indy 500 last chance qualifying

Three of these drivers will comprise Row 11, and one will not make the race

'It’s gonna be high pressure': Ericsson, Rahal, Coyne compete for final spots in Indy 500

(28) Marcus Ericsson (W), Honda, Andretti Global, 230.603

(51) Katherine Legge, Honda, Dale Coyne, 230.830

(15) Graham Rahal, Honda, Rahal Letterman Lanigan, 230.685

(18) Nolan Siegel (R), Honda, Dale Coyne, 228.276

2024 Indy 500 Row 5

13. (26) Colton Herta, Honda, Andretti Global, 232.316

14. (10) Alex Palou, Honda, Chip Ganassi Racing, 232.306

15. (6) Callum Ilott, Chevrolet, Arrow McLaren, 232.230

2024 Indy 500 Row 6

16. (11) Marcus Armstrong (R), Honda, Chip Ganassi Racing, 232.183

17. (20) Ed Carpenter, Chevrolet, Ed Carpenter Racing, 232.017

18. (4) Kyffin Simpson (R), Honda, Chip Ganassi Racing, 231.948

2024 Indy 500 Row 7

19. (98) Marco Andretti, Honda, Andretti Global, 231.890

20. (06) Helio Castroneves (W), Honda, Meyer Shank, 231.871

21. (9) Scott Dixon (W), Honda, Chip Ganassi Racing, 231.851

2024 Indy 500 Row 8

22. (78) Agustin Canapino, Chevrolet, Juncos Hollinger Racing, 231.847

23. (41) Sting Ray Robb, Chevrolet, AJ Foyt Racing, 231.826

24. (33) Christian Rasmussen (R), Chevrolet, Ed Carpenter Racing, 231.851

2024 Indy 500 Row 9

25. (66) Tom Blomqvist (R), Honda, Meyer Shank, 231.578

26. (77) Romain Grosjean, Chevrolet, Juncos Hollinger Racing, 231.514

27. (8) Linus Lundqvist (R), Honda, Chip Ganassi Racing, 231.506

2024 Indy 500 Row 10

28. (45) Christian Lundgaard, Honda, Rahal Letterman Lanigan, 231.465

29. (24) Conor Daly, Chevrolet, Dreyer & Reinbold-Cusick, 231.243

30. (30) Pietro Fittipaldi, Honda, Rahal Letterman Lanigan, 231.100

Indy 500 qualifying schedule, procedure

Listen to the action on IndyCar Radio or SiriusXM Channel 218

Sunday, May 19

(Practices will be on Peacock)

Noon-1 p.m. : Top 12 practice

1-2 p.m. : Last chance qualifiers practice

(Qualifying on NBC)

3:05-4:05 p.m. : The fastest 12 cars from Saturday will get one attempt each to post an additional time. The slowest of those 12 goes first, then the 11th, etc. Positions 7-12 during this sessions establish their starting positions for the race. The six fastest will have one more chance to earn the pole position.

4:15-5:15 p.m. : Last chance qualifying will determine the 11th row (positions 31-33). Each of the four slowest qualifiers from Saturday will be guaranteed at least one four-lap run. Any can make multiple attempts as needed before the clock expires. The slowest car in this session does not make the Indy 500.

5:25-5:55 p.m. : The Fast Six determines the first two rows. Each car gets one four-lap attempt, starting with the 6th-fastest from the 3:05 p.m. session, then the 5th, etc. Fastest in this session starts the race from the pole position, and the rest fill Rows 1 and 2 based their attempts in this session.