claimed hypothesis mean calculator

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Hypothesis Test for a Mean

Use the calculator below to analyze the results of a hypothesis test for a mean. Enter your null hypothesis's mean, sample mean, sample standard deviation, sample size, test type, and significance level to find your results.

You will find a description of how to conduct a hypothesis test of a mean below the calculator.

Define the t-test

Sample mean under the null distribution, conducting single mean hypothesis tests.

A hypothesis test of a sample mean can help you make inferences about the population from which you drew it. It is a tool to determine what is probably true about an event or phenomena.

Testing a Mean

For the results of a hypothesis test of a mean to be valid, you should follow these steps:

Check Your Conditions

State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.

To use the testing procedure described below, you should check the following conditions:

• Simple Random Sampling - You should collect your sample with simple random sampling. This type of sampling requires that every occurrence of a value in a population has an equal chance of being selected when taking a sample.
• Normal Sampling Distribution -The sampling distribution should follow the Normal or a nearly Normal distribution. A sampling distribution will be nearly Normal when the samples are collected independently and when the population distribution is nearly Normal. Generally, the larger the sample size, the more normally distributed the sampling distribution. Additionally, outlier data points can make a distribution less Normal, so if your data contains many outliers, exercise caution when verifying this condition.

You must state a null hypothesis and an alternative hypothesis to conduct a hypothesis test for a mean.

The null hypothesis, is a skeptical claim that you would like to test. It is defined by the null hypothesis's mean, which is often labeled μ 0 .

The alternative hypothesis represents an alternative claim to the null hypothesis.

Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.

To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:

• Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of μ ≠ μ 0 requires a two-tail test.
• One-tail tests place the rejection region entirely on one side of the distribution i.e. to the right or left tail of the null sampling distribution. For example, in a one-tail test evaluating if the sampling distribution is above the null sampling distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. μ > μ 0 and μ 0 alternative hypotheses require one-tail tests.

The graphical results section of the calculator above shades rejection regions blue.

After checking your conditions, stating your hypothesis, determining your significance level, and collecting your sample, you are ready to analyze your hypothesis.

Sample means follow the Normal Distribution with the following parameters:

• The Population Mean, μ - The population mean is assumed to be the null hypothesis's mean in a single mean hypothesis test.
• The Standard Error, SE - For samples that are much smaller than the population, the standard error can be computed as follows: SE = s / sqrt(n), with s being the sample standard deviation and n being the sample size. It defines how sample means are expected to vary around the null hypothesis's mean given the sample size and under the assumption that the null hypothesis is true.
• Degrees of Freedom, DF - For hypothesis tests for a single mean, the degrees of freedom equals n – 1, with n being the sample size.

In a hypothesis test for a mean, we calculate the probability that we would observe the sample mean, x̄, assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.

You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the t-score, or t-statistic, as follows: t = (x̄ - μ 0 ) / SE

The t-score is a test statistic that tells us how far our observation is from the null hypothesis's mean under the null distribution. Using any t-score table, we can look up the probability of observing the results under the null distribution. You will need to look up the t-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for a mean is sometimes known as a t-test because of the use of a t-score in analyzing results.

If you find the probability is below the significance level, we reject the null hypothesis.

The conclusion of a hypothesis test for a mean is always either:

• Reject the null hypothesis
• Do not reject the null hypothesis

If you reject the null hypothesis, you cannot say that your sample mean is the true population mean. If you do not reject the null hypothesis, you cannot say that the null hypothesis is true.

A hypothesis test is simply a way to look at a sample and conclude if it provides sufficient evidence to reject the null hypothesis.

Example: Hypothesis Test for a Mean

Let’s say that you manage a clothing store with a historical average transaction amount of $53.24.

You believe the best way to improve your business is to increase your average sale amount. So, you have been working hard on training your sales staff on how sell more items to customers to increase sales.

To test if your sales training has increased your average sale amount, you decide to run a hypothesis test for a mean with a sample of 50 transactions to see if your average sale amount has increased.

• Check the conditions - You collect your sample using simple random sampling , and you know that historically your transactions are normally distributed about the average transaction. So, your conditions for running a hypothesis test for a mean are satisfied.
• State Your Hypothesis - Your null hypothesis is that your average transaction amount is the same or less than the historical average, formally stated μ ≤ $53.24. Your alternative hypothesis is that your average is greater than the historical average, formally stated μ > $53.24.
• Determine Your Analysis Plan - You believe that a 5% significance level is reasonable. As your test is one-tail test, you will evaluate if your sample mean would occur at the upper 5% of the null distribution.
• Analyze Your Sample - After collecting your sample (which you do after steps 1-3), you find that the sample mean, x̄, transaction amount is $61.02 with a standard deviation of $39.12. Using the calculator above, you find that a sample mean of $61.02 would results in a t-score of 1.41 under the null distribution, which translates to a p-value of 8.30%.
• Interpret Your Results - Since your p-value of 8.30% is greater than the significance level of 5%, you do not have sufficient evidence to reject the null hypothesis.

In this example, you found that you cannot reject the claim that your current transaction amount is less than or equal to your historical transaction amount of $53.24. Your results do not guarantee that your transaction amount is $53.24 or below, but they do indicate that your sales training has likely not had the effect that you wanted on your store's average sale amount.

Teach yourself statistics

Hypothesis Test for a Mean

This lesson explains how to conduct a hypothesis test of a mean, when the following conditions are met:

• The sampling method is simple random sampling .
• The sampling distribution is normal or nearly normal.

Generally, the sampling distribution will be approximately normally distributed if any of the following conditions apply.

• The population distribution is normal.
• The population distribution is symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population distribution is moderately skewed , unimodal, without outliers, and the sample size is between 16 and 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of hypotheses. Each makes a statement about how the population mean μ is related to a specified value M . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the one-sample t-test to determine whether the hypothesized mean differs significantly from the observed sample mean.

Analyze Sample Data

Using sample data, conduct a one-sample t-test. This involves finding the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = s * sqrt{ ( 1/n ) * [ ( N - n ) / ( N - 1 ) ] }

SE = s / sqrt( n )

• Degrees of freedom. The degrees of freedom (DF) is equal to the sample size (n) minus one. Thus, DF = n - 1.

t = ( x - μ) / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, given the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Sample Size Calculator

As you probably noticed, the process of hypothesis testing can be complex. When you need to test a hypothesis about a mean score, consider using the Sample Size Calculator. The calculator is fairly easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a mean score. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

An inventor has developed a new, energy-efficient lawn mower engine. He claims that the engine will run continuously for 5 hours (300 minutes) on a single gallon of regular gasoline. From his stock of 2000 engines, the inventor selects a simple random sample of 50 engines for testing. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes. Test the null hypothesis that the mean run time is 300 minutes against the alternative hypothesis that the mean run time is not 300 minutes. Use a 0.05 level of significance. (Assume that run times for the population of engines are normally distributed.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

Null hypothesis: μ = 300

Alternative hypothesis: μ ≠ 300

• Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method is a one-sample t-test .

SE = s / sqrt(n) = 20 / sqrt(50) = 20/7.07 = 2.83

DF = n - 1 = 50 - 1 = 49

t = ( x - μ) / SE = (295 - 300)/2.83 = -1.77

where s is the standard deviation of the sample, x is the sample mean, μ is the hypothesized population mean, and n is the sample size.

Since we have a two-tailed test , the P-value is the probability that the t statistic having 49 degrees of freedom is less than -1.77 or greater than 1.77. We use the t Distribution Calculator to find P(t < -1.77) is about 0.04.

• If you enter 1.77 as the sample mean in the t Distribution Calculator, you will find the that the P(t < 1.77) is about 0.04. Therefore, P(t >  1.77) is 1 minus 0.96 or 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
• Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the population was normally distributed, and the sample size was small relative to the population size (less than 5%).

Problem 2: One-Tailed Test

Bon Air Elementary School has 1000 students. The principal of the school thinks that the average IQ of students at Bon Air is at least 110. To prove her point, she administers an IQ test to 20 randomly selected students. Among the sampled students, the average IQ is 108 with a standard deviation of 10. Based on these results, should the principal accept or reject her original hypothesis? Assume a significance level of 0.01. (Assume that test scores in the population of engines are normally distributed.)

Null hypothesis: μ >= 110

Alternative hypothesis: μ < 110

• Formulate an analysis plan . For this analysis, the significance level is 0.01. The test method is a one-sample t-test .

SE = s / sqrt(n) = 10 / sqrt(20) = 10/4.472 = 2.236

DF = n - 1 = 20 - 1 = 19

t = ( x - μ) / SE = (108 - 110)/2.236 = -0.894

Here is the logic of the analysis: Given the alternative hypothesis (μ < 110), we want to know whether the observed sample mean is small enough to cause us to reject the null hypothesis.

The observed sample mean produced a t statistic test statistic of -0.894. We use the t Distribution Calculator to find P(t < -0.894) is about 0.19.

• This means we would expect to find a sample mean of 108 or smaller in 19 percent of our samples, if the true population IQ were 110. Thus the P-value in this analysis is 0.19.
• Interpret results . Since the P-value (0.19) is greater than the significance level (0.01), we cannot reject the null hypothesis.

Hypothesis Testing Calculator Online

Hypothesis testing is a foundational method used in statistics to infer the validity of a hypothesis about a population parameter. The Hypothesis Testing Calculator facilitates this process by automating the computations necessary for the t-test , a method used to compare sample means against a hypothesized mean or against each other. Let’s delve into the formulas this calculator uses to execute one-sample and two-sample t-tests.

One-Sample t-Test

This test is used to determine if the mean (x̄) of your sample is statistically different from a hypothesized population mean (μ₀).

• t is the test statistic
• x̄ is the sample mean
• μ₀ is the hypothesized population mean
• s is the sample standard deviation
• n is the sample size (number of observations)

Two-Sample t-Test

This formula compares the means of two independent groups (x̄₁ and x̄₂), with variations for equal and unequal variances.

Equal Variances:

• x̄₁ and x̄₂ are the means of the first and second sample, respectively
• s pooled is the pooled standard deviation (calculated from both samples)
• n₁ and n₂ are the sizes of the first and second sample, respectively

Unequal Variances (Welch’s t-Test):

t = (x̄₁ – x̄₂) / (√((s₁² / n₁) + (s₂² / n₂)))

• x̄₁ is the mean of the first sample
• x̄₂ is the mean of the second sample
• s₁ and s₂ are the standard deviations of the first and second sample, respectively

Table of Critical t-Values

The following table provides critical t-values for different confidence levels and degrees of freedom which are typically use to determine the cutoff points at which the null hypothesis is reject.

These values are crucial in hypothesis testing as they help define the threshold for significance, assisting users of the calculator in interpreting their results accurately.

Consider a scenario where a school administrator wants to test if the average test score of the students this semester differs from a hypothesized mean of 70%. Using the one-sample t-test:

• Sample mean (x̄) = 74%
• Hypothesized mean (μ₀) = 70%
• Sample standard deviation (s) = 8%
• Sample size (n) = 36

Using the one-sample t-test formula:

t = (74 – 70) / (8 / √36) = (4 / 1.333) = 3.00

The calculated t-value is 3.00. Using the critical t-values table, at 95% confidence level and 35 degrees of freedom, the critical value is approximately 2.030. Since 3.00 > 2.030, the null hypothesis is reject, indicating a significant difference from the hypothesize mean.

Most Common FAQs

The p-value represents the probability of obtaining test results at least as extreme as the results observed, under the assumption that the null hypothesis is correct. A low p-value (typically below 0.05) indicates strong evidence against the null hypothesis, hence it is usually rejected.

Use a one-sample t-test when comparing the mean of a single sample to a known standard or hypothesized mean. Use a two-sample t-test when comparing the means of two independent groups to see if there is a statistically significant difference between them.

Yes, while the t-test is specifically design for means, the principles of hypothesis testing apply to other parameters such as proportions and variances. Which can also be tested using appropriate versions of hypothesis tests such as the z-test and F-test.

🚀 Upgrade Your Calculations with AI-Powered Precision!

Solve any problem in a snap with Calculatorshub Ai Calculator.

Related Calculators

Le Chatelier’s Principle Calculator Online

K and J Magnetics Calculator Online

Mass of Moon Calculator Online

Electrostatic Calculator Online

WKG Calculator Online

Richter Scale Calculator Online

Fick’s Calculator Online

Viscosity of Air Calculator Online

Young Modulus Calculator Online

Reduced Mass Calculator Online

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Learning about Electronics

• Programming
• Calculators

Hypothesis Testing Calculator

Related Resources

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a mean.

A population mean is an average of value a population.

Hypothesis tests are used to check a claim about the size of that population mean.

Hypothesis Testing a Mean

The following steps are used for a hypothesis test:

• Check the conditions
• Define the claims
• Decide the significance level
• Calculate the test statistic

For example:

• Population : Nobel Prize winners
• Category : Age when they received the prize.

And we want to check the claim:

"The average age of Nobel Prize winners when they received the prize is more than 55"

By taking a sample of 30 randomly selected Nobel Prize winners we could find that:

The mean age in the sample (\(\bar{x}\)) is 62.1

The standard deviation of age in the sample (\(s\)) is 13.46

From this sample data we check the claim with the steps below.

1. Checking the Conditions

The conditions for calculating a confidence interval for a proportion are:

• The sample is randomly selected
• The population data is normally distributed
• Sample size is large enough

A moderately large sample size, like 30, is typically large enough.

In the example, the sample size was 30 and it was randomly selected, so the conditions are fulfilled.

Note: Checking if the data is normally distributed can be done with specialized statistical tests.

2. Defining the Claims

We need to define a null hypothesis (\(H_{0}\)) and an alternative hypothesis (\(H_{1}\)) based on the claim we are checking.

The claim was:

In this case, the parameter is the mean age of Nobel Prize winners when they received the prize (\(\mu\)).

The null and alternative hypothesis are then:

Null hypothesis : The average age was 55.

Alternative hypothesis : The average age was more than 55.

Which can be expressed with symbols as:

\(H_{0}\): \(\mu = 55 \)

\(H_{1}\): \(\mu > 55 \)

This is a ' right tailed' test, because the alternative hypothesis claims that the proportion is more than in the null hypothesis.

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

Advertisement

3. Deciding the Significance Level

The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

• \(\alpha = 0.1\) (10%)
• \(\alpha = 0.05\) (5%)
• \(\alpha = 0.01\) (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

4. Calculating the Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

The formula for the test statistic (TS) of a population mean is:

\(\displaystyle \frac{\bar{x} - \mu}{s} \cdot \sqrt{n} \)

\(\bar{x}-\mu\) is the difference between the sample mean (\(\bar{x}\)) and the claimed population mean (\(\mu\)).

\(s\) is the sample standard deviation .

\(n\) is the sample size.

In our example:

The claimed (\(H_{0}\)) population mean (\(\mu\)) was \( 55 \)

The sample mean (\(\bar{x}\)) was \(62.1\)

The sample standard deviation (\(s\)) was \(13.46\)

The sample size (\(n\)) was \(30\)

So the test statistic (TS) is then:

\(\displaystyle \frac{62.1-55}{13.46} \cdot \sqrt{30} = \frac{7.1}{13.46} \cdot \sqrt{30} \approx 0.528 \cdot 5.477 = \underline{2.889}\)

You can also calculate the test statistic using programming language functions:

With Python use the scipy and math libraries to calculate the test statistic.

With R use built-in math and statistics functions to calculate the test statistic.

5. Concluding

There are two main approaches for making the conclusion of a hypothesis test:

• The critical value approach compares the test statistic with the critical value of the significance level.
• The P-value approach compares the P-value of the test statistic and with the significance level.

Note: The two approaches are only different in how they present the conclusion.

The Critical Value Approach

For the critical value approach we need to find the critical value (CV) of the significance level (\(\alpha\)).

For a population mean test, the critical value (CV) is a T-value from a student's t-distribution .

This critical T-value (CV) defines the rejection region for the test.

The rejection region is an area of probability in the tails of the standard normal distribution.

Because the claim is that the population mean is more than 55, the rejection region is in the right tail:

The student's t-distribution is adjusted for the uncertainty from smaller samples.

This adjustment is called degrees of freedom (df), which is the sample size \((n) - 1\)

In this case the degrees of freedom (df) is: \(30 - 1 = \underline{29} \)

Choosing a significance level (\(\alpha\)) of 0.01, or 1%, we can find the critical T-value from a T-table , or with a programming language function:

With Python use the Scipy Stats library t.ppf() function find the T-Value for an \(\alpha\) = 0.01 at 29 degrees of freedom (df).

With R use the built-in qt() function to find the t-value for an \(\alpha\) = 0.01 at 29 degrees of freedom (df).

Using either method we can find that the critical T-Value is \(\approx \underline{2.462}\)

For a right tailed test we need to check if the test statistic (TS) is bigger than the critical value (CV).

If the test statistic is bigger than the critical value, the test statistic is in the rejection region .

When the test statistic is in the rejection region, we reject the null hypothesis (\(H_{0}\)).

Here, the test statistic (TS) was \(\approx \underline{2.889}\) and the critical value was \(\approx \underline{2.462}\)

Here is an illustration of this test in a graph:

Since the test statistic was bigger than the critical value we reject the null hypothesis.

This means that the sample data supports the alternative hypothesis.

And we can summarize the conclusion stating:

The sample data supports the claim that "The average age of Nobel Prize winners when they received the prize is more than 55" at a 1% significance level .

The P-Value Approach

For the P-value approach we need to find the P-value of the test statistic (TS).

If the P-value is smaller than the significance level (\(\alpha\)), we reject the null hypothesis (\(H_{0}\)).

The test statistic was found to be \( \approx \underline{2.889} \)

For a population proportion test, the test statistic is a T-Value from a student's t-distribution .

Because this is a right tailed test, we need to find the P-value of a t-value bigger than 2.889.

The student's t-distribution is adjusted according to degrees of freedom (df), which is the sample size \((30) - 1 = \underline{29}\)

We can find the P-value using a T-table , or with a programming language function:

With Python use the Scipy Stats library t.cdf() function find the P-value of a T-value bigger than 2.889 at 29 degrees of freedom (df):

With R use the built-in pt() function find the P-value of a T-Value bigger than 2.889 at 29 degrees of freedom (df):

Using either method we can find that the P-value is \(\approx \underline{0.0036}\)

This tells us that the significance level (\(\alpha\)) would need to be bigger than 0.0036, or 0.36%, to reject the null hypothesis.

This P-value is smaller than any of the common significance levels (10%, 5%, 1%).

So the null hypothesis is rejected at all of these significance levels.

The sample data supports the claim that "The average age of Nobel Prize winners when they received the prize is more than 55" at a 10%, 5%, or 1% significance level .

Note: An outcome of an hypothesis test that rejects the null hypothesis with a p-value of 0.36% means:

For this p-value, we only expect to reject a true null hypothesis 36 out of 10000 times.

Calculating a P-Value for a Hypothesis Test with Programming

Many programming languages can calculate the P-value to decide outcome of a hypothesis test.

Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.

The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.

With Python use the scipy and math libraries to calculate the P-value for a right tailed hypothesis test for a mean.

Here, the sample size is 30, the sample mean is 62.1, the sample standard deviation is 13.46, and the test is for a mean bigger than 55.

With R use built-in math and statistics functions find the P-value for a right tailed hypothesis test for a mean.

Left-Tailed and Two-Tailed Tests

This was an example of a right tailed test, where the alternative hypothesis claimed that parameter is bigger than the null hypothesis claim.

You can check out an equivalent step-by-step guide for other types here:

• Left-Tailed Test
• Two-Tailed Test

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

Other calculators ...

Free statistical calculators, test for one mean calculator, description, required input, computational notes.

This procedure calculates the difference of an observed mean with a hypothesized value. A significance value (P-value) and 95% Confidence Interval (CI) of the observed mean is reported. The P-value is the probability of obtaining the observed mean in the sample if the null hypothesis value were the true value.

The P-value is the area of the t distribution with n −1 degrees of freedom, that falls outside ± t (see Values of the t distribution table).

How to cite this page

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.26: Hypothesis Test for a Population Mean (5 of 5)

• Last updated
• Save as PDF
• Page ID 14164

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Interpret the P-value as a conditional probability.

We finish our discussion of the hypothesis test for a population mean with a review of the meaning of the P-value, along with a review of type I and type II errors.

Review of the Meaning of the P-value

At this point, we assume you know how to use a P-value to make a decision in a hypothesis test. The logic is always the same. If we pick a level of significance (α), then we compare the P-value to α.

• If the P-value ≤ α, reject the null hypothesis. The data supports the alternative hypothesis.
• If the P-value > α, do not reject the null hypothesis. The data is not strong enough to support the alternative hypothesis.

In fact, we find that we treat these as “rules” and apply them without thinking about what the P-value means. So let’s pause here and review the meaning of the P-value, since it is the connection between probability and decision-making in inference.

Birth Weights in a Town

Let’s return to the familiar context of birth weights for babies in a town. Suppose that babies in the town had a mean birth weight of 3,500 grams in 2010. This year, a random sample of 50 babies has a mean weight of about 3,400 grams with a standard deviation of about 500 grams. Here is the distribution of birth weights in the sample.

Obviously, this sample weighs less on average than the population of babies in the town in 2010. A decrease in the town’s mean birth weight could indicate a decline in overall health of the town. But does this sample give strong evidence that the town’s mean birth weight is less than 3,500 grams this year?

We now know how to answer this question with a hypothesis test. Let’s use a significance level of 5%.

Let μ = mean birth weight in the town this year. The null hypothesis says there is “no change from 2010.”

• H 0 : μ < 3,500
• H a : μ = 3,500

Since the sample is large, we can conduct the T-test (without worrying about the shape of the distribution of birth weights for individual babies.)

Statistical software tells us the P-value is 0.082 = 8.2%. Since the P-value is greater than 0.05, we fail to reject the null hypothesis.

Our conclusion: This sample does not suggest that the mean birth weight this year is less than 3,500 grams ( P -value = 0.082). The sample from this year has a mean of 3,400 grams, which is 100 grams lower than the mean in 2010. But this difference is not statistically significant. It can be explained by the chance fluctuation we expect to see in random sampling.

What Does the P-Value of 0.082 Tell Us?

A simulation can help us understand the P-value. In a simulation, we assume that the population mean is 3,500 grams. This is the null hypothesis. We assume the null hypothesis is true and select 1,000 random samples from a population with a mean of 3,500 grams. The mean of the sampling distribution is at 3,500 (as predicted by the null hypothesis.) We see this in the simulated sampling distribution.

In the simulation, we can see that about 8.6% of the samples have a mean less than 3,400. Since probability is the relative frequency of an event in the long run, we say there is an 8.6% chance that a random sample of 500 babies has a mean less than 3,400 if the population mean is 3,500. We can see that the corresponding area to the left of T = −1.41 in the T-model (with df = 49) also gives us a good estimate of the probability. This area is the P-value, about 8.2%.

If we generalize this statement, we say the P-value is the probability that random samples have results more extreme than the data if the null hypothesis is true. (By more extreme, we mean further from value of the parameter, in the direction of the alternative hypothesis.) We can also describe the P-value in terms of T-scores. The P-value is the probability that the test statistic from a random sample has a value more extreme than that associated with the data if the null hypothesis is true.

What Does a P-Value Mean?

Do women who smoke run the risk of shorter pregnancy and premature birth? The mean pregnancy length is 266 days. We test the following hypotheses.

• H 0 : μ = 266
• H a : μ < 266

Suppose a random sample of 40 women who smoke during their pregnancy have a mean pregnancy length of 260 days with a standard deviation of 21 days. The P-value is 0.04.

What probability does the P-value of 0.04 describe? Label each of the following interpretations as valid or invalid.

https://assessments.lumenlearning.co...sessments/3654

https://assessments.lumenlearning.co...sessments/3655

https://assessments.lumenlearning.co...sessments/3656

Review of Type I and Type II Errors

We know that statistical inference is based on probability, so there is always some chance of making a wrong decision. Recall that there are two types of wrong decisions that can be made in hypothesis testing. When we reject a null hypothesis that is true, we commit a type I error. When we fail to reject a null hypothesis that is false, we commit a type II error.

The following table summarizes the logic behind type I and type II errors.

It is possible to have some influence over the likelihoods of committing these errors. But decreasing the chance of a type I error increases the chance of a type II error. We have to decide which error is more serious for a given situation. Sometimes a type I error is more serious. Other times a type II error is more serious. Sometimes neither is serious.

Recall that if the null hypothesis is true, the probability of committing a type I error is α. Why is this? Well, when we choose a level of significance (α), we are choosing a benchmark for rejecting the null hypothesis. If the null hypothesis is true, then the probability that we will reject a true null hypothesis is α. So the smaller α is, the smaller the probability of a type I error.

It is more complicated to calculate the probability of a type II error. The best way to reduce the probability of a type II error is to increase the sample size. But once the sample size is set, larger values of α will decrease the probability of a type II error (while increasing the probability of a type I error).

General Guidelines for Choosing a Level of Significance

• If the consequences of a type I error are more serious, choose a small level of significance (α).
• If the consequences of a type II error are more serious, choose a larger level of significance (α). But remember that the level of significance is the probability of committing a type I error.
• In general, we pick the largest level of significance that we can tolerate as the chance of a type I error.

Let’s return to the investigation of the impact of smoking on pregnancy length.

Recap of the hypothesis test: The mean human pregnancy length is 266 days. We test the following hypotheses.

https://assessments.lumenlearning.co...sessments/3778

https://assessments.lumenlearning.co...sessments/3779

https://assessments.lumenlearning.co...sessments/3780

Let’s Summarize

In this “Hypothesis Test for a Population Mean,” we looked at the four steps of a hypothesis test as they relate to a claim about a population mean.

Step 1: Determine the hypotheses.

• The hypotheses are claims about the population mean, µ.
• The null hypothesis is a hypothesis that the mean equals a specific value, µ 0 .

Step 2: Collect the data.

Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the t-model is a good fit for the sampling distribution of sample means. To use the t-model, the variable must be normally distributed in the population or the sample size must be more than 30. In practice, it is often impossible to verify that the variable is normally distributed in the population. If this is the case and the sample size is not more than 30, researchers often use the t-model if the sample is not strongly skewed and does not have outliers.

Step 3: Assess the evidence.

• If a t-model is appropriate, determine the t-test statistic for the data’s sample mean.
• Use the test statistic, together with the alternative hypothesis, to determine the P-value.
• The P-value is the probability of finding a random sample with a mean at least as extreme as our sample mean, assuming that the null hypothesis is true.
• As in all hypothesis tests, if the alternative hypothesis is greater than, the P-value is the area to the right of the test statistic. If the alternative hypothesis is less than, the P-value is the area to the left of the test statistic. If the alternative hypothesis is not equal to, the P-value is equal to double the tail area beyond the test statistic.

Step 4: Give the conclusion.

The logic of the hypothesis test is always the same. To state a conclusion about H 0 , we compare the P-value to the significance level, α.

• If P ≤ α, we reject H 0 . We conclude there is significant evidence in favor of H a .
• If P > α, we fail to reject H 0 . We conclude the sample does not provide significant evidence in favor of H a .
• We write the conclusion in the context of the research question. Our conclusion is usually a statement about the alternative hypothesis (we accept H a or fail to acceptH a ) and should include the P-value.

Other Hypothesis Testing Notes

• Remember that the P-value is the probability of seeing a sample mean at least as extreme as the one from the data if the null hypothesis is true. The probability is about the random sample; it is not a “chance” statement about the null or alternative hypothesis.
• If our test results in rejecting a null hypothesis that is actually true, then it is called a type I error.
• If our test results in failing to reject a null hypothesis that is actually false, then it is called a type II error.
• If rejecting a null hypothesis would be very expensive, controversial, or dangerous, then we really want to avoid a type I error. In this case, we would set a strict significance level (a small value of α, such as 0.01).
• Finally, remember the phrase “garbage in, garbage out.” If the data collection methods are poor, then the results of a hypothesis test are meaningless.

Contributors and Attributions

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Hypothesis Testing Calculator

Understanding Hypothesis Testing: A Guide to the Hypothesis Testing Calculator

Hypothesis testing is a crucial statistical method used to make informed decisions about data and draw conclusions. Whether you’re a student, researcher, or professional, a Hypothesis Testing Calculator can be an invaluable tool in your statistical toolkit. Let’s explore what hypothesis testing is and how this calculator can assist you:

Hypothesis Testing Basics:

• Null Hypothesis (H0): This is the default assumption or claim that there is no significant difference or effect. It’s often denoted as H0.
• Alternative Hypothesis (Ha): This is the statement that contradicts the null hypothesis. It suggests that there is a significant difference or effect. It’s denoted as Ha.
• Significance Level (α): This is the predetermined threshold (e.g., 0.05 or 5%) used to determine statistical significance. If the calculated p-value is less than α, you reject the null hypothesis.
• p-value: This is the probability of observing the results (or more extreme results) if the null hypothesis is true. A small p-value suggests that the results are unlikely under the null hypothesis.

Key Features of the Hypothesis Testing Calculator:

• Input Parameters: The calculator typically requires you to input sample data, choose the type of test (e.g., t-test, chi-square test), specify the null and alternative hypotheses, and set the significance level.
• Calculations: Once you input the data and parameters, the calculator performs the necessary statistical tests and calculations. It generates results such as the test statistic, degrees of freedom, and the p-value.
• Interpretation: Based on the results, the calculator helps you determine whether to reject or fail to reject the null hypothesis. It provides an interpretation of the findings, which is crucial for drawing conclusions.
• Visual Representation: Some calculators may offer visual aids like graphs or charts to help you better understand the data distribution and test results.

Significance of the Hypothesis Testing Calculator:

• Scientific Research: Researchers across various fields use hypothesis testing to validate their hypotheses and draw meaningful conclusions from data.
• Quality Control: Industries use hypothesis testing to ensure the quality and consistency of products and processes.
• Medical Studies: In medical research, hypothesis testing helps assess the effectiveness of treatments or interventions.
• Academics: Students and educators use hypothesis testing to teach and learn statistical concepts and conduct experiments.
• Data-Driven Decisions: Businesses use hypothesis testing to make data-driven decisions, such as whether to launch a new product based on market research.

Conclusion:

The Hypothesis Testing Calculator is a powerful tool that simplifies complex statistical analysis and enables data-driven decision-making. Whether you’re conducting experiments, analyzing survey data, or performing quality control, understanding hypothesis testing and using this calculator can help you make informed choices and contribute to evidence-based research and decision-making.

Hypothesis Testing Calculator

Navigating hypothesis testing: unveiling the potential of the hypothesis testing calculator.

Embarking on the journey of statistical exploration, hypothesis testing stands out as an indispensable method for informed decision-making and drawing meaningful conclusions from data. Whether you find yourself in the academic realm, engaged in research endeavors, or navigating the professional landscape, having a trustworthy Hypothesis Testing Calculator in your statistical toolkit can prove to be a game-changer. Let’s delve into the intricacies of hypothesis testing and uncover how this calculator can be your ally in statistical analyses.

Demystifying Hypothesis Testing:

Null Hypothesis (H0): Positioned as the default assumption, the null hypothesis asserts the absence of any significant difference or effect and is commonly represented as H0.

Alternative Hypothesis (Ha): In direct contradiction to the null hypothesis, the alternative hypothesis posits the existence of a noteworthy difference or effect, denoted as Ha.

Significance Level (α): Acting as the predetermined threshold, typically set at 0.05 or 5%, the significance level plays a pivotal role in determining statistical significance. Should the calculated p-value fall below α, the null hypothesis is rejected.

p-value: Representing the likelihood of observing the results, or more extreme outcomes, under the assumption of the null hypothesis being true, a smaller p-value suggests the unlikelihood of the results occurring by chance.

Features that Define the Hypothesis Testing Calculator:

Input Parameters: The calculator demands input of sample data, selection of the test type (e.g., t-test, chi-square test), specification of null and alternative hypotheses, and determination of the significance level.

Calculations: Once armed with the requisite data and parameters, the calculator diligently executes statistical tests and computations. The output encompasses crucial details like the test statistic, degrees of freedom, and the all-important p-value.

Interpretation: Armed with the results, the calculator aids in the decision-making process, guiding whether to reject or accept the null hypothesis. An interpretation of the findings is provided, playing a pivotal role in drawing insightful conclusions.

Visual Representation: Some calculators go the extra mile by offering visual aids such as graphs or charts, facilitating a deeper understanding of data distribution and test outcomes.

Unveiling the Significance of the Hypothesis Testing Calculator:

In Scientific Research: Researchers spanning diverse fields leverage hypothesis testing to validate their hypotheses, thereby extracting meaningful insights from data.

In Quality Control: Industries rely on hypothesis testing as a quality assurance mechanism, ensuring the consistency and excellence of products and processes.

In Medical Studies: Within the realm of medical research, hypothesis testing serves as a critical tool for evaluating the effectiveness of treatments or interventions.

In Academics: Both students and educators find value in hypothesis testing as an educational tool, enabling the comprehension of statistical concepts and the conduct of experiments.

In Data-Driven Decision-Making: Businesses, keen on making decisions grounded in data, turn to hypothesis testing to navigate choices such as launching a new product based on comprehensive market research.

Concluding Insights:

The Hypothesis Testing Calculator emerges as a formidable ally, simplifying intricate statistical analyses and fostering data-driven decision-making. Whether you are in the midst of experimental undertakings, scrutinizing survey data, or overseeing quality control protocols, a solid understanding of hypothesis testing coupled with the use of this calculator empowers you to make well-informed choices. In doing so, you not only contribute to evidence-based research but also play a pivotal role in shaping decision-making processes across various domains.

One Sample T Test Calculator

Enter sample data, reporting results in apa style, one sample t-test, what is a one sample t-test, how to use the one sample t test calculator, calculators.

Test Statistic Calculator

$$ \frac{\overline{x} - μ_0}{\frac{σ}{\sqrt{n}}} $$

$$ \frac{\overline{x} - \overline{y}}{\sqrt{\frac{σ^2_x}{n_1} + \frac{σ^2_y}{n_2}}} $$

$$ \frac{\stackrel{\text{^}}{p} - \ p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} $$

$$ \frac{\stackrel{\text{^}}{p_1} - \stackrel{\text{^}}{p_2}}{\sqrt{\stackrel{\text{^}}{p}(1-\stackrel{\text{^}}{p})(\frac{1}{n_1} + \frac{1}{n_2})}} $$

Table of Content

In order to calculate the test statistics for one population mean, compare two means, a single population proportion, and two population proportions the test statistic calculator is used. It has the ability to summarize your data into a single number. 

What Is Test Statistics?

“The measurement that evaluates the strength of evidence by refuting the hypothesis is known as test statistics”.  

It helps to determine the population hypothesis and helps us to summarize the data. Therefore it is also known as the significance hypothesis. 

Test Statistics Formula:

The test statistic formula calculator is used to evaluate the strength of evidence from the sample. However, the formula varies with the size of the population and the sample, and with these, you can evaluate how far your observed data is from the null hypothesis. 

One Population Mean:

For one population mean the test statistics formula is as follows:

$$ \frac{\overline{x} - μ_0}{\frac{σ}{\sqrt{n}}} $$

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

Comparing Two Means: 

The formula to evaluate the independent samples are given below:

$$ \frac{\overline{x} - \overline{y}}{\sqrt{\frac{σ^2_x}{n_1} + \frac{σ^2_y}{n_2}}} $$

• x and y are the means 
• σx are the standard deviation of the x values
• σy are the standard deviation of the y values
• n1 is the sample size of the x 
• n2 is the sample size of the y

Single Population Portion: 

• P is the sample proportion
• P0  is the claimed proportion
• n is the sample size

Two Population Portions: 

• P1 and  P2 are the populations
• n1 and n2 are the sample sizes

How to Calculate Test Statistic?

In this type of statistics, the quantitative measures assess the strength of evidence against the hypothesis. So look at the below example which indicates how the value of test statistic calculator summarizes your data into a single number. 

Suppose a cricket series was held against Pakistan and Sri Lanka in Colombo in which Baber Azam makes an average score of about 78 in five matches. As you know the average batting for a player is 40. In this case, the deviation in scoring is 4, what are the performance stats of Baber Azam?

Given Data:

• Deviation = 4

$$ \text{Test Statistic}=\frac{78 – 40}{\frac{4}{\sqrt{5}}} $$

$$ \text{Test Statistic}=\frac{38}{\frac{4}{2.236}} $$

$$ \text{Test Statistic}=\frac{26}{1.79} $$

$$ \text{Test Statistic}= 14.53 $$

Suppose there is a 3% and it means that the performance for 5 matches is considerably better than average. 

Working of Sample Test Statistic Calculator:

The test value calculator transforms the data analysis by simplifying the hypothesis testing. Attach to the guide below to utilize the test statistics calculator.

• Choose the point that you want to calculate 
• Put the values according to the chosen value 
• Tap on “Calculate”

Our standardized test statistic calculator will give you the following results. 

• Test statistics for sample and population mean 
• Complete calculation in the steps given 

Test Statistics Table:

One tail table:, two tail table:, what indicates the negative test statistics.

A negative test statistics value indicates that it occurs on the left side of the mean. All left values are negative and all right values are positive. A negative test is just like a standard normal that has a zero mean. 

What are the applications of test statistics related to data sets?

• Product quality with the sample measurement 
• Market research to analyze the survey data 
• Strategies of investment and impact of market trends also analyzed 
• Determination of significant change and physiological experiments 

What does a 0 test value mean?

If the test statistics value is equal to zero it means that sample results are equal to the null hypothesis.  

References:

From the source Wikipedia: Test statistic , Example.

From the source Khan Academy: Significance tests (hypothesis testing), 

Alan Walker

Studies mathematics sciences, and Technology. Tech geek and a content writer. Wikipedia addict who wants to know everything. Loves traveling, nature, reading. Math and Technology have done their part, and now it's the time for us to get benefits.

Submit Your Review

Related converters.

Follow Us on Social Media

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

Single Sample T-Test Calculator

A single sample t-test (or one sample t-test) is used to compare the mean of a single sample of scores to a known or hypothetical population mean. So, for example, it could be used to determine whether the mean diastolic blood pressure of a particular group differs from 85, a value determined by a previous study.

Requirements

• The data is normally distributed
• Scale of measurement should be interval or ratio
• A randomized sample from a defined population

Null Hypothesis

H 0 : M - μ = 0, where M is the sample mean and μ is the population or hypothesized mean.

As above, the null hypothesis is that there is no difference between the sample mean and the known or hypothesized population mean.

p-value Calculator

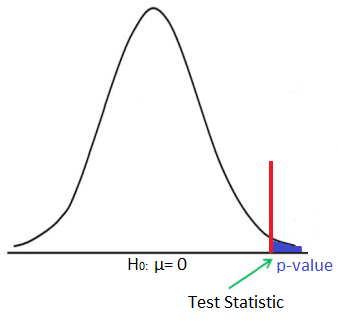
Test Statistic:

Sample Size:

Test Type: Left-tail (Ha: μ < H0) Right-tail (Ha: μ > H0) Two-tail (Ha: μ ≠ H0)

Significance Level, α: 0.1% 0.5% 1% 2.5% 5% 10% 20% 25% 40%

Determining the p-value allows us to determine whether we should reject or not reject a claimed hypothesis.

Related Resources