chance problem solving year 5

Maths Year 5 with Ms Szalek: Probability

• X (formerly Twitter)

Hey mathematicians! My name's Ms Szalek and welcome to maths. Today we're going to focus on probability.

For this lesson, you'll need a pencil, paper, a die, and a coin.

First, let's get into our warm up. I'm going to be flipping a coin, so I'd love you to get a coin and flip along with me. Now, if you look at our coin, we have heads and we have tails. That means we have two possible outcomes. I'm going to be flipping my coin four times and I'd love you to flip along. Are you ready? Okay, here we go. Let's see what we get.

Heads. How did you go? I got heads again. What did you get? Oh, tails. Okay our last one. Whoa, tails. So I got two heads and two tails. How did you go at home? Do you think if we did this again, we would get two heads and two tails every time? Well, let's get into today's lesson and find out.

Our learning intention for today is to determine and represent probabilities of equally likely events as fractions.

But first, what is probability? Well, probability is the likelihood or chance that an event can occur. What are some of the words we already know about probability? Let's take a look together. We have impossible, unlikely, equally likely, likely, and certain. So impossible, what does that mean? Well, that means something is impossible. The event cannot happen. There is no chance. It is definitely not going to happen. On the other end of the scale we have certain which means that our event is certain. It is absolutely definitely going to happen. When we look into the middle, we can see equally likely. And when we think about it like a scale, there is an equal chance that it will either happen or not happen. Then, when we see likely we're closer to certain, which means there's more of a chance that it will happen. And unlikely being closer to impossible means that there is less of a chance of our event occurring.

But what do these look like when we write them as fractions? If we look at impossible, well, we already said that there was a zero chance that our event can occur. Which means that impossible is zero.

When we look at equally likely, well, just like when we looked with our coin, we had heads and we had tails. That's right. So out of our total outcomes, we had heads and tails. We had two outcomes. That means our denominator is two. Two represents our total outcomes. When we flip our coin, we can only land on either a head or a tail. We can't land on both, which means that we have a one out of two chance of getting a head and a one out of two chance of getting a tail. So equally likely comes down as one half. So we have a half chance of our event happening and a half chance of it not happening.

When we look at certain, well, we know that it is absolutely going to happen. So out of two, it means that we have a two out of two chance that our event's going to occur. And we know that two halves make a whole, so certain is actually the same as one whole. So our scale of probability goes from zero at impossible to one, certain.

When we're looking at our likely and unlikely, well, we're halfway between a half and a whole, and halfway between a half and a whole is actually three quarters, as we can see here. And when we move to unlikely, well, that's halfway between zero and a half, which means that we have one quarter. And this is how we represent probability using fractions.

What will these fractions look like if we put them into action? Well, let's do an activity now. I've got a coin here and I'm going to flip it eight times. I'd love for you to get a coin and flip along with me at home. Before we start, let's look at what we might expect to happen. Well, I've got a head on one side and a tail on the other. So every time I flip the coin, two times I would expect that one of them would be a head and the other would be a tail. Do you think that's actually what's going to happen though? Well, let's find out together.

Heads. Heads again. Are you ready? What did you get at home? Whoa, I got heads again. Do you think the next one's going to be a head? Well, that might not be the case because chance has no memory. So our probability resets each time. So for every flip, there's still a one in two chance that I will get a head or a tail. Oh, look at that, I got tails. Heads. Tails. Tails. Heads.

Now we're going to look at our actual outcomes. Our actual outcomes are out of eight because we flipped the coin eight times. How many heads did you get out of your eight flips? Well, I got one, two, three, four, five. So I'm going to write five out of eight, which means that my actual outcome was five eighths. How many tails did you get? Well, as you can see, I got one, two, three, so I got three tails. So I'm going to do three out of eight. Now, that's not quite what we expected because we know that four eighths are a half and I didn't get four eighths on either of my flips, which means that our actual outcomes are not always the same as our expected outcomes. They can be different. What if we have more possible outcomes? What if we had say six? What if instead of flipping a coin, we rolled a die.

With a die, we know that there are six sides and on each side is a different number. That means that our total number of outcomes is six. Our probability of rolling, say, a four, that would be one in, you guessed it, that would be one in six. My favourite number is three. Do you think that I'd have a higher probability of rolling a three? Well, that's not actually the case because probability doesn't take into account our favourites. Remember that probability is the likelihood or chance that an event can occur. Let's roll and find out. Whoa, I rolled a four, but I want to see how many times I can roll a three, cause remember it is my favourite. And let's look at the board. If I want to roll a three, I expect to roll it one out of every six times. So let's roll it five more times and see how we go. Another four. And a two. And another four. Two more rolls here. Another two and one more, a six. So we didn't even roll a three out of our six trials. That means that our expected outcome is not the same as our actual outcome. What do you think might happen if we rolled it 50 or a hundred or a thousand or even a million times? Well, in the long run, our actual outcomes would get closer and closer to our expected outcomes.

Now it's your turn to try at home. Grab a die and choose a number between one and six. Try to work out what your expected probability is, and then describe it using a fraction. Then the challenge is to roll your die 12, 24 or even 50 times, and see if your actual outcome matches the expected probability that you wrote before. Thanks for joining me today to learn how we can use fractions to describe probability. My name's Ms Szalek. Have a great day.

SUBJECTS:  Maths

YEARS:  5–6

Learn how to use fractions to describe probability outcomes.

Ms Szalek explains some of the words used in probability, and then she suggests how you can investigate using fractions to find expected and actual outcomes in an experiment.

Acknowledgements

Special thanks to Ms Szalek, The Victorian Department of Education and Training, and Hillsmeade Primary School.

Production Date: 2021

Metadata © Australian Broadcasting Corporation 2020 (except where otherwise indicated). Digital content © Australian Broadcasting Corporation (except where otherwise indicated). Video © Australian Broadcasting Corporation and Department of Education and Training (Victoria). All images copyright their respective owners. Text © Australian Broadcasting Corporation and Department of Education and Training (Victoria).

Maths Year 6 with Ms Szalek: Probability

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Statistics >

Probability Worksheets

Navigate through this assortment of printable probability worksheets that includes exercises on basic probability based on more likely, less likely, equally likely, certain and impossible events, pdf worksheets based on identifying suitable events, simple spinner problems, for students in grade 4, grade 5, and grade 6. With the required introduction, the beginners get to further their knowledge with skills like probability on single coin, two coins, days in a week, months in a year, fair die, pair of dice, deck of cards, numbers and more. Mutually exclusive and inclusive events, probability on odds and other challenging probability worksheets are useful for grade 7, grade 8, and high school. Grab some of these probability worksheets for free!

Probability on Coins

Simple probability worksheets based on tossing single coin or two coins. Identify the proper sample space before finding probability.

Probability in a single coin toss

Probability in pair of coin - 1

Probability in pair of coin - 2

Probability on Days and Months

Fun filled worksheet pdfs based on days in a week and months in a year. Sample space is easy to find but care is required in identifying like events.

Days of a week

Months of a year - 1

Months of a year - 2

Probability on Fair Die

Fair die is numbered from 1 to 6. Understand the multiples, divisors and factors and apply it on these probability worksheets.

Simple numbers

Multiples and divisors

Mutually exclusive and inclusive

Probability on Pair of Dice

Sample space is little large which contains 36 elements. Write all of them in papers before start answering on probability questions for grade 7 and grade 8.

Based on numbers

Based on sum and difference

Based on multiples and divisors

Based on factors

Probability on Numbers

Students should learn the concepts of multiples, divisors and factors before start practicing these printable worksheets.

Probability on numbers - 1

Probability on numbers - 2

Probability on numbers - 3

Probability on numbers - 4

Probability on numbers - 5

Probability on Deck of Cards

Deck of cards contain 52 cards, 26 are black, 26 are red, four different flowers, each flower contain 13 cards such as A, 1, 2, ..., 10, J, Q, K.

Deck of cards worksheet - 1

Deck of cards worksheet - 2

Deck of cards worksheet - 3

Probability on Spinners

Interactive worksheets for 4th grade and 5th grade kids to understand the probability using spinners. Colorful spinners are included for more fun.

Spinner worksheets on numbers

Spinner worksheets on colors

Probability on Odds

Probability on odds worksheets can be broadly classifieds as favorable to the events or against the events.

Odds worksheet - 1

Odds worksheet - 2

Odds worksheet - 3

Probability on Independent and Dependent

Here comes our challenging probability worksheets set for 8th grade and high school students based on dependent and independent events with various real-life applications.

Based on deck of cards

Based on marbles

Based on cards

Probability on Different Events

Basic probability worksheets for beginners in 6th grade and 7th grade to understand the different type of events such as more likely, less likely, equally likely and so on.

Balls in container

Identify suitable events

Mutually inclusive and exclusive events

Related Worksheets

» Permutation

» Combination

» Permutation and Combination

» Venn Diagram

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

Free delivery on all orders over £40* (ex VAT) Order by phone:  03451 203 603 | Mon - Fri 08:00 - 17:00 PM

• Mathematics
• Maths Teaching Resources

Maths Problem Solving Cards Year 5 - Statistics and Chance from Hope Education

Product code: HE1593886

Product Description

Hope Statistics and Chance - Year 5 Problem Solving Strategies and Skills Maths Cards Embed Mathematical Problem-Solving and Reasoning.

The Problem-Solving Strategies and Skills Maths Cards provide a wide variety of motivating and high-interest problem-solving activities.

There are three boxes for each year level, Year 1 to Year 6, comprising:

• 30 Number and Algebra cards, plus answers 
• 30 Measurement and Geometry cards, plus answers
• 30 Statistics and Chance cards, plus answers

Each box also includes a problem-solving process card, and a problem-solving strategies card, to guide and provide support to children as they progress through each stage and box set.

The front of each card has a mathematics word problem for pupils to solve and the reverse of each card has an extension activity for more able pupils. The problems involve one or several steps, require the use of a variety of strategies and skills and are supported by colourful artwork.

The features of the Problem-Solving boxes include:

• Excellent resources to support problem-solving, an essential component of the maths curriculum;
• Varied, real-life and challenging problems
• Activities that enable pupils to practise maths concepts taught in class through problems.

The Problem-solving cards also provide lots of opportunities for reflective teaching and focus on pupil thinking in problem-solving.

Year 5 Statistics and Chance

Visual data and information is displayed in more complex formats, including further use of keys to incorporate multiple sources and in varied formats that require to be studied and interpreted.

Mathematical learning from the areas of number, algebra and geometry are introduced alongside the statistics and chance analysis to bring together the overall mathematical process and use of skills.

The continued use of real-life/business life applications to the problems both retain an interest level as well as support and stimulate the opportunity for debate and discussion around the topics to encourage the formation and expression of opinion by pupils.

Further Information

You may also like.

Shopping from Overseas?

We have detected that your IP address is not UK based.

We have a specific international website which deals with all non-UK transactions and deliveries. Please select which website you would like to continue with.

For International Delivery

For delivery in the uk.

Problem-solving strategies and skills — Statistics and chance — Year 5

Core concepts in each statistics and chance box:.

Account required

Already have a Studyladder account?   Log In

New to Studyladder? Get a free trial account!   Join Now

Chance Problem Solving

• Grade: Year 5 Activity type: Assessment

To save results or sets tasks for your students you need to be logged in. Join Now, Free

• Course Mathematics
• Grade Year 5
• Section Chance and Probability
• Outcome Chance and Probability (as fractions)
• Activity Type Assessment
• Activity ID 4382

Activity: View similar activities

• Chance and probability

Testimonials

What a brilliant site you have!!! I love it, especially as it saves me hours and hours of hard work. Others who haven't found your site yet don't know what they are missing! Patricia Celikbilek, Teacher Read More

It is quite frankly the best money I have ever spent on my child. I really cannot thank you enough for providing this, it really is brilliant. Vanessa Wills, Parent Read More

You have the most amazing program. Everybody loves it and the student's results have been in the high 90%'s, it's definitely due to your program. Chris Rayment, School Principal Read More

Awarded June 2012 “Best Educational Website for Teaching and Learning”

Australia – australian curriculum, statistics and probability.

ACMSP116 – List outcomes of chance experiments involving equally likely outcomes and represent probabilities of those outcomes using fractions

Samples: Chance and Probability (as fractions). Chance Fraction. Chance Problem Solving. Chance Problem Solving. 

ACMSP145 – Conduct chance experiments with both small and large numbers of trials using appropriate digital technologies

Samples: Chance and Probability (as fractions). Chance from 0 to 1. Describe probabilities using decimals. 

ACMSP146 – Compare observed frequencies across experiments with expected frequencies

New Zealand – National Standards

6 – year 6, 6.s – statistics.

6.S.1 – Order the likelihoods of outcomes for situations involving chance, considering experimental results and models of all possible outcomes.

Samples: Order probability (impossible - certain). Chance - one cannot happen if the other happens. 

7 – Year 7

7.s – statistics.

7.S.2 – Order the likelihoods of outcomes for situations involving chance, checking for consistency between experimental results and models of all possible outcomes.

United Kingdom – National Curriculum

Ks2.y6 – ks2 year 6, year 6 programme of study.

KS2.Y6.G.S – Statistics

Pupils should be taught to:

KS2.Y6.G.S.2 – Calculate and interpret the mean as an average

Samples: Median, Range and Mean. Chance and Probability (as fractions). Chance from 0 to 1. Chance Fraction. 

United States – Common Core State Standards

You can go to an overview of all the curricula here .

Parent/Teacher Only

Login required.

This activity requires an account to enable as it customises it questions to individual students

Free Parent & Teacher Access

You can join Studyladder FREE!

Your account will have additional material that tracks students progress to provide individual focused material and reports. Also it includes fun incentives to encourage students to learn more all customised to each students needs.

I would like to register for a:

• Parent Account
• Homeschooling Account
• School Teacher Account

I would like to:

• Browse All / Search
• Mathematics
• Visual Arts and Music
• Health, Safety & Citizenship
• Language & Culture
• Information Communication Technology
• Theme Based Learning
• Forgot password

Studyladder World Teaser

Studyladder home tutor trailer.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Great Expectations: Probability Through Problems

Probability articles.

Probability Through Problems: a new approach to teaching probability

Introducing Probability

What is our approach about?

Why Start with Tree Diagrams?

Why the tree diagram is fundamental to studying probability - and why it should be introduced right from the start.

Probability Calculations from Tree Diagrams

Progression from natural frequencies to proportions to the multiplication rule, and hence to probability trees.

Learning Probability Through Mathematical Modelling

Moving from the particular to the general, then revisiting the particular in that light, and so generalising further.

Tree Diagrams, 2-way Tables and Venn Diagrams

Representing frequencies and probabilities diagrammatically, and using the diagrams as interpretive tools.

Independence and Dependence

When are events independent of each other? Sampling with and without replacement.

Conditional Probability Is Important for All Students!

Understanding statistics about testing for cancer or the chance that two babies in a family could die of SIDS is a crucial skill for ALL students.

Probability Resources for Teaching the Curriculum

Which Team Will Win?

A practical experiment which will introduce students to tree diagrams, and help them to understand that outcomes may not be equally likely.

The Dog Ate My Homework!

A practical experiment which uses tree diagrams to help students understand the nature of questions in conditional probability.

Who Is Cheating?

A practical experiment provides data. Moving onto expected results provides a context to establish the multiplication rule in probability, and an intuitive approach to conditional probability.

Prize Giving

What's the fairest way to choose 2 from 8 potential prize winners? How likely are you to be chosen?

Exploring the Mathematisation of Probability

The Wisdom of the Crowd

Who's closest to the correct number of sweets in a jar - an individual guess or the average of many individuals' guesses? Which average?

Capture and Recapture

How do scientists or mathematicians estimate the size of a population of wild animals?

How Confident Are You?

What proportion of people make 90% confident guesses which actually contain the correct answer?

Louis' Ice Cream Business

Should Louis go for the safer options, hoping to limit his losses, or would he be better off with a riskier strategy, focusing on maximising his profit?

To Insure or Not to Insure

Should you insure your mobile phone? It rather depends on whether you focus on the long-term pay-off or the effect of a single event.

Mastery-Aligned Maths Tutoring

“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."

FREE daily maths challenges

A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

18 Word Problems For Year 5: Develop Their Problem Solving Skills Across Single and Mixed KS2 Topics

Emma Johnson

Word problems for Year 5 are a great way to assess pupils’ number fluency. By the time primary school children reach Upper Key Stage 2, they will be building on their knowledge and understanding of the number system and place value, working with larger integers. An increased understanding of the connections between the different maths concepts is crucial, as children will be expected to tackle more complex, multi-step problems.

It is important children are regularly provided with the opportunity to solve a range of word problems and Year 5 maths worksheets with reasoning and problem solving incorporated alongside fluency, into all lessons.

To help you with this, we have put together a collection of 18 word problems aimed at Year 5 maths pupils.

Place value 

Addition and subtraction , multiplication and division , fractions, decimals and percentages, measurement , why are word problems important in year 5 maths, how to teach problem solving in year 5, addition word problems for year 5, subtraction word problems for year 5,  multiplication word problems for year 5, division word problems for year 5, fraction and decimal word problems in year 5, mixed four operation word problems, word problem resources.

All Kinds of Word Problems

Download this free pack of multiplication word problems to help your Year 5 class grow their problem solving skills

Year 5 maths word problems in the national curriculum

The National Curriculum states that by Year 5, pupils should develop their ability to solve a wider range of problems, including increasingly complex properties of numbers and arithmetic, and problems demanding efficient written and mental methods of calculation. Children also begin to use the language of algebra for solving a range of problems.

By Year 5, pupils should be starting to gain confidence in solving more complex two-step and multi-step word problems, covering topics across the Year 5 curriculum.

Solve number and practical problems involving ordering and comparing numbers to at least 1,00,000; counting forwards or backwards in steps of powers of 10; interpreting negative numbers in context and rounding to the nearest 10,100, 1000, 10,000 and 100,000.

Solve addition and subtraction word problems and a combination of these, including understanding the meaning of the equals sign.

Solve problems involving multiplication and division, including using knowledge of factors, multiples, squares and cubes and scaling by simple fractions.

Solve problems involving numbers up to 3 decimal places and problems which require knowing percentage and decimal equivalents.

Solve time word problems and those involving converting between units of time and problems involving measure (for example, length, mass, volume and money word problems ) using decimal notation and scaling.

Solve comparison, sum and difference problems, using information presented in a line graph.

Word problems are an important element of the Year 5 curriculum. By this stage, children need to be building confidence in approaching a range of one, two and multi-step word problems . They require children to be creative and apply the skills they have learnt to a range of real-life situations. 

Children need to be taught the skills for successfully approaching and tackling word problems. Reading the question carefully and identifying the key information needed to tackle the problem, is the first step, followed by identifying which calculations are required for solving it and deciding whether it will be helpful to draw a picture/ visual representation to understand and answer the question. 

Using mental maths skills to round and estimate an answer is also very helpful for children to establish whether their final answer is realistic. Children need to also be able to calculate the inverse, to be able to check their answer, once the problem has been completed.

See also: Mental maths year 5

Here is an example:

A transport museum has 1243 visitors on Monday morning and another 1387 visitors in the afternoon. On Tuesday 736 fewer visitors go to the museum than who visited on Monday.

How many visitors were there altogether on Tuesday?

How to solve:

What do you already know?

• The number of visitors on Monday morning and Monday afternoon are given separately. They need to be added together to give the total number of visitors for Monday.
• ‘Fewer’ means I will need to subtract the number of fewer visitors on Tuesday from the total number of visitors on Monday.
• Column addition and subtraction will be needed to solve this question.

How can this be drawn/represented pictorially?

We can draw a bar model to represent this problem:

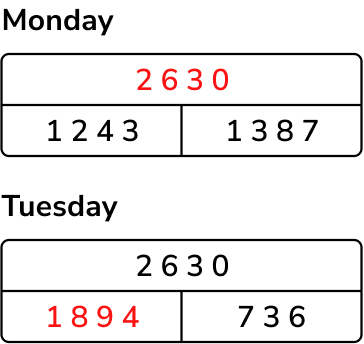
• To calculate the total number of visitors on Monday, we need to add 1243 and 1387 together. 1243 + 1387 = 2630
• The number of fewer visitors on Tuesday needs to be subtracted from Monday’s total: 2630 – 736 = 1894.
• The total number of visitors on Tuesday was 1894.

In Year 5, addition word problems can involve whole numbers with over 4 digits and decimal numbers. Children should be able to round number to check the accuracy and begin to solve two step number problems 

Addition question 1

Gemma picks two cards from the cards below and adds them together.  She is able to make three different totals. What will they be?

2365     6281      9782

Answer (2 marks) : 12,147   16,063  8646

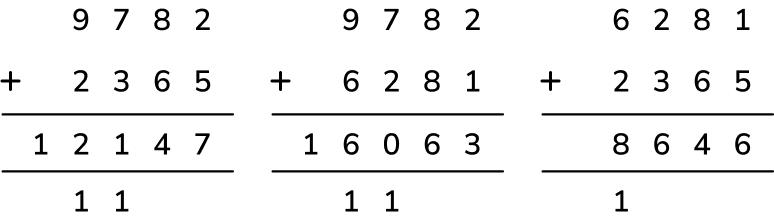
Addition question 2

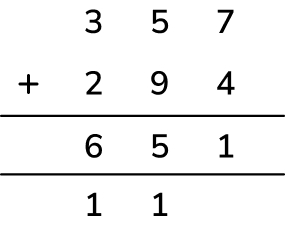
Ahmed adds two of these numbers mentally.

357         280          294          232

In his calculation, he exchanges twice to create one ten and one hundred. Write Ahmed’s calculation and work out the total.

Answer (1 mark) : 357 + 294 = 651

Addition question 3

Change one digit in the calculation below, so that the answer is a multiple of 10.

Answer (1 mark) : 723 + 347 = 1070

Subtraction word problems in Year 5 require pupils to be confident subtracting numbers over 4 digits and problems involving decimal numbers. Pupils need to be able to round numbers to check accuracy and to use subtraction when solving mixed word problems. 

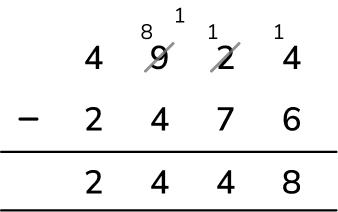
Subtraction question 1

A coach is travelling 4924 km across the USA It has 2476 km to go. How many kilometres has the coach already travelled?

Answer (1 mark) : 2448 km

Subtraction question 2

A primary school printed 7283 maths worksheets in the Summer term. 2156 were for Key Stage 1 pupils. How many were printed for Key Stage 2?

Answer (1 mark): 5127 worksheets

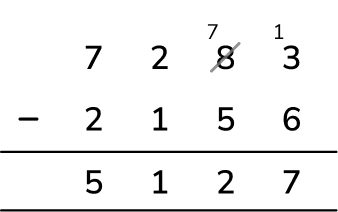
Subtraction question 3

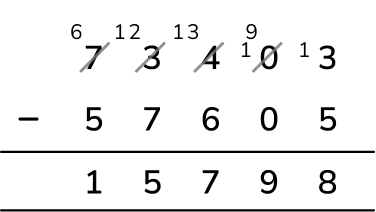
 A clothing company made £57,605 profit in 2021 and £73,403 in 2022.  How much more profit did the company make in 2022 than in 2021?

Answer (1 mark): £15,798

In year 5, multiplication word problems include problems involving times tables and multiplying whole numbers up to 4-digits by 1 or 2-digit numbers. Pupils also need to be able to combine multiplication with other operations, in order to solve two-step word problems. 

Multiplication question 1

In this diagram, the numbers in the circles are multiplied together to make the answer in the square between them.

Complete the missing numbers.

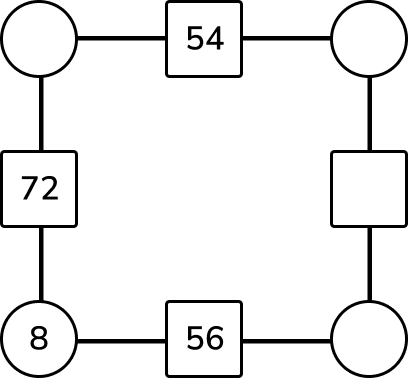
Answer (1 mark)

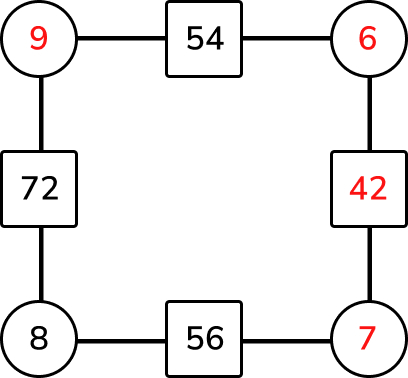
Multiplication question 2

Mrs Jones was printing the end of year maths test. Each test had 18 pages and 89 pupils were sitting the test. Mrs Jones also needed to print out 12 copies for the teachers and Teaching Assistants who were helping to run the test. 

How many pieces of paper did Mrs Jones need to put in the photocopier, to make sure she had enough for all the tests?

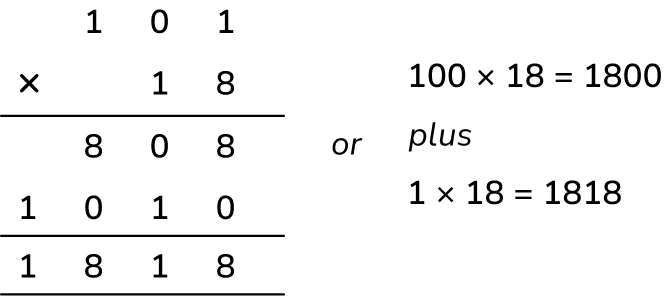
Multiplication question 3

A school is booking a trip to Alton Towers. Tickets cost £22 per pupil. There are 120 children in each year group and all the children from 3 year groups will be going.

What will be the total price for all the tickets?

Answer (2 marks): £7920

Third Space Learning often ties word problems into our online one-to-one tutoring. Each lesson is personalised to the needs of the individual student, growing maths knowledge and problem solving skills.

In Year 5, division word problems can involve whole numbers up to 4 digits being divided by 1-digit numbers. Pupils need to understand how to answer word problems, when the answer involves a remainder.

Division question 1

Tom has 96 cubes and makes 12 equal towers. Masie has 63 cubes and makes 9 equal towers. Whose towers are tallest and by how many cubes?

Answer (2 marks): Tom

Tom’s tower has more cubes. His towers have 1 more cube than Maise’s towers.

96 ÷ 12 = 8

Division question 2

A cake factory has made cakes to deliver to a large event. 265 cakes have been baked. How many boxes of 8 cakes can be delivered to the event?

Answer (2 marks) : 33 boxes

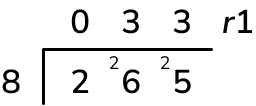
Division question 3

Lily collected 1256 stickers. She shared them between her 8 friends. How many stickers did each friend get

Answer (1 mark): 157 stickers

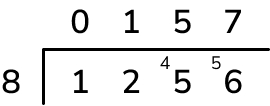
In Year 5, fractions word problems and decimals can include questions involving ordering, addition and subtraction of fractions. They can also involve converting between fractions and decimals. 

Fraction and decimal question 1

Isobel collected 24 conkers. She gave \frac{1}{8} of the conkers to her brother. How many conkers did she have left?

Answer (1 mark): 21 conkers left

\frac{1}{8} of 24 = 3

24 – 4 = 21

Fraction and decimal question 2

Ahmed counted out 32 sweets. He gave \frac{1}{4} of the sweets to his brother and \frac{3}{8} of the sweets to his friend. How many sweets did he have left?

Answer (2 marks): 12 sweets

\frac{1}{4} of 32 = 8

\frac{3}{8} of 32 = 12

He gave away 20 sweets, so had 12 left for himself.

Fraction and decimal question 3

Two friends shared some pizzas, 1 ate 1 \frac{1}{2} pizzas, whilst the other ate \frac{5}{8} of a pizza. How much did they eat altogether?

Answer (1 mark): 2 \frac{1}{8} of pizza

1 \frac{1}{2} = \frac{12}{8}

\frac {12}{8} + \frac{5}{8} = \frac{17}{8} = 2 \frac{1}{8} pizzas

Problems with mixed operations, or ‘multi-step’ word problems, require two or more operations to solve them. A range of concepts can be covered within mixed problems, including the four operations, fractions, decimals and measures. These are worth more marks than some of the more straightforward, one-step problems.

Mixed operation question 1

At the cake sale, Sam buys 6 cookies and a cupcake . He pays £2.85 altogether. Naya buys 2 cookies and pays 90p altogether.

How much does the cupcake cost?

Answer (2 marks): 60p for one cupcake

Mixed operation question 2

Large biscuit tin – 48 biscuits (picture of boxes here) Small biscuit tin – 30 biscuits Ben bought 2 large tins of biscuits and 3 small tins.

How many biscuits did he buy altogether?

Answer (2 marks): 186 biscuits

2 x 48 = 96

3 x 30 = 90

96 + 90 = 186 biscuits

Mixed operation question 3

The owner of a bookshop bought a box of 15 books for £150.

He sold the books individually for £12 each. 

How much profit did he make?

Answer (2 marks)

Third Space Learning offers a wide array of maths and word problems resources for other year groups such as word problems for year 6 , word problems for year 3 and word problems for year 4 . Our word problem collection covers all four operations and other specific maths topics such as ratio word problems and percentage word problems .

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn how tutors develop pupils’ maths fluency or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils

What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

FREE Guide to Maths Mastery

All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.

Ideal for running staff meetings on mastery or sense checking your own approach to mastery.

Privacy Overview

Probability

How likely something is to happen.

Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability.

Tossing a Coin

When a coin is tossed, there are two possible outcomes:

Heads (H) or Tails (T)

• the probability of the coin landing H is ½
• the probability of the coin landing T is ½

Throwing Dice

When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6 .

The probability of any one of them is 1 6

In general:

Probability of an event happening = Number of ways it can happen Total number of outcomes

Example: the chances of rolling a "4" with a die

Number of ways it can happen: 1 (there is only 1 face with a "4" on it)

Total number of outcomes: 6 (there are 6 faces altogether)

So the probability = 1 6

Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked?

Number of ways it can happen: 4 (there are 4 blues)

Total number of outcomes: 5 (there are 5 marbles in total)

So the probability = 4 5 = 0.8

Probability Line

We can show probability on a Probability Line :

Probability is always between 0 and 1

Probability is Just a Guide

Probability does not tell us exactly what will happen, it is just a guide

Example: toss a coin 100 times, how many Heads will come up?

Probability says that heads have a ½ chance, so we can expect 50 Heads .

But when we actually try it we might get 48 heads, or 55 heads ... or anything really, but in most cases it will be a number near 50.

Learn more at Probability Index .

Some words have special meaning in Probability:

Experiment : a repeatable procedure with a set of possible results.

Example: Throwing dice

We can throw the dice again and again, so it is repeatable.

The set of possible results from any single throw is {1, 2, 3, 4, 5, 6}

Outcome: A possible result.

Example: "6" is one of the outcomes of a throw of a die.

Trial: A single performance of an experiment.

Example: I conducted a coin toss experiment. After 4 trials I got these results:

Three trials had the outcome "Head", and one trial had the outcome "Tail"

Sample Space: all the possible outcomes of an experiment.

Example: choosing a card from a deck

There are 52 cards in a deck (not including Jokers)

So the Sample Space is all 52 possible cards : {Ace of Hearts, 2 of Hearts, etc... }

The Sample Space is made up of Sample Points:

Sample Point: just one of the possible outcomes

Example: Deck of Cards

• the 5 of Clubs is a sample point
• the King of Hearts is a sample point

"King" is not a sample point. There are 4 Kings, so that is 4 different sample points.

There are 6 different sample points in that sample space.

Event: one or more outcomes of an experiment

Example Events:

An event can be just one outcome:

• Getting a Tail when tossing a coin
• Rolling a "5"

An event can include more than one outcome:

• Choosing a "King" from a deck of cards (any of the 4 Kings)
• Rolling an "even number" (2, 4 or 6)

Hey, let's use those words, so you get used to them:

Example: Alex wants to see how many times a "double" comes up when throwing 2 dice.

The Sample Space is all possible Outcomes (36 Sample Points):

{1,1} {1,2} {1,3} {1,4} ... ... ... {6,3} {6,4} {6,5} {6,6}

The Event Alex is looking for is a "double", where both dice have the same number. It is made up of these 6 Sample Points :

{1,1} {2,2} {3,3} {4,4} {5,5} and {6,6}

These are Alex's Results:

 After 100 Trials , Alex has 19 "double" Events ... is that close to what you would expect?