what is quantum hypothesis

• Structure of Atom
• Planks Quantum Theory

Planck's Quantum Theory - Quantization Of Energy

Introduction.

Before learning about Planck’s quantum theory, we need to know a few things.

As progress in the science field was happening, Maxwell’s suggestion about the wave nature of electromagnetic radiation was helpful in explaining phenomena such as interference, diffraction, etc. However, he failed to explain various other observations such as the nature of emission of radiation from hot bodies, photoelectric effect, i.e. ejection of electrons from a metal compound when electromagnetic radiation strikes it, the dependence of heat capacity of solids upon temperature, line spectra of atoms (especially hydrogen).

Table of Contents

Black body radiation, recommended videos.

• Planck’s quantum theory
• Frequently Asked Questions – FAQs

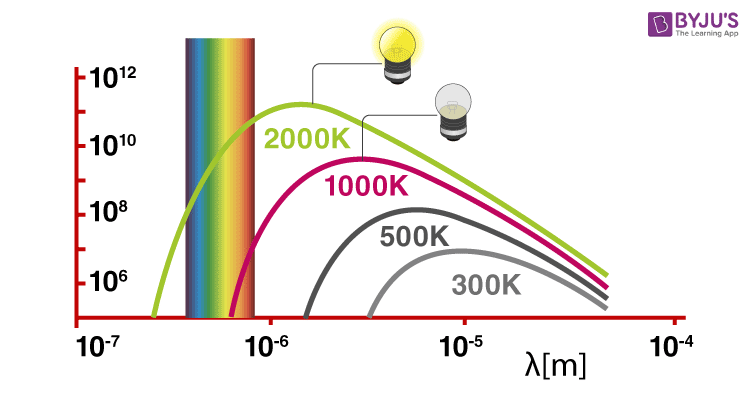
Solids, when heated, emit radiation varying over a wide range of wavelengths. For example: when we heat solid colour, changes continue with a further increase in temperature. This change in colour happens from a lower frequency region to a higher frequency region as the temperature increases. For example, in many cases, it changes from red to blue. An ideal body which can emit and absorb radiation of all frequencies is called a black body. The radiation emitted by such bodies is called black body radiation.

Thus, we can say that variation of frequency for black body radiation depends on the temperature. At a given temperature, the intensity of radiation is found to increase with an increase in the wavelength of radiation which increases to a maximum value and then decreases with an increase in the wavelength. This phenomenon couldn’t be explained with the help of Maxwell’s suggestions. Hence, Planck proposed Planck’s quantum theory to explain this phenomenon.

Black body Radiation

Planck’s Quantum Theory

According to Planck’s quantum theory,

• Different atoms and molecules can emit or absorb energy in discrete quantities only. The smallest amount of energy that can be emitted or absorbed in the form of electromagnetic radiation is known as quantum.
• The energy of the radiation absorbed or emitted is directly proportional to the frequency of the radiation.

Meanwhile, the energy of radiation is expressed in terms of frequency as,

E = Energy of the radiation

h = Planck’s constant (6.626×10 –34  J.s)

ν = Frequency of radiation

Interestingly, Planck has also concluded that these were only an aspect of the processes of absorption and emission of radiation. They had nothing to do with the physical reality of the radiation itself. Later in the year 1905, famous German physicist, Albert Einstein also reinterpreted Planck’s theory to further explain the photoelectric effect. He was of the opinion that if some source of light was focused on certain materials, they can eject electrons from the material. Basically, Planck’s work led Einstein in determining that light exists in discrete quanta of energy, or photons.

Related Videos

Electromagnetic radiations & planck’s quantum theory.

Frequently Asked Questions on Black Body Radiation

What is a planck curve.

A black body’s energy density between λ and λ + dλ is the energy of a mode E = hc / λ times the density of photon states, times the probability that the mode is filled. This is the famous formula from Planck for a black body’s energy density.

What is Stefan’s law of radiation?

The law of Stefan-Boltzmann states that the overall radiant heat power released from a surface is proportional to its fourth absolute temperature power. The rule only refers to black bodies, imaginary surfaces that collect heat radiation from all events.

How is blackbody radiation produced?

Electromagnetic radiation is produced from all objects according to their temperature. An idealised object that consumes the electromagnetic energy that it comes into contact with is a black body. In a continuous continuum, which then emits thermal radiation according to its temperature.

What is Planck’s constant in simple terms?

The Planck constant compares the sum of energy a photon bears with its electromagnetic wave frequency. It is named after Max Planck, the physicist. In quantum mechanics, it is an essential quantity.

What is Planck’s number?

Planck’s constant is currently calculated by scientists to be 6.62607015 x 10 -34 joule-seconds. In 1900, Planck identified his game-changing constant by describing how the smallest bits of matter release energy in discrete bundles called quanta, essentially placing the “quanta” in quantum mechanics.

To learn more about the  quantum theory of light and other topics you can register with BYJU’S or download BYJU’s – The Learning App.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Chemistry related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

i liked your material you have given

Thank you so much.

I like it. It helps with my chemistry homework.

Good job keep it.

It’s good

softly captured, keep it up

thnx a lott

love you BYJU’S FOREVER

thank you so much, helped with my essay on Max Planck

Thank you byjus awesome it helped me a lot in my project

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

21.1 Planck and Quantum Nature of Light

Section learning objectives.

By the end of this section, you will be able to do the following:

• Describe blackbody radiation
• Define quantum states and their relationship to modern physics
• Calculate the quantum energy of lights
• Explain how photon energies vary across divisions of the electromagnetic spectrum

Teacher Support

The learning objectives in this section will help your students master the following standards:

• (D) : explain the impacts of the scientific contributions of a variety of historical and contemporary scientists on scientific thought and society.
• (B) : compare and explain the emission spectra produced by various atoms; and
• (D) : give examples of applications of atomic and nuclear phenomena such as radiation therapy, diagnostic imaging, and nuclear power, and examples of quantum phenomena such as digital cameras.

Section Key Terms

Blackbodies.

• Prior to beginning this section, it would be a good idea to review wave concepts including frequency, wavelength, and amplitude. Have students write down a list of equations or statements that relate to the three concepts.
• [BL] [OL] Discuss what could be meant by the term blackbody . Why do some objects appear black? Furthermore, why do we see objects that are red as red? It is said that black is the absence of color , but what does that mean in terms of the light reflected into our eyes?
• [AL] Discuss what can happen to energy when it strikes a surface. Discuss how it can be reflected or transmitted. If a blackbody is perfectly black, what must be happening to all of the energy incident upon it?
• [EL]Reinforce that the term blackbody is nothing more than its name suggests—that is, a body that is perfectly black. Discuss what perfectly black means. Is a black piece of paper perfectly black ?

Our first story of curious significance begins with a T-shirt. You are likely aware that wearing a tight black T-shirt outside on a hot day provides a significantly less comfortable experience than wearing a white shirt. Black shirts, as well as all other black objects, will absorb and re-emit a significantly greater amount of radiation from the sun. This shirt is a good approximation of what is called a blackbody .

Occasionally, texts refer to blackbody and perfect blackbody as two different concepts. It is likely best to refer to anything that is not a perfect blackbody as an approximation of a blackbody in order to avoid confusion.

A perfect blackbody is one that absorbs and re-emits all radiated energy that is incident upon it. Imagine wearing a tight shirt that did this! This phenomenon is often modeled with quite a different scenario. Imagine carving a small hole in an oven that can be heated to very high temperatures. As the temperature of this container gets hotter and hotter, the radiation out of this dark hole would increase as well, re-emitting all energy provided it by the increased temperature. The hole may even begin to glow in different colors as the temperature is increased. Like a burner on your stove, the hole would glow red, then orange, then blue, as the temperature is increased. In time, the hole would continue to glow but the light would be invisible to our eyes. This container is a good model of a perfect blackbody.

It is the analysis of blackbodies that led to one of the most consequential discoveries of the twentieth century. Take a moment to carefully examine Figure 21.2 . What relationships exist? What trends can you see? The more time you spend interpreting this figure, the closer you will be to understanding quantum physics!

It is important for students to make sense of Figure 21.2 before progressing further. Have students independently create a list of observations from the graph. When presenting their observations, press the students on the specifics of their observations.

[BL] Discuss what variables are being graphed. Have them complete the statement: ________ is dependent upon ________. Discuss what is meant by intensity. What is the difference between being mad and intensely mad ?

[OL] Discuss what the peak of each graph refers to. Ask if the radiation intensity depends upon the wavelength of the radiation. How do they know this? What do the peaks on each graph mean?

[AL] Discuss why there are three lines on the graph. Does it make sense that an increase in temperature would cause the line of the graph to be raised? Why does this make sense? A good challenging exercise would be to have the students re-graph the information in order to represent EM radiation intensity against frequency.

Tips For Success

When encountering a new graph, it is best to try to interpret the graph before you read about it. Doing this will make the following text more meaningful and will help to remind yourself of some of the key concepts within the section.

Understanding Blackbody Graphs

Figure 21.2 is a plot of radiation intensity against radiated wavelength. In other words, it shows how the intensity of radiated light changes when a blackbody is heated to a particular temperature.

It may help to just follow the bottom-most red line labeled 3,000 K, red hot. The graph shows that when a blackbody acquires a temperature of 3,000 K, it radiates energy across the electromagnetic spectrum. However, the energy is most intensely emitted at a wavelength of approximately 1000 nm. This is in the infrared portion of the electromagnetic spectrum. While a body at this temperature would appear red-hot to our eyes, it would truly appear ‘infrared-hot’ if we were able to see the entire spectrum.

A few other important notes regarding Figure 21.2 :

• As temperature increases, the total amount of energy radiated increases. This is shown by examining the area underneath each line.
• Regardless of temperature, all red lines on the graph undergo a consistent pattern. While electromagnetic radiation is emitted throughout the spectrum, the intensity of this radiation peaks at one particular wavelength.
• As the temperature changes, the wavelength of greatest radiation intensity changes. At 4,000 K, the radiation is most intense in the yellow-green portion of the spectrum. At 6,000 K, the blackbody would radiate white hot, due to intense radiation throughout the visible portion of the electromagnetic spectrum. Remember that white light is the emission of all visible colors simultaneously.
• As the temperature increases, the frequency of light providing the greatest intensity increases as well. Recall the equation v = f λ . v = f λ . Because the speed of light is constant, frequency and wavelength are inversely related. This is verified by the leftward movement of the three red lines as temperature is increased.

Discuss the bullet points above. Why does an increase in temperature result in an increase in the total amount of energy radiated? Do you have personal experience with the relationship described in bullet point #3? Students may not have answers as to the causal factors for some of the observations in the above bullet points. Remind them that this is okay as these why questions were the big questions being asked by physicists at the turn of the twentieth century!

[BL] [OL] Do you have personal evidence to show that as temperature increases the energy radiated increases as well?

[AL] Remind students that temperature is just a measure of the average kinetic energy of particles in a gas. Does this definition support bullet point #1?

While in science it is important to categorize observations, theorizing as to why the observations exist is crucial to scientific advancement. Why doesn’t a blackbody emit radiation evenly across all wavelengths? Why does the temperature of the body change the peak wavelength that is radiated? Why does an increase in temperature cause the peak wavelength emitted to decrease? It is questions like these that drove significant research at the turn of the twentieth century. And within the context of these questions, Max Planck discovered something of tremendous importance.

Planck’s Revolution

Planck’s revolution is very much the story of the scientific method—reconciling disconnects between theory and experimental results. Encourage the students to think of other events—either historical or within their own lives—in which a predominant theory was shown to be incorrect when confronted with overwhelming evidence to the contrary. Possible examples include the geocentric model, the ether, or the four elements.

The prevailing theory at the time of Max Planck’s discovery was that intensity and frequency were related by the equation I = 2 k T λ 2 . I = 2 k T λ 2 . This equation, derived from classical physics and using wave phenomena, infers that as wavelength increases, the intensity of energy provided will decrease with an inverse-squared relationship. This relationship is graphed in Figure 21.3 and shows a troubling trend. For starters, it should be apparent that the graph from this equation does not match the blackbody graphs found experimentally. Additionally, it shows that for an object of any temperature, there should be an infinite amount of energy quickly emitted in the shortest wavelengths. When theory and experimental results clash, it is important to re-evaluate both models. The disconnect between theory and reality was termed the ultraviolet catastrophe .

Due to concerns over the ultraviolet catastrophe, Max Planck began to question whether another factor impacted the relationship between intensity and wavelength. This factor, he posited, should affect the probability that short wavelength light would be emitted. Should this factor reduce the probability of short wavelength light, it would cause the radiance curve to not progress infinitely as in the classical theory, but would instead cause the curve to precipitate back downward as is shown in the 5,000 K, 4,000 K, and 3,000 K temperature lines of the graph in Figure 21.3 . Planck noted that this factor, whatever it may be, must also be dependent on temperature, as the intensity decreases at lower and lower wavelengths as the temperature increases.

The determination of this probability factor was a groundbreaking discovery in physics, yielding insight not just into light but also into energy and matter itself. It would be the basis for Planck’s 1918 Nobel Prize in Physics and would result in the transition of physics from classical to modern understanding. In an attempt to determine the cause of the probability factor, Max Planck constructed a new theory. This theory, which created the branch of physics called quantum mechanics , speculated that the energy radiated by the blackbody could exist only in specific numerical, or quantum , states. This theory is described by the equation E = n h f , E = n h f , where n is any nonnegative integer (0, 1, 2, 3, …) and h is Planck’s constant , given by h = 6.626 × 10 −34 J ⋅ s , h = 6.626 × 10 −34 J ⋅ s , and f is frequency.

Through this equation, Planck’s probability factor can be more clearly understood. Each frequency of light provides a specific quantized amount of energy. Low frequency light, associated with longer wavelengths would provide a smaller amount of energy, while high frequency light, associated with shorter wavelengths, would provide a larger amount of energy. For specified temperatures with specific total energies, it makes sense that more low frequency light would be radiated than high frequency light. To a degree, the relationship is like pouring coins through a funnel. More of the smaller pennies would be able to pass through the funnel than the larger quarters. In other words, because the value of the coin is somewhat related to the size of the coin, the probability of a quarter passing through the funnel is reduced!

Furthermore, an increase in temperature would signify the presence of higher energy. As a result, the greater amount of total blackbody energy would allow for more of the high frequency, short wavelength, energies to be radiated. This permits the peak of the blackbody curve to drift leftward as the temperature increases, as it does from the 3,000 K to 4,000 K to 5,000 K values. Furthering our coin analogy, consider a wider funnel. This funnel would permit more quarters to pass through and allow for a reduction in concern about the probability factor .

In summary, it is the interplay between the predicted classical model and the quantum probability that creates the curve depicted in Figure 21.3 . Just as quarters have a higher currency denomination than pennies, higher frequencies come with larger amounts of energy. However, just as the probability of a quarter passing through a fixed diameter funnel is reduced, so is the probability of a high frequency light existing in a fixed temperature object. As is often the case in physics, it is the balancing of multiple incredible ideas that finally allows for better understanding.

Quantization

[EL]Quantum is related to the word quantity, a measure of the amount of something. Discuss why the term quantum would be useful in this context.

[ BL , OL , AL ]Quantum vs. continuous states is well described when considering clocks. A digital clock represents quantum states—it reads 11:14 a.m., then 11:15 a.m. An analog clock with a continually gliding second hand is a good representation of continuous states—it does not appear to pause at any one instant. What would you consider an analog clock that ticks each second? What would you consider a grandfather clock?

It may be helpful at this point to further consider the idea of quantum states. Atoms, molecules, and fundamental electron and proton charges are all examples of physical entities that are quantized —that is, they appear only in certain discrete values and do not have every conceivable value. On the macroscopic scale, this is not a revolutionary concept. A standing wave on a string allows only particular harmonics described by integers. Going up and down a hill using discrete stair steps causes your potential energy to take on discrete values as you move from step to step. Furthermore, we cannot have a fraction of an atom, or part of an electron’s charge, or 14.33 cents. Rather, everything is built of integral multiples of these substructures.

That said, to discover quantum states within a phenomenon that science had always considered continuous would certainly be surprising. When Max Planck was able to use quantization to correctly describe the experimentally known shape of the blackbody spectrum, it was the first indication that energy was quantized on a small scale as well. This discovery earned Planck the Nobel Prize in Physics in 1918 and was such a revolutionary departure from classical physics that Planck himself was reluctant to accept his own idea. The general acceptance of Planck’s energy quantization was greatly enhanced by Einstein’s explanation of the photoelectric effect (discussed in the next section), which took energy quantization a step further.

Worked Example

How many photons per second does a typical light bulb produce.

Assuming that 10 percent of a 100-W light bulb’s energy output is in the visible range (typical for incandescent bulbs) with an average wavelength of 580 nm, calculate the number of visible photons emitted per second.

The number of visible photons per second is directly related to the amount of energy emitted each second, also known as the bulb’s power. By determining the bulb’s power, the energy emitted each second can be found. Since the power is given in watts, which is joules per second, the energy will be in joules. By comparing this to the amount of energy associated with each photon, the number of photons emitted each second can be determined.

The power in visible light production is 10.0 percent of 100 W, or 10.0 J/s. The energy of the average visible photon is found by substituting the given average wavelength into the formula

E = n h f = n h c λ . E = n h f = n h c λ .

By rearranging the above formula to determine energy per photon, this produces

The number of visible photons per second is thus

p h o t o n s sec = 10.0 J / s 3.43 × 10 − 19 J / p h o t o n = 2.92 × 10 19 p h o t o n s / s. p h o t o n s sec = 10.0 J / s 3.43 × 10 − 19 J / p h o t o n = 2.92 × 10 19 p h o t o n s / s.

This incredible number of photons per second is verification that individual photons are insignificant in ordinary human experience. However, it is also a verification of our everyday experience—on the macroscopic scale, photons are so small that quantization becomes essentially continuous.

How does Photon Energy Change with Various Portions of the EM Spectrum?

Refer to the Graphs of Blackbody Radiation shown in the first figure in this section. Compare the energy necessary to radiate one photon of infrared light and one photon of visible light.

To determine the energy radiated, it is necessary to use the equation E = n h f . E = n h f . It is also necessary to find a representative frequency for infrared light and visible light.

According to the first figure in this section, one representative wavelength for infrared light is 2000 nm (2.000 × 10 -6 m). The associated frequency of an infrared light is

Using the equation E = n h f E = n h f , the energy associated with one photon of representative infrared light is

The same process above can be used to determine the energy associated with one photon of representative visible light. According to the first figure in this section, one representative wavelength for visible light is 500 nm.

This example verifies that as the wavelength of light decreases, the quantum energy increases. This explains why a fire burning with a blue flame is considered more dangerous than a fire with a red flame. Each photon of short-wavelength blue light emitted carries a greater amount of energy than a long-wavelength red light. This example also helps explain the differences in the 3,000 K, 4,000 K, and 6,000 K lines shown in the first figure in this section. As the temperature is increased, more energy is available for a greater number of short-wavelength photons to be emitted.

Practice Problems

An AM radio station broadcasts at a frequency of 1,530 kHz . What is the energy in Joules of a photon emitted from this station?

• 10.1 × 10 -26 J
• 1.01 × 10 -28 J
• 1.01 × 10 -29 J
• 1.01 × 10 -27 J

A photon travels with energy of 1.0 eV. What type of EM radiation is this photon?

• visible radiation
• microwave radiation
• infrared radiation
• ultraviolet radiation

Check Your Understanding

Do reflective or absorptive surfaces more closely model a perfect blackbody?

• reflective surfaces
• absorptive surfaces
• The T-shirt reflects some light.
• The T-shirt absorbs all incident light.
• The T-shirt re-emits all the incident light.
• The T-shirt does not reflect light.

Why do we not notice quantization of photons in everyday experience?

• because the size of each photon is very large
• because the mass of each photon is so small
• because the energy provided by photons is very large
• because the energy provided by photons is very small
• The red flame is hotter because red light has lower frequency.
• The red flame is hotter because red light has higher frequency.
• The blue flame is hotter because blue light has lower frequency.
• The blue flame is hotter because blue light has higher frequency.
• Increase, because more high-energy UV photons can enter the eye.
• Increase, because less high-energy UV photons can enter the eye.
• Decrease, because more high-energy UV photons can enter the eye.
• Decrease, because less high-energy UV photons can enter the eye.
• The wavelength of the most intense radiation will vary randomly.
• The wavelength of the most intense radiation will increase.
• The wavelength of the most intense radiation will remain unchanged.
• The wavelength of the most intense radiation will decrease.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-physics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/physics/pages/1-introduction

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: Physics
• Publication date: Mar 26, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/physics/pages/1-introduction
• Section URL: https://openstax.org/books/physics/pages/21-1-planck-and-quantum-nature-of-light

© Jun 7, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

The Many-Worlds Theory, Explained

Quantum physics is strange. At least, it is strange to us, because the rules of the quantum world, which govern the way the world works at the level of atoms and subatomic particles (the behavior of light and matter, as the renowned physicist Richard Feynman put it), are not the rules that we are familiar with — the rules of what we call “common sense.”

The quantum rules, which were mostly established by the end of the 1920s, seem to be telling us that a cat can be both alive and dead at the same time, while a particle can be in two places at once. But to the great distress of many physicists, let alone ordinary mortals, nobody (then or since) has been able to come up with a common-sense explanation of what is going on. More thoughtful physicists have sought solace in other ways, to be sure, namely coming up with a variety of more or less desperate remedies to “explain” what is going on in the quantum world.

These remedies, the quanta of solace, are called “interpretations.” At the level of the equations, none of these interpretations is better than any other, although the interpreters and their followers will each tell you that their own favored interpretation is the one true faith, and all those who follow other faiths are heretics. On the other hand, none of the interpretations is worse than any of the others, mathematically speaking. Most probably, this means that we are missing something. One day, a glorious new description of the world may be discovered that makes all the same predictions as present-day quantum theory, but also makes sense. Well, at least we can hope.

Meanwhile, I thought I might provide an agnostic overview of one of the more colorful of the hypotheses, the many-worlds, or multiple universes, theory. For overviews of the other five leading interpretations, I point you to my book, “ Six Impossible Things .” I think you’ll find that all of them are crazy, compared with common sense, and some are more crazy than others. But in this world, crazy does not necessarily mean wrong, and being more crazy does not necessarily mean more wrong.

If you have heard of the Many Worlds Interpretation (MWI), the chances are you think that it was invented by the American Hugh Everett in the mid-1950s. In a way that’s true. He did come up with the idea all by himself. But he was unaware that essentially the same idea had occurred to Erwin Schrödinger half a decade earlier. Everett’s version is more mathematical, Schrödinger’s more philosophical, but the essential point is that both of them were motivated by a wish to get rid of the idea of the “collapse of the wave function,” and both of them succeeded.

As Schrödinger used to point out to anyone who would listen, there is nothing in the equations (including his famous wave equation) about collapse. That was something that Bohr bolted on to the theory to “explain” why we only see one outcome of an experiment — a dead cat or a live cat — not a mixture, a superposition of states. But because we only detect one outcome — one solution to the wave function — that need not mean that the alternative solutions do not exist. In a paper he published in 1952, Schrödinger pointed out the ridiculousness of expecting a quantum superposition to collapse just because we look at it. It was, he wrote, “patently absurd” that the wave function should “be controlled in two entirely different ways, at times by the wave equation, but occasionally by direct interference of the observer, not controlled by the wave equation.”

Although Schrödinger himself did not apply his idea to the famous cat, it neatly resolves that puzzle. Updating his terminology, there are two parallel universes, or worlds, in one of which the cat lives, and in one of which it dies. When the box is opened in one universe, a dead cat is revealed. In the other universe, there is a live cat. But there always were two worlds that had been identical to one another until the moment when the diabolical device determined the fate of the cat(s). There is no collapse of the wave function. Schrödinger anticipated the reaction of his colleagues in a talk he gave in Dublin, where he was then based, in 1952. After stressing that when his eponymous equation seems to describe different possibilities (they are “not alternatives but all really happen simultaneously”), he said:

Nearly every result [the quantum theorist] pronounces is about the probability of this or that or that … happening — with usually a great many alternatives. The idea that they may not be alternatives but all really happen simultaneously seems lunatic to him, just impossible. He thinks that if the laws of nature took this form for, let me say, a quarter of an hour, we should find our surroundings rapidly turning into a quagmire, or sort of a featureless jelly or plasma, all contours becoming blurred, we ourselves probably becoming jelly fish. It is strange that he should believe this. For I understand he grants that unobserved nature does behave this way—namely according to the wave equation. The aforesaid alternatives come into play only when we make an observation — which need, of course, not be a scientific observation. Still it would seem that, according to the quantum theorist, nature is prevented from rapid jellification only by our perceiving or observing it … it is a strange decision.

In fact, nobody responded to Schrödinger’s idea. It was ignored and forgotten, regarded as impossible. So Everett developed his own version of the MWI entirely independently, only for it to be almost as completely ignored. But it was Everett who introduced the idea of the Universe “splitting” into different versions of itself when faced with quantum choices, muddying the waters for decades.

It was Hugh Everett who introduced the idea of the Universe “splitting” into different versions of itself when faced with quantum choices, muddying the waters for decades.

Everett came up with the idea in 1955, when he was a PhD student at Princeton. In the original version of his idea, developed in a draft of his thesis, which was not published at the time, he compared the situation with an amoeba that splits into two daughter cells. If amoebas had brains, each daughter would remember an identical history up until the point of splitting, then have its own personal memories. In the familiar cat analogy, we have one universe, and one cat, before the diabolical device is triggered, then two universes, each with its own cat, and so on. Everett’s PhD supervisor, John Wheeler, encouraged him to develop a mathematical description of his idea for his thesis, and for a paper published in the Reviews of Modern Physics in 1957, but along the way, the amoeba analogy was dropped and did not appear in print until later. But Everett did point out that since no observer would ever be aware of the existence of the other worlds, to claim that they cannot be there because we cannot see them is no more valid than claiming that the Earth cannot be orbiting around the Sun because we cannot feel the movement.

Everett himself never promoted the idea of the MWI. Even before he completed his PhD, he had accepted the offer of a job at the Pentagon working in the Weapons Systems Evaluation Group on the application of mathematical techniques (the innocently titled game theory) to secret Cold War problems (some of his work was so secret that it is still classified) and essentially disappeared from the academic radar. It wasn’t until the late 1960s that the idea gained some momentum when it was taken up and enthusiastically promoted by Bryce DeWitt, of the University of North Carolina, who wrote: “every quantum transition taking place in every star, in every galaxy, in every remote corner of the universe is splitting our local world on Earth into myriad copies of itself.” This became too much for Wheeler, who backtracked from his original endorsement of the MWI, and in the 1970s, said: “I have reluctantly had to give up my support of that point of view in the end — because I am afraid it carries too great a load of metaphysical baggage.” Ironically, just at that moment, the idea was being revived and transformed through applications in cosmology and quantum computing.

“Every quantum transition taking place in every star, in every galaxy, in every remote corner of the universe is splitting our local world on Earth into myriad copies of itself.”

The power of the interpretation began to be appreciated even by people reluctant to endorse it fully. John Bell noted that “persons of course multiply with the world, and those in any particular branch would experience only what happens in that branch,” and grudgingly admitted that there might be something in it:

The “many worlds interpretation” seems to me an extravagant, and above all an extravagantly vague, hypothesis. I could almost dismiss it as silly. And yet … It may have something distinctive to say in connection with the “Einstein Podolsky Rosen puzzle,” and it would be worthwhile, I think, to formulate some precise version of it to see if this is really so. And the existence of all possible worlds may make us more comfortable about the existence of our own world … which seems to be in some ways a highly improbable one.

The precise version of the MWI came from David Deutsch, in Oxford, and in effect put Schrödinger’s version of the idea on a secure footing, although when he formulated his interpretation, Deutsch was unaware of Schrödinger’s version. Deutsch worked with DeWitt in the 1970s, and in 1977, he met Everett at a conference organized by DeWitt — the only time Everett ever presented his ideas to a large audience. Convinced that the MWI was the right way to understand the quantum world, Deutsch became a pioneer in the field of quantum computing, not through any interest in computers as such, but because of his belief that the existence of a working quantum computer would prove the reality of the MWI.

This is where we get back to a version of Schrödinger’s idea. In the Everett version of the cat puzzle, there is a single cat up to the point where the device is triggered. Then the entire Universe splits in two. Similarly, as DeWitt pointed out, an electron in a distant galaxy confronted with a choice of two (or more) quantum paths causes the entire Universe, including ourselves, to split. In the Deutsch–Schrödinger version, there is an infinite variety of universes (a Multiverse) corresponding to all possible solutions to the quantum wave function. As far as the cat experiment is concerned, there are many identical universes in which identical experimenters construct identical diabolical devices. These universes are identical up to the point where the device is triggered. Then, in some universes the cat dies, in some it lives, and the subsequent histories are correspondingly different. But the parallel worlds can never communicate with one another. Or can they?

Deutsch argues that when two or more previously identical universes are forced by quantum processes to become distinct, as in the experiment with two holes, there is a temporary interference between the universes, which becomes suppressed as they evolve. It is this interaction that causes the observed results of those experiments. His dream is to see the construction of an intelligent quantum machine — a computer — that would monitor some quantum phenomenon involving interference going on within its “brain.” Using a rather subtle argument, Deutsch claims that an intelligent quantum computer would be able to remember the experience of temporarily existing in parallel realities. This is far from being a practical experiment. But Deutsch also has a much simpler “proof” of the existence of the Multiverse.

What makes a quantum computer qualitatively different from a conventional computer is that the “switches” inside it exist in a superposition of states. A conventional computer is built up from a collection of switches (units in electrical circuits) that can be either on or off, corresponding to the digits 1 or 0. This makes it possible to carry out calculations by manipulating strings of numbers in binary code. Each switch is known as a bit, and the more bits there are, the more powerful the computer is. Eight bits make a byte, and computer memory today is measured in terms of billions of bytes — gigabytes, or Gb. Strictly speaking, since we are dealing in binary, a gigabyte is 2 30 bytes, but that is usually taken as read. Each switch in a quantum computer, however, is an entity that can be in a superposition of states. These are usually atoms, but you can think of them as being electrons that are either spin up or spin down. The difference is that in the superposition, they are both spin up and spin down at the same time — 0 and 1. Each switch is called a qbit, pronounced “cubit.”

Using a rather subtle argument, Deutsch claims that an intelligent quantum computer would be able to remember the experience of temporarily existing in parallel realities.

Because of this quantum property, each qbit is equivalent to two bits. This doesn’t look impressive at first sight, but it is. If you have three qbits, for example, they can be arranged in eight ways: 000, 001, 010, 011, 100, 101, 110, 111. The superposition embraces all these possibilities. So three qbits are not equivalent to six bits (2 x 3), but to eight bits (2 raised to the power of 3). The equivalent number of bits is always 2 raised to the power of the number of qbits. Just 10 qbits would be equivalent to 2 10 bits, actually 1,024, but usually referred to as a kilobit. Exponentials like this rapidly run away with themselves. A computer with just 300 qbits would be equivalent to a conventional computer with more bits than there are atoms in the observable Universe. How could such a computer carry out calculations? The question is more pressing since simple quantum computers, incorporating a few qbits, have already been constructed and shown to work as expected. They really are more powerful than conventional computers with the same number of bits.

Deutsch’s answer is that the calculation is carried out simultaneously on identical computers in each of the parallel universes corresponding to the superpositions. For a three-qbit computer, that means eight superpositions of computer scientists working on the same problem using identical computers to get an answer. It is no surprise that they should “collaborate” in this way, since the experimenters are identical, with identical reasons for tackling the same problem. That isn’t too difficult to visualize. But when we build a 300-qbit machine—which will surely happen—we will, if Deutsch is right, be involving a “collaboration” between more universes than there are atoms in our visible Universe. It is a matter of choice whether you think that is too great a load of metaphysical baggage. But if you do, you will need some other way to explain why quantum computers work.

Most quantum computer scientists prefer not to think about these implications. But there is one group of scientists who are used to thinking of even more than six impossible things before breakfast — the cosmologists. Some of them have espoused the Many Worlds Interpretation as the best way to explain the existence of the Universe itself.

Their jumping-off point is the fact, noted by Schrödinger, that there is nothing in the equations referring to a collapse of the wave function. And they do mean the wave function; just one, which describes the entire world as a superposition of states — a Multiverse made up of a superposition of universes.

Some cosmologists have espoused the Many Worlds Interpretation as the best way to explain the existence of the Universe itself.

The first version of Everett’s PhD thesis (later modified and shortened on the advice of Wheeler) was actually titled “The Theory of the Universal Wave Function.” And by “universal” he meant literally that, saying:

Since the universal validity of the state function description is asserted, one can regard the state functions themselves as the fundamental entities, and one can even consider the state function of the whole universe. In this sense this theory can be called the theory of the “universal wave function,” since all of physics is presumed to follow from this function alone.

… where for the present purpose “state function” is another name for “wave function.” “All of physics” means everything, including us — the “observers” in physics jargon. Cosmologists are excited by this, not because they are included in the wave function, but because this idea of a single, uncollapsed wave function is the only way in which the entire Universe can be described in quantum mechanical terms while still being compatible with the general theory of relativity. In the short version of his thesis published in 1957, Everett concluded that his formulation of quantum mechanics “may therefore prove a fruitful framework for the quantization of general relativity.” Although that dream has not yet been fulfilled, it has encouraged a great deal of work by cosmologists since the mid-1980s, when they latched on to the idea. But it does bring with it a lot of baggage.

The universal wave function describes the position of every particle in the Universe at a particular moment in time. But it also describes every possible location of those particles at that instant. And it also describes every possible location of every particle at any other instant of time, although the number of possibilities is restricted by the quantum graininess of space and time. Out of this myriad of possible universes, there will be many versions in which stable stars and planets, and people to live on those planets, cannot exist. But there will be at least some universes resembling our own, more or less accurately, in the way often portrayed in science fiction stories. Or, indeed, in other fiction. Deutsch has pointed out that according to the MWI, any world described in a work of fiction, provided it obeys the laws of physics, really does exist somewhere in the Multiverse. There really is, for example, a “Wuthering Heights” world (but not a “Harry Potter” world).

That isn’t the end of it. The single wave function describes all possible universes at all possible times. But it doesn’t say anything about changing from one state to another. Time does not flow. Sticking close to home, Everett’s parameter, called a state vector, includes a description of a world in which we exist, and all the records of that world’s history, from our memories, to fossils, to light reaching us from distant galaxies, exist. There will also be another universe exactly the same except that the “time step” has been advanced by, say, one second (or one hour, or one year). But there is no suggestion that any universe moves along from one time step to another. There will be a “me” in this second universe, described by the universal wave function, who has all the memories I have at the first instant, plus those corresponding to a further second (or hour, or year, or whatever). But it is impossible to say that these versions of “me” are the same person. Different time states can be ordered in terms of the events they describe, defining the difference between past and future, but they do not change from one state to another. All the states just exist. Time, in the way we are used to thinking of it, does not “flow” in Everett’s MWI.

John Gribbin, described by the Spectator as “one of the finest and most prolific writers of popular science around,” is the author of, among other books, “ In Search of Schrödinger’s Cat ,” “ The Universe: A Biography ,” and “ Six Impossible Things ,” from which this article is excerpted. He is a Visiting Fellow in Astronomy at the University of Sussex, UK.

• Humanities ›
• History & Culture ›
• The 20th Century ›
• People & Events ›

Max Planck Formulates Quantum Theory

Bettmann / Getty Images

• People & Events
• Fads & Fashions
• Early 20th Century
• American History
• African American History
• African History
• Ancient History and Culture
• Asian History
• European History
• Latin American History
• Medieval & Renaissance History
• Military History
• Women's History
• B.A., History, University of California at Davis

In 1900, German theoretical physicist Max Planck revolutionized the field of physics by discovering that energy does not flow evenly but is instead released in discrete packets. Planck created an equation to predict this phenomenon, and his discovery ended the primacy of what many people now call "classical physics" in favor of the study of quantum physics .

The Problem

Despite feeling that all was already known in the field of physics, there was still one problem that had plagued physicists for decades: They could not understand the surprising results they continued to get from heating surfaces that absorb all frequencies of light that hit them, otherwise known as black bodies .

Try as they might, scientists could not explain the results using classical physics.

The Solution

Max Planck was born in Kiel, Germany, on April 23, 1858, and was considering becoming a professional pianist before a teacher turned his attention to science. Planck went on to receive degrees from the University of Berlin and the University of Munich.

After spending four years as an associate professor of theoretical physics at Kiel University, Planck moved to the University of Berlin, where he became a full professor in 1892.

Planck's passion was thermodynamics. While researching black-body radiation, he too kept running into the same problem as other scientists. Classical physics could not explain the results he was finding.

In 1900, 42-year-old Planck discovered an equation that explained the results of these tests: E=Nhf, with E=energy, N=integer, h=constant, f=frequency. In determining this equation, Planck came up with the constant (h), which is now known as " Planck's constant ."

The amazing part of Planck's discovery was that energy, which appears to be emitted in wavelengths, is actually discharged in small packets he called "quanta".

This new theory of energy revolutionized physics and opened the way for Albert Einstein's theory of relativity .

Life After Discovery

At first, the magnitude of Planck's discovery was not fully understood. It wasn't until Einstein and others used quantum theory for even further advancements in physics that the revolutionary nature of his discovery was realized.

By 1918, the scientific community was well aware of the importance of Planck's work and awarded him the Nobel Prize in Physics.

He continued to conduct research and contribute further to the advancement of physics, but nothing compared to his 1900 findings.

Tragedy in His Personal Life

While he achieved much in his professional life, Planck's personal life was marked by tragedy. His first wife died in 1909, his oldest son, Karl, during  World War I . Twin girls, Margarete and Emma, both later died in childbirth. And his youngest son, Erwin, was implicated in the failed  July Plot to kill Hitler and was hanged.

In 1911, Planck did remarry and had one son, Hermann.

Planck decided to remain in Germany during World War II . Using his clout, the physicist tried to stand up for Jewish scientists, but with little success. In protest, Planck resigned as president of the Kaiser Wilhelm Institute in 1937.

In 1944, a bomb dropped during an Allied air raid hit his house, destroying many of his possessions, including all his scientific notebooks. 

Max Planck died on October 4, 1947, at the age of 89.

• Most Influential Scientists of the 20th Century
• 10 Things You Don't Know About Albert Einstein
• Biography of Albert Einstein, Theoretical Physicist
• Biography of Enrico Fermi
• Cold War Glossary
• Sigmund Freud
• Clarence Darrow, Famous Defense Attorney and Crusader for Justice
• Sinking of the Lusitania
• What Is Communism? Definition and Examples
• A Timeline of the Genocide in Rwanda
• 100 Famous Women of the 20th Century
• Life and Work of H.L. Mencken: Writer, Editor, and Critic
• History of the Sacco and Vanzetti Case
• A Short Guide to the Vietnam War
• The Day the Mona Lisa Was Stolen
• Biography of Helen Keller, Deaf and Blind Spokesperson and Activist