
- Google OR-Tools
- Español – América Latina
- Português – Brasil
- Tiếng Việt

Solving an Assignment Problem
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.
In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .
The costs of assigning workers to tasks are shown in the following table.
| Worker | Task 0 | Task 1 | Task 2 | Task 3 |
|---|---|---|---|---|
| 90 | 80 | 75 | 70 | |
| 35 | 85 | 55 | 65 | |
| 125 | 95 | 90 | 95 | |
| 45 | 110 | 95 | 115 | |
| 50 | 100 | 90 | 100 |
The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.
MIP solution
The following sections describe how to solve the problem using the MPSolver wrapper .
Import the libraries
The following code imports the required libraries.
Create the data
The following code creates the data for the problem.
The costs array corresponds to the table of costs for assigning workers to tasks, shown above.
Declare the MIP solver
The following code declares the MIP solver.
Create the variables
The following code creates binary integer variables for the problem.
Create the constraints
Create the objective function.
The following code creates the objective function for the problem.
The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.
Invoke the solver
The following code invokes the solver.
Print the solution
The following code prints the solution to the problem.
Here is the output of the program.
Complete programs
Here are the complete programs for the MIP solution.
CP SAT solution
The following sections describe how to solve the problem using the CP-SAT solver.
Declare the model
The following code declares the CP-SAT model.
The following code sets up the data for the problem.
The following code creates the constraints for the problem.
Here are the complete programs for the CP-SAT solution.
Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.
Last updated 2024-08-28 UTC.
- DSA Tutorial
- Data Structures
- Linked List
- Dynamic Programming
- Binary Tree
- Binary Search Tree
- Divide & Conquer
- Mathematical
- Backtracking
- Branch and Bound
- Pattern Searching
Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Do the same (as step 1) for all columns.
- Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
- Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Try it before moving to see the solution
Explanation for above simple example:
An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).
Space complexity : O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.
In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY
Please Login to comment...
Similar reads.
- How to Get a Free SSL Certificate
- Best SSL Certificates Provider in India
- Elon Musk's xAI releases Grok-2 AI assistant
- What is OpenAI SearchGPT? How it works and How to Get it?
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
- WolframAlpha.com
- WolframCloud.com
- All Sites & Public Resources...
- Wolfram|One
- Mathematica
- Wolfram|Alpha Notebook Edition
- Finance Platform
- System Modeler
- Wolfram Player
- Wolfram Engine
- WolframScript
- Enterprise Private Cloud
- Application Server
- Enterprise Mathematica
- Wolfram|Alpha Appliance
- Corporate Consulting
- Technical Consulting
- Wolfram|Alpha Business Solutions
- Data Repository
- Neural Net Repository
- Function Repository
- Wolfram|Alpha Pro
- Problem Generator
- Products for Education
- Wolfram Cloud App
- Wolfram|Alpha for Mobile
- Wolfram|Alpha-Powered Apps
- Paid Project Support
- Summer Programs
- All Products & Services »
- Wolfram Language Revolutionary knowledge-based programming language. Wolfram Cloud Central infrastructure for Wolfram's cloud products & services. Wolfram Science Technology-enabling science of the computational universe. Wolfram Notebooks The preeminent environment for any technical workflows. Wolfram Engine Software engine implementing the Wolfram Language. Wolfram Natural Language Understanding System Knowledge-based broadly deployed natural language. Wolfram Data Framework Semantic framework for real-world data. Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more. Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha.
- All Technologies »
- Aerospace & Defense
- Chemical Engineering
- Control Systems
- Electrical Engineering
- Image Processing
- Industrial Engineering
- Mechanical Engineering
- Operations Research
- Actuarial Sciences
- Bioinformatics
- Data Science
- Econometrics
- Financial Risk Management
- All Solutions for Education
- Machine Learning
- Multiparadigm Data Science
- High-Performance Computing
- Quantum Computation Framework
- Software Development
- Authoring & Publishing
- Interface Development
- Web Development
- All Solutions »
- Wolfram Language Documentation
- Fast Introduction for Programmers
- Videos & Screencasts
- Wolfram Language Introductory Book
- Webinars & Training
- Support FAQ
- Wolfram Community
- Contact Support
- All Learning & Support »
- Company Background
- Wolfram Blog
- Careers at Wolfram
- Internships
- Other Wolfram Language Jobs
- Wolfram Foundation
- Computer-Based Math
- A New Kind of Science
- Wolfram Technology for Hackathons
- Student Ambassador Program
- Wolfram for Startups
- Demonstrations Project
- Wolfram Innovator Awards
- Wolfram + Raspberry Pi
- All Company »
Wolfram Language ™
Optimal assignment problem.
Find the amount of electricity a company must send from its four power plants to five cities so as to maximize profit and minimize cost while meeting the cities' peak demands.
This example demonstrates how LinearFractionalOptimization may be used to minimize the ratio of cost to profit within given constraints. Use of a matrix-valued variable makes the modeling relatively simple.
As an example, here is the cost of transporting one million kilowatt hours (kWh) of electricity from four plants to five cities.
The profit that each power plant generates by selling 1 million kWh to each city is shown here.
The cities have a peak demand of 45, 20, 30, 30 and 40 million kWh, respectively, and a minimum demand of 5 million kWh.
The power plants can supply a minimum of 35, 50, 40 and 40 million kWh of electricity, respectively.
The optimal amount of electricity to send each city by each plant can be found by minimizing the ratio of cost to profit.
The breakdown of electricity supplied is shown.
Related Examples

- Wolfram|Alpha Notebook Edition
- Mobile Apps
- Wolfram Workbench
- Volume & Site Licensing
- View all...
- For Customers
- Online Store
- Product Registration
- Product Downloads
- Service Plans Benefits
- User Portal
- Your Account
- Customer Service
- Get Started with Wolfram
- Fast Introduction for Math Students
- Public Resources
- Wolfram|Alpha
- Resource System
- Connected Devices Project
- Wolfram Data Drop
- Wolfram Science
- Computational Thinking
- About Wolfram
- Legal & Privacy Policy

Index Assignment problem Hungarian algorithm Solve online
Solve an assignment problem online
Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given.
Fill in the cost matrix ( random cost matrix ):
Don't show the steps of the Hungarian algorithm Maximize the total cost
HungarianAlgorithm.com © 2013-2024
Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.
Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
|
|
|---|
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
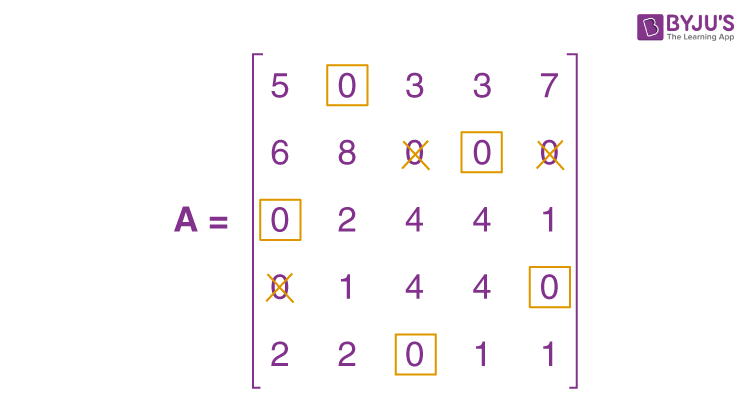
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
The Quadratic Assignment Problem
- First Online: 01 January 2015
Cite this chapter

- Zvi Drezner 4
4712 Accesses
9 Citations
The quadratic assignment problem is reviewed in this chapter. Weights between pairs of facilities and distances between the same number of locations are given. The problem is to find the assignment of facilities to locations that minimizes the weighted sum of distances. This problem is considered to be one of the most difficult combinatorial optimization problems. The construction of efficient solution algorithms (exact or heuristic) is challenging and has been extensively investigated by the communities working in Operations Research/Management Science, Industrial Engineering, or Computer Science. Examples of applications are given, the related layout problem is briefly described, exact and heuristic solution algorithms are reviewed, and a list of test problem instances and results are reported.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Similar content being viewed by others

Extensions and Related Problems
A linear formulation with \(o(n^2)\) variables for quadratic assignment problems with manhattan distance matrices.

Quadratic Assignment Problems
Adams W, Guignard M, Hahn P, Hightower W (2007) A level-2 reformulation-linearization technique bound for the quadratic assignment problem. Eur J Oper Res 180:983–996
Google Scholar
Ahuja R, Orlin J, Tiwari A (2000) A descent genetic algorithm for the quadratic assignment problem. Comput Oper Res 27:917–934
Amin S (1999) Simulated jumping. Ann Oper Res 84:23–38
Anstreicher K, Brixius N, Gaux JP, Linderoth J (2002) Solving large quadratic assignment problems on computational grids. Math Program 91:563–588
Anstreicher KM, Brixius NW (2001) A new bound for the quadratic assignment problem based on convex quadratic programming. Math Program 89:341–357
Armour GC, Buffa ES (1963) A heuristic algorithm and simulation approach to relative location of facilities. Manag Sci 9:294–309
Battiti R, Tecchiolli G (1994) The reactive tabu search. ORSA J Comput 6:126–140
Bos J (1993) Zoning in forest management: a quadratic assignment problem solved by simulated annealing. J Environ Manag 37:127–145
Buffa ES, Armour GC, Vollmann TE (1962) Allocating facilities with CRAFT. Harv Bus Rev 42:136–158
Burer S, Vandenbussche D (2006) Solving lift-and-project relaxations of binary integer programs. SIAM J Optimiz 16:726–750
Burkard R, Rendl F (1984) A thermodynamically motivated simulation procedure for combinatorial optimization problems. Eur J Oper Res 17:169–174
Burkard RE (1990) Locations with spatial interactions: the quadratic assignment problem. In: Mirchandani PB, Francis RL (eds) Discrete location theory. Wiley, New York, pp 387–437
Burkard RE, Cela E (1999) Linear assignment problems and extensions. In: Pardalos P, Du D-Z (eds) Handbook of combinatorial optimization. Springer, Dordrecht, pp 75–149
Burkard RE (2013) Quadratic assignment problems. In: Pardalos P, Du D-Z (eds) Handbook of combinatorial optimization, 2nd edn. Springer, New York, pp 2741–2814
Burkard RE, Offermann J (1977) Entwurf von schreibmaschinentastaturen mittels quadratischer zuordnungsprobleme. Math Method Oper Res 21:121–132
Cantú-Paz E (2001) Migration policies, selection pressure, and parallel evolutionary algorithms. J Heuristics 7:311–334
de Carvalho Jr SA, Rahmann S (2006) Microarray layout as a quadratic assignment problem. In: Huson D, Kohlbacher O, Lupas A, Nieselt K, Zell A (eds) Proceedings of the German conference on bioinformatics, vol 83. Gesellschaft für Informatik, Bonn, pp 11–20
Cela E (1998) The quadratic assignment problem: theory and algorithms. Kluwer Academic Publishers, Dordrecht
Connoly D (1990) An improved annealing scheme for the QAP. Eur J Oper Res 46:93–100
Cordeau JF, Gaudioso M, Laporte G, Moccia L (2006) A memetic heuristic for the generalized quadratic assignment problem. INFORMS J Comput 18:433–443
Coxeter HSM (1973) Regular polytopes. Dover Publications, New York
Cung VD, Mautor T, Michelon P, Tavares AI (1997) A scatter search based approach for the quadratic assignment problem. In: Proceedings of the IEEE international conference on evolutionary computation and evolutionary programming (ICEC’97), Indianapolis, pp 165–170
Dickey JW, Hopkins JW (1972) Campus building arrangement using topaz. Transp Res 6:59–68
Drezner T, Drezner Z (2005) Genetic algorithms: mimicking evolution and natural selection in optimization models. In: Bar-Cohen Y (ed) Biomimetics—biologically inspired technologies. CRC Press, Boca Raton, pp 157–175
Drezner T, Drezner Z (2006) Gender specific genetic algorithms. INFOR Inform Syst Oper Res 44:117–127
Drezner Z (1975) Problems in non-linear programming (the allocation problem). Ph.D. thesis, The Technion, Haifa
Drezner Z (1980) DISCON—a new method for the layout problem. Oper Res 28:1375–1384
Drezner Z (1987) A heuristic procedure for the layout of a large number of facilities. Manag Sci 33:907–915
Drezner Z (2002) A new heuristic for the quadratic assignment problem. J Appl Math Decis Sci 6:163–173
Drezner Z (2003) A new genetic algorithm for the quadratic assignment problem. INFORMS J Comput 15:320–330
Drezner Z (2005a) A distance based rule for removing population members in genetic algorithms. 4OR-Q J Oper Res 3:109–116
Drezner Z (2005b) The extended concentric tabu for the quadratic assignment problem. Eur J Oper Res 160:416–422
Drezner Z (2006) Finding a cluster of points and the grey pattern quadratic assignment problem. OR Spectr 28:417–436
Drezner Z (2008a) Extensive experiments with hybrid genetic algorithms for the solution of the quadratic assignment problem. Comput Oper Res 35:717–736
Drezner Z (2008b) Tabu search and hybrid genetic algorithms for quadratic assignment problems. In: Jaziri W (ed) Tabu search, in-tech, pp 89–108. Available free on: http://books.i-techonline.com
Drezner Z (2010) On the unboundedness of facility layout problems. Math Method Oper Res 72:205–216
Drezner Z, Marcoulides GA (2003) A distance-based selection of parents in genetic algorithms. In: Resende MGC, de Sousa JP (eds) Metaheuristics: computer decision-making. Kluwer Academic Publishers, Boston, pp 257–278
Drezner Z, Misevičius A (2013) Enhancing the performance of hybrid genetic algorithms by differential improvement. Comput Oper Res 40:1038–1046
Drezner Z, Suzuki A (2010) Covering continuous demand in the plane. J Oper Res Soc 61:878–881
Drezner Z, Zemel E (1992) Competitive location in the plane. Ann Oper Res 40:173–193
Drezner Z, Hahn PM, Taillard ÉD (2005) Recent advances for the quadratic assignment problem with special emphasis on instances that are difficult for meta-heuristic methods. Ann Oper Res 139:65–94
Drezner Z, Misevičius A, Palubeckis G (2014) Exact algorithms for the solution of the grey pattern quadratic assignment problem. In review
Duman E, Uysal M, Alkaya AF (2012) Migrating birds optimization: a new metaheuristic approach and its performance on quadratic assignment problem. Inform Sci 217:65–77
Elshafei AN (1977) Hospital layout as a quadratic assignment problem. Oper Res Q 28:167–179
Fischetti M, Monaci M, Salvagnin D (2012) Three ideas for the quadratic assignment problem. Oper Res 60:954–964
Fleurent C, Ferland J (1994) Genetic hybrids for the quadratic assignment problem. In: Pardalos P, Wolkowicz H (eds) Quadratic assignment and related problems, DIMACS series in discrete mathematics and theoretical computer science, vol 16. American Methematical Society, Providence, pp 173–187
Fox BR, McMahon MB (1991) Genetic operators for sequencing problems. In: Rawlins G (ed) Foundations of genetic algorithms. Morgan-Kaufmann, San Mateo, pp 284–300
Francis RL, McGinnis LF Jr, White JA (1992) Facility layout and location: an analytical approach, 2nd edn. Prentice Hall, Englewood Cliffs
Gambardella L, Taillard ÉD, Dorigo M (1999) Ant colonies for the quadratic assignment problem. J Oper Res Soc 50:167–176
Geoffrion AM, Graves GW (1976) Scheduling parallel production lines with changeover costs: practical application of a quadratic assignment/lp approa ch. Oper Res 24:595–610
Gilmore P (1962) Optimal and suboptimal algorithms for the quadratic assignment problem. J SIAM 10:305–313
Glover F (1977) Heuristics for integer programming using surrogate constraints. Decis Sci 8:156–166
Glover F (1986) Future paths for integer programming and links to artificial intelligence. Comput Oper Res 13:533–549
Glover F, Laguna M (1997) Tabu search. Kluwer Academic Publishers, Boston
Hahn P, Grant T (1998) Lower bounds for the quadratic assignment problem based upon a dual formulation. Oper Res 46:912–922
Hahn P, Krarup J (2001) A hospital facility problem finally solved. J Intell Manuf 12:487–496
Hahn PM, Kim BJ, Guignard M, Smith JM, Zhu YR (2008) An algorithm for the generalized quadratic assignment problem. Comput Optim Appl 40:351–372
Hahn PM, Zhu YR, Guignard M, Hightower WL, Saltzman MJ (2012) A level-3 reformulation-linearization technique-based bound for the quadratic assignment problem. INFORMS J Comput 24:202–209
Heffley DR (1977) Assigning runners to a relay team. In: Ladany SP, Machol RE (eds) Optimal strategies in sports. North-Holland, Amsterdam, pp 169–171
Hilbert D, Cohn-Vossen S (1956) Geometry and the imagination (english translation of Anschauliche Geometrie, 1932). Chelsea Publishing Company, New York
Hillier FS, Connors MM (1966) Quadratic assignment problem algorithms and the location of indivisible facilities. Manag Sci 13:42–57
Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor
Koopmans TC, Beckmann MJ (1957) Assignment problems and the location of economic activities. Econometrica 25:53–76
Laporte G, Mercure H (1988) Balancing hydraulic turbine runners: a quadratic assignment problem. Eur J Oper Res 35:378–381
Lawler EL (1973) Optimal sequencing of a single machine subject to precedence constraints. Manag Sci 19:544–546
Lee CG, Ma Z (2005) The generalized quadratic assignment problem. Department of Mechanical and Industrial Engineering, University of Toronto, MIE OR Technical Reports (TR2005-01)
Li Y, Pardalos PM (1992) Generating quadratic assignment test problems with known optimal permutations. Comput Optim Appl 1:163–184
Li Y, Pardalos PM, Resende MGC (1994) A greedy randomized adaptive search procedure for the quadratic assignment problem. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems, DIMACS series in discrete mathematics and theoretical computer science, vol 16, American Mathematical Society, Providence, pp 237–261
Loiola EM, de Abreu NMM, Boaventura-Netto PO, Hahn P, Querido T (2007) A survey for the quadratic assignment problem. Eur J Oper Res 176:657–690
Love RF, Wong JY (1976) Solving quadratic assignment problems with rectangular distances and integer programming. Nav Res Logist Q 23:623–627
Misevičius A (2003) A modified simulated annealing algorithm for the quadratic assignment problem. Informatica 14:497–514
Misevičius A (2011) Generation of grey patterns using an improved genetic-evolutionary algorithm: some new results. Inf Technol Control 40:330–343
Misevičius A (2012) An implementation of the iterated tabu search algorithm for the quadratic assignment problem. OR Spectr 34:665–690
Misevičius A, Blonskis J (2005) Experiments with tabu search for random quadratic assignment problems. Inf Technol Control 34:237–244
Misevičius A, Guogis E (2012) Computational study of four genetic algorithm variants for solving the quadratic assignment problem. In: Skersys T, Butkienè R, Butleris R (eds) Communications in computer and information science (CCIS). Proceedings of 18th international conference on information and software technologies ICIST 2012, vol 319. Springer, Berlin, pp 24–37
Misevičius A, Tomkevičius A, Karbauskas J (2006) Stagnation-protected tabu search variants for unstructured quadratic assignment problems. Inf Technol Control 35:363–370
Misevičius A, Guogis E, Stanevičienè E (2013) Computational algorithmic generation of high-quality colour patterns. In: Skersys T, Butkienè R, Butleris R (eds) Communications in computer and information science (CCIS). Proceedings of 19th international conference in information and software technologies ICIST 2013. Springer, Berlin, pp 285–296
Misevičius A (2004) An improved hybrid genetic algorithm: new results for the quadratic assignment problem. Knowl-Based Syst 17:65–73
Misevičius A (2005) A tabu search algorithm for the quadratic assignment problem. Comput Optim Appl 30:95–111
Misevičius A (2008) Restart-based genetic algorithm for the quadratic assignment problem. In: Bramer M, Coenen F, Petridis M (eds) Research and development in intelligent systems. Proceedings of AI-2008, the 28th SGAI international conference on innovative techniques and applications of artificial intelligence. Springer, London, pp 91–104
Misevičius A, Rubliauskas D (2009) Testing of hybrid genetic algorithms for structured quadratic assignment problems. Informatica 20:255–272
Misevičius A, Rubliauskas D, Barkauskas V (2009) Some further experiments with the genetic algorithm for the quadratic assignment problem. Inf Technol Control 38:325–332
Nugent C, Vollman T, Ruml T (1968) An experimental comparison of techniques for the assignment of facilities to locations. Oper Res 16:150–173
Nyberg A, Westerlund T (2012) A new exact discrete linear reformulation of the quadratic assignment problem. Eur J Oper Res 220:314–319
Nyström M (1999) Solving certain large instances of the quadratic assignment problem: Steinberg’s examples. Technical report, California Institute of Technology. http://resolver.caltech.edu/CaltechCSTR:2001.010
Okabe A, Suzuki A (1987) Stability of spatial competition for a large number of firms on a bounded two-dimensional space. Environ Plann A 16:107–114
Oliveira CAS, Pardalos PM, Resende MGC (2004) GRASP with path-relinking for the quadratic assignment problem. In: Ribeiro CC, Martins SL (eds) Efficient and experimental algorithms. Springer, Berlin/Heidelberg, pp 237–261
Pierce JF, Crowston WB (1971) Tree-search algorithms for quadratic assignment problems. Nav Res Logist Q 18:1–36
Pierskalla WP (1967) The tri-substitution method for the three-dimensional assignment problem. CORS J 5:71–81
Pierskalla WP (1968) The multidimensional assignment problem. Oper Res 16:422–431
Ramakrishnan KG, Resende M, Ramachandran B, Pekny J (2002) Tight QAP bounds via linear programming. In: Pardalos PM, Migdalas A, Burkard R (eds) Combinatorial and global optimization. World Scientific Publishing, Singapore, pp 297–303
Rendl F (2002) The quadratic assignment problem. In: Drezner Z, Hamacher H (eds) Facility location: applications and theory. Springer, Berlin
Rendl F, Sotirov R (2007) Bounds for the quadratic assignment problem using the bundle method. Math Program 109:505–524
Resende M, Ramakrishnan K, Drezner Z (1995) Computational experiments with the lower bound for the quadratic assignment problem based on linear programming. Oper Res 43:781–791
Roupin F (2004) From linear to semidefinite programming: an algorithm to obtain semidefinite relaxations for bivalent quadratic problems. J Comb Optim 8:469–493
Sahni S, Gonzalez T (1976) P-complete approximation problems. J ACM 23:555–565
Schaffer JD, Caruana RA, Eshelman LJ (1989) A study of control parameters affecting online performance of genetic algorithms. In: Schaffer JD (ed) Proceedings of the 3rd international conference on genetic algorithms. Morgan Kaufmann, San Mateo, pp 51–60
Sherali HD, Adams WP (1990) A hierarchy of relaxations between the continuous and convex hull representations for zero-one programming problems. SIAM J Discret Math 3:411–430
Sherali HD, Adams WP (1998) A reformulation-linearization technique for solving discrete and continuous nonconvex problems. Springer, Berlin
Skorin-Kapov J (1990) Tabu search applied to the quadratic assignment problem. ORSA J Comput 2:33–45
Steinberg L (1961) The backboard wiring problem: a placement algorithm. SIAM Rev 3:37–50
Suzuki A, Drezner Z (1996) The p-center location problem in an area. Locat Sci 4:69–82
Suzuki A, Okabe A (1995) Using Voronoi diagrams. In: Drezner Z (ed) Facility location: a survey of applications and methods. Springer, New York, pp 103–118
Szabo PG, Markot M, Csendes T, Specht E (2007) New approaches to circle packing in a square: with program codes. Springer, New York
Taillard ÉD (1991) Robust tabu search for the quadratic assignment problem. Parallel Comput 17:443–455
Taillard ÉD (1995) Comparison of iterative searches for the quadratic assignment problem. Locat Sci 3:87–105
Taillard ÉD (1998) Fant: fast ant system. Technical report, Istituto Dalle Molle Di Studi Sull Intelligenza Artificiale, iDSIA Technical Report IDSIA-46-98
Taillard ÉD (2000) An introduction to ant systems. In: Laguna M, González-Velarde J (eds) Computing tools for modeling, optimization and simulation. Wiley, New York, pp 131–144
Talbi EG, Roux O, Fonlupt C, Robillard D (2001) Parallel ant colonies for the quadratic assignment problem. Futur Gener Comput Syst 17:441–449
Tate D, Smith A (1995) A genetic approach to the quadratic assignment problem. Comput Oper Res 22:73–83
Thonemann U, Bölte A (1994) An improved simulated annealing algorithm for the quadratic assignment problem. Technical report, working paper, School of Business, Department of Production and Operations Research, University of Paderborn, Germany
Wilhelm M, Ward T (1987) Solving quadratic assignment problems by simulated annealing. IIE Trans 19:107–119
Wu Y, Ji P (2008) Solving the quadratic assignment problems by a genetic algorithm with a new replacement strategy. Int J Comput Intell 4:225–229
Download references
Author information
Authors and affiliations.
California State University, Fullerton, CA, 92834, USA
Zvi Drezner
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Zvi Drezner .
Editor information
Editors and affiliations.
HEC Montréal, Montréal, Canada
Gilbert Laporte
Institute of Operations Research (IOR), Karlsruhe Institute of Technology, Karlsruhe, Germany
Stefan Nickel
DEIO-FCUL, University of Lisbon, Lisbon, Portugal
Francisco Saldanha da Gama
Rights and permissions
Reprints and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Drezner, Z. (2015). The Quadratic Assignment Problem. In: Laporte, G., Nickel, S., Saldanha da Gama, F. (eds) Location Science. Springer, Cham. https://doi.org/10.1007/978-3-319-13111-5_13
Download citation
DOI : https://doi.org/10.1007/978-3-319-13111-5_13
Published : 21 January 2015
Publisher Name : Springer, Cham
Print ISBN : 978-3-319-13110-8
Online ISBN : 978-3-319-13111-5
eBook Packages : Business and Economics Business and Management (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research
Chapter: 12th business maths and statistics : chapter 10 : operations research.
Solution of assignment problems (Hungarian Method)
First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.
Step :1 Choose the least element in each row and subtract it from all the elements of that row.
Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.
Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.
Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.
Example 10.7
Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.
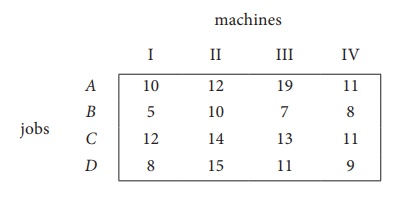
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced. Now let us find the solution.
Step 1: Select a smallest element in each row and subtract this from all the elements in its row.
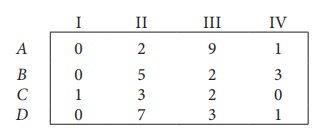
Look for atleast one zero in each row and each column.Otherwise go to step 2.
Step 2: Select the smallest element in each column and subtract this from all the elements in its column.
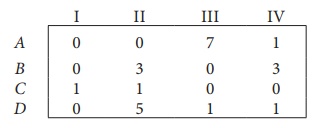
Since each row and column contains atleast one zero, assignments can be made.
Step 3 (Assignment):
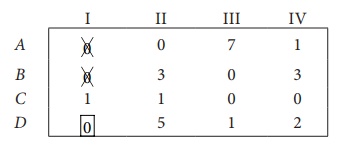
Thus all the four assignments have been made. The optimal assignment schedule and total cost is
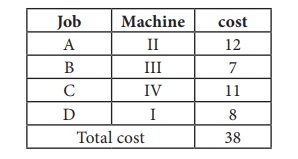
The optimal assignment (minimum) cost
Example 10.8
Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.
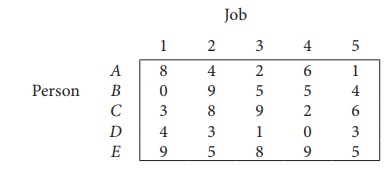
∴ The given assignment problem is balanced.
Now let us find the solution.
The cost matrix of the given assignment problem is
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is
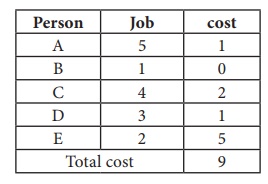
The optimal assignment (minimum) cost = ` 9
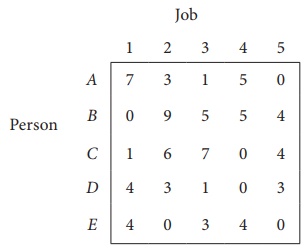
Example 10.9
Solve the following assignment problem.
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is
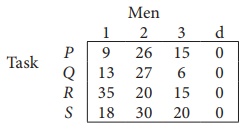
Here only 3 tasks can be assigned to 3 men.
Step 1: is not necessary, since each row contains zero entry. Go to Step 2.
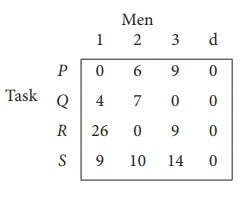
Step 3 (Assignment) :
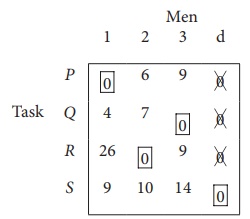
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is
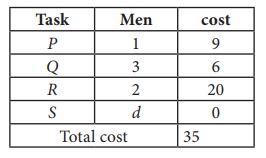
The optimal assignment (minimum) cost = ₹ 35
Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.
You must enable JavaScript in order to use this site.

IMAGES
VIDEO
COMMENTS
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: ... Fortunately, there are many algorithms for finding the optimal assignment in time polynomial in n. The assignment problem is a special case of the transportation problem, ...
The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3). ... The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them. The problem ...
Best known bounds. O(mn1/2) deterministic; O(n 2.376) randomized. Planar weighted bipartite matching. O(n3/2 log5 n). Weighted Bipartite Matching m edges, n nodes A lg or ithmD es nb y v aT dsJ Keier ¥Cp ©205 Wey S ev e Input Queued Switching 19 Input-Queued Switching Input-queued switch.! n inputs and n outputs in an n-by-n crossbar layout.!
6.2 Problem Let N be a networkobtained from Km;m by giving eachedge e an integer weight w(e). Find a perfect matching of maximum weight in N. As in most optimization problems, animportant step in nding an algorithm for solving this problem is to give a criterion for recognising an optimal solution.
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver. Example. In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview.
The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our problem is a special case of binary integer linear programming problem (which is NP-hard). ... Mike Dawes "The Optimal ...
Then X∗ solves the assignment problem specified by C since z(X∗)=0and z(X) ≥ 0 for any other solution X.ByExample5,X∗ is also an optimal solution to the assignment problem specified by C.NotethatX∗ corresponds to the permutation 132. The method used to obtain an optimal solution to the assignment problem specified by C
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for ...
The Assignment Problem: Suppose we have n resources to which we want to assign to n tasks on a one-to-one basis. Suppose also that we know the cost of assigning a given resource to a given task. We wish to find an optimal assignment-one which minimizes total cost. 29
The problem is a special form of the transportation problem and, as such, has an optimal solution in which each variable is either zero or one. The problem can be solved by the simplex method, but special assignment problem algorithms tend to be computationally more efficient. ... Assignment Problem. In: Gass, S.I., Fu, M.C. (eds) Encyclopedia ...
In this lesson we learn what is an assignment problem and how we can solve it using the Hungarian method.
The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
The Hungarian algorithm, aka Munkres assignment algorithm, utilizes the following theorem for polynomial runtime complexity (worst case O(n 3)) and guaranteed optimality: If a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an ...
Hungarian algorithm steps for minimization problem. Step 1: For each row, subtract the minimum number in that row from all numbers in that row. Step 2: For each column, subtract the minimum number in that column from all numbers in that column. Step 3: Draw the minimum number of lines to cover all zeroes.
H. W. KUHN 87 The largest number of jobs that can be assigned to qualified individuals is equal to the smallest total allotment of any adequate budget. Any assignment is optimal if and only if it is complete after every possible transfer. 3. THE GENERAL ASSIGNMENT PROBLEM Suppose n individuals (i = 1, . . ., n) are available for n jobs (I = 1, . . .
Problem 4. Job shop needs to assign 4 jobs to 4 workers. The cost of performing a job is a function of the skills of the workers. Table summarizes the cost of the assignments. Worker1 cannot do job3, and worker 3 cannot do job 4. Determine the optimal assignment using the Hungarian method. Job.
Optimal Assignment Problem. Find the amount of electricity a company must send from its four power plants to five cities so as to maximize profit and minimize cost while meeting the cities' peak demands. This example demonstrates how LinearFractionalOptimization may be used to minimize the ratio of cost to profit within given constraints. Use ...
Thus, worker 1 should perform job 3, worker 2 job 2, worker 3 job 1, and worker 4 should perform job 4. The total cost of this optimal assignment is to 69 + 37 + 11 + 23 = 140. Solve your own problem online
Solve an assignment problem online. Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given. Fill in the cost matrix (random cost matrix):
The problem in this work will consider the case n=k. Mathematically stated the assignment problem is as follows: Let R be an n x n matrix with positive integer entries. The optimal assignment problem consists of choosing n entries, so that no two chosen entries come from the same row or column and such that the sum of the entries is maximized.
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
The quadratic assignment problem (QAP) is considered one of the most difficult optimization problems to solve optimally. The QAP is a combinatorial optimization problem stated for the first time by Koopmans and Beckmann ().Early papers on the subject include Gilmore (), Pierce and Crowston (), Lawler (), and Love and Wong ().The problem is defined as follows.
The optimal assignment (minimum) cost = ` 9. Example 10.9. Solve the following assignment problem. Solution: Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is
OpenStax offers free college textbooks for all types of students, making education accessible & affordable for everyone. Browse our list of available subjects!