Rate Problems
The Unit Conversion Tables should be helpful for this section. (The link will open in a new window, so you can keep this information close by.)
Here are some examples of rates:
$\displaystyle\frac{\$5}{\text{hr}}$, also commonly seen as $\,\$5/\text{hr}\,,$ and read as ‘five dollars per hour’
$\displaystyle\frac{40\text{ miles}}{3\text{ days}}$, read as ‘forty miles per three days’
$\displaystyle\frac{10\text{ kg}}{{\text{ in}}^3}$, read as ‘ten kilograms per cubic inch’
A rate is a mathematical expression, and like all types of mathematical expressions, rates have lots of different names. For example,
Notice that each of these names has a unit of currency (a money unit) in the numerator, and a unit of time in the denominator.
A rate can be renamed to a new desired name, providing the type of units in the numerator and denominator (e.g., length, time, volume, mass/weight) remain the same.
For example, suppose a rate has a unit of length in the numerator, and a unit of volume in the denominator. Then, it can only be renamed to rates that have length in the numerator and volume in the denominator.
Which name should you use? It depends! If you're earning \$5 per hour, and want to know how much you'll earn in $\,30\,$ minutes, then $\displaystyle\,\frac{\$2.50}{30\text{ min}}\,$ is a good name. You can get whatever name you need just by multiplying by one, as you'll see below!
Try not to be intimidated by the ‘fractions within fractions’. If you give this method a chance, you'll be solving an incredible variety of problems quickly and efficiently.
Two versions of the solution are given: a one-sentence solution and a two-sentence solution. Both solutions have the same beginning steps — to make sure you know what you're starting with, and what you want to end up with!

Both Versions of the Solution Start Off the Same Way
- Step 1: Identify the original rate. Answer: $\displaystyle\frac{2\text{ ft}}{1\text{ hr}}$
- Step 2: Identify the name for the rate that you want . Use $\,x\,$ for any number that is unknown. Answer: $\displaystyle\frac{7\text{ in}}{x\text{ min}}$
- Step 3: Check that the original rate and its desired new name are ‘compatible’; i.e., same types of units in both numerator and denominator. Answer: Both rates have units of length upstairs (feet and inches), and units of time downstairs (hours and minutes). They're compatible!
This one-sentence solution is ultra-fast and efficient, once you get used to working with fractions within fractions.
First, you multiply by $\,1\,$ in appropriate forms to get the units you want. Then, you get rid of the numbers you don't want. Then, you introduce the number you do want! All by just multiplying by $\,1\,$!
If you're not seeing what's going on here, there are lots more details in the text (starting on page 172).

Here it is again, in the most compact form. This is the form you'll use when you get really good at this method!
Here's the two-sentence solution. The first sentence renames the rate with the desired units. The second sentence sets up a proportion, which is then solved for the unknown number.
First sentence: Convert the given rate to the desired units. Answer: $$ \begin{align} \cssId{s99}{\frac{2\text{ ft}}{1\text{ hr}}}\ &\cssId{s100}{= \frac{2\text{ ft}}{1\text{ hr}} \cdot \frac{12\text{ in}}{1\text{ ft}} \cdot \frac{1\text{ hr}}{60\text{ min}}}\cr\cr &\cssId{s101}{= \frac{24\text{ in}}{60\text{ min}}} \end{align} $$
Second sentence: Set up a proportion to solve for the unknown number. Answer: $$ \cssId{s105}{\frac{24\text{ in}}{60\text{ min}}} \cssId{s106}{= \frac{7\text{ in}}{x\text{ min}}} $$
Now, solve for $\,x\,.$ Ignore all the units; just work with the numbers.
| $\displaystyle 24x = 420 $ | (cross-multiply) |
| $\displaystyle x = \frac{420}{24} = 17.5 $ | (solve for $\,x\,$) |
Thus, it takes $\,17.5\,$ minutes for the snail to crawl $\,7\,$ inches.
An object travels $\,5\text{ ft}\,$ in $\,8\text{ min}\,.$
Feel free to use scrap paper and a calculator to compute your answers.
In this problem set, you will not type in your answers. You will just compare your answer with the one given here.
Depending on how you do the unit conversion, you may get a slightly different answer than the answer reported here. Do not despair! If your answer is close, then you're fine!
For this exercise, use only the conversion information given in the Unit Conversion Tables to compute your answers.
All answers are either exact, or rounded to six decimal places. It is possible to get $\,0.000000\,$ as an answer.


How To Solve Rate Problems: A Step-By-Step Guide For Math Students
How do you solve a problem involving rates.
To solve a problem involving rates, follow these steps:
1. Identify what you are trying to find: Before you begin solving a problem involving rates, you need to identify what you are trying to find. This will help guide you in setting up the problem.
2. Write down the formula: Once you have identified what you are trying to find, write down the formula for the rate you need to calculate. This formula may be given to you in the problem or you may need to derive it from the information given.
3. Plug in the values: Now that you have the formula, plug in the values given in the problem. Make sure to match units (e.g., time, distance, weight) so that they cancel out appropriately.
4. Solve for the unknown: Once you have plugged in all the values, solve for the unknown variable (the one you’re trying to find).
5. Check your answer: Always double-check your work to ensure that your answer makes sense and is reasonable given the context of the problem.
6. Convert units: Finally, convert your answer to the required units if necessary.
More Answers:
Recent posts, ramses ii a prominent pharaoh and legacy of ancient egypt.
Ramses II (c. 1279–1213 BCE) Ramses II, also known as Ramses the Great, was one of the most prominent and powerful pharaohs of ancient Egypt.
Formula for cyclic adenosine monophosphate & Its Significance
Is the formula of cyclic adenosine monophosphate (cAMP) $ce{C_{10}H_{11}N_{5}O_{6}P}$ or $ce{C_{10}H_{12}N_{5}O_{6}P}$? Does it matter? The correct formula for cyclic adenosine monophosphate (cAMP) is $ce{C_{10}H_{11}N_{5}O_{6}P}$. The
Development of a Turtle Inside its Egg
How does a turtle develop inside its egg? The development of a turtle inside its egg is a fascinating process that involves several stages and
The Essential Molecule in Photosynthesis for Energy and Biomass
Why does photosynthesis specifically produce glucose? Photosynthesis is the biological process by which plants, algae, and some bacteria convert sunlight, carbon dioxide (CO2), and water
How the Human Body Recycles its Energy Currency
Source for “The human body recycles its body weight of ATP each day”? The statement that “the human body recycles its body weight of ATP
Don't Miss Out! Sign Up Now!
Sign up now to get started for free!

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 9: Radicals
9.10 Rate Word Problems: Work and Time
If it takes Felicia 4 hours to paint a room and her daughter Katy 12 hours to paint the same room, then working together, they could paint the room in 3 hours. The equation used to solve problems of this type is one of reciprocals. It is derived as follows:
[latex]\text{rate}\times \text{time}=\text{work done}[/latex]
For this problem:
[latex]\begin{array}{rrrl} \text{Felicia's rate: }&F_{\text{rate}}\times 4 \text{ h}&=&1\text{ room} \\ \\ \text{Katy's rate: }&K_{\text{rate}}\times 12 \text{ h}&=&1\text{ room} \\ \\ \text{Isolating for their rates: }&F&=&\dfrac{1}{4}\text{ h and }K = \dfrac{1}{12}\text{ h} \end{array}[/latex]
To make this into a solvable equation, find the total time [latex](T)[/latex] needed for Felicia and Katy to paint the room. This time is the sum of the rates of Felicia and Katy, or:
[latex]\begin{array}{rcrl} \text{Total time: } &T \left(\dfrac{1}{4}\text{ h}+\dfrac{1}{12}\text{ h}\right)&=&1\text{ room} \\ \\ \text{This can also be written as: }&\dfrac{1}{4}\text{ h}+\dfrac{1}{12}\text{ h}&=&\dfrac{1 \text{ room}}{T} \\ \\ \text{Solving this yields:}&0.25+0.083&=&\dfrac{1 \text{ room}}{T} \\ \\ &0.333&=&\dfrac{1 \text{ room}}{T} \\ \\ &t&=&\dfrac{1}{0.333}\text{ or }\dfrac{3\text{ h}}{\text{room}} \end{array}[/latex]
Example 9.10.1
Karl can clean a room in 3 hours. If his little sister Kyra helps, they can clean it in 2.4 hours. How long would it take Kyra to do the job alone?
The equation to solve is:
[latex]\begin{array}{rrrrl} \dfrac{1}{3}\text{ h}&+&\dfrac{1}{K}&=&\dfrac{1}{2.4}\text{ h} \\ \\ &&\dfrac{1}{K}&=&\dfrac{1}{2.4}\text{ h}-\dfrac{1}{3}\text{ h}\\ \\ &&\dfrac{1}{K}&=&0.0833\text{ or }K=12\text{ h} \end{array}[/latex]
Example 9.10.2
Doug takes twice as long as Becky to complete a project. Together they can complete the project in 10 hours. How long will it take each of them to complete the project alone?
[latex]\begin{array}{rrl} \dfrac{1}{R}+\dfrac{1}{2R}&=&\dfrac{1}{10}\text{ h,} \\ \text{where Doug's rate (} \dfrac{1}{D}\text{)}& =& \dfrac{1}{2}\times \text{ Becky's (}\dfrac{1}{R}\text{) rate.} \\ \\ \text{Sum the rates: }\dfrac{1}{R}+\dfrac{1}{2R}&=&\dfrac{2}{2R} + \dfrac{1}{2R} = \dfrac{3}{2R} \\ \\ \text{Solve for R: }\dfrac{3}{2R}&=&\dfrac{1}{10}\text{ h} \\ \text{which means }\dfrac{1}{R}&=&\dfrac{1}{10}\times\dfrac{2}{3}\text{ h} \\ \text{so }\dfrac{1}{R}& =& \dfrac{2}{30} \\ \text{ or }R &= &\dfrac{30}{2} \end{array}[/latex]
This means that the time it takes Becky to complete the project alone is [latex]15\text{ h}[/latex].
Since it takes Doug twice as long as Becky, the time for Doug is [latex]30\text{ h}[/latex].
Example 9.10.3
Joey can build a large shed in 10 days less than Cosmo can. If they built it together, it would take them 12 days. How long would it take each of them working alone?
[latex]\begin{array}{rl} \text{The equation to solve:}& \dfrac{1}{(C-10)}+\dfrac{1}{C}=\dfrac{1}{12}, \text{ where }J=C-10 \\ \\ \text{Multiply each term by the LCD:}&(C-10)(C)(12) \\ \\ \text{This leaves}&12C+12(C-10)=C(C-10) \\ \\ \text{Multiplying this out:}&12C+12C-120=C^2-10C \\ \\ \text{Which simplifies to}&C^2-34C+120=0 \\ \\ \text{Which will factor to}& (C-30)(C-4) = 0 \end{array}[/latex]
Cosmo can build the large shed in either 30 days or 4 days. Joey, therefore, can build the shed in 20 days or −6 days (rejected).
The solution is Cosmo takes 30 days to build and Joey takes 20 days.
Example 9.10.4
Clark can complete a job in one hour less than his apprentice. Together, they do the job in 1 hour and 12 minutes. How long would it take each of them working alone?
[latex]\begin{array}{rl} \text{Convert everything to hours:} & 1\text{ h }12\text{ min}=\dfrac{72}{60} \text{ h}=\dfrac{6}{5}\text{ h}\\ \\ \text{The equation to solve is} & \dfrac{1}{A}+\dfrac{1}{A-1}=\dfrac{1}{\dfrac{6}{5}}=\dfrac{5}{6}\\ \\ \text{Therefore the equation is} & \dfrac{1}{A}+\dfrac{1}{A-1}=\dfrac{5}{6} \\ \\ \begin{array}{r} \text{To remove the fractions, } \\ \text{multiply each term by the LCD} \end{array} & (A)(A-1)(6)\\ \\ \text{This leaves} & 6(A)+6(A-1)=5(A)(A-1) \\ \\ \text{Multiplying this out gives} & 6A-6+6A=5A^2-5A \\ \\ \text{Which simplifies to} & 5A^2-17A +6=0 \\ \\ \text{This will factor to} & (5A-2)(A-3)=0 \end{array}[/latex]
The apprentice can do the job in either [latex]\dfrac{2}{5}[/latex] h (reject) or 3 h. Clark takes 2 h.
Example 9.10.5
A sink can be filled by a pipe in 5 minutes, but it takes 7 minutes to drain a full sink. If both the pipe and the drain are open, how long will it take to fill the sink?
The 7 minutes to drain will be subtracted.
[latex]\begin{array}{rl} \text{The equation to solve is} & \dfrac{1}{5}-\dfrac{1}{7}=\dfrac{1}{X} \\ \\ \begin{array}{r} \text{To remove the fractions,} \\ \text{multiply each term by the LCD}\end{array} & (5)(7)(X)\\ \\ \text{This leaves } & (7)(X)-(5)(X)=(5)(7)\\ \\ \text{Multiplying this out gives} & 7X-5X=35\\ \\ \text{Which simplifies to} & 2X=35\text{ or }X=\dfrac{35}{2}\text{ or }17.5 \end{array}[/latex]
17.5 min or 17 min 30 sec is the solution
For Questions 1 to 8, write the formula defining the relation. Do Not Solve!!
- Bill’s father can paint a room in 2 hours less than it would take Bill to paint it. Working together, they can complete the job in 2 hours and 24 minutes. How much time would each require working alone?
- Of two inlet pipes, the smaller pipe takes four hours longer than the larger pipe to fill a pool. When both pipes are open, the pool is filled in three hours and forty-five minutes. If only the larger pipe is open, how many hours are required to fill the pool?
- Jack can wash and wax the family car in one hour less than it would take Bob. The two working together can complete the job in 1.2 hours. How much time would each require if they worked alone?
- If Yousef can do a piece of work alone in 6 days, and Bridgit can do it alone in 4 days, how long will it take the two to complete the job working together?
- Working alone, it takes John 8 hours longer than Carlos to do a job. Working together, they can do the job in 3 hours. How long would it take each to do the job working alone?
- Working alone, Maryam can do a piece of work in 3 days that Noor can do in 4 days and Elana can do in 5 days. How long will it take them to do it working together?
- Raj can do a piece of work in 4 days and Rubi can do it in half the time. How long would it take them to do the work together?
- A cistern can be filled by one pipe in 20 minutes and by another in 30 minutes. How long would it take both pipes together to fill the tank?
For Questions 9 to 20, find and solve the equation describing the relationship.
- If an apprentice can do a piece of work in 24 days, and apprentice and instructor together can do it in 6 days, how long would it take the instructor to do the work alone?
- A carpenter and his assistant can do a piece of work in 3.75 days. If the carpenter himself could do the work alone in 5 days, how long would the assistant take to do the work alone?
- If Sam can do a certain job in 3 days, while it would take Fred 6 days to do the same job, how long would it take them, working together, to complete the job?
- Tim can finish a certain job in 10 hours. It takes his wife JoAnn only 8 hours to do the same job. If they work together, how long will it take them to complete the job?
- Two people working together can complete a job in 6 hours. If one of them works twice as fast as the other, how long would it take the slower person, working alone, to do the job?
- If two people working together can do a job in 3 hours, how long would it take the faster person to do the same job if one of them is 3 times as fast as the other?
- A water tank can be filled by an inlet pipe in 8 hours. It takes twice that long for the outlet pipe to empty the tank. How long would it take to fill the tank if both pipes were open?
- A sink can be filled from the faucet in 5 minutes. It takes only 3 minutes to empty the sink when the drain is open. If the sink is full and both the faucet and the drain are open, how long will it take to empty the sink?
- It takes 10 hours to fill a pool with the inlet pipe. It can be emptied in 15 hours with the outlet pipe. If the pool is half full to begin with, how long will it take to fill it from there if both pipes are open?
- A sink is ¼ full when both the faucet and the drain are opened. The faucet alone can fill the sink in 6 minutes, while it takes 8 minutes to empty it with the drain. How long will it take to fill the remaining ¾ of the sink?
- A sink has two faucets: one for hot water and one for cold water. The sink can be filled by a cold-water faucet in 3.5 minutes. If both faucets are open, the sink is filled in 2.1 minutes. How long does it take to fill the sink with just the hot-water faucet open?
- A water tank is being filled by two inlet pipes. Pipe A can fill the tank in 4.5 hours, while both pipes together can fill the tank in 2 hours. How long does it take to fill the tank using only pipe B?
Answer Key 9.10
Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
You are using an outdated browser and it's not supported. Please upgrade your browser to improve your experience.
- LOGIN FOR PROGRAM PARTICIPANTS
- PROGRAM SUPPORT
Problem Solving Using Rates, Unit Rates, and Conversions
Description.
There may be cases when our downloadable resources contain hyperlinks to other websites. These hyperlinks lead to websites published or operated by third parties. UnboundEd and EngageNY are not responsible for the content, availability, or privacy policies of these websites.
- Grade 6 Mathematics Module 1, Topic C, Lesson 23: Student Version
- Grade 6 Mathematics Module 1, Topic C, Lesson 23: Teacher Version
Prerequisites
- CCSS Standard:
- 6.RP.A.3.B ,
Related Guides and Multimedia
Our professional learning resources include teaching guides, videos, and podcasts that build educators' knowledge of content related to the standards and their application in the classroom.
There are no related guides or videos. To see all our guides, please visit the Enhance Instruction section here .
Work Rate Problems with Solutions
A set of problems related to work and rate of work is presented with detailed solutions.
| | It takes 1.5 hours for Tim to mow the lawn. Linda can mow the same lawn in 2 hours. How long will it take John and Linda, work together, to mow the lawn? John: 1 / 1.5 and Linda 1 / 2 R = 1 / 4.8 , rate of pump C. t × (1 / 4.8) = 1 t = 4.8 hours , the time it takes pump C to fill the tank. t = 7 / 3 hours = 2.3 hours = 2 hours 20 minutes. 9 + 2:20 = 11:20 More in this site. |
Please log in to save materials. Log in
- Resource Library
- 6th Grade Mathematics
Education Standards
Wyoming standards for mathematics.
Learning Domain: Ratios and Proportional Relationships
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0, and use rate language in the context of a ratio relationship.
Standard: Use ratio and rate reasoning to solve real-world and mathematical problems.
Standard: Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.
Standard: Solve unit rate problems including those involving unit pricing and constant speed.
Maryland College and Career Ready Math Standards
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ‰äĘ 0 (b not equal to zero), and use rate language in the context of a ratio relationship. For example, "This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar." "We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger." (Expectations for unit rates in this grade are limited to non-complex fractions.)
Standard: Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
Standard: Solve unit rate problems including those involving unit pricing and constant speed. For example, If it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?
Common Core State Standards Math
Cluster: Understand ratio concepts and use ratio reasoning to solve problems
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0 (b not equal to zero), and use rate language in the context of a ratio relationship. For example, "This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar." "We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger." (Expectations for unit rates in this grade are limited to non-complex fractions.)
Distance, Time, and Speed
Dollars and pesos, hours, speed, and miles, prepare a presentation, price per gallon, stack of books, using rates to solve problems.

Students use their knowledge of rates to solve problems.
Key Concepts
Given any two values in a rate situation, you can find the third value.
These three equations are equivalent, and they all describe rate relationships:
y = rx , r = yx , x = yr
At the beginning of this lesson (or for homework), students will revise their work on the pre-assessment Self Check. Their revised work will provide data that you and your students can use to reassess students' understanding of rate. You can use this information to clear up any remaining misconceptions and to help students integrate their learning from the past several days into a deeper and more coherent whole.
The work students do in this lesson and in revising their pre-assessments will help you and your students decide how to help them during the Gallery. In this lesson, students will reveal the depth and clarity of their understanding of rate.
- Students whose understanding of rate is still delicate should get extra help during the Gallery.
- Students who feel that they have a robust understanding of rate may choose from any of the problem-solving or deeper mathematics problems in the Gallery.
Goals and Learning Objectives
- Uncover any partial understandings and misconceptions about rate.
- Develop a more robust understanding of rate.
- Identify which Gallery problems to work on.
Revise and Extend Your Work
Lesson guide.
Have students work in pairs to revise their work from the Self Check. Encourage students to incorporate ideas from their partner in their revisions. Then students will work together on a similar task.
Students have worked with rate in a variety of contexts. At this point, their understanding is still very delicate, containing a mix of good conceptualization, partial conceptions, and some misconceptions.
While students work with their partners, note different approaches to the task:
- How do they organize their work?
- Do they notice if they have chosen a strategy that does not seem to be productive? If so, what do they do?
- He can multiply the rate $3.00 per pound by 5.75 pounds to find the price in dollars.
- She can divide 12 miles by 1.5 hours to find her speed in miles per hour.
- He can divide 325 square feet of wall by 85 square feet per quart to find the number of quarts.
- She can divide 13.1 miles by 2.6 hours to find her speed in miles per hour.
Work with your partner to revise your work on the Self Check.
- Explain what calculation the person can perform to find what he or she wants to know.
- Explain what the unit of the answer is.
- At the store, Jason sees that the price of cherries is $3.00 per pound. What calculation can he perform to find the price of 5.75 pounds of cherries?
- Rosa knows that she can skate to the park in 1.5 hours. The park is 12 miles away. What calculation can she perform to find her speed?
- Denzel knows that 1 quart of paint will cover about 85 square feet of wall. He needs enough paint to cover 325 square feet of wall. What calculation can Denzel perform to find how many quarts of paint he will need?
- Mina ran a half marathon (13.1 miles) this weekend. She completed the run in 2.6 hours. What calculation can Mina perform to find her speed during this run?
Math Mission
Discuss the Math Mission. Students will work through several rate problems using what they have learned about rates.
Use what you know about rates to work through problems.
Pay attention to how students are finding values for their tables. Do they start with the first row? With some other row? How are students navigating between the rows?
The different approaches you notice will allow you to engage students in a rich conversation during Ways of Thinking.
SWD: Consider the prerequisite skills for this Putting it Together lesson. Students with disabilities may need direct instruction and/or guided practice with the skills needed to complete the tasks in this lesson. It may be helpful to pull individual students and/or a small group for direct instruction or guided practice with the skills they have learned thus far in this unit.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- In these problems, students can enter any numbers into the tables as long as the relationship between the numbers is correct. As students work, identify a variety of work with an eye to making connections among different methods. For example, look for the following different approaches:
- Choosing a speed and a time, and then calculating distance; choosing a distance and a time, and then calculating speed; and choosing a speed and a distance, and then calculating time.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Look for students who understand that they can choose any two numbers to find the third number; these students are using a general method to solve all rate problems.
Interventions
Student has difficulty connecting the problem to familiar situations.
- What do you think a typical bike riding speed might be?
- How long might you ride your bike? If you ride for that length of time at that speed, how far would you ride?
- What is the relationship among speed, distance, and time?
- What is a common rate for the speed of a car?
- If a car travels for two hours, how far would it go at that constant speed?
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- Can you use your definition of rate to help you get started?
Student has an incorrect solution.
- Have you checked your work?
- Do your answers make sense?
- Explain the relationship among your numbers in this problem.
- Where do you see the rate in this problem? Describe it.
Student has a solution.
- Why did you approach this problem in the way that you did?
- Could you have used another method to solve this problem? Explain.
- What still confuses you about rate?
- Answers will vary, but the relationships should show that speed is equal to distance divided by the time.
In this problem, you will work with three quantities: distance, time, and speed.
Create a set of three numbers that shows the relationship among the quantities. For instance, if you chose a time of 3 hours and a speed of 25 miles per hour, the distance would be 75 miles.
- The first set contains any numbers.
- The second set contains numbers greater than 10.
- The third set contains decimal numbers.
INTERACTIVE: Distance, Time, and Speed
Students will fill in a table showing the relationship between gallons, total price, and price per gallon.
- Students can enter any numbers into the tables as long as the relationship between the numbers is correct. As students work, identify a variety of work with an eye to making connections among different methods. For example, look for the following different approaches:
- Choosing a number of gallons and a total price, and then calculating unit price; choosing a total price and a unit price, and then calculating a number of gallons; and choosing a number of gallons and a unit price, and then calculating total price.
- Answers will vary, but the relationships should show that price per gallon is equal to price divided by gallons.
In this problem, you will work with three quantities: gallons, total price, and price per gallon.
Create a set of three numbers that shows the relationship among the quantities.
INTERACTIVE: Price per Gallon
Have the students look up the current exchange rate of pesos per dollar or dollars per peso. Students fill in a table reflecting one of those rates.
- Choosing a number of dollars and a rate, and then calculating a number of pesos
- Choosing a number of pesos and a rate, and then calculating a number of dollars.
- Answers will vary, but the relationships should show that dollars per peso is equal to dollars divided by pesos.
In this problem, you will work with three quantities: dollars, pesos, and dollars per peso.
Create a set of three numbers that show the relationship among the quantities.
INTERACTIVE: Dollars and Pesos
Student will fill in a table showing the relationship of hours, speed, and miles.
- Answers will vary, but the relationships should show that speed is equal to the miles divided by the hours.
In this problem, you will work with three quantities: hours, speed, and miles.
Lesson guide
Students will fill in a table showing the relationship of the number of books in a stack, the height of the stack, and the thickness of each book (inches per book).
- Answers will vary, but the relationships should show that the thickness of a book is equal to the height of the stack divided by the number of books.
In this problem, you will work with three quantities: the number of books in a stack, the height of the stack, and the thickness of each book (inches per book).
INTERACTIVE: Stack of Books
Students fill in a table on a runner to find out if a runner runs at a constant speed. Then they prepare a presentation on their method.
Preparing for Ways of Thinking
Look for students who understand that they can choose any two numbers to find the third number. These students are using a general method to solve all rate problems.
- Did you remember to convert minutes to hours?
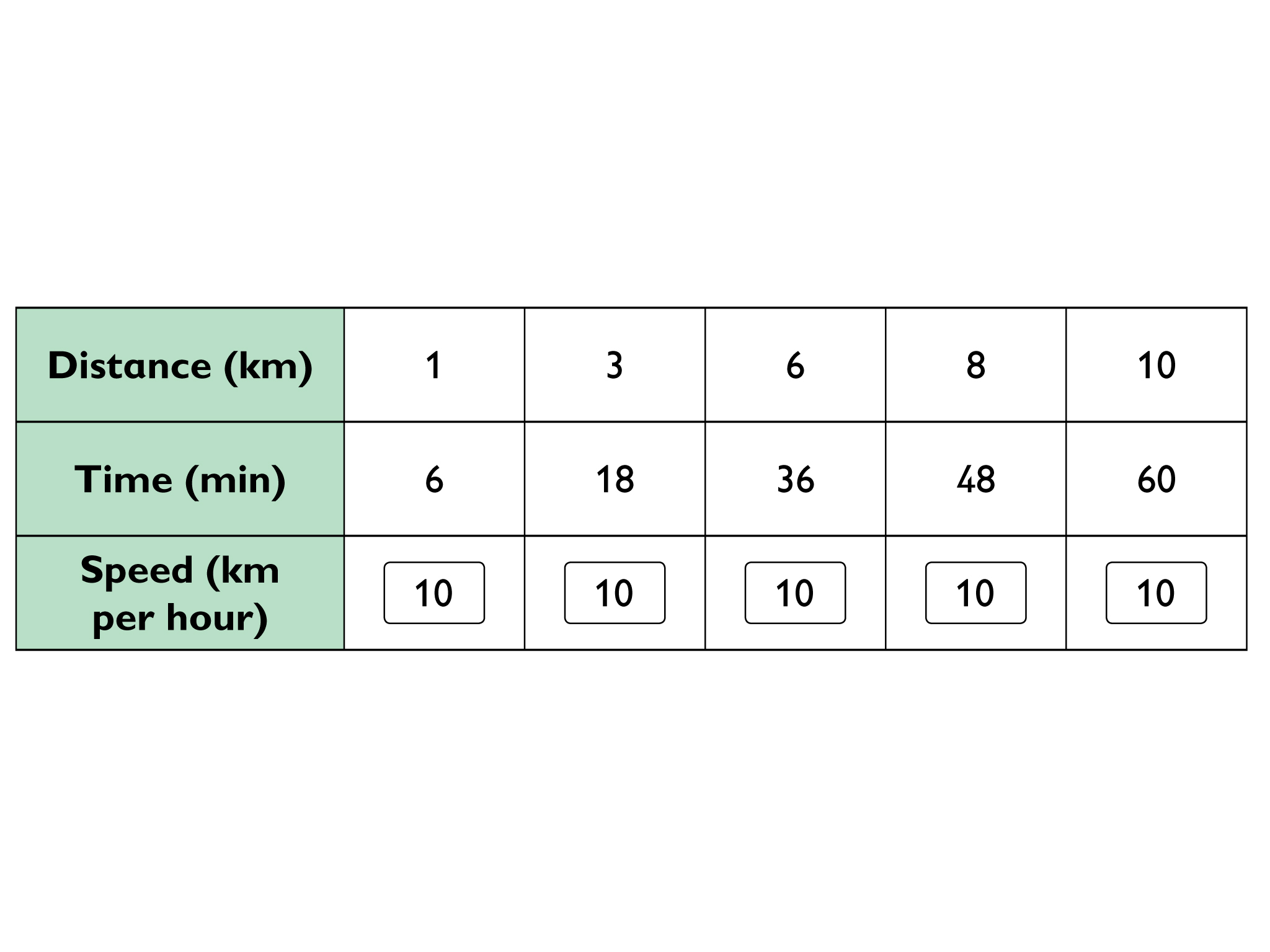
10 kilometers per hour
Prepare a presentation of your work.
- Does the table support this statement?
- Complete the table.
- Express the speed of the runner in kilometers per hour.
INTERACTIVE: Prepare a Presentation
Make Connections
By the end of the discussion, students should understand each other's methods and make connections between methods. All students should also understand that given any two values in a rate situation, they can find the third value. Encourage students to critique each method.
Mathematics
Discuss the different approaches students use. Ask questions such as the following to help students critique each other's work and to help them see relationships among the different methods:
- How did the student make sense of the problem?
- What was similar about their approaches?
- What was different?
- Did anyone try a method that did not work? What did you do? Why didn't your method work?
Performance Task
Ways of thinking: make connections.
As you listen to other students present their work, find ways to understand how to think about rate.
As your classmates present, ask questions such as:
- Where is the rate in your numbers?
- Where do you see the other two quantities?
- How would you describe the relationship among the three numbers?
Reflect On Your Work
Have each student write a brief reflection before the end of class. Review students' reflections.
If any reflections look interesting enough to pursue later, share them with the class at an appropriate time.
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I still wonder about rates is …
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Ratio problem solving
Here you will learn about ratio problem solving, including how to set up and solve problems. You will also look at real life ratio word problems.
Students will first learn about ratio problem solving as part of ratio and proportion in 6 th grade and 7 th grade.
What is ratio problem solving?
Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.
A ratio is a relationship between two or more quantities. They are usually written in the form a : b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are:
- What is the ratio involved?
- What order are the quantities in the ratio?
- What is the total amount / what is the part of the total amount known?
- What are you trying to calculate ?
As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that you can use to help you find an answer.
The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.
Let’s look at a couple of methods you can use when given certain pieces of information.
When solving ratio word problems, it is very important that you are able to use ratios. This includes being able to use ratio notation.
For example, Charlie and David share some sweets in the ratio of 3 : 5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.
Charlie and David share 40 sweets, how many sweets do they each get?
You use the ratio to divide 40 sweets into 8 equal parts.
40 \div 8=5
Then you multiply each part of the ratio by 5.
3\times 5:5\times 5=15 : 25
This means that Charlie will get 15 sweets and David will get 25 sweets.
There can be ratio word problems involving different operations and types of numbers.
Here are some examples of different types of ratio word problems:
| Dividing ratios | A bag of sweets is shared between boys and girls in |
| Ratios and fractions (proportion word problems) | If \frac{9}{10} students are right handed, write the ratio of |
| Simplifying ratios | Simplify the ratio 10:15. |
| Equivalent ratios | Write the ratio 4:15 in the form 1:n. |
| Units and conversions | If £1:\$1.37, how much is £10 in US dollars? |
| Percents | In a class of 30 students, the ratio of boys to girls is |

Common Core State Standards
How does this relate to 6 th and 7 th grade math?
- Grade 6 – Ratios and Proportional Relationships (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
- Grade 7 – Ratio and Proportional Relationships (7.RP.A.2) Recognize and represent proportional relationships between quantities.
How to do ratio problem solving
In order to solve problems including ratios:
Identify key information within the question.
Know what you are trying to calculate.
Use prior knowledge to structure a solution.
![math problem solving rates [FREE] Ratio Problem Solving Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/05/Ratio-Problem-Solving-Worksheet-listing-image.png)
[FREE] Ratio Problem Solving Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of ratio problem solving. 15 questions with answers to identify areas of strength and support!
Ratio problem solving examples
Example 1: part:part ratio.
Within a school, the total number of students who have school lunches to packed lunches is 5 : 7. If 465 students have a school lunch, how many students have a packed lunch?
Within a school, the number of students who have school lunches to packed lunches is \textbf{5 : 7} . If \textbf{465} students have a school lunch, how many students have a packed lunch?
Here you can see that the ratio is 5 : 7, where the first part of the ratio represents school lunches (S) and the second part of the ratio represents packed lunches (P).
You could write this as:
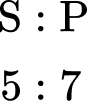
Where the letter above each part of the ratio links to the question.
You know that 465 students have school lunch.
2 Know what you are trying to calculate.
From the question, you need to calculate the number of students that have a packed lunch, so you can now write a ratio below the ratio 5 : 7 that shows that you have 465 students who have school lunches, and p students who have a packed lunch.
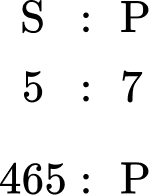
You need to find the value of p.
3 Use prior knowledge to structure a solution.
You are looking for an equivalent ratio to 5 : 7. So you need to calculate the multiplier.
You do this by dividing the known values on the same side of the ratio by each other.
465\div 5 = 93
This means to create an equivalent ratio, you can multiply both sides by 93.
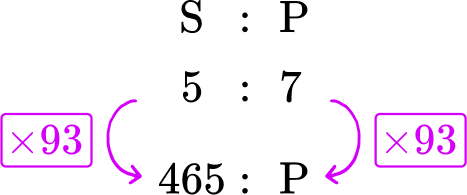
So the value of p is equal to 7 \times 93=651.
There are 651 students that have a packed lunch.
Example 2: unit conversions
The table below shows the currency conversions on one day.
| GBP | 1.00 |
| USD | 1.37 |
| EUR | 1.17 |
| AUD | 1.88 |
Use the table above to convert £520 \; (GBP) to Euros € \; (EUR).
| \colorbox{yellow}{GBP} | \colorbox{yellow}{1.00} |
| USD | 1.37 |
| \colorbox{yellow}{EUR} | \colorbox{yellow}{1.17} |
| AUD | 1.88 |
Use the table above to convert \bf{£520} \textbf{ (GBP)} to Euros \textbf{€ } \textbf{(EUR)}.
The two values in the table that are important are \text{GBP} and EUR. Writing this as a ratio, you can state,
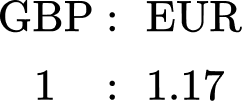
You know that you have £520.
You need to convert GBP to EUR and so you are looking for an equivalent ratio with GBP=£520 and EUR=E.

To get from 1 to 520, you multiply by 520 and so to calculate the number of Euros for £520, you need to multiply 1.17 by 520.
1.17 \times 520=608.4
So £520=€608.40.

Example 3: writing a ratio 1 : n
Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500 \, ml of concentrated plant food must be diluted into 2 \, l of water. Express the ratio of plant food to water, respectively, in the ratio 1 : n.
Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500 \, ml} of concentrated plant food must be diluted into \bf{2 \, l} of water. Express the ratio of plant food to water respectively as a ratio in the form 1 : n.
Using the information in the question, you can now state the ratio of plant food to water as 500 \, ml : 2 \, l. As you can convert liters into milliliters, you could convert 2 \, l into milliliters by multiplying it by 1000.
2 \, l=2000 \, ml
So you can also express the ratio as 500 : 2000 which will help you in later steps.
You want to simplify the ratio 500 : 2000 into the form 1:n.
You need to find an equivalent ratio where the first part of the ratio is equal to 1. You can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).
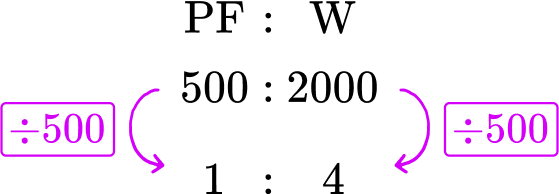
So the ratio of plant food to water in the form 1 : n is 1 : 4.
Example 4: forming and solving an equation
Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives \$ 8 allowance, how much money do the three siblings receive in total?
Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their ages. Kieran is \bf{3} years older than Josh. Luke is twice Josh’s age. If Luke receives \bf{\$ 8} allowance, how much money do the three siblings receive in total?
You can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, you have:
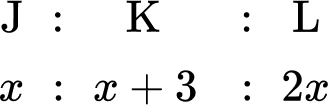
You also know that Luke receives \$ 8.
You want to calculate the total amount of allowance for the three siblings.
You need to find the value of x first. As Luke receives \$ 8, you can state the equation 2x=8 and so x=4.
Now you know the value of x, you can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.
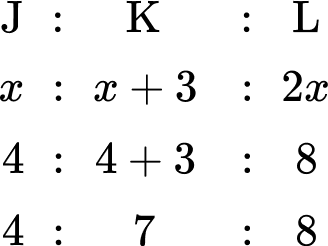
The total amount of allowance is therefore 4+7+8=\$ 19.
Example 5: simplifying ratios
Below is a bar chart showing the results for the colors of counters in a bag.
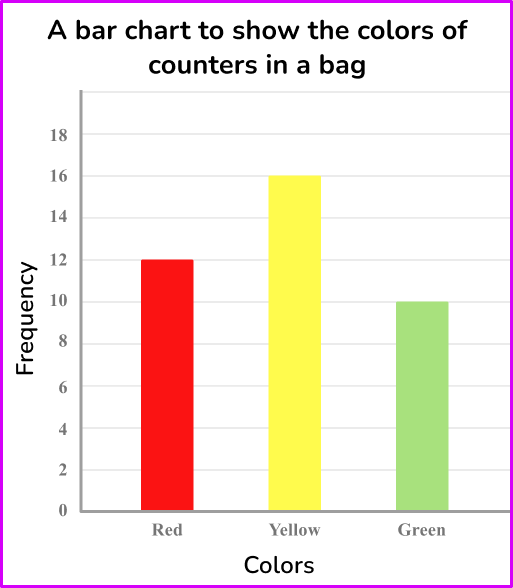
Express this data as a ratio in its simplest form.
From the bar chart, you can read the frequencies to create the ratio.

You need to simplify this ratio.
To simplify a ratio, you need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.
\begin{aligned} & 12 = 1, {\color{red}2}, 3, 4, 6, 12 \\\\ & 16 = 1, {\color{red}2}, 4, 8, 16 \\\\ & 10 = 1, {\color{red}2}, 5, 10 \end{aligned}
HCF(12,16,10) = 2
Dividing all the parts of the ratio by 2, you get
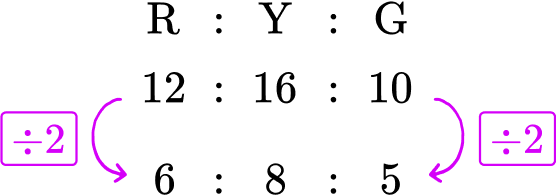
Our solution is 6 : 8 : 5.
Example 6: combining two ratios
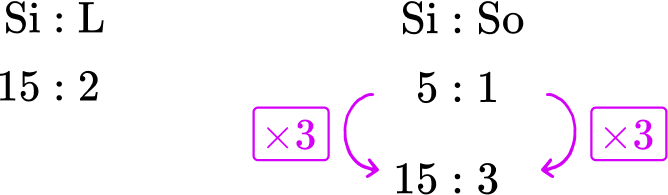
Glass is made from silica, lime and soda. The ratio of silica to lime is 15 : 2. The ratio of silica to soda is 5 : 1. State the ratio of silica:lime:soda.
Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15 : 2}. The ratio of silica to soda is \bf{5 : 1}. State the ratio of silica:lime:soda.
You know the two ratios

You are trying to find the ratio of all 3 components: silica, lime and soda.
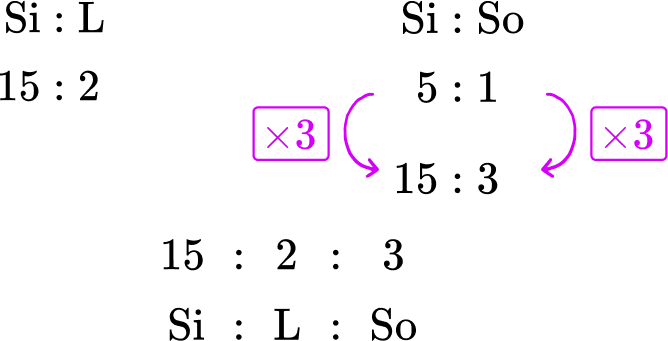
Using equivalent ratios you can say that the ratio of Silica:Soda is equivalent to 15 : 3 by multiplying the ratio by 3.
You now have the same amount of silica in both ratios and so you can now combine them to get the ratio 15 : 2 : 3.
Example 7: using bar modeling
India and Beau share some popcorn in the ratio of 5 : 2. If India has 75 \, g more popcorn than Beau, what was the original quantity?
India and Beau share some popcorn in the ratio of \bf{5 : 2} . If India has \bf{75 \, g} more popcorn than Beau, what was the original quantity?
You know that the initial ratio is 5 : 2 and that India has three more parts than Beau.
You want to find the original quantity.
Drawing a bar model of this problem, you have:

Where India has 5 equal shares, and Beau has 2 equal shares.
Each share is the same value and so if you can find out this value, you can then find the total quantity.
From the question, India’s share is 75 \, g more than Beau’s share so you can write this on the bar model.
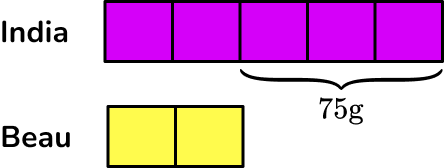
You can find the value of one share by working out 75 \div 3=25 \, g.
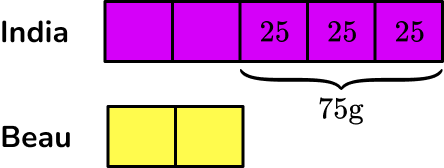
You can fill in each share to be 25 \, g.
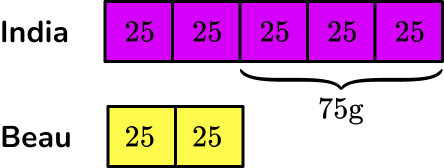
Adding up each share, you get
India=5 \times 25=125 \, g
Beau=2 \times 25=50 \, g
The total amount of popcorn was 125+50=175 \, g.
Teaching tips for ratio problem solving
- Continue to remind students that when solving ratio word problems, it’s important to identify the quantities being compared and express the ratio in its simplest form.
- Create practice problems for students using the information in your classroom. For example, ask students to find the ratio of boys to the ratio of girls using the total number of students in your classroom, then the school.
- To find more practice questions, utilize educational websites and apps instead of worksheets. Some of these may also provide tutorials for struggling students. These can also be helpful for test prep as they are more engaging for students.
- Use a variety of numbers in your ratio word problems – whole numbers, fractions, decimals, and mixed numbers – to give students a variety of practice.
- Provide students with a step-by-step process for problem solving, like the one shown above, that can be applied to every ratio word problem.
Easy mistakes to make
- Mixing units Make sure that all the units in the ratio are the same. For example, in example 6, all the units in the ratio were in milliliters. You did not mix ml and l in the ratio.
- Writing ratios in the wrong order For example, the number of dogs to cats is given as the ratio 12 : 13 but the solution is written as 13 : 12.

- Counting the number of parts in the ratio, not the total number of shares For example, the ratio 5 : 4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.
- Ratios of the form \bf{1 : \textbf{n}} The assumption can be incorrectly made that n must be greater than 1, but n can be any number, including a decimal.
Related ratio lessons
- Unit rate math
- Simplifying ratios
- Ratio to fraction
- How to calculate exchange rates
- Ratio to percent
- How to write a ratio
- Dividing ratios
- How to find the unit rate
- Ratio scale
- Constant of proportionality
Practice ratio problem solving questions
1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3 : 8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.
2. The ratio of prime numbers to non-prime numbers from 1-200 is 45 : 155. Express this as a ratio in the form 1 : n.
You need to simplify the ratio so that the first number is 1. That means you need to divide each number in the ratio by 45.
45 \div 45=1
155\div{45}=3\cfrac{4}{9}
3. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2 : 3 and the ratio of cloud to rain was 9 : 11. State the ratio that compares sunshine:cloud:rain for the month.
3 \times S : C=6 : 9
4. The angles in a triangle are written as the ratio x : 2x : 3x. Calculate the size of each angle.
You should know that the 3 angles in a triangle always equal 180^{\circ}.
\begin{aligned} & x+2 x+3 x=180 \\\\ & 6 x=180 \\\\ & x=30^{\circ} \\\\ & 2 x=60^{\circ} \\\\ & 3 x=90^{\circ} \end{aligned}
5. A clothing company has a sale on tops, dresses and shoes. \cfrac{1}{3} of sales were for tops, \cfrac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.
\cfrac{1}{3}+\cfrac{1}{5}=\cfrac{5+3}{15}=\cfrac{8}{15}
1-\cfrac{8}{15}=\cfrac{7}{15}
6. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75 \, l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?
The given ratio in the word problem is 2. 75 \mathrm{~L}: 18^{\circ} \mathrm{K}
Divide 45 by 18 to see the relationship between the two temperatures.
45 \div 18=2.5
45 is 2.5 times greater than 18. So we multiply 2.75 by 2.5 to get the amount of gas.
2.75 \times 2.5=6.875 \mathrm{~l}
Ratio problem solving FAQs
A ratio is a comparison of two or more quantities. It shows how much one quantity is related to another.
A recipe calls for 2 cups of flour and 1 cup of sugar. What is the ratio of flour to sugar? (2 : 1)
In middle school ( 7 th grade and 8 th grade), students transition from understanding basic ratios to working with more complex and real-life applications of ratios and proportions. They gain a deeper understanding of how ratios relate to different mathematical concepts, making them more prepared for higher-level math topics in high school.
The next lessons are
- Converting fractions, decimals and percentages
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!
Privacy Overview
- WordPress.org
- Documentation
- Learn WordPress
SingaporeMathSource
- Singapore Math Source Quick Start Guide
- Singapore Math Curriculum
- Scope and Sequences
- In the News
- Schools in the News
- Favorite Printable Resources
- Primary Mathematics vs. Math in Focus
- Best Books to Support Singapore Math in the Classroom
- Best Books for Grown-Ups Wanting to Learn Singapore Math
- Fun Math Practice Sites
- Math Wall ideas
- Assessments
- Handouts from Trainings
- Jumpstart Your Singapore Math 2024
- Jumpstart your Singapore Math Online
- Member Access – Jumpstart Your Singapore Math For Schools
- Math Champions Professional Development
- What attendees are saying!
Speed and Rate Problems
Rate problems provide some of the biggest challenges to students and adults. These come from Problem-Solving Processes in Mathematics -6 B by Fabian Ng.
- At 10:15 am, a car left Town X for Town Y at an average speed of 86 km/h, while a truck left Town Y for Town X at an average speed of 74 km/h. At 3:15 pm, the two vehicles were 12 km apart. How far apart were the two towns?
- At 10:30 am, a cyclist started traveling on a road at an average speed of 60 km/h. At 2:30 pm, a motorist started from the same place, traveling on the same road. If the motorist took 4 hours to catch up with the cyclist, find his average speed.
- The distance from Town P to Town Q was 312 km. Winston started from Town P at an average speed of 76 km/h. He maintained this speed for 2 hours before increasing it by 4 km/ for the rest of the journey to Town Q.
Can you draw a model or diagram to illustrate each of these problems?
(Answers next week!)
Passionate about Singapore Math + Teacher Trainer and Coach + Treasure Hunter + Learner. Answer to the ultimate question? 42.
Speak Your Mind Cancel reply
This site uses Akismet to reduce spam. Learn how your comment data is processed .
Your Host, Cassandra Turner

Find Us Near You
Find us on the web.

We’ve trained teachers in 47 States!
What Teachers are Saying
We’re on instagram.

mathchampions
Customized math training/coaching PD for your school. How can we help you improve your math instruction?

Blog Categories
- Implementing Singapore Math (29)
- Masters (1)
- Math Events (64)
- Math Resources (158)
- Schools (15)
- Singapore Math Problems (41)
- Tales from the classroom (41)
- Training (47)
- Uncategorized (3)
- Word Problem Wednesday (31)

Pinterest Faves

Copyright © 2008 - 2024 · Cassandra Turner · Site Design by Heather Mackan Creative · Built on Genesis
Return to top of page
Solving Problems Involving Distance, Rate, and Time
- Pre Algebra & Algebra
- Math Tutorials
- Exponential Decay
- Worksheets By Grade
In math, distance, rate, and time are three important concepts you can use to solve many problems if you know the formula. Distance is the length of space traveled by a moving object or the length measured between two points. It is usually denoted by d in math problems .
The rate is the speed at which an object or person travels. It is usually denoted by r in equations . Time is the measured or measurable period during which an action, process, or condition exists or continues. In distance, rate, and time problems, time is measured as the fraction in which a particular distance is traveled. Time is usually denoted by t in equations.
Solving for Distance, Rate, or Time
When you are solving problems for distance, rate, and time, you will find it helpful to use diagrams or charts to organize the information and help you solve the problem. You will also apply the formula that solves distance, rate, and time, which is distance = rate x tim e. It is abbreviated as:
There are many examples where you might use this formula in real life. For example, if you know the time and rate a person is traveling on a train, you can quickly calculate how far he traveled. And if you know the time and distance a passenger traveled on a plane, you could quickly figure the distance she traveled simply by reconfiguring the formula.
Distance, Rate, and Time Example
You'll usually encounter a distance, rate, and time question as a word problem in mathematics. Once you read the problem, simply plug the numbers into the formula.
For example, suppose a train leaves Deb's house and travels at 50 mph. Two hours later, another train leaves from Deb's house on the track beside or parallel to the first train but it travels at 100 mph. How far away from Deb's house will the faster train pass the other train?
To solve the problem, remember that d represents the distance in miles from Deb's house and t represents the time that the slower train has been traveling. You may wish to draw a diagram to show what is happening. Organize the information you have in a chart format if you haven't solved these types of problems before. Remember the formula:
distance = rate x time
When identifying the parts of the word problem, distance is typically given in units of miles, meters, kilometers, or inches. Time is in units of seconds, minutes, hours, or years. Rate is distance per time, so its units could be mph, meters per second, or inches per year.
Now you can solve the system of equations:
50t = 100(t - 2) (Multiply both values inside the parentheses by 100.) 50t = 100t - 200 200 = 50t (Divide 200 by 50 to solve for t.) t = 4
Substitute t = 4 into train No. 1
d = 50t = 50(4) = 200
Now you can write your statement. "The faster train will pass the slower train 200 miles from Deb's house."
Sample Problems
Try solving similar problems. Remember to use the formula that supports what you're looking for—distance, rate, or time.
d = rt (multiply) r = d/t (divide) t = d/r (divide)
Practice Question 1
A train left Chicago and traveled toward Dallas. Five hours later another train left for Dallas traveling at 40 mph with a goal of catching up with the first train bound for Dallas. The second train finally caught up with the first train after traveling for three hours. How fast was the train that left first going?
Remember to use a diagram to arrange your information. Then write two equations to solve your problem. Start with the second train, since you know the time and rate it traveled:
Second train t x r = d 3 x 40 = 120 miles First train t x r = d 8 hours x r = 120 miles Divide each side by 8 hours to solve for r. 8 hours/8 hours x r = 120 miles/8 hours r = 15 mph
Practice Question 2
One train left the station and traveled toward its destination at 65 mph. Later, another train left the station traveling in the opposite direction of the first train at 75 mph. After the first train had traveled for 14 hours, it was 1,960 miles apart from the second train. How long did the second train travel? First, consider what you know:
First train r = 65 mph, t = 14 hours, d = 65 x 14 miles Second train r = 75 mph, t = x hours, d = 75x miles
Then use the d = rt formula as follows:
d (of train 1) + d (of train 2) = 1,960 miles 75x + 910 = 1,960 75x = 1,050 x = 14 hours (the time the second train traveled)
- Distance, Rate, and Time Worksheets
- Quadratic Formula Worksheets with Answers
- Rate of Change Worksheet with Solutions
- Converting Radians and Degrees
- Algebra Age-Related Word Problem Worksheets
- How to Solve Algebra Problems Step-By-Step
- Algebra: Using Mathematical Symbols
- Using the Quadratic Formula With No X-intercept
- What Type of Mathematical Function Is This?
- Quadratic Functions
- What You Need to Know About Consecutive Numbers
- Algebra Definition
- Adding and Subtracting Polynomials
- The Significance of Negative Slope
- Simplifying Expressions With the Distributive Property Law
- What Slope-Intercept Form Means and How to Find It
- Our Mission
Using Video Projects to Reinforce Learning in Math
A collaborative project can help students deeply explore math concepts, explain problem-solving strategies, and demonstrate their learning.

Problem-solving, and the creativity that generates and fuels it, lies at the heart of mathematics. Mathematics is essentially about reasoning and much less about memorization or even procedural skills, although both processes are meaningful and useful to simplify and support problem-solving. The National Council of Teachers of Mathematics (NCTM) has consistently advocated to keep problem-solving as the centerpiece of mathematics teaching, and global trends in mathematics education have increasingly emphasized problem-solving and mathematical modeling.
Problem-solving allows students to deepen their conceptual comprehension and appreciate the usefulness and relevance of mathematics. Thus, it generates and fosters interest, engagement, and a deeper understanding of the world around them. Because problem-solving is often used in the mathematics classroom, it’s particularly important to find fresh and interesting ways to attract and maintain students’ engagement.
Video Projects Support Interest in Problem-Solving
To this end, I assign video projects to my students. In groups of two or three, they solve a set of problems on a topic and then choose one to illustrate, solve, and explain their favorite problem-solving strategy in detail, along with the reasons they chose it. The student-created videos are collected and stored on a Padlet even after I have evaluated them—kept as a reference, keepsake, and support. I have a library of student-created videos that benefit current and future students when they have some difficulties with a topic and associated problems.
Some topics in mathematics are well-suited for applications and problem-solving. These are usually multistep problems that require a combination of strategies and procedural fluency. Typical examples are the motion, work, and mixture problems in algebra, the optimization problems in precalculus or calculus, and related rates problems in calculus.
This collection of student-created videos is about related rates problems (note that some links may not work, as this collection is old). Video activities based on problem-solving can be done at any level of mathematics, as problem-solving is a task in which children are engaged in math class from an early age.
Useful Recording Tools
Some examples of useful recording apps include Screencastify , ScreenPal , iMovie , and QuickTime . Each of them has pros and cons, so I suggest looking at the particular specifications of each tool in terms of the number and length of videos allowed by the free version of those apps. I let my students choose what app they want to use to create their videos—they are generally very familiar with this sort of technology and may be more at ease with one tool over another. All they have to produce is a usable link to their video that will be posted on the common Padlet.
Loom is an intuitive, user-friendly screen recording tool that can record audio, video, browser windows, or entire screens in a Chrome extension, desktop app, or mobile app. You can sign up for a free Loom for Education account; students don’t need an account to watch a teacher’s videos, but they will in order to create their own videos.
Loom’s training module is thorough and includes tutorials, special feature descriptions, and examples. Once you click the Loom icon, there’s a short countdown that precedes the recording. When you stop the recording, a link automatically saves to your clipboard and can be easily shared via email, social media, or an embed code.
The videos will also save to your personal library and can be shared to a team library to make them easily accessible to colleagues. Editing features are quite limited (trimming and changing playback speed), which means you may have to do multiple takes, but teachers can control the settings for comment and download options.
4 Problem-Solving Strategies
Mathematician George Polya outlined a four-step model in his famous book, How to Solve It . It involves understanding the problem, devising a plan, carrying it out, and finally looking back and reflecting. These are the strategies that my students must demonstrate while creating their videos.
- Understand the problem: Students reread the problem carefully, summarize and rewrite the information in mathematical notation, use keyword analysis, draw a picture or a diagram, or even act out the scenario.
- Devise a plan: Looking for patterns and solving a simpler problem are my favorite approaches, but other ideas—guess-and-check, working backward, eliminating possibilities, using a formula and solving an equation—can work well too, depending on the circumstances. Most often, for good problems, several of these strategies have to be employed at the same time and help support confidence in the solution.
- Carry out the plan: This is where “show your work” comes in with full force. Communicating their thoughts and ideas is paramount: Students should be systematic, show their thinking in a logical progression, check their work, and be flexible and persistent.
- Look back and reflect: It’s important to consider which part of the problem was the most challenging and why, which process was most effective, and other strategies that could have worked. This makes for more efficient and deeper learning.
Related rates problems can be intimidating at first, and it is useful for students to write out explicitly the steps and strategies they take to solve the first few problems.
My students come up with a model that follows the previously mentioned steps. It includes labeling the rates with their units and sign, an understanding of the rate they must find, finding at least one equation that binds the variables together, differentiating this equation with respect to time, plugging in the given information, and, finally, writing a short sentence that summarizes their conclusion (including sign and units).
Benefits of the Video Activity
My students and I have experienced several benefits of this task.
Students are encouraged to communicate mathematically. The importance of communication among learners is also heavily emphasized in the NCTM publication Principles and Standards for School Mathematics .
Student collaboration. Viewing learning as a collective endeavor , rather than an individual competition, helps students develop their social and collaborative skills. When students take joint responsibility for their learning—sharing ideas and resources—it fosters a safe environment where they perceive each other as allies rather than competitors, which increases engagement and academic achievement.
Problem-solving skills are strengthened. As reported in the Executive Summary of the NCTM Principles and Standards for School Mathematics , when solving mathematical problems, students acquire ways of thinking, habits of persistence and curiosity, and confidence in unfamiliar situations that serve them well beyond the classroom.
Teachers can clearly see students’ understanding. This includes conceptual understanding, procedural precision, logical and analytical thinking, problem-solving strategies, and clarity of communication.
A sense of belonging in math class is cemented. The experience generates positive, affirmative memories—the goal of social and emotional learning—and “ encourages student focus and motivation, improves relationships between students and teachers, and increases student confidence and success .” It should be promoted, particularly in the STEM disciplines.
In other words, it’s a keeper.
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
What can QuickMath do?
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.
- The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
- The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
- The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
- The calculus section will carry out differentiation as well as definite and indefinite integration.
- The matrices section contains commands for the arithmetic manipulation of matrices.
- The graphs section contains commands for plotting equations and inequalities.
- The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions

IMAGES
VIDEO
COMMENTS
Here are two different ways to solve this problem: Compare dollars per kilogram. The large bag costs $8 per kilogram, because 16 ÷ 2 = 8 16 ÷ 2 = 8. The small bag holds 12 1 2 pound of cheese, because there are 16 ounces in 1 pound, and 8 ÷ 16 = 12 8 ÷ 16 = 1 2. The small bag costs $4 per pound, because 2 ÷ 12 = 4 2 ÷ 1 2 = 4.
One method to solve unit rate problems is setting up a table. In this method, setting up the table is the first and most important step in solving a unit rate problem. Set up a rate table. The ...
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/cc-sixth-grade-math/x0267d782:c...
Step 1: Identify the original rate. Answer: 2 ft 1 hr 2 ft 1 hr. Step 2: Identify the name for the rate that you want. Use x x for any number that is unknown. Answer: 7 in x min 7 in x min. Step 3: Check that the original rate and its desired new name are 'compatible'; i.e., same types of units in both numerator and denominator.
Unit Rate Math - Math Steps, Examples & Questions
While solving rate problems, it is crucial to identify the given information, set up the appropriate equation or proportion, and solve for the unknown variable. ... This means you are capable of solving around 0.88 math problems every minute. Explanation: To find out your unit rate per minute, you can simply divide the total number of problems ...
In general, to find the total distance traveled, multiply the total time spent traveling by the rate of travel. This can be expressed as an equation: d = rt where d = total distance, r = rate of travel, and t = time. Using this equation, we can write r and t in terms of the other variables: r = and t =. Make sure units are consistent.
The key to solving rate problems is to figure out the context of the problem and then identify a formula that relates all of the information in the problem. In this problem, our context is distance: we have two objects traveling at different rates and in opposite directions. We can relate all of the information using the simple formula distance ...
1. Identify what you are trying to find: Before you begin solving a problem involving rates, you need to identify what you are trying to find. This will help guide you in setting up the problem. 2. Write down the formula: Once you have identified what you are trying to find, write down the formula for the rate you need to calculate.
Basic Rate ProblemWatch the next lesson: https://www.khanacademy.org/math/algebra/solving-linear-equations-and-inequalities/More-equation-practice/v/early-tr...
Welcome to Unit Rates with Mr. J! Need help with how to solve unit rate problems? You're in the right place!Whether you're just starting out, or need a quick...
Watch a video that explains how to solve rate problems using ratios and unit rates, and practice with interactive exercises.
9.10 Rate Word Problems: Work and Time
Math / Grade 6 G6 / Module 1 M1 / Topic C TC / Lesson 23 lesson 23. lesson 23. 1 hour. Problem Solving Using Rates, Unit Rates, and Conversions. Students solve constant rate problems. Download Lesson Related Resources. Math Grade 6 Curriculum Map. module 1 - topic A. topic B. topic C. topic D. module 2 - module 3 - module 4 - ...
Solution to Problem 2: The rates of pumps A and B can be calculated as follows: A: 1 / 6 and B: 1 / 8. Let R be the rate of pump C. When working together for 2 hours, we have. 2 ( 1 / 6 + 1 / 8 + R ) = 1. Solve for R. R = 1 / 4.8 , rate of pump C. Let t be the time it takes pump C, used alone, to fill the tank.
Cluster: Understand ratio concepts and use ratio reasoning to solve problems Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0 (b not equal to zero), and use rate language in the context of a ratio relationship. For example, "This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar."
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/cc-sixth-grade-math/x0267d782:...
Free ratio problem solving math topic guide, including step-by-step examples, free practice questions, teaching tips and more! Math Tutoring for Schools. How it Works; Impact; Tutors; ... Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double ...
Rate problems provide some of the biggest challenges to students and adults. These come from Problem-Solving Processes in Mathematics -6 B by Fabian Ng. At 10:15 am, a car left Town X for Town Y at an average speed of 86 km/h, while a truck left Town Y for Town X at an average speed of 74 km/h. At 3:15 pm, the two vehicles were 12 km apart.
Rate is distance per time, so its units could be mph, meters per second, or inches per year. Now you can solve the system of equations: 50t = 100 (t - 2) (Multiply both values inside the parentheses by 100.) 50t = 100t - 200. 200 = 50t (Divide 200 by 50 to solve for t.) t = 4. Substitute t = 4 into train No. 1.
This collection of student-created videos is about related rates problems (note that some links may not work, as this collection is old). Video activities based on problem-solving can be done at any level of mathematics, as problem-solving is a task in which children are engaged in math class from an early age.
Welcome to Solving Unit Rate Word Problems with Mr. J! Need help with unit rates? You're in the right place!Whether you're just starting out, or need a quick...
Solve - Step-by-Step Math Problem Solver
Mathway | Algebra Problem Solver