hypothesis mathematical modeling

Maël Montévil

A Primer on Mathematical Modeling in the Study of Organisms and Their Parts

Systems Biology

How do mathematical models convey meaning? What is required to build a model? An introduction for biologists and philosophers.

Mathematical modeling is a very powerful tool for understanding natural phenomena. Such a tool carries its own assumptions and should always be used critically. In this chapter, we highlight the key ingredients and steps of modeling and focus on their biological interpretation. In particular, we discuss the role of theoretical principles in writing models. We also highlight the meaning and interpretation of equations. The main aim of this chapter is to facilitate the interaction between biologists and mathematical modelers. We focus on the case of cell proliferation and motility in the context of multicellular organisms.

Keywords: Equations, Mathematical modeling, Parameters, Proliferation, Theory

A primer on mathematical modeling in the study of organisms and their parts

Mathematical modeling is a very powerful tool to understand natural phenomena. Such a tool carries its own assumptions and should always be used critically. In this chapter we highlight the key ingredients and steps of modeling and focus on their biological interpretation. In particular, we discuss the role of theoretical principles in writing models. We also highlight the meaning and interpretation of equations. The main aim of this chapter is to facilitate the interaction between biologists and mathematical modelers. We focus on the case of cell proliferation and motility in the context of multicellular organisms.

Keywords : mathematical modeling, proliferation, theory, equations, parameters

1 Introduction

Mathematical modeling may serve many purposes such as performing quantitative predictions or making sense of a situation where reciprocal interactions are beyond informal analyses. For example, describing the properties of the diferent ionic channels of a neuron individually is not sufficient to understand how their combination entails the formation of action potentials. We need a mathematical analysis such as the one performed by the Hodgkin-Huxley model to gain such an understanding [ 1 ]. In this sense, mathematical modeling is required at some point in order to understand many biological phenomena. Let us emphasize that the perspective of modelers is usually different than the one of many experimentalists, especially in molecular biology. The latter field tends to emphasize the contribution of individual parts, but traditional reductionism [ 2 ] involves both the analysis of parts and the theoretical composition of parts to understand the whole, usually by means of mathematical analysis. Without the latter move, it is never clear whether the parts analyzed individually are sufficient to explain how the phenomenon under study comes to be or whether key processes are missing.

We want to emphasize the difference between mathematical models on the one side and theories on the other side. Of course modelization belongs to the broad category of theoretical work by contrast with experimental work. However, in this text, we will refer to theory in the precise sense of a broad conceptual framework such as evolutionary theory. Evolutionary theory has been initially formulated without explicit mathematics. Evolutionary theory has actually led to different categories of mathematical analyses such as population genetics or phyllogenetic analysis which are very different mathematically. Theoretical frameworks typically guide modelization and contributes to justify mathematical models.

Mathematical modeling raises several difficulties in the study of organisms.

The first one is that most biologists do not have the mathematical or physical background to assess the meaning and the validity of models. The division of labor in interdisciplinary projects is an efficient way to work but it should at least be completed by an understanding of the principles at play in every part of the work. Otherwise, the coherence of the knowledge that result from this work is not ensured.

The second difficulty is intrinsic. Living objects have theoretical specificities that make mathematical modeling difficult or at least limit its meaning. These specificities are at least of two kinds.

• Current organisms are the result of an evolutive and developmental history which means that many contingent events are deeply inscribed in the organization of living being. By contrast the aim of mathematical modeling is usually to make explicit the necessity of an outcome. For more on this issue, see [ 3 ].
• The study of a part X of an organism is not completely meaningful by itself. Instead, the inscription of this part inside the organism and in particular the role that this part plays is a mandatory object of study to assess the biological relevance of the properties of X that are under study. As such, the modelization of X per se is insufficient and requires a supplementary discussion [ 4 ].

The third difficulty is that there are no well established theoretical principles to frame model writing in physiology or developmental biology [ 5 ]. In particular, cells are elementary objects since the cell theory states that there is no living things without cells. However, cells have complex organizations themselves. Modeling their behavior (note 1 ) is therefore challenging and requires appropriate theoretical assumptions to ensure that this modeling has a robust biological meaning.

A theoretical way to organize the mathematical modeling of cell behaviors is to propose a default state, that is to say to make explicit a state of reference that takes place without the need of particular constraints, input or signal. We think that proliferation with variation and motility should be used as a default state [ 6 , 7 ]. Under this assumption, cells spontaneously proliferate. By contrast, quiescence should be explained by constraints explicitly limiting or even preventing cell proliferation. The same reasoning applies mutadis mutandis to motility. This assumption has been used to model mammary gland morphogenesis and helps to systematize the mathematical analysis of cellular populations [ 8 ].

In this chapter we will focus on model writing. Our aim is not to emphasize the technical aspects of mathematical analysis. Instead, this text aims to help biologists to understand modelization in order to better interact with modelers. Reciprocally, we also highlight theoretical specificities of biology which may be of help to modelers. Of course, the usual way to divide chapters in this book series is not entirely appropriate for the topic of our chapter. We still kept this structure and follow it in a metaphorical sense. In materials, we are describing key conceptual and mathematical ingredients of models. In methods, we will focus on the writing and analysis of models per se .

2 Materials

2.1 parameters and states, 2.1.1 parameters.

Parameters are quantities that play a role in the system but which are not significantly impacted by the system’s behavior at the time scale of the phenomenon under study. From an experimentalist’s point of view, there are two kinds of parameters. Some parameters correspond to a quantity that is explicitly set by the experimenter such as the temperature, the size of a plate or the concentration of a relevant compound in the media. Other parameters correspond to properties of parts under study, such as the speed of a chemical reaction, the elasticity of collagen or the division rate τ of a cell without constraints. Changing the value of these parameters require to change the part in question, see also note 2 .

Identifying relevant parameters has actually two different meaning :

• Parameters that will be used explicitly in the model are parameters whose value is required to deduce the behavior of the system. The dynamics of the system depends explicitly on the value of these parameters. A fortiori , parameters that correspond to different treatments leading to a response will fall under this category. Note that the importance of some parameters usually appear in other steps of modeling.
• Theoretical parameters correspond to parameters that we know are relevant and even mandatory for the process to take place but that we can keep implicit in our model. For example, the concentration of oxygen in the media is usually not made explicit in a model of an in vitro experiment even though it is relevant for the very survival of the cells studied. Of course, there is usually a cornucopia of this sort of parameters, for example the many components of the serum.

2.1.2 State space

The state of an object describes its situation at a given time. The state is composed of one or several quantities, see note 3 . By contrast with parameters, the notion of state is restricted to those aspects of the system which will change as a result of explicit causes or randomness intrinsic to the system described. The usual approach, inherited from physics, is to propose a set of possible states that does not change during the dynamics. Then the changes of the system will be changes of states while staying among these possible states. For example, we can describe a cell population in a very simple manner by the number of cells n(t) . Then, the state space is all the possible values for n , that is to say the positive integers.

Usually, the changes of state depend on the state of the system which means that the state has a causal power, which can be either direct or indirect. A direct causal power is illustrated by n which is the number of cells that are actively proliferating in the example above and thus trigger the changes in n . An indirect causal power corresponds, for example, to the position of a cell provided that some positions are too crowded for cells to proliferate.

2.1.3 Parameter versus state

Deciding whether a given quantity should be described as a parameter or as an element of the state space is a theoretical decision that is sometimes difficult, see also note 4 . The heart of the matter is to analyze the role of this quantity but it also depends on the modeling aims.

• Does this quantity change in a quantitatively significant way at the time scale of the phenomenon of interest ? If no it should be a parameter. If yes :
• Are the changes of this quantity required to observe the phenomenon one wants to explain ? If yes, it should be a part of the state space. If no :
• Do we want to perform precise quantitative predictions ? If yes, then the quantity should be a part of the state space and a parameter otherwise.

In the following, we will call “description space” the combination of the state space and parameters.

2.2 Equations

Equations are often seen as intimidating by experimental biologists. Our aim here and in the following subsection is to help demystify them. In the modeling process, equations are the final explicitation of how changes occur and causes act in a model. As a result understanding them is of paramount importance to understand the assumptions of a model.

The basic rule of modeling is extremely simple. Parameters do not require equations since they are set externally. However, the value of states are unspecified. As a result, equations are required to describe how states change. More precisely, modelers require an equation for each quantity describing the state. Quantities of the state space are degrees of freedom, and these degrees of freedom have to be “removed” by equations for the model to perform predictions. These equations need to be independent in the sense that they need to capture different aspects of the system : copying twice the same equation obviously does not constrain the states. Equations typically come in two kinds :

• Equations that relate different quantities of the state space. For example, if we have n the total number of cells and two possible cell types with cell counts n 1 and n 2 , then we will always have n=n 1 +n 2 . As a result, it is sufficient to describe how two of these variables change in order obtain the third one.
• Equations that describe a change of state as a function of the state. These equations typically take two different forms, depending on the representation of time which may be either continuous or discrete, see note 5 . In continuous time, modelers use differential equations, for example dn ∕ dt=n ∕ τ . This equation means that the change of n ( dn) during a short time ( dt) is equal to ndt/ τ . This change follows from cell proliferation and we will expand on this equation in the next section. In discrete time, n t+ Δ t − n t is the change of state which relates to the current state by n t+ Δ t − n t =n t Δ t ∕ τ . Alternatively and equivalently, the future state can be written as a function of the current state : n t+ Δ t =n t Δ t ∕ τ +n t . Defining a dynamics requires at least one such equation to bind together the different time points, that is to say to bind causes and their effects.

2.3 Invariants and symmetries

We have discussed the role of equations, now let us expand on their structure. Let us start with the equation mentioned above : dn ∕ dt=n ∕ τ . What is the meaning of such an equation ? This equation states that the change of n, dn/dt, is proportional to n . 1) In conformity, with the cell theory, there is no spontaneous generation. There is no migration from outside the system described, which is an assumption proper to a given situation. The only source of cells is then cell proliferation. 2) Every cell divides at a given rate, independently. As a conclusion, the appearance of new cells is proportional to the number of cells which are dividing unconstrained, that is to say n . A cell needs a duration of τ to generate two cells (that is to say increase the cell count by one) which is exemplified by the fact that for n=1, dn/dt=1/ τ .

Alternatively, this equation is equivalent to dn ∕ dt × 1 ∕ n= 1 ∕ τ , and the latter relation shows that the equation is equivalent to the existence of an invariant quantity : dn ∕ dt × 1 ∕ n which is equal to 1/ τ for all values of n. Doubling n thus requires to double dn/dt. In this sense, the joint transformation dn ∕ dt → 2 dn ∕ dt and n → 2 n is a symmetry, that is to say a transformation that leaves invariant a key aspect of the system . This transformation leads from one time point to another. Discussing symmetries of equations is a method to show their meaning. Here, in a sense, the size of the population does not matter. Symmetries can also be multi-scale, for example fractal analysis is based on a symmetry between the different scales that is very fruitful in biology [ 9 , 10 ].

Probabilities may also be analyzed on the basis of symmetries. Randomness may be defined as unpredictability in a given theoretical frame and is more general than probabilities. To define probabilities, two steps have to be performed. The modeler needs to define a space of possibilities and then to define the probabilities of these possibilities. The most meaningful way to do the latter is to figure out possibilities that are equivalent, that is to say symmetric. For example, in a homogeneous environment, all directions are equivalent and thus would be assigned the same probabilities. A cell, in this situation, would have the same chance to choose any of these directions assuming that the cell’s organization is not already oriented in space, see also note 6 . In physics, a common assumption is to consider that states which have the same energy have the same probabilities.

Now there are several ways to write equations, independently of their deterministic or stochastic nature :

• Symmetry based writing is exemplified by the model of exponential growth above. In this case, the equation has a genuine meaning. Of course the model conveys approximations which are not always valid, but the terms of the equation are biologically meaningful. This also ensure that all mathematical outputs of the model may be interpreted biologically.

where k is the maximum of the population. Le us remark that we have written the equation in two different forms, we come back on this in note 7 . The solution of this equation is the classical logistic function.

Note however that this equation has symmetries which are dubious from a biological viewpoint : the way the population takes off is identical to the way it saturates because the logistic equation has a center of symmetry, A in figure, see also [ 11 ].

• The last way to write equations is called heuristic. The idea is to use functions that mimic quantitatively and to some extent qualitatively the phenomenon under study. Of course this method is less meaningful that the others but it is often required when the knowledge of the underlying phenomenon is not sufficient.

2.4 Theoretical principles

Theoretical principles are powerful tools to write equations that convey biological meaning. Let us provide a few examples.

• Cell theory implies that cells come from the proliferation of other cells and excludes spontaneous generation.
• Classical mechanics aims to understand movements in space. The acceleration of an object requires that a mechanical force is exerted on this object. Note that the principle of reaction states that if A exerts a force on B, then B exerts the same force with opposite direction on A. Therefore, there is an equivalence between “A exerts a force” and “a force is exerted on A” from the point of view of classical mechanics. The difficulty lies in the forces exerted by cells as cells can consume free energy to exert many kinds of forces. Cells are neither an elastic nor a bag of water, they possess agency which leads us to the next point.
• As explained in introduction, the reference to a default state helps to write equations that pertain to cellular behaviors. There are many aspects that contribute to cellular proliferation and motility. The writing of an equation such as the logistic model is not about all these factors and should not be interpreted as such. Instead, it assumes proliferation on the one side and one or several factors that constrain proliferation on the other side.

3.1 Model writing

Model writing may have different levels of precision and ambition. Models can be a proof of concept, that is to say the genuine proof that some hypotheses explain a given behavior or even proofs of the theoretical possibility of a behavior. Proof of concept do not include a complete proof that the natural phenomenon genuinely behave like the model. On the opposite end of the spectrum, models may aim at quantitative predictions. Usually, it is good practice to start from a crude model and after that to go for more detailed and quantitative analyses depending on the experimental possibilities.

We will now provide a short walkthrough for writing an initial model :

• Specify the aims of the model. Models cannot answer all questions at once, and it is crucial to be clear on the aim of a model before attempting to write it. Of course, these aims may be adjusted afterwards. The scope of the model should also depend on the experimental methods that link it to reality.
• Analyze the level of description that is mandatory for the model to explain the target phenomenon. Usually, the simplest the description is the better. When cells do not constrain each other, describing cells by their count n is sufficient. By contrast, if cells constrain each other, for example if they are in organized 3d structures it can be necessary to take into account the position of each individual cell which leads to a list of positions x → 1, x → 2, x → 3, . . . . Note that in this case the state space is far larger than before, see note 8 . A fortiori, it is necessary to represent space to understand morphogenesis. Note that the notion of level of description is different from the notion of scale. A level of description pertains to qualitative aspects such as the individual cell, the tissue, the organ, the organism, etc. By contrast, a scale is defined by a quantity.
• List the theoretical principles that are relevant to the phenomenon. These principles can be properly biological and pertain to cell theory, the notion of default state, biological organization or evolution. Physico-chemical principles may also be useful such as mechanics or the balance of chemical reactions.
• List the relevant states and parameters. These quantities are the ones that are expected to play a causal role that pertains to the aim of the model. This list will probably not be definitive, and will be adjusted in further steps. In all cases, we cannot emphasize enough that aiming for exhaustivity is the modeler’s worst enemy. Biologists need to take many factors into account when designing an experimental protocol, it is a mistake to try to model all of these factors.
• The crucial step is to propose mathematical relations between states and their changes. We have described in sections 2.2 and 2.3 what kinds of relation can be used. Usually these relations will involve supplementary parameters whose relevance was not obvious initially. Let us emphasize here that the key to robust models is to base it on sufficiently solid grounds. A model where all relations are heuristic will probably not be robust. As such, figuring out the robust and meaningful relations that can be used is crucial.
• The last step is to analyze the consequences of the model. We describe this step with more details below. What matters here is that the models may work as intended, in which case it may be refined by adding further details. The model may also lead to unrealistic consequences and not lead to the expected results. In these latter cases, the issue may lie in the formulation of the relations above, in the choice of the variables or in oversimplifications. In all cases the model requires a revision.

Writing a model is similar to the chess game in that the anticipation of all these steps from the beginning helps. The steps that we have described are all required but a central aspect of modeling is to gain a precise intuition of what determines the system’s behavior. Once this intuition is gained, it guides the specification of the model at all step. Reciprocally, these steps help to gain such an intuition.

3.2 Model analysis

In this section, we will not cover all the main ways to analyze model since this subject is far too vast and depends on the mathematical structures used in the models. Instead, we will focus on the outcome of model analyses.

3.2.1 Analytic methods

Analytic methods consist in the mathematical analysis of a model. They should always be preferred to simulations when the model is tractable, even at the cost of using simplifying hypotheses.

• Asymptotic reasoning is a fundamental method to study models. The underlying idea is that models are always a bit complicated. To make sense of them, we can look at the dynamics after enough time which simplifies the outcome. For example, the outcome of the logistic function discussed above will always be an equilibrium point, where the population is at a maximum. Mathematically, “enough” time means infinite time, hence the term asymptotic. In practice “infinite” means “large in comparison with the characteristic times of the dynamics”, which may not be long from a human point of view. For example, a typical culture of bacteria reaches a maximum after less than day. Asymptotic behaviors may be more complicated such as oscillations or strange attractors.
• Steady states analysis. In fairly complex situations, for example when both space and time are involved, a usual approach is to analyze states that are sustained over time. For example, in the analysis of epithelial morphogenesis, it is possible to consider how the shape of a duct is sustained over time.

Near 0, n= 0 + Δ n and dn ∕ dt ≃ Δ n ∕ τ . The small variation Δ n leads to a positive dn ∕ dt therefore this variation is amplified and this equilibrium is not stable. We should not forget the biology here. For a population of cells or animals of a given large size, a small variation is possible. However, a small variation from a population of size 0 is only possible through migration because spontaneous generation does not happen. Nevertheless this analysis shows that a small population, close to n=0 , should not collapse but instead will expand.

Near k , let us write n=k+ Δ n

• Special cases. In some situations, qualitatively remarkable behaviors appear for specific values of the parameters. Studying these cases is interesting per se, e ven though the odds for parameters to have specific value are slim without an explicit reason for this paramter to be set at this value. However, in biology the value of some parameters are the result of biological evolution and specific value can become relevant when the associated qualitative behavior is biologically meaningful [ 13 , 14 ].
• Parameter rewriting. One of the major practical advantages of analytical methods is to prove the relevance of parameters that are key to understand the behavior of a system. These “new” parameters are usually combinations of the initial parameters. We have implicitly done this operation in section 2.3 . Instead of writing an+bn 2 we have written n ∕ τ − n 2 ∕ k τ . The point here is to introduce τ the characteristic time for a cell division and k which is the maximum size of the population. By contrast, a and especially b are less meaningful. These key parameters and their meaning are an outcome of models and at the same time should be the target of precise experiments to explore the validity of models.

3.2.2 Numerical methods – simulations

Simulations have a major strength and a major weakness. Their strength lies in their ability to handle complicated situations that are not tractable analytically. Their weakness is that each simulation run provides a particular trajectory which cannot a priori be assumed to be representative of the dynamical possibilities of the model.

In this sense, the outcome of simulations may be compared to empirical results, except that simulation are transparent : it is possible to track all variables of interest over time. Of course, the outcome of simulations is artificial and only as good as the initial model.

Last, there is almost always a loss when going from a mathematical model to a computer simulation. Computer simulation are always about discrete objects and deterministic functions. Randomness and continua are always approximated in simulations and mathematical care is required to ensure that the qualitative features of simulations are feature of the mathematical model and not artifacts of the transposition of the model into a computer program. A subfield of mathematics, numerical analysis, is devoted to this issue.

3.2.3 Results

We want to emphasize two points to conclude this section.

First, it is not sufficient for a model to provide the qualitative or even quantitative behavior expected for this model to be correct. The validation of a model is based on the validation of a process and of the way this process takes place. As a result, it is necessary to explore the predictions of the model to verify them experimentally. All outcomes that we have described in 3.2.1 may be used to do so on top of a direct verification of the assumptions of the model themselves. Of course, it is never possible to verify everything experimentally, therefore the focus should be on aspects that are unlikely except in the light of the model.

Second, modeling focuses on a specific part and a specific process. However, this part and this process take place in an organism. Their physiological meaning, or possible lack thereof, should be analyzed. We are developing a framework to perform this kind of analysis [ 15 , 4 ] but it can also be performed informally by looking at the consequences of the part considered for the rest of the organism.

• In biology, behavior usually has an ethological meaning and evolution refers to the theory evolution. In the mathematical context, these words have a broader meaning. They both typically refer to the properties of dynamics. For example, the behavior of a population without constrain is exponential growth.
• Parameters that play a role in an equation are defined in two different ways. They are defined by their role in the equation and by their biological interpretation. For example, the division rate τ corresponds to the division rate of the cells without the constraint that is represented by k . τ may also embed constant constraints on cell proliferation, for example chemical constraints from the serum or the temperature. Thus, τ is what physicists call an effective parameter it carries implicitly constraints beyond the explicit constraints of the model.
• A state may be composed of several quantities, let’s say k, n, m . It is possible to write the state by the three quantities independently or to join them in one vector X=(k,n,m) . The two viewpoints are of course equivalent but they lead to different mathematical methods and ways to see the problem. The second viewpoint shows that it is always valid to consider that the state is a single mathematical object and not just a plurality of quantities.
• The notion of organization in the sense of a specific interdependence between parts [ 4 ] implies that most parameters are a consequence of others parts, at other time scales. As a result, modeling a given quantity as a parameter is only valid for some time scales, and is acceptable when these time scales are the ones at which the process modeled takes place.
• The choice between a model based on discrete or on continuous time is base on several criteria. For example, if the proliferation of cells is synchronized, there is a discrete nature of the phenomenon that strongly suggests to represent the dynamics in discrete time. In this case the discrete time corresponds to an objective aspect of the phenomenon. On the opposite, when cells divide at all times in the population, a representation in continuous time is more adequate. In order to perform simulations, time may still be discretized but the status of the discrete structure is then different than in the first case : discretization is then arbitrary and serves the purpose of approximating the continuum. To distinguish the two situations, a simple question should be asked. What is the meaning of the time difference between two time points. In the first case, this time difference has a biological meaning, in the second it is arbitrary and just small enough for the approximation to be acceptable.
• Probabilities over continuous possibilities are somewhat subtle. Let us show why : let us say that all directions are equivalent, thus all angles in the interval [0,360[ are equivalent. They are equivalent, so their probabilities are all the same value p. However, there is an infinite number of possible angles, so the sum of all the probabilities of all possibilities would be infinite. Over the continuum, probabilities are assigned to sets and in particular to intervals, not individual possibilities.
• There are many equivalent ways to write a mathematical term. The choice of a specific way to write a term conveys meaning and corresponds to an interpretation of this term. For example, in the text, we transformed dn ∕ dt=n ∕ τ − n 2 ∕ k τ because this expression has little biological meaning. By contrast, dn ∕ dt=n 1 − n ∕ k ∕ τ implies that when n/k is very small by comparison with 1, cells are not constraining each other. On the opposite, when n=k there is no proliferation. The consequence of cells constraining each other can be interpreted as a proportion 1-n/k of cells proliferating and a proportion n/k of cells not proliferating. Now, there is another way to write the same term which is : dn ∕ dt=n ∕ τ ∕ 1 − n ∕ k . Here, the division time becomes τ /(1-n/k) and the more cells there are, the longer the division time becomes. This division time becomes infinite when n=k which means that cells are quiescent. These two interpretations are biologically different. In the first interpretation, a proportion of cells are completely constrained while the other proliferate freely. In the second, all cells are impacted equally. Nevertheless, the initial term is compatible with both interpretations and they hhave the same consequences at this level of analysis.
• The number of quantities that form the state space is called its dimension. The dimension of the phase space is a crucial matter for its mathematical analysis. Basically, low dimensions such as 3 or below are more tractable and easier to represent. High dimensions may also be tractable if many dimensions play equivalent roles (even in infinite dimension). A large number of heterogeneous quantities (10 or 20) is complicated to analyze even with computer simulations because this situation is associated with many possibilities for the initial conditions and for the parameters making it difficult to “probe” the different qualitative possibilities of the model.
• It is very common in modeling to use the words “small” and “large”. A small (resp. large) quantity is a quantity that is assumed to be small (resp. large) enough so that a given approximation can be performed. For example, a large time in the context of the logistic equation means that the population is approximately at the maximum k . Similarly, infinite and large are very close notions in most practical cases. For example, a very large capacity k leads to dn ∕ dt=n ∕ τ 1 − n ∕ k ≃ n ∕ τ which is an exponential growth as long as n is far smaller than k.
• Beeman, D. (2013). Hodgkin-Huxley Model, pages 1–13. Encyclopedia of Computational Neuroscience. Springer New York, New York, NY. Doi : 10.1007/978-1-4614-7320-6_127-3
• Descartes, R. (2016). Discours de la méthode. Flammarion.
• Montévil, M., Mossio, M., Pocheville, A., and Longo, G. (2016a). Theoretical principles for biology : Variation. Progress in Biophysics and Molecular Biology, 122(1) : 36 – 50. Doi : 10.1016/j.pbiomolbio.2016.08.005
• Mossio, M., Montévil, M., and Longo, G. (2016). Theoretical principles for biology : Organization. Progress in Biophysics and Molecular Biology, 122(1) : 24 – 35. Doi : 10.1016/j.pbiomolbio.2016.07.005
• Noble, D. (2010). Biophysics and systems biology. Philosophical Transactions of the Royal Society A : Mathematical, Physical and Engineering Sciences, 368(1914) : 1125. Doi : 10.1098/rsta.2009.0245
• Sonnenschein, C. and Soto, A. (1999). The society of cells : cancer and control of cell proliferation. Springer Verlag, New York.
• Soto, A. M., Longo, G., Montévil, M., and Sonnenschein, C. (2016). The biological default state of cell proliferation with variation and motility, a fundamental principle for a theory of organisms. Progress in Biophysics and Molecular Biology, 122(1) : 16 – 23. Doi : 10.1016/j.pbiomolbio.2016.06.006
• Montévil, M., Speroni, L., Sonnenschein, C., and Soto, A. M. (2016b). Modeling mammary organogenesis from biological first principles : Cells and their physical constraints. Progress in Biophysics and Molecular Biology, 122(1) : 58 – 69. Doi : 10.1016/j.pbiomolbio.2016.08.004
• D’Anselmi, F., Valerio, M., Cucina, A., Galli, L., Proietti, S., Dinicola, S., Pasqualato, A., Manetti, C., Ricci, G., Giuliani, A., and Bizzarri, M. (2011). Metabolism and cell shape in cancer : A fractal analysis. The International Journal of Biochemistry & Cell Biology, 43(7) : 1052 – 1058. Metabolic Pathways in Cancer. Doi : 10.1016/j.biocel.2010.05.002
• Longo, G. and Montévil, M. (2014). Perspectives on Organisms : Biological time, symmetries and singularities. Lecture Notes in Morphogenesis. Springer, Dordrecht. Doi : 10.1007/978-3-642-35938-5
• Tjørve, E. (2003). Shapes and functions of species–area curves : a review of possible models. Journal of Biogeography, 30(6) : 827 – 835. Doi : 10.1046/j.1365-2699.2003.00877.x
• Hoehler, T. M. and Jorgensen, B. B. (2013). Microbial life under extreme energy limitation. Nat Rev Micro, 11(2) : 83 – 94. Doi : 10.1038/nrmicro2939
• Camalet, S., Duke, T., Julicher, F., and Prost, J. (2000). Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proceedings of the National Academy of Sciences, pages 3183 – 3188. Doi : 10.1073/pnas.97.7.3183
• Lesne, A. and Victor, J.-M. (2006). Chromatin fiber functional organization : Some plausible models. Eur Phys J E Soft Matter, 19(3) : 279 – 290. Doi : 10.1140/epje/i2005-10050-6
• Montévil, M. and Mossio, M. (2015). Biological organisation as closure of constraints. Journal of Theoretical Biology, 372(0) : 179 – 191. Doi : 10.1016/j.jtbi.2015.02.029

∗ Montévil M. (2018) A Primer on Mathematical Modeling in the Study of Organisms and Their Parts. In: Bizzarri M. (eds) Systems Biology. Methods in Molecular Biology, vol 1702. Humana Press, New York, NY. Doi : 10.1007/978-1-4939-7456-6_4

† Laboratoire "Matière et Systèmes Complexes" (MSC), UMR 7057 CNRS, Université Paris 7 Diderot, 75205 Paris Cedex 13, France and Institut d’Histoire et de Philosophie des Sciences et des Techniques (IHPST) - UMR 8590 Paris, France.

Loading metrics

Open Access

Essays articulate a specific perspective on a topic of broad interest to scientists.

See all article types »

Not Just a Theory—The Utility of Mathematical Models in Evolutionary Biology

* E-mail: [email protected]

Affiliation Department of Biology, University of North Carolina, Chapel Hill, North Carolina, United States of America

Affiliation Department of Plant Biology, University of Minnesota, Twin Cities, St. Paul, Minnesota, United States of America

Affiliation National Evolutionary Synthesis Center (NESCent), Durham, North Carolina, United States of America

Affiliation Department of Ecology, Evolution, and Behavior, University of Minnesota, Twin Cities, St. Paul, Minnesota, United States of America

Affiliations Department of Biology, University of North Carolina, Chapel Hill, North Carolina, United States of America, Santa Fe Institute, Santa Fe, New Mexico, United States of America

Affiliations National Evolutionary Synthesis Center (NESCent), Durham, North Carolina, United States of America, Department of Biology, University of Kentucky, Lexington, Kentucky, United States of America

• Maria R. Servedio, 
• Yaniv Brandvain, 
• Sumit Dhole, 
• Courtney L. Fitzpatrick, 
• Emma E. Goldberg, 
• Caitlin A. Stern, 
• Jeremy Van Cleve, 
• D. Justin Yeh

Published: December 9, 2014

• https://doi.org/10.1371/journal.pbio.1002017
• Reader Comments

Citation: Servedio MR, Brandvain Y, Dhole S, Fitzpatrick CL, Goldberg EE, Stern CA, et al. (2014) Not Just a Theory—The Utility of Mathematical Models in Evolutionary Biology. PLoS Biol 12(12): e1002017. https://doi.org/10.1371/journal.pbio.1002017

Copyright: © 2014 Servedio et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Funding: MRS was supported by the National Science Foundation (NSF) grants DEB-0919018 and DEB-1255777, and CF and JV were supported by the National Evolutionary Synthesis Center (NESCent), NSF EF-0423641. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Competing interests: The authors have declared that no competing interests exist.

Progress in science often begins with verbal hypotheses meant to explain why certain biological phenomena exist. An important purpose of mathematical models in evolutionary research, as in many other fields, is to act as “proof-of-concept” tests of the logic in verbal explanations, paralleling the way in which empirical data are used to test hypotheses. Because not all subfields of biology use mathematics for this purpose, misunderstandings of the function of proof-of-concept modeling are common. In the hope of facilitating communication, we discuss the role of proof-of-concept modeling in evolutionary biology.

A Conceptual Gap: Models and Misconceptions

Recent advances in many fields of biology have been driven by a synergistic approach involving observation, experiment, and mathematical modeling (see, e.g., [1] ). Evolutionary biology has long required this approach, due in part to the complexity of population-level processes and to the long time scales over which evolutionary processes occur. Indeed, the “modern evolutionary synthesis” of the 1930s and 40s—a pivotal moment of intellectual convergence that first reconciled Mendelian genetics and gene frequency change with natural selection—hinged on elegant mathematical work by RA Fisher, Sewall Wright, and JBS Haldane. Formal (i.e., mathematical) evolutionary theory has continued to mature; models can now describe how evolutionary change is shaped by genome-scale properties such as linkage and epistasis [2] , [3] , complex demographic variability [4] , environmental variability [5] , and individual and social behavior [6] , [7] within and between species.

Despite their integral role in evolutionary biology, the purpose of certain types of mathematical models is often questioned [8] . Some view models as useful only insofar as they generate immediately testable quantitative predictions [9] , and others see them as tools to elaborate empirically-derived biological patterns but not to independently make substantial new advances [10] . Doubts about the utility of mathematical models are not limited to present day studies of evolution—indeed, this is a topic of discussion in many fields including ecology [11] , [12] , physics [13] , and economics [14] , and has been debated in evolution previously [15] . We believe that skepticism about the value of mathematical models in the field of evolution stems from a common misunderstanding regarding the goals of particular types of models. While the connection between empiricism and some forms of theory (e.g., the construction of likelihood functions for parameter inference and model choice) is straightforward, the importance of highly abstract models—which might not make immediately testable predictions—can be less evident to empiricists. The lack of a shared understanding of the purpose of these “proof-of-concept” models represents a roadblock for progress and hinders dialogue between scientists studying the same topics but using disparate approaches. This conceptual gap obstructs the stated goals of evolutionary biologists; a recent survey of evolutionary biologists and ecologists reveals that the community wants more interaction between theoretical and empirical research than is currently perceived to occur [16] .

To promote this interaction, we clarify the role of mathematical models in evolutionary biology. First, we briefly describe how models fall along a continuum from those designed for quantitative prediction to abstract models of biological processes. Then, we highlight the unique utility of proof-of-concept models, at the far end of this continuum of abstraction, presenting several examples. We stress that the development of rigorous analytical theory with proof-of-concept models is itself a test of verbal hypotheses [11] , [17] , and can in fact be as strong a test as an elegant experiment.

Degrees of Abstraction in Evolutionary Theory

Good evolutionary theory always derives its motivation from the natural world and relates its conclusions back to biological questions. Building such theory requires different degrees of biological abstraction depending on the specific question. Some questions are best addressed by building models to interface directly with data. For example, DNA substitution models in molecular evolution can be built to take into account the biochemistry of DNA, including variation in guanine and cytosine (GC) content [18] and the structure of the genetic code [19] . These substitution models form the basis of the likelihood functions used to infer phylogenetic relationships from sequence data. Models can also provide baseline expectations against which to compare empirical observations (e.g., coalescent genealogies under simple demographic histories [20] or levels of genetic diversity around selective sweeps [21] ).

In contrast, higher degrees of abstraction are required when models are built to qualitatively, as opposed to quantitatively, describe a set of processes and their expected outcomes. Though not mathematical, verbal or pictorial models have long been used in evolutionary biology to form abstract hypotheses about processes that operate among diverse species and across vast time scales. Darwin's [22] theory of natural selection represents one such model, and many others have followed since; for example, Muller proposed that genetic recombination might evolve to prevent the buildup of deleterious mutations (“Muller's ratchet”) [23] , and the “Red Queen hypothesis” proposes that coevolution between antagonistically interacting species can proceed without either species achieving a long-term increase in fitness [24] . A clear verbal model lays out explicitly which biological factors and processes it is (and is not) considering and follows a chain of logic from these initial assumptions to conclusions about how these factors interact to produce biological patterns.

However, evolutionary processes and the resulting patterns are often complex, and there is much room for error and oversight in verbal chains of logic. In fact, verbal models often derive their influence by functioning as lightning rods for debate about exactly which biological factors and processes are (or should be) under consideration and how they will interact over time. At this stage, a mathematical framing of the verbal model becomes invaluable. It is this proof-of-concept modeling on which we focus below.

Proof-of-Concept Models: Testing Verbal Logic in Evolutionary Biology

Proof-of-concept models, used in many fields, test the validity of verbal chains of logic by laying out the specific assumptions mathematically. The results that follow from these assumptions emerge through the principles of mathematics, which reduces the possibility of logical errors at this step of the process. The appropriateness of the assumptions is critical, but once they are established, the mathematical analysis provides a precise mapping to their consequences.

A clear analogy exists between proof-of-concept models and other forms of hypothesis testing. In general, the hypotheses generated by verbal models must ultimately be tested as part of the scientific process ( Figure 1A ). Empirical research tests a hypothesis by gathering data in order to determine whether those data match predicted outcomes ( Figure 1B ). Proof-of-concept models function very similarly ( Figure 1C ): to test the validity of a verbal model, precise predictions from a mathematical analysis of the assumptions are compared against verbal predictions. This important function of mathematical modeling is commonly misunderstood, as theoreticians are often asked how they might test their proof-of-concept models empirically. The models themselves are tests of whether verbal models are sound; if their predictions do not match, the verbal model is flawed, and that form of the hypothesis is disproved.

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

This flowchart shows the steps in the scientific process, emphasizing the relationship between experimental empirical techniques and proof-of-concept modeling. Other approaches, including ones that combine empirical and mathematical techniques, are not shown. We note that some questions are best addressed by one or the other of these techniques, while others might benefit from both approaches. Proof-of-concept models, for example, are best suited to testing the logical correctness of verbal hypotheses (i.e., whether certain assumptions actually lead to certain predictions), while only empirical approaches can address hypotheses about which assumptions are most commonly met in nature. (A) A general description of the scientific process. (B) Steps in the scientific process as approached by experimental empirical techniques. In this case, statistical techniques are often used to analyze the gathered data. (C) Steps in the scientific process as approached by proof-of-concept modeling. Here, techniques such as invasion and stability analyses, stochastic simulations, and numerical analyses are employed to analyze the expected outcomes of a model. In both cases, the hypothesis can be evaluated by comparing the results of the analyses to the original predictions.

https://doi.org/10.1371/journal.pbio.1002017.g001

That is not to say, however, that proof-of-concept models do not need to interact with natural systems or with empirical work; in fact, quite the contrary is true. There are vital links between theory and natural systems at the assumption stage ( Box 1 ), and there can also be important connections at the predictions stage ( Box 2 ); connections also occur at the discussion stage, where empirical results are synthesized into a broader conceptual framework. Additionally, theoretical models often point to promising new directions for empirical research, even if these models do not provide immediately testable predictions (see below). When empirical results run counter to theoretical expectations, theorists and empiricists have an opportunity to discover unknown or underappreciated phenomena with potentially important consequences.

Box 1. A Critical Connection—Assumptions

Although the steps between assumptions and predictions in proof-of-concept models do not need to be empirically tested, empirical support is essential to ensure that key assumptions of mathematical models are biologically realistic. The process of matching assumptions to data is a two-way street; if a model demonstrates that a certain assumption is very important, it should motivate empirical work to see if it is met. Importantly, however, not all assumptions must be fully realistic for a model to inform our understanding of the natural world.

We can group assumptions into three general categories (with some overlap between them): we name these 1) critical, 2) exploratory, and 3) logistical. Critical assumptions are those that are integral to the hypothesis, analogous to the factors that an empirical scientist varies in an experiment (they would be part of the purple “hypothesis” box of Figure 1 ). These assumptions are crucial in order to properly test the verbal model; if they do not match the intent of the verbal hypothesis, then the mathematical model is not a true test of the verbal one. To illustrate this category of assumptions (and those below), consider the mathematical model by Rice [35] , which tests the verbal model that “antagonistic selection between the sexes can maintain sexual dimorphism.” In this model, assumptions that fall into the critical category are that (i) antagonistic selection at a locus results in higher fitness for alternate alleles in each sex, and (ii) sexual dimorphism results from a polymorphism between these alleles. If critical assumptions cannot be supported by underlying data or observation, and are therefore biologically unrealistic, then the entire modeling exercise is devoid of biological meaning [36] .

The second category, exploratory assumptions, may be important to vary and test, but are not at the core of the verbal hypothesis. These assumptions are analogous to factors that an empiricist wishes to control for, but that are not the primary variables. Examining the effects of these assumptions may give new insights and breadth to our understanding of a biological phenomenon. (These assumptions, and those below, might best fit in the blue “assumptions” box of Figure 1C .) Returning to Rice's [35] model of sexual dimorphism, two exploratory assumptions are the dominance relationship between the alleles under antagonistic selection and whether the locus is autosomal or sex linked. Analysis of the model shows that dominance does not affect the conditions for sexual dimorphism when the locus is autosomal, but it does when the locus is sex linked.

Finally, every mathematical modeling exercise requires that logistical assumptions be made. These assumptions are partly necessary for tractability. Additionally, proof-of-concept models in evolutionary biology, as in other fields, are not meant to replicate the real world; their purpose instead is to identify the effects of certain assumptions (critical and exploratory ones) by isolating them and placing them in a simplified and abstract context. A key to creating a meaningful model is to be certain that logistical assumptions made to reduce complexity do not qualitatively alter the model's results. In many cases, theoreticians know enough about the effects of an assumption to be able to make it safely. In Rice's [35] sexual dimorphism example, the logistical assumptions include random mating, infinitely large population size, and nonoverlapping generations. These are common and well-understood assumptions in many population genetic models. In other cases, the robustness of logistical assumptions must be tested in a specific model to understand their effects in that context. Because assumptions in mathematical models are explicit, potential limitations in applicability caused by the remaining assumptions can be identified; it is important that modelers acknowledge the potential effects of relaxing these assumptions to make these issues more transparent. As with the other categories of assumptions above, logistical assumptions have an analogy in empirical work; many experiments are conducted in lab environments, or under altered field conditions, with the same purpose of reducing biological complexity to pinpoint specific effects.

Much of the doubt about the applicability of models may stem from a mistrust of the effects of logistical assumptions. It is the responsibility of the theoretician to make his or her knowledge of the robustness of these assumptions transparent to the reader; it may not always be obvious which assumptions are critical versus logistical, and whether the effects of the latter are known. It is likewise the responsibility of the empirically-minded reader to approach models with the same open mind that he or she would an experiment in an artificial setting, rather than immediately dismiss them because of the presence of logistical assumptions.

Box 2. The Complete Picture—Testing Predictions

The predictions of some proof-of-concept models can be evaluated empirically. These tests are not “tests of the model”; the model is correct in that its predictions follow mathematically from its assumptions. They are, though, tests of the relevance or applicability of the model to empirical systems, and in that sense another way of testing whether the assumptions of the model are met in nature (i.e., an indirect test of the assumptions).

A well-known example of an empirical test of theoretically-derived predictions arises in local mate competition theory, which makes predictions about the sex ratio females should produce in their offspring in order to maximize fitness in structured populations, based on the intensity of local competition for mates [37] . These predictions have been assessed, for example, using experimental evolution in spider mites ( Tetranychus urticae ) [38] . The predictions of other evolutionary models might be best suited to comparative tests rather than tests in a single system. For example, inclusive fitness models suggest that, all else being equal, cooperation will be most likely to evolve within groups of close kin [6] . In support of this idea, comparative analyses suggest that mating with a single male (monandry), rather than polyandry, was the ancestral state for eusocial hymenoptera, meaning that this extreme form of cooperation arose within groups of full siblings [39] .

In other cases, comparative data might be very difficult to collect. Theoretical models, for example, have demonstrated that speciation is greatly facilitated if isolating mechanisms that occur before and after mating are controlled by the same genes (e.g., are pleiotropic) [40] . While this condition is found in an increasing number of case studies [41] , each case requires manipulative tests of selection and/or identification of specific genes, so that a rigorous comparative test of how often such pleiotropy is involved in speciation remains far in the future.

Proof-of-concept models can both bring to light hidden assumptions present in verbal models and generate counterintuitive predictions. When a verbal model is converted into a mathematical one, casual or implicit assumptions must be made explicit; in doing so, any unintended assumptions are revealed. Once these hidden assumptions are altered or removed, the predicted outcomes and resulting inferences of the formal model may differ from, or even contradict, those of the verbal model ( Box 3 ). This benefit of mathematical models has brought clarity and transparency to virtually all fields of evolutionary biology. Additionally, in spite of their abstract simplicity, proof-of-concept models, much like simple, elegant experiments, have the capacity to surprise. Even formalizations of seemingly straightforward verbal models can yield outcomes that are unanticipated using a verbal chain of logic ( Box 4 ). Proof-of-concept models thus have the ability both to reinforce the foundations of evolutionary explanations and to advance the field by introducing new predictions.

Box 3. Uncovering Hidden Assumptions

A striking example of the utility of mathematical models comes from the literature on the evolution of indiscriminate altruism (the provision of benefits to others, at a cost to oneself, without discriminating between partners who cooperate and partners who do not). Hamilton [6] proposed that indiscriminate altruism can evolve in a population if individuals are more likely to interact with kin. He also suggested that population viscosity—the limited dispersal of individuals from their birthplace—can increase the probability of interacting with kin. For a long time after Hamilton's original work, it was assumed, often without any explicit justification, that limited dispersal alone could facilitate the evolution of altruism [42] . A simple mathematical model by Taylor [43] , however, showed that population viscosity alone cannot facilitate the evolution of altruism, because the benefits of close proximity to kin are exactly balanced by the costs of competition with those kin. Taylor's model revealed the importance of kin competition and clarified that additional assumptions about life history, such as age structure and the timing of dispersal relative to reproduction, are required for population viscosity to promote (or even inhibit) the evolution of altruism.

Box 4. A Proof-of-Concept Model Finds a Flaw and Introduces a New Twist

In stalk-eyed flies, males' exaggerated eyestalks play two roles in sexual selection: they are used in male–male competition and are the object of female choice. Researchers noticed that generations of experimental selection for less exaggerated eyestalks resulted in males that fathered proportionally fewer sons than expected [44] . Both verbal intuition and preliminary evidence led the research group to propose that females preferred males with long eyestalks because this exaggerated trait resided on a Y chromosome that was resistant to an X chromosome driver with biased transmission [45] . However, a proof-of-concept model highlighted the flawed logic of this verbal model; the mathematical model showed that females choosing to mate with males bearing a drive-resistant Y chromosome (as putatively indicated by long eyestalks) would have lower fitness than nonchoosy females, and therefore this preference would not evolve [46] . In contrast, female choice for long eyestalks could be favored if long eyestalks were genetically associated with a nondriving allele at the (X-linked) drive locus [46] , so long as the eyestalk-length and drive loci were tightly linked [47] . These proof-of-concept models provided a new direction for empirical work, leading to the collection of new evidence demonstrating that the X-driver is linked to the eyestalk-length locus by an inversion [48] , with the nondriver and long eyestalk in coupling phase (i.e., on the same haplotype).

Investigating Evolutionary Puzzles through Proof-of-Concept Modeling

Proof-of-concept models have proven to be an essential tool for investigating some of the classic and most enduring puzzles in the study of evolutionary biology, such as “why is there sex?” and “how do new species originate?” These areas of research remain highly active in part because the relevant time scales are long and the processes are intricate. They represent excellent examples of topics in which mathematical approaches allow investigators to explore the effects of biologically complex factors that are difficult or impossible to manipulate experimentally.

Why Is There Sex?

A century after Darwin [25] published his comprehensive treatment of sexual reproduction, John Maynard Smith [26] used a simple mathematical formalization to identify a biological paradox: why is sexual reproduction ubiquitous, given that asexual organisms can reproduce at a higher rate than sexual ones by not producing males (the “2-fold cost of sex”)? Increased genetic variation resulting from sexual reproduction is widely thought to counteract this cost, but simple proof-of-concept models quickly revealed both a flaw in this verbal logic and an unexpected outcome: sex need not increase variation, and even when it does, the increased variation need not increase fitness [27] . Subsequent theoretical work has illuminated many factors that facilitate the evolution and maintenance of sex. Otto and Nuismer [28] , for example, used a population genetic model to examine the effects on the evolution of sex of antagonistic interactions between species. Such interactions were long thought to facilitate the evolution of sex [29] , [30] . They found, however, that these interactions only select for sex under particular circumstances that are probably relatively rare. Although these predictions might be difficult to test empirically, their implications are important for our conceptual understanding of the evolution of sex.

How Do New Species Originate?

Speciation is another research area that has benefitted from extensive proof-of-concept modeling. Even under the conditions most unfavorable to speciation (e.g., continuous contact between individuals from diverging types), one can weave plausible-sounding verbal speciation scenarios [22] . Verbal models, however, can easily underestimate the strength of biological factors that maintain species cohesion (e.g., gene flow and genetic constraints). Mathematical models have allowed scientists to explicitly outline the parameter space in which speciation can and cannot occur, highlighting many critical determinants of the speciation process that were previously unrecognized [31] . Felsenstein [32] , for example, revolutionized our understanding of the difficulties of speciation with gene flow by using a proof-of-concept model to identify hitherto unconsidered genetic constraints. Speciation models in general have made it clear that the devil is in the details; there are many important biological conditions that combine to determine whether speciation is more or less likely to occur. Because speciation is exceedingly difficult to replicate experimentally, theoretical developments such as these have been particularly valuable.

Pitfalls and Promise

Although mathematical models are potentially enlightening, they share with experimental tests the danger of possible overinterpretation. Mathematical models can clearly outline the parameter space in which an evolutionary phenomenon such as speciation or the evolution of sex can occur under certain assumptions, but is this space “big” or “little”? As with any scientific study, the impression that a model leaves can be misleading, either through faults in the presentation or improper citation in subsequent literature.

Overgeneralization from what a model actually investigates, and claims to investigate, is strikingly common in this age when time for reading is short [33] , and this problem is exacerbated when the presentation is not accessible to readers with a more limited background in theoretical analysis [34] . Indeed, these problems, universal to many fields of science, introduce the greatest potential for error in the conclusions that the research community draws from evolutionary theory.

We follow this word of caution with a final positive thought: in addition to the roles of mathematical models in testing verbal logic, the ability of theory to circumvent practical obstructions of experimental tractability in order to tackle virtually any problem is a benefit that should not be underestimated. Science is a quest for knowledge, and if a problem is, at least currently, empirically intractable, it is very unsatisfactory to collectively throw up our hands and accept ignorance. Surely it is far better, in such cases, to use mathematical models to explore how evolution might have proceeded, illuminating the conditions under which certain evolutionary paths are possible.

Acknowledgments

We thank Haven Wiley, Ben Haller, and Mark Peifer for stimulating discussion and insightful comments on the manuscript.

• View Article
• Google Scholar
• 7. Frank SA (1998) Foundations of Social Evolution. Princeton: Princeton University Press. 268 pp.
• 9. Peters RH (1991) A Critique for Ecology. Cambridge: Cambridge University Press. 366. pp
• 17. Kokko H (2007) Modelling for Field Biologists and other Interesting People. Cambridge: Cambridge University Press. 230 pp.
• 22. Darwin C (1859) The Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: J. Murray. 490 pp
• 25. Darwin CR (1878) The effects of cross and self-fertilisation in the vegetable kingdom. 2nd edition. London: J. Murray.
• 26. Smith JM (1978) The Evolution of Sex. Cambridge: Cambridge University Press. 236 pp
• 31. Coyne JA, Orr HA (2004) Speciation. Sunderland: Sinauer Associates. 545. pp
• 40. Gavrilets S (2004) Fitness Landscapes and the Origin of Species. Princeton: Princeton University Press. 476 pp.

HYPOTHESIS AND THEORY article

Strong inference in mathematical modeling: a method for robust science in the twenty-first century.

• 1 Department of Microbiology, University of Tennessee, Knoxville, TN, USA
• 2 Department of Mathematics, University of Tennessee, Knoxville, TN, USA
• 3 National Institute for Mathematical and Biological Synthesis, University of Tennessee, Knoxville, TN, USA

While there are many opinions on what mathematical modeling in biology is, in essence, modeling is a mathematical tool, like a microscope, which allows consequences to logically follow from a set of assumptions. Only when this tool is applied appropriately, as microscope is used to look at small items, it may allow to understand importance of specific mechanisms/assumptions in biological processes. Mathematical modeling can be less useful or even misleading if used inappropriately, for example, when a microscope is used to study stars. According to some philosophers ( Oreskes et al., 1994 ), the best use of mathematical models is not when a model is used to confirm a hypothesis but rather when a model shows inconsistency of the model (defined by a specific set of assumptions) and data. Following the principle of strong inference for experimental sciences proposed by Platt (1964) , I suggest “strong inference in mathematical modeling” as an effective and robust way of using mathematical modeling to understand mechanisms driving dynamics of biological systems. The major steps of strong inference in mathematical modeling are (1) to develop multiple alternative models for the phenomenon in question; (2) to compare the models with available experimental data and to determine which of the models are not consistent with the data; (3) to determine reasons why rejected models failed to explain the data, and (4) to suggest experiments which would allow to discriminate between remaining alternative models. The use of strong inference is likely to provide better robustness of predictions of mathematical models and it should be strongly encouraged in mathematical modeling-based publications in the Twenty-First century.

1. The Core of Mathematical Modeling

What is the use of mathematical modeling in biology? The answer likely depends on the background of the responder as mathematicians or physicists may have a different answer than biologists, and the answer may also depend on the researcher's definition of a “model.” In some cases models are useful for estimation of parameters underlying biological processes when such parameters are not directly measurable. For example, by measuring the number of T lymphocytes over time and by utilizing a simple model, assuming exponential growth, we can estimate the rate of expansion of T cell populations ( De Boer et al., 2001 ). In other cases, making the model may help think more carefully about contribution of multiple players and their interactions in the observed phenomenon. In general, however, mathematical models are most useful when they provide important insights into underlying biological mechanisms. In this opinion article, I would to provide my personal thoughts on the current state and future of mathematical modeling in biology with the focus on the dynamics of infectious diseases. As a disclosure I must admit that I am taking an extreme, provocative view, based on personal experience as a reader and a reviewer. I hope that this work will generate the much needed discussion on uses and misuses of mathematical models in biology and perhaps will result in quantitative data on this topic.

In my experience, in the area of dynamical systems/models of the within-host and between-host dynamics of infectious diseases, the two most commonly given answers to the question of the “use of mathematical models” are (1) models help us understand biology better; and (2) models help us predict the impact of interventions (e.g., gene knockouts/knockins, cell depletions, vaccines, treatments) on the population dynamics. Although there is some truth to these answers the way mathematical modeling in biology is generally taught and applied rarely allows one to better understand biology. In some cases mathematical models generate predictions which are difficult or impossible to test, the latter making such models unscientific per the definition of a scientific theory according to one of the major philosophers of science in the Twentieth Century Karl Popper ( Popper, 2002 ). Moreover, mathematical modeling may result in questionable recommendations for public health-related policies. My main thesis is that while, in my experience, much of current research in mathematical biology is aimed at finding the right model for a given biological system, we should pay more attention to understanding which biologically reasonable models do not work, i.e., are not able to describe the biological phenomenon in question. According to Karl Popper, proving a given hypothesis to be correct is impossible while rejecting hypotheses is feasible ( Oreskes et al., 1994 ; Popper, 2002 ).

What is a mathematical model? In essence, mathematical model is a hypothesis regarding a phenomenon in question. While any specific model always has an underlying hypothesis (or in some cases, a set of hypotheses), the converse is not true as multiple mathematical models could be formulated for a given hypothesis. In this essay I will use words “hypothesis” and “model” interchangeably. The core of a mathematical model is the set of model assumptions. These assumptions could be based on some experimental observations or simply be a logical thought based on everyday experience. For example, for an ordinary differential equation (ODE)-based model, the assumptions are the formulated equations which include functional terms of interactions between species in the model, parameters associated with these functions, and initial conditions of the model. The utility of mathematics lies in our ability to logically follow from the assumptions to conclusions on the system's dynamics. Thus, mathematical modeling is a logical path from a set of assumptions to conclusions. Such a logical path from axioms to theorems was termed by some as a mathematical revolution in the Twentieth Century ( Quinn, 2012 ). However, while in mathematics it is vital to formulate a complete set of axioms/assumptions to establish verifiable, true statements such as theorems ( Quinn, 2012 ), a complete set of assumptions is impossible in any biology-based mathematical model due to the openness of biological systems (or any other natural system, Oreskes et al., 1994 ). Therefore, biological conclusions stemming from analysis of mathematical models are inherently incomplete and are in general strongly dependent on the assumptions of the model ( De Boer, 2012 ). While such dependency of model conclusions on model assumptions may be viewed as a weakness but it is instead the most significant strength of mathematical modeling! By varying model assumptions one can vary model predictions and subsequently by comparing predictions to experimental observations, sets of assumptions which generate predictions consistent and inconsistent with the data can be identified. This is the core of mathematical modeling which can provide profound insights into biological processes. While it is often possible to provide mechanistic explanations for some biological phenomena from intuition—and many biologists do it—it is often hard to identify sets of implicit assumptions made during such a verbal process. Mathematical modeling by requiring one to define the model specifies such assumptions explicitly. Inherent to this interpretation of mathematical modeling is the need to consider multiple sets of assumptions (or models) to determine which are consistent and, more importantly, which are not consistent with experimental observations. Rather than a thorough expedition to test multiple alternative models, in my experience as a reader and a reviewer many studies utilizing mathematical modeling in biology have been a quest to find (and analyze) a single “correct” model.

I would argue that studies in which a single model was considered and in which the developed model was not rigorously tested against experimental data, do not provide robust biological insights (see below). Pure mathematical analysis of the model and its behavior (e.g., often performed steady state stability analyses for ODE-based models) often provides little insight into the mechanisms driving dynamics in specific biological systems. Failure to consider alternative models often results in biased interpretation of biological observations. Let me give two examples.

Discussion of predator-prey interactions in ecology often starts with the Lotka-Volterra model which is built on very simple and yet powerful basic assumptions ( Mooney and Swift, 1999 ; Kot, 2001 ). The dynamics of the model can be understood analytically and predictions on the dynamics of predator and prey abundances can be easily generated. The observation of the hares and lynx dynamics in Canada has been often presented as evidence that predator-prey interactions driven the dynamics of this biological system ( Mooney and Swift, 1999 ). While it is possible that the dynamics was driven by predator-prey interactions, recent studies also suggest that the dynamics could be driven by self-regulating factors and weather activities influencing independently each of the species ( Brauer and Castillo-Chávez, 2001 ; Zhang et al., 2007 ). A more robust modeling approach would be to start with observations of lynx and hare dynamics and ask about biological mechanisms which could be driving such dynamics including predator-prey interactions, seasonality, or both ( Hilborn and Mangel, 1997 ). The data can then be used to test which of these sets of assumptions is more consistent with experimental data using standard model selection tools ( Burnham and Anderson, 2002 ).

In immunology, viral infections often lead to generation of a large population of virus-specific effector CD8 T cells, and following clearance of the infection, there is formation of memory CD8 T cells ( Ahmed and Gray, 1996 ; Kaech and Cui, 2012 ). However, how memory CD8 T cells are formed during the infection has been a subject of a debate ( Ahmed and Gray, 1996 ). One of the earlier models assumed that memory precursors proliferate during the infection and produce terminally differentiated, nondividing effector T cells, which then die following clearance of the infection ( Wodarz et al., 2000 ; Bocharov et al., 2001 ; Wodarz and Nowak, 2002 ; Fearon et al., 2006 ). While this model was used to explain several biological phenomena, later studies have shown that this model failed to accurately explain experimental data on the dynamics of CD8 T cell response to lymphocytic choriomengitis virus ( Antia et al., 2005 ; Ganusov, 2007 ). More precisely, the model was able to accurately fit experimental data but it required unphysiologically rapid interdivision time for activated CD8 T cells [e.g., 25 min in Ganusov (2007) ] which was inconsistent with other measurements made to date. Constraining the interdivision time to a larger value (e.g., 3 h) resulted in a poor model fit of the data. Therefore, development of adequate mathematical models cannot be all based on “basic principles” and must include comparison with quantitative experimental data.

These examples illustrate how mathematical modeling can teach us about mechanisms underlying biological processes. When a model is developed using some basic biological assumptions/mechanisms and yet such a model is unable to accurately describe quantitative biological data, we learn something. We learn that the mechanisms that we thought should be important in explaining the phenomenon are incorrect (or that we modeled them incorrectly). In this case, modeling provides important information that some aspects of biology that we thought we knew we actually do not know. In the case of memory CD8 T cell differentiation, the poor assumption was that effector T cells do not proliferate ( Ganusov, 2007 ). An alternative situation is when it is believed that only one mechanism explains a biological phenomenon, and yet several different models can be formulated and all models are able to accurately describe experimental data. Again, such a result would illustrate that specific data can be explained by more than one mechanism and additional experiments are needed to further discriminate between alternative models. Although this has not been formally done, two alternative mechanisms (predator-prey and seasonality) may be reasonable explanations of the hare-lynx dynamics in Canada.

2. Strong Inference in Mathematical Modeling

Strong inference was proposed over 50 years ago to promote rapid science ( Platt, 1964 ). Platt suggested that despite a commonly spread “…polite fiction that all science is equal…some areas of science progress faster than others” ( Platt, 1964 ). Platt (1964) proposed that by choosing well formulated questions and hypotheses and by designing discriminatory experiments, one can progress faster with understanding of the underlying phenomena. According to strong inference, the following steps must be taken to investigate a given scientific question ( Platt, 1964 ):

1. Devising alternative hypotheses;

2. Devising a crucial experiment (or several of them), with alternative possible outcomes, each of which will, as nearly as possible, exclude one or more of the hypotheses;

3. Carrying out the experiment so as to get a clean result;

1'. Recycling the procedure, making subhypotheses or sequential hypotheses to refine the possibilities that remain; and so on.

These recommendations were highly influential as judged by the number of citation (1439 in Web of Science or 2867 in Google scholar as of April 5th, 2016); however, it does not appear that they have been widely adopted in biological sciences ( Jewett, 2005 ). Two major points of these recommendations include (1) formulation of a set of alternative hypotheses and (2) attempt to reject, not to confirm, these hypotheses. The idea of formulating multiple hypotheses goes back to another important paper on “The method of multiple working hypotheses” ( Chamberlin, 1890 ) which recently received an update ( Elliott and Brook, 2007 ). The idea of testing hypotheses to reject them goes back to Karl Popper, who proposed that falsification of hypotheses is the core of the scientific method ( Popper, 2002 ). Strong inference received its share of criticism suggesting that it cannot be applied in some areas of research and that it does not promote rapid science ( O'Donohue and Buchanan, 2001 ). Indeed, testing n > 1 multiple hypotheses is unlikely to provide rapid progress because it would probably take n times longer to find the answer as compared to that if there were only one hypothesis to start with. However, strong inference will likely result in more robust results than results based on a single hypothesis, and therefore, overall, multiple hypotheses-driven research provides more rapid progress for the field as it cuts out early wrong leads. One author suggested that the use of strong inference may occur more frequently in industry than in academia due to a higher focus of industrial research on robustness rather than novelty ( Ehlers, 2016 ). Robust conclusions rather than novel results are also viewed as a feature of good scientists both by general public and professional researchers ( Ebersole et al., 2016 ).

In my view, not all mathematical modeling studies are equal and some provide better insights into biological mechanisms than others. By extending Platt's ideas to mathematical modeling I propose the following steps for “strong inference in mathematical modeling” in biology:

1. For a given biological question and associated experimental data, formulate several alternative mathematical models aimed at explaining the data;

2. Compare model predictions with experimental data with the goal of excluding as many of the alternative models as possible;

3. For the rejected models, determine reasons why the models were not able to accurately describe the data;

4. For the models that are consistent with the data, generate predictions for experiments which would allow one to discriminate between these alternative models;

1'. As new data are available, recycle the procedure by making sub-models, alternative models, and so on.

To avoid misinterpretation two issues must be explained further: what different models are and what it means to reject a model.

There are two levels at which alternative models can be defined. One is the basic/core mechanism of the mathematical model and another is specific model formulations within such a core mechanism. Using hare-lynx dynamics as an example, two core mechanisms could include predator-prey interactions or season-driven dynamics. (Perhaps the reader already came up with a third core mechanism?) Using a given specific core mechanism one now can write different formulations of the model, for example, how predator consumes the prey and how the prey biomass translates into predator biomass. Multiple formulations are possible and these all are alternative models, and yet they all have the same basic core mechanism. In essence, the model core is an equivalent of the main hypothesis responsible for the observed phenomenon. Similarly, seasonality can enter the model directly assuming time-dependent birth/death rates of hares and lynx or indirectly by assuming time-dependent variability in resources. These formulations also can be viewed as alternative models. Rejection of a specific mathematical model does not necessarily invalidate the core mechanism but rejection of a set of alternative models based on a given core mechanism will raise doubts whether such a core mechanism is responsible for the observed phenomenon. The best use of strong inference is a rejection of a core mechanism.

Criteria of model rejection are not well established and rejection can be done on absolute or relative grounds. When comparing model predictions and data one could ask if the model is adequately describing the data. Two tests could be of particular importance such as goodness of fit test and lack of fit test ( Bates and Watts, 1988 ). These tests require data with sufficient richness but in some cases, incompatibility between model and data can be determined ( Noecker et al., 2015 ). When using a set of alternative models other tests such as likelihood ratio test or information criteria (AIC, BIC, etc.) can be also used ( Bates and Watts, 1988 ; Burnham and Anderson, 2002 ; Johnson and Omland, 2004 ) to determine which of the models are less likely to be consistent with the data. Similarly, comparison with data may allow to reject a core mechanism or more commonly, reject specific formulations of the core mechanism. Issues associated with identifiability of mathematical models and precise estimation of model parameters in some case may not allow to reject specific models ( Meshkat et al., 2009 ; Raue et al., 2009 ).

Proper application of strong inference in mathematical modeling depends critically on choosing a “good” question which has only a limited number of possible core mechanisms. It is clear that “big” fundamental questions often have many potential answers ( O'Donohue and Buchanan, 2001 ) and from the perspective of strong inference, big questions can rarely be exhaustively explored. As continuous application of the method of multiple working hypotheses “develops a habit of parallel or complex thought” ( Chamberlin, 1890 ), continuous application of strong inference allows development of a skill of asking the “good” questions and recognition when asked questions are “bad.”

As the method of multiple working hypotheses has a “danger of vacillation” ( Chamberlin, 1890 ), strong inference may fail when none of the alternative models can be rejected. In fact, it has been argued that inability to reject hypotheses/models may be a feature of ecological studies ( Hobbs and Hilborn, 2006 ). One proposed solution is to use model averaging where predictions of different models are “weighted” based on the models' consistency with experimental data ( Hoeting et al., 1999 ; Burnham and Anderson, 2002 ). Model averaging is not without problems, however, including situations where alternative models generate contradictory predictions ( Grueber et al., 2011 ). In my view, inability to apply principles of strong inference to reject some of the alternative models indicates two potential problems: (1) the data are poor and insufficient to discriminate between alternative models (so more and better data need to be collected), and (2) the formulated question is “bad” (so a better formulated question is needed).

One useful example of the use of strong inference comes from the analysis of movement patterns of activated CD8 T cells in murine brains ( Harris et al., 2012 ). Using intravital imaging the authors recorded coordinates of T cells in the brain over long periods of time. By comparing predictions of multiple mathematical models the authors concluded that only one in the list of several alternative models, based on generalized Levy walks, could explain all data with reasonable quality ( Harris et al., 2012 ). Future studies utilizing further strong inference would need to discriminate between cell-intrinsic vs. environment-driven core mechanisms explaining this type of walk of T cells in the brain.

With principles of strong inference the power of mathematical modeling can be truly revealing. Closer collaborations between experimentalists and modelers leading to discrimination between alternative models using data would likely result in substantial robust gains in our understanding of biological processes.

3. Dangers of Single Hypothesis/Model-Driven Research

While scientific benefits of multiple hypotheses/models-driven research are hard to deny, dangers of using single hypotheses in research have not been widely emphasized. Already in 1890, Chamberlin (1890) warned about biases resulting from “dominant theory” or “single hypothesis”-driven research and why thinking in terms of multiple hypotheses must extend beyond science and be common practice for everyone in the world. I would like to present three examples, in which single hypothesis/mathematical model-driven research limits and sometimes biases our understanding of biology. These examples represent my hypothesis on limited robustness of single mathematical model-based studies; this hypothesis will have to be tested and perhaps rejected in the future.

3.1. Biased Predictions

One of the virtues of mathematical models is often cited their predictive power. Indeed, mathematical models are used to make predictions in many areas of science including biology. The types of models used to make predictions vary in their complexity from simple, few equations-based models to models including hundreds of variables. How robust are predictions of such models? My thesis is that predictions based on a single mathematical model are unlikely to be robust ( De Boer, 2012 ).

Recently, Evans et al. (2013) questioned whether general, very simple models are useful in making quantitative predictions on vital, public-health related issues. The authors argued that such general models by design are relatively simple and are aimed at describing as many situations as possible. The authors also argued that models that are designed for specific systems and parameterized from specific experimental data, are likely to be more precise in predictions. Such case-specific models are thought to be more useful in guiding policies for control of infectious diseases ( Evans et al., 2013 ). The authors illustrated their point by discussing the predictions of two mathematical models on the level of vaccination required to eradicate rabies in the fox populations in Europe ( Anderson et al., 1981 ; Eisinger and Thulke, 2008 ). Evans et al. (2013) argued that simple, susceptible-infected-recovered mathematical model overestimated the level of vaccination needed for rabies eradication ( Anderson et al., 1981 ). Such a simple model predicted that 70% of foxes had to be vaccinated for efficient control. A more complex model, including details of the local spread of the infection from rabid to susceptible foxes, predicted a lower vaccination level of 60% ( Eisinger and Thulke, 2008 ). Although such a 10% difference may appear small, Eisinger and Thulke (2008) suggested that the vaccination campaign based on the prediction of the simple model may have cost over several millions of euros more than was needed. The authors concluded that in order to make public health-related predictions for a specific biological system, the models should include sufficient detail about that system so the model predictions are accurate and precise ( Evans et al., 2013 ). Thus, predictions of a single model may not be robust, and in some cases, predicted interventions may cost more than needed.

Another example comes from early predictions of potential size of the Ebola virus epidemics in Africa in 2014–2016 ( Butler, 2014 ). Initial studies by considering simple models predicted devastating impact of the epidemic on human population which luckily did not occur ( Butler, 2014 ; Pandey et al., 2014 ). Later analyses revealed that simple models were inadequate by ignoring potential heterogeneity in behavior which translated into large variability in transmission efficacy ( Drake et al., 2015 ). Although there is a consensus that mathematical modeling is needed to understand biological phenomena including epidemiology of infectious diseases ( Lofgren et al., 2014 ), non-robust model predictions which overestimate risks are perhaps even more harmful than models that underestimate the risks. In fact, good modeling practice is in general to provide minimal estimates of the risk. Examples of wrong predictions may fuel unwarranted public debate on trustworthiness of mathematical models, for example, predicting climate change. Taken together, studies that are based on the analysis of a single model are not expected to produce robust predictions ( Oreskes et al., 1994 ). Predictive studies illustrating which alternative models have been considered in the analysis, which models have been rejected and why, and whether predictions of the remaining models are self-consistent, will lead to robust predictions and should be encouraged.

3.2. Unreproducible Science

The great feature of science is its self-correcting nature. Some theories have persisted for decades but have been shown later to be incorrect as new ideas and data accumulated. While exceptions clearly exist and there are still common myths despite experimental evidence otherwise ( Scudellari, 2015 ), science has been mostly self-correcting. I would argue that in some cases consideration of a single hypothesis and failure to consider and reject alternatives has caused dominance of an eventually wrong theory. In some cases, self-correction in sciences took long time with resources wasted and lives affected. One example is on the development of understanding of motions of planets with a complete dominance of Ptolemy's theory of immotile Earth with Sun and planets moving in circular orbits ( Danielson and Graney, 2014 ). If Tycho Brahe, one of the major astronomers collecting data to support Ptolemy's circular orbits-based theory, and other scientists at the time considered alternatives of elliptic circles and movable Earth, perhaps science would progress faster, reach more robust conclusions, and Bruno and Galileo would not have suffered ( Danielson and Graney, 2014 ). There is more recent, perhaps an extreme example of a crime conviction of an innocent person based on consideration of a single hypothesis ( Nuzzo, 2015 ).

The common practice of considering a single hypothesis and collecting data to “prove” it can bias interpretation and may result in unreproducible results. In recent years it has been noted by several groups of investigators that many of the results in biological sciences are unreproducible ( Prinz et al., 2011 ; Begley and Ellis, 2012 ; Collaboration, 2015 ; Freedman and Gibson, 2015 ; Freedman et al., 2015 ). In particular, biotech company Amgen attempted to reproduce 53 “landmark” papers from cancer biology and was able to reproduce only 6 ( Begley and Ellis, 2012 ). Overall, a recent review suggests that at least 50% of reanalyzed studies are unreproducible ( Freedman et al., 2015 ). If these findings can be extrapolated to the whole field of biomedical research one study estimates that over $28B are wasted on unreproducible studies, and half of those expenditures are suggested to result from inappropriate study design and data analysis ( Freedman et al., 2015 ).

It remains unknown whether reproducibility of mathematical modeling-based studies is different from that of science in general (or biology in particular, Boulesteix et al., 2015 ). For example, one recent study could reproduce less than half of bioinformatic analyses of published microarray gene expression data ( Ioannidis et al., 2009 ). The definition of reproducibility may be difficult in general as it may vary by researcher ( Goodman et al., 2016 ). For one type of mathematical modeling studies which do not involve any experimental data we generally expect full reproducibility if the authors correctly wrote and analyzed their model and/or appropriately simulated its dynamics. However, programing errors may still occur. A lower level of reproducibility may be expected for studies utilizing both mathematical models and analysis of experimental data. I analyzed a subset of data from a recent survey by Nature ( Baker, 2016 ) by focusing on responses by scientists from the field of “Biology” with expertise in “Bioinformatics and Computational Biology” ( n 1 = 36) or “Systems Biology” ( n 2 = 9, n = n 1 + n 2 = 45 surveys in total). I found that computational biologists are at least as skeptical about the state of reproducibility of studies in their fields as compared to all scientists surveyed. In particular, computational biologists believe that on average only 50% of studies in their field are reproducible (compared to 58% for general population, Mann-Whitney test, p = 0.02), 27% believe that computational biology has similar level of reproducibility compared to other fields (vs. 21% for all scientists, χ ( 1 ) 2 = 0 . 76 , p = 0.38), and 73% of computational biologists believe that failure to reproduce results is the major problem in the field (as compared to 59% of all scientists surveyed, χ ( 1 ) 2 = 3 . 85 , p = 0.05). Interestingly, 20% of computational biologists were told that someone could not reproduce their work (vs. 18% for all scientists, χ ( 1 ) 2 = 0 . 12 , p = 0.73). Thus, there is a general concern about the level of reproducibility of mathematical modeling-based studies.

A large number of unreproducible studies is paralleled by a recent increase in percentage of retracted peer-reviewed papers ( Fang et al., 2012 ; Grieneisen and Zhang, 2012 ; Fanelli, 2013 ; Castillo, 2014 ). While increased scrutiny of published papers may have contributed to the rise in the number of retracted articles ( Fanelli, 2013 ), the increased competition in research, especially in biomedical sciences, leading to the “publish-or-perish” culture is a very like cause for the growing number of unreproducible studies and retracted papers ( Steen et al., 2013 ). The number of retracted mathematical modeling-based papers remains relatively low (a simple search for “mathematical model” on RetractionWatch.com yielded under ten hits as of April 5th, 2016).

The need for more robust ways of doing science, including mathematical modeling, is well recognized ( Begley and Ellis, 2012 ; Fang and Casadevall, 2012 ). By focusing mathematical modeling analyses on a single model and by showing qualitative consistency of the model and data we commit a cognitive/confirmation bias ( Kaptchuk, 2003 ; Editorial, 2015 ). Confirmation bias appears to be widespread in the mathematical modeling literature where consistency of a model with experimental observations occurs much more frequently than rejection of models. Even in cases when model predictions match qualitatively other, potentially independent data, there is a risk of so-called “therapeutic illusion” ( Casarett, 2016 ), an inability to recognize that alternative mechanisms, not included in the model, could explain additional data too. Several suggestions have been made to improve reproducibility and robustness of science including use of strong inference ( Nuzzo, 2015 ), improved trainings ( Moher and Altman, 2015 ), performing blind analyses of the data ( MacCoun and Perlmutter, 2015 ), the need for independent analyses of the same data/models by different teams prior to publication ( Silberzahn and Uhlmann, 2015 ), and standardization of tools ( Baker, 2015 ). There is also a need to reduce overoptimistic reporting in mathematical modeling-based studies ( Boulesteix, 2015 ) and reduce uncertainties in predictions of mathematical models ( Kirk et al., 2015 ). The use of principles of strong inference should increase robustness of predictions of mathematical models and in general, should reduce the amount of unreproducible research in biology.

3.3. Development of Large Models

The formulation and analysis of multiple alternative mathematical models can clearly increase robustness of conclusions and improve our ability to make accurate predictions. Robustness of predictions of mathematical models for public health-related policies is particularly important. To avoid the need to formulate multiple alternative models for a given phenomenon researchers often construct models that include many of known mechanisms in the biological system of interest. Such a model is then expected to be able to explain a large number of different phenomena, and there is a hope that at some choice of parameters the model behavior will capture true biological forces at play. Such a model is viewed as useful to make specific predictions of the impact of interventions on population dynamics ( Bru and Cardona, 2010 ; Cilfone et al., 2015 ). This trend for “systems” view on biological phenomena is becoming more popular and it is now being questioned whether simple models which include only a few major details about biological system are useful in making relevant forecasts ( Evans et al., 2013 ). One of the major problems of large and complex models is that by including many mechanisms and details these models become as complex as phenomena they are trying to explain precluding detailed understanding of such models. Furthermore, by including multiple details such large models can rarely if ever be rejected which essentially makes them unscientific per Karl Popper ( Popper, 2002 ; Ellis and Silk, 2014 ).

Large complex models are often compared to data to illustrate their plausibility. However, with tens to hundreds of parameters complex models can easily explain one or several datasets. Such model overfitting of the data should never be viewed as model confirmation ( Oreskes et al., 1994 ). Only few parameters are needed to generate complex patterns as famous saying states: “with four parameters I can fit an elephant, and with five, I can make him wiggle his trunk” ( Mayer et al., 2010 ; Ditlev et al., 2013 ). Development of large, complex models can be useful if such models show inconsistency of specific mechanisms with sets of experimental observations. Predictions of large models should be treated with caution unless it has been established which alternative models/mechanisms have been rejected during model development ( Oreskes et al., 1994 ). Iterative process of model development, testing, and calibration using sufficiently extensive datasets may result in large mathematical models of robust predictive power; mathematical models predicting weather are one good example ( Bauer et al., 2015 ). Yet, even well calibrated weather prediction models have reasonable accuracy only for relatively short-term predictions ( Bauer et al., 2015 ).

4. Changing Training in Mathematical Biology

Given intuitive benefits of multiple models-driven research it is perhaps strange to realize that it remains quite rare. In part this is due to widely adopted approach to find models which explain phenomena. I believe that “the approach to find the right model” starts very early in education of a mathematical biologist, probably during undergraduate or early graduate career. Many of the classical textbooks on mathematical modeling in biology have a similar theme: (1) identify a biological problem, (2) develop a mathematical model for the problem; the degree of complexity of the model should depend on the complexity of the problem and/or underlying biology, (3) analyze the model; (4) draw the conclusions from the model behaviors and extrapolate the conclusions to the actual biological system ( Segel, 1984 ; Mooney and Swift, 1999 ; Kot, 2001 ; Ellner and Guckenheimer, 2006 ; Vries et al., 2006 ; Percus, 2012 ). In this approach the developed model is often treated as a very good representation of the actual biological system and rarely the basic assumptions of the model are challenged. Education in physics and engineering proceeds in a similar fashion where complex mathematical models are derived from basic principles which are accepted to be true either because of some fundamental experiments or simply because of intuition. This approach, although being relatively straightforward, fosters an impression that if one starts with a good set of assumptions this will lead to a model which should not be questioned. Experimental data are often brought as support of the model, and when the model predictions are consistent with some, often qualitative data, the model appears to be a strong reflection of the reality ( Simberloff, 2007 ). However, rarely the basic feature of mathematical models—that predictions are the direct consequences of the model assumptions—is investigated thoroughly by identifying model assumptions which are most critical for the “consistency” between the model and experimental observations, and which assumptions would allow the model to “fail” at explaining the data. Furthermore, in many cases consistency between models and data is indicated by qualitative or semi-quantitative comparison which does not allow to investigate in a rigorous sense whether the model is indeed an accurate enough representation of the data ( Jin et al., 1999 ; Wang et al., 2015 ).

While many methods are likely to improve robustness of mathematical modeling-based (and other scientific) studies, the widespread use of strong inference is likely to be important in this endeavor ( Nuzzo, 2015 ). Design of multiple alternative models forces the researcher to deeply understand the underlying biological question and not be satisfied with standard answers that “this is well known” but to require solid experimental support for major model assumptions. Education of future generations of students in mathematical modeling should focus more on deeper understanding of biological details and on investigating which aspects of their models could be wrong. If we substitute “theory” with “model,” it was very nicely said by Ellis and Silk (2014) that research often “boils down to clarifying one question: what potential observational or experimental evidence is there that would persuade you that the theory is wrong and lead you to abandoning it? If there is none, it is not a scientific theory.” Finding boundaries when the model “breaks” at explaining the phenomenon in question would reveal limitations of the model and of its predictions. Therefore, future mathematical modelers should be able to understand details of biological experiments, how the data are collected and analyzed, so such data are used with most efficiency for model development and testing. Such training thus must extend beyond traditional education in mathematics, engineering, and computer science .

One of the major difficulties with multiple models-driven research and strong inference is to identify the number of alternative models/hypotheses one needs to consider to satisfy principles of strong inference ( Platt, 1964 ). Choosing a “good” question is key in this process. Wise application of strong inference requires selection of “good” questions for which only a limited number of alternative hypotheses (or core mechanisms) exist ( Platt, 1964 ). Choosing the “good” question is an endeavor and skill on its own; it is a part of scientific method and it requires specific training. Education in mathematical modeling should focus more on developing skills on identifying biological problems which have a limited number of possible answers and which can be addressed using mathematical modeling. For example, if one finds too many alternative explanations for his/her question, perhaps he/she is not asking a “good” question. In practice, consideration of two or more models would be likely to be better than study with a single model, and formulation and analysis of models with alternative core mechanisms is most preferable per strong inference.

It has to be realized that predictions of any single model for a biological system are not likely to be robust due to inherent openness of biological systems ( Oreskes et al., 1994 ). Therefore, any single model is very limited in its use. However, a collection of alternative models is more likely to generate robust predictions; alternatively, analysis of such models could suggest inability to make robust predictions due to lack of appropriate data to reject alternative models. In this case, such multiple models-driven analysis may suggest areas for further experimental investigations. The idea of limited robustness of mathematical models in describing biological phenomena needs to be percolated in educational curriculum of undergraduate and graduate students, and this notion needs to be more widely stated in the professional modeling community. Realization that for every biological problem there are likely several alternative mechanisms/models needs to be eventually translated in research where it is not acceptable anymore to have a publication with only one mathematical model analyzed. We need to see mathematical biology research to move to the stage where in most publications the authors propose multiple models and discriminate between these models using quantitative biological data. Education of future generation of mathematical modelers must include training in building of alternative mathematical models and in techniques to discriminate between alternative models using experimental data ( Burnham and Anderson, 2002 ; Johnson and Omland, 2004 ). When presented with results from a mathematical modeling-based study we should always ask the question (adapted from Platt, 1964 ): “But Sir/Madam, which mathematical models/mechanisms have you rejected in your study?”

Training of a new generation of scientists in mathematical biology should involve more reading and discussion of the basics of scientific method. Three papers are of particular importance and they should form the core of the graduate curriculum in graduate schools and specifically, of programs on mathematical modeling ( Chamberlin, 1890 ; Platt, 1964 ; Oreskes et al., 1994 ). While I have discussed the ideas of the papers by Chamberlin (1890) and Platt (1964) , an essay by Oreskes et al. (1994) clearly defined usefulness and limitations of mathematical modeling of open natural systems. In particular, the authors strongly cautioned against use of the words “verification” and “validation” to indicate “quality” of mathematical models as these terms exaggerate the limited ability of models to make robust predictions. In fact, “verification” of models is impossible per word definition due to the openness of natural systems, and in most cases the use of the word “validation” is synonymous to “verification” and thus is also inappropriate. The authors discussed in detail why verification/validations of models (or any logical statement) is impossible in natural sciences, and highlighted many philosophical developments on the nature of scientific method in the early Twentieth Century that is rarely discussed in graduate programs nowadays.

An important component of learning about mathematical modeling in biology is a realization that good modeling requires good understanding of the developed mathematical models. When does one understand the model, in a true sense of understanding? I believe that for simple models with a few parameters, true understanding is realized when one intuitively can predict the impact of the change in a model parameter or a combination of parameters on the model dynamics. Such an detailed understanding of the model also allows for insights in situations when the model is not able to fit/describe experimental data—i.e., why isn't the model able to explain experimental data? What is wrong with it? Deeper understanding of the model can point to parts of the model that are responsible for such discrepancy. Intuitive understanding of the model is very difficult or impossible for models with tens to hundreds of parameters. Yet, such an understanding is needed if the model fails to explain well some experimental data. How can one understand such a model? The traditional approach for understanding complex models is sensitivity analysis ( Marino and Kirschner, 2004 ). Sensitivity analysis can allow to rank parameters of the model or the combination of parameters in terms of their impact on behavior of specific model components, e.g., density of species at some time point. I would argue, however, that in many cases sensitivity analyses do not give a good understanding of the model behavior because answers may depend on the method used and because sensitivity analysis often does not specify why this and not another parameter is the most important in the model dynamics. However, analyses which provide rational explanations of why specific parameters or parameter combinations drive model dynamics will likely reveal relative importance of different biological mechanisms. Education of future mathematical modelers should include basics of sensitivity analyses and understanding when such analyses are informative and when they are not .

5. Conclusions

A simple and effective critique of multiple hypotheses/models-driven research is to make counter examples of studies utilizing a single mathematical model and yet providing important biological insights. For instance, very well known studies utilizing a single ODE-based mathematical model estimated the rate of turnover of HIV and HIV-infected cells ( Ho et al., 1995 ; Wei et al., 1995 ). Although the success of this pioneering work to accurately estimate the life-span of infected cells is well known, the failure of the model to accurately predict turnover of CD4 T cells due to incorrect assumption of CD4 T cell recovery due to production of new T cells is rarely acknowledged ( Ho et al., 1995 ; Pabst and Rosenberg, 1998 ; Bucy et al., 1999 ). Furthermore, because we tend to remember “winners” and forget “losers,” it is very likely that many predictions of single mathematical modeling-based studies are incorrect or not robust to changes in the model assumption. It would be useful to generate data on the frequency of “correct" vs. “incorrect” predictions of studies based on single vs. multiple mathematical models although it may be difficult to define “correctness” of predictions.

Even in the absence of such data I propose that in order for mathematical modeling to become more robust, more practical and relevant for infectious disease biology we, mathematical modelers, need to re-think how we do research and how we train new generations of students. It is possible that the current format in which students, taking mathematical modeling in biology courses, get exposed to sets of standard models and their properties needs to be changed to observation-driven training where students develop models to explain particular experimental observations. Basic biological principles can be used to drive the development of models with variable levels of complexity and models the alternative mechanisms. Comparison to quantitative experimental data then can be used to test which of the models (i.e., mechanisms) are not consistent with the data and why ( Popper, 2002 ).

Given that mathematical models are increasingly playing an important role in policy decision making ( Christley et al., 2013 ), it is the time to change the way many mathematicians approach modeling, and we need to change the way we teach mathematical modeling at universities. Devising as many as possible alternative models for every biological question and comparing model predictions with quantitative experimental data to reject the models will allow mathematical modeling to become a scientific procedure generating more robust predictions.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I would like to thank many colleagues who have influenced my view on mathematical modeling including Rustom Antia, Rob De Boer, Alan Perelson, past and present members of my group, Sivan Leviyang for comments on earlier versions of the paper, and reviewers who raised important points on uses of mathematical modeling. This work was in part supported by the AHA grant to VG.

Ahmed, R., and Gray, D. (1996). Immunological memory and protective immunity: understanding their relation. Science 272, 54–60. doi: 10.1126/science.272.5258.54

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, R. M., Jackson, H. C., May, R. M., and Smith, A. M. (1981). Population dynamics of fox rabies in Europe. Nature 289, 765–771. doi: 10.1038/289765a0

CrossRef Full Text | Google Scholar

Antia, R., Ganusov, V. V., and Ahmed, R. (2005). The role of models in understanding CD8+ T-cell memory. Nat. Rev. Immunol. 5, 101–111. doi: 10.1038/nri1550

Baker, M. (2015). Reproducibility crisis: blame it on the antibodies. Nature 521, 274–276. doi: 10.1038/521274a

Baker, M. (2016). Is there a reproducibility crisis? Nature 533, 452–454. doi: 10.1038/533452a

Bates, D. M., and Watts, D. G. (1988). Nonlinear Regression Analysis and Its Applications. Hoboken, NJ: John Wiles & Sons, Inc. doi: 10.1002/9780470316757

CrossRef Full Text

Bauer, P., Thorpe, A., and Brunet, G. (2015). The quiet revolution of numerical weather prediction. Nature 525, 47–55. doi: 10.1038/nature14956

Begley, C. G., and Ellis, L. M. (2012). Drug development: raise standards for preclinical cancer research. Nature 483, 531–533. doi: 10.1038/483531a

Bocharov, G., Klenerman, P., and Ehl, S. (2001). Predicting the dynamics of antiviral cytotoxic T-cell memory in response to different stimuli: cell population structure and protective function. Immunol. Cell. Biol. 79, 74–86. doi: 10.1046/j.1440-1711.2001.00985.x

Boulesteix, A.-L. (2015). Ten simple rules for reducing overoptimistic reporting in methodological computational research. PLoS Comput. Biol. 11:e1004191. doi: 10.1371/journal.pcbi.1004191

Boulesteix, A.-L., Stierle, V., and Hapfelmeier, A. (2015). Publication bias in methodological computational research. Cancer Inform. 14(Suppl 5), 11–19. doi: 10.4137/CIN.S30747

Brauer, F., and Castillo-Chávez, C. (2001). Mathematical Models in Population Biology and Epidemiology, Texts in Applied Mathematics . New York, NY: Springer.

Google Scholar

Bru, A., and Cardona, P.-J. (2010). Mathematical modeling of tuberculosis bacillary counts and cellular populations in the organs of infected mice. PLoS ONE 5:e12985. doi: 10.1371/journal.pone.0012985

Bucy, R. P., Hockett, R. D., Derdeyn, C. A., Saag, M. S., Squires, K., Sillers, M., et al. (1999). Initial increase in blood CD4(+) lymphocytes after HIV antiretroviral therapy reflects redistribution from lymphoid tissues. J. Clin. Invest. 103, 1391–1398. doi: 10.1172/JCI5863

Burnham, K. P., and Anderson, D. R. (2002). Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. New York, NY: Springer-Verlag.

Butler, D. (2014). Models overestimate Ebola cases. Nature 515:18. doi: 10.1038/515018a

Casarett, D. (2016). The science of choosing wisely–overcoming the therapeutic illusion. New Engl. J. Med. 374, 1203–1205. doi: 10.1056/NEJMp1516803

Castillo, M. (2014). The fraud and retraction epidemic. AJNR Am. J. Neuroradiol. 35, 1653–1654. doi: 10.3174/ajnr.A3835

Chamberlin, T. C. (1890). The method of multiple working hypotheses: with this method the dangers of parental affection for a favorite theory can be circumvented. Science 15, 92–96.

Christley, R. M., Mort, M., Wynne, B., Wastling, J. M., Heathwaite, A. L., Pickup, R., et al. (2013). “Wrong, but useful”: negotiating uncertainty in infectious disease modelling. PLoS ONE 8:e76277. doi: 10.1371/journal.pone.0076277

Cilfone, N. A., Ford, C. B., Marino, S., Mattila, J. T., Gideon, H. P., Flynn, J. L., et al. (2015). Computational modeling predicts IL-10 control of lesion sterilization by balancing early host immunity-mediated antimicrobial responses with caseation during Mycobacterium tuberculosis infection. J. Immunol. 194, 664–677. doi: 10.4049/jimmunol.1400734

Collaboration, O. S. (2015). PSYCHOLOGY. Estimating the reproducibility of psychological science. Science 349:aac4716. doi: 10.1126/science.aac4716

Danielson, D., and Graney, C. M. (2014). The case against Copernicus. Sci. Am. 310, 72–77. doi: 10.1038/scientificamerican0114-72

De Boer, R. J. (2012). Which of our modeling predictions are robust? PLoS Comput. Biol. 8:e1002593. doi: 10.1371/journal.pcbi.1002593

De Boer, R. J., Oprea, M., Antia, R., Murali-Krishna, K., Ahmed, R., and Perelson, A. S. (2001). Recruitment times, proliferation, and apoptosis rates during the CD8(+) T-cell response to lymphocytic choriomeningitis virus. J. Virol. 75, 10663–10669. doi: 10.1128/JVI.75.22.10663-10669.2001

Ditlev, J. A., Mayer, B. J., and Loew, L. M. (2013). There is more than one way to model an elephant. Experiment-driven modeling of the actin cytoskeleton. Biophys. J. 104, 520–532. doi: 10.1016/j.bpj.2012.12.044

Drake, J. M., Kaul, R. B., Alexander, L. W., O'Regan, S. M., Kramer, A. M., Pulliam, J. T., et al. (2015). Ebola cases and health system demand in Liberia. PLoS Biol. 13:e1002056. doi: 10.1371/journal.pbio.1002056

Ebersole, C. R., Axt, J. R., and Nosek, B. A. (2016). Scientists' reputations are based on getting it right, not being right. PLoS Biol. 14:e1002460. doi: 10.1371/journal.pbio.1002460

Editorial (2015). Let's think about cognitive bias. Nature 526:163. doi: 10.1038/526163a

PubMed Abstract | CrossRef Full Text

Ehlers, M. D. (2016). Lessons from a recovering academic. Cell 165, 1043–1048. doi: 10.1016/j.cell.2016.05.005

Eisinger, D., and Thulke, H.-H. (2008). Spatial pattern formation facilitates eradication of infectious diseases. J. Appl. Ecol. 45, 415–423. doi: 10.1111/j.1365-2664.2007.01439.x

Elliott, L. P., and Brook, B. W. (2007). Revisiting chamberlin: multiple working hypotheses for the 21st century. BioScience 57, 608–614. doi: 10.1641/B570708

Ellis, G., and Silk, J. (2014). Defend the integrity of physics. Nature 516, 321–323. doi: 10.1038/516321a

Ellner, S. P., and Guckenheimer, J. (2006). Dynamics Models in Biology . Princeton, NJ: Princeton University Press.

Evans, M. R., Grimm, V., Johst, K., Knuuttila, T., de Langhe, R., Lessells, C. M., et al. (2013). Do simple models lead to generality in ecology? Trends Ecol. Evol. 28, 578–583. doi: 10.1016/j.tree.2013.05.022

Fanelli, D. (2013). Why growing retractions are (mostly) a good sign. PLoS Med. 10:e1001563. doi: 10.1371/journal.pmed.1001563

Fang, F. C., and Casadevall, A. (2012). Reforming science: structural reforms. Infect. Immun. 80, 897–901. doi: 10.1128/IAI.06184-11

Fang, F. C., Steen, R. G., and Casadevall, A. (2012). Misconduct accounts for the majority of retracted scientific publications. Proc. Natl. Acad. Sci. U.S.A 109, 17028–17033. doi: 10.1073/pnas.1212247109

Fearon, D., Carr, J., Telaranta, A., Carrasco, M., and Thaventhiran, J. (2006). The rationale for the IL-2-independent generation of the self-renewing central memory CD8+ T cells. Immunol. Rev. 211, 104–118. doi: 10.1111/j.0105-2896.2006.00390.x

Freedman, L. P., Cockburn, I. M., and Simcoe, T. S. (2015). The economics of reproducibility in preclinical research. PLoS Biol. 13:e1002165. doi: 10.1371/journal.pbio.1002165

Freedman, L. P., and Gibson, M. C. (2015). The impact of preclinical irreproducibility on drug development. Clin. Pharmacol. Ther. 97, 16–18. doi: 10.1002/cpt.9

Ganusov, V. V. (2007). Discriminating between different pathways of memory CD8+ T cell differentiation. J. Immunol. 179, 5006–5013. doi: 10.4049/jimmunol.179.8.5006

Goodman, S. N., Fanelli, D., and Ioannidis, J. P. A. (2016). What does research reproducibility mean? Sci. Transl. Med. 8, 1–6. doi: 10.1126/scitranslmed.aaf5027

Grieneisen, M. L., and Zhang, M. (2012). A comprehensive survey of retracted articles from the scholarly literature. PLoS ONE 7:e44118. doi: 10.1371/journal.pone.0044118

Grueber, C. E., Nakagawa, S., Laws, R. J., and Jamieson, I. G. (2011). Multimodel inference in ecology and evolution: challenges and solutions. J. Evol. Biol. 24, 699–711. doi: 10.1111/j.1420-9101.2010.02210.x

Harris, T. H., Banigan, E. J., Christian, D. A., Konradt, C., Wojno, E. D. T., Norose, K., et al. (2012). Generalized Lévy walks and the role of chemokines in migration of effector CD8+ T cells. Nature 486, 545–548. doi: 10.1038/nature11098

Hilborn, R., and Mangel, M. (1997). The Ecological Detective: Confronting Models with Data . Princeton NJ: Princeton University Press.

Ho, D., Neumann, A., Perelson, A., Chen, W., Leonard, J., and Markowitz, M. (1995). Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 373, 123–126. doi: 10.1038/373123a0

Hobbs, N. T., and Hilborn, R. (2006). Alternatives to statistical hypothesis testing in ecology: a guide to self teaching. Ecol. Appl. 16, 5–19. doi: 10.1890/04-0645

Hoeting, J. A., Madigan, D., Raftery, A. E., and Volinsky, C. T. (1999). Bayesian model averaging: a tutorial. Stat. Sci. 14, 382–401.

Ioannidis, J. P. A., Allison, D. B., Ball, C. A., Coulibaly, I., Cui, X., Culhane, A. C., et al. (2009). Repeatability of published microarray gene expression analyses. Nat. Genet. 41, 149–155. doi: 10.1038/ng.295

Jewett, D. L. (2005). What's wrong with single hypotheses?: why it is time for strong-inference-PLUS. Scientist 19:10.

PubMed Abstract | Google Scholar

Jin, X., Bauer, D. E., Tuttleton, S. E., Lewin, S., Gettie, A., Blanchard, J., et al. (1999). Dramatic rise in plasma viremia after CD8(+) T cell depletion in simian immunodeficiency virus-infected macaques. J. Exp. Med. 189, 991–998. doi: 10.1084/jem.189.6.991

Johnson, J. B., and Omland, K. S. (2004). Model selection in ecology and evolution. Trends Ecol. Evol. 19, 101–108. doi: 10.1016/j.tree.2003.10.013

Kaech, S. M., and Cui, W. (2012). Transcriptional control of effector and memory CD8+ T cell differentiation. Nat. Rev. Immunol. 12, 749–761. doi: 10.1038/nri3307

Kaptchuk, T. J. (2003). Effect of interpretive bias on research evidence. BMJ 326, 1453–1455. doi: 10.1136/bmj.326.7404.1453

Kirk, P. D. W., Babtie, A. C., and Stumpf, M. P. H. (2015). SYSTEMS BIOLOGY. Systems biology (un)certainties. Science 350, 386–388. doi: 10.1126/science.aac9505

Kot, M. (2001). Elements of Mathematical Ecology . Cambridge, UK: Cambridge University Press. doi: 10.1017/cbo9780511608520

Lofgren, E. T., Halloran, M. E., Rivers, C. M., Drake, J. M., Porco, T. C., Lewis, B., et al. (2014). Opinion: mathematical models: a key tool for outbreak response. Proc. Natl. Acad. Sci. U.S.A. 111, 18095–18096. doi: 10.1073/pnas.1421551111

MacCoun, R., and Perlmutter, S. (2015). Blind analysis: hide results to seek the truth. Nature 526, 187–189. doi: 10.1038/526187a

Marino, S., and Kirschner, D. (2004). The human immune response to M ycobacterium tuberculosis in lung and lymph node. J. Theor. Biol. 227, 463–486. doi: 10.1016/j.jtbi.2003.11.023

Mayer, J., Khairy, K., and Howard, J. (2010). Drawing an elephant with four complex parameters. Am. J. Phys. 78, 648–649. doi: 10.1119/1.3254017

Meshkat, N., Eisenberg, M., and Distefano, III. J. J. (2009). An algorithm for finding globally identifiable parameter combinations of nonlinear ODE models using Gröbner Bases. Math. Biosci. 222, 61–72. doi: 10.1016/j.mbs.2009.08.010

Moher, D., and Altman, D. G. (2015). Four proposals to help improve the medical research literature. PLoS Med. 12:e1001864. doi: 10.1371/journal.pmed.1001864

Mooney, D., and Swift, R. (1999). A Course in Mathematical Modeling . Mathematical Association of America.

Noecker, C., Schaefer, K., Zaccheo, K., Yang, Y., Day, J., and Ganusov, V. V. (2015). Simple mathematical models do not accurately predict early SIV dynamics. Viruses 7, 1189–1217. doi: 10.3390/v7031189

Nuzzo, R. (2015). How scientists fool themselves - and how they can stop. Nature 526, 182–185. doi: 10.1038/526182a

O'Donohue, W., and Buchanan, J. A. (2001). The weaknesses of strong inference. Behav. Philos. 29, 1–20.

Oreskes, N., Shrader-Frechette, K., and Belitz, K. (1994). Verification, validation, and confirmation of numerical models in the Earth sciences. Science 263, 641–646. doi: 10.1126/science.263.5147.641

Pabst, R., and Rosenberg, Y. J. (1998). Interpreting data on lymphocyte subsets in the blood of HIV patients - organ distribution, proliferation and migration kinetics are critical factors. Pathobiology 66, 117–122. doi: 10.1159/000028006

Pandey, A., Atkins, K. E., Medlock, J., Wenzel, N., Townsend, J. P., Childs, J. E., et al. (2014). Strategies for containing Ebola in West Africa. Science 346, 991–995. doi: 10.1126/science.1260612

Percus, J. (2012). Mathematical Methods in Immunology, Courant Lecture Notes Series . American Mathematical Soc.

Platt, J. R. (1964). Strong inference: certain systematic methods of scientific thinking may produce much more rapid progress than others. Science 146, 347–353. doi: 10.1126/science.146.3642.347

Popper, K. (2002). The logic of scientific discovery . New York, NY: Routledge Classics. Taylor & Francis.

Prinz, F., Schlange, T., and Asadullah, K. (2011). Believe it or not: how much can we rely on published data on potential drug targets? Nat. Rev. Drug Discov. 10:712. doi: 10.1038/nrd3439-c1

Quinn, F. (2012). A revolution in mathematics? What really happened a century ago and why it matters today. Notices AMS 59, 31–37. doi: 10.1090/noti787

Raue, A., Kreutz, C., Maiwald, T., Bachmann, J., Schilling, M., Klingmüller, U., et al. (2009). Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 25, 1923–1929. doi: 10.1093/bioinformatics/btp358

Scudellari, M. (2015). The science myths that will not die. Nature 528, 322–325. doi: 10.1038/528322a

Segel, L. A. (1984). Modeling Dynamic Phenomena in Molecular and Cellular Biology . New York, NY: Cambridge University Press.

Silberzahn, R., and Uhlmann, E. L. (2015). Crowdsourced research: many hands make tight work. Nature 526, 189–191. doi: 10.1038/526189a

Simberloff, D. (2007). An angry indictment of mathematical modeilng. Bioscience 57, 884–885.

Steen, R. G., Casadevall, A., and Fang, F. C. (2013). Why has the number of scientific retractions increased? PLoS ONE 8:e68397. doi: 10.1371/journal.pone.0068397

Vries, G. D., Hillen, T., Lewis, M., and Schõnfisch, B. (2006). A Course in Mathematical Biology: Quantitative Modeling with Mathematical and Computational (Monographs on Mathematical Modeling and Computation) . SIAM. doi: 10.1137/1.9780898718256

Wang, S., Hottz, P., Schechter, M., and Rong, L. (2015). Modeling the slow CD4+ T cell decline in HIV-infected individuals. PLoS Comput. Biol. 11:e1004665. doi: 10.1371/journal.pcbi.1004665

Wei, X., Ghosh, S., Taylor, M., Johnson, V., Emini, E., Deutsch, P., et al. (1995). Viral dynamics in human immunodeficiency virus type 1 infection. Nature 373, 117–122. doi: 10.1038/373117a0

Wodarz, D., May, R. M., and Nowak, M. A. (2000). The role of antigen-independent persistence of memory cytotoxic T lymphocytes. Int. Immunol. 12, 467–477. doi: 10.1093/intimm/12.4.467

Wodarz, D., and Nowak, M. A. (2002). Mathematical models of HIV pathogenesis and treatment. Bioessays 24, 1178–1187. doi: 10.1002/bies.10196

Zhang, Z., Tao, Y., and Li, Z. (2007). Factors affecting harelynx dynamics in the classic time series of the Hudson Bay Company, Canada. Clim. Res. 34, 83–89. doi: 10.3354/cr034083

Keywords: robust science, mathematical modeling, immunology, microbiology, public health, scientific method

Citation: Ganusov VV (2016) Strong Inference in Mathematical Modeling: A Method for Robust Science in the Twenty-First Century. Front. Microbiol . 7:1131. doi: 10.3389/fmicb.2016.01131

Received: 22 April 2016; Accepted: 07 July 2016; Published: 22 July 2016.

Reviewed by:

Copyright © 2016 Ganusov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Vitaly V. Ganusov, [email protected]

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Introduction to Mathematical Modelling

What is a Mathematical Model? #

A mathematical model is a mathematical representation of a system used to make predictions and provide insight about a real-world scenario, and mathematical modelling is the process of constructing, simulating and evaluating mathematical models.

Why do we construct mathematical models? It can often be costly (or impossible!) to conduct experiments to study a real-world problem and so a mathematical model is a way to describe the behaviour of a system and predict outcomes using mathematical equations and computer simulations .

Check out the following resources to get started with mathematical modelling:

Chapter 1: What is Mathematical Modelling? in Principles of Mathematical Modeling

What is Math Modeling?

Wikipedia: Mathematical Model

Outline of the Modelling Process #

Mathematical modelling involves observing some real-world phenomenon and formulating a mathematical representation of the system. But how do we even know where to start? Or how to find a solution? The modelling process is a systematic approach:

Clearly state the problem

Identify variables and parameters

Make assumptions and identify constraints

Build solutions

Analyze and assess

Report the results

Models can have a wide range of complexity ! More complex does not necessarily mean better and we can sometimes work with more simplistic models to achieve good results. In many instances, we often start with a simple model and then build-up the complexity by iterating through the steps in modelling process until the model accurately describes the real-world application.

Check out Math Modeling: Getting Started and Getting Solutions to read more about the modelling process.

Types of Models #

There are many different types of mathematical models! In this course we focus on the following:

Deterministic models predict future based on current information and do not include randomness. These kinds of models often take the from of systems of differential equations which describe the evolution of a system over time.

Stochastic models include randomness and are based on probability distributions and stochastic processes .

Data-driven models look for patterns in observed data to predict the output of a system. These kinds of models often take the form of functions with parameters computed to fit observed data.

• Search Menu
• Browse content in Arts and Humanities
• Browse content in Archaeology
• Anglo-Saxon and Medieval Archaeology
• Archaeological Methodology and Techniques
• Archaeology by Region
• Archaeology of Religion
• Archaeology of Trade and Exchange
• Biblical Archaeology
• Contemporary and Public Archaeology
• Environmental Archaeology
• Historical Archaeology
• History and Theory of Archaeology
• Industrial Archaeology
• Landscape Archaeology
• Mortuary Archaeology
• Prehistoric Archaeology
• Underwater Archaeology
• Urban Archaeology
• Zooarchaeology
• Browse content in Architecture
• Architectural Structure and Design
• History of Architecture
• Residential and Domestic Buildings
• Theory of Architecture
• Browse content in Art
• Art Subjects and Themes
• History of Art
• Industrial and Commercial Art
• Theory of Art
• Biographical Studies
• Byzantine Studies
• Browse content in Classical Studies
• Classical History
• Classical Philosophy
• Classical Mythology
• Classical Literature
• Classical Reception
• Classical Art and Architecture
• Classical Oratory and Rhetoric
• Greek and Roman Epigraphy
• Greek and Roman Law
• Greek and Roman Archaeology
• Greek and Roman Papyrology
• Late Antiquity
• Religion in the Ancient World
• Digital Humanities
• Browse content in History
• Colonialism and Imperialism
• Diplomatic History
• Environmental History
• Genealogy, Heraldry, Names, and Honours
• Genocide and Ethnic Cleansing
• Historical Geography
• History by Period
• History of Agriculture
• History of Education
• History of Emotions
• History of Gender and Sexuality
• Industrial History
• Intellectual History
• International History
• Labour History
• Legal and Constitutional History
• Local and Family History
• Maritime History
• Military History
• National Liberation and Post-Colonialism
• Oral History
• Political History
• Public History
• Regional and National History
• Revolutions and Rebellions
• Slavery and Abolition of Slavery
• Social and Cultural History
• Theory, Methods, and Historiography
• Urban History
• World History
• Browse content in Language Teaching and Learning
• Language Learning (Specific Skills)
• Language Teaching Theory and Methods
• Browse content in Linguistics
• Applied Linguistics
• Cognitive Linguistics
• Computational Linguistics
• Forensic Linguistics
• Grammar, Syntax and Morphology
• Historical and Diachronic Linguistics
• History of English
• Language Acquisition
• Language Variation
• Language Families
• Language Evolution
• Language Reference
• Lexicography
• Linguistic Theories
• Linguistic Typology
• Linguistic Anthropology
• Phonetics and Phonology
• Psycholinguistics
• Sociolinguistics
• Translation and Interpretation
• Writing Systems
• Browse content in Literature

Bibliography

• Children's Literature Studies
• Literary Studies (Asian)
• Literary Studies (European)
• Literary Studies (Eco-criticism)
• Literary Studies (Modernism)
• Literary Studies (Romanticism)
• Literary Studies (American)
• Literary Studies - World
• Literary Studies (1500 to 1800)
• Literary Studies (19th Century)
• Literary Studies (20th Century onwards)
• Literary Studies (African American Literature)
• Literary Studies (British and Irish)
• Literary Studies (Early and Medieval)
• Literary Studies (Fiction, Novelists, and Prose Writers)
• Literary Studies (Gender Studies)
• Literary Studies (Graphic Novels)
• Literary Studies (History of the Book)
• Literary Studies (Plays and Playwrights)
• Literary Studies (Poetry and Poets)
• Literary Studies (Postcolonial Literature)
• Literary Studies (Queer Studies)
• Literary Studies (Science Fiction)
• Literary Studies (Travel Literature)
• Literary Studies (War Literature)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Browse content in Media Studies
• Browse content in Music
• Applied Music
• Dance and Music
• Ethics in Music
• Ethnomusicology
• Gender and Sexuality in Music
• Medicine and Music
• Music Cultures
• Music and Religion
• Music and Culture
• Music and Media
• Music Education and Pedagogy
• Music Theory and Analysis
• Musical Scores, Lyrics, and Libretti
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Performance Practice and Studies
• Race and Ethnicity in Music
• Sound Studies
• Browse content in Performing Arts
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• Epistemology
• Feminist Philosophy
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Non-Western Philosophy
• Philosophy of Science
• Philosophy of Action
• Philosophy of Law
• Philosophy of Religion
• Philosophy of Language
• Philosophy of Mind
• Philosophy of Perception
• Philosophy of Mathematics and Logic
• Practical Ethics
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• East Asian Religions
• History of Religion
• Judaism and Jewish Studies
• Qumran Studies
• Religion and Education
• Religion and Health
• Religion and Politics
• Religion and Science
• Religion and Law
• Religion and Art, Literature, and Music
• Religious Studies
• Browse content in Society and Culture
• Cookery, Food, and Drink
• Cultural Studies
• Customs and Traditions
• Ethical Issues and Debates
• Hobbies, Games, Arts and Crafts
• Lifestyle, Home, and Garden
• Natural world, Country Life, and Pets
• Popular Beliefs and Controversial Knowledge
• Sports and Outdoor Recreation
• Technology and Society
• Travel and Holiday
• Visual Culture
• Browse content in Law
• Arbitration
• Browse content in Company and Commercial Law
• Commercial Law
• Company Law
• Browse content in Comparative Law
• Systems of Law
• Competition Law
• Browse content in Constitutional and Administrative Law
• Government Powers
• Judicial Review
• Local Government Law
• Military and Defence Law
• Parliamentary and Legislative Practice
• Construction Law
• Contract Law
• Browse content in Criminal Law
• Criminal Procedure
• Criminal Evidence Law
• Sentencing and Punishment
• Employment and Labour Law
• Environment and Energy Law
• Browse content in Financial Law
• Banking Law
• Insolvency Law
• History of Law
• Human Rights and Immigration
• Intellectual Property Law
• Browse content in International Law
• Private International Law and Conflict of Laws
• Public International Law
• IT and Communications Law
• Jurisprudence and Philosophy of Law
• Law and Politics
• Law and Society
• Browse content in Legal System and Practice
• Courts and Procedure
• Legal Skills and Practice
• Primary Sources of Law
• Regulation of Legal Profession
• Medical and Healthcare Law
• Browse content in Policing
• Criminal Investigation and Detection
• Police and Security Services
• Police Procedure and Law
• Police Regional Planning
• Browse content in Property Law
• Personal Property Law
• Study and Revision
• Terrorism and National Security Law
• Browse content in Trusts Law
• Wills and Probate or Succession
• Browse content in Medicine and Health
• Browse content in Allied Health Professions
• Arts Therapies
• Clinical Science
• Dietetics and Nutrition
• Occupational Therapy
• Operating Department Practice
• Physiotherapy
• Radiography
• Speech and Language Therapy
• Browse content in Anaesthetics
• General Anaesthesia
• Neuroanaesthesia
• Browse content in Clinical Medicine
• Acute Medicine
• Cardiovascular Medicine
• Clinical Genetics
• Clinical Pharmacology and Therapeutics
• Dermatology
• Endocrinology and Diabetes
• Gastroenterology
• Genito-urinary Medicine
• Geriatric Medicine
• Infectious Diseases
• Medical Oncology
• Medical Toxicology
• Pain Medicine
• Palliative Medicine
• Rehabilitation Medicine
• Respiratory Medicine and Pulmonology
• Rheumatology
• Sleep Medicine
• Sports and Exercise Medicine
• Clinical Neuroscience
• Community Medical Services
• Critical Care
• Emergency Medicine
• Forensic Medicine
• Haematology
• History of Medicine
• Browse content in Medical Dentistry
• Oral and Maxillofacial Surgery
• Paediatric Dentistry
• Restorative Dentistry and Orthodontics
• Surgical Dentistry
• Medical Ethics
• Browse content in Medical Skills
• Clinical Skills
• Communication Skills
• Nursing Skills
• Surgical Skills
• Medical Statistics and Methodology
• Browse content in Neurology
• Clinical Neurophysiology
• Neuropathology
• Nursing Studies
• Browse content in Obstetrics and Gynaecology
• Gynaecology
• Occupational Medicine
• Ophthalmology
• Otolaryngology (ENT)
• Browse content in Paediatrics
• Neonatology
• Browse content in Pathology
• Chemical Pathology
• Clinical Cytogenetics and Molecular Genetics
• Histopathology
• Medical Microbiology and Virology
• Patient Education and Information
• Browse content in Pharmacology
• Psychopharmacology
• Browse content in Popular Health
• Caring for Others
• Complementary and Alternative Medicine
• Self-help and Personal Development
• Browse content in Preclinical Medicine
• Cell Biology
• Molecular Biology and Genetics
• Reproduction, Growth and Development
• Primary Care
• Professional Development in Medicine
• Browse content in Psychiatry
• Addiction Medicine
• Child and Adolescent Psychiatry
• Forensic Psychiatry
• Learning Disabilities
• Old Age Psychiatry
• Psychotherapy
• Browse content in Public Health and Epidemiology
• Epidemiology
• Public Health
• Browse content in Radiology
• Clinical Radiology
• Interventional Radiology
• Nuclear Medicine
• Radiation Oncology
• Reproductive Medicine
• Browse content in Surgery
• Cardiothoracic Surgery
• Gastro-intestinal and Colorectal Surgery
• General Surgery
• Neurosurgery
• Paediatric Surgery
• Peri-operative Care
• Plastic and Reconstructive Surgery
• Surgical Oncology
• Transplant Surgery
• Trauma and Orthopaedic Surgery
• Vascular Surgery
• Browse content in Science and Mathematics
• Browse content in Biological Sciences
• Aquatic Biology
• Biochemistry
• Bioinformatics and Computational Biology
• Developmental Biology
• Ecology and Conservation
• Evolutionary Biology
• Genetics and Genomics
• Microbiology
• Molecular and Cell Biology
• Natural History
• Plant Sciences and Forestry
• Research Methods in Life Sciences
• Structural Biology
• Systems Biology
• Zoology and Animal Sciences
• Browse content in Chemistry
• Analytical Chemistry
• Computational Chemistry
• Crystallography
• Environmental Chemistry
• Industrial Chemistry
• Inorganic Chemistry
• Materials Chemistry
• Medicinal Chemistry
• Mineralogy and Gems
• Organic Chemistry
• Physical Chemistry
• Polymer Chemistry
• Study and Communication Skills in Chemistry
• Theoretical Chemistry
• Browse content in Computer Science
• Artificial Intelligence
• Computer Architecture and Logic Design
• Game Studies
• Human-Computer Interaction
• Mathematical Theory of Computation
• Programming Languages
• Software Engineering
• Systems Analysis and Design
• Virtual Reality
• Browse content in Computing
• Business Applications
• Computer Security
• Computer Games
• Computer Networking and Communications
• Digital Lifestyle
• Graphical and Digital Media Applications
• Operating Systems
• Browse content in Earth Sciences and Geography
• Atmospheric Sciences
• Environmental Geography
• Geology and the Lithosphere
• Maps and Map-making
• Meteorology and Climatology
• Oceanography and Hydrology
• Palaeontology
• Physical Geography and Topography
• Regional Geography
• Soil Science
• Urban Geography
• Browse content in Engineering and Technology
• Agriculture and Farming
• Biological Engineering
• Civil Engineering, Surveying, and Building
• Electronics and Communications Engineering
• Energy Technology
• Engineering (General)
• Environmental Science, Engineering, and Technology
• History of Engineering and Technology
• Mechanical Engineering and Materials
• Technology of Industrial Chemistry
• Transport Technology and Trades
• Browse content in Environmental Science
• Applied Ecology (Environmental Science)
• Conservation of the Environment (Environmental Science)
• Environmental Sustainability
• Environmentalist Thought and Ideology (Environmental Science)
• Management of Land and Natural Resources (Environmental Science)
• Natural Disasters (Environmental Science)
• Nuclear Issues (Environmental Science)
• Pollution and Threats to the Environment (Environmental Science)
• Social Impact of Environmental Issues (Environmental Science)
• History of Science and Technology
• Browse content in Materials Science
• Ceramics and Glasses
• Composite Materials
• Metals, Alloying, and Corrosion
• Nanotechnology
• Browse content in Mathematics
• Applied Mathematics
• Biomathematics and Statistics
• History of Mathematics
• Mathematical Education
• Mathematical Finance
• Mathematical Analysis
• Numerical and Computational Mathematics
• Probability and Statistics
• Pure Mathematics
• Browse content in Neuroscience
• Cognition and Behavioural Neuroscience
• Development of the Nervous System
• Disorders of the Nervous System
• History of Neuroscience
• Invertebrate Neurobiology
• Molecular and Cellular Systems
• Neuroendocrinology and Autonomic Nervous System
• Neuroscientific Techniques
• Sensory and Motor Systems
• Browse content in Physics
• Astronomy and Astrophysics
• Atomic, Molecular, and Optical Physics
• Biological and Medical Physics
• Classical Mechanics
• Computational Physics
• Condensed Matter Physics
• Electromagnetism, Optics, and Acoustics
• History of Physics
• Mathematical and Statistical Physics
• Measurement Science
• Nuclear Physics
• Particles and Fields
• Plasma Physics
• Quantum Physics
• Relativity and Gravitation
• Semiconductor and Mesoscopic Physics
• Browse content in Psychology
• Affective Sciences
• Clinical Psychology
• Cognitive Neuroscience
• Cognitive Psychology
• Criminal and Forensic Psychology
• Developmental Psychology
• Educational Psychology
• Evolutionary Psychology
• Health Psychology
• History and Systems in Psychology
• Music Psychology
• Neuropsychology
• Organizational Psychology
• Psychological Assessment and Testing
• Psychology of Human-Technology Interaction
• Psychology Professional Development and Training
• Research Methods in Psychology
• Social Psychology
• Browse content in Social Sciences
• Browse content in Anthropology
• Anthropology of Religion
• Human Evolution
• Medical Anthropology
• Physical Anthropology
• Regional Anthropology
• Social and Cultural Anthropology
• Theory and Practice of Anthropology
• Browse content in Business and Management
• Business Strategy
• Business History
• Business Ethics
• Business and Government
• Business and Technology
• Business and the Environment
• Comparative Management
• Corporate Governance
• Corporate Social Responsibility
• Entrepreneurship
• Health Management
• Human Resource Management
• Industrial and Employment Relations
• Industry Studies
• Information and Communication Technologies
• International Business
• Knowledge Management
• Management and Management Techniques
• Operations Management
• Organizational Theory and Behaviour
• Pensions and Pension Management
• Public and Nonprofit Management
• Strategic Management
• Supply Chain Management
• Browse content in Criminology and Criminal Justice
• Criminal Justice
• Criminology
• Forms of Crime
• International and Comparative Criminology
• Youth Violence and Juvenile Justice
• Development Studies
• Browse content in Economics
• Agricultural, Environmental, and Natural Resource Economics
• Asian Economics
• Behavioural Finance
• Behavioural Economics and Neuroeconomics
• Econometrics and Mathematical Economics
• Economic Systems
• Economic Methodology
• Economic History
• Economic Development and Growth
• Financial Markets
• Financial Institutions and Services
• General Economics and Teaching
• Health, Education, and Welfare
• History of Economic Thought
• International Economics
• Labour and Demographic Economics
• Law and Economics
• Macroeconomics and Monetary Economics
• Microeconomics
• Public Economics
• Urban, Rural, and Regional Economics
• Welfare Economics
• Browse content in Education
• Adult Education and Continuous Learning
• Care and Counselling of Students
• Early Childhood and Elementary Education
• Educational Equipment and Technology
• Educational Strategies and Policy
• Higher and Further Education
• Organization and Management of Education
• Philosophy and Theory of Education
• Schools Studies
• Secondary Education
• Teaching of a Specific Subject
• Teaching of Specific Groups and Special Educational Needs
• Teaching Skills and Techniques
• Browse content in Environment
• Applied Ecology (Social Science)
• Climate Change
• Conservation of the Environment (Social Science)
• Environmentalist Thought and Ideology (Social Science)
• Natural Disasters (Environment)
• Social Impact of Environmental Issues (Social Science)
• Browse content in Human Geography
• Cultural Geography
• Economic Geography
• Political Geography
• Browse content in Interdisciplinary Studies
• Communication Studies
• Museums, Libraries, and Information Sciences
• Browse content in Politics
• African Politics
• Asian Politics
• Chinese Politics
• Comparative Politics
• Conflict Politics
• Elections and Electoral Studies
• Environmental Politics
• European Union
• Foreign Policy
• Gender and Politics
• Human Rights and Politics
• Indian Politics
• International Relations
• International Organization (Politics)
• International Political Economy
• Irish Politics
• Latin American Politics
• Middle Eastern Politics
• Political Methodology
• Political Communication
• Political Philosophy
• Political Sociology
• Political Theory
• Political Behaviour
• Political Economy
• Political Institutions
• Politics and Law
• Public Administration
• Public Policy
• Quantitative Political Methodology
• Regional Political Studies
• Russian Politics
• Security Studies
• State and Local Government
• UK Politics
• US Politics
• Browse content in Regional and Area Studies
• African Studies
• Asian Studies
• East Asian Studies
• Japanese Studies
• Latin American Studies
• Middle Eastern Studies
• Native American Studies
• Scottish Studies
• Browse content in Research and Information
• Research Methods
• Browse content in Social Work
• Addictions and Substance Misuse
• Adoption and Fostering
• Care of the Elderly
• Child and Adolescent Social Work
• Couple and Family Social Work
• Developmental and Physical Disabilities Social Work
• Direct Practice and Clinical Social Work
• Emergency Services
• Human Behaviour and the Social Environment
• International and Global Issues in Social Work
• Mental and Behavioural Health
• Social Justice and Human Rights
• Social Policy and Advocacy
• Social Work and Crime and Justice
• Social Work Macro Practice
• Social Work Practice Settings
• Social Work Research and Evidence-based Practice
• Welfare and Benefit Systems
• Browse content in Sociology
• Childhood Studies
• Community Development
• Comparative and Historical Sociology
• Economic Sociology
• Gender and Sexuality
• Gerontology and Ageing
• Health, Illness, and Medicine
• Marriage and the Family
• Migration Studies
• Occupations, Professions, and Work
• Organizations
• Population and Demography
• Race and Ethnicity
• Social Theory
• Social Movements and Social Change
• Social Research and Statistics
• Social Stratification, Inequality, and Mobility
• Sociology of Religion
• Sociology of Education
• Sport and Leisure
• Urban and Rural Studies
• Browse content in Warfare and Defence
• Defence Strategy, Planning, and Research
• Land Forces and Warfare
• Military Administration
• Military Life and Institutions
• Naval Forces and Warfare
• Other Warfare and Defence Issues
• Peace Studies and Conflict Resolution
• Weapons and Equipment

• < Previous chapter
• Next chapter >

21 Mathematical Modeling

Daniel R. Cavagnaro, Department of Psychology, The Ohio State University, Columbus, OH

Jay I. Myung, Department of Psychology, The Ohio State University, Columbus, OH

Mark A. Pitt, Department of Psychology, The Ohio State University, Columbus, OH

• Published: 01 October 2013
• Cite Icon Cite
• Permissions Icon Permissions

Explanations of human behavior are most often presented in a verbal form as theories. Psychologists can also harness the power and precision of mathematics by explaining behavior quantitatively. This chapter introduces the reader to how this is done and the advantages of doing so. It begins by contrasting mathematical modeling with hypothesis testing to highlight how the two methods of knowledge acquisition differ. The many styles of modeling are then surveyed, along with their advantages and disadvantages. This is followed by an in-depth example of how to create a mathematical model and fit it to experimental data. Issues in evaluating models are discussed, including a survey of quantitative methods of model selection. Particular attention is paid to the concept of generalizability and the trade-off of model fit with model complexity. The chapter closes by describing some of the challenges for the discipline in the years ahead.

Introduction

Psychologists study behavior. Data, acquired through experimentation, are used to build theories that explain behavior, which in turn provide meaning and understanding. Because behavior is complex, a complete theory of any behavior (e.g., depression, reasoning, motivation) is likely to be complex as well, having many variables and conditions that influence it.

Mathematical models are tools that assist in theory development and testing. Models are theories, or parts of theories, formalized mathematically. They complement theorizing in many ways, as discussed in the following pages, but their ultimate goal is to promote understanding of the theory, and thus behavior, by taking advantage of the precision offered by mathematics. Although they have been part of psychology since its inception, their popularity began to rise in the 1950s and has increased substantially since the 1980s, in part because of the

introduction of personal computers. This interest is not an accident or fad. Every style of model that has been introduced has had a significant impact in its discipline, and sometimes far beyond that. After reading this chapter, the reader should begin to understand why.

This chapter is written as a first introduction to mathematical modeling in psychology for those with little or no prior experience with the topic. Our aim is to provide a good conceptual understanding of the topic and make the reader aware of some of the fundamental issues in mathematical modeling but not necessarily to provide an in-depth step-by-step tutorial on how to actually build and evaluate a mathematical model from scratch. In doing so, we assume no more of the reader than a year-long course in graduate-level statistics. For related publications on the topic, the reader is directed to Busemeyer and Diederich (2010) , Fum, Del Missier, and Stocco (2007) , and Myung and Pitt (2002) . In particular, the present chapter may be viewed as an updated version of the last of these. The focus of the first half of the chapter is on the advantages of mathematical modeling. By turning what may be vague notions or ideas into precise quantities, significant clarity can be gained to reveal new insights that push science forward. In the next section , we highlight some of the benefits of mathematical modeling relative to the method of investigation that currently dominates psychological research: verbal modeling. After that, we provide a brief overview of the styles of mathematical modeling. The second half of the chapter focuses on algebraic models, discussing in detail how to build them and how to evaluate them. We conclude with a list of recommended readings for many of the topics covered.

From Verbal Modeling to Mathematical Modeling

Verbal modeling.

To understand the importance and contribution of mathematical modeling, it is useful to contrast it with the way scientific investigation commonly proceeds in psychology. The typical investigation proceeds as follows. First, a hypothesis is generated from a theory in the form of differences across conditions. These could be as general as higher ratings in the experimental condition compared to a control condition or a V-shaped pattern of responses across three levels of an independent variable such as task difficulty (e.g., low, medium, high). The hypothesis is usually coarse-grained and expressed verbally (e.g., “memory will be worse in condition A compared with condition B,” or “one’s self-image is more affected by negative than positive reinforcement”), hence it is referred to as a verbal model. To test the hypothesis, it is contrasted with the hypothesis that there is absolutely no difference among conditions. After data collection, inferential statistics are used to pass judgment on only this latter, “null” hypothesis. A statistically significant difference leads one to reject it (which is not the same as confirming the hypothesis of interest), whereas on the other hand, a difference that is not statistically significant leads one to fail to reject the null, effectively returning one to the same state of knowledge as before the experiment was conducted.

This verbal modeling ritual is played out over and over again in the psychology literature. It is usually the case that a great deal of mileage can be gained from it when testing a new theory because correctly predicting qualitative differences (e.g., A ¿ B) can be decisive in keeping a theory alive. However, a point of diminishing returns will eventually be reached once a majority of the main claims have been tested. The theory must expand in some way if it is to be advanced. After all, models should provide insight and explain behavior at a level of abstraction that goes beyond a redescription of the data. Moreover, although the data collected are analyzed numerically using statistics, numerical differences are rarely predicted nor of primary interest in verbal models, which predict qualitative differences among conditions. To take the theory a step further and ask the degree to which performance should differ between two conditions goes beyond the level of detail provided in verbal models.

Mathematical modeling offers a means for going beyond verbal modeling by using mathematics in a very direct manner, to instantiate theory, rather than a supplementary manner, to test simple, additive effects predicted by the theory. In quantifying a theory, the details provided in its mathematical specification push the theory in new directions and make possible new means of theory evaluation. In a mathematical model, hypotheses about the relations between the underlying mental processes and behavioral responses are expressed in the form of mathematical equations, computer algorithms, or other simulation procedures. Accordingly, mathematical models can go beyond qualitative predictions such as “performance in condition A will be greater than performance in condition B” to make quantifiable predictions such as “performance in condition A will be two times greater than in condition B,” which can be tested experimentally. Furthermore, using mathematics to instantiate theory opens the door to models with nonlinear relationships and dynamic processes, which are capable of more accurately reflecting the complexity of the psychological processes that they are intended to model.

Shifting the Scientific Reasoning Process

Mathematical modeling also aids scientific investigation by freeing it from the confines of null hypothesis significance testing (NHST) of qualitative predictions in verbal models. The wisdom of NHST has been criticized repeatedly over the years ( Rozeboom, 1960 ; Bakan, 1966 ; Lykken, 1968 ; Nickerson, 2000 ; Wagenmakers, 2007 ). In NHST, decisions pertain only to the null hypothesis. Decisions about the accuracy of the experimental hypothesis in which the researcher is interested are not made. Statistically significant results merely keep the theory alive, making it a contender among others. In the end, the theory should be the only one standing if it is correct, but with NHST, commitment to one’s theory is never made and evidence is only indirectly viewed as accumulating in favor of the theory of interest. This mode of reasoning makes NHST very conservative.

Although the landscape of statistical modeling in psychology is changing to make increasing use of NHST of quantitative predictions in conjunction with mathematical models, as in structural equations modeling and multilevel modeling, the dominant application of NHST is still to test qualitative predictions derived from verbal models. Continuous use of NHST in this way can hinder scientific progress by creating a permanent dependence on statistical techniques such as linear regression or ANOVA, rather than at some point switching over to using mathematics to model the psychological processes of interest. Further, statistical tests are used in NHST in a way that gives the illusion of being impartial or objective about the null hypothesis, when in fact all such tests make more explicit assumptions about the underlying mental process, the most obvious being that behavior is linearly related to the independent variables. If one is not careful, then theories can end up resembling the statistical procedures themselves. Gigerenzer (1991) refers to this approach to theory building as tools-to-theories. Researchers take an available statistical method and postulate it as a psychological explanation of data. However, unless one thinks that the mind operates as a regression model or other statistical procedure, these tools should not be intended to reflect the inner workings of psychological mechanisms ( Marewski & Olsson, 2009 ).

When engaged in mathematical modeling, there is an explicit change in the scientific reasoning process away from that of NHST-based verbal modeling. The focus in mathematical modeling is on assessing the viability of a particular model, rather than rejecting or failing to reject the status quo. Correctly predicted outcomes are taken as evidence in favor of the model. Although it is recognized that alternative models could potentially make the same predictions (this issue is discussed more thoroughly below), a model that passes this “sufficiency test” is pursued and taken seriously until evidence against it is generated or a viable contender is proposed.

Types of Mathematical Models

This section offers a brief overview of the various types of mathematical models that are used in different subfields of psychology.

Core Modeling Approaches

The styles of modeling listed under this heading were popularized before the advent of modern computing in the 1980s. Far from being obsolete, the models described here comprise the backbone of modern theories in psychophysics, measurement, and decision making, among others, and important progress is still being made with these methods.

psychophysical models

The earliest mathematical models in psychology came from psychophysicists, in their efforts to describe the relationship between the physical magnitudes of stimuli and their perceived intensities (e.g., does a 20-pound weight feel twice as heavy as a 10-pound weight?). One of the pioneers in this field was Ernst Heinrich Weber (1795–1878). Weber was interested in the fact that very small changes in the intensity of a stimulus, such as the brightness of a light or the loudness of a sound, were imperceptible to human participants. The threshold at which the difference can be perceived is called the just-noticeable difference . Weber noticed that the just-noticeable difference depends on the stimulus’ magnitude (e.g., 5%) rather than being an absolute value (e.g., 5 grams). This relationship is formalized mathematically in terms of the differential equation known as Weber’s Law: Δ J N D x = k W x , where, Δ J N D x is the just-noticeable difference (JND) in the physical intensity of the stimulus, x is the current intensity of the stimulus, and k W is an empirically determined constant known as the Weber fraction. That is, the JND is equal to a constant times the physical intensity of the stimulus. For example, a Weber fraction of 0.01 means that participants can detect a 1% change in the stimulus intensity. The value of the Weber fraction varies depending on the nature of the stimulus (e.g., light, sound, heat).

Gustav Fechner (1801–1887) rediscovered the same relationship in the 1850s and formulated what is now known as Fechner’s law: ψ ( x ) = k *ln(x), where ψ (x) denotes the perceived intensity (i.e., the perceived intensity of the stimulus is equal to a constant times the log of the physical intensity of the stimulus). Because Fechner’s law can be derived from Webers Law as an integral expression of the latter, they are essentially one and the same and are often referred to collectively as the Weber-Fechner Law. For more details on these and other psychophysical laws, see   Stevens (1975) .

The early psychophysical laws were extended by Louis Thurstone (1887–1955), who considered the more general question of how the mind assigns numerical values to items, even abstract items such as attitudes and values, so that they can be meaningfully compared. He published his paper on the “law” of paired comparisons in 1927. Although Thurstone referred to it as a law, it is more aptly described as a model because it constitutes a scientific hypothesis regarding the outcomes of pairwise comparisons among a collection of objects. If data agree with the model, then it is possible to produce a scale from the data. Thurstone’s model is the foundation of modern psychometrics, which is the general study of psychological measurement. For more details, see   Thurstone (1974) .

axiomatic models

The axiomatic method of mathematical modeling involves replacing the phenomenon to be modeled with a collection of simple propositions, or axioms , which are designed in such a way that the observed pattern of behavior can be deduced logically from them. Each axiom by itself represents a fundamental assumption about the process under investigation and often takes the form of an ordinal restriction or existence statement, such as “The choice threshold is always greater than zero” or “There exists a value x greater than zero such that a participant will not be able to distinguish between A units and A + x units.” Taken together, a set of axioms can constrain the variables sufficiently for a model to be uniquely identified.

Axiomatic models are especially prevalent in the field of judgment and decision making. For example, the Expected Utility model of decision making under uncertainty ( Morgenstern & Von Neumann, 1947 ) states that any decision maker’s preferences can be characterized according to an internal utility function that they use to evaluate uncertain prospects. This utility function has the form of an expected utility in the sense that a gamble G offering x dollars with probability p and y dollars with probability ( 1 - p ), would have expected utility U ( G ) = p v ( x ) + ( 1 - p ) v ( y ) , where v ( x ) represents the subjective value of money to the participant. That is, the utility of the gamble is equal to a weighted sum of the possible payoffs, where they weight attached to each payoff is its probability of occurring. The model predicts that a decision maker will always choose the gamble with higher expected utility.

On the face of it, the existence of such a utility function that fully defines a decision maker’s preferences over all possible gambles is a difficult assumption to justify. However, its existence can be derived by assuming the following three, reasonable axioms ( see , e.g., Fishburn, 1982 ):

1. Ordering : Preferences are weak orders (i.e., rankings with ties).

2. Continuity : For any choice B such that choice A is preferred to choice B, which is in turn preferred to choice C, there exists a unique probability q such that one is indifferent between choice B and a gamble composed of q chance of A and a ( 1 - q ) chance of C, in which A is chosen with probability q and C is chosen with probability ( 1 - q ).

3. Independence : If choices A and B are equally preferable, then a gamble composed of a q chance of A and a ( 1 - q ) chance of C is equally preferable to a gamble composed of a q chance of B and a ( 1 - q ) chance of C for any choice C and all q ( 0 < q < 1 ) .

The axiomatic method is very much the “slow-and-steady” approach to mathematical modeling. Progress is often slow in this area because of the mathematical complexities involved in constructing coherent and justifiable axioms for psychological phenomena of interest. However, because all of the assumptions are spelled out explicitly in behaviorally verifiable axioms, axiomatic models are highly transparent in how they generate predictions. Moreover, because of the logical rigor of their construction, axiomatic models are long-lasting. That is, unlike other types of mathematical models that we will discuss later, axiomatic models are not prone to being deposed by competing models that perform “just a little bit better.” For these reasons, many scientists consider the knowledge gained from axiomatic modeling to be of the highest quality. For more details on axiomatic modeling, the reader is referred to Luce (2000) .

algebraic models

Algebraic models are probably what come to mind first for most people when they think of mathematical models. An algebraic model is essentially a generalization of the standard linear regression model in the sense that it describes exactly how the input stimuli and model parameters are combined to produce the output (behavioral response), in terms of a closed-form algebraic expression. Algebraic models are usually easy to understand because of this tight link between the descriptive (verbal) theory and its computational instantiation. Further, their assumptions can usually be well justified, often axiomatically or through functional equations (e.g., Aczel, 1966 ).

The simplest example of an algebraic models is the general linear model, which is restricted to linear combinations of input stimuli, such as y = a x + b , in which the tunable, free parameters ( a , b ) measure the relative extent to which the output response y is sensitive to the input stimulus dimension x . In general, however, algebraic models may include nonlinear terms and parameters that can describe various psychological factors.

For example, it is well known among memory researchers that a person’s ability to retain in memory what was just learned (e.g., a list of words) drops quickly at first and then levels off. The exponential model of memory retention (e.g., Wixted & Ebbesen, 1991 ) states this relationship between time and amount remembered with the equation p = a e - b x , where p is the probability of a participant being able to correctly recall the learned item (e.g., a word), x is the length of time since learning it, and a and b are model parameters. This means that the probability of correct recall is found by first multiplying the length of time since learning by - b , exponentiating the result, and then multiplying the resulting value by a . When x = 0 , the value of this equation is a , which means that the parameter a ( 0 < a < 1 ) represents the baseline retention probability before any time passed. The parameter b ( b 〉 0 ) represents the rate at which retention performance drops with time, which is a psychological process. We could, of course, entertain other model equation that can capture this decreasing trend of retention memory, such as power ( p = a ( x + 1 ) - b ), hyperbolic ( p = 1 ∕ ( a + b x ) ), or logarithmic models, to name a few ( see , e.g., Rubin & Wenzel, 1996 ).

Other examples of algebraic models include the Diffusion Model of Memory Retrieval ( Ratcliff, 1978 ), Generalized Context Model of category learning ( Nosofsky, 1986 ), Multinomial Processing Tree models of source monitoring ( Batchelder & Riefer, 1999 ), and the Scale-Independent Memory, Perception, and Learning model (SIMPLE) of memory retrieval ( Brown, Neath, & Chater, 2007 ).

Computational Modeling Approaches

Modern-day mathematical models are characterized by an increased reliance on the computational power provided by the rise of modern computing in the 1980s.

algorithmic models

An algorithmic model is defined in terms of a simulation procedure that describes how specific internal processes interact with one another to yield an output behavior. The processes involved are often so complicated that the model’s predictions cannot be obtained by simply evaluating an equation at the appropriate values of the parameters and independent variables, as in algebraic models. Rather, deriving predictions from the model requires simulating dynamic processes on a computer with the help of random number generators. The process begins with an activation stimulus, and then runs through a sequence of probabilistic interactions that are meant to represent corresponding mental activity, finally yielding an output value that usually corresponds to a decision or an action taken by a participant.

When building an algorithmic model, the primary concern is that the system accurately reproduces human data. In contrast to the axiomatic modeling approach, in which each assumption is well grounded theoretically, algorithmic models often make many assumptions about the mental processes involved in a behavior, which cannot be verified empirically because they are not directly observable. This gives scientists considerable leeway to tweak the internal structure of a model and quickly observe its behavior.

One advantage of this approach is that it allows scientists to work with ideas that cannot yet be expressed in precise mathematical form ( Estes, 1975 ). This extends the domain of what can be modeled to include very complex cognitive and neural processes. Moreover, this type of model can provide a great deal of insight into the mental processes that are involved in behavior. For example, an algorithmic model such as the Decision Field Theory model of decision making ( Busemeyer & Townsend, 1993 ) predicts not only the final action taken by a participant but also the amount of time elapsed before taking that action. Another excellent example of this type of model is the retrieving-effectively-from-memory (REM) model of recognition memory ( Shiffrin & Steyvers, 1997 ).

The main drawback of algorithmic modeling is a lack of transparency between the parts of the model and their mental counterparts. The same flexibility that allows them to be built and tested quickly also allows them to create a host of assumptions that often serve no other purpose than simply to fit the data. To minimize this problem, algorithmic models should be designed with as few assumptions as possible, and care should be taken to ensure that all of the assumptions are well justified and psychologically plausible.

connectionist models

Connectionist models make up a class of cognitive models in which mental phenomena are described by multilayer networks of interconnected units, or nodes . Model predictions are generated by encoding a stimulus in the activation of a set of “input nodes,” which then pass the activation across a series of “hidden nodes,” which transform the original stimulus into new codes or features, until the activation finally reaches an “output node” representing a response. This structure is often meant to simulate the way the brain works, with the nodes representing neurons and the connections between nodes representing synapses, but other interpretations are also possible. For example, in a connectionist model of language acquisition, the nodes could represent words, with connections indicating semantic similarity. Examples of connectionist models include the TRACE model of speech perception ( McClelland & Elman, 1986 ), the ALCOVE model of category learning ( Kruschke, 1992 ), the Connectionist Model of Word Reading ( Plaut, McClelland, Seidenberg, & Patterson, 1996 ), and the Temporal Context Model of episodic memory ( Howard & Kahana, 2002 ).

Connectionist models can be characterized as a particular subclass of algorithmic models. The key difference is that connectionist models make even fewer explicit assumptions about the underlying processes and instead focus on learning the regularities in the data through training. Essentially, the network learns to produce the correct data pattern by adapting itself from experience with the input, strengthening and weakening connections in a manner similar to the way learning occurs in the human brain. This flexibility allows connectionist models to predict highly complex data patterns. In fact, certain connectionist models have been proved by mathematicians to have literally unlimited flexibility. That is, a connectionist model with a sufficiently large number of hidden units can approximate any continuous nonlinear input–output relationship to any desired degree of accuracy ( Hornik, Stinchcombe, & White, 1989 , 1990 ). Unfortunately, this means that connectionist models are prone to fit not only the underlying regularities in the data but also spurious, random noise that has no psychological meaning. Consequently, care must be taken to make sure that the model learns only the underlying regularities and does not degenerate into a mere redescription of the idiosyncrasies in the data, which would provide little insight into mental functioning.

bayesian modeling

The term Bayesian model has become somewhat of a buzz phrase in recent years, and it is now used very broadly in reference to any model that takes advantage of the Bayesian statistical approach to processing information ( Chater, Tenenbaum, & Yuille, 2006 ; Kruschke, 2010 ; Lee, 2011 ). However, because the Bayesian approach can be utilized in diverse ways to the aid of mathematical modeling, there are actually a few different classes of models, all of which are referred to as Bayesian models.

Briefly, a Bayesian model is defined in terms of two components: (1) the prior distribution , which is a probability distribution representing the investigator’s initial uncertainty about the parameters before the data are collected, and (2) the likelihood function , which specifies the likelihood of the observed data as a function of the parameters. From these, the posterior distribution , which is a probability distribution that expresses an updated uncertainty about the parameters in light of the data, is obtained by applying Bayes rule. A specific inference procedure is then constructed or performed on the basis of the posterior distribution depending on the inference problem at hand. For further details of Bayesian inference, the reader is directed to other sources (e.g., Gill, 2008 ; Gelman, Carlin, Stern, & Rubin, 2004 ).

Two types of Bayesian models that we will briefly discuss here are Bayesian statistical models (those that use Bayesian statistics as a tool for data analysis) and Bayesian theoretical models (those that use Bayesian statistics as a theoretical analogy for the inner workings of the mind). Bayesian statistical models often use Bayesian statistics as a method of conducting standard analyses of data, as an alternative to frequentist statistical methods such as NHST (for a review, see , Kruschke, 2010 ). Bayesian hypothesis testing using the Bayes factor, for example, extends NHST to allow accumulation of evidence in favor of a null hypothesis ( Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009 ; Wagenmakers, Lodewyckx, Kuriyal, & Grasman, 2010 ). It also provides the necessary machinery for doing inference on unobservable, or “latent,” psychological parameters, as opposed to just measured dependent variables such as recall rate and response time. This style of Bayesian modeling, called Hierarchical Bayes, accounts for additional sources of variation, such as individual differences, in a rigorous way using latent parameters ( Rouder & Lu, 2005 ; Rouder, Sun, Speckman, Lu, & Zhou, 2003 ; Lee, 2008 ; Lee, in press). Because of their popularity, specialized software packages have been developed for building and testing them ( Lunn, Thomas, Best & Speigelhalter, 2000 ).

Bayesian theoretical models, on the other hand, utilize Bayesian statistics as a working assumption for how the mind makes inferences. In this style of modeling, Bayesian inference is used to provide a rational account of why people behave the way they do, often without accounting for the cognitive mechanisms that produce the behavior. Bayesian statistics as a theoretical analogy has been an influential position for the last decade or so in cognitive science, and it has led to the development of impressive new models addressing a wide range of important theoretical questions in psychological science (e.g., Chater et al., 2006 ; Tenenbaum, Griffiths & Kemp, 2006 ; Griffiths, Steyvers & Tenenbaum, 2007 ; Steyvers, Lee & Wagenmakers, 2009 ; Xu & Griffiths, 2010 ; Lee & Sarnecka, 2010 ).

How to Build and Evaluate Mathematical Models

Just as verbal models are built from interpretation of past data and intuitions about the psychological process of interest, mathematical models require one to make more of these same decisions but at a much finer level of precision. This can make a first-time modeler uncomfortable because of the many decisions that must be made, which force the practitioner to make important choices and think about critical issues at a high level of specificity. However, the process can be tremendously insightful and cause the practitioner to rethink past assumptions, viewpoints, and interpretations of data. In this section, we walk through the process of mathematical modeling, from model specification through fitting data, model comparison, and finally model revision. Before that, it is important to explain the logic of modeling.

Logic of Model Testing

The generally accepted criterion for a model to be “correct” is that it is both necessary and sufficient for its predictions about the data to be true. Estes (2002) has succinctly illustrated how this criterion can be scrutinized more carefully by considering it in the framework of formal logic, some key points of which we review here. Following the standard logical notation ( Suppes, 1957 ), let P denote the model of interest, collectively referring to the assumptions the model makes, and let Q denote the predictions being made about possible observations in a given experimental setting. The sufficiency of the model can be assessed by examining the logical statement P → Q , which reads “P implies Q,” and the necessity can be assessed by examining the logical statement ~ P → ~ Q , which reads “not P implies not Q.”

The sufficiency condition, P → Q , is equivalent to the informal statement that under the assumptions of the model, the predictions of the data follow. For model testing, this means that if the predictions are shown to be accurate (i.e., confirmed by observed data), then the model is said to be sufficient to predict the data. On the other hand, if the predictions are shown to be inaccurate and thus unconfirmed, then the model must be false (incorrect). In short, the model can be tested, and possibly falsified, by observing experiment data ( Estes, 2002 , p. 5).

It is important to emphasize that confirming sufficiency alone does not validate the model. This is because one might be able to construct another model, with a different set of assumptions from those of the original model, that may also make exactly the same predictions—that is, P’ → Q, where P’ denotes the competing model. Consequently, confirming Q does not constitute the unequivocal confirmation of the model P. To establish the model as valid, the necessity of the model in accounting for the data must also be established.

The necessity condition, ~ P → ~ Q , is equivalent to the informal statement that every possible deviation from the original model (e.g., by replacing the assumptions of the model with different ones) fails to generate the predictions of the data. If this condition is satisfied, then the model is said to be necessary to predict the data.

The reality of model testing is that establishing the necessity of a model is generally not an achievable goal in practice. This is because testing it requires individual examinations of the assumptions of the model, which are not typically amenable to empirical verification. This means that in model testing, one is almost always restricted to confirming or disconfirming the sufficiency of a model.

Model Specification

Modeling can be a humbling experience because it makes one realize how incomplete the corresponding theory is. Given how little is actually known about the psychological process under study (how many outstanding questions have yet to be answered), could it be any other way? This state of affairs highlights the fact that models should be considered to be only approximations of the “true” theory. To expect a model to be correct on the first try is not only unrealistic but impossible.

In contrast to predictions of verbal models, which are qualitative in nature and expressed verbally, the predictions made by mathematical models characterize quantitative relationships that clearly specify the effect on one variable that would result from a change in the other and are expressed in, of course, mathematical language—that is, equations. Translating a verbal prediction into a mathematical language is one of the first challenges of creating mathematical models.

To illustrate the process, we will examine a model of lexical decision making. The lexical decision task is a procedure used in many psychology and psycholinguistics experiments ( Perea, Rosa, & Gomez, 2002 ). The basic procedure involves measuring how quickly participants can classify stimuli as words or non-words. It turns out that speed of classification depends on the frequency with which the stimulus word is used in the English language. A simple, verbal prediction for this task could be stated as “the higher the word frequency, the faster the response time.” This verbal prediction describes a qualitative relationship between word frequency and response time, whereby response time decreases monotonically as a function of word frequency. This qualitative relationship could be captured by many different mathematical functions, but different functions make different quantitative predictions that can be tested empirically.

There are many different models related to this task ( see , e.g., Adelman & Brown, 2008). One example of a model for the lexical decision task is a power function, which uses the equation

where RT is the response time measured in an appropriate unit, WF is the word frequency and a , b , and c are parameters ( a , b , c 〉 0 ). That is, the response time is found by adding one to the word frequency, raising that value to the - b power, multiplying the result by the parameter a , and then adding the parameter c . Like all algebraic models, this one can be broken down into “observables,” whose values are a priori known or obtained from an experiment, and “non-observables,” which must be inferred from the observables. Here, the observables are RT and WF , whereas the non-observables are the three parameters a , b , and c . A typical prediction of this model is illustrated in Figure 21.1 .

Writing the model equation is an important first step in specifying the model, but it is not the end of the process. The next step is to account for random variability in the data. A naïve view of modeling is that the data would directly and perfectly reveal the underlying process, but this view is unrealistic because people are neither perfect nor identical, which means that experiment data will inevitably contain random variability between participants and even within the data for individual participants. It is therefore important that a mathematical model specify not only the hypothesized regularity behind the data but also the error structure of the data. For example, the above power function for the lexical decision task could be made into a probabilistic model by adding an error term, e , yielding

The error term e is a random variable whose value is drawn from a probability distribution, often a normal distribution, centered at 0 and with variance σ 2 . With the error term e , the model now predicts a data pattern in which the response times are not identical on every trial even with the same word frequency but, rather, normally distributed with mean a ( W F + 1 ) - b + c , and with the variance σ 2 , as shown in Figure 21.1 . Other error specifications are, of course, possible.

Technically speaking in more formal terms, a model is defined as a parameterized family of probability distributions M = { f ( y | w ) , w ∈ W } , where y = ( y 1 , … , y n ) is the data vector of n observations; w is the parameter vector defining model parameters (e.g., w = [ a , b , c , σ ] for the above power model); and f ( y | w ) is the probability density function specifying the probability of observing y given w ; and, finally, W is the parameter space. From this viewpoint, the model consists of a collection of probability distributions indexed by its parameters so that each parameter value is associated with a probability distribution of responses.

Model Fitting

Once a model has been fully specified with a model equation and an error structure, the next step is to assess its descriptive adequacy. The descriptive adequacy of a model is measured by how closely its predictions can be aligned with the observed pattern of data from an experiment. Given that the model can describe a range of data patterns by varying the values of its parameters, the first step in assessing the descriptive adequacy of a model is to find the set of parameter values for which the model fits the data “best” in some defined sense. This step is called parameter estimation.

Behavior predicted by the power model of lexical decisions with a = 0 . 7 8 , b = 0 . 5 0 , c = 0 , and σ = 0 . 1 0 .

There are two general methods of parameter estimation in statistics, least-squares estimation (LSE) and maximum likelihood estimation (MLE). Both of these methods are similar in spirit but differ from one another in implementation ( see   Myung, 2003 , for a tutorial).

Specifically, the goal of LSE is to identify the parameter values that most accurately describe the data, whereas in MLE the goal is to find the parameter values that are most likely to have generated the data. Least-squares estimation is tied with familiar statistical concepts in psychology such as the sum of squares error, the percent variance accounted for, and the root mean squared deviation. Formally, the LSE estimate, denoted by w L S E , minimizes the sum of squares error between observed and predicted data and is obtained using the formula

where the symbol “argmin” stands for the argument of the minimum, referring to the argument value (i.e., w ) that minimizes the given expression. The expression is a sum over n observations, indexed by i , of the squared difference between the value predicted by the model and the actual observed value. Least-squares estimation is primarily a descriptive measure, often associated with linear models with normal error.

On the other hand, MLE is the standard method of parameter estimation in statistics and forms a basis for many inferential statistical methods such as the chi-square test and several model comparison methods (described in the next section ). The central idea in MLE estimation is the notion of the likelihood of the observed data given a parameter value. For each parameter value of a model, there is a corresponding likelihood that the model generated the data. Together, these likelihoods constitute the likelihood function of the model. The MLE estimate, denoted by w M L E , is obtained by maximizing the likelihood function,

which entails finding the value of w that maximizes the likelihood of y o b s given w . Figure 21.2 displays a hypothetical likelihood function for the power model of lexical decision, highlighting the model likelihoods of three parameter values.

It is not generally possible to find an analytic form solution (i.e., single equation) for the LSE or MLE estimate. As such, the solution must be sought numerically using search algorithms implemented on computer, such as the Newton-Raphson algorithm and the gradient descent algorithm (e.g., Press, Teukolsky, Vetterling, & Flannery, 1992 ).

Model Comparison

Specifying a mathematical model and justifying all of its assumptions is a difficult task. Completing it, and then going further to show that it provides an adequate fit to a set of experimental data, is a feat worthy of praise (and maybe a journal publication). However, these steps are only the beginning of the journey. The next question to ask of this model is why anyone should use it instead of someone else’s model that also has justifiable assumptions and also fits the data well. This is the problem of model comparison, and it arises from what we discussed earlier about the logic of mode testing—namely, that it is almost never possible to establish the necessity of a model (only the sufficiency), because someone can almost always come up with a competing model based on different assumptions that produces exactly the same predictions and, hence, an equally good fit to the data. Given the difficulty in establishing the necessity of a model, how should we choose between differing explanations (i.e., models) given a finite sample of noisy observations?

A hypothetical likelihood function. The curve indicates the likelihood of the model ( y -axis) for each possible parameter value ( y -axis). In this case, the parameter ranges from 0 to 12. This likelihood function has local maxima at 2.8, 9.2, and 12. The global maximum, (MLE) is at 6.5. When using an automated search algorithm to find the MLE, it is important to avoid getting stuck in a local maximum.

The ultimate goal of model comparison is to identify, among a set of candidate models, the one that actually generated the data you are fitting. However, this is not possible in general because of at least two difficulties in practice: (1) there are never enough observations in a data set to pin down the truth exactly and uniquely; and (2) the truth may be quite complex and beyond the descriptive power of any of the models under consideration. Given these limitations, a more realistic goal is to choose the model that provides the closest approximation to the truth in some defined sense.

In defining the “best” or “closest approximation,” there are many different model evaluation criteria from which to choose (e.g., Jacobs & Grainger, 1994 ). Table 21.1 summarizes six of these. Among these six criteria, three are qualitative and the other three are quantitative. In the rest of this section, we focus on the three quantitative criteria: goodness of fit, complexity or simplicity, and generalizability.

goodness of fit, complexity (simplicity), and generalizability

The goodness-of-fit criterion (GOF) is defined as a model’s best fit to the observed data, obtained by searching the model’s parameter space for the best-fitting parameter values that maximize or minimize a specific objective function. The common measures of GOF include the root mean squared error (RMSE), the percent variance accounted for , and the maximum likelihood (ML).

One cannot use GOF alone for comparing models because of what is called the overfitting problem ( Myung, 2000 ). Overfitting arises when a model captures not only the underlying regularities in a dataset, which is good, but also random noise, which is not good. It is inevitable that behavioral data include random noise from a number of sources, including sampling error, human error, and individual differences, among others. A model’s ability to fit that noise is meaningless because, being random, the noise pattern will be different from one data set to another. Fitting the noise reveals nothing of psychological relevance and can actually hinder the identification of more meaningful patterns in the data.

Because GOF measures the model’s fit to both regularity and noise, properties of the model that have nothing to do with its ability to fit the underlying regularity can improve GOF. One such property is complexity. Intuitively, complexity is defined as a model’s inherent flexibility in fitting a wide range of data patterns ( Myung & Pitt, 1997 ). It can be understood by contrasting the data-fitting capabilities of simple and complex models. A simple model will have few parameters and make clear and easily falsifiable predictions. A simple model predicts that a specific pattern will be found in the data, and if this pattern is found then the model will fit well, otherwise it will fit poorly. On the other hand, a complex model will have many more parameters, making it more flexible and able to predict with high accuracy many different data patterns by finely tuning those parameters. A highly complex model is not easily falsifiable because its parameters can be tuned to fit almost any pattern of data including random noise. As such, a complex model can often provide superior fits by capitalizing on random noise, which is specific to the particular data sample, but not necessarily by capturing the regularity underlying the data.

Desired in model comparison is a yardstick by which a model is measured by its ability to capture the underlying regularity only rather than idiosyncratic noise. This is the generalizability criterion ( Pitt, Myung, & Zhang, 2002 ). Generalizability refers to a model’s ability to fit the current data sample (i.e., actual observations) and all “future” data samples (i.e., replications of the experiment) from the same underlying process that generated the current data. Generalizability is often called predictive accuracy or generality ( Hitchcock & Sober, 2004 ). An important goal of modeling is to identify hypotheses that generate accurate predictions; hence, the goal of model comparison is to choose the model that best generalizes, not the one that provides the best fit to a single data set.

Figure 21.3 illustrates the relationship between complexity and generalizabilityand shows the fits of three different models to a data set from a lexical decision experiment. The linear model (top left graph) underfits the data because it does not have sufficient complexity to capture the underlying regularities. When underfitting occurs, increasing the complexity of the model not only improves GOF, it will also improve generalizability because the additional complexity captures unaccounted-for, underlying regularities in the data. However, too much complexity, as in the Spline model (top right graph), will cause the model to pick up on not just the underlying regularities but also idiosyncratic noise that does not generalize to future datasets (bottom graph). This will result in overfitting and reduce generalizability. Thus the dilemma in trying to maximize generalizability is a delicate balance between complexity and GOF.

To summarize, what is needed in model comparison is a method that estimates a model’s generalizability by accounting for the effects of its complexity. Various measures of generalizability have been proposed in statistics, which we discuss next. For more thorough treatments of the topic, the reader is directed to two Journal of Mathematical Psychology special issues ( Myung, Forester, & Browne, 2000 ; Wagenmakers & Waldorp, 2006 ) and a recent review article ( Shiffrin, Lee, Kim, & Wagenmakers, 2008 ).

methods of model comparison

Akaike Information Criterion and Bayesian Information Criterion: The Akaike Information Criterion (AIC; Akaike, 1973 ) and the Bayesian Information Criterion (BIC; Schwartz, 1978 ) address the most salient dimension of model complexity, the number of free parameters, and are defined as

The first term in each of these expressions assesses the model’s GOF (as –2 times the natural logarithm of the value of the likelihood function at the MLE estimate), whereas the second term penalizes the model for complexity. Specifically, the second term includes a count of the number of parameters, k . The AIC and BIC penalize a model more as the number of parameters increases. Under each criterion, the smaller the criterion value is, the better the model is judged to generalize. Consequently, to be selected as more generalizable, a more complex model must overcome this penalty with a much better GOF to the data than the simpler model with fewer parameters.

Bayesian Model Selection and Minimum Description Length . Another feature that affects model complexity is functional form, which refers to the way in which the model’s parameters are combined in the model equation. More sophisticated selection methods, such as Bayesian model selection (BMS; Kass & Raftery, 1995 ; Wasserman, 2000 ) and minimum description length (MDL; Rissanen, 1996 ; Pitt, Myung, & Zhang, 2002 ; Hansen & Yu, 2001 ) are sensitive to a model’s functional form as well as the number of parameters, and are defined as

Top row: Three models of the lexical decision task with their fits to a fictitious data set—from left to right: linear model, power model, Spline model. Bottom row: Generalizability of the fits in the top row to the data from a different participant.

where π ( w ) is the parameter prior and I( w ) is the Fisher information matrix. The effects of functional form on model complexity are reflected in the third term of the MDL equation, whereas in BMS it is hidden inside the integral.

Cross-Validation and Accumulative Prediction Error . Two other measures, cross-validation (CV; Browne, 2000 ) and accumulative prediction error (APE; Dawid, 1984 ; Wagenmakers, Grunwald, & Steyvers, 2006 ) assess generalizability by actually evaluating the model’s performance against “future” data. The basic idea of CV is to partition the data sample into two complementary subsets. One subset, called the training or calibration set, is used to fit the model via LSE or MLE. The other subset, called the validation set, is treated as a “future” data set and is used to test the estimates from the training set. If the parameters estimated from the training set also provide a good fit to the validation set, then the conclusion is that the model generalizes well.

Accumulative prediction error is similar to CV in spirit but differs from it in implementation. In APE, the size of the training set is increased successively one observation at a time while maintaining the size of the validation set fixed to one. The litmus test for generalizability is performed by assessing how well the model predicts the next “unseen” data point y o b s , j + 1 using the best-fit parameter value obtained based on the first j observations { y o b s , 1 , y o b s , 2 , … , y o b s , j } for j = k + 1 , … , n - 1 . Accumulative predictive error then estimates the model’s generalizability by the sum of the prediction errors for the validation data.

Both CV and APE are thought to be sensitive to number of parameters as well as functional form.

Model Revision

When a model is found to be inappropriate, in terms of a lack of fit or lack of generalizability, steps must be taken to revise it, perhaps substantially, or even replace it with a new model ( Shiffrin & Nobel, 1997 , p. 7). This could be emotionally difficult for the investigator, especially if the person has invested substantial resources into developing the model (e.g., years of work). In these situations, it is best to put aside personal attachment and make the goals of science paramount.

In the words of Meehl (1990) , “Even the best theories are likely to be approximations of reality.” However, mathematical models can still be very useful, even in this limited capacity. Many people have heard the famous quote, “All models are false, but some are useful,” credited to George E. P. Box (1975). The nature of that usefulness was summed up by Karlin (1983) , who said, “The purpose of models is not to fit the data but to sharpen the questions.” In a sense, a model is only as valuable as the insights it provides and the research hypotheses that it generates. This means that mathematical models are not ends in themselves but, rather, steps on the road to scientific understanding. We will always need new models to expand on the knowledge and insights gained from previous models.

One viable approach in model revision is to selectively add and remove relevant features to and from the model. In taking this course of action, one should be mindful of the important but often neglected issues of model faithfulness ( Myung et al., 1999 ) and irrelevant specification ( Lewandowsky, 1993 ). Model faithfulness refers to the issue of whether a model’s success in mimicking human behavior results from the theoretical principles embodied in the model or merely from its computational instantiation. In other words, even if a model provides an excellent description of human data in the simplest manner possible, it is often difficult to determine whether the theoretical principles that the model originally intended to implement are critical for its performance or if less central choices in model instantiation are instead responsible for good performance.

Irrelevant specification, which is similar to the concept of model faithfulness, refers to the case in which a model’s performance is strongly affected by irrelevant modeling details that are theoretically neutral and fully interchangeable with any viable alternatives. Examples of irrelevant details include input coding methods, the specification of error structure, and idiosyncratic features of the simulation schedule ( Fum et al., 2007 ).

The science of mathematical modeling involves converting the ideas, assumptions, and principles embodied in psychological theory into mathematical abstraction. Mathematics is used to craft precise representations of human behavior. The specificity inherent in models opens up new avenues of research. Their usefulness is evident in the rapid rate at which models are appearing in psychology, as well as in related fields such as human factors, behavioral economics, and cognitive neuroscience. Mathematical modeling has become an essential tool for understanding human behavior, and any researcher with an inclination toward theory building would be well served to begin practicing it.

Future Directions

Mathematical modeling has contributed substantially to advancing the study of mind and brain. Modeling has opened up new ways of thinking about problems, provided a framework for studying complex interactions among causal and correlational variables, provided insight needed to tie together seemingly inconsistent findings, and increased the precision of prediction in experimentation.

Despite these advances, for the field to move forward and beyond the current state of affairs, there remain many challenges to overcome and problems to be solved. Below we list four challenges for the next decade of mathematical modeling.

1. At present, mathematical modeling is confined to a relatively small group of mostly self-selected researchers. To impact the mainstream of psychological science, an effort should be made to ensure that frontline psychologists learn to practice the art of modeling. Examples of such efforts include writing tutorial articles in journals and publishing graduate-level textbooks.

2. Modeling begins in a specific domain, whether it be a phenomenon, task, or process. Modelers eventually face the challenge of expanding the scope of their models to explain performance on other tasks, account for additional phenomena, or to bridge multiple levels of description (e.g., brain activity and behavior responses). Model expansion is difficult because the perils of complexity multiply. The development of methods for doing so will be an important step in the discipline.

3. Model faithfulness, discussed above, concerns determining what properties of a model are critical for explaining human performance and what properties serve lesser roles. Failure to make this distinction runs the risk of erroneously attributing a model’s behavior to its underlying theoretical principles. In the worst case, computational complexity is mistaken for theoretical accuracy. A method should be developed to formalize and assess a model’s faithfulness such that the relative contribution of each modeling assumption to the model’s data-fitting ability is quantified in some justifiable sense.

4. Models can be difficult to discriminate experimentally because of their complexity and the extent to which they mimic each other. A method for identifying an “optimal” experimental design that would produce the most informative, differentiating outcome between the models of interest needs to be developed. Related to this, quantitative methods of model comparison have their limits. Empirical data alone may not be sufficient to discriminate highly similar models. Modeling would benefit from the introduction of new and more powerful measures of model adequacy. In particular, it would be desirable to quantify the qualitative dimensions described in Table 21.1 .

Author Note

This research is supported in part by National Institute of Health Grant R01-MH57472.

Aczel, J. ( 1966 ). Lectures on Functional Equations and their Applications . New York, NY: Academic Press.

Google Scholar

Google Preview

Akaike, H. ( 1973 ). Information theory and an extension of the maximum likelihood principle. In Petrov, B. N. & Caski, F. , (Eds.), Proceedings of the Second International Symposium on Information Theory , (pp. 267–281), Budapest. Akademiai Kiado.

Bakan, D. ( 1966 ). Statistical significance in psychological research.   Psychological Bulletin , 66 , 423–437.

Batchelder, W. H. & Riefer, D. M. ( 1999 ). Theoretical and empirical review of multinomial process tree modeling.   Psychonomic Bulletin and Review , 6 , 57–86.

Brown, G. D. A. , Neath, I. & Chater, N. ( 2007 ). A temporal ratio model of memory.   Psychological Review , 114 , 539–576.

Browne, M. W. ( 2000 ). Cross-validation methods.   Journal of Mathematical Psychology , 44 , 108–132.

Busemeyer, J. R. & Diederich, A. ( 2010 ). Cognitive Modeling . Thousand Oaks, CA: Sage Publications.

Busemeyer, J. R. & Townsend, J. T. ( 1993 ). Decision field theory: A dynamic- cognitive approach to decision making in an uncertain environment. Psychological Review, 100 , 432–459.

Chater, N. , Tenenbaum, J. , & Yuille, A. ( 2006 ). Probabilistic models of cognition: Conceptual foundations.   Trends in Cognitive Sciences , 10 , 287–291.

Dawid, A. P. ( 1984 ). Statistical theory: The prequential approach.   Journal of the Royal Statistical Society, Series A , 147 , 278–292.

Estes, W. K. ( 1975 ). Some targets for mathematical psychology.   Journal of Mathematical Psychology , 12, 263–282.

Estes, W. K. ( 2002 ). Traps in the route to models of memory and decision.   Psychonomic Bulletin & Review , 9: 3–25.

Fishburn, P. ( 1982 ). The Foundations of Expected Utility . Dordrecht, Holland: Kluwer.

Fum, D. , Del Missier, F. , & Stocco, A. ( 2007 ). The cognitive modeling of human behavior: Why a model is (sometimes) better than 10 ,000 words. Cognitive Systems Research , 8 , 135–142.

Gelman, A. , Carlin, J. B. , Stern, H. S. & Rubin, D. B. ( 2004 ). Bayesian Data Analysis (2nd edition) . Boca Raton, FL: Chapman & Hall/CRC.

Gigerenzer, G. ( 1991 ). From tools to theories: A heuristic of discovery in cognitive psychology.   Psychological Review , 98 , 254–267.

Gill, J. ( 2008 ). Bayesian Methods: A Social and Behavioral Sciences Approach (2nd ed.). Boca Raton, FL: Chapman & Hall/CRC.

Griffiths, T. L. , Steyvers, M. , & Tenenbaum, J. B. ( 2007 ). Topics in semantic representation.   Psychological Review , 114 , 211–244.

Hansen, M. & Yu, B. ( 2001 ). Model selection and the principle of minimum description length.   Journal of the American Statistical Association , 96 , 746–774.

Hitchcock, C. & Sober, E. ( 2004 ). Prediction versus accommodation and the risk of overfitting.   British Journal for the Philosophy of Science , 55 , 1–34.

Hornik, K. , Stinchcombe, M. , & White, H. ( 1989 ). Multilayer feedforward networks are universal approximators.   Neural Networks , 2 , 359–368.

Hornik, K. , Stinchcombe, M. , & White, H. ( 1990 ). Universal approximations of an unknown mapping and its derivatives using multilayer feedforward networks.   Neural Networks , 3 , 551–560.

Howard, M. & Kahana, M. ( 2002 ). A distributed representation of temporal context.   Journal of Mathematical Psychology , 46 , 269–299.

Jacobs, A. & Grainger, J. ( 1994 ). Models of visual word recognition: Sampling the state of the art.   Journal of Experimental Psychology: Human Perception and Performance , 29 , 1311–1334.

Karlin, S. ( 1983 ). The 11th R. A. Fisher Memorial Lecture given at the Royal Society 20 Meeting in April, 1983.

Kass, R. E. & Raftery, A. E. ( 1995 ). Bayes factors.   Journal of the American Statistical Association , 90 , 773–795.

Kruschke, J. K. ( 1992 ). Alcove: An exemplar-based connectionist model of category learning.   Psychological Review , 99 , 22–44.

Kruschke, J. K. ( 2010 ). What to believe: Bayesian methods for data analysis.   Trends in Cognitive Sciences , 14 , 293–300.

Lee, M. D. ( 2008 ). Three case studies in the Bayesian analysis of cognitive models.   Psychonomic Bulletin & Review , 15 , 1–15.

Lee, M. D. ( 2011 ). How cognitive modeling can benefit from hierarchical Bayesian models.   Journal of Mathematical Psychology , 55 , 1–7.

Lee, M. D. , & Sarnecka, B. W. ( 2010 ). A model of knower-level behavior in number-concept development.   Cognitive Science , 34 , 51–67.

Lewandowsky, S. ( 1993 ). The rewards and hazards of computer simulations.   Psychological Science , 4 , 236–243.

Luce, R. D. ( 2000 ). Utility of Gains and Losses: Measurement-theoretical and Experimental Approaches . Mahwah, NJ: Lawrence Erlbaum.

Lunn, D. J. , Thomas, A. , Best, N. , & Spiegelhalter, D. ( 2000 ). WinBUGS—a Bayesian modeling framework: Concepts, structure and extensibility.   Statistics and Computing , 10 , 325–337.

Lykken, D. ( 1968 ). Statistical significance in psychological research.   Psychological Bulletin , 70 , 151–159.

Marewski, J. N. & Olsson, H. ( 2009 ). Beyond the null ritual.   Zeitschrift fur Psychologie , 217 , 49–60.

McClelland, J. L. & Elman, J. L. ( 1986 ). The trace model of speech perception.   Cognitive Psychology , 18 , 1–86.

Meehl, P. ( 1990 ). Appraising and amending theories: The strategy of Lakatosian defense and two principles that warrant it.   Psychological Inquiry , 1 , 108–141.

Morgenstern, O. & Von Neumann, J. ( 1947 ). Theory of Games and Economic Behavior . Princeton, NJ: Princeton University Press.

Myung, I. J. ( 2000 ). The importance of complexity in model selection.   Journal of Mathematical Psychology , 44 , 190–204.

Myung, I. J. ( 2003 ). Tutorial on maximum likelihood estimation.   Journal of Mathematical Psychology , 47 , 90–100.

Myung, I. , J. Brunsman IV, A. , & Pitt, M. A. ( 1999 ). True to thyself: Assessing whether computational models of cognition remain faithful to their theoretical principles. In M. Hahn & S. C. Stoness (Eds.), Proceedings of the Twenty-first Annual Conference of the Cognitive Science Society (pp. 462–467). Mahwah, NJ: Lawrence Erlbaum Associates.

Myung, I. J. , Forster, M. , & Browne, M. W. ( 2000 ). Special issue on model selection.   Journal of Mathematical Psychology , 44 , 1–2.

Myung, I. J. & Pitt, M. A. ( 1997 ). Applying Occam’s razor in modeling cognition: A Bayesian approach.   Psychonomic Bulletin & Review , 4 , 79–95.

Myung, I. J. , & Pitt, M. A. ( 2002 ). Mathematical modeling. In J. Wixted (Ed.), Stevens’ Handbook of Experimental Psychology (Third Edition), Volume IV (Methodology) (pp. 429–459). New York: John Wiley & Sons.

Nickerson, R. ( 2000 ). Null hypothesis statistical testing: A review of an old and continuing controversy.   Psychological Methods , 5 , 241–301.

Nosofsky, R. M. ( 1986 ). Attention, similarity and the identification-categorization relationship.   Journal of Experimental Psychology: General , 115 , 39–57.

Perea, M. , Rosa, E. , & Gomez, C. ( 2002 ). Is the go/no-go lexical decision task an alternative to the yes/no lexical decision task?   Memory & Cognition , 30 , 34–45.

Pitt, M. A. , Myung, I. J. , & Zhang, S. ( 2002 ). Toward a method of selecting among computational models of cognition.   Psychological Review , 190 , 472–491.

Plaut, D. C. , McClelland, J. L. , Seidenberg, M. S. & Patterson, K. ( 1996 ). Understanding normal and impaired word reading: Computational principles in quasi-regular domains.   Psychological Review , 103 , 56–115.

Press, W. H. , Teukolsky, S. A. , Vetterling, W. T. & Flannery, B. R. ( 1992 ). Numerical Recipes in C: The Art of Scientific Computing (2nd edition) . Cambridge, UK: Cambridge University Press.

Ratcliff, R. ( 1978 ). A theory of memory retrieval.   Psychological Review , 85 , 59–108.

Rissanen, J. ( 1996 ). Fisher information and stochastic complexity.   IEEE Transaction on Information Theory , 42 , 40–47.

Rouder, J. & Lu, J. ( 2005 ). An introduction to Bayesian hierarchical models with an application in the theory of signal detection.   Psychonomic Bulletin & Review , 12 , 573–604.

Rouder, J. N. , Sun, D. , Speckman, P. , Lu, J. , & Zhou, D. ( 2003 ). A hierarchical Bayesian statistical framework for response time distributions.   Psychometrika , 68 , 589–606.

Rozeboom, W. ( 1960 ). The fallacy of the null-hypothesis significance test.   Psychological Bulletin , 57 , 416–428.

Rubin, D. & Wenzel, A. ( 1996 ). One hundred years of forgetting: A quantitative description of retention.   Psychological Review , 103 , 734–760.

Schwarz, G. ( 1978 ). Estimating the dimension of a model.   Annals of Statistics , 6 , 461–464.

Shiffrin, R. M. & Nobel, P. A. . ( 1997 ). The art of model development and testing.   Behavior Research Methods, Instruments, and Computers, 29(1), 6–14.

Shiffrin, R. M. & Steyvers, M. ( 1997 ). A model for recognition memory: REM-retrieving effectively from memory.   Psychonomic Bulletin & Review , 4 , 145–166.

Shiffrin, R. M. , Lee, M. D. , Kim, W. , & Wagenmakers, E-J. ( 2008 ). A survey of model evaluation approaches with a tutorial on hierarchical Bayesian methods.   Cognitive Science , 32 , 1248–1284.

Stevens, S. ( 1975 ). Psychophysics: Introduction to its Perceptual, Neural, and Social Prospects . New York: John Wiley & Sons.

Steyvers, M. , Lee, M. D. , & Wagenmakers, E-J. ( 2009 ). A Bayesian analysis of human decision-making on bandit problems.   Journal of Mathematical Psychology , 53 , 168–179.

Suppes, P. ( 1957 ). Introduction to Logic . Mineola, NY: Dover Publications.

Tenenbaum, J. B. , Griffiths, T. L. , & Kemp, C. ( 2006 ). Theory-based Bayesian models of inductive learning and reasoning.   Trends in Cognitive Science , 10 , 309–318.

Thurstone, L. ( 1974 ). The Measurement of Values . Chicago: The University of Chicago Press.

Wagenmakers, E.-J. ( 2007 ). A practical solution to the pervasive problems of p values.   Psychonomic Bulletin and Review , 14 , 779–804.

Wagenmakers, E.-J. , Grunwald, P. , & Steyvers, M. ( 2006 ). Accumulative prediction error and the selection of time series models.   Journal of Mathematical Psychology , 50 , 149–166.

Wagenmakers, E-J. , Lodewyckx, T. , Kuriyal, H. , & Grasman, R. ( 2010 ). Bayesian hypothesis testing for psychologists: A tutorial on the Savage-Dickey method.   Cognitive Psychology , 60 , 158–189.

Wagenmakers, E.-J. & Waldorp, L. ( 2006 ). Editors’ introduction.   Journal of Mathematical Psychology , 50 , 99–100.

Wasserman, L. ( 2000 ). Bayesian model selection and model averaging.   Journal of Mathematical Psychology , 44 , 92–107.

Wetzels, R. , Raaijmakers, J. , Jakab, E. , & Wagenmakers, E.-J. ( 2009 ). How to quantify support for and against the null hypothesis: A flexible WINBUGS implementation of a default Bayesian t-test.   Psychonomic Bulletin & Review , 16 , 752–760.

Wixted, J. , & Ebbesen, E. ( 1991 ). On the form of forgetting.   Psychological Science , 2 , 409–415.

Xu, J. , & Griffiths, T. L. ( 2010 ). A rational analysis of the effects of memory biases on serial reproduction.   Cognitive Psychology , 60 , 107–126.

• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.1: Introduction to Modeling

• Last updated
• Save as PDF
• Page ID 93900

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

Students will be able to:

• Express the relationship between the input and output variable for a function
• Use function notation to evaluate a function for a given input
• Represent a function as a table, graph, or formula

in order to apply mathematical modeling to solve real-world applications.

In this section, we will introduce the basics for creating mathematical models which enable us to make predictions and understand the relationships that exist between two different factors called variables. We will first discuss functions which give us the tools needed to describe relationships between two variables, and we will then introduce key concepts such as correlation which enable us to create our models.

Given two sets \(A\) and \(B\) a set with elements that are ordered pairs \((x,y)\) where \(x\) is an element of \(A\) and \(y\) is an element of \(B,\) is a relation from \(A\) to \(B\). A relation from \(A\) to \(B\) defines a relationship between those two sets. A function is a special type of relation in which each element of the first set is related to exactly one element of the second set. The element of the first set is called the input ; the element of the second set is called the output . Functions are used all the time in mathematics to describe relationships between two sets. For any function, when we know the input, the output is determined, so we say that the output is a function of the input. For example, the area of a square is determined by its side length, so we say that the area (the output) is a function of its side length (the input). The velocity of a ball thrown in the air can be described as a function of the amount of time the ball is in the air. The cost of mailing a package is a function of the weight of the package. Since functions have so many uses, it is important to have precise definitions and terminology to study them.

Definition: Functions

A function \(f\) consists of a set of inputs, a set of outputs, and a rule for assigning each input to exactly one output. The set of inputs is called the domain of the function. The set of outputs is called the range of the function .

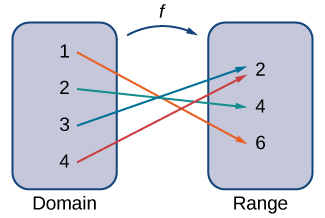
For example, consider the function \(f\), where the domain is the set of all real numbers and the rule is to square the input. Then, the input \(x=3\) is assigned to the output \(3^2=9\).

Since every nonnegative real number has a real-value square root, every nonnegative number is an element of the range of this function. Since there is no real number with a square that is negative, the negative real numbers are not elements of the range. We conclude that the range is the set of nonnegative real numbers.

For a general function \(f\) with domain \(D\), we often use \(x\) to denote the input and \(y\) to denote the output associated with \(x\). When doing so, we refer to \(x\) as the independent variable and \(y\) as the dependent variable , because it depends on \(x\). Using function notation, we write \(y=f(x)\), and we read this equation as “\(y\) equals \(f\) of \(x.”\) For the squaring function described earlier, we write \(f(x)=x^2\).

The concept of a function can be visualized using Figures \(\PageIndex{1}\) - \(\PageIndex{3}\).

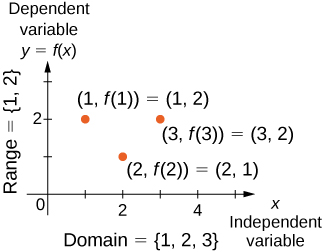
We can also visualize a function by plotting points \((x,y)\) in the coordinate plane where \(y=f(x)\). The graph of a function is the set of all these points. For example, consider the function \(f\), where the domain is the set \(D=\{1,2,3\}\) and the rule is \(f(x)=3−x\). In Figure \(\PageIndex{4}\), we plot a graph of this function.

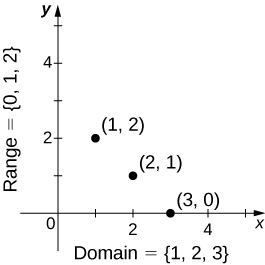
Every function has a domain. However, sometimes a function is described by an equation, as in \(f(x)=x^2\), with no specific domain given. In this case, the domain is taken to be the set of all real numbers \(x\) for which \(f(x)\) is a real number. For example, since any real number can be squared, if no other domain is specified, we consider the domain of \(f(x)=x^2\) to be the set of all real numbers. On the other hand, the square root function \(f(x)=\sqrt{x}\) only gives a real output if \(x\) is nonnegative. Therefore, the domain of the function \(f(x)=\sqrt{x}\) is the set of nonnegative real numbers, sometimes called the natural domain.

For the functions \(f(x)=x^2\) and \(f(x)=\sqrt{x}\), the domains are sets with an infinite number of elements. Clearly we cannot list all these elements. When describing a set with an infinite number of elements, it is often helpful to use set-builder or interval notation. When using set-builder notation to describe a subset of all real numbers, denoted \(R\), we write

\[\{x\,|\,\textit{x has some property}\}.\]

We read this as the set of real numbers \(x\) such that \(x\) has some property. For example, if we were interested in the set of real numbers that are greater than one but less than five, we could denote this set using set-builder notation by writing

\[\{x\,|\,1<x<5\}.\]

A set such as this, which contains all numbers greater than \(a\) and less than \(b,\) can also be denoted using the interval notation \((a,b)\). Therefore,

\[(1,5)=\{x\,|\,1<x<5\}.\]

The numbers \(1\) and \(5\) are called the endpoints of this set. If we want to consider the set that includes the endpoints, we would denote this set by writing

\[[1,5]=\{x\,|\,1<x<5\}.\]

We can use similar notation if we want to include one of the endpoints, but not the other. To denote the set of nonnegative real numbers, we would use the set-builder notation

\[\{x\,|\,x\ge 0\}.\]

The smallest number in this set is zero, but this set does not have a largest number. Using interval notation, we would use the symbol \(∞,\) which refers to positive infinity, and we would write the set as

\[[0,∞)=\{x\,|\,x\ge 0\}.\]

It is important to note that \(∞\) is not a real number. It is used symbolically here to indicate that this set includes all real numbers greater than or equal to zero. Similarly, if we wanted to describe the set of all nonpositive numbers, we could write

\[(−∞,0]=\{x\,|\,x≤0\}.\]

Here, the notation \(−∞\) refers to negative infinity, and it indicates that we are including all numbers less than or equal to zero, no matter how small. The set

\[(−∞,∞)=\{\textit{x} \,|\, \textit{x is any real number}\}\]

refers to the set of all real numbers.Some functions are defined using different equations for different parts of their domain. These types of functions are known as piecewise-defined functions. For example, suppose we want to define a function \(f\) with a domain that is the set of all real numbers such that \(f(x)=3x+1\) for \(x≥2\) and \(f(x)=x^2\) for\( x<2\).We denote this function by writing

\[f(x)=\begin{cases} 3x+1, & \text{if } x≥2 \\ x^2, & \text{if } x<2 \end{cases}\]

When evaluating this function for an input \(x\),the equation to use depends on whether \(x≥2\) or \(x<2\). For example, since \(5>2\), we use the fact that \(f(x)=3x+1\) for \(x≥2\) and see that \(f(5)=3(5)+1=16\). On the other hand, for \(x=−1\), we use the fact that \(f(x)=x^2\) for \(x<2\) and see that \(f(−1)=1\).

Example \(\PageIndex{1}\): Evaluating Functions

For the function \(f(x)=3x^2+2x−1\), evaluate:

• \(f(−2)\)

Substitute the given value for \(x\) in the formula for \(f(x)\).

• \(f(−2)=3(−2)^2+2(−2)−1=12−4−1=7\)
• \(f(3)=3(3)^2+2(3)−1=18+6−1=23\)

Exercise \(\PageIndex{2}\)

For \(f(x)=x^2−3x+5\), evaluate \(f(1)\) and \(f(-1)\).

Substitute \(1\) and \(-3\) for \(x\) in the formula for \(f(x)\).

\(f(1)=(1)^2-3(1)+5=1-3+5=3\) and \(f(-1)=(-1)^2-3(-1)+5=1+3+5=9\)

Representing Functions

Typically, a function is represented using one or more of the following tools:

We can identify a function in each form, but we can also use them together. For instance, we can plot on a graph the values from a table or create a table from a formula.

Functions described using a table of values arise frequently in real-world applications. Consider the following simple example. We can describe temperature on a given day as a function of time of day. Suppose we record the temperature every hour for a 24-hour period starting at midnight. We let our input variable \(x\) be the time after midnight, measured in hours, and the output variable \(y\) be the temperature \(x\) hours after midnight, measured in degrees Fahrenheit. We record our data in Table \(\PageIndex{1}\).

We can see from the table that temperature is a function of time, and the temperature decreases, then increases, and then decreases again. However, we cannot get a clear picture of the behavior of the function without graphing it.

Given a function \(f\) described by a table, we can provide a visual picture of the function in the form of a graph. Graphing the temperatures listed in Table \(\PageIndex{1}\) can give us a better idea of their fluctuation throughout the day. Figure \(\PageIndex{5}\) shows the plot of the temperature function.

From the points plotted on the graph in Figure \(\PageIndex{5}\), we can visualize the general shape of the graph. It is often useful to connect the dots in the graph, which represent the data from the table. In this example, although we cannot make any definitive conclusion regarding what the temperature was at any time for which the temperature was not recorded, given the number of data points collected and the pattern in these points, it is reasonable to suspect that the temperatures at other times followed a similar pattern, as we can see in Figure \(\PageIndex{6}\).

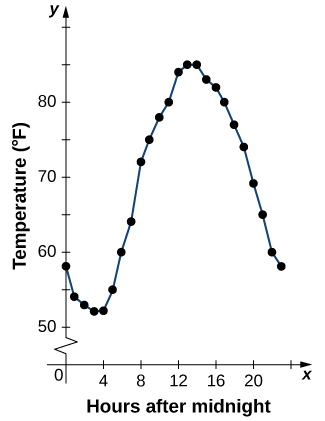
Algebraic Formulas

Sometimes we are not given the values of a function in table form, rather we are given the values in an explicit formula. Formulas arise in many applications. For example, the area of a circle of radius \(r\) is given by the formula \(A(r)=πr^2\). When an object is thrown upward from the ground with an initial velocity \(v_{0}\) ft/s, its height above the ground from the time it is thrown until it hits the ground is given by the formula \(s(t)=−16t^2+v_{0}t\). When \(P\) dollars are invested in an account at an annual interest rate \(r\) compounded continuously, the amount of money after \(t\) years is given by the formula \(A(t)=Pe^{rt}\). Algebraic formulas are important tools to calculate function values. Often we also represent these functions visually in graph form.

Given an algebraic formula for a function \(f\), the graph of \(f\) is the set of points \((x,f(x))\), where \(x\) is in the domain of \(f\) and \(f(x)\) is in the range. To graph a function given by a formula, it is helpful to begin by using the formula to create a table of inputs and outputs. If the domain of \(f\) consists of an infinite number of values, we cannot list all of them, but because listing some of the inputs and outputs can be very useful, it is often a good way to begin.

When creating a table of inputs and outputs, we typically check to determine whether zero is an output. Those values of \(x\) where \(f(x)=0\) are called the zeros of a function. For example, the zeros of \(f(x)=x^2−4\) are \(x=±2\). The zeros determine where the graph of \(f\) intersects the \(x\)-axis, which gives us more information about the shape of the graph of the function. The graph of a function may never intersect the \(x\)-axis, or it may intersect multiple (or even infinitely many) times.

Another point of interest is the \(y\) -intercept, if it exists. The \(y\)-intercept is given by \((0,f(0))\).

Since a function has exactly one output for each input, the graph of a function can have, at most, one \(y\)-intercept. If \(x=0\) is in the domain of a function \(f,\) then \(f\) has exactly one \(y\)-intercept. If \(x=0\) is not in the domain of \(f,\) then \(f\) has no \(y\)-intercept. Similarly, for any real number \(c,\) if \(c\) is in the domain of \(f\), there is exactly one output \(f(c),\) and the line \(x=c\) intersects the graph of \(f\) exactly once. On the other hand, if \(c\) is not in the domain of \(f,\) \(f(c)\) is not defined and the line \(x=c\) does not intersect the graph of \(f\).

Example \(\PageIndex{3}\): Finding the Height of a Free-Falling Object

If a ball is dropped from a height of 100 ft, its height s at time \(t\) is given by the function \(s(t)=−16t^2+100\), where s is measured in feet and \(t\) is measured in seconds. The domain is restricted to the interval \([0,c],\) where \(t=0\) is the time when the ball is dropped and \(t=c\) is the time when the ball hits the ground.

• Create a table showing the height s(t) when \(t=0,\, 0.5,\, 1,\, 1.5,\, 2,\) and \(2.5\). Using the data from the table, determine the domain for this function. That is, find the time \(c\) when the ball hits the ground.
• Sketch a graph of \(s\).

Since the ball hits the ground when \(t=2.5\), the domain of this function is the interval \([0,2.5]\).

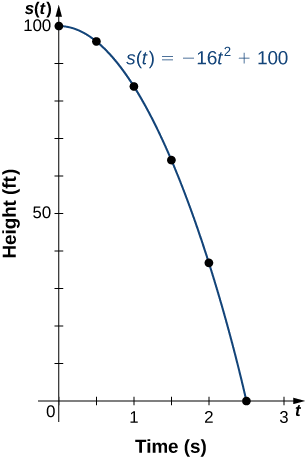
• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Entry Contents

Bibliography

Academic tools.

• Friends PDF Preview
• Author and Citation Info
• Back to Top

Model Theory

Model theory began with the study of formal languages and their interpretations, and of the kinds of classification that a particular formal language can make. Mainstream model theory is now a sophisticated branch of mathematics (see the entry on first-order model theory ). But in a broader sense, model theory is the study of the interpretation of any language, formal or natural, by means of set-theoretic structures, with Alfred Tarski’s truth definition as a paradigm. In this broader sense, model theory meets philosophy at several points, for example in the theory of logical consequence and in the semantics of natural languages.

1. Basic notions of model theory

2. model-theoretic definition, 3. model-theoretic consequence, 4. expressive strength, 5. models and modelling, 6. model theory as a source of philosophical questions, other internet resources, related entries.

Sometimes we write or speak a sentence \(S\) that expresses nothing either true or false, because some crucial information is missing about what the words mean. If we go on to add this information, so that \(S\) comes to express a true or false statement, we are said to interpret \(S\), and the added information is called an interpretation of \(S\). If the interpretation \(I\) happens to make \(S\) state something true, we say that \(I\) is a model of \(S\), or that \(I\) satisfies \(S\), in symbols ‘\(I \vDash S\)’. Another way of saying that \(I\) is a model of \(S\) is to say that \(S\) is true in \(I\), and so we have the notion of model-theoretic truth , which is truth in a particular interpretation. But one should remember that the statement ‘\(S\) is true in \(I\)’ is just a paraphrase of ‘\(S\), when interpreted as in \(I\), is true’; so model-theoretic truth is parasitic on plain ordinary truth, and we can always paraphrase it away.

For example I might say

He is killing all of them,

and offer the interpretation that ‘he’ is Alfonso Arblaster of 35 The Crescent, Beetleford, and that ‘them’ are the pigeons in his loft. This interpretation explains (a) what objects some expressions refer to, and (b) what classes some quantifiers range over. (In this example there is one quantifier: ‘all of them’). Interpretations that consist of items (a) and (b) appear very often in model theory, and they are known as structures . Particular kinds of model theory use particular kinds of structure; for example mathematical model theory tends to use so-called first-order structures , model theory of modal logics uses Kripke structures , and so on.

The structure \(I\) in the previous paragraph involves one fixed object and one fixed class. Since we described the structure today, the class is the class of pigeons in Alfonso’s loft today, not those that will come tomorrow to replace them. If Alfonso Arblaster kills all the pigeons in his loft today, then \(I\) satisfies the quoted sentence today but won’t satisfy it tomorrow, because Alfonso can’t kill the same pigeons twice over. Depending on what you want to use model theory for, you may be happy to evaluate sentences today (the default time), or you may want to record how they are satisfied at one time and not at another. In the latter case you can relativise the notion of model and write ‘\(I \vDash_t S\)’ to mean that \(I\) is a model of \(S\) at time \(t\). The same applies to places, or to anything else that might be picked up by other implicit indexical features in the sentence. For example if you believe in possible worlds, you can index \(\vDash\) by the possible world where the sentence is to be evaluated. Apart from using set theory, model theory is completely agnostic about what kinds of thing exist.

Note that the objects and classes in a structure carry labels that steer them to the right expressions in the sentence. These labels are an essential part of the structure.

If the same class is used to interpret all quantifiers, the class is called the domain or universe of the structure. But sometimes there are quantifiers ranging over different classes. For example if I say

One of those thingummy diseases is killing all the birds.

you will look for an interpretation that assigns a class of diseases to ‘those thingummy diseases’ and a class of birds to ‘the birds’. Interpretations that give two or more classes for different quantifiers to range over are said to be many-sorted , and the classes are sometimes called the sorts .

The ideas above can still be useful if we start with a sentence \(S\) that does say something either true or false without needing further interpretation. (Model theorists say that such a sentence is fully interpreted .) For example we can consider misinterpretations \(I\) of a fully interpreted sentence \(S\). A misinterpretation of \(S\) that makes it true is known as a nonstandard or unintended model of \(S\). The branch of mathematics called nonstandard analysis is based on nonstandard models of mathematical statements about the real or complex number systems; see Section 4 below.

One also talks of model-theoretic semantics of natural languages, which is a way of describing the meanings of natural language sentences, not a way of giving them meanings. The connection between this semantics and model theory is a little indirect. It lies in Tarski’s truth definition of 1933. See the entry on Tarski’s truth definitions for more details.

A sentence \(S\) divides all its possible interpretations into two classes, those that are models of it and those that are not. In this way it defines a class, namely the class of all its models, written \(\Mod(S)\). To take a legal example, the sentence

The first person has transferred the property to the second person, who thereby holds the property for the benefit of the third person.

defines a class of structures which take the form of labelled 4-tuples, as for example (writing the label on the left):

• the first person = Alfonso Arblaster;
• the property = the derelict land behind Alfonso’s house;
• the second person = John Doe;
• the third person = Richard Roe.

This is a typical model-theoretic definition, defining a class of structures (in this case, the class known to the lawyers as trusts ).

We can extend the idea of model-theoretic definition from a single sentence \(S\) to a set \(T\) of sentences; \(\Mod(T)\) is the class of all interpretations that are simultaneously models of all the sentences in \(T\). When a set \(T\) of sentences is used to define a class in this way, mathematicians say that \(T\) is a theory or a set of axioms , and that \(T\) axiomatises the class \(\Mod(T)\).

Take for example the following set of first-order sentences:

Here the labels are the addition symbol ‘+’, the minus symbol ‘\(-\)’ and the constant symbol ‘0’. An interpretation also needs to specify a domain for the quantifiers. With one proviso, the models of this set of sentences are precisely the structures that mathematicians know as abelian groups . The proviso is that in an abelian group \(A\), the domain should contain the interpretation of the symbol 0, and it should be closed under the interpretations of the symbols + and \(-\). In mathematical model theory one builds this condition (or the corresponding conditions for other function and constant symbols) into the definition of a structure.

Each mathematical structure is tied to a particular first-order language. A structure contains interpretations of certain predicate, function and constant symbols; each predicate or function symbol has a fixed arity. The collection \(K\) of these symbols is called the signature of the structure. Symbols in the signature are often called nonlogical constants , and an older name for them is primitives . The first-order language of signature \(K\) is the first-order language built up using the symbols in \(K\), together with the equality sign =, to build up its atomic formulas. (See the entry on classical logic .) If \(K\) is a signature, \(S\) is a sentence of the language of signature \(K\) and \(A\) is a structure whose signature is \(K\), then because the symbols match up, we know that \(A\) makes \(S\) either true or false. So one defines the class of abelian groups to be the class of all those structures of signature \(+\), \(-\), \(0\) which are models of the sentences above. Apart from the fact that it uses a formal first-order language, this is exactly the algebraists’ usual definition of the class of abelian groups; model theory formalises a kind of definition that is extremely common in mathematics.

Now the defining axioms for abelian groups have three kinds of symbol (apart from punctuation). First there is the logical symbol = with a fixed meaning. Second there are the nonlogical constants, which get their interpretation by being applied to a particular structure; one should group the quantifier symbols with them, because the structure also determines the domain over which the quantifiers range. And third there are the variables \(x, y\) etc. This three-level pattern of symbols allows us to define classes in a second way. Instead of looking for the interpretations of the nonlogical constants that will make a sentence true, we fix the interpretations of the nonlogical constants by choosing a particular structure \(A\), and we look for assignments of elements of \(A\) to variables which will make a given formula true in \(A\).

For example let \(\mathbb{Z}\) be the additive group of integers. Its elements are the integers (positive, negative and 0), and the symbols \(+\), \(-\), \(0\) have their usual meanings. Consider the formula

If we assign the number \(-3\) to \(v_1\) and the number \(-6\) to \(v_2\), the formula works out as true in \(\mathbb{Z}\). We express this by saying that the pair \((-3,-6)\) satisfies this formula in \(\mathbf{Z}\). Likewise (15,30) and (0,0) satisfy it, but \((2,-4)\) and (3,3) don’t. Thus the formula defines a binary relation on the integers, namely the set of pairs of integers that satisfy it. A relation defined in this way in a structure \(A\) is called a first-order definable relation in \(A\). A useful generalisation is to allow the defining formula to use added names for some specific elements of \(A\); these elements are called parameters and the relation is then definable with parameters .

This second type of definition, defining relations inside a structure rather than classes of structure, also formalises a common mathematical practice. But this time the practice belongs to geometry rather than to algebra. You may recognise the relation in the field of real numbers defined by the formula

It’s the circle of radius 1 around the origin in the real plane. Algebraic geometry is full of definitions of this kind.

During the 1940s it occurred to several people (chiefly Anatolii Mal’tsev in Russia, Alfred Tarski in the USA and Abraham Robinson in Britain) that the metatheorems of classical logic could be used to prove mathematical theorems about classes defined in the two ways we have just described. In 1950 both Robinson and Tarski were invited to address the International Congress of Mathematicians at Cambridge Mass. on this new discipline (which as yet had no name – Tarski proposed the name ‘theory of models’ in 1954). The conclusion of Robinson’s address to that Congress is worth quoting:

[The] concrete examples produced in the present paper will have shown that contemporary symbolic logic can produce useful tools – though by no means omnipotent ones – for the development of actual mathematics, more particularly for the development of algebra and, it would appear, of algebraic geometry. This is the realisation of an ambition which was expressed by Leibniz in a letter to Huyghens as long ago as 1679. (Robinson 1952, 694)

In fact Mal’tsev had already made quite deep applications of model theory in group theory several years earlier, but under the political conditions of the time his work in Russia was not yet known in the West. By the end of the twentieth century, Robinson’s hopes had been amply fulfilled; see the entry on first-order model theory .

There are at least two other kinds of definition in model theory besides these two above. The third is known as interpretation (a special case of the interpretations that we began with). Here we start with a structure \(A\), and we build another structure \(B\) whose signature need not be related to that of \(A\), by defining the domain \(X\) of \(B\) and all the labelled relations and functions of \(B\) to be the relations definable in \(A\) by certain formulas with parameters. A further refinement is to find a definable equivalence relation on \(X\) and take the domain of \(B\) to be not \(X\) itself but the set of equivalence classes of this relation. The structure \(B\) built in this way is said to be interpreted in the structure \(A\).

A simple example, again from standard mathematics, is the interpretation of the group \(\mathbb{Z}\) of integers in the structure \(\mathbb{N}\) consisting of the natural numbers 0, 1, 2 etc. with labels for 0, 1 and +. To construct the domain of \(\mathbb{Z}\) we first take the set \(X\) of all ordered pairs of natural numbers (clearly a definable relation in \(\mathbb{N})\), and on this set \(X\) we define the equivalence relation \(\sim\) by

(again definable). The domain of \(\mathbb{Z}\) consists of the equivalence classes of this relation. We define addition on \(\mathbb{Z}\) by

The equivalence class of \((a,b)\) becomes the integer \(a - b\).

When a structure \(B\) is interpreted in a structure \(A\), every first-order statement about \(B\) can be translated back into a first-order statement about \(A\), and in this way we can read off the complete theory of \(B\) from that of \(A\). In fact if we carry out this construction not just for a single structure \(A\) but for a family of models of a theory \(T\), always using the same defining formulas, then the resulting structures will all be models of a theory \(T'\) that can be read off from \(T\) and the defining formulas. This gives a precise sense to the statement that the theory \(T'\) is interpreted in the theory \(T\). Philosophers of science have sometimes experimented with this notion of interpretation as a way of making precise what it means for one theory to be reducible to another. But realistic examples of reductions between scientific theories seem generally to be much subtler than this simple-minded model-theoretic idea will allow. See the entry on intertheory relations in physics .

The fourth kind of definability is a pair of notions, implicit definability and explicit definability of a particular relation in a theory. See section 3.3 of the entry on first-order model theory .

Unfortunately there used to be a very confused theory about model-theoretic axioms, that also went under the name of implicit definition. By the end of the nineteenth century, mathematical geometry had generally ceased to be a study of space, and it had become the study of classes of structures which satisfy certain ‘geometric’ axioms. Geometric terms like ‘point’, ‘line’ and ‘between’ survived, but only as the primitive symbols in axioms; they no longer had any meaning associated with them. So the old question, whether Euclid’s parallel postulate (as a statement about space) was deducible from Euclid’s other assumptions about space, was no longer interesting to geometers. Instead, geometers showed that if one wrote down an up-to-date version of Euclid’s other assumptions, in the form of a theory \(T\), then it was possible to find models of \(T\) which fail to satisfy the parallel postulate. (See the entry on geometry in the 19th century for the contributions of Lobachevski and Klein to this achievement.) In 1899 David Hilbert published a book in which he constructed such models, using exactly the method of interpretation that we have just described.

Problems arose because of the way that Hilbert and others described what they were doing. The history is complicated, but roughly the following happened. Around the middle of the nineteenth century people noticed, for example, that in an abelian group the minus function is definable in terms of 0 and + (namely: \(-a\) is the element \(b\) such that \(a + b = 0)\). Since this description of minus is in fact one of the axioms defining abelian groups, we can say (using a term taken from J. D. Gergonne, who should not be held responsible for the later use made of it) that the axioms for abelian groups implicitly define minus. In the jargon of the time, one said not that the axioms define the function minus, but that they define the concept minus. Now suppose we switch around and try to define plus in terms of minus and 0. This way round it can’t be done, since one can have two abelian groups with the same 0 and minus but different plus functions. Rather than say this, the nineteenth century mathematicians concluded that the axioms only partially define plus in terms of minus and 0. Having swallowed that much, they went on to say that the axioms together form an implicit definition of the concepts plus, minus and 0 together, and that this implicit definition is only partial but it says about these concepts precisely as much as we need to know.

One wonders how it could happen that for fifty years nobody challenged this nonsense. In fact some people did challenge it, notably the geometer Moritz Pasch who in section 12 of his Vorlesungen über Neuere Geometrie (1882) insisted that geometric axioms tell us nothing whatever about the meanings of ‘point’, ‘line’ etc. Instead, he said, the axioms give us relations between the concepts. If one thinks of a structure as a kind of ordered \(n\)-tuple of sets etc., then a class \(\Mod(T)\) becomes an \(n\)-ary relation, and Pasch’s account agrees with ours. But he was unable to spell out the details, and there is some evidence that his contemporaries (and some more recent commentators) thought he was saying that the axioms may not determine the meanings of ‘point’ and ‘line’, but they do determine those of relational terms such as ‘between’ and ‘incident with’! Frege’s demolition of the implicit definition doctrine was masterly, but it came too late to save Hilbert from saying, at the beginning of his Grundlagen der Geometrie , that his axioms give ‘the exact and mathematically adequate description’ of the relations ‘lie’, ‘between’ and ‘congruent’. Fortunately Hilbert’s mathematics speaks for itself, and one can simply bypass these philosophical faux pas. The model-theoretic account that we now take as a correct description of this line of work seems to have surfaced first in the group around Giuseppe Peano in the 1890s, and it reached the English-speaking world through Bertrand Russell’s Principles of Mathematics in 1903.

Suppose \(L\) is a language of signature \(K, T\) is a set of sentences of \(L\) and \(\phi\) is a sentence of \(L\). Then the relation

expresses that every structure of signature \(K\) which is a model of \(T\) is also a model of \(\phi\). This is known as the model-theoretic consequence relation , and it is written for short as

The double use of \(\vDash\) is a misfortune. But in the particular case where \(L\) is first-order, the completeness theorem (see the entry on classical logic ) tells us that ‘\(T \vDash \phi\)’ holds if and only if there is a proof of \(\phi\) from \(T\), a relation commonly written

Since \(\vDash\) and \(\vdash\) express exactly the same relation in this case, model theorists often avoid the double use of \(\vDash\) by using \(\vdash\) for model-theoretic consequence. But since what follows is not confined to first-order languages, safety suggests we stick with \(\vDash\) here.

Before the middle of the nineteenth century, textbooks of logic commonly taught the student how to check the validity of an argument (say in English) by showing that it has one of a number of standard forms, or by paraphrasing it into such a form. The standard forms were syntactic and/or semantic forms of argument in English. The process was hazardous: semantic forms are almost by definition not visible on the surface, and there is no purely syntactic form that guarantees validity of an argument. For this reason most of the old textbooks had a long section on ‘fallacies’ – ways in which an invalid argument may seem to be valid.

In 1847 George Boole changed this arrangement. For example, to validate the argument

All monarchs are human beings. No human beings are infallible. Therefore no infallible beings are monarchs.

Boole would interpret the symbols \(P, Q, R\) as names of classes:

\(P\) is the class of all monarchs. \(Q\) is the class of all human beings. \(R\) is the class of all infallible beings.

Then he would point out that the original argument paraphrases into a set-theoretic consequence:

(This example is from Stanley Jevons, 1869. Boole’s own account is idiosyncratic, but I believe Jevons’ example represents Boole’s intentions accurately.) Today we would write \(\forall x(Px \rightarrow Qx)\) rather than \(P \subseteq Q\), but this is essentially the standard definition of \(P \subseteq Q\), so the difference between us and Boole is slight.

Insofar as they follow Boole, modern textbooks of logic establish that English arguments are valid by reducing them to model-theoretic consequences. Since the class of model-theoretic consequences, at least in first-order logic, has none of the vaguenesses of the old argument forms, textbooks of logic in this style have long since ceased to have a chapter on fallacies.

But there is one warning that survives from the old textbooks: If you formalise your argument in a way that is not a model-theoretic consequence, it doesn’t mean the argument is not valid . It may only mean that you failed to analyse the concepts in the argument deeply enough before you formalised. The old textbooks used to discuss this in a ragbag section called ‘topics’ (i.e. hints for finding arguments that you might have missed). Here is an example from Peter of Spain’s 13th century Summulae Logicales :

‘There is a father. Therefore there is a child.’ … Where does the validity of this argument come from? From the relation. The maxim is: When one of a correlated pair is posited, then so is the other.

Hilbert and Ackermann, possibly the textbook that did most to establish the modern style, discuss in their section III.3 a very similar example: ‘If there is a son, then there is a father’. They point out that any attempt to justify this by using the symbolism

is doomed to failure. “A proof of this statement is possible only if we analyze conceptually the meanings of the two predicates which occur”, as they go on to illustrate. And of course the analysis finds precisely the relation that Peter of Spain referred to.

On the other hand if your English argument translates into an invalid model-theoretic consequence, a counterexample to the consequence may well give clues about how you can describe a situation that would make the premises of your argument true and the conclusion false. But this is not guaranteed.

One can raise a number of questions about whether the modern textbook procedure does really capture a sensible notion of logical consequence. For example in Boole’s case the set-theoretic consequences that he relies on are all easily provable by formal proofs in first-order logic, not even using any set-theoretic axioms; and by the completeness theorem (see the entry on classical logic ) the same is true for first-order logic. But for some other logics it is certainly not true. For instance the model-theoretic consequence relation for some logics of time presupposes some facts about the physical structure of time. Also, as Boole himself pointed out, his translation from an English argument to its set-theoretic form requires us to believe that for every property used in the argument, there is a corresponding class of all the things that have the property. This comes dangerously close to Frege’s inconsistent comprehension axiom!

In 1936 Alfred Tarski proposed a definition of logical consequence for arguments in a fully interpreted formal language. His proposal was that an argument is valid if and only if: under any allowed reinterpretation of its nonlogical symbols, if the premises are true then so is the conclusion. Tarski assumed that the class of allowed reinterpretations could be read off from the semantics of the language, as set out in his truth definition . He left it undetermined what symbols count as nonlogical; in fact he hoped that this freedom would allow one to define different kinds of necessity, perhaps separating ‘logical’ from ‘analytic’. One thing that makes Tarski’s proposal difficult to evaluate is that he completely ignores the question we discussed above, of analysing the concepts to reach all the logical connections between them. The only plausible explanation I can see for this lies in his parenthetical remark about

the necessity of eliminating any defined signs which may possibly occur in the sentences concerned, i.e. of replacing them by primitive signs.

This suggests to me that he wants his primitive signs to be by stipulation unanalysable. But then by stipulation it will be purely accidental if his notion of logical consequence captures everything one would normally count as a logical consequence.

Historians note a resemblance between Tarski’s proposal and one in section 147 of Bernard Bolzano’s Wissenschaftslehre of 1837. Like Tarski, Bolzano defines the validity of a proposition in terms of the truth of a family of related propositions. Unlike Tarski, Bolzano makes his proposal for propositions in the vernacular, not for sentences of a formal language with a precisely defined semantics.

On all of this section, see also the entry on logical consequence .

A sentence \(S\) defines its class \(\Mod(S)\) of models. Given two languages \(L\) and \(L'\), we can compare them by asking whether every class \(\Mod(S)\), with \(S\) a sentence of \(L\), is also a class of the form \(\Mod(S')\) where \(S'\) is a sentence of \(L'\). If the answer is Yes, we say that \(L\) is reducible to \(L'\), or that \(L'\) is at least as expressive as \(L\).

For example if \(L\) is a first-order language with identity, whose signature consists of 1-ary predicate symbols, and \(L'\) is the language whose sentences consist of the four syllogistic forms (All \(A\) are \(B\), Some \(A\) are \(B\), No \(A\) are \(B\), Some \(A\) are not \(B)\) using the same predicate symbols, then \(L'\) is reducible to \(L\), because the syllogistic forms are expressible in first-order logic. (There are some quarrels about which is the right way to express them; see the entry on the traditional square of opposition .) But the first-order language \(L\) is certainly not reducible to the language \(L'\) of syllogisms, since in \(L\) we can write down a sentence saying that exactly three elements satisfy \(Px\), and there is no way of saying this using just the syllogistic forms. Or moving the other way, if we form a third language \(L''\) by adding to \(L\) the quantifier \(Qx\) with the meaning “There are uncountably many elements \(x\) such that …”, then trivially \(L\) is reducible to \(L''\), but the downward Loewenheim-Skolem theorem shows at once that \(L''\) is not reducible to \(L\).

These notions are useful for analysing the strength of database query languages. We can think of the possible states of a database as structures, and a simple Yes/No query becomes a sentence that elicits the answer Yes if the database is a model of it and No otherwise. If one database query language is not reducible to another, then the first can express some query that can’t be expressed in the second.

So we need techniques for comparing the expressive strengths of languages. One of the most powerful techniques available consists of the back-and-forth games of Ehrenfeucht and Fraïssé between the two players Spoiler and Duplicator; see the entry on logic and games for details. Imagine for example that we play the usual first-order back-and-forth game \(G\) between two structures \(A\) and \(B\). The theory of these games establishes that if some first-order sentence \(\phi\) is true in exactly one of \(A\) and \(B\), then there is a number \(n\), calculable from \(\phi\), with the property that Spoiler has a strategy for \(G\) that will guarantee that he wins in at most \(n\) steps. So conversely, to show that first-order logic can’t distinguish between \(A\) and \(B\), it suffices to show that for every finite \(n\), Duplicator has a strategy that will guarantee she doesn’t lose \(G\) in the first \(n\) steps. If we succeed in showing this, it follows that any language which does distinguish between \(A\) and \(B\) is not reducible to the first-order language of the structures \(A\) and \(B\).

These back-and-forth games are immensely flexible. For a start, they make just as much sense on finite structures as they do on infinite; many other techniques of classical model theory assume that the structures are infinite. They can also be adapted smoothly to many non-first-order languages.

In 1969 Per Lindström used back-and-forth games to give some abstract characterisations of first-order logic in terms of its expressive power. One of his theorems says that if \(L\) is a language with a signature \(K, L\) is closed under all the first-order syntactic operations, and \(L\) obeys the downward Loewenheim-Skolem theorem for single sentences, and the compactness theorem, then \(L\) is reducible to the first-order language of signature \(K\). These theorems are very attractive; see Chapter XII of Ebbinghaus, Flum and Thomas for a good account. But they have never quite lived up to their promise. It has been hard to find any similar characterisations of other logics. Even for first-order logic it is a little hard to see exactly what the characterisations tell us. But very roughly speaking, they tell us that first-order logic is the unique logic with two properties: (1) we can use it to express arbitrarily complicated things about finite patterns, and (2) it is hopeless for discriminating between one infinite cardinal and another.

These two properties (1) and (2) are just the properties of first-order logic that allowed Abraham Robinson to build his nonstandard analysis . The background is that Leibniz, when he invented differential and integral calculus, used infinitesimals, i.e. numbers that are greater than 0 and smaller than all of 1/2, 1/3, 1/4 etc. Unfortunately there are no such real numbers. During the nineteenth century all definitions and proofs in the Leibniz style were rewritten to talk of limits instead of infinitesimals. Now let \(\mathbb{R}\) be the structure consisting of the field of real numbers together with any structural features we care to give names to: certainly plus and times, maybe the ordering, the set of integers, the functions sin and log, etc. Let \(L\) be the first-order language whose signature is that of \(\mathbb{R}\). Because of the expressive strength of \(L\), we can write down any number of theorems of calculus as sentences of \(L\). Because of the expressive weakness of \(L\), there is no way that we can express in \(L\) that \(\mathbb{R}\) has no infinitesimals. In fact Robinson used the compactness theorem to build a structure \(\mathbb{R}'\) that is a model of exactly the same sentences of \(L\) as \(\mathbb{R}\), but which has infinitesimals. As Robinson showed, we can copy Leibniz’s arguments using the infinitesimals in \(\mathbb{R}'\), and so prove that various theorems of calculus are true in \(\mathbb{R}'\). But these theorems are expressible in \(L\), so they must also be true in \(\mathbb{R}\).

Since arguments using infinitesimals are usually easier to visualise than arguments using limits, nonstandard analysis is a helpful tool for mathematical analysts. Jacques Fleuriot in his Ph.D. thesis (2001) automated the proof theory of nonstandard analysis and used it to mechanise some of the proofs in Newton’s Principia .

To model a phenomenon is to construct a formal theory that describes and explains it. In a closely related sense, you model a system or structure that you plan to build, by writing a description of it. These are very different senses of ‘model’ from that in model theory: the ‘model’ of the phenomenon or the system is not a structure but a theory, often in a formal language. The Unified Modeling Language , UML for short, is a formal language designed for just this purpose. It’s reported that the Australian Navy once hired a model theorist for a job ‘modelling hydrodynamic phenomena’. (Please don’t enlighten them!)

A little history will show how the word ‘model’ came to have these two different uses. In late Latin a ‘modellus’ was a measuring device, for example to measure water or milk. By the vagaries of language, the word generated three different words in English: mould, module, model. Often a device that measures out a quantity of a substance also imposes a form on the substance. We see this with a cheese mould, and also with the metal letters (called ‘moduli’ in the early 17th century) that carry ink to paper in printing. So ‘model’ comes to mean an object in hand that expresses the design of some other objects in the world: the artist’s model carries the form that the artist depicts, and Christopher Wren’s ‘module’ of St Paul’s Cathedral serves to guide the builders.

Already by the late 17th century the word ‘model’ could mean an object that shows the form, not of real-world objects, but of mathematical constructs. Leibniz boasted that he didn’t need models in order to do mathematics. Other mathematicians were happy to use plaster or metal models of interesting surfaces. The models of model theory first appeared as abstract versions of this kind of model, with theories in place of the defining equation of a surface. On the other hand one could stay with real-world objects but show their form through a theory rather than a physical copy in hand; ‘modelling’ is building such a theory.

We have a confusing halfway situation when a scientist describes a phenomenon in the world by an equation, for example a differential equation with exponential functions as solutions. Is the model the theory consisting of the equation, or are these exponential functions themselves models of the phenomenon? Examples of this kind, where theory and structures give essentially the same information, provide some support for Patrick Suppes’ claim that “the meaning of the concept of model is the same in mathematics and the empirical sciences” (1969, 12). Several philosophers of science have pursued the idea of using an informal version of model-theoretic models for scientific modelling. Sometimes the models are described as non-linguistic – this might be hard to reconcile with our definition of models in section 1 above.

Cognitive science is one area where the difference between models and modelling tends to become blurred. A central question of cognitive science is how we represent facts or possibilities in our minds. If one formalises these mental representations, they become something like ‘models of phenomena’. But it is a serious hypothesis that in fact our mental representations have a good deal in common with simple set-theoretic structures, so that they are ‘models’ in the model-theoretic sense too. In 1983 two influential works of cognitive science were published, both under the title Mental Models . The first, edited by Dedre Gentner and Albert Stevens, was about people’s ‘conceptualizations’ of the elementary facts of physics; it belongs squarely in the world of ‘modelling of phenomena’. The second, by Philip Johnson-Laird, is largely about reasoning, and makes several appeals to ‘model-theoretic semantics’ in our sense. Researchers in the Johnson-Laird tradition tend to refer to their approach as ‘model theory’, and to see it as allied in some sense to what we have called model theory.

Pictures and diagrams seem at first to hover in the middle ground between theories and models. In practice model theorists often draw themselves pictures of structures, and use the pictures to think about the structures. On the other hand pictures don’t generally carry the labelling that is an essential feature of model-theoretic structures. There is a fast growing body of work on reasoning with diagrams, and the overwhelming tendency of this work is to see pictures and diagrams as a form of language rather than as a form of structure. For example Eric Hammer and Norman Danner (1996) describe a ‘model theory of Venn diagrams’; the Venn diagrams themselves are the syntax, and the model theory is a set-theoretical explanation of their meaning. (A curious counterexample is the horizontal line diagrams of the 12th century Baghdad Jewish scholar Abū l-Barakāt they represent structures and not propositions, and Abū l-Barakāt uses them to express model-theoretic consequence in syllogisms. Further details are in Hodges 2018 on model-theoretic consequence.)

The model theorist Yuri Gurevich introduced abstract state machines (ASMs) as a way of using model-theoretic ideas for specification in computer science. According to the Abstract State Machine website (see Other Internet Resources below),

any algorithm can be modeled at its natural abstraction level by an appropriate ASM. … ASMs use classical mathematical structures to describe states of a computation; structures are well-understood, precise models.

The book of Börger and Stärk cited below is an authoritative account of ASMs and their uses.

Today you can make your name and fortune by finding a good representation system. There is no reason to expect that every such system will fit neatly into the syntax/semantics framework of model theory, but it will be surprising if model-theoretic ideas don’t continue to make a major contribution in this area.

The sections above considered some of the basic ideas that fed into the creation of model theory, noting some ways in which these ideas appeared either in mathematical model theory or in other disciplines that made use of model theory. None of this is particularly philosophical, except in the broad sense that philosophers work with ideas. But as mathematical model theory has become more familiar to philosophers, it has increasingly become a source of material for philosophical questions. In 2018 two books appeared that directly addressed this philosophical use of model theory, though in very different ways.

In the first book, Button and Walsh 2018, the authors present an invitation to the reader to help create a discipline, ‘philosophy and model theory’, which is gradually coming into existence. (This is partly belied by the large amount of carefully-worked material in the book.) Mathematics in general is a source of fundamental philosophical worries. For example mathematicians refer to entities that we have no causal interaction with (such as the number π or the set of real numbers), and this creates questions about how we can identify these entities to ourselves or each other, and how we can discover facts about them. These problems are not new or peculiar to model theory; but mathematical model theory is the part of mathematics most concerned with ‘reference’ and ‘isomorphism types’ and ‘indiscernibility’, notions which go directly to the philosophical problem areas. The authors give clear analyses of exactly what the issues are in key discussions in these areas.

The second book, Baldwin 2018, presents mathematical model theory of the period from 1970 to today as a source of material for the discipline of philosophy of mathematical practice. This discipline studies the work of particular mathematicians within their historical context, and asks such questions as: Why did this mathematician prefer classifications in terms of X to classifications in terms of Y ? Why did this group of mathematical researchers choose to formalise their subject matter using such-and-such a language or set of symbols? How did they decide what to formalise and what to leave unformalised? The discipline is partly historical, but it looks for conceptual justifications of the historical choices made. (See the entries mathematical style and explanation in mathematics .) Baldwin has a long history of work in mathematical model theory, so he can answer questions like those above from personal knowledge. This book gives a rich supply of examples, explained with helpful pictures and remarkably little technical notation.

Introductory texts

• Doets, K., 1996, Basic Model Theory , Stanford: CSLI Publications.
• Hodges, W., 1997, A Shorter Model Theory , Cambridge: Cambridge University Press.
• Manzano, M., 1999, Model Theory , Oxford: Oxford University Press.
• Rothmaler, P., 2000, Introduction to Model Theory , Amsterdam: Gordon and Breach.

Model-theoretic definition

• Frege, G., 1906, “Grundlagen der Geometrie”, Jahresbericht der deutschen Mathematikervereinigung , 15: 293–309, 377–403, 423–430.
• Gergonne, J., 1818, “Essai sur la théorie de la définition”, Annales de Mathématiques Pures et Appliquées , 9: 1–35.
• Hilbert, D., 1899, Grundlagen der Geometrie , Leipzig: Teubner.
• Hodges, W., 2008, “Tarski’s theory of definition”, in Patterson, D. New Essays on Tarski and Philosophy , Oxford: Oxford University Press, pp. 94–132.
• Lascar, D., 1998, “Perspective historique sur les rapports entre la théorie des modèles et l’algèbre”, Revue d’histoire des mathématiques , 4: 237–260.
• Mancosu, P., Zach, R. and Badesa, C., 2009, “The development of mathematical logic from Russell to Tarski”, in L. Haaparanta (ed.), The Development of Modern Logic , Oxford: Oxford University Press, pp. 318–470.
• Pasch, M., 1882, Vorlesungen über Neuere Geometrie , Berlin: Springer-Verlag.
• Robinson, A., 1952, “On the application of symbolic logic to algebra”, Proceedings of the International Congress of Mathematicians (Cambridge, MA, 1950, Volume 1), Providence, RI: American Mathematical Society, pp. 686–694.
• Suppes, P., 1957, “Theory of definition” in Introduction to Logic (Chapter 8), Princeton, NJ: Van Nostrand.
• Tarski, A., 1954, “Contributions to the theory of models, I”, Indagationes Mathematicae , 16: 572–581.

Model-theoretic consequence

• Blanchette, P., 1996, “Frege and Hilbert on consistency”, The Journal of Philosophy , 93: 317–336.
• –––, 2012, Frege’s Conception of Logic , New York: Oxford University Press.
• Boole, G., 1847, The Mathematical Analysis of Logic , Cambridge: Macmillan, Barclay and Macmillan.
• Etchemendy, J., 1990, The Concept of Logical Consequence , Cambridge, MA: Harvard University Press.
• Frege, G., 1971, On the Foundations of Geometry, and Formal Theories of Arithmetic , E. Kluge (trans.), New Haven: Yale University Press.
• Gómez-Torrente, M., 1996, “Tarski on logical consequence”, Notre Dame Journal of Formal Logic , 37: 125–151.
• Hodges, W. 2004, “The importance and neglect of conceptual analysis: Hilbert-Ackermann iii.3”, in V. Hendricks et al . (eds.), First-Order Logic Revisited , Berlin: Logos, pp. 129–153.
• –––, 2018, “Two early Arabic applications of model-theoretic consequence”, Logica Universalis , 12: 37–54.
• Kreisel, G., 1969, “Informal rigour and completeness proofs”, in J. Hintikka (ed.), The Philosophy of Mathematics , London: Oxford University Press, pp. 78–94.
• Tarski, A., 1983, “On the concept of logical consequence”, translated in A. Tarski, Logic, Semantics, Metamathematics , J. Corcoran (ed.), Indianapolis: Hackett, pp. 409–420.
• van Benthem, J., 1991 [1983], The Logic of Time: A Model-Theoretic Investigation into the Varieties of Temporal Ontology and Temporal Discourse , Dordrecht: Reidel, 1983; second edition, Springer, 1991.

Expressive strength

• Cutland, N., 2009, Nonstandard Analysis and its Applications , Cambridge: Cambridge University Press.
• Ebbinghaus, H.-D., and Flum, J., 1999, Finite Model Theory , Berlin: Springer-Verlag.
• Ebbinghaus, H.-D., Flum, J. and Thomas, W., 1984, Mathematical Logic , New York: Springer-Verlag.
• Fleuriot, J., 2001, A Combination of Geometry Theorem Proving and Nonstandard Analysis, with Application to Newton’s Principia , New York: Springer-Verlag.
• Immerman, N., 1999, Descriptive Complexity , New York: Springer-Verlag.
• Libkin, L., 2004, Elements of Finite Model Theory , Berlin: Springer-Verlag.
• Lindström, P., 1969, “On extensions of elementary logic”, Theoria , 35:1–11.
• Loeb, P. and Wolff, M. (eds.), 2000, Nonstandard Analysis for the Working Mathematician , Dordrecht: Kluwer.
• Robinson, A., 1967, “The metaphysics of the calculus”, in Problems in the Philosophy of Mathematics , I. Lakatos (ed.), Amsterdam : North-Holland, pp. 28–40.

Models and modelling

• Allwein, G. and Barwise, J. (eds.), 1996, Logical Reasoning with Diagrams , New York: Oxford University Press.
• Börger, E. and Stärk, R., 2003, Abstract State Machines: A Method for High-Level System Design and Analysis , Berlin: Springer-Verlag.
• Fowler, M., 2000, UML Distilled , Boston: Addison-Wesley.
• Garnham, A., 2001, Mental Models and the Interpretation of Anaphora , Philadelphia: Taylor and Francis.
• Gentner, D. and Stevens, A. (eds.), 1983, Mental Models , Hillsdale, NJ: Lawrence Erlbaum.
• Gurevich, Yuri, 1993, “Evolving Algebras: An Attempt to Discover Semantics”, in E. Börger (ed.), Specification and Validation Methods , pp. 9–36, Oxford: Oxford University Press.
• Hammer, E. and Danner, N., 1996, “Towards a Model Theory of Venn Diagrams”, in Allwein and Barwise (eds.) 1996, pp. 109–128.
• Johnson-Laird, P., 1983, Mental Models: Towards a cognitive science of language, inference, and consciousness , Cambridge: Cambridge University Press.
• Meijers, A. (ed.), 2009, Philosophy of Technology and Engineering Sciences , Amsterdam: Elsevier; see chapters W. Hodges, “Functional modelling and mathematical models”; R. Müller, “The notion of a model, theories of models and history”; and N. Nersessian, “Model based reasoning in interdisciplinary engineering”.
• Moktefi, A. and Shin, S.-J. (eds.), 2013, Visual Reasoning with Diagrams , Basel: Birkhäuser.
• Morgan, M. S. and Morrison, M. (eds.), 1999, Models as Mediators , Cambridge: Cambridge University Press.
• Pullum, G. K. and Scholz, B. C., 2001, “On the distinction between model-theoretic and generative-enumerative syntactic frameworks”, in Logical Aspects of Computational Linguistics (Lecture Notes in Computer Science: Volume 2099), P. De Groote et al . (eds.), Berlin: Springer-Verlag, pp. 17–43.
• Stenning, K., 2002, Seeing Reason , Oxford: Oxford University Press.
• Suppes, P., 1969, Studies in the Methodology and Foundations of Science , Dordrecht: Reidel.

Philosophy of model theory

• Baldwin, J., 2018, Model Theory and the Philosophy of Mathematical Practice: Formalization without Foundationalism , Cambridge: Cambridge University Press.
• Button, T. and Walsh, S., 2018, Philosophy and Model Theory , Oxford: Oxford University Press.

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

• mentalmodelsblog: Mental Models in Human Thinking and Reasoning , by Ruth Byrne.
• Algorithmic Model Theory , by E. Graedel, D. Berwanger and M. Hoelzel (Mathematische Grundlagen der Informatik, RWTH Aachen)
• Abstract State Machines , by Jim Huggins (no longer maintained)

diagrams | geometry: in the 19th century | logic: classical | logical consequence | logical truth | mathematics, philosophy of | models in science | physics: intertheory relations in | physics: structuralism in | square of opposition | Tarski, Alfred | Tarski, Alfred: truth definitions

Copyright © 2020 by Wilfrid Hodges < wilfrid . hodges @ btinternet . com >

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2023 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

• Conferences

Mathematical Theory and Modeling

• Current Issue
• Back Issues

Announcements

• Full List of Journals
• Migrate a Journal
• Special Issue Service
• Conference Publishing
• Editorial Board
• OPEN ACCESS Policy
• Other Journals

Mathematical Theory and Modeling is a peer reviewed journal published by IISTE. The journal publishes original papers at the forefront of mathematical theories, modelings, and applications. The journal is published in both printed and online versions. The online version is free access and download.

IISTE is a member of  CrossRef .

The DOI of the journal is:  https://doi.org/10.7176/MTM

Vol 14, No 1 (2024)

Table of contents.

Paper submission email: [email protected]

ISSN (Paper)2224-5804 ISSN (Online)2225-0522

Please add our address "[email protected]" into your email contact list.

This journal follows ISO 9001 management standard and licensed under a Creative Commons Attribution 3.0 License.

Copyright © www.iiste.org

• {{subColumn.name}}

AIMS Public Health

• {{newsColumn.name}}
• Share facebook twitter google linkedin

On mathematical modelling of measles disease via collocation approach

• Shahid Ahmed 1 , 
• Shah Jahan 1 ,  ,  , 
• Kamal Shah 2 , 
• Thabet Abdeljawad 2
• 1. Department of Mathematics, Central University of Haryana, Mohindergarh-123031, India
• 2. Department of Mathematics and Sciences, Prince Sultan University, Riyadh 11586, Saudi Arabia
• Received: 04 February 2024 Accepted: 11 April 2024 Published: 06 May 2024
• Full Text(HTML)
• Download PDF

Measles, a highly contagious viral disease, spreads primarily through respiratory droplets and can result in severe complications, often proving fatal, especially in children. In this article, we propose an algorithm to solve a system of fractional nonlinear equations that model the measles disease. We employ a fractional approach by using the Caputo operator and validate the model's by applying the Schauder and Banach fixed-point theory. The fractional derivatives, which constitute an essential part of the model can be treated precisely by using the Broyden and Haar wavelet collocation methods (HWCM). Furthermore, we evaluate the system's stability by implementing the Ulam-Hyers approach. The model takes into account multiple factors that influence virus transmission, and the HWCM offers an effective and precise solution for understanding insights into transmission dynamics through the use of fractional derivatives. We present the graphical results, which offer a comprehensive and invaluable perspective on how various parameters and fractional orders influence the behaviours of these compartments within the model. The study emphasizes the importance of modern techniques in understanding measles outbreaks, suggesting the methodology's applicability to various mathematical models. Simulations conducted by using MATLAB R2022a software demonstrate practical implementation, with the potential for extension to higher degrees with minor modifications. The simulation's findings clearly show the efficiency of the proposed approach and its application to further extend the field of mathematical modelling for infectious illnesses.

• fractional SEIR modeling ,
• fixed point theory ,
• Haar wavelet ,
• numerical analysis ,
• Ulam-Hyers stability

Citation: Shahid Ahmed, Shah Jahan, Kamal Shah, Thabet Abdeljawad. On mathematical modelling of measles disease via collocation approach[J]. AIMS Public Health, 2024, 11(2): 628-653. doi: 10.3934/publichealth.2024032

Related Papers:

• This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 ) -->

Supplements

Access history.

• Corresponding author: * Correspondence: Email: [email protected] .; 

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 103 ) PDF downloads( 11 ) Cited by( 0 )

Figures and Tables

Figures( 11 )  /  Tables( 1 )

Associated material

Other articles by authors.

• Shahid Ahmed
• Thabet Abdeljawad

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

• Figure 1.  Flow chart
• Figure 2.  Graphical presentation of sensitivity index
• Figure 3.  Susceptible population by HWCM at $\chi=1$
• Figure 4.  Plot of exposed peoples by HWCM at $\chi=1$
• Figure 5.  Plot of infected people by HWCM at $\chi=1$
• Figure 6.  Plot of recovered people by HWCM at $\chi=1$
• Figure 7.  Plot of $\mathbb{S}(\tau)$ for various values of $\chi$
• Figure 8.  Plot of $\mathbb{E}(\tau)$ for various values of $\chi$
• Figure 9.  Plot of infected population $\mathbb{I}(\tau)$ for various values of $\chi$
• Figure 10.  Plot of $\mathbb{R}(\tau)$ for various values of $\chi$
• Figure 11.  Dynamics of the SEIR system at $\chi=1$

share this!

May 17, 2024

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

trusted source

Tracing the history of perturbative expansion in quantum field theory

by Samuel Jarman, SciencePOD

Perturbative expansion is a valuable mathematical technique which is widely used to break down descriptions of complex quantum systems into simpler, more manageable parts. Perhaps most importantly, it has enabled the development of quantum field theory (QFT): a theoretical framework that combines principles from classical, quantum, and relativistic physics, and serves as the foundation of the Standard Model of particle physics.

Yet despite its importance in shaping our understanding of the universe, the role of perturbative expansion has often been understated when discussing the mathematical and philosophical foundations of QFT. Through new analysis published in EPJ H, James Fraser at the University of Wuppertal, together with Kasia Rejzner at the University of York, bring the special status of perturbative expansions into sharper focus, by highlighting their deep-rooted relationship with the foundations of QFT.

The findings are published in The European Physical Journal H .

In fundamental physics , perturbative expansion is used extensively to extract accurate experimental predictions from QFT, which have gone on to shape the theory to its current form. All the same, the simplified descriptions offered by the technique have widely been viewed as irrelevant when discussing the mathematical and philosophical framework of the theory.

In contrast , Fraser and Rejzner argue that the mathematics of perturbative expansion has played a central role in the development QFT: often engaging directly with its foundational mathematical structure. Because of this, its importance cannot be understated when discussing the fundamental nature of the universe through QFT.

Through their paper, the duo brings the history of this relationship into sharper focus; tracing the history of the use of perturbative expansion in foundational developments in QFT. Their work could ultimately help physicists gain a deeper understanding of the implications of theories they have developed using perturbative expansion.

Provided by SciencePOD

Explore further

Feedback to editors

Blue Origin flies thrill seekers to space, including oldest astronaut

5 hours ago

Composition of gut microbiota could influence decision-making

May 18, 2024

Researchers realize multiphoton electron emission with non-classical light

Saturday Citations: Mediterranean diet racks up more points; persistent quantum coherence; vegan dogs

Physicists propose path to faster, more flexible robots

Scientists develop new geochemical 'fingerprint' to trace contaminants in fertilizer

Study reveals how a sugar-sensing protein acts as a 'machine' to switch plant growth—and oil production—on and off

Researchers develop world's smallest quantum light detector on a silicon chip

How heat waves are affecting Arctic phytoplankton

Horse remains show Pagan-Christian trade networks supplied horses from overseas for the last horse sacrifices in Europe

Relevant physicsforums posts, motivation behind the operator-formalism in qm.

2 hours ago

Color charge is not scalar -- do their components have dimensions?

8 hours ago

The Dirac equation as a linear tensor equation for one component

21 hours ago

Generalized Eigenvalues of Pauli Matrices

Eigenstates of particle with 1/2 spin (qbit), if the gravitational constant had a different value.

May 16, 2024

More from Quantum Physics

Related Stories

Modeling high-harmonic generation without resorting to perturbation theory

Feb 8, 2022

The quantum theory of gravitation, effective field theories and strings: Past and present

May 7, 2024

Examining recent developments in quantum chromodynamics

Dec 23, 2021

The end of the quantum tunnel: Exact instanton transseries for quantum mechanics

Apr 26, 2024

A theory of strong-field non-perturbative physics driven by quantum light

Sep 5, 2023

Using holograms to illuminate de Sitter space

Jul 20, 2022

Recommended for you

Scientists use generative AI to answer complex questions in physics

Scientists demonstrate the survival of quantum coherence in a chemical reaction involving ultracold molecules

Researchers call for a new measurement of time for tunneling particles

Quantum experts review major techniques for isolating Majoranas

Let us know if there is a problem with our content.

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Springer Nature - PMC COVID-19 Collection

Mathematical modeling applied to epidemics: an overview

Angélica s. mata.

1 Departamento de Física, Universidade Federal de Lavras, 37200-900 Lavras, MG Brazil

Stela M. P. Dourado

2 Departamento de Ciências da Saúde, Universidade Federal de Lavras, 37200-900 Lavras, MG Brazil

This work presents an overview of the evolution of mathematical modeling applied to the context of epidemics and the advances in modeling in epidemiological studies. In fact, mathematical treatments have contributed substantially in the epidemiology area since the formulation of the famous SIR (susceptible-infected-recovered) model, in the beginning of the 20th century. We presented the SIR deterministic model and we also showed a more realistic application of this model applying a stochastic approach in complex networks. Nowadays, computational tools, such as big data and complex networks, in addition to mathematical modeling and statistical analysis, have been shown to be essential to understand the developing of the disease and the scale of the emerging outbreak. These issues are fundamental concerns to guide public health policies. Lately, the current pandemic caused by the new coronavirus further enlightened the importance of mathematical modeling associated with computational and statistical tools. For this reason, we intend to bring basic knowledge of mathematical modeling applied to epidemiology to a broad audience. We show the progress of this field of knowledge over the years, as well as the technical part involving several numerical tools.

Introduction

Studies involving epidemiology were consolidated in the 19th century although the mortality from infectious diseases has been investigated mathematically since the Eighteenth century [ 20 ]. But it was only in 1927, with the formulation of a mathematical model known as SIR (susceptible-infected-recovered) model [ 45 ], by the biochemist Kermack and the physician McKendrick , that the modern mathematical epidemiology indeed began.

Afterwards, many increasingly complex models were created to model epidemic processes, but most of them are based on the concepts of the SIR model [ 8 , 47 ]. In general, such models are extremely useful for finding out how rapidly the etiological agent, for example, a virus, can spread, how many people will be affected, what containment measures can be taken, what proportion of a population should be vaccinated, etc.

The study of infectious disease dynamics has become very interdisciplinary, in the last decades. The contributions of mathematics, physics, biology, computer science, statistics and epidemiology are essential to provide effective responses for the development and improvement of public health. In this context, mathematical modeling appears with a huge potential to clarify the complexity of the dynamics of infectious diseases [ 30 , 40 ].

Infectious diseases emerge due to environmental, social and demographic factors because we are always in contact with microorganisms or animals that host them [ 58 ]. According to World Health Organization (WHO), research and development efforts must prioritize a set of diseases, all of them caused by virus, including ebola virus [ 16 ], Zika virus [ 2 ], Middle East respiratory syndrome coronavirus (MERS) [ 39 ] and severe acute respiratory syndrome (SARS) [ 28 , 50 ].

Recently, due to the current pandemic caused by the new coronavirus, the importance of mathematical modeling have become increasingly remarkable. Jargons of the area such as basic reproductive number, infection rate, epidemic threshold, etc., are frequently mentioned in news and in social media posts. In this context, our aim is to provide basic information of mathematical modeling applied to epidemiology to a broad audience and more detailed references for those who would like to learn deeper the topic.

This manuscript is divided as follows: in Sect.  2 , we presented a historical background about epidemiology and multicausality. In Sect.  3 we presented the advances of mathematical models in the context of epidemiological analysis. In Sect.  4 , we presented the mathematical development of the SIR model, its usefulness for modeling a pandemic, its unfolding in other more complex epidemic models and its implementation using complex networks. Finally, in Sect.  5 , we closed this issue presenting some perspectives and challenges of the mathematical modeling related to pandemics, public health, vaccines and infodemic.

Historical background of epidemiology and multicausality

Researches involving epidemiology were well-established in the Nineteenth century with pioneering studies about the London cholera epidemic (1849–1854) by the sanitarist medical-doctor John Snow. He became known as the father of epidemiology because he was able to determine the source of infection from a disease, even without knowing its etiological agent [ 63 ]. Afterward, the scientist Louis Pasteur determined the etiological agent of diseases, which enabled the introduction of prevention and treatment measures [ 72 ].

Previously, this research area had already had contributions from experts as John Graunt, in the Fifteenth century, who quantified the patterns of mortality and birth rates [ 68 ]. In the Sixteenth century, Louis Villermé investigated the impact of poverty and bad working conditions on the health of the population [ 43 ] and Pierre Louis used the epidemiological method in clinical investigations [ 56 ]. Edward Jenner, in 1796, discovered the first smallpox vaccine, almost a hundred years before the virus was discovered. Fortunately, this disease was permanently eradicated from the planet in 1980 due to mass vaccination [ 67 ]. Ignaz Semmelweis, in the 19h century, was the first health professional to associate the contamination of hands with transmission disease and he introduced hygiene measures to reduce the spread of pathogens, significantly decreasing the number of deaths from infection in hospitals [ 77 ].

Therefore, infectious diseases are a ubiquitous part of human life. The bubonic plague, caused by a bacteria transmitted to human by the rat flea, reached Europe in the Fourteenth century leaving 50 million dead. Cholera, known since ancient times and transmitted to people through contaminated water and food, had a first epidemic outbreak in the early Nineteenth century killing hundreds of thousands of people. Tuberculosis is highly contagious because it is transmitted from one person to another through the respiratory tract [ 58 , 60 ]. This disease killed a billion people between 1850 and 1950 although trace elements of the disease were found in skeletons 7000 years ago. In recent years, the infection has resurfaced in underdeveloped countries and currently, together with malaria, they are considered the most important re-emerging infectious diseases in the world [ 80 ].

Epidemics of new and old infectious diseases, also known as emerging and reemerging diseases, periodically emerge [ 57 ]. They remain among the leading causes of death and can be associated with human behaviours and environmental perturbation [ 25 ]. There are many infectious diseases that have plagued humanity for years such as bubonic plague, cholera, tuberculosis, smallpox, Spanish flu, dengue fever, AIDS, etc. Many of them have caused terrible epidemics and/or cause worrying endemics, especially in tropical and underdeveloped countries [ 60 ].

Remarkably, major epidemics of the Twentieth and Twenty first centuries are caused by virus. The World Health Organization (WHO) has indicated that vector-borne diseases account for more than 17 % of infectious diseases in the world, causing more than 700,000 deaths per year. Many of them are transmitted by a virus through a vector, such as dengue, yellow fever and Zika [ 80 ]. Such infections affect more the poorest populations of underdeveloped countries, being classified as neglected tropical diseases [ 80 ]. The Zika virus, for example was identified in 1947 among primates in the Zika forest in Uganda but the major outbreak happened in Brazil between 2015 and 2016 and subsequently spread to other countries in South America, Central America and the Caribbean. Brazil led the discovery of the relationship between the Zika virus and the increase cases of microcephaly in newborns [ 12 ].

Another viral disease of global importance is Acquired Immunodeficiency Syndrome (AIDS), whose outbreak began in the 1980s, that is caused by HIV virus and it attacks the immune system. There is no vaccine, but treatment can be done with antiretroviral drugs, which also greatly reduces the chance of transmission through sexual relations [ 32 ]. In Africa, it is estimated that 17 % of adults have the virus, according to WHO [ 80 ]. This continent is also the most affected by the ebola virus. This disease can be transmitted through contaminated meat (bats are usuallys the primary hosts) or body fluids from infected people. As it manifests severe symptoms, it is easy to identify and isolate the infected individual. The same does not happen with diseases caused by viruses like influenza and coronavirus [ 16 ].

Some strains of the influenza virus, for example, were responsible for the Spanish flu in 1918 [ 75 ], killing millions of people worldwide and for swine flu in 2009. Different strains of the coronavirus were responsible for the 2002 epidemic when SARS-CoV virus caused an outbreak of severe acute respiratory syndrome (SARS) [ 28 , 50 ]. In 2012 MERS-CoV virus caused Middle East respiratory syndrome (MERS) [ 39 ] and finally, in 2019 , the pandemic caused by the new coronavirus SARS-CoV2, responsible for the corona virus disease (COVID-19) [ 48 ], infected 25 million people and killed 848,000 people around the world until August 2020, according to WHO [ 80 ].

In general, the symptoms of these diseases are similar and in the beggining not much severe. People usually present clinical symptoms as fever, cough and difficulty in breathing. The delay in the manifestation of symptoms (about a week after contagion) combined with mild symptoms that affect the majority of the population are key ingredients that promote a fast spreading of the disease [ 49 ]. In addition to these ingredients, the way as the virus is transmitted from one person to another also facilitates the spread. Transmission occurs through physical contact with contaminated people or surfaces, such as shaking hands or touching a contaminated surface and then touching the eyes, mouth or nose, for example. Sneezing, coughing and saliva droplets from infected people also transmit the virus, that is why the use of masks and measures related to social distance are so required by health surveillance [ 80 ].

In this context, mathematical modeling offers valuable tools for understanding the disease spreading, quantifying the total number of people being infected over time and, consequently, investigating the impact of humans mobility, environmental changes and also the effectiveness of prevention and control measures for developing and evaluating evidence for decision-making in global health [ 8 , 30 ].

Advances in mathematical models

The SIR model is one of the most basic models to investigate epidemic process. In this scenario, each individual can be in one of three epidemiological states at any given time: susceptible, infected and infectious, or removed which can mean immunized (recovered) or dead [ 45 ]. The model specifies the rates at which individual changes their state, as detailed in the netx section.

Originally, epidemic models did not taking into account the heterogeneity in contact behavior not even the mobility of the agents involved in the disease transmission process. The simplest theory of epidemic spreading assumes that the population can be divided into different compartments according to the stage of the disease as susceptible, infected or removed, for the SIR model, for example. However, individuals are assumed to be identical and have approximately the same number of neighbors. From this elementary approach, we are able to write a time evolution equation for the number of infected individuals and finally, we can obtain relevant informations about the disease spreading. This characterizes the homogenenous mean-field theory [ 7 ] and the complete analysis of this algebraic development is shown in Sect.  4 .

Over the past few decades, the increase sophistication of epidemic models, the advance in the computational system and the use of complex network tools combine with big data provide opportunities to predict epidemic outbreaks and control strategies in an accurate and increasingly realistic way [ 8 , 11 , 40 , 47 ].

There are many works in the literature that can exemplify the advancement in mathematical modeling [ 3 , 44 ]. For instance, to model the measles outbreak in children, the models considered age groups, spatial and temporal features and metapopulation structured [ 24 , 38 , 82 ]. Metapopulation is a set of populations, separated in space, but connected with each other allowing the movement of people between them [ 21 ].

When it concerns about infectious diseases transmitted by a vector, such as malaria, dengue fever, Zika and leishmaniasis, the modeling involves at least two host species and environmental conditions should be considered. In this case, multilayer networks [ 37 ] have shown to be useful because they are composed by two distinc layers, for instance, one representing the human population and its mobility, and the other representing the same for the vector—a mosquito, for example—that transmits the disease to humans. The disease propagation between layers since one infected human can infect a insect which, in turn, can sting a healthy human and infects him [ 37 ].

Novel emerging infections such as SARS, MERS, and SARS-Cov2 required models that take into account contact tracing, quarantine, human mobility patterns, intervetions measures, latency period, comorbidities, age groups and impact of vaccines. Besides that, social mixing patterns, the urban demography and spatial dynamics also have to be taken into account as they directly impact on the transmission of infectious diseases. [ 46 , 51 , 53 ].

To implement and to investigate the spread of infectious diseases we can used a set of approaches: deterministic, stochastic, agent-based, or a mixed of them. These alternative perspectives allowing researchers to gain complementary insights about infectious diseases and investigate strategies for combating them. Most of them are based on compartment models, this means, the populations of individuals are divided in different compartments, where each compartment represents a specific stage of the disease [ 30 ]. In a stochastic framework, the transition probabilities of one compartment to another can be modeled by a continuous time Markov process [ 1 , 76 ]. However, these probabilities can be approximated, in the deterministic approach, by a differential form. In this case, the set of ordinary differential equations describe how the system evolve in time [ 69 , 74 ]. Besides that, statistical approaches can also be used to model epidemic dynamics, mainly when it involves concerns related to the spatio-temporal behavior of the disease [ 6 , 41 , 66 ]. In general, all of these models try to capture the complexity of the real-world such as mobility patterns, social contacts, age stratification and spatial distribution of the population.

The deterministic investigation of epidemic models is already sufficient to provide us a basic description of an epidemic, such as the existence of an epidemic threshold that separates a phase where the epidemic grows exponentially from a disease-free state [ 54 ]. It is due to the existence of this threshold that disease control measures can be introduced. On the other hand, stochastic models, associated with Monte Carlos simulations, are useful to investigate epidemic models on networks [ 4 , 36 , 62 , 64 ]. In this scenario, each individual of a population is represented by a vertex or a node of the network and the transmission of the disease occurs through edges connecting them. This framework provides a more realistic perspective, since we are able to investigate the epidemic spreading on large and highly heterogeneous systems. In the next section, we describe both deterministic and stochastic approaches to explore the SIR model.

Epidemic modeling

How to model the evolution of the dynamic disease and how to mitigate its growth? [ 45 ] An epidemic outbreak usually starts with just one infected person—called zero individual—that is the first one takes the virus. As mentioned previously, we can use the SIR model [ 45 ] to investigate this dynamic. The SIR model becomes a famous epidemic model because despite its simplicity, it is able to predict an essential feature for epidemiology: epidemic threshold. It separates two distinct states of the epidemic: disease free scenario and a state of there are a significant quantity of infected people [ 54 ]. There are many other models more complex than the SIR model, but almost all of them are based on the SIR rules, that describes very well the dynamic of an epidemic [ 62 ]. We firstly investigated this successful model using a deterministic approach and after we implemented this model in networks using the stochastic framework.

The SIR deterministic model

In this model [ 45 ], the population is divided in three compartments: susceptible S , infected I or removed R . Susceptible individuals are at risk of getting the disease, if they have some contact with an infected one. If it happens, the susceptible individual becomes infected and, consequently, he/she is able to disseminate the virus. Generally, there are two possibilities for infected people, to heal and become immune or, unfortunately, to die. Both of cases are equivalent from a mathematical point of view because they do not transmit the virus anymore and pass to the removed class.

Besides the SIR model, there are other models that include more compartments and that can be useful depending on the type of disease one wants to model. For example, in the SEIR model, we consider a latent period, called Exposed (E), in which an individual is infected but it still does not transmit the virus. This stage corresponds to an intermediate period between susceptible and infected. We can also include a differentiation between recovered and dead individuals through the inclusion of compartment D (dead). In this case, we have a SEIRD model. Another example is the famous SIRS model, in which the individual has only temporary immunity, and may become susceptible to the disease again after a certain time [ 64 ]. Recently, Arenas and collaborators [ 5 ] proposed a model to study the spreading of the COVID-19 pandemic based on 10 compartments. According to this work, the population is divided into: susceptible (S), exposed (E), asymptomatic infectious (A), symptomatic infectious (I), to be admitted in ICU (pre hospitalized in ICU,PH), fatal prognosis (predeceased,PD), admitted in ICU that will recover (HR) or decease (HD), recovered (R), and deceased(D) .

Thus we can then conclude that, according to the complexity of the investigated disease, many compartments can be incorporated into the model. However, it is interesting to note that, despite its simplicity, the SIR model is able to capture essential features of an ordinary epidemic, such as the fact that social distancing measures work very well and that vaccination is really the best strategy to contain its spreading, as we will show below. Therefore, in this work we are going to focus on this model. If the reader wants to know more details about the other models, we recommend reading references [ 30 , 64 ].

In the SIR model, we considered that the size N of population remains constant, this means: N = S ( t ) + I ( t ) + R ( t ) , where X ( t ) represents the population of the compartment X in a given time step t . So, S ( t )/ N is the fraction of the population that can be infected. Let’s suppose that each infected individual has, on average, μ contacts, then μ S ( t ) I ( t ) / N daily meetings can result in contagion. However, it is reasonable to assume that only a fraction of those meetings τ < 1 effectively results in contagion. Consequently, the number of new infected people in the next day will be [ 45 ]:

But the number of infected people also decreases as long as they become recovered or dead. If the mean recovered time is D days, a fraction β = 1 / D of infected will become recovered every day. Finally, the number of total infected in the next day can given by:

where Δ t is the unit of time that corresponds to an specific time interval, which can denote, for example, one day. If N has a large value, we can consider that the variables are continuous when we make the interval of time smaller and smaller, that is:

In the beginning of a new epidemic, that corresponds to t = 0 in our mathematical approach, we can assume a commonly hypothesis that practically all individuals are susceptible 1 - except the zero individual—it means S ( t = 0 ) ≈ N . This value remains pretty constant in the first steps of the contagion. For example we can cite the number of infected people with the new coronavirus (SARS-CoV-2).The first reported case occurs in Wuhan, China on December 31, 2019. After one month, in January 31, 2020, there were 9826 infected individuals, according to the Situation Report 11 of WHO [ 80 ]. This correspond to a tiny fraction of the global population - more than seven billion of people according to the United Nations Organization. Considering this approximation, we have

which gives,

as a solution of the evolution of the number of infected people in the beginning of the epidemic. We can obtain a valuable information with this expression. If λ S ( 0 ) - β > 0 , the number of infected grows exponentially. However, if λ S ( 0 ) - β < 0 , the number of infected people decreases until the complete extinction of the epidemic. The value λ S ( 0 ) / β = 1 is the epidemic threshold, which separates two distinct phases of the epidemic. When the initial condition corresponds to all susceptible people, as happened in the COVID-19 spreading for example, we have a particular case when the value λ S ( 0 ) / β = λ N / β is known as the basic reproductive number and it measures the “intensity of the contagion” , this means, the quantity of contagion that each infected person can cause. It means that the number of infected will increase because λ S ( t ) / β > 1 . On the other hand, when we look at how the number of susceptible people changes over time, we concluded that this quantity will always decreases with time because

Therefore, there will be a time when the quantity λ S ( t ) / β will become smaller than one, and consequently, the number of infected will start to decrease. That is, the number of infected individuals grows exponentially fast at the beginning of the epidemic, reaches a peak and begins to decline as we show in Fig.  1 a. This is the natural behavior of an epidemic. However, waiting for a large part of the population to become infected in order to mitigate the epidemic is certainly not the best strategy, especially when the disease presents high mortality and lethality rates.

a The evolution of density of infected, susceptible and removed individuals over time. The number of infected individuals grows exponentially fast at the beginning of the epidemic, reaches a peak and begins to decline, showing the natural behavior of an epidemic. b The graph is the same as represented in ( a ) but here is a simple demonstration of the effectiveness of vaccination. A small portion initially immunized (about 10 % of individuals at t = 0 ) is already enough to drastically decrease the number of people infected over time and it is also decrease the peak of the epidemic (Color figure online)

We can remember that λ = μ τ / N , β = 1 / D and, in the beginning of the epidemic S ( t ) ≈ N , then if

the epidemic starts to reduce. This shows us there are other strategies that can be adopted by governments and the entire population to mitigate the epidemic.

Indeed, the most efficient measure that would cause minor impact on society is mass vaccination. If that happened at the beginning of the epidemic, few people would be infected because the quantity S ( t ) would already start with a reduced value, quickly extinguishing the epidemic (see Fig.  1 b). This measure has worked for many cases as we mentioned in historical background, but unfortunately this strategy is not always possible especially when it comes to new emerging diseases, such as SARS-COV-2.

To reduce the contagion we can also reduce μ , the number of contact promoting measures of social distance, or we can minimize τ which implies reducing contagious encounters, that is, wearing masks, not touching infected people, and washing hands frequently. When these rates μ and τ are reduced, the curve of infected people changes becoming more flattened and with a lower peak, as we show in Fig.  2 . This explain why such measures of social distance are very important: the peak reduction, that is, the reduction of people that are infected simultaneously, avoids overloading health systems. How long a person remains infected is also a relevant factor. The faster the individual is cured, the less the transmission.

We show the difference between the infected curve over time when the contagion is reduced. The peak becomes more attenuated and consequently the epidemic lasts longer (Color figure online)

From these analyzes, we can observe how mathematical modeling can influence public health policies. However, when we investigate a pandemic, which affects several countries at the same time, the situation is more complex. Countries, states and cities have completely different demographic, economic and social configurations; therefore, other elements must be considered in the diagnosis of the evolution of the disease and in the insertion of control measures. To cover all this complexity, stochastic models are more robust as we will see in the simplest example showed below.

The SIR stochastic model running on top of complex networks

In the previous analysis we were not concern about the connection between infected, susceptible and recovered individuals. However to cover a more realistic situation we can take into account different patterns of connectivity between them. We can make this assumption considering a network where each individual is represented by a vertex or a node and the transmission of the disease occurs through edges connecting them [ 4 , 36 , 62 ].

The simplest scenario can be represent by a random graph as the model proposed by Erdős and Rényi (ER) [ 29 ], where a network is constructed starting from a set of N nodes and all pair of nodes have the same probability of connecting. This generates a homogeneous graph (see Fig.  3 a) in which the vertices have a number of neighbors, named k degree, that do not differ much from the average degree ⟨ k ⟩ . The connectivity distribution for this graph can be represent by a Poisson distribution, as showed in Fig.  4 . Here we compared this homogeneous network with a heterogeneous one. This comparison, despite its simplicity, it is useful enough to show how the topology of the network, this mean, the pattern of connection can highly impact on the epidemic spreading.

An illustration of ( a ) Erdős and Rényi and ( b ) Barabàsi-Albert networks. Both with N = 20 nodes. It is possible to observe the difference between the connectivity patterns. While the former has nodes with almost the same number of links, the latter has a few of nodes with many edges (Color figure online)

The degree distribution of networks generated by Erdős and Rényi (blue circles) and Barabàsi-Albert (red circles) networks. The inset (log-log scale) shows clearly the heavy-tail of the heterogeneous distribution compared with the homogeneous one (Color figure online)

As an example of heterogeneous network, we used the most well-known complex network model: Barabàsi-Albert (BA) model [ 9 ]. In this system, new nodes are added to the network and they are connected to those nodes already present in the network with a probability proportional to their degrees, promoting the emergence of hubs, it means, nodes with a large number of connections ( k ≫ ⟨ k ⟩ ) as we showed in Fig.  3 b. These growth and preferential attachment rules provide a network with a power law degree distribution P ( k ) ∼ k - γ , with γ = 3 in the thermodynamic limit (see Fig.  4 ). This connectivity distribution, known as heavy-tail distribution indicates that there is a low probability, but different from zero, to find hubs in the network. This is an important feature of heterogeneous networks since hubs can spread the disease to a larger number of neighbors, thus contributing to the speed of infection. Despite the addition of new nodes, when we investigate epidemic process in this network, we consider it a static network since it is grown first and after the dynamics run through the substrate.

To investigate the role of connectivity pattern, we can rewrite Eq. ( 2 ) using a heterogeneous mean-field (HMF) approach, in which dynamical quantities, as the density of infected individuals, depend only of the vertex degree. Then, we named i k ( t ) the density of infected nodes with a given degree k and the dynamical mean-field equation describing the system can thus be written as [ 62 ]:

The first term on the right-side considers the event that a node with k links is healthy, s k ( t ) , and gets the infection via a nearest neighbor. The probability of this event is proportional to the infection rate λ , the number of connections k and the density of infected neighbors Θ k ( t ) . The second term considers nodes becoming healthy at rate β . To solve this equation we should consider there is no degree correlations, this means the probability that a link between a node with degree k and other node with degree k ′ can be expressed as P ( k ′ | k ) = k ′ P ( k ′ ) / ⟨ k ⟩  [ 10 ]. So, Θ k ( t ) can be expressed as

The term k ′ - 1 considers that at least one link of an infected node points to other infected node, through which it got infected and this node can not be reinfected again, because, once infected, it becomes removed at a rate β and it can not return to the susceptible compartment [ 62 ]. We can replace s k ( t ) with 1 - r k ( t ) - i k ( t ) , where r k ( t ) is the number of recovered nodes with degree k in the time t . Performing the linearization of Eq. ( 7 ), we obtain the epidemic threshold, this means, the value of λ / β delimiting the transition between the absorbing phase ( i k ( t → ∞ ) = r k ( t → ∞ ) = 0 ) and the active phase ( i k ( t → ∞ ) = 0 and r k ( t → ∞ ) = finite), and it is given by [ 10 , 62 ]:

Other mean-field approaches can be used to calculate the epidemic threshold, as for example, the quenched mean-field theory [ 17 ], that explicitly takes into account the actual connectivity of the network through its adjacency matrix, whose elements A ij = 1 if the vertices i and j are connected, and A ij = 0 , otherwise [ 10 ]. However, for the scope of this work, the previous analysis is quite enough.

We can estimate now the epidemic threshold of the SIR model running on top of the Erdős-Rényi and the Barabàsi-Albert networks. For the homogeneous model, we obtain a finite threshold, however, for the heterogeneous network, we obtain a vanishing one, since scale-free networks, characterized by a power-law degree distribution with exponent 2 < γ ≤ 3 , has ⟨ k 2 ⟩ → ∞ when the network goes to an infinite size [ 15 ]. This simple analysis shows us how the connection structure of individuals in a network plays a fundamental role in the spread of the disease, which shows how complex the study of an epidemic can become.

To verify this prediction we can simulate the SIR model running on the top of both networks. Numerical simulations is an important tool to check the accuracy of mean-field approaches. The Gillespie algorithm [ 34 ] is the standard algorithm to implement continuous-time Markov processes [ 4 , 36 ]. In a Markov chain process the physical state at a given time t depends only on the state at the previous time. We can associated independent spontaneous processes to each dynamical transition, infection and cure, for example. However, in each change of state, a list of all possible spontaneous processes must be updated. For very large networks this task is computationally unsustainable. Cota and Ferreira [ 23 ] proposed an optimized version of the Gillespie recipe and the SIR dynamics can be simulated according to the following steps [ 33 ]:

• To keep and constantly to update a list P with the positions of all infected vertices where changes will take place;
• the time step is incremented by Δ t = 1 / ( R + J ) ;
• With probability p = R / ( R + J ) an infected vertex i is selected randomly and turns it to removed;
• With complementary probability q = J / ( R + J ) an infected vertex is selected at random and accepted with probability proportional to its degree. In the infection attempt, a neighbor of the selected vertex is randomly chosen and if susceptible, it is infected. Otherwise nothing happens and simulations run to the next time step.

The total rate that an infected vertex becomes removed in the whole network is R = β N i , where N i is the number of infected vertices and the total rate that one susceptible vertex is infected is given by J = λ N e , where N e is the number of vertices emanating from infected nodes.

In the Fig.  5 we show the density of removed individuals as a function of the parameter control λ . In this simulation we fixed β = 1 and named λ c the threshold, without loss of generality, just to simplify the notation. Note that the density of recovered nodes changes from a null value (absorbing state) to a finite value (active state) for a specific value of λ that is known as λ c , the epidemic threshold. 2 For BA network, this happen for a smaller value of λ , near to zero, as expected because λ c = 0 when N → ∞ . While for ER network, it is necessary a bigger value of infection rate λ to start the spreading of the disease to the entire network, confirming how the network topology influences the dynamics of the epidemic. For both networks, we used N = 10 4 and ⟨ k ⟩ = 5 . It is well-known that real systems are much more similar to BA network than ER one [ 15 ]. This elucidates many real-world phenomena such as the fact that only one infected individual, called individual zero, is enough to spread an epidemic to the entire world, as happened in the COVID-19 pandemic [ 30 , 48 ].

Density of recovered (or removed) nodes (individuals)— ρ r - in function of the infection rate λ , also known as control parameter. For BA network, a small value of the infection rate is enough to start the disease spreading while for ER network, it is necessary a bigger value of λ to start the spreading of the disease to the entire network. The value of λ c is the epidemic threshold for the SIR model running on top of these different substrates. Here, we used both networks with N = 10 4 nodes (Color figure online)

As we mentioned previously, despite the simplicity of this comparison, we hope that it has become clear to the reader the relevance of complex networks in epidemic modeling and how this issue gets more and more refined and intricate depending on the substrate used. However, as we discussed in Sect.  2 , more sophisticated network models such as metapopulations [ 21 ], multilayer networks [ 26 , 37 , 59 ], models that include agent mobility patterns, age stratification social mixing patterns, spatial structure, interventions measures [ 30 , 46 , 51 , 53 ] are even more realistic and, when they are used in combination with big data and statistical tools, they are able to provide increasingly accurate outcomes.

Non-compartmental models

Most of studies to model epidemic spreading are based on compartmental models. However, other methodologies, for example, statistical analyses, can also be used. Typically, at the beginning of disease spreading, compartmental models are useful to predict the development of the epidemic. This is important to help the government make decisions related to containment measures and also to prevent the population from the risk of contagion [ 5 , 42 , 81 ]. But spatial statistics methods is able to obtain more appreciable insights related to the spreading pattern of the disease in space and time, taking into account geographic, social and demographic factors. Indeed, there are many different types of statistical approaches that can be used to investigate epidemic spreading processes. It would be unfeasible to discuss in greater detail all of them in this work. However, we would like to mention some important aspects of this kind of approach.

For example, there are recent studies using statistical tools to investigate the spatio-temporal spreading of the COVID-19 disease. Wells and collaborators [ 79 ] used maximum likelihood to predict the impact of travels on the dynamic of this pandemic. Azevedo and colleagues [ 6 ] analyzed the spatial and temporal dynamics of the disease by mapping the infection rates in the municipalities of Portugal through maps of the interpolation of this rate over time. Ribeiro et al. [ 66 ] predicted the cumulative cases of COVID-19 in ten Brazilian states. Zhao et al. [ 84 ] used correlational analysis to quantify the relation between the number of passengers from Wuhan with the number of infected people in a set of ten nearby cities.

In other recent study, the authors [ 78 ] observed 1212 patients in China and they evaluated the incubation period using maximum likelihood estimation. The authors of reference [ 70 ] also investigated the spatial and temporal associations of the incidence, mortality, and the rate of two different kinds of tests in a specific region from Brazil. Pedrosa and collaborators [ 65 ] also analysed the COVID-19 cases spatially and related to the number of intensive care beds in the region investigated.

Despite extensive efforts to predict and contain an epidemic, we must always remember that the spread of a disease involves an exponential growth of infected people and this is intrinsically unpredictable. In addition, such events are directly related to the individual and collective behavior of the population, which makes it even more complex [ 18 ].

Final remarks: challenges and perspectives

In this paper, we briefly reviewed epidemics from the perspective of historical background and mathematical modeling. Our aim was to introduce this topic for a broad audience, on the purpose of summarizing the evolution of the use of mathematical modeling, complex networks and statistical tools in epidemiology. We synthesized the primary literature on this topic over the years and we provided a comprehensive list of citations for those who desire to go beyond.

We believe that it became clear to the reader the importance of computational tools in predicting epidemics, in helping governments to implement safe and efficient public policies and in implementing different vaccination strategies [ 40 ]. This is essential to think about public health policies and, above all, to make the population aware of the importance of control measures such as social isolation, quarantine, wearing masks, constant hand hygiene, etc. Infectious diseases are challenging in the scope of public health policies because their prevention and control involve national and regional efforts coordinated worldwide [ 27 ].

Scientific community has done great efforts to search for specific antiviral therapeutics and vaccines against many virus such as SARS-CoV-2. The main idea, explaining in a trivial way, is found a method to inhibit the activity of the main protease of the virus – in this specific example, the new coronavirus - and consequently to block viral replication. In this context, complex networks can also help to answer questions related to protein structure and functioning (useful surveys related to this topic can be found in the references [ 13 , 31 ]).

It is important to emphasize that epidemic models–despite their usefulness to predict and to better understand dynamical diseases—present limitations of modeling related to uncertainties in predictions since, however sophisticated they are, they are not able to capture all the complexity of social interactions [ 27 , 40 ]. In addition, there are other challenges such as synthesizing data in real time, underreporting of cases and deaths, new policies to vaccinate the most vulnerable population, missing information on the influence of control measures to comprehension human responses, etc [ 35 ].

Besides the challenges inherent in predicting and controlling any epidemic, lately we have a major obstacle related to the large amount of information we receive daily, especially from social media. WHO classified this phenomena as an infodemic  [ 80 ], this means, the volume of information related to an specific topic, such as the COVID-19 pandemic, has grown exponentially fast in a short period of time, mainly because social media. This huge quantify of information—not always accurate - negatively affects human health making people confused, and increasing mental health problems like depression and anxiety. It makes hard for people to find trusted sources and consequently it impacts in the community engagement and its well-being [ 83 ].

In conclusion, we emphasized that the progress in the epidemiological modeling area has grown incredibly fast and it is not possible to discuss all recent surveys, but we mentioned the main advances in this field. The relevance of studying epidemic models becomes more evident when faced with alarming situations such as the recent pandemic of COVID-19 [ 30 , 48 ]. Recently, there have been several innovative and interesting works on the modeling of SARS-CoV-2 using different substrates related to complex networks [ 19 , 22 , 52 , 71 , 73 ]. It is also relevant to mention that the use of mathematical and computational tools presented here can be expanded and applied to other disease spreading such as livestock and vector-borne diseases [ 14 , 80 ]. We are aware that there are many challenges in modeling spreading diseases mainly related to public health and global transmission [ 55 ]. However, we hope that this survey identifies our current situation and what we still need to do to improve our mathematical and computational tools and, consequently, to fight better future epidemics.

Acknowledgements

Angélica S. Mata acknowledges the support from FAPEMIG (Grant No. APQ-02482-18) and CNPq (Grant No. 423185/2018-7).

Declarations

The authors declare there is no conflict of interest.

1 Here we are considering an approximation to simplify the mathematical calculations. We know that there are several biological factors that can, for example, make a fraction of the population naturally immune to some new epidemic. However, to attend our aim, this assumption is quite reasonable.

2 In fact, any realization of the epidemic dynamics in finite networks reaches the absorbing state sooner or later because of dynamic fluctuations inherent to stochastic process, even above the critical point. This simulation difficulty was traditionally overcome by quasi stationary methods. For further details, the reader can consult the following references: [ 54 , 61 ]

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

New work extends the thermodynamic theory of computation

Every computing system, biological or synthetic, from cells to brains to laptops, has a cost. This isn't the price, which is easy to discern, but an energy cost connected to the work required to run a program and the heat dissipated in the process.

Researchers at SFI and elsewhere have spent decades developing a thermodynamic theory of computation, but previous work on the energy cost has focused on basic symbolic computations -- like the erasure of a single bit -- that aren't readily transferable to less predictable, real-world computing scenarios.

In a paper published in Physical Review X on May 13, a quartet of physicists and computer scientists expand the modern theory of the thermodynamics of computation. By combining approaches from statistical physics and computer science, the researchers introduce mathematical equations that reveal the minimum and maximum predicted energy cost of computational processes that depend on randomness, which is a powerful tool in modern computers.

In particular, the framework offers insights into how to compute energy-cost bounds on computational processes with an unpredictable finish. For example: A coin-flipping simulator may be instructed to stop flipping once it achieves 10 heads. In biology, a cell may stop producing a protein once it elicits a certain reaction from another cell. The "stopping times" of these processes, or the time required to achieve the goal for the first time, can vary from trial to trial. The new framework offers a straightforward way to calculate the lower bounds on the energy cost of those situations.

The research was conducted by SFI Professor David Wolpert, Gonzalo Manzano (Institute for Cross-Disciplinary Physics and Complex Systems, Spain), Édgar Roldán (Institute for Theoretical Physics, Italy), and SFI graduate fellow Gülce Kardes (CU Boulder). The study uncovers a way to lower-bound the energetic costs of arbitrary computational processes. For example: an algorithm that searches for a person's first or last name in a database might stop running if it finds either, but we don't know which one it found. "Many computational machines, when viewed as dynamical systems, have this property where if you jump from one state to another you really can't go back to the original state in just one step," says Kardes.

Wolpert began investigating ways to apply ideas from nonequilibrium statistical physics to the theory of computation about a decade ago. Computers, he says, are a system out of equilibrium, and stochastic thermodynamics gives physicists a way to study nonequilibrium systems. "If you put those two together, it seemed like all kinds of fireworks would come out, in an SFI kind of spirit," he says.

In recent studies that laid the groundwork for this new paper, Wolpert and colleagues introduced the idea of a "mismatch cost," or a measure of how much the cost of a computation exceeds Landauer's bound. Proposed in 1961 by physicist Rolf Landauer, this limit defines the minimum amount of heat required to change information in a computer. Knowing the mismatch cost, Wolpert says, could inform strategies for reducing the overall energy cost of a system.

Across the Atlantic, co-authors Manzano and Roldán have been developing a tool from the mathematics of finance -- the martingale theory -- to address the thermodynamic behavior of small fluctuating systems at stopping times. Roldán et. al.'s "Martingales for Physicists" helped pave the way to successful applications of such a martingale approach in thermodynamics.

Wolpert, Kardes, Roldán, and Manzano extend these tools from stochastic thermodynamics to the calculation of a mismatch cost to common computational problems in their PRX paper.

Taken together, their research point to a new avenue for finding the lowest energy needed for computation in any system, no matter how it's implemented. "It's exposing a vast new set of issues," Wolpert says.

It may also have a very practical application, in pointing to new ways to make computing more energy efficient. The National Science Foundation estimates that computers use between 5% and 9% of global generated power, but at current growth rates, that could reach 20% by 2030. But previous work by SFI researchers suggests modern computers are grossly inefficient: Biological systems, by contrast, are about 100,000 times more energy-efficient than human-built computers. Wolpert says that one of the primary motivations for a general thermodynamic theory of computation is to find new ways to reduce the energy consumption of real-world machines.

For instance, a better understanding of how algorithms and devices use energy to do certain tasks could point to more efficient computer chip architectures. Right now, says Wolpert, there's no clear way to make physical chips that can carry out computational tasks using less energy.

"These kinds of techniques might provide a flashlight through the darkness," he says.

• Thermodynamics
• Energy Technology
• Solar Energy
• Computer Science
• Computer Modeling
• Computers and Internet
• Distributed Computing
• Cryptography
• John von Neumann
• Computer simulation
• Quantum computer
• Mathematical model
• Game theory
• Artificial intelligence

Story Source:

Materials provided by Santa Fe Institute . Note: Content may be edited for style and length.

Journal Reference :

• Gonzalo Manzano, Gülce Kardeş, Édgar Roldán, David H. Wolpert. Thermodynamics of Computations with Absolute Irreversibility, Unidirectional Transitions, and Stochastic Computation Times . Physical Review X , 2024; 14 (2) DOI: 10.1103/PhysRevX.14.021026

Cite This Page :

Explore More

• High-Efficiency Photonic Integrated Circuit
• Life Expectancy May Increase by 5 Years by 2050
• Toward a Successful Vaccine for HIV
• Highly Efficient Thermoelectric Materials
• Toward Human Brain Gene Therapy
• Whale Families Learn Each Other's Vocal Style
• AI Can Answer Complex Physics Questions
• Otters Use Tools to Survive a Changing World
• Monogamy in Mice: Newly Evolved Type of Cell
• Sustainable Electronics, Doped With Air

Trending Topics

Strange & offbeat.

• Computer Vision
• Federated Learning
• Reinforcement Learning
• Natural Language Processing
• New Releases
• AI Dev Tools
• Advisory Board Members
• 🐝 Partnership and Promotion

In conclusion, researchers introduced a mathematical explanation for the rise of Fourier features in learning systems like neural networks. Also, they proved that if a machine learning model of a specific kind is invariant to a finite group, then its weights are closely related to the Fourier transform on that group, and the algebraic structure of an unknown group can be recovered from an invariant model. Future work includes the study of analogs of the proposed theory on real numbers which is an interesting area that will be aligned more towards the current practices in the field.

Check out the  Paper . All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on  Twitter . Join our  Telegram Channel ,   Discord Channel , and  LinkedIn Gr oup .

If you like our work, you will love our  newsletter..

Don’t Forget to join our  42k+ ML SubReddit

Sajjad Ansari

Sajjad Ansari is a final year undergraduate from IIT Kharagpur. As a Tech enthusiast, he delves into the practical applications of AI with a focus on understanding the impact of AI technologies and their real-world implications. He aims to articulate complex AI concepts in a clear and accessible manner.

This AI Paper from Huawei Introduces a Theoretical Framework Focused on the Memorization Process and Performance Dynamics of Transformer-based Language Models (LMs)

• Consistency Large Language Models (CLLMs): A New Family of LLMs Specialized for the Jacobi Decoding Method for Latency Reduction
• FastGen: Cutting GPU Memory Costs Without Compromising on LLM Quality
• Researchers from Princeton and Meta AI Introduce 'Lory': A Fully-Differentiable MoE Model Designed for Autoregressive Language Model Pre-Training

RELATED ARTICLES MORE FROM AUTHOR

Cinepile: a novel dataset and benchmark specifically designed for authentic long-form video understanding, alpine: autoregressive learning for planning in networks, google ai described new machine learning methods for generating differentially private synthetic data, planning architectures for autonomous robotics, this ai paper from stanford university evaluates the performance of multimodal foundation models scaling from few-shot to many-shot-in-context learning icl, this ai paper from huawei introduces a theoretical framework focused on the memorization process....

• AI Magazine
• Privacy & TC
• Cookie Policy

🐝 🐝 Join the Fastest Growing AI Research Newsletter Read by Researchers from Google + NVIDIA + Meta + Stanford + MIT + Microsoft and many others...

Thank You 🙌

Privacy Overview

Assessment of the Attractiveness of Large Russian Cities for Residents, Tourists, and Business

• URBAN STUDIES
• Published: 16 December 2020
• Volume 10 , pages 538–548, ( 2020 )

Cite this article

• R. V. Fattakhov 1 ,
• M. M. Nizamutdinov 2 &
• V. V. Oreshnikov 2  

148 Accesses

4 Citations

Explore all metrics

The article proposes an approach to assessing the attractiveness of large cities of the Russian Federation for residents, businesses, and tourists. As part of the development of this approach, particular parameters of the attractiveness of cities for individual economic agents were determined and an integral indicator was calculated. The hypothesis of the study is based on the fact that high positions of a city in a particular rating do not always guarantee its leadership in other areas; however, in general, the differentiation of places in case of a particular city is more inherent to ratings outsiders than to leading cities. Systemic analysis; factorial, statistical, structural, and dynamic analysis; classification, correlation, and regression analysis; and economic and mathematical modeling were used as research tools. The approach was tested on data for large Russian cities. Both sets of particular indicators characterizing certain areas of research and the approach to forming an integral indicator of the level of attractiveness of cities necessary for a generalized assessment have been determined. The presented results generally confirm the proffered hypothesis. In modern conditions, public authorities should pay special attention not only to the development of individual cities, but to the integrated development of the spatial framework of a territory where cities play a decisive role. The proposed approach to assessing the level of attractiveness of Russian cities makes it possible to obtain logical meaningful results that can be applied to solve problems in these areas.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price excludes VAT (USA) Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Impact of tourism development upon environmental sustainability: a suggested framework for sustainable ecotourism

Understanding the Relationship between Urban Public Space and Social Cohesion: A Systematic Review

Urbanisation and Land Use Change

Regions of Russia. Main Socioeconomic Indicators of Cities. 2018: Statistical Digest / Rosstat. Moscow, 2018. 443 p.

Alekseev, A.I. and Zubarevich, N.V., The urbanization crisis: the formation of a new way of life, Probl. Prognoz ., 2000, no. 4, pp. 138–146.

Akhmetov, T.R., The innovation cycle and the evolutionary model of social development with an innovative determinant at various levels, Fundam. Issled ., 2016, no. 4-2, pp. 350–354.

Barinova, Yu.A. and Suslov, S.A., Food security, development of agriculture and demographic trends for individual territories of the Russian Federation, Vestn. Nizhegorod. Gos. Inzh.-Ekon. Univ ., 2013, no. 1 (20), pp. 3–24.

Granberg, A.G. and Suspitsyn, S.A., Vvedenie v sistemnoe modelirovanie narodnogo khozyaistva (Introduction into Systemic Modeling of National Economics), Novosibirsk: Nauka, 1988.

Ivanov, P.A., The concept of municipal finances and a retrospective analysis of their development in Russia, Mezhdunar. Zh. Prikl. Fundam. Issled ., 2015, no. 12-4, pp. 697–701.

Kabashova, E.V., Use of multiple regression models for the analysis of population income, Aktual. Probl. Persp. Razvit. Ekon.: Ross. Zarubezhnyi Opyt , 2016, no. 2, pp. 8–10.

Kleiner, G.B., Systems management in a transforming economy, Eff. Antikrizisnoe Upr ., 2014, no. 5, pp. 54–59.

Las’ko, A.I., Urbanization as a reason of the economic crisis, Ekon. Menedzhment Innovatsionnykh Tekhnol ., 2014, no. 7 (34), pp. 51–53.

Popov, A.V., Salary as a tool to stimulate labor activity, Sotsiol. Issled ., 2016, no. 7, pp. 40–47.

Stroev, P.V., Transformation of spatial structure of Russia, Vestn. Inst. Ekon., Ross. Akad. Nauk , 2014, no. 4, pp. 61–70.

Tatarkin, A.I., The hidden potential of Russian cities: from agglomeration associations to program and project strategies for the development of territories, Ekon. Nauka Sovrem. Ross ., 2014, no. 2 (65), pp. 7–25.

Toguzaev, P.A. and Gubanov, E.V., Assessment of the investment attractiveness of Kaluga oblast using the quantitative method, Sist. Upr ., 2015, no. 4 (29), p. 37.

Ulyaeva, A.G. and Ataeva, A.G., Formation and development of urban agglomerations as a direction for strengthening interterritorial interaction in the region, Ekon. Predprinimatel’stvo , 2015, no. 12-1 (65), pp. 369–373.

Fattakhov, R.V., Abdulova, L.R., and Oreshnikov, V.V., Analysis and assessment of the mutual influence of the parameters of the demographic and economic development of regions and cities, case study of the Volga Federal District, Ekon. Anal.: Teor. Prakt ., 2016, no. 2 (449), pp. 77–90.

Fattakhov, R.V., Nizamutdinov, M.M., and Oreshnikov, V.V., Substantiation of the strategic development parameters of the region based on adaptive simulation modeling, Reg.: Ekon. Sotaiol ., 2017, no. 1 (93), pp. 101–120.

Cherkesova, E.Yu., Pakhomova, A.I., and Buryakov, S.A., Adaptation of a modern city to technological challenges, Ekon. Predprinimatel’stvo , 2017, no. 8-2 (85), pp. 332–335.

Chernyakhovskaya, L.R., Fedorova, N.I., and Vladimirova, I.P., Management of interacting processes based on an integrated knowledge representation model, Trudy Tret’ei Mezhdunarodnoi nauchnoi konferentsii “Informatsionnye tekhnologii i sistemy” (Proc. Third Int. Sci. Conf. “Information Technologies and Systems”), Chelyabinsk, 2014, pp. 95–96.

Amisano, G. and Geweke, J., Prediction Using Several Macroeconomic Models: Working Paper no. 1537 , Frankfurt am Main: European Central Bank, 2013. https://doi.org/10.1162/REST_a_00655 . http://www.ecb.europa.eu/pub/pdf/scpwps/ecbwp1537.pdf. Accessed May 15, 2016.

Glaeser, E., Triumph of the City: How Our Greatest Invention Makes Us Richer, Smarter, Greener, Healthier, and Happier , New York: Penguin, 2011.

Google Scholar  

Li, C., Wei, L., and Hao, Y., Research on characteristics of city agglomeration compound traffic network, J. Syst. Simul ., 2016, vol. 28, no. 12, pp. 2958–2965. https://doi.org/10.16182/j.issn1004731x.joss.201612012

Article   Google Scholar  

Martin, R., Rebalancing the spatial economy: the challenge for regional theory, Territ., Politics, Governance . 2015, vol. 3, no. 3, pp. 235–272. https://doi.org/10.1080/21622671.2015.1064825

Scott, A.J. and Storper, M., The nature of cities: the scope and limits of urban theory, Int. J. Urban Reg. Res ., 2015, vol. 39, no. 1, pp. 1–15. https://doi.org/10.1111/1468-2427.12134

Download references

The study was carried out under the state task of the UFRC RAS no. 075-01211-20-01 for 2020.

Author information

Authors and affiliations.

Department of Public Finance of the Financial University under the Government of the Russian Federation, 125993, Moscow, Russia

R. V. Fattakhov

Institute for Socioeconomic Research, Ufa Federal Research Center, Russian Academy of Sciences, 450054, Ufa, Russia

M. M. Nizamutdinov & V. V. Oreshnikov

You can also search for this author in PubMed   Google Scholar

Corresponding authors

Correspondence to R. V. Fattakhov , M. M. Nizamutdinov or V. V. Oreshnikov .

Ethics declarations

The authors declare no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Fattakhov, R.V., Nizamutdinov, M.M. & Oreshnikov, V.V. Assessment of the Attractiveness of Large Russian Cities for Residents, Tourists, and Business. Reg. Res. Russ. 10 , 538–548 (2020). https://doi.org/10.1134/S2079970520040036

Download citation

Received : 15 February 2019

Revised : 10 July 2020

Accepted : 20 July 2020

Published : 16 December 2020

Issue Date : October 2020

DOI : https://doi.org/10.1134/S2079970520040036

The Unique Burial of a Child of Early Scythian Time at the Cemetery of Saryg-Bulun (Tuva)

<< Previous page

Pages:  379-406

In 1988, the Tuvan Archaeological Expedition (led by M. E. Kilunovskaya and V. A. Semenov) discovered a unique burial of the early Iron Age at Saryg-Bulun in Central Tuva. There are two burial mounds of the Aldy-Bel culture dated by 7th century BC. Within the barrows, which adjoined one another, forming a figure-of-eight, there were discovered 7 burials, from which a representative collection of artifacts was recovered. Burial 5 was the most unique, it was found in a coffin made of a larch trunk, with a tightly closed lid. Due to the preservative properties of larch and lack of air access, the coffin contained a well-preserved mummy of a child with an accompanying set of grave goods. The interred individual retained the skin on his face and had a leather headdress painted with red pigment and a coat, sewn from jerboa fur. The coat was belted with a leather belt with bronze ornaments and buckles. Besides that, a leather quiver with arrows with the shafts decorated with painted ornaments, fully preserved battle pick and a bow were buried in the coffin. Unexpectedly, the full-genomic analysis, showed that the individual was female. This fact opens a new aspect in the study of the social history of the Scythian society and perhaps brings us back to the myth of the Amazons, discussed by Herodotus. Of course, this discovery is unique in its preservation for the Scythian culture of Tuva and requires careful study and conservation.

Keywords: Tuva, Early Iron Age, early Scythian period, Aldy-Bel culture, barrow, burial in the coffin, mummy, full genome sequencing, aDNA

Information about authors: Marina Kilunovskaya (Saint Petersburg, Russian Federation). Candidate of Historical Sciences. Institute for the History of Material Culture of the Russian Academy of Sciences. Dvortsovaya Emb., 18, Saint Petersburg, 191186, Russian Federation E-mail: [email protected] Vladimir Semenov (Saint Petersburg, Russian Federation). Candidate of Historical Sciences. Institute for the History of Material Culture of the Russian Academy of Sciences. Dvortsovaya Emb., 18, Saint Petersburg, 191186, Russian Federation E-mail: [email protected] Varvara Busova  (Moscow, Russian Federation).  (Saint Petersburg, Russian Federation). Institute for the History of Material Culture of the Russian Academy of Sciences.  Dvortsovaya Emb., 18, Saint Petersburg, 191186, Russian Federation E-mail:  [email protected] Kharis Mustafin  (Moscow, Russian Federation). Candidate of Technical Sciences. Moscow Institute of Physics and Technology.  Institutsky Lane, 9, Dolgoprudny, 141701, Moscow Oblast, Russian Federation E-mail:  [email protected] Irina Alborova  (Moscow, Russian Federation). Candidate of Biological Sciences. Moscow Institute of Physics and Technology.  Institutsky Lane, 9, Dolgoprudny, 141701, Moscow Oblast, Russian Federation E-mail:  [email protected] Alina Matzvai  (Moscow, Russian Federation). Moscow Institute of Physics and Technology.  Institutsky Lane, 9, Dolgoprudny, 141701, Moscow Oblast, Russian Federation E-mail:  [email protected]

Shopping Cart Items: 0 Cart Total: 0,00 € place your order

Price pdf version

student - 2,75 € individual - 3,00 € institutional - 7,00 €

Copyright В© 1999-2022. Stratum Publishing House