assignment problem using branch and bound

Branch and Bound Algorithm

Last updated: March 18, 2024

Baeldung Pro comes with both absolutely No-Ads as well as finally with Dark Mode , for a clean learning experience:

>> Explore a clean Baeldung

Once the early-adopter seats are all used, the price will go up and stay at $33/year.

1. Overview

In computer science, there is a large number of optimization problems which has a finite but extensive number of feasible solutions. Among these, some problems like finding the shortest path in a graph or Minimum Spanning Tree can be solved in polynomial time .

A significant number of optimization problems like production planning , crew scheduling can’t be solved in polynomial time, and they belong to the NP-Hard class . These problems are the example of NP-Hard combinatorial optimization problem .

Branch and bound (B&B) is an algorithm paradigm widely used for solving such problems.

In this tutorial, we’ll discuss the branch and bound method in detail.

2. Basic Idea

Branch and bound algorithms are used to find the optimal solution for combinatory, discrete, and general mathematical optimization problems. In general, given an NP-Hard problem, a branch and bound algorithm explores the entire search space of possible solutions and provides an optimal solution.

A branch and bound algorithm consist of stepwise enumeration of possible candidate solutions by exploring the entire search space. With all the possible solutions, we first build a rooted decision tree. The root node represents the entire search space:

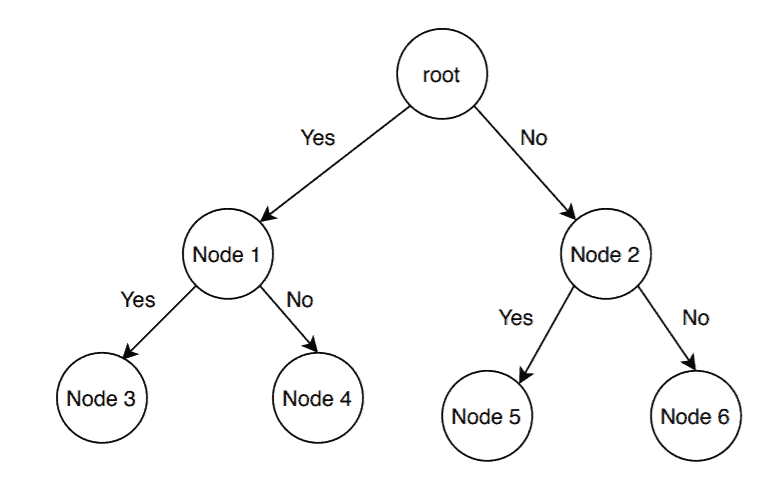
Here, each child node is a partial solution and part of the solution set. Before constructing the rooted decision tree, we set an upper and lower bound for a given problem based on the optimal solution. At each level, we need to make a decision about which node to include in the solution set. At each level, we explore the node with the best bound. In this way, we can find the best and optimal solution fast.

Now it is crucial to find a good upper and lower bound in such cases. We can find an upper bound by using any local optimization method or by picking any point in the search space. On the other hand, we can obtain a lower bound from convex relaxation or duality .

In general, we want to partition the solution set into smaller subsets of solution. Then we construct a rooted decision tree, and finally, we choose the best possible subset (node) at each level to find the best possible solution set.

3. When Branch and Bound Is a Good Choice?

We already mentioned some problems where a branch and bound can be an efficient choice over the other algorithms. In this section, we’ll list all such cases where a branch and bound algorithm is a good choice.

If the given problem is a discrete optimization problem, a branch and bound is a good choice. Discrete optimization is a subsection of optimization where the variables in the problem should belong to the discrete set. Examples of such problems are 0-1 Integer Programming or Network Flow problem .

Branch and bound work efficiently on the combinatory optimization problems. Given an objective function for an optimization problem, combinatory optimization is a process to find the maxima or minima for the objective function. The domain of the objective function should be discrete and large. Boolean Satisfiability , Integer Linear Programming are examples of the combinatory optimization problems.

4. Branch and Bound Algorithm Example

In this section, we’ll discuss how the job assignment problem can be solved using a branch and bound algorithm.

4.1. Problem Statement

	Job 1	Job 2	Job 3
A	9	3	4
B	7	8	4
C	10	5	2

We can assign any of the available jobs to any worker with the condition that if a job is assigned to a worker, the other workers can’t take that particular job. We should also notice that each job has some cost associated with it, and it differs from one worker to another.

Here the main aim is to complete all the jobs by assigning one job to each worker in such a way that the sum of the cost of all the jobs should be minimized.

4.2. Branch and Bound Algorithm Pseudocode

Now let’s discuss how to solve the job assignment problem using a branch and bound algorithm.

Let’s see the pseudocode first:

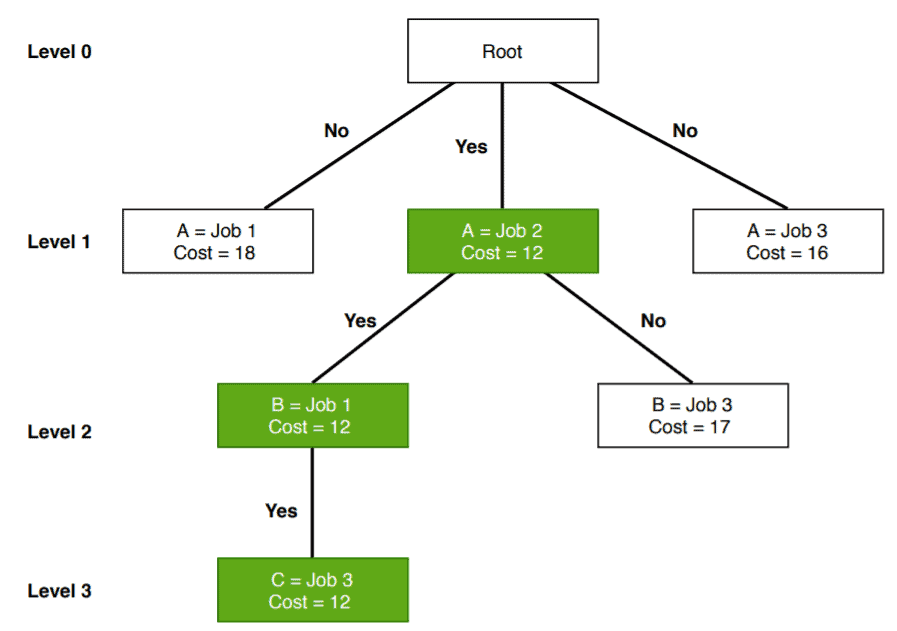
In the search space tree, each node contains some information, such as cost, a total number of jobs, as well as a total number of workers.

Now let’s run the algorithm on the sample example we’ve created:

4. Advantages

In a branch and bound algorithm, we don’t explore all the nodes in the tree. That’s why the time complexity of the branch and bound algorithm is less when compared with other algorithms.

If the problem is not large and if we can do the branching in a reasonable amount of time, it finds an optimal solution for a given problem.

The branch and bound algorithm find a minimal path to reach the optimal solution for a given problem. It doesn’t repeat nodes while exploring the tree.

5. Disadvantages

The branch and bound algorithm are time-consuming. Depending on the size of the given problem, the number of nodes in the tree can be too large in the worst case.

Also, parallelization is extremely difficult in the branch and bound algorithm.

6. Conclusion

One of the most popular algorithms used in the optimization problem is the branch and bound algorithm. We’ve discussed it thoroughly in this tutorial.

We’ve explained when a branch and bound algorithm would be the right choice for a user to use. Furthermore, we’ve presented a branch and bound based algorithm for solving the job assignment problem.

Finally, we mentioned some advantages and disadvantages of the branch and bound algorithm.

Press ESC to close

Or check our popular categories..., branch and bound | set 4 (job assignment problem).

Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.

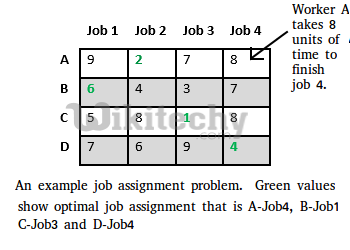
Let us explore all approaches for this problem.

Solution 1: Brute Force We generate n! possible job assignments and for each such assignment, we compute its total cost and return the less expensive assignment. Since the solution is a permutation of the n jobs, its complexity is O(n!).

Solution 2: Hungarian Algorithm The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3).

Solution 3: DFS/BFS on state space tree A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem. We can perform depth-first search on state space tree and but successive moves can take us away from the goal rather than bringing closer. The search of state space tree follows leftmost path from the root regardless of initial state. An answer node may never be found in this approach. We can also perform a Breadth-first search on state space tree. But no matter what the initial state is, the algorithm attempts the same sequence of moves like DFS.

Solution 4: Finding Optimal Solution using Branch and Bound The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.

There are two approaches to calculate the cost function:

For each worker, we choose job with minimum cost from list of unassigned jobs (take minimum entry from each row).
For each job, we choose a worker with lowest cost for that job from list of unassigned workers (take minimum entry from each column).

In this article, the first approach is followed.

Let’s take below example and try to calculate promising cost when Job 2 is assigned to worker A.

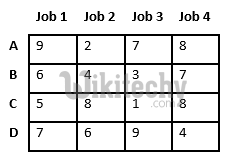
Since Job 2 is assigned to worker A (marked in green), cost becomes 2 and Job 2 and worker A becomes unavailable (marked in red).

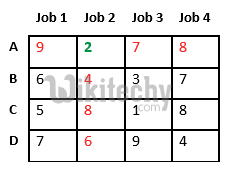
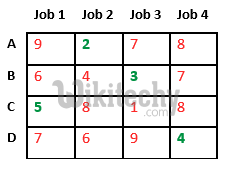
Now we assign job 3 to worker B as it has minimum cost from list of unassigned jobs. Cost becomes 2 + 3 = 5 and Job 3 and worker B also becomes unavailable.

Finally, job 1 gets assigned to worker C as it has minimum cost among unassigned jobs and job 4 gets assigned to worker C as it is only Job left. Total cost becomes 2 + 3 + 5 + 4 = 14.

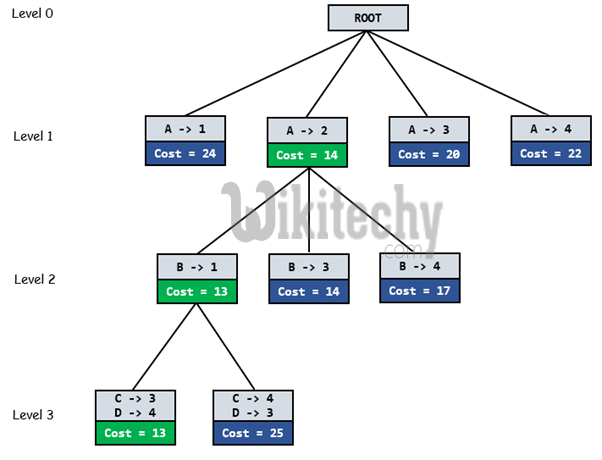
Below diagram shows complete search space diagram showing optimal solution path in green.

Complete Algorithm:

Below is its C++ implementation.

Categorized in:

Venkatesan Prabu

Wikitechy Founder, Author, International Speaker, and Job Consultant. My role as the CEO of Wikitechy, I help businesses build their next generation digital platforms and help with their product innovation and growth strategy. I'm a frequent speaker at tech conferences and events.

Save my name, email, and website in this browser for the next time I comment.

10 steps to quickly learn programming in c#, c program print bst keys in the given range, java program print bst keys in the given range, cpp algorithm – length of the longest valid substring, other stories, c programming – inserting a node in linked list | set 2, c++ program check if a number is multiple of 9 using bitwise operators, summer offline internship.

Internship for cse students
Internship for it students
Internship for ece students
Internship for eee students
Internship for mechanical engineering students
Internship for aeronautical engineering students
Internship for civil engineering students
Internship for bcom students
Internship for mcom students
Internship for bca students
Internship for mca students
Internship for biotechnology students
Internship for biomedical engineering students
Internship for bsc students
Internship for msc students
Internship for bba students
Internship for mba students

Summer Online Internship

Online internship for cse students
Online internship for ece students
Online internship for eee students
Online internship for it students
Online internship for mechanical engineering students
Online internship for aeronautical engineering students
Online internship for civil engineering students
Online internship for bcom students
Online internship for mcom students
Online internship for bca students
Online internship for mca students
Online internship for biotechnology students
Online internship for biomedical engineering students
Online internship for bsc students
Online internship for msc students
Online internship for bba students
Online internship for mba students

Internship in Chennai

Intenship in Chennai
Intenship in Chennai for CSE Students
Internship in Chennai for IT Students
Internship in Chennai for ECE Students
Internship in Chennai for EEE Students
Internship in Chennai for EIE Students
Internship in Chennai for MECH Students
Internship in Chennai for CIVIL Students
Internship in Chennai for BIOTECH Students
Internship in Chennai for AERO Students
Internship in Chennai for BBA Students
Internship in Chennai for MBA Students
Internship in Chennai for MBA HR Students
Internship in Chennai for B.Sc Students
Internship in Chennai for M.Sc Students
Internship in Chennai for BCA Students
Internship in Chennai for MCA Students
Internship in Chennai for B.Com Students
Internship in Chennai for M.Com Students

Programming / Technology Internship in Chennai

Data Science Internship in Chennai
Artificial Intelligence Internship in Chennai
Web Development Internship in Chennai
Android Internship in Chennai
Cloud Computing Internship in Chennai
.Net Internship in Chennai
JAVA Internship in Chennai
Ethical Hacking Internship in Chennai
IOT Internship in Chennai
Machine Learning Internship in Chennai
Networking Internship in Chennai
Robotics Internship in Chennai
Matlab Internship in Chennai

Job Sequencing using Branch and Bound

by codecrucks · Published 03/04/2022 · Updated 20/01/2023

Job Sequencing using Branch and Bound: Given n jobs with profit, execution time, and deadline, achieve the schedule which maximizes the profit.

We will solve the problem using the FIFO branch and bound with the variable tuple and fixed tuple representations. Each job i is represented by the tuple (Pi, di, ti), where Pi, di, and ti represent profit, deadline, and execution time associated with job i. If job i is completed on or before its deadline, profit Pi is earned. But if the job i finish after its deadline, then a penalty Pi will incur. The brute force method finds 2 n schedules for n jobs and finds the best from them. Branch and bound is a more efficient way of finding the optimal schedule.

Examples on Job Sequencing using Branch and Bound

Example: Select optimal subset J with an optimal penalty for the following data. What will be the penalty corresponding to the optimal solution?


1	5	1	1
2	10	3	2
3	6	2	1
4	3	1	1

The cost function for node x in state space tree for job sequencing problem is defined as,

Where, m = max{i | i ∈ S x }

S x is the subset of jobs selected at node x.

Upper bound u(x) for node x is defined as,

Computation of cost and bound for each node using variable tuple size is shown in the following table.

Node	S = Set of selected jobs at node x	m = max(i \| i ∈ S )	\[ hat{c}(x) = sum_{i<m ; & ; i notin S_x} P_i \]	\[ u(x) = sum_{i notin S_x} P_i \]
1	{ }	1	0	5 + 10 + 6 + 3 = 24
2	{1}	1	0	10 + 6 + 3 = 19
3	{2}	2	5	5 + 6 + 3 = 14
4	{3}	3	5 + 10 = 15	5 + 10 + 3 = 18
5	{4}	4	5 + 10 + 6 = 21	5 + 10 + 6 = 21
6	{1, 2}	2	0	6 + 3 = 9
7	{1, 3}	3	10	10 + 3 = 13
8	{1, 4}	4	10 + 6 = 16	10 + 6 = 16
9	{2, 3}	3	5	5 + 3 = 8
10	{2, 4}	4	5 + 6 = 11	5 + 6 = 11
11	{3, 4}	4	5 + 10 = 15	5 + 10 = 15

State-space tree for variable tuple formulation and fixed tuple formulation is depicted in Fig. (a) and Fig. (b), respectively

In the fixed tuple formulation, x i = 1 indicates the inclusion of job i, and xi = 0 indicates the exclusion of job i. For example, at node 6, job 1 is omitted and job 2 is selected, so the penalty at that node is 5. At node 11, job 1 is included but jobs 2 and 3 are excluded, so the penalty incurred at node 11 is P 2 + P 3 = 16. The cost for node x is computed in a similar way.

Tags: algorithm branch and bound job scheduling

Next story Knapsack Problem using Branch and Bound
Previous story FIFO Branch and Bound
Pingbacks 0

How did you converted profits to penalties?

Solving Generalized Assignment Problem using Branch-And-Price

Oct 27, 2021

Generalized assignment problem, dantzig-wolfe decomposition, column generation, standalone model, initial solution, branching rule, branch-and-price.

One of the best known and widely researched problems in combinatorial optimization is Knapsack Problem:

given a set of items, each with its weight and value,
select a set of items maximizing total value
that can fit into a knapsack while respecting its weight limit.

The most common variant of a problem, called 0-1 Knapsack Problem can be formulated as follows:

$m$ - number of items;
$x_i$ - binary variable indicating whether item is selected;
$v_i$ - value of each items;
$w_i$ - weight of each items;
$W$ - maximum weight capacity.

As often happens in mathematics, or science in general, an obvious question to ask is how the problem can be generalized. One of generalization is Generalized Assignment Problem. It answers question - how to find a maximum profit assignment of $m$ tasks to $n$ machines such that each task ($i=0, \ldots, m$) is assigned to exactly one machine ($j=1, \ldots, n$), and one machine can have multiple tasks assigned to subject to its capacity limitation. Its standard formulation is presented below:

$n$ - number of machines;
$m$ - number of tasks;
$x_{ij}$ - binary variable indicating whether task $i$ is assigned to machine $j$;
$v_{ij}$ - value/profit of assigning task $i$ to machine $j$;
$w_{ij}$ - weight of assigning task $i$ to machine $j$;
$c_j$ - capacity of machine $j$.

Branch-and-price

Branch-and-price is generalization of branch-and-bound method to solve integer programs (IPs),mixed integer programs (MIPs) or binary problems. Both branch-and-price, branch-and-bound, and also branch-and-cut, solve LP relaxation of a given IP. The goal of branch-and-price is to tighten LP relaxation by generating a subset of profitable columns associated with variables to join the current basis.

Branch-and-price builds at the top of branch-and-bound framework. It applies column generation priori to branching. Assuming maximization problem, branching occurs when:

Column Generation is finished (i.e. no profitable columns can be found).
Objective value of the current solution is greater than best lower bound.
The current solution does not satisfy integrality constraints.

However, if only first two conditions are met but not the third one, meaning the current solution satisfies integrality constraints, then the best solution and lower bound are updated (lower bound is tightened) with respectively the current solution and its objective value.

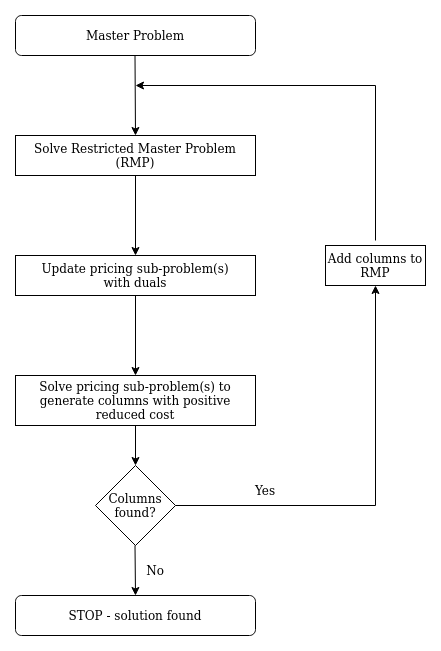
The crucial element needed to apply branch-and-price successfully is to find branching scheme. It is tailored to specific problem to make sure that it does not destroy problem structure and can be used in pricing subproblem to effectively generate columns that enter Restricted Master Problem (RMP) while respecting branching rules .

Below is flow diagram describing branch-and-price method:

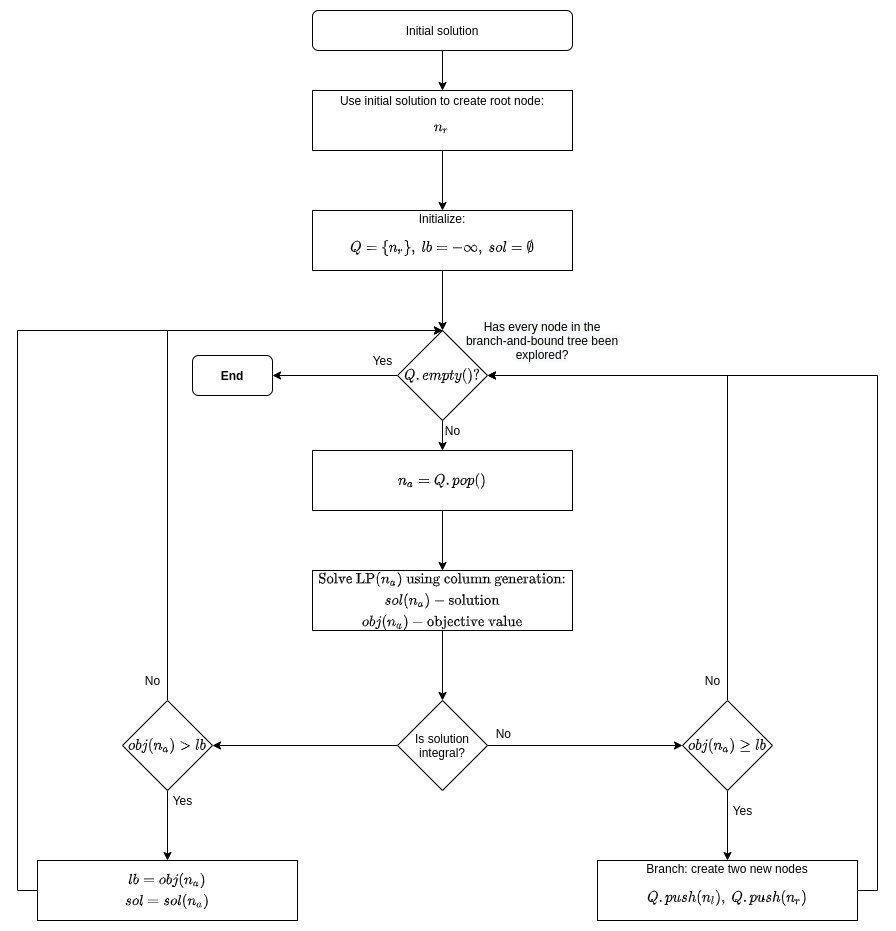
The successful application B&P depends on tight/strong model formulation. Model formulation is considered tight if solution of its LP relaxation satisfies (frequently) integrality constraints. One of structured approaches to come up with such a formulation is to use Dantzig-Wolfe Decomposition technique. We will see example of it applied to Generalized Assignment Problem (GAP).

A standard formulation was described above. Now, let’s try to reformulate problem. Let

be a set containing all feasible solutions to Knapsack problem for $j$-th machine. Clearly, $S_j$ contains finite number of points, so $S_j = \{ \mathbf{z}_j^1, \ldots, \mathbf{z}_j^{K_j} \}$, where $\mathbf{z}_j^k \in \{0, 1\}^{m}$. You can think about $\mathbf{z}_j^k \in \{0, 1\}^{m}$ as 0-1 encoding of tasks that form $k$-th feasible solution for machine $j$. Now, let $S = \{ \mathbf{z}_1^1, \ldots, \mathbf{z}_1^{K_1}, \ldots, \mathbf{z}_n^1, \ldots, \mathbf{z}_n^{K_n} \}$ be a set of all feasible solution to GAP. It, potentially, contains a very large number of elements. Then, every point $x_{ij}$ can be expressed by the following convex combination:

where $z_{ij}^k \in \{0, 1\}$, and $z_{ij}^k = 1$ iff task $i$ is assigned to machine $j$ in $k$-th feasible solution for the machine.

Now, let’s use this representation to reformulate GAP:

Note that we do not need capacity restrictions as they are embedded into definition of feasible solution for machine $j$.

Now that we have formulation that is suitable for column generation, let’s turn our attention to it.

Column generation is another crucial component of branch-and-price. There are many great resources devoted to column generation so I will mention only core points:

Column generation is useful when a problem’s pool of feasible solutions contains many elements but only small subset will be present in the optimal solution.
There exists subproblem (called often pricing problem) that can be used to effectively generate columns that should enter RMP.
Column generation starts with initial feasible solution.
Pricing subproblem objective function is updated with dual of the current solution.
Columns with positive reduced cost, in case of maximization problem, enter problem.
Procedure continues until such columns exist.

Below is flow diagram describing column generation method:

Implementation

Let’s see how one can approach implementation of B&P to solve Generalized Assignment Problem. Below is discussion about main concepts and few code excerpts, a repository containing all code can be found on github .

An example of problem instance taken from [1] is:

It is always good idea to have a reference simple(r) implementation that can be used to validate our results using more sophisticated methods. In our case it is based on standard problem formulation. Implementation can be found in repo by checking classes GAPStandaloneModelBuilder and GAPStandaloneModel . Formulation for a problem instance presented above looks as follows:

Now let’s try to examine building blocks of B&P to discus main part at the end, once all the puzzles are there.

To start column generation process, we need to have an initial solution. One possible way to derive it is to use two-phase Simplex method. In first step, you add slack variables to each constraint and set objective function as their sum. Then you minimize the problem. If your solution has objective value $0$, then first of all you have initial solution and you know that your problem is feasible. In case you end up with positive value for any of slack variables, you can conclude that the problem is infeasible. You can stop here.

I took a different approach and came up with simple heuristic that generate initial solution. I have not analyzed it thoroughly so I am not sure if it is guaranteed to always return feasible solution if one exists. Its idea is quite simple:

Construct bipartite graph defined as $G=(V, A)$, where $V = T \cup M$ – $T$ is set of tasks and obviously $M$ is set of machines. There exists arc $a = (t, m)$ if $w_{tm} \le rc_{m}$, where $rc_{m}$ is remaining capacity for machine $m$. Initially remaining capacity is equal to capacity of machine and with each iteration, and assignment of task to machine it is being update. If $\vert A \vert = 0$, then stop.
Solve a minimum weight matching problem.
Update assignments – say that according to solution task $t_0$ should be assigned to machine $m_0$, then $\overline{rc}_{m_0} = rc_{m_0} - w_{t_0 m_0}$.
Find a machine where task is contributing with the lowest weight – say machine $m_0 = \arg\min \{ m: w_{t_0 m} \}$.
Free up remaining capacity so there is enough space for $t_0$ on machine $m_0$. Any tasks that were de-assigned in a process are added to pool of unassigned tasks.
Repeat until there are no unassigned tasks.

See details on github .

As we said before the most important piece needed to implement B&P is branching rules which does not destroy structure of subproblem. Let’s consider non-integral solution to RMP. Given convexity constraint it means that there exists machine $j_0$ and at least two, and for sake of example say exactly two, $0 < \lambda_{j_0} ^{k_1} < 1$ and $0 < \lambda_{j_0} ^{k_2} < 1$ such that $\lambda_{j_0} ^{k_1} + \lambda_{j_0} ^{k_2} = 1$. Since with each of $\lambda$s is connected different assignment (set of tasks), then it leads us to a conclusion that there exists task $i_0$ such that $x_{i_0 j_0} < 1$ expressed in variables from the original formulation. Now, let’s use this information to formulate branching rule:

left child node: a task $i_0$ must be assigned to a machine $j_0$.
right child node: a task $i_0$ cannot be assigned to a machine $j_0$.

We can say that branching is based on $x_{ij}$ from standard formulation. And it can be represented by:

Note that we can use the branching rule to easily to filter out initial columns for each node that do not satisfy those conditions:

$j = j_0$ and task $i_0 \in T_{j_0}$, or
$j \neq j_0$ and task $i_0 \notin T_{j}$.
$j = j_0$ and task $i_0 \in T_{j_0}$.

See on github .

Based on the same principle, subproblem’s pool of feasible solution are created - i.e. on left child node:

knapsack subproblem for machine $j_0$ – variable representing task $i_0$ is forced to be $1$.
knapsack subproblem for machine $j \neq j_0$ – variable representing task $i_0$ is forced to be $0$.

Similarly for right childe node. See on github .

Below is an outline of main loop of column generation. It is an implementation of flow diagram from above so I will not spend too much time describing it. The only part maybe worth commenting is stop_due_to_no_progress - it evaluates whether column generation did not make any progress in last $k$-iterations and it should be stop.

Now, let’s see how constructing subproblems, solving them and then adding back column(s) to RMP looks like. We have as many subproblems as machines. Once a solution is available, we check whether it has positive reduced cost. A solution to knapsack problem corresponds to column in RMP. So if the column with positive reduced cost was identified and added, then new iteration of column generation will be executed. Gurobi allows to query information about all other identified solutions, so we can utilize this feature and add all columns that have the same objective value as optimal solution, potentially adding more than one column and hoping it will positively impact solution time.

Note that each subproblem is independent so in principle they could be solved in parallel. However due to Python Global Interpreter Lock (GIL) that prevent CPU-bounded threads to run in parallel, they are solved sequentially. Additionally depending on your Gurobi license, you might not be allowed to solve all those models in parallel even if Python would allow it.

Below you can find example of one of the RMPs:

and subproblem with dual information passed:

Now that we have all building blocks prepared, then let’s turn our attention back to B&P.

In the blog post, Branch-and-Price technique for solving MIP was explained. An example of applying B&P for Generalized Assignment Problem was presented. The solution approach used Python as programming language and Gurobi as solver.

[1] Der-San Chen, Robert G. Batson, Yu Dang (2010), Applied Integer Programming - Modeling and Solution, Willey. [2] Lasdon, Leon S. (2002), Optimization Theory for Large Systems, Mineola, New York: Dover Publications. [3] Cynthia Barnhart, Ellis L. Johnson, George L. Nemhauser, Martin W. P. Savelsbergh, Pamela H. Vance, (1998) Branch-and-Price: Column Generation for Solving Huge Integer Programs. Operations Research 46(3):316-329.

Branch and Bound

I. introduction, ii. illustration on the job assignment problem, iii. the general branch and bound algorithm, iv. criteria for the choice of approximate cost functions, v. implementation of the b&b job assignment algorithm, the general branch and bound algorithm.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

Notifications You must be signed in to change notification settings

Solved the Job Assignment Problem using a branch and bound algorithm

Valor-boop/Job-Assignment-Problem

Folders and files.

Name		Name
4 Commits

Repository files navigation

Job-assignment-problem.

Solved the Job Assignment Problem using both brute force as well as branch and bound. The code contains 5 functions:

job_assignment(cost_matrix): Find an optimal solution to the job assignment problem using branch and bound. Input: an nxn matrix where a row represents a person and a column represents the cost each person takes to complete the jobs. Return: the minimal cost, an optimal solution, and the number of partial or full solutions evaluated.

get_csf(cost_matrix, partial_solution): Input: an nxn cost matrix and a partial solution. Return: the partial solution's Cost So Far (CSF). A partial solution is represented as a list of n elements, where an undecided element is denoted by a -1. For instance, a partial solution [2, -1, -1] represents assigning job 2 to person 0 and leaving the assignments of person 1 and person 2 undecided.

get_gfc(cost_matrix, partial_solution): Input: an nxn cost matrix and a partial solution. Return: the partial solution's Guaranteed Future Cost (GFC).

get_ffc(cost_matrix, partial_solution): Input: an nxn cost matrix and a partial solution. Return: the partial solution's Feasible Futre Cost (FFC)

brute_force(cost_matrix): This function finds an optimal solution for the job assignment problem using brute force. Input: an nxn cost matrix. Return: the minimal total cost, an optimal solution, and the number of full solutions investigated.

Python 100.0%

DAA Tutorial
DAA Algorithm
Need of Algorithm
Complexity of Algorithm
Algorithm Design Techniques
Asymptotic Analysis
Analyzing Algorithm Control Structure
Recurrence Relation
Recursion Tree Method
Master Method

Analysis of Sorting

Bubble Sort
Selection Sort
Insertion Sort

Divide and Conquer

Introduction
Max-Min Problem
Binary Search
Tower of Hanoi
Binary Heap
Stable Sorting
Lower bound Theory

Sorting in Linear Time

Linear Time
Counting Sort
Bucket Sort
Hash Tables
Hashing Method
Open Addressing Techniques
Hash Function

Binary Search Trees

Red Black Tree
Dynamic Programming
Divide & Conquer Method vs Dynamic Programming
Fibonacci sequence
Matrix Chain Multiplication
Matrix Chain Multiplication Example
Matrix Chain Multiplication Algorithm
Longest Common Sequence
Longest Common Sequence Algorithm
0/1 Knapsack Problem
DUTCH NATIONAL FLAG
Longest Palindrome Subsequence
Longest Increasing Subsequence
Longest Common Subsequence
Tabulation vs Memoization
How to solve a dynamic programming problem
Optimal Substructure Property
Overlapping sub-problems
Dynamic programming vs Greedy approach
Regular Expression Matching
Branch and bound vs backtracking
Branch and bound
Longest Repeated Subsequence
Longest Common Substring
Shortest Common Supersequence
Dynamic Programming vs Divide and Conquer
Maximum Sum Increasing Subsequence
Wildcard Pattern Matching
Largest Sum Contiguous Subarray
Shortest Sum Contiguous Subarray
Dynamic programming vs Backtracking
Brute force approach
Fractional vs 0/1 knapsack problem
Traveling Salesperson problem using branch and bound
Integer Partition Problem
Kruskal Algorithm

Greedy Algorithm

Greedy Algorithms
Activity Selection Problem
Fractional Knapsack problem
Huffman Codes
Algorithm of Huffman Code
Activity or Task Scheduling Problem
Travelling Sales Person Problem
Dynamic Programming vs Greedy Method

Backtracking

Backtracking Introduction
Recursive Maze Algorithm
Hamiltonian Circuit Problems
Subset Sum Problems
N Queens Problems
MST Introduction
MST Applications
Kruskal's Algorithm
Prim's Algorithm

Shortest Path

Negative Weight Edges
Representing Shortest Path
Dijkstra's Algorithm
Bellman-Ford Algorithm
Single Source Shortest Path in a directed Acyclic Graphs

All-Pairs Shortest Paths

Floyd-Warshall Algorithm
Johnson's Algorithm

Maximum Flow

Flow networks and Flows
Network Flow Problems
Ford Fulkerson Algorithm
Maximum bipartite matching

Sorting Networks

Comparison Network
Bitonic Sorting Network
Merging Network

Complexity Theory

Complexity Classes
Polynomial Time Verification
NP-Completeness
Circuit Satisfiability
3-CNF Satisfiability
Clique Problem
Vertex Cover Problem
Subset-Sum Problem

Approximation Algo

Vertex Cover
Travelling Salesman Problem

String Matching

Naive String Matching Algorithm
Rabin-Karp-Algorithm
String Matching with Finite Automata
Knuth-Morris-Pratt Algorithm
Boyer-Moore Algorithm
Kosaraju Algorithm
Hashing algorithm
Huffman Coding Algorithm
Kadane's Algorithm
Dijkstra Algorithm Example
Euclidean algorithm
Floyd's Algorithm
Properties of Algorithm
Time Complexity of Kruskals Algorithm
Kosaraju's Algorithm
Characteristics of an Algorithm
Algorithm Examples
Searching Algorithms
Algorithm for Binary Search
Sorting Algorithms: Slowest to Fastest
Extended Euclidian Algorithm
How to Write an Algorithm
Recursive Algorithm
Sliding Window Algorithm
Difference Between Algorithms and Flowcharts
PageRank Algorithm
Greedy Algorithm Example

Interview Questions

DAA Interview Questions

Branch and bound is one of the techniques used for problem solving. It is similar to the backtracking since it also uses the state space tree. It is used for solving the optimization problems and minimization problems. If we have given a maximization problem then we can convert it using the Branch and bound technique by simply converting the problem into a maximization problem.

Jobs = {j1, j2, j3, j4}

P = {10, 5, 8, 3}

d = {1, 2, 1, 2}

The above are jobs, problems and problems given. We can write the solutions in two ways which are given below:

Suppose we want to perform the jobs j1 and j2 then the solution can be represented in two ways:

The first way of representing the solutions is the subsets of jobs.

S1 = {j1, j4}

The second way of representing the solution is that first job is done, second and third jobs are not done, and fourth job is done.

S2 = {1, 0, 0, 1}

The solution s1 is the variable-size solution while the solution s2 is the fixed-size solution.

As we can observe in the above figure that the breadth first search is performed but not the depth first search. Here we move breadth wise for exploring the solutions. In backtracking, we go depth-wise whereas in branch and bound, we go breadth wise.

Now one level is completed. Once I take first job, then we can consider either j2, j3 or j4. If we follow the route then it says that we are doing jobs j1 and j4 so we will not consider jobs j2 and j3.

The above is the state space tree for the solution s1 = {j1, j4}

We will see another way to solve the problem to achieve the solution s1.

First, we consider the node 1 shown as below:

Now, we will expand the node 1. After expansion, the state space tree would be appeared as:

On each expansion, the node will be pushed into the stack shown as below:

There is one more method that can be used to find the solution and that method is Least cost branch and bound. In this technique, nodes are explored based on the cost of the node. The cost of the node can be defined using the problem and with the help of the given problem, we can define the cost function. Once the cost function is defined, we can define the cost of the node.

Now we will expand the node 1. The node 1 will be expanded into four nodes named as 2, 3, 4 and 5 shown as below:

Since it is the least cost branch n bound, so we will explore the node which is having the least cost. In the above figure, we can observe that the node with a minimum cost is node 3. So, we will explore the node 3 having cost 12.

Since the node 3 works on the job j2 so it will be expanded into two nodes named as 6 and 7 shown as below:

Latest Courses

We provides tutorials and interview questions of all technology like java tutorial, android, java frameworks

Contact info

G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India

[email protected] .

Online Compiler

An official website of the United States government

Here’s how you know

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock A locked padlock ) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.

https://www.nist.gov/publications/branch-and-bound-algorithm-growing-datasets-large-scale-parameter-estimation

A branch-and-bound algorithm with growing datasets for large-scale parameter estimation

Download paper, additional citation formats.

Google Scholar

If you have any questions about this publication or are having problems accessing it, please contact [email protected] .

Branch and Bound Tutorial
Backtracking Vs Branch-N-Bound
0/1 Knapsack
8 Puzzle Problem
Job Assignment Problem
N-Queen Problem
Travelling Salesman Problem

Why do we use branch and bound algorithm?

The Branch and Bound algorithm is used to solve optimization problems where the goal is to find the best solution out of all possible solutions. It is efficient as it eliminates the need to check all solutions by ruling out those that cannot possibly lead to the best solution.

What is Branch and Bound Algorithm?

The Branch and Bound algorithm is a method used for solving combinatorial optimization problems. These are problems where you’re trying to find the best solution out of a set of possible solutions.

The algorithm works by dividing (branching) the problem into subproblems and solving them independently. The solutions to the subproblems are then combined to give a solution to the original problem.

Efficiency of the Branch and Bound Algorithm

Branch and Bound algorithm is efficient due to discarding (bound) certain solutions without fully exploring them. It does this by estimating the best possible solution that can be obtained from a subproblem. If this estimate is worse than the best solution found so far, the subproblem is discarded.

This bounding step is what makes the Branch and Bound algorithm more efficient than brute force methods, which would require checking all possible solutions.

The Branch and Bound algorithm is widely used in various fields of computer science and operations research, including:

Efficiently solves combinatorial optimization problems by exploring only promising subproblems
Helps in reducing the search space by pruning branches that cannot lead to an optimal solution
Useful for problems with an exponential number of possible solutions
Can handle large instances of problems effectively

Standard Problems of Branch and Bound algorithm:

1. Traveling Salesman Problem : This is a classic problem in computer science, where the goal is to find the shortest possible route that a traveling salesman can take to visit a certain number of cities and return to the origin city. The Branch and Bound algorithm can be used to find the optimal solution.

2. Knapsack Problem : This is a problem in combinatorial optimization, where the goal is to maximize the total value of items placed in a knapsack, subject to a weight constraint. The Branch and Bound algorithm can be used to find the optimal set of items.

3. Job Scheduling Problem : This is a problem in operations research, where the goal is to schedule a set of jobs on a set of machines so as to minimize the total time taken. The Branch and Bound algorithm can be used to find the optimal schedule.

4. N Queen Problem : Involves placing N queens on an N x N chessboard such that no two queens threaten each other. The objective is to find all possible distinct configurations of placing N queens on the board without any queen attacking another along rows, columns, or diagonals.

In conclusion, the Branch and Bound algorithm is a powerful method for solving optimization problems. It offers a balance between exhaustive search and intelligent pruning, allowing it to solve problems that would be infeasible to solve by brute force. By understanding the principles and applications of the Branch and Bound algorithm, one can tackle a wide range of complex optimization problems in computer science and operations research.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

IMAGES

Assignment Problem using Branch and Bound
Assignment problem
Solved 2. (a) Solve the given Assignment problem with Branch
how to solve job assignment problem using branch and bound method
Job Assignment Problem using Branch And Bound
Assignment problem by branch and bound method

VIDEO

Assignment Problem-Branch and Bound
Assignment Problem ( Brute force method) Design and Analysis of Algorithm
Assignment Problem using Branch and Bound
Introduction to Branch and Bound
Assignment Problem
Assignment Problem

COMMENTS

Job Assignment Problem using Branch And Bound
Learn how to solve the job assignment problem using branch and bound algorithm, a technique that prunes the search tree by estimating the cost of each node. See the cost matrix, the search space diagram, and the C++, Java, Python, and C# implementations.
Assignment Problem using Branch and Bound
This Video demonstrates the Concept of Branch and Bound and the Operation of Assignment Problem using Branch and Bound
Branch and Bound Algorithm
Learn how to use branch and bound algorithm to solve the job assignment problem, a discrete optimization problem with finite but extensive solutions. See the pseudocode, the example, and the advantages and disadvantages of this algorithm.
Branch And Bound
Learn how to use branch and bound algorithm to solve the job assignment problem, where N workers and N jobs have to be matched with minimum cost. See the cost matrix, the search space tree, the cost function, and the C++ code implementation.
how to solve job assignment problem using branch and bound method
Learn how to tackle job assignment problems using the branch and bound method with a step-by-step guide.
Assignment Problem using Branch and Bound
This video lecture is produced by S. Saurabh. He is B.Tech from IIT and MS from USA.Assignment problem using Branch and BoundThere are a number of agents and...
Introduction to Branch and Bound
Job Assignment Problem using Branch And Bound. Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total ...
Branch and Bound Algorithm
Learn how to use branch and bound to solve combinatorial optimization problems like the traveling salesman and job scheduling. See examples of branch and bound applications, such as the 0/1 knapsack, the 8 puzzle, the queen problem, and the job assignment problem.
Job Sequencing using Branch and Bound
1. Solution: The cost function for node x in state space tree for job sequencing problem is defined as, Misplaced &. Where, m = max {i | i ∈ S x } S x is the subset of jobs selected at node x. Upper bound u (x) for node x is defined as, u(x) = suminotinSxPi. Computation of cost and bound for each node using variable tuple size is shown in the ...
PDF Branch and Bound Algorithms -Principles and Examples
the Quadratic Assignment problem. 1 Introduction. Solving NP-hard discrete optimization problems to optimality is often an im-mense job requiring very e cient algorithms, and the B&B paradigm is one of the main tools in construction of these. A B&B algorithm searches the complete space of solutions for a given problem for the best solution.
Solving Generalized Assignment Problem using Branch-And-Price
Branch-and-price is generalization of branch-and-bound method to solve integer programs (IPs),mixed integer programs (MIPs) or binary problems. Both branch-and-price, branch-and-bound, and also branch-and-cut, solve LP relaxation of a given IP. The goal of branch-and-price is to tighten LP relaxation by generating a subset of profitable columns ...
PDF Branch and Bound
Learn how to use branch and bound technique to solve hard optimization problems. See examples of graph coloring, bin packing, knapsack and travelling salesman problems with pseudocode and illustrations.
PDF Branch and bound: Method Method, knapsack problemproblem
1.204 Lecture 16 Branch and bound: Method Method, knapsack problemproblem Branch and bound • Technique for solving mixed (or pure) integer programming problems, based on tree search - Yes/no or 0/1 decision variables, designated x i - Problem may have continuous, usually linear, variables - O(2n) complexity • Relies on upper and lower bounds to limit the number of
Branch and Bound
Branch and bound is a systematic method for solving optimization problems. B&B is a rather general optimization technique that applies where the greedy method and dynamic programming fail. However, it is much slower. Indeed, it often leads to exponential time complexities in the worst case.
Valor-boop/Job-Assignment-Problem
Solved the Job Assignment Problem using both brute force as well as branch and bound. The code contains 5 functions: job_assignment(cost_matrix): Find an optimal solution to the job assignment problem using branch and bound. Input: an nxn matrix where a row represents a person and a column represents the cost each person takes to complete the jobs.
PDF Branch and Bound
Job Assignment Problem. Given n tasks and n agents. Each agent has a cost to complete each task. Assign each agent a task to minimize cost. lub: 73 glb: 58. then add the smallest values in each a:1 (60) column. This is a lower bound on the size of the solution with a assigned to job 1.
Branch and bound
Learn how to use branch and bound technique to solve optimization and minimization problems using state space tree. See examples of variable-size and fixed-size solutions, and least cost branch and bound method.
Assignment Problem using Branch and Bound
This tutorial shows you how to solve the assignment problem using branch and bound method using an example
Traveling Salesman Problem using Branch And Bound
A TSP tour in the graph is 0-1-3-2-0. The cost of the tour is 10+25+30+15 which is 80. We have discussed following solutions. 1) Naive and Dynamic Programming. 2) Approximate solution using MST. Branch and Bound Solution. As seen in the previous articles, in Branch and Bound method, for current node in tree, we compute a bound on best possible ...
A branch-and-bound algorithm with growing datasets for large-scale
The solution of nonconvex parameter estimation problems with deterministic global optimization methods is desirable but challenging, especially if large measurement data sets are considered. We propose to exploit the structure of this class of optimization problems to enable their solution with the spatial branch-and-bound algorithm.
Assignment problem using branch and bound
#assignmentproblem #branchandbound #algorithmdesign #branchandboundassignmentproblem
Why do we use branch and bound algorithm?
The Branch and Bound algorithm is a method used for solving combinatorial optimization problems. These are problems where you're trying to find the best solution out of a set of possible solutions. The algorithm works by dividing (branching) the problem into subproblems and solving them independently. The solutions to the subproblems are then ...
Assignment problem
Hi there,I hope you liked this video. Please hit like, share and subscribe. It will motivate me to do more of these. Thanks!