unit fraction problem solving

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Fraction word prob.

Fraction word problems

Here you will learn about fraction word problems, including solving math word problems within a real-world context involving adding fractions, subtracting fractions, multiplying fractions, and dividing fractions.

Students will first learn about fraction word problems as part of number and operations—fractions in 4 th grade.

What are fraction word problems?

Fraction word problems are math word problems involving fractions that require students to use problem-solving skills within the context of a real-world situation.

To solve a fraction word problem, you must understand the context of the word problem, what the unknown information is, and what operation is needed to solve it. Fraction word problems may require addition, subtraction, multiplication, or division of fractions.

After determining what operation is needed to solve the problem, you can apply the rules of adding, subtracting, multiplying, or dividing fractions to find the solution.

For example,

Natalie is baking 2 different batches of cookies. One batch needs \cfrac{3}{4} cup of sugar and the other batch needs \cfrac{2}{4} cup of sugar. How much sugar is needed to bake both batches of cookies?

You can follow these steps to solve the problem:

Step-by-step guide: Adding and subtracting fractions

Step-by-step guide: Adding fractions

Step-by-step guide: Subtracting fractions

Step-by-step guide: Multiplying and dividing fractions

Step-by-step guide: Multiplying fractions

Step-by-step guide: Dividing fractions

Common Core State Standards

How does this relate to 4 th grade math to 6 th grade math?

• Grade 4: Number and Operations—Fractions (4.NF.B.3d) Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
• Grade 4: Number and Operations—Fractions (4.NF.B.4c) Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. For example, if each person at a party will eat \cfrac{3}{8} of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
• Grade 5: Number and Operations—Fractions (5.NF.A.2) Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers. For example, recognize an incorrect result \cfrac{2}{5}+\cfrac{1}{2}=\cfrac{3}{7} by observing that \cfrac{3}{7}<\cfrac{1}{2} .
• Grade 5: Number and Operations—Fractions (5.NF.B.6) Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
• Grade 5: Number and Operations—Fractions (5.NF.B.7c) Solve real world problems involving division of unit fractions by non-zero whole numbers and division of whole numbers by unit fractions, e.g., by using visual fraction models and equations to represent the problem. For example, how much chocolate will each person get if 3 people share \cfrac{1}{2} \: lb of chocolate equally? How many \cfrac{1}{3} cup servings are in 2 cups of raisins?
• Grade 6: The Number System (6.NS.A.1) Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for \cfrac{2}{3} \div \cfrac{4}{5} and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that \cfrac{2}{3} \div \cfrac{4}{5}=\cfrac{8}{9} because \cfrac{3}{4} of \cfrac{8}{9} is \cfrac{2}{3}. (In general, \cfrac{a}{b} \div \cfrac{c}{d}=\cfrac{a d}{b c} \, ) How much chocolate will each person get if 3 people share \cfrac{1}{2} \: lb of chocolate equally? How many \cfrac{3}{4} cup servings are in \cfrac{2}{3} of a cup of yogurt? How wide is a rectangular strip of land with length \cfrac{3}{4} \: m and area \cfrac{1}{2} \: m^2?

[FREE] Fraction Operations Worksheet (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!

How to solve fraction word problems

In order to solve fraction word problems:

Determine what operation is needed to solve.

Write an equation.

Solve the equation.

State your answer in a sentence.

Fraction word problem examples

Example 1: adding fractions (like denominators).

Julia ate \cfrac{3}{8} of a pizza and her brother ate \cfrac{2}{8} of the same pizza. How much of the pizza did they eat altogether?

The problem states how much pizza Julia ate and how much her brother ate. You need to find how much pizza Julia and her brother ate altogether , which means you need to add.

2 Write an equation.

3 Solve the equation.

To add fractions with like denominators, add the numerators and keep the denominators the same.

4 State your answer in a sentence.

The last step is to go back to the word problem and write a sentence to clearly say what the solution represents in the context of the problem.

Julia and her brother ate \cfrac{5}{8} of the pizza altogether.

Example 2: adding fractions (unlike denominators)

Tim ran \cfrac{5}{6} of a mile in the morning and \cfrac{1}{3} of a mile in the afternoon. How far did Tim run in total?

The problem states how far Tim ran in the morning and how far he ran in the afternoon. You need to find how far Tim ran in total , which means you need to add.

To add fractions with unlike denominators, first find a common denominator and then change the fractions accordingly before adding.

\cfrac{5}{6}+\cfrac{1}{3}= \, ?

The least common multiple of 6 and 3 is 6, so 6 can be the common denominator.

That means \cfrac{1}{3} will need to be changed so that its denominator is 6. To do this, multiply the numerator and the denominator by 2.

\cfrac{1 \times 2}{3 \times 2}=\cfrac{2}{6}

Now you can add the fractions and simplify the answer.

\cfrac{5}{6}+\cfrac{2}{6}=\cfrac{7}{6}=1 \cfrac{1}{6}

Tim ran a total of 1 \cfrac{1}{6} miles.

Example 3: subtracting fractions (like denominators)

Pia walked \cfrac{4}{7} of a mile to the park and \cfrac{3}{7} of a mile back home. How much farther did she walk to the park than back home?

The problem states how far Pia walked to the park and how far she walked home. Since you need to find the difference ( how much farther ) between the two distances, you need to subtract.

To subtract fractions with like denominators, subtract the numerators and keep the denominators the same.

\cfrac{4}{7}-\cfrac{3}{7}=\cfrac{1}{7}

Pia walked \cfrac{1}{7} of a mile farther to the park than back home.

Example 4: subtracting fractions (unlike denominators)

Henry bought \cfrac{7}{8} pound of beef from the grocery store. He used \cfrac{1}{3} of a pound of beef to make a hamburger. How much of the beef does he have left?

The problem states how much beef Henry started with and how much he used. Since you need to find how much he has left , you need to subtract.

To subtract fractions with unlike denominators, first find a common denominator and then change the fractions accordingly before subtracting.

\cfrac{7}{8}-\cfrac{1}{3}= \, ?

The least common multiple of 8 and 3 is 24, so 24 can be the common denominator.

That means both fractions will need to be changed so that their denominator is 24.

To do this, multiply the numerator and the denominator of each fraction by the same number so that it results in a denominator of 24. This will give you an equivalent fraction for each fraction in the problem.

\begin{aligned}&\cfrac{7 \times 3}{8 \times 3}=\cfrac{21}{24} \\\\ &\cfrac{1 \times 8}{3 \times 8}=\cfrac{8}{24} \end{aligned}

Now you can subtract the fractions.

\cfrac{21}{24}-\cfrac{8}{24}=\cfrac{13}{24}

Henry has \cfrac{13}{24} of a pound of beef left.

Example 5: multiplying fractions

Andre has \cfrac{3}{4} of a candy bar left. He gives \cfrac{1}{2} of the remaining bit of the candy bar to his sister. What fraction of the whole candy bar does Andre have left now?

It could be challenging to determine the operation needed for this problem; many students may automatically assume it is subtraction since you need to find how much of the candy bar is left.

However, since you know Andre started with a fraction of the candy bar and you need to find a fraction OF a fraction, you need to multiply.

The difference here is that Andre did NOT give his sister \cfrac{1}{2} of the candy bar, but he gave her \cfrac{1}{2} of \cfrac{3}{4} of a candy bar.

To solve the word problem, you can ask, “What is \cfrac{1}{2} of \cfrac{3}{4}? ” and set up the equation accordingly. Think of the multiplication sign as meaning “of.”

\cfrac{1}{2} \times \cfrac{3}{4}= \, ?

To multiply fractions, multiply the numerators and multiply the denominators.

\cfrac{1}{2} \times \cfrac{3}{4}=\cfrac{3}{8}

Andre gave \cfrac{1}{2} of \cfrac{3}{4} of a candy bar to his sister, which means he has \cfrac{1}{2} of \cfrac{3}{4} left. Therefore, Andre has \cfrac{3}{8} of the whole candy bar left.

Example 6: dividing fractions

Nia has \cfrac{7}{8} cup of trail mix. How many \cfrac{1}{4} cup servings can she make?

The problem states the total amount of trail mix Nia has and asks how many servings can be made from it.

To solve, you need to divide the total amount of trail mix (which is \cfrac{7}{8} cup) by the amount in each serving ( \cfrac{1}{4} cup) to find out how many servings she can make.

To divide fractions, multiply the dividend by the reciprocal of the divisor.

\begin{aligned}& \cfrac{7}{8} \div \cfrac{1}{4}= \, ? \\\\ & \downarrow \downarrow \downarrow \\\\ &\cfrac{7}{8} \times \cfrac{4}{1}=\cfrac{28}{8} \end{aligned}

You can simplify \cfrac{28}{8} to \cfrac{7}{2} and then 3 \cfrac{1}{2}.

Nia can make 3 \cfrac{1}{2} cup servings.

Teaching tips for fraction word problems

• Encourage students to look for key words to help determine the operation needed to solve the problem. For example, subtracting fractions word problems might ask students to find “how much is left” or “how much more” one fraction is than another.
• Provide students with an answer key to word problem worksheets to allow them to obtain immediate feedback on their solutions. Encourage students to attempt the problems independently first, then check their answers against the key to identify any mistakes and learn from them. This helps reinforce problem-solving skills and confidence.
• Be sure to incorporate real-world situations into your math lessons. Doing so allows students to better understand the relevance of fractions in everyday life.
• As students progress and build a strong foundational understanding of one-step fraction word problems, provide them with multi-step word problems that involve more than one operation to solve.
• Take note that students will not divide a fraction by a fraction as shown above until 6 th grade (middle school), but they will divide a unit fraction by a whole number and a whole number by a fraction in 5 th grade (elementary school), where the same mathematical rules apply to solving.
• There are many alternatives you can use in place of printable math worksheets to make practicing fraction word problems more engaging. Some examples are online math games and digital workbooks.

Easy mistakes to make

• Misinterpreting the problem Misreading or misunderstanding the word problem can lead to solving for the wrong quantity or using the wrong operation.
• Not finding common denominators When adding or subtracting fractions with unlike denominators, students may forget to find a common denominator, leading to an incorrect answer.
• Forgetting to simplify Unless a problem specifically says not to simplify, fractional answers should always be written in simplest form.

Related fractions operations lessons

• Fractions operations
• Multiplicative inverse
• Reciprocal math
• Fractions as divisions

Practice fraction word problem questions

1. Malia spent \cfrac{5}{6} of an hour studying for a math test. Then she spent \cfrac{1}{3} of an hour reading. How much longer did she spend studying for her math test than reading?

Malia spent \cfrac{1}{2} of an hour longer studying for her math test than reading.

Malia spent \cfrac{5}{18} of an hour longer studying for her math test than reading.

Malia spent \cfrac{1}{2} of an hour longer reading than studying for her math test.

Malia spent 1 \cfrac{1}{6} of an hour longer studying for her math test than reading.

To find the difference between the amount of time Malia spent studying for her math test than reading, you need to subtract. Since the fractions have unlike denominators, you need to find a common denominator first.

You can use 6 as the common denominator, so \cfrac{1}{3} becomes \cfrac{3}{6}. Then you can subtract.

\cfrac{3}{6} can then be simplified to \cfrac{1}{2}.

Finally, you need to choose the answer that correctly answers the question within the context of the situation. Therefore, the correct answer is “Malia spent \cfrac{1}{2} of an hour longer studying for her math test than reading.”

2. A square garden is \cfrac{3}{4} of a meter wide and \cfrac{8}{9} of a meter long. What is its area?

The area of the garden is 1\cfrac{23}{36} square meters.

The area of the garden is \cfrac{27}{32} square meters.

The area of the garden is \cfrac{2}{3} square meters.

The perimeter of the garden is \cfrac{2}{3} meters.

To find the area of a square, you multiply the length and width. So to solve, you multiply the fractional lengths by mulitplying the numerators and multiplying the denominators.

\cfrac{24}{36} can be simplified to \cfrac{2}{3}. 

Therefore, the correct answer is “The area of the garden is \cfrac{2}{3} square meters.”

3. Zoe ate \cfrac{3}{8} of a small cake. Liam ate \cfrac{1}{8} of the same cake. How much more of the cake did Zoe eat than Liam?

Zoe ate \cfrac{3}{64} more of the cake than Liam.

Zoe ate \cfrac{1}{4} more of the cake than Liam.

Zoe ate \cfrac{1}{8} more of the cake than Liam.

Liam ate \cfrac{1}{4} more of the cake than Zoe.

To find how much more cake Zoe ate than Liam, you subtract. Since the fractions have the same denominator, you subtract the numerators and keep the denominator the same.

\cfrac{2}{8} can be simplified to \cfrac{1}{4}. 

Therefore, the correct answer is “Zoe ate \cfrac{1}{4} more of the cake than Liam.”

4. Lila poured \cfrac{11}{12} cup of pineapple and \cfrac{2}{3} cup of mango juice in a bottle. How many cups of juice did she pour into the bottle altogether?

Lila poured 1 \cfrac{7}{12} cups of juice in the bottle altogether.

Lila poured \cfrac{1}{4} cups of juice in the bottle altogether.

Lila poured \cfrac{11}{18} cups of juice in the bottle altogether.

Lila poured 1 \cfrac{3}{8} cups of juice in the bottle altogether.

To find the total amount of juice that Lila poured into the bottle, you need to add. Since the fractions have unlike denominators, you need to find a common denominator first.

You can use 12 as the common denominator, so \cfrac{2}{3} becomes \cfrac{8}{12}.  Then you can add.

\cfrac{19}{12} can be simplified to 1 \cfrac{7}{12}. 

Therefore, the correct answer is “Lila poured 1 \cfrac{7}{12} cups of juice in the bottle altogether.”

5. Killian used \cfrac{9}{10} of a gallon of paint to paint his living room and \cfrac{7}{10} of a gallon to paint his bedroom. How much paint did Killian use in all?

Killian used \cfrac{2}{10} gallons of paint in all.

Killian used \cfrac{1}{5} gallons of paint in all.

Killian used \cfrac{63}{100} gallons of paint in all.

Killian used 1 \cfrac{3}{5} gallons of paint in all.

To find the total amount of paint Killian used, you add the amount he used for the living room and the amount he used for the kitchen. Since the fractions have the same denominator, you add the numerators and keep the denominators the same.

\cfrac{16}{10} can be simplified to 1 \cfrac{6}{10} and then further simplified to 1 \cfrac{3}{5}.

Therefore, the correct answer is “Killian used 1 \cfrac{3}{5} gallons of paint in all.”

6. Evan pours \cfrac{4}{5} of a liter of orange juice evenly among some cups.

He put \cfrac{1}{10} of a liter into each cup. How many cups did Evan fill?

Evan filled \cfrac{2}{25} cups.

Evan filled 8 cups.

Evan filled \cfrac{9}{10} cups.

Evan filled 7 cups.

To find the number of cups Evan filled, you need to divide the total amount of orange juice by the amount being poured into each cup. To divide fractions, you mulitply the first fraction (the dividend) by the reciprocal of the second fraction (the divisor).

\cfrac{40}{5} can be simplifed to 8.

Therefore, the correct answer is “Evan filled 8 cups.”

Fraction word problems FAQs

Fraction word problems are math word problems involving fractions that require students to use problem-solving skills within the context of a real-world situation. Fraction word problems may involve addition, subtraction, multiplication, or division of fractions.

To solve fraction word problems, first you need to determine the operation. Then you can write an equation and solve the equation based on the arithmetic rules for that operation.

Fraction word problems and decimal word problems are similar because they both involve solving math problems within real-world contexts. Both types of problems require understanding the problem, determining the operation needed to solve it (addition, subtraction, multiplication, division), and solving it based on the arithmetic rules for that operation.

The next lessons are

Still stuck.

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

Unit Fraction

Unit fractions are those whose numerator is 1 and the denominator is any natural number. It is of the form 1/x, where x∈N. Few examples of unit fractions are 1/2, 1/5, 1/34, etc.

What is a Unit Fraction?

All the fractions with 1 as the numerator are known as unit fractions. In these fractions, we take only one part of the whole which is divided equally into a finite number of parts. Unit denotes one. Therefore, they are known as unit fractions. For example, if a pizza is divided into 8 equal parts and Joseph is eating one part of it, then it will be represented as 1/8 which is a unit fraction.

In the image below, 1/2, 1/4, and 1/7 are unit fractions.

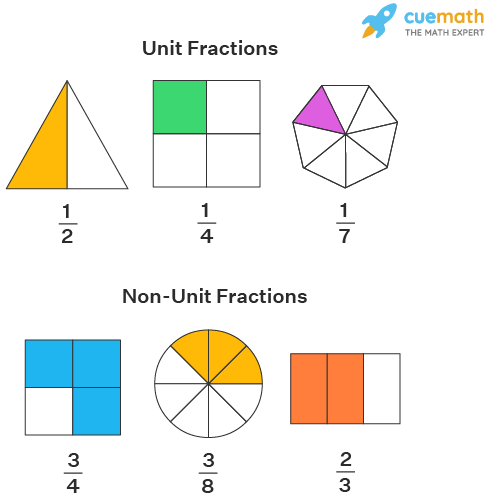
What is Non-Unit Fraction?

Any fraction with a numerator other than 1 is a non-unit fraction. For example, 3/4, 3/8, 2/3, etc are all non-unit fractions. Here, it is important to understand that fractions that can be reduced to 1 in the numerator are also non-unit fractions that can be expressed as a unit fraction after simplification. For example, 2/4 is a non-unit fraction, which can be expressed as a unit fraction with a different denominator 1/2. The idea behind unit fractions is that we are taking 1 part out of a whole, so if we have taken 2 parts out of 4, that is surely not what we are asked for. But yes, if we consider that whole divided into 2 parts, then we can say that we are considering 1 part out of 2, which is a unit fraction.

Unit Fraction Divided by Whole Number

Dividing unit fractions by whole numbers is done by multiplying the whole number with the denominator of the given fraction. Follow the steps given below to understand the division of a unit fraction by the whole number in detail:

• Step 1: Find the reciprocal of the whole number.
• Step 2: Change the division fact to multiplication by changing the sign and multiplying the reciprocal with the unit fraction.
• Step 3: Find the product and write the answer.

Let us take an example of dividing 1/7 by 8.

Step 1: The reciprocal of 8 is 1/8.

Step 2: 1/7 ÷ 8 = 1/7 × 1/8

Step 3: 1/7 × 1/8 = 1/56.

Therefore, dividing 1/7 by 8 gives us 1/56. If you observe carefully, we are just multiplying the given whole number to the denominator of the fraction. It's easy, isn't it? Now, let us learn about dividing a whole number by a unit fraction. To do that, we will just have to multiply the whole number with the denominator of the fraction. It will always give us a whole number as the answer. For example, 5 ÷ 1/6 can be written as 5 × 6, which is 30. So, 5 ÷ 1/6 = 30.

Unit Fraction Related Articles

Check these interesting articles related to the concept of the unit fraction.

• Types of Fractions
• Multiplication of Fractions
• Improper Fractions

Unit Fractions Examples

Example 1: Write the fraction of the shaded part for each of the given circles, and find which fraction can be represented as a unit fraction?

Solution: Let us first write the fraction of the shaded portion of each of the given circles starting from the left.

Fraction 1 - 2/3

Fraction 2 - 3/5

Fraction 3 - 2/4

Fraction 4 - 5/8

Fraction 5 - 5/6

Out of these fractions, only 2/4 can be reduced to a unit fraction, as 2/4 = 1/2. Therefore, 2/4 is the answer.

Example 2: Divide 1/9 by 15.

Solution: To divide a unit fraction by a whole number, we need to multiply the number to the denominator of the fraction and write the answer in fractional form. So, 1/9 ÷ 15 = 1/(9 × 15) = 1/135. Therefore, 1/9 ÷ 15 = 1/135.

Example 3: What will be the answer if 20 is divided by 1/20?

Solution: To divide a whole number by a unit fraction, multiply the number with the denominator of the fraction. So, we get, 20 ÷ 1/20 = 20 × 20 = 400. Therefore, 20 ÷ 1/20 = 400.

go to slide go to slide go to slide

Book a Free Trial Class

Unit Fraction Practice Questions

go to slide go to slide

FAQs on Unit Fraction

What are a unit fraction and a non-unit fraction.

A unit fraction is a fraction with 1 as the numerator. While a non-unit fraction has a numerator other than 1. Examples of unit fractions are 1/2, 1/3, 1/4, etc. Examples of non-unit fractions are 2/3, 4/9, 12/15, etc.

Why is it called a Unit Fraction?

Unit fractions mean we are considering one part out of the total parts of the whole. Unit means one. Therefore, it is called a unit fraction.

What is a Product of a Whole Number and a Unit Fraction?

The product of a whole number 'a' and a unit fraction '1/b' is 'a/b'. For example, 3 × 1/5 = 3/5.

How to Divide a Whole Number by a Unit Fraction?

To divide a whole number by a unit fraction, we just have to multiply it by the denominator of the fraction. It always results in a whole number. For example, 10 ÷ 1/4 = 10 × 4 = 40.

How to Decompose a Fraction into Unit Fractions?

To write a fraction as a sum of unit fractions, we write it in the form of the addition of two unit fractions with two unknown integers in the denominators. For example, 7/10 = 1/A + 1/B. This implies, 7/10 = (A+B)/AB. Now, we can simply equate numerators and denominators separately. So, A+B=7, and AB=10. Solving these two equations, we get A= 2 or 5, and B = 5 or 2. Therefore, 7/10 can be decomposed as the sum of two unit fractions 1/2 and 1/5.

Is Unit Fraction a Proper Fraction?

Unit fractions are always proper fractions except 1/1 (which is an improper fraction ). This is because, for unit fractions, the numerator is always 1 which is the smallest natural number . So, any natural number in the denominator greater than 1 forms a proper fraction.

Is 1 a Unit Fraction?

Yes, 1 is a unit fraction as it can be represented as 1/1. And we know that any fraction with 1 as the numerator is a unit fraction.

What is a Multiple of a Unit Fraction?

We can write any fraction as a multiple of a unit fraction. For example, 7/8 is 7 × 1/8. So it is the seventh multiple of 1/8.