problem solving elimination method

Elimination Method

The elimination method of solving a system of linear equations algebraically is the most widely used method out of all the methods to solve linear equations. In the elimination method, we eliminate any one of the variables by using basic arithmetic operations and then simplify the equation to find the value of the other variable. Then we can put that value in any of the equations to find the value of the variable eliminated.

The elimination method is easy to use because here we eliminate one of the terms that make our calculations simple. In this article, we will learn how to solve systems of equations using the elimination method. We shall solve various examples based on the concept for a better understanding. 

What is Elimination Method?

As per the elimination method definition, it is about eliminating one of the terms containing any of the variables to make the calculations easier. This is done by multiplying or dividing a number by the equation(s) such that the coefficients of any one of the variable terms become the same. Then, we add or subtract both the equations to eliminate or remove that term from the result. That is why the elimination method is also called the addition method. For example, let us solve two linear equations containing two variables using the elimination method.

Solving Systems of Equations by Elimination

The elimination method is used to solve systems of equations by eliminating a variable and determining the value of the variable to find the solution. Given below is an image showing the application of the elimination method to solve a system of equations with two variables. Consider two equations x - 2y = 8 and 2x + y = 5. 

Steps to Use Elimination Method

The elimination method is useful to solve linear equations containing two or three variables . We can solve three equations as well using this method. But it can only be applied to two equations at a time. Let us look at the steps to solve a system of equations using the elimination method.

• Step-1: The first step is to multiply or divide both the linear equations with a non-zero number to get a common coefficient of any one of the variables in both equations.
• Step-2: Add or subtract both the equations such that the same terms will get eliminated.
• Step-3: Simplify the result to get a final answer of the left out variable (let's say, y) such that we will only get an answer in the form of y=c, where c is any constant.
• Step-4: At last, substitute this value in any of the given equations to find the value of the other given variable.

These are the elimination method steps to solve simultaneous linear equations . Let us take an example of two linear equations x+y=8 and 2x-3y=4 to understand it better.

Let, x + y = 8 → (1) and 2x - 3y = 4 → (2)

Step 1: To make the coefficients of x equal, multiply equation (1) by 2 and equation (2) by 1. We get,

(x+y=8) × 2 → (1)

(2x-3y=4) × 1 → (2)

So, the two equations we have now are 2x + 2y = 16 → (1) and 2x - 3y = 4 → (2).

Step 2: Subtract equation 2 from 1, we get, y=12/5.

Step 3: Substitute the value of y in equation 1, we get, x + 12/5 = 8

x = 8 - 12/5

Therefore, x = 28/5 and y=12/5.

But what if while multiplying a non-zero constant, we get the coefficients of both the variables equal? What if both the terms got eliminated while adding or subtracting? We get such cases while solving equations of parallel and coincident lines. Equations of two intersecting lines will have only two solutions that are consistent, but the equations of two parallel lines have no solutions as these lines never intersect each other. And the equations of coincident lines have infinitely many solutions as they lie on each other so every point is the intersection or the common point of those lines. Let us discuss each of these two cases in detail.

Elimination Method: No Solutions

As we know that equations of two parallel lines have no solutions. So, if we solve any such equations using the elimination method we get the answer as two unequal numbers on both sides of the unequal sign. For example, 0≠8, -2≠0, etc. In such cases, we cannot eliminate only one variable. Both the variables get eliminated. For example, let us solve two equations 2x - y = 4 → (1) and 4x - 2y = 7 → (2) by the elimination method. In order to make the x coefficients equal in both the equations, we multiply equation (1) by 2 and equation (2) by 1. By doing so we get, 4x - 2y = 8 → (3) and 4x - 2y = 7 → (4). Now, if we try to subtract equation 4 from equation 3, we get, 0=1 as both the variables are getting eliminated. There is no other way to solve these equations as the solutions are inconsistent. So, in the elimination method when there is no solution, we get the result in this form.

Elimination Method: Infinitely Many Solutions

Two equations of coincident lines have infinitely many solutions possible. So, if by the elimination method we solve a system of equations of coincident lines, we get a consistent system with infinite solutions. In such cases, we get an answer in the form of 0=0 if we apply the elimination method. For example, try to solve equations x+y=2 and 2x+2y-4=0. If you multiply any non-zero constant with both equations, you will find that every time x-variable terms and y-variable terms are getting canceled or eliminated. So, in the elimination method when there are infinitely many solutions possible, we get the result in the form of 0=0. It is advisable to check whether the given linear equations are of intersecting lines, parallel lines, or coincident lines before trying to solve them. Check this article to know about the solutions of linear equations .

Solving System of 3 Equations Using Elimination Method

To solve a system of three linear equations with the elimination method, first, make sure that the equations are written in the standard form Ax+By+C=0 or Ax+By=C without any fractional coefficient. Take any two equations as per your comfortability and select a variable to eliminate. Eliminate the chosen variable. Now, select another pair of equations out of the given three equations and eliminate the same variable. This way you will get two equations with only two variables. Solve those using the elimination method steps mentioned above and find the values of those 2 variables. Substitute the values in any of the given equations to find the value of the third variable.

Let's solve three equations 3x-y+2z=5, 4x+2y-z=6, and 5x-3y+z=1 for a better understanding.

Now, we have found that x=1. Substitute this value in equation P, we get 9×(1)-y=7.

Now put the values of x and y in the third equation 5x-3y+z=1, and we get z=2. Therefore, x=1, y=2, and z=2.

Important Notes on Elimination Method

• The elimination method is used to solve a system of equations.
• This method is easy and makes the calculations easier as it eliminates one variable and hence, reduces the calculations.
• We make the coefficient of a variable identical to eliminate the corresponding variable.

Related Articles

• Elimination Method Calculator
• Substitution Method
• System of Equations Solver
• Cross Multiplication Method
• Graphically Solving a Pair of Linear Equations
• Solving Linear Equations

Elimination Method Examples

Example 1: Dorion was given two equations 5m−2n=17 and 3m+n=8 and asked to find the value of m and n. Can you help him in finding the value of m and n using the elimination method?

Solution: Given equations are 5m − 2n = 17 → (1) and 3m + n = 8 → (2). It is easy to make the coefficients of the n variable term equal, so let us multiply equation (1) by 1 and equation (2) by 2. We will get,

5m−2n=17 → (1)

6m+2n=16 → (2)

Add both the equations to eliminate the n variable term.

Hence, m=3. Now put the value of m in equation 1, and we get, 5×3−2n=17

Answer:  Therefore, m=3 and n=-1.

Example 2: Emma has two numbers such that their sum is 9 and the difference between them is 5. Can you find the numbers by the elimination method?

Solution: Let the greater number be x and the smaller number be y. It is given that, x+y=9 → (1) and x-y=5 → (2). Add both the equations to eliminate y variable terms. We get,

Now, put the value of x in equation 1. We get y=9-7 = 2.

Answer:  Therefore, the numbers are 7 and 2.

Example 3: Solve the given system of linear equations using the elimination method:

2x - 3y = 12 → (1)

3x - 4y + 10 = 0 → (2)

Solution: Writing both the equations in the form of Ax+By=C, we get, 2x - 3y = 12 → (1) and 3x - 4y = –10 → (2). Multiply the first equation by 3 and second equation by 2, we get,

(2x - 3y = 12) × 3 → (1)

(3x - 4y = –10) × 2 → (2)

After simplifying, we have,

6x - 9y = 36 → (1)

6x - 8y = –20 → (2)

Subtract equation 1 from equation 2, we get,

Substitute the value of y in equation 1, we get 2x - 3 × (-56) = 12

Answer:  Therefore, by using the elimination method we have found that x = –78 and y = –56.

go to slide go to slide go to slide

Book a Free Trial Class

Elimination Method Questions

go to slide go to slide

FAQs on Elimination Method

What is the elimination method in math.

In math, the elimination method is used to solve a system of linear equations. It is the most widely used and simple method as it involves fewer calculations and steps. In this method, we eliminate one of the two variables and try to solve equations with one variable. The value found here can be substituted in any of the given equations to find the value of the other variable as well.

How do you Solve Linear Equations Using the Elimination Method?

Simultaneous linear equations can be solved using the elimination method. First of all, make sure that the equations are written in the standard form either Ax+By=C or Ax+By+C=0. In this method, we multiply both the equations with a non-zero number to make the coefficients of any one variable equal. Then we add or subtract the equations to eliminate one of the variables to find the value of the other variable. This is how we solve linear equations by the elimination method.

What are the Steps Involved in the Elimination Method?

The steps involved in the elimination method are given below:

• Choose any one variable to eliminate. Multiply or divide both the equations with a non-zero constant to make the coefficients of that variable equal.
• Add or subtract the resultant equations such that the chosen variable gets eliminated.
• Simplify and find the value of the other variable.
• Substitute that value in any of the given equations to find the value of the eliminated variable.

Can the Elimination Method be Used to Solve the System of Equations in Three Variables?

Yes, the elimination method can be used to solve linear equations with three variables. With three equations, we take any two equations and select the variable to be eliminated. Then we repeat the same process by taking another pair of equations and eliminate the same variable. In this way, we will be left with two equations in two variables only that can be solved using the elimination method. At last, we put the values of those two variables in any of the given equations to find the value of the third variable.

When Should you Use the Elimination Method?

It is better to use the elimination method when the coefficients of any one variable in the equations are the same. For example, 3x+7y+2=0 and 3x-4y+5=0. The other methods of solving linear equations are substitution method , cross multiplication method , graphical method , and matrix method.

What is the Difference Between the Elimination Method and the Substitution Method?

The difference between the substitution and the elimination method is that in the substitution method we find the value of one variable in terms of the other variable. Then, we substitute that value in the second equation to find the value of the other variable. But in the elimination method, we eliminate any one variable and then find the value of the other variable.

How Do You Solve Systems of Equations Using the Elimination Method?

To solve systems of equations using the elimination method, we make the coefficient of one of the variables involved identical and then add/subtract the equations in order to eliminate that variable and find the value of the other variable.

Why is Elimination Method Better?

The elimination method is considered better than other methods for solving a system of equations because it makes the calculations easier by eliminating a variable. Once a variable is eliminated, it becomes easier to determine the value of another variable and then use this value to find the value of the eliminated variable. 

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Solving System of Linear Equations

Elimination Method

The elimination method of solving systems of equations is also called the addition method. To solve a system of equations by elimination we transform the system such that one variable "cancels out".

Example 1: Solve the system of equations by elimination

In this example we will "cancel out" the y term. To do so, we can add the equations together.

Now we can find: $x = 2$

In order to solve for y, take the value for x and substitute it back into either one of the original equations.

The solution is $(x, y) = (2, 1)$.

Example 2: Solve the system using elimination

Look at the x - coefficients. Multiply the first equation by -4, to set up the x-coefficients to cancel.

Now we can find: $y = -2$

Take the value for y and substitute it back into either one of the original equations.

The solution is $(x, y) = (1, -2)$.

Example 3: Solve the system using elimination method

In this example, we will multiply the first row by -3 and the second row by 2 ; then we will add down as before.

Now we can find: y = -1

Substitute y = -1 back into first equation:

The solution is $(x, y) = (3, -1)$.

Exercise: Solve the following systems using elimination method

• Roots and Radicals Simplify Expression Adding and Subtracting Multiplying and Dividing
• Complex Numbers Arithmetic Polar representation
• Polynomials Multiplying Polynomials Division of Polynomials Zeros of Polynomials
• Rational Expressions Simplifying Multiplying and Dividing Adding and Subtracting
• Solving Equations Linear Equations Absolute Value Equations Quadratic Equation Equations with Radicals
• Systems of Equations Substitution Method Elimination Method Row Reduction Cramers Rule Inverse Matrix Method
• Exponential Functions Introduction Exponential Equations Logarithmic Functions
• Trigonometry Trigonometric Formulas Trigonometric Equations Law of Cosines
• Progressions Arithmetic Progressions Geometric Progressions
• Differentiation Common formulas Product and Quotient Rule Chain Rule
• Limits Properties of Limits Rational Function Irrational Functions Trigonometric Functions L'Hospital's Rule
• Integrals Integration Formulas Exercises
• Integral techniques Substitution Integration by Parts Integrals with Trig. Functions Trigonometric Substitutions
• Integral Applications Area Volume Arc Length

Analytic geometry

• Analytic Geometry 2D Basic Concepts Lines Parallel and Perpendicular Lines Polar Coordinates
• Conic Sections Circle Ellipse Hyperbola
• Analytic Geometry 3D Line in 3D Planes

Linear Algebra

• Matrices Definitions Addition and Multiplication Gauss-Jordan elimination
• Determinants Introduction to Determinants Applications of Determinants
• Vectors Basic Operations Dot Product Cross Product

Random Quote

The human mind has never invented a labor-saving machine equal to algebra.

Author Unknown

If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is.

John Louis von Neumann

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

4. Systems of Equations

4.3 Solve Systems of Equations by Elimination

Lynn Marecek and MaryAnne Anthony-Smith

Learning Objectives

By the end of this section it is expected that you will be able to:

• Solve a system of equations by elimination
• Solve applications of systems of equations by elimination
• Choose the most convenient method to solve a system of linear equations

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

Solve a System of Equations by Elimination

The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For any expressions a , b , c , and d ,

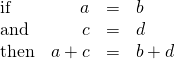
To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.

Notice how that works when we add these two equations together:

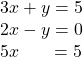
Let’s try another one:

This time we don’t see a variable that can be immediately eliminated if we add the equations.

But if we multiply the first equation by −2, we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2.

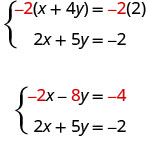
Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.

Add the equations yourself—the result should be −3 y = −6. And that looks easy to solve, doesn’t it? Here is what it would look like.

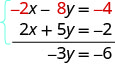
We’ll do one more:

It doesn’t appear that we can get the coefficients of one variable to be opposites by multiplying one of the equations by a constant, unless we use fractions. So instead, we’ll have to multiply both equations by a constant.

We can make the coefficients of x be opposites if we multiply the first equation by 3 and the second by −4, so we get 12 x and −12 x .

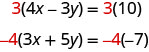
This gives us these two new equations:

When we add these equations,

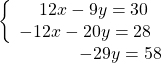
the x ’s are eliminated and we just have −29 y = 58.

Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.

Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.

The steps are listed below for easy reference.

How to solve a system of equations by elimination.

• Write both equations in standard form. If any coefficients are fractions, clear them.
• Decide which variable you will eliminate.
• Multiply one or both equations so that the coefficients of that variable are opposites.
• Add the equations resulting from Step 2 to eliminate one variable.
• Solve for the remaining variable.
• Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
• Write the solution as an ordered pair.
• Check that the ordered pair is a solution to both original equations.

First we’ll do an example where we can eliminate one variable right away.

In the next example, we will be able to make the coefficients of one variable opposites by multiplying one equation by a constant.

Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.

In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by a constant to get the opposites.

What other constants could we have chosen to eliminate one of the variables? Would the solution be the same?

When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by its LCD.

In this example, both equations have fractions. Our first step will be to multiply each equation by its LCD to clear the fractions.

When we were solving systems of linear equations by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.

Solve the system by elimination:

no solution

Solve Applications of Systems of Equations by Elimination

Some applications problems translate directly into equations in standard form, so we will use the elimination method to solve them. As before, we use our Problem Solving Strategy to help us stay focused and organized.

The sum of two numbers is 39. Their difference is 9. Find the numbers.

The sum of two numbers is 42. Their difference is 8. Find the numbers.

The numbers are 25 and 17.

Joe stops at a burger restaurant every day on his way to work. Monday he had one order of medium fries and two small sodas, which had a total of 620 calories. Tuesday he had two orders of medium fries and one small soda, for a total of 820 calories. How many calories are there in one order of medium fries? How many calories in one small soda?

Malik stops at the grocery store to buy a bag of diapers and 2 cans of formula. He spends a total of $37. The next week he stops and buys 2 bags of diapers and 5 cans of formula for a total of $87. How much does a bag of diapers cost? How much is one can of formula?

The bag of diapers costs ?11 and the can of formula costs ?13.

Choose the Most Convenient Method to Solve a System of Linear Equations

When you will have to solve a system of linear equations in a later math class, you will usually not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

a) Since both equations are in standard form, using elimination will be most convenient.

Access these online resources for additional instruction and practice with solving systems of linear equations by elimination.

• Instructional Video-Solving Systems of Equations by Elimination
• Instructional Video-Solving by Elimination
• Instructional Video-Solving Systems by Elimination

Key Concepts

4.3 exercise set.

In the following exercises, solve the systems of equations by elimination.

In the following exercises, translate to a system of equations and solve.

• The sum of two numbers is 65. Their difference is 25. Find the numbers .
• The sum of two numbers is −27. Their difference is −59. Find the numbers.
• Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?
• The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?

In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.

• infinitely many solutions
• inconsistent, no solution
• The numbers are 20 and 45.
• The numbers are 16 and −43.
• A shirt costs $16 and a sweater costs $33.
• There are 860 mg in a hot dog. There are 1,000 mg in a cup of cottage cheese.
• elimination
• substitution

Business/Technical Mathematics Copyright © 2021 by Lynn Marecek and MaryAnne Anthony-Smith is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

7.6 Solving Systems with Gaussian Elimination

Learning objectives.

In this section, you will:

• Write the augmented matrix of a system of equations.
• Write the system of equations from an augmented matrix.
• Perform row operations on a matrix.
• Solve a system of linear equations using matrices.

Carl Friedrich Gauss lived during the late 18th century and early 19th century, but he is still considered one of the most prolific mathematicians in history. His contributions to the science of mathematics and physics span fields such as algebra, number theory, analysis, differential geometry, astronomy, and optics, among others. His discoveries regarding matrix theory changed the way mathematicians have worked for the last two centuries.

We first encountered Gaussian elimination in Systems of Linear Equations: Two Variables . In this section, we will revisit this technique for solving systems, this time using matrices.

Writing the Augmented Matrix of a System of Equations

A matrix can serve as a device for representing and solving a system of equations. To express a system in matrix form, we extract the coefficients of the variables and the constants, and these become the entries of the matrix. We use a vertical line to separate the coefficient entries from the constants, essentially replacing the equal signs. When a system is written in this form, we call it an augmented matrix .

For example, consider the following 2 × 2 2 × 2 system of equations.

We can write this system as an augmented matrix:

We can also write a matrix containing just the coefficients. This is called the coefficient matrix .

A three-by-three system of equations such as

has a coefficient matrix

and is represented by the augmented matrix

Notice that the matrix is written so that the variables line up in their own columns: x -terms go in the first column, y -terms in the second column, and z -terms in the third column. It is very important that each equation is written in standard form a x + b y + c z = d a x + b y + c z = d so that the variables line up. When there is a missing variable term in an equation, the coefficient is 0.

Given a system of equations, write an augmented matrix.

• Write the coefficients of the x -terms as the numbers down the first column.
• Write the coefficients of the y -terms as the numbers down the second column.
• If there are z -terms, write the coefficients as the numbers down the third column.
• Draw a vertical line and write the constants to the right of the line.

Writing the Augmented Matrix for a System of Equations

Write the augmented matrix for the given system of equations.

The augmented matrix displays the coefficients of the variables, and an additional column for the constants.

Write the augmented matrix of the given system of equations.

Writing a System of Equations from an Augmented Matrix

We can use augmented matrices to help us solve systems of equations because they simplify operations when the systems are not encumbered by the variables. However, it is important to understand how to move back and forth between formats in order to make finding solutions smoother and more intuitive. Here, we will use the information in an augmented matrix to write the system of equations in standard form.

Writing a System of Equations from an Augmented Matrix Form

Find the system of equations from the augmented matrix.

When the columns represent the variables x , x , y , y , and z , z ,

Write the system of equations from the augmented matrix.

Performing Row Operations on a Matrix

Now that we can write systems of equations in augmented matrix form, we will examine the various row operations that can be performed on a matrix, such as addition, multiplication by a constant, and interchanging rows.

Performing row operations on a matrix is the method we use for solving a system of equations. In order to solve the system of equations, we want to convert the matrix to row-echelon form , in which there are ones down the main diagonal from the upper left corner to the lower right corner, and zeros in every position below the main diagonal as shown.

We use row operations corresponding to equation operations to obtain a new matrix that is row-equivalent in a simpler form. Here are the guidelines to obtaining row-echelon form.

• In any nonzero row, the first nonzero number is a 1. It is called a leading 1.
• Any all-zero rows are placed at the bottom on the matrix.
• Any leading 1 is below and to the right of a previous leading 1.
• Any column containing a leading 1 has zeros in all other positions in the column.

To solve a system of equations we can perform the following row operations to convert the coefficient matrix to row-echelon form and do back-substitution to find the solution.

• Interchange rows. (Notation: R i ↔ R j R i ↔ R j )
• Multiply a row by a constant. (Notation: c R i c R i )
• Add the product of a row multiplied by a constant to another row. (Notation: R i + c R j ) R i + c R j )

Each of the row operations corresponds to the operations we have already learned to solve systems of equations in three variables. With these operations, there are some key moves that will quickly achieve the goal of writing a matrix in row-echelon form. To obtain a matrix in row-echelon form for finding solutions, we use Gaussian elimination, a method that uses row operations to obtain a 1 as the first entry so that row 1 can be used to convert the remaining rows.

Gaussian Elimination

The Gaussian elimination method refers to a strategy used to obtain the row-echelon form of a matrix. The goal is to write matrix A A with the number 1 as the entry down the main diagonal and have all zeros below.

The first step of the Gaussian strategy includes obtaining a 1 as the first entry, so that row 1 may be used to alter the rows below.

Given an augmented matrix, perform row operations to achieve row-echelon form.

• The first equation should have a leading coefficient of 1. Interchange rows or multiply by a constant, if necessary.
• Use row operations to obtain zeros down the first column below the first entry of 1.
• Use row operations to obtain a 1 in row 2, column 2.
• Use row operations to obtain zeros down column 2, below the entry of 1.
• Use row operations to obtain a 1 in row 3, column 3.
• Continue this process for all rows until there is a 1 in every entry down the main diagonal and there are only zeros below.
• If any rows contain all zeros, place them at the bottom.

Solving a 2 × 2 2 × 2 System by Gaussian Elimination

Solve the given system by Gaussian elimination.

First, we write this as an augmented matrix.

We want a 1 in row 1, column 1. This can be accomplished by interchanging row 1 and row 2.

We now have a 1 as the first entry in row 1, column 1. Now let’s obtain a 0 in row 2, column 1. This can be accomplished by multiplying row 1 by −2 , −2 , and then adding the result to row 2.

We only have one more step, to multiply row 2 by 1 5 . 1 5 .

Use back-substitution. The second row of the matrix represents y = 1. y = 1. Back-substitute y = 1 y = 1 into the first equation.

The solution is the point ( 3 2 , 1 ) . ( 3 2 , 1 ) .

Using Gaussian Elimination to Solve a System of Equations

Use Gaussian elimination to solve the given 2 × 2 2 × 2 system of equations .

Write the system as an augmented matrix .

Obtain a 1 in row 1, column 1. This can be accomplished by multiplying the first row by 1 2 . 1 2 .

Next, we want a 0 in row 2, column 1. Multiply row 1 by −4 −4 and add row 1 to row 2.

The second row represents the equation 0 = 4. 0 = 4. Therefore, the system is inconsistent and has no solution.

Solving a Dependent System

Solve the system of equations.

Perform row operations on the augmented matrix to try and achieve row-echelon form .

The matrix ends up with all zeros in the last row: 0 y = 0. 0 y = 0. Thus, there are an infinite number of solutions and the system is classified as dependent. To find the generic solution, return to one of the original equations and solve for y . y .

So the solution to this system is ( x , 3 − 3 4 x ) . ( x , 3 − 3 4 x ) .

Performing Row Operations on a 3×3 Augmented Matrix to Obtain Row-Echelon Form

Perform row operations on the given matrix to obtain row-echelon form.

The first row already has a 1 in row 1, column 1. The next step is to multiply row 1 by −2 −2 and add it to row 2. Then replace row 2 with the result.

Next, obtain a zero in row 3, column 1.

Next, obtain a zero in row 3, column 2.

The last step is to obtain a 1 in row 3, column 3.

Write the system of equations in row-echelon form.

Solving a System of Linear Equations Using Matrices

We have seen how to write a system of equations with an augmented matrix , and then how to use row operations and back-substitution to obtain row-echelon form . Now, we will take row-echelon form a step farther to solve a 3 by 3 system of linear equations. The general idea is to eliminate all but one variable using row operations and then back-substitute to solve for the other variables.

Solve the system of linear equations using matrices.

First, we write the augmented matrix.

Next, we perform row operations to obtain row-echelon form.

The easiest way to obtain a 1 in row 2 of column 1 is to interchange R 2 R 2 and R 3 . R 3 .

The last matrix represents the equivalent system.

Using back-substitution, we obtain the solution as ( 4 , −3 , 1 ) . ( 4 , −3 , 1 ) .

Solving a Dependent System of Linear Equations Using Matrices

Solve the following system of linear equations using matrices.

Write the augmented matrix.

First, multiply row 1 by −1 −1 to get a 1 in row 1, column 1. Then, perform row operations to obtain row-echelon form.

The last matrix represents the following system.

We see by the identity 0 = 0 0 = 0 that this is a dependent system with an infinite number of solutions. We then find the generic solution. By solving the second equation for y y and substituting it into the first equation we can solve for z z in terms of x . x .

Now we substitute the expression for z z into the second equation to solve for y y in terms of x . x .

The generic solution is ( x , 2 −2 x 3 , 1 − x 3 ) . ( x , 2 −2 x 3 , 1 − x 3 ) .

Solve the system using matrices.

Can any system of linear equations be solved by Gaussian elimination?

Yes, a system of linear equations of any size can be solved by Gaussian elimination.

Given a system of equations, solve with matrices using a calculator.

• Save the augmented matrix as a matrix variable [ A ] , [ B ] , [ C ] ,   … . [ A ] , [ B ] , [ C ] ,   … .
• Use the ref( function in the calculator, calling up each matrix variable as needed.

Solving Systems of Equations with Matrices Using a Calculator

Write the augmented matrix for the system of equations.

On the matrix page of the calculator, enter the augmented matrix above as the matrix variable [ A ] . [ A ] .

Use the ref( function in the calculator, calling up the matrix variable [ A ] . [ A ] .

Using back-substitution, the solution is ( 61 187 , − 92 187 , − 24 187 ) . ( 61 187 , − 92 187 , − 24 187 ) .

Applying 2 × 2 Matrices to Finance

Carolyn invests a total of $12,000 in two municipal bonds, one paying 10.5% interest and the other paying 12% interest. The annual interest earned on the two investments last year was $1,335. How much was invested at each rate?

We have a system of two equations in two variables. Let x = x = the amount invested at 10.5% interest, and y = y = the amount invested at 12% interest.

As a matrix, we have

Multiply row 1 by −0.105 −0.105 and add the result to row 2.

So 12,000 −5,000 = 7,000. 12,000 −5,000 = 7,000.

Thus, $5,000 was invested at 12% interest and $7,000 at 10.5% interest.

Applying 3 × 3 Matrices to Finance

Ava invests a total of $10,000 in three accounts, one paying 5% interest, another paying 8% interest, and the third paying 9% interest. The annual interest earned on the three investments last year was $770. The amount invested at 9% was twice the amount invested at 5%. How much was invested at each rate?

We have a system of three equations in three variables. Let x x be the amount invested at 5% interest, let y y be the amount invested at 8% interest, and let z z be the amount invested at 9% interest. Thus,

Now, we perform Gaussian elimination to achieve row-echelon form.

The third row tells us − 1 3 z = −2,000 ; − 1 3 z = −2,000 ; thus z = 6,000. z = 6,000.

The second row tells us y + 4 3 z = 9,000. y + 4 3 z = 9,000. Substituting z = 6,000 , z = 6,000 , we get

The first row tells us x + y + z = 10 , 000. x + y + z = 10 , 000. Substituting y = 1 , 000 y = 1 , 000 and z = 6 , 000 , z = 6 , 000 , we get

The answer is $3,000 invested at 5% interest, $1,000 invested at 8%, and $6,000 invested at 9% interest.

A small shoe company took out a loan of $1,500,000 to expand their inventory. Part of the money was borrowed at 7%, part was borrowed at 8%, and part was borrowed at 10%. The amount borrowed at 10% was four times the amount borrowed at 7%, and the annual interest on all three loans was $130,500. Use matrices to find the amount borrowed at each rate.

Access these online resources for additional instruction and practice with solving systems of linear equations using Gaussian elimination.

• Solve a System of Two Equations Using an Augmented Matrix
• Solve a System of Three Equations Using an Augmented Matrix
• Augmented Matrices on the Calculator

7.6 Section Exercises

Can any system of linear equations be written as an augmented matrix? Explain why or why not. Explain how to write that augmented matrix.

Can any matrix be written as a system of linear equations? Explain why or why not. Explain how to write that system of equations.

Is there only one correct method of using row operations on a matrix? Try to explain two different row operations possible to solve the augmented matrix [ 9 3 1 − 2   |   0 6 ] . [ 9 3 1 − 2   |   0 6 ] .

Can a matrix whose entry is 0 on the diagonal be solved? Explain why or why not. What would you do to remedy the situation?

Can a matrix that has 0 entries for an entire row have one solution? Explain why or why not.

For the following exercises, write the augmented matrix for the linear system.

8 x −37 y = 8 2 x + 12 y = 3 8 x −37 y = 8 2 x + 12 y = 3

   16 y = 4 9 x − y = 2    16 y = 4 9 x − y = 2

3 x + 2 y + 10 z = 3 −6 x + 2 y + 5 z = 13              4 x + z = 18 3 x + 2 y + 10 z = 3 −6 x + 2 y + 5 z = 13              4 x + z = 18

  x + 5 y + 8 z = 19 12 x + 3 y = 4 3 x + 4 y + 9 z = −7   x + 5 y + 8 z = 19 12 x + 3 y = 4 3 x + 4 y + 9 z = −7

6 x + 12 y + 16 z = 4   19 x −5 y + 3 z = −9              x + 2 y = −8 6 x + 12 y + 16 z = 4   19 x −5 y + 3 z = −9              x + 2 y = −8

For the following exercises, write the linear system from the augmented matrix.

[ −2 5 6 −18   |   5 26 ] [ −2 5 6 −18   |   5 26 ]

[ 3 4 10 17   |   10 439 ] [ 3 4 10 17   |   10 439 ]

[ 3 2 0 −1 −9 4 8 5 7   |   3 −1 8 ] [ 3 2 0 −1 −9 4 8 5 7   |   3 −1 8 ]

[ 8 29 1 −1 7 5 0 0 3   |   43 38 10 ] [ 8 29 1 −1 7 5 0 0 3   |   43 38 10 ]

[ 4 5 −2 0 1 58 8 7 −3   |   12 2 −5 ] [ 4 5 −2 0 1 58 8 7 −3   |   12 2 −5 ]

For the following exercises, solve the system by Gaussian elimination.

[ 1 0 0 0   |   3 0 ] [ 1 0 0 0   |   3 0 ]

[ 1 0 1 0   |   1 2 ] [ 1 0 1 0   |   1 2 ]

[ 1 2 4 5   |   3 6 ] [ 1 2 4 5   |   3 6 ]

[ −1 2 4 −5   |   −3 6 ] [ −1 2 4 −5   |   −3 6 ]

[ −2 0 0 2   |   1 −1 ] [ −2 0 0 2   |   1 −1 ]

  2 x − 3 y = − 9 5 x + 4 y = 58   2 x − 3 y = − 9 5 x + 4 y = 58

6 x + 2 y = −4 3 x + 4 y = −17 6 x + 2 y = −4 3 x + 4 y = −17

2 x + 3 y = 12   4 x + y = 14 2 x + 3 y = 12   4 x + y = 14

−4 x −3 y = −2   3 x −5 y = −13 −4 x −3 y = −2   3 x −5 y = −13

−5 x + 8 y = 3 10 x + 6 y = 5 −5 x + 8 y = 3 10 x + 6 y = 5

  3 x + 4 y = 12 −6 x −8 y = −24   3 x + 4 y = 12 −6 x −8 y = −24

−60 x + 45 y = 12   20 x −15 y = −4 −60 x + 45 y = 12   20 x −15 y = −4

11 x + 10 y = 43 15 x + 20 y = 65 11 x + 10 y = 43 15 x + 20 y = 65

2 x − y = 2 3 x + 2 y = 17 2 x − y = 2 3 x + 2 y = 17

−1.06 x −2.25 y = 5.51 −5.03 x −1.08 y = 5.40 −1.06 x −2.25 y = 5.51 −5.03 x −1.08 y = 5.40

3 4 x − 3 5 y = 4 1 4 x + 2 3 y = 1 3 4 x − 3 5 y = 4 1 4 x + 2 3 y = 1

1 4 x − 2 3 y = −1 1 2 x + 1 3 y = 3 1 4 x − 2 3 y = −1 1 2 x + 1 3 y = 3

[ 1 0 0 0 1 1 0 0 1   |   31 45 87 ] [ 1 0 0 0 1 1 0 0 1   |   31 45 87 ]

[ 1 0 1 1 1 0 0 1 1   |   50 20 −90 ] [ 1 0 1 1 1 0 0 1 1   |   50 20 −90 ]

[ 1 2 3 0 5 6 0 0 8   |   4 7 9 ] [ 1 2 3 0 5 6 0 0 8   |   4 7 9 ]

[ −0.1 0.3 −0.1 −0.4 0.2 0.1 0.6 0.1 0.7   |   0.2 0.8 −0.8 ] [ −0.1 0.3 −0.1 −0.4 0.2 0.1 0.6 0.1 0.7   |   0.2 0.8 −0.8 ]

−2 x + 3 y − 2 z = 3       4 x + 2 y − z = 9 4 x − 8 y + 2 z = −6 −2 x + 3 y − 2 z = 3       4 x + 2 y − z = 9 4 x − 8 y + 2 z = −6

      x + y − 4 z = −4   5 x − 3 y − 2 z = 0   2 x + 6 y + 7 z = 30       x + y − 4 z = −4   5 x − 3 y − 2 z = 0   2 x + 6 y + 7 z = 30

      2 x + 3 y + 2 z = 1   −4 x − 6 y − 4 z = −2 10 x + 15 y + 10 z = 5       2 x + 3 y + 2 z = 1   −4 x − 6 y − 4 z = −2 10 x + 15 y + 10 z = 5

    x + 2 y − z = 1 − x − 2 y + 2 z = −2 3 x + 6 y − 3 z = 5     x + 2 y − z = 1 − x − 2 y + 2 z = −2 3 x + 6 y − 3 z = 5

    x + 2 y − z = 1 − x −2 y + 2 z = −2 3 x + 6 y −3 z = 3     x + 2 y − z = 1 − x −2 y + 2 z = −2 3 x + 6 y −3 z = 3

x + y = 2    x + z = 1 − y − z = −3 x + y = 2    x + z = 1 − y − z = −3

x + y + z = 100     x + 2 z = 125 − y + 2 z = 25 x + y + z = 100     x + 2 z = 125 − y + 2 z = 25

1 4 x − 2 3 z = − 1 2 1 5 x + 1 3 y = 4 7 1 5 y − 1 3 z = 2 9 1 4 x − 2 3 z = − 1 2 1 5 x + 1 3 y = 4 7 1 5 y − 1 3 z = 2 9

− 1 2 x + 1 2 y + 1 7 z = − 53 14    1 2 x − 1 2 y + 1 4 z = 3     1 4 x + 1 5 y + 1 3 z = 23 15 − 1 2 x + 1 2 y + 1 7 z = − 53 14    1 2 x − 1 2 y + 1 4 z = 3     1 4 x + 1 5 y + 1 3 z = 23 15

− 1 2 x − 1 3 y + 1 4 z = − 29 6    1 5 x + 1 6 y − 1 7 z = 431 210 − 1 8 x + 1 9 y + 1 10 z = − 49 45 − 1 2 x − 1 3 y + 1 4 z = − 29 6    1 5 x + 1 6 y − 1 7 z = 431 210 − 1 8 x + 1 9 y + 1 10 z = − 49 45

For the following exercises, use Gaussian elimination to solve the system.

x −1 7 + y −2 8 + z −3 4 = 0 x + y + z = 6 x + 2 3 + 2 y + z −3 3 = 5 x −1 7 + y −2 8 + z −3 4 = 0 x + y + z = 6 x + 2 3 + 2 y + z −3 3 = 5

x −1 4 − y + 1 4 + 3 z = −1   x + 5 2 + y + 7 4 − z = 4          x + y − z −2 2 = 1 x −1 4 − y + 1 4 + 3 z = −1   x + 5 2 + y + 7 4 − z = 4          x + y − z −2 2 = 1

x −3 4 − y −1 3 + 2 z = −1 x + 5 2 + y + 5 2 + z + 5 2 = 8 x + y + z = 1 x −3 4 − y −1 3 + 2 z = −1 x + 5 2 + y + 5 2 + z + 5 2 = 8 x + y + z = 1

x −3 10 + y + 3 2 −2 z = 3 x + 5 4 − y −1 8 + z = 3 2 x −1 4 + y + 4 2 + 3 z = 3 2 x −3 10 + y + 3 2 −2 z = 3 x + 5 4 − y −1 8 + z = 3 2 x −1 4 + y + 4 2 + 3 z = 3 2

x −3 4 − y −1 3 + 2 z = −1 x + 5 2 + y + 5 2 + z + 5 2 = 7 x + y + z = 1 x −3 4 − y −1 3 + 2 z = −1 x + 5 2 + y + 5 2 + z + 5 2 = 7 x + y + z = 1

Real-World Applications

For the following exercises, set up the augmented matrix that describes the situation, and solve for the desired solution.

Every day, Angeni's cupcake store sells 5,000 cupcakes in chocolate and vanilla flavors. If the chocolate flavor is 3 times as popular as the vanilla flavor, how many of each cupcake does the store sell per day?

At Bakari's competing cupcake store, $4,520 worth of cupcakes are sold daily. The chocolate cupcakes cost $2.25 and the red velvet cupcakes cost $1.75. If the total number of cupcakes sold per day is 2,200, how many of each flavor are sold each day?

You invested $10,000 into two accounts: one that has simple 3% interest, the other with 2.5% interest. If your total interest payment after one year was $283.50, how much was in each account after the year passed?

You invested $2,300 into account 1, and $2,700 into account 2. If the total amount of interest after one year is $254, and account 2 has 1.5 times the interest rate of account 1, what are the interest rates? Assume simple interest rates.

Bikes’R’Us manufactures bikes, which sell for $250. It costs the manufacturer $180 per bike, plus a startup fee of $3,500. After how many bikes sold will the manufacturer break even?

A major appliance store has agreed to order vacuums from a startup founded by college engineering students. The store would be able to purchase the vacuums for $86 each, with a delivery fee of $9,200, regardless of how many vacuums are sold. If the store needs to start seeing a profit after 230 units are sold, how much should they charge for the vacuums?

The three most popular ice cream flavors are chocolate, strawberry, and vanilla, comprising 83% of the flavors sold at an ice cream shop. If vanilla sells 1% more than twice strawberry, and chocolate sells 11% more than vanilla, how much of the total ice cream consumption are the vanilla, chocolate, and strawberry flavors?

At an ice cream shop, three flavors are increasing in demand. Last year, banana, pumpkin, and rocky road ice cream made up 12% of total ice cream sales. This year, the same three ice creams made up 16.9% of ice cream sales. The rocky road sales doubled, the banana sales increased by 50%, and the pumpkin sales increased by 20%. If the rocky road ice cream had one less percent of sales than the banana ice cream, find out the percentage of ice cream sales each individual ice cream made last year.

A bag of mixed nuts contains cashews, pistachios, and almonds. There are 1,000 total nuts in the bag, and there are 100 less almonds than pistachios. The cashews weigh 3 g, pistachios weigh 4 g, and almonds weigh 5 g. If the bag weighs 3.7 kg, find out how many of each type of nut is in the bag.

A bag of mixed nuts contains cashews, pistachios, and almonds. Originally there were 900 nuts in the bag. 30% of the almonds, 20% of the cashews, and 10% of the pistachios were eaten, and now there are 770 nuts left in the bag. Originally, there were 100 more cashews than almonds. Figure out how many of each type of nut was in the bag to begin with.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/7-6-solving-systems-with-gaussian-elimination

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Simultaneous Equations Using Elimination Method

Last Updated: November 28, 2022 Fact Checked

This article was reviewed by Joseph Meyer . Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 115,305 times.

Have you ever had a simultaneous problem equation you needed to solve? When you use the elimination method, you can achieve a desired result in a very short time. This article can explain how to perform to achieve the solution for both variables.

• 3x - y = 12
• 2x + y = 13

• + 2x + y = 13
• -------------

• 3(5) - 3 = 12
• 15 - 3 = 12

Community Q&A

• You can solve it horizontally as well. Thanks Helpful 1 Not Helpful 1
• Remember that if the unknown terms have the same signs you must subtract and if they have different signs you must add the equations. Thanks Helpful 3 Not Helpful 0
• The easiest of all is the elimination method and fastest as well. It is simple and can be learned much more easily then the other two. It is usually used when the equations have the same variable/unknown term disregarding the sign. Thanks Helpful 3 Not Helpful 1

You Might Also Like

• ↑ https://flexbooks.ck12.org/cbook/ck-12-cbse-math-class-10/section/3.6/primary/lesson/solving-simultaneous-linear-equations-by-elimination/
• ↑ https://www.youtube.com/watch?v=O-rrOPPmFgM
• ↑ https://www.youtube.com/watch?v=7Ja_H6a8ltY
• ↑ https://www.mathsteacher.com.au/year10/ch04_simultaneous/03_elimination_method/elim.htm
• ↑ https://www.bbc.co.uk/bitesize/guides/z9y9jty/revision/1
• ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:systems-of-equations/x2f8bb11595b61c86:solving-systems-elimination/a/elimination-method-review

About This Article

• Send fan mail to authors

Reader Success Stories

Jul 27, 2016

Did this article help you?

Featured Articles

Trending Articles

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• elimination\:x+y+z=25,\:5x+3y+2z=0,\:y-z=6
• elimination\:x+2y=2x-5,\:x-y=3
• elimination\:5x+3y=7,\:3x-5y=-23
• elimination\:x+z=1,\:x+2z=4

elimination-system-of-equations-calculator

• High School Math Solutions – Systems of Equations Calculator, Nonlinear In a previous post, we learned about how to solve a system of linear equations. In this post, we will learn how...

Please add a message.

Message received. Thanks for the feedback.

Gauss Elimination Method

Gauss elimination method is used to solve a system of linear equations. Let’s recall the definition of these systems of equations. A system of linear equations is a group of linear equations with various unknown factors. As we know, unknown factors exist in multiple equations. Solving a system involves finding the value for the unknown factors to verify all the equations that make up the system.

If there is a single solution that means one value for each unknown factor, then we can say that the given system is a consistent independent system. If multiple solutions exist, the system has infinitely many solutions; then we say that it is a consistent dependent system. If there is no solution for unknown factors, and this will happen if there are two or more equations that can’t be verified simultaneously, then we say that it’s an inconsistent system.

This can be summarized in a table as given below:

Now, let’s have a look at the method that can be used to find the solution(s) of the given system of equations.

What is the Gauss Elimination Method?

In mathematics, the Gaussian elimination method is known as the row reduction algorithm for solving linear equations systems. It consists of a sequence of operations performed on the corresponding matrix of coefficients. We can also use this method to estimate either of the following:

• The rank of the given matrix
• The determinant of a square matrix
• The inverse of an invertible matrix

To perform row reduction on a matrix, we have to complete a sequence of elementary row operations to transform the matrix till we get 0s (i.e., zeros) on the lower left-hand corner of the matrix as much as possible. That means the obtained matrix should be an upper triangular matrix. There are three types of elementary row operations; they are:

• Swapping two rows and this can be expressed using the notation ↔, for example, R 2 ↔ R 3
• Multiplying a row by a nonzero number, for example, R 1 → kR 2 where k is some nonzero number
• Adding a multiple of one row to another row, for example, R 2 → R 2 + 3R 1

Learn more about the elementary operations of a matrix here.

The obtained matrix will be in row echelon form. The matrix is said to be in reduced row-echelon form when all of the leading coefficients equal 1, and every column containing a leading coefficient has zeros elsewhere. This final form is unique; that means it is independent of the sequence of row operations used. We can understand this in a better way with the help of the example given below.

Gauss Elimination Method with Example

Let’s have a look at the gauss elimination method example with a solution.

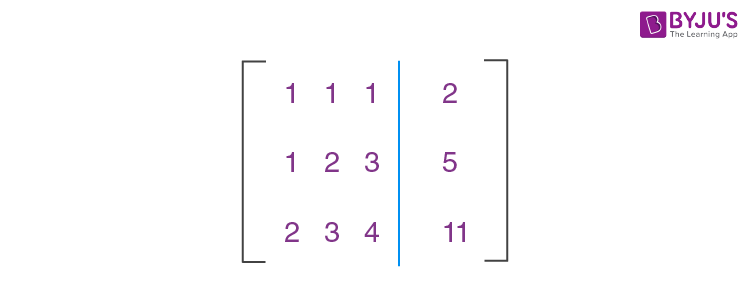
Solve the following system of equations:

x + y + z = 2

x + 2y + 3z = 5

2x + 3y + 4z = 11

Given system of equations are:

Let us write these equations in matrix form.

Subtracting R 1 from R 2 to get the new elements of R 2 , i.e. R 2 → R 2 – R 1 .

From this we get,

Let us make another operation as R 3 → R 3 – 2R 1

Subtract R 2 from R 1 to get the new elements of R 1 , i.e. R 1 → R 1 – R 2 .

Now, subtract R 2 from R 3 to get the new elements of R 3 , i.e. R 3 → R 3 – R 2 .

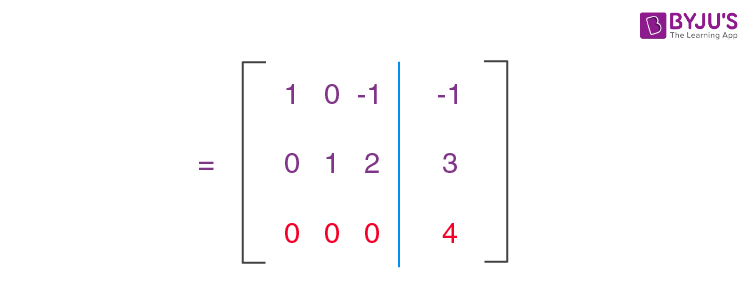
x – z = -1

That means, there is no solution for the given system of equations.

Gauss Elimination Method Problems

1. Solve the following system of equations using Gauss elimination method.

x + y + z = 9

2x + 5y + 7z = 52

2x + y – z = 0

2. Solve the following linear system using the Gaussian elimination method.

4x – 5y = -6

2x – 2y = 1

3. Using Gauss elimination method, solve:

2x – y + 3z = 9

x + y + z = 6

Frequently Asked Questions on Gauss Elimination Method

Why gauss elimination method is used.

The Gauss elimination method is used for solving a given system of linear equations. Other methods of solving system of linear equations are the Jacobi method, Cramer’s rule, Gauss-Seidel method etc.

What type of method is the Gauss elimination method?

The Gauss Elimination method is a direct method for solving a system of linear equations because, within a finite number of determined steps, we can solve the given system of linear equations.

What are the steps of the Gauss elimination method?

The steps of the Gauss elimination method are (1) Write the given system of linear equations in matrix form AX = B, where A is the coefficient matrix, X is a column matrix of unknowns and B is the column matrix of the constants. (2) Reduce the augmented matrix [A : B] by elementary row operations to get [A’ : B’]. (3) We get A’ as an upper triangular matrix. (4) By the backward substitution in A’X = B’, we get the solution of the given system of linear equations.

How Gauss-Jordan Method is different from the Gauss-Elimination method?

Both Gauss-Jordan and Gauss elimination are somewhat similar methods, the only difference is in the Gauss elimination method the matrix is reduced into an upper-triangular matrix whereas in the Gauss-Jordan method is reduced into a diagonal matrix.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

The Elimination Method

Learning Objective(s)

·          Solve a system of equations when no multiplication is necessary to eliminate a variable.

·          Solve a system of equations when multiplication is necessary to eliminate a variable.

·          Recognize systems that have no solution or an infinite number of solutions.

·          Solve application problems using the elimination method.

Introduction

The elimination method for solving systems of linear equations uses the addition property of equality. You can add the same value to each side of an equation.

So if you have a system: x – 6 = −6 and x + y = 8, you can add x + y to the left side of the first equation and add 8 to the right side of the equation. And since x + y = 8, you are adding the same value to each side of the first equation.

Using Addition to Eliminate a Variable

If you add the two equations, x – y = −6 and x + y = 8 together, as noted above, watch what happens.

You have eliminated the y term, and this equation can be solved using the methods for solving equations with one variable.

Let’s see how this system is solved using the elimination method.

Unfortunately not all systems work out this easily. How about a system like 2 x + y = 12 and − 3 x + y = 2. If you add these two equations together, no variables are eliminated.

But you want to eliminate a variable. So let’s add the opposite of one of the equations to the other equation.

 2 x + y =12      →        2 x + y = 12      →       2 x + y = 12

           − 3 x + y = 2      →      − ( − 3 x + y ) = − (2)   →  3 x – y = − 2

                                                                                    5 x + 0 y = 10

You have eliminated the y variable, and the problem can now be solved. See the example below.

The following are two more examples showing how to solve linear systems of equations using elimination.

Notice the coefficients of each variable in each equation. If you add these two equations, the x term will be eliminated since

−2 x + 2 x = 0.

Add and solve for y .

2 x + 5 y = 25

2 x + 5(3) = 25

2 x + 15 = 25

Substitute y = 3 into one of the original equations.

−2x + 3y = −1

−2(5) + 3(3) = −1

−10 + 9 = −1

2(5) + 5(3) = 25

10 + 15 = 25

Check solutions.

The answers check.

The solution is (5, 3).

Notice the coefficients of each variable in each equation. You will need to add the opposite of one of the equations to eliminate the variable y , as 2 y + 2y = 4 y , but

2 y + (−2 y ) = 0.

Change one of the equations to its opposite, add and solve for x .

4 x + 2 y = 14

4(2) + 2 y = 14

8 + 2 y = 14

Substitute x = 2 into one of the original equations and solve for y .

The solution is (2, 3).

Go ahead and check this last example—substitute (2, 3) into both equations. You get two true statements: 14 = 14 and 16 = 16!

Notice that you could have used the opposite of the first equation rather than the second equation and gotten the same result.

Using Multiplication and Addition to Eliminate a Variables

Many times adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below.

3 x + 4 y = 52

5 x + y = 30

If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So let’s now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will result in the coefficient of one of the variables being the opposite of the same variable in the other equation.

This is where multiplication comes in handy. Notice that the first equation contains the term 4 y , and the second equation contains the term y . If you multiply the second equation by −4, when you add both equations the y variables will add up to 0.

3 x + 4 y = 52    →        3 x + 4 y = 52                →             3 x + 4 y =    52

5 x + y = 30      →      − 4(5 x + y ) = − 4(30)      →        − 20 x – 4 y = − 120

                                                                                                − 17 x + 0 y = − 68

See the example below.

Look for terms that can be eliminated. The equations do not have any x or y terms with the same coefficients.

Multiply the second equation by − 4 so they do have the same coefficient.

Rewrite the system, and add the equations.

Solve for x .

3(4) + 4 y = 52

12 + 4 y = 52

Substitute x = 4 into one of the original equations to find y .

3(4) + 4(10) = 52

12 + 40 = 52

5(4) + 10 = 30

20 + 10 = 30

Check your answer.

The solution is (4, 10).

There are other ways to solve this system. Instead of multiplying one equation in order to eliminate a variable when the equations were added, you could have multiplied both equations by different numbers.

Let’s remove the variable x this time. Multiply Equation A by 5 and Equation B by − 3.

Look for terms that can be eliminated. The equations do not have any x or y terms with the same coefficient.

In order to use the elimination method, you have to create variables that have the same coefficient—then you can eliminate them. Multiply the top equation by 5.

Now multiply the bottom equation by −3.

Next add the equations, and solve for y .

3 x + 4(10) = 52

3 x + 40 = 52

Substitute y = 10 into one of the original equations to find x .

You arrive at the same solution as before.

These equations were multiplied by 5 and − 3 respectively, because that gave you terms that would add up to 0. Be sure to multiply all of the terms of the equation.

Special Situations

Just as with the substitution method, the elimination method will sometimes eliminate both v ariables, and you end up with either a true statement or a false statement. Recall that a false statement means that there is no solution.

Let’s look at an example.

Graphing these lines shows that they are parallel lines and as such do not share any point in common, verifying that there is no solution.

If both variables are eliminated and you are left with a true statement, this indicates that there are an infinite number of ordered pairs that satisfy both of the equations. In fact, the equations are the same line.

Graphing these two equations will help to illustrate what is happening.

Solving Application Problems Using the Elimination Method

The elimination method can be applied to solving systems of equations that model real situations. Two examples of using the elimination method in problem solving are shown below.

Combining equations is a powerful tool for solving a system of equations. Adding or subtracting two equations in order to eliminate a common variable is called the elimination (or addition) method. Once one variable is eliminated, it becomes much easier to solve for the other one. Multiplication can be used to set up matching terms in equations before they are combined. When using the multiplication method, it is important to multiply all the terms on both sides of the equation—not just the one term you are trying to eliminate.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.6: Solving Systems with Gaussian Elimination

• Last updated
• Save as PDF
• Page ID 1388

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Write the augmented matrix of a system of equations.
• Write the system of equations from an augmented matrix.
• Perform row operations on a matrix.
• Solve a system of linear equations using matrices.

Carl Friedrich Gauss lived during the late \(18^{th}\) century and early \(19^{th}\) century, but he is still considered one of the most prolific mathematicians in history. His contributions to the science of mathematics and physics span fields such as algebra, number theory, analysis, differential geometry, astronomy, and optics, among others. His discoveries regarding matrix theory changed the way mathematicians have worked for the last two centuries.

We first encountered Gaussian elimination in Systems of Linear Equations: Two Variables . In this section, we will revisit this technique for solving systems, this time using matrices.

Writing the Augmented Matrix of a System of Equations

A matrix can serve as a device for representing and solving a system of equations. To express a system in matrix form, we extract the coefficients of the variables and the constants, and these become the entries of the matrix. We use a vertical line to separate the coefficient entries from the constants, essentially replacing the equal signs. When a system is written in this form, we call it an augmented matrix .

For example, consider the following \(2 × 2\) system of equations.

\[\begin{align*} 3x+4y&= 7\\ 4x-2y&= 5 \end{align*}\]

We can write this system as an augmented matrix:

\(\left[ \begin{array}{cc|c} 3&4&7\\4&-2&5\end{array} \right]\)

We can also write a matrix containing just the coefficients. This is called the coefficient matrix.

\(\begin{bmatrix}3&4\\4&−2\end{bmatrix}\)

A three-by-three system of equations such as

\[\begin{align*} 3x-y-z&= 0\\ x+y&= 5\\ 2x-3z&= 2 \end{align*}\]

has a coefficient matrix

\(\begin{bmatrix}3&−1&−1\\1&1&0\\2&0&−3\end{bmatrix}\)

and is represented by the augmented matrix

\(\left[ \begin{array}{ccc|c}3&−1&−1&0\\1&1&0&5\\2&0&−3&2\end{array} \right]\)

Notice that the matrix is written so that the variables line up in their own columns: \(x\)-terms go in the first column, \(y\)-terms in the second column, and \(z\)-terms in the third column. It is very important that each equation is written in standard form \(ax+by+cz=d\) so that the variables line up. When there is a missing variable term in an equation, the coefficient is \(0\).

How to: Given a system of equations, write an augmented matrix

• Write the coefficients of the \(x\)-terms as the numbers down the first column.
• Write the coefficients of the \(y\)-terms as the numbers down the second column.
• If there are \(z\)-terms, write the coefficients as the numbers down the third column.
• Draw a vertical line and write the constants to the right of the line.

Example \(\PageIndex{1}\): Writing the Augmented Matrix for a System of Equations

Write the augmented matrix for the given system of equations.

\[\begin{align*} x+2y-z&= 3\\ 2x-y+2z&= 6\\ x-3y+3z&= 4 \end{align*}\]

The augmented matrix displays the coefficients of the variables, and an additional column for the constants.

\(\left[ \begin{array}{ccc|c}1&2&−1&3\\2&−1&2&6\\1&−3&3&4\end{array} \right]\)

Exercise \(\PageIndex{1}\)

Write the augmented matrix of the given system of equations.

\[\begin{align*} 4x-3y&= 11\\ 3x+2y&= 4 \end{align*}\]

\(\left[ \begin{array}{cc|c} 4&−3&11\\3&2&4\end{array} \right]\)

Writing a System of Equations from an Augmented Matrix

We can use augmented matrices to help us solve systems of equations because they simplify operations when the systems are not encumbered by the variables. However, it is important to understand how to move back and forth between formats in order to make finding solutions smoother and more intuitive. Here, we will use the information in an augmented matrix to write the system of equations in standard form.

Example \(\PageIndex{2}\): Writing a System of Equations from an Augmented Matrix Form

Find the system of equations from the augmented matrix.

\(\left[ \begin{array}{ccc|c}1&−3&−5&-2\\2&−5&−4&5\\−3&5&4&6 \end{array} \right]\)

When the columns represent the variables \(x\), \(y\), and \(z\),

\[\left[ \begin{array}{ccc|c}1&-3&-5&-2\\2&-5&-4&5\\-3&5&4&6 \end{array} \right] \rightarrow \begin{align*} x-3y-5z&= -2\\ 2x-5y-4z&= 5\\ -3x+5y+4z&= 6 \end{align*}\]

Exercise \(\PageIndex{2}\)

Write the system of equations from the augmented matrix.

\(\left[ \begin{array}{ccc|c}1&−1& 1&5\\2&−1&3&1\\0&1&1&-9\end{array}\right]\)

\(\begin{align*} x-y+z&= 5\\ 2x-y+3z&= 1\\ y+z&= -9 \end{align*}\)

Performing Row Operations on a Matrix

Now that we can write systems of equations in augmented matrix form, we will examine the various row operations that can be performed on a matrix, such as addition, multiplication by a constant, and interchanging rows.

Performing row operations on a matrix is the method we use for solving a system of equations. In order to solve the system of equations, we want to convert the matrix to row-echelon form, in which there are ones down the main diagonal from the upper left corner to the lower right corner, and zeros in every position below the main diagonal as shown.

Row-echelon form \(\begin{bmatrix}1&a&b\\0&1&d\\0&0&1\end{bmatrix}\)

We use row operations corresponding to equation operations to obtain a new matrix that is row-equivalent in a simpler form. Here are the guidelines to obtaining row-echelon form.

• In any nonzero row, the first nonzero number is a \(1\). It is called a leading \(1\).
• Any all-zero rows are placed at the bottom on the matrix.
• Any leading \(1\) is below and to the right of a previous leading \(1\).
• Any column containing a leading \(1\) has zeros in all other positions in the column.

To solve a system of equations we can perform the following row operations to convert the coefficient matrix to row-echelon form and do back-substitution to find the solution.

• Interchange rows. (Notation: \(R_i ↔ R_j\))
• Multiply a row by a constant. (Notation: \(cR_i\))
• Add the product of a row multiplied by a constant to another row. (Notation: \(R_i+cR_j\))

Each of the row operations corresponds to the operations we have already learned to solve systems of equations in three variables. With these operations, there are some key moves that will quickly achieve the goal of writing a matrix in row-echelon form. To obtain a matrix in row-echelon form for finding solutions, we use Gaussian elimination, a method that uses row operations to obtain a \(1\) as the first entry so that row \(1\) can be used to convert the remaining rows.

GAUSSIAN ELIMINATION

The Gaussian elimination method refers to a strategy used to obtain the row-echelon form of a matrix. The goal is to write matrix \(A\) with the number \(1\) as the entry down the main diagonal and have all zeros below.

\(A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}\xrightarrow{After\space Gaussian\space elimination} A=\begin{bmatrix}1&b_{12}& b_{13}\\0&1&b_{23}\\0&0&1\end{bmatrix}\)

The first step of the Gaussian strategy includes obtaining a \(1\) as the first entry, so that row \(1\) may be used to alter the rows below.

How to: Given an augmented matrix, perform row operations to achieve row-echelon form

• The first equation should have a leading coefficient of \(1\). Interchange rows or multiply by a constant, if necessary.
• Use row operations to obtain zeros down the first column below the first entry of \(1\).
• Use row operations to obtain a \(1\) in row 2, column 2.
• Use row operations to obtain zeros down column 2, below the entry of 1.
• Use row operations to obtain a \(1\) in row 3, column 3.
• Continue this process for all rows until there is a \(1 in every entry down the main diagonal and there are only zeros below.
• If any rows contain all zeros, place them at the bottom.

Example \(\PageIndex{3}\): Solving a \(2×2\) System by Gaussian Elimination

Solve the given system by Gaussian elimination.

\[\begin{align*} 2x+3y&= 6\\ x-y&= \dfrac{1}{2} \end{align*}\]

First, we write this as an augmented matrix.

\(\left[ \begin{array}{cc|c} 2&3&6\\1&−1&12\end{array} \right]\)

We want a \(1\) in row 1, column 1. This can be accomplished by interchanging row 1 and row 2.

\(R_1\leftrightarrow R_2\rightarrow \left[ \begin{array}{cc|c} 1&−1&12\\2&3&6\end{array} \right]\)

We now have a \(1\) as the first entry in row 1, column 1. Now let’s obtain a \(0\) in row 2, column 1. This can be accomplished by multiplying row 1 by \(−2\), and then adding the result to row 2.

\(-2R_1+R_2=R_2\rightarrow \left[ \begin{array}{cc|c} 1&−1&12\\0&5&5\end{array} \right]\)

We only have one more step, to multiply row 2 by \(\dfrac{1}{5}\).

\(\dfrac{1}{5}R_2=R_2\rightarrow \left[ \begin{array}{cc|c} 1&−1&12\\0&1&1\end{array} \right]\)

Use back-substitution. The second row of the matrix represents \(y=1\). Back-substitute \(y=1\) into the first equation.

\[\begin{align*} x-(1)&= \dfrac{1}{2}\\ x&= \dfrac{3}{2} \end{align*}\]

The solution is the point \(\left(\dfrac{3}{2},1\right)\).

Exercise \(\PageIndex{3}\)

\[\begin{align*} 4x+3y&= 11\\ x-3y&= -1 \end{align*}\]

Example \(\PageIndex{4}\): Using Gaussian Elimination to Solve a System of Equations

Use Gaussian elimination to solve the given \(2 × 2\) system of equations .

\[\begin{align*} 2x+y&= 1\\ 4x+2y&= 6 \end{align*}\]

Write the system as an augmented matrix .

\(\left[ \begin{array}{cc|c} 2&1&1\\4&2&6\end{array} \right]\)

Obtain a \(1\) in row 1, column 1. This can be accomplished by multiplying the first row by \(\dfrac{1}{2}\).

\(\dfrac{1}{2} R_1=R_1\rightarrow \left[ \begin{array}{cc|c} 1&\dfrac{1}{2}&\dfrac{1}{2}\\4&2&6\end{array} \right]\)

Next, we want a \(0\) in row 2, column 1. Multiply row 1 by \(−4\) and add row 1 to row 2.

\(-4R_1+R_2=R_2\rightarrow \left[ \begin{array}{cc|c} 1&\dfrac{1}{2}&\dfrac{1}{2}\\0&0&4\end{array} \right]\)

The second row represents the equation \(0=4\). Therefore, the system is inconsistent and has no solution.

Example \(\PageIndex{5}\): Solving a Dependent System

Solve the system of equations.

\[\begin{align*} 3x+4y&= 12\\ 6x+8y&= 24 \end{align*}\]

Perform row operations on the augmented matrix to try and achieve row-echelon form .

\(A=\left[ \begin{array}{cc|c} 3&4&12\\6&8&24\end{array} \right]\)

\(-\dfrac{1}{2}R_2+R_1=R_1\rightarrow \left[ \begin{array}{cc|c} 0&0&0\\6&8&24\end{array} \right]\)

\(R_1\leftrightarrow R_2=\left[ \begin{array}{cc|c} 6&8&24\\0&0&0\end{array} \right]\)

The matrix ends up with all zeros in the last row: \(0y=0\). Thus, there are an infinite number of solutions and the system is classified as dependent. To find the generic solution, return to one of the original equations and solve for \(y\).

\[\begin{align*} 3x+4y&= 12\\ 4y&= 12-3x\\ y&= 3-\dfrac{3}{4}x \end{align*}\]

So the solution to this system is \(\left(x,3−\dfrac{3}{4}x\right)\).

Example \(\PageIndex{6}\): Performing Row Operations on a \(3×3\) Augmented Matrix to Obtain Row-Echelon Form

Perform row operations on the given matrix to obtain row-echelon form.

\(\left[ \begin{array}{ccc|c} 1&-3&4&3\\2&-5&6&6\\-3&3&4&6\end{array} \right]\)

The first row already has a \(1\) in row 1, column 1. The next step is to multiply row 1 by \(−2\) and add it to row 2. Then replace row 2 with the result.

\(-2R_1+R_2=R_2 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\-3&3&4&6\end{array} \right]\)

Next, obtain a zero in row 3, column 1.

\(3R_1+R_3=R_3 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\0&-6&16&15\end{array} \right]\)

Next, obtain a zero in row 3, column 2.

\(6R_2+R_3=R_3 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\0&0&4&15\end{array} \right]\)

The last step is to obtain a 1 in row 3, column 3.

\(\dfrac{1}{3}R_3=R_3 \left[ \begin{array}{ccc|c} 1&-3&4&3\\0&1&-2&0\\0&0&1&\dfrac{21}{2}\end{array} \right]\)

Exercise \(\PageIndex{4}\)

Write the system of equations in row-echelon form.

\[\begin{align*} x−2y+3z &= 9 \\ −x+3y &= −4 \\ 2x−5y+5z &= 17 \end{align*}\]

\(\left[ \begin{array}{ccc|c} 1&-\dfrac{5}{2}&\dfrac{5}{2}&\dfrac{17}{2}\\0&1&5&9\\0&0&1&2\end{array} \right]\)

Solving a System of Linear Equations Using Matrices

We have seen how to write a system of equations with an augmented matrix , and then how to use row operations and back-substitution to obtain row-echelon form. Now, we will take row-echelon form a step farther to solve a \(3\) by \(3\) system of linear equations. The general idea is to eliminate all but one variable using row operations and then back-substitute to solve for the other variables.

Example \(\PageIndex{7}\): Solving a System of Linear Equations Using Matrices

Solve the system of linear equations using matrices.

\[\begin{align*} x-y+z&= 8\\ 2x+3y-z&= -2\\ 3x-2y-9z&= 9 \end{align*}\]

First, we write the augmented matrix.

\(\left[ \begin{array}{ccc|c} 1&-1&1&8\\2&3&-1&-2\\3&-2&-9&9\end{array} \right]\)

Next, we perform row operations to obtain row-echelon form.

\(−2R_1+R_2=R_2\rightarrow \left[ \begin{array}{ccc|c} 1&-1&1&8\\0&5&-3&-18\\3&-2&-9&9\end{array} \right]\)

\(−3R_1+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&-1&1&8\\0&5&-3&-18\\0&1&-12&-15\end{array} \right]\)

The easiest way to obtain a \(1\) in row 2 of column 1 is to interchange \(R_2\) and \(R_3\).

\(Interchange\space R_2\space and\space R_3\rightarrow\left[ \begin{array}{ccc|c} 1&-1&1&8\\0&1&-12&-15\\0&5&-3&-18\end{array} \right]\)

\(−5R_2+R_3=R_3\rightarrow\left[ \begin{array}{ccc|c} 1&-1&1&8\\0&1&-12&-15\\0&0&57&57\end{array} \right]\)

\(−\dfrac{1}{57}R_3=R_3\rightarrow\left[ \begin{array}{ccc|c} 1&-1&1&8\\0&1&-12&-15\\0&0&1&1\end{array} \right]\)

The last matrix represents the equivalent system.

\[\begin{align*} x−y+z &= 8 \\ y−12z &= −15 \\ z &= 1 \end{align*}\]

Using back-substitution, we obtain the solution as \((4,−3,1)\).

Example \(\PageIndex{8}\): Solving a Dependent System of Linear Equations Using Matrices

Solve the following system of linear equations using matrices.

\[\begin{align*} −x−2y+z &= −1 \\ 2x+3y &= 2 \\ y−2z &= 0 \end{align*}\]

Write the augmented matrix.

\(\left[ \begin{array}{ccc|c} -1&-2&1&-1\\2&3&0&2\\0&1&-2&0\end{array} \right]\)

First, multiply row 1 by \(−1\) to get a \(1\) in row 1, column 1. Then, perform row operations to obtain row-echelon form.

\(-R_1\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\2&3&0&2\\0&1&-2&0\end{array} \right]\)

\(R_2\leftrightarrow R_3\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\0&1&-2&0\\2&3&0&2\end{array} \right]\)

\(−2R_1+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\0&1&-2&0\\0&-1&2&0\end{array} \right]\)

\(R_2+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&2&-1&1\\0&1&-2&0\\0&0&0&0\end{array} \right]\)

The last matrix represents the following system.

\[\begin{align*} x+2y−z &= 1 \\ y−2z &= 0 \\ 0 &= 0 \end{align*}\]

We see by the identity \(0=0\) that this is a dependent system with an infinite number of solutions. We then find the generic solution. By solving the second equation for \(y\) and substituting it into the first equation we can solve for \(z\) in terms of \(x\).

\[\begin{align*} x+2y−z &= 1 \\ y &= 2z \\ x+2(2z)−z &= 1 \\ x+3z &= 1 \\ z &=\dfrac{1−x}{3} \end{align*}\]

Now we substitute the expression for \(z\) into the second equation to solve for \(y\) in terms of \(x\).

\[\begin{align*} y−2z &= 0 \\ z &= \dfrac{1−x}{3} \\ y−2\left(\dfrac{1−x}{3}\right) &= 0 \\ y &= \dfrac{2−2x}{3} \end{align*}\]

The generic solution is \(\left(x,\dfrac{2−2x}{3},\dfrac{1−x}{3}\right)\).

Exercise \(\PageIndex{5}\)

Solve the system using matrices.

\[\begin{align*} x+4y-z&= 4\\ 2x+5y+8z&= 1\\ 5x+3y-3z&= 1 \end{align*}\]

\((1,1,1)\)

Q&A: Can any system of linear equations be solved by Gaussian elimination?

Yes, a system of linear equations of any size can be solved by Gaussian elimination.

How to: Given a system of equations, solve with matrices using a calculator

• Save the augmented matrix as a matrix variable \([A], [B], [C], ….\)
• Use the ref( function in the calculator, calling up each matrix variable as needed.

Example \(\PageIndex{9A}\): Solving Systems of Equations with Matrices Using a Calculator

\[\begin{align*} 5x+3y+9z&= -1\\ -2x+3y-z&= -2\\ -x-4y+5z&= 1 \end{align*}\]

Write the augmented matrix for the system of equations.

\(\left[ \begin{array}{ccc|c} 5&3&9&-1\\-2&3&-1&-2\\-1&-4&5&1\end{array} \right]\)

On the matrix page of the calculator, enter the augmented matrix above as the matrix variable \([A]\).

\([A]=\left[ \begin{array}{ccc|c} 5&3&9&-1\\-2&3&-1&-2\\-1&-4&5&1\end{array} \right]\)

Use the ref( function in the calculator, calling up the matrix variable \([A]\).

\[\begin{array}{cc} {\left[ \begin{array}{ccc|c} 1&\dfrac{3}{5}&\dfrac{9}{5}&\dfrac{1}{5}\\0&1&\dfrac{13}{21}&-\dfrac{4}{7}\\0&0&1&-\dfrac{24}{187}\end{array} \right] \rightarrow} & {\begin{align*} x+\dfrac{3}{5}y+\dfrac{9}{5}z &= -\dfrac{1}{5} \\ y+\dfrac{13}{21}z &= -\dfrac{4}{7} \\ z &= -\dfrac{24}{187} \end{align*}} \end{array}\]

Using back-substitution, the solution is \(\left(\dfrac{61}{187},−\dfrac{92}{187},−\dfrac{24}{187}\right)\).

Example \(\PageIndex{9B}\): Applying \(2×2\) Matrices to Finance

Carolyn invests a total of \($12,000\) in two municipal bonds, one paying \(10.5%\) interest and the other paying \(12%\) interest. The annual interest earned on the two investments last year was \($1,335\). How much was invested at each rate?

We have a system of two equations in two variables. Let \(x=\) the amount invested at \(10.5%\) interest, and \(y=\) the amount invested at \(12%\) interest.

\[\begin{align*} x+y&= 12,000\\ 0.105x+0.12y&= 1,335 \end{align*}\]

As a matrix, we have

\(\left[ \begin{array}{cc|c} 1&1&12,000\\0.105&0.12&1,335\end{array} \right]\)

Multiply row 1 by \(−0.105\) and add the result to row 2.

\(\left[ \begin{array}{cc|c} 1&1&12,000\\0&0.015&75\end{array} \right]\)

\[\begin{align*} 0.015y &= 75 \\ y &= 5,000 \end{align*}\]

So \(12,000−5,000=7,000\).

Thus, \($5,000\) was invested at \(12%\) interest and \($7,000\) at \(10.5%\) interest.

Example \(\PageIndex{10}\): Applying \(3×3\) Matrices to Finance

Ava invests a total of \($10,000\) in three accounts, one paying \(5%\) interest, another paying \(8%\) interest, and the third paying \(9%\) interest. The annual interest earned on the three investments last year was \($770\). The amount invested at \(9%\) was twice the amount invested at \(5%\). How much was invested at each rate?

We have a system of three equations in three variables. Let \(x\) be the amount invested at \(5%\) interest, let \(y\) be the amount invested at \(8%\) interest, and let \(z\) be the amount invested at \(9%\) interest. Thus,

\[\begin{align*} x+y+z &= 10,000 \\ 0.05x+0.08y+0.09z &= 770 \\ 2x−z &= 0 \end{align*}\]

\(\left[ \begin{array}{ccc|c} 1&1&1&10,000\\0.05&0.08&0.09&770\\2&0&-1&0\end{array} \right]\)

Now, we perform Gaussian elimination to achieve row-echelon form.

\(−0.05R_1+R_2=R_2\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&0.03&0.04&270\\2&0&-1&0\end{array} \right]\)

\(−2R_1+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&0.03&0.04&270\\0&-2&-3&-20,000\end{array} \right]\)

\(\dfrac{1}{0.03}R_2=R_2\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&1&\dfrac{4}{3}&9,000\\0&-2&-3&-20,000\end{array} \right]\)

\(2R_2+R_3=R_3\rightarrow \left[ \begin{array}{ccc|c} 1&1&1&10,000\\0&1&\dfrac{4}{3}&9,000\\0&0&-\dfrac{1}{3}&-2,000\end{array} \right]\)

The third row tells us \(−\dfrac{1}{3}z=−2,000\); thus \(z=6,000\).

The second row tells us \(y+\dfrac{4}{3}z=9,000\). Substituting \(z=6,000\),we get

\[\begin{align*} y+\dfrac{4}{3}(6,000) &= 9,000 \\ y+8,000 &= 9,000 \\ y &= 1,000 \end{align*}\]

The first row tells us \(x+y+z=10,000\). Substituting \(y=1,000\) and \(z=6,000\),we get

\[\begin{align*} x+1,000+6,000 &= 10,000 \\ x &= 3,000 \end{align*}\]

The answer is \($3,000\) invested at \(5%\) interest, \($1,000\) invested at \(8%\), and \($6,000\) invested at \(9%\) interest.

Exercise \(\PageIndex{6}\)

A small shoe company took out a loan of \($1,500,000\) to expand their inventory. Part of the money was borrowed at \(7%\), part was borrowed at \(8%\), and part was borrowed at \(10%\). The amount borrowed at \(10%\) was four times the amount borrowed at \(7%\), and the annual interest on all three loans was \($130,500\). Use matrices to find the amount borrowed at each rate.

\($150,000\) at \(7%\), \($750,000\) at \(8%\), \($600,000\) at \(10%\)

Access these online resources for additional instruction and practice with solving systems of linear equations using Gaussian elimination.

• Solve a System of Two Equations Using an Augmented Matrix
• Solve a System of Three Equations Using an Augmented Matrix
• Augmented Matrices on the Calculator

Key Concepts

• An augmented matrix is one that contains the coefficients and constants of a system of equations. See Example \(\PageIndex{1}\).
• A matrix augmented with the constant column can be represented as the original system of equations. See Example \(\PageIndex{2}\).
• Row operations include multiplying a row by a constant, adding one row to another row, and interchanging rows.
• We can use Gaussian elimination to solve a system of equations. See Example \(\PageIndex{3}\), Example \(\PageIndex{4}\), and Example \(\PageIndex{5}\).
• Row operations are performed on matrices to obtain row-echelon form. See Example \(\PageIndex{6}\).
• To solve a system of equations, write it in augmented matrix form. Perform row operations to obtain row-echelon form. Back-substitute to find the solutions. See Example \(\PageIndex{7}\) and Example \(\PageIndex{8}\).
• A calculator can be used to solve systems of equations using matrices. See Example \(\PageIndex{9}\).
• Many real-world problems can be solved using augmented matrices. See Example \(\PageIndex{10}\) and Example \(\PageIndex{11}\).

Elimination Calculator

gives you step-by-step help on solving systems by elimination.

What do you want to calculate?

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

• Enter your equations separated by a comma in the box, and press Calculate!
• Or click the example.

About Elimination

Need more problem types? Try MathPapa Algebra Calculator

Clear Elimination Calculator »