hypothesis theorem formula

Pythagoras' Theorem

Over 2000 years ago there was an amazing discovery about triangles:

When a triangle has a right angle (90°) ...

... and squares are made on each of the three sides, ...

... then the biggest square has the exact same area as the other two squares put together!

It is called "Pythagoras' Theorem" and can be written in one short equation:

a 2 + b 2 = c 2

• c is the longest side of the triangle
• a and b are the other two sides

The longest side of the triangle is called the "hypotenuse", so the formal definition is:

In a right angled triangle: the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Let's see if it really works using an example.

Example: A "3, 4, 5" triangle has a right angle in it.

Why Is This Useful?

If we know the lengths of two sides of a right angled triangle, we can find the length of the third side . (But remember it only works on right angled triangles!)

How Do I Use it?

Write it down as an equation:

Then we use algebra to find any missing value, as in these examples:

Example: Solve this triangle

Read Builder's Mathematics to see practical uses for this.

Also read about Squares and Square Roots to find out why √ 169 = 13

Example: Solve this triangle.

Example: what is the diagonal distance across a square of size 1.

It works the other way around, too: when the three sides of a triangle make a 2 + b 2 = c 2 , then the triangle is right angled.

Example: Does this triangle have a Right Angle?

Does a 2 + b 2 = c 2 ?

• a 2 + b 2 = 10 2 + 24 2 = 100 + 576 = 676
• c 2 = 26 2 = 676

They are equal, so ...

Yes, it does have a Right Angle!

Example: Does an 8, 15, 16 triangle have a Right Angle?

Does 8 2 + 15 2 = 16 2 ?

• 8 2 + 15 2 = 64 + 225 = 289 ,
• but 16 2 = 256

So, NO, it does not have a Right Angle

Yes, it does!

So this is a right-angled triangle

And You Can Prove The Theorem Yourself !

Get paper pen and scissors, then using the following animation as a guide:

• Draw a right angled triangle on the paper, leaving plenty of space.
• Draw a square along the hypotenuse (the longest side)
• Draw the same sized square on the other side of the hypotenuse
• Draw lines as shown on the animation, like this:

• Cut out the shapes
• Arrange them so that you can prove that the big square has the same area as the two squares on the other sides

Another, Amazingly Simple, Proof

Here is one of the oldest proofs that the square on the long side has the same area as the other squares.

Watch the animation, and pay attention when the triangles start sliding around.

You may want to watch the animation a few times to understand what is happening.

The purple triangle is the important one.

We also have a proof by adding up the areas .

Right Triangles

Rules, Formula and more

Pythagorean Theorem

The sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse .

Usually, this theorem is expressed as $$ A^2 + B^2 = C^2 $$ .

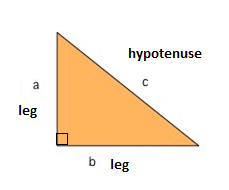
Right Triangle Properties

A right triangle has one $$ 90^{\circ} $$ angle ($$ \angle $$ B in the picture on the left) and a variety of often-studied formulas such as:

• The Pythagorean Theorem
• Trigonometry Ratios (SOHCAHTOA)
• Pythagorean Theorem vs Sohcahtoa (which to use)

SOHCAHTOA only applies to right triangles ( more here ) .

A Right Triangle's Hypotenuse

The hypotenuse is the largest side in a right triangle and is always opposite the right angle.

In the triangle above, the hypotenuse is the side AB which is opposite the right angle, $$ \angle C $$.

Online tool calculates the hypotenuse (or a leg) using the Pythagorean theorem.

Practice Problems

Below are several practice problems involving the Pythagorean theorem, you can also get more detailed lesson on how to use the Pythagorean theorem here .

Find the length of side t in the triangle on the left.

Substitute the two known sides into the Pythagorean theorem's formula : A² + B² = C²

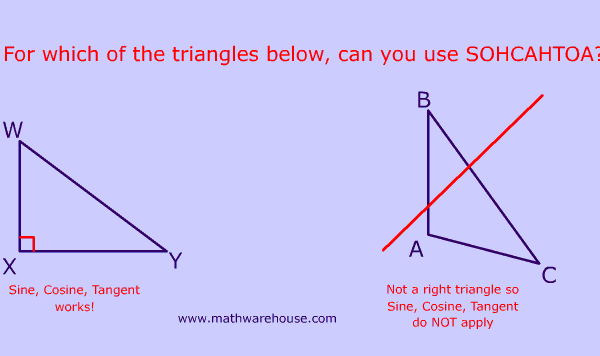
What is the value of x in the picture on the left?

Set up the Pythagorean Theorem : 14 2 + 48 2 = x 2 2,500 = X 2

$$ x = \sqrt{2500} = 50 $$

$$ x^2 = 21^2 + 72^2 \\ x^2= 5625 \\ x = \sqrt{5625} \\ x =75 $$

Find the length of side X in the triangle on on the left?

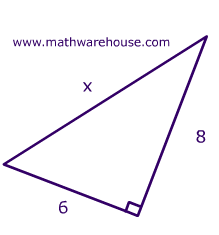
Substitue the two known sides into the pythagorean theorem's formula : $$ A^2 + B^2 = C^2 \\ 8^2 + 6^2 = x^2 \\ x = \sqrt{100}=10 $$

What is x in the triangle on the left?

x 2 + 4 2 = 5 2 x 2 + 16 = 25 x 2 = 25 - 16 = 9 x = 3

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

A free service from Mattecentrum

The Pythagorean Theorem

• Catheters I
• Catheters II
• Catheters III

One of the best known mathematical formulas is Pythagorean Theorem, which provides us with the relationship between the sides in a right triangle. A right triangle consists of two legs and a hypotenuse. The two legs meet at a 90° angle and the hypotenuse is the longest side of the right triangle and is the side opposite the right angle.

The Pythagorean Theorem tells us that the relationship in every right triangle is:

$$a^{2}+b^{2}=c^{2}$$

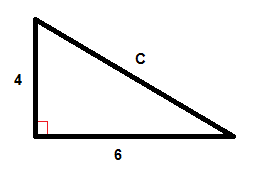
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\approx 7.2$$

There are a couple of special types of right triangles, like the 45°-45° right triangles and the 30°-60° right triangle.

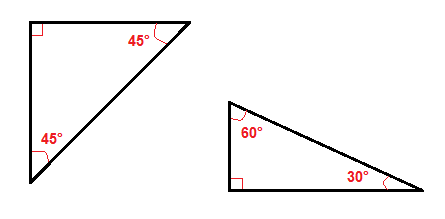
Because of their angles it is easier to find the hypotenuse or the legs in these right triangles than in all other right triangles.

In a 45°-45° right triangle we only need to multiply one leg by √2 to get the length of the hypotenuse.

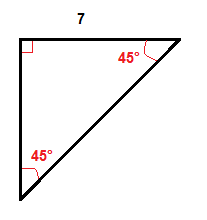
We multiply the length of the leg which is 7 inches by √2 to get the length of the hypotenuse.

$$7\cdot \sqrt{2}\approx 9.9$$

In a 30°-60° right triangle we can find the length of the leg that is opposite the 30° angle by using this formula:

$$a=\frac{1}{2}\cdot c$$

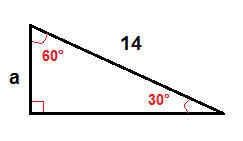
To find a, we use the formula above.

$$a=\frac{1}{2}\cdot 14$$

Video lesson

Find the sides of this right triangle

• Algebra 1 Overview
• Algebra 2 Overview
• Geometry Overview
• SAT Overview
• ACT Overview

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

7.4.1 - hypothesis testing, five step hypothesis testing procedure section  .

In the remaining lessons, we will use the following five step hypothesis testing procedure. This is slightly different from the five step procedure that we used when conducting randomization tests. 

• Check assumptions and write hypotheses.  The assumptions will vary depending on the test. In this lesson we'll be confirming that the sampling distribution is approximately normal by visually examining the randomization distribution. In later lessons you'll learn more objective assumptions. The null and alternative hypotheses will always be written in terms of population parameters; the null hypothesis will always contain the equality (i.e., \(=\)).
• Calculate the test statistic.  Here, we'll be using the formula below for the general form of the test statistic.
• Determine the p-value.  The p-value is the area under the standard normal distribution that is more extreme than the test statistic in the direction of the alternative hypothesis.
• Make a decision.  If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
• State a "real world" conclusion.  Based on your decision in step 4, write a conclusion in terms of the original research question.

General Form of a Test Statistic Section  

When using a standard normal distribution (i.e., z distribution), the test statistic is the standardized value that is the boundary of the p-value. Recall the formula for a z score: \(z=\frac{x-\overline x}{s}\). The formula for a test statistic will be similar. When conducting a hypothesis test the sampling distribution will be centered on the null parameter and the standard deviation is known as the standard error.

This formula puts our observed sample statistic on a standard scale (e.g., z distribution). A z score tells us where a score lies on a normal distribution in standard deviation units. The test statistic tells us where our sample statistic falls on the sampling distribution in standard error units.

Hypotenuse Calculator

Table of contents

With this hypotenuse calculator, you will quickly find the longest side of a right triangle. If you want to know what is the hypotenuse of a right triangle, how to find it, and what is the hypotenuse of a triangle formula, you'll find the answer below, with a simple example to clear things up. Don't wait any longer; give this hypotenuse calculator a try!

How to use this hypotenuse calculator

The following instructions will show you how to use this calculator with ease:

Select which set of parameters is known. You can choose between:

An angle and one side.

Area and one side.

Enter the known parameters , following the labels in the diagram. To input a parameter in a different unit than the default option, click on the unit, change it, and then enter the parameter value.

The tool will immediately calculate the hypotenuse (and any other missing dimensions). Click on the unit to change it to anyone you like.

Consider a right triangle with angle α = 60° and side a = 5 cm. First, we select the option angle and one side and enter these values. Instantly, the calculator determines that:

• Side b = 2.887 cm;
• Angle β = 30°; and
• Hypotenuse c = 5.774 cm.

The calculator is usable in reverse, too. Suppose you must find an unknown side using the hypotenuse (13 cm) and a known side (12 cm). Select two sides as the given parameters, and enter the hypotenuse c = 13 cm and side a = 12 cm. Instantly, you can learn that side b = 5 cm.

The following article explains what the hypotenuse is and how it is calculated using different parameters. It is fun and informative, so we recommend you read it to internalize this concept well.

What is the hypotenuse of a triangle?

A hypotenuse is the longest side of a right triangle . It's the side that is opposite to the right angle (90°). Hypotenuse length may be found, for example, from the Pythagorean theorem. You can learn more about this in our pythagorean theorem calculator .

Hypotenuse of a triangle formula

This hypotenuse calculator has a few formulas implemented - this way, we made sure it fits different scenarios you may encounter. You can find the hypotenuse:

• Given two right triangle legs

Use the Pythagorean theorem to calculate the hypotenuse from the right triangle sides. Take a square root of sum of squares:

• c = √(a² + b²)

• Given an angle and one leg
• c = a / sin(α) = b / sin(β) , explained in our law of sines calculator .
• Given the area and one leg

As the area of a right triangle is equal to a × b / 2 , then

• c = √(a² + b²) = √(a² + (area × 2 / a)²) = √((area × 2 / b)² + b²) .

To learn more about calculations involving right triangles visit our area of a right triangle calculator and the right triangle side and angle calculator .

Ladder example — How to find the hypotenuse of a right triangle with this hypotenuse calculator

Let's calculate how long the ladder should be if we want to rescue a kitten from a 10 ft roof. The calculator helps to find the ladder length from the ground to the edge of the roof, but don't forget about the part of the ladder which should extend over the edge!

• Choose the option needed for your calculations . We know that our roof is 10 ft in height and that the safest angle for a ladder is ~75.5°. From the dropdown list of the given box, select the option: angle ∡ and one side .
• Change the units to feet .

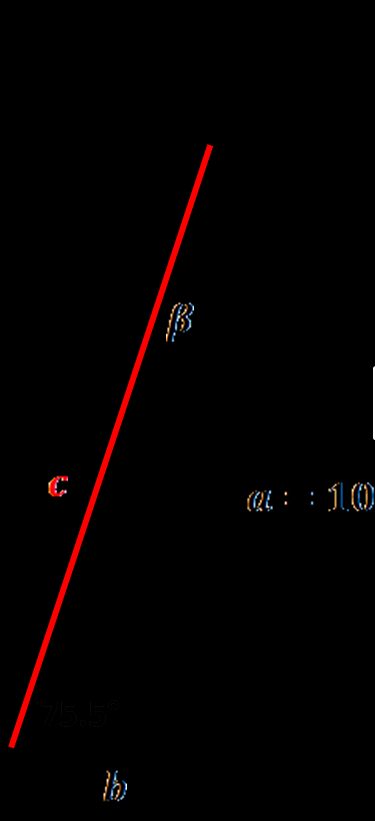
Enter the given values . Our leg a is 10 ft long, and the α angle between the ladder and the ground equals 75.5°.

Ladder length, our right triangle hypotenuse, appears! It's equal to 10.33 ft.

The angle β = 14.5° and leg b = 2.586 ft are displayed as well. The second leg is also an important parameter, as it tells you how far you should place the ladder from the wall (or rather from a roof edge). The general principle to remember is a 4:1 rule – for every four feet of vertical height, the ladder foot should move one foot from the wall.

Creating the hypotenuse calculator

I'm Hanna, a long-time creator at Omni Calculator, having made numerous useful scientific tools besides this one that resonate and help a wide range of people every day! The idea for this calculator came to me while I was calculating the correct length for a ladder to climb up to my roof. Struck by the ubiquitousness of right triangles in our daily lives, I was determined to make this tool so it may help everyone!

We at Omni exercise extreme care to ensure the quality of our content so that it is as accurate and reliable as possible. Each tool is peer-reviewed by a trained expert and then proofread by a native speaker. You can learn more about our standards in our Editorial Policies page.

How do I find hypotenuse with sin?

• Perform the sin operation on the angle (not the right angle).
• Divide the length of the side opposite the angle used in step 1 by the result of step 1.
• The result is the hypotenuse .

Is the hypotenuse always the longest side?

Yes, the hypotenuse is always the longest side , but only for right-angled triangles. For isosceles triangles, the two equal sides are known as the legs, while in an equilateral triangle, all sides are known simply as sides.

How do I find the hypotenuse adjacent and opposite?

• Find the longest side and label it the hypotenuse .
• You can only find the adjacent and opposite sides if you choose one angle less than 90 degrees.
• The adjacent is the side that forms the angle of choice along with the hypotenuse.
• The opposite is the side that does not form the angle of choice.

How do you find the altitude of a hypotenuse?

• Draw the altitude of the hypotenuse on the triangle. The two new triangles you have created are similar to each other and the main triangle.
• Divide the length of the shortest side of the main triangle by the hypotenuse of the main triangle.
• Multiply the result by the length of the remaining side to get the length of the altitude.
• Alternatively, the angles within the smaller triangles will be the same as the angles of the main one, so you can perform trigonometry to find it another way.

What should I do if the hypotenuse is the opposite?

If the hypotenuse is the opposite, then you are considering the wrong angle - you cannot use trigonometry with the right angle of a triangle. Consider one of the other angles. This is as the adjacent angle. The opposite will be the side that does not form that angle.

How do I construct a line perpendicular to the hypotenuse?

• Acquire a pair of compasses, a ruler, and a pen or pencil.
• Set your pair of compasses to the length of the hypotenuse (or any length, as long as it stays constant).
• Draw a circle that has its center at one of the ends of the hypotenuse.
• Draw another circle with its center at the other end of the hypotenuse.
• Draw a line joining the two points where these circles meet. This line is perpendicular to the hypotenuse.

How do I find the hypotenuse of isosceles right triangle?

• Find the length of one of the non-hypotenuse sides .
• Square the length of the side.
• Double the result of the previous step.
• Square root the result of step 3. This is the length of the hypotenuse .

What is the hypotenuse angle theorem?

The hypotenuse angle theorem is a way of testing if two right-angled triangles are congruent or not. It states that if two right-angled triangles have a hypotenuse and an acute angle that is the same, they are congruent.

Where does the word hypotenuse come from?

The word hypotenuse comes from the Ancient Greek hypoteinousa , meaning ‘stretching under (a right angle)’. This, in turn, comes from hypo- ‘under’ and teinein ‘to stretch’. Another thing we have to thank the Ancient Greeks for!

How do I solve a right triangle with only the hypotenuse?

You cannot solve a right-angled triangle with only the hypotenuse . This is because the other two sides and angles are still undefined, so the triangle can still have many forms.

Side length a

Side length b

.css-slt4t3.css-slt4t3{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-slt4t3.css-slt4t3:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-slt4t3 .js-external-link-button.link-like,.css-slt4t3 .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-slt4t3 .js-external-link-button.link-like:hover,.css-slt4t3 .js-external-link-anchor:hover,.css-slt4t3 .js-external-link-button.link-like:active,.css-slt4t3 .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-slt4t3 .js-external-link-button.link-like:focus-visible,.css-slt4t3 .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-slt4t3 p,.css-slt4t3 div{margin:0px;display:block;}.css-slt4t3 pre{margin:0px;display:block;}.css-slt4t3 pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-slt4t3 pre:not(:first-child){padding-top:8px;}.css-slt4t3 ul,.css-slt4t3 ol{display:block margin:0px;padding-left:20px;}.css-slt4t3 ul li,.css-slt4t3 ol li{padding-top:8px;}.css-slt4t3 ul ul,.css-slt4t3 ol ul,.css-slt4t3 ul ol,.css-slt4t3 ol ol{padding-top:0px;}.css-slt4t3 ul:not(:first-child),.css-slt4t3 ol:not(:first-child){padding-top:4px;} .css-4okk7a{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-4okk7a code,.css-4okk7a kbd,.css-4okk7a pre,.css-4okk7a samp{font-family:monospace;}.css-4okk7a code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-4okk7a figcaption,.css-4okk7a caption{text-align:center;}.css-4okk7a figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-4okk7a h3{font-size:1.75rem;}.css-4okk7a h4{font-size:1.5rem;}.css-4okk7a .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-4okk7a .mathBlock .katex{font-size:24px;text-align:left;}.css-4okk7a .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-4okk7a .videoBlock,.css-4okk7a .imageBlock{margin-bottom:16px;}.css-4okk7a .imageBlock__image-align--left,.css-4okk7a .videoBlock__video-align--left{float:left;}.css-4okk7a .imageBlock__image-align--right,.css-4okk7a .videoBlock__video-align--right{float:right;}.css-4okk7a .imageBlock__image-align--center,.css-4okk7a .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-4okk7a .imageBlock__image-align--none,.css-4okk7a .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-4okk7a .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-4okk7a .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-4okk7a .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-4okk7a .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-4okk7a .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-4okk7a .katex .katex-version::after{content:'0.13.13';}.css-4okk7a .katex .katex-mathml{position:absolute;clip:rect(1px, 1px, 1px, 1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-4okk7a .katex .katex-html>.newline{display:block;}.css-4okk7a .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-4okk7a .katex .strut{display:inline-block;}.css-4okk7a .katex .textbf{font-weight:bold;}.css-4okk7a .katex .textit{font-style:italic;}.css-4okk7a .katex .textrm{font-family:KaTeX_Main;}.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .texttt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-4okk7a .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-4okk7a .katex .mathrm{font-style:normal;}.css-4okk7a .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-4okk7a .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-4okk7a .katex .amsrm{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathbb,.css-4okk7a .katex .textbb{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-4okk7a .katex .mathfrak,.css-4okk7a .katex .textfrak{font-family:KaTeX_Fraktur;}.css-4okk7a .katex .mathtt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathscr,.css-4okk7a .katex .textscr{font-family:KaTeX_Script;}.css-4okk7a .katex .mathsf,.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .mathboldsf,.css-4okk7a .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-4okk7a .katex .mathitsf,.css-4okk7a .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-4okk7a .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-4okk7a .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-4okk7a .katex .vlist-r{display:table-row;}.css-4okk7a .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-4okk7a .katex .vlist>span{display:block;height:0;position:relative;}.css-4okk7a .katex .vlist>span>span{display:inline-block;}.css-4okk7a .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-4okk7a .katex .vlist-t2{margin-right:-2px;}.css-4okk7a .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-4okk7a .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-4okk7a .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-4okk7a .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-4okk7a .katex .msupsub{text-align:left;}.css-4okk7a .katex .mfrac>span>span{text-align:center;}.css-4okk7a .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .mfrac .frac-line,.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline,.css-4okk7a .katex .hdashline,.css-4okk7a .katex .rule{min-height:1px;}.css-4okk7a .katex .mspace{display:inline-block;}.css-4okk7a .katex .llap,.css-4okk7a .katex .rlap,.css-4okk7a .katex .clap{width:0;position:relative;}.css-4okk7a .katex .llap>.inner,.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{position:absolute;}.css-4okk7a .katex .llap>.fix,.css-4okk7a .katex .rlap>.fix,.css-4okk7a .katex .clap>.fix{display:inline-block;}.css-4okk7a .katex .llap>.inner{right:0;}.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{left:0;}.css-4okk7a .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-4okk7a .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-4okk7a .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-4okk7a .katex .sizing.reset-size1.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-4okk7a .katex .sizing.reset-size1.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size1.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-4okk7a .katex .sizing.reset-size1.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size1.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size1.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-4okk7a .katex .sizing.reset-size1.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size1.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size1.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-4okk7a .katex .sizing.reset-size1.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-4okk7a .katex .sizing.reset-size1.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-4okk7a .katex .sizing.reset-size2.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size2.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-4okk7a .katex .sizing.reset-size2.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-4okk7a .katex .sizing.reset-size2.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size2.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size2.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-4okk7a .katex .sizing.reset-size2.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-4okk7a .katex .sizing.reset-size2.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size2.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size2.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-4okk7a .katex .sizing.reset-size2.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-4okk7a .katex .sizing.reset-size3.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-4okk7a .katex .sizing.reset-size3.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-4okk7a .katex .sizing.reset-size3.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-4okk7a .katex .sizing.reset-size3.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-4okk7a .katex .sizing.reset-size3.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-4okk7a .katex .sizing.reset-size3.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-4okk7a .katex .sizing.reset-size3.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-4okk7a .katex .sizing.reset-size3.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-4okk7a .katex .sizing.reset-size3.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-4okk7a .katex .sizing.reset-size4.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size4.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size4.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-4okk7a .katex .sizing.reset-size4.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-4okk7a .katex .sizing.reset-size4.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-4okk7a .katex .sizing.reset-size4.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-4okk7a .katex .sizing.reset-size4.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size4.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size4.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-4okk7a .katex .sizing.reset-size4.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-4okk7a .katex .sizing.reset-size4.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-4okk7a .katex .sizing.reset-size5.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size5.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size5.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-4okk7a .katex .sizing.reset-size5.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-4okk7a .katex .sizing.reset-size5.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-4okk7a .katex .sizing.reset-size5.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-4okk7a .katex .sizing.reset-size5.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size5.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size5.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-4okk7a .katex .sizing.reset-size5.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-4okk7a .katex .sizing.reset-size5.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-4okk7a .katex .sizing.reset-size6.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size6.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-4okk7a .katex .sizing.reset-size6.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-4okk7a .katex .sizing.reset-size6.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-4okk7a .katex .sizing.reset-size6.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-4okk7a .katex .sizing.reset-size6.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-4okk7a .katex .sizing.reset-size6.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size6.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size6.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-4okk7a .katex .sizing.reset-size6.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-4okk7a .katex .sizing.reset-size6.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-4okk7a .katex .sizing.reset-size7.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size7.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size7.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-4okk7a .katex .sizing.reset-size7.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size7.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size7.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size7.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-4okk7a .katex .sizing.reset-size7.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size7.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size7.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-4okk7a .katex .sizing.reset-size7.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-4okk7a .katex .sizing.reset-size8.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size8.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size8.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-4okk7a .katex .sizing.reset-size8.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size8.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size8.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size8.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size8.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-4okk7a .katex .sizing.reset-size8.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size8.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-4okk7a .katex .sizing.reset-size8.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-4okk7a .katex .sizing.reset-size9.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-4okk7a .katex .sizing.reset-size9.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size9.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-4okk7a .katex .sizing.reset-size9.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-4okk7a .katex .sizing.reset-size9.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-4okk7a .katex .sizing.reset-size9.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-4okk7a .katex .sizing.reset-size9.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size9.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size9.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-4okk7a .katex .sizing.reset-size9.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-4okk7a .katex .sizing.reset-size9.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-4okk7a .katex .sizing.reset-size10.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-4okk7a .katex .sizing.reset-size10.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-4okk7a .katex .sizing.reset-size10.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-4okk7a .katex .sizing.reset-size10.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-4okk7a .katex .sizing.reset-size10.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-4okk7a .katex .sizing.reset-size10.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-4okk7a .katex .sizing.reset-size10.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-4okk7a .katex .sizing.reset-size10.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-4okk7a .katex .sizing.reset-size10.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-4okk7a .katex .sizing.reset-size10.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-4okk7a .katex .sizing.reset-size10.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-4okk7a .katex .sizing.reset-size11.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-4okk7a .katex .sizing.reset-size11.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-4okk7a .katex .sizing.reset-size11.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-4okk7a .katex .sizing.reset-size11.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-4okk7a .katex .sizing.reset-size11.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-4okk7a .katex .sizing.reset-size11.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-4okk7a .katex .sizing.reset-size11.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-4okk7a .katex .sizing.reset-size11.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-4okk7a .katex .sizing.reset-size11.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-4okk7a .katex .sizing.reset-size11.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-4okk7a .katex .sizing.reset-size11.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-4okk7a .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-4okk7a .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-4okk7a .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-4okk7a .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-4okk7a .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-4okk7a .katex .delimcenter{position:relative;}.css-4okk7a .katex .op-symbol{position:relative;}.css-4okk7a .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-4okk7a .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-4okk7a .katex .op-limits>.vlist-t{text-align:center;}.css-4okk7a .katex .accent>.vlist-t{text-align:center;}.css-4okk7a .katex .accent .accent-body{position:relative;}.css-4okk7a .katex .accent .accent-body:not(.accent-full){width:0;}.css-4okk7a .katex .overlay{display:block;}.css-4okk7a .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-4okk7a .katex .mtable .arraycolsep{display:inline-block;}.css-4okk7a .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-4okk7a .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-4okk7a .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-4okk7a .katex .svg-align{text-align:left;}.css-4okk7a .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-4okk7a .katex svg path{stroke:none;}.css-4okk7a .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-4okk7a .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-4okk7a .katex .stretchy::before,.css-4okk7a .katex .stretchy::after{content:'';}.css-4okk7a .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-4okk7a .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-4okk7a .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .x-arrow-pad{padding:0 0.5em;}.css-4okk7a .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-4okk7a .katex .x-arrow,.css-4okk7a .katex .mover,.css-4okk7a .katex .munder{text-align:center;}.css-4okk7a .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-4okk7a .katex .fbox,.css-4okk7a .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-4okk7a .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-4okk7a .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-4okk7a .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-4okk7a .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-4okk7a .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-4okk7a .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-4okk7a .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-4okk7a .katex .mtr-glue{width:50%;}.css-4okk7a .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-4okk7a .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-4okk7a .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-4okk7a .katex-display{display:block;margin:1em 0;text-align:center;}.css-4okk7a .katex-display>.katex{display:block;white-space:nowrap;}.css-4okk7a .katex-display>.katex>.katex-html{display:block;position:relative;}.css-4okk7a .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-4okk7a .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-4okk7a .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-4okk7a body{counter-reset:katexEqnNo mmlEqnNo;}.css-4okk7a table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-4okk7a .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-4okk7a .tableBlock thead,.css-4okk7a .tableBlock thead th{border-bottom:1px solid #333!important;}.css-4okk7a .tableBlock th,.css-4okk7a .tableBlock td{padding:10px;text-align:left;}.css-4okk7a .tableBlock th{font-weight:bold!important;}.css-4okk7a .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-4okk7a .tableBlock caption>p{margin:0;}.css-4okk7a .tableBlock th>p,.css-4okk7a .tableBlock td>p{margin:0;}.css-4okk7a .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-4okk7a .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-4okk7a .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-4okk7a .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-4okk7a .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-4okk7a .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-4okk7a .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-4okk7a .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-4okk7a .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-4okk7a .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-4okk7a .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-4okk7a .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-4okk7a .tableBlock [data-text-align='center']{text-align:center;}.css-4okk7a .tableBlock [data-text-align='left']{text-align:left;}.css-4okk7a .tableBlock [data-text-align='right']{text-align:right;}.css-4okk7a .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-4okk7a .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-4okk7a .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-4okk7a .tableBlock__font-size--xxsmall{font-size:10px;}.css-4okk7a .tableBlock__font-size--xsmall{font-size:12px;}.css-4okk7a .tableBlock__font-size--small{font-size:14px;}.css-4okk7a .tableBlock__font-size--large{font-size:18px;}.css-4okk7a .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--bordered td,.css-4okk7a .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--borderless tbody+tbody,.css-4okk7a .tableBlock__border--borderless td,.css-4okk7a .tableBlock__border--borderless th,.css-4okk7a .tableBlock__border--borderless tr,.css-4okk7a .tableBlock__border--borderless thead,.css-4okk7a .tableBlock__border--borderless thead th{border:0!important;}.css-4okk7a .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-4okk7a .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-4okk7a .tableBlock__table-compactl th,.css-4okk7a .tableBlock__table-compact td{padding:3px!important;}.css-4okk7a .tableBlock__full-size{width:100%;}.css-4okk7a .textBlock{margin-bottom:16px;}.css-4okk7a .textBlock__text-formatting--finePrint{font-size:12px;}.css-4okk7a .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-4okk7a .textBlock__text-infoBox p{margin:0;}.css-4okk7a .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-4okk7a .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-4okk7a .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-4okk7a .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-4okk7a .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-4okk7a .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-4okk7a .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-4okk7a .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-4okk7a.css-4okk7a{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-4okk7a.css-4okk7a:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-4okk7a .js-external-link-button.link-like,.css-4okk7a .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-4okk7a .js-external-link-button.link-like:hover,.css-4okk7a .js-external-link-anchor:hover,.css-4okk7a .js-external-link-button.link-like:active,.css-4okk7a .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-4okk7a .js-external-link-button.link-like:focus-visible,.css-4okk7a .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-4okk7a p,.css-4okk7a div{margin:0px;display:block;}.css-4okk7a pre{margin:0px;display:block;}.css-4okk7a pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-4okk7a pre:not(:first-child){padding-top:8px;}.css-4okk7a ul,.css-4okk7a ol{display:block margin:0px;padding-left:20px;}.css-4okk7a ul li,.css-4okk7a ol li{padding-top:8px;}.css-4okk7a ul ul,.css-4okk7a ol ul,.css-4okk7a ul ol,.css-4okk7a ol ol{padding-top:0px;}.css-4okk7a ul:not(:first-child),.css-4okk7a ol:not(:first-child){padding-top:4px;} Hypotenuse

Side length c

4.4 The Mean Value Theorem

Learning objectives.

• 4.4.1 Explain the meaning of Rolle’s theorem.
• 4.4.2 Describe the significance of the Mean Value Theorem.
• 4.4.3 State three important consequences of the Mean Value Theorem.

The Mean Value Theorem is one of the most important theorems in calculus. We look at some of its implications at the end of this section. First, let’s start with a special case of the Mean Value Theorem, called Rolle’s theorem.

Rolle’s Theorem

Informally, Rolle’s theorem states that if the outputs of a differentiable function f f are equal at the endpoints of an interval, then there must be an interior point c c where f ′ ( c ) = 0 . f ′ ( c ) = 0 . Figure 4.21 illustrates this theorem.

Theorem 4.4

Let f f be a continuous function over the closed interval [ a , b ] [ a , b ] and differentiable over the open interval ( a , b ) ( a , b ) such that f ( a ) = f ( b ) . f ( a ) = f ( b ) . There then exists at least one c ∈ ( a , b ) c ∈ ( a , b ) such that f ′ ( c ) = 0 . f ′ ( c ) = 0 .

Let k = f ( a ) = f ( b ) . k = f ( a ) = f ( b ) . We consider three cases:

• f ( x ) = k f ( x ) = k for all x ∈ ( a , b ) . x ∈ ( a , b ) .
• There exists x ∈ ( a , b ) x ∈ ( a , b ) such that f ( x ) > k . f ( x ) > k .
• There exists x ∈ ( a , b ) x ∈ ( a , b ) such that f ( x ) < k . f ( x ) < k .

Case 1: If f ( x ) = k f ( x ) = k for all x ∈ ( a , b ) , x ∈ ( a , b ) , then f ′ ( x ) = 0 f ′ ( x ) = 0 for all x ∈ ( a , b ) . x ∈ ( a , b ) .

Case 2: Since f f is a continuous function over the closed, bounded interval [ a , b ] , [ a , b ] , by the extreme value theorem, it has an absolute maximum. Also, since there is a point x ∈ ( a , b ) x ∈ ( a , b ) such that f ( x ) > k , f ( x ) > k , the absolute maximum is greater than k . k . Therefore, the absolute maximum does not occur at either endpoint. As a result, the absolute maximum must occur at an interior point c ∈ ( a , b ) . c ∈ ( a , b ) . Because f f has a maximum at an interior point c , c , and f f is differentiable at c , c , by Fermat’s theorem, f ′ ( c ) = 0 . f ′ ( c ) = 0 .

Case 3: The case when there exists a point x ∈ ( a , b ) x ∈ ( a , b ) such that f ( x ) < k f ( x ) < k is analogous to case 2, with maximum replaced by minimum.

An important point about Rolle’s theorem is that the differentiability of the function f f is critical. If f f is not differentiable, even at a single point, the result may not hold. For example, the function f ( x ) = | x | − 1 f ( x ) = | x | − 1 is continuous over [ −1 , 1 ] [ −1 , 1 ] and f ( −1 ) = 0 = f ( 1 ) , f ( −1 ) = 0 = f ( 1 ) , but f ′ ( c ) ≠ 0 f ′ ( c ) ≠ 0 for any c ∈ ( −1 , 1 ) c ∈ ( −1 , 1 ) as shown in the following figure.

Let’s now consider functions that satisfy the conditions of Rolle’s theorem and calculate explicitly the points c c where f ′ ( c ) = 0 . f ′ ( c ) = 0 .

Example 4.14

Using rolle’s theorem.

For each of the following functions, verify that the function satisfies the criteria stated in Rolle’s theorem and find all values c c in the given interval where f ′ ( c ) = 0 . f ′ ( c ) = 0 .

• f ( x ) = x 2 + 2 x f ( x ) = x 2 + 2 x over [ −2 , 0 ] [ −2 , 0 ]
• f ( x ) = x 3 − 4 x f ( x ) = x 3 − 4 x over [ −2 , 2 ] [ −2 , 2 ]

Checkpoint 4.14

Verify that the function f ( x ) = 2 x 2 − 8 x + 6 f ( x ) = 2 x 2 − 8 x + 6 defined over the interval [ 1 , 3 ] [ 1 , 3 ] satisfies the conditions of Rolle’s theorem. Find all points c c guaranteed by Rolle’s theorem.

The Mean Value Theorem and Its Meaning

Rolle’s theorem is a special case of the Mean Value Theorem. In Rolle’s theorem, we consider differentiable functions f f defined on a closed interval [ a , b ] [ a , b ] with f ( a ) = f ( b ) f ( a ) = f ( b ) . The Mean Value Theorem generalizes Rolle’s theorem by considering functions that do not necessarily have equal value at the endpoints. Consequently, we can view the Mean Value Theorem as a slanted version of Rolle’s theorem ( Figure 4.25 ). The Mean Value Theorem states that if f f is continuous over the closed interval [ a , b ] [ a , b ] and differentiable over the open interval ( a , b ) , ( a , b ) , then there exists a point c ∈ ( a , b ) c ∈ ( a , b ) such that the tangent line to the graph of f f at c c is parallel to the secant line connecting ( a , f ( a ) ) ( a , f ( a ) ) and ( b , f ( b ) ) . ( b , f ( b ) ) .

Theorem 4.5

Mean value theorem.

Let f f be continuous over the closed interval [ a , b ] [ a , b ] and differentiable over the open interval ( a , b ) . ( a , b ) . Then, there exists at least one point c ∈ ( a , b ) c ∈ ( a , b ) such that

The proof follows from Rolle’s theorem by introducing an appropriate function that satisfies the criteria of Rolle’s theorem. Consider the line connecting ( a , f ( a ) ) ( a , f ( a ) ) and ( b , f ( b ) ) . ( b , f ( b ) ) . Since the slope of that line is

and the line passes through the point ( a , f ( a ) ) , ( a , f ( a ) ) , the equation of that line can be written as

Let g ( x ) g ( x ) denote the vertical difference between the point ( x , f ( x ) ) ( x , f ( x ) ) and the point ( x , y ) ( x , y ) on that line. Therefore,

Since the graph of f f intersects the secant line when x = a x = a and x = b , x = b , we see that g ( a ) = 0 = g ( b ) . g ( a ) = 0 = g ( b ) . Since f f is a differentiable function over ( a , b ) , ( a , b ) , g g is also a differentiable function over ( a , b ) . ( a , b ) . Furthermore, since f f is continuous over [ a , b ] , [ a , b ] , g g is also continuous over [ a , b ] . [ a , b ] . Therefore, g g satisfies the criteria of Rolle’s theorem. Consequently, there exists a point c ∈ ( a , b ) c ∈ ( a , b ) such that g ′ ( c ) = 0 . g ′ ( c ) = 0 . Since

we see that

Since g ′ ( c ) = 0 , g ′ ( c ) = 0 , we conclude that

In the next example, we show how the Mean Value Theorem can be applied to the function f ( x ) = x f ( x ) = x over the interval [ 0 , 9 ] . [ 0 , 9 ] . The method is the same for other functions, although sometimes with more interesting consequences.

Example 4.15

Verifying that the mean value theorem applies.

For f ( x ) = x f ( x ) = x over the interval [ 0 , 9 ] , [ 0 , 9 ] , show that f f satisfies the hypothesis of the Mean Value Theorem, and therefore there exists at least one value c ∈ ( 0 , 9 ) c ∈ ( 0 , 9 ) such that f ′ ( c ) f ′ ( c ) is equal to the slope of the line connecting ( 0 , f ( 0 ) ) ( 0 , f ( 0 ) ) and ( 9 , f ( 9 ) ) . ( 9 , f ( 9 ) ) . Find these values c c guaranteed by the Mean Value Theorem.

We know that f ( x ) = x f ( x ) = x is continuous over [ 0 , 9 ] [ 0 , 9 ] and differentiable over ( 0 , 9 ) . ( 0 , 9 ) . Therefore, f f satisfies the hypotheses of the Mean Value Theorem, and there must exist at least one value c ∈ ( 0 , 9 ) c ∈ ( 0 , 9 ) such that f ′ ( c ) f ′ ( c ) is equal to the slope of the line connecting ( 0 , f ( 0 ) ) ( 0 , f ( 0 ) ) and ( 9 , f ( 9 ) ) ( 9 , f ( 9 ) ) ( Figure 4.27 ). To determine which value(s) of c c are guaranteed, first calculate the derivative of f . f . The derivative f ′ ( x ) = 1 ( 2 x ) . f ′ ( x ) = 1 ( 2 x ) . The slope of the line connecting ( 0 , f ( 0 ) ) ( 0 , f ( 0 ) ) and ( 9 , f ( 9 ) ) ( 9 , f ( 9 ) ) is given by

We want to find c c such that f ′ ( c ) = 1 3 . f ′ ( c ) = 1 3 . That is, we want to find c c such that

Solving this equation for c , c , we obtain c = 9 4 . c = 9 4 . At this point, the slope of the tangent line equals the slope of the line joining the endpoints.

One application that helps illustrate the Mean Value Theorem involves velocity. For example, suppose we drive a car for 1 h down a straight road with an average velocity of 45 mph. Let s ( t ) s ( t ) and v ( t ) v ( t ) denote the position and velocity of the car, respectively, for 0 ≤ t ≤ 1 0 ≤ t ≤ 1 h. Assuming that the position function s ( t ) s ( t ) is differentiable, we can apply the Mean Value Theorem to conclude that, at some time c ∈ ( 0 , 1 ) , c ∈ ( 0 , 1 ) , the speed of the car was exactly

Example 4.16

Mean value theorem and velocity.

If a rock is dropped from a height of 100 ft, its position t t seconds after it is dropped until it hits the ground is given by the function s ( t ) = −16 t 2 + 100 . s ( t ) = −16 t 2 + 100 .

• Determine how long it takes before the rock hits the ground.
• Find the average velocity v avg v avg of the rock for when the rock is released and the rock hits the ground.
• Find the time t t guaranteed by the Mean Value Theorem when the instantaneous velocity of the rock is v avg . v avg .
• When the rock hits the ground, its position is s ( t ) = 0 . s ( t ) = 0 . Solving the equation −16 t 2 + 100 = 0 −16 t 2 + 100 = 0 for t , t , we find that t = ± 5 2 sec . t = ± 5 2 sec . Since we are only considering t ≥ 0 , t ≥ 0 , the ball will hit the ground 5 2 5 2 sec after it is dropped.
• The average velocity is given by v avg = s ( 5 / 2 ) − s ( 0 ) 5 / 2 − 0 = 0 − 100 5 / 2 = −40 ft/sec . v avg = s ( 5 / 2 ) − s ( 0 ) 5 / 2 − 0 = 0 − 100 5 / 2 = −40 ft/sec .

Checkpoint 4.15

Suppose a ball is dropped from a height of 200 ft. Its position at time t t is s ( t ) = −16 t 2 + 200 . s ( t ) = −16 t 2 + 200 . Find the time t t when the instantaneous velocity of the ball equals its average velocity.

Corollaries of the Mean Value Theorem

Let’s now look at three corollaries of the Mean Value Theorem. These results have important consequences, which we use in upcoming sections.

At this point, we know the derivative of any constant function is zero. The Mean Value Theorem allows us to conclude that the converse is also true. In particular, if f ′ ( x ) = 0 f ′ ( x ) = 0 for all x x in some interval I , I , then f ( x ) f ( x ) is constant over that interval. This result may seem intuitively obvious, but it has important implications that are not obvious, and we discuss them shortly.

Theorem 4.6

Corollary 1: functions with a derivative of zero.

Let f f be differentiable over an interval I . I . If f ′ ( x ) = 0 f ′ ( x ) = 0 for all x ∈ I , x ∈ I , then f ( x ) = f ( x ) = constant for all x ∈ I . x ∈ I .

Since f f is differentiable over I , I , f f must be continuous over I . I . Suppose f ( x ) f ( x ) is not constant for all x x in I . I . Then there exist a , b ∈ I , a , b ∈ I , where a ≠ b a ≠ b and f ( a ) ≠ f ( b ) . f ( a ) ≠ f ( b ) . Choose the notation so that a < b . a < b . Therefore,

Since f f is a differentiable function, by the Mean Value Theorem, there exists c ∈ ( a , b ) c ∈ ( a , b ) such that

Therefore, there exists c ∈ I c ∈ I such that f ′ ( c ) ≠ 0 , f ′ ( c ) ≠ 0 , which contradicts the assumption that f ′ ( x ) = 0 f ′ ( x ) = 0 for all x ∈ I . x ∈ I .

From Corollary 1: Functions with a Derivative of Zero , it follows that if two functions have the same derivative, they differ by, at most, a constant.

Theorem 4.7

Corollary 2: constant difference theorem.

If f f and g g are differentiable over an interval I I and f ′ ( x ) = g ′ ( x ) f ′ ( x ) = g ′ ( x ) for all x ∈ I , x ∈ I , then f ( x ) = g ( x ) + C f ( x ) = g ( x ) + C for some constant C . C .

Let h ( x ) = f ( x ) − g ( x ) . h ( x ) = f ( x ) − g ( x ) . Then, h ′ ( x ) = f ′ ( x ) − g ′ ( x ) = 0 h ′ ( x ) = f ′ ( x ) − g ′ ( x ) = 0 for all x ∈ I . x ∈ I . By Corollary 1, there is a constant C C such that h ( x ) = C h ( x ) = C for all x ∈ I . x ∈ I . Therefore, f ( x ) = g ( x ) + C f ( x ) = g ( x ) + C for all x ∈ I . x ∈ I .

The third corollary of the Mean Value Theorem discusses when a function is increasing and when it is decreasing. Recall that a function f f is increasing over I I if f ( x 1 ) < f ( x 2 ) f ( x 1 ) < f ( x 2 ) whenever x 1 < x 2 , x 1 < x 2 , whereas f f is decreasing over I I if f ( x ) 1 > f ( x 2 ) f ( x ) 1 > f ( x 2 ) whenever x 1 < x 2 . x 1 < x 2 . Using the Mean Value Theorem, we can show that if the derivative of a function is positive, then the function is increasing; if the derivative is negative, then the function is decreasing ( Figure 4.29 ). We make use of this fact in the next section, where we show how to use the derivative of a function to locate local maximum and minimum values of the function, and how to determine the shape of the graph.

This fact is important because it means that for a given function f , f , if there exists a function F F such that F ′ ( x ) = f ( x ) ; F ′ ( x ) = f ( x ) ; then, the only other functions that have a derivative equal to f f are F ( x ) + C F ( x ) + C for some constant C . C . We discuss this result in more detail later in the chapter.

Theorem 4.8

Corollary 3: increasing and decreasing functions.

Let f f be continuous over the closed interval [ a , b ] [ a , b ] and differentiable over the open interval ( a , b ) . ( a , b ) .

• If f ′ ( x ) > 0 f ′ ( x ) > 0 for all x ∈ ( a , b ) , x ∈ ( a , b ) , then f f is an increasing function over [ a , b ] . [ a , b ] .
• If f ′ ( x ) < 0 f ′ ( x ) < 0 for all x ∈ ( a , b ) , x ∈ ( a , b ) , then f f is a decreasing function over [ a , b ] . [ a , b ] .

We will prove i.; the proof of ii. is similar. Suppose f f is not an increasing function on I . I . Then there exist a a and b b in I I such that a < b , a < b , but f ( a ) > f ( b ) . f ( a ) > f ( b ) . Since f f is a differentiable function over I , I , by the Mean Value Theorem there exists c ∈ ( a , b ) c ∈ ( a , b ) such that

Since f ( a ) > f ( b ) , f ( a ) > f ( b ) , we know that f ( b ) − f ( a ) < 0 . f ( b ) − f ( a ) < 0 . Also, a < b a < b tells us that b − a > 0 . b − a > 0 . We conclude that

However, f ′ ( x ) > 0 f ′ ( x ) > 0 for all x ∈ I . x ∈ I . This is a contradiction, and therefore f f must be an increasing function over I . I .

Section 4.4 Exercises

Why do you need continuity to apply the Mean Value Theorem? Construct a counterexample.

Why do you need differentiability to apply the Mean Value Theorem? Find a counterexample.

When are Rolle’s theorem and the Mean Value Theorem equivalent?

If you have a function with a discontinuity, is it still possible to have f ′ ( c ) ( b − a ) = f ( b ) − f ( a ) ? f ′ ( c ) ( b − a ) = f ( b ) − f ( a ) ? Draw such an example or prove why not.

For the following exercises, determine over what intervals (if any) the Mean Value Theorem applies. Justify your answer.

y = sin ( π x ) y = sin ( π x )

y = 1 x 3 y = 1 x 3

y = 4 − x 2 y = 4 − x 2

y = x 2 − 4 y = x 2 − 4

y = ln ( 3 x − 5 ) y = ln ( 3 x − 5 )

For the following exercises, graph the functions on a calculator and draw the secant line that connects the endpoints. Estimate the number of points c c such that f ′ ( c ) ( b − a ) = f ( b ) − f ( a ) . f ′ ( c ) ( b − a ) = f ( b ) − f ( a ) .

[T] y = 3 x 3 + 2 x + 1 y = 3 x 3 + 2 x + 1 over [ −1 , 1 ] [ −1 , 1 ]

[T] y = tan ( π 4 x ) y = tan ( π 4 x ) over [ − 3 2 , 3 2 ] [ − 3 2 , 3 2 ]

[T] y = x 2 cos ( π x ) y = x 2 cos ( π x ) over [ −2 , 2 ] [ −2 , 2 ]

[T] y = x 6 − 3 4 x 5 − 9 8 x 4 + 15 16 x 3 + 3 32 x 2 + 3 16 x + 1 32 y = x 6 − 3 4 x 5 − 9 8 x 4 + 15 16 x 3 + 3 32 x 2 + 3 16 x + 1 32 over [ −1 , 1 ] [ −1 , 1 ]

For the following exercises, use the Mean Value Theorem and find all points 0 < c < 2 0 < c < 2 such that f ( 2 ) − f ( 0 ) = f ′ ( c ) ( 2 − 0 ) . f ( 2 ) − f ( 0 ) = f ′ ( c ) ( 2 − 0 ) .

f ( x ) = x 3 f ( x ) = x 3

f ( x ) = sin ( π x ) f ( x ) = sin ( π x )

f ( x ) = cos ( 2 π x ) f ( x ) = cos ( 2 π x )

f ( x ) = 1 + x + x 2 f ( x ) = 1 + x + x 2

f ( x ) = ( x − 1 ) 10 f ( x ) = ( x − 1 ) 10

f ( x ) = ( x − 1 ) 9 f ( x ) = ( x − 1 ) 9

For the following exercises, show there is no c c such that f ( 1 ) − f ( −1 ) = f ′ ( c ) ( 2 ) . f ( 1 ) − f ( −1 ) = f ′ ( c ) ( 2 ) . Explain why the Mean Value Theorem does not apply over the interval [ −1 , 1 ] . [ −1 , 1 ] .

f ( x ) = | x − 1 2 | f ( x ) = | x − 1 2 |

f ( x ) = 1 x 2 f ( x ) = 1 x 2

f ( x ) = | x | f ( x ) = | x |

f ( x ) = ⌊ x ⌋ f ( x ) = ⌊ x ⌋ ( Hint : This is called the floor function and it is defined so that f ( x ) f ( x ) is the largest integer less than or equal to x . ) x . )

For the following exercises, determine whether the Mean Value Theorem applies for the functions over the given interval [ a , b ] . [ a , b ] . Justify your answer.

y = e x y = e x over [ 0 , 1 ] [ 0 , 1 ]

y = ln ( 2 x + 3 ) y = ln ( 2 x + 3 ) over [ − 3 2 , 0 ] [ − 3 2 , 0 ]

f ( x ) = tan ( 2 π x ) f ( x ) = tan ( 2 π x ) over [ 0 , 2 ] [ 0 , 2 ]

y = 9 − x 2 y = 9 − x 2 over [ −3 , 3 ] [ −3 , 3 ]

y = 1 | x + 1 | y = 1 | x + 1 | over [ 0 , 3 ] [ 0 , 3 ]

y = x 3 + 2 x + 1 y = x 3 + 2 x + 1 over [ 0 , 6 ] [ 0 , 6 ]

y = x 2 + 3 x + 2 x y = x 2 + 3 x + 2 x over [ −1 , 1 ] [ −1 , 1 ]

y = x sin ( π x ) + 1 y = x sin ( π x ) + 1 over [ 0 , 1 ] [ 0 , 1 ]

y = ln ( x + 1 ) y = ln ( x + 1 ) over [ 0 , e − 1 ] [ 0 , e − 1 ]

y = x sin ( π x ) y = x sin ( π x ) over [ 0 , 2 ] [ 0 , 2 ]

y = 5 + | x | y = 5 + | x | over [ −1 , 1 ] [ −1 , 1 ]

For the following exercises, consider the roots of the equation.

Show that the equation y = x 3 + 4 x + 16 y = x 3 + 4 x + 16 has exactly one real root. What is it?

Find the conditions for exactly one root (double root) for the equation y = x 2 + b x + c y = x 2 + b x + c

Find the conditions for y = e x − b y = e x − b to have one root. Is it possible to have more than one root?

For the following exercises, use a calculator to graph the function over the interval [ a , b ] [ a , b ] and graph the secant line from a a to b . b . Use the calculator to estimate all values of c c as guaranteed by the Mean Value Theorem. Then, find the exact value of c , c , if possible, or write the final equation and use a calculator to estimate to four digits.

[T] y = tan ( π x ) y = tan ( π x ) over [ − 1 4 , 1 4 ] [ − 1 4 , 1 4 ]

[T] y = 1 x + 1 y = 1 x + 1 over [ 0 , 3 ] [ 0 , 3 ]

[T] y = | x 2 + 2 x − 4 | y = | x 2 + 2 x − 4 | over [ −4 , 0 ] [ −4 , 0 ]

[T] y = x + 1 x y = x + 1 x over [ 1 2 , 4 ] [ 1 2 , 4 ]

[T] y = x + 1 + 1 x 2 y = x + 1 + 1 x 2 over [ 3 , 8 ] [ 3 , 8 ]

At 10:17 a.m., you pass a police car at 55 mph that is stopped on the freeway. You pass a second police car at 55 mph at 10:53 a.m., which is located 39 mi from the first police car. If the speed limit is 60 mph, can the police cite you for speeding?

Two cars drive from one stoplight to the next, leaving at the same time and arriving at the same time. Is there ever a time when they are going the same speed? Prove or disprove.

Show that y = sec 2 x y = sec 2 x and y = tan 2 x y = tan 2 x have the same derivative. What can you say about y = sec 2 x − tan 2 x ? y = sec 2 x − tan 2 x ?

Show that y = csc 2 x y = csc 2 x and y = cot 2 x y = cot 2 x have the same derivative. What can you say about y = csc 2 x − cot 2 x ? y = csc 2 x − cot 2 x ?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution-NonCommercial-ShareAlike License and you must attribute OpenStax.

Access for free at https://openstax.org/books/calculus-volume-1/pages/1-introduction

• Authors: Gilbert Strang, Edwin “Jed” Herman
• Publisher/website: OpenStax
• Book title: Calculus Volume 1
• Publication date: Mar 30, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/calculus-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/calculus-volume-1/pages/4-4-the-mean-value-theorem

© Feb 5, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

17.2: Bayesian Hypothesis Tests

• Last updated
• Save as PDF
• Page ID 4050

• Danielle Navarro
• University of New South Wales

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In Chapter 11 I described the orthodox approach to hypothesis testing. It took an entire chapter to describe, because null hypothesis testing is a very elaborate contraption that people find very hard to make sense of. In contrast, the Bayesian approach to hypothesis testing is incredibly simple. Let’s pick a setting that is closely analogous to the orthodox scenario. There are two hypotheses that we want to compare, a null hypothesis h 0 and an alternative hypothesis h 1 . Prior to running the experiment we have some beliefs P(h) about which hypotheses are true. We run an experiment and obtain data d. Unlike frequentist statistics Bayesian statistics does allow to talk about the probability that the null hypothesis is true. Better yet, it allows us to calculate the posterior probability of the null hypothesis , using Bayes’ rule:

\(\ P(h_0 | d) = \dfrac{P(d | h_0)P(h_0)}{P(d)}\)

This formula tells us exactly how much belief we should have in the null hypothesis after having observed the data d. Similarly, we can work out how much belief to place in the alternative hypothesis using essentially the same equation. All we do is change the subscript:

\(\ P(h_1 | d) = \dfrac{P(d | h_1)P(h_1)}{P(d)}\)

It’s all so simple that I feel like an idiot even bothering to write these equations down, since all I’m doing is copying Bayes rule from the previous section. 259

Bayes factor

In practice, most Bayesian data analysts tend not to talk in terms of the raw posterior probabilities P(h 0 |d) and P(h 1 |d). Instead, we tend to talk in terms of the posterior odds ratio. Think of it like betting. Suppose, for instance, the posterior probability of the null hypothesis is 25%, and the posterior probability of the alternative is 75%. The alternative hypothesis is three times as probable as the null, so we say that the odds are 3:1 in favour of the alternative. Mathematically, all we have to do to calculate the posterior odds is divide one posterior probability by the other:

\(\ \dfrac{P(h_1 | d)}{P(h_0 | d)}=\dfrac{0.75}{0.25}=3\)

Or, to write the same thing in terms of the equations above:

\(\ \dfrac{P(h_1 | d)}{P(h_0 | d)} = \dfrac{P(d | h_1)}{P(d | h_0)} \times \dfrac{P(h_1)}{P(h_0)}\)

Actually, this equation is worth expanding on. There are three different terms here that you should know. On the left hand side, we have the posterior odds, which tells you what you believe about the relative plausibilty of the null hypothesis and the alternative hypothesis after seeing the data. On the right hand side, we have the prior odds , which indicates what you thought before seeing the data. In the middle, we have the Bayes factor , which describes the amount of evidence provided by the data:

The Bayes factor (sometimes abbreviated as BF ) has a special place in the Bayesian hypothesis testing, because it serves a similar role to the p-value in orthodox hypothesis testing: it quantifies the strength of evidence provided by the data, and as such it is the Bayes factor that people tend to report when running a Bayesian hypothesis test. The reason for reporting Bayes factors rather than posterior odds is that different researchers will have different priors. Some people might have a strong bias to believe the null hypothesis is true, others might have a strong bias to believe it is false. Because of this, the polite thing for an applied researcher to do is report the Bayes factor. That way, anyone reading the paper can multiply the Bayes factor by their own personal prior odds, and they can work out for themselves what the posterior odds would be. In any case, by convention we like to pretend that we give equal consideration to both the null hypothesis and the alternative, in which case the prior odds equals 1, and the posterior odds becomes the same as the Bayes factor.

Interpreting Bayes factors

One of the really nice things about the Bayes factor is the numbers are inherently meaningful. If you run an experiment and you compute a Bayes factor of 4, it means that the evidence provided by your data corresponds to betting odds of 4:1 in favour of the alternative. However, there have been some attempts to quantify the standards of evidence that would be considered meaningful in a scientific context. The two most widely used are from Jeffreys (1961) and Kass and Raftery (1995). Of the two, I tend to prefer the Kass and Raftery (1995) table because it’s a bit more conservative. So here it is:

And to be perfectly honest, I think that even the Kass and Raftery standards are being a bit charitable. If it were up to me, I’d have called the “positive evidence” category “weak evidence”. To me, anything in the range 3:1 to 20:1 is “weak” or “modest” evidence at best. But there are no hard and fast rules here: what counts as strong or weak evidence depends entirely on how conservative you are, and upon the standards that your community insists upon before it is willing to label a finding as “true”.

In any case, note that all the numbers listed above make sense if the Bayes factor is greater than 1 (i.e., the evidence favours the alternative hypothesis). However, one big practical advantage of the Bayesian approach relative to the orthodox approach is that it also allows you to quantify evidence for the null. When that happens, the Bayes factor will be less than 1. You can choose to report a Bayes factor less than 1, but to be honest I find it confusing. For example, suppose that the likelihood of the data under the null hypothesis P(d|h 0 ) is equal to 0.2, and the corresponding likelihood P(d|h 0 ) under the alternative hypothesis is 0.1. Using the equations given above, Bayes factor here would be:

\(\ BF=\dfrac{P(d | h_1)}{P(d | h_0}=\dfrac{0.1}{0.2}=0.5\)

Read literally, this result tells is that the evidence in favour of the alternative is 0.5 to 1. I find this hard to understand. To me, it makes a lot more sense to turn the equation “upside down”, and report the amount op evidence in favour of the null . In other words, what we calculate is this:

\(\ BF^{\prime} = \dfrac{P(d | h_0)}{P(d | h_1)}=\dfrac{0.2}{0.1}=2\)

And what we would report is a Bayes factor of 2:1 in favour of the null. Much easier to understand, and you can interpret this using the table above.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• CBSE Class 12 Maths Notes: Chapter Wise Notes PDF 2024

Chapter 1: Relations and Functions

• Types of Functions
• Composite functions - Relations and functions
• Invertible Functions
• Composition of Functions
• Inverse Functions
• Verifying Inverse Functions by Composition

Chapter 2: Inverse Trigonometric Functions

• Inverse Trigonometric Functions
• Graphs of Inverse Trigonometric Functions - Trigonometry | Class 12 Maths
• Properties of Inverse Trigonometric Functions
• Inverse Trigonometric Identities

Chapter 3: Matrices

• Types of Matrices
• Matrix Operations
• Matrix Addition
• Matrix Multiplication - How to Multiply Matrices, Methods, Examples
• Transpose of a Matrix
• Symmetric and Skew Symmetric Matrices
• Elementary Operations on Matrices
• Inverse of a Matrix by Elementary Operations - Matrices | Class 12 Maths
• Invertible Matrix

Chapter 4: Determinants

• Determinant of a Matrix with Solved Examples
• Properties of Determinants
• Area of a Triangle using Determinants
• Minors and Cofactors
• Adjoint of a Matrix
• Applications of Matrices and Determinants

Chapter 5: Continuity and Differentiability

• Continuity and Discontinuity in Calculus - Class 12 CBSE
• Differentiability of a Function | Class 12 Maths
• Derivatives of Inverse Functions
• Derivatives of Implicit Functions - Continuity and Differentiability | Class 12 Maths
• Derivatives of Composite Functions
• Derivatives of Inverse Trigonometric Functions | Class 12 Maths
• Derivative of Exponential Functions
• Logarithmic Differentiation - Continuity and Differentiability
• Proofs for the derivatives of eˣ and ln(x) - Advanced differentiation
• Rolle's Theorem and Lagrange's Mean Value Theorem
• Derivative of Functions in Parametric Forms
• Second Order Derivatives: Rules , Formula and Examples (Class 12 Maths)
• Mean Value Theorem
• Algebra of Continuous Functions - Continuity and Differentiability | Class 12 Maths

Chapter 6: Applications of Derivatives

• Critical Points
• Derivatives as Rate of Change
• Increasing and Decreasing Functions
• Increasing and Decreasing Intervals
• Tangents and Normals
• Equation of Tangents and Normals
• Relative Minima and Maxima
• Absolute Minima and Maxima
• Concave Function
• Inflection Point
• Curve Sketching
• Approximations & Maxima and Minima - Application of Derivatives | Class 12 Maths
• Higher Order Derivatives

Chapter 7: Integrals

• Integration by Substitution Method
• Integration by Partial Fractions
• Integration by Parts
• Integration of Trigonometric Functions
• Functions Defined by Integrals
• Definite Integral
• Computing Definite Integrals
• Fundamental Theorem of Calculus
• Finding Derivative with Fundamental Theorem of Calculus
• Evaluating Definite Integrals
• Properties of Definite Integrals
• Definite Integrals of Piecewise Functions
• Improper Integrals
• Riemann Sums
• Riemann Sums in Summation Notation
• Trapezoidal Rule
• Definite Integral as the Limit of a Riemann Sum
• Antiderivatives
• Indefinite Integrals
• Particular Solutions to Differential Equations
• Integration by U-substitution
• Reverse Chain Rule
• Partial Fraction Expansion
• Trigonometric Substitution: Method, Formula and Solved Examples

Chapter 8: Applications of Integrals

• Area under Simple Curves
• Area Between Two Curves - Calculus
• Area between Polar Curves
• Area as Definite Integral

Chapter 9: Differential Equations

• Differential Equations
• Homogeneous Differential Equations
• Separable Differential Equations
• Exact Equations and Integrating Factors
• Implicit Differentiation
• Implicit differentiation - Advanced Examples
• Advanced Differentiation
• Disguised Derivatives - Advanced differentiation | Class 12 Maths
• Derivative of Inverse Trig Functions
• Logarithmic Differentiation

Chapter 10: Vector Algebra

• Vector Algebra
• Dot and Cross Products on Vectors
• How to Find the Angle Between Two Vectors?
• Section Formula - Vector Algebra

Chapter 11: Three-dimensional Geometry

• Direction Cosines and Direction Ratios
• Equation of a Line in 3D
• Angles Between two Lines in 3D Space: Solved Examples
• Shortest Distance Between Two Lines in 3D Space | Class 12 Maths
• Points, Lines and Planes

Chapter 12: Linear Programming

• Linear Programming
• Graphical Solution of Linear Programming Problems

Chapter 13: Probability

• Conditional Probability and Independence - Probability | Class 12 Maths
• Multiplication Theorem
• Dependent and Independent Events
• Bayes' Theorem
• Probability Distribution - Function, Formula, Table
• Binomial Distribution in Probability
• Binomial Mean and Standard Deviation - Probability | Class 12 Maths
• Bernoulli Trials and Binomial Distribution
• Discrete Random Variable
• Expected Value
• NCERT Solution for Class 12 Math PDF 2024-25
• RD Sharma Class 12 Solutions for Maths

Bayes’ Theorem

Bayes’ Theorem is used to determine the conditional probability of an event. It was named after an English statistician, Thomas Bayes who discovered this formula in 1763. Bayes Theorem is a very important theorem in mathematics, that laid the foundation of a unique statistical inference approach called the Bayes’ inference. It is used to find the probability of an event, based on prior knowledge of conditions that might be related to that event.

For example, if we want to find the probability that a white marble drawn at random came from the first bag, given that a white marble has already been drawn, and there are three bags each containing some white and black marbles, then we can use Bayes’ Theorem.

This article explores the Bayes theorem including its statement, proof, derivation, and formula of the theorem, as well as its applications with various examples.

What is Bayes’ Theorem?

Bayes theorem (also known as the Bayes Rule or Bayes Law) is used to determine the conditional probability of event A when event B has already occurred.

The general statement of Bayes’ theorem is “ The conditional probability of an event A, given the occurrence of another event B, is equal to the product of the event of B, given A and the probability of A divided by the probability of event B.” i.e.

P(A|B) = P(B|A)P(A) / P(B)

where, P(A) and P(B) are the probabilities of events A and B P(A|B) is the probability of event A when event B happens P(B|A) is the probability of event B when A happens

Check: Bayes’s Theorem for Conditional Probability

Bayes Theorem Statement

Bayes’ Theorem for n set of events is defined as,

Let E 1 , E 2 ,…, E n be a set of events associated with the sample space S, in which all the events E 1 , E 2 ,…, E n have a non-zero probability of occurrence. All the events E 1 , E 2 ,…, E form a partition of S. Let A be an event from space S for which we have to find probability, then according to Bayes’ theorem,

P(E i |A) = P(E i )P(A|E i ) / ∑ P(E k )P(A|E k ) for k = 1, 2, 3, …., n

Bayes Theorem Formula

For any two events A and B, then the formula for the Bayes theorem is given by: (the image given below gives the Bayes’ theorem formula)

Bayes’ Theorem Formula

• P(A) and P(B) are the probabilities of events A and B also P(B) is never equal to zero.
• P(A|B) is the probability of event A when event B happens
• P(B|A) is the probability of event B when A happens

Bayes Theorem Derivation

The proof of Bayes’ Theorem is given as, according to the conditional probability formula,

P(E i |A) = P(E i ∩A) / P(A)…..(i)

Then, by using the multiplication rule of probability, we get

P(E i ∩A) = P(E i )P(A|E i )……(ii)

Now, by the total probability theorem,

P(A) = ∑ P(E k )P(A|E k )…..(iii)

Substituting the value of P(E i ∩A) and P(A) from eq (ii) and eq(iii) in eq(i) we get,

P(E i |A) = P(E i )P(A|E i ) / ∑ P(E k )P(A|E k )

Bayes’ theorem is also known as the formula for the probability of “causes” . As we know, the E i ‘s are a partition of the sample space S, and at any given time only one of the events E i occurs. Thus we conclude that the Bayes’ theorem formula gives the probability of a particular E i , given the event A has occurred.

Terms Related to Bayes Theorem

After learning about Bayes theorem in detail, let us understand some important terms related to the concepts we covered in formula and derivation.

• Hypotheses: Events happening in the sample space E 1 , E 2 ,… E n is called the hypotheses
• Priori Probability: Priori Probability is the initial probability of an event occurring before any new data is taken into account. P(E i ) is the priori probability of hypothesis E i .
• Posterior Probability: Posterior Probability is the updated probability of an event after considering new information. Probability P(E i |A) is considered as the posterior probability of hypothesis E i .

Conditional Probability

• The probability of an event A based on the occurrence of another event B is termed conditional Probability .
• It is denoted as P(A|B) and represents the probability of A when event B has already happened.

Joint Probability

When the probability of two more events occurring together and at the same time is measured it is marked as Joint Probability. For two events A and B, it is denoted by joint probability is denoted as, P(A∩B).

Random Variables

Real-valued variables whose possible values are determined by random experiments are called random variables. The probability of finding such variables is the experimental probability.

Bayes’ Theorem Applications

Bayesian inference is very important and has found application in various activities, including medicine, science, philosophy, engineering, sports, law, etc., and Bayesian inference is directly derived from Bayes’ theorem.

Example: Bayes’ theorem defines the accuracy of the medical test by taking into account how likely a person is to have a disease and what is the overall accuracy of the test.

Difference Between Conditional Probability and Bayes Theorem

The difference between Conditional Probability and Bayes Theorem can be understood with the help of the table given below,

Theorem of Total Probability

Let E 1 , E 2 , . . ., E n is mutually exclusive and exhaustive events associated with a random experiment and lets E be an event that occurs with some E i . Then, prove that 

P(E) = n ∑ i=1 P(E/E i ) . P(E j )

Let S be the sample space. Then, S = E 1 ∪ E 2 ∪ E 3  ∪ . . . ∪ En and E i ∩ E j = ∅ for i ≠ j. E = E ∩ S  ⇒ E = E ∩ (E 1 ∪ E 2 ∪ E 3 ∪ . . . ∪ E n ) ⇒ E = (E ∩ E 1 ) ∪ (E ∩ E 2 ) ∪ . . . ∪ (E ∩ E n ) P(E) = P{(E ∩ E 1 ) ∪ (E ∩ E 2 )∪ . . . ∪(E ∩ E n )} ⇒ P(E) = P(E ∩ E 1 ) + P(E ∩ E 2 ) + . . . + P(E ∩ E n ) {Therefore, (E ∩ E 1 ), (E ∩ E 2 ), . . . ,(E ∩ E n )} are pairwise disjoint} ⇒ P(E) = P(E/E 1 ) . P(E 1 ) + P(E/E 2 ) . P(E 2 ) + . . . + P(E/E n ) . P(E n )  [by multiplication theorem] ⇒ P(E) = n ∑ i=1 P(E/E i ) . P(E i )

Articles Related to Bayes’ Theorem

Probability Distribution Bayes’ Theorem for Conditional Probability Permutations and Combinations Binomial Theorem

Conclusion – Bayes’ Theorem

Bayes’ Theorem offers a powerful framework for updating the probability of a hypothesis based on new evidence or information. By incorporating prior knowledge and updating it with observed data, Bayes’ Theorem allows for more accurate and informed decision-making in a wide range of fields, including statistics, machine learning, medicine, and finance. Its applications span from medical diagnosis and risk assessment to spam filtering and natural language processing.

Understanding and applying Bayes’ Theorem enables us to make better predictions, estimate uncertainties, and draw meaningful insights from data, ultimately enhancing our ability to make informed decisions in complex and uncertain situations.

Also Check:

• Bayes’ Theorem in Data Mining
• Bayes Theorem in Artificial Intelligence
• Bayes Theorem in Machine learning

Bayes Theorem Examples

Example 1: A person has undertaken a job. The probabilities of completion of the job on time with and without rain are 0.44 and 0.95 respectively. If the probability that it will rain is 0.45, then determine the probability that the job will be completed on time.

Let E 1 be the event that the mining job will be completed on time and E 2 be the event that it rains. We have, P(A) = 0.45, P(no rain) = P(B) = 1 − P(A) = 1 − 0.45 = 0.55 By multiplication law of probability, P(E 1 ) = 0.44, and P(E 2 ) = 0.95 Since, events A and B form partitions of the sample space S, by total probability theorem, we have P(E) = P(A) P(E 1 ) + P(B) P(E 2 ) ⇒ P(E) = 0.45 × 0.44 + 0.55 × 0.95 ⇒ P(E) = 0.198 + 0.5225 = 0.7205 So, the probability that the job will be completed on time is 0.7205

Example 2: There are three urns containing 3 white and 2 black balls; 2 white and 3 black balls; 1 black and 4 white balls respectively. There is an equal probability of each urn being chosen. One ball is equal probability chosen at random. what is the probability that a white ball is drawn?

Let E 1 , E 2 , and E 3 be the events of choosing the first, second, and third urn respectively. Then, P(E 1 ) = P(E 2 ) = P(E 3 ) =1/3 Let E be the event that a white ball is drawn. Then, P(E/E 1 ) = 3/5, P(E/E 2 ) = 2/5, P(E/E 3 ) = 4/5 By theorem of total probability, we have P(E) = P(E/E 1 ) . P(E 1 ) + P(E/E 2 ) . P(E 2 ) + P(E/E 3 ) . P(E 3 ) ⇒ P(E) = (3/5 × 1/3) + (2/5 × 1/3) + (4/5 × 1/3) ⇒ P(E) = 9/15 = 3/5

Example 3: A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both hearts. find the probability of the lost card being a heart.

Let E 1 , E 2 , E 3, and E 4 be the events of losing a card of hearts, clubs, spades, and diamonds respectively. Then P(E 1 ) = P(E 2 ) = P(E 3 ) = P(E 4 ) = 13/52 = 1/4. Let E be the event of drawing 2 hearts from the remaining 51 cards. Then, P(E|E 1 ) = probability of drawing 2 hearts, given that a card of hearts is missing ⇒ P(E|E 1 ) = 12 C 2 / 51 C 2 = (12 × 11)/2! × 2!/(51 × 50) = 22/425 P(E|E 2 ) = probability of drawing 2 clubs ,given that a card of clubs is missing ⇒ P(E|E 2 ) = 13 C 2 / 51 C 2 = (13 × 12)/2! × 2!/(51 × 50) = 26/425 P(E|E 3 ) = probability of drawing 2 spades ,given that a card of hearts is missing ⇒ P(E|E 3 ) = 13 C 2 / 51 C 2 = 26/425 P(E|E 4 ) = probability of drawing 2 diamonds ,given that a card of diamonds is missing ⇒ P(E|E 4 ) = 13 C 2 / 51 C 2 = 26/425 Therefore, P(E 1 |E) = probability of the lost card is being a heart, given the 2 hearts are drawn from the remaining 51 cards ⇒ P(E 1 |E) = P(E 1 ) . P(E|E 1 )/P(E 1 ) . P(E|E 1 ) + P(E 2 ) . P(E|E 2 ) + P(E 3 ) . P(E|E 3 ) + P(E 4 ) . P(E|E 4 ) ⇒ P(E 1 |E) = (1/4 × 22/425) / {(1/4 × 22/425) + (1/4 × 26/425) + (1/4 × 26/425) + (1/4 × 26/425)} ⇒ P(E 1 |E) = 22/100 = 0.22 Hence, The required probability is 0.22.

Example 4: Suppose 15 men out of 300 men and 25 women out of 1000 are good orators. An orator is chosen at random. Find the probability that a male person is selected. Assume that there are equal numbers of men and women.

Gievn, Total Men = 300 Total Women = 1000 Good orators among Men = 15 Good orators among Women = 25 Total number of good orators = 15 (from men) + 25 (from women) = 40 Probability of selecting a male orator: P(Male Orator) = Numbers of male orators / total no of orators = 15/40

Example 5: A man is known to speak the lies 1 out of 4 times. He throws a die and reports that it is a six. Find the probability that is actually a six.

In a throw of a die, let E 1 = event of getting a six, E 2 = event of not getting a six and E = event that the man reports that it is a six. Then, P(E 1 ) = 1/6, and P(E 2 ) = (1 – 1/6) = 5/6 P(E|E 1 ) = probability that the man reports that six occurs when six has actually occurred  ⇒ P(E|E 1 ) = probability that the man speaks the truth ⇒ P(E|E 1 ) = 3/4 P(E|E 2 ) = probability that the man reports that six occurs when six has not actually occurred ⇒ P(E|E 2 ) = probability that the man does not speak the truth ⇒ P(E|E 2 ) = (1 – 3/4) = 1/4 Probability of getting a six ,given that the man reports it to be six  P(E 1 |E) = P(E|E 1 ) × P(E 1 )/P(E|E 1 ) × P(E 1 ) + P(E|E 2 ) × P(E 2 )     [by Bayes’ theorem] ⇒ P(E 1 |E) = (3/4 × 1/6)/{(3/4 × 1/6) + (1/4 × 5/6)} ⇒ P(E 1 |E) = (1/8 × 3) = 3/8 Hence the probability required is 3/8.

FAQs on Bayes’ Theorem

What is bayes’ theorem.

Bayes, theorem as the name suggest is a mathematical theorem which is used to find the conditionality probability of an event. Conditional probability is the probability of the event which will occur in future. It is calculated based on the previous outcomes of the events.

When is Bayes’ theorem used?

Bayes’ theorem has a wide range of applications, especially in fields that deal with updating probabilities based on new data. Bayes rule lets you calculate the posterior (or updated) probability. It is used to calculate conditional probability of events.

What are some key terms to understand Bayes’ theorem?

Some of the key terms are: Prior Probability (P(A)) Posterior Probability (P(A | B)) Likelihood (P(B | A)) Marginal Probability (P(B))

When to use Bayes’ theorem?

Bayes’ theorem is applicable when the conditional probability of an event is given, it is used to find the reverse probability of the event.

How is Bayes’ theorem different from conditional probability?

Bayes’ theorem is used to define the probability of an event based on the previous conditions of the event. Whereas, Bayes’ Theorem uses conditional probability to find the reverse probability of the event.

What is the formula for Bayes’ theorem?

Bayes theorem formula is explained below, P(A|B) = [P(B|A) P(A)] / P(B)

Please Login to comment...

Similar reads.

• Maths-Class-12
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Hypotenuse Formula

The hypotenuse formula is used in a right-angled triangle, to calculate the longest side that is called the hypotenuse. The hypotenuse is always the side that is opposite to the right angle in a right triangle. We use the Pythagoras theorem to find the hypotenuse, and thus the hypotenuse formula.

What Is Hypotenuse Formula?

Hypotenuse formula or the  Pythagoras theorem  is defined as the square of the hypotenuse is equal to the sum of the squares of the other two sides (legs). Let us understand the derivation of the hypotenuse formula with the help of the Pythagoras theorem.

Pythagoras Theorem

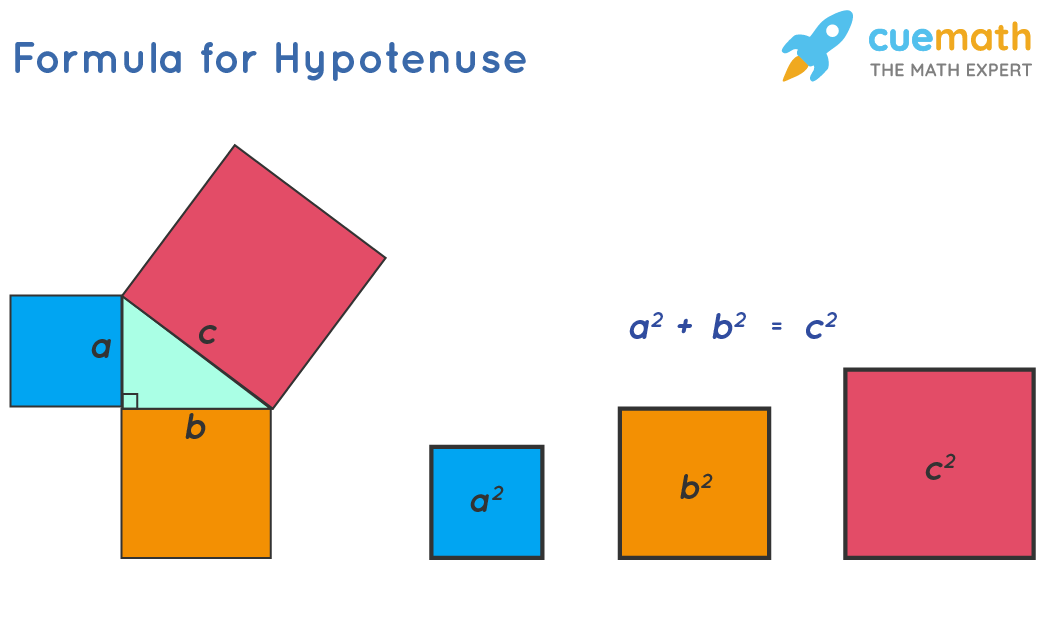
• c = hypotenuse
• a = height (a leg)
• b = base (a leg)

From Pythagoras theorem, (hypotenuse) 2  = (base) 2  + (height) 2

If we take the square root on both sides, we get the formula of the hypotenuse.

Hypotenuse formula = √((base) 2  + (height) 2 ) (or) c =  √ (a 2  + b 2 )

Book a Free Trial Class

Examples on Hypotenuse Formula

Let us solve some interesting problems using the hypotenuse formula.

Example 1: Using hypotenuse formula solve for the longest side of the given bread slice that is similar to a right-angle triangle. Its height is 13 units and its base is 5 units.

To find: The longest side (hypotenuse) of the bread slice.

Its height = 13 units.

Its base = 5 units.

By using the hypotenuse formula,

hypotenuse formula = √ ((base) 2  + (height  2 )

=√(5 2 +13 2 ) =√25+169 =√194 =13.98

Answer: The longest side of the bread slice = 13.928 units.

Example 2: The hypotenuse of a right triangle is 5 units. Its base is 3 units. Find its height using the hypotenuse formula.

To find: The height of the right triangle. Let us assume it to be 'h' Its hypotenuse = 5 units. Its base = 3 units. By using the hypotenuse formula, hypotenuse 2  = (base) 2  + (height) 2

5 2  = 3 2  + h 2 25 = 9 + h 2 25−9 = h 2 16 = h 2 4 = h

Answer: The height of the right triangle = 4 units.

Example 3: Using the hypotenuse formula, solve for the longest side of the given bread slice that is similar to a right-angle triangle. Its height is 14 units and its base is 8 units.

Solution:  

Its height = 14 units.

Its base = 8 units.

hypotenuse formula = √((base) 2  + (height  2 )

=√(8 2 +14 2 ) =√64+196 =√260 =16.124

Answer: The longest side of the bread slice = 16.124 units.

FAQs on Hypotenuse Formula 

How do you find the hypotenuse of a triangle using the hypotenuse formula .

By using the Pythagorean theorem (Hypotenuse) 2  = (Base) 2  + (Altitude) 2 ,  we can calculate the hypotenuse. If the values of the other two sides are known, the hypotenuse can be easily calculated with this formula. It is also known as the hypotenuse formula.

How Do you Find the Longest Side of a Triangle Using the Hypotenuse Formula? 

The hypotenuse is termed as the longest side of a right-angled triangle. To find the longest side we use the hypotenuse formula that can be easily driven from the Pythagoras theorem, (Hypotenuse) 2  = (Base) 2  + (Altitude) 2 . Hypotenuse formula = √((base) 2  + (height) 2 ) (or) c = √(a 2  + b 2 ).

How Do You Find the Hypotenuse Formula Using the Pythagoras Theorem?

The Pythagoras theorem is represented by the formula (Hypotenuse) 2  = (Base) 2  + (Altitude) 2 . The longest side of the right triangle is the hypotenuse and the other two sides are the base and the altitude of the triangle. Thus the hypotenuse formula is expressed as: Hypotenuse formula = √((base) 2  + (height) 2 ) 

• Math Article
• Bayes Theorem

Bayes' Theorem

Bayes’ theorem describes the probability of occurrence of an event related to any condition. It is also considered for the case of conditional probability . Bayes theorem is also known as the formula for the probability of “causes”. For example: if we have to calculate the probability of taking a blue ball from the second bag out of three different bags of balls, where each bag contains three different colour balls viz. red, blue, black. In this case, the probability of occurrence of an event is calculated depending on other conditions is known as conditional probability.  In this article, let us discuss the statement and proof for Bayes theorem, its derivation, formula, and many solved examples.

Table of Contents:

• Applications
• Practice problems

Bayes Theorem Statement

Let E 1 , E 2 ,…, E n  be a set of events associated with a sample space S , where all the events E 1 , E 2 ,…, E n  have nonzero probability of occurrence and they form a partition of S . Let A  be any event associated with S , then according to Bayes theorem,

\(\begin{array}{l}P(E_i│A)~=~\frac{P(E_i)P(A│E_i)}{\sum\limits_{k=1}^{n}P(E_k)P(A| E_k)}\end{array} \)

for any k = 1, 2, 3, …., n

Bayes Theorem Proof

According to the conditional probability formula,

\(\begin{array}{l}P(E_i│A)~=~\frac{P(E_i ∩ A)}{P(A)}…(1)\end{array} \)

Using the multiplication rule of probability, \(\begin{array}{l}P(E_i ∩ A)~= ~P(E_i)P(A │E_i)…(2)\end{array} \)

Using total probability theorem, \(\begin{array}{l}P(A)~=~\sum\limits_{k=1}^{n}~P(E_k)P(A| E_k)…(3)\end{array} \)

Putting the values from equations (2) and (3) in equation 1, we get

\(\begin{array}{l}P(E_i│A)~=~\frac{P(E_i)P(A│E_i)}{\sum\limits_{k=1}^n~P(E_k)P(A| E_k)}\end{array} \)

The following terminologies are also used when the Bayes theorem is applied:

Hypotheses: The events E 1 , E 2 ,… E n is called the hypotheses

Priori Probability: The probability P(E i ) is considered as the priori probability of hypothesis E i

Posteriori Probability: The probability P(E i |A) is considered as the posteriori probability of hypothesis E i Bayes’ theorem is also called the formula for the probability of “causes”. Since the E i ‘s are a partition of the sample space S, one and only one of the events E i occurs (i.e. one of the events E i must occur and the only one can occur). Hence, the above formula gives us the probability of a particular E i (i.e. a “Cause”), given that the event A has occurred.

Bayes Theorem Formula

If A and B are two events, then the formula for the Bayes theorem is given by:

Where P(A|B) is the probability of condition when event A is occurring while event B has already occurred. Also, get the Bayes Theorem Calculator here.

Bayes Theorem Derivation

Bayes Theorem can be derived for events and random variables separately using the definition of conditional probability and density.

From the definition of conditional probability, Bayes theorem can be derived for events as given below:

P(A|B) = P(A ⋂ B)/ P(B), where P(B) ≠ 0

P(B|A) = P(B ⋂ A)/ P(A), where P(A) ≠ 0

Here, the joint probability P(A ⋂ B) of both events A and B being true such that,

P(B ⋂ A) = P(A ⋂ B)

P(A ⋂ B) = P(A | B) P(B) = P(B | A) P(A)

P(A|B) = [P(B|A) P(A)]/ P(B), where P(B) ≠ 0

Similarly, from the definition of conditional density, Bayes theorem can be derived for two continuous random variables namely X and Y as given below:

\(\begin{array}{l}f_{X|Y=y}(x)=\frac{f_{X,Y(x,y)}}{f_Y(y)}\\f_{Y|X=x}(y)=\frac{f_{X,Y(x,y)}}{f_X(x)}\end{array} \)

Therefore, 

\(\begin{array}{l}f_{X|Y=y}(x)=\frac{f_{Y|X=x}(y)f_X(x)}{f_Y(y)}\end{array} \)

Examples and Solutions

Some illustrations will improve the understanding of the concept.

A bag I contains 4 white and 6 black balls while another Bag II contains 4 white and 3 black balls. One ball is drawn at random from one of the bags, and it is found to be black. Find the probability that it was drawn from Bag I.

Let E 1 be the event of choosing bag I, E 2 the event of choosing bag II, and A be the event of drawing a black ball.

Then, \(\begin{array}{l}P(E_1)~ = ~P(E_2)~ =~\frac{1}{2}\end{array} \)

Also, P(A|E 1 ) = P(drawing a black ball from Bag I) = 6/10 = 3/5

P(A|E 2 ) = P(drawing a black ball from Bag II) = 3/7

By using Bayes’ theorem, the probability of drawing a black ball from bag I out of two bags,

\(\begin{array}{l}P(E_1 |A)~ =~\frac{P(E_1)P(A|E_1)}{P(E_1 )P(A│E_1 )+ P(E_2)P(A|E_2)}\end{array} \)

\(\begin{array}{l}=\large\frac{\frac{1}{2}~\times~\frac{3}{5}}{\frac{1}{2}~\times~\frac{3}{5}~+~\frac{1}{2}~ ×~\frac{3}{7}}\end{array} \)

\(\begin{array}{l}=\frac{7}{12}\end{array} \)

A man is known to speak the truth 2 out of 3 times. He throws a die and reports that the number obtained is a four. Find the probability that the number obtained is actually a four.

Let A be the event that the man reports that number four is obtained.

Let E 1 be the event that four is obtained and E 2 be its complementary event.

Then, P(E 1 ) = Probability that four occurs = 1/6.

P(E 2 ) = Probability that four does not occur = 1- P(E 1 ) = 1 – (1/6) = 5/6.

Also, P(A|E 1 ) = Probability that man reports four and it is actually a four = 2/3

P(A|E 2 )  = Probability that man reports four and it is not a four = 1/3.

By using Bayes’ theorem, probability that number obtained is actually a four, P(E 1 |A)

\(\begin{array}{l}= \large \frac{P(E_1)P(A|E_1)}{P(E_1 )P(A│E_1 )~+~ P(E_2)P(A|E_2)}~ =~\frac{\frac{1}{6} ~ ×~ \frac{2}{3}}{\frac{1}{6} ~×~ \frac{2}{3}~ +~ \frac{5}{6}~ ×~\frac{1}{3}}\end{array} \)

\(\begin{array}{l}=\frac{2}{7}\end{array} \)

Bayes Theorem Applications

One of the many applications of Bayes’ theorem is Bayesian inference, a particular approach to statistical inference. Bayesian inference has found application in various activities, including medicine, science, philosophy, engineering, sports, law, etc. For example, we can use Bayes’ theorem to define the accuracy of medical test results by considering how likely any given person is to have a disease and the test’s overall accuracy. Bayes’ theorem relies on consolidating prior probability distributions to generate posterior probabilities. In Bayesian statistical inference, prior probability is the probability of an event before new data is collected.

Practice Problems

Solve the following problems using Bayes Theorem.

• A bag contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted, and again the ball is returned to the bag. Also, 2 additional balls of the colour drawn are put in the bag. After that, the ball is drawn at random from the bag. What is the probability that the second ball drawn from the bag is red?
• Of the students in the college, 60% of the students reside in the hostel and 40% of the students are day scholars. Previous year results report that 30% of all students who stay in the hostel scored A Grade and 20% of day scholars scored A grade. At the end of the year, one student is chosen at random and found that he/she has an A grade. What is the probability that the student is a hosteler? 
• From the pack of 52 cards, one card is lost. From the remaining cards of a pack, two cards are drawn and both are found to be diamond cards. What is the probability that the lost card is a diamond?

Frequently Asked Questions on Bayes Theorem

What is meant by bayes theorem in probability.

In Probability, Bayes theorem is a mathematical formula, which is used to determine the conditional probability of the given event. Conditional probability is defined as the likelihood that an event will occur, based on the occurrence of a previous outcome.

How is Bayes theorem different from conditional probability?

As we know, Bayes theorem defines the probability of an event based on the prior knowledge of the conditions related to the event. In case, if we know the conditional probability, we can easily find the reverse probabilities using the Bayes theorem.

When can we use Bayes theorem?

Bayes theorem is used to find the reverse probabilities if we know the conditional probability of an event.

What is the formula for Bayes theorem?

The formula for Bayes theorem is: P(A|B)= [P(B|A). P(A)]/P(B) Where P(A) and P(B) are the probabilities of events A and B. P(A|B) is the probability of event A given B P(B|A) is the probability of event B given A.

Where can we use Bayes theorem?

Bayes rule can be used in the condition while answering the probabilistic queries conditioned on the piece of evidence.

Students, are you struggling to find a solution to a specific question from Bayes theorem? We will make it easy for you. For a detailed discussion on the concept of Bayes’ theorem, download BYJU’S – The Learning App.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Superb explanation. Thanks to bujy’s🙂

very nicely explained.

Well explained theory.

thank you for explaining really good

well explained

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.