what is the contrastive analysis hypothesis

• Linguistics
• Join Newsletter

Our Promise to you

Founded in 2002, our company has been a trusted resource for readers seeking informative and engaging content. Our dedication to quality remains unwavering—and will never change. We follow a strict editorial policy , ensuring that our content is authored by highly qualified professionals and edited by subject matter experts. This guarantees that everything we publish is objective, accurate, and trustworthy.

Over the years, we've refined our approach to cover a wide range of topics, providing readers with reliable and practical advice to enhance their knowledge and skills. That's why millions of readers turn to us each year. Join us in celebrating the joy of learning, guided by standards you can trust.

What Is Contrastive Analysis?

Contrastive analysis is the study and comparison of two languages. For example, this can be comparing English with Latin or Basque with Iroquois. This is done by looking at the structural similarities and differences of the studied languages. There are two central aims to contrastive analysis; the first is to establish the inter-relationships of languages in order to create a linguistic family tree. The second aim is to aid second language acquisition.

The idea of contrastive analysis grew out of observing students learning a second language. Each student or group of students tended to repeat the same linguistic mistakes as previous groups. This turned into an assumption that the mistakes were caused by the student’s first language interfering with the second. This interference happened because the student applied the first language’s rules to the second language, much in the same way children apply the rules of regular words to irregular ones.

Serious studies into contrastive analysis began with Robert Lado’s 1957 book, “ Linguistics Across Culture.” Its central tenets and other observations on second language acquisition became increasingly influential in the 1960s and 70s. It built upon ideas set out in linguistic relativity , also known as the Sapir-Whorf Hypothesis , which believed that language structures affect cognitive thinking. This led to the automatic transferring of one language’s rules to another.

The ideas of contrastive analysis regarding second language acquisition are considered simplistic. They assume all students studying one language, who speak the same mother tongue, will make the same mistakes as one another. It does not factor in the possibility of individual differences. It also does not help students avoid systematic mistakes. The only help for such students is lists of common mistakes.

Contrastive analysis fails to distinguish between the written rules of formal language and the unwritten rules of informal language. It also fails to take into account differences between dialects. Most contrastive studies take into account basic building blocks of languages such as phonics and vocabulary and also the structural natures of many languages including how they form sentences and change word forms.

Studies comparing and contrasting different languages still have a role to play in language formation and history. The production of language family trees and genealogies are useful for explaining how different languages were formed and where they came from. It is also used to connect different languages together.

Some languages such as the Slavic, Germanic and Romance languages have obvious connections with one another and hark back to general proto-languages. The theory is that each language started as a dialect and became more distinct over time. Some languages are more isolated and harder to explain like Basque and Hungarian. Others, like Japanese, cause controversy because some think Japanese is unique, while others draw comparisons with Korean and a plethora of related languages such as Okinawan, Yaeyama and Yonaguni.

Editors' Picks

Related Articles

• What Is Linguistic Relativity?
• What Is Critical Discourse Analysis?
• What Is Political Discourse Analysis?
• What Is a Degree of Comparison?
• What Is Comparative Literature?
• What Is Discourse Analysis?
• What is American Sign Language?

Our latest articles, guides, and more, delivered daily.

Literary Articles

• A Farewell to Arms (1)
• Absurd Drama (5)
• African Literature (11)
• Agamemnon (2)
• Agha Shahid Ali (1)
• American Literature (32)
• Amitav Ghosh (6)
• Anita Desai (1)
• Aristotle (6)
• Bengali Literature (4)
• British Fiction (20)
• Charles Dickens (8)
• Chaucer (1)
• Chomsky (11)
• Classics (12)
• Clear Light of the Day (1)
• Cotton Mather (1)
• Death of a Salesman (5)
• Derek Walcott (3)
• Derrida (1)
• Descartes (1)
• Dr. Samuel Johnson (7)
• Edward Said (1)
• Elaine Showalter (2)
• ELT Terms Difined (20)
• Emily Bronte (6)
• Emily Dickinson (3)
• English History (9)
• English Language (2)
• English Literature (2)
• Great Expectations (7)
• Greek Literature (7)
• Heart of Darkness (2)
• History of English Language (15)
• History of English literature (9)
• Indian Literature (18)
• Indian Literature in English (2)
• Indian Poetry in English (23)
• Irish Literature (4)
• John Donne (2)
• John Keats (5)
• John Locke (2)
• Kamala Das (17)
• Kim by Kipling (2)
• Latin American Literature (2)
• Life and time of Michael K (3)
• Linguistics (13)
• Literary Criticism (28)
• Literary Terms (7)
• Literary Theories (19)
• Love Song of J. Alfred Prufrock (1)
• Machiavelli (2)
• Magic Realism (2)
• Marvell (2)
• Maupassant (1)
• Measure for Measure (3)
• Metaphysical poetry (3)
• Native Son (1)
• Nissim Ezekiel (4)
• Oedipus Rex (2)
• Othello (5)
• Phaedra by Seneca (3)
• Philosophy short notes (1)
• Postcolonial Reading (1)
• Postmodernist reading (2)
• Pride and Prejudice (4)
• Psychoanalytic Reading (1)
• Quartet (1)
• R K Narayan's The Guide (10)
• Red Badge of Courage (1)
• Riders to the Sea (1)
• Robert Frost (4)
• Roland Barthes (3)
• Romantic Literature (13)
• Romantic Poetry (4)
• Ronald Barthes (3)
• S .T . Coleridge (4)
• Samuel Beckett (1)
• Saul Bellow’s Seize the Day (1)
• Seamus Heaney (1)
• Seize the Day by Saul Bellow (4)
• Shakespeare (22)
• Shakespeare's Sonnets (6)
• Shelley (2)
• Song of Myself by Whitman (3)
• Sonnets (3)
• Sons and Lovers (5)
• Sophocles (2)
• South Asian Literature (2)
• Strange Pilgrims by Gabriel Garcia Marquez (3)
• T. S . Eliot (10)
• Teaching Language Through Literature (5)
• Tempest (4)
• Tennyson (1)
• The Ancient Mariner (5)
• The Great Gatsby (3)
• The Iliad (1)
• The Old Man And The Sea (1)
• The Playboy of the Western World (3)
• The Return of the Native (4)
• The Scarlet Letter (2)
• The Spanish Tragedy (1)
• The Turn of the Screw (3)
• The Waste Land (2)
• The Zoo Story by Adward Albee (4)
• Things Fall Apart (4)
• Thomas Hardy (4)
• Victorian Literature (5)
• W. J. Mitchell (1)
• W.B. Yeats (11)
• Waiting for Godot (3)
• Western Philosophy (13)
• William Blake (3)
• Wole Soyinka (5)
• Wordsworth (11)
• Workhouse Ward (1)

Saturday, November 16, 2013

What is contrastive analysis hypothesis in sla what are its major limitations, litarticles channel.

• YouTube Channel

• Subject List
• Take a Tour
• For Authors
• Subscriber Services
• Publications
• African American Studies
• African Studies
• American Literature
• Anthropology
• Architecture Planning and Preservation
• Art History
• Atlantic History
• Biblical Studies
• British and Irish Literature
• Childhood Studies
• Chinese Studies
• Cinema and Media Studies
• Communication
• Criminology
• Environmental Science
• Evolutionary Biology
• International Law
• International Relations
• Islamic Studies
• Jewish Studies
• Latin American Studies
• Latino Studies

Linguistics

• Literary and Critical Theory
• Medieval Studies
• Military History
• Political Science
• Public Health
• Renaissance and Reformation
• Social Work
• Urban Studies
• Victorian Literature
• Browse All Subjects

How to Subscribe

• Free Trials

In This Article Expand or collapse the "in this article" section Contrastive Analysis in Linguistics

Introduction, informal beginnings of contrastive linguistics.

• Comparative Stylistics
• Contrastive Linguistics in the United States (1945 to c . 1970)
• Contrastive Linguistics in Europe (1970 to c . 1990)
• Contrastive Pragmatics and Discourse Analysis
• Typological Comparison of Language Pairs
• Corpus-Based Contrastive Analysis
• Corpus-Based Contrastive Interlanguage Research
• Prospects for the Future
• Bibliographies
• Corpora and Digital Resources

Related Articles Expand or collapse the "related articles" section about

About related articles close popup.

Lorem Ipsum Sit Dolor Amet

Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia Curae; Aliquam ligula odio, euismod ut aliquam et, vestibulum nec risus. Nulla viverra, arcu et iaculis consequat, justo diam ornare tellus, semper ultrices tellus nunc eu tellus.

• Acceptability Judgments
• Accessibility Theory in Linguistics
• Acoustic Phonetics
• Acquisition of Possessives
• Anaphora Resolution in Second Language Acquisition
• Articulatory Phonetics
• Auxiliaries
• Bilingual Lexicography
• Bilingualism and Multilingualism
• Classifiers
• Cognitive Grammar
• Compounding
• Cross-Language Speech Perception and Production
• Distinctive Features
• Early Child Phonology
• Educational Linguistics
• English as a Lingua Franca
• Existential
• Languages of the World
• Lexical Semantics
• Linguistic Profiling and Language-Based Discrimination
• Linguistic Relativity
• Mass-Count Distinction
• Nasals and Nasalization
• Politeness in Language
• Reciprocals
• Reduplication
• Reflexives and Reflexivity
• Second Language Listening
• Second Language Writing
• Second-Language Reading
• Sentence Processing in Monolingual and Bilingual Speakers
• Sociolinguistics
• Speech Perception
• Structural Borrowing
• Teaching Pragmatics
• Translation
• Word Classes

Other Subject Areas

Forthcoming articles expand or collapse the "forthcoming articles" section.

• Attention and Salience
• Edward Sapir
• Text Comprehension
• Find more forthcoming articles...
• Export Citations
• Share This Facebook LinkedIn Twitter

Contrastive Analysis in Linguistics by Christian Mair LAST REVIEWED: 26 October 2023 LAST MODIFIED: 26 October 2023 DOI: 10.1093/obo/9780199772810-0214

In its core sense, contrastive linguistics can be defined as the theoretically grounded, systematic and synchronic comparison of usually two languages, or at most no more than a small number of languages. In the early stages of the development of the field, comparisons were usually carried out with a view to applying the findings for the benefit of the community, for example in foreign-language teaching or in translation. In recent years, this applied orientation has persisted, but it has been complemented by a growing body of contrastive research with a more theoretical orientation. The languages compared can be genetically related or unrelated, as well as typologically similar or dissimilar. Some comparisons, in particular those with a more theoretical orientation, are symmetrical in the sense that they cover the specifics of one language viewed against another in a balanced way. Applied contrastive comparisons of languages, on the other hand, are often asymmetrical or “directed.” This is typically the case in pedagogically oriented contrastive research, where the focus is on differences in L2, which are seen as potential sources of difficulty in foreign-language learning. Contrastive linguistics emerged as a major subfield of applied linguistics in the 1940s and consolidated quickly throughout the 1950s and 1960s. When it became clear that contrastive linguistics was not going to provide the foundation for a comprehensive theory of foreign-language learning, the field started showing signs of strain. Over time, however, it has avoided disintegration and managed to reposition itself successfully—not as a clearly demarcated subfield, but rather as an approach that has continued to prove its usefulness to a wide range of applied- and theoretical-linguistic domains, such as second-language acquisition (SLA) research, translation studies and translation theory, lexicography, the study of cross-cultural communication, and even cultural studies. Progress in contrastive linguistics has manifested itself on the conceptual level, for example through the constant refinement of notions such as L1 transfer and interference, or through fruitful interdisciplinary dialogue with language typology, but also in contrastivists’ active contribution to the construction of digital research tools such as learner corpora and translation corpora. The following annotated bibliography charts the development of the field on the basis of publications that stand out either because they have become classic points of reference for other work or because they have raised important theoretical and methodological points. Studies of specific phenomena in individual language pairs are mentioned for illustrative purposes. No comprehensive coverage of such largely descriptive work is attempted, however.

The practical usefulness of a contrastive approach to the teaching of foreign languages was obvious to instructors centuries before contrastive linguistics established itself as a distinct subdiscipline within academic linguistics. For example, Lewis 1671 contains the following informal statement of the contrastive hypothesis : “The most facil way of introducing any in a Tongue unknown , is to shew what Grammar it hath beyond, or short of his Mother-Tongue ; following that Maxime, to proceed a noto ad ignotum , making what we know, a step to what we are to learn.” A more or less explicit contrastive approach also informs many publications emanating from the language-teaching reform movements of the late nineteenth and early twentieth centuries, which polemicized against the use of the grammar-and-translation method for the teaching of the modern languages. Works such as Viëtor 1894 , with its three-way comparison of the phonetics of German, French, and English, or Sommer 1921 , with its grammatical comparison of German with the four foreign languages commonly taught in German schools at the time (English, French, Latin, Greek), still contain insights that are of interest beyond their merely historical value. Published more than seventy years after Sommer’s work, Glinz 1994 offers a much-expanded contrastive grammar of the same four languages. Work of the Prague school on linguistic characterology, such as Mathesius 1964 , clearly foreshadows later work on theoretically and typologically informed contrastive linguistics. Works such as Levý 1957 , Levý 1969 , Levý 2011 , and Wandruszka 1969 are representative of a copious literature on translation criticism that contains numerous contrastive-linguistic observations.

Glinz, Hans. 1994. Grammatiken im Vergleich: Deutsch – Französisch – Englisch – Latein, Formen –Bedeutungen – Verstehen . Tübingen, Germany: Niemeyer.

DOI: 10.1515/9783110914801

This monumental contrastive grammar of the four languages presents a summary of the author’s lifelong work on semantically and pragmatically motivated syntax. It contains a wealth of fascinating descriptive insights, but stands somewhat apart from the contemporary mainstream of contrastive linguistics and language typology in its terminology and conceptual structure.

Levý, Jiří. 1957. České theorie překladu . Prague: SNKLHU.

Written in Czech, this massive tome, about a thousand pages in length, presents the sum of the work of this experienced translator and early translation theorist.

Levý, Jiří. 1969. Die literarische Übersetzung . Bonn, Germany: Athenäum.

Selections from Levý’s writings in German translation, with a focus on the translation of literary works. For the present-day reader, the book is worth consulting mainly for its rich illustrative material and experience-based commentary. It is written in a witty and accessible essayistic style.

Levý, Jiří. 2011. The art of translation . Amsterdam: John Benjamins.

DOI: 10.1075/btl.97

Selections from Levý’s writings in English translation.

Lewis, Mark. 1671. Institutio grammaticae puerilis: Or The rudiments of the Latine and Greek tongues; Fitted to childrens capacities as an introduction to larger grammars . London.

Quoted above (from Early English Books Online, original held in the Folger Shakespeare Library, Washington DC) for its early informal formulation of the contrastive hypothesis, this book also contains the controversial assertion that “ Whatever Tongue hath less Grammar than the English, is not intelligible: Whatever hath more, is superfluous ,” which has never been seriously followed up on in later contrastive work.

Mathesius, Vilém. 1964. On linguistic characterology with illustrations from modern English. In A Prague school reader in linguistics . Edited by Josef Vachek, 59–67. Bloomington: Indiana Univ. Press.

A reprint of Mathesius’s original 1928 paper, which introduces the type of theoretically driven comparison of languages that came to be known as “linguistic characterology” in the Prague school tradition.

Sommer, Ferdinand. 1921. Vergleichende Syntax der Schulsprachen (Deutsch, Englisch, Französisch, Griechisch, Lateinisch) mit besonderer Berücksichtigung des Deutschen . Leipzig: Teubner.

Features parallel descriptions of the grammars of German, English, French, (Classical) Greek, and Latin, with numerous contrastive observations.

Viëtor, Wilhelm. 1894. Elemente der Phonetik des Deutschen, Englischen und Französischen: Mit Rücksicht auf die Bedürfnisse der Lehrpraxis . 3d ed. Leipzig: O. R. Reisland.

Viëtor (b. 1850–d. 1918) wrote this book to draw attention to what he saw as the deplorable neglect of pronunciation and the spoken language in the classroom. The contrastive approach is considered to raise awareness of the causes of learner accents and thus improve teaching. The first edition of this work appeared under a slightly different title in 1884; for an adapted English version, see Laura Soames and Wilhelm Viëtor, Introduction to English, French and German Phonetics , 2d ed. (London: Swan Sonnenschein, 1899).

Wandruszka, Mario. 1969. Sprachen, vergleichbar und unvergleichlich . Munich: Piper.

Translation criticism, focusing mainly on lexical and phraseological contrasts, with examples mostly from English, German, and the Romance languages; erudite and essayistic.

back to top

Users without a subscription are not able to see the full content on this page. Please subscribe or login .

Oxford Bibliographies Online is available by subscription and perpetual access to institutions. For more information or to contact an Oxford Sales Representative click here .

• About Linguistics »
• Meet the Editorial Board »
• Acquisition, Second Language, and Bilingualism, Psycholin...
• Adpositions
• African Linguistics
• Afroasiatic Languages
• Algonquian Linguistics
• Altaic Languages
• Ambiguity, Lexical
• Analogy in Language and Linguistics
• Animal Communication
• Applicatives
• Applied Linguistics, Critical
• Arawak Languages
• Argument Structure
• Artificial Languages
• Australian Languages
• Austronesian Linguistics
• Balkans, The Languages of the
• Baudouin de Courtenay, Jan
• Berber Languages and Linguistics
• Biology of Language
• Borrowing, Structural
• Caddoan Languages
• Caucasian Languages
• Celtic Languages
• Celtic Mutations
• Chomsky, Noam
• Chumashan Languages
• Clauses, Relative
• Clinical Linguistics
• Cognitive Linguistics
• Colonial Place Names
• Comparative Reconstruction in Linguistics
• Comparative-Historical Linguistics
• Complementation
• Complexity, Linguistic
• Compositionality
• Comprehension, Sentence
• Computational Linguistics
• Conditionals
• Conjunctions
• Connectionism
• Consonant Epenthesis
• Constructions, Verb-Particle
• Contrastive Analysis in Linguistics
• Conversation Analysis
• Conversation, Maxims of
• Conversational Implicature
• Cooperative Principle
• Coordination
• Creoles, Grammatical Categories in
• Critical Periods
• Cyberpragmatics
• Default Semantics
• Definiteness
• Dementia and Language
• Dene (Athabaskan) Languages
• Dené-Yeniseian Hypothesis, The
• Dependencies
• Dependencies, Long Distance
• Derivational Morphology
• Determiners
• Dialectology
• Dravidian Languages
• Endangered Languages
• English, Early Modern
• English, Old
• Eskimo-Aleut
• Euphemisms and Dysphemisms
• Evidentials
• Exemplar-Based Models in Linguistics
• Existential Wh-Constructions
• Experimental Linguistics
• Fieldwork, Sociolinguistic
• Finite State Languages
• First Language Attrition
• Formulaic Language
• Francoprovençal
• French Grammars
• Gabelentz, Georg von der
• Genealogical Classification
• Generative Syntax
• Genetics and Language
• Grammar, Categorial
• Grammar, Cognitive
• Grammar, Construction
• Grammar, Descriptive
• Grammar, Functional Discourse
• Grammars, Phrase Structure
• Grammaticalization
• Harris, Zellig
• Heritage Languages
• History of Linguistics
• History of the English Language
• Hmong-Mien Languages
• Hokan Languages
• Humor in Language
• Hungarian Vowel Harmony
• Idiom and Phraseology
• Imperatives
• Indefiniteness
• Indo-European Etymology
• Inflected Infinitives
• Information Structure
• Interface Between Phonology and Phonetics
• Interjections
• Iroquoian Languages
• Isolates, Language
• Jakobson, Roman
• Japanese Word Accent
• Jones, Daniel
• Juncture and Boundary
• Khoisan Languages
• Kiowa-Tanoan Languages
• Kra-Dai Languages
• Labov, William
• Language Acquisition
• Language and Law
• Language Contact
• Language Documentation
• Language, Embodiment and
• Language for Specific Purposes/Specialized Communication
• Language, Gender, and Sexuality
• Language Geography
• Language Ideologies and Language Attitudes
• Language in Autism Spectrum Disorders
• Language Nests
• Language Revitalization
• Language Shift
• Language Standardization
• Language, Synesthesia and
• Languages of Africa
• Languages of the Americas, Indigenous
• Learnability
• Lexical Access, Cognitive Mechanisms for
• Lexical-Functional Grammar
• Lexicography
• Lexicography, Bilingual
• Linguistic Accommodation
• Linguistic Anthropology
• Linguistic Areas
• Linguistic Landscapes
• Linguistic Prescriptivism
• Linguistics, Educational
• Listening, Second Language
• Literature and Linguistics
• Machine Translation
• Maintenance, Language
• Mande Languages
• Mathematical Linguistics
• Mayan Languages
• Mental Health Disorders, Language in
• Mental Lexicon, The
• Mesoamerican Languages
• Minority Languages
• Mixed Languages
• Mixe-Zoquean Languages
• Modification
• Mon-Khmer Languages
• Morphological Change
• Morphology, Blending in
• Morphology, Subtractive
• Munda Languages
• Muskogean Languages
• Niger-Congo Languages
• Non-Pama-Nyungan Languages
• Northeast Caucasian Languages
• Oceanic Languages
• Papuan Languages
• Penutian Languages
• Philosophy of Language
• Phonetics, Acoustic
• Phonetics, Articulatory
• Phonological Research, Psycholinguistic Methodology in
• Phonology, Computational
• Phonology, Early Child
• Policy and Planning, Language
• Positive Discourse Analysis
• Possessives, Acquisition of
• Pragmatics, Acquisition of
• Pragmatics, Cognitive
• Pragmatics, Computational
• Pragmatics, Cross-Cultural
• Pragmatics, Developmental
• Pragmatics, Experimental
• Pragmatics, Game Theory in
• Pragmatics, Historical
• Pragmatics, Institutional
• Pragmatics, Second Language
• Pragmatics, Teaching
• Prague Linguistic Circle, The
• Presupposition
• Psycholinguistics
• Quechuan and Aymaran Languages
• Reading, Second-Language
• Register and Register Variation
• Relevance Theory
• Representation and Processing of Multi-Word Expressions in...
• Salish Languages
• Sapir, Edward
• Saussure, Ferdinand de
• Second Language Acquisition, Anaphora Resolution in
• Semantic Maps
• Semantic Roles
• Semantic-Pragmatic Change
• Semantics, Cognitive
• Sign Language Linguistics
• Sociolinguistics, Variationist
• Sociopragmatics
• Sound Change
• South American Indian Languages
• Specific Language Impairment
• Speech, Deceptive
• Speech Production
• Speech Synthesis
• Switch-Reference
• Syntactic Change
• Syntactic Knowledge, Children’s Acquisition of
• Tense, Aspect, and Mood
• Text Mining
• Tone Sandhi
• Transcription
• Transitivity and Voice
• Translanguaging
• Trubetzkoy, Nikolai
• Tucanoan Languages
• Tupian Languages
• Usage-Based Linguistics
• Uto-Aztecan Languages
• Valency Theory
• Verbs, Serial
• Vocabulary, Second Language
• Voice and Voice Quality
• Vowel Harmony
• Whitney, William Dwight
• Word Formation in Japanese
• Word Recognition, Spoken
• Word Recognition, Visual
• Word Stress
• Writing, Second Language
• Writing Systems
• Zapotecan Languages
• Privacy Policy
• Cookie Policy
• Legal Notice
• Accessibility

Powered by:

• [185.66.15.189]
• 185.66.15.189

• DOI: 10.17776/CSJ.29353
• Corpus ID: 61076600

An Overview of Contrastive Analysis Hypothesis

• Mahboobeh Joze Tajareh
• Published 13 May 2015
• Linguistics, Education

9 Citations

Relative clause transfer strategy and the implication on contrastive analysis hypothesis, contrastive analysis and its implications for bengali learners of esl, a contrastive analysis of articles in english and demonstratives in isizulu, contrastive analysis of french and nubian: noun phrase constructions, an attempt to a contrastive analysis of igbo and tongan conditional clauses, teaching english phonemes to moore efl students using phonemic awareness activities: a contrastive analysis approach, equal opportunity interference: both l1 and l2 influence l3 morpho-syntactic processing, english versus zambian languages:  exploring some similarities and differences with their implication on the teaching of literacy and language in primary schools.

• Highly Influenced

A Cognitive Investigation into the Love-life Relationship Expressed in Poetry

10 references, the contrastive analysis hypothesis..

• Highly Influential

The grammatical structures of English and Spanish

Contrastive rhetoric: cross-cultural aspects of second language writing, linguistics across cultures: applied linguistics for language teachers, language structures in contrast, related papers.

Showing 1 through 3 of 0 Related Papers

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

Download Free PDF

Contrastive Analysis Hypothesis and Second Language Learning

Journal of ELT Research

This article aims to provide an overview of some of the issues related to contrastive analysis hypothesis in second language learning. Contrastive hypothesis is one of the branches of applied linguistics which concerns with the study of two systems of languages between first language and target language. Contrastive hypothesis has fairly played an important role in language studies. Thus, in recent years, contrastive analysis has been used in language teaching contexts, syllabus design, and language classrooms by language teachers over the world. Many research works have been done by many language researchers in different aspects of contrastive hypothesis and also error analysis in the world. Language teachers always see contrastive analysis as a pedagogical imperative in target language and they use it as a functional approach in language classroom. However, contrastive hypothesis follows the errors of language learners in second language education.

Related papers

Italica. Vol. 70, No. 2. Pp. 228-229., 1993

This review of Danesi and Di Pietro's volume on Contrastive Analysis is the definitive statement on this topic. This volume features an innovation, which the authors label the "stage hypothesis", which is designed to illustrate that CA is not a comprehensive theory of second-language acquisition, but rather a mechanism for the earliest stages of second-language instruction.

Italica, 1993

International Journal of Education (IJE), 2020

Contrastive analysis (CA) was primarily used in the 1950’s as an effective means to address second or foreign language teaching and learning. In this context, it was used to compare pairs of languages, identify similarities and differences in order to predict learning difficulties, with the ultimate goal of addressing them (Fries, 1943; Lado, 1957). Yet, in the 1980’s and 1990’s the relevance of CA has been disputed. Many studies have pointed out the limit of CA with respect to its weak and strong versions (Oller and Ziahosseiny, 1970), (Wardhaugh, 1970) (Brown, 1989), (Hughes, 1980), (Yang, 1992), and (Whitman and Jackson, 1972). To answer the limits of CA with regards to its weak, strong, and moderate versions, many language teachers used CA with a new approach. Kupferberg and Olshtain (1996), James (1996), and Ruzhekova-Rogozherova (2007). Here, salient contrastive linguistic input (CLI) is presented to learners for an effective noticing. Yet, mere exposition of contrastive lingu...

International Letters of Social and Humanistic Sciences, 2013

The current paper reflects on the evolving course and place of contrastive aspects of second language research. It attempts to give a concise overview of the related cross-linguistic perspectives over the last decades and elucidates their ascribed nuts and bolts in order to shed further light on the role and significance of cross-linguistic studies in second language research from the past up until now. To this end, the author expressly elaborates on different versions of Contrastive Analysis (CA) to come up with a clear picture of…

Theory and Practice in Language Studies, 2014

This study problematizes contrastive linguistics by highlighting the connection between interlanguage and error analysis. A qualitative method for data collection and analysis was used. The study applied the theories of Contrastive Analysis (CA) to compare and contrast linguistic and socio-cultural data between the Shona and the English languages. It was revealed that although there are similarities in the Subject Verb Agreement (SVO) between the two languages, there are also differences in that the Shona language is implicit in addressing the gender of the subject whereas the English language is explicit in identifying the gender of the subject by the use of explicit pronouns. The study concludes that the difficulties in language learning emanate from the differences between the new language (L2) and learners first language (L1) interference. In addition to that, the two languages under this study have differences in typological features. The study recommends the prescription of contrastive analysis theories in the teaching and learning of language.

The major aim of the current paper is to review and discuss three prevailing approaches to the study of Second Language Acquisition (SLA) since the middle of the twentieth century: Contrastive Analysis (CA, henceforth), Error Analysis (EA) and Interlanguage (IL). It begins with a general overview of how the CA approach was formulated and developed and discusses the three versions of CA which were displaced later by other approaches, such as EA and IL. The paper also provides an in-depth theoretical discussion of the notion of EA in terms of its definitions, goals, significance, development, causes and procedures. The discussion about the SLA approaches concludes with a review of IL which claims that language learners produce a separate linguistic system with its own salient features, which differs from their L1 and target language. Additionally, a bulk of previous studies conducted on EA in different contexts are reviewed throughout the paper.

Contrastive linguistics and language teacher. Oxford: …, 1981

Loading Preview

Sorry, preview is currently unavailable. You can download the paper by clicking the button above.

Readings on English as a Second language for Teachers and Teacher Trainers, 1980

univagro-iasi.ro

Theory and Practice in Language Studies

Journal of Humanities and Cultural Studies R&D, 2018

Dictionaries of Linguistics and Communication Science: Linguistic theory and methodology, 2012

Lahivordlusi Lahivertailuja, 2012

SWS Journal of SOCIAL SCIENCES AND ART, 2020

Proceedings of the 1st Yogyakarta International Conference on Educational Management/Administration and Pedagogy (YICEMAP 2017), 2017

English Language Teaching, 2017

Related topics

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

A Historical Development of Contrastive Analysis: A Relevant Review in Second and Foreign Language Teaching

• December 2020
• This person is not on ResearchGate, or hasn't claimed this research yet.

Discover the world's research

• 25+ million members
• 160+ million publication pages
• 2.3+ billion citations

No full-text available

To read the full-text of this research, you can request a copy directly from the author.

• James Jensen

• Donna Reseigh Long

• Ronald Wardhaugh
• Terence Odlin

• William E. Rutherford
• Nick C. Ellis

• Arthur Hughes
• Charles C. Fries
• Ivan Poldauf
• STUD SECOND LANG ACQ
• Soile Oikkenon
• Claudia Fernández

• Walter Lehn
• William R. Slager
• Randal L. Whitman
• Kenneth L. Jackson

• B Gnalibouly
• N Djiguimkoudre
• SCI STUD READ
• R Fielding-Barnsley
• I Kupferberg
• Sharwood Smith
• Recruit researchers
• Join for free
• Login Email Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google Welcome back! Please log in. Email · Hint Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google No account? Sign up

Professor Jack C. Richards

Contrastive analysis.

Submitted by Syvia, Brazil

Is contrastive analysis still relevant in language teaching?

Dr. Richards responds:

The contrastive analysis hypothesis (CA), states that where the first language and the target language are similar, learners will generally acquire structures with ease, and where they are different, learners will have difficulty. CA was based on the related theory of language transfer: difficulty in second language learning results from transfer of features of the first language to the second language. Transfer (also known as interference ) was considered the main explanation for learners’ errors. Teachers were encouraged to spend time on features of English that were most likely to be affected by first-language transfer. Today, transfer is considered only one of many possible causes of learners’ errors. However, in the 1960s the contrastive analysis hypothesis was criticized, as research began to reveal that second language learners use simple structures ‘that are very similar across learners from a variety of backgrounds, even if their respective first languages are different from each other and different from the target languages’ (Lightbown and Spada, 2006.) My early work on error analysis supported this view (Richards, 1974). Behaviourism as an explanation for language learning was subsequently rejected by advocates of more cognitive theories of language and of language learning that appeared in the 1960s and 1970s. One of the first people to develop a cognitive perspective on language was the prominent American linguist Noam Chomsky. His critique of Skinner’s views (Chomsky, 1959) was extremely influential and introduced the view that language learning should be seen not simply as something that comes from outside but is determined by internal processes of the mind, i.e. by cognitive processes.

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• « Iran March 2016
• Role of Schema »

Multilingual Pedagogy and World Englishes

Linguistic Variety, Global Society

Contrastive Analysis

In linguistics, the term c ontrastive analysis refers to “a theoretically grounded, systematic and synchronic comparison of usually two languages, or at most no more than a small number of languages” (Mair). Such comparisons frequently reveal similarities and dissimilarities between or among those languages.

The purpose is not only to understand the languages themselves better, but also to understand characteristics that might make language learning easier or more challenging for speakers of those languages. For example, contrastive analysis of English and Chinese would reveal that while the two languages share the same word order (Subject-Verb-Object), Chinese–unlike English–does not have a system of definite and indefinite articles (a, an, the). Consequently, when instructors or tutors see an English language learner from China struggling to produce articles or place them correctly, a little research and analysis would reveal that the L1 in this case is causing some L2 interference because of linguistic transfer.

Application

If an instructor is working in an EFL context or with a specific population in an ESL context, contrastive analysis is a fairly simple and useful tool. In an ESL context in which many different populations are represented, instructors may find such analysis to still be useful, but also time-consuming and challenging because of the diversity of students. Where and when possible, teachers ought to find ways to learn more about their students’ L1 as such activity can promote better teacher-student relationships and provide teachers with material for more incisive feedback in assessment.

Bibliography

Mair, Christian.  Oxford Bibliographies , Oxford University Press, 22 Feb. 2018, DOI: 10.1093/OBO/9780199772810-0214. Accessed 12 Apr. 2019.

Explaining outliers and anomalous groups via subspace density contrastive loss

• Open access
• Published: 23 September 2024

Cite this article

You have full access to this open access article

• Fabrizio Angiulli 1   na1 ,
• Fabio Fassetti 1   na1 ,
• Simona Nisticò 1   na1 &
• Luigi Palopoli 1   na1  

76 Accesses

1 Altmetric

Explore all metrics

Explainable AI refers to techniques by which the reasons underlying decisions taken by intelligent artifacts are single out and provided to users. Outlier detection is the task of individuating anomalous objects within a given data population they belong to. In this paper we propose a new technique to explain why a given data object has been singled out as anomalous. The explanation our technique returns also includes counterfactuals, each of which denotes a possible way to “repair” the outlier to make it an inlier. Thus, given in input a reference data population and an object deemed to be anomalous, the aim is to provide possible explanations for the anomaly of the input object, where an explanation consists of a subset of the features, called choice , and an associated set of changes to be applied, called mask , in order to make the object “behave normally”. The paper presents a deep learning architecture exploiting a features choice module and mask generation module in order to learn both components of explanations. The learning procedure is guided by an ad-hoc loss function that simultaneously maximizes (minimizes, resp.) the isolation of the input outlier before applying the mask (resp., after the application of the mask returned by the mask generation module) within the subspace singled out by the features choice module, all that while also minimizing the number of features involved in the selected choice. We consider also the case in which a common explanation is required for a group of outliers provided together in input. We present experiments on both artificial and real data sets and a comparison with competitors validating the effectiveness of the proposed approach.

Similar content being viewed by others

Counterfactuals Explanations for Outliers via Subspaces Density Contrastive Loss

Outlier Explanation Through Masking Models

Abstraction-Based Outlier Detection for Image Data

Explore related subjects.

• Artificial Intelligence

Avoid common mistakes on your manuscript.

1 Introduction

In this paper, we focus on the problem of finding the motivations underlying the abnormality of a given anomalous sample as compared to the normal ones, also referred to as the Outlier Explanation problem.

Unfortunately, despite the importance of the outlier explanation task, in the literature this problem has attracted less attention than that of outlier detection. The huge number of papers appeared in the last years on the outlier (aka “anomaly”) detection topic (see, e.g., (Pang et al., 2021 ; Bhuyan et al., 2014 ; Chandola et al., 2012 ; Steinwart et al., 2005 ; Angiulli et al., 2022 )) witnesses the interest on this problem. Many are applications in which outlier detection plays a fundamental role, including environmental monitoring (Russo et al., 2020 ; Hill & Minsker, 2010 ; Leigh et al., 2019 ), cyber-security (Kruegel & Vigna, 2003 ; Xu et al., 2018 ), fraud detection (Hilal et al., 2021 ; Abdallah et al., 2016 ), healthcare (Duraj & Chomatek, 2017 ; Hauskrecht et al., 2013 ), and others (Narayanan & Bobba, 2018 ).

As already pointed out, explaining to users what makes an anomalous observation (either known in advance or computationally detected) different from the rest of the data population it belongs to is as important as the detection task. As a matter of fact, having a full understanding of the unique characteristics of outliers is important to gain new knowledge and give support information to the decision process. For example, users can benefit from the availability of anomaly explanations since this will enhance their comprehension of the outliers, which is a crucial factor for taking right decisions. Indeed, by acquiring awareness about the nature of an outlier, they could decide to trust or not an alert about the anomalous nature of the sample. Moreover, domain experts, by having an explanation coupled to the anomalous sample, can effectively identify false positives and make decision more effectively. Additionally, if anomalous samples represent the observation of an unknown phenomenon, a deeper analysis of their characterizing peculiarities helps in the process of finding new knowledge.

Different are the ways in which one can try to explain why a sample is an outlier (Panjei et al. 2022 ). Approaches to outlier explanation in the literature can be basically grouped into two main families, namely feature-selection-based approaches, aimed at finding a set of features well characterizing the outlier, and score-and-search-based approaches, which are instead designed to assign an importance score to the features to establish a ranking.

While all the existing outlier explanation methods focus on singling out groups of attributes mostly characterizing the abnormality of the observation to explain, in this work we introduce a novel notion of outlier explanation, that we refer to as transformation-based . Our explanation consists of two components, namely the choice , a subset of features to be modified, and the mask , a set of offsets to be applied on the choice feature values. Thus, according to our approach an outlier explanation is a minimal choice-mask pair whose application makes the outlier indistinguishable from inliers. From what stated, our approach does not fall in any of the above mentioned families of approaches.

The key aspect of this novel form of explanation is that it provides the user with the information about how the features characterizing the outliers differ from what can be considered a normal behaviour, and also provides indications on how to “repair” the outlier; all that, we would argue, provides the user with a much intelligible knowledge about the nature of the anomalies characterizing the given object. Furthermore, by applying the suggested transformation, the user is provided with a counterfactual which, in this context, provides an example of “normality” that shares some characteristics with the analyzed sample.

To search for the above described explanation, we propose a new approach exploiting artificial neural networks. The proposed architecture receives a training-set consisting of a set of pairs, each one composed of the outlier to explain and of a normal example coming from a reference subset of the dataset, and outputs the choice and the mask as a results of the optimization of an ad-hoc Subspace Density Contrastive Loss. We employ as reference subset the set of the outlier nearest-neighbors. Our approach is able to deal both with single outliers and with groups of outliers. In the latter case, we return explanations that are widely shared by the group to be explained.

Before going into the details, we point out here that in the rest of the paper we will use the terms “outlier” and “anomaly” interchangeably, as also we shall do with“attribute”, “feature” and “dimension”.

Summarizing, we next list the main contributions of this work:

We present a new perspective for the Outlier Explanation problem, where a concept of transformation is introduced to provide features characterizing the abnormal behavior together with a suggested modification indicating how the object should look like in order to be considered normal;

The technique Masking Models for Outlier Explanation , shortly \(\text {M}^2\text {OE}\) , is presented. An innovative aspect of this technique is that the explanations also includes counterfactuals, which shows possible ways to transform the outlier to make it an inlier;

We also consider scenarios where is of interest detecting explanations to simultaneously characterize the abnormality of a group of anomalies.

A study of the effectiveness of our proposal is performed considering synthetic as well as real data sets, comparing the results with the ones achieved by competitors.

The rest of the paper is organized as follows: Sect.  2 gives a brief description of the state of the art, Sect.  3 expounds the \(\text {M}^2\text {OE}\) technique, Sect.  4 describe how \(\text {M}^2\text {OE}\) has been extended to explain groups of anomalies, Sect.  5 comments on the experimental results and, finally, Sect.  6 concludes this work.

2 Related works

As already stated in the previous section, the transformation-based explanation that we adopt in this paper has not been proposed before in the context of the outlier explanation task, except for the preliminary version of this paper (Angiulli et al. 2023 ). We will better discuss on the peculiarities of our approach in the following of this section.

We point out that transformation-based approaches have been used in other tasks, like that of post-hoc model explanation (Angiulli et al. 2022 ) and the use of counterfactuals in the explanation process (Guidotti 2022 ).

It can be noted that most existing outlier explanation methods basically work according to two kinds of approaches, we will discuss in the following.

Approaches of the first kind are characterized by exploiting feature selection techniques, which are widely used in classification problems, and are based on the idea of returning, as an explanation, a set of features in which the sample outlierness is maximized. The methods acting according to this mechanism are known as f eature-selection-based techniques.

As for the approaches of the other kind, they associate each feature with a score that measures the level of importance of that feature for assessing the outlierness of the sample. The techniques implementing this strategy are known as s core-and-search-based methods.

Generally speaking, however, as it will be clear in the rest of this section, all the methodologies at the state-of-the-art only provide users with a set of attributes or an attribute ranking adding no additional information about why those features are deemed to cause the anomaly.

2.1 Feature-selection-based approaches

Features selection techniques are conceived to reduce the data set dimensionality to improve model performance in classification tasks. To reach this goal, they need to retrieve the features that better characterize the sample with respect to the class label. In the context considered here, its declination is that of searching for a group of features that characterize the point outlierness the most, so that, generally speaking, a feature is just either included in the explanation or not without providing a measure of their relevance. This approach is also referred to in the literature as Outlier Aspect Mining . In the following, we describe several methods belonging to this group.

The paper (Kriegel et al. 2009 ) simultaneously addresses the detection and explanation problems by exploiting the Subspace Outlier Degree (SOD) algorithm. In this approach, whose final result is to compute an outlierness score, a reference set is used, which is looked at as possibly defining a subspace cluster (or a part of such a cluster). To find the best subspace, SOD research focuses on subspaces in which the reference samples fall in a dense region. If the query point deviates considerably from the reference set in the latter attributes, that point is singled out as an outlier in that corresponding subspace.

The idea that good separability between inliers and outliers is indicative of good explanatory subspaces is explored in Micenková et al. ( 2013 ), where the outlier detection problem is converted into a two-class classification problem. Then, to find the most suitable subspace, the authors employ a feature selection method.

Local Outliers with Graph Projection (LOGP), proposed in Dang et al. ( 2014 ), deals both with outlier detection and outlier explanation by exploiting concepts borrowed from the spectral graph embedding theory. In particular, LOGP constructs a projection on a space of reduced dimensionality in which the outlier is well-recognisable and the neighbourhood relationships between samples are left unchanged. To achieve this goal, authors employ an invertible function that allows them to retrieve the features that allow to distinguish the outlier from the individuated spaces.

Given a categorical data set and an outlier o , the k attributes associated with the highest outlier score represent the explanation provided by the approach proposed in Angiulli et al. ( 2009 ). To search for these attributes, the authors present a criterion aimed at evaluating the abnormality of combinations of attribute values featured by the given abnormal individual with respect to the reference data population. An extension of the approach to numerical data sets is presented in Angiulli et al. ( 2017 ).

A method explaining outliers using sample-based sequential explanations is presented in Mokoena et al. ( 2022 ). The strategy employed in this method is that of using known supervised feature selection methods to explain one outlying sample. Since those algorithms do not work well on unbalanced data, they propose a sampling method to create a balanced data collection for the explanation task. The inlier set of this data collection is defined as the union of the normal samples whose distance to the outlier is less than or equal to the distance between the outlier and its k -nearest inlier, referred to by the paper as k -distance, and some randomly chosen samples. To create an outlier class, a set of objects is drawn from a normal distribution, whose mean is given by the outlier to explain and whose standard deviation depends on the k -distance.

Moreover, some approaches are found in the literature which consider groups of outliers, thus finding an explanation summarizing the characteristics of more samples. One of these is eXplaining Patterns of Anomalies with Characterizing Subspaces (X-PACS) (Macha & Akoglu, 2018 ), which approach is that of exploiting the known anomalies in order to find the patterns distinguishing them and the characteristic subspace t whose features separate each anomalous pattern from normal instances.

2.2 Score-and-search-based approaches

The group of score-and-search-based approaches comprises all those methods that use some measure as features outlierness metric. Thus, each feature is associated with a score characterizing its relevance rate in sample outlierness and, in this, they are clearly separated from those techniques, discussed above, returning bare feature selection. The strength of these latter approaches is that the concept of “feature ranking” provides more detailed information, while its weakness is that scores are computed considering single features only, thus ignoring possible interaction among them.

One technique falling in the group at hand is HOS-Miner (Zhang et al. 2004 ). This method detects the outlying features by exploiting the Outlying Degree distance function, defined as the sum of the distances between the query data point and its k-nearest neighbours.

Reference (Duan et al. 2015 ) uses the subspace density as the score criterion where, in order to rank an attribute subspace, it exploites kernel-density estimation.

It is worth noting that methods in this family are characterized by the presence of a common problem, that is, they heavily rely on the distance function which may suffer from the dimensionality bias problem that makes larger subspaces preferable if we look only at the distance function. To avoid this phenomenon, (Vinh et al. 2016 ) presents the Z-score and the Isolation Path score (iPath), two dimensional-unbiased measures. The latter score is inspired by Isolation Forest (Liu et al. 2008 ), an outlier detection algorithm, based on the idea that anomalies are “few” and isolated from the rest of the data. Additionally, this work proposes a procedure for searching for attribute subspaces characterizing anomalies. The proposed research procedure first inspects all 1-D spaces, then exhaustively searches between all the 2-D subspaces and, finally, performs a beam search for subspaces with a dimension larger than 2.

In Wells and Ting ( 2019 ), sGrid is presented, which is a grid-based density estimator that leverages results from Silverman ( 2018 ). This method aims at making mining algorithms faster, a goal attained by sacrificing the estimation space unbiasedness.

A notable further form of scoring is the Simple Isolation score Using Nearest Neighbor Ensemble (SiNNE) (Samariya et al. 2020 ), whose definition is related to an outlier detection algorithm named Isolation using Nearest Neighbor Ensembles (iNNE) Bandaragoda et al. ( 2018 ).

Contextual Outlier INterpretation (COIN) framework (Liu et al. 2018 ), exploits the neighbourhood of anomalous samples. It first divides the normal samples into clusters in order to, then, learn, for each of them, a simple classification model. The parameters of these models are finally combined to compute a score for each feature.

2.3 Other approaches

The architecture named OARank has been developed (Vinh et al. 2015 ) in the attempt to combine the strength of both features-selection-based and score-and-search-based approaches. Because of this, it has been labelled by Samariya et al. ( 2020 ) as an hybrid approach, the only one proposed up to date. Generally speaking, OARank uses a feature-selection-based technique to find a set of features Sf and, then, apply a score-and-search-based algorithm to Sf to fine-tune the result of the feature-selection step.

A visualization-based explanation is considered by LookOut (Gupta et al. 2019 ), which explain outliers by providing users with a few focus-plots. The focus-plots are pairwise feature plots, in which the couples of features to show are selected following an objective promoting plots in which outliers are better recognisable and that, at the same time, characterize multiple outliers and minimize the overlap of the outliers covered by each plot.

Finally, a Deep-Learning-based approach is provided by the Attention-guided Triplet deviation network for Outlier interpretatioN (ATON) method (Xu et al. 2021 ), which leverages the concept of deviation between outliers and normal samples to learn an embedding space in which the analyzed outlier can be easily detected. An attention layer is used to build the transformation to the embedding space and to distil the set of outlying features from that space.

2.4 Why are we looking for transformation-based explanations?

We have already pointed out that transformation-based explanations , introduced in the preliminary version of this work (Angiulli et al. 2023 ), represent a novelty for the Outlier Explanation task, and the description of the literature presented up to this point goes in the direction of supporting the above claim.

The research for enriched forms of explanations arises from the need to have a deeper understanding of the reasons that locate an outlier sample far from the behaviour of the normal data.

To elaborate, methods returning set of features as an explanation must rely on the assumption that the returned features represent subspaces where the outlier is mostly isolated. Moreover, in order to meet the succinctness desiderata of explanations, these methods are likely to return an explanation consisting of a set of features for which the outlier behaves normally in any of its subsets. However, it is worth noting that, in several cases, it may be sufficient to modify a strict subset of the above features, or even just a single one, to make the anomaly indistinguishable from the rest of the population. Such an information, deemed to be useful indeed, is not captured using other methods the literature describes, while our method returns it correctly.

Being able to capture such an information helps understanding the characteristics of outliers and, as known in psychology, when people reason about something they are observing, they spontaneously create alternatives and imagine how the reality would change under different conditions (Byrne 2016 ).

For example, consider the two dimensional dataset in Fig.  1 a. The point in orange is an outlier in the full space, so an outlier explanation method would return \(\{x,y\}\) as the explanation. However note that the outlier does not exhibit exceptional values on both features as considered one by one. Indeed, if only the x value of the point were modified and the y value were left unchanged, the point would dive into the inliers. The same holds if only the y value is changed.

Moreover, having both the choice and the mask is useful not only for the reasons above discussed but also because in some cases there is more than one way to “fix” the anomaly. For example, consider Fig.  1 b, where outlier point (in orange) can be made inlier by applying two different transformations.

Summarizing, traditional methods are tailored to detect as more important those features that maximize the anomaly of the object which, in general, are not the features that minimize the alterations to be applied to the object to make it inlier. Thus, on the one hand the features returned are not necessarily those most suitable to be modified in order to make the object an inlier, since there is no guarantee that they are a superset of the right ones nor that they are scored in the right order. On the other hand, even if the right features were provided, and we note that it is not likely to be the case, it anyway remains the non-trivial problem of singling out the right mask to be applied, a problem that can also have more solutions.

With respect to the original conference version of this paper (Angiulli et al. 2023 ), this extended version presents several improvements and add-on, including a more extensive survey of the literature, improved motivations for the proposed approach, an improved formalization of the problem, the extension of the approach in order to manage groups of anomalies and not just single ones and a widened set of experiments. In particular, it is worth noting that extending the method in order to manage groups of anomalies required a re-design of the whole architecture.

3 The proposed technique

The purpose of this section is to describe our technique for solving the outlier explanation problem introduced in Sect.  1 .

In order to present the notion of outlier explanation , we need to introduce the transformation of an object. In the following \(\mathcal {F}= \{f_1\dots ,f_n\}\) denotes a set of n real-valued features, that is, a set of identifiers with value domains (in our case, that of real numbers for all of them) associated to them. A dataset DS defined over \(\mathcal {F}\) is a set of data objects (or, more simply, objects) over \(\mathcal {F}\) , where an object o is a mapping from \(\mathcal {F}\) to \(\mathcal {R}^n\) . For any object \(o\in DS\) , \(o[f] \in \mathbb {R}\) denotes the value that o assumes on the feature \(f\in \mathcal {F}\) .

Definition 1

Given an object \(o\in DS\) and a set e of feature-value pairs \(e = \{ (f_{i_1}, v_{i_1}), \dots , (f_{i_k}, v_{i_k}) \}\) , the transformation \(t_{e}(o)\) of o according to e is a new object \(o'\) such that \(o'[f_j] = o[f_j] + v_j\) for \(j \in \{i_1, \dots , i_k\}\) and \(o'[f_j] = o[f_j]\) otherwise.

Next, we formally define the explanation of an outlier which, roughly speaking, is a set of value-pairs that can lead to transform an outlier into an inlier.

Definition 2

Given an object \(o\in DS\) known to be an outlier, a set of feature-value pairs \(e = \{ (f_{i_1}, v_{i_1}), \dots , (f_{i_k}, v_{i_k}) \}\) is said to be an explanation for o if the transformation \(o'=t_{e}(o)\) of o according to e is an inlier in DS .

In the following, given an explanation \(e = \{(f_{i_1}, v_{i_1}), \dots (f_{i_k}, v_{i_k}) \}\) , we call choice \(c_e\) associated with e the \(|\mathcal {F}|\) -dimensional binary vector such that \(c_e[j] = 1\) if \(j\in \{i_1,\ldots ,i_k\}\) and \(c_e[j] = 0\) otherwise. Analogously, we call mask \(m_e\) associated with e the \(\mathcal {F}\) -dimensional real vector such that \(m_e[j] = v_j\) if \(j \in \{i_1,\ldots ,i_k\}\) , \(m_e[j] = 0\) otherwise.

Thus, the explanation e can be also identified by means of its associated choice-mask pair, namely \(e=\langle c_e,m_e\rangle\) .

Note that, for a given outlier object, according to the definition, many explanations may exist, whose associated features sets may partially overlap or be strict super/sub sets of each other.

In this paper, we address the outlier explanation problem whose goal is to find a set of minimal disjoint explanations for an outlier object provided in input. In the rest of this section we shall provide details on how our technique, called \(\text {M}^2\text {OE}\) , tackles this problem.

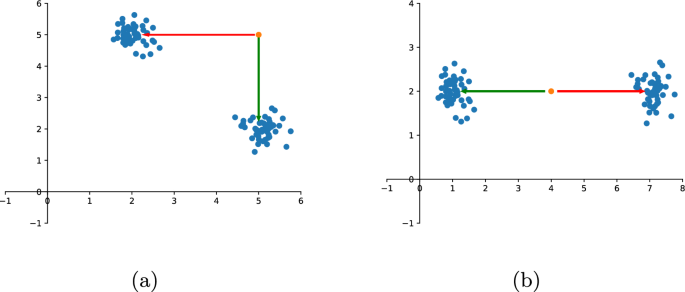
Example of different choices and masks

Before illustrating our techniques, however, it is worth pinpointing why, in general, it is needed to detect different choices and masks for a single given outlier (see Fig.  1 ). Specifically, consider a bidimensional set of data, the blue points, and the outlier object, the orange point. Figure  1 a shows how two equally relevant possible choices may exist, in this case \(c_1=[1,0]\) and \(c_2=[0,1]\) , as if only the x -feature or, equivalently, only the y -feature, is altered the red point is moved within the cloud of normal objects. Conversely, Fig.  1 b shows how, for a same choice, in this case \(c=[1,0]\) , two possible masks, namely \(m_1 = [-3,0]\) and \(m_2=[3,0]\) , can be applied to the outlier in order to transform it in an inlier.

Note that, as the example highlights, even if the outlier is anomalous in a subspace ( \(\mathbb {R}^2\) in the example) the interesting choices might refer to strict subsets of the features characterizing that subspace (a single feature in the example), witnessing that the features in the choice do not identify the anomalous subspace but, rather, represent the minimal set of features that has to be modified in order to make the outlier indistinguishable from normal objects.

3.1 Architecture pipeline description

At the basis of our \(\text {M}^2\text {OE}\) there is a deep neural network (purposely designed to compute explanations) that cooperates with a shallow module designed to build a set of minimal disjoint explanations starting from those individuated by the deep neural network module.

Figure  2 depicts the structure of the pipeline underlying our proposal.

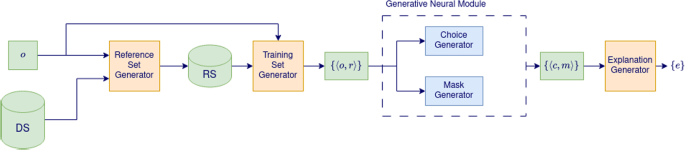
\(\text {M}^2\text {OE}\) pipeline

The first part of the pipeline is devoted to preparing the training data. The method receives in input the outlier o to be explained and the dataset DS .

First, the Reference Set Generator takes charge of selecting a Reference Set RS for the outlier o , namely a subset of k dataset objects to be used as prototype of the normality concept to conform with.

The Training Set Generator receives the outlier o and the reference set RS and builds the training set TS for the subsequent modules, consisting of the set of the k pairs \(\{ \langle o,r\rangle : r\in RS\}\)

The training set TS is then processed by the Generative Neural Module composed by two generative networks acting in parallel, namely the Choice Generator and the Mask Generator .

After the training phase, the Generative Neural Module outputs a set of k choice-mask pairs \(\langle c,m\rangle\) , each associated with a different example in TS . Finally, the Explanations Generator combines such pairs in order to build a set of minimal disjoint explanations for the outlier o .

3.1.1 Generative neural module

The Choice Generator module is a feed-forward dense neural network consisting of \(l_g\ge 3\) layers. The input layer has size 2 d in that it receives a pair of observations, namely the outlier to be explained and a reference inlier example. The hidden layers employ a ReLU activation function. The first input layer maps inputs into a larger latent space \(n_{g1}\cdot d\) ( \(n_{g1}\ge 3\) ) and then the latent space is progressively reduced by the following hidden layers. The output layer employs the sigmoid as the activation function and returns the d -dimensional real-valued choice vector \(\tilde{c}\) . The values of the elements \(\tilde{c}_i\in [0,1]\) of the vector \(\tilde{c}\) are eventually converted into binary values \(c_i\in \{0,1\}\) by means of a thresholding operation.

Also the Mask Generation module is a feed-forward deep neural network. The architecture of this module is almost identical to that of the Choice Generator , the only difference being that the output layer employs a linear activation function and, moreover, activation functions other than the ReLU can be adopted for the intermediate hidden layers.

3.1.2 Explanation computation module

Given the current reference set RS having size k , the statistics vector s associated with RS is the vector whose i -th feature ( \(1\le i\le d\) ) contains the mean feature-wise squared differences between normal points, that is:

Moreover, let \(\tilde{o}'\) denote the point

where o is the given outlier object and \(\odot\) indicates the element-by-element multiplication, representing the approximate (differentiable) version of the transformed point \(o'=t_e(o)\) for the explanation \(e=\langle c,m \rangle\) .

The loss function we employ is defined as follows:

where \(\alpha _1\) , \(\alpha _2\) and \(\alpha _3\) are values used to weigh the contributes of the three terms appearing in the loss function and \(\epsilon\) is a small constant to avoid division by zero.

The first term of the loss (having weight \(\alpha _1\) ) represents the ratio between the mean squared distance among normal points in the feature subspace identified by the choice \(\tilde{c}\) and the squared distance between the outlier and the reference point in the same feature subspace. Minimizing this terms corresponds to search for subspaces where the outlier deviates the most from the normal behavior. Thus, intuitively, this term guides the selection of the choice .

The second term of the loss (having weight \(\alpha _2\) ) represents the distance between \(\tilde{o}'\) and the inlier sample r in the feature subspace identified by the choice \(\tilde{c}\) . Minimizing this terms corresponds to finding the transformation values that make the outlier similar to inlier instances in the subspace. Since \(\tilde{o}_i' = o_i + \tilde{c}_i\cdot m_i\) , intuitively, this term guides the selection of the mask .

The last term of the loss (having weight \(\alpha _3\) ) has the purpose of reducing the number of selected outlying features, in compliance with the Occam razor principle.

Once the training phase of the neural module is completed, we collect the set \({{\mathcal {C}}}\) consisting of all the choices associated with objects of the reference set RS . The frequent itemsets \(\mathcal{F}_{{\mathcal {C}}}\) in \({\mathcal {C}}\) , where items represent single features, are then computed. Next, for each frequent itemset (aka, frequent choice) f in \({{\mathcal {F}}}_{{\mathcal {C}}}\) a clustering algorithm Footnote 1 is executed on the reference set points whose corresponding choice contains f . Finally, for each of the above determined clusters, our network is feed with inputs o and med , the medoid of the cluster, and returned choice and mask form one of the explanations to be returned to the user.

4 Dealing with anomaly groups

Till now we have focused on the explanation of a single input outlier. A very interesting extension of that application context concerns the simultaneous explanation of a set of anomalies provided together as a single input. For example, suppose you are given a set of healthy individuals and a small set of unhealthy patients. It is of great interest for analysts to detect features characterizing the pathology and, then, features able to discriminate healthy individuals from all unhealthy patients.

Next we introduce a modification to the basic \(\text {M}^2\text {OE}\) architecture, we shall refer to this new one simply as \(\text {M}^2\text {OE-groups}\) , able to deal with the above depicted scenario. Let \(o_1, \ldots , o_n\) denote the set of anomalies to be explained.

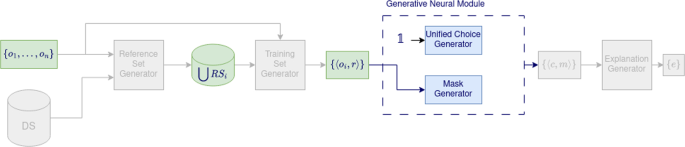
\(\text {M}^2\text {OE}\) –group pipeline

To solve the novel problem, we need to bring some modifications to the \(\text {M}^2\text {OE}\) architecture, as shown in Fig.  3 . Firstly, the Reference Set Generator selects a subset \(RS_i\) of k reference objects for any outlier \(o_i\) and, then, the training set now consists of all the pairs \(\langle o_i,r \rangle\) ( \(1\le i\le n\) ) with \(r\in RS_i\) and \(RS = \bigcup _i RS_i\) .

Furthermore, the novel Unified Generative Neural Module consists again of the Choice Generator and Mask Generator , with the substantial difference that the Choice Generator is trained to output a unified choice, namely to produce the same output for any input. Thus, the output of the module is, for any input pair \(\langle o_i, r \rangle\) , a unified choice and a different mask.

However, in practical cases, there is not a common explanations for all the outliers since different sources of anomalies can exist. In the above example, you can have that the pathology arise for two different reasons and then a group of patients share one explanation while the second group of patients share a different one.

In order to deal with this scenario, we propose an iterative procedure, reported as Algorithm 1, which works via grouping outliers into a tree of clusters each associated with a choice.

Specifically, it starts by considering each outlier as a singleton and it is used to train the architecture. Next, the algorithm repeatedly executes the following steps: ( i ) identify the two groups of objects \(s_p\) and \(s_q\) scoring the highest value of the score \(\sigma\) with respect to the choice associated with \(s_p\) (see below for its formal definition); ( ii ) merge \(s_p\) and \(s_q\) in one group and ( iii ) train the architecture on this group. Algorithm continues these steps until all groups are merged together.

As for the score \(\sigma\) we employ to select the pair of groups to merge at the current iteration, it evaluates the loss function \({{\mathcal {L}}}_{s_p}\) of the neural module trained on the subgruop \(s_p\) on the instances of the subgroup \(s_q\) with respect to the reference set points:

The rationale of this score is that these instances are the most likely to show a similar behavior after being grouped together.

It is worth noticing that since the architecture is retrained on the merged group, it is able to find the optimal choice for the group which can be, in general, different from the choices associated with subgroups and from a choice obtained by a form of combination between subgroup choices.

Algorithm 1, then, computes a hierarchical series of nested groups in a form of dendograms , where groups composed by single anomalies are the leafs, and each node identifies a group of outliers with an associated choice. Note that each outlier in a group is associated with its own mask.

The set \({\mathcal {G}}\) is used to store the dendrogram structure. It consists of pairs ( sg ,  g ), where sg denotes a child group and g its a parent group. Once such a dendogram is built, relevant group explanations are identified by cutting the tree at the point that individuates a partition \(G^*=\{g_1,\ldots ,g_{m}\}\) of the set of outliers minimizing the following equation:

Indeed, note that the loss is likely to increase when the outliers are grouped since the Generative Neural Module has to search for the optimal common choice for the group and then it is, in general, not the optimal one for each single outlier.

Thus, the average loss tends to be inversely proportional to the number of the selected groups. We can conclude that, according to the proposed formulation, the above criterion allows to select the set of groups as a trade-off between the minimization of the average loss and the minimization of the number of groups.

\(\text {M}^2\text {OE}\) – group

5 Experiments

In this section, an assessment of the quality of our technique is carried out through an experimental campaign which focuses both on studying how hyper-parameter values affect \(\text {M}^2\text {OE}\) performances and comparing its results with competitors.

Since, as stated above, this is the first method employing an explanation based on a concept of transformation, there are no other methods that are directly comparable to ours.

Thus, in order to anyway develop a comparison with other methods, we selected the two competitors sharing most commonalities with our proposal. The first of them is ATON (Xu et al. 2021 ) which uses a Neural Network in the explanation process. The second one is COIN (Liu et al. 2018 ) which also exploits the neighbourhood of the outlier to find an explanation.

We note that, since none of the techniques presented to date gives information about how to modify the outlier (see Sect.  2 ), only the choice c is taken into account for comparison purposes.

For experiments, we consider both synthetic and real data sets. Synthetic data comes from the collection of benchmarking data sets published in Keller et al. ( 2012 ), which contain subspace clusters and outliers generated in subspaces having dimensions ranging from 2 to 5. Each of these subspaces characterizes a group of anomalies for which it represents the outlierness ground truth. The peculiarity of these data sets is that the outliers have been generated in such a way that they are not observable in any lower dimensional sub-space projection, which results in building suitable explanations more challenging. This collection contains data sets with 10, 20, 30, 40, 50 and 75 dimensions and, in particular, it contains three data sets for each size. Each data set consists of 100 normal data points and includes from 19 to 111 outliers.

For what concerns real data, we have considered 7 data sets from the ODDS repository (Rayana 2016 ), that are, vowels , cardio , breast , ionosphere , satimage-2 , musk and arrhythmia , whose number of dimensions ranges from 12 to 274. More details about these data sets are provided in Table  1 .

The rest of the section is organized as follows: Sect.  5.1 describes the metrics used for the evaluation, Sect.  5.2 shows the results of the parameter study and Sect.  5.3 compares \(\text {M}^2\text {OE}\) with its competitors, finally, Sect.  5.4 discusses the results of the comparison of \(\text {M}^2\text {OE-groups}\) with other methods devoted to solve the outlier group explanation task.

5.1 Employed metrics

In order to globally evaluates our techniques, it is needed to measure both the quality of the set of features retrieved and the effectiveness of the mask suggested to obtain a normal point, so that the experimental campaign follows this two-fold objective. Indeed, given an object o and an explanation e for o , in order for e to be significant, o should be clearly an outlier in the subspace \(e_c\) and the object \(o'\) , obtained by transforming o through e , should be normal in \(e_c\) and, furthermore, \(e_c\) should be as small as possible.

In order to evaluate the quality of the set of features singled out as anomalous, it is necessary to distinguish the situation where an annotation of which actually are the outlying features is available in the first place for the evaluation purposes, from the case in which this information is not available. In the first case, to evaluate the performances of our techniques, we use the Precision and Jaccard measures:

where \(e_t\) is the true choice while \(e_c\) is the choice predicted by the method.

Counter-wisely, if there are no information available about which are the true choices (as it happens for the real data sets considered in this work) a proxy measure for subspaces outlierness is needed. In this work we employ the iForest score (Liu et al. 2008 ) to evaluate the quality of the set of features retrieved in this setting. The idea underlying this method is that anomalies are better isolated from normal data so that, if binary trees are considered, they need fewer splits to be isolated as compared to normal data.

The iForest score is used also to evaluate the quality of the transformation suggested by the model (which gives an indication of mask effectiveness). Particularly, the score \(s_o\) of the outlier o and the score \(s_{o'}\) of its “patched” version are considered. A transformation is considered successful if the value \(s_{o'}\) is lower then \(s_o\) : indeed, in this situation, the transformation has lowered the point outlierness of at least the \(5\%\) of the original value. For each of the considered data set, we will take the percentage of successful transformation to measure the quality of the mask. Since one of the key contributions of this paper is that of providing transformation-based explanations, this test is important because it measures the proposed method’s effectiveness in answering the user’s question about how to change the outlier (introduced in Sect.  2.4 ).

As a further assessment, in order to quantify the degree of abnormality of an observation o in a given subspace S , we compute \(\rho _S(o)\) , the mean distance separating o to its k nearest neighbors in the subspace S , divided by \(\sqrt{|S|}\) as a normalization factor. Then the \(Z_S(o)\) denotes the Z-score computed with respect to the dataset population, namely

Furthermore, in order to assess the compliance of subspaces with the available ground truth, we exploit the Fisher exact test , providing the probability that a randomly generated subset ss of the whole set of features \(\mathcal {F}\) shows a certain degree of overlap \(|ss\cap ss_t|\) with a target subspace \(ss_t\) . Given the set of features \(\mathcal {F}\) , the outlying subspace \(ss_t\) and the subspace \(ss\) returned by a method, a \(2\times 2\) contingency table can be built as

The null hypothesis is that such a table is obtained by chance from the hypergeometric distribution with parameters \(|\mathcal {F}|\) , \(|ss_t|\) and \(|ss|\) . The Fisher exact test can, thus, be used to evaluate the probability of observing a more extreme table, namely the p-value .

5.2 Parameters tuning

This section aims at illustrating how the performances of the method changes for different hyper-parameters configuration. In particular, we let the values of \(\alpha _1\) , \(\alpha _2\) and \(\alpha _3\) , which, we recall, are used to weigh the terms of the loss function, to vary and exploit all the synthetic data sets for the analysis purposes. For each dimensionality value, we computed the result as the arithmetic mean taken on all the data sets which points have that certain number of features.

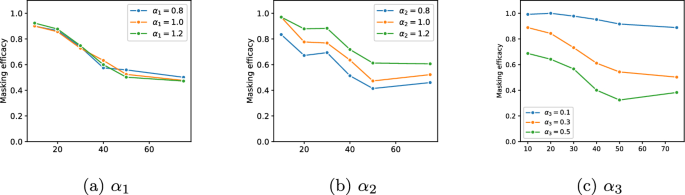
Trend of transformation success for different values of \(\alpha _1\) (5a), \(\alpha _2\) (5b) and \(\alpha _3\) (5c). Results are obtained by changing one hyper-parameters at a time, where their default values, when fixed, are, respectively: \(\alpha _1=1.0\) , \(\alpha _2=1.0\) and \(\alpha _3=0.3\) . Abscissa shows the number of dimensions of the considered data

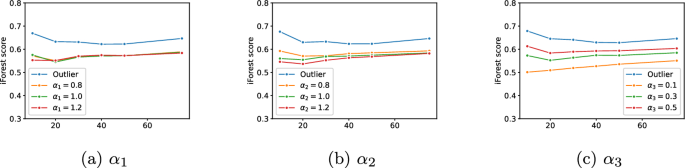
Value of the iForest score of the outlier in the space highlighted by the ground truth (blue line), and after the transformation found by using different values of \(\alpha _1\) (5a), \(\alpha _2\) (5b) and \(\alpha _3\) (5c). Results are obtained by changing one hyper-parameters at a time, where their default values, when fixed, are, respectively: \(\alpha _1=1.0\) , \(\alpha _2=1.0\) and \(\alpha _3=0.3\) . Abscissa shows the number of dimensions of the considered data

Table  2 shows the ratio between the Precision and Jaccard values achieved by \(\text {M}^2\text {OE}\) when the loss weights are equal to \(\alpha _1=1.0\) , \(\alpha _2=1.0\) and \(\alpha _3=0.3\) and when these values are changed. This analysis is performed to evaluate the sensitivity of the proposed methodology to different values of the parameters. From these results, it is possible to notice how the values of the Precision and Jaccard metrics are poorly affected by changes in the values of the loss parameters values. Indeed, their values are always near to 1, suggesting that there are no significant changes. The only exception is represented by the parameter \(\alpha _3\) , whose effect is visible in the measured precision and recall. This behaviour is the one we expect to observe, since this parameter directly affects the number of features included in the explanation by making the insertion more or less restrictive.

The trend of the transformation success is depicted in Fig.  4 , which shows that \(\alpha _2\) and \(\alpha _3\) affect most the value of this metric. In Fig.  5 , the iForrest score of the ground truth and of the set of features included in the explanation are reported, in this measurement, which is, as a consequence of the structure of these synthetic data sets, closely related to the number of features retrieved, the parameter \(\alpha _3\) is that influencing the results the most.

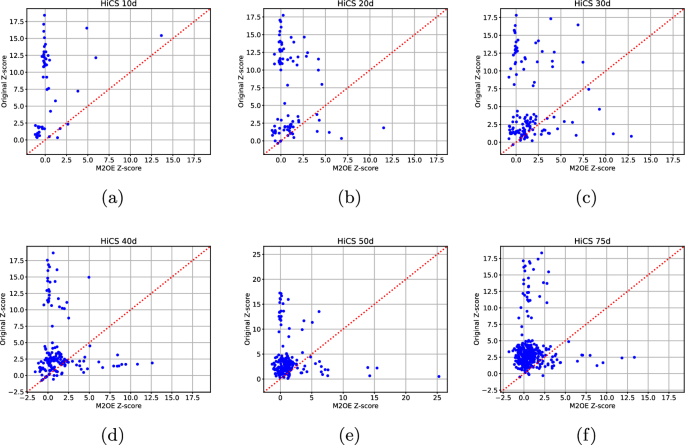
Experiments on synthetic data. Each figure reports, on the ordinate axis, the samples’ Z-scores computed in the subspace given by the choices of \(\text {M}^2\text {OE}\) , and, on the ordinate axis, the Z-score value computed on the same subspace after the transformation application

5.3 Comparison with ATON and COIN

In this section, we compare our techniques with two outlier explanation methods ATON and COIN referred to in Sect.  2 . The evaluation is carried out first on the same synthetic data sets used to study the behaviour of the method for different hyper parameters and then on some real world data sets.

5.3.1 Synthetic data sets

We begin by considering again the HiCS data sets where the ground truths for anomalous features are available so that performances are computed in terms of Precision and Jaccard. Results are obtained following the same methodology of Sect.  5.2 .

In order to compare the choice returned by \(\text {M}^2\text {OE}\) and the subspaces returned by competitors, we perform a Fisher Exact Test to measure the degree of compliance with the ground truth and collect p-values associated with \(\text {M}^2\text {OE}\) , ATON and COIN. We disregard objects where both our method and the competitor have a p-value above a significative threshold (in particular, we fix it to \(3\permille\) ) since, in those cases, results are to consider not significant. Table  3 reports the results of such comparison and, in particular, for each dataset dimensionality and for each competitor we compute the fraction of wins, where \(\text {M}^2\text {OE}\) “wins” if the p-value associated with it is lower than that associated with the competitor.

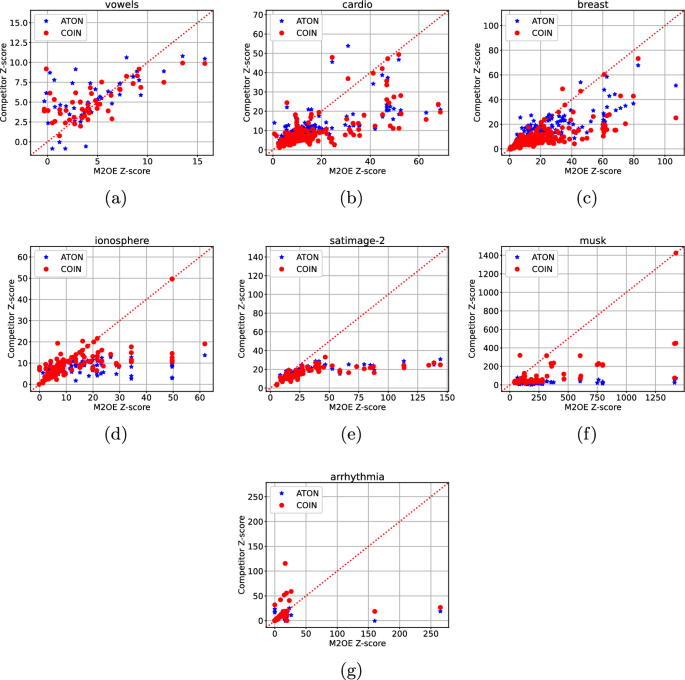
Experiments on real data sets. Each figure reports, on the ordinate axis, samples’ Z-scores computed in competitors’ subspaces, and, on the abscissa axis, the Z-scores value computed on the subspace given by the \(\text {M}^2\text {OE}\) choices

Regarding the quality of the transformation provided by \(\text {M}^2\text {OE}\) , Fig.  6 reports on the ordinate the Z-score associated with each outlier o in the subspace defined by its choice c and on the abscissa the Z-score associated with \(o'\) , the object obtained after the application of the mask m , in the same subspace. The various plots concern synthetic datasets having number of dimensions varying from 10 to 75. Results highlight that the choices c returned by \(\text {M}^2\text {OE}\) isolate subspaces in which the outlier o exhibits an significant degree of separation from the rest of the data and that the transformation associated with the choice c and the mask m is able to sensibly reduce that separation, in the great majority of points has y-values larger than x-values.

5.3.2 Real data sets

Here we considered the real data sets introduced in Sect.  5 and described in Table  1 . Since, in this setting, no information related to the outlying features is available, the iForest score is employed to perform evaluation, as described in Sect.  5.1 . All the values are obtained by performing 5 runs and then computing the mean and the standard deviation of the results.

Table  4 shows the quality score achieved by the subspaces retrieved by each of the considered methods. For each data set, the maximum value is highlighted in bold while the second maximum is highlighted in italics, the global baseline value represents the anomaly score computed in the whole feature space. From these data, it is possible to notice how \(\text {M}^2\text {OE}\) almost always reaches the maximum score, thus outperforming his competitors and, when this does not happen, it ranks second. We also note that the value of all the techniques is greater than the global baseline.

Figure  7 compares the Z-scores associated with the choice returned by \(\text {M}^2\text {OE}\) and the Z-scores associated with the subspaces returned by ATON and COIN. Larger Z-scores indicate that the outliers are better separated from the rest of the data. Since both point clouds (the blue concerning comparison with ATON and the red concerning comparison with COIN) lie mostly below the bisector, it follows that \(\text {M}^2\text {OE}\) is able to detect set of features for which outliers exhibit a more abnormal behavior. The only exception is represented by the vowel dataset, where the points lay mostly near the bisector, as, in this case, if we look at the Z-scores, \(\text {M}^2\text {OE}\) and its competitors have comparable performances.

To check if \(\text {M}^2\text {OE}\) is able to patch also real data set outliers, the percentage of successfully-patched outliers is computed and results are reported in Table  5 . This table shows that \(\text {M}^2\text {OE}\) patches a good percentage of anomalies, so we can conclude that it can provide users with effective explanations describing how to change the outliers even in this context.

5.4 Explanation of group of anomalies

Here we describe the experiments performed to test the quality of our extension of \(\text {M}^2\text {OE}\) to explain groups of anomalies. In this assessment, together with X-PACS, which is the only competitor that deals with such a setting, we also consider the single outlier version of \(\text {M}^2\text {OE}\) , ATON and COIN. For these latter methods, to obtain a single explanation for each group, we have considered three different strategies to combine returned explanations, that are, the intersection among all the explanations, which will not be reported because it always results in an empty set, the union of all the features included in the explanations (to which we will refer with a \(\cup\) subscript) and the frequent feature sets (to which we will refer with a fi subscript). In the following, we discuss the results collected for synthetic as well as real data sets.

5.4.1 Synthetic data sets

In order to check how the number of dimensions affects the explanations of groups of anomalies, we have considered one of the HiCS data sets, previously used in the assessment of the explanations of single outliers, having 75 dimensions and we have built a series of data sets having 10, 20, 30, 40, 50 and 75 dimensions by taking the anomalous dimensions characterizing each group of anomalies together with some random normal features. So, for each previously mentioned number of dimensions, we have obtained 22 data sets that include the anomalies belonging to a certain group and all the normal samples of the data set.

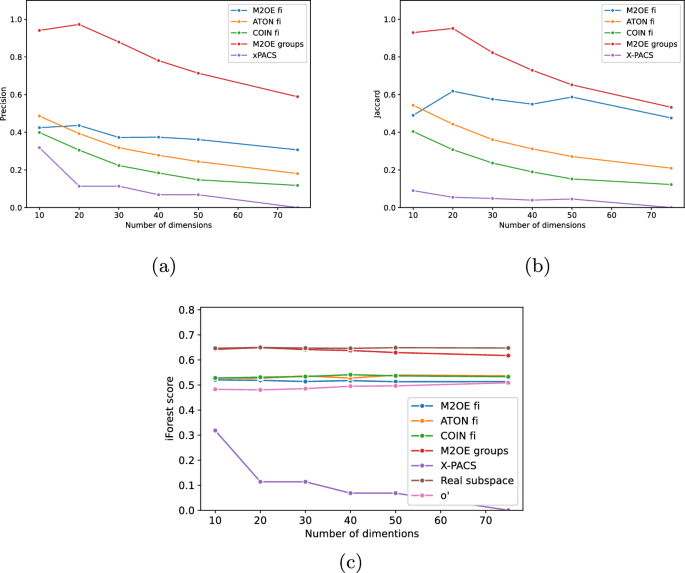
Results on the set of data sets built from one of the HiCS data sets having 75 dimensions by taking, for each group of anomalies, the anomalous features and some random normal ones. Each data set contains the anomalies belonging to one of the 22 groups included in the original data set. Figure  8 a reports the precision, Fig. 8 b reports the Jaccard score and   8 c reports the Forest score. In the latter figure, the pink line highlights the iForest score in the subspace denoted by the ground truth of the outliers after being modified according to the explanation provided by \(\text {M}^2\text {OE-groups}\)

Figure  8 depicts the results collected on these datasets. From these results, it is possible to notice how, despite not being designed to provide subspace-based explanations, \(\text {M}^2\text {OE-groups}\) heavily outperforms the other methods involved in the evaluation both considering precision, Jaccard and iForest scores. Additionally, it maintains good scores even when the number of features of the data set increases. Moreover, it is worth observing from Fig.  8 c, that the iForest score of the outliers computed in the subspace corresponding to the ground truth (brown line) consistently decreases after the application of the transformation suggested by \(\text {M}^2\text {OE-groups}\) (pink line). This result is important for the assessment of our method since it is focused on providing transformation-based explanations.

5.4.2 Real data sets

To test the performances of \(\text {M}^2\text {OE-groups}\) we consider again the real data sets employed in Sect.  5.3.2 to assess the ability of \(\text {M}^2\text {OE}\) to explain single anomalies. For these experiments, we have set a large time window fixed to 3 days, after which the explanation is deemed unsuccessful. Notwithstanding this ample time interval, X-PACS exceeded the available time for ionosphere, satimage-2 and musk data sets. Thus, we also considered a modified version of these data sets in which the number of dimensions has been reduced to 10. We refer to these data sets as \(\text {ION}_\text {R}\) , \(\text {SAT}_\text {R}\) and \(\text {MUS}_\text {R}\) . To perform the dimensionality reduction we have employed the PCA (FRS & Pearson, 1901 ).

Table  6 reports the results of the tests on the real data sets. It is worth noticing how \(\text {M}^2\text {OE-groups}\) almost always manages to provide a set of features achieving the best results in terms of iForest score, and when it is not the best one, it ranks second. Moreover, the scores of the other method that explains groups of anomalies are almost always less than those of the methodology we propose (the only exception is given by the vowels data set). It is worth point out here that, actually, our methodology was not designed to find outlying subspaces: for this reason, the obtained results must be considered particularly positive and significant.

As previously anticipated, due to its excessive demands on time, X-PACS has not been able to provide an explanation for the ionosphere, satimage-2 and musk data sets. Unfortunately, for the first of these three data sets, it was not been able to produce an explanation even after a dimensionality reduction.

Since the \(\text {M}^2\text {OE-groups}\) method is focused on transformation-based explanations, it is important to evaluate the impact that the suggested transformation has on the outliers. Table  7 reports the percentage of correctly-fixed outliers. From the results reported it is possible to observe how \(\text {M}^2\text {OE-groups}\) is always able to achieve good results according to this metric.

6 Conclusions

In this paper, a new technique to explain why a given data object has to be considered anomalous has been presented. One main novelty of our proposal is that its explanations include counterfactuals, denoting possible ways to “repair” the outlier to make it an inlier, which can provide users with a deeper understanding of data point characteristics. Thanks to the summarization performed, \(\text {M}^2\text {OE}\) is able to provide diverse explanations which account for the peculiarities of the outlier w.r.t the normal points leveraged for the explanation.

Moreover, we have presented a variant of \(\text {M}^2\text {OE}\) , called \(\text {M}^2\text {OE-groups}\) , aimed at finding an explanation justifying the outlierness of a group of anomalies. Thanks to the iterative procedure used to group the outliers, the variant gives to users the opportunity to inspect different ways to aggregate the outliers.

The extensive experimental campaign carried out on synthetic and real data sets provides empirical evidence demonstrating the quality of the results returned by \(\text {M}^2\text {OE}\) for explaining single outliers and \(\text {M}^2\text {OE-groups}\) for explaining outlier groups.

As for the limitations of the technique, we mention that sometimes the technique may experience difficulties in reporting an high-quality explanation. We verified that, although the technique is always able to decrease the outlierness of the object to be explained, in these difficult cases the object is put towards the border of normality rather than inside the normal distribution. We associated this behavior with an imperfect selection of the reference subset, which may be associated with the peculiarities of the data distribution at hand in the locality of the object. Thus, an interesting future direction of investigation concerns the proper selection of the reference set to be employed during the generative learning process of the technique in order to improve result quality. To conclude, we point out that our method has be designed in order to deal with numerical data and extending it to categorical domains represents an open challenge.

Availability of data and material

Not Applicable.

DBSCAN (Ester et al. 1996 ) has been used in the present work.

Abdallah, A., Maarof, M. A., & Zainal, A. (2016). Fraud detection system: A survey. Journal of Network and Computer Applications, 68 , 90–113.

Article   Google Scholar  

Angiulli, F., Fassetti, F., & Ferragina, L. (2022). Latent o ut: An unsupervised deep anomaly detection approach exploiting latent space distribution. Machine Learning, 112 , 1–27.

Google Scholar  

Angiulli, F., Fassetti, F., Manco, G., & Palopoli, L. (2017). Outlying property detection with numerical attributes. Data Mining and Knowledge Discovery, 31 (1), 134–163.

Article   MathSciNet   Google Scholar  

Angiulli, F., Fassetti, F., & Palopoli, L. (2009). Detecting outlying properties of exceptional objects. Acm Transactions on Database Systems (TODS), 34 (1), 1–62.

Angiulli, F., Fassetti, F., Nisticó, S., & Palopoli, L. (2023). Counterfactuals explanations for outliers via subspaces density contrastive loss. In International Conference on Discovery Science, pp 159–173. Springer

Angiulli, F., Fassetti, F., Nisticò, S., & Palopoli, L. (2022). Outlier explanation through masking models. In European Conference on Advances in Databases and Information Systems, pp 392–406. Springer

Bandaragoda, T. R., Ting, K. M., Albrecht, D., Liu, F. T., Zhu, Y., & Wells, J. R. (2018). Isolation-based anomaly detection using nearest-neighbor ensembles. Computational Intelligence, 34 (4), 968–998.

Bhuyan, M. H., Bhattacharyya, D. K., & Kalita, J. K. (2014). Network anomaly detection: Methods, systems and tools. IEEE Communications Surveys Tutorials, 16 (1), 303–336. https://doi.org/10.1109/SURV.2013.052213.00046

Byrne, R. M. (2016). Counterfactual thought. Annual Review of Psychology, 67 (1), 135–157.

Chandola, V., Banerjee, A., & Kumar, V. (2012). Anomaly detection for discrete sequences: A survey. IEEE Transactions on Knowledge and Data Engineering, 24 (5), 823–839. https://doi.org/10.1109/TKDE.2010.235

Dang, X.H., Assent, I., Ng, R.T., Zimek, A., & Schubert, E. (2014). Discriminative features for identifying and interpreting outliers. In 2014 IEEE 30th International Conference on Data Engineering, pp 88–99. IEEE

Duan, L., Tang, G., Pei, J., Bailey, J., Campbell, A., & Tang, C. (2015). Mining outlying aspects on numeric data. Data Mining and Knowledge Discovery, 29 (5), 1116–1151.

Duraj, A., & Chomatek, L. (2017). Supporting breast cancer diagnosis with multi-objective genetic algorithm for outlier detection. In International Conference on Diagnostics of Processes and Systems, pp 304–315. Springer

Ester, M., Kriegel, H.-P., Sander, J., & Xu, X., et al. (1996). A density-based algorithm for discovering clusters in large spatial databases with noise. In: Kdd, vol. 96, pp 226–231

FRS., & Pearson, K. (1901). Liii. on lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 2 (11), 559–572. https://doi.org/10.1080/14786440109462720

Guidotti, R. (2022). Counterfactual explanations and how to find them: Literature review and benchmarking. Data Mining and Knowledge Discovery, 22 , 1–55.

Gupta, N., Eswaran, D., Shah, N., Akoglu, L., & Faloutsos, C. (2019). Beyond outlier detection: Lookout for pictorial explanation. In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2018, Dublin, Ireland, September 10–14, 2018, Proceedings, Part I 18, pp 122–138. Springer

Hauskrecht, M., Batal, I., Valko, M., Visweswaran, S., Cooper, G. F., & Clermont, G. (2013). Outlier detection for patient monitoring and alerting. Journal of Biomedical Informatics, 46 (1), 47–55.

Hilal, W., Gadsden, S. A., & Yawney, J. (2021). A review of anomaly detection techniques and applications in financial fraud. Expert Systems with Applications, 193 , 116429.

Hill, D. J., & Minsker, B. S. (2010). Anomaly detection in streaming environmental sensor data: A data-driven modeling approach. Environmental Modelling & Software, 25 (9), 1014–1022.

Keller, F., Muller, E., & Bohm, K. (2012). Hics: High contrast subspaces for density-based outlier ranking. In 2012 IEEE 28th International Conference on Data Engineering, pp 1037–1048. IEEE

Kriegel, H.-P., Kröger, P., Schubert, E., & Zimek, A. (2009). Outlier detection in axis-parallel subspaces of high dimensional data. In Pacific-asia Conference on Knowledge Discovery and Data Mining, pp 831–838. Springer

Kruegel, C., & Vigna, G. (2003). Anomaly detection of web-based attacks. In Proceedings of the 10th ACM Conference on Computer and Communications Security, pp 251–261

Leigh, C., Alsibai, O., Hyndman, R. J., Kandanaarachchi, S., King, O. C., McGree, J. M., Neelamraju, C., Strauss, J., Talagala, P. D., Turner, R. D., et al. (2019). A framework for automated anomaly detection in high frequency water-quality data from in situ sensors. Science of the Total Environment, 664 , 885–898.

Liu, F.T., Ting, K.M., & Zhou, Z.-H. (2008). Isolation forest. In 2008 Eighth IEEE International Conference on Data Mining, pp 413–422. IEEE

Liu, N., Shin, D., & Hu, X. (2018). Contextual outlier interpretation. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, pp 2461–2467

Macha, M., & Akoglu, L. (2018). Explaining anomalies in groups with characterizing subspace rules. Data Mining and Knowledge Discovery, 32 , 1444–1480.

Micenková, B., Ng, R.T., Dang, X.-H., & Assent, I. (2013). Explaining outliers by subspace separability. In 2013 IEEE 13th International Conference on Data Mining, pp 518–527. IEEE

Mokoena, T., Celik, T., & Marivate, V. (2022). Why is this an anomaly? Explaining anomalies using sequential explanations. Pattern Recognition, 121 , 108227.

Narayanan, V., & Bobba, R.B. (2018). Learning based anomaly detection for industrial arm applications. In Proceedings of the 2018 Workshop on Cyber-Physical Systems Security and PrivaCy, pp 13–23

Pang, G., Shen, C., Cao, L., & Hengel, A. V. D. (2021). Deep learning for anomaly detection: A review. ACM Computing Surveys . https://doi.org/10.1145/3439950

Panjei, E., Gruenwald, L., Leal, E., Nguyen, C., & Silvia, S. (2022). A survey on outlier explanations. The VLDB Journal, 31 (5), 977–1008.

Rayana, S. (2016). ODDS library. http://odds.cs.stonybrook.edu

Russo, S., Lürig, M., Hao, W., Matthews, B., & Villez, K. (2020). Active learning for anomaly detection in environmental data. Environmental Modelling & Software, 134 , 104869.

Samariya, D., Aryal, S., Ting, K.M., & Ma, J. (2020). A new effective and efficient measure for outlying aspect mining. In International Conference on Web Information Systems Engineering, pp 463–474. Springer

Samariya, D., Ma, J., & Aryal, S. (2020). A comprehensive survey on outlying aspect mining methods. arXiv preprint arXiv:2005.02637

Silverman, B. W. (2018). Density Estimation for Statistics and Data Analysis . England: Routledge.

Book   Google Scholar  

Steinwart, I., Hush, D., & Scovel, C. (2005). A classification framework for anomaly detection. Journal of Machine Learning Research, 6 (2), 211.

MathSciNet   Google Scholar  

Vinh, N. X., Chan, J., Romano, S., Bailey, J., Leckie, C., Ramamohanarao, K., & Pei, J. (2016). Discovering outlying aspects in large datasets. Data Mining and Knowledge Discovery, 30 (6), 1520–1555.

Vinh, N.X., Chan, J., Bailey, J., Leckie, C., Ramamohanarao, K., & Pei, J. (2015). Scalable outlying-inlying aspects discovery via feature ranking. In Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp 422–434. Springer

Wells, J. R., & Ting, K. M. (2019). A new simple and efficient density estimator that enables fast systematic search. Pattern Recognition Letters, 122 , 92–98.

Xu, H., Chen, W., Zhao, N., Li, Z., Bu, J., Li, Z., Liu, Y., Zhao, Y., Pei, D., & Feng, Y., et al. (2018). Unsupervised anomaly detection via variational auto-encoder for seasonal kpis in web applications. In Proceedings of the 2018 World Wide Web Conference, pp 187–196

Xu, H., Wang, Y., Jian, S., Huang, Z., Wang, Y., Liu, N., & Li, F. (2021). Beyond outlier detection: Outlier interpretation by attention-guided triplet deviation network. In Proceedings of the Web Conference 2021. WWW ’21, pp 1328–1339. Association for Computing Machinery, New York, NY, USA. https://doi.org/10.1145/3442381.3449868 .

Zhang, J., Lou, M., Ling, T.W., & Wang, H. (2004). Hos-miner: A system for detecting outlying subspaces of high-dimensional data. In Proceedings of the 30th International Conference on Very Large Data Bases (VLDB’04), pp 1265–1268. Morgan Kaufmann Publishers Inc.

Download references

Acknowledgements

We acknowledge the support of the PNRR project FAIR - Future AI Research (PE00000013), Spoke 9 - Green-aware AI, under the NRRP MUR program funded by the NextGenerationEU.

Open access funding provided by Università della Calabria within the CRUI-CARE Agreement. No funding was received for conducting this study.

Author information

Fabrizio Angiulli, Fabio Fassetti, Simona Nisticò and Luigi Palopoli have contributed equally to this work.

Authors and Affiliations

DIMES, University of Calabria, Rende, Italy

Fabrizio Angiulli, Fabio Fassetti, Simona Nisticò & Luigi Palopoli

You can also search for this author in PubMed   Google Scholar

Contributions

Fabrizio Angiulli, Fabio Fassetti, Simona Nisticò and Luigi Palopoli contributed to the study conception and design. Material preparation, data collection and analysis were performed by all the authors. The first draft of the manuscript was written by all the authors. All authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Simona Nisticò .

Ethics declarations

Conflict of interest.

No conflicts to declare.

Ethics approval

Consent to participate, consent for publication, code availability.

The current version of the code is available at https://github.com/simona-nistico/M2OE

Additional information

Editors: Albert Bifet, Rita Ribeiro, Ana Carolina Lorena.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Angiulli, F., Fassetti, F., Nisticò, S. et al. Explaining outliers and anomalous groups via subspace density contrastive loss. Mach Learn (2024). https://doi.org/10.1007/s10994-024-06618-8

Download citation

Received : 28 March 2024

Revised : 13 August 2024

Accepted : 27 August 2024

Published : 23 September 2024

DOI : https://doi.org/10.1007/s10994-024-06618-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Outlier explanation
• Explainable artificial intelligence
• Deep learning

Advertisement

• Find a journal
• Publish with us
• Track your research