type 1 error in research

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Type i and type ii errors and statistical power.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Healthcare professionals, when determining the impact of patient interventions in clinical studies or research endeavors that provide evidence for clinical practice, must distinguish well-designed studies with valid results from studies with research design or statistical flaws. This article will help providers determine the likelihood of type I or type II errors and judge the adequacy of statistical power (see Table. Type I and Type II Errors and Statistical Power). Then one can decide whether or not the evidence provided should be implemented in practice or used to guide future studies.

• Issues of Concern

Having an understanding of the concepts discussed in this article will allow healthcare providers to accurately and thoroughly assess the results and validity of medical research. Without an understanding of type I and II errors and power analysis, clinicians could make poor clinical decisions without evidence to support them.

Type I and Type II Errors

Type I and Type II errors can lead to confusion as providers assess medical literature. A vignette that illustrates the errors is the Boy Who Cried Wolf. First, the citizens commit a type I error by believing there is a wolf when there is not. Second, the citizens commit a type II error by believing there is no wolf when there is one.

A type I error occurs when in research when we reject the null hypothesis and erroneously state that the study found significant differences when there indeed was no difference. In other words, it is equivalent to saying that the groups or variables differ when, in fact, they do not or having false positives. [1]  An example of a research hypothesis is below:

Drug 23 will significantly reduce symptoms associated with Disease A  compared to Drug 22.

For our example, if we were to state that Drug 23 significantly reduced symptoms of Disease A compared to Drug 22 when it did not, this would be a type I error. Committing a type I error can be very grave in specific scenarios. For example, if we did, move ahead with Drug 23 based on our research findings even though there was actually was no difference between groups, and the drug costs significantly more money for patients or has more side effects, then we would raise healthcare costs, cause iatrogenic harm, and not improve clinical outcomes. If a p-value is used to examine type I error, the lower the p-value, the lower the likelihood of the type I error to occur.

A type II error occurs when we declare no differences or associations between study groups when, in fact, there was. [2]  As with type I errors, type II errors in certain cause problems. Picture an example with a new, less invasive surgical technique that was developed and tested in comparison to the more invasive standard care. Researchers would seek to show no differences between patients receiving the two treatment methods in health outcomes (noninferiority study). If, however, the less invasive procedure resulted in less favorable health outcomes, it would be a severe error. Table 1 provides a depiction of type I and type II errors.

(See Type I and Type II Errors and Statistical Power Table 1) 

A concept closely aligned to type II error is statistical power. Statistical power is a crucial part of the research process that is most valuable in the design and planning phases of studies, though it requires assessment when interpreting results. Power is the ability to correctly reject a null hypothesis that is indeed false. [3]  Unfortunately, many studies lack sufficient power and should be presented as having inconclusive findings. [4]  Power is the probability of a study to make correct decisions or detect an effect when one exists. [3] [5]

The power of a statistical test is dependent on: the level of significance set by the researcher, the sample size, and the effect size or the extent to which the groups differ based on treatment. [3]  Statistical power is critical for healthcare providers to decide how many patients to enroll in clinical studies. [4]  Power is strongly associated with sample size; when the sample size is large, power will generally not be an issue. [6]  Thus, when conducting a study with a low sample size, and ultimately low power, researchers should be aware of the likelihood of a type II error. The greater the N within a study, the more likely it is that a researcher will reject the null hypothesis. The concern with this approach is that a very large sample could show a statistically significant finding due to the ability to detect small differences in the dataset; thus, utilization of p values alone based on a large sample can be troublesome.

It is essential to recognize that power can be deemed adequate with a smaller sample if the  effect size is large. [6]  What is an acceptable level of power? Many researchers agree upon a power of 80% or higher as credible enough for determining the actual effects of research studies. [3]  Ultimately, studies with lower power will find fewer true effects than studies with higher power; thus, clinicians should be aware of the likelihood of a power issue resulting in a type II error. [7]  Unfortunately, many researchers, and providers who assess medical literature, do not scrutinize power analyses. Studies with low power may inhibit future work as they lack the ability to detect actual effects with variables; this could lead to potential impacts remaining undiscovered or noted as not effective when they may be. [7]

Medical researchers should invest time in conducting power analyses to sufficiently distinguish a difference or association. [3]  Luckily, there are many tables of power values as well as statistical software packages that can help to determine study power and guide researchers in study design and analysis. If choosing to utilize statistical software to calculate power, the following are necessary for entry: the predetermined alpha level, proposed sample size, and effect size the investigator(s) is aiming to detect. [2]  By utilizing power calculations on the front end, researchers can determine adequate sample size to compute effect, and determine based on statistical findings; sufficient power was actually observed. [2]

• Clinical Significance

By limiting type I and type II errors, healthcare providers can ensure that decisions based on research outputs are safe for patients. [8]  Additionally, while power analysis can be time-consuming, making inferences on low powered studies can be inaccurate and irresponsible. Through the utilization of adequately designed studies through balancing the likelihood of type I and type II errors and understanding power, providers and researchers can determine which studies are clinically significant and should, therefore, implemented into practice.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts of Type I and II errors and power. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. They will also more effectively work in teams with other professionals. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Type I and Type II Errors and Statistical Power  Contributed by M Huecker, MD and J Shreffler, PhD

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Type I and Type II Errors and Statistical Power. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The future of Cochrane Neonatal. [Early Hum Dev. 2020] The future of Cochrane Neonatal. Soll RF, Ovelman C, McGuire W. Early Hum Dev. 2020 Nov; 150:105191. Epub 2020 Sep 12.
• Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas. [Cochrane Database Syst Rev. 2022] Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas. Crider K, Williams J, Qi YP, Gutman J, Yeung L, Mai C, Finkelstain J, Mehta S, Pons-Duran C, Menéndez C, et al. Cochrane Database Syst Rev. 2022 Feb 1; 2(2022). Epub 2022 Feb 1.
• Review Low power and type II errors in recent ophthalmology research. [Can J Ophthalmol. 2016] Review Low power and type II errors in recent ophthalmology research. Khan Z, Milko J, Iqbal M, Masri M, Almeida DRP. Can J Ophthalmol. 2016 Oct; 51(5):368-372. Epub 2016 Sep 3.
• The Effectiveness of Integrated Care Pathways for Adults and Children in Health Care Settings: A Systematic Review. [JBI Libr Syst Rev. 2009] The Effectiveness of Integrated Care Pathways for Adults and Children in Health Care Settings: A Systematic Review. Allen D, Gillen E, Rixson L. JBI Libr Syst Rev. 2009; 7(3):80-129.
• Review Impact of summer programmes on the outcomes of disadvantaged or 'at risk' young people: A systematic review. [Campbell Syst Rev. 2024] Review Impact of summer programmes on the outcomes of disadvantaged or 'at risk' young people: A systematic review. Muir D, Orlando C, Newton B. Campbell Syst Rev. 2024 Jun; 20(2):e1406. Epub 2024 Jun 13.

Recent Activity

• Type I and Type II Errors and Statistical Power - StatPearls Type I and Type II Errors and Statistical Power - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

Type 1 and Type 2 Errors in Statistics

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

On This Page:

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty). Because a p -value is based on probabilities, there is always a chance of making an incorrect conclusion regarding accepting or rejecting the null hypothesis ( H 0 ).

Anytime we make a decision using statistics, there are four possible outcomes, with two representing correct decisions and two representing errors.

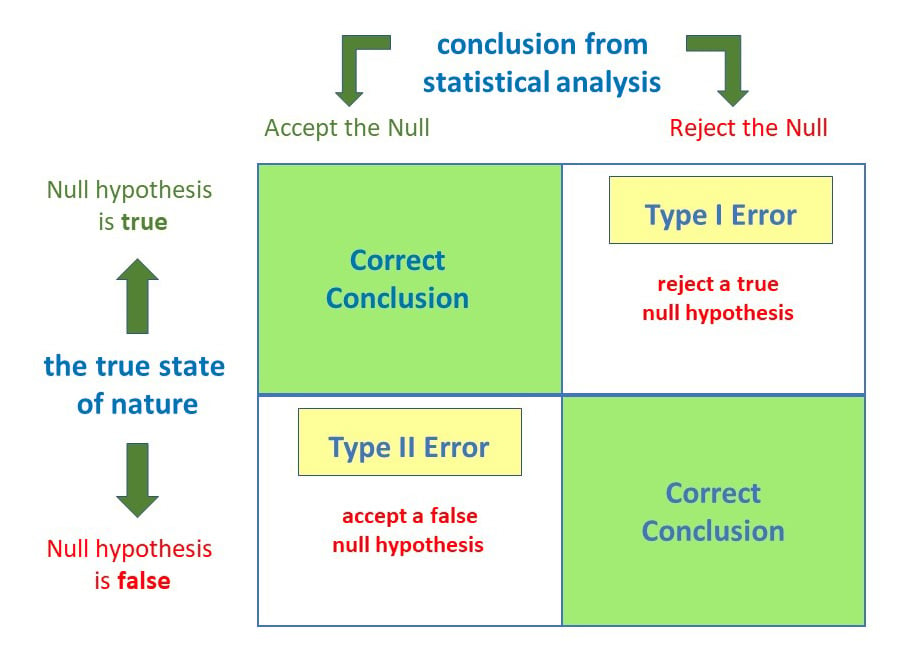
The chances of committing these two types of errors are inversely proportional: that is, decreasing type I error rate increases type II error rate and vice versa.

As the significance level (α) increases, it becomes easier to reject the null hypothesis, decreasing the chance of missing a real effect (Type II error, β). If the significance level (α) goes down, it becomes harder to reject the null hypothesis , increasing the chance of missing an effect while reducing the risk of falsely finding one (Type I error).

Type I error 

A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. Simply put, it’s a false alarm.

This means that you report that your findings are significant when they have occurred by chance.

The probability of making a type 1 error is represented by your alpha level (α), the p- value below which you reject the null hypothesis.

A p -value of 0.05 indicates that you are willing to accept a 5% chance of getting the observed data (or something more extreme) when the null hypothesis is true.

You can reduce your risk of committing a type 1 error by setting a lower alpha level (like α = 0.01). For example, a p-value of 0.01 would mean there is a 1% chance of committing a Type I error.

However, using a lower value for alpha means that you will be less likely to detect a true difference if one really exists (thus risking a type II error).

Scenario: Drug Efficacy Study

Imagine a pharmaceutical company is testing a new drug, named “MediCure”, to determine if it’s more effective than a placebo at reducing fever. They experimented with two groups: one receives MediCure, and the other received a placebo.

• Null Hypothesis (H0) : MediCure is no more effective at reducing fever than the placebo.
• Alternative Hypothesis (H1) : MediCure is more effective at reducing fever than the placebo.

After conducting the study and analyzing the results, the researchers found a p-value of 0.04.

If they use an alpha (α) level of 0.05, this p-value is considered statistically significant, leading them to reject the null hypothesis and conclude that MediCure is more effective than the placebo.

However, MediCure has no actual effect, and the observed difference was due to random variation or some other confounding factor. In this case, the researchers have incorrectly rejected a true null hypothesis.

Error : The researchers have made a Type 1 error by concluding that MediCure is more effective when it isn’t.

Implications

Resource Allocation : Making a Type I error can lead to wastage of resources. If a business believes a new strategy is effective when it’s not (based on a Type I error), they might allocate significant financial and human resources toward that ineffective strategy.

Unnecessary Interventions : In medical trials, a Type I error might lead to the belief that a new treatment is effective when it isn’t. As a result, patients might undergo unnecessary treatments, risking potential side effects without any benefit.

Reputation and Credibility : For researchers, making repeated Type I errors can harm their professional reputation. If they frequently claim groundbreaking results that are later refuted, their credibility in the scientific community might diminish.

Type II error

A type 2 error (or false negative) happens when you accept the null hypothesis when it should actually be rejected.

Here, a researcher concludes there is not a significant effect when actually there really is.

The probability of making a type II error is called Beta (β), which is related to the power of the statistical test (power = 1- β). You can decrease your risk of committing a type II error by ensuring your test has enough power.

You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.

Scenario: Efficacy of a New Teaching Method

Educational psychologists are investigating the potential benefits of a new interactive teaching method, named “EduInteract”, which utilizes virtual reality (VR) technology to teach history to middle school students.

They hypothesize that this method will lead to better retention and understanding compared to the traditional textbook-based approach.

• Null Hypothesis (H0) : The EduInteract VR teaching method does not result in significantly better retention and understanding of history content than the traditional textbook method.
• Alternative Hypothesis (H1) : The EduInteract VR teaching method results in significantly better retention and understanding of history content than the traditional textbook method.

The researchers designed an experiment where one group of students learns a history module using the EduInteract VR method, while a control group learns the same module using a traditional textbook.

After a week, the student’s retention and understanding are tested using a standardized assessment.

Upon analyzing the results, the psychologists found a p-value of 0.06. Using an alpha (α) level of 0.05, this p-value isn’t statistically significant.

Therefore, they fail to reject the null hypothesis and conclude that the EduInteract VR method isn’t more effective than the traditional textbook approach.

However, let’s assume that in the real world, the EduInteract VR truly enhances retention and understanding, but the study failed to detect this benefit due to reasons like small sample size, variability in students’ prior knowledge, or perhaps the assessment wasn’t sensitive enough to detect the nuances of VR-based learning.

Error : By concluding that the EduInteract VR method isn’t more effective than the traditional method when it is, the researchers have made a Type 2 error.

This could prevent schools from adopting a potentially superior teaching method that might benefit students’ learning experiences.

Missed Opportunities : A Type II error can lead to missed opportunities for improvement or innovation. For example, in education, if a more effective teaching method is overlooked because of a Type II error, students might miss out on a better learning experience.

Potential Risks : In healthcare, a Type II error might mean overlooking a harmful side effect of a medication because the research didn’t detect its harmful impacts. As a result, patients might continue using a harmful treatment.

Stagnation : In the business world, making a Type II error can result in continued investment in outdated or less efficient methods. This can lead to stagnation and the inability to compete effectively in the marketplace.

How do Type I and Type II errors relate to psychological research and experiments?

Type I errors are like false alarms, while Type II errors are like missed opportunities. Both errors can impact the validity and reliability of psychological findings, so researchers strive to minimize them to draw accurate conclusions from their studies.

How does sample size influence the likelihood of Type I and Type II errors in psychological research?

Sample size in psychological research influences the likelihood of Type I and Type II errors. A larger sample size reduces the chances of Type I errors, which means researchers are less likely to mistakenly find a significant effect when there isn’t one.

A larger sample size also increases the chances of detecting true effects, reducing the likelihood of Type II errors.

Are there any ethical implications associated with Type I and Type II errors in psychological research?

Yes, there are ethical implications associated with Type I and Type II errors in psychological research.

Type I errors may lead to false positive findings, resulting in misleading conclusions and potentially wasting resources on ineffective interventions. This can harm individuals who are falsely diagnosed or receive unnecessary treatments.

Type II errors, on the other hand, may result in missed opportunities to identify important effects or relationships, leading to a lack of appropriate interventions or support. This can also have negative consequences for individuals who genuinely require assistance.

Therefore, minimizing these errors is crucial for ethical research and ensuring the well-being of participants.

Further Information

• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Statistical notes for clinical researchers: Type I and type II errors in statistical decision

Hae-young kim.

• Author information
• Article notes
• Copyright and License information

Correspondence to Hae-Young Kim, DDS, PhD. Associate Professor, Department of Health Policy and Management, College of Health Science, and Department of Public Health Sciences, Graduate School, Korea University, 145 Anam-ro, Seongbukgu, Seoul, Korea 136-701. TEL, +82-2-3290-5667; FAX, +82-2-940-2879; [email protected]

Corresponding author.

Issue date 2015 Aug.

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License ( http://creativecommons.org/licenses/by-nc/3.0/ ) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Statistical inference is a procedure that we try to make a decision about a population by using information from a sample which is a part of it. In modern statistics it is assumed that we never know about a population, and there is always a possibility to make errors. Theoretically a sample statistic may have values in a wide range because we may select a variety of different samples, which is called a sampling variation. To get practically meaningful inference we preset a certain level of error. In statistical inference we presume two types of error, type I and type II errors.

Null hypothesis and alternative hypothesis

The first step of statistical testing is the setting of hypotheses. When comparing multiple group means we usually set a null hypothesis. For example, "There is no true mean difference," is a general statement or a default position. The other side is an alternative hypothesis such as "There is a true mean difference." Often the null hypothesis is denoted as H 0 and the alternative hypothesis as H 1 or H a . To test a hypothesis, we collect data and measure how much the data support or contradict the null hypothesis. If the measured results are similar to or only slightly different from the condition stated by the null hypothesis, we do not reject and accept H 0 . However, if the dataset shows a big and significant difference from the condition stated by the null hypothesis, we regard that there is enough evidence that the null hypothesis is not true and reject H 0 . When a null hypothesis is rejected, the alternative hypothesis is adopted.

Type I and type II errors

As we assume that we never directly know the information of the population, we never know whether the statistical decision is right or wrong. Actually, the H 0 may be right or wrong and we could make a decision of the acceptance or the rejection of H 0 . In a situation of statistical decision, there may be four different occasions as presented in Table 1 . Two situations lead correct conclusions that true H 0 is accepted and false H 0 is rejected. However, the others are two incorrect erroneous situations that false H 0 is accepted and true H 0 is rejected. A Type I error or alpha (α) error refers to an erroneous rejection of true H 0 . Conversely, a Type II error or beta (β) error refers to an erroneous acceptance of false H 0 .

Table 1. Possible results of hypothesis testing.

Making some level of error is unavoidable because fundamental uncertainty lies in a statistical inference procedure. As allowing errors is basically harmful, we need to control or limit the maximum level of errors. Which type of error is more risky between type I and type II errors? Traditionally, committing type I error has been considered more risky, and thus more strict control of type I error has been performed in statistical inference.

When we have interest in the null hypothesis only, we may think about type I error only. Let's consider a situation that someone develops a new method and insists that it is more efficient than conventional methods but the new method is actually not more efficient. The truth is H 0 that says "The effects of conventional and newly developed methods are equal." Let's suppose the statistical test results support the efficiency of the new method, which is an erroneous conclusion that the true H 0 is rejected (type I error). According to the conclusion, we consider adopting the newly developed method and making effort to construct a new production system. The erroneous statistical inference with type I error would result in an unnecessary effort and vain investment for nothing better. Otherwise, if the statistical conclusion was made correctly that the conventional and newly developed methods were equal, then we could comfortably stay with the familiar conventional method. Therefore, type I error has been strictly controlled to avoid such useless effort for an inefficient change to adopt new things.

In other example, let's think that we are interested in a safety issue. Someone developed a new method which is actually safer compared to the conventional method. In this situation, null hypothesis states that "Degrees of safety of both methods are equal", when the alternative hypothesis that "The new method is safer than conventional method" is true. Let's suppose that we erroneously accept the null hypothesis (type II error) as the result of statistical inference. We erroneously conclude equal safety and we stay on the less safe conventional environment and have to be exposed to risks continuously. If the risk is a serious one, we would stay in a danger because of the erroneous conclusion with type II error. Therefore, not only type I error but also type II error need to be controlled.

Schematic example of type I and type II errors

Figure 1 shows a schematic example of relative sampling distributions under a null hypothesis (H 0 ) and an alternative hypothesis (H 1 ). Let's suppose they are two sampling distributions of sample means ( X ). H 0 states that sample means are normally distributed with population mean zero. H 1 states the different population mean of 3 under the same shape of sampling distribution. For simplicity, let's assume the standard error of two distributions is one. Therefore, the sampling distribution under H 0 is assumed as the standard normal distribution in this example. In statistical testing on H 0 with an alpha level 0.05, the critical values are set at ± 2 (or exactly 1.96). If the observed sample mean from the dataset lies within ± 2, then we accept H 0 , because we don't have enough evidence to deny H 0 . Or, if the observed sample mean lies beyond the range, we reject H 0 and adopt H 1 . In this example we can say that the probability of alpha error (two-sided) is set at 0.05, because the area beyond ± 2 is 0.05, which is the probability of rejecting the true H 0 . As seen in Figure 1 , extreme values larger than absolute 2 can appear under H 0 with the standard normal distribution ranging to infinity. However, we practically decide to reject H 0 , because the extreme values are too different from the assumed mean, zero. Though the decision includes a probability of error of 0.05, we allow the risk of error because the difference is considered sufficiently big to reach a reasonable conclusion that the null hypothesis is false. As we never know the truth whether the sample dataset we have is from the population H 0 or H 1 , we can make decision only based on the value we observe from the sample data.

Figure 1. Illustration of type I (α) and type II (β) errors.

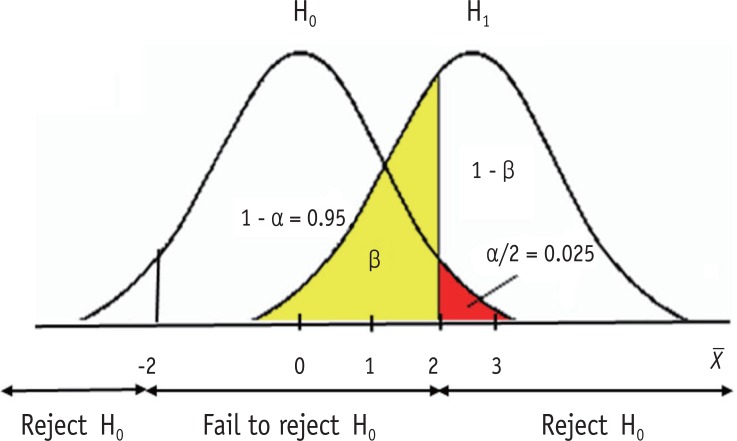
Type II error is shown as the area lower than 2 under the distribution of H 1 . The amount of type II error can be calculated only when the alternative hypothesis suggest a definite value. In Figure 1 , a definite mean value of 3 is used in the alternative hypothesis. The critical value 2 is one standard error (= 1) smaller than mean 3 and is standardized to z = - 1 = 2 - 3 1 in a standard normal distribution. The area less than z = -1 is 0.16 (yellow area) in standard normal distribution. Therefore, the amount of type II error is obtained as 0.16 in this example.

Relationship and affecting factors on type I and type II errors

1. related change of both errors.

Type I and type II errors are closely related. If all other conditions are the same, the reduction of Type I error level accompanies the increase of type II error level. When we decrease alpha error level from 0.05 to 0.01, the critical value moves outward to around ± 2.58. As the result, beta level will increase to around 0.34 in Figure 1 , if all other conditions are the same. Conversely, moving the determinant line to the left side will cause both decrease of type II error level and increase of type I error level. Therefore, the determination of error level should be a procedure considering both error types simultaneously.

2. Effect of distance between H 0 and H 1

If H 1 suggest a bigger center, e.g., 4 instead of 3, then the distribution moves to the right. If we fix the alpha level as 0.05, then the beta level gets smaller than ever. If the center value is 4 then z value is -2 and the area less than -2 in the standard normal distribution is obtained as 0.025. If all other condition is the same, the increase of distance between H 0 and H 1 decrease the beta error level.

3. Effect of sample size

Then how do we maintain both error levels lower? Increasing the sample size is one answer, because a large sample size reduce standard error (standard deviation/√sample size) when all other conditions retained as the same. Smaller standard error can produce more concentrated sampling distributions with slender curve under both null and alternative hypothesis and the consequent overlapping area gets smaller. As sample size increases, we can get satisfactory low levels of both alpha and beta errors.

Statistical significance level

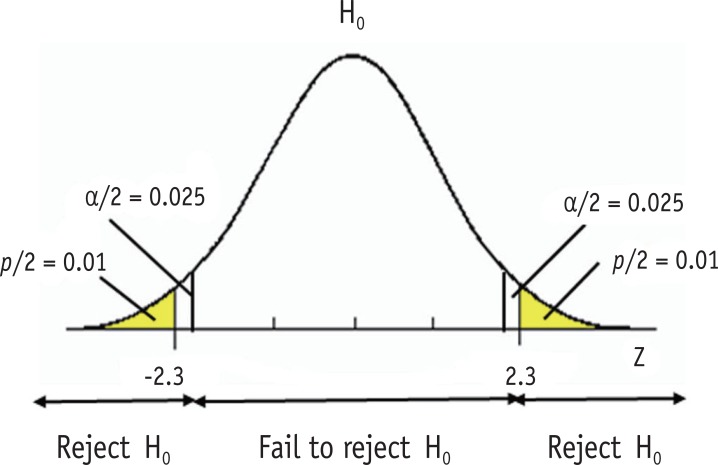
Type I error level of is often called a significance level. In a statistical testing, we reject the null hypothesis when the observed value from the dataset is located in area of extreme 0.05 and conclude there is evidence of difference from the null hypothesis when we set the alpha level at 0.05. As we consider the difference over the level is statistically significant, the level is called a significance level. Sometimes the significance level is expressed using p value, e.g., "Statistical significance was determined as p < 0.05." P value is defined as the probability of obtaining the observed value or more extreme values when the null hypothesis is true. Figure 2 shows that type I error level at 0.05 and a two-sided p value of 0.02. The observed z value 2.3 was located in the rejection region with p value of 0.02, which is smaller than the significance level 0.05. Small p value indicates that the probability of observing such a dataset or more extreme cases is very low under the assumed null hypothesis.

Figure 2. Significance level and p value.

Statistical power

Power is the probability of rejecting a false null hypothesis, which is the other side of type II error. Power is calculated as 1- Type II error (β). In Figure 1 , type II error level is 0.16 and power is obtained as 0.84. Usually a power level of 0.8 - 0.9 is required in experimental studies. Because of the relationship between type I and type II errors, we need to keep a minimum required level of both errors. Sufficient sample size is needed to keep the type I error low as 0.05 or 0.01 and the power high as 0.8 or 0.9.

• 1. Rosner B. Fundamentals of Biostatistics. 6th ed. Belmont: Duxbury Press; 2006. pp. 226–252. [ Google Scholar ]
• View on publisher site
• PDF (548.6 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

• Search Search Please fill out this field.

What Is a Type I Error?

• How It Works

The Bottom Line

• Business Leaders
• Math and Statistics

Type 1 Error: Definition, False Positives, and Examples

Investopedia / Julie Bang

In simple terms, a type I error is a false positive result. If a person was diagnosed with a medical condition that they do not have, this would be an example of a type I error. Similarly, if a person was convicted of a crime, a type I error occurs if they were innocent.

Within the field of statistics, a type 1 error is when the null hypothesis — the assumption that no relationship exists between different variables—is incorrectly rejected. In the event of a type I error, the results are flawed if a relationship is found between the given variables when in fact no relationship is present.

Key Takeaways

• A type I error is a false positive leading to an incorrect rejection of the null hypothesis.
• The null hypothesis assumes no cause-and-effect relationship between the tested item and the stimuli applied during the test.
• A false positive can occur if something other than the stimuli causes the outcome of the test.

How Does a Type I Error Occur?

A type I error can result across a wide range of scenarios, from medical diagnosis to statistical research, particularly when there is a greater degree of uncertainty.

In statistical research, hypothesis testing is designed to provide evidence that the hypothesis is supported by the data being tested. To do so, it starts with a null hypothesis, which is the assumption that there is no statistical significance between two data sets, variables, or populations . In many cases, a researcher generally tries to disprove the null hypothesis.

For example, consider a null hypothesis that states that ethical investment strategies perform no better than the S&P 500 . To analyze this, an analyst would take samples of data and test the historical performance of ethical investment strategies to determine if they outperformed the S&P 500. If they conclude that ethical investment strategies outperform the S&P 500, when in fact they perform no better than the index, the null hypothesis would be rejected and a type I error would occur. These wrongful conclusions may have resulted from unrelated factors or incorrect data analysis.

Often, researchers will determine a probability of achieving their results, called the significance level. Typically, the significance level is set at 5%, meaning the likelihood of obtaining your result is 5% in the case that the null hypothesis is valid. Going further, by reducing the significance level, it reduces the odds of a type I error from occurring.

Ideally, a null hypothesis should never be rejected if it's found to be true. However, there are situations when errors can occur.

Examples of Type I Errors

Let's look at a couple of hypothetical examples to show how type I errors occur.

Criminal Trials

Type I errors commonly occur in criminal trials, where juries are required to come up with a verdict of either innocent or guilty. In this case, the null hypothesis is that the person is innocent, while the alternative is guilty. A jury may come up with a type I error if the members find that the person is found guilty and is sent to jail, despite actually being innocent.

Medical Testing

In medical testing, a type I error would cause the appearance that a treatment for a disease has the effect of reducing the severity of the disease when, in fact, it does not. When a new medicine is being tested, the null hypothesis will be that the medicine does not affect the progression of the disease.

Let's say a lab is researching a new cancer drug . Their null hypothesis might be that the drug does not affect the growth rate of cancer cells.

After applying the drug to the cancer cells, the cancer cells stop growing. This would cause the researchers to reject their null hypothesis that the drug would have no effect. If the drug caused the growth stoppage, the conclusion to reject the null, in this case, would be correct.

However, if something else during the test caused the growth stoppage instead of the administered drug, this would be an example of an incorrect rejection of the null hypothesis (i.e., a type I error).

How Does a Type I Error Arise?

A type I error occurs when the null hypothesis, which is the belief that there is no statistical significance or effect between the data sets considered in the hypothesis, is mistakenly rejected. The type I error should never be rejected even though it's accurate. It is also known as a false positive result.

What Is the Difference Between a Type I and Type II Error?

Type I and type II errors occur during statistical hypothesis testing. While the type I error (a false positive) rejects a null hypothesis when it is, in fact, correct, the type II error (a false negative) fails to reject a false null hypothesis. For example, a type I error would convict someone of a crime when they are actually innocent. A type II error would acquit a guilty individual when they are guilty of a crime.

What Is a Null Hypothesis?

A null hypothesis occurs in statistical hypothesis testing. It states that no relationship exists between two data sets or populations. When a null hypothesis is accurate and rejected, the result is a false positive or a type I error. When it is false and fails to be rejected, a false negative occurs. This is also referred to as a type II error.

What's the Difference Between a Type I Error and a False Positive?

A type I error is often called a false positive. This occurs when the null hypothesis is rejected even though it's correct. The rejection takes place because of the assumption that there is no relationship between the data sets and the stimuli. As such, the outcome is assumed to be incorrect.

Type I errors, which incorrectly reject the null hypothesis when it is in fact true, are present in many areas, such as making investment decisions or deciding the fate of a person in a criminal trial.

Most commonly, the term is used in statistical research that applies hypothetical testing. In this method, data sets are used to either accept or determine a specific outcome using a null hypothesis. Although we often don't realize it, we use hypothesis testing in our everyday lives to determine whether the results are valid or an outcome is true.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.1 - type i and type ii errors.

When conducting a hypothesis test there are two possible decisions: reject the null hypothesis or fail to reject the null hypothesis. You should remember though, hypothesis testing uses data from a sample to make an inference about a population. When conducting a hypothesis test we do not know the population parameters. In most cases, we don't know if our inference is correct or incorrect.

When we reject the null hypothesis there are two possibilities. There could really be a difference in the population, in which case we made a correct decision. Or, it is possible that there is not a difference in the population (i.e., \(H_0\) is true) but our sample was different from the hypothesized value due to random sampling variation. In that case we made an error. This is known as a Type I error.

When we fail to reject the null hypothesis there are also two possibilities. If the null hypothesis is really true, and there is not a difference in the population, then we made the correct decision. If there is a difference in the population, and we failed to reject it, then we made a Type II error.

Rejecting \(H_0\) when \(H_0\) is really true, denoted by \(\alpha\) ("alpha") and commonly set at .05

     \(\alpha=P(Type\;I\;error)\)

Failing to reject \(H_0\) when \(H_0\) is really false, denoted by \(\beta\) ("beta")

     \(\beta=P(Type\;II\;error)\)

Example: Trial Section  

A man goes to trial where he is being tried for the murder of his wife.

We can put it in a hypothesis testing framework. The hypotheses being tested are:

• \(H_0\) : Not Guilty
• \(H_a\) : Guilty

Type I error  is committed if we reject \(H_0\) when it is true. In other words, did not kill his wife but was found guilty and is punished for a crime he did not really commit.

Type II error  is committed if we fail to reject \(H_0\) when it is false. In other words, if the man did kill his wife but was found not guilty and was not punished.

Example: Culinary Arts Study Section  

A group of culinary arts students is comparing two methods for preparing asparagus: traditional steaming and a new frying method. They want to know if patrons of their school restaurant prefer their new frying method over the traditional steaming method. A sample of patrons are given asparagus prepared using each method and asked to select their preference. A statistical analysis is performed to determine if more than 50% of participants prefer the new frying method:

• \(H_{0}: p = .50\)
• \(H_{a}: p>.50\)

Type I error  occurs if they reject the null hypothesis and conclude that their new frying method is preferred when in reality is it not. This may occur if, by random sampling error, they happen to get a sample that prefers the new frying method more than the overall population does. If this does occur, the consequence is that the students will have an incorrect belief that their new method of frying asparagus is superior to the traditional method of steaming.

Type II error  occurs if they fail to reject the null hypothesis and conclude that their new method is not superior when in reality it is. If this does occur, the consequence is that the students will have an incorrect belief that their new method is not superior to the traditional method when in reality it is.