regression general linear hypothesis

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.2.1: Hypothesis Test for Linear Regression

• Last updated
• Save as PDF
• Page ID 34850

• Rachel Webb
• Portland State University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

To test to see if the slope is significant we will be doing a two-tailed test with hypotheses. The population least squares regression line would be \(y = \beta_{0} + \beta_{1} + \varepsilon\) where \(\beta_{0}\) (pronounced “beta-naught”) is the population \(y\)-intercept, \(\beta_{1}\) (pronounced “beta-one”) is the population slope and \(\varepsilon\) is called the error term.

If the slope were horizontal (equal to zero), the regression line would give the same \(y\)-value for every input of \(x\) and would be of no use. If there is a statistically significant linear relationship then the slope needs to be different from zero. We will only do the two-tailed test, but the same rules for hypothesis testing apply for a one-tailed test.

We will only be using the two-tailed test for a population slope.

The hypotheses are:

\(H_{0}: \beta_{1} = 0\) \(H_{1}: \beta_{1} \neq 0\)

The null hypothesis of a two-tailed test states that there is not a linear relationship between \(x\) and \(y\). The alternative hypothesis of a two-tailed test states that there is a significant linear relationship between \(x\) and \(y\).

Either a t-test or an F-test may be used to see if the slope is significantly different from zero. The population of the variable \(y\) must be normally distributed.

F-Test for Regression

An F-test can be used instead of a t-test. Both tests will yield the same results, so it is a matter of preference and what technology is available. Figure 12-12 is a template for a regression ANOVA table,

where \(n\) is the number of pairs in the sample and \(p\) is the number of predictor (independent) variables; for now this is just \(p = 1\). Use the F-distribution with degrees of freedom for regression = \(df_{R} = p\), and degrees of freedom for error = \(df_{E} = n - p - 1\). This F-test is always a right-tailed test since ANOVA is testing the variation in the regression model is larger than the variation in the error.

Use an F-test to see if there is a significant relationship between hours studied and grade on the exam. Use \(\alpha\) = 0.05.

Hours Studied for Exam 20 16 20 18 17 16 15 17 15 16 15 17 16 17 14 Grade on Exam 89 72 93 84 81 75 70 82 69 83 80 83 81 84 76

The hypotheses are:

\(H_{0}: \beta_{1} = 0\)
\(H_{1}: \beta_{1} \neq 0\)

Compute the sum of squares.

\(SS_{xx} = 41.6\), \(SS_{yy} = 631.7333\), \(SS_{xy} = 133.8\), \(n = 15\) and \(p = 1\)

\(SSR = \frac{\left(SS_{xy}\right)^{2}}{SS_{xx}} = \frac{(133.8)^{2}}{41.6} = 430.3471154\)

\(SSE = SST - SSR = 631.7333 - 430.3471154 = 201.3862\)

\(SST = SS_{yy} = 631.7333\)

Compute the degrees freedom.

\(df_{T} = n - 1 = 14 \quad\quad df_{E} = n - p - 1 = 15 - 1 - 1 = 13\)

Compute the mean squares.

\(MSR = \frac{SSR}{p} = \frac{430.3471154}{1} = 430.3471154 \quad\quad MSE = \frac{SSE}{n-p-1} = \frac{201.3862}{13} = 15.4912\)

Compute the Test Statistic

\(F = \frac{MSR}{MSE} = \frac{430.3471154}{15.4912} = 27.7801\)

Substitute the numbers into the ANOVA table:

This is a right-tailed F-test with \(df = 1, 13\) and \(\alpha\) = 0.05, which gives a critical value of 4.667.

In Excel we can find the critical value by using the function =F.INV.RT(0.05,1,13) = 4.667.

Or use the online calculator at to visualize the critical value, as shown in Figure 12-13. It is hard to see the shaded tail in the following picture above the test statistic since the F-distribution is so close to the \(x\)-axis after 3, but it has the right-tail shaded from 4.667 and greater.

The test statistic 27.78 is even further out in the tail than the critical value, so we would reject \(H_{0}\). At the 5% level of significance, there is a statistically significant relationship between hours studied and grade on a student’s final exam.

The p-value could also be used to make the decision. The p-value method would use the function =F.DIST.RT(27.78,1,13) = 0.00015 in Excel. The p-value is less than \(\alpha\) = 0.05, which also verifies that we reject \(H_{0}\).

The following is the output from Excel and SPSS. Note the same ANOVA table information is shown but the columns are in a different order.

T-Test for Regression

If the regression equation has a slope of zero, then every \(x\) value will give the same \(y\) value and the regression equation would be useless for prediction. We should perform a t-test to see if the slope is significantly different from zero before using the regression equation for prediction. The numeric value of t will be the same as the t-test for a correlation. The two test statistic formulas are algebraically equal; however, the formulas are different and we use a different parameter in the hypotheses.

The formula for the t-test statistic is \(t = \frac{b_{1}}{\sqrt{ \left(\frac{MSE}{SS_{xx}}\right) }}\)

Use the t-distribution with degrees of freedom equal to \(n - p - 1\).

The t-test for slope has the same hypotheses as the F-test:

Use a t-test to see if there is a significant relationship between hours studied and grade on the exam, use \(\alpha\) = 0.05.

Hours Studied for Exam 20 16 20 18 17 16 15 17 15 16 15 17 16 17 14 Grade on Exam 89 72 93 84 81 75 70 82 69 83 80 83 81 84 76

The hypotheses are:

\(H_{0}: \beta_{1} = 0\)
\(H_{1}: \beta_{1} \neq 0\)

Find the critical value using \(df_{E} = n - p - 1 = 13\) for a two-tailed test \(\alpha\) = 0.05 inverse t-distribution to get the critical values \(\pm 2.160\).

Draw the sampling distribution and label the critical values, as shown in Figure 12-14.

The critical value is the same as we found using the t-test for correlation.

Next, find the test statistic \(t = \frac{b_{1}}{\sqrt{ \left(\frac{MSE}{SS_{xx}}\right) }} = \frac{3.216346}{\sqrt{ \left(\frac{15.4912}{41.6}\right) }}\) = 5.271\).

The test statistic value is the same value of the t-test for correlation even though they used different formulas. We look in the same place using technology as the correlation test.

The test statistic is greater than the critical value of 2.160 and in the rejection region. The decision is to reject \(H_{0}\).

Summary: At the 5% significance level, there is enough evidence to support the claim that there is a significant linear relationship (correlation) between the number of hours studied for an exam and exam scores. The p-value method could also be used to find the same decision.

The p-value = 0.00015, the same as the previous tests. We will use technology for the p-value method. In the SPSS output, they use Sig. for the p-value.

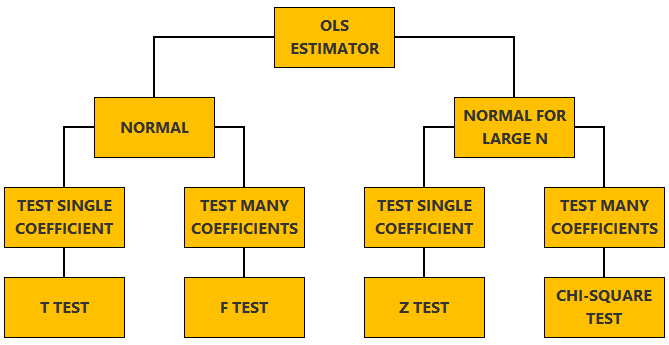
Linear regression - Hypothesis testing

by Marco Taboga , PhD

This lecture discusses how to perform tests of hypotheses about the coefficients of a linear regression model estimated by ordinary least squares (OLS).

Table of contents

Normal vs non-normal model

The linear regression model, matrix notation, tests of hypothesis in the normal linear regression model, test of a restriction on a single coefficient (t test), test of a set of linear restrictions (f test), tests based on maximum likelihood procedures (wald, lagrange multiplier, likelihood ratio), tests of hypothesis when the ols estimator is asymptotically normal, test of a restriction on a single coefficient (z test), test of a set of linear restrictions (chi-square test), learn more about regression analysis.

The lecture is divided in two parts:

in the first part, we discuss hypothesis testing in the normal linear regression model , in which the OLS estimator of the coefficients has a normal distribution conditional on the matrix of regressors;

in the second part, we show how to carry out hypothesis tests in linear regression analyses where the hypothesis of normality holds only in large samples (i.e., the OLS estimator can be proved to be asymptotically normal).

We also denote:

We now explain how to derive tests about the coefficients of the normal linear regression model.

It can be proved (see the lecture about the normal linear regression model ) that the assumption of conditional normality implies that:

How the acceptance region is determined depends not only on the desired size of the test , but also on whether the test is:

one-tailed (only one of the two things, i.e., either smaller or larger, is possible).

For more details on how to determine the acceptance region, see the glossary entry on critical values .

The F test is one-tailed .

A critical value in the right tail of the F distribution is chosen so as to achieve the desired size of the test.

Then, the null hypothesis is rejected if the F statistics is larger than the critical value.

In this section we explain how to perform hypothesis tests about the coefficients of a linear regression model when the OLS estimator is asymptotically normal.

As we have shown in the lecture on the properties of the OLS estimator , in several cases (i.e., under different sets of assumptions) it can be proved that:

These two properties are used to derive the asymptotic distribution of the test statistics used in hypothesis testing.

The test can be either one-tailed or two-tailed . The same comments made for the t-test apply here.

Like the F test, also the Chi-square test is usually one-tailed .

The desired size of the test is achieved by appropriately choosing a critical value in the right tail of the Chi-square distribution.

The null is rejected if the Chi-square statistics is larger than the critical value.

Want to learn more about regression analysis? Here are some suggestions:

R squared of a linear regression ;

Gauss-Markov theorem ;

Generalized Least Squares ;

Multicollinearity ;

Dummy variables ;

Selection of linear regression models

Partitioned regression ;

Ridge regression .

How to cite

Please cite as:

Taboga, Marco (2021). "Linear regression - Hypothesis testing", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/linear-regression-hypothesis-testing.

Most of the learning materials found on this website are now available in a traditional textbook format.

• F distribution
• Beta distribution
• Conditional probability
• Central Limit Theorem
• Binomial distribution
• Mean square convergence
• Delta method
• Almost sure convergence
• Mathematical tools
• Fundamentals of probability
• Probability distributions
• Asymptotic theory
• Fundamentals of statistics
• About Statlect
• Cookies, privacy and terms of use
• Loss function
• Almost sure
• Type I error
• Precision matrix
• Integrable variable
• To enhance your privacy,
• we removed the social buttons,
• but don't forget to share .

• Skip to secondary menu
• Skip to main content
• Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

Linear Regression Explained with Examples

By Jim Frost 13 Comments

What is Linear Regression?

Linear regression models the relationships between at least one explanatory variable and an outcome variable. This flexible analysis allows you to separate the effects of complicated research questions, allowing you to isolate each variable’s role. Additionally, linear models can fit curvature and interaction effects.

Statisticians refer to the explanatory variables in linear regression as independent variables (IV) and the outcome as dependent variables (DV). When a linear model has one IV, the procedure is known as simple linear regression. When there are more than one IV, statisticians refer to it as multiple regression. These models assume that the average value of the dependent variable depends on a linear function of the independent variables.

Linear regression has two primary purposes—understanding the relationships between variables and prediction.

• The coefficients represent the estimated magnitude and direction (positive/negative) of the relationship between each independent variable and the dependent variable.
• The equation allows you to predict the mean value of the dependent variable given the values of the independent variables that you specify.

Linear regression finds the constant and coefficient values for the IVs for a line that best fit your sample data. The graph below shows the best linear fit for the height and weight data points, revealing the mathematical relationship between them. Additionally, you can use the line’s equation to predict future values of the weight given a person’s height.

Linear regression was one of the earliest types of regression analysis to be rigorously studied and widely applied in real-world scenarios. This popularity stems from the relative ease of fitting linear models to data and the straightforward nature of analyzing the statistical properties of these models. Unlike more complex models that relate to their parameters in a non-linear way, linear models simplify both the estimation and the interpretation of data.

In this post, you’ll learn how to interprete linear regression with an example, about the linear formula, how it finds the coefficient estimates , and its assumptions .

Learn more about when you should use regression analysis  and independent and dependent variables .

Linear Regression Example

Suppose we use linear regression to model how the outside temperature in Celsius and Insulation thickness in centimeters, our two independent variables, relate to air conditioning costs in dollars (dependent variable).

Let’s interpret the results for the following multiple linear regression equation:

Air Conditioning Costs$ = 2 * Temperature C – 1.5 * Insulation CM

The coefficient sign for Temperature is positive (+2), which indicates a positive relationship between Temperature and Costs. As the temperature increases, so does air condition costs. More specifically, the coefficient value of 2 indicates that for every 1 C increase, the average air conditioning cost increases by two dollars.

On the other hand, the negative coefficient for insulation (–1.5) represents a negative relationship between insulation and air conditioning costs. As insulation thickness increases, air conditioning costs decrease. For every 1 CM increase, the average air conditioning cost drops by $1.50.

We can also enter values for temperature and insulation into this linear regression equation to predict the mean air conditioning cost.

Learn more about interpreting regression coefficients and using regression to make predictions .

Linear Regression Formula

Linear regression refers to the form of the regression equations these models use. These models follow a particular formula arrangement that requires all terms to be one of the following:

• The constant
• A parameter multiplied by an independent variable (IV)

Then, you build the linear regression formula by adding the terms together. These rules limit the form to just one type:

Dependent variable = constant + parameter * IV + … + parameter * IV

This formula is linear in the parameters. However, despite the name linear regression, it can model curvature. While the formula must be linear in the parameters, you can raise an independent variable by an exponent to model curvature . For example, if you square an independent variable, linear regression can fit a U-shaped curve.

Specifying the correct linear model requires balancing subject-area knowledge, statistical results, and satisfying the assumptions.

Learn more about the difference between linear and nonlinear models and specifying the correct regression model .

How to Find the Linear Regression Line

Linear regression can use various estimation methods to find the best-fitting line. However, analysts use the least squares most frequently because it is the most precise prediction method that doesn’t systematically overestimate or underestimate the correct values when you can satisfy all its assumptions.

The beauty of the least squares method is its simplicity and efficiency. The calculations required to find the best-fitting line are straightforward, making it accessible even for beginners and widely used in various statistical applications. Here’s how it works:

• Objective : Minimize the differences between the observed and the linear regression model’s predicted values . These differences are known as “ residuals ” and represent the errors in the model values.
• Minimizing Errors : This method focuses on making the sum of these squared differences as small as possible.
• Best-Fitting Line : By finding the values of the model parameters that achieve this minimum sum, the least squares method effectively determines the best-fitting line through the data points. 

By employing the least squares method in linear regression and checking the assumptions in the next section, you can ensure that your model is as precise and unbiased as possible. This method’s ability to minimize errors and find the best-fitting line is a valuable asset in statistical analysis.

Assumptions

Linear regression using the least squares method has the following assumptions:

• A linear model satisfactorily fits the relationship.
• The residuals follow a normal distribution.
• The residuals have a constant scatter.
• Independent observations.
• The IVs are not perfectly correlated.

Residuals are the difference between the observed value and the mean value that the model predicts for that observation. If you fail to satisfy the assumptions, the results might not be valid.

Learn more about the assumptions for ordinary least squares and How to Assess Residual Plots .

Yan, Xin (2009),  Linear Regression Analysis: Theory and Computing

Share this:

Reader Interactions

May 9, 2024 at 9:10 am

Why not perform centering or standardization with all linear regression to arrive at a better estimate of the y-intercept?

May 9, 2024 at 4:48 pm

I talk about centering elsewhere. This article just covers the basics of what linear regression does.

A little statistical niggle on centering creating a “better estimate” of the y-intercept. In statistics, there’s a specific meaning to “better estimate,” relating to precision and a lack of bias. Centering (or standardizing) doesn’t create a better estimate in that sense. It can create a more interpretable value in some situations, which is better in common usage.

August 16, 2023 at 5:10 pm

Hi Jim, I’m trying to understand why the Beta and significance changes in a linear regression, when I add another independent variable to the model. I am currently working on a mediation analysis, and as you know the linear regression is part of that. A simple linear regression between the IV (X) and the DV (Y) returns a statistically significant result. But when I add another IV (M), X becomes insignificant. Can you explain this? Seeking some clarity, Peta.

August 16, 2023 at 11:12 pm

This is a common occurrence in linear regression and is crucial for mediation analysis.

By adding M (mediator), it might be capturing some of the variance that was initially attributed to X. If M is a mediator, it means the effect of X on Y is being channeled through M. So when M is included in the model, it’s possible that the direct effect of X on Y becomes weaker or even insignificant, while the indirect effect (through M) becomes significant.

If X and M share variance in predicting Y, when both are in the model, they might “compete” for explaining the variance in Y. This can lead to a situation where the significance of X drops when M is added.

I hope that helps!

July 31, 2022 at 7:56 pm

July 30, 2022 at 2:49 pm

Jim, Hi! I am working on an interpretation of multiple linear regression. I am having a bit of trouble getting help. is there a way to post the table so that I may initiate a coherent discussion on my interpretation?

April 28, 2022 at 3:24 pm

Is it possible that we get significant correlations but no significant prediction in a multiple regression analysis? I am seeing that with my data and I am so confused. Could mediation be a factor (i.e IVs are not predicting the outcome variables because the relationship is made possible through mediators)?

April 29, 2022 at 4:37 pm

I’m not sure what you mean by “significant prediction.” Typically, the predictions you obtain from regression analysis will be a fitted value (the prediction) and a prediction interval that indicates the precision of the prediction (how close is it likely to be to the correct value). We don’t usually refer to “significance” when talking about predictions. Can you explain what you mean? Thanks!

March 25, 2022 at 7:19 am

I want to do a multiple regression analysis is SPSS (creating a predictive model), where IQ is my dependent variable and my independent variables contains of different cognitive domains. The IQ scores are already scaled for age. How can I controlling my independent variables for age, whitout doing it again for the IQ scores? I can’t add age as an independent variable in the model.

I hope that you can give me some advise, thank you so much!

March 28, 2022 at 9:27 pm

If you include age as an independent variable, the model controls for it while calculating the effects of the other IVs. And don’t worry, including age as an IV won’t double count it for IQ because that is your DV.

March 2, 2022 at 8:23 am

Hi Jim, Is there a reason you would want your covariates to be associated with your independent variable before including them in the model? So in deciding which covariates to include in the model, it was specified that covariates associated with both the dependent variable and independent variable at p<0.10 will be included in the model.

My question is why would you want the covariates to be associated with the independent variable?

March 2, 2022 at 4:38 pm

In some cases, it’s absolutely crucial to include covariates that correlate with other independent variables, although it’s not a sufficient reason by itself. When you have a potential independent variable that correlates with other IVs and it also correlates with the dependent variable, it becomes a confounding variable and omitting it from the model can cause a bias in the variables that you do include. In this scenario, the degree of bias depends on the strengths of the correlations involved. Observational studies are particularly susceptible to this type of omitted variable bias. However, when you’re performing a true, randomized experiment, this type of bias becomes a non-issue.

I’ve never heard of a formalized rule such as the one that you mention. Personally, I wouldn’t use p-values to make this determination. You can have low p-values for weak correlation in some cases. Instead, I’d look at the strength of the correlations between IVs. However, it’s not a simple as a single criterial like that. The strength of the correlation between the potential IV and the DV also plays a role.

I’ve written an article about that discusses these issues in more detail, read Confounding Variables Can Bias Your Results .

February 28, 2022 at 8:19 am

Jim, as if by serendipity: having been on your mailing list for years, I looked up your information on multiple regression this weekend for a grad school advanced statistics case study. I’m a fan of your admirable gift to make complicated topics approachable and digestible. Specifically, I was looking for information on how pronounced the triangular/funnel shape must be–and in what directions it may point–to suggest heteroscedasticity in a regression scatterplot of standardized residuals vs standardized predicted values. It seemed to me that my resulting plot of a 5 predictor variable regression model featured an obtuse triangular left point that violated homoscedasticity; my professors disagreed, stating the triangular “funnel” aspect would be more prominent and overt. Thus, should you be looking for a new future discussion point, my query to you then might be some pearls on the nature of a qualifying heteroscedastic funnel shape: How severe must it be? Is there a quantifiable magnitude to said severity, and if so, how would one quantify this and/or what numeric outputs in common statistical software would best support or deny a suspicion based on graphical interpretation? What directions can the funnel point; are only some directions suggestive, whereby others are not? Thanks for entertaining my comment, and, as always, thanks for doing what you do.

Comments and Questions Cancel reply

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

General linear hypothesis test statistic: equivalence of two expressions

Assume a general linear model $y = X \beta + \epsilon$ with observations in an $n$-vector $y$, a $(n \times p)$-design matrix $X$ of rank $p$ for $p$ parameters in a $p$-vector $\beta$. A general linear hypothesis (GLH) about $q$ of these parameters ($q < p$) can be written as $\psi = C \beta$, where $C$ is a $(q \times p)$ matrix. An example for a GLH is the one-way ANOVA hypothesis where $C \beta = 0$ under the null.

The GLH-test uses a restricted model with design matrix $X_{r}$ where the $q$ parameters are set to 0, and the corresponding $q$ columns of $X$ are removed. The unrestricted model with design matrix $X_{u}$ makes no restrictions, and thus contains $q$ free parameters more - its parameters are a superset of those from the restricted model, and the columns of $X_{u}$ are a superset of those from $X_{r}$.

$P_{u} = X_{u}'(X_{u}'X_{u})^{-1} X'$ is the orthogonal projection onto subspace $V_{u}$ spanned by $X_{u}$, and analogously $P_{r}$ onto $V_{r}$. Then $V_{r} \subset V_{u}$. The parameter estimates of a model are $\hat{\beta} = X^{+} y = (X'X)^{-1} X' y$, the predictions are $\hat{y} = P y$, the residuals are $(I-P)y$, the sum of squared residuals SSE is $||e||^{2} = e'e = y'(I-P)y$, and the estimate for $\psi$ is $\hat{\psi} = C \hat{\beta}$. The difference $SSE_{r} - SSE_{u}$ is $y'(P_{u}-P_{r})y$. Now the univariate $F$ test statistic for a GLH that is familiar (and understandable) to me is: $$ F = \frac{(SSE_{r} - SSE_{u}) / q}{\hat{\sigma}^{2}} = \frac{y' (P_{u} - P_{r}) y / q}{y^{t} (I - P_{u}) y / (n - p)} $$

There's an equivalent form that I don't yet understand: $$ F = \frac{(C \hat{\beta})' (C(X'X)^{-1}C')^{-1} (C \hat{\beta}) / q}{\hat{\sigma}^{2}} $$

As a start $$ \begin{array}{rcl} (C \hat{\beta})' (C(X'X)^{-1}C')^{-1} (C \hat{\beta}) &=& (C (X'X)^{-1} X' y)' (C(X'X)^{-1}C')^{-1} (C (X'X)^{-1} X' y) \\ ~ &=& y' X (X'X)^{-1} C' (C(X'X)^{-1}C')^{-1} C (X'X)^{-1} X' y \end{array} $$

• How do I see that $P_{u} - P_{r} = X (X'X)^{-1} C' (C(X'X)^{-1}C')^{-1} C (X'X)^{-1} X'$?
• What is the explanation for / motivation behind the numerator of the 2nd test statistic? - I can see that $C(X'X)^{-1}C'$ is $V(C \hat{\beta}) / \sigma^{2} = (\sigma^{2} C(X'X)^{-1}C') / \sigma^{2}$, but I can't put these pieces together.
• linear-model

2 Answers 2

For your second question, you have $\mathbf{y}\sim N(\mathbf{X}\boldsymbol{\beta},\sigma^2 \mathbf{I})$ and suppose you're testing $\mathbf{C}\boldsymbol{\beta}=\mathbf{0}$. So, we have that (the following is all shown through matrix algebra and properties of the normal distribution -- I'm happy to walk through any of these details)

$ \mathbf{C}\hat{\boldsymbol{\beta}}\sim N(\mathbf{0}, \sigma^2 \mathbf{C(X'X)^{-1}C'}). $

$ \textrm{Cov}(\mathbf{C}\hat{\boldsymbol{\beta}})=\sigma^2 \mathbf{C(X'X)^{-1}C}. $

which leads to noting that

$ F_1 = \frac{(\mathbf{C}\hat{\boldsymbol{\beta}})'[\mathbf{C(X'X)^{-1}C'}]^{-1}\mathbf{C}\hat{\boldsymbol{\beta}}}{\sigma^2}\sim \chi^2 \left(q\right). $

You get the above result because $F_1$ is a quadratic form and by invoking a certain theorem. This theorem states that if $\mathbf{x}\sim N(\boldsymbol{\mu}, \boldsymbol{\Sigma})$, then $\mathbf{x'Ax}\sim \chi^2 (r,p)$, where $r=\textrm{rank}(A)$ and $p=\frac{1}{2}\boldsymbol{\mu}'\mathbf{A}\boldsymbol{\mu}$, iff $\mathbf{A}\boldsymbol{\Sigma}$ is idempotent. [The proof of this theorem is a bit long and tedious, but it's doable. Hint: use the moment generating function of $\mathbf{x'Ax}$].

So, since $\mathbf{C}\hat{\boldsymbol{\beta}}$ is normally distributed, and the numerator of $F_1$ is a quadratic form involving $\mathbf{C}\hat{\boldsymbol{\beta}}$, we can use the above theorem (after proving the idempotent part).

$ F_2 = \frac{\mathbf{y}'[\mathbf{I} - \mathbf{X(X'X)^{-1}X'}]\mathbf{y}}{\sigma^2}\sim \chi^2(n-p-1) $

Through some tedious details, you can show that $F_1$ and $F_2$ are independent. And from there you should be able to justify your second $F$ statistic.

• $\begingroup$ Thanks for your fast reply! Could you please explain the "which leads to noting that" step to $F_{1}$ a little bit further? That's the one I'm not getting... $\endgroup$ –  caracal Commented Oct 18, 2011 at 17:26
• 1 $\begingroup$ @caracal Sure. I edited my response to add in some details. $\endgroup$ –  user5594 Commented Oct 18, 2011 at 17:41
• $\begingroup$ I'll accept this answer, but I'd still be very happy about an answer to my first question as well - literature tips are of course welcome! $\endgroup$ –  caracal Commented Oct 20, 2011 at 12:57
• $\begingroup$ Related: stats.stackexchange.com/q/188626/119261 . $\endgroup$ –  StubbornAtom Commented Jun 25, 2020 at 19:07

Since nobody has done so yet, I will address your first question. I also could not find a reference for [a proof of] this result anywhere, so if anyone knows a reference please let us know.

The most general test that this $F$-test can handle is $H_0 : C \beta = \psi$ for some $q \times p$ matrix $C$ and $q$-vector $\psi$. This allows you to test hypotheses like $H_0 : \beta_1 + \beta_2 = \beta_3 + 4$.

However, it seems you are focusing on testing hypotheses like $H_0 : \beta_2 = \beta_4 = \beta_5 = 0$, which is a special case with $\psi=0$ and $C$ being a matrix with one $1$ in each row, and all other entries being $0$. This allows you to more concretely view the smaller model as obtained by simply dropping some columns of your design matrix (i.e. going from $X_u$ to $X_r$), but in the end the result you are seeking is in terms of an abstract $C$ anyway.

Since it happens to be true that the formula $(C\hat{\beta})' (C (X'X)^{-1} C') (C \hat{\beta})$ works for arbitrary $C$ and $\psi=0$, I will prove it in that level of generality. Then you can consider your situation as a special case, as described in the previous paragraph.

If $\psi \ne 0$, the formula needs to be modified to $(C\hat{\beta} - \psi)' (C (X'X)^{-1} C') (C \hat{\beta} - \psi)$, which I also prove at the end of this post.

First I consider the case $\psi=0$. I will try to keep some of your notation. Let $V_u = \text{colspace}(X) = \{X\beta : \beta \in \mathbb{R}^p\}$. Let $V_r := \{X\beta : C\beta=0\}$. (This would be the column space of your $X_r$ in your special case.)

Let $P_u$ and $P_r$ be the projections on these two subspaces. As you noted, $P_u y$ and $P_r y$ are the predictions under the full model and the null model respectively. Moreover, you can show $\|(P_u - P_r) y\|^2$ is the difference in the sum of squares of residuals.

Let $V_l$ be the orthogonal complement of $V_r$ when viewed as a subspace of $V_u$. (In your special case, $V_l$ would be the span of the columns of the removed columns of $X_u$.) Then $V_r \oplus V_l = V_u$, and moreover, In particular, if $P_l$ is the projection onto $V_l$, then $P_u = P_r + P_l$.

Thus, the difference in the sum of squares of residuals is $$\|P_l y\|^2.$$ If $\tilde{X}$ is a matrix whose columns span $V_l$, then $P_l = \tilde{X} (\tilde{X}'\tilde{X})^{-1} \tilde{X}'$ and thus $$\|P_l y\|^2 = y'\tilde{X} (\tilde{X}'\tilde{X})^{-1} \tilde{X}' y.$$

In view of your attempt at the bottom of your post, all we have to do is show that choosing $\tilde{X} := X(X'X)^{-1} C'$ works, i.e., that $V_l$ is the span of this matrix's columns. Then that will conclude the proof.

• It is clear that $\text{colspace}(\tilde{X}) \subseteq \text{colspace}(X)=V_u$.
• Moreover, if $v \in V_r$ then it is of the form $v=X\beta$ with $C\beta=0$, and thus $v' \tilde{X} = \beta' X' X (X'X)^{-1} C' = (C \beta)' = 0$, which shows $\text{colspace}(\tilde{X})$ is in the orthogonal complement of $V_r$, i.e. $\text{colspace}(\tilde{X}) \subseteq V_l$.
• Finally, suppose $X\beta \in V_l$. Then $(X\beta)'(X\beta_0)=0$ for any $\beta_0 \in \text{nullspace}(C)$. This implies $X'X\beta \in \text{nullspace}(C)^\perp = \text{colspace}(C')$, so $X'X\beta=C'v$ for some $v$. Then, $X(X'X)^{-1} C' v = X\beta$, which shows $V_l \subseteq \text{colspace}(\tilde{X})$.

The more general case $\psi \ne 0$ can be obtained by slight modifications to the above proof. The fit of the restricted model would just be the projection $\tilde{P}_r$ onto the affine space $\tilde{V}_r = \{X \beta : C \beta = \psi\}$, instead of the projection $P_r$ onto the subspace $V_r =\{X\beta : C \beta = 0\}$. The two are quite related however, as one can write $\tilde{V}_r = V_r + \{X \beta_1\}$, where $\beta_1$ is an arbitrarily chosen vector satisfying $C \beta_1 = \psi$, and thus $$\tilde{P}_r y = P_r(y - X\beta_1) + X \beta_1.$$

Then, using the fact that $P_u X \beta_1 = X \beta_1$, we have $$(P_u - \tilde{P}_r) y = P_u y - P_r(y - X \beta_1) - X \beta_1 = (P_u - P_r)(y - X\beta_1) = P_l(y - X \beta_1).$$ Recalling $P_l = \tilde{X} (\tilde{X}'\tilde{X})^{-1} \tilde{X}'$ with $\tilde{X} = X(X'X)^{-1} C'$, the difference in sum of squares of residuals can be shown to be $$(y - X \beta_1)' P_l (y - X \beta_1) = (C \hat{\beta} - \psi)'(C (X'X)^{-1} C') (C\hat{\beta} - \psi).$$

Your Answer

Sign up or log in, post as a guest.

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged regression anova linear-model or ask your own question .

• Featured on Meta
• Upcoming sign-up experiments related to tags

Hot Network Questions

• Was Croatia the first country to recognize the sovereignity of the USA? Was Croatia expecting military help from USA that didn't come?
• Possible negative connotations of "Messy Kitchen" for a blog and social media project name
• What can I add to my too-wet tuna+potato patties to make them less mushy?
• What aspects define how present the garlic taste in an aglio e olio pasta becomes?
• What is the most general notion of exactness for functors between triangulated categories?
• What happens if you don't appear for jury duty for legitimate reasons in the state of California?
• Could Jordan have saved his company and avoided arrest if he hadn’t made that mistake?
• Could a Google Chrome extension read my password?
• Is it correct to call a room with a bath a "toilet"?
• Ideal test/p-value calculation for difference in means with small sample size and right skewed data?
• tnih neddih eht kcehc
• What was the first modern chess piece?
• How should I end a campaign only the passive players are enjoying?
• How to see image size in Firefox?
• Can my grant pay for a conference marginally related to award?
• Starship IFT-4: whatever happened to the fin tip camera feed?
• Error using simpleEmail REST API: UNKNOWN_EXCEPTION with error ID
• Why is the Newcomb problem confusing?
• Creating a property list. I'm new to expl3
• How much time is needed to judge an Earth-like planet to be safe?
• A deceiving simple question of combinations about ways of selecting 5 questions with atleast 1 question from each sections
• Could alien species with blood based on different elements eat the same food?
• Door latch can be forced out of strike plate without turning handle
• How to temporarily disable a primary IP without losing other IPs on the same interface

Statistical Thinking for the 21st Century

Chapter 14 the general linear model.

Remember that early in the book we described the basic model of statistics:

\[ data = model + error \] where our general goal is to find the model that minimizes the error, subject to some other constraints (such as keeping the model relatively simple so that we can generalize beyond our specific dataset). In this chapter we will focus on a particular implementation of this approach, which is known as the general linear model (or GLM). You have already seen the general linear model in the earlier chapter on Fitting Models to Data, where we modeled height in the NHANES dataset as a function of age; here we will provide a more general introduction to the concept of the GLM and its many uses. Nearly every model used in statistics can be framed in terms of the general linear model or an extension of it.

Before we discuss the general linear model, let’s first define two terms that will be important for our discussion:

• dependent variable : This is the outcome variable that our model aims to explain (usually referred to as Y )
• independent variable : This is a variable that we wish to use in order to explain the dependent variable (usually referred to as X ).

There may be multiple independent variables, but for this course we will focus primarily on situations where there is only one dependent variable in our analysis.

A general linear model is one in which the model for the dependent variable is composed of a linear combination of independent variables that are each multiplied by a weight (which is often referred to as the Greek letter beta - \(\beta\) ), which determines the relative contribution of that independent variable to the model prediction.

Figure 14.1: Relation between study time and grades

As an example, let’s generate some simulated data for the relationship between study time and exam grades (see Figure 14.1 ). Given these data, we might want to engage in each of the three fundamental activities of statistics:

• Describe : How strong is the relationship between grade and study time?
• Decide : Is there a statistically significant relationship between grade and study time?
• Predict : Given a particular amount of study time, what grade do we expect?

In the previous chapter we learned how to describe the relationship between two variables using the correlation coefficient. Let’s use our statistical software to compute that relationship for these data and test whether the correlation is significantly different from zero:

The correlation is quite high, but notice that the confidence interval around the estimate is very wide, spanning nearly the entire range from zero to one, which is due in part to the small sample size.

14.1 Linear regression

We can use the general linear model to describe the relation between two variables and to decide whether that relationship is statistically significant; in addition, the model allows us to predict the value of the dependent variable given some new value(s) of the independent variable(s). Most importantly, the general linear model will allow us to build models that incorporate multiple independent variables, whereas the correlation coefficient can only describe the relationship between two individual variables.

The specific version of the GLM that we use for this is referred to as as linear regression . The term regression was coined by Francis Galton, who had noted that when he compared parents and their children on some feature (such as height), the children of extreme parents (i.e. the very tall or very short parents) generally fell closer to the mean than did their parents. This is an extremely important point that we return to below.

The simplest version of the linear regression model (with a single independent variable) can be expressed as follows:

\[ y = x * \beta_x + \beta_0 + \epsilon \] The \(\beta_x\) value tells us how much we would expect y to change given a one-unit change in \(x\) . The intercept \(\beta_0\) is an overall offset, which tells us what value we would expect y to have when \(x=0\) ; you may remember from our early modeling discussion that this is important to model the overall magnitude of the data, even if \(x\) never actually attains a value of zero. The error term \(\epsilon\) refers to whatever is left over once the model has been fit; we often refer to these as the residuals from the model. If we want to know how to predict y (which we call \(\hat{y}\) ) after we estimate the \(\beta\) values, then we can drop the error term:

\[ \hat{y} = x * \hat{\beta_x} + \hat{\beta_0} \] Note that this is simply the equation for a line, where \(\hat{\beta_x}\) is our estimate of the slope and \(\hat{\beta_0}\) is the intercept. Figure 14.2 shows an example of this model applied to the study time data.

Figure 14.2: The linear regression solution for the study time data is shown in the solid line The value of the intercept is equivalent to the predicted value of the y variable when the x variable is equal to zero; this is shown with a dotted line. The value of beta is equal to the slope of the line – that is, how much y changes for a unit change in x. This is shown schematically in the dashed lines, which show the degree of increase in grade for a single unit increase in study time.

We will not go into the details of how the best fitting slope and intercept are actually estimated from the data; if you are interested, details are available in the Appendix.

14.1.1 Regression to the mean

The concept of regression to the mean was one of Galton’s essential contributions to science, and it remains a critical point to understand when we interpret the results of experimental data analyses. Let’s say that we want to study the effects of a reading intervention on the performance of poor readers. To test our hypothesis, we might go into a school and recruit those individuals in the bottom 25% of the distribution on some reading test, administer the intervention, and then examine their performance on the test after the intervention. Let’s say that the intervention actually has no effect, such that reading scores for each individual are simply independent samples from a normal distribution. Results from a computer simulation of this hypothetic experiment are presented in Table 14.1 .

Table 14.1: Reading scores for Test 1 (which is lower, because it was the basis for selecting the students) and Test 2 (which is higher because it was not related to Test 1).

	Score
Test 1	88
Test 2	101

If we look at the difference between the mean test performance at the first and second test, it appears that the intervention has helped these students substantially, as their scores have gone up by more than ten points on the test! However, we know that in fact the students didn’t improve at all, since in both cases the scores were simply selected from a random normal distribution. What has happened is that some students scored badly on the first test simply due to random chance. If we select just those subjects on the basis of their first test scores, they are guaranteed to move back towards the mean of the entire group on the second test, even if there is no effect of training. This is the reason that we always need an untreated control group in order to interpret any changes in performance due to an intervention; otherwise we are likely to be tricked by regression to the mean. In addition, the participants need to be randomly assigned to the control or treatment group, so that there won’t be any systematic differences between the groups (on average).

14.1.2 The relation between correlation and regression

There is a close relationship between correlation coefficients and regression coefficients. Remember that Pearson’s correlation coefficient is computed as the ratio of the covariance and the product of the standard deviations of x and y:

\[ \hat{r} = \frac{covariance_{xy}}{s_x * s_y} \] whereas the regression beta for x is computed as:

\[ \hat{\beta_x} = \frac{covariance_{xy}}{s_x*s_x} \]

Based on these two equations, we can derive the relationship between \(\hat{r}\) and \(\hat{beta}\) :

\[ covariance_{xy} = \hat{r} * s_x * s_y \]

\[ \hat{\beta_x} = \frac{\hat{r} * s_x * s_y}{s_x * s_x} = r * \frac{s_y}{s_x} \] That is, the regression slope is equal to the correlation value multiplied by the ratio of standard deviations of y and x. One thing this tells us is that when the standard deviations of x and y are the same (e.g. when the data have been converted to Z scores), then the correlation estimate is equal to the regression slope estimate.

14.1.3 Standard errors for regression models

If we want to make inferences about the regression parameter estimates, then we also need an estimate of their variability. To compute this, we first need to compute the residual variance or error variance for the model – that is, how much variability in the dependent variable is not explained by the model. We can compute the model residuals as follows:

\[ residual = y - \hat{y} = y - (x*\hat{\beta_x} + \hat{\beta_0}) \] We then compute the sum of squared errors (SSE) :

\[ SS_{error} = \sum_{i=1}^n{(y_i - \hat{y_i})^2} = \sum_{i=1}^n{residuals^2} \] and from this we compute the mean squared error :

\[ MS_{error} = \frac{SS_{error}}{df} = \frac{\sum_{i=1}^n{(y_i - \hat{y_i})^2} }{N - p} \] where the degrees of freedom ( \(df\) ) are determined by subtracting the number of estimated parameters (2 in this case: \(\hat{\beta_x}\) and \(\hat{\beta_0}\) ) from the number of observations ( \(N\) ). Once we have the mean squared error, we can compute the standard error for the model as:

\[ SE_{model} = \sqrt{MS_{error}} \]

In order to get the standard error for a specific regression parameter estimate, \(SE_{\beta_x}\) , we need to rescale the standard error of the model by the square root of the sum of squares of the X variable:

\[ SE_{\hat{\beta}_x} = \frac{SE_{model}}{\sqrt{{\sum{(x_i - \bar{x})^2}}}} \]

14.1.4 Statistical tests for regression parameters

Once we have the parameter estimates and their standard errors, we can compute a t statistic to tell us the likelihood of the observed parameter estimates compared to some expected value under the null hypothesis. In this case we will test against the null hypothesis of no effect (i.e.  \(\beta=0\) ):

\[ \begin{array}{c} t_{N - p} = \frac{\hat{\beta} - \beta_{expected}}{SE_{\hat{\beta}}}\\ t_{N - p} = \frac{\hat{\beta} - 0}{SE_{\hat{\beta}}}\\ t_{N - p} = \frac{\hat{\beta} }{SE_{\hat{\beta}}} \end{array} \]

In general we would use statistical software to compute these rather than computing them by hand. Here are the results from the linear model function in R:

In this case we see that the intercept is significantly different from zero (which is not very interesting) and that the effect of studyTime on grades is marginally significant (p = .09) – the same p-value as the correlation test that we performed earlier.

14.1.5 Quantifying goodness of fit of the model

Sometimes it’s useful to quantify how well the model fits the data overall, and one way to do this is to ask how much of the variability in the data is accounted for by the model. This is quantified using a value called \(R^2\) (also known as the coefficient of determination ). If there is only one x variable, then this is easy to compute by simply squaring the correlation coefficient:

\[ R^2 = r^2 \] In the case of our study time example, \(R^2\) = 0.4, which means that we have accounted for about 40% of the variance in grades.

More generally we can think of \(R^2\) as a measure of the fraction of variance in the data that is accounted for by the model, which can be computed by breaking the variance into multiple components:

THIS IS CONFUSING, CHANGE TO RESIDUAL RATHER THAN ERROR

\[ SS_{total} = SS_{model} + SS_{error} \] where \(SS_{total}\) is the variance of the data ( \(y\) ) and \(SS_{model}\) and \(SS_{error}\) are computed as shown earlier in this chapter. Using this, we can then compute the coefficient of determination as:

\[ R^2 = \frac{SS_{model}}{SS_{total}} = 1 - \frac{SS_{error}}{SS_{total}} \]

A small value of \(R^2\) tells us that even if the model fit is statistically significant, it may only explain a small amount of information in the data.

14.2 Fitting more complex models

Often we would like to understand the effects of multiple variables on some particular outcome, and how they relate to one another. In the context of our study time example, let’s say that we discovered that some of the students had previously taken a course on the topic. If we plot their grades (see Figure 14.3 ), we can see that those who had a prior course perform much better than those who had not, given the same amount of study time. We would like to build a statistical model that takes this into account, which we can do by extending the model that we built above:

\[ \hat{y} = \hat{\beta_1}*studyTime + \hat{\beta_2}*priorClass + \hat{\beta_0} \] To model whether each individual has had a previous class or not, we use what we call dummy coding in which we create a new variable that has a value of one to represent having had a class before, and zero otherwise. This means that for people who have had the class before, we will simply add the value of \(\hat{\beta_2}\) to our predicted value for them – that is, using dummy coding \(\hat{\beta_2}\) simply reflects the difference in means between the two groups. Our estimate of \(\hat{\beta_1}\) reflects the regression slope over all of the data points – we are assuming that regression slope is the same regardless of whether someone has had a class before (see Figure 14.3 ).

Figure 14.3: The relation between study time and grade including prior experience as an additional component in the model. The solid line relates study time to grades for students who have not had prior experience, and the dashed line relates grades to study time for students with prior experience. The dotted line corresponds to the difference in means between the two groups.

14.3 Interactions between variables

In the previous model, we assumed that the effect of study time on grade (i.e., the regression slope) was the same for both groups. However, in some cases we might imagine that the effect of one variable might differ depending on the value of another variable, which we refer to as an interaction between variables.

Let’s use a new example that asks the question: What is the effect of caffeine on public speaking? First let’s generate some data and plot them. Looking at panel A of Figure 14.4 , there doesn’t seem to be a relationship, and we can confirm that by performing linear regression on the data:

But now let’s say that we find research suggesting that anxious and non-anxious people react differently to caffeine. First let’s plot the data separately for anxious and non-anxious people.

As we see from panel B in Figure 14.4 , it appears that the relationship between speaking and caffeine is different for the two groups, with caffeine improving performance for people without anxiety and degrading performance for those with anxiety. We’d like to create a statistical model that addresses this question. First let’s see what happens if we just include anxiety in the model.

Here we see there are no significant effects of either caffeine or anxiety, which might seem a bit confusing. The problem is that this model is trying to use the same slope relating speaking to caffeine for both groups. If we want to fit them using lines with separate slopes, we need to include an interaction in the model, which is equivalent to fitting different lines for each of the two groups; this is often denoted by using the \(*\) symbol in the model.

From these results we see that there are significant effects of both caffeine and anxiety (which we call main effects ) and an interaction between caffeine and anxiety. Panel C in Figure 14.4 shows the separate regression lines for each group.

Figure 14.4: A: The relationship between caffeine and public speaking. B: The relationship between caffeine and public speaking, with anxiety represented by the shape of the data points. C: The relationship between public speaking and caffeine, including an interaction with anxiety. This results in two lines that separately model the slope for each group (dashed for anxious, dotted for non-anxious).

One important point to note is that we have to be very careful about interpreting a significant main effect if a significant interaction is also present, since the interaction suggests that the main effect differs according to the values of another variable, and thus is not easily interpretable.

Sometimes we want to compare the relative fit of two different models, in order to determine which is a better model; we refer to this as model comparison . For the models above, we can compare the goodness of fit of the model with and without the interaction, using what is called an analysis of variance :

This tells us that there is good evidence to prefer the model with the interaction over the one without an interaction. Model comparison is relatively simple in this case because the two models are nested – one of the models is a simplified version of the other model, such that all of the variables in the simpler model are contained in the more complex model. Model comparison with non-nested models can get much more complicated.

14.4 Beyond linear predictors and outcomes

It is important to note that despite the fact that it is called the general linear model, we can actually use the same machinery to model effects that don’t follow a straight line (such as curves). The “linear” in the general linear model doesn’t refer to the shape of the response, but instead refers to the fact that model is linear in its parameters — that is, the predictors in the model only get multiplied the parameters, rather than a nonlinear relationship like being raised to a power of the parameter. It’s also common to analyze data where the outcomes are binary rather than continuous, as we saw in the chapter on categorical outcomes. There are ways to adapt the general linear model (known as generalized linear models ) that allow this kind of analysis. We will explore these models later in the book.

14.5 Criticizing our model and checking assumptions

The saying “garbage in, garbage out” is as true of statistics as anywhere else. In the case of statistical models, we have to make sure that our model is properly specified and that our data are appropriate for the model.

When we say that the model is “properly specified”, we mean that we have included the appropriate set of independent variables in the model. We have already seen examples of misspecified models, in Figure 5.3 . Remember that we saw several cases where the model failed to properly account for the data, such as failing to include an intercept. When building a model, we need to ensure that it includes all of the appropriate variables.

We also need to worry about whether our model satisfies the assumptions of our statistical methods. One of the most important assumptions that we make when using the general linear model is that the residuals (that is, the difference between the model’s predictions and the actual data) are normally distributed. This can fail for many reasons, either because the model was not properly specified or because the data that we are modeling are inappropriate.

We can use something called a Q-Q (quantile-quantile) plot to see whether our residuals are normally distributed. You have already encountered quantiles — they are the value that cuts off a particular proportion of a cumulative distribution. The Q-Q plot presents the quantiles of two distributions against one another; in this case, we will present the quantiles of the actual data against the quantiles of a normal distribution fit to the same data. Figure 14.5 shows examples of two such Q-Q plots. The left panel shows a Q-Q plot for data from a normal distribution, while the right panel shows a Q-Q plot from non-normal data. The data points in the right panel diverge substantially from the line, reflecting the fact that they are not normally distributed.

Figure 14.5: Q-Q plotsof normal (left) and non-normal (right) data. The line shows the point at which the x and y axes are equal.

Model diagnostics will be explored in more detail in a later chapter.

14.6 What does “predict” really mean?

When we talk about “prediction” in daily life, we are generally referring to the ability to estimate the value of some variable in advance of seeing the data. However, the term is often used in the context of linear regression to refer to the fitting of a model to the data; the estimated values ( \(\hat{y}\) ) are sometimes referred to as “predictions” and the independent variables are referred to as “predictors”. This has an unfortunate connotation, as it implies that our model should also be able to predict the values of new data points in the future. In reality, the fit of a model to the dataset used to obtain the parameters will nearly always be better than the fit of the model to a new dataset ( Copas 1983 ) .

As an example, let’s take a sample of 48 children from NHANES and fit a regression model for weight that includes several regressors (age, height, hours spent watching TV and using the computer, and household income) along with their interactions.

Table 14.2: Root mean squared error for model applied to original data and new data, and after shuffling the order of the y variable (in essence making the null hypothesis true)

Data type	RMSE (original data)	RMSE (new data)
True data	3.0	25
Shuffled data	7.8	59

Here we see that whereas the model fit on the original data showed a very good fit (only off by a few kg per individual), the same model does a much worse job of predicting the weight values for new children sampled from the same population (off by more than 25 kg per individual). This happens because the model that we specified is quite complex, since it includes not just each of the individual variables, but also all possible combinations of them (i.e. their interactions ), resulting in a model with 32 parameters. Since this is almost as many coefficients as there are data points (i.e., the heights of 48 children), the model overfits the data, just like the complex polynomial curve in our initial example of overfitting in Section 5.4 .

Another way to see the effects of overfitting is to look at what happens if we randomly shuffle the values of the weight variable (shown in the second row of the table). Randomly shuffling the value should make it impossible to predict weight from the other variables, because they should have no systematic relationship. The results in the table show that even when there is no true relationship to be modeled (because shuffling should have obliterated the relationship), the complex model still shows a very low error in its predictions on the fitted data, because it fits the noise in the specific dataset. However, when that model is applied to a new dataset, we see that the error is much larger, as it should be.

14.6.1 Cross-validation

One method that has been developed to help address the problem of overfitting is known as cross-validation . This technique is commonly used within the field of machine learning, which is focused on building models that will generalize well to new data, even when we don’t have a new dataset to test the model. The idea behind cross-validation is that we fit our model repeatedly, each time leaving out a subset of the data, and then test the ability of the model to predict the values in each held-out subset.

Figure 14.6: A schematic of the cross-validation procedure.

Let’s see how that would work for our weight prediction example. In this case we will perform 12-fold cross-validation, which means that we will break the data into 12 subsets, and then fit the model 12 times, in each case leaving out one of the subsets and then testing the model’s ability to accurately predict the value of the dependent variable for those held-out data points. Most statistical software provides tools to apply cross-validation to one’s data. Using this function we can run cross-validation on 100 samples from the NHANES dataset, and compute the RMSE for cross-validation, along with the RMSE for the original data and a new dataset, as we computed above.

Table 14.3: R-squared from cross-validation and new data, showing that cross-validation provides a reasonable estimate of the model’s performance on new data.

	R-squared
Original data	0.95
New data	0.34
Cross-validation	0.60

Here we see that cross-validation gives us an estimate of predictive accuracy that is much closer to what we see with a completely new dataset than it is to the inflated accuracy that we see with the original dataset – in fact, it’s even slightly more pessimistic than the average for a new dataset, probably because only part of the data are being used to train each of the models.

Note that using cross-validation properly is tricky, and it is recommended that you consult with an expert before using it in practice. However, this section has hopefully shown you three things:

• “Prediction” doesn’t always mean what you think it means
• Complex models can overfit data very badly, such that one can observe seemingly good prediction even when there is no true signal to predict
• You should view claims about prediction accuracy very skeptically unless they have been done using the appropriate methods.

14.7 Learning objectives

Having read this chapter, you should be able to:

• Describe the concept of linear regression and apply it to a dataset
• Describe the concept of the general linear model and provide examples of its application
• Describe how cross-validation can allow us to estimate the predictive performance of a model on new data

14.8 Suggested readings

• The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd Edition) - The “bible” of machine learning methods, available freely online.

14.9 Appendix

14.9.1 estimating linear regression parameters.

We generally estimate the parameters of a linear model from data using linear algebra , which is the form of algebra that is applied to vectors and matrices. If you aren’t familiar with linear algebra, don’t worry – you won’t actually need to use it here, as R will do all the work for us. However, a brief excursion in linear algebra can provide some insight into how the model parameters are estimated in practice.

First, let’s introduce the idea of vectors and matrices; you’ve already encountered them in the context of R, but we will review them here. A matrix is a set of numbers that are arranged in a square or rectangle, such that there are one or more dimensions across which the matrix varies. It is customary to place different observation units (such as people) in the rows, and different variables in the columns. Let’s take our study time data from above. We could arrange these numbers in a matrix, which would have eight rows (one for each student) and two columns (one for study time, and one for grade). If you are thinking “that sounds like a data frame in R” you are exactly right! In fact, a data frame is a specialized version of a matrix, and we can convert a data frame to a matrix using the as.matrix() function.

We can write the general linear model in linear algebra as follows:

\[ Y = X*\beta + E \] This looks very much like the earlier equation that we used, except that the letters are all capitalized, which is meant to express the fact that they are vectors.

We know that the grade data go into the Y matrix, but what goes into the \(X\) matrix? Remember from our initial discussion of linear regression that we need to add a constant in addition to our independent variable of interest, so our \(X\) matrix (which we call the design matrix ) needs to include two columns: one representing the study time variable, and one column with the same value for each individual (which we generally fill with all ones). We can view the resulting design matrix graphically (see Figure 14.7 ).

Figure 14.7: A depiction of the linear model for the study time data in terms of matrix algebra.

The rules of matrix multiplication tell us that the dimensions of the matrices have to match with one another; in this case, the design matrix has dimensions of 8 (rows) X 2 (columns) and the Y variable has dimensions of 8 X 1. Therefore, the \(\beta\) matrix needs to have dimensions 2 X 1, since an 8 X 2 matrix multiplied by a 2 X 1 matrix results in an 8 X 1 matrix (as the matching middle dimensions drop out). The interpretation of the two values in the \(\beta\) matrix is that they are the values to be multipled by study time and 1 respectively to obtain the estimated grade for each individual. We can also view the linear model as a set of individual equations for each individual:

\(\hat{y}_1 = studyTime_1*\beta_1 + 1*\beta_2\)

\(\hat{y}_2 = studyTime_2*\beta_1 + 1*\beta_2\)

\(\hat{y}_8 = studyTime_8*\beta_1 + 1*\beta_2\)

Remember that our goal is to determine the best fitting values of \(\beta\) given the known values of \(X\) and \(Y\) . A naive way to do this would be to solve for \(\beta\) using simple algebra – here we drop the error term \(E\) because it’s out of our control:

\[ \hat{\beta} = \frac{Y}{X} \]

The challenge here is that \(X\) and \(\beta\) are now matrices, not single numbers – but the rules of linear algebra tell us how to divide by a matrix, which is the same as multiplying by the inverse of the matrix (referred to as \(X^{-1}\) ). We can do this in R:

Anyone who is interested in serious use of statistical methods is highly encouraged to invest some time in learning linear algebra, as it provides the basis for nearly all of the tools that are used in standard statistics.

Linear Hypothesis Tests

Most regression output will include the results of frequentist hypothesis tests comparing each coefficient to 0. However, in many cases, you may be interested in whether a linear sum of the coefficients is 0. For example, in the regression

You may be interested to see if \(GoodThing\) and \(BadThing\) (both binary variables) cancel each other out. So you would want to do a test of \(\beta_1 - \beta_2 = 0\).

Alternately, you may want to do a joint significance test of multiple linear hypotheses. For example, you may be interested in whether \(\beta_1\) or \(\beta_2\) are nonzero and so would want to jointly test the hypotheses \(\beta_1 = 0\) and \(\beta_2=0\) rather than doing them one at a time. Note the and here, since if either one or the other is rejected, we reject the null.

Keep in Mind

• Be sure to carefully interpret the result. If you are doing a joint test, rejection means that at least one of your hypotheses can be rejected, not each of them. And you don’t necessarily know which ones can be rejected!
• Generally, linear hypothesis tests are performed using F-statistics. However, there are alternate approaches such as likelihood tests or chi-squared tests. Be sure you know which on you’re getting.
• Conceptually, what is going on with linear hypothesis tests is that they compare the model you’ve estimated against a more restrictive one that requires your restrictions (hypotheses) to be true. If the test you have in mind is too complex for the software to figure out on its own, you might be able to do it on your own by taking the sum of squared residuals in your original unrestricted model (\(SSR_{UR}\)), estimate the alternate model with the restriction in place (\(SSR_R\)) and then calculate the F-statistic for the joint test using \(F_{q,n-k-1} = ((SSR_R - SSR_{UR})/q)/(SSR_{UR}/(n-k-1))\).

Also Consider

• The process for testing a nonlinear combination of your coefficients, for example testing if \(\beta_1\times\beta_2 = 1\) or \(\sqrt{\beta_1} = .5\), is generally different. See Nonlinear hypothesis tests .

Implementations

Linear hypothesis test in R can be performed for most regression models using the linearHypothesis() function in the car package. See this guide for more information.

Tests of coefficients in Stata can generally be performed using the built-in test command.

Statistics Made Easy

Understanding the Null Hypothesis for Linear Regression

Linear regression is a technique we can use to understand the relationship between one or more predictor variables and a response variable .

If we only have one predictor variable and one response variable, we can use simple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x

• ŷ: The estimated response value.
• β 0 : The average value of y when x is zero.
• β 1 : The average change in y associated with a one unit increase in x.
• x: The value of the predictor variable.

Simple linear regression uses the following null and alternative hypotheses:

• H 0 : β 1 = 0
• H A : β 1 ≠ 0

The null hypothesis states that the coefficient β 1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.

The alternative hypothesis states that β 1 is not equal to zero. In other words, there is a statistically significant relationship between x and y.

If we have multiple predictor variables and one response variable, we can use multiple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x 1 + β 2 x 2 + … + β k x k

• β 0 : The average value of y when all predictor variables are equal to zero.
• β i : The average change in y associated with a one unit increase in x i .
• x i : The value of the predictor variable x i .

Multiple linear regression uses the following null and alternative hypotheses:

• H 0 : β 1 = β 2 = … = β k = 0
• H A : β 1 = β 2 = … = β k ≠ 0

The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically significant relationship with the response variable, y.

The alternative hypothesis states that not every coefficient is simultaneously equal to zero.

The following examples show how to decide to reject or fail to reject the null hypothesis in both simple linear regression and multiple linear regression models.

Example 1: Simple Linear Regression

Suppose a professor would like to use the number of hours studied to predict the exam score that students will receive in his class. He collects data for 20 students and fits a simple linear regression model.

The following screenshot shows the output of the regression model:

The fitted simple linear regression model is:

Exam Score = 67.1617 + 5.2503*(hours studied)

To determine if there is a statistically significant relationship between hours studied and exam score, we need to analyze the overall F value of the model and the corresponding p-value:

• Overall F-Value:  47.9952
• P-value:  0.000

Since this p-value is less than .05, we can reject the null hypothesis. In other words, there is a statistically significant relationship between hours studied and exam score received.

Example 2: Multiple Linear Regression

Suppose a professor would like to use the number of hours studied and the number of prep exams taken to predict the exam score that students will receive in his class. He collects data for 20 students and fits a multiple linear regression model.

The fitted multiple linear regression model is:

Exam Score = 67.67 + 5.56*(hours studied) – 0.60*(prep exams taken)

To determine if there is a jointly statistically significant relationship between the two predictor variables and the response variable, we need to analyze the overall F value of the model and the corresponding p-value:

• Overall F-Value:  23.46
• P-value:  0.00

Since this p-value is less than .05, we can reject the null hypothesis. In other words, hours studied and prep exams taken have a jointly statistically significant relationship with exam score.

Note: Although the p-value for prep exams taken (p = 0.52) is not significant, prep exams combined with hours studied has a significant relationship with exam score.

Additional Resources

Understanding the F-Test of Overall Significance in Regression How to Read and Interpret a Regression Table How to Report Regression Results How to Perform Simple Linear Regression in Excel How to Perform Multiple Linear Regression in Excel

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “Understanding the Null Hypothesis for Linear Regression”

Thank you Zach, this helped me on homework!

Great articles, Zach.

I would like to cite your work in a research paper.

Could you provide me with your last name and initials.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

Linear regression hypothesis testing: Concepts, Examples

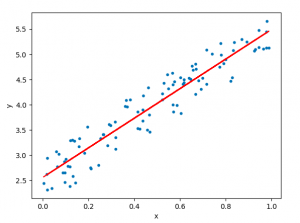
In relation to machine learning , linear regression is defined as a predictive modeling technique that allows us to build a model which can help predict continuous response variables as a function of a linear combination of explanatory or predictor variables. While training linear regression models, we need to rely on hypothesis testing in relation to determining the relationship between the response and predictor variables. In the case of the linear regression model, two types of hypothesis testing are done. They are T-tests and F-tests . In other words, there are two types of statistics that are used to assess whether linear regression models exist representing response and predictor variables. They are t-statistics and f-statistics. As data scientists , it is of utmost importance to determine if linear regression is the correct choice of model for our particular problem and this can be done by performing hypothesis testing related to linear regression response and predictor variables. Many times, it is found that these concepts are not very clear with a lot many data scientists. In this blog post, we will discuss linear regression and hypothesis testing related to t-statistics and f-statistics . We will also provide an example to help illustrate how these concepts work.

Table of Contents

What are linear regression models?

A linear regression model can be defined as the function approximation that represents a continuous response variable as a function of one or more predictor variables. While building a linear regression model, the goal is to identify a linear equation that best predicts or models the relationship between the response or dependent variable and one or more predictor or independent variables.

There are two different kinds of linear regression models. They are as follows:

• Simple or Univariate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and one predictor or independent variable. The form of the equation that represents a simple linear regression model is Y=mX+b, where m is the coefficients of the predictor variable and b is bias. When considering the linear regression line, m represents the slope and b represents the intercept.
• Multiple or Multi-variate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and more than one predictor or independent variable. The form of the equation that represents a multiple linear regression model is Y=b0+b1X1+ b2X2 + … + bnXn, where bi represents the coefficients of the ith predictor variable. In this type of linear regression model, each predictor variable has its own coefficient that is used to calculate the predicted value of the response variable.

While training linear regression models, the requirement is to determine the coefficients which can result in the best-fitted linear regression line. The learning algorithm used to find the most appropriate coefficients is known as least squares regression . In the least-squares regression method, the coefficients are calculated using the least-squares error function. The main objective of this method is to minimize or reduce the sum of squared residuals between actual and predicted response values. The sum of squared residuals is also called the residual sum of squares (RSS). The outcome of executing the least-squares regression method is coefficients that minimize the linear regression cost function .

The residual e of the ith observation is represented as the following where [latex]Y_i[/latex] is the ith observation and [latex]\hat{Y_i}[/latex] is the prediction for ith observation or the value of response variable for ith observation.

[latex]e_i = Y_i – \hat{Y_i}[/latex]

The residual sum of squares can be represented as the following:

[latex]RSS = e_1^2 + e_2^2 + e_3^2 + … + e_n^2[/latex]

The least-squares method represents the algorithm that minimizes the above term, RSS.

Once the coefficients are determined, can it be claimed that these coefficients are the most appropriate ones for linear regression? The answer is no. After all, the coefficients are only the estimates and thus, there will be standard errors associated with each of the coefficients.  Recall that the standard error is used to calculate the confidence interval in which the mean value of the population parameter would exist. In other words, it represents the error of estimating a population parameter based on the sample data. The value of the standard error is calculated as the standard deviation of the sample divided by the square root of the sample size. The formula below represents the standard error of a mean.

[latex]SE(\mu) = \frac{\sigma}{\sqrt(N)}[/latex]

Thus, without analyzing aspects such as the standard error associated with the coefficients, it cannot be claimed that the linear regression coefficients are the most suitable ones without performing hypothesis testing. This is where hypothesis testing is needed . Before we get into why we need hypothesis testing with the linear regression model, let’s briefly learn about what is hypothesis testing?

Train a Multiple Linear Regression Model using R

Before getting into understanding the hypothesis testing concepts in relation to the linear regression model, let’s train a multi-variate or multiple linear regression model and print the summary output of the model which will be referred to, in the next section. 

The data used for creating a multi-linear regression model is BostonHousing which can be loaded in RStudioby installing mlbench package. The code is shown below:

install.packages(“mlbench”) library(mlbench) data(“BostonHousing”)

Once the data is loaded, the code shown below can be used to create the linear regression model.

attach(BostonHousing) BostonHousing.lm <- lm(log(medv) ~ crim + chas + rad + lstat) summary(BostonHousing.lm)

Executing the above command will result in the creation of a linear regression model with the response variable as medv and predictor variables as crim, chas, rad, and lstat. The following represents the details related to the response and predictor variables:

• log(medv) : Log of the median value of owner-occupied homes in USD 1000’s
• crim : Per capita crime rate by town
• chas : Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
• rad : Index of accessibility to radial highways
• lstat : Percentage of the lower status of the population

The following will be the output of the summary command that prints the details relating to the model including hypothesis testing details for coefficients (t-statistics) and the model as a whole (f-statistics) 

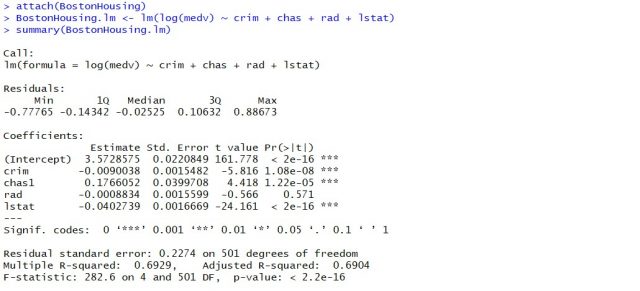
Hypothesis tests & Linear Regression Models

Hypothesis tests are the statistical procedure that is used to test a claim or assumption about the underlying distribution of a population based on the sample data. Here are key steps of doing hypothesis tests with linear regression models:

• Hypothesis formulation for T-tests: In the case of linear regression, the claim is made that there exists a relationship between response and predictor variables, and the claim is represented using the non-zero value of coefficients of predictor variables in the linear equation or regression model. This is formulated as an alternate hypothesis. Thus, the null hypothesis is set that there is no relationship between response and the predictor variables . Hence, the coefficients related to each of the predictor variables is equal to zero (0). So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis for each test states that a1 = 0, a2 = 0, a3 = 0 etc. For all the predictor variables, individual hypothesis testing is done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. Thus, if there are, say, 5 features, there will be five hypothesis tests and each will have an associated null and alternate hypothesis.
• Hypothesis formulation for F-test : In addition, there is a hypothesis test done around the claim that there is a linear regression model representing the response variable and all the predictor variables. The null hypothesis is that the linear regression model does not exist . This essentially means that the value of all the coefficients is equal to zero. So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis states that a1 = a2 = a3 = 0.
• F-statistics for testing hypothesis for linear regression model : F-test is used to test the null hypothesis that a linear regression model does not exist, representing the relationship between the response variable y and the predictor variables x1, x2, x3, x4 and x5. The null hypothesis can also be represented as x1 = x2 = x3 = x4 = x5 = 0. F-statistics is calculated as a function of sum of squares residuals for restricted regression (representing linear regression model with only intercept or bias and all the values of coefficients as zero) and sum of squares residuals for unrestricted regression (representing linear regression model). In the above diagram, note the value of f-statistics as 15.66 against the degrees of freedom as 5 and 194. 
• Evaluate t-statistics against the critical value/region : After calculating the value of t-statistics for each coefficient, it is now time to make a decision about whether to accept or reject the null hypothesis. In order for this decision to be made, one needs to set a significance level, which is also known as the alpha level. The significance level of 0.05 is usually set for rejecting the null hypothesis or otherwise. If the value of t-statistics fall in the critical region, the null hypothesis is rejected. Or, if the p-value comes out to be less than 0.05, the null hypothesis is rejected.
• Evaluate f-statistics against the critical value/region : The value of F-statistics and the p-value is evaluated for testing the null hypothesis that the linear regression model representing response and predictor variables does not exist. If the value of f-statistics is more than the critical value at the level of significance as 0.05, the null hypothesis is rejected. This means that the linear model exists with at least one valid coefficients. 
• Draw conclusions : The final step of hypothesis testing is to draw a conclusion by interpreting the results in terms of the original claim or hypothesis. If the null hypothesis of one or more predictor variables is rejected, it represents the fact that the relationship between the response and the predictor variable is not statistically significant based on the evidence or the sample data we used for training the model. Similarly, if the f-statistics value lies in the critical region and the value of the p-value is less than the alpha value usually set as 0.05, one can say that there exists a linear regression model.

Why hypothesis tests for linear regression models?

The reasons why we need to do hypothesis tests in case of a linear regression model are following:

• By creating the model, we are establishing a new truth (claims) about the relationship between response or dependent variable with one or more predictor or independent variables. In order to justify the truth, there are needed one or more tests. These tests can be termed as an act of testing the claim (or new truth) or in other words, hypothesis tests.
• One kind of test is required to test the relationship between response and each of the predictor variables (hence, T-tests)
• Another kind of test is required to test the linear regression model representation as a whole. This is called F-test.

While training linear regression models, hypothesis testing is done to determine whether the relationship between the response and each of the predictor variables is statistically significant or otherwise. The coefficients related to each of the predictor variables is determined. Then, individual hypothesis tests are done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. If at least one of the null hypotheses is rejected, it represents the fact that there exists no relationship between response and that particular predictor variable. T-statistics is used for performing the hypothesis testing because the standard deviation of the sampling distribution is unknown. The value of t-statistics is compared with the critical value from the t-distribution table in order to make a decision about whether to accept or reject the null hypothesis regarding the relationship between the response and predictor variables. If the value falls in the critical region, then the null hypothesis is rejected which means that there is no relationship between response and that predictor variable. In addition to T-tests, F-test is performed to test the null hypothesis that the linear regression model does not exist and that the value of all the coefficients is zero (0). Learn more about the linear regression and t-test in this blog – Linear regression t-test: formula, example .

Recent Posts

• Python Pickle Security Issues / Risk - May 31, 2024
• Pricing Analytics in Banking: Strategies, Examples - May 15, 2024
• How to Learn Effectively: A Holistic Approach - May 13, 2024

Ajitesh Kumar

One response.

Very informative

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Search for:
• Excellence Awaits: IITs, NITs & IIITs Journey

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Python Pickle Security Issues / Risk
• Pricing Analytics in Banking: Strategies, Examples
• How to Learn Effectively: A Holistic Approach
• How to Choose Right Statistical Tests: Examples
• Data Lakehouses Fundamentals & Examples

Data Science / AI Trends

• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable
• • Machine learning in finance

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Linear hypothesis test on generalized linear regression model coefficients

Description

p = coefTest( mdl ) computes the p -value for an F test that all coefficient estimates in mdl , except the intercept term, are zero.

p = coefTest( mdl , H ) performs an F -test that H × B = 0 , where B represents the coefficient vector. Use H to specify the coefficients to include in the F -test.

p = coefTest( mdl , H , C ) performs an F -test that H × B = C .

[ p , F ] = coefTest( ___ ) also returns the F -test statistic F using any of the input argument combinations in previous syntaxes.

[ p , F , r ] = coefTest( ___ ) also returns the numerator degrees of freedom r for the test.

collapse all

Test Significance of Generalized Linear Regression Model

Fit a generalized linear regression model, and test the coefficients of the fitted model to see if they differ from zero.

Generate sample data using Poisson random numbers with two underlying predictors X(:,1) and X(:,2) .

Create a generalized linear regression model of Poisson data.

Test whether the fitted model has coefficients that differ significantly from zero.

The small p -value indicates that the model fits significantly better than a degenerate model consisting of only an intercept term.

Test Significance of Generalized Linear Regression Model Coefficient

Fit a generalized linear regression model, and test the significance of a specified coefficient in the fitted model.

Test the significance of the x1 coefficient. According to the model display, x1 is the second predictor. Specify the coefficient by using a numeric index vector.

The returned p -value indicates that x1 is statistically significant in the fitted model.

Input Arguments

Mdl — generalized linear regression model generalizedlinearmodel object | compactgeneralizedlinearmodel object.

Generalized linear regression model, specified as a GeneralizedLinearModel object created using fitglm or stepwiseglm , or a CompactGeneralizedLinearModel object created using compact .

H — Hypothesis matrix numeric index matrix

Hypothesis matrix, specified as a full-rank numeric index matrix of size r -by- s , where r is the number of linear combinations of coefficients being tested, and s is the total number of coefficients.

If you specify H , then the output p is the p -value for an F -test that H × B = 0 , where B represents the coefficient vector.

If you specify H and C , then the output p is the p -value for an F -test that H × B = C .

Example: [1 0 0 0 0] tests the first coefficient among five coefficients.

Data Types: single | double

C — Hypothesized value numeric vector

Hypothesized value for testing the null hypothesis, specified as a numeric vector with the same number of rows as H .

If you specify H and C , then the output p is the p -value for an F -test that H × B = C , where B represents the coefficient vector.

Output Arguments

P — p -value for f -test numeric value in the range [0,1].

p -value for the F -test, returned as a numeric value in the range [0,1].

F — Value of test statistic for F -test numeric value

Value of the test statistic for the F -test, returned as a numeric value.

r — Numerator degrees of freedom for F -test positive integer

Numerator degrees of freedom for the F -test, returned as a positive integer. The F -statistic has r degrees of freedom in the numerator and mdl.DFE degrees of freedom in the denominator.

The p -value, F -statistic, and numerator degrees of freedom are valid under these assumptions:

The data comes from a model represented by the formula in the Formula property of the fitted model.

The observations are independent, conditional on the predictor values.

Under these assumptions, let β represent the (unknown) coefficient vector of the linear regression. Suppose H is a full-rank numeric index matrix of size r -by- s , where r is the number of linear combinations of coefficients being tested, and s is the total number of coefficients. Let c be a column vector with r rows. The following is a test statistic for the hypothesis that Hβ  =  c :

F = ( H β ^ − c ) ′ ( H V H ′ ) − 1 ( H β ^ − c ) / r .

Here β ^ is the estimate of the coefficient vector β , stored in the Coefficients property, and V is the estimated covariance of the coefficient estimates, stored in the CoefficientCovariance property. When the hypothesis is true, the test statistic F has an F Distribution with r and u degrees of freedom, where u is the degrees of freedom for error, stored in the DFE property.

Alternative Functionality

The values of commonly used test statistics are available in the Coefficients property of a fitted model.

Extended Capabilities

Gpu arrays accelerate code by running on a graphics processing unit (gpu) using parallel computing toolbox™..

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox) .

Version History

Introduced in R2012a

GeneralizedLinearModel | CompactGeneralizedLinearModel | linhyptest | coefCI | devianceTest

• Generalized Linear Model Workflow
• Generalized Linear Models

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

• Stack Overflow Public questions & answers
• Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
• Talent Build your employer brand
• Advertising Reach developers & technologists worldwide
• Labs The future of collective knowledge sharing
• About the company

Collectives™ on Stack Overflow

Find centralized, trusted content and collaborate around the technologies you use most.

Q&A for work

Connect and share knowledge within a single location that is structured and easy to search.

Get early access and see previews of new features.

How to interpret the results of linearHypothesis function when comparing regression coefficients?

I used linearHypothesis function in order to test whether two regression coefficients are significantly different. Do you have any idea how to interpret these results?

Here is my output:

• 1 Pr(>F) is the p-value of the test, and this is the output of interest. You want the interpretation of every output ? –  Stéphane Laurent Commented Feb 11, 2019 at 12:40

3 Answers 3

Short Answer

Your F statistic is 104.34 and its p-value 2.2e-16. The corresponding p-value suggests that we can reject the null hypothesis that both coefficients cancel each other at any level of significance commonly used in practice.

Were your p-value greater than 0.05, it is accustomed that you would not reject the null hypothesis.

Long Answer

The linearHypothesis function tests whether the difference between the coefficients is significant. In your example, whether the two betas cancel each other out β1 − β2 = 0.

Linear hypothesis tests are performed using F-statistics. They compare your estimated model against a restrictive model which requires your hypothesis (restriction) to be true.

An alternative linear hypothesis testing would be to test whether β1 or β2 are nonzero, so we jointly test the hypothesis β1=0 and β2 = 0 rather than testing each one at a time. Here the null is rejected when one is rejected. Rejection here means that at least one of your hypotheses can be rejected. In other words provide both linear restrictions to be tested as strings

Here are few examples of the multitude of ways you can test hypothese:

You can test a linear combination of coeffecients

joint probability

Aside from the t statistics, which test for the predictive power of each variable in the presence of all the others, another test which can be used is the F-test. (this is the F-test that you would get at the bottom of a linear model)

This tests the null hypothesis that all of the β’s are equal to zero against the alternative that allows them to take any values. If we reject this null hypothesis (which we do because the p-value is small), then this is the same as saying there is enough evidence to conclude that at least one of the covariates has predictive power in our linear model, i.e. that using a regression is predictively ‘better’ than just guessing the average.

So basically, you are testing whether all coefficients are different from zero or some other arbitrary linear hypothesis, as opposed to a t-test where you are testing individual coefficients.

The answer given above is detailed enough except that for this test we are more interested in the two variables hence the linear hypothesis does not investigate the null hypothesis that all of the β’s are equal to zero against the alternative that allows them to take any values but just for two variables of interest which makes this test equivalent to a t-test.

• 1 As it’s currently written, your answer is unclear. Please edit to add additional details that will help others understand how this addresses the question asked. You can find more information on how to write good answers in the help center . –  Community Bot Commented Sep 14, 2022 at 19:22

Your Answer

Reminder: Answers generated by artificial intelligence tools are not allowed on Stack Overflow. Learn more

Sign up or log in

Post as a guest.

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged r regression or ask your own question .

• Featured on Meta
• Upcoming sign-up experiments related to tags
• The 2024 Developer Survey Is Live
• The return of Staging Ground to Stack Overflow
• Policy: Generative AI (e.g., ChatGPT) is banned

Hot Network Questions

• Ideal test/p-value calculation for difference in means with small sample size and right skewed data?
• Starship IFT-4: whatever happened to the fin tip camera feed?
• Convention of parameter naming - undocumented options
• Error using simpleEmail REST API: UNKNOWN_EXCEPTION with error ID
• Project Euler 127 - abc-hits
• Is it possible for Mathematica to output the name of a matrix as opposed to its matrix form?
• Blend a list of colors with hues from 0 to 1 in increments of 0.1
• Could Jordan have saved his company and avoided arrest if he hadn’t made that mistake?
• What can I add to my too-wet tuna+potato patties to make them less mushy?
• A deceiving simple question of combinations about ways of selecting 5 questions with atleast 1 question from each sections
• How to replace sequences in a list based on specific patterns?
• Would you be able to look directly at the Sun if it were a red giant?
• A short story about an ancient anaerobic civilisation on Earth
• Is there a name for books in which the narrator isn't the protagonist but someone who know them well?
• Simulation of a battery with lifting up and role of salt bridge
• Do sus24 chords exist?
• Why do we need unit vectors in a differential bit of area?
• What is PS1 prompt \[\e]0; vs \[\e]2; , it looks like one is for title name of tab, one is for title name of windows
• What was Jessica and the Bene Gesserit's game plan if Paul failed the test?
• What happens after electrons get ejected in the photoelectric effect?
• UTF-8 characters in POSIX shell script *comments* - anything against it?
• How to use SSReflect to prove commutativity and associativity of addition idiomatically?
• Show sixel images inside Vim terminal
• Can the laser light, in principle, take any wavelength in the EM spectrum?

• Advanced search

Regression, ANOVA, and the general linear model : a statistics primer / Peter Vik, Idaho State University

Full Text available online

Availability

Finding items...

• Analysis of variance
• Regression analysis
• Linear models (Statistics)

8: Regression (General Linear Models Part I)

Case-study: land development.

The first step is for Bob to look at his data. He wants to use the number of critical areas to predict the dollar amount in the proposal. Both of these variables are quantitative. Below are the descriptive statistics for Bob’s data.

Descriptive Statistics: Critical Areas, Cost

Variable	N	N*	Mean	SE Mean	StDev	Minimum	Q1	Median	Q3	Maximum
Critical Areas	95	0	4.7990	0.0979	0.9539	2.1296	4.0708	4.8344	5.4800	6.7657
Cost	95	0	99.53	1.03	9.99	72.71	92.56	100.71	106.17	118.04

Bob is looking to predict a quantitative variable based on what he knows about a his actual value of a quantitative variable. Because he wants to predict, he needs to consider a regression.

Before we get started thinking about regression, let’s take a step back. A regression is a simple linear model. If that sounds strange to you, you can think about a linear model as an equation where we consider Y to be some function of X. In other words, Y = f(X). Both the topic in this unit (regression) and that in the next unit (ANOVA) are linear models. With advances in both computing power and the complexity of designs, separating regression and ANOVA are really a matter of semantics than substance. That said, this unit will focus on regression, with ANOVA coming later in the course. Let’s get back to Bob.

Bob did a great job understanding correlations and scatterplots, so he creates a scatterplot of the data.

He recognizes the fact that he has two quantitative variables, dollar amount and number of critical areas and that they have a positive strong linear relationship. However, he learned that the limitation of correlation is that the technique cannot lead to insights about causality between variables. Now he needs a new statistical technique.

Regression analysis provides the evidence that Bob is seeking, specifically how a specific variable of interest is affected by one or more variables. For Bob’s example, he is using number of critical areas to predict dollar amount.

Before we get starting with regression, it is important to distinguish between the variable of interest and the variable(s) we will use to predict the variable of interest.

When there is only one predictor variable, we refer to the regression model as a simple linear regression model.

In statistics, we can describe how variables are related using the mathematical function as we described as a linear model. We refer to this model as the simple linear regression model.

• Identify the slope,  intercept, and coefficient of determination
• Calculate predicted and residual (error) values
• Test the significance of the slope, including statement of the null hypothesis for the slope
• State the assumptions for regression

8.1 - Linear Relationships

To define a useful model, we must investigate the relationship between the response and the predictor variables. As mentioned before, the focus of this Lesson is linear relationships. For a brief review of linear functions, recall that the equation of a line has the following form:

where m is the slope and b is the y-intercept.

Given two points on a line, \(\left(x_1,y_1\right)\) and \(\left(x_2, y_2\right)\), the slope is calculated by:

\begin{align} m&=\dfrac{y_2-y_1}{x_2-x_1}\\&=\dfrac{\text{change in y}}{\text{change in x}}\\&=\frac{\text{rise}}{\text{run}} \end{align}

The slope of a line describes a lot about the linear relationship between two variables. If the slope is positive, then there is a positive linear relationship, i.e., as one increases, the other increases. If the slope is negative, then there is a negative linear relationship, i.e., as one increases the other variable decreases. If the slope is 0, then as one increases, the other remains constant.

8.2 - Simple Linear Regression

For Bob’s simple linear regression example, he wants to see how changes in the number of critical areas (the predictor variable) impact the dollar amount for land development (the response variable). If the value of the predictor variable (number of critical areas) increases, does the response (cost) tend to increase, decrease, or stay constant? For Bob, as the number of critical features increases, does the dollar amount increase, decrease or stay the same?

We test this by using the characteristics of the linear relationships, particularly the slope as defined above. Remember from hypothesis testing, we test the null hypothesis that a value is zero. We extend this principle to the slope, with a null hypothesis that the slope is equal to zero. Non-zero slopes indicate a significant impact of the predictor variable from the response variable, whereas zero slope indicates change in the predictor variable do not impact changes in the response.

Let’s take a closer look at the linear model producing our regression results.

8.2.1 - Assumptions for the SLR Model

Before we get started in interpreting the output it is critical that we address specific assumptions for regression.  Not meeting these assumptions is a flag that the results are not valid (the results cannot be interpreted with any certainty because the model may not fit the data).  

In this section, we will present the assumptions needed to perform the hypothesis test for the population slope:

\(H_0\colon \ \beta_1=0\)

\(H_a\colon \ \beta_1\ne0\)

We will also demonstrate how to verify if they are satisfied. To verify the assumptions, you must run the analysis in Minitab first.

Assumptions for Simple Linear Regression

Check this assumption by examining a scatterplot of x and y.

Check this assumption by examining a scatterplot of “residuals versus fits”; the correlation should be approximately 0. In other words, there should not look like there is a relationship.

Check this assumption by examining a normal probability plot; the observations should be near the line. You can also examine a histogram of the residuals; it should be approximately normally distributed.

Check this assumption by examining the scatterplot of “residuals versus fits”; the variance of the residuals should be the same across all values of the x-axis. If the plot shows a pattern (e.g., bowtie or megaphone shape), then variances are not consistent, and this assumption has not been met.

8.2.2 - The SLR Model

The errors referred to in the assumptions are only one component of the linear model. The basis of the model, the observations are considered as coordinates, \((x_i, y_i)\), for \(i=1, …, n\). The points, \(\left(x_1,y_1\right), \dots,\left(x_n,y_n\right)\), may not fall exactly on a line, (like the cost and number of critical areas). This gap is the error!

The graph below is an example of a scatter plot showing height as the explanatory variable for height. Select the + icons to view the explanations of the different parts of the scatterplot and the least-squares regression line.

The graph below summarizes the least-squares regression for Bob's data. We will define what we mean by least squares regression in more detail later in the Lesson, for now, focus on how the red line (the regression line) "fits" the blue dots (Bob's data)

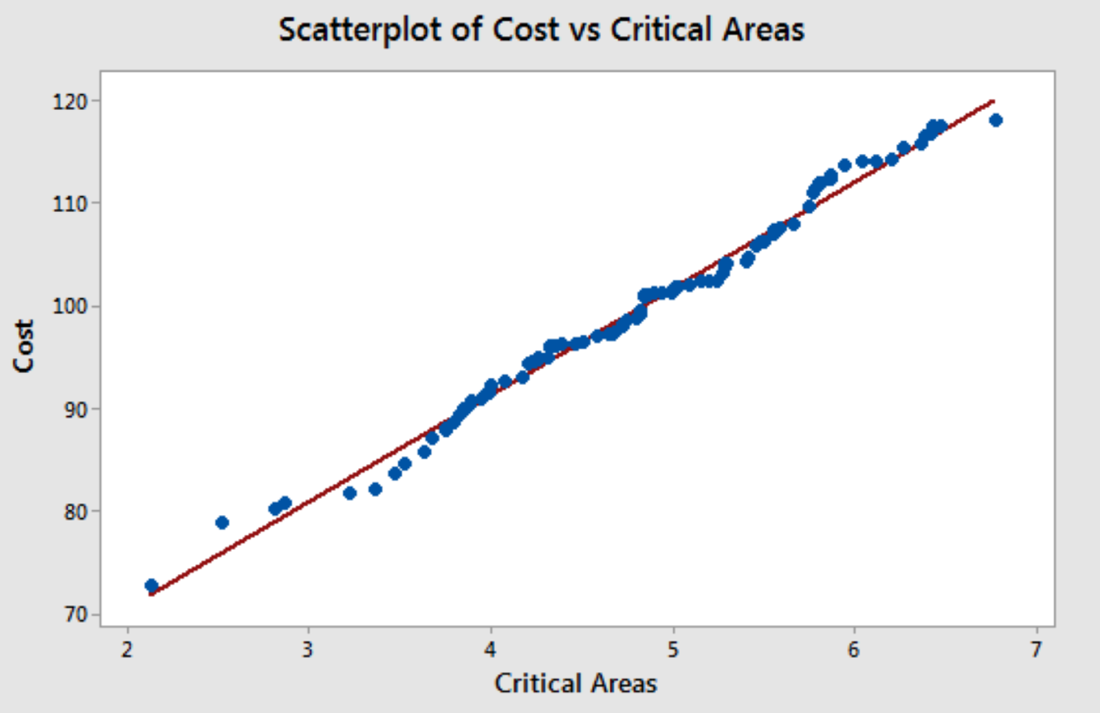
We combine the linear relationship along with the error in the simple linear regression model.

Simple Linear Regression Model

The general form of the simple linear regression model is...

\(Y=\beta_0+\beta_1X+\epsilon\)

For an individual observation,

\(y_i=\beta_0+\beta_1x_i+\epsilon_i\)

• \(\beta_0\) is the population y-intercept,
• \(\beta_1\) is the population slope, and
• \(\epsilon_i\) is the error or deviation of \(y_i\) from the line, \(\beta_0+\beta_1x_i\)

To make inferences about these unknown population parameters (namely the slope and intercept), we must find an estimate for them. There are different ways to estimate the parameters from the sample. This is where we get to n the least-squares method.

Least Squares Line

The least-squares line is the line for which the sum of squared errors of predictions for all sample points is the least.

Using the least-squares method, we can find estimates for the two parameters.

The formulas to calculate least squares estimates are:

The least squares line for Bob’s data is the red line on the scatterplot below.

Let’s jump ahead for a moment and generate the regression output. Below we will work through the content of the output. The regression output for Bob’s data look like this:

Coefficients

Predictor	Coef	SE Coef	T-Value	P-Value	VIF
Constant	49.542	0.560	88.40	0.000
Critical Areas	10.417	0.115	90.92	0.000	1.00

Regression Equation

Cost = 49.542 + 10.417 Critical Areas

8.2.3 - Interpreting the Coefficients

Once we have the estimates for the slope and intercept, we need to interpret them. For Bob’s data, the estimate for the slope is 10.417 and the estimate for the intercept (constant) is 49.542. Recall from the beginning of the Lesson what the slope of a line means algebraically. If the slope is denoted as \(m\), then

\(m=\dfrac{\text{change in y}}{\text{change in x}}\)

Going back to algebra, the intercept is the value of y when \(x = 0\). It has the same interpretation in statistics.

Interpreting the intercept of the regression equation, \(\hat{\beta}_0\) is the \(Y\)-intercept of the regression line. When \(X = 0\) is within the scope of observation, \(\hat{\beta}_0\) is the estimated value of Y when \(X = 0\).

Note, however, when \(X = 0\) is not within the scope of the observation, the Y-intercept is usually not of interest. In Bob’s example, \(X = 0\) or 49.542 would be a plot of land with no critical areas. This might be of interest in establishing a baseline value, but specifically, in looking at land that HAS critical areas, this might not be of much interest to Bob.

As we already noted, the slope of a line is the change in the y variable over the change in the x variable. If the change in the x variable is one, then the slope is:

\(m=\dfrac{\text{change in y}}{1}\)

The slope is interpreted as the change of y for a one unit increase in x. In Bob’s example, for every one unit change in critical areas, the cost of development increases by 10.417.

Interpreting the slope of the regression equation, \(\hat{\beta}_1\)

\(\hat{\beta}_1\) represents the estimated change in Y per unit increase in X

Note that the change may be negative which is reflected when \(\hat{\beta}_1\) is negative or positive when \(\hat{\beta}_1\) is positive.

If the slope of the line is positive, as it is in Bob’s example, then there is a positive linear relationship, i.e., as one increases, the other increases. If the slope is negative, then there is a negative linear relationship, i.e., as one increases the other variable decreases. If the slope is 0, then as one increases, the other remains constant, i.e., no predictive relationship.

Therefore, we are interested in testing the following hypotheses:

\(H_0\colon \beta_1=0\\H_a\colon \beta_1\ne0\)

Let’s take a closer look at the hypothesis test for the estimate of the slope. A similar test for the population intercept, \(\beta_0\), is not discussed in this class because it is not typically of interest.

8.2.4 - Hypothesis Test for the Population Slope

As mentioned, the test for the slope follows the logic for a one sample hypothesis test for the mean. Typically (and will be the case in this course) we test the null hypothesis that the slope is equal to zero. However, it is possible to test the null hypothesis that the slope is zero or less than zero OR test the null hypothesis that the slope is zero or greater than zero.

Research Question	Is there a linear relationship?	Is there a positive linear relationship?	Is there a negative linear relationship?
Null Hypothesis	\(\beta_1=0\)	\(\beta_1=0\)	\(\beta_1=0\)
Alternative Hypothesis	\(\beta_1\ne0\)	\(\beta_1>0\)	\(\beta_1<0\)
Type of Test	Two-tailed, non-directional	Right-tailed, directional	Left-tailed, directional

The test statistic for the test of population slope is:

\(t^*=\dfrac{\hat{\beta}_1}{\hat{SE}(\hat{\beta}_1)}\)

where \(\hat{SE}(\hat{\beta}_1)\) is the estimated standard error of the sample slope (found in Minitab output). Under the null hypothesis and with the assumptions shown in the previous section, \(t^*\) follows a \(t\)-distribution with \(n-2\) degrees of freedom.

Take another look at the output from Bob’s data.

Here we can see that the “T-Value” is 90.92, a very large t value indicating the difference between the null value for the slope (zero) is very different from the value for the slope calculated by the least-squares method (10.417). This results in a small probability value that the null is true (P-Value is less then .05), so Bob can reject the null, and conclude that the slope is not zero. Therefore, the number of critical areas significantly predicts the cost of development.

He can be more specific and conclude that for every one unit change in critical areas, the cost of development increases by 10.417.

As with most of our calculations, we need to allow some room for imprecision in our estimate. We return to the concept of confidence intervals to build in some error around the estimate of the slope.

The \( (1-\alpha)100\%\) confidence interval for \(\beta_1\) is:

\(\hat{\beta}_1\pm t_{\alpha/2}\left(\hat{SE}(\hat{\beta}_1)\right)\)

where \(t\) has \(n-2\) degrees of freedom.

The final piece of output from Minitab is the Least Squares Regression Equation. Remember that Bob is interested in being able to predict the development cost of land given the number of critical areas. Bob can use the equation to do this.

If a given piece of land has 10 critical areas, Bob can “plug in” the value of “10” for X, the resulting equation

\(Cost = 49.542 + 10.417 * 10\)

Results in a predicted cost of:

\(153.712 = 49.542 + 10.417 * 10\)

So, if Bob knows a piece of land has 10 critical areas, he can predict the development cost will be about 153 dollars!

Using the 10 critical features allowed Bob to predict the development cost, but there is an important distinction to make about predicting an “AVERAGE” cost, or a “SPECIFIC” cost. These are represented by ‘CONFIDENCE INTERVALS” versus ‘PREDICTION INTERVALS’ for new observations. (notice the difference here is that we are referring to a new observation as opposed to above when we used confidence intervals for the estimate of the slope!)

The mean response at a given X value is given by:

\(E(Y)=\beta_0+\beta_1X\)

Inferences about Outcome for New Observation

• The point estimate for the outcome at \(X = x\) is provided above.
• The interval to estimate the mean response is called the confidence interval. Minitab calculates this for us.
• The interval used to estimate (or predict) an outcome is called prediction interval.

For a given x value, the prediction interval and confidence interval have the same center, but the width of the prediction interval is wider than the width of the confidence interval. That makes good sense since it is harder to estimate a value for a single subject (for example a particular piece of land in Bob’s town that may have some unique features)  than it would be to estimate the average for all pieces of land. Again, Minitab will calculate this interval as well.

8.2.5 - SLR with Minitab

Minitab ®, simple linear regression with minitab.

• Select Stat > Regression > Regression > Fit Regression Model
• In the box labeled " Response ", specify the desired response variable.
• In the box labeled " Predictors ", specify the desired predictor variable.
• Select OK . The basic regression analysis output will be displayed in the session window.

To check assumptions...

• Click Graphs .
• In 'Residuals plots, choose 'Four in one.'
• Select OK .

8.3 - Cautions with Linear Regression

Extrapolation is applying a regression model to X-values outside the range of sample X-values to predict values of the response variable Y. For example, Bob would not want to use the number of critical features to predict dollar amount using a regression model based on an urban area if Bob’s town is rural.

Second, if no linear relationship (i.e. correlation is zero) exists it does not imply there is no relationship . The scatter plot will reveal whether other possible relationships may exist. The figure below gives an example where X, Y are related, but not linearly related i.e. the correlation is zero.

Outliers and Influential Observations

Influential observations are points whose removal causes the regression equation to change considerably. It is flagged by Minitab in the unusual observation list and denoted as X. Outliers are points that lie outside the overall pattern of the data. Potential outliers are flagged by Minitab in the unusual observation list and denoted as R. The following is the Minitab output for the unusual observations within Bob’s study:

Fits and Diagnostics for Unusual Observations

Obs	Cost	Fit	Resid	Std Resid
1	72.714	71.725	0.989	0.98		X
2	78.825	75.829	2.996	2.93	R	X
6	81.967	84.507	-2.540	-2.44	R
7	83.490	85.640	-2.150	-2.06	R
85	113.540	111.440	2.100	2.01	R

R Large Residual

X Unusual X

Some observations may be both outliers and influential, and these are flagged by R. Those observational points will merit particular attention because these points are not well “fit” by the model and maybe influencing conclusions or indicate an alternative model is needed.

8.4 - Estimating the standard deviation of the error term

Our simple linear regression model is:

The errors for the \(n\) observations are denoted as \(\epsilon_i\), for \(i=1, …, n\). One of our assumptions is that the errors have equal variance (or equal standard deviation). We can estimate the standard deviation of the error by finding the standard deviation of the residuals, \(\hat{\epsilon}_i=\hat{y}_i-y_i\). Minitab also provides the estimate for us, denoted as \(S\), under the Model Summary. We can also calculate it by:

\(s=\sqrt{\text{MSE}}\)

Find the MSE in the ANOVA table, under the Adj MS column and the Error row. The value of 1.12 represents the average squared error. This becomes the denominator for the F test.

Analysis of Variance

Source	DF	Adj SS	Adj MS	F-Value	P-Value
Regression	1	9281.7	9281.72	8267.30	0.000
Critical Areas	1	9287.7	9281.72	8267.30	0.000
Error	93	104.4	1.12
Total	94	9386.1

8.5 - Coefficient of Determination

Now that we know how to estimate the coefficients and perform the hypothesis test, is there any way to tell how useful the model is?

One measure is the coefficient of determination, denoted \(R^2\).

Therefore, a value close to 100% means that the model is useful and a value close to zero indicates that the model is not useful. It can be shown by mathematical manipulation that:

\(\text{SST }=\text{ SSR }+\text{ SSE}\)

\(\sum (y_i-\bar{y})^2=\sum (\hat{y}_i-\bar{y})^2+\sum (y_i-\hat{y}_i)^2\)

Total variability in the y value = Variability explained by the model + Unexplained variability

To get the total, explained and unexplained variability, first we need to calculate corresponding deviances. Drag the slider on the image below to see how the total deviance \((y_i-\bar{y})\) is split into explained \((\hat{y}_i-\bar{y})\) and unexplained deviances \((y_i-\hat{y}_i)\).

he breakdown of variability in the above equation holds for the multiple regression model also.

\(R^2=\dfrac{\text{variability explained by the model}}{\text{total variability in the y values}}\)

\(R^2\) represents the proportion of total variability of the \(y\)-value that is accounted for by the independent variable \(x\).

For the specific case when there is only one independent variable \(X\) (i.e., simple linear regression), one can show that \(R^2 =r^2\), where \(r\) is correlation coefficient between \(X\) and \(Y\). For Bob’s data, the correlation of the two variable is 0.994 and the R2 value is 98.89.

Correlations

Pearson correlation	0.994
P-value	0.000

Model Summary

S	R-sq	R-sq(adj)	R-sq(pred)
1.05958	98.89%	98.88%	98.82%

Finding Correlation

• Select Stat > Basic statistics > Correlation
• Pearson correlation is the default.  An optional Spearman rho method is also available. 
• If it isn't already checked, put a checkmark in the box labeled Display p-values by clicking once on the box.
• Select OK . The output will appear in the session window.

8.6 - Lesson Summary

Now that you have seen what the components of a regression are, you can see that a regression is a linear model (following the form \(y=b_0+b_1+ \text{error}\)). In our next lesson, we will learn that this same linear model can analyze a categorical variable’s impact on a quantitative (y) variable.

Let’s return to Bob. Bob can now state with confidence that the number of critical features does significantly impact the dollar amount of a land development proposal. Hopefully growing statistical skills will make his work with developers more effective and efficient!

Optimal Rates for Functional Linear Regression with General Regularization

• Gupta, Naveen
• Sivananthan, S.
• Sriperumbudur, Bharath K.

Functional linear regression is one of the fundamental and well-studied methods in functional data analysis. In this work, we investigate the functional linear regression model within the context of reproducing kernel Hilbert space by employing general spectral regularization to approximate the slope function with certain smoothness assumptions. We establish optimal convergence rates for estimation and prediction errors associated with the proposed method under a Hölder type source condition, which generalizes and sharpens all the known results in the literature.

• Mathematics - Statistics Theory

API Reference #

This is the class and function reference of scikit-learn. Please refer to the full user guide for further details, as the raw specifications of classes and functions may not be enough to give full guidelines on their uses. For reference on concepts repeated across the API, see Glossary of Common Terms and API Elements .

Object	Description
	.
	for simple transformers.
	kernel takes two kernels \(k_1\) and \(k_2\)
	kernel takes two kernels \(k_1\) and \(k_2\)
	.
	.
	score function, fraction of log loss explained.
	regression score function, fraction of absolute error explained.
	regression score function, fraction of pinball loss explained.
	regression score function, fraction of Tweedie deviance explained.
	(coefficient of determination) regression score function.
	from the given estimators.
	from the given transformers.
	.
	elements from 0 to .
	evenly spaced slices going up to .
	is joblib.Memory-like.
	is in a multilabel format.
	Request} instance from the given object.
	.
	that propagates the scikit-learn configuration.
	.
	.