problem solving using venn diagram grade 7 ppt

Introduction to Sets PowerPoint

https://drive.google.com/file/d/16obKRFE34kXhs8xia_uS42jEKFXOERwk/view

Introduction to Sets Video Tutorial

Definition, notation and properties of Sets

Representation of a set

Numerical Sets

Subsets and proper subsets

Super set, power set, empty/null set and universal set

Complement and cardinality of sets

Solving problems involving sets using venn diagram.

Solving Problems Involving Sets Using Venn Diagram Video Tutorial

What is venn diagram powerpoint.

What is Venn Diagram Video Tutorial

YouTube: https://youtu.be/qjHMKS3WuCQ

Union and Intersection

Solving Set Problems Using Venn Diagram Sample Problem 1

Solving Set Problems Using Venn Diagram Sample Problem 2

Solving Set Problems Using Venn Diagram Sample Problem 3

Concept of absolute value: simplified ppt.

Concept of Absolute Value Video Tutorial

Adding integers ppt.

Adding integers Video Tutorial

Subtracting integers ppt.

Subtracting integers Video Tutorial

Multiplication and division of integers ppt.

Multiplication and Division of Integers Video Tutorial

Conversions and operations, fraction to decimal ppt.

Fraction to Decimal Video Tutorial

Decimal to fraction ppt.

Decimal to Fraction Video Tutorial

Adding and subtracting fractions ppt.

Adding and Subtracting fractions Video Tutorial

Scientific notation ppt.

Scientific Notation Video Tutorial

• International
• Education Jobs
• Schools directory
• Resources Education Jobs Schools directory News Search

Problem solving with Venn diagrams

Subject: Mathematics

Age range: 14 - 18

Resource type: Other

Last updated

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Tes paid licence How can I reuse this?

Get this resource as part of a bundle and save up to 29%

A bundle is a package of resources grouped together to teach a particular topic, or a series of lessons, in one place.

Sets theory and Venn diagrams

% Power point presentations on: Introduction to set theory The number sets Union and intersection of sets Shading regions in Venn diagrams Solving rpoblem using Venn diagrams

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

This resource hasn't been reviewed yet

To ensure quality for our reviews, only customers who have purchased this resource can review it

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• Inspiration

• Skills by Standard
• Skills by Grade
• Skills by Category

Go to profile

• Assignments
• Assessments
• Report Cards
• Our Teachers

Remove ads and gain access to the arcade and premium games!

Unlock harder levels by getting an average of 80% or higher.

Earn up to 5 stars for each level The more questions you answer correctly, the more stars you'll unlock!

Each game has 10 questions. Green box means correct. Yellow box means incorrect.

Need some help or instruction on how to do this skill?

Want a paper copy? Print a generated PDF for this skill.

Share MathGames with your students, and track their progress.

See how you scored compared to other students from around the world.

Learn Math Together.

Grade 7 - Mathematical Process Standards

Standard 7.MPS.111.27.b.1B - Use venn diagrams to solve word problems.

Included Skills:

Use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution.

If you notice any problems, please let us know .

• Preferences

How To Solve a Word Problem Using Venn Diagrams - PowerPoint PPT Presentation

How To Solve a Word Problem Using Venn Diagrams

... skateboarding, one set for bicycling, and one set for college student chat rooms. ... all the students who joined the bicycling chat room or n(bicycling) ... – powerpoint ppt presentation.

• Suppose that a group of 200 students are surveyed and ask which chatrooms they have joined. There are three chatrooms in our survey one for skateboarding, one for bicycling, and one for college students.
• 90 students joined the room for skateboarding
• 50 students joined the room for bicycling
• 70 students joined the room for college students
• 15 students joined rooms for skateboarding and college students
• 12 students joined rooms for bicycling and college students
• 25 students joined rooms for skateboarding and bicycling
• 10 students joined all three rooms.
• 1.) How many students joined the room for skateboarding OR bicycling?
• 2.) How many students did not join any of these three rooms?
• 3.) How many students joined the bicycling AND skateboarding rooms BUT NOT the room for college students?
• 4.) How many students joined EXACTLY 1 of these rooms?
• 5.) How many students joined AT MOST 2 of these rooms?
• This problem seems too difficult to solve! But it isnt. You just need to use a Venn Diagram to represent the relationship between the three chat rooms and the answers to all 5 of these questions will be perfectly clear.
• For this type of problem we fill in our regions for our Venn Diagram. We use the information given to fill in the number of students in each region. We start from the bottom and work our way to the top.
• First we draw our Venn Diagram representing three sets, one set for Skateboarding, one set for Bicycling, and one set for College Student chat rooms. Then we label our regions and start putting in the number of elements or students for each region. 10 students joined all three rooms means these 10 students are in all three circles - the intersection of circles for skateboarding, bicycling, and college students. This is represented by region 5 - we need to put in a 10 in region 5.
• Our next piece of information is
• What do these 25 students represent? They are the the set of students who joined the Skateboarding chatroom AND the Bicycling chatroom or n(Skateboarding n Bicycling). These 25 students are in both the Skateboarding circle AND the Bicycling circle. This intersection is represented by regions 2 5 - we already have 10 students in region 5 so the number of students to put in region 2 25-10 or 15.
• What do these 12 students represent? They are the the students who joined the Bicycling chatroom AND the College Students chatroom or n(Bicycling n College Students). These 12 students are in both the Bicycling circle AND the College Student circle. This intersection is represented by regions 5 6 - we already have 10 students in region 5 so the number of students to put in region 6 12-10 or 2.
• What do these 15 students represent? They represent the students who joined the Skateboarding chatroom AND the students who joined the College Students chatroom or
• n(Skateboarding n College Students). These 15 students are in both the Skateboarding circle AND the College Student circle. This intersection is represented by regions 4 5 - we already have 10 students in region 5 so the number of students to put in region 4 15-10 or 5.
• What do these 70 students represent? They represent ALL the students who joined the College Students chat room or n(College Students). This is represented by regions 4 5 6 7 - the sum of the students in these four regions 70. We already have 5 students in region 4, 10 students in region 5, and 2 students in region 6 so the number of students to put in region 7 70-(1052) 53.
• What do these 50 students represent? They represent ALL the students who joined the Bicycling chat room or n(Bicycling). This is represented by regions 2 3 5 6 - the sum of the students in these four regions 50. We already have 15 students in region 2, 10 students in region 5, and 2 students in region 6 so the number of students to put in region 3 50-(15102) 23.
• What do these 90 students represent? They represent ALL the students who joined the Skateboarding chatroom or n(Skateboarding). This is represented by regions 1 2 4 5 - the sum of the students in these four regions 90. We already have 15 students in region 2, 5 students in region 4, and 10 students in region 5 so the number of students to put in region 1 90-(15510) 60.
• We have now filled in regions 1 thru 7, we only have to fill in region 8. What students does region 8 represent? Region 8 represents the students surveyed who did not join any of the three chatrooms in our survey. These students are not in any of the circles that represent our sets. The sum of ALL 8 regions must add up to all the students we surveyed - our universe - or 200 students. Therefore, the number of students in region 8 200-(601523510253)32.
• Now that we have all our regions filled in we can answer our five questions.
• How many students joined the room for skateboarding OR bicycling?
• This is asking us for the union of the skateboarding and bicycling chatrooms or n(Skateboarding U Bicycling). For union we bring all the members of the skateboarding and bicycling chatrooms together. We want all the regions in the skateboarding and bicycling circle (remember dont count regions more than once). So the students we are interested in are in regions 1 2 3 4 5 6 or
• 60 15 23 5 10 2 115 students
• How many students did not join any of these three rooms?
• The students who did not join any groups are not in ANY of the three circles. These students are in region 8. So the number of students who did not join any of these three chatrooms 32 students
• How many students joined the bicycling AND skateboarding rooms BUT NOT the room for college students?
• We want the students who joined bicycling AND skateboarding - this represents the intersection of the skateboarding and bicycling sets - regions 2 5. The next part of the question tells us that we do not want students in the College Students set, so we do not want region 5 since this region while it is in the intersection of skateboarding and bicycling it is also in the college students circle, we only want region 2. The answer is 15 students.
• How many students joined EXACTLY 1 of these rooms?
• The students who joined EXACTLY 1 of the rooms will be in regions that are only in 1 circle. These regions include 1, 3, and 7, we will add all the students in these regions to get our answer.
• 60 23 53 136 students
• Students who joined exactly 2 chatrooms will be in regions in exactly 2 circles, these regions are 2,4, and 6.
• Students who joined exactly 3 chatrooms will be in regions in exactly 3 circles, this region is 5.
• How many students joined AT MOST 2 of these rooms?
• AT MOST 2 means the number of rooms we want a student to join is LESS THAN OR EQUAL TO 2. ( 2 rooms). We want regions that are in 2 circles, 1 circle, or none of the circles. These include regions 1,2,3,4,6,7,and 8. We add up all these regions to get our answer.
• 601523525332 190 students
• NOTE If the question had asked for the number of students who joined AT LEAST 2 of these rooms we would be interested in regions that are in 2 OR MORE circles (at least mean means 2). We would want to add together the students in regions 2,4,5,and 6.

PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.

You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.

About the Developers

PowerShow.com is brought to you by  CrystalGraphics , the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.

• Skills by Standard
• Skills by Grade
• Skills by Category

Go to profile

• Assignments
• Assessments
• Report Cards
• Our Teachers

Remove ads and gain access to the arcade and premium games!

Unlock harder levels by getting an average of 80% or higher.

Earn up to 5 stars for each level The more questions you answer correctly, the more stars you'll unlock!

Each game has 10 questions. Green box means correct. Yellow box means incorrect.

Need some help or instruction on how to do this skill?

Want a paper copy? Print a generated PDF for this skill.

Share MathGames with your students, and track their progress.

See how you scored compared to other students from around the world.

Learn Math Together.

Grade 7 - Expressions & Equations

Standard 7.EE.B.3 - Use venn diagrams to solve word problems.

Included Skills:

Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies. For example: If a woman making $25 an hour gets a 10% raise, she will make an additional 1/10 of her salary an hour, or $2.50, for a new salary of $27.50. If you want to place a towel bar 9 3/4 inches long in the center of a door that is 27 1/2 inches wide, you will need to place the bar about 9 inches from each edge; this estimate can be used as a check on the exact computation.

If you notice any problems, please let us know .

Home Blog Presentation Ideas Venn Diagram Ideas for PowerPoint Presentations

Venn Diagram Ideas for PowerPoint Presentations

Venn Diagrams are widely used for business presentations to show the relationship between a collection of sets. Venn Diagrams can be made using PowerPoint shapes or SmartArt Graphics, however, they can appear confusing if the color combinations and display layout do not follow presentation best practices. You can save time and effort in making Professional Venn Diagrams for your presentations with the help of readymade Venn Diagram Templates for PowerPoint .

Whether you’re a student or a professional, you may have heard of Venn diagrams. Perhaps you’re required to demonstrate the logic in boolean expressions, describe the commonalities and differences between two communities, or want to show how your company is different from the competition; Venn diagrams can be a great tool to organize all of this data. These diagrams are a great tool to visually demonstrate the commonalities and differences between two or more entities.

In this article, we will discuss what Venn diagrams are? their history, their purpose, and where they are used.

Table of Contents:

What is a Venn Diagram?

A brief history of venn diagrams, quick guide to venn diagrams, what are venn diagrams used for.

• Grunge Venn Diagram For PowerPoint
• Grunge Concentric Circles For PowerPoint
• Ecosystem Diagram PowerPoint Template
• Gradient Venn Diagram for PowerPoint
• Multi-Layer Diagram Concept for PowerPoint
• Hexagon Venn Diagram PowerPoint Template
• Venn Diagram Material Design for PowerPoint

Interactive Venn Diagrams: Engaging Your Audience in Presentations

The future of venn diagrams in a data-driven world, f.a.q. section — venn diagrams explained.

• Final Words

A Venn Diagram is an illustration representing sets and the relationship between them. Venn diagrams consist of circles, each representing a set. Everything inside a particular circle is considered an element of the set, while everything that is outside is not considered an element of the set. If there are elements that belong to two or more sets, the circles are overlapped such that the elements become part of two or more entities.

Venn diagrams are part of Euler diagrams and are used in mathematics to demonstrate the set theory. Moreover, these diagrams are used to illustrate relationships between sets in logic, probability, statistics, computer science, and linguistics.

Other Names For Venn Diagrams may include primary diagrams, logic diagrams, or set diagrams.

The pioneer of Venn diagrams was John Venn , who made these diagrams popular in 1880. John Venn published a titled On the Diagrammatic and Mechanical Representation of Propositions and Reasoning in the Journal of Science and the Philosophical Magazine. The diagrams introduced by Venn gave various ways to illustrate propositions by diagrams.

According to Mark Wetson and Frank Ruskey , these diagrams had been used in formal logic much before Venn. However, they are correctly associated with him as he had comprehensively studied these diagrams, formalized them, and generalized their usage.

At first, Venn did not call his diagrams Venn Diagrams but rather referred to them as Eulerian Circles. However, Lewis Carroll included Venn’s Method of Diagrams and Euler’s Method of Diagrams in the appendix of his book titled Symbolic Logic in 1896. Moreover, in his book entitled A Survey of Symbolic Logic in 1918, Clarence Irving Lewis used the term Venn Diagram .

Leonhard Euler developed Euler Diagrams in the 18th century; Venn diagrams are quite similar to Euler Diagrams. Moreover, M.E. Baron stated that Leibniz, in the 17th century, made similar diagrams to Euler diagrams. However, much of the work remained unpublished. She also noted that early Euler-like diagrams had been around since the 13th century by Ramon Lull.

We will analyze how Venn diagrams are used in real-life scenarios. 

Let’s think of 2 items that most people have in their homes or offices: Smartphones and Laptops. Both devices do some similar tasks and also show some significant differences. We can explain how they share features as much as how they can be different —taking this into account: 

• Circle A: Smartphone: small form factor, allows phone connectivity, includes a high-definition camera
• Circle B: Laptop: large form factor, requires Wi-Fi access, includes a keyboard 

To understand the intersection of both, we will add the features they both share, including the internet browser, games, work, and video calls. 

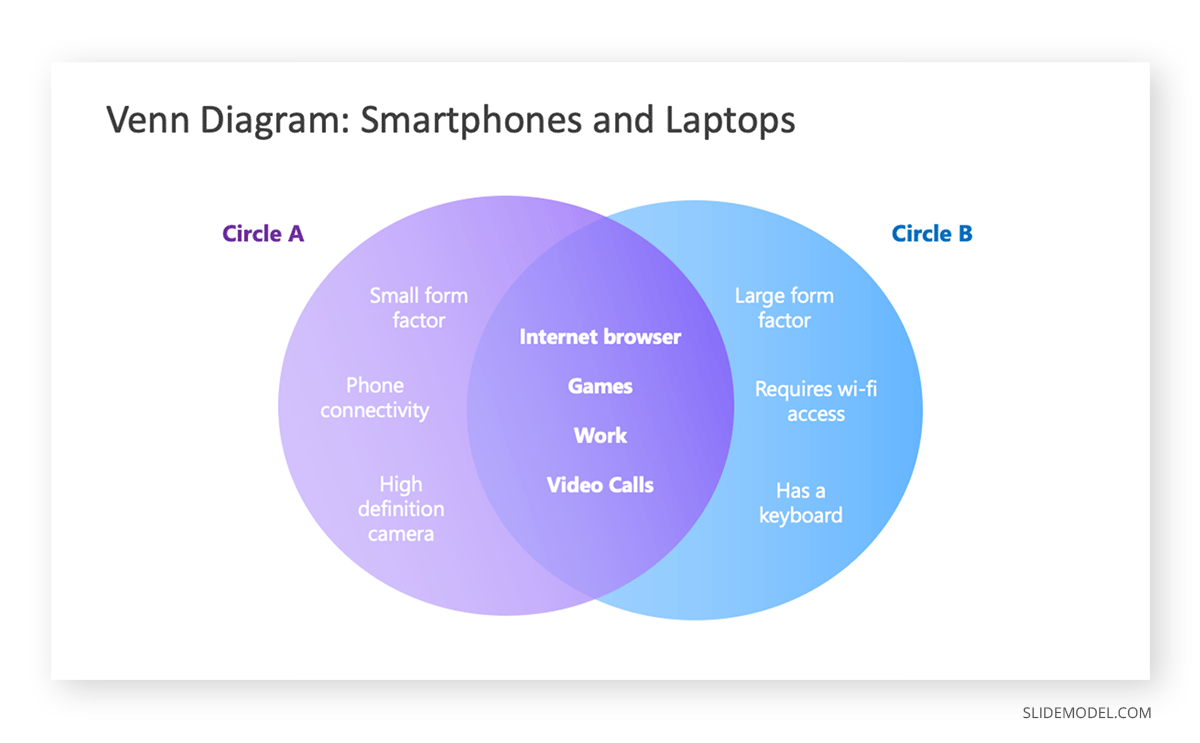
We now understand both devices are different, as they do additional things, but they also have in common a set of features that allow for cross-usage. 

When creating a Venn Diagram, generally, we think about 2 circles side by side, but we might realize that 2 circles will come off short, and we need more when defining the information that will go into them. Therefore, many interesting variations of Venn Diagrams have been created to portray different element sets, and you can include as many circles and information as needed.

You can check our Venn Diagram PPT Templates and select a ready made Venn Diagram design for your presentation

Venn diagrams are used for various purposes. They show the relationship between multiple sets of entities and organize the data visually. You can add all kinds of different Venn Diagrams either with SmartArt from PowerPoint or any of the SlideModel templates in presentations. Even during a meeting or a work session, you can actively workshop with your team information to be included in a presentation that will later be given to a client to confer relevant ideas. Due to the flexibility of Venn diagrams, they can be added with few explanations when explaining 2 or more sets of information.

Venn Diagrams in Education 

Students, as well as professionals, may use these diagrams to show the logic governing a concept as well as to aid visual communication. They may be able to demonstrate the similarities and differences between the two concepts in a visual manner.

With Venn diagrams, you may be able to show the commonalities and differences between two or more entities in business or marketing. This may be used for selecting a service or product for purchase. They will also come in handy while teaching regular subjects: Mathematics, logic, probability, and statistics.

Venn Diagrams in Math

If you’re a mathematician or a student studying mathematics, you can use these diagrams to solve complex problems, visualize the prediction of probabilities, and correlations, and compare data sets. These diagrams may also be used to give reasons for the logic in statements, such as in Boolean logic.

Venn Diagrams in Computer Science 

This type of diagram is great for showing the overlaps between sets of data in Computer Science.

Venn Diagrams in Business. 

We want to share with you another day-to-day example, but this time we want to frame out a prevalent set of terms used in marketing, sales, or an investor pitch. You might have heard about TAM, SAM, and SOM, but in case you haven’t, we will add a brief explanation alongside how we can create this model with Venn Diagrams. 

When working to roll out any commercial plan, it’s crucial to understand the market size. TAM, Total Addressable market, means the whole universe of people who can be potential buyers; this is to be represented as a large outer circle. Afterward, we need to define the SAM, Service Addressable Market, or the market to reach realistically with the current business model in a second internal circle. Finally, we will build a smaller circle inside the SAM to represent the SOM, or Serviceable Obtainable Market, a faithful portion of the market to be reached with available resources. 

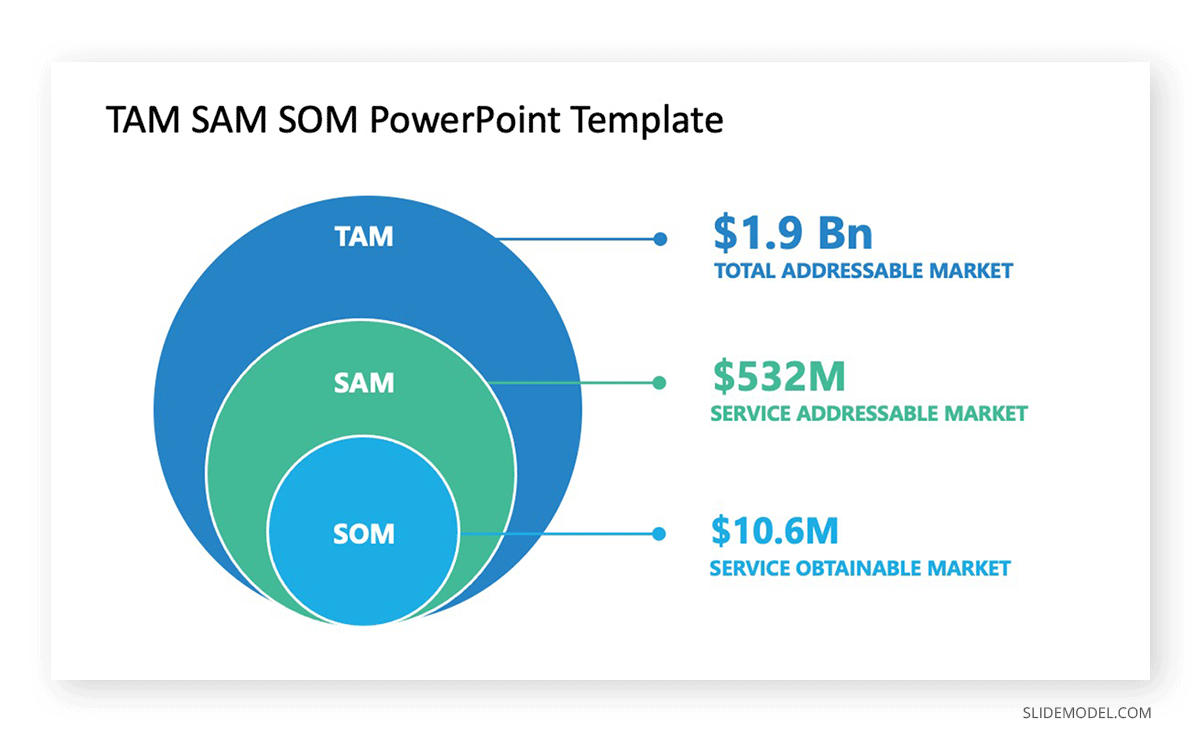
Check our market segmentation ppt article for more information about Market Segmentation Presentations.

PowerPoint Venn Diagram Template Examples

Since we’ve added some examples of how you can use Venn Diagrams in presentations, we want to share how you can create PowerPoint presentations with a varied array of premade designs and formats, including an editable Venn Diagram template, available at our gallery.

1. Grunge Venn Diagram For PowerPoint

The Grunge Venn Diagram PowerPoint Template is a professionally designed template that provides highly customizable sample slides for making Venn Diagrams.

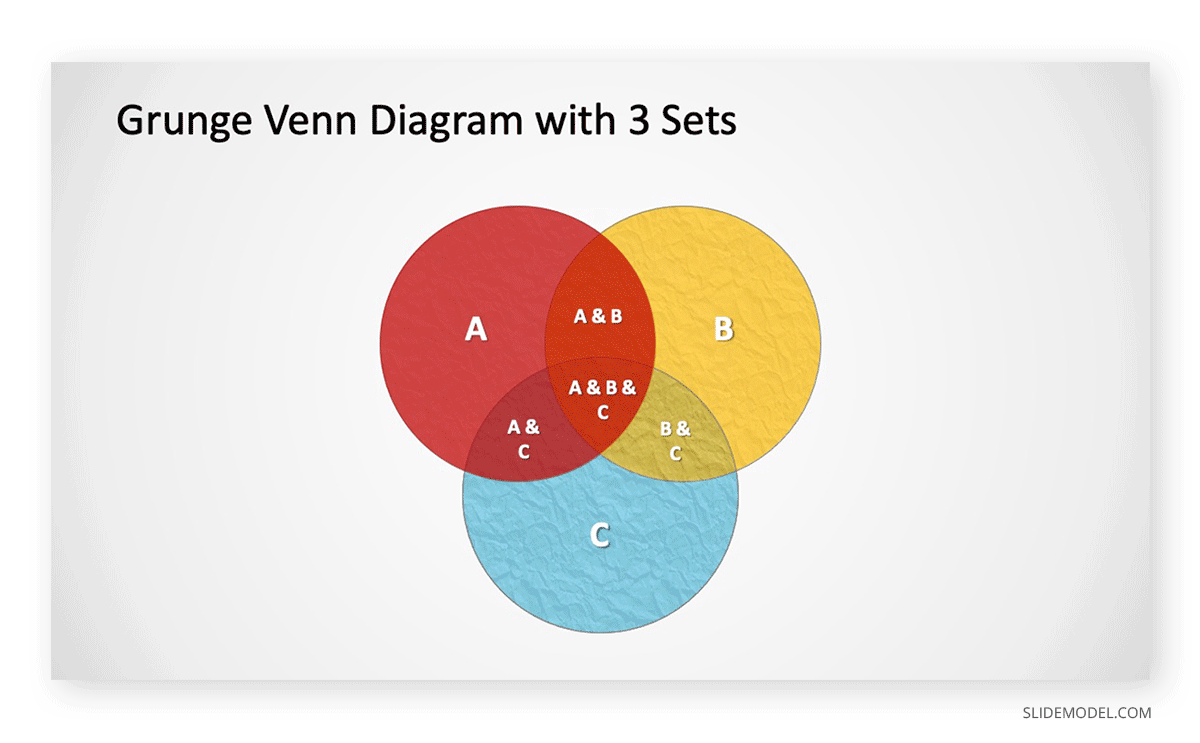
The overlapping circles in this template come with different color combinations and a clean layout; which can be customized right down to the very basic objects in the given sample slides.

This template is available in both Standard and Widescreen formats.

2. Grunge Concentric Circles For PowerPoint

Another Grunge-based template for PowerPoint that can be quite handy in quickly constructing Venn Diagrams is the Grunge Concentric Circles PowerPoint Template. This template comes with textured objects and different shapes for making different types of Venn Diagrams. In this example, we are using the Golden Circle created by Simon Sinek, which seeks to explain the purpose (Why), method (How), and solution (What).

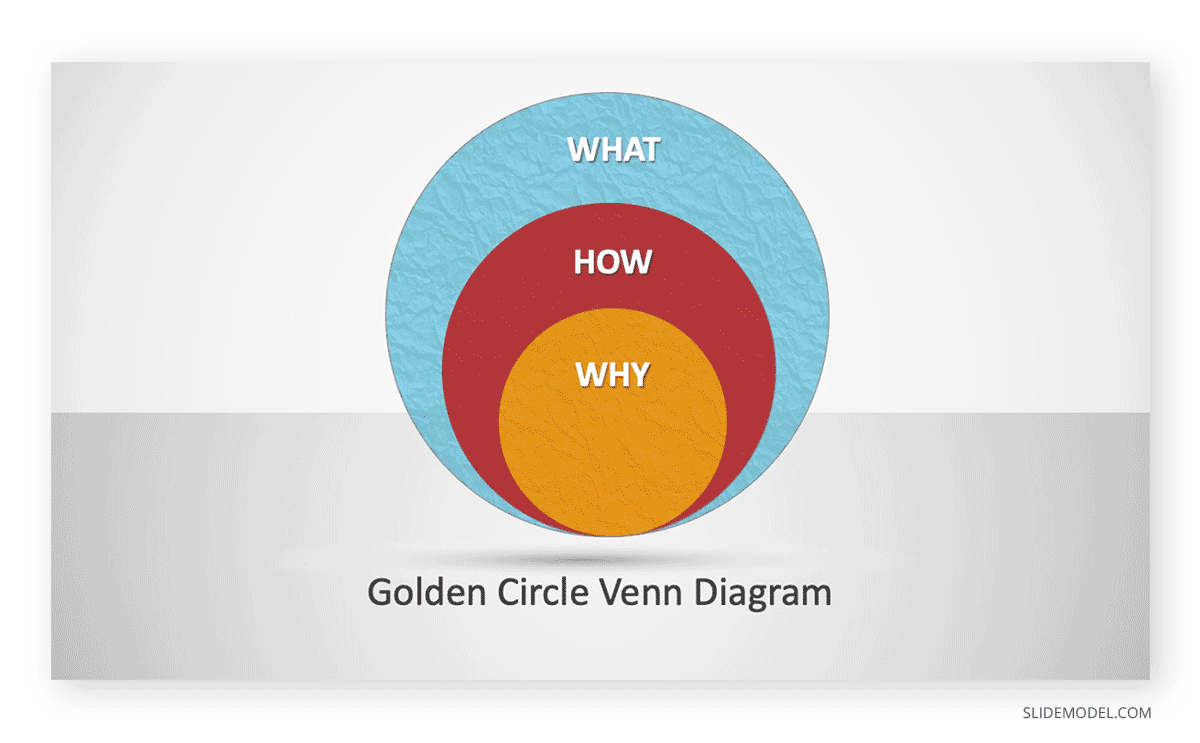
The diversity in shapes can be useful in constructing diagrams for representing a diverse range of processes and can also be helpful in differentiating one type of process from another (during a PowerPoint presentation).

3. Ecosystem Diagram PowerPoint Template

This is another fine template for making Venn Diagrams. It provides 6 awesome slide designs in the form of circular diagrams.

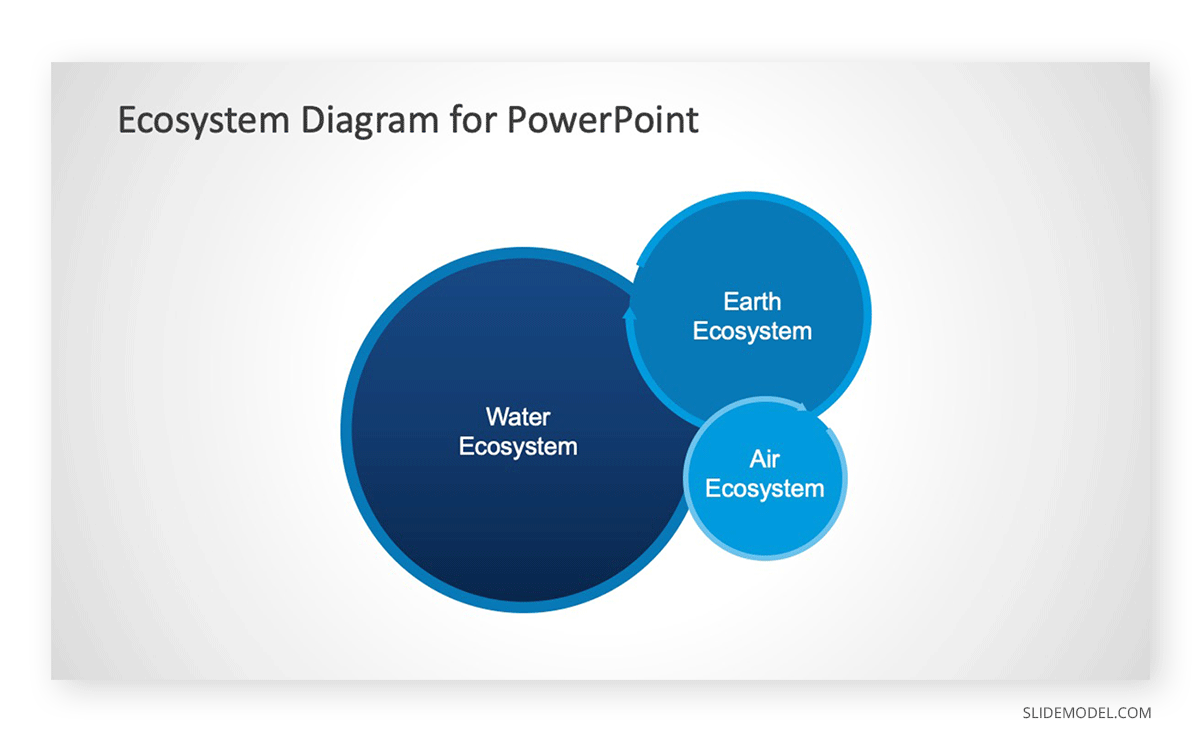
While this template has been designed mainly for biology or eco-system-related presentations, however, you can also use this template to create Venn Diagrams related to business or production processes, a community, a network of objects or people, etc.

To see an example of sample slides and to download this template, check out the link given below.

Go to Download Ecosystem Diagram PowerPoint Template

4. Gradient Venn Diagram for PowerPoint

The gradient Venn diagram is an aesthetically pleasing template that allows you to create a comparison or connection between 2 main ideas, including the intersection of both and the universe of surrounding concepts. 

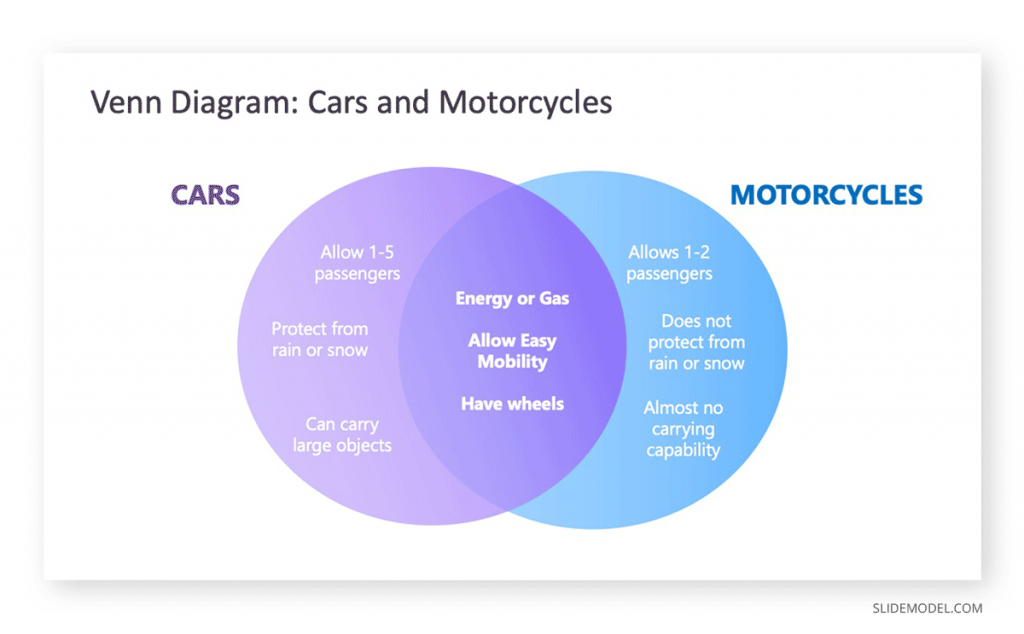
Go to Download Gradient Venn Diagram Template and try this modern Venn Diagram Template.

5. Multi-Layer Diagram Concept for PowerPoint

When seeking to create a Venn diagram that shows multiple levels and several processes, this is a great option. This template allows you to build upon different levels of information, including an infographic format that explains further in a more visually pleasing design. 

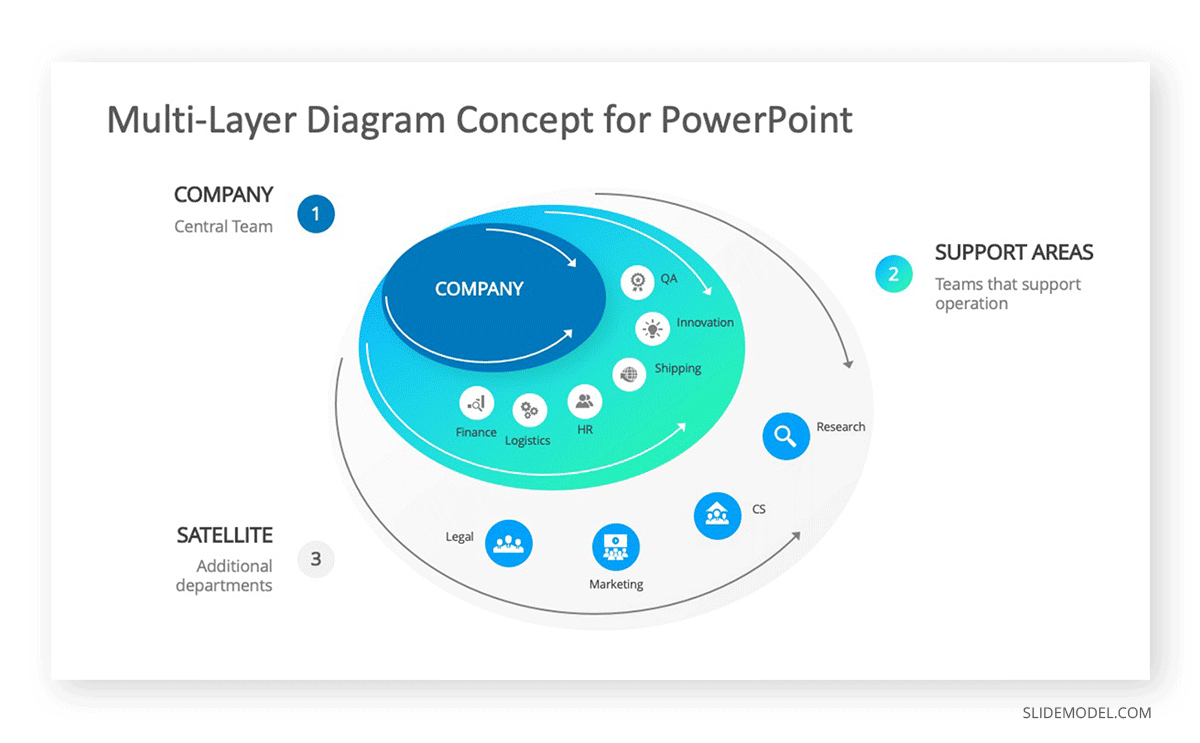
The multi-layer diagram uses modern gradient colors and fine details in the shapes. Ideal for modern executive audiences.

Go to Download Multi-Layer Diagram Concept Template and check the additional slides provided.

6. Hexagon Venn Diagram PowerPoint Template

A Venn Diagram can become increasingly complex and become an infographic and the set up of the information; this is why a template like the 5 Hexagon Venn Diagram for PowerPoint is an excellent choice if you need to present a large number of interactions. 

Providing dark and white contrast backgrounds the hexagonal Venn diagram can be used in infographic designs or traditional business presentations.

Go to Download 5 Hexagon Venn Diagram PowerPoint Template and experiment with this modern design.

7. Venn Diagram Material Design for PowerPoint

After the 2-circle Venn Diagram, the 3-circle version is almost as popular, therefore to be able to build not only an intriguing but clear presentation is mandatory when working with 3 elements. The Venn Diagram Material Design PowerPoint Diagram will be helpful when it’s necessary to create a graphic that not only allows more information, a basic one but also needs to be eye-catching and practical. 

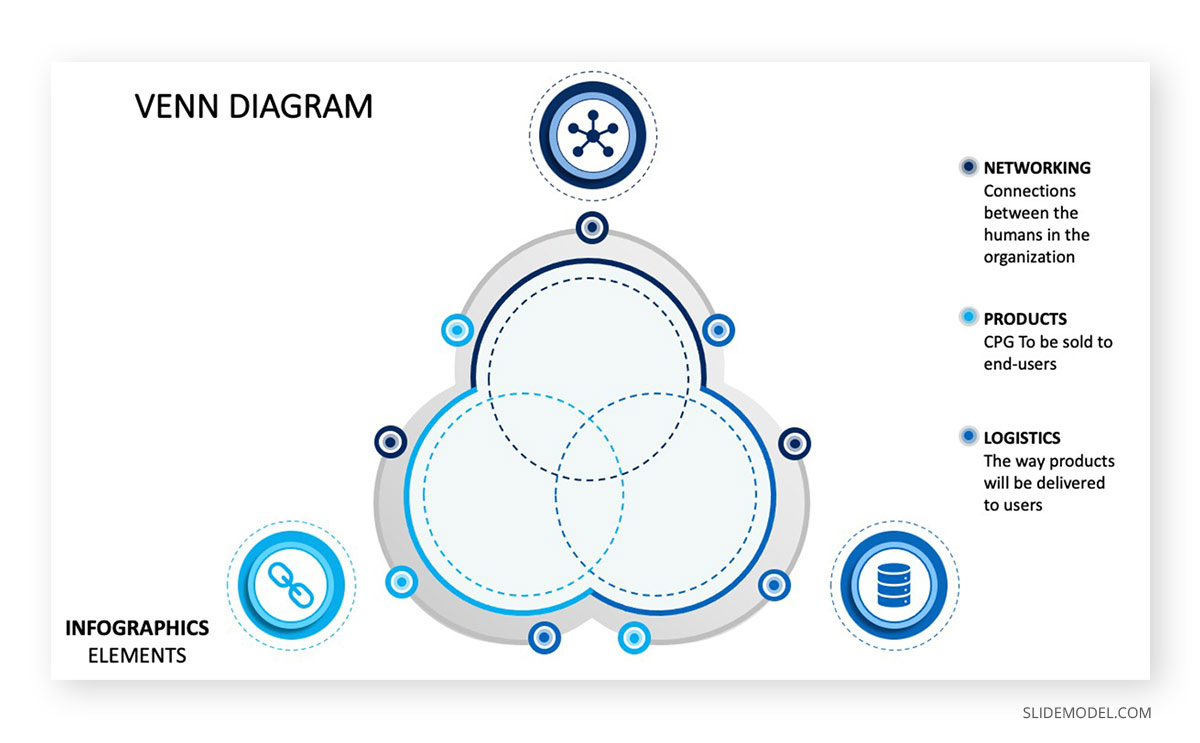
This diagram provides vertexes over the circle vector that help the presenter add additional data points over the set information.

Go to Venn Diagram Material Design for PowerPoint to check the different layouts provided.

In today’s world of dynamic presentations, engagement is key to getting your message across effectively. Venn diagrams, traditionally static visual aids, can be transformed into interactive tools to captivate your audience. Here’s how to make your Venn diagrams interactive and take your presentations to the next level.

• Clickable Elements: Instead of static circles use clickable elements within your Venn diagram. This can be achieved through hyperlinks or interactive objects in your presentation software. When clicked, these elements can reveal additional information or take the audience to a different part of your presentation.
• Animated Transitions: Animate the transitions between different sections of your Venn diagram to create a sense of movement and flow. This can make your presentation more dynamic and engaging.
• Drag-and-Drop Functionality: Introduce drag-and-drop features to allow the audience to move elements within the Venn diagram. This can be a useful tool for educational presentations, problem-solving scenarios, or group discussions.
• Pop-up Descriptions: When a user hovers their cursor over a specific part of the Venn diagram, a pop-up description can appear, providing additional details, context, or insights. This interactive feature keeps the audience engaged and informed.
• User-Generated Content: Encourage audience participation by allowing them to contribute to the Venn diagram. This can be particularly effective in brainstorming sessions, surveys, or collaborative decision-making.
• Quizzes and Polls: Incorporate interactive quizzes or polls within your Venn diagrams. This not only engages the audience but also provides valuable feedback and insights.
• Navigation Buttons: Include navigation buttons that allow the audience to explore the Venn diagram at their own pace. This empowers viewers to focus on areas of interest and navigate through the content as they see fit.

By making your Venn diagrams interactive, you transform them into engaging, educational, and participatory tools that can enhance your presentations and leave a lasting impact on your audience.

As we move further into the 21st century, the role of Venn diagrams in our data-driven world is evolving. These timeless visual aids are adapting to meet the demands of an increasingly complex and data-rich environment. Here’s a glimpse into the future of Venn diagrams:

Big Data Visualization

Venn diagrams are taking on a pivotal role in visualizing big data. In various fields such as business, science, and technology, the volume of data has exploded. Venn diagrams are becoming essential for simplifying complex data relationships and patterns. They help distill vast datasets into manageable and comprehensible insights. In business, for instance, they can represent market segmentation, customer preferences, and the overlap between different target audiences. In scientific research, Venn diagrams can be used to identify commonalities and differences in large datasets, facilitating data-driven discoveries.

Artificial Intelligence Integration

Venn diagrams are harnessing the power of artificial intelligence (AI). AI-powered tools are beginning to enhance the capabilities of Venn diagrams. These tools can automatically identify overlaps, correlations, and patterns within data. This automation makes the diagram creation process more efficient and insightful. For instance, in data analysis, AI can analyze large datasets and generate Venn diagrams that highlight significant intersections, enabling faster decision-making and uncovering hidden relationships within the data.

Real-Time Data Representation

Venn diagrams are adapting to the need for real-time data representation. They are becoming valuable tools for monitoring and decision-making. Businesses and organizations are using them to track market trends, customer behavior, and more. With real-time data integration, Venn diagrams enable decision-makers to respond promptly to changing situations. For example, in e-commerce, Venn diagrams can illustrate the dynamic relationship between customer preferences and inventory levels, helping businesses optimize their supply chain and stock management in real-time.

Cross-Platform Accessibility

Venn diagrams are becoming more versatile and accessible across different platforms and devices. They are no longer confined to static presentations. Mobile apps and web applications are adopting Venn diagrams for data analysis, collaboration, and decision support. This accessibility ensures that data-driven insights can be shared and accessed conveniently across teams and devices, making collaboration more efficient and informed.

Customization and Personalization

Users are gaining more control over the design and functionality of Venn diagrams. They can tailor these visuals to their specific needs. This personalization is catering to a wide range of industries and applications. Users can customize the appearance of Venn diagrams to match their brand identity or specific requirements. For instance, in educational settings, educators can adapt Venn diagrams to suit their teaching style and the complexity of the subject matter. This customization empowers users to create diagrams that are highly relevant to their unique contexts.

Q. Can I create a Venn diagram with more than two circles? 

A. Traditionally, Venn diagrams have 2 circles intersecting; however, depending on the amount of information that needs to be shown, we can add more circles. If you are looking to display many circles more than 4 or 5 to increment the data, it might be a good idea to rethink the type of diagram and perhaps include 3D shapes. 

Alternatively, discover our guide on how to make a Venn Diagram in PowerPoint .

Q. How to use a Venn diagram in the classroom? 

A. Venn diagrams are great for teaching science, social studies, biology, or even math, as they are flexible and can be built on the go. When teachers want to show what makes several concepts similar or different, this type of diagram will support a clear and visual explanation that will suit all learners of all sorts. If the subject is too detailed, perhaps a Venn Diagram is not the ideal tool, as this works better with precise information. 

Q. What are the advantages of Venn Diagram Templates? 

A. First of all, Venn Diagrams are very visual, which will help the relationship between elements become easier to understand. Second, this type of diagram’s elegant simplicity allows fewer words to explain complex information. Finally, the combination of the above will help retention overall through the association of colors and shapes.  

Q. What is the middle of the Venn Diagram called?

A. The middle section of the Venn Diagram is called an intersection. This area is where concepts intersect, it´s used to add the shared information between 2 ideas.  What are Venn diagrams used for? Venn diagrams are excellent for visually organizing information due to their graphic nature, comparing or contrasting 2 or more choices, understanding or solving math problems, comparing information sets for computer science, teaching, or even using Boolean logic. 

Final Words 

Explaining almost any complex information gets easier when including compelling graphic elements. Venn Diagrams have been around for centuries and have been used for nearly every industry in dozens of contexts. Nevertheless, the popularity of these diagrams continues to grow, especially today, where we see more data than ever. 

Something is true, different visual formats will only grow in variability shortly, and with the shift to remote work, virtual communications require the synthesis of ideas faster in another way of presenting. The beauty of well-built models like Venn Diagrams surpasses the tests of technology and innovation, bringing to the table flexibility and pragmatism, not just today but probably for decades to come. 

1. 4-Step Petal Venn Diagram PowerPoint Template

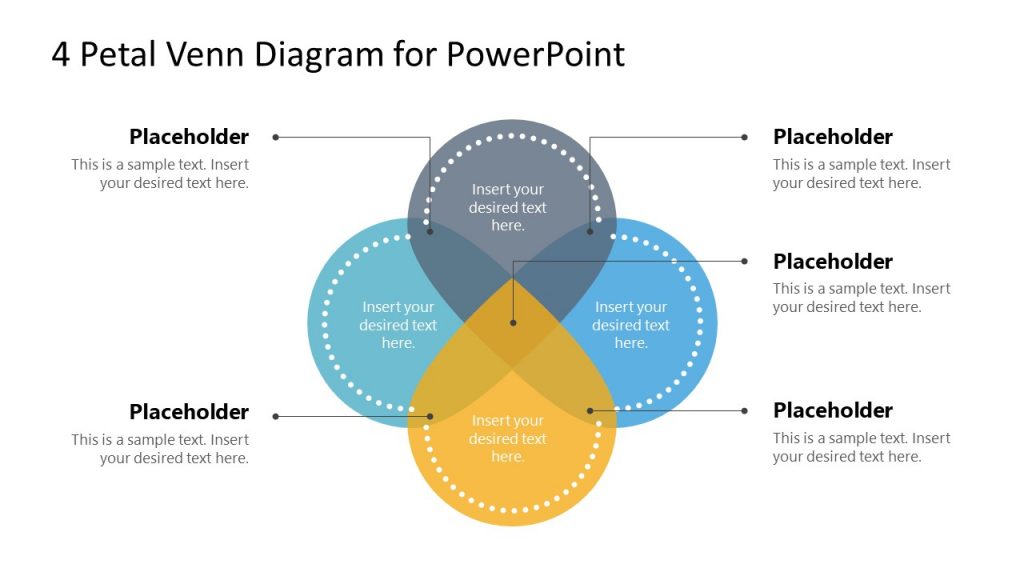
Venn diagrams can have more than 2 circles, they can even include different shapes or be similar to organic or non organic shapes. In this case, the 4 Step Petal can be useful to explain 4 sets of information in a visually appealing format.

Use This Template

2. 4 Hexagon Venn Diagram PowerPoint Template

Working with 4 relevant sets of information might require a Venn Diagram to support the analysis of a presentation. This template provides a creative format to present data that is interconnected.

3. Simple Flat Venn Diagram PowerPoint Template

If you are working on a Venn Diagram and you have 3 sets of very relevant information, this template can help you present your data in a functional, yet aesthetic way.

4. 4 Circle Venn Diagram PowerPoint Template

This is a 4 circle Venn diagram design that you can use to represent four overlapping ideas in a PowerPoint presentation.

5. Modern Venn Diagram Infographics

This slide bundle contains 14 slides with modern diagram infographics and includes a Venn diagram design.

6. Rhombus Venn Diagram PowerPoint Template

Like this article? Please share

Analysis Templates, Business Analysis Tools, Business Diagrams, Business Ideas, Business PowerPoint Templates, Business Presentations, Business Templates, Diagram Templates, Templates, Venn Diagrams Filed under Presentation Ideas

Related Articles

Filed under Design • August 14th, 2024

Creating Custom Themes for PowerPoint and Google Slides

Do you want your slides to go beyond the average result from a template? If so, learn how to create custom themes for presentations with this guide.

Filed under Business • August 8th, 2024

How to Create Engaging and Persuasive Proposal Presentations

Secure your business deals and build your brand’s reputation by mastering the art of proposal presentations. Tips and recommended PPT templates included.

Filed under Presentation Ideas • June 28th, 2024

Key Insights on How To End a Presentation Effectively

Learn key insights on how to end a presentation, with professional tips, PowerPoint templates examples and real life experiences.

Leave a Reply

Section SV.3 – Practice Problems

For problems 1 – 1 2 , create a Venn diagram to illustrate each of the following.

1. [latex]\bar{C}[/latex]

2. [latex]A~\cup~B[/latex]

3. [latex]A~\cap~B[/latex]

4. [latex]A~\cap~\bar{B}[/latex]

5. [latex]A~\cup~B~\cup~C[/latex]

6. [latex]A~\cap~B~\cap~C[/latex]

7. [latex](A~\cup~B)~\cap~C[/latex]

8. [latex](C~\cap~B)~\cup~A[/latex]

9. [latex](C~\cap~\bar{A})~\cup~B[/latex]

10. [latex](A~\cup~\bar{B})~\cap~C[/latex]

11. [latex](\bar{A}~\cap~\bar{B})~\cap~C[/latex]

12. [latex](A~\cap~B)~\cup~(A~\cap~\bar{C})[/latex]

13. Draw a Venn Diagram to represent the sets U = {q, w, e, r, t, y, u}, A = {w, e, u}, and B = {r, t, e, u}.

14. Draw a Venn Diagram to represent the sets U = {a, b, c, d, e, f, g, h, i, j, k}, A = {a, b, h, i, j}, B = {c, d, f, i, j}, and C = {f, g, h, j}.

15. Draw a Venn Diagram to represent the sets U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {4, 5, 6, 8}, B = {1, 2, 4, 5, 6, 7}, and C = {3, 4, 7}

For pro blems 1 6 – 1 9 , write an expression for the shaded region. There may be more than one way to write an expression for each of the shaded regions.

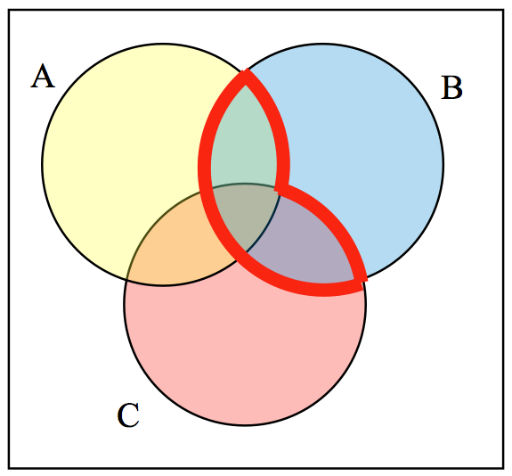
20. Use the Venn diagram to write each of the sets below in roster form.

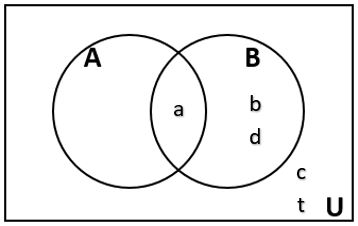
a. [latex]\bar{A}~\cap~B[/latex]

b. [latex]\bar{B}~\cup~A[/latex]

21. Use the Venn diagram to write each of the sets below in roster form.

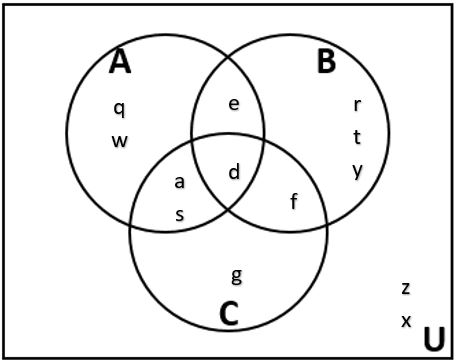
a. [latex]\cup[/latex] (the universal set)

b. [latex]A[/latex]

c. [latex]A~\cap~C[/latex]

d. [latex]B~\cup~C[/latex]

e. [latex]\overline{(A~\cup~B)}[/latex]

f. [latex](A~\cap~B)~\cap~\bar{C}[/latex]

g. [latex]\overline{(A~\cup~C)}~\cap~B[/latex]

h. [latex](\bar{B}~\cap~\bar{C})~\cup~\overline{(B~\cup~A)}[/latex]

22. Use the Venn diagram to write each of the sets below in roster form.

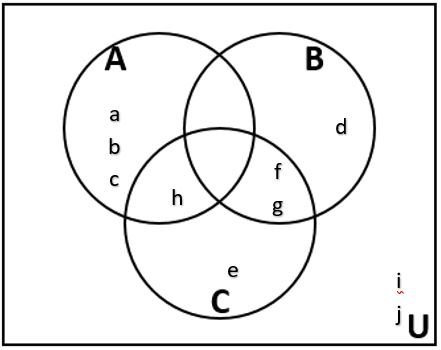
b. [latex]B[/latex]

c. [latex]B~\cap~C[/latex]

d. [latex]A~\cup~C[/latex]

e. [latex]\overline{(B~\cup~C)}[/latex]

f. [latex]A~\cap~B~\cap~\bar{C}[/latex]

g. [latex]\overline{A~\cup~B}~\cap~C[/latex]

College Mathematics - MAT14X - 3rd Edition Copyright © by Adam Avilez; Shelley Ceinaturaga; and Terri D. Levine is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License , except where otherwise noted.

Share This Book