

Solving Quadratics by the Quadratic Formula
How to solve quadratic equations using the quadratic formula.
There are times when we are stuck solving a quadratic equation of the form [latex]a{x^2} + bx + c = 0[/latex] because the trinomial on the left side can’t be factored out easily. It doesn’t mean that the quadratic equation has no solution. At this point, we need to call upon the straightforward approach of the quadratic formula to find the solutions of the quadratic equation or put simply, determine the values of [latex]x[/latex] that can satisfy the equation.
In order use the quadratic formula, the quadratic equation that we are solving must be converted into the “standard form”, otherwise, all subsequent steps will not work. The goal is to transform the quadratic equation such that the quadratic expression is isolated on one side of the equation while the opposite side only contains the number zero, [latex]0[/latex].
Take a look at the diagram below.
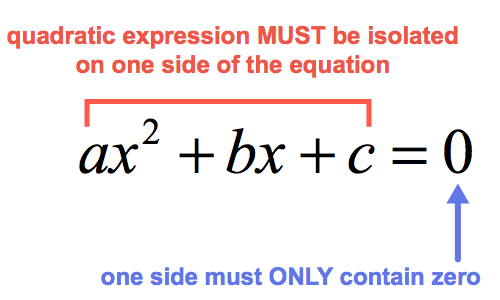
In this convenient format, the numerical values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are easily identified! Upon knowing those values, we can now substitute them into the quadratic formula then solve for the values of [latex]x[/latex].
The Quadratic Formula
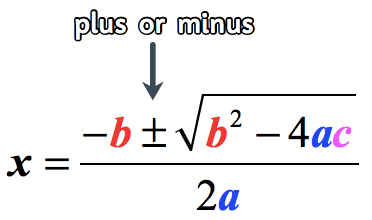
- Where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are the coefficients of an arbitrary quadratic equation in the standard form, [latex]a{x^2} + bx + c = 0[/latex].
Slow down if you need to. Be careful with every step while simplifying the expressions. This is where common mistakes usually happen because students tend to “relax” which results to errors that could have been prevented, such as in the addition, subtraction, multiplication and/or division of real numbers.
Examples of How to Solve Quadratic Equations by the Quadratic Formula
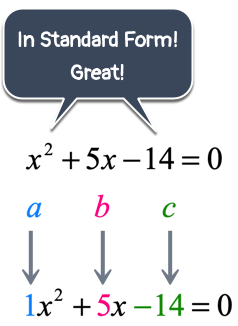
Example 1 : Solve the quadratic equation below using the Quadratic Formula.
By inspection, it’s obvious that the quadratic equation is in the standard form since the right side is just zero while the rest of the terms stay on the left side. In other words, we have something like this

This is great! What we need to do is simply identify the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] then substitute into the quadratic formula.
That’s it! Make it a habit to always check the solved values of [latex]x[/latex] back into the original equation to verify.
Example 2 : Solve the quadratic equation below using the Quadratic Formula.
This quadratic equation is absolutely not in the form that we want because the right side is NOT zero. I need to eliminate that [latex]7[/latex] on the right side by subtracting both sides by [latex]7[/latex]. That takes care of our problem. After doing so, solve for [latex]x[/latex] as usual.
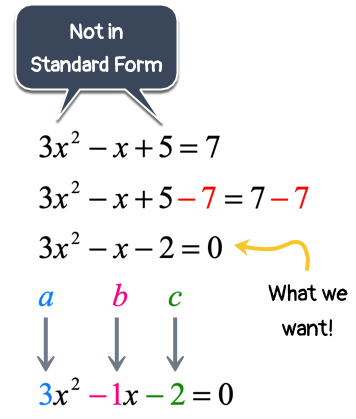
The final answers are [latex]{x_1} = 1[/latex] and [latex]{x_2} = – {2 \over 3}[/latex].
Example 3 : Solve the quadratic equation below using the Quadratic Formula.
This quadratic equation looks like a “mess”. I have variable [latex]x[/latex]’s and constants on both sides of the equation. If we are faced with something like this, always stick to what we know. Yes, it’s all about the Standard Form. We have to force the right side to be equal to zero. We can do just that in two steps.
I will first subtract both sides by [latex]5x[/latex], and followed by the addition of [latex]8[/latex].

Values we need:
[latex]a = – 1[/latex], [latex]b = – \,8[/latex], and [latex]c = 2[/latex]
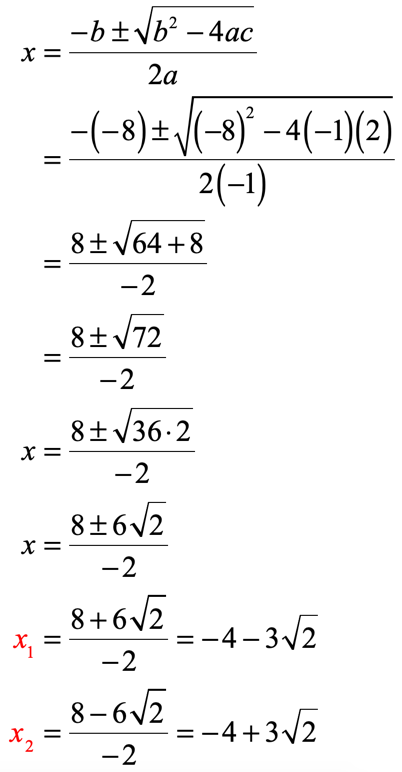
Example 4 : Solve the quadratic equation below using the Quadratic Formula.
Well, if you think that Example [latex]3[/latex] is a “mess” then this must be even “messier”. However, you’ll soon realize that they are really very similar.
We first need to perform some cleanup by converting this quadratic equation into standard form. Sounds familiar? Trust me, this problem is not as bad as it looks, as long as we know what to do.
Just to remind you, we want something like this

Therefore, we must do whatever it takes to make the right side of the equation equal to zero. Since we have three terms on the right side, it follows that three steps are required to make it zero.
The solution below starts by adding both sides by [latex]3{x^2}[/latex], followed by subtraction of [latex]3x[/latex], and finally the addition of [latex]5[/latex]. Done!
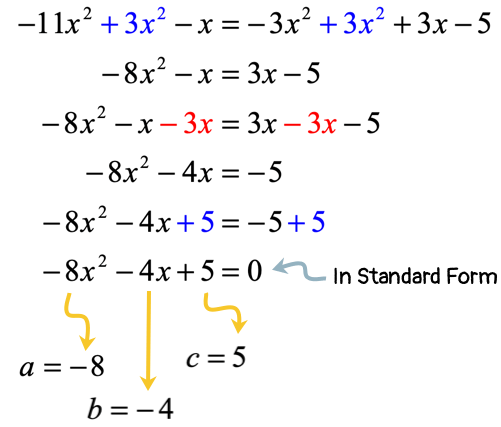
After making the right side equal to zero, the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are easy to identify. Plug those values into the quadratic formula, and simplify to get the final answers!

Example 5 : Solve the quadratic equation below using the Quadratic Formula.
First, we need to rewrite the given quadratic equation in Standard Form, [latex]a{x^2} + bx + c = 0[/latex].
- Eliminate the [latex]{x^2}[/latex] term on the right side.
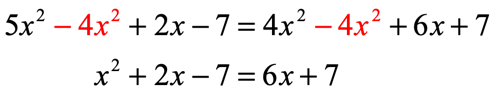
- Eliminate the [latex]x[/latex] term on the right side.
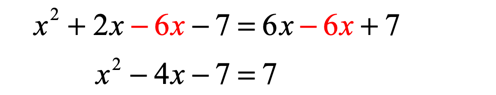
- Eliminate the constant on the right side.
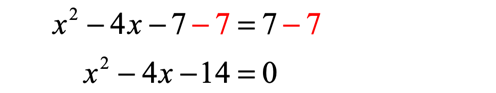
After getting the correct standard form in the previous step, it’s now time to plug the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] into the quadratic formula to solve for [latex]x[/latex].
- From the converted standard form, extract the required values.
[latex]a = 1[/latex], [latex]b = – \,4[/latex], and [latex]c = – \,14[/latex]
- Then evaluate these values into the quadratic formula.

You may also be interested in these related math lessons or tutorials:
Quadratic Formula Practice Problems with Answers
Solving Quadratic Equations by Square Root Method Solving Quadratic Equations by Factoring Method Solving Quadratic Equations by Completing the Square

Quadratic Formula Practice Questions
Click here for questions, click here for answers.
GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
10.3 Solve Quadratic Equations Using the Quadratic Formula
Learning objectives.
By the end of this section, you will be able to:
- Solve quadratic equations using the quadratic formula
- Use the discriminant to predict the number of solutions of a quadratic equation
- Identify the most appropriate method to use to solve a quadratic equation
Be Prepared 10.7
Before you get started, take this readiness quiz.
Simplify: −20 − 5 10 −20 − 5 10 . If you missed this problem, review Example 1.74 .
Be Prepared 10.8
Simplify: 4 + 121 4 + 121 . If you missed this problem, review Example 9.29 .
Be Prepared 10.9
Simplify: 128 128 . If you missed this problem, review Example 9.12 .
When we solved quadratic equations in the last section by completing the square, we took the same steps every time. By the end of the exercise set, you may have been wondering ‘isn’t there an easier way to do this?’ The answer is ‘yes.’ In this section, we will derive and use a formula to find the solution of a quadratic equation.
We have already seen how to solve a formula for a specific variable ‘in general’ so that we would do the algebraic steps only once and then use the new formula to find the value of the specific variable. Now, we will go through the steps of completing the square in general to solve a quadratic equation for x . It may be helpful to look at one of the examples at the end of the last section where we solved an equation of the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 as you read through the algebraic steps below, so you see them with numbers as well as ‘in general.’
| We start with the standard form of a quadratic equation and solve it for by completing the square. | |
| Isolate the variable terms on one side. | |
| Make leading coefficient 1, by dividing by a. | |
| Simplify. | |
| To complete the square, find and add it to both sides of the equation. | |
| The left side is a perfect square, factor it. | |
| Find the common denominator of the right side and write equivalent fractions with the common denominator. | |
| Simplify. | |
| Combine to one fraction. | |
| Use the square root property. | |
| Simplify. | |
| Add to both sides of the equation. | |
| Combine the terms on the right side. |
This last equation is the Quadratic Formula.
- Quadratic Formula
The solutions to a quadratic equation of the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 , a ≠ 0 a ≠ 0 are given by the formula:
To use the Quadratic Formula, we substitute the values of a , b , and c a , b , and c into the expression on the right side of the formula. Then, we do all the math to simplify the expression. The result gives the solution(s) to the quadratic equation.
Example 10.28
How to solve a quadratic equation using the quadratic formula.
Solve 2 x 2 + 9 x − 5 = 0 2 x 2 + 9 x − 5 = 0 by using the Quadratic Formula.
Try It 10.55
Solve 3 y 2 − 5 y + 2 = 0 3 y 2 − 5 y + 2 = 0 by using the Quadratic Formula.
Try It 10.56
Solve 4 z 2 + 2 z − 6 = 0 4 z 2 + 2 z − 6 = 0 by using the Quadratic Formula.
Solve a quadratic equation using the Quadratic Formula.
- Step 1. Write the Quadratic Formula in standard form. Identify the a a , b b , and c c values.
- Step 2. Write the Quadratic Formula. Then substitute in the values of a a , b b , and c . c .
- Step 3. Simplify.
- Step 4. Check the solutions.
If you say the formula as you write it in each problem, you’ll have it memorized in no time. And remember, the Quadratic Formula is an equation. Be sure you start with ‘ x = x = ’.
Example 10.29
Solve x 2 − 6 x + 5 = 0 x 2 − 6 x + 5 = 0 by using the Quadratic Formula.
| This equation is in standard form. | ||
| Identify the values. | ||
| Write the Quadratic Formula. | ||
| Then substitute in the values of | ||
| Simplify. | | |
| Rewrite to show two solutions. | ||
| Simplify. | | |
| Check. | ||
Try It 10.57
Solve a 2 − 2 a − 15 = 0 a 2 − 2 a − 15 = 0 by using the Quadratic Formula.
Try It 10.58
Solve b 2 + 10 b + 24 = 0 b 2 + 10 b + 24 = 0 by using the Quadratic Formula.
When we solved quadratic equations by using the Square Root Property, we sometimes got answers that had radicals. That can happen, too, when using the Quadratic Formula. If we get a radical as a solution, the final answer must have the radical in its simplified form.
Example 10.30
Solve 4 y 2 − 5 y − 3 = 0 4 y 2 − 5 y − 3 = 0 by using the Quadratic Formula.
We can use the Quadratic Formula to solve for the variable in a quadratic equation, whether or not it is named ‘ x ’.
| This equation is in standard form. | ||
| Identify the values. | ||
| Write the Quadratic Formula. | ||
| Then substitute in the values of | ||
| Simplify. | | |
| Rewrite to show two solutions. | ||
| Check. We leave the check to you. | ||
Try It 10.59
Solve 2 p 2 + 8 p + 5 = 0 2 p 2 + 8 p + 5 = 0 by using the Quadratic Formula.
Try It 10.60
Solve 5 q 2 − 11 q + 3 = 0 5 q 2 − 11 q + 3 = 0 by using the Quadratic Formula.
Example 10.31
Solve 2 x 2 + 10 x + 11 = 0 2 x 2 + 10 x + 11 = 0 by using the Quadratic Formula.
| This equation is in standard form. | ||
| Identify the values. | ||
| Write the Quadratic Formula. | ||
| Then substitute in the values of | ||
| Simplify. | | |
| Simplify the radical. | ||
| Factor out the common factor in the numerator. | ||
| Remove the common factors. | ||
| Rewrite to show two solutions. | ||
| Check. We leave the check to you. | ||
Try It 10.61
Solve 3 m 2 + 12 m + 7 = 0 3 m 2 + 12 m + 7 = 0 by using the Quadratic Formula.
Try It 10.62
Solve 5 n 2 + 4 n − 4 = 0 5 n 2 + 4 n − 4 = 0 by using the Quadratic Formula.
We cannot take the square root of a negative number. So, when we substitute a a , b b , and c c into the Quadratic Formula, if the quantity inside the radical is negative, the quadratic equation has no real solution. We will see this in the next example.
Example 10.32
Solve 3 p 2 + 2 p + 9 = 0 3 p 2 + 2 p + 9 = 0 by using the Quadratic Formula.
| This equation is in standard form. | ||
| Identify the values. | ||
| Write the Quadratic Formula. | ||
| Then substitute in the values of | ||
| Simplify. | ||
| Simplify the radical. | ||
| We cannot take the square root of a negative number. | There is no real solution. | |
Try It 10.63
Solve 4 a 2 − 3 a + 8 = 0 4 a 2 − 3 a + 8 = 0 by using the Quadratic Formula.
Try It 10.64
Solve 5 b 2 + 2 b + 4 = 0 5 b 2 + 2 b + 4 = 0 by using the Quadratic Formula.
The quadratic equations we have solved so far in this section were all written in standard form, a x 2 + b x + c = 0 a x 2 + b x + c = 0 . Sometimes, we will need to do some algebra to get the equation into standard form before we can use the Quadratic Formula.
Example 10.33
Solve x ( x + 6 ) + 4 = 0 x ( x + 6 ) + 4 = 0 by using the Quadratic Formula.
| Distribute to get the equation in standard form. | ||
| This equation is now in standard form. | ||
| Identify the values. | ||
| Write the Quadratic Formula. | ||
| Then substitute in the values of | ||
| Simplify. | ||
| Simplify inside the radical. | ||
| Simplify the radical. | ||
| Factor out the common factor in the numerator. | ||
| Remove the common factors. | ||
| Rewrite to show two solutions. | ||
| Check. We leave the check to you. | ||
Try It 10.65
Solve x ( x + 2 ) − 5 = 0 x ( x + 2 ) − 5 = 0 by using the Quadratic Formula.
Try It 10.66
Solve y ( 3 y − 1 ) − 2 = 0 y ( 3 y − 1 ) − 2 = 0 by using the Quadratic Formula.
When we solved linear equations, if an equation had too many fractions we ‘cleared the fractions’ by multiplying both sides of the equation by the LCD. This gave us an equivalent equation—without fractions—to solve. We can use the same strategy with quadratic equations.
Example 10.34
Solve 1 2 u 2 + 2 3 u = 1 3 1 2 u 2 + 2 3 u = 1 3 by using the Quadratic Formula.
| Multiply both sides by the LCD, 6, to clear the fractions. | ||
| Multiply. | ||
| Subtract 2 to get the equation in standard form. | ||
| Identify the values. | ||
| Write the Quadratic Formula. | ||
| Then substitute in the values of | ||
| Simplify. | | |
| Simplify the radical. | ||
| Factor out the common factor in the numerator. | ||
| Remove the common factors. | ||
| Rewrite to show two solutions. | ||
| Check. We leave the check to you. | ||
Try It 10.67
Solve 1 4 c 2 − 1 3 c = 1 12 1 4 c 2 − 1 3 c = 1 12 by using the Quadratic Formula.
Try It 10.68
Solve 1 9 d 2 − 1 2 d = − 1 2 1 9 d 2 − 1 2 d = − 1 2 by using the Quadratic Formula.
Think about the equation ( x − 3 ) 2 = 0 ( x − 3 ) 2 = 0 . We know from the Zero Products Principle that this equation has only one solution: x = 3 x = 3 .
We will see in the next example how using the Quadratic Formula to solve an equation with a perfect square also gives just one solution.
Example 10.35
Solve 4 x 2 − 20 x = −25 4 x 2 − 20 x = −25 by using the Quadratic Formula.
| Add 25 to get the equation in standard form. | ||
| Identify the values. | ||
| Write the Quadratic Formula. | ||
| Then substitute in the values of | ||
| Simplify. | | |
| Simplify the radical. | ||
| Simplify the fraction. | ||
| Check. We leave the check to you. | ||
Did you recognize that 4 x 2 − 20 x + 25 4 x 2 − 20 x + 25 is a perfect square?
Try It 10.69
Solve r 2 + 10 r + 25 = 0 r 2 + 10 r + 25 = 0 by using the Quadratic Formula.
Try It 10.70
Solve 25 t 2 − 40 t = −16 25 t 2 − 40 t = −16 by using the Quadratic Formula.
Use the Discriminant to Predict the Number of Solutions of a Quadratic Equation
When we solved the quadratic equations in the previous examples, sometimes we got two solutions, sometimes one solution, sometimes no real solutions. Is there a way to predict the number of solutions to a quadratic equation without actually solving the equation?
Yes, the quantity inside the radical of the Quadratic Formula makes it easy for us to determine the number of solutions. This quantity is called the discriminant .
Discriminant
In the Quadratic Formula x = − b ± b 2 − 4 a c 2 a x = − b ± b 2 − 4 a c 2 a , the quantity b 2 − 4 a c b 2 − 4 a c is called the discriminant .
Let’s look at the discriminant of the equations in Example 10.28 , Example 10.32 , and Example 10.35 , and the number of solutions to those quadratic equations.
| + | 2 | |||
| 0 | 1 | |||
| − | 0 |
When the discriminant is positive ( x = − b ± + 2 a ) ( x = − b ± + 2 a ) the quadratic equation has two solutions .
When the discriminant is zero ( x = − b ± 0 2 a ) ( x = − b ± 0 2 a ) the quadratic equation has one solution .
When the discriminant is negative ( x = − b ± − 2 a ) ( x = − b ± − 2 a ) the quadratic equation has no real solutions .
Use the discriminant, b 2 − 4 a c b 2 − 4 a c , to determine the number of solutions of a Quadratic Equation.
For a quadratic equation of the form a x 2 + b x + c = 0 a x 2 + b x + c = 0 , a ≠ 0 a ≠ 0 ,
- if b 2 − 4 a c > 0 b 2 − 4 a c > 0 , the equation has two solutions.
- if b 2 − 4 a c = 0 b 2 − 4 a c = 0 , the equation has one solution.
- if b 2 − 4 a c < 0 b 2 − 4 a c < 0 , the equation has no real solutions.

Example 10.36
Determine the number of solutions to each quadratic equation:
ⓐ 2 v 2 − 3 v + 6 = 0 2 v 2 − 3 v + 6 = 0 ⓑ 3 x 2 + 7 x − 9 = 0 3 x 2 + 7 x − 9 = 0 ⓒ 5 n 2 + n + 4 = 0 5 n 2 + n + 4 = 0 ⓓ 9 y 2 − 6 y + 1 = 0 9 y 2 − 6 y + 1 = 0
To determine the number of solutions of each quadratic equation, we will look at its discriminant.
| The equation is in standard form, identify , , . | |
| Write the discriminant. | |
| Substitute in the values of , , . | |
| Simplify. | |
| Because the discriminant is negative, there are no real solutions to the equation. |
| The equation is in standard form, identify , , . | |
| Write the discriminant. | |
| Substitute in the values of , , . | |
| Simplify. | |
| Because the discriminant is positive, there are two solutions to the equation. |
The equation is in standard form, identify , , . | |
| Write the discriminant. | |
| Substitute in the values of , , . | |
| Simplify. | |
| Because the discriminant is negative, there are no real solutions to the equation. |
The equation is in standard form, identify , , . | |
| Write the discriminant. | |
| Substitute in the values of , , . | |
| Simplify. | |
| Because the discriminant is 0, there is one solution to the equation. |
Try It 10.71
ⓐ 8 m 2 − 3 m + 6 = 0 8 m 2 − 3 m + 6 = 0 ⓑ 5 z 2 + 6 z − 2 = 0 5 z 2 + 6 z − 2 = 0 ⓒ 9 w 2 + 24 w + 16 = 0 9 w 2 + 24 w + 16 = 0 ⓓ 9 u 2 − 2 u + 4 = 0 9 u 2 − 2 u + 4 = 0
Try It 10.72
ⓐ b 2 + 7 b − 13 = 0 b 2 + 7 b − 13 = 0 ⓑ 5 a 2 − 6 a + 10 = 0 5 a 2 − 6 a + 10 = 0 ⓒ 4 r 2 − 20 r + 25 = 0 4 r 2 − 20 r + 25 = 0 ⓓ 7 t 2 − 11 t + 3 = 0 7 t 2 − 11 t + 3 = 0
Identify the Most Appropriate Method to Use to Solve a Quadratic Equation
We have used four methods to solve quadratic equations:
- Square Root Property
- Completing the Square
You can solve any quadratic equation by using the Quadratic Formula, but that is not always the easiest method to use.
Identify the most appropriate method to solve a Quadratic Equation.
- Step 1. Try Factoring first. If the quadratic factors easily, this method is very quick.
- Step 2. Try the Square Root Property next. If the equation fits the form a x 2 = k a x 2 = k or a ( x − h ) 2 = k a ( x − h ) 2 = k , it can easily be solved by using the Square Root Property.
- Step 3. Use the Quadratic Formula . Any quadratic equation can be solved by using the Quadratic Formula.
What about the method of completing the square? Most people find that method cumbersome and prefer not to use it. We needed to include it in this chapter because we completed the square in general to derive the Quadratic Formula. You will also use the process of completing the square in other areas of algebra.
Example 10.37
Identify the most appropriate method to use to solve each quadratic equation:
ⓐ 5 z 2 = 17 5 z 2 = 17 ⓑ 4 x 2 − 12 x + 9 = 0 4 x 2 − 12 x + 9 = 0 ⓒ 8 u 2 + 6 u = 11 8 u 2 + 6 u = 11
ⓐ 5 z 2 = 17 5 z 2 = 17
Since the equation is in the a x 2 = k a x 2 = k , the most appropriate method is to use the Square Root Property.
ⓑ 4 x 2 − 12 x + 9 = 0 4 x 2 − 12 x + 9 = 0
We recognize that the left side of the equation is a perfect square trinomial, and so Factoring will be the most appropriate method.
ⓒ 8 u 2 + 6 u = 11 8 u 2 + 6 u = 11
Put the equation in standard form. 8 u 2 + 6 u − 11 = 0 8 u 2 + 6 u − 11 = 0
While our first thought may be to try Factoring, thinking about all the possibilities for trial and error leads us to choose the Quadratic Formula as the most appropriate method
Try It 10.73
ⓐ x 2 + 6 x + 8 = 0 x 2 + 6 x + 8 = 0 ⓑ ( n − 3 ) 2 = 16 ( n − 3 ) 2 = 16 ⓒ 5 p 2 − 6 p = 9 5 p 2 − 6 p = 9
Try It 10.74
ⓐ 8 a 2 + 3 a − 9 = 0 8 a 2 + 3 a − 9 = 0 ⓑ 4 b 2 + 4 b + 1 = 0 4 b 2 + 4 b + 1 = 0 ⓒ 5 c 2 = 125 5 c 2 = 125
Access these online resources for additional instruction and practice with using the Quadratic Formula:
- Solving Quadratic Equations: Solving with the Quadratic Formula
- How to solve a quadratic equation in standard form using the Quadratic Formula (example)
- Solving Quadratic Equations using the Quadratic Formula—Example 3
- Solve Quadratic Equations using Quadratic Formula
Section 10.3 Exercises
Practice makes perfect.
Solve Quadratic Equations Using the Quadratic Formula
In the following exercises, solve by using the Quadratic Formula.
4 m 2 + m − 3 = 0 4 m 2 + m − 3 = 0
4 n 2 − 9 n + 5 = 0 4 n 2 − 9 n + 5 = 0
2 p 2 − 7 p + 3 = 0 2 p 2 − 7 p + 3 = 0
3 q 2 + 8 q − 3 = 0 3 q 2 + 8 q − 3 = 0
p 2 + 7 p + 12 = 0 p 2 + 7 p + 12 = 0
q 2 + 3 q − 18 = 0 q 2 + 3 q − 18 = 0
r 2 − 8 r − 33 = 0 r 2 − 8 r − 33 = 0
t 2 + 13 t + 40 = 0 t 2 + 13 t + 40 = 0
3 u 2 + 7 u − 2 = 0 3 u 2 + 7 u − 2 = 0
6 z 2 − 9 z + 1 = 0 6 z 2 − 9 z + 1 = 0
2 a 2 − 6 a + 3 = 0 2 a 2 − 6 a + 3 = 0
5 b 2 + 2 b − 4 = 0 5 b 2 + 2 b − 4 = 0
2 x 2 + 3 x + 9 = 0 2 x 2 + 3 x + 9 = 0
6 y 2 − 5 y + 2 = 0 6 y 2 − 5 y + 2 = 0
v ( v + 5 ) − 10 = 0 v ( v + 5 ) − 10 = 0
3 w ( w − 2 ) − 8 = 0 3 w ( w − 2 ) − 8 = 0
1 3 m 2 + 1 12 m = 1 4 1 3 m 2 + 1 12 m = 1 4
1 3 n 2 + n = − 1 2 1 3 n 2 + n = − 1 2
16 c 2 + 24 c + 9 = 0 16 c 2 + 24 c + 9 = 0
25 d 2 − 60 d + 36 = 0 25 d 2 − 60 d + 36 = 0
5 m 2 + 2 m − 7 = 0 5 m 2 + 2 m − 7 = 0
8 n 2 − 3 n + 3 = 0 8 n 2 − 3 n + 3 = 0
p 2 − 6 p − 27 = 0 p 2 − 6 p − 27 = 0
25 q 2 + 30 q + 9 = 0 25 q 2 + 30 q + 9 = 0
4 r 2 + 3 r − 5 = 0 4 r 2 + 3 r − 5 = 0
3 t ( t − 2 ) = 2 3 t ( t − 2 ) = 2
2 a 2 + 12 a + 5 = 0 2 a 2 + 12 a + 5 = 0
4 d 2 − 7 d + 2 = 0 4 d 2 − 7 d + 2 = 0
3 4 b 2 + 1 2 b = 3 8 3 4 b 2 + 1 2 b = 3 8
1 9 c 2 + 2 3 c = 3 1 9 c 2 + 2 3 c = 3
2 x 2 + 12 x − 3 = 0 2 x 2 + 12 x − 3 = 0
16 y 2 + 8 y + 1 = 0 16 y 2 + 8 y + 1 = 0
In the following exercises, determine the number of solutions to each quadratic equation.
- ⓐ 4 x 2 − 5 x + 16 = 0 4 x 2 − 5 x + 16 = 0
- ⓑ 36 y 2 + 36 y + 9 = 0 36 y 2 + 36 y + 9 = 0
- ⓒ 6 m 2 + 3 m − 5 = 0 6 m 2 + 3 m − 5 = 0
- ⓓ 18 n 2 − 7 n + 3 = 0 18 n 2 − 7 n + 3 = 0
- ⓐ 9 v 2 − 15 v + 25 = 0 9 v 2 − 15 v + 25 = 0
- ⓑ 100 w 2 + 60 w + 9 = 0 100 w 2 + 60 w + 9 = 0
- ⓒ 5 c 2 + 7 c − 10 = 0 5 c 2 + 7 c − 10 = 0
- ⓓ 15 d 2 − 4 d + 8 = 0 15 d 2 − 4 d + 8 = 0
- ⓐ r 2 + 12 r + 36 = 0 r 2 + 12 r + 36 = 0
- ⓑ 8 t 2 − 11 t + 5 = 0 8 t 2 − 11 t + 5 = 0
- ⓒ 4 u 2 − 12 u + 9 = 0 4 u 2 − 12 u + 9 = 0
- ⓓ 3 v 2 − 5 v − 1 = 0 3 v 2 − 5 v − 1 = 0
- ⓐ 25 p 2 + 10 p + 1 = 0 25 p 2 + 10 p + 1 = 0
- ⓑ 7 q 2 − 3 q − 6 = 0 7 q 2 − 3 q − 6 = 0
- ⓒ 7 y 2 + 2 y + 8 = 0 7 y 2 + 2 y + 8 = 0
- ⓓ 25 z 2 − 60 z + 36 = 0 25 z 2 − 60 z + 36 = 0
In the following exercises, identify the most appropriate method (Factoring, Square Root, or Quadratic Formula) to use to solve each quadratic equation. Do not solve.
ⓐ x 2 − 5 x − 24 = 0 x 2 − 5 x − 24 = 0 ⓑ ( y + 5 ) 2 = 12 ( y + 5 ) 2 = 12 ⓒ 14 m 2 + 3 m = 11 14 m 2 + 3 m = 11
ⓐ ( 8 v + 3 ) 2 = 81 ( 8 v + 3 ) 2 = 81 ⓑ w 2 − 9 w − 22 = 0 w 2 − 9 w − 22 = 0 ⓒ 4 n 2 − 10 = 6 4 n 2 − 10 = 6
ⓐ 6 a 2 + 14 = 20 6 a 2 + 14 = 20 ⓑ ( x − 1 4 ) 2 = 5 16 ( x − 1 4 ) 2 = 5 16 ⓒ y 2 − 2 y = 8 y 2 − 2 y = 8
ⓐ 8 b 2 + 15 b = 4 8 b 2 + 15 b = 4 ⓑ 5 9 v 2 − 2 3 v = 1 5 9 v 2 − 2 3 v = 1 ⓒ ( w + 4 3 ) 2 = 2 9 ( w + 4 3 ) 2 = 2 9
Everyday Math
A flare is fired straight up from a ship at sea. Solve the equation 16 ( t 2 − 13 t + 40 ) = 0 16 ( t 2 − 13 t + 40 ) = 0 for t t , the number of seconds it will take for the flare to be at an altitude of 640 feet.
An architect is designing a hotel lobby. She wants to have a triangular window looking out to an atrium, with the width of the window 6 feet more than the height. Due to energy restrictions, the area of the window must be 140 square feet. Solve the equation 1 2 h 2 + 3 h = 140 1 2 h 2 + 3 h = 140 for h h , the height of the window.
Writing Exercises
Solve the equation x 2 + 10 x = 200 x 2 + 10 x = 200 ⓐ by completing the square ⓑ using the Quadratic Formula ⓒ Which method do you prefer? Why?
Solve the equation 12 y 2 + 23 y = 24 12 y 2 + 23 y = 24 ⓐ by completing the square ⓑ using the Quadratic Formula ⓒ Which method do you prefer? Why?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Elementary Algebra 2e
- Publication date: Apr 22, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/elementary-algebra-2e/pages/10-3-solve-quadratic-equations-using-the-quadratic-formula
© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Real World Examples of Quadratic Equations
A Quadratic Equation looks like this:
Quadratic equations pop up in many real world situations!
Here we have collected some examples for you, and solve each using different methods:
- Factoring Quadratics
- Completing the Square
- Graphing Quadratic Equations
- The Quadratic Formula
- Online Quadratic Equation Solver
Each example follows three general stages:
- Take the real world description and make some equations
- Use your common sense to interpret the results

Balls, Arrows, Missiles and Stones
When you throw a ball (or shoot an arrow, fire a missile or throw a stone) it goes up into the air, slowing as it travels, then comes down again faster and faster ...
... and a Quadratic Equation tells you its position at all times!
Example: Throwing a Ball
A ball is thrown straight up, from 3 m above the ground, with a velocity of 14 m/s. when does it hit the ground.
Ignoring air resistance, we can work out its height by adding up these three things: (Note: t is time in seconds)
| The height starts at 3 m: | 3 | |
| It travels upwards at 14 meters per second (14 m/s): | 14t | |
| Gravity pulls it down, changing its position by 5 m per second squared: | −5t | |
| is simplified from -(½)at with a=9.8 m/s ) |
Add them up and the height h at any time t is:
h = 3 + 14t − 5t 2
And the ball will hit the ground when the height is zero:
3 + 14t − 5t 2 = 0
Which is a Quadratic Equation !
In "Standard Form" it looks like:
−5t 2 + 14t + 3 = 0
It looks even better when we multiply all terms by −1 :
5t 2 − 14t − 3 = 0
Let us solve it ...
There are many ways to solve it, here we will factor it using the "Find two numbers that multiply to give ac , and add to give b " method in Factoring Quadratics :
ac = −15 , and b = −14 .
The factors of −15 are: −15, −5, −3, −1, 1, 3, 5, 15
By trying a few combinations we find that −15 and 1 work (−15×1 = −15, and −15+1 = −14)
The "t = −0.2" is a negative time, impossible in our case.
The "t = 3" is the answer we want:
The ball hits the ground after 3 seconds!
Here is the graph of the Parabola h = −5t 2 + 14t + 3
It shows you the height of the ball vs time
Some interesting points:
(0,3) When t=0 (at the start) the ball is at 3 m
(−0.2,0) says that −0.2 seconds BEFORE we threw the ball it was at ground level. This never happened! So our common sense says to ignore it.
(3,0) says that at 3 seconds the ball is at ground level.
Also notice that the ball goes nearly 13 meters high.
Note: You can find exactly where the top point is!
The method is explained in Graphing Quadratic Equations , and has two steps:
Find where (along the horizontal axis) the top occurs using −b/2a :
- t = −b/2a = −(−14)/(2 × 5) = 14/10 = 1.4 seconds
Then find the height using that value (1.4)
- h = −5t 2 + 14t + 3 = −5(1.4) 2 + 14 × 1.4 + 3 = 12.8 meters
So the ball reaches the highest point of 12.8 meters after 1.4 seconds.
Example: New Sports Bike

You have designed a new style of sports bicycle!
Now you want to make lots of them and sell them for profit.
Your costs are going to be:
- $700,000 for manufacturing set-up costs, advertising, etc
- $110 to make each bike
Based on similar bikes, you can expect sales to follow this "Demand Curve":
Where "P" is the price.
For example, if you set the price:
- at $0, you just give away 70,000 bikes
- at $350, you won't sell any bikes at all
- at $300 you might sell 70,000 − 200×300 = 10,000 bikes
So ... what is the best price? And how many should you make?
Let us make some equations!
How many you sell depends on price, so use "P" for Price as the variable
Profit = −200P 2 + 92,000P − 8,400,000
Yes, a Quadratic Equation. Let us solve this one by Completing the Square .
Solve: −200P 2 + 92,000P − 8,400,000 = 0
Step 1 Divide all terms by -200
Step 2 Move the number term to the right side of the equation:
Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:
(b/2) 2 = (−460/2) 2 = (−230) 2 = 52900
Step 4 Take the square root on both sides of the equation:
Step 5 Subtract (-230) from both sides (in other words, add 230):
What does that tell us? It says that the profit is ZERO when the Price is $126 or $334
But we want to know the maximum profit, don't we?
It is exactly half way in-between! At $230
And here is the graph:
The best sale price is $230 , and you can expect:
- Unit Sales = 70,000 − 200 x 230 = 24,000
- Sales in Dollars = $230 x 24,000 = $5,520,000
- Costs = 700,000 + $110 x 24,000 = $3,340,000
- Profit = $5,520,000 − $3,340,000 = $2,180,000
A very profitable venture.
Example: Small Steel Frame
Your company is going to make frames as part of a new product they are launching.
The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm 2
The inside of the frame has to be 11 cm by 6 cm
What should the width x of the metal be?
Area of steel before cutting:
Area of steel after cutting out the 11 × 6 middle:
Let us solve this one graphically !
Here is the graph of 4x 2 + 34x :
The desired area of 28 is shown as a horizontal line.
The area equals 28 cm 2 when:
x is about −9.3 or 0.8
The negative value of x make no sense, so the answer is:
x = 0.8 cm (approx.)
Example: River Cruise
A 3 hour river cruise goes 15 km upstream and then back again. the river has a current of 2 km an hour. what is the boat's speed and how long was the upstream journey.
There are two speeds to think about: the speed the boat makes in the water, and the speed relative to the land:
- Let x = the boat's speed in the water (km/h)
- Let v = the speed relative to the land (km/h)
Because the river flows downstream at 2 km/h:
- when going upstream, v = x−2 (its speed is reduced by 2 km/h)
- when going downstream, v = x+2 (its speed is increased by 2 km/h)
We can turn those speeds into times using:
time = distance / speed
(to travel 8 km at 4 km/h takes 8/4 = 2 hours, right?)
And we know the total time is 3 hours:
total time = time upstream + time downstream = 3 hours
Put all that together:
total time = 15/(x−2) + 15/(x+2) = 3 hours
Now we use our algebra skills to solve for "x".
First, get rid of the fractions by multiplying through by (x-2) (x+2) :
3(x-2)(x+2) = 15(x+2) + 15(x-2)
Expand everything:
3(x 2 −4) = 15x+30 + 15x−30
Bring everything to the left and simplify:
3x 2 − 30x − 12 = 0
It is a Quadratic Equation!
Let us solve it using the Quadratic Formula :
Where a , b and c are from the Quadratic Equation in "Standard Form": ax 2 + bx + c = 0
Solve 3x 2 - 30x - 12 = 0
Answer: x = −0.39 or 10.39 (to 2 decimal places)
x = −0.39 makes no sense for this real world question, but x = 10.39 is just perfect!
Answer: Boat's Speed = 10.39 km/h (to 2 decimal places)
And so the upstream journey = 15 / (10.39−2) = 1.79 hours = 1 hour 47min
And the downstream journey = 15 / (10.39+2) = 1.21 hours = 1 hour 13min
Example: Resistors In Parallel
Two resistors are in parallel, like in this diagram:
The total resistance has been measured at 2 Ohms, and one of the resistors is known to be 3 ohms more than the other.
What are the values of the two resistors?
The formula to work out total resistance "R T " is:
1 R T = 1 R 1 + 1 R 2
In this case, we have R T = 2 and R 2 = R 1 + 3
1 2 = 1 R 1 + 1 R 1 +3
To get rid of the fractions we can multiply all terms by 2R 1 (R 1 + 3) and then simplify:
Yes! A Quadratic Equation!
Let us solve it using our Quadratic Equation Solver .
- Enter 1, −1 and −6
- And you should get the answers −2 and 3
R 1 cannot be negative, so R 1 = 3 Ohms is the answer.
The two resistors are 3 ohms and 6 ohms.
Quadratic Equations are useful in many other areas:

For a parabolic mirror, a reflecting telescope or a satellite dish, the shape is defined by a quadratic equation.
Quadratic equations are also needed when studying lenses and curved mirrors.
And many questions involving time, distance and speed need quadratic equations.

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Solving Quadratic Equations with the Quadratic Formula
Factoring Roots Completing the Square Formula Graphing Examples
Somebody (possibly in seventh-century India ) was solving a lot of quadratic equations by completing the square. At some point, he (and, yes, it would have been a guy back then) noticed that he was always doing the exact same steps in the exact same order for every equation.
The great power of algebra is that it provides us with the ability to deal with abstractions, such as formulas that always work. This can relieve us from the burden and messiness of having to muck about with the numbers every single time we do the exact same thing. Using this power with respect to solving quadratics by completing the square, he made a formula out of what he'd been doing; namely, the Quadratic Formula, which states:
Content Continues Below
MathHelp.com
The Quadratic Formula
The Quadratic Formula: Given a quadratic equation in the following form:
ax 2 + bx + c = 0
...where a , b , and c are the numerical coefficients of the terms of the quadratic, the value of the variable x is given by the following equation:
The nice thing about the Quadratic Formula is that the Quadratic Formula always works. There are some quadratics (most of them, actually) that we can't solve by factoring. But the Quadratic Formula will always spit out an answer, whether or not the quadratic expression was factorable.
Let's try that first problem from the previous page again, but this time we'll use the Quadratic Formula instead of the laborious process of completing the square:
Use the Quadratic Formula to solve x 2 − 4 x − 8 = 0
The Quadratic Formula requires that I have the quadratic expression on one side of the "equals" sign, with "zero" on the other side. They've given me the equation already in that form. Also, the Formula is stated in terms of the numerical coefficients of the terms of the quadratic expression. Looking at the coefficients in this equation, I see that a = 1 , b = −4 , and c = −8 . I'll plug these numbers into the Formula, and simplify. (I should get the same answer as I previously have.)
This is the same answer as I got before, which confirms that the Quadratic Formula works as intended. Once again, my final answer is:
The nice thing about the Quadratic Formula (as compared to completing the square) is that we're just plugging into a formula. There are no "steps" to remember, and thus there are fewer opportunities for mistakes. That being said:
Take care not to omit the " ± " sign in front of the radical.
Don't draw the fraction line as being only under the square root, because it's under the initial " − b " part, too.
Don't forget that the denominator of the Formula is " 2 a ", not just " 2 ". That is, when the leading term is something like " 5 x 2 ", you will need to remember to put the " a = 5 " value in the denominator.
Use parentheses around the coefficients when you're first plugging them into the Formula, especially when any of those coefficients is negative, so you don't lose any "minus" signs.
Solve 4 x 2 + 3 x − 2 = 0 using the Quadratic Formula.
First, I'll read off the values of the coefficients that I'll be plugging into the Formula:
c = − 2
Now all I have to do is plug these values into the Formula, and simplify to get my answer:
x = [−(3) ± sqrt{(3) 2 − 4(4)(−2}]/[2(4)]
= [−3 ± sqrt{9 + 32}]/[8]
= [−3 ± sqrt{41}]/[8]
Absolutely nothing will simplify here, so I'm done. My answer is:
x = [−3 ± sqrt{41}]/[8]
You should definitely memorize the Quadratic Formula. I don't care if your teacher says she's going to give it to you on the next test; memorize it anyway, because you'll be needing it later. It's not that long, and there's even a song to help you remember it, set to the tune of "Pop Goes the Weasel":
X is equal to negative B Plus or minus the square root Of B-squared minus four A C All over two A
(The above song isn't original to me. I learned it elsewhere .)
When using the Formula, take the time to be careful because, as long as you do your work neatly, the Quadratic Formula will give you the right answer every time.
I have a lesson on the Quadratic Formula , which provides worked examples and shows the connection between the discriminant (the " b 2 − 4 ac " part inside the square root), the number and type of solutions of the quadratic equation, and the graph of the related parabola. If you're wanting more help with the Formula, then please study the lesson at the above hyperlink.
You can use the Mathway widget below to practice solving quadratic equations by using the Quadratic Formula. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve using the Quadratic Formula" to compare your answer to Mathway's. (Or skip the widget and continue on the next page.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/solvquad4.htm
Page 1 Page 2 Page 3 Page 4 Page 5 Page 6
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles

The Quadratic Formula
What it is, what it does, and how to use it
What is the Quadratic Formula?
The quadratic formula is:

What does this formula tell us?
The quadratic formula calculates the solutions of any quadratic equation.
What is a quadratic equation?
A quadratic equation is an equation that can be written as ax ² + bx + c where a ≠ 0 . In other words, a quadratic equation must have a squared term as its highest power.
Examples of quadratic equations
$$ y = 5x^2 + 2x + 5 \\ y = 11x^2 + 22 \\ y = x^2 - 4x +5 \\ y = -x^2 + + 5 $$
Non Examples
$$ y = 11x + 22 \\ y = x^3 -x^2 +5x +5 \\ y = 2x^3 -4x^2 \\ y = -x^4 + 5 $$
Ok, but what is a 'solution'?
Well a solution can be thought in two ways:
| For any quadratic equation of the form f(x) = ax +bx+c, the solution is when f(x) = 0. | |
| The solution is where the graph of a quadratic equation (a ) is intersects the x-axis. This, of course, only applies to real solutions. |
Example of the quadratic formula to solve an equation
Use the formula to solve theQuadratic Equation: $$ y = x^2 + 2x + 1 $$ .
Just substitute a,b, and c into the general formula:
$$ a = 1 \\ b = 2 \\ c = 1 $$
Below is a picture representing the graph of y = x² + 2x + 1 and its solution.
Quadratic Formula Song
A catchy way to remember the quadratic formula is this song (pop goes the weasel).
Practice Problems
Use the quadratic formula to find the solutions to the following equation: y = x² − 2x + 1 and its solution.
- b = − 2
Use the quadratic formula to find the solutions to the following equation: y = x² − x − 2 and its solution .
In this quadratic equation, y = x² − x − 2 and its solution:
- b = − 1
- c = − 2
Use the quadratic formula to find the solutions to the following equation: y = x² − 1 and its solution.
In this quadratic equation, y = x² − 1 and its solution:
- c = −1
Calculate the solutions of the the quadratic equation below by using the quadratic formula : y = x² + 2x − 3 and its solution.
In this quadratic equation, y = x² + 2x − 3 and its solution:
- c = −3
Below is a picture of the graph of the quadratic equation and its two solutions.
Use the quadratic formula to find the solutions to the following equation: y = x² + 4x − 5 and its solution.
In this quadratic equation, y = x² + 4x − 5 and its solution:
- c = −5
Use the quadratic formula to find the solutions to the following equation: y = x² − 4x + 5 and its solution.
In this quadratic equation, y = x² − 4x + 5 and its solution:
- b = −4
Below is a picture of this quadratic's graph.
- Solving Quadratic Equations

- Discriminant
- Completing the Square in Math
Completing The Square Calculator
Solves Equation and lets you print image to Desktop!

- Quadratic Formula Calculator
- Formula for Sum and Product of Roots
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.


IMAGES
VIDEO
COMMENTS
This is a quadratic equation; rewrite it in standard form. Solve the equation using the Quadratic Formula. Identify the \(a,b,c\) values. Write the Quadratic Formula. Then substitute in the values of \(a,b,c\). Simplify. Figure 9.5.13: Rewrite to show two solutions. Approximate the answers using a calculator. We eliminate the negative solution ...
The more you use the formula to solve quadratic equations, the more you become expert at it! Use the illustration below as a guide. Notice that in order to apply the quadratic formula, we must transform the quadratic equation into the standard form, that is, [latex]a{x^2} + bx + c = 0[/latex] where [latex]a \ne 0[/latex].
Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere. ... Worked example: quadratic formula (negative coefficients) Report a problem. Loading...
First we need to identify the values for a, b, and c (the coefficients). First step, make sure the equation is in the format from above, a x 2 + b x + c = 0 : x 2 + 4 x − 21 = 0. is what makes it a quadratic). Then we plug a , b , and c into the formula: x = − 4 ± 16 − 4 ⋅ 1 ⋅ ( − 21) 2. solving this looks like:
If you say the formula as you write it in each problem, you'll have it memorized in no time! And remember, the Quadratic Formula is an EQUATION. Be sure you start with "\(x=\)". ... How to solve a quadratic equation using the Quadratic Formula. Write the quadratic equation in standard form, \(a x^{2}+b x+c=0\). Identify the values of \(a ...
Try It 9.48. Solve by using the Quadratic Formula: 5b2 + 2b + 4 = 0 5 b 2 + 2 b + 4 = 0. Remember, to use the Quadratic Formula, the equation must be written in standard form, ax2 + bx + c = 0. Sometimes, we will need to do some algebra to get the equation into standard form before we can use the Quadratic Formula.
Solve by completing the square: Non-integer solutions. Worked example: completing the square (leading coefficient ≠ 1) Solving quadratics by completing the square: no solution. Proof of the quadratic formula. Solving quadratics by completing the square. Completing the square review. Quadratic formula proof review.
The solutions to a quadratic equation of the form ax2 + bx + c = 0, where a ≠ 0 are given by the formula: x = −b ± √b2 − 4ac 2a. To use the Quadratic Formula, we substitute the values of a, b, and c from the standard form into the expression on the right side of the formula. Then we simplify the expression. The result is the pair of ...
Example 5: Solve the quadratic equation below using the Quadratic Formula. First, we need to rewrite the given quadratic equation in Standard Form, [latex]a{x^2} + bx + c = 0[/latex]. Eliminate the [latex]{x^2}[/latex] term on the right side. Eliminate the [latex]x[/latex] term on the right side. Eliminate the constant on the right side.
The Corbettmaths Practice Questions on the Quadratic Formula. Next: Rounding Significant Figures Practice Questions
Introduction; 2.1 Solve Equations Using the Subtraction and Addition Properties of Equality; 2.2 Solve Equations using the Division and Multiplication Properties of Equality; 2.3 Solve Equations with Variables and Constants on Both Sides; 2.4 Use a General Strategy to Solve Linear Equations; 2.5 Solve Equations with Fractions or Decimals; 2.6 Solve a Formula for a Specific Variable
The quadratic formula helps us solve any quadratic equation. First, we bring the equation to the form ax²+bx+c=0, where a, b, and c are coefficients. Then, we plug these coefficients in the formula: (-b±√ (b²-4ac))/ (2a) . See examples of using the formula to solve a variety of equations. Created by Sal Khan.
Directions: Solve the following questions, for the indicated variable, using the quadratic formula. It is possible that some of these problems can also be solved by factoring, but for right now, we are practicing the quadratic formula. 1. Solve using the quadratic formula: x2 - 2 x - 24 = 0. Choose:
Step 5. Solve the equation using algebra techniques. Step 6. Check the answer in the problem and make sure it makes sense. Step 7. Answer the question with a complete sentence. We have solved number applications that involved consecutive even and odd integers, by modeling the situation with linear equations.
Yes! A Quadratic Equation! Let us solve it using our Quadratic Equation Solver. Enter 1, −1 and −6; And you should get the answers −2 and 3; R 1 cannot be negative, so R 1 = 3 Ohms is the answer. The two resistors are 3 ohms and 6 ohms. Others. Quadratic Equations are useful in many other areas:
Use the quadratic formula to solve the equation, 0 is equal to negative 7q squared plus 2q plus 9. Now, the quadratic formula, it applies to any quadratic equation of the form-- we could put the 0 on the left hand side. 0 is equal to ax squared plus bx plus c. And we generally deal with x's, in this problem we're dealing with q's.
You can use the Mathway widget below to practice solving quadratic equations by using the Quadratic Formula. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve using the Quadratic Formula" to compare your answer to Mathway's. (Or skip the widget and continue on the next page.)
Example of the quadratic formula to solve an equation. Use the formula to solve theQuadratic Equation: y = x2 + 2x + 1 y = x 2 + 2 x + 1 . Just substitute a,b, and c into the general formula: a = 1 b = 2 c = 1 a = 1 b = 2 c = 1. Below is a picture representing the graph of y = x² + 2x + 1 and its solution.
The solutions to a quadratic equation of the form ax2 + bx + c = 0 a x 2 + b x + c = 0, a ≥ 0 a ≥ 0 are given by the formula: x = −b± b2−4ac√ 2a x = − b ± b 2 − 4 a c 2 a. To use the Quadratic Formula, we substitute the values of a, b, and c into the expression on the right side of the formula. Then, we do all the math to ...
The 25/4 and 7 is the result of completing the square method. To factor the equation, you need to first follow this equation: x^ 2 + 2ax + a^2. In x^2 +5x = 3/4, The a^2 is missing. To figure out the a, you need to take the 5 and divide it by 2 (because 2ax), which becomes 5/2. a=5/2. Then you need to square it, (because a^2) which becomes 5^2/2^2.
Calculator Use. This online calculator is a quadratic equation solver that will solve a second-order polynomial equation such as ax 2 + bx + c = 0 for x, where a ≠ 0, using the quadratic formula. The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots.
Subtract c from both sides. ax2 + bx = − c. Divide both sides by a, the coefficient of x2. x2 + b ax = − c a. Now we have the proper form to complete the square. Take one half the coefficient of x, square it, and add the result to both sides of the equation found in step 2.