
- Math Forum/Help
- Problem Solver
- College Math
- Word Problems

Math Word Problems and Solutions - Distance, Speed, Time
Problem 1 A salesman sold twice as much pears in the afternoon than in the morning. If he sold 360 kilograms of pears that day, how many kilograms did he sell in the morning and how many in the afternoon? Click to see solution Solution: Let $x$ be the number of kilograms he sold in the morning.Then in the afternoon he sold $2x$ kilograms. So, the total is $x + 2x = 3x$. This must be equal to 360. $3x = 360$ $x = \frac{360}{3}$ $x = 120$ Therefore, the salesman sold 120 kg in the morning and $2\cdot 120 = 240$ kg in the afternoon.
Problem 2 Mary, Peter, and Lucy were picking chestnuts. Mary picked twice as much chestnuts than Peter. Lucy picked 2 kg more than Peter. Together the three of them picked 26 kg of chestnuts. How many kilograms did each of them pick? Click to see solution Solution: Let $x$ be the amount Peter picked. Then Mary and Lucy picked $2x$ and $x+2$, respectively. So $x+2x+x+2=26$ $4x=24$ $x=6$ Therefore, Peter, Mary, and Lucy picked 6, 12, and 8 kg, respectively.
Problem 3 Sophia finished $\frac{2}{3}$ of a book. She calculated that she finished 90 more pages than she has yet to read. How long is her book? Click to see solution Solution: Let $x$ be the total number of pages in the book, then she finished $\frac{2}{3}\cdot x$ pages. Then she has $x-\frac{2}{3}\cdot x=\frac{1}{3}\cdot x$ pages left. $\frac{2}{3}\cdot x-\frac{1}{3}\cdot x=90$ $\frac{1}{3}\cdot x=90$ $x=270$ So the book is 270 pages long.
Problem 4 A farming field can be ploughed by 6 tractors in 4 days. When 6 tractors work together, each of them ploughs 120 hectares a day. If two of the tractors were moved to another field, then the remaining 4 tractors could plough the same field in 5 days. How many hectares a day would one tractor plough then? Click to see solution Solution: If each of $6$ tractors ploughed $120$ hectares a day and they finished the work in $4$ days, then the whole field is: $120\cdot 6 \cdot 4 = 720 \cdot 4 = 2880$ hectares. Let's suppose that each of the four tractors ploughed $x$ hectares a day. Therefore in 5 days they ploughed $5 \cdot 4 \cdot x = 20 \cdot x$ hectares, which equals the area of the whole field, 2880 hectares. So, we get $20x = 2880$ $ x = \frac{2880}{20} = 144$. Hence, each of the four tractors would plough 144 hectares a day.
Problem 5 A student chose a number, multiplied it by 2, then subtracted 138 from the result and got 102. What was the number he chose? Click to see solution Solution: Let $x$ be the number he chose, then $2\cdot x - 138 = 102$ $2x = 240$ $x = 120$
Problem 6 I chose a number and divide it by 5. Then I subtracted 154 from the result and got 6. What was the number I chose? Click to see solution Solution: Let $x$ be the number I chose, then $\frac{x}{5}-154=6$ $\frac{x}{5}=160$ $x=800$
| V (km/hr) | t (hr) | S (km) | |
| Car | x + 5 | 4 | 4(x +5) |
| Truck | X | 4 | 4x |
Problem 8 One side of a rectangle is 3 cm shorter than the other side. If we increase the length of each side by 1 cm, then the area of the rectangle will increase by 18 cm 2 . Find the lengths of all sides. Click to see solution Solution: Let $x$ be the length of the longer side $x \gt 3$, then the other side's length is $x-3$ cm. Then the area is S 1 = x(x - 3) cm 2 . After we increase the lengths of the sides they will become $(x +1)$ and $(x - 3 + 1) = (x - 2)$ cm long. Hence the area of the new rectangle will be $A_2 = (x + 1)\cdot(x - 2)$ cm 2 , which is 18 cm 2 more than the first area. Therefore $A_1 +18 = A_2$ $x(x - 3) + 18 = (x + 1)(x - 2)$ $x^2 - 3x + 18 = x^2 + x - 2x - 2$ $2x = 20$ $x = 10$. So, the sides of the rectangle are $10$ cm and $(10 - 3) = 7$ cm long.
Problem 9 The first year, two cows produced 8100 litres of milk. The second year their production increased by 15% and 10% respectively, and the total amount of milk increased to 9100 litres a year. How many litres were milked from each cow each year? Click to see solution Solution: Let x be the amount of milk the first cow produced during the first year. Then the second cow produced $(8100 - x)$ litres of milk that year. The second year, each cow produced the same amount of milk as they did the first year plus the increase of $15\%$ or $10\%$. So $8100 + \frac{15}{100}\cdot x + \frac{10}{100} \cdot (8100 - x) = 9100$ Therefore $8100 + \frac{3}{20}x + \frac{1}{10}(8100 - x) = 9100$ $\frac{1}{20}x = 190$ $x = 3800$ Therefore, the cows produced 3800 and 4300 litres of milk the first year, and $4370$ and $4730$ litres of milk the second year, respectively.
Problem 10 The distance between stations A and B is 148 km. An express train left station A towards station B with the speed of 80 km/hr. At the same time, a freight train left station B towards station A with the speed of 36 km/hr. They met at station C at 12 pm, and by that time the express train stopped at at intermediate station for 10 min and the freight train stopped for 5 min. Find: a) The distance between stations C and B. b) The time when the freight train left station B. Click to see solution Solution a) Let x be the distance between stations B and C. Then the distance from station C to station A is $(148 - x)$ km. By the time of the meeting at station C, the express train travelled for $\frac{148-x}{80}+\frac{10}{60}$ hours and the freight train travelled for $\frac{x}{36}+\frac{5}{60}$ hours. The trains left at the same time, so: $\frac{148 - x}{80} + \frac{1}{6} = \frac{x}{36} + \frac{1}{12}$. The common denominator for 6, 12, 36, 80 is 720. Then $9(148 - x) +120 = 20x +60$ $1332 - 9x + 120 = 20x + 60$ $29x = 1392$ $x = 48$. Therefore the distance between stations B and C is 48 km. b) By the time of the meeting at station C the freight train rode for $\frac{48}{36} + \frac{5}{60}$ hours, i.e. $1$ hour and $25$ min. Therefore it left station B at $12 - (1 + \frac{25}{60}) = 10 + \frac{35}{60}$ hours, i.e. at 10:35 am.
Problem 11 Susan drives from city A to city B. After two hours of driving she noticed that she covered 80 km and calculated that, if she continued driving at the same speed, she would end up been 15 minutes late. So she increased her speed by 10 km/hr and she arrived at city B 36 minutes earlier than she planned. Find the distance between cities A and B. Click to see solution Solution: Let $x$ be the distance between A and B. Since Susan covered 80 km in 2 hours, her speed was $V = \frac{80}{2} = 40$ km/hr. If she continued at the same speed she would be $15$ minutes late, i.e. the planned time on the road is $\frac{x}{40} - \frac{15}{60}$ hr. The rest of the distance is $(x - 80)$ km. $V = 40 + 10 = 50$ km/hr. So, she covered the distance between A and B in $2 +\frac{x - 80}{50}$ hr, and it was 36 min less than planned. Therefore, the planned time was $2 + \frac{x -80}{50} + \frac{36}{60}$. When we equalize the expressions for the scheduled time, we get the equation: $\frac{x}{40} - \frac{15}{60} = 2 + \frac{x -80}{50} + \frac{36}{60}$ $\frac{x - 10}{40} = \frac{100 + x - 80 + 30}{50}$ $\frac{x - 10}{4} = \frac{x +50}{5}$ $5x - 50 = 4x + 200$ $x = 250$ So, the distance between cities A and B is 250 km.
Problem 12 To deliver an order on time, a company has to make 25 parts a day. After making 25 parts per day for 3 days, the company started to produce 5 more parts per day, and by the last day of work 100 more parts than planned were produced. Find how many parts the company made and how many days this took. Click to see solution Solution: Let $x$ be the number of days the company worked. Then 25x is the number of parts they planned to make. At the new production rate they made: $3\cdot 25 + (x - 3)\cdot 30 = 75 + 30(x - 3)$ Therefore: $25 x = 75 + 30(x -3) - 100$ $25x = 75 +30x -90 - 100$ $190 -75 = 30x -25$ $115 = 5x$ $x = 23$ So the company worked 23 days and they made $23\cdot 25+100 = 675$ pieces.
Problem 13 There are 24 students in a seventh grade class. They decided to plant birches and roses at the school's backyard. While each girl planted 3 roses, every three boys planted 1 birch. By the end of the day they planted $24$ plants. How many birches and roses were planted? Click to see solution Solution: Let $x$ be the number of roses. Then the number of birches is $24 - x$, and the number of boys is $3\times (24-x)$. If each girl planted 3 roses, there are $\frac{x}{3}$ girls in the class. We know that there are 24 students in the class. Therefore $\frac{x}{3} + 3(24 - x) = 24$ $x + 9(24 - x) = 3\cdot 24$ $x +216 - 9x = 72$ $216 - 72 = 8x$ $\frac{144}{8} = x$ $x = 18$ So, students planted 18 roses and 24 - x = 24 - 18 = 6 birches.
Problem 14 A car left town A towards town B driving at a speed of V = 32 km/hr. After 3 hours on the road the driver stopped for 15 min in town C. Because of a closed road he had to change his route, making the trip 28 km longer. He increased his speed to V = 40 km/hr but still he was 30 min late. Find: a) The distance the car has covered. b) The time that took it to get from C to B. Click to see solution Solution: From the statement of the problem we don't know if the 15 min stop in town C was planned or it was unexpected. So we have to consider both cases. A The stop was planned. Let us consider only the trip from C to B, and let $x$ be the number of hours the driver spent on this trip. Then the distance from C to B is $S = 40\cdot x$ km. If the driver could use the initial route, it would take him $x - \frac{30}{60} = x - \frac{1}{2}$ hours to drive from C to B. The distance from C to B according to the initially itinerary was $(x - \frac{1}{2})\cdot 32$ km, and this distance is $28$ km shorter than $40\cdot x$ km. Then we have the equation $(x - 1/2)\cdot 32 + 28 = 40x$ $32x -16 +28 = 40x$ $-8x = -12$ $8x = 12$ $x = \frac{12}{8}$ $x = 1 \frac{4}{8} = 1 \frac{1}{2} = 1 \frac{30}{60} =$ 1 hr 30 min. So, the car covered the distance between C and B in 1 hour and 30 min. The distance from A to B is $3\cdot 32 + \frac{12}{8}\cdot 40 = 96 + 60 = 156$ km. B Suppose it took $x$ hours for him to get from C to B. Then the distance is $S = 40\cdot x$ km. The driver did not plan the stop at C. Let we accept that he stopped because he had to change the route. It took $x - \frac{30}{60} + \frac{15}{60} = x - \frac{15}{60} = x - \frac{1}{4}$ h to drive from C to B. The distance from C to B is $32(x - \frac{1}{4})$ km, which is $28$ km shorter than $40\cdot x$, i.e. $32(x - \frac{1}{4}) + 28 = 40x$ $32x - 8 +28 = 40x$ $20= 8x$ $x = \frac{20}{8} = \frac{5}{2} = 2 \text{hr } 30 \text{min}.$ The distance covered equals $ 40 \times 2.5 = 100 km$.
Problem 15 If a farmer wants to plough a farm field on time, he must plough 120 hectares a day. For technical reasons he ploughed only 85 hectares a day, hence he had to plough 2 more days than he planned and he still has 40 hectares left. What is the area of the farm field and how many days the farmer planned to work initially? Click to see solution Solution: Let $x$ be the number of days in the initial plan. Therefore, the whole field is $120\cdot x$ hectares. The farmer had to work for $x + 2$ days, and he ploughed $85(x + 2)$ hectares, leaving $40$ hectares unploughed. Then we have the equation: $120x = 85(x + 2) + 40$ $35x = 210$ $x = 6$ So the farmer planned to have the work done in 6 days, and the area of the farm field is $120\cdot 6 = 720$ hectares.
Problem 16 A woodworker normally makes a certain number of parts in 24 days. But he was able to increase his productivity by 5 parts per day, and so he not only finished the job in only 22 days but also he made 80 extra parts. How many parts does the woodworker normally makes per day and how many pieces does he make in 24 days? Click to see solution Solution: Let $x$ be the number of parts the woodworker normally makes daily. In 24 days he makes $24\cdot x$ pieces. His new daily production rate is $x + 5$ pieces and in $22$ days he made $22 \cdot (x + 5)$ parts. This is 80 more than $24\cdot x$. Therefore the equation is: $24\cdot x + 80 = 22(x +5)$ $30 = 2x$ $x = 15$ Normally he makes 15 parts a day and in 24 days he makes $15 \cdot 24 = 360$ parts.
Problem 17 A biker covered half the distance between two towns in 2 hr 30 min. After that he increased his speed by 2 km/hr. He covered the second half of the distance in 2 hr 20 min. Find the distance between the two towns and the initial speed of the biker. Click to see solution Solution: Let x km/hr be the initial speed of the biker, then his speed during the second part of the trip is x + 2 km/hr. Half the distance between two cities equals $2\frac{30}{60} \cdot x$ km and $2\frac{20}{60} \cdot (x + 2)$ km. From the equation: $2\frac{30}{60} \cdot x = 2\frac{20}{60} \cdot (x+2)$ we get $x = 28$ km/hr. The intial speed of the biker is 28 km/h. Half the distance between the two towns is $2 h 30 min \times 28 = 2.5 \times 28 = 70$. So the distance is $2 \times 70 = 140$ km.
Problem 18 A train covered half of the distance between stations A and B at the speed of 48 km/hr, but then it had to stop for 15 min. To make up for the delay, it increased its speed by $\frac{5}{3}$ m/sec and it arrived to station B on time. Find the distance between the two stations and the speed of the train after the stop. Click to see solution Solution: First let us determine the speed of the train after the stop. The speed was increased by $\frac{5}{3}$ m/sec $= \frac{5\cdot 60\cdot 60}{\frac{3}{1000}}$ km/hr = $6$ km/hr. Therefore, the new speed is $48 + 6 = 54$ km/hr. If it took $x$ hours to cover the first half of the distance, then it took $x - \frac{15}{60} = x - 0.25$ hr to cover the second part. So the equation is: $48 \cdot x = 54 \cdot (x - 0.25)$ $48 \cdot x = 54 \cdot x - 54\cdot 0.25$ $48 \cdot x - 54 \cdot x = - 13.5$ $-6x = - 13.5$ $x = 2.25$ h. The whole distance is $2 \times 48 \times 2.25 = 216$ km.
Problem 19 Elizabeth can get a certain job done in 15 days, and Tony can finish only 75% of that job within the same time. Tony worked alone for several days and then Elizabeth joined him, so they finished the rest of the job in 6 days, working together. For how many days have each of them worked and what percentage of the job have each of them completed? Click to see solution Solution: First we will find the daily productivity of every worker. If we consider the whole job as unit (1), Elizabeth does $\frac{1}{15}$ of the job per day and Tony does $75\%$ of $\frac{1}{15}$, i.e. $\frac{75}{100}\cdot \frac{1}{15} = \frac{1}{20}$. Suppose that Tony worked alone for $x$ days. Then he finished $\frac{x}{20}$ of the total job alone. Working together for 6 days, the two workers finished $6\cdot (\frac{1}{15}+\frac{1}{20}) = 6\cdot \frac{7}{60} = \frac{7}{10}$ of the job. The sum of $\frac{x}{20}$ and $\frac{7}{10}$ gives us the whole job, i.e. $1$. So we get the equation: $\frac{x}{20}+\frac{7}{10}=1$ $\frac{x}{20} = \frac{3}{10}$ $x = 6$. Tony worked for 6 + 6 = 12 days and Elizabeth worked for $6$ days. The part of job done is $12\cdot \frac{1}{20} = \frac{60}{100} = 60\%$ for Tony, and $6\cdot \frac{1}{15} = \frac{40}{100} = 40\%$ for Elizabeth.
Problem 20 A farmer planned to plough a field by doing 120 hectares a day. After two days of work he increased his daily productivity by 25% and he finished the job two days ahead of schedule. a) What is the area of the field? b) In how many days did the farmer get the job done? c) In how many days did the farmer plan to get the job done? Click to see solution Solution: First of all we will find the new daily productivity of the farmer in hectares per day: 25% of 120 hectares is $\frac{25}{100} \cdot 120 = 30$ hectares, therefore $120 + 30 = 150$ hectares is the new daily productivity. Lets x be the planned number of days allotted for the job. Then the farm is $120\cdot x$ hectares. On the other hand, we get the same area if we add $120 \cdot 2$ hectares to $150(x -4)$ hectares. Then we get the equation $120x = 120\cdot 2 + 150(x -4)$ $x = 12$ So, the job was initially supposed to take 12 days, but actually the field was ploughed in 12 - 2 =10 days. The field's area is $120 \cdot 12 = 1440$ hectares.
Problem 21 To mow a grass field a team of mowers planned to cover 15 hectares a day. After 4 working days they increased the daily productivity by $33 \times \frac{1}{3}\%$, and finished the work 1 day earlier than it was planned. A) What is the area of the grass field? B) How many days did it take to mow the whole field? C) How many days were scheduled initially for this job? Hint : See problem 20 and solve by yourself. Answer: A) 120 hectares; B) 7 days; C) 8 days.
Problem 22 A train travels from station A to station B. If the train leaves station A and makes 75 km/hr, it arrives at station B 48 minutes ahead of scheduled. If it made 50 km/hr, then by the scheduled time of arrival it would still have 40 km more to go to station B. Find: A) The distance between the two stations; B) The time it takes the train to travel from A to B according to the schedule; C) The speed of the train when it's on schedule. Click to see solution Solution: Let $x$ be the scheduled time for the trip from A to B. Then the distance between A and B can be found in two ways. On one hand, this distance equals $75(x - \frac{48}{60})$ km. On the other hand, it is $50x + 40$ km. So we get the equation: $75(x - \frac{48}{60}) = 50x + 40$ $x = 4$ hr is the scheduled travel time. The distance between the two stations is $50\cdot 4 +40 = 240$ km. Then the speed the train must keep to be on schedule is $\frac{240}{4} = 60$ km/hr.
Problem 23 The distance between towns A and B is 300 km. One train departs from town A and another train departs from town B, both leaving at the same moment of time and heading towards each other. We know that one of them is 10 km/hr faster than the other. Find the speeds of both trains if 2 hours after their departure the distance between them is 40 km. Click to see solution Solution: Let the speed of the slower train be $x$ km/hr. Then the speed of the faster train is $(x + 10)$ km/hr. In 2 hours they cover $2x$ km and $2(x +10)$km, respectively. Therefore if they didn't meet yet, the whole distance from A to B is $2x + 2(x +10) +40 = 4x +60$ km. However, if they already met and continued to move, the distance would be $2x + 2(x + 10) - 40 = 4x - 20$km. So we get the following equations: $4x + 60 = 300$ $4x = 240$ $x = 60$ or $4x - 20 = 300$ $4x = 320$ $x = 80$ Hence the speed of the slower train is $60$ km/hr or $80$ km/hr and the speed of the faster train is $70$ km/hr or $90$ km/hr.
Problem 24 A bus travels from town A to town B. If the bus's speed is 50 km/hr, it will arrive in town B 42 min later than scheduled. If the bus increases its speed by $\frac{50}{9}$ m/sec, it will arrive in town B 30 min earlier than scheduled. Find: A) The distance between the two towns; B) The bus's scheduled time of arrival in B; C) The speed of the bus when it's on schedule. Click to see solution Solution: First we will determine the speed of the bus following its increase. The speed is increased by $\frac{50}{9}$ m/sec $= \frac{50\cdot60\cdot60}{\frac{9}{1000}}$ km/hr $= 20$ km/hr. Therefore, the new speed is $V = 50 + 20 = 70$ km/hr. If $x$ is the number of hours according to the schedule, then at the speed of 50 km/hr the bus travels from A to B within $(x +\frac{42}{60})$ hr. When the speed of the bus is $V = 70$ km/hr, the travel time is $x - \frac{30}{60}$ hr. Then $50(x +\frac{42}{60}) = 70(x-\frac{30}{60})$ $5(x+\frac{7}{10}) = 7(x-\frac{1}{2})$ $\frac{7}{2} + \frac{7}{2} = 7x -5x$ $2x = 7$ $x = \frac{7}{2}$ hr. So, the bus is scheduled to make the trip in $3$ hr $30$ min. The distance between the two towns is $70(\frac{7}{2} - \frac{1}{2}) = 70\cdot 3 = 210$ km and the scheduled speed is $\frac{210}{\frac{7}{2}} = 60$ km/hr.
120 Math Word Problems To Challenge Students Grades 1 to 8
Written by Marcus Guido
- Teaching Tools

- Subtraction
- Multiplication
- Mixed operations
- Ordering and number sense
- Comparing and sequencing
- Physical measurement
- Ratios and percentages
- Probability and data relationships
You sit at your desk, ready to put a math quiz, test or activity together. The questions flow onto the document until you hit a section for word problems.
A jolt of creativity would help. But it doesn’t come.
Whether you’re a 3rd grade teacher or an 8th grade teacher preparing students for high school, translating math concepts into real world examples can certainly be a challenge.
This resource is your jolt of creativity. It provides examples and templates of math word problems for 1st to 8th grade classes . ( See our entire list of back to school resources for teachers here .)
There are 120 examples in total.
The list of examples is supplemented by tips to create engaging and challenging math word problems.
120 Math word problems, categorized by skill
Addition word problems.

Best for: 1st grade, 2nd grade
1. Adding to 10: Ariel was playing basketball. 1 of her shots went in the hoop. 2 of her shots did not go in the hoop. How many shots were there in total?
2. Adding to 20: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store to get 3 more pieces of gum. How many pieces of gum does Adrianna have now?
3. Adding to 100: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store and got 70 pieces of strawberry gum and 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?
4. Adding Slightly over 100: The restaurant has 175 normal chairs and 20 chairs for babies. How many chairs does the restaurant have in total?
5. Adding to 1,000: How many cookies did you sell if you sold 320 chocolate cookies and 270 vanilla cookies?
6. Adding to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In June, the hobby store sold 15,498 more trading cards than normal. In total, how many trading cards did the hobby store sell in June?
7. Adding 3 Numbers: Billy had 2 books at home. He went to the library to take out 2 more books. He then bought 1 book. How many books does Billy have now?
8. Adding 3 Numbers to and over 100: Ashley bought a big bag of candy. The bag had 102 blue candies, 100 red candies and 94 green candies. How many candies were there in total?
Subtraction word problems
Best for: 1st grade, second grade
9. Subtracting to 10: There were 3 pizzas in total at the pizza shop. A customer bought 1 pizza. How many pizzas are left?
10. Subtracting to 20: Your friend said she had 11 stickers. When you helped her clean her desk, she only had a total of 10 stickers. How many stickers are missing?
11. Subtracting to 100: Adrianna has 100 pieces of gum to share with her friends. When she went to the park, she shared 10 pieces of strawberry gum. When she left the park, Adrianna shared another 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

Practice math word problems with Prodigy Math
Join millions of teachers using Prodigy to make learning fun and differentiate instruction as they answer in-game questions, including math word problems from 1st to 8th grade!
12. Subtracting Slightly over 100: Your team scored a total of 123 points. 67 points were scored in the first half. How many were scored in the second half?
13. Subtracting to 1,000: Nathan has a big ant farm. He decided to sell some of his ants. He started with 965 ants. He sold 213. How many ants does he have now?
14. Subtracting to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In July, the hobby store sold a total of 20,777 trading cards. How many more trading cards did the hobby store sell in July compared with a normal month?
15. Subtracting 3 Numbers: Charlene had a pack of 35 pencil crayons. She gave 6 to her friend Theresa. She gave 3 to her friend Mandy. How many pencil crayons does Charlene have left?
16. Subtracting 3 Numbers to and over 100: Ashley bought a big bag of candy to share with her friends. In total, there were 296 candies. She gave 105 candies to Marissa. She also gave 86 candies to Kayla. How many candies were left?
Multiplication word problems

Best for: 2nd grade, 3rd grade
17. Multiplying 1-Digit Integers: Adrianna needs to cut a pan of brownies into pieces. She cuts 6 even columns and 3 even rows into the pan. How many brownies does she have?
18. Multiplying 2-Digit Integers: A movie theatre has 25 rows of seats with 20 seats in each row. How many seats are there in total?
19. Multiplying Integers Ending with 0: A clothing company has 4 different kinds of sweatshirts. Each year, the company makes 60,000 of each kind of sweatshirt. How many sweatshirts does the company make each year?
20. Multiplying 3 Integers: A bricklayer stacks bricks in 2 rows, with 10 bricks in each row. On top of each row, there is a stack of 6 bricks. How many bricks are there in total?
21. Multiplying 4 Integers: Cayley earns $5 an hour by delivering newspapers. She delivers newspapers 3 days each week, for 4 hours at a time. After delivering newspapers for 8 weeks, how much money will Cayley earn?
Division word problems
Best for: 3rd grade, 4th grade, 5th grade
22. Dividing 1-Digit Integers: If you have 4 pieces of candy split evenly into 2 bags, how many pieces of candy are in each bag?
23. Dividing 2-Digit Integers: If you have 80 tickets for the fair and each ride costs 5 tickets, how many rides can you go on?
24. Dividing Numbers Ending with 0: The school has $20,000 to buy new computer equipment. If each piece of equipment costs $50, how many pieces can the school buy in total?
25. Dividing 3 Integers: Melissa buys 2 packs of tennis balls for $12 in total. All together, there are 6 tennis balls. How much does 1 pack of tennis balls cost? How much does 1 tennis ball cost?
26. Interpreting Remainders: An Italian restaurant receives a shipment of 86 veal cutlets. If it takes 3 cutlets to make a dish, how many cutlets will the restaurant have left over after making as many dishes as possible?
Mixed operations word problems

27. Mixing Addition and Subtraction: There are 235 books in a library. On Monday, 123 books are taken out. On Tuesday, 56 books are brought back. How many books are there now?
28. Mixing Multiplication and Division: There is a group of 10 people who are ordering pizza. If each person gets 2 slices and each pizza has 4 slices, how many pizzas should they order?
29. Mixing Multiplication, Addition and Subtraction: Lana has 2 bags with 2 marbles in each bag. Markus has 2 bags with 3 marbles in each bag. How many more marbles does Markus have?
30. Mixing Division, Addition and Subtraction: Lana has 3 bags with the same amount of marbles in them, totaling 12 marbles. Markus has 3 bags with the same amount of marbles in them, totaling 18 marbles. How many more marbles does Markus have in each bag?
Ordering and number sense word problems
31. Counting to Preview Multiplication: There are 2 chalkboards in your classroom. If each chalkboard needs 2 pieces of chalk, how many pieces do you need in total?
32. Counting to Preview Division: There are 3 chalkboards in your classroom. Each chalkboard has 2 pieces of chalk. This means there are 6 pieces of chalk in total. If you take 1 piece of chalk away from each chalkboard, how many will there be in total?
33. Composing Numbers: What number is 6 tens and 10 ones?
34. Guessing Numbers: I have a 7 in the tens place. I have an even number in the ones place. I am lower than 74. What number am I?
35. Finding the Order: In the hockey game, Mitchell scored more points than William but fewer points than Auston. Who scored the most points? Who scored the fewest points?
Fractions word problems

Best for: 3rd grade, 4th grade, 5th grade, 6th grade
36. Finding Fractions of a Group: Julia went to 10 houses on her street for Halloween. 5 of the houses gave her a chocolate bar. What fraction of houses on Julia’s street gave her a chocolate bar?
37. Finding Unit Fractions: Heather is painting a portrait of her best friend, Lisa. To make it easier, she divides the portrait into 6 equal parts. What fraction represents each part of the portrait?
38. Adding Fractions with Like Denominators: Noah walks ⅓ of a kilometre to school each day. He also walks ⅓ of a kilometre to get home after school. How many kilometres does he walk in total?
39. Subtracting Fractions with Like Denominators: Last week, Whitney counted the number of juice boxes she had for school lunches. She had ⅗ of a case. This week, it’s down to ⅕ of a case. How much of the case did Whitney drink?
40. Adding Whole Numbers and Fractions with Like Denominators: At lunchtime, an ice cream parlor served 6 ¼ scoops of chocolate ice cream, 5 ¾ scoops of vanilla and 2 ¾ scoops of strawberry. How many scoops of ice cream did the parlor serve in total?
41. Subtracting Whole Numbers and Fractions with Like Denominators: For a party, Jaime had 5 ⅓ bottles of cola for her friends to drink. She drank ⅓ of a bottle herself. Her friends drank 3 ⅓. How many bottles of cola does Jaime have left?
42. Adding Fractions with Unlike Denominators: Kevin completed ½ of an assignment at school. When he was home that evening, he completed ⅚ of another assignment. How many assignments did Kevin complete?
43. Subtracting Fractions with Unlike Denominators: Packing school lunches for her kids, Patty used ⅞ of a package of ham. She also used ½ of a package of turkey. How much more ham than turkey did Patty use?
44. Multiplying Fractions: During gym class on Wednesday, the students ran for ¼ of a kilometre. On Thursday, they ran ½ as many kilometres as on Wednesday. How many kilometres did the students run on Thursday? Write your answer as a fraction.
45. Dividing Fractions: A clothing manufacturer uses ⅕ of a bottle of colour dye to make one pair of pants. The manufacturer used ⅘ of a bottle yesterday. How many pairs of pants did the manufacturer make?
46. Multiplying Fractions with Whole Numbers: Mark drank ⅚ of a carton of milk this week. Frank drank 7 times more milk than Mark. How many cartons of milk did Frank drink? Write your answer as a fraction, or as a whole or mixed number.
Decimals word problems
Best for: 4th grade, 5th grade
47. Adding Decimals: You have 2.6 grams of yogurt in your bowl and you add another spoonful of 1.3 grams. How much yogurt do you have in total?
48. Subtracting Decimals: Gemma had 25.75 grams of frosting to make a cake. She decided to use only 15.5 grams of the frosting. How much frosting does Gemma have left?
49. Multiplying Decimals with Whole Numbers: Marshall walks a total of 0.9 kilometres to and from school each day. After 4 days, how many kilometres will he have walked?
50. Dividing Decimals by Whole Numbers: To make the Leaning Tower of Pisa from spaghetti, Mrs. Robinson bought 2.5 kilograms of spaghetti. Her students were able to make 10 leaning towers in total. How many kilograms of spaghetti does it take to make 1 leaning tower?
51. Mixing Addition and Subtraction of Decimals: Rocco has 1.5 litres of orange soda and 2.25 litres of grape soda in his fridge. Antonio has 1.15 litres of orange soda and 0.62 litres of grape soda. How much more soda does Rocco have than Angelo?
52. Mixing Multiplication and Division of Decimals: 4 days a week, Laura practices martial arts for 1.5 hours. Considering a week is 7 days, what is her average practice time per day each week?
Comparing and sequencing word problems

Best for: Kindergarten, 1st grade, 2nd grade
53. Comparing 1-Digit Integers: You have 3 apples and your friend has 5 apples. Who has more?
54. Comparing 2-Digit Integers: You have 50 candies and your friend has 75 candies. Who has more?
55. Comparing Different Variables: There are 5 basketballs on the playground. There are 7 footballs on the playground. Are there more basketballs or footballs?
56. Sequencing 1-Digit Integers: Erik has 0 stickers. Every day he gets 1 more sticker. How many days until he gets 3 stickers?
57. Skip-Counting by Odd Numbers: Natalie began at 5. She skip-counted by fives. Could she have said the number 20?
58. Skip-Counting by Even Numbers: Natasha began at 0. She skip-counted by eights. Could she have said the number 36?
59. Sequencing 2-Digit Numbers: Each month, Jeremy adds the same number of cards to his baseball card collection. In January, he had 36. 48 in February. 60 in March. How many baseball cards will Jeremy have in April?
Time word problems
66. Converting Hours into Minutes: Jeremy helped his mom for 1 hour. For how many minutes was he helping her?
69. Adding Time: If you wake up at 7:00 a.m. and it takes you 1 hour and 30 minutes to get ready and walk to school, at what time will you get to school?
70. Subtracting Time: If a train departs at 2:00 p.m. and arrives at 4:00 p.m., how long were passengers on the train for?
71. Finding Start and End Times: Rebecca left her dad’s store to go home at twenty to seven in the evening. Forty minutes later, she was home. What time was it when she arrived home?
Money word problems
Best for: 1st grade, 2nd grade, 3rd grade, 4th grade, 5th grade
60. Adding Money: Thomas and Matthew are saving up money to buy a video game together. Thomas has saved $30. Matthew has saved $35. How much money have they saved up together in total?
61. Subtracting Money: Thomas has $80 saved up. He uses his money to buy a video game. The video game costs $67. How much money does he have left?
62. Multiplying Money: Tim gets $5 for delivering the paper. How much money will he have after delivering the paper 3 times?
63. Dividing Money: Robert spent $184.59 to buy 3 hockey sticks. If each hockey stick was the same price, how much did 1 cost?
64. Adding Money with Decimals: You went to the store and bought gum for $1.25 and a sucker for $0.50. How much was your total?
65. Subtracting Money with Decimals: You went to the store with $5.50. You bought gum for $1.25, a chocolate bar for $1.15 and a sucker for $0.50. How much money do you have left?
67. Applying Proportional Relationships to Money: Jakob wants to invite 20 friends to his birthday, which will cost his parents $250. If he decides to invite 15 friends instead, how much money will it cost his parents? Assume the relationship is directly proportional.
68. Applying Percentages to Money: Retta put $100.00 in a bank account that gains 20% interest annually. How much interest will be accumulated in 1 year? And if she makes no withdrawals, how much money will be in the account after 1 year?
Physical measurement word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade
72. Comparing Measurements: Cassandra’s ruler is 22 centimetres long. April’s ruler is 30 centimetres long. How many centimetres longer is April’s ruler?
73. Contextualizing Measurements: Picture a school bus. Which unit of measurement would best describe the length of the bus? Centimetres, metres or kilometres?
74. Adding Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Last year, Micha’s dad used 100 litres of gas. This year, her dad used 90 litres of gas. How much gas did he use in total for the two years?
75. Subtracting Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Over the past two years, Micha’s dad used 200 litres of gas. This year, he used 100 litres of gas. How much gas did he use last year?
76. Multiplying Volume and Mass: Kiera wants to make sure she has strong bones, so she drinks 2 litres of milk every week. After 3 weeks, how many litres of milk will Kiera drink?
77. Dividing Volume and Mass: Lillian is doing some gardening, so she bought 1 kilogram of soil. She wants to spread the soil evenly between her 2 plants. How much will each plant get?
78. Converting Mass: Inger goes to the grocery store and buys 3 squashes that each weigh 500 grams. How many kilograms of squash did Inger buy?
79. Converting Volume: Shad has a lemonade stand and sold 20 cups of lemonade. Each cup was 500 millilitres. How many litres did Shad sell in total?
80. Converting Length: Stacy and Milda are comparing their heights. Stacy is 1.5 meters tall. Milda is 10 centimetres taller than Stacy. What is Milda’s height in centimetres?
81. Understanding Distance and Direction: A bus leaves the school to take students on a field trip. The bus travels 10 kilometres south, 10 kilometres west, another 5 kilometres south and 15 kilometres north. To return to the school, in which direction does the bus have to travel? How many kilometres must it travel in that direction?
Ratios and percentages word problems
Best for: 4th grade, 5th grade, 6th grade
82. Finding a Missing Number: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. Jenny has 28 trophies. How many does Meredith have?
83. Finding Missing Numbers: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. The difference between the numbers is 12. What are the numbers?
84. Comparing Ratios: The school’s junior band has 10 saxophone players and 20 trumpet players. The school’s senior band has 18 saxophone players and 29 trumpet players. Which band has the higher ratio of trumpet to saxophone players?
85. Determining Percentages: Mary surveyed students in her school to find out what their favourite sports were. Out of 1,200 students, 455 said hockey was their favourite sport. What percentage of students said hockey was their favourite sport?
86. Determining Percent of Change: A decade ago, Oakville’s population was 67,624 people. Now, it is 190% larger. What is Oakville’s current population?
87. Determining Percents of Numbers: At the ice skate rental stand, 60% of 120 skates are for boys. If the rest of the skates are for girls, how many are there?
88. Calculating Averages: For 4 weeks, William volunteered as a helper for swimming classes. The first week, he volunteered for 8 hours. He volunteered for 12 hours in the second week, and another 12 hours in the third week. The fourth week, he volunteered for 9 hours. For how many hours did he volunteer per week, on average?
Probability and data relationships word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade
89. Understanding the Premise of Probability: John wants to know his class’s favourite TV show, so he surveys all of the boys. Will the sample be representative or biased?
90. Understanding Tangible Probability: The faces on a fair number die are labelled 1, 2, 3, 4, 5 and 6. You roll the die 12 times. How many times should you expect to roll a 1?
91. Exploring Complementary Events: The numbers 1 to 50 are in a hat. If the probability of drawing an even number is 25/50, what is the probability of NOT drawing an even number? Express this probability as a fraction.
92. Exploring Experimental Probability: A pizza shop has recently sold 15 pizzas. 5 of those pizzas were pepperoni. Answering with a fraction, what is the experimental probability that he next pizza will be pepperoni?
93. Introducing Data Relationships: Maurita and Felice each take 4 tests. Here are the results of Maurita’s 4 tests: 4, 4, 4, 4. Here are the results for 3 of Felice’s 4 tests: 3, 3, 3. If Maurita’s mean for the 4 tests is 1 point higher than Felice’s, what’s the score of Felice’s 4th test?
94. Introducing Proportional Relationships: Store A is selling 7 pounds of bananas for $7.00. Store B is selling 3 pounds of bananas for $6.00. Which store has the better deal?
95. Writing Equations for Proportional Relationships: Lionel loves soccer, but has trouble motivating himself to practice. So, he incentivizes himself through video games. There is a proportional relationship between the amount of drills Lionel completes, in x , and for how many hours he plays video games, in y . When Lionel completes 10 drills, he plays video games for 30 minutes. Write the equation for the relationship between x and y .
Geometry word problems
Best for: 4th grade, 5th grade, 6th grade, 7th grade, 8th grade
96. Introducing Perimeter: The theatre has 4 chairs in a row. There are 5 rows. Using rows as your unit of measurement, what is the perimeter?
97. Introducing Area: The theatre has 4 chairs in a row. There are 5 rows. How many chairs are there in total?
98. Introducing Volume: Aaron wants to know how much candy his container can hold. The container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. What is the container’s volume?
99. Understanding 2D Shapes: Kevin draws a shape with 4 equal sides. What shape did he draw?
100. Finding the Perimeter of 2D Shapes: Mitchell wrote his homework questions on a piece of square paper. Each side of the paper is 8 centimetres. What is the perimeter?
101. Determining the Area of 2D Shapes: A single trading card is 9 centimetres long by 6 centimetres wide. What is its area?
102. Understanding 3D Shapes: Martha draws a shape that has 6 square faces. What shape did she draw?
103. Determining the Surface Area of 3D Shapes: What is the surface area of a cube that has a width of 2cm, height of 2 cm and length of 2 cm?
104. Determining the Volume of 3D Shapes: Aaron’s candy container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. Bruce’s container is 25 centimetres tall, 9 centimetres long and 9 centimetres wide. Find the volume of each container. Based on volume, whose container can hold more candy?
105. Identifying Right-Angled Triangles: A triangle has the following side lengths: 3 cm, 4 cm and 5 cm. Is this triangle a right-angled triangle?
106. Identifying Equilateral Triangles: A triangle has the following side lengths: 4 cm, 4 cm and 4 cm. What kind of triangle is it?
107. Identifying Isosceles Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 5 cm. What kind of triangle is it?
108. Identifying Scalene Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 6 cm. What kind of triangle is it?
109. Finding the Perimeter of Triangles: Luigi built a tent in the shape of an equilateral triangle. The perimeter is 21 metres. What is the length of each of the tent’s sides?
110. Determining the Area of Triangles: What is the area of a triangle with a base of 2 units and a height of 3 units?
111. Applying Pythagorean Theorem: A right triangle has one non-hypotenuse side length of 3 inches and the hypotenuse measures 5 inches. What is the length of the other non-hypotenuse side?
112. Finding a Circle’s Diameter: Jasmin bought a new round backpack. Its area is 370 square centimetres. What is the round backpack’s diameter?
113. Finding a Circle's Area: Captain America’s circular shield has a diameter of 76.2 centimetres. What is the area of his shield?
114. Finding a Circle’s Radius: Skylar lives on a farm, where his dad keeps a circular corn maze. The corn maze has a diameter of 2 kilometres. What is the maze’s radius?
Variables word problems

Best for: 6th grade, 7th grade, 8th grade
115. Identifying Independent and Dependent Variables: Victoria is baking muffins for her class. The number of muffins she makes is based on how many classmates she has. For this equation, m is the number of muffins and c is the number of classmates. Which variable is independent and which variable is dependent?
116. Writing Variable Expressions for Addition: Last soccer season, Trish scored g goals. Alexa scored 4 more goals than Trish. Write an expression that shows how many goals Alexa scored.
117. Writing Variable Expressions for Subtraction: Elizabeth eats a healthy, balanced breakfast b times a week. Madison sometimes skips breakfast. In total, Madison eats 3 fewer breakfasts a week than Elizabeth. Write an expression that shows how many times a week Madison eats breakfast.
118. Writing Variable Expressions for Multiplication: Last hockey season, Jack scored g goals. Patrik scored twice as many goals than Jack. Write an expression that shows how many goals Patrik scored.
119. Writing Variable Expressions for Division: Amanda has c chocolate bars. She wants to distribute the chocolate bars evenly among 3 friends. Write an expression that shows how many chocolate bars 1 of her friends will receive.
120. Solving Two-Variable Equations: This equation shows how the amount Lucas earns from his after-school job depends on how many hours he works: e = 12h . The variable h represents how many hours he works. The variable e represents how much money he earns. How much money will Lucas earn after working for 6 hours?
How to easily make your own math word problems & word problems worksheets

Armed with 120 examples to spark ideas, making your own math word problems can engage your students and ensure alignment with lessons. Do:
- Link to Student Interests: By framing your word problems with student interests, you’ll likely grab attention. For example, if most of your class loves American football, a measurement problem could involve the throwing distance of a famous quarterback.
- Make Questions Topical: Writing a word problem that reflects current events or issues can engage students by giving them a clear, tangible way to apply their knowledge.
- Include Student Names: Naming a question’s characters after your students is an easy way make subject matter relatable, helping them work through the problem.
- Be Explicit: Repeating keywords distills the question, helping students focus on the core problem.
- Test Reading Comprehension: Flowery word choice and long sentences can hide a question’s key elements. Instead, use concise phrasing and grade-level vocabulary.
- Focus on Similar Interests: Framing too many questions with related interests -- such as football and basketball -- can alienate or disengage some students.
- Feature Red Herrings: Including unnecessary information introduces another problem-solving element, overwhelming many elementary students.
A key to differentiated instruction , word problems that students can relate to and contextualize will capture interest more than generic and abstract ones.
Final thoughts about math word problems
You’ll likely get the most out of this resource by using the problems as templates, slightly modifying them by applying the above tips. In doing so, they’ll be more relevant to -- and engaging for -- your students.
Regardless, having 120 curriculum-aligned math word problems at your fingertips should help you deliver skill-building challenges and thought-provoking assessments.
The result?
A greater understanding of how your students process content and demonstrate understanding, informing your ongoing teaching approach.
Try Prodigy
There's no cost to you or your students and Prodigy is fully aligned with state standards for grades 1-8 math.
Share this article
Table of Contents
Popular Posts

Related Categories
- Teacher Activities (5)
- Teacher Resources (74)
Hey teachers! 👋
Use Prodigy to spark a love for math in your students – including when solving word problems!
32 Examples of Real-World Math Problems

- • Published: April 23, 2024
- • Last update: June 14, 2024
- • Grades: All grades
Introduction

8th grade algebra problem:
Farmer Alfred has three times as many chickens as cows. In total, there are 60 legs in the barn. How many cows does Farmer Alfred have? [1]
Does this sound like a real-world math problem to you? We’ve got chickens, cows, and Farmer Alfred – it’s a scenario straight out of everyday life, isn’t it?
But before you answer, let me ask you something: If you wanted to figure out the number of cows, would you:
- Count their legs, or
- Simply count their heads ( or even just ask Farmer Alfred, “Hey Alfred, how many cows do you have?” )
Chances are, most people would go with option B.
So, why do our math books contain so many “real-world math problems” like the one above?
In this article, we’ll dive into what truly makes a math problem a real-world challenge.
Understanding 'Problems' in Daily Life and Mathematics
The word “problem” carries different meanings in everyday life and in the realm of mathematics, which can sometimes lead to confusion. In our daily lives, when we say “ I have a problem ,” we typically mean that something undesirable has occurred – something challenging to resolve or with potential negative consequences.
For instance:
- “I have a problem because I’ve lost my wallet.”
- “I have a problem because I forgot my keys at home, and I won’t be able to get into the house when I return from school.”
- “I have a problem because I was sick and missed a few weeks of school, which means I’ll likely fail my math test.”
These are examples of everyday problems we encounter. However, once the problem is solved, it often ceases to be a problem:
- “I don’t have a problem getting into my house anymore because my mom gave me her keys.”
In mathematics, the term “problem” takes on a different meaning. According to the Cambridge dictionary [2], it’s defined as “ a question in mathematics that needs an answer. “
Here are a few examples:
- If x + 2 = 4, what is the value of x?
- How do you find the common denominator for fractions 1/3 and 1/4?
- What is the length of the hypotenuse in a right triangle if two legs are 3 and 4 feet long?
These are all examples of math problems.
It’s important to note that in mathematics, a problem remains a problem even after it’s solved. Math problems are universal, regardless of who encounters them [3]. For instance, both John and Emma could face the same math problem, such as “ If x + 2 = 4, then what is x? ” After they solve it, it still remains a math problem that a teacher could give to somebody else.
Understanding Real-World Math Problems
So, what exactly is a “real-world math problem”? We’ve established that in our daily lives, we refer to a situation as a “problem” when it could lead to unpleasant consequences. In mathematics, a “problem” refers to a mathematical question that requires a mathematical solution.
With that in mind, we can define a real-world math problem as:
A situation that could have negative consequences in real life and that requires a mathematical solution (i.e. mathematical solution is preferred over other solutions).
Consider this example:

Could miscalculating the flour amount lead to less-than-ideal results? Absolutely. Messing up the flour proportion could result in a less tasty cake – certainly an unpleasant consequence.
Now, let’s explore the methods for solving this. While traditional methods, like visually dividing the flour or measuring multiple times, have their place, they may not be suitable for larger-scale events, such as catering for a wedding with 250 guests. In such cases, a mathematical solution is not only preferred but also more practical.
By setting up a simple proportion – 1 1/2 cups of flour for 8 people equals x cups for 20 people – we can quickly find the precise amount needed: 3 3/4 cups of flour. In larger events, like the wedding, the mathematical approach provides even more value, yielding a requirement of nearly 47 cups of flour.
This illustrates why a mathematical solution is faster, more accurate, and less error-prone, making it the preferred method. Coupled with the potential negative consequences of inaccuracies, this makes the problem a real-world one, showcasing the practical application of math in everyday scenarios.
Identifying Non-Real-World Math Problems
Let’s revisit the example from the beginning of this article:
Farmer Alfred has three times as many chickens as cows. In total, there are 60 legs in the barn. How many cows does Farmer Alfred have?
3rd grade basic arithmetic problem:
Noah has $56, and Olivia has 8 times less. How much money does Olivia have?

Once more, in our daily routines, do we handle money calculations this way? Why would one prefer to use mathematical solution ($56 : 8 =$7). More often than not, we’d simply ask Olivia how much money she has. While the problem can theoretically be solved mathematically, it’s much more practical, efficient, and reliable to resolve it by directly asking Olivia.
Examples like these are frequently found in math textbooks because they aid in developing mathematical thinking. However, the scenarios they describe are uncommon in real life and fail to explicitly demonstrate the usefulness of math. In essence, they don’t showcase what math can actually be used for. Therefore, there are two crucial aspects of true real-world math problems: they must be commonplace in real life, and they must explicitly illustrate the utility of math.
To summarize:
Word problems that are uncommon in real life and fail to convincingly demonstrate the usefulness of math are not real-world math problems.
Real-World Math Problems Across Professions
Many professions entail encountering real-world math problems on a regular basis. Consider the following examples:

Nurses often need to calculate accurate drug dosage amounts using proportions, a task solved through mathematical methods. Incorrect dosage calculations can pose serious risks to patient health, leading to potentially harmful consequences.
Construction engineers frequently need to determine whether a foundation will be sturdy enough to support a building, employing mathematical solving techniques and specialized formulas. Errors in these calculations can result in structural issues such as cracks in walls due to foundation deformation, leading to undesirable outcomes.

Marketers often rely on statistical analysis to assess the performance of online advertisements, including metrics like click-through rates and the geographical distribution of website visitors. Mathematical analysis guides decision-making in this area. Inaccurate analyses may lead to inefficient allocation of advertisement budgets, resulting in less-than-optimal outcomes.
These examples illustrate real-world math problems encountered in various professions. While there are numerous instances of such problems, they are often overlooked in educational settings. At DARTEF, we aim to bridge this gap by compiling a comprehensive list of real-world math problems, which we’ll explore in the following section.
32 Genuine Real-World Math Problems
In this section, we present 32 authentic real-world math problems from diverse fields such as safety and security, microbiology, architecture, engineering, nanotechnology, archaeology, creativity, and more. Each of these problems meets the criteria we’ve outlined previously. Specifically, a problem can be classified as a real-world math problem if:
- It is commonly encountered in real-life scenarios.
- It has the potential for undesirable consequences.
- A mathematical solution is preferable over alternative methods.
- It effectively illustrates the practical utility of mathematics.
All these problems stem from actual on-the-job situations, showcasing the application of middle and high school math in various professions.
Math Problems in Biology
Real-world math problems in biology often involve performing measurements or making predictions. Mathematics helps us understand various biological phenomena, such as the growth of bacterial populations, the spread of diseases, and even the reconstruction of ancient human appearances. Here are a couple of specific examples:
1. Reconstructing Human Faces Using Parallel and Perpendicular Lines:

Archeologists and forensic specialists often reconstruct human faces based on skeletal remains. They utilize parallel and perpendicular lines to create symmetry lines on the face, aiding in the recovery of facial features and proportions. Our article, “ Parallel and Perpendicular Lines: A Real-Life Example (From Forensics and Archaeology) ,” provides a comprehensive explanation and illustrates how the shape of the nose can be reconstructed using parallel and perpendicular lines, line segments, tangent lines, and symmetry lines.
2. Measuring Bacteria Size Using Circumference and Area Formulas:

Microbiology specialists routinely measure bacteria size to monitor and document their growth rates. Since bacterial shapes often resemble geometric shapes studied in school, mathematical methods such as calculating circumference or area of a circle are convenient for measuring bacteria size. Our article, “ Circumference: A Real-Life Example (from Microbiology) ,” delves into this process in detail.
Math Problems in Construction and Architecture
Real-world math problems are abundant in architecture and construction projects, where mathematics plays a crucial role in ensuring safety, efficiency, and sustainability. Here are some specific case studies that illustrate the application of math in these domains:
3. Calculating Central Angles for Safe Roadways:

Central angle calculations are a fundamental aspect of roadway engineering, particularly in designing curved roads. Civil engineers use these calculations to determine the degree of road curvature, which significantly impacts road safety and compliance with regulations. Mathematical concepts such as radius, degrees, arc length, and proportions are commonly employed by civil engineers in their daily tasks. Our article, “ How to Find a Central Angle: A Real-Life Example (from Civil Engineering) ,” provides further explanation and demonstrates the calculation of central angles using a real road segment as an example.
4. Designing Efficient Roof Overhang Using Trigonometry

Trigonometry is a powerful tool in architecture and construction, providing a simple yet effective way to calculate the sizes of building elements, including roof overhangs. For example, the tangent function is used to design the optimal length of a roof overhang that blocks the high summer sun while allowing the lower winter sun to enter . Our article, “ Tangent (Trigonometry): A Real-Life Example (From Architecture and Construction) ,” provides a detailed use case with two methods of calculation and also includes a worksheet.
5. Designing Efficient Roofs for Solar Panels Using Angle Geometry:

Mathematics plays a crucial role in architecture, aiding architects and construction engineers in designing energy-efficient building structures. For example, when considering the installation of solar panels on a building’s roof, understanding geometric properties such as adjacent and alternate angles is essential for maximizing energy efficiency . By utilizing mathematical calculations, architects can determine the optimal angle for positioning solar panels and reflectors to capture maximum sunlight. Our article, “ A Real-Life Example of How Angles are Used in Architecture ,” provides explanations and illustrations, including animations.
6. Precision Drilling of Oil Wells Using Trigonometry:

Petroleum engineers rely on trigonometric principles such as sines, cosines, tangents, and right-angle triangles to drill oil wells accurately. Trigonometry enables engineers to calculate precise angles and distances necessary for drilling vertical, inclined, and even horizontal wells. For instance, when drilling at an inclination of 30°, engineers can use trigonometry to calculate the vertical depth corresponding to each foot drilled horizontally. Our article, “ CosX: A Real-Life Example (from Petroleum Engineering) ,” provides examples, drawings of right triangle models, and necessary calculations.
7. Calculating Water Flow Rate Using Composite Figures:

Water supply specialists frequently encounter the task of calculating water flow rates in water canals, which involves determining the area of composite figures representing canal cross-sections . Many canal cross-sections consist of composite shapes, such as rectangles and triangles. By calculating the areas of these individual components and summing them, specialists can determine the total cross-sectional area and subsequently calculate the flow rate of water. Our article, “ Area of Composite Figures: A Real-Life Example (from Water Supply) ,” presents necessary figures, cross-sections, and an example calculation.
Math Problems in Business and Marketing
Mathematics plays a crucial role not only in finance and banking but also in making informed decisions across various aspects of business development, marketing analysis, growth strategies, and more. Here are some real-world math problems commonly encountered in business and marketing:
8. Analyzing Webpage Position in Google Using Polynomials and Polynomial Graphs:

Polynomials and polynomial graphs are essential tools for data analysis. They are useful for a wide variety of people, not only data analysts, but literally everyone who ever uses Excel or Google Sheets. Our article, “ Graphing Polynomials: A Real-World Example (from Data Analysis) ,” describes this and provides an authentic case study. The case study demonstrates how polynomials, polynomial functions of varying degrees, and polynomial graphs are used in internet technologies to analyze the visibility of webpages in Google and other search engines.”
9. Making Informed Business Development Decisions Using Percentages:

In business development, math problems often revolve around analyzing growth and making strategic decisions. Understanding percentages is essential, particularly when launching new products or services. For example, determining whether a startup should target desktop computer, smartphone, or tablet users for an app requires analyzing installation percentages among user groups to gain insights into consumer behavior. Math helps optimize marketing efforts, enhance customer engagement, and drive growth in competitive markets. Check out our article “ A Real-Life Example of Percent Problems in Business ” for a detailed description of this example.
10. Analyzing Customer Preferences Using Polynomials:

Marketing involves not only creative advertising but also thorough analysis of customer preferences and marketing campaigns. Marketing specialists often use simple polynomials for such analysis, as they help analyze multiple aspects of customer behavior simultaneously. For instance, marketers may use polynomials to determine whether low price or service quality is more important to hotel visitors. Smart analysis using polynomials enables businesses to make informed decisions. If you’re interested in learning more, our article “ Polynomials: A Real Life Example (from Marketing) ” provides a real-world example from the hotel industry.
11. Avoiding Statistical Mistakes Using Simpson’s Paradox:

Data gathering and trend analysis are essential in marketing, but a good understanding of mathematical statistics helps avoid intuitive mistakes . For example, consider an advertising campaign targeting Android and iOS users. Initial data may suggest that iOS users are more responsive. However, a careful statistical analysis, as described in our article “ Simpson’s Paradox: A Real-Life Example (from Marketing) ,” may reveal that Android users, particularly tablet users, actually click on ads more frequently. This contradiction highlights the importance of accurate statistical interpretation and the careful use of mathematics in decision-making.
Math Problems in Digital Agriculture
In the modern era, agriculture is becoming increasingly digitalized, with sensors and artificial intelligence playing vital roles in farm management. Mathematics is integral to this digital transformation, aiding in data analysis, weather prediction, soil parameter measurement, irrigation scheduling, and more. Here’s an example of a real-world math problem in digital agriculture:
12. Combatting Pests with Negative Numbers:

Negative numbers are utilized in agriculture to determine the direction of movement, similar to how they’re used on a temperature scale where a plus sign indicates an increase and a minus sign indicates a decrease. In agricultural sensors, plus and minus signs may indicate whether pests are moving towards or away from plants. For instance, a plus sign could signify movement towards plants, while a minus sign indicates movement away from plants. Understanding these directional movements helps farmers combat pests effectively. Our article, “ Negative Numbers: A Real-Life Example (from Agriculture) ,” provides detailed explanations and examples of how negative numbers are applied in agriculture.
Math Problems in DIY Projects
In do-it-yourself (DIY) projects, mathematics plays a crucial role in measurements, calculations, and problem-solving. Whether you’re designing furniture, planning home renovations, crafting handmade gifts, or landscaping your garden, math provides essential tools for precise measurements, material estimations, and budget management. Here’s an example of a real-world math problem in DIY:
13. Checking Construction Parts for Right Angles Using the Pythagorean Theorem:

The converse of the Pythagorean theorem allows you to check whether various elements – such as foundations, corners of rooms, garage walls, or sides of vegetable patches – form right angles. This can be done quickly using Pythagorean triples like 3-4-5 or 6-8-10, or by calculating with square roots. This method ensures the creation of right angles or verifies if an angle is indeed right. Our article, “ Pythagorean Theorem Converse: A Real-Life Example (from DIY) ,” explains this concept and provides an example of how to build a perfect 90° foundation using the converse of the Pythagorean theorem.
Math Problems in Entertainment and Creativity
Mathematics plays a surprisingly significant role in the creative industries, including music composition, visual effects creation, and computer graphic design. Understanding and applying mathematical concepts is essential for producing engaging and attractive creative works. Here’s an example of a real-world math problem in entertainment:
14. Controlling Stage Lamps with Linear Functions:

Linear and quadratic functions are essential components of the daily work of lighting specialists in theaters and event productions. These professionals utilize specialized software and controllers that rely on algorithms based on mathematical functions. Linear functions, in particular, are commonly used to control stage lamps, ensuring precise and coordinated lighting effects during performances. Our article, “ Linear Function: A Real-Life Example (from Entertainment) ,” delves into this topic in detail, complete with animations that illustrate how these functions are applied in practice.
Math Problems in Healthcare
Mathematics plays a crucial role in solving numerous real-world problems in healthcare, ranging from patient care to the design of advanced medical devices. Here are several examples of real-world math problems in healthcare:
15. Calculating Dosage by Converting Time Units:

Nurses frequently convert between hours, minutes, and seconds to accurately administer medications and fluids to patients. For example, if a patient requires 300mL of fluid over 2.5 hours, nurses must convert hours to minutes to calculate the appropriate drip rate for an IV bag. Understanding mathematical conversions and solving proportions are essential skills in nursing. Check out our article, “ Converting Hours to Minutes: A Real-Life Example (from Nursing) ,” for further explanation.
16. Predicting Healthcare Needs Using Quadratic Functions:

Mathematical functions, including quadratic functions, are used to make predictions in public health. These predictions are vital for estimating the need for medical services, such as psychological support following traumatic events. Quadratic functions can model trends in stress symptoms over time, enabling healthcare systems to anticipate and prepare for increased demand. Our article, “ Parabola Equation: A Real-Life Example (from Public Health) ,” provides further insights and examples.
17. Predicting Healthcare Needs Using Piecewise Linear Functions:

Piecewise linear functions are useful for describing real-world trends that cannot be accurately represented by other functions. For instance, if stress symptoms fluctuate irregularly over time, piecewise linear functions can define periods of increased and decreased stress levels. Our article, “ Piecewise Linear Function: A Real-Life Example (From Public Health) ,” offers an example of how these functions are applied.
18. Designing Medical Prostheses Using the Pythagorean Theorem:

The Pythagorean theorem is applied in the design of medical devices , particularly prostheses for traumatic recovery. Components of these devices often resemble right triangles, allowing engineers to calculate movement and placement for optimal patient comfort and stability during rehabilitation. For a detailed explanation and animations, see our article, “ The 3-4-5 Triangle: A Real-Life Example (from Mechatronics) .”
19. Illustrating Disease Survival Rates Using Cartesian Coordinate Plane:

In medicine, Cartesian coordinate planes are utilized for analyzing historical data, statistics, and predictions. They help visualize relationships between independent and dependent variables, such as survival rates and diagnostic timing in diseases like lung cancer. Our article, “ Coordinate Plane: A Real-Life Example (from Medicine) ,” offers a detailed exploration of this concept, including analyses for both non-smoking and smoking patients.
Math Problems in Industry
Mathematics plays a vital role in solving numerous real-world problems across various industries. From designing industrial robots to analyzing production quality and planning logistics, math is indispensable for optimizing processes and improving efficiency. Here are several examples of real-world math problems in industry:
20. Precise Movements of Industrial Robots Using Trigonometry:

Trigonometry is extensively utilized to direct and control the movements of industrial robots. Each section of an industrial robot can be likened to a leg or hypotenuse of a right triangle, allowing trigonometry to precisely control the position of the robot head. For instance, if the robot head needs to move 5 inches to the right, trigonometry enables calculations to ensure each section of the robot moves appropriately to achieve the desired position. For detailed examples and calculations, refer to our article, “ Find the Missing Side: A Real-life Example (from Robotics) .”
21. Measuring Nanoparticle Size via Cube Root Calculation:

Mathematics plays a crucial role in nanotechnology, particularly in measuring the size of nanoparticles. Cube roots are commonly employed to calculate the size of cube-shaped nanoparticles. As nanoparticles are extremely small and challenging to measure directly, methods in nanotechnology determine nanoparticle volume, allowing for the calculation of cube root to determine the size of the nanoparticle cube side. Check out our article, “ Cube Root: A Real-Life Example (from Nanotechnology) ,” for explanations, calculations, and insights into the connection between physics and math.
22. Understanding Human Emotions Using Number Codes for Robots:

Mathematics is employed to measure human emotions effectively, which is essential for building smart robots capable of recognizing and responding to human emotions. Each human emotion can be broken down into smaller features, such as facial expressions, which are assigned mathematical codes to create algorithms for robots to recognize and distinguish emotions. Explore our article, “ Psychology and Math: A Real-Life Example (from Smart Robots) ,” to understand this process and its connection to psychology.
23. Systems of Linear Equations in Self-Driving Cars:

In the automotive industry, mathematics is pivotal for ensuring the safety and efficiency of self-driving cars. Systems of linear equations are used to predict critical moments in road safety, such as when two cars are side by side during an overtaking maneuver. By solving systems of linear equations, self-driving car computers can assess the safety of overtaking situations. Our article, “ Systems of Linear Equations: A Real-Life Example (from Self-Driving Cars) ,” provides a comprehensive explanation, including animated illustrations and interactive simulations, demonstrating how linear functions and equations are synchronized with car motion.
Math Problems in Information Technology (IT)
Mathematics serves as a fundamental tool in the field of information technology (IT), underpinning various aspects of software development, cybersecurity, and technological advancements. Here are some real-world math problems encountered in IT:
24. Selecting the Right Word in Machine Translation Using Mathematical Probability:

Theoretical probability plays a crucial role in AI machine translation systems, such as Google Translate, by aiding in the selection of the most appropriate words. Words often have multiple translations, and theoretical probability helps analyze the frequency of word appearances in texts to propose the most probable translation. Dive deeper into this topic in our article, “ Theoretical Probability: A Real-Life Example (from Artificial Intelligence) .”
25. Creating User-Friendly Music Streaming Websites Using Mathematical Probability:

Probability is utilized in user experience (UX) design to enhance the usability of digital products , including music streaming websites. Recommendation algorithms calculate theoretical probability to suggest songs that users are likely to enjoy, improving their overall experience. Learn more about this application in our article, “ Theoretical Probability: A Real-Life Example (from Digital Design) .”
26. Developing Realistic Computer Games with Vectors:

Mathematics is essential in animating objects and simulating real-world factors in computer games. Vectors enable game developers to incorporate realistic elements like gravity and wind into the gaming environment. By applying vector addition, developers can accurately depict how external forces affect object trajectories, enhancing the gaming experience. Explore this concept further in our article, “ Parallelogram Law of Vector Addition: A Real-Life Example (from Game Development) .”
27. Detecting Malicious Bots in Social Media Using Linear Inequalities:

Mathematical inequalities are valuable tools in cybersecurity for identifying malicious activity on social media platforms. By analyzing behavioral differences between real users and bots—such as friend count, posting frequency, and device usage—cybersecurity experts can develop algorithms to detect and block suspicious accounts. Discover more about this application in our article, “ How to Write Inequalities: A Real-life Example (from Social Media) .”
28. Increasing Computational Efficiency Using Algebraic and Rational Expressions

Algebraic and rational expressions are crucial in computer technology for increasing computational efficiency . Every step in a computer program’s algorithm requires valuable time and energy for execution. This is especially important for programs used in various safety and security systems. Simplifying these expressions helps boost computational performance. Our article, “ Algebraic and Rational Expressions: A Real-Life Example (from Computer Technology) ,” explains this in detail.
Math Problems in Legal Issues
In legal proceedings, mathematics plays a crucial role in analyzing data and making informed decisions. Here’s a real-world math problem encountered in legal work:
29. Proving the Reliability of Technology in Court Using Percentages:

In certain court cases, particularly those involving new technologies like autonomous cars, lawyers may need to employ mathematical methods to justify evidence. Percentage analysis can be utilized to assess the reliability of technology in court. For instance, in cases related to self-driving cars, lawyers may compare the percentage of errors made by autonomous vehicles with those made by human drivers to determine the technology’s safety. Delve deeper into this topic in our article, “ Solving Percent Problems: A Real-Life Example (from Legal) .”
Math Problems in Safety and Security
In the realm of safety and security, mathematics plays a vital role in protecting people, nature, and assets. Real-world math problems in this field can involve reconstructing crime scenes, analyzing evidence, creating effective emergency response plans, and predicting and responding to natural disasters. Here are two examples:
30. Reconstructing a Crime Scene with Inverse Trigonometry:

Forensic specialists rely on mathematical methods, such as inverse trigonometry, to uncover details of crimes long after they’ve occurred. Inverse trigonometric functions like arcsin, arccos, and arctan enable forensic specialists to calculate precise shooting angles or the trajectory of blood drops at crime scenes. Dive into this topic in our article, “ Arctan: A Real-Life Example (from Criminology) .”
31. Responding to Wildfires with Mathematical Variables:

Variables in mathematical language are also prevalent in real-world scenarios like firefighting. For instance, when dealing with wildfires, independent variables like forest type, wind speed and direction, rainfall, and terrain slope influence fire spread speed (dependent variable) . By utilizing specialized formulas incorporating these variables, fire protection specialists can accurately predict fire paths and optimize firefighting efforts. Explore this practical application in our article, “ Dependent and Independent Variables: A Real-Life Example (from Fire Protection) .”
Math Problems in Weather and Climate
In the realm of weather and climate, mathematics is crucial for creating mathematical models of Earth’s atmosphere, making weather forecasts, predicting weather patterns, and assessing long-term climate trends. Here’s an example:
32. Forecasting Thunderstorms with Negative Numbers:

Negative numbers play a significant role in forecasting thunderstorms. The probability of thunderstorms is closely tied to the temperature differences between air masses in the atmosphere. By subtracting negative numbers (representing temperature values) and analyzing the results, meteorologists can forecast the likelihood of thunderstorms based on the temperature differentials. Dive deeper into this concept in our article, “ Subtracting Negative Numbers: A Real-Life Example (from Weather Forecast). “
Conclusions
Many students perceive math as disconnected from the real world, leading them to question its relevance. Admittedly, maintaining this relevance is no easy feat—it requires collective effort. Farmer Alfred can’t tackle this challenge alone. However, introducing more real-world math examples into the school curriculum is a crucial step. Numerous studies have demonstrated that such examples significantly enhance students’ motivation to learn math. Our own pilot tests confirm this, showing that a clear connection between real-world problems and math education profoundly influences how young people view their future careers.
Therefore, to increase the overall relevance of math education and motivate students, we must prioritize the integration of real-world examples into our teaching practices. At DARTEF, we are dedicated to this cause, striving to bring authenticity to mathematics education worldwide.
- Vos, Pauline. ““How real people really need mathematics in the real world”—Authenticity in mathematics education.” Education Sciences 8.4 (2018): 195.
- Cambridge dictionary, Meaning of problem in English.
- Reif, Frederick. Applying cognitive science to education: Thinking and learning in scientific and other complex domains . MIT press, 2008.
Privacy Overview
What real-life math topic interests you.
Interested in seeing how a specific math topic is applied in the real world?
Let us know your preferred topic, and we’ll create a blog post and video showcasing its practical applications.
If you’d like, you can also let us know which real-world domain you’d like us to explore!
Math Problem Solving Strategies
In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.
Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons
Problem Solving Strategies
The strategies used in solving word problems:
- What do you know?
- What do you need to know?
- Draw a diagram/picture
Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.
Solving Word Problems
Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check
Problem Solving Strategy: Guess And Check
Using the guess and check problem solving strategy to help solve math word problems.
Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?
Problem Solving : Make A Table And Look For A Pattern
- Identify - What is the question?
- Plan - What strategy will I use to solve the problem?
- Solve - Carry out your plan.
- Verify - Does my answer make sense?
Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?
Find A Pattern Model (Intermediate)
In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.
Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?
| Rectangles | Pattern | Total dots |
| 1 | 10 | 10 |
| 2 | 10 + 7 | 17 |
| 3 | 10 + 14 | 24 |
| 4 | 10 + 21 | 31 |
| 5 | 10 + 28 | 38 |
| 6 | 10 + 35 | 45 |
| 7 | 10 + 42 | 52 |
| 8 | 10 + 49 | 59 |
| 9 | 10 + 56 | 66 |
| 10 | 10 + 63 | 73 |
a) The number of dots required for 7 rectangles is 52.
b) If the figure has 73 dots, there would be 10 rectangles.
Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.
| Layers | Pattern | Total dots |
| 1 | 3 | 3 |
| 2 | 3 + 3 | 6 |
| 3 | 3 + 3 + 4 | 10 |
| 4 | 3 + 3 + 4 + 5 | 15 |
| 5 | 3 + 3 + 4 + 5 + 6 | 21 |
| 6 | 3 + 3 + 4 + 5 + 6 + 7 | 28 |
| 7 | 3 + 3 + 4 + 5 + 6 + 7 + 8 | 36 |
The number of dots for 7 layers of triangles is 36.
Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269
| I | 1 | 7 | 13 | 19 | 25 |
| II | 2 | 8 | 14 | 20 | 26 |
| III | 3 | 9 | 15 | 21 | 27 |
| IV | 4 | 10 | 16 | 22 | |
| V | 5 | 11 | 17 | 23 | |
| VI | 6 | 12 | 18 | 24 |
Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)
Example: The following figures were formed using matchsticks.
a) Based on the above series of figures, complete the table below.
| Number of squares | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of triangles | 4 | 6 | 8 | 10 | ||||
| Number of matchsticks | 12 | 19 | 26 | 33 |
b) How many triangles are there if the figure in the series has 9 squares?
c) How many matchsticks would be used in the figure in the series with 11 squares?
| Number of squares | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of triangles | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| Number of matchsticks | 12 | 19 | 26 | 33 | 40 | 47 | 54 | 61 |
b) The pattern is +2 for each additional square. 18 + 2 = 20 If the figure in the series has 9 squares, there would be 20 triangles.
c) The pattern is + 7 for each additional square 61 + (3 x 7) = 82 If the figure in the series has 11 squares, there would be 82 matchsticks.
Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?
| A | B | C | D | E | F | G | |
| A | |||||||
| B | ● | ||||||
| C | ● | ● | |||||
| D | ● | ● | ● | ||||
| E | ● | ● | ● | ● | |||
| F | ● | ● | ● | ● | ● | ||
| G | ● | ● | ● | ● | ● | ● | |
| HS | 6 | 5 | 4 | 3 | 2 | 1 |
Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.
The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?
The following are some other examples of problem solving strategies.
Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)
Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry
Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”
Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents
Problem Solving in Mathematics
- Math Tutorials
- Pre Algebra & Algebra
- Exponential Decay
- Worksheets By Grade
The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.
Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.
Use Established Procedures
Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.
Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.
Look for Clue Words
Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.
Common clue words for addition problems:
Common clue words for subtraction problems:
- How much more
Common clue words for multiplication problems:
Common clue words for division problems:
Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.
Read the Problem Carefully
This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:
- Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
- What did you need to do in that instance?
- What facts are you given about this problem?
- What facts do you still need to find out about this problem?
Develop a Plan and Review Your Work
Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:
- Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
- If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.
If it seems like you’ve solved the problem, ask yourself the following:
- Does your solution seem probable?
- Does it answer the initial question?
- Did you answer using the language in the question?
- Did you answer using the same units?
If you feel confident that the answer is “yes” to all questions, consider your problem solved.
Tips and Hints
Some key questions to consider as you approach the problem may be:
- What are the keywords in the problem?
- Do I need a data visual, such as a diagram, list, table, chart, or graph?
- Is there a formula or equation that I'll need? If so, which one?
- Will I need to use a calculator? Is there a pattern I can use or follow?
Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.
- Examples of Problem Solving with 4 Block
- Using Percents - Calculating Commissions
- What to Know About Business Math
- Parentheses, Braces, and Brackets in Math
- How to Solve a System of Linear Equations
- How to Solve Proportions to Adjust a Recipe
- Calculate the Exact Number of Days
- What Is a Ratio? Definition and Examples
- Changing From Base 10 to Base 2
- Finding the Percent of Change Between Numbers
- Learn About Natural Numbers, Whole Numbers, and Integers
- How to Calculate Commissions Using Percents
- Overview of the Stem-and-Leaf Plot
- Understanding Place Value
- Probability and Chance
- Evaluating Functions With Graphs

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
5 Teaching Mathematics Through Problem Solving
Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)
What is a problem in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.
According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.
There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.
Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.
Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.
Teaching through problem solving focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.
Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):
- The problem has important, useful mathematics embedded in it.
- The problem requires high-level thinking and problem solving.
- The problem contributes to the conceptual development of students.
- The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
- The problem can be approached by students in multiple ways using different solution strategies.
- The problem has various solutions or allows different decisions or positions to be taken and defended.
- The problem encourages student engagement and discourse.
- The problem connects to other important mathematical ideas.
- The problem promotes the skillful use of mathematics.
- The problem provides an opportunity to practice important skills.
Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.
Key features of a good mathematics problem includes:
- It must begin where the students are mathematically.
- The feature of the problem must be the mathematics that students are to learn.
- It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.
It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.
When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!
Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task
Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:
- Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
- What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
- Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks
By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].
The strengths of using Low Floor High Ceiling Tasks:
- Allows students to show what they can do, not what they can’t.
- Provides differentiation to all students.
- Promotes a positive classroom environment.
- Advances a growth mindset in students
- Aligns with the Standards for Mathematical Practice
Examples of some Low Floor High Ceiling Tasks can be found at the following sites:
- YouCubed – under grades choose Low Floor High Ceiling
- NRICH Creating a Low Threshold High Ceiling Classroom
- Inside Mathematics Problems of the Month
Math in 3-Acts
Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:
Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.
In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.
Act Three is the “reveal.” Students share their thinking as well as their solutions.
“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:
- Dan Meyer’s Three-Act Math Tasks
- Graham Fletcher3-Act Tasks ]
- Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete
Number Talks
Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:
- The teacher presents a problem for students to solve mentally.
- Provide adequate “ wait time .”
- The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
- For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
- Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.
“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:
- Inside Mathematics Number Talks
- Number Talks Build Numerical Reasoning

Saying “This is Easy”
“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.
When the teacher says, “this is easy,” students may think,
- “Everyone else understands and I don’t. I can’t do this!”
- Students may just give up and surrender the mathematics to their classmates.
- Students may shut down.
Instead, you and your students could say the following:
- “I think I can do this.”
- “I have an idea I want to try.”
- “I’ve seen this kind of problem before.”
Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.
Using “Worksheets”
Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?
What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.
Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.
One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”
You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can
- Provide your students a bridge between the concrete and abstract
- Serve as models that support students’ thinking
- Provide another representation
- Support student engagement
- Give students ownership of their own learning.
Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.
any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method
should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning
involves teaching a skill so that a student can later solve a story problem
when we teach students how to problem solve
teaching mathematics content through real contexts, problems, situations, and models
a mathematical activity where everyone in the group can begin and then work on at their own level of engagement
20 seconds to 2 minutes for students to make sense of questions
Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book
- PRINT TO PLAY
- DIGITAL GAMES

Problem-Solving Strategies
October 16, 2019
There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.
Problem-solving strategies
1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.
Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.
Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?
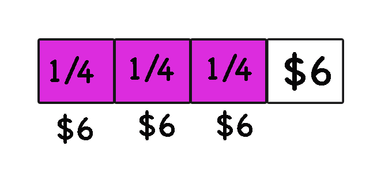
2. Guess and check
Teach students the same strategy research mathematicians use.
With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly. By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.
Find two numbers that have sum 11 and product 24.
Try/guess 5 and 6 the product is 30 too high
adjust to 4 and 7 with product 28 still high
adjust again 3 and 8 product 24
3. Make a table or a list
Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.
To make sure you are listing all the information correctly read the problem carefully.
Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.
Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?
A table or list is useful in solving logic problems.
| Thomas | Lucky | Not gray, the cat is black |
| Helen | Not Moo, not Buddy, not Lucky so Fifi | White |
| Bill | Moo | Gray |
| Mary | Buddy | Brown |
Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.
Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.
Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.
5. Find a pattern.
Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.
The “rule” can then be used to find the answer to the question and complete the table/list.
Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?
| Sunday | 5 |
| Monday | 10 |
| Tuesday | 20 |
| Wednesday | 40 |
| Thursday | |
| Friday | |
| Saturday |
6. Working backward
Problems that can be solved with this strategy are the ones that list a series of events or a sequence of steps .
In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.
Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.
For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.
The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.
8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took
8+31+5+4= 48 Answer: The box came with 48 pieces of candy.
Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.

Print and digital activities
I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.
sample below

How to use the activity cards
Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.
Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.
For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.
Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.
Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions
There are 2 versions of the resource
70 google slides with explanations + 70 printable task cards
70 google slides with explanations + 11 worksheets
You might also like
Multiplying fractions/mixed numbers/simplifying
Adding and subtracting fractions
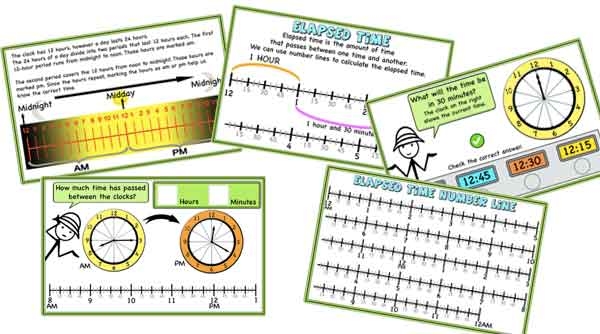
AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities
Teaching area, ideas, games, print, and digital activities
Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems
Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division
Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike
Diving into Division -Teaching division conceptually

Expressions with arrays
Decimals, Decimal fractions, Percentages – print and digital
Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital
Check out our best selling card games now available at amazon.com and amazon.ca.

Chicken Escape
A multiplayer card game that makes mental math practice fun! Chicken Escape is a fast-paced multiplayer card game. While playing…

Dragon Times – A math Adventure card game
Dragon Times is an educational fantasy card game that aims to motivate children to practice multiplication and division facts while…

Problem Solving Activities: 7 Strategies
- Critical Thinking

Problem solving can be a daunting aspect of effective mathematics teaching, but it does not have to be! In this post, I share seven strategic ways to integrate problem solving into your everyday math program.
In the middle of our problem solving lesson, my district math coordinator stopped by for a surprise walkthrough.
I was so excited!
We were in the middle of what I thought was the most brilliant math lesson– teaching my students how to solve problem solving tasks using specific problem solving strategies.
It was a proud moment for me!
Each week, I presented a new problem solving strategy and the students completed problems that emphasized the strategy.
Genius right?
After observing my class, my district coordinator pulled me aside to chat. I was excited to talk to her about my brilliant plan, but she told me I should provide the tasks and let my students come up with ways to solve the problems. Then, as students shared their work, I could revoice the student’s strategies and give them an official name.
What a crushing blow! Just when I thought I did something special, I find out I did it all wrong.
I took some time to consider her advice. Once I acknowledged she was right, I was able to make BIG changes to the way I taught problem solving in the classroom.
When I Finally Saw the Light
To give my students an opportunity to engage in more authentic problem solving which would lead them to use a larger variety of problem solving strategies, I decided to vary the activities and the way I approached problem solving with my students.
Problem Solving Activities
Here are seven ways to strategically reinforce problem solving skills in your classroom.

Seasonal Problem Solving
Many teachers use word problems as problem solving tasks. Instead, try engaging your students with non-routine tasks that look like word problems but require more than the use of addition, subtraction, multiplication, and division to complete. Seasonal problem solving tasks and daily challenges are a perfect way to celebrate the season and have a little fun too!
Cooperative Problem Solving Tasks
Go cooperative! If you’ve got a few extra minutes, have students work on problem solving tasks in small groups. After working through the task, students create a poster to help explain their solution process and then post their poster around the classroom. Students then complete a gallery walk of the posters in the classroom and provide feedback via sticky notes or during a math talk session.
Notice and Wonder
Before beginning a problem solving task, such as a seasonal problem solving task, conduct a Notice and Wonder session. To do this, ask students what they notice about the problem. Then, ask them what they wonder about the problem. This will give students an opportunity to highlight the unique characteristics and conditions of the problem as they try to make sense of it.
Want a better experience? Remove the stimulus, or question, and allow students to wonder about the problem. Try it! You’ll gain some great insight into how your students think about a problem.

Math Starters
Start your math block with a math starter, critical thinking activities designed to get your students thinking about math and provide opportunities to “sneak” in grade-level content and skills in a fun and engaging way. These tasks are quick, designed to take no more than five minutes, and provide a great way to turn-on your students’ brains. Read more about math starters here !
Create your own puzzle box! The puzzle box is a set of puzzles and math challenges I use as fast finisher tasks for my students when they finish an assignment or need an extra challenge. The box can be a file box, file crate, or even a wall chart. It includes a variety of activities so all students can find a challenge that suits their interests and ability level.
Calculators
Use calculators! For some reason, this tool is not one many students get to use frequently; however, it’s important students have a chance to practice using it in the classroom. After all, almost everyone has access to a calculator on their cell phones. There are also some standardized tests that allow students to use them, so it’s important for us to practice using calculators in the classroom. Plus, calculators can be fun learning tools all by themselves!
Three-Act Math Tasks
Use a three-act math task to engage students with a content-focused, real-world problem! These math tasks were created with math modeling in mind– students are presented with a scenario and then given clues and hints to help them solve the problem. There are several sites where you can find these awesome math tasks, including Dan Meyer’s Three-Act Math Tasks and Graham Fletcher’s 3-Acts Lessons .
Getting the Most from Each of the Problem Solving Activities
When students participate in problem solving activities, it is important to ask guiding, not leading, questions. This provides students with the support necessary to move forward in their thinking and it provides teachers with a more in-depth understanding of student thinking. Selecting an initial question and then analyzing a student’s response tells teachers where to go next.
Ready to jump in? Grab a free set of problem solving challenges like the ones pictured using the form below.
Which of the problem solving activities will you try first? Respond in the comments below.

Shametria Routt Banks

- Assessment Tools
- Content and Standards
- Differentiation
- Math & Literature
- Math & Technology
- Math Routines
- Math Stations
- Virtual Learning
- Writing in Math
You may also like...

2 Responses
This is a very cool site. I hope it takes off and is well received by teachers. I work in mathematical problem solving and help prepare pre-service teachers in mathematics.
Thank you, Scott! Best wishes to you and your pre-service teachers this year!
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
This site uses Akismet to reduce spam. Learn how your comment data is processed .
©2024 The Routty Math Teacher. All Rights Reserved. Designed by Ashley Hughes.
Privacy overview, grade level.
- Math tutors
- Math classes
- 1st Grade Math Worksheets
- 2nd Grade Math Worksheets
- 3rd Grade Math Worksheets
- 4th Grade Math Worksheets
- 5th Grade Math Worksheets
- 6th Grade Math Worksheets
- 7th Grade Math Worksheets
- 8th Grade Math Worksheets
- Knowledge Base
10 Strategies for Problem-Solving in Math
reviewed by Jo-ann Caballes
Updated on August 21, 2024

It’s not surprising that kids who lack problem-solving skills feel stuck in math class. Students who are behind in problem-solving may have difficulties identifying and carrying out a plan of action to solve a problem. Math strategies for problem-solving allow children to use a range of approaches to work out math problems productively and with ease. This article explores math problem-solving strategies and how kids can use them both in traditional classes and in a virtual classroom.
What are problem-solving strategies in math?
Problem-solving strategies for math make it easier to tackle math and work up an effective solution. When we face any kind of problem, it’s usually impossible to solve it without carrying out a good plan.In other words, these strategies were designed to make math for kids easier and more manageable. Another great benefit of these strategies is that kids can spend less time cracking math problems.
Here are some problem-solving methods:
- Drawing a picture or diagram (helps visualize the problem)
- Breaking the problem into smaller parts (to keep track of what has been done)
- Making a table or a list (helps students to organize information)
When children have a toolkit of math problem-solving strategies at hand, it makes it easier for them to excel in math and progress faster.
How to solve math problems?
To solve math problems, it’s worth having strategies for math problem-solving that include several steps, but it doesn’t necessarily mean they are failproof. They serve as a guide to the solution when it’s difficult to decide where and how to start. Research suggests that breaking down complex problems into smaller stages can reduce cognitive load and make it easier for students to solve problems. Essentially, a suitable strategy can help kids to find the right answers fast.
Here are 5 math problem-solving strategies for kids:
- Recognize the Problem
- Work up a Plan
- Carry Out the Plan
- Review the Work
- Reflect and Analyze
Understanding the Problem
Understanding the problem is the first step in the journey of solving it. Without doing this, kids won’t be able to address it in any way. In the beginning, it’s important to read the problem carefully and make sure to understand every part of it. Next, when kids know what they are asked to do, they have to write down the information they have and determine what essentially they need to solve.
Work Out a Plan
Working out a plan is one of the most important steps to solving math problems. Here, the kid has to choose a good strategy that will help them with a specific math problem. Outline these steps either in mind or on paper.
Carry Out the Plan
Being methodical at that stage is key. It involves following the plan and performing calculations with the correct operations and rules. Finally, when the work is done, the child can review and show their work to a teacher or tutor.
Review the Work
This is where checking if the answer is correct takes place. If time allows, children and the teacher can choose other methods and try to solve the same problem again with a different approach.
Reflect and Analyze
This stage is a great opportunity to think about how the problem was solved: did any part cause confusion? Was there a more efficient method? It’s important to let the child know that they can use the insights gained for future reference.
Ways to solve math problems
The ways to solve math problems for kids are numerous, but it doesn’t mean they all work the same for everybody. For example, some children may find visual strategies work best for them; some prefer acting out the problem using movements. Finding what kind of method or strategy works best for your kid will be extremely beneficial both for school performance and in real-life scenarios where they can apply problem-solving.
Online tutoring platforms like Brighterly offer personalized assistance, interactive tools, and access to resources that help to determine which strategies are best for your child. Expertise-driven tutors know how to guide your kid so they won’t be stuck with the same fallacies that interfere with effective problem-solving. For example, tutors can assist kids with drawing a diagram, acting a problem out with movement, or working backward. All of these ways are highly effective, especially with a trusted supporter by your side.

Your child will fall in love with math after just one lesson!
Choose 1:1 online math tutoring.

What are 10 strategies for solving math problems?
There are plenty of different problem-solving strategies for mathematical problems to help kids discover answers. Let’s explore 10 popular problem-solving strategies:
Understand the Problem
Figuring out the nature of math problems is the key to solving them. Kids need to identify what kind of issue this is (fraction problem, word problem, quadratic equation, etc.) and work up a plan to solve it.
Guess and Check
With this approach, kids simply need to keep guessing until they get the answer right. While this approach may seem irrelevant, it illustrates what the kid’s thinking process is.
Work It Out
This method encourages students to write down or say their problem-solving process instead of going straight to solving it without preparation. This minimizes the probability of mistakes.
Work Backwords
Working backward is a great problem-solving strategy to acquire a fresh perspective. It requires one to come up with a probable solution and decide which step to take to come to that solution.
A visual representation of a math problem may help kids to understand it in full. One way to visualize a problem is to use a blank piece of paper and draw a picture, including all of the aspects of the issue.
Find a Pattern
By helping students see patterns in math problems, we help them to extract and list relevant details. This method is very effective in learning shapes and other topics that need repetition.
It may be self-explanatory, but it’s quite helpful to ask, “What are some possible solutions to this issue?”. By giving kids time to think and reflect, we help them to develop creative and critical thinking.
Draw a Picture or Diagram
Instead of drawing the math problem yourself, ask the kid to draw it themselves. They can draw pictures of the ideas they have been taught to help them remember the concepts better.
Trial and Error Method
Not knowing clear formulas or instructions, kids won’t be able to solve anything. Ask them to make a list of possible answers based on rules they already know. Let them learn by making mistakes and trying to find a better solution.
Review Answers with Peers
It’s so fun to solve problems alongside your peers. Kids can review their answers together and share ideas on how each problem can be solved.
Help your kid achieve their full math potential
The best Brighterly tutors are ready to help with that.
Math problem-solving strategies for elementary students
5 problem-solving strategies for elementary students include:
Using Simple Language
Ask students to explain the problem in their own words to make sure they understand the problem correctly.
Using Visuals and Manipulatives
Using drawing and manipulatives like counters, blocks, or beads can help students grasp the issue faster.
Simplifying the Problem
Breaking the problem into a step-by-step process and smaller, manageable steps will allow students to find the solution faster.
Looking for Patterns
Identifying patterns in numbers and operations is a great strategy to help students gain more confidence along the way.
Using Stories

Turning math problems into stories will surely engage youngsters and make them participate more actively.
To recap, students need to have effective math problem-solving strategies up their sleeves. Not only does it help them in the classroom, but it’s also an essential skill for real-life situations. Productive problem-solving strategies for math vary depending on the grade. But what they have in common is that kids have to know how to break the issue into smaller parts and apply critical and creative thinking to solve it.
If you want your kid to learn how to thrive in STEM and apply problem-solving strategies to both math and real life, book a free demo lesson with Brighterly today! Make your child excited about math!

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

As adults, we take numbers for granted, but preschoolers and kindergartners have no idea what these symbols mean. Yet, we often demand instant understanding and flawless performance when we start teaching numbers to our children. If you don’t have a clue about how to teach numbers for kids, browse no more. You will get four […]
May 19, 2022

Teaching strategies aren’t something that is set in stone and continue to evolve every year. Even though traditional educational strategies like teachers teaching in front of the classroom seemed to work for decades with little to no adjustments, the digital age has brought along numerous challenges. Teaching methods for kids require new strategies, so educators […]
Math homework help for grade 1-8
Get the homework support your child needs!

Choose kid's grade
Math Program Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!
After-school math classes for grades 1-8
Personalized lessons for kids & teens.

Our after-school math curriculum includes
Related posts.

100 Silly Math Jokes and Math Puns for Kids!
In the wonderful world of numbers and logic, there’s no shortage of fun to be had! Welcome to Brighterly, where we believe that learning math should be as enjoyable as it is educational. So, here’s an assortment of 100 Silly Math Jokes and Math Puns for Kids that will surely get your little ones giggling […]
Jul 26, 2023

Common Core Math Standards
Math isn’t an easy field of knowledge — it requires that kids dig deeper into the subject, investigate, and try to understand topics (instead of simply memorizing them). Luckily, there are math wizards who can help untangle all the math complexities. After decades of solving math problems a certain way, teachers now use a new […]
Apr 05, 2022

15 Best Outdoor Math Games for Your Child
Math doesn’t come naturally to most kids. If your young one has trouble understanding math, taking lessons outside to do some outdoor math activities can be beneficial to break the learning barrier. In this piece, we will discover the 15 best outside math games and how they can be beneficial for both children and educators. […]
Want your kid to excel in math?
Kid’s grade

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More
Problem Solving Skills: Meaning, Examples & Techniques
Table of Contents
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. |
26 January 2021
Reading Time: 2 minutes
Do your children have trouble solving their Maths homework?
Or, do they struggle to maintain friendships at school?
If your answer is ‘Yes,’ the issue might be related to your child’s problem-solving abilities. Whether your child often forgets his/her lunch at school or is lagging in his/her class, good problem-solving skills can be a major tool to help them manage their lives better.
Children need to learn to solve problems on their own. Whether it is about dealing with academic difficulties or peer issues when children are equipped with necessary problem-solving skills they gain confidence and learn to make healthy decisions for themselves. So let us look at what is problem-solving, its benefits, and how to encourage your child to inculcate problem-solving abilities
Problem-solving skills can be defined as the ability to identify a problem, determine its cause, and figure out all possible solutions to solve the problem.
- Trigonometric Problems
What is problem-solving, then? Problem-solving is the ability to use appropriate methods to tackle unexpected challenges in an organized manner. The ability to solve problems is considered a soft skill, meaning that it’s more of a personality trait than a skill you’ve learned at school, on-the-job, or through technical training. While your natural ability to tackle problems and solve them is something you were born with or began to hone early on, it doesn’t mean that you can’t work on it. This is a skill that can be cultivated and nurtured so you can become better at dealing with problems over time.
Problem Solving Skills: Meaning, Examples & Techniques are mentioned below in the Downloadable PDF.
| 📥 |
|
Benefits of learning problem-solving skills
Promotes creative thinking and thinking outside the box.
Improves decision-making abilities.
Builds solid communication skills.
Develop the ability to learn from mistakes and avoid the repetition of mistakes.
Problem Solving as an ability is a life skill desired by everyone, as it is essential to manage our day-to-day lives. Whether you are at home, school, or work, life throws us curve balls at every single step of the way. And how do we resolve those? You guessed it right – Problem Solving.
Strengthening and nurturing problem-solving skills helps children cope with challenges and obstacles as they come. They can face and resolve a wide variety of problems efficiently and effectively without having a breakdown. Nurturing good problem-solving skills develop your child’s independence, allowing them to grow into confident, responsible adults.
Children enjoy experimenting with a wide variety of situations as they develop their problem-solving skills through trial and error. A child’s action of sprinkling and pouring sand on their hands while playing in the ground, then finally mixing it all to eliminate the stickiness shows how fast their little minds work.
Sometimes children become frustrated when an idea doesn't work according to their expectations, they may even walk away from their project. They often become focused on one particular solution, which may or may not work.
However, they can be encouraged to try other methods of problem-solving when given support by an adult. The adult may give hints or ask questions in ways that help the kids to formulate their solutions.
Encouraging Problem-Solving Skills in Kids
Practice problem solving through games.
Exposing kids to various riddles, mysteries, and treasure hunts, puzzles, and games not only enhances their critical thinking but is also an excellent bonding experience to create a lifetime of memories.
Create a safe environment for brainstorming
Welcome, all the ideas your child brings up to you. Children learn how to work together to solve a problem collectively when given the freedom and flexibility to come up with their solutions. This bout of encouragement instills in them the confidence to face obstacles bravely.
Invite children to expand their Learning capabilities
Whenever children experiment with an idea or problem, they test out their solutions in different settings. They apply their teachings to new situations and effectively receive and communicate ideas. They learn the ability to think abstractly and can learn to tackle any obstacle whether it is finding solutions to a math problem or navigating social interactions.
Problem-solving is the act of finding answers and solutions to complicated problems.
Developing problem-solving skills from an early age helps kids to navigate their life problems, whether academic or social more effectively and avoid mental and emotional turmoil.
Children learn to develop a future-oriented approach and view problems as challenges that can be easily overcome by exploring solutions.
About Cuemath
Cuemath, a student-friendly mathematics and coding platform, conducts regular Online Classes for academics and skill-development, and their Mental Math App, on both iOS and Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath Fee structure and sign up for a free trial.
Frequently Asked Questions (FAQs)
How do you teach problem-solving skills.
Model a useful problem-solving method. Problem solving can be difficult and sometimes tedious. ... 1. Teach within a specific context. ... 2. Help students understand the problem. ... 3. Take enough time. ... 4. Ask questions and make suggestions. ... 5. Link errors to misconceptions.
What makes a good problem solver?
Excellent problem solvers build networks and know how to collaborate with other people and teams. They are skilled in bringing people together and sharing knowledge and information. A key skill for great problem solvers is that they are trusted by others.
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Circle theorems
Here you will learn about circle theorems, including their application, proof, and how to use them to problem solve. You will learn how these theorems apply to angles formed by secant and tangent lines and how they apply to properties within a circle.
Students first learn about circle theorems in geometry where they learn how to apply the theorems to problem solve. Students use the concepts taught in precalculus and calculus as well as on standardized tests such as SATs and state assessments.
What are circle theorems?
Circle theorems verify properties that show relationships between angles formed by special lines and line segments and arcs within a circle. These theorems along with prior knowledge of other angle properties are used together to problem solve.
Let’s take a look in greater depth at the following:
Central angles
Chords of a circle.
- Circle and chord theorems
Subtended angles
Tangents of a circle.
Below is a summary of each theorem, along with a diagram. You need to remember all of these circle theorems and be able to describe each one in a sentence.
![problem solving examples in mathematics [FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Central angles are angles that have a vertex at the center of the circle and the sides of the angle are the radii of the circle.
Angle ABC is a central angle of circle B.

The degree measurement of a central angle is equal to the arc it intercepts.
Angle ABC=60^{\circ} and arc AC=60^{\circ}
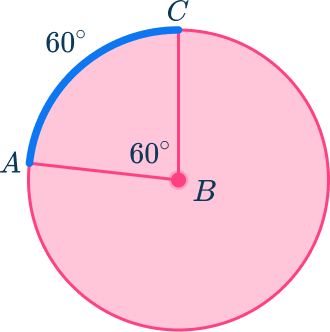
Inscribed angles are angles that have a vertex on the edge of the circle and the sides are chords of the circle. The measurement of the inscribed angle is \cfrac{1}{2} the measurement of the arc it intercepts.
Angle CEA is an inscribed angle (subtended angle) and the measurement of this inscribed angle is 30^{\circ} because it intercepts an arc that is 60^{\circ}.
The inscribed angle is always \cfrac{1}{2} the measurement of the arc it intercepts.
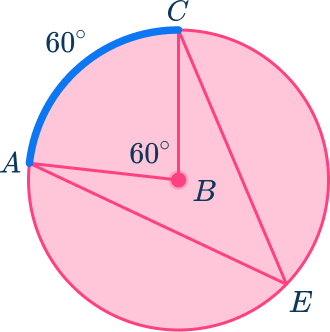
Remember: A subtended angle is an angle inside a circle that is created by two chords that meet at a point on the circle.
Step-by-step guide: Central Angle
Chords are line segments inside a circle that have endpoints on the edge of the circle. The longest chord in a circle is the diameter. Chords create situations within a circle that can help us to solve problems.

If BO is perpendicular to LM and if BP is perpendicular to NQ and BO is congruent in length to BP, you can conclude that LM is congruent to NQ.
Step-by-step guide: Chords of circles
Step-by-step guide: Circle and chord theorems
Subtended angles of a circle form inscribed angles. When inscribed angles intercept the same arc they are congruent.
Angle KGM, angle KEM and angle KLM all intercept the same arc, arc KM. If arc KM is 60^{\circ}, then angle KGM=30^{\circ}, angle KEM=30^{\circ} and angle KLM=30^{\circ}.
So, \text{ angle } KGM \approx \text { angle } KEM \approx \text{ angle } KLM.

Subtended angles can form inscribed quadrilaterals and triangles.
A quadrilateral can be inscribed in a circle, meaning that all four vertices are on the edge of the circle, if the opposite angles of a quadrilateral are supplementary (sum to 180^{\circ} ).
Inscribed quadrilaterals are also called cyclic quadrilaterals.

Quadrilateral HIJG is inscribed in circle F , so opposite angles must be supplementary.
Inscribed triangle ABC has one side as the diameter of the circle D.
Triangle ABC is a right triangle because the intercepted arc of angle A is semi-circle CB which is 180^{\circ}.
The measure of the intercepted arc is half the measure of the arc it intercepts, so in this case, angle A=90^{\circ}
This is also known as the semicircle theorem.

Step-by-step guide: Subtended angles
Tangent lines are lines that touch the circle at one point called the point of tangency.
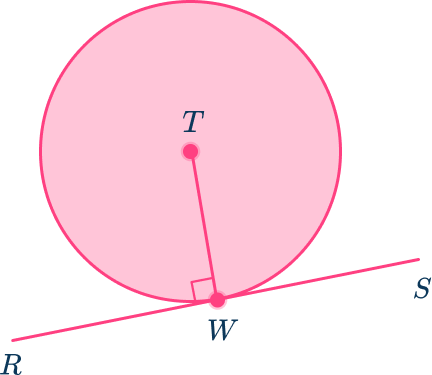
Line RS is tangent to circle T if and only if the line is perpendicular to the radius at point W. Point W is the point of tangency.
If two lines are tangent to a circle from an external point, the tangent lines will be congruent in length. The tangent line must be perpendicular to the radius at the point of tangency, so using congruent triangles, you can prove that the tangent lines are congruent.
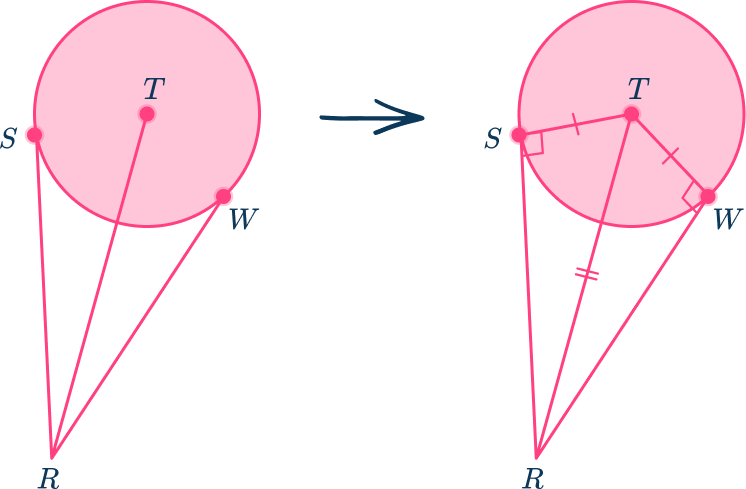
Through HL (Hypotenuse Leg) you can prove that triangle STR is congruent to triangle WTR.
Therefore, by CPTPC (Corresponding parts of congruent triangles are congruent) you can conclude that segment SR is congruent to segment WR, which are the tangent segments.
Step-by-step guide: Tangents of a circle
Common Core State Standards
How does this apply to geometry?
- High School Geometry – Circles (HSG-C.A.2) Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.
How to use circle theorems to solve problems
There are several ways to apply circle theorems to problem solve. For more specific step-by-step guides, check out the pages linked in the “What are circle theorems?” section above or read through the examples below.
In order to problem solve using circle theorems:
Recall the theorem.
Solve the problem.
Circle theorem examples
Example 1: central angle theorem.
Find the measure of angle A in circle D.
Angle A is an inscribed angle and is half the measure of the arc it intercepts.
2 Solve the problem.
Arc PC is the intercepted arc of angle A. Arc PC=42^{\circ} and angle A is an inscribed angle.
Angle A=21^{\circ}
Find the measure of arc WV in circle R.
Angle Angle W is an inscribed angle and is half the measure of the arc it intercepts.
Also, chord WV is congruent to chord WZ so the arcs they intercept are also congruent, meaning that arc WV is congruent to arc WZ.
Since angle W is 32^{\circ}, arc ZV is double that measurement.
32 \times 2=64
Arc ZV=64^{\circ}
The measurement of a full circle is 360^{\circ}, subtract 64^{\circ} from that, 360-64=296.
That means that the two congruent arcs, arc WZ and arc WV together equal 296^{\circ}.
Since both arcs are congruent, to find the measure of one of them divide 296 in half.
296 \div 2=148, arc WV=148^{\circ}
Find the value of x.
Segment LM and segment LN are tangent segments of circle P. When two lines come from the same external point and are tangent to the same circle, the tangent lines (segments) are congruent. In this case, LM is congruent to LN.
Since LN and LM are congruent, they are also equal.
LM=5x-9 and LN=3x+7
\begin{aligned}& 5 x-9=3 x+7 \\\\ & 2 x=16 \\\\ & x=8 \end{aligned}
In circle E, find the value of angle G.
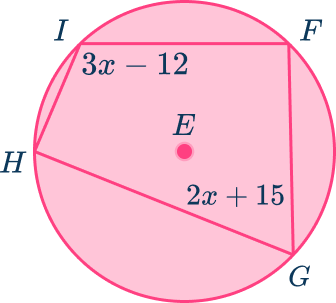
Quadrilateral HIFG is inscribed in circle E. Inscribed quadrilaterals have opposite angles that are supplementary (sum to 180 ). Angle I \, + angle G=180
Since angle I \, + angle G=180 and angle I=3x-12 and angle G= 2x+15, you can write and solve the equation:
\begin{aligned}& 3 x-12=2 x+15 \\\\ & x=27 \end{aligned}
Since x=27, substitute that value in for x,
Angle G=2x+15=2(27)+15=69
Angle G=69^{\circ}
Triangle TQR is inscribed in circle P and TQ=QR=10. Find the length of the diameter, TR.

Angle Q is an inscribed angle of circle P and also an angle of the inscribed triangle TQR. The inscribed angle is half the measure of the arc it intercepts and in this case, angle Q intercepts semi-circle TR.
The semi-circle is 180^{\circ} , so angle Q=\cfrac{1}{2} \times 180=90. Angle Q is a right angle, so triangle TQR is an inscribed right triangle.
Using the Pythagorean theorem, you can solve for the diameter which is also the hypotenuse of the right triangle.
Pythagorean theorem, a^2+b^2=c^2 where TQ and RQ are a and b.
\begin{aligned}& 10^2+10^2=c^2 \\\\ & 100+100=c^2 \\\\ & 200=c^2 \\\\ & 14.1=c \text { (rounded to } 1 \text { decimal place }) \end{aligned}
The diameter, TR, length is 14.1 units.
In circle C, the diameter is 14 units and JK is 3 units. Find the length of GH.

In circle C, since the diameter is 14 units the radius is half of that. So, the radius length is 7 units. The diameter is also perpendicular to GH, so it also bisects GH meaning that it cuts it in half, GJ=JH.
Triangle CJG is a right triangle because the diameter is perpendicular to GH forming a right triangle.
Using the fact that CJG is a right triangle, apply the Pythagorean theorem to find the missing side, JG.
CG is the radius of the circle which is 7 units.
CK is also a radius of the circle which is 7 units. If you subtract JK from CK you get the value of CJ (given the information that JK=3 units).
Using the Pythagorean theorem, a^2+b^2=c^2 where CJ is a and the radius (CG) is c.
\begin{aligned}& 4^2+b^2=7^2 \\\\ & 16+b^2=49 \\\\ & b^2=33 \\\\ & b \approx 5.7 \text { (rounded to } 1 \text { decimal place) } \end{aligned}
GJ=5.7 which means that JH=5.7 So, GH=5.7+5.7=11.4
Teaching tips for circle theorems
- Provide opportunity for students to discover the theorems and make conjectures using compasses and protractors.
- Use digital platforms such as Desmos so students can investigate strategies to problem solve using the circle theorems.
- Have students use online platforms such as Khan Academy which contain tutorials created by math tutors to practice exam questions and to prepare for the SAT.
- Although worksheets provide an opportunity for students to practice skills, using digital platforms that focus on gameplay is more effective in engaging students.
Easy mistakes to make
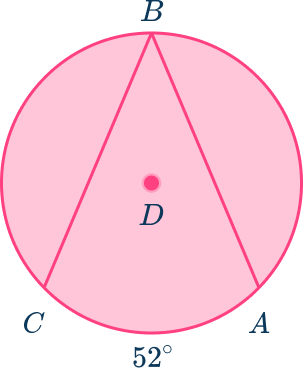
Practice circle theorems questions
1. In circle B, find the measure of angle ABC.
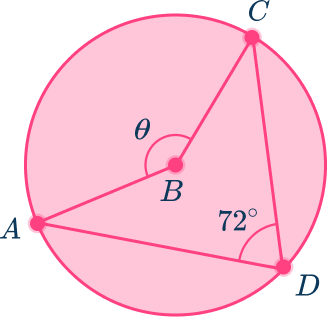
Angle D is an inscribed angle and intercepts arc AC. Inscribed angles are half the measure of the arcs they intercept so arc AC=72 \times 2=144^{\circ}.
Angle ABC is a central angle and the central angle is equal in measure to the arc it intercepts. So, if arc AC is 144^{\circ}, then angle ABC=144^{\circ}.
2. Find the measure of \theta.

Inscribed angles that intercept the same arc are congruent to each other.
Angle DAC and angle CBD are inscribed angles that both intercept arc CD. This means that angle DAC is equal to angle CBD.
So, if angle DAC=11^{\circ}, then angle CBD=11^{\circ}.
3. Triangle ABC is inscribed in circle D. Find the measure of ϴ.
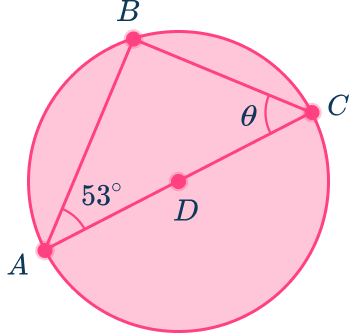
AC is the diameter of circle D and the inscribed angle ABC intercepts semi-circle AC. The semi-circle is 180^{\circ}.
Inscribed angles are half the measure of the arcs they intercept. So, angle ABC=90^{\circ}, angles in a triangle sum to 180^{\circ}.
To find \theta (angle ACB ) =180-(90+53)=37^{\circ}.
4. Quadrilateral ABCD is inscribed in the circle, find the value \theta.

Quadrilaterals inscribed in circles have interior angles where the opposite angles are supplementary (sum to 180^{\circ} ).
In this case, angle D \, + angle B=180^{\circ}, so to find the missing angle, 63^{\circ}+\theta=180^{\circ}, \theta=117^{\circ}.
5. In circle C, \, GH=16 units and CJ=6 units, find the length of the diameter DK.
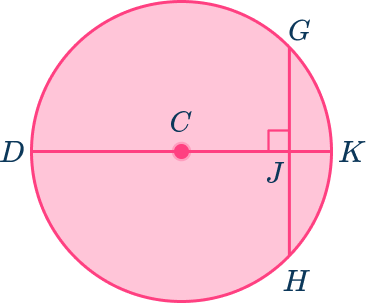
Since the diameter is perpendicular to chord GH it also bisects chord GH so GJ=JH. \, GH=16 so half of that is 8, \, GJ=8 and JH=8.
Draw in a radius to make a right triangle and use the Pythagorean theorem.

Triangle GJC is a right triangle where sides CJ=6, \, GJ=8 and the hypotenuse is CG (also the radius). Using the Pythagoras’ theorem, 6^2+8^2=c^2, 36+64=c^2, 100=c^2, \mathrm{~c}=10.
Since the radius is equal to 10, the diameter is equal to 2 \times 10=20.
6. Find MP in circle L.
Two lines that are coming from the same external point and are tangent to the same circle are congruent. In this case, MP=NP, so the equation to solve for x is,
Substitute the value of x into the algebraic expression that represents MP. \, M P=6 x-3,6(10)-3=57.
Circle theorem FAQs
Arc length is the distance between the two endpoints of an arc. The arc length is part of the circumference of a circle which should not be confused with the measure of an arc. An arc can have a degree measure because it is a portion of the full 360^{\circ} of a circle and it can also have length.

The definition of a circle is a locus of points. This means it is the set of all points that are the same distance from a fixed point. The distance of the set of points from a fixed point is the radius length of a circle and the fixed point is the centre of the circle.
Yes, sometimes with the different circles, you need to use trigonometry to find the size of the angles within the triangle.
The next lessons are
- Types of data
- Averages and range
- Representing data
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!
Privacy Overview
Problem Solving
Handbooks, special collections, etc.
- Brown, S. I.: M.I. Walter (1990). The Art of Problem Posing . Hillsdale, New Jersey, Hove and London: Lawrence Erlbaum Associates, Publishers
- Karp, A., & Wasserman, N. (2015). Mathematics in Middle and Secondary School. A problem solving approach . Charlotte, NC: Information Age.
- Krulik, S. & Reys, R. E. (1980). Problem Solving in School Mathematics, 1980 Yearbook of the National Council of Teachers of Mathematics , Reston, VA: NCTM.
- Liljedahl. P., Santos-Trigo, M., Malaspina, U., Bruder, R. (2016). Problem Solving in Mathematics Education . Springer.
- Newell, A; H. Simon (1972). Human problem solving . Englewood Cliffs, NJ: Prentice Hall.
- Polya, G. (1973). How to solve it . Princeton, NJ: Princeton University Press.
- Polya, G. (1981). Mathematical discovery . New York: John Wiley & Sons.
- Polya, G. (1954). Mathematics and plausible reasoning; Vol. 1. Introduction and analogy in mathematics; Vol. 2. Patterns of plausible inference . Princeton, NJ: Princeton University Press.
- Schoenfeld, A. (1985). Mathematical problem solving . New York, NY: Academic Press.
- Schoenfeld, A. (1992). Learning to think mathematically: problem solving, metacognition, and sense-making in mathematics. In D. A. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 334-370). Reston, VA: NCTM.
- Watson, A., Mason, J. (2005). Mathematics as a constructive activity. Learners Generating examples. Mahwah, NJ – London: Lawrence Erlbaum Associates, Publishers.
- Watson, A., Ohtani, M. (2015). Task design in mathematics education . Springer.
Papers and chapters
- Bernardo, A. B. (2001). Analogical problem construction and transfer in mathematical problem solving. Educational Psychology , 21(2), 137-150.
- Cai, J., Hwang, S., Jiang, C., & Silber, S. (2015). Problem posing research in mathematics: Some answered and unanswered questions. In F.M. Singer, N. Ellerton, & J. Cai (Eds.), Mathematical problem posing: From research to effective practice (pp. 3–34). Springer.
- Cooney, Thomas J. (1985). A Beginning Teacher's View of Problem Solving. Journal for Research in Mathematics Education, Vol. 16, No. 5, 324-336.
- English, L. D. & Gainsburg, J. (2016). Problem solving in a 21st- Century mathematics education.In L. D. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (pp. 313–335). NY: Routledge.
- Kilpatrick, J. (1978) Variables and methodologies in research on problem solving. In L. Hartfield (Ed.), Mathematical problem solving . Columbus, OH: ERIC, 7-20.
- Kilpatrick, J. (1985) A retrospective account of the past twenty-five years of research on teaching mathematical problem solving. In E.A.Silver (ed), Teaching and learning mathematical problem solving: Multiple research perspectives (1-16). Hillsdale, NJ: Lawrence Erlbaum.
- Kilpatrick, J. (1987). Problem formulating: Where do good problem come from? In A.H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 123–147). Hillsdale,NJ: Erlbaum.
- Novick, L., & Holyoak, K. (1991). Mathematical problem solving by analogy. Journal of Experimental Psychology, 17(3), 398–415.
- Santos-Trigo, M. (2007). Mathematical problem solving: An evolving research and practice domain. ZDM—The International Journal on Mathematics Education , 39(5, 6): 523–536.
- Schoenfeld, A. H. (1982). Some thoughts on problem-solving research and mathematics education. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 27–37). Philadelphia: Franklin Institute Press.
- Schoenfeld, A. (1987). What’s all the fuss about metacognition. In Cognitive Science and Mathematics Education /edited by A.Schoenfeld. New Jersey-London: Lawrence Erlbaum Associates, Publishers.
- Schoenfeld, A. (1989).Explorations of Students' Mathematical Beliefs and Behavior Journal for Research in Mathematics Education , Vol. 20, No. 4, 338-355.
- Silver, E. (1982). Knowledge organization and mathematical problem solving. In F. K. Lester &J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 15–25). Philadelphia: Franklin Institute Press.
- Silver, E.; J. Mamona-Downs, S. Leung; P. Kenney (1996). Posing mathematical problems: an exploratory study. Journal for Research in Mathematics Education , 27 (3), 293-309.
- Singer, F., Ellerton, N., & Cai, J. (2013). Problem posing research in mathematics education: New questions and directions. Educational Studies in Mathematics, 83(1), 9–26.
- Stanic G; J. Kilpatrick (1989). Historical Perspectives on problem solving in the mathematics curriculum. In R. Charles & E. Silver (Eds.), The teaching and assessing of mathematical problem solving. Reston, VA: National Council of Teachers of Mathematics, 1-22.
Faculty publications
- Karp, A. (2002). Math problems in blocks: How to write them and why. PRIMUS , 12(4), 289-304.
- Karp, A. (2006). And now put aside your pens and calculators...: On mental problem solving in the high school mathematics lesson. Focus on Learning Problems in Mathematics , 28(1), 23-36.
- Karp, A., & Marcantonio, N. (2010). “The number which is always positive, even if it is negative” (On studying the concept of absolute value). Investigations in Mathematics Learning, 2(3), 43-68.
- Karp, A. (2015). Problems in old Russian textbooks: How they were selected In K. Bjarnadottir et al. (Eds.) “ Dig where you stand” 3 (pp. 203-218). Uppsala: Uppsala University
A few TC dissertations
- DeGraaf, E. (2015). What makes a good problem? Perspectives of students, teachers, and mathematicians.
- McCarron, Craig S. (2011). Comparing the Effects of Metacognitive Prompts and Contrasting Cases on Transfer in Solving Algebra Problems.
- Nahornick, Ashley. (2014). The effect of group dynamics on high-school students' creativity and problem-solving strategies with investigative open-ended non-routine problems.
- Smith, J.P. (1973). The effect of general versus specific heuristics in mathematical problem solving tasks .
- Tjoe, Hartono Hardi (2011). Which approaches do students prefer? Analyzing the mathematical problem solving behavior of mathematically gifted students .
Members of the TSG
Alexander Karp
Philip Smith
Program Director : Professor Alexander Karp
Teachers College, Columbia University 323 Thompson
Phone: (212) 678-3381 Fax: (212) 678-8319
Email: tcmath@tc.edu

Mathematics as a Complex Problem-Solving Activity
By jacob klerlein and sheena hervey, generation ready.
By the time young children enter school they are already well along the pathway to becoming problem solvers. From birth, children are learning how to learn: they respond to their environment and the reactions of others. This making sense of experience is an ongoing, recursive process. We have known for a long time that reading is a complex problem-solving activity. More recently, teachers have come to understand that becoming mathematically literate is also a complex problem-solving activity that increases in power and flexibility when practiced more often. A problem in mathematics is any situation that must be resolved using mathematical tools but for which there is no immediately obvious strategy. If the way forward is obvious, it’s not a problem—it is a straightforward application.
Mathematicians have always understood that problem-solving is central to their discipline because without a problem there is no mathematics. Problem-solving has played a central role in the thinking of educational theorists ever since the publication of Pólya’s book “How to Solve It,” in 1945. The National Council of Teachers of Mathematics (NCTM) has been consistently advocating for problem-solving for nearly 40 years, while international trends in mathematics teaching have shown an increased focus on problem-solving and mathematical modeling beginning in the early 1990s. As educators internationally became increasingly aware that providing problem-solving experiences is critical if students are to be able to use and apply mathematical knowledge in meaningful ways (Wu and Zhang 2006) little changed at the school level in the United States.
“Problem-solving is not only a goal of learning mathematics, but also a major means of doing so.”
(NCTM, 2000, p. 52)
In 2011 the Common Core State Standards incorporated the NCTM Process Standards of problem-solving, reasoning and proof, communication, representation, and connections into the Standards for Mathematical Practice. For many teachers of mathematics this was the first time they had been expected to incorporate student collaboration and discourse with problem-solving. This practice requires teaching in profoundly different ways as schools moved from a teacher-directed to a more dialogic approach to teaching and learning. The challenge for teachers is to teach students not only to solve problems but also to learn about mathematics through problem-solving. While many students may develop procedural fluency, they often lack the deep conceptual understanding necessary to solve new problems or make connections between mathematical ideas.
“A problem-solving curriculum, however, requires a different role from the teacher. Rather than directing a lesson, the teacher needs to provide time for students to grapple with problems, search for strategies and solutions on their own, and learn to evaluate their own results. Although the teacher needs to be very much present, the primary focus in the class needs to be on the students’ thinking processes.”
(Burns, 2000, p. 29)
Learning to problem solve
To understand how students become problem solvers we need to look at the theories that underpin learning in mathematics. These include recognition of the developmental aspects of learning and the essential fact that students actively engage in learning mathematics through “doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning” (Copley, 2000, p. 29). The concept of co-construction of learning is the basis for the theory. Moreover, we know that each student is on their unique path of development.
Beliefs underpinning effective teaching of mathematics
- Every student’s identity, language, and culture need to be respected and valued.
- Every student has the right to access effective mathematics education.
- Every student can become a successful learner of mathematics.
Children arrive at school with intuitive mathematical understandings. A teacher needs to connect with and build on those understandings through experiences that allow students to explore mathematics and to communicate their ideas in a meaningful dialogue with the teacher and their peers.
Learning takes place within social settings (Vygotsky, 1978). Students construct understandings through engagement with problems and interaction with others in these activities. Through these social interactions, students feel that they can take risks, try new strategies, and give and receive feedback. They learn cooperatively as they share a range of points of view or discuss ways of solving a problem. It is through talking about problems and discussing their ideas that children construct knowledge and acquire the language to make sense of experiences.
Students acquire their understanding of mathematics and develop problem-solving skills as a result of solving problems, rather than being taught something directly (Hiebert1997). The teacher’s role is to construct problems and present situations that provide a forum in which problem-solving can occur.
Why is problem-solving important?
Our students live in an information and technology-based society where they need to be able to think critically about complex issues, and “analyze and think logically about new situations, devise unspecified solution procedures, and communicate their solution clearly and convincingly to others” (Baroody, 1998). Mathematics education is important not only because of the “gatekeeping role that mathematics plays in students’ access to educational and economic opportunities,” but also because the problem-solving processes and the acquisition of problem-solving strategies equips students for life beyond school (Cobb, & Hodge, 2002).
The importance of problem-solving in learning mathematics comes from the belief that mathematics is primarily about reasoning, not memorization. Problem-solving allows students to develop understanding and explain the processes used to arrive at solutions, rather than remembering and applying a set of procedures. It is through problem-solving that students develop a deeper understanding of mathematical concepts, become more engaged, and appreciate the relevance and usefulness of mathematics (Wu and Zhang 2006). Problem-solving in mathematics supports the development of:
- The ability to think creatively, critically, and logically
- The ability to structure and organize
- The ability to process information
- Enjoyment of an intellectual challenge
- The skills to solve problems that help them to investigate and understand the world
Problem-solving should underlie all aspects of mathematics teaching in order to give students the experience of the power of mathematics in the world around them. This method allows students to see problem-solving as a vehicle to construct, evaluate, and refine their theories about mathematics and the theories of others.
Problems that are “Problematic”
The teacher’s expectations of the students are essential. Students only learn to handle complex problems by being exposed to them. Students need to have opportunities to work on complex tasks rather than a series of simple tasks devolved from a complex task. This is important for stimulating the students’ mathematical reasoning and building durable mathematical knowledge (Anthony and Walshaw, 2007). The challenge for teachers is ensuring the problems they set are designed to support mathematics learning and are appropriate and challenging for all students. The problems need to be difficult enough to provide a challenge but not so difficult that students can’t succeed. Teachers who get this right create resilient problem solvers who know that with perseverance they can succeed. Problems need to be within the students’ “Zone of Proximal Development” (Vygotsky 1968). These types of complex problems will provide opportunities for discussion and learning.
Students will have opportunities to explain their ideas, respond to the ideas of others, and challenge their thinking. Those students who think math is all about the “correct” answer will need support and encouragement to take risks. Tolerance of difficulty is essential in a problem-solving disposition because being “stuck” is an inevitable stage in resolving just about any problem. Getting unstuck typically takes time and involves trying a variety of approaches. Students need to learn this experientially. Effective problems:
- Are accessible and extendable
- Allow individuals to make decisions
- Promote discussion and communication
- Encourage originality and invention
- Encourage “what if?” and “what if not?” questions
- Contain an element of surprise (Adapted from Ahmed, 1987)
“Students learn to problem solve in mathematics primarily through ‘doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning.”
(Copley, 2000, p. 29)
“…as learners investigate together. It becomes a mini- society – a community of learners engaged in mathematical activity, discourse and reflection. Learners must be given the opportunity to act as mathematicians by allowing, supporting and challenging their ‘mathematizing’ of particular situations. The community provides an environment in which individual mathematical ideas can be expressed and tested against others’ ideas.…This enables learners to become clearer and more confident about what they know and understand.”
(Fosnot, 2005, p. 10)
Research shows that ‘classrooms where the orientation consistently defines task outcomes in terms of the answers rather than the thinking processes entailed in reaching the answers negatively affects the thinking processes and mathematical identities of learners’ (Anthony and Walshaw, 2007, page 122).
Effective teachers model good problem-solving habits for their students. Their questions are designed to help children use a variety of strategies and materials to solve problems. Students often want to begin without a plan in mind. Through appropriate questions, the teacher gives students some structure for beginning the problem without telling them exactly what to do. In 1945 Pólya published the following four principles of problem-solving to support teachers with helping their students.
- Understand and explore the problem
- Find a strategy
- Use the strategy to solve the problem
- Look back and reflect on the solution
Problem-solving is not linear but rather a complex, interactive process. Students move backward and forward between and across Pólya’s phases. The Common Core State Standards describe the process as follows:
“Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary”. (New York State Next Generation Mathematics Learning Standards 2017).
Pólya’s Principals of Problem-Solving
Students move forward and backward as they move through the problem-solving process.
The goal is for students to have a range of strategies they use to solve problems and understand that there may be more than one solution. It is important to realize that the process is just as important, if not more important, than arriving at a solution, for it is in the solution process that students uncover the mathematics. Arriving at an answer isn’t the end of the process. Reflecting on the strategies used to solve the problem provides additional learning experiences. Studying the approach used for one problem helps students become more comfortable with using that strategy in a variety of other situations.
When making sense of ideas, students need opportunities to work both independently and collaboratively. There will be times when students need to be able to work independently and other times when they will need to be able to work in small groups so that they can share ideas and learn with and from others.
Getting real
Effective teachers of mathematics create purposeful learning experiences for students through solving problems in relevant and meaningful contexts. While word problems are a way of putting mathematics into contexts, it doesn’t automatically make them real. The challenge for teachers is to provide students with problems that draw on their experience of reality, rather than asking them to suspend it. Realistic does not mean that problems necessarily involve real contexts, but rather they make students think in “real” ways.
Planning for talk
By planning for and promoting discourse, teachers can actively engage students in mathematical thinking. In discourse-rich mathematics classes, students explain and discuss the strategies and processes they use in solving mathematical problems, thereby connecting their everyday language with the specialized vocabulary of mathematics.
Students need to understand how to communicate mathematically, give sound mathematical explanations, and justify their solutions. Effective teachers encourage their students to communicate their ideas orally, in writing, and by using a variety of representations. Through listening to students, teachers can better understand what their students know and misconceptions they may have. It is the misconceptions that provide a window into the students’ learning process. Effective teachers view thinking as “the process of understanding,” they can use their students’ thinking as a resource for further learning. Such teachers are responsive both to their students and to the discipline of mathematics.
“Mathematics today requires not only computational skills but also the ability to think and reason mathematically in order to solve the new problems and learn the new ideas that students will face in the future. Learning is enhanced in classrooms where students are required to evaluate their own ideas and those of others, are encouraged to make mathematical conjectures and test them, and are helped to develop their reasoning skills.”
(John Van De Walle)
“Equity. Excellence in mathematics education requires equity—high expectations and strong support for all students.”
How teachers organize classroom instruction is very much dependent on what they know and believe about mathematics and on what they understand about mathematics teaching and learning. Teachers need to recognize that problem-solving processes develop over time and are significantly improved by effective teaching practices. The teacher’s role begins with selecting rich problem-solving tasks that focus on the mathematics the teacher wants their students to explore. A problem-solving approach is not only a way for developing students’ thinking, but it also provides a context for learning mathematical concepts. Problem-solving allows students to transfer what they have already learned to unfamiliar situations. A problem-solving approach provides a way for students to actively construct their ideas about mathematics and to take responsibility for their learning. The challenge for mathematics teachers is to develop the students’ mathematical thinking process alongside the knowledge and to create opportunities to present even routine mathematics tasks in problem-solving contexts.
Given the efforts to date to include problem-solving as an integral component of the mathematics curriculum and the limited implementation in classrooms, it will take more than rhetoric to achieve this goal. While providing valuable professional learning, resources, and more time are essential steps, it is possible that problem-solving in mathematics will only become valued when high-stakes assessment reflects the importance of students’ solving of complex problems.
- Our Mission
There has been an error with the video.
Using a Plan of Attack for Math Problem-Solving
Spending the majority of their time modeling problems and making sense of relationships in math can help students move beyond a surface-level grasp.
At every grade level, math teachers in the Success Academy Charter Schools Network in New York City ask students to spend the lion’s share of their time during math lessons deeply examining the question they are being asked to solve. Students start by asking themselves questions like, “What are the mathematical relationships in the problem?” “What is this problem asking me to do?” and “How can I model my thinking?” Every classroom even has a formula—a problem-solving plan for math, printed out and displayed on the wall—called the “Plan of Attack,” which includes three parts: using 80 percent of the allotted time to conceptualize the question by reading the problem multiple times, then modeling the relationships and actions in the problems; 10 percent to answer the question by determining a strategy they will use to solve it and then computing; and finally double-checking in the last 10 percent of their time—by rereading the problem, evaluating their own reasoning, and checking computations for accuracy.
First-grade teacher Evelyn Gonzales and eighth-grade teacher Fei Liu both reinforce this strategy during precious class time by working through the problem as a whole with their students first, emphasizing the importance of this step before rushing in to solve. As a result, their students develop a much stronger understanding of the mathematical concepts at hand. “In my classroom, I don’t really care for the answer,” says Liu. “They can double-check once they have the answer. What we really need to focus on is why we set the things up, so that when they see a problem, they have an idea of where to start to think.”
The network led the state for math test scores in the 2023–2024 school year, with with 49 percent of Black and 55 percent of Hispanic students earning fours, the highest possible mark.
See all of Edutopia’s coverage of Success Academy Charter Schools to learn more about the network.
Success Academy Charter Schools

- How It Works
- In Center Learning
- Online Tutoring
- The Mathnasium Method
- How We Compare
- Homework Help
- Our Instructors
- Our History
- Overview of Programs
- Summer at Mathnasium
- Early Childhood
- Elementary School
- Middle School
- High School
- Own a Mathnasium

- (813) 655-6284
- About this Center
- Promotions & Special Offers
- Hours & Holiday Information
- Careers @ this Center
- Enrolled Student & Parent Center
- Request Info

- Schedule Free Assessment
What Is PEMDAS? Explained for Elementary School Students

Math expressions can be confusing, especially when they consist of several different operations.
Which one should you do first, and which comes next?
Whether you're just starting to learn the order of operations, or you are helping your student with their homework, PEMDAS can make solving most math expressions a piece of cake.
Read on to find everything you need to know about PEMDAS: when and how we use it, tips for remembering it, examples to practice with, and a fun quiz to test your skills.
Find Top-Rated K-12 Math Tutors Near You
What Is PEMDAS?
PEMDAS is an acronym that helps us remember the order of operations in math .
It stands for:
- P arentheses
- M ultiplication
- S ubtraction
We use this acronym in the United States.
In other countries, you are more likely to encounter different, but similar acronyms:
- In the UK, Australia, India, Pakistan, and Bangladesh , this order is known as BODMAS (Brackets, Orders, Division, Multiplication, Addition, Subtraction)
- In Canada , it's called BEDMAS (Brackets, Exponents, Division, Multiplication, Addition, Subtraction).
When Do We Use PEMDAS?
We use PEMDAS when we come across math problems with multiple operations in one expression.
To solve these expressions correctly, we follow PEMDAS.
This means we handle:
- Parentheses first
- Exponents second
- Multiplication and division next
- Addition and subtraction last
Let’s put PEMDAS into action with a simple example:
6 + 3 x (2 + 1)
Without PEMDAS, we may make a mistake and start solving the expression from left to right like so:
9 x (2 + 1) --> 9 x 3 = 27
Using PEMDAS, we can remember that we need to start with parenthesis, then do the multiplication, and finally do the addition, like so:
First, we solve the expression inside the parentheses:
(2 + 1) = 3
After we’ve solved the parentheses, our expression looks like this: 6 + 3 x 3
Then, we do the multiplication:
3 x 3 = 9
Now, our expression looks like this: 6 + 9
Finally, when we add the two, we get:
So, the correct answer is 15.
Let's see all that in one sequence:
6 + 3 x (2 + 1) --> 6 + 3 x 3 --> 6 + 9 = 15
A Trick to Memorizing PEMDAS Rules
Sometimes, students struggle to memorize the order of operations in PEMDAS.
To make it easier, they use playful mnemonics . A mnemonic is a tool that helps you remember something by using a pattern of letters, ideas, or associations.
One popular mnemonic for PEMDAS is: " Please Excuse My Dear Aunt Sally ." Each word in this phrase helps remember the steps:
- P lease ( Parentheses )
- E xcuse ( E xponents)
- M y ( M ultiplication)
- D ear ( D ivision)
- A unt ( A ddition)
- S ally ( S ubtraction)
Examples of PEMDAS
Here are a couple more challenging examples to help you understand how to use order of operations better.
3 2 + 4 x 5 + 22
Let's break it down using PEMDAS:
1. First , we do the exponent (in this case multiply 3 by itself):
So, the expression becomes:
9 + 4 x 5 + 22
2. Next , multiply
4 x 5 = 20
3. Finally , add:
So, the answer is 51.
12 2 – 4 x 2 ÷ (3 + 1)
Let's use PEMDAS step-by-step:
1. First, do the addition inside the parentheses:
(3 + 1) = 4
12 2 – 4 x 2 ÷ 4
2. Next, do the exponent:
144 – 4 x 2 ÷ 4
3. Then, multiply:
144 – 8 ÷ 4
4. After this, divide:
5. Finally, subtract:
144 – 2 = 142
So, the answer is 142.
Quiz Time! Recap What You've Learned About PEMDAS
Ready to show what you’ve learned about PEMDAS? Try our 2-minute quiz.
PEMDAS FAQs
PEMDAS is especially helpful when we’re working with more complicated math problems. Here are a couple of tricky examples to help you understand better.
Can PEMDAS be applied to all mathematical problems?
Yes, PEMDAS is a universal rule for solving mathematical expressions with multiple operations. It ensures consistency and accuracy in calculations.
Can the order of operations change in different countries?
No, PEMDAS (or its equivalents, such as BODMAS, BEDMAS, etc.) is universally recognized and used in mathematical operations worldwide.
How does PEMDAS help us in everyday life?
Whether you’re doing a science experiment, budgeting, or solving puzzles that involve mathematical expressions, PEMDAS helps ensure that anyone, anywhere in the world can look at an expression and know how to simplify it.
Learn & Master Elementary School Math at Mathnasium
Mathnasium’s specially trained elementary school tutors work with students of all skill levels to help them master any math subject and topic including PEMDAS.
Discover our approach to elementary school tutoring :
- 1 st Grade Math Tutors
- 2 nd Grade Math Tutors
- 3 rd Grade Math Tutors
- 4 th Grade Math Tutors
- 5 th Grade Math Tutors
At Mathnasium, we evaluate each student’s current skills and consider their unique academic goals to develop personalized learning plans that will put them on the best path towards math excellence.
Whether your student is looking to catch up, keep up, or get ahead in your math class, find a Mathnasium Learning Center near you, schedule an assessment, and enroll them today!
Find a Math Tutor Near You
Related Articles
How do we measure rainfall a fun diy guide.
Discover how we measure rainfall, why it is important, what units and math we use for measuring, and how you can set up your own rain gauge at home.
Geometric Transformations – Definitions, Types, Examples, and Quiz
In this middle- and high-school-friendly introduction to geometric transformations, you’ll find simple definitions, examples, and a fun quiz. Enjoy!
What Is Rotation in Math? Definition, Examples & How-to Guide
Find simple definitions, key terms, solved examples, and practice materials in our middle-school-friendly guide to rotation in math.

- Mathnasium Method
- International Locations
- Our Results
- About Mathnasium
- Own a Franchise
- Math Tutors Near Me
- Accessibility
- Privacy Policy
- Cookie Settings
- Terms of Use
Contact Us ×
By clicking "Submit," you agree to receive recurring advertising emails, text messages and calls from Mathnasium and its independently owned learning centers about our offerings to the phone number/email provided above, including calls and texts placed using an automatic telephone dialing system. Consent to receive advertising text messages and calls is not required to purchase goods or services. Message frequency varies. Message and data rates may apply. Reply STOP to no longer receive messages. Email [email protected] for assistance. By clicking "Submit," you also consent to Mathnasium's Terms and Conditions of Use and Privacy Policy .
To revisit this article, visit My Profile, then View saved stories .
- The Big Story
- Newsletters
- Steven Levy's Plaintext Column
- WIRED Classics from the Archive
- WIRED Insider
- WIRED Consulting
OpenAI Announces a New AI Model, Code-Named Strawberry, That Solves Difficult Problems Step by Step
OpenAI made the last big breakthrough in artificial intelligence by increasing the size of its models to dizzying proportions, when it introduced GPT-4 last year. The company today announced a new advance that signals a shift in approach—a model that can “reason” logically through many difficult problems and is significantly smarter than existing AI without a major scale-up.
The new model, dubbed OpenAI o1, can solve problems that stump existing AI models, including OpenAI’s most powerful existing model, GPT-4o . Rather than summon up an answer in one step, as a large language model normally does, it reasons through the problem, effectively thinking out loud as a person might, before arriving at the right result.
“This is what we consider the new paradigm in these models,” Mira Murati , OpenAI’s chief technology officer, tells WIRED. “It is much better at tackling very complex reasoning tasks.”
The new model was code-named Strawberry within OpenAI, and it is not a successor to GPT-4o but rather a complement to it, the company says.
Murati says that OpenAI is currently building its next master model, GPT-5, which will be considerably larger than its predecessor. But while the company still believes that scale will help wring new abilities out of AI, GPT-5 is likely to also include the reasoning technology introduced today. “There are two paradigms,” Murati says. “The scaling paradigm and this new paradigm. We expect that we will bring them together.”
LLMs typically conjure their answers from huge neural networks fed vast quantities of training data. They can exhibit remarkable linguistic and logical abilities, but traditionally struggle with surprisingly simple problems such as rudimentary math questions that involve reasoning.
Murati says OpenAI o1 uses reinforcement learning, which involves giving a model positive feedback when it gets answers right and negative feedback when it does not, in order to improve its reasoning process. “The model sharpens its thinking and fine tunes the strategies that it uses to get to the answer,” she says. Reinforcement learning has enabled computers to play games with superhuman skill and do useful tasks like designing computer chips . The technique is also a key ingredient for turning an LLM into a useful and well-behaved chatbot.
Mark Chen, vice president of research at OpenAI, demonstrated the new model to WIRED, using it to solve several problems that its prior model, GPT-4o, cannot. These included an advanced chemistry question and the following mind-bending mathematical puzzle: “A princess is as old as the prince will be when the princess is twice as old as the prince was when the princess’s age was half the sum of their present age. What is the age of the prince and princess?” (The correct answer is that the prince is 30, and the princess is 40).
“The [new] model is learning to think for itself, rather than kind of trying to imitate the way humans would think,” as a conventional LLM does, Chen says.
OpenAI says its new model performs markedly better on a number of problem sets, including ones focused on coding, math, physics, biology, and chemistry. On the American Invitational Mathematics Examination (AIME), a test for math students, GPT-4o solved on average 12 percent of the problems while o1 got 83 percent right, according to the company.

The new model is slower than GPT-4o, and OpenAI says it does not always perform better—in part because, unlike GPT-4o, it cannot search the web and it is not multimodal, meaning it cannot parse images or audio.
Improving the reasoning capabilities of LLMs has been a hot topic in research circles for some time. Indeed, rivals are pursuing similar research lines. In July, Google announced AlphaProof , a project that combines language models with reinforcement learning for solving difficult math problems.
AlphaProof was able to learn how to reason over math problems by looking at correct answers. A key challenge with broadening this kind of learning is that there are not correct answers for everything a model might encounter. Chen says OpenAI has succeeded in building a reasoning system that is much more general. “I do think we have made some breakthroughs there; I think it is part of our edge,” Chen says. “It’s actually fairly good at reasoning across all domains.”
Noah Goodman , a professor at Stanford who has published work on improving the reasoning abilities of LLMs, says the key to more generalized training may involve using a “carefully prompted language model and handcrafted data” for training. He adds that being able to consistently trade the speed of results for greater accuracy would be a “nice advance.”
Yoon Kim , an assistant professor at MIT, says how LLMs solve problems currently remains somewhat mysterious, and even if they perform step-by-step reasoning there may be key differences from human intelligence. This could be crucial as the technology becomes more widely used. “These are systems that would be potentially making decisions that affect many, many people,” he says. “The larger question is, do we need to be confident about how a computational model is arriving at the decisions?”
The technique introduced by OpenAI today also may help ensure that AI models behave well. Murati says the new model has shown itself to be better at avoiding producing unpleasant or potentially harmful output by reasoning about the outcome of its actions. “If you think about teaching children, they learn much better to align to certain norms, behaviors, and values once they can reason about why they’re doing a certain thing,” she says.
Oren Etzioni , a professor emeritus at the University of Washington and a prominent AI expert, says it’s “essential to enable LLMs to engage in multi-step problem solving, use tools, and solve complex problems.” He adds, “Pure scale up will not deliver this.” Etzioni says, however, that there are further challenges ahead. “Even if reasoning were solved, we would still have the challenge of hallucination and factuality.”
OpenAI’s Chen says that the new reasoning approach developed by the company shows that advancing AI need not cost ungodly amounts of compute power. “One of the exciting things about the paradigm is we believe that it’ll allow us to ship intelligence cheaper,” he says, “and I think that really is the core mission of our company.”
You Might Also Like …
In your inbox: The best and weirdest stories from WIRED’s archive
How the brain decides what to remember
The Big Story: Meet Priscila, queen of the rideshare mafia
Silicon Valley's soulless plutocrats flip for Donald Trump
Event: Join us for The Big Interview on December 3 in San Francisco


COMMENTS
Click to see solution. Problem 17. A biker covered half the distance between two towns in 2 hr 30 min. After that he increased his speed by 2 km/hr. He covered the second half of the distance in 2 hr 20 min. Find the distance between the two towns and the initial speed of the biker. Click to see solution. Problem 18.
In 1945, Pólya published the short book How to Solve It, which gave a four-step method for solving mathematical problems: First, you have to understand the problem. After understanding, then make a plan. Carry out the plan. ... Problem Solving Strategy 6 (Make a List) Example 1: Can perfect squares end in a 2 or a 3?
It provides examples and templates of math word problems for 1st to 8th grade classes. (See our entire list of back to school resources for teachers here.) There are 120 examples in total. The list of examples is supplemented by tips to create engaging and challenging math word problems. 120 Math word problems, categorized by skill
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
32 Genuine Real-World Math Problems. In this section, we present 32 authentic real-world math problems from diverse fields such as safety and security, microbiology, architecture, engineering, nanotechnology, archaeology, creativity, and more. Each of these problems meets the criteria we've outlined previously.
The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information. Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern.
Khan Academy's 100,000+ free practice questions give instant feedback, don't need to be graded, and don't require a printer. Math Worksheets. Khan Academy. Math worksheets take forever to hunt down across the internet. Khan Academy is your one-stop-shop for practice from arithmetic to calculus. Math worksheets can vary in quality from ...
Problem Solving Strategy 6 (Work Systematically). If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated. For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how ...
The very first Mathematical Practice is: Make sense of problems and persevere in solving them. Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of ...
Step-by-Step Examples. Basic Math. Pre-Algebra. Algebra. Finding the Start Point Given the Mid and End Points. Finding the End Point Given the Start and Mid Points. Finding the Slope of the Perpendicular Line to the Line Through the Two Points. Finding the Degree, Leading Term, and Leading Coefficient.
Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.
Examples for. Mathematical Word Problems. Math word problems is one of the most complex parts of the elementary math curriculum since translating text into symbolic math is required to solve the problem. Because the Wolfram Language has powerful symbolic computation ability, Wolfram|Alpha can interpret basic mathematical word problems and give ...
Teaching about problem solving begins with suggested strategies to solve a problem. For example, "draw a picture," "make a table," etc. You may see posters in teachers' classrooms of the "Problem Solving Method" such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no ...
1. Create a Diagram/draw a picture. Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution. Example.
When students participate in problem solving activities, it is important to ask guiding, not leading, questions. This provides students with the support necessary to move forward in their thinking and it provides teachers with a more in-depth understanding of student thinking. Selecting an initial question and then analyzing a student's ...
Here are some problem-solving methods: Drawing a picture or diagram (helps visualize the problem) Breaking the problem into smaller parts (to keep track of what has been done) Making a table or a list (helps students to organize information) When children have a toolkit of math problem-solving strategies at hand, it makes it easier for them to ...
Problem-solving is the ability to use appropriate methods to tackle unexpected challenges in an organized manner. The ability to solve problems is considered a soft skill, meaning that it's more of a personality trait than a skill you've learned at school, on-the-job, or through technical training. While your natural ability to tackle ...
Free math problem solver answers your algebra homework questions with step-by-step explanations.
Problem solving in mathematics education has been a prominent research field that aims at understanding and relating the processes involved in solving problems to students' development of mathematical knowledge and problem solving competencies. ... such a scenario is the definition of a problem. For example, Resnick and Glaser define a ...
1. Link problem-solving to reading. When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools ...
Learn how to solve equations and inequalities with different strategies and techniques. Find out the conditions for no solution or infinite solutions.
Example 27. Solution; Example 28. Solution; Try it Now 6; Finally, we will bring together the mathematical tools we've reviewed, and use them to approach more complex problems. In many problems, it is tempting to take the given information, plug it into whatever formulas you have handy, and hope that the result is what you were supposed to find.
How to use circle theorems to solve problems. There are several ways to apply circle theorems to problem solve. For more specific step-by-step guides, check out the pages linked in the "What are circle theorems?" section above or read through the examples below. In order to problem solve using circle theorems: Recall the theorem. Solve the ...
Mathematical problem solving: An evolving research and practice domain. ZDM—The International Journal on Mathematics Education, 39(5, 6): 523-536. Schoenfeld, A. H. (1982). Some thoughts on problem-solving research and mathematics education. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 27-37 ...
Problem-solving in mathematics supports the development of: The ability to think creatively, critically, and logically. The ability to structure and organize. The ability to process information. Enjoyment of an intellectual challenge. The skills to solve problems that help them to investigate and understand the world.
Every classroom even has a formula—a problem-solving plan for math, printed out and displayed on the wall—called the "Plan of Attack," which includes three parts: using 80 percent of the allotted time to conceptualize the question by reading the problem multiple times, then modeling the relationships and actions in the problems; 10 ...
PEMDAS is especially helpful when we're working with more complicated math problems. Here are a couple of tricky examples to help you understand better. Can PEMDAS be applied to all mathematical problems? Yes, PEMDAS is a universal rule for solving mathematical expressions with multiple operations. It ensures consistency and accuracy in ...
Example 2. Simple Math Problems. Create a tape diagram example that represents each equation. ( a ) 3 + 9 = 12 ( b ) 10 + 4 = 14. Solution (a ) To create a tape diagram for 3 + 9 = 12, we must make three equal cells and nine more. An alternative illustration would be a rectangle with two parts, as shown below.
On the American Invitational Mathematics Examination (AIME), a test for math students, GPT-4o solved on average 12 percent of the problems while o1 got 83 percent right, according to the company ...