hypothesis testing calculator binomial

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

Binomial Test Calculator

This binomial test calculator determines the probability of a particular outcome (K) across a certain number of trials ( n ), where there are precisely two possible outcomes.

To use the calculator, enter the values of n , K and p into the table below ( q will be calculated automatically), where n is the number of trials or observations, K is number of occasions the actual (or stipulated) outcome occurred, and p is the probability the outcome will occur on any particular occasion.

Things to remember: (a) the binomial test is appropriate only when you've got just two possible outcomes (or categories, etc.); (b) n and K will be frequencies; and (c) the value for p will fall somewhere between 0 and 1 - it's a proportion.

Descriptive Statistics

Hypothesis test, binomial test calculator.

The domain of statistics is vast, with numerous tests and tools designed to decode the complexities of data. Among these, the binomial test stands out as a powerful technique to test the probability of observed outcomes. Whether you're examining the success rate of a new drug, the likelihood of customers choosing a product, or any scenario involving two potential outcomes, the Binomial Test Calculator is your analytical companion. This post delves into the significance of the binomial test and how our calculator simplifies its execution.

Understanding the Binomial Test

At its core, the binomial test determines whether the observed proportion of successes in a sample matches a pre-defined expectation. It's especially handy when you're dealing with yes/no, success/failure, or any other dichotomous outcomes.

Key Features of the Binomial Test Calculator

• User-Friendly Interface: Regardless of your statistical prowess, our calculator is designed for ease of use, ensuring every user can quickly input data and derive results.
• Quick Analysis: The need for manual calculations or complex software setups is eliminated. Input your data, and obtain results promptly.
• Detailed Outputs: Along with the p-value, the calculator provides clear interpretations, helping you gauge whether the observed outcomes significantly deviate from expectations.
• Graphical Illustration: Visual learners can benefit from the distribution graphs, making it easier to understand the data's significance in a graphical context.

How to Navigate the Binomial Test Calculator

• Data Input: Begin by inputting the number of trials, the number of observed successes, and the expected probability of success.
• Calculation: After feeding the data, click 'Calculate'. The calculator promptly processes the data and provides the results.
• Interpreting Results: A crucial metric provided is the p-value. Typically, a p-value less than 0.05 indicates that the observed data is significantly different from what was expected under the null hypothesis.

Practical Applications

The binomial test and our calculator find usage in various fields:

• Medical Research: To analyze the effectiveness of a treatment when compared to a known success rate.
• Marketing Studies: To determine if a new advertisement has a significant impact on product choices.
• Quality Control: To assess if the defect rate in a production batch deviates from acceptable standards.

The Binomial Test Calculator transforms these analytical tasks into smooth operations, ensuring accuracy and efficiency.

In Conclusion

The realm of statistics offers profound insights, provided we have the right tools in our arsenal. The Binomial Test Calculator serves as a bridge between complex statistical principles and actionable insights. Whether you're a researcher, a student, or a professional looking to make data-driven decisions, our calculator ensures you do so with confidence and clarity. Dive into the fascinating world of binomial tests and let our calculator guide your explorations!

For optimal use, please visit DATAtab on your desktop PC!

Metric Variables:

Ordinal variables:, nominal variables:, binomial test calculator.

You can calculate a binomial test with a few clicks right here online, just select a categorical variable with two values and enter the probability of success.

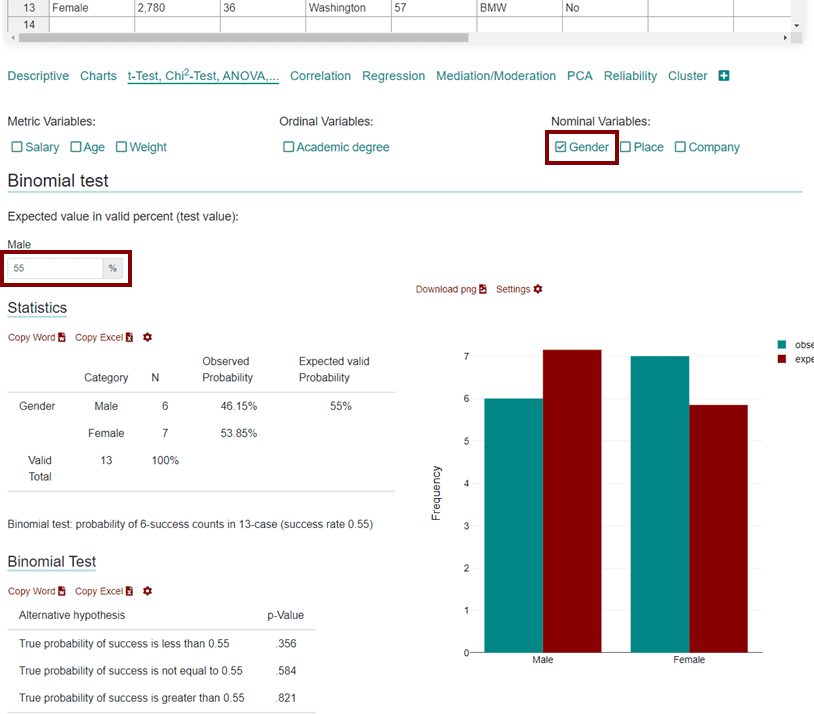
The binomial test calculator then gives you a statement as to whether the expected frequency matches the observed frequency.

Calculate binomial test

With the help of the binomial test, you can calculate whether the frequency distribution of a sample matches that of the population or not. To check whether your result is significant or not, DATAtab gives you the p-value . If the p-value is smaller than the significance level, usually 0.05, then the frequency distribution does not match significantly.

If you have a categorical variable with more than two values, just use the Chi2 test calculator . Click here for the binomial test tutorial

Binomial Test

A binomial test is a statistical test used to determine whether the proportion of successes in a binary outcome differs significantly from a specified value or from another proportion. It is applicable when dealing with categorical data with two possible outcomes, often referred to as success and failure.

The binomial test is based on the binomial distribution, which models the probability of obtaining a specific number of successes in a fixed number of independent Bernoulli trials (experiments with two possible outcomes). The test is used to assess whether the observed proportion of successes significantly deviates from what would be expected by chance.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

Hypothesis Testing with the Binomial Distribution

Contents Toggle Main Menu 1 Hypothesis Testing 2 Worked Example 3 See Also

Hypothesis Testing

To hypothesis test with the binomial distribution, we must calculate the probability, $p$, of the observed event and any more extreme event happening. We compare this to the level of significance $\alpha$. If $p>\alpha$ then we do not reject the null hypothesis. If $p<\alpha$ we accept the alternative hypothesis.

Worked Example

A coin is tossed twenty times, landing on heads six times. Perform a hypothesis test at a $5$% significance level to see if the coin is biased.

First, we need to write down the null and alternative hypotheses. In this case

The important thing to note here is that we only need a one-tailed test as the alternative hypothesis says “in favour of tails”. A two-tailed test would be the result of an alternative hypothesis saying “The coin is biased”.

We need to calculate more than just the probability that it lands on heads $6$ times. If it landed on heads fewer than $6$ times, that would be even more evidence that the coin is biased in favour of tails. Consequently we need to add up the probability of it landing on heads $1$ time, $2$ times, $\ldots$ all the way up to $6$ times. Although a calculation is possible, it is much quicker to use the cumulative binomial distribution table. This gives $\mathrm{P}[X\leq 6] = 0.058$.

We are asked to perform the test at a $5$% significance level. This means, if there is less than $5$% chance of getting less than or equal to $6$ heads then it is so unlikely that we have sufficient evidence to claim the coin is biased in favour of tails. Now note that our $p$-value $0.058>0.05$ so we do not reject the null hypothesis. We don't have sufficient evidence to claim the coin is biased.

But what if the coin had landed on heads just $5$ times? Again we need to read from the cumulative tables for the binomial distribution which shows $\mathrm{P}[X\leq 5] = 0.021$, so we would have had to reject the null hypothesis and accept the alternative hypothesis. So the point at which we switch from accepting the null hypothesis to rejecting it is when we obtain $5$ heads. This means that $5$ is the critical value .

Selecting a Hypothesis Test

4.3 Binomial Distribution

There are three characteristics of a binomial experiment.

• There are a fixed number of trials. Think of trials as repetitions of an experiment. The letter n denotes the number of trials.
• There are only two possible outcomes, called "success" and "failure," for each trial. The letter p denotes the probability of a success on one trial, and q denotes the probability of a failure on one trial. p + q = 1.
• The n trials are independent and are repeated using identical conditions. Because the n trials are independent, the outcome of one trial does not help in predicting the outcome of another trial. Another way of saying this is that for each individual trial, the probability, p , of a success and probability, q , of a failure remain the same. For example, randomly guessing at a true-false statistics question has only two outcomes. If a success is guessing correctly, then a failure is guessing incorrectly. Suppose Joe always guesses correctly on any statistics true-false question with probability p = 0.6. Then, q = 0.4. This means that for every true-false statistics question Joe answers, his probability of success ( p = 0.6) and his probability of failure ( q = 0.4) remain the same.

The outcomes of a binomial experiment fit a binomial probability distribution . The random variable X = the number of successes obtained in the n independent trials.

The mean, μ , and variance, σ 2 , for the binomial probability distribution are μ = np and σ 2 = npq . The standard deviation, σ , is then σ = n p q n p q .

Any experiment that has characteristics two and three and where n = 1 is called a Bernoulli Trial (named after Jacob Bernoulli who, in the late 1600s, studied them extensively). A binomial experiment takes place when the number of successes is counted in one or more Bernoulli Trials.

Example 4.9

At ABC College, the withdrawal rate from an elementary physics course is 30% for any given term. This implies that, for any given term, 70% of the students stay in the class for the entire term. A "success" could be defined as an individual who withdrew. The random variable X = the number of students who withdraw from the randomly selected elementary physics class.

The state health board is concerned about the amount of fruit available in school lunches. Forty-eight percent of schools in the state offer fruit in their lunches every day. This implies that 52% do not. What would a "success" be in this case?

Example 4.10

Suppose you play a game that you can only either win or lose. The probability that you win any game is 55%, and the probability that you lose is 45%. Each game you play is independent. If you play the game 20 times, write the function that describes the probability that you win 15 of the 20 times. Here, if you define X as the number of wins, then X takes on the values 0, 1, 2, 3, ..., 20. The probability of a success is p = 0.55. The probability of a failure is q = 0.45. The number of trials is n = 20. The probability question can be stated mathematically as P ( x = 15).

Try It 4.10

A trainer is teaching a rescued dolphin to catch live fish before returning it to the wild. The probability that the dolphin successfully catches a fish is 35%, and the probability that the dolphin does not successfully catch the fish is 65%. Out of 20 attempts, you want to find the probability that the dolphin succeeds 12 times. State the probability question mathematically.

Example 4.11

A coin is has been altered to weight the outcome from 0.5 to 0.25 and flipped 5 times. Each flip is independent. What is the probability of getting more than 3 heads? Let X = the number of heads in 5 flips of the fair coin. X takes on the values 0, 1, 2, 3, 4, 5. Since the coin is altered to result in p = 0.25, q is 0.75. The number of trials is n = 5. State the probability question mathematically.

First develop fully the probability density function and graph the probability density function. With the fully developed probability density function we can simply read the solution to the question P x > 3 P x > 3 heads. P x > 3 = P x = 4 + P x = 5 = 0 . 0146 + 0 . 0007 = 0 . 0153 . P x > 3 = P x = 4 + P x = 5 = 0 . 0146 + 0 . 0007 = 0 . 0153 . We have added the two individual probabilities because of the addition rule from Probability Topics .

Figure 4.2 also allows us to see the link between the probability density function and probability and area. We also see in Figure 4.2 the skew of the binomial distribution when p is not equal to 0.5. In Figure 4.2 the distribution is skewed right as a result of μ = n p = 1 . 25 μ = n p = 1 . 25 because p = 0 . 25 p = 0 . 25 .

Try It 4.11

A fair, six-sided die is rolled ten times. Each roll is independent. You want to find the probability of rolling a one more than three times. State the probability question mathematically.

Example 4.12

Approximately 70% of statistics students do their homework in time for it to be collected and graded. Each student does homework independently. In a statistics class of 50 students, what is the probability that at least 40 will do their homework on time? Students are selected randomly.

a. This is a binomial problem because there is only a success or a __________, there are a fixed number of trials, and the probability of a success is 0.70 for each trial.

b. If we are interested in the number of students who do their homework on time, then how do we define X ?

c. What values does x take on?

d. What is a "failure," in words?

e. If p + q = 1, then what is q ?

f. The words "at least" translate as what kind of inequality for the probability question P ( x ____ 40).

b. X = the number of statistics students who do their homework on time

c. 0, 1, 2, …, 50

d. Failure is defined as a student who does not complete their homework on time.

The probability of a success is p = 0.70. The number of trials is n = 50.

e. q = 0.30

f. greater than or equal to (≥) The probability question is P ( x ≥ 40).

Try It 4.12

Sixty-five percent of people pass the state driver’s exam on the first try. A group of 50 individuals who have taken the driver’s exam is randomly selected. Give two reasons why this is a binomial problem.

Notation for the Binomial: B = Binomial Probability Distribution Function

X ~ B ( n , p )

Read this as " X is a random variable with a binomial distribution." The parameters are n and p ; n = number of trials, p = probability of a success on each trial.

Example 4.13

It has been stated that about 41% of adult workers have a high school diploma but do not pursue any further education. If 20 adult workers are randomly selected, find the probability that at most 12 of them have a high school diploma but do not pursue any further education. How many adult workers do you expect to have a high school diploma but do not pursue any further education?

Let X = the number of workers who have a high school diploma but do not pursue any further education.

X takes on the values 0, 1, 2, ..., 20 where n = 20, p = 0.41, and q = 1 – 0.41 = 0.59. X ~ B (20, 0.41)

Find P ( x ≤ 12). P ( x ≤ 12) = 0.9738. (calculator or computer)

Using the TI-83, 83+, 84, 84+ Calculator

Go into 2 nd DISTR. The syntax for the instructions are as follows:

To calculate ( x = value): binompdf( n , p , number) if "number" is left out, the result is the binomial probability table. To calculate P ( x ≤ value): binomcdf( n , p , number) if "number" is left out, the result is the cumulative binomial probability table. For this problem: After you are in 2 nd DISTR , arrow down to binomcdf . Press ENTER . Enter 20,0.41,12). The result is P ( x ≤ 12) = 0.9738.

If you want to find P ( x = 12), use the pdf (binompdf). If you want to find P ( x > 12), use 1 - binomcdf(20,0.41,12).

The probability that at most 12 workers have a high school diploma but do not pursue any further education is 0.9738.

The graph of X ~ B (20, 0.41) is as follows:

The y -axis contains the probability of x , where X = the number of workers who have only a high school diploma.

The number of adult workers that you expect to have a high school diploma but not pursue any further education is the mean, μ = np = (20)(0.41) = 8.2.

The formula for the variance is σ 2 = npq . The standard deviation is σ = n p q n p q . σ = ( 20 ) ( 0.41 ) ( 0.59 ) ( 20 ) ( 0.41 ) ( 0.59 ) = 2.20.

Try It 4.13

About 32% of students participate in a community volunteer program outside of school. If 30 students are selected at random, find the probability that at most 14 of them participate in a community volunteer program outside of school. Use the TI-83+ or TI-84 calculator to find the answer.

Example 4.14

In the 2013 Jerry’s Artarama art supplies catalog, there are 560 pages. Eight of the pages feature signature artists. Suppose we randomly sample 100 pages. Let X = the number of pages that feature signature artists.

• What values does x take on?
• the probability that two pages feature signature artists
• the probability that at most six pages feature signature artists
• the probability that more than three pages feature signature artists.
• Using the formulas, calculate the (i) mean and (ii) standard deviation.
• x = 0, 1, 2, 3, 4, 5, 6, 7, 8
• P ( x = 2) = binompdf ( 100 , 8 560 , 2 ) ( 100 , 8 560 , 2 ) = 0.2466
• P ( x ≤ 6) = binomcdf ( 100 , 8 560 , 6 ) ( 100 , 8 560 , 6 ) = 0.9994
• P ( x > 3) = 1 – P ( x ≤ 3) = 1 – binomcdf ( 100 , 8 560 , 3 ) ( 100 , 8 560 , 3 ) = 1 – 0.9443 = 0.0557
• Mean = np = (100) ( 8 560 ) ( 8 560 ) = 800 560 800 560 ≈ 1.4286
• Standard Deviation = n p q n p q = ( 100 ) ( 8 560 ) ( 552 560 ) ( 100 ) ( 8 560 ) ( 552 560 ) ≈ 1.1867

Try It 4.14

According to a Gallup poll, 60% of American adults prefer saving over spending. Let X = the number of American adults out of a random sample of 50 who prefer saving to spending.

• What is the probability distribution for X ?
• the probability that 25 adults in the sample prefer saving over spending
• the probability that at most 20 adults prefer saving
• the probability that more than 30 adults prefer saving
• Using the formulas, calculate the (i) mean and (ii) standard deviation of X .

Example 4.15

The lifetime risk of developing cancer is about one in 67 (1.5%). Suppose we randomly sample 200 people. Let X = the number of people who will develop cancer.

• Use your calculator to find the probability that at most eight people develop cancer
• Is it more likely that five or six people will develop cancer? Justify your answer numerically.
• X   ~   B 200 , 0 . 015 X   ~   B 200 , 0 . 015
• Mean = n p = 200 0 . 015   = 3 Mean = n p = 200 0 . 015   = 3 Standard   Deviation = n p q = 200 ( 0 . 015 ) ( 0 . 985 ) = 1 . 719 Standard   Deviation = n p q = 200 ( 0 . 015 ) ( 0 . 985 ) = 1 . 719
• P x ≤ 8   = 0 . 9965 P x ≤ 8   = 0 . 9965
• The probability that five people develop cancer is 0.1011. The probability that six people develop cancer is 0.0500.

Try It 4.15

During a certain NBA season, a player for the Los Angeles Clippers had the highest field goal completion rate in the league. This player scored with 61.3% of his shots. Suppose you choose a random sample of 80 shots made by this player during the season. Let X = the number of shots that scored points.

• Use your calculator to find the probability that this player scored with 60 of these shots.
• Find the probability that this player scored with more than 50 of these shots.

Example 4.16

The following example illustrates a problem that is not binomial. It violates the condition of independence. ABC College has a student advisory committee made up of ten staff members and six students. The committee wishes to choose a chairperson and a recorder. What is the probability that the chairperson and recorder are both students? The names of all committee members are put into a box, and two names are drawn without replacement . The first name drawn determines the chairperson and the second name the recorder. There are two trials. However, the trials are not independent because the outcome of the first trial affects the outcome of the second trial. The probability of a student on the first draw is 6 16 6 16 . The probability of a student on the second draw is 5 15 5 15 , when the first draw selects a student. The probability is 6 15 6 15 , when the first draw selects a staff member. The probability of drawing a student's name changes for each of the trials and, therefore, violates the condition of independence.

Try It 4.16

A lacrosse team is selecting a captain. The names of all the seniors are put into a hat, and the first three that are drawn will be the captains. The names are not replaced once they are drawn (one person cannot be two captains). You want to see if the captains all play the same position. State whether this is binomial or not and state why.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics 2e
• Publication date: Dec 13, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics-2e/pages/4-3-binomial-distribution

© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Teach yourself statistics

Binomial Probability Calculator

Use the Binomial Calculator to compute individual and cumulative binomial probabilities. For help in using the calculator, read the Frequently-Asked Questions or review the Sample Problems .

To learn more about the binomial distribution, go to Stat Trek's tutorial on the binomial distribution .

• Enter a value in each of the first three text boxes (the unshaded boxes).
• Click the Calculate button to compute binomial and cumulative probabilities.

Frequently-Asked Questions

Instructions: To find the answer to a frequently-asked question, simply click on the question.

What is a binomial experiment?

A binomial experiment has the following characteristics:

• The experiment involves repeated trials.
• Each trial has only two possible outcomes - a success or a failure.
• The probability that any trial will result in success is constant.
• All of the trials in the experiment are independent.

A series of coin tosses is a perfect example of a binomial experiment. Suppose we toss a coin three times. Each coin flip represents a trial, so this experiment would have 3 trials. Each coin flip also has only two possible outcomes - a Head or a Tail. We could call a Head a success; and a Tail, a failure. The probability of a success on any given coin flip would be constant (i.e., 50%). And finally, the outcome on any coin flip is not affected by previous or succeeding coin flips; so the trials in the experiment are independent.

What is a binomial distribution?

A binomial distribution is a probability distribution . It refers to the probabilities associated with the number of successes in a binomial experiment .

For example, suppose we toss a coin three times and suppose we define Heads as a success. This binomial experiment has four possible outcomes: 0 Heads, 1 Head, 2 Heads, or 3 Heads. The probabilities associated with each possible outcome are an example of a binomial distribution , as shown below.

What is the number of trials?

The number of trials refers to the number of replications in a binomial experiment.

Suppose that we conduct the following binomial experiment. We flip a coin and count the number of Heads. We classify Heads as success; tails, as failure. If we flip the coin 3 times, then 3 is the number of trials. If we flip it 20 times, then 20 is the number of trials.

Note: Each trial results in a success or a failure. So the number of trials in a binomial experiment is equal to the number of successes plus the number of failures.

What is the number of successes?

Each trial in a binomial experiment can have one of two outcomes. The experimenter classifies one outcome as a success; and the other, as a failure. The number of successes in a binomial experient is the number of trials that result in an outcome classified as a success.

What is the probability of success on a single trial?

In a binomial experiment, the probability of success on any individual trial is constant. For example, the probability of getting Heads on a single coin flip is always 0.50. If "getting Heads" is defined as success, the probability of success on a single trial would be 0.50.

What is the binomial probability?

A binomial probability refers to the probability of getting EXACTLY r successes in a specific number of trials. For instance, we might ask: What is the probability of getting EXACTLY 2 Heads in 3 coin tosses. That probability (0.375) would be an example of a binomial probability.

In a binomial experiment, the probability that the experiment results in exactly x successes is indicated by the following notation: P(X=x);

What is the cumulative binomial probability?

Cumulative binomial probability refers to the probability that the value of a binomial random variable falls within a specified range.

The probability of getting AT MOST 2 Heads in 3 coin tosses is an example of a cumulative probability. It is equal to the probability of getting 0 heads (0.125) plus the probability of getting 1 head (0.375) plus the probability of getting 2 heads (0.375). Thus, the cumulative probability of getting AT MOST 2 Heads in 3 coin tosses is equal to 0.875.

Notation associated with cumulative binomial probability is best explained through illustration. The probability of getting FEWER THAN 2 successes is indicated by P(X<2); the probability of getting AT MOST 2 successes is indicated by P(X≤2); the probability of getting AT LEAST 2 successes is indicated by P(X≥2); the probability of getting MORE THAN 2 successes is indicated by P(X>2).

Sample Problem

• The probability of success (i.e., getting a Head) on any single trial is 0.5.
• The number of trials is 12.
• The number of successes is 7 (since we define getting a Head as success).

Therefore, we plug those numbers into the Binomial Calculator and hit the Calculate button.

The calculator reports that the binomial probability is 0.193. That is the probability of getting EXACTLY 7 Heads in 12 coin tosses. (The calculator also reports the cumulative probabilities. For example, the probability of getting AT MOST 7 heads in 12 coin tosses is a cumulative probability equal to 0.806.)

• The probability of success for any individual student is 0.6.
• The number of trials is 3 (because we have 3 students).
• The number of successes is 2.

The calculator reports that the probability that two or fewer of these three students will graduate is 0.784.

Oops! Something went wrong.

Two sample t test

Kruskal wallis

Pearson product moment

Two sample f test

One way anova

Bartlett test

Chi square goodness of fit

Fligner killeen

Hypothesis Test Calculator

Upload your data set below to get started

Or input your data as csv

Sharing helps us build more free tools

Video Crash Courses

Junior Math

Math Essentials

Tutor-on-Demand

Encyclopedia

Digital Tools

How to Do Hypothesis Testing with Binomial Distribution

A hypothesis test has the objective of testing different results against each other. You use them to check a result against something you already believe is true. In a hypothesis test, you’re checking if the new alternative hypothesis  H A would challenge and replace the already existing null hypothesis  H 0 .

Hypothesis tests are either one-sided or two-sided. In a one-sided test, the alternative hypothesis is left-sided with p < p 0 or right-sided with p > p 0 . In a two-sided test, the alternative hypothesis is p ≠ p 0 . In all three cases, p 0 is the pre-existing probability of what you’re comparing, and p is the probability you are going to find.

Note! In hypothesis testing, you calculate the alternative hypothesis to say something about the null hypothesis.

Hypothesis Testing Binomial Distribution

For example, you would have a reason to believe that a high observed value of p , makes the alternative hypothesis H a : p > p 0 seem reasonable.

There is a drug on the market that you know cures 8 5 % of all patients. A company has come up with a new drug they believe is better than what is already on the market. This new drug has cured 92 of 103 patients in tests. Determine if the new drug is really better than the old one.

This is a classic case of hypothesis testing by binomial distribution. You now follow the recipe above to answer the task and select 5 % level of significance since it is not a question of medication for a serious illness.

The alternative hypothesis in this case is that the new drug is better. The reason for this is that you only need to know if you are going to approve for sale and thus the new drug must be better:

This result indicates that there is a 1 3 . 6 % chance that more than 92 patients would be cured with the old medicine.

so H 0 cannot be rejected. The new drug does not enter the market.

If the p value had been less than the level of significance, that would mean that the new drug represented by the alternative hypothesis is better, and that you are sure of this with statistical significance.