Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .
- Payment Plans
- Product List
- Partnerships

- Try Free Trial
- Study Packages
- Levels I, II & III Lifetime Package
- Video Lessons
- Study Notes
- Practice Questions
- Levels II & III Lifetime Package
- About the Exam
- About your Instructor
- Part I Study Packages
- Parts I & II Packages
- Part I & Part II Lifetime Package
- Part II Study Packages
- Exams P & FM Lifetime Package
- Quantitative Questions
- Verbal Questions
- Data Insight Questions
- Live Tutoring
- About your Instructors
- EA Practice Questions
- Data Sufficiency Questions
- Integrated Reasoning Questions

Hypothesis Tests and Confidence Intervals in Multiple Regression
After completing this reading you should be able to:
- Construct, apply, and interpret hypothesis tests and confidence intervals for a single coefficient in a multiple regression.
- Construct, apply, and interpret joint hypothesis tests and confidence intervals for multiple coefficients in a multiple regression.
- Interpret the \(F\)-statistic.
- Interpret tests of a single restriction involving multiple coefficients.
- Interpret confidence sets for multiple coefficients.
- Identify examples of omitted variable bias in multiple regressions.
- Interpret the \({ R }^{ 2 }\) and adjusted \({ R }^{ 2 }\) in a multiple regression.
Hypothesis Tests and Confidence Intervals for a Single Coefficient
This section is about the calculation of the standard error, hypotheses testing, and confidence interval construction for a single regression in a multiple regression equation.
Introduction
In a previous chapter, we looked at simple linear regression where we deal with just one regressor (independent variable). The response (dependent variable) is assumed to be affected by just one independent variable. M ultiple regression, on the other hand , simultaneously considers the influence of multiple explanatory variables on a response variable Y. We may want to establish the confidence interval of one of the independent variables. We may want to evaluate whether any particular independent variable has a significant effect on the dependent variable. Finally, We may also want to establish whether the independent variables as a group have a significant effect on the dependent variable. In this chapter, we delve into ways all this can be achieved.
Hypothesis Tests for a single coefficient
Suppose that we are testing the hypothesis that the true coefficient \({ \beta }_{ j }\) on the \(j\)th regressor takes on some specific value \({ \beta }_{ j,0 }\). Let the alternative hypothesis be two-sided. Therefore, the following is the mathematical expression of the two hypotheses:
$$ { H }_{ 0 }:{ \beta }_{ j }={ \beta }_{ j,0 }\quad vs.\quad { H }_{ 1 }:{ \beta }_{ j }\neq { \beta }_{ j,0 } $$
This expression represents the two-sided alternative. The following are the steps to follow while testing the null hypothesis:
- Computing the coefficient’s standard error.
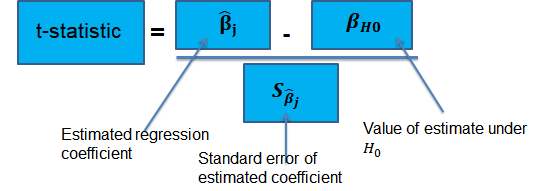
$$ p-value=2\Phi \left( -|{ t }^{ act }| \right) $$
- Also, the \(t\)-statistic can be compared to the critical value corresponding to the significance level that is desired for the test.
Confidence Intervals for a Single Coefficient
The confidence interval for a regression coefficient in multiple regression is calculated and interpreted the same way as it is in simple linear regression.
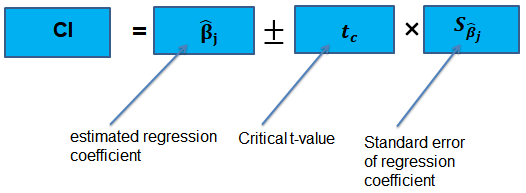
The t-statistic has n – k – 1 degrees of freedom where k = number of independents
Supposing that an interval contains the true value of \({ \beta }_{ j }\) with a probability of 95%. This is simply the 95% two-sided confidence interval for \({ \beta }_{ j }\). The implication here is that the true value of \({ \beta }_{ j }\) is contained in 95% of all possible randomly drawn variables.
Alternatively, the 95% two-sided confidence interval for \({ \beta }_{ j }\) is the set of values that are impossible to reject when a two-sided hypothesis test of 5% is applied. Therefore, with a large sample size:
$$ 95\%\quad confidence\quad interval\quad for\quad { \beta }_{ j }=\left[ { \hat { \beta } }_{ j }-1.96SE\left( { \hat { \beta } }_{ j } \right) ,{ \hat { \beta } }_{ j }+1.96SE\left( { \hat { \beta } }_{ j } \right) \right] $$
Tests of Joint Hypotheses
In this section, we consider the formulation of the joint hypotheses on multiple regression coefficients. We will further study the application of an \(F\)-statistic in their testing.
Hypotheses Testing on Two or More Coefficients
Joint null hypothesis.
In multiple regression, we canno t test the null hypothesis that all slope coefficients are equal 0 based on t -tests that each individual slope coefficient equals 0. Why? individual t-tests do not account for the effects of interactions among the independent variables.
For this reason, we conduct the F-test which uses the F-statistic . The F-test tests the null hypothesis that all of the slope coefficients in the multiple regression model are jointly equal to 0, .i.e.,
\(F\)-Statistic
The F-statistic, which is always a one-tailed test , is calculated as:
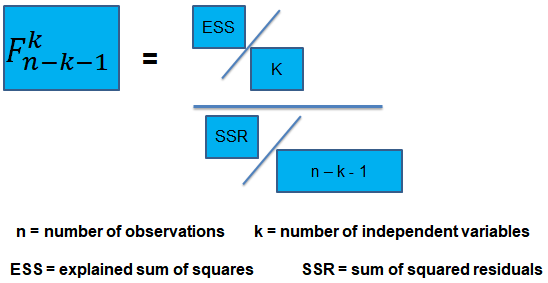
To determine whether at least one of the coefficients is statistically significant, the calculated F-statistic is compared with the one-tailed critical F-value, at the appropriate level of significance.
Decision rule:

Rejection of the null hypothesis at a stated level of significance indicates that at least one of the coefficients is significantly different than zero, i.e, at least one of the independent variables in the regression model makes a significant contribution to the dependent variable.
An analyst runs a regression of monthly value-stock returns on four independent variables over 48 months.
The total sum of squares for the regression is 360, and the sum of squared errors is 120.
Test the null hypothesis at the 5% significance level (95% confidence) that all the four independent variables are equal to zero.
\({ H }_{ 0 }:{ \beta }_{ 1 }=0,{ \beta }_{ 2 }=0,\dots ,{ \beta }_{ 4 }=0 \)
\({ H }_{ 1 }:{ \beta }_{ j }\neq 0\) (at least one j is not equal to zero, j=1,2… k )
ESS = TSS – SSR = 360 – 120 = 240
The calculated test statistic = (ESS/k)/(SSR/(n-k-1))
=(240/4)/(120/43) = 21.5
\({ F }_{ 43 }^{ 4 }\) is approximately 2.44 at 5% significance level.
Decision: Reject H 0 .
Conclusion: at least one of the 4 independents is significantly different than zero.
Omitted Variable Bias in Multiple Regression
This is the bias in the OLS estimator arising when at least one included regressor gets collaborated with an omitted variable. The following conditions must be satisfied for an omitted variable bias to occur:
- There must be a correlation between at least one of the included regressors and the omitted variable.
- The dependent variable \(Y\) must be determined by the omitted variable.
Practical Interpretation of the \({ R }^{ 2 }\) and the adjusted \({ R }^{ 2 }\), \({ \bar { R } }^{ 2 }\)
To determine the accuracy within which the OLS regression line fits the data, we apply the coefficient of determination and the regression’s standard error .
The coefficient of determination, represented by \({ R }^{ 2 }\), is a measure of the “goodness of fit” of the regression. It is interpreted as the percentage of variation in the dependent variable explained by the independent variables

\({ R }^{ 2 }\) is not a reliable indicator of the explanatory power of a multiple regression model.Why? \({ R }^{ 2 }\) almost always increases as new independent variables are added to the model, even if the marginal contribution of the new variable is not statistically significant. Thus, a high \({ R }^{ 2 }\) may reflect the impact of a large set of independents rather than how well the set explains the dependent.This problem is solved by the use of the adjusted \({ R }^{ 2 }\) (extensively covered in chapter 8)
The following are the factors to watch out when guarding against applying the \({ R }^{ 2 }\) or the \({ \bar { R } }^{ 2 }\):
- An added variable doesn’t have to be statistically significant just because the \({ R }^{ 2 }\) or the \({ \bar { R } }^{ 2 }\) has increased.
- It is not always true that the regressors are a true cause of the dependent variable, just because there is a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
- It is not necessary that there is no omitted variable bias just because we have a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
- It is not necessarily true that we have the most appropriate set of regressors just because we have a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
- It is not necessarily true that we have an inappropriate set of regressors just because we have a low \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
An economist tests the hypothesis that GDP growth in a certain country can be explained by interest rates and inflation.
Using some 30 observations, the analyst formulates the following regression equation:
$$ GDP growth = { \hat { \beta } }_{ 0 } + { \hat { \beta } }_{ 1 } Interest+ { \hat { \beta } }_{ 2 } Inflation $$
Regression estimates are as follows:
|
|
| |
| Intercept | 0.10 | 0.5% |
| Interest rates | 0.20 | 0.05 |
| Inflation | 0.15 | 0.03 |
Is the coefficient for interest rates significant at 5%?
- Since the test statistic < t-critical, we accept H 0 ; the interest rate coefficient is not significant at the 5% level.
- Since the test statistic > t-critical, we reject H 0 ; the interest rate coefficient is not significant at the 5% level.
- Since the test statistic > t-critical, we reject H 0 ; the interest rate coefficient is significant at the 5% level.
- Since the test statistic < t-critical, we accept H 1 ; the interest rate coefficient is significant at the 5% level.
The correct answer is C .
We have GDP growth = 0.10 + 0.20(Int) + 0.15(Inf)
Hypothesis:
$$ { H }_{ 0 }:{ \hat { \beta } }_{ 1 } = 0 \quad vs \quad { H }_{ 1 }:{ \hat { \beta } }_{ 1 }≠0 $$
The test statistic is:
$$ t = \left( \frac { 0.20 – 0 }{ 0.05 } \right) = 4 $$
The critical value is t (α/2, n-k-1) = t 0.025,27 = 2.052 (which can be found on the t-table).
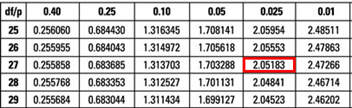
Conclusion : The interest rate coefficient is significant at the 5% level.
Offered by AnalystPrep

Modeling Cycles: MA, AR, and ARMA Models
Empirical approaches to risk metrics and hedging, futures markets.
After completing this reading, you should be able to: Define and describe the... Read More
Bond Yields and Return Calculations
After completing this reading, you should be able to: Distinguish between gross, and... Read More
Modeling and Forecasting Seasonality
After completing this reading you should be able to: Describe the sources of... Read More
Modeling and Hedging Non-Parallel Term ...
After completing this reading you should be able to: Describe principal components analysis... Read More
Leave a Comment Cancel reply
You must be logged in to post a comment.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Multiple Linear Regression | A Quick Guide (Examples)
Published on February 20, 2020 by Rebecca Bevans . Revised on June 22, 2023.
Regression models are used to describe relationships between variables by fitting a line to the observed data. Regression allows you to estimate how a dependent variable changes as the independent variable(s) change.
Multiple linear regression is used to estimate the relationship between two or more independent variables and one dependent variable . You can use multiple linear regression when you want to know:
- How strong the relationship is between two or more independent variables and one dependent variable (e.g. how rainfall, temperature, and amount of fertilizer added affect crop growth).
- The value of the dependent variable at a certain value of the independent variables (e.g. the expected yield of a crop at certain levels of rainfall, temperature, and fertilizer addition).
Table of contents
Assumptions of multiple linear regression, how to perform a multiple linear regression, interpreting the results, presenting the results, other interesting articles, frequently asked questions about multiple linear regression.
Multiple linear regression makes all of the same assumptions as simple linear regression :
Homogeneity of variance (homoscedasticity) : the size of the error in our prediction doesn’t change significantly across the values of the independent variable.
Independence of observations : the observations in the dataset were collected using statistically valid sampling methods , and there are no hidden relationships among variables.
In multiple linear regression, it is possible that some of the independent variables are actually correlated with one another, so it is important to check these before developing the regression model. If two independent variables are too highly correlated (r2 > ~0.6), then only one of them should be used in the regression model.
Normality : The data follows a normal distribution .
Linearity : the line of best fit through the data points is a straight line, rather than a curve or some sort of grouping factor.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

Multiple linear regression formula
The formula for a multiple linear regression is:
- … = do the same for however many independent variables you are testing
To find the best-fit line for each independent variable, multiple linear regression calculates three things:
- The regression coefficients that lead to the smallest overall model error.
- The t statistic of the overall model.
- The associated p value (how likely it is that the t statistic would have occurred by chance if the null hypothesis of no relationship between the independent and dependent variables was true).
It then calculates the t statistic and p value for each regression coefficient in the model.
Multiple linear regression in R
While it is possible to do multiple linear regression by hand, it is much more commonly done via statistical software. We are going to use R for our examples because it is free, powerful, and widely available. Download the sample dataset to try it yourself.
Dataset for multiple linear regression (.csv)
Load the heart.data dataset into your R environment and run the following code:
This code takes the data set heart.data and calculates the effect that the independent variables biking and smoking have on the dependent variable heart disease using the equation for the linear model: lm() .
Learn more by following the full step-by-step guide to linear regression in R .
To view the results of the model, you can use the summary() function:
This function takes the most important parameters from the linear model and puts them into a table that looks like this:
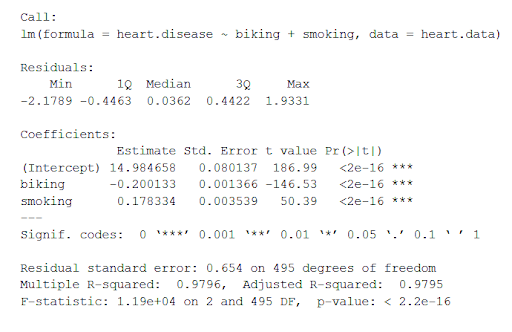
The summary first prints out the formula (‘Call’), then the model residuals (‘Residuals’). If the residuals are roughly centered around zero and with similar spread on either side, as these do ( median 0.03, and min and max around -2 and 2) then the model probably fits the assumption of heteroscedasticity.
Next are the regression coefficients of the model (‘Coefficients’). Row 1 of the coefficients table is labeled (Intercept) – this is the y-intercept of the regression equation. It’s helpful to know the estimated intercept in order to plug it into the regression equation and predict values of the dependent variable:
The most important things to note in this output table are the next two tables – the estimates for the independent variables.
The Estimate column is the estimated effect , also called the regression coefficient or r 2 value. The estimates in the table tell us that for every one percent increase in biking to work there is an associated 0.2 percent decrease in heart disease, and that for every one percent increase in smoking there is an associated .17 percent increase in heart disease.
The Std.error column displays the standard error of the estimate. This number shows how much variation there is around the estimates of the regression coefficient.
The t value column displays the test statistic . Unless otherwise specified, the test statistic used in linear regression is the t value from a two-sided t test . The larger the test statistic, the less likely it is that the results occurred by chance.
The Pr( > | t | ) column shows the p value . This shows how likely the calculated t value would have occurred by chance if the null hypothesis of no effect of the parameter were true.
Because these values are so low ( p < 0.001 in both cases), we can reject the null hypothesis and conclude that both biking to work and smoking both likely influence rates of heart disease.
When reporting your results, include the estimated effect (i.e. the regression coefficient), the standard error of the estimate, and the p value. You should also interpret your numbers to make it clear to your readers what the regression coefficient means.
Visualizing the results in a graph
It can also be helpful to include a graph with your results. Multiple linear regression is somewhat more complicated than simple linear regression, because there are more parameters than will fit on a two-dimensional plot.
However, there are ways to display your results that include the effects of multiple independent variables on the dependent variable, even though only one independent variable can actually be plotted on the x-axis.
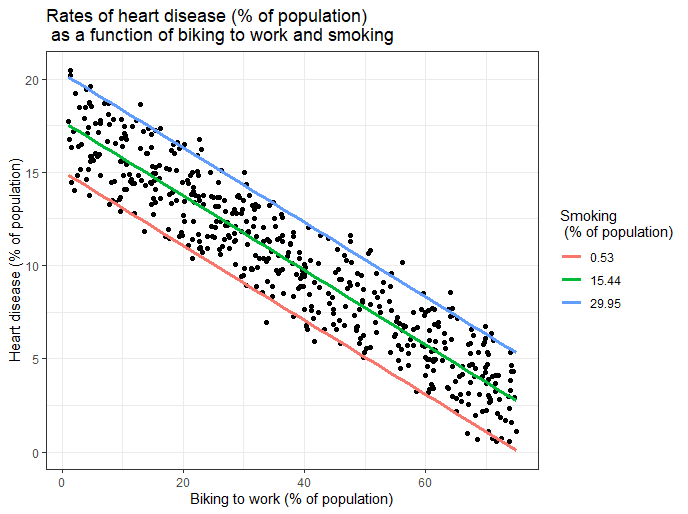
Here, we have calculated the predicted values of the dependent variable (heart disease) across the full range of observed values for the percentage of people biking to work.
To include the effect of smoking on the independent variable, we calculated these predicted values while holding smoking constant at the minimum, mean , and maximum observed rates of smoking.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Chi square test of independence
- Statistical power
- Descriptive statistics
- Degrees of freedom
- Pearson correlation
- Null hypothesis
Methodology
- Double-blind study
- Case-control study
- Research ethics
- Data collection
- Hypothesis testing
- Structured interviews
Research bias
- Hawthorne effect
- Unconscious bias
- Recall bias
- Halo effect
- Self-serving bias
- Information bias
A regression model is a statistical model that estimates the relationship between one dependent variable and one or more independent variables using a line (or a plane in the case of two or more independent variables).
A regression model can be used when the dependent variable is quantitative, except in the case of logistic regression, where the dependent variable is binary.
Multiple linear regression is a regression model that estimates the relationship between a quantitative dependent variable and two or more independent variables using a straight line.
Linear regression most often uses mean-square error (MSE) to calculate the error of the model. MSE is calculated by:
- measuring the distance of the observed y-values from the predicted y-values at each value of x;
- squaring each of these distances;
- calculating the mean of each of the squared distances.
Linear regression fits a line to the data by finding the regression coefficient that results in the smallest MSE.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Multiple Linear Regression | A Quick Guide (Examples). Scribbr. Retrieved September 25, 2024, from https://www.scribbr.com/statistics/multiple-linear-regression/
Is this article helpful?
Rebecca Bevans
Other students also liked, simple linear regression | an easy introduction & examples, an introduction to t tests | definitions, formula and examples, types of variables in research & statistics | examples, what is your plagiarism score.
Multiple linear regression
Multiple linear regression #.
Fig. 11 Multiple linear regression #
Errors: \(\varepsilon_i \sim N(0,\sigma^2)\quad \text{i.i.d.}\)
Fit: the estimates \(\hat\beta_0\) and \(\hat\beta_1\) are chosen to minimize the residual sum of squares (RSS):
Matrix notation: with \(\beta=(\beta_0,\dots,\beta_p)\) and \({X}\) our usual data matrix with an extra column of ones on the left to account for the intercept, we can write
Multiple linear regression answers several questions #
Is at least one of the variables \(X_i\) useful for predicting the outcome \(Y\) ?
Which subset of the predictors is most important?
How good is a linear model for these data?
Given a set of predictor values, what is a likely value for \(Y\) , and how accurate is this prediction?
The estimates \(\hat\beta\) #
Our goal again is to minimize the RSS: $ \( \begin{aligned} \text{RSS}(\beta) &= \sum_{i=1}^n (y_i -\hat y_i(\beta))^2 \\ & = \sum_{i=1}^n (y_i - \beta_0- \beta_1 x_{i,1}-\dots-\beta_p x_{i,p})^2 \\ &= \|Y-X\beta\|^2_2 \end{aligned} \) $
One can show that this is minimized by the vector \(\hat\beta\) : $ \(\hat\beta = ({X}^T{X})^{-1}{X}^T{y}.\) $
We usually write \(RSS=RSS(\hat{\beta})\) for the minimized RSS.
Which variables are important? #
Consider the hypothesis: \(H_0:\) the last \(q\) predictors have no relation with \(Y\) .
Based on our model: \(H_0:\beta_{p-q+1}=\beta_{p-q+2}=\dots=\beta_p=0.\)
Let \(\text{RSS}_0\) be the minimized residual sum of squares for the model which excludes these variables.
The \(F\) -statistic is defined by: $ \(F = \frac{(\text{RSS}_0-\text{RSS})/q}{\text{RSS}/(n-p-1)}.\) $
Under the null hypothesis (of our model), this has an \(F\) -distribution.
Example: If \(q=p\) , we test whether any of the variables is important. $ \(\text{RSS}_0 = \sum_{i=1}^n(y_i-\overline y)^2 \) $
| Res.Df | RSS | Df | Sum of Sq | F | Pr(>F) |
|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| 494 | 11336.29 | NA | NA | NA | NA |
| 492 | 11078.78 | 2 | 257.5076 | 5.717853 | 0.003509036 |
The \(t\) -statistic associated to the \(i\) th predictor is the square root of the \(F\) -statistic for the null hypothesis which sets only \(\beta_i=0\) .
A low \(p\) -value indicates that the predictor is important.
Warning: If there are many predictors, even under the null hypothesis, some of the \(t\) -tests will have low p-values even when the model has no explanatory power.
How many variables are important? #
When we select a subset of the predictors, we have \(2^p\) choices.
A way to simplify the choice is to define a range of models with an increasing number of variables, then select the best.
Forward selection: Starting from a null model, include variables one at a time, minimizing the RSS at each step.
Backward selection: Starting from the full model, eliminate variables one at a time, choosing the one with the largest p-value at each step.
Mixed selection: Starting from some model, include variables one at a time, minimizing the RSS at each step. If the p-value for some variable goes beyond a threshold, eliminate that variable.
Choosing one model in the range produced is a form of tuning . This tuning can invalidate some of our methods like hypothesis tests and confidence intervals…
How good are the predictions? #
The function predict in R outputs predictions and confidence intervals from a linear model:
| fit | lwr | upr |
|---|---|---|
| 9.409426 | 8.722696 | 10.09616 |
| 14.163090 | 13.708423 | 14.61776 |
| 18.916754 | 18.206189 | 19.62732 |
Prediction intervals reflect uncertainty on \(\hat\beta\) and the irreducible error \(\varepsilon\) as well.
| fit | lwr | upr |
|---|---|---|
| 9.409426 | 2.946709 | 15.87214 |
| 14.163090 | 7.720898 | 20.60528 |
| 18.916754 | 12.451461 | 25.38205 |
These functions rely on our linear regression model $ \( Y = X\beta + \epsilon. \) $
Dealing with categorical or qualitative predictors #
For each qualitative predictor, e.g. Region :
Choose a baseline category, e.g. East
For every other category, define a new predictor:
\(X_\text{South}\) is 1 if the person is from the South region and 0 otherwise
\(X_\text{West}\) is 1 if the person is from the West region and 0 otherwise.
The model will be: $ \(Y = \beta_0 + \beta_1 X_1 +\dots +\beta_7 X_7 + \color{Red}{\beta_\text{South}} X_\text{South} + \beta_\text{West} X_\text{West} +\varepsilon.\) $
The parameter \(\color{Red}{\beta_\text{South}}\) is the relative effect on Balance (our \(Y\) ) for being from the South compared to the baseline category (East).
The model fit and predictions are independent of the choice of the baseline category.
However, hypothesis tests derived from these variables are affected by the choice.
Solution: To check whether region is important, use an \(F\) -test for the hypothesis \(\beta_\text{South}=\beta_\text{West}=0\) by dropping Region from the model. This does not depend on the coding.
Note that there are other ways to encode qualitative predictors produce the same fit \(\hat f\) , but the coefficients have different interpretations.
So far, we have:
Defined Multiple Linear Regression
Discussed how to test the importance of variables.
Described one approach to choose a subset of variables.
Explained how to code qualitative variables.
Now, how do we evaluate model fit? Is the linear model any good? What can go wrong?
How good is the fit? #
To assess the fit, we focus on the residuals $ \( e = Y - \hat{Y} \) $
The RSS always decreases as we add more variables.
The residual standard error (RSE) corrects this: $ \(\text{RSE} = \sqrt{\frac{1}{n-p-1}\text{RSS}}.\) $
Fig. 12 Residuals #
Visualizing the residuals can reveal phenomena that are not accounted for by the model; eg. synergies or interactions:
Potential issues in linear regression #
Interactions between predictors
Non-linear relationships
Correlation of error terms
Non-constant variance of error (heteroskedasticity)
High leverage points
Collinearity
Interactions between predictors #
Linear regression has an additive assumption: $ \(\mathtt{sales} = \beta_0 + \beta_1\times\mathtt{tv}+ \beta_2\times\mathtt{radio}+\varepsilon\) $
i.e. An increase of 100 USD dollars in TV ads causes a fixed increase of \(100 \beta_2\) USD in sales on average, regardless of how much you spend on radio ads.
We saw that in Fig 3.5 above. If we visualize the fit and the observed points, we see they are not evenly scattered around the plane. This could be caused by an interaction.
One way to deal with this is to include multiplicative variables in the model:
The interaction variable tv \(\cdot\) radio is high when both tv and radio are high.
R makes it easy to include interaction variables in the model:
Non-linearities #
Fig. 13 A nonlinear fit might be better here. #
Example: Auto dataset.
A scatterplot between a predictor and the response may reveal a non-linear relationship.
Solution: include polynomial terms in the model.
Could use other functions besides polynomials…
Fig. 14 Residuals for Auto data #
In 2 or 3 dimensions, this is easy to visualize. What do we do when we have too many predictors?
Correlation of error terms #
We assumed that the errors for each sample are independent:
What if this breaks down?
The main effect is that this invalidates any assertions about Standard Errors, confidence intervals, and hypothesis tests…
Example : Suppose that by accident, we duplicate the data (we use each sample twice). Then, the standard errors would be artificially smaller by a factor of \(\sqrt{2}\) .
When could this happen in real life:
Time series: Each sample corresponds to a different point in time. The errors for samples that are close in time are correlated.
Spatial data: Each sample corresponds to a different location in space.
Grouped data: Imagine a study on predicting height from weight at birth. If some of the subjects in the study are in the same family, their shared environment could make them deviate from \(f(x)\) in similar ways.
Correlated errors #
Simulations of time series with increasing correlations between \(\varepsilon_i\)

Non-constant variance of error (heteroskedasticity) #
The variance of the error depends on some characteristics of the input features.
To diagnose this, we can plot residuals vs. fitted values:
If the trend in variance is relatively simple, we can transform the response using a logarithm, for example.
Outliers from a model are points with very high errors.
While they may not affect the fit, they might affect our assessment of model quality.
Possible solutions: #
If we believe an outlier is due to an error in data collection, we can remove it.
An outlier might be evidence of a missing predictor, or the need to specify a more complex model.
High leverage points #
Some samples with extreme inputs have an outsized effect on \(\hat \beta\) .
This can be measured with the leverage statistic or self influence :
Studentized residuals #
The residual \(e_i = y_i - \hat y_i\) is an estimate for the noise \(\epsilon_i\) .
The standard error of \(\hat \epsilon_i\) is \(\sigma \sqrt{1-h_{ii}}\) .
A studentized residual is \(\hat \epsilon_i\) divided by its standard error (with appropriate estimate of \(\sigma\) )
When model is correct, it follows a Student-t distribution with \(n-p-2\) degrees of freedom.
Collinearity #
Two predictors are collinear if one explains the other well:
Problem: The coefficients become unidentifiable .
Consider the extreme case of using two identical predictors limit : $ \( \begin{aligned} \mathtt{balance} &= \beta_0 + \beta_1\times\mathtt{limit} + \beta_2\times\mathtt{limit} + \epsilon \\ & = \beta_0 + (\beta_1+100)\times\mathtt{limit} + (\beta_2-100)\times\mathtt{limit} + \epsilon \end{aligned} \) $
For every \((\beta_0,\beta_1,\beta_2)\) the fit at \((\beta_0,\beta_1,\beta_2)\) is just as good as at \((\beta_0,\beta_1+100,\beta_2-100)\) .
If 2 variables are collinear, we can easily diagnose this using their correlation.
A group of \(q\) variables is multilinear if these variables “contain less information” than \(q\) independent variables.
Pairwise correlations may not reveal multilinear variables.
The Variance Inflation Factor (VIF) measures how predictable it is given the other variables, a proxy for how necessary a variable is:
Above, \(R^2_{X_j|X_{-j}}\) is the \(R^2\) statistic for Multiple Linear regression of the predictor \(X_j\) onto the remaining predictors.
| Multiple Regression: Estimation and Hypothesis Testing In this chapter we considered the simplest of the multiple regression models, namely, the three-variable linear regression model—one dependent variable and two explanatory variables. Although in many ways a straightforward extension of the two-variable linear regression model, the three-variable model introduced several new concepts, such as partial regression coefficients, adjusted and unadjusted multiple coefficient of determination, and multicollinearity. Insofar as estimation of the parameters of the multiple regression coefficients is concerned, we still worked within the framework of the classical linear regression model and used the method of ordinary least squares (OLS). The OLS estimators of multiple regression, like the two-variable model, possess several desirable statistical properties summed up in the Gauss-Markov property of best linear unbiased estimators (BLUE). With the assumption that the disturbance term follows the normal distribution with zero mean and constant variance σ , we saw that, as in the two-variable case, each estimated coefficient in the multiple regression follows the normal distribution with a mean equal to the true population value and the variances given by the formulas developed in the text. Unfortunately, in practice, σ is not known and has to be estimated. The OLS estimator of this unknown variance is . But if we replace σ by , then, as in the two-variable case, each estimated coefficient of the multiple regression follows the distribution, not the normal distribution. The knowledge that each multiple regression coefficient follows the distribution with d.f. equal to ( ), where is the number of parameters estimated (including the intercept), means we can use the distribution to test statistical hypotheses about each multiple regression coefficient individually. This can be done on the basis of either the test of significance or the confidence interval based on the distribution. In this respect, the multiple regression model does not differ much from the two-variable model, except that proper allowance must be made for the d.f., which now depend on the number of parameters estimated. However, when testing the hypothesis that all partial slope coefficients are simultaneously equal to zero, the individual testing referred to earlier is of no help. Here we should use the analysis of variance (ANOVA) technique and the attendant test. Incidentally, testing that all partial slope coefficients are simultaneously equal to zero is the same as testing that the multiple coefficient of determination is equal to zero. Therefore, the test can also be used to test this latter but equivalent hypothesis. We also discussed the question of when to add a variable or a group of variables to a model, using either the test or the test. In this context we also discussed the method of restricted least squares. All the concepts introduced in this chapter have been illustrated by numerical examples and by concrete economic applications.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

IMAGES
VIDEO
COMMENTS
As in simple linear regression, under the null hypothesis t 0 = βˆ j seˆ(βˆ j) ∼ t n−p−1. We reject H 0 if |t 0| > t n−p−1,1−α/2. This is a partial test because βˆ j depends on all of the other predictors x i, i 6= j that are in the model. Thus, this is a test of the contribution of x j given the other predictors in the model.
Confidence Intervals for a Single Coefficient. The confidence interval for a regression coefficient in multiple regression is calculated and interpreted the same way as it is in simple linear regression. The t-statistic has n - k - 1 degrees of freedom where k = number of independents. Supposing that an interval contains the true value of ...
Testing that individual coefficients take a specific value such as zero or some other value is done in exactly the same way as with the simple two variable regression model. Now suppose we wish to test that a number of coefficients or combinations of coefficients take some particular value. In this case we will use the so called "F-test".
Multiple linear regression formula. The formula for a multiple linear regression is: = the predicted value of the dependent variable. = the y-intercept (value of y when all other parameters are set to 0) = the regression coefficient () of the first independent variable () (a.k.a. the effect that increasing the value of the independent variable ...
A population model for a multiple linear regression model that relates a y -variable to p -1 x -variables is written as. y i = β 0 + β 1 x i, 1 + β 2 x i, 2 + … + β p − 1 x i, p − 1 + ϵ i. We assume that the ϵ i have a normal distribution with mean 0 and constant variance σ 2. These are the same assumptions that we used in simple ...
a hypothesis test for testing that a subset — more than one, but not all — of the slope parameters are 0. In this lesson, we also learn how to perform each of the above three hypothesis tests. Key Learning Goals for this Lesson: Be able to interpret the coefficients of a multiple regression model. Understand what the scope of the model is ...
You would then proceed to generate the ANOVA table for hypothesis testing. Rcmdr: Models → Hypothesis testing → ANOVA tables. ... Absence of multicollinearity is important assumption of multiple regression. A partial test is to calculate product moment correlations among predictor variables. For example, when we calculate the correlation ...
Hypothesis Test for Predictors. One of the fundamental questions that should be answered while running Multiple Linear Regression is, whether or not, at least one of the predictors is useful in predicting the output. We saw that the three predictors TV, radio and newspaper had a different degree of linear relationship with the sales.
Solution: To check whether region is important, use an \(F\)-test for the hypothesis \(\beta_\text{South}=\beta_\text{West}=0\) by dropping Region from the model. This does not depend on the coding. ... Defined Multiple Linear Regression. Discussed how to test the importance of variables. Described one approach to choose a subset of variables.
There is a statistical test we can use to determine the overall significance of the regression model. The F-test in Multiple Linear Regression test the following hypotheses: \ (H_0\colon \beta_1=...=\beta_k=0\) \ (H_a\colon \text { At least one }\beta_i\text { is not equal to zero}\) The test statistic for this test, denoted \ (F^*\), follows ...
Multiple Regression: Estimation and Hypothesis Testing. In this chapter we considered the simplest of the multiple regression models, namely, the three-variable linear regression model—one dependent variable and two explanatory variables. Although in many ways a straightforward extension of the two-variable linear regression model, the three ...
can use its P-value to test the null hypothesis that the true value of the coefficient is 0. Using the coefficients from this table, we can write the regression model:. ... Second, multiple regression is an extraordinarily versatile calculation, underly-ing many widely used Statistics methods. A sound understanding of the multiple
12-2 Hypothesis Tests in Multiple Linear Regression R 2 and Adjusted R The coefficient of multiple determination • For the wire bond pull strength data, we find that R2 = SS R /SS T = 5990.7712/6105.9447 = 0.9811. • Thus, the model accounts for about 98% of the variability in the pull strength response.
• Multiple regression in matrix notation • Least squares estimation of model parameters • Maximum likelihood estimation of model parameters • Hypothesis testing. 2 Multiple linear regression We are now considering the model y i = ...
In contrast, the simple regression slope is called the marginal (or unadjusted) coefficient. The multiple regression model can be written in matrix form. To estimate the parameters b 0, b 1,..., b p using the principle of least squares, form the sum of squared deviations of the observed yj's from the regression line:
Okay, suppose you've estimated your regression model. The first hypothesis test you might want to try is one in which the null hypothesis that there is no relationship between the predictors and the outcome, ... 4.354 on 97 degrees of freedom Multiple R-squared: 0.8161, Adjusted R-squared: 0.8123 F-statistic: 215.2 on 2 and 97 DF, p-value ...
The hypotheses are: Find the critical value using dfE = n − p − 1 = 13 for a two-tailed test α = 0.05 inverse t-distribution to get the critical values ± 2.160. Draw the sampling distribution and label the critical values, as shown in Figure 12-14. Figure 12-14: Graph of t-distribution with labeled critical values.
For the simple linear regression model, there is only one slope parameter about which one can perform hypothesis tests. For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are: Hypothesis test for testing that all of the slope parameters are 0.
2. I struggle writing hypothesis because I get very much confused by reference groups in the context of regression models. For my example I'm using the mtcars dataset. The predictors are wt (weight), cyl (number of cylinders), and gear (number of gears), and the outcome variable is mpg (miles per gallon). Say all your friends think you should ...
We will now explore multiple hypothesis testing, or what happens when multiple tests are conducted on the same family of data. We will set things up as before, with the false positive rate α= 0.05 α = 0.05 and false negative rate β =0.20 β = 0.20. library (pwr) library (ggplot2) set.seed(1) mde <- 0.1 # minimum detectable effect.
xi: The value of the predictor variable xi. Multiple linear regression uses the following null and alternative hypotheses: H0: β1 = β2 = … = βk = 0. HA: β1 = β2 = … = βk ≠ 0. The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically ...
Lesson 5: Multiple Linear Regression. Overview. In this lesson, we make our first (and last?!) major jump in the course. We move from the simple linear regression model with one predictor to the multiple linear regression model with two or more predictors. That is, we use the adjective "simple" to denote that our model has only predictors, and ...
This test is called the overall F-test in MLR and is very similar to the F F -test in a reference-coded One-Way ANOVA model. It tests the null hypothesis that involves setting every coefficient except the y y -intercept to 0 (so all the slope coefficients equal 0). We saw this reduced model in the One-Way material when we considered setting all ...
I am familiar with using multiple linear regressions to create models of various variables. However, I was curious if regression tests are ever used to do any sort of basic hypothesis testing. If so, what would those scenarios/hypotheses look like? regression. hypothesis-testing.
Whatever levels are chosen, testing at multiple alphas is subject to the qualifications needed for any application of P-values, which only indicate the degree to which data are unusual if a test hypothesis together with all other modelling assumptions are correct. Data from a repeat of a trial may still, with the same assumptions and tests ...