unit 12 probability homework 5 conditional probability answer key

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics > unit 7.

Conditional probability and independence
Conditional probability with Bayes' Theorem

Conditional probability using two-way tables

Calculate conditional probability
Conditional probability tree diagram example
Tree diagrams and conditional probability
Your answer should be
an integer, like 6 ‍
a simplified proper fraction, like 3 / 5 ‍
a simplified improper fraction, like 7 / 4 ‍
a mixed number, like 1 3 / 4 ‍
an exact decimal, like 0.75 ‍
a multiple of pi, like 12 pi ‍ or 2 / 3 pi ‍
(Choice A) True A True
(Choice B) False B False
(Choice A) About 62 % ‍ of females chose invisibility as their superpower. A About 62 % ‍ of females chose invisibility as their superpower.
(Choice B) About 62 % ‍ of people who chose invisibility as their superpower were female. B About 62 % ‍ of people who chose invisibility as their superpower were female.

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

5.E: Basic Concepts of Probability (Exercises)

Last updated
Save as PDF
Page ID 28387

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

These are homework exercises to accompany the Textmap created for "Introductory Statistics" by Shafer and Zhang.

3.1: Sample Spaces, Events, and Their Probabilities

A box contains $10$ white and $10$ black marbles. Construct a sample space for the experiment of randomly drawing out, with replacement, two marbles in succession and noting the color each time. (To draw “with replacement” means that the first marble is put back before the second marble is drawn.)

A box contains $16$ white and $16$ black marbles. Construct a sample space for the experiment of randomly drawing out, with replacement, three marbles in succession and noting the color each time. (To draw “with replacement” means that each marble is put back before the next marble is drawn.)

A box contains $8$ red, $8$ yellow, and $8$ green marbles. Construct a sample space for the experiment of randomly drawing out, with replacement, two marbles in succession and noting the color each time.

A box contains $6$ red, $6$ yellow, and $6$ green marbles. Construct a sample space for the experiment of randomly drawing out, with replacement, three marbles in succession and noting the color each time.

In the situation of Exercise 1 , list the outcomes that comprise each of the following events.

At least one marble of each color is drawn.
No white marble is drawn.

In the situation of Exercise 2 , list the outcomes that comprise each of the following events.

More black than white marbles are drawn.

In the situation of Exercise 3 , list the outcomes that comprise each of the following events.

No yellow marble is drawn.
The two marbles drawn have the same color.

In the situation of Exercise 4 , list the outcomes that comprise each of the following events.

The three marbles drawn have the same color.

Assuming that each outcome is equally likely, find the probability of each event in Exercise 5 .

Assuming that each outcome is equally likely, find the probability of each event in Exercise 6 .

Assuming that each outcome is equally likely, find the probability of each event in Exercise 7 .

Assuming that each outcome is equally likely, find the probability of each event in Exercise 8 .

A sample space is $S=\{a,b,c,d,e\}$. Identify two events as $U=\{a,b,d\}$ and $V=\{b,c,d\}$. Suppose $P(a)$ and $P(b)$ are each $0.2$ and $P(c)$ and $P(d)$ are each $0.1$.

Determine what $P(e)$ must be.
Find $P(U)$.
Find $P(V)$

A sample space is $S=\{u,v,w,x\}$. Identify two events as $A=\{v,w\}$ and $B=\{u,w,x\}$. Suppose $P(u)=0.22$, $P(w)=0.36$, and $P(x)=0.27$.

Determine what $P(v)$ must be.
Find $P(A)$.
Find $P(B)$.

A sample space is $S=\{m,n,q,r,s\}$. Identify two events as $U=\{m,q,s\}$ and $V=\{n,q,r\}$. The probabilities of some of the outcomes are given by the following table: \[\begin{array}{c|c c c c c} Outcome &m &n &q &r &s \\ \hline Probability &0.18 &0.16 & &0.24 &0.21\\ \end{array}\]

Determine what $P(q)$ must be.
Find $P(V)$.

A sample space is $S=\{d,e,f,g,h\}$. Identify two events as $M=\{e,f,g,h\}$ and $N=\{d,g\}$. The probabilities of some of the outcomes are given by the following table: \[\begin{array}{c|c c c c c} Outcome &d &e &f &g &h \\ \hline Probability &0.22 &0.13 &0.27 & &0.19\\ \end{array}\]

Determine what $P(g)$ must be.
Find $P(M)$.
Find $P(N)$.

Applications

The sample space that describes all three-child families according to the genders of the children with respect to birth order was constructed in "Example 3.1.4". Identify the outcomes that comprise each of the following events in the experiment of selecting a three-child family at random.

At least one child is a girl.
At most one child is a girl.
All of the children are girls.
Exactly two of the children are girls.
The first born is a girl.

The sample space that describes three tosses of a coin is the same as the one constructed in "Example 3.1.4" with “boy” replaced by “heads” and “girl” replaced by “tails.” Identify the outcomes that comprise each of the following events in the experiment of tossing a coin three times.

The coin lands heads more often than tails.
The coin lands heads the same number of times as it lands tails.
The coin lands heads at least twice.
The coin lands heads on the last toss.

Assuming that the outcomes are equally likely, find the probability of each event in Exercise 17 .

Assuming that the outcomes are equally likely, find the probability of each event in Exercise 18 .

Additional Exercises

The following two-way contingency table gives the breakdown of the population in a particular locale according to age and tobacco usage:

A person is selected at random. Find the probability of each of the following events.

The person is a smoker.
The person is under $30$.
The person is a smoker who is under $30$.

The following two-way contingency table gives the breakdown of the population in a particular locale according to party affiliation ($A, B, C,\; \text{or None}$) and opinion on a bond issue:

The person is affiliated with party $B$.
The person is affiliated with some party.
The person is in favor of the bond issue.
The person has no party affiliation and is undecided about the bond issue.

The following two-way contingency table gives the breakdown of the population of married or previously married women beyond child-bearing age in a particular locale according to age at first marriage and number of children:

A woman is selected at random. Find the probability of each of the following events.

The woman was in her twenties at her first marriage.
The woman was $20$ or older at her first marriage.
The woman had no children.
The woman was in her twenties at her first marriage and had at least three children.

The following two-way contingency table gives the breakdown of the population of adults in a particular locale according to highest level of education and whether or not the individual regularly takes dietary supplements:

An adult is selected at random. Find the probability of each of the following events.

The person has a high school diploma and takes dietary supplements regularly.
The person has an undergraduate degree and takes dietary supplements regularly.
The person takes dietary supplements regularly.
The person does not take dietary supplements regularly.

Large Data Set Exercises

Large Data Set 4 and Data Set 4A record the results of $500$ tosses of a coin. Find the relative frequency of each outcome $1, 2, 3, 4, 5,\; and\; 6$. Does the coin appear to be “balanced” or “fair”?

Large Data Set 6, Data Set 6A, and Data Set 6B record results of a random survey of $200$ voters in each of two regions, in which they were asked to express whether they prefer Candidate $A$ for a U.S. Senate seat or prefer some other candidate.

Find the probability that a randomly selected voter among these $400$ prefers Candidate $A$.
Find the probability that a randomly selected voter among the $200$ who live in Region $1$ prefers Candidate $A$ (separately recorded in $\text{Large Data Set 6A}$).
Find the probability that a randomly selected voter among the $200$ who live in Region $2$ prefers Candidate $A$ (separately recorded in $\text{Large Data Set 6B}$).

$S=\{bb,bw,wb,ww\}$

$S=\{rr,ry,rg,yr,yy,yg,gr,gy,gg\}$

$\{bw,wb\}$
$\{rr,rg,gr,gg\}$
$\{rr,yy,gg\}$
$\varnothing $
$\{gbb,gbg,ggb,ggg\}$
$\{bgg,gbg,ggb\}$
$\{ggg\}$
$\{bbb,bbg,bgb,gbb\}$
$\{bbg,bgb,bgg,gbb,gbg,ggb,ggg\}$

The relative frequencies for $1$ through $6$ are $0.16, 0.194, 0.162, 0.164, 0.154\; and\; 0.166$. It would appear that the die is not balanced.

3.2: Complements, Intersections and Unions

$A=\{a,d,e\}$
$B=\{b,c,d,e\}$
$R=\{t,u\}$
$T=\{r\}$
$\varnothing$ (the “empty” set that has no elements)
List the outcomes that comprise $H$ and $M$.
List the outcomes that comprise $H\cap M$, $H\cup M$, and $H^c$.
Assuming all outcomes are equally likely, find $P(H\cap M)$, $P(H\cup M)$, and $P(H^c)$.
Determine whether or not $H^c$ and $M$ are mutually exclusive. Explain why or why not.
List the outcomes that comprise $T$ and $G$.
List the outcomes that comprise $T\cap G$, $T\cup G$, $T^c$, and $(T\cup G)^c$.
Assuming all outcomes are equally likely, find $P(T\cap G)$, $P(T\cup G)$, and $P(T^c)$.
Determine whether or not $T$ and $G$ are mutually exclusive. Explain why or why not.
List the outcomes that comprise $B$, $R$, and $N$.
List the outcomes that comprise $B\cap R$, $B\cup R$, $B\cap N$, $R\cup N$, $B^c$, and $(B\cup R)^c$.
Assuming all outcomes are equally likely, find the probabilities of the events in the previous part.
Determine whether or not $B$ and $N$ are mutually exclusive. Explain why or why not.
List the outcomes that comprise $Y$, $I$, and $J$.
List the outcomes that comprise $Y\cap I$, $Y\cup J$, $I\cap J$, $I^c$, and $(Y\cup J)^c$.
Determine whether or not $I^c$ and $J$ are mutually exclusive. Explain why or why not.
The Venn diagram provided shows a sample space and two events $A$ and $B$. Suppose $P(a)=0.13, P(b)=0.09, P(c)=0.27, P(d)=0.20,\; \text{and}\; P(e)=0.31$. Confirm that the probabilities of the outcomes add up to $1$, then compute the following probabilities.

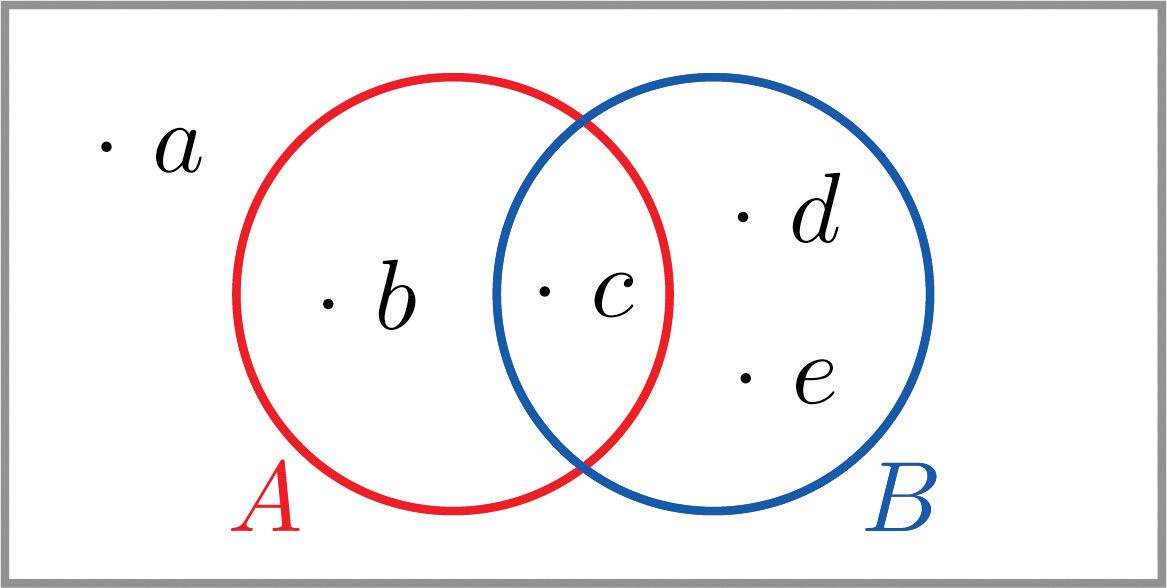
$P(A^c)$. Two ways: (i) by finding the outcomes in $A^c$ and adding their probabilities, and (ii) using the Probability Rule for Complements.
$P(A\cap B)$.
$P(A\cup B)$ Two ways: (i) by finding the outcomes in $A\cup B$ and adding their probabilities, and (ii) using the Additive Rule of Probability.
The Venn diagram provided shows a sample space and two events $A$ and $B$. Suppose $P(a)=0.32, P(b)=0.17, P(c)=0.28,\; \text{and}\; P(d)=0.23$. Confirm that the probabilities of the outcomes add up to $1$, then compute the following probabilities.

Confirm that the probabilities in the two-way contingency table add up to $1$, then use it to find the probabilities of the events indicated.
$P(A), P(B), P(A\cap B)$.
$P(U), P(W), P(U\cap W)$.
$P(U\cup W)$.
$P(V^c)$.
Determine whether or not the events $A$ and $U$ are mutually exclusive; the events $A$ and $V$.
$P(R), P(S), P(R\cap S)$.
$P(M), P(N), P(M\cap N)$.
$P(R\cup S)$.
$P(R^c)$.
Determine whether or not the events $N$ and $S$ are mutually exclusive; the events $N$ and $T$.
In the roll of a die: “five or more.”
In a roll of a die: “an even number.”
In two tosses of a coin: “at least one heads.”
In the random selection of a college student: “Not a freshman.”
In the roll of a die: “two or less.”
In the roll of a die: “one, three, or four.”
In two tosses of a coin: “at most one heads.”
In the random selection of a college student: “Neither a freshman nor a senior.”
The person is male.
The person is not in favor.
The person is either male or in favor.
The person is female and neutral.
A tourist who speaks English and German but no other language visits a region of Slovenia. If $35\%$ of the residents speak English, $15\%$ speak German, and $3\%$ speak both English and German, what is the probability that the tourist will be able to talk with a randomly encountered resident of the region?
In a certain country $43\%$ of all automobiles have airbags, $27\%$ have anti-lock brakes, and $13\%$ have both. What is the probability that a randomly selected vehicle will have both airbags and anti-lock brakes?
A manufacturer examines its records over the last year on a component part received from outside suppliers. The breakdown on source (supplier $A$, supplier $B$) and quality ($\text{H: high, U: usable, D: defective}$) is shown in the two-way contingency table.

The record of a part is selected at random. Find the probability of each of the following events.

The part was defective.
The part was either of high quality or was at least usable, in two ways: (i) by adding numbers in the table, and (ii) using the answer to (a) and the Probability Rule for Complements.
The part was defective and came from supplier $B$.
The part was defective or came from supplier $B$, in two ways: by finding the cells in the table that correspond to this event and adding their probabilities, and (ii) using the Additive Rule of Probability.
Individuals with a particular medical condition were classified according to the presence ($T$) or absence ($N$) of a potential toxin in their blood and the onset of the condition ($\text{E: early, M: midrange, L: late}$). The breakdown according to this classification is shown in the two-way contingency table.

One of these individuals is selected at random. Find the probability of each of the following events.

The person experienced early onset of the condition.
The onset of the condition was either midrange or late, in two ways: (i) by adding numbers in the table, and (ii) using the answer to (a) and the Probability Rule for Complements.
The toxin is present in the person’s blood.
The person experienced early onset of the condition and the toxin is present in the person’s blood.
The person experienced early onset of the condition or the toxin is present in the person’s blood, in two ways: (i) by finding the cells in the table that correspond to this event and adding their probabilities, and (ii) using the Additive Rule of Probability.
The breakdown of the students enrolled in a university course by class ($\text{F: freshman, So: sophomore, J: junior, Se: senior}$) and academic major ($\text{S: science, mathematics, or engineering, L: liberal arts, O: other}$) is shown in the two-way classification table.

A student enrolled in the course is selected at random. Adjoin the row and column totals to the table and use the expanded table to find the probability of each of the following events.

The student is a freshman.
The student is a liberal arts major.
The student is a freshman liberal arts major.
The student is either a freshman or a liberal arts major.
The student is not a liberal arts major.
The table relates the response to a fund-raising appeal by a college to its alumni to the number of years since graduation.

An alumnus is selected at random. Adjoin the row and column totals to the table and use the expanded table to find the probability of each of the following events.

The alumnus responded.
The alumnus did not respond.
The alumnus graduated at least $21$ years ago.
The alumnus graduated at least $21$ years ago and responded.
List the outcomes that correspond to the statement “All the coins are heads.”
List the outcomes that correspond to the statement “Not all the coins are heads.”
List the outcomes that correspond to the statement “All the coins are not heads.”
$\{b,c\}$
$\varnothing$
$H=\{hhh,hht,hth,htt,thh,tht,tth\},\; M=\{hhh,hht,hth,thh\}$
$H\cap M=\{hhh,hht,hth,thh\}, H\cup M=H, H^c=\{ttt\}$
$P(H\cap M)=4/8, P(H\cup M)=7/8, P(H^c)=1/8$
Mutually exclusive because they have no elements in common.
$B=\{b1,b2,b3,b4\},\; R=\{r1,r2,r3,r4\},\; N=\{b1,b2,y1,y2,g1,g2,r1,r2\}$
$B\cap R=\varnothing , B\cup R=\{b1,b2,b3,b4,r1,r2,r3,r4\},\; B\cap N=\{b1,b2\},\\ R\cup N=\{b1,b2,y1,y2,g1,g2,r1,r2,r3,r4\},\\ B^c=\{y1,y2,y3,y4,g1,g2,g3,g4,r1,r2,r3,r4\},\; (B\cup R)^c=\{y1,y2,y3,y4,g1,g2,g3,g4\}$
$P(B\cap R)=0,\; P(B\cup R)=8/16,\; P(B\cap N)=2/16,\; P(R\cup N)=10/16,\; P(B^c)=12/16,\; P((B\cup R)^c)=8/16$
Not mutually exclusive because they have an element in common.
$P(A)=0.38,\; P(B)=0.62,\; P(A\cap B)=0$
$P(U)=0.37,\; P(W)=0.33,\; P(U\cap W)=0$
$A$ and $U$ are not mutually exclusive because $P(A\cap U)$ is the nonzero number $0.15$. $A$ and $V$ are mutually exclusive because $P(A\cap V)=0$.
“four or less”
“an odd number”
“no heads” or “all tails”
“a freshman”
“All the children are boys.” Event: $\{bbg,bgb,bgg,gbb,gbg,ggb,ggg\}$, Complement: $\{bbb\}$
“At least two of the children are girls” or “There are two or three girls.” Event: $\{bbb,bbg,bgb,gbb\}$, Complement: $\{bgg,gbg,ggb,ggg\}$
“At least one child is a boy.” Event: $\{ggg\}$, Complement: $\{bbb,bbg,bgb,bgg,gbb,gbg,ggb\}$
“There are either no girls, exactly one girl, or three girls.” Event: $\{bgg,gbg,ggb\}$, Complement: $\{bbb,bbg,bgb,gbb,ggg\}$
“The first born is a boy.” Event: $\{gbb,gbg,ggb,ggg\}$, Complement: $\{bbb,bbg,bgb,bgg\}$
$920/1671$
$668/1671$
$368/1671$
$1220/1671$
$1003/1671$
$\{hhh\}$
$\{hht,hth,htt,thh,tht,tth,ttt\}$
$\{ttt\}$

3.3: Conditional Probability and Independent Events

Find $P(A\mid B)$.
Find $P(B\mid A)$.
Determine whether or not $A$ and $B$ are independent.
The probability that the roll is even.
The probability that the roll is even, given that it is not a two.
The probability that the roll is even, given that it is not a one.
The probability that the second toss is heads.
The probability that the second toss is heads, given that the first toss is heads.
The probability that the second toss is heads, given that at least one of the two tosses is heads.
The probability that the card drawn is red.
The probability that the card is red, given that it is not green.
The probability that the card is red, given that it is neither red nor yellow.
The probability that the card is red, given that it is not a four.
The probability that the card drawn is a two or a four.
The probability that the card is a two or a four, given that it is not a one.
The probability that the card is a two or a four, given that it is either a two or a three.
The probability that the card is a two or a four, given that it is red or green.
$P(A),\; P(R),\; P(A\cap B)$.
Based on the answer to (a), determine whether or not the events $A$ and $R$ are independent.
Based on the answer to (b), determine whether or not $P(A\mid R)$ can be predicted without any computation. If so, make the prediction. In any case, compute $P(A\mid R)$ using the Rule for Conditional Probability.
$P(A\cap B)$, with the extra information that $A$ and $B$ are independent.
$P(A\cap B)$, with the extra information that $A$ and $B$ are mutually exclusive.
$P(A\cap B\cap C)$.
$P(A^c\cap B^c\cap C^c)$.

The sample space that describes all three-child families according to the genders of the children with respect to birth order is \[S=\{bbb,bbg,bgb,bgg,gbb,gbg,ggb,ggg\}\] In the experiment of selecting a three-child family at random, compute each of the following probabilities, assuming all outcomes are equally likely.

The probability that the family has at least two boys.
The probability that the family has at least two boys, given that not all of the children are girls.
The probability that at least one child is a boy.
The probability that at least one child is a boy, given that the first born is a girl.

The following two-way contingency table gives the breakdown of the population in a particular locale according to age and number of vehicular moving violations in the past three years:

A person is selected at random. Find the following probabilities.

The person is under $21$.
The person has had at least two violations in the past three years.
The person has had at least two violations in the past three years, given that he is under $21$.
The person is under $21$, given that he has had at least two violations in the past three years.
Determine whether the events “the person is under $21$” and “the person has had at least two violations in the past three years” are independent or not.

The following two-way contingency table gives the breakdown of the population in a particular locale according to party affiliation ($A, B, C, \text{or None}$) and opinion on a bond issue:

A person is selected at random. Find each of the following probabilities.

The person is in favor of the bond issue, given that he is affiliated with party $A$.
The person is in favor of the bond issue, given that he is affiliated with party $B$.

The following two-way contingency table gives the breakdown of the population of patrons at a grocery store according to the number of items purchased and whether or not the patron made an impulse purchase at the checkout counter:

A patron is selected at random. Find each of the following probabilities.

The patron made an impulse purchase.
The patron made an impulse purchase, given that the total number of items purchased was many.
Determine whether or not the events “few purchases” and “made an impulse purchase at the checkout counter” are independent.

The following two-way contingency table gives the breakdown of the population of adults in a particular locale according to employment type and level of life insurance:

An adult is selected at random. Find each of the following probabilities.

The person has a high level of life insurance.
The person has a high level of life insurance, given that he does not have a professional position.
The person has a high level of life insurance, given that he has a professional position.
Determine whether or not the events “has a high level of life insurance” and “has a professional position” are independent.

The sample space of equally likely outcomes for the experiment of rolling two fair dice is \[\begin{matrix} 11 & 12 & 13 & 14 & 15 & 16\\ 21 & 22 & 23 & 24 & 25 & 26\\ 31 & 32 & 33 & 34 & 35 & 36\\ 41 & 42 & 43 & 44 & 45 & 46\\ 51 & 52 & 53 & 54 & 55 & 56\\ 61 & 62 & 63 & 64 & 65 & 66 \end{matrix}\] Identify the events $\text{N: the sum is at least nine, T: at least one of the dice is a two, and F: at least one of the dice is a five}$.

Find $P(N\mid F)$.
Find $P(N\mid T)$.
Determine from the previous answers whether or not the events $N$ and $F$ are independent; whether or not $N$ and $T$ are.

The sensitivity of a drug test is the probability that the test will be positive when administered to a person who has actually taken the drug. Suppose that there are two independent tests to detect the presence of a certain type of banned drugs in athletes. One has sensitivity $0.75$; the other has sensitivity $0.85$. If both are applied to an athlete who has taken this type of drug, what is the chance that his usage will go undetected?

A man has two lights in his well house to keep the pipes from freezing in winter. He checks the lights daily. Each light has probability $0.002$ of burning out before it is checked the next day (independently of the other light).

If the lights are wired in parallel one will continue to shine even if the other burns out. In this situation, compute the probability that at least one light will continue to shine for the full $24$ hours. Note the greatly increased reliability of the system of two bulbs over that of a single bulb.
If the lights are wired in series neither one will continue to shine even if only one of them burns out. In this situation, compute the probability that at least one light will continue to shine for the full $24$ hours. Note the slightly decreased reliability of the system of two bulbs over that of a single bulb.

An accountant has observed that $5\%$ of all copies of a particular two-part form have an error in Part I, and $2\%$ have an error in Part II. If the errors occur independently, find the probability that a randomly selected form will be error-free.

A box contains $20$ screws which are identical in size, but $12$ of which are zinc coated and $8$ of which are not. Two screws are selected at random, without replacement.

Find the probability that both are zinc coated.
Find the probability that at least one is zinc coated.

Events $A$ and $B$ are mutually exclusive. Find $P(A\mid B)$.

The city council of a particular city is composed of five members of party $A$, four members of party $B$, and three independents. Two council members are randomly selected to form an investigative committee.

Find the probability that both are from party $A$.
Find the probability that at least one is an independent.
Find the probability that the two have different party affiliations (that is, not both $A$, not both $B$, and not both independent).

A basketball player makes $60\%$ of the free throws that he attempts, except that if he has just tried and missed a free throw then his chances of making a second one go down to only $30\%$. Suppose he has just been awarded two free throws.

Find the probability that he makes both.
Find the probability that he makes at least one. (A tree diagram could help.)

An economist wishes to ascertain the proportion $p$ of the population of individual taxpayers who have purposely submitted fraudulent information on an income tax return. To truly guarantee anonymity of the taxpayers in a random survey, taxpayers questioned are given the following instructions.

Flip a coin.
If the coin lands heads, answer “Yes” to the question “Have you ever submitted fraudulent information on a tax return?” even if you have not.
If the coin lands tails, give a truthful “Yes” or “No” answer to the question “Have you ever submitted fraudulent information on a tax return?”

The questioner is not told how the coin landed, so he does not know if a “Yes” answer is the truth or is given only because of the coin toss.

The only information that the economist sees are the entries in the following table: \[\begin{array}{c|c|c} Response & "Yes" & "No" \\ \hline Proportion &r &s\\ \end{array}\]Equate the entry in the one cell in the table in (a) that corresponds to the answer “No” to the number s to obtain the formula that expresses the unknown number $p$ in terms of the known number $s$.
Equate the sum of the entries in the three cells in the table in (a) that together correspond to the answer “Yes” to the number r to obtain the formula that expresses the unknown number $p$ in terms of the known number $r$.
Use the fact that $r+s=1$(since they are the probabilities of complementary events) to verify that the formulas in (b) and (c) give the same value for $p$. (For example, insert $s=1-r$into the formula in (b) to obtain the formula in (c)).
Suppose a survey of $1,200$ taxpayers is conducted and $690$ respond “Yes” (truthfully or not) to the question “Have you ever submitted fraudulent information on a tax return?” Use the answer to either (b) or (c) to estimate the true proportion $p$ of all individual taxpayers who have purposely submitted fraudulent information on an inc ome tax return.
not independent
$P(A)=0.3,\; P(R)=0.4,\; P(A\cap R)=0.12$
independent
without computation $0.3$
Insufficient information. The events A and B are not known to be either independent or mutually exclusive.

Contributor

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

8.4.1: Conditional Probability (Exercises)

Last updated
Save as PDF
Page ID 37915

Rupinder Sekhon and Roberta Bloom
De Anza College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

SECTION 8.4 PROBLEM SET: CONDITIONAL PROBABILITY

Questions 1 - 4: Do these problems using the conditional probability formula: $P(A | B)=\frac{P(A \cap B)}{P(B)}$.

Questions 5 - 8 refer to the following: The table shows the distribution of Democratic and Republican U.S. Senators by gender in the 114 th Congress as of January 2015.

Use this table to determine the following probabilities:

Do the following conditional probability problems.

At a college, 72% of courses have final exams and 46% of courses require research papers. 32% of courses have both a research paper and a final exam. Let $F$ be the event that a course has a final exam and $R$ be the event that a course requires a research paper.

Consider a family of three children. Find the following probabilities.

Questions 21 - 26 refer to the following: The table shows highest attained educational status for a sample of US residents age 25 or over:

PAYMENT PLANS ARE NOW AVAILABLE! • VISIT THE SHOP TO LEARN MORE!

All Things Algebra®

unit 12 probability homework 5 conditional probability answer key

Geometry Unit 12: Probability

This unit includes 50 pages of guided notes, homework assignments, two quizzes, a study guide, and a unit test that cover the topics listed in the description below.

Description
Additional Information
What Educators Are Saying

This unit contains the following topics:

• Introduction to Sets (Universal Set, Complement of a Set, Subsets, Union, Intersection – just basic!) • Venn Diagrams • Counting Outcomes (Fundamental Counting Principle) • Theoretical Probability • Experimental Probability • Geometric Probability (Segments, Area, and Volume) • Compound Probability: Independent Events • Compound Probability: Dependent Events • Conditional Probability • Two-Way Tables • Relative Frequency Two-Way Tables • Probability with Two-Way Tables • Permutations • Combinations • Probability with Permutations and Combinations

This unit does not contain activities.

This is the guided notes, homework assignments, quizzes, study guide, and unit test only. For suggested activities to go with this unit, check out the ATA Activity Alignment Guides .

This resource is included in the following bundle(s):

Geometry Curriculum Geometry Curriculum (with Activities)

License Terms:

This purchase includes a single non-transferable license, meaning it is for one teacher only for personal use in their classroom and can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. A t ransferable license is not available for this resource.

Copyright Terms:

No part of this resource may be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

What standards is this curriculum aligned to?

What format are the files in, will i have access to materials if they are updated, are answer keys included, are videos included.

This is a major upgrade from the resources my school provided for our probability unit! My students find the notes/assignments easy to work with and enjoy the similarity in the notes and homework that make it easy for them to find examples to refer to when they need help!

Lots of great examples showing various types of probability problems, including using Venn Diagrams. The geometry probability problems are nice and challenging too. As usual, great product.

This was a lifesaver the last few weeks of school. I had no desire to create a whole unit from scratch the last unit and this was very helpful. As usual, I love that the answer keys were included. Having the videos included was also very helpful for making sub plans.

Conditional Probability Worksheets

What Is Conditional Probability? The probability that is defined as the possibility for the likelihood of the following event based on the result of the previous event. Conditional probability is found out by multiplying the probability of the previous into the probability of the succeeding event. For example: You have event A that represents that there is a 20% chance of rain today. You have event B that represents that you have to go outside and has the probability of 60%. The conditional probability will give you the outcome based on the relationship between these two events. That is the probability that represents both, you need to go outside, and it is raining. Independent events are events that are not affected by one another. For example, tossing a coin. In a coin toss, each toss is an independent event and an isolated outcome. Events can also be dependent. That is, both the events are affected by each other. The next event is affected by the probability of the previous event. For example, 2 blue and 3 red balls are in the bag. The probability of getting a blue ball is 2 in 5. But if we got a red ball before, then the probability of getting a blue is 2 in 4.

Basic Lesson

Introduces the application of conditional probability with playing cards. One card is drawn from a standard deck of cards. Find the probability of drawing a club or spade card?

Intermediate Lesson

This lesson focuses on conditional probability within random numbers. A number is selected from 1 to 15 at random. What is the probability of getting a number that is a multiple of 5?

Independent Practice 1

Students practice with 20 conditional probability problems. The answers can be found below. In a middle school of 200 students, 100 are seniors, 50 students take part in a play, and 30 students are seniors and are also taking part in play. What is the probability that a randomly chosen student is a senior and is taking part in play?

Independent Practice 2

Another 20 conditional probability problems. The answers can be found below. If the student selected is an 8th grade student, what is the probability that the student prefers Science or History?

Homework Worksheet

Reviews all skills in the unit. A great take home sheet. Also provides a practice problem.

10 problems that test Conditional Probability skills.

Homework and Quiz Answer Key

Answers for the homework and quiz.

Answers for the lesson and practice sheets.

What Are The Odds?

A statistician was stopped because she had a bomb in her carry-on. The official said, "Why would you want to blow up a plane?" The woman replied, "I wasn't going to use it, but the odds of there being 2 bombs on one plane is 1 in 100,000."

Conditional Probability Questions

Conditional probability questions with solutions are given here for students to practice and understand the concept of conditional probability. By conditional probability, we mean the possibility of happening an event after the occurrence of an event already. For example, a dice is rolled, and the outcome is an odd number, now we have to find the probability of the outcome being a prime number, then,

A ≡ Odd outcome for rolling a dice

B ≡ Outcome being a prime number

Clearly, A already happened thereafter; we have to find the probability of happening B.

Thus, P(B|A) = P(A ∩ B)/P(A), where P(A) ≠ 0 and

P(B|A) = probability of occurrence of B given A already happened

P(A ∩ B) = probability of occurrence of A and B together

P(A) = probability of occurrence of A.

Learn more about conditional probability .

Conditional Probability Questions with Solutions

Let us solve some questions based on conditional probability with detailed solutions.

Question 1:

Ten numbered cards are there from 1 to 15, and two cards a chosen at random such that the sum of the numbers on both the cards is even. Find the probability that the chosen cards are odd-numbered.

Let, A ≡ event of selecting two odd-numbered cards

B ≡ event of selecting cards whose sum is even.

n(B) = number of ways of choosing two numbers whose sum is even = 8 C 2 + 7 C 2 .

n(A ∩ B) = number of ways of choosing odd-numbered cards such that their sum is even.

Now, P(A|B) = P(A ∩ B)/P(B) = n(A ∩ B)/n(B)

= 8 C 2 / ( 8 C 2 + 7 C 2 ) = 4/7.

Question 2:

Let E and F are events of a experiment such that P(E) = 3/10 P(F) = ½ and P(F|E) = ⅖. Find the value of (i) P(E ∩ F) (ii) P(E|F) (iii) P(E U F)

We know that P(A|B) = P(A ∩ B)/P(B) ⇒ P(A ∩ B) = P(A|B).P(B)

∴ P(E ∩ F) = P(F|E).P(E) =⅖ × 3/10 = 3/25

(ii) P(E|F) = P(E ∩ F)/P(F) = (3/25) ÷ (½) = 6/25

(iii) P(E U F) = P(E) + P(F) – P(E ∩ F) = 3/10 + ½ – 3/25 = 17/25.

Question 3:

The probability of a student passing in science is ⅘ and the of the student passing in both science and maths is ½. What is the probability of that student passing in maths knowing that he passed in science?

Let A ≡ event of passing in science

B ≡ event of passing in maths

Given, P(B) = ⅘ and P(A ∩ B) = ½

Then, probability of passing maths after passing in science = P(B|A) = P(A ∩ B)/P(A)

= ½ ÷ ⅘ = ⅝

∴ the probability of passing in maths is ⅝.

Question 4:

In a survey among few people, 60% read Hindi newspaper, 40% read English newspaper and 20% read both. If a person is chosen at random and if he already reads English newspaper find the probability that he also reads Hindi newspaper.

Let there be 100 people in the survey, then

Number of people read Hindi newspaper = n(A) = 60

Number of people read English newspaper = n(B) = 40

Number of people read both = n(A ∩ B) = 20

Probability of the person reading Hindi newspaper when he already reads English newspaper is given by –

P(A|B) = n(A ∩ B)/n(B) = 20/40 = ½.

Bayes Theorem
Probability for Class 12
Basic Probability Formulas
Mutually Exclusive Events

Question 5:

A fair coin is tossed twice such that E: event of having both head and tail, and F: event of having atmost one tail. Find P(E), P(F) and P(E|F)

The sample space S = { HH, HT, TH, TT}

E = {HT, TH}

F = {HH, HT, TH}

E ∩ F = {HT, TH}

P(E) = 2/4 = ½

P(E ∩ F) = 2/4 = ½

P(E|F) = P(E ∩ F)/P(F) = ½ ÷ ¾ = ⅔.

Question 6:

In a class, 40% of the students like Mathematics and 25% of students like Physics and 15% like both the subjects. One student select at random, find the probability that he likes Physics if it is known that he likes Mathematics.

Let there be 100 students, then,

Number of students like Mathematics = n(A) = 40

Number of students like Physics = n(B) = 25

Number of students like both Mathematics and Physics = n(A ∩ B) = 15

Now, the probability that the student likes Physics if it is known that he likes Mathematics is given by –

P(B|A) = n(A ∩ B)/n(A) = 15/40 = ⅜.

Question 7:

Two dice are rolled, if it is known that atleast one of the dice always shows 4, find the probability that the numbers appeared on the dice have a sum 8.

A: one of the outcomes is always 4

B: sum of the outcomes is 8

Then, A = {(1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6)}

B{(4, 4), (5, 3), (3, 5), (6, 2), (2, 6)}

n(A) = 11, n(B) = 5, n(A ∩ B) = 1

P(B|A) = n(A ∩ B)/n(A) = 1/11.

Question 8:

A bag contains 3 red and 7 black balls. Two balls are drawn at randon without replacement. If the second ball is red, what is the probability that the first ball is also red?

Let A: event of selecting a red ball in first draw

B: event of selecting a red ball in second draw

P(A ∩ B) = P(selecting both red balls) = 3/10 × 2/9 = 1/15

P(B) = P(selecting a red ball in second draw) = P(red ball and rad ball or black ball and red ball)

= P(red ball and red ball) + P(black ball and red ball)

= 3/10 × 2/9 + 7/10 × 3/9 = 3/10

∴ P(A|B) = P(A ∩ B)/P(B) = 1/15 ÷ 3/10 = 2/9.

Question 9:

If a family has two children, what is the conditional probability that both are girls if there is atleast one girl?

Let A: both being girls

B: Atleast one girl

n(A ∩ B) = 1

P(A|B) = n(A ∩ B)/n(B) = ⅓.

Question 10:

A dice and a coin are tossed simultaneously. Find the probability of obtaining a 6, given that a head came up.

Let A: six coming with a heads

B: coin shows a head

A ={(6, H))

B = {(1, H), (2, H), (3, H), (4, H), (5, H), (6, H)}

n(A ∩ B) = 1 and n(B) = 6

∴ Probability of getting a six when there is a head is given by –

P(A|B) = n(A ∩ B)/n(B) = ⅙.

Practice Questions on Conditional Probability

1. If P(A) = 2P(B) = 4/13 and P(A|B) = ⅔, find the value of P(A U B).

2. In a survey among few people, 60% read Hindi newspaper, 40% read English newspaper and 20% read both. If a person is chosen at random and if he already reads Hindi newspaper find the probability that he also reads English newspaper.

3. A fair coin is tossed twice such that E: event of having both head and tail, and F: event of having atmost one head. Find P(E ∩ F) and P(F|E).

4. In a class, 60% of the students like Mathematics and 35% of students like Physics and 25% like both the subjects. One student select at random, find the probability that he likes Physics if it is known that he likes Mathematics.

5. Two dice are rolled, if it is known that the second dice always shows 4, find the probability that the numbers appeared on the dice have a sum 6.

Learn about various mathematical concepts in a simple manner with detailed information, along with step by step solutions to all questions, only at BYJU’S. Download BYJU’S – The Learning App to get personalised videos.

Register with BYJU'S & Download Free PDFs

Common Core Algebra II - Unit #12 Probability

Description

Probability is developed in this 6 lesson unit by using sets, their intersections, and their unions. Two way frequency charts are extensively used to introduce the concept of conditional probabilities. The multiplication of probabilities is used to find the probability of complex events and the product test for independence is developed and applied.

To access the lesson videos on YouTube use your smartphone or tablet to scan the QR code at the top of each lesson.

Questions & Answers

Emathinstruction.

We're hiring
Help & FAQ
Privacy policy
Student privacy
Terms of service
Tell us what you think

IMAGES

Conditional Probability and Tree Diagrams with Answer Key (Editable)
Solutions Conditional Probability Homework
Conditional Probability (Year 2 A Level Maths): class notes + questions
6+ Chapter 12 Probability And Statistics Answer Key
Probability Worksheet With Answers Pdf
Conditional Probability Worksheet Form

VIDEO

conditional probabilities example 2
Ch 13 Probability One Shot
Chapter 13 Probability NCERT Solutions I EX 13.1 I New NCERT Solutions Class 12 I Class 12 I A4S
Conditional Probability Explained with Examples, Probability & Statistics
[PDF] Probability
Conditional Probability : ExamSolutions

COMMENTS

Unit 12
Assessment. Unit 12 Mid-Unit Quiz (Through Lesson 4) - Form C. ASSESSMENT. ANSWER KEY. EDITABLE ASSESSMENT. EDITABLE KEY.
G.Unit 12 Lesson 5- "Conditional Probability" Flashcards
Conditional Probability. the probability of an event ( A ), given that another ( B ) has already occurred. Venn Diagram. A diagram that uses circles to display elements of different sets. Overlapping circles show common elements. Keep Change Flip. Method used to divide a fraction BY a fraction. ATA Learn with flashcards, games, and more — for ...
Conditional Probability: assignment Flashcards
A: The conditional probability formula is. P (X │ Y) = p (x n y)/p (y) C: The notation P (R │ S) indicates the probability of event R, given that event S has already occurred. E: Conditional probabilities can be calculated using a Venn diagram. Click the card to flip 👆. 1 / 9.
Unit 12: Probability
Download Unit 12 Homework answers here. 12.1 Notes Probability and Measurement: ... 12.5 Notes Mutually Exclusive Events and Probability: 12.6 Notes Two-Way Frequency Tables: Unit 12 Review Key. Powered by Create your own unique website with customizable templates.
Unit 12: Probability Flashcards
Probability. likelihood that a particular event will occur. Experiment. a set of controlled observations that test the hypothesis. Trial. each repetition or observation of an experiment. Outcome. A result of a trial. Sample Space.
Conditional probability and independence (article)
What is conditional probability and how does it relate to independence? Learn how to use formulas and tables to calculate conditional probabilities and check if two events are independent. Khan Academy is a free online learning platform that covers various topics in math, science, and more.
Conditional probability using two-way tables
This two-way table displays data for the sample of students who responded to the survey: A student will be chosen at random. Find the probability that the student chose to fly as their superpower. Find the probability that the student was male. Find the probability that the student was male, given the student chose to fly as their superpower.
PDF Advanced Algebra Name Conditional Probability Day 5 Homework of 100
Conditional Probability Day 5 Homework 1. A two-way frequency table is shown below displaying the relationship between age and baldness. A sample of 100 male subjects was randomly selected. Each man was asked their age and a notation was made as to whether or not the man was bald. Two-way Frequency Table Bald Age Younger than 45 Age 45 or older
7.2: Conditional Probability
The probability that the second card is a spade, given the first was a spade, is 12 51 12 51, since there is one less spade in the deck, and one less total cards. The probability that both cards are spades is 13 52 ⋅ 12 51 = 156 2652 ≈ 0.0588 13 52 ⋅ 12 51 = 156 2652 ≈ 0.0588. You Try It 7.2.1 7.2. 1. If you draw 2 cards from a standard ...
Probability (Geometry Curriculum
Geometry (Second Semester) Notes, Homework, Quizzes, TestsThis bundle contains the following units:• Right Triangles & Trigonometry• Polygons & Quadrilaterals• Transformations• Circles• Volume & Surface Area• ProbabilityThese units contain notes, homework assignments, quizzes, stu. 6. Products. $79.00 $105.80 Save $26.80.
5.5: Conditional Probabilities
We want to draw a face card and an ace so use multiplication. P(1st face card and 2nd ace) = 12 52 ⋅ 4 51 = 48 2652 ≈ 0.018 P ( 1st face card and 2nd ace) = 12 52 ⋅ 4 51 = 48 2652 ≈ 0.018. The probability that the first card is a face card and the second card an ace is approximately 0.018 or 1.8%. Solution c. There are two ways for this ...
3.2: Problems on Conditional Probability
Note that if A ⊂ B then P(AB) = P(A). Answer. Exercise 3.2.4. From 100 cards numbered 00, 01, 02, ⋅ ⋅ ⋅, 99, one card is drawn. Suppose Ai is the event the sum of the two digits on a card is i, 0 ≤ i ≤ 18, and Bj is the event the product of the two digits is j. Determine P(Ai | B0) for each possible i. Answer.
Probability Homework (Algebra 2
☑ Conditional Probability (2 pages) ☑ Compound Events (3 pages) **(3/3/2022) Corrected homework key for Lesson 12.5 #15 and #16A **(3/3/2022) Corrected homework key for Lesson 12.4 #5 and #18, changed wording on #13. Click HERE to SAVE 20% by buying all PROBABILITY products, including cooperative activities, in UNIT 12 MEGA BUNDLE.
PDF Independent and Dependent Events
Find the probability. 5) You flip a coin and then roll a fair six-sided die. The coin lands heads-up and the die shows an even number. 6) You roll a fair six-sided die twice. The first roll shows a five and the second roll shows a six. 7) There are eight shirts in your closet, four blue and four green. You randomly select one to wear on Monday ...
5.E: Basic Concepts of Probability (Exercises)
The probability that the roll is even, given that it is not a two. The probability that the roll is even, given that it is not a one. Q3.3.1Compute the following probabilities in connection with two tosses of a fair coin. The probability that the second toss is heads. The probability that the second toss is heads, given that the first toss is ...
8.4.1: Conditional Probability (Exercises)
Questions 1 - 4: Do these problems using the conditional probability formula: P(A|B) = P(A∩B) P(B) P ( A | B) = P ( A ∩ B) P ( B). A card is drawn from a deck. Find the conditional probability of P P (a queen | a face card). A card is drawn from a deck. Find the conditional probability of P P (a queen | a club). A die is rolled.
Geometry Unit 12: Probability
This unit contains the following topics: • Introduction to Sets (Universal Set, Complement of a Set, Subsets, Union, Intersection - just basic!) • Venn Diagrams. • Counting Outcomes (Fundamental Counting Principle) • Theoretical Probability. • Experimental Probability.
Conditional Probability Worksheets
Independent Practice 1. Students practice with 20 conditional probability problems. The answers can be found below. In a middle school of 200 students, 100 are seniors, 50 students take part in a play, and 30 students are seniors and are also taking part in play. What is the probability that a randomly chosen student is a senior and is taking ...
Conditional Probability Questions With Solutions
Conditional Probability Questions with Solutions. Let us solve some questions based on conditional probability with detailed solutions. Question 1: Ten numbered cards are there from 1 to 15, and two cards a chosen at random such that the sum of the numbers on both the cards is even. Find the probability that the chosen cards are odd-numbered.
Common Core Algebra II
Description. Probability is developed in this 6 lesson unit by using sets, their intersections, and their unions. Two way frequency charts are extensively used to introduce the concept of conditional probabilities. The multiplication of probabilities is used to find the probability of complex events and the product test for independence is ...
Solved Name: Date: Unit 11: Probability & Statistics
Question: Name: Date: Unit 11: Probability & Statistics Homework 3: Conditional Probability Bell: ** This is a 2-page document! ** Use for questions 1-2: A bucket contains 50 lottery balls numbered 1-50. One is drawn at random. Find each probability. 1. P (multiple of 6 | 2-digit number) 2. P (at least 20 | prime number) 3. Marti rolls two dice.
Algebra 2 Unit 12: Probability Flashcards
P (A and B and C) = P (A) P (B) P (C) Probability of Dependent Events. The probability of two or more dependent events A and B is the probability of A times the probability of B after A occurs. P (A and B) = P (A) * P (B after A) Study with Quizlet and memorize flashcards containing terms like event, probability, theoretical probability and more.
Unit 8: Probability and Statistics Flashcards
An event made up of two or more simple events. Uses multiplication of the number of ways each event in an experiment can occur to find the number of possible outcomes in a sample space. Study with Quizlet and memorize flashcards containing terms like compound event, Probability, random sample and more.

AP®︎/College Statistics

Conditional probability using two-way tables

Want to join the conversation?

Margin Size

5.E: Basic Concepts of Probability (Exercises)

3.1: Sample Spaces, Events, and Their Probabilities

Applications

Additional Exercises

Large Data Set Exercises

3.2: Complements, Intersections and Unions

3.3: Conditional Probability and Independent Events

Contributor

Margin Size

8.4.1: Conditional Probability (Exercises)

Geometry Unit 12: Probability

This unit contains the following topics:

This unit does not contain activities.

This resource is included in the following bundle(s):

License Terms:

Copyright Terms:

What standards is this curriculum aligned to?

Conditional Probability Worksheets

Basic Lesson

Intermediate Lesson

Independent Practice 1

Independent Practice 2

Homework Worksheet

Homework and Quiz Answer Key

What Are The Odds?

Conditional Probability Questions

Conditional Probability Questions with Solutions

Practice Questions on Conditional Probability

Leave a Comment Cancel reply

Register with BYJU'S & Download Free PDFs

Common Core Algebra II - Unit #12 Probability

Description

Questions & Answers

IMAGES

VIDEO

COMMENTS