Advertisement

The impact of centroid connectors on transit assignment outcomes
- Original Paper
- Published: 20 August 2020
- Volume 12 , pages 611–629, ( 2020 )
Cite this article

- Ouassim Manout ORCID: orcid.org/0000-0002-7688-7934 1 , 2 ,
- Patrick Bonnel 1 &
- François Pacull 3
300 Accesses
Explore all metrics
In transit modeling, access and egress conditions are often overlooked. The most common modeling technique of these conditions relies on the use of centroid connectors. This definition often uses the geographic position of zone centroids and sets constraints on the maximum number and length of connectors. This definition is subject to spatial aggregation issues and has already been proven to bias car assignment outcomes. The impact on transit assignment outcomes has not yet been demonstrated. The current paper investigates the statistical impact of connectors on transit assignment outcomes in an urban model of Lyon in France. Findings suggest that transit ridership, total passenger-kilometers and transit transfers are dependent on the definition of centroid connectors. Setting arbitrary values for the maximum number and length of connectors statistically affects transit results. The pattern and magnitude of this impact vary, however, between transit modes. The bus and rapid bus systems have been shown to be more sensitive towards the definition of connectors than the subway and the light rail systems. These findings question, to a certain extent, the validity and reliability of transit modeling outcomes.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions

Similar content being viewed by others
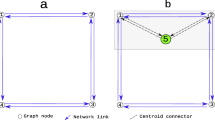
Spatial Aggregation Issues in Traffic Assignment Models
Examining the performance of transit systems in large US metropolitan areas
Adjusting the service? Understanding the factors affecting bus ridership over time at the route level in Montréal, Canada
Explore related subjects.
- Automotive Engineering
In fact, the calibration of transportation models often relies on “fine-tuning” the definition of connectors. In our case, this practice would mask the impact of the definition of centroid connectors on assignment outcomes.
Onboard Travel Surveys were conducted by the local transit authority between 2012 and 2016.
A trip is considered here as a travel, journey or movement between an origin and a destination using a specific travel mode or a combination of modes.
The Gaussian form is derived from a Gaussian Kernel-density estimation (KDE) method.
For these zones, all their centroid connectors are drawn but not necessarily used. Travel demand is distributed between connectors that produce shortest travel strategies.
Abrantes PA, Wardman MR (2011) Meta-analysis of UK values of travel time: an update. Transp Res Part A Policy Pract 45:1–17. https://doi.org/10.1016/j.tra.2010.08.003
Article Google Scholar
Alshalalfah B, Shalaby AS (2007) Case study: relationship of walk access distance to transit with service, travel, and personal characteristics. J Urban Plan Dev 133:114–118. https://doi.org/10.1061/(ASCE)0733-9488(2007)133:2(114)
Bell MG (2009) Hyperstar: a multi-path Astar algorithm for risk averse vehicle navigation. Transp Res Part B Methodol 43:97–107. https://doi.org/10.1016/j.trb.2008.05.010
Bollinger CR, Ihlanfeldt KR (1997) The impact of rapid rail transit on economic development: the case of Atlanta’s MARTA. J Urban Econ 42:179–204. https://doi.org/10.1006/juec.1996.2020
Brown MB, Forsythe AB (1974a) Robust tests for the equality of variances. J Am Stat Assoc 69:364–367. https://doi.org/10.1080/01621459.1974.10482955
Brown MB, Forsythe AB (1974b) The small sample behavior of some statistics which test the equality of several means. Technometrics 16:129–132. https://doi.org/10.1080/00401706.1974.10489158
Chang K-T, Khatib Z, Ou Y (2002) Effects of zoning structure and network detail on traffic demand modeling. Environ Plan B Plan Des 29:37–52. https://doi.org/10.1068/b2742
Chowdhury S, Zhai K, Khan A (2016) The effects of access and accessibility on public transport users’ attitudes. J Public Transp 19:97–113. https://doi.org/10.5038/2375-0901.19.1.7
Daniels R, Mulley C (2013) Explaining walking distance to public transport: the dominance of public transport supply. J Transp Land Use 6:5–20. https://doi.org/10.5198/jtlu.v6i2.308
De Cea J, Fernandez L (1989) Transit assignment to minimal routes: an efficient new algorithm. Traffic Eng Control 30:491–494
Google Scholar
Delbosc A, Currie G (2011) Exploring the relative influences of transport disadvantage and social exclusion on well-being. Transp Policy 18:555–562. https://doi.org/10.1016/j.tranpol.2011.01.011
El-Geneidy A, Grimsrud M, Wasfi R, Tétreault P, Surprenant-Legault J (2014) New evidence on walking distances to transit stops: identifying redundancies and gaps using variable service areas. Transportation 41:193–210. https://doi.org/10.1007/s11116-013-9508-z
Farhan B, Murray AT (2006) Distance decay and coverage in facility location planning. Ann Reg Sci 40:279–295. https://doi.org/10.1007/s00168-005-0041-7
Friedrich M, Galster M (2009) Methods for generating connectors in transport planning models. Transp Res Rec J Transp Res Board 2132:133–142. https://doi.org/10.3141/2132-15
Gentile G, Noekel K (2016) Modelling public transport passenger flows in the era of intelligent transport systems. Springer International Publishing, New York. https://doi.org/10.1007/978-3-319-25082-3
Book Google Scholar
Gutiérrez J, Cardozo OD, García-Palomares JC (2011) Transit ridership forecasting at station level: an approach based on distance-decay weighted regression. J Transp Geogr 19:1081–1092. https://doi.org/10.1016/j.jtrangeo.2011.05.004
Higgins C, Ferguson M, Kanaroglou P (2014) Light rail and land use change: rail transit’s role in reshaping and revitalizing cities. J Public Transp 17:5. https://doi.org/10.5038/2375-0901.17.2.5
Jeon J-H, Kho S-Y, Park JJ, Kim D-K (2012) Effects of spatial aggregation level on an urban transportation planning model. KSCE J Civ Eng 16:835–844. https://doi.org/10.1007/s12205-012-1400-4
Kurauchi F, Schmöcker J-D, Shimamoto H, Hassan SM (2013) Variability of commuters’ bus line choice: an analysis of oyster card data. Public Transp 6:21–34. https://doi.org/10.1007/s12469-013-0080-x
Leurent F, Benezech V, Samadzad M (2011) A stochastic model of trip end disaggregation in traffic assignment to a transportation network. Proced Soc Behav Sci 20:485–494. https://doi.org/10.1016/j.sbspro.2011.08.055
Lucas K, Musso A (2014) Policies for social inclusion in transportation: an introduction to the special issue. Case Stud Transp Policy 2:37–40. https://doi.org/10.1016/j.cstp.2014.06.002
Ma J, Fukuda D, Schmöcker J-D (2013) Faster hyperpath generating algorithms for vehicle navigation. Transportmetr A Transp Sci 9:925–948. https://doi.org/10.1080/18128602.2012.719165
Manout O, Bonnel P, Bouzouina L (2018) Transit accessibility: a new definition of transit connectors. Transp Res Part A Policy Pract 113:88–100. https://doi.org/10.1016/j.tra.2018.03.028
McFadden D (1978) Modelling the choice of residential location. University of California, San Francisco
Nguyen S, Pallottino S (1988) Equilibrium traffic assignment for large scale transit networks. Eur J Oper Res 37:176–186. https://doi.org/10.1016/0377-2217(88)90327-x
Noekel K, Gentile G, Nathanail E, Fonzone A (2016) From transit systems to models: data representation and collection. In Modelling public transport passenger flows in the era of intelligent transport systems. Springer International Publishing, New York, pp 235–284. https://doi.org/10.1007/978-3-319-25082-3_5
Qian SZ, Zhang H (2012) On centroid connectors in static traffic assignment: their effects on flow patterns and how to optimize their selections. Transp Res Part B Methodol 46:1489–1503. https://doi.org/10.1016/j.trb.2012.07.006
Redman L, Friman M, Gärling T, Hartig T (2013) Quality attributes of public transport that attract car users: a research review. Transp Policy 25:119–127. https://doi.org/10.1016/j.tranpol.2012.11.005
Snedecor GW, Cochran WG (1989) Statistical methods, 8th edn. Iowa State University Press, Iowa
Spiess H, Florian M (1989) Optimal strategies: a new assignment model for transit networks. Transp Res Part B Methodol 23:83–102. https://doi.org/10.1016/0191-2615(89)90034-9
Wardman M (2001) A review of British evidence on time and service quality valuations. Transp Res Part E Logist Transp Rev 37:107–128. https://doi.org/10.1016/S1366-5545(00)00012-0
Welch BL (1947) The generalization of “student’s” problem when several different population variances are involved. Biometrika 34:28–35. https://doi.org/10.1093/biomet/34.1-2.28
Zhao F, Chow L-F, Li M-T, Ubaka I, Gan A (2003) Forecasting transit walk accessibility: regression model alternative to buffer method. Transp Res Rec J Transp Res Board 1835:34–41. https://doi.org/10.3141/1835-05
Download references
Acknowledgements
The authors are grateful to the reviewers of this paper. Their valuable comments and suggestions have contributed to the final version of this paper.
This work has been funded by ForCity, Agence Nationale de la Recherche et de la Technologie (ANRT), and Laboratoire Aménagement Economie Transports (LAET) under the CIFRE funding Grant no. 2015/0341. This financial support is gratefully acknowledged.
Author information
Authors and affiliations.
LAET, University of Lyon, ENTPE, CNRS, Lyon, France
Ouassim Manout & Patrick Bonnel
Polytechnique, Montreal, Quebec, Canada
Ouassim Manout
Architecture and Performance, Lyon, France
François Pacull
You can also search for this author in PubMed Google Scholar

Corresponding author
Correspondence to Ouassim Manout .
Ethics declarations
Conflict of interest.
On behalf of all authors, the corresponding author states that there is no conflict of interest. None of the authors of this paper has a financial or personal relationship with other people or organizations.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Reprints and permissions
About this article
Manout, O., Bonnel, P. & Pacull, F. The impact of centroid connectors on transit assignment outcomes. Public Transp 12 , 611–629 (2020). https://doi.org/10.1007/s12469-020-00246-w
Download citation
Accepted : 06 August 2020
Published : 20 August 2020
Issue Date : October 2020
DOI : https://doi.org/10.1007/s12469-020-00246-w
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
JEL Classification
- Find a journal
- Publish with us
- Track your research

TRID the TRIS and ITRD database
On Centroid Connectors in Static Traffic Assignment: Their Effects on Flow Patterns and How to Optimize
In this paper, the authors investigate to what extent the results of static traffic assignment (STA) are influenced by centroid connectors and how to optimize their selections. Three networks are used to evaluate the impact of different centroid connector configurations on the resulting traffic flow pattern: a synthetic grid network, the California SR-41 corridor network and a large Sacramento area network. From the STA results of these three networks, the authors observe large fluctuations on resultant link volumes, maximum volume capacity (V/C) ratios, average V/C ratios and total travel time with respect to randomized connector selections. The fluctuations seem to indicate that STA results are unstable with respect to arbitrary connector selections, and this cannot be improved by simply increasing the number of connectors. In fact, more connectors often result in serious under-estimation of total travel time and average link load. The authors infer that, if provided little information of access/egress nodes of trips, randomly generated connectors lead to artificial over- or under-utilization on network links. The authors therefore propose a connector optimization algorithm in which the connectors and their travel times are chosen in such a way that the maximum V/C ratio of some characteristic links, ``direct links'', is minimized. As the numerical example on the SR-41 network indicates, this connector optimization algorithm seems to reduce the artificial over- and under-utilization of network links, and obtain a flow pattern more consistent with the one derived from a more refined network where trip access/egress nodes are known in more details.
Transportation Research Board
- Zhang, H Michael
- Transportation Research Board 89th Annual Meeting
- Location: Washington DC, United States
- Date: 2010-1-10 to 2010-1-14
- Media Type: DVD
- Features: Figures; Maps; References;
- Pagination: 22p
- Monograph Title: TRB 89th Annual Meeting Compendium of Papers DVD
Subject/Index Terms
- TRT Terms: Highway capacity ; Highway operations ; Optimization ; Traffic assignment ; Traffic flow ; Traffic volume ; Travel time
- Uncontrolled Terms: Static traffic assignment (STA)
- Geographic Terms: Sacramento (California)
- Subject Areas: Highways; Operations and Traffic Management; I71: Traffic Theory;
Filing Info
- Accession Number: 01154410
- Record Type: Publication
- Report/Paper Numbers: 10-2887
- Files: TRIS, TRB
- Created Date: Apr 14 2010 7:14AM

IMAGES
COMMENTS
In assignment it is first necessary to describe the transport network to which trips are being assigned. The network is described as a series of nodes .and con necting links; in a highway network the nodes would be the junctions and the links the connecting highways. Centroids of traffic zones, at which it is assumed that all
Recently, subarea traffic assignment was proposed to reduce the effect of centroid connectors on assignment results (Mann, 2002). In that study, up to 12 subzones are created automatically within each traffic zone, and the trip table is subdivided according the new "subzones".
In a comprehensive research conducted by Chang et al. , the authors find out that traffic assignment outcomes are dependent on the definition of zone centroids, and thus on the definition of centroid connectors. Four different configurations of centroid connectors are tested and explored in a statewide model of Idaho, USA.
Traffic assignment is the process by which a set of trip desires (a matrix of zone to zone interchanges) is allocated to a represen tation of the transportation network in a rational and orderly way. Land areas are aggregated into zones and all trips are assumed to originate and terminate at the zone centroid.
For this reason, centroid connectors could have significant impacts on the main outputs of transport models and particularly on the outcome of the traffic assignment procedure ( Chang et al., 2002 ...
Three strategies to improve the computational efficiency of path‐based algorithms for solving the static user equilibrium traffic assignment problem (STA) by providing a simple method to preclude the through‐routing via the zone centroid and helping to avoid unrealistic flow without affecting the flow update process of a PBA are proposed.
Advanced traffic assignment models, such as simulation-based dynamic traffic assignment, typically incorporate more detailed network representations than do traditional planning models. ... On Centroid Connectors in Static Traffic Assignment: Their Effects on Flow Patterns and How to Optimize Their Selections. Transportation Research Part B ...
Assignment of Centroids A centroid represents the "center of activity" of a TAZ and is used as the specific location of the origin and destination for all trips to and from the TAZ. A centroid may be a city, a town, or a ... number of centroid connectors on traffic demand forecast. As mentioned earlier, a centroid may.
In this paper, the authors investigate to what extent the results of static traffic assignment (STA) are influenced by centroid connectors and how to optimize their selections. Three networks are used to evaluate the impact of different centroid connector configurations on the resulting traffic flow pattern: a synthetic grid network, the ...
centroid connectors that improves on the "nearest node" paradigm. The goal of automating the process is to better enable the transi- tion between static traffic assignment models and dynamic ...