problem solving with bar models

What are bar models and how to use them to solve problems

What are bar models where did they come from.

Bar models have been part of the Singapore Ministry of Education’s mathematics’ concrete, pictorial, abstract process since the late 1980s.

Their origins date back further than the late 1980s, though. They were used as part of the American psychologist and educationalist, Jerome Bruner’s three-part lesson process in the late-1960s. (To learn more about three-part lessons, please read our blog that delves deeper into the concrete, pictorial, abstract approach to mathematics teaching and learning.)

Bar models have more recently become popularised in the UK and North America due to the push for better PISA rankings for mathematics by the governments of the UK, US and Canada, specifically by applying Singaporean teaching and learning strategies in their schools.

Different ways of using bar models

Bar models can be used by children (and grown-ups, too!) for a variety of uses: partitioning numbers in place value, all four operations individually (addition, subtraction, multiplication and division), multi-step and mixed operation questions, fractions, percentage increases and decreases, times tables, calculating missing angles and much, much more!

When it comes to progressing from using physical equipment (concrete), to pictorial (sketched) learning into abstract mathematics, bar models are one of the key structures that work as a bridge throughout the process. They can be used with concrete equipment, in a purely pictorial way, and as an aide-memoire when writing abstract number sentences.

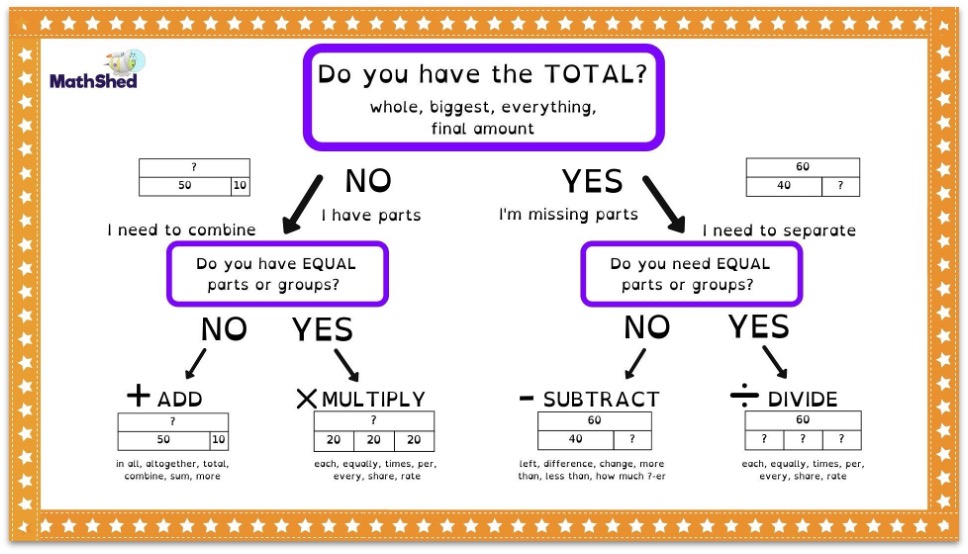
Using the bar model flow chart to unpack RUCSAC

RUCSAC is an acronym that has been popular for teachers to help children unpick word problems.

Read the question carefully Underline keywords in the question Choose the required operation(s) Solve the problem Answer the problem Check your answer

Many teachers have fallen out of love with RUCSAC, particularly because underlining the keywords is quite a vague instruction. (Or, on some posters, even worse, understanding the question.)

The following flow chart helps to unpack and repurpose RUCSAC to the point of usefulness once more.

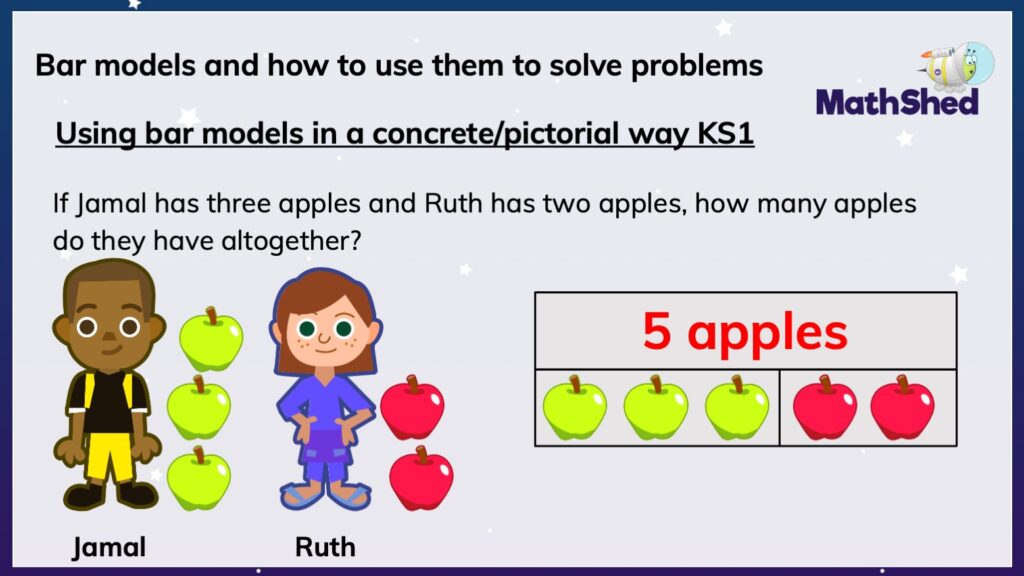
Using bar models in a concrete/pictorial way in KS1

Take the following word problem:

If Jamal has three apples and Ruth has two apples, how many apples do they have altogether?

To help children solve this problem, we could use a bar model and mathematical equipment. You could use either real apples, counters, cubes, or similar, as represented in the solution below. Shown in the Number Stacks video later in the blog is another handy resource: prepared bar model frames.

Using bar models in the “standard” pictorial way in KS1

We are presented with the same word problem, but this time, the bar model itself carries the pictorial nature of the solution.

Both parts hold numbers and the total bar holds also a number by itself, without the familiar unit of measurement (apples).

Using bar models in a pictorial/abstract way in KS1

Finally, with the same word problem in mind, we can see how using the bar model supports children in progressing to using abstract number sentences, with the + and = symbols employed in this scenario.

Using bar models in a concrete/pictorial way in KS2

If a picture is worth a thousand words, this wonderful video by Number Stacks is worth at least a million words in demonstrating best practices in using bar models in a concrete/pictorial manner in KS2. In this instance, focusing on fractions of amounts.

When it comes to bar models… plain paper is better than grid/squared paper!

Ultimately, bar models should lower the cognitive load of children. Using bar models should allow them to work through problems more quickly, not slow them down.

If a child is working out how many squares in their grid/square paper exercise book they need to use to draw the bar model, then this thinking is slowing them down.

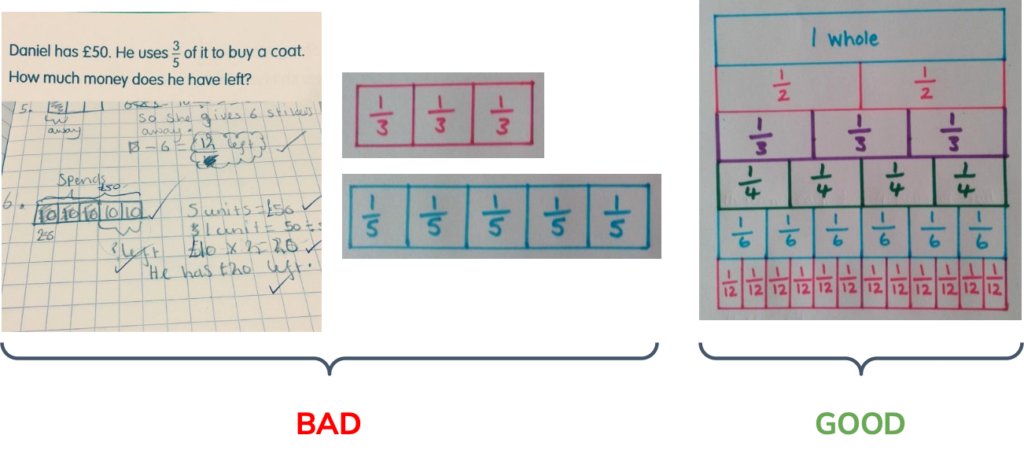
The only time you want a series of bar models to have a difference in width between their total length is if children are using comparison bars or are working on a multi-step problem and have subtracted an amount in a previous step (or enlarged the total part if adding or multiplying later on in a multi-step problem).

Regardless, using plain paper allows children to create approximate equivalence and difference between bar models while maintaining a fluent, or near-fluent, pace in their working out.

Fixed policy vs. varied bar model presentation

Some schools and schemes will advocate for one type of bar model usage over another.

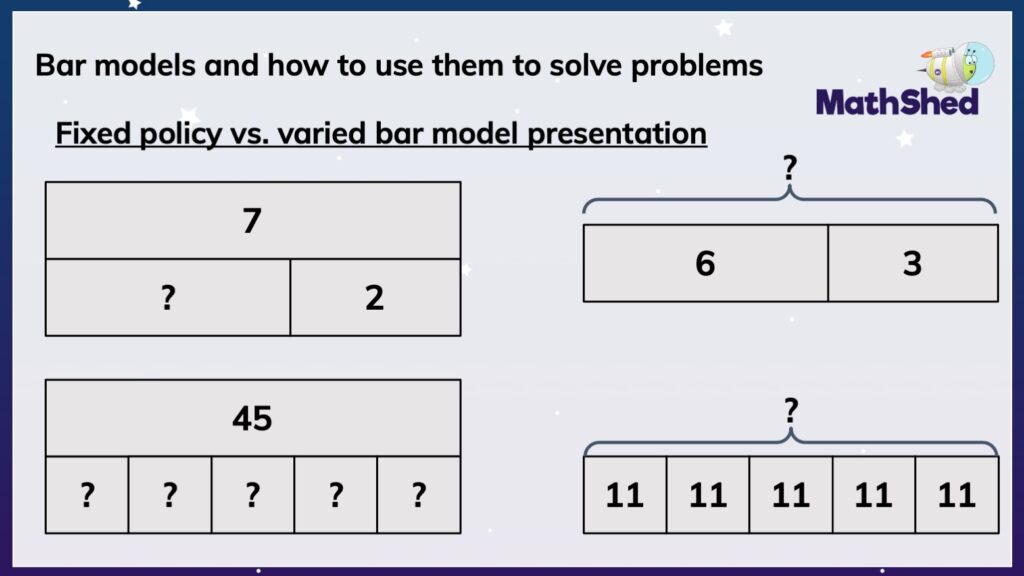
Some might exclusively use bar models like those shown on the left of the slide above, while others might favour bars curly brackets, and double arrow-headed lines, as on the right-hand side of the slide.

There is certainly strength in having a consistent and preferred set of representations for children to become confident with initially; however, ultimately, it serves children best to be aware of a range of representations, especially given the various familiar and less familiar ways bar models are presented in the end of key stage assessment papers.

Part-part-whole bars vs. comparison bar models

The use of part-part-whole bars versus bars with curly brackets is particularly apparent when performing subtraction calculations.

Here, the following word problem has been posed: “If Ahmed and Eve have 8 oranges in total and Ahmed has five oranges, how many oranges does Eve have?”

So, using our bar model flow chart, we can draw up a part-part-whole bar model.

Do you have the total? Yes. So, we put 8 in the total bar.

Do we have parts or are we missing a part? We are missing Eve’s part.

Are the parts equal or unequal? We do not know yet, but it is likely that they are unequal. So, we know to draw a bar model for subtraction, as shown above (on the left-hand side of the slide).

Similarly, we can use a comparison bar model, as we are seeking to find the difference between the total amount of eight apples and Ahmed’s five apples. (Shown on the right-hand side of the slide.)

Either way, an adult modelling or children solving the word problem using either type of bar model should arrive at the correct answer. Eve has three apples.

Using bar models for subtraction in KS2

Bar models can be used for each of the four operations in KS2 (as well as multi-step, mixed operation problems, and more).

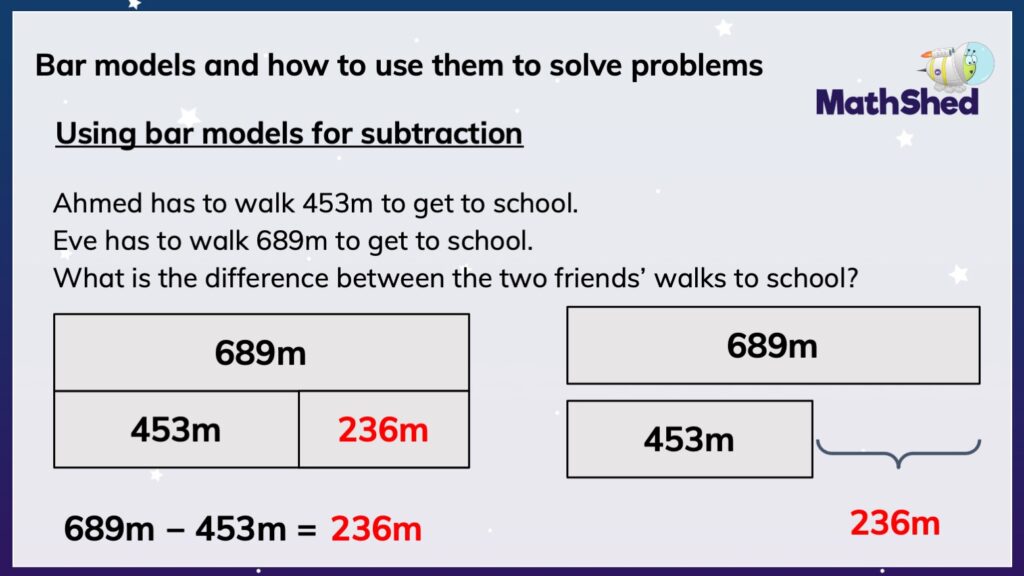
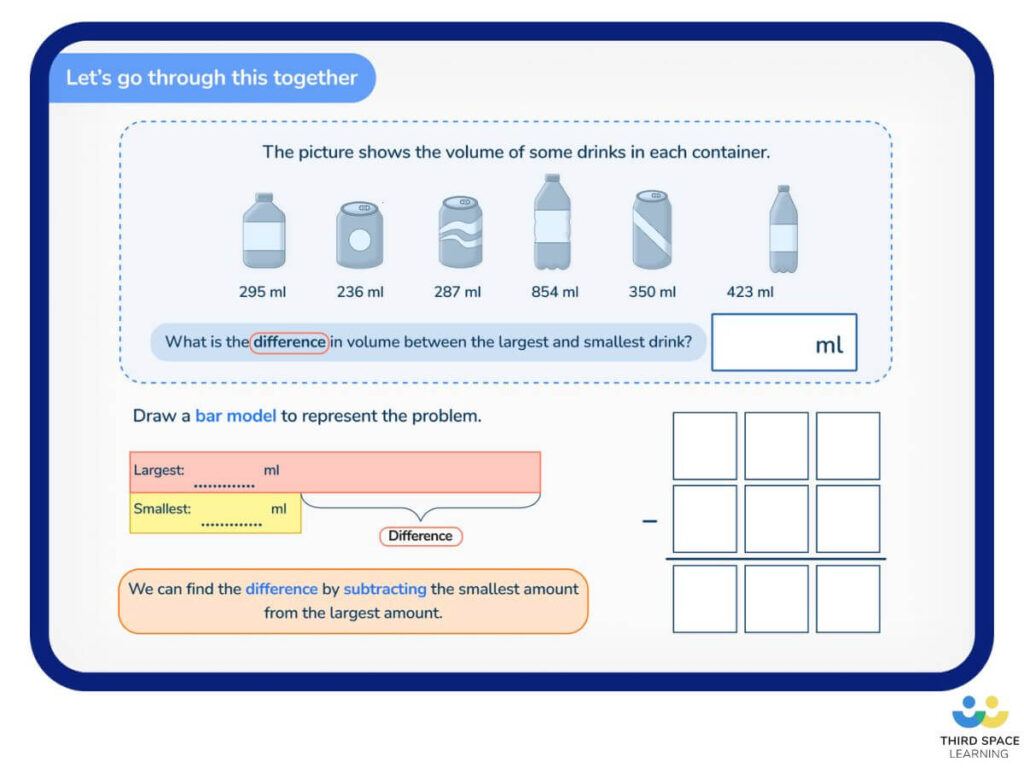
We have provided a similar subtraction word problem. Now the complexity has increased, as we are dealing with three-digit numbers and a unit of measurement, too.

Ahmed has to walk 453m to get to school. Eve has to walk 689m to get to school. What is the difference between the two friends’ walks to school?

Again, using our bar model flow chart, we can draw up a part-part-whole bar model.

Do you have the total? Yes. We know that Eve’s walk to school is the greatest distance. So, we will put 689m in the total bar.

Do we have parts or are we missing a part? We are missing the difference amount between the two friends’ walking distances to school. So, we will place Ahmed’s measurement of 453m in the known part bar.

Are the parts equal or unequal? Again, we do not know yet, but it is likely that they are unequal. So, we know to draw a bar model for subtraction, as shown above (on the left-hand side of the slide).

Much like the simpler subtraction word problem above, we can use a comparison bar model, as we are seeking to find the difference between Eve’s walk to school and Ahmed’s walk to school. Shown on the right-hand side of the slide is the comparison bar model.

Whether adults or children use the part-part-whole bar model or comparison bar model, assuming no transcription or calculation errors are made, the correct solution will be found: 236m.

Using bar models for addition

Bar models can be used to help solve addition calculations for all primary year groups.

Once more, we can use the bar model flow chart to help draw the bar model.

The word problem is: James has 237 tokens. Yasmin has 342 tokens. In total, how many tokens do the two friends have?

Do we know the total? No.

Are the parts equal? No, so we know it will be a bar model for addition.

Children should then draw two unequal parts, with 237 going into the smaller part and 342 going into the larger part.

Once they have completed the calculation, they will know that 579 is the sum (total). So, 579 goes into the whole bar.

Using bar models for multiplication

Bar models can be used for multiplication, from the 2 times table, all the way through to multi-digit by single-digit multiplication.

The word problem is: Farmer Sam has four cows. On average, each cow weighs 360 kg. How much do the cows weigh combined?

Here, we can use the bar model flow chart questions to help with demonstrating using bar models for multiplication.

Are the parts equal? Yes, so it is a multiplication calculation.

Next, do we know how many parts there are and how much each part is worth? Yes, four lots of 360kg.

So, using this information, children should be able to draw a bar model with four equal parts with 360kg in each part. Doing so should help them either mentally multiply or make jottings of repeated addition. The result, as shown, is 1,440kg.

Using bar models for division

Just as we have seen bar models used for addition, subtraction and multiplication, they work wonders for division, too!

The word problem is along a similar farmyard theme as the previous word problem: Farmer Sam has six rams that are all the same weight. In total, the six rams weigh 672 kg. How much does one ram weigh?

Do we know the total? Yes.

Are the parts going to be equal? Yes.

(And, into how many parts do we need to split the total? Six.)

So, in this case, children should then be able to start drawing their bar model with the total bar holding 672kg. They should then know to draw six equal part bars beneath the total bar.

If they are using mental strategies or a quick bus stop division calculation, children should then be able to write 112kg in each of the six parts, as well as after the equals symbol in a number sentence.

Using bar models for fractions of amounts

Bar models being used for fractions of amounts are covered in the Number Stacks video above, too.

When working with fractions of amounts, children will either be asked to find a unit fraction amount (one-third, one-fifth etc.) or a non-unit fraction amount (three-quarters, seven-tenths etc.). If it is a unit fraction of an amount problem, it requires the same as a division bar model solution, but when it is a non-unit fraction of an amount word problem, it requires a multi-step solution.

The word problem is: James had 355 marbles at the beginning of the year. By the end of the year, he has two-fifths of his marbles left. How many marbles has James lost? 

We can use the bar model flow chart questions to start helping us solve the problem.

Do we know the total? Yes. So, we can start by drawing a total bar with 355 written inside it.

Are there equal parts? Yes, we know we are going to be working with fifths, so there will be five equal parts.

Initially, the total, 355, needs to be divided by 5, meaning each of the five parts is worth 71.

We then know that James has two-fifths of his marbles left, meaning he has lost three-fifths of his marbles.

So, the final step (shown above by a curly bracket, but could have been a second bar model), demonstrates three equal parts of 71.

3 × 71 = 213. Therefore, James lost 213 marbles.

Using bar models to calculate percentages

Calculating percentages with bar models is a derivative of the division bar model.

The word problem is:

At full price, a pair of shoes cost £60. The price is reduced by 20% in the summer sale. How much do the shoes cost in the summer sale?

Again, we can work through the bar model flow chart questions.

Do we know the total? Yes, £60. So, £60 goes into the total bar.

Is there equal or unequal parts? Using known facts, that 20% is equivalent to one fifth, children should then know to split the part bar into five equal parts.

Children can then use their times tables knowledge to divide 60 by 5, to state that 20% of the full price is £12.

Then, there is the option to either multiple £12 by 4, or subtract £12 from £60. Either way, the correct solution can be found: the shoes will cost £48 in the sale.

Using bar models for algebra

Bar models work wonderfully for algebra. They can be used for working with formulae, expressing rules, solving equations and much more!

Here, we look at using bar models to work out an unknown value.

We can answer the initial bar model flow chart question to start with…

Do we know the total? Yes. So, we can put 22 into the total bar.

Do we know any of the parts? Are any of them equal? Well, we know one of the parts is 4. We also know that there are two equal unknown parts, too.

So, we draw the topmost bar model on the right-hand side of the slide above to start.

We can then subtract the known part value, 4, from the total, 22, to get the difference, 18.

Then, we can draw a second bar model, as shown on the bottom right-hand side of the slide. Initially, as 18 in the total bar, and a ‘y’ in each of the two equal, unknown part bars.

Then, it’s a matter of dividing 18 by 2 to solve the equation and know that each ‘y’ is worth 9.

Using bar models to solve multi-step word problems

A bar model, or series of bar models, is a great structure for solving multi-step word problems.

A papaya weighs 700g. A watermelon weighs twice as much. a) What is the weight of the watermelon? b) What is the total weight of the papaya and watermelon combined?

Here, we can see the pupil is using free-form bar models and curly brackets, rather than the part-part-whole bar models we have seen in the majority of the blog.

The pupil has drawn what is known already: a bar representing the weight of a papaya, 700g.

He has then drawn two bars each roughly as wide as the papaya bar. He knows that the weight of the watermelon is double the weight of the papaya. So, he can calculate that 700g × 2 = 1,400g to find the weight of the watermelon.

Next, all he has to do is combine the two weights together to solve the second part of the word problem. Then, he is ready to show that the total weight of a papaya and a watermelon combined is 2,100g.

Using bar models to calculate missing angles

The strength of bar models is their versatility. It isn’t just when teaching addition, subtraction, multiplication and division that they are helpful! They can be used for many areas of the curriculum, including calculating missing angles.

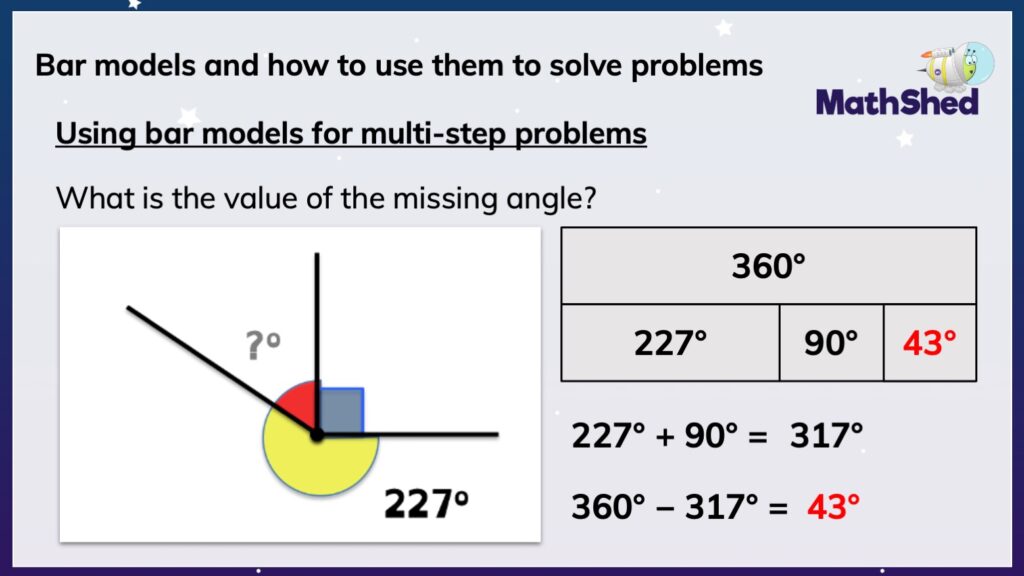
Again, we can return to the bar model flow chart questions.

Do we know the total? Yes, it should be a known fact that a full turn is equal to 360 degrees. So, we can start by writing 360 degrees into the total bar.

Do we know any of the parts’ values? Are the parts equal? Yes, we do know some of the parts. No, they are not equal.

So, then we know to draw three unequal part bars. The largest part represents 227 degrees, the next largest is the right-angle value of 90 degrees, and the smallest part should be empty to start with…

Then, it is apparent from the bar model that 227 and 90 degrees need to be combined, then subtracted from 360 degrees. So, the missing angle is 43 degrees.

Further Festive Bar Model Practice

Subscribers and non-subscribers alike can download our Advent CalenBAR resources.

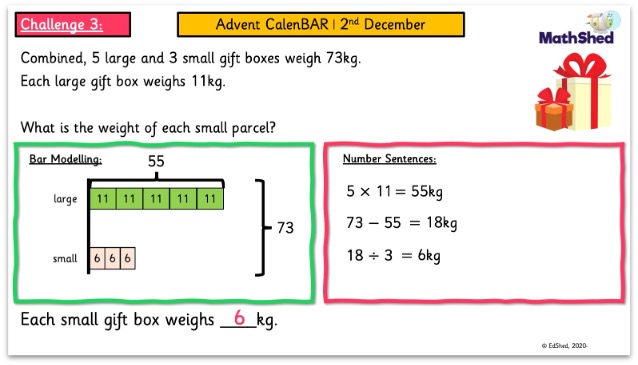
There are four daily challenges to encourage the use of bar models to solve problems. They come in PowerPoint and PDF format, with a handwriting and dyslexia-font, as well as providing question and answer pages!

BONUS: FREE Bar Model CPD Slides

Bonus: free bar model cpd webinar recording.

Teach Starter, part of Tes Teach Starter, part of Tes

Search  everything  in all resources

What Is a Bar Model? How to Use This Math Problem-Solving Method in Your Classroom

Written by B

Teaching mathematical problem-solving to your students is a crucial element of mathematical understanding. They must be able to decipher word problems and recognize the correct operation to use in order to solve the problem correctly (rather than freaking out as soon as they see a mathematical problem in words!!!). But what is the best strategy for embedding this knowledge into your students? Enter the Bar Model Method , also known in education as a tape diagram, strip diagram, or tape model.

The model has gained traction in classrooms around the world, so you may be thinking it’s time to introduce it in your classroom. But what is the bar model all about, and what are the advantages of using this method with elementary students? The math teachers on the Teach Starter team are here with a quick primer to help you decide if this is the right path for your math class!

Explore the latest math teaching resources from Teach Starter!

What Is a Bar Model?

The Bar Model is a mathematical diagram that is used to represent and solve problems involving quantities and their relationships to one another.

It was developed in Singapore in the 1980s when data showed Singapore’s elementary school students were lagging behind their peers in math. An analysis of testing data at the time showed less than half of Singapore’s students in grades 2-4 could solve word problems that were presented without keywords such as “altogether” or “left.” Something had to be done, and that something was the introduction of the bar model, which has been widely credited with rocketing the kids of Singapore to the top of math scores for kids all around the globe.

At its core, the bar model is an explicit teaching and learning strategy for problem-solving. The actual bar model consists of a set of bars or rectangles that represent the quantities in the problem, and the operations are represented by the lengths and arrangements of the bars. Among its strengths is the fact that it can be applied to all operations, including multiplication and division. They’re also useful when it comes to teaching students more advanced math concepts, such as ratios and proportionality.

The Bar Model combines the concrete (drawings) and the abstract (algorithms or equations) to help the student solve the problem.

How to Use a Bar Model in Math

Whether you’re calling it a bar model, a strip diagram, or a tape diagram, the concept is the same – you have rectangular bars (or strips) that are laid out horizontally to represent quantities and the relationships between them.

• The bars themselves — horizontal rectangles—  represent the problem.
• The length of the bar(s) represents the quantity.
• The locations of the bars show the relationship between the quantities.

Visualizing this relationship helps students decide which operation to use to solve the problem. The student then labels the known quantities with numbers and labels the unknown quantities with question marks.

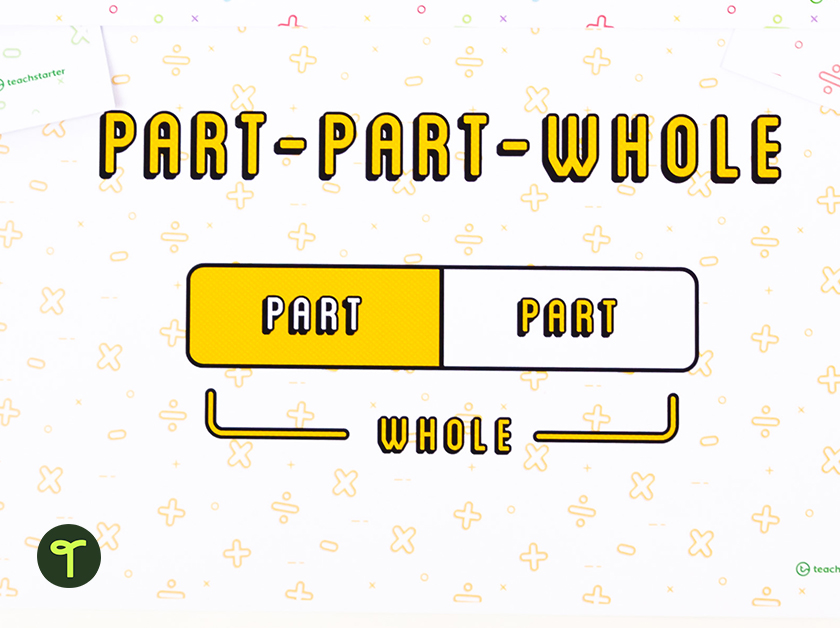
The three basic structures are:

• Part-Part-Whole
• Equal Parts

Many teachers (particularly in the elementary grades) will recognize elements of the Bar Model as being similar to the Part-Part-Whole method we’ve been teaching forever.

The Bar Model could be looked at as an extension of this concept. It can be used by students right through elementary school (and beyond) not only to solve addition and subtraction problems but to tackle multiplication and division word-based problems as well.

Teaching with the Bar Model

The Bar Model can easily be incorporated into your elementary math instruction, from simple addition to more complex multiplication and division and so on. Here are just a few ideas from our teacher team:

• Use part–whole bar models to show word problems with a missing number element to teach addition or subtraction.

• Use the bar model method to help students see how a bar must be cut into equal parts when multiplying and dividing.
• Help students visualize fractions with the bar model — Use the rectangles to help students see how the fractions relate to whole numbers by showing the relationship between the numerator and denominator.

Explore our complete collection of curriculum-aligned resources for teaching about operations !

Banner image via Shutterstock/Komuso Colorsandia

30 Buzzing Facts About Bees to Excite Kids About Nature

Everyone benefits from the busyness of bees which is why these bee facts will help inspire your students to appreciate and protect them!

21 Epic Last Day of School Activities to Kick Off Summer Break

Looking for easy last day of school ideas for elementary or middle school? These quick and fun end of year classroom activities will help you finish off your year just right!

70 1st Grade Books to Add to Your Classroom Reading Corner This Year

Wondering which 1st grade books you should add to your classroom library? Look no further! We have a list of 70 that are teacher (and student) approved!

22 Fun Groundhog Facts to Share With Your Class on Groundhog Day

Need fun groundhog facts to share with your students this Groundhog Day? Find out what groundhogs eat, where they live and why we let them predict the weather!

How to Teach 1st Grade — The Ultimate Guide to What to Do, What to Buy and What to Teach

Looking for tips on teaching first grade? Our comprehensive 1st grade teacher guide will answer all your questions from what to buy to how to prepare for the first day of school and what to do throughout the school year.

10 Best Pencil Sharpeners for the Classroom — Recommended by Teachers

Need new pencil sharpeners in your classroom? We've rounded up 10 best pencil sharpeners recommended by teachers to get you started.

Get more inspiration delivered to your inbox!

Sign up for a free membership and receive tips, news and resources directly to your email!

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

The Ultimate Guide To The Bar Model: How To Teach It And Use It In Elementary School

Pete Richardson

Teaching the bar model in elementary school is essential if you want students to do well in their reasoning and problem solving skills. Here’s your step-by-step guide on how to teach the bar model using math mastery lessons from Pre-K and Kindergarten right up to 5th grade level questions.

First we will look at the four operations and a progression of bar model representations that can be applied across all grades in elementary school.

Then we will look at more complex bar model examples, including how to apply bar models to other concepts such as fraction and equations.

What is a bar model in math?

How to draw a bar model, bar models: pre-k to third grade, bar models: 3rd grade to 5th grade, bar models: middle school and beyond.

Fun Math Games and Activities Packs for Kindergarten to 5th Grade

Individual packs for K-5 containing fun math games and activities to do with your students

What is a bar model ? In math a bar model, also known as a strip diagram , is a pictorial representation of a problem or concept where bars or boxes are used to represent the known and unknown quantities. Bar models are most often used to solve number problems with the four operations – addition and subtraction , multiplication and division.

In word problems, bar models help children visualize the problem and decide which operations to use.

The bar model is the pictorial stage in the concrete pictorial abstract (CPA) approach to learning and is central to math mastery. Bar models will not, however, do the calculations for the students; they simply make it easier for learners to work out which equation must be done to solve the problem.

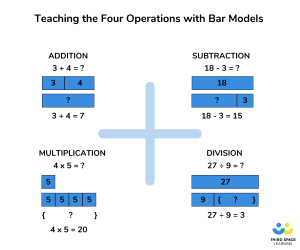
What is the bar model in math?

The bar model is used by drawing out a bar to represent the known and unknown quantities in a given problem. Encouraging a child to use the bar model in a problem can help them to understand conceptually what math operation is required from the problem, and how each part combines to make the whole.

An understanding of bar models is essential for teaching word problems , especially those using four operations (addition, subtraction, multiplication, division), fractions and algebra. Here the bar model shows us that if 2 rectangles out of 3 rectangles are green, then two thirds of 12 must be 8.

Why use the bar model method in math?

The bar model is used in Singapore and Asian Math textbooks and is an essential part of the mastery math approach used by schools at all stages.

By using the bar method to visualize problems, students are able to tackle any kind of number problem or complex word problem.

Because bar models only require pencils and paper, they are highly versatile and can be very useful for tests.

The use of bar models are also useful for learning at an early stage, from showing number bonds to ten or partitioning numbers as part of your place value work. 

Once a child is secure in their use of the bar model for the four operations and can conceptualize its versatility, they can start to use it to visualize many other math topics and problems, such as statistics and data handling .

The Singapore Bar Model Method

‘The Singapore Math Model’ is another name for the bar model method. Despite this name however the Singapore bar model (like most of the math mastery approach) is based heavily on the work of Bruner, Dienes and Bishop about the best way to help children learn: teaching for mastery. 

Bar models act as a ‘bridge’ between the concrete, pictorial and abstract (CPA in math); once children are secure with using pictorial versions of their concrete materials, they can progress to using bars as visual representations.  

Bars are a more abstract way of representing amounts, making the transition to using wholly abstract numbers significantly less difficult. 

The Part Whole Method

Also known as the ‘part part whole’ method or the comparison model, this kind of bar model uses rectangles to represent the known and unknown quantities as parts of a whole. This is an excellent method to help students represent the very common ‘missing number’ problems. 

This can be done in two ways:

• As discrete parts to a whole – each unit in the problem has its own individual box, similar to using Numicon cubes. 
• As continuous parts to a whole – units are grouped into one box for each amount in the problem e.g. in 26 + 52, 26 would have one long bar, not 26 smaller rectangles joined together.

When using the part-whole method, proportionality is key; all the bars must be roughly proportional to each other e.g. 6 should be about twice the length of 3. 

Part-whole models are generally used to visually represent the four operations, fractions, measurement, algebra and ratios, but can be applied to many more topics in the common core (as long as they’re relevant!).

Read more: What Is The Part Whole Model ?

There are a few steps involved in drawing a bar model and using it to solve a problem:

• Read the question carefully
• Circle the important information
• Determine the variables: who? what?
• Make a plan for solving the problem: what operation needs to be used?
• Draw the unit bars based on the information
• Re-read the problem to make sure that the bar models match the information given
• Complete the problem using the determined operation.

Bar model addition

Students in Pre-K and Kindergarten will routinely come across expressions such as 4+3.

Often, these expressions will be presented as word problems: Aliya has 4 oranges. Alfie has 3 oranges. How many oranges are there altogether? To help children fully understand later stages of the bar model, it is crucial they begin with concrete representations.

There are 2 models that can be used to represent addition:

Once they are used to the format and able to represent word problems with models in this way themselves (assigning ‘labels’ verbally), the next stage is to replace the ‘real’ objects with objects that represent what is being discussed (in this case, we replace the ‘real’ oranges with button counters):

The next stage is to move away from the concrete to the pictorial. As with all the stages, when students are ready for the next stage is a judgment call that is best decided upon within your school.

A general rule of thumb would be that towards the end of kindergarten or start of first grade, students should be able to understand and represent simple addition and subtraction problems pictorially and assign written labels in a bar model.

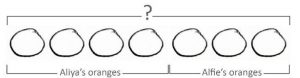
The penultimate stage is to represent each object as part of a bar, in preparation for the final stage:

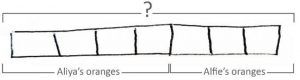
The final stage moves away from the 1:1 representation. Each quantity is represented approximately as a rectangular bar:

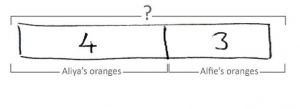
As mentioned before, it is a judgment call for your school to make, but if you want students to use the bar model to support them at the end of semester tests towards the later stage of their early years, they are going to need to have had a fair amount of experience in this final stage.

Bar model subtraction

The same concrete to pictorial stages can be applied to subtraction. However, whereas with addition it is really down to the student’s preference as to which of the 2 bar representations to use, with subtraction the teacher can nudge students to one or the other.

The reason? One represents a ‘part-part-whole’ model, the other a ‘find the difference’ model. Each will be more suited to different word problems and different learners. Let’s examine those at the final stage of the bar model:

Part-part-whole

Austin has 18 lego bricks. He used 15 pieces to build a small car. How many pieces does he have left?

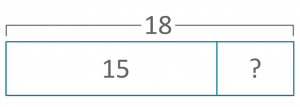
Equation: 18 – 15 =

Find the difference

Austin has 18 lego bricks. Lionel has 3 lego bricks. How many more lego bricks does Austin have than Lionel?

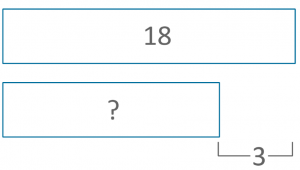
Equation: 18 – 3 =

Bar model multiplication

Bar model multiplication starts with the same ‘real’ and ‘representative counters’ stages as addition and subtraction. Then it moves to its final stage, drawing rectangular bars to represent each group:

Each box contains 5 cookies. Lionel buys 4 boxes. How many cookies does Lionel have?

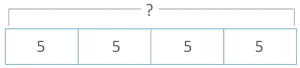
Bar model division

Due to the complexity of division, it is recommended to keep grouping and sharing until the final stage of the bar model is understood. Then word problems such as the 2 below can be introduced:

Grace has 27 lollipops. She wants to share them amongst 9 friends by putting them in party bags. How many lollipops will go into each party bag?

Grace has 27 lollipops for her party friends. She wants each friend to have 3 lollipops. How many friends can she invite to her party?

Bar models in assessments

The key question at any grade level is, “what do we know?” By training students to ask this when presented with word problems themselves, they quickly become independent at drawing bar models.

For example, in the problem: Egg boxes can hold 6 eggs. We need to fill 7 boxes. How many eggs will we need?

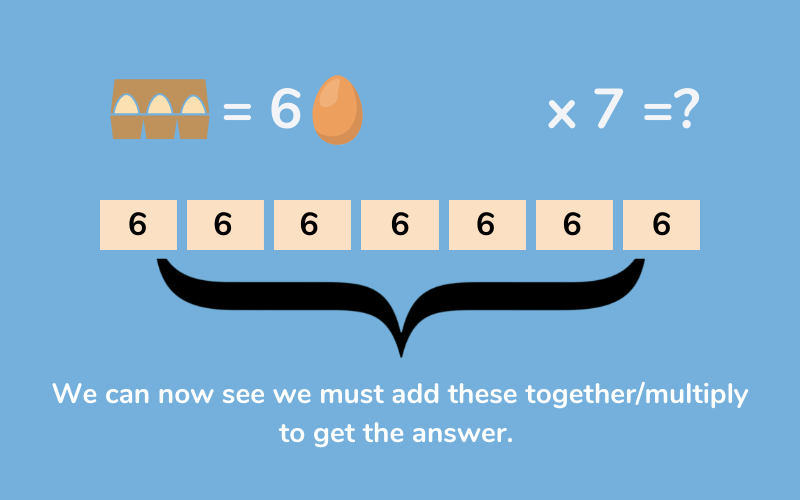
We know that there will be 7 egg boxes, so we know we can draw 7 rectangular bars. We know that each box holds 6 eggs, so we can write ‘6 eggs’ or ‘6’ in each of those 7 rectangular bars. We know we need to find the amount of eggs we have altogether. We can see we will need to use repeated addition or multiplication to solve the problem.

Bar model for the four operations word problems

Let’s ramp up the difficulty a little. In a sample assessment, students are asked:

A bag of 5 lemons costs $1. A bag of 4 oranges costs $1.80. How much more does one orange cost than one lemon?

Students could represent this problem in the below bar model, simply by asking and answering ‘what do we know?’

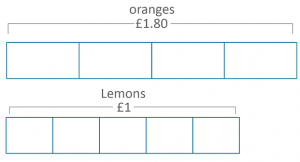
From here it should be straightforward for the students to ‘see’ or visualize their next step. Namely, dividing $1.80 by 4 and $1 by 5. Some students will not need the bar model to represent the next stage, but if they do, they would solve and then allocate the cost onto the model:

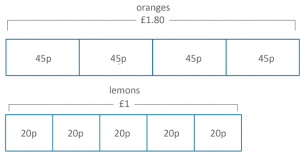
Then those students that needed this stage, should be able to see that to answer the question, they need to solve 45¢ – 20¢. With the answer of 25¢.

Bar model for word problems with fractions

Here’s another example from tests involving fractions and how it can be solved using a fraction bar model . 

On Saturday Lara read two fifths of her book. On Sunday, she read the other 90 pages to finish the book. How many pages are there in Lara’s book? If we create our bar model for what we know:

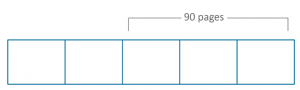
Students will then see that they can divide 90 by 3:

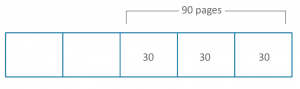
As fractions are ‘equal parts’ – a concept they should be familiar with from third grade – they know that the other 2 fifths (Saturday’s reading) will be 30 pages each:

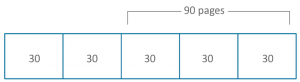
Then they can solve 30 x 5 = 150

Equations with the bar model

There are lots of other areas where bar models can assist student’s understanding such as ratio, percentages and equations. In this final example, we look at how an equation can be demystified using the comparison model:

2a + 7 = a + 11

Let’s draw what we know in a comparison model, as we know both sides of the equation will equal the same total:

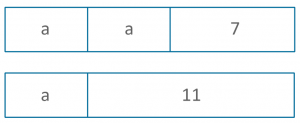
The bars showing 7 and 11 could have been a lot smaller or larger as we don’t know their relative value to ‘a’ at this stage. However, it is crucial that the ‘a’ appearing first in both bars is understood to be equal (even if it is only approximately equal when drawn freehand in the bar). This allows the student to ‘see’ that to work out the second ‘a’ in the top bar, they can solve 11-7.

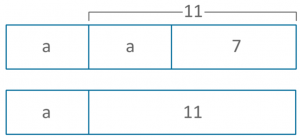
So if that ‘a’ is 4, then both the other ‘a’s will also be 4. So each side of the equation will total 15. The below model shows all sections completed. This is not necessary for the students to do, the representation is merely useful until they can see the steps necessary to solve whatever they are faced with:

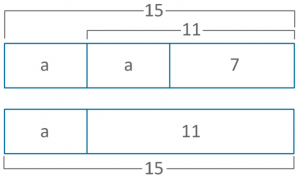
Where next?

Now you’re persuaded (we hope!) that the bar model in math is going to revolutionize problem solving across your school from early years onwards.

If you don’t believe me, use this problem to grab their attention:

Hussain wins first prize for his spectacular cake version of the Eiffel Tower. He generously gives three fifths of his winnings to his children and spends a third of what he had left. He has $80 left. How much money did he win?

With or without bar models? Which is easier? My guess is your staff will be hooked!

More on the bar model and math mastery techniques

• Third Space Sample Lessons on the Bar Model
• Benefits of following a mastery in math approach
• Bar model applied to improper fractions

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by primary school deputy head teacher Pete Richardson and has since been revised and adapted for US schools by elementary math teacher Jaclyn Wassell.

Related articles

Retrieval Practice: A Foolproof Method To Improve Student Retention and Recall

5 Tried And Tested Strategies To Increase Student Engagement

Rote Memorization: Is It Effective In Education?

5 Effective Instructional Strategies Educators Can Use In Every Classroom

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

2-Step Word Problems and Bar Models

These lessons, with videos, examples, solutions and worksheets, help students learn how to solve 2-step word problems using bar models in Singapore Math . Bar models are similar to tape diagrams used in Common Core Math.

Related Pages Comparison Word Problems 2-Step Word Problems More Word Problems & Singapore Math

The following diagrams show the Part-Part-Whole Models and Comparison Models. Scroll down the page for examples and solutions.

Weight Word Problems Liquid Volume Word Problems Measurement Word Problems

Words to Equations (Multiply/Divide) 2-Step Word Problems (Multiply/Divide) 2-Step Word Problems (Multiply/Divide/Add/Subtract)

Singapore Math: Grade 3a Unit 2 Some 2-step word problems.

• Jamie picked 17 flowers and Lindsey picked 12. They gave away 20 of the flowers. How many flowers were left?
• 125 children took part in a mathematics competition. 54 of them were girls. How many more boys than girls were there?
• Ali collected 137 stamps. He collected 27 stamps less than his sister. How many stamps did they collect altogether?

Singapore Math: Grade 3 How to solve a simple 2 step word problem using Bar Models?

Example: A washing machine costs $700, It costs $800 less than a refrigerator. Find the total cost of the two items?

Two-Step word problems

Example: 50 children attended the birthday party. 13 children left during the first hour. 9 children came in during the second hour. How many children were at the birthday party then?

Singapore Math: Grade 3 - 2 Step Basic Word Problems This presentation shows how bar models are used for simple word problems.

• 30 apples were harvested from a plantation. 5 were rotten. How many good apples were there?
• At a fruit store, there were 250 oranges. If 100 were small oranges, how many big oranges were there?
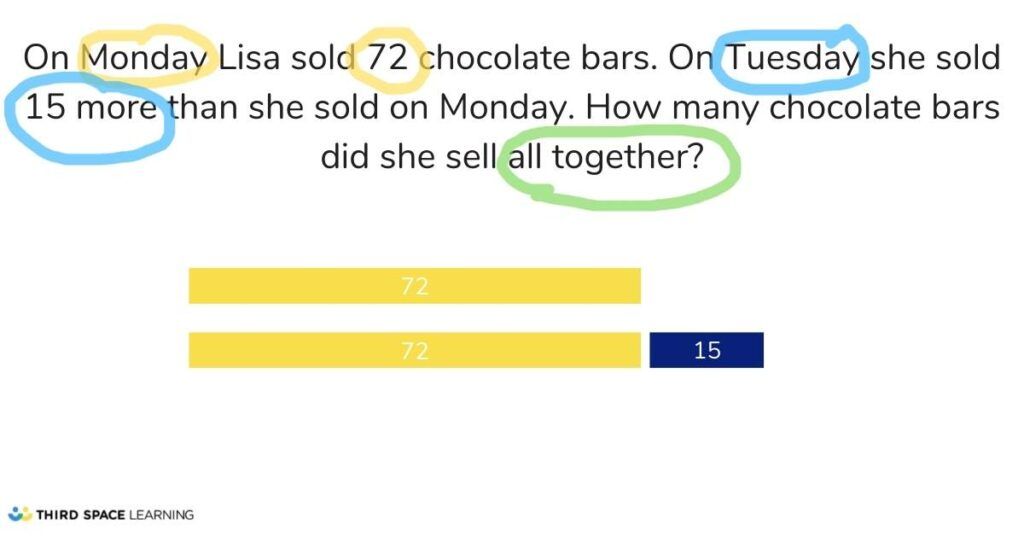
• Shop A sold 50 shirts in January. Shop B sold 25 more than shop A in the same month. How many shirts did they sell altogether?
• At Clara’s art exhibition, 120 visitors came on the first day. 20 fewer visitors came on the second day. How many visitors came to the exhibition on the two days?

4th Grade Word Problems and Bar Models

Example: Dad bought two hammers. One cost $18, the other cost $28 more. What was his total bill?

Example: Kim has 78 boxes of apples and 130 boxes of oranges. She sells some boxes of oranges. Now she has 159 boxes of apples and oranges left. a) How many boxes did she have at first? b) How many boxes of oranges did she sell?

Bar Models: Solving Word Problems (Singapore Math 5A)

Example: Rowan and Emma each had an equal number of popsicles. After Rowan ate 25 popsicles and Emma ate 31 popsicles, Rowan had twice as many as Emma. How many popsicles did they each have at first?

Example: In a basketball game, Marc, Jackson, and Cole scored 106 points altogether. Marc scored 15 more points than Jackson. Jackson scored 7 fewer than Cole. How many points did Cole score?

Example: Peter bought 32 chocolate bars at 4 for $3. He ate 2two of them and sold the rest at 3 for $4. How much money did he earn?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Bar Model in Math – Definition with Examples

What is a bar model in math, types of bar models , bar model fractions, solved examples, practice problems, frequently asked questions.

A bar model is one such tool that helps us visualize the given math problem using different-sized rectangles or bars. The size of the bars are proportional to the numbers that it represents.

Let’s take up some bar model examples to understand them better.

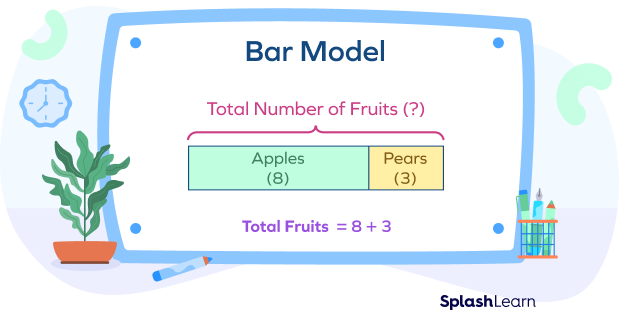
In the given example, the green bar represents 8 apples, and the yellow bar represents 3 pears. And their combination represents the total number of fruits, that is, $8 + 3$.

We can represent other operations like subtraction, multiplication, and division using a bar model, too. We can also show a comparison of numbers using this model. 

Recommended Games

The different types of bar models include 

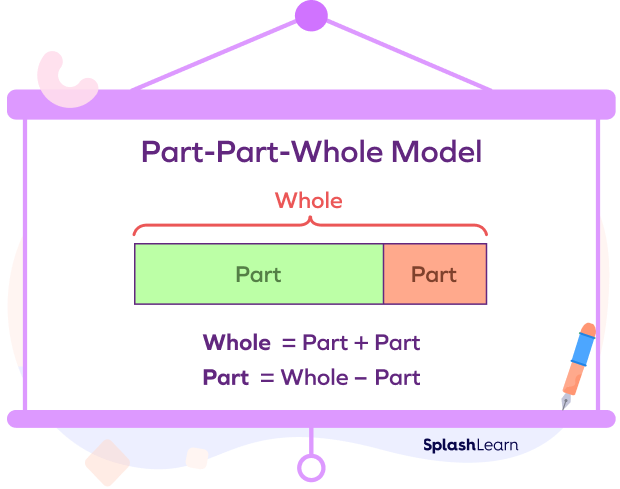
Part-Part-Whole Model

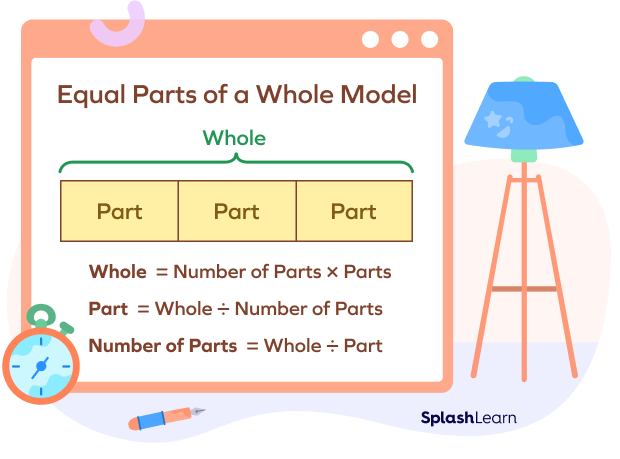
Equal parts of a whole model, comparison model.

The part-part-whole model consists of two parts that together form a whole. This model can be used to show addition and subtraction.

The equal parts of a whole model consist of multiple equal parts that together form a whole. This model can be used to show multiplication and division.

The comparison model consists of two or more bars placed one below the other to compare the quantities.

Recommended Worksheets

More Worksheets

Making Bar Models to Solve Word Problems

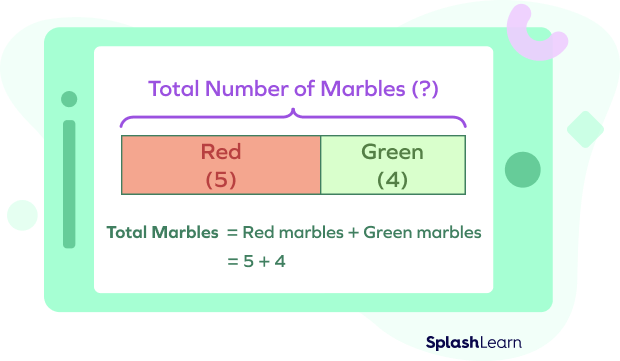
Bar model addition.

Sam has 5 red marbles and 4 green marbles. Find the total number of marbles with Sam.

In this example, we are given a number of red and green marbles, and we need to find the total number of marbles. This means that the parts are known and the whole is unknown. So, we add the parts to find the whole.

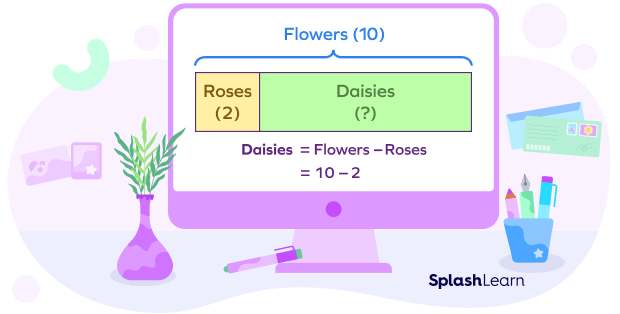
Bar Model Subtraction

Kate has 10 flowers, out of which 2 are roses and the rest are daisies. How many daisies does Kate have?

In this example, we are given a total number of flowers and the number of roses, and we need to find the number of daisies. This means the whole and one part are known, and the other part is unknown. So, we subtract the given part from the whole to find the other part using the subtraction bar model.

Multiplication Bar model

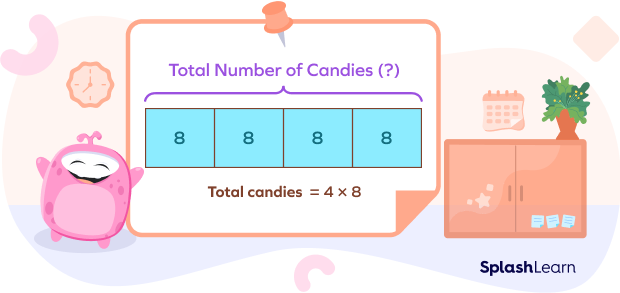
Beth has 4 bags of 8 candies each. How many candies does she have?

In this example, we have candies divided equally among 4 bags. We know the number of bags and the number of candies in each bag. So, we need to find the total number of candies. 

According to the model, we know the number of equal parts and the size of each part. So, we multiply them to find the unknown whole. 

Division Bar Model

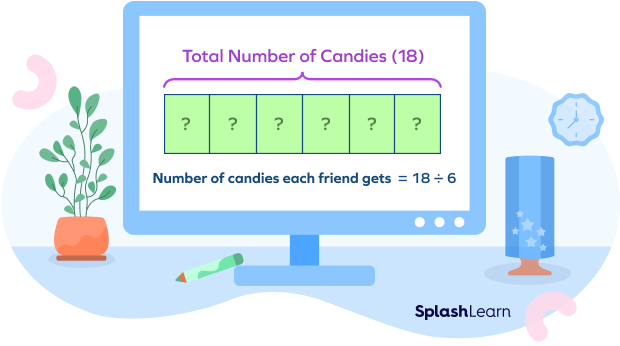
Tim had 18 candies, which he distributed equally among 6 of his friends. How many candies did each friend get? 

In this example, we know the total number of candies and the number of friends. That is, the whole and the number of equal parts is known. We need to find the number of candies each friend will get, that is, the size of each part is unknown. We divide the whole by the number of parts to get the answer. 

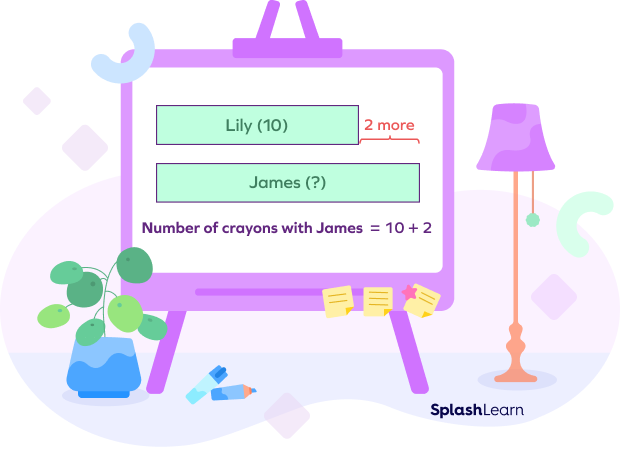
Lily has 10 crayons. James has 2 more crayons than Lily. How many crayons does James have?  

In this example, the number of crayons with Lily (Quantity A) and how many more crayons James has (difference) is known. We need to find the number of crayons with James (Quantity B).

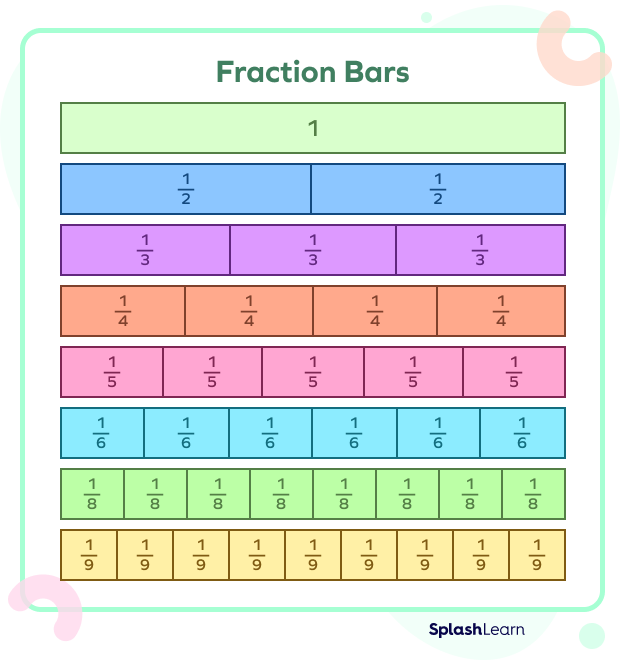
Bar models can also be used to show fractions, as shown below:

Bar models are a great way to visualize math problems and understand operations like subtraction, addition, multiplication, and division. They can help us compare different amounts and understand parts of a whole.

They can make word problems much easier to solve. Let’s try it!

Example 1: Write an equation for the given bar model.

The model clearly shows that the parts are known, and the whole is unknown. 

So the equation that represents this model is:

$8 + 12 =$ ? = Total Number of Candies

Example 2: Write an equation for the given bar model.

The model clearly shows that the total and one of the parts are known, while the second part is unknown. 

$56 +$ girls $= 85$ 

$85 – 56 =$ ? $=$ girls 

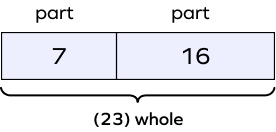
Example 3:  What would be the bar model for this equation: $7 + 16 = 23$ ?

Solution : There are two parts, 7 and 16, that together make 23. So the model would be as follows:

Example 4: Grant has 40 fruit bars. Ken has 15 less fruit bars than Grant. How many fruit bars does Ken have?

Represent this situation using a bar model to find the answer.

We know Grant’s number of fruit bars and how many more bars he has than Ken. Clearly, this is a comparison model and can be represented as: 

Number of fruit bars with Ken $=$ Number of fruit bars with Grant $– 15$ 

                                                $= 40 – 15 = 25$ fruit bars

Example 5: Create a word problem for the given model. 

Nina sells chocolate and vanilla ice cream cones. On a particular day, she sold 13 ice cream cones out of which 10 were vanilla. How many chocolate cones did she sell?

(Please note that there can be multiple answers to this problem.)

Bar Model in Math - Definition with Examples

Attend this quiz & Test your knowledge.

Which of the following equations correctly represents the given model?

Find the correct value for the missing number.

Alex has 84 berries. He wants to eat them over 7 days, eating the same number of berries daily. Use the bar model to find how many berries he should eat daily.

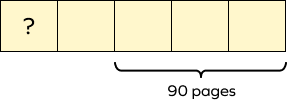
A book consists of 5 chapters. Each chapter has an equal number of pages. Katie has read the first chapter. How many pages has Katie read if the last three chapters are 90 pages altogether? Draw a bar model to find the answer.

Why do bar models have different-sized boxes?

Bar models have different-sized boxes because the boxes represent different values or quantities. The size of each part shows how much it is as a proportion of the whole.

How can we write an addition statement where the whole and one part in the bar model are known?

We can write it like this:  $3 +$ ? $= 24$?

How do bar models help solve math problems?

Bar models help solve math problems because they show us a visual representation of the problem and help us understand the missing number. They also help us compare different numbers or quantities and see how they relate to each other.

Can we represent different forms of numbers such as fractions, percentages, and decimals using a bar model?

Yes, we can represent fractions, percentages, and decimals using bar models.

RELATED POSTS

• Area in Math – Definition, Composite Figures, FAQs, Examples
• Horizontal – Definition with Examples
• Vertices – Definition with Examples
• Fraction – Definition, Types, FAQs, Examples
• Subtracting Decimals – Definition With Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Bar Modelling

Bar modelling is an essential maths mastery strategy. A Singapore-style of maths model, bar modelling allows pupils to draw and visualize mathematical concepts to solve problems.

At a glance

• A versatile maths model strategy that can be used across a wide range of concepts and topics
• Gives pupils a powerful and adaptable strategy for solving increasingly difficult problems
• Allows pupils to understand on a conceptual level what occurs when using complex formulas (for example, algebra)
• Draws on the Concrete, Pictorial, Abstract approach
• Used extensively in Singapore-style maths mastery textbooks and workbooks
• Based on three pedagogical theorists — Jerome Bruner, Zoltan Dienes, and Alan J Bishop

Bar modelling and the CPA approach

The bar model method draws on the Concrete, Pictorial, Abstract (CPA) approach — an essential maths mastery concept. The process begins with pupils exploring problems via concrete objects. Pupils then progress to drawing pictorial diagrams, and then to abstract algorithms and notations (such as the +, -, x and / symbols).

The example below explains how bar modelling moves from concrete maths models to pictorial representations.

As shown, the bar method is primarily pictorial. Pupils will naturally develop from handling concrete objects, to drawing pictorial representations, to creating abstract rectangles to illustrate a problem. With time and practice, pupils will no longer need to draw individual boxes/units. Instead, they will label one long rectangle/bar with a number. At this stage, the bars will be somewhat proportional. So, in the example above, the purple bar representing 12 cookies is longer than the orange bar representing 8 cookies.

The lasting advantages of bar modelling

On one hand, the Singapore maths model method — bar modelling — provides pupils with a powerful tool for solving word problems. However, the lasting power of bar modelling is that once pupils master the approach, they can easily use bar models year after year across many maths topics. For example, bar modelling is an excellent technique (but not the only one!) for tackling ratio problems, volume problems, fractions, and more.

Importantly, bar modelling leads students down the path towards mathematical fluency and number sense. Maths models using concrete or pictorial rectangles allow pupils to understand complex formulas (for example, algebra) on an intuitive, conceptual level. Instead of simply following the steps of any given formula, students will possess a strong understanding of what is actually happening when applying or working with formulas.

The result? A stable, transferable, and solid mathematical framework for approaching abstract concepts. Combined with other [ Error: Link is empty → essential maths mastery strategies and concepts ← ] (https://mathsnoproblem.com/en/approach/number-bonds/), bar modelling sets students up for long-term maths success.

Find out how proven mastery strategies, world-class training, and step-by-step teacher guides can give you and your school a maths boost.

Unlocking the power of problem-solving.

For the community, by the community 28 November at The Royal Society, London.

By clicking “Accept All” , you agree to the storing of cookies on your device to enhance site navigation, analyze site usage and assist in our marketing efforts.

• WordPress.org
• Documentation
• Learn WordPress
• Members Newsfeed

What Is a Bar Model? How to Use This Maths Problem-Solving Method in Your Classroom

• Math Education

The bar model is a powerful visual strategy for solving arithmetic problems, commonly used in Singapore Math and other mathematics curricula around the world. It helps students understand the relationship between numbers and the operations that connect them. But what exactly is a bar model, and how can it be effectively employed in the classroom to enhance students’ problem-solving skills?

A bar model is a pictorial representation of numerical situations or problems. It involves drawing bars or boxes to represent known and unknown quantities, making it easier to visualize complex arithmetic problems. The bars are drawn to scale to reflect the value of each amount, with longer bars representing larger amounts and shorter bars for smaller quantities.

To use this method in your class, introduce it step by step:

1. Start with simple addition and subtraction problems – Use physical objects at first (like blocks or counters) to help students see how numbers can be represented visually, then transition to drawing these representations as models.

2. Teach students to label their bar models – Each part of the bar or box should be labeled with the corresponding value or variable. For example, if students are working on a problem involving the total number of apples, each section of their model could be labeled with ‘apples’.

3. Progress to more complex problems – Once your students are comfortable with basic problems, introduce varied types such as multiplication, division, ratios, or even algebraic expressions and equations into bar modeling exercises.

4. Encourage creativity and flexibility – There is often more than one way to draw a model for a given problem. Encourage students to experiment with different models until they find one that helps them understand and solve the problem best.

5. Practice regularly – Include bar modeling in regular practice exercises so that students develop familiarity with this approach and gain confidence in using it.

6. Word Problems – Bar models thrive in breaking down word problems into digestible parts. Have students identify what they know, what they need to find out, and how the parts of the problem relate to each other before drawing their models.

In practice, here’s how you might use a bar model:

Suppose your objective is to solve a word problem like “John has 20 apples; he gives 5 to Mary. How many does he have left?” A bar would be drawn representing John’s 20 apples. Then a smaller section (representing the 5 apples he gives away) would be shaded or separated from the rest of this bar. The length of the unshaded part of the bar represents how many apples John has left.

The strength of teaching through bar models comes from its capacity to provide an external aid in understanding abstract concepts. Fluency with this technique allows students not only to answer textbook questions but also equips them with analytical tools that apply far beyond formal math problems—into everyday numeracy.

Integrating this tool into your math instruction encourages strategic thinking, deepens comprehension, and fosters an environment where mathematical discussion and exploration are part of everyday class activities.

Related Articles

Connecting mathematics to fun and practical applications can make it a favorite…

Mathematics forms an integral part of educational curriculums around the world, establishing…

Composite numbers are integers that have more than two distinct positive divisors.…

Pedagogue is a social media network where educators can learn and grow. It's a safe space where they can share advice, strategies, tools, hacks, resources, etc., and work together to improve their teaching skills and the academic performance of the students in their charge.

If you want to collaborate with educators from around the globe, facilitate remote learning, etc., sign up for a free account today and start making connections.

Pedagogue is Free Now, and Free Forever!

• New? Start Here
• Frequently Asked Questions
• Privacy Policy
• Terms of Service

Are you sure you want to delete post?

This post cannot be restored anymore.

• Registration

Don't you have an account? Register Now! it's really simple and you can start enjoying all the benefits!

We just sent you an Email. Please Open it up to activate your account.

I allow this website to collect and store submitted data.

Singapore math support and resources

Bar Modeling 101

Bar Modeling, or sometimes called Model Method, uses rectangular bars to represent relative quantitative values, and was first developed by the Ministry of Education in Singapore in the 1980s to help students solve word problems. It is a very powerful visual problem-solving heuristic that serves as a foundation to algebraic thinking, and is used as early as first grade.

Lower Elementary

While ten frames and number bonds help kids develop basic facts in addition and subtraction for a single quantity, bar models help them visualize relationships between quantities that may belong to two different entities. For example, the problem below is usually taught by bar modeling in second grade.

There are 824 girls in the auditorium. There are 125 more girls than boys. How many boys are there?

Without pictorial modeling, students often assume the word “more” means “add” and make the mistake of adding instead of subtracting. With the bar model, they can clearly see how the numbers in the word problem relate to each other.

Upper Elementary

Bar models are also used when solving multiplication, division or fraction of a set problems in upper elementary. Here, students are introduced to the concept of defining a “unit” in the bar models, which is a basic place-holder for some unknown quantity. The following example illustrates how the bar model can help students visualize a word problem.

Amy has some flowers. Bob has 3 times as many flowers as Amy. Together, they have 120 flowers. How many flowers does Amy have?

4 units = 120 1 unit = 120 ÷ 4 = 30 Amy has 30 flowers.

Again, without the aid of the visual models, many students make the mistake of dividing by 3 instead of 4.

Here you also see why bar models are used in developing the foundation in algebraic thinking in elementary levels.

Middle School

Algebra is often seen as a formidable topic in middle school and students panicked when numbers are replaced by symbols. However, since they were exposed to defining unknown “units” in bar models early on, they are more comfortable dealing with symbols as temporary place-holders and can also more easily visualize word problems. For example, the same problem above may also appear as an algebra question in middle school.

Let x be the number of flowers Amy has. 4 x = 120 x = 120 ÷ 4 = 30 Amy has 30 flowers.

Many middle school students have problem transferring the simple word problem into algebraic equations. With the help of bar models, the problem is laid out visually which may be less intimidating!

More Resources

For more in-depth reading on bar-models, our favorite reference is Dr Yeap Ban-Har’s book “ Bar Modeling – a Problem-solving Tool ”.

Related Resources

For more related resources, please refer to our Bar Models page.

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *