problem solving lesson 12.8

Solve equations and inequalities
Simplify expressions
Factor polynomials
Graph equations and inequalities
Advanced solvers
All solvers
Arithmetics
Determinant
Percentages
Scientific Notation
Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
The calculus section will carry out differentiation as well as definite and indefinite integration.
The matrices section contains commands for the arithmetic manipulation of matrices.
The graphs section contains commands for plotting equations and inequalities.
The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

Add Fractions
Simplify Fractions

Chapter 12: Two-Dimensional Geometry

Chapter 12 Essential Question:

Chapter 12 objectives:.

Use defining attributes to sort shapes.
Describe attributes of two-dimensional shapes.
Use objects to compose new two-dimensional shapes.
Compose a new shape by combining two-dimensional shapes.
Make new shapes from composite two-dimensional shapes using the strategy act it out.
Decompose combined shapes into shapes.
Decompose two-dimensional shapes into parts.
Identify equal and unequal parts (or shares) in two-dimensional shapes.
Partition circles and rectangles into two equal shares (half of, halves).
Partition circles and rectangles into four equal shares (fourth of, fourths, quarter of, quarters).

GO Math! is Online

iTools Primary

Interactive Student Edition-This is a great way to preview or review the math skills for the chapter!

Lesson 12.1- Sort Two-Dimensional Shapes
Lesson 12.2- Hands On: Describe Two-Dimensional Shapes
Lesson 12.3- Hands On: Combine Two-Dimensional Shapes
Lesson 12.4- Combine More Shapes
Lesson 12.5- Problem Solving: Make New Two-Dimensional Shapes
Lesson 12.6- Hands On: Find Shapes in Shapes
Lesson 12.7- Take Apart Two-Dimensional Shapes
Lesson 12.8- Equal or Unequal Parts
Lesson 12.9- Halves
Lesson 12.10- Fourths

Math On the Spot Videos-Cute videos that model problems within each lesson.

Animated Math Models-Practice some of your math skills with Curious George!

Lesson 12.1, 12.2 (Skill 48)- Sort and Classify Plane Figures
Lesson 12.3, 12.4 (Skill 49)- Combine Plane Figures
Lesson 12.5, 12.6, 12.7 (Skill 50)- Combine and Separate Plane Figures

Mega Math Games-Fun games that reinforce concepts taught within the chapter.

Lesson 12.1- Shapes Ahoy, Ship Shapes- Level G
Lesson 12.1- Shapes Ahoy, Sea Caves- Level K
Lesson 12.2- Shapes Ahoy, Ship Shapes- Level H
Lesson 12.2- Shapes Ahoy, Ship Shapes- Level J
Lesson 12.2- Shapes Ahoy, Undersea 3D- Level G
Lesson 12.3- Shapes Ahoy, Ship Shapes- Level K
Lesson 12.8- Shapes Ahoy, Ship Shapes- Level Q

First Grade Team

Location: East Heritage Elementary School, East Constitution Way, Fontana, CA, United States Phone: 909-823-5696

Texas Go Math
Big Ideas Math
Engageny Math
McGraw Hill My Math
enVision Math
180 Days of Math
Math in Focus Answer Key
Math Expressions Answer Key
Privacy Policy

$CCSS Math Answers$

Eureka Math Grade 8 Module 3 Lesson 12 Answer Key

Engage ny eureka math 8th grade module 3 lesson 12 answer key, eureka math grade 8 module 3 lesson 12 example answer key.

$Engage NY Math 8th Grade Module 3 Lesson 12 Example Answer Key 1$

→ Where would the shadow of the flagpole be? → On the ground, some distance from the base of the flagpole

$Engage NY Math 8th Grade Module 3 Lesson 12 Example Answer Key 2$

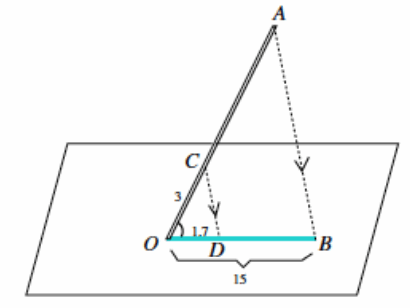
→ Now that we know △COD~△AOB, how can we find the length of the flagpole? → Since the triangles are similar, then we know that the ratios of their corresponding sides must be equal. Therefore, if we let x represent the length of the flagpole (i.e., OA), then $\frac{x}{3}$=$\frac{15}{1.7}$

→ We are looking for the value of x that makes the fractions equivalent. → Therefore, 1.7x=45, and x≈26.47. The length of the flagpole is approximately 26.47 feet.

Eureka Math Grade 8 Module 3 Lesson 12 Exercise Answer Key

Mathematical Modeling Exercises 1–3

$Eureka Math Grade 8 Module 3 Lesson 12 Exercise Answer Key 20$

c. What is the distance from the mirror to the building? Answer: 1750 ft.-7.2 ft.=1742.8 ft.

d. Do you have enough information to determine the approximate height of the building? If yes, determine the approximate height of the building. If not, what additional information is needed? Answer: Yes, there is enough information about the similar triangles to determine the height of the building. Since x represents the height of the building, then $\frac{x}{5.3}$ = $\frac{1,742.8}{7.2}$ We are looking for the value of x that makes the fractions equivalent. Then, 7.2x=9236.84, and x≈1282.9. The height of the building is approximately 1,282.9 feet.

$Eureka Math Grade 8 Module 3 Lesson 12 Exercise Answer Key 21.1$

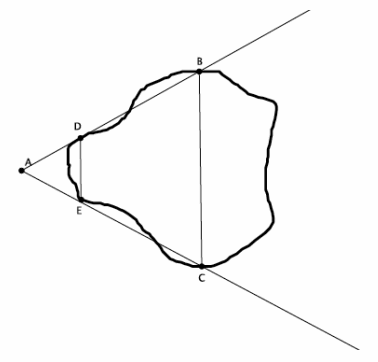
a. Has the geologist done enough work so far to use similar triangles to help measure the widest part of the lake? Explain. Answer: Yes, based on the sketch, the geologist found a center of dilation at point A. The geologist marked points around the lake that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠DAE is equal to itself. Since there are two pairs of corresponding angles that are equal, then △DAE~△BAC.

b. The geologist has made the following measurements: |DE|=5 feet, |AE|=7 feet, and |EC|=15 feet. Does she have enough information to complete the task? If so, determine the length across the widest part of the lake. If not, state what additional information is needed. Answer: Yes, there is enough information about the similar triangles to determine the distance across the widest part of the lake. Let x represent the length of segment BC; then $\frac{x}{5}$=$\frac{22}{7}$ We are looking for the value of x that makes the fractions equivalent. Therefore, 7x=110, and x≈15.7. The distance across the widest part of the lake is approximately 15.7 feet.

c. Assume the geologist could only measure a maximum distance of 12 feet. Could she still find the distance across the widest part of the lake? What would need to be done differently? Answer: The geologist could still find the distance across the widest part of the lake. However, she would have to select different points D and E at least 3 feet closer to points B and C, respectively. That would decrease the length of $\overline{\boldsymbol{E C}}$ to, at most, 12 feet. Then $\overline{\boldsymbol{D E}}$, in its new position, would still have to be contained within a line that was parallel to the line containing $\overline{\boldsymbol{B C}}$ in order to calculate the desired distance.

$Eureka Math Grade 8 Module 3 Lesson 12 Exercise Answer Key 30$

b. Assume that the sun casts a shadow 32 feet long from a point on top of the house to a point in front of the house. The distance from the end of the house’s shadow to the base of the tree is 53 feet. If the house is 16 feet tall, how tall must the tree get to provide shade for the house? Answer: If we let x represent the height the tree must be, then $\frac{16}{x}$=$\frac{32}{53}$ We are looking for the value of x that makes the fractions equivalent. Therefore, 32x=848, and x=26.5. The tree must grow to a height of 26.5 feet to provide the desired shade for the house.

c. Assume that the tree grows at a rate of 2.5 feet per year. If the tree is now 7 feet tall, about how many years will it take for the tree to reach the desired height? Answer: The tree needs to grow an additional 19.5 feet to reach the desired height. If the tree grows 2.5 feet per year, then it will take the tree 7.8 years or about 8 years to reach a height of 26.5 feet.

Eureka Math Grade 8 Module 3 Lesson 12 Problem Set Answer Key

Students practice solving real-world problems using properties of similar triangles.

$Eureka Math Grade 8 Module 3 Lesson 12 Problem Set Answer Key 50$

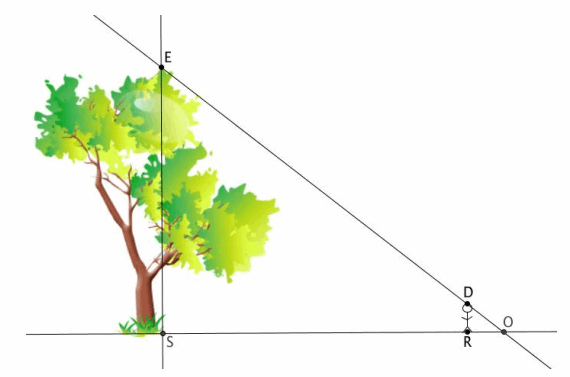
b. Assume △ESO~△DRO. A friend stands in the shadow of the tree. He is exactly 5.5 feet tall and casts a shadow of 12 feet. Is there enough information to determine the height of the tree? If so, determine the height. If not, state what additional information is needed. Answer: No, there is not enough information to determine the height of the tree. I need either the total length of the shadow that the tree casts or the distance between the base of the tree and the friend.

c. Your friend stands exactly 477 feet from the base of the tree. Given this new information, determine about how many feet taller the world’s tallest tree is compared to the one in the local park. Let x represent the height of the tree; then $\frac{x}{5.5}$=$\frac{489}{12}$ We are looking for the value of x that makes the fractions equivalent. Therefore, 12x=2689.5, and x=224.125. The world’s tallest tree is about 146 feet taller than the tree in the park.

d. Assume that your friend stands in the shadow of the world’s tallest redwood, and the length of his shadow is just 8 feet long. How long is the shadow cast by the tree? Answer: Let x represent the length of the shadow cast by the tree; then $\frac{x}{8}$=$\frac{370}{5.5}$ We are looking for the value of x that makes the fractions equivalent. Therefore, 5.5x=2960, and x≈538.2. The shadow cast by the world’s tallest tree is about 538 feet in length.

$Eureka Math Grade 8 Module 3 Lesson 12 Problem Set Answer Key 50.1$

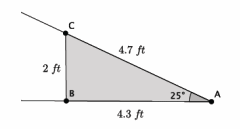
c. What length of wood is required to go from the ground to the top of the 5-foot height to make the ramp? Explain your answer using properties of similar triangles. Answer: If we let y represent the length of the wood needed to make the ramp, then $\frac{4.7}{y}$=$\frac{2}{5}$ We are looking for the value of y that makes the fractions equivalent. Therefore, 2y=23.5, and y=11.75. The length of wood needed to make the ramp is 11.75 feet.

Eureka Math Grade 8 Module 3 Lesson 12 Exit Ticket Answer Key

$Eureka Math Grade 8 Module 3 Lesson 12 Exit Ticket Answer Key 31$

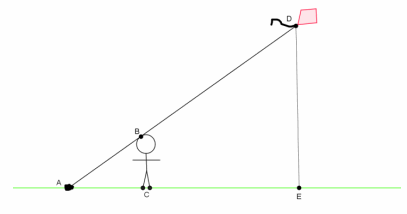
a. Has Henry done enough work so far to use similar triangles to help measure the height of the kite? Explain. Answer: Yes Based on the sketch, Henry found a center of dilation, point A. Henry has marked points so that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠BAC is equal to itself. Since there are two pairs of corresponding angles that are equal, then △BAC~△DAE.

b. Henry knows he is 5$\frac{1}{2}$ feet tall. Henry measures the string from the rock to his head and finds it to be 8 feet. Does he have enough information to determine the height of the kite? If so, find the height of the kite. If not, state what other information would be needed. Answer: Yes, there is enough information. Let x represent the height DE. Then, $\frac{8}{150}$=$\frac{5.5}{x}$ We are looking for the value of x that makes the fractions equivalent. Therefore, 8x=825, and x=103.125 feet. The height of the kite is approximately 103 feet high in the air.

Go Math Grade 8 Answer Key Chapter 13 Volume

Gather all the Go Math Grade 8 Questions and answers along with the explanations are provided for all the students. The best math practice will come with the Go Math Grade 8 Answer Key Chapter 13 Volume. Everyday learning is easy with the practice of the Go Math Grade 8 Chapter 13 Volume Solution Key. Get a free pdf of Go Math Grade 8 Answer Key now to practice maths offline. Be the first to grab your HMH Go Math Grade 8 Answer Key and read all the questions of maths.

Go Math Grade 8 Chapter 13 Volume Answer Key

Refer to Go Math Grade 8 Answer Key Chapter 13 Volume for answers and explanations. It is very easy to get good marks in the exam by practicing with the help of Go Math Grade 8 Solution Key. Top-ranked student’s first choice is Go Math Grade 8 Answer Key Chapter 13 Volume. Learn and practice the maths in the best way using Go Math Grade 8 Answer Key.

Lesson 1: Volume of Cylinders

Volume of Cylinders – Page No. 402
Volume of Cylinders – Page No. 403
Volume of Cylinders – Page No. 404

Lesson 2: Volume of Cones

Volume of Cones – Page No. 408
Volume of Cones – Page No. 409
Volume of Cones – Page No. 410

Lesson 3: Volume of Spheres

Volume of Spheres – Page No. 414
Volume of Spheres – Page No. 415
Volume of Spheres – Page No. 416

Model Quiz :

Model Quiz – Page No. 417
Mixed Review – Page No. 418

Guided Practice – Volume of Cylinders – Page No. 402

Question 1. Vocabulary Describe the bases of a cylinder. Type below: ____________

Answer: The ends of a cylinder are the bases of the cylinder of the two flat surfaces.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 1: Volume of Cylinders img 1$

Explanation: Number of inch cubes that fit in the base of the cylinder = 61 Number of inch cubes that fit in the length of the cylinder = 7 The volume of cylinder = base area x height V= 61 x 7 V = 427 cubic units. Volume of each cube = 1 in³ Volume of cylinder = 427in³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 1: Volume of Cylinders img 2$

Answer: The volume of the cylinder is approximately 1695.6 m 3 . 1695.6m³

Explanation: V = πr²h V = π . 6² . 15 V = 3.14 × 36 × 15 V = 1695.6m³

Question 4. A Japanese odaiko is a very large drum that is made by hollowing out a section of a tree trunk. A museum in Takayama City has three odaikos of similar size carved from a single tree trunk. The largest measures about 2.7 meters in both diameter and length, and weighs about 4.5 metric tons. Using the volume formula for a cylinder, approximate the volume of the drum to the nearest tenth. The radius of the drum is about _____ m. The volume of the drum is about _____ m 3 . The radius of the drum is about ___________ m The volume of the drum is about ___________ m 3

Answer: The radius of the drum is about 1.35 m. The volume of the drum is about 15.5 m 3 .

Explanation: Diameter of base of drum = 2.7 m The radius of the base of the drum = 2.7/2 R = 1.35 m The volume of cylinder = πr²h Height (h) = 2.7 m Radius (R) = 1.35 m Volume = 3.14 × (1.35) × 2.7 V = 15.4511 m³ V = 15.5 m³

ESSENTIAL QUESTION CHECK-IN

Question 5. How do you find the volume of a cylinder? Describe which measurements of a cylinder you need to know. Type below: ____________

Answer: The volume of the cylinder is = πr²h

Explanation: We need to find the radius of the base, r, and the height of the cylinder, h. The volume of the cylinder is = πr²h

13.1 Independent Practice – Volume of Cylinders – Page No. 403

Find the volume of each figure. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 1: Volume of Cylinders img 3$

Answer: 569.9 cm³

Explanation: Radius of base = 11 cm Height of cylinder = 1.5 cm The volume of the cylinder = πr²h V = 3.14 × (11)² × 1.5 V = 569.91 V = 569.9 cm³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 1: Volume of Cylinders img 4$

Answer: 1205.8 in³

Explanation: Radius of base = 4 in Height of cylinder = 24 in The volume of cylinder = πr²h V = 3.14 × (4)² × 24 V = 1205.76 V = 1205.8 in³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 1: Volume of Cylinders img 5$

Answer: 1256 m³

Explanation: Radius of base = 5 m Height of cylinder = 16 m The volume of the cylinder = πr²h V = 3.14 × (5)² × 16 V = 1256 V = 1256 m³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 1: Volume of Cylinders img 6$

Answer: 942 in³

Explanation: Diameter of base = 10 in Radius of base = 5 in Height of cylinder = 12 in The volume of the cylinder = πr²h V = 3.14 × (5)² × 12 V = 942 in³

Question 10. A cylinder has a radius of 4 centimeters and a height of 40 centimeters. _________ cm 3

Answer: 2009.6 cm³

Explanation: Radius of base = 4 cm Height of cylinder = 40 cm The volume of cylinder = πr²h V = 3.14 × (4)² × 40 V = 2009.6 cm³

Question 11. A cylinder has a radius of 8 meters and a height of 4 meters. _________ m 3

Answer: 803.8 m³

Explanation: The radius of base = 8 m Height of cylinder = 4 m The volume of the cylinder = πr²h V = 3.14 × (8)² × 4 V = 803.84 m³ V = 803.8 m³

Round your answer to the nearest tenth, if necessary. Use 3.14 for π.

Question 12. The cylindrical Giant Ocean Tank at the New England Aquarium in Boston is 24 feet deep and has a radius of 18.8 feet. Find the volume of the tank. _________ ft 3

Answer: 26635.2 ft³

Explanation: The base radius of the tank = 18.8 ft Depth of the tank in the ocean = 24 ft The volume of the cylinder = πr²h V = 3.14 × (18.8)² × 24 V = 3.14 × 354.44 × 24 V = 26635.2384 ft³ V = 26635.2 ft³

Question 13. A standard-size bass drum has a diameter of 22 inches and is 18 inches deep. Find the volume of this drum. _________ in 3

Answer: 6838.9 in³

Explanation: The base diameter of the drum = 22 in Base radius of the drum = 22/2 = 11 in Depth of the bass drum = 18 in The volume of the bass drum = πr²h V = 3.14 × (11)² × 18 V = 3.14 × 121 × 18 V = 6838.92 in³ V = 6838.9 in³

Question 14. Grain is stored in cylindrical structures called silos. Find the volume of a silo with a diameter of 11.1 feet and a height of 20 feet. _________ ft 3

Answer: 1934.4 ft³

Explanation: Base diameter of silo = 11.1 ft Base radius of the silo = 11.1/2 = 5.55 ft Depth of the silo = 20 ft Volume of the silo = πr²h V = 3.14 × (5.55)² × 18 V = 3.14 × 30.8025 × 18 V = 1934.397 ft³ V = 1934.4 ft³

Question 15. The Frank Erwin Center, or “The Drum,” at the University of Texas in Austin can be approximated by a cylinder that is 120 meters in diameter and 30 meters in height. Find its volume. _________ m 3

Answer: 339120 m³

Explanation: Base diameter of the drum = 120 m Base radius of the drum = 120/2 = 60 m Height of the drum = 30 m Volume of the drum = πr²h V = 3.14 × (60)² × 30 V = 3.14 × 3600 × 30 V = 339120 m³

Volume of Cylinders – Page No. 404

Question 16. A barrel of crude oil contains about 5.61 cubic feet of oil. How many barrels of oil are contained in 1 mile (5280 feet) of a pipeline that has an inside diameter of 6 inches and is completely filled with oil? How much is “1 mile” of oil in this pipeline worth at a price of $100 per barrel? __________ barrels $ __________

Answer: 184.7 barrels $18470

Explanation: Volume of barrel = 5.61 cubic feet Length of the pipe = 1 mile = 5280 feet Diameter of the pipe = 6 inches = 0.5 feet Radius of the pipe = 6/2 inches = 3 inches = 0.25 feet Volume of oil in the pipe = πr²h = 3.14 × (0.25)² × 5280 = 1036.2 cubic feet Number of barrels in the pipe = 1036.2/5.61 = 184.7 barrels Cost of one barrel = $100 Cost of 184.7 barrels =184.7 × $100 = $18470

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 1: Volume of Cylinders img 7$

Answer: 57.697 in³

Explanation: The length of the pan = 12 in The diameter of the pan = 3.5 in Radius = 3.5/2 = 1.75 in The volume of uncooked dough = Half the volume of the full cylinder of the above dimensions. = (πr²h)/2 = (3.14 × (1.75)² × 12)/2 = 115.395/2 = 57.697 in³

FOCUS ON HIGHER ORDER THINKING

Question 18. Explain the Error A student said the volume of a cylinder with a 3-inch diameter is two times the volume of a cylinder with the same height and a 1.5-inch radius. What is the error? Type below: _______________

Answer: The volume of the cylinder of 3 in is four times the volume of the new cylinder of radius 1.5 in

Explanation: The volume of a cylinder is directly proportional to the square of the radius of the cylinder. The volume does not depend on the radius linearly. Volume = πr²h V1 = π(3)²h V2 = π(1.5)²h V1/V2 = (π(3)²h)/(π(1.5)²h) V1/V2 = 4 V1 = 4V2

Volume of Cylinders and Cones Mini Quiz Answer Key Question 19. Communicate Mathematical Ideas Explain how you can find the height of a cylinder if you know the diameter and the volume. Include an example with your explanation. Type below: _______________

Answer: Let the diameter be D. Radius r = D/2 Volume = πr²h Volume = π(D/2)²h V = π((D)²/4)h h = 4V/π(D)² To find the height of a cylinder with diameter D = 2 m Let the volume be 10 m³ h = 4V/π(D)² h = (4 × 10)/(3.14 × 2²) h = 3.18 m³

Question 20. Analyze Relationships Cylinder A has a radius of 6 centimeters. Cylinder B has the same height and a radius half as long as cylinder A. What fraction of the volume of cylinder A is the volume of cylinder B? Explain. Fraction: $\frac{□}{□}$

Answer: $\frac{VA}{4}$

Explanation: rA = 6 cm rB = half of the radius of cylinder A = 3 cm hA = hB VA = πrA²h VB = πrB²h VA/VB = (πrA²h)/(πrB²h) VA/VB = 6²/3² = 36/9 = 4 Thus VB = VA/4

Guided Practice – Volume of Cones – Page No. 408

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 2: Volume of Cones img 8$

Answer: 150 in³

Explanation: In the question, the area of the base of the cylinder, B = 45 in² Height of the cylinder, h = 10 inch Volume of the cylinder, V cylinder = B × h = 45 × 10 = 450 inch³ Volume of the cone, V Cone = 1/3 V cylinder =1/3(450 inch) = 150 inch³ So, the volume of the cone is Vcone = 150 in³

Volume of Cylinders and Cones Mini Quiz Answer Key Question 2. A cone and a cylinder have congruent heights and bases. The volume of the cone is 18 m 3 . What is the volume of the cylinder? Explain. _________ m 3

Answer: 54 m 3

Explanation: The volume of the cone is 18 m 3 . Vcone = 1/3 Vcylinder Vcylinder = 3Vcone Vcylinder = 3.18 Vcylinder = 54 m 3

Find the volume of each cone. Round your answer to the nearest tenth if necessary. Use 3.14 for π.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 2: Volume of Cones img 9$

Answer: 65.94 ft³

Explanation: the diameter of the cone is 6ft. so, the radius of the cone is 3ft. the height of the cone is 7ft. the volume of the cone = 1/3 × πr²h = 1/3 × 3.14 × 3² × 7 = 65.94 ft³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 2: Volume of Cones img 10$

Answer: 113982in³

Explanation: The radius is 33inch and the height is 100 inch Volume of the cone = 1/3 × πr²h = 1/3 × π(33)²100 = 113982in³

Question 5. Gretchen made a paper cone to hold a gift for a friend. The paper cone was 15 inches high and had a radius of 3 inches. Find the volume of the paper cone to the nearest tenth. Use 3.14 for π. _________ in 3

Answer: 141.3in³

Explanation: the radius of the cone is 3inch and the height of the cone is 15inch. Volume of the cone = 1/3 × πr²h = 1/3 × π(3)² × 15 = 141.3in³

Question 6. A cone-shaped building is commonly used to store sand. What would be the volume of a cone-shaped building with a diameter of 50 meters and a height of 20 meters? Round your answer to the nearest tenth. Use 3.14 for π. _________ m 3

Answer: 13083.33 m³

Explanation: The diameter of the cone is 50 meters. So, the radius of the cone is 25 meters. The height of the cone is 20 meters. Volume of the cone = 1/3 × πr²h = 1/3 × π(25)² × 20 = 13083.33 m³

Question 7. How do you find the volume of a cone? Type below: ____________

Answer: V cone = 1/3 V cylinder V cone = 1/3 πr²h

13.2 Independent Practice – Volume of Cones – Page No. 409

Find the volume of each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 2: Volume of Cones img 11$

Answer: 410.3 mm³

Explanation: Radius r = 7 mm height = 8 mm Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(7)²(8) Volume = 410.29 mm³ Volume = 410.3 mm³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 2: Volume of Cones img 12$

Answer: 25.1 in 3

Explanation: Radius r = 2 in Height = 6 in Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(2)²(6) Volume = 25.12 in 3 Volume = 25.1 in 3

Lesson 2 Extra Practice Volume of Cones Answers Key Question 10. A cone has a diameter of 6 centimeters and a height of 11.5 centimeters. _________ cm 3

Answer: 108.3 cm 3

Explanation: Diameter of base = 6 cm Radius = 6/2 cm = 3 cm Height = 11.5 cm Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(3)² (11.5) Volume = 108.33 cm 3 Volume = 108.3 cm 3

Question 11. A cone has a radius of 3 meters and a height of 10 meters. _________ m 3

Answer: 94.2 m 3

Explanation: Radius r = 3 m Height = 10 m Volume of cone = 1/3 πr²h Volume = 1/3(3.14)(3)²(10) Volume = 94.2 m 3

Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 12. Antonio is making mini waffle cones. Each waffle cone is 3 inches high and has a radius of $\frac{3}{4}$ inch. What is the volume of a waffle cone? _________ in 3

Answer: 1.8 in 3

Explanation: Radius = 3/4 in Radius r = 0.75 in Height = 3 in Volume of each waffle cone = 1/3 πr²h Volume = 1/3 (3.14) (0.75)² (3) Volume = 1.76625 in 3 Volume = 1.8 in 3

Question 13. A snack bar sells popcorn in cone-shaped containers. One container has a diameter of 8 inches and a height of 10 inches. How many cubic inches of popcorn does the container hold? _________ in 3

Answer: 167.5 in 3

Explanation: Diameter of base = 8 in Radius = 8/2 in = 4 in Height = 10 in Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (4)² (10) Volume = 167.466 in 3 Volume = 167.5 in 3

Question 14. A volcanic cone has a diameter of 300 meters and a height of 150 meters. What is the volume of the cone? _________ m 3

Answer: 3534291.7 m 3

Explanation: Diameter of base = 300 m Radius = 300/2 m = 150 m Height = 150 m Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (150)² (150) Volume = 3534291.735 m 3 Volume = 3534291.7 m 3

The volume of Cones Answers Key Question 15. Multistep Orange traffic cones come in a variety of sizes. Approximate the volume, in cubic inches, of a traffic cone that has a height of 2 feet and a diameter of 10 inches. Use 3.14 for π. _________ in 3

Answer: 628 in³

Explanation: The radius of the cone is Diameter/2 = 10/2 = 5 The height of the cone is 2 ft = 2 . 12 = 24 in Vcone = 1/3 πr²h Vcone = 1/3 (3.14) (5)² (24) Vcone = 628 in³

Find the missing measure for each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

Question 16. radius = _______ height = 6 in. volume = 100.48 in3 _________ in.

Answer: radius = 4 in. 4 in.

Explanation: Let radius be R. Height = 6 in Volume = 100.4 in Volume of cone = 1/3 πr²h √(3v/hπ) = R √((3 × 100.48)/(18.84)) = R √(301.44/18.84) = R R = √(16) R = 4 in

Question 17. diameter = 6 cm height = _______ volume = 56.52 cm 3 _______ cm

Answer: height = 6 cm h = 6 cm

Explanation: Let height be h Diameter = 6 cm Radius = 6/2 = 3 cm Volume = 56.52 cm Volume of cone = 1/3 πr²h (3V/r²h) = h (3 × 56.52)/(3² × 3.14) = h 169.56/28.26 = h h = 6 cm

Question 18. The diameter of a cone-shaped container is 4 inches, and its height is 6 inches. How much greater is the volume of a cylinder-shaped container with the same diameter and height? Round your answer to the nearest hundredth. Use 3.14 for π. Type below: ____________

Answer: The volume of the cylinder is 50.24 in³ greater than the volume of the cone.

Explanation: The diameter of a cone, d = 4 inch radius of a cone, r = d/2 = 4/2 = 2 inches height of a cone, h = 6 inches. So, the volume of a cone, V cone = 1/3 πr²h = 1/3 (3.14) (2)² (6) = 25.12 in³ And the volume of a cylinder with the same diameter and height, V cylinder = πr²h = (3.14) (2)² (6) = 75.36 in³ The volume of the cylinder is 50.24 in³ greater than the volume of the cone.

FOCUS ON HIGHER ORDER THINKING – Volume of Cones – Page No. 410

Question 19. Alex wants to know the volume of sand in an hourglass. When all the sand is in the bottom, he stands a ruler up beside the hourglass and estimates the height of the cone of sand. a. What else does he need to measure to find the volume of sand? ____________

Answer: To find the volume of the sand, he needs to measure the radius of the base of the hourglass.

Question 19. b. Make a Conjecture If the volume of sand is increasing at a constant rate, is the height increasing at a constant rate? Explain. ____________

Answer: The volume of the cone is linearly proportional to the height of the cone. Therefore, if the volume is increasing at a constant rate, the height is also increasing at a constant rate.

Question 20. Problem Solving The diameter of a cone is x cm, the height is 18 cm, and the volume is 301.44 cm 3 . What is x? Use 3.14 for π. ________ cm

Answer: 8 cm

Explanation: V cone = 1/3 πr²h 301.44 = 1/3 . 3.14 . r² . 18 r² = 904.32/56.52 r² = 16 r = 4 cm The diameter of the circle is twice its radius, therefore x = 2 . r x = 2 . 4 x = 8 cm

Question 21. Analyze Relationships A cone has a radius of 1 foot and a height of 2 feet. How many cones of liquid would it take to fill a cylinder with a diameter of 2 feet and a height of 2 feet? Explain. ________ cones

Answer: 3 cones

Explanation: The diameter of the base of the cylinder is 2 feet, which means that its radius is 1 foot. Its height is 2 feet. The volume of this cylinder is V cylinder = πr²h V cylinder = (3.14) (1)² (2) V cylinder = 6.28 The radius of the cone is 1 foot and the height of the cone is 2 feet. The volume of the cone is: V cone = 1/3 πr²h V cone = 1/3 (3.14) (1)² (2) V cone = 1/3 × 6.28 V cone = 1/3 . V cylinder V cone = 2.09 It would take 3 cones of liquid to fill the cylinder.

Question 22. Critique Reasoning Herb knows that the volume of a cone is one third that of a cylinder with the same base and height. He reasons that a cone with the same height as a given cylinder but 3 times the radius should therefore have the same volume as the cylinder, since $\frac{1}{3}$ ⋅ 3 = 1. Is Herb correct? Explain. ____________

Answer: The volume of the given cylinder is V cylinder = πr²h The volume of the cone with the same height h as a given cylinder but 3 times the radius r is V cone = 1/3 π(3r)²h V cone = 3 πr²h V cone = 3 V cylinder As we can see, Herb is not correct. The volume of the cone is not equal to the volume of the cylinder. But it is three times the volume of the cylinder.

Guided Practice – Volume of Spheres – Page No. 414

Question 1. Vocabulary A sphere is a three-dimensional figure with all points _____ from the center. Type below: ____________

Answer: A sphere is a three-dimensional figure with all points at equal distances from the center.

Lesson 13.2 Volume of Cones Practice and Problem Solving a/b Answers Question 2. Vocabulary The _____ is the distance from the center of a sphere to a point on the sphere. Type below: ____________

Answer: radius

Explanation: The radius is the distance from the center f the sphere to a point on the sphere

Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Volume of Spheres img 13$

Answer: 4.12 in 3

Explanation: V = 4/3πr³ V = 4/3 (3.14) (1)³ V = 4.12 in 3

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Volume of Spheres img 14$

Answer: 4186.7 cm³

Explanation: Diameter = 20 cm Radius r = 20/2 = 10 cm Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (10)³ Volume = 4186.66 cm³ Volume = 4186.7 cm³

Question 5. A sphere has a radius of 1.5 feet. _______ ft 3

Answer: 14.1 ft³

Explanation: Radius r = 1.5 ft The volume of the sphere = 4/3πr³ Volume = 4/3 (3.14) (1.5)³ Volume = 14.13 ft³ Volume = 14.1 ft³

Question 6. A sphere has a diameter of 2 yards. _______ yd 3

Answer: 4.2 yd³

Explanation: Diameter = 2 yards Radius r = 2/2 yards Radius r = 1 yd Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (1)³ Volume = 4.1866 yd³ Volume = 4.2 yd³

Question 7. A baseball has a diameter of 2.9 inches. Find the volume of the baseball. Round your answer to the nearest tenth if necessary. Use 3.14 for π. _______ in 3

Answer: 12.8 in³

Explanation: Diameter of baseball = 2.9 in Radius r = 2.9/2 in Radius of baseball = 1.45 in The volume of the sphere = 4/3πr³ Volume = 4/3 (3.14) (1.45)³ Volume = 12.763 in³ Volume = 12.8 in³

Lesson 13.3 Volume of Spheres Practice and Problem Solving a/b Question 8. A basketball has a radius of 4.7 inches. What is its volume to the nearest cubic inch? Use 3.14 for π. _______ in 3

Answer: 1304 in³

Explanation: Radius of baseball = 4.7 in The volume of the sphere = 4/3πr³ Volume = 4/3 (3.14) (4.7)³ Volume = 1304.0168 in³ Volume = 1304 in³

$Go Math Grade 8 Answer Key Chapter 13 Volume Go Math Grade 8 Answer Key Chapter 13 Volume img 15 img 15$

Answer: The volume of the cylinder is V cylinder = πr²h Since the ball touches the bottom, top, and sides, then the height of the cylinder will be equal to 2r. V cylinder = πr²(2r) = 2πr³ On the other hand, the volume of the sphere is V sphere = 4/3 πr³ The volume of the empty space inside the cylindrical box is found by subtracting the volume of the sphere from the volume of the cylinder V cylinder – V sphere = 2πr³ – 4/3 πr³ = (2 – 4/3)πr³ = 2/3πr³

Question 9. b. Find an expression for the volume of the cubic box. Type below: _______________

Answer: The volume of a cube with side a is V cube = a³ Since the ball touches the bottom, top, and sides, then the side of the cube will be equal to 2r. V cube = (2r)³ V cube = 8r³

Question 9. c. About what portion of the space inside the cubic box is empty? Explain Type below: _______________

Answer: The volume of the empty space inside the cubical box is found by subtracting the volume of the sphere from the volume of the cube: V cube – V sphere = 8r³ – 4/3 πr³ = (8 – 4/3π)r³ = (8 – 4.2)r³ = 3.8r³

Question 10. Explain the steps you use to find the volume of a sphere. Type below: _______________

Answer: Step 1: The radius of the sphere is found out. Step 2: The volume of the sphere is 4/3 πr³; where R is the radius. Step 3: Put the value of radius in the equation of volume. Step 4: Calculate the volume.

13.3 Independent Practice – Volume of Spheres – Page No. 415

Question 11. radius of 3.1 meters _______ m 3

Answer: 124.7 m³

Explanation: The volume of the sphere with a radius of 3.1 meter is 4/3 πr³ V = 4/3 . (3.14) . (3.1)³ V = 124.7 m³

Question 12. diameter of 18 inches _______ in 3

Answer: 3052.1 in³

Explanation: The diameter of the sphere is 18 inches, which means that its radius is 9 inches. The volume of the sphere is V = 4/3 πr³ V = 4/3 . (3.14) . (9)³ V = 3052.08 in³ V = 3052.1 in³

Volume of Cylinders Cones and Spheres Iready Answers Question 13. r = 6 in. _______ in 3

Answer: 904.3 in³

Explanation: The volume of the sphere with a radius of 6 inches is V = 4/3 πr³ V = 4/3 (3.14) (6)³ V = 904.32 V = 904.3 in³

Question 14. d = 36 m _______ m 3

Answer: 24416.6 m³

Explanation: d = 36 m radius r = 36/2 = 18 m Volume = 4/3 πr³ = 4/3 (3.14) (18)³ = 24416.64 Volume = 24416.6 m³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Volume of Spheres img 16$

Answer: 5572.5 cm³

Explanation: The volume of the sphere with a radius of 11 centimeters is V = 4/3 πr³ V = 4/3 (3.14) (11)³ V = 5572.5 cm³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Volume of Spheres img 17$

Answer: 8.2 feet³

Explanation: The diameter of the sphere is 2.5 feet, which means that its radius is 1.25 feet. The volume of the sphere is V = 4/3 πr³ V = 4/3 . (3.14) . (1.25)³ V = 8.2 feet³

The eggs of birds and other animals come in many different shapes and sizes. Eggs often have a shape that is nearly spherical. When this is true, you can use the formula for a sphere to find their volume.

Question 17. The green turtle lays eggs that are approximately spherical with an average diameter of 4.5 centimeters. Each turtle lays an average of 113 eggs at one time. Find the total volume of these eggs, to the nearest cubic centimeter. _______ cm 3

Answer: 5389 cm³

Explanation: The diameter of an egg (sphere) is 4.5 centimeters, which means that its radius is 2.25 centimeters. The volume of a single egg is V = 4/3 πr³ V = 4/3 (3.14) (2.25)³ V = 47.68875 cm³ Therefore, the total volume of 113 eggs is 113 . V = 113(47.68875) = 5388.82875 = 5389 cm³

Question 18. Hummingbirds lay eggs that are nearly spherical and about 1 centimeter in diameter. Find the volume of an egg. Round your answer to the nearest tenth. _______ cm 3

Answer: 0.5 cm³

Explanation: The diameter of an egg (sphere) is 1 centimeter, which means that its radius is 0.5 centimeters. The volume of a single egg is V = 4/3 πr³ V = 4/3 (3.14) (0.5)³ V = 0.5 cm³

Question 19. Fossilized spherical eggs of dinosaurs called titanosaurid sauropods were found in Patagonia. These eggs were 15 centimeters in diameter. Find the volume of an egg. Round your answer to the nearest tenth. _______ cm 3

Answer: 1766.25 cm³

Explanation: Diameter of an egg = 15 cm Its radius = 15/2 = 7.5 cm Volume = 4/3 πr³ V = 4/3 (3.14) (7.5)³ V = 1766.25 cm³

Volume and Surface Area of Spheres Question 20. Persevere in Problem Solving An ostrich egg has about the same volume as a sphere with a diameter of 5 inches. If the eggshell is about $\frac{1}{12}$ inch thick, find the volume of just the shell, not including the interior of the egg. Round your answer to the nearest tenth. _______ in 3

Answer: 6.8 in³

Explanation: Diameter including the eggshell = 5 + (2 . 1/2) = (5 + 1/6) in = 5.166 in Radius including eggshell = 5.166/2 = 2.5833 in Volume = 4/3 πr³ Volume = 4/3 (3.14) (2.5833)³ =72.176 in³ Volume with shell = 72.2 in³ Radius excluding shell = 5/2 = 2.5 in Volume = 4/3 (3.14) (2.5)³ = 65.416 in³ Volume (without shell) = 65.4 in³ Volume of shell = Total volume – Inner Volume = 72.2 – 65.4 = 6.8 in³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Volume of Spheres img 18$

Answer: 5/3πr³

Explanation: The radius of the hemisphere = r The radius of cylinder = r Height of cylinder = r Step 1: Find the formula for the volume of a hemisphere The volume of hemisphere = 4/3 π/2 r³ = 2/3πr³ Step 2: Find the formula for the volume of a cylinder The volume of the cylinder = πr²h =πr³ Step 3: Add both the volume expressions: Total volume = 2/3πr³ + πr³ = 5/3πr³

Volume of Spheres – Page No. 416

Question 22. Critical Thinking Explain what happens to the volume of a sphere if you double the radius. Type below: _____________

Answer: Let Radius = r Volume V1 = 4/3πr³ Radius = 2r Volume V2 = 4/3π(2r)³ = 8 . 4/3πr³ = 8 V1 = 8(initial volume) By doubling the radius of the sphere we make the volume 8 times the initial value.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Volume of Spheres img 19$

Answer: 12.3 in³

Explanation: Radius of the ball = 1.25 inch Height of the cylinder = (2 × 1.25) × 3 = (2.5) × 3 = 7.5 in radius of base of cylinder = 1.25 in. Volume of cylinder = πr²h = (3.14) (1.25)² (7.5) = 36.7968 = 36.8 in³ Volume of a ball (all three) = 3 × 4/3πr³ = 4 (3.14) (1.25)³ = 24.53125 in³ = 24.5 in³ Volume of empty space = Volume of cylinder – Volume of ball = 36.8 – 24.5 = 12.3 in³

Question 24. Critique Reasoning A sphere has a radius of 4 inches, and a cube-shaped box has an edge length of 7.5 inches. J.D. says the box has a greater volume, so the sphere will fit in the box. Is he correct? Explain. _____________

Answer: The volume of sphere = 4/3πr³ = 4/3 (3.14) (4)³ = 267.9466 = 268 The volume of cube = (7.5)³ = 421.875 =421.9 The volume of cube > Volume of a sphere But the base of the cube has an area of (7.5 × 7.5) = 56.25 while the cross-action area of the sphere. πr² = (3.14) (4)² = 50.24 The cross-section area of the cube is less than that of a sphere. thus J.D. is wrong and the ball (sphere) will not fit in the cube.

Question 25. Critical Thinking Which would hold the most water: a bowl in the shape of a hemisphere with radius r, a cylindrical glass with radius r and height r, or a cone-shaped drinking cup with radius r and height r? Explain. _____________

Answer: The volume of a sphere with radius r is V sphere = 4/3πr³ Therefore, the volume of a hemisphere is V hemisphere = V sphere/2 V hemisphere = 2/3πr³ The volume of a cylinder with radius r and height r is V cylinder = πr²h V cylinder = πr³ The volume of a cone with radius r and height r is V cone = 1/3πr²h V cone = 1/3πr³ V cone < V hemisphere < V cylinder Therefore, the cylindrical glass with radius r and height r will hold the most water.

8th Grade Review for Volume of Cylinders, Cones, and Spheres Answer Key Question 26. Analyze Relationships Hari has models of a sphere, a cylinder, and a cone. The sphere’s diameter and the cylinder’s height are the same, 2r. The cylinder has radius r. The cone has diameter 2r and height 2r. Compare the volumes of the cone and the sphere to the volume of the cylinder. Type below: _____________

Answer: Radius of sphere = 2r/2 = r Volume of sphere = 4/3πr³ The radius of cylinder = r Height of cylinder = 2r volume of cylinder = πr²(2r) V cylinder = 2πr³ Radius of cone = 2r/2 = r Height of cone = 2r Volume of cone = 1/3 πr²(2r) V cone = 2/3πr³ Volume of cylinder > Volume of sphere > Volume of cone 2πr³ > 4/3πr³ > 2/3πr³

Question 27. A spherical helium balloon that is 8 feet in diameter can lift about 17 pounds. What does the diameter of a balloon need to be to lift a person who weighs 136 pounds? Explain. _______ feet

Answer: Diameter of ballon = 8 ft Weight it could lift = 17 pound Volume = 4/3 π(8/2)³ = 4³(4π/3) 4³/x(4π/3) = 17/36 1/x = 1/8 × 3/4π × 1/48 x = 4π/3 . 4³ . 2³ x = 4/3. π . 8³ The volume of ballon which can lift 136 pounds is equal to 4/3. π . 8³ The radius of that ballon = 8ft Diameter = 8 . 2 = 16 ft

Ready to Go On ? – Model Quiz – Page No. 417

13.1 Volume of Cylinders

Find the volume of each cylinder. Round your answers to the nearest tenth if necessary. Use 3.14 for π.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Model Quiz img 20$

Answer: 904.8 ft³

Explanation: Radius of base = 6 ft Height of cylinder = 8 ft The volume of cylinder = πr²h Volume = (3.14) (6)² (8) Volume = 904.77 ft³ Volume = 904.8 ft³

Volume of Cylinders, Cones, and Spheres Iready Answers Question 2. A can of juice has a radius of 4 inches and a height of 7 inches. What is the volume of the can? _______ in 3

Answer: 351.7 in³

Explanation: Radius if cylindrical can = 4 in Height of cylindrical can = 7 in The volume of cylinder = πr²h Volume = (3.14) (4)² (7) Volume = 351.68 in³ Volume = 351.7 in³

13.2 Volume of Cones

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Model Quiz img 21$

Answer: 565.2 cm³

Explanation: Radius of base of cone = 6 cm Height of cone = 15 cm Volume of cone = 1/3πr²h Volume = 1/3 (3.14) (4)² (7) Volume = 565.2 cm³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Model Quiz img 22$

Answer: 3014.4 in³

Explanation: The radius of the base of cone = 12 in Height of cone = 20 in The volume of cone = 1/3πr²h Volume = 1/3 (3.14) (12)² (20) Volume = 3014.4 in³

13.3 Volume of Spheres

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Model Quiz img 23$

Answer: 113 in³

Explanation: Radius of sphere = 3 ft Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (3)³ Volume = 113.04 ft³ Volume = 113 in³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Model Quiz img 24$

Answer: 1149.8 cm³

Explanation: Diameter = 13 cm Radius = 13/2 cm = 6.5 cm Volume of sphere = 4/3πr³ Volume = 4/3 (3.14) (6.5)³ Volume = 1149.7633 cm³ Volume = 1149.8 cm³

ESSENTIAL QUESTION

Question 7. What measurements do you need to know to find the volume of a cylinder? a cone? a sphere? Type below: ___________

Answer: Sphere: To find the volume of the sphere, the radius is to be measured. Cylinder: To measure the volume of the cylinder, we need to find out the base radius of the base of the cylinder along with the height of the cylinder. Cone: To calculate the volume of the cone, we need to calculate the base radius of the base of the cone along with the height of the cone.

Explanation: The volume of sphere = 4/3 πr³ Sphere: For finding the volume of the sphere, the radius is to be measured The volume of Cylinder = πr²h Cylinder: To calculate the volume of the cylinder, we need to find out the base radius of the base of the cylinder along with the height of the cylinder The volume of Cone = 1/3 πr²h Cone: To calculate the volume of the cone, we need to measure the base radius of the base of the cone along with the height of the cone

Selected Response – Mixed Review – Page No. 418

Question 1. The bed of a pickup truck measures 4 feet by 8 feet. To the nearest inch, what is the length of the longest thin metal bar that will lie flat in the bed? Options: a. 11 ft 3 in. b. 10 ft 0 in. c. 8 ft 11 in. d. 8 ft 9 in.

Answer: d. 8 ft 9 in.

Explanation: The length of the longest thin metal bar that will lie flat in the bed’s equal to the length of the bed’s hypotenuse. Let a = 4 and b = 8. Using the Pythagorean Theorem a² + b² = c² 4² + 8² = c² 16 + 64 = c² 80 = c² Rounding the length of the hypotenuse to the nearest tenth of a foot c = 8.9 ft Therefore, the length of the longest thin metal bar that will lie flat in the bed is 8 ft. 9 in.

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Mixed Review img 25$

Answer: c. 1,091.6 cubic yards

Explanation: Diameter of the base of the cylinder = 11.4 yd Radius = 11.4/2 yd = 5.7 yd Height = 10.7 ys Volume of cylinder = πr²h Volume = (3.14) (5.7)² (10.7) Volume = 1091.599 yd³ Volume = 1091.6 yd³

Question 3. Rhett made mini waffle cones for a birthday party. Each waffle cone was 3.5 inches high and had a radius of 0.8 inches. What is the volume of each cone to the nearest hundredth? Options: a. 1.70 cubic inches b. 2.24 cubic inches c. 2.34 cubic inches d. 8.79 cubic inches

Answer: c. 2.34 cubic inches

Explanation: Height of each waffle cone = 3.5 in Radius of base = 0.8 in Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (0.8)² (3.5) Volume = 2.344533 in³ Volume = 2.34 in³

Question 4. What is the volume of a cone that has a height of 17 meters and a base with a radius of 6 meters? Use 3.14 for π and round to the nearest tenth. Options: a. 204 cubic meters b. 640.6 cubic meters c. 2,562.2 cubic meters d. 10,249 cubic meters

Answer: b. 640.6 cubic meters

Explanation: Height of the cone = 17 m Radius of base = 6 m Volume of cone = 1/3 πr²h Volume = 1/3 (3.14) (6)² (17) Volume = 640.56 m³ Volume = 640.6 m³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Mixed Review img 26$

Answer: b. 5,572.5 cubic centimeters

Explanation: Diameter of the base of the sphere = 22 cm Radius = 22/2 yd = 11 cm Volume of sphere = 4/3 πr³ Volume = 4/3 (3.14) (11)³ Volume = 5572.4533 cm³ Volume = 5572.5 cm³

$Go Math Grade 8 Answer Key Chapter 13 Volume Lesson 3: Mixed Review img 27$

Answer: 8.574 cm³

Explanation: The radius of the cylinder as well as the hemisphere = 1.6 cm Height = 6.2 cm the volume of the hemisphere = 2/3 πr³ the volume of the hemisphere = 2/3 (3.14) (1.6)³ the volume of the hemisphere = 8.574 cm³

Question 6. b. What is the volume of the cylinder? _______ cm 3

Answer: 49.838 cm³

Explanation: The volume of cylinder = πr²h = (3.14) (1.6)² (6.2) = 49.838 cm³

Question 6. c. What is the volume of the whole figure? _______ cm 3

Answer: 58.4 cm³

Explanation: Total volume = Volume of cylinder + volume of a hemisphere Total volume = 8.574 cm³ + 49.838 cm³ Total volume = 58.4 cm³

Conclusion:

Download Go Math Grade 8 Answer Key Chapter 13 Volume for free of cost. Self-study is also possible with the help of HMH Go Math Grade 8 Solution Key. Begin your practice now by referring to Go Math Grade 8 Chapter 13 Volume Solution Key. Every student love to practice maths with the help of the Go Math Grade 8 Solution Key. Each and every problem is explained in a detailed way to help the students to practice in the best way.

Problem-Solving # 2 Storytime : Games & Activities for Special Ed NO PREP

Description

NO PREP! This lesson plan is designed to engage special education students in problem-solving through interactive story reading and related games and activities. The goal is to promote critical thinking, communication, and teamwork skills in a fun and accessible way. It requires minimal preparation, making it ideal for busy teachers looking for creative and effective teaching strategies.

Questions & Answers

Engage excite explore.

We're hiring
Help & FAQ
Privacy policy
Student privacy
Terms of service
Tell us what you think

An Introduction to Relational Frame Theory (Standard)

15.29 problem solving example part 8, problem solving.

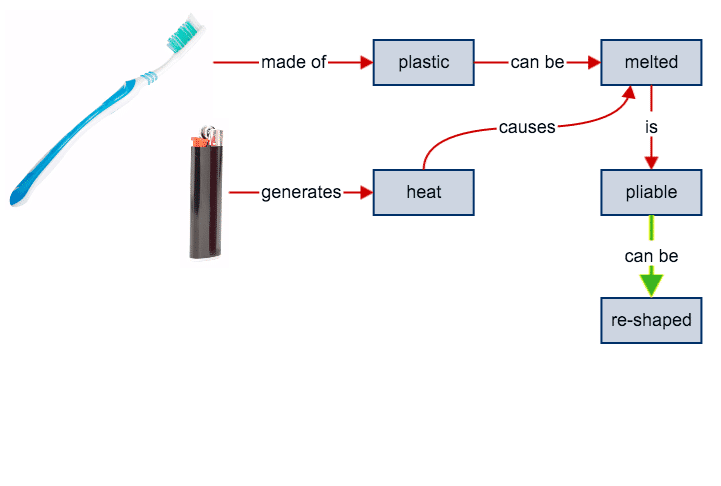
…which means that the melted plastic can be re-shaped. Re-shaping the end of the toothbrush to fit the head of the screw might be a good idea, eh?

A diagram illustrating the production process of a toothbrush.

Lesson Plans

General Archive
Health & Safety
Interdisciplinary
Language Arts
PE & Sports
Social Science
Special Ed & Guidance
Special Themes
Top LP Features
Article Archive
User Submitted LPs
Box Cars Math Games
Every Day Edits
Five Minute Fillers
Holiday Lessons
News for Kids
ShowBiz Science
Student Engagers
Work Sheet Library
More LP Features
Calculator Lessons
Coloring Calendars
Friday Fun Lessons
Math Machine
Month of Fun
Reading Machine
Tech Lessons
Writing Bug
All Work Sheets
Critical Thinking Work Sheets
Animals A to Z
Backpacktivities
EveryDay Edits
Hunt the Fact Monster
It All Adds Up Math Puzzles
Make Your Own Work Sheets
Math Cross Puzzles
Mystery State
Math Practice 4 You
Phonics Word Search Puzzles
Readers Theater Scripts
Sudoku Puzzles
Vocabulous!
Back to School
Back to School Archive
Icebreaker Activities
Preparing for the First Day
Ideas for All Year
The Homework Dilemma
First Year Teachers
Don't Forget the Substitute
More Great Ideas for the New School Year
Early Childhood
Best Books for Educators
Assessments
Award Certificates
Bulletin Board Resources
Classroom Organizers
Graphic Organizers
Newsletters
Parent Teacher Communications
More Templates

Search form

Lesson plan: stem project - solving a problem.

Subject : Science

Grade : 3-5

Lesson Objective: To solve a real-world problem

Next Gen Science Standard: 3-5-ETS1-2. Generate and compare multiple possible solutions to a problem based on how well each is likely to meet the criteria and constraints of the problem.

Preparation Needed:

Make up small groups of students to work together on the project
What do you think is the most important thing to remember when working together? (Allow the students to answer.)
Today, you are going to be split into small groups of students to work on solving a problem that I will give you.
While solving the problem, you are going to need to use everything that you have learned about what different materials are good for.
Now, I am going to read a situation to you. I need you to listen carefully because in this situation is the problem that you will need to solve.
There are two different situations. Listen to each carefully and then you will decide with your group which problem you would like to solve.

Read the following situations to the students:

A musician who plays the trumpet has to practice for a concert that she has coming up. She lives in a house with four other people. The other people do not like to listen to her practice. The musician needs a room that she can practice in that will not bother the other people. She needs the room to be soundproof.
A chef has started a new business. He cooks food for people and then takes it to them so that they do not have to cook. He makes the food ahead of time and keeps it in a refrigerator. He needs to take the food to the people’s homes and keep it cold. He needs a way to safely transport the cold food.
Listen carefully to the students you will be working with (provide the students with their groups). Then, take your notebook and something to write with, get up and find a space in the room to work with your group. (Allow time to read the list of groups and have the students find their groups and a place to sit together).
The first thing that you will be doing is choosing whether you want to figure out how to sound proof a room or safely transport cold food.
Then, you will start by figuring how what questions to ask and what your hypothesis will be.

Ask: "Does anyone have any questions"? (Allow about 15 minutes for the students to start working on the problem that they chose.)

What are you having a difficult time with as you start to work on solving your problem? (Allow the students to answer.)
What do you think is the best way to share the solution that you came up with to your problem? (Allow the students to answer.)
We are going to talk about how to present the solution to your problem to the rest of the class.
You will finish solving your problem as a group and then present what you found.
A good way to present information is by talking about it, but also by showing something.
You can draw a picture of what you came up with to show as you talk about your solution.
You have about 10 minutes to finish working and get ready to present your solution to the rest of the class. You are now going to present your solution to the class. Please choose one person to tell the class which problem you chose and the solution you came up with.
Raise your hand if your group would like to first. (Allow about 20 minutes for the students to present their solution to the rest of the class.)
Do you think any of the solutions that were presented would really work? Why or why not? (Allow the students to answer.)

Written by Kimberly Greacen, Education World® Contributing Writer

Kimberly is an educator with extensive experience in curriculum writing and developing instructional materials to align with Common Core State Standards and Bloom's Taxonomy.

EW Lesson Plans

EW Professional Development

Ew worksheets.

top education news, lesson ideas, teaching tips and more!

No thanks, I don't need to stay current on what works in education!

SchoolNotes.com
The Educator's Network

IMAGES

Stages of Problem Solving
PPT
15 Fun Activities To Teach Problem Solving To Kids
Problem Solving Exercise Problem Solving Worksheets Problem Solving
Mastering 8D Problem Solving: A Comprehensive Guide
Problem Solving Classroom Guidance Lesson: I Can Solve Problems

VIDEO

Problem Solving Lesson 10-B Thursday 05 16 2024
EFTY ACADEMY PROBLEM SOLVING
Problem Solving
Problem Solving Lesson 2 Thursday 11 16 2023
5th Gr
Problem Solving Lesson 2

COMMENTS

3rd grade GO Math: Lesson 12.8 Problem Solving-Classify Plane Shapes
This video covers Lesson 12.8 Problem Solving-Classify Plane Shapes on pages 535-538 of the 3rd grade GO Math textbook.
PDF Lesson 12.8 Problem Solving • Classify Plane Shapes
Lesson 12.8 Practice and Homework Chapter 12 745 1. Steve drew the shapes below. Write the letter of each shape where it belongs in the Venn diagram. 2. Janice drew the shapes below. Write the letter of each shape where it belongs in the Venn diagram. 3. WRITE Math Draw a Venn diagram with one circle labeled Quadrilaterals and the other circle ...
Go Math Lesson 12.8 Problem Solving: Classify Plane Shapes
This video covers Lesson 12.8 in the third-grade Go Math curriculum. In this lesson, students learn how to use the vocabulary from this chapter and apply it ...
PDF PROBLEM SOLVING Lesson 12.8 Try Another Problem Problem Solving
Read the Problem A Venn diagram shows how sets of things are related. In the Venn diagram at the right, one circle has shapes that are rectangles. Shapes that ... PROBLEM SOLVING Lesson 12.8 Geometry 3.G.A.1 MATHEMATICAL PRACTICES MP1, MP2, MP4, MP7 ath alk MATHEMATICAL PRACTICES 1 Make Sense of Problems Does a fit in the Venn diagram? Explain.
PDF The Pythagorean Theorem 12-1 Practice and Problem Solving: A/B
Part is an alternate interior angle to a 45° angle, and part is an alternate interior angle to a 35° angle. I can use those measures to add because the angles are congruent. 4. m∠x = 70° − 30° = 40° The angle marked 70° and the angles marked x and 30° are alternate interior angles and therefore congruent.
Step-by-Step Math Problem Solver
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
Area of right triangles (practice)
units 2. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Go Math!
Lesson 12.5- Problem Solving: Make New Two-Dimensional Shapes; Lesson 12.6- Hands On: Find Shapes in Shapes; Lesson 12.7- Take Apart Two-Dimensional Shapes; Lesson 12.8- Equal or Unequal Parts; Lesson 12.9- Halves; Lesson 12.10- Fourths; zoom_out_map . Math On the Spot Videos-Cute videos that model problems within each lesson.
PDF Making Predictions with Experimental Probability
LESSON 12-4 Practice and Problem Solving: A/B 1. 140 times 2. 135 serves 3. 64 days 4. 330 people 5. 298 times 6. 49 shots 7. in Classes 1 and 3, because the percents preferring digital were 80% and 81% Practice and Problem Solving: C 1. Yes, they should keep their plans. The location is likely to provide over 9 days without rain. 2.
problem solving lesson 12.8
Texas Go Math; Big Ideas Math; Engageny Math; McGraw Hill My Math; enVision Math; 180 Days of Math; Math in Focus Answer Key; Math Expressions Answer Key; Privacy ...
Geometry, Volume 2
Now, with expert-verified solutions from Geometry, Volume 2 1st Edition, you'll learn how to solve your toughest homework problems. Our resource for Geometry, Volume 2 includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. With Expert Solutions for thousands of practice problems ...
McDougal Littell Pre-Algebra: Practice Workbook
Now, with expert-verified solutions from McDougal Littell Pre-Algebra: Practice Workbook 1st Edition, you'll learn how to solve your toughest homework problems. Our resource for McDougal Littell Pre-Algebra: Practice Workbook includes answers to chapter exercises, as well as detailed information to walk you through the process step by step.
PDF Lesson 12.7 Name Metric Units of Mass and Liquid Volume
Lesson 12.8 Units of Time Chapter 12 P215 Complete. 1. 6 minutes = __ seconds Think: 1 minute = 60 seconds, so 6 minutes = 6 3 60 seconds, or 360 seconds 8. 2 years 14 months 9. 3 hours 300 minutes Compare using ,, ., or 5. Problem SolvingProblem Solving 14. Jody practiced a piano piece for 500 seconds. Bill practiced a piano piece for 8 minutes.
Eureka Math Grade 8 Module 3 Lesson 12 Answer Key
Eureka Math Grade 8 Module 3 Lesson 12 Problem Set Answer Key. Students practice solving real-world problems using properties of similar triangles. Question 1. The world's tallest living tree is a redwood in California. It's about 370 feet tall. In a local park, there is a very tall tree.
Go Math Grade 8 Answer Key Chapter 13 Volume
Lesson 13.1 Volume of Cylinders Practice and Problem Solving a/b Question 3. Find the volume of the cylinder to the nearest tenth. Use 3.14 for π. ... Lesson 13.2 Volume of Cones Practice and Problem Solving a/b Answers Question 2. Vocabulary The _____ is the distance from the center of a sphere to a point on the sphere. Type below ...
High School Math 2012 Common-core Algebra 1 Practice And Problem
Textbook solutions for High School Math 2012 Common-core Algebra 1 Practice And… 1st Edition Prentice Hall and others in this series. View step-by-step homework solutions for your homework. Ask our subject experts for help answering any of your homework questions!
Team Problem-Solving Fun
Team Problem-Solving Fun ... Lesson Plan Source Education World Submitted By Gary Hopkins National Standards LANGUAGE ARTS: EnglishGRADES K - 12NL-ENG.K-12.2 Reading for UnderstandingNL-ENG.K-12.8 Developing Research SkillsNL-ENG.K-12.9 Multicultural UnderstandingNL-ENG.K-12.12 Applying Language Skills SOCIAL SCIENCES: EconomicsGRADES K - 4NSS ...
Problem-Solving # 2 Storytime : Games & Activities for Special Ed ...
NO PREP! This lesson plan is designed to engage special education students in problem-solving through interactive story reading and related games and activities. The goal is to promote critical thinking, communication, and teamwork skills in a fun and accessible way. It requires minimal preparatio...
15.29 Problem Solving Example Part 8
An Introduction to Relational Frame Theory (Standard) Lesson 15: Implications and Applications 15.29 Problem Solving Example Part 8. This is the open-access version of this module and your progress is not tracked or recorded. which means that the melted plastic can be re-shaped. Re-shaping the end of the toothbrush to fit the head of the screw ...
Problem 12.8 Flashcards
Problem 12.8. a. Click the card to flip 👆. the proposal that seems most reasonable for the issue is between Gomez and Wu. Police should get training for biases and how to treat people of different races with caution. Also, when people are stopped.. they should not even have to question why they were pulled over.
Lesson Plan: STEM Project Solving a Problem
Lesson Plan: STEM Project - Solving a Problem. Subject: Science. Grade: 3-5. Lesson Objective: To solve a real-world problem. Next Gen Science Standard: 3-5-ETS1-2. Generate and compare multiple possible solutions to a problem based on how well each is likely to meet the criteria and constraints of the problem. Preparation Needed: PART 1. Starter: