non parametric test in research

Nonparametric Tests

•   1  
• |   2  
• |   3  
• |   4  
• |   5  
• |   6  
• |   7  
• |   8  
• |   9  

All Modules

Introduction to Nonparametric Testing

This module will describe some popular nonparametric tests for continuous outcomes. Interested readers should see Conover 3 for a more comprehensive coverage of nonparametric tests.      

The techniques described here apply to outcomes that are ordinal, ranked, or continuous outcome variables that are not normally distributed. Recall that continuous outcomes are quantitative measures based on a specific measurement scale (e.g., weight in pounds, height in inches). Some investigators make the distinction between continuous, interval and ordinal scaled data. Interval data are like continuous data in that they are measured on a constant scale (i.e., there exists the same difference between adjacent scale scores across the entire spectrum of scores). Differences between interval scores are interpretable, but ratios are not. Temperature in Celsius or Fahrenheit is an example of an interval scale outcome. The difference between 30º and 40º is the same as the difference between 70º and 80º, yet 80º is not twice as warm as 40º. Ordinal outcomes can be less specific as the ordered categories need not be equally spaced. Symptom severity is an example of an ordinal outcome and it is not clear whether the difference between much worse and slightly worse is the same as the difference between no change and slightly improved. Some studies use visual scales to assess participants' self-reported signs and symptoms. Pain is often measured in this way, from 0 to 10 with 0 representing no pain and 10 representing agonizing pain. Participants are sometimes shown a visual scale such as that shown in the upper portion of the figure below and asked to choose the number that best represents their pain state. Sometimes pain scales use visual anchors as shown in the lower portion of the figure below.

 Visual Pain Scale

In the upper portion of the figure, certainly 10 is worse than 9, which is worse than 8; however, the difference between adjacent scores may not necessarily be the same. It is important to understand how outcomes are measured to make appropriate inferences based on statistical analysis and, in particular, not to overstate precision.

Assigning Ranks

The nonparametric procedures that we describe here follow the same general procedure. The outcome variable (ordinal, interval or continuous) is ranked from lowest to highest and the analysis focuses on the ranks as opposed to the measured or raw values. For example, suppose we measure self-reported pain using a visual analog scale with anchors at 0 (no pain) and 10 (agonizing pain) and record the following in a sample of n=6 participants:

                                                                      7               5               9              3             0               2                  

 The ranks, which are used to perform a nonparametric test, are assigned as follows: First, the data are ordered from smallest to largest. The lowest value is then assigned a rank of 1, the next lowest a rank of 2 and so on. The largest value is assigned a rank of n (in this example, n=6). The observed data and corresponding ranks are shown below:

A complicating issue that arises when assigning ranks occurs when there are ties in the sample (i.e., the same values are measured in two or more participants). For example, suppose that the following data are observed in our sample of n=6:

Observed Data:       7         7           9            3           0           2                  

The 4 th and 5 th ordered values are both equal to 7. When assigning ranks, the recommended procedure is to assign the mean rank of 4.5 to each (i.e. the mean of 4 and 5), as follows:

Suppose that there are three values of 7.   In this case, we assign a rank of 5 (the mean of 4, 5 and 6) to the 4 th , 5 th and 6 th values, as follows:

Using this approach of assigning the mean rank when there are ties ensures that the sum of the ranks is the same in each sample (for example, 1+2+3+4+5+6=21, 1+2+3+4.5+4.5+6=21 and 1+2+3+5+5+5=21). Using this approach, the sum of the ranks will always equal n(n+1)/2. When conducting nonparametric tests, it is useful to check the sum of the ranks before proceeding with the analysis.

To conduct nonparametric tests, we again follow the five-step approach outlined in the modules on hypothesis testing.  

• Set up hypotheses and select the level of significance α. Analogous to parametric testing, the research hypothesis can be one- or two- sided (one- or two-tailed), depending on the research question of interest.
• Select the appropriate test statistic. The test statistic is a single number that summarizes the sample information. In nonparametric tests, the observed data is converted into ranks and then the ranks are summarized into a test statistic.
• Set up decision rule. The decision rule is a statement that tells under what circumstances to reject the null hypothesis. Note that in some nonparametric tests we reject H 0 if the test statistic is large, while in others we reject H 0 if the test statistic is small. We make the distinction as we describe the different tests.
• Compute the test statistic. Here we compute the test statistic by summarizing the ranks into the test statistic identified in Step 2.
• Conclusion. The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule.   The final conclusion is either to reject the null hypothesis (because it is very unlikely to observe the sample data if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely if the null hypothesis is true).  

return to top | previous page | next page

Content ©2017. All Rights Reserved. Date last modified: May 4, 2017. Wayne W. LaMorte, MD, PhD, MPH

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Korean J Anesthesiol
• v.69(1); 2016 Feb

Nonparametric statistical tests for the continuous data: the basic concept and the practical use

Francis sahngun nahm.

Department of Anesthesiology and Pain Medicine, Seoul National University Bundang Hospital, Seongnam, Korea.

Conventional statistical tests are usually called parametric tests. Parametric tests are used more frequently than nonparametric tests in many medical articles, because most of the medical researchers are familiar with and the statistical software packages strongly support parametric tests. Parametric tests require important assumption; assumption of normality which means that distribution of sample means is normally distributed. However, parametric test can be misleading when this assumption is not satisfied. In this circumstance, nonparametric tests are the alternative methods available, because they do not required the normality assumption. Nonparametric tests are the statistical methods based on signs and ranks. In this article, we will discuss about the basic concepts and practical use of nonparametric tests for the guide to the proper use.

Introduction

Statistical analysis is a universal method with which to assess the validity of a conclusion. It is one of the most important aspects of a medical paper. Statistical analysis grants meaning to otherwise meaningless series of numbers and allow researchers to draw conclusions from uncertain facts. Hence, it is a work of creation that breathes life into data. However, the inappropriate use of statistical techniques results in faulty conclusions, inducing errors and undermining the significance of the article. Moreover, medical researchers must pay more attention to acquiring statistical validity as evidence-based medicine has taken center stage on the medicine scene in these days. Recently, rapid advances in statistical analysis packages have opened doors to more convenient analyses. However, easier methods of performing statistical analyses, such as inputting data on software and simply pressing the "analysis" or "OK" button to compute the P value without understanding the basic concepts of statistics, have increased the risk of using incorrect statistical analysis methods or misinterpreting analytical results [ 1 ].

Several journals, including the Korean Journal of Anesthesiology , have been striving to identify and to reduce statistical errors overall in medical journals [ 2 , 3 , 4 , 5 ]. As a result, a wide array of statistical errors has been found in many papers. This has further motivated the editors of each journal to enhance the quality of their journals by developing checklists or guidelines for authors and reviewers [ 6 , 7 , 8 , 9 ] to reduce statistical errors. One of the most common statistical errors found in journals is the application of parametric statistical techniques to nonparametric data [ 4 , 5 ]. This is presumed to be due to the fact that medical researchers have had relatively few opportunities to use nonparametric statistical techniques as compared to parametric techniques because they have been trained mostly on parametric statistics, and many statistics software packages strongly support parametric statistical techniques. Therefore, the present paper seeks to boost our understanding of nonparametric statistical analysis by providing actual cases of the use of nonparametric statistical techniques, which have only been introduced rarely in the past.

The History of Nonparametric Statistical Analysis

John Arbuthnott, a Scottish mathematician and physician, was the first to introduce nonparametric analytical methods in 1710 [ 10 ]. He performed a statistical analysis similar to the sign test used today in his paper "An Argument for divine providence, taken from the constant regularity observ'd in the Births of both sexes." Nonparametric analysis was not used for a while after that paper, until Jacob Wolfowitz used the term "nonparametric" again in 1942 [ 11 ]. Then, in 1945, Frank Wilcoxon introduced a nonparametric analysis method using rank, which is the most commonly used method today [ 12 ]. In 1947, Henry Mann and his student Donald Ransom Whitney expanded on Wilcoxon's technique to develop a technique for comparing two groups of different number of samples [ 13 ]. In 1951, William Kruskal and Allen Wallis introduced a nonparametric test method to compare three or more groups using rank data [ 14 ]. Since then, several studies have reported that nonparametric analyses are just as efficient as parametric methods; it is known that the asymptotic relative efficiency of nonparametric statistical analysis, specifically Wilcoxon's signed rank test and the Mann-Whitney test, is 0.955 against the t-test when the data satisfies the assumption of normality [ 15 , 16 ]. Ever since when Tukey developed a method to compute confidence intervals using a nonparametric method, nonparametric analysis was established as a commonly used analytical method in medical and natural science research [ 17 ].

The Basic Principle of Nonparametric Statistical Analysis

Traditional statistical methods, such as the t-test and analysis of variance, of the types that are widely used in medical research, require certain assumptions about the distribution of the population or sample. In particular, the assumption of normality, which specifies that the means of the sample group are normally distributed, and the assumption of equal variance, which specifies that the variances of the samples and of their corresponding population are equal, are two most basic prerequisites for parametric statistical analysis. Hence, parametric statistical analyses are conducted on the premise that the above assumptions are satisfied. However, if these assumptions are not satisfied, that is, if the distribution of the sample is skewed toward one side or the distribution is unknown due to the small sample size, parametric statistical techniques cannot be used. In such cases, nonparametric statistical techniques are excellent alternatives.

Nonparametric statistical analysis greatly differs from parametric statistical analysis in that it only uses + or - signs or the rank of data sizes instead of the original values of the data. In other words, nonparametric analysis focuses on the order of the data size rather than on the value of the data per se. For example, let's pretend that we have the following five data for a variable X.

After listing the data in the order of their sizes, each instance of data is ranked from one to five; the data with the lowest value (18) is ranked 1, and the data with the greatest value (99) is ranked 5. There are two data instances with values of 32, and these are accordingly given a rank of 2.5. Furthermore, the signs assigned to each data instance are a + for those values greater than the reference value and a − for those values less than the reference value. If we assign a reference value of 50 for these instances, there would only be one value greater than 50, resulting in one + and four − signs. While parametric analysis focuses on the difference in the means of the groups to be compared, nonparametric analysis focuses on the rank, thereby putting more emphasis differences of the median values than the mean.

As shown above, nonparametric analysis converts the original data in the order of size and only uses the rank or signs. Although this can result in a loss of information of the original data, nonparametric analysis has more statistical power than parametric analysis when the data are not normally distributed. In fact, as shown in the above example, one particular feature of nonparametric analysis is that it is minimally affected by extreme values because the size of the maximum value (99) does not affect the rank or the sign even if it is greater than 99.

Advantages and Disadvantages of Nonparametric Statistical Analysis

Nonparametric statistical techniques have the following advantages:

- There is less of a possibility to reach incorrect conclusions because assumptions about the population are unnecessary. In other words, this is a conservative method.

- It is more intuitive and does not require much statistical knowledge.

- Statistics are computed based on signs or ranks and thus are not greatly affected by outliers.

- This method can be used even for small samples.

On the other hand, nonparametric statistical techniques are associated with the following disadvantages:

- Actual differences in a population cannot be known because the distribution function cannot be stated.

- The information acquired from nonparametric methods is limited compared to that from parametric methods, and it is more difficult to interpret it.

- Compared to parametric methods, there are only a few analytical methods.

- The information in the data is not fully utilized.

- Computation becomes complicated for a large sample.

In summary, using nonparametric analysis methods reduces the risk of drawing incorrect conclusions because these methods do not make any assumptions about the population, whereas can have lower statistical power. In other words, nonparametric methods are "always valid, but not always efficient," while parametric methods are "always efficient, but not always valid." Therefore, parametric methods are recommended when they can in fact be used.

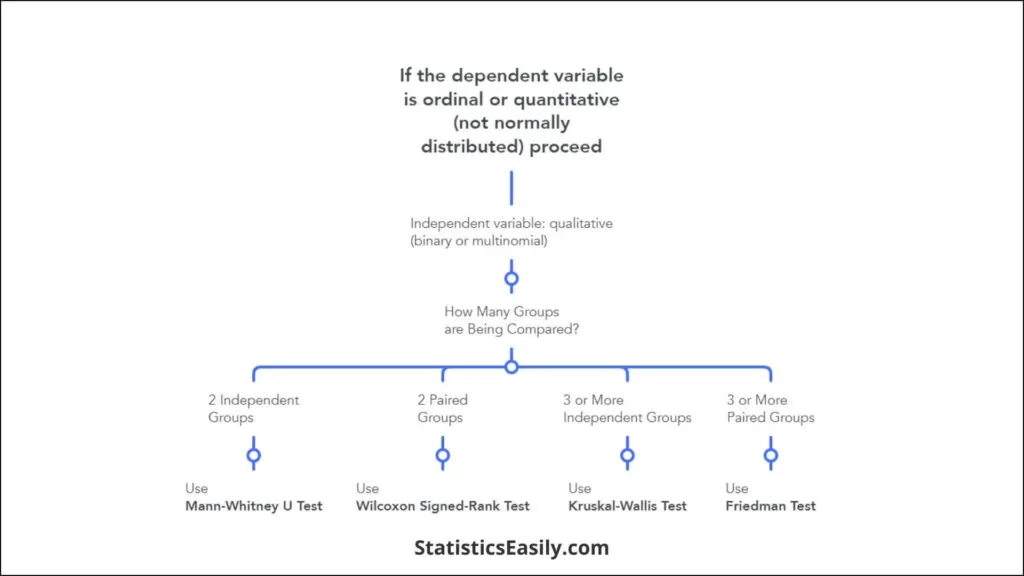
Types of Nonparametric Statistical Analyses

In this section, I explain the median test for one sample, a comparison of two paired samples, a comparison of two independent samples, and a comparison of three or more samples. The types of nonparametric analysis techniques and the corresponding parametric analysis techniques are delineated in Table 1 .

Median test for one sample: the sign test and Wilcoxon's signed rank test

The sign test and Wilcoxon's signed rank test are used for median tests of one sample. These tests examine whether one instance of sample data is greater or smaller than the median (reference value).

The sign test is the simplest test among all nonparametric tests regarding the location of a sample. This test examines the hypothesis about the median θ 0 of a population, and it involves testing the null hypothesis H 0 : θ = θ 0 . If the observed value (X i ) is greater than the reference value (θ 0 ), it is marked as +, and it is given a − sign if the observed value is smaller than the reference value, after which the number of + values is calculated. If there is an observed value in the sample that is equal to the reference value (θ 0 ), the said observed value is eliminated from the sample. Accordingly, the size of the sample is then reduced to proceed with the sign test. The number of sample data instances given the + sign is denoted as 'B' and is referred to as the sign statistic. If the null hypothesis is true, the number of + signs and the number of − signs are equal. The sign test ignores the actual values of the data and only uses + or − signs. Therefore, it is useful when it is difficult to measure the values.

Wilcoxon's signed rank test

The sign test has one drawback in that it may lead to a loss of information because only + or − signs are used in the comparison of the given data with the reference value of θ 0 . In contrast, Wilcoxon's signed rank test not only examines the observed values in comparison with θ 0 but also considers the relative sizes, thus mitigating the limitation of the sign test. Wilcoxon's signed rank test has more statistical power because it can reduce the loss of information that arises from only using signs. As in the sign test, if there is an observed value that is equal to the reference value θ 0 , this observed value is eliminated from the sample and the sample size is adjusted accordingly. Here, given a sample with five data points (X i ), as shown in Table 2 , we test whether the median (θ 0 ) of this sample is 50.

Let the median (θ 0 ) is 50. The original data were transformed into rank and sign data. +/- mean X i > 50 and < 50 respectively. The round bracket means rank.

In this case, if we subtract θ 0 from each data point (R i = X i - θ 0 ), find the absolute value, and rank the values in increasing order, the resulting rank is equal to the value in the parenthesis in Table 2 . With Wilcoxon's signed rank test, only the ranks with positive values are added as per the following equation:

Comparison of a paired sample: sign test and Wilcoxon's signed rank test

In the previously described one-sample sign test, the given data was compared to the median value (θ 0 ). The sign test for a paired sample compares the scores before and after treatment, with everything else identical to how the one-sample sign test is run. The sign test does not use ranks of the scores but only considers the number of + or − signs. Thus, it is rarely affected by extreme outliers. At the same time, it cannot utilize all of the information in the given data. Instead, it can only provide information about the direction of the difference between two samples, but not about the size of the difference between two samples.

This test is a nonparametric method of a paired t test. The only difference between this test and the previously described one-sample test is that the one-sample test compares the given data to the reference value (θ 0 ), while the paired test compares the pre- and post-treatment scores. In the example with five paired data instances (X ij ), as shown in Table 3 , which shows scores before and after education, X 1j refers to the pre-score of student j, and X 2j refers to the post-score of student j. First, we calculate the change in the score before and after education (R j = X 1j - X 2j ). When R j is listed in the order of its absolute values, the resulting rank is represented by the values within the parentheses in Table 3 . Wilcoxon's signed rank test is then conducted by adding the number of + signs, as in the one-sample test. If the null hypothesis is true, the number of + signs and the number of − signs should be nearly equal.

Under the null hypothesis (no difference between the pre/post scores), test statistics (W + , the sum of the positive rank) would be close to 7.5 ( = ∑ k = 1 5 k 2 ), but get far from 7.5 when the alternative hypothesis is true. According to the table for Wilcoxon's rank sum test, the P value = 0. 1363 when test statistics (W + ) 3 under α = 0.05 (two tailed test) and the sample size = 5. Therefore, null hypothesis cannot be rejected.

The sign test is limited in that it cannot reflect the degree of change between paired scores. Wilcoxon's signed rank test has more statistical power than the sign test because it not only considers the direction of the change but also ranks the degree of change between the paired scores, providing more information for the analysis.

Comparison of two independent samples: Wilcoxon's rank sum test, the Mann-Whitney test, and the Kolmogorov-Smirnov test

Wilcoxon's rank sum test and mann-whitney test.

Wilcoxon's rank sum test ranks all data points in order, calculates the rank sum of each sample, and compares the difference in the rank sums ( Table 4 ). If two groups have similar scores, their rank sums will be similar; however, if the score of one group is higher or lower than that of the other group, the rank sums between the two groups will be farther apart.

There are two independent groups with the sample sizes of group X (m) is 5 and group Y (n) is 4. Under the null hypothesis (no difference between the 2 groups), the rank sum of group X (W X ) and group Y (W Y ) would be close to 22.5 ( = ∑ k = 1 9 k 2 , but get far from 22.5 when the alternative hypothesis is true. According to the table for Wilcoxon's rank sum test, the P value = 0. 0556 when test statistics (W Y ) = 13 under α = 0.05 (two tailed test) at m = 5 and n = 4. Therefore, null hypothesis cannot be rejected.

On the other hand, the Mann-Whitney test compares all data x i belonging in the X group and all data y i belonging in the Y group and calculates the probability of xi being greater than y i : P(x i > y i ). The null hypothesis states that P(x i > y i ) = P(x i < y i ) = ½, while the alternative hypothesis states that P(x i > y i ) ≠ ½. The process of the Mann-Whitney test is illustrated in Table 5 . Although the Mann-Whitney test and Wilcoxon's rank sum test differ somewhat in their calculation processes, they are widely considered equal methods because they use the same statistics.

There are two independent groups with the sample sizes of group X (m) is 5 and group Y (n) is 4. Under the null hypothesis (no difference between the 2 groups), the test statistics (U) gets closer to 10 ( = m × n 2 ), but gets more extreme (smaller in this example) when the alternative hypothesis is true. The test statistics of this data is U = 3, which is greater than the reference value of 1 under α = 0.05 (two tailed test) at m = 5 and n = 4. Therefore, null hypothesis cannot be rejected.

Kolmogorov-Smirnov test (K-S test)

The K-S test is commonly used to examine the normality of a data set. However, it is originally a method that examines the cumulative distributions of two independent samples to examine whether the two samples are extracted from two populations with an equal distribution or the same population. If they were extracted from the same population, the shapes of their cumulative distributions would be equal. In contrast, if the two samples show different cumulative distributions, it can be assumed that they were extracted from different populations. Let's use the example in Table 6 for an actual analysis. First, we need to identify the distribution pattern of two samples in order to compare two independent samples. In Table 6 , the range of the samples is 43 with a minimum value of 50 and a maximum value of 93. The statistical power of the K-S test is affected by the interval that is set. If the interval is too wide, the statistical power can be reduced due to a small number of intervals; similarly, if the interval is too narrow, the calculations become too complicated due to the excessive number of intervals. The data shown in Table 6 has a range of 43; hence, we will establish an interval range of 4 and set the number of intervals to 11. As shown in Table 6 , a cumulative probability distribution table must be created for each interval (S X , S Y ), and the value with the greatest difference between the cumulative distributions of two variables (Max(S X - S Y )) must be determined. This maximum difference is the test statistic. We compare this difference to the reference value to test the homogeneity of the two samples. The actual analysis process is described in Table 6 .

There are two independent groups with the sample sizes of group X (N X ) and group Y (N Y ) are 15. The maximal difference between the cumulative probability density of X (S X ) and Y (S Y ) is 8/15 (0.533), which is greater than the rejection value of 0.467 under α = 0.05 (two tailed test) at N X = N Y = 15. Therefore, there is a significant difference between the group X and group Y.

Comparison of k independent samples: the Kruskal-Wallis test and the Jonckheere test

Kruskal-wallis test.

The Kruskal-Wallis test is a nonparametric technique with which to analyze the variance. In other words, it analyzes whether there is a difference in the median values of three or more independent samples. The Kruskal-Wallis test is similar to the Mann-Whitney test in that it ranks the original data values. That is, it collects all data instances from the samples and ranks them in increasing order. If two scores are equal, it uses the average of the two ranks to be given. The rank sums are then calculated and the Kruskal-Wallis test statistic (H) is calculated as per the following equation [ 14 ]:

Jonckheere test

Greater statistical power can be acquired if a rank alternative hypothesis is established using prior information. Let's think about a case in which we can predict the order of the effects of a treatment when increasing the degree of the treatment. For example, when we are evaluating the efficacy of an analgesic, we can predict that the effect will increase depending on the dosage, dividing the groups into a control group, a low-dosage group, and a high-dosage group. In this case, the null hypothesis H 2 is better than the null hypothesis H 1 .

H 0 : [τ 1 = τ 2 = τ 3 ]

H 1 : [τ 1 , τ 2 , τ 3 not all equal]

H 2 : [τ 1 ≤ τ 2 ≤ τ 3 , with at least strict inequality]

The Jonckheere test is a nonparametric technique that can be used to test such a rank alternative hypothesis [ 18 ].

The actual analysis process is described with illustration in Table 7 .

The test statistic J = 55 and P (J ≥ 55) = 0.035. Therefore, the null hypothesis (τ 1 = τ 2 = τ 3 ) is rejected and the alternative hypothesis (τ 1 ≤ τ 2 ≤ τ 3 , with at least strict inequality) is accepted under α = 0.05.

Nonparametric tests and parametric tests: which should we use?

As there is more than one treatment modality for a disease, there is also more than one method of statistical analysis. Nonparametric analysis methods are clearly the correct choice when the assumption of normality is clearly violated; however, they are not always the top choice for cases with small sample sizes because they have less statistical power compared to parametric techniques and difficulties in calculating the "95% confidence interval," which assists the understanding of the readers. Parametric methods may lead to significant results in some cases, while nonparametric methods may result in more significant results in other cases. Whatever methods can be selected to support the researcher's arguments most powerfully and to help the reader's easy understandings, when parametric methods are selected, researchers should ensure that the required assumptions are all satisfied. If this is not the case, it is more valid to use nonparametric methods because they are "always valid, but not always efficient," while parametric methods are "always efficient, but not always valid".

LEARN STATISTICS EASILY

Learn Data Analysis Now!

Non-Parametric Statistics: A Comprehensive Guide

Exploring the Versatile World of Non-Parametric Statistics: Mastering Flexible Data Analysis Techniques.

Introduction

Non-parametric statistics  serve as a critical toolset in data analysis. They are known for their adaptability and the capacity to provide valid results without the stringent prerequisites demanded by parametric counterparts. This article delves into the fundamentals of non-parametric techniques, shedding light on their operational mechanisms, advantages, and scenarios of optimal application. By equipping readers with a solid grasp of  non-parametric statistics , we aim to enhance their analytical capabilities, enabling the effective handling of diverse datasets, especially those that challenge conventional parametric assumptions. Through a precise, technical exposition, this guide seeks to elevate the reader’s proficiency in applying non-parametric methods to extract meaningful insights from data, irrespective of its distribution or scale.

• Non-parametric statistics bypass assumptions for true data integrity.
• Flexible methods in non-parametric statistics reveal hidden data patterns.
• Real-world applications of non-parametric statistics solve complex issues.
• Non-parametric techniques like Mann-Whitney U bring clarity to data.
• Ethical data analysis through non-parametric statistics upholds truth.

Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

Understanding Non-Parametric Statistics

Non-parametric statistics  are indispensable in data analysis, mainly due to their capacity to process data without the necessity for predefined distribution assumptions. This distinct attribute sets non-parametric methods apart from parametric ones, which mandate that data adhere to certain distribution norms, such as the normal distribution. The utility of non-parametric techniques becomes especially pronounced with datasets where the distribution is either unknown, non-normal, or insufficient sample size to validate any distributional assumptions.

The cornerstone of  non-parametric statistics  is their reliance on the ranks or order of data points instead of the actual data values. This approach renders them inherently resilient to outliers and aptly suited for analyzing non-linear relationships within the data. Such versatility makes non-parametric methods applicable across diverse data types and research contexts, including situations involving ordinal data or instances where scale measurements are infeasible.

By circumventing the assumption of a specific underlying distribution, non-parametric methods facilitate a more authentic data analysis, capturing its intrinsic structure and characteristics. This capability allows researchers to derive conclusions that are more aligned with the actual nature of their data, which is particularly beneficial in disciplines where data may not conform to the conventional assumptions underpinning parametric tests.

Non-Parametric Statistics Flexibility

The core advantage of Non-Parametric Statistics lies in its inherent flexibility, which is crucial for analyzing data that doesn’t conform to the assumptions required by traditional parametric methods. This flexibility stems from the ability of non-parametric techniques to make fewer assumptions about the data distribution, allowing for a broader application across various types of data structures and distributions.

For instance, non-parametric methods do not assume a specific underlying distribution (such as normal distribution), making them particularly useful for skewed, outliers, or ordinal data. This is a significant technical benefit when dealing with real-world data, often deviating from idealized statistical assumptions.

Moreover, non-parametric statistics are adept at handling small sample sizes where the central limit theorem might not apply, and parametric tests could be unreliable. This makes them invaluable in fields where large samples are difficult to obtain, such as in rare disease research or highly specialized scientific studies.

Another technical aspect of non-parametric methods is their use in hypothesis testing, particularly with the Wilcoxon Signed-Rank Test for paired data and the Mann-Whitney U Test for independent samples. These tests are robust alternatives to the t-test when the data does not meet the necessary parametric assumptions, providing a means to conduct meaningful statistical analysis without the stringent requirements of normality and homoscedasticity.

The flexibility of non-parametric methods extends to their application in correlation analysis with Spearman’s rank correlation and in estimating distribution functions with the Kaplan-Meier estimator, among others. These tools are indispensable in fields ranging from medical research to environmental studies, where the nature of the data and the research questions do not fit neatly into parametric frameworks.

Techniques and Methods

In  non-parametric statistics , several essential techniques and methods stand out for their utility and versatility across various types of data analysis. This section delves into six standard non-parametric tests, providing a technical overview of each method and its application.

Mann-Whitney U Test : Often employed as an alternative to the t-test for independent samples, the Mann-Whitney U test is pivotal when comparing two independent groups. It assesses whether their distributions differ significantly, relying not on the actual data values but on the ranks of these values. This test is instrumental when the data doesn’t meet the normality assumption required by parametric tests.

Wilcoxon Signed-Rank Test : This test is a non-parametric alternative to the paired t-test, used when assessing the differences between two related samples, matched samples, or repeated measurements on a single sample. The Wilcoxon test evaluates whether the median differences between pairs of observations are zero. It is ideal for the paired differences that do not follow a normal distribution.

Kruskal-Wallis Test : As the non-parametric counterpart to the one-way ANOVA, the Kruskal-Wallis test extends the Mann-Whitney U test to more than two independent groups. It evaluates whether the populations from which the samples are drawn have identical distributions. Like the Mann-Whitney U, it bases its analysis on the rank of the data, making it suitable for data that does not follow a normal distribution.

Friedman Test : Analogous to the repeated measures ANOVA in parametric statistics, the Friedman test is a non-parametric method for detecting differences in treatments across multiple test attempts. It is beneficial for analyzing data from experiments where measurements are taken from the same subjects under different conditions, allowing for assessing the effects of other treatments on a single sample population.

Spearman’s Rank Correlation : Spearman’s rank correlation coefficient offers a non-parametric measure of the strength and direction of association between two variables. It is especially applicable in scenarios where the variables are measured on an ordinal scale or when the relationship between variables is not linear. This method emphasizes the monotonic relationship between variables, providing insights into the data’s behavior beyond linear correlations.

Kendall’s Tau : Kendall’s Tau is a correlation measure designed to assess the association between two measured quantities. It determines the strength and direction of the relationship, much like Spearman’s rank correlation, but focuses on the concordance and discordance between data points. Kendall’s Tau is particularly useful for data that involves ordinal or ranked variables, providing insight into the monotonic relationship without assuming linearity.

Chi-square Test:  The Chi-square test is a non-parametric statistical tool used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories. It is beneficial in categorical data analysis, where the variables are nominal or ordinal, and the data are in the form of frequencies or counts. This test is valuable when evaluating hypotheses on the independence of two variables or the goodness of fit for a particular distribution.

Non-Parametric Statistics Real-World Applications

The practical utility of  Non-Parametric Statistics  is vast and varied, spanning numerous fields and research disciplines. This section showcases real-world case studies and examples where non-parametric methods have provided insightful solutions to complex problems, highlighting the depth and versatility of these techniques.

Environmental Science : In a study examining the impact of industrial pollution on river water quality, researchers employed the Kruskal-Wallis test to compare the pH levels across multiple sites. This non-parametric method was chosen due to the non-normal distribution of pH levels and the presence of outliers caused by sporadic pollution events. The test revealed significant differences in water quality, guiding policymakers in identifying pollution hotspots.

Medical Research : In a longitudinal study on chronic pain management, the Wilcoxon Signed-Rank Test was employed to assess the effectiveness of a novel therapy compared to conventional treatment. Each patient underwent both treatments in different periods, with pain scores recorded on an ordinal scale before and after each treatment phase. Given the non-normal distribution of differences in pain scores before and after each treatment for the same patient, the Wilcoxon test facilitated a statistically robust analysis. It revealed a significant reduction in pain intensity with the new therapy compared to conventional treatment, thereby demonstrating its superior efficacy in a manner that was both robust and suited to the paired nature of the data.

Market Research : A market research firm used Spearman’s Rank Correlation to analyze survey data to understand customer satisfaction across various service sectors. The ordinal ranking of satisfaction levels and the non-linear relationship between service features and customer satisfaction made Spearman’s correlation an ideal choice, uncovering critical drivers of customer loyalty.

Education : In educational research, the Friedman test was utilized to assess the effectiveness of different teaching methods on student performance over time. With data collected from the same group of students under three distinct teaching conditions, the test provided insights into which method led to significant improvements, informing curriculum development.

Social Sciences : Kendall’s Tau was applied in a sociological study to examine the relationship between social media usage and community engagement among youths. Given the ordinal data and the interest in understanding the direction and strength of the association without assuming linearity, Kendall’s Tau offered nuanced insights, revealing a weak but significant negative correlation.

Non-Parametric Statistics Implementation in R

Implementing non-parametric statistical methods in R involves a systematic approach to ensure accurate and ethical analysis. This step-by-step guide will walk you through the process, from data preparation to result interpretation, while emphasizing the importance of data integrity and ethical considerations.

1. Data Preparation:

• Begin by importing your dataset into R using functions like read.csv() for CSV files or read.table() for tab-delimited data.
• Perform initial data exploration using functions like summary(), str(), and head() to understand your data’s structure, variables, and any apparent issues like missing values or outliers.

2. Choosing the Right Test:

• Determine the appropriate non-parametric test based on your data type and research question. For two independent samples, consider the Mann-Whitney U test (wilcox.test() function); for paired samples, use the Wilcoxon Signed-Rank test (wilcox.test() with paired = TRUE); for more than two independent groups, use the Kruskal-Wallis test (kruskal.test()); and for correlation analysis, use Spearman’s rank correlation (cor.test() with method = “spearman”).

3. Executing the Test:

• Execute the chosen test using its corresponding function. Ensure your data meets the test’s requirements, such as correctly ranked or categorized.
• For example, to run a Mann-Whitney U test, use wilcox.test(group1, group2), replacing group1 and group2 with your actual data vectors.

4. Result Interpretation:

• Carefully interpret the output, paying attention to the test statistic and p-value. A p-value less than your significance level (commonly 0.05) indicates a statistically significant difference or correlation.
• Consider the effect size and confidence intervals to assess the practical significance of your findings.

5. Data Integrity and Ethical Considerations:

• Ensure data integrity by double-checking data entry, handling missing values appropriately, and conducting outlier analysis.
• Maintain ethical standards by respecting participant confidentiality, obtaining necessary permissions for data use, and reporting findings honestly without data manipulation.

6. Reporting:

• When documenting your analysis, include a detailed methodology section that outlines the non-parametric tests used, reasons for their selection, and any data preprocessing steps.
• Present your results using visual aids like plots or tables where applicable, and discuss the implications of your findings in the context of your research question.

Throughout this article, we have underscored the significance and value of  non-parametric statistics  in data analysis. These methods enable us to approach data sets with unknown or non-normal distributions, providing genuine insights and unveiling the truth and beauty hidden within the data. We encourage readers to maintain an  open mind  and a steadfast commitment to uncovering authentic insights when applying statistical methods to their research and projects. We invite you to explore the potential of  non-parametric statistics  in your endeavors and to share your findings with the scientific and academic community, contributing to the collective enrichment of knowledge and the advancement of science.

Recommended Articles

Discover more about the transformative power of data analysis in our collection of articles. Dive deeper into the world of statistics with our curated content and join our community of truth-seeking analysts.

• Understanding the Assumptions for Chi-Square Test of Independence
• What is the difference between t-test and Mann-Whitney test?
• Mastering the Mann-Whitney U Test: A Comprehensive Guide
• A Comprehensive Guide to Hypotheses Tests in Statistics
• A Guide to Hypotheses Tests

Frequently Asked Questions (FAQs)

Q1: What Are Non-Parametric Statistics?  Non-parametric statistics are methods that don’t rely on data from specific distributions. They are used when data doesn’t meet the assumptions of parametric tests.

Q2: Why Choose Non-Parametric Methods?  They offer flexibility in analyzing data with unknown distributions or small sample sizes, providing a more ethical approach to data analysis.

Q3: What Is the Mann-Whitney U Test?  It’s a non-parametric test for assessing whether two independent samples come from the same distribution, especially useful when data doesn’t meet normality assumptions.

Q4: How Do Non-Parametric Methods Enhance Data Integrity?  By not imposing strict assumptions on data, non-parametric methods respect the natural form of data, leading to more truthful insights.

Q5: Can Non-Parametric Statistics Handle Outliers?  Yes, non-parametric statistics are less sensitive to outliers, making them suitable for datasets with extreme values.

Q6: What Is the Kruskal-Wallis Test?  This test is a non-parametric method for comparing more than two independent samples, proper when the ANOVA assumptions are not met.

Q7: How Does Spearman’s Rank Correlation Work?  Spearman’s rank correlation measures the strength and direction of association between two ranked variables, ideal for non-linear relationships.

Q8: What Are the Real-World Applications of Non-Parametric Statistics?  They are widely used in fields like environmental science, education, and medicine, where data may not follow standard distributions.

Q9: What Are the Benefits of Using Non-Parametric Statistics in Data Analysis?  They provide a more inclusive data analysis, accommodating various data types and distributions and revealing deeper insights.

Q10: How to Get Started with Non-Parametric Statistical Analysis?  Begin by understanding the nature of your data and choosing appropriate non-parametric methods that align with your analysis goals.

Similar Posts

Pearson Correlation Coefficient Statistical Guide

Master the Pearson Correlation Coefficient with our statistical guide. Discover how to measure and interpret linear relationships.

Florence Nightingale: How Data Visualization in the Form of Pie Charts Saved Lives

Discover how Florence Nightingale used data visualization and pie charts to revolutionize healthcare during the Crimean War.

Outlier Detection and Treatment: A Comprehensive Guide

Master Outlier Detection and Treatment to enhance your data analysis skills. A definitive guide for data scientists seeking accuracy.

How Statistical Fallacies Influenced the Perception of the Mozart Effect

Explore the influence of statistical fallacies on the Mozart Effect in education. Discover more insights on our blog!

A Comprehensive Guide to Levels of Measurement in Data Analysis

Dive deep into the foundations of data analysis, exploring the four fundamental levels of measurement: nominal, ordinal, interval, and ratio scales.

How to Create Regression Lines in Excel

Master the art of creating Regression Lines in Excel with our guide. Discover step-by-step instructions for powerful data analysis.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Section 9.1: Nonparametric Definitions

Learning Objectives

At the end of this section you should be able to answer the following questions:

• How would you define non-parametric methods?
• What types of assumptions are made for non-parametric methods?

Non-Parametric Methods

What can be done when the assumptions we have discussed in past lessons (t-tests, correlation etc.) are not maintained? There are tests used when a number of assumptions are not maintained for regular tests like t-tests or correlations (e.g. nonnormal distribution or small sample sizes). These tests – called non-parametric tests – use the same type of comparisons but with different assumptions.

Parametric Assumptions

Parametric statistics is a branch of statistics that assumes that sample data comes from a population that follows parameters and assumptions that hold true in most, in not all, cases. Most well-known elementary statistical methods are parametric, many of which we have discussed on this webpage.

Parametric Assumptions and the Normal Distribution

Normal distribution is a common assumption for many tests, including t-tests, ANOVAs and regression. Recall that parametric tests we have discussed here met the following assumptions of the normal distribution: minimal or no skewness and kurtosis of variables and error terms are independent across variables.

These assumptions allow us to infer a normal distribution in the population.

Statistical methods which do not require us to make distributional assumptions about the data are called non-parametric methods. Non-parametric, as a term, actually does not apply to the data, but to the method used to analyse the data. These tests use rankings to analyse differences. Non-parametric methods can be used for different types of comparisons or models

Nonparametric Assumptions

• Nonparametric tests make assumptions about sampling (that it is generally random).
• There are assumptions about the independence or dependence of samples, depending on which nonparametric test is used, there are no assumptions about the population distribution of scores.

Nonparametric Tests and Level of Measurement

Variables at particular categorical levels of measurement may require Nonparametric Tests

Consider variables like autonomy, skill, income. Would such variables always follow a normal distribution? It is possible that when looking at income, you would expect the data to be skewed, as there are a small minority of the population who earn extremely high salaries.

Mean vs Median

When a distribution is highly skewed, the mean is affected by the high number of relative outliers. For example, when measuring something like income, where there are few high-income earners but many middle and low-income earners, the center of the distribution is quite skewed. This means that the median (i.e., the middle amount with 50% above and below this amount) is best used.

Sample Size

Sample size is another consideration when deciding if one should use a parametric or nonparametric test. Often, researchers will want to run a certain type of parametric test, but might not have the recommended minimum number of participants. Additionally, if the sample is very small, tests of normality often cannot be run. This is due to the lack of power needed to provide an interpretable result. When this is coupled with non-normal distributions of data, researchers might decide to use nonparametric tests.

As discussed in previous chapters, parametric tests can only use continuous data for the dependant variable. This data should be normally distributed and not have any spurious outliers. However, some nonparametric tests can use data that is ordinal, or ranked for the dependant variable. These tests may also not be impacted severely by non-normal data or outliers. Each parametric test has its own requirements, so it is advisable to check the assumptions for each test.

Statistics for Research Students Copyright © 2022 by University of Southern Queensland is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Parametric vs. Non-Parametric Tests and When to Use Them

The fundamentals of data science include computer science, statistics and math. It’s very easy to get caught up in the latest and greatest, most powerful algorithms —  convolutional neural nets, reinforcement learning, etc.

As an ML/health researcher and algorithm developer, I often employ these techniques. However, something I have seen rife in the data science community after having trained ~10 years as an electrical engineer is that if all you have is a hammer, everything looks like a nail. Suffice it to say that while many of these exciting algorithms have immense applicability, too often the statistical underpinnings of the data science community are overlooked. 

What is the Difference Between Parametric and Non-Parametric Tests?

A parametric test makes assumptions about a population’s parameters, and a non-parametric test does not assume anything about the underlying distribution.

I’ve been lucky enough to have had both undergraduate and graduate courses dedicated solely to statistics , in addition to growing up with a statistician for a mother. So this article will share some basic statistical tests and when/where to use them.

A parametric test makes assumptions about a population’s parameters:

• Normality  : Data in each group should be normally distributed.
• Independence  : Data in each group should be sampled randomly and independently.
• No outliers  : No extreme outliers in the data.
• Equal Variance  : Data in each group should have approximately equal variance.

If possible, we should use a parametric test. However, a non-parametric test (sometimes referred to as a distribution free test ) does not assume anything about the underlying distribution (for example, that the data comes from a normal (parametric distribution).

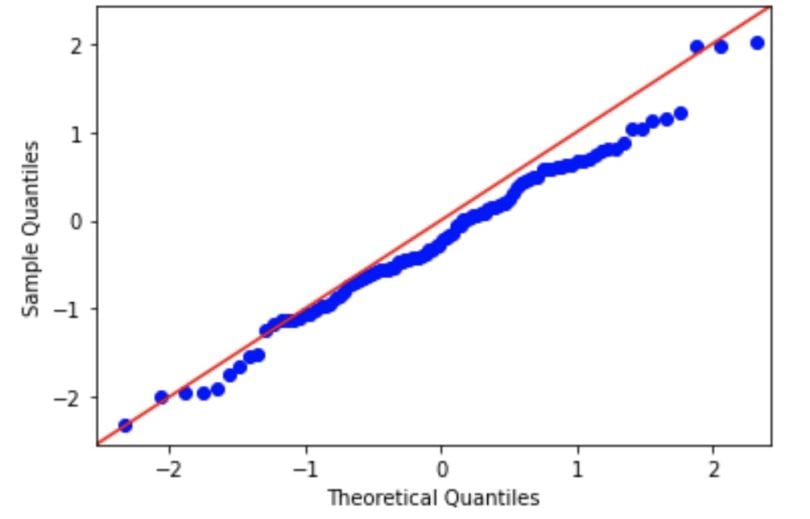
We can assess normality visually using a Q-Q (quantile-quantile) plot. In these plots, the observed data is plotted against the expected quantile of a normal distribution . A demo code in Python is seen here, where a random normal distribution has been created. If the data are normal, it will appear as a straight line.

Read more about data science Random Forest Classifier: A Complete Guide to How It Works in Machine Learning

Tests to Check for Normality

• Shapiro-Wilk
• Kolmogorov-Smirnov

The null hypothesis of both of these tests is that the sample was sampled from a normal (or Gaussian) distribution. Therefore, if the p-value is significant, then the assumption of normality has been violated and the alternate hypothesis that the data must be non-normal is accepted as true.

Selecting the Right Test

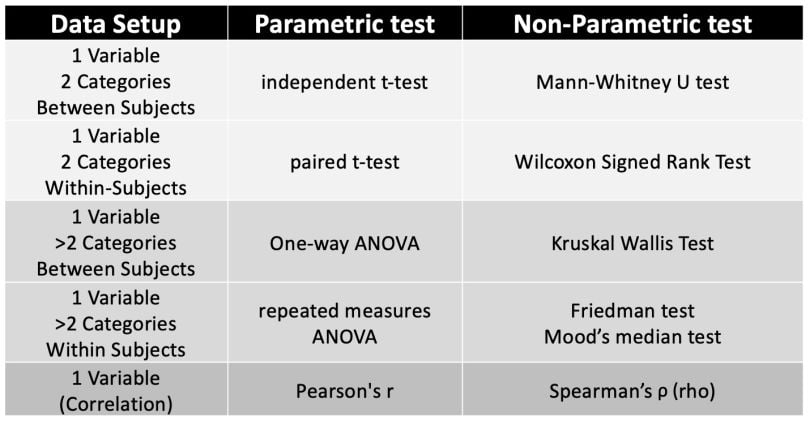
You can refer to this table when dealing with interval level data for parametric and non-parametric tests.

Read more about data science Statistical Tests: When to Use T-Test, Chi-Square and More

Advantages and Disadvantages

Non-parametric tests have several advantages, including:

• More statistical power when assumptions of parametric tests are violated.
• Assumption of normality does not apply.
• Small sample sizes are okay.
• They can be used for all data types, including ordinal, nominal and interval (continuous).
• Can be used with data that has outliers.

Disadvantages of non-parametric tests:

• Less powerful than parametric tests if assumptions haven’t been violated

[1] Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences , Wiley.

[2] Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics , Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

[3] Rumsey, D. J. (2003). Statistics for dummies, 18th edition  

Built In’s expert contributor network publishes thoughtful, solutions-oriented stories written by innovative tech professionals. It is the tech industry’s definitive destination for sharing compelling, first-person accounts of problem-solving on the road to innovation.

Great Companies Need Great People. That's Where We Come In.

• Search Search Please fill out this field.
• Corporate Finance
• Financial Analysis

Nonparametric Statistics: Overview, Types, and Examples

Investopedia / Zoe Hansen

What Are Nonparametric Statistics?

Nonparametric statistics refers to a statistical method in which the data are not assumed to come from prescribed models that are determined by a small number of parameters; examples of such models include the normal distribution model and the linear regression model. Nonparametric statistics sometimes uses data that is ordinal, meaning it does not rely on numbers, but rather on a ranking or order of sorts. For example, a survey conveying consumer preferences ranging from like to dislike would be considered ordinal data.

Nonparametric statistics includes nonparametric descriptive statistics , statistical models, inference, and statistical tests. The model structure of nonparametric models is not specified a priori but is instead determined from data. The term nonparametric is not meant to imply that such models completely lack parameters, but rather that the number and nature of the parameters are flexible and not fixed in advance. A histogram is an example of a nonparametric estimate of a probability distribution.

Key Takeaways

• Nonparametric statistics are easy to use but do not offer the pinpoint accuracy of other statistical models.
• This type of analysis is often best suited when considering the order of something, where even if the numerical data changes, the results will likely stay the same.

Understanding Nonparametric Statistics

In statistics, parametric statistics includes parameters such as the mean, standard deviation, Pearson correlation, variance, etc. This form of statistics uses the observed data to estimate the parameters of the distribution. Under parametric statistics, data are often assumed to come from a normal distribution with unknown parameters μ (population mean) and σ2 (population variance), which are then estimated using the sample mean and sample variance.

Nonparametric statistics makes no assumption about the sample size or whether the observed data is quantitative.

Nonparametric statistics does not assume that data is drawn from a normal distribution. Instead, the shape of the distribution is estimated under this form of statistical measurement. While there are many situations in which a normal distribution can be assumed, there are also some scenarios in which the true data generating process is far from normally distributed.

Examples of Nonparametric Statistics

In the first example, consider a financial analyst who wishes to estimate the value-at-risk (VaR) of an investment. The analyst gathers earnings data from 100’s of similar investments over a similar time horizon. Rather than assume that the earnings follow a normal distribution, they use the histogram to estimate the distribution nonparametrically. The 5th percentile of this histogram then provides the analyst with a nonparametric estimate of VaR.

For a second example, consider a different researcher who wants to know whether average hours of sleep is linked to how frequently one falls ill. Because many people get sick rarely, if at all, and occasional others get sick far more often than most others, the distribution of illness frequency is clearly non-normal, being right-skewed and outlier-prone. Thus, rather than use a method that assumes a normal distribution for illness frequency, as is done in classical regression analysis, for example, the researcher decides to use a nonparametric method such as quantile regression analysis.

Special Considerations

Nonparametric statistics have gained appreciation due to their ease of use. As the need for parameters is relieved, the data becomes more applicable to a larger variety of tests. This type of statistics can be used without the mean, sample size, standard deviation, or the estimation of any other related parameters when none of that information is available.

Since nonparametric statistics makes fewer assumptions about the sample data, its application is wider in scope than parametric statistics. In cases where parametric testing is more appropriate, nonparametric methods will be less efficient. This is because nonparametric statistics discard some information that is available in the data, unlike parametric statistics.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Non-parametric Tests for Psychological Data

• First Online: 28 August 2019

Cite this chapter

• J. P. Verma 2  

2233 Accesses

2 Citations

In most of the psychological studies, data that is generated is non-metric; hence, it is essential to know various non-parametric tests that are available for different situations. Non-parametric tests are used for non-metric data, but if assumptions of the parametric tests are violated, these tests can be used for addressing research questions. Several non-parametric tests are available as a substitute for many parametric tests. For example, chi-square test is an option for correlation coefficient; sign test and median/Mann–Whitney U tests are the options for one-sample t-test and two-sample t-test, respectively; Kruskal–Wallis H test is an option for one-way ANOVA; and Friedman’s test is an option for one-way repeated measures ANOVA. The procedure of these tests has been discussed in this chapter by means of examples. After going through this chapter, one should be able to apply chi-square test, runs test, sign test, median test, Mann–Whitney test, Kruskal–Wallis H test, and Friedman’s test.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Parametric Tests

Writing about Non-parametric Tests

Author information

Authors and affiliations.

Department of Sport Psychology, Lakshmibai National Institute of Physical Education, Gwalior, India

Prof. J. P. Verma

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to J. P. Verma .

Rights and permissions

Reprints and permissions

Copyright information

© 2019 Springer Nature Singapore Pte Ltd.

About this chapter

Verma, J.P. (2019). Non-parametric Tests for Psychological Data. In: Statistics and Research Methods in Psychology with Excel. Springer, Singapore. https://doi.org/10.1007/978-981-13-3429-0_12

Download citation

DOI : https://doi.org/10.1007/978-981-13-3429-0_12

Published : 28 August 2019

Publisher Name : Springer, Singapore

Print ISBN : 978-981-13-3428-3

Online ISBN : 978-981-13-3429-0

eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• > Statistics

Non-Parametric Statistics: Types, Tests, and Examples

• Pragya Soni
• May 12, 2022

Statistics, an essential element of data management and predictive analysis , is classified into two types, parametric and non-parametric. 

Parametric tests are based on the assumptions related to the population or data sources while, non-parametric test is not into assumptions, it's more factual than the parametric tests. Here is a detailed blog about non-parametric statistics.

What is the Meaning of Non-Parametric Statistics ?

Unlike, parametric statistics, non-parametric statistics is a branch of statistics that is not solely based on the parametrized families of assumptions and probability distribution. Non-parametric statistics depend on either being distribution free or having specified distribution, without keeping any parameters into consideration.

Non-parametric statistics are defined by non-parametric tests; these are the experiments that do not require any sample population for assumptions. For this reason, non-parametric tests are also known as distribution free tests as they don’t rely on data related to any particular parametric group of probability distributions.

In other terms, non-parametric statistics is a statistical method where a particular data is not required to fit in a normal distribution. Usually, non-parametric statistics used the ordinal data that doesn’t rely on the numbers, but rather a ranking or order. For consideration, statistical tests, inferences, statistical models, and descriptive statistics.

Non-parametric statistics is thus defined as a statistical method where data doesn’t come from a prescribed model that is determined by a small number of parameters. Unlike normal distribution model,  factorial design and regression modeling, non-parametric statistics is a whole different content.

Unlike parametric models, non-parametric is quite easy to use but it doesn’t offer the exact accuracy like the other statistical models. Therefore, non-parametric statistics is generally preferred for the studies where a net change in input has minute or no effect on the output. Like even if the numerical data changes, the results are likely to stay the same.

Also Read | What is Regression Testing?

How does Non-Parametric Statistics Work ?

Parametric statistics consists of the parameters like mean,  standard deviation , variance, etc. Thus, it uses the observed data to estimate the parameters of the distribution. Data are often assumed to come from a normal distribution with unknown parameters.

While, non-parametric statistics doesn’t assume the fact that the data is taken from a same or normal distribution. In fact, non-parametric statistics assume that the data is estimated under a different measurement. The actual data generating process is quite far from the normally distributed process.

Types of Non-Parametric Statistics

Non-parametric statistics are further classified into two major categories. Here is the brief introduction to both of them:

1. Descriptive Statistics

Descriptive statistics is a type of non-parametric statistics. It represents the entire population or a sample of a population. It breaks down the measure of central tendency and central variability.

2. Statistical Inference

Statistical inference is defined as the process through which inferences about the sample population is made according to the certain statistics calculated from the sample drawn through that population.

Some Examples of Non-Parametric Tests

In the recent research years, non-parametric data has gained appreciation due to their ease of use. Also, non-parametric statistics is applicable to a huge variety of data despite its mean, sample size, or other variation. As non-parametric statistics use fewer assumptions, it has wider scope than parametric statistics.

Here are some common  examples of non-parametric statistics :

Consider the case of a financial analyst who wants to estimate the value of risk of an investment. Now, rather than making the assumption that earnings follow a normal distribution, the analyst uses a histogram to estimate the distribution by applying non-parametric statistics.

Consider another case of a researcher who is researching to find out a relation between the sleep cycle and healthy state in human beings. Taking parametric statistics here will make the process quite complicated. 

So, despite using a method that assumes a normal distribution for illness frequency. The researcher will opt to use any non-parametric method like quantile regression analysis.

Similarly, consider the case of another health researcher, who wants to estimate the number of babies born underweight in India, he will also employ the non-parametric measurement for data testing.

A marketer that is interested in knowing the market growth or success of a company, will surely employ a non-statistical approach.

Any researcher that is testing the market to check the consumer preferences for a product will also employ a non-statistical data test. As different parameters in nutritional value of the product like agree, disagree, strongly agree and slightly agree will make the parametric application hard.

Any other science or social science research which include nominal variables such as age, gender, marital data, employment, or educational qualification is also called as non-parametric statistics. It plays an important role when the source data lacks clear numerical interpretation.

Also Read | Applications of Statistical Techniques

What are Non-Parametric Tests ?

Types of Non-Parametric Tests

  Here is the list of non-parametric tests that are conducted on the population for the purpose of statistics tests :

Wilcoxon Rank Sum Test

The Wilcoxon test also known as rank sum test or signed rank test. It is a type of non-parametric test that works on two paired groups. The main focus of this test is comparison between two paired groups. The test helps in calculating the difference between each set of pairs and analyses the differences.

The Wilcoxon test is classified as a statistical  hypothesis tes t and is used to compare two related samples, matched samples, or repeated measurements on a single sample to assess whether their population mean rank is different or not.

Mann- Whitney U Test

The Mann-Whitney U test also known as the Mann-Whitney-Wilcoxon test, Wilcoxon rank sum test and Wilcoxon-Mann-Whitney test. It is a non-parametric test based on null hypothesis. It is equally likely that a randomly selected sample from one sample may have higher value than the other selected sample or maybe less.

Mann-Whitney test is usually used to compare the characteristics between two independent groups when the dependent variable is either ordinal or continuous. But these variables shouldn’t be normally distributed. For a Mann-Whitney test, four requirements are must to meet. The first three are related to study designs and the fourth one reflects the nature of data.

Kruskal Wallis Test

Sometimes referred to as a one way ANOVA on ranks, Kruskal Wallis H test is a nonparametric test that is used to determine the statistical differences between the two or more groups of an independent variable. The word ANOVA is expanded as Analysis of variance.

The test is named after the scientists who discovered it, William Kruskal and W. Allen Wallis. The major purpose of the test is to check if the sample is tested if the sample is taken from the same population or not.

Friedman Test

The Friedman test is similar to the Kruskal Wallis test. It is an alternative to the ANOVA test. The only difference between Friedman test and ANOVA test is that Friedman test works on repeated measures basis. Friedman test is used for creating differences between two groups when the dependent variable is measured in the ordinal.

The Friedman test is further divided into two parts, Friedman 1 test and Friedman 2 test. It was developed by sir Milton Friedman and hence is named after him. The test is even applicable to complete block designs and thus is also known as a special case of Durbin test.

Distribution Free Tests

Distribution free tests are defined as the mathematical procedures. These tests are widely used for testing statistical hypotheses. It makes no assumption about the probability distribution of the variables. An important list of distribution free tests is as follows:

•  Anderson-Darling test: It is done to check if the sample is drawn from a given distribution or not.
• Statistical bootstrap methods: It is a basic non-statistical test used to estimate the accuracy and sampling distribution of a statistic.
• Cochran’s Q: Cochran’s Q is used to check constant treatments in block designs with 0/1 outcomes.
• Cohen’s kappa: Cohen kappa is used to measure the inter-rater agreement for categorical items.
• Kaplan-Meier test: Kaplan Meier test helps in estimating the survival function from lifetime data, modeling, and censoring.
• Two-way analysis Friedman test: Also known as ranking test, it is used to randomize different block designs.
• Kendall’s tau: The test helps in defining the statistical dependency between two different variables.
• Kolmogorov-Smirnov test: The test draws the inference if a sample is taken from the same distribution or if two or more samples are taken from the same sample.
• Kendall’s W: The test is used to measure the inference of an inter-rater agreement .
• Kuiper’s test: The test is done to determine if the sample drawn from a given distribution is sensitive to cyclic variations or not.
• Log Rank test: This test compares the survival distribution of two right-skewed and censored samples.
• McNemar’s test: It tests the contingency in the sample and revert when the row and column marginal frequencies are equal to or not.
• Median tests: As the name suggests, median tests check if the two samples drawn from the similar population have similar median values or not.
• Pitman’s permutation test: It is a statistical test that yields the value of p variables. This is done by examining all possible rearrangements of labels.
• Rank products: Rank products are used to detect expressed genes in replicated microarray experiments.
• Siegel Tukey tests: This test is used for differences in scale between two groups.
• Sign test: Sign test is used to test whether matched pair samples are drawn from distributions from equal medians.
• Spearman’s rank: It is used to measure the statistical dependence between two variables using a monotonic function.
• Squared ranks test: Squared rank test helps in testing the equality of variances between two or more variables.
• Wald-Wolfowitz runs a test: This test is done to check if the elements of the sequence are mutually independent or random.

Also Read | Factor Analysis

Advantages and Disadvantages of Non-Parametric Tests

The benefits of non-parametric tests are as follows:

It is easy to understand and apply.

It consists of short calculations.

The assumption of the population is not required.

Non-parametric test is applicable to all data kinds

The limitations of non-parametric tests are:

It is less efficient than parametric tests.

Sometimes the result of non-parametric data is insufficient to provide an accurate answer.

Applications of Non-Parametric Tests

Non-parametric tests are quite helpful, in the cases :

Where parametric tests are not giving sufficient results.

When the testing hypothesis is not based on the sample.

For the quicker analysis of the sample.

When the data is unscaled.

The current scenario of research is based on fluctuating inputs, thus, non-parametric statistics and tests become essential for in-depth research and data analysis .

Share Blog :

Be a part of our Instagram community

Trending blogs

5 Factors Influencing Consumer Behavior

Elasticity of Demand and its Types

What is PESTLE Analysis? Everything you need to know about it

An Overview of Descriptive Analysis

What is Managerial Economics? Definition, Types, Nature, Principles, and Scope

5 Factors Affecting the Price Elasticity of Demand (PED)

6 Major Branches of Artificial Intelligence (AI)

Scope of Managerial Economics

Dijkstra’s Algorithm: The Shortest Path Algorithm

Different Types of Research Methods

Latest Comments

brenwright30

THIS IS HOW YOU CAN RECOVER YOUR LOST CRYPTO? Are you a victim of Investment, BTC, Forex, NFT, Credit card, etc Scam? Do you want to investigate a cheating spouse? Do you desire credit repair (all bureaus)? Contact Hacker Steve (Funds Recovery agent) asap to get started. He specializes in all cases of ethical hacking, cryptocurrency, fake investment schemes, recovery scam, credit repair, stolen account, etc. Stay safe out there! [email protected] https://hackersteve.great-site.net/

Non-Parametric Test

Non-parametric test is a statistical analysis method that does not assume the population data belongs to some prescribed distribution which is determined by some parameters. Due to this, a non-parametric test is also known as a distribution-free test. These tests are usually based on distributions that have unspecified parameters.

A non-parametric test acts as an alternative to a parametric test for mathematical models where the nature of parameters is flexible. Usually, when the assumptions of parametric tests are violated then non-parametric tests are used. In this article, we will learn more about a non-parametric test, the types, examples, advantages, and disadvantages.

What is Non-Parametric Test in Statistics?

A non-parametric test in statistics does not assume that the data has been taken from a normal distribution . A normal distribution belongs to a parametrized family of probability distributions and includes parameters such as mean, variance, standard deviation, etc. Thus, a non-parametric test does not make assumptions about the probability distribution's parameters.

Non-Parametric Test Definition

A non-parametric test can be defined as a test that is used in statistical analysis when the data under consideration does not belong to a parametrized family of distributions. When the data does not meet the requirements to perform a parametric test, a non-parametric test is used to analyze it.

Reasons to Use Non-Parametric Tests

It is important to access when to apply parametric and non-parametric tests in order to arrive at the correct statistical inference. The reasons to use a non-parametric test are given below:

• When the distribution is skewed, a non-parametric test is used. For skewed distributions, the mean is not the best measure of central tendency, hence, parametric tests cannot be used.
• If the size of the data is too small then validating the distribution of the data becomes difficult. Thus, in such cases, a non-parametric test is used to analyze the data.
• If the data is nominal or ordinal, a non-parametric test is used. This is because a parametric test can only be used for continuous data.

Types of Non-Parametric Tests

Parametric tests are those that assume that the data follows a normal distribution. Examples include ANOVA and t-tests. There are many different methods available to perform a non-parametric test. These tests can also be used in hypothesis testing. Some common non-parametric tests are given as follows:

Mann-Whitney U Test

This non-parametric test is analogous to t-tests for independent samples. To conduct such a test the distribution must contain ordinal data. It is also known as the Wilcoxon rank sum test.

Null Hypothesis: \(H_{0}\): The two populations under consideration must be equal.

Test Statistic: U should be smaller of

\(U_{1} = n_{1}n_{2}+\frac{n_{1}(n_{1}+1)}{2}-R_{1}\) or \(U_{2} = n_{1}n_{2}+\frac{n_{2}(n_{2}+1)}{2}-R_{2}\)

where, \(R_{1}\) is the sum of ranks in group 1 and \(R_{2}\) is the sum of ranks in group 2.

Decision Criteria: Reject the null hypothesis if U < critical value.

Wilcoxon Signed Rank Test

This is the non-parametric test whose counterpart is the parametric paired t-test . It is used to compare two samples that contain ordinal data and are dependent. The Wilcoxon signed rank test assumes that the data comes from a symmetric distribution.

Null Hypothesis: \(H_{0}\): The difference in the median is 0.

Test Statistic: W. W is defined as the smaller of the sums of the negative and positive ranks.

Decision Criteria: Reject the null hypothesis if W < critical value.

This non-parametric test is the parametric counterpart to the paired samples t-test. The sign test is similar to the Wilcoxon sign test.

Test Statistic: The smaller value among the number of positive and negative signs.

Decision Criteria: Reject the null hypothesis if the test statistic < critical value.

Kruskal Wallis Test

The parametric one-way ANOVA test is analogous to the non-parametric Kruskal Wallis test. It is used for comparing more than two groups of data that are independent and ordinal.

Null Hypothesis: \(H_{0}\): m population medians are equal

Test Statistic: H = \(\left ( \frac{12}{N(N+1)}\sum_{1}^{m} \frac{R_{j}^{2}}{n_{j}}\right ) - 3(N+1)\)

where, N = total sample size, \(n_{j}\) and \(R_{j}\) are the sample size and the sum of ranks of the j th group

Decision Criteria: Reject the null hypothesis if H > critical value

Non-Parametric Test Example

The best way to understand how to set up and solve a hypothesis involving a non-parametric test is by taking an example.

Suppose patients are suffering from cancer. They are divided into three groups and different drugs were administered. The platelet count for the patients is given in the table below. It needs to be checked if the population medians are equal. The significance level is 0.05.

As the size of the 3 groups is not same the Kruskal Wallis test is used.

\(H_{0}\): Population medians are same

\(H_{1}\): Population medians are different

\(n_{1}\) = 5, \(n_{2}\) = 3, \(n_{3}\) = 4

N = 5 + 3 + 4 = 12

Now ordering the groups and assigning ranks

\(R_{1}\) = 18.5, \(R_{2}\) = 21, \(R_{3}\) = 38.5,

Substituting these values in the test statistic formula, \(\left ( \frac{12}{N(N+1)}\sum_{1}^{m} \frac{R_{j}^{2}}{n_{j}}\right ) - 3(N+1)\)

H = 6.0778.

Using the critical value table, the critical value will be 5.656.

As H < critical value, the null hypothesis is rejected and it is concluded that there is no significant evidence to show that the population medians are equal.

Difference between Parametric and Non-Parametric Test

Depending upon the type of distribution that the data has been obtained from both, a parametric test and a non-parametric test can be used in hypothesis testing. The table given below outlines the main difference between parametric and non-parametric tests.

Advantages and Disadvantages of Non-Parametric Test

Non-parametric tests are used when the conditions for a parametric test are not satisfied. In some cases when the data does not match the required assumptions but has a large sample size then a parametric test can still be used. Some of the advantages and disadvantages of a non-parametric test are listed as follows:

Advantages of Non-Parametric Test

The advantages of a non-parametric test are listed as follows:

• Knowledge of the population distribution is not required.
• The calculations involved in such a test are shorter.
• A non-parametric test is easy to understand.
• These tests are applicable to all data types.

Disadvantages of Non-Parametric Test

The disadvantages of a non-parametric test are given below:

• They are not as efficient as their parametric counterparts.
• As these are distribution-free tests the level of accuracy is reduced.

Related Articles:

• Summary Statistics
• Probability and Statistics
• T-Distribution

Important Notes on Non-Parametric Test

• A non-parametric test is a statistical test that is performed on data belonging to a distribution whose parameters are unknown.
• It is used on skewed distributions and the measure of central tendency used is the median.
• Kruskal Wallis test, sign test, Wilcoxon signed test and the Mann Whitney u test are some important non-parametric tests used in hypothesis testing.

Examples on Non-Parametric Test

Example 1: A surprise quiz was taken and the scores of 6 students are given as follows:

After giving a month's time to practice, the same quiz was taken again and the following scores were obtained.

Assigning signed ranks to the differences

\(H_{0}\): Median difference is 0. \(H_{1}\): Median difference is positive. W1: Sum of positive ranks = 17.5 W2: Sum of negative ranks = 3.5 As W2 < W1, thus, W2 is the test statistic. Now from the table, the critical value is 2. Since W2 > 2, thus, the null hypothesis cannot be rejected and it can be concluded that there is no difference between the scores of the two tests. Answer: Fail to reject the null hypothesis

\(H_{0}\): Two groups report same number of cases \(H_{1}\): Two groups report different number of cases \(R_{1}\) = 15.5, \(R_{2}\) = 39.5 \(n_{1}\) = \(n_{2}\) = 5 Using the formulas, \(U_{1} = n_{1}n_{2}+\frac{n_{1}(n_{1}+1)}{2}-R_{1}\) and \(U_{2} = n_{1}n_{2}+\frac{n_{2}(n_{2}+1)}{2}-R_{2}\) \(U_{1}\) = 24.5, \(U_{2}\) = 0.5 As \(U_{2}\) < \(U_{1}\), thus, \(U_{2}\) is the test statistic. From the table the critical value is 2 As \(U_{2}\) < 2, the null hypothesis is rejected and it is concluded that there is no evidence to prove that the two groups have the same number of sleepwalking cases. Answer: Null hypothesis is rejected

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Non-Parametric Test

What is a non-parametric test.

A non-parametric test in statistics is a test that is performed on data belonging to a distribution that has flexible parameters. Thus, they are also known as distribution-free tests.

When Should a Non-Parametric Test be Used?

A non-parametric test should be used under the following conditions.

• The distribution is skewed.
• The size of the distribution is small.
• The data is nominal or ordinal.

What is the Test Statistic Used for the Mann-Whitney U Non-Parametric Test?

The Mann Whitney U non-parametric test is the non parametric version of the sample t-test. The test statistic used for hypothesis testing is U . U should be smaller of \(U_{1} = n_{1}n_{2}+\frac{n_{1}(n_{1}+1)}{2}-R_{1}\) or \(U_{2} = n_{1}n_{2}+\frac{n_{2}(n_{2}+1)}{2}-R_{2}\)

What is the Test Statistic Used for the Kruskal Wallis Non-Parametric Test?

The parametric counterpart of the Kruskal Wallis non parametric test is the one way ANOVA test. The test statistic used is H = \(\left ( \frac{12}{N(N+1)}\sum_{1}^{m} \frac{R_{j}^{2}}{n_{j}}\right ) - 3(N+1)\).

What is the Test Statistic Used for the Sign Non-Parametric Test?

The smaller value among the number of positive and negative signs is the test statistic that is used for the sign non-parametric test.

What is the Difference Between a Parametric and Non-Parametric Test?

A parametric test is conducted on data that is obtained from a parameterized distribution such as a normal distribution. On the other hand, a non-parametric test is conducted on a skewed distribution or when the parameters of the population distribution are not known.

What are the Advantages of a Non-Parametric Test?

A non-parametric test does not rely on the assumed parameters of a distribution and is applicable to all data types. Furthermore, they are easy to understand.

• Math Article
• Non Parametric Test

Non-Parametric Test

Non-parametric tests are experiments that do not require the underlying population for assumptions. It does not rely on any data referring to any particular parametric group of probability distributions . Non-parametric methods are also called distribution-free tests since they do not have any underlying population.  In this article, we will discuss what a non-parametric test is, different methods, merits, demerits and examples of non-parametric testing methods.

Table of Contents:

• Non-parametric T Test
• Non-parametric Paired T-Test

Mann Whitney U Test

Wilcoxon signed-rank test, kruskal wallis test.

• Advantages and Disadvantages
• Applications

What is a Non-parametric Test?

Non-parametric tests are the mathematical methods used in statistical hypothesis testing, which do not make assumptions about the frequency distribution of variables that are to be evaluated. The non-parametric experiment is used when there are skewed data, and it comprises techniques that do not depend on data pertaining to any particular distribution.

The word non-parametric does not mean that these models do not have any parameters. The fact is, the characteristics and number of parameters are pretty flexible and not predefined. Therefore, these models are called distribution-free models.

Non-Parametric T-Test

Whenever a few assumptions in the given population are uncertain, we use non-parametric tests, which are also considered parametric counterparts. When data are not distributed normally or when they are on an ordinal level of measurement, we have to use non-parametric tests for analysis. The basic rule is to use a parametric t-test for normally distributed data and a non-parametric test for skewed data.

Non-Parametric Paired T-Test

The paired sample t-test is used to match two means scores, and these scores come from the same group. Pair samples t-test is used when variables are independent and have two levels, and those levels are repeated measures.

Non-parametric Test Methods

The four different techniques of parametric tests, such as Mann Whitney U test, the sign test, the Wilcoxon signed-rank test, and the Kruskal Wallis test are discussed here in detail. We know that the non-parametric tests are completely based on the ranks, which are assigned to the ordered data. The four different types of non-parametric test are summarized below with their uses, null hypothesis , test statistic, and the decision rule. 

Kruskal Wallis test is used to compare the continuous outcome in greater than two independent samples.

Null hypothesis, H 0 :  K Population medians are equal.

Test statistic:

If N is the total sample size, k is the number of comparison groups, R j is the sum of the ranks in the jth group and n j is the sample size in the jth group, then the test statistic, H is given by:

\(\begin{array}{l}H = \left ( \frac{12}{N(N+1)}\sum_{j=1}^{k} \frac{R_{j}^{2}}{n_{j}}\right )-3(N+1)\end{array} \)

Decision Rule: Reject the null hypothesis H 0 if H ≥ critical value

The sign test is used to compare the continuous outcome in the paired samples or the two matches samples.

Null hypothesis, H 0 : Median difference should be zero 

Test statistic: The test statistic of the sign test is the smaller of the number of positive or negative signs.

Decision Rule: Reject the null hypothesis if the smaller of number of the positive or the negative signs are less than or equal to the critical value from the table.

Mann Whitney U test is used to compare the continuous outcomes in the two independent samples. 

Null hypothesis, H 0 : The two populations should be equal.

If R 1 and R 2 are the sum of the ranks in group 1 and group 2 respectively, then the test statistic “U” is the smaller of:

\(\begin{array}{l}U_{1}= n_{1}n_{2}+\frac{n_{1}(n_{1}+1)}{2}-R_{1}\end{array} \)

\(\begin{array}{l}U_{2}= n_{1}n_{2}+\frac{n_{2}(n_{2}+1)}{2}-R_{2}\end{array} \)

Decision Rule: Reject the null hypothesis if the test statistic, U is less than or equal to critical value from the table.

Wilcoxon signed-rank test is used to compare the continuous outcome in the two matched samples or the paired samples.

Null hypothesis, H 0 : Median difference should be zero.

Test statistic: The test statistic W, is defined as the smaller of W+ or W- .

Where W+ and W- are the sums of the positive and the negative ranks of the different scores.

Decision Rule: Reject the null hypothesis if the test statistic, W is less than or equal to the critical value from the table.

Advantages and Disadvantages of Non-Parametric Test

The advantages of the non-parametric test are:

• Easily understandable
• Short calculations
• Assumption of distribution is not required
• Applicable to all types of data

The disadvantages of the non-parametric test are:

• Less efficient as compared to parametric test
• The results may or may not provide an accurate answer because they are distribution free

Applications of Non-Parametric Test

The conditions when non-parametric tests are used are listed below:

• When parametric tests are not satisfied.
• When testing the hypothesis, it does not have any distribution.
• For quick data analysis.
• When unscaled data is available.

Frequently Asked Questions on Non-Parametric Test

What is meant by a non-parametric test.

The non-parametric test is one of the methods of statistical analysis, which does not require any distribution to meet the required assumptions, that has to be analyzed. Hence, the non-parametric test is called a distribution-free test.

What is the advantage of a non-parametric test?

The advantage of nonparametric tests over the parametric test is that they do not consider any assumptions about the data.

Is Chi-square a non-parametric test?

Yes, the Chi-square test is a non-parametric test in statistics, and it is called a distribution-free test.

Mention the different types of non-parametric tests.

The different types of non-parametric test are: Kruskal Wallis Test Sign Test Mann Whitney U test Wilcoxon signed-rank test

When to use the parametric and non-parametric test?

If the mean of the data more accurately represents the centre of the distribution, and the sample size is large enough, we can use the parametric test. Whereas, if the median of the data more accurately represents the centre of the distribution, and the sample size is large, we can use non-parametric distribution.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 02 May 2024

Effectiveness of social media-assisted course on learning self-efficacy

• Jiaying Hu 1 ,
• Yicheng Lai 2 &
• Xiuhua Yi 3  

Scientific Reports volume  14 , Article number:  10112 ( 2024 ) Cite this article

1 Altmetric

Metrics details

• Human behaviour

The social media platform and the information dissemination revolution have changed the thinking, needs, and methods of students, bringing development opportunities and challenges to higher education. This paper introduces social media into the classroom and uses quantitative analysis to investigate the relation between design college students’ learning self-efficacy and social media for design students, aiming to determine the effectiveness of social media platforms on self-efficacy. This study is conducted on university students in design media courses and is quasi-experimental, using a randomized pre-test and post-test control group design. The study participants are 73 second-year design undergraduates. Independent samples t-tests showed that the network interaction factors of social media had a significant impact on college students learning self-efficacy. The use of social media has a significant positive predictive effect on all dimensions of learning self-efficacy. Our analysis suggests that using the advantages and value of online social platforms, weakening the disadvantages of the network, scientifically using online learning resources, and combining traditional classrooms with the Internet can improve students' learning self-efficacy.

Similar content being viewed by others

Determinants of behaviour and their efficacy as targets of behavioural change interventions

Impact of artificial intelligence on human loss in decision making, laziness and safety in education

Toolbox of individual-level interventions against online misinformation

Introduction.

Social media is a way of sharing information, ideas, and opinions with others one. It can be used to create relationships between people and businesses. Social media has changed the communication way, it’s no longer just about talking face to face but also using a digital platform such as Facebook or Twitter. Today, social media is becoming increasingly popular in everyone's lives, including students and researchers 1 . Social media provides many opportunities for learners to publish their work globally, bringing many benefits to teaching and learning. The publication of students' work online has led to a more positive attitude towards learning and increased achievement and motivation. Other studies report that student online publications or work promote reflection on personal growth and development and provide opportunities for students to imagine more clearly the purpose of their work 2 . In addition, learning environments that include student publications allow students to examine issues differently, create new connections, and ultimately form new entities that can be shared globally 3 , 4 .

Learning self-efficacy is a belief that you can learn something new. It comes from the Latin word “self” and “efficax” which means efficient or effective. Self-efficacy is based on your beliefs about yourself, how capable you are to learn something new, and your ability to use what you have learned in real-life situations. This concept was first introduced by Bandura (1977), who studied the effects of social reinforcement on children’s learning behavior. He found that when children were rewarded for their efforts they would persist longer at tasks that they did not like or had low interest in doing. Social media, a ubiquitous force in today's digital age, has revolutionized the way people interact and share information. With the rise of social media platforms, individuals now have access to a wealth of online resources that can enhance their learning capabilities. This access to information and communication has also reshaped the way students approach their studies, potentially impacting their learning self-efficacy. Understanding the role of social media in shaping students' learning self-efficacy is crucial in providing effective educational strategies that promote healthy learning and development 5 . Unfortunately, the learning curve for the associated metadata base modeling methodologies and their corresponding computer-aided software engineering (CASE) tools have made it difficult for students to grasp. Addressing this learning issue examined the effect of this MLS on the self-efficacy of learning these topics 6 . Bates et al. 7 hypothesize a mediated model in which a set of antecedent variables influenced students’ online learning self-efficacy which, in turn, affected student outcome expectations, mastery perceptions, and the hours spent per week using online learning technology to complete learning assignments for university courses. Shen et al. 8 through exploratory factor analysis identifies five dimensions of online learning self-efficacy: (a) self-efficacy to complete an online course (b) self-efficacy to interact socially with classmates (c) self-efficacy to handle tools in a Course Management System (CMS) (d) self-efficacy to interact with instructors in an online course, and (e) self-efficacy to interact with classmates for academic purposes. Chiu 9 established a model for analyzing the mediating effect that learning self-efficacy and social self-efficacy have on the relationship between university students’ perceived life stress and smartphone addiction. Kim et al. 10 study was conducted to examine the influence of learning efficacy on nursing students' self-confidence. The objective of Paciello et al. 11 was to identify self-efficacy configurations in different domains (i.e., emotional, social, and self-regulated learning) in a sample of university students using a person-centered approach. The role of university students’ various conceptions of learning in their academic self-efficacy in the domain of physics is initially explored 12 . Kumar et al. 13 investigated factors predicting students’ behavioral intentions towards the continuous use of mobile learning. Other influential work includes 14 .

Many studies have focused on social networking tools such as Facebook and MySpace 15 , 16 . Teachers are concerned that the setup and use of social media apps take up too much of their time, may have plagiarism and privacy issues, and contribute little to actual student learning outcomes; they often consider them redundant or simply not conducive to better learning outcomes 17 . Cao et al. 18 proposed that the central questions in addressing the positive and negative pitfalls of social media on teaching and learning are whether the use of social media in teaching and learning enhances educational effectiveness, and what motivates university teachers to use social media in teaching and learning. Maloney et al. 3 argued that social media can further improve the higher education teaching and learning environment, where students no longer access social media to access course information. Many studies in the past have shown that the use of modern IT in the classroom has increased over the past few years; however, it is still limited mainly to content-driven use, such as accessing course materials, so with the emergence of social media in students’ everyday lives 2 , we need to focus on developing students’ learning self-efficacy so that they can This will enable students to 'turn the tables and learn to learn on their own. Learning self-efficacy is considered an important concept that has a powerful impact on learning outcomes 19 , 20 .

Self-efficacy for learning is vital in teaching students to learn and develop healthily and increasing students' beliefs in the learning process 21 . However, previous studies on social media platforms such as Twitter and Weibo as curriculum support tools have not been further substantiated or analyzed in detail. In addition, the relationship between social media, higher education, and learning self-efficacy has not yet been fully explored by researchers in China. Our research aims to fill this gap in the topic. Our study explored the impact of social media on the learning self-efficacy of Chinese college students. Therefore, it is essential to explore the impact of teachers' use of social media to support teaching and learning on students' learning self-efficacy. Based on educational theory and methodological practice, this study designed a teaching experiment using social media to promote learning self-efficacy by posting an assignment for post-course work on online media to explore the actual impact of social media on university students’ learning self-efficacy. This study examines the impact of a social media-assisted course on university students' learning self-efficacy to explore the positive impact of a social media-assisted course.

Theoretical background

• Social media

Social media has different definitions. Mayfield (2013) first introduced the concept of social media in his book-what is social media? The author summarized the six characteristics of social media: openness, participation, dialogue, communication, interaction, and communication. Mayfield 22 shows that social media is a kind of new media. Its uniqueness is that it can give users great space and freedom to participate in the communication process. Jen (2020) also suggested that the distinguishing feature of social media is that it is “aggregated”. Social media provides users with an interactive service to control their data and information and collaborate and share information 2 . Social media offers opportunities for students to build knowledge and helps them actively create and share information 23 . Millennial students are entering higher education institutions and are accustomed to accessing and using data from the Internet. These individuals go online daily for educational or recreational purposes. Social media is becoming increasingly popular in the lives of everyone, including students and researchers 1 . A previous study has shown that millennials use the Internet as their first source of information and Google as their first choice for finding educational and personal information 24 . Similarly, many institutions encourage teachers to adopt social media applications 25 . Faculty members have also embraced social media applications for personal, professional, and pedagogical purposes 17 .

Social networks allow one to create a personal profile and build various networks that connect him/her to family, friends, and other colleagues. Users use these sites to stay in touch with their friends, make plans, make new friends, or connect with someone online. Therefore, extending this concept, these sites can establish academic connections or promote cooperation and collaboration in higher education classrooms 2 . This study defines social media as an interactive community of users' information sharing and social activities built on the technology of the Internet. Because the concept of social media is broad, its connotations are consistent. Research shows that Meaning and Linking are the two key elements that make up social media existence. Users and individual media outlets generate social media content and use it as a platform to get it out there. Social media distribution is based on social relationships and has a better platform for personal information and relationship management systems. Examples of social media applications include Facebook, Twitter, MySpace, YouTube, Flickr, Skype, Wiki, blogs, Delicious, Second Life, open online course sites, SMS, online games, mobile applications, and more 18 . Ajjan and Hartshorne 2 investigated the intentions of 136 faculty members at a US university to adopt Web 2.0 technologies as tools in their courses. They found that integrating Web 2.0 technologies into the classroom learning environment effectively increased student satisfaction with the course and improved their learning and writing skills. His research focused on improving the perceived usefulness, ease of use, compatibility of Web 2.0 applications, and instructor self-efficacy. The social computing impact of formal education and training and informal learning communities suggested that learning web 2.0 helps users to acquire critical competencies, and promotes technological, pedagogical, and organizational innovation, arguing that social media has a variety of learning content 26 . Users can post digital content online, enabling learners to tap into tacit knowledge while supporting collaboration between learners and teachers. Cao and Hong 27 investigated the antecedents and consequences of social media use in teaching among 249 full-time and part-time faculty members, who reported that the factors for using social media in teaching included personal social media engagement and readiness, external pressures; expected benefits; and perceived risks. The types of Innovators, Early adopters, Early majority, Late majority, Laggards, and objectors. Cao et al. 18 studied the educational effectiveness of 168 teachers' use of social media in university teaching. Their findings suggest that social media use has a positive impact on student learning outcomes and satisfaction. Their research model provides educators with ideas on using social media in the education classroom to improve student performance. Maqableh et al. 28 investigated the use of social networking sites by 366 undergraduate students, and they found that weekly use of social networking sites had a significant impact on student's academic performance and that using social networking sites had a significant impact on improving students' effective time management, and awareness of multitasking. All of the above studies indicate the researcher’s research on social media aids in teaching and learning. All of these studies indicate the positive impact of social media on teaching and learning.

• Learning self-efficacy

For the definition of concepts related to learning self-efficacy, scholars have mainly drawn on the idea proposed by Bandura 29 that defines self-efficacy as “the degree to which people feel confident in their ability to use the skills they possess to perform a task”. Self-efficacy is an assessment of a learner’s confidence in his or her ability to use the skills he or she possesses to complete a learning task and is a subjective judgment and feeling about the individual’s ability to control his or her learning behavior and performance 30 . Liu 31 has defined self-efficacy as the belief’s individuals hold about their motivation to act, cognitive ability, and ability to perform to achieve their goals, showing the individual's evaluation and judgment of their abilities. Zhang (2015) showed that learning efficacy is regarded as the degree of belief and confidence that expresses the success of learning. Yan 32 showed the extent to which learning self-efficacy is viewed as an individual. Pan 33 suggested that learning self-efficacy in an online learning environment is a belief that reflects the learner's ability to succeed in the online learning process. Kang 34 believed that learning self-efficacy is the learner's confidence and belief in his or her ability to complete a learning task. Huang 35 considered self-efficacy as an individual’s self-assessment of his or her ability to complete a particular task or perform a specific behavior and the degree of confidence in one’s ability to achieve a specific goal. Kong 36 defined learning self-efficacy as an individual’s judgment of one’s ability to complete academic tasks.

Based on the above analysis, we found that scholars' focus on learning self-efficacy is on learning behavioral efficacy and learning ability efficacy, so this study divides learning self-efficacy into learning behavioral efficacy and learning ability efficacy for further analysis and research 37 , 38 . Search the CNKI database and ProQuest Dissertations for keywords such as “design students’ learning self-efficacy”, “design classroom self-efficacy”, “design learning self-efficacy”, and other keywords. There are few relevant pieces of literature about design majors. Qiu 39 showed that mobile learning-assisted classroom teaching can control the source of self-efficacy from many aspects, thereby improving students’ sense of learning efficacy and helping middle and lower-level students improve their sense of learning efficacy from all dimensions. Yin and Xu 40 argued that the three elements of the network environment—“learning content”, “learning support”, and “social structure of learning”—all have an impact on university students’ learning self-efficacy. Duo et al. 41 recommend that learning activities based on the mobile network learning community increase the trust between students and the sense of belonging in the learning community, promote mutual communication and collaboration between students, and encourage each other to stimulate their learning motivation. In the context of social media applications, self-efficacy refers to the level of confidence that teachers can successfully use social media applications in the classroom 18 . Researchers have found that self-efficacy is related to social media applications 42 . Students had positive experiences with social media applications through content enhancement, creativity experiences, connectivity enrichment, and collaborative engagement 26 . Students who wish to communicate with their tutors in real-time find social media tools such as web pages, blogs, and virtual interactions very satisfying 27 . Overall, students report their enjoyment of different learning processes through social media applications; simultaneously, they show satisfactory tangible achievement of tangible learning outcomes 18 . According to Bandura's 'triadic interaction theory’, Bian 43 and Shi 44 divided learning self-efficacy into two main elements, basic competence, and control, where basic competence includes the individual's sense of effort, competence, the individual sense of the environment, and the individual's sense of control over behavior. The primary sense of competence includes the individual's Sense of effort, competence, environment, and control over behavior. In this study, learning self-efficacy is divided into Learning behavioral efficacy and Learning ability efficacy. Learning behavioral efficacy includes individuals' sense of effort, environment, and control; learning ability efficacy includes individuals' sense of ability, belief, and interest.

In Fig.  1 , learning self-efficacy includes learning behavior efficacy and learning ability efficacy, in which the learning behavior efficacy is determined by the sense of effort, the sense of environment, the sense of control, and the learning ability efficacy is determined by the sense of ability, sense of belief, sense of interest. “Sense of effort” is the understanding of whether one can study hard. Self-efficacy includes the estimation of self-effort and the ability, adaptability, and creativity shown in a particular situation. One with a strong sense of learning self-efficacy thinks they can study hard and focus on tasks 44 . “Sense of environment” refers to the individual’s feeling of their learning environment and grasp of the environment. The individual is the creator of the environment. A person’s feeling and grasp of the environment reflect the strength of his sense of efficacy to some extent. A person with a shared sense of learning self-efficacy is often dissatisfied with his environment, but he cannot do anything about it. He thinks the environment can only dominate him. A person with a high sense of learning self-efficacy will be more satisfied with his school and think that his teachers like him and are willing to study in school 44 . “Sense of control” is an individual’s sense of control over learning activities and learning behavior. It includes the arrangement of individual learning time, whether they can control themselves from external interference, and so on. A person with a strong sense of self-efficacy will feel that he is the master of action and can control the behavior and results of learning. Such a person actively participates in various learning activities. When he encounters difficulties in learning, he thinks he can find a way to solve them, is not easy to be disturbed by the outside world, and can arrange his own learning time. The opposite is the sense of losing control of learning behavior 44 . “Sense of ability” includes an individual’s perception of their natural abilities, expectations of learning outcomes, and perception of achieving their learning goals. A person with a high sense of learning self-efficacy will believe that he or she is brighter and more capable in all areas of learning; that he or she is more confident in learning in all subjects. In contrast, people with low learning self-efficacy have a sense of powerlessness. They are self-doubters who often feel overwhelmed by their learning and are less confident that they can achieve the appropriate learning goals 44 . “Sense of belief” is when an individual knows why he or she is doing something, knows where he or she is going to learn, and does not think before he or she even does it: What if I fail? These are meaningless, useless questions. A person with a high sense of learning self-efficacy is more robust, less afraid of difficulties, and more likely to reach their learning goals. A person with a shared sense of learning self-efficacy, on the other hand, is always going with the flow and is uncertain about the outcome of their learning, causing them to fall behind. “Sense of interest” is a person's tendency to recognize and study the psychological characteristics of acquiring specific knowledge. It is an internal force that can promote people's knowledge and learning. It refers to a person's positive cognitive tendency and emotional state of learning. A person with a high sense of self-efficacy in learning will continue to concentrate on studying and studying, thereby improving learning. However, one with low learning self-efficacy will have psychology such as not being proactive about learning, lacking passion for learning, and being impatient with learning. The elements of learning self-efficacy can be quantified and detailed in the following Fig.  1 .

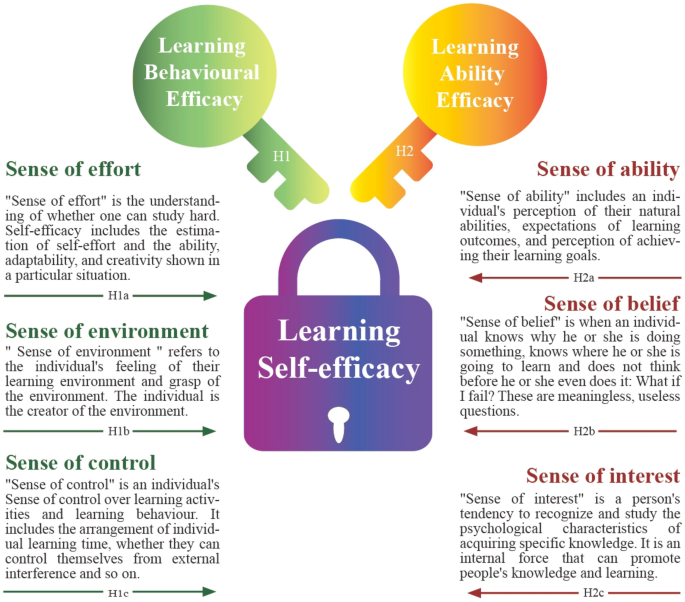
Learning self-efficacy research structure in this paper.

Research participants

All the procedures were conducted in adherence to the guidelines and regulations set by the institution. Prior to initiating the study, informed consent was obtained in writing from the participants, and the Institutional Review Board for Behavioral and Human Movement Sciences at Nanning Normal University granted approval for all protocols.

Two parallel classes are pre-selected as experimental subjects in our study, one as the experimental group and one as the control group. Social media assisted classroom teaching to intervene in the experimental group, while the control group did not intervene. When selecting the sample, it is essential to consider, as far as possible, the shortcomings of not using randomization to select or assign the study participants, resulting in unequal experimental and control groups. When selecting the experimental subjects, classes with no significant differences in initial status and external conditions, i.e. groups with homogeneity, should be selected. Our study finally decided to select a total of 44 students from Class 2021 Design 1 and a total of 29 students from Class 2021 Design 2, a total of 74 students from Nanning Normal University, as the experimental subjects. The former served as the experimental group, and the latter served as the control group. 73 questionnaires are distributed to measure before the experiment, and 68 are returned, with a return rate of 93.15%. According to the statistics, there were 8 male students and 34 female students in the experimental group, making a total of 44 students (mirrors the demographic trends within the humanities and arts disciplines from which our sample was drawn); there are 10 male students and 16 female students in the control group, making a total of 26 students, making a total of 68 students in both groups. The sample of those who took the course were mainly sophomores, with a small number of first-year students and juniors, which may be related to the nature of the subject of this course and the course system offered by the university. From the analysis of students' majors, liberal arts students in the experimental group accounted for the majority, science students and art students accounted for a small part. In contrast, the control group had more art students, and liberal arts students and science students were small. In the daily self-study time, the experimental and control groups are 2–3 h. The demographic information of research participants is shown in Table 1 .

Research procedure

Firstly, the ADDIE model is used for the innovative design of the teaching method of the course. The number of students in the experimental group was 44, 8 male and 35 females; the number of students in the control group was 29, 10 male and 19 females. Secondly, the classes are targeted at students and applied. Thirdly, the course for both the experimental and control classes is a convenient and practice-oriented course, with the course title “Graphic Design and Production”, which focuses on learning the graphic design software Photoshop. The course uses different cases to explain in detail the process and techniques used to produce these cases using Photoshop, and incorporates practical experience as well as relevant knowledge in the process, striving to achieve precise and accurate operational steps; at the end of the class, the teacher assigns online assignments to be completed on social media, allowing students to post their edited software tutorials online so that students can master the software functions. The teacher assigns online assignments to be completed on social media at the end of the lesson, allowing students to post their editing software tutorials online so that they can master the software functions and production skills, inspire design inspiration, develop design ideas and improve their design skills, and improve students' learning self-efficacy through group collaboration and online interaction. Fourthly, pre-tests and post-tests are conducted in the experimental and control classes before the experiment. Fifthly, experimental data are collected, analyzed, and summarized.

We use a questionnaire survey to collect data. Self-efficacy is a person’s subjective judgment on whether one can successfully perform a particular achievement. American psychologist Albert Bandura first proposed it. To understand the improvement effect of students’ self-efficacy after the experimental intervention, this work questionnaire was referenced by the author from “Self-efficacy” “General Perceived Self Efficacy Scale” (General Perceived Self Efficacy Scale) German psychologist Schwarzer and Jerusalem (1995) and “Academic Self-Efficacy Questionnaire”, a well-known Chinese scholar Liang 45 .  The questionnaire content is detailed in the supplementary information . A pre-survey of the questionnaire is conducted here. The second-year students of design majors collected 32 questionnaires, eliminated similar questions based on the data, and compiled them into a formal survey scale. The scale consists of 54 items, 4 questions about basic personal information, and 50 questions about learning self-efficacy. The Likert five-point scale is the questionnaire used in this study. The answers are divided into “completely inconsistent", “relatively inconsistent”, “unsure”, and “relatively consistent”. The five options of “Completely Meet” and “Compliant” will count as 1, 2, 3, 4, and 5 points, respectively. Divided into a sense of ability (Q5–Q14), a sense of effort (Q15–Q20), a sense of environment (Q21–Q28), a sense of control (Q29–Q36), a sense of Interest (Q37–Q45), a sense of belief (Q46–Q54). To demonstrate the scientific effectiveness of the experiment, and to further control the influence of confounding factors on the experimental intervention. This article thus sets up a control group as a reference. Through the pre-test and post-test in different periods, comparison of experimental data through pre-and post-tests to illustrate the effects of the intervention.

Reliability indicates the consistency of the results of a measurement scale (See Table 2 ). It consists of intrinsic and extrinsic reliability, of which intrinsic reliability is essential. Using an internal consistency reliability test scale, a Cronbach's alpha coefficient of reliability statistics greater than or equal to 0.9 indicates that the scale has good reliability, 0.8–0.9 indicates good reliability, 7–0.8 items are acceptable. Less than 0.7 means to discard some items in the scale 46 . This study conducted a reliability analysis on the effects of the related 6-dimensional pre-test survey to illustrate the reliability of the questionnaire.

From the Table 2 , the Cronbach alpha coefficients for the pre-test, sense of effort, sense of environment, sense of control, sense of interest, sense of belief, and the total questionnaire, were 0.919, 0.839, 0.848, 0.865, 0.852, 0.889 and 0.958 respectively. The post-test Cronbach alpha coefficients were 0.898, 0.888, 0.886, 0.889, 0.900, 0.893 and 0.970 respectively. The Cronbach alpha coefficients were all greater than 0.8, indicating a high degree of reliability of the measurement data.

The validity, also known as accuracy, reflects how close the measurement result is to the “true value”. Validity includes structure validity, content validity, convergent validity, and discriminative validity. Because the experiment is a small sample study, we cannot do any specific factorization. KMO and Bartlett sphericity test values are an important part of structural validity. Indicator, general validity evaluation (KMO value above 0.9, indicating very good validity; 0.8–0.9, indicating good validity; 0.7–0.8 validity is good; 0.6–0.7 validity is acceptable; 0.5–0.6 means poor validity; below 0.45 means that some items should be abandoned.

Table 3 shows that the KMO values of ability, effort, environment, control, interest, belief, and the total questionnaire are 0.911, 0.812, 0.778, 0.825, 0.779, 0.850, 0.613, and the KMO values of the post-test are respectively. The KMO values are 0.887, 0.775, 0.892, 0.868, 0.862, 0.883, 0.715. KMO values are basically above 0.8, and all are greater than 0.6. This result indicates that the validity is acceptable, the scale has a high degree of reasonableness, and the valid data.

In the graphic design and production (professional design course), we will learn the practical software with cases. After class, we will share knowledge on the self-media platform. We will give face-to-face computer instruction offline from 8:00 to 11:20 every Wednesday morning for 16 weeks. China's top online sharing platform (APP) is Tik Tok, micro-blog (Micro Blog) and Xiao hong shu. The experiment began on September 1, 2022, and conducted the pre-questionnaire survey simultaneously. At the end of the course, on January 6, 2023, the post questionnaire survey was conducted. A total of 74 questionnaires were distributed in this study, recovered 74 questionnaires. After excluding the invalid questionnaires with incomplete filling and wrong answers, 68 valid questionnaires were obtained, with an effective rate of 91%, meeting the test requirements. Then, use the social science analysis software SPSS Statistics 26 to analyze the data: (1) descriptive statistical analysis of the dimensions of learning self-efficacy; (2) Using correlation test to analyze the correlation between learning self-efficacy and the use of social media; (3) This study used a comparative analysis of group differences to detect the influence of learning self-efficacy on various dimensions of social media and design courses. For data processing and analysis, use the spss26 version software and frequency statistics to create statistics on the basic situation of the research object and the basic situation of the use of live broadcast. The reliability scale analysis (internal consistency test) and use Bartlett's sphericity test to illustrate the reliability and validity of the questionnaire and the individual differences between the control group and the experimental group in demographic variables (gender, grade, Major, self-study time per day) are explained by cross-analysis (chi-square test). In the experimental group and the control group, the pre-test, post-test, before-and-after test of the experimental group and the control group adopt independent sample T-test and paired sample T-test to illustrate the effect of the experimental intervention (The significance level of the test is 0.05 two-sided).

Results and discussion

Comparison of pre-test and post-test between groups.

To study whether the data of the experimental group and the control group are significantly different in the pre-test and post-test mean of sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief. The research for this situation uses an independent sample T-test and an independent sample. The test needs to meet some false parameters, such as normality requirements. Generally passing the normality test index requirements are relatively strict, so it can be relaxed to obey an approximately normal distribution. If there is serious skewness distribution, replace it with the nonparametric test. Variables are required to be continuous variables. The six variables in this study define continuous variables. The variable value information is independent of each other. Therefore, we use the independent sample T-test.

From the Table 4 , a pre-test found that there was no statistically significant difference between the experimental group and the control group at the 0.05 confidence level ( p  > 0.05) for perceptions of sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief. Before the experiment, the two groups of test groups have the same quality in measuring self-efficacy. The experimental class and the control class are homogeneous groups. Table 5 shows the independent samples t-test for the post-test, used to compare the experimental and control groups on six items, including the sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief.

The experimental and control groups have statistically significant scores ( p  < 0.05) for sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief, and the experimental and control groups have statistically significant scores (t = 3.177, p  = 0.002) for a sense of competence. (t = 3.177, p  = 0.002) at the 0.01 level, with the experimental group scoring significantly higher (3.91 ± 0.51) than the control group (3.43 ± 0.73). The experimental group and the control group showed significance for the perception of effort at the 0.01 confidence level (t = 2.911, p  = 0.005), with the experimental group scoring significantly higher (3.88 ± 0.66) than the control group scoring significantly higher (3.31 ± 0.94). The experimental and control groups show significance at the 0.05 level (t = 2.451, p  = 0.017) for the sense of environment, with the experimental group scoring significantly higher (3.95 ± 0.61) than the control group scoring significantly higher (3.58 ± 0.62). The experimental and control groups showed significance for sense of control at the 0.05 level of significance (t = 2.524, p  = 0.014), and the score for the experimental group (3.76 ± 0.67) would be significantly higher than the score for the control group (3.31 ± 0.78). The experimental and control groups showed significance at the 0.01 level for sense of interest (t = 2.842, p  = 0.006), and the experimental group's score (3.87 ± 0.61) would be significantly higher than the control group's score (3.39 ± 0.77). The experimental and control groups showed significance at the 0.01 level for the sense of belief (t = 3.377, p  = 0.001), and the experimental group would have scored significantly higher (4.04 ± 0.52) than the control group (3.56 ± 0.65). Therefore, we can conclude that the experimental group's post-test significantly affects the mean scores of sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief. A social media-assisted course has a positive impact on students' self-efficacy.

Comparison of pre-test and post-test of each group

The paired-sample T-test is an extension of the single-sample T-test. The purpose is to explore whether the means of related (paired) groups are significantly different. There are four standard paired designs: (1) Before and after treatment of the same subject Data, (2) Data from two different parts of the same subject, (3) Test results of the same sample with two methods or instruments, 4. Two matched subjects receive two treatments, respectively. This study belongs to the first type, the 6 learning self-efficacy dimensions of the experimental group and the control group is measured before and after different periods.

Paired t-tests is used to analyze whether there is a significant improvement in the learning self-efficacy dimension in the experimental group after the experimental social media-assisted course intervention. In Table 6 , we can see that the six paired data groups showed significant differences ( p  < 0.05) in the pre and post-tests of sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief. There is a level of significance of 0.01 (t = − 4.540, p  = 0.000 < 0.05) before and after the sense of ability, the score after the sense of ability (3.91 ± 0.51), and the score before the Sense of ability (3.41 ± 0.55). The level of significance between the pre-test and post-test of sense of effort is 0.01 (t = − 4.002, p  = 0.000). The score of the sense of effort post-test (3.88 ± 0.66) will be significantly higher than the average score of the sense of effort pre-test (3.31 ± 0.659). The significance level between the pre-test and post-test Sense of environment is 0.01 (t = − 3.897, p  = 0.000). The average score for post- Sense of environment (3.95 ± 0.61) will be significantly higher than that of sense of environment—the average score of the previous test (3.47 ± 0.44). The average value of a post- sense of control (3.76 ± 0.67) will be significantly higher than the average of the front side of the Sense of control value (3.27 ± 0.52). The sense of interest pre-test and post-test showed a significance level of 0.01 (− 4.765, p  = 0.000), and the average value of Sense of interest post-test was 3.87 ± 0.61. It would be significantly higher than the average value of the Sense of interest (3.25 ± 0.59), the significance between the pre-test and post-test of belief sensing is 0.01 level (t = − 3.939, p  = 0.000). Thus, the average value of a post-sense of belief (4.04 ± 0.52) will be significantly higher than that of a pre-sense of belief Average value (3.58 ± 0.58). After the experimental group’s post-test, the scores for the Sense of ability, effort, environment, control, interest, and belief before the comparison experiment increased significantly. This result has a significant improvement effect. Table 7 shows that the control group did not show any differences in the pre and post-tests using paired t-tests on the dimensions of learning self-efficacy such as sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief ( p  > 0.05). It shows no experimental intervention for the control group, and it does not produce a significant effect.

The purpose of this study aims to explore the impact of social media use on college students' learning self-efficacy, examine the changes in the elements of college students' learning self-efficacy before and after the experiment, and make an empirical study to enrich the theory. This study developed an innovative design for course teaching methods using the ADDIE model. The design process followed a series of model rules of analysis, design, development, implementation, and evaluation, as well as conducted a descriptive statistical analysis of the learning self-efficacy of design undergraduates. Using questionnaires and data analysis, the correlation between the various dimensions of learning self-efficacy is tested. We also examined the correlation between the two factors, and verifies whether there was a causal relationship between the two factors.

Based on prior research and the results of existing practice, a learning self-efficacy is developed for university students and tested its reliability and validity. The scale is used to pre-test the self-efficacy levels of the two subjects before the experiment, and a post-test of the self-efficacy of the two groups is conducted. By measuring and investigating the learning self-efficacy of the study participants before the experiment, this study determined that there was no significant difference between the experimental group and the control group in terms of sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief. Before the experiment, the two test groups had homogeneity in measuring the dimensionality of learning self-efficacy. During the experiment, this study intervened in social media assignments for the experimental group. The experiment used learning methods such as network assignments, mutual aid communication, mutual evaluation of assignments, and group discussions. After the experiment, the data analysis showed an increase in learning self-efficacy in the experimental group compared to the pre-test. With the test time increased, the learning self-efficacy level of the control group decreased slightly. It shows that social media can promote learning self-efficacy to a certain extent. This conclusion is similar to Cao et al. 18 , who suggested that social media would improve educational outcomes.

We have examined the differences between the experimental and control group post-tests on six items, including the sense of ability, sense of effort, sense of environment, sense of control, sense of interest, and sense of belief. This result proves that a social media-assisted course has a positive impact on students' learning self-efficacy. Compared with the control group, students in the experimental group had a higher interest in their major. They showed that they liked to share their learning experiences and solve difficulties in their studies after class. They had higher motivation and self-directed learning ability after class than students in the control group. In terms of a sense of environment, students in the experimental group were more willing to share their learning with others, speak boldly, and participate in the environment than students in the control group.

The experimental results of this study showed that the experimental group showed significant improvement in the learning self-efficacy dimensions after the experimental intervention in the social media-assisted classroom, with significant increases in the sense of ability, sense of effort, sense of environment, sense of control, sense of interest and sense of belief compared to the pre-experimental scores. This result had a significant improvement effect. Evidence that a social media-assisted course has a positive impact on students' learning self-efficacy. Most of the students recognized the impact of social media on their learning self-efficacy, such as encouragement from peers, help from teachers, attention from online friends, and recognition of their achievements, so that they can gain a sense of achievement that they do not have in the classroom, which stimulates their positive perception of learning and is more conducive to the awakening of positive effects. This phenomenon is in line with Ajjan and Hartshorne 2 . They argue that social media provides many opportunities for learners to publish their work globally, which brings many benefits to teaching and learning. The publication of students' works online led to similar positive attitudes towards learning and improved grades and motivation. This study also found that students in the experimental group in the post-test controlled their behavior, became more interested in learning, became more purposeful, had more faith in their learning abilities, and believed that their efforts would be rewarded. This result is also in line with Ajjan and Hartshorne's (2008) indication that integrating Web 2.0 technologies into classroom learning environments can effectively increase students' satisfaction with the course and improve their learning and writing skills.

We only selected students from one university to conduct a survey, and the survey subjects were self-selected. Therefore, the external validity and generalizability of our study may be limited. Despite the limitations, we believe this study has important implications for researchers and educators. The use of social media is the focus of many studies that aim to assess the impact and potential of social media in learning and teaching environments. We hope that this study will help lay the groundwork for future research on the outcomes of social media utilization. In addition, future research should further examine university support in encouraging teachers to begin using social media and university classrooms in supporting social media (supplementary file 1 ).

The present study has provided preliminary evidence on the positive association between social media integration in education and increased learning self-efficacy among college students. However, several avenues for future research can be identified to extend our understanding of this relationship.

Firstly, replication studies with larger and more diverse samples are needed to validate our findings across different educational contexts and cultural backgrounds. This would enhance the generalizability of our results and provide a more robust foundation for the use of social media in teaching. Secondly, longitudinal investigations should be conducted to explore the sustained effects of social media use on learning self-efficacy. Such studies would offer insights into how the observed benefits evolve over time and whether they lead to improved academic performance or other relevant outcomes. Furthermore, future research should consider the exploration of potential moderators such as individual differences in students' learning styles, prior social media experience, and psychological factors that may influence the effectiveness of social media in education. Additionally, as social media platforms continue to evolve rapidly, it is crucial to assess the impact of emerging features and trends on learning self-efficacy. This includes an examination of advanced tools like virtual reality, augmented reality, and artificial intelligence that are increasingly being integrated into social media environments. Lastly, there is a need for research exploring the development and evaluation of instructional models that effectively combine traditional teaching methods with innovative uses of social media. This could guide educators in designing courses that maximize the benefits of social media while minimizing potential drawbacks.

In conclusion, the current study marks an important step in recognizing the potential of social media as an educational tool. Through continued research, we can further unpack the mechanisms by which social media can enhance learning self-efficacy and inform the development of effective educational strategies in the digital age.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request. The data are not publicly available due to privacy or ethical restrictions.

Rasheed, M. I. et al. Usage of social media, student engagement, and creativity: The role of knowledge sharing behavior and cyberbullying. Comput. Educ. 159 , 104002 (2020).

Article   Google Scholar  

Ajjan, H. & Hartshorne, R. Investigating faculty decisions to adopt Web 2.0 technologies: Theory and empirical tests. Internet High. Educ. 11 , 71–80 (2008).

Maloney, E. J. What web 2.0 can teach us about learning. The Chronicle of Higher Education 53 , B26–B27 (2007).

Ustun, A. B., Karaoglan-Yilmaz, F. G. & Yilmaz, R. Educational UTAUT-based virtual reality acceptance scale: A validity and reliability study. Virtual Real. 27 , 1063–1076 (2023).

Schunk, D. H. Self-efficacy and classroom learning. Psychol. Sch. 22 , 208–223 (1985).

Cheung, W., Li, E. Y. & Yee, L. W. Multimedia learning system and its effect on self-efficacy in database modeling and design: An exploratory study. Comput. Educ. 41 , 249–270 (2003).

Bates, R. & Khasawneh, S. Self-efficacy and college students’ perceptions and use of online learning systems. Comput. Hum. Behav. 23 , 175–191 (2007).

Shen, D., Cho, M.-H., Tsai, C.-L. & Marra, R. Unpacking online learning experiences: Online learning self-efficacy and learning satisfaction. Internet High. Educ. 19 , 10–17 (2013).

Chiu, S.-I. The relationship between life stress and smartphone addiction on taiwanese university student: A mediation model of learning self-efficacy and social self-Efficacy. Comput. Hum. Behav. 34 , 49–57 (2014).

Kim, S.-O. & Kang, B.-H. The influence of nursing students’ learning experience, recognition of importance and learning self-efficacy for core fundamental nursing skills on their self-confidence. J. Korea Acad.-Ind. Coop. Soc. 17 , 172–182 (2016).

Google Scholar  

Paciello, M., Ghezzi, V., Tramontano, C., Barbaranelli, C. & Fida, R. Self-efficacy configurations and wellbeing in the academic context: A person-centred approach. Pers. Individ. Differ. 99 , 16–21 (2016).

Suprapto, N., Chang, T.-S. & Ku, C.-H. Conception of learning physics and self-efficacy among Indonesian University students. J. Balt. Sci. Educ. 16 , 7–19 (2017).

Kumar, J. A., Bervell, B., Annamalai, N. & Osman, S. Behavioral intention to use mobile learning: Evaluating the role of self-efficacy, subjective norm, and WhatsApp use habit. IEEE Access 8 , 208058–208074 (2020).

Fisk, J. E. & Warr, P. Age-related impairment in associative learning: The role of anxiety, arousal and learning self-efficacy. Pers. Indiv. Differ. 21 , 675–686 (1996).

Pence, H. E. Preparing for the real web generation. J. Educ. Technol. Syst. 35 , 347–356 (2007).

Hu, J., Lee, J. & Yi, X. Blended knowledge sharing model in design professional. Sci. Rep. 13 , 16326 (2023).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Moran, M., Seaman, J. & Tintikane, H. Blogs, wikis, podcasts and Facebook: How today’s higher education faculty use social media, vol. 22, 1–28 (Pearson Learning Solutions. Retrieved December, 2012).

Cao, Y., Ajjan, H. & Hong, P. Using social media applications for educational outcomes in college teaching: A structural equation analysis: Social media use in teaching. Br. J. Educ. Technol. 44 , 581–593 (2013).

Artino, A. R. Academic self-efficacy: From educational theory to instructional practice. Perspect. Med. Educ. 1 , 76–85 (2012).

Article   PubMed   PubMed Central   Google Scholar  

Pajares, F. Self-efficacy beliefs in academic settings. Rev. Educ. Res. 66 , 543–578 (1996).

Zhao, Z. Classroom Teaching Design of Layout Design Based on Self Efficacy Theory (Tianjin University of Technology and Education, 2021).

Yılmaz, F. G. K. & Yılmaz, R. Exploring the role of sociability, sense of community and course satisfaction on students’ engagement in flipped classroom supported by facebook groups. J. Comput. Educ. 10 , 135–162 (2023).

Nguyen, N. P., Yan, G. & Thai, M. T. Analysis of misinformation containment in online social networks. Comput. Netw. 57 , 2133–2146 (2013).

Connaway, L. S., Radford, M. L., Dickey, T. J., Williams, J. D. A. & Confer, P. Sense-making and synchronicity: Information-seeking behaviors of millennials and baby boomers. Libri 58 , 123–135 (2008).

Wankel, C., Marovich, M. & Stanaityte, J. Cutting-edge social media approaches to business education : teaching with LinkedIn, Facebook, Twitter, Second Life, and blogs . (Global Management Journal, 2010).

Redecker, C., Ala-Mutka, K. & Punie, Y. Learning 2.0: The impact of social media on learning in Europe. Policy brief. JRC Scientific and Technical Report. EUR JRC56958 EN . Available from http://bit.ly/cljlpq [Accessed 6 th February 2011] 6 (2010).

Cao, Y. & Hong, P. Antecedents and consequences of social media utilization in college teaching: A proposed model with mixed-methods investigation. Horizon 19 , 297–306 (2011).

Maqableh, M. et al. The impact of social media networks websites usage on students’ academic performance. Commun. Netw. 7 , 159–171 (2015).

Bandura, A. Self-Efficacy (Worth Publishers, 1997).

Karaoglan-Yilmaz, F. G., Ustun, A. B., Zhang, K. & Yilmaz, R. Metacognitive awareness, reflective thinking, problem solving, and community of inquiry as predictors of academic self-efficacy in blended learning: A correlational study. Turk. Online J. Distance Educ. 24 , 20–36 (2023).

Liu, W. Self-efficacy Level and Analysis of Influencing Factors on Non-English Major Bilingual University Students—An Investigation Based on Three (Xinjiang Normal University, 2015).

Yan, W. Influence of College Students’ Positive Emotions on Learning Engagement and Academic Self-efficacy (Shanghai Normal University, 2016).

Pan, J. Relational Model Construction between College Students’ Learning Self-efficacy and Their Online Autonomous Learning Ability (Northeast Normal University, 2017).

Kang, Y. The Study on the Relationship Between Learning Motivation, Self-efficacy and Burnout in College Students (Shanxi University of Finance and Economics, 2018).

Huang, L. A Study on the Relationship between Chinese Learning Efficacy and Learning Motivation of Foreign Students in China (Huaqiao University, 2018).

Kong, W. Research on the Mediating Role of Undergraduates’ Learning Self-efficacy in the Relationship between Professional Identification and Learning Burnout (Shanghai Normal University, 2019).

Kuo, T. M., Tsai, C. C. & Wang, J. C. Linking web-based learning self-efficacy and learning engagement in MOOCs: The role of online academic hardiness. Internet High. Educ. 51 , 100819 (2021).

Zhan, Y. A Study of the Impact of Social Media Use and Dependence on Real-Life Social Interaction Among University Students (Shanghai International Studies University, 2020).

Qiu, S. A study on mobile learning to assist in developing English learning effectiveness among university students. J. Lanzhou Inst. Educ. 33 , 138–140 (2017).

Yin, R. & Xu, D. A study on the relationship between online learning environment and university students’ learning self-efficacy. E-educ. Res. 9 , 46–52 (2011).

Duo, Z., Zhao, W. & Ren, Y. A New paradigm for building mobile online learning communities: A perspective on the development of self-regulated learning efficacy among university students, in Modern distance education 10–17 (2019).

Park, S. Y., Nam, M.-W. & Cha, S.-B. University students’ behavioral intention to use mobile learning: Evaluating the technology acceptance model: Factors related to use mobile learning. Br. J. Educ. Technol. 43 , 592–605 (2012).

Bian, Y. Development and application of the Learning Self-Efficacy Scale (East China Normal University, 2003).

Shi, X. Between Life Stress and Smartphone Addiction on Taiwanese University Student (Southwest University, 2010).

Liang, Y. Study On Achievement Goals、Attribution Styles and Academic Self-efficacy of Collage Students (Central China Normal University, 2000).

Qiu, H. Quantitative Research and Statistical Analysis (Chongqing University Press, 2013).

Download references

Acknowledgements

This work is supported by the 2023 Guangxi University Young and middle-aged Teachers' Basic Research Ability Enhancement Project—“Research on Innovative Communication Strategies and Effects of Zhuang Traditional Crafts from the Perspective of the Metaverse” (Grant Nos. 2023KY0385), and the special project on innovation and entrepreneurship education in universities under the “14th Five-Year Plan” for Guangxi Education Science in 2023, titled “One Core, Two Directions, Three Integrations - Strategy and Practical Research on Innovation and Entrepreneurship Education in Local Universities” (Grant Nos. 2023ZJY1955), and the 2023 Guangxi Higher Education Undergraduate Teaching Reform General Project (Category B) “Research on the Construction and Development of PBL Teaching Model in Advertising” (Grant Nos.2023JGB294), and the 2022 Guangxi Higher Education Undergraduate Teaching Reform Project (General Category A) “Exploration and Practical Research on Public Art Design Courses in Colleges and Universities under Great Aesthetic Education” (Grant Nos. 2022JGA251), and the 2023 Guangxi Higher Education Undergraduate Teaching Reform Project Key Project “Research and Practice on the Training of Interdisciplinary Composite Talents in Design Majors Based on the Concept of Specialization and Integration—Taking Guangxi Institute of Traditional Crafts as an Example” (Grant Nos. 2023JGZ147), and the2024 Nanning Normal University Undergraduate Teaching Reform Project “Research and Practice on the Application of “Guangxi Intangible Cultural Heritage” in Packaging Design Courses from the Ideological and Political Perspective of the Curriculum” (Grant Nos. 2024JGX048),and the 2023 Hubei Normal University Teacher Teaching Reform Research Project (Key Project) -Curriculum Development for Improving Pre-service Music Teachers' Teaching Design Capabilities from the Perspective of OBE (Grant Nos. 2023014), and the 2023 Guangxi Education Science “14th Five-Year Plan” special project: “Specialized Integration” Model and Practice of Art and Design Majors in Colleges and Universities in Ethnic Areas Based on the OBE Concept (Grant Nos. 2023ZJY1805), and the 2024 Guangxi University Young and Middle-aged Teachers’ Scientific Research Basic Ability Improvement Project “Research on the Integration Path of University Entrepreneurship and Intangible Inheritance - Taking Liu Sanjie IP as an Example” (Grant Nos. 2024KY0374), and the 2022 Research Project on the Theory and Practice of Ideological and Political Education for College Students in Guangxi - “Party Building + Red”: Practice and Research on the Innovation of Education Model in College Student Dormitories (Grant Nos. 2022SZ028), and the 2021 Guangxi University Young and Middle-aged Teachers’ Scientific Research Basic Ability Improvement Project - "Research on the Application of Ethnic Elements in the Visual Design of Live Broadcast Delivery of Guangxi Local Products" (Grant Nos. 2021KY0891).

Author information

Authors and affiliations.

College of Art and Design, Nanning Normal University, Nanning, 530000, Guangxi, China

Graduate School of Techno Design, Kookmin University, Seoul, 02707, Korea

Yicheng Lai

College of Music, Hubei Normal University, Huangshi, 435000, Hubei, China

You can also search for this author in PubMed   Google Scholar

Contributions

The contribution of H. to this paper primarily lies in research design and experimental execution. H. was responsible for the overall framework design of the paper, setting research objectives and methods, and actively participating in data collection and analysis during the experimentation process. Furthermore, H. was also responsible for conducting literature reviews and played a crucial role in the writing and editing phases of the paper. L.'s contribution to this paper primarily manifests in theoretical derivation and the discussion section. Additionally, author L. also proposed future research directions and recommendations in the discussion section, aiming to facilitate further research explorations. Y.'s contribution to this paper is mainly reflected in data analysis and result interpretation. Y. was responsible for statistically analyzing the experimental data and employing relevant analytical tools and techniques to interpret and elucidate the data results.

Corresponding author

Correspondence to Jiaying Hu .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary information., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Hu, J., Lai, Y. & Yi, X. Effectiveness of social media-assisted course on learning self-efficacy. Sci Rep 14 , 10112 (2024). https://doi.org/10.1038/s41598-024-60724-0

Download citation

Received : 02 January 2024

Accepted : 26 April 2024

Published : 02 May 2024

DOI : https://doi.org/10.1038/s41598-024-60724-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Design students
• Online learning
• Design professional

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

• Open access
• Published: 27 May 2024

Comparative genomic analysis of Planctomycetota potential for polysaccharide degradation identifies biotechnologically relevant microbes

• Dominika Klimek 1 , 2 ,
• Malte Herold 1 &
• Magdalena Calusinska 1  

BMC Genomics volume  25 , Article number:  523 ( 2024 ) Cite this article

Metrics details

Members of the Planctomycetota phylum harbour an outstanding potential for carbohydrate degradation given the abundance and diversity of carbohydrate-active enzymes (CAZymes) encoded in their genomes. However, mainly members of the Planctomycetia class have been characterised up to now, and little is known about the degrading capacities of the other Planctomycetota . Here, we present a comprehensive comparative analysis of all available planctomycetotal genome representatives and detail encoded carbohydrolytic potential across phylogenetic groups and different habitats.

Our in-depth characterisation of the available planctomycetotal genomic resources increases our knowledge of the carbohydrolytic capacities of Planctomycetota . We show that this single phylum encompasses a wide variety of the currently known CAZyme diversity assigned to glycoside hydrolase families and that many members encode a versatile enzymatic machinery towards complex carbohydrate degradation, including lignocellulose. We highlight members of the Isosphaerales, Pirellulales, Sedimentisphaerales and Tepidisphaerales orders as having the highest encoded hydrolytic potential of the Planctomycetota . Furthermore, members of a yet uncultivated group affiliated to the Phycisphaerales order could represent an interesting source of novel lytic polysaccharide monooxygenases to boost lignocellulose degradation. Surprisingly, many Planctomycetota from anaerobic digestion reactors encode CAZymes targeting algal polysaccharides – this opens new perspectives for algal biomass valorisation in biogas processes.

Conclusions

Our study provides a new perspective on planctomycetotal carbohydrolytic potential, highlighting distinct phylogenetic groups which could provide a wealth of diverse, potentially novel CAZymes of industrial interest.

Peer Review reports

Introduction

Modern society generates enormous amount of waste organic matter that requires specific and well-defined disposal procedures [ 1 ]. Instead, waste biomass could be valorised into added-value products and energy [ 2 ]. In the light of global threats like environmental pollution and climate change, the bioconversion of organic waste into biofuels and sustainable, added-value products has been gaining considerable attention [ 3 ]. Microorganisms possess a broad repertoire of hydrolytic enzymes for aerobic and anaerobic degradation of organic matter [ 4 ]. The enzymes involved in carbohydrate breakdown are known as carbohydrate-active enzymes (CAZymes) and are currently classified into five classes that include glycoside hydrolases (GH), carbohydrate esterases (CE), polysaccharide lyases (PL) and enzymes with auxiliary activities (AA) [ 5 ]. Carbohydrate binding modules (CBMs) are non-catalytic modules, generally defined as accessory CAZymes, and their main role is to recognise the substrates by binding carbohydrates [ 6 ]. Several different industrial sectors, such as food industries and biorefineries, rely on the application of CAZymes from bacterial and fungal strains [ 7 ]. The increasing availability of genomic data provides promising avenue to discover novel strains and enzymes for scientific and industrial applications for e.g., heterologous expression [ 8 ]. Although a number of metagenomic studies have revealed a high diversity of microorganisms capable of degrading complex polysaccharides in distinct biomass-rich habitats, little attention has been paid to Planctomycetota [ 4 , 9 , 10 ]. According to a recent analysis of the global distribution of carbohydrate utilisation potential in the tree of life, alongside Bacteroidota and a few other phyla, Planctomycetota was identified as one of the most versatile phyla in degrading diverse biopolymers of cellulosic and non-cellulosic origin [ 11 ]. Planctomycetota , previously known as Planctomycetes , is one of the phyla within the Planctomycetota-Verrucomicrobiota-Chlamydiota superphylum (PVC). They are characterised with distinctive features not commonly detected in other prokaryotes, such as enlarged periplasm, outer membrane complexes in the form of crateriform structures, and a non-FtsZ based division mode [ 12 , 13 ]. Besides these cellular particularities, bacteria belonging to this widespread phylum have been highlighted in different environments for their hydrolytic potential [ 14 ]. Uncultured Planctomycetota have been identified as primary degraders of extracellular polymeric substances in soil and complex carbohydrates in marine sediments [ 15 , 16 , 17 ]. Certain members of this phylum can attach to algal surfaces and have been proposed to depolymerise algae-derived polymers [ 18 , 19 ]. Accordingly, Rhodopirellula is widely known for producing multiple and diverse sulphatases engaged in sulphated polysaccharides degradation like algal polysaccharides [ 20 ]. Metatranscriptomic studies also revealed the contribution of Planctomycetota to complex polysaccharide degradation in Sphagnum -dominated areas [ 21 ]. However, so far, only a limited number of Planctomycetota have been identified as potential candidates for biotechnological applications such as the bioactive compound production [ 22 ], and most of the characterised strains derive from the Planctomycetia class only [ 23 , 24 ].

In this study we investigate the encoded carbohydrolytic capacities of Planctomycetota , including the Planctomycetia and Phycisphaerae classes, as well as other less characterised members of this phylum. Through bioinformatics analysis of 1425 non-redundant genomes, we unveil a number of diverse CAZymes across planctomycetotal orders, emphasising their versatile encoded capabilities in carbohydrate degradation. High incidence of CAZyme gene clusters and presence of potentially extracellular enzymes, point to the existence of coordinated strategies for complex polysaccharide degradation, including lignocellulose and algal biomasses.

Dataset acquisition and classification of planctomycetotal genomes

Over 3000 publicly available draft and complete planctomycetotal genomes were downloaded from GenBank in June 2021 ( http://www.ncbi.nlm.nih.gov/genbank/ ), using ncbi-genome-download ( https://github.com/kblin/ncbi-genome-download ). The initial genome database was complemented with the metagenome-assembled genomes (MAGs) from own studies (see Additional File 1 , Table S1 for further details) as well as genomes from the catalogue of Earth’s Microbiomes (GEM) available from the JGI [ 25 ]. Unless stated otherwise, we will refer to both individual genomes and MAGs as genomes. All genomes were assessed for redundancy using dRep v3.2.2 with the -con 10 --checkM_method taxonomy_wf parameters [ 26 ]. The resulting 1457 non-redundant genomes were classified taxonomically with GTDB-tk v1.2.0 against GTDB database release 89 [ 27 ] and only hits designated as Planctomycetota were retained. A few changes were introduced to the taxonomic designations. The Planctomycetes class was renamed Planctomycetia as originally proposed by NL Ward 2011 (Bergey’s Manual) and formally adopted in Oren and Garrity 2020 [ 28 , 29 ]. Furthermore, the candidate order UBA1161 was renamed Tepidisphaerales [ 30 ], as proposed by Dedysh et al. [ 31 ]. CheckM v1.2.0 was used to determine genome completeness and contamination [ 32 ] and only genomes meeting the MIMAG standard of medium to high quality level (i.e. completeness above 75% and contamination below 10%) were retained for further analyses [ 33 ]. At this stage, our database contained 1451 non-redundant planctomycetotal genomes. We further reduced this number to 1425, by excluding the genomes encoding less than 10 carbohydrate active enzymes (CAZymes). To simplify the analysis, we designated classes with fewer than 10 sequenced genomes as “other class”. The final database of 1425 non-redundant genomes was additionally complemented with the respective metadata retrieved from NCBI using the rentrez script [ 34 ], followed by manual curation for conflicting information. Environmental metadata from the GEM catalogue was retrieved directly from the deposited repository and unified with the NCBI entries for the different habitat categories (Additional File 1 , Table S2 ).

Functional annotation of planctomycetotal genomes

Genomes were gene-called by prodigal v2.6.3 [ 35 ] and CAZymes were annotated by dbCAN2 v2.0.11 [ 36 ] against the dbCAN database v9 [ 5 ] using the three integrated tools (DIAMOND, Hotpep and, HMMER) with default parameters [ 37 , 38 , 39 ]. Genome annotation was also performed using Prokka v1.14.6 with its default databases [ 40 ]. To determine clusters of co-localised CAZymes, we applied a modified version of the CGCFinder module of dbCAN2 to detect CAZyme gene clusters (CGCs) [ 36 ]. CGCs were predicted as consisting of at least one CAZyme coding gene with at least one auxiliary gene (e.g. transcription factor or transporter) or another CAZyme separated by at most two other genes. Positive hits were assigned to CAZyme families if annotated by HMMER v3.1.2 and multiple CAZyme assignments were considered as separate functional domains or modules. For searching putatively novel CAZymes, only hits annotated either by DIAMOND v0.9.19 or Hotpep, but not HMMER, were retained (as so-called unclassified CAZymes). To assess the novelty of predicted CAZymes (assigned by HMMER), we searched the protein sequences against the CAZy database with DIAMOND and amino acid sequence identity of the best hit was inferred. Signal peptides were detected using signalP v6 [ 41 ]. Glycosyltransferase coding genes were excluded from the analysis as they are not involved in polysaccharide degradation. The raw output files of dbCAN2, CGCFinder and signalP are available in Additional File 4, 5, and 6, respectively.

Data analysis

Statistical analyses and visualisations were performed with the R software v 4.0.2 [ 42 ]. For multivariate analyses, a presence-absence table of CAZyme content for each genome was transformed into a Jaccard distance matrix (Additional File 2, Table S3 ). CAZyme dissimilarity was assessed using principal coordinate analysis (PCoA) and permutational ANOVA (PERMANOVA) as well as analysis of similarities (ANOSIM) with the vegan v 2.5.7 package in R [ 43 ]. Linear discriminant analysis (LDA) was performed with a nonparametric Kruskal Wallis test using the microbial v0.0.22 package in R (logarithmic LDA score > 4) [ 44 ]. A phylogenetic tree of genomes was constructed from the alignment of default marker genes using PhyloPhlAn v3.0.60 (--diversity medium supertree_aa) [ 45 ]. The alignment of protein sequences was calculated using the MUSCLE algorithm with default parameters [ 46 ]. Pairwise comparisons between protein sequences and Neighbor-Joining consensus were calculated for constructing the tree using Geneious Prime v 2019.0.3 [ 47 ]. The Spearman’s rank correlation was calculated in R using package stats. Unless otherwise stated, the significance of differences between tested groups was assessed using either a non-parametric Kruskal-Wallis or Wilcoxon test (R package stats). The obtained p -values were adjusted for multiple testing using the Benjamini–Hochberg procedure (false-discovery rate).

Annotation of CAZyme family activities

The substrate database (CAZyme families assigned to substrates) was framed according to [ 11 ] and the CAZy database [ 5 ] (Additional File 3 ). For CAZyme functional analysis, entries assigned to GH and PL families were classified based on their main characterised enzymatic activities into four categories according to the main target: algal biomass (algae-derived polymers), plant biomass (plant storage polysaccharides, oligosaccharides, and cellulose-hemicellulose fractions), algal/plant biomass and other activities (all the remaining polysaccharide targets were grouped together). Further, the categories were subdivided based on the substrate specificity: algal polysaccharides, glucans (α- and β-glucans), oligosaccharides, lignocellulose (cellulosic and/or hemicellulosic backbone), NAG-based polysaccharides (based on N-acetylglucosamine, including bacterial and host glycans), pectin, and other polysaccharides. The detailed annotations of substrates are available in the Additional File 3 . The ratio of CAZymes for polysaccharide target specificity was calculated by comparing the number of CAZymes (GHs and/or PLs) with assigned function to the number of all predicted CAZymes (GHs and/or PLs).

Results and discussion

Database of planctomycetotal genomes.

In this study, we investigated the metabolic potential of Planctomycetota for polysaccharide degradation. We tried to identify the primary trends across Planctomycetota by concentrating the analysis on the class and order taxonomic levels (Fig.  1 ). We argue that lower than phylum taxonomic level genomic comparisons provide a more nuanced and detailed perspective on the carbohydrolytic potential, enabling us to investigate common patterns that may not be as evident when carrying out a comparison at the bacterial phylum levels only.

To characterise the carbohydrate degrading potential of Planctomycetota , we created a database of 1425 non-redundant and medium to high quality genomes of different fragmentation level, recovered from both metagenomics and isolate sequencing studies (Fig.  1 a-d; Additional File 1, Table S1 ). Our database reflects all currently known as well as putatively novel classes of Planctomycetota (Fig.  1 a), allowing us to largely complement another recent study of microbial CAZymes, which included only 243 planctomycetotal genomes [ 11 ]. Specifically, the database includes 662 genomes of the Planctomycetia class with the following orders: Gemmatales (number of genomes, n  = 87), Isosphaerales ( n  = 28), Pirellulales ( n  = 408), and Planctomycetales ( n  = 137). Furthermore, it includes 463 genomes of the Phycisphaerae class including the Phycisphaerales ( n  = 246), Sedimentisphaerales ( n  = 118), and Tepidisphaerales ( n  = 13), as well as putative UBA1845 ( n  = 64) and SM23-33 ( n  = 22) orders. Planctomycetia and Phycisphaerae are the two biggest and widely described classes of the Planctomycetota phylum, and a few isolated representatives are the only so far cultured and characterised carbohydrate degrading Planctomycetota [ 13 ]. Additionally, 46 genomes of the Brocadiae candidate class are included, which are commonly known as anaerobic ammonium oxidising (anammox) bacteria widely employed in wastewater treatment settings [ 48 ]. Other genomes ( n  = 172) represent novel, not yet assigned planctomycetotal classes, including UBA8742, UBA8108, UBA1135 and UBA11346, which we labelled “putatively novel classes” (Fig.  1 a). Genomes that represent other less populated classes of Planctomycetota (< 10 genomes) were grouped together as “other class” (see Methods, n  = 65).

According to the environmental metadata, half of the planctomycetotal genomes in our database originate from marine and freshwater habitats (51%) while the remaining genomes were retrieved from extreme environments including thermal springs, hydrothermal vents and saline/alkaline habitats (13%), wastewater (8%), terrestrial (7%), animal digestive systems (4%), anammox (2%), AD reactors (4%) and other environments (11%) (Fig.  1 c; Additional File 1, Table S2 ).

Overview of planctomycetotal genomes included in the study, grouped and coloured at the class level. ( a ) The phylogenetic distribution of planctomycetotal genomes. The grey colour on the outer circle represents genomes assigned to “other class”. ( b ) Histogram of the genome fragmentation level c-d. Environmental origin, further called “habitat” ( c ) and genome size in Mb ( d ) of planctomycetotal genomes

Phylum- and class-level distribution of planctomycetotal CAZymes

The complete deconstruction of polysaccharides requires GH interaction with other CAZymes, including PLs responsible for the non-hydrolytic cleavage of glycosidic bonds and carbohydrate esters hydrolysing CEs, as well as other redox enzymes with auxiliary activities, such as AAs and including the lytic polysaccharide monooxygenases (LPMOs) [ 49 ]. Therefore, we first assessed the set of CAZyme families in the Planctomycetota genomes to estimate their catalytic potential. Globally, we detected 232 CAZyme families and 132 CAZyme subfamilies (Additional File 2, Table S3 ), demonstrating that this phylum alone covers 80% of the known GH family diversity at the time of analysis (September 2022). In turn, the diversity of AAs, CEs, PLs and CBMs represents 53%, 70%, 69% and 43% of the family diversity described, respectively. By examining the distribution of CAZymes across planctomycetotal classes, we found 129 CAZyme families that are shared between all the classes of Planctomycetota (Fig.  2 a). The Phycisphaerae class displays the greatest encoded diversity, including unique families such as β-agarases GH118, mannan-targeting GH47 and GH134, xylanases GH11 and α-L-arabinofuranosidases GH54 (Fig.  2 a). Conversely, the CAZyme families in UBA8742 exhibit little diversity, but families including GH44, putatively engaged in hemicellulose degradation, and pectin-targeting PL9 are frequently encoded in representative genomes of this class (Additional File 7, Fig. S1 ). Genomes belonging to the Planctomycetia class are deprived of genes that encode GH102 (peptidoglycan lyase), which are present in all other classes of Planctomycetota (Additional File 7, Fig. S1 ). Certain planctomycetotal genomes encode CAZymes assigned to the AA12 family representing putative oxidoreductases; which have never before been detected in any prokaryote [ 5 ], thus representing an interesting avenue for future studies.

To further compare CAZyomes at the planctomycetotal class level, we employed principal coordinate analysis (PCoA, Fig.  2 b-c) applied to the CAZyme occurrence matrix. We observed a moderate separation between the different planctomycetotal classes, especially visible for GH families (Fig.  2 b), which was further supported by statistical tests (PERMANOVA p  < 0.01 and ANOSIM R  = 0.45 p  < 0.01). We found that genome origin (habitat) has only a low impact on the carbohydrate degrading potential (Additional File 7, Fig. S2 ; ANOSIM R  = 0.06 p  < 0.01).

Characterisation of planctomycetotal CAZyomes (CAZyme repertoires) coloured by class affiliation. For a, b, c and d , the colour code corresponds to planctomycetotal classes, as indicated at the top of the figure. a. Bar plot (left) and upset plot (right), representing the number of CAZyme families and intersections between the planctomycetotal classes. b-c. Principal coordinates analysis (PCoA) ordination based on the Jaccard distance presence-absence matrix of GHs ( b , ANOSIM = 0.45) and all the other CAZyme families ( c , ANOSIM = 0.41) encoded in planctomycetotal genomes. d. Alluvial plot representing the number of significantly enriched GH and PL families in planctomycetotal orders ( p  < 0.05) with assigned functions towards either type of biomass. Only selected CAZyme families are highlighted. e. Bar plot representing the functional assignment of GHs and PLs, grouped at the order level and coloured by the substrate category

Redundant hydrolytic potentials of distinct planctomycetotal orders

To specifically assess the differences in the carbohydrate degrading potentials, we further detected enriched CAZyme families in planctomycetotal genomes, identifying a panel of 101 differentially encoded CAZymes within the Planctomycetota orders (Fig.  2 d; Additional File 2, Table S4 ). Considering the fact that different GH families may catalyse the hydrolysis of structurally similar substrates and seemingly diverse CAZyomes could be functionally redundant [ 50 ], we broadly classified the differentially enriched CAZymes in planctomycetotal genomes into different biomass and substrate categories (Fig.  2 e). These functional categories were assigned to CAZyme families based on the main described prevailing enzyme activities (see Methods). However, this approach may be limited by the broad diversity of catalytic activities within known families, particularly GHs. Future investigations should be supplemented with more detailed bioinformatic approaches and experimental validation.

While different CAZyme families are preferentially encoded in different groups with notable differences between taxonomic orders, all Planctomycetota seem equally well equipped for the degradation of main biomass and substrate categories, regardless of their phylogenetic origin and habitat specificity. Interestingly, the planctomycetotal genomes of marine bacteria are enriched with lignocellulose-degrading CAZymes (Fig.  3 a), even though marine polysaccharides differ from terrestrial carbohydrates, and are often highly sulphated, especially in algal polysaccharides [ 51 ]. Planctomycetotal genomes retrieved from diverse environments such as freshwater and engineered systems, including anammox and AD reactors, encode a similar potential for algae-derived polysaccharides as average marine Planctomycetota , suggesting they are equally well-suited to targeting algal biomass. Across the phylum, we also detected GH families 29, 107, 139, 151 and 168, as well as other polyspecific families such as GH95, and GH141 that may target diverse sulphated fucan-based polysaccharides e.g. fucoidans, primarily found in various species of brown seaweeds [ 52 ] as well as other fucose-containing oligosaccharides (Fig.  3 a). Although some members of the Planctomycetota phylum are already well-known utilisers of sulphated compounds including carrageenans and fucoidans [ 20 , 53 ], little is known about the planctomycetotal enzymatic systems involved in the degradation of algal biomass in general. For instance, the complexity of fucoidans pressure bacteria to possess highly specialised enzymatic systems in order to fully degrade them, as described in ‘Lentimonas’ sp. CC4 [ 52 ]. Arguably, Planctomycetota might also be a key player in the degradation of various structurally complex fucoidans, given the widespread distribution of CAZymes targeting the backbone of sulphated polysaccharides in their genomes.

Diversity of encoded GHs in individual Planctomycetota

We next examined the potential hydrolytic capacity of individual microorganisms by looking at the diversity profiles of CAZymes in genomes (number of distinct CAZyme families) assigned to the same phylogenetic class (Fig.  3 b) and order (Fig.  3 c; only GHs shown). The high diversity of CAZymes points to an extended capacity of the microorganisms to hydrolyse a wide range of complex polysaccharides in diverse environments [ 54 ]. Therefore, members of the unclassified UBA11346 class, planctomycetial ( Isosphaerales, Pirellulales ) and phycisphaeral ( Sedimentisphaerales, Tepidisphaerales ) orders demonstrate the largest potential to target diverse polysaccharides. The highest diversity of GHs is attributed to the UBA11346 putative class (38 ± 8 GHs per genome) while the lowest GH-encoding potential (between 4 and 13 different GHs) is typical for members of Brocadiae and the other yet unclassified classes (Fig.  3 b; Additional File 2, Table S5 ). Comparing members at the order level, genomes assigned to Sedimentisphaerales ( Phycisphaerae class) encode the highest number of hydrolysing enzymes assigned to GH and PL families, with an average of 47 ± 19 and 7 ± 4 distinct subfamilies per genome, respectively (Fig.  3 c; Additional File 2, Table S5 ). Specifically, genomes assigned to the SG8-4 putative family of Sedimentisphaerales are characterised with one of the highest GH and PL diversities of all the Planctomycetota (Additional File 7, Fig. S3 ). The Sedimentisphaerales order also encodes up to 11 distinct GH families putatively targeting a different backbone of lignocellulosic polymers acting as “endo”- or “exo” enzymes (Additional File 7, Fig. S4 ). In comparison, most of the planctomycetotal genomes are characterised with at maximum six distinct CAZymes targeting the backbone of lignocellulose. Commonly found in terrestrial habitats Isosphaerales ( Planctomycetia class; GH diversity 32 ± 16) and Tepidisphaerales ( Phycisphaerae class; GH diversity 41 ± 11) also show multiple distinct GH modules, indicating their capacity to degrade diverse carbohydrates (Fig.  3 c). The genomes assigned to the Pirellulales and Gemmatales orders correspond to the diversity of subfamilies in the range of 27 ± 15 and 15 ± 6, respectively. Pirellulales genomes assigned to the Pirellulaceae family are characterised with a much higher GH family diversity than the order average and could represent interesting “outliers” possibly targeting a wider range of polysaccharides (Additional File 7, Fig. S3 ). Furthermore, Pirellulales among all the Planctomycetota encode the highest number of GHs and PLs targeting algal carbohydrates, i.e. up to 13 different families (Additional File 7, Fig. S4 ).

Diversity of accessory modules and rare CAZymes

Compared to other CAZyme classes, AAs are only occasionally detected in planctomycetotal genomes (Fig.  3 b). Nevertheless, certain representatives of the Planctomycetia class encode up to six different AA families, including putative lignin peroxidases from the AA2 family (Additional File 7, Fig. S1 ). However, the AA2 family is mainly encoded in unclassified Planctomycetota from the UBA8742 and UBA1135 classes, equipping these members with a plausible capacity to degrade lignin and lignin derivates. All LPMOs identified are assigned to the AA10 family, which is the only LPMO family present in bacteria. They are mainly detected in genomes of uncultured members of the phycisphaeral SM1A02 putative family, and sporadically in other members of the phylum (Fig.  4 ). Importantly, SM1A02 genomes are particularly enriched in rare CAZymes e.g., present in < 5% of all planctomycetotal genomes. Of the 223 SM1A02 genomes used in our study, we identified 132 distinct CAZyme families, which corresponds to a wide diversity of CAZymes just within one family of bacteria, while per genome, on average only six different CAZyme families are encoded (Additional File 7, Figure S3 ). The representatives of the Planctomycetia class display a higher diversity of CE families than other Planctomycetota (Fig.  3 b), encoding on average from 7 to 9 different CE families per genome. Overall, Planctomycetales and Pirellulales trend towards a higher number of esterases, including CEs and sulphatases (Additional File 7, Fig. S5 ), which are critical enzymes for debranching algal polysaccharides. Considering a rich selection of algae-degrading enzymes of Pirellulales , as well as a high number of CEs and sulphatases encoded in their genomes, we could infer the presence of a system designed to scavenge the algal biomass, reinforcing the earlier observations [ 55 ].

Multi-modularity of planctomycetotal CAZymes

The variety of CBM modules seems to well reflect the diversity of GH families in some planctomycetotal genomes (Additional File 2, Table S6 ). Accordingly, planctomycetial Isosphaerales (rho = 0.70) and phycisphaeral Sedimentisphaerales (rho = 0.82), UBA1845 (rho = 0.76) and SM23-33 (rho = 0.70) show a strong correlation ( p  < 0.05) between GH and CBM family diversity (number of encoded GH and CBM families). However, members of Tepidisphaerales , characterised with one of the highest GH family diversities, do not follow this trend (rho = 0.21, p  = 0.49). High correlation values could also result from some GH enzymes containing additional domains that accommodate other CAZyme modules, including CBMs, forming multi-modular enzymes [ 6 ]. For instance, members of Sedimentisphaerales encode on average 10% of CAZymes with multi-modular characteristics, including the highest number of unique module combinations (Additional File 7, Fig. S6 ). The most common combinations for all Planctomycetota are two-module CAZymes, but certain genomes encode regularly CAZymes with three and more modules (Additional File 2, Table S7 ). Although GHs are commonly associated with CBMs in different bacteria [ 6 ], the occurrence of complex CAZymes containing other enzymatic modules is relatively less frequent. However, such complexity may represent an adaptation strategy in competitive environments [ 56 ]. Of particular interests are CAZymes with four or five modules, encompassing a variety of endo-acting polysaccharides, including cellulases GH5 and GH9, as well as xylanases GH10 and GH62. These CAZymes often feature diverse appended CBMs, sometimes occurring in multiple instances, and are encoded by Gemmatales, Pirellulales (mainly cellulases) and Sedimentisphaerales (mainly xylanases).

Multiple catalytic domains within single polypeptides suggest that individual enzymes might independently target and degrade different components of the biomass, likely improving its overall hydrolysis rate, thus representing biotechnologically relevant targets [ 57 , 58 ]. Previously, various bacteria have been demonstrated to secrete multi-modular CAZymes, either as free or membrane-bound enzymes, capable of acting on a diverse array of complex substrates [ 59 , 60 ]. This includes modular cellulases featuring multiple catalytic domains (such as GH5 and GH9) along with non-catalytic domains, representing a novel arrangement distinct from the cellulosome expressed by some well-known cellulolytic microorganisms [ 61 ]. Unfortunately, the only planctomycetotal CAZyme characterised so far is a unimodular cellulase belonging to GH44 encoded by Telmatocola sphagniphila SP2T ( Gemmatales ) [ 62 ]. Therefore, the need for characterised multi-modular enzymes persists, and members of Planctomycetota hold promise for future discoveries.

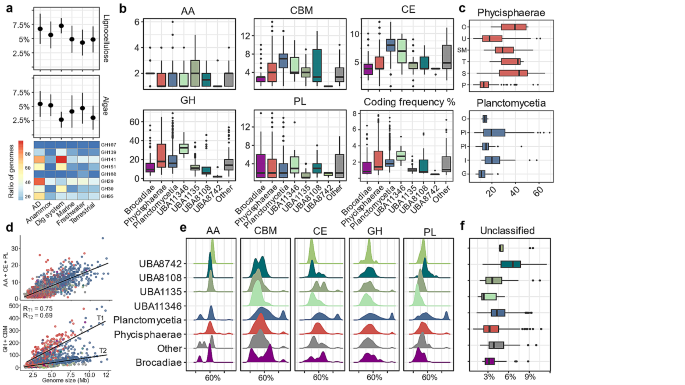
CAZyme family diversity, coding frequency and protein sequence identity of planctomycetotal genomes coloured by class affiliation. ( a ) Ratio of algalytic and lignocellulolytic CAZymes encoded by individual planctomycetotal genomes, grouped by the environmental origin. The heatmap illustrates the number of genomes encoding the listed CAZyme families. ( b ) CAZyme family diversity at the class level. Bottom right panel: CAZyme coding frequency (ratio of CAZymes to protein-coding genes) at the class level. ( c ) GH family diversity at the order level for two main classes of Planctomycetota. Phycisphaeral orders from the top: O – Other, U – UBA1845, SM – SM23-33, T – Tepidisphaerales, S – Sedimentisphaerales, P – Phycisphaerales; Planctomycetial orders from the top: O – Other, Pi – Pirellulales, Pl – Planctomycetales, I – Isosphaerales, G – Gemmatales. ( d ) Genome size versus number of CAZyme coding genes for each planctomycetotal genome. Trends for GH + CBM families were established based on the thresholds for low (T2, < 2%) and medium to high (T1, > 2%) CAZyme coding frequencies. ( e ) CAZyme protein sequence identity to public databases. ( f ) Ratio of unclassified CAZymes

CAZyme gene coding frequency varies based on phylogeny and genome size

The Planctomycetia class has the largest genomes of all Planctomycetota (5.8 Mb on average; Fig.  1 d) while phycisphaeral and brocadial genomes are among the smallest (3.6–3.9 Mb on average). However, regardless of the different genome sizes, members of the Phycisphaerae and Planctomycetia classes display similar CAZyme coding frequencies (Fig.  3 b). A higher number of functionalities encoded in bacterial genomes was proposed to make up the larger genome size, shifting the potential for the discovery of new functionalities towards bigger genomes [ 63 ]. Previously, a positive correlation between the planctomycetotal genome size and the number of biosynthetic gene clusters (BGCs) was observed [ 22 ] that could not be extrapolated to their carbohydrate degrading potential. Here, we observed an unexpected tendency of Planctomycetota to discriminate between two main trends (T1 and T2), owing to the different number of encoded GHs and CBMs among the bacteria within the same range of genome size (Fig.  3 d). The number of AAs, CEs and PLs simply correlates with the genome sizes as expected ( R  = 0.73, p  < 0.01) and does not follow the aforementioned trends. Planctomycetotal genomes characterised with T1 trend, rich in CAZymes, represent a subset of microorganisms from AD, animal digestive tract and extreme environments which were previously recognised as promising sources for the discovery of biomass-degrading enzymes [ 9 , 64 , 65 ]. Considering individual genomes, the highest CAZyme coding frequency was attributed to an uncultivated member of the Thermoguttaceae family within the Pirellulales order (9.1%), followed by the SG8-4 putative family genome (8.7%) and an Anaerohalophaeraceae member (8.3%), with the latter two representing Sedimentisphaerales (Additional File 2, Table S8 ). These genomes were retrieved from the ruminant gastrointestinal tract system ( Thermoguttaceae ) and lab-scale anaerobic digestion studies ( Sedimentisphaerales ), respectively. Overall, there is a tendency for microorganisms inhabiting animal digestive systems to encode a significant fraction of CAZymes in their genomes, likely reflecting the adaptation and response to the diversity of dietary polysaccharides present in these environments [ 66 ]. In AD environments, the similarity in patterns is likely due to the presence of complex carbohydrates within their organic matter.

The potential for the discovery of novel and unique CAZymes in Planctomycetota

At present, planctomycetotal CAZymes remain largely uncharacterised and to further prospect new functionalities in planctomycetotal genomes we evaluated the novelty of CAZymes by comparing their sequences to the entries in the CAZy database [ 5 ]. Overall, CAZymes encoded in Planctomycetota are distantly related to other bacterial CAZymes with the protein sequence identity ranging on average between 40% and 60% (Fig.  3 e). A relatively large number of planctomycetotal CAZymes show very low sequence identity to any previously characterised enzyme, i.e. below 30% (Additional File 2, Table S9 ). For example, among the CBM modules with the lowest sequence identity are versatile CBM51 and CBM57, rhamnose-binding GH67, fucose-binding CBM47 and cellulose-binding CBM9 and CBM16. Below the set threshold we found only a single PL8 family, putatively involved in the breakdown of various polysaccharides such as xanthan, chondroitin sulphate, alginate, and CE15 which typically displays ligninolytic activity by cleaving ester bonds between lignin and hemicellulose components (CAZy database). The planctomycetotal AA10 are also distantly related to other currently described LPMOs and accordingly, their sequence similarity to other publicly accessible proteins is assessed at between 28% and 68% (Additional File 7, Fig. S7 ). Furthermore, the protein sequence alignment of all the planctomycetotal AA10 proteins revealed only moderate coverage in a few regions (pairwise identity median of 25.8%), advocating for high intra-specialisation within this group (Additional File 2, Table S10 ).

The high degree of novelty within planctomycetotal CAZyomes is in line with a previous study analysing a large group of β-galactosidase homologues from planctomycetotal genomes, which highlighted the presence of multiple, poorly characterised CAZymes, almost exclusively present in the PVC superphylum and some Bacteroidota [ 67 ]. Another recent study described the diversity of α-l-arabinofuranosidase homologues (GH51) from subantarctic intertidal sediments in different bacteria including Planctomycetota [ 68 ]. Similarly, further investigation of unclassified CAZymes, and CAZymes with a low sequence homology to known proteins, shall, in the future, allow the discovery of novel CAZyme functionalities as highlighted in the past by Naumoff and Dedysh [ 69 ].

Finally, we also evaluated the abundance of what we called unclassified GHs, PLs, and CEs, that is, enzymes which were not classified to any of the currently recognised CAZyme families (see Methods). We revealed that Planctomycetota typically encode between 1 and 5% of unclassified CAZymes in their genomes (Fig.  3 f). Currently, comprehensive research data covering all bacterial phyla are not available, which prevents us from placing these findings within the broader context.

The phylogeny of planctomycetotal AA10 protein sequences retrieved from Planctomycetota genomes and the additional 15 AA10 protein sequences from bacteria representing other phyla with the LPMO activity described (highlighted in light red box). Bootstrap values are shown on branches. Additional metadata for planctomycetotal AA10 are presented: multi-modularity, presence of signal peptides, occurrence in CAZyme Gene Clusters (CGCs), taxonomic assignment and environmental origin (habitat)

Potential strategies for complex polysaccharide deconstruction – clustering of CAZymes in planctomycetotal genomes

Certain bacteria tend to cluster their CAZymes with complementary functions into so-called CAZyme gene clusters (CGCs) [ 66 ]. The most widely studied example is the polysaccharide utilisation locus (PUL) of Bacteroidota [ 70 , 71 , 72 ], however, similar gene clusters were also discovered in other bacterial phyla [ 73 ]. To the best of our knowledge, CAZyme clusters have not yet been characterised functionally in Planctomycetota although distinct groups within this phylum frequently encode co-localised CAZymes (Fig.  5 ). Most members of the Brocadiae , Phycisphaerae and putative UBA11346 classes co-localise more than 50% of their GHs on average. For comparison, up to 51% of predicted GHs are clustered in Bacteroidetes cellulolysiticus , which represents one of the highest scores in the bacterial domain [ 50 ]. Knowing that some planctomycetotal genomes in our database are incomplete and fragmented (Fig.  1 b), the predicted number of CAZymes falling within gene clusters is likely a conservative estimate. We also looked at the portion of hypothetical genes as well as unclassified CAZymes within CGCs that could potentially represent novel enzymatic functions. Planctomycetotal orders encode between 30% and 34% of unassigned hits within CGCs that were not classified either as CAZymes or as regulatory/transport proteins (Fig.  5 a). In general, research focusing on the functional characterisation of PULs, including analysis of genes previously categorised as hypothetical, can reveal new biocatalysts or led to the establishment of completely novel CAZyme families [ 74 , 75 , 76 ]. Further investigation of comparable systems in Planctomycetota is of high priority.

The CAZymes targeting different fractions of lignocellulose are regularly found within CGCs in almost all planctomycetotal classes, except for some unclassified UBA11346 and “other” class members, whose genomes show significant co-localisation only for glucan-targeting CAZymes, likely involved in the cellular metabolism (Fig.  5 b). Among unclassified Planctomycetota , members assigned to UBA11346 deserve some attention. Despite the limited number of genomes in our database (only 16), they show a wide diversity and high coding frequency of CAZyme families, and their CAZyme distribution beyond CGCs suggest potentially a different enzymatic strategy to other generalist Planctomycetota . While genomes of Isosphaerales and Pirellulales have frequently co-localised diverse CAZymes, Gemmatales and Planctomycetales do not encode significantly more co-localised lignocellulolytic, pectinolytic and algalytic CAZymes ( p  < 0.01) than other orders (Additional File 2, Table S11 ). Finally, we also examined the putative CAZyme clusters involving LPMO coding genes and found that in most genomes, i.e. 80%, AA10 is not found within CGCs (Fig.  4 ).

The CAZymes found within planctomycetotal CGCs. ( a ) Left panel: A mean fraction of hypothetical proteins, unclassified GHs and all CAZymes within CGCs for each planctomycetotal class. Right panel: A mean fraction of CAZyme coding genes co-localised within CGCs for each planctomycetotal class. ( b ) Ratio of functionally assigned CAZymes within or beyond CGCs in the individual genomes, estimated for the Planctomycetota classes. In light grey, CAZymes outside CGCs

Cellular localisation of planctomycetotal CAZymes

To estimate the potential secretion of planctomycetotal CAZymes, either extracellularly or membrane-bound, we verified the presence of signal peptides in their enzymes [ 77 ]. The majority of Planctomycetota representatives were predicted to harbour N-terminal SPI (Sec) or Twin Arginine Transport (TAT) pathway signal peptides in more than 50% of their CAZymes (Additional File 7, Fig. S8 ). Phylum-wise, almost all of lignocellulose-, pectin- or algae-targeting enzymes are putatively secreted while CAZymes targeting α-glucans are much less common to incorporate signal peptides, mainly expected to be geared towards internal metabolism (Fig.  6 a). Representatives of Sedimentisphaerales, Pirellulales , and Isosphaerales encode on average 76.1% ± 16.9, 74.4% ± 21.9, 72.9% ± 18.4 of their lignocellulolytic CAZymes as putatively extracellular enzymes, respectively (Fig.  6 b). Differences between taxonomic classes could also be observed in pectinolytic and algalytic potentials. Members of Planctomycetia , including the Planctomycetales (85.7% ± 19.9), Gemmatales (82.2% ± 22.8) and Isosphaerales (81.6% ± 20.4) orders, encode the highest ratio of putatively secreted pectinases. Despite a low number of CAZymes targeting algae in the genomes belonging to Isosphaerales , they are predicted to be localised extracellularly (85.5% ± 18.8), while Pirellulales would putatively secrete half of the encoded algalytic repertoire (49.7% ± 33.8), on average.

Extracellular enzymes play an important role in initiating the hydrolysis of complex carbohydrates to shorter oligosaccharides, ready for cellular uptake [ 78 ]. Enzyme-secreting bacteria are beneficial to the whole community, as they pre-degrade larger fibres into smaller components which can be used by other microbes [ 79 , 80 ]. Although in our analysis most of the planctomycetotal genomes flank their CAZymes with signal peptides to indicate the export of the proteins for the extracellular degradation, it was suggested that certain Planctomycetota selfishly import marine polysaccharides via an unknown mechanism [ 53 ]. In such cases, CAZymes flanked with the N-terminal peptide would only be transported to the periplasm, where the main saccharification would take place. Looking at the other types of signal peptides, we predicted that most of the planctomycetotal classes also encode in their genomes CAZymes with lipoprotein signal peptides cleaved by Lsp (leader peptidase or signal peptidase II; Additional File 7, Fig. S8 ). This type of signal peptide often serves for intracellular localisation [ 41 ], thus putatively supports the anchoring of their enzymes to either the inner or the outer cell membrane. The membrane anchored extracellular CAZymes would benefit the host more than the other community members, allowing the higher share of the liberated oligosaccharides to be taken by the main enzyme producer. An interesting feature, exclusive to Planctomycetota , was further observed by Boedecker et al. [ 12 ], who described an extreme enlargement of the periplasmic space in Planctopirus limnophila ( Planctomycetales order), accompanied by its ability to bind sugar moieties using crateriform structures when feeding on complex, branched glucan (dextran). Likewise, type IV pili of Fimbriiglobus ruber ( Gemmatales order) were shown to enhance bacterial adhesion to chitin and other biopolymers [ 81 ]. So far, these mechanisms have only been proven experimentally for some species from the Planctomycetia class, and any further ecological relevance, directly or indirectly related to polysaccharide uptake and degradation, remains to be scrutinised.

Predicted localisation of CAZymes putatively engaged in the degradation of specific polysaccharides, in the individual planctomycetotal genomes. ( a ) Ratio of CAZymes with any type of predicted signal peptide illustrated for the Planctomycetota classes. ( b ) Ratio of CAZymes with any type of predicted signal peptide illustrated for the Planctomycetia (blue) and Phycisphaerae (red) orders

Perspectives on biotechnological applications

There is a viable interest in exploring how microorganisms utilise polysaccharides, as understanding these mechanisms can help us not only to unveil their environmental interactions, but also reinforce the current solutions or develop new industrial technologies [ 56 , 73 , 82 ]. For instance, the arrangement of the CAZymes in clusters allows the coordination of gene expression, resulting in the protein ensembles required for a complex carbohydrate saccharification [ 70 , 83 , 84 ]. As such, the synergistically acting enzymatic complexes could be extracted together, simplifying the enzymatic cocktail design [ 85 ]. Similarly, the role of extracellular enzymes extends to various biotechnology applications, mainly as nature-inspired enzymatic cocktails that simplify the extraction and downstream processing [ 86 , 87 ]. In view of this, we think that the as yet uncultured members of phycisphaeral Sedimentisphaerales and planctomycetial Pirellulales characterised with putatively extracellular, diverse and frequently co-localised CAZymes are among the high-priority targets for extending the strategies to be applied to biomass-based biorefineries. Nevertheless, the carbohydrolytic potential encoded by Planctomycetota cannot fully reflect their microbial capabilities in the environment and a deeper understanding of planctomycetotal metabolism and ecology is essential for their effective biotechnological application in the developing biorefinery sector. Contextualising the genomic measurements to metabolic traits remains difficult; yet, the novel approaches present a promising avenue for overcoming this challenge, enabling the accurate prediction of microbial phenotypes from genomic data exclusively [ 88 ]. It is worth noting that slow growth rates are a hallmark of Planctomycetota , exhibited by many isolated strains of this phylum [ 89 ], and one of the key considerations for developing specific applications lies in the continued optimisation of their growth. Culture-based methods are still required for optimising and scaling up biotechnological processes [ 90 ], posing an ongoing challenge, however a few methods have already been established for Planctomycetota [ 91 , 92 ]. On the other hand, for the discovery of novel CAZymes, genomic approaches provide an alternative to culturing microorganisms [ 85 ].

Lignocellulose, despite being generally common and abundant resource, is an untapped biomass feedstock due to its recalcitrance [ 93 ]. In consequence, this so-called second-generation feedstock still lacks economic viability at the industrial scale and new approaches are needed to improve the enzymatic hydrolysis of diverse plant biomasses [ 87 ]. It has been suggested that LPMOs help degrade the recalcitrant lignocellulose fractions efficiently by boosting the overall activity of common GHs [ 94 , 95 ]. Here, we identified LPMO coding genes in Planctomycetota genomes exhibiting high diversity of homology, which likely reflects their different origins or evolutionary history. Based on protein phylogeny, AA10 sequences retrieved from Planctomycetota form separate cluster than other, even phylogenetically unrelated bacteria representing different phyla such as Actinomycetota, Pseudomonadota and Bacillota (Fig.  4 ; Additional File 7, Fig. S7 ). Thus, as yet uncharacterised planctomycetotal AA10 family might represent new hydrolytic functionalities that are not only distantly related to existing sequences in public databases, but also functionally diverse. We argue that LPMOs co-localised with other GHs might represent an evolutionary optimised version of an efficient enzymatic machinery, possibly targeting complex polysaccharides like crystalline cellulose or chitin. However, while LPMOs might specifically enhance the activity of co-localised GHs, LPMOs encoded beyond clusters might be universal boosters helping diverse enzymes to attack glycosidic bonds within the polysaccharide moieties. Cellular investment in a single enzyme production would offer an interesting cost-saving strategy compared to the expression of the whole enzyme cluster. Thus, such potent LPMOs would represent an interesting component of industrially relevant enzymatic preparations that could significantly reduce the cost of the enzymatic biomass processing technologies, e.g. for bioethanol production [ 96 ]. So far, none of the planctomycetotal LPMOs have ever been analysed, therefore their enzymatic activities should be further studied to determine their effectiveness for biomass processing.

Algae, considered a third-generation biomass, could offer potential advantages over lignocellulose such as negligible presence of lignin, making it less resistant to degradation and reducing the need for intensive pre-treatments [ 97 , 98 ]. However, the diversity of unique algal polysaccharides, particularly the recalcitrant fucoidans produced by brown algae, seem to become the major obstacle for developing biorefineries [ 52 , 99 ]. It is therefore crucial to design an individual approach for each type of biomass, and nature-inspired cocktails seem to be a promising alternative for the complete conversion of different biomasses to fermentable sugars [ 100 , 101 , 102 ]. Initially, we expected the Planctomycetota retrieved from marine environments to serve as a reservoir for diverse algalytic CAZymes, due to the abundance of algal biomass in seawater. Contrary to our expectations, genomes of Planctomycetota retrieved from engineered systems such as AD, encode a similar algae-targeting potential to marine-sourced members of the phylum. Furthermore, their potential specialisation towards specific algal fractions such as fucan-based compounds, is particularly intriguing given the possibilities for its harnessing to develop well-defined applications. Overall, the capacity of anaerobic microbes to degrade algal biomass directly in AD reactors opens up a new perspective for its valorisation in the context of biogas production and the development of biorefineries. As the field of green biotechnology continues to advance, the interest in the planctomycetotal-based applications is likely to grow.

The Planctomycetota phylum offers a wealth of diverse, novel CAZymes of potential industrial interest. Our study provides a new perspective on the planctomycetotal carbohydrolytic potential, highlighting the presence of distinct phylogenetic groups with both general and specialised abilities to break down complex carbohydrates. We identified planctomycetotal families affiliated to the Sedimentisphaerales and Pirellulales orders that are not yet well characterised as suitable candidates for applications in second generation biomass transformation technologies, due to their diverse CAZymes, including extracellular lignocellulose targeting enzymes. In addition, we showed that some Planctomycetota possess LPMOs, which can be further employed to boost the overall activity of GHs in lignocellulose hydrolysis. To our surprise, AD-sourced Planctomycetota appeared to be well-equipped for degrading algal-derived polysaccharides, thus representing a perspective for a direct algal biomass transformation to bioenergy in methanogenic reactors. Overall, our findings have implications for directing bioprospecting ventures to enable a more effective discovery of CAZymes in Planctomycetota . Although the most interesting planctomycetotal models represent still uncultivated bacteria, their enzymes can already be explored for specific applications thanks to their identification and characterisation through in silico studies.

Data availability

All data generated or analysed during this study are included in this article and its supplementary information files. Accession numbers of public genomes used in this study are listed in the Additional File 1, Table S1 . Remaining genomes from previous, own studies are available upon request.

Abbreviations

Anaerobic Digestion

Carbohydrate Active Enzyme(s)

Carbohydrate Gene Cluster(s)

Glycoside Hydrolases

Carbohydrate Esterases

Polysaccharide Lyases

Enzymes with auxiliary activities

Principal Coordinates Analysis

Hoornweg D, Bhada-Tata P. What a Waste: A Global Review of Solid Waste Management. 2012.

Achinas S, Achinas V, Euverink GJW. A Technological overview of Biogas Production from Biowaste. Engineering. 2017;3:299–307.

Article   Google Scholar  

Chavan S, Yadav B, Atmakuri A, Tyagi RD, Wong JWC, Drogui P. Bioconversion of organic wastes into value-added products: a review. Bioresour Technol. 2022;344:126398.

Article   CAS   PubMed   Google Scholar  

Alessi AM, Bird SM, Oates NC, Li Y, Dowle AA, Novotny EH, et al. Defining functional diversity for lignocellulose degradation in a microbial community using multi-omics studies. Biotechnol Biofuels. 2018;11:166.

Article   PubMed   PubMed Central   Google Scholar  

Drula E, Garron M-L, Dogan S, Lombard V, Henrissat B, Terrapon N. The carbohydrate-active enzyme database: functions and literature. Nucleic Acids Res. 2022;50:D571–7.

Guillén D, Sánchez S, Rodríguez-Sanoja R. Carbohydrate-binding domains: multiplicity of biological roles. Appl Microbiol Biotechnol. 2010;85:1241–9.

Article   PubMed   Google Scholar  

Jaramillo PMD, Gomes HAR, Monclaro AV, Silva COG, Filho EXF. Lignocellulose-degrading enzymes. Fungal biomolecules. John Wiley & Sons, Ltd; 2015. pp. 73–85.

Lopes AMM, Martins M, Goldbeck R. Heterologous expression of lignocellulose-modifying enzymes in microorganisms: current status. Mol Biotechnol. 2021;63:184–99.

Bertucci M, Calusinska M, Goux X, Rouland-Lefèvre C, Untereiner B, Ferrer P et al. Carbohydrate hydrolytic potential and redundancy of an anaerobic digestion Microbiome exposed to Acidosis, as uncovered by Metagenomics. Appl Environ Microbiol. 2019;85.

Stewart RD, Auffret MD, Warr A, Walker AW, Roehe R, Watson M. Compendium of 4,941 rumen metagenome-assembled genomes for rumen microbiome biology and enzyme discovery. Nat Biotechnol. 2019;37:953–61.

Article   CAS   PubMed   PubMed Central   Google Scholar  

López-Mondéjar R, Tláskal V, da Rocha UN, Baldrian P. Global Distribution of Carbohydrate Utilization Potential in the Prokaryotic Tree of Life. mSystems. 2022;7:e0082922.

Boedeker C, Schüler M, Reintjes G, Jeske O, van Teeseling MCF, Jogler M, et al. Determining the bacterial cell biology of Planctomycetes. Nat Commun. 2017;8:14853.

Wiegand S, Jogler M, Jogler C. On the maverick Planctomycetes. FEMS Microbiol Rev. 2018;42:739–60.

Dedysh SN, Ivanova AA. Planctomycetes in boreal and subarctic wetlands: diversity patterns and potential ecological functions. FEMS Microbiol Ecol. 2019;95.

Wang X, Sharp CE, Jones GM, Grasby SE, Brady AL, Dunfield PF. Stable-isotope probing identifies uncultured Planctomycetes as primary degraders of a Complex Heteropolysaccharide in Soil. Appl Environ Microbiol. 2015;81:4607–15.

Probandt D, Knittel K, Tegetmeyer HE, Ahmerkamp S, Holtappels M, Amann R. Permeability shapes bacterial communities in sublittoral surface sediments. Environ Microbiol. 2017;19:1584–99.

Suominen S, van Vliet DM, Sánchez-Andrea I, van der Meer MTJ, Sinninghe Damsté JS, Villanueva L. Organic Matter Type defines the composition of active Microbial communities originating from anoxic Baltic Sea sediments. Front Microbiol. 2021;12.

Bengtsson MM, Øvreås L. Planctomycetes dominate biofilms on surfaces of the kelp Laminaria hyperborea. BMC Microbiol. 2010;10:261.

Faria M, Bordin N, Kizina J, Harder J, Devos D, Lage OM. Planctomycetes attached to algal surfaces: insight into their genomes. Genomics. 2018;110:231–8.

Wegner C-E, Richter-Heitmann T, Klindworth A, Klockow C, Richter M, Achstetter T, et al. Expression of sulfatases in Rhodopirellula baltica and the diversity of sulfatases in the genus Rhodopirellula. Mar Genom. 2013;9:51–61.

Ivanova AA, Wegner C-E, Kim Y, Liesack W, Dedysh SN. Metatranscriptomics reveals the hydrolytic potential of peat-inhabiting Planctomycetes. Antonie Van Leeuwenhoek. 2018;111:801–9.

Kallscheuer N, Jogler C. The bacterial phylum Planctomycetes as novel source for bioactive small molecules. Biotechnol Adv. 2021;53:107818.

Wiegand S, Jogler M, Boedeker C, Pinto D, Vollmers J, Rivas-Marín E, et al. Cultivation and functional characterization of 79 planctomycetes uncovers their unique biology. Nat Microbiol. 2020;5:126–40.

Vitorino IR, Lage OM. The Planctomycetia: an overview of the currently largest class within the phylum Planctomycetes. Antonie Van Leeuwenhoek. 2022;115:169–201.

Nayfach S, Roux S, Seshadri R, Udwary D, Varghese N, Schulz F, et al. A genomic catalog of Earth’s microbiomes. Nat Biotechnol. 2021;39:499–509.

Olm MR, Brown CT, Brooks B, Banfield JF. dRep: a tool for fast and accurate genomic comparisons that enables improved genome recovery from metagenomes through de-replication. ISME J. 2017;11:2864–8.

Chaumeil P-A, Mussig AJ, Hugenholtz P, Parks DH. GTDB-Tk: a toolkit to classify genomes with the genome taxonomy database. Bioinformatics. 2020;36:1925–7.

Article   CAS   Google Scholar  

Oren A, Garrity GM. Valid publication of the names of forty-two phyla of prokaryotes. Int J Syst Evol Microbiol. 2021;71.

Krieg NR, Staley JT, Brown DR, Hedlund BP, Paster BJ, Ward NL, et al. editors. Bergey’s Manual® of systematic bacteriology: volume four the Bacteroidetes, Spirochaetes, Tenericutes (Mollicutes), Acidobacteria, Fibrobacteres, Fusobacteria, Dictyoglomi, Gemmatimonadetes, Lentisphaerae, Verrucomicrobia, Chlamydiae, and Planctomycetes. New York, NY: Springer New York; 2010.

Google Scholar  

Kovaleva OL, Merkel AYu, Novikov AA, Baslerov RV, Toshchakov SV, Bonch-Osmolovskaya EA. Tepidisphaera mucosa gen. nov., sp. nov., a moderately thermophilic member of the class Phycisphaerae in the phylum Planctomycetes, and proposal of a new family, Tepidisphaeraceae fam. nov., and a new order, Tepidisphaerales ord. nov. International Journal of Systematic and Evolutionary Microbiology. 2015;65 Pt_2:549–55.

Dedysh SN, Beletsky AV, Ivanova AA, Kulichevskaya IS, Suzina NE, Philippov DA, et al. Wide distribution of Phycisphaera-like planctomycetes from WD2101 soil group in peatlands and genome analysis of the first cultivated representative. Environ Microbiol. 2021;23:1510–26.

Parks DH, Imelfort M, Skennerton CT, Hugenholtz P, Tyson GW. CheckM: assessing the quality of microbial genomes recovered from isolates, single cells, and metagenomes. Genome Res. 2015;25:1043–55.

Bowers RM, Kyrpides NC, Stepanauskas R, Harmon-Smith M, Doud D, Reddy TBK, et al. Minimum information about a single amplified genome (MISAG) and a metagenome-assembled genome (MIMAG) of bacteria and archaea. Nat Biotechnol. 2017;35:725–31.

Winter DJ. rentrez: An R package for the NCBI eUtils API. 2017;9.

Hyatt D, Chen G-L, LoCascio PF, Land ML, Larimer FW, Hauser LJ. Prodigal: prokaryotic gene recognition and translation initiation site identification. BMC Bioinformatics. 2010;11:119.

Zhang H, Yohe T, Huang L, Entwistle S, Wu P, Yang Z, et al. dbCAN2: a meta server for automated carbohydrate-active enzyme annotation. Nucleic Acids Res. 2018;46:W95–101.

Xie C, Huson DH, Buchfink B. Fast and sensitive protein alignment using DIAMOND. Nat Methods. 2015;12.

Busk PK, Pilgaard B, Lezyk MJ, Meyer AS, Lange L. Homology to peptide pattern for annotation of carbohydrate-active enzymes and prediction of function. BMC Bioinformatics. 2017;18:214.

Finn RD, Clements J, Eddy SR. HMMER web server: interactive sequence similarity searching. Nucleic Acids Res. 2011;39 suppl2:W29–37.

Seemann T. Prokka: rapid prokaryotic genome annotation. Bioinformatics. 2014;30:2068–9.

Teufel F, Almagro Armenteros JJ, Johansen AR, Gíslason MH, Pihl SI, Tsirigos KD, et al. SignalP 6.0 predicts all five types of signal peptides using protein language models. Nat Biotechnol. 2022;40:1023–5.

R Core Team. R: A language and environment for statistical computing R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/ . 2020.

Jari, Oksanen et al. Vegan: Community Ecology Package. R package version 2.5-7.

Kai Guo and Pan Gao. Microbial: Do 16s Data Analysis and Generate Figures. R package version 0.0.22. 2021.

Asnicar F, Thomas AM, Beghini F, Mengoni C, Manara S, Manghi P, et al. Precise phylogenetic analysis of microbial isolates and genomes from metagenomes using PhyloPhlAn 3.0. Nat Commun. 2020;11:2500.

Edgar RC. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–7.

Geneious Basic. An integrated and extendable desktop software platform for the organization and analysis of sequence data | Bioinformatics | Oxford Academic. https://academic-oup-com.proxy.bnl.lu/bioinformatics/article/28/12/1647/267326 . Accessed 19 Jan 2023.

Kartal B, van Niftrik L, Keltjens JT, Op den Camp HJM, Jetten MSM. Anammox—Growth Physiology, Cell Biology, and metabolism. Advances in Microbial Physiology. Elsevier; 2012. pp. 211–62.

Terrapon N, Lombard V, Drula E, Coutinho PM, Henrissat B. The CAZy Database/the carbohydrate-active enzyme (CAZy) database: principles and usage guidelines. In: Aoki-Kinoshita KF, editor. A practical guide to using Glycomics databases. Tokyo: Springer Japan; 2017. pp. 117–31.

Chapter   Google Scholar  

Terrapon N, Lombard V, Drula É, Lapébie P, Al-Masaudi S, Gilbert HJ, et al. PULDB: the expanded database of polysaccharide utilization loci. Nucleic Acids Res. 2018;46:D677–83.

Helbert W. Marine Polysaccharide sulfatases. Front Mar Sci. 2017;4.

Sichert A, Corzett CH, Schechter MS, Unfried F, Markert S, Becher D, et al. Verrucomicrobia use hundreds of enzymes to digest the algal polysaccharide fucoidan. Nat Microbiol. 2020;5:1026–39.

Reintjes G, Arnosti C, Fuchs B, Amann R. Selfish, sharing and scavenging bacteria in the Atlantic Ocean: a biogeographical study of bacterial substrate utilisation. ISME J. 2019;13:1119–32.

Berlemont R, Martiny AC. Genomic potential for polysaccharide deconstruction in Bacteria. Appl Environ Microbiol. 2015;81:1513–9.

Bondoso J, Godoy-Vitorino F, Balagué V, Gasol JM, Harder J, Lage OM. Epiphytic Planctomycetes communities associated with three main groups of macroalgae. FEMS Microbiol Ecol. 2017;93.

Tomazetto G, Pimentel AC, Wibberg D, Dixon N, Squina FM. Multi-omic Directed Discovery of cellulosomes, polysaccharide utilization loci, and Lignocellulases from an enriched Rumen Anaerobic Consortium. Appl Environ Microbiol. 2020;86:e00199–20.

Brunecky R, Chung D, Sarai NS, Hengge N, Russell JF, Young J, et al. High activity CAZyme cassette for improving biomass degradation in thermophiles. Biotechnol Biofuels. 2018;11:22.

Glasgow E, Vander Meulen K, Kuch N, Fox BG. Multifunctional cellulases are potent, versatile tools for a renewable bioeconomy. Curr Opin Biotechnol. 2021;67:141–8.

Lu Z, Kvammen A, Li H, Hao M, Inman AR, Bulone V, et al. A polysaccharide utilization locus from Chitinophaga pinensis simultaneously targets chitin and β-glucans found in fungal cell walls. mSphere. 2023;8:e00244–23.

Krska D, Larsbrink J. Investigation of a thermostable multi-domain xylanase-glucuronoyl esterase enzyme from Caldicellulosiruptor kristjanssonii incorporating multiple carbohydrate-binding modules. Biotechnol Biofuels. 2020;13:68.

Naas AE, Solden LM, Norbeck AD, Brewer H, Hagen LH, Heggenes IM, et al. Candidatus Paraporphyromonas polyenzymogenes encodes multi-modular cellulases linked to the type IX secretion system. Microbiome. 2018;6:44.

Rakitin AL, Naumoff DG, Beletsky AV, Kulichevskaya IS, Mardanov AV, Ravin NV, et al. Complete genome sequence of the cellulolytic planctomycete Telmatocola Sphagniphila SP2T and characterization of the first cellulolytic enzyme from planctomycetes. Syst Appl Microbiol. 2021;44:126276.

Nayfach S, Pollard KS. Average genome size estimation improves comparative metagenomics and sheds light on the functional ecology of the human microbiome. Genome Biol. 2015;16:51.

Shu W-S, Huang L-N. Microbial diversity in extreme environments. Nat Rev Microbiol. 2022;20:219–35.

Reichart NJ, Bowers RM, Woyke T, Hatzenpichler R. High potential for biomass-degrading enzymes revealed by Hot Spring Metagenomics. Front Microbiol. 2021;12.

Zheng J, Hu B, Zhang X, Ge Q, Yan Y, Akresi J, et al. dbCAN-seq update: CAZyme gene clusters and substrates in microbiomes. Nucleic Acids Res. 2022. gkac1068.

Naumoff DG, Dedysh SN. Bacteria from poorly studied Phyla as a potential source of new enzymes: β-Galactosidases from Planctomycetes and Verrucomicrobia. Microbiology. 2018;87:796–805.

Dionisi HM, Lozada M, Campos E. Diversity of GH51 α-L-arabinofuranosidase homolog sequences from subantarctic intertidal sediments. Biologia. 2023;78:1899–918.

Naumoff DG, Dedysh SN. Lateral gene transfer between the Bacteroidetes and Acidobacteria: the case of α-l-rhamnosidases. FEBS Lett. 2012;586:3843–51.

Grondin JM, Tamura K, Déjean G, Abbott DW, Brumer H. Polysaccharide utilization loci: fueling Microbial communities. J Bacteriol. 2017;199:e00860–16.

McKee LS, La Rosa SL, Westereng B, Eijsink VG, Pope PB, Larsbrink J. Polysaccharide degradation by the Bacteroidetes: mechanisms and nomenclature. Environ Microbiol Rep. 2021;13:559–81.

Lapébie P, Lombard V, Drula E, Terrapon N, Henrissat B. Bacteroidetes use thousands of enzyme combinations to break down glycans. Nat Commun. 2019;10:2043.

Calusinska M, Marynowska M, Bertucci M, Untereiner B, Klimek D, Goux X, et al. Integrative omics analysis of the termite gut system adaptation to Miscanthus diet identifies lignocellulose degradation enzymes. Commun Biol. 2020;3:1–12.

Garron M-L, Henrissat B. The continuing expansion of CAZymes and their families. Curr Opin Chem Biol. 2019;53:82–7.

Cabral L, Persinoti GF, Paixão DAA, Martins MP, Morais MAB, Chinaglia M, et al. Gut microbiome of the largest living rodent harbors unprecedented enzymatic systems to degrade plant polysaccharides. Nat Commun. 2022;13:629.

Ndeh D, Rogowski A, Cartmell A, Luis AS, Baslé A, Gray J, et al. Complex pectin metabolism by gut bacteria reveals novel catalytic functions. Nature. 2017;544:65–70.

Owji H, Nezafat N, Negahdaripour M, Hajiebrahimi A, Ghasemi Y. A comprehensive review of signal peptides: structure, roles, and applications. Eur J Cell Biol. 2018;97:422–41.

Arnosti C. Microbial extracellular enzymes and the Marine Carbon Cycle. Annu Rev Mar Sci. 2011;3:401–25.

Orsi WD. Ecology and evolution of seafloor and subseafloor microbial communities. Nat Rev Microbiol. 2018;16:671–83.

Arnosti C, Wietz M, Brinkhoff T, Hehemann J-H, Probandt D, Zeugner L, et al. The Biogeochemistry of Marine polysaccharides: sources, inventories, and bacterial drivers of the Carbohydrate cycle. Annu Rev Mar Sci. 2021;13:81–108.

Ravin NV, Rakitin AL, Ivanova AA, Beletsky AV, Kulichevskaya IS, Mardanov AV et al. Genome analysis of Fimbriiglobus ruber SP5T, a planctomycete with confirmed chitinolytic capability. Appl Environ Microbiol. 2018;84.

Liu N, Li H, Chevrette MG, Zhang L, Cao L, Zhou H, et al. Functional metagenomics reveals abundant polysaccharide-degrading gene clusters and cellobiose utilization pathways within gut microbiota of a wood-feeding higher termite. ISME J. 2019;13:104–17.

Hemsworth GR, Déjean G, Davies GJ, Brumer H. Learning from microbial strategies for polysaccharide degradation. Biochem Soc Trans. 2016;44:94–108.

Berlemont R. The supragenic organization of glycoside hydrolase encoding genes reveals distinct strategies for carbohydrate utilization in bacteria. Front Microbiol. 2023;14.

Chettri D, Verma AK, Verma AK. Innovations in CAZyme gene diversity and its modification for biorefinery applications. Biotechnol Rep. 2020;28:e00525.

Sharma H, Upadhyay SK. Chapter 3 - enzymes and their production strategies. In: Singh SP, Pandey A, Singhania RR, Larroche C, Li Z, editors. Biomass, Biofuels, Biochemicals. Elsevier; 2020. pp. 31–48.

Xu N, Liu S, Xin F, Zhou J, Jia H, Xu J et al. Biomethane production from lignocellulose: Biomass Recalcitrance and its impacts on anaerobic digestion. Front Bioeng Biotechnol. 2019;7.

Li Z, Selim A, Kuehn S. Statistical prediction of microbial metabolic traits from genomes. PLoS Comput Biol. 2023;19:e1011705.

Lage O, Bondoso J. Bringing Planctomycetes into pure culture. Front Microbiol. 2012;3.

Pandhal J, Noirel J. Synthetic microbial ecosystems for biotechnology. Biotechnol Lett. 2014;36:1141–51.

Jogler C, Glöckner FO, Kolter R. Characterization of Planctomyces limnophilus and development of genetic tools for its manipulation establish it as a Model species for the Phylum Planctomycetes. Appl Environ Microbiol. 2011;77:5826–9.

Jeske O, Surup F, Ketteniß M, Rast P, Förster B, Jogler M et al. Developing techniques for the utilization of Planctomycetes as producers of Bioactive molecules. Front Microbiol. 2016;7.

Singhvi MS, Gokhale DV. Lignocellulosic biomass: hurdles and challenges in its valorization. Appl Microbiol Biotechnol. 2019;103:9305–20.

Rani Singhania R, Dixit P, Kumar Patel A, Shekher Giri B, Kuo C-H, Chen C-W, et al. Role and significance of lytic polysaccharide monooxygenases (LPMOs) in lignocellulose deconstruction. Bioresour Technol. 2021;335:125261.

Hemsworth GR, Johnston EM, Davies GJ, Walton PH. Lytic Polysaccharide monooxygenases in Biomass Conversion. Trends Biotechnol. 2015;33:747–61.

Barbosa FC, Silvello MA, Goldbeck R. Cellulase and oxidative enzymes: new approaches, challenges and perspectives on cellulose degradation for bioethanol production. Biotechnol Lett. 2020;42:875–84.

Behera S, Singh R, Arora R, Sharma NK, Shukla M, Kumar S. Scope of Algae as Third Generation Biofuels. Front Bioeng Biotechnol. 2015;2.

Rodriguez C, Alaswad A, Mooney J, Prescott T, Olabi AG. Pre-treatment techniques used for anaerobic digestion of algae. Fuel Process Technol. 2015;138:765–79.

Neto JM, Komesu A, da Silva Martins LH, Gonçalves VOO, de Oliveira JAR, Rai M. Chapter 10 - third generation biofuels: an overview. In: Rai M, Ingle AP, editors. Sustainable Bioenergy. Elsevier; 2019. pp. 283–98.

Li J, He Z, Liang Y, Peng T, Hu Z. Insights into Algal polysaccharides: a review of their structure, depolymerases, and metabolic pathways. J Agric Food Chem. 2022;70:1749–65.

Montingelli ME, Tedesco S, Olabi AG. Biogas production from algal biomass: a review. Renew Sustain Energy Rev. 2015;43:961–72.

Bhushan S, Jayakrishnan U, Shree B, Bhatt P, Eshkabilov S, Simsek H. Biological pretreatment for algal biomass feedstock for biofuel production. J Environ Chem Eng. 2023;11:109870.

Download references

Acknowledgements

We thank Lindsey Stokes for her English proofreading.

This study was supported by the National Research Fund, Luxembourg (AFR Grant, ref. 14583934).

Author information

Authors and affiliations.

Environmental Research and Innovation Department, Luxembourg Institute of Science and Technology (LIST), 41 rue du Brill, Belvaux, L-4422, Luxembourg

Dominika Klimek, Malte Herold & Magdalena Calusinska

The Faculty of Science, Technology and Medicine (FSTM), University of Luxembourg, 2 Avenue de l’Université, Esch-sur-Alzette, L-4365, Luxembourg

Dominika Klimek

You can also search for this author in PubMed   Google Scholar

Contributions

D.K. and M.C. designed the study. D.K. and M.H. handled the data analysis. D.K. and M.C. wrote the manuscript and M.H. revised it. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Dominika Klimek .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary Material 1

Supplementary material 2, supplementary material 3, supplementary material 4, supplementary material 5, supplementary material 6, supplementary material 7, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Klimek, D., Herold, M. & Calusinska, M. Comparative genomic analysis of Planctomycetota potential for polysaccharide degradation identifies biotechnologically relevant microbes. BMC Genomics 25 , 523 (2024). https://doi.org/10.1186/s12864-024-10413-z

Download citation

Received : 26 January 2024

Accepted : 15 May 2024

Published : 27 May 2024

DOI : https://doi.org/10.1186/s12864-024-10413-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Planctomycetota
• Carbohydrate-active enzymes (CAZymes)
• Carbohydrolytic potential
• Algal and lignocellulosic biomass degradation
• Bioprospecting

BMC Genomics

ISSN: 1471-2164

• Submission enquiries: [email protected]
• General enquiries: [email protected]